























Preview text:
1. 2. 3. 4.
HĐ1. Nhận biết dãy có giới hạn là 0 Cho dãy số với
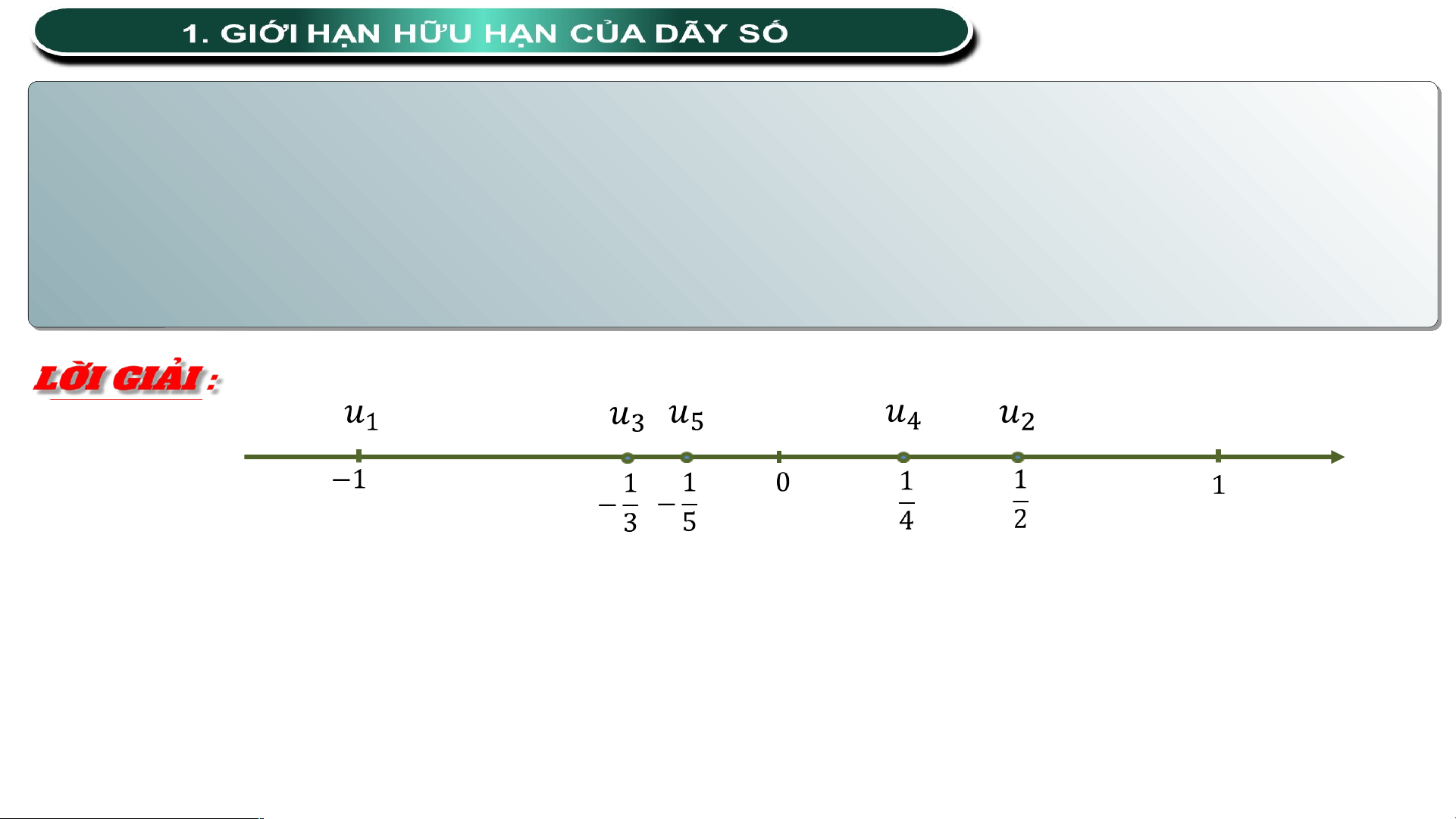
a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ đến 0 nhỏ hơn 0,01? a)
b) Khoảng cách từ đến 0 là Ta có
Vậy từ số hạng của dãy trở đi thì khoảng cách từ đến 0 nhỏ hơn 0,01
Dãy số có giới hạn là 0 khi dần tới dương vô cực, nếu có thể nhỏ hơn
một số dương bé tùy ý, kể từ số hạng nào đó trở đi, ký hiệu hay khi
Vì sao dãy số có giới hạn là 0?
Dãy số có giới hạn là 0 bởi vì có thể nhỏ hơn một số dương bé tùy ý khi 𝑛 đủ lớn.
Vậy từ số hạng của dãy trở đi có giá trị tuyệt đối nhỏ hơn 0,0001 nguyên dương; nếu
Nếu với mọi và thì Chứng minh rằng Xét dãy với Ta có: Và nên
HĐ2. Nhận biết dãy có giới hạn hữu hạn
Cho dãy số với . Xét dãy xác định bởi . Tính Ta có . Do đó
Dãy số có giới hạn là khi n dần tới dương vô cực, nếu , ký hiệu hay khi Cho dãy số với . CMR Ta có Vậy
Nếu ( là hằng số) thì
Cho dãy số với . Chứng minh rằng Ta có Vậy
Một quả bóng thả từ độ cao 5m xuống sàn. Sau mỗi lần chạm sàn, quả bóng
nảy lên độ cao bằng 2/3 độ cao trước đó. Giả sử quả bóng luôn chuyển
động vuông góc với mặt sàn và quá trình diễn ra vô hạn lần. Giả sử là độ cao (m) Sa củau qlần uả nả bó y n thứ g n sau hấ lầ t, n b nảóyng lê có n độ thứ . ca C o M là R d ; ãy số có giới hạn là 0. Lần hai là Lần ba là … Lần là Ta có nên
HĐ3. Hình thành quy tắc tính giới hạn Cho hai dãy số và với ; Tìm và so sánh và
. Vậy 𝑛→+∞ khi . Nên 𝑛→+∞ Và khi . Nên 𝑛→+∞ Khi đó ta có:
𝒏→+∞
𝒏→+∞ 𝒏→+∞ Tìm Ta có Tì m √𝟐 𝟏
+ 𝒏𝟐 Ta có 𝐥
𝐢𝐦 √ 𝟐 𝒏𝟐+𝟏 𝒏+𝟏 = 𝐥𝐢𝐦 𝟏 𝟏 + 𝒏
𝐥𝐢𝐦 √𝟐 𝟏 + 𝐧𝟐 ¿ =√ 𝟐 𝐥𝐢𝐦 𝟏 (𝟏 + 𝐧 )
HĐ4. Làm quen việc tính tổng vô hạn
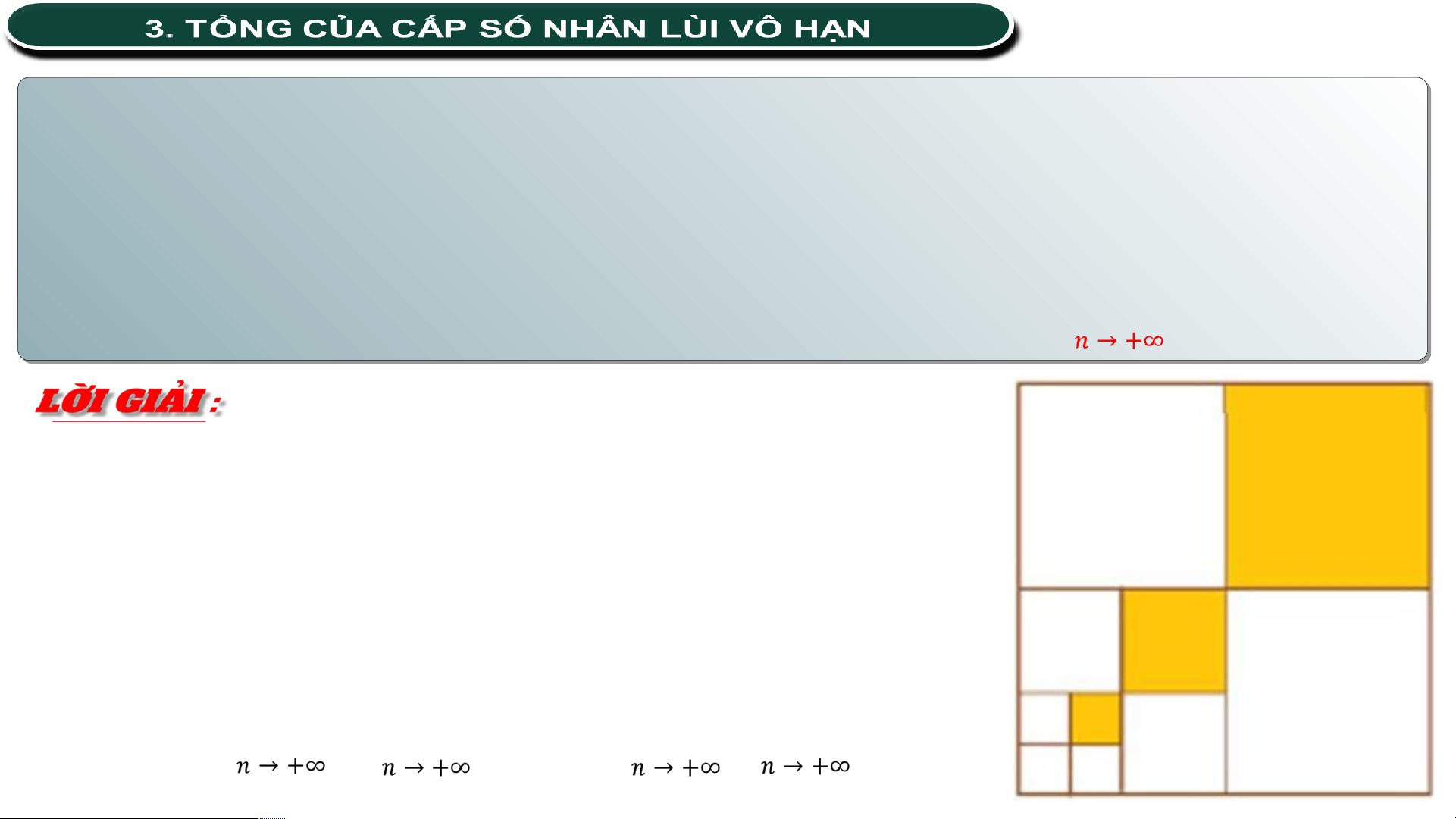
Cho hình vuông cạnh 1 (đvdd). Chia hình vuông thành bốn hình vuông nhỏ
bằng nhau, sau đó tô màu hình vuông nhỏ góc trên bên phải. Giả sử quá
trình trên tiếp diễn vô hạn. Gọi lần lượt là độ dài cạnh các hình vuông được tô màu.
a) Tính tổng b) Tìm
a) Ta có: là độ dài cạnh hình vuông đầu tiên được tô màu, ; ; ;……
Lập thành CSN ; . Do đó, tổngsố hạng đầu tiên là: . b) Ta có:
Cấp số nhân vô hạn có công bội với là cấp số nhân lùi vô hạn Ta có: Vì nên khi . Do đó :
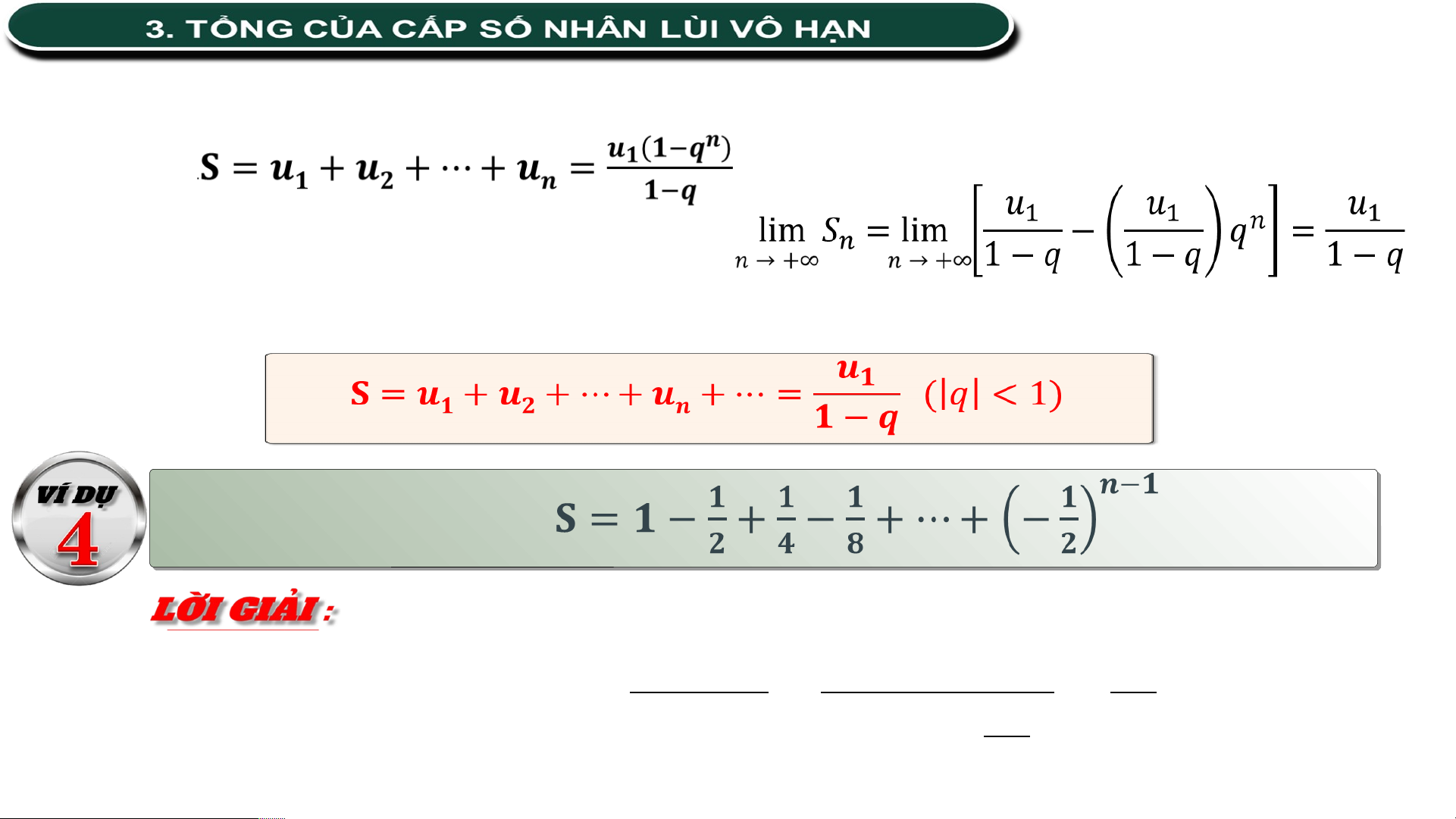
Giới hạn này gọi là tổng của cấp số nhân lùi vô hạn. Như vậy ta có: Tính tổng
S là tổng của cấp số nhân lùi vô hạn với ; 𝒖 𝟏 𝟐 Nên ta 𝐒 𝟏 = 𝟏 = − 𝒒 = 𝟏 𝟑 có:
𝟏 − (− 𝟐 )
Biểu diễn số thập phân vô hạn tuần hoàn dưới dạng phân số Ta có
là tổng của cấp số nhân lùi vô hạn với ; 𝑢 2 𝟐𝟎 V 2. ậy 222 … 1 = = = 1 −𝑞 1 𝟗 1 − 10 𝟐 𝟐 𝟐
Tính tổng 𝐒=𝟐+ 𝟕+ 𝟒𝟗 +…+ 𝟕𝒏−𝟏
S là tổng của cấp số nhân lùi vô hạn với ; 𝑢 V 𝑺 1 2 𝟕 ậy = = 1 −𝑞 = 1 𝟑 1− 7
(Giải thích nghịch lí Zeno) Giả sử Achil es chạy với vận tốc 100 km/h, vận
tốc rùa là 1 km/h, khoảng cách ban đầu là a = 100 (km).
a) Tính thời gian t , t , ..., t , ... để Achil es chạy từ A đến A , từ A đến A , ... 1 2 n 1 2 2 3
b) Tính tổng thời gian để Achil es chạy hết các quãng đường
c) Sai lầm trong lập luận của Zeno là gì? A A 1 2 A 3 A A 4 5 A … 6 R R R R R … 1 2 3 4 5
a) Với t = 1h: Achil es chạy đoạn A A = 100(km); Rùa chạy đoạn A A = 1(km) 1 1 2 2 3
Với t = (h) Achil es chạy đoạn A A = 1(km); Rùa đã chạy đoạn A A = (km) 2 2 3 3 4
Cứ như vậy, Achil es mất t = (h) để chạy đoạn A A = (km) n n n+1
(Giải thích nghịch lí Zeno) Giả sử Achil es chạy với vận tốc 100 km/h, vận
tốc rùa là 1 km/h, khoảng cách ban đầu là a = 100 (km).
a) Tính thời gian t , t , ..., t , ... để Achil es chạy từ A đến A , từ A đến A , ... 1 2 n 1 2 2 3
b) Tính tổng thời gian để Achil es chạy hết các quãng đường
c) Sai lầm trong lập luận của Zeno là gì? A A 1 2 A 3 A A 4 5 A … 6 R R R R R … 1 2 3 4 5 1 1 1 1 𝐓 =1+ 100 + +…+ + 1002
100𝑛−1 100𝑛 + … 𝑢
là tổng của cấp số nhân lùi vô hạn với ; nên 𝐓 1 = =𝟏 𝟏 1 −𝑞 𝟗𝟗 (h)
c) Nghịch lý Zeno chỉ đúng với điều kiện tổng thời gian Achilles chạy hết các
quãng đường để đuổi kịp Rùa là vô hạn. Nếu nó hữu hạn thì là khoảng thời
gian mà Achilles đuổi kịp Rùa.
HĐ5. Nhận biết giới hạn vô cực: Một loại vi khuẩn được nuôi cấy với số
lượng ban đầu là 50. Sau mỗi chu kì 4 giờ, số lượng của chúng sẽ tăng gấp đôi.
a) Dự đoán công thức tính số vi khuẩn sau chu kì thứ .
b) Sau bao lâu, số lượng vi khuẩn sẽ vượt con số 10 000?
a) Ta có số lượng ban đầu của vi khuẩn là
Sau chu kì thứ nhất, số lượng vi khuẩn là
Sau chu kì thứ hai, số lượng vi khuẩn là
Cứ tiếp tục như vậy, dự đoán sau chu kì thứ , số lượng vi khuẩn là
b) Giả sử sau chu kì thứ , số lượng vi khuẩn sẽ vượt con số 10 000. Khi đó ta có
Vậy sau 8 chu kỳ (khoảng 32 giờ) số lượng vi khuẩn sẽ vượt con số 10 000 Tính a) Ta có:
nên 𝐥𝐢𝐦 (𝒏 𝟐− 𝟐𝒏)=+∞ 𝟏 𝟏
b) Ta có: (𝒏− √𝒏)=𝒏(𝟏− √𝒏);𝐥𝐢𝐦𝒏=+∞;𝐥𝐢𝐦(𝟏− √𝒏)=𝟏 nên
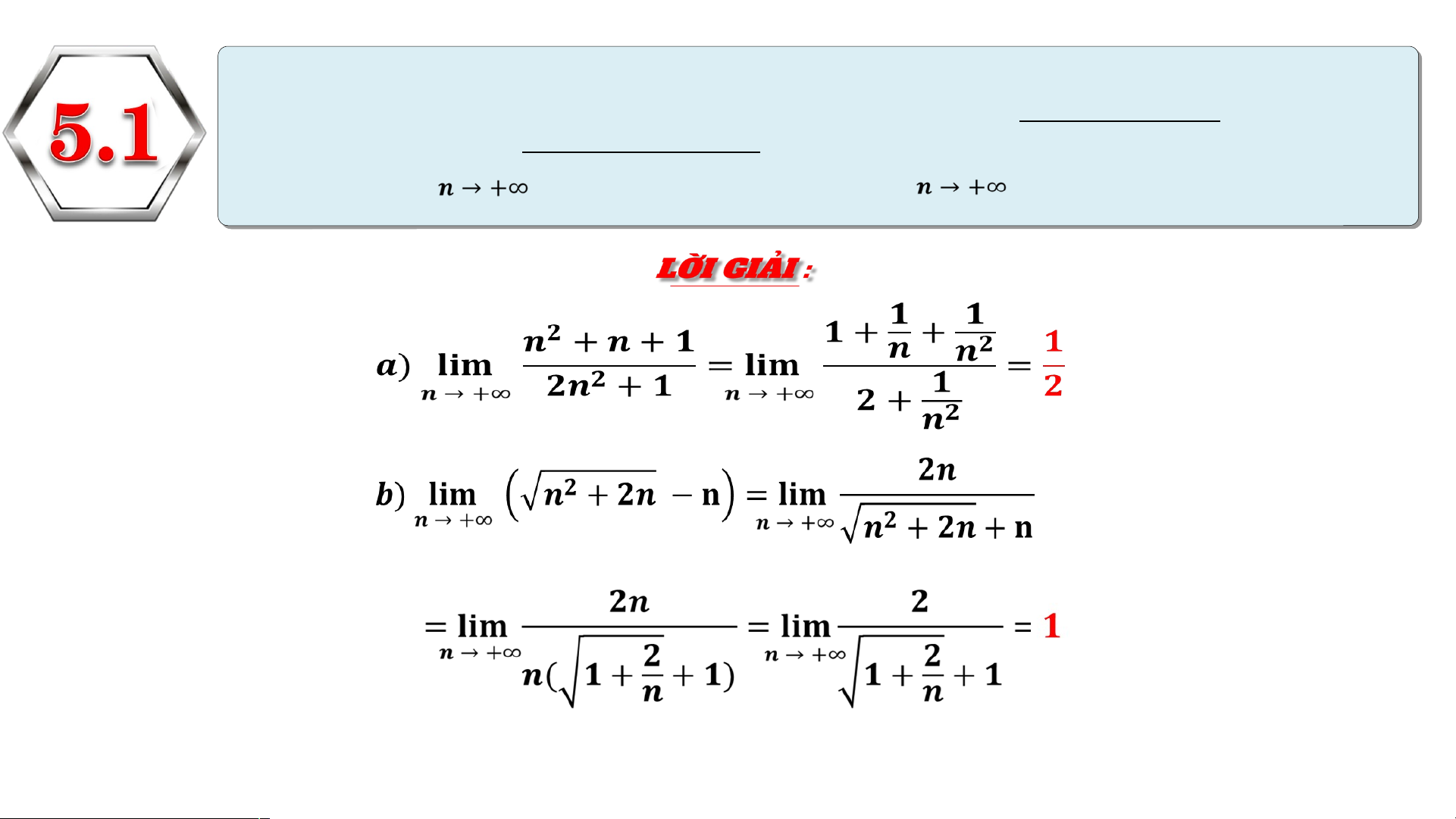
Tính các giới hạn sau: 𝒏𝟐 𝒂
+𝒏 +𝟏 ¿ 𝐥𝐢𝐦
𝒃 ¿ 𝐥𝐢𝐦 (√ 𝒏𝟐+𝟐 𝒏 − 𝐧 )
𝟐𝒏𝟐 +𝟏 𝒗 𝟐 𝒂 𝒏 ¿ 𝐥𝐢𝐦 𝒃 𝒗 ¿ 𝐥𝐢𝐦 − 𝒖
√𝒖𝒏 +𝟐 𝒗 𝒏 𝒏 𝒏
Áp dụng các Quy tắc tính giới hạn để giải. b) Ta có nên
Tính các giới hạn của các dãy số cho bởi 𝒏𝟐 𝒂 +𝟏 ¿ 𝒖𝒏 = 𝒃 𝟐 𝒏 ¿ 𝒗 − 𝟏
𝒏 =√ 𝟐 𝒏𝟐 +𝟏 − 𝐧 a) Ta có và với mọi nên b) Ta có
Viết các số thập phân vô hạn tuần hoàn sau dưới dạng phân số: a) b) . Vậy 𝑆2=¿ . Vậy 3,(102) = 3 +
Một bệnh nhân mỗi ngày uống viên thuốc 150 mg. Sau ngày đầu,
trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính
lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước
tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc lâu dài.
Cho tam giác vuông ABC vuông tại A, có AB = và góc B bằng (Hình.5.3). Từ A kẻ AA ⊥ BC, từ A kẻ A A ⊥ AC, sau đó lại kẻ 1 1 1 2 A A
⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn 2 3
AA A A ... Tính độ dài đường gấp khúc này theo và . 1 2 3
A A = AA sin𝛼 = .sin. sin = sin2. A A = A A .sin = sin2 .sin = sin3. 1 2 1 2 3 1 2
A A = A A .sin = sin3sin = sin4. B 3 4 2 3
Tiếp tục như vậy, ta có A A = sinn. n – 1 n A1
AA A A ... = AA + A A + A A +...+ A 1 2 3 1 1 2 2 3 n – A3 A +... 1 n A5
= sin + sin2 +sin3 + ... +sinn+ ... Do đó, AA A A ... = 1 2 3 A A C A A2 4 6 Hình.5.3
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29




