






Preview text:
1. Hình thang. Hình thang cân • Khái niệm:
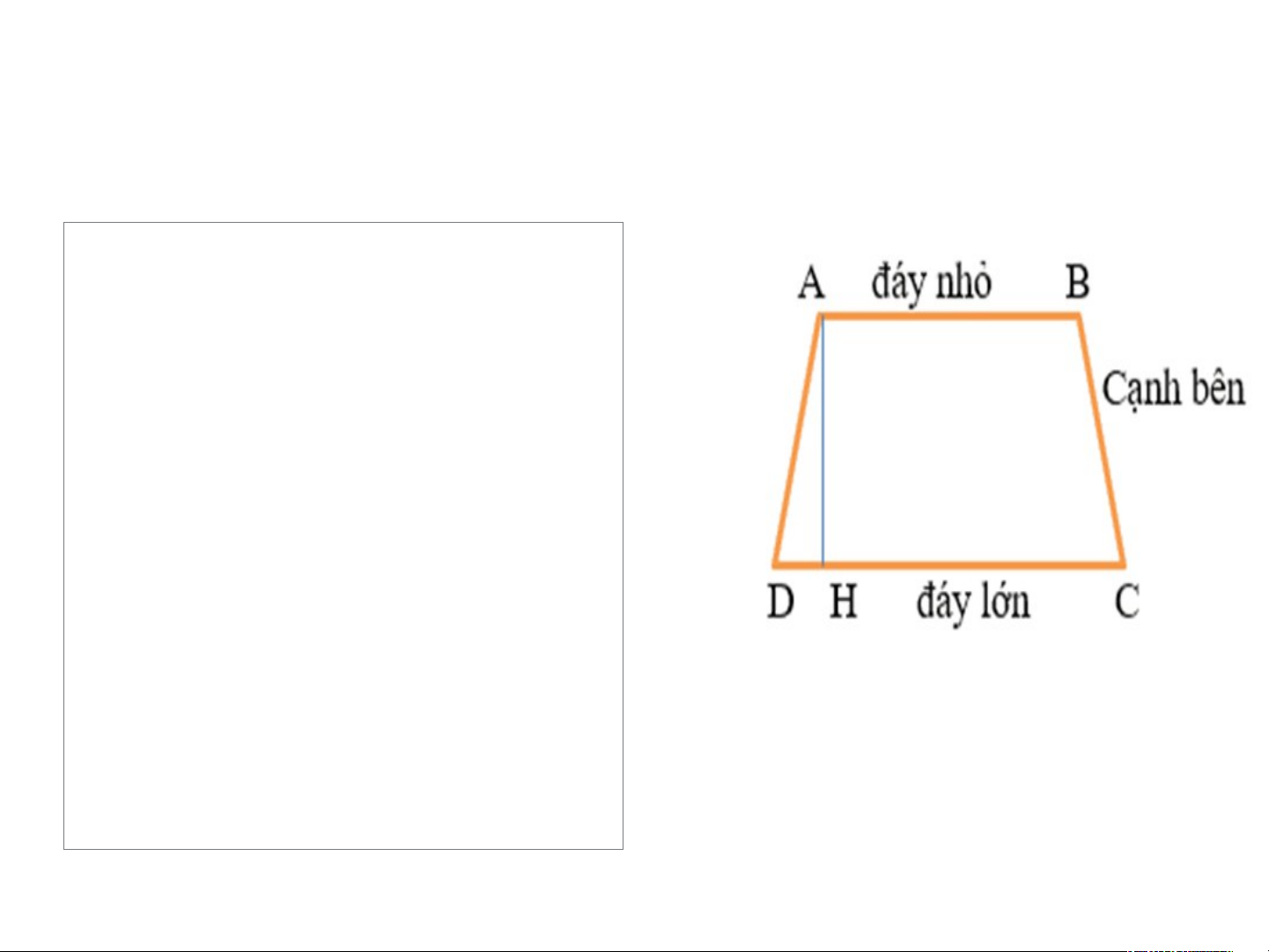
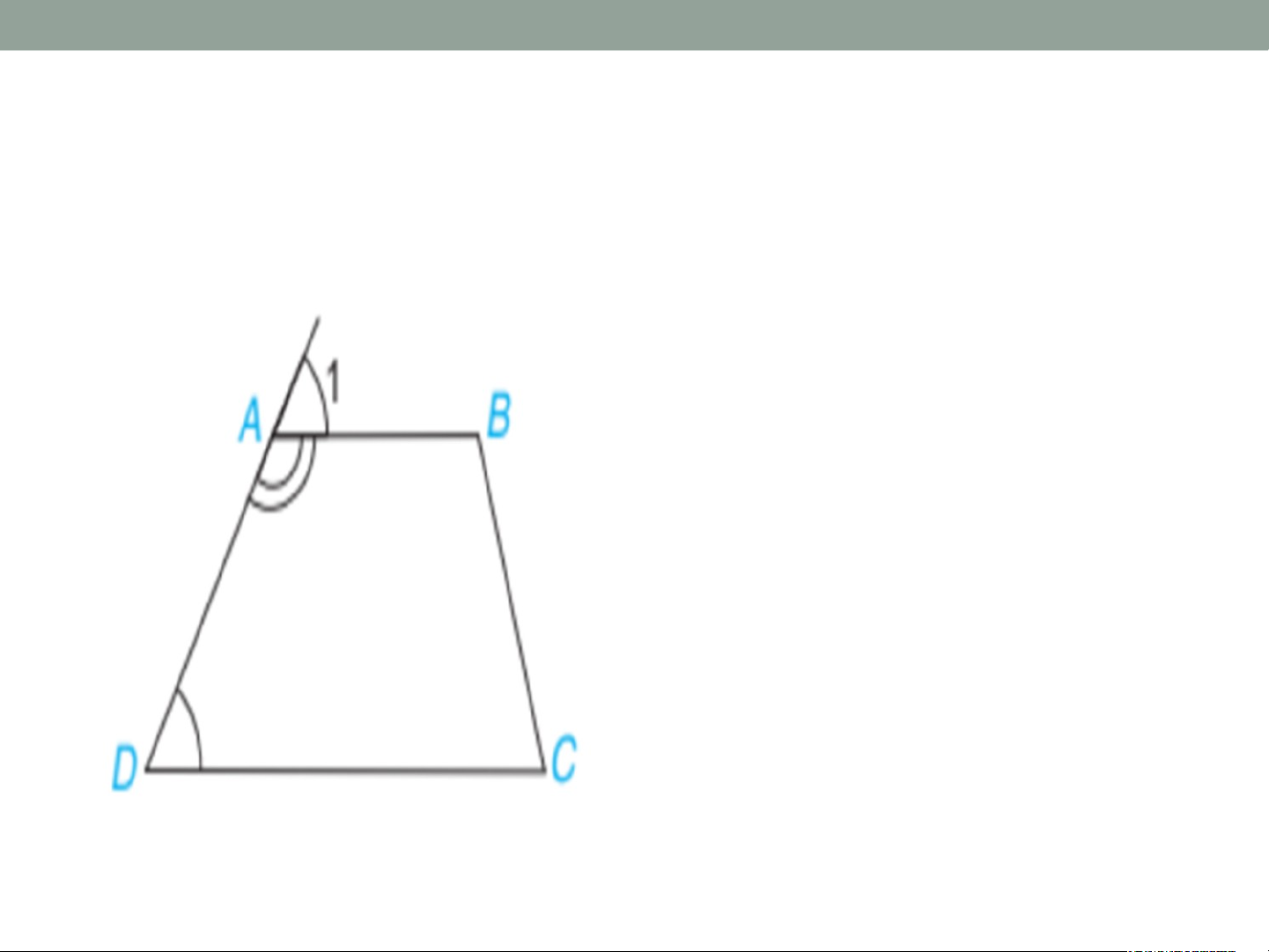
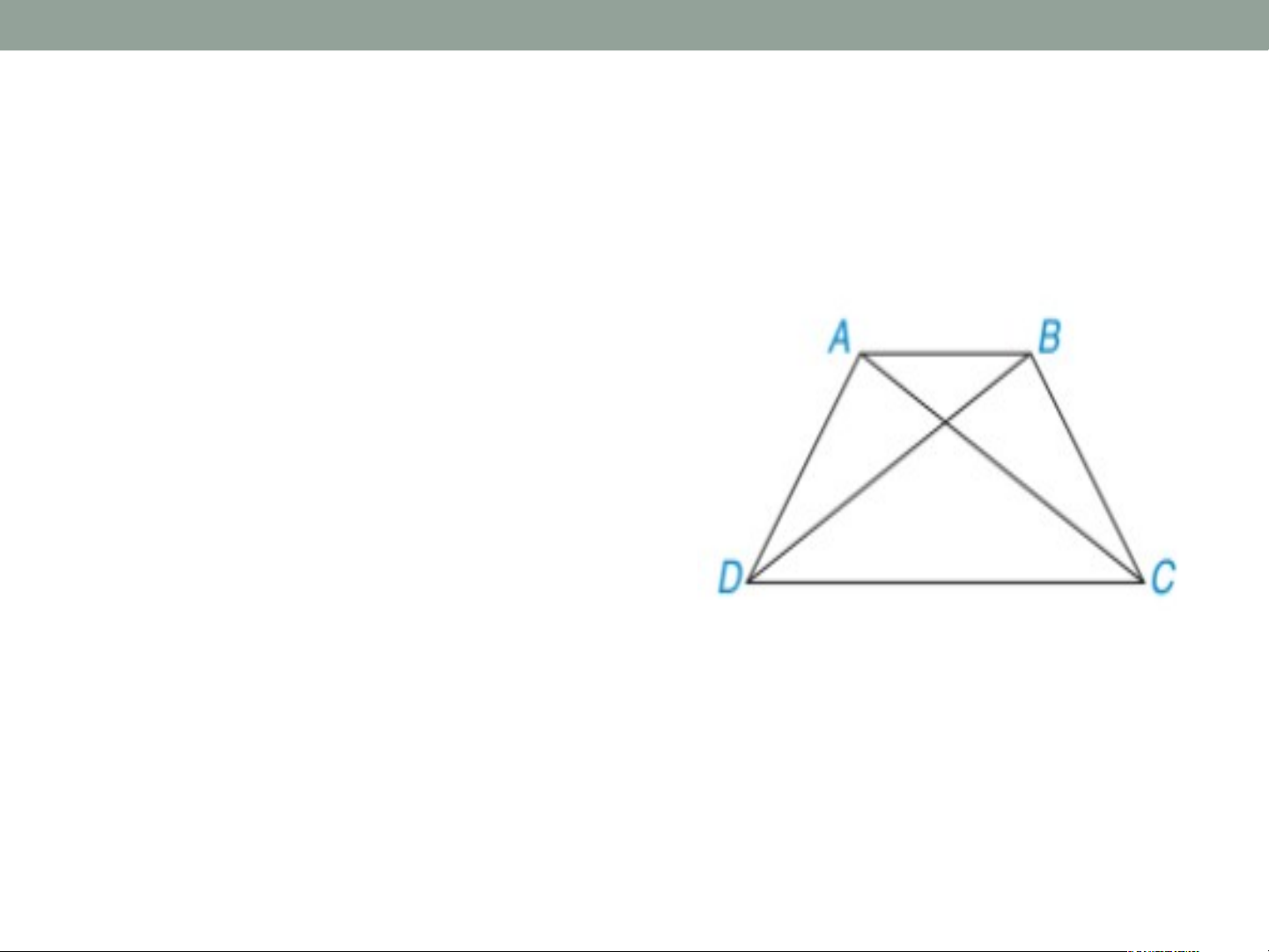
Hình thang là tứ giác có hai cạnh đối song song. Hình thang ABCD có:
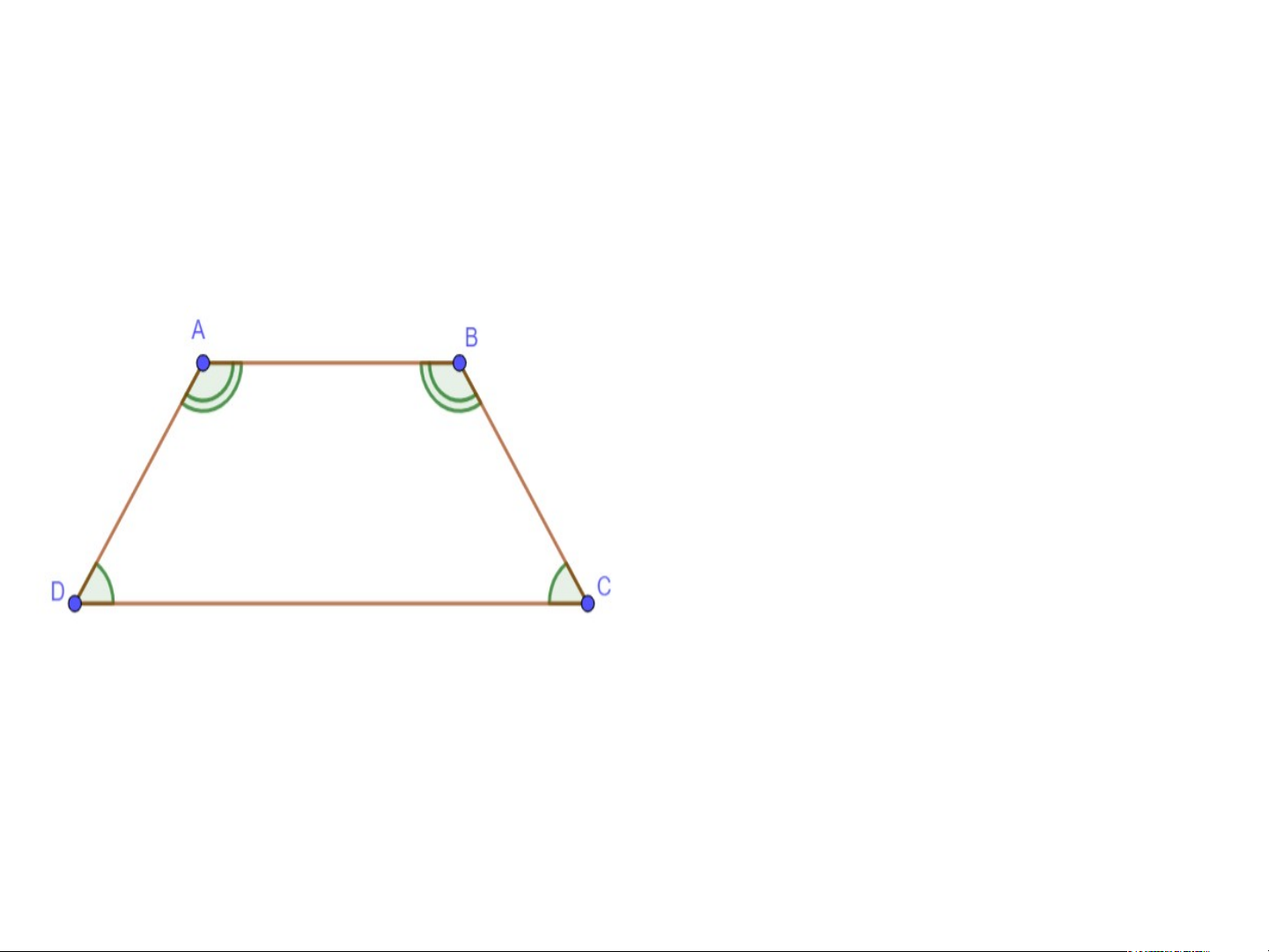
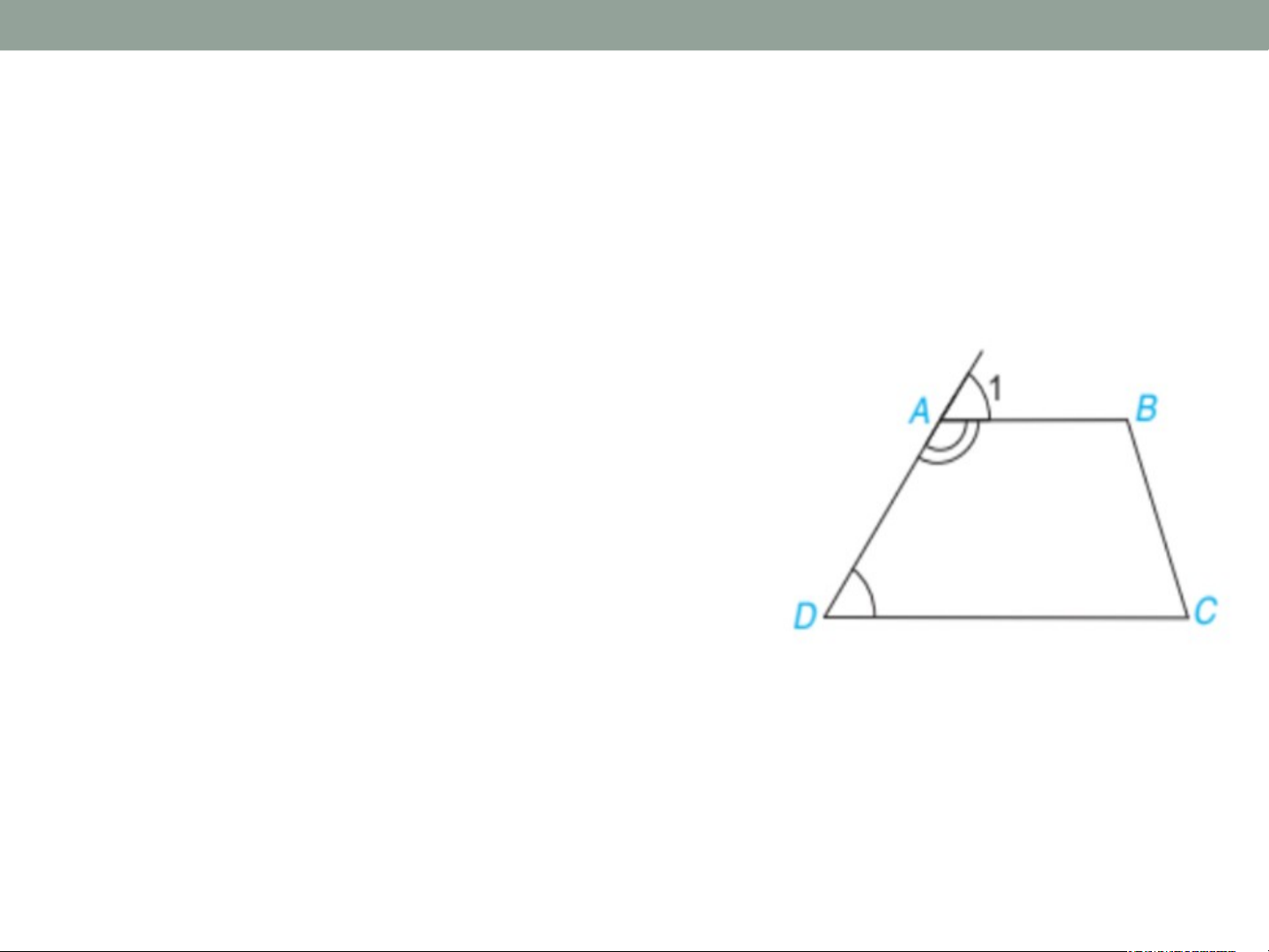
+ Đáy nhỏ AB song song với đáy lớn CD. + Cạnh bên AD và BC. + Đường cao AH. Khái niệm hình thang cân • Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. - Nhận xét Hình Hình tha t ng n AB g C AB D C c ó: c AB ó: // // CD. C + + Vì Vì và và là là hai ha góc góc kề kề cùng c ùng một m đáy đá nhỏ n AB AB nên nê hình hìn tha th ng a ABC AB D là D là hình hình tha t ng ha c ng ân. â Ví dụ 1. •Chứng minh rằng hai góc kề một cạnh bên của hình thang bù nhau Lời giải ví dụ 1. Vì ABCD là hình thang (AB // CD) nên: (đồng vị). Do (hai góc kề bù) Suy ra: .
Luyện tập 1 trang 53 Toán 8 Tập 1
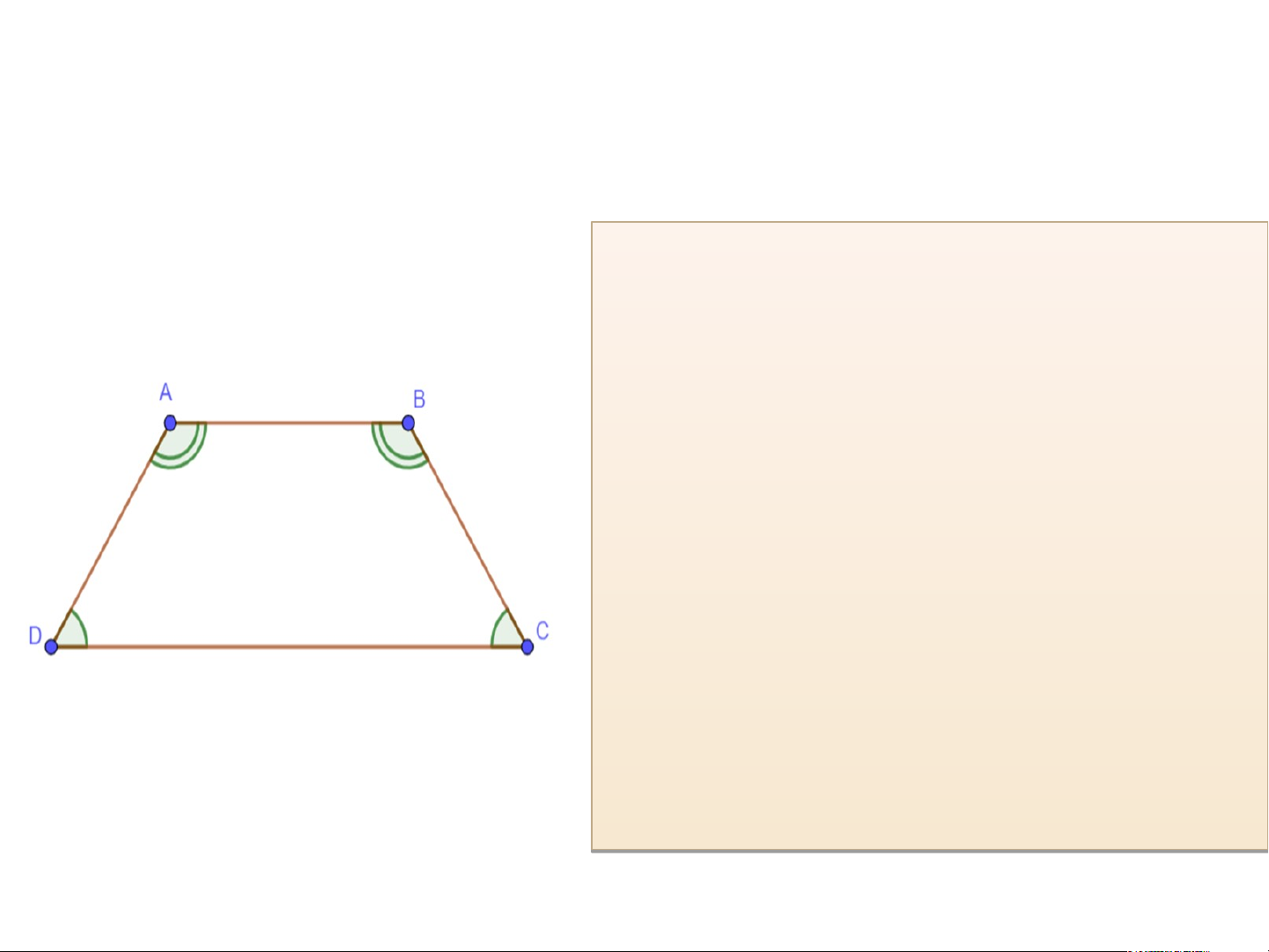
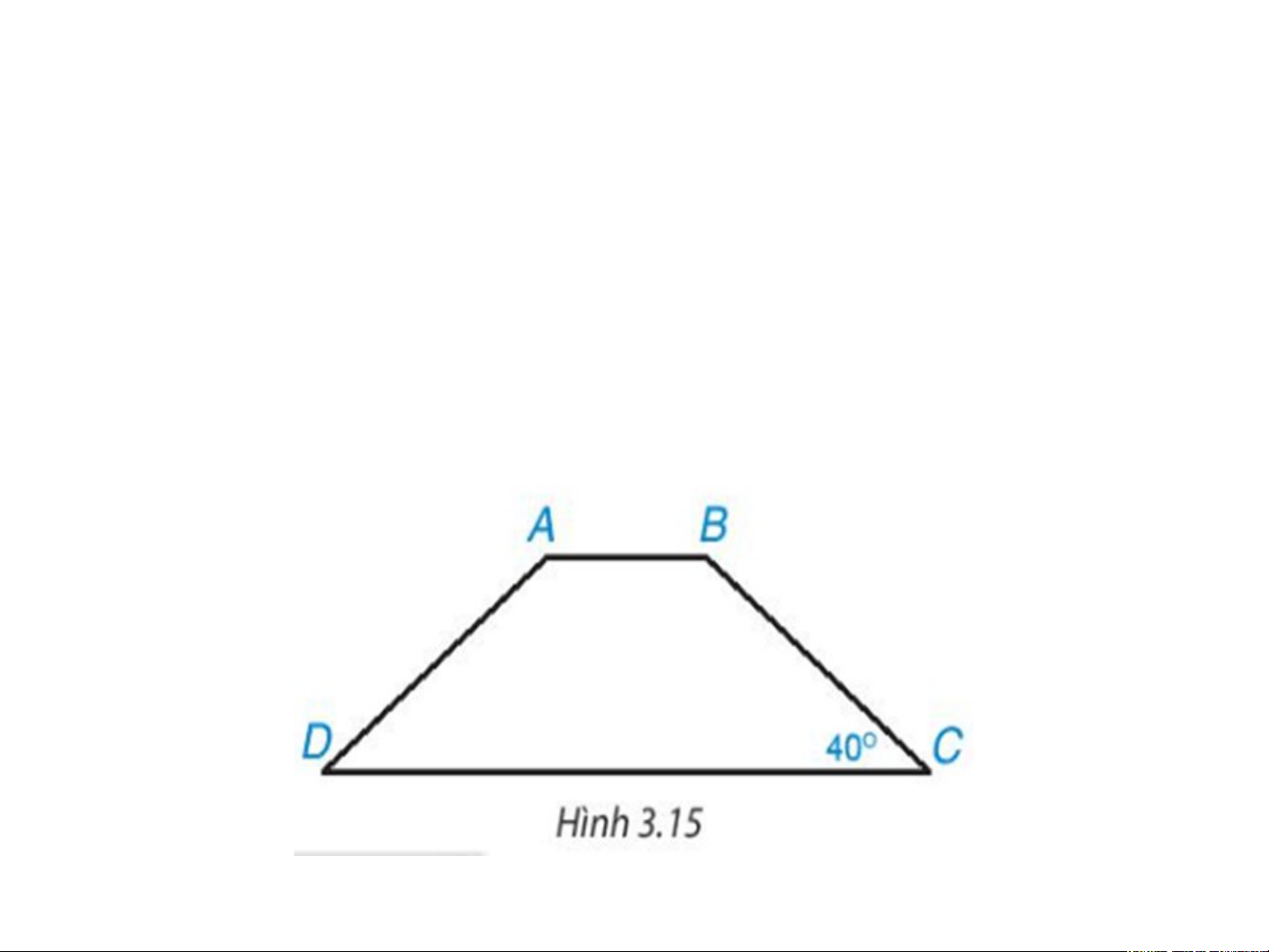
Tính các góc của hình thang cân ABCD
(AB // CD), biết góc C =40° (H.3.15). Đáp án luyện tập 1
Hình thang cân ABCD (AB // CD) nên ta có: Ta có: => =>
2. Tính chất của hình thang cân
Tính chất về cạnh bên của hình thanh cân
• HĐ1 trang 53 Toán 8 Tập
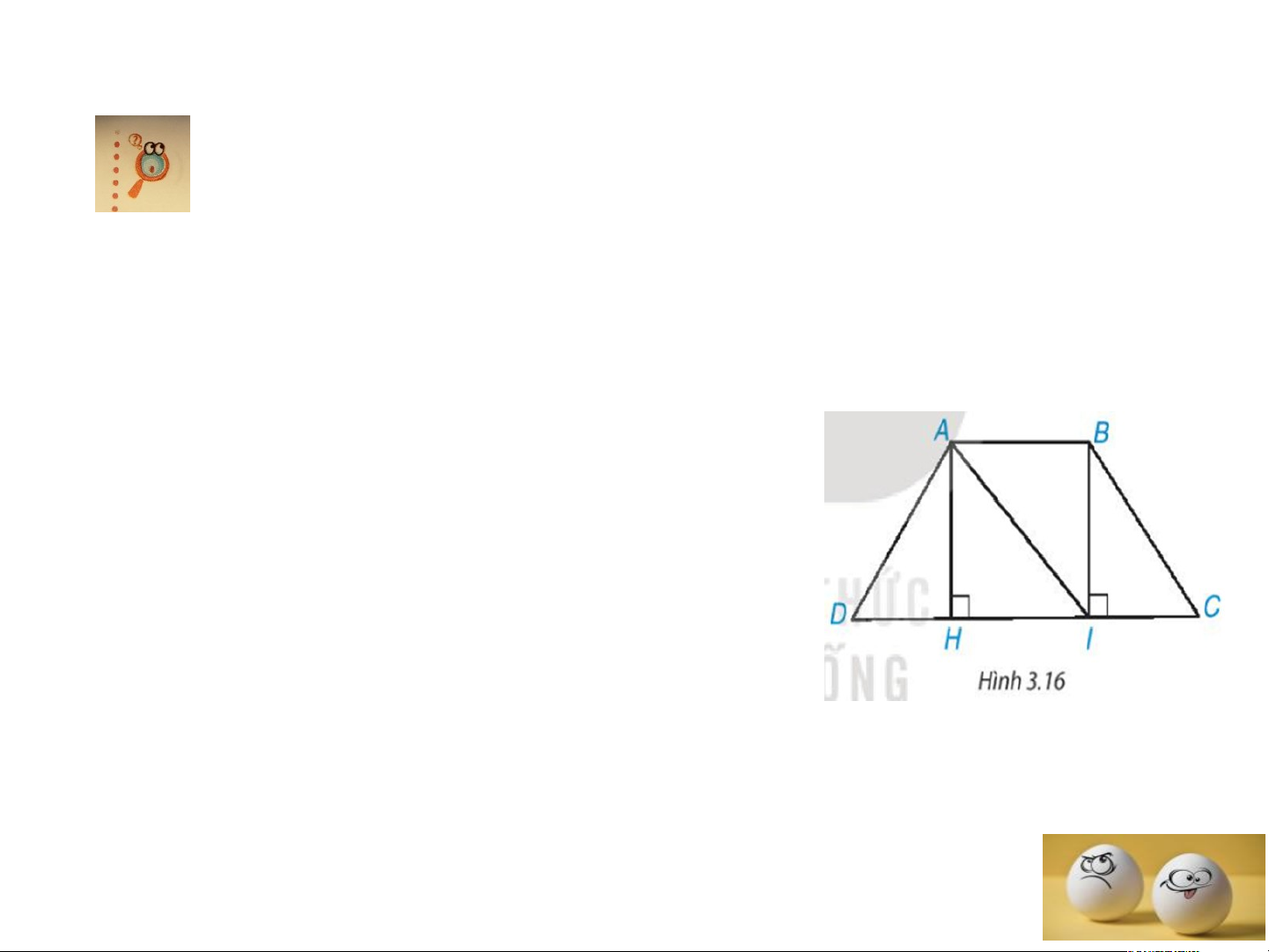
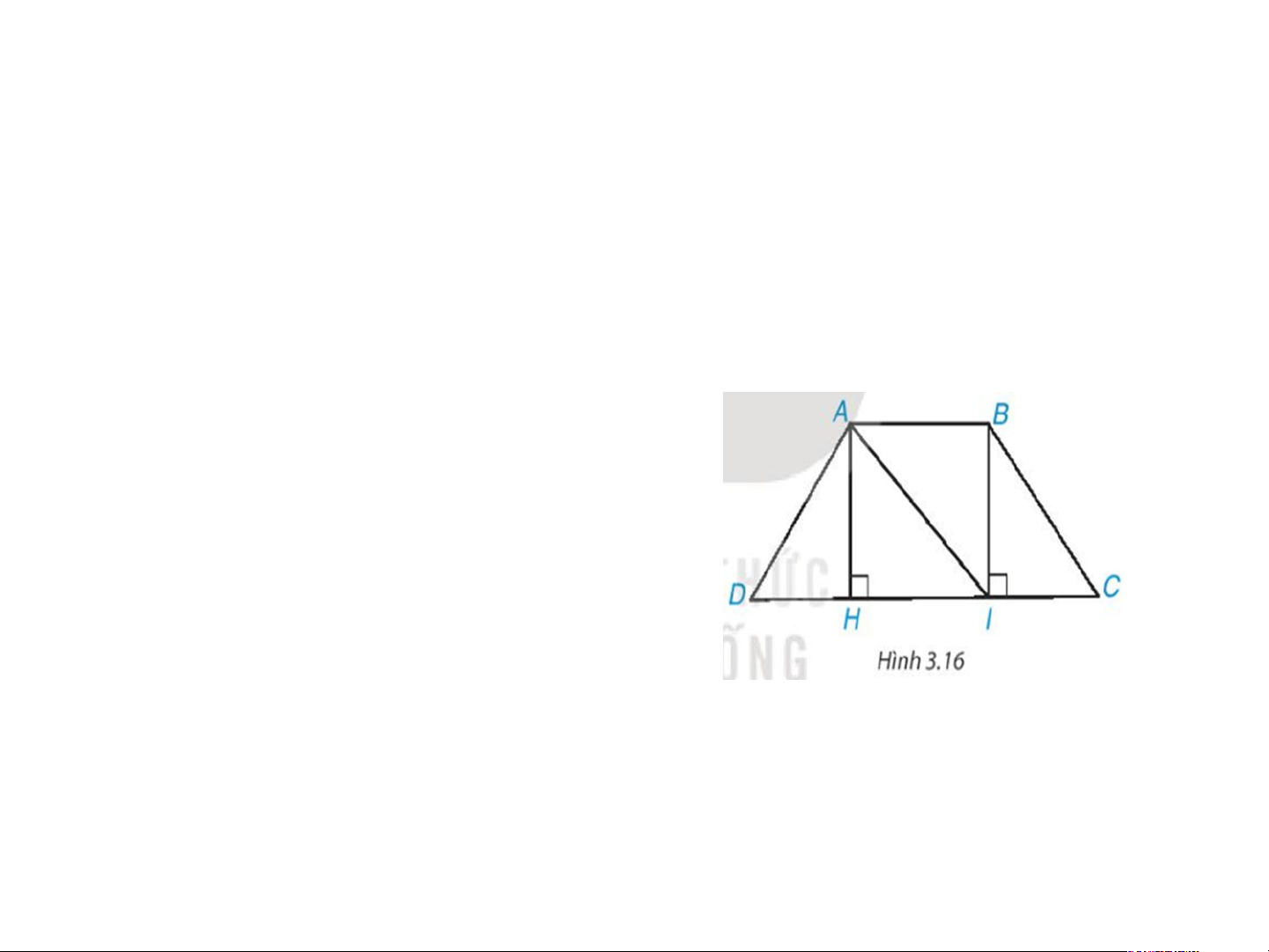
1: Cho hình thang cân ABCD,
AB // CD và AB < CD (H.3.16).
• a) Từ A và B kẻ AH ⊥ DC, BI
⊥ DC, H ∈ CD, I ∈ CD. Chứng
minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.
• b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC. HĐ1 ( Đáp án ý a)
a) Ta có AB // CD (gt) mà (gt) => . Suy ra . Xét và có: (so le trong) AI chung => (g.c.g) => AH = BI. HĐ1 ( Đáp án ý b) b) Xét và có: (ABCD là hình thang cân) AH = BI (theo a) => (g.c.g) => AD = BC. Tính chất về cạnh bên của hình thang cân. • Định lí 1. A B
Trong hình thang cân, hai
cạnh bên bằng nhau.
Cụ thể, hình thang cân
ABCD có hai cạnh bên là
AD và BC thì AD = BC D C
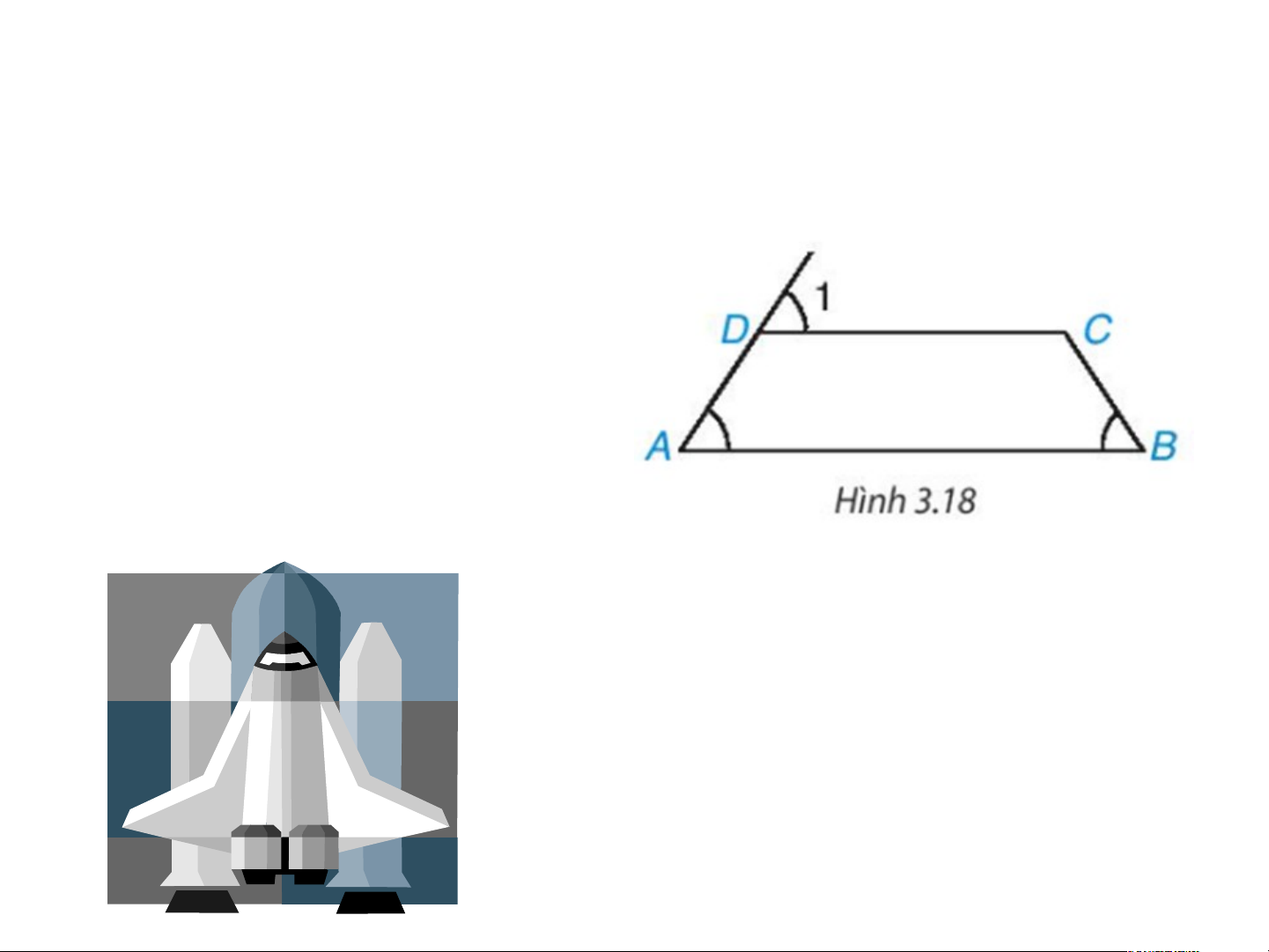
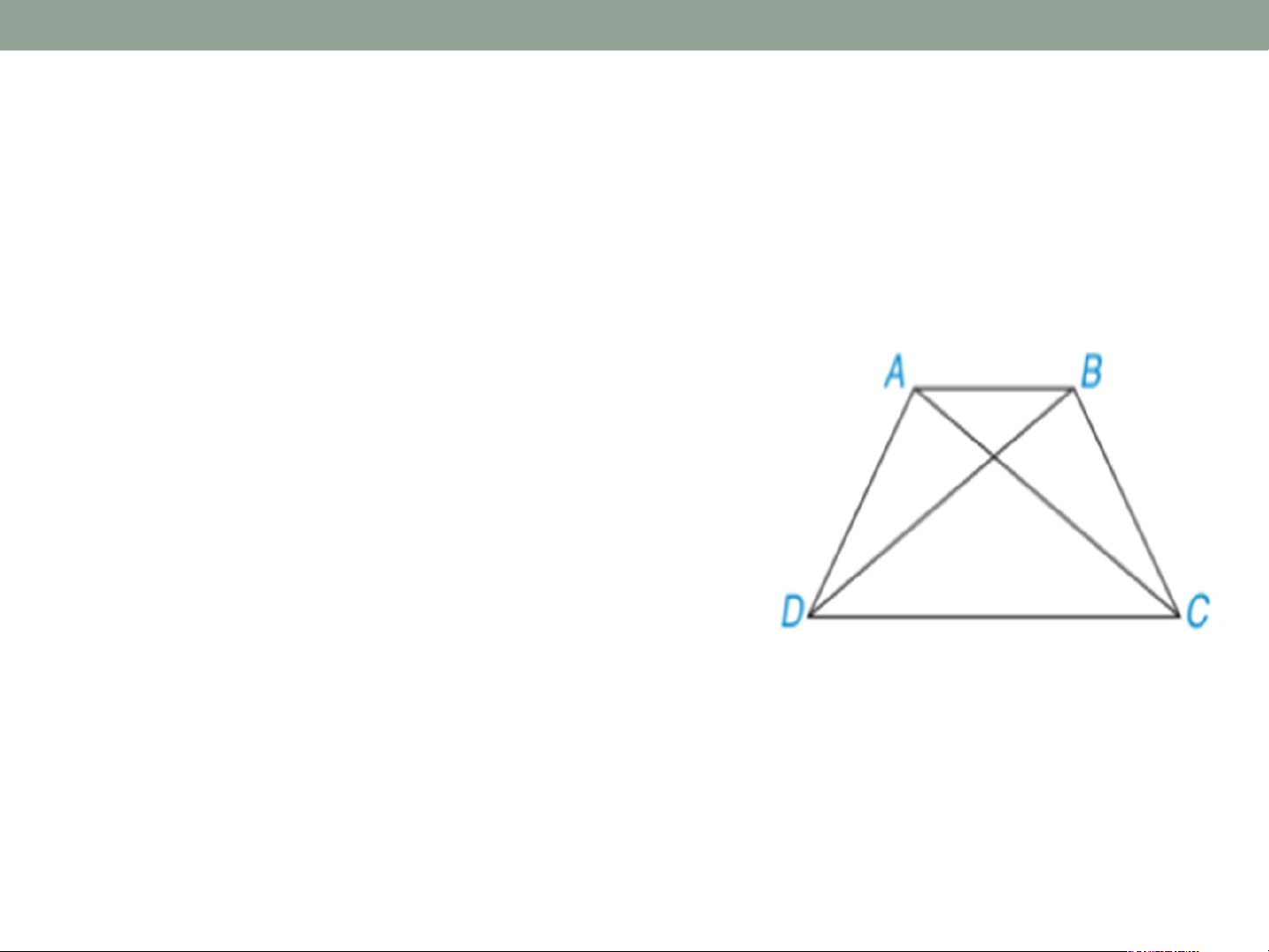
Luyện tập 2 ( SGK-tr53) • Cho tứ giác ABCD như Hình 3.18. Biết rằng góc Chứng minh rằng AD = BC. ĐÁP ÁN LUYỆN TẬP 2
• Ta có: (gt) mà hai góc này ở vị trí đồng vị, nên suy ra: DC // AB.
Vậy tứ giác ABCD là hình thang.
Lại có => hình thang ABCD cân. => AD = BC. Đáp án Xét và có: CD chung AD = BC => (c.g.c) => DC = BD.
Tính chất về đường chéo của hình thang cân
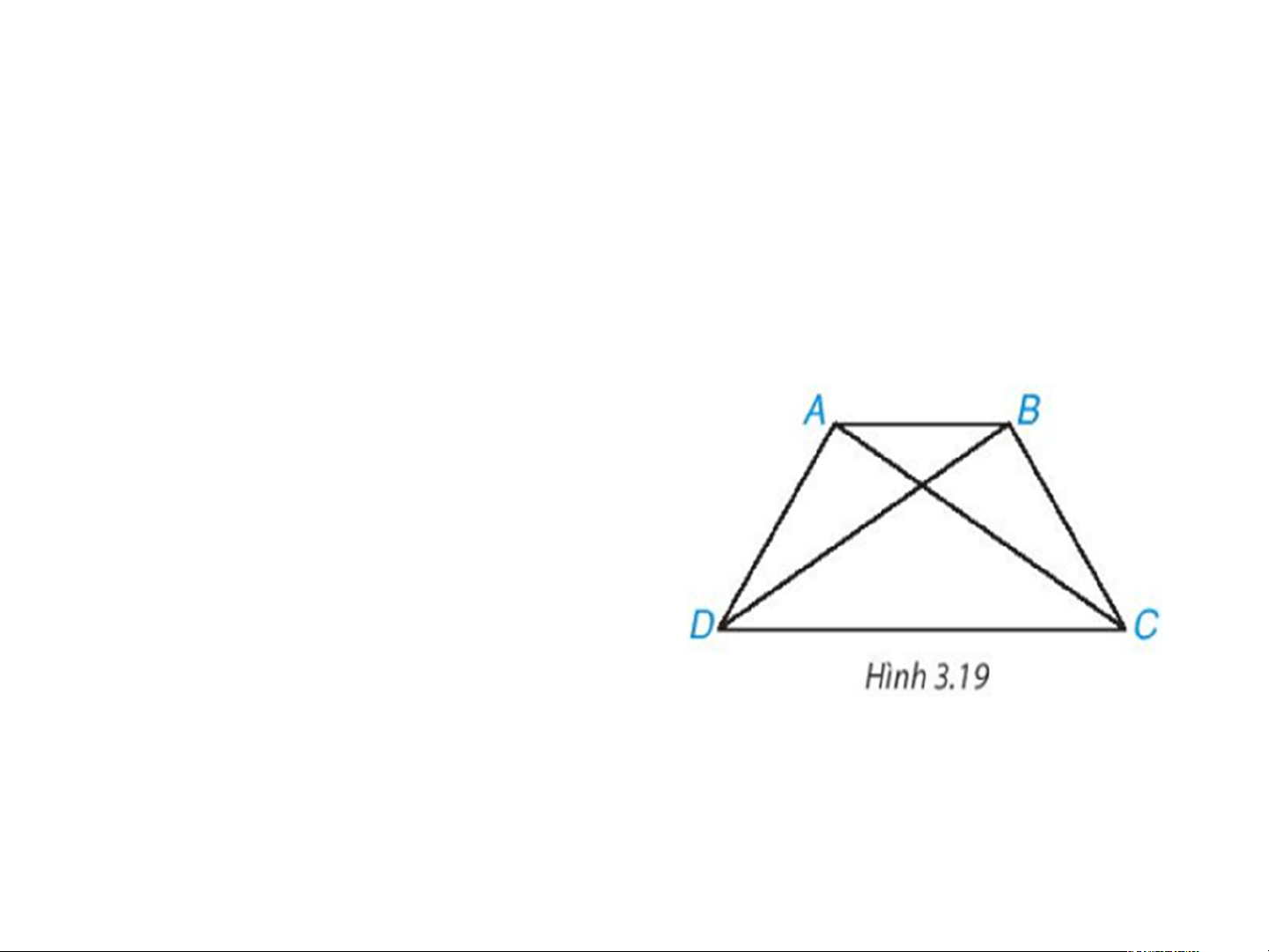
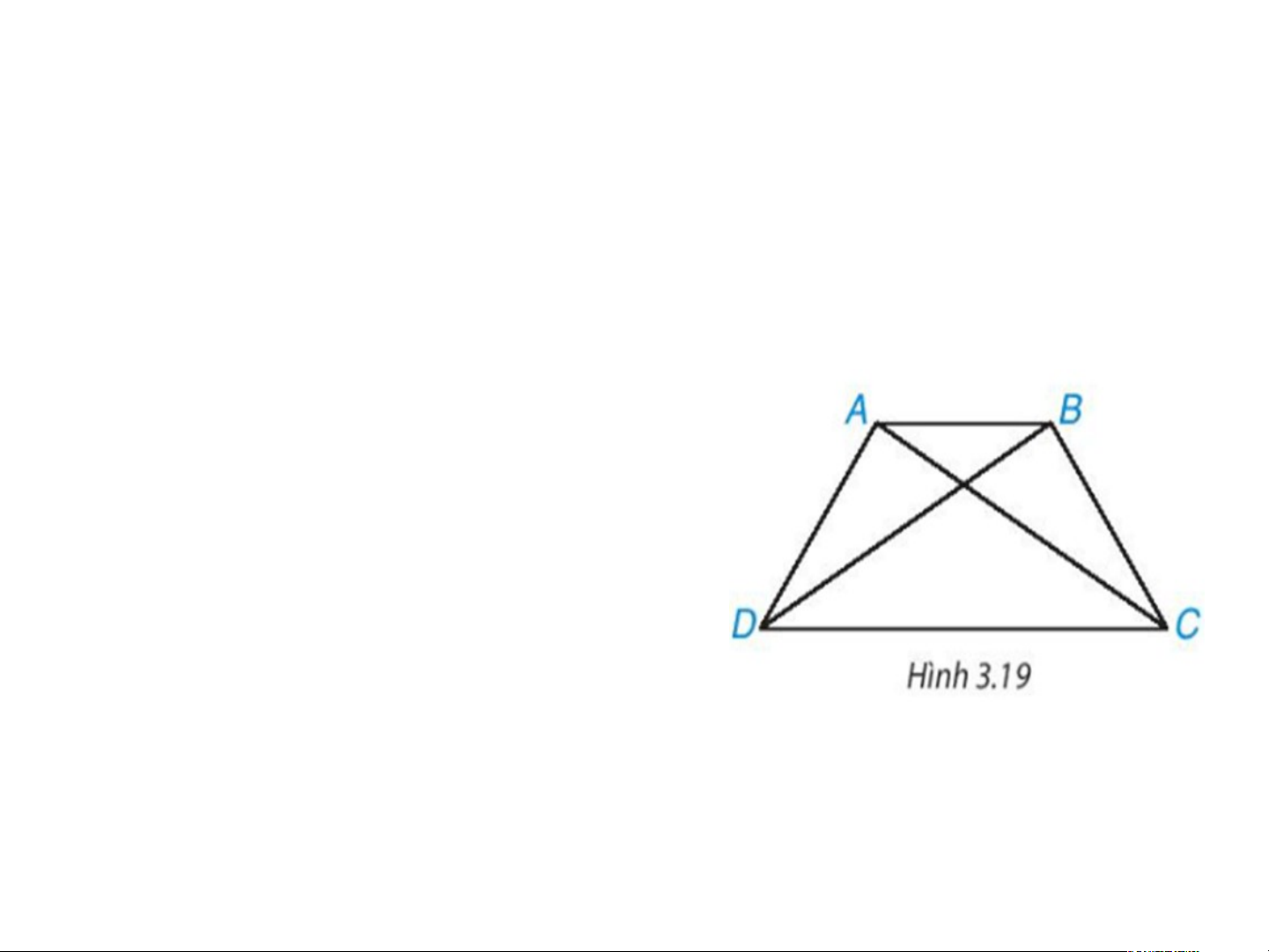
• HĐ2 trang 54 Toán 8
Tập 1: Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ACD = ∆BDC. Từ đó suy ra AC = BD.
Tính chất về đường chéo của hình thang cân.
• Định lí 2
Trong hình thang cân, hai
đường chéo bằng nhau.
Cụ thể: hình thang cân
ABCD có hai đường chéo
là AC và DB thì AC = BD
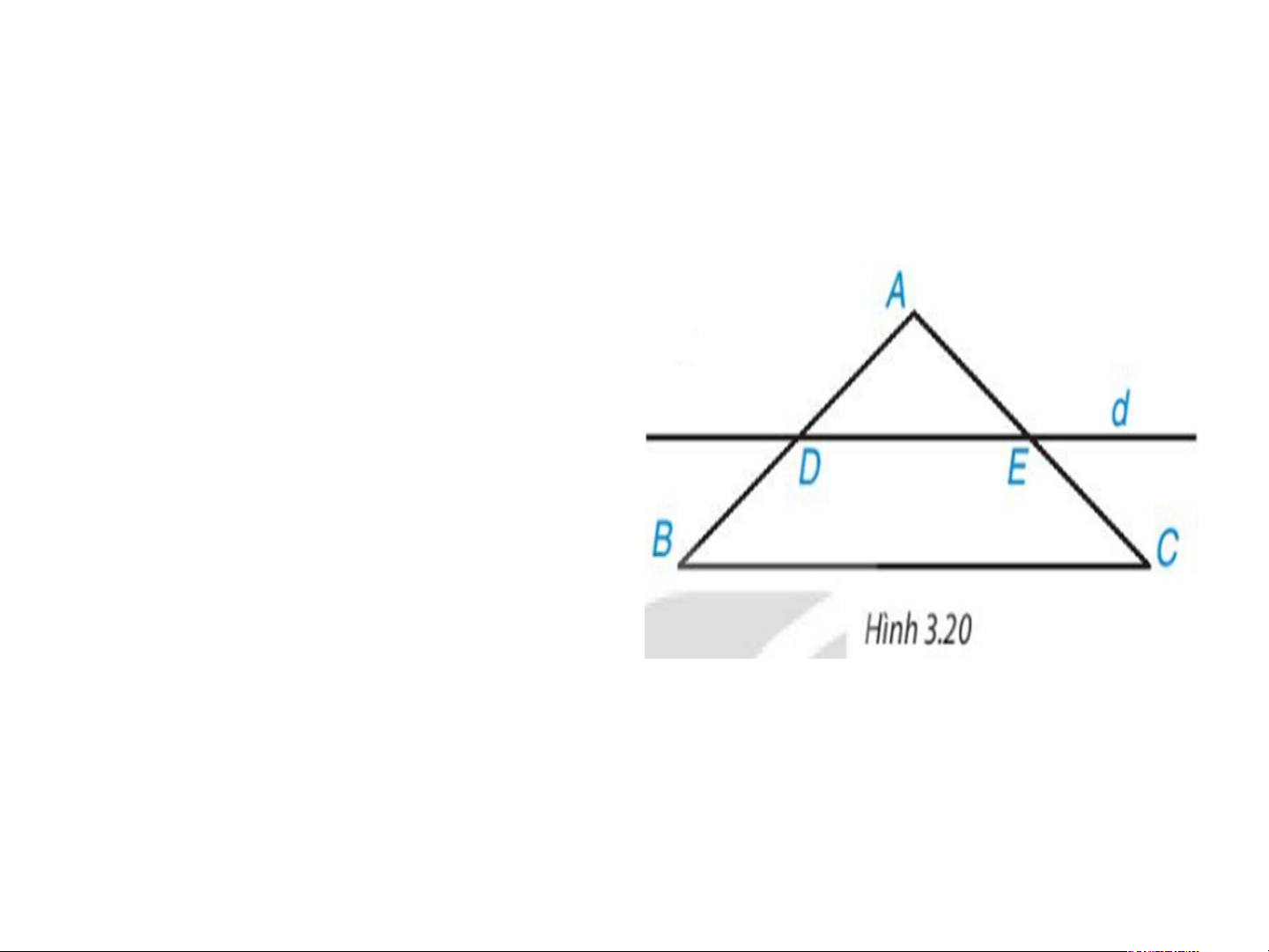
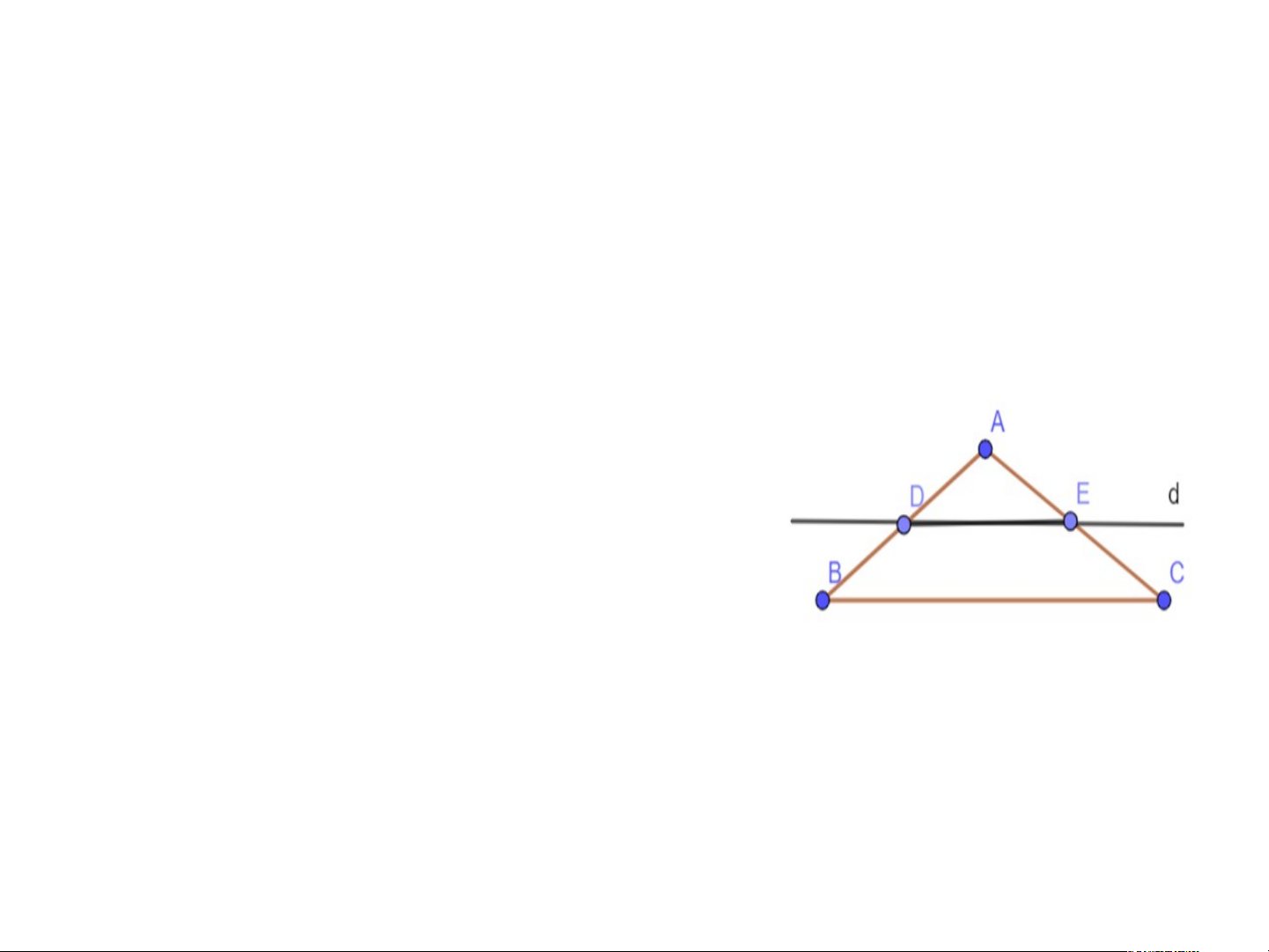
Luyện tập 3 trang 54 Toán 8 Tập 1 Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20). a) Tứ giác DECB là hình gì? b) Chứng minh BE = CD
Đáp án luyện tập 3a. Sgk-tr54
a) Vì DE // BC nên tứ giác DECB là hình thang. Lại có cân tại A =>
Suy ra hình thang DECB có hai
góc kề 1 đáy bằng nhau nên là hình thang cân.
DẤU HIỆU NHẬN BIẾT HÌNH THANG CÂN • .
• Định lí 3:
Nếu một hình thang có hai đường
chéo bằng nhau thì hình thang đó là hình thang cân.
Cụ thể: Hình thang ABCD có hai
đường chéo bằng nhau là AC =
DB thì ABCD là hình thang cân Ví dụ 2. sgk – tr 54 • Cho hình thang ABCD
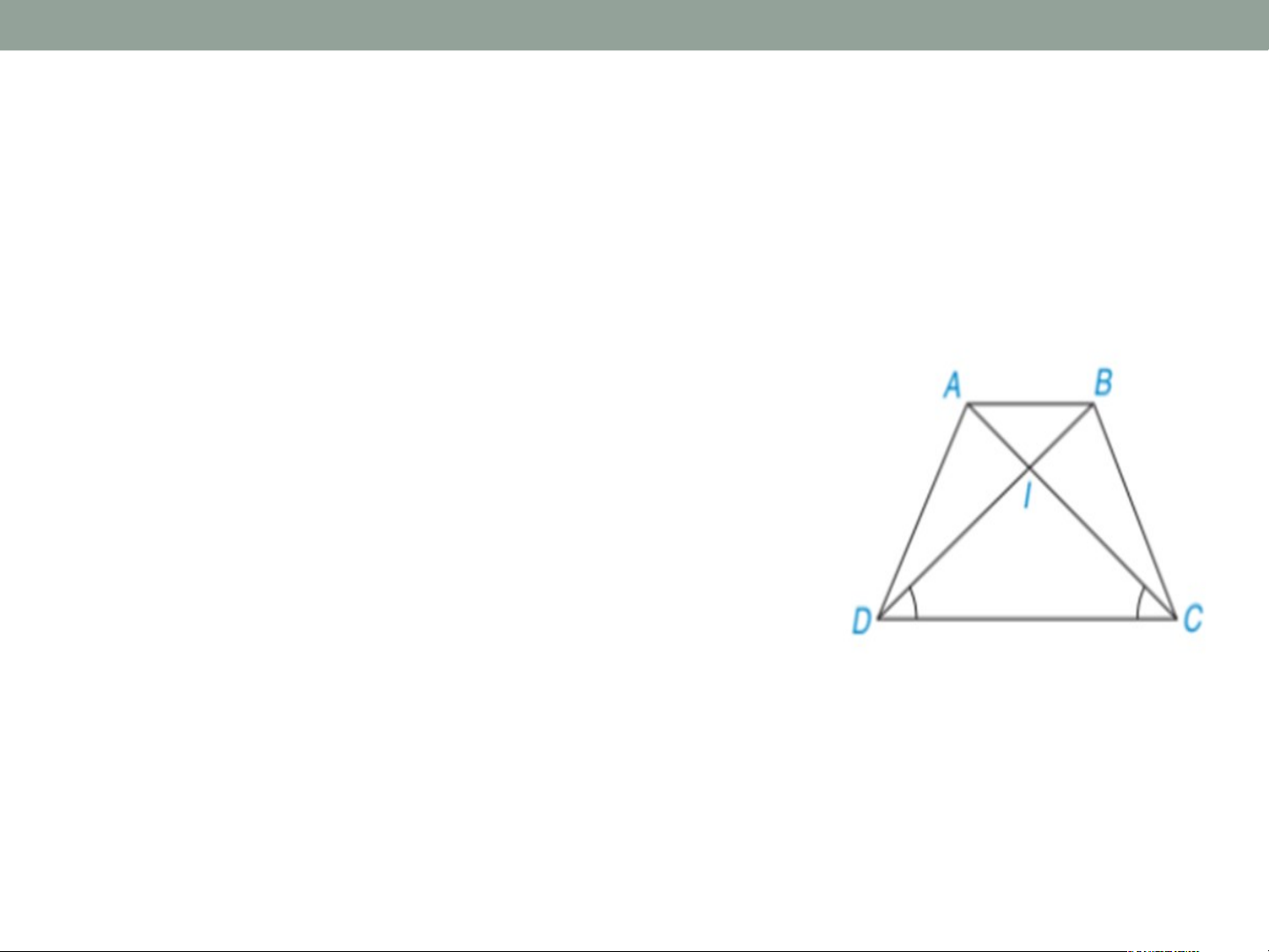
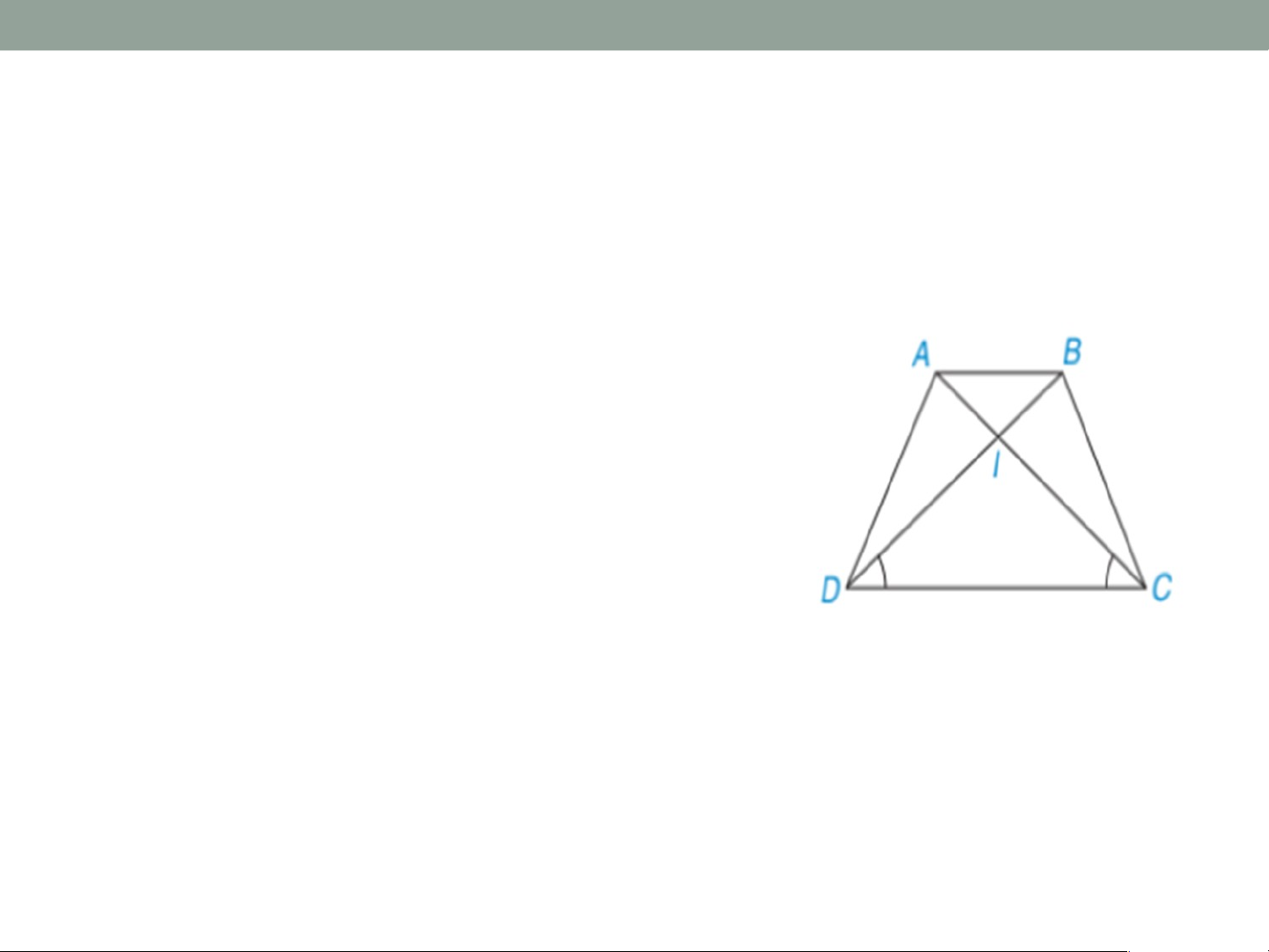
(AB//CD) có góc ACD = góc BDC) Chứng minh rằng hình thang ABCD là hình thang cân Lời giải ví dụ 2
Hình thang ABCD có 2 đường chéo AC và BD cắt nhau tai I. Vì AB//DC nên suy ra ( so le trong) ( so le trong)
Theo giả thiết ta có
Þ Tam giác AIB cân tại I => IA=IB
Tam giác DIC cân tại I => ID=IC
Ta có: DB = DI+IB = CI+IA = AC hay DB = AC
Hình thang ABCD có hai đường chéo bằng nhau
DB =AC nên là hình thang cân
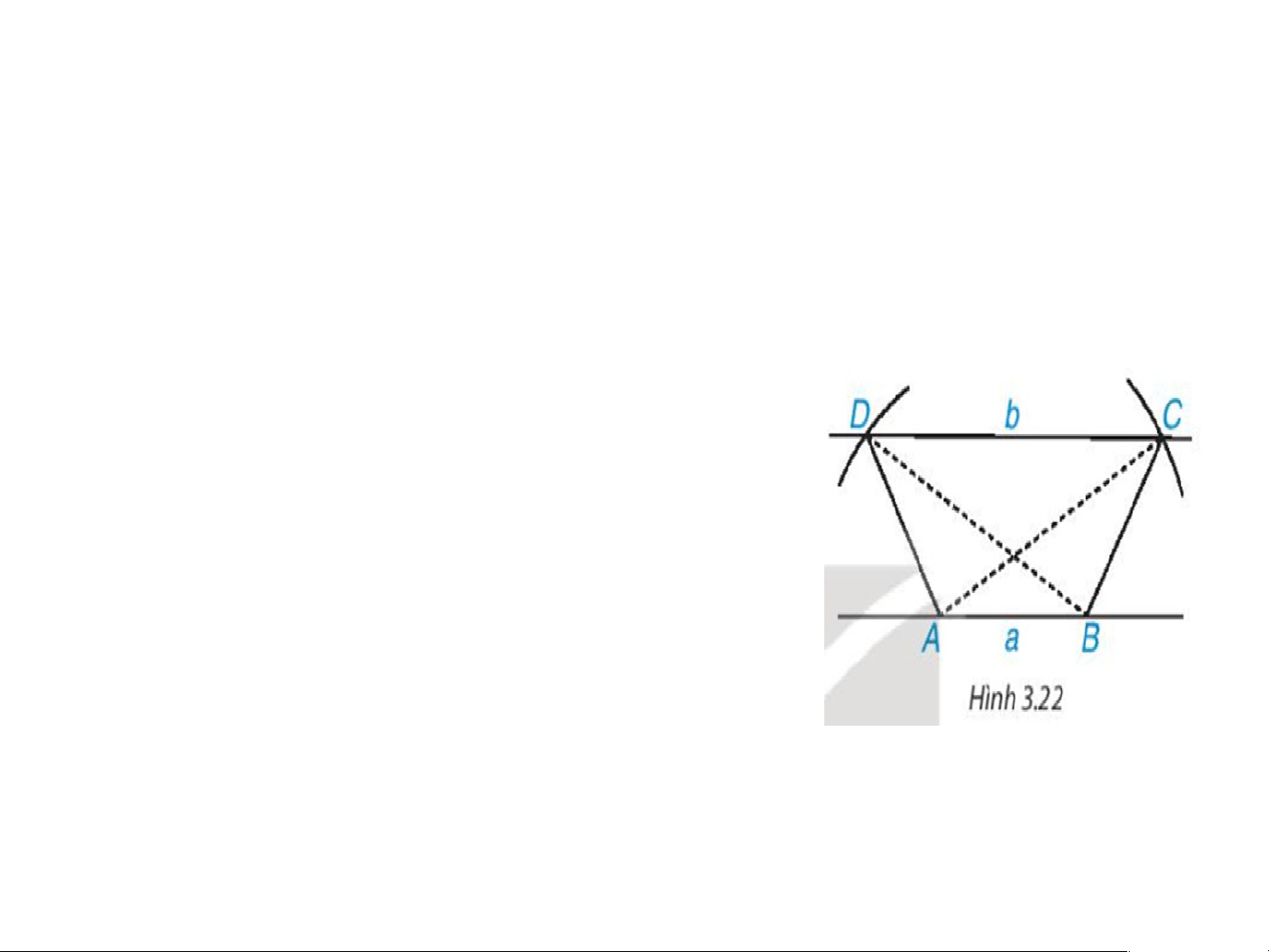
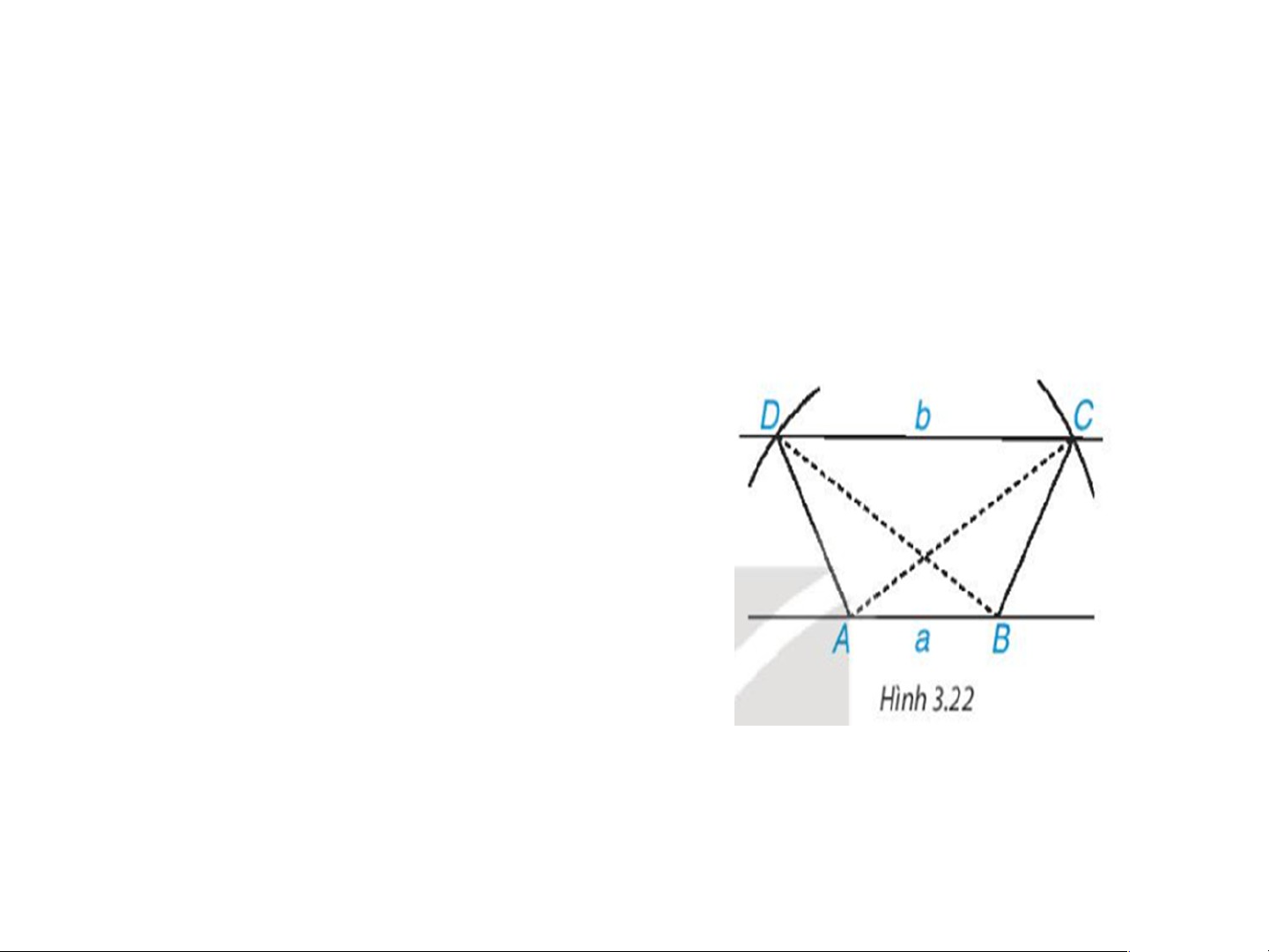
Thực hành trang 55 Toán 8 Tập 1: (H.3.22)
a) Vẽ hình thang có hai đường chéo
bằng nhau theo các bước sau:
- Vẽ hai đường thẳng song song a,
b. Trên a lấy hai điểm A, B.
- Vẽ hai cung tròn tâm A và B có
cùng bán kính sao cho cung tròn
tâm A cắt b tại C; cung tròn tâm B
cắt b tại D và hai đoạn thẳng AC,
BD cắt nhau. Hình thang ABCD có
hai đường chéo AC và BD bằng nhau.
b) Hình thang ABCD có là hình thang cân không? Vì sao?
Thực hành trang 55 Toán 8 Tập 1: (H.3.22) lời giải a) Học sinh vẽ hình theo các bước đã nêu ở đề bài. b) Hình thang ABCD có hai đường chéo AC = BD. Do đó ABCD là hình thang cân.
Vận dụng trang 55 Toán 8 Tập 1:
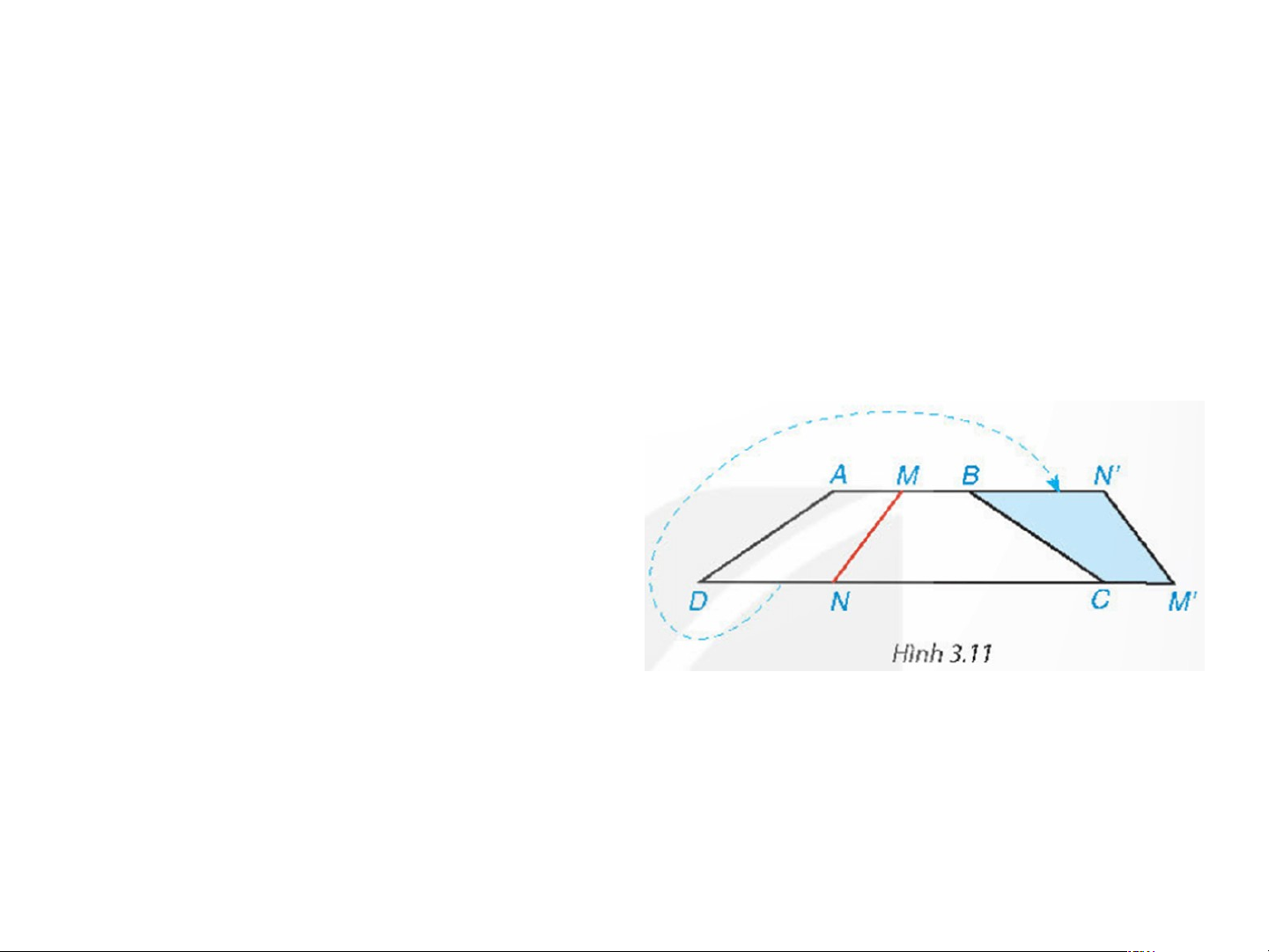
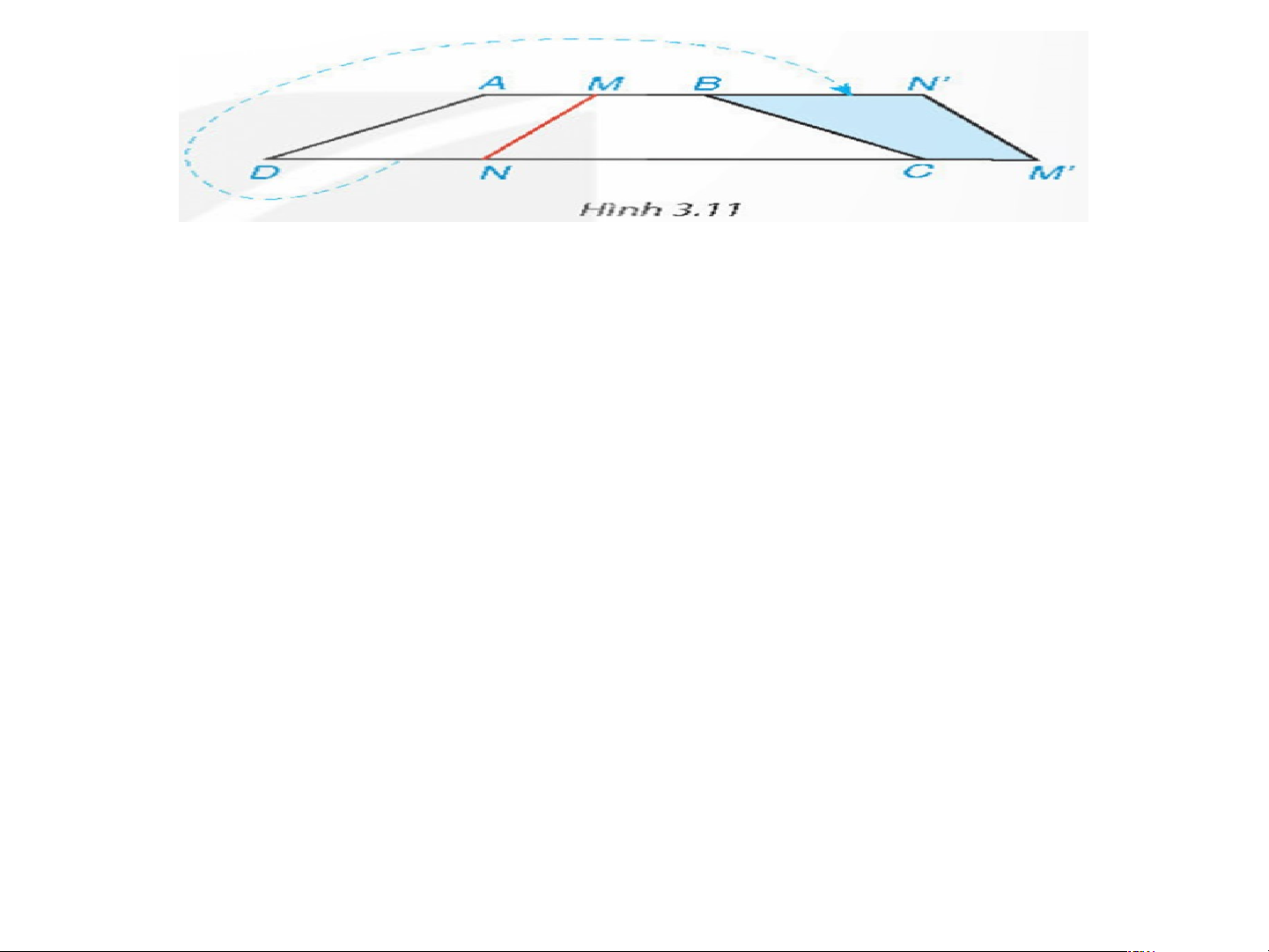
• Hãy giải bài toán mở đầu.
Cắt một mảnh giấy hình thang cân bằng một nhát
thẳng cắt cả hai cạnh đáy
thì được hai hình thang. Lật
một trong hai hình thang đó
rồi ghép với hình thang còn
lại dọc theo các cạnh bên của hình thang ban đầu
(Hình 3.11). Hãy giải thích
tại sao hình tạo thành cũng là một hình thang cân.
Theo hình 3.11 ta có hình thang mới là: MN’M’N. Ta có:
+ Hình thang AMND có: M’N’ là cạnh mới cắt ; AD là cạnh bên.
+ Hình thang MBCN có: MN là cạnh mới cắt; BC là cạnh bên. => (so le trong)
=> Lật hình thang AM’N’D để ghép vào hình thang MBCN thì
cạnh DA trùng với BC. Thì hình mới là MN’M’N có
Vậy nó là hình thang cân.
Document Outline
- 1. Hình thang. Hình thang cân
- Khái niệm hình thang cân
- - Nhận xét
- Slide 4
- Ví dụ 1.
- Lời giải ví dụ 1.
- Luyện tập 1 trang 53 Toán 8 Tập 1
- Đáp án luyện tập 1
- Slide 9
- HĐ1 ( Đáp án ý a)
- HĐ1 ( Đáp án ý b)
- Tính chất về cạnh bên của hình thang cân.
- Luyện tập 2 ( SGK-tr53)
- ĐÁP ÁN LUYỆN TẬP 2
- Slide 15
- Đáp án
- Tính chất về đường chéo của hình thang cân
- Tính chất về đường chéo của hình thang cân.
- Luyện tập 3 trang 54 Toán 8 Tập 1
- Đáp án luyện tập 3a. Sgk-tr54
- Slide 21
- DẤU HIỆU NHẬN BIẾT HÌNH THANG CÂN
- Ví dụ 2. sgk – tr 54
- Lời giải ví dụ 2
- Thực hành trang 55 Toán 8 Tập 1: (H.3.22)
- Thực hành trang 55 Toán 8 Tập 1: (H.3.22) lời giải
- Vận dụng trang 55 Toán 8 Tập 1:
- Slide 28
- Slide 29



