Nh n ữ g đ i l ạ n ượ g nào đ c ặ tr n ư g cho dao đ n ộ g điều hoà ? Chúc m ng b ừ n đ ạ ư c ợ 8 đi m ể  Biên đ . ộ  Chu kì.  Tần số.
 Tần số góc. GO HOME Ch n c ọ âu đúng khi nói v ề dao đ ng ộ đi u ề hòa? A. S ố dao đ n ộ g toàn ph n ầ th c ự hi n
ệ trong 1 giây là chu kì c a ủ dao đ n ộ g đi u ề hòa. B. C ứ sau m t ộ kho ng ả th i ờ gian là m t ộ chu kì thì v t ậ tr ở v ề vị trí ban đ u ầ . C. C ứ sau m t ộ kho ng ả th i ờ gian là m t
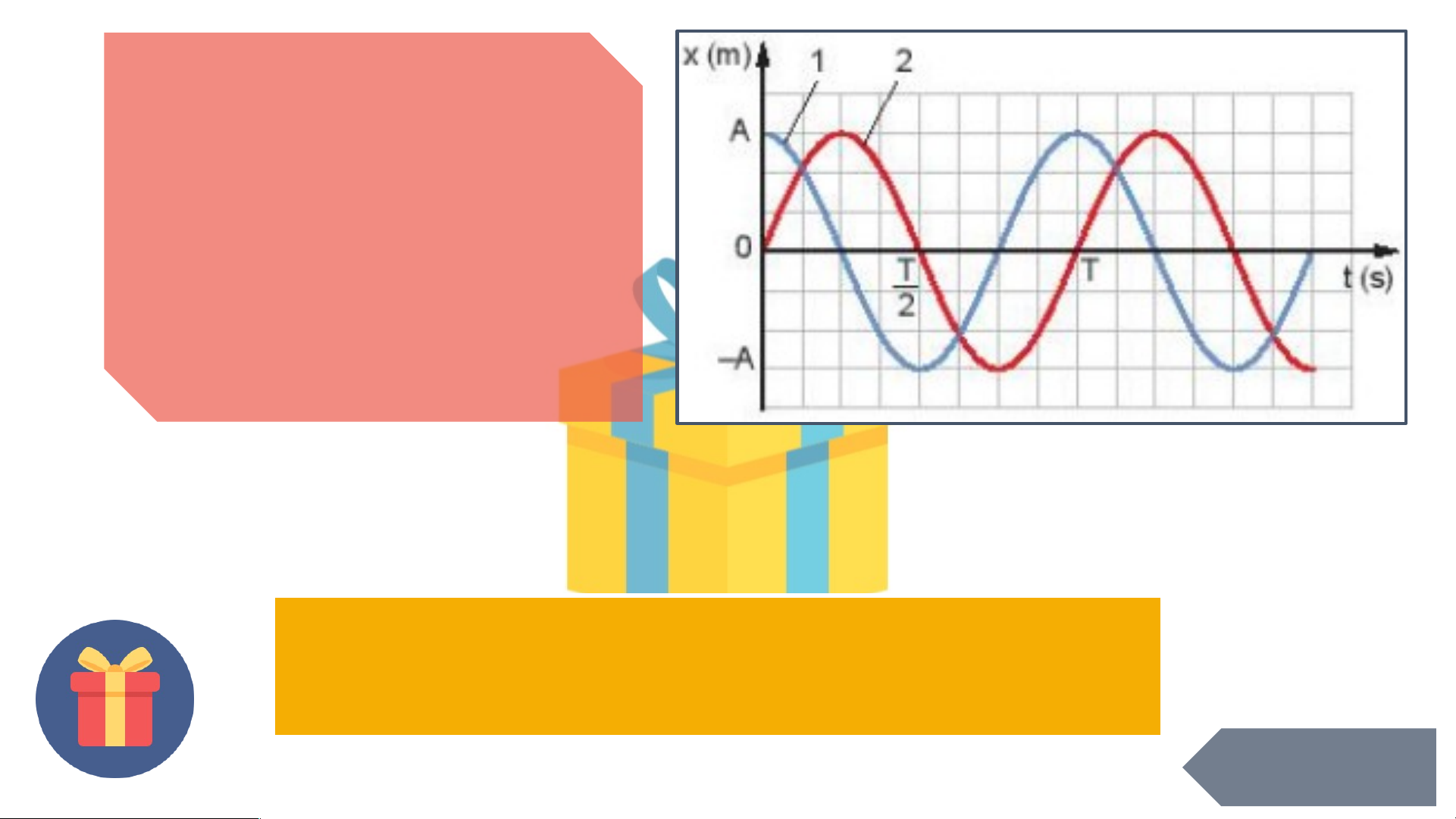
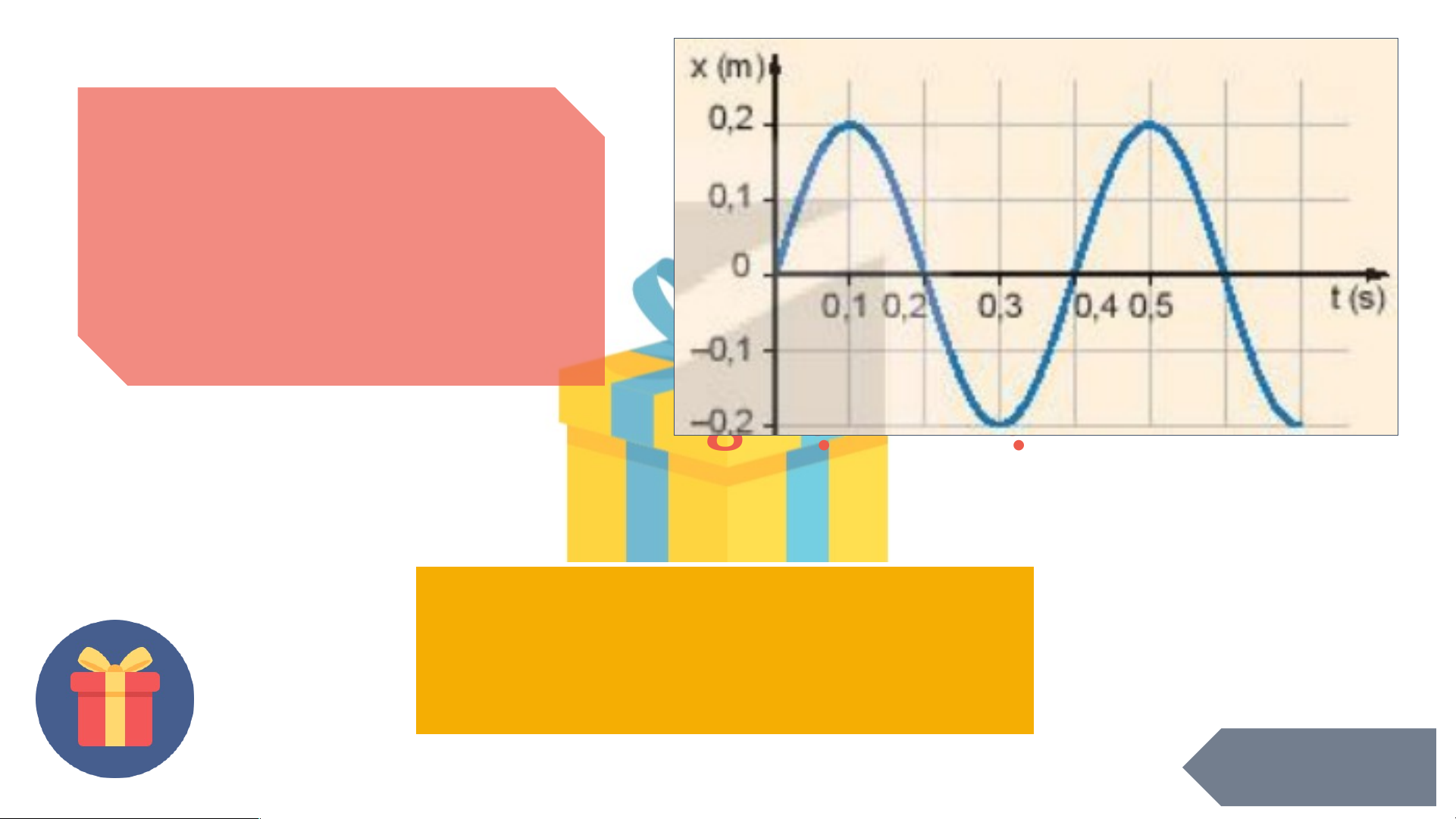
ộ chu kì thì biên đ ộ c a ủ v t ậ tr ở v ề giá tr ị ban đ u ầ . Chúc m ng ừ b n ạ nh n ậ đ c ượ D. Kho ng ả th i ờ gian đ ể v t ậ th c ự hi n ệ m t ộ dao đ ng ộ toàn ph n ầ là m t ộ chu kì. 1 đi m c ể n ộ g Đáp án: D GO HOME Trong dao đ n ộ g đi u ề hòa, đ i ạ l n ượ g luôn thay đ i ổ theo th i ờ gian là A. biên đ . ộ B. pha dao đ n ộ g. C. t n ầ s ố góc. D. pha ban đ u. ầ Chúc m ng ừ b n ạ nh n ậ đ c ượ 5 viên k o ẹ ! Đáp án: B GO HOME Cho đồ thị nh ư hình vẽ. Đ ộ l ch ệ pha c a ủ hai dao đ n ộ g này là bao nhiêu? A. 0 rad. B.  rad C. rad.D. rad. Chúc m n ừ g b n nh ạ n đ ậ c ượ 9 đi m! ể Đáp án: C GO HOME Đại lư n ợ g nào dư i ớ đây đ c ặ tr n ư g cho đ ộ l ch ệ v ề th i ờ gian gi a ữ hai dao đ n ộ g đi u ề hoà cùng chu kì? A. Li đ . ộ B. Pha. C. Độ l ch ệ pha. D. Pha ban đ u. ầ Chúc m ng b ừ n đ ạ ư c ợ 8 đi m ể Đáp án: C GO HOME Cho đ ồ th ị nh ư hình vẽ. T ừ đ ồ th ị xác định biên đ ộ và chu kì c a ủ v t ậ . Chúc m n ừ g b n nh ạ n ậ
được một tràng pháo tay Từ đ ồ th : ị A = 0,2 m; T = 0,4 s. GO HOME Trong DĐĐH, Trong dao + khi đi t ừ biên v ề VTCB v t ậ động điều chuy n ể đ n ộ g hoà c a ủ v t ậ nhanh dần, có sinh ra gia + đi t ừ VTCB v ề tốc không? Vì biên v t ậ chuy n ể sao? đ n ộ g ch m ậ d n ầ  t c ứ có s ự bi n ế đ i v ổ n ậ t c ố . V y ậ trong DĐĐH có sinh ra gia t c ố . BÀI 3: V N Ậ T C Ố , GIA T C Ố TRONG DAO Đ N Ộ G ĐI U Ề HÒA Bài 3: V N Ậ T C Ố , GIA T C Ố TRONG DAO Đ N Ộ G ĐI U Ề HÒA I. V N Ậ T C Ố C A Ủ V T Ậ DAO Đ N Ộ G 1. Phương trình v n ậ t c ố ĐI U Ề HOÀ 2. Đồ th ị v n ậ t c ố .
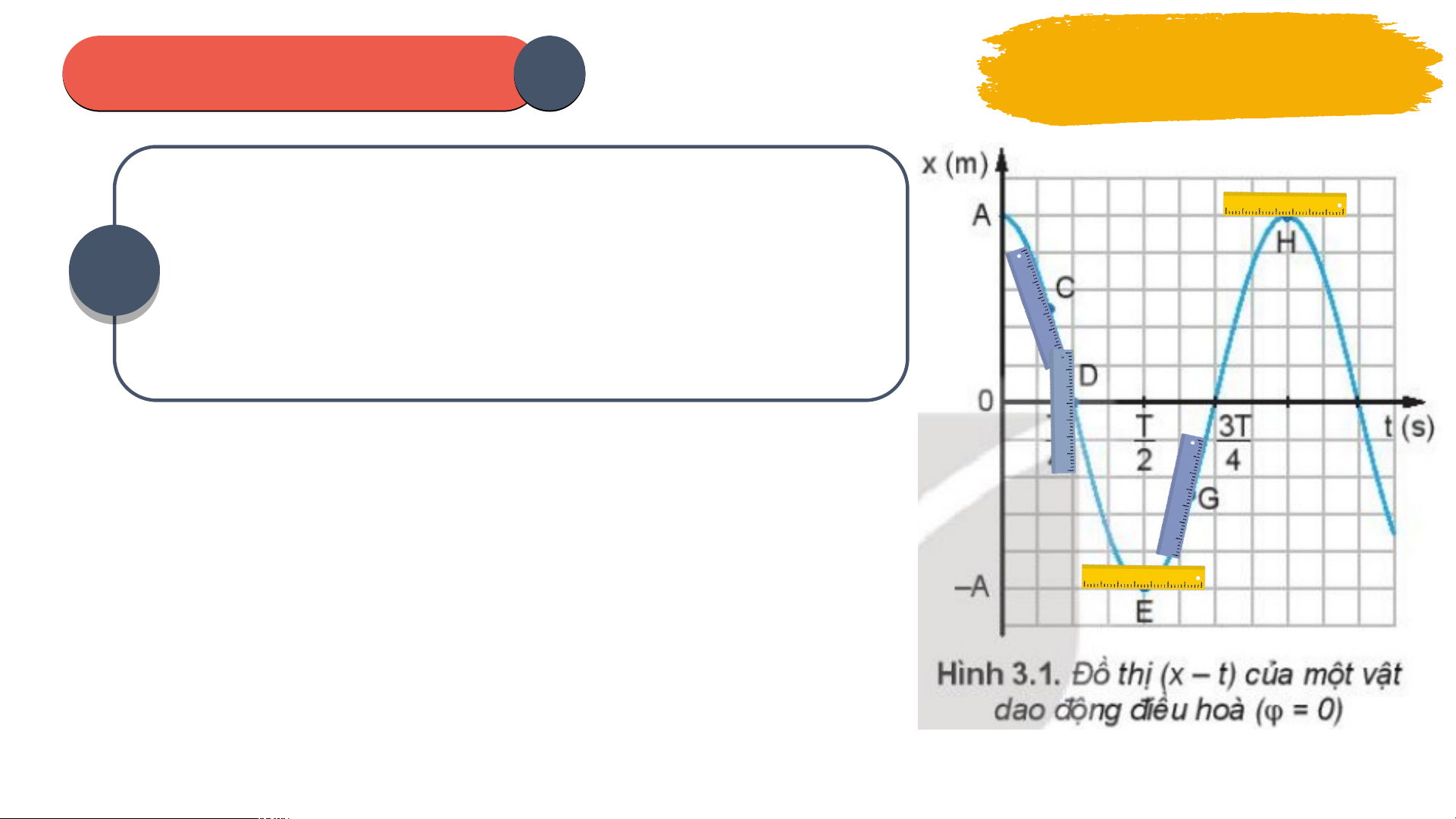
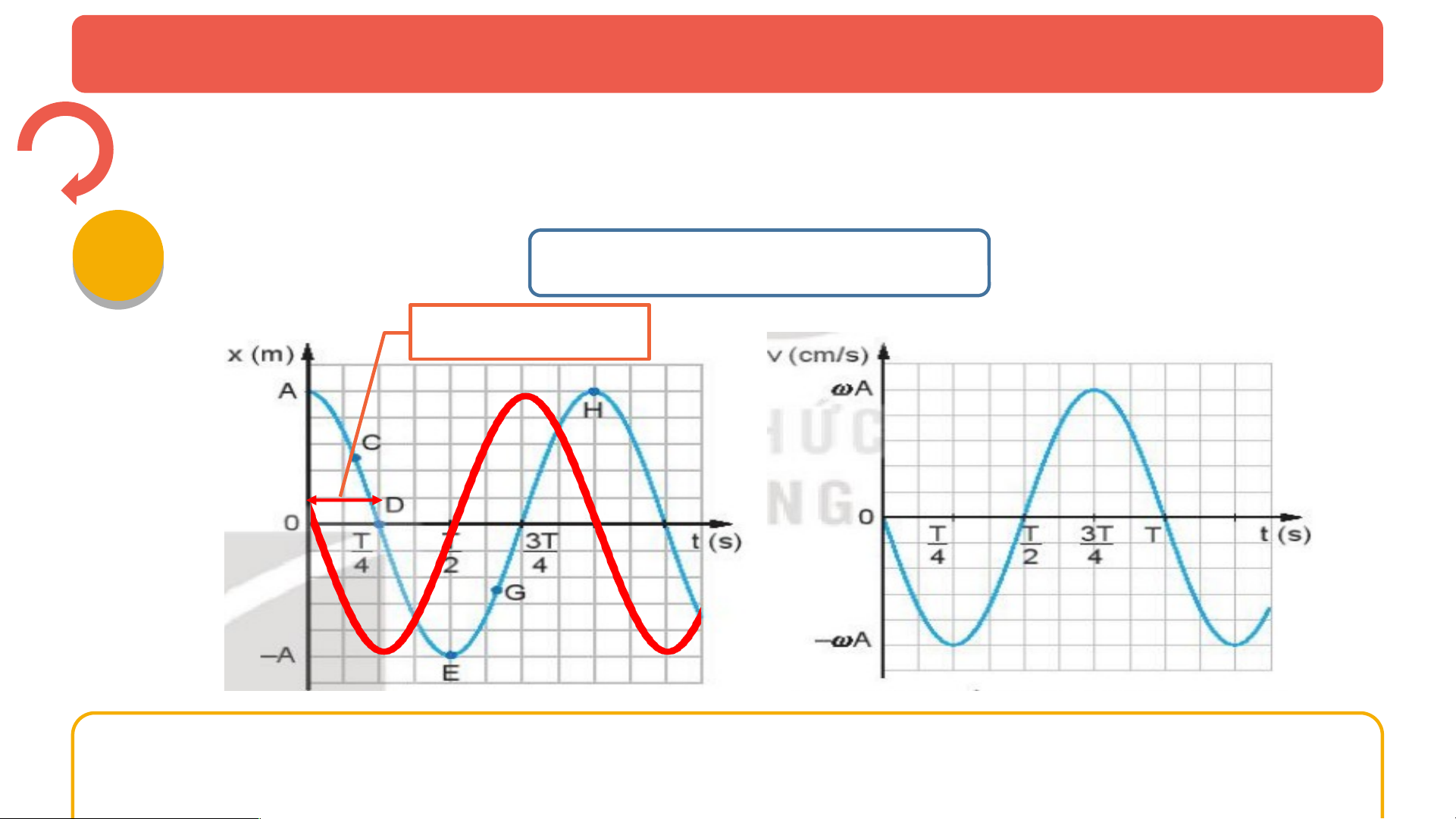
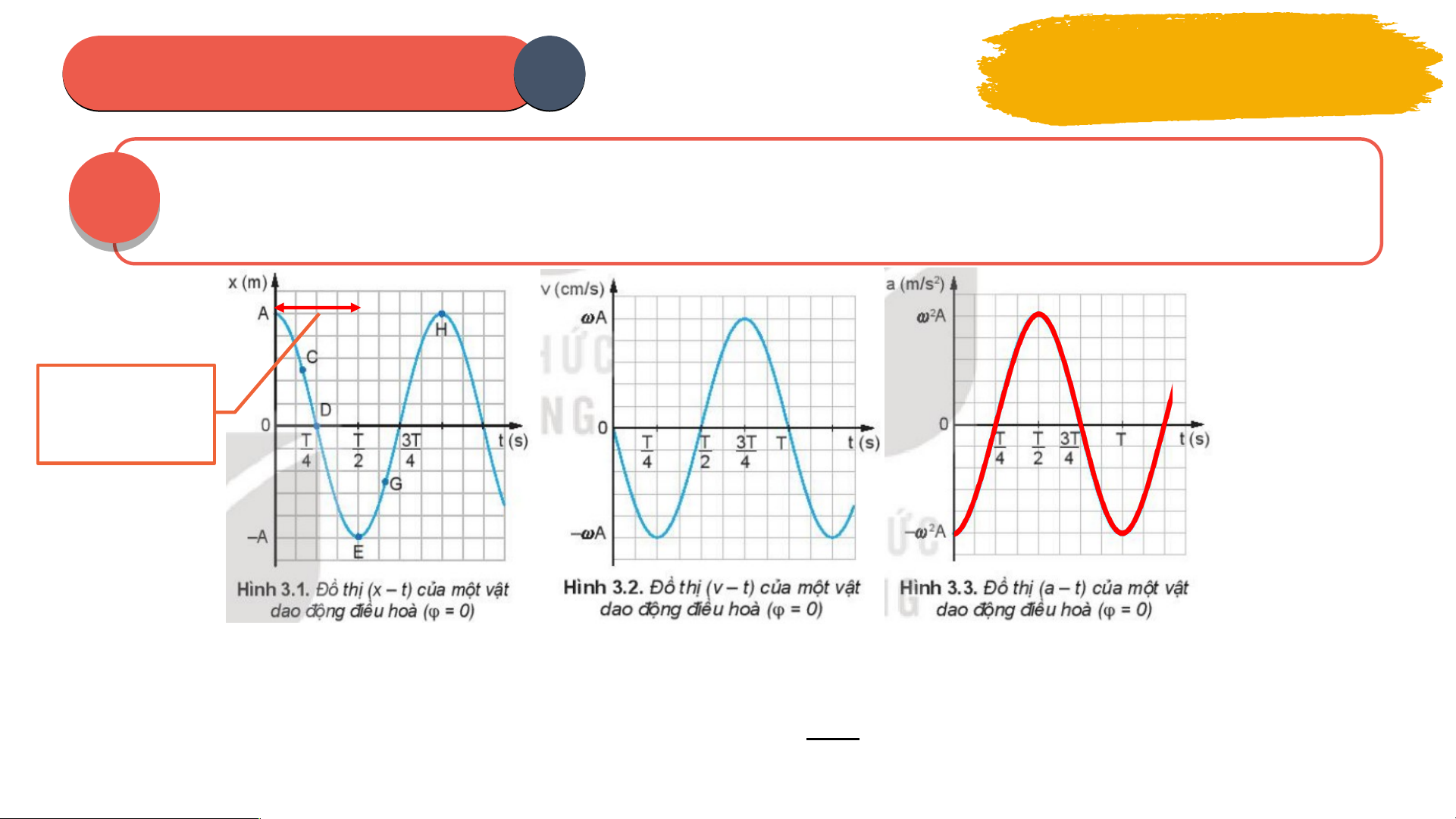
1. Phương trình gia t c ố II. GIA T C Ố CỦA V T Ậ 2. Đ ồ th ị gia t c ố . DAO Đ NG Ộ ĐI U Ề HOÀ Bài 3: V N Ậ T C Ố , GIA T C Ố TRONG DAO Đ N Ộ G ĐI U Ề HÒA I VẬN T C Ố C A Ủ V T Ậ DAO Đ N Ộ G ĐI U Ề HOÀ Thảo luận PHIẾ H U IẾ H ỌC TẬP 1 nhóm 01 02 03 04 05 06 PHIẾU I HỌ H C TẬ T P 1 Thảo luận nhóm Vi t ế công th c ứ v n ậ t c ố t c ứ th i ờ c a ủ m t ộ v t? ậ Trong công th c ứ 01 vận tốc t c ứ th i, ờ vì th i ờ gian ta xét là r t ấ nh ỏ ch n ứ g t ỏ v n ậ t c ố t c ứ th i b ờ n ằ g đ ộ d c ố c a ủ đ ồ th ịnào? Hư ng ớ dẫn: Công th c ứ v n ậ t c ố t c ứ th i ờ c a ủ m t ộ v t: ậ Vì   t r t ấ nh , ỏ ch n ứ g t ỏ v n ậ t c ố t c ứ th i ờ b n ằ g đ ộ d c ố c a ủ đ ồ thị to đ ạ ộ (x – t) t i ạ đi m ể đang xét. PHIẾU I HỌ H C TẬ T P 1 Thảo luận nhóm Đ t ặ m t ộ thư c ớ k ẻ lo i ạ 20 cm cho mép c a ủ thư c ớ ti p ế xúc v i ớ đ ồ th ịli đ ộ th i ờ gian nh ư 02 hình 3.1 ở m t ộ s ố đi m ể C, D, E, G, H. T ừ đ ộ d c ố của thư c ớ hãy so sánh đ ộ l n ớ v n ậ t c ố c a ủ v t ậ t i ạ các đi m ể trên ? Hướng d n ẫ : + Ở đi m ể C và G thư c ớ có đ ộ d c ố nh ư nhau  v n ậ t c ố có đ l ộ n ớ nh nh ư au. + Ở đi m ể D thư c c ớ ó đ d ộ c ố nhi u ề nh t ấ  v n ậ t c ố có đ l ộ n ớ c c ự đ i. ạ + Ở đi m ể E và H thư c ớ n m ằ ngang, không có đ d ộ c ố  v n ậ t c ố b ng ằ 0. PHIẾU I HỌ H C TẬ T P 1 Thảo luận nhóm Khi h c ọ phép tính đ o ạ hàm, v i ớ t r t ấ nh ỏ thì v n ậ t c ố v và li đ ộ x 03 có mối quan h ệ nh ư th ế nào v i ớ nhau? Hư ng ớ dẫn: Khi h c ọ phép tính đ o ạ hàm, (v i ớ  t r t ấ nh ) ỏ chính là đ o ạ hàm c a ủ li đ ộ x theo th i ờ gian. PHIẾU I HỌ H C TẬ T P 1 Thảo luận nhóm  B ng ằ phép đ o
ạ hàm, hãy xác định phư n ơ g trình v n ậ t c ố c a ủ v t ậ dao đ ng ộ điều hoà? Gi i t
ả hích ý nghĩa và nêu đ n v ơ đ ị o t n ừ g đ i l ạ ư ng ợ .  Từ phư n ơ g trình v n ậ t c ố , đ n ồ g th i ờ v n ậ d ng ụ bi n ế đ i ổ toán h c ọ đ ể ch ng ứ 04 minh công th c đ ứ c ộ l p ậ th i g ờ ian: .  Qua đó xác đ nh ị giá tr c ị a v ủ n ậ t c ố ở v ịtrí cân b ng ằ và v t ị rí biên?  Từ phư n ơ g trình v n ậ t c ố , cho bi t ế d ng ạ đ ồ th ị v n ậ t c ố c a ủ dao đ n ộ g đi u ề hoà? Hư n ớ g d n: ẫ  Ta có: Trong đó: x = Acos( t +  )  v: v n t ậ c ố t c ứ th i ờ t ở h i ờ đi m ể t (m/s). v = x’ = -  Asin( t +  )   : t n s ầ ố góc (rad/s).  A: biên đ c ộ a d ủ ao đ n ộ g (cm).   : pha ban đầu c a ủ li đ ( ộ rad).  ( t +  ): pha của li đ ộ t ở h i ờ đi m ể t (rad). PHIẾU I HỌ H C TẬ T P 1 Thảo luận nhóm  B ng ằ phép đ o
ạ hàm, hãy xác định phư n ơ g trình v n ậ t c ố c a ủ v t ậ dao đ ng ộ điều hoà? Gi i t
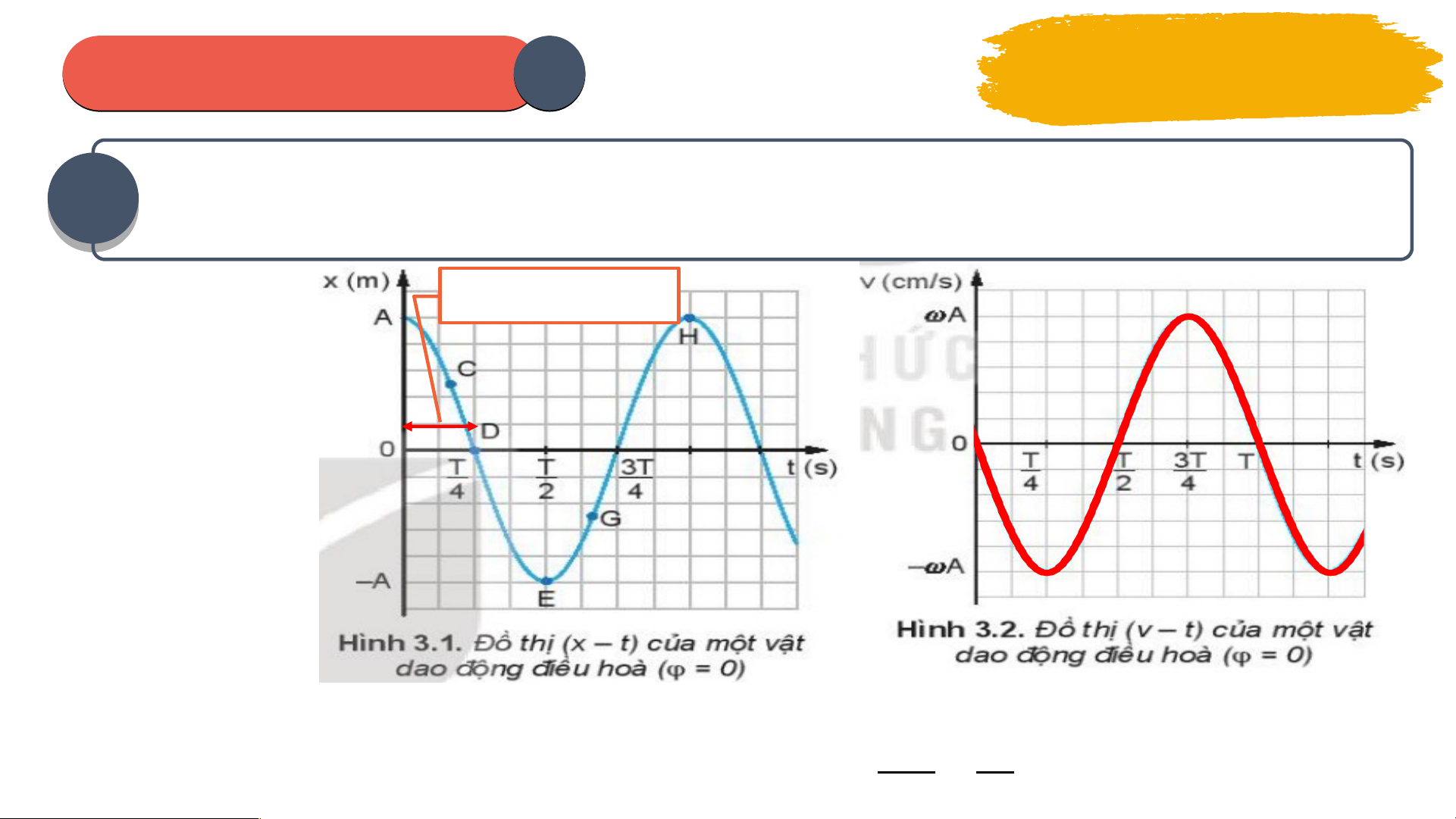
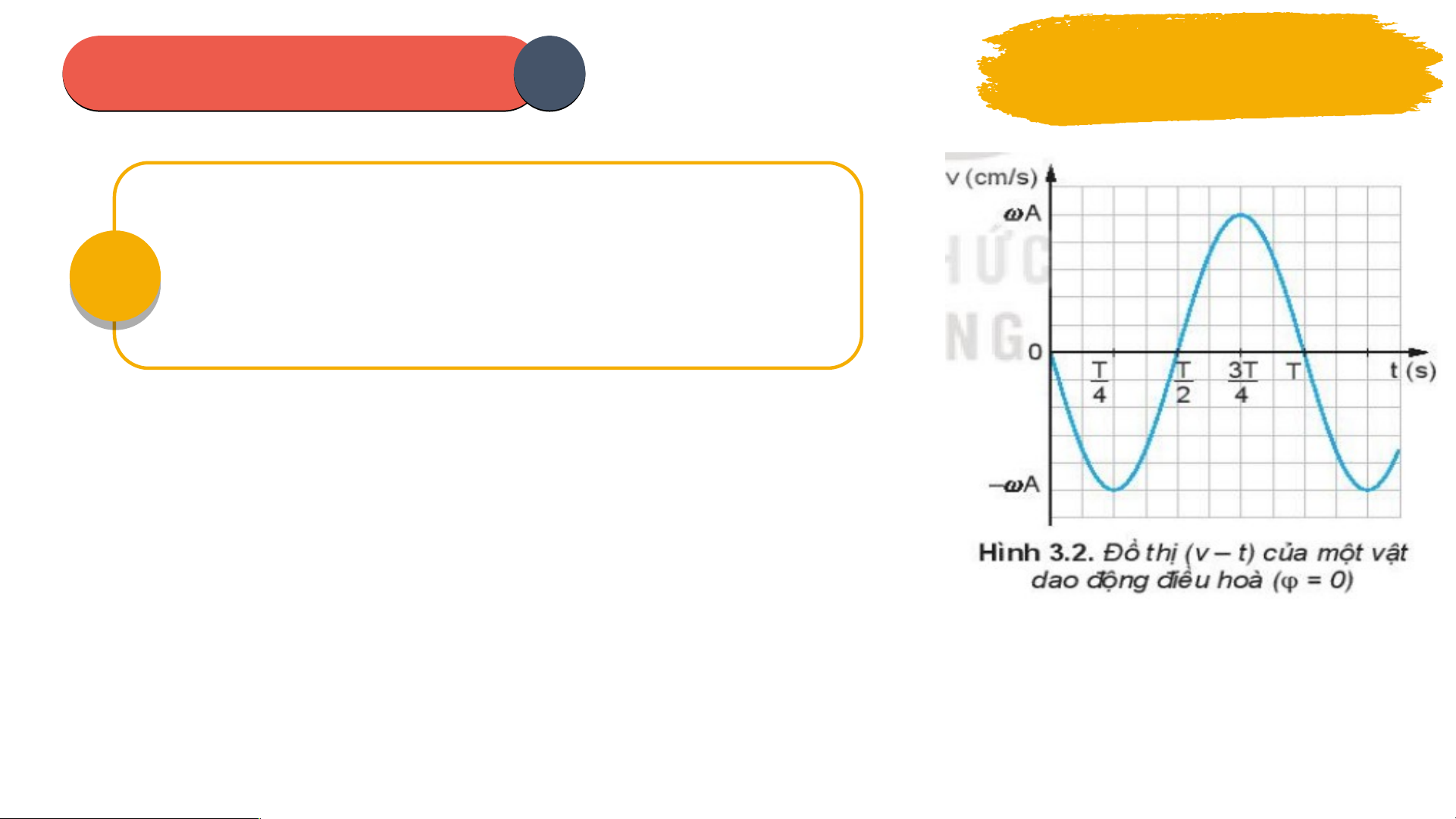
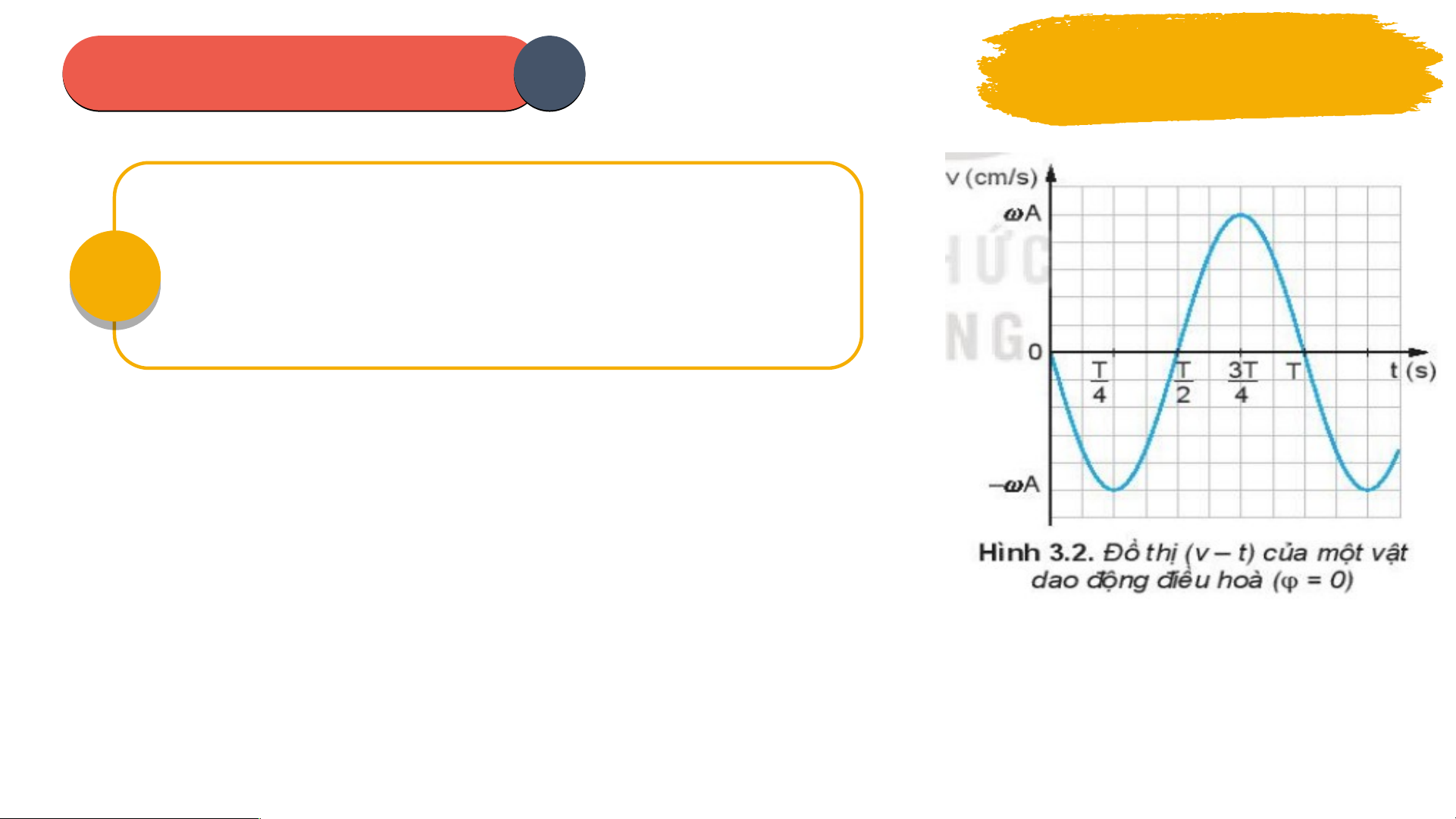
ả hích ý nghĩa và nêu đ n v ơ đ ị o t n ừ g đ i l ạ ư ng ợ .  Từ phư n ơ g trình v n ậ t c ố , đ n ồ g th i ờ v n ậ d ng ụ bi n ế đ i ổ toán h c ọ đ ể ch ng ứ 04 minh công th c đ ứ c ộ l p ậ th i g ờ ian: .  Qua đó xác đ nh ị giá tr c ị a v ủ n ậ t c ố ở v ịtrí cân b ng ằ và v t ị rí biên?  Từ phư n ơ g trình v n ậ t c ố , cho bi t ế d ng ạ đ ồ th ị v n ậ t c ố c a ủ dao đ n ộ g đi u ề hoà? Hư n ớ g d n: ẫ v = x’ = -  Asin( t +  )  v =  Phư ng ơ trình v n ậ t c: ố v = -  Asin( t +  ) là  m t ộ hàm sin nên đ ồ th ị   Khi v t ậ VT ở CB: v =   A  |v| = max  A. của nó cũng là m t ộ  Khi v t ậ VT ở biên: v = 0 đường hình sin. min PHIẾU I HỌ H C TẬ T P 1 Thảo luận nhóm 05 T ừ đồ thị v n ậ t c ố (3.2) và đ ồ th ịli đ
ộ (3.1) hãy so sánh pha c a ủ v n ậ tốc v i ớ li đ ? ộ Hư ng d ớ ẫn: Thời gian  t Ta thấy v bi n ế thiên s m ớ h n ơ x m t ộ kho n ả g , suy ra, v n ậ t c ố s m ớ pha h n ơ li đ ộ m t ộ góc Δ𝑡 𝜋
Δ 𝜑=2 𝜋 𝑇 = 2 (𝑟𝑎𝑑) PHIẾU I HỌ H C TẬ T P 1 Thảo luận nhóm T đ ừ t
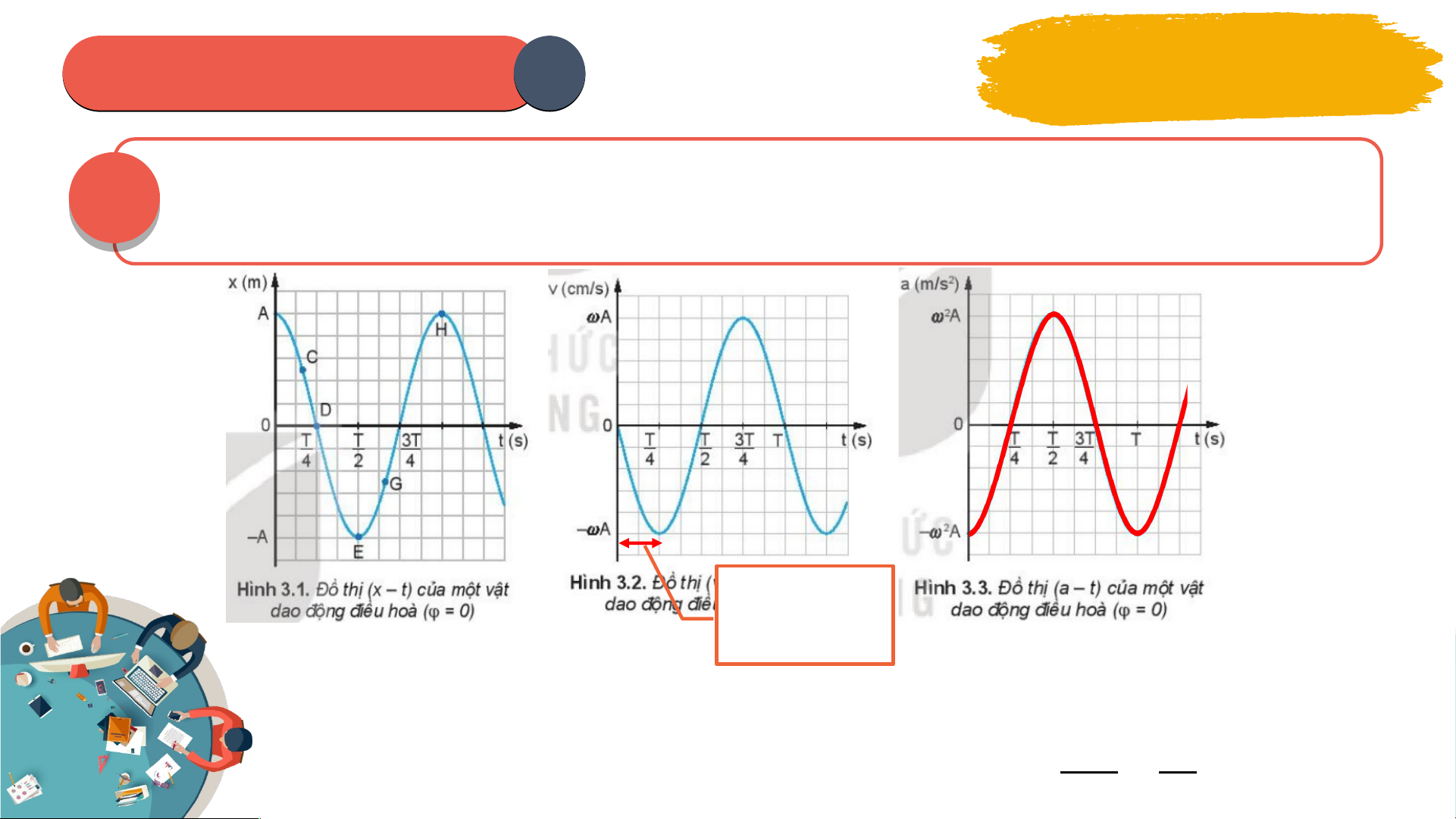
ồ h ị3.2, trong các kho ng ả th i g ờ ian t ừ 0 đến ; t ừ đ n ế ; t ừ đ n ế ; t ừ đ n ế T, v n ậ 06 tốc của dao đ n ộ g đi u ề hoà thay đ i ổ nh ư th nà ế o? Hư n ớ g dẫn:  Từ 0 đ n ế T/4: v n ậ t c ố có hư ng ớ t ừ biên v ề vị trí cân b ng ằ ngư c ợ chi u ề dư ng ơ , đ ộ l n ớ tăng dần t 0 v ừ à đ t ạ giá tr ịl n ớ nh t ấ t i T ạ /4  T ừ T/4 đ n ế T/2: v n ậ t c ố có hư ng ớ t ừ v ịtrí cân b ng ằ v ề biên ngư c ợ v i ớ chi u ề dư ng ơ , đ ộ l n ớ gi m ả d n ầ t ừ giá tr ịl n ớ nh t ấ v ề 0 t i ạ T/2 PHIẾU I HỌ H C TẬ T P 1 Thảo luận nhóm T đ ừ t
ồ h ị3.2, trong các kho ng ả th i g ờ ian t ừ 0 đến ; t ừ đ n ế ; t ừ đ n ế ; t ừ đ n ế T, v n ậ 06 tốc của dao đ n ộ g đi u ề hoà thay đ i ổ nh ư th nà ế o? Hư n ớ g dẫn:  Từ T/2 đ n ế 3T/4: v n ậ t c ố có hư ng ớ t ừ v ị trí biên v ề v ị trí cân b ng ằ cùng chi u ề dư n ơ g, đ ộ l n ớ tăng d n ầ t ừ 0 và đ t ạ giá trị l n n ớ hất t i 3T ạ /4.  Từ 3T/4 đ n ế T: v n ậ t c ố có hư n ớ g t ừ v ịtrí cân b n ằ g v ề biên cùng chi u ề dư ng ơ , đ ộ l n ớ gi m ả dần t ừ giá tr ịl n ớ nh t ấ v ề 0 t i ạ T Bài 3: V N Ậ T C Ố , GIA T C Ố TRONG DAO Đ N Ộ G ĐI U Ề HÒA I VẬN T C Ố C A Ủ V T Ậ DAO Đ N Ộ G ĐI U Ề HOÀ 01 Phư n ơ g trình v n ậ t c: ố V n ậ t c ố t c ứ th i ờ c a ủ m t ộ v t: ậ (v i ớ   t r t ấ nh ), ỏ t c ứ là b n ằ g đ ộ d c ố c a ủ đ t ồ h t ị o đ ạ ộ (x – t) t i ạ đi m ể đang xét. v = x’ = -  Asin( t +  ) Trong đó:  v: v n ậ tốc t c ứ th i ờ ở th i ờ đi m ể t (m/s).   : tần s g ố óc (rad/s)  A: biên đ ộ c a ủ dao đ n ộ g (cm).   : pha ban đ u ầ c a l ủ i đ ộ (rad).  ( t +  ): pha c a ủ li đ ộ ở th i ờ đi m ể t (rad). Bài 3: V N Ậ T C Ố , GIA T C Ố TRONG DAO Đ N Ộ G ĐI U Ề HÒA I VẬN T C Ố C A Ủ V T Ậ DAO Đ N Ộ G ĐI U Ề HOÀ 01 Phư n ơ g trình v n ậ t c: ố v = x’ = -  Asin( t +  ) - Công th c ứ đ c ộ l p ậ th i g ờ ian liên h ệ gi a ữ v và x:  Khi v t ậ ở VTCB: v =   A  |v| = max  A.  Khi v t ậ ở VT biên: v = 0. min * Nh n ậ xét: V n ậ tốc c a v ủ t ậ dao đ n ộ g s m ớ pha so v i ớ li đ . ộ Bài 3: V N Ậ T C Ố , GIA T C Ố TRONG DAO Đ N Ộ G ĐI U Ề HÒA I VẬN T C Ố C A Ủ V T Ậ DAO Đ N Ộ G ĐI U Ề HOÀ 02 Đồ thị v n ậ t c ố : v = x’ = -  Asin( t +  ) Thời gian  t Đồ thị v n ậ t c ố c a ủ dao đ n ộ g đi u ề hoà theo th i g ờ ian là đư n ờ g hình sin. Bài 3: V N Ậ T C Ố , GIA T C Ố TRONG DAO Đ N Ộ G ĐI U Ề HÒA II GIA TỐC C A Ủ V T Ậ DAO Đ N Ộ G ĐI U Ề HOÀ Thảo luận PHIẾ H U IẾ H ỌC TẬP 2 nhóm 01 02 03 04 05 06 PHIẾU I HỌ H C TẬ T P 2 Thảo luận nhóm Vi t ế công th c ứ gia t c ố t c ứ th i ờ c a ủ m t ộ v t ậ ? Trong công th c ứ gia 01 tốc t c ứ th i, ờ vì th i ờ gian ta xét là r t ấ nh ỏ ch n ứ g t ỏ gia t c ố t c ứ th i ờ b n ằ g đ ộ d c ố c a ủ đ ồ th ịnào ? Hư ng ớ dẫn: Gia tốc t c ứ th i ờ c a m ủ t ộ v t ậ : Vì  t r t ấ nh , ỏ ch n ứ g t ỏ gia t c ố t c ứ th i ờ b n ằ g đ ộ d c ố c a ủ đ ồ thị v n ậ tốc (v – t) t i ạ đi m ể đang xét. PHIẾU I HỌ H C TẬ T P 2 Thảo luận nhóm Khi h c ọ phép tính đ o ạ hàm, v i ớ   t r t ấ nh ỏ thì gia t c ố a và v n ậ t c ố 02 v có mối quan h ệ nh ư th n ế ào v i ớ nhau ? Hư n ớ g d n: ẫ Khi h c ọ phép tính đ o ạ hàm,
chính là đạo hàm c a v ủ n ậ t c ố v theo th i ờ gian. PHIẾU I HỌ H C TẬ T P 2 Thảo luận nhóm  B ng ằ phép đ o ạ hàm, hãy xác đ n ị h phư ng ơ trình gia t c ố c a ủ v t ậ dao đ ng ộ đi u ề hoà ? Gi i t
ả hích ý nghĩa và nêu đ n ơ v đ ị o t ng ừ đ i l ạ ư n ợ g. 03  Từ phư ng ơ trình gia t c ố và li đ ộ hãy ch ng ứ minh công th c ứ đ c ộ l p ậ th i ờ gian: a = - 2x. Qua đó xác đ n ị h giá tr g ị ia t c ố v ở t ị rí cân b n ằ g và v t ị rí biên ?  Từ phư ng ơ trình gia t c, ố hãy cho bi t ế đ ồ th ịgia t c ố c a ủ dao đ n ộ g đi u ề hoà? Hư n ớ g d n: ẫ Ta có: v = - Asin( t +  ) Trong đó: 2).  a: gia t c t ố c t ứ h i ờ t ở h i đ ờ i m ể t (m/s  a = v’ = -  2Acos( t +  )   : tần s g ố óc (rad/s).  A: biên đ c ộ a d ủ ao đ ng ộ (cm).   : pha ban đầu c a li đ ủ ( ộ rad).  ( t +  ): pha c a ủ li đ ộ ở th i đ ờ i m ể t (rad). PHIẾU I HỌ H C TẬ T P 2 Thảo luận nhóm  B ng ằ phép đ o ạ hàm, hãy xác đ n ị h phư ng ơ trình gia t c ố c a ủ v t ậ dao đ ng ộ đi u ề hoà ? Gi i t
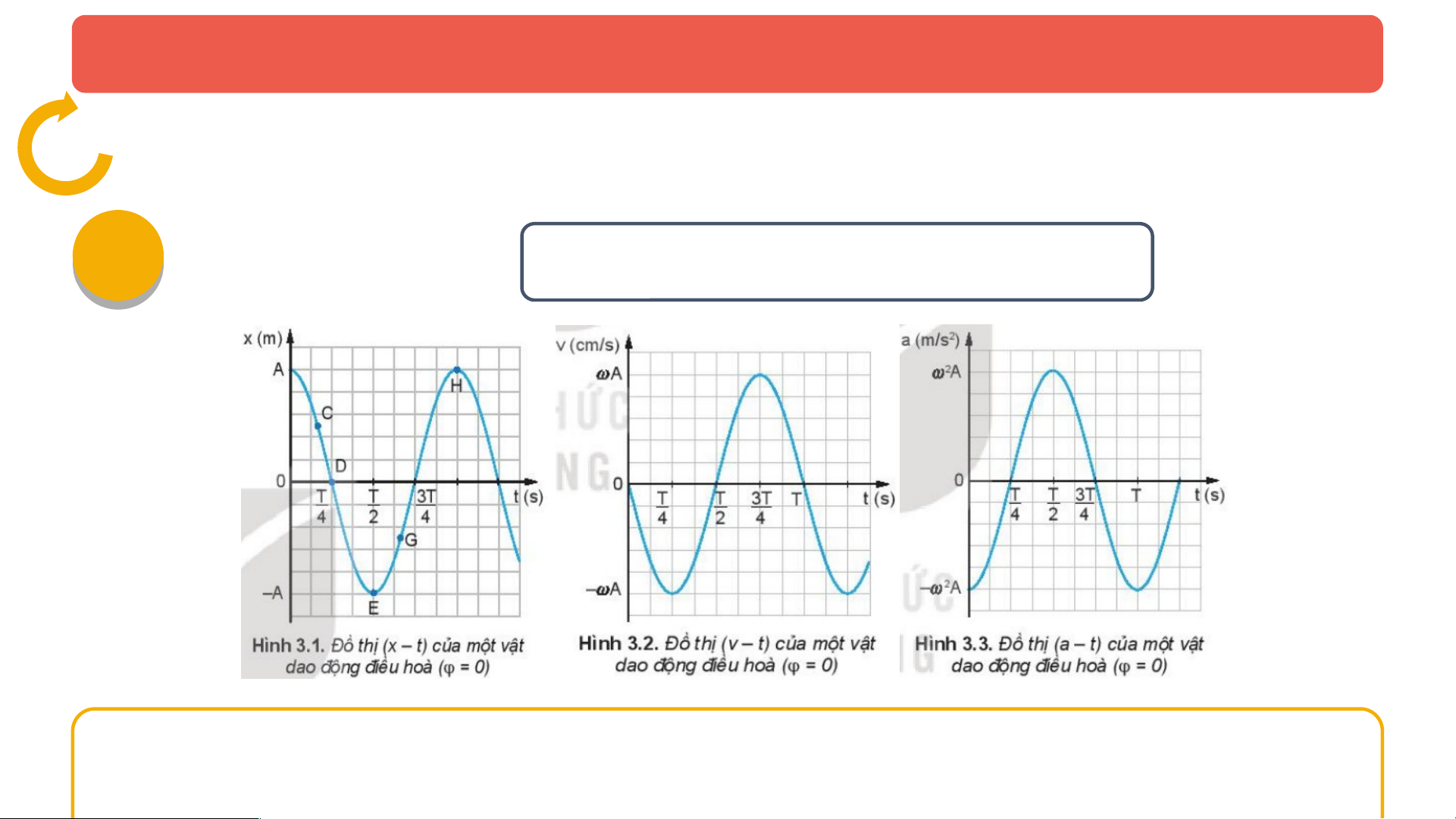
ả hích ý nghĩa và nêu đ n ơ v đ ị o t ng ừ đ i l ạ ư n ợ g. 03  Từ phư ng ơ trình gia t c ố và li đ ộ hãy ch ng ứ minh công th c ứ đ c ộ l p ậ th i ờ gian: a = - 2x. Qua đó xác đ n ị h giá tr g ị ia t c ố v ở t ị rí cân b n ằ g và v t ị rí biên ?  Từ phư ng ơ trình gia t c, ố hãy cho bi t ế đ ồ th ịgia t c ố c a ủ dao đ n ộ g đi u ề hoà? Hư n ớ g a = v’ = -  2Acos( t +  ) d n: ẫ Mà: x = Acos( t +  )  a = - 2x  Khi v t ậ VT ở CB: a = 0. min  Khi v t ậ VT ở biên: a =   2A  |a| = max  2A. Phư n ơ g trình gia t c ố : a = -  2Acos( t +  ) là m t ộ hàm sin nên đ ồ th ị của nó cũng là m t ộ đư ng ờ hình sin. PHIẾU I HỌ H C TẬ T P 2 Thảo luận nhóm T đ ừ th ồ g ị ia t c ố (3.3), đ ồ th ịv n ậ t c ố (3.2) và đ t ồ h l ị i đ ộ (3.1) hãy 04 so sánh pha c a ủ gia t c ố v i ớ v n ậ t c ố và li đ ? ộ Thời gian  t Ta thấy, gia t c ố bi n ế thiên s m ớ h n ơ li đ ộ m t ộ kho ng ả Suy ra, gia t c ố và li đ l ộ ch ệ pha nhau 1 góc: Δ𝑡
Δ 𝜑=2 𝜋 𝑇 =(𝑟𝑎𝑑)  gia t c ố và li đ ng ộ ư c ợ pha nhau. PHIẾU I HỌ H C TẬ T P 2 Thảo luận nhóm T đ ừ th ồ g ị ia t c ố (3.3), đ ồ th ịv n ậ t c ố (3.2) và đ t ồ h l ị i đ ộ (3.1) hãy 04 so sánh pha c a ủ gia t c ố v i ớ v n ậ t c ố và li đ ? ộ Thời Hư n ớ g d n: ẫ gian  t Ta thấy, gia t c b ố i n ế thiên s m ớ h n ơ v n ậ t c ố m t ộ kho ng ả Suy ra, gia t c ố s m ớ pha h n v ơ n ậ t c 1 g ố óc: Δ 𝑡 𝜋
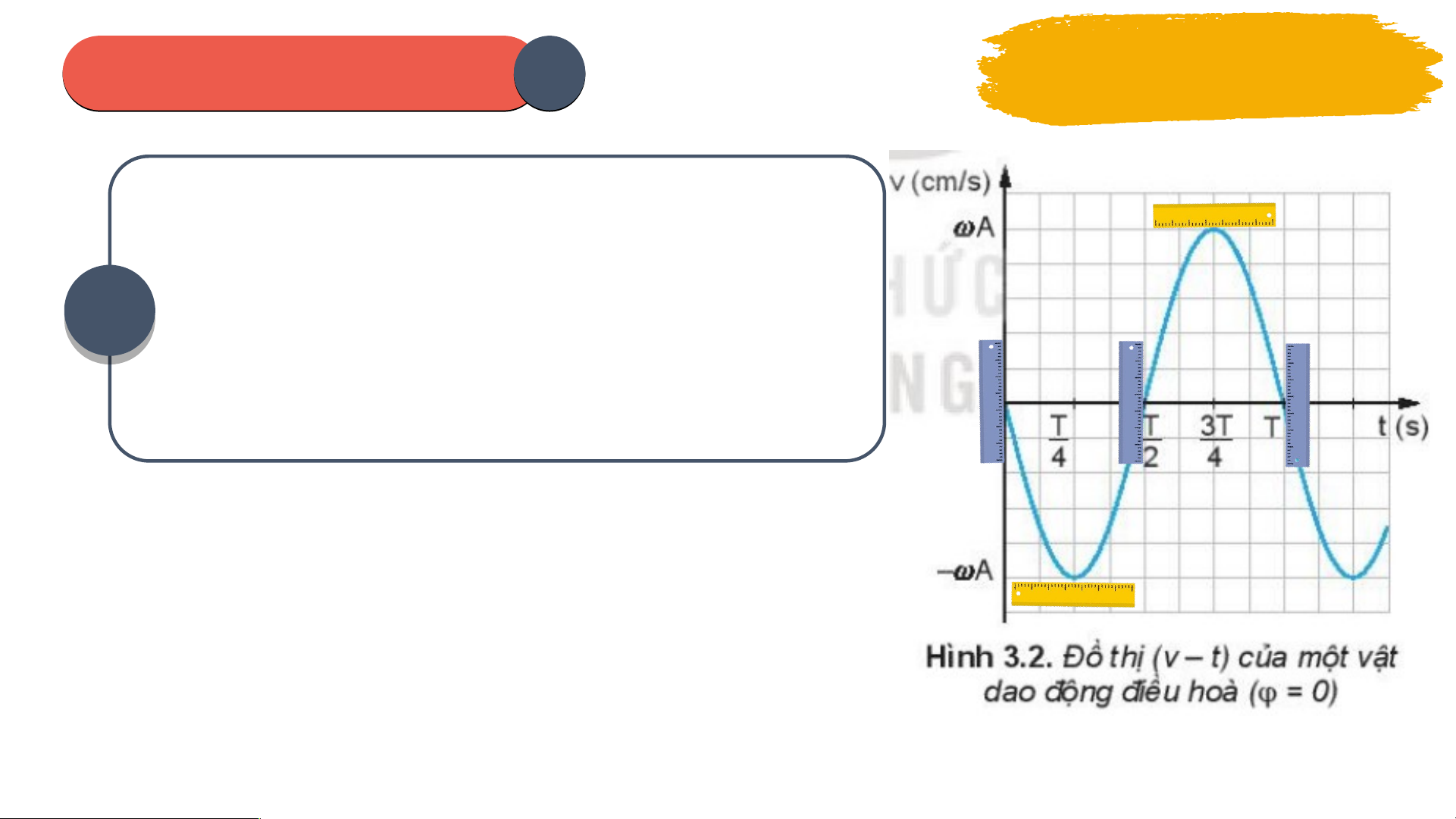
Δ 𝜑=2 𝜋 𝑇 = 2 (𝑟𝑎𝑑) PHIẾU I HỌ H C TẬ T P 2 Thảo luận nhóm Dùng thư c ớ k ẻ lo i ạ 20 cm đ ể xác đ nh ị xem trên đ ồ th ị(v – t) nh ư hình 3.2, t i ạ th i ờ đi m ể nào đ ộ d c ố c a ủ đ ồ th ị b ng ằ 0 và t i ạ th i ờ 05 điểm nào đ d ộ c c ố a ủ đ t ồ h c ị c ự đ i. ạ T ừ đó, so sánh đ ộ l n ớ gia t c ố trên đ ồ th ị(a – t) hình 3.3 các t ở h i đ ờ i m ể tư ng ơ n ứ g. Hư n ớ g dẫn: + Đ ộ d c ố c a ủ đ ồ th ịb ng ằ 0 t i ạ các th i ờ điểm: ; . + Đ ộ d c ố c a ủ đ ồ th ị c c ự đ i ạ t i ạ các th i đ ờ i m ể : 0; ; T. PHIẾU I HỌ H C TẬ T P 2 Thảo luận nhóm 05 Hư n ớ g d n: ẫ + Độ dốc c a ủ đ ồ th ịb ng ằ 0 t i ạ các th i ờ đi m ể : ; . a = 0. min + Độ dốc c a ủ đ ồ th ịc c ự đ i ạ t i ạ các th i ờ đi m ể : 0; ; T. |a| = max  2A. PHIẾU I HỌ H C TẬ T P 2 Thảo luận nhóm T
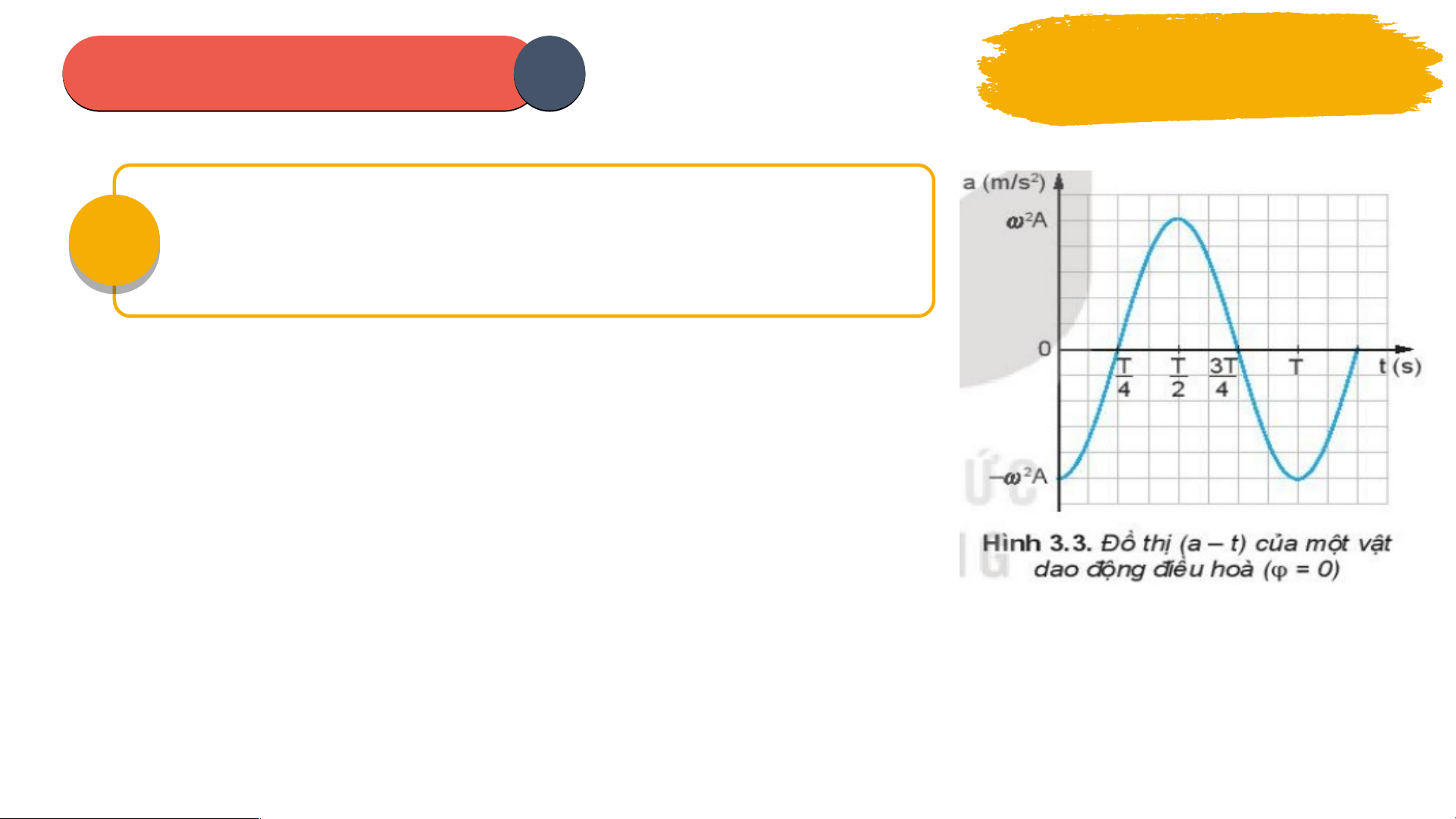
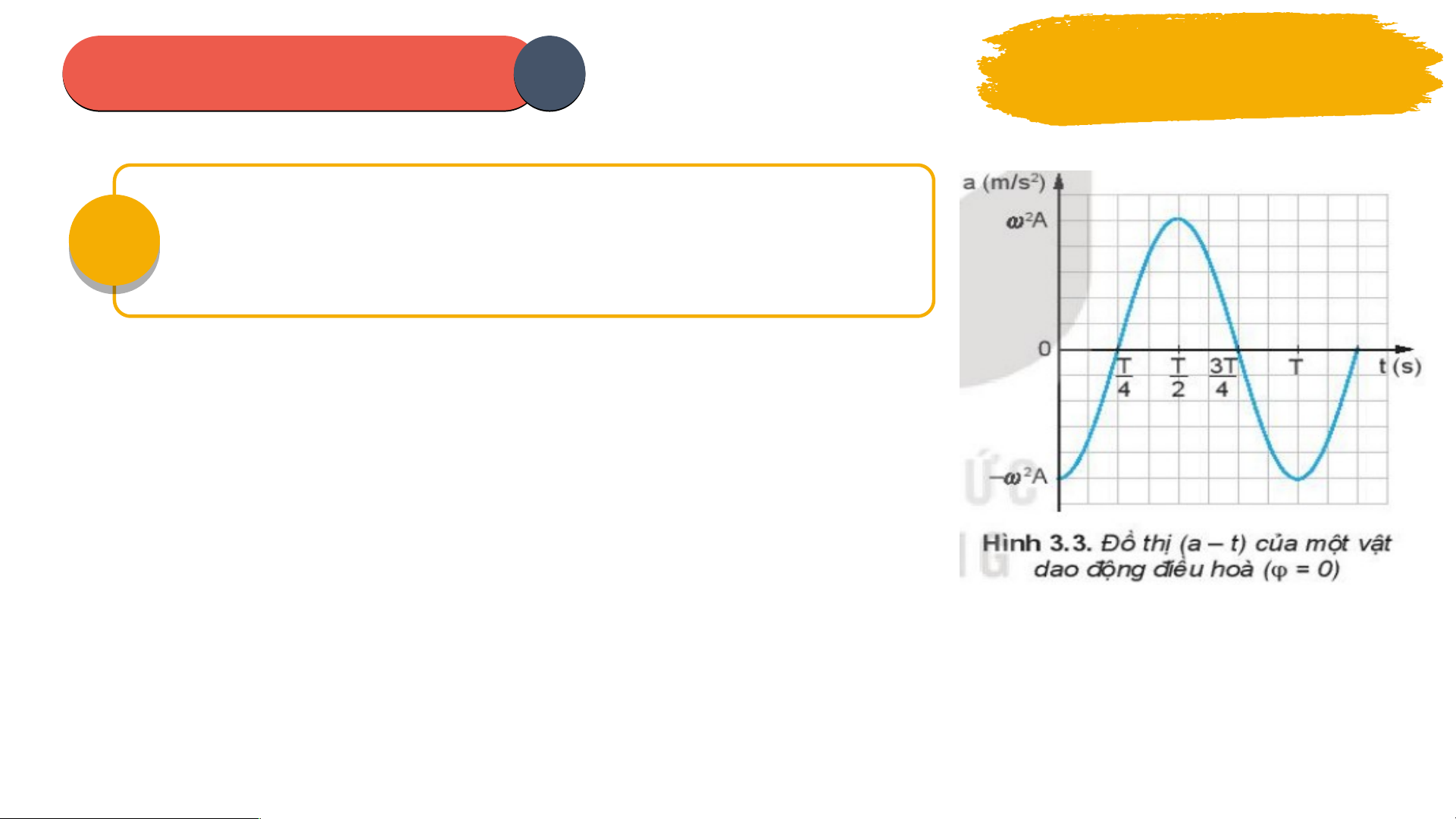
ừ đồ th ị 3.3, trong các kho ng ả th i ờ gian t ừ 0 06 đến ; t ừ đ n ế ; t ừ đ n ế ; t ừ đ n ế T, gia t c ố c a ủ dao đ ng ộ đi u ề hoà thay đ i n ổ h t ư h ế nào? Hư n ớ g d n: ẫ  Từ 0 đ n ế T/4: v n ậ t c ố có hư ng ớ t ừ biên về v ịtrí cân b ng ằ ngư c ợ chi u ề dư n ơ g, đ ộ l n ớ gia t c ố tăng dần t 0 ừ và đ t ạ giá tr l ị n ớ nhất t i T ạ /4  T ừ T/4 đ n ế T/2: v n ậ t c ố có hư n ớ g t ừ v ị trí cân b n ằ g v ề biên ngư c ợ v i ớ chi u ề dư ng ơ , đ ộ l n ớ gia t c ố gi m ả dần t ừ giá tr ị l n nh ớ ất v 0 t ề i ạ T/2 PHIẾU I HỌ H C TẬ T P 2 Thảo luận nhóm T
ừ đồ th ị 3.3, trong các kho ng ả th i ờ gian t ừ 0 06 đến ; t ừ đ n ế ; t ừ đ n ế ; t ừ đ n ế T, gia t c ố c a ủ dao đ ng ộ đi u ề hoà thay đ i n ổ h t ư h ế nào? Hư n ớ g d n: ẫ  Từ T/2 đ n ế 3T/4: v n ậ t c ố có hư n ớ g t ừ v ị trí biên v ề v ị trí cân b ng ằ cùng chi u ề dư ng ơ , đ ộ l n ớ gia t c ố tăng dần từ 0 và đ t ạ giá tr l ị n ớ nh t ấ t i ạ 3T/4  Từ 3T/4 đ n ế T: v n ậ t c ố có hư n ớ g t ừ v ịtrí cân b n ằ g v ề biên cùng chi u ề dư n ơ g, đ ộ l n ớ gia t c ố gi m ả d n ầ t ừ giá tr ị l n ớ nh t ấ về 0 t i T ạ Bài 3: V N Ậ T C Ố , GIA T C Ố TRONG DAO Đ N Ộ G ĐI U Ề HÒA II GIA TỐC C A Ủ V T Ậ DAO Đ N Ộ G ĐI U Ề HOÀ 01 Phư n ơ g trình gia t c: ố Gia tốc t c ứ th i ờ c a ủ m t ộ v t ậ : (v i ớ   t r t ấ nh ), ỏ t c ứ là b n ằ g đ ộ d c ố c a ủ đồ th ịv n ậ tốc (v – t) t i ạ đi m ể đang xét. a = v’ = -  2Acos( t +  ) Trong đó:  a: gia t c ố t c ứ th i ờ ở th i ờ đi m ể t (m/s2).   : tần số góc (rad/s).  A: biên đ ộ c a ủ dao đ n ộ g (cm).   : pha ban đ u ầ c a ủ li đ ( ộ rad).  ( t +  ): pha c a ủ li đ ộ ở th i ờ đi m ể t (rad). Bài 3: V N Ậ T C Ố , GIA T C Ố TRONG DAO Đ N Ộ G ĐI U Ề HÒA II GIA TỐC C A Ủ V T Ậ DAO Đ N Ộ G ĐI U Ề HOÀ 01 Phư n ơ g trình gia t c: ố a = v’ = -  2Acos( t +  ) - Công th c ứ đ c ộ l p ậ th i g ờ ian liên h ệ gi a ữ a và x: a = - 2x  Khi v t ậ ở VTCB: a = 0. min  Khi v t ậ ở VT biên: a =   2A  |a| = max  2A. * Nh n ậ xét: + Gia tốc c a ủ v t ậ dao đ n ộ g và li đ ộ ngư c ợ pha nhau.  Véc t ơ gia t c ố luôn hư n ớ g v ề v ịtrí cân b n ằ g và có đ ộ l n ớ t ỉl ệ v i ớ đ ộ l n ớ c a ủ li đ . ộ + Gia tốc c a ủ v t ậ dao đ n ộ g s m ớ pha so v i ớ v n ậ t c ố . Bài 3: V N Ậ T C Ố , GIA T C Ố TRONG DAO Đ N Ộ G ĐI U Ề HÒA II GIA TỐC C A Ủ V T Ậ DAO Đ N Ộ G ĐI U Ề HOÀ 02 Đồ thị gia t c: ố a = v’ = -  2Acos( t +  ) = -  2x Đồ thị gia tốc c a ủ dao đ n ộ g đi u ề hoà theo th i ờ gian là đư n ờ g hình sin. C N Ủ G CỐ v = -  Asin( t +  )  V
Ở TCB: x = 0; a = 0; v = min min max  2A Đ ồ thị: đư ng ờ hình sin.  V
Ở T biên: |x| = A; |a| = = 0; max max  2A; vmin V n ậ t c ố Gia t c ố DĐĐH DĐĐH  v s m ớ pha   /2 so v i ớ x. a = -  2Acos( t +  )  a s m ớ pha   /2 so v i ớ v. a = - 2x.  a, x: ngư c ợ pha nhau. Đ ồ thị: đư ng ờ hình sin. TRÒ CH I: Ơ GI I Ả M T Ậ LUYỆN T P Ậ THƯ
 Các nhóm nhận m t ậ th ư s ố 1 (b ng ằ 1 bài t p ậ ): Có 5 m t ậ th ư gi ng ố nhau đư c ợ giao cho t ng H ừ S c a ủ nhóm
01  Cá nhân HS ghi tên và gi i ả bài t p ậ trong m t ậ th ư trong th i ờ gian 2 phút.
 Thảo luận nhóm chung trong 1 phút.  02 GV g i ọ bất kì s ố th t ứ nà ự o đem m t ậ th lê ư n ch p ậ t i ạ v t ị rí c a ủ tổ  HS ti p ế t c ụ lấy m t ậ th s ư 2 v ố à th c ự hi n nh ệ t ư rên …
03  GV chấm đi m ể mật th t ư rên b n ả g (đi m
ể thành viên là đi m ể c a ủ t ) ổ  H t ế mật th k ư t ế thúc trò ch i ơ
04  Trình chi u ế k t ế qu , ả h c ọ sinh s a ử phi u ế h c ọ t p ậ và t ng k ổ t ế đi m ể LUYỆN T P Ậ M T Ậ TH Ư S Ố 1 Phư ng ơ trình dao đ n ộ g c a m ủ t ộ v t ậ là x = 5cos4 t (cm). a. Xác đ n ị h t c đ ố c ộ c đ ự i c ạ a ủ v t ậ .
01 b. Hãy vi tế phư ng ơ trình v n t ậ c, ố gia t c. ố c. Vẽ đ t ồ h li đ ị , ộ v n ậ t c, ố gia t c t ố heo th i ờ gian c a v ủ t ậ Hư n ớ g d n: ẫ
Từ phương trình: x = 5cos4 t (cm). Ta có: A = 5 cm;  = 4 rad/s;  = 0.
a. Tốc độ cực đại của vật: v =  A = 4 .5 = 20 cm/s. max
b. Phương trình vận tốc: v = - Asin( t +  ) = - 4 .5.sin4 t = - 20 .sin4 t (cm/s).
Phương trình gia tốc: a = -  2Acos( t +  ) = - (4 )2.5cos4 t = - 800.cos4 t (cm/s2). LUYỆN T P Ậ M T Ậ TH Ư S Ố 1 Phư ng ơ trình dao đ n ộ g c a m ủ t ộ v t ậ là x = 5cos4 t (cm). a. Xác đ n ị h t c đ ố c ộ c đ ự i c ạ a ủ v t ậ .
01 b. Hãy vi tế phư ng ơ trình v n t ậ c, ố gia t c. ố c. Vẽ đ t ồ h li đ ị , ộ v n ậ t c, ố gia t c t ố heo th i ờ gian c a v ủ t ậ Hư n ớ g d c. n: ẫTa có:  = 4 rad/s  T = s. Từ phương trình: t = 0 x = 5cos4  t (cm). (s) v = - 20 .sin4 t (cm/s). a = - 800.cos4 t (cm/s2). x (cm) 5 0 -5 0 5
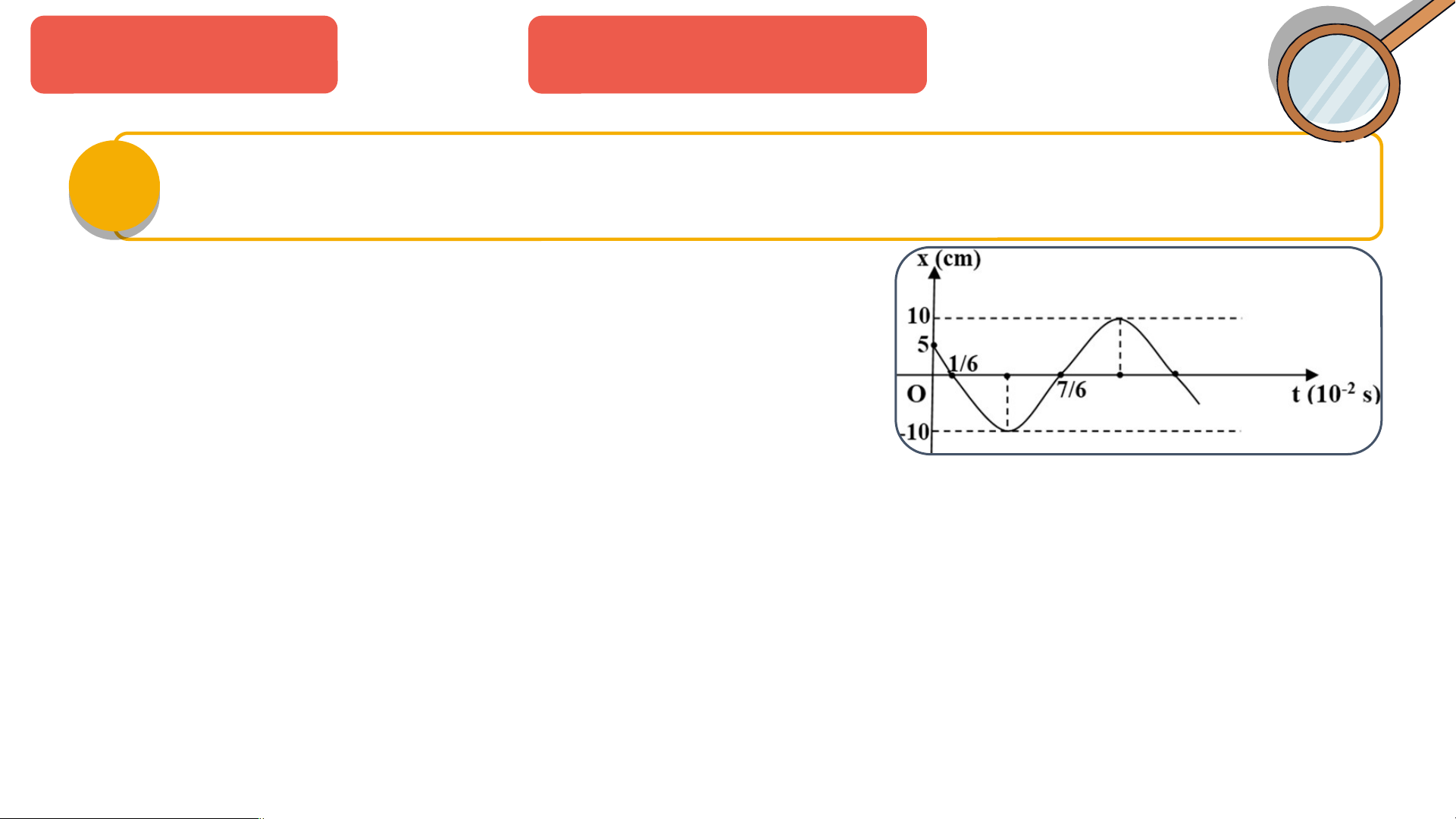
Ta lập bảng số liệu v (cm/s) 0 -20 0 20 0 a (cm/s2) -800 0 800 0 -800 LUYỆN T P Ậ M T Ậ TH Ư S Ố 1 t = 0 01 (s) x (cm) 5 0 -5 0 5 v (cm/s) 0 -20 0 20 0 a (cm/s2) -800 0 800 0 -800 LUYỆN T P Ậ M T Ậ TH Ư S Ố 2 Cho đ ồ th ịdao đ ng ộ c a ủ m t ộ v t ậ nh ư hình vẽ. Vi t ế phư n ơ g trình li đ , ộ v n ậ 02 t c v ố à gia t c ố c a ủ v t ậ .
Từ đồ thị ta thấy:  A = 10 cm; 
T/2 = (7/6-1/6).10-2 = 10-2 s  T = 0,02 s   = 100 (rad/s).  Lúc t = 0: 
Phương trình li độ:
Phương trình vận tốc:
Phương trình gia tốc: LUYỆN T P Ậ M T Ậ TH Ư S Ố 3 M t ộ v t ậ dao đ n ộ g đi u ề hoà trên tr c ụ Ox. Khi v t ậ qua v ịtrí cân b ng ằ thì t c ố 03 đ ộ c a ủ nó là 20 cm/s. Khi v t ậ có t c ố đ ộ 10 cm/s thì gia t c ố c a ủ nó có đ ộ l n ớ cm/s2. Tính biên đ d ộ ao đ ng ộ c a ủ v t ậ .
Ta có: v = 20 cm/s =  A. max v = 10 cm/s; a = cm/s2. Từ: ; a = - 2x   = 4 rad/s. Vậy: NHI M Ệ V Ụ V Ề NHÀ
 Làm bài tập trong SGK, sách bài t p ậ  Tư ng ơ t ự nh ư cách vẽ đ ồ th
ị x – t, xét phư n ơ g trình dao đ ng ộ x = Acos( t +  ). Hãy xác đ nh ị v n ậ t c ố và gia t c ố t i ạ các th i ờ đi m
ể t = 0, t = T/4, t = T/2, t = 3T/4, t = T. T ừ d ữ li u ệ này hãy vẽ đ ồ th v ị - t, a – t
 Ôn bài 1, 2, 3 chu n ẩ b c ị ho ti t ế bài t p ậ hôm sau
Document Outline