






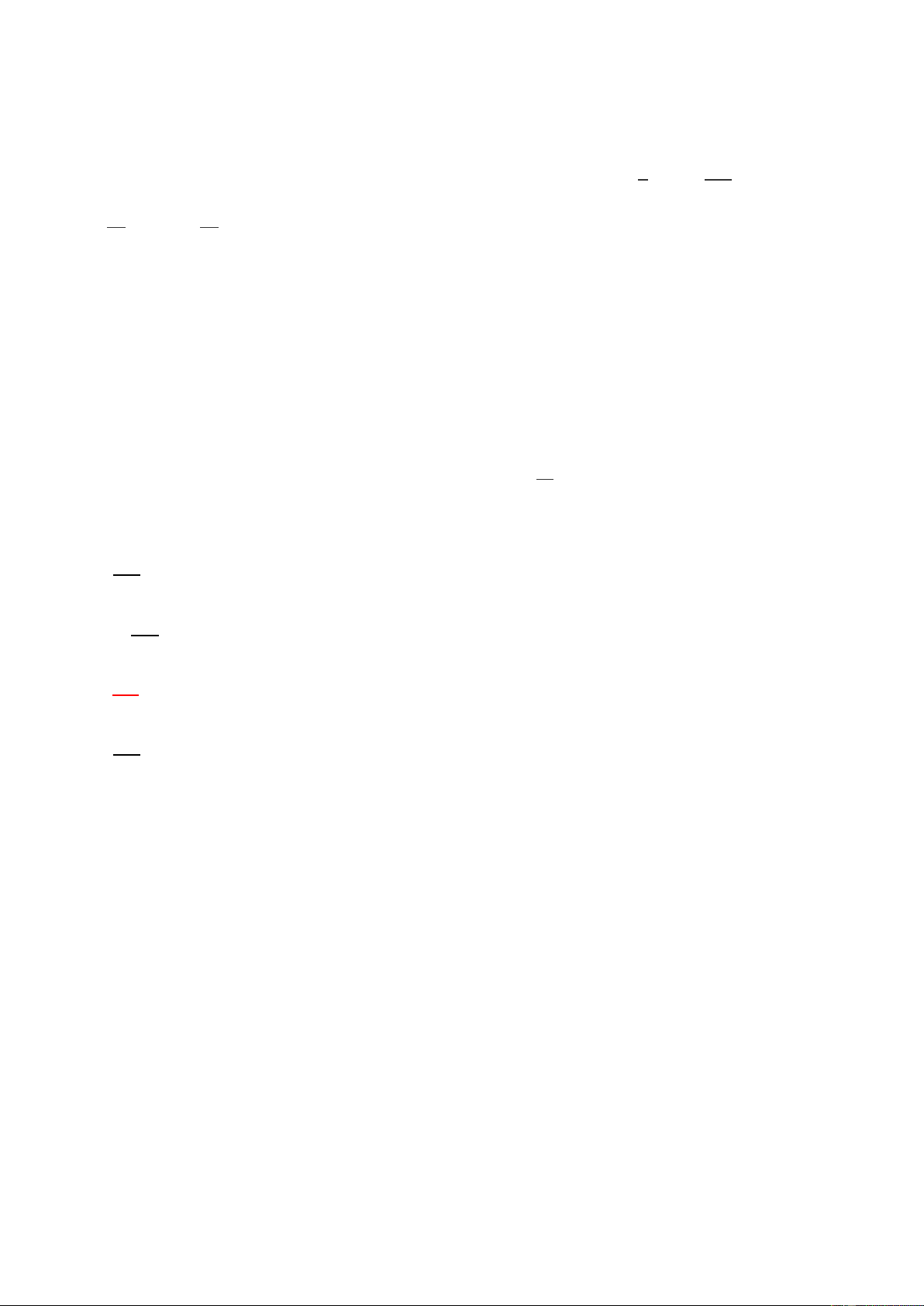











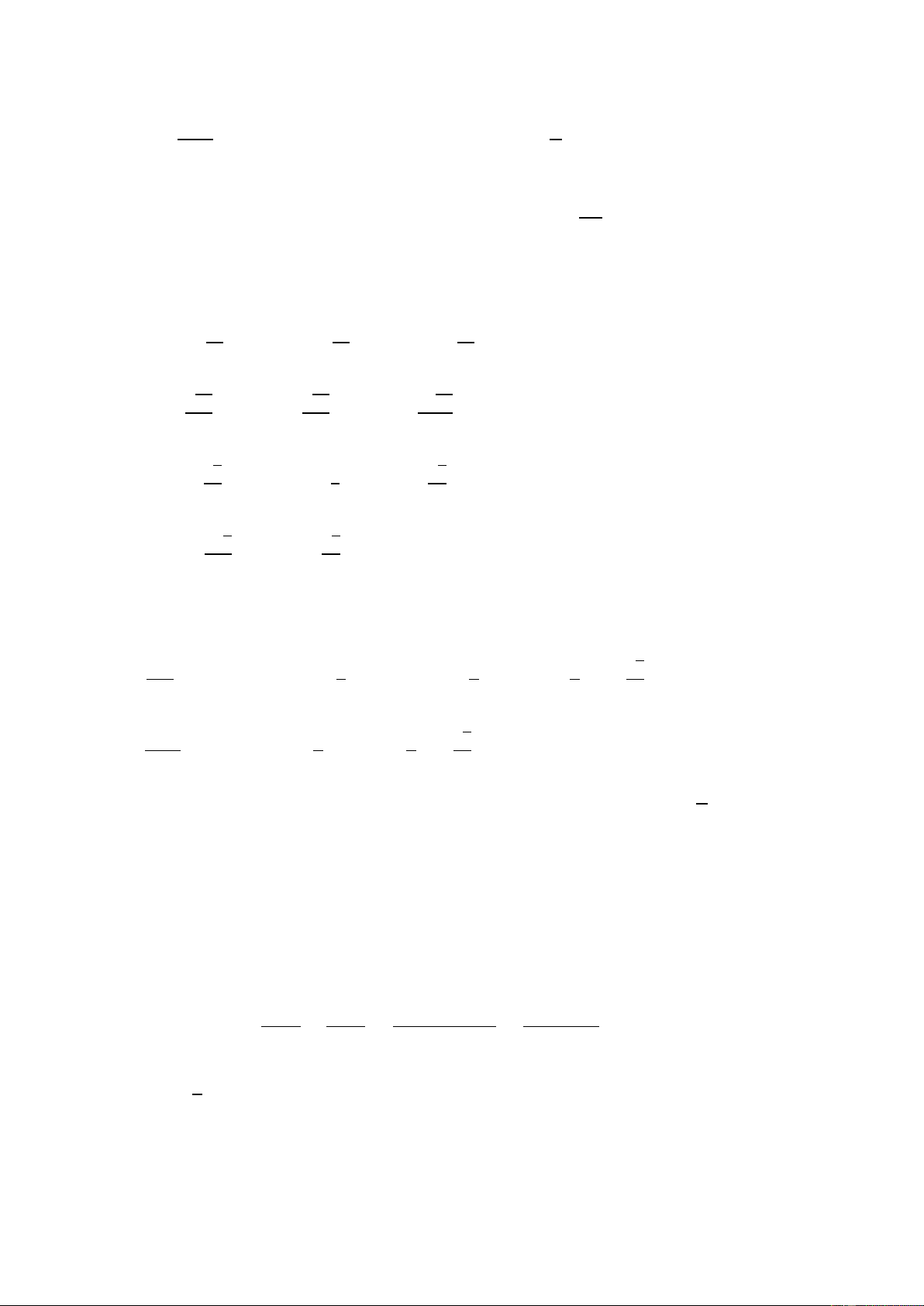













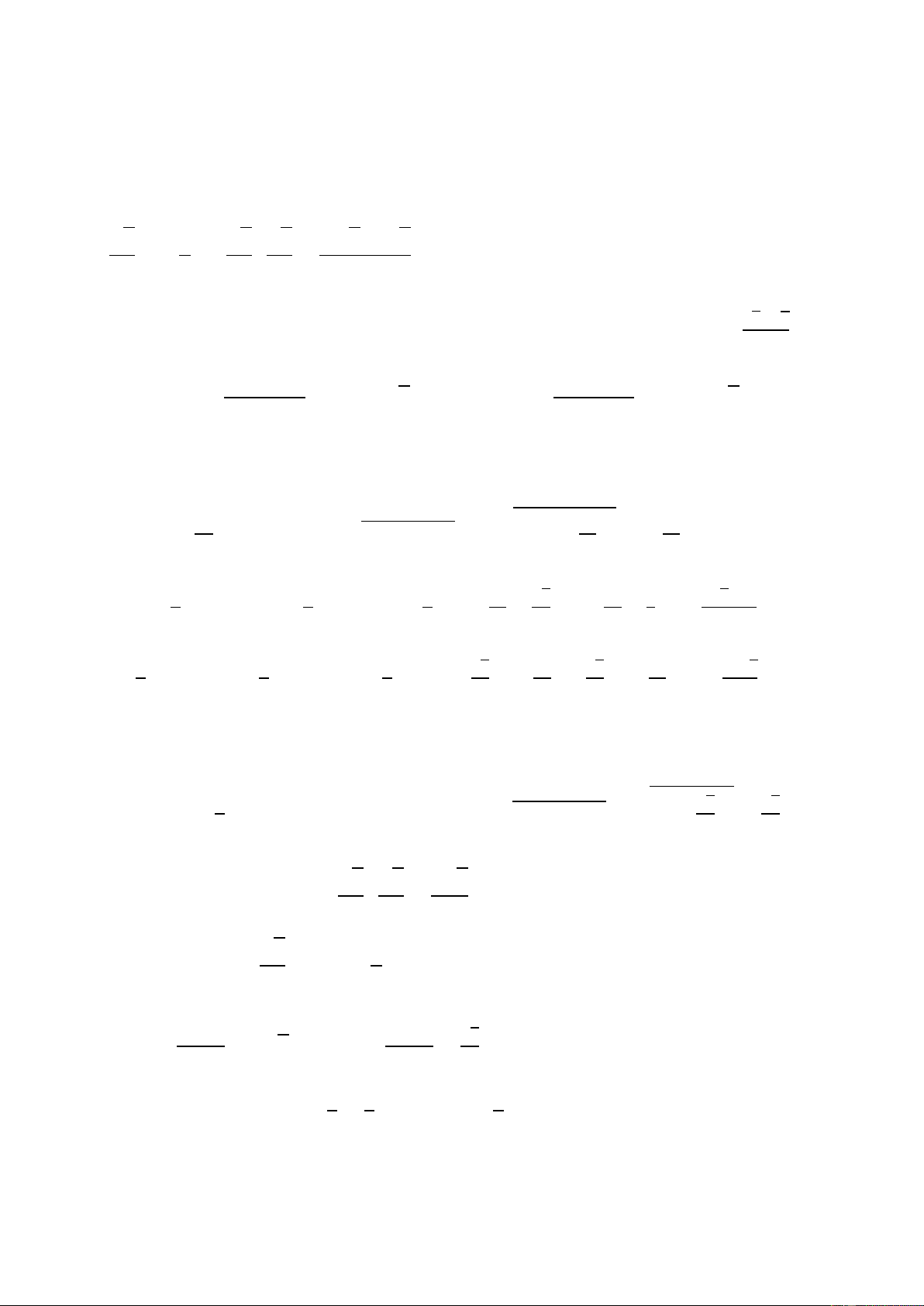

















































































































Preview text:
Ngày soạn: .../.../... Ngày dạy: .../.../...
CHƯƠNG I: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
BÀI 1: GÓC LƯỢNG GIÁC (1 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết các khái niệm cơ bản về góc lượng giác: góc lượng giác, số đo của
góc lượng giác, hệ thức Chasles cho các góc lượng giác, đường tròn lượng giác.
- Biểu diễn các góc lượng giác trên đường tròn lượng giác.
- Đổi số đo góc từ độ sang radian và ngược lại. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học, giải quyết vấn đề toán học: nhận biết và thể hiện
được các khái niệm cơ bản của góc lượng giác, sử dụng hệ thức Chales, biểu diễn
các góc lượng giác.
- Mô hình hóa toán học: Vận dụng góc lượng giác trong các mô hình bài toán thực tế đơn giản.
- Giải quyết vấn đề toán học, 1 - Giao tiếp toán học.
- Sử dụng công cụ, phương tiện học toán. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
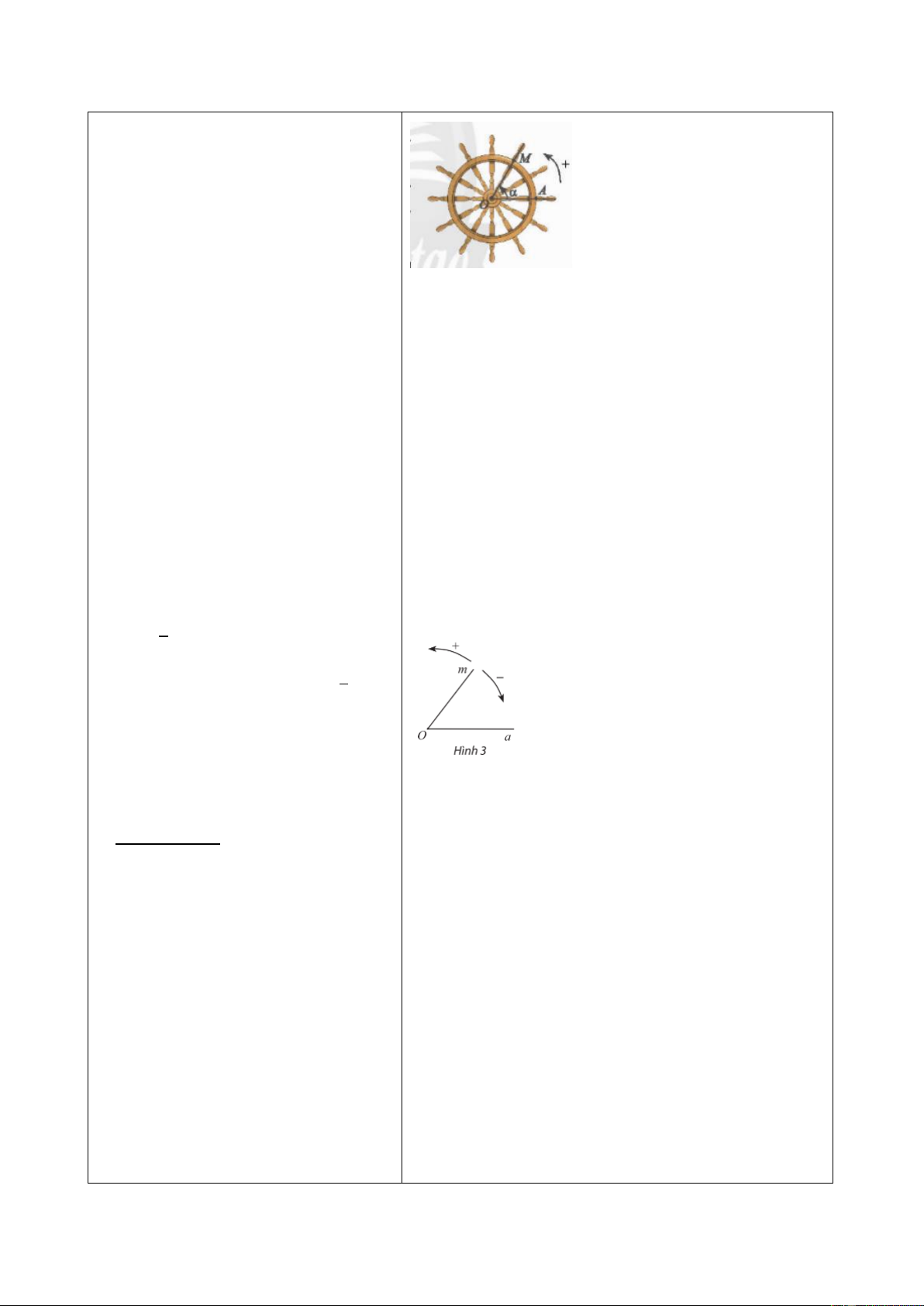
- Dựa vào hình ảnh trực quan về một chuyển động quay của bánh lái tàu để giúp HS có
được hình dung ban đầu về nhu cầu sử dụng góc lượng giác để mô tả chuyển động quay.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS đưa ra được câu trả lời.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu 2 - GV gợi mở:
+ Xác định điểm đầu, điểm cuối của chuyển động, xác định số vòng quay của chuyển động.
+ Từ đó so sánh sự giống và khác nhau về điểm đầu, điểm cuối, chiều chuyển động, số vòng quay.
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung. Dự kiến câu trả lời
Các chuyển động có cùng điểm đầu là 𝐴 và điểm cuối là 𝐵, mỗi chuyển động quay theo
một chiều cố định, tuy nhiên số vòng quay và chiều quay không như nhau:
• Trong trường hợp a, bánh lái quay ngược chiều kim đồng hồ từ 𝐴 đến 𝐵 sau đó
quay thêm một vòng để gặp 𝐵 lần thứ 2 (quay ngược chiều kim đồng hồ 1 1 6 vòng).
• Trong trường hợp b, bánh lái quay cùng chiều kim đồng hồ từ 𝐴 đến 𝐵, gặp 𝐵
đúng 1 lần (quay cùng chiều kim đồng hồ 5 vòng). 6
• Trong trường hợp c, bánh lái quay ngược chiều kim đồng hồ từ 𝐴 đến 𝐵, gặp 𝐵
đúng 1 lần (quay ngược chiều kim đồng hồ 1 vòng) 6 3
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học mới “Chuyển động quay của một điểm trên bánh lái từ 𝐴 đến 𝐵 tương ứng
với chuyển động quay của một thanh bánh lái từ vị trí đầu 𝑂𝐴 đến vị trí cuối 𝑂𝐵. Tuy
nhiên góc hình học 𝐴𝑂𝐵
̂ không mô tả được chiều quay và số vòng quay của các chuyển
động này. Để mô tả được các yếu tố này trong chuyển động quay, người ta sử dụng góc
lượng giác. Bài học hôm nay chúng ta cùng đi tìm hiểu các khái niệm cơ bản về góc lượng giác”.
Bài 1: Góc lượng giác.
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Góc lượng giác a) Mục tiêu:
- HS nhận biết và thể hiện được khái niệm góc lượng giác, số đo góc lượng giác.
- HS hiểu, phát biểu và vận dụng được hệ thức Chasles. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động khám phá, thực hành, vận dụng, đọc hiểu ví dụ.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi,
HS xác định được số đo góc lượng giác, vận dụng hệ thức Chasles.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ: 1. Góc lượng giác
Nhiệm vụ 1: Tìm hiểu Khái niệm a) Khái niệm góc lượng giác
góc lượng giác HĐKP 1: 4
- GV yêu cầu HS thảo luận nhóm
đôi, hoàn thành HĐKP 1.
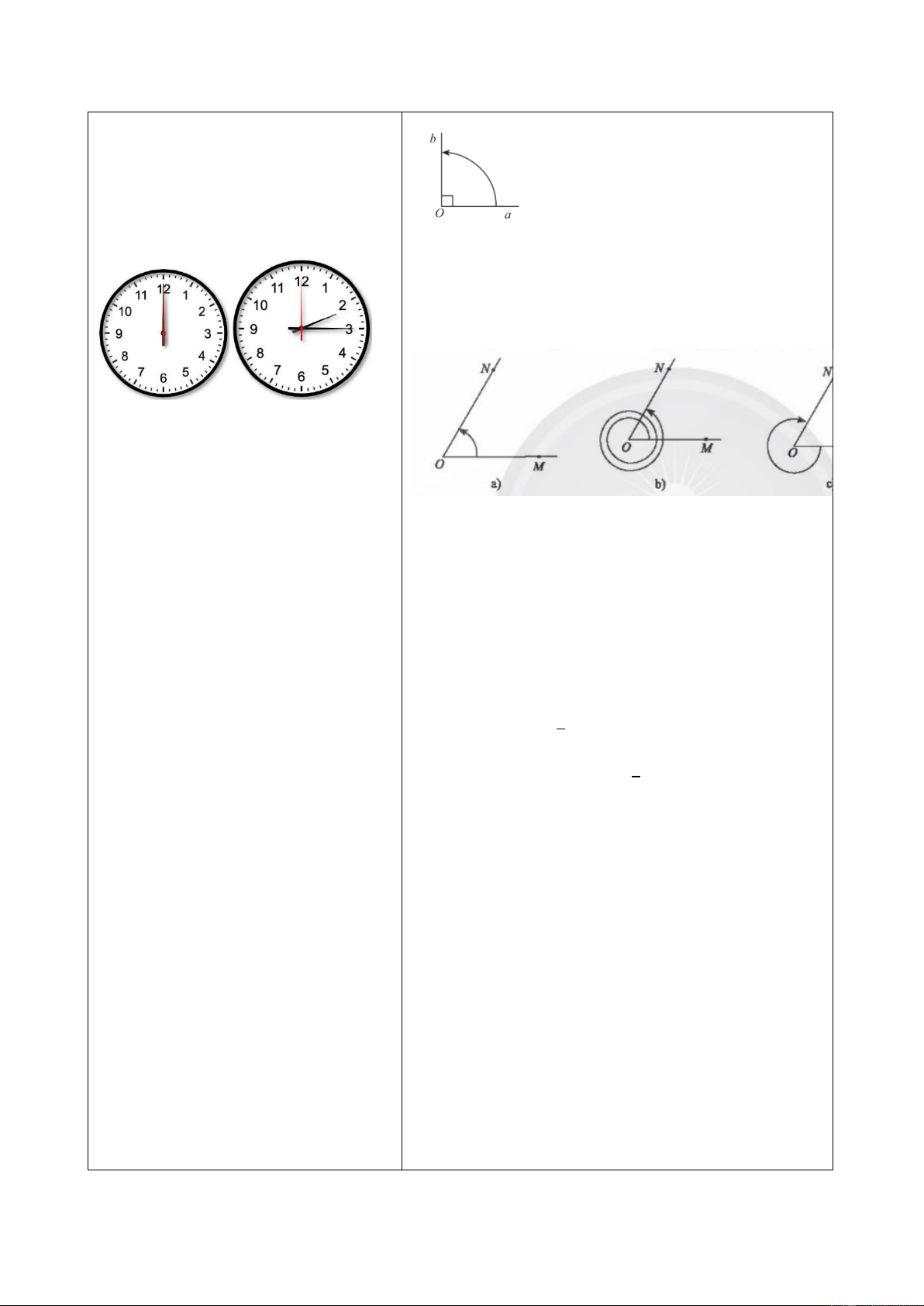
a) Cứ mỗi giây, thanh 𝑂𝑀 quay được 60∘ nên
mỗi giây góc quay được cộng thêm 60∘.
b) Cứ mỗi giây, thanh 𝑂𝑀 quay được −60∘ nên
mỗi giây góc quay được cộng thêm −60∘.
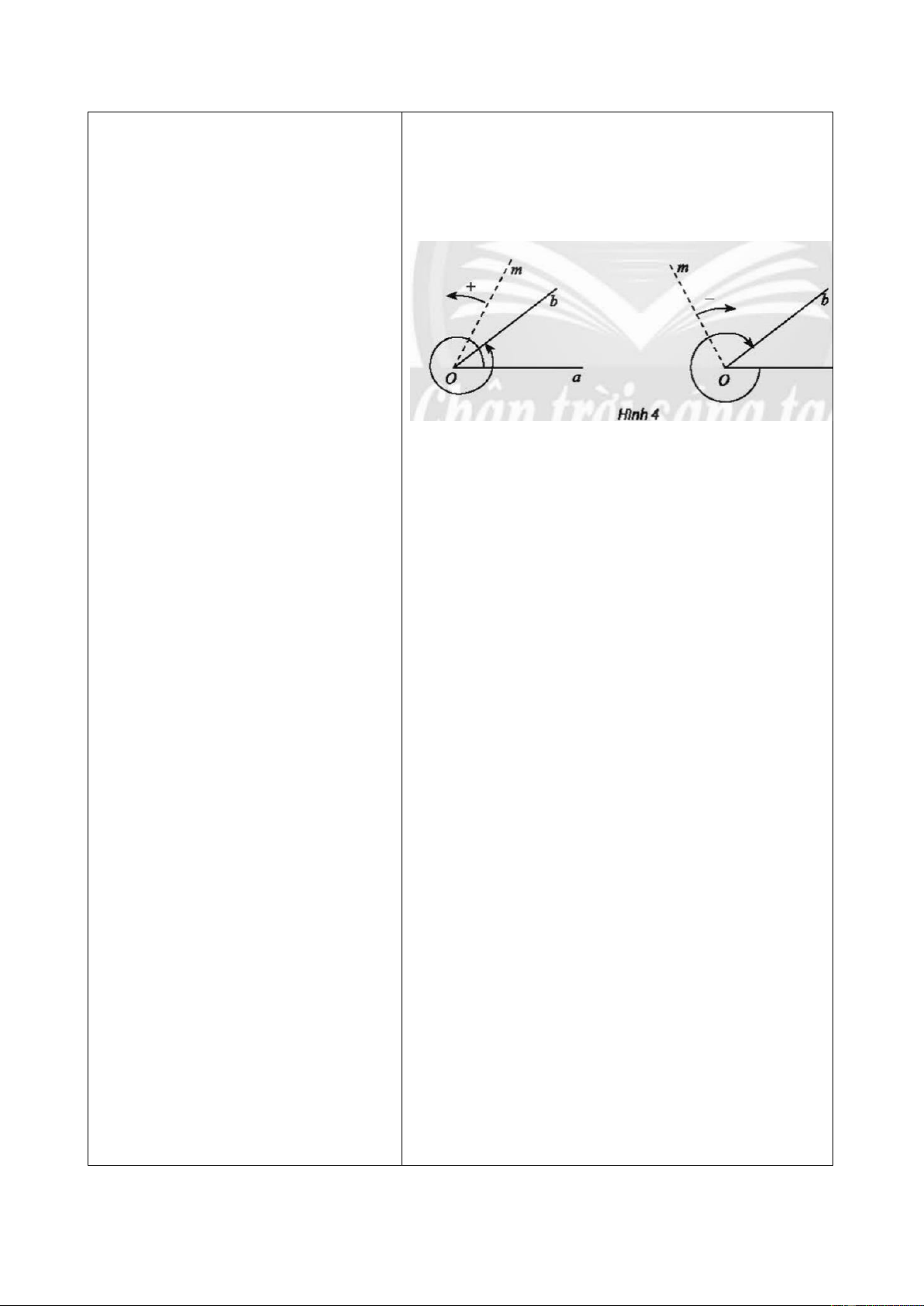
- GV giới thiệu về chuyển động
quay của tia Om quanh gốc O, tính (Bảng dưới)
từ vị trí ban đầu sẽ có sự quy ước về - Quy ước: Chiều quay ngược chiều kim đồng
chiều âm và chiều dương.
hồ là chiều dương, chiều quay cùng chiều kim
+ Ví dụ khi quay Om theo chiều đồng hồ là chiều âm.
dương 1 vòng thì ta nói Om quay 4 đượ 1
c góc 90𝑜; theo chiều âm vòng 4
thì ta nói Om quay được góc −90𝑜.
- GV giới thiệu về góc lượng giác
và số đo của một góc lượng giác. Kết luận
+ Nhấn mạnh: một góc lượng giác - Cho hai tia Oa, Ob.
cần xác định được tia đầu, tia cuối và chiều quay.
+ Nếu một tia Om quay quanh gốc O của nó theo
+ Số đo góc lượng giác có thể âm một chiều cố định bắt đầu từ vị trí tia 𝑂𝑎 và
hoặc dương phụ thuộc chiều quay; dừng ở vị trí tia 𝑂𝑏 thì ta nói tia 𝑂𝑚 quét một
có thể lớn hoặc bé tùy vào số vòng góc lượng giác có tia đầu 𝑂𝑎, tia cuối 𝑂𝑏, kí hiệu quay của tia cuối. (𝑂𝑎, 𝑂𝑏). 5
- Khi tia 𝑂𝑚 quay một góc 𝛼, ta nói số đo của
góc lượng giác (𝑂𝑎, 𝑂𝑏) bằng 𝛼, kí hiệu - GV đặt câu hỏi:
𝑠đ(𝑂𝑎, 𝑂𝑏) = 𝛼.
+ Với hai tia Oa và Ob cho trước
có bao nhiêu góc lượng giác có tia
đầu là Oa và tia cuối Ob? (Có vô số).
- GV cho HS quan sát, giải thích Ví dụ 1.
+ Xác định chiều, tia đầu và tia cuối Chú ý: Với hai tia Oa và Ob cho trước:
của góc lượng giác. - GV đặt câu hỏi:
+ Có vô số góc lượng giác có tia đầu là Oa và tia
+ Quan sát các hình 5a, 5b, 5c, 5d; cuối Ob.
khi các góc lượng giác đều có cùng + Kí hiệu: (Oa,Ob).
tia đầu và tia cuối, thì số đo góc
lượng giác của chúng có mối quan Ví dụ 1 (SGK -tr.8) hệ gì?
(Sai khác một bội nguyên của 360𝑜) Nhận xét:
+ GV lưu ý: để thể hiện sự sai khác Số đo của các góc lượng giác có cùng tia đầu Oa
một bội nguyên ta sử dụng 𝑘 ∈ ℤ; và tia cuối Ob sai khác một bội nguyên của
giá trị k có thể âm hoặc dương. 360∘.
- HS thực hiện Thực hành 1 theo 𝑠đ(𝑂𝑎, 𝑂𝑏) = αo + 𝑘360∘(𝑘 ∈ ℤ) nhóm đôi.
Hoặc (𝑂𝑎, 𝑂𝑏) = αo + 𝑘360∘(𝑘 ∈ ℤ).
Với αo là số đo của một góc lượng giác bất kì có
tia đầu Oa và tia cưới Ob. Ví dụ: 6
- HS thực hiện Vận dụng 1. GV gợi
𝑠đ(𝑂𝑎, 𝑂𝑏) = 90𝑜 + 𝑘360𝑜(𝑘 ∈ ý: ℤ) Thực hành 1:
+ Kim phút quay theo chiều nào?
+ Kim phút quay từ vị trí 0 giờ đến
2h15 thì quay được bao nhiêu vòng? a) 60∘;
Nhiệm vụ 2: Tìm hiểu hệ thức b) 60∘ + 2 ⋅ 360∘ = 780∘; Chasles c) −300∘.
- HS thực hiện HĐKP 2. Vận dụng 1:
Kim phút quay 2 1 vòng theo chiều âm nên số đo 4
góc lượng giác là 𝛼 = −2 1 ⋅ 360∘ = −810∘. 4 b) Hệ thức Chasles 7 HĐKP 2:
- Từ đó GV giới thiệu về hệ thức
Chasles với ba tia Oa, Ob, Oc bất kì
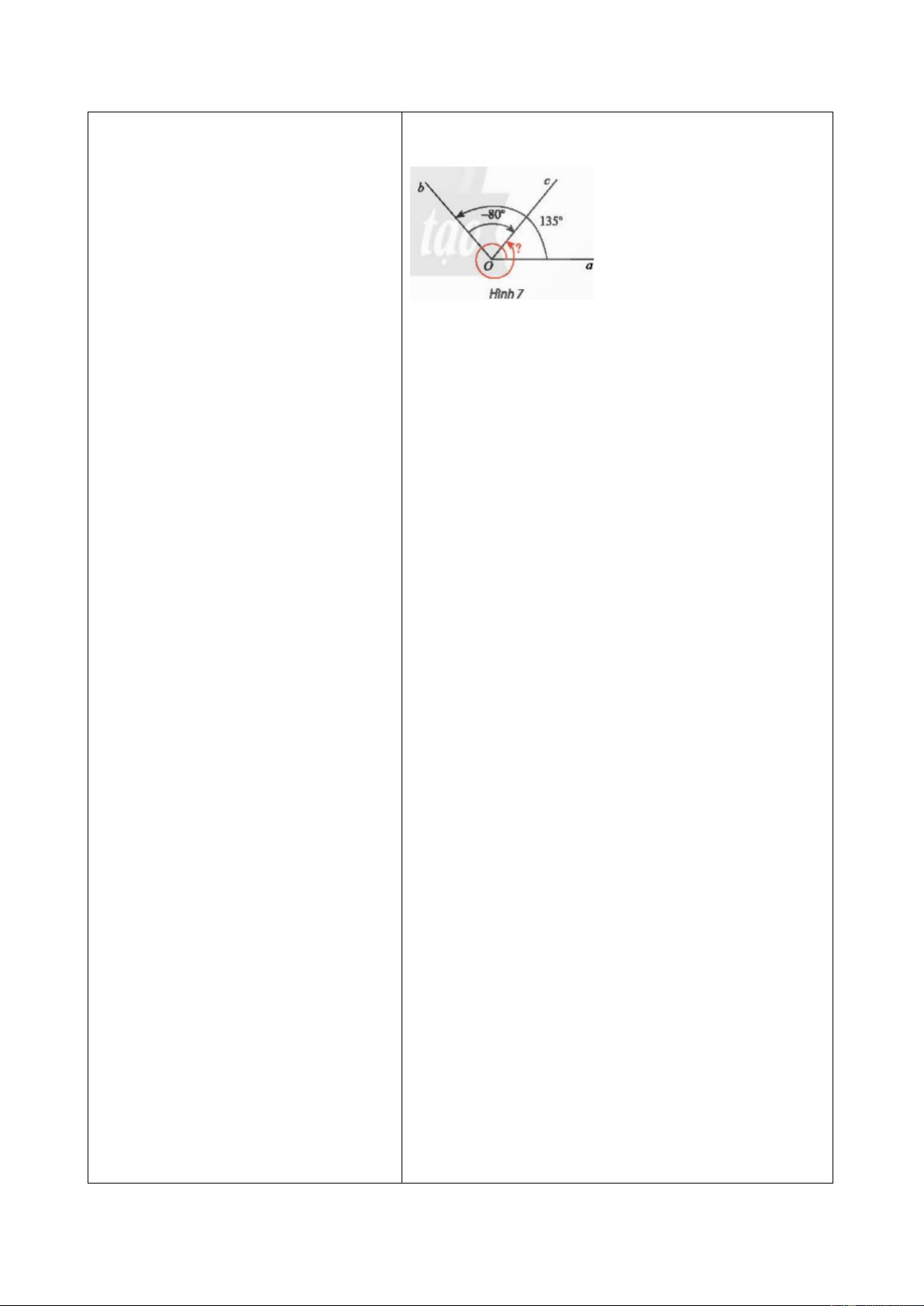
- HS thảo luận nhóm đôi, thực hiện a) Số đo góc lượng giác (𝑂𝑎, 𝑂𝑏) trong hình là
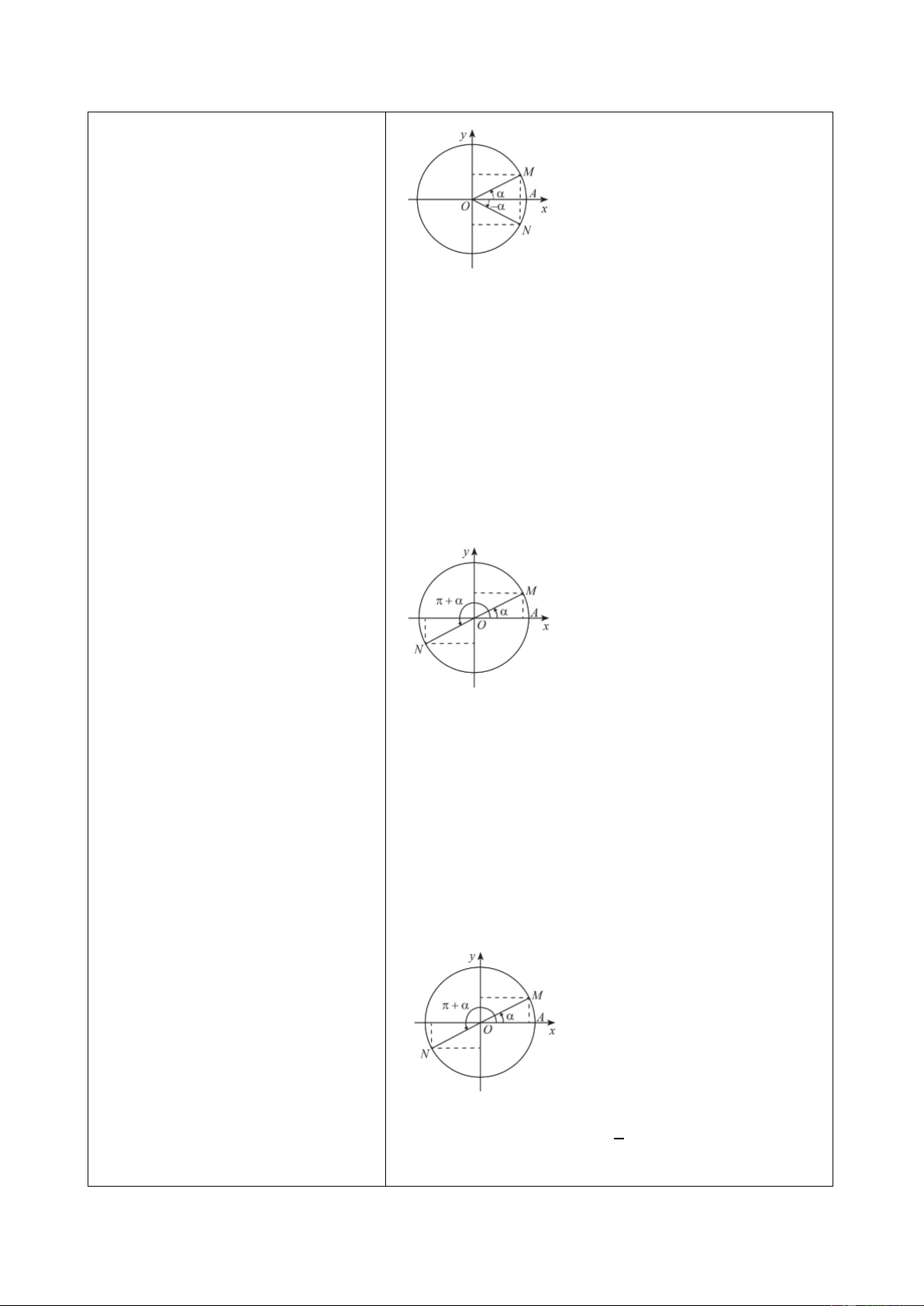
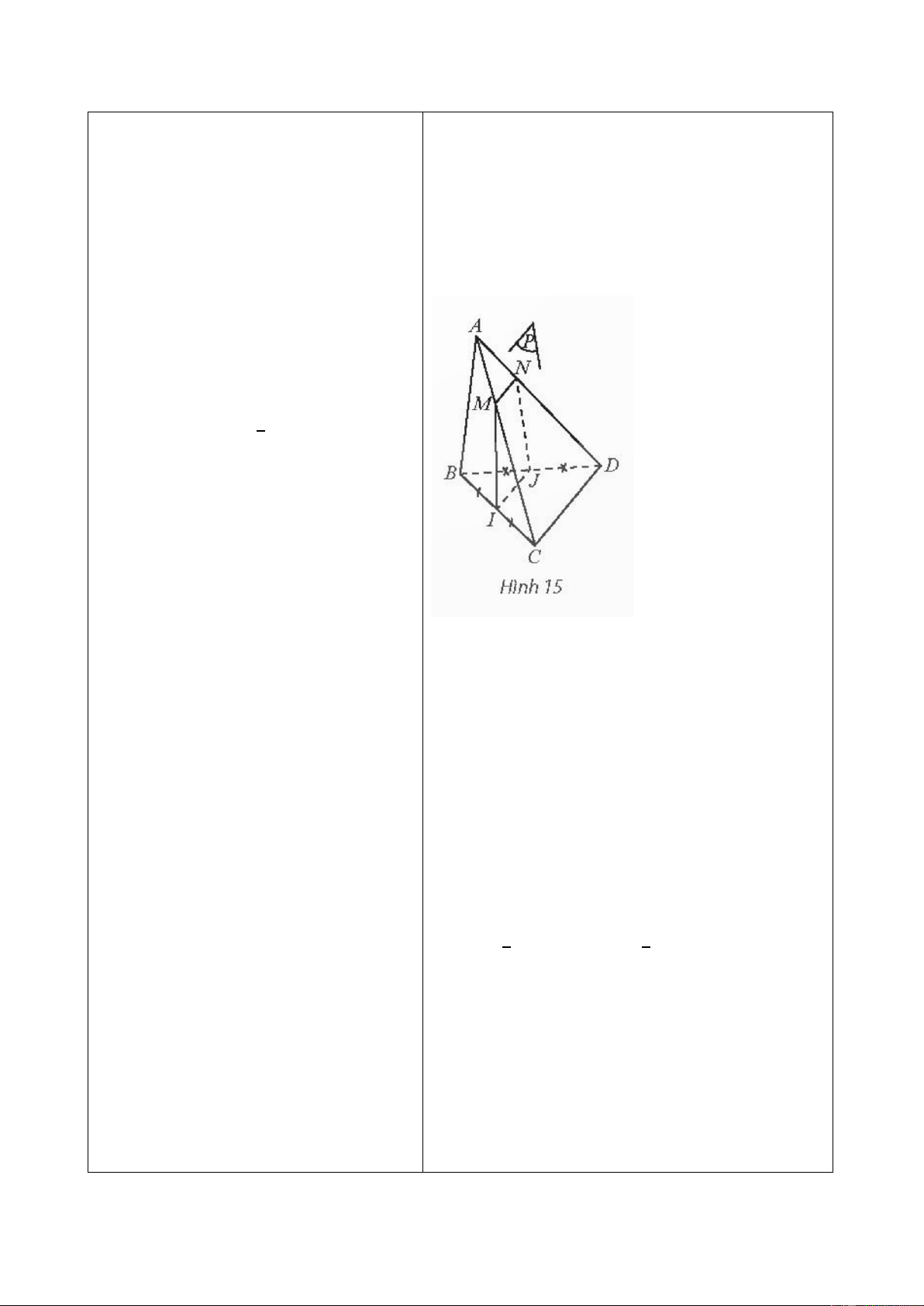
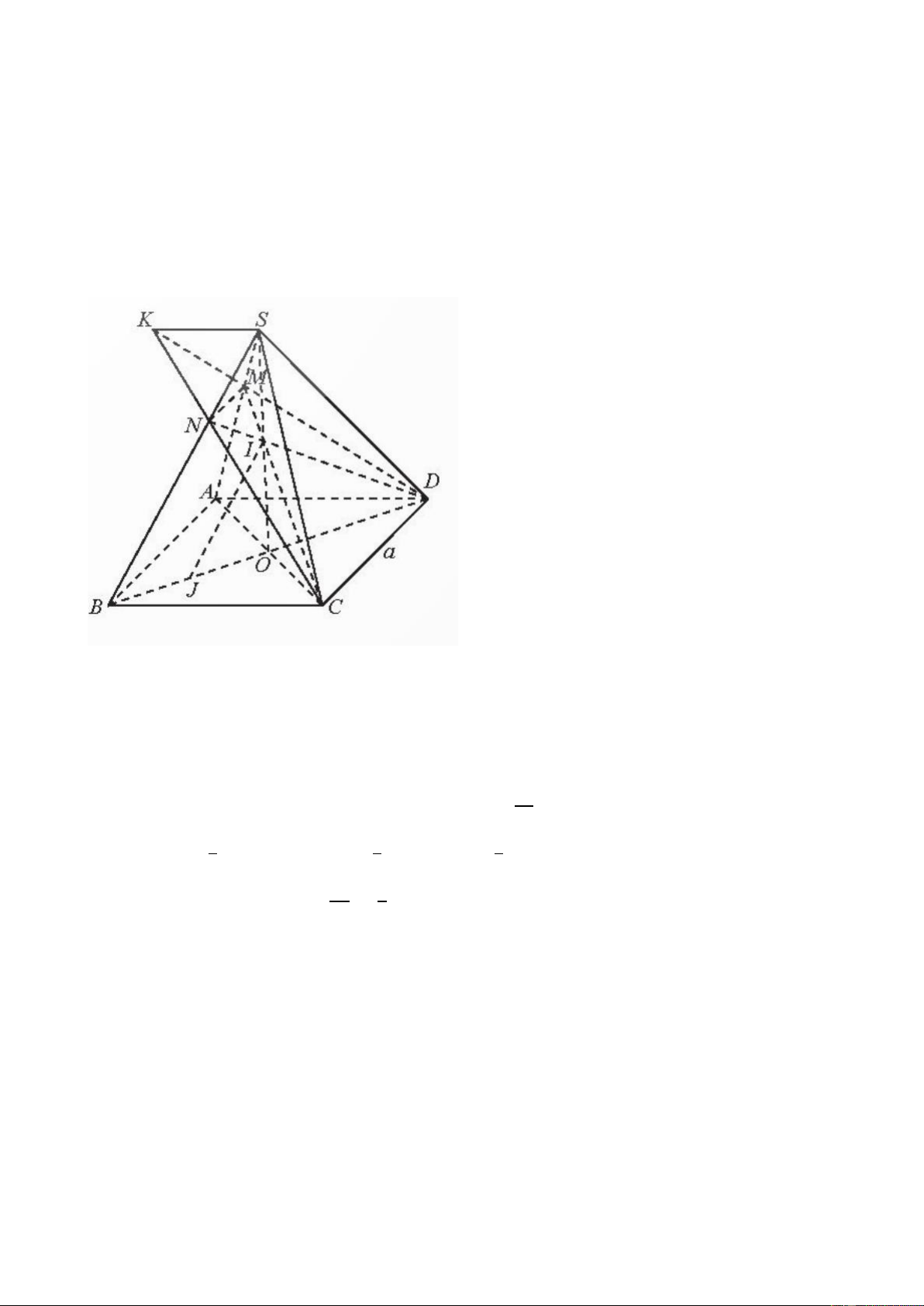
Vận dụng 2. GV gợi ý: 135∘. + Tính số đo các góc
Số đo góc lượng giác (𝑂𝑏, 𝑂𝑐) trong hình là 𝑀𝑂𝑁 ̂ , 𝑀𝑂𝑃 ̂ , 𝑃𝑂𝑁 ̂ . −80∘.
+ Để tính được (𝑂𝑥, 𝑂𝑁) ta có thể
sử dụng định lí nào với ba tia Dựa vào hình, ta có 𝑎𝑂𝑐
̂ = 135∘ − 80∘ = 55∘. 𝑂𝑥, 𝑂𝑀, 𝑂𝑁?
Trong hình, góc lượng giác (𝑂𝑎, 𝑂𝑐) tương ứng
với chuyển động quay theo chiều dương từ 𝑂𝑎
Bước 2: Thực hiện nhiệm vụ:
đến 𝑂𝑐, sau đó quay thêm 1 vòng. Do đó số đo
- HS theo dõi SGK, chú ý nghe, tiếp góc lượng giác (𝑂𝑎, 𝑂𝑐) trong hình là 55∘ +
nhận kiến thức, hoàn thành các yêu 360∘ = 415∘. cầu, thảo luận nhóm.
b) Như vậy đối với ba góc trong hình, ta có tổng - GV quan sát hỗ trợ.
số đo góc lượng giác (𝑂𝑎, 𝑂𝑏) và (𝑂𝑏, 𝑂𝑐)
Bước 3: Báo cáo, thảo luận:
chênh lệch với số đo góc lượng giác (𝑂𝑎, 𝑂𝑐) là
- HS giơ tay phát biểu, lên bảng một số nguyên lần 360∘. trình bày Kết luận
- Một số HS khác nhận xét, bổ sung cho bạn.
- Hệ thức Chasles: Với ba tia 𝑂𝑎, 𝑂𝑏, 𝑂𝑐 bất kì,
Bước 4: Kết luận, nhận định: GV ta có 𝑠đ(𝑂𝑎, 𝑂𝑏) + 𝑠đ(𝑂𝑏, 𝑂𝑐) = 𝑠đ(𝑂𝑎, 𝑂𝑐) +
tổng quát lưu ý lại kiến thức trọng 𝑘360∘(𝑘 ∈ ℤ)
tâm và yêu cầu HS ghi chép đầy đủ Vận dụng 2: vào vở. 8
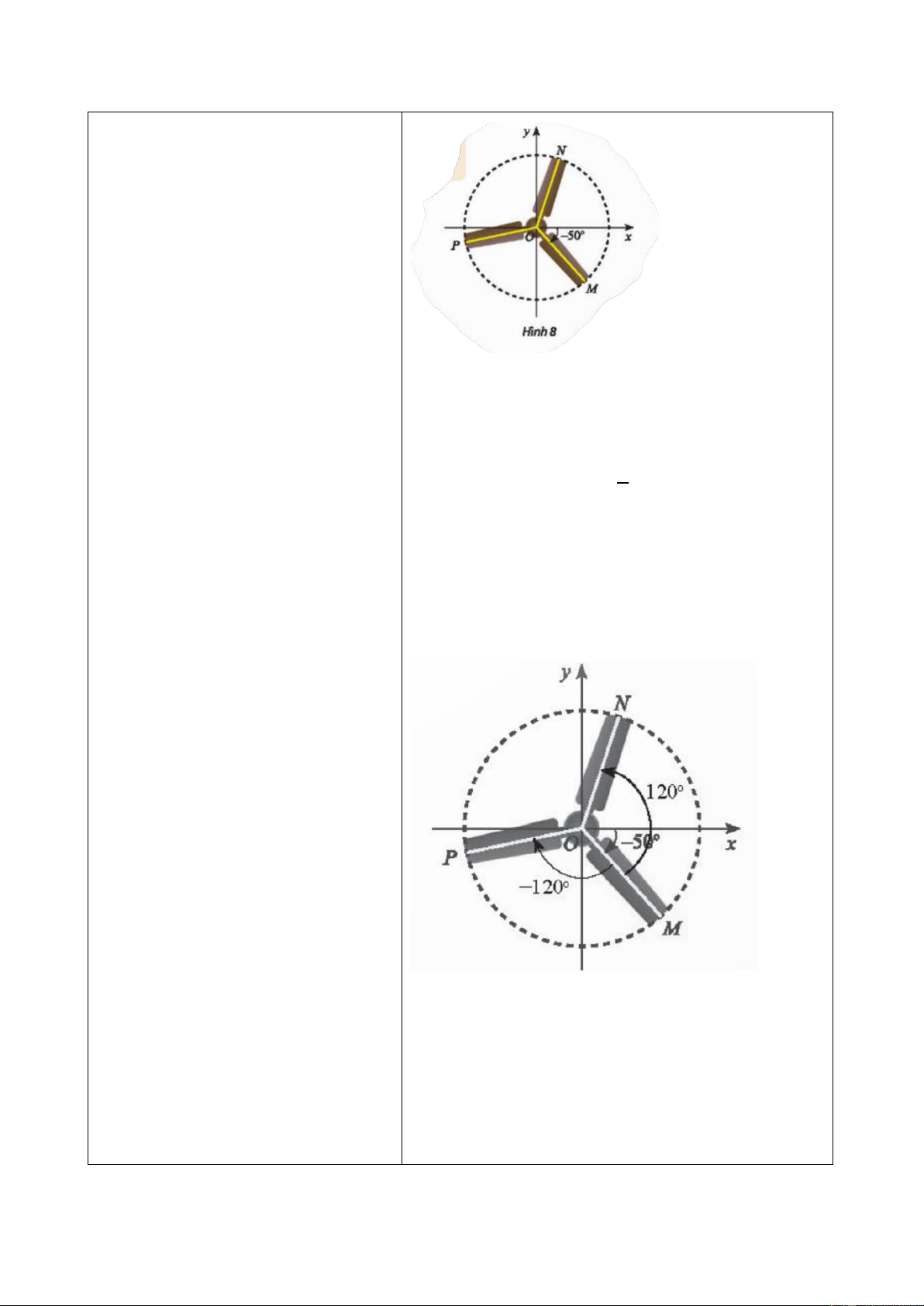
Vì chiếc quạt có ba cánh được phân bố đều nhau nên 1 𝑀𝑂𝑁 ̂ = 𝑀𝑂𝑃 ̂ = ⋅ 360∘ = 120∘. 3
Do đó số đo các góc lượng giác (𝑂𝑀, 𝑂𝑁) và
(𝑂𝑀, 𝑂𝑃) được vẽ trong hình lần lượt là 120∘ và −120∘. Ta có:
(𝑂𝑥, 𝑂𝑁) = (𝑂𝑥, 𝑂𝑀) + (𝑂𝑀, 𝑂𝑁) + 𝑘360∘(𝑘 ∈ ℤ)
= −50∘ + 120∘ + 𝑘360∘(𝑘 ∈ ℤ)
= 70∘ + 𝑘360∘(𝑘 ∈ ℤ). 9 (𝑂𝑥, 𝑂𝑃)
= (𝑂𝑥, 𝑂𝑀) + (𝑂𝑀, 𝑂𝑃) + 𝑘360∘(𝑘 ∈ ℤ)
= −50∘ − 120∘ + 𝑘360∘(𝑘 ∈ ℤ)
= −170∘ + 𝑘360∘(𝑘 ∈ ℤ). HĐKP 1 a) Thời gian 𝑡 (giây) 1 2 3 4 5 6 Góc quay 𝛼 60∘ 120∘ 180∘ 240∘ 300∘ 360∘ b) Thời gian 𝑡 1 2 3 4 5 6 (giây) Góc quay 𝛼 −60∘ −120∘ −180∘ −240∘ −300∘ −360∘
Hoạt động 2: Đơn vị radian a) Mục tiêu:
- HS nhận biết đơn vị radian.
- HS chuyển đổi số đo góc lượng giác từ đơn vị radian sang đơn vị độ và ngược lại.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động của mục 2.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi,
HS đổi được đơn vị đo theo yêu cầu.
d) Tổ chức thực hiện: 10
HOẠT ĐỘNG CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN Bướ 2. Đơn vị
c 1: Chuyển giao nhiệm vụ: radian HĐKP 3:
- GV yêu cầu HS thảo luận nhóm đôi, hoàn thành HĐKP 3. Số đo 𝐴𝑂𝐵
̂ không phụ thuộc vào đường tròn đượ
- Từ đó GV giới thiệu về đơn vị đo
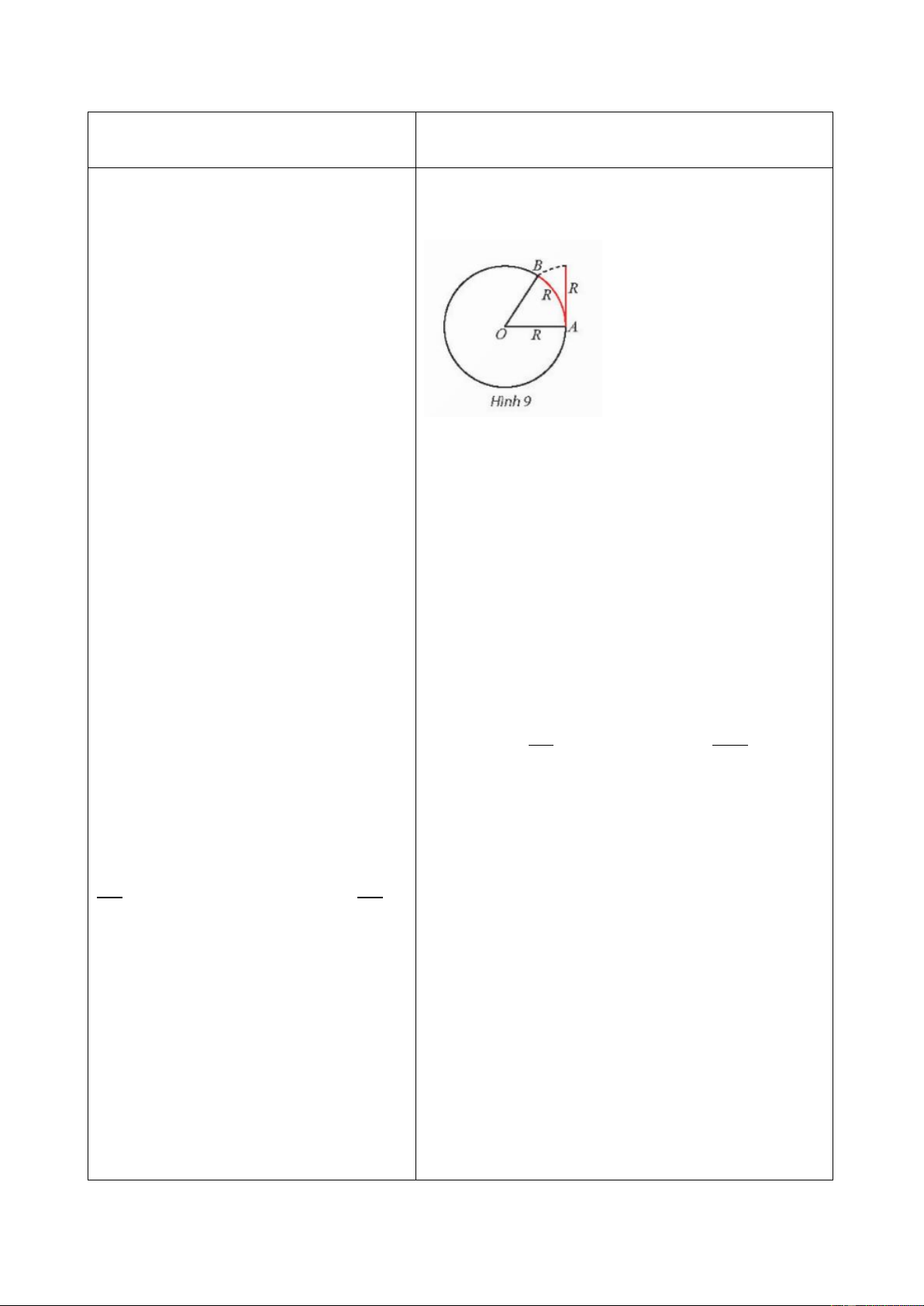
c vẽ và bằng khoảng 57∘. radian. Kết luận
Trên đường tròn bán kính 𝑅 tùy ý, góc ở tâm
chắn một cung có độ dài đúng bằng 𝑅 được gọi - GV gợi mở
là một góc có số đo 1 radian.
+ Một góc ở tâm có số đo 𝛼 rad thì Viết tắt: 1 rad.
chắn một cung có độ dài bao nhiêu? ∘ (Độ dài: 𝛼𝑅) a∘ = 𝜋𝑎 rad 180α và 𝛼 𝑟𝑎𝑑 = ( ) 180 𝜋
+ GV hướng dẫn tính góc bẹt. Từ đó
có mối liên hệ 180𝑜 = 𝜋 𝑟𝑎𝑑.
+ Vậy có mối liên hệ giữa 1∘ = 𝜋 ∘
𝑟𝑎𝑑 và ngược lại 1𝑟𝑎𝑑 = 180 ( ) . 180 𝜋
- GV cho HS nêu công thức tổng quát
đổi độ sang rad và ngược lại.
- HS quan sát Ví dụ 2.
- HS luyện tập làm Thực hành 2.
- GV cho HS chú ý về cách viết đơn
vị rad và công thức số đo tổng quát Ví dụ 2 (SGK -tr.10) theo rad. 11 Bướ Thực hành 2:
c 2: Thực hiện nhiệm vụ:
- HS theo dõi SGK, chú ý nghe, tiếp Đơn vị độ Đơn vị rad
nhận kiến thức, suy nghĩ trả lời câu 0𝑜 0 𝑟𝑎𝑑
hỏi, hoàn thành các yêu cầu.
- GV: quan sát và trợ giúp HS. 30𝑜 𝜋 rad 6
Bước 3: Báo cáo, thảo luận: 45𝑜 𝜋 rad
- HS giơ tay phát biểu, lên bảng trình 4 bày 60𝑜 𝜋 rad
- Một số HS khác nhận xét, bổ sung 3 cho bạn. 90𝑜 𝜋
Bước 4: Kết luận, nhận định: GV rad 2
tổng quát lưu ý lại kiến thức trọng 120𝑜 2𝜋
tâm và yêu cầu HS ghi chép đầy đủ rad 3 vào vở. 135𝑜 3𝜋 rad 4 150𝑜 5𝜋 rad 6 180𝑜 π rad Chú ý: 𝜋
+ 𝛼 𝑟𝑎𝑑 có thể được viết là 𝛼. Ví dụ: 𝑟𝑎𝑑 2 đượ 𝜋 c viết là . 2
+ (𝑂𝑎, 𝑂𝑏) = α + 𝑘2𝜋 (𝑘 ∈ ℤ)
Trong đó 𝛼 là số đo theo radian của một góc
lượng giác bất kì có tia đầu Oa và tia cuối Ob.
Hoạt động 3: Đường tròn lượng giác 12 a) Mục tiêu:
- HS nhận biết và thể hiện được khái niệm đường tròn lượng giác.
- HS biểu diễn góc lượng giác với số đo cho trước trên đường tròn lượng giác.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động của mục 3.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi,
HS biểu diễn được góc lượng giác.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN Bướ
3. Đường tròn lượ
c 1: Chuyển giao nhiệm vụ: ng giác HĐKP 4:
- GV yêu cầu HS thảo luận nhóm đôi,
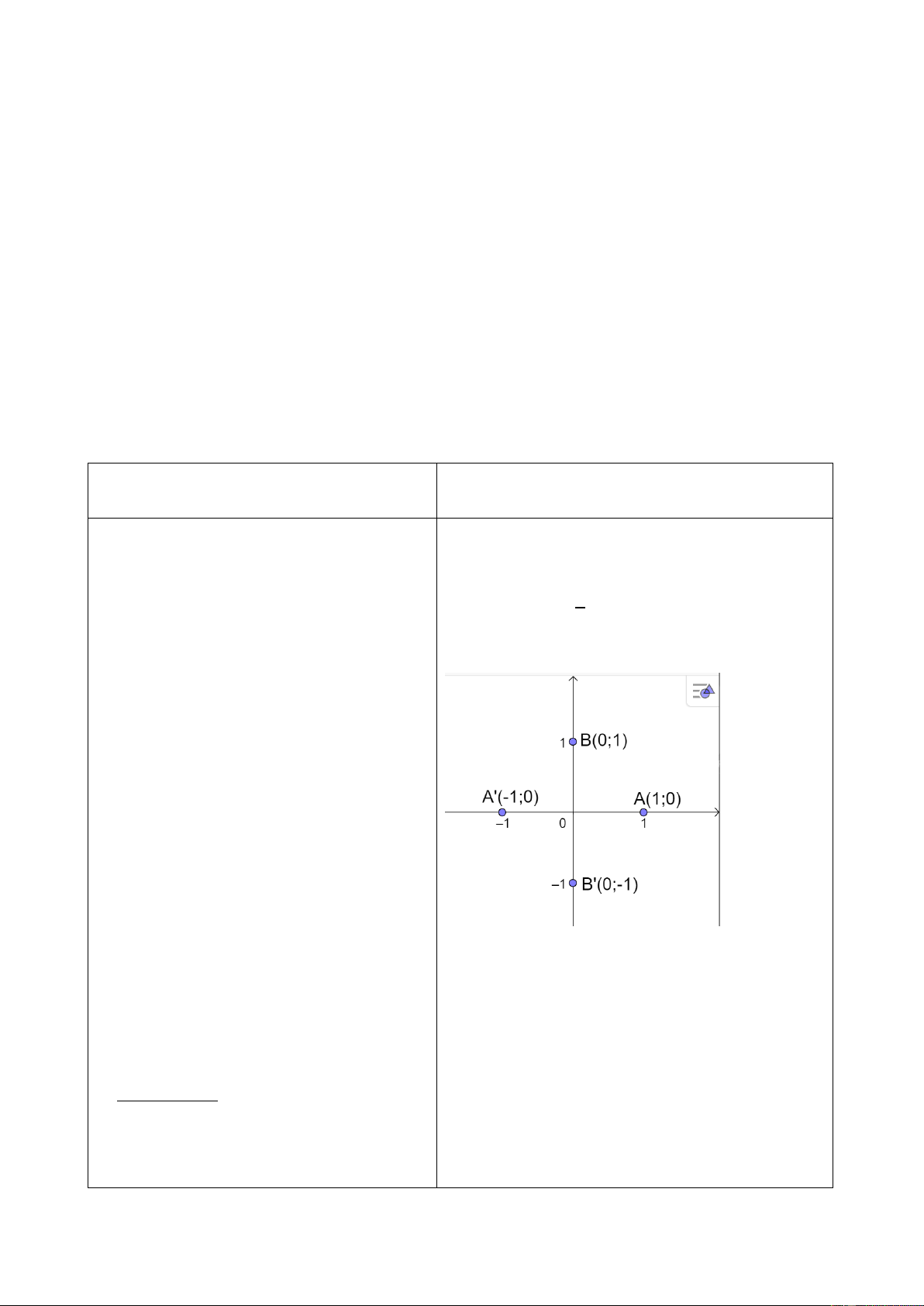
a) (𝑂𝐴, 𝑂𝐵) = 𝜋 + 𝑘2𝜋 rad, 𝑘 ∈ ℤ hoàn thành HĐKP 4 2
b) 𝐴′(−1; 0) và 𝐵′(0; −1). Kết luận
Trong mặt phẳng tọa độ Oxy, cho đường
- GV giới thiệu về khái niệm đường tròn tròn tâm O bán kính bằng 1. Trên đường tròn lượng giác.
này, chọn điểm A(1; 0) làm gốc, chiều
+ Nhấn mạnh: đường tròn lượng giác dương là chiều ngược chiều kim đồng hồ và
tâm O, bán kính bằng 1; xác định chiều chiều âm là chiều cùng chiều kim đồng hồ. âm, chiều dương. 13
Đường tròn cùng với gốc và chiều như trên
được gọi là đường tròn lượng giác. - GV đặt câu hỏi:
+ Nếu cho góc 𝛼 bất kì, có bao nhiêu
điểm M trên đường tròn lượng giác để - Trên đường tròn lượng giác, ta xác định
𝑠đ(𝑂𝐴; 𝑂𝑀) = 𝛼? đượ
c duy nhất một điểm M sao cho số đo (Xác đị góc lượ nh duy nhất điểm M).
ng giác (𝑂𝐴, 𝑂𝑀) = 𝛼. Khi đó điểm
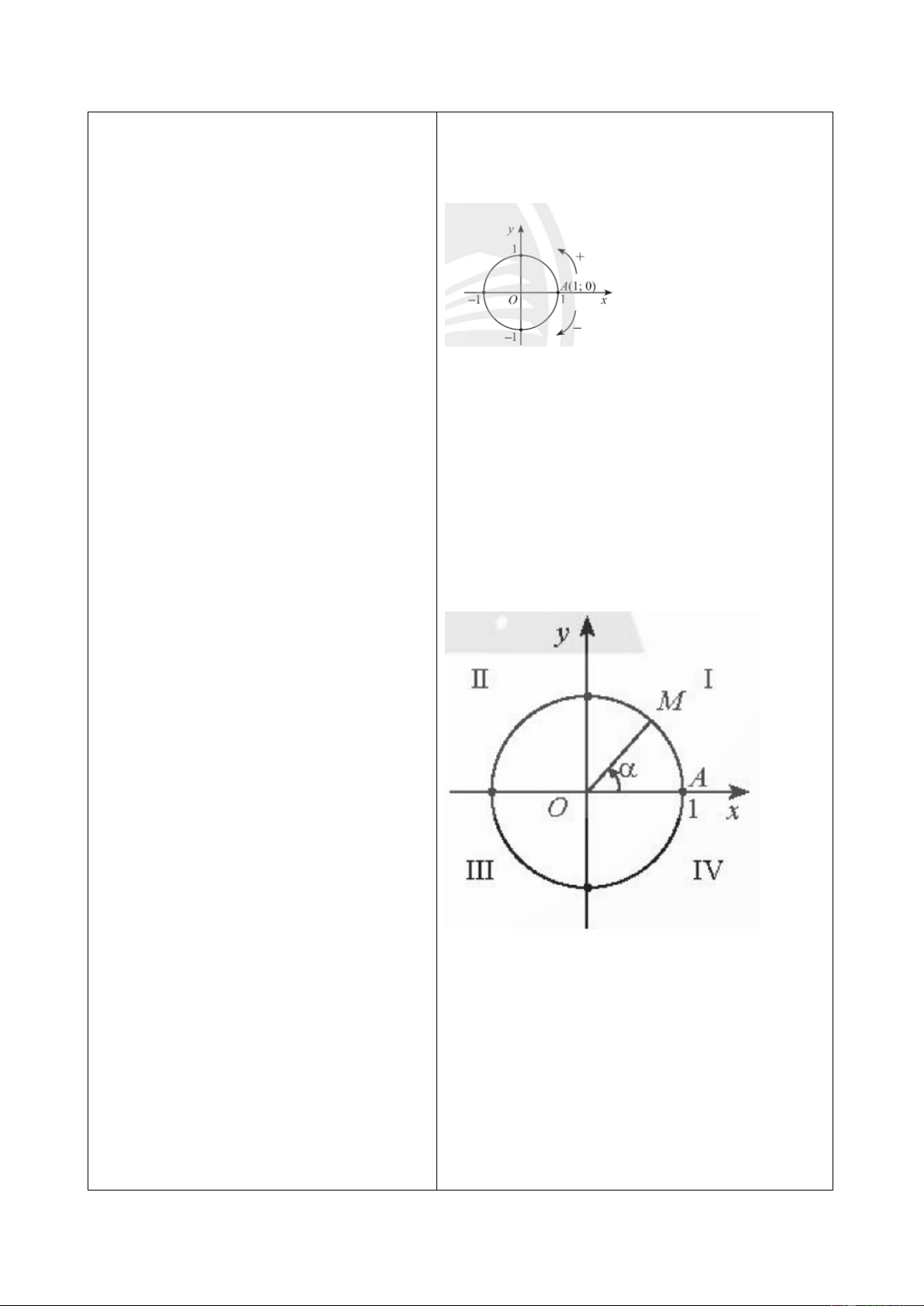
- GV giới thiệu về các góc phần tư.
M gọi là điểm biểu diễn của góc có số đo 𝛼
trên đường tròn lượng giác. Chú ý:
Các góc phần tư, kí hiệu I, II, III, IV
- GV hướng dẫn HS thực hiện Ví dụ 3
+ Để biểu diễn góc lượng giác: ta cần
xác định góc đó có là chứa bội của 360𝑜
hoặc 2𝜋 hay không; rồi xác định chiều
quay của góc; xác định điểm biểu diễn thỏa mãn góc đã cho.
Ví dụ 3 (SGK -tr.11)
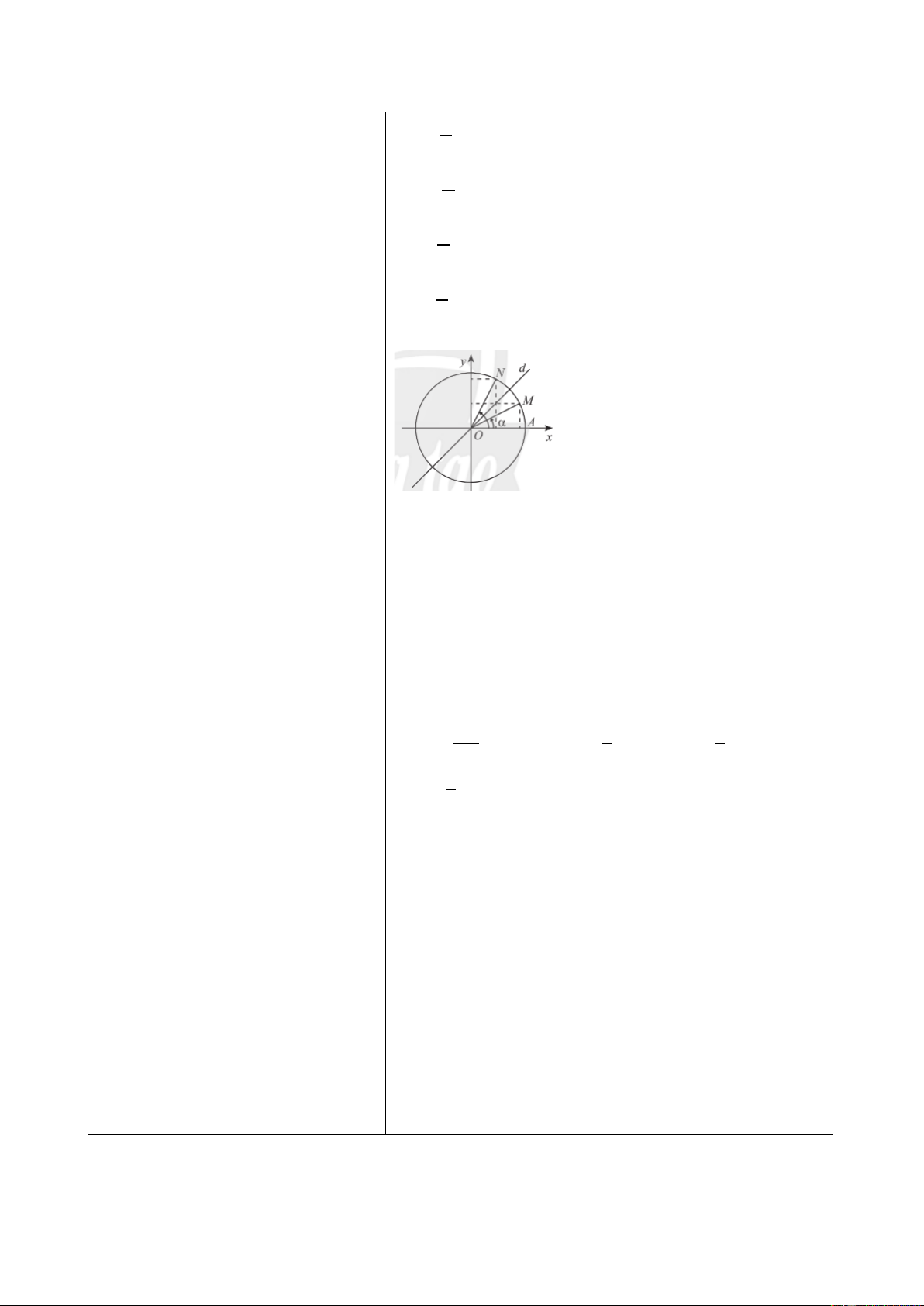
- HS thực hiện Thực hành 3. Thực hành 3 Bướ
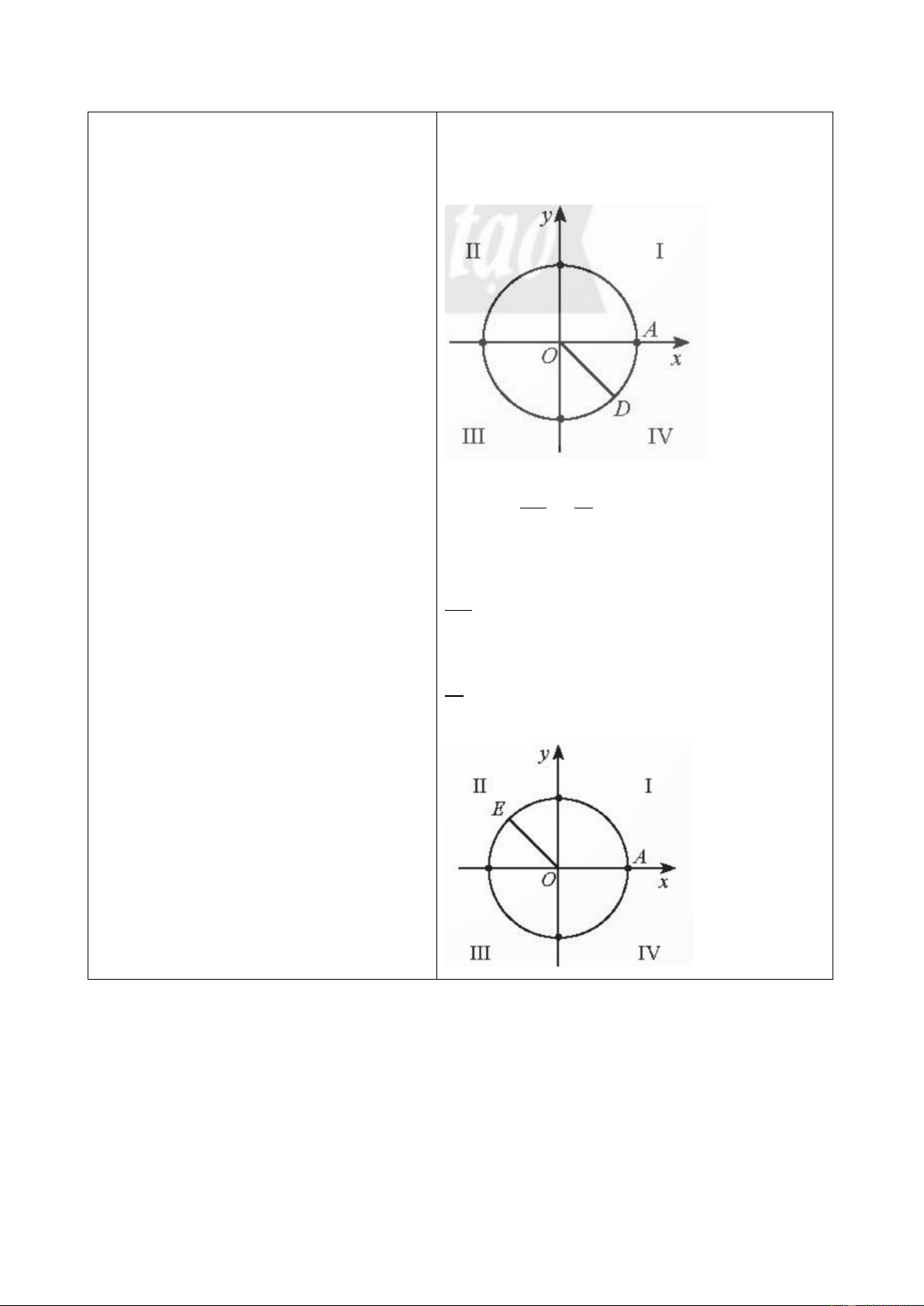
a) Ta có −1485∘ = −45∘ − 4 ⋅ 360∘.
c 2: Thực hiện nhiệm vụ:
- HS theo dõi SGK, chú ý nghe, tiếp Vậy điểm biễu diễn góc lượng giác có số đo
nhận kiến thức, suy nghĩ trả lời câu hỏi, −1485∘ là điểm 𝐷 trên phần đường tròn hoàn thành các yêu cầu. 14
- GV: quan sát và trợ giúp HS.
lượng giác thuộc góc phần tư thứ IV sao cho
Bước 3: Báo cáo, thảo luận: 𝐴𝑂𝐷 ̂ = 45∘.
- HS giơ tay phát biểu, lên bảng trình bày
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận định: GV tổng
quát lưu ý lại kiến thức trọng tâm và yêu
cầu HS ghi chép đầy đủ vào vở. 19𝜋 b) Ta có = 3𝜋 + 4𝜋 4 4
Vậy điểm biểu diễn góc lượng giác có số đo
19𝜋 là điểm 𝐸 trên phần đường tròn lượng 4
giác thuộc góc phần tư thứ II sao cho 𝐴𝑂𝐸 ̂ = 3𝜋. 4
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học. 15
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập Bài 1, 2, 3, 4, 5, 7 (SGK -tr12+13) và câu hỏi TN.
c) Sản phẩm học tập: Câu trả lời của HS.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS trả lời các câu hỏi TN nhanh
Câu 1. Đổi 4𝜋 rad sang độ bằng 5 A. 114𝑜 B. 114𝑜 C. 104𝑜 D. 141𝑜
Câu 2. Trong khoảng thời gian từ 3 giờ đến 6 giờ 30 phút, kim phút quét một góc lượng giác bao nhiêu độ? A. −1060𝑜 B. −1160𝑜 C. −1260𝑜 D. −1360𝑜
Câu 3. Cho số đo các góc lượng giác: (𝑂𝑎, 𝑂𝑏) = 120𝑜, (𝑂𝑏, 𝑂𝑐) = 75𝑜. Số đo góc
lượng giác (𝑂𝑎, 𝑂𝑐) bằng: A. −135𝑜 B. −145𝑜 C. −155𝑜 16 D. −165𝑜
Câu 4. Cho bốn góc lượng giác (trên cùng một đường tròn): 𝛼 = 𝜋 , 𝛽 = 10𝜋 , 𝛾 = 3 3
− 5𝜋 , 𝛿 = − 7𝜋. Các góc lượng giác có điểm biểu diễn trùng nhau là 3 3 A. α và β
B. α và γ C. α và δ D. β và δ
Câu 5. Cho góc lượng giác (OA; OB) có số đo bằng 𝜋
. Trong các số sau đây, số nào là 12
số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác (OA; OB)? A. 13𝜋 12 B. − 25𝜋 12 C. 49𝜋 12 D. 19𝜋 12
- GV tổ chức cho HS hoạt động thực hiện Bài 1, 2, 3, 4, 5, 7 (SGK -tr.12+13).
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định: 17
- GV nhận xét thái độ làm việc, phương án trả lời của các học sinh, ghi nhận và tuyên dương. Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 B C D B C Bài 1. a) 38∘ = 19𝜋 rad; 90 b) −115∘ = 23𝜋 rad 36 0 c) 3 ( ) = 1 rad. 𝜋 60 Bài 2. a) 𝜋 rad = 15∘, 12 ∘ b) −5 = 900 ( ) ≈ 286, 479∘ 𝜋 c) 13𝜋 = 260∘. 9 Bài 3.
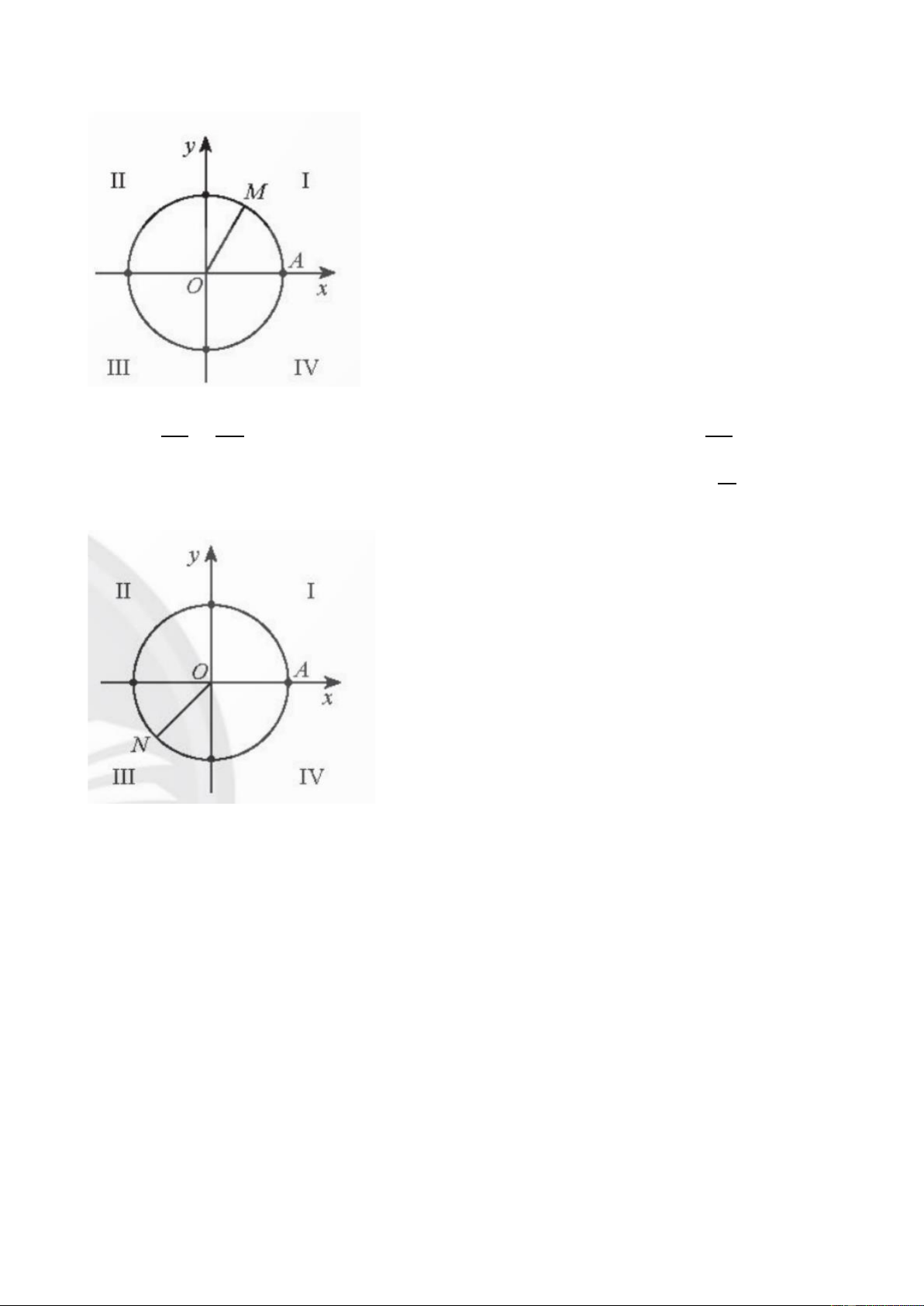
a) Tacó −17𝜋 = 𝜋 − 3.2𝜋. 3 3
Vậy điểm biểu diễn góc lượng giác có số đo −17𝜋 là điểm 𝑀 trên phần đường tròn 3
lượng giác thuộc góc phần tư thứ I sao cho 𝐴𝑂𝑀 ̂ = 𝜋. 3 18
b) Ta có 13𝜋 = −3𝜋 + 2 ⋅ 2𝜋. Vậy điễm biểu diễn góc lượng giác có số đo 13𝜋 là điểm 𝑁 4 4 4
trên phần đường tròn lượng giác thuộc góc phần tư thứ III sao cho 𝐴𝑂𝑁 ̂ = 3𝜋. 4
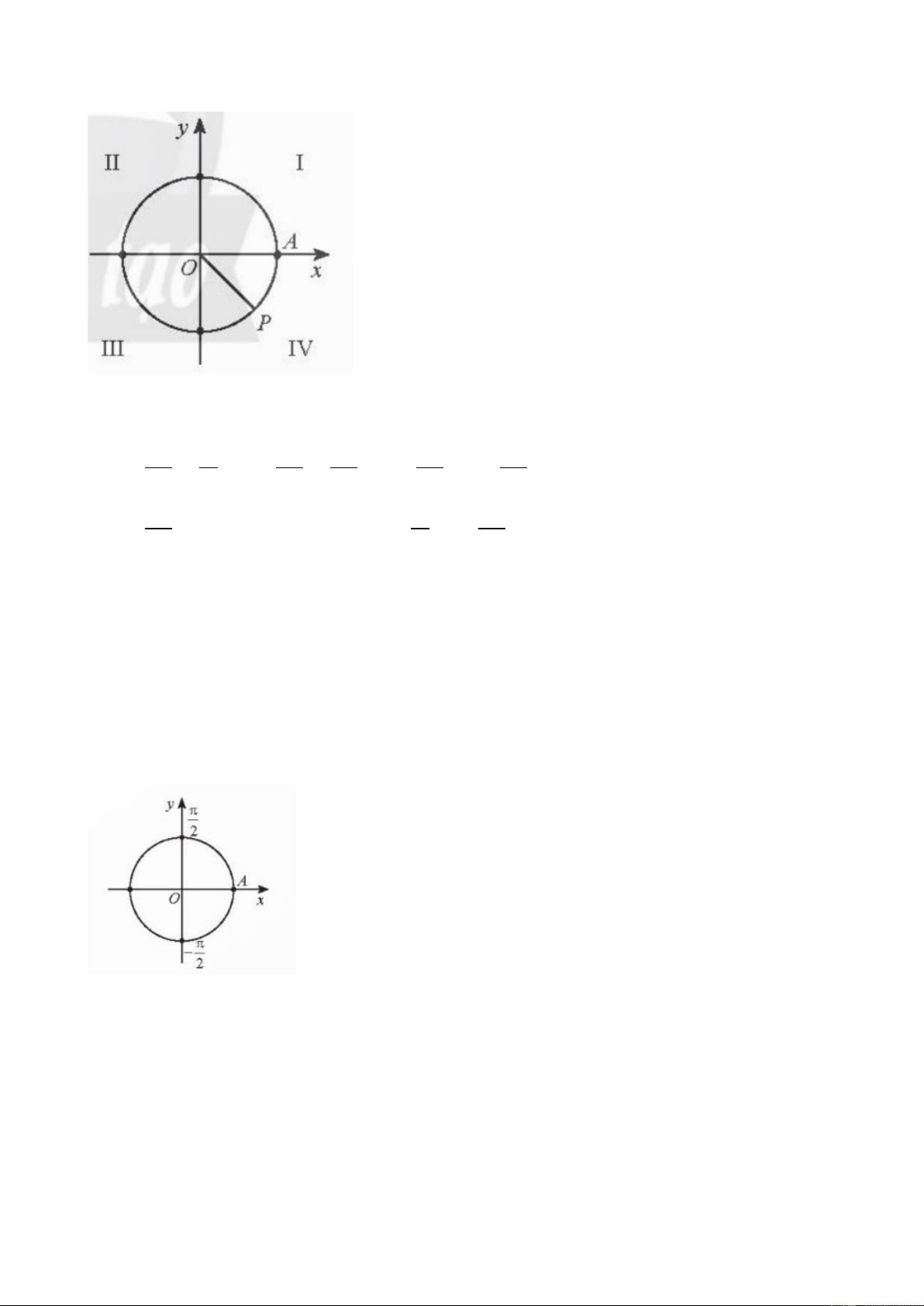
c) Ta có −765∘ = −45∘ − 2 ⋅ 360∘.
Vậy điểm biểu diễn góc lượng giác có số đo-765 là điểm 𝑃 trên phần đường tròn lượng
giác thuộc góc phần tư thứ IV sao cho 𝐴𝑂𝑃 ̂ = 45∘. 19 Bài 4.
Ta có: 31𝜋 = 3𝜋 + 4𝜋; 31𝜋 = 10𝜋 + 3𝜋; 31𝜋 = (− 25𝜋) + 8𝜋. 7 7 7 7 7 7
Do đó 31𝜋 có cùng điểm biểu diễn với 3𝜋 và − 25𝜋. 7 7 7 Bài 5.
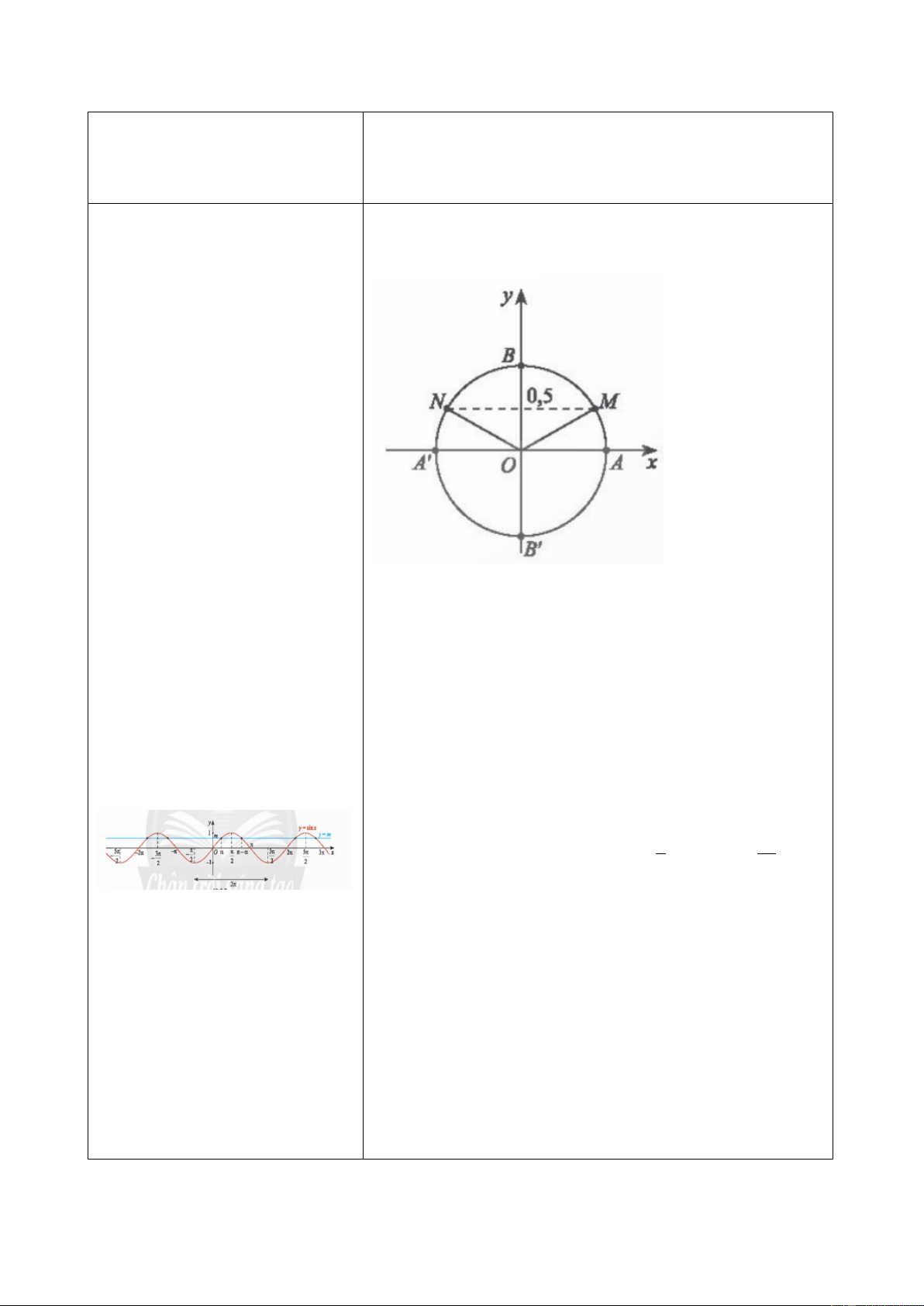
(𝑂𝐴, 𝑂𝑀) = 120∘ + 𝑘360∘(𝑘 ∈ ℤ); (𝑂𝐴, 𝑂𝑁) = −75∘ + 𝑘360∘(𝑘 ∈ ℤ). Bài 7. a) b) 20
D. HOẠT ĐỘNG VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập.
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 6, 8, 9 (SGK -tr.12).
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: Bài 6.
(𝑂𝑥, 𝑂𝑁) = (𝑂𝑥, 𝑂𝑀) + (𝑂𝑀, 𝑂𝑁) + 𝑘360∘(𝑘 ∈ ℤ) 21 2
= 45∘ − ⋅ 360∘ + 𝑘360∘(𝑘 ∈ ℤ) 5
= −99∘ + 𝑘360∘(𝑘 ∈ ℤ). Bài 8.
𝜋 + 𝑘 2𝜋 (𝑘 ∈ ℤ) và − 𝜋 + 𝑘 2𝜋 (𝑘 ∈ ℤ). 2 3 6 3 Bài 9. Ta có 1 𝜋 𝜋 𝛼 = ⋅ = (rad). 60 180 10800
Vì mỗi radian chắn một cung bằng bán kính trái đất 𝑅 ≈ 6371 km, nên 𝛼 chắn cung có
độ dài 𝜋 ⋅ 6371 ≈ 1,85( km). 10800
Vậy một hải lí dài khoảng 1,85 km.
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: “Bài 2. Giá trị lượng giác của một góc lượng giác”. 22 Ngày soạn: .../.../... Ngày dạy: .../.../...
BÀI 2: GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC (1 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết khái niệm giá trị lượng giác của một góc lượng giác.
- Mô tả bảng giá trị lượng giác của một số góc lượng giác thường gặp; hệ thức cơ
bản giữa các giá trị lượng giác của một góc lượng giác; quan hệ giữa các giá trị
lượng giác của các góc lượng giác có liên quan đặc biệt: bù nhau, phụ nhau, đối nhau, hơn kém nhau 𝜋.
- Sử dụng máy tinh cầm tay để tính giá trị lượng giác của một góc lượng giác khi
biết số đo của góc đó.
- Giải quyết một số vấn đề thực tiễn gắn với giá trị lượng giác của góc lượng giác. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học, giải quyết vấn đề toán học: Nhận biết được khái niệm
giá trị lượng giác của góc lượng giác, vận dụng các hệ thức cơ bản của giá trị
lượng giác, quan hệ giữa các giá trị lượng giác có liên quan đặc biệt.
- Mô hình hóa toán học: Giải quyết một số vấn đề thực tiễn gắn với giá trị lượng
giác của góc lượng giác. 23 - Giao tiếp toán học.
- Sử dụng công cụ, phương tiện học toán. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học. Thông qua bài toán thực tế và tích
hợp Toán học với Vật lí để dẫn đến việc mở rộng khái iệm giá trị lượng giác cho góc lượng giác.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS đưa ra dự đoán cho câu hỏi.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu
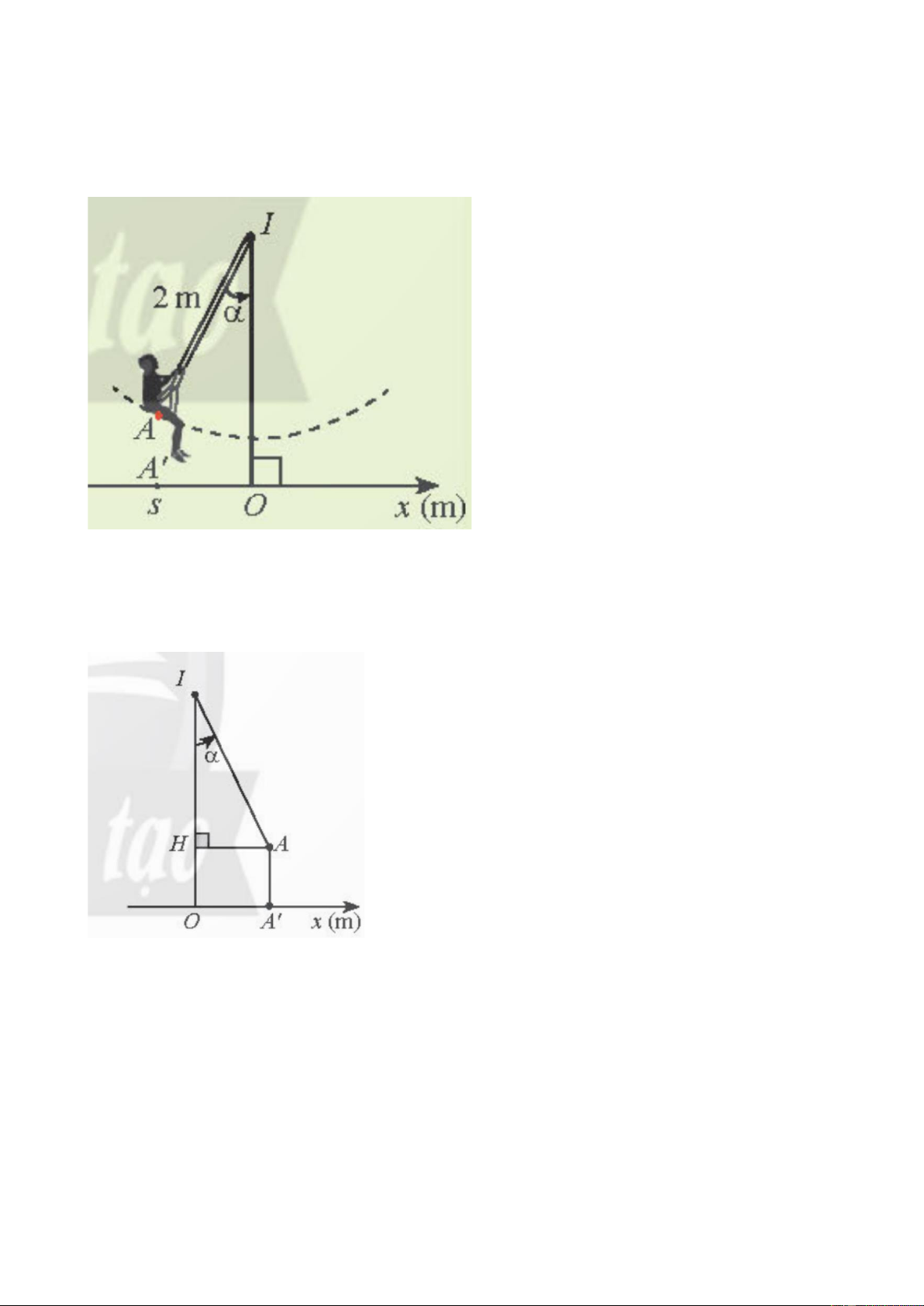
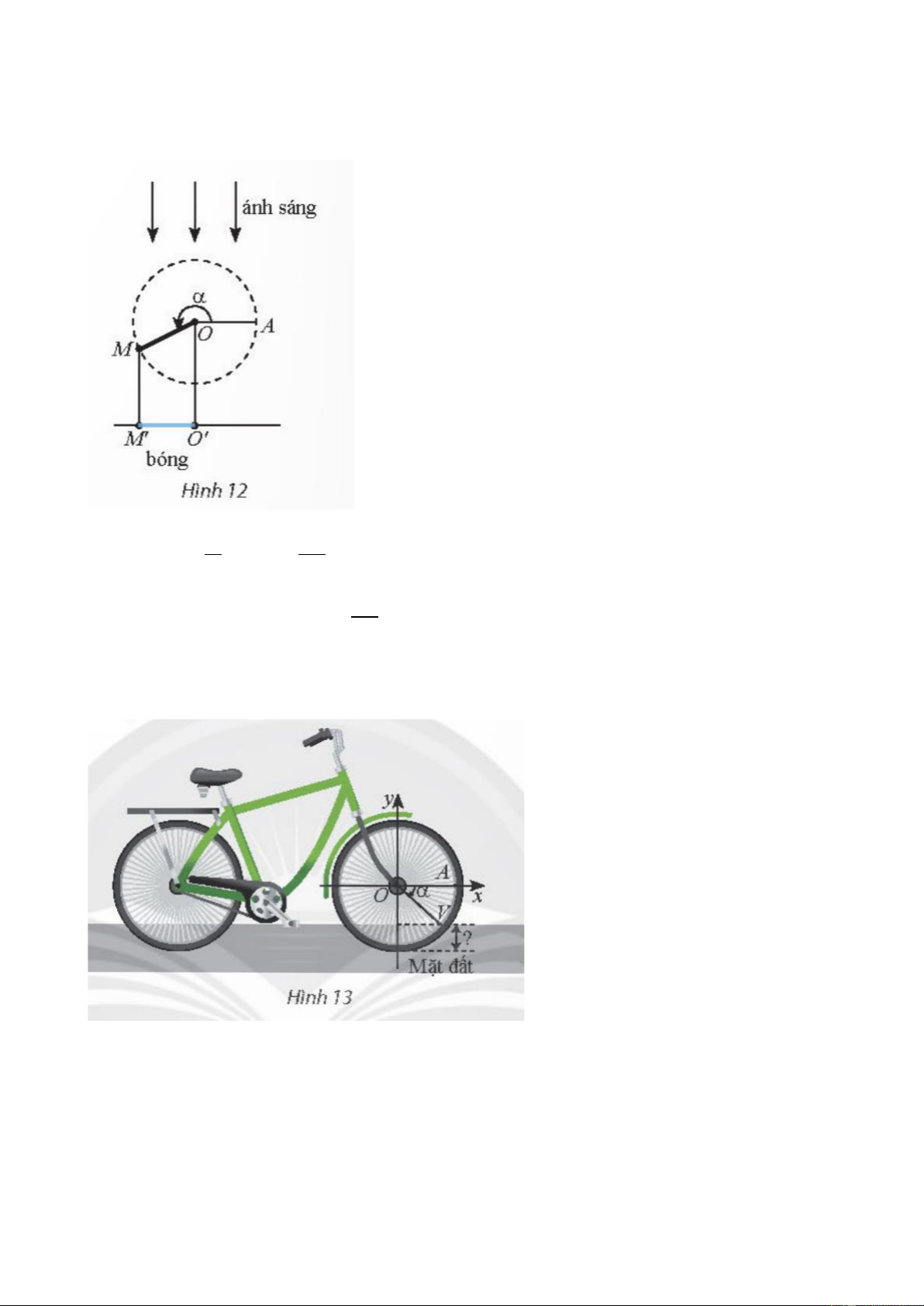
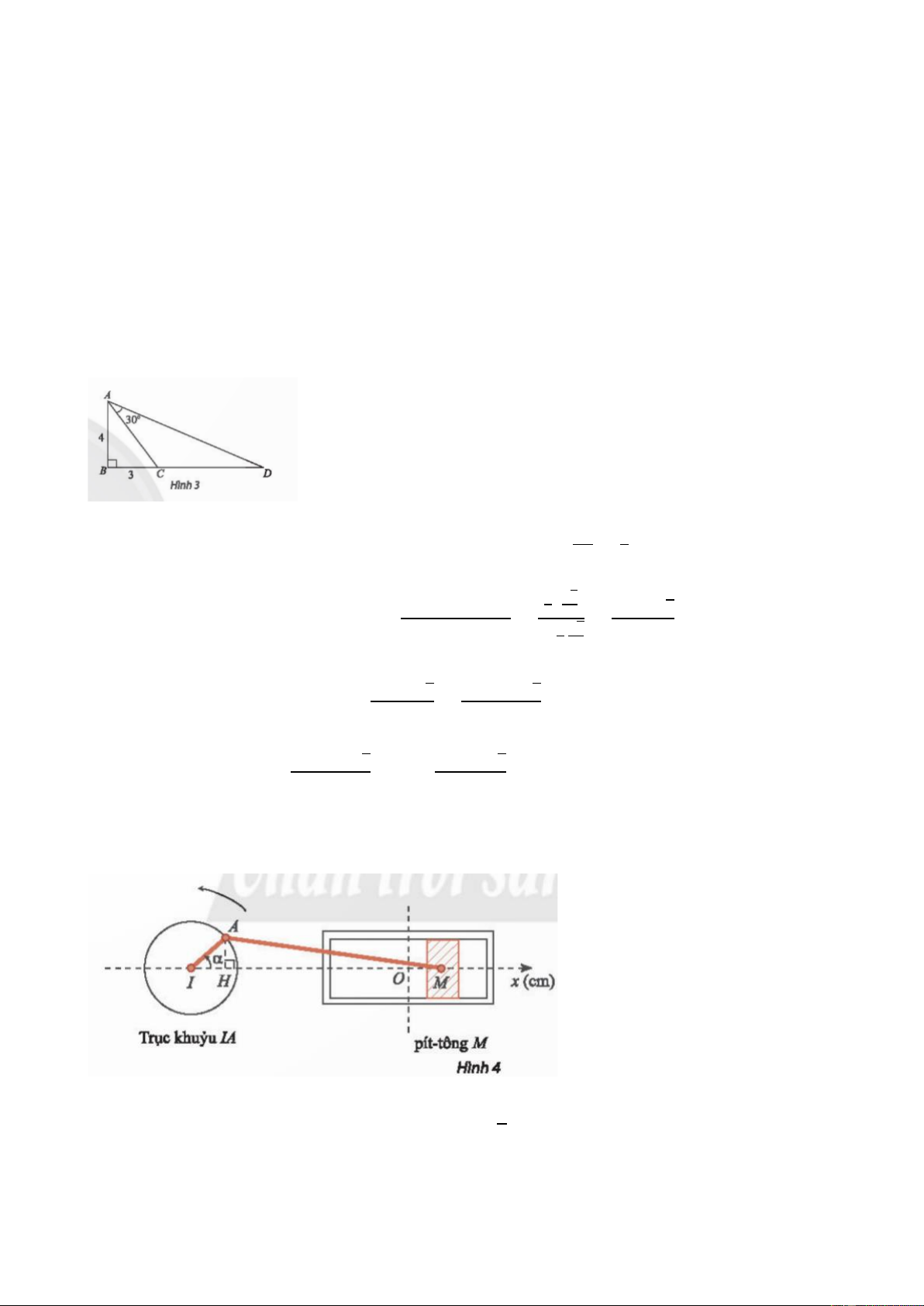
Hình bên biểu diễn xích đu IA có độ dài 2 m dao động quanh trục IO vuông góc với trục
Ox trên mặt đất và A’ là hình chiếu của A lên Ox. Tọa độ s của A’ trên trục Ox được gọi 24
là li độ của A và (𝐼𝑂; 𝐼𝐴) = 𝛼 được gọi là li độ góc của A. Làm cách nào để tính li độ dựa vào li độ góc?
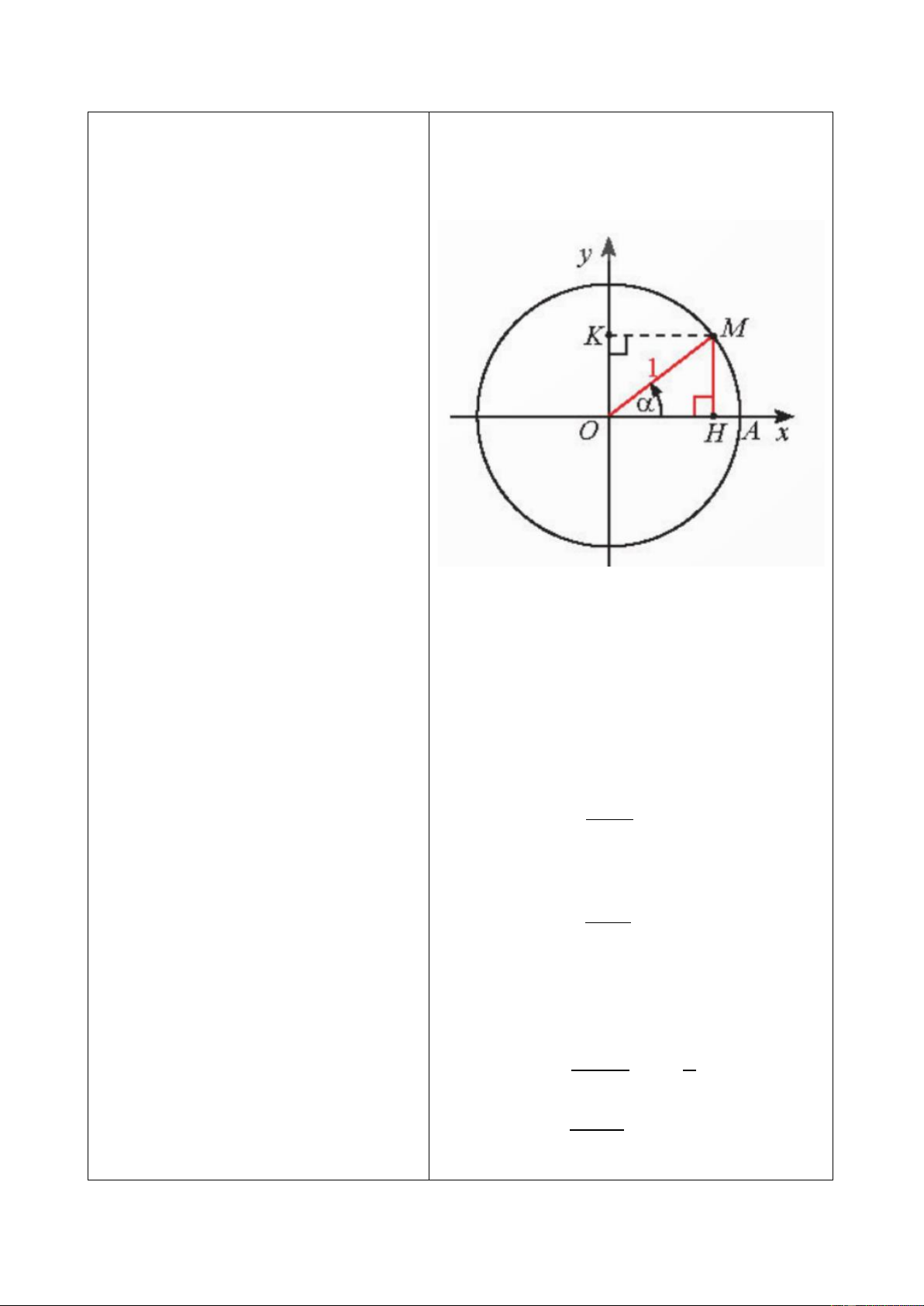
- GV hướng dẫn HS tìm hiểu với góc 𝛼 sao cho −90𝑜 ≤ 𝛼 ≤ 90𝑜.
+ Khi 0𝑜 ≤ 𝛼 ≤ 90𝑜 ta có thể biểu diễn góc 𝛼 như sau
Tọa độ s mang dấu gì? Có độ lớn bằng độ dài đoạn nào? (𝑠 > 0, 𝑠 = 𝑂𝐴′ = 𝐴𝐻 = 𝐼𝐴𝑠𝑖𝑛 𝛼 )
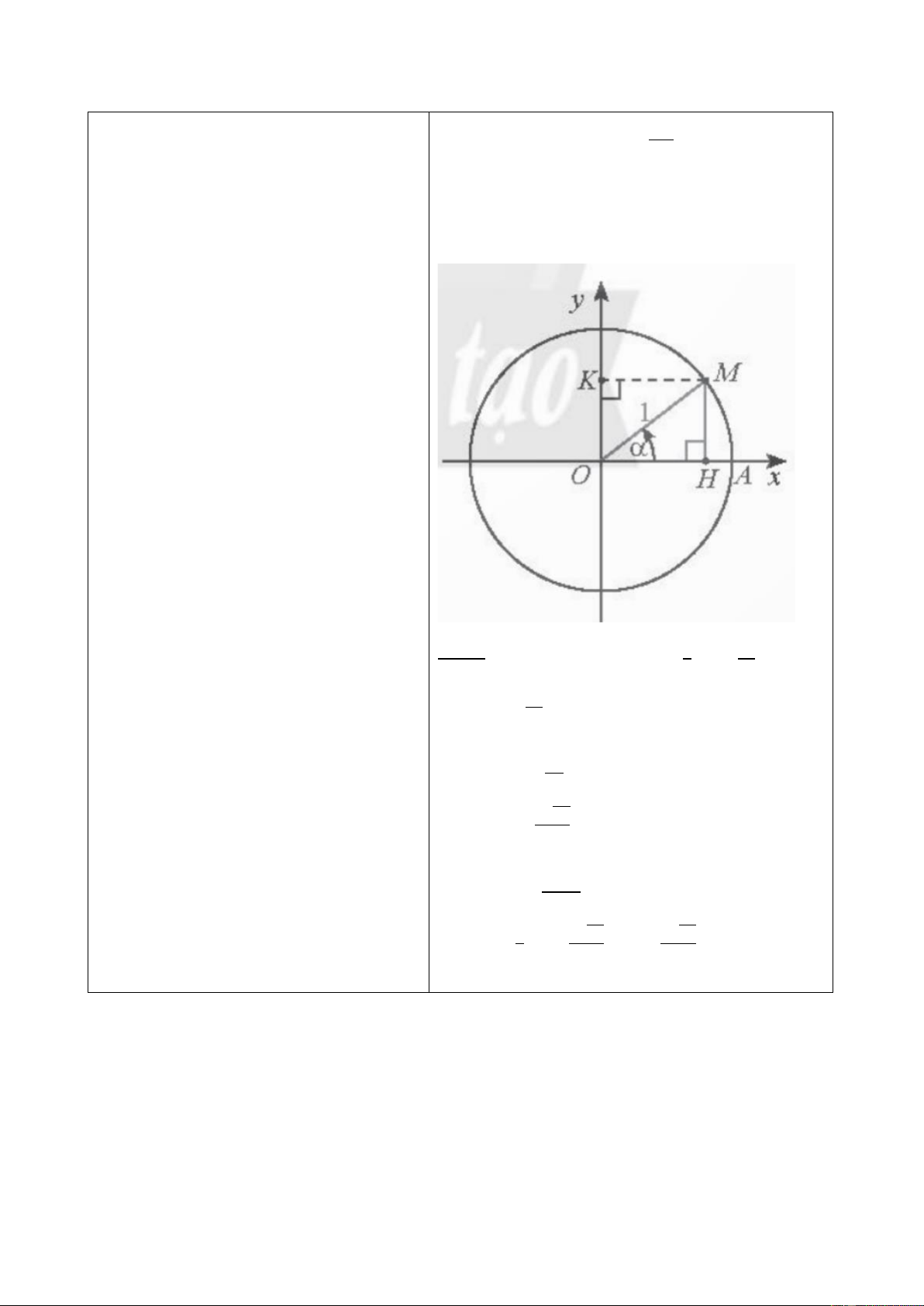
+ Khi −90𝑜 ≤ 𝛼 ≤ 0𝑜 ta có thể biểu diễn góc 𝛼 như sau 25
Tọa độ s mang dấu gì? Có độ lớn bằng độ dài đoạn nào? (𝑠 < 0, |𝑠| = 𝑂𝐴′ = 𝐴𝐻 =
|𝐼𝐴. 𝑠𝑖𝑛 𝛼| ).
→ Ở đây không thể sử dung công thức của trường hợp trên để tính vì chưa có khái niệm
sin của góc âm. Có thể mở rộng khái niệm giá trị lượng giác cho góc lượng giác bất kì
để thống nhất công thức tính.
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học mới: “Bài học hôm nay chúng ta cùng đi tìm hiểu mối quan hệ giữa góc
lượng giác và tọa độ của điểm biểu diễn góc lượng giác đó và các tính chất liên quan”.
Bài 2: Giá trị lượng giác của một góc lượng giác.
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Giá trị lượng giác của góc lượng giác a) Mục tiêu:
- HS nhận biết khái niệm giá trị lượng giác của một góc lượng giác, b) Nội dung: 26
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động khám phá, thực hành, vận dụng mục 1.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi,
HS nhận biết và thể hiện được giá trị lượng giác.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm 1. Giá trị lượng giác của góc lượng giác vụ: HĐKP 1:
- GV yêu cầu HS thảo luận
nhóm đôi, hoàn thành HĐKP 1. GV hướng dẫn
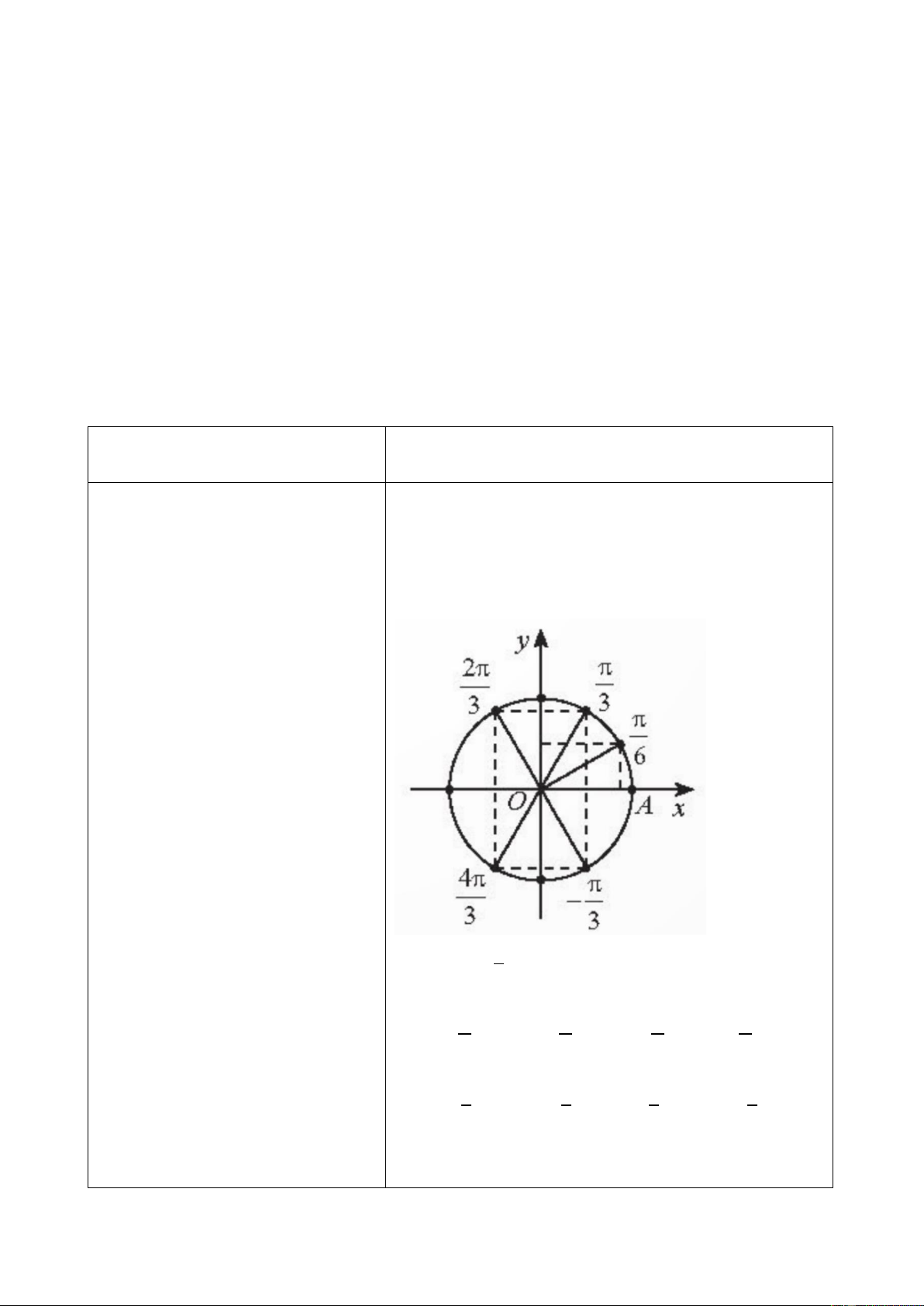
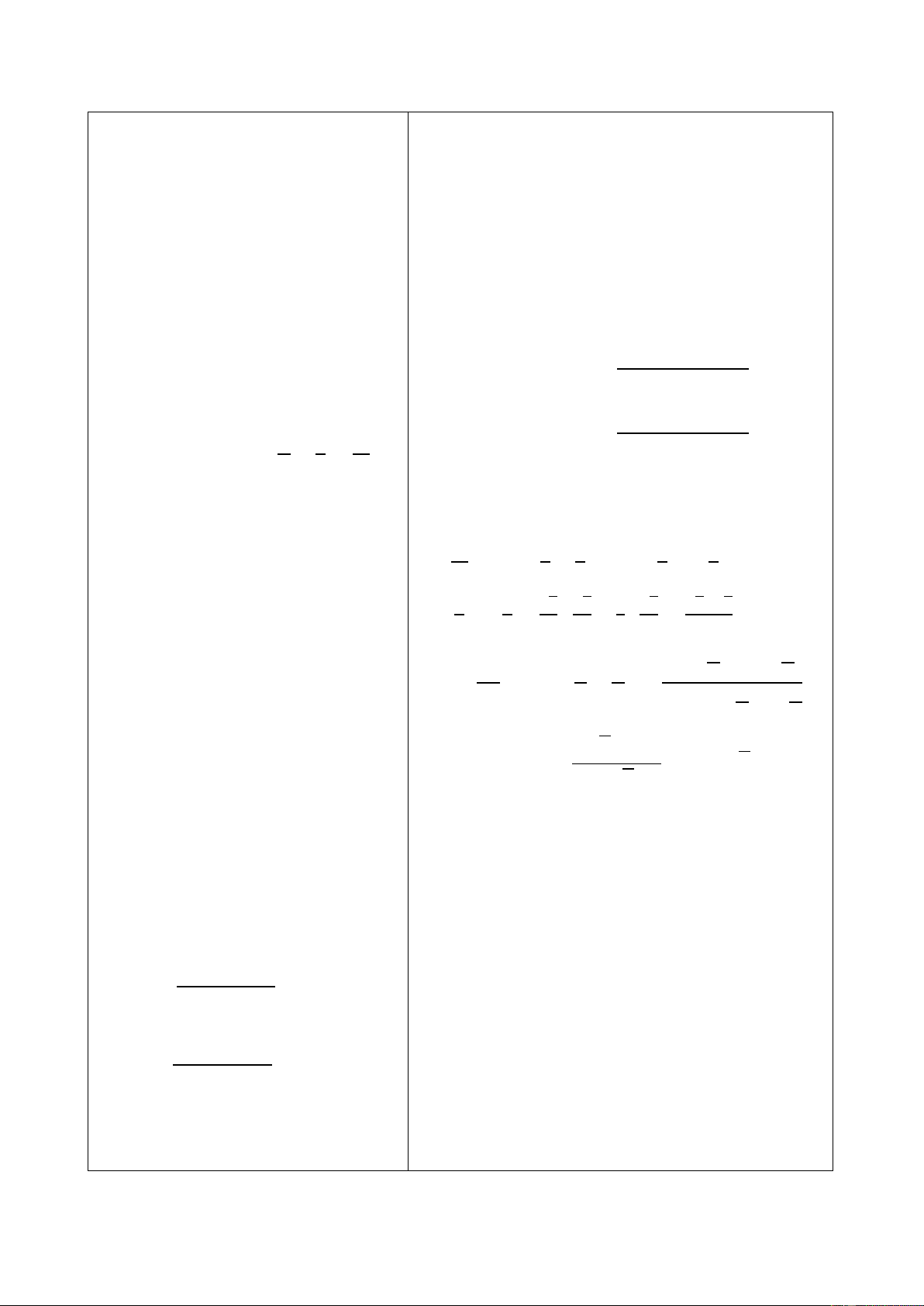
+ Sử dụng kiến thức về giá trị
lượng giác của các góc 0𝑜 ≤
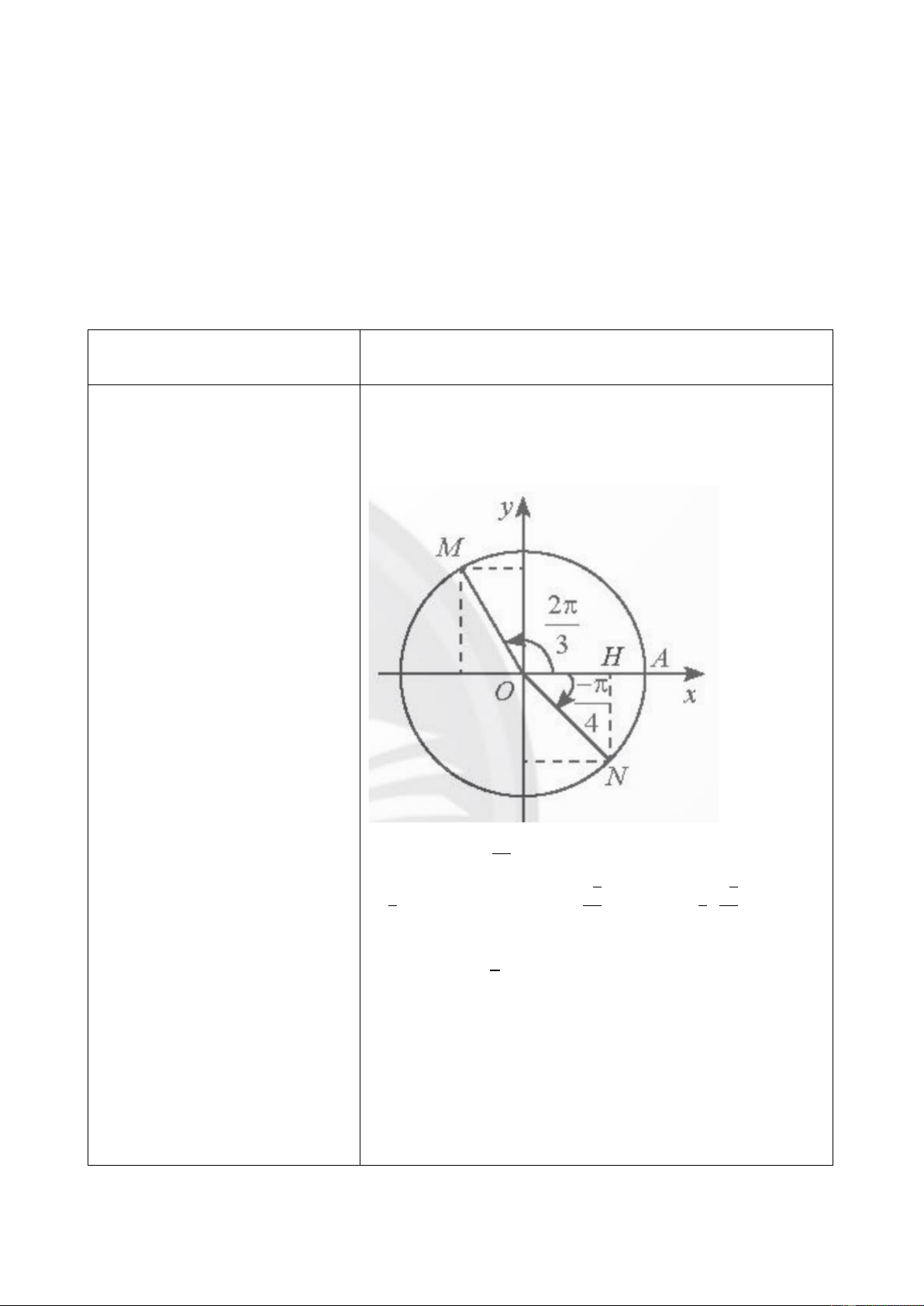
𝛼 ≤ 180𝑜, ta tính được tọa độ 𝑥𝑀; 𝑦𝑀 theo sin 120𝑜 ; cos 120𝑜.
+ Dựng tam giác vuông OHN
vuông tại H. để tính tọa độ
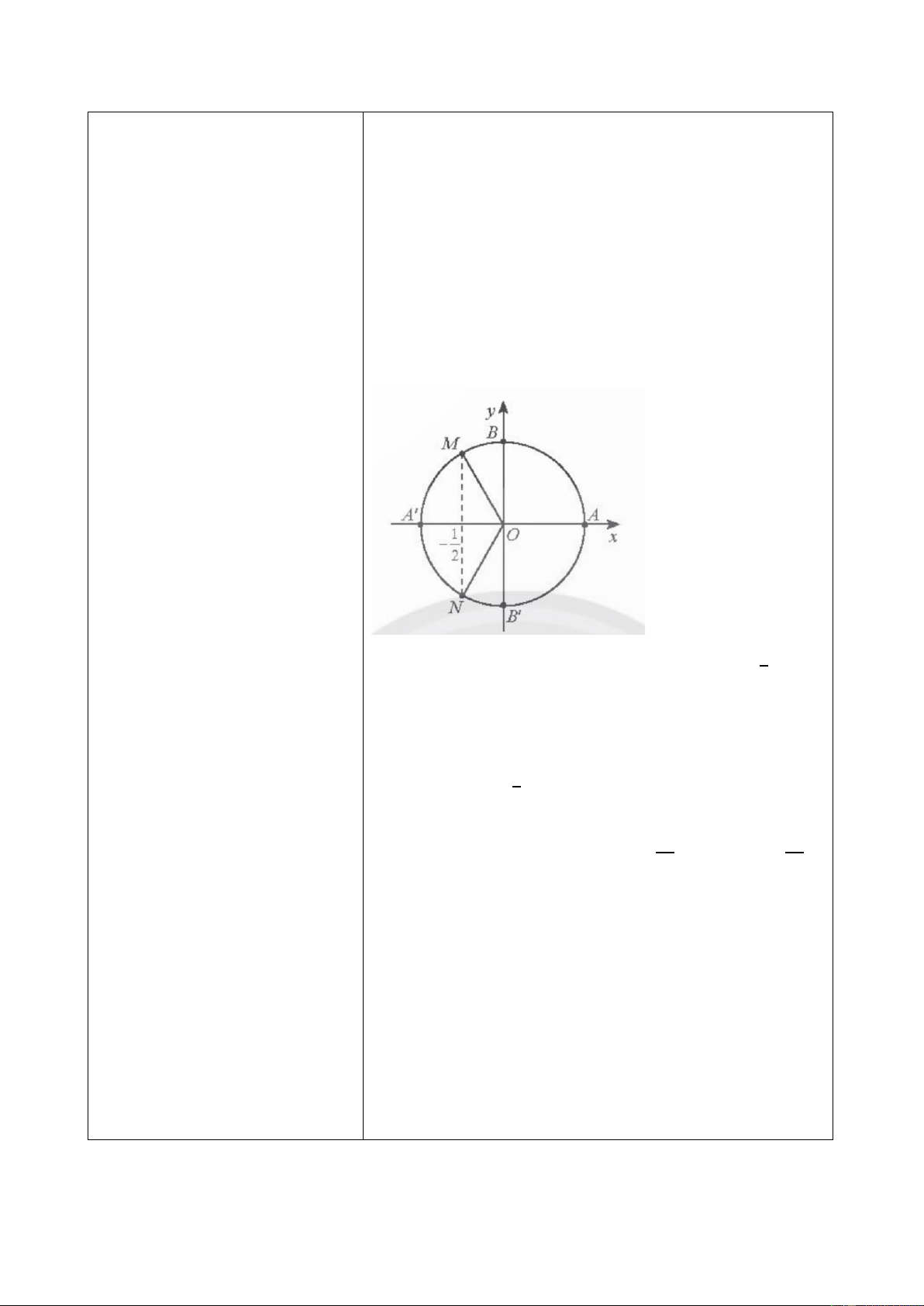
điểm N ta phải tính độ dài Ta có 𝑥𝑂𝑀
̂ = 2𝜋 = 120∘. Do đó, 𝑥 3 𝑀 = cos 120∘ =
đoạn nào? (Tính được NH và −1 và 𝑦𝑀 = sin 120∘ = √3, hay 𝑀(−1;√3). OH). 2 2 2 2 Ta có 𝑥𝑂𝑁
̂ = 𝜋 = 45∘ nên △ 𝑂𝐻𝑁 là tam giác vuông 4
cân với cạnh huyền 𝑂𝑁 = 1. 27
Do đó 𝑂𝐻 = 𝑁𝐻 = √2. Vì 𝑁 nằm trong góc phần tư 2 thứ IV, nên ta có 𝑥 và 𝑦 𝑁 = 𝑂𝐻 = √2 2 𝑁 = −𝑁𝐻 =
− √2. Do đó 𝑁 (√2 ; − √2). 2 2 2
- Từ đó GV giới thiệu giá trị Kết luận
lượng giác của góc bất kì.
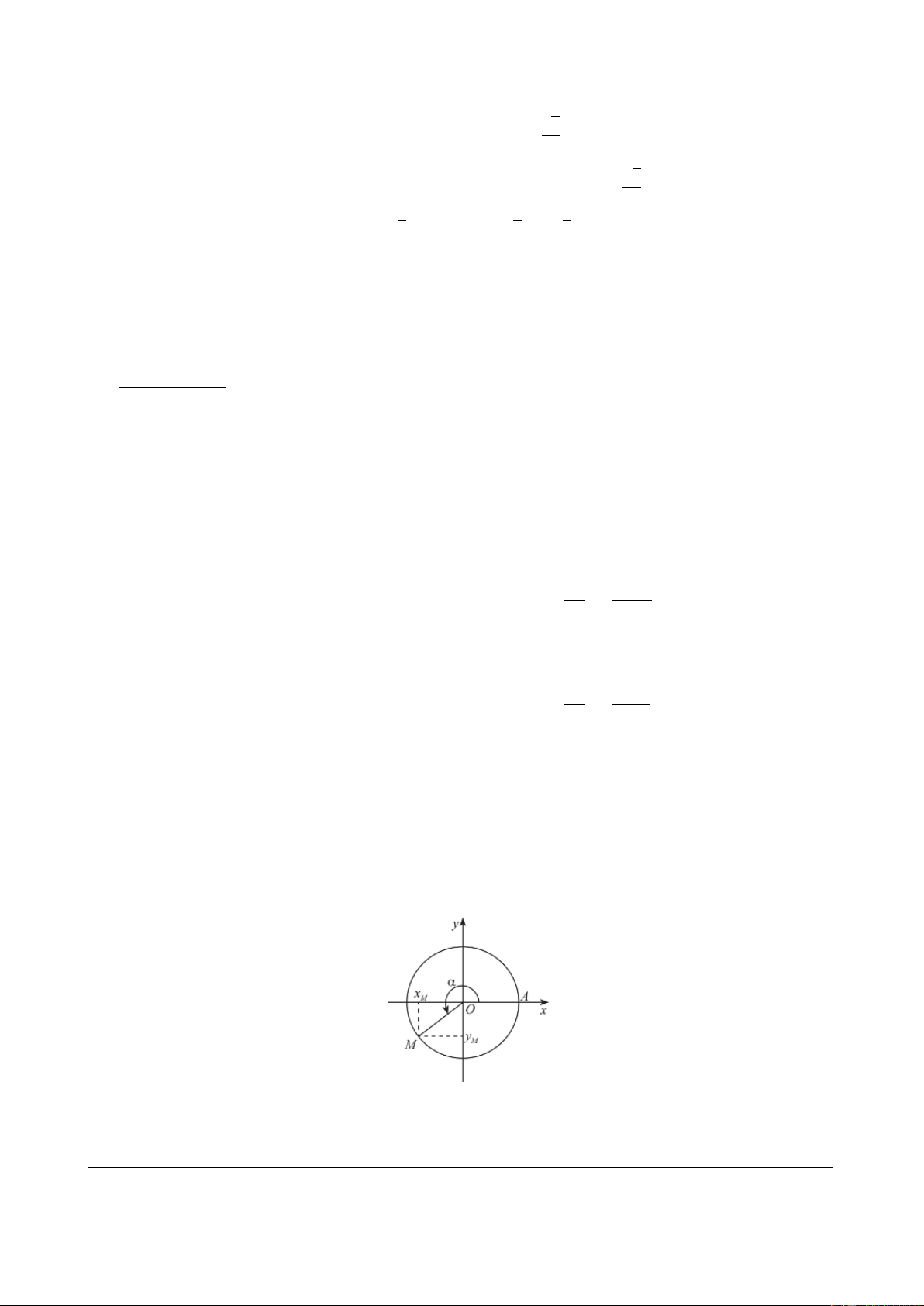
Trên đường tròn lượng giác, gọi M là điểm biểu diễn
+ Nhấn mạnh: Điều kiện để góc lượng giác có số đo 𝛼. Khi đó tang và côtang tồn tại. - GV có thể lưu ý thêm:
+ Tung độ 𝑦𝑀 của M gọi là sin của 𝛼, kí hiệu sin 𝛼. + Giá trị của
+ Hoành độ 𝑥𝑀 của M gọi là côsin của 𝛼, kí hiệu
𝑠𝑖𝑛 𝛼 , 𝑐𝑜𝑠 𝛼 thuộc khoảng, cos 𝛼.
đoạn giá trị nào? (Thuộc đoạn [−1; 1]) 𝑦 + Nếu 𝑥 𝑀 𝑀 ≠ 0 thì tỉ số
= sin 𝛼 gọi là tang của 𝛼, kí 𝑥𝑀 cos 𝛼 hiệu tan 𝛼. 𝑥 + Nếu 𝑦 𝑀 𝑀 ≠ 0 thì tỉ số
= cos 𝛼 gọi là côtang của 𝑦𝑀 sin 𝛼 𝛼, kí hiệu cot 𝛼.
Các giá trị sin 𝛼 , cos 𝛼 , tan 𝛼 , cot 𝛼 được gọi là các
giá trị lượng giác của góc lượng giác 𝛼. Chú ý: 28
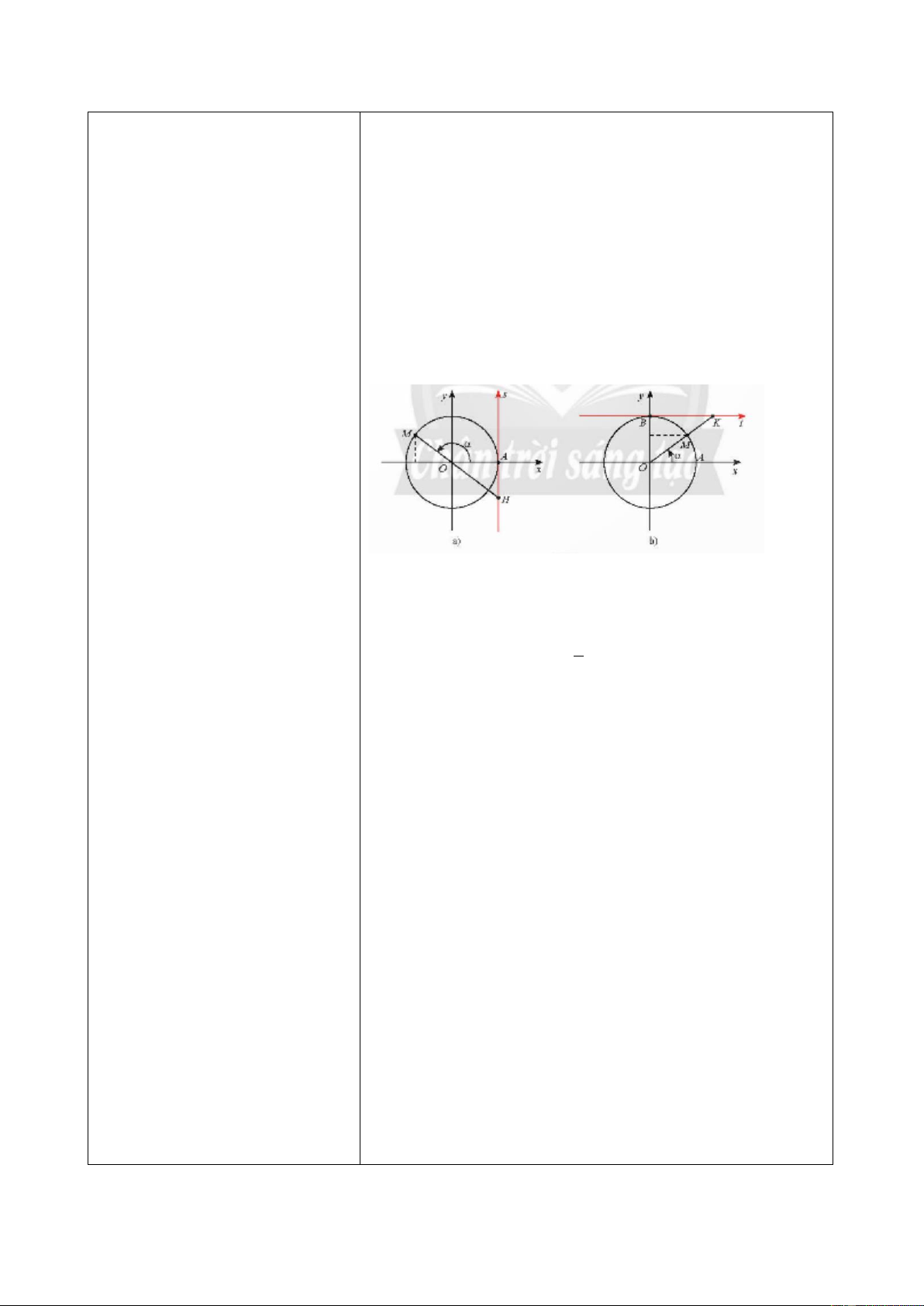
a) Ta gọi trục hoành là trục côsin, còn trục tung là trục sin.
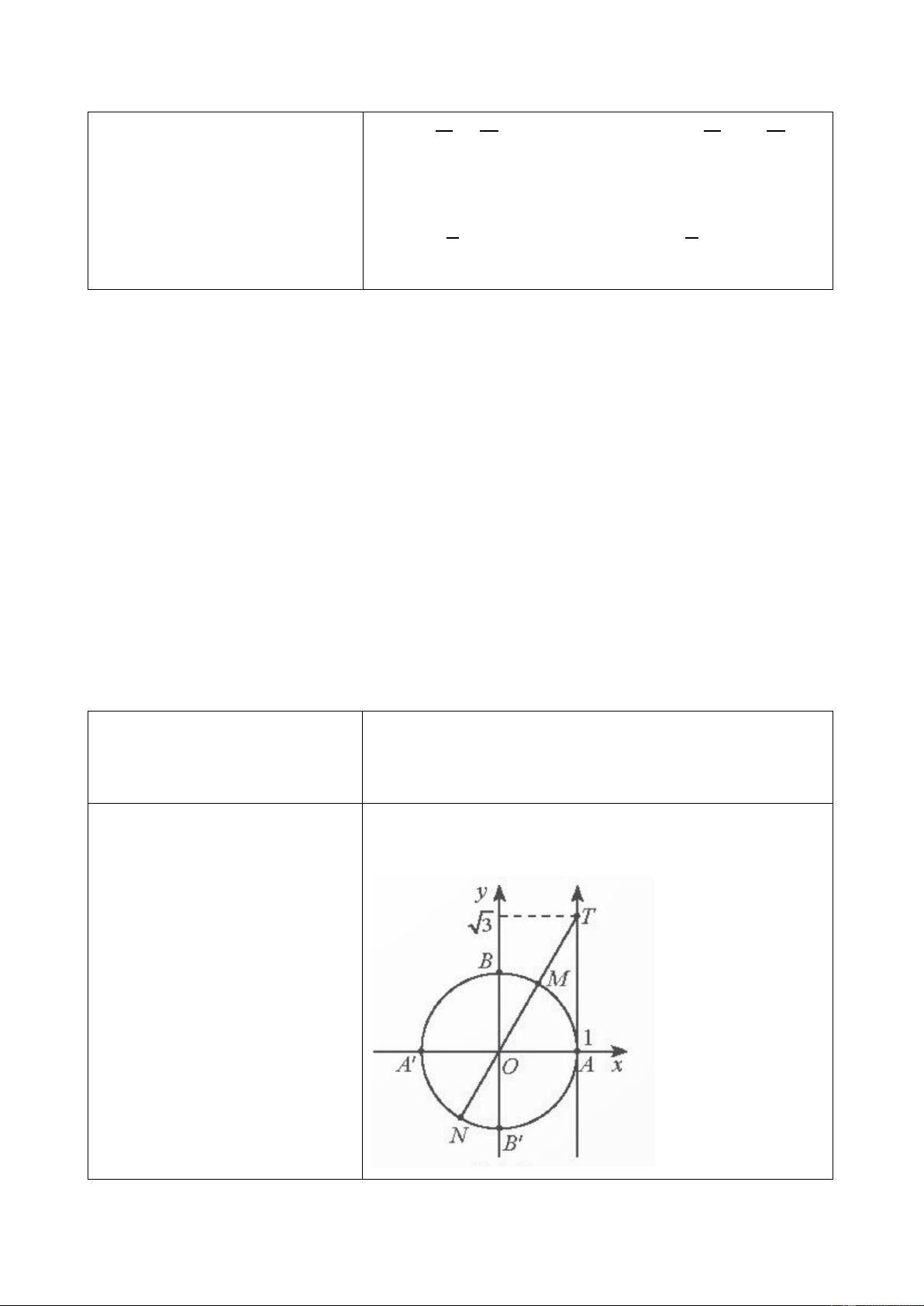
b) Trục As có gốc ở điểm A(1; 0) và song song với
- GV giới thiệu về trục côsin, trục sin gọi là trục tang.
trục sin, trục tang, trục côtang;
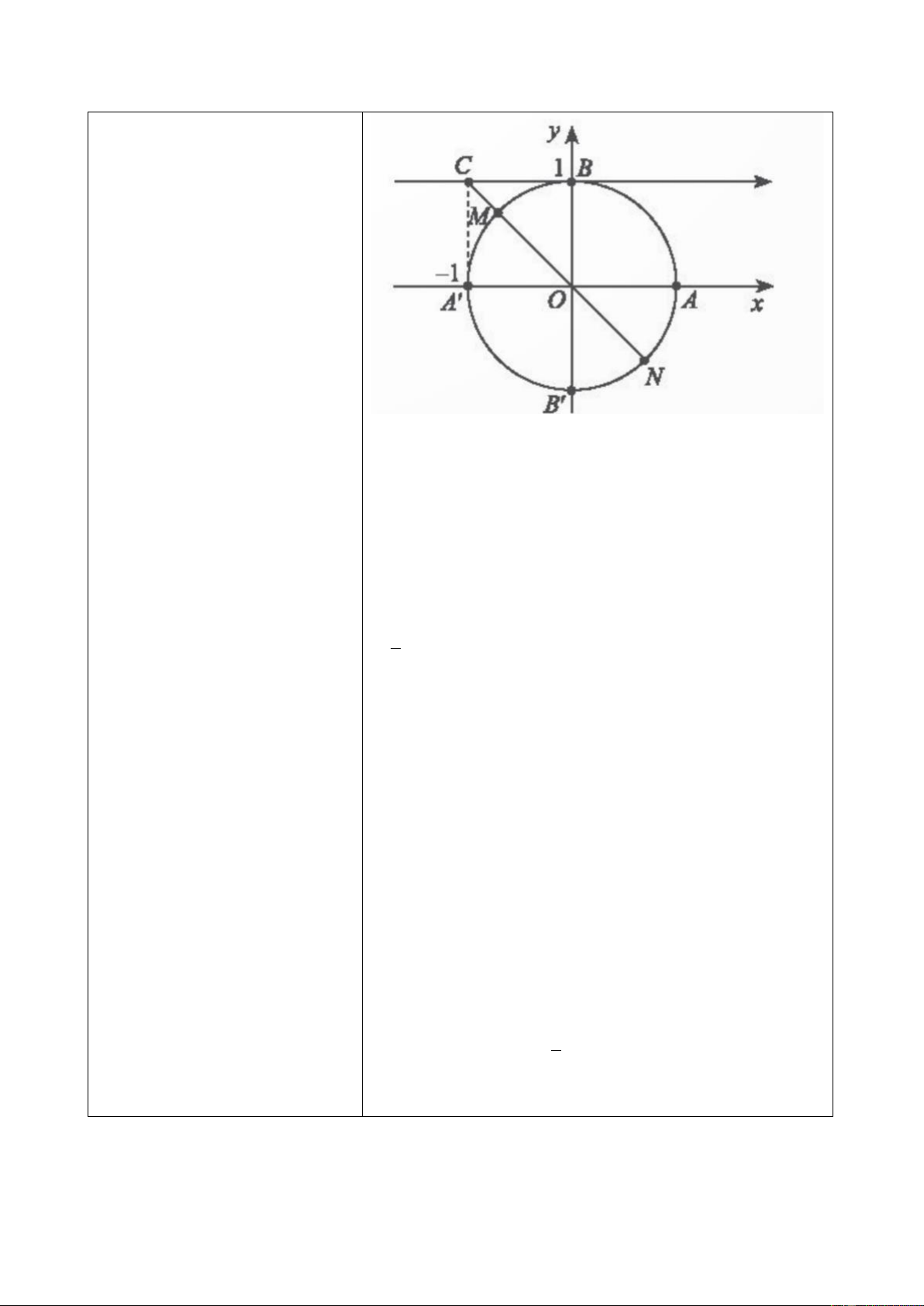
đây là ý nghĩa về mặt hình học Trục Bt có gốc là điểm B(0;1) và song song với trục
của các giá trị lượng giác.
côsin gọi là trục côtang.
+ Khi có điểm 𝑀(𝑥𝑀; 𝑦𝑀) trên
đường tròn lượng giác, biểu
diễn góc 𝛼; thì hoành độ và
tung độ của M lần lượt là côsin và sin của góc 𝛼.
+ OM giao với trục tang tại
điểm H thì tung độ của H là b) sin 𝛼 và cos 𝛼 xác định với mọi 𝛼 ∈ ℝ; tan 𝛼.
tan 𝛼 xác định khi 𝛼 ≠ 𝜋 + 𝑘𝜋(𝑘 ∈ ℤ).
+ OM giao với trục côtang tại 2
K thì hoành độ của K là cot 𝛼.
cot 𝛼 xác định khi 𝛼 ≠ 𝑘𝜋(𝑘 ∈ ℤ).
- GV giới thiệu điều kiện góc
để tan và cot xác định.
c) Với mọi góc lượng giác 𝛼 và số nguyên k, ta có: - GV đặt câu hỏi:
sin(𝛼 + 𝑘2𝜋) = sin 𝛼 (𝑘 ∈ ℤ);
+ Góc 𝛼 và 𝛼 + 𝑘2𝜋 có điểm cos (𝛼 + 𝑘2𝜋) = cos 𝛼 (𝑘 ∈ ℤ).
biểu diễn như thế nào với nhau?
tan(𝛼 + 𝑘𝜋) = tan 𝛼 (𝑘 ∈ ℤ). ; (Cùng điểm biểu diễn)
cot (𝛼 + 𝑘𝜋) = cot 𝛼 (𝑘 ∈ ℤ).
Từ đó nêu mối quan hệ sin, cos giữa hai góc.
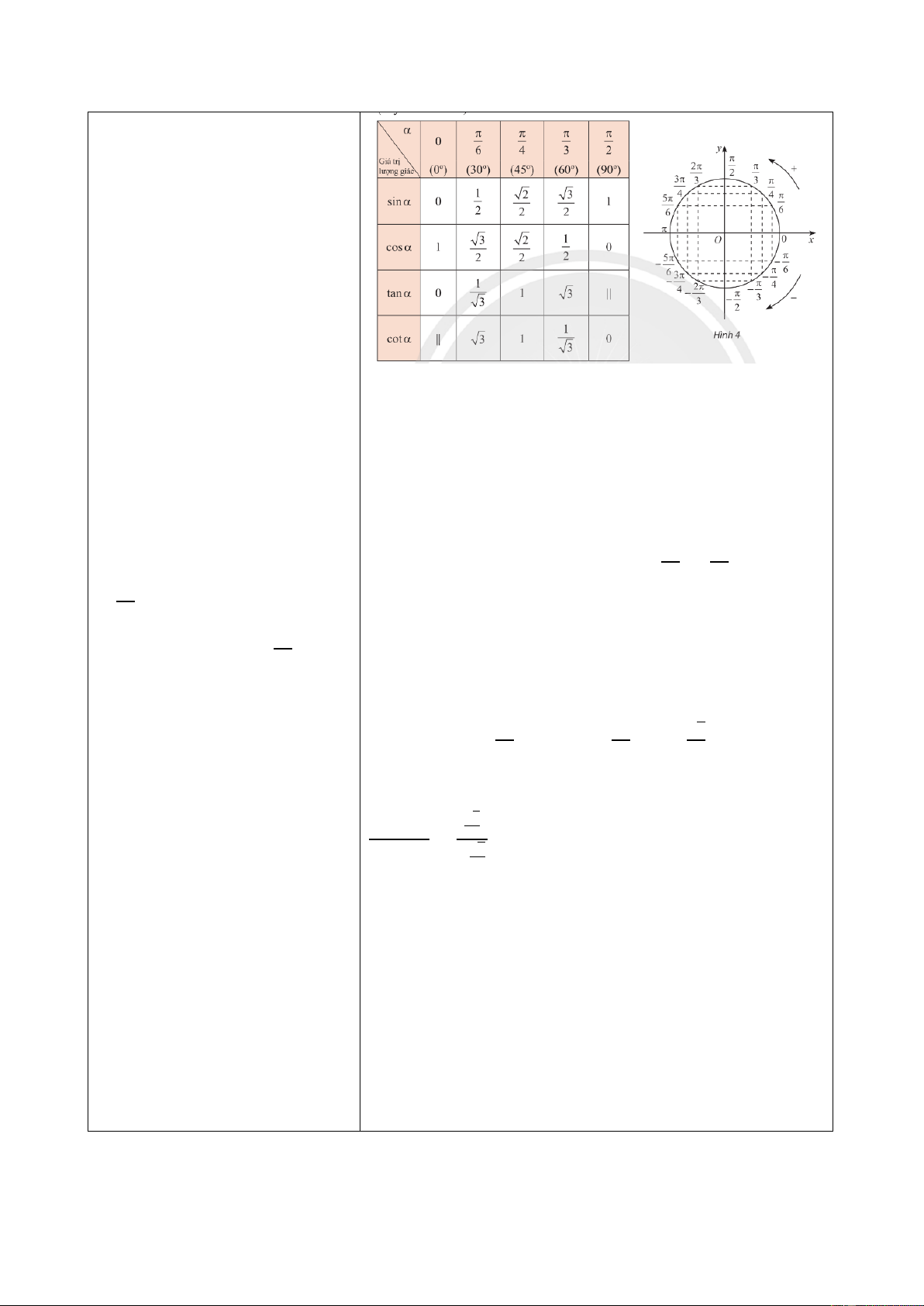
d) Bảng giá trị lượng giác của một số góc lượng giác
+ GV hướng dẫn biểu diễn góc
𝛼 và 𝛼 + 𝑘𝜋 có điểm biểu diễn
là M và M’ khi đó O, M, M’ 29
thẳng hàng. Từ đó nêu mối
quan hệ giữa tan, cot giữa góc 𝛼 và 𝛼 + 𝑘𝜋.
- GV giới thiệu một số giá trị
lượng giác của góc đặc biệt.
- HS đọc hiểu Ví dụ 1. GV Ví dụ 1 (SGK -tr.15) hướng dẫn. Thực hành 1
- HS thực hiện Thực hành 1. 2𝜋
+ HS biểu diển góc lượng giác + Vì điểm biểu diễn của hai góc − 2𝜋 và trên 3 3
− 2𝜋 trên đường tròn, xác định đường tròn lượng giác đối xứng nhau qua trục hoành, 3 2𝜋 nên chúng có hoành độ mối quan hệ với góc .
bằng nhau và tung độ đối 3 nhau.
+ Viết góc 495∘ = 135∘ + 360∘. Do đó, sin 2𝜋
(− 2𝜋) = −sin ( ) = − √3. 3 3 2
Vì 495∘ = 135∘ + 360∘ nên tan 495∘ = tan 135∘ = √2
- GV hướng dẫn HS tính giá trị sin 135∘ = 2 = −1 cos 135∘ −√2
lượng giác bằng máy tính cầm 2 tay.
2. Tính giá trị lượng giác của một góc bằng máy
+ Lưu ý cách tính giá trị cot tính cầm tay.
thông qua cách tính giá trị tan.
Ví dụ 2 (SGK – tr. 15)
Bước 2: Thực hiện nhiệm vụ: Thực hành 2 - HS theo dõi SGK, chú ý
nghe, tiếp nhận kiến thức, 30
hoàn thành các yêu cầu, thảo √6 − √2 −19𝜋 √3 cos 75∘ = ≈ 0,259; tan ( ) = − luận nhóm. 4 6 3 ≈ −0,577. - GV quan sát hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình bày
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận định:
GV tổng quát lưu ý lại kiến
thức trọng tâm và yêu cầu HS
ghi chép đầy đủ vào vở.
Hoạt động 2: Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác a) Mục tiêu:
- HS phát biểu được các hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác.
- HS vận dụng được các hệ thức cơ bản.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động khám phá, thực hành mục 3.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi,
vận dụng hệ thức cơ bản để tính giá trị lượng giác.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN 31
Bước 1: Chuyển giao nhiệm vụ:
3. Hệ thức cơ bản giữa các giá trị lượng giác
của một góc lượng giác
- GV yêu cầu HS thảo luận nhóm đôi, HĐKP 2: hoàn thành HĐKP 2.
a) Trong Hình 5 , tam giác 𝑂𝑀𝐻 vuông tại 𝐻,
ta có 𝑂𝐻 = cos 𝛼, 𝑀𝐻 = sin 𝛼 và 𝑂𝑀 = 1.
Áp dụng định lí Pythagore ta có 𝑂𝐻2 +
𝑀𝐻2 = 𝑂𝑀2 hay cos2 𝛼 + sin2 𝛼 = 1.
- Từ đó GV giới thiệu một số công thức
b) Chia cả hai vế cho cos2 𝛼(cos 𝛼 ≠ 0), ta lượng giác cơ bản. có 1 + tan2 𝛼 = 1 . cos2 𝛼
c) Chia cå hai vế cho sin2 𝛼(sin 𝛼 ≠ 0), ta có cot2 𝛼 + 1 = 1 . sin2 𝛼 Kết luận
- Áp dụng công thức ta tính ví dụ 3.
𝑠𝑖𝑛2 𝛼 + 𝑐𝑜𝑠2 𝛼 = 1
+ Để tính sin 𝛼 khi biết cos 𝛼 ta dùng 1 𝜋 1 + 𝑡𝑎𝑛2 𝛼 = (𝛼 ≠ + 𝑘𝜋, 𝑘 ∈ ℤ) công thức nào? 𝑐𝑜𝑠2 𝛼 2
+ Để xác định được dấu của sin 𝛼 ta 1 1 + 𝑐𝑜𝑡2 𝛼 =
(𝛼 ≠ 𝑘𝜋, 𝑘 ∈ ℤ) 𝑠𝑖𝑛2 𝛼 dựa vào điều gì? 32
+ Để tính tan và cot ta làm thế nào? 𝑘𝜋
𝑡𝑎𝑛 𝛼 . 𝑐𝑜𝑡 𝛼 = 1 (𝛼 ≠ , 𝑘 ∈ ℤ)
- Tương tự HS thực hiện Thực hành 3. 2
Bước 2: Thực hiện nhiệm vụ:
Ví dụ 3 (SGK -tr. 17) Thực hành 3
- HS theo dõi SGK, chú ý nghe, tiếp
nhận kiến thức, suy nghĩ trả lời câu hỏi, hoàn thành các yêu cầu.
- GV: quan sát và trợ giúp HS.
Bước 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình bày
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận định: GV
tổng quát lưu ý lại kiến thức trọng tâm 1 2 = 1 + tan2 𝛼 = 1 + 2 ( ) = 13. Suy ra
và yêu cầu HS ghi chép đầy đủ vào vở. cos2 𝛼 3 9 cos2 𝛼 = 9 . 13
Vì 𝜋 < 𝛼 < 3𝜋 nên cos 𝛼 < 0. Suy ra 2 cos 𝛼 = − 3√13. 13
Vì tan 𝛼 = sin 𝛼 nên sin 𝛼 = tan 𝛼 ⋅ cos 𝛼
cos 𝛼 = 2 ⋅ (− 3√13) = − 2√13. 3 13 13
Hoạt động 3: Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt a) Mục tiêu:
- HS phát biểu được mối liên hệ giữa giá trị lượng giác của các góc lượng giác liên quan đặc biệt. 33
- HS vận dụng được mối liên hệ giữa các giá trị lượng giác. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động mục 4.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi,
vận dụng các mối liên hệ giữa giá trị lượng giác của góc lượng giác.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ: 4. Giá trị lượng giác của các góc lượng giác có liên quan đặ
- GV yêu cầu HS thảo luận nhóm c biệt
bốn, hoàn thành HĐKP 3. HĐKP 3:
+ Dựa vào điểm biểu diễn, tìm
mối quan hệ giữa tọa độ các điểm. 𝜋 +) −𝛼 = − 3 𝜋 𝜋 𝜋 𝜋
sin (− ) = −sin ; cos (− ) = cos 3 3 3 3
tan (− 𝜋) = −tan 𝜋 ; cot (− 𝜋) = −cot 𝜋. 3 3 3 3 34 4𝜋 +) 𝛼 + 𝜋 = 3 4𝜋 𝜋 4𝜋 𝜋 sin = −sin ; cos = −cos ; 3 3 3 3
tan 4𝜋 = tan 𝜋 ; cot 4𝜋 = cot 4𝜋. 3 3 3 3 2𝜋 +) − 𝛼 = 3 2𝜋 𝜋 2𝜋 𝜋 sin = sin ; cos = − cos ; 3 3 3 3
tan 2𝜋 = −tan 𝜋 ; cot 2𝜋 = −cot 𝜋. 3 3 3 3 𝜋 𝜋 +) − 𝛼 = 2 6 𝜋 𝜋 𝜋 𝜋 sin = cos ; cos = sin ; 6 3 6 3
tan 𝜋 = cot 𝜋 ; cot 𝜋 = tan 𝜋. 6 3 6 3
- GV hướng dẫn HS vẽ hình các
trường hợp các góc liên quan đặc Kết luận
biệt. Từ đó nêu mối quan hệ.
a) Hai góc đối nhau 𝛼 và −𝛼
- GV có thể nêu cách nhớ:
Cos đối, sin bù, phụ chéo, tan và cos(−𝛼) = cos 𝛼 cot hơn kém. sin(−𝛼) = − sin 𝛼 tan(−𝛼) = − tan 𝛼 cot(−𝛼) = − cot 𝛼 35
b) Hai góc hơn kém 𝜋: 𝛼 và 𝛼 + 𝜋
sin(𝜋 + 𝛼) = −sin 𝛼
cos (𝜋 + 𝛼) = −cos 𝛼 tan (𝜋 + 𝛼) = tan 𝛼 cot (𝜋 + 𝛼) = cot 𝛼
c) Hai góc bù nhau 𝛼 và 𝜋 − 𝛼
sin (𝜋 − 𝛼) = sin 𝛼
cos (𝜋 − 𝛼) = −cos 𝛼
tan (𝜋 − 𝛼) = −tan 𝛼
cot (𝜋 − 𝛼) = −cot 𝛼 𝜋
d) Hai góc phụ nhau 𝛼 và − 𝛼 2 36 𝜋 sin ( − 𝛼) = cos𝛼 2
- HS thực hiện Ví dụ 4. GV 𝜋
hướng dẫn HS viết theo các góc cos ( − 𝛼) = sin 𝛼 2 liên quan đặc biệt. 𝜋 tan ( − 𝛼) = −tan 𝛼 2
- HS làm Thực hành 4. 𝜋 cot ( − 𝛼) = −cot 𝛼 2
- HS thảo luận nhóm đôi thực hiện Vận dụng.
+ a) Chiều cao từ B đến mặt đất
bằng độ dài đoạn nào? Tính theo Ví dụ 4 (SGK -tr.18) tọa độ các điểm? Thực hành 4
+ b) sử dụng công thức đã có ở a) cos 638∘ = cos (−82∘ + 2 ⋅ 360∘) =
câu a, xét trường hợp góc 𝛼 thuộc cos (−82∘) = cos 82∘ = sin (90∘ − 82∘) =
góc phần tư thứ III và IV. sin 8∘;
Bước 2: Thực hiện nhiệm vụ:
b) cot 19𝜋 = cot (4𝜋 − 𝜋) = cot (− 𝜋) = 5 5 5
- HS theo dõi SGK, chú ý nghe, −cot 𝜋. 5
tiếp nhận kiến thức, hoàn thành Vận dụng
các yêu cầu, thảo luận nhóm. - GV quan sát hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình bày
- Một số HS khác nhận xét, bổ sung cho bạn. 37
Bước 4: Kết luận, nhận định:
GV tổng quát lưu ý lại kiến thức
trọng tâm và yêu cầu HS ghi chép
đầy đủ vào vở.
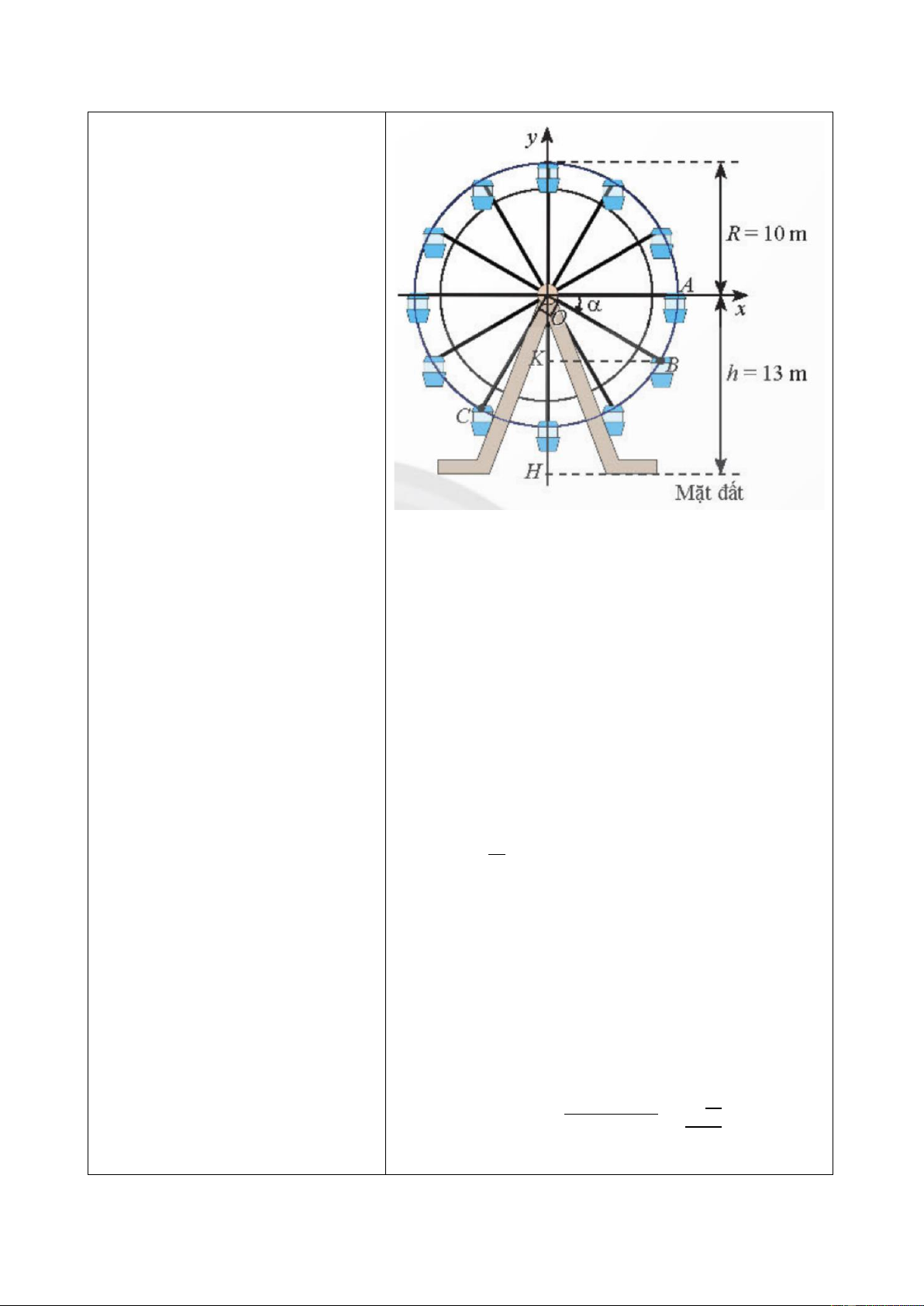
a) Tung độ của 𝐻 và 𝐾 lần lượt là 𝑦𝐻 = −13 và
𝑦𝐾 = 𝑂𝐵 ⋅ sin (𝑂𝐴, 𝑂𝐵) = 10sin 𝛼.
Suy ra độ cao của điểm 𝐵 so vói mặt đất là 𝐾𝐻 =
𝑦𝐾 − 𝑦𝐻 = 10sin 𝛼 + 13.
Khi 𝛼 = −30∘ thì 𝐾𝐻 = 13 + 10sin (−30∘) = 8( m).
b) Ta có 𝐾𝐻 = 4 hay 13 + 10sin 𝛼 = 4, suy ra
sin 𝛼 = − 9 , suy ra 𝛼 thuộc góc phần tư thứ III 10
hoặc góc phần tư thứ IV. Khi đó độ cao của cabin
𝐶 là ℎ = 13 + 10sin (𝑂𝐴, 𝑂𝐶) = 13 +
10sin (𝛼 − 90∘) = 13 − 10cos 𝛼.
Trường hợp 1: 𝛼 thuộc góc phần tur thứ III nên cos 𝛼 < 0.
Do đó, cos 𝛼 = −√1 − sin2 𝛼 = −√19. 10 38
Suy ra ℎ = 13 − 10 ⋅ (− √19) ≈ 17,36( m). 10
Trường hợp 2: 𝛼 thuộc góc phần tư thứ IV nên
cos 𝛼 > 0. Do đó, cos 𝛼 = √1 − sin2 𝛼 = √19. 10
Suy ra ℎ = 13 − 10 ⋅ √19 ≈ 8,64( m). 10
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 1 đến 6 (SGK -tr.20) và các câu hỏi TN.
c) Sản phẩm học tập: Câu trả lời của HS. HS sử dụng kiến thức đã học tính giá trị lượng
giác, chứng minh đẳng thức, rút gọn biểu thức.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS trả lời các câu hỏi TN nhanh
Câu 1. Giá trị của 𝑐𝑜𝑡81𝜋 là: 4 A. √2 2 B. 1 C. −√2 2 D. -1
Câu 2. Giá trị của biểu thức: 𝐴 = 𝑡𝑎𝑛10𝑜. 𝑡𝑎𝑛20𝑜. 𝑡𝑎𝑛30𝑜. . . tan 80𝑜 là: 39 A. 1 B. -1 C. 8 D. -8
Câu 3. Cho sin 𝛼 = − 4 và 𝜋 < 𝛼 < 3𝜋. Giá trị của 𝑐𝑜𝑠𝛼 là: 5 2 A. 3 5 B. − 3 5 C. ± 3 5 D. 9 25
Câu 4. Cho 𝑐𝑜𝑡𝛼 = 5. Giá trị của 𝐴 = 2 cos2 𝛼 + 5 sin 𝛼 cos 𝛼 + 1 bằng: A. 10 26 B. 100 26 C. 101 26 D. 50 26
Câu 5. Cho 𝑐𝑜𝑡𝛼 = 3, giá trị của 𝑠𝑖𝑛 (2𝛼 − 𝜋) là: 4 A. −2 B. 2√2 C. −2√10 D. 2√10 40
- GV tổ chức cho HS hoạt động thực hiện Bài 1 đến 6 (SGK -tr.20)
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định:
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác. Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 B A B C C Bài 1. 2 2 a) Có. Vì 3 3
( ) + (− 4) = 1, nên tồn tại điểm 𝑀 ( ; − 4) nằm trên đường tròn lượng 5 5 5 5
giác biểu diê̄n góc 𝛼.
b) Không. Vì sin 𝛼 = 1 và cot 𝛼 = 1 không thoả mãn đằng thức 1 = cot2 𝛼 + 1. 3 2 sin2 𝛼
c) Có. Chọn 𝛼 là một góc có tan 𝛼 = 3 thi cot 𝛼 = 1 = 1 nên thoả mãn diều kiện. tan 𝛼 3 Bài 2. 41 15𝜋 𝜋 sin (−
− 𝛼) − cos (13𝜋 + 𝛼) = sin (−8𝜋 +
− 𝛼) − cos (12𝜋 + 𝜋 + 𝛼) 2 2 10
= cos 𝛼 + cos 𝛼 = 2cos 𝛼 = − . 13 Bài 3.
a) cos 𝛼 = − 12 ; tan 𝛼 = − 5 ; cot 𝛼 = − 12; 13 12 5
b) sin 𝛼 = √21 ; tan 𝛼 = √21 ; cot 𝛼 = 2√21; 5 2 21
c) sin 𝛼 = − √3 ; cos 𝛼 = − 1 ; cot 𝛼 = √3 2 2 3
d) sin 𝛼 = − 2√5 ; cos 𝛼 = √5 ; tan 𝛼 = −2. 5 5 Bài 4. a) 31𝜋 𝜋 𝜋 𝜋 cos
= cos (4𝜋 + 𝜋 + ) = cos (𝜋 + ) = −cos = − √3. 6 6 6 6 2 b) sin 129𝜋 = sin 𝜋
(32𝜋 + 𝜋) = sin ( ) = √2. 4 4 4 2
c) tan 1020∘ = tan (3.360∘ − 60∘) = tan (−60∘) = −cot (30∘) = −√3. Bài 5.
a) sin4 𝛼 − cos4 𝛼 = (sin2 𝛼 + cos2 𝛼)(sin2 𝛼 − cos2 𝛼) = sin2 𝛼 − cos2 𝛼 =
(1 − cos2 𝛼) − cos2 𝛼 = 1 − 2cos2 𝛼.
b) tan 𝛼 + cot 𝛼 = sin 𝛼 + cos 𝛼 = sin2 𝛼+cos2 𝛼 = 1 . cos 𝛼 sin 𝛼 sin 𝛼cos 𝛼 sin 𝛼cos 𝛼
c) sin (𝛼 − 𝜋) + cos (−𝛼 + 6𝜋) − tan (𝛼 + 𝜋) ⋅ cot (3𝜋 − 𝛼) 2 Bài 6. 42 a) 1 1 cos 𝛼 sin 𝛼 + = + = 1. tan 𝛼+1 cot 𝛼+1 sin 𝛼+cos 𝛼 cos 𝛼+sin 𝛼 𝜋
= −sin ( − 𝛼) + cos (−𝛼) − tan 𝛼 ⋅ (−cot 𝛼) 2 b) cos 𝜋
( − 𝛼) − sin (𝜋 + 𝛼) = sin 𝛼 + sin 𝛼 = 2sin 𝛼 2
= −cos 𝛼 + cos 𝛼 + tan 𝛼 ⋅ cot 𝛼 = tan 𝛼 ⋅ cot 𝛼 = 1.
D. HOẠT ĐỘNG VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập 7, 8 (SGK -tr.20).
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: 43 Bài 7.
Ta có 𝛼 = (3 1 ) ⋅ 2𝜋 = 31𝜋 (rad). 10 5
𝑂′𝑀′ = |𝑂𝑀cos 𝛼| = |15cos 31𝜋| ≈ 8,8( cm). 5 Bài 8.
Khoảng cách từ van đến mặt đất là ℎ = 𝑅 + 𝑅sin 𝛼 = 𝑅(1 + sin 𝛼).
Vì bánh xe quay cùng chiểu kim đồng hồ (chiều âm) với tốc góc là 11rad/s, nên sau 1
phút = 60 giây, ta có 𝛼 = (−11).60 = −660 (rad). 44
Do đó ℎ = 58[1 + sin (−660)] ≈ 42,8( cm).
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: "Bài 3 Các công thức lượng giác." 45 Ngày soạn: .../.../... Ngày dạy: .../.../...
BÀI 3: CÁC CÔNG THỨC LƯỢNG GIÁC (2 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học xong bài này, HS đạt các yêu cầu sau:
- Mô tả các phép biến đổi lượng giác cơ bản: công thức cộng; công thức góc nhân
đôi; công thức biến đồi tich thành tồng và công thức biến đổi tổng thành tích.
- Giải quyết một số vấn đề thực tiễn gắn với giá trị lượng giác của góc lượng giác
và các phép biến đổi lượng giác. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học, giải quyết vấn đề toán học: So sánh, phân tích dữ
liệu tìm ra mối liên hệ giữa các đối tượng đã cho và nội dung bài học về các công
thức lượng giác từ đó có thể áp dụng kiến thức đã học để giải quyết các bài toán.
- Mô hình hóa toán học: Mô tả được các dữ liệu liên quan đến yêu cầu trong thực
tiễn, lựa chọn các công thức lượng giác phù hợp để giải quyết bài toán. - Giao tiếp toán học.
- Sử dụng công cụ, phương tiện học toán. 3. Phẩm chất 46
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học. Thông qua bài toán thực tế trong
xây dựng để dẫn đến các phép biến đổi lượng giác, cụ thể là công thức nhân đôi.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS dự đoán, đưa ra câu trả lời cho câu hỏi mở đầu.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu:
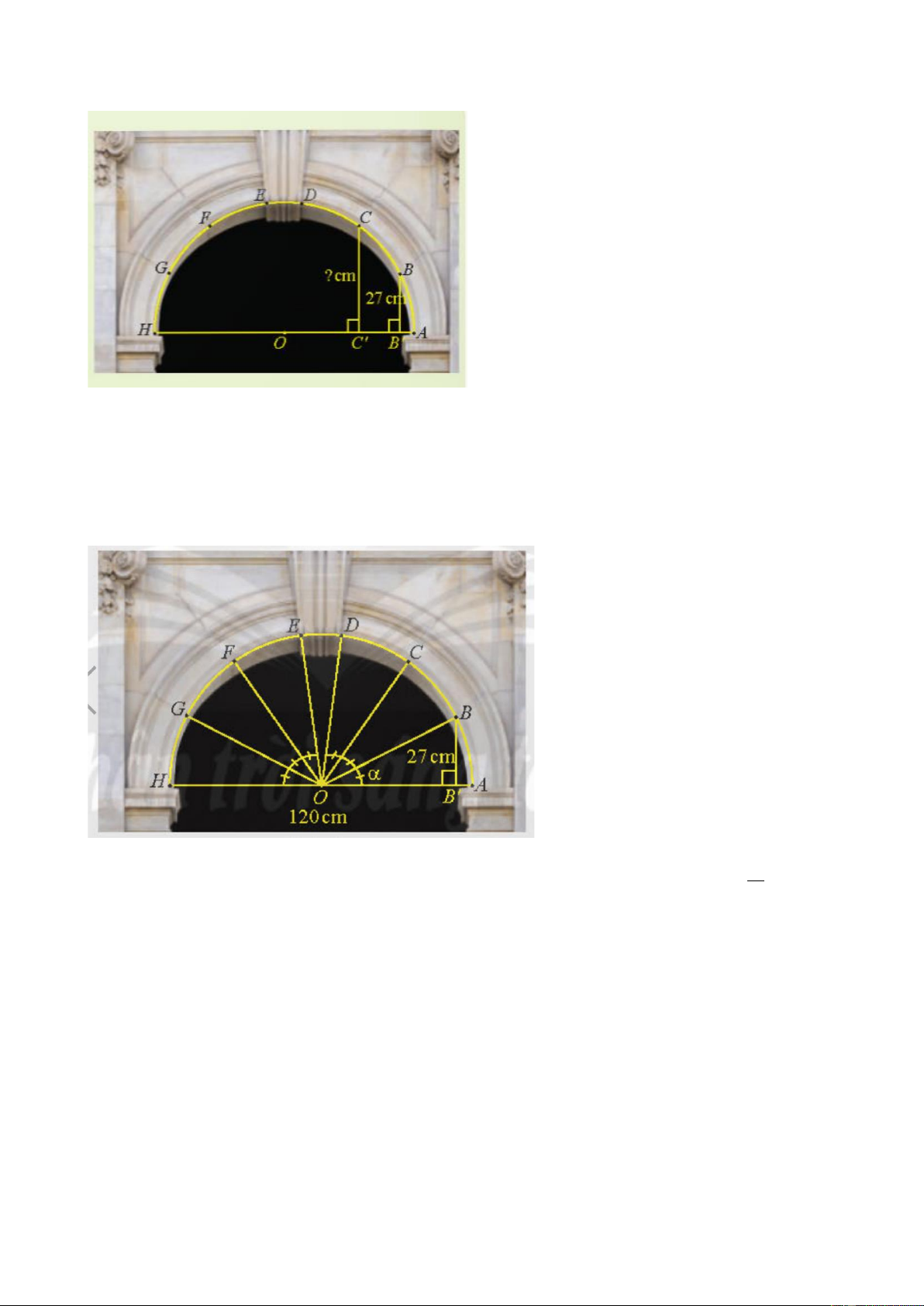
Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu
lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đã hai bên tạo thành các cung
AB, BC, CD, EF, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng
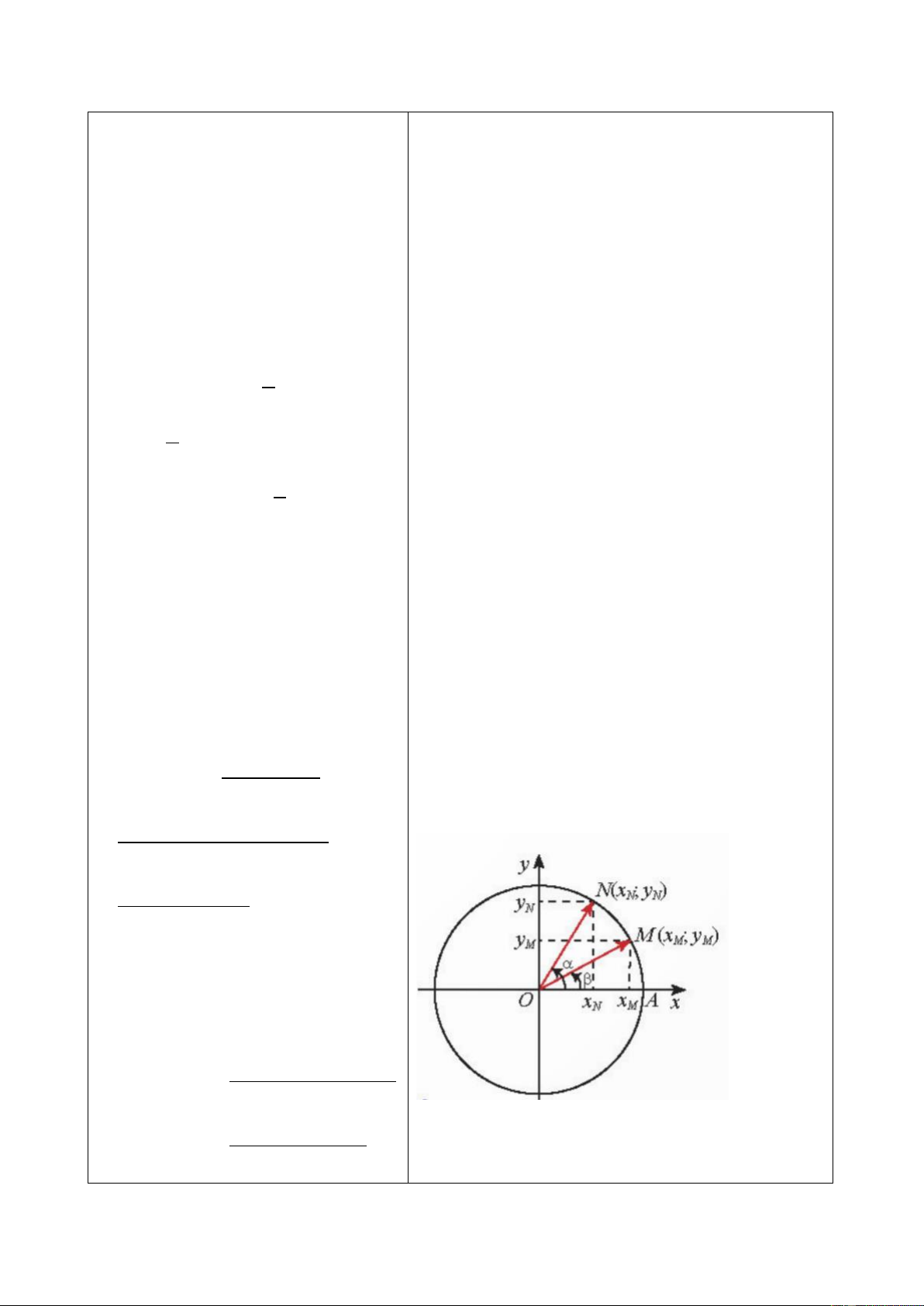
và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH? 47 - GV hướng dẫn:
+ Sử dụng hình vẽ sau, với dữ kiện chiều rộng cổng 𝐴𝐻 = 120 𝑐𝑚, khoảng cách từ
điểm B đến đường kính AH là 𝐵𝐵’ = 27 𝑐𝑚. + Giả sử 𝐴𝑂𝐵
̂ = 𝛼. Ta có khoảng cách từ 𝐵 đến 𝐴𝐻 bằng 27 cm nên sin 𝛼 = 27. 60
Với 𝛼 là góc nhọn nên có thể tính được tất cả các giá tri lượg giác của góc 𝛼.
Mặt khác, các cung 𝐴𝐵 và 𝐵𝐶 bằng nhau nên 𝐴𝑂𝐶 ̂ = 2𝐴𝑂𝐵
̂ = 2𝛼 và khoảng cách từ 𝐶
đến 𝐴𝐻 là 60sin 2𝛼.
Do đó để tính được khoảng cách từ 𝐶 đến 𝐴𝐻, cần có công thức biểu diễn sin 2𝛼 qua
các giá trị lượng giác của góc 𝛼. 48
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học mới: “Bài học hôm nay chúng ta cùng đi tìm hiểu về các công thức biến đổi
lượng giác để tính toán được linh hoạt, vận dụng vào nhiều bài toán.”
Bài 3. Các công thức lượng giác.
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Công thức cộng. Công thức góc nhân đôi a) Mục tiêu:
- HS mô tả được công thức cộng, công thức góc nhân đôi lượng giác.
- HS vận dụng vào một số bài toán. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động mục 1 và mục 2.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi,
HS vận dụng vào bài tập tính giá trị lượng giác sử dụng công thức cộng, công thức nhân đôi.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ: 1. Công thức cộng
Nhiệm vụ 1: Tìm hiểu công thức HĐKP 1 cộng 49
- GV yêu cầu HS thảo luận nhóm 𝑂𝑀
⃗ ⋅ 𝑂𝑁⃗ = |𝑂𝑀||𝑂𝑁⃗ |cos 𝑀𝑂𝑁 ̂ (định nghĩa
đôi, hoàn thành HĐKP 1. của tích vô hướng)
- GV có thể cho HS tìm hiểu, xây = |𝑂𝑀
⃗ ||𝑂𝑁⃗ | cos(𝛼 − 𝛽)
dựng thêm công thức cộng của sin = cos(𝛼 − 𝛽)
và tan bằng cách sử dụng công thức (vì 𝑀𝑂𝑁 ̂ = 𝑥𝑂𝑁 ̂ − 𝑥𝑂𝑀 ̂ = 𝛼 − 𝛽)
cộng cos và giá trị lượng giác của
các góc liên quan đặc biệt.
( vì 𝑀, 𝑁 thuộc đường trò̀n lượng giác nên |𝑂𝑀 ⃗ | 𝜋
sin(𝛼 + 𝛽) = cos ( − 𝛼 − 𝛽) = |𝑂𝑁 ⃗ | = 1). 2 𝜋 = cos ( − 𝛼) cos 𝛽
Vì 𝑀 và 𝑁 lần lượt là điểm biểu diễn của các 2 𝜋
góc lượng giác 𝛽 và 𝛼 trên đường tròn lượng + sin ( − 𝛼) sin 𝛽 2
giác, nên toạ độ của các điểm này là
= sin 𝛼cos 𝛽 + cos 𝛼sin 𝛽
𝑀(cos 𝛽; sin 𝛽) và 𝑁(cos 𝛼; sin 𝛼). Do đó
sin(𝛼 − 𝛽) = sin[𝛼 + (−𝛽)] 𝑂𝑀
⃗ ⋅ 𝑂𝑁⃗ = cos 𝛽cos 𝛼 + sin 𝛽sin 𝛼
= sin 𝛼 cos(−𝛽) + cos 𝛼 sin(−𝛽)
Vậy cos (𝛼 − 𝛽) = cos 𝛼cos 𝛽 + sin 𝛼sin 𝛽.
= sin 𝛼cos 𝛽 − cos 𝛼sin 𝛽;
Suy ra cos (𝛼 + 𝛽) = cos [𝛼 − (−𝛽)] = sin(𝛼 + 𝛽)
cos 𝛼cos (−𝛽) + sin 𝛼sin (−𝛽) = tan(𝛼 + 𝛽) = cos(𝛼 + 𝛽)
cos 𝛼cos 𝛽 − sin 𝛼sin 𝛽.
sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽 =
cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽 tan 𝛼 + tan 𝛽 = 1 − tan 𝛼 tan 𝛽
(chia tử và mẫu cho 𝛼cos 𝛽
tan(𝛼 − 𝛽) = tan [𝛼 + (−𝛽)] tan 𝛼 + tan (−𝛽) = 1 − tan 𝛼tan (−𝛽) tan 𝛼 − tan 𝛽 = 1 + tan 𝛼tan 𝛽 50
- GV chốt lại công thức cộng.
- GV có thể giới thiệu một số cách Kết luận: Công thức cộng nhớ công thức.
𝑐𝑜𝑠(𝛼 + 𝛽) = cos 𝛼 cos 𝑏 − sin 𝛼 sin 𝑏
𝑐𝑜𝑠(𝛼 − 𝛽) = cos 𝛼 cos 𝑏 + sin 𝛼 sin 𝑏
𝑠𝑖𝑛(𝛼 − 𝛽) = sin 𝛼 cos 𝛽 − cos 𝛼 sin 𝛽
𝑠𝑖𝑛(𝛼 + 𝛽) = sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽
- HS quan sát và nêu cách làm Ví dụ tan 𝛼 − tan 𝛽 tan(𝛼 − 𝛽) = 1. 1 + tan 𝛼 tan 𝛽
- HS thực hiện Thực hành 1, sử tan 𝛼 + tan 𝛽 tan(𝛼 + 𝛽) =
dụng cộng thức cộng 𝜋 − 𝜋 = 𝜋 . 1 − tan 𝛼 tan 𝛽 3 4 12
Ví dụ 1 (SGK -tr.21) Thực hành 1 𝜋
sin 𝜋 = sin ( − 𝜋) = sin 𝜋 cos 𝜋 − 12 3 4 3 4
cos 𝜋 sin 𝜋 = √3 ⋅ √2 − 1 ⋅ √2 = √6−√2; 3 4 2 2 2 2 4 𝜋 𝜋 𝜋 𝜋 𝜋 tan − tan
Nhiệm vụ 2: Tìm hiểu công thức tan = tan ( − ) = 3 4 12 3 4 𝜋 𝜋 góc nhân đôi 1 + tan tan 3 4
- HS thực hiện HĐKP 2, từ đó xây √3 − 1 = = 2 − √3
dựng được công thức góc nhân đôi. 1 + √3 ⋅ 1
- GV có thể cho HS viết 𝑐𝑜𝑠 𝛼, 𝑠𝑖𝑛 𝛼 2. Công thức góc nhân đôi
theo 𝑐𝑜𝑠 2𝛼. Giới thiệu công thức hạ HĐKP 2: bậc. cos 2𝛼 = cos(𝛼 + 𝛼) Công thức hạ bậc
= cos 𝛼 cos 𝛼 − sin 𝛼 sin 𝛼 1 + cos 2𝛼 cos2𝛼 = 2 = cos2 𝛼 − sin2 𝛼. 1 − cos 2𝛼 sin2𝛼 =
Mà cos2 𝛼 − sin2 𝛼 = cos2 𝛼 − (1 − 2
cos2 𝛼) = 2cos2 𝛼 − 1. 51
Hoặc cos2 𝛼 − sin2 𝛼 = (1 − sin2 𝛼) − sin2 𝛼 = 1 − 2sin2 𝛼.
+) sin 2𝛼 = sin (𝛼 + 𝛼) = sin 𝛼cos 𝛼 +
cos 𝛼sin 𝛼 = 2sin 𝛼cos 𝛼.
+) tan 2𝛼 = tan (𝛼 + 𝛼) = tan 𝛼+tan 𝛼 = 1−tan 𝛼tan 𝛼 2tan 𝛼 . 1−tan2 𝛼 Kết luận
sin 2𝛼 = 2 sin 𝛼 cos 𝛼
cos 2𝛼 = cos2 𝛼 − sin2 𝛼 = 2 cos2 𝛼 − 1 = 1 − 2𝛼
- HS thực hiện Ví dụ 2, sử dụng 2tan 𝛼
công thức góc nhân đôi. tan 2𝛼 = 1 − tan2 𝛼
- Tương tự HS thực hiện Thực hành Ví dụ 2 (SGK -tr.22) 2. Bướ Thực hành 2:
c 2: Thực hiện nhiệm vụ: 𝜋 √2
- HS theo dõi SGK, chú ý nghe, tiếp 𝜋 cos + 1 + 1 2 + √2 +) cos2 = 4 = 2 =
nhận kiến thức, hoàn thành các yêu 8 2 2 4 cầu, thảo luận nhóm.
Vì 0 < 𝜋 < 𝜋 nên cos 𝜋 > 0. Do đó cos 𝜋 = 8 2 8 8 - GV quan sát hỗ trợ. √2+√2. 2
Bước 3: Báo cáo, thảo luận: 𝜋 1 4 +) tan2 = 𝜋 − 1 = − 1 = 3 − 2√2.
- HS giơ tay phát biểu, lên bảng trình 8 cos2 2+√2 8 bày 𝜋
Vì 0 < 𝜋 < 𝜋 nênt tan > 0.
- Một số HS khác nhận xét, bổ sung 8 2 8 cho bạn.
Do đó tan 𝜋 = √3 − 2√2 = √2 − 1. 8
Bước 4: Kết luận, nhận định: GV
tổng quát lưu ý lại kiến thức trọng 52
tâm và yêu cầu HS ghi chép đầy đủ vào vở.
Hoạt động 2: Công thức biến đổi tích thành tổng. Công thức biến đổi tổng thành tích. a) Mục tiêu:
- HS mô tả được công thức biến tích thành tổng và tổng thành tích.
- HS vận dụng công thức vào giải quyết bài toán.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động mục 3 và 4.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi,
HS tính giá trị lượng giác, giá trị biểu thức sử dụng công thức biến đổi tích thành tổng
hoặc tổng thành tích.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV
SẢN PHẨM DỰ KIẾN VÀ HS
Bước 1: Chuyển giao 3. Công thức biến đổi tích thành tổng. HĐKP 3 nhiệm vụ: a)
Nhiệm vụ 1: Tìm hiểu công cos (𝛼 − 𝛽) + cos (𝛼 + 𝛽)
thức biến đổi tích thành = (cos 𝛼cos 𝛽 + sin 𝛼sin 𝛽) + (cos 𝛼cos 𝛽 tổng. − sin 𝛼sin 𝛽)
- GV yêu cầu HS thực hiện
HĐKP 3. Sử dụng công thức = 2 cos 𝛼 cos 𝛽
cộng, tính tổng hiệu theo yêu cos (𝛼 − 𝛽) − cos (𝛼 + 𝛽) cầu. 53
= (cos 𝛼cos 𝛽 + sin 𝛼sin 𝛽) − (cos 𝛼cos 𝛽 − sin 𝛼sin 𝛽) = 2sin 𝛼sin 𝛽 b)
sin(𝛼 − 𝛽) + sin(𝛼 + 𝛽)
= (sin 𝛼cos 𝛽 − cos 𝛼sin 𝛽) + (sin 𝛼cos 𝛽 + cos 𝛼sin 𝛽) = 2 sin 𝛼 cos 𝛽
sin(𝛼 − 𝛽) − sin(𝛼 + 𝛽)
= (sin 𝛼cos 𝛽 − cos 𝛼sin 𝛽) − (sin 𝛼cos 𝛽 + cos 𝛼sin 𝛽) = −2cos 𝛼sin 𝛽. Kết luận:
- GV chốt công thức biến 1
cos 𝛼 cos 𝛽 = [cos(𝛼 − β) + cos(𝛼 + β)] tích thành tổng. 2
- HS đọc hiểu Ví dụ 3, giải 1 thích.
sin 𝛼 sin 𝛽 = [cos(𝛼 − β) − cos(𝛼 + β)] 2
- HS thực hiện Thực hành 3. 1
sin 𝛼cos β = [sin (𝛼 − β) + sin (𝛼 + β)] 2
Ví dụ 3 (SGK -tr.22) Thực hành 3 𝜋 5𝜋 sin cos 24 24 1 𝜋 5𝜋 𝜋 5𝜋 = [sin ( − ) + sin ( + )] 2 24 24 24 24 54 1 𝜋 𝜋 = [sin (− ) + sin ] 2 6 4 1 1 √2 −1 + √2 = (− + ) = 2 2 2 4 7𝜋 5𝜋 sin sin 8 8 1 7𝜋 5𝜋 7𝜋 5𝜋 = [cos ( − ) − cos ( + )] 2 8 8 8 8 1 𝜋 3𝜋 = (cos − cos ) 2 4 2 = 1 ⋅ √2 = √2. 2 2 4
4. Công thức biến đổi tổng thành tích.
Nhiệm vụ 2: Tìm hiểu công HĐKP 4
thức biến đổi tổng thành 𝛼+𝛽 𝛼−𝛽 1 𝛼+𝛽 𝛼−𝛽 +) cos cos = [cos ( − ) + 2 2 2 2 2 tích cos 𝛼+𝛽 (
+ 𝛼−𝛽)] = 1 (cos 𝛽 + cos 𝛼).
- HS thực hiện HĐKP 4 theo 2 2 2
nhóm đôi vào phiếu bài tập
+) sin 𝛼+𝛽 sin 𝛼−𝛽 = 1 𝛼+𝛽 [cos ( − 𝛼−𝛽) − 2 2 2 2 2
- GV cho HS nêu công thức cos 𝛼+𝛽 (
+ 𝛼−𝛽)] = 1 (cos 𝛽 − cos 𝛼). biến tổng thành tích. 2 2 2 𝛼 + 𝛽 𝛼 − 𝛽 +) sin cos 2 2 1 𝛼 + 𝛽 𝛼 − 𝛽 𝛼 + 𝛽 𝛼 − 𝛽 = [sin ( − ) + sin ( + )] 2 2 2 2 2 1 = (sin 𝛽 + sin 𝛼) 2 Kết luận 𝛼 + β 𝛼 − β cos 𝛼 + cos β = 2cos cos 2 2 55 𝛼 + β 𝛼 − β
cos 𝛼 − cos β = −2sin sin 2 2 𝛼 + β 𝛼 − β sin 𝛼 + sin β = 2sin cos 2 2 𝛼 + β 𝛼 − β sin 𝛼 − sin β = 2cos sin 2 2
Ví dụ 4 (SGK -tr.23) Thực hành 4
- HS đọc hiểu, giải thích cách 7𝜋 𝜋 cos + cos 12 12 làm Ví dụ 4.
- HS áp dụng thực hiện Thực 7𝜋 𝜋 7𝜋 𝜋 + − 12 12 12 12 hành 4. = 2 cos cos 2 2 - HS làm Vận dụng
+Tính khoảng cách từ C đến = 2cos 𝜋 cos 𝜋 = 2 ⋅ 1 ⋅ √2 = √2. 3 4 2 2 2 AH thông qua công thức Vận dụng nào?
Từ đó phải sử dụng mối quan hệ nào với sin 𝛼.
Bước 2: Thực hiện nhiệm vụ: - HS theo dõi SGK, chú ý
nghe, tiếp nhận kiến thức,
suy nghĩ trả lời câu hỏi, hoàn Đặt 𝛼 = 𝐵𝑂𝐵′
̂ . Ta có sin 𝛼 = 𝐵𝐵′ = 27 = 9 . 𝑂𝐵 60 20 thành các yêu cầu.
Vì 0 < 𝛼 < 90∘ nên cos 𝛼 > 0, suy ra cos 𝛼 =
- GV: quan sát và trợ giúp HS. √1 − sin2 𝛼 = √319. 20
Bước 3: Báo cáo, thảo luận: 56
- HS giơ tay phát biểu, lên Khoảng cách từ 𝐶 đến 𝐴𝐻 là ℎ𝐶 = 60 ⋅ sin 2𝛼 = bảng trình bày
60.2sin 𝛼cos 𝛼 = 27√319 ≈ 48,2( cm). 10
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận
định: GV tổng quát lưu ý lại
kiến thức trọng tâm và yêu
cầu HS ghi chép đầy đủ vào vở.
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập TN và bài 1 đến 6 (SGK tr.23+24)
c) Sản phẩm học tập: Câu trả lời của HS. HS tính được giá trị lượng giác, tính giá trị
biểu thức, chứng minh đẳng thức sử dụng các công thức lượng giác.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS trả lời các câu hỏi TN nhanh
Câu 1. Biến đổi 𝐴 = 2𝑠𝑖𝑛𝑥. 𝑠𝑖𝑛2𝑥. 𝑠𝑖𝑛3𝑥 thành tổng: A. 1
𝑠𝑖𝑛2𝑥 + 1 𝑠𝑖𝑛4𝑥 + 1 𝑠𝑖𝑛6𝑥 2 2 2 B. 1
𝑠𝑖𝑛2𝑥 + 1 𝑠𝑖𝑛4𝑥 − 1 𝑠𝑖𝑛6𝑥 2 2 2 C. 1
𝑠𝑖𝑛2𝑥 − 1 𝑠𝑖𝑛4𝑥 − 1 𝑠𝑖𝑛6𝑥 2 2 2 D. 1
𝑠𝑖𝑛2𝑥 − 1 𝑠𝑖𝑛4𝑥 + 1 𝑠𝑖𝑛6𝑥 2 2 2
Câu 2. Cho 𝛼 = 1, giá trị của biểu thức 𝐴 = 𝑠𝑖𝑛(𝛼 − 𝜋) − 𝑐𝑜𝑠(𝛼 − 𝜋) là: 3 4 4 57 A. √2 3 B. −√2 3 C. 2√2 − 1 3 3 D. −2√2 − 1 3 3
Câu 3. Biểu thức thu gọn của biểu thức 𝐴 = sin 𝑎+sin3𝑎+sin5𝑎 là: cos 𝑎+cos 3𝑎+cos 5𝑎 A. 𝑠𝑖𝑛3𝑎 B. 𝑐𝑜𝑠3𝑎
C. 𝑡𝑎𝑛3𝑎 D. 𝑐𝑜𝑡3𝑎
Câu 4. Tính 𝒔𝒊𝒏𝟐 𝟐𝒙 biết 𝟏 + 𝟏 + 𝟏 + 𝟏 = 𝟕 𝒕𝒂𝒏𝟐𝒙 𝒄𝒐𝒕𝟐𝒙 𝒔𝒊𝒏𝟐𝒙 𝒄𝒐𝒔𝟐𝒙 A. 4 9 B. 8 9 C. 2 9 D. 16 9 Câu 5. Cho 𝜋
< 𝛼 < 𝜋 và 𝑐𝑜𝑠𝛼 = − 2. Biết 𝐴 = 𝑠𝑖𝑛2𝛼 + 𝑐𝑜𝑠2𝛼 = 𝑎 + 𝑏√5 (𝑎, 𝑏 ∈ 2 3 𝑄) và 𝑎
= 𝑝 là phân số tối giản. Tính 𝑝 − 𝑞? 𝑏 𝑞 A. 3 B. 1 C. -3 58 D. -1
- GV tổ chức cho HS hoạt động thực hiện Bài 1 đến 6 (SGK tr.23+24).
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định:
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác. Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 B B C B C Bài 1. a) sin 5𝜋 = sin 𝜋
( + 𝜋) = sin 𝜋 cos 𝜋 + cos 𝜋 sin 𝜋 = √2 ⋅ √3 + √2 ⋅ 1 = √6+√2; 12 4 6 4 6 4 6 2 2 2 2 4 5𝜋 𝜋 𝜋 𝜋 𝜋 𝜋 𝜋 1 cos
= cos ( + ) = cos cos − sin sin = √2 ⋅ √3 − √2 ⋅ = √6−√2; 12 4 6 4 6 4 6 2 2 2 2 4 5𝜋 5𝜋 sin tan = 12 = 2 + √3 12 5𝜋 cos 12 cot 5𝜋 = 1 = 1 = 2 − √3. 12 5𝜋 tan 2+√3 12 59
b) sin (−555∘) = sin (165∘ − 2 ⋅ 360∘) = sin 165∘ = sin (45∘ + 120∘)
= sin 45∘cos 120∘ + cos 45∘sin 120∘ √2 1 √2 √3 −√2 + √6 = ⋅ (− ) + ⋅ = 2 2 2 2 4
cos (−555∘) = cos (45∘ + 120∘) = cos 45∘cos 120∘ − sin 45∘sin 120∘ = √2−√6; 4
tan (−555∘) = sin (−645∘) = −2 + √3; cot (−555∘) = 1 = −2 − √3. cos (−645∘) tan (−555∘) Bài 2. 2
Vì 𝜋 < 𝛼 < 3𝜋 nên cos 𝛼 = −√1 − sin2 𝛼 = −√1 − (− 5 ) = − 12. 2 13 13
sin (𝛼 + 𝜋) = sin 𝛼cos 𝜋 + cos 𝛼sin 𝜋 = (− 5 ) ⋅ √3 + (− 12) ⋅ 1 = − 5√3+12. 6 6 6 13 2 13 2 26 𝜋 𝜋 𝜋 12 5 17
cos ( − 𝛼) = cos cos 𝛼 + sin sin 𝛼 = √2 ⋅ (− ) + √2 ⋅ (− ) = − √2. 4 4 4 2 13 2 13 26 Bài 3. 2
a) Vì 0 < 𝛼 < 𝜋 nên cos 𝛼 > 0, suy ra cos 𝛼 = √1 − sin2 𝛼 = √1 − (√3) = √6. 2 3 3 √3 √6 2√2
sin 2𝛼 = 2sin 𝛼cos 𝛼 = 2 ⋅ ⋅ = ; cos 2𝛼 = 2cos2 𝛼 − 1 3 3 3 2 √6 1 = 2 ⋅ ( ) − 1 = ; 3 3
tan 2𝛼 = sin 2𝛼 = 2√2; cot 2𝛼 = 1 = √2. cos 2𝛼 tan 2𝛼 4
b) Ta có 𝜋 < 𝛼 < 2𝜋 suy ra 𝜋 < 𝛼 < 𝜋 nên cos 𝛼 < 0. 2 2 2 60 2 Do đó cos 𝛼 = − 3
√1 − sin2 𝛼 = −√1 − ( ) = − √7. 2 2 4 4 2
sin 𝛼 = 2sin 𝛼 cos 𝛼 = 2 ⋅ 3 ⋅ 3
(− √7) = − 3√7 ; cos 𝛼 = 1 − 2sin2 𝛼 = 1 − 2 ( ) = 2 2 4 4 8 2 4 − 1. 8 3√7 1 3√7
sin 2𝛼 = 2sin 𝛼cos 𝛼 = 2 (− ) (− ) = ; cos 2𝛼 = 2cos2 𝛼 − 1 8 8 32 1 2 31 = 2 ⋅ (− ) − 1 = − ; 8 32
tan 2𝛼 = sin 2𝛼 = − 3√7 ; cot 2𝛼 = 1 = − 31√7. cos 2𝛼 31 tan 2𝛼 21 Bài 4.
a) √2sin (𝛼 + 𝜋) − cos 𝛼 = √2 (sin 𝛼cos 𝜋 + cos 𝛼sin 𝜋) − cos 𝛼 4 4 4
= (sin 𝛼 + cos 𝛼) − cos 𝛼 = sin 𝛼.
b) (cos 𝛼 + sin 𝛼)2 − sin 2𝛼 = cos2 𝛼 + 2cos 𝛼sin 𝛼 + sin2 𝛼 − 2sin 𝛼cos 𝛼 = 1. Bài 5. 2 1−
a) cos 2𝛼 = 1 − 2sin2 𝛼. Do đó sin2 𝛼 = 1−cos 2𝛼 = 5 = 3 . 2 2 10
Vì − 𝜋 < 𝛼 < 0 nên sin 𝛼 < 0. Do đó sin 𝛼 = − √30. 2 10
Vì − 𝜋 < 𝛼 < 0 nên cos 𝛼 > 0. Do đó cos 𝛼 = √1 − sin2 𝛼 = √70. 2 10
tan 𝛼 = sin 𝛼 = − √21 ; cot 𝛼 = 1 = − √21. cos 𝛼 7 tan 𝛼 3
b) Vì 𝜋 < 𝛼 < 3𝜋 nên 𝜋 < 2𝛼 < 3𝜋. Do đó cos 2𝛼 < 0. 2 4 2 61 2
cos 2𝛼 = −√1 − sin2 2𝛼 = −√1 − (− 4) = − √65. 9 9
Vì 𝜋 < 𝛼 < 3𝜋 nên sin 𝛼 > 0. Do đó sin 𝛼 = √1−cos 2𝛼 = √9+√65. 2 4 2 18
Vì 𝜋 < 𝛼 < 3𝜋 nên cos 𝛼 < 0. Do đó cos 𝛼 = −√1 − sin2 𝛼 = −√9−√65. 2 4 18
tan 𝛼 = sin 𝛼 = −√9+√65 ; cot 𝛼 = 1 = −√9−√65. cos 𝛼 9−√65 tan 𝛼 9+√65 Bài 6.
Trong tam giác 𝐴𝐵𝐶, ta có 𝐴̂ + 𝐵̂ + 𝐶̂ = 180∘.
Do đó sin 𝐴 = sin (180∘ − (𝐵 + 𝐶)) = sin (𝐵 + 𝐶) = sin 𝐵cos 𝐶 + sin 𝐶cos 𝐵.
D. HOẠT ĐỘNG VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập.
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 7, 8, 9 (SGK -tr. 24)
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ. 62
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: Bài 7. Đặt 𝛼 = 𝐵𝐴𝐶
̂. Vì tam giác 𝐴𝐵𝐶 vuông tại 𝐵 nên tan 𝛼 = 𝐵𝐶 = 3. 𝐴𝐵 4 3+√3 Suy ra tan 𝐵𝐴𝐷
̂ = tan (𝛼 + 30∘) = tan 𝛼+tan 30∘ = 4 3 = 48+25√3. 1−tan 𝛼tan 30∘ 3 1− ⋅√3 39 4 3
Ta có 𝐵𝐷 = 𝐴𝐵 ⋅ tan 𝐵𝐴𝐷
̂ = 4 ⋅ 48+25√3 = 192+100√3. 39 39
Vậy 𝐶𝐷 = 𝐵𝐷 − 𝐵𝐶 = 192+100√3 − 3 = 75+100√3. 39 39 Bài 8.
a) Vì độ dài 𝐻𝑀 xem như không đổi và khi 𝛼 = 𝜋 thì 𝐻𝑀 = 𝐼𝑂, nên ta xem như 𝐻𝑀 2 luôn bằng 𝐼𝑂. 63 Do đó 𝑂𝑀
⃗ = 𝐼𝐻, hay toạ độ 𝑥𝑀 của 𝑀 trên trục 𝑂𝑥 bằng tọa độ của 𝐻 trên trục 𝐼𝑥.
Suy ra 𝑥𝑀 ≈ 𝐼𝐴 ⋅ cos 𝛼 = 8cos 𝛼(cm).
b) Giả sử sau 1 phút chuyển động, 𝐼𝐴 quay được một góc 𝛽 thì sau 2 phút chuyển động,
𝐼𝐴 quay được một góc 2𝛽.
Ta có sau 1 phút chuyển động thì 𝑥𝑀 ≈ 8cos 𝛽 = −3. Suy ra cos 𝛽 = − 3. 8
Do đó sau 2 phút chuyển động thì 23
𝑥𝑀 ≈ 8cos 2𝛽 = 8(2cos2 𝛽 − 1) = − = 4 −5,75( cm). Bài 9.
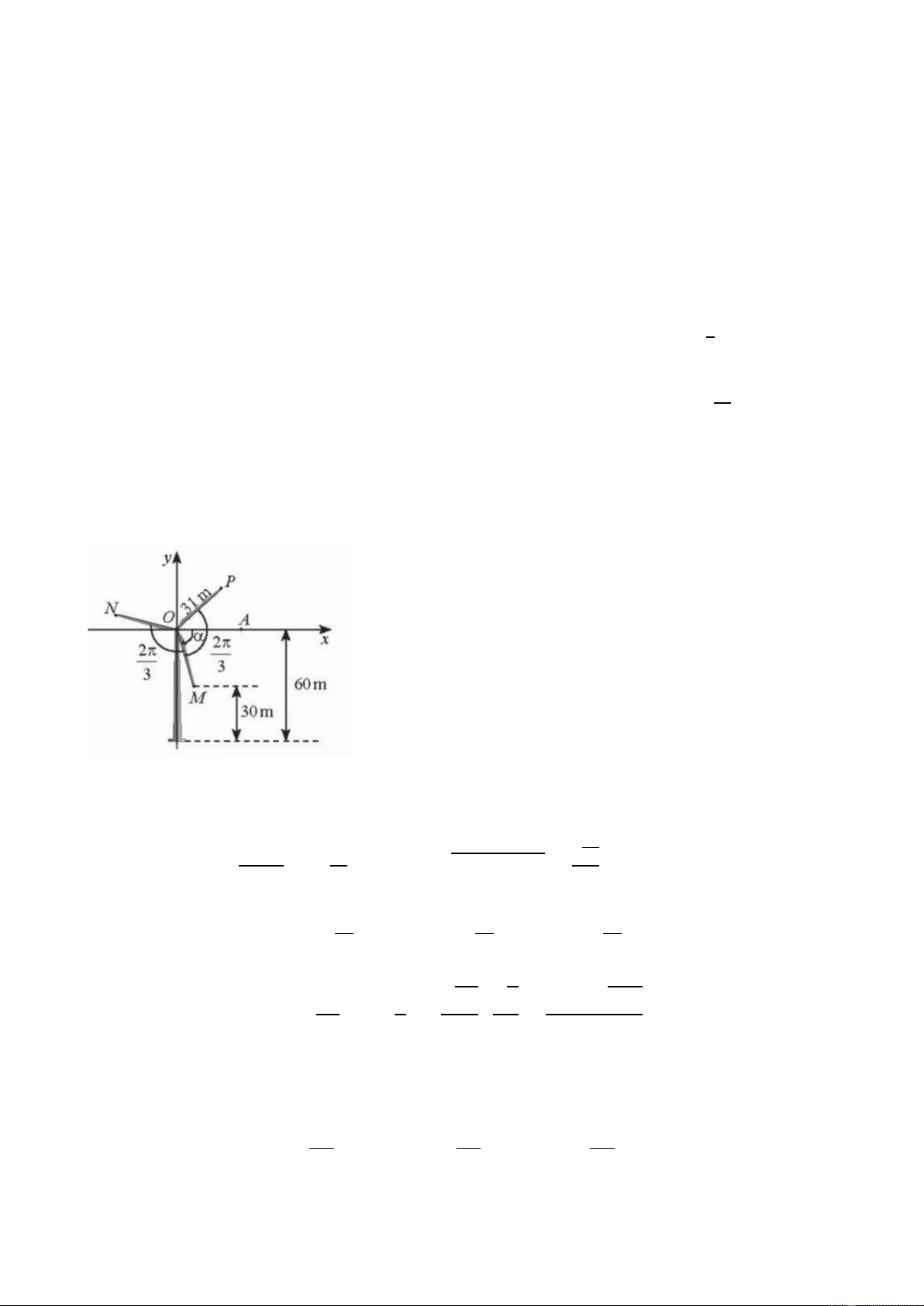
a) Trong hệ truc toạ đô 𝑥𝑂𝑦 như hình, ta có điểm 𝑀 nằm ở góc phần tư thứ IV.
Do đó sin 𝛼 = − 60−30 = − 30 ; cos 𝛼 = √1 − sin2 𝛼 = √61. 31 31 31
b) sin (𝑂𝐴, 𝑂𝑁) = sin (𝛼 − 2𝜋) = sin 𝛼cos 2𝜋 − cos 𝛼sin 2𝜋 3 3 3 30 1 √61 √3 30 − √183 = (− ) ⋅ (− ) − ⋅ = . 31 2 31 2 62
Khoảng cách từ 𝑁 đến mặt đất là 60 + 31sin (𝑂𝐴, 𝑂𝑁) ≈ 68,24( m). 2𝜋 2𝜋 2𝜋
sin (𝑂𝐴, 𝑂𝑃) = sin (𝛼 + ) = sin 𝛼cos + cos 𝛼sin 3 3 3 64 30 1 30+ = − ⋅ (− ) + √61 ⋅ √3 = √183. 31 2 31 2 62
Khoảng cách từ 𝑃 đến mặt đất là 60 + 31sin (𝑂𝐴, 𝑂𝑃) ≈ 81,76( m).
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: "Bài 4. Hàm số lượng giác và đồ thị" 65 Ngày soạn: .../.../... Ngày dạy: .../.../...
BÀI 4. HÀM SỐ LƯỢNG GIÁC VÀ ĐỒ THỊ (2 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết các khái niệm về hàm số chẵn, hàm số lẻ, hàm số tuần hoàn.
- Nhận biết các đặc trưng hình học của đồ thị hàm số chẵn, hàm số lẻ, hàm số tuần hoàn.
- Nhận biết các hàm số lượng giác 𝑦 = 𝑠𝑖𝑛 𝑥 , 𝑦 = 𝑐𝑜𝑠 𝑥 , 𝑦 = 𝑡𝑎𝑛 𝑥 , 𝑦 = 𝑐𝑜𝑡 𝑥
thông qua đường tròn lượng giác.
- Mô tả bảng giá trị của bốn hàm lượng giác đó trên một chu kì.
- Vẽ được đồ thị của các hàm số 𝑦 = 𝑠𝑖𝑛 𝑥 , 𝑦 = 𝑐𝑜𝑠 𝑥 , 𝑦 = 𝑡𝑎𝑛 𝑥 , 𝑦 = 𝑐𝑜𝑡 𝑥
- Giải thích được: tập xác định, tập giá trị, tính chẵn lẻ, tính tuần hoàn, chu kì,
khoảng đồng biến, nghịch biến của các hàm số lượng giác.
- Giải quyết một số vấn đề thực tiễn gắn với hàm số lượng giác. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học, giải quyết vấn đề toán học: So sánh, phân tích dữ
liệu tìm ra mối liên hệ giữa các đối tượng đã cho và nội dung bài học hàm số lương
giác, từ đó có thể áp dụng kiến thức đã học để giải quyết các bài toán.
- Mô hình hóa toán học: giải quyết một số vấn đề thực tiễn gắn với hàm số lượng giác. 66 - Giao tiếp toán học.
- Sử dụng công cụ, phương tiện học toán. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Khơi gợi sự hứng thú của HS về đồ thị hàm số lượng giác thông qua việc liên hệ giữa
thuật ngữ “Dạng hình sin” thường gặp trong khoa học và cuộc sống với đồ thị hàm số
sin sẽ được học trong bài.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS trả lời được câu hỏi mở đầu.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu
Vì sao mặt cắt của sóng nước trên mặt hồ được gọi là dạng hình sin? 67
- GV hướng dẫn, giới thiệu về “dạng hình sin” cho HS. (Có thể HS đã được tiếp cận ở
môn Vật lí lớp 11 trong bài Dao động điều hòa).
Một số hình ảnh về dạng hình sin trong vật lí
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung. 68
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học mới: “Bài học hôm nay chúng ta cùng tìm hiểu về hàm số và đồ thị của các
hàm số lượng giác cơ bản”.
Bài 4. Hàm số lượng giác và đồ thị.
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Hàm số lượng giác. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn. a) Mục tiêu:
- HS nhận biết khái niệm hàm số lượng giác.
- HS nhận biết được khái niệm hàm số chẵn, hàm số lẻ, hàm số tuần hoàn.
- HS nhận biết được đặc trưng hình học của hàm số chẵn, hàm số lẻ, hàm số tuần hoàn. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động mục 1 và 2.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi,
HS xác định được hàm số lượng giác là hàm số chẵn, hàm số lẻ, hàm số tuần hoàn.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ:
1. Hàm số lượng giác
Nhiệm vụ 1: Tìm hiểu hàm số lượng HĐKP 1 giác
- GV yêu cầu HS thảo luận nhóm đôi, hoàn HĐKP 1 69
Lưu ý: nhấn mạnh đơn vị đo góc được sử dụng là radian.
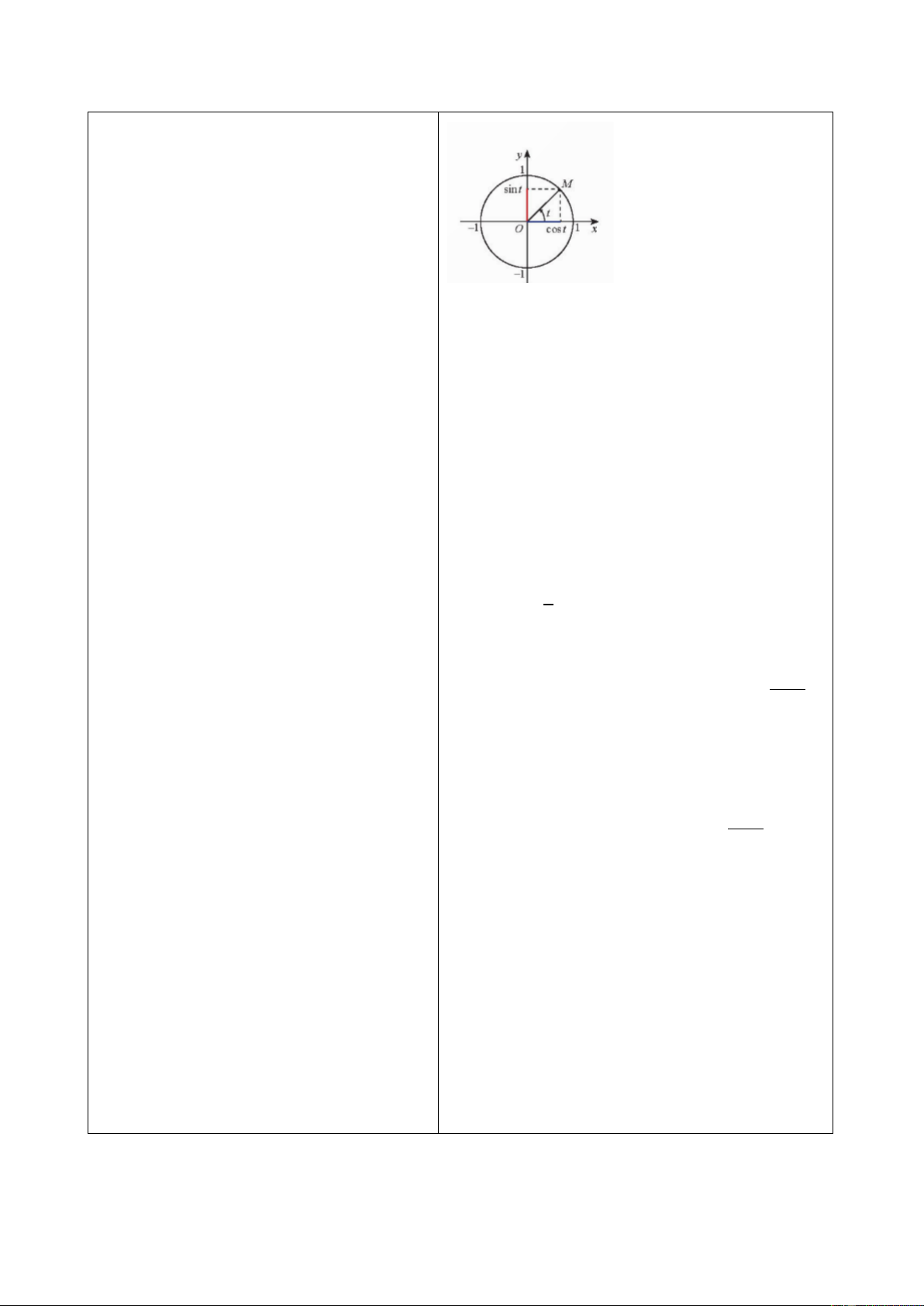
a) Với mỗi số thực 𝑡, góc lượng giác 𝑡 rad
được biểu diễn bởi một điểm duy nhất trên
đường tròn lượng giác, mỗi điểm như vậy
đều có một tung độ và một hoành độ duy
nhất, chính là sin 𝑡 và cos 𝑡.
Do đó xác định duy nhất giá trị sin 𝑡 và cos 𝑡.
b) Với 𝑡 ≠ 𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ thì cos 𝑡 ≠ 0. Vì 2 xác đị
nh duy nhất giá trị cos 𝑡 và sin 𝑡 nên
cũng xác định duy nhất giá trị tan 𝑡 = sin 𝑡. cos 𝑡
Với 𝑡 ≠ 𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ thì sin 𝑡 ≠ 0. Vỉ xác
định duy nhất giá trị cos 𝑡 và sin 𝑡 nên cũng
xác định duy nhất giá trị cot 𝑡 = cos 𝑡. sin 𝑡
Như vậy 𝑦 = sin 𝑡, 𝑦 = cos 𝑡, 𝑦 = tan 𝑡 và
𝑦 = cot 𝑡 là các hàm số.
- GV: ứng với mỗi giá trị t có một giá Kết luận
trị sin 𝑡, tương tự với các giá trị lượng
- Hàm số sin là quy tắc đặt tương ứng mỗi số
giác khác. Quy tắc đặt tương ứng đó
thực x với số thực sin 𝑥, kí hiệu 𝑦 = sin 𝑥.
thõa mãn định nghĩa hàm số. 70
Từ đó hình thành khái niệm hàm số
- Hàm số côsin là quy tắc đặt tương ứng mỗi lượng giác.
số thực x với số thực cos 𝑥, kí hiệu 𝑦 = cos 𝑥.
- Hàm số tang là hàm số được xác định bởi công thức
𝑦 = sin 𝑥 với 𝑥 ≠ 𝜋 + 𝑘𝜋(𝑘 ∈ ℤ), kí hiệu cos 𝑥 2 𝑦 = tan 𝑥.
- Hàm số côtang là hàm số được xác định bởi công thức
𝑦 = cos 𝑥 với 𝑥 ≠ 𝜋 + 𝑘𝜋(𝑘 ∈ ℤ), kí hiệu sin 𝑥 𝑦 = cot 𝑥. Nhận xét
- Tập xác định của hàm số 𝑦 = sin 𝑥 và 𝑦 =
- GV đặt câu hỏi: Nêu tập xác định của cos 𝑥 là ℝ.
các hàm số lượng giác đó?
- Tập xác định của hàm số 𝑦 = tan 𝑥 là 𝐷 = ℝ\ 𝜋 { + 𝑘𝜋|𝑘 ∈ ℤ} 2
- Tập xác định của hàm số 𝑦 = cot 𝑥 là 𝐷 = ℝ\{𝑘𝜋|𝑘 ∈ ℤ}.
2. Hàm số chẵn, hàm số lẻ, hàm số tuần
Nhiệm vụ 2: Tìm hiểu về hàm số chẵn, hoàn hàm số lẻ.
a) Hàm số chẵn, hàm số lẻ
- HS thực hiện HĐKP 2.
- GV tổng quát hai trường hợp: HĐKP 2 71
+ Tổng quát, đồ thị của một hàm số đối
xứng qua trục 𝑂𝑦 khi và chủ khi với
mồi điểm " (𝑥; 𝑓(𝑥)) thuộc đồ thị hàm
số thì điểm (−𝑥; 𝑓(𝑥)) cũng thuộc đồ
thị hàm số, nói cách khác, nếu 𝑥 thuộc
tập xác định thì −𝑥 cũng thuộc tập xác
định và 𝑓(−𝑥) = 𝑓(𝑥). Tử đây, ta có
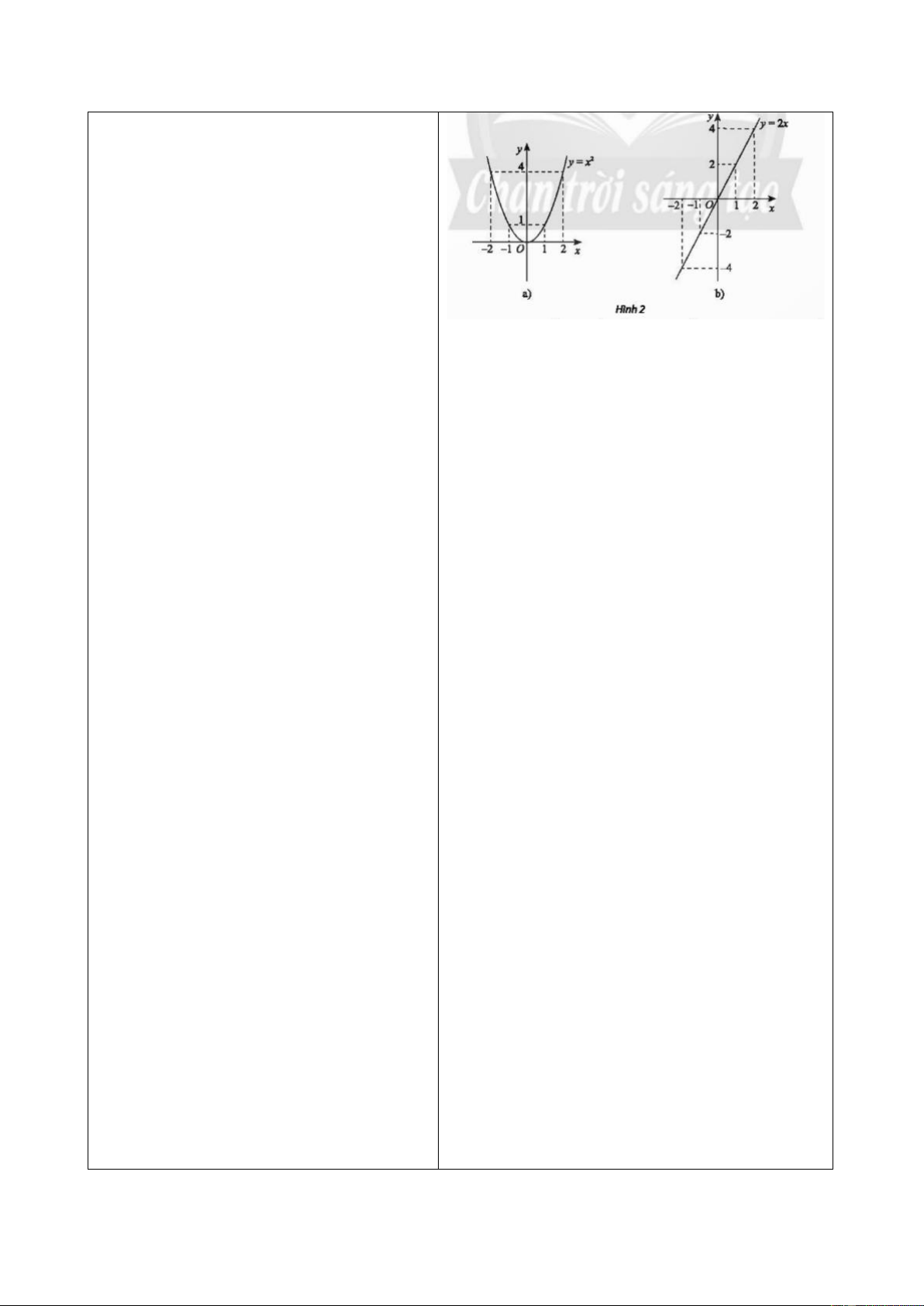
a) 𝑦(−1) = 𝑦(1) và 𝑦(−2) = 𝑦(2).
khái niệm , hàm số chẵn.
Quan sát Hình 2a, ta thấy đồ thị hàm số 𝑦 =
+ Tổng quát, đồ thị của một hàm số đối 𝑥2 đối xứng qua trục 𝑂𝑦. Điều này có được
xứng qua gốc toạ độ 𝑂 khi và chỉ khi
vì giá trị hàm số 𝑦 = 𝑥2 tại 𝑥 và −𝑥 là bằng
với mỗi điễm (𝑥; 𝑓(𝑥)) thuộc đồ thị
nhau với mọi 𝑥 ∈ ℝ.
hàm số thì điểm (−𝑥; −𝑓(𝑥)) cũng
thuộc đồ thị hàm số, nói cách khác, nếu b) 𝑦(−1) = −𝑦(1) và 𝑦(−2) = −𝑦(2).
𝑥 thuộc tập xác định thì −𝑥 cũng thuộc Quan sát Hình 2𝑏, ta thấy đồ thị hàm số 𝑦 =
tập xác định và 𝑓(−𝑥) = −𝑓(𝑥). Từ
2𝑥 đối xúng qua gốc tọa độ 𝑂. Điều này có
đây, ta có khái niệm hàm số lẻ.
được vì giá trị hàm số 𝑦 = 2𝑥 ại 𝑥 và −𝑥 là
đối nhau với mọi 𝑥 ∈ ℝ.
- GV giới thiệu định nghĩa hàm số chẵn, hàm số lẻ. Định nghĩa
- GV chú ý về đồ thị hàm số chẵn, lẻ.
Cho hàm số 𝑦 = 𝑓(𝑥) có tập xác định là 𝐷.
- GV lưu ý: Có hàm số không lẻ, không
+ Hàm số 𝑦 = 𝑓(𝑥) với tập xác định D được chẵn. + Các bước cơ bản để
gọi là hàm số chẵn nếu với mọi 𝑥 ∈ 𝐷 ta có xác định hàm số −𝑥 ∈ 𝐷 chẵn, lẻ:
và 𝑓(−𝑥) = 𝑓(𝑥).
Tìm tập xác định của hàm số.
+ Hàm số 𝑦 = 𝑓(𝑥) với tập xác định D được
Xét x và – x có thuộc vào tập xác định gọi là hàm số lẻ nếu với mọi 𝑥 ∈ 𝐷 ta có D không
−𝑥 ∈ 𝐷 và 𝑓(−𝑥) = −𝑓(𝑥).
Tính 𝑓(−𝑥) và 𝑓(𝑥) và so sánh. Nhận xét
- HS đọc hiểu Ví dụ 1 72
- HS thực hiện Thực hành 1.
Đồ thị của hàm số chẵn nhận trục tung là trục đối xứng.
Đồ thị của hàm số lẻ nhận gốc tọa độ là tâm đối xứng.
Ví dụ 1 (SGK -tr.27) Thực hành 1
+) Hàm số 𝑦 = sin 𝑥 có tập xác định là ℝ.
Với mọi 𝑥 ∈ ℝ thì −𝑥 ∈ ℝ và sin (−𝑥) = −sin 𝑥.
Do đó 𝑦 = sin 𝑥 là hàm số lẻ.
+) Hàm số 𝑦 = cot 𝑥 có tập xác định là ℝ ∖ {𝑘𝜋 ∣ 𝑘 ∈ ℤ).
Với mọi 𝑥 ≠ 𝑘𝜋, 𝑘 ∈ ℤ thì −𝑥 ≠ −𝑘𝜋, 𝑘 ∈
ℤ, cũng có nghĩa là −𝑥 ≠ 𝑘𝜋, 𝑘 ∈ ℤ. Hơn
nũa, cot (−𝑥) = −cot 𝑥. Do đó 𝑦 = cot 𝑥 là hàm số lẻ.
Nhiệm vụ 3: Tìm hiểu hàm số tuần b) Hàm số tuần hoàn hoàn HĐKP 3
- HS thực hiện HĐKP 3.
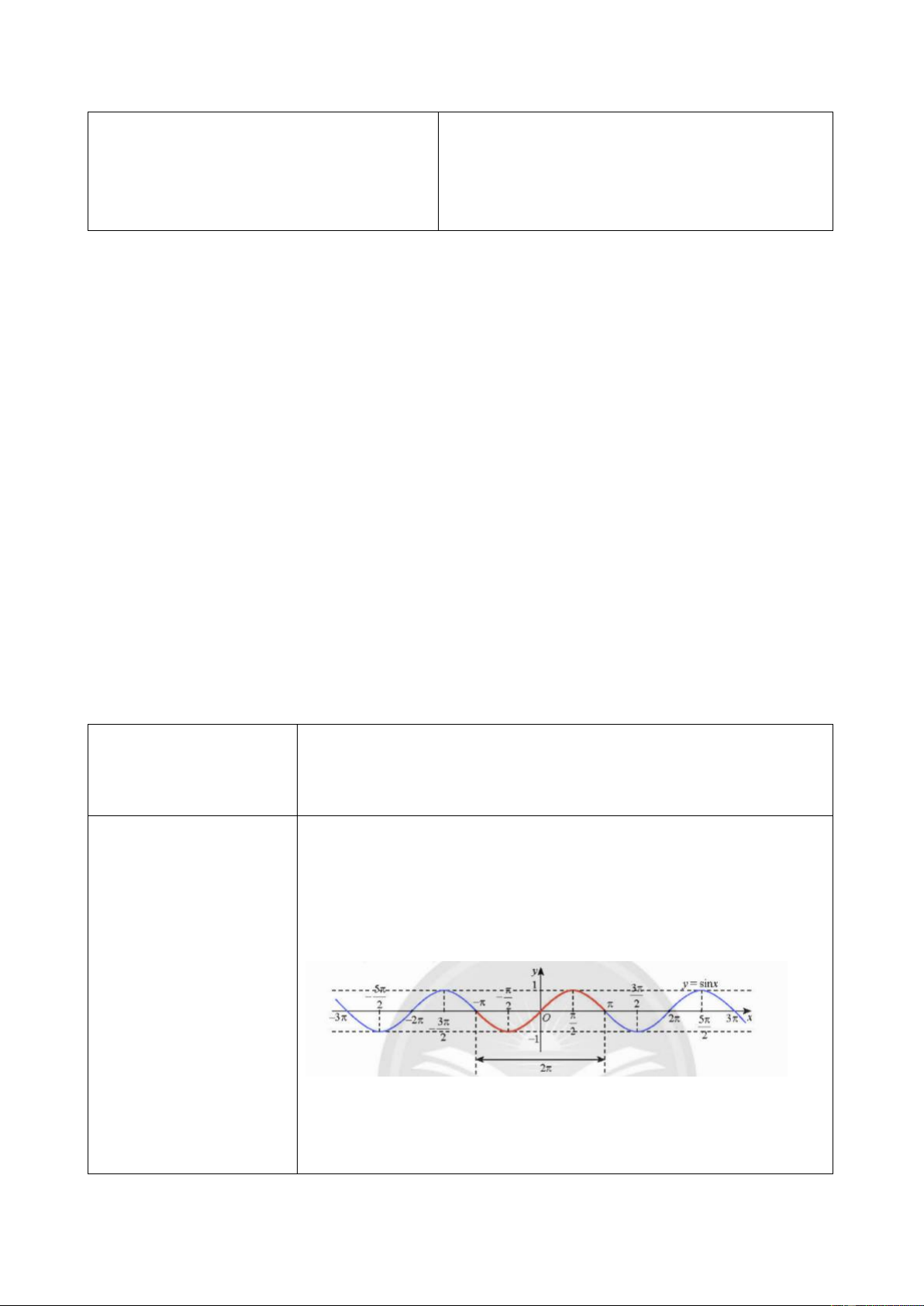
- GV giới thiệu về hàm số tuần hoàn và 𝑇 bằng 2𝜋 hoặc một bội bất kì khác của 2𝜋.
chu kì tuần hoàn của hàm số.
Như vậy giá trị của hàm số sin lặp lại trên
+ Chú ý về đồ thị của hàm số tuần hoàn. từng đoạn có độ dài 2𝜋.
(có thể cho HS dự đoán trước). Kết luận
Hàm số y = f(x) có tập xác định D được gọi
là hàm số tuần hoàn nếu tồn tại 𝑇 ≠ 0 sao 73
cho: với mọi 𝑥 ∈ 𝐷, ta có 𝑥 ± 𝑇 ∈ 𝐷 và
𝑓(𝑥 + 𝑇) = 𝑓(𝑥), ∀𝑥 ∈ 𝐷.
Số T dương nhỏ nhất thỏa mãn các điều kiện
trên (nếu có) được gọi là chu kì của hàm số tuần hoàn y = f(x). Chú ý:
Đồ thị của hàm số tuần hoàn chu kì T được
lặp lại trên từng đoạn giá trị của x có độ dài T.
- HS đọc hiểu Ví dụ 2.
Ví dụ 2 (SGK -tr.27)
- HS thực hiện Thực hành 2.
- HS nhắc lại tính chất của Thực hành 2
sin 𝛼 𝑣à sin(𝛼 + 𝑘2𝜋) ;
Hàm số 𝑦 = cos 𝑥 là hàm số tuần hoàn vì
tan 𝛼 𝑣à tan(𝛼 + 𝑘𝜋).
với mọi 𝑥 ∈ ℝ ta có 𝑥 + 2𝜋 ∈ ℝ và Từ đó có chú ý.
cos (𝑥 + 2𝜋) = cos 𝑥.
Bước 2: Thực hiện nhiệm vụ:
Hàm số 𝑦 = cot 𝑥 là hàm số tuần hoàn vì
- HS theo dõi SGK, chú ý nghe, tiếp với mọi 𝑥 ∈ ℝ ∖ {𝑘𝜋 ∣ 𝑘 ∈ ℤ} ta có
nhận kiến thức, hoàn thành các yêu cầu, thảo luận nhóm.
𝑥 + 𝜋 ∈ ℝ ∖ {𝑘𝜋 ∣ 𝑘 ∈ ℤ} và cot (𝑥 + 𝜋) = cot 𝑥. - GV quan sát hỗ trợ.
Bước 3: Báo cáo, thảo luận: Chú ý:
- HS giơ tay phát biểu, lên bảng trình a) Các hàm số 𝑦 = sin 𝑥 và 𝑦 = cos 𝑥 là các bày
hàm số tuần hoàn với chu kì 2𝜋.
- Một số HS khác nhận xét, bổ sung cho
b) Các hàm số 𝑦 = tan 𝑥 và 𝑦 = cot 𝑥 là các bạn.
hàm số tuần hoàn với chu kì 𝜋. 74
Bước 4: Kết luận, nhận định: GV tổng
quát lưu ý lại kiến thức trọng tâm và yêu
cầu HS ghi chép đầy đủ vào vở.
Hoạt động 2: Đồ thị của các hàm số lượng giác a) Mục tiêu:
- HS vẽ được đồ thị của các hàm số lượng giác cơ bản.
- HS giải thích được: tập xác định, tập giá trị, tính chất chẵn lẻ, chu kì, tínhđồng biến,
nghịch biến của hàm số lượng giác cơ bản.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động mục 3.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi và hoạt động.
d) Tổ chức thực hiện: HOẠT ĐỘNG CỦA
SẢN PHẨM DỰ KIẾN GV VÀ HS Bướ 3. Đồ c 1: Chuyển giao
thị của các hàm số lượng giác nhiệm vụ:
a) Hàm số 𝒚 = 𝐬𝐢𝐧 𝒙
HĐKP 4 (Bảng dưới)
- GV yêu cầu HS thảo Kết luận luận nhóm 4, hoàn thành HĐKP 4 - Từ đó GV giới thiệu
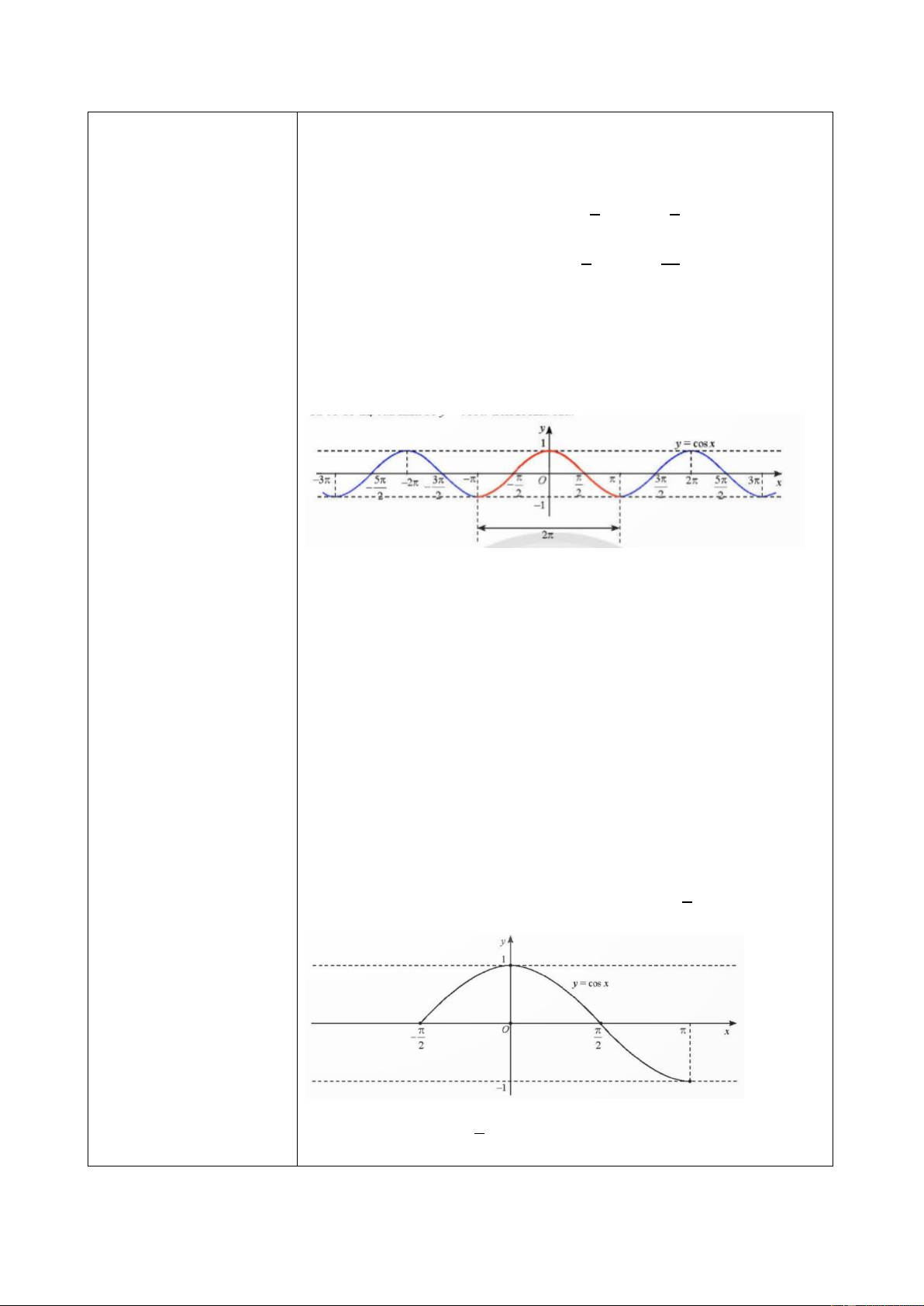
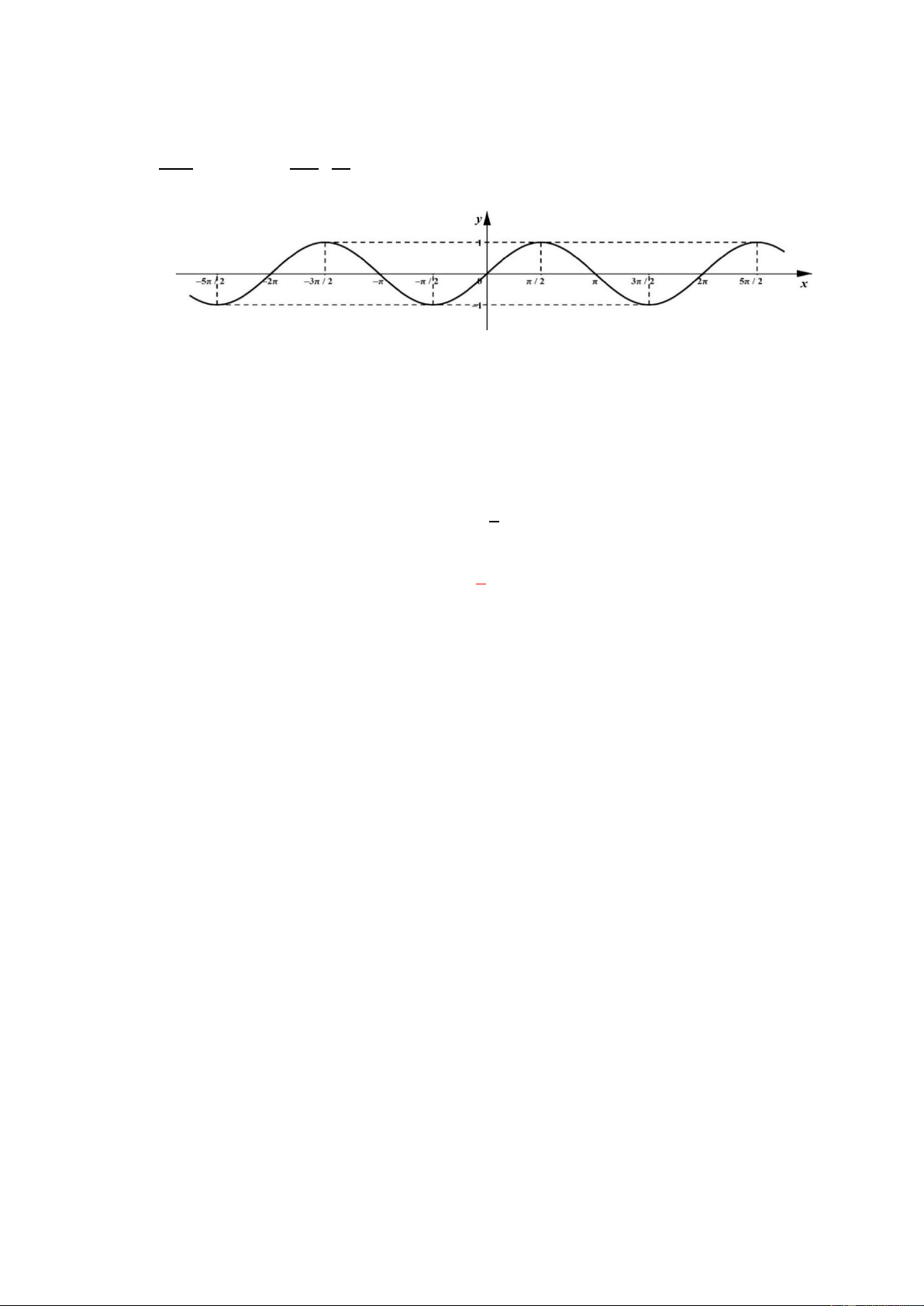
về đồ thị hàm số của
hàm lượng giác cơ bản. • TXĐ: 𝐷 = ℝ.
• Tập giá trị: [−1; 1]. 75
- Tương tự HS có thể • Hàm số tuần hoàn với chu kì 2𝜋.
thực hiện tìm hiểu các • Là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O.
HĐKP 5. Từ đó rút ra • Đồng biến trên mỗi khoảng (−𝜋 + 𝑘2𝜋;𝜋 + 𝑘2𝜋) và
kết luận về đồ thị hàm 2 2 𝜋 số y = cos x.
nghịch biến trên mỗi khoảng ( + 𝑘2𝜋; 3𝜋 + 𝑘2𝜋) , 𝑘 ∈ ℤ. 2 2
- HS đọc hiểu ví dụ 3. b) Hàm số 𝒚 = 𝐜𝐨𝐬 𝒙
- Áp dụng HS thực HĐKP 5 (bảng dưới)
hiện Thực hành 3, Kết luận Vận dụng 1. - HS tìm hiểu HĐKP 6, HĐKP 7 theo nhóm 4.
- GV cho HS nêu kết • TXĐ: 𝐷 = ℝ.
luận về đồ thị hàm số y • Tập giá trị: [−1;1]. =tan x và y = cot x. •
- HS đọc, giải thích ví
Hàm số tuần hoàn với chu kì 2𝜋. dụ 4
Là hàm số chẵn và đồ thị đối xứng qua trục tung Oy.
- HS thực hiện Thực • Đồng biến trên mỗi khoảng (−𝜋 + 𝑘2𝜋; 𝑘2𝜋) và nghịch hành 4 và Vận dụng 2.
biến trên mỗi khoảng (𝑘2𝜋; 𝜋 + 𝑘2𝜋), 𝑘 ∈ ℤ.
Bước 2: Thực hiện Ví dụ 3 (SGK -tr.29) nhiệm vụ: Thực hành 3
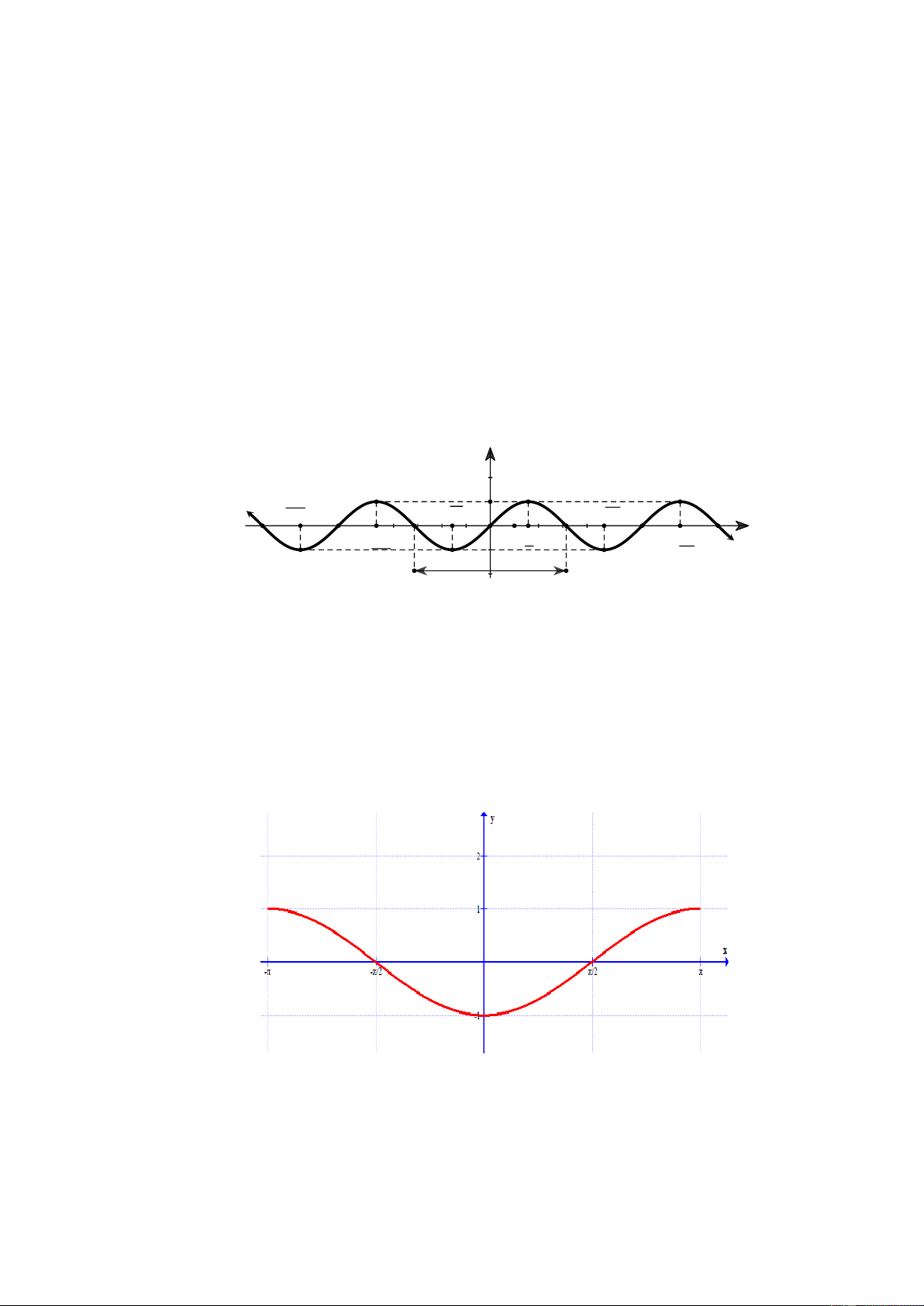
- HS theo dõi SGK, a) Ta có đồ thị hàm số 𝑦 = cos 𝑥 với 𝑥 ∈ [− 𝜋 ; 𝜋] 2 chú ý nghe, tiếp nhận
kiến thức, suy nghĩ trả
lời câu hỏi, hoàn thành các yêu cầu. - GV: quan sát và trợ giúp HS.
b) Xét trên đoạn [− 𝜋 ; 𝜋] 2 76
Bước 3: Báo cáo, thảo Tại điểm có hoành độ 𝑥 = 0 thì hàm số đạt giá trị lớn nhất là luận: 𝑦 = 1 .
- HS giơ tay phát biểu, c) Khi 𝑥 ∈ [− 𝜋 ; 𝜋] thì sin (𝑥 − 𝜋) < 0. 4 4 4 lên bảng trình bày Vận dụng 1:
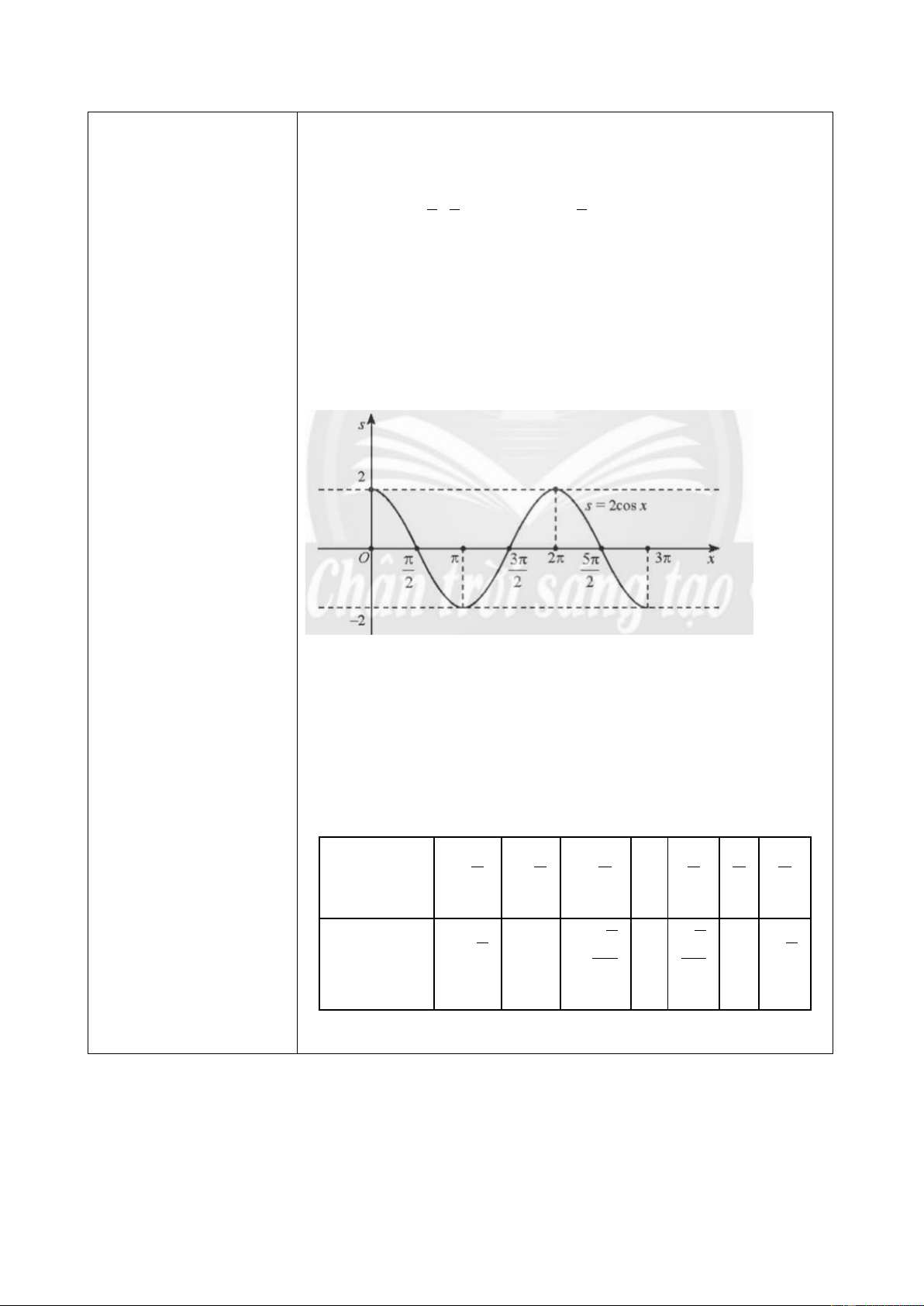
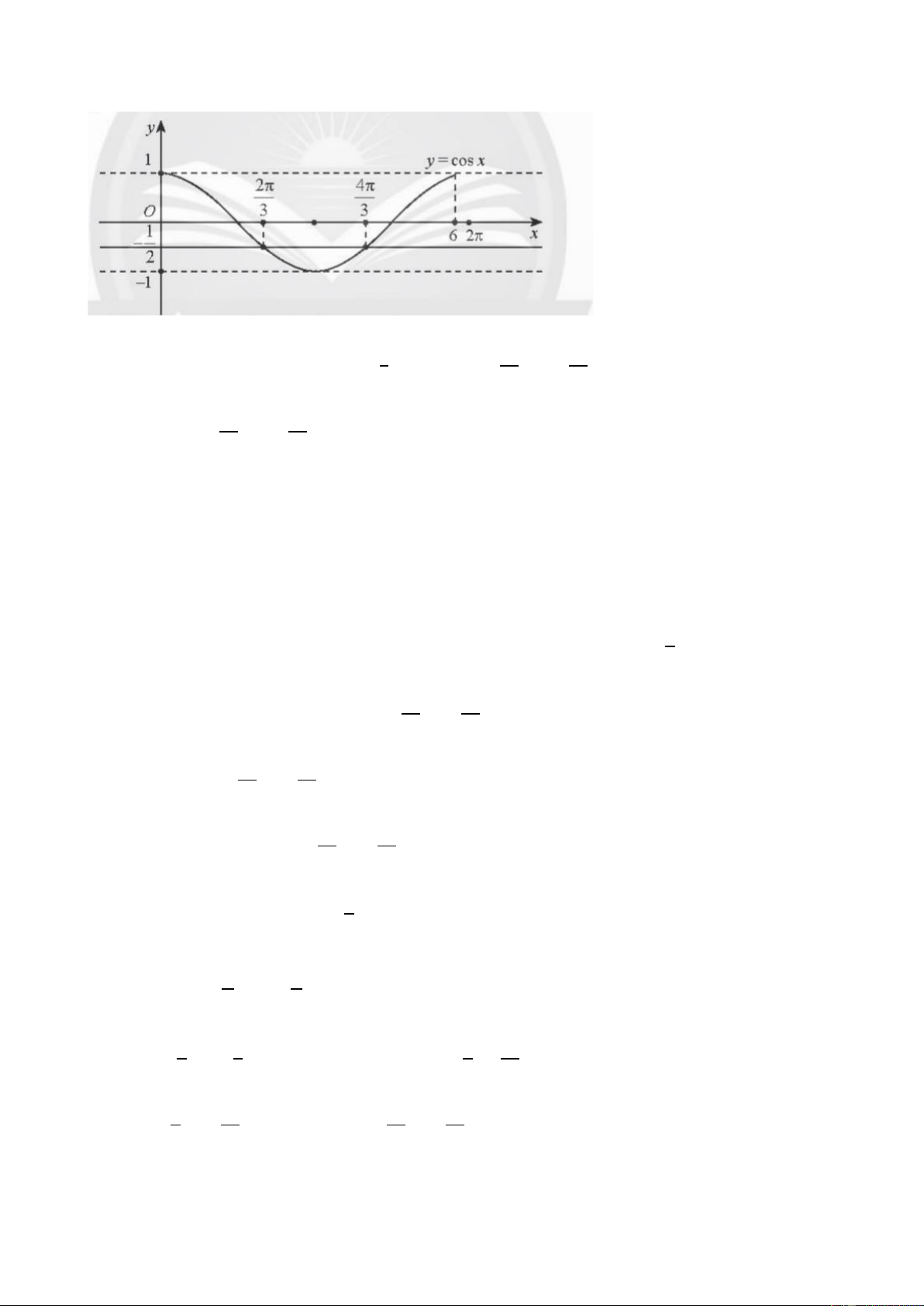
- Một số HS khác nhận Trong 3 giây đầu, ta có 0 ≤ 𝑡 ≤ 3, nên 0 ≤ 𝜋𝑡 ≤ 3𝜋. Đặt xét, bổ sung cho bạn.
𝑥 = 𝜋𝑡 và từ đồ thị hàm số côsin, ta có đồ thị hàm 𝑠 =
Bước 4: Kết luận, 2cos 𝑥 trên đoạn [0;3𝜋] như sau:
nhận định: GV tổng
quát lưu ý lại kiến thức trọng tâm và yêu cầu HS ghi chép đầy đủ vào vở.
Ta thấy 𝑠 đạt giá trị lớn nhất khi 𝑥 = 0 hoặc 𝑥 = 2𝜋. Khi dó 𝑡 = 0 hoặ 𝑡 = 2.
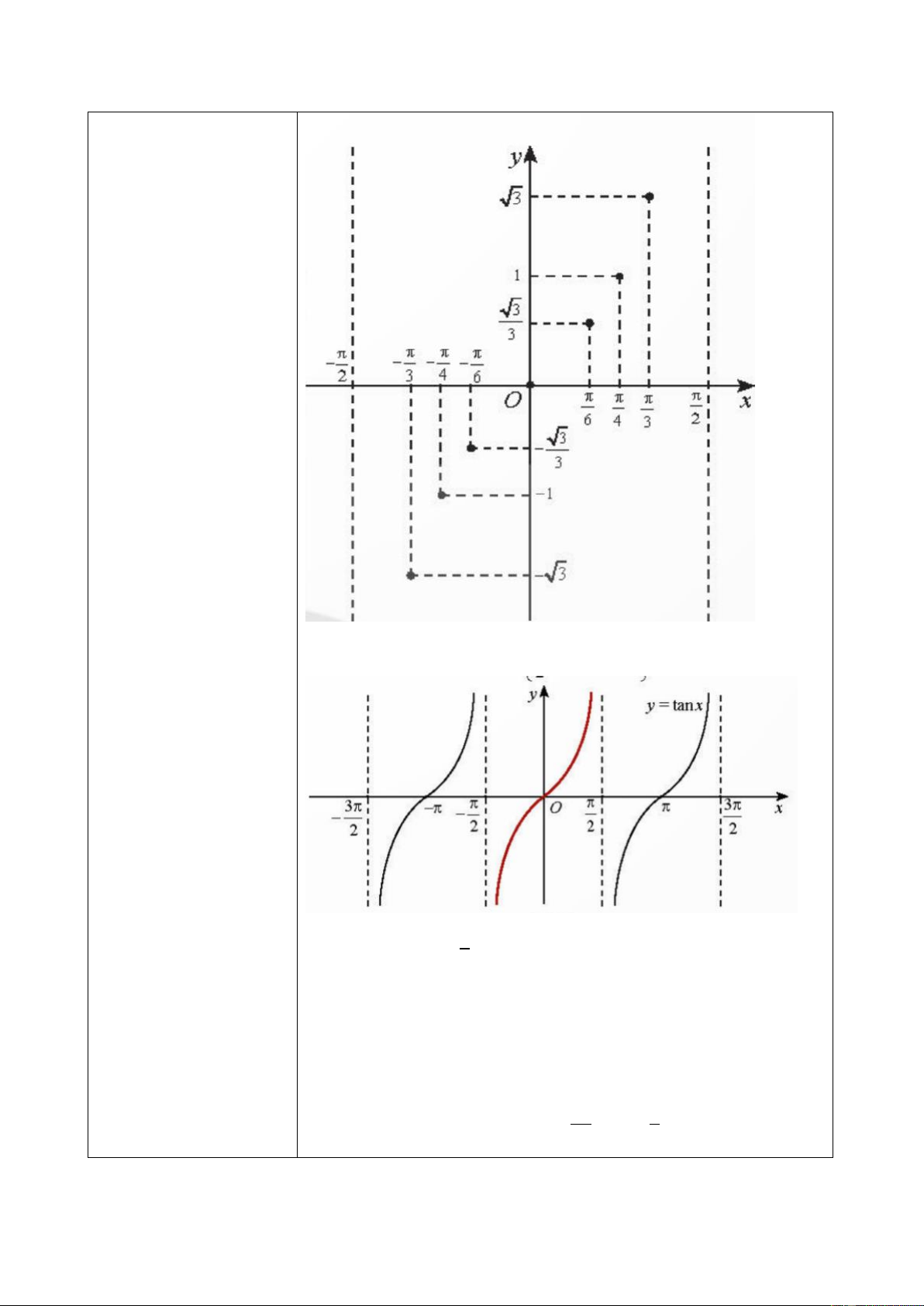
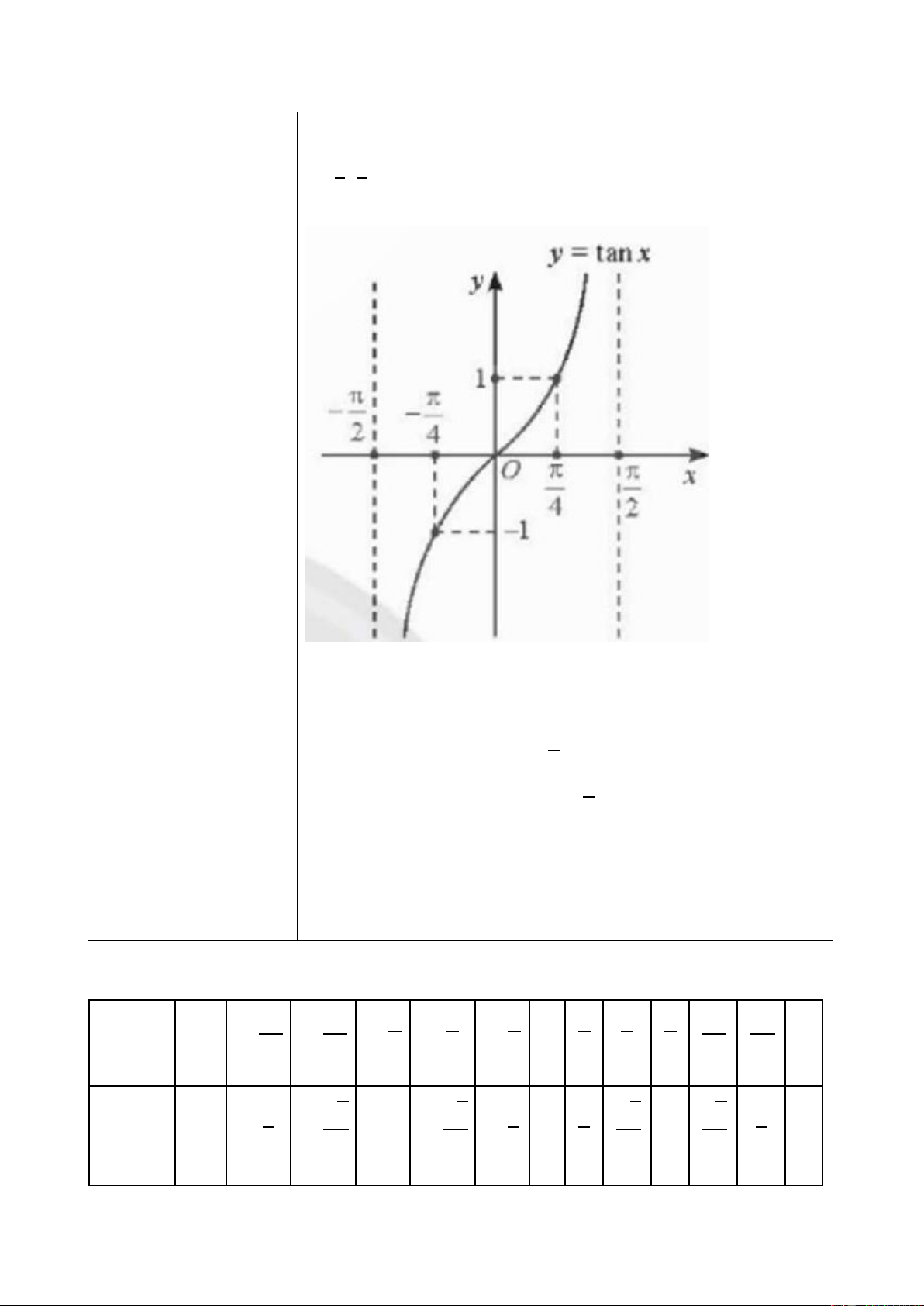
c) Hàm số 𝒚 = 𝐭𝐚𝐧 𝒙 HĐKP 6: 𝜋 𝜋 𝜋 𝜋 𝜋 𝜋 𝑥 − − − 0 3 4 6 6 4 3 𝑦 = tan 𝑥 √3 √3 −√3 -1 − 0 1 √3 3 3 77 Kết luận • 𝜋
TXĐ: 𝐷 = ℝ\ { + 𝑘𝜋|𝑘 ∈ ℤ}. 2
• Tập giá trị: ℝ.
• Hàm số tuần hoàn với chu kì 𝜋.
• Hàm số lẻ, đồ thị đối xứng qua gốc tọa độ O. • −𝜋
Đồng biến trên mỗi khoảng (
+ 𝑘𝜋; 𝜋 + 𝑘𝜋) , 𝑘 ∈ ℤ 2 2 78
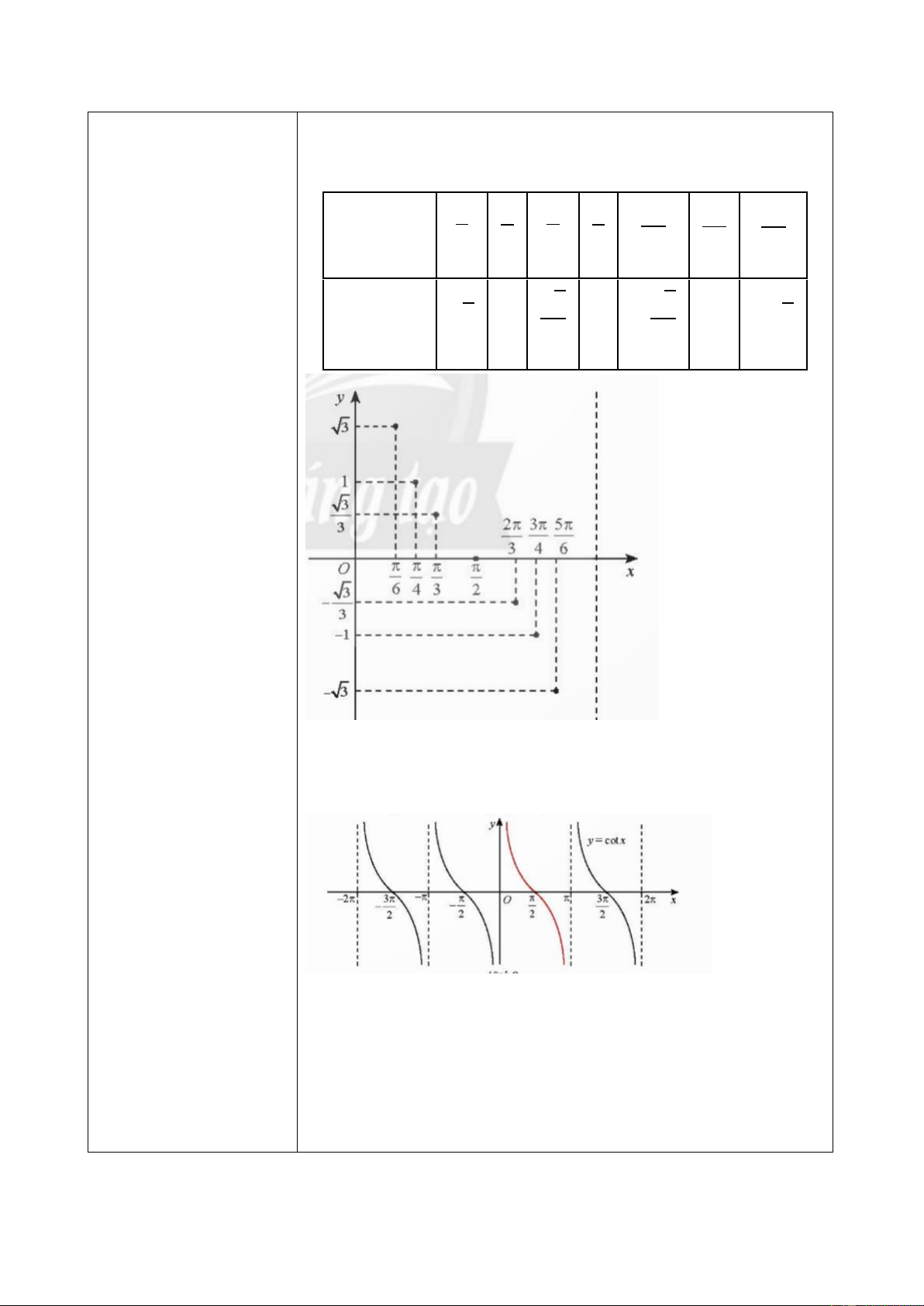
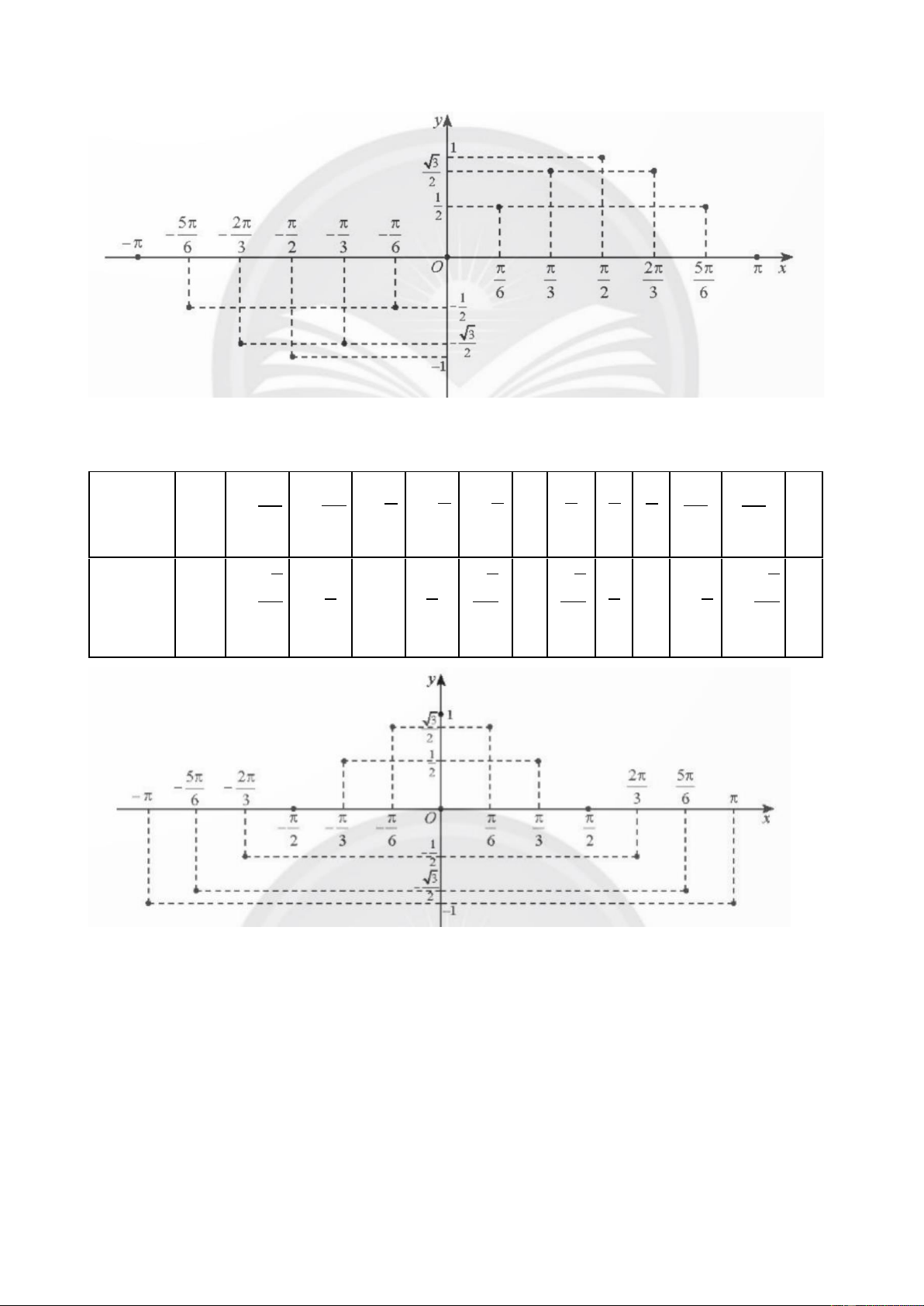
d) Hàm số 𝒚 = 𝐜𝐨𝐭 𝒙 HĐKP 7 𝜋 𝜋 𝜋 𝜋 2𝜋 3𝜋 5𝜋 𝑥 6 4 3 2 3 4 6 𝑦 = cot 𝑥 √3 √3 √3 1 0 − -1 −√3 3 3 Kết luận
• TXĐ: 𝐷 = ℝ\{𝑘𝜋|𝑘 ∈ ℤ}.
• Tập giá trị: ℝ.
• Hàm số tuần hoàn với chu kì 𝜋.
• Hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ. 79
• Nghịch biến trên mỗi khoảng (𝑘𝜋; 𝜋 + 𝑘𝜋), 𝑘 ∈ ℤ
Ví dụ 4 (SGk -tr.32) Thực hành 4
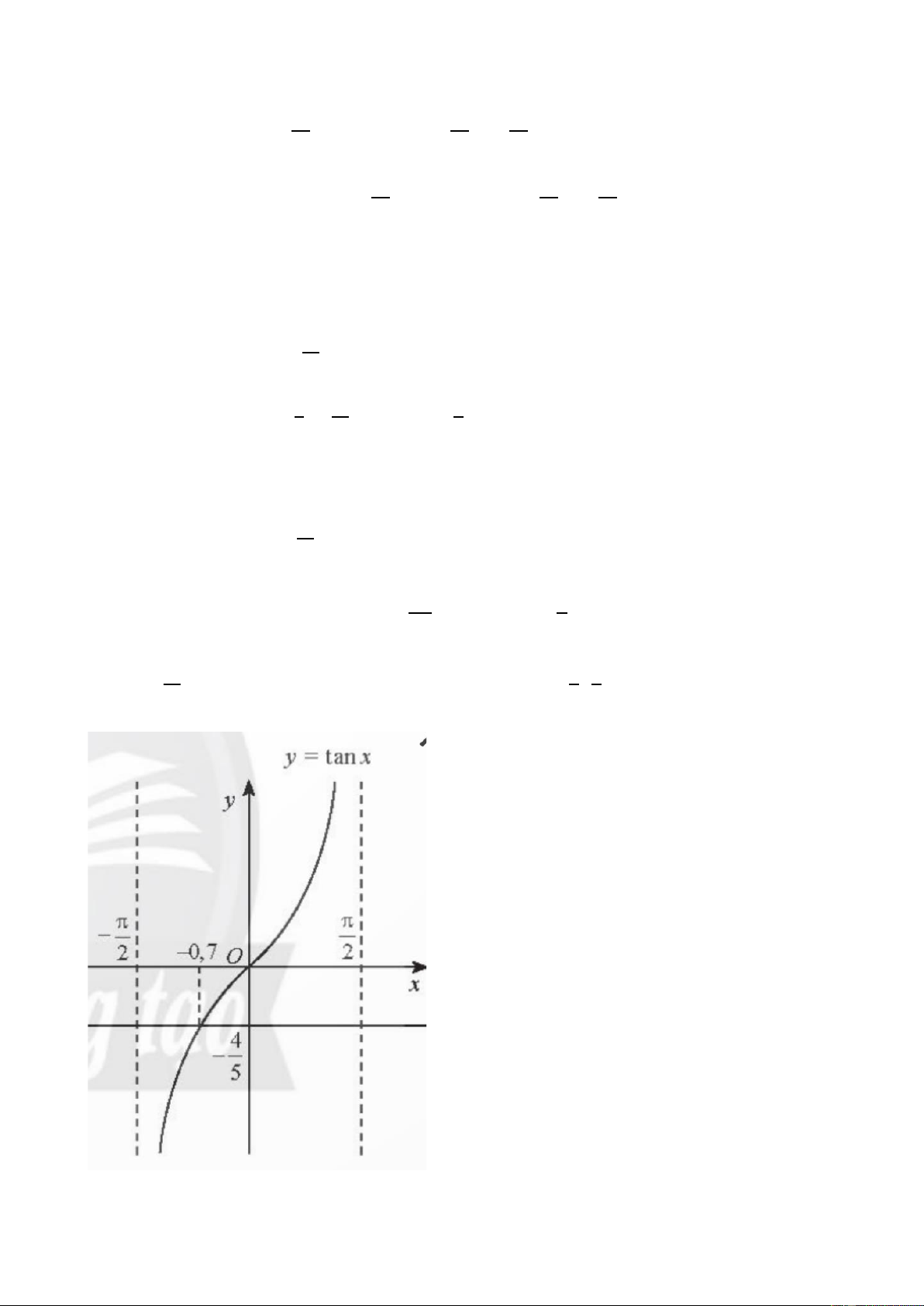
a) Ta có đồ thị hàm số 𝑦 = cot 𝑥 với 𝑥 ∈ (− 𝜋 ; 2𝜋) và 𝑥 ≠ 2 𝑘𝜋(𝑘 ∈ ℤ)
b) Trong hình dưới đây, ta thấy đồ thị hàm số 𝑦 = cot 𝑥 cắt
đường thẳng 𝑦 = 2 tại hai điểm phân biệt. Do đó, có hai giá
trị x mà tại đó giá trị hàm số bằng 2. Vận dụng 2
Điểm nằm cách xích đạo 20 cm có 𝑦 = 20 hoặc 𝑦 = −20, nghĩa là tan 𝜋 𝜋 ( 𝜑) = 1 hoặc tan ( 𝜑) = −1. 180 180
Vì − 90 < 𝜑 < 90 nên − 𝜋 < 𝜋 𝜑 < 𝜋. 2 180 2 80 Đặ 𝜋 t 𝑥 =
𝜑 và xét đồ thị hàm số 𝑦 = tan 𝑥 trên khoảng 180
(− 𝜋 ; 𝜋), ta có đồ thị như hình: 2 2
Dựa vào đồ thị, ta thấy: 𝜋 𝑦 = 1 khi 𝑥 = , suy ra 𝜑 = 45; 4 𝜋
𝑦 = −1 khi 𝑥 = − , suy ra 𝜑 = −45. 4
Vậy trên bản đồ, các điểm nằm ở vĩ độ 45∘ Bắc và 45∘ Nam
nằm cách xích đạo 20 cm. HĐKP 4 5𝜋 2𝜋 𝜋 𝜋 𝜋 𝜋 𝜋 𝜋 2𝜋 5𝜋 𝑥 −𝜋 − − − − − 0 𝜋 6 3 2 3 6 6 3 2 3 6 𝑦 1 1 1 1 0 √3 √3 √3 √3 − − -1 − − 0 1 0 = sin 𝑥 2 2 2 2 2 2 2 2 81 HĐKP 5 5𝜋 2𝜋 𝜋 𝜋 𝜋 𝜋 𝜋 𝜋 2𝜋 5𝜋 𝑥 −𝜋 − − − − − 0 𝜋 6 3 2 3 6 6 3 2 3 6 𝑦 1 1 1 1 - -1 √3 √3 √3 √3 − − 0 1 0 − − = cos 𝑥 2 2 2 2 2 2 2 2 1 HĐKP 7
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học. 82
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 1 đến 4 (SGK -tr.32+33) và các câu hỏi TN.
c) Sản phẩm học tập: Câu trả lời của HS.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS trả lời các câu hỏi TN nhanh
Câu 1. Đồ thị trong hình vẽ dưới đây là của hàm số nào? y -5 - 3 -2 - 2 3 2 2 2 x 1 -3 -3 5 O 2 2 2 2
A. 𝑦 = 𝑐𝑜𝑡 𝑥. B. 𝑦 = 𝑠𝑖𝑛 2 𝑥.
C. 𝑦 = 𝑠𝑖𝑛 𝑥.
D. 𝑦 = 𝑐𝑜𝑠 2 𝑥.
Câu 2. Cho đồ thị với 𝑥 ∈ [−𝜋; 𝜋]. Đây là đồ thị của hàm số của hàm số nào?
A. 𝑦 = 𝑐𝑜𝑠 𝑥. B. 𝑦 = − 𝑐𝑜𝑠 𝑥.
C. 𝑦 = 𝑠𝑖𝑛 𝑥 D. 𝑦 = 𝑐𝑜𝑠|𝑥|. 83
Câu 3. Dựa vào đồ thị của hàm số 𝑦 = 𝑠𝑖𝑛 𝑥, hãy tìm số nghiệm của phương trình:
𝑠𝑖𝑛 𝑥 = 1 trên đoạn −5𝜋 [ ; 5𝜋]. 2018 2 2
A. 4. B. 6. C. 10. D. 5.
Câu 4. Tìm mệnh đề sai trong các mệnh đề sau.
A. Hàm số 𝑦 = 𝑐𝑜𝑠 𝑥 tuần hoàn với chu kì 2𝜋. B. Hàm số 𝜋
𝑦 = 𝑠𝑖𝑛 𝑥 nghịch biến trên khoảng ( ; 𝜋). 2 C. Hàm số 𝜋
𝑦 = 𝑐𝑜𝑡 𝑥 đồng biến trên khoảng ( ; 𝜋). 2
D. Hàm số 𝑦 = 𝑡𝑎𝑛 𝑥 tuần hoàn với chu kì 𝜋.
Câu 5. Hàm số nào sau đây là hàm số chẵn?
A. 𝑦 = −2 𝑠𝑖𝑛 𝑥.
B. 𝑦 = 2 𝑠𝑖𝑛 2 𝑥.
C. 𝑦 = 𝑠𝑖𝑛 𝑥 − 𝑐𝑜𝑠 𝑥.
D. 𝑦 = −2 𝑐𝑜𝑠 𝑥
- GV tổ chức cho HS hoạt động thực hiện Bài tập 1 đến 4 (SGK -tr.32+33)
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng. 84
Bước 4: Kết luận, nhận định:
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác.
- GV chú ý cho HS các lỗi sai hay mắc phải
- GV nhận xét thái độ làm việc, phương án trả lời của các học sinh, ghi nhận và tuyên dương Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 C B D C D Bài 1 a) Hàm số chẵn vì
Hàm số 𝑦 = 5 sin2 𝑥 + 1 có tập xác định là ℝ.
Với mọi 𝑥 ∈ ℝ thì −𝑥 ∈ ℝ và 5 sin2(−𝑥) + 1 = 5 sin2 𝑥 + 1
b) Không là hàm số chẵn, không là hàm số lẻ;
Hàm số 𝑦 = cos 𝑥 + sin 𝑥 có tập xác định là ℝ.
Với mọi 𝑥 ∈ ℝ thì −𝑥 ∈ ℝ và cos(−𝑥) + sin(−𝑥) = cos 𝑥 − sin 𝑥 c) Hàm số lẻ.
Hàm số 𝑦 = tan 2𝑥 có tập xác định là 𝐷 = ℝ \ 𝜋 { + 𝑘𝜋} , 𝑘 ∈ ℝ. 4 2
Với mọi 𝑥 ∈ 𝐷 thì −𝑥 ∈ 𝐷 và 5 sin2(−𝑥) + 1 = 5 sin2 𝑥 + 1 Bài 2. 85
a) Hàm số đã cho xác định khi 𝜋
cos 𝑥 ≠ 0, hay 𝑥 ≠ + 𝑘𝜋, 𝑘 ∈ ℤ. 2
Tập xác định 𝐷 = ℝ ∖ 𝜋
{ + 𝑘𝜋 ∣ 𝑘 ∈ ℤ}. 2
b) Hàm số đã cho xác định khi 𝑥 + 𝜋 ≠ 𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ hay 𝑥 ≠ 𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ. 4 2 4
Tập xác định 𝐷 = ℝ ∖ 𝜋
{ + 𝑘𝜋 ∣ 𝑘 ∈ ℤ}. 4
c) Vì 0 ≤ sin2 𝑥 ≤ 1 với mọi 𝑥 ∈ ℝ, nên 2 − sin2 𝑥 ≠ 0 với mọi 𝑥 ∈ ℝ. Do đó 𝐷 = ℝ. Bài 3.
Do −1 ≤ 𝑐𝑜𝑠 𝑥 ≤ 1 nên 2. (−1) + 1 ≤ 2 𝑐𝑜𝑠 𝑥 + 1 ≤ 2.1 + 1
Vậy tập giá trị của hàm số là [−1; 3]. Bài 4.
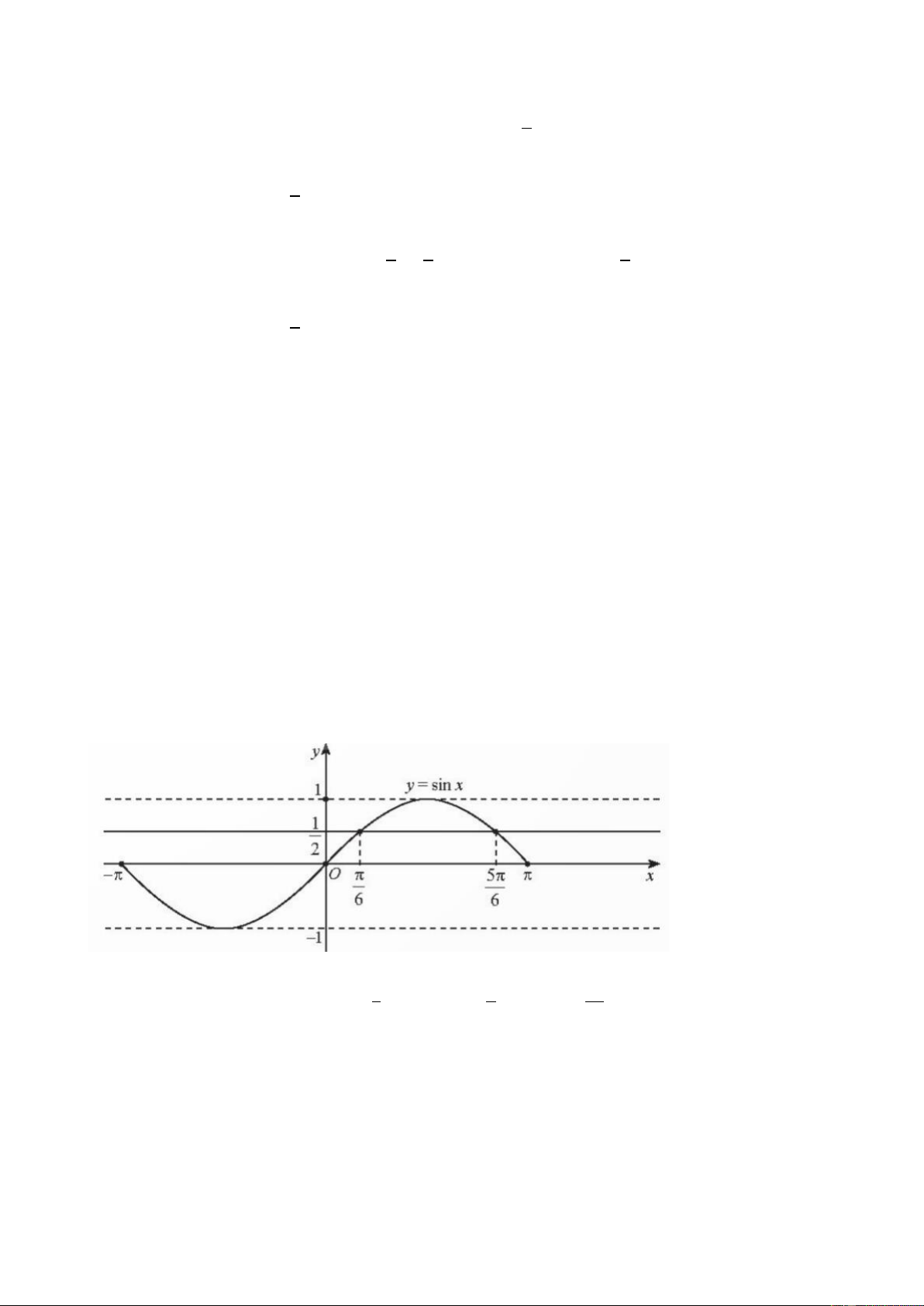
Ta có đồ thị hàm số 𝑦 = 𝑠𝑖𝑛 𝑥 trên đoạn [−𝜋; 𝜋]
Trên đoạn [−𝜋; 𝜋], ta có sin 𝑥 = 1, suy ra 𝑥 = 𝜋 hoặc 𝑥 = 5𝜋. 2 6 6
D. HOẠT ĐỘNG VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức. 86
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập.
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 5, 6, 7 (SGK -tr.33).
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: Bài 5.
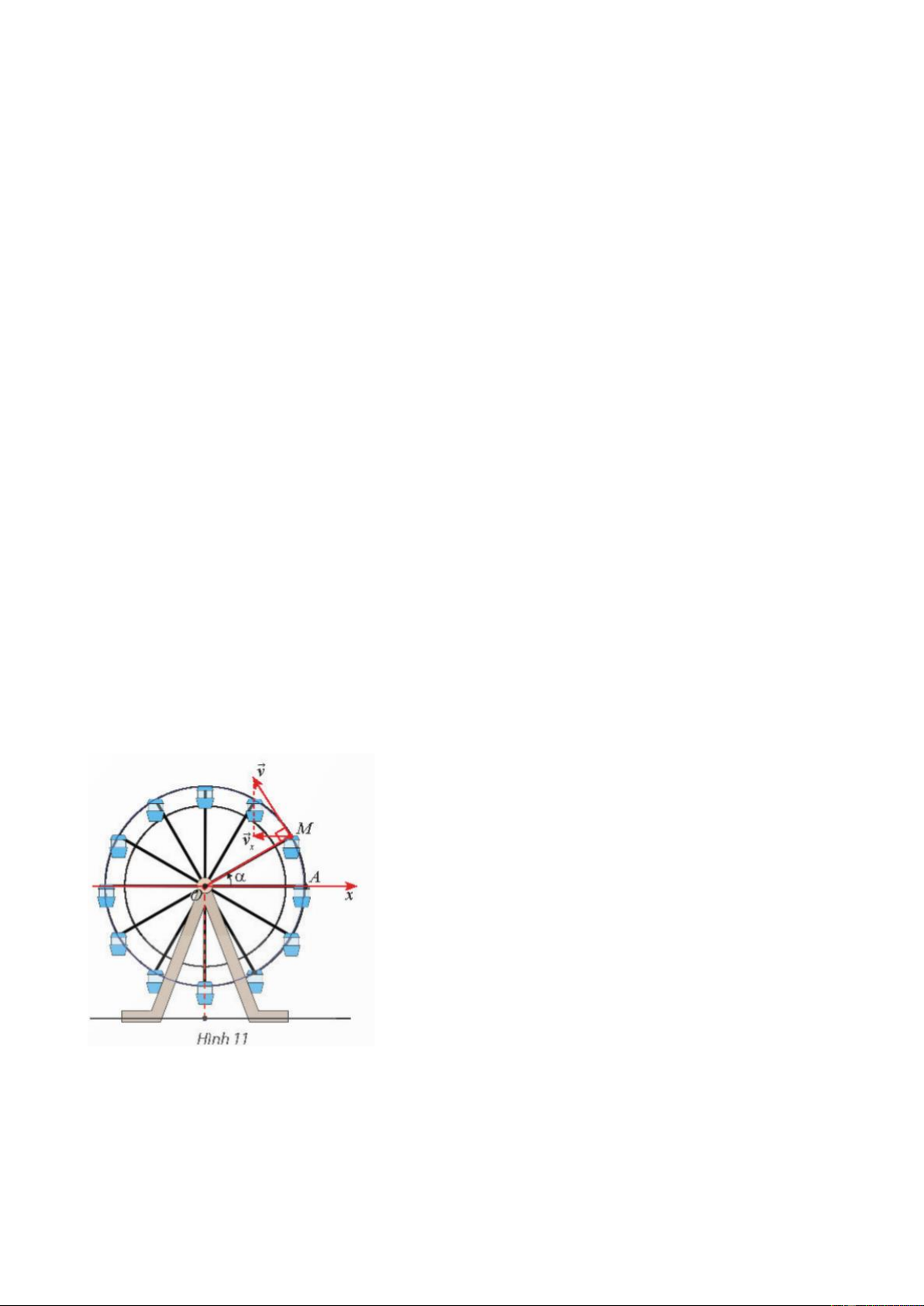
a) Ta có 𝑣𝑥 ∈ [−0,3; 0,3] với mọi 𝛼 ∈ ℝ. Do đó, giá trị lớn nhất của 𝑣𝑥 là 0,3 m/s, giá
trị nhỏ nhất của 𝑣𝑥 là −0,3 m/s. 87
b) Vì 𝑣𝑥 = 0,3sin 𝛼 nên 𝑣𝑥 tăng khi và chỉ khi sin 𝛼 tăng. Do đó, dựa vào đồ thị của
hàm sin 𝛼 trên đoạn [0; 2𝜋] trong hình dưới đây, vận tốc 𝑣𝑥 tăng khi và chỉ khi 0 <
𝛼 < 𝜋 , 3𝜋 < 𝛼 < 2𝜋. 2 2 Bài 6.
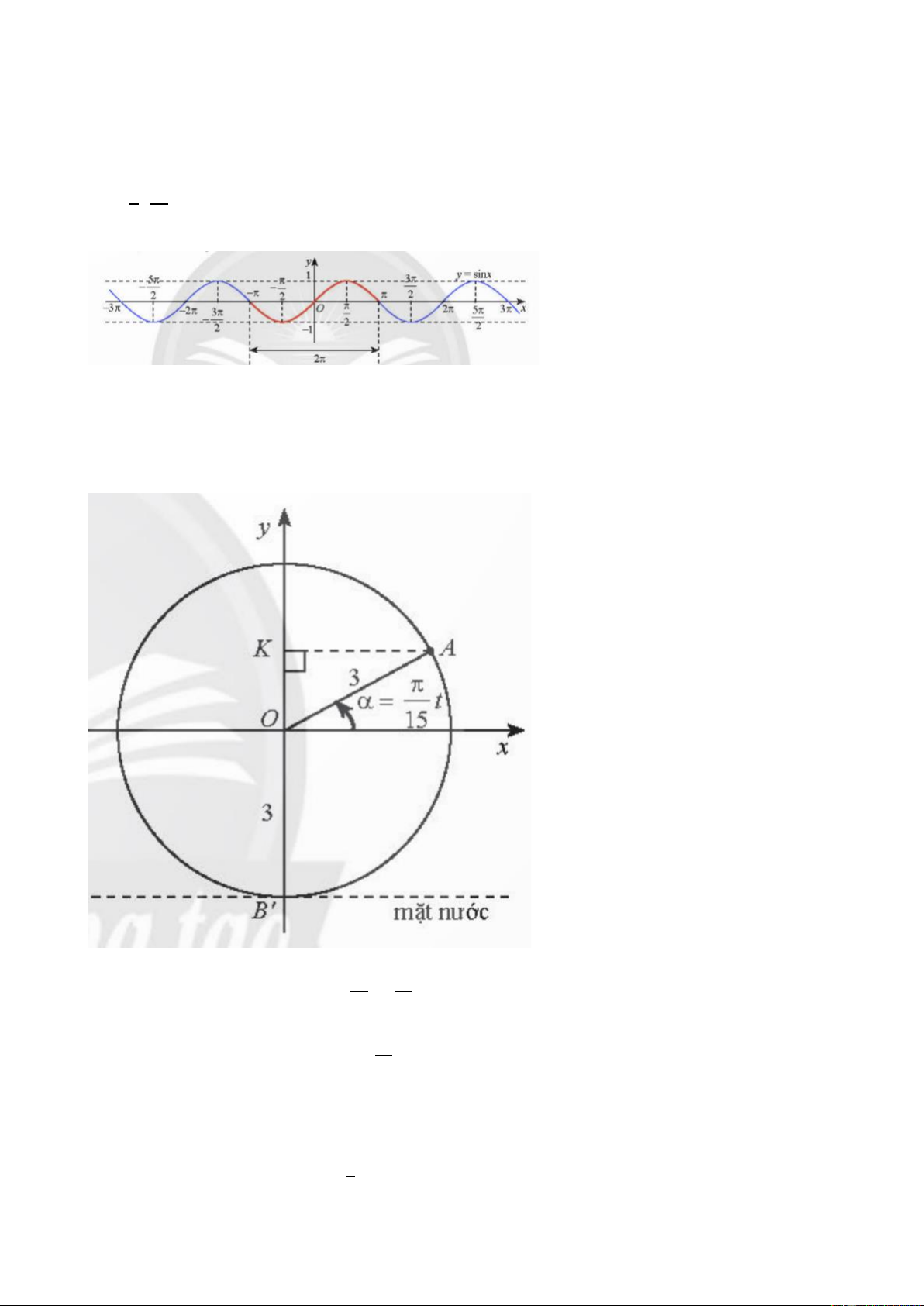
a) ℎ(𝛼) = 3 + 3sin 𝛼 = 3(1 + sin 𝛼)
b) Vận tốc góc của gàu là 𝜔 = 2𝜋 = 𝜋 (rad/s). 30 15
Góc quay của gàu 𝐺 là 𝛼 = 𝜔𝑡 = 𝜋 𝑡. 15
Trong 1 phút đầu, ta có 0 ≤ 𝑡 ≤ 60 (giây) suy ra 0 ≤ 𝛼 ≤ 4𝜋.
Vì ℎ(𝛼) = 1,5 nên sin 𝛼 = − 1. 2 88
Xét đồ thị hàm số 𝑦 = sin 𝛼 trong đoạn [0; 4𝜋] như hình, ta thấy có bốn giá trị 𝛼 thoả mãn là 𝛼 ∈ 7𝜋 { ; 11𝜋 ; 19𝜋 ; 23𝜋}. 6 6 6 6
Do đó 𝑡 ∈ {17,5; 27,5; 47,5; 57,5}. Bài 7.
a) 𝑥𝐻 = 𝐴𝐻cot 𝛼 = 500cot 𝛼.
b) Dựa vào đồ thị hàm số 𝑦 = cot 𝛼, ta thấy khi 𝜋 < 𝛼 < 2𝜋 thì − √3 < cot 𝛼 < √3. 6 3 3
Do đó − 500√3 < 500cot 𝛼 < 500√3, hay −288,7 < 𝑥 3 𝐻 < 866( m).
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: "Bài 5. Phương trình lượng giác cơ bản". 89 Ngày soạn: .../.../... Ngày dạy: .../.../...
BÀI 5: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN (2 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết công thức nghiệm của phương trình lượng giác cơ bản bằng cách vận
dụng đồ thị hàm số lượng giác tương ứng.
- Tính nghiệm gần đúng của phương trình lượng giác cơ bản bằng máy tính cầm tay.
- Giải phương trình lượng giác ở dạng vận dụng trực tiếp phương trình lượng giác cơ bản.
- Giải quyết một số vấn đề thực tiễn gắn với phương trình lượng giác. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học, giải quyết vấn đề toán học: So sánh, phân tích dữ
liệu tìm ra mối liên hệ giữa các đối tượng đã có để giải phương trình lượng giác cơ bản.
- Mô hình hóa toán học: Mô tả được các dữ liệu liên quan đến yêu cầu trong thực
tiễn, vận dụng vào phương trình lượng giác giải quyết bài toán. - Giao tiếp toán học. 90
- Sử dụng công cụ, phương tiện học toán: Tính nghiệm gần đúng của phương trình
lượng giác cơ bản bằng máy tính cầm tay. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Khơi gợi nhu cầu giải phương trình lượng giác thông qua bài toán thực tế về chuyển
động quay và dao động điều hòa.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS trả lời được câu hỏi mở đầu.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu
Trong hình, khi bàn đạp xe đạp quay, bóng M của đầu trục quay dao động trên mặt đất
quanh điểm O theo phương trình 𝑠 = 17 cos 5𝜋𝑡 với 𝑠(𝑐𝑚) là tọa độ của điểm M trên
trục Ox và t (giây) là thời gian bàn đạp quay. Làm cách nào để xác định được các thời
điểm mà tại đó độ dài bóng OM bằng 10 cm? 91
- GV gợi mở: Nếu độ dài bóng OM bằng 10 cm thì s bằng bao nhiêu? (s = 10)
=> Từ đó ta có mối quan hệ: 10 = 17 cos 5𝜋𝑡. Đây là một phương trình lượng giác.
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học mới: “Bài học hôm nay chúng ta cùng đi tìm hiểu cách để tìm các nghiệm
của một phương trình lượng giác cơ bản.”
Bài 5. Phương trình lượng giác cơ bản.
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Phương trình tương đương a) Mục tiêu:
- HS nhận biết và thể hiện được khái niệm phương trình tương đương. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động mục 1. 92
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ: 1. Phương trình tương đương
- GV yêu cầu HS thảo luận thực HĐKP 1 hiện HĐKP 1.
a) Tập nghiệm của phương trình 𝑥 − 1 = 0 là 𝑆1 = {1}.
Tập nghiệm của phương trình 𝑥2 − 1 = 0 là 𝑆2 = {−1; 1}.
Tập nghiệm của phương trình √2𝑥2 − 1 = 𝑥 là 𝑆3 = {1}.
Ta có 𝑆1 = 𝑆3 ≠ 𝑆2.
- GV giới thiệu về hai phương Kết luận trình tương tương.
Hai phương trình được gọi là tưong
đưong nếu chúng có cùng tập nghiệm.
- HS đọc Ví dụ 1, giải thích vì sao Ví dụ 1 (SGK -tr.34)
hai phương trình tương đương, Chú ý:
hoặc không tương đương.
- Một số phép biến đổi tương đương thường sử
- GV cho HS nhắc lại các phép dụng
biến đổi để giải phương trình đã
+ Cộng hoặc trừ hai vế của phương trình cùng với
học lớp dưới (cộng hoặc trừ hai vế
một số hoặc cùng một biểu thức mà không làm
với cùng số khác 0 và nhân hoặc thay đổi điều kiện của phương trình.
chia hai vế với cùng một số khác 0). 93
- HS thực hiện Thực hành 1.
+ Nhân hoặc chia hai vế của phương trình với cùng
Bước 2: Thực hiện nhiệm vụ: một số khác 0 hoặc cùng một biểu thức luôn có giá
- HS theo dõi SGK, chú ý nghe, trị khác 0 mà không thay đổi điều kiện của phương
tiếp nhận kiến thức, hoàn thành
các yêu cầu, thảo luận nhóm. trình. - GV quan sát hỗ trợ.
- Để chỉ sự tương đương của các phương trình, dùng
Bước 3: Báo cáo, thảo luận: kí hiệu ⇔.
- HS giơ tay phát biểu, lên bảng trình bày Thực hành 1
- Một số HS khác nhận xét, bổ Phép biến đổi đầu tiên không là biến đổi tương sung cho bạn.
đương, do khi chia cả hai vế của phương trình cho
𝑥 = 0 thì làm mất đi nghiệm này.
Bước 4: Kết luận, nhận định: Phương trình đầu tiên có hai nghiệm 𝑥 = 0 và 𝑥 =
GV tổng quát lưu ý lại kiến thức
2, còn phương trình thứ hai chỉ có nghiệm 𝑥 = 0.
trọng tâm và yêu cầu HS ghi chép đầy đủ vào vở.
Hoạt động 2: Phương trình 𝒔𝒊𝒏 𝒙 = 𝒎. Phương trình 𝒄𝒐𝒔 𝒙 = 𝒎 a) Mục tiêu:
- Nhận biết công thức nghiệm của phương trình lượng giác cơ bản
sin 𝑥 = 𝑚, cos 𝑥 = 𝑚 bằng cách vận dụng đồ thị hàm số lượng giác tương ứng.
- Giải phương trình lượng giác ở dạng vận dụng trực tiếp phương trình lượng giác cơ bản.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện: 94
HOẠT ĐỘNG CỦA GV VÀ
SẢN PHẨM DỰ KIẾN HS
Bước 1: Chuyển giao nhiệm 2. Phương trình 𝐬𝐢𝐧 𝒙 = 𝒎 HĐKP 2 vụ:
Nhiệm vụ 1: Tìm hiểu phương
trình 𝒔𝒊𝒏 𝒙 = 𝒎
- GV yêu cầu HS thảo luận
nhóm đôi, hoàn thành HĐKP 2
- GV đặt câu hỏi: phương trình sin x = m có nghiệm khi m
thuộc đoạn giá trị nào?
- GV chốt lại kiến thức về cách
a) Không có giá trị nào của 𝑥 đễ sin 𝑥 = 1,5 vì −1 ≤
giải phương trình sin x = m.
sin 𝑥 ≤ 1 với mọi 𝑥 ∈ ℝ.
+ Giới thiệu về hình ảnh giữa
đồ thị hàm số y =sin x với b) Đường thẳng vuông góc trục sin tại điểm 0,5 cắt
đường thẳng y = m. Để thấy đường tròn lượng giác tại hai điểm 𝑀 và 𝑁. Do đó 𝑀
được tập nghiệm của phương và 𝑁 là điểm biểu diễn các góc lượng giác trình. 𝑥 có sin 𝑥 = 0,5.
Các góc lượng giác đó lần lượ 𝜋 5𝜋 t là + 𝑘2𝜋 và + 6 6 𝑘2𝜋, 𝑘 ∈ ℤ. - GV yêu cầu:
+ Tìm nghiệm cho phương Kết luận
trình sin x = 1; sin x = -1; sin x Xét phương trình sin 𝑥 = 𝑚 = 0.
+ Nếu có sin u = sin v thì có thể +) Nếu |𝑚| > 1 thì phương trình vô nghiệm.
viết mối quan hệ của u và v như
+) Nếu |𝑚| ≤ 1 thì phương trình có nghiệm thế nào? 95
+ GV hướng dẫn cách trình bày
𝑥 = 𝛼 + 𝑘2𝜋, 𝑘 ∈ ℤ
khi tính theo đơn vị độ.
Và 𝑥 = 𝜋 − 𝛼 + 𝑘2𝜋, 𝑘 ∈ ℤ
- HS đọc và thực hiện Ví dụ 2. GV hướng dẫn:
Với 𝛼 ∈ [− 𝜋 ; 𝜋] sao cho sin 𝛼 = 𝑚. 2 2
+ Xác định giá trị m trong các
trường hợp, xét xem có nghiệm Chú ý: hay không.
a) Một số trường hợp đặc biệt:
+ c) áp dụng công thức viết
mối quan hệ của 2x và 3x.
• sin 𝑥 = 0 ⇔ 𝑥 = 𝑘𝜋, 𝑘 ∈ ℤ.
- HS thực hiện Thực hành 2.
• sin 𝑥 = 1 ⇔ 𝑥 = 𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ.
Nhiệm vụ 2: Tìm hiểu phương 2
trình 𝒄𝒐𝒔 𝒙 = 𝒎
• sin 𝑥 = −1 ⇔ 𝑥 = − 𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ Tương tự 2 với phương trình sin x = m. b) sin 𝑢 = sin 𝑣
GV hướng dẫn HS thực hiện. u = v + 𝑘2𝜋 ⇔ [ (𝑘 ∈ ℤ) u = 𝜋 − 𝑣 + k2π c)sin 𝑥 = sin 𝑎∘
- HS thực hiện Ví dụ 3 và 𝑥 = 𝑎∘ + 𝑘360∘ Thực hành 3. ⇔ [ (𝑘 ∈ ℤ)
𝑥 = 180∘ − 𝑎∘ + 𝑘360∘
Bước 2: Thực hiện nhiệm vụ: Ví dụ 2 (SGK -tr.35)
- HS theo dõi SGK, chú ý nghe, Thực hành 2
tiếp nhận kiến thức, suy nghĩ a)
trả lời câu hỏi, hoàn thành các a) sin 𝑥 = √3 ⇔ sin 𝑥 = sin 𝜋 2 3 yêu cầu.
- GV: quan sát và trợ giúp HS. ⇔ 𝑥 = 𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 𝑥 = 2𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ. 3 3
Bước 3: Báo cáo, thảo luận: b) sin (𝑥 + 30∘) = sin (𝑥 + 60∘)
- HS giơ tay phát biểu, lên bảng trình bày 96
- Một số HS khác nhận xét, bổ ⇔ 𝑥 + 30∘ = 𝑥 + 60∘ + 𝑘360∘, 𝑘 ∈ ℤ hoặc 𝑥 + sung cho bạn.
30∘ = 180∘ − 𝑥 − 60∘ + 𝑘360∘, 𝑘 ∈ ℤ
Bước 4: Kết luận, nhận định: ⇔ 𝑥 + 30∘ = 120∘ − 𝑥 + 𝑘360∘,𝑘 ∈ ℤ
GV tổng quát lưu ý lại kiến
thức trọng tâm và yêu cầu HS ⇔ 𝑥 = 45∘ + 𝑘180∘, 𝑘 ∈ ℤ.
ghi chép đầy đủ vào vở.
3. Phương trình 𝐜𝐨𝐬 𝒙 = 𝒎 HĐKP 3
Đường thẳng vuông góc trục côsin tại điểm − 1 cắt 2
đường tròn lượng giác tại hai điểm 𝑀 và 𝑁. Do đó 𝑀
và 𝑁 là điểm biểu diễn các góc lượng giác 𝑥 có cos 𝑥 = − 1. 2
Các góc lượng giác đó lần lượ 2𝜋 t là + 𝑘2𝜋 và − 2𝜋 + 3 3 𝑘2𝜋, 𝑘 ∈ ℤ. Kết luận
Xét phương trình cos 𝑥 = 𝑚
+) Nếu |𝑚| > 1 thì phương trình vô nghiệm.
+) Nếu |𝑚| ≤ 1 thì phương trình có nghiệm 97
𝑥 = 𝛼 + 𝑘2𝜋, 𝑘 ∈ ℤ
Và 𝑥 = −𝛼 + 𝑘2𝜋, 𝑘 ∈ ℤ
Với 𝛼 ∈ [0; 𝜋] sao cho cos 𝛼 = 𝑚. Chú ý:
a) Một số trường hợp đặc biệt:
• cos 𝑥 = 0 ⇔ 𝑥 = 𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ. 2
• cos 𝑥 = 1 ⇔ 𝑥 = 𝑘2𝜋, 𝑘 ∈ ℤ.
• cos 𝑥 = −1 ⇔ 𝑥 = 𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ b) u = v + 𝑘2𝜋 cos 𝑢 = cos 𝑣 ⇔ [ (𝑘 ∈ ℤ) v = −v + k2π c) 𝑥 = 𝑎∘ + 𝑘360∘ cos 𝑥 = cos 𝑎∘ ⇔ [ (𝑘 ∈ ℤ) 𝑥 = −𝑎∘ + 𝑘360∘
Ví dụ 3 (SGK -tr.37) Thực hành 3
a) cos 𝑥 = −3 vô nghiệm; b) cos 𝑥 = cos 15∘
⇔ 𝑥 = 15∘ + 𝑘360∘, 𝑘 ∈ ℤ hoặc 𝑥 = −15∘ + 𝑘360∘, 𝑘 ∈ ℤ.
c) cos (𝑥 + 𝜋 ) = cos 3𝜋 12 12 98 𝜋 3𝜋 𝜋 3𝜋 ⇔ 𝑥 + =
+ 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 𝑥 + = − + 12 12 12 12 𝑘2𝜋, 𝑘 ∈ ℤ 𝜋 𝜋 ⇔ 𝑥 =
+ 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 𝑥 = − + 𝑘2𝜋, 𝑘 ∈ ℤ 6 3
Hoạt động 3: Phương trình 𝒕𝒂𝒏 𝒙 = 𝒎. Phương trình 𝒄𝒐𝒕 𝒙 = 𝒎 a) Mục tiêu:
- Nhận biết công thức nghiệm của phương trình lượng giác cơ bản
tan 𝑥 = 𝑚, cot 𝑥 = 𝑚 bằng cách vận dụng đồ thị hàm số lượng giác tương ứng.
- Giải phương trình lượng giác ở dạng vận dụng trực tiếp phương trình lượng giác cơ bản.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động mục 4 và 5.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV VÀ
SẢN PHẨM DỰ KIẾN HS Bướ
4. Phương trình 𝐭𝐚𝐧 𝒙 = 𝒎
c 1: Chuyển giao nhiệm HĐKP 4 vụ:
Nhiệm vụ 1: Tìm hiểu phương
trình 𝒕𝒂𝒏 𝒙 = 𝒎
- GV yêu cầu HS thảo luận
nhóm đôi, hoàn thành HĐKp 4.
- GV hướng dẫn HS tương tự
như hai phương trình trên. 99
- HS thực hiện Ví dụ 4 và Thực Đường thẳng đi qua gốc tọa độ và điểm 𝑇(1; √3) cắt hành 4.
đường tròn lượng giác tại hai điểm 𝑀 và 𝑁. Do đó 𝑀
Nhiệm vụ 2: Tìm hiểu phương và 𝑁 là điểm biểu diễn các góc lượng giác 𝑥 có tan 𝑥 =
trình 𝐜𝐨𝐭 𝒙 = 𝒎
√3. Công thức tổng quát của các góc lượng giác đó là 𝜋 - GV hướng dẫn HS. + 𝑘𝜋, 𝑘 ∈ ℤ. 3
- HS thực hiện Ví dụ 5 và Thực Kết luận hành 5.
Với mọi số thực m, phương trình tan 𝑥 = 𝑚 có nghiệm
Bước 2: Thực hiện nhiệm vụ: 𝑥 = 𝛼 + 𝑘𝜋(𝑘 ∈ ℤ).
- HS theo dõi SGK, chú ý nghe, Với 𝛼 ∈ (− 𝜋 ; 𝜋) sao cho tan 𝛼 = 𝑚. 2 2
tiếp nhận kiến thức, suy nghĩ
trả lời câu hỏi, hoàn thành các Chú ý: yêu cầu.
tan 𝑥 = tan 𝑎∘ ⇔ 𝑥 = 𝑎∘ + 𝑘180∘ (𝑘 ∈ ℤ).
- GV: quan sát và trợ giúp HS. Ví dụ 4 (SGK -tr.38)
Bước 3: Báo cáo, thảo luận: Thực hành 4
- HS giơ tay phát biểu, lên bảng trình bày
a) tan 𝑥 = 0 ⇔ 𝑥 = 𝑘𝜋, 𝑘 ∈ ℤ.
- Một số HS khác nhận xét, bổ b) tan(30∘ − 3𝑥) = tan75∘ sung cho bạn.
Bước 4: Kết luận, nhận định: ⇔ 30∘ − 3𝑥 = 75∘ + 𝑘180∘, 𝑘 ∈ ℤ
GV tổng quát lưu ý lại kiến
⇔ 𝑥 = −15∘ + 𝑘60∘, 𝑘 ∈ ℤ
thức trọng tâm và yêu cầu HS
ghi chép đầy đủ vào vở.
5. Phương trình 𝐜𝐨𝐭 𝒙 = 𝒎 HĐKP 5 100
Đường thẳng đi qua gốc toạ độ và điểm 𝐶(−1; 1) cắt
đường tròn lượng giác tại hai điểm 𝑀 và 𝑁. Do đó 𝑀
và 𝑁 là điểm biểu diễn các góc lương giác 𝑥có cot 𝑥 = −1.
Công thức tổng quát của các góc lượng giác đó là
− 𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ. 4 Kết luận
- Với mọi số thực , phương trình cot 𝑥 = 𝑚 có nghiệm
𝑥 = 𝛼 + 𝑘𝜋(𝑘 ∈ ℤ)
với 𝛼 ∈ (0; 𝜋) sao cho cot 𝛼 = 𝑚. Chú ý
cot 𝑥 = cot 𝑎∘ ⇔ 𝑥 = 𝑎∘ + 𝑘180∘ (𝑘 ∈ ℤ).
Ví dụ 5 (SGK -tr.39) Thực hành 5
a) cot 𝑥 = 1 ⇔ 𝑥 = 𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ; 4
b) cot (3𝑥 + 30∘) = tan 75∘ ⇔ 3𝑥 + 30∘ = 75∘ + 101 𝑘180∘, 𝑘 ∈ ℤ
⇔ 𝑥 = 15∘ + 𝑘60∘, 𝑘 ∈ ℤ. Hoạt động 2: a) Mục tiêu:
- Tính nghiệm gần đúng của phương trình lượng giác cơ bản bằng máy tính cầm tay.
- Giải phương trình lượng giác ở dạng vận dụng trực tiếp phương trình lượng giác cơ bản.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động mục 6.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ:
6. Giải phương trình lượng giác bằng máy tính cầm tay
- GV hướng dẫn HS sử dụng máy tính Ví dụ 6 (SGK -tr.40) cầm tay Chú ý:
+ Tìm góc thỏa mãn giá trị lượng giác mà Để giải phương trình cot𝑥 = 𝑚(𝑚 ≠ 0), ta phương trình cho.
giải phương trình tan 𝑥 = 1 .
+ Rồi viết công thức nghiệm. 𝑚
- Chú ý: khi giải phương trình cot x = m. Thực hành 6
- Tương tự HS thực hiện Thực hành 6 và a) cos 𝑥 = 0,4 ⇔ 𝑥 ≈ 1,16 + 𝑘2𝜋, 𝑘 ∈ ℤ Vận dụng.
hoặc 𝑥 ≈ −1,16 + 𝑘2𝜋, 𝑘 ∈ ℤ.
Bước 2: Thực hiện nhiệm vụ:
b) tan 𝑥 = √3 ⇔ 𝑥 = 𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ. 3 Vận dụng 102
- HS theo dõi SGK, chú ý nghe, tiếp nhận Ta có |𝑥| = 10 ⇔ 17cos 5𝜋𝑡 = 10 hoặc
kiến thức, suy nghĩ trả lời câu hỏi, hoàn 17cos 5𝜋𝑡 = −10. thành các yêu cầu. +) 17cos 5𝜋𝑡 = 10
- GV: quan sát và trợ giúp HS. 10
Bước 3: Báo cáo, thảo luận: ⇔ cos 5𝜋𝑡 = 17
- HS giơ tay phát biểu, lên bảng trình bày ⇔ 5𝜋𝑡 ≈ 0,94 + 𝑘2𝜋,𝑘 ∈ ℤ hoặc 5𝜋𝑡 ≈
- Một số HS khác nhận xét, bổ sung cho −0,94 + 𝑘2𝜋,𝑘 ∈ ℤ bạn.
Bước 4: Kết luận, nhận định: GV tổng ⇔ 𝑡 ≈ 0,06 + 0,4𝑘, 𝑘 ∈ ℤ hoăc 𝑡 ≈
quát lưu ý lại kiến thức trọng tâm và yêu −0,06 + 0,4𝑘, 𝑘 ∈ ℤ.
cầu HS ghi chép đầy đủ vào vở. +) 17 cos 5𝜋𝑡 = −10 10 ⇔ cos 5𝜋𝑡 = − 17
⇔ 5𝜋𝑡 ≈ 2,2 + 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 5𝜋𝑡 ≈
−2,2 + 𝑘2𝜋, 𝑘 ∈ ℤ
⇔ 𝑡 ≈ 0,14 + 0,4𝑘, 𝑘 ∈ ℤ hoặc 𝑡 ≈
−0,14 + 0,4𝑘, 𝑘 ∈ ℤ.
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 1 đến 5 (SGk -tr.40+41) và các câu hỏi TN.
c) Sản phẩm học tập: Câu trả lời của HS.
d) Tổ chức thực hiện: 103
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS trả lời các câu hỏi TN nhanh
Câu 1. Gọi 𝑆 là tập nghiệm của phương trình 2 𝑐𝑜𝑠 𝑥 = √3. Khẳng định nào sau đây là đúng?
A. 𝟓𝝅 ∈ 𝑺.
B. 𝟏𝟏𝝅 ∈ 𝑺.
C. 𝟏𝟑𝝅 ∉ 𝑺.
D. − 𝟏𝟑𝝅 ∉ 𝑺. 𝟔 𝟔 𝟔 𝟔
Câu 2. Trong các phương trình sau, phương trình nào tương đương với phương trình 2 𝑐𝑜𝑠2 𝑥 = 1? A. 𝑠𝑖𝑛 𝑥 = √2.
B. 2 𝑠𝑖𝑛 𝑥 + √2 = 0. 2 C. 𝑡𝑎𝑛 𝑥 = 1. D. 𝑡𝑎𝑛2 𝑥 = 1.
Câu 3. Có bao nhiêu giá trị nguyên của tham số 𝑚 thuộc đoạn 2 − 108;201 8 để phương
trình 𝑚 𝑐𝑜𝑠 𝑥 + 1 = 0 có nghiệm?
A. 𝟐𝟎𝟏𝟖.
B. 𝟐𝟎𝟏𝟗.
C. 𝟒𝟎𝟑𝟔.
D. 𝟒𝟎𝟑𝟖.
Câu 4. Tìm giá trị thực của tham số 𝑚 để phương trình (𝑚 − 2) 𝑠𝑖𝑛 2 𝑥 = 𝑚 + 1 nhận 𝑥 = 𝜋 làm nghiệm. 12 𝟐(√𝟑+𝟏)
A. 𝒎 ≠ 𝟐. B. 𝒎 =
. C. 𝒎 = −𝟒.
D. 𝒎 = −𝟏. √𝟑−𝟐
Câu 5. Giải phương trình 4 𝑠𝑖𝑛2 𝑥 = 3. 𝒙 = 𝝅 + 𝒌𝟐𝝅 𝒙 = 𝝅 + 𝒌𝟐𝝅 𝟑 A. [ 𝟑 𝝅 , (𝒌 ∈ ℤ). B. [
, (𝒌 ∈ ℤ). 𝒙 = − + 𝒌𝟐𝝅 𝒙 = 𝟐𝝅 + 𝒌𝟐𝝅 𝟑 𝟑 𝒙 = 𝝅 + 𝒌𝝅 𝒙 = 𝒌𝝅 C. { 𝟑
𝟑 (𝒌, 𝓵 ∈ ℤ). D. {
𝟑 (𝒌, 𝓵 ∈ ℤ). 𝒌 ≠ 𝟑𝓵 𝒌 ≠ 𝟑𝓵
- GV tổ chức cho HS hoạt động thực hiện Bài tập 1 đến 5 (SGk -tr.40+41) 104
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định:
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác. Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 B B A C D Bài 1
a) sin 2𝑥 = 1 ⇔ 2𝑥 = 𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ hoăc 2𝑥 = 5𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ 2 6 6 𝜋 5𝜋 ⇔ 𝑥 =
+ 𝑘𝜋, 𝑘 ∈ ℤ hoăc 𝑥 = + 𝑘𝜋, 𝑘 ∈ ℤ; 12 12
b) sin (𝑥 − 𝜋) = sin 2𝜋 ⇔ 𝑥 − 𝜋 = 2𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 𝑥 − 𝜋 = 5𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ 7 7 7 7 7 7 3𝜋 6𝜋 ⇔ 𝑥 =
+ 𝑘2𝜋, 𝑘 ∈ ℤ họ̆c 𝑥 = + 𝑘2𝜋, 𝑘 ∈ ℤ 7 7 c) sin 4𝑥 − cos 𝜋
(𝑥 + 𝜋) = 0 ⇔ sin 4𝑥 = cos (𝑥 + 𝜋) ⇔ sin 4𝑥 = sin ( − 𝑥) 6 6 3 105 𝜋 2𝜋 ⇔ 4𝑥 =
− 𝑥 + 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 4𝑥 =
+ 𝑥 + 𝑘2𝜋, 𝑘 ∈ ℤ 3 3 𝜋 2𝜋 2𝜋 2𝜋 ⇔ 𝑥 = + 𝑘 , 𝑘 ∈ ℤ hoăc 𝑥 = + 𝑘 , 𝑘 ∈ ℤ. 15 5 9 3 Bài 2.
a) cos (𝑥 + 𝜋) = √3 ⇔ 𝑥 + 𝜋 = 𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 𝑥 + 𝜋 = − 𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ 3 2 3 6 3 6 𝜋 𝜋
⇔ 𝑥 = − + 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 𝑥 = − + 𝑘2𝜋, 𝑘 ∈ ℤ; 6 2
b) cos 4𝑥 = cos 5𝜋 ⇔ 4𝑥 = 5𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 4𝑥 = − 5𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ 12 12 12 5𝜋 𝜋 5𝜋 𝜋 ⇔ 𝑥 =
+ 𝑘 , 𝑘 ∈ ℤ hoặc 𝑥 = − + 𝑘 , 𝑘 ∈ ℤ 48 2 48 2
c) cos2 𝑥 = 1 ⇔ cos 𝑥 = 1 hoặc cos 𝑥 = −1
⇔ 𝑥 = 𝑘𝜋, 𝑘 ∈ ℤ Bài 3.
a) tan 𝑥 = tan 55∘ ⇔ 𝑥 = 55∘ + 𝑘180∘, 𝑘 ∈ ℤ;
b) tan (2𝑥 + 𝜋) = 0 ⇔ 2𝑥 + 𝜋 = 𝑘𝜋, 𝑘 ∈ ℤ ⇔ 𝑥 = − 𝜋 + 𝑘 𝜋 , 𝑘 ∈ ℤ. 4 4 8 2 Bài 4. a) cot 1
( 𝑥 + 𝜋) = −1 ⇔ 1 𝑥 + 𝜋 = − 𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ ⇔ 𝑥 = −𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ; 2 4 2 4 4
b) cot 3𝑥 = − √3 ⇔ 3𝑥 = − 𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ ⇔ 𝑥 = − 𝜋 + 𝑘 𝜋 , 𝑘 ∈ ℤ. 3 3 9 3 Bài 5.
cos 𝑥 = sin 𝑥 ⇔ tan 𝑥 = 1 (hiển nhiên cos 𝑥 ≠ 0 ) 𝜋 ⇔ 𝑥 = + 𝑘𝜋, 𝑘 ∈ ℤ 4 106
D. HOẠT ĐỘNG VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập.
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 6, 7 (SGK -tr.41).
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: Bài 6. 𝜋
𝑠 = −5√3 ⇔ 10sin (10𝑡 + ) = −5√3 2 𝜋 √3 ⇔ sin (10𝑡 + ) = − 2 2 𝜋 𝜋 𝜋 4𝜋 ⇔ 10𝑡 +
= − + 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 10𝑡 + = + 𝑘2𝜋, 𝑘 ∈ ℤ 2 3 2 3 𝜋 𝜋 𝜋 𝜋 ⇔ 𝑡 = −
+ 𝑘 , 𝑘 ∈ ℤ hoăc 𝑡 = + 𝑘 , 𝑘 ∈ ℤ. 12 5 12 5 107
Vậy tại các thời điểm 𝜋 𝜋 𝜋 𝜋 𝑡 = −
+ 𝑘 , 𝑘 ∈ ℤ và 𝑡 =
+ 𝑘 , 𝑘 ∈ ℤ thì 𝑠 = −5√3 cm. 12 5 12 5 Bài 7.
a) Góc quay của đèn hải đăng sau 𝑡 giây là 𝛼 = 𝜋 𝑡 rad. 10
Do đó 𝑦𝑀 = 𝐻𝑂tan 𝛼 = tan 𝜋 𝑡( km). 10
b) Đèn chiếu vào ngôi nhà 𝑁 khi và chỉ khi 𝑦𝑀 = −1 hay tan 𝜋 𝑡 = −1. 10
tan 𝜋 𝑡 = −1 ⇔ 𝜋 𝑡 = 3𝜋 + 𝑘𝜋, 𝑘 ∈ ℤ (vì 𝑡 > 0 nên ta chi xét 𝑘 ≥ 0 ) 10 10 4
⇔ 𝑡 = 7,5 + 10𝑘, 𝑘 ∈ ℕ.
Vậy đèn hải đăng chiếu vào ngôi nhà vào các thời điểm 𝑡 = 7,5 + 10𝑘 (giây), 𝑘 ∈ ℕ.
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài: “Bài tập cuối chương I”.
• GV chia lớp thành 4 – 5 nhóm, chuẩn bị nội dung vẽ sơ đồ tóm tắt nội dung của chương I.
HS chuẩn bị bài tập cuối chương I. 108 Ngày soạn: .../.../... Ngày dạy: .../.../...
BÀI TẬP CUỐI CHƯƠNG I (2 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học sinh củng cố, ôn tập lại các kiến thức, kĩ năng về - Góc lượng giác
- Giá trị lượng giác của một góc lượng giác.
- Các công thức lượng giác
- Hàm số lượng giác và đồ thị
- Phương trình lượng giác cơ bản. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học, giải quyết vấn đề toán học: So sánh, phân tích dữ
liệu tìm ra mối liên hệ giữa các đối tượng đã cho và nội dung bài học về góc lượng
giác, giá trị lượng giác, các công thức lượng giác, hàm số lượng giác, phương trình lượng giác.
- Mô hình hóa toán học: vận dụng các kiến thức vào bài toán thực tế. - Giao tiếp toán học. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác. 109
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo tâm thế HS vào bài học. HS nhớ lại các kiến thức đã học ở chương I.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS trả lời được câu hỏi về hàm số lượng giác, phương trình lượng giác.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS trả lời các câu hỏi TN 1 đến 6 (SGK -tr.42)
Bước 2: Thực hiện nhiệm vụ: HS suy nghĩ trả lời nhanh các câu hỏi, giải thích các đáp án.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học mới. Đáp án
1.C, 2. A, 3. B, 4. A, 5.B, 6.C
B. HÌNH THÀNH KIẾN THỨC MỚI 110
Hoạt động 1: Ôn tập kiến thức đã học của chương I. a) Mục tiêu:
- HS nhắc lại và tổng hợp được các kiến thức đã học theo một sơ đồ nhất định. a) Mục tiêu:
- HS nhắc lại và tổng hợp được các kiến thức đã học theo một sơ đồ nhất định. b) Nội dung
HS tổng hợp lại kiến thức dựa theo SGK và ghi chép trên lớp theo nhóm đã được phân công của buổi trước.
c) Sản phẩm: Sơ đồ mà HS đã vẽ.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ:
- - GV mời đại diện từng nhóm lên
trình bày về sơ đồ tư duy của nhóm.
+ Hệ thức Chasles: Với ba tia 𝑂𝑎, 𝑂𝑏, 𝑂𝑐 bất
- GV có thể đặt các câu hỏi thêm về
kì, ta có 𝑠đ(𝑂𝑎, 𝑂𝑏) + 𝑠đ(𝑂𝑏, 𝑂𝑐) = nội dung kiến thức:
𝑠đ(𝑂𝑎, 𝑂𝑐) + 𝑘360∘(𝑘 ∈ ℤ) + Nêu hệ thức Chasles. + Công thức cộng
+ Nêu các công thức lượng giác:
𝑐𝑜𝑠(𝛼 + 𝛽) = cos 𝛼 cos 𝑏 − sin 𝛼 sin 𝑏
công thức cộng, công thức góc nhân
𝑐𝑜𝑠(𝛼 − 𝛽) = cos 𝛼 cos 𝑏 + sin 𝛼 sin 𝑏
đôi, công thức biến tổng thành tích.
𝑠𝑖𝑛(𝛼 − 𝛽) = sin 𝛼 cos 𝛽 − cos 𝛼 sin 𝛽
+ Nêu mối liên hệ về giá trị lượng
𝑠𝑖𝑛(𝛼 + 𝛽) = sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽
giác của các góc phụ nhau, bù nhau, tan 𝛼 − tan 𝛽 tan(𝛼 − 𝛽) = đố 1 + tan 𝛼 tan 𝛽 i nhau. tan 𝛼 + tan 𝛽
+ Nêu cách giải phương trình cơ bản tan(𝛼 + 𝛽) = 1 − tan 𝛼 tan 𝛽
sin 𝑥 = 𝑚, tan 𝑥 = 𝑚
(giả thiết biểu thức đều có nghĩa) 111
Bước 2: Thực hiện nhiệm vụ:
+ Công thức góc nhân đôi
sin 2𝛼 = 2 sin 𝛼 cos 𝛼
- HS tự phân công nhóm trưởng và
cos 2𝛼 = cos2 𝛼 − sin2 𝛼 = 2 cos2 𝛼 − 1
nhiệm vụ phải làm để hoàn thành sơ = 1 − 2𝛼 đồ. 2tan 𝛼 tan 2𝛼 =
- GV hỗ trợ, hướng dẫn thêm. 1 − tan2 𝛼
Bước 3: Báo cáo, thảo luận:
+ Công thức biến đổi tổng thành tích 𝛼 + β 𝛼 − β
- Đại diện nhóm trình bày, các HS cos 𝛼 + cos β = 2cos cos 2 2
chú ý lắng nghe và cho ý kiến. 𝛼 + β 𝛼 − β
- HS trả lời câu hỏi của GV.
cos 𝛼 − cos β = −2sin sin 2 2
Bước 4: Kết luận, nhận định: 𝛼 + β 𝛼 − β sin 𝛼 + sin β = 2sin cos
- GV nhận xét các sơ đồ, nêu ra điểm 2 2
tốt và chưa tốt, cần cải thiện. 𝛼 + β 𝛼 − β sin 𝛼 − sin β = 2cos sin
- GV chốt lại kiến thức của chương. 2 2
+ Hai góc đối nhau 𝜶 và −𝜶 cos(−𝛼) = cos 𝛼 sin(−𝛼) = − sin 𝛼 tan(−𝛼) = − tan 𝛼 cot(−𝛼) = − cot 𝛼
+) Hai góc bù nhau 𝛼 và 𝜋 − 𝛼
sin (𝜋 − 𝛼) = sin 𝛼
cos (𝜋 − 𝛼) = −cos 𝛼
tan (𝜋 − 𝛼) = −tan 𝛼
cot (𝜋 − 𝛼) = −cot 𝛼 112 𝜋
+) Hai góc phụ nhau 𝛼 và − 𝛼 2 𝜋 sin ( − 𝛼) = cos𝛼 2 𝜋 cos ( − 𝛼) = sin 𝛼 2 𝜋 tan ( − 𝛼) = −tan 𝛼 2 𝜋 cot ( − 𝛼) = −cot 𝛼 2
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 7 đến 11 (SGK - tr.42+43).
c) Sản phẩm học tập: Câu trả lời của HS.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS hoạt động thực hiện Bài 7 đến 11 (SGK -tr.42+43).
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định:
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác. 113 Kết quả: Bài 7
Trong 1 giây, quạt quay được 45 = 3 (vòng). 60 4
Trong 3 giây, quạt quay được 3 ⋅ 3 = 9 (vòng). 4 4
Vì quạt quay theo chiều durơng nên góc quay của quạt sau 3 giây có số đo là 9 ⋅ 2𝜋 = 4 9𝜋. 2 Bài 8. 2 a) sin 𝛼 = − 1
√1 − cos2 𝛼 = −√1 − ( ) = − 2√2; 3 3
b) sin 2𝛼 = 2sin 𝛼cos 𝛼 = 2 ⋅ (− 2√2) ⋅ 1 = − 4√2; 3 3 9
c) cos (𝛼 + 𝜋) = cos 𝛼cos 𝜋 − sin 𝛼sin 𝜋 = 1 ⋅ 1 + 2√2 ⋅ √3 = 1+2√6. 3 3 3 3 2 3 2 6 Bài 9.
a) sin (𝛼 + 𝛽)sin (𝛼 − 𝛽) = (sin 𝛼cos 𝛽 + cos 𝛼sin 𝛽)(sin 𝛼cos 𝛽 − cos 𝛼sin 𝛽)
= sin2 𝛼cos2 𝛽 − cos2 𝛼sin2 𝛽
= sin2 𝛼(1 − sin2 𝛽) − (1 − sin2 𝛼)sin2 𝛽 = sin2 𝛼 − sin2 𝛽;
b) cos4 𝛼 − cos4 (𝛼 − 𝜋) = cos4 𝛼 − sin4 𝛼 = (cos2 𝛼 − sin2 𝛼)(cos2 𝛼 + 2 sin2 𝛼)
= cos2 𝛼 − sin2 𝛼 = cos 2𝛼. Bài 10. 114 𝜋 𝜋
sin (𝑥 + ) − sin 2𝑥 = 0 ⇔ sin (𝑥 + ) = sin 2𝑥 6 6 𝜋 𝜋 ⇔ 𝑥 +
= 2𝑥 + 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 𝑥 +
= 𝜋 − 2𝑥 + 𝑘2𝜋, 𝑘 ∈ ℤ 6 6 𝜋 5𝜋 2𝜋 ⇔ 𝑥 =
+ 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 𝑥 = + 𝑘 , 𝑘 ∈ ℤ. 6 18 3
Với 𝑥 = 𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ, ta có 𝑥 ∈ {… ; − 11𝜋 ; 𝜋 ; 13𝜋 ; … }. 6 6 6 6
Với 𝑥 = 5𝜋 + 𝑘 2𝜋 , 𝑘 ∈ ℤ, ta có 𝑥 ∈ {… ; − 7𝜋 ; 5𝜋 ; 17𝜋 ; … }. 18 3 18 18 18
Vậy nghiệm durơng nhỏ nhất của phương trình đã cho là 𝜋. 6 Bài 11.
a) sin 2𝑥 + cos 3𝑥 = 0 ⇔ cos 3𝑥 = −sin 2𝑥 ⇔ cos 3𝑥 = cos (2𝑥 + 𝜋) 2 𝜋 𝜋 ⇔ 3𝑥 = 2𝑥 +
+ 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 3𝑥 = −2𝑥 − + 𝑘2𝜋, 𝑘 ∈ ℤ 2 2 𝜋 𝜋 2𝜋 ⇔ 𝑥 =
+ 𝑘2𝜋, 𝑘 ∈ ℤ hoăc 𝑥 = − + 𝑘 , 𝑘 ∈ ℤ; 2 10 5
b) sin 𝑥cos 𝑥 = √2 ⇔ sin 2𝑥 = √2 4 2 𝜋 3𝜋 ⇔ 2𝑥 =
+ 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 2𝑥 = + 𝑘2𝜋, 𝑘 ∈ ℤ 4 4 𝜋 3𝜋 ⇔ 𝑥 =
+ 𝑘𝜋, 𝑘 ∈ ℤ hoăc 𝑥 = + 𝑘𝜋, 𝑘 ∈ ℤ; 8 8
c) sin 𝑥 + sin 2𝑥 = 0 ⇔ sin 2𝑥 = −sin 𝑥 ⇔ sin 2𝑥 = sin (𝑥 + 𝜋)
⇔ 2𝑥 = 𝑥 + 𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 2𝑥 = −𝑥 + 𝑘2𝜋, 𝑘 ∈ ℤ 2𝜋
⇔ 𝑥 = 𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ hoặc 𝑥 = 𝑘 , 𝑘 ∈ ℤ. 3
D. HOẠT ĐỘNG VẬN DỤNG 115 a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập.
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 12, 13, 14 (SGK -tr.43)
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: Bài 12.
a) Vào thời điểm 𝑡 = 2, dộ sâu của nước là ℎ(2) = 0,8cos (0,5.2) + 4 ≈ 4,43( m).
b) ℎ(𝑡) ≥ 3,6 ⇔ 0,8cos 0,5𝑡 + 4 ≥ 3,6 ⇔ cos 0,5𝑡 ≥ − 1. 2
Vì 0 ≤ 𝑡 ≤ 12 nện 0 ≤ 0,5𝑡 ≤ 6. Đặt 𝑥 = 0,5t và xét đồ thị hàm số 𝑦 = cos 𝑥 trên
đoạn [0; 6] thư hình dưới đây. 116
Dựa vào đồ thị, ta thấy cos 𝑥 ≥ − 1 ⇔ 0 ≤ 𝑥 ≤ 2𝜋 hoăc 4𝜋 ≤ 𝑥 ≤ 6. 2 3 3
Do đó 0 ≤ 𝑡 ≤ 4𝜋 hoăc 8𝜋 ≤ 𝑡 ≤ 12 ⇔ 0 ≤ 𝑡 ≤ 4,19 hoặc 8,38 ≤ 𝑡 ≤ 12. 3 3
Vậy có thể hạ thuỷ tàu sau 𝑡 giờ tính từ lúc thuỷ triều lên với 𝑡 thuọc [0; 4,19] hoặc [8,38; 12] (giờ). Bài 13.
a) Vận tốc của con lắc đạt giá trị lớn nhất là 3 cm/s khi sin (1,5𝑡 + 𝜋) = −1. 3
Giải phương trình này ta dược 𝑡 = − 5𝜋 + 𝑘 4𝜋 , 𝑘 ∈ ℤ. 9 3
Vì 𝑡 ≥ 0 nên 𝑡 = 7𝜋 + 𝑘 4𝜋 , 𝑘 ∈ ℕ. 9 3
Vậy vào các thời điểm 𝑡 = 7𝜋 + 𝑘 4𝜋 , 𝑘 ∈ ℕ thì vận tốc của con lắc đạt giá trị lớn nhất. 9 3
b) 𝑣 = 1,5 ⇔ −3sin (1,5𝑡 + 𝜋) = 1,5 3 𝜋 1 ⇔ sin (1,5𝑡 + ) = − 3 2
⇔ 1,5𝑡 + 𝜋 = − 𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ họ̆c 1,5𝑡 + 𝜋 = 7𝜋 + 𝑘2𝜋, 𝑘 ∈ ℤ 3 6 3 6
⇔ 𝑡 = − 𝜋 + 𝑘 4𝜋 , 𝑘 ∈ ℤ hoặc 𝑡 = 5𝜋 + 𝑘 4𝜋 , 𝑘 ∈ ℤ. 3 3 9 3 117 Vì 4𝜋 5𝜋 4𝜋
𝑡 ≥ 0 nên 𝑡 = 𝜋 + 𝑘 , 𝑘 ∈ ℕ hoă̆ 𝑡 = + 𝑘 , 𝑘 ∈ ℕ. 3 9 3
Vậy vào các thời điểm 𝑡 = 𝜋 + 𝑘 4𝜋 , 𝑘 ∈ ℕ hoặc 𝑡 = 5𝜋 + 𝑘 4𝜋 , 𝑘 ∈ ℕ thì vận tốc con 3 9 3 lắc bằng 1,5 cm/s. Bài 14.
a) 𝑥𝐸 = 5tan 𝜃𝑧 = 5tan 𝜋 (𝑡 − 12) 12
b) Vì 6 < 𝑡 < 18 nên − 𝜋 < 𝜋 (𝑡 − 12) < 𝜋. 2 12 2
Bóng cây phủ qua vị trí tường rào 𝑁 khi và chỉ khi 𝑥𝑔 ≤ −4.
Ta có 𝑥𝑅 ≤ −4 ⇔ 5tan 𝜋 (𝑡 − 12) ≤ −4 12 𝜋 4 ⇔ tan (𝑡 − 12) ≤ − 12 5 Đặt 𝜋 𝜋 𝜋 𝑢 =
(𝑡 − 12) xét đồ thì hàm số 𝑦 = tan 𝑢 trên (− ; ) như hình vẽ 12 2 2 118
Dựa vào đồ thị, ta thấy 4 𝜋 tan 𝑢 ≤ − ⇔ < 𝑢 ≤ −0,7 5 2
Hay − 𝜋 < 𝜋 (𝑡 − 12) ≤ −0,7. Suy ra 𝑡 ∈ (6; 9,3] 2 12
Vậy trong khoáng từ 6 giờ dến khoảng 9,3 giờ ( 9 giờ 18 phút) thì bóng cây phủ qua vị trí tường rào 𝑁.
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: "Bài 1. Dãy số". 119 Ngày soạn: .../.../... Ngày dạy: .../.../...
CHƯƠNG II: DÃY SỐ. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN
BÀI 1: DÃY SỐ (2 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết dãy số hữu hạn, dãy số vô hạn.
- Thể hiện cách cho dãy số bằng liệt kê các số hạng; bằng công thức tổng quát;
bằng hệ thức truy hồi; bằng cách mô tả.
- Nhận biết tính chất tăng, giảm, bị chặn của dãy số trong những trường hợp đơn giản. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học: So sánh, phân tích dữ liệu tìm ra mối liên hệ giữa
các đối tượng đã cho và dãy số, nhận biết dãy số, thể hiện dãy số theo yêu cầu,
nhận biết tính chất tăng, giảm, bị chặn của dãy số.
- Mô hình hóa toán học: Mô tả được các dữ liệu liên quan đến yêu cầu trong thực
tiễn để lựa chọn các đối tượng phù hợp về dãy số để giải quyết bài toán.
- Giải quyết vấn đề toán học, giao tiếp toán học.
- Sử dụng công cụ, phương tiện học toán. 120 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học. HS có cơ hội thảo luận về nhu cầu
xuất hiện khái niệm dãy số thông qua việc biểu diễn diện tích các hình vuông.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS trả lời được câu hỏi mở đầu.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu 121
Gọi 𝑢1; 𝑢2; 𝑢3; … . ; 𝑢𝑛 lần lượt là diện tích các hình vuông có độ dài cạnh là 1; 2; 3; ..; n. Tính 𝑢3 và 𝑢4.
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung. Dự kiến câu trả lời: - 𝑢(3) = 9; 𝑢(4) = 16.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học mới: “Các số thể hiện diện tích một dãy các hình vuông được gọi là một dãy
số. Bài học hôm nay chúng ta cùng đi tìm hiểu thế nào là một dãy số và các tính chất cơ
bản của một dãy số”. Bài 1. Dãy số
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Tìm hiểu về dãy số. a) Mục tiêu:
- HS nhận biết dãy số hữu hạn, dãy số vô hạn.
- HS thể hiện được cách cho dãy số theo các cách. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động mục 1 và 2.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN 122
Bước 1: Chuyển giao nhiệm vụ: 1. Dãy số là gì?
Nhiệm vụ 1: Tìm hiểu về khái HĐKP 1
niệm dãy số
𝑢(1) = 1; 𝑢(2) = 4; 𝑢(50) = 2500;
- GV yêu cầu HS hoàn thành 𝑢(100) = 10000 HĐKP 1. Kết luận
- GV giới thiệu; trong thực tiễn
- Hàm số u xác định trên tập hợp ℕ∗ được gọi là
chúng ta có nhu cầu đánh số thứ
một dãy số vô hạn (gọi tắt là dãy số), nghĩa là
tự một loạt các giá trị số, khi đó có 𝑢: ℕ∗ → ℝ khái niệm dãy số. 𝑛 ↦ 𝑢
- GV giới thiệu về dãy số. 𝑛 = 𝑢(𝑛)
+ Dãy số trên kí hiệu (𝑢 + kí hiệu. 𝑛).
+ Dạng khai triển của dãy số (𝑢 + Dạng khai triển.
𝑛): 𝑢1, 𝑢2, … , 𝑢𝑛, … Chú ý:
+ Số hạng đầu, số hạng cuối. + Dãy không đổ + Số 𝑢 i.
1 = 𝑢(1) gọi là số hạng đầu, 𝑢𝑛 = 𝑢(𝑛) là
số hạng thứ 𝑛 và gọi là số hạng tổng quát của dãy
- GV cho HS đưa ra ví dụ về dãy số. số. + (u
- HS đọc Ví dụ 1, xác định số hạng
n) là dãy số không đổi: ∀𝑛 ∈ ℕ∗, 𝑢𝑛 = 𝐶.
Ví dụ 1 (SGK -tr.45)
thứ 1, 2, 3 và số hạng tổng quát. HĐKP 2
+ GV giới thiệu số hạng tổng quát 𝑣(1) = 2.1 = 2 thứ n.
- HS thực hiện HĐKP 2. 𝑣(2) = 2.2 = 4
+ Dãy số trên có bao nhiêu phần tử? 𝑣(3) = 2.3 = 6
Từ đó giới thiệu dãy hữu hạn. 𝑣(4) = 2.4 = 8
- HS đọc Ví dụ 2.
- HS thực hiện Thực hành 1 và 𝑣(5) = 2.5 = 10 Vận dụng 1. Kết luận 123
- Hàm số 𝑢 xác định trên tâp 𝑀 = {1; 2; 3; … , 𝑚}
được gọi là một dãy số hữu hạn.
+ Dạng khai triển của dãy số hữu hạn là
𝑢1, 𝑢2, … , 𝑢𝑚, trong đó 𝑢1 gọi là số hạng đầu, số
𝑢𝑚 gọi là số hạng cuối.
Ví dụ 2 (SGK -tr.46) Thực hành 1
a) Dãy số trên là dãy số vô hạn b) 𝑢1 = 13 = 1 𝑢2 = 23 = 8 𝑢3 = 33 = 27 𝑢4 = 43 = 64 𝑢5 = 53 = 125 Vận dụng 1
a) 𝜋; 4𝜋; 9 𝜋; 16 𝜋; 25 𝜋
b) Số hạng đầu là 𝜋; số hạng cuối là 25𝜋.
Nhiệm vụ 2: Tìm hiểu cách xác
2. Cách xác định dãy số
định dãy số HĐKP 3
- HS thực hiện HĐKP 3, sau đó
Bốn số hạng đầu tiên của các dãy số quan sát và trả lời: 𝑎
+ Các cách cho một dãy số ở
1 = 0; 𝑎2 = 1; 𝑎3 = 2; 𝑎4 = 3 HĐKP 3 là gì?
𝑏1 = 2; 𝑏2 = 4; 𝑏3 = 6; 𝑏4 = 8 124
- GV chốt lại kiến thức.
𝑐1 = 1; 𝑐2 = 2; 𝑐3 = 3; 𝑐4 = 4
+ Yêu cầu HS đưa ra ví dụ về mỗi 𝑑 cách cho.
1 = 2𝜋; 𝑑2 = 4𝜋; 𝑑3 = 6𝜋; 𝑑4 = 8𝜋
- HS đọc hiểu Ví dụ 3, Ví dụ 4. Kết luận
- HS thực hiện Thực hành 2 và Thông thường một dãy số có thể được cho bằng các Vận dụng 2. cách sau:
Bước 2: Thực hiện nhiệm vụ:
Cách 1: Liệt kê các số hạng (với các dãy số hữu hạn)
- HS theo dõi SGK, chú ý nghe, Cách 2: Cho công thức của số hạng tổng quát 𝑢𝑛
tiếp nhận kiến thức, hoàn thành
các yêu cầu, thảo luận nhóm.
Cách 3: Cho hệ thức truy hồi, nghĩa là - GV quan sát hỗ trợ.
+ Cho số hạng thứ nhất 𝑢1 (hoặc một vài số hạng đầu tiền);
Bước 3: Báo cáo, thảo luận:
+ Cho một công thức tính 𝑢𝑛 theo 𝑢𝑛−1 (hoặc theo
- HS giơ tay phát biểu, lên bảng
một vài số hạng đứng ngay trước nó). trình bày
- Một số HS khác nhận xét, bổ Cách 4: Cho bằng cách mô tả. sung cho bạn.
Ví dụ 3 (SGK -tr.47)
Bước 4: Kết luận, nhận định: Ví dụ 4 (SGK -tr.47)
GV tổng quát lưu ý lại kiến thức Thực hành 2
trọng tâm và yêu cầu HS ghi chép a) 𝑢2 = 2.𝑢1 = 2.3
đầy đủ vào vở.
𝑢3 = 2. 𝑢2 = 2.2.3 = 22. 3
𝑢4 = 2. 𝑢3 = 2.22. 3 = 23. 3 b) 𝑢𝑛 = 2𝑛−1. 3 Vận dụng 2 a) 𝑢𝑛 = 13 + 𝑛 125 𝑢 b) { 1 = 14 𝑢𝑛 = 𝑢𝑛−1 + 1
Hoạt động 2: Dãy số tăng, dãy số giảm. Dãy số bị chặn a) Mục tiêu:
- HS nhận biết tính chất tăng, giảm, bị chặn của dãy số trong những trường hợp đơn giản.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động mục 3 và 4.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV VÀ
SẢN PHẨM DỰ KIẾN HS
Bước 1: Chuyển giao nhiệm vụ: 3. Dãy số tăng, dãy số giảm. HĐKP 4
- GV yêu cầu HS thảo luận nhóm a) 𝑎
đôi, hoàn thành HĐKP 4
𝑛 = 3𝑛 + 1; 𝑎𝑛+1 = 3(𝑛 + 1) + 1 = 3𝑛 + 4
Suy ra 𝑎𝑛 < 𝑎𝑛+1
- GV giới thiệu về dãy số tăng,
b) 𝑏𝑛 = −5𝑛; 𝑏𝑛+1 = −5(𝑛 + 1) = −5𝑛 − 5 dãy số giảm Suy ra 𝑏 + Lưu ý: để 𝑛 > 𝑏𝑛+1 là dãy số tăng thì Kết luận
𝑢𝑛+1 > 𝑢𝑛 ∀𝑛 ∈ ℕ∗, chứ không - Dãy số (𝑢
phải là một vài giá trị của dãy số.
𝑛) được gọi là dãy số tăng nếu 𝑢𝑛+1 > 𝑢
- HS đọc hiểu, giải thích ví dụ 5, 𝑛 ∀𝑛 ∈ ℕ∗. ví dụ 6
- Dãy số (𝑢𝑛) được gọi là dãy số giảm 𝑢𝑛+1 < 𝑢𝑛
- GV tổng kết lại một số cách để ∀𝑛 ∈ ℕ∗.
xét tính tăng giảm của dãy số.
Ví dụ 5 (SGK -tr.48)
Ví dụ 6 (SGK -tr.48) 126
+ Cách 1: Dùng định nghĩa, bằng Thực hành 3
cách xét hiệu 𝑢𝑛+1 − 𝑢𝑛.
a) Ta có: 𝑢𝑛 = 2𝑛−1 = 2 − 3 < 𝑢 𝑛+1 𝑛+1 𝑛+1 = 2 −
+ Cách 2: Nếu 𝑢𝑛 > 0, mọi 𝑛 ∈ 3 , ∀𝑛 ∈ ℕ∗ 𝑛+2
ℕ ∗thì tính 𝑇 = 𝑢𝑛+1 𝑢𝑛
- HS thực hiện Thực hành 3.
Vậy (𝑢𝑛) là dãy số tăng
+ Ta nên sử dụng cách nào (xét b) Ta nhận thấy các số hạng của dãy (xn) đều là số
hiệu hay xét thương) với các dãy dương. Ta lập tỉ số hai số hạng liên tiếp của dãy: số?
+ c) HS tính 3 giá trị đầu tiên của 𝑥𝑛+1 = 𝑛+2 < 1, ∀𝑛 ∈ ℕ∗ 𝑥 4(𝑛+1) dãy để 𝑛
so sánh. Từ đó tổng quát
về tính tăng giảm của dãy.
Suy ra 𝑥𝑛+1 < 𝑥𝑛, ∀𝑛 ∈ ℕ∗
- HS làm Vận dụng 3.
Vậy (𝑥𝑛) là dãy số giảm
c) Ta có: 𝑡1 = −1; 𝑡2 = 4; 𝑡3 = −9. Suy ra 𝑡1 < 𝑡2, 𝑡2 > 𝑡3.
Vậy (𝑡𝑛) không là dãy số tăng, cũng không là dãy số giảm. Vận dụng 3
a) Ta có: 𝑢𝑛 = 26 − 𝑛 > 𝑢𝑛+1 = 26 − 𝑛 − 1 = 25 − 𝑛
Vậy dãy số (un) là dãy số giảm
b) Ta có: 𝑣𝑛 = 13 + 𝑛 < 𝑣𝑛+1 = 13 + 𝑛 + 1 = 14 + 𝑛
Vậy dãy số (un) là dãy số tăng.
- HS thực hiện HĐKP 4.
4. Dãy số bị chặn HĐKP 5 127
- GV giới thiệu về dãy số bị chặn
∀𝑛 ∈ ℕ∗, 0 < 𝑢𝑛 ≤ 1
trên bị chặn dưới và dãy bị chặn. Kết luận
- HS đọc ví dụ 7, GV hướng dẫn. - Dãy số (𝑢𝑛) được gọi là bị chặn trên nếu tồn tại
- HS thực hiện Thực hành 4.
một số 𝑀 sao cho 𝑢𝑛 ≤ 𝑀 ∀𝑛 ∈ ℕ∗.
+ a) Sử dụng tính chất về tập giá
- Dãy số (𝑢𝑛) được gọi là bị chặn dưới nếu tồn tại
trị của hàm 𝑦 = cos 𝑥.
một số 𝑚 sao cho 𝑢𝑛 ≥ 𝑚 ∀𝑛 ∈ ℕ∗.
+) b) So sánh tử số và mẫu số, từ
đó đánh giá tập giá trị của bn .
- Dãy số (𝑢𝑛) được gọi là bị chặn nếu nó vừa bị
Bước 2: Thực hiện nhiệm vụ:
chặn trên vừa bi chặn dưới, tức là tồn tại các só
𝑚, 𝑀 sao cho 𝑚 ≤ 𝑢
- HS theo dõi SGK, chú ý nghe,
𝑛 ≤ 𝑀 ∀𝑛 ∈ ℕ∗.
tiếp nhận kiến thức, suy nghĩ trả Ví dụ 7 (SGK -tr.49)
lời câu hỏi, hoàn thành các yêu Thực hành 4 cầu.
a) Ta có −1 ≤ cos 𝜋 ≤ 1 𝑛
- GV: quan sát và trợ giúp HS.
Suy ra −1 ≤ 𝑎𝑛 ≤ 1. Vậy (𝑎𝑛) bị chặn. Bướ 𝑛
c 3: Báo cáo, thảo luận: b) Ta có = 1 − 1 𝑛+1 𝑛+1
- HS giơ tay phát biểu, lên bảng Suy ra 0≤ 𝑏𝑛 ≤ 1. Vậy (𝑏𝑛) bị chặn. trình bày
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận định:
GV tổng quát lưu ý lại kiến thức
trọng tâm và yêu cầu HS ghi chép
đầy đủ vào vở.
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 1 đến 4 (SGK -tr.50) và các câu hỏi TN. 128
c) Sản phẩm học tập: Câu trả lời của HS.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS trả lời các câu hỏi TN nhanh
Câu 1. Cho dãy số (𝑦𝑛) xác định bởi 𝑦𝑛 = 𝑠𝑖𝑛2 𝑛𝜋 + 𝑐𝑜𝑠 2𝑛𝜋. Bốn số hạng đầu của dãy 4 3 số đó là:
A. 0, 1 , 3 , − 1.
B. 1, 1 , 3 , 1. 2 2 2 2 2 2
C. 1, 1 , 3 , 3.
D. 0, 1 , − 1 , 1. 2 2 2 2 2 2
Câu 2. Cho dãy số (𝑢𝑛) có 𝑢𝑛 = 𝑛+1 . Số 8 là số hạng thứ bao nhiêu của dãy số (𝑢 2𝑛+1 15 𝑛) ? A. 8 B. 6. C. 5. D. 7.
Câu 3. Trong các dãy số dưới đây dãy số nào là dãy số tăng ? A. Dãy ( 𝜋
𝑎𝑛), với 𝑎𝑛 = (−1)𝑛+1. 𝑠𝑖𝑛 , ∀𝑛 ∈ ℕ ∗. 𝑛
B. Dãy (𝑏𝑛), với 𝑏𝑛 = (−1)2𝑛. (5𝑛 + 1), ∀𝑛 ∈ ℕ ∗.
C. Dãy (𝑐𝑛), với 𝑐𝑛 = 1 , ∀𝑛 ∈ ℕ ∗. 𝑛+√𝑛+1
D. Dãy (𝑑𝑛), với 𝑑𝑛 = 𝑛 , ∀𝑛 ∈ ℕ ∗. 𝑛2+1
Câu 4. Trong các dãy số sau đây, dãy số nào là dãy số giảm ? 𝑛
A. Dãy (𝑎𝑛), với 𝑎𝑛 = (− 1) . B. Dãy (𝑏 . 2 𝑛) với 𝑏𝑛 = 𝑛2+1 𝑛
C. Dãy (𝑐𝑛), với 𝑐𝑛 = 1 . D. Dãy (𝑑 𝑛3+1
𝑛), với 𝑑𝑛 = 3. 2𝑛.
Câu 5. Trong các dãy số sau dãy số nào là dãy bị chặn ?
A. Dãy (𝑎𝑛), với 𝑎𝑛 = √𝑛2 + 16, ∀𝑛 ∈ ℕ ∗.
B. Dãy (𝑏𝑛), với 𝑏𝑛 = 𝑛 + 1 , ∀𝑛 ∈ ℕ ∗. 2𝑛
C. Dãy (𝑐𝑛), với 𝑐𝑛 = 2𝑛 + 3, ∀𝑛 ∈ ℕ ∗. 129 D. Dãy ( 𝑛 𝑑𝑛), với 𝑑𝑛 = , ∀𝑛 ∈ ℕ ∗. 𝑛2+4
- GV tổ chức cho HS hoạt động thực hiện Bài 1 đến 4 (SGK -tr.50)
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định:
- GV nhận xét thái độ làm việc, phương án trả lời của các học sinh, ghi nhận và tuyên dương Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 A D B C D Bài 1. 𝑢2 = 1 ; 𝑢 . 2 3 = 1 3
Ta cũng tính được 𝑢4 = 1 ; 𝑢 ; 𝑢 ; … 4 5 = 1 5 6 = 1 6
Vậy ta dự đoán 𝑢𝑛 = 1. 𝑛 Bài 2. Ta có : 𝑢1 = 1 = 1 1.2 2 130 1 1 1 1 1 1 1 1 2 𝑢2 = + = ( − ) + ( − ) = − = ; 1 ⋅ 2 2 ⋅ 3 1 2 2 3 1 3 3 1 1 1 1 1 1 1 1 1 1 1 3 𝑢3 = + +
= ( − ) + ( − ) + ( − ) = − = ; 1.2 2.3 3.4 1 2 2 3 3 4 1 4 4
Công thức số hạng tổng quát: 𝑢 1 1 1 𝑛 = 1 + 1 + ⋯ + 1
= ( − 1) + ( − 1) + ⋯ + ( − 1 ) = 1 − 1 = 𝑛 . 1⋅2 2⋅3 𝑛(𝑛+1) 1 2 2 3 𝑛 𝑛+1 1 𝑛+1 𝑛+1 Bài 3.
𝑦𝑛 = √𝑛 + 1 − √𝑛 = 𝑛+1−𝑛 = 1 ; 𝑦𝑛+1 = 1 . √𝑛+1+√𝑛 √𝑛+1+√𝑛 √𝑛+2+√𝑛+1 Ta có: 𝑦𝑛+1 = 1 < 1
= 𝑦𝑛, ∀𝑛 ∈ ℕ∗. Vậy (𝑦𝑛) là dãy số giảm. √𝑛+2+√𝑛+1 √𝑛+1+√𝑛 Bài 4.
a) Ta có: −1 ≤ 𝑎𝑛 ≤ 2, ∀𝑛 ∈ ℕ∗. Vậy dãy số (𝑎𝑛) bị chặn.
b) Ta có: 𝑢𝑛 = 6𝑛−4 > 6−4 = 2 > 0, ∀𝑛 ∈ ℕ′. Vậy dãy số (𝑢 𝑛+2 𝑛+2 𝑛+2 𝑛) bị chặn dưới.
𝑢𝑛 = 6𝑛−4 = 6𝑛+12−16 = 6 − 16 < 6, ∀𝑛 ∈ ℕ∗. Vậy dãy số (𝑢 𝑛+2 𝑛+2 𝑛+2 𝑛) bị chặn trên.
Suy ra dãy số (𝑢𝑛) bị chặn.
D. HOẠT ĐỘNG VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập.
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ. 131
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: Bài 5.
Ta có 𝑢𝑛+1 − 𝑢𝑛 = 2𝑛+1 − 2𝑛−1 = 3 > 0, ∀𝑛 ∈ ℕ∗. 𝑛+2 𝑛+1 (𝑛+2)(𝑛+1)
Suy ra 𝑢𝑛+1 > 𝑢𝑛, ∀𝑛 ∈ ℕ∗. Vậy (𝑢𝑛) là dãy số tăng.
Ta có: 𝑢𝑛 > 2−1 = 1 > 0, ∀𝑛 ∈ ℕ+. Vậy dãy số (𝑢 𝑛+1 𝑛+1 𝑛) bị chặn dưới.
𝑢𝑛 = 2𝑛−1 = 2𝑛+2−3 = 2 − 3 < 2, ∀𝑛 ∈ ℕ∗. Vậy dãy số (𝑢 𝑛+1 𝑛+1 𝑛+1 𝑛) bị chặn trên.
Suy ra dãy số (𝑢𝑛) bị chặn.
Vậy (𝑢𝑛) là dãy số tăng và bị chặn. Bài 6.
Ta có 𝑢𝑛+1 − 𝑢𝑛 = 𝑎(𝑛+1)+2 − 𝑎𝑛+2 = 𝑎−2 . 𝑛+2 𝑛+1 (𝑛+2)(𝑛+1)
a) (𝑢𝑛) là dãy số tăng khi và chỉ khi 𝑎 > 2.
b) (𝑢𝑛) là dãy số giảm khi và chỉ khi 𝑎 < 2. Bài 7. 132
Ta có dãy số: 1; 1; 2; 3; 5; 8; 13; 21.
Nhận xét: Kể từ số hạng thứ ba, mỗi số hạng của dãy bằng tổng của hai số hạng liền trước.
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: "Bài 2. Cấp số cộng". 133 Ngày soạn: .../.../... Ngày dạy: .../.../...
BÀI 2: CẤP SỐ CỘNG (2 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết một dãy số là cấp số cộng.
- Giải thích được công thức xác định số hạng tổng quát của cấp số cộng.
- Tính tổng của n số hạng đầu của cấp số cộng.
- Giải quyết một số vấn đề thực tiễn gắn với cấp số cộng để giải một số bài toán
liên quan đến thực tiễn (ví dụ: vấn đề trong Sinh học, trong Giáo dục dân số,..). 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học: So sánh, phân tích dữ liệu tìm ra mối liên hệ giữa
các đối tượng đã cho và nội dung bài học cấp số cộng, nhận biết và thể hiện cấp
số cộng, tìm công sai và số hạng đầu, tìm số hạng thứ n của cấp số cộng.
- Mô hình hóa toán học: mô tả thiết lập các đối tượng bài toán, sử dụng tính chất
cấp số cộng để giải quyết.
- Giải quyết vấn đề toán học, giao tiếp toán học.
- Sử dụng công cụ, phương tiện học toán. 3. Phẩm chất 134
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học. Giúp HS có cơ hội nhận biết một
dãy số là cấp số cộng thông qua việc đếm số ghế ở các hàng trong một rạp hát có số ghế
tăng dần tính từ sân khấu.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS trả lời được câu hỏi mở đầu.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu:
Một rạp hát có 20 hàng ghế. Tính từ sân khấu, số lượng ghế của các hàng tăng dần như
trong hình minh hoạ dưới đây. 135 - GV đặt câu hỏi:
+ Bạn hãy đếm và nêu nhận xét về số ghế của năm hàng đầu tiên.
(Số ghế 5 hàng đầu tiên lần lượt là: 14; 17; 20; 23; 26.)
(HS dự đoán về tính chất của dãy số trên).
+ Làm thế nào để biết được số ghế của một hàng bất kì và tính được tổng số ghế trong rạp hát đó?
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học mới: “Bài học hôm trước chúng ta đã cùng tìm hiểu thế nào là một dãy số.
Bài học hôm nay chúng ta cùng đi tìm hiểu về một loại dãy số có tính chất như dãy số phần mở đầu”.
Bài 1. Cấp số cộng
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Cấp số cộng. Số hạng tổng quát của cấp số cộng a) Mục tiêu:
- Nhận biết một dãy số là cấp số cộng.
- Giải thích được công thức xác định số hạng tổng quát của cấp số cộng. b) Nội dung: 136
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động mục 1 và 2.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao 1. Cấp số cộng nhiệm vụ: HĐKP 1
- GV yêu cầu HS hoàn Các dãy số trên có điểm giống nhau: thành HĐKP 1
Trong cùng một dãy số, số liền sau bằng tổng của số liền
- GV giới thiệu dãy trên trước với một số không đổi.
được gọi là một cấp số cộng. Kết luận
+ HS khái quát thế nào là Cấp số cộng là một dãy số (hữa hạn hay vô hạn), trong đó cấp số cộng.
kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số
- GV nhấn mạnh để xác hạng đứng ngay trước nó với một số d không đổi.
định cấp số cộng cần xác
𝑢𝑛 = 𝑢𝑛−1 + 𝑑 với 𝑛 ∈ ℕ∗.
định số hạng đầu và công sai.
Số 𝑑 được gọi là công sai của cấp số cộng.
- HS đọc Ví dụ 1, chỉ ra Ví dụ 1 (SGK -tr.52)
cấp số cộng và công sai.
Ví dụ 2 (SGK -tr.53)
- HS đọc Ví dụ 2, chỉ ra
Ví dụ 3 (SGK -tr.53)
số hạng đầu, công sai.
HS đọc hiểu và giải thích Ví dụ 4 (SGK -tr.53) Ví dụ 3, 4.
+ Ví dụ 3: Để chứng minh
là cấp số cộng ta chỉ ra 137
𝑢𝑛+1 − 𝑢𝑛 = 𝑑 là số Nhận xét: Nếu (𝑢𝑛) là cấp số cộng thì kể từ số hạng thứ không đổi.
hai, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng hữu
- Từ kết quả ví dụ 4, ta hạn) đều là trung bình cộng của hai số hạng đứng kề nó trong
khái quát mối quan hệ dãy:
giữa ba số liên nhau trong 𝑢𝑘 = 𝑢𝑘−1+𝑢𝑘+1 ,∀𝑘 ≥ 2 2 cấp số cộng.
- HS thực hiện Thực Thực hành 1
hành 1, 2 và Vận dụng 1. a) Dãy số 3; 7; 11; 15; 19; 23 là cấp số cộng vì kể từ số
hạng hứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với 4. b) Ta có: 𝑢
𝑛+1 = 9(𝑛 + 1) − 9 = 9𝑛 − 9 + 9 = 𝑢𝑛 + 9
Vậy dãy số (𝑢𝑛) là cấp số cộng có công sai d = 9
c) Ta có: 𝑣𝑛+1 = 𝑎(𝑛 + 1) − 𝑏 = 𝑎𝑛 − 𝑏 + 𝑎 = 𝑣𝑛 + 𝑎
Vậy dãy số (𝑣𝑛) là cấp số cộng có công sai d = a. Thực hành 2
3 góc của tam giác lập thành cấp số cộng, gọi 3 góc đó là:
𝑎; 𝑎 + 𝑑; 𝑎 + 2𝑑 (𝑎, 𝑑 > 0) Ta có:
𝑎 + (𝑎 + 𝑑) + (𝑎 + 2𝑑) = 180𝑜 ⇔ 3𝑎 + 3𝑑 = 180𝑜 ⇔ 𝑎 + 𝑑 = 60𝑜 (1)
Do tam giác đó là tam giác vuông nên có 1 góc bằng 90𝑜.
Suy ra 𝑎 + 2𝑑 = 90𝑜 (2) 138
Từ (1) và (2), ta tính được 𝑎 = 30𝑜, 𝑑 = 30𝑜
Vậy số đo 3 góc là 30𝑜; 60𝑜; 90𝑜. Vận dụng 1
Số ô trên các vòng là: 𝑢1 = 6; 𝑢2 = 12; 𝑢3 = 18
Ta thấy 𝑢𝑛+1 = 𝑢𝑛 + 6
Vậy các ô trên vòng theo thứ tự tạo thành cấp số cộng có
- GV đặt câu hỏi: Để tính công sai là 6.
số hạng thứ 100 của một 2. Số hạng tổng quát của cấp số cộng
cấp số cộng 𝑢𝑛 thì ta phải HĐKP 2
làm thế nào? Có phải cần 𝑢2 − 𝑢1 = 𝑑
tìm tất cả 99 số hạng đứng trướ 𝑢 c nó? 3 − 𝑢1 = 2𝑑
- HS thực hiện HĐKP 2. 𝑢4 − 𝑢1 = 3𝑑
- Từ đó có số hạng tổng
quát của cấp số cộng. .....
- HS đọc hiểu Ví dụ 5, 𝑢𝑛 − 𝑢1 = (𝑛 − 1)𝑑
thực hiện Thực hành 3, Vận dụng 2. Định lí 1
+ Để tìm số hạng tổng
quát theo đề bài, ta biểu Nếu cấp số cộng (𝑢𝑛) có số hạng đầu 𝑢1 và công sai 𝑑 thì
diễn các số hạng đã cho số hạng tổng quát 𝑢𝑛 của nó được xác định theo công thức theo 𝑢1 và 𝑑.
𝑢𝑛 = 𝑢1 + (𝑛 − 1)𝑑, 𝑛 ≥ 2.
Bước 2: Thực hiện nhiệm vụ:
Ví dụ 5 (SGK -tr.54)
- HS theo dõi SGK, chú ý Thực hành 3
nghe, tiếp nhận kiến thức, 139
hoàn thành các yêu cầu, a) 𝑎𝑛 = 5 + (𝑛 − 1). (−5) = −5𝑛 + 10 thảo luận nhóm.
b) 𝑏10 = 𝑏1 + 9𝑑 ⇔ 20 = 2 + 9𝑑 ⇔ 𝑑 = 2 - GV quan sát hỗ trợ. Bướ
Suy ra số hạng tổng quát c 3: Báo cáo, thảo 𝑏 luận:
𝑛 = 2 + (𝑛 − 1).2 = 2𝑛 Vận dụng 2
- HS giơ tay phát biểu, lên bảng trình bày
𝑐4 = 𝑐1 + 3𝑑 ⇔ 𝑐1 + 3𝑑 = 80 - Một số HS khác nhận 𝑐 xét, bổ sung cho bạn.
6 = 𝑐1 + 5𝑑 ⇔ 𝑐1 + 5𝑑 = 40
Bước 4: Kết luận, nhận Suy ra 𝑐1 = 140 𝑣à 𝑑 = −20
định: GV tổng quát lưu ý 𝑐
lại kiến thức trọng tâm và
𝑛 = 140 + (𝑛 − 1). (−20) = −20𝑛 + 160
yêu cầu HS ghi chép đầy Vậy số hạng tổng quát của cấp số cộng là đủ vào vở. 𝑐𝑛 = −20𝑛 + 160
Hoạt động 2: Tổng của n số hạng đầu tiên của cấp số cộng a) Mục tiêu:
- HS tính được tổng của n số hạng đầu tiên của cấp số cộng.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động mục 3.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ:
3. Tổng của n số hạng đầu tiên của cấp số cộng 140
- GV yêu cầu HS thảo luận nhóm đôi, HĐKP 3 hoàn thành HĐKP 3. a)
- GV hướng dẫn HS để có công thức tổng 𝑢1 + 𝑢𝑛 = 𝑢1 + 𝑢1 + (𝑛 − 1)𝑑
quát về tổng n số hạng đầu của dãy. = 2𝑢1 + (𝑛 − 1)𝑑
- Áp dụng HS làm Ví dụ 6, Thực hành 4 𝑢 và Vận dụng 3.
2 + 𝑢𝑛−1 = 𝑢1 + 𝑑 + 𝑢1 + (𝑛 − 2)𝑑 = 2𝑢1 + (𝑛 − 1)𝑑
Bước 2: Thực hiện nhiệm vụ:
- HS theo dõi SGK, chú ý nghe, tiếp nhận 𝑢3 + 𝑢𝑛−2 = 𝑢1 + 2𝑑 + 𝑢1 + (𝑛 − 3)𝑑
kiến thức, suy nghĩ trả lời câu hỏi, hoàn = 2𝑢1 + (𝑛 − 1)𝑑 thành các yêu cầu. ….
- GV: quan sát và trợ giúp HS. 𝑢 Bướ
𝑘 + 𝑢𝑛−𝑘+1 = 2𝑢1 + (𝑛 − 1)𝑑
c 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình bày b) Theo a ta có
- Một số HS khác nhận xét, bổ sung cho 2(𝑢1 + 𝑢2+. . . +𝑢𝑛) = 𝑛(2𝑢1 + (𝑛 − 1)𝑑) bạn. ⇔ 2(𝑢 Bướ
1 + 𝑢2+. . . +𝑢𝑛) = 𝑛(𝑢1 + 𝑢𝑛)
c 4: Kết luận, nhận định: GV tổng Định lí 2
quát lưu ý lại kiến thức trọng tâm và yêu Cho cấp số cộng (𝑢𝑛) với công sai d. Đặt
cầu HS ghi chép đầy đủ vào vở.
𝑆𝑛 = 𝑢1 + 𝑢2 + ⋯ + 𝑢𝑛. Khi đó 𝑛(𝑢 𝑆 1 + 𝑢𝑛) 𝑛 = 2 Hay 𝑆𝑛 = 𝑛 [2𝑢 2 1 + (𝑛 − 1)𝑑]
Ví dụ 6 (SGK -tr.55) Thực hành 4
a) Tổng 50 số tự nhiên chẵn đầu tiên là: 50[2.0 + (50 − 1). 2] 𝑆50 = = 2450 2 141
b) 𝑢3 + 𝑢28 = 𝑢1 + 2𝑑 + 𝑢1 + 27𝑑 =
𝑢1 + 𝑢1 + 29𝑑 = 𝑢1 + 𝑢30 = 100 𝑛(𝑢 𝑆 1 + 𝑢30) 30 = = 30.1002 = 1500 2
c) 𝑆6 = 6(2𝑢1+5𝑑) = 18 ⇔ 2𝑢 2 1 + 5𝑑 = 6 10(2𝑢 𝑆 1 + 9𝑑) 10 = = 110 ⇔ 2𝑢 2 1 + 9𝑑 = 22 Suy ra 𝑢1 = −7; 𝑑 = 4 20(2𝑢 𝑆 1 + 19𝑑) 20 = = 620 2 Vận dụng 3
Ta có: 𝑢1 = 17; 𝑢2 = 20; 𝑢3 = 23
Suy ra 𝑑 = 3 và 𝑢𝑛 = 17 + (𝑛 − 1).3 = 3𝑛 + 14 a) 𝑢20 = 3.20 + 14 = 74 b) 𝑆20 = 20. (17+74) = 910 2
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 1 đến 5 (SGK -tr.56) và các câu hỏi TN.
c) Sản phẩm học tập: Câu trả lời của HS. 142
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS trả lời các câu hỏi TN nhanh
Câu 1. Trong các dãy số sau, dãy số nào là cấp số cộng? A. −3,1,5,9,14.
B. 5,2, −1, −4, −7. 5
C. , 1, 1 , − 1 , −3.
D. − 7 , − 5 , −2, − 1 , 1. 3 3 3 2 2 2 2
Câu 2. Cho cấp số cộng (𝑢𝑛) xác định bởi 𝑢3 = −2; 𝑢𝑛+1 = 𝑢𝑛 + 3, ∀𝑛 ∈ ℕ∗. Xác định
số hạng tổng quát của cấp số cộng đó.
A. 𝑢𝑛 = 3𝑛 − 11.
B. 𝑢𝑛 = 3𝑛 − 8.
C. 𝑢𝑛 = 2𝑛 − 8.
D. 𝑢𝑛 = 𝑛 − 5.
Câu 3. Cho cấp số cộng 6, 𝑥, −2, 𝑦. Khẳng định nào sau đây đúng? A. 𝑥 = 2; 𝑦 = 5. B. 𝑥 = 4; 𝑦 = 6.
C. 𝑥 = 2; 𝑦 = −6.
D. 𝑥 = 4; 𝑦 = −6.
Câu 4. Cho cấp số cộng (𝑢𝑛) có 𝑢4 = −3u = 3
− và tổng của 9 số hạng đầu tiên là 𝑆 4 9 =
45. Cấp số cộng trên có A. 𝑆10 = 92. B. 𝑆20 = 980. C. 𝑆3 = −56. D. 𝑆16 = 526.
Câu 5. Người ta trồng 3003 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây,
hàng thứ hai có 2 cây, hàng thứ ba có 3 cây,… Hỏi trồng được bao nhiêu hàng cây theo cách này? A. 77 hàng. B. 76 hàng. C. 78 hàng. D. 79 hàng.
- GV tổ chức cho HS hoạt động thực hiện Bài 1 đến 5 (SGK -tr.56). 143
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định:
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác. Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 B A C B A Bài 1
Kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với (−4)
nên dãy số 1; −3; −7; −11; −15 là một cấp số cộng. Bài 2.
𝑢𝑛 = 𝑢1 + (𝑛 − 1)𝑑 = 4 + (𝑛 − 1)(−10) = −10𝑛 + 14 Bài 3.
a) 𝑢12 = 𝑢1 + 11𝑑 = −3 + 11 ⋅ 2 = 19;
b) Ta có: 𝑢𝑛 = −3 + 2(𝑛 − 1) = 195 ⇒ 𝑛 = 100. Vậy 195 là số hạng thứ 100 . Bài 4. 144
a) (𝑢𝑛) là cấp số cộng với số hạng đầu 𝑢1 = −1 và công sai 𝑑 = −4.
b) (𝑢𝑛) là cấp số cộng với số hạng đầu 𝑢1 = − 7 và công sai 𝑑 = 1. 2 2
c) (𝑢𝑛) không phải là cấp số cộng vì có 𝑢1 = 5; 𝑢2 = 25; 𝑢3 = 125; 𝑢2 − 𝑢1 ≠ 𝑢3 − 𝑢2.
d) (𝑢𝑛) là cấp số cộng với số hạng đầu 𝑢1 = 4 và công sai 𝑑 = − 5. 3 3 Bài 5. 𝑢 2𝑑 = 20 𝑑 = 10 a) { 3 − 𝑢1 = 20 ⇔ { ⇔ { 𝑢2 + 𝑢5 = 54 2𝑢1 + 5𝑑 = 54 𝑢1 = 2; 𝑢 2𝑢 𝑑 = 40
b) { 2 + 𝑢3 = 0 ⇔ { 1 + 3𝑑 = 0 ⇔ { 𝑢2 + 𝑢5 = 80 2𝑢1 + 5𝑑 = 80 𝑢1 = −60; 𝑢 3𝑑 = 3 𝑑 = 1 c) { 5 − 𝑢2 = 3 ⇔ { ⇔ { ⇔ 𝑢 2 8 ⋅ 𝑢3 = 24
(𝑢1 + 7𝑑)(𝑢1 + 2𝑑) = 24 𝑢1 + 9𝑢1 − 10 = 0 𝑑 = 1 {
𝑢1 = 1 hoặc 𝑢1 = −10.
D. HOẠT ĐỘNG VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập.
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 6, 7, 8 (SGK -tr.56).
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ. 145
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: Bài 6.
a) Chiều dài các thanh ngang của cái thang (tính từ bậc dưới cùng) tạo thành một cấp số
cộng có: 𝑢1 = 45; 𝑑 = −2. Suy ra 𝑛 = 45−31 + 1 = 8. 2 Vậy cái thang có 8 bậc.
b) 𝑆8 = 8(45+31) = 304. Vậy người đó cần mua thanh gỗ có chiều dài 304 cm. 2 Bài 7. a) 𝑑 = 32.
b) 𝑆10 = 10(2⋅16+9.32) = 1600 (feet). 2 Bài 8.
Chiều cao của các cây có số alen trội từ 0 đến 4 tạo thành 5 số hạng liên tiếp của một
cấp số cộng với 𝑢1 = 100 và 𝑑 = 5, suy ra 𝑢5 = 100 + 4.5 = 120.
Vậy cây cao nhất với kiểu gene AABB có chiều cao 120 cm.
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: "Bài 3. Cấp số nhân" 146 Ngày soạn: .../.../... Ngày dạy: .../.../...
BÀI 3. CẤP SỐ NHÂN (2 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết một dãy số là cấp số nhân.
- Giải thích được công thức xác định số hạng tổng quát của cấp số nhân.
- Tính tổng của n số hạng đầu của cấp số nhân.
- Giải quyết một số vấn đề thực tiễn gắn với cấp số nhân để giải một số bài toán
liên quan đến thực tiễn (ví dụ: vấn đề trong Sinh học, trong Giáo dục dân số,..). 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học: So sánh, phân tích dữ liệu tìm ra mối liên hệ giữa
các đối tượng đã cho và nội dung bài học cấp số nhân, nhận biết và thể hiện cấp
số nhân, tìm công bội và số hạng đầu, tìm số hạng thứ n của cấp số nhân.
- Mô hình hóa toán học: mô tả thiết lập các đối tượng bài toán, sử dụng tính chất
cấp số nhân để giải quyết.
- Giải quyết vấn đề toán học, giao tiếp toán học. 147
- Sử dụng công cụ, phương tiện học toán. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học. Giúp HS có cơ hội thảo luận về
cấp số nhân thông qua việc xét dãy số biểu diễn các độ cao nảy lên của một quả bóng.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS trả lời được câu hỏi mở đầu.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu: 148
Một quả bóng rơi từ một vị trí có độ cao 120 cm. Khi chạm đất, nó luôn nảy lên độ cao
bằng một nửa độ cao của lần rơi trước đó.
Gọi 𝑢1 = 120 là độ cao của lần rơi đầu tiên và 𝑢2; 𝑢3; . . . ; 𝑢𝑛; . .. là độ cao của các lần
rơi kế tiếp. Tìm 5 số hạng đầu tiên của dãy (un) và tìm điểm đặc biệt của dãy số đó.
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học mới. Bài 3. Cấp số nhân.
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Cấp số nhân. Số hạng tổng quát của cấp số nhân a) Mục tiêu:
- Nhận biết một dãy số là cấp số nhân.
- Giải thích được công thức xác định số hạng tổng quát của cấp số nhân. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi. 149
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ: 1. Cấp số nhân
- GV yêu cầu HS thảo luận nhóm đôi, HĐKP 1 hoàn thành HĐKP 1
a) Thương của 2 số hạng liên tiếp trong dãy là
- GV giới thiệu dãy số như trên được 2. gọi là cấp số nhân.
b) Điểm giống nhau của các dãy số là:
Từ đó HS khái quát thế nào là cấp số Trong mỗi dãy số, mỗi số hạng đều bằng tích nhân.
của số hạng liền trước với một số không đổi.
+ Nhấn mạnh: cấp số nhân xác định Kết luận
khi biết số hạng đầu và công bội.
Cấp số nhân là một dãy số (hữu hạn hay vô
- HS đọc, giải thích Ví dụ 1, 2, 3.
hạn), trong đó kể tử số hạng thứ hai mỗi số
- Từ kết quả của Ví dụ 3, khái quát về
hạng đều bằng tích của số hạng đứng ngay
tính chất của ba số liên tiếp trong một trước nó với một số không đổi 𝑞. cấp số nhân.
- HS thực hiện Thực hành 1.
𝑢𝑛 = 𝑢𝑛−1 ⋅ 𝑞 với 𝑛 ∈ ℕ∗.
+ vì m, n, p lập thành cấp số cộng,
Số q được gọi là công bội của cấp số nhân.
viết mối quan hệ của m, n, p.
Ví dụ 1 (SGK -tr.57)
+ Từ đó viết mối quan hệ của
Ví dụ 2 (SGK -tr.58) 2𝑚, 2𝑛, 2𝑝.
Ví dụ 3 (SGK -tr.58)
- HS thực hiện Vận dụng 1, 2.
Chú ý: Dãy số (𝑢
+ VD1: Viết dân số các năm theo P
𝑛) là cấp số nhân thì 𝑢 2 = 𝑢
và a%, từ đó xác định được số hạng 𝑘
𝑘−1. 𝑢𝑘+1, ∀𝑘 ≥ 2. đầ Thực hành 1 u, công bội.
Vì 3 số m, n, p theo thứ tự lập thành 1 cấp số
+ VD2: Viết tần số ba phím đã cho cộng.
theo một cấp số nhân, rồi tìm công bội. 150
Gọi d là công sai của cấp số công. Ta có: 𝑛 =
𝑚 + 𝑑, 𝑝 = 𝑛 + 𝑑
Ta có: 2𝑛 = 2𝑚+𝑑 = 2𝑚. 2𝑑
Và 2𝑝 = 2𝑛+𝑑 = 2𝑛. 2𝑑
Vậy 2𝑚, 2𝑛, 2𝑝 theo thứ tự lập thành cấp số
nhân có công bội là 2𝑑. Vận dụng 1 Dân số qua các năm là: 𝑢2011 = 𝑃
𝑢2012 = 𝑃 + 𝑎𝑃 = 𝑃(1 + 𝑎) = 𝑢2011. (1 + 𝑎)
𝑢2013 = 𝑃(1 + 𝑎) + 𝑎𝑃(1 + 𝑎) = 𝑃(1 + 𝑎)2 = 𝑢2012. (1 + 𝑎) .....
𝑢𝑛+1 = 𝑢𝑛(1 + 𝑎)
Vậy dân số các năm tạo thành cấp số nhân có công bội là 1 + 𝑎. Vận dụng 2
Do tần số của ba phím Sol, La, Si tạo thành
cấp số nhân nên gọi tần số 3 phím lần lượt
là: 𝑎, 𝑎𝑞, 𝑎𝑞2
Ta có: 𝑎 = 415 và 𝑎𝑞2 = 466. Nên 𝑞 = 1,06 151 Suy ra: 𝑎𝑞 = 440
Vậy tần số của phím La là 440 Hz.
2. Số hạng tổng quát của cấp số nhân
- HS thực hiện HĐKP 2, để tìm ra số HĐKP 2
hạng tổng quát của cấp số nhân. 𝑢
- GV chốt lại kiến thức: định lí 1. 2 = 𝑢1. 𝑞
- HS thực hiện Ví dụ 4, Thực hành
𝑢3 = 𝑢2. 𝑞 = 𝑢1. 𝑞2 2, Vận dụng 3.
+ TH4: xác định số hạng đầu và công
𝑢4 = 𝑢3. 𝑞 = 𝑢1. 𝑞3 bội của cấp số nhân 𝑢 + VD3: Xác đị 10 = 𝑢1. 𝑞9
nh công bội và số hạng Định lí 1
đầu. Rồi tính chu kì bán rã trong mỗi
Nếu một cấp số nhân có số hạng đầu 𝑢1 và câu a, b.
công bội 𝑞 thì số hạng tổng quát 𝑢𝑛 của nó
Bước 2: Thực hiện nhiệm vụ:
được xác định bởi công thức
- HS theo dõi SGK, chú ý nghe, tiếp
𝑢𝑛 = 𝑢1 ⋅ 𝑞𝑛−1 với 𝑛 ≥ 2.
nhận kiến thức, hoàn thành các yêu cầu, thảo luận nhóm.
Ví dụ 4 (SGK -tr.59) - GV quan sát hỗ trợ. Thực hành 2 a) 𝑢 Bướ 𝑛 = 5.2𝑛−1
c 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình 1 𝑛−1 b) 𝑢𝑛 = 1. ( ) 10 bày
- Một số HS khác nhận xét, bổ sung Vận dụng 3 cho bạn.
a) Sau 690 = 138.5 ngày, tức là sau 5 chu kì
Bước 4: Kết luận, nhận định: GV bán rã, khối lượng nguyên tố Poloni còn lại là:
tổng quát lưu ý lại kiến thức trọng 4
tâm và yêu cầu HS ghi chép đầy đủ 20 ⋅ 1 ( ) = 1,25( g); 2 vào vở. 152
b) Sau 7314 = 138.53 ngày, tức là sau 53 chu
kì bán rã, khối lượng nguyên tố Poloni còn lại là: 52 20 ⋅ 1 ( ) ≈ 4,44 ⋅ 10−15( g). 2 Hoạt động 2: a) Mục tiêu:
- HS tính được tổng của n số hạng đầu tiên của cấp số nhân.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV VÀ
SẢN PHẨM DỰ KIẾN HS
Bước 1: Chuyển giao nhiệm 3. Tổng của n số hạng đầu tiên của cấp số nhân HĐKP 3 vụ:
𝑆𝑛 = 𝑢1 + 𝑢2 + ⋯ + 𝑢𝑛
- GV yêu cầu HS thảo luận
nhóm đôi, hoàn thành HĐKP 3.
= 𝑢1 + 𝑢1. 𝑞 + 𝑢1. 𝑞2+. . . . +𝑢1. 𝑞𝑛−1
- Từ đó có công thức tính tổng a) Ta có:
n số hạng đầu của dãy.
- HS áp dụng thực hiện Ví dụ 5,
𝑞. 𝑆𝑛 = 𝑢1. 𝑞 + 𝑢1. 𝑞2+. . . . +𝑢1. 𝑞𝑛
Thực hành 3, Vận dụng 4. 153
+ TH3: xác định công bội của
(𝑢2 + ⋯ + 𝑢𝑛) + 𝑞. 𝑢𝑛
dãy số, giá trị n, rồi áp dụng
= 𝑢1. 𝑞 + 𝑢1. 𝑞2+. . . . +𝑢1. 𝑞𝑛−1 công thức tính. + 𝑢1. 𝑞𝑛
+ VD4: xác định số hạng đầu, Vậy 𝑞. 𝑆
công bội, giá trị n bằng bao
𝑛 = (𝑢2 + ⋯ + 𝑢𝑛) + 𝑞. 𝑢𝑛 nhiêu.
b) Ta có: 𝑢1 + 𝑞. 𝑆𝑛 = 𝑢1 + (𝑢2 + ⋯ + 𝑢𝑛) + 𝑞. 𝑢𝑛
Bước 2: Thực hiện nhiệm vụ:
= (𝑢1 + 𝑢2+. . +𝑢𝑛) + 𝑞. 𝑢𝑛 = 𝑆𝑛 + 𝑢1. 𝑞𝑛
- HS theo dõi SGK, chú ý nghe,
tiếp nhận kiến thức, suy nghĩ Vậy 𝑢1 + 𝑞. 𝑆𝑛 = 𝑆𝑛 + 𝑢1. 𝑞𝑛
trả lời câu hỏi, hoàn thành các Định lí 2 yêu cầu.
Giả sử (𝑢𝑛) là một cấp số nhân với công bội 𝑞 ≠ 1.
- GV: quan sát và trợ giúp HS. Đặt 𝑆𝑛 = 𝑢1 + 𝑢2 + ⋯ + 𝑢𝑛. Khi đó
Bước 3: Báo cáo, thảo luận: 𝑢 𝑆 1(1 − 𝑞𝑛) 𝑛 = . 1 − 𝑞
- HS giơ tay phát biểu, lên bảng trình bày
Chú ý: Khi 𝑞 = 1 thì 𝑆𝑛 = 𝑛. 𝑢1
- Một số HS khác nhận xét, bổ Ví dụ 5 (SGK -tr.60) sung cho bạn. Thực hành 3
Bước 4: Kết luận, nhận định: a) 𝑆5 = 105(1−0,15) = 11110 1−0,1
GV tổng quát lưu ý lại kiến
thức trọng tâm và yêu cầu HS b) 𝑢2 = −20 = 𝑢1. 𝑞.
ghi chép đầy đủ vào vở. Suy ra 𝑞 = −2 10. (1 − (−2)5) 𝑆5 = = 110 1 − (−2) Vận dụng 4
Ta có: 𝑢1 = 120; 𝑞 = 1 2 154 1 10 120. (1 − (2) ) 𝑆10 = = 239,8 1 1 − 2
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 1 đến 4 (SGK tr.60) và các câu hỏi TN.
c) Sản phẩm học tập: Câu trả lời của HS.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS trả lời các câu hỏi TN nhanh
Câu 1. Trong các dãy số được cho dưới đây, dãy số nào là cấp số nhân?
A. Dãy số (𝑢𝑛), với 𝑢𝑛 = 7 − 3𝑛.
B. Dãy số (𝑣𝑛), với 𝑣𝑛 = 7 − 3𝑛.
C. Dãy số (𝑤𝑛), với w = 7.3 .n D. Dãy số (𝑡 . n 𝑛), với 𝑡𝑛 = 7 3𝑛
Câu 2. Cho dãy số (𝑢𝑛)(u xác định bởi 𝑢
, ∀𝑛 ≥ 1. Tìm số hạng n )
1 = 3 và 𝑢𝑛+1 = 𝑢𝑛 4 tổng quát của dãy số.
A. 𝒖𝒏 = 𝟑. 𝟒−𝒏.
B. 𝒖𝒏 = 𝟑. 𝟒𝟏−𝒏.
C. 𝒖𝒏 = 𝟑. 𝟒𝒏−𝟏.
D. 𝒖𝒏 = 𝟑. 𝟒−𝒏−𝟏.
Câu 3. Cho cấp số nhân (𝑥𝑛) có 𝑥2 = −3 và 𝑥4 = −27. Tính số hạng đầu 𝑥1 và công
bội 𝑞 q của cấp số nhân.
A. 𝒙𝟏 = −𝟏, 𝒒 = −𝟑 hoặc 𝑥1 = 1, 𝑞 = 3.
B. 𝒙𝟏 = −𝟏, 𝒒 = 𝟑 hoặc 𝑥1 = 1, 𝑞 = −3.
C. 𝒙𝟏 = 𝟑, 𝒒 = −𝟏 hoặc 𝑥1 = −3, 𝑞 = 1.
D. 𝒙𝟏 = 𝟑, 𝒒 = 𝟏 hoặc 𝑥1 = −3, 𝑞 = −1.
Câu 4. Cho cấp số nhân (𝑢𝑛) có 𝑆2 = 4 và 𝑆3 = 13. Tìm 𝑆5. 155 A. 181 35 𝑆5 = 121 hoặc 𝑆5 = . B. 𝑆 . 16 5 = 121 hoặc 𝑆5 = 16
C. 𝑆5 = 114 hoặc 𝑆5 = 185. D. 𝑆 . 16 5 = 141 hoặc 𝑆5 = 183 16 𝑢
Câu 5. Cho cấp số nhân (𝑢 4 + 𝑢6 = −540 𝑛) có { . Tính 𝑆 𝑢 21. 3 + 𝑢5 = 180
A. 𝑆21 = 1 (321 + 1) B. 𝑆 2 21 = 321 − 1.
C. 𝑆21 = 1 − 321. D. 𝑆21 = − 1 (321 + 1). 2
- GV tổ chức cho HS hoạt động thực hiện Bài 1 đến 4 (SGK tr.60)
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định:
- GV nhận xét thái độ làm việc, phương án trả lời của các học sinh, ghi nhận và tuyên dương. Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 C B B A A Bài 1. 156
a) (𝑢𝑛) là một cấp số nhân với số hạng đầu 𝑢1 = −6 và công bội 𝑞 = −2.
b) (𝑢𝑛) là một cấp số nhân với số hạng đầu 𝑢1 = 7 và công bội 𝑞 = −7.
c)Ta có: 𝑢1 = 1; 𝑢2 = 5; 𝑢3 = 13. Vì 𝑢2 ≠ 𝑢3 nên (𝑢 𝑢
𝑛) không phải là cấp số nhân. 1 𝑢2 Bài 2. a) 𝑢 15 𝑢 𝑢 1(𝑞4 − 1) = 15 𝑢
{ 5 − 𝑢1 = 15 ⇔ { 1(𝑞4 − 1) = 15 ⇔ { 𝑞4 − 1 15 ⇔ { 1 = (𝑞4 − 1) 𝑢4 − 𝑢2 = 6 𝑢1𝑞(𝑞2 − 1) = 6 = 𝑞(𝑞2 − 1) 6 2𝑞2 − 5𝑞 + 2 = 0 1 𝑞 = 2 𝑞 = ⇔ { hoặc { 𝑢 2 1 = 1 𝑢1 = −16. b) 𝑢 325 𝑢 𝑢 1(1 + 𝑞6) = 325 𝑢
{ 1 − 𝑢3 + 𝑢5 = 65 ⇔ { 1(1 − 𝑞2 + 𝑞4) = 65 ⇔ { 1 + 𝑞6 325 ⇔ { 1 = 1 + 𝑞6 𝑢 𝑢 = 1 + 𝑢7 = 325 1(1 + 𝑞6) = 325 1 − 𝑞2 + 𝑞4 65 1 + 𝑞2 = 5 𝑞 = 2 𝑞 = −2 ⇔ { hoặc { 𝑢1 = 5 𝑢1 = 5. Bài 3.
a) Gọi số đo bốn góc của tứ giác lập thành cấp số nhân là 𝑢1; 𝑢2; 𝑢3; 𝑢4. Ta có: 𝑢
{ 1 + 𝑢2 + 𝑢3 + 𝑢4 = 360 𝑢4 = 8𝑢1 360 𝑢
⇔ { 1 = 1 + 𝑞 + 𝑞2 + 𝑞3 𝑞3 = 8 𝑢 𝑢
⇔ { 1 + 𝑢1𝑞 + 𝑢1𝑞2 + 𝑢1𝑞3 = 360 ⇔ { 1 = 24 𝑢 𝑞 = 2. 1𝑞3 = 8𝑢1
Vậy số đo bốn góc của tứ giác là 24∘; 48∘; 96∘; 192∘.
b) 𝑞 = −2. Vậy sáu số cần tìm là: 4; −8; 16; −32; 64; −128. 157
Số hạng thứ 15 là: -32768 . Bài 4.
Ta có 2 , 1 , 2 lập thành cấp số cộng, suy ra: 𝑏−𝑎 𝑏 𝑏−𝑐 2 2 2 2𝑏 − 𝑎 − 𝑐 1 + = ⇒ =
⇒ 𝑏(2𝑏 − 𝑎 − 𝑐) = (𝑏 − 𝑎)(𝑏 − 𝑐) ⇒ 𝑏2 𝑏 − 𝑎 𝑏 − 𝑐 𝑏 (𝑏 − 𝑎)(𝑏 − 𝑐) 𝑏 = 𝑎𝑐.
Suy ra 𝑎, 𝑏, 𝑐 lập thành cấp số nhân.
D. HOẠT ĐỘNG VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập.
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 5, 6, 7, 8 (SGK -tr.60+61).
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: 158 Bài 5. 1 1⋅(1− a) (3𝑛+1−3) 𝑆 3𝑛+1) 𝑛 = 1 + 1 + 1 + ⋯ + 1 = = ; 3 32 3𝑛 1 1− 2⋅3𝑛 3 b)
𝑆𝑛 = 9 + 99 + 999 + ⋯ + 99 … .9 (𝑛 𝑠ố 9)
= (101 − 1) + (102 − 1) + (103 − 1) + ⋯ + (10𝑛 − 1) 10(1 − 10𝑛) 10𝑛+1 − 10
= (101 + 102 + 103 + ⋯ + 10𝑛) − (1 + 1 + 1 + ⋯ + 1) = − 𝑛 = − 𝑛. 1 − 10 9 Bài 6.
𝑢1 = 1; 𝑞 = 2; 𝑢21 = 1 ⋅ 220 = 1048576. Bài 7.
a) Dân số của thành phố vào năm thứ n là: 𝑢𝑛 = 2,1.1,0075𝑛−2022
2,1(1 + 0,75%)10 ≈ 2,26 (triệu người).
b) Khi 𝑢𝑛 = 2. 𝑢2022 ⇔ 1,0075𝑛−2022 = 2 ⇔ 𝑛 = 2115
Vậy đến năm 2115, dân số thành phố gấp đôi so với năm 2022 Bài 8. a) 9 ⋅ (0,6)2 = 3,24( m). b) 9⋅(1−0,65) 𝑆5 = ≈ 20,75( m). 1−0,6
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài tập cuối chương II.
• GV chia lớp thành 4 – 5 tổ thực hiện vẽ sơ đồ tóm tắt kiến thức chương II.
• HS chuẩn bị bài tập cuối chương II – SGK – tr.61+62. 159 Ngày soạn: .../.../... Ngày dạy: .../.../...
BÀI TẬP CUỐI CHƯƠNG II (2 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học sinh ôn tập và củng cố về - Dãy số - Cấp số cộng. - Cấp số nhân. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học, giải quyết vấn đề toán học: So sánh, phân tích dữ
liệu tìm ra mối liên hệ giữa các đối tượng đã cho và nội dung bài học về dãy số,
cấp số cộng, cấp số nhân, tính chất dãy số, số hạng tổng quát, công thức tính tổng
dãy của cấp số cộng và cấp số nhân.
- Mô hình hóa toán học: vận dụng các kiến thức vào bài toán thực tế. - Giao tiếp toán học. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV. 160
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo tâm thế cho HS vào bài học. Ôn lại kiến thức đã học.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS trả lời được câu hỏi mở đầu.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS trả lời và giải thích các câu hỏi TN 1, 2, 3, 4, 5, 6, 7, 8 (SGK -tr.61+62).
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, trả lời câu hỏi và giải thích đáp án.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học: Bài tập cuối chương II. Đáp án
1.B, 2. C, 3. A, 4. D, 5. C, 6. D, 7. B, 8. D
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Ôn tập các kiến thức đã học ở chương II a) Mục tiêu: 161
- HS nhắc lại và tổng hợp được các kiến thức đã học theo một sơ đồ nhất định. b) Nội dung
HS tổng hợp lại kiến thức dựa theo SGK và ghi chép trên lớp theo nhóm đã được phân công của buổi trước.
c) Sản phẩm: Sơ đồ mà HS đã vẽ.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ:
+) Hàm số u xác định trên tập hợp ℕ∗
được gọi là một dãy số vô hạn,
- GV mời đại diện từng nhóm lên trình bày về 𝑢: ℕ∗ → ℝ
sơ đồ tư duy của nhóm.
𝑛 ↦ 𝑢𝑛 = 𝑢(𝑛)
- GV có thể đặt các câu hỏi thêm về nội dung Kí hiệu (𝑢𝑛). kiến thức:
+) Cách xác định dãy số
+ Thế nào là một dãy số? Nêu các cách cho một dãy số?
- Liệt kê các số hạng (chỉ dùng cho
+ Nêu số hạng tổng quát của cấp số nhân.
các däy hữu hạn và có ít số hạng);
Công thức tính tổng n số hạng đầu của cấp số - Công thức của số hạng tổng quát; nhân.
+ Một HS cho ví dụ về cấp số cộng. - Phương pháp mô tả
HS khác xác định số hạng đầu và công sai - Phương pháp truy hồi
của cấp số cộng đó.
HS khác tính tổng của 10 số hạng đầu của
+) Nếu một cấp số nhân có số hạng
cấp số cộng đó.
đầu 𝑢1 và công bội 𝑞 thì số hạng tổng
- GV có thể đưa ra sơ đồ chung để HS hình
quát 𝑢𝑛 của nó được xác định bởi dung hơn. công thức
Bước 2: Thực hiện nhiệm vụ:
𝑢𝑛 = 𝑢1 ⋅ 𝑞𝑛−1 với 𝑛 ≥ 2. 162
- HS tự phân công nhóm trưởng và nhiệm vụ
+) Cho cấp số nhân (𝑢𝑛) với công bội
phải làm để hoàn thành sơ đồ.
𝑞 ≠ 1. Đặt 𝑆𝑛 = 𝑢1 + 𝑢2 + ⋯ + 𝑢𝑛. Khi đó
- GV hỗ trợ, hướng dẫn thêm.
Bước 3: Báo cáo, thảo luận: 𝑢 𝑆 1(1 − 𝑞𝑛) 𝑛 = . 1 − 𝑞
- Đại diện nhóm trình bày, các HS chú ý lắng nghe và cho ý kiến.
Chú ý: Khi 𝑞 = 1 thì 𝑆𝑛 = 𝑛. 𝑢1
- HS trả lời câu hỏi của GV.
Bước 4: Kết luận, nhận định:
- GV nhận xét các sơ đồ, nêu ra điểm tốt và
chưa tốt, cần cải thiện.
- GV chốt lại kiến thức của chương.
C. HOẠT ĐỘNG LUYỆN TẬP, VẬN DỤNG
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập
c) Sản phẩm học tập: Câu trả lời của HS.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS hoạt động thực hiện Bài 9-15 (SGK -tr.62)
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng. 163
Bước 4: Kết luận, nhận định:
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác. Bài 9.
Ta có 𝑢𝑛+1 − 𝑢𝑛 = 3𝑛+1−1 − 3𝑛−1 = 3𝑛+1 > 0, ∀𝑛 ∈ ℕ∗. Vậy (𝑢 2𝑛+1 2𝑛 2𝑛+1 𝑛) là dãy số tăng. 𝑛 𝑛 𝑢 3 1 𝑛 = 3𝑛−1 = ( )
− ( ) > 0, ∀𝑛 ∈ ℕ∗. Vậy dãy số (𝑢 2𝑛 2 2 𝑛) bị chặn dưới.
Suy ra dãy số (𝑢𝑛) tăng và bị chặn dưới. Bài 10.
0 < 2𝑛+1 = 2 − 3 < 2, ∀𝑛 ∈ ℕ∗. Vậy dãy số (𝑢 𝑛+2 𝑛+2 𝑛) bị chặn. Bài 11. 5𝑢 15𝑢 15𝑢 𝑢 a) { 1 + 10𝑢𝑠 = 0 ⇔ { 1 + 40𝑑 = 0 ⇔ { 1 + 40𝑑 = 0 ⇔ { 1 = 8 𝑆4 = 14 2(2𝑢1 + 3𝑑) = 14 2𝑢1 + 3𝑑 = 7 𝑑 = −3; 𝑢 2𝑢 𝑢 b) { 7 + 𝑢15 = 60 ⇔ {
1 + 20𝑑 = 60 ⇔ { 1 = 30 − 10𝑑 𝑢2 2 2 2 4 + 𝑢12 = 1170 𝑢4 + 𝑢12 = 1170
(30 − 7𝑑)2 + (30 + 𝑑)2 = 1170 21 𝑢 𝑑 = 3 𝑑 = ⇔ { 1 = 30 − 10𝑑 ⇔ { hay { 5 5𝑑2 − 36𝑑 + 63 = 0 𝑢1 = 0 𝑢1 = −12 Bài 12. 𝑢 𝑢 𝑞 = 2
a) { 5 = 96 ⇔ { 1𝑞4 = 96 ⇔ { 𝑢6 = 192 𝑢 𝑢 1𝑞5 = 192 1 = 6; 𝑢 𝑢 𝑞 = 2
b) { 4 + 𝑢2 = 72 ⇔ { 1𝑞(𝑞2 + 1) = 72 ⇔ { . 𝑢 36 5 + 𝑢3 = 144 𝑢 𝑢 1𝑞2(𝑞2 + 1) = 144 1 = 5 Bài 13.
Tỉ lệ gia tăng số lượng cá thể của quần thể là: 12% − 2% − 8% = 2%.
Sau 2 năm số lượng cá thể của quần thể là: 110000 ⋅ (1 + 2%)2 = 114444 (cá thể). Bài 14. 164
Ta có 800 = 400 ⋅ 𝑞12, suy ra 𝑞 ≈ 1,06. Bài 15.
Đổi 97,6 triệu người = 97600000 người.
Ước tính dân số Việt Nam năm 2040 là 97600000. (1 + 1,14%)20 ≈ 122400000 (người).
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: “Bài 1. Giới hạn dãy số” 165 Ngày soạn: .../.../... Ngày dạy: .../.../...
CHƯƠNG IV: ĐƯỜNG THẲNG VÀ MẶT PHẲNG. QUAN HỆ SONG SONG TRONG KHÔNG GIAN
BÀI 1. ĐIỂM, ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN (3 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết các quan hệ liên thuộc cơ bản giữa điểm, đường thẳng, mặt phẳng trong không gian.
- Mô tả được ba cách xác định mặt phẳng (qua ba điểm không thẳng hàng; qua
một đường thẳng và một điểm không thuộc đường thẳng đó; qua hai đường thẳng cắt nhau.
- Xác định giao tuyến của hai mặt phẳng, giao điểm của đường thẳng và mặt phẳng.
- Vận dụng được các tính chất về giao tuyến của hai mặt phẳng; giao điểm của
đường thẳng và mặt phẳng vào giải bài tập.
- Nhận biết hình chóp và hình tứ diện.
- Vận dụng được kiến thức về đường thẳng, mặt phẳng trong không gian để mô tả
một số hình ảnh trong thực tiễn. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng: 166
- Tư duy và lập luận toán học, giải quyết vấn đề toán học: xác định được giao tuyến
của hai mặt phẳng, giao điểm của đường thẳng và mặt phẳng, vận dụng các tính
chất về giao tuyến, giao điểm; nhận biết hình chóp, hình tứ diện.
- Mô hình hóa toán học: Vận dụng được kiến thức về đường thẳng, mặt phẳng trong
không gian để mô tả một số hình ảnh trong thực tiễn. - Giao tiếp toán học.
- Sử dụng công cụ, phương tiện học toán. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học. HS có cơ hội phân biệt giữa hình
học không gian và hình học phẳng thông qua so sánh các hình hai chiều và ba chiều.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS trả lời được câu hỏi mở đầu.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ: 167
- GV yêu cầu HS đọc tình huống mở đầu
Môn học Hình học phẳng tìm hiểu tính chất của các hình cùng thuộc một mặt phẳng.
Môn học Hình học không gian tìm hiểu tính chất của các hình trong không gian, những
hình này có thể chứa những điểm không cùng thuộc một mặt phẳng. Hãy phân loại các
hình sau đâu thành hai nhóm hình khác nhau.
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung. Nhóm Hình học phẳng:
Nhóm Hình học không gian:
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học mới: “Trong chương này, chúng ta cùng đi tìm hiểu về điểm, đường thẳng,
mặt phẳng trong không gian; mối quan hệ song song trong không gian có khác gì hình 168
học phẳng; cũng như các ứng dụng của chúng. Bài đầu tiên của chương chúng ta đi tìm
hiểu về những yếu tố cơ bản: điểm, đường thẳng và mặt phẳng trong không gian.”
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Mặt phẳng trong không gian. Các tính chất thừa nhận của hình học không gian. a) Mục tiêu:
- Nhận biết các quan hệ liên thuộc cơ bản giữa điểm, đường thẳng, mặt phẳng trong không gian.
- Nhận biết các tính chất được thừa nhận của hình học không gian.
- Vận dụng được các tính chất đó. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động mục 1 và mục 2.
c) Sản phẩm: HS hình thành được kiến thức bài học về mặt phẳng trong không gian, câu
trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm 1. Mặt phẳng trong không gian vụ: HĐKP 1
- GV yêu cầu HS thảo luận Ví dụ về hình ảnh của mặt phẳng:
nhóm đôi, hoàn thành HĐKP - mặt tivi, trang giấy, mặt gương,.. 1. Kết luận:
- Điểm, đường thẳng và mặt phẳng là ba đối tượng cơ
bản của hình học phẳng. 169
- GV giới thiệu về các đối - Mặt phẳng không có bề dày và không có giới hạn
tượng cơ bản của hình học không gian.
+ Lưu ý: không định nghĩa về
điểm, đường, mặt phẳng.
+ Giới thiệu về cách biểu diễn
mặt phẳng phẳng và kí hiệu. Chú ý:
Mặt phẳng (P) còn được viết tắt mp(P) hoặc (P).
- GV cho HS quan sát hình ảnh *) Điểm thuộc mặt phẳng
điểm thuộc mặt phẳng và - Nếu điểm 𝐴 thuộc mặt phằng (𝑃), thì ta nói A nằm không thuộc.
trên (P) hay (P) chứa A, kí hiệu 𝐴 ∈ (𝑃).
- Nếu điểm 𝐵 không thuộc mặt phẳng (𝑃), thì ta nói
B nằm ngoài (P) hay (P) không chứa B, kí hiệu 𝐵 ∉ (𝑃). từ đó có
khái quát về cách gọi, kí hiệu.
*) Biểu diễn các hình trong không gian lên mặt phẳng
- GV cho HS thực hành biểu + Hình biểu diễn của đường thẳng là đường thẳng,
diễn các hình trong không gian. của đoạn thẳng là đoạn thẳng.
+ Lưu ý nét đứt, nét liền; giữ + Giữ nguyên tính liên thuộc giữa điểm với đường
nguyên tính song song, cắt nha, thẳng hoặc với đoạn thẳng. liên thuộc.
+ Giữ nguyên tính song song, tính cắt nhau giữa các đường thẳng.
+ Đường nhìn thấy: vẽ nét liền. Đường bị che khuất: vẽ nét đứt. 170
- Hình biểu diễn của một số hình thường gặp Thực hành 1 a) Hình hộp chữ nhật
- HS thực hành biểu diễn hình
hộp chữ nhật và xác định tính
liên thuộc trong Thực hành 1.
b) Điểm thuộc mặt phẳng (P) là: A'; B'; C'; D'
Điểm không thuộc mặt phẳng (P) là: A; B; C; D
c) Điểm thuộc mặt phẳng (Q) là: A; C; D 171
Điểm không thuộc mặt phẳng (Q) là: B
- GV cho HS thực hiện theo 2. Các tính chất thừa nhận của hình học không
nhóm đôi, làm phiếu bài tập các gian
HĐKP 2, 3, 4, 5, 6, 7. HĐKP 2 - Sau khi HS hoàn thành, GV
chữa bài lần lượt và đi đến các Dựa vào hai điểm trên hai cọc đỡ.
kết luận về tính chất. Tính chất 1 - GV chữa HĐKP 2.
Từ đó HS khái quát: qua hai Có một và chỉ một đường thẳng đi qua hai điểm phân
điểm phân biệt cho trước có biệt cho trước. bao nhiêu đường thẳng?
+ Kí hiệu đường thẳng qua hai điểm phân biệt A, B
- HS áp dụng đọc hiểu Ví dụ 1 là AB.
và làm Thực hành 2.
Ví dụ 1 (SGK -tr.90) Thực hành 2 Có 6 đường thẳng. HĐKP 3
Giá đỡ máy ảnh tiếp đất tại 3 điểm.
Giá đỡ máy ảnh thường có ba chân vì khi đó giá đỡ - GV chữa HĐKP 3. Khái quát: qua ba điể
tiếp đất tại 3 điểm. Mà 3 điểm thì sẽ xác định một m không mặt phẳng.
thẳng hàng cho trước có bao Tính chất 2 nhiêu mặt phẳng? Có một và chỉ
- HS áp dụng đọc hiểu Ví dụ 2
một mặt phẳng đi qua ba điểm không thẳng hàng.
và làm Thực hành 3. Chú ý:
Mặt phẳng qua ba điểm A, B, C không thẳng hàng
được kí hiệu là (ABC). 172
Ví dụ 2 (SGK -tr.90) Thực hành 3:
Có duy nhất một mặt phẳng. HĐKP 4
Đặt câu thước có hai điểm chung với mặt bàn, cây
thước phải hoàn toàn nằm trên mặt bàn. Tính chất 3 - GV chữa HĐKP 4
Nếu một đường thẳng có hai điểm phân biệt thuộc Khái quát tính chất 3.
một mặt phẳng thì mọi điểm của đường thẳng đều
+ GV lưu ý: kí hiệu đường thuộc mặt phẳng đó.
thẳng thuộc mặt phẳng dùng kí
hiệu tập con: 𝑑 ⊂ (𝑃).
- HS áp dụng đọc hiểu Ví dụ 3
và làm Thực hành 4.
Chú ý: đường thẳng d nằm trong mặt phẳng (P)
thường được kí hiệu là 𝑑 ⊂ (𝑃) hoặc (𝑃) ⊂ 𝑑.
Ví dụ 3 (SGK -tr.91) Thực hành 4
Áp dụng tính chất 3, ta có mọi điểm thuộc hai đường
thẳng AC, BD đều thuộc mặt phẳng (P). HĐKP 5 - GV chữa HĐKP 5 Đặ
Bốn đỉnh của cái bánh giò không cùng nằm trong
t câu hỏi: Có phải bốn điểm cùng mặt phẳng.
phân biệt luôn cùng nằm trên
- Tính chất 4: Tồn tại bốn điểm không cùng nằm
một mặt phẳng hay không? trên một mặt phẳng. Chú ý: 173
+ GV lưu ý: về đồng phẳng và Nếu có nhiều điểm cùng thuộc một mặt phẳng thì ta không đồng phẳng.
nói những điểm đó đồng phẳng.
- HS áp dụng đọc hiểu Ví dụ 4 Nếu không có mặt phẳng nào chứa các điểm đó thì ta
và làm Thực hành 5.
nói chúng không đồng phẳng.
+ TH5: để xác định mặt phẳng Ví dụ 4 (SGK -tr.91)
cần lấy mấy điểm phân biệt? Thực hành 5
(Cần 3 điểm phân biệt).
Có bốn mặt phẳng: (OMN), (ONP), (OPM), (MNP). - GV chữa HĐKP 6 HĐKP 6: Khái quát tính chất 5.
Phần giao nhau của hai bức tường là một đường
+ GV giới thiệu về giao tuyến thẳng. và kí hiệu.
- Tính chất 5: Nếu hai mặt phẳng phân biệt có một
- HS áp dụng đọc hiểu Ví dụ 5 điểm chung thì chúng có một đường thẳng chung duy
và làm Thực hành 6.
nhất chứa tất cả các điểm chung của hai phẳng đó.
Chú ý: đường thẳng chung d (nếu có) của hai mặt
phẳng phân biệt (P) và (Q) được gọi là giao tuyến
của hai mặt phẳng đó. Kí hiệu 𝑑 = (𝑃) ∩ (𝑄).
Ví dụ 5 (SGK -tr.92) Thực hành 6:
A, B, C cùng thuộc một giao tuyến của hai mặt
phẳng phân biệt nên thẳng hàng với nhau. 174 HĐKP 7: - GV chữa HĐKP 7
𝑀𝑁 = 1 (tính chất đường trung bình của tam giác). Khái quát tính chất 6. 𝐵𝐶 2
+ GV lưu ý: Sử dụng các kết - Tính chất 6: Trên mỗi mặt phẳng, tất cả các kết đã
quả của hình học phẳng để biết trong hình học phẳng đều đúng.
chứng minh, tính toán trong Ví dụ 6 (SGK -tr.93) hình học phẳng. Vận dụng 1
- HS áp dụng đọc hiểu Ví dụ 6
+ Sử dụng tính chất trọng tâm Sử dụng tính chất 5, ta có nếu 3 điểm đều nằm trên trong các tam giác.
cùng một đường thẳng thì đường thẳng đó chính là
Từ ví dụ 6 và các tính chất đã giao tuyến của hai mặt phẳng là mặt phẳng chứa
học. GV lưu ý HS 1 cách để cánh cửa và mặt phẳng chứa bức tường.
chứng minh các điểm thẳng
hàng: chứng minh các điểm là
Đều là điểm chung của hai mặt
phẳng đó, khi đó các điểm phải
cùng nằm trên 1 đường thẳng là giao tuyến.
- HS làm Vận dụng 1, áp dụng
tính chất về giao hai mặt phẳng (tính chất 5).
Bước 2: Thực hiện nhiệm vụ: 175
- HS theo dõi SGK, chú ý nghe,
tiếp nhận kiến thức, hoàn thành
các yêu cầu, thảo luận nhóm. - GV quan sát hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình bày
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận định:
GV tổng quát lưu ý lại kiến
thức trọng tâm và yêu cầu HS
ghi chép đầy đủ vào vở. PHIẾU BÀI TẬP 1. HĐKP 2
Quan sát Hình 5 và cho biết muốn gác một cây
sào tập nhảy cao, người ta cần dựa nó vào mấy điểm trên 2 cọc đỡ.
………………………………………………………………………
……………………………………………………………………… 176 2. HĐKP 3
Quan sát Hình 7 và cho biết giá đỡ máy ảnh tiếp đất
tại mấy điểm. Tại sao giá đỡ máy ảnh thường có ba chân?
………………………………………………………………………
……………………………………………………………………… 3. HĐKP 4
Quan sát Hình 10 và cho biết người thợ mộc kiểm tra
mặt bàn có phẳng hay không bằng một cây thước thẳng như thế nào?
………………………………………………………………………
……………………………………………………………………… 4. HĐKP 5
Quan sát Hình 13 và cho biết bốn đỉnh A,B,C,D của cái
bánh giò có cùng nằm trên một mặt phẳng hay không.
………………………………………………………………………
……………………………………………………………………… 177 5. HĐKP 6
Quan sát Hình 14 và mô tả phần giao nhau của hai bức tường.
………………………………………………………………………
……………………………………………………………………… 6. HĐKP 7
Trong mặt phẳng (P), cho tam giác ABC có M, N
lần lượt là trung điểm của các đoạn thẳng AB, AC
(Hình 17). Tính tỉ số 𝑀𝑁 . 𝐵𝐶
………………………………………………………………………
………………………………………………………………………
Hoạt động 2: Cách xác định mặt phẳng a) Mục tiêu:
- Mô tả được ba cách xác định mặt phẳng (qua ba điểm không thẳng hàng; qua
một đường thẳng và một điểm không thuộc đường thẳng đó; qua hai đường thẳng cắt nhau.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động mục 3.
c) Sản phẩm: HS hình thành được kiến thức bài học về cách xác định mặt phẳng, câu
trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện: 178
HOẠT ĐỘNG CỦA GV VÀ
SẢN PHẨM DỰ KIẾN HS Bướ 3. Cách xác đị
c 1: Chuyển giao nhiệm nh mặt phẳng Cách xác đị vụ: nh 1:
Một mặt phẳng được xác định nếu biết nó chứa ba
- GV yêu cầu HS thảo luận trả lời điểm không thẳng hàng. câu hỏi: Ví dụ:
+ Trong hình học phẳng, đường Mặt phẳng xác định bởi ba điểm A, B, C không
thẳng xác định khi biết ít nhất hai thẳng hàng kí hiều là mp(ABC) hay (ABC).
điểm phân biệt. Vậy trong không
gian, mặt phẳng xác định khi có
ít nhất những yếu tố nào?
+ HS nhắc lại tính chất 2, từ đó
phát hiện một cách xác định mặt phẳng trong không gian.
Ví dụ 7 (SGK -tr.94) HĐKP 8
- HS đọc, giải thích Ví dụ 7. Đườ
- HS thực hiện HĐKP 8.
ng thẳng a nằm trong mặt phẳng (P).
+ Sử dụng các tính chất về đường Vì qua ba điểm xác định duy nhất một mặt phẳng
thẳng, điểm thuộc mặt phẳng. (tính chất 2).
B, C thuộc mặt phẳng (P) mà đường thẳng a qua B,
C nên mọi điểm thuộc đường thẳng a đề
u thuộc (P) (tính chất 3). Cách xác đị nh 2:
- HS khái quát về cách xác định Một mặt phẳng được xác định nếu biết nó chứa một đườ
mặt phẳng thứ 2 khi biết đường
ng thẳng và một điểm không thuộc đường
thẳng và điểm không thuộc thẳng đó. đường đó. Ví dụ: 179
Mặt phẳng xác định bởi điểm A và đường thẳng a
không qua điểm A, kí hiệu mp(A,a) hay (A,a).
Ví dụ 8 (SGk -tr.94)
- Áp dụng HS đọc và giải thích Ví dụ 8. HĐKP 9
- HS thực hiện HĐKP 9.
Đường thẳng a và b nằm trong mặt phẳng (P) vì
+ (P) đi qua hai điểm N, O nên (P) chứa đường thẳng a.
+ (P) đi qua hai điểm M, O nên (P) chứa đường thẳng b.
Từ đó khái quát cách xác định Cách xác định 3:
mặt phẳng khi biết hai đường
- Một mặt phẳng được xác định nếu biết nó chứa thẳng cắt nhau.
hai đường thẳng cắt nhau. Ví dụ:
Mặt phẳng xác định bởi hai đường thwangr a, b cắt nhau kí hiệu là mp(a,b).
- Áp dụng HS thực hiện Ví dụ 9. Ví dụ 9 (SGK -tr.95) Thực hành 7
a) Ta có: 𝑀 ∈ (𝑀, 𝑎) và 𝑀 ∈ (𝑀, 𝑏). 180
- HS thảo luận theo nhóm đôi
𝑂 ∈ 𝑎 ⇒ 𝑂 ∈ (𝑀, 𝑎)
thực hiện Thực hành 7, Vận
𝑂 ∈ 𝑏 ⇒ 𝑂 ∈ (𝑀, 𝑏)
dụng 2, Vận dụng 3.
Vậy MO là giao tuyến cần tìm.
+ TH7: Để tìm giao tuyến hai mặt
phẳng ta xác định ít nhất hai điểm chung.
c) Chỉ ra A, B, C đều thuộc 2 mặt phẳng.
+ VD 2: vận dụng tính chất và
cách xác định mặt phẳng.
b) 𝐴, 𝐵 ∈ (𝑀𝐴𝐵);
+ VD 3: xác định mặt phẳng tạo
𝐴 ∈ 𝑎 ⇒ 𝐴 ∈ (𝑎, 𝑏) bởi OA, OB.
𝐵 ∈ 𝑏 ⇒ 𝑏 ∈ (𝑎, 𝑏) Từ đó tìm giao tuyến.
Bước 2: Thực hiện nhiệm vụ:
- HS theo dõi SGK, chú ý nghe,
tiếp nhận kiến thức, suy nghĩ trả
lời câu hỏi, hoàn thành các yêu cầu.
- GV: quan sát và trợ giúp HS.
Bước 3: Báo cáo, thảo luận:
Vậy AB là giao tuyến cần tìm.
- HS giơ tay phát biểu, lên bảng c) Giao tuyến của mặt phẳng (MAB) và mp(a,b) là trình bày AB
- Một số HS khác nhận xét, bổ Mà C là giao của A’B’ với (a,b) nên C cũng thuộc sung cho bạn.
giao tuyến của hai mặt phẳng (MAB) và (a,b).
Bước 4: Kết luận, nhận định: Suy ra A, B, C thẳng hàng.
GV tổng quát lưu ý lại kiến thức
trọng tâm và yêu cầu HS ghi chép
đầy đủ vào vở. 181 Vận dụng 2
- Qua ba điểm không thẳng hàng có một và chỉ một mặt phẳng.
- Bốn điểm thì có thể không cùng nằm trên một mặt phẳng. Vận dụng 3
+) Giao tuyến của (OA, OB) với hai mặt tường lần lượt là AC và BC.
Hoạt động 3: Hình chóp và hình tứ diện a) Mục tiêu:
- HS nhận biết được hình chóp và hình tứ diện.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động mục 4.
c) Sản phẩm: HS hình thành được kiến thức bài học về hình chóp và hình tứ diện, câu
trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV
SẢN PHẨM DỰ KIẾN VÀ HS 182
Bước 1: Chuyển giao nhiệm 4. Hình chóp và hình tứ diện vụ: a) Hình chóp HĐKP 10
- GV yêu cầu HS thực hiện a) Hình tam giác HĐKP 10.
b) Các mặt bên đều là tam giác và có chung một đỉnh. Kết luận: Các hình 31.a, b, c
- Cho đa giác lồi 𝐴1𝐴2 … 𝐴𝑛 nằm trong mặt phẳng
(𝛼) và một điểm 𝑆 không thuộc (𝛼). Nối 𝑆 với các
đỉnh 𝐴1, 𝐴2, … , 𝐴𝑛 để được 𝑛 tam giác
được gọi là hình chóp
𝑆𝐴1𝐴2, 𝑆𝐴2𝐴3, … , 𝑆𝐴𝑛𝐴1. Hình gồm 𝑛 tam giác đó và
- HS khái quát thế nào là hình đa giác 𝐴1𝐴2 … 𝐴𝑛 được gọi là hình chóp và kí hiệu là chóp.
𝑆. 𝐴1𝐴2 … 𝐴𝑛.
- Trong hình chóp 𝑆. 𝐴1𝐴2 … 𝐴𝑛,
- GV giới thiệu về các yếu tố
của hình chóp: đỉnh, mặt bên, + Điểm 𝑆 được gọi là đỉnh;
mặt đáy, cạnh bên, cạnh đáy. + Đa giác 𝐴
+ Nhấn mạnh: mặt bên là tam
1𝐴2 … 𝐴𝑛 được gọi là mặt đáy,
các giác giác, mặt đáy có thể + Các tam giác 𝑆𝐴1𝐴2, 𝑆𝐴2𝐴3, … , 𝑆𝐴𝑛𝐴1 được gọi là
là đa giác ví dụ tam giác, tứ các mặt bên; giác, ngũ giác,… + Các đoạn 𝑆𝐴
1, 𝑆𝐴2, … , 𝑆𝐴𝑛 được gọi là các cạnh bên;
+ Các cạnh 𝐴1𝐴2, 𝐴2𝐴3, … , 𝐴𝑛𝐴1 được gọi là các cạnh đáy. 183
- HS thực đọc Ví dụ 10. Nêu - Ta gọi hình chóp có đáy tam giác, tứ giác, ngũ
các yếu tố của hình chóp.
giác,… lần lượt là hình chóp tam giác, hình chóp tứ
giác, hình chóp ngũ giác,…
- HS thực hiện HĐKP 11.
Ví dụ 10 (SGK -tr.96) b) Hình tứ diện HĐKP 11
- GV giới thiệu về tứ diện và Hình 34a có số mặt ít nhất
các yếu tố của tứ diện. Kết luận
- Cho bốn điểm 𝐴, 𝐵, 𝐶, 𝐷 không đồng phẳng. Hình
gồm bốn tam giác 𝐴𝐵𝐶, 𝐴𝐶𝐷, 𝐴𝐵𝐷 và 𝐵𝐶𝐷 được gọi
là hình tứ diện (hay tứ diện), kí hiệu là 𝐴𝐵𝐶𝐷. 184
Trong hình tứ diện 𝐴𝐵𝐶𝐷:
+ Các điểm 𝐴, 𝐵, 𝐶, 𝐷 các đỉnh.
+ Các đoạn thẳng 𝐴𝐵, 𝐵𝐶, 𝐶𝐷, 𝐷𝐴, 𝐴𝐶, 𝐵𝐷 : các cạnh của tứ diện,
+ Hai cạnh không đi qua cùng một đỉnh là hai cạnh đối diện.
+ Các tam giác 𝐴𝐵𝐶, 𝐴𝐶𝐷, 𝐴𝐵𝐷, 𝐵𝐶𝐷 : các mặt của tứ diện.
+ Đỉnh không thuộc một mặt của tứ diện là đỉnh đối diện với mặt đó.
Ví dụ 11 (SGK -tr97) Chú ý
- HS làm Ví dụ 11: nêu các a) Hình tứ diện có bốn mặt là các tam giác đều được
mặt và cặp cạnh đối diện của gọi là hình tứ diện đều. tứ diện.
b) Một tứ diện có thể xem là hình chóp tam giác. - Chú ý: +Tứ diện đều.
Ví dụ 12 (SGK -tr.98)
+ Tứ diện có thể xem là một
hình chóp, ta có thể chọn đỉnh Thực hành 8
và mặt đáy tương ứng.
a) Trong mặt phẳng (SAC), kéo dài HK cắt AC tại E.
- GV hướng dẫn HS thực hiện Ví dụ 12.
Ta có 𝐸 ∈ 𝐴𝐶 suy ra 𝐸 ∈ (𝑆𝐴𝐶).
+ Cách xác định giao điểm: Vậy giao điểm của đường thẳng HK và mặt phẳng
tìm điểm chung giữa đường (SAC) là E.
thẳng và mặt phẳng. Nếu 185
chưa có sẵn thì ta tìm xem
đường thẳng đó có cắt được
đường thẳng nào trong mặt phẳng không.
+ Cách xác định giao tuyến: tìm hai điểm chung.
- HS trao đổi, thảo luận, thực
hiện Thực hành 8 và Vận b) Ta có BK cắt SI tại M. A và M là điểm chung của
dụng 4, Vận dụng 5.
hai mặt phẳng (SAI) và (ABK) nên giao tuyến của
Bước 2: Thực hiện nhiệm (SAI) và (ABK) là AM. vụ:
Ta có H và I là điểm chung của hai mặt phẳng (SAI) - HS theo dõi SGK, chú ý
và (BCH) nên giao tuyến của (SAI) và (BCH) là HI.
nghe, tiếp nhận kiến thức, suy
nghĩ trả lời câu hỏi, hoàn thành các yêu cầu.
- GV: quan sát và trợ giúp HS.
Bước 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình bày
- Một số HS khác nhận xét, bổ Vận dụng 4 sung cho bạn. Bướ
c 4: Kết luận, nhận đị
nh: GV tổng quát lưu ý lại
kiến thức trọng tâm và yêu
cầu HS ghi chép đầy đủ vào vở. 186
a)Ta có: S và O là điểm chung của hai mặt phẳng
(SAC) và (SBD) nên giao tuyến của (SAC) và (SBD) là SO
Ta có: S và O' là điểm chung của hai mặt phẳng
(SA'C') và (SB'D') nên giao tuyến của (SA'C') và (SB'D') là SO'
Mà (𝑆𝐴𝐶) ≡ (𝑆𝐴′𝐶′), (𝑆𝐵𝐷) ≡ (𝑆𝐵′𝐷′) nên 𝑆𝑂 ≡ 𝑆𝑂′ Hay S, O, O' thẳng hàng
b) Ta có: S và E là điểm chung của hai mặt phẳng
(SAB) và (SCD) nên giao tuyến của (SAB) và (SCD) là SE
Ta có: S và E' là điểm chung của hai mặt phẳng
(SA'B') và (SC'D') nên giao tuyến của (SA'B') và (SC'D') là SE'. 187
Mà (𝑆𝐴𝐵) ≡ (𝑆𝐴′𝐵′), (𝑆𝐶𝐷) ≡ (𝑆𝐶′𝐷′) nên S𝐸 ≡ 𝑆𝐸′. Hay S, E, E' thẳng hàng. Vận dụng 5
Gấp theo các cạnh AB, BC, CA để ba điểm S, S’, S’’ trùng nhau.
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 1, 2, 3 (SGK -tr.99) và các câu hỏi TN.
c) Sản phẩm học tập: Câu trả lời của HS.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS trả lời các câu hỏi TN nhanh
Câu 1. Trong mp(𝛼), cho bốn điểm 𝐴, 𝐵, 𝐶, 𝐷 trong đó không có ba điểm nào thẳng
hàng. Điểm 𝑆 ∉ 𝑚𝑝(𝛼). Có mấy mặt phẳng tạo bởi 𝑆 và hai trong số bốn điểm nói trên? A. 4 . B. 5. C. 6 . D. 8 .
Câu 2. Cho hình chóp S.ABCD. Gọi I là giao điểm của AC và BD, J là giao điểm của
AB và CD, K là giao điểm của AD và BC. Trong các khẳng định sau, khẳng định nào sai?
A. (𝑆𝐴𝐶) ∩ (𝑆𝐵𝐷) = 𝑆𝐼 188
B. (𝑆𝐴𝐵) ∩ (𝑆𝐶𝐷) = 𝑆𝐽
C. (𝑆𝐴𝐷) ∩ (𝑆𝐵𝐶) = 𝑆𝐾
D. (𝑆𝐴𝐶) ∩ (𝑆𝐴𝐷) = 𝐴𝐵
Câu 3. Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là : A. 5 mặt, 5 cạnh. B. 6 mặt, 5 cạnh. C. 6 mặt, 10 cạnh. D. 5 mặt, 10 cạnh.
Câu 4. Cho bốn điểm 𝐴, 𝐵, 𝐶, 𝐷 không cùng nằm trong một mặt phẳng. Trên 𝐴𝐵, 𝐴𝐷lần
lượt lấy các điểm 𝑀 và 𝑁 sao cho 𝑀𝑁 cắt 𝐵𝐷 tại 𝐼. Điểm 𝐼 không thuộc mặt phẳng nào sao đây: A. (𝐵𝐶𝐷). B. (𝐴𝐵𝐷)
C. (𝐶𝑀𝑁). D. (𝐴𝐶𝐷).
Câu 5. Cho tứ diện 𝑆. 𝐴𝐵𝐶. Trên S ,
A SB và SC lấy các điểm 𝐷, 𝐸 và 𝐹 sao cho 𝐷𝐸 cắt
𝐴𝐵 tại 𝐼,𝐸𝐹 cắt 𝐵𝐶 tại 𝐽, 𝐹𝐷 cắt 𝐶𝐴 tại 𝐾.Khẳng định nào sau đây đúng?
A. Ba điểm 𝐵, 𝐽 , 𝐾thẳng hàng
B. Ba điểm 𝐼, 𝐽, 𝐾 thẳng hàng
C. Ba điểm 𝐼, 𝐽, 𝐾 không thẳng hàng
D. Ba điểm 𝐼, 𝐽, 𝐶thẳng hàng
- GV tổ chức cho HS hoạt động thực hiện Bài 1, 2, 3 (SGK -tr.99).
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định: 189
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác. Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 C D C D B Bài 1
a) Ta có: 𝑀 ∈ 𝑆𝐴, suy ra 𝑀 ∈ (𝑆𝐴𝐶) (1);
𝑁 ∈ 𝑆𝐶, suy ra 𝑁 ∈ (𝑆𝐴𝐶) (2).
Từ (1) và (2), suy ra 𝑀𝑁 nằm trong mặt phẳng (𝑆𝐴𝐶).
b) Điểm 𝑂 thuộc 𝐴𝐶 và 𝐵𝐷, suy ra 𝑂 là điểm chung của hai mặt phẳng (𝑆𝐴𝐶) và (𝑆𝐵𝐷). Bài 2. 190
a) Gọi 𝑂 là giao điểm của 𝐴𝐶 và 𝐵𝐷.
Trong △ 𝑆𝐴𝐶, hai trung tuyến 𝐴𝑀 và 𝑆𝑂 cắt nhau tại trọng tâm 𝐼. Do 𝑆𝑂 ⊂ (𝑆𝐵𝐷) nên
𝐴𝑀 ∩ (𝑆𝐵𝐷) = 𝐼 và do 𝐼 là trọng tâm của △ 𝑆𝐴𝐶 nên 𝐼𝐴 = 2𝐼𝑀.
b) Trong mặt phẳng (𝑆𝐵𝐷), vẽ giao điểm 𝐸 của 𝐵𝐼 và 𝑆𝐷. Do 𝐵𝐼 ⊂ (𝐴𝐵𝑀) nên 𝑆𝐷 ∩ (𝐴𝐵𝑀) = 𝐸
c) Trong mặt phẳng (𝐴𝐵𝑀), vẽ giao điểm 𝐹 của 𝑀𝑁 và 𝐵𝐼. Do 𝐵𝐼 ⊂ (𝑆𝐵𝐷) nên
𝑀𝑁 ∩ (𝑆𝐵𝐷) = 𝐹. Bài 3. 191
a) Trong mặt phẳng (SBD), vẽ giao điểm 𝐸 của 𝑀𝑁 và 𝑆𝑂.
Do 𝑀𝑁 ⊂ (𝑀𝑁𝑃) nên 𝑆𝑂 ∩ (𝑀𝑁𝑃) = 𝐸.
b) Trong mặt phẳng (𝑆𝐴𝐶), vẽ giao điểm 𝑄 của 𝑃𝐸 và 𝑆𝐴.
Do 𝑃𝐸 ⊂ (𝑀𝑁𝑃) nên 𝑆𝐴 ∩ (𝑀𝑁𝑃) = 𝑄.
c) 𝐼, 𝐽, 𝐾 là ba điểm chung của hai mặt phẳng (𝑀𝑁𝑃) và (𝐴𝐵𝐶𝐷) suy ra 𝐼, 𝐽, 𝐾 thẳng hàng.
D. HOẠT ĐỘNG VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập.
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 4, 5 (SGK – tr.99)
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: Bài 4. 192
a) 𝐺𝐼 = (𝐸𝐹𝐺) ∩ (𝐵𝐶𝐷); 𝐹𝐻 = (𝐸𝐹𝐺) ∩ (𝐴𝐶𝐷).
b) Trong mặt phẳng (𝐸𝐹𝐺), vẽ giao điểm 𝑀 của 𝐼𝐺 và 𝐹𝐻. Ta có 𝑀 là điểm chung của
hai mặt phẳng (𝐴𝐶𝐷) và (𝐵𝐶𝐷), suy ra giao tuyến 𝐶𝐷 của hai mặt phẳng (𝐴𝐶𝐷) và
(𝐵𝐶𝐷) phải đi qua 𝑀. Vậy 𝐶𝐷, 𝐼𝐺, 𝐻𝐹 cùng đi qua một điểm. Bài 5.
Giao tuyến của mặt phẳng ánh sáng với mặt tường hoặc mặt sàn là một đường thẳng,
do đó thước kẻ laser sẽ giúp người thơ xây dửng kẻ được đường thẳng trên tường hoặc sàn nhà.
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: "" 193 194 Ngày soạn: .../.../... Ngày dạy: .../.../...
BÀI 2: HAI ĐƯỜNG THẲNG SONG SONG (3 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng:
Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết vị trí tương đối của hai đường thẳng trong không gian: hai đường
thẳng trùng nhau, song song, cắt nhau, chéo nhau.
- Giải thích tích chất cơ bản của hai đường thẳng song song trong không gian.
- Vận dụng kiến thức về hai đường thẳng song song để mô tả một số hình ảnh trong thực tiễn. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Năng lực tư duy và lập luận toán học: trong quá trình khám phá, hình thành kiến
thức toán học về hai đường thẳng song song, thực hành và vận dụng kiến thức.
- Năng lực giao tiếp toán học: thông qua sử dụng các thuật ngữ, khái niệm, công
thức, kí hiệu toán học trong trình bày, thảo luận, làm việc nhóm.
- Sử dụng công cụ, phương tiện học toán. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV. 195
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS trả lời được câu hỏi mở đầu, bước đầu hình dung về nội dung bài học.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu:
Mô tả vị trí giữa các cặp đường thẳng a và b, b và c, c và d có trong hình bên dưới.
- GV đặt câu hỏi gợi mở:
+ Nhắc lại khái niệm hai đường thẳng song song?
(Hai đường thẳng song song: là hai đường thẳng không có điểm chung).
+ Em hãy nêu vị trí tương đối giữa đường thẳng a và b, c và d
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung. 196
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học mới: “Trong chương này, chúng ta sẽ tìm hiểu về các vị trí tương đối của hai
đường thẳng trong không gian và tính chất của nó”.
Bài mới: Hai đường thẳng song song.
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Vị trí tương đối của hai đường thẳng trong không gian. a) Mục tiêu:
- HS nhận biết được vị trí tương đối của hai đường thẳng trong không gian: hai đường
thẳng trung nhau, song song, cắt nhau, chéo nhau. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động HĐKP 1, Thực hành 1, Vận dụng 1 đọc hiểu Ví dụ 1.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
HS trả lời các câu hỏi về vị trí tương đối của đường thẳng trong không gian để hình thành
khái niệm hai đường thẳng song song, hai đường thẳng chéo nhau.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao 1. Vị trí tương đối của hai đường thẳng trong không gian nhiệm vụ: HĐKP 1: - GV yêu cầu HS thảo a)
luận nhóm đôi, hoàn - Hình 1a: Hai đường thẳng trùng nhau thành HĐKP 1.
- Hình 1b: Hai đường thẳng cắt nhau.
- Hình 1c: Hai đường thẳng song song.
→ Khi hai đường thẳng a và b cùng nằm trên một mặt phẳng
thì a và b có thể trùng nhau, song song hoặc cắt nhau. b) 197
AB và CD không cùng nằm trên một mặt phẳng. - GV giới thiệu: Kết luận Hai đườ Cho hai đườ ng thẳng trong
ng thẳng trong không gian. Khi đó có thể xảy ra không gian có thể đồng
một trong hai trường hợp sau:
phẳng tức là cùng thuộc - Trường hợp 1: Có một mặt phẳng chứa 𝑎 và b. Khi đó a và một mặt phẳng hoặc b đồng phẳng. không đồng phẳng.
+ Nếu 𝑎 và 𝑏 có hai điểm chung thì a trùng b, kí hiệu 𝑎 ≡ 𝑏. Ví dụ hình 1.
+ Nếu 𝑎 và b có một điểm chung là M thì a và b cắt nhau tại
- GV cho HS khái quát M, kí hiệu 𝑎 ∩ 𝑏 = 𝑀.
các vị trí tương đối của hai đường thẳng.
+ Nếu a và b không có điểm chung thì a và b song song với
+ Nhấn mạnh sử dụng nhau, 𝑎 ∕∕ 𝑏.
việc đồng phẳng hay - Trường hợp 2: Không có mặt phẳng nào chứa a và b. không và số điểm chung
để xét vị trí tương đối.
Khi đó, ta cũng nói a chéo với 𝑏, hoặc 𝑏 chéo với 𝑎.
Hai đường thẳng gọi là song song nếu chúng nằm trong
cùng một mặt phẳng và không có điểm chung
- GV cho HS đọc chú ý Chú ý: 198
a) Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng.
b) Cho hai đường thẳng song song a và b. Có duy nhất một
mặt phẳng chứa hai đường thẳng đó, kí hiệu mp(a,b)
- GV cho HS tìm hiểu Ví Ví dụ 1 (SGK – tr.64)
dụ 1. GV hướng dẫn:
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB,
a) Để xét vị trí của tương AC. Xét vị trí tương đối của các cặp đường thẳng sau đây:
đối của MN và BC, ta a) MN và BC
xét xem MN và BC có b) AN và CD
cùng thuộc một mặt c) MN và CD phẳng hay không? Giải
+ Điểm M, N lần lượt là trung điểm của AB, AC nên MN thuộc mặt phẳng (ABC). Từ đó suy ra MN // BC
b) Để xét vị trí tương đối
của AN và CD, ta xét
xem AN và CD có cùng a) Trong mặt phẳng (ABC), ta có MN là đường trung bình
thuộc một mặt phẳng của tam giác ABC, suy ra MN // BC hay không?
b) Trong mặt phẳng (ACD), ta có AN cắt CD tại điểm C.
+ N là trung điểm AC c) Giả sử MN và CD cùng nằm trong một mặt phẳng (P),
nên AN nằm trong mặt suy ra đường thẳng NC nằm trong (P), suy ra (P) chứa điểm
phẳng (ACD). Từ đó A. Tương tự, ta cũng có AM nằm trong (P), suy ra (P) chứa
suy ra AN cắt CD tại C. điểm B. Suy ra (P) chứa cả bốn đỉnh của tứ diện ABCD.
c) Để xét xem vị trí Điều này vô lí.
tương đối của MN và Vậy hai đường thẳng MN và CD không nằm trong bất kì
CD, ta xét xem MN và mặt phẳng nào, suy ra MN chéo với CD. Thực hành 1: 199
CD có cùng thuộc một Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Xét
mặt phẳng hay không?
vị trí tương đối của các cặp đường thẳng sau đây:
+ MN nằm trong mặt a) AB và CD
phẳng (ABC) và CD b) SA và SC
nằm trong mặt phẳng c) SA và BC (ACD), (BCD) nên MN và CD không cùng nằm trong một mặt phẳng. Từ đó suy ra MN và CD chéo nhau. - HS thảo luận nhóm
đôi, làm Thực hành 1, giải thích. Giải
a) Trong mặt phẳng (ABCD) ta có hình bình hành ABCD nên AB // CD
b) Trong mặt phẳng (SAC), ta có SA cắt SC tại điểm S.
c) Giả sử SA và BC cùng nằm trong một mặt phẳng (P). Suy
ra đường thẳng AC nằm trong (P). Suy ra (P) chứa cả 4 điểm S, A, B, C.
Mà theo khái niệm hình chóp thì S không đồng phẳng với A, B, C.
Vậy SA và BC không nằm trong bất kì mặt phẳng nào, suy ra SA chéo với BC.
- HS suy nghĩ cá nhân Vận dụng 1:
thực hiện Vận dụng 1. Hãy chỉ ra các ví dụ về hai đường thẳng song song, cắt nhau GV gợi mở:
và chéo nhau trong hình cầu sắt ở Hình 6.
+ Có thể lấy đường
thẳng là thanh ngang 200
(đường a) và xác định
đường thẳng nào chéo nhau,
+ Để tìm hai đường song song, cắt nhau,
trước hết ta tìm hai
đường thẳng cùng mặt phẳng.
Bước 2: Thực hiện Giải nhiệm vụ: b, c cắt nhau;
- HS theo dõi SGK, chú b, d song song;
ý nghe, tiếp nhận kiến a, b chéo nhau.
thức, hoàn thành các yêu cầu, thảo luận nhóm. - GV quan sát hỗ trợ.
Bước 3: Báo cáo, thảo luận: - HS giơ tay phát biểu, lên bảng trình bày - Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận
định: GV tổng quát lưu ý lại kiến thức : Hai đường thẳng song song nếu chúng nằm trong cùng một mặt
phẳng và không có điểm chung 201
Hoạt động 2: Tính chất cơ bản về hai đường thẳng song song a) Mục tiêu:
- HS giải thích được tích chất cơ bản của hai đường thẳng song song trong không gian.
- HS vận dụng được kiến thức về hai đường thẳng song song để mô tả một số hình ảnh trong thực tiễn.
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động HĐKP 2, 3, Thực hành 2, 3, Vận dụng 2, đọc hiểu
các ví dụ 2, 3, 4, 5.
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
HS khám phá được các định lí và hệ quả của hai đường thẳng song song trong không
gian, vận dụng được định lí và hệ quả của hai đường thẳng song song để giải quyết bài toán.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ:
2. Tính chất cơ bản về hai đường thẳng song
- GV yêu cầu HS thảo luận nhóm đôi, song
hoàn thành HĐKP 2. GV gợi ý: HĐKP 2:
a) Mặt phẳng (Q) có chứa điểm M a) Hai mặt phẳng (P) và (Q) trùng nhau.
không? Từ đó (P) và (Q) có mối quan b) Nếu a và b có điểm chung M thì điểm M có hệ gì? thuộc c.
b) Nếu a và b cắt nhau tại M thì M
thuộc các mặt phẳng nào? Từ đó M có thuộc c không?
- Từ kết quả của HĐKP 2a, GV đưa Định lí 1 ra Định lí 1
Trong không gian, qua một điểm nằm ngoài
một đường thẳng, có một và chỉ một đường
thẳng song song với đường thẳng đó.
- HS tìm hiểu Ví dụ 2. GV hướng dẫn: Ví dụ 2 (SGK – tr.102) 202
Từ hình bình hành ACBE suy ra AE // Cho tứ diện ABCD. Trong mặt phẳng (ABC)
BC, áp dụng định lí 1 suy ra AE trùng vẽ hình bình hành ACBE. Gọi d là đường thẳng
với d (d là đường thẳng đi qua A và trong không gian đi qua A và song song với BC. song song với BC).
Chứng minh điểm E thuộc đường thẳng d. Giải
Ta có ACBE là hình bình hành, suy ra AE //
BC. Do trong không gian chỉ có duy nhất một
đường thẳng đi qua A và song song với BC, suy
ra AE phải trùng d, vậ điểm E phải thuộc d.
- Áp dụng HS làm Thực hành 2. Thực hành 2:
+ Chứng minh đường thẳng d trùng Cho hình chóp S.ABCD. Vẽ hình thang
ADMS có hai đáy là AD và MS. Gọ với đường thẳng SM i d là
đường thẳng trong không gian đi qua S và
song song với AD. Chứng minh đường thẳng
d nằm trong mặt phẳng (SAD) Giải 203
Ta có hình thang ADMS có đáy là AD và MS nên AD // MS
Trong không gian, chỉ có duy nhất 1 đường
thẳng đi qua S và song song với AD nên d phải trùng SM.
Mà SM ⊂ (ADMS) nên d ⊂ (ADMS), hay d ⊂ (SAD)
- Từ kết quả của HĐKP 2b, GV đưa Định lí 2 ra Định lí 2
Nếu ba mặt phẳng đôi một cắt nhau the oba
giao tuyến phân biệt thì ba giao tuyến ấy hoặc
đồng quy hoặc đôi một song song.
- HS tìm hiểu Ví dụ 3. GV hướng dẫn: Ví dụ 3 (SGK – tr.103)
a) Xác định ba mặt phẳng giao nhau
tạo ra ba đường thẳng cắt nhau. Chẳng hạn:
(BAC) ∩ (BAD) = BA
(BAC) ∩ (BCD) = BC
(BCD) ∩ (BAD) = BD
→ BA ∩ BC ∩ BD = B 204
b) Xác định ba mặt phẳng giao nhau
tạo ra ba đường thẳng song song. Chẳng hạn:
(ABCD) ∩ (ABMN) = AB
(ABCD) ∩ (CDMN) = CD
(CDMN) ∩ (ABMN) = MN Mà AB // CD // MN
- Từ Định lí 2, GV dẫn dắt đưa ra hệ Hệ quả
quả, yêu cầu HS giải thích hệ quả dựa Nếu hai mặt phẳng phân biệt lần lượt đi qua vào định lí.
hai đường thẳng song song thì giao tuyến của
chúng (nếu có) song song với hai đường thẳng
đó hoặc trùng với một trong hai đường thẳng
- HS đọc hiểu Ví dụ 4. đó.
+ Xác định điểm chung của hai mặt Ví dụ 4 (SGK – tr.104) phẳng (SBC) và (SAD).
+ Áp dụng định lí 2, tìm đoạn thẳng song song với BC và AD
- GV yêu cầu HS thảo luận nhóm đôi, hoàn thành HĐKP 3. HĐKP 3:
+ Xác định d giao tuyến của mp(a,c)
và mp(M,b). Từ đó suy ra M ∈ d.
+ Áp dụng định lí 1, d trùng với a suy ra a // b
Ta có: d là giao tuyến của mp(a,c) và mp(M,b)
Hay d là giao tuyến của mp(a.,c) và mp(a,b)
Mà a cũng nằm trong mp(a, c) và mp(a, b) Suy ra d trùng a. Do đó, a//b.
- GV cho HS phát biểu Định lí 3. Định lí 3 205
Hai đường thẳng phân biệt cùng song song
với một đường thẳng thứ ba thì song song với nhau. - HS đọc chú ý.
Chú ý: Khi hai đường thẳng phân biệt a, b
cùng song song với đường thẳng c thì ta có thể
kí hiệu là a // b // c và gọi là ba đường thẳng song song.
- GV cho HS tìm hiểu Ví dụ 5. GV Ví dụ 5 (SGK – tr.104) hướng dẫn:
Gọi M, N, P, Q, R, S là trung điểm các cạnh
+ Chứng minh MPNQ là hình bình của tứ diện ABCD như Hình 14. Chứng minh
hành. Từ đó suy ra MN và PQ cắt rằng các đoạn thẳng MN, PQ, RS có cùng trung điể
nhau tại trung điểm mỗi đường. m.
+ Chứng minh MRNS là hình bình Giải
hành. Từ đó suy ra MN và RS cắt nhau
tại trung điểm mỗi đường.
+ Từ đó suy ra điều phải chứng minh. Ta có MP là đườ
ng trung bình của tam giác 𝐴𝐶 ABC, suy ra MP // AC và MP = . 2
Ta cũng có QN là đường trung bình của tam 𝐴𝐶
giác ADC, suy ra QN // AC và QN = 2
MP và QN cùng song song với AC suy ra MP
// QN. Tứ giác MPNQ có hai cạnh đối song
song và bằng nhau nên là hình bình hành, suy 206
ra MN và QP có cùng trung điểm I. Chứng
minh tương tự ta cũng có MN và RS có cùng
trung điểm I. Vậy các đoạn thẳng MN, PQ, RS có cùng trung điểm.
- Áp dụng HS làm Thực hành 3. Thực hành 3:
a) Chứng minh MN // IJ // CD. Từ đó
suy ra IJMN là hình bình hành.
b) Áp dụng tích chất đường trung bình 1
chứng minh MN = CD. Từ đó suy ra 2
vị trí của điểm M Giải
a) Ta có ba mặt phẳng (P), (ACD), (BCD) cắt
nhau theo ba giao tuyến phân biệt là IJ, MN và CD. Mà IJ//CD
Nên (P) giao với (ACD) tại MN // IJ // CD.
Vậy IJMN là hình thang có đáy là MN và IJ
b) Để IJMN là hình bình hành thì IJ = MN 1 1 Mà IJ = CD nên MN = CD 2 2
Vậy M là trung điểm của AC.
- HS thảo luận nhóm đôi, thực hiện Vận dụng 2 Vận dụng 2. 207 Giải
a) Ba mặt phẳng cắt nhau từng đôi một theo
Bước 2: Thực hiện nhiệm vụ:
giao tuyến song song là: (P), (Q), (R)
- HS theo dõi SGK, chú ý nghe, tiếp b) Ba mặt phẳng cắt nhau từng đôi một theo
nhận kiến thức, suy nghĩ trả lời câu giao tuyến đồng quy là: (P), (R), (S).
hỏi, hoàn thành các yêu cầu.
- GV: quan sát và trợ giúp HS.
Bước 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng trình bày
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận định: GV
tổng quát lưu ý lại kiến thức trọng tâm
và yêu cầu HS ghi chép đầy đủ vào vở.
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập trắc nghiệm và bài 1, 2, 3 (SGK – tr.105, 106).
c) Sản phẩm học tập: Câu trả lời của HS. HS xác định được vị trí tương đối của hai đường thẳng.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ: 208
- GV cho HS trả lời nhanh các câu trắc nghiệm:
Câu 1. Cho ba mặt phẳng phân biệt cắt nhau từng đôi một theo ba giao tuyến 𝑑1, 𝑑2, 𝑑3
trong đó d song song với 𝑑 1
2. Khi đó vị trí tương đối của 𝑑2 và 𝑑3 là? A. Chéo nhau. B. Cắt nhau. C. Song song. D. trùng nhau.
Câu 2. Cho hình tứ diện 𝐴𝐵𝐶𝐷. Khẳng định nào sau đây đúng?
A. 𝑨𝑩 và 𝐶𝐷 cắt nhau.
B. 𝑨𝑩 và 𝐶𝐷 chéo nhau.
C. 𝑨𝑩 và 𝐶𝐷 song song. D. Tồn tại một mặt phẳng chứa 𝑨𝑩 và 𝐶𝐷
Câu 3. Cho tứ diện 𝐴𝐵𝐶𝐷 và 𝑀, 𝑁 lần lượt là trọng tâm của tam giác 𝐴𝐵𝐶, 𝐴𝐵𝐷. Khẳng
định nào sau đây là đúng? A. 𝑴𝑵//𝑪𝑫. B. 𝑴𝑵//𝑨𝑫. C. 𝑴𝑵//𝑩𝑫. D. 𝑴𝑵//𝑪𝑨.
Câu 4. Trong không gian cho ba đường thẳng phân biệt 𝑎, 𝑏, 𝑐 trong đó 𝑎 song song với
b . Khẳng định nào sau đây sai?
A. Nếu 𝑏 song song với 𝑐 thì 𝑎 song song với 𝑐.
B. Tồn tại duy nhất một mặt phẳng chứa cả hai đường thẳng 𝑎 và 𝑏.
C. Nếu 𝑐 cắt 𝑎 thì 𝑐 cắt 𝑏.
D. Nếu điểm 𝐴 thuộc 𝑎 và điểm 𝐵 thuộc 𝑏 thì ba đường thẳng 𝑎, 𝑏 và 𝐴𝐵 cùng ở trên một mặt phẳng.
Câu 5. Cho tứ diện 𝐴𝐵𝐶𝐷. 𝑃, 𝑄 lần lượt là trung điểm của 𝐴𝐵, 𝐶𝐷. Điểm 𝑅 nằm trên
cạnh 𝐵𝐶 sao cho 𝐵𝑅 = 2𝑅𝐶. Gọi 𝑆 là giao điểm của mặt phẳng (𝑃𝑄𝑅) và 𝐴𝐷. Khi đó A. 𝑆𝐴 = 3SD. B. 𝑆𝐴 = 2SD. C. 𝑆𝐴 = SD. D. 2𝑆𝐴 = 3SD.
- GV tổ chức cho HS hoạt động thực hiện hoat động cá nhân làm bài 1, 2, 3 (SGK – tr.105, 106).
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận, hoàn thành
các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ. 209
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định:
- GV nhận xét thái độ làm việc, phương án trả lời của các học sinh, ghi nhận và tuyên dương Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 C B A C B Bài 1. a) Mệnh đề sai.
Ví dụ: Xét tứ diện SABC với M, N lần lượt là trung điểm của SA và SB. Ta có AB //
MN, CA cắt AB nhưng CA không cắt MN. b) Mệnh đề sai.
Ví dụ: Xét tứ diện SABC với M, N lần lượt là trung điểm của SA và SA. Ta có AB //
MN, CA chéo với MN nhưng CA cắt AB. Bài 2. 210
Trong mặt phẳng (𝐴𝐵𝐶), vẽ giao điểm 𝑃 của 𝐴𝑀 và 𝐵𝐶. Ta có 𝑀 ∈ (𝑆𝐴𝑃) và 𝑀𝑁 song
song với 𝑆𝐴 nằm trong (𝑆𝐴𝑃), suy ra 𝑀𝑁 ⊂ (𝑆𝐴𝑃).
Trong mặt phẳng (𝑆𝐴𝑃), qua 𝑀 vẽ đường thẳng 𝑑 song song với 𝑆𝐴 và cắt 𝑆𝑃 tại 𝑁.
Ta có: 𝑆𝐴//𝑀𝑁, 𝐶 là điểm chung của (𝑆𝐴𝐶) và (𝐶𝑀𝑁), suy ra giao tuyến của (𝑆𝐴𝐶)
và (𝐶𝑀𝑁) là đường thẳng 𝑑′ đi qua 𝐶 và 𝑑′//𝑆𝐴//𝑀𝑁. Bài 3.
a) Ta có: 𝐴𝐵//𝐶𝐷, 𝑆 là điểm chung của (𝑆𝐶𝐷) và (𝑆𝐴𝐵), suy ra giao tuyến (𝑆𝐶𝐷) và
(𝑆𝐴𝐵) là đường thẳng 𝑑 đi qua 𝑆 và 𝑑//𝐴𝐵//𝐶𝐷.
b) Ta có 𝐴𝐷//𝐵𝐶, suy ra giao tuyến của hai mặt phẳng (𝑀𝐵𝐶) và (𝑆𝐴𝐷) là đường
thẳng 𝑀𝑁 sao cho 𝑀𝑁//𝐵𝐶//𝐴𝐷.
Vậy tứ giác 𝐶𝐵𝑀𝑁 là hình thang.
D. HOẠT ĐỘNG VẬN DỤNG a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập 4, 5, 6 (SGK – tr.106). 211
c) Sản phẩm: Kết quả thực hiện các bài tập. HS vận dụng các tính chất cơ bản về hai
đường thẳng song song để chứng minh hai đường thẳng song song trong mặt phẳng và
giải quyết bài toán thực tế.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 4, 5, 6 (SGK – tr.106).
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: Bài 4.
Gọi 𝑂 giao điểm của 𝐴𝐶 và 𝐵𝐷. Ta có 𝐼𝑂//𝑆𝐵 (vì 𝐼𝑂 là đường trung bình của △ 𝑆𝐷𝐵 ). 212
Hai mặt phẳng (𝐼𝐴𝐶) và (𝑆𝐵𝐷) lần lượt chứa hai đường thẳng song song 𝐼𝑂, 𝑆𝐵 và có
điểm chung 𝐶 nên (𝐼𝐴𝐶) và (𝑆𝐵𝐶) cắt nhau theo giao tuyến 𝐶𝑥 và 𝐶𝑥//𝑆𝐵//𝐼𝑂.
Do đó 𝐶𝑥//𝑆𝐵. Bài 5.
a) Trong mặt phẳng (𝑆𝐵𝐷), 𝐷𝐼 cắt 𝑆𝐵 tại 𝑁. Trong mặt phẳng (𝑆𝐴𝐶), 𝐶𝐼 cắt 𝑆𝐴 tại 𝑀.
Khi đó 𝑀, 𝑁 lần lượt là giao điểm của 𝑆𝐴 và 𝑆𝐵 với mặt phẳng (𝐼𝐶𝐷).
Ta có 𝐶𝐷//𝐴𝐵, suy ra 𝑀𝑁//𝐴𝐵//𝐶𝐷.
Gọi 𝐽 là trung điểm của 𝑂𝐵. Ta có 𝐼𝐽//𝑆𝐵 và 𝐼𝐽 = 𝑆𝐵. 2
Ta lại có 𝐼𝐽 = 3 𝐵𝑁, suy ra 𝐵𝑁 = 2 𝑆𝐵 và 𝑆𝑁 = 1 𝑆𝐵. 4 3 3
Mà 𝑀𝑁//𝐴𝐵, suy ra 𝑀𝑁 = 𝐴𝐵 = 𝑎. 3 3
b) Ta có 𝑆 và 𝐾 là hai điểm chung của hai mặt phẳng (𝑆𝐵𝐶) và (𝑆𝐴𝐷), suy ra 𝑆𝐾 là
giao tuyến của hai mặt phẳng (𝑆𝐵𝐶) và (𝑆𝐴𝐷). Ta lại có 𝐴𝐷//𝐵𝐶, suy ra 𝑆𝐾//𝐴𝐷//𝐵𝐶. Bài 6. 213
Hình a: Các dây điện song song với nhau
Hình b: Các mép của viên gạch lát song song với nhau
Hình c: Các mép của bậc thang song song với nhau
Hình d: Các mép của phím đàn song song với nhau
Hình e: Các mép của từng ngăn kệ song song với nhau
Hình g: Các mép của viên gạch song song với nhau
Một số ví dụ khác về đường thẳng song song: Các gáy của quyền sách trong chồng
sách, Các mép của chân bàn thẳng đứng,...
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: "Đường thẳng và mặt phẳng song song". 214 Ngày soạn: .../.../... Ngày dạy: .../.../...
BÀI 3: ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG (3 TIẾT) I. MỤC TIÊU:
1. Kiến thức, kĩ năng: Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết đường thẳng song song với mặt phẳng.
- Giải thích được điều kiện để đường thẳng song song với mặt phẳng.
- Giải thích được tính chất cơ bản về đường thẳng song song với mặt phẳng.
- Vận dụng điều kiện để chứng minh đường thẳng song song với mặt phẳng, vận
dụng tính chất cơ bản của đường thẳng song song với mặt phẳng vào các bài
toán chứng minh, tính toán, bài toán thực tế….
- Mô tả một số hình ảnh trong thực tiễn có liên quan đến đường thẳng song song với mặt phẳng. 2. Năng lực
Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.
Năng lực riêng:
- Tư duy và lập luận toán học, giải quyết vấn đề toán học: Giải thích được điều kiện
và tính chất đường thẳng song song mặt phẳng. Vận dụng điều kiện để chứng minh
đường thẳng song song với mặt phẳng, vận dụng tính chất cơ bản của đường thẳng
song song với mặt phẳng vào các bài toán chứng minh, tính toán, bài toán thực tế…. 215
- Mô hình hóa toán học: Vận dụng được kiến thức về đường thẳng song song với
mặt phẳng để giải quyết bài toán thực tế, mô tả một số hình ảnh thực tế. - Giao tiếp toán học. 3. Phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm,
tôn trọng ý kiến các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức
theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với GV: SGK, Tài liệu giảng dạy, giáo án, đồ dùng dạy học.
2. Đối với HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
c) Sản phẩm: HS trả lời được câu hỏi mở đầu.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV yêu cầu HS đọc tình huống mở đầu
Đường thẳng a trên mép hiên của toà nhà có điểm nào chung với mặt phẳng (P) của
phố đi bộ Nguyễn Huệ không? 216
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm đôi hoàn thành yêu cầu.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS
vào bài học mới : “Trong không gian có những vị trí tương đối nào của đường thẳng và
mặt phẳng? Khi đường thẳng và mặt phẳng không có điểm chung thì vị trí của chúng là
gì? Có tính chất gì? Bài học hôm nay chúng ta cùng đi tìm hiểu”
Bài 3. Đường thẳng và mặt phẳng song song.
B. HÌNH THÀNH KIẾN THỨC MỚI
Hoạt động 1: Đường thẳng song song với mặt phẳng. Điều kiện để một đường thẳng
song song với một mặt phẳng. a) Mục tiêu:
- Nhận biết đường thẳng song song với mặt phẳng.
- Giải thích được điều kiện để đường thẳng song song với mặt phẳng. b) Nội dung:
HS đọc SGK, nghe giảng, thực hiện các nhiệm vụ được giao, suy nghĩ trả lời câu hỏi,
thực hiện các hoạt động mục 1 và 2.
c) Sản phẩm: HS hình thành được kiến thức bài học về đường thẳng song song mặt
phẳng, điều kiện song song, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện: 217 HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm 1. Đường thẳng song song với mặt phẳng vụ: HĐKP 1
- GV yêu cầu HS thảo luận nhóm Số giao điểm của mặt phẳng (ABCD) với MN, MA,
đôi, hoàn thành HĐKP 1.
AC lần lượt là 0, 1, vô số giao điểm.
GV khái quát giới thiệu về các vị Kết luận
trí tương đối của đường thẳng và Cho đườ mặt phẳng.
ng thẳng a và mặt phẳng (P).
Dựa vào số điểm chung giữa + a ⊂ (P)⇔ a và (P) có hai điểm chung phân biệt
đường thẳng và mặt phẳng để xác trở lên.
định vị trí tương đối.
+ a ∩ (P)=A ⇔ a và (P) có 1 điểm chung duy nhất là A.
+ a // (P) ⇔ a và (P) không có điểm chung.
Đường thẳng a song song với mặt phẳng (P) nếu
chúng không có điểm chung.
Ví dụ 1 (SGK -tr.107+108)
- Áp dụng chỉ ra vị trí tương đối Thực hành 1 trong Ví dụ 1.
- HS thực hiện Thực hành 1.
+ EF có tính chất gì? Từ đó EF
có điểm chung nào vs (BCD) hay không? 218
- GV dẫn dắt: để chỉ ra đường
thẳng song song với mặt phẳng
thì việc chỉ ra chúng không có
điểm chung nào nói chung là khó khăn.
Ta cùng tìm hiểu một số định lí ,
𝐵𝐶 ⊂ (𝐵𝐶𝐷), 𝐴𝐷 ∩ (𝐵𝐶𝐷) = 𝐷, 𝐸𝐹 ∕∕ (𝐵𝐶𝐷)
tính chất thường gặp để chỉ ra đườ
2. Điều kiện để một đường thẳng song song với
ng thẳng song song với mặt một mặt phẳng. phẳng.
- HS thực hiện HĐKP 2. HĐKP 2
Từ đây ta thấy nếu a song song a) Giao tuyến của hai mặt phẳng (P) và (Q) là b.
với đường thẳng b thuộc (P) thì a b) Nếu a có điểm chung M với (P) thì điểm M phải
không có điểm chung nào với nằm trên đường thẳng b (Do hai mặt phẳng chỉ giao (P). nhau tại 1 giao tuyến) - HS khái quát định lí.
→Sử dụng định lí để chứng minh Điều này trái với giả thiết a//b.
đường thẳng song song với mặt Định lí 1
phẳng. Ta chỉ cần chỉ ra điều gì? Nếu đường thẳng 𝑎 không nằm trong mặt phẳng
(a//b và 𝑎 ⊄ (𝑃), 𝑏 ⊂ (𝑃) ⇒ 𝑎 ∕ (𝑃) và song song với một đường thẳng nằm trong ∕ (𝑃)).
(𝑃) thì a song song với (𝑃).
- HS áp dụng đọc, giải thích Ví dụ 2.
+ Xác định số điểm chung của
các đường thẳng với mặt phẳng,
từ đó xác định vị trí tương đối. 219
+ 𝑑3 song song với đường thẳng Ví dụ 2 (SGK -tr.108)
nào? Từ đó mối quan hệ của 𝑑3và Thực hành 2 (P).
Các đường thẳng SA, SB, SC cắt mặt phẳng
- HS thực hiện Thực hành 2, (ABC). Vận dụng 1.
+ TH2: Vận dụng tính chất Các đường thẳng AB, BC, CA nằm trong mặt đường trung bình. phẳng (ABC).
+ VD 1: tìm các đường thẳng có
Các đường thẳng A'B', B'C', C'A' song song với
số điểm chung lần lượt là vô số, mặt phẳng (ABC).
0,1 so với mặt phẳng sàn. Bướ Vận dụng 1
c 2: Thực hiện nhiệm vụ:
- HS theo dõi SGK, chú ý nghe,
tiếp nhận kiến thức, hoàn thành
các yêu cầu, thảo luận nhóm. - GV quan sát hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- HS giơ tay phát biểu, lên bảng
a nằm trong (P), c song song với (P); (b) cắt (P). trình bày
- Một số HS khác nhận xét, bổ sung cho bạn.
Bước 4: Kết luận, nhận định:
GV tổng quát lưu ý lại kiến thức
trọng tâm và yêu cầu HS ghi chép
đầy đủ vào vở.
Hoạt động 2: Tính chất cơ bản của đường thẳng và mặt phẳng song song a) Mục tiêu: 220
- Giải thích được tính chất cơ bản về đường thẳng song song với mặt phẳng.
- Vận dụng tính chất cơ bản của đường thẳng song song với mặt phẳng vào các bài
toán chứng minh, tính toán, bài toán thực tế….
b) Nội dung: HS đọc SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV, chú ý
nghe giảng, thực hiện các hoạt động mục 3.
c) Sản phẩm: HS hình thành được kiến thức bài học về tính chất cơ bản của đường thẳng
và mặt phẳng song song, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện:
HOẠT ĐỘNG CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
Bước 1: Chuyển giao nhiệm vụ:
3. Tính chất cơ bản của đường thẳng và
- GV yêu cầu HS hoạt động cá nhân mặt phẳng song song HĐKP 3 hoàn thành HĐKP 3. Hai đườ
ng thẳng a và b không có điểm chung nào. Đị
- HS khái quát: Nếu đường thẳng a song nh lí 2
song với (P) và a thuộc (Q) thì giao Cho đường thẳng a song song với mặt phẳng
tuyến của (P) và (Q) có tính chất gì?
(P). Nếu mặt phẳng (Q) chứa a và cắt (P)
- Áp dụng định lí 2 HS đọc và giải thích theo giao tuyến b thì b song song với a. Ví dụ 3.
- GV lưu ý: định lí 2 là một cách để
chứng minh hai đường thẳng song song.
Ví dụ 3 (SGK -tr.109) Hệ quả 1
- GV đặt câu hỏi để dẫn đến hệ quả
Cho đường thẳng a song song với mặt phẳng
+ Cho đường thẳng a song song với (P) (P). Nếu qua điểm M thuộc (P) ta vẽ đường
và điểm M thuộc (P). Qua M vẽ đường 221
thẳng b song song với a thì b thuộc mặt thẳng b song song với a thì b phải nằm trong
phẳng (P) hay không? Giải thích (P). (b thuộc (P), Vì
Gọi giao tuyến của (P) và (M,a) là
đường thẳng m. Suy ra m // a theo định lí 2.
Mà trong (M,a) tồn tại b và m đều qua
M và song song với a. Suy ra 𝑚 ≡ 𝑏 hay b thuộc (P).)
+ Nếu a song song với mặt phẳng (P) và
(Q) thì giao tuyến b của hai mặt phẳng Hệ quả 2:
có mối quan hệ gì với a?
Nếu hai mặt phẳng phân biệt cùng song song
(a//b, Gọi M là điểm thuộc giao tuyến b. với một đường thẳng thì giao tuyến của
Khi đó b chính là giao tuyến của mặt chúng (nếu có) cũng song song với đường
phẳng (M, a) và (P); b là giao tuyến của thẳng đó. (M, a) và (Q)).
- HS áp dụng, giải thích Ví dụ 4.
Ví dụ 4(SGK -tr.110)
- GV lưu ý: từ hệ quả 1, 2 có thể dùng để
*) Mặt phẳng đi qua một trong hai đường
dựng giao tuyến giữa hai mặt phẳng
thẳng chéo nhau và song song với đường còn có yếu tố song song. lại
- HS thực hiện HĐKP 4 theo nhóm đôi HĐKP 4 222
- Từ đó HS khái quát định lí 3.
a) 𝑏′ ⊂ (𝑃), 𝑏′//𝑏 𝑛ê𝑛 𝑏//(𝑃) b) 𝑏′ ⊂ (𝑃′)
- Áp dụng làm Ví dụ 5. (P) và (P') trùng nhau.
+ b) tìm điểm chung thứ nhất giữa hai Định lí 3:
mặt phẳng; phát hiện (P) song song với Nếu a và b là hai đường thẳng chéo nhau thì
CD từ đó sử dụng định lí 2.
qua a, có một và chỉ một mặt phẳng song song
- HS thực hiện Thực hành 3 và Vận với b. dụng 2.
Ví dụ 5 (SGK -tr.111)
+ Để chứng minh đường thẳng song Thực hành 3
song với mặt phẳng phải chỉ ra điều gì?
Tìm xem MN song song với đường thẳng nào. Tương tự với câu b.
Bước 2: Thực hiện nhiệm vụ:
- HS theo dõi SGK, chú ý nghe, tiếp
nhận kiến thức, suy nghĩ trả lời câu hỏi, hoàn thành các yêu cầu.
- GV: quan sát và trợ giúp HS.
a) Ta có hình bình hành ABCD; M, N lần
lượt là trung điểm của AB, CD nên
Bước 3: Báo cáo, thảo luận: MN//BC//AD
- HS giơ tay phát biểu, lên bảng trình bày
Do 𝐵𝐶 ⊂ (𝑆𝐵𝐶) nên 𝑀𝑁//(𝑆𝐵𝐶) 223
- Một số HS khác nhận xét, bổ sung cho Do 𝐴𝐷 ⊂ (𝑆𝐴𝐷) nên 𝑀𝑁//(𝑆𝐴𝐷) bạn.
b) Trong tam giác SAB có M, E lần lượt là
Bước 4: Kết luận, nhận định: GV tổng trung điểm của AB và SA nên ME//SB quát lưu ý lạ
i kiến thức trọng tâm và yêu
cầu HS ghi chép đầy đủ vào vở.
Mà 𝑀𝐸 ⊂ (𝑀𝑁𝐸) nên 𝑆𝐵//(𝑀𝑁𝐸)
Gọi O là giao của AC, BD và MN
Do ABCD là hình bình hành nên O là trung điểm của AC
Trong tam giác SAC có O, E lần lượt là
trung điểm của AC và SA nên OE//SC
Mà 𝑂𝐸 ⊂ (𝑀𝑁𝐸) nên 𝑆𝐶//(𝑀𝑁𝐸) Vận dụng 2
Đặt mép thước kẻ a song song với đường thẳng gáy sách.
C. HOẠT ĐỘNG LUYỆN TẬP
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập 1, 2, 3 (SGK -tr.112) và các câu hỏi TN nhanh.
c) Sản phẩm học tập: Câu trả lời của HS.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV tổ chức cho HS trả lời các câu hỏi TN nhanh
Câu 1. Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b? 224 A. 0 B. 1 C. 2 D. Vô số
Câu 2. Cho tứ diện ABCD. Gọi 𝐺1 và 𝐺2 lần lượt là trọng tâm các tam giác BCD và ACD. Chọn câu sai:
A. 𝐺1𝐺2 ∕∕ (𝐴𝐵𝐷)
B. 𝐺1𝐺2 ∕∕ (𝐴𝐵𝐷)
C. 𝐵𝐺1, 𝐴𝐺2 và CD đồng quy
D. 𝑮𝟏𝑮𝟐 = 𝟐 𝑨𝑩 𝟑
Câu 3. Cho hình chóp tứ giác S.ABCD. Gọi M và N lần lượt là trung điểm của SA và
SC. Khẳng định nào sau đây đúng? A. MN // (ABCD) B. MN // (SAB) C. MN // (SCD) D. MN // (SBC)
Câu 4. Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng
tâm của tam giác SAB và SAD. E, F lần lượt là trung điểm của AB và AD. Trong các
mệnh đề sau, mệnh đề nào đúng? A. IJ // (SBD) B. IJ // (SEF) 225 C. IJ // (SAB) D. IJ // (SAD)
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm của
tam giác SAB, I là trung điểm của AB. Lấy điểm M trên đoạn AD sao cho AD = 3AM.
Đường thẳng qua M và song song với AB cắt CI tại J. Đường thẳng JG không song song với mặt phẳng: A. (SCD) B. (SAD) C. (SBC) D. (SAC)
- GV tổ chức cho HS hoạt động thực hiện Bài 1, 2, 3 (SGK -tr.112).
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm, hoàn
thành các bài tập GV yêu cầu.
- GV quan sát và hỗ trợ.
Bước 3: Báo cáo, thảo luận:
- Câu hỏi trắc nghiệm: HS trả lời nhanh, giải thích, các HS chú ý lắng nghe sửa lỗi sai.
- Mỗi bài tập GV mời HS trình bày. Các HS khác chú ý chữa bài, theo dõi nhận xét bài trên bảng.
Bước 4: Kết luận, nhận định:
- GV chữa bài, chốt đáp án, tuyên dương các hoạt động tốt, nhanh và chính xác. Kết quả:
Đáp án trắc nghiệm 1 2 3 4 5 226 B D A A B Bài 1.
a) 𝑂𝑀 là đường trung bình của tam giác 𝑆𝐴𝐶, suy ra 𝑂𝑀//𝑆𝐴. Ta có 𝑂𝑀 không nằm
trong mặt phẳng (𝑆𝐴𝐷) và 𝑂𝑀 song song với 𝑆𝐴 nằm trong (𝑆𝐴𝐷), suy ra 𝑂𝑀//(𝑆𝐴𝐷).
Tương tự, 𝑂𝑀//(𝑆𝐵𝐴).
b) Ta có 𝐷 là điểm chung của hai mặt phẳng (𝑂𝑀𝐷) và (𝑆𝐴𝐷). Ta lại có (𝑂𝑀𝐷) chứa
𝑂𝑀 và 𝑂𝑀//(𝑆𝐴𝐷), suy ra giao tuyến của (𝑂𝑀𝐷) với (SAD) là đường thẳng 𝑑 đi qua
điểm 𝐷 và 𝑑//𝑂𝑀. Bài 2.
a) Ta có 𝐸𝐹//𝐴𝐵 và 𝐸𝐹 = 𝐴𝐵, 𝐶𝐷//𝐴𝐵 và 𝐶𝐷 = 𝐴𝐵, suy ra 𝐸𝐹//𝐶𝐷 và 𝐸𝐹 = 𝐶𝐷, suy
ra 𝐸𝐹𝐷𝐶 là hình bình hành, suy ra 𝐷𝐹//𝐶𝐸.
Ta có 𝑂𝑂′ là đường trung bình của tam giác 𝐵𝐹𝐷, suy ra 𝑂𝑂′//𝐷𝐹//𝐶𝐸. Vậy 𝑂𝑂′
song song với các mặt phẳng (𝐶𝐷𝐹𝐸), (𝐴𝐷𝐹) và (𝐵𝐶𝐸).
b) Trong hình bình hành ABEF có M, N lần lượt là trung điểm của AE và
BF nên 𝑀𝑁//𝐸𝐹//𝐴𝐵. 227
Suy ra 𝑀𝑁//(𝐶𝐷𝐸𝐹).
c) Ta có 𝐴𝐵//𝑀𝑁 và 𝑂 là điểm chung của hai mặt phẳng (𝑂𝑀𝑁) và (𝐴𝐵𝐶𝐷), suy ra
giao tuyến của hai mặt phẳng (𝑂𝑀𝑁) và (𝐴𝐵𝐶𝐷) là đường thẳng 𝑑 đi qua 𝑂 và 𝑑//𝐴𝐵. Bài 3.
a) Ta có (𝑆𝐶𝐷) ∩ (𝐴𝐵𝐶𝐷) = 𝐶𝐷; (𝛼) ∩ (𝑆𝐶𝐷) = 𝑃𝑄;
(𝛼) ∩ (𝐴𝐵𝐶𝐷) = 𝑀𝑁. Ta lại có 𝐶𝐷//(𝛼), suy ra 𝑀𝑁//𝑃𝑄.
Vậy 𝑀𝑁𝑃𝑄 là hình thang.
b) Ta có 𝐵𝐶//𝐴𝐷 và 𝑆 là điểm chung của hai mặt phẳng (𝑆𝐵𝐶) và (𝑆𝐴𝐷), suy ra giao
tuyến của hai mặt phẳng (𝑆𝐵𝐶) và (𝑆𝐴𝐷) là đường thẳng 𝑑 cố định đi qua 𝑆 và
𝑑//𝐵𝐶//𝐴𝐷. Ta có 𝐼 là điểm chung của hai mặt phẳng (𝑆𝐵𝐶) và (𝑆𝐴𝐷), suy ra 𝐼 luôn
thuộc đường thẳng 𝑑 cố định.
D. HOẠT ĐỘNG VẬN DỤNG a) Mục tiêu: 228
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: HS sử dụng SGK và vận dụng kiến thức đã học để làm bài tập.
c) Sản phẩm: Kết quả thực hiện các bài tập.
d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động hoàn thành bài tập 4, 5, 6 (SGK -tr.139).
Bước 2: Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Bước 3: Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Bước 4: Kết luận, nhận định
- GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hay mắc phải. Gợi ý đáp án: Bài 4. 229
a) Ta có (𝛼) ∩ (𝐴𝐵𝐶) = 𝑀𝑁; (𝛼) ∩ (𝐵𝐶𝐷) = 𝑃𝑄;
(𝐴𝐵𝐶) ∩ (𝐵𝐶𝐷) = 𝐵𝐶. Ta lại có 𝐵𝐶//(𝛼), suy ra
𝑀𝑁//𝑃𝑄. Tương tư, ta có 𝑀𝑄//𝑁𝑃. Vậy tứ giác 𝑀𝑁𝑃𝑄 là hình bình hành.
b) 𝑀𝑁𝑃𝑄 là hình thoi khi 𝐴𝐷 = 𝐵𝐶 và 𝑀 là trung điểm của 𝐴𝐵. Bài 5. 230
Qua 𝑀 kẻ 𝑀𝑁//𝐵𝐶(𝑁 ∈ 𝐴𝐵); qua 𝑁 kẻ 𝑁𝑃//𝑆𝐴(𝑃 ∈ 𝑆𝐵); qua 𝑃 vẽ 𝑃𝑄//𝐵𝐶; nối 𝑀 với 𝑄.
Ta được các giao tuyến của mặt phẳng (𝑃) với các mặt của hình chóp là
𝑀𝑁, 𝑁𝑃, 𝑃𝑄, 𝑄𝑀. Bài 6.
Các đường thẳng 𝑎, 𝑏, 𝑐 song song với mặt phẳng (𝑃). Đường thẳng 𝑑 cắt mặt phẳng
(𝑃) và đường thẳng 𝑒 nằm trong mặt phẳng (𝑃).
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: "Bài 4. Hai mặt phẳng song song” 231 232




