Giáo án Toán 8 HK1 Kết nối tri thức

Trang 1

Tuần 2

Tiết 1; 2; 3

Ngày soạn 20/8/2023

Lớp

8A

1

8A

2

8A

3

Ngày dạy:

ÔN TẬP BÀI 1,2: ĐƠN THỨC, ĐA THỨC

I. MỤC TIÊU

1. Về kiến thức:

-Học sinh nhận biết được đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn

thức.

-Học sinh thu gọn được được đơn thức, nhận biết được đơn thức đồng dạng và cộng,

trừ hai đơn thức đồng dạng.

-Nhận biết được đa thức, hạng tử của đa thức, đa thức thu gọn.

-Thu gọn được đa thức, tìm được bậc của đa thức.

-Biết tìm giá trị của đa thức khi biết giá trị của biến.

2. Về năng lực:

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được đơn thức, đa thức, bậc của

đơn thức, đa thức

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng hợp,

tính toán,

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, máy chiếu.

2. Học sinh: SGK, vở ghi.

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

1) Đơn thức.

Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến hoặc có dạng tích của

những số và biến

2) Đơn thức thu gọn, bậc của một đơn thức.

Trang 2

 Đơn thức thu gọn là đơn thức chỉ gồm một số hoặc có dạng tích của một số với

những biến, mỗi biến chỉ xuất hiện một lần và đã được nâng lên lũy thừa với số

mũ nguyên dương.

 Tổng các số mũ của các biến trong một đơn thức thu gọn với hệ số khác

0

gọn

là bậc của đơn thức đó.

 Trong một đơn thức thu gọn, phần số còn gọi là hệ số, phần còn lại gọi là phần

biến.

VD: Với đơn thức

( )

7

35

2 x y z−

thì phần hệ số là

( )

7

2−

còn phần biến là

35

x y z

 Với các đơn thức có hệ số là

1

hay

1−

ta không viết số

1.

VD: Với đơn thức

5

xy−

có hệ số là

1−

 Mỗi số khác

0

cũng là một đơn thức thu gọn với bậc là

0

 Số

0

cũng được gọi là một đơn thức, đơn thức này không có bậc.

3) Đơn thức đồng dạng.

 Hai đơn thức đồng dạng là hai đơn thức có hệ số khác

0

và có phần biến giống

nhau.

 Hai đơn thức đồng dạng thì có cùng bậc.

 Để thực hiện phép cộng, trừ các đơn thức đồng dạng, ta cộng, trừ phần hệ số và

giữ nguyên phần biến.

4) Đa thức.

 Đa thức là tổng của những đơn thức, mỗi đơn thức trong tổng gọi là một hạng

tử của đa thức đó.

 Mỗi đơn thức cũng được gọi là một đa thức.

5) Thu gọn đa thức.

 Đa thức thu gọn là đa thức không có hai hạng tử nào đồng dạng.

 Bậc của một đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của

đa thức đó.

 Một số khác

0

cũng được coi là một đa thức bậc

0

 Số

0

cũng là một đa thức, gọi là đa thức

0

và không có bậc xác định.

2. BÀI TẬP

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ

- GV chiếu bài tập lên máy chiếu yêu cầu

học sinh trả lời nhanh bài tập trắc nghiệm

- HS tìm hiểu bài toán 1

Dạng 1: Nhận biết đơn thức, đơn thức

đồng dạng, đa thức, bậc và hệ số của

đơn thức, đa thức

Bài 1: Bài tập trắc nghiệm

a) Trong các biểu thức sau, biểu thức nào là đơn thức?

A.

2xy−

B.

22xy−

C.

4 x

D.

4xy −

b) Trong các biểu thức sau, biểu thức nào là đa thức?

A.

36xy xy−

B.

1

2

x

−

C.

3

2

x

y−

D.

15

2

xy

xy−+

c) Tìm đơn thức đồng dạng với đơn thức

2

4xy−

.

Trang 3

A.

2

xy−

B,

2

4xy

C.

2

1

4xy−

D.

2

4

xy

−

d) Hệ số của đơn thức

2

2 xyz−

là:

A.

2

B.

2−

C.

xyz

D.

4−

*Thực hiện nhiệm vụ

-GV yêu cầu hS hoạt động cá nhân

- Giáo viên gọi lần lượt HS đứng tại chỗ

trả lời và giải thích

HS đứng tại chỗ trả lời các câu hỏi trả lời

các câu hỏi

a) Đáp án B

b) Đáp án C

c) Đáp án B

d) Đáp án D

- HS chốt được kiến thức: Đơn thức là

biểu thức đại số chỉ gồm một số hoặc một

biến hoặc có dạng tích của những số và

biến

*Kết luận, nhận định:

-Tại sao

4 x

không là đơn thức?

- Vì biểu thức đó gồm tích của một số với

căn bậc hai của 1 biến.

a) Trong các biểu thức sau, biểu thức nào

là đơn thức?

A.

2xy−

B.

22xy−

C.

4 x

D.

4xy −

Ta có:

2xy−

,

4xy −

là đa thức

4 x

không là đơn thức

b) Trong các biểu thức sau, biểu thức nào

là đa thức?

A.

36xy xy−

B.

1

2

x

−

C.

3

2

x

y−

D.

15

2

xy

xy−+

Ta có:

3 6 3xy xy xy− = −

là đơn thức

1 1 2

2

x

xx

−

−=

không là đa thức

29

15

22

xy

xy xy

−

− + =

là đơn thức

c) Tìm đơn thức đồng dạng với đơn

thức

2

4xy−

.

A.

2

xy−

B,

2

4xy

C.

2

1

4xy−

D.

2

4

xy

−

Ta có đơn thức

2

4xy−

và

2

xy−

có cùng

phần biến

2

xy

và hệ số khác 0.

d) Hệ số của đơn thức

2

2 xyz−

là:

A.

2

B.

2−

C.

xyz

D.

4−

Ta có:

2

24− = −

nên đơn thức đó có hệ

số là

4−

.

*Giao nhiệm vụ

- GV chiếu bài tập lên máy chiếu, gọi một

HS đứng tại chỗ đọc đề bài.

Bài 2:

Phương pháp:

-Bước 1: Thu gọn đơn thức.

Trang 4

-Một HS đứng tại chỗ đọc đề bài

Bài 2. Tìm bậc và hệ số của các biểu thức

đại số sau:

a)

43xy xy−−

b)

33

1

2

x y x y−

c)

2 4 8xy xy xy+−

d)

2

( ).( 5x )xy yz−−

e)

2

3

.( 2 )

2

xy xy−

*Thực hiện nhiệm vụ

-GV yêu cầu HS hoạt động cá nhân

-Hs hoạt động cá nhân

- Em hãy nêu cách làm?

-Một hS đứng tại chỗ nêu cách làm

-Muốn tìm bậc của đơn thức làm như thế

nào?

-Muốn tìm bậc của đơn thức ta cộng số mũ

của các biến lại.

- GV gọi 5 HS lên bảng trình bày

*Kết luận, nhận định:

- HS khác ở dưới nhận xét

GV chốt phương pháp giải của dạng toán

và một số lưu ý

-HS nắm được lưu ý: Trước khi tìm bậc

và hệ số của đơn thức cần thu gọn đơn

thức.

-Bước 2: Tìm bậc và hệ số của đơn thức.

a)

43xy xy−−

( 4 3) 7xy xy= − − = −

Đơn thức có hệ số là

7−

, bậc là

2

b)

33

1

2

x y x y−

33

11

( 1) y

22

x x y− = −

Đơn thức có hệ số là , bậc là

4

c)

2 4 8xy xy xy+−

(2 4 8) 2xy xy= + − = −

Đơn thức có hệ số là

2−

, bậc là

2

d)

2

( ).( 5 )xy x yz−−

2 3 2

( 1).( 5).( . ).( . ). 5x x y y z x y z= − − =

Đơn thức có hệ số là

5

, bậc là

6

e)

2

3

.( 2 )

2

xy xy−

2 2 3

3

.( 2).( . ).( y) 3x

2

x x y y= − = −

Đơ thức có hệ số là

3−

, bậc là

5

*Giao nhiệm vụ

Bài 3

Trang 5

-GV đưa bài tập lên yêu cầu hoạt động cá

nhân

-HS nhận nhiệm vụ

Bài 3. Phân thành các nhóm đơn thức

đồng dạng trong các đơn thức sau:

32

3xy

,

5 4 2

11

x y z

,

33

6

xy−

33

11xy−

,

5 4 2

6x y z−

,

32

1

6

2

xy

.

*Thực hiện nhiệm vụ

-HS hoạt động cá nhân, suy nghĩ bài làm

-Hãy nêu cách làm?

-GV gọi một hS lên bảng trình bày

-Một HS lên bảng trình bày

*Kết luận, nhận định

-GV chốt kiến thức và lưu ý: Hai đơn thức

đồng dạng thì cùng bậc với nhau nhưng

hai đơn thức cùng bậc với nhau thì chưa

chắc đã đồng dạng với nhau

-HS nắm được lưu ý

Phương pháp:

-Chọn các đơn thức có cùng phần biến với

nhau thành một nhóm. Lưu ý cần rút gọn

đơn thức trước ( nếu cần)

N1:

32

3xy

,

32

1

6

2

xy

N2:

5 4 2

11

x y z

,

5 4 2

6x y z−

N3:

33

6

xy−

,

33

11xy−

*Lưu ý:

Hai đơn thức đồng dạng thì cùng bậc với

nhau nhưng hai đơn thức cùng bậc với

nhau thì chưa chắc đã đồng dạng với nhau

VD:

32

3xy

và

23

6xy

có cùng bậc là

5

nhưng không đồng dạng với nhau vì

không cùng phần biến (

3 2 2 3

x y x y

*Giao nhiệm vụ

-GV yêu cầu hS đọc bài toán

-HS đứng tại chỗ đọc bài

Bài 4: Thu gọn rồi tìm bậc

của các đa thức sau

6 5 4 4 4 4

1A x y x y x y= + + + −

( )

5 4 5

7 2 1 7B x x x= − − + −

4 2 2 4

2 3 5C x x y xy x= − + + −

*Thực hiện nhiệm vụ

-GV yêu cầu hS hoạt động cá nhân

-HS hoạt động cá nhân

-Em hãy nêu cách làm? Thế nào là bậc của

đa thức?

- Bậc của một đa thức là bậc của hạng tử

có bậc cao nhất trong dạng thu gọn của đa

Bài 4.

Phương pháp

-Nhóm các đơn thức đồng dạng với nhau

rồi thu gọn.

-Tìm bậc của từng hạng tử ( đơn thức).

Đơn thức nào có bậc cao nhất chính là bậc

của đa thức

Trang 6

thức đó.

-GV gọi 3 HS lên bảng trình bày

-3 HS lên bảng trình bày

*Kết luận, nhận định

-HS khác ở dưới nhận xét

-GV chốt kiến thức và lưu ý: Trước khi

tìm bậc của đa thức cần thu gọn đa thức

đó.

-HS nắm được lưu ý

6 5 4 4 4 4

1A x y x y x y= + + + −

6 5 4 4 4 4

( ) 1x y x y x y= + + − +

65

1xy= + +

(

6

x

có bậc là

6

,

5

y

có bậc là

5

,

1

có bậc

là

0

)

Đa thức

A

có bậc là

6

.

( )

5 4 5

7 2 1 7B x x x= − − + −

5 5 4

7 ( 7 ) 2 1x x x



= + − − −



4

21x= − −

(

4

2x−

có bậc là

4

,

1−

có bậc là

0

) Đa thức

B

có bậc là

4

4 2 2 4

2 3 5C x x y xy x= − + + −

4 4 2 2

( ) 2 3 5x x x y xy= − − + +

22

2 3 5x y xy= − + +

(

22

2xy−

có bậc là

4

,

3xy

có bậc là

2

,

5

có bậc là

0

)

Đa thức

C

có bậc là

4

Lưu ý: Trước khi tìm bậc cần thu gọn đa

thức

*GV giao nhiệm vụ

-GV chiếu bài tập lên yêu cầu một hS

đứng tại chỗ đọc

-Một HS đứng tại chỗ đọc đề bài

Dạng 2: Thực hiện phép tính

Bài 5: Bài tập Trắc nghiệm

Bài 5. Chọn đáp án đúng

a) Kết quả của phép tính

( )

5xy xy xy− − +

là:

A.

5xy

B.

6xy

C.

7xy

D.

5xy−

b) Thực hiện phép tính

( )

2

5 . 3xy y−

được kết quả:

A.

2x

B.

4

15xy−

C.

4

45xy−

D.

4

45xy

c) Kết quả của phép tính

2

3.xyz xz yz−−

là:

A.

2

4xyz−

B.

2

3xyz−

C.

2

xyz−

D.

2

4xyz

*Thực hiện nhiệm vụ

a) Đáp án C

Trang 7

-GV yêu cầu HS thực hiện cá nhân trả lời

nhanh

- HS thực hiện các nhân

-Nhắc lại cách cộng, trừ hai đơn thức đồng

dạng?

-Muốn cộng, trừ hai đơn thức đồng dạng ta

cộn, trừ các hệ số với nhau và giữ nguyên

phần biến

-GV gọi lần lượt hS đứng tại chỗ trả lời

-3 HS lần lượt đứng tại chỗ trả lời

-Hãy nêu cách làm ý c)

-Bước 1: Tính

2

3 . 3xz yz xyz=

-Bước 2: Trừ hai đơn thức đồng dạng

*Kết luận, nhận định

-HS khác nhận xét

-GV nhận xét và chốt kiến thức

b) Đáp án D

c) Đáp án A

a)Kết quả của phép tính

( )

5xy xy xy− − +

là:

A.

5xy

B.

6xy

C.

7xy

D.

5xy−

Ta có:

( )

5xy xy xy− − +

7xy=

b) Thực hiện phép tính

( )

2

5 . 3xy y−

được kết quả:

A.

2x

B.

4

15xy−

C.

4

45xy−

D.

4

45xy

Ta có:

( )

2

5 . 3xy y−

22

5 .9yxy=

4

45xy=

c) Kết quả của phép tính

2

3.xyz xz yz−−

là:

A.

2

4xyz−

B.

2

3xyz−

C.

2

xyz−

D.

2

4xyz

Ta có:

2

3.xyz xz yz−−

22

3xyz xyz= − −

2

4xyz=−

*GV giao nhiệm vụ

-GV chiếu bài tập lên

-HS đọc đề bài

Bài 6: Thực hiện phép tính:

a)

( )

2

8.x y x xy−−

b)

( )

2 2 2

4 . 12xy x x y−−

c)

( )

2 3 2

5

3

6

xy x y x y−

d)

4 4 2 2

15 7 20 .x x x x+−

*Thực hiện nhiệm vụ

-GV yêu cầu hS hoạt động cặp đôi

-HS hoạt động cặp đôi

-Hãy nêu cách làm?

-Một HS nêu cách làm

-GV gọi đại diện của 4 cặp nhanh nhất lên

Bài 6: Thực hiện phép tính

Phương pháp:

-Bước 1: Thu gọn các hạng tử

-Bước 2: Nhóm các hệ số với nhau và giữ

nguyên phần biến(Nếu đơn thức đồng

dạng)

a)

( )

2

8.x y x xy−−

22

8x y x y= − −

Trang 8

trình bày

-4 HS lên bảng trình bày

*Kết luận, nhận định

-HS khác nhận xét

-GV nhận xét và chốt kiến thức.

2

( 8 1)xy= − −

2

9xy=−

b)

( )

2 2 2

4 . 12xy x x y−−

2 2 2 2

4 12x y x y=+

22

16xy=

c)

( )

2 3 2

5

3

6

xy x y x y−

3 2 3 2

5

3

6

x y x y=−

32

5

3

6

xy



=−





32

13

6

xy=

d)

4 4 2 2

15 7 20 .x x x x+−

4 4 4

(15 7 ) 20x x x= + −

4

(15 7 20)x= + −

4

2x=

*Giao nhiệm vụ

-GV yêu cầu hS đọc bài toán

-Một HS đứng tại chỗ đọc bài toán

Bài 7: Tìm hiệu

AB−

biết

a)

2 2 2 2

2 3 4x y A xy B x y xy− + + − = −

b)

2 2 2 2

5 6 7 8xy A yx B xy x y− − + = − +

c)

2 3 3 2 2 3 3 2

3 5 8 4x y A x y B x y x y− − + = −

*Thực hiện nhiệm vụ

-GV yêu cầu hS hoạt động theo bàn

-HS thực hiện theo bàn

-Một em đại diện nêu cách làm?

-Một hS đứng tại chỗ nêu cách làm:

B1: Chuyển các hạng tử sang vế phải

B2: Áp dụng qui tắc công, trừ đa thức để

thu gọn vế phải

B3: Tìm

AB−

-GV gọi đại diện 3 bàn nhanh nhất lên

bảng

-3 HS lên bảng trình bày

-Để làm bài tập này em cần áp dụng những

kiến thức nào đã học?

-HS: -Cần áp dụng quy tắc chuyển vế,

cách cộng, trừ hai đơn thức và quy tắc dấu

ngoặc (theo chiều ngược lại)

Bài 7:

Phương pháp

Bước 1: Chuyển các hạng tử sang vế phải

Bước 2: Áp dụng qui tắc công, trừ đa thức

để thu gọn vế phải

Bước 3: Tìm

AB−

a)

2 2 2 2

2 3 4x y A xy B x y xy− + + − = −

2 2 2 2

3 4 2A B x y xy x y xy− = − + −

2 2 2 2

(3 ) (4 2 )x y x y xy xy= + − +

22

46x y xy=−

Trang 9

*Kết luận, nhận định

-Các HS ở dưới nhận xét

-GV nhận xét và chốt kiến thức

-Hãy nhắc lại qui tắc chuyển vế ?

-Một HS đứng tại chỗ nhắc lại qui tác

chuyển vế.

-GV lưu ý:

()A B A B− = − − +

b)

2 2 2 2

5 6 7 8xy A yx B xy x y− − + = − +

2 2 2 2

7 8 5 6A B xy x y xy x y− + = − + − +

2 2 2 2

( 7 5 ) (8 6 )xy xy x y x y= − − + +

22

12 14xy x y= − +

Suy ra

()A B A B− = − − +

22

( 12 14 )xy x y= − − +

22

12 14xy x y=−

c)

2 3 3 2 2 3 3 2

3 5 8 4x y A x y B x y x y− − + = −

2 3 3 2 2 3 3 2

8 4 3 5A B x y x y x y x y− + = − − +

2 3 2 3 3 2 3 2

(8 3 ) (5 4 )x y x y x y x y= − + −

2 3 3 2

5x y x y=+

Sy ra:

()A B A B− = − − +

2 3 3 2

(5 )x y x y= − +

2 3 3 2

5x y x y= − −

*Lưu ý:

()A B A B− = − − +

* Giao nhiệm vụ

- GV chiếu bài tập lên

-Một HS đứng tại chỗ đọc bài

-Các HS khác tìm hiểu bài toán

Dạng 3: Toán tổng hợp

Bài 8: Bài tập trắc nghiệm

Bài 8. Cho đa thức

6 5 4 4 4 4

1A x y x y x y= + + + −

a) Thu gọn đa thức được kết quả:

A.

65

1x y xy+ + +

B.

6 5 0 0

1x y x y+ + +

C.

65

1A x y= + +

D.

6 5 4 4

21A x y x y= + + +

b) Bậc của đa thức là:

Trang 10

A.

1

B.

2

C.

5

D.

6

c) Giá trị của đa thức tại

1, 1xy= = −

là:

A.

1

B.

2

C.

3

D.

4

*Thực hiện nhiệm vụ

-GV yêu cầu hS hoạt động cá nhân

-HS hoạt động cá nhân

-Hãy nêu cách thu gọn đa thức?

-Muốn thu gọn đa thức ta nhóm các hạng

tử( đơn thức) đồng dạng với nhau

-Thế nào là bậc của đa thức?

-Bậc của đa thức là bậc của hạng tử có bậc

cao nhất

-Muốn tính giá trị của đa thức em làm như

nào?

-Ta thay giá trị của biến vào đa thức

-GV gọi các hS đứng tại chỗ trả lời nhanh

-3 HS đứng tại chỗ trả lời nhanh

a) Đáp án C

b) Đáp án D

c) Đáp án A

*Kết luận, nhận định

-Các hS khác nhận xét

-GV nhận xét và lưu ý:

Trước khi tìm bậc của đa thức cần thu gọn

đa thức

-HS nắm lưu ý

a)Thu gọn đa thức được kết quả:

A.

65

1x y xy+ + +

B.

6 5 0 0

1x y x y+ + +

C.

65

1A x y= + +

D.

6 5 4 4

21A x y x y= + + +

Ta có:

6 5 4 4 4 4

1A x y x y x y= + + + −

6 5 4 4 4 4

( ) 1x y x y x y= + + − +

65

1xy= + +

Đáp án C

b)Bậc của đa thức là:

A.

1

B.

2

C.

5

D.

6

Ta có:

6

x

có bậc là

6

5

y

có bậc là

5

1

có bậc là

0

Vậy đa thức có bậc là

6

Đáp án D.

c) Giá trị của đa thức tại

1, 1xy= = −

là:

A.

1

B.

2

C.

3

D.

4

Thay

1, 1xy= = −

vào đa thức

65

1xy++

ta được

65

1 ( 1) 1A = + − +

1 1 1A = − +

1=

Đáp án A

*Lưu ý: Trước khi tìm bậc của đa thức

cần thu gọn đa thức.

Trang 11

*Giao nhiệm vụ

-GV yêu cầu hS đọc đề bài

-HS tìm hiểu đề bài

Bài 9: Cho hai đơn thức

32

3

2

x y z

−

và

( )

35

6xy z−

.

a)Tính tích hai đơn thức trên

b)Chỉ ra hệ số, phần biến và bậc của đơn

thức tích.

*Thực hiện nhiệm vụ

-GV yêu cầu hS hoạt động cá nhân

-HS hoạt động cá nhân

-Muốn nhân hai đơn thức em làm như thế

nào?

-Muốn nhân hai đơn thức em nhân hệ số

với hệ số, nhận phần biến với phần biến

-Hãy nêu các bước làm?

-Một HS nêu cách làm

-GV gọi hai HS lên bảng(mỗi HS một ý)

-HS lên bảng trình bày

*Kết luận, nhận định

-HS khác nhận xét

-GV nhận xét và chốt kiến thức

-GV lưu ý cho HS: Đối với đơn thức có

dạng

xy

hoặc

xy−

thì hệ số là

1

hoặc

1−

.(nhiều hS cho hệ số bằng

0

là sai)

-HS nắm lưu ý

Bài 9.

Phương pháp:

Bước 1: Áp dụng qui tắc nhân hai đơn

thức

Bước 2: Thu gọn đơn thức

Bước 3: Tìm hệ số (phần số), phần biến

và bậc (tổng số mũ của các biến)

a)

3 2 3 5

3

.( 6 )

2

x y z xy z

−

3 2 3 5

3

[( ).( 6)].( . )

2

x y z xy z

−

=−

4 5 6

9x y z=

b)Hệ số:

9

Phần biến:

4 5 6

x y z

Bậc:

4 5 6 15+ + =

*Lưu ý: Đối với đơn thức có dạng

xy

hoặc

xy−

thì hệ số là

1

hoặc

1−

*Giao nhiệm vụ

-GV chiếu bài tập lên và yêu cầu HS đọc

bài

-Một HS đọc bài, cả lớp tìm hiểu bài

Bài 10: Thu gọn, tìm bậc rồi tính giá trị

Bài 10.

Phương pháp

Bước 1: Nhóm các đơn thức đồng dạn

với nhau

Bước 2: Thu gọn đa thức

Trang 12

của các đa thức sau

2 2 2 2

1 1 1

5

3 2 3

A x y xy xy xy xy x y= + − + − −

Tại

1

,1

2

xy==

2 2 2

2

12

23

1

2

3

B xy x y xy xy

x y xy

= + − +

−+

tại

1

,1

2

xy==

*Thực hiện nhiệm vụ

-GV yêu cầu HS hoạt động cá nhân

-HS hoạt động cá nhân

?Muốn thu gọn đa thức em làm như thế

nào?

-Muốn thu gọn đa thức ta nhóm các hạng

tử (đơn thức) đồng dạng với nhau.

-Một em hãy nêu cách làm

-Một hS nêu cách làm

-GV gọi hai HS lên bảng trình bày

-Hai HS lên bảng.

Bước 3: Tìm bậc của đa thức

Bước 4: Thay giá trị của

,xy

vào đa thức

trên ta được giá trị cần tìm

22

1

3

11

5

23

A x y xy xy

xy xy x y

= + −

+ − −

22

11

()

33

1

( ) ( 5 )

2

x y x y

xy xy xy xy

= − +

+ − +

2

3

6

2

xy xy=−

-Bậc của đa thức là

3

Tại

1

,1

2

xy==

thì

2

3 1 1

. .1 6. .1

2 2 2

A =−

9

4

A =−

22

12

23

1

2

3

B xy x y xy

xy x y xy

= + −

+ − +

Trang 13

*Kết luận, nhận định

-Hai HS đứng tại chỗ nhận xét

-GV nhận xét và chốt kiến thức

-HS lắng nghe

22

1

()

2

21

( ) ( 2 )

33

B xy xy

x y x y xy xy

= + +

− − −

22

31

23

B xy x y xy= + +

Tại

1

,1

2

xy==

thì

2

3 1 1 1 1

. .1 . .1 .1

2 2 3 2 2

B



= + +





4

3

B =

IV. PHIẾU BÀI TẬP BỔ TRỢ

1. TRẮC NGHIỆM

Câu 1. Trong các biểu thức sau, biểu thức nào là đơn thức?

A.

2

xy

B.

31x−−

C.

2

1

5

xy−

D.

1

6 x−

Câu 2. Trong các biểu thức sau, biểu thức nào là đơn thức?

A.

2

6

x

B.

2

xy

xy z

−

C.

4

5

−

D.

( )

2

1

2

x −

Câu 3. Phần hệ số và bậc của các đơn thức

( )

25

.x y xy−−

là:

A.

1;7−

B.

1;9−

C.

1;7

D.

1;9

Câu 4. Kết quả thu gọn của đơn thức

32

2

.

7

xy y xy−−

là:

A.

3

9

7

xy−

B.

3

9

7

xy

C.

3

9

7

xy−

D.

3

9

7

xy

Câu 5. Trong các biểu thức sau, đâu là đa thức

A.

2

xy

B.

1

x

C.

2

2xy

z

+

D.

2xy+

Câu 6. Trong các biểu thức sau, đâu không là đa thức

A.

2

1

23

x

xy −

B.

2

5

xy+

C.

2

1

62xy

x

−+

D.

0

Câu 7. Bậc của các đa thức

( )

2

1 x−

là:

A.

2

B.

3

C.

4

D.

5

2. TỰ LUẬN

Trang 14

Bài 1: Phân thành các nhóm đơn thức đồng dạng trong các đơn thức sau:

2

12xy−

3

8

xyz−

100−

3yxz−

2.xy x−

1

.

3

y xy



−





Bài 2: Thực hiện phép tính:

1)

( )

5xy xy xy− − +

2)

2 2 2

6 3 12xy xy xy−−

3)

( )

2 3 4 2 3 4

34x y z x y z+−

4)

( )

22

48x y x y+−

5)

( )

22

25 55x y x y+−

6)

2 2 2

34x y x y x y+−

7)

( )

2 2 2

2xy x y xy+ + −

8)

( )

2 3 4 2 3 4

12 7x y z x y z+−

9)

( )

3 3 3

6 6 6xy xy x y− − − +

Bài 3: Cho đơn thức:

2 2 2

81

.

34

A x y x y

−



=





.

a) Thu gọn đơn thức

A

rồi xác định hệ số và tìm bậc của đơn thức.

b) Tính giá trị của

A

tại

1, 1xy= − =

.

Bài 4: Cho đơn thức

2 2 2

37

79

D x y x y

−

  

=

  

  

.

a) Thu gọn đơn thức

D

rồi xác định hệ số và phần biến của đơn thức.

b) Tính giá trị của đơn thức

D

tại

1, 2xy= − =

.

Bài 5: Cho đơn thức

2

23

3 20

.

5 27

F xy x y

−

   

=

   

   

a) Thu gọn đơn thức và tìm bậc của đơn thức

F

b) Tính giá trị của biểu thức

F

biết

3

x

y

−

=

và

2xy+=

.

Bài 6: Thu gọn rồi tìm bậc của các đa thức sau

1)

2 2 2 2 2

5 .2 5 .3 6A x y x xy x y x y= − − +

2)

4 3 2 3 2 2

3 . 4 . 5 5 .B x x x x x x x x= + − −

3)

2 2 2 2

2 4 5C x yz xy z x yz xy z xyz= + − + −

4)

3 2 2 2 3 2 2 3 2

5 4 8 5D x y x y x x y x y= + − + −

5)

22

1 1 1

3 1 3

4 2 4

E x y xy x y xy xy= − + − + −

6)

5 2 2 5 2

1 3 3

33

2 4 4

F x x y xy x x y= − − − −

7)

3 3 2 2

1

53

2

G x xy x xy x xy x= − + + − + −

8)

5 6 7 2 5 6 7

1

3 3 3 3

2

H xy x y x y xy x y= − + − +

Bài 7: Cho hai đơn thức:

3 4 5

18A x y z=−

và

( )

2

52

2

9

B x yz=

.

a) Đơn thức

C

là tích của đơn thức

A

và

.B

Xác định phần biến, phần hệ số,

bậc của

.C

b) Tính giá trị của đơn thức

C

khi

1, 1, 1x y z= − = = −

.

Bài 8: Thu gọn rồi tính giá trị của các đa thức sau

a)

5 3 4 3 4 3 5 3

3 4 2 3B x y x y x y x y= − + −

tại

1; 2xy= = −

b)

2 4 2 2 4 9

2 4 2 5 3 4 3C x y xyz x x y xyz y= + − − + − + −

tại

1, 1xy= = −

Tuần 3

Tiết 4; 5; 6

Trang 15

Ngày soạn 01/11/2023

Lớp

8A

1

8A

2

8A

3

Ngày dạy:

ÔN TẬP TỨ GIÁC LỒI . HÌNH THANG CÂN

I. MỤC TIÊU

1. Về kiến thức:

- Củng cố định nghĩa tứ giác, hình thang, hình thang cân.

- Củng cố các định lí về tổng các góc trong của tứ giác, tính chất của hình thang cân

2. Về năng lực:

- Nhận biết và giải thích được tứ giác là hình thang, hình thang cân

- Lập luận và chứng minh hình học trong những trường hợp đơn giản.

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được tứ giác là hình thang,

hình thang cân.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng hợp

khi làm các bài tập về hình thang, hình thang cân.

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

Trang 16

1. Tứ giác, tứ giác lồi

a) Định nghĩa

+ Tứ giác

ABCD

là một hình gồm bốn đoạn thẳng

AB

,

BC

,

CD

,

DA

trong đó

không có hai đoạn thẳng nào cùng nằm trên một đường thẳng.

+ Tứ giác lồi là tứ giác mà hai đỉnh thuộc một cạnh bất kì luôn nằm về một phía của

đường thẳng đi qua hai đỉnh còn lại.

b) Định lý tổng các góc của một tứ giác:

Tổng các góc của một tứ giác bằng

o

360

.

2. Hình thang, hình thang cân

a) Hình thang: Hình thang là tứ giác có hai cạnh đối song song.

-Nhận xét:

+ Hai góc kề một cạnh bên của hình thang có tổng bằng

o

180

.

b) Hình thang cân: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

- Tính chất:

+ Trong hình thang cân, hai cạnh bên bằng nhau.

+ Trong hình thang cân, hai đường chéo bằng nhau.

- Dấu hiệu nhận biết:

+ Hình thang có hai góc kề một đáy bằng nhau thì hình thang đó là hình thang cân.

+ Hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.

2. BÀI TẬP

Hoạt động của giáo viên và HS

Nội dung

* Giao nhiệm vụ

- GV yêu cầu HS hoạt động cá nhân thực hiện

Bài 1: Bài tập trắc nghiệm

D

C

A

B

A

C

D

Trang 17

bài tập trắc nghiệm 1.

Kiểm tra củng cố lý thuyết cho HS

- HS nhận nhiệm vụ được giao

Đáp án:

1

2

3

4

5

C

B

C

A

Câu 1 . Các góc của tứ giác có thể là:

A. Bốn góc nhọn.

B. Bốn góc tù.

C. Bốn góc vuông.

D. Một góc vuông và ba góc nhọn.

Câu 2. Hình thang là tứ giác có:

A. Hai cạnh đối bằng nhau.

B. Hai cạnh đối song song với nhau.

C. Một góc vuông.

D. Hai đường chéo bằng nhau.

Câu 3. Khẳng định nào sau đây là sai:

A. Tổng các góc của một tứ giác bằng

o

360

B. Tổng các góc của hình thang bằng

o

360

.

C. Hình thang có các góc đối bằng nhau.

D. Hình thang có hai góc kề cạnh bên bù

nhau.

Câu 4. Hình thang cân là hình thang có:

A. Hai góc kề một cạnh đáy bằng nhau.

B. Hai góc đối bằng nhau.

C. Hai cạnh bên song song.

D. Hai cạnh bên bằng nhau

Câu 5 Số đo các góc của tứ giác

ABCD

theo

tỉ lệ:

: : : 4:3:2:1A B C D =

Số đo các góc theo thứ tự đó là:

A.

o o o o

120 ;90 ;60 ;30

.

B.

o o o o

140 ;105 ;70 ;35

.

C.

o o o o

144 ;108 ;72 ;36

.

Trang 18

D. Cả

,,A B C

đều sai.

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

GV: Cho HS đọc đầu bài trắc nghiệm trên

màn hình .

- GV yêu cầu HS hoạt động nhóm đôi thực

hiện bài tập trắc nghiệm 1

- HS HĐ cá nhân thực hiện bài 1.

- HS báo cáo kết quả.

- Nhận xét, đánh giá câu trả lời của nhau.

GV: Để chọn phương án đúng ở câu 1,2,3,4,5

ta dựa vào kiến thức nào đã học ?

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 2:

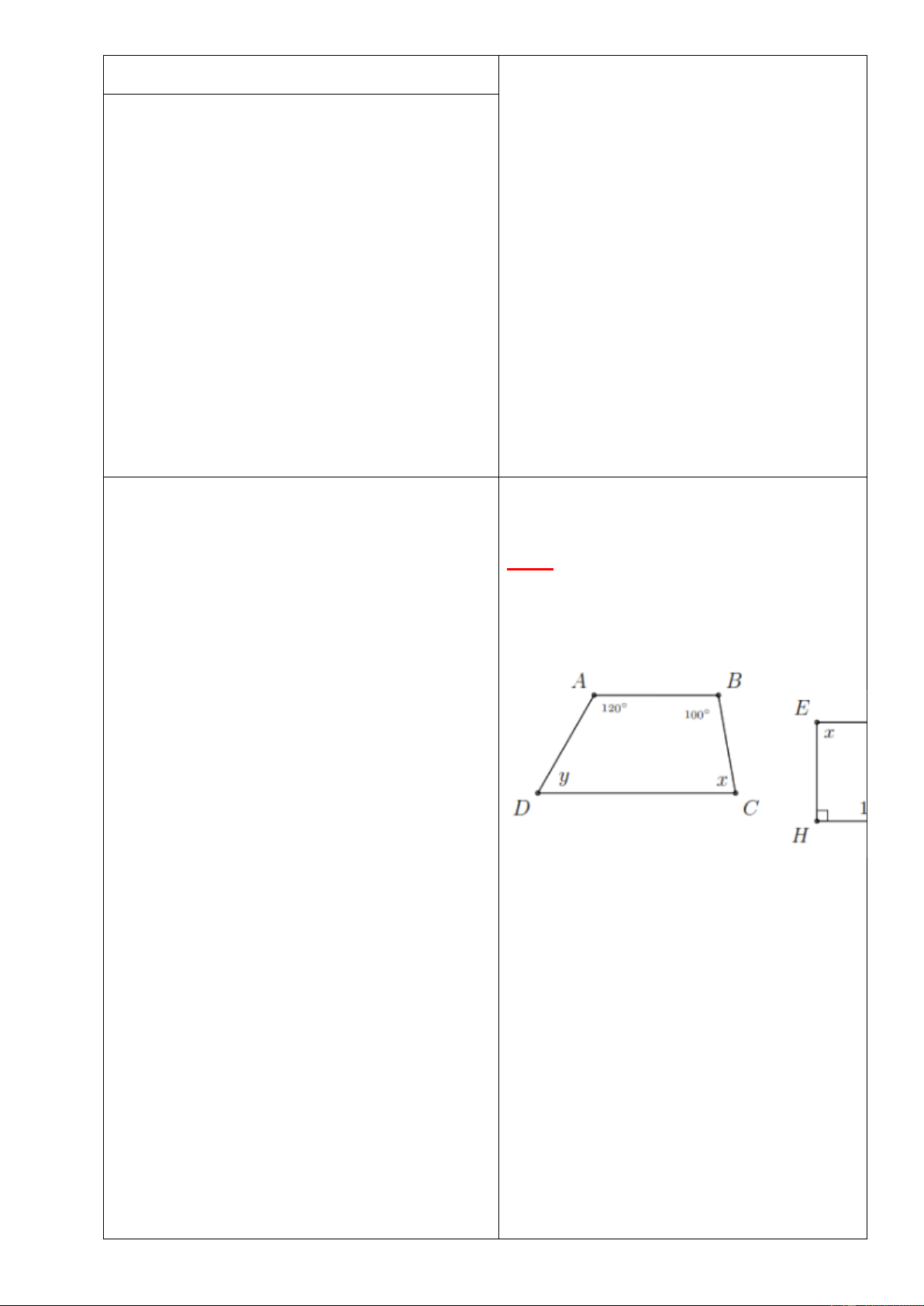
Tìm

x

và

y

ở hình vẽ dưới biết các hình

thang

ABCD

và

EFGH

có đáy lần lượt là

AB

và

CD

;

EF

và

GH

- HS tìm hiểu bài toán

2.

HS: Đọc đầu bài 2

.*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện.

GV: Nêu cách tính các góc

x

và

y

.

GV: Áp dụng kiến thức nào đã học?

HS: Áp dụng tính chất của hai đường thẳng

song song và tổng các góc trong tứ giác

HS: Hoạt động trình bày tính góc

HS: Lên bảng trình bày.

GV: Gọi HS nhận xét

*Kết luận, nhận định: Khi có giả thiết hình

thang, các em ghi nhớ tính chất của các góc kề

cạnh bên, tổng các góc trong tứ giác bằng

360

Dạng 1: Tính các góc của tứ giác, hình

thang

Bài 2: Tìm

x

và

y

ở hình vẽ dưới biết

các hình thang

ABCD

và

EFGH

có đáy

lần lượt là

AB

và

CD

;

EF

và

GH

.

Lời giải

a) Vì

AB

//

CD

nên

180AD+= 

hay

120 180D +  = 

60Dy = = 

.

Tương tự,

180BC+ = 

180 100 80Cx = =  −  = 

c) Vì

EF

//

HG

nên

180EH+ = 

.

180 90 90Ex = =  −  = 

Tương tự

180FG+= 

.

Trang 19

180 50F y G  = =  − =

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 3

Cho hình thang

ABCD

(

// AB CD

) có

10BC− = 

Tính số đo góc

B

?

- HS tìm hiểu bài toán 3.

HS: Đọc đầu bài 3

.*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện.

GV: Nêu cách tính góc

B

GV: Áp dụng kiến thức nào đã học?

- HS trả lời theo từng câu hỏi được GV đề

xuất.

- HS phản biện câu trả lời của nhau.

*Kết luận, nhận định: Khi có giả thiết hình

thang, các em ghi nhớ tính chất của các góc kề

cạnh bên, tìm hai góc khi biết tổng và hiệu của

hai góc

Bài 3: Cho hình thang

ABCD

(

// AB CD

) có

10BC− = 

Tính số đo góc

B

?

Lời giải

Vì

ABCD

là hình thang có

// AB CD

nên

180BC+ = 

Và theo GT

10BC− = 



180 10

95

2

B

 + 

= = 

Dạng 2

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 4:

Tứ giác

ABCD

có

BC CD=

và

DB

là phân

giác của góc

D

. Chứng minh

ABCD

là hình

thang.

HS tìm hiểu bài toán 4

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

GV: Hình vẽ cho biết yếu tố nào bằng nhau?

Dạng 2: Chứng minh tứ giác là hình

thang, hình thang cân

Bài 4:

Tứ giác

ABCD

có

BC CD=

và

DB

là

phân giác của góc

D

. Chứng minh

ABCD

là hình thang.

Lời giải

Trang 20

HS quan sát hình vẽ

GV: Dự đoán đáy của hình thang và chứng

minh

// BC AD

như thế nào? Áp dụng kiến

thức nào đã học?

HS: dự đoán

// BC AD

HS: Chứng minh hai góc so le trong bằng

nhau qua góc khác.

*Kết luận, nhận định: cách chứng minh tứ

giác là hình thang: cần tìm một cặp cạnh

song song

Xét

BCD

Có

BC CD=

nên

BCD

cân tại

C

suy ra

DBC BDC=

Mà

DB

là phân giác của

D

nên

CDB BDA=

.

Suy ra

( )

ADB DBC CDB==

nên

// BC AD

hay

ABCD

là hình thang.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 5

* Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

HS thực hiện NV GV giao

GV: Nêu cách nhận biết hình thang cân

GV: Yêu cầu HS hoạt động tìm ra những đk

để khẳng định tứ giác là hình thang cân

HS: Để chứng minh tứ giác là hình thang cân

cần chứng minh: hai cạnh đáy song song và

hai góc kề đáy bằng nhau

HS hoạt động theo yêu cầu của GV.

HS: Lên bảng trình bày

GV: gọi HS nhận xét.

*Kết luận, nhận định: Dấu hiệu nhận biết

HTC

Bước 1. Chứng minh hai cạnh đối song song

Bước 2. Chứng minh hai góc kề đáy bằng

nhau hoặc hai đường chéo bằng nhau

- Nêu tính chất về góc trong hình thang cân

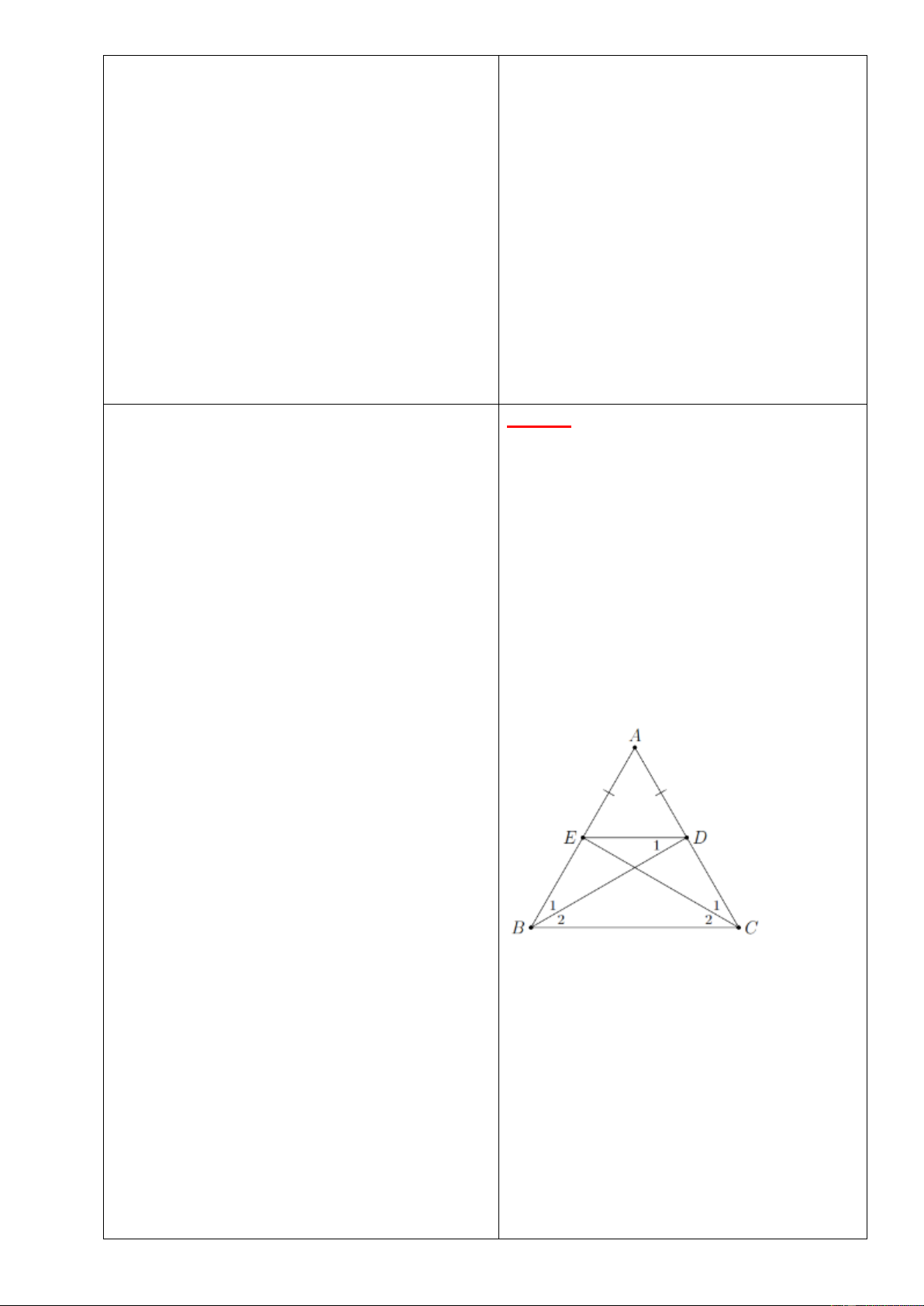
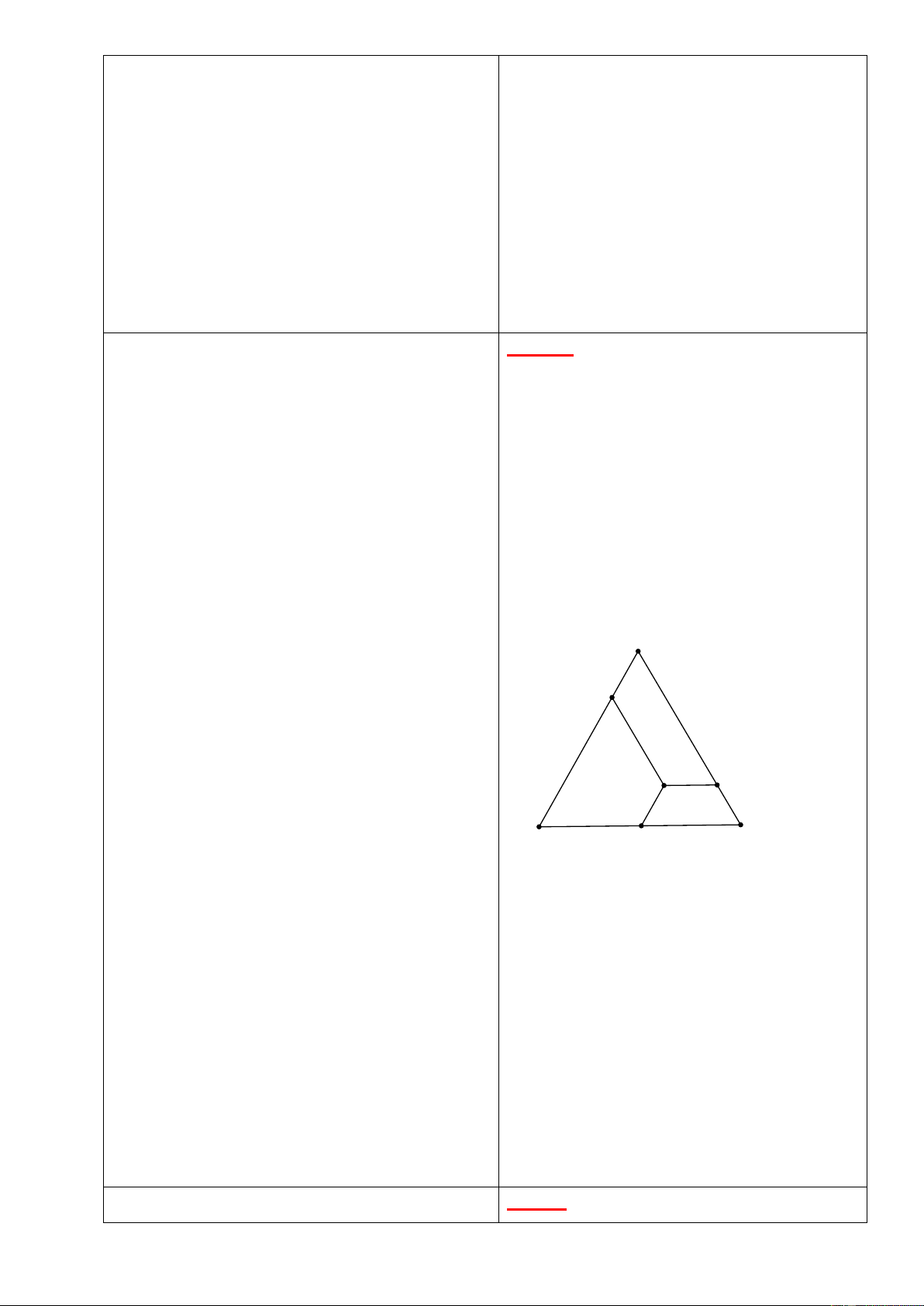
Bài 5: Cho tam giác

ABC

cân tại

A

, các

đường phân giác

BD

,

CE

(

D AC

,

E AB

).

a) Chứng minh

BEDC

là hình thang cân;

b) Tính các góc của hình thang cân

BEDC

, biết

50C



=

.

Lời giải

a) Do

ABC

cân tại

A

và

BD

,

CE

là các

đường phân giác suy ra hai tam giác

BCE

và

CDB

có

▪

EBC DCB=

,

▪

BC

chung,

▪

BCE DBC=

.

Vậy

BCE CBD = 

(g.c.g).

Trang 21

22

BC=

,

BD EC=

,

BE DC=

;

ADE

cân tại A

BEDC

là hình

thang cân.

b) Do

BCDE

là hình thang cân có

50C = 

50

180 130 .

BC

E D C



==







= = − =









* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 6

HS thực hiện NV GV giao

* Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

GV: Nêu cách nhận biết hình thang cân

HS: Để chứng minh tứ giác là hình thang cân

cần chứng minh: hai cạnh đáy song song và

hai góc kề đáy bằng nhau

GV: Yêu cầu HS hoạt động tìm ra những đk

để khẳng định tứ giác là hình thang cân

- nêu tính chất về góc và cạnh của tam giác

đều, của hình thang cân

HS: - Tam giác đều có 3 cạnh bằng nhau và

ba góc bằng

60

HS: Lên bảng trình bày

GV: gọi HS nhận xét.

*Kết luận, nhận định: Dấu hiệu nhận biết

HTC

Bước 1. Chứng minh 2 cạnh đối song song

Bước 2. Chứng minh hai góc kề đáy bằng

nhau hoặc hai đường chéo bằng nhau

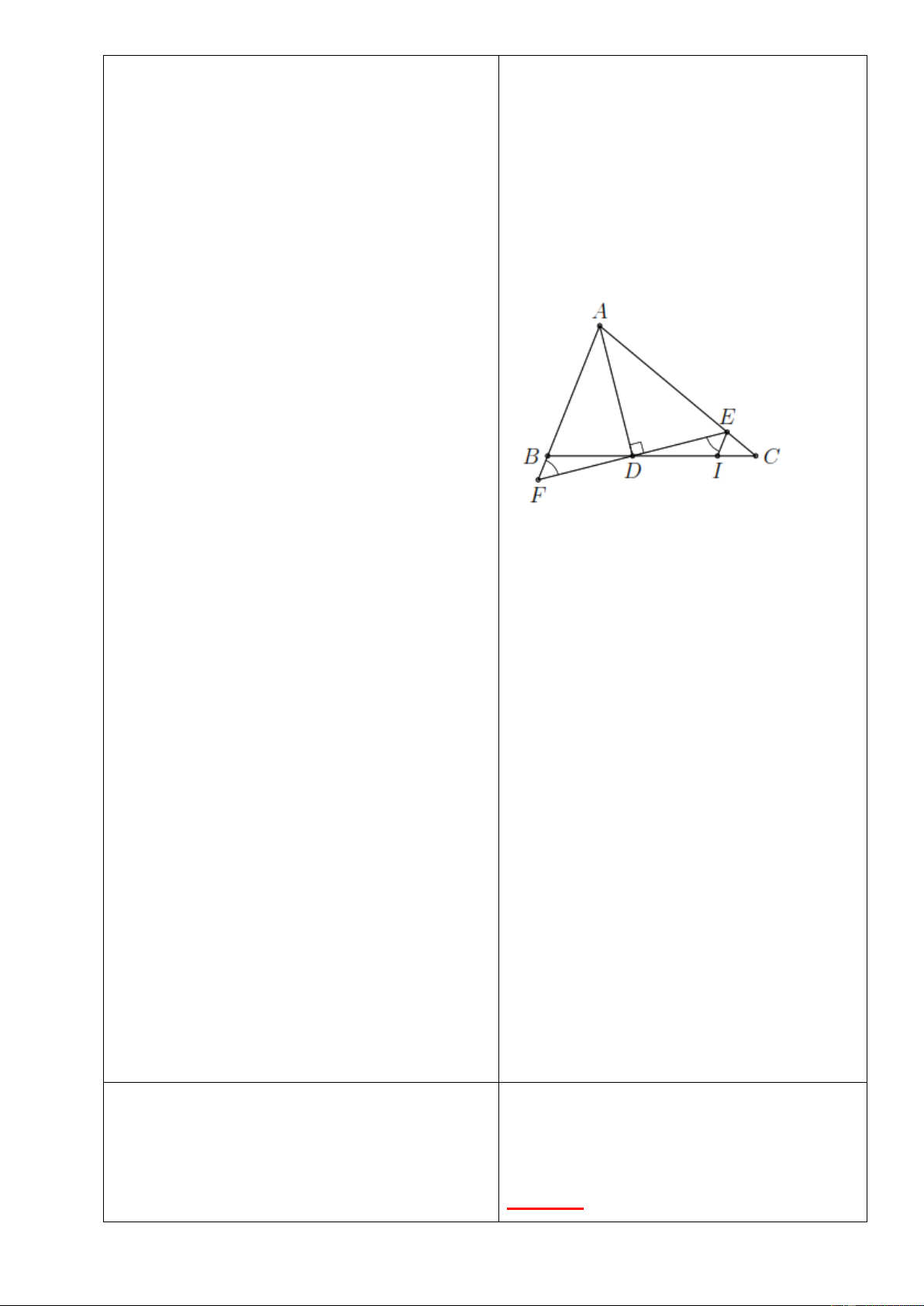
Bài 6: Cho ∆ đều

ABC

. Từ điểm

O

trong

tam giác kẻ đường thẳng song song với

BC

cắt

AC

ở

D

, kẻ đường thẳng song

song với AB cắt

BC

ở

E

, kẻ đường

thẳng song song với

AC

cắt

AB

ở

F

.

Chứng minh tứ giác

ODAF

là hình thang

cân và

OB EF=

Lời giải

Có

// OF AC



tứ giác

ODAF

là hình

thang (1)



ABC

đều



60AC= = 

Mà

// OD BC



60ADO C= = 



60A ADO= = 

(2)

Từ (1) và (2)



ODAF

là hình thang cân

* Chứng minh tương tự

BEOF

là hình

thang cân



OB EF=

* Giao nhiệm vụ

Bài 7: Cho tam giác

ABC

có

AB AC

,

F

E

D

A

B

C

O

Trang 22

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 7

HS tìm hiểu bài toán 7

* Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

GV: Nêu cách chứng minh hình thang

HS: Để chứng minh tứ giác là hình thang cần

chứng minh: hai cạnh đáy

//EI AB

GV: Yêu cầu HS hoạt động tìm ra những đk

để khẳng định tứ giác là hình thang

- Khai thác giải thiết:

AD

là phân giác góc

BAC

và

AD DE⊥

như thế nào ?

GV: gọi HS nhận xét.

HS hoạt động theo yêu cầu của GV.

HS:

AD

là phân giác góc

BAC

và

AD DE⊥

Nên

AD

là đường đặc biệt từ đỉnh của



cân

Do đó nghĩ đến việc tạo ra tam giác cân đó

bằng cách vẽ

ED

kéo dài cắt

AB

tại

F

HS: Lên bảng trình bày

*Kết luận, nhận định:

Trong bài đã khai thác đường đặc biệt

AD

vừa là đg cao, đường phân giác của một tam

giác nên tam giác đó cân

đường phân giác

AD

. Đường vuông góc

với

AD

tại

D

cắt

AB

và

AC

lần lượt tại

F

và

E

. Trên cạnh

DC

lấy điểm

I

sao

cho

DI DB=

. Chứng minh

AEIB

là hình

thang.

Lời giải

Kéo

dài

ED

cắt

AB

tại

F

AD

là phân giác và là đường cao của

AEF

.

AEF

cân tại

A

.

AD

là đường trung tuyến.

DE DF=

.

Xét

BDF

và

IDE

có

DI DB=

(giả thiết);

BDF EDI=

(đối đỉnh);

DE DF=

(chứng minh trên).

BDF IDE  = 

(c.g.c).

IED DFB=

//  EI AB



AEIB

là hình thang.

Dạng 3

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 8

Dạng 3: Sử dụng tính chất hình thang,

hình thang cân chứng minh các yếu tố

khác

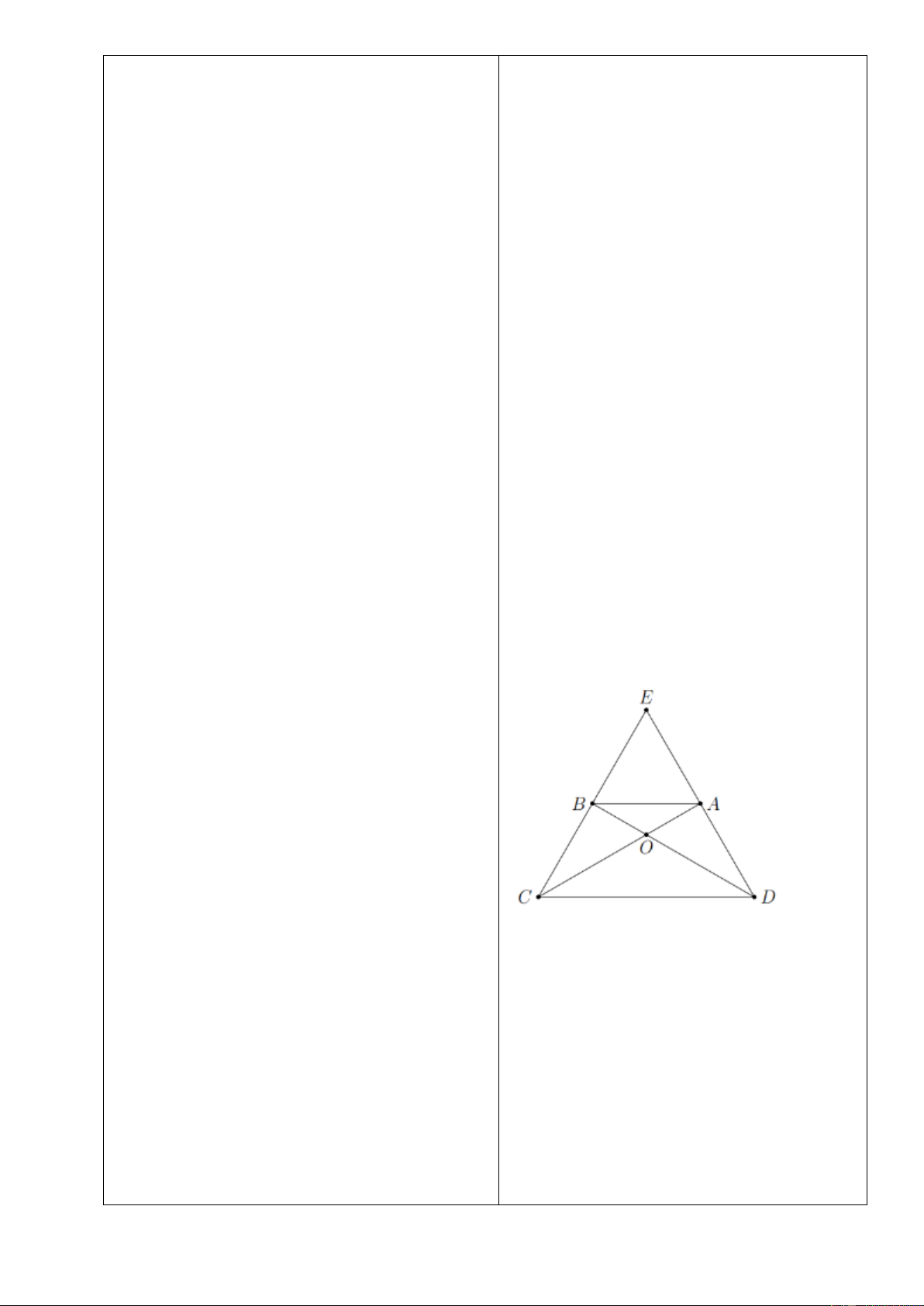
Bài 8: Cho hình thang cân

ABCD

có

Trang 23

HS tìm hiểu bài toán 8

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

HS thực hiện nhiệm vụ GV giao

GV:

, , ,OA OB OC OD

là cạnh của tam giác

nào?

HS: Chứng minh

OA OB=

qua

OAB

cân

GV: Nêu cách chứng minh

OAB

và

OCD

cân

HS: chứng minh



cân qua dấu hiệu hai góc

đáy bằng nhau

GV: Hãy c/m

ABD BAC = 

HS: chứng minh

ABD BAC = 

(cgc)

HS: Chứng minh

,EO

cùng cách đều

A

và

B

Chứng minh:

E

và

O

cùng cách đều

C

và

D

GV: Quan sát hướng dẫn.

b) GV: Cách chứng minh

EO

là đường trung

trực của

AB

và

CD

*Kết luận, nhận định:

Trong bài đã khai thác tính chất về cạnh, góc,

đường chéo của hình thang cân. Ngoài ra các

em cần ghi nhớ cách chứng minh đường trung

trực của đoạn thẳng bằng phương pháp tìm ra

hai điểm thuộc đường thẳng cách đều hai đầu

mút của đoạn thẳng đó.

//AB CD

,

O

là giao điểm của hai đường

chéo,

E

là giao điểm của hai đường thẳng

chứa cạnh bên

AD

và

BC

Chứng minh

a)

OA OB=

,

OC OD=

;

b)

EO

là đường trung trực của hai đáy

hình thang

ABCD

.

Lời giải

a) Do

ABCD

là hình thang cân



// AB CD

AD BC

BAD ABC

=









=





.

Xét

ABD

và

BAC

có

AD BC=

( vì

ABCD

là hình thang cân)

BAD ABC=

(

ABCD

là hình thang cân);

AB

là cạnh chung.

(c.g.c)ABD BAC  = 

.

ABD BAC=

(cặp góc tương ứng).

Suy ra

OAB

cân tại

O OA OB=

.

Chứng minh tư tương tự với

OC OD=

.

b)

EBA

,

EDC

cân tại

E

AE BE=

,

ED EC=

E

thuộc trung trực

AB

,

DC

. (1)

Mà

OA OB=

;

OC OD=

(cmt)

O

thuộc trung trực

AB

,

DC

. (2)

Từ

(1)

và

(2) OE

là đường trung trực

của

AB

,

CD

.

Trang 24

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 9

HS tìm hiểu bài toán 9

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

HS: Thực hiện nhiệm vụ theo yêu cầu của GV.

HS đọc đầu bài và vẽ hình, ghi GT,KL

GV: Chú ý giải thiết

DB

vuông góc với

BC

và

DB

là phân giác góc

ADC

gợi đến kiến

thức nào ?

HS: nghĩ đến tính chất của tam giác cân, nên

từ đó làm xuất hiện tam giác cân bằng cách

kéo dài

BC

cắt

AD

tại

O

HS thực hiện nhiệm vụ.

theo nhóm

GV: Quan sát hướng dẫn

Hãy so sánh các cạnh của hình thang

ABCD

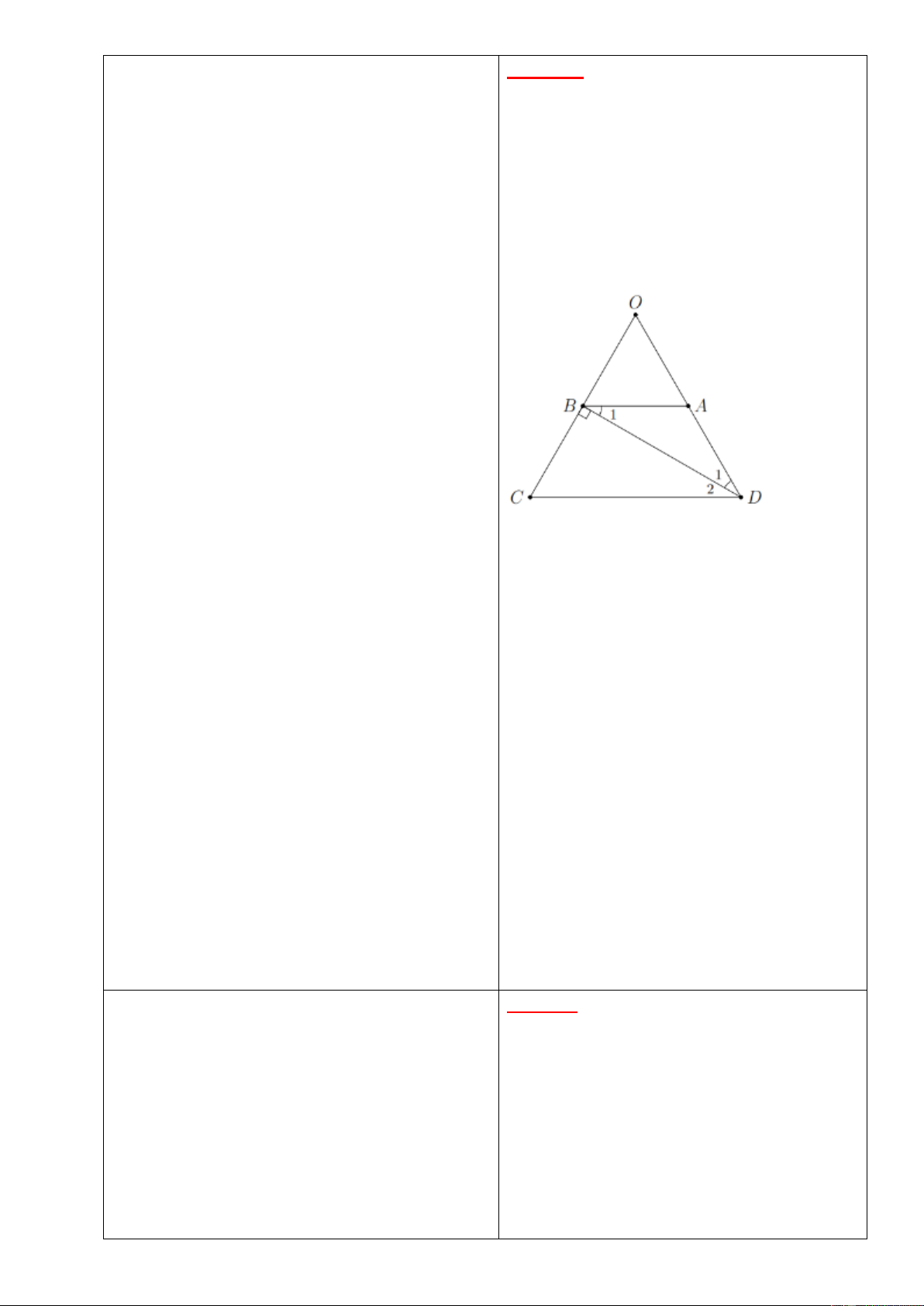
Bài 9: Cho hình thang cân

ABCD

có

// AB CD

, đường chéo

DB

vuông góc với

cạnh bên

BC

,

DB

là tia phân giác góc

D

.

Tính chu vi của hình thang, biết

3BC =

cm.

Lời giải

Trong hình thang cân

ABCD

có

180BC+ = 

1 1 2

90 180B D D + + =+

1

3 90B = 

1

30B = 

60 =C

.

Gọi

O BC AD=

OCD

đều

nên

60AOB =

.

OAB

có

OA OB=

,

60AOB =

OAB

đều

BA AD BC = =

.

Chu vi của hình thang

ABCD

là

3 3 6 3 18+ + + =

cm.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 10

HS tìm hiểu bài toán 10

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện.

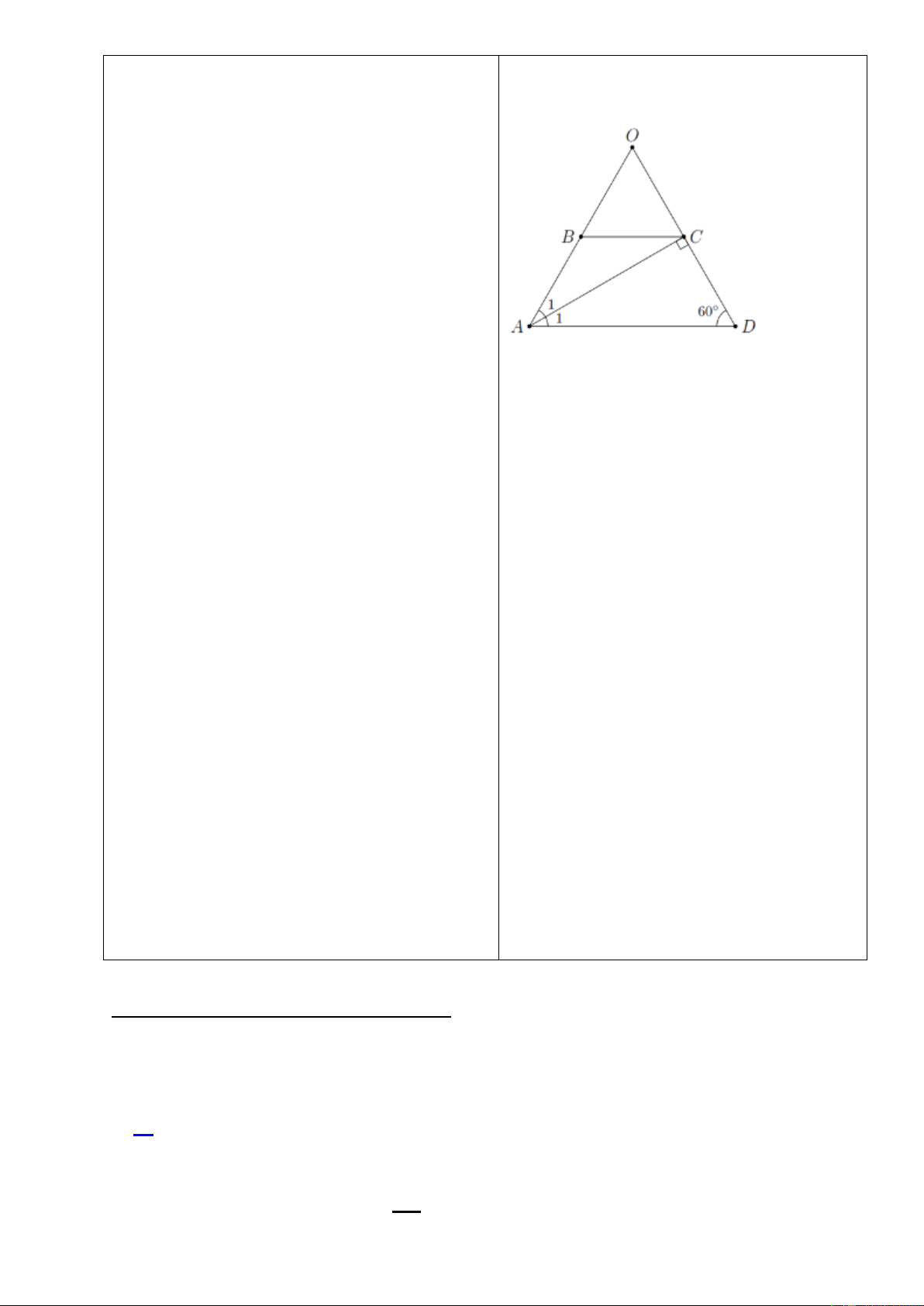
Bài 10: Cho hình thang

ABCD

(

// AD CB

,

AD BC

) có đường chéo

AC

vuông góc với cạnh bên

CD

,

AC

là

tia phân giác góc

BAD

và

60D =

.

a) Chứng minh

ABCD

là hình thang cân;

b) Tính độ dài cạnh

AD

, biết chu vi hình

thang bằng

20

cm.

Trang 25

HS: Thực hiện nhiệm vụ theo yêu cầu của GV.

HS hoạt động theo nhóm

GV: các em thấy nội dung bài toán 10 và 9 có

liên quan như thế nào với nhau

GV: Quan sát hướng dẫn HS thực hiện nhiệm

vụ trên gợi ý của bài tập số 9

HS trình bày lời giải , các HS khác nhận xét

Lời giải

a) Gọi

O BD DC=

. Tam giác

OAD

có

AC

vừa là phân giác vừa là đường cao nên

OAD

cân tại

A

.

Lại có

60D =

nên

OAD

là tam giác

đều. Suy ra

ABCD

là hình thang cân.

b) Theo phần

)a

C

là trung điểm

OD

, mà

OAD

đều

22AD CD AB = =

.

Lại có

// BC AD

BCA CAD=

OAD

đều mà

AC

là đường cao

BAC CAD=

Nên

BAC BCA=



ABC

cân tại

B



AB BC=

Do chu vi hình thang

ABCD

là

20AD DC CB BA+ + + =

5 20BC=

48BC AD =  =

cm.

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ….. :

1. TRẮC NGHIỆM

Câu 1. Tứ giác

ABCD

có

50

o

A =

;

o

95B =

;

o

135C =

. Số đo góc

D

là:

A.

o

80D =

. B.

o

90D =

. C.

o

100D =

. D.

o

130D =

.

Câu 2 Khằng định nào sau đây là sai ?

Trang 26

A. Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

B. Hình thang có hai cạnh bên bằng nhau là hình thang cân.

C. Hình thang có hai đường chéo bằng nhau là hình thang cân.

D. Tứ giác có hai cạnh đối song song và hai đường chéo bằng nhau là hình thang

cân.

Câu 3 . Cho hình thang

ABCD

(

// AB CD

) có

70AD− = 

. Số đo

A

và

D

lần lượt

bằng:

A.

oo

125 ;55

. B.

oo

115 ;65

. C.

oo

105 ;75

. D.

oo

95 ;85

.

Câu 4. Cho thang cân

ABCD

(

// AB CD

) có

50

o

A =

. Số đo

B

bằng:

A.

o

50

. B.

o

100

. C.

o

90

. D.

o

130

.

Câu 5. Góc kề cạnh bên của hình thang có số đo là

o

70

. Góc kề còn lại của cạnh bên

đó là:

A.

o

70

. B.

o

90

. C.

o

110

. D.

o

170

.

Câu 6. Cho tứ giác

ABCD

có

o

180AD+=

và

o

180AC+=

thì tứ giác

ABCD

là

hình gì?

A. Hình thang. B. Hình thang vuông.

C. Hình thang cân. D. Không có câu nào đúng.

Câu 7. Cho

ABC

cân tại A. Trên các cạnh

AB

,

AC

lấy các điểm

,MN

sao cho

BM CN=

. Tứ giác

BMNC

là hình gì?

A. Hình thang. B. Hình thang cân. C. Hình thang vuông. D. Cả A, B, C đều

sai.

2. TỰ LUẬN

Bài tập 1 : Cho hình thang

ABCD

có hai đáy là

AB

và

CD

. Biết

30BC− = 

và

3AD=

. Tính các góc của hình thang.

Bài tập 2: Tính các góc của hình thang cân, biết một góc bằng

40



.

Bài tập 3. Cho hình thang cân

ABCD

có

// AB CD

(

)AB CD

. Kẻ các đường cao

AH

,

BK

. Chứng minh

DH CK=

.

Bài tập 4 . Cho hình thang

ABCD

(

// AB CD

,

AB CD

). Hai tia phân giác của góc

C

và

D

cắt nhau tại

K

thuộc đáy

AB

. Chứng minh

a)

ADK

cân ở

A

,

BKC

cân ở

B

; b)

AB AD BC=+

.

Trang 27

Bài tập 5. Cho hình thang

ABCD

(

// AB CD

) , biết

Ax

,

Dy

lần lượt là phân giác

của góc

A

, góc

D

của hình thang. Chứng minh

Ax Dy⊥

.

Bài tập 6 . Cho tam giác

ABC

cân tại

A

. Lấy điểm

D

trên cạnh

AB

, điểm

E

trên

cạnh

AC

sao cho

AD AE=

.

a) Tứ giác

BDEC

là hình gì? Vì sao?

b) Các điểm

D

,

E

ở vị trí nào thì

BD DE EC==

?

Tuần 4

Tiết 7; 8; 9

Ngày soạn 01/11/2023

Lớp

8A

1

8A

2

8A

3

Ngày dạy:

ÔN TẬP BÀI 3: PHÉP CỘNG VÀ PHÉP TRỪ ĐA THỨC

I. MỤC TIÊU

1. Về kiến thức:

- Nhận biết được tổng và hiệu của hai đa thức.

- Nhận biết được nếu

A B C−=

thì

;A B C=+

ngược lại, nếu

A B C=+

thì

A B C−=

(

,,A B C

là những đa thức tùy ý).

2. Về năng lực:

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được quy tắc cộng, trừ hai đa

thức

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng

hợp, khái quát hóa, …

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, bảng nhóm.

Trang 28

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

Tổng hợp kiến thức cần nhớ:

- Muốn cộng (hay trừ) hai đa thức, ta nối hai đa thức đã cho bởi dấu ‘+’ (hay dấu “-”)

rồi bỏ dấu ngoặc (nếu có) và thu gọn đa thức nhận được.

- Phép cộng đa thức cũng có các tính chất giao hoán và kết hợp tương tự như phép

cộng các số.

- Với

,,A B C

là những đa thức tùy ý, ta có:

( ) ( )A B C A B C A B C+ + = + + = + +

.

- Nếu

A B C−=

thì

;A B C=+

ngược lại, nếu

A B C=+

thì

A B C−=

.

2. BÀI TẬP

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài

toán trắc nghiệm 1

Dạng 1: Thu gọn đa thức, tìm bậc của

đa thức

Bài 1: Bài tập trắc nghiệm

Câu 1: Bậc của đa thức

5 2 2 2 5

5 3 2A x x y x y x= − + − +

sau khi thu gọn có bậc mấy?

A.

5.

B.

4.

C.

2.

D.

1.

Câu 2: Rút gọn biểu thức

( ) ( ) ( )x y y z z x+ − + − +

có kết quả là

A.

2.x−

B.

2.y−

C.

2.z−

D.

.xz−

Câu 3: Thu gọn đa thức

22

12

52

23

B xy x y xy x y= + − +

có kết quả là

A.

2

13 5

.

32

xy x y−

B.

2

13 5

.

32

xy x y

−

+

C.

2

13 5

.

32

xy x y+

D.

2

13 5

.

32

xy x y

−

+

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện (đưa

ra một số gợi ý)

HS trả lời các câu hỏi được GV đề xuất

hoặc nêu cách giải 1 bài toán

*Kết luận, nhận định:

GV khai thác các câu hỏi theo các hướng

khác nhau (nếu được)

Trả lời

Câu 1

5 2 2 2 5

5 5 2 2 2

2 2 2

5 3 2

( ) 5 3 2

5 3 2

A x x y x y x

x x x y x y

x y x y

= − + − +

= − − + +

= − + +

Đáp án: B.

4.

Câu 2

( ) ( ) ( ) 2x y y z z x x y y z z x z+ − + − + = + − − − − = −

Đáp án: C.

2.z−

Câu 3

22

12

52

23

B xy x y xy x y= + − +

22

21

52

32

xy xy x y x y

   

= − + +

   

   

Trang 29

2

13 5

32

xy x y=+

Đáp án: C.

2

13 5

.

32

xy x y+

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu bài toán 2

Bài 2: Thu gọn các đa thức sau

a)

22

1

25

2

A x x x x= + − +

b)

22

2 3 6 5B xy x y xy x y= − − −

c)

3 2 2 3

1

2 2 5

2

C x xy x xy x x= − + + − −

HS tìm hiểu bài toán 2

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện đưa

ra một số gợi ý, suy luận logic.

HS trả lời theo từng câu hỏi được GV đề

xuất hoặc nêu cách giải 1 ý của bài toán

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Bài 2: Thu gọn các đa thức sau

Lời giải

a)

( )

22

2 2 2

1

25

2

13

2 5 6

22

A x x x x

x x x x x x

= + − +



= − + + = +





b)

22

2

2 3 6 5

(2 6 ) (3 5 )

48

B xy x y xy x y

xy xy x y x y

xy x y

= − − −

= − − +

= − −

c)

( )

3 2 2 3

3 3 2 2

1

2 2 5

2

1

2 2 5

2

C x xy x xy x x

x x x x xy xy

= − + + − −



= − + − + − +





3

2

x xy=+

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu bài toán 3

Bài 3:

a) Cho đa thức

2 3 2

3A x y x xy= + − +

và

32

6.B x xy xy= + − −

Thu gọn và tìm

bậc của đa thức

=+.Q A B

b) Cho đa thức

( )

3

11

2;

33

C a b a b

æö

÷

ç

÷

= - - +

ç

÷

ç

÷

ç

èø

và

( )

3

11

( ) .

33

D a b a b= + - -

Thu gọn và

Bài 3:

Trang 30

tìm bậc của đa thức

=+.RCD

HS tìm hiểu bài toán 3

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện đưa

ra một số gợi ý, suy luận logic.

HS trả lời theo từng câu hỏi được GV đề

xuất hoặc nêu cách giải 1 ý của bài toán

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Lời giải

a)

=+Q A B

= + − +

2 3 2

( 3)x y x xy

+

+ − −

32

( 6)x xy xy

=

+ − −

32

2 3.x x y xy

Đa thức

Q

có bậc

3.

b)

=+RCD

( )

3

11

2

33

a b a b

æö

÷

ç

÷

= - - +

ç

÷

ç

÷

ç

èø

( )

3

11

()

33

a b a b+ + - -

4

.

3

ab= - -

Đa thức

R

có bậc

1.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu bài toán 4

Bài 4: Tính tổng hai đa thức sau

a)

2 3 2

3E x y x xy= − − −

và

32

36F x xy xy= − + −

b)

2 3 3 2 3

x y 0,5xy 7,5x y xM = + − +

và

3 2 3 2

3xy 5,5N x y x y= − +

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện đưa

ra một số gợi ý, suy luận logic.

HS trả lời theo từng câu hỏi được GV đề

xuất hoặc nêu cách giải 1 ý của bài toán

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Dạng 2: Tìm tổng của các đa thức

Bài 4: Tính tổng hai đa thức sau

Lời giải

a)

( ) ( )

2 3 2 3 2

3 3 6

E F x y x xy x xy xy

x y x xy x xy xy

+ = − − − + − + −

= − − − + − + −

( ) ( )

( )

2 3 3 2 2

3

36

x y x x xy xy

xy

= + − + + − −

+ + − −

2 3 2

2 2 9x y x xy xy= + − + −

Vậy

2 3 2

2 2 9E F x y x xy xy+ = + − + −

b)

( ) ( )

2 3 3 2 3 3 2 3 2

x y 0,5xy 7,5x y x 3xy 5,5

MN

x y x y

+

= + − + + − +

2 3 3 2 3 3 2 3 2

0,5 7,5 3 5,5x y xy x y x xy x y x y= + − + + − +

( ) ( ) ( )

2 2 3 3 3 2 3 2 3

0,5 3 5,5 7,5x y x y xy xy x y x y x= − + + + − +

3 3 2 3

3,5 2xy x y x= − +

Vậy

3 3 2 3

3,5 2M N xy x y x+ = − +

* Giao nhiệm vụ

Trang 31

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu bài toán 5

Bài 5: Cho hai đa thức

22

5x 6xP y y= + -

và

22

2 2x 6xQ y y= - -

. Chứng minh rằng

không tồn tại giá trị nào của

x

và

y

để hai

đa thức

P

và

Q

cùng có giá trị âm.

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện đưa

ra một số gợi ý, suy luận logic.

HS trả lời theo từng câu hỏi được GV đề

xuất hoặc nêu cách giải 1 ý của bài toán

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Bài 5:

Lời giải

Ta có:

( )

2 2 2 2

(5x 6x ) 2 2x 6xP Q y y y y+ = + − + − −

2 2 2 2

5x 6x 2 2x 6xy y y y= + − + − −

22

30xy= + 

Do đó

P

,

Q

không thể cùng có giá trị âm.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu bài toán 6

Bài 6: Cho hai đa thức:

2

3 3 5 1;M xyz x xy= − + −

và

2

5 5 3 .N x xyz xy y= + − + −

Tính

;MN−

.NM−

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện đưa

ra một số gợi ý, suy luận logic.

HS trả lời theo từng câu hỏi được GV đề

xuất hoặc nêu cách giải 1 ý của bài toán

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Dạng 3: Tìm hiệu của các đa thức

Bài 6:

Đáp án

a)

2

8 2 10 4 ;M N x xyz xy y− = − + + − +

b)

2

N M 8x 2 10 4 .xyz xy y− = − − + −

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu bài toán 7

Bài 7: Tính hiệu của hai đa thức

A

và

B

a)

22

2;A x y xy= + −

22

2B x y xy= + +

.

b)

32

2 3 1;A x xy x= − + + +

32

3 4 5B x xy x= − + −

.

Bài 7:

Lời giải

a)

( ) ( )

2 2 2 2

22A B x y xy x y xy− = + − − + +

2 2 2 2

22x y xy x y xy= + − − − −

Trang 32

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện đưa

ra một số gợi ý, suy luận logic.

HS trả lời theo từng câu hỏi được GV đề

xuất hoặc nêu cách giải 1 ý của bài toán

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

( ) ( )

( )

2 2 2 2

22x x y y xy xy= − + − + − −

4xy=−

.

Vậy

4A B xy− = −

b)

( ) ( )

3 2 3 2

2 3 1 3 4 5A B x xy x x xy x− = − + + + − − + −

3 2 3 2

2 3 1 3 4 5x xy x x xy x= − + + + − + − +

( ) ( )

3 3 2 2

2 3 3 4 1 5x x xy xy x x= − − + + + − + + +

32

5 2 6x xy x= − + + − +

Vậy

32

5 2 6A B x xy x− = − + − +

.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu bài toán 8

Bài 8: Tìm đa thức M biết

a)

( )

2 2 2 2 2

6x 3x 2x ;y M x y y- + = + -

b)

( )

2 2 2

2x 4 5x 7 .M y y y x y- - = + -

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện đưa

ra một số gợi ý, suy luận logic.

HS trả lời theo từng câu hỏi được GV đề

xuất hoặc nêu cách giải 1 ý của bài toán

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Dạng 4: Tổng hợp và nâng cao

Bài 8:

Đáp án

a)

2 2 2

5;M x y xy= - + +

b)

22

7 11 .M xy x y= + -

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu bài toán c

Bài 9: Cho các đa thức :

3 2 2 2

5 4 6A x y xy x y= - -

;

3 2 2 2

84B xy xy x y= - + -

3 3 3 2 2 2

4 6 4 5C x x y xy xy x y= + - - +

. Hãy

tính:

a)

A B C−−

b)

B A C+−

c)

C A B−−

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện đưa

ra một số gợi ý, suy luận logic.

HS trả lời theo từng câu hỏi được GV đề

xuất hoặc nêu cách giải 1 ý của bài toán

*Kết luận, nhận định:

Bài 9

Lời giải

a.

3 2 2 2

3 3 3 2 2 2

(5 4 6 )

( 8 4 )

( 4 6 4 5 )

A B C x y xy x y

xy xy x y

x x y xy xy x y

- - = - -

- - + -

- + - - +

3 2 2 2

3 2 2 2 3

3 3 2 2 2

5 4 6

84

4 6 4 5

x y xy x y

xy xy x y x

x y xy xy x y

= - -

+ - + -

- + + -

3 2 2 2 3 3

7 14x y xy x y xy x= - - + -

b.

3 2 2 2

3 3 3 2 2 2

( 8 4 )

(5 4 6 )

( 4 6 4 5 )

B A C xy xy x y

x y xy x y

x x y xy xy x y

+ - = - + -

+ - -

- + - - +

Trang 33

GV chốt phương pháp giải của dạng toán

và một số lưu ý

3 2 2 2

3 3 3 2 2 2

84

5 4 6

4 6 4 5

xy xy x y

x y xy x y

x x y xy xy x y

= - + -

+ - -

- - + + -

3 2 2 2 3 3

2 15xy xy x y x y x= - + - + -

c.

3 3 3 2 2 2

3 2 2 2

( 4 6 4 5 )

(5 4 6 )

( 8 4 )

C A B x x y xy xy x y

x y xy x y

xy xy x y

- - = + - - +

- - -

- - + -

3 3 3 2 2 2

3 2 2 2

4 6 4 5

5 4 6

84

x x y xy xy x y

x y xy x y

xy xy x y

= + - - +

- + +

+ - +

3 3 3 2 2 2

2 15x x y xy xy x y= - + - +

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu bài toán 10

Bài 10: Tính giá trị của các đa thức sau

a)

( )

6 12 2 6 .A x y y= − + +

Biết

1xy=−

.

b)

3 2 2 2

3 4 2.B x x y x xy y y x= − + − + − + +

Biết

3 0.xy− + =

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện đưa

ra một số gợi ý, suy luận logic.

HS trả lời theo từng câu hỏi được GV đề

xuất hoặc nêu cách giải 1 ý của bài toán

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Bài 10

Lời giải

a) Khi biết

1xy=−

ta có

( ) ( ) ( )

6 12 2 6 6 1 12 2 6 30.A x y y y y y= − + + = − − + + = −

b)

3 2 2 2

3 4 2A x x y x xy y y x= − + − + − + +

( ) ( )

2

3 3 2x x y y x y y x= − + − − + − + +

( ) ( ) ( )

2

3 3 3 1x x y y x y x y= − + − − + + − + −

( )

2

3 1 1x y x y= − + − + −

Nên với

30xy− + =

suy ra

0 1 1.A = − = −

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ 02

1. TRẮC NGHIỆM

Câu 1: Thu gọn đa thức

2 4 2 2 4 2 2

3 2 1

5 3 6

5 5 5

A x y x y x y x y xy x y= − − + + −

có kết quả là

A.

42

2 6 .x y xy+

B.

42

2 6 .x y xy−−

C.

42

2 6 .x y xy−+

D.

42

2 6 .x y xy−

Câu 2: Cho đa thức

22

2;A x y xy= + −

22

2.B x y xy= + +

BA−

có kết quả là

A.

4.xy−

B.

4.xy

C.

2.xy−

D.

2.xy

Trang 34

Câu 3: Đa thức

M

trong biểu thức

2 2 2 2

2 3 4 2 4 4+ − + = − + − +M xy x y xy x y xy x xy

là đa

thức nào dưới đây ?

A.

22

4.x y xy x−−

B.

22

4.x y xy x+−

C.

22

4.x y xy x−+

D.

22

4.x y xy x++

Câu 4: Đa thức

N

trong biểu thức

( )

3 2 2 2 2 2 2 3

2 3 2 5 2 3N xy xy x y x y xy x y x y y− + − + = − + −

là đa thức nào dưới đây ?

A.

2 2 3 2 3

3x y 3xy x y 7xy y .− + + + +

B.

2 2 3 2 3

3x y 3xy x y 7xy y .− + + + −

C.

2 2 3 2 3

3x y 3xy x y 7xy y .− − + + −

D.

2 2 3 2 3

3x y 3xy x y 7xy y .− + − + −

Câu 5: Cho biết

( )

2 2 2 2 2

6 3 2 .x xy M x y xy− + = + −

Đa thức

M

là đa thức nào

dưới đây?

A.

2 2 2

5.x y xy− + +

B.

2 2 2

5.x y xy++

C.

2 2 2

5.x y xy− − +

D.

2 2 2

5.x y xy− + −

2. TỰ LUẬN

Bài 1. Tìm đa thức

M

sao cho tổng của

M

và đa thức

3 2 2

3 5 7 2x x y xy xy+ − − −

là đa thức bậc

0

. Có tất cả bao nhiêu đa thức

M

thỏa mãn điều kiện như vậy.

Bài 2. Cho các đa thức

22

6 5 13M x xy y= − + −

;

22

52N x xy y= − +

. Chứng tỏ rằng

M

,

N

không thể cùng có giá trị dương.

Bài 3. Cho hai đa thức:

3 2 3 2

2 1; .A x x x B x x= − − + = − +

a) Tính

;M A B=+

b) Tính giá trị của

M

tại

1;x =

c) Tìm

x

để

0.M =

Bài 4. Cho các đa thức

22

2 1;A x y xy= − + +

2 2 2 2

1.B x y x y= + − −

Tìm C sao cho

a)

;C A B=+

b)

.C A B+=

Bài 5. Cho các đa thức sau

3 2 2 3 2

4 2 1 à 3 2 5 à 4 5 3 1M x x y xy v N x y xy v P x x y xy= − + + = + − = − + +

Tính a) M – N – P;

b) P – N – M.

Tuần 5

Trang 35

Tiết 10; 11; 12

Ngày soạn 01/11/2023

Lớp

8A

1

8A

2

8A

3

Ngày dạy:

ÔN TẬP HÌNH BÌNH HÀNH. DẤU HIỆU NHẬN BIẾT HÌNH BÌNH HÀNH

I. MỤC TIÊU

1. Về kiến thức:

- Nhận biết được hình bình hành.

- Hiểu về các tính chất và dấu hiệu nhận biết hình bình hành.

2. Về năng lực:

- Nhận biết và giải thích được tứ giác là hình tbình hành.

- Lập luận và chứng minh hình học trong những trường hợp đơn giản.

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được tứ giác là hình bình hành.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng hợp

khi làm các bài tập về hình bình hành.

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

1. Hình bình hành và tính chất

a. Khái niệm hình bình hành

Trang 36

Hình bình hành là tứ giác có các cạnh đối song song.

b. Tính chất của hình bình hành

Trong hình bình hành:

a) Các cạnh đối bằng nhau.

b) Các góc đối bằng nhau.

c) Hai đường chéo cắt nhau tại trung điểm của mỗi đường

2. Dấu hiệu nhận biết

a. Dấu hiệu nhận biết hình bình hành theo cạnh

• Tứ giác có các cạnh đối bằng nhau là một hình bình hành.

• Tứ giác có một cặp cạnh đối song song và bằng nhau là một hình bình hành.

b. Dấu hiệu nhận biết hình bình hành theo góc và đường chéo

• Tứ giác có các góc đối bằng nhau là một hình bình hành.

• Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là một hình bình

hành.

2. BÀI TẬP

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ

- GV yêu cầu HS hoạt động cá nhân thực

hiện bài tập trắc nghiệm 1.

Kiểm tra củng cố lý thuyết cho HS

HS nhận nhiệm vụ GV giao

Bài 1: Bài tập trắc nghiệm

Đáp án:

1

2

3

4

5

C

B

C

A

1.1: Phát biểu nào dưới đây đúng?

A. Hình bình hành là tứ giác có các cạnh

bằng nhau.

B. Hình bình hành là tứ giác có các góc

bằng nhau.

C. Hình bình hành là tứ giác hai cạnh kề

bằng nhau.

D. Hình bình hành là tứ giác có hai cạnh đối

song song và bằng nhau.

1.2: Cho hình bình hành

ABCD

biết

Trang 37

75A =

. Các góc còn lại có giá trị bằng bao

nhiêu?

A.

105B =

,

105C =

,

75D =

.

B.

105B =

,

75C =

,

105D =

.

C.

85B =

,

95C =

,

105D =

.

D.

75B =

,

105C =

,

105D =

.

1.3: Cho hình bình hành

ABCD

biết

40AB− = 

. Tính số đo góc

A

.

A.

60A =

. B.

110A =

.

C.

90A =

. D.

120A =

.

1.4: Cho hình bình hành

ABCD

, gọi

I

là

giao điểm của hai đường chéo

,AC BD

.

Chọn phát biểu đúng.

A.

2AC IB=

. B.

1

2

ID AC=

.

C.

1

2

IC AC=

. D.

IA IB ID==

.

1.5: Cho hình bình hành

ABCD

có

6AB cm=

,

8BC cm=

. Tính chu vi hình bình

hành

ABCD

.

A. 10. B. 14.

C. 28. D. 24.

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

GV: Cho HS đọc đầu bài trắc nghiệm trên

màn hình .

- HS HĐ cá nhân thực hiện bài 1.

- GV yêu cầu HS hoạt động nhóm đôi thực

hiện bài tập trắc nghiệm 1

- HS báo cáo kết quả.

- Nhận xét, đánh giá câu trả lời của nhau

Trang 38

GV: Để chọn phương án đúng ở câu

1,2,3,4,5 ta dựa vào kiến thức nào đã học ?

HS: Trả lời

Dạng 1

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 2:

- HS tìm hiểu bài toán 2.

HS: Đọc đầu bài 2

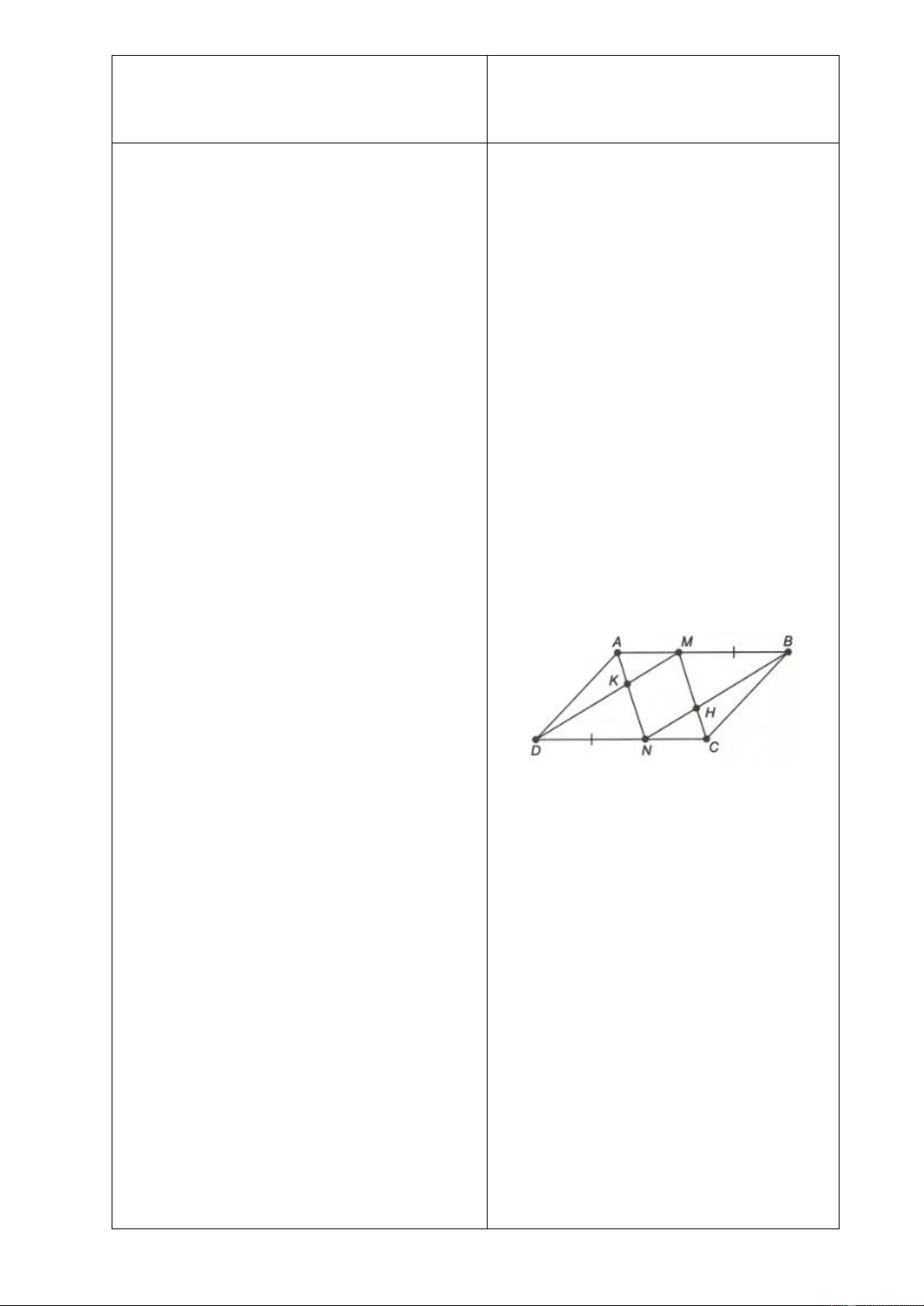
Chứng minh các tứ giác

BMDN

,

AMCN

,

MKNH

là hình bình hành.

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện.

GV: Nêu các dấu hiệu nhận biết hình bình

hành.

GV: Trong bài toán này chúng ta sử dụng

dấu hiệu nhận biết nào?

- HS trả lời theo từng câu hỏi được GV đề

xuất.

GV: Gọi HS nhận xét

- HS phản biện câu trả lời của nhau.

HS: Hoạt động trình bày chứng minh tứ

giác là hình bình hành.

HS: Lên bảng trình bày.

HS: Nhận xét.

*Kết luận, nhận định: Khi có giả thiết

hình thang, các em ghi nhớ tính chất của các

góc kề cạnh bên, tổng các góc trong tứ giác

360

°

=

Dạng 1. Chứng minh một tứ giác là

hình bình hành

Bài 2: Cho hình bình hành

ABCD

. Trên

cạnh

AB

lấy điểm

M

, trên cạnh

CD

lấy

điểm

N

sao cho

MB DN=

.

a) Chứng minh

BMDN

là hình bình

hành.

b) Chứng minh

AMCN

là hình bình

hành.

c) Gọi

K

là giao điểm của

DM

và

AN

và

H

là giao điểm của

BN

và

CM

.

Chứng minh tứ giác

MKNH

là hình bình

hành.

Hướng dẫn giải:

a) Xét tứ giác BMDN ta có:

BM DN=

(giả thiết),

//BM DN

(tứ giác ABCD là

hình bình hành)



Tứ giác BMDN là hình bình hành

(dấu hiệu nhận biết hình bình hành)

b) Ta có

AB CD=

(tứ giác ABCD là hình

bình hành),

BM DN=

(giả thiết),

AB BM CD DN − = −

AM CN=

.

Xét tứ giác AMCN, ta có

AM CN=

(chứng minh trên),

Trang 39

//AM CN

(tứ giác ABCD là

hình bình hành)



Tứ giác AMCN là hình bình hành vì

có hai cạnh đối vừa song song vừa bằng

nhau.

c) Xét tứ giác MKNH, ta có

//KM NH

(tứ giác BMDN là

hình bình hành),

//MH KN

(tứ giác AMCN là

hình bình hành)



Tứ giác MKNH là hình bình hành vì

có hai cặp cạnh đối song song.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 3

- HS tìm hiểu bài toán 3.

HS: Đọc đầu bài 3

Tứ giác

MNPQ

là hình gì? .

Chứng minh

EQ MP=

.*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện.

GV: Dự đoán

MNPQ

là hình gì?

GV: Áp dụng kiến thức nào đã học để

chứng minh?

GV: Sử dụng tính chất gì để chứng minh

EQ MP=

- HS trả lời theo từng câu hỏi được GV đề

xuất.

- HS phản biện câu trả lời của nhau.

*Kết luận, nhận định:

Các bước chứng minh tứ giác là hình

bình hành:

Bước 1. Xác định đoạn thẳng thuộc các

Bài 3: Cho tam giác

ABC

, các trung tuyến

BM

và

CN

cắt nhau ở

G

. Gọi

P

là điểm

sao cho G là trung điểm của MP. Gọi

Q

là

điểm sao cho G là trung điểm của NQ .

a) Tứ giác

MNPQ

là hình gì? Vì sao?

b) Trên tia đối của tia

MN

, lấy điểm

E

sao

cho

AM NM=

. Chứng minh

EQ MP=

.

Hướng dẫn giải:

a) Xét tứ giác MNPQ, ta có

G là trung điểm của MP

G là trung điểm của NQ



Tứ giác MNPQ là hình bình hành vì có

hai đường chéo cắt nhau tại trung điểm mỗi

đường.

b) Ta có:

EM MN=

(giả thiết)

PQ MN=

(Tứ giác MNPQ là hình

bình hành)

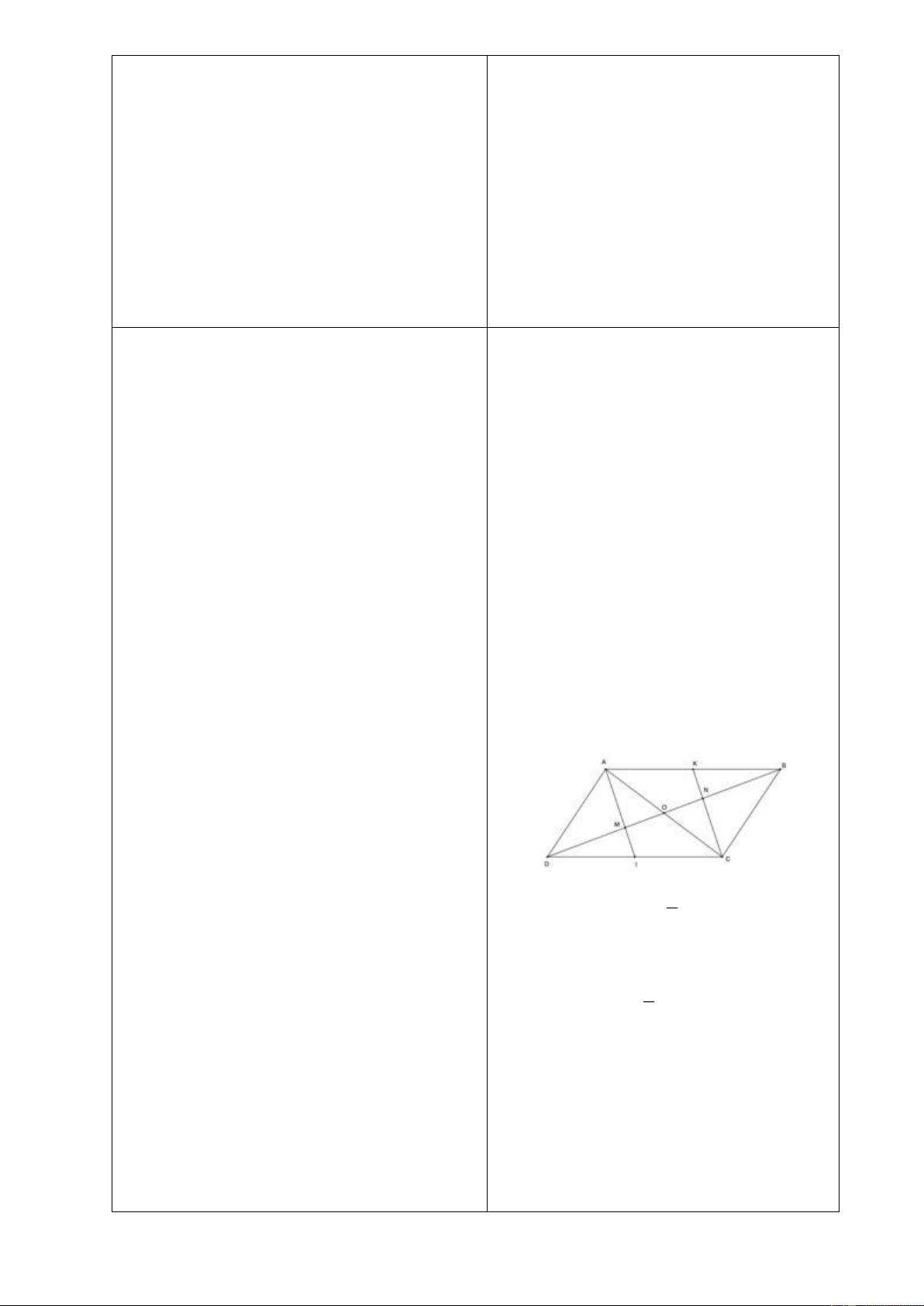
Trang 40

cạnh có tính chất đặc biệt như song song,

trung điểm.

Bước 2. Sử dụng định nghĩa và tính chất về

cạnh, góc và đường chéo của hình bình

hành.

( )

EM PQ MN = =

Xét tứ giác EMPQ, ta có

EM PQ=

(chứng minh trên)

( )

// //EM PQ MN PQ



Tứ giác EMPQ là hình bình hành vì có

hai cạnh đối vừa song song vừa bằng nhau.

Suy ra

EQ MP=

.

Dạng 2

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 4

HS tìm hiểu bài toán 4

Chứng minh

AKCI

là hình thang.

Chứng minh

DM MN NB==

.

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

GV: Hình vẽ cho biết yếu tố nào bằng

nhau?

HS quan sát hình vẽ

GV: Dự đoán sử dụng dấu hiệu nhận biết

nào để chứng minh

AKCI

là hình bình

hành?

HS: dự đoán

GV: Dự đoán dử dụng kiến thức nào để

chứng minh

DM MN NB==

HS thực hiện nhiệm vụ

*Kết luận, nhận định: cách chứng minh

tứ giác là hình thang: cần tìm 1 cặp cạnh

song song

Dạng 2. Vận dụng tính chất của hình

bình hành để chứng minh tính chất

hình học

Bài 4: Cho hình bình hành

ABCD

. Gọi

K

là trung điểm

AB

,

I

là trung điểm

của

,DC BD

lần lượt cắt

AI

và

CK

tại

,MN

. Gọi

O

là giao điểm của hai đường

chéo

AC

và

BD

.

a) Chứng minh tứ giác

AKCI

là hình

bình hành.

b) Chứng minh

DM MN NB==

.

Hướng dẫn giải:

a) Ta có:

1

2

KA KB AB==

(

K

là trung

điểm của

AB

)

1

2

ID IC DC==

(

I

là trung điểm

của

DC

)

Mà

AB DC=

(

ABCD

là hình bình hành)

nên

KA KB ID IC= = =

.

Xét tứ giác AKCI, ta có:

AK IC=

(chứng minh trên)

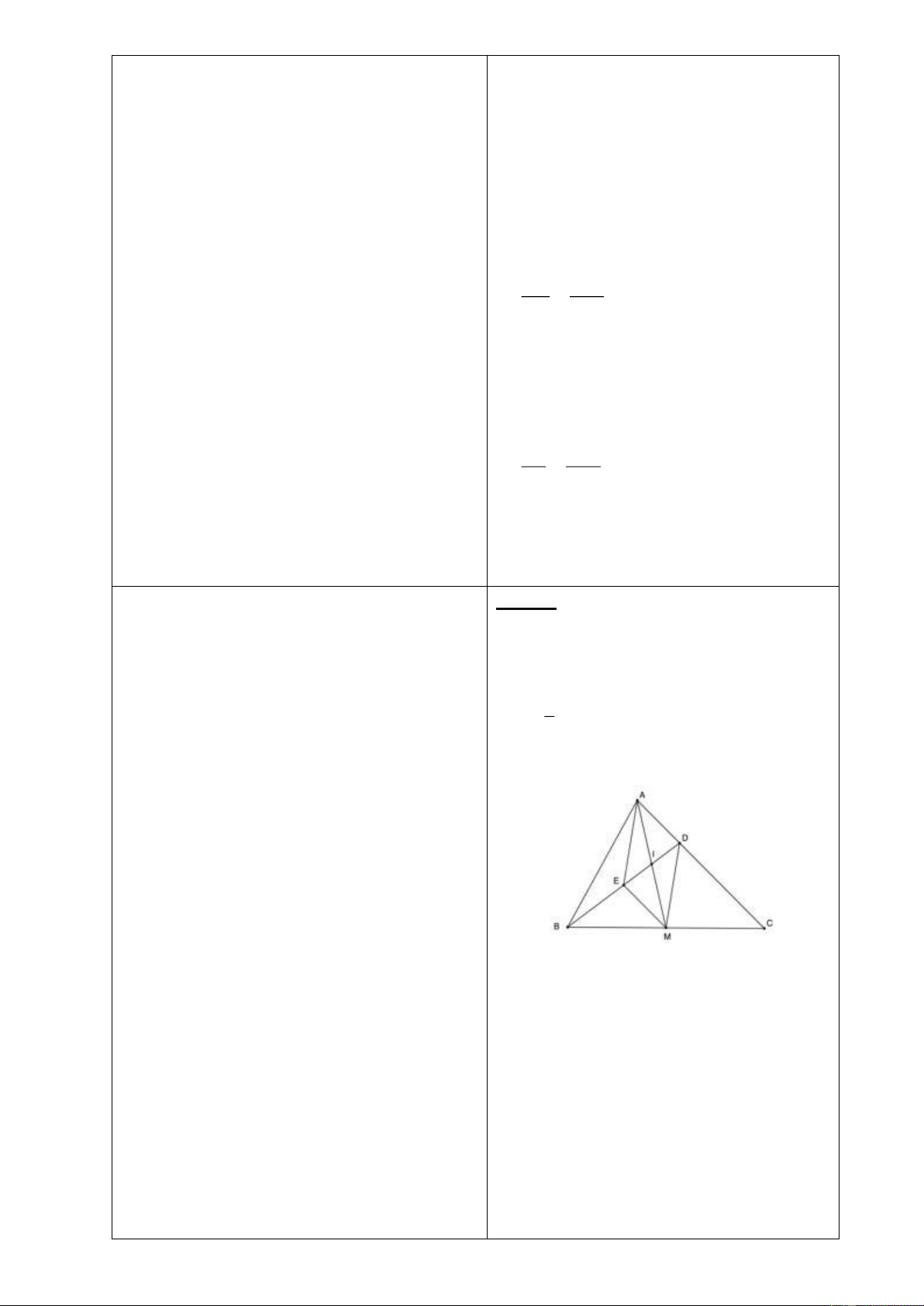
Trang 41

( )

// //AK IC AB DC

Suy ra tứ giác

AKCI

là hình bình hành

vì có hai cạnh đối vừa song song vừa

bằng nhau.

b) Xét

BAM

ta có:

//KN AM

(

AKIC

là hình bình hành)

1

BK BN

KA NM

 = =

NB MN=

( )

1

.

Xét

DCN

ta có:

//IM CN

(

AKCI

lả hình bình hành)

1

DI DM

IC MN

 = =

DM MN=

( )

2

.

Từ

( )

1

và

( )

2

suy ra

DM MN NB==

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 5

HS tìm hiểu bài toán 5

* Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

GV: Yêu cầu HS quan sát hình vẽ xem có

hình nào là hình bình hành không?

HS thực hiện NV GV giao

HS: Tứ giác

ADME

là hình bình hành.

GV: Yêu cầu HS hoạt động tìm ra những

đk để khẳng định tứ giác là hình thình bình

hành.

HS: Để chứng minh tứ giác là hình bình

hành ta sử dụng dấu hiệu nhận biết: hai

đường chéo cắt nhau tại trung điểm của mỗi

đường.

GV: gọi HS nhận xét.

Bài 5: Cho

ABC

, trung tuyến

AM

.

Gọi

I

là trung điểm của

AM

,

D

là giao

điểm của

BI

và

AC

. Chứng minh rằng

1

3

AD AC=

Hướng dẫn giải:

Do

I

là trung điểm của

AM

theo giả

thiết nên chọn

AM

là một đường chéo

Vẽ thêm điểm

E

sao cho

I

là trung điểm

của

ED

thì tứ giác

ADME

có hai đường

chéo cắt nhau tại trung điểm của mỗi

đường nên nó là hình bình hành

Áp dụng định nghĩa và tính chất về cạnh

vào hình bình hành

ADME

, ta được

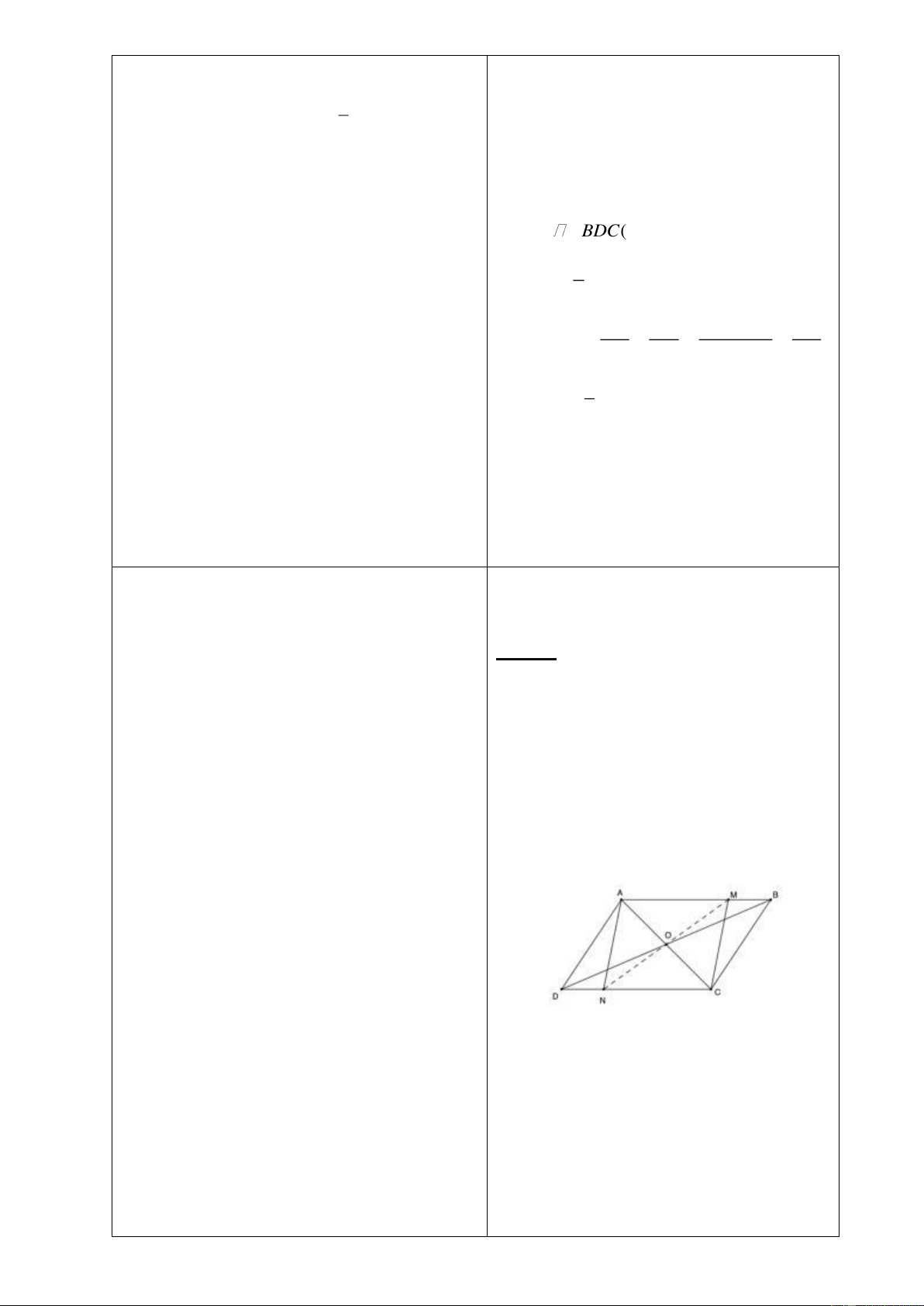
Trang 42

GV: Sử dụng tính chất nào của hình bình

hành để chứng minh

1

3

AD AC=

?

HS hoạt động theo yêu cầu của GV.

HS: Lên bảng trình bày

HS nhận xét.

*Kết luận, nhận định: Phương pháp

giải:

Bước 1. Xác định đoạn thẳng thuộc các

cạnh có tính chất đặc biệt như song song,

trung điểm.

Bước 2. Sử dụng định nghĩa và tính chất về

cạnh, góc và đường chéo của hình bình

hành.

ME AD=

(1)

Và

( )

/ / , / / 2ME AD ME DC

Lại có

( )

3BM MC=

Từ

( )( )

23 BE ED=

( . )BEM BDC g g

( )

1

4

2

ME CD=

Từ

( )( )

14

1 2 3 3

AD DC AD DC AC+

 = = =

.

Vậy

1

3

AD AC=

.

Dạng 3

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 6

HS tìm hiểu bài toán 6

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

HS thực hiện nhiệm vụ GV giao

HS đọc đề bài và vẽ hình vào vở.

GV: Nêu cách chứng minh tứ giác

AMCN

là hình bình hành

HS: Tứ giác AMCN là hình bình hành vì có

hai cạnh đối vừa song song vừa bằng nhau

GV: Sử dụng kiến thức gì để chứng minh

,,M O N

thẳng hàng.

HS: Tính chất đường chéo của hình bình

hành.

Dạng 3: Chứng minh ba điểm thẳng

hàng, các đường thẳng đồng quy

Bài 6: Cho hình bình hành

ABCD

là

hình bình hành. Trên cạnh

AB

lấy điểm

M

, trên cạnh

CD

lấy điểm

N

sao cho

DM CN=

. Gọi

O

là giao điểm của

AC

và

BD

. Chứng minh

,,M O N

thẳng

hàng.

Hướng dẫn giải:

Tứ giác

ABCD

là hình bình hành và

O

là giao điểm của hai đường chéo

,AC BD



O

là trung điểm của

,AC BD

.

Xét tứ giác

AMCN

ta có

AM CN=

(giả thiết),

//AM CN

(tứ giác ABCD là

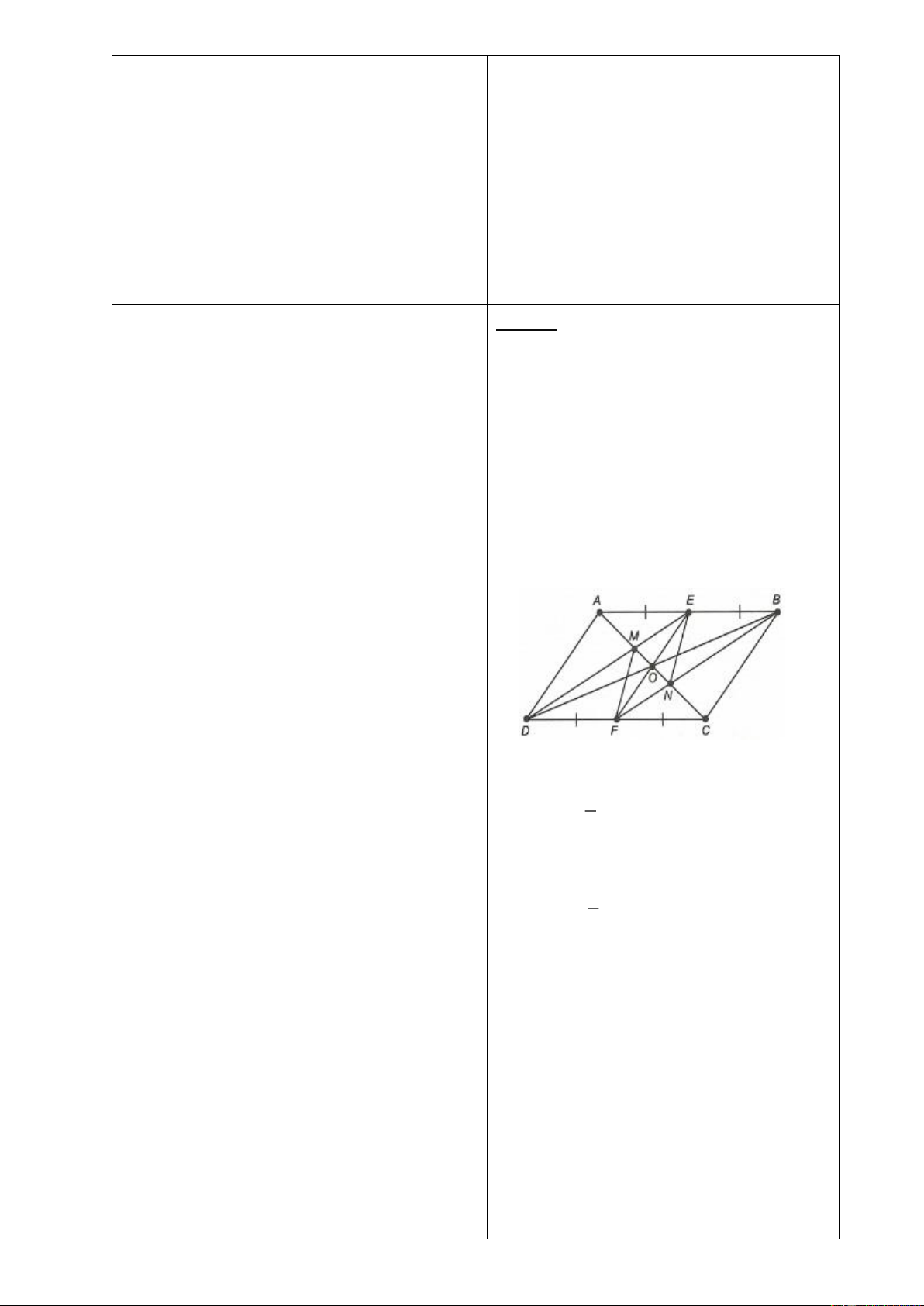
Trang 43

GV: Quan sát hướng dẫn.

*Kết luận, nhận định:

Trong bài đã khai thác tính chất về đường

chéo của hình bình hành để chứng minh 3

điểm thẳng hàng. Đây là một trong nhũng

cácc phổ biến để chứng minh 3 điểm thẳng

hàng.

hình bình hành)



tứ giác

AMCN

là

hình bình hành vì có hai cạnh đối vừa

song song vừa bằng nhau.

Mà

O

là trung điểm của đường chéo

AC

nên

O

là trung điểm của đường chéo

MN

.

Hay

,,M O N

thẳng hàng.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 7

HS tìm hiểu bài toán 7

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

HS: Thực hiện nhiệm vụ theo yêu cầu của

GV.

HS đọc đề bài và vẽ hình, ghi GT, KL

GV: Tứ giác DEBF là hình gì?

HS: sử dụng tính chất hai cạnh đối vừa

song song vừa bằng nhau để chứng minh

DEBF là hình bình hành.

GV: Sử dụng dấu hiệu nhận biết nào để

chứng minh?

HS: Chứng minh giao điểm của BC và AD

thuộc EF.

GV: Có những cách nào để chứng minh 3

đường thẳng đồng quy?

GV: Trong bài toán này chúng ta sử dụng

cách nào?

Bài 7: Cho hình bình hành

ABCD

. Gọi

,EF

lần lượt là trung điểm của

AB

và

CD

.

a) Tứ giác

DEBF

là hình gì? Vì sao?

b) Chứng minh ba đường thẳng

,,BD AC EF

đồng quy.

Hướng dẫn giải:

a) Ta có:

1

2

AE EB AB==

(

E

là trung điểm của

AB

)

1

2

DF FC DC==

(

F

là trung điểm của

DC

)

Mà

AB CD=

(tứ giác ABCD là hình bình

hành) nên

AE EB DF FC= = =

.

Xét tứ giác DEBF, ta có

BE DF=

(chứng minh trên)

//BE DF

(tứ giác

ABCD

là hình bình

hành)



Tứ giác

DEBF

là hình bình hành vì

Trang 44

có hai cạnh đối vừa song song vừa bằng

nhau.

b) Gọi

O

là giao điểm của

AC

và

BD

.

Do tứ giác

ABCD

là hình bình hành nên

O

là trung điểm của hai đường chéo

,AC BD

( )

1

Tứ giác

DEBF

là hình bình hành có

O

là trung điểm của đường chéo

BD

nên

O

là trung điểm của đường chéo

EF

.

Suy ra

,,O E F

thẳng hàng.

( )

2

Từ

( )

1

và

( )

2

suy ra ba đường thẳng

,,BD AC EF

đồng quy tại

O

.

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ ….

1. TRẮC NGHIỆM

Bài 1: Phát biểu nào dưới đây đúng?

A. Hình bình hành là tứ giác có các cạnh bằng nhau.

B. Hình bình hành là tứ giác có các góc bằng nhau.

C. Hình bình hành là tứ giác hai cạnh kề bằng nhau.

D. Hình bình hành là tứ giác có hai cạnh đối song song và bằng nhau.

Bài 2: Cho hình bình hành

ABCD

biết

75A =

. Các góc còn lại có giá trị bằng bao

nhiêu?

A.

105B =

,

105C =

,

75D =

. B.

105B =

,

75C =

,

105D =

.

C.

85B =

,

95C =

,

105D =

. D.

75B =

,

105C =

,

105D =

.

Bài 3: Cho hình bình hành ABCD biết

40AB− = 

. Tính số đo góc

A

.

A.

60A =

. B.

110A =

. C.

90A =

. D.

120A =

.

Bài 4: Cho hình bình hành

ABCD

, gọi

I

là giao điểm của hai đường chéo

,AC BD

.

Chọn phát biểu đúng.

A.

2AC IB=

. B.

1

2

ID AC=

.

Trang 45

C.

1

2

IC AC=

. D.

IA IB ID==

.

Bài 5: Cho hình bình hành

ABCD

có

6AB cm=

,

8BC cm=

. Tính chu vi hình bình

hành

ABCD

.

A. 10. B. 14. C. 28. D. 24.

2. TỰ LUẬN

Bài 1: Cho hình bình hành

ABCD

. Gọi E là trung điểm của AB, F là trung điểm của

DC.

a) Chứng minh

BE DF=

b) Chứng minh tứ giác BEDF là hình bình hành.

Bài 2: Cho hình bình hành

ABCD

, đường chéo

BD

. Từ

A

và

C

kẻ

,AE CF

vuông

góc với

BD

ở

H

và

K

. Chứng minh tứ giác

AHCK

là hình bình hành.

Bài 3: Cho hình bình hành

ABCD

. Gọi

,KI

lần lượt là trung điểm của các cạnh

AB

và

CD

. Gọi

M

và

N

lần lượt là giao điểm của

AI

và

CK

với

BD

. Chứng minh

a.

ADM CBN = 

b.

, / /MAC NCA IM CN=

Bài 4: Cho hình bình hành

ABCD

, hai đường chéo

,AC BD

cắt nhau tại

O

. Kẻ

BH AC⊥

tại

H

cắt

DC

tại

N

và kẻ

DK AC⊥

tại

K

cắt

AB

tại

M

.

a) Chứng minh tứ giác

BMDN

là hình bình hành.

b) Chứng minh tứ giác

BKDH

là hình bình hành.

c) Chứng minh

,,AC BD MN

đồng quy.

Bài 5: Cho tam giác

ABC

có ba góc nhọn. Gọi

M

là trung điểm của

BC

, trên tia

AM

lấy điểm

K

sao cho

M

là trung điểm của

AK

.

a) Chứng minh tứ giác

ABKC

là hình bình hành.

b) Gọi

I

là trung điểm của

AB

và

E

là trung điểm của

AC

. Trên tia

IE

lấy điểm

H

sao cho

E

là trung điểm của

IH

. Chứng minh tứ giác

AHCI

là hình bình hành.

c) Chứng minh K thẳn

,,K C H

hàng.

Trang 46

Bài 6: Cho hình bình hành

ABCD

. Lấy hai điểm

,EF

theo thứ tự thuộc

AB

và

CD

sao cho

AE CF=

. Lấy hai điểm

,MN

theo thứ tự thuộc

BC

và

AD

sao cho

CM AN=

. Chứng minh rằng:

a) Tứ giác

AECF

là hình bình hành.

b) Tứ giác

ANCM

là hình bình hành.

c) Ba đường thẳng

,,MN BD EF

đồng quy.

Bài 7: Cho điểm

P

nằm trong

ABC

. Gọi

,,D E F

lần lượt là trung điểm của các

cạnh

,,BC CA AB

. Từ

A

vẽ đường thẳng song song với

PD

cắt đường thẳng kẻ từ

B

song song với

PE

tại

S

. Chứng minh rằng nếu

2BS EP=

thì

//CS PF

Tuần 6

Tiết 13; 14; 15

Ngày soạn 01/11/2023

Lớp

8A

1

8A

2

8A

3

Ngày dạy:

ÔN TẬP PHÉP NHÂN, PHÉP CHIA ĐA THỨC

I. MỤC TIÊU

1. Về kiến thức:

Học sinh biết cách nhân đơn thức với đa thức, nhân đa thức với đa thức.

Học sinh biết chia đơn thức cho đơn thức, chia đa thức cho đơn thức, chia đa thức cho

đa thức.

2. Về năng lực:

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu được các quy tắc nhân đa thức với đơn

thức, đa thức với đa thức, chia đa thức cho đơn thức.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: Học sinh làm thành thạo các phép tính nhân, chia đa thức. Biết

đưa lạ về quen, rèn kĩ năng trình bày, tính toán chính xác, cẩn thận.

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

Trang 47

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

- Muốn nhân một đa thức với một đa thức ta nhân mỗi hạng tử của đa thức này với

từng hạng tử của đa thức kia rồi cộng các tích với nhau.

- Đơn thức

A

chia hết cho đơn thức

( )

0BB

khi mỗi biến của B đều là biến của A

với số mũ không lớn hơn số mũ của nó trong

.A

- Muốn chia đơn thức

A

cho đơn thức

B

(trường hợp chia hết), ta chia hệ số cho hệ

số, biến số cho biến số rồi nhân các kết quả với nhau.

- Đa thức

A

chia hết cho đơn thức

B

nếu mọi hạng tử của

A

đều chia hết cho

.B

- Muốn chia đa thức

A

cho đơn thức

B

(trường hợp chia hết) ta chia từng hạng tử của

A

cho

B

rồi cộng các kết quả với nhau.

2. BÀI TẬP

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài toán

trắc nghiệm 1

Dạng 1: Thực hiện phép tính

Bài 1: Bài tập trắc nghiệm

Câu 1. Kết quả của phép tính

( )

2

1xy x x+−

là:

A.

32

x y x y xy++

B.

32

–x y x y xy+

C.

32

––x y x y xy

D.

32

–x y x y xy+

Câu 2. Trong các phép chia dưới đây, phép chia hết là:

A.

3

– 6 :5x y xy

B.

( )

3 2 2

:x x x x++

C.

( )

32

:x y x z xy xy++

D.

( )

2

1 : –1xx+

Câu 3. Kết quả của phép tính

4 2 4

27 :9x y z x y

là:

A.

3xyz

B.

3xz

C.

3yz

D.

3 xy

Câu 4. Kết quả của phép tính

( )

2

6 2 3xy x y−

là

A.

22

12 18 x y xy+

B.

32

12 18x y xy−

C.

32

12 18x y xy+

D.

22

12 18x y xy−

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

Con sử dụng các quy tắc nào?

Trả lời

Đáp án

1D, 2A, 3C, 4B

Trang 48

Câu 1, 4 sử dụng quy tắc nhân đơn thức với đa

thức

Câu 3: Quy tắc chia đa thức

- Phép chia hết là phép chia như thế nào?

Phép chia hết là phép chia mà mỗi biến của đơn

thức bị chia đều có số mũ lớn hơn hoặc bằng số

mũ trong biến của đơn thức chia,

*Kết luận, nhận định:

Đáp án

1D, 2A, 3C, 4B

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 2

Bài 2: Thực hiện phép tính

a)

( )( )

22

– 2 3x y xy x y−

b)

( )

2 3 2 2 3

2 . 2 5xy x y x y xy− − +

c)

( )

2

4

3 – 6 9

3

.x y xy x xy



+−





d)

3

2 1 1

10 .

5 3 2

x y z xy

   

− + − −

   

   

*Thực hiện nhiệm vụ

- Các phép tính thuộc dạng toán nào?

Nhân đơn thức với đa thức.

- Muốn nhân đơn thức với đa thức ta phải làm

gì?

1 HS phát biểu quy tắc nhân đơn thức với đa

thức.

*Kết luận, nhận định:

Khi thực hiện phép nhân hai số nguyên cần chú

ý tránh nhầm dấu.

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 3

Bài 3: Thực hiện phép tính

a)

( )( )

–21x xy+ −

b)

( )

2

2 2 3xy x xy−+

c)

2

15

23

34

x x xy x

  

− + −

  

  

d)

( ) ( )

2 2 2 2 2

3 . 2 – – 2 – . 2x y x y x x y y

Bài 2: Thực hiện phép tính

Lời giải

a)

4 2 3 2

36x y x y−+

b)

4 3 3 4 2 5

2 4 10x y x y x y− + −

c)

3 2 2 2 2

4 8 12x y x y x y− + −

d)

42

11

5

56

x y xy xyz−+

- Muốn nhân đơn thức với đa thức ta nhân

đơn thức với từng hạng tử của đa thức rồi

cộng các kết quả với nhau.

Bài 3: Thực hiện phép tính

Lời giải

a)

2

2x xy x y− − − −

b)

2 2 3 2

2 3 4 6x y x y x xy+ − −

c)

3 3 2 2

1 5 5 15

23

3 12 2 4

x y x x y x xy x− − + + −

Trang 49

*Thực hiện nhiệm vụ

- Các phép tính thuộc dạng toán nào?

Nhân đa thức với đa thức.

- Muốn nhân đa thức với đa thức ta phải làm gì?

*Kết luận, nhận định:

Khi thực hiện phép nhân hai số nguyên cần chú

ý tránh nhầm dầu.

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 4.

Bài 4: Thực hiện phép tính

a)

( )

5 3 3 2 4 4 2 2

15 10 20 :5x y x y x y x y−+

b)

( )

4 3 2 2 3 2

3 9 15 :x y x y xy xy−+

c)

3 2 2 3

(18 12 6 ):6x y x y xy xy−+

d)

( )

2

2 4 3 3 2

2 3 6 :x y x y x y xy



+−





e)

5 4 4 2 3 3 2 2

11

5 2 :

24

x y z x y z xy z xy z



+−





f)

2 3 3 4 2 2

10 15 5

5:

3 2 3

x yz xy z xyz xyz



− + −





Yêu cầu HS phát biểu quy tắc chia đa thức cho

đơn thức.

Yêu cầu HS làm cá nhân bài tập 4, chọn 3 ý làm

vào vở

*Kết luận, nhận định:

- Đa thức

A

chia hết cho đơn thức

B

nếu mọi

hạng tử của

A

đều chia hết cho

.B

- Muốn chia đa thức

A

cho đơn thức

B

(trường

hợp chia hết) ta chia từng hạng tử của

A

cho

B

rồi cộng các kết quả với nhau.

d)

4 2 2 4 2 2

4 2 2

6 3 4 2

2

x y x y x y x y

x y x y

− − +

=−

Bài 4: Thực hiện phép tính

Lời giải

a)

3 2 2

3 2 4x y x x y−+

b)

3

3 9 15x y x y−+

c)

22

32x xy y−+

d)

22

4 3 6x x y x+−

e)

4 2 3 2

20 2 8x y x z yz+−

f)

22

9

23

2

xz y z− + −

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 5

Bài 5: Rút gọn các biểu thức sau:

a)

( )

( ) ( )

22

1

1 2 4 1 2

2

x x x x x x x− − + + − + + −

b)

( ) ( ) ( )

11x xy y xy xy x y+ + − − +

HS tìm hiểu bài toán 5

Dạng 2: Rút gọn biểu thức

Bài 5: Hướng dẫn giải

a)

( )

( ) ( )

22

3 2 3 2 2

1

1 2 4 1 2

2

2 2 2

x x x x x x x

− − + + − + + −

= − + − + − + + − = −

b)

Trang 50

*Thực hiện nhiệm vụ

- GV yêu cầu HS làm việc cá nhân vào vở

*Kết luận, nhận định:

Sử dụng quy tắc nhân đa thức để thu gọn biểu

thức.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 6, bài 7

Bài 6: Rút gọn biểu thức:

a)

( )

22

2x xy y xy

xy x xy y

+ + −

+ − +

b)

( )( ) ( )( )

( )( )

3 2 2 4 1 3

2 2 2

x x x x

xx

− − + − −

− − +

c)

( )( )

( )

22

33

,

n n n n n n

nn

x y x x y y

x y n

+ − +

−

Bài 7: Tính giá trị của biểu thức

5 4 3

2

100 100

100 100 9

A x x x

xx

= − +

− + −

một cách hợp lý tại

99x =

.

Yêu cầu HS làm việc nhóm

- Để tính giá trị của biểu thức ta cần làm gì?

- Có thể thay giá trị

99x =

trực tiếp vào biểu

thức không?

- Các hệ số của A như thế nào với giá trị cần

thay vào?

- Có cách nào để tính A đơn giản hơn không?

*Kết luận, nhận định:

Ở dạng toán này ta thấy x = 99 rất gần với hệ số

100 của đa thức ban đầu, từ đó ta nghĩ rằng có

thể thay 100 = x + 1 như ở cách 1, hoặc chuyển

thành x – 99 = 0 như ở cách 2

2 2 2 2

( 1) ( 1) ( )x xy y xy xy x y

x y x xy y x y xy

xy

+ + − − +

= + + − − −

=−

Bài 6.

a)

3 2 2 3

2 2 2x y x y xy

x y x y xy

= − − −

+ − +

3 2 2 3

3x y x y xy= − − −

b)

22

2

3 6 2 4 4

12 4 12 2 8

x x x x

x x x

= − − + +

− − + − +

9 14x= − +

c)

( )

3 2 2 2 2 3

33

n n n n n n n n n n

nn

x x y x y x y x y y

xy

= − + + − +

−

( )( )

3 3 3 3

6 3 3 3 3 6

66

n n n n

n n n n n n

nn

x y x y

x x y x y y

xy

= + −

= − + +

=−

Bài 7.

Cách 1: Ta có

99 1 100xx=  + =

.

Thay

100 1x=+

, vào biểu

thức ta tính được

90A =

Cách 2:

99 99 0xx=  − =

do đó ta biến đổi

biểu thức về dạng:

5 4 4 3 3

22

99 99

99 99 9

A x x x x x

x x x x

= − − + +

− − + + −

( ) ( )

43

2

99 99

99 99 9

90

A x x x x

x x x x x

= − − −

+ − − − + −

=

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 8, 9, 10

Yêu cầu HS chọn 1 trong 3 bài làm vào vở

Bài 8: Chứng minh rằng các biểu thức sau

Dạng 3: Chứng minh rằng các biểu thức

sau không phụ thuộc vào giá trị của biến

Bài 8:

a)

Trang 51

không phụ thuộc vào biến x, y:

a)

2 2 2

5 ( 2 ) 5(1 ) 10A x y x y x x= − + − − +

b)

( ) ( )

( )

2 2 2 3 3

4 – 3 6 2 – 2 3 2B xy x y x x y x y= + + +

Bài 9: Chứng minh rằng các biểu thức sau

không phụ thuộc vào biến x; y

a)

( )

( )( )

( )

2

3 1 1 1

34

xy x y xy y y

xy x

+ − − − +

− − +

b)

( ) ( )( )

( )

2 2 2 2 2

44

x y a b ax by ay bx

ab x y

− + + + +

−+

Bài 10: Chứng minh rằng biểu thức sau luôn

dương với mọi giá trị của biến:

( ) ( ) ( )

( )

5 4 3

4 4 4

3

4

1 2 1 3 1

:1

x x x

x



+ − + + +





+

- Biểu thức có như thế nào được gọi là có giá trị

không phụ thuộc vào biến?

Giá trị của biểu thức là một số thực.

- Biểu thức luôn dương là biểu thức như thế

nào?

Biểu thức có giá trị lớn hơn 0.

- Chúng ta đã biết những biểu thức nào luôn

không âm

Lũy thừa chẵn của một biểu thức, giá trị tuyệt

đối của biểu thức và căn bậc hai của một biểu

thức.

*Kết luận, nhận định:

Để chứng minh biểu thức có giá trị không phụ

thuộc vào giá trị của biến ta thu gọn biểu thức

và được kết quả là một số thực.

2 2 2

2 2 2 2

5 ( 2 ) 5(1 ) 10

5 10 5 5 10

5

A x y x y x x

xy x xy x

= − + − − +

= − − − + +

=−

Vậy

A

không phụ thuộc vào giá trị của

biến.

b)

( ) ( )

( )

2 2 2 3

3

4 – 3 6 2

–2 3 2

B xy x y x x y

xy

= + +

+

3 3 3

46

12 6 4

0

–12yx

x

x xy

xy x y

=+

+ − −

=

Vậy

B

không phụ thuộc vào giá trị của

biến.

Bài 9

a)

( )

( )( )

( )

2

3 1 1 1

34

xy x y xy y y

xy x

+ − − − +

− − +

( )

32

22

33

1 3 3 12

xy xy xy x

xy y xy x

= − + −

− − − + −

12=−

Vậy biểu thức có giá trị không phụ thuộc

vào giá trị của biến.

b)

( ) ( )( )

( )

2 2 2 2 2

44

x y a b ax by ay bx

ab x y

− + + + +

−+

2 2 2 2 2 2 4 2

2 2 4 2

a x y b x y a x y abx aby

b x y abx aby

= − − + + +

+ − −

0=

Vậy biểu thức có giá trị không phụ thuộc

vào giá trị của biến.

Bài 10

Ta có

( ) ( ) ( ) ( )

5 4 3 3

4 4 4 4

1 2 1 3 1 : 1x x x x



+ − + + + +





( ) ( )

2

44

1 2 1 3xx= + − + +

8 4 4

2 1 2 2 3x x x= − + − − +

8

2x=+

Ta thấy

8

0x 

với mọi

x

, khi đó

8

20x +

với mọi

.x

Trang 52

Vậy biểu thức đã cho luôn dương với mọi

giá trị của biến

2. TỰ LUẬN

Bài 1. Thực hiện các phép tính sau:

a)

( )

23

3 2 5x x x−+

b)

( )

4 2 2 2

2

29

3

x x y x y

−

− − −

c)

2 3 4

32

2 .10

85

x y y xy xy



− + −





Giải

a)

( )

2 3 5 3 2

3 2 5 6 3 15x x x x x x− + = − +

b)

( )

4 2 2 2 5 2 3 2

2 2 4

2 9 6

3 3 3

x x y x y x y x xy

−

− − − = + +

c)

2 3 4 3 4 5 2 2

3 2 15

2 .10 20 4

8 5 4

x y y xy xy x y xy x y



− + − = − + −





Bài 2. Thực hiện phép tính

a)

( )

2

3 3 5x x x+ + −

b)

( )( )

22

12x x x−+

c)

( )( )( )

2 1 3 2 3x x x− + −

Lời giải

a)

( )

2

3 3 5x x x+ + −

22

. .3 .5 3. 3.3 3.5x x x x x x x= + − + + −

32

6 4 15x x x= + + −

b)

( )( )

22

12x x x−+

2 2 2 2

. .2 2x x x x x x= + − −

4 3 2

22x x x x= + − −

c)

( )( )( )

2 1 3 2 3x x x− + −

( )( )

2 .3 2 .2 3 2 3x x x x x= + − − −

( )

2

6 2 3x x x= + − −

22

6 .3 6 . .3 . 2.3 2.x x x x x x x= − + − − +

2 3 2

18 6 3 6 2x x x x x= − + − − +

32

6 17 5 6x x x= − + + −

Bài 3. Làm phép chia:

a.

2 4 3

9 :12x y z xy

b.

2 2 2 1 2 4

1

:

5

n n n n

x y x y

−−

c.

4 3 5 4 2

12 4

:

25 5

x y z x yz



−





Lời giải

a)

3

4

xyz

b)

4

5xy

c)

23

3

5

yz

−

Bài 4. Tìm x, biết:

Trang 53

a)

( ) ( )

43

3 2 3 2

3 1 :3 1 15a x a x− − =

b)

( ) ( )

21

3 3 5 2

2 1 : x 2 1 3 :3 0

mm

x x x

+−

− − − =

Lời giải

a)

( ) ( )

43

3 2 3 2

3 1 :3 1 15a x a x− − =

( ) ( )

43

3 2 3 2

3 1 :3 1 15a x a x− − =

2

1 15x −=

4, 4xx= = −

b)

( ) ( )

21

3 3 5 2

2 1 : x 2 1 3 :3 0

mm

x x x

+−

− − − =

( )

3

2 1 3 0x − − =

2 1 3x −=

2x =

Bài 5. Thực hiện phép tính

a)

3 5 4 4 5 2 3 2

(15 20 5 ):( 5 )x y x y x y x y− − −

b)

( ) ( ) ( ) ( )

5 4 3 3

15 10 20 :5x y x y y x y x



− − − − − −



Lời giải

a)

3 2 2

34y xy x− + +

b)

( ) ( ) ( ) ( )

5 4 3 3

15 10 20 :5y x y x y x y x



− − − − − − −



( ) ( )

2

3 2 4y x y x= − − − − −

Bài 6. Thực hiện phép tính

a)

( )

4 2 3 3 2 2 2 2

8 2 4 :2A x y x y x y x y= − +

b)

3 2 2 3 2 2

1 2 3

:

2 3 4

B x y x y xy xy



= − +





c)

( )

4 2 3 3 2 2 2 4 5 3

11

8 2 : 2 4 3 :

23

C x y x y x y x y xy xy



= − − −





Lời giải

a)

( )

4 2 3 3 2 2 2 2

8 2 4 :2A x y x y x y x y= − +

2

42x xy= − +

.

b)

3 2 2 3 2 2

1 2 3

:

2 3 4

B x y x y xy xy



= − +





2

4 2 8

3 3 9

x xy= − +

Trang 54

c)

( )

4 2 3 3 2 2 2 4 5 3

11

8 2 : 2 4 3 :

23

C x y x y x y x y xy xy



= − − −





22

27

49

2

x xy xy y= − − +

22

29

49

2

x xy y= − +

Bài 7. Rút gọn các biểu thức sau

a)

( )

2 2 2

2 3 5 1x x x x x− − + +

b)

( ) ( )

( )

2

3 5 5 1 8 3x x x x x− − − − −

c)

( ) ( )

22

1 1 1

6 5 2 6

2 2 2

x x x x x



− − + + +





Lời giải

a)

( )

2 2 2

2 3 5 1x x x x x− − + +

3 3 2 2

2 3 5x x x x x= − − − +

3

33xx= − −

b)

( ) ( )

( )

2

3 5 5 1 8 3x x x x x− − − − −

2 2 2

3 15 5 5 8 24x x x x x= − − + − +

20 24x= − +

c)

( ) ( )

22

1 1 1

6 5 2 6

2 2 2

x x x x x



− − + + +





3 2 3

5 1 1

3 2 3

2 2 2

x x x x x= − − − + +

32

5

3

2

xx= − +

Bài 8. Rút gọn rồi tính giá trị các biểu thức sau

a)

( ) ( )

2 2 2

2 3 5 3A x x x x x x= + − − −

tại

2x =

.

b)

( )

2 2 2

6 4 2 4 2 3C x x x x x x x= − − − + − +

tại

4x =−

.

Lời giải

a) Ta có:

( ) ( )

2 2 2 2 2 2

2 3 5 3 2 .3 2 .5 .3 .A x x x x x x x x x x x x x x= + − − − = + − + −

3 2 3 2 3 2

6 10 3 7 4 10x x x x x x x x= + − + − = − +

Tại

2x =

thay vào ta được:

32

7.2 4.2 10.2 56 16 20 60A = − + = − + =

Vậy

60A =

tại

2x =

b) Ta có:

( )

2 2 2

6 4 2 4 2 3C x x x x x x x= − − − + − +

2 3 2 3 2

6 6 4 2 4 8 12x x x x x x x= − − + + − +

12 6 6x x x= − =

Trang 55

Tại

4x =−

thay vào ta được:

( )

6 4 24C = − = −

Vậy

24C =−

. tại

4x =−

Bài 9. Tính giá trị các biểu thức sau

a)

( )

14 13 12 11 2

10 10 10 ... 10 10 10P x x x x x x x= − + − + + − +

tại

9x =

b)

( )

15 14 3 12 2

8 8 8 ... 8 8 5Q x x x x x x x= − + − + − + −

tại

7x =

Lời giải

a) Vì

9x =

nên

1 10x +=

do đó

( )

14 13 12 11 2

10 10 10 ... 10 10 10P x x x x x x x= − + − + + − +

( ) ( ) ( ) ( )

14 13 12 11

1 1 1 ... 1 1x x x x x x x x x x= − + + + − + + − + + +

14 14 13 13 12 12 11 3 2 2

... 1x x x x x x x x x x x x= − − + + − − + + + − − + +

1=

Vậy giá trị của

( )

14 13 12 11 2

10 10 10 ... 10 10 10P x x x x x x x= − + − + + − +

tại

9x =

là

1

b)

( )

15 14 13 12 2

8 8 8 ... 8 8 5Q x x x x x x x= − + − + − + −

tại

7x =

Vì

7x =

nên

18x +=

do đó

( )

15 14 13 12 2

8 8 8 ... 8 8 5Q x x x x x x x= − + − + − + −

( ) ( ) ( ) ( ) ( )

15 14 13 12 2

1 1 1 ... 1 1 5x x x x x x x x x x x= − + + + − + + − + + + −

15 15 14 14 13 13 12 3 2 2

... 5x x x x x x x x x x x= − − + + − − + − − + + −

5x=−

Thay

7x =

vào biểu thức

5x −

ta được

7 5 2−=

Vậy giá trị của

( )

15 14 13 12 2

8 8 8 ... 8 8 5Q x x x x x x x= − + − + − + −

tại

7x =

là

2

.

Bài 10. Tìm x, biết:

a)

3(2 1) 5( 3) 6(3 4) 24x x x− − − + − =

c)

2 (5 3 ) 2 (3 5) 3( 7) 3x x x x x− + − − − =

b)

22

2 3( 1) 5 ( 1)x x x x+ − = +

d)

3 ( 1) 2 ( 2) 1x x x x x+ − + = − −

.

Giải

a)

3(2 1) 5( 3) 6(3 4) 24x x x− − − + − =

6 3 5 15 18 24 24x x x− − + + − =

36

19 36

19

xx=  =

b)

22

2 3( 1) 5 ( 1)x x x x+ − = +

22

5 3 5 5x x x− = +

53x =−

3

5

x =−

c)

2 (5 3 ) 2 (3 5) 3( 7) 3x x x x x− + − − − =

22

10 6 6 10 3 21 3x x x x x− + − − + =

3 18 6xx− = −  =

Trang 56

d)

3 ( 1) 2 ( 2) 1x x x x x+ − + = − −

22

3 3 2 4 1x x x x x+ − − = − −

2

1x =−

Không tồn tại x vì

2

0x 

với mọi x.

Bài 11. Chứng minh rằng giá trị các biểu thức sau không phụ thuộc vào biến

x

.

a)

( ) ( )

( )

22

5 3 1 6 10 3x x x x x x x x− − − + − − +

b)

( )

22

1 1 5x x x x x x+ + − + − +

Lời giải

a)

( ) ( )

( )

22

5 3 1 6 10 3x x x x x x x x− − − + − − +

2 3 2 3 2

5 3 6 10 3x x x x x x x= − − + + − − +

10=−

Vậy biểu thức trên không phụ thuộc vào biến

x

.

b)

( )

22

1 1 5x x x x x x+ + − + − +

3 2 3 2

5x x x x x x= + + − − − +

5=

Vậy biểu thức sau không phụ thuộc vào biến

x

.

Bài 12. Chứng minh rằng: Với mọi số nguyên

n

, ta có:

a)

( )

23

3 1 2 2 5n n n n+ − + − +

.

b)

( )( ) ( )( )

6 1 5 3 5 2 1 2n n n n+ + − + −

.

c)

( ) ( )( )

5 3 2 6n n n n+ − − +

.

Lời giải

a)

( )

23

3 1 2 2 5n n n n+ − + − +

Ta có:

( )

23

3 1 2 2n n n n+ − + − +

2 2 33

223 6 2n n n n nn+ − += + − + −

2

5 5n n= +

( )

5 15nn= +

b)

( )( ) ( )( )

6 1 5 3 5 2 1 2n n n n+ + − + −

Ta có:

( )( ) ( )( )

6 1 5 3 5 2 1n n n n+ + − + −

22

6 30 5 6 3 10 5n n n n nn= + + + − + − +

Trang 57

24 10n=+

( )

2. 12 5 2n=+

c)

( ) ( )( )

5 3 2 6n n n n+ − − +

Ta có:

( ) ( )( )

5 3 2n n n n+ − − +

22

5 2 3 6n n n n n= + − − + +

66n=+

( )

661n= +

Bài 13. Tìm ba số tự nhiên liên tiếp, biết tích của hai số sau lớn hơn tích của hai số

đầu là 52.

Lời giải

Gọi 3 số tự nhiên liên tiếp lần lượt là

( )

; 1; 2x x x x+ + 

Tích hai số sau là:

( )( )

12xx++

tích hai số đầu là

( )

1xx+

Theo bài ra ta có

( )( ) ( )

1 2 1 52x x x x+ + − + =

Giải ta tìm được

25x =

(thỏa mãn).

Vậy ba số cần tìm là 25; 26; 27.

Bài 14. Cho

( )

2

5 25P x ax bx= + + +

và

( )

3

125Q x x=+

. Với giá trị nào của a và b

thì

PQ=

với mọi x.

Lời giải

Để thì

PQ=

với mọi x thì

( ) ( )

3 2 3

5 5 25 125 125ax a b x b x x+ + + + + = +

với mọi

x

1

50

5 25 0

a

ab

b

=





+=





+=



1, 5ab= = −

Tuần 7

Tiết 16; 17; 18

Ngày soạn 01/11/2023

Lớp

8A

8B

Ngày dạy:

ÔN TẬP HÌNH CHỮ NHẬT

I. MỤC TIÊU

1. Về kiến thức:

- Củng cố định nghĩa hình chữ nhật là tứ giác có 4 góc vuông, liên hệ được hình chữ

nhật cũng là hình bình hành, hình thang cân.

- Giải thích được hình chữ nhật có 2 đường chéo bằng nhau.

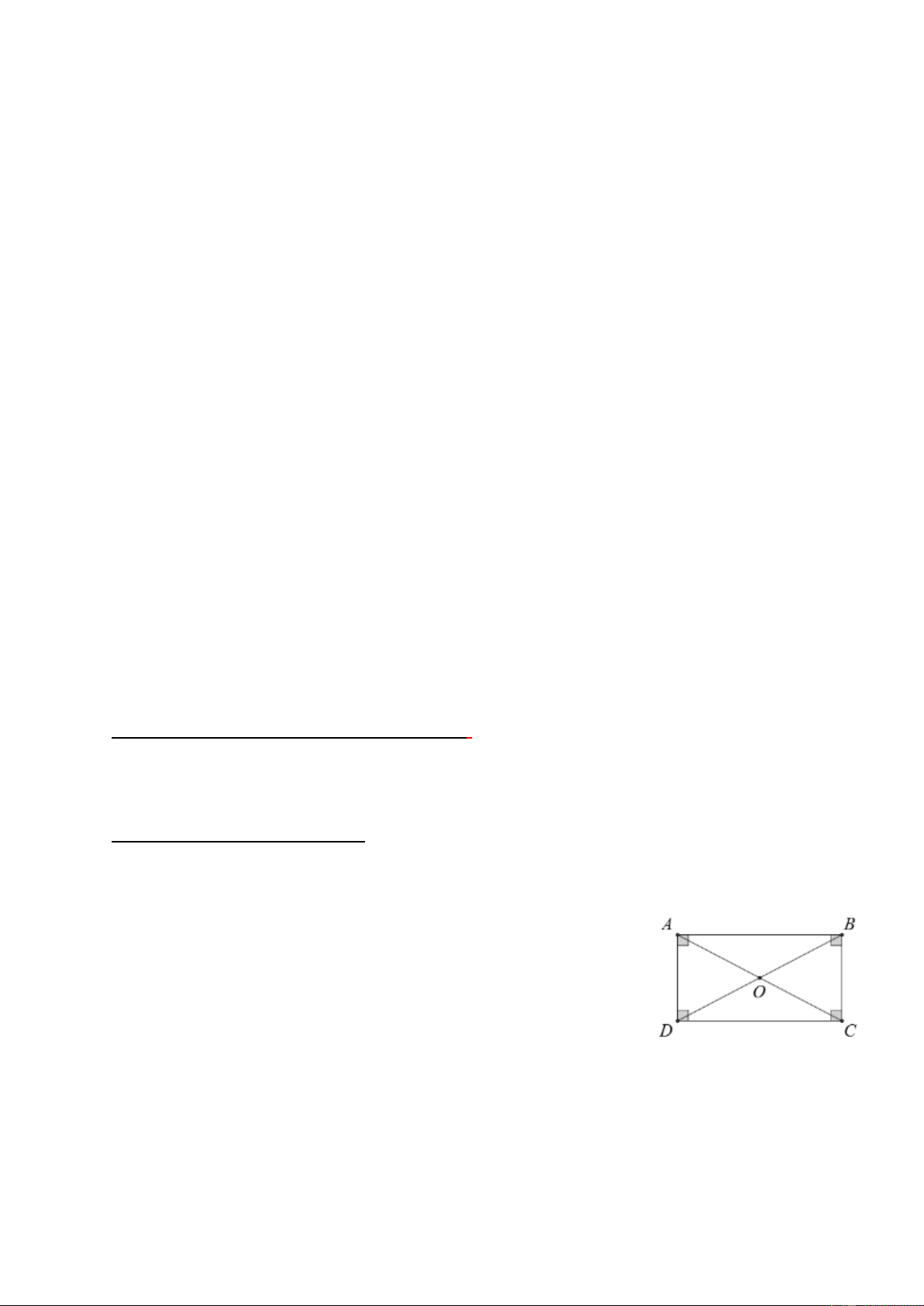
Trang 58

- Củng cố được dấu hiệu hình bình hành có 2 đường chéo bằng nhau là hình chữ nhật.

2. Về năng lực:

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu được định nghĩa hình chữ nhật là tứ giác

có 4 góc vuông, nhận biết và giải thích được tính chất 2 đường chéo của hình chữ

nhật, nhận biết được để một hình bình hành là hình chữ nhật.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng

hợp, khái quát hóa, …

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

 Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông.

Tứ giác

ABCD

là hình chữ nhật

ˆˆ

90 .A B C D = = = = 

 Nhận xét: Hình chữ nhật cũng là một hình bình hành, một hình thang cân.

 Tính chất:

- Hình chữ nhật có tất cả các tính chất của hình bình hành.

- Hình chữ nhật có tất cả các tính chất của hình thang cân.

Trang 59

- Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi

đường.

Nhận xét:

- Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền,

ta có:

1

2

BM AC=

- Nếu một tam giác có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy thì tam

giác đó là tam giác vuông:

Nếu

1

2

BM AC ABC=  

vuông tại

A

 Dấu hiệu nhận biết:

- Hình bình hành có một góc vuông là hình chữ nhật.

- Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

GV: Cho học sinh tóm tắt kiến thức thông qua sơ đồ tư duy

+ Đại diện học sinh lên thuyết trình lại bản đồ tư duy của mình. HS cả lớp ôn lại kiến

thức toàn bài.

M

C

B

A

Trang 60

2. BÀI TẬP

Hoạt động của giáo viên – Học sinh

Nội dung

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài

toán trắc nghiệm 1

-- HS nhận nhiệm vụ GV giao.

- HS tìm hiểu bài toán 1.

Bài tập trắc nghiệm

Câu 1. Chọn phương án đúng nhất:

A. Hình chữ nhật là tứ giác có 4 cạnh bằng

nhau.

B. Hình chữ nhật là tứ giác có 4 góc vuông.

C. Hình chữ nhật là tứ giác có hai góc

vuông.

D. Các phương án trên đều không đúng.

Câu 2. Tìm câu sai trong các câu sau

A. Trong hình chữ nhật hai đường chéo bằng

Dạng 1: Chứng minh 1 tứ giác là

hình chữ nhật

Bài 1: Bài tập trắc nghiệm

Đáp án:

1. B

2. C

3. A

Trang 61

nhau.

B. Trong hình chữ nhật hai đường chéo cắt

nhau tại trung điểm của mỗi đường.

C. Trong hình chữ nhật hai cạnh kề bằng

nhau.

D. Trong hình chữ nhật giao của hai đường

chéo là tâm của hình chữ nhật đó.

Câu 3. Các dấu hiệu sau dấu hiệu nhận biết

nào chưa đúng

A. Hình bình hành có hai đường chéo cắt

nhau tại trung điểm của mỗi đường là hình

chữ nhật.

B. Tứ giác có ba góc vuông là hình chữ nhật.

C.Hình thang cân có một góc vuông là hình

chữ nhật.

D. Hình bình hành có hai đường chéo bằng

nhau là hình chữ nhật.

* Thực hiện nhiệm vụ:

- Yêu cầu HS hoạt động cá nhân trả lời câu

hỏi trắc nghiệm của bài toán 1.

HS trả lời các câu hỏi được GV đề xuất

trong bài toán 1

+ Trong HCN hai cạnh đối bằng.

*Kết luận, nhận định:

- GV đánh giá, nhận xét đáp án chính xác

của bài tập.

- GV khai thác thêm:

+ Câu 2: Vì sao ý B lại sai? Em hãy sửa lại

cho đúng?

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 2

“ Cho tứ giác

ABCD

có

AC BD O⊥

.

Gọi

, , ,E F G H

lần lượt là trung điểm của các

Bài 2: Hướng dẫn giải

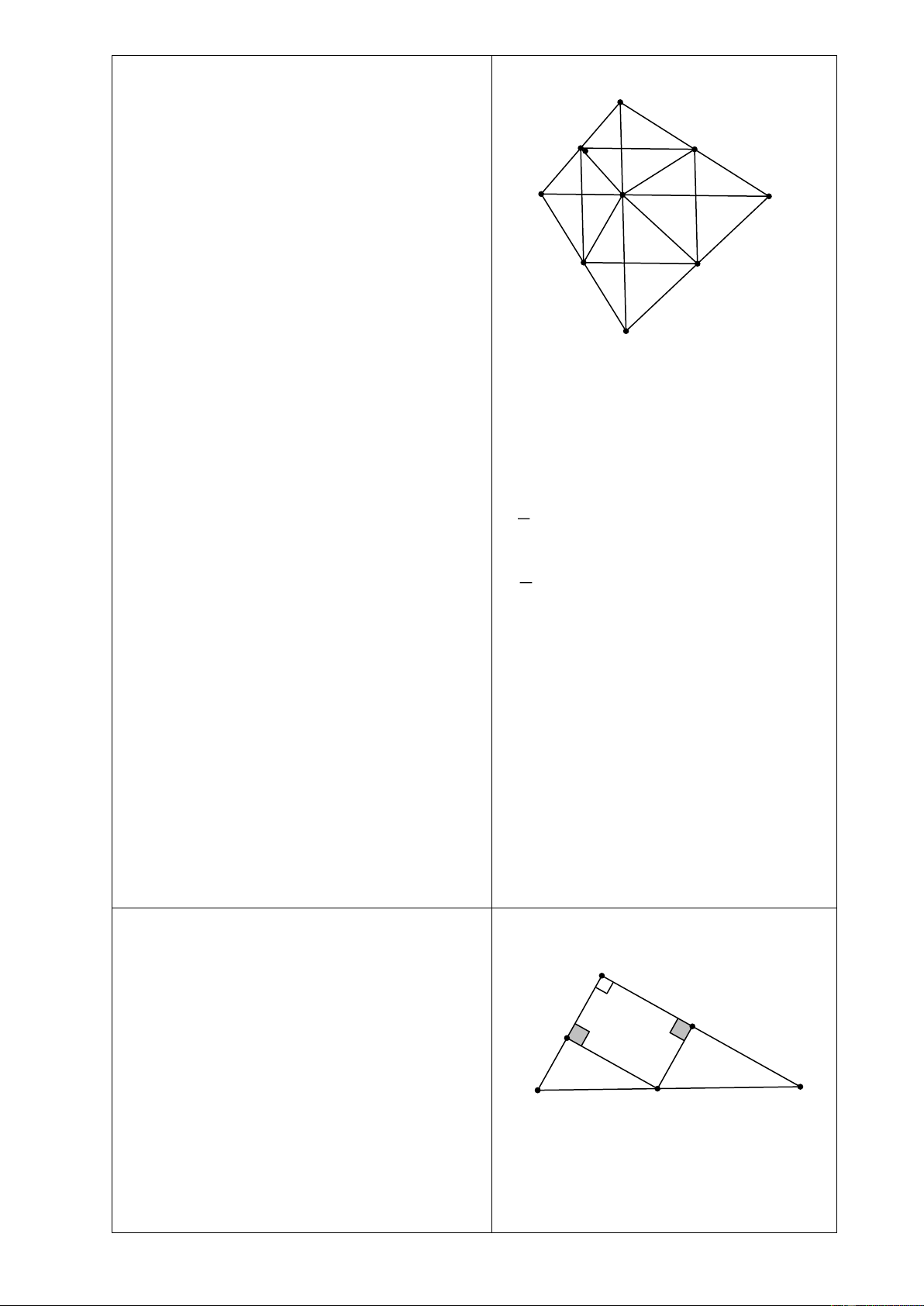
Trang 62

cạnh

, , ,AB BC CD DA

.

Chứng minh rằng

a.

OE OF OG OH+ + +

bằng nửa chu vi tứ

giác

ABCD

b. Tứ giác

EFGH

là hình chữ nhật.

- HS tìm hiểu bài toán 2. Xác định GT-KL

của bài toán.

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện (đưa ra

một số gợi ý)

- HS hoạt động cá nhân vẽ hình vào vở. Một

HS lên bảng vẽ hình

- HS trả lời các câu hỏi của GV:

+

, , ,OE OF OG OH

có quan hệ như thế nào

với

, , ,AB BC CD DA

+ Chứng minh

EFGH

là hình chữ nhật theo

dấu hiệu hình bình hành có 1 góc vuông.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và

một số lưu ý

- HS tìm hiểu bài toán 2. Xác định GT-KL

của bài toán.

a. Ta có

OE OF OG OH+ + +

1

= ( )

2

AB BC CD DA+ + +

1

2

ABCD

P=

b. Có

//EF GH

EF GH







=



EFGH

là hình

bình hành (dấu hiệu nhận biết)

Mặt khác

//EF //

AC BD BD EF

AC BD EH

⊥⊥









EH EF EFGH ⊥ 

là hình chữ

nhật (dhnb)

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 3

Cho tam giác

ABC

vuông cân tại

C

. Trên

cạnh

,AC BC

lấy lần lượt các điểm

,PQ

sao

cho

AP CQ=

. Từ điểm

P

vẽ

//PM BC

(

M

thuộc

AB

).

Chứng minh tứ giác

PCQM

là hình chữ

nhật

- HS tìm hiểu bài toán 3. Xác định GT-KL

Bài 3

Ta có

ABC

vuông cân

45A APM =   

vuông cân

H

G

F

D

E

C

B

A

Q

P

M

C

B

A

Trang 63

của bài toán.

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện (đưa ra

một số gợi ý)

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và

một số lưu ý

AP PM=

Theo giả thiết

AP CQ PM CQ=  =

Lại có

//PM CQ PMCQ

là hình

bình hành

Mặt khác

ˆ

90C PMCQ=   

là hình

chữ nhật (dhnb)

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 4

Cho tam giác

ABC

cân tại

A

, các đường

trung tuyến

,BD CE

cắt nhau tại

O

. Gọi

D

là trung điểm của

MO

,

E

là trung điểm của

ON

Tứ giác

BNMC

là hình gì? Vì sao?

- HS tìm hiểu bài toán 4. Xác định GT-KL

của bài toán.

- HS hoạt động cá nhân vẽ hình vào vở. Một

HS lên bảng vẽ hình

- HS trả lời các câu hỏi của GV:

Dự đoán tứ giác

BNMC

là hình chữ nhật

theo dấu hiệu nhận biết hình bình hành có 2

đường chéo bằng nhau.

.

Bài 4

Tứ giác

BNMC

là hình chữ nhật

Giải thích:

OD DM=

O

là trọng tâm của

ABC

nên

2BO OD BO OM=  =

Chứng minh tương tự ta có:

CO ON=

Tứ giác

BNMC

có hai đường chéo cắt

nhau tại trung điểm của mỗi đường nên

là hình bình hành

Có

( )

11

..BDC CEB c g c B C =   =

BO CO BM CN =  =

Hình bình hành

BNMC

có hai đường

chéo bằng nhau nên là hình chữ nhật.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 5

Cho

ABC

vuông tại

A

, có

AM

là đường

Dạng 2: Vận dụng tính chất của

HCN để chứng minh quan hệ bằng

nhau, song song, vuông góc, đồng

quy, tính độ dài các đoạn thẳng

D

E

O

N

M

C

B

A

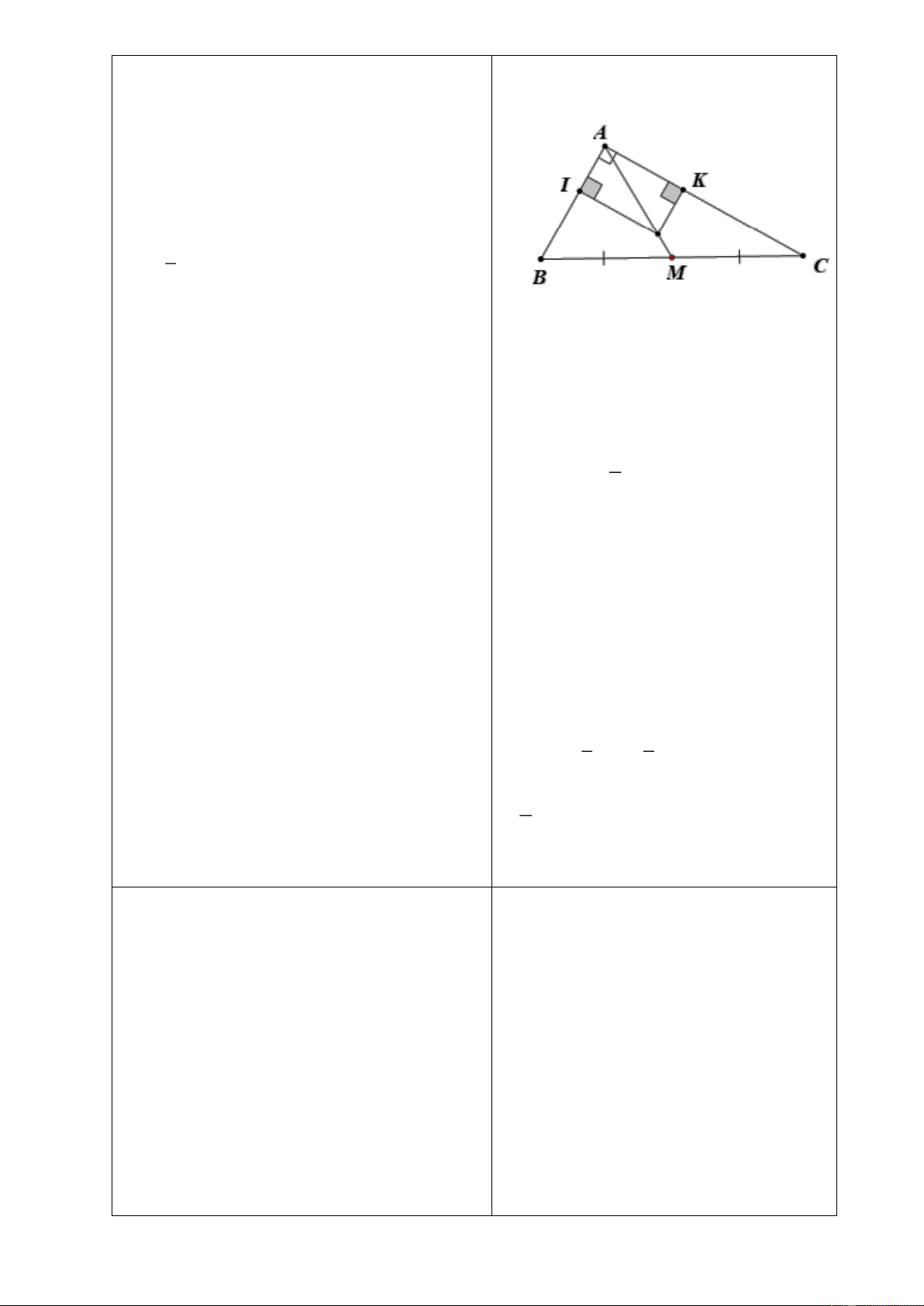
Trang 64

trung tuyến. Gọi

D

là một điểm thuộc

AM

.

Kẻ

DI

vuông góc với

AB

,

DK

vuông góc

với

AC

a) Chứng minh rằng

//IK BC

b) Xác định vị trí điểm

D

trên

AM

sao cho

1

3

IK BC=

- HS tìm hiểu bài toán 5. Xác định GT-KL

của bài toán.

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện :

Cách giải: Áp dụng các tính chất của hình

chữ nhật

- Áp dụng tính chất đường trung tuyến trong

tam giác vuông

- HS hoạt động cá nhân vẽ hình vào vở. Một

HS lên bảng vẽ hình

- HS dưới lớp trình bày vào vở

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và

một số lưu ý

Bài 5: Hướng dẫn giải

a) Dễ dàng chứng minh được

AIKD

là

DAI KAI=

ABC

vuông tại

A

có

1

2

AM MB BC==

( do

AM

là trung

tuyến ứng với cạnh huyền

BC



AMB

cân (tính chất)

//

DAI MBA

KIA MBA IK BC

=

 = 

b)

11

.2

33

IK AD

AD BC AM

=

 = =

2

3

AM D=

là trọng tâm của

ABC

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 7

Cho tam giác

ABC

vuông tại

A

, đường cao

AH

. Gọi

,IK

theo thứ tự là trung điểm của

,AB AC

. Chứng minh

a.

90IHK =

b. Chu vi tam giác

IHK

bằng nửa chu vi

tam giác

ABC

Dạng 3:

Sử dụng định lí thuận và đảo của

đường trung tuyến ứng với cạnh

huyền trong tam giác vuông

Bài 6

D

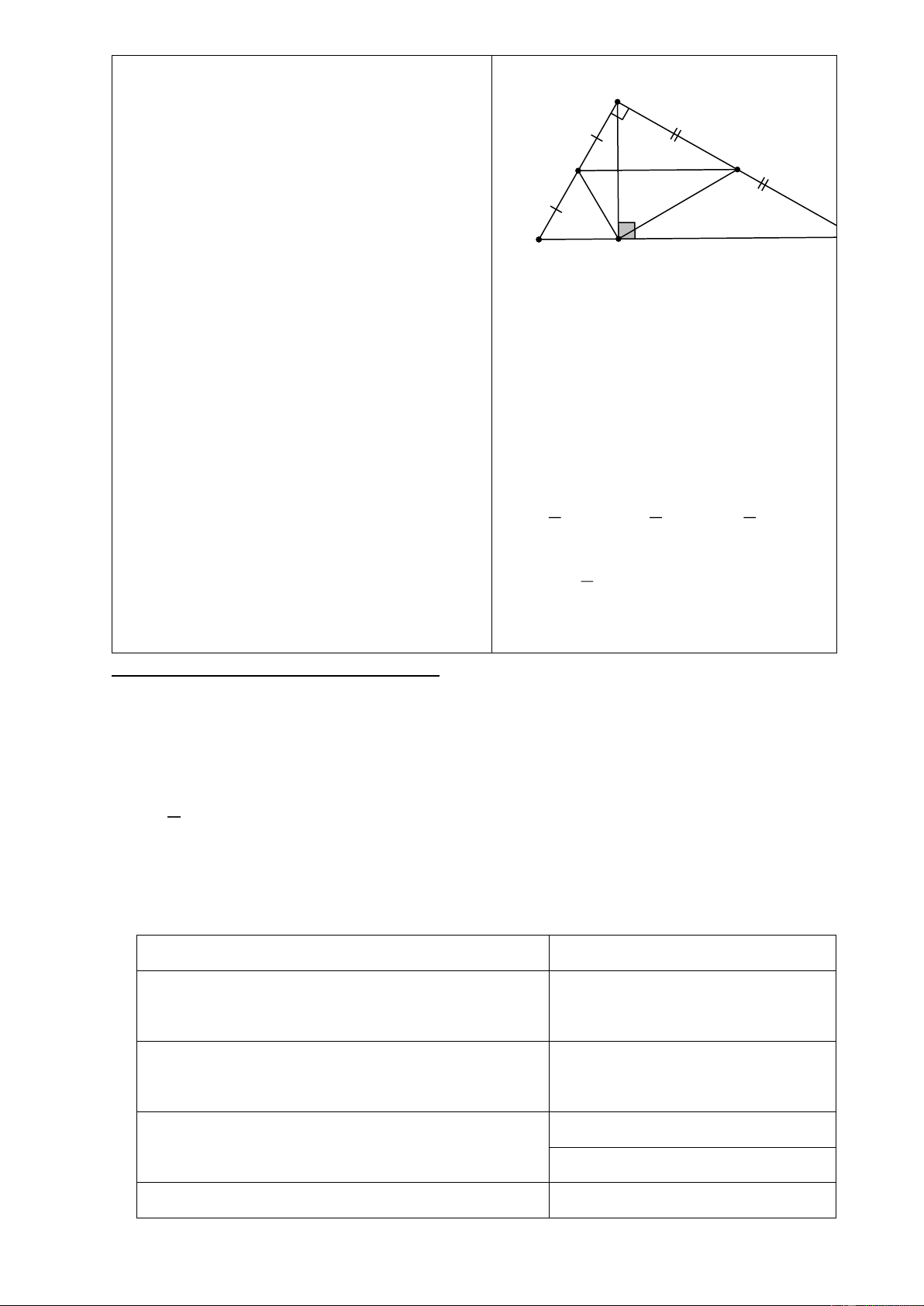
Trang 65

- HS tìm hiểu bài toán 7. Xác định GT-KL

của bài toán.

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện :

Cách giải: Sử dụng định lý về tính chất

đường trung tuyến ứng với cạnh huyền của

tam giác vuông để chứng minh các hình

bằng nhau hoặc chứng minh tam giác vuông

- HS dưới lớp trình bày vào vở

- HS hoạt động cá nhân vẽ hình vào vở. Một

HS lên bảng vẽ hình

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và

một số lưu ý

a) Ta có:

,IAH KAH

cân tại

I

và

K

,IHA IAH HAK AHK = =

90IHK = 

b. Ta có

1 1 1

,,

2 2 2

IH AB HK BC IK BC= = =

1

2

IHK ABC

PP=

(đpcm)

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ ….

1. TRẮC NGHIỆM

Câu 1. Hãy chọn câu trả lời đúng. Hình bình hành ABCD là hình chữ nhật khi:

A.

AB BC=

B.

AC BD=

C.

BC CD=

D.

AC BD⊥

Câu 2. Nối các ý ở cột A với mỗi ý ở cột B để được kết luận đúng

A

B

a. Tứ giác có hai cạnh đối song song, hai cạnh

đối kia bằng nhau và không song song

1. là hình thoi

b. Tứ giác có hai đường chéo cắt nhau tại trung

điểm của mỗi đường

2. là hình thang cân

c. Tứ giác có hai cạnh đối song song và hai góc

đối bằng

90 .

3. là hình bình hành

4. là hình chữ nhật

Đáp án: a - 2; b – 3; c - 4

H

K

I

C

B

A

Trang 66

Câu 3. Cho hình chữ nhật

ABCD

có

8cm, 6cmAB BC==

(hình 2). Các điểm

, , ,M N P Q

là trung điểm của các cạnh hình chữ nhật. Tổng diện tích các tam giác

trong hình bên là

A.

2

4cm .

B.

2

6cm .

C.

2

12cm .

D.

2

24cm .

Câu 4. Trong tam giác vuông trung tuyến ứng với cạnh huyền có độ dài là 5

cm khi đó độ dài cạnh huyền là:

A. 10 cm.

B. 2,5 cm.

C. 5 cm.

D. Cả A,B,C đều sai.

Câu 5: Chọn câu sai. Tứ giác

ABCD

là hình chữ nhật khi:

A.

90

ˆˆ

A B C= = = 

.

B.

90

ˆˆ

A B C= = = 

;

// AB CD

.

C.

AB CD AD BC= = =

.

D.

// ; AB CD AB CD=

và

AC BD=

.

Câu 6: Cho tam giác

ABC

vuông tại

A

,

6AC cm=

, điểm

M

thuộc cạnh

BC

.

Gọi

,DE

theo thứ tự là các chân đường vuông góc kẻ từ

M

đến

,AB AC

. Chu vi

của tứ giác

ADME

bằng:

A.

6cm

.

B.

36cm

.

C.

18cm

.

D.

12cm

.

2. TỰ LUẬN

Bài 1. Cho tam giác

ABC

, đường cao

AH

. Gọi

I

là trung điểm của

AC

. Lấy

I

là

trung điểm

IH

. Gọi

,MN

lần lượt là trung điểm của

,HC CE

. Các đường thẳng

,AM AN

cắt

HE

tại

G

và

K

a. Chứng minh tứ giác

AHCE

là hình chữ nhật.

D

N

Q

P

M

C

B

A

Trang 67

b. Chứng minh

HG GK KE==

.

Bài 2.

Cho tam giác

ABC

vuông tại

A

,

M

thuộc

BC

. Gọi

D

và

E

là chân đường vuông

góc kẻ từ

M

đến

AB

và

AC

a. Định dạng tứ giác

ADME

.

b. Gọi

I

là trung điểm của

DE

. Chứng minh

,,A I M

thẳng hàng.

c. Điểm

M

nằm ở đâu trên

BC

thì

DE

nhỏ nhất. Tính

DE

trong trường hợp đó biết

15cm,AB =

20cmAC =

Bài 3

Cho tam giác

ABC

vuông tại

A

. Về phía ngoài tam giác

ABC

, vẽ hai tam giác vuông

cân

( )

ADB DA DB=

và

( )

ACE AE EC=

. Gọi

M

là trung điểm của

BC

,

I

là giao

điểm của

DM

với

AB

, và

K

là giao điểm của

EM

với

AC

. Chứng minh:

a) Ba điểm

,,D A E

thẳng hàng.

b) Tứ giác

IAKM

là hình chữ nhật.

c) Tam giác

DME

là tam giác vuông cân.

Bài 4

Cho hình thang vuông

ABCD

(

90AD= = 

) có các điểm

E

và

F

thuộc cạnh

AD

sao cho

AE DF=

và

90BFC =

. Chứng minh

90BEC =

Hướng dẫn

Bài 1

a. Chứng minh tứ giác

AHCE

là hình bình hành, có

90AHC AHCE=   

là hình chữ nhật

b. Chứng minh

,GK

lần lượt là các trọng tâm của tam giác

,AHC AEC

và sử dụng

tính chất 2 đường chéo của hình chữ nhật

Bài 2

K

I

H

E

N

G

M

C

B

A

Trang 68

HD

a. Tứ giác

ADME

có 3 góc vuông nên là hình chữ nhật

c. DE nhỏ nhất khi

AM

nhỏ nhất (

DE AM=

).

AM

nhỏ nhất khi và chỉ khi

AM AH=

khi

M

trùng

H

Xét

ABC

vuông tại

A

25cm( )BC pytago=

11

..

22

ABC

S AH BC AB AC = =

. 15.20

12 cm

25

AB AC

AH

BC

 = = = ()

Bài 3

HD

a) Chứng minh

180DEA =

b) Chứng minh

90AIM AKM IAK= = = 

c) Chứng minh

DME

có

45EDM DEM= = 

DME

vuông cân ở

M

.

Bài 4

HD

I

H

D

E

M

C

B

A

K

I

D

E

M

C

B

A

Trang 69

Gọi

,IK

lần lượt là trung điểm của

,BC AD

Chú ý

FEI

cân ở

I

Chứng minh:

IE IB IC EBC− =  

vuông tại

90E BEC = 

.

Tuần 8

Tiết 19; 20; 21

Ngày soạn 01/11/2023

Lớp

8A

8B

Ngày dạy:

ÔN TẬP BÀI TẬP CUỐI CHƯƠNG I

I. MỤC TIÊU

1. Về kiến thức:

- Nhận biết được các đơn thức, đa thức

- Thu gọn được các đơn thức, các đa thức

- Thực hiện được các phép tính cộng, trừ, nhân, chia các đơn thức, các đa thức

2. Về năng lực:

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được các đơn thức, đa thức.

D

K

D

F

E

C

B

A

Trang 70

- Năng lực tư duy và lập luận toán học: HS thu gọn được các đơn thức, các đa thức.

- Năng lực giải quyết vấn đề toán học: Thực hiện được các phép tính cộng, trừ, nhân,

chia các đơn thức, các đa thức.

- Năng lực mô hình hóa toán học: Sử dụng được các kí hiệu, cách diễn đạt toán học

để thu gọn được một đa thức, tính toán được các phép tính về đa thức thu gọn, đơn

thức đồng dạng.

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: Có ý thức trong hoạt động làm việc nhóm, hoàn thành đầy đủ, có chất

lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm, đồ dùng học tập.

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

- Khái niệm về đơn thức, đa thức

+ Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của

những số và biến.

Ví dụ:

24

1

, , ,...

2

x xy xyx−

là những đơn thức

+ Hai đơn thức đồng dạng là hai đơn thức với hệ số khác 0 và có phần biến giống

nhau

Ví dụ:

55

2

,5

5

xx−

là hai đơn thức đồng dạng

+ Đa thức là tổng của những đơn thức, mỗi đơn thức trong tổng gọi là một hạng tử của

đa thức đó.

Ví dụ:

5 3 2 3

3x 9x 2,5x 4xy, 9xy 3y− + − − +

, ... là các đa thức

+ Cộng (hay trừ) hai đa thức là thu gọn đa thức nhận được sau khi nối hai đa thức đã

cho bởi dấu “+” (hay dấu “-“)

+ Muốn nhân hai đơn thức, ta nhân hai hệ số với nhau và nhân hai phần biến với nhau.

+ Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa

thức rồi cộng các tích với nhau.

+ Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với

hạng tử của đa thức kia rồi cộng các tích với nhau.

2. BÀI TẬP

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài toán trắc

Dạng 1: Nhận biết các đơn

thức, tính giá trị biểu thức của

Trang 71

nghiệm 1

các đơn thức.

Bài 1: Bài tập trắc nghiệm

Đáp án

1)C 2) B 3) B 4) D 5) A

Bài 1: Trắc nghiệm

1) Biểu thức nào sau đây không là đơn thức:

A.

( )

2

42x y x−

B. 2x C.

2

2xy x−

D. 2022

2) Giá trị của biểu thức M = - 3x

2

y

3

tại x = -1, y = 1 là:

A. 3 B. -3 C. 18 D. -18

3) Đơn thức nào sau đây đồng dạng với đơn thức

2

3xy−

A.

2

3xy−

B.

( 3 )xy y−

C.

2

3( )xy−

D.

3xy−

4) Đơn thức đồng dạng với đơn thức 5x

3

y là :

A. 0x

3

y B. 5x

2

y C. 5x

3

y

2

D. – 3x

3

y .

5) Trong các biểu thức sau đâu là đơn thức:

A. 4xy

2

B. 3-2y

C. 10x +y

D. 5(x+y)

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trả lời câu hỏi trắc

nghiệm của bài toán 1.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 1

1)C 2)B

3)B 4)D 5) A

*Kết luận, nhận định:

GV đánh giá, nhận xét đáp án chính xác của bài

tập.

Đáp án

1)C 2) B 3) B 4) D 5) A

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 2

Bài 2: Thu gọn và chỉ ra phần hệ số, phần biến

và tìm bậc của các đơn thức sau:

1)

22

5x .3xy

2)

( )

3

23

2y . 2y .y

3)

( )

23

1

x y . 2xy

3

−







4)

( )

23

3

x y . xy

4

−



−





5)

4 3 2

5x .4x .3x .2x

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 2.

HS trả lời các câu hỏi được GV đề xuất trong bài

Bài 2: Hướng dẫn giải

Chi tiết

1)

32

15xy

, hệ số là 15, biến là

32

xy

, bậc là 5

2)

12

16y

, hệ số là 16, biến là

12

y

, bậc là 12

3)

34

2

3

xy

−

, hệ số là

2

3

−

, biến

là

34

xy

, bậc là 7

4)

34

3

4

xy

, hệ số là

3

4

, biến là

34

xy

, bậc là 7

5)

10

120x

, hệ số là 120, biến là

10

x

, bậc là 10

- Chốt phương pháp giải:

Áp dụng nguyên tắc về thu gọn

đơn thức rồi sau đó chỉ ra phần

Trang 72

toán 2

1)

32

15xy

2)

12

16y

3)

34

2

3

xy

−

4)

34

3

4

xy

5)

10

120x

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

biến, hệ số và xác định bậc của

đơn thức đó.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 3

Bài 3: Cho đơn thức:

2 2 2

81

A .x y . x y

34

−



=





.

a, Thu gọn đơn thức A, rồi xác định hệ số và tìm

bậc của đơn thức.

b, Tính giá trị của A tại

x 1,y 1= − =

.

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 3.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 3

a)

2 2 2 4 3

8 1 2

A .x y . x y x y

3 4 3

−−



==





hệ số là

2

3

−

, bậc là 7

b) giá trị của biếu thức

43

2

A x y

3

−

=

tại

x 1,y 1= − =

là

2

3

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

Bài 3: Hướng dẫn giải

Chi tiết

a)

2 2 2 4 3

8 1 2

A .x y . x y x y

3 4 3

−−



==





hệ số là

2

3

−

, bậc là 7

b) Thay

x 1,y 1= − =

vào biểu thức

43

2

A x y

3

−

=

ta được:

43

22

A 1 ( 1)

33

−

= − =

Vậy giá trị của biếu thức

43

2

A x y

3

−

=

tại

x 1,y 1= − =

là

2

3

- Chốt phương pháp giải:

Thu gọn đơn thức rồi mới thay

giá trị cho trước của biến để tính

giá trị của đơn thức đã được thu

gọn.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 4

Bài 4: Cho hai đơn thức:

2

3

xy

4

−

và

2

xy z

3

.

a, Tính tích hai đơn thức trên.

b, Xác định hệ số, phần biến, bậc của đơn thức

tích.

Bài 4: Hướng dẫn giải

Chi tiết

a)

2 2 3 3

3 2 1

x y . xy z x y z

4 3 2

−−

   

=

   

   

b)

Hệ số là

1

2

−

Phần biến là

33

x y z

,

bậc của đơn thức là 7

Trang 73

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 4.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 4

a)

2 2 3 3

3 2 1

x y . xy z x y z

4 3 2

−−

   

=

   

   

b) Hệ số là

1

2

−

Phần biến là

33

x y z

, bậc của đơn

thức là 7

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

- Chốt phương pháp giải:

Thực hiện nhân hai đơn thức theo

quy tắc nhân hai đơn thức rồi sau

đó xác định phần biến, hệ số, bậc

của đơn thức tích đã được thu

gọn.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 5

Bài 5: Sắp xếp các đơn thức sau thành nhóm các

đơn thức đồng dạng và tính tổng mỗi nhóm:

32

3x y

,

1

3

2

−

,

5 4 2

x y z

11

,

33

xy

6

−

,

32

1

6 x y

2

,

33

11x y−

,

5 4 2

6x y z−

,

6

1

−

.

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 5.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 5

a)

16

3;

21

−−

1 6 19

3

2 1 2

−

   

− + − =

   

   

b)

3 2 3 2

1

3x y ;6 x y

2

3 2 3 2

32

1

3x y 6 x y

2

19

xy

2

+

=

c)

5 4 2

x y z

; 6x y z

11

−

( )

5 4 2

x y z

6x y z

11

65

x y z

11

+−

−

=

Bài 5: Hướng dẫn giải

Chi tiết

Nhóm đơn thức đồng dạng là:

a)

16

3;

21

−−

ta có:

1 6 19

3

2 1 2

−

   

− + − =

   

   

b)

3 2 3 2

1

3x y ;6 x y

2

ta có:

3 2 3 2 3 2

1 19

3x y 6 x y x y

22

+=

c)

5 4 2

x y z

; 6x y z

11

−

ta có:

( )

5 4 2

5 4 2 5 4 2

x y z 65

6x y z x y z

11 11

−

+ − =

d)

33

xy

; 11x y

6

−

ta có:

( )

33

3 3 3 3

x y 67

11x y x y

66

−−

+ − =

- Chốt phương pháp giải:

Xác định các đơn thức đồng dạng

và sắp xếp vào cùng một nhóm

sau đó tính tổng các đơn thức

đồng dạng đã được sắp xếp theo

nhóm.

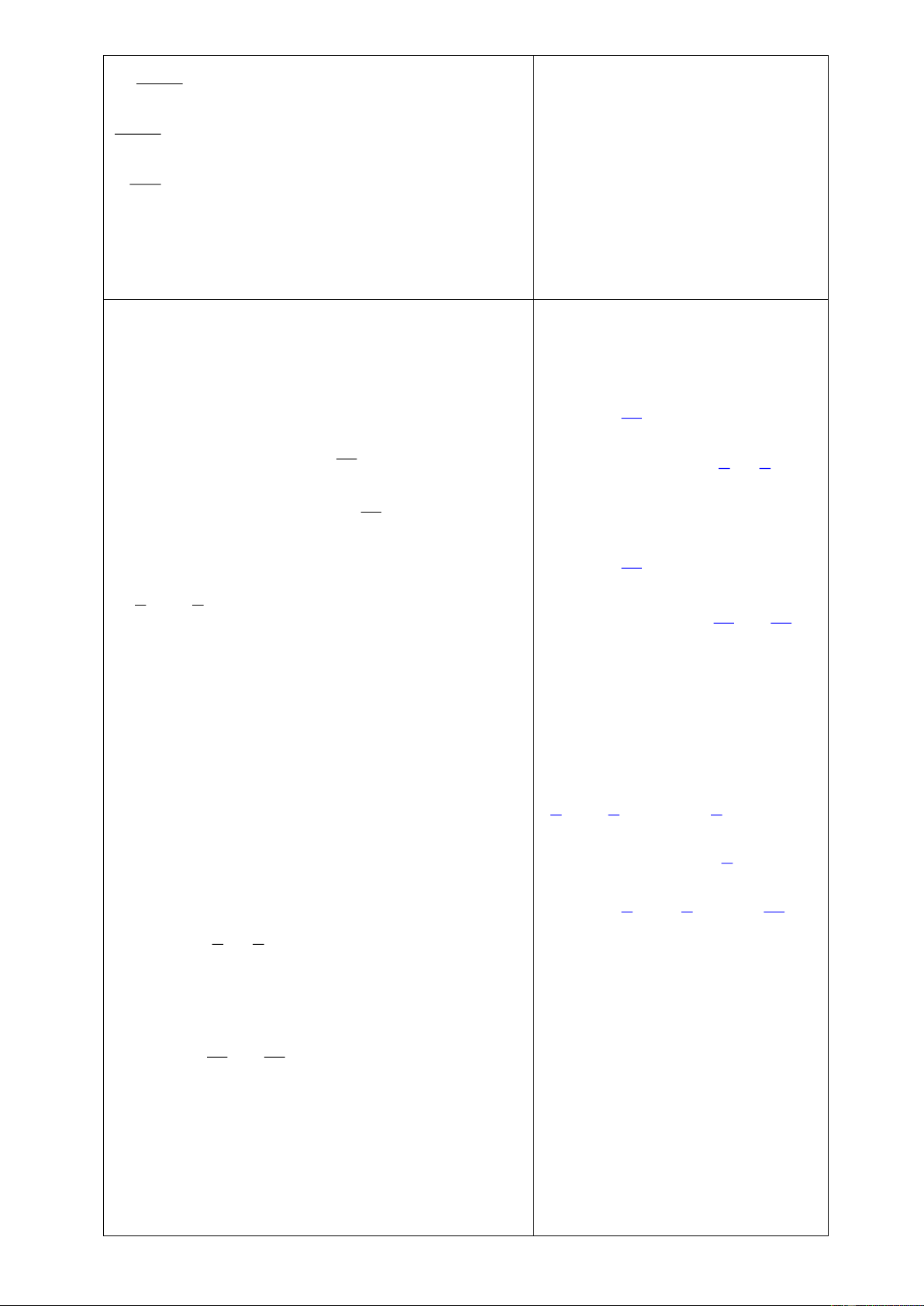
Trang 74

d)

33

xy

; 11x y

6

−

( )

33

xy

11x y

6

67

xy

6

−

+−

−

=

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 6

Bài 6: Thu gọn rồi tính giá trị tổng các đơn thức

sau:

a,

5x 7x 3x 2x− + − −

tại

1

x

2

−

=

.

b,

2 2 2 2

4x 3x 2x x− − + −

tại

1

x

2

−

=

.

c,

( )

4 4 2 2

15x 7x 20x .x+ + −

tại

x1=−

.

d,

5 5 5

13

x y x y x y

24

−+

tại

x 1,y 1= − =

.

e,

2 5 2 5 2 5

13x y 2x y x y−+

tại

x 1,y 2= = −

.

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 6.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 6

a)

5x 7x 3x 2x

3x

− + − −

=−

13

3x 3.

22



− = − − =





b)

2 2 2 2

2

4x 3x 2x x

6x

− − + −

=−

2

13

6x 6.

22

−−



− = − =





c)

( )

4 4 2 2

4

15x 7x 20x .x

2x

+ + −

=

( )

4

2x 2. 1 2= − =

Bài 6: Hướng dẫn giải

Chi tiết

a)Ta có:

5x 7x 3x 2x 3x− + − − = −

Thay

1

x

2

−

=

vào

3x−

ta được:

13

3x 3.

22



− = − − =





b) Ta có:

2 2 2 2 2

4x 3x 2x x 6x− − + − = −

Thay

1

x

2

−

=

vào

2

6x−

ta được:

2

13

6x 6.

22

−−



− = − =





c) Ta có:

( )

4 4 2 2 4

15x 7x 20x .x 2x+ + − =

Thay

x1=−

vào

2

6x−

ta được:

( )

4

2x 2. 1 2= − =

d) Ta có:

5 5 5 5

1 3 3

x y x y x y x y

2 4 4

− + =

Thay

x 1,y 1= − =

vào

5

3

xy

4

ta được:

( )

5

3 3 3

x y 1 1

4 4 4

−

= − =

e) Ta có:

2 5 2 5 2 5 2 5

13x y 2x y x y 12x y− + =

Thay

x 1,y 2= = −

vào

25

12x y

ta được:

( )

5

2 5 2

12x y 12.1 . 2 384= − = −

- Chốt phương pháp giải:

Thu gọn các đơn thức đã cho

trước khi thay giá trị đã cho của

biến để tính giá trị biểu thức đã

được thu gọn,

Trang 75

d)

5 5 5

5

13

x y x y x y

24

3

xy

4

−+

=

( )

5

3 3 3

x y 1 1

4 4 4

−

= − =

e)

2 5 2 5 2 5

25

13x y 2x y x y

12x y

−+

=

( )

5

2 5 2

12x y 12.1 . 2

384

=−

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài toán trắc

nghiệm 1

Dạng 2: Dạng 2: Nhận biết các

đơn thức, tính giá trị biểu thức

của các đa thức.

Bài 1: Bài tập trắc nghiệm

Đáp án

1)C 2) A 3) B 4) C 5) C

Bài 1: Trắc nghiệm

1) Giá trị của biểu thức tại là:

A.0 B. 9 C. -1 D. -2

2) Thu gọn đa thức P = x

3

y – 5xy

3

+ 2 x

3

y + 5 xy

3

bằng

A. 3 x

3

y

B. – x

3

y

C. x

3

y + 10

D. 3 x

3

y - 10xy

3

3) Đa thức

3 2 2 3

2 1 2 5x x x x x x− + + + − + −

có bậc là :

A. 3 B. 2 C.1 D. 5

4) Tổng các hệ số của đa thức 2x

2

– x – 1 là:

A.-1 B.1 C.0 D.2

5) Bậc của đa thức là

A. 7

B. 6

C. 5

D. 4.

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trả lời câu hỏi trắc

nghiệm của bài toán 1.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 1

1)C 2)A

3)B 4)C 5) C

Đáp án

1)C 2) A 3) B 4) C 5) C

2

45x−

1x =−

3 4 3

7 11Q x x y xy= − + −

Trang 76

*Kết luận, nhận định:

GV đánh giá, nhận xét đáp án chính xác của bài

tập.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 2

Bài 2: Trong các biểu thức sau đâu là đa thức:

2

3x

,

2

5x 4xy−

, 18,

3

9xy 3y−+

,

2

4x y 2xy

y5

+

, 0,

2

3

5

−

,

2

6

xy

−

+

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 2.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 2

Các đa thức là:

23

5x 4xy; 9xy 3y− − +

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

Bài 2: Hướng dẫn giải

Chi tiết

Các đa thức là:

23

5x 4xy; 9xy 3y− − +

- Chốt phương pháp giải:

Dựa vào định nghĩa đa thức để

xác định các đa thức trong bài.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 3

Bài 3: Thu gọn rồi tìm bậc của các đa thức sau:

a)

6 5 4 4

A x y x y 1= + + +

b)

( )

22

B 3y x xy 7x y xy= − − +

c)

22

C x 2xy 5x 1= − + −

( )

3 2 2 2 2 2

D 4x yz 4xy z xyz x y z= − − +

d)

22

1

E 3x x 1 2x x

2

= − + + −

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 3.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 3

a)đa thức A có bậc là 6

b)

2 2 3

B 4x y 3xy 7x y= − − −

đa thức B có bậc là 4

Bài 3: Hướng dẫn giải

Chi tiết

a)

6 5 4 4

A x y x y 1= + + +

,

đa thức A có bậc là 6

b)

( )

22

2 2 2 3

2 2 3

B 3y x xy 7x y xy

3x y 3xy 7x y 7x y

4x y 3xy 7x y

= − − +

= − − −

đa thức B có bậc là 4

c)

22

2

C x 2xy 5x 1

6x 2xy 1

= − + −

= − −

đa thức C có bậc là 2

d)

( )

3 2 2 2 2 2

D 4x yz 4xy z xyz x y z

4x yz 4xy z xyz x y z

= − − +

= − − −

đa thức D có bậc là 6

e)

2 2 2

13

E 3x x 1 2x x 2x x 1

22

= − + + − = + +

đa thức E có bậc là 2

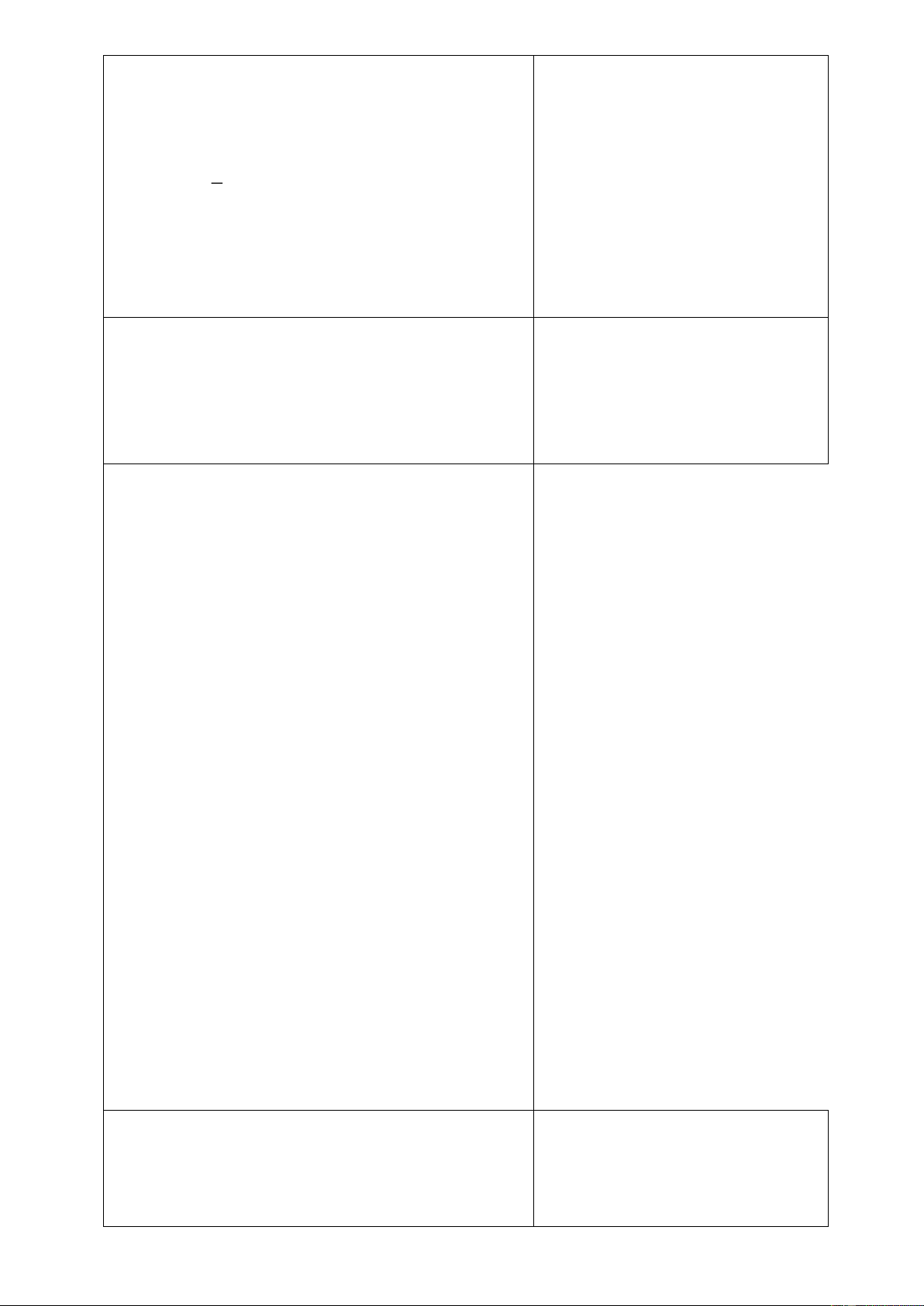
Trang 77

c)

2

C 6x 2xy 1= − −

đa thức C có bậc là 2

d)

3 2 2 2 2 2

D 4x yz 4xy z xyz x y z= − − −

đa thức D có

bậc là 6

e)

2

3

E 2x x 1

2

= + +

đa thức E có bậc là 2

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

- Chốt phương pháp giải:

Thu gọn đa thức trước khi tìm bậc

của đa thức

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài toán trắc

nghiệm 1

Dạng 3: Cộng, trừ đa thức

Bài 1: Bài tập trắc nghiệm

Đáp án

1)A 2) B 3) A 4) D

Bài 1: Trắc nghiệm

1) Tính hiệu hai đa thức

( ) ( )

3x y z 4x 2y 6z+ − − − +

A.

37x y z− + −

B.

37x y z+−

C.

37x y z− + +

D.

37x y z− − −

2) Thu gọn đa thức

( ) ( )

2 2 2 2

3x y 2xy 6 x y 5xy 1− − + + − + −

A.

22

4 3 5x y xy− − +

B.

22

4 3 5x y xy− + +

C.

22

4 3 5x y xy− − −

D.

22

3 3 5x y xy− + +

3)Cho hai đa thức:

22

M x 2yz z= − +

và

22

N 3yz z 5x= − +

.

Tính

MN+

A.

2

6x yz+

B.

2

6x yz−+

C.

22

62x yz z+−

D.

22

6x yz z++

4) Cho hai đa thức:

22

A x 2xy y= − +

và

22

B y 2xy x 1= + + +

.Tính

AB−

.

A.

41xy +

B

4xy−

C.

41xy−−

D.

41xy−+

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trả lời câu hỏi trắc

nghiệm của bài toán 1.

HS trả lời các câu hỏi được GV đề xuất trong bài

Đáp án

1)A 2) B 3) A 4) D

Trang 78

toán 1

1)A 2)B

3)A 4)D

*Kết luận, nhận định:

GV đánh giá, nhận xét đáp án chính xác của bài

tập.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 2

Bài 2: Tính

1)

( ) ( )

3 2 3 3 3

x 6x 5y 2x 5x 7y+ + − − +

2)

( ) ( )

2 2 2 2 2 2

15x y 7xy 6y 2x 12x y 7xy− − + − +

3)

( ) ( )

2 2 3 2

5x y 3xy 7 6x y 4xy 5− + + + − + −

4)

( ) ( )

( )

2 2 2 2

x y 2xy x y 2xy 4xy 1+ − − + + + −

5)

( ) ( ) ( )

2 2 2 2 2 2

3x 2xy y x xy 2y 4x y− + + − + − −

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 2.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 2

1)

3 2 3

x 6x 5x 2y− + − −

2)

2 2 2

3x y 6y 2x−+

3)

2 3 2

5x y 6x y 7xy 5− − + −

4)

1−

5)

2

3xy 2y−+

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

Bài 2: Hướng dẫn giải

Chi tiết

1)

3 2 3

x 6x 5x 2y− + − −

2)

2 2 2

3x y 6y 2x−+

3)

2 3 2

5x y 6x y 7xy 5− − + −

4)

1−

5)

2

3xy 2y−+

- Chốt phương pháp giải:

Áp dụng nguyên tắc cộng trừ các

đa thức rồi tính kết quả

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 3

Bài 3: Tìm x biết:

1)

.14

2

1

).4

2

1

(

4

1

2

−=−− xxx

2)

( )( )

3 1 4 1

4 3 2 3 27

xx

−−

+ − + = −

Bài 3: Hướng dẫn giải

Chi tiết

1)

2 14 7xx= −  = −

2)

43 27 27 0xx− = −  =

3)

1

21 7

3

xx=  =

- Chốt phương pháp giải:

Thu gọn đa thức rồi tìm giá trị của

x.

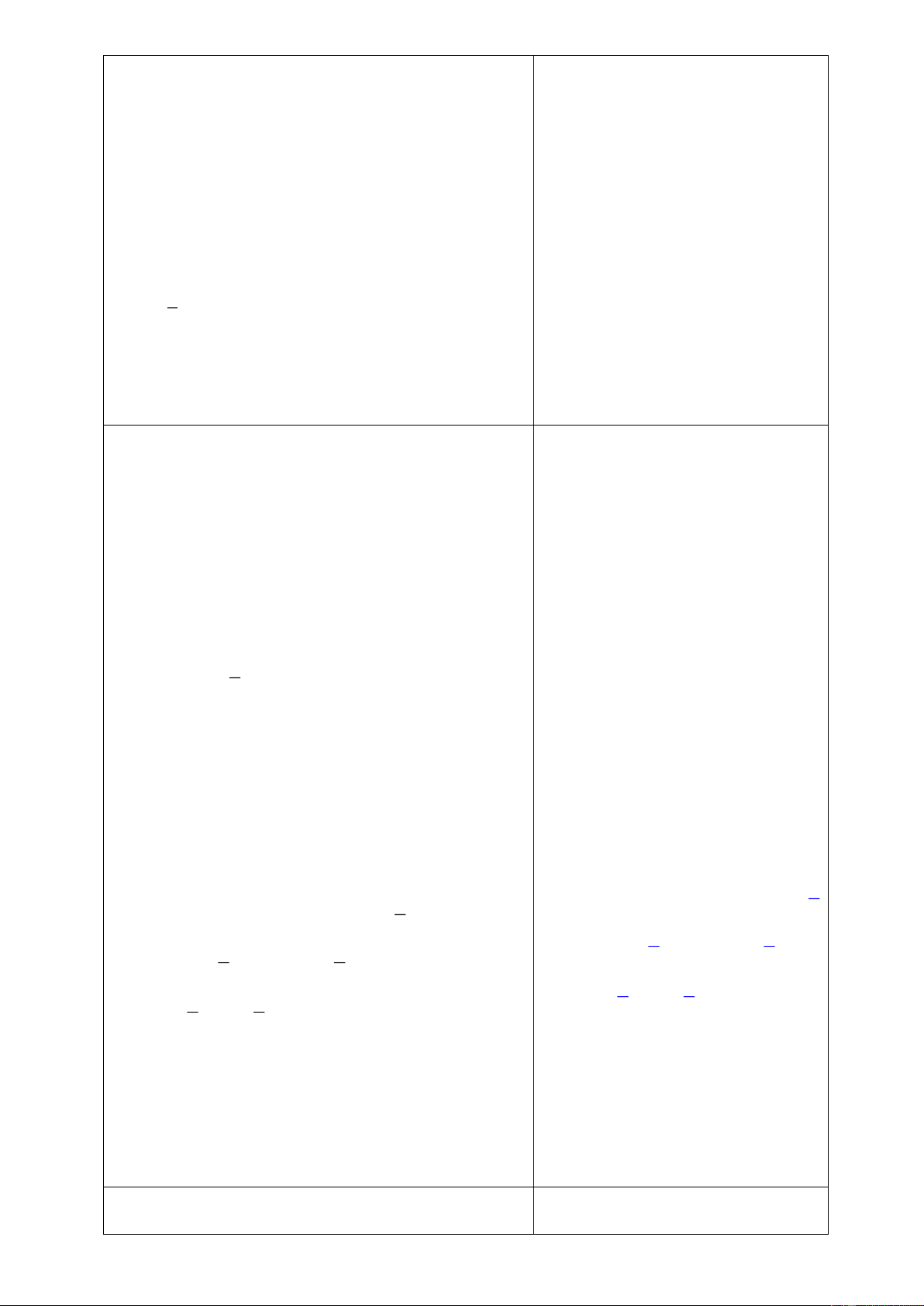
Trang 79

3)

( ) ( )

6 5 3 3 1 – 10 7x x x x+ + =

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 3.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 3

1)

7x =−

2)

0x =

3)

1

3

x =

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 4

Bài 4: Bài 4: Cho các đa thức:

( )

2

3 – 1f x x x=+

và

( )

– 1g x x=

a)Tính

( ) ( )

.f x g x

b)Tìm x để

( ) ( ) ( )

2

. 1 – 3.

5

2

f x g x x g x





+

=



*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 4.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 4

a)

( ) ( )

32

. 3 – 4 2 – 1f x g x x x x=+

b)

( ) ( ) ( )

2

5

. 1 – 3.

2

f x g x x g x+=





55

2 – 1 2 1

22

77

2 x=

24

xx

x

 =  = +

 = 

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

Bài 4: Hướng dẫn giải

Chi tiết

a)Ta có:

( ) ( )

( )

2

3 2 2

32

.

3 – 1 – 1

3 – 3 – – 1

3 – 4 2 – 1

f x g x

x x x

x x x x x

x x x

=+

= + +

=+

b)Ta có:

( ) ( ) ( )

( )

2

32

2

3 2 2

3 2 2 3 2

. 1 – 3.

3 – 4 2 – 1

1 – 3 – 1

3 – 4 2 – 1 1 – 3 3

3 – 4 2 – 1 – 3 3

2 – 1 .

f x g x x g x

x x x

xx

x x x x x

x x x x x x

x

+





=+

+





= + + +

=

Do đó,

( ) ( ) ( )

2

5

. 1 – 3.

2

f x g x x g x+=





55

2 – 1 2 1

22

77

2 x=

24

xx

x

 =  = +

 = 

- Chốt phương pháp giải:

Thực hiện nhân hai đơn thức theo

quy tắc nhân hai đơn thức rồi sau

đó xác định phần biến, hệ số, bậc

của đơn thức tích đã được thu

gọn.

* Giao nhiệm vụ

Bài 5: Hướng dẫn giải

Chi tiết

Trang 80

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 3

Bài 5: Chứng minh các biểu thức sau không phụ

thuộc vào biến số:

1)

( )( )

3 5 2 11

2 3 3 7

A x x

xx

= − +

− + +

2)

( )( )

( )

5 2 3

– 2 – 3 7

B x x

x x x

= − +

++

3)

( ) ( )

( )

2

3

C 2 1 – 2

– 3

x x x x

xx

= + +

++

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 5.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 5

a) a)

76A =−

b

8B =−

c)

3C =

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

a)

( )( )

22

3 5 2 11

2 3 3 7

6 33 10 55 6 14 9 21

76

A x x

xx

A x x x x x x

A

= − +

− + +

= + − − − − − −

=−

b)

( )( ) ( )

22

5 2 3 – 2 – 3

7

2 3 10 15 2 6 7

8

B x x x x

x

B x x x x x x

B

= − +

++

= + − − − + + +

=−

c)

( ) ( )

( )

2

3

2 3 2 3

C 2 1 – 2

– 3

223

3

x x x x

xx

C x x x x x x

C

= + +

++

= + − − + − +

=

- Chốt phương pháp giải:

Thu gọn các đa thức và kết quả là

1 số và không còn biến x

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 6

Bài 6: Chứng minh đẳng thức sau:

a)

( ) ( ) ( )

– – –

2

a b c b a c c a b

bc

++

=−

b)

( )

( ) ( )

22

1 – – 1 – a b a a a a b+=

c)

( ) ( ) ( )

– a b x x a b b a x+ + = +

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 6.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 6

a)

2VT VP bc= = −

b)

( )

2

– VT VP a a b==

c)

( )

VT VP b a x= = +

*Kết luận, nhận định:

Bài 6: Hướng dẫn giải

Chi tiết

a)Ta có:

( ) ( ) ( )

– – –

– – – –

2

VT a b c b a c c a b

ab ac ab bc ac bc

bc VP

= + +

=+

= − =

Vậy đẳng thức được chứng minh

b) Ta có:

( )

3

2

– –

–

VT a ab a a

a ab

a a b

VP

=+

=

Vậy đẳng thức được chứng minh

c) Ta có:

( )

–

VT ab ax ax bx

ab bx

b a x

VP

= + +

=+

=

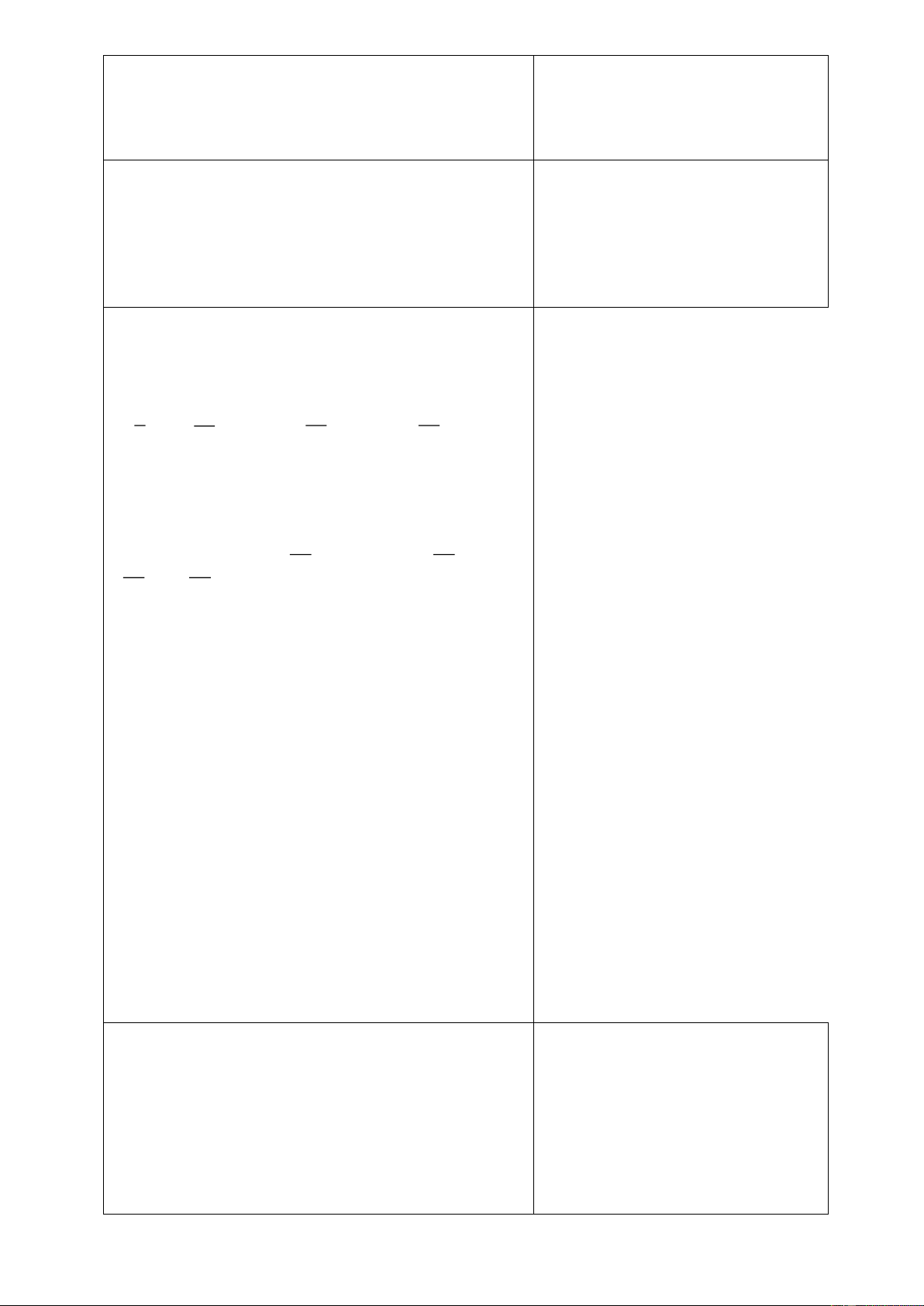
Trang 81

GV chốt phương pháp giải của dạng toán và một

số lưu ý

Vậy đẳng thức được chứng minh

- Chốt phương pháp giải:

Chứng minh VT=VP của đẳng

thức.

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài toán trắc

nghiệm 1

Dạng 5: Phép chia các đa thức

Bài 1: Bài tập trắc nghiệm

Đáp án

1)C 2) A 3) A 4) A 5) C

Bài 1: Trắc nghiệm

1) Kết quả của phép chia

( )

3 2 2

10 : 4 x y z xy z−

là :

A.

2

5

2

x

B.

2

5

2

x yz

−

C.

2

5

2

x

−

D.

2

5

2

xy

−

2) Kết quả của phép chia

( ) ( )

54

35 : 12xy z xy−−

là :

A.

35

12

yz

B.

35

12

xyz

C.

35

12

xy

D.

35

2

yz

3) Kết quả của phép chia

( ) ( )

5 3 3

4 – 8 : 2x x x−

là :

A.

2

24x−+

B.

2

24x−−

C.

2

24xx−+

D.

2

24x +

4) Kết quả của phép chia

( )

32

9 – 12 3 : 3x x x x+−

là :

A.

2

3 4 1xx− + −

B

2

3 4 1xx− + +

C.

2

3 4 1xx+−

D.

2

3 4 1xx− − −

5) Thực hiện phép tính

( ) ( )

2 2 3 3 4 2

4 – 3 : 2xy x y x y xy+−

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trả lời câu hỏi trắc

nghiệm của bài toán 1.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 1

1)C 2)A

3)A 4)A 5) C

Đáp án

1)C 2) A 3) A 4) A 5) C

Trang 82

*Kết luận, nhận định:

GV đánh giá, nhận xét đáp án chính xác của bài

tập.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 2

Bài 2: Thực hiện phép tính:

1)

( ) ( )

5 4 2

12 : 4x y x y−−

2)

( )

4 5 3 2

25 : 3x y z xy z−

3)

22

18 : 6x y z xyz

4)

4 2 4

27 : 9x y z x y

5)

( ) ( )

54

35 : 12xy z xy−−

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 2.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 2

1)

33

3xy

2)

3 3 2

25

3

x y z

−

3)

3xy

4)

3yz

5)

35

12

yz

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

Bài 2: Hướng dẫn giải

Chi tiết

1)

( ) ( )

5 4 2 3 3

12 : 4 3x y x y x y− − =

2)

( )

4 5 3 2 3 3 2

25

25 : 3

3

x y z xy z x y z

−

−=

3)

22

18 : 6 3x y z xyz xy=

4)

4 2 4

27 : 9 3x y z x y yz=

5)

( ) ( )

54

35

35 : 12

12

xy z xy yz− − =

- Chốt phương pháp giải:

Áp dụng nguyên tắc chia đa thức.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 3

Bài 3: Thực hiện phép tính:

1)

( ) ( )

5 3 3

4 – 8 : 2x x x−

2)

( )

32

9 – 12 3 : 3x x x x+−

3)

( ) ( )

2 3 3 4 4 5 2 3

3 4 – x :x y x y y x y− + −

4)

( ) ( ) ( ) ( )

32

2 – – 7 – – – : – x y y x y x x y





5)

( ) ( ) ( )

( )

5 4 2

2

3 – – 2 – 3 –

: 5 –

x y x y x y

xy









+

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

Bài 3: Hướng dẫn giải

Chi tiết

1)

2

24x−+

2)

2

3 4 1xx− + −

3)

22

34xy x y−+

4)

( ) ( )

2

2 – 7 – 1x y x y−+

5)

( ) ( )

32

3 2 3

– –

5 5 5

x y x y−+

- Chốt phương pháp giải:

Áp dụng nguyên tắc chia đa thức.

Trang 83

của bài toán 3.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 3

1)

2

24x−+

2)

2

3 4 1xx− + −

3)

22

34xy x y−+

4)

( ) ( )

2

2 – 7 – 1x y x y−+

5)

( ) ( )

32

3 2 3

– –

5 5 5

x y x y−+

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 4

Bài 4: Tìm x biết:

1)

( )

( ) ( )

2

8 – 4 : 4 – 2 8x x x x− + =

2)

( ) ( ) ( )

4 3 2 2 2

2 – 3 : 4 2 1 0x x x x x x+ − + − + =

*Thực hiện nhiệm vụ

- Yêu cầu HS hoạt động cá nhân trình bày lời giải

của bài toán 4.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 4

a)

3x =−

b)

1x =

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán và một

số lưu ý

Bài 4: Hướng dẫn giải

Chi tiết

a)

( )

( ) ( )

2

8 – 4 : 4 – 2 8

2 1 2 8

3 9 3

x x x x

xx

− + =

 − + − − =

 − =  = −

b)

( ) ( ) ( )

4 3 2 2 2

22

2 – 3 : 2 2 1 0

2 3 1 2 4 2 0

1 0 1

x x x x x x

x x x x

xx

+ − + − + =

 − + − + − + =

 − + =  =

- Chốt phương pháp giải:

Thu gọn rồi tìm giá trị của x

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ ….

1. TRẮC NGHIỆM

1) Đơn thức nào sau đây đồng dạng với đơn thức

2

3xy−

A.

2

3xy−

B.

( 3 )xy y−

C.

2

3( )xy−

D.

3xy−

2) Trong các biểu thức sau đâu là đơn thức:

A. 4xy

2

B. 3-2y

C. 10x +y

D. 5(x+y)

3) Tích của hai đơn thức là

23

3x y z

trong đó có một đơn thức là

2

4xy

, đơn thức còn

lại là :

Trang 84

A.

2

3

4

xy z

B.

4

3

xyz

C.

3

4

xyz

D.

3

4

xy

4) Thu gọn đa thức P = x

3

y – 5xy

3

+ 2 x

3

y + 5 xy

3

bằng

A. 3 x

3

y

B. – x

3

y

C. x

3

y + 10 xy

3

D. 3 x

3

y - 10xy

3

.

5) Đa thức

3 2 2 3

2 1 2 5x x x x x x− + + + − + −

có bậc là :

A. 3 B. 2 C.1 D.

5

6) Đơn thức A ở đẳng thức

2

2 . 4x A x y=−

là:

A.

2A xy=

B.

2

2A x y=−

C.

2A xy=−

D.

2

4A x y=−

7) Tích của 2 đơn thức -

4

1

x

2

và -8xy

2

là :

A. 2x

3

y

2

B. – 2 x

3

y

2

C. 32 x

3

y

2

D. 2 x

2

y

2

.

8) Kết quả của phép chia

( )

32

9 – 12 3 : 3x x x x+−

là :

A.

2

3 4 1xx− + −

B

2

3 4 1xx− + +

C.

2

3 4 1xx+−

D.

2

3 4 1xx− − −

9) Bậc của đa thức 4 x

5

y + x

3

y - 2 x

2

- 4 x

5

y + 3x y – 1 là :

A. 6 B. 4 C. 5 D. 3 .

10) Kết quả của phép chia

( ) ( )

54

35 : 12xy z xy−−

là :

A.

35

12

yz

B.

35

12

xyz

C.

35

12

xy

D.

35

2

yz

2. TỰ LUẬN

Bài 1: Thu gọn và chỉ ra phần biến, phần hệ số và tìm bậc của các đơn thức sau:

1)

( )

3

23

2y . 2y .y

2)

( )

3 3 4

1

x y . 2x y

4



−





3)

( )

2 4 5 5 4 2

5x y z . 2x y z−−

4)

3 4 8 5

18

3 x y . x y

85

5)

2 5 3 2

32

x y . x y

53

−







Bài 2: Cho đơn thức

2 2 2

37

M x y . x y

79

−

   

=

   

   

.

a, Thu gọn đơn thức M rồi xác định hệ số và phần biến của đơn thức.

b, Tính giá trị của đơn thức M tại

x 1,y 2= − =

.

Bài 3: Thu gọn rồi tìm bậc các đa thức sau:

Trang 85

1)

2 5 6 7 3 5 6 7

1

A 3x y 4y 3x y x y 3xy 3x y

2

= + − + − +

2)

2 4 2 2 4 9

B 2x y 4xyz 2x 5 3x y 4xyz 3 y= + − − + − + −

3)

4 2 3 2 2 2 4 2 2 2

1

C x x y x y z x x y z

2

= − + − −

4)

5 3 2 5 2

1 3 3

D 3x x y xy 3x x y

2 4 4

= − − − −

5)

22

1 1 1

E 3x y xy 1 3x y xy xy

4 2 4

= − + − + −

Bài 4: Cho hai đa thức:

( )

32

2 6 3 9f x x x x x= − + + +

và

( )

2 3 2

3 2 8 4 5g x x x x= − + − −

1.Sắp xếp hai đa thức

( )

fx

và

( )

gx

theo lũy thừa giàm dần của biến.

2.Tính

( ) ( )

f x g x+

và

( ) ( )

f x g x−

Bài 5: Cho hai đa thức:

( )

24

3 2 2 7A x x x x= − − − +

và

( )

24

3 4 5 2B x x x x= + − +

a) Hãy sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến.

b) Tính

( ) ( ) ( )

M x A x B x=+

. Tìm x để

( )

4Mx=

c) Tìm đa thức

( )

Cx

sao cho

( ) ( ) ( )

C x B x A x− = −

Bài 6: Cho các đa thức:

( )

2 2 3

5 1 3 5F x x x x x= − + + −

và

( )

3 2 3

2 3 6 5 2G x x x x x x= − + + − −

a) Thu gọn và sắp xếp hai đa thức F(x) và G(x) theo lũy thừa giảm dần của biến.

b) Tính

( ) ( ) ( )

M x F x G x=−

và tìm nghiệm của đa thức

( )

Mx

.

c) Tìm đa thức

( )

Nx

biết

( ) ( ) ( )

N x F x G x+ = −

.

Bài 7: Chứng tỏ rằng các đa thức sau không phụ thuộc vào biến:

1)

( ) ( )

( )

23

2 1 – 2 – 3F x x x x x x= + + + +

2)

( ) ( ) ( ) ( )

22

4 – 6 – 2 3 5 – 4 3 – 1G x x x x x x x= + + +

Bài 8: Bà Khanh dự định mua x hộp sữa, mỗi hộp giá y đồng. Nhưng khi đến cửa

hàng bà Khanh thấy giá sữa giảm 1500 đồng mỗi hộp nên quyết định mua thêm 3 hộp

nữa.

Tìm đa thức biểu thị số tiền bà Khanh phải trả cho tổng số hộp sữa đã mua.

Bài 9: Trong một khách sạn có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có

chiều sâu là 1,2m, đáy là hình chữ nhật có chiều dài x mét, chiều rộng y mét. Bể thứ

hai có chiều sâu là 1,5m, hai kích thước đáy gấp 5 lần hai kích thước đáy của bể thứ

nhất.

a) Hãy tìm đơn thức (hai biến x và y) biểu thị số mét khối nước cần có để bơm

đầy cả hai bể bơi.

b) Tính lượng nước bơm đầy hai bể nếu x=5m, y=3m.

Trang 86

Bài 10: Chuyện rằng Rùa chạy đua với Thỏ. Thỏ chạy nhanh gấp 60 lần Rùa, nhưng

chỉ sau t phút chạy, Thỏ đã dừng lại mặc dù chưa đến đích. Do mải chơi, thỏ không

biết rằng Rùa vẫn cần mẫn chạy liên tục trong 90t phút và đến đích trước Thỏ.

a) Gọi v (m/phút) là vận tốc chạy của Rùa. Hãy viết các đơn thức biểu thị quãng

đường mà Thỏ và Rùa đã chạy.

b) Hỏi Rùa đã chạy được quang đường dài gấp bao nhiêu lần quãng đường Thỏ đã

chạy?

Tuần 9

Tiết 22; 23; 24

Ngày soạn 01/11/2023

Lớp

8A

8B

Ngày dạy:

ÔN TẬP HÌNH THOI VÀ HÌNH VUÔNG

I. MỤC TIÊU

1. Về kiến thức:

- Mô tả được khái niệm hình thoi, hình vuông từ tứ giác.

- Biết và giải thích được các tính chất của hình thoi và hình vuông.

- Biết dấu hiệu nhận biết một hình chữ nhật là hình thoi, hình vuông.

2. Về năng lực:

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu được khái niệm, tính chất và dấu hiệu

nhận biết của hình thoi và hình vuông.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng

hợp, khái quát hóa, vận dụng các tính chất và dấu hiệu nhận biết hình thoi và hình

vuông để giải toán.

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

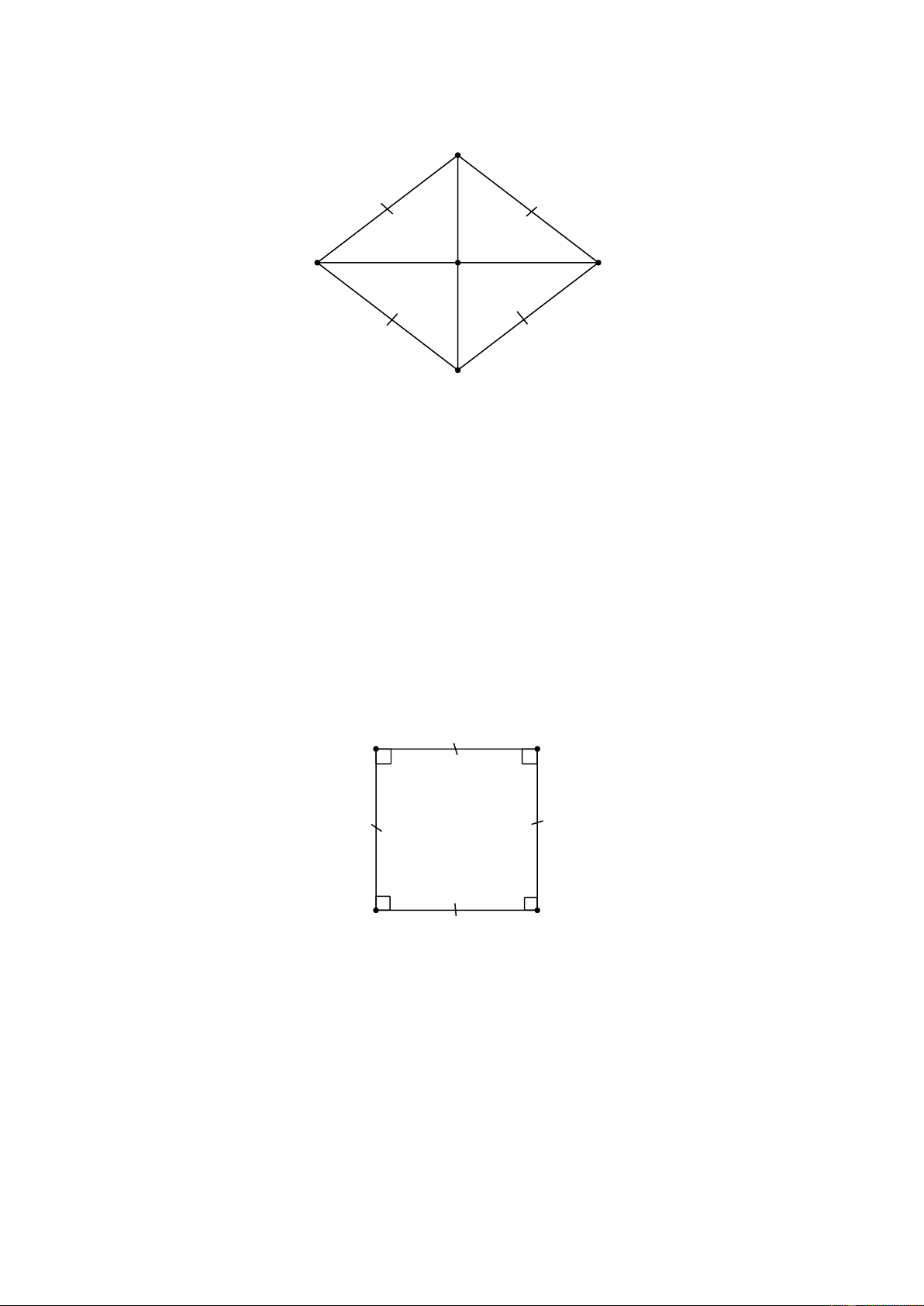
Trang 87

1. KIẾN THỨC CẦN NHỚ

a. Hình thoi:

* Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.

* Tính chất về đường chéo: Trong hình thoi:

- Hai đường chéo của hình thoi vuông góc với nhau.

- Hai đường chéo là các đường phân giác của các góc của hình thoi.

* Dấu hiệu nhận biết:

-Tứ giác có bốn cạnh bằng nhau.

- Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

- Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

b. Hình vuông:

* Định nghĩa: Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.

* Tính chất về đường chéo:

- Trong hình vuông, hai đường chéo bằng nhau, vuông góc với nhau, cắt nhau tại

trung điểm của mỗi đường và là các đường phân giác của các góc của hình vuông.

* Dấu hiệu nhận biết:

- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

- Hình chữ nhật có hai đường chéo vuông góc là hình vuông.

- Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

- Hình thoi có một góc vuông là hình vuông.

- Hình thoi có hai đường chéo bằng nhau là hình vuông.

O

D

C

B

A

D

C

B

A

Trang 88

2. BÀI TẬP

Hoạt động của giáo viên

- học sinh

Nội dung

* Giao nhiệm vụ:

- GV tổ chức hoạt động, trả lời nhanh bài toán trắc

nghiệm 1:

- HS nhận nhiệm vụ GV giao.

- HS tìm hiểu bài toán 1.

Dạng 1: Nhận biết và chứng

minh một tứ giác là hình thoi

Bài 1: Bài tập trắc nghiệm

Đáp án:

1. D

2. C

3. D

Chốt phương pháp: Quan sát

hình, tìm các yếu tố đã có trên hình

vẽ. Bám chặt vào dấu hiệu nhận

biết.

Chọn phương án trả lời đúng:

Câu 1: Trong các tứ giác sau, tứ giác nào không

phải là hình thoi?

Hình 1

D

C

B

A

Hình 2

H

G

F

E

Hình 3

N

M

I

K

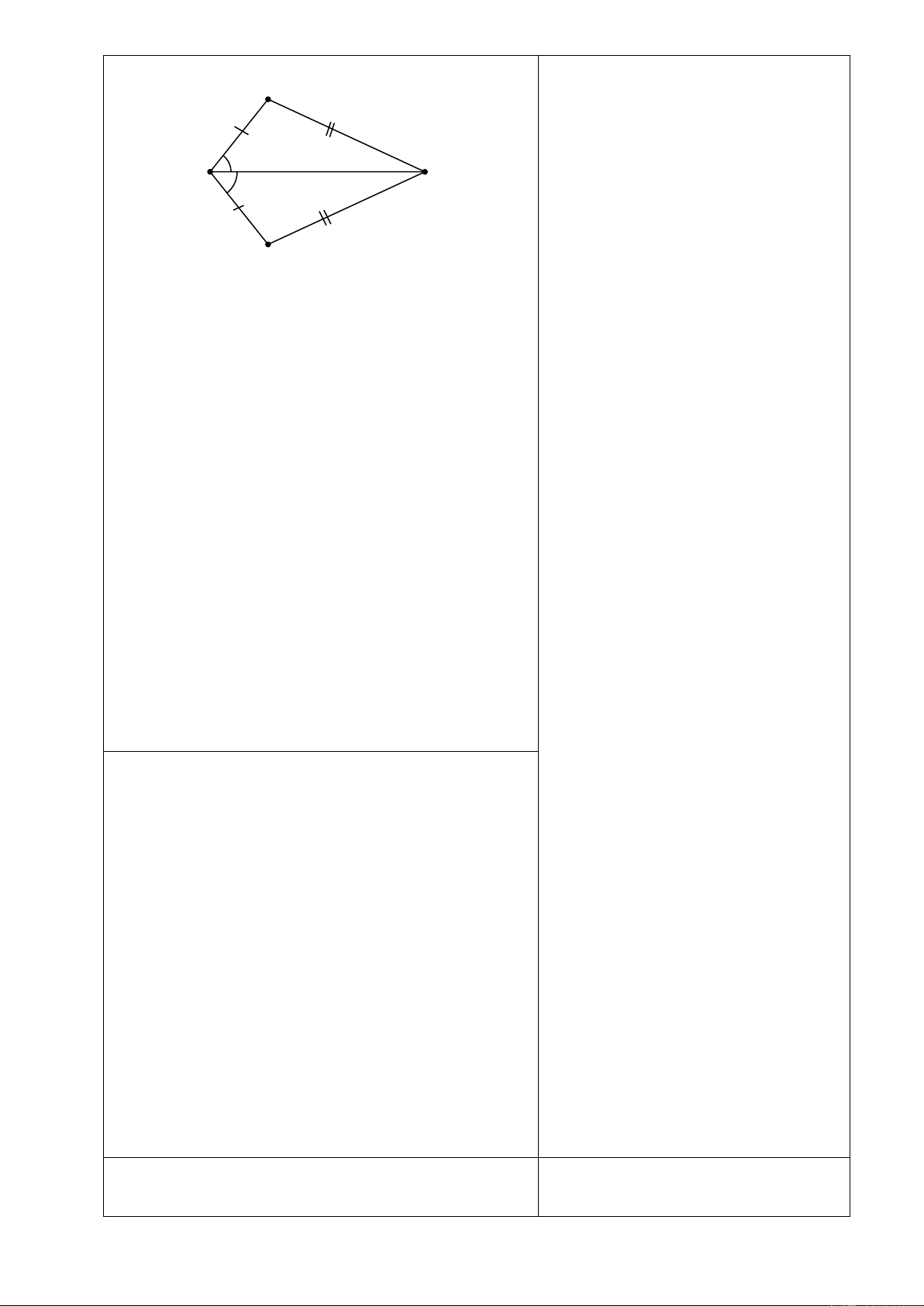
Trang 89

A. Hình 1 B. Hình 2

C. Hình 3 D. Hình 4

Câu 2: Khẳng định nào đúng:

A. Hình thoi là tứ giác có bốn góc bằng nhau.

B. Hình thoi là tứ giác có hai góc đối bằng nhau.

C. Hình thoi là tứ giác có bốn cạnh bằng nhau.

D. Hình thoi là tứ giác có 3 góc vuông.

Câu 3: Chọn câu trả lời sai:

A. Hình bình hành có hai cạnh kề bằng nhau là

hình thoi.

B. Hình bình hành có một đường chéo là đường

phân giác của một góc là hình thoi.

C. Hình bình hành có hai đường chéo vuông góc

với nhau là hình thoi.

D. Tứ giác có bốn góc bằng nhau là hình thoi.

* Thực hiện nhiệm vụ:

- Yêu cầu HS hoạt động cá nhân trả lời câu hỏi trắc

nghiệm của bài toán 1.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 1

*Kết luận, nhận định:

- GV đánh giá, nhận xét đáp án chính xác của bài

tập.

- GV khai thác thêm:

+ Câu 1: Vì sao các tứ giác ở hình 1, 2, 3 là hình

thoi? Dựa vào dấu hiệu nhận biết nào

- HS được củng cố lại các dấu hiệu nhận biết hình

thoi

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

Bài 2: Hướng dẫn giải

S

R

Q

P

Hình 4

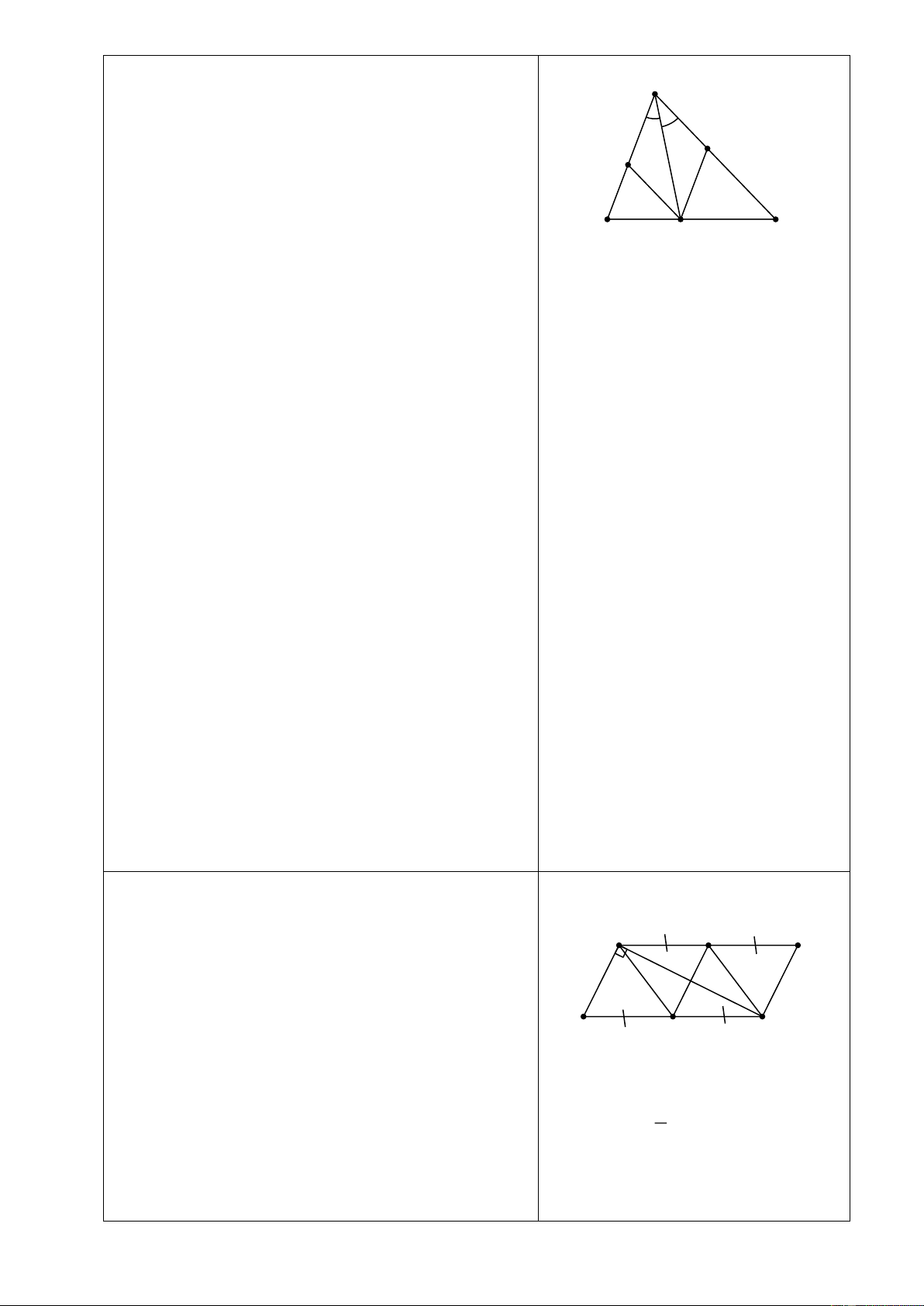
Trang 90

bài toán 2:

Cho tam giác

ABC

, tia phân giác

AD

. Qua

D

kẻ

đường thẳng song song với

AC

cắt

AB

ở

E

, qua

D

kẻ đường thẳng song song với

AB

cắt

AC

ở

F

. Tứ giác

AEDF

là hình gì? Vì sao?

- HS tìm hiểu bài toán 2. Xác định GT-KL của bài

toán.

* Thực hiện nhiệm vụ:

- GV yêu cầu HS vẽ hình, vào vở.

- GV hướng dẫn HS thực hiện nhiệm vụ:

+ Dự đoán tứ giác

AEDF

là hình gì? Dựa vào dấu

hiệu nhận biết nào?

+ Để chứng minh tứ giác

AEDF

là hình bình hành

em làm thế nào?

- GV yêu cầu HS hoạt động cá nhân trình bày lời

giải vào vở. Một HS lên bảng trình bày.

- HS hoạt động cá nhân vẽ hình vào vở. Một HS

lên bảng vẽ hình

- HS trả lời các câu hỏi của GV:

+ Dự đoán tứ giác

AEDF

là hình thoi. Dựa vào

dấu hiệu: Hình bình hành có một đường chéo là

đường phân giác của một góc là hình thoi.

+ Chứng minh

AEDF

là hình bình hành theo dấu

hiệu tứ giác có hai cặp cạnh đối song song

* Kết luận, nhận định:

- GV chốt phương pháp giải của dạng toán và một

số lưu ý

Xét tứ giác

AEDF

có:

//AE DF

(GT)

//AF DE

(GT)



AEDF

là hình bình hành

Lại có

AD

là phân giác của

BAC

(GT)



AEDF

là hình thoi

Chốt phương pháp: Quan sát

hình, tìm các yếu tố đã có trên hình

vẽ. Bám chặt vào dấu hiệu nhận biết

hình bình hành và hình thoi.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 3:

Cho hình bình hành

ABCD

có

AC

vuông góc với

AD

. Gọi

M

,

N

theo thứ tự là trung điểm của

AB

và

CD

. Tứ giác

AMCN

là hình gì? Vì sao?

- HS tìm hiểu bài toán 3. Xác định GT-KL của bài

toán

* Thực hiện nhiệm vụ:

- GV yêu cầu HS vẽ hình, vào vở.

- GV hướng dẫn HS thực hiện nhiệm vụ:

+ Dự đoán tứ giác

AMCN

là hình gì? Dựa vào dấu

Bài 3: Hướng dẫn giải

Ta có:

1

2

AM MB AB==

(

M

là trung

điểm của

AB

)

F

E

D

C

B

A

N

M

D

C

B

A

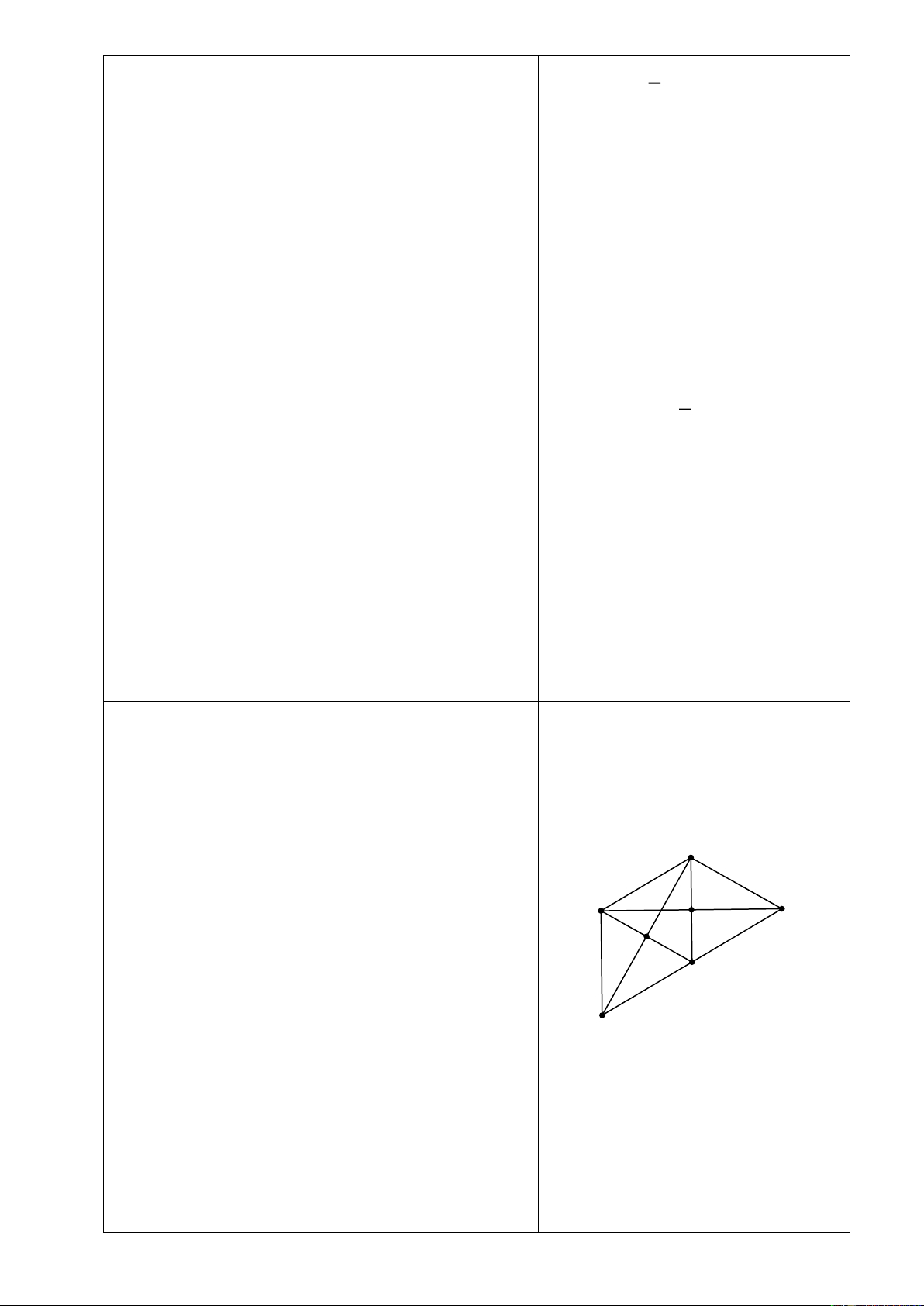
Trang 91

hiệu nhận biết nào?

+ Trước hết, để chứng minh

AMCN

là hình bình

hành, em làm thế nào?

- HS hoạt động cá nhân vẽ hình vào vở. Một HS

lên bảng vẽ hình

- HS trả lời các câu hỏi của GV:

+ Dự đoán tứ giác

AEDF

là hình thoi. Có thể sử

dụng dấu hiệu: Hình bình hành có hai cạnh kề

bằng nhau là hình thoi. Hoặc dấu hiệu: Hình bình

hành có hai đường chéo vuông góc với nhau là

hình thoi.

+ HS chứng minh

AMCN

là hình bình hành theo

dấu hiệu tứ giác có cặp cạnh đối song song và bằng

nhau.

Sau đó HS có thể chứng minh

AN CN=

hoặc

AC MN⊥

* Kết luận, nhận định:

- GV chốt phương pháp giải của dạng toán và một

số lưu ý

1

2

CN ND AC==

(

N

là trung điểm

của

CD

)

Mà

AB CD=

(

ABCD

là hình bình

hành)



AM CN=

Lại có

//AM CN

(vì

//AB CD

)



AMCN

là hình bình hành (1)

Xét

ACD

vuông tại

A

có:

AN

là đường trung tuyến ứng với

cạnh huyền

CD



1

2

AN CN CD==

(2)

Từ (1) và (2) suy ra

AMCN

là hình

thoi.

Chốt phương pháp: Quan sát

hình, tìm các yếu tố đã có trên hình

vẽ. Bám chặt vào dấu hiệu nhận biết

về cạnh của hình bình hành và hình

thoi.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 4:

Cho hình thoi

ABCD

có

60A =

, vẽ

BH

vuông

góc với

AD

rồi kéo dài một đoạn

HE HB=

. Nối

E

với

A

,

E

với

D

a. Chứng minh rằng tứ giác

ABDE

là hình thoi.

b.

D

là trung điểm của

EC

.

c.

EB AC=

.

HS tìm hiểu bài toán 4. Xác định GT-KL của bài

toán.

* Thực hiện nhiệm vụ:

- Giáo viên hướng dẫn HS thực hiện:

a. Chứng minh

ABDE

là hình thoi dựa vào dấu

hiệu nhận biết nào? Cần chứng minh thêm điều gì?

- HS hoạt động cá nhân vẽ hình vào vở. Một HS

lên bảng vẽ hình

- HS trả lời các câu hỏi được GV đề xuất:

Dạng 2: Vận dụng tính chất của

hình thoi để chứng minh các quan

hệ hình học

Bài 4: Hướng dẫn giải

a.

ABD

có

AB AD=

(vì

ABCD

là hinh thoi)

ABD

cân tại

A

Lại có

60A ABD=   

đều

Mà

BH AD⊥

AH HD=

E

H

D

C

B

A

Trang 92

a. Chứng minh

ABDE

là hình thoi theo dấu hiệu

Hình bình hành có hai đường chéo vuông góc với

nhau là hình thoi.

ABDE

có:

BE AD⊥

và

HE HB=

, do đó cần

chứng minh thêm

AH HD=

.

b. Để

D

là trung điểm của

EC

thì cần 2 điều kiện:

b. Để

D

là trung điểm của

EC

thì cần mấy điều

kiện?

Chứng minh các điều kiện đó bằng cách nào?

c. Nếu HS gặp khó khăn thì GV định hướng chứng

minh

ABCE

là hình thang cân.

+ c/m

,,E D C

thẳng hàng dựa vào tiên đề Euclid.

+ c/m

DE DC=

(cùng bằng

AB

)

c. Chứng minh

ABCE

là hình thang cân theo dấu

hiệu hình thang có hai góc kề một đáy bằng nhau.

*Kết luận, nhận định:

- GV chốt lại: theo tính chất của hình thoi, ta có

thể suy ra được các cặp đoạn thẳng bằng nhau, cặp

góc bằng nhau, hai đường thẳng song song.

- GV lưu ý ở câu b HS thường mắc sai lầm là chỉ

chứng minh

DE DC=

, không chứng minh

,,E D C

thẳng hàng.

Tứ giác

ABDE

có hai đường chéo

cắt nhau tại trung điểm của mỗi

đường và vuông góc với nhau nên là

hình thoi (dấu hiệu nhận biết)

b. Có

ABCD

là hình thoi

//CD AB

Có

ABDE

là hình thoi

//DE AB

,,E D C

thẳng hàng (1)

Có

DE AB=

và

//CD AB

DE DC=

(2)

Từ (1) và (2) suy ra

D

là trung

điểm của

EC

.

c. Xét tứ giác

ABCE

có

//AB CE

ABEC

là hình thang

Lại có

60CE= = 

ABCE

là hình thang cân

AC BE=

* Giao nhiệm vụ:

- GV tổ chức hoạt động, trả lời nhanh bài toán trắc

nghiệm 5:

- HS nhận nhiệm vụ GV giao.

- HS tìm hiểu bài toán 5.

Dạng 3: Nhận biết và chứng

minh một tứ giác là hình vuông

Bài 5: Bài tập trắc nghiệm

Đáp án:

1. A

2. B

3. D

4. D

Chọn phương án trả lời đúng:

Câu 1: Khẳng định nào đúng?

A. Hình vuông là tứ giác có bốn góc vuông và bốn

cạnh bằng nhau.

B. Hình vuông là tứ giác có bốn góc bằng nhau.

C. Hình vuông là tứ giác có bốn cạnh bằng nhau.

D. Hình vuông là tứ giác có hai cạnh kề bằng nhau.

Câu 2: Khẳng định nào sai?

A. Trong hình vuông hai đường chéo bằng nhau và

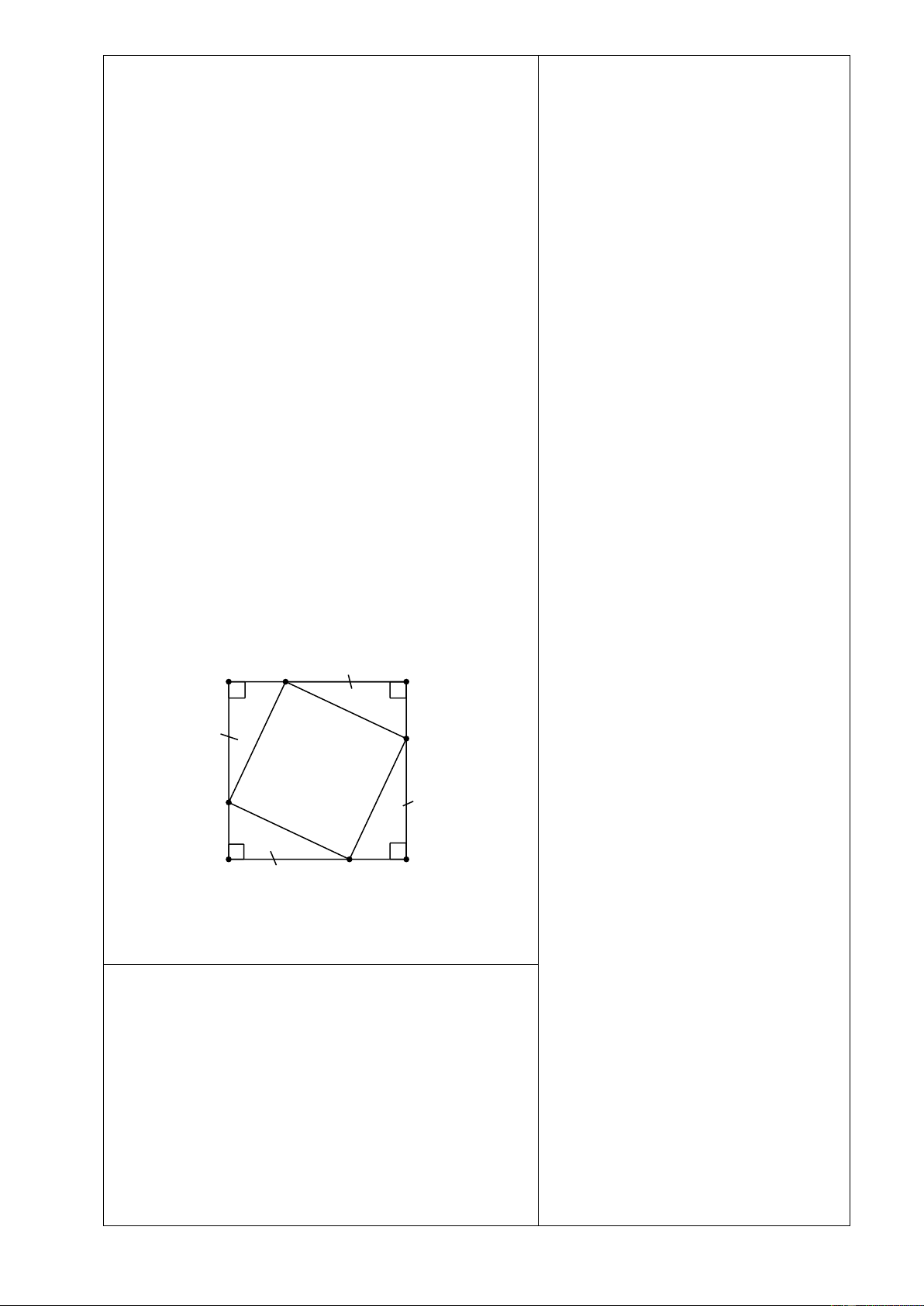
Trang 93

cắt nhau tại trung điểm của mỗi đường.

B. Trong hình vuông hai đường chéo không vuông

góc với nhau

C. Trong hình vuông hai đường chéo đồng thời là

hai trục đối xứng của hình vuông.

D. Trong hình vuông hai đường chéo vuông góc

với nhau và bằng nhau

Câu 3: Các dấu hiệu nhận biết sau, dấu hiệu nào

không đủ để kết luận tứ giác đó là hình vuông

A. Hình chữ nhật có hai cạnh kề bằng nhau là hình

vuông.

B. Hình chữ nhật có hai đường chéo vuông góc với

nhau là hình vuông

C. Hình chữ nhật có một đường chéo là phân giác

của một góc là hình vuông.

D. Hình bình hành có hai đường chéo bằng nhau là

hình vuông

Câu 4: Trên hình vẽ cho hình vuông

ABCD

. Biết

BM CN DP AQ= = =

. Tứ giác

MNPQ

là hình

gì?

A. Hình bình hành B. Hình chữ nhật

C. Hình thoi D. Hình vuông

* Thực hiện nhiệm vụ:

- Yêu cầu HS hoạt động cá nhân trả lời câu hỏi trắc

nghiệm của bài toán 5.

HS trả lời các câu hỏi được GV đề xuất trong bài

toán 5

HS được củng cố lại các dấu hiệu nhận biết hình

vuông

* Kết luận, nhận định:

- GV đánh giá, nhận xét đáp án chính xác của bài

Q

N

P

M

D

C

B

A

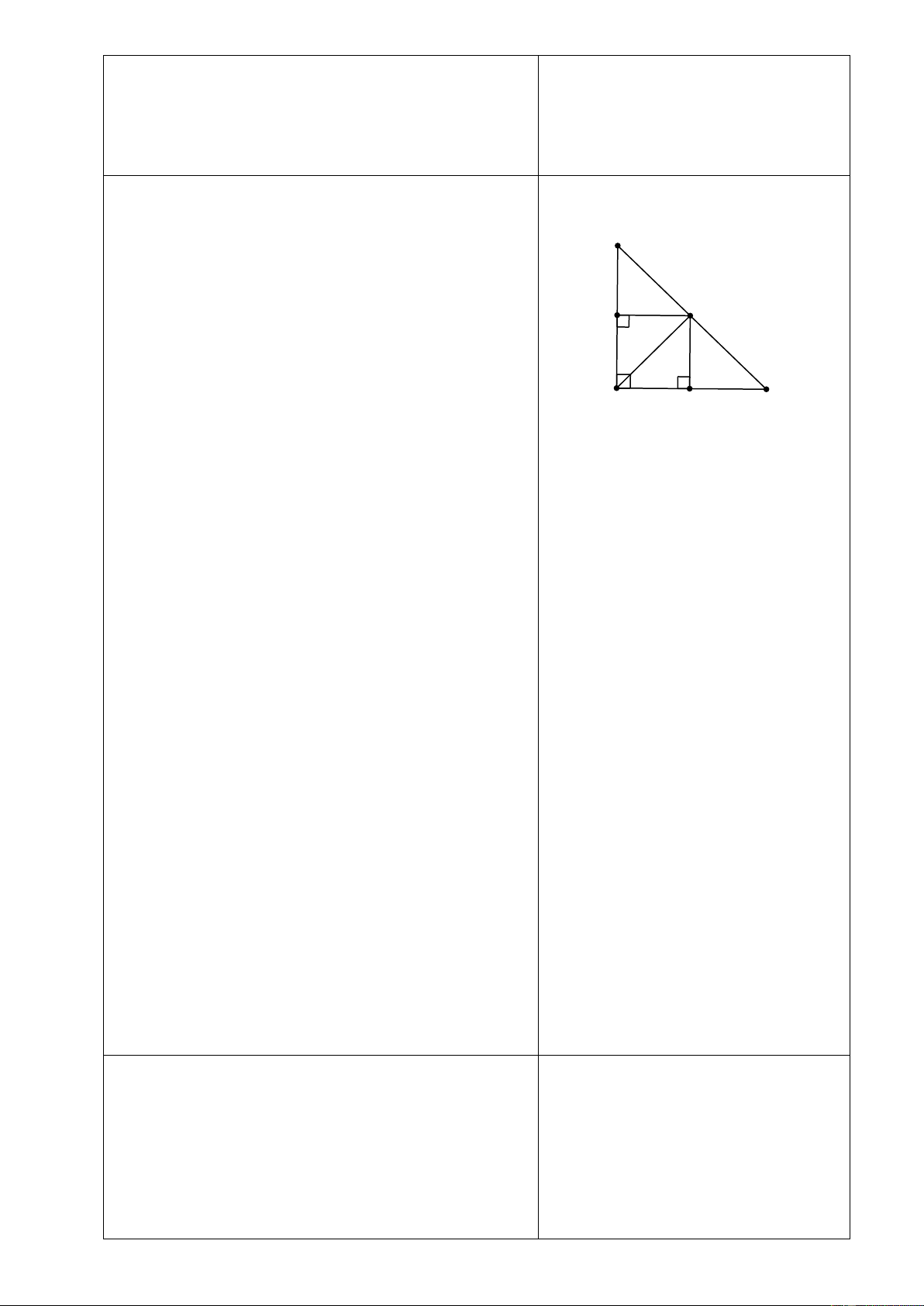
Trang 94

tập.

- GV khai thác thêm:

+ Câu 4: Vì sao

MNPQ

là hình vuông? Dựa vào

dấu hiệu nhận biết nào.

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 6:

Cho tam giác

ABC

vuông tại

A

, đường phân giác

AD

. Gọi

,MN

lần lượt là hình chiếu của

D

trên

,AB

AC

. Chứng minh tứ giác

AMDN

là hình

vuông.

- HS tìm hiểu bài toán 6. Xác định GT-KL của bài

toán

* Thực hiện nhiệm vụ:

- GV yêu cầu HS vẽ hình, vào vở.

- GV hướng dẫn HS thực hiện nhiệm vụ:

+ Chứng minh tứ giác

AMDN

là hình vuông theo

dấu hiệu nhận biết nào?

+ Để chứng minh

AMDN

là hình chữ nhật, ta sử

dụng dấu hiệu nhận biết nào?

- HS hoạt động cá nhân vẽ hình vào vở. Một HS

lên bảng vẽ hình

- HS trả lời các câu hỏi được GV đề xuất:

+

AMDN

là hình vuông theo dấu hiệu: Hình chữ

nhật có một đường chéo là đường phân giác của

một góc là hình vuông

+

AMDN

là hình chữ nhật theo dấu hiệu nhận biết

tứ giác có ba góc vuông.

* Kết luận, nhận định:

- GV chốt phương pháp giải của dạng toán và một

số lưu ý

Bài 6:

Tứ giác

AMDN

có:

90MAN =

(GT)

90AMD =

(vì

DM AB⊥

)

90AND =

(vì

DN AC⊥

)

AMDN

là hình chữ nhật

Lại có

AD

là phân giác của

MAN

AMDN

là hình vuông

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 7:

Cho hình chữ nhật

ABCD

có

2AB AD=

. Gọi

,PQ

theo thứ tự là trung điểm của

,AB CD

. Gọi

H

là giao điểm của

AQ

và

DP

, gọi

K

là giao

Bài 7:

N

M

D

C

B

A

Trang 95

điểm của

CP

và

BQ

. Chứng minh

PHQK

là hình

vuông.

HS tìm hiểu bài toán 7. Xác định GT-KL của bài

toán.

* Thực hiện nhiệm vụ:

- GV yêu cầu HS vẽ hình, vào vở.

- GV hướng dẫn HS thực hiện nhiệm vụ:

- HS hoạt động cá nhân vẽ hình vào vở. Một HS

lên bảng vẽ hình.

- HS trả lời các câu hỏi được GV đề xuất:

+ Chứng minh

PHQK

là hình vuông theo dấu

hiệu: hình chữ nhật có hai cạnh kề bằng nhau

+ Chứng minh

PHQK

là hình vuông theo dấu hiệu

nhận biết nào?

+ GV có thể hướng dẫn theo sơ đồ chứng minh.

* Kết luận, nhận định:

- GV chốt phương pháp giải của dạng toán và một

số lưu ý

Tứ giác

APCQ

có

// AP CQ

,

AP CQ=

APCQ

là hình bình hành

//AQ PC

C/m tương tự có

//BQ PD

Tứ giác

PHQK

có

//AQ PC

,

//BQ PD

nên là hình bình hành

Tứ giác

APQD

có

// DAP Q

,

AP DQ=

APQD

là hình bình hành

Mà

90PAD =

APQD

là hình

chữ nhật

Lại có

1

2

AP AD AB



==





APQD

là hình vuông

90PHQ = 

và

PH PQ=

(tính

chất đường chéo của hình vuông)

Hình bình hành

PHQK

có

90PHQ =

và

PH PQ=

PHQK

là hình vuông

* Giao nhiệm vụ

- GV tổ chức hoạt động, hướng dẫn HS tìm hiểu

bài toán 8:

Cho hình vuông

ABCD

. Trên cạnh

AD

lấy điểm

F

trên cạnh

DC

lấy điểm E sao cho

AF DE=

.

Chứng minh

AE BF=

và

AE BF⊥

.

- HS tìm hiểu bài toán 8. Xác định GT-KL của bài

toán.

* Thực hiện nhiệm vụ:

Dạng 4: Vận dụng tính chất của

hình thoi để chứng minh các quan

hệ hình học

Bài 8:

K

H

Q

P

D

C

B

A

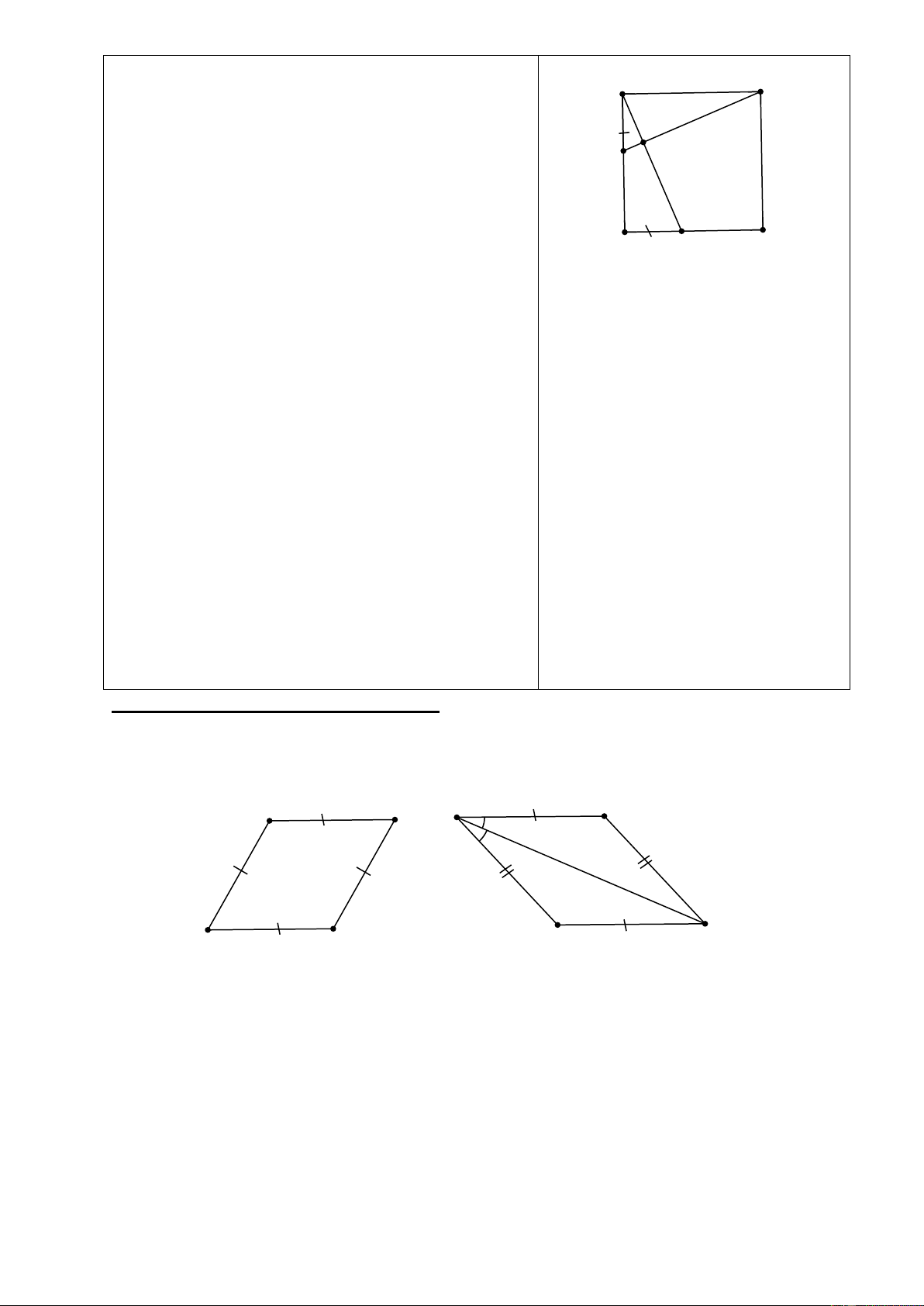
Trang 96

- HS hoạt động cá nhân vẽ hình vào vở. Một HS

lên bảng vẽ hình.

- HS trả lời các câu hỏi được GV đề xuất:

+ Chứng minh

AE BF=

bằng cách chứng minh

hai tam giác bằng nhau.

- GV yêu cầu HS vẽ hình, vào vở.

- GV hướng dẫn HS thực hiện nhiệm vụ:

+ Để chứng minh

AE BF=

ta làm thế nào?

+ Nếu HS gặp khó khăn trong việc chứng minh

AE BF⊥

thì GV có thể định hướng chứng minh

ABH

vuông.

* Kết luận, nhận định:

- GV chốt phương pháp giải của dạng toán và một

số lưu ý

- GV chốt lại: theo tính chất của hình vuông, ta có

thể suy ra được các cặp đoạn thẳng bằng nhau, cặp

góc bằng nhau.

Xét

ADE

và

BAF

có:

AD BA=

(

ABCD

là hình vuông)

90ADE BAF= = 

(

ABCD

là hình

vuông)

DE AF=

(GT)

ADE BAF  = 

(c.g.c)

AE BF=

,

11

AB=

Lại có

12

90AA+ = 

12

90BA + = 

Gọi

H

là giao điểm của

AE

và

BF

ABH

có

12

90BA+ = 

0

90AHB=



AE BF⊥

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ ….

1. TRẮC NGHIỆM

Câu 1: Trong các tứ giác sau, tứ giác nào không phải là hình thoi?

1

E

H

2

1

F

A

B

C

D

Hình 1

D

C

B

A

Hình 2

H

G

F

E

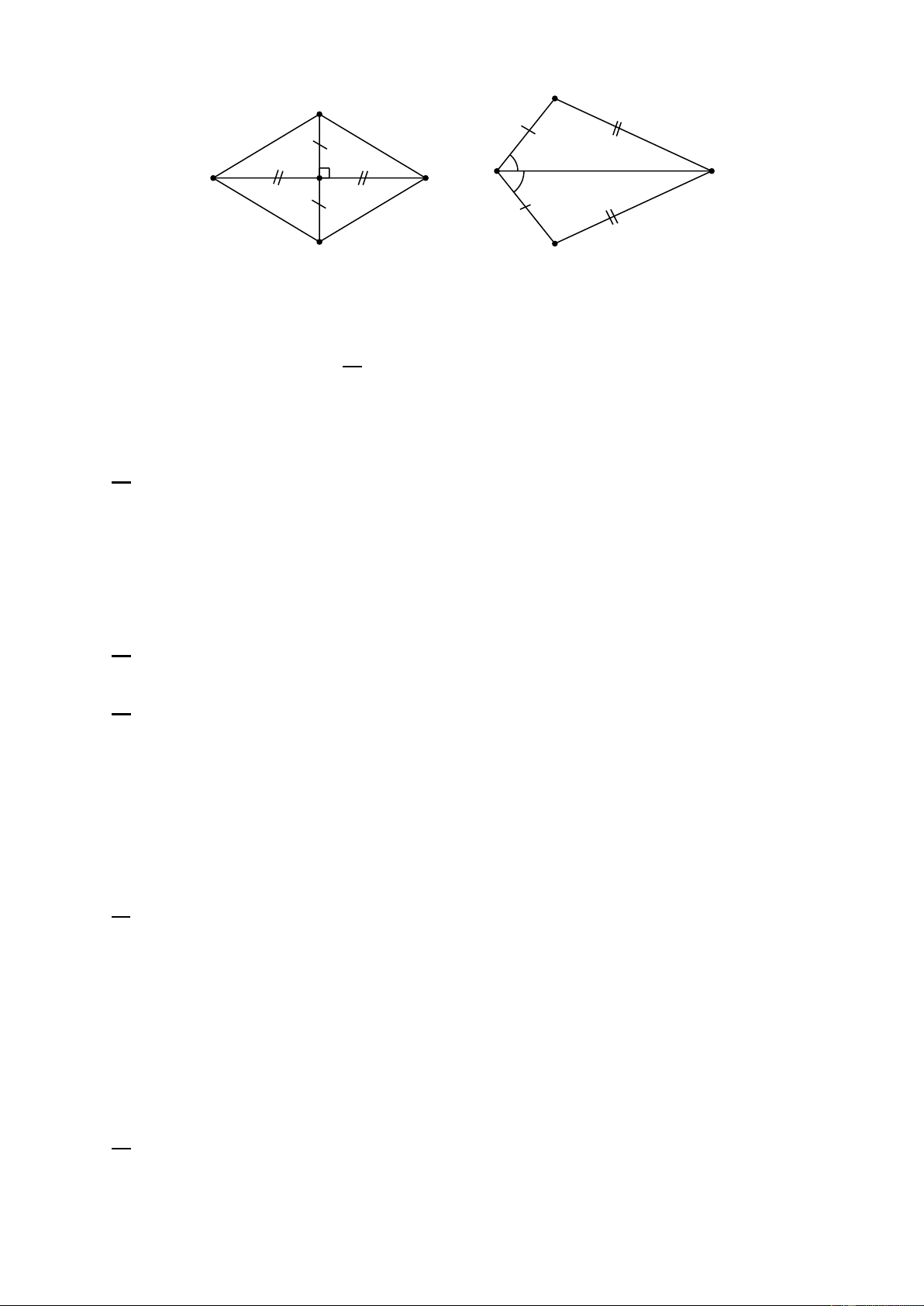
Trang 97

A. Hình 1 B. Hình 2

C. Hình 3 D. Hình 4

Câu 2: Khẳng định nào đúng:

A. Hình thoi là tứ giác có bốn góc bằng nhau.

B. Hình thoi là tứ giác có hai góc đối bằng nhau.

C. Hình thoi là tứ giác có bốn cạnh bằng nhau.

D. Hình thoi là tứ giác có 3 góc vuông.

Câu 3: Chọn câu trả lời sai:

A. Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

B. Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

C. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

D. Tứ giác có bốn góc bằng nhau là hình thoi.

Câu 4: Khẳng định nào đúng?

A. Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

B. Hình vuông là tứ giác có bốn góc bằng nhau.

C. Hình vuông là tứ giác có bốn cạnh bằng nhau.

D. Hình vuông là tứ giác có hai cạnh kề bằng nhau.

Câu 5: Khẳng định nào sai?

A. Trong hình vuông hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi

đường.

B. Trong hình vuông hai đường chéo không vuông góc với nhau

C. Trong hình vuông hai đường chéo đồng thời là hai trục đối xứng của hình vuông.

D. Trong hình vuông hai đường chéo vuông góc với nhau và bằng nhau

Câu 6: Các dấu hiệu nhận biết sau, dấu hiệu nào không đủ để kết luận tứ giác đó là

hình vuông

A. Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

B. Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông

C. Hình chữ nhật có một đường chéo là phân giác của một góc là hình vuông.

D. Hình bình hành có hai đường chéo bằng nhau là hình vuông

Câu 7: Trên hình vẽ cho hình vuông

ABCD

. Biết

BM CN DP AQ= = =

. Tứ giác

MNPQ

là hình gì?

Hình 3

N

M

I

K

S

R

Q

P

Hình 4

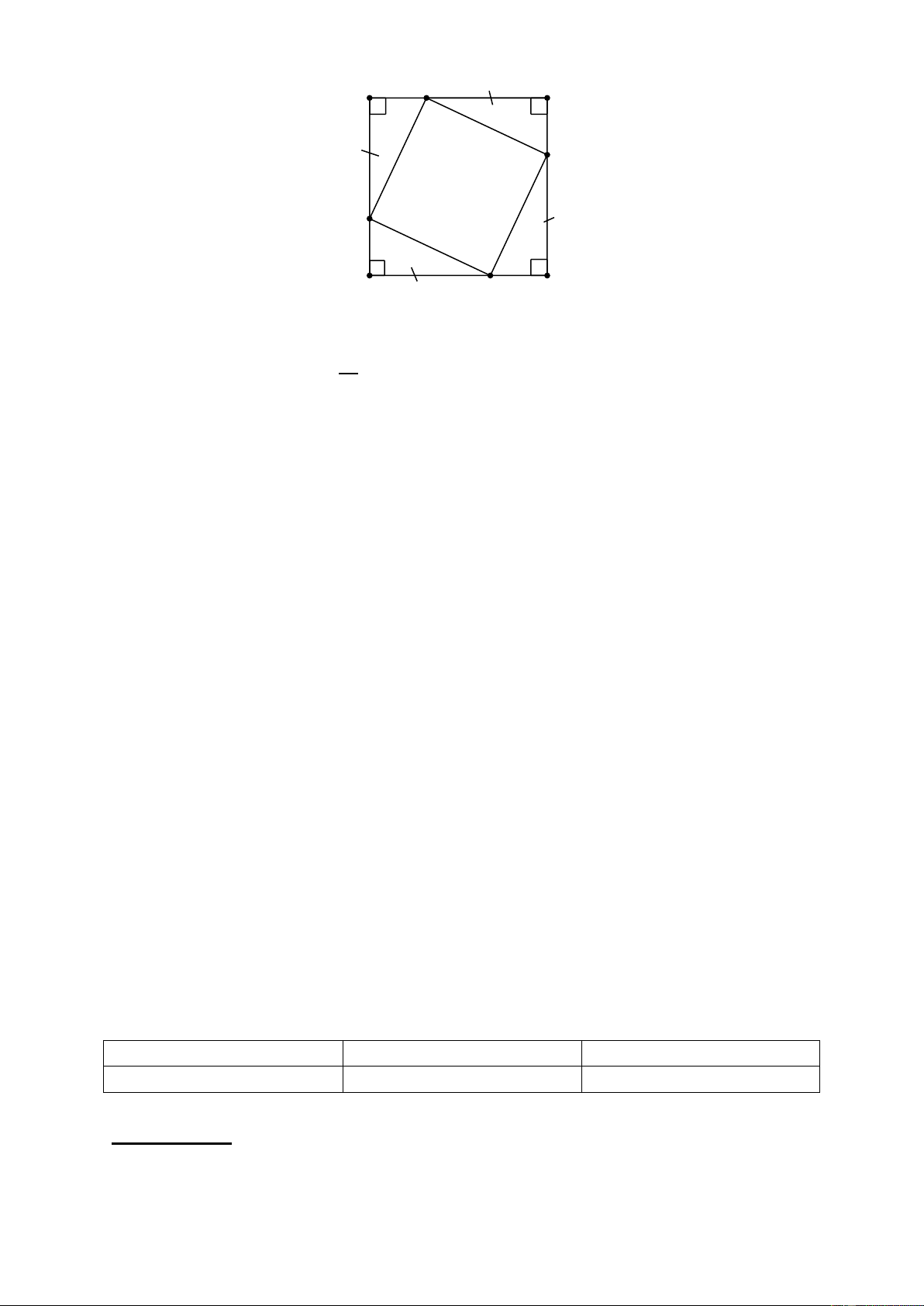
Trang 98

A. Hình bình hành B. Hình chữ nhật

C. Hình thoi D. Hình vuông

2. TỰ LUẬN

Bài 1: Cho tam giác

ABC

, tia phân giác

AD

. Qua

D

kẻ đường thẳng song song với

AC

cắt

AB

ở

E

, qua

D

kẻ đường thẳng song song với

AB

cắt

AC

ở

F

. Tứ giác

AEDF

là hình gì? Vì sao?

Bài 2: Cho hình bình hành

ABCD

có

AC

vuông góc với

AD

. Gọi

M

,

N

theo thứ

tự là trung điểm của

AB

và

CD

. Tứ giác

AMCN

là hình gì? Vì sao?

Bài 3: Cho hình thoi

ABCD

có

60A =

, vẽ

BH

vuông góc với

AD

rồi kéo dài một

đoạn

HE HB=

. Nối

E

với

A

,

E

với

D

.

a. Chứng minh rằng tứ giác

ABDE

là hình thoi.

b.

D

là trung điểm của

EC

.

c.

EB AC=

Bài 4: Cho tam giác

ABC

vuông tại

A

, đường phân giác

AD

. Gọi

,MN

lần lượt là

hình chiếu của

D

trên

,AB

AC

. Chưng minh tứ giác

AMDN

là hình vuông.

Bài 5: Cho hình chữ nhật

ABCD

có

2AB AD=

. Gọi

,PQ

theo thứ tự là trung điểm

của

,AB CD

. Gọi

H

là giao điểm của

AQ

và

DP

, gọi

K

là giao điểm của

CP

và

BQ

. Chứng minh

PHQK

là hình vuông.

Bài 6: Cho hình vuông

ABCD

. Trên cạnh

AD

lấy điểm

F

trên cạnh

DC

lấy điểm E

sao cho

AF DE=

. Chứng minh

AE BF=

và

AE BF⊥

.

Tuần 10

Tiết 25; 26; 27

Ngày soạn 01/11/2023

Lớp

8A

8B

Ngày dạy:

ÔN TẬP HẰNG ĐẲNG THỨC ĐÁNG NHỚ

I. MỤC TIÊU

1. Về kiến thức:

- HS được củng cố, nâng cao một số kiến thức về công thức lũy thừa.

- HS được củng cố một số kiến thức về bảy hằng đẳng thức đáng nhớ.

Q

N

P

M

D

C

B

A

Trang 99

2. Về năng lực:

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được công thức bảy hằng đẳng

thức đáng nhớ.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng

hợp, khái quát hóa, …

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

Các công thức lũy thừa:

1.

n

a =a.a.a...a

5.

m

a

m-n

=a

n

a

2.

a

0

1=

a 0 

6.

n n n

(a.b) a .b=

3.

1

-n

a=

n

a

7.

n

aa

=

n

b







4.

m n m+n

a .a =a

8.

m n n m m.n

(a ) =(a ) =a

Năm hằng đẳng thức đáng nhớ:

( )

2

22

2A+B = A + AB+B

( )

2

22

A B A 2AB B− = − +

( )( )

22

A -B = A+B A-B

( )

3

3 2 2 3

= A +3A B+3AB +B+AB

( )

3

3 2 2 3

3 3−−− = +A B A A B AB B

2. BÀI TẬP

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ

Dạng 1: Thực hiện các phép tính:

Trang 100

- GV tổ chức hoạt động, trả lời nhanh bài

toán trắc nghiệm 1

- HS đứng tại chỗ trả lời:

+ HS1: Đáp án cần chọn là: C

+ HS2: Đáp án cần chọn là: A

+ HS3: Đáp án cần chọn là: B

- Gọi HS khác nhận xét.

- GV nhận xét, đánh giá.

Biến đổi tích thành tổng

Phương pháp:

- Xem biểu thức đã cho có dạng hằng

đẳng thức nào.

- Biến đổi biểu thức đã cho để xuất hiện

dạng hằng đẳng thức.

- Thực hiện các hằng đẳng thức hợp lý ta

có kết quả (có thể kết quả không gọn).

Bài 1: Trắc nghiệm (3-5 câu)

Câu 1: Chọn câu sai.

A.

( )

2

22

2 4 4 + = + +x y x xy y

B.

( )

2

22

– 2 – 4 4=+x y x xy y

C.

( )

2

2 2

– 2 = – 4x y x y

D.

( )( )

22

– 2 2 – 4 +=x y x y x y

Câu 2: Khai triển

( )

2

3 – 4 xy

ta được:

A.

22

9 – 24 16+x xy y

B.

22

9 – 12 16+x xy y

C.

22

9 – 24 4 +x xy y

D.

22

9 – 6 16+x xy y

Câu 3: Khai triển

2

-2

2







x

y

ta được

2

A. 4

4

−+

x

xy y

2

B. 2 4

4

−+

x

xy y

2

C. 2 2

4

−+

x

xy y

2

D. 4

2

−+

x

xy y

Đáp án

Câu 1: Đáp án cần chọn là: C

Câu 2: Đáp án cần chọn là: A

Câu 3: Đáp án cần chọn là: B

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

+ Biểu thức đã cho có dạng hằng đẳng thức

Bài 2: Thực hiện phép tính

( )

1)

2

+aa

2

1

)-

2







bx

Trang 101

nào?

- HS trả lời các câu hỏi:

a)

( )

2

22

2A+B = A + AB+B

b)

( )

2

22

A B A 2AB B− = − +

c)

( )

3

3 2 2 3

= A +3A B+3AB +B+AB

d)

( )

3

3 2 2 3

3 3−−− = +A B A A B AB B

- GV gọi HS lên bảng giải:

( )

2

) 1 2 1+ = + +a a a a

2

11

2

) - -

24

b x x x







=+

( )

)

3

2c xy+

3 2 2 3

8 12 6= + + +x x y xy y

3

1

)-

3







dx

11

32

--

3 27

x x x=+

- HS nhận xét

- GV nhận xét

*Kết luận: Để thực hiện phép tính:

- Xem biểu thức đã cho có dạng hằng đẳng

thức nào.

- Biến đổi biểu thức đã cho để xuất hiện

dạng hằng đẳng thức.

- Thực hiện các hằng đẳng thức hợp lý ta có

kết quả (có thể kết quả không gọn)

( )

3

) 2 +c xy

3

1

)-

3







dx

Lời giải

( )

2

) 1 2 1+ = + +a a a a

22

1 1 1

2

) - -2. .

2 2 2

b x x x

   

   

   

==

1

2

-

4

xx=+

( )

)

3

2c xy+

( ) ( )

32

23

2 3. 2 . 3.2 .x x y x y y= + + +

3 2 2 3

8 12 6= + + +x x y xy y

3

1

)-

3







dx

11

32

--

3 27

x x x=+

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

+ Biểu thức đã cho có dạng hằng đẳng thức

nào?

- HS trả lời các câu hỏi:

a)

( )

3

3 2 2 3

= A +3A B+3AB +B+AB

( )

2

22

2A+B = A + AB+B

b)

( )

2

22

2A+B = A + AB+B

( )

2

22

A B A 2AB B− = − +

c)

( )

3

3 2 2 3

3 3−−− = +A B A A B AB B

- GV gọi HS lên bảng giải:

3 2 3 2

)( 2) ( 2) 7 8 12x x x x x=+ + − + + +a

b)

22

( 1) .( 1)xx+−

24

4 4 1xxx= − − −

Bài 3. Thực hiện phép tính

a)

32

( 2) ( 2)xx+ + −

b)

22

( 1) .( 1)xx+−

c)

( )

4

3

x

−

Lời giải

32

)( 2) ( 2)xx+ + −a

23 2

( 6 12 ))4 48(xx xxx= + + + +−+

23

7 8 12x x x+ + +=

22

)( 1) .( 1)xx+−b

22

2 1).((2 1)x x xx +=−++

Trang 102

c)

( )

2

4

3

9 27 27

3

x

x x x

x

−

= − + −

−

- HS nhận xét

- GV nhận xét

*Kết luận: Để thực hiện phép tính:

- Xem biểu thức đã cho có dạng hằng đẳng

thức nào.

- Biến đổi biểu thức đã cho để xuất hiện

dạng hằng đẳng thức.

- Thực hiện các hằng đẳng thức hợp lý ta có

kết quả (có thể kết quả không gọn).

( )

2

21xx= − +

24

4 4 1xxx= − − −

( )

4

3

23

3

)3

3

9 27 27

x

c

xx

−

=−

−

= − + −

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài

toán trắc nghiệm 1

- HS đứng tại chỗ trả lời:

HS 1: Đáp án cần chọn là: B

HS 2: Đáp án cần chọn là: A

HS 3: Đáp án cần chọn là: A

HS 4: Đáp án cần chọn là: C

HS 5: Đáp án cần chọn là: D

- Gọi HS khác nhận xét.

- GV nhận xét, đánh giá.

Dạng 2: Rút gọn biểu thức và tính giá

trị biểu thức:

Phương pháp rút gọn biểu thức:

Xem biểu thức đã cho có dạng hằng đẳng

thức nào.

Biến đổi biểu thức đã cho để xuất hiện

dạng hằng đẳng thức.

Thực hiện các hằng đẳng thức hợp lý ta

có kết qủa thường thì kết quả rất gọn).

Bài 1: Trắc nghiệm (3-5 câu)

Câu 1: Biểu thức

22

1

4

x y xy++

bằng

2

1

.1

4

A xy



+





2

1

.1

2

B xy



+





2

1

.-

2

C xy







2

1

. -1

2

D xy







Câu 2: Viết biểu thức

22

25 – 20 4 x xy y+

dưới dạng bình phương của một hiệu

( )

2

. 5 – 2A x y

Trang 103

( )

2

. 2 – 5B x y

( )

2

. 25 – 4C x y

( )

2

. 5 2D x y+

Câu 3: Rút gọn biểu thức

( ) ( )

2

3 –1 – 9 1A x x x=+

ta được

. 15 1Ax−+

B. 1

. 15 1 Cx+

D. – 1

Câu 4: Rút gọn biểu thức

( ) ( ) ( )( )

22

5 4 4 – 5 – 9 4 – 4A x x x x= + + +

, ta được:

A. 342

B. 243

C. 324

D. 324−

Câu 5: Rút gọn biểu thức

( )( ) ( ) ( )

2

2 – 3 1 – – 4 – 7B a a a a a= + +

ta được

A. 0

B. 1

C. 19

D. – 19

Đáp án

Câu 1: Đáp án cần chọn là: B

Câu 2: Đáp án cần chọn là: A

Câu 3: Đáp án cần chọn là: A

Câu 4: Đáp án cần chọn là: C

Câu 5: Đáp án cần chọn là: D

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

+ Biểu thức đã cho có dạng hằng đẳng thức

nào?

- HS trả lời các câu hỏi:

a)

( )

2

22

2A + AB+B A+B=

b)

( )( )

22

A -B = A+B A-B

c)

( )

3

3 2 2 3

3 3A A B AB B A B− − =+−

- GV gọi HS lên bảng giải:

( )

2

4 2) 4a x x x+ + = +

( )( )

2

1 -1 -1) xxb x+=

3 2 2 3 3

-6 12 -8 - 2) ( )c x x y xy y x y=+

Bài 2: Rút gọn biểu thức

2

4) 4a x x++

( )( )

1) 1 -xb x+

3 2 2 3

-6 2 -8) 1c x x y xy y+

Lời giải

2 2 2

4 4 2. .2 2)a x x x x+ + = + +

( )

2

2x=+

( )( )

2 2 2

1 -1 -1 -1) x x xb x+ = =

3 2 2 3 3

-6 12 -8 -2) ( )c x x y xy y x y=+

Trang 104

- HS nhận xét

- GV nhận xét

*Kết luận: Phương pháp rút gọn biểu

thức:

Xem biểu thức đã cho có dạng hằng đẳng

thức nào.

Biến đổi biểu thức đã cho để xuất hiện dạng

hằng đẳng thức.

Thực hiện các hằng đẳng thức hợp lý ta có

kết qủa thường thì kết quả rất gọn).

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài

toán trắc nghiệm 1

- HS đứng tại chỗ trả lời:

HS 1: Đáp án cần chọn là: B

HS 2: Đáp án cần chọn là: C

HS 3: Đáp án cần chọn là: A

- Gọi HS khác nhận xét.

- GV nhận xét, đánh giá.

Phương pháp tính giá trị biểu thức:

Dựa vào hằng đẳng thức thu gọn biểu

thức.

Thay giá trị của biến vào biểu thức thu

gọn.

Thực hiện phép tính các số ta có kết quả.

Bài 1: Trắc nghiệm (3-5 câu)

a) Tính giá trị

2

21xx−+

tại

1x =

A. 0

B. 1

C. 2

D. 3

b) Tính giá trị

2

21xx++

tại

1x =

A. 0

B. 2

C. 4

D. 6

c) Tính giá trị

32

3 3 1x x x+ + +

tại

1x =

A. 2

B. 4

C. 6

D. 8

Đáp án

a) Đáp án cần chọn là: A

b) Đáp án cần chọn là: B

Trang 105

c) Đáp án cần chọn là: D

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

+ Biểu thức đã cho có dạng hằng đẳng thức

nào?

- HS trả lời các câu hỏi:

a)

( )

3

3 2 2 3

A +3A B+3AB +B AB= +

b)

( )

3

3 2 2 3

33A A B AB B A B−+ = −−

c)

( )

2

22

2A+B = A + AB+B

sau khi rút

gọn thì biến đổi xuất hiện tổng và tích

của a;b.

d)

( )

2

22

A B A 2AB B− = − +

sau khi rút

gọn thì biến đổi xuất hiện hiệu và tích

của a;b.

- GV gọi HS lên bảng giải:

- HS nhận xét

- GV nhận xét

*Kết luận: Phương pháp tính giá trị biểu

thức:

Dựa vào hằng đẳng thức thu gọn biểu thức.

Thay giá trị của biến vào biểu thức thu gọn.

Thực hiện phép tính các số ta có kết quả.

Bài 2: Tính giá trị biểu thức

a)

32

2

8 4

3

1

27

x x x+ + +

khi

1

6

x =

b)

3 2 2 3

27 54 36 8x x y xy y− + −

khi

1; 1xy==

c)

( )

2

ab−

biết

7ab+=

và

. 12ab=

d)

( )

2

ab+

biết

20ab−=

và

.3ab=

Lời giải

a)

3

32

11

27

2

8 2

3 3

4x x x x



=





++



++

Thay

1

6

x =

vào biểu thức

3

2

3

1

x







+

:

3 3 3

1 1 1 1 2 8

6 3 3 3

2

27

.

3

     

= = =

    

++



     

3 2 2 3

27 54 36 8)b x x y xy y− + −

( )

3

32xy= −

Thay

1; 1xy==

vào biểu thức

( )

3

3 - 2xy

:

( ) ( )

33

3

3.1- 2.1 3- 2 11= = =

c) Ta có:

( ) ( )

22

2

4 7 4.12a b a b ab− = + − = − =

49 48 1= − =

d) Ta có:

( ) ( )

22

2

a b a b 4ab 20 4.3+ = − + = +

400 12 412= + =

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài

toán trắc nghiệm 1

- HS đứng tại chỗ trả lời:

+ HS1: Đáp án cần chọn là: B

+ HS2: Đáp án cần chọn là: C

Dạng 3: Tính nhanh:

Phương pháp:

Xem biểu thức đã cho có dạng hằng đẳng

thức nào.

Biến đổi hoặc thêm, bớt vào biểu thức đã

cho để xuất hiện dạng hằng đẳng thức.

Trang 106

+ HS3: Đáp án cần chọn là: A

- Gọi HS khác nhận xét.

- GV nhận xét, đánh giá.

Thực hiện hằng đẳng thức và các phép

tính ta có kết quả.

Bài 1: Trắc nghiệm (3-5 câu)

Câu 1: Giá trị của

2

101

là:

A. 10101

B. 10201

C. 10301

D. 10401

Câu 2: Không dùng máy tính, hãy tính

2

199

:

A.39401

B.39501

C.39601

D.39701

Câu 3: Không dùng máy tính, hãy tính

47.53

:

A.2491

B. 2591

C. 2691

D. 2791

Đáp án

a) Đáp án cần chọn là: A

b) Đáp án cần chọn là: B

c) Đáp án cần chọn là: D

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

+ Biểu thức đã cho có dạng hằng đẳng thức

nào?

- HS trả lời các câu hỏi:

a)

( )

2

22

2A+B = A + AB+B

b)

( )

2

22

A B A 2AB B− = − +

c)

( )( )

22

A -B = A+B A-B

d)

( )

2

22

2A+B = A + AB+B

e)

( )( )

22

A -B = A+B A-B

- GV gọi HS lên bảng giải:

( )

2

a 301 = 300+1 =9) 0601

( )

2

99 = 100-1 =b) 9801

( )( )

22

c 56.64= 60-4 60+4 =

=60 -4

)

=3584

Bài 2: Tính nhanh

2

a)301

2

b) 99

c) 56.64

22

d 53 + 47 + 47.) 106

( )( )

4 4 2 2

e 5 . 3 – 15 – 1 15) + 1

Lời giải

( )

2

a 301 = 300+1)

22

=300 +2.300.1+1

=90000+600+1 =90601

( )

2

99 = 1b 00-1) =

22

=100 -2.100.1+1 =9801.

( )( )

c 56.64= 60-4 6) 0+4 =

22

=60 -4 =3584

Trang 107

( )

( )( )

22

2

4 4 2 2

44

d 53 + 47 + 47. 106

= 53 + 47 + 2. 47. 53

= 53 + 47 = 100 = 10000

e 5 . 3 – 15 – 1 15 +

)

(

1

= 15 – 1 )5 – 1 = 1

- HS nhận

xét

- GV nhận xét

*Kết luận: Để tính nhanh:

Xem biểu thức đã cho có dạng hằng đẳng

thức nào.

Biến đổi hoặc thêm, bớt vào biểu thức đã

cho để xuất hiện dạng hằng đẳng thức.

Thực hiện hằng đẳng thức và các phép tính

ta có kết quả.

22

d 53 + 47 + 47.) 106

22

= 53 + 47 + 2. 47. 53

( )

2

= 53 + 47 = 100 = 10000

( )( )

4 4 2 2

e 5 . 3 – 15 – 1 15) + 1

44

= 15 – 15()– 1 = 1

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài

toán trắc nghiệm 1

- HS đứng tại chỗ trả lời:

+ HS1: Đáp án cần chọn là: C

+ HS2: Đáp án cần chọn là: D

+ HS3: Đáp án cần chọn là: D

- Gọi HS khác nhận xét.

- GV nhận xét, đánh giá.

Dạng 4: Chứng minh đẳng thức:

Phương pháp:

Để chứng minh đẳng thức: A = B

- Đưa dạng A về dạng B ( hoặc đưa dạng

B về dạng A)

- So sánh A = B rồi kết luận.

Bài 1: Trắc nghiệm (3-5 câu)

Câu 1: Chọn câu đúng

( ) ( ) ( )( )

22

. – – A c d a b c d a b c d a b+ + = + + + + +

( ) ( ) ( )( )

22

. – – – – – B c d a b c d a b c d a b+ = + + +

( )( ) ( ) ( )

22

. – – – – C a b c d a b c d a b c d+ + + + = +

( )( ) ( ) ( )

22

. – – – – C a b c d a b c d a b c d+ + + + = +

Câu 2: Chọn câu đúng

( ) ( )( )

2

. 4 – 2 2 – A a b a b a b+ = + + +

( ) ( )( )

2

. 4 – 4 4 – – B a b a b a b+ = + +

( ) ( )( )

2

. 4 – 2 – 2 – C a b a b a b+ = + +

( ) ( )( )

2

. 4 – 2 2 – – D a b a b a b+ = + +

Trang 108

Câu 3: So sánh

A = 2019.2021.a

và

( )

2

B = 2019 + 2.2019 + 1 a

(với

a > 0

)

. A A B=

. B A B

. C A B

. D A B

Đáp án

Câu 1: Đáp án cần chọn là: C

Câu 2: Đáp án cần chọn là: D

Câu 3: Đáp án cần chọn là: D

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

+ Biểu thức đã cho có dạng hằng đẳng thức

nào?

- HS trả lời các câu hỏi:

a)

( )

2

22

A B A 2AB B− = − +

( )

2

22

2A+B = A + AB+B

b)

( )

2

22

A B A 2AB B− = − +

- GV gọi HS lên bảng giải:

( )

2

22

2

22

) - 4 - 2 4

2

a Xét a b ab a ab b ab

a ab b a b

+ = + +

= + + = +

Vậy

( ) ( )

22

- -4a b a b ab=+

( ) ( )

22

2 2 2 2

- -

2-

)

2 - 4

a b a b

a ab b a a a

b

b b b

+

= + + + =

- HS nhận xét

- GV nhận xét

*Kết luận: Để chứng minh đẳng thức: A

= B

- Đưa dạng A về dạng B ( hoặc đưa dạng B

về dạng A)

- So sánh A = B rồi kết luận.

Bài 2: Chứng minh:

a)

( ) ( )

22

-4a b a b ab+ = +

( ) ( )

22

- - 4) a b a bb ab+=

Lời giải

( )

2

22

) - 4 -2 4a Xét a b ab a ab b ab+ = + +

( )

2

22

2a ab b a b= + + = +

Vậy

( ) ( )

22

- - 4a b a b ab=+

( ) ( )

22

) - -b a b a b+

2 2 2 2

2 - 2 - 4a ab b a ab b ab= + + + =

IV. PHIẾU BÀI TẬP BỔ TRỢ

1. TRẮC NGHIỆM

Câu 1: Chọn câu đúng.

( )

3

3 2 2 3

. 3 3 A A B A A B AB B+ = + + +

( )

3

3 2 2 3

. - - 3 - 3 - B A B A A B AB B=

( )

3

33

. C A B A B+ = +

Trang 109

( )

3

33

. - - D A B A B=

Câu 2: Chọn câu đúng

( )

3

– 2xy

bằng:

3 2 3

. – 3 3 A x xy x y y++

3 2 2 3

. – 6 12 – 8B x x y xy y+

3 2 2 3

. – 6 12 – 4C x x y xy y+

3 2 2 3

. – 3 12 – 8D x x y xy y+

Câu 3: Chọn câu sai.

( )

3 3 2 2

. – A A B A B A AB B+ = + +

( )

3 3 2 2

. - - B A B A B A AB B= + +

( ) ( )

33

. C A B B A+ = +

( ) ( )

33

. – – D A B B A=

Câu 4: Chọn câu đúng.

( )

2 3 3

. 8 12 6 8 A y y y y+ + + = +

( )

3

32

. 3 3 1 1B a a a a+ + + = +

( )

3

3 2 3

. 2 – 2 – 6 6 – C x y x x y xy y=+

( )

3

32

. 3 1 3 9 3 1D a a a a+ = + + +

Câu 5: Chọn câu sai.

( ) ( )

3

33

. - – - – 3 – A b a a ab a b b=+

( ) ( )

3

33

. – – 3 – B c d c d cd d c=+

( ) ( )

3

. – 2 – 8 – 6 2C y y y y=+

( ) ( )

3

. – 1 – 1 3 – 1D y y y y=−

Câu 6: Viết biểu thức

32

x + 12x + 48x + 64

dưới dạng lập phương của một tổng

( )

3

. 4Ax+

( )

3

. – 4Bx

( )

3

. – 8 Cx

( )

3

. 8Dx+

Câu 7: Viết biểu thức

32

8 36 54 27x x x+ + +

dưới dạng lập phương của một tổng

( )

3

. 2 9Ax+

( )

3

. 2 3Bx+

( )

3

. 4 3Cx+

Trang 110

( )

3

. 4 9Dx+

Câu 8: Viết biểu thức

32

– 6 12 – 8x x x+

dưới dạng lập phương của một hiệu

( )

3

. 4 Ax+

( )

3

. – 4Bx

( )

3

. 2 Cx+

( )

3

. - 8Dx

Câu 9: Viết biểu thức

3 2 2 3

8 – 12 6 – x x y xy y+

dưới dạng lập phương của một

hiệu

( )

3

. 2 – A x y

( )

3

. – 2B x y

( )

3

. 4 – C x y

( )

3

. 2 Dxy+

2. TỰ LUẬN

Câu 10: Cho

( ) ( )

22

2

55

25

xx

C

x

+ + −

=

+

và

( ) ( )

22

2

2 5 5 2

1

xx

D

x

+ + −

=

+

. Tìm mối quan

hệ giữa C và D.

Câu 11: Cho

( ) ( ) ( )( )

22

4 1 2 1 – 8 – 1 1 – 12 M x x x x x= + + + +

Tìm mối quan hệ

giữa M và N

Câu 12: Tìm x thỏa mãn

( ) ( )

22

2 – 1 – 5 – 5 0xx=

Câu 13: Tìm giá trị x thỏa mãn

( ) ( )

22

2 1 – 4 3 0xx+ + =

Câu 14: Tìm x biết

( )( ) ( )

2

– 6 6 – 3 9x x x+ + =

Câu 15: Tìm x biết

( ) ( ) ( )( )

22

3 – 1 2 3 11 1 1 – 6x x x x+ + + + =

Câu 16: So sánh

A 2016.2018.a và B 2017.a==

(với a > 0)

Câu 17: So sánh

( )

2

2019.2021. 2019 2.2019 1A a và B a= = + +

(với a > 0)

Câu 18: So sánh

( )

( )( )( )( )

32 2 4 8 16

2 2 1 2 1 2 1 2 1 2 1M và N= = + + + + +

Tuần 11

Tiết 28; 29; 30

Ngày soạn 01/11/2023

Lớp

8A

8B

Ngày dạy:

ÔN TẬP CHƯƠNG III

Trang 111

I. MỤC TIÊU

1. Về kiến thức:

- Khái niệm tứ giác, tứ giác lồi. Các yếu tố của tứ giác lồi. Tính chất của tứ giác lồi.

- Khái niệm hình thang, hình thang cân. Tính chất hình thang cân. Dấu hiệu nhận biết

hình thang cân.

- Khái niệm hình bình hành. Tính chất hình bình hành. Dấu hiệu nhận biết hình bình

hành.

- Khái niệm và tính chất hình chữ nhật. Dấu hiệu nhận biết hình chữ nhật.

- Khái niệm và tính chất hình thoi, hình vuông. Dấu hiệu nhận biết hình thoi và hình

vuông.

2. Về năng lực:

* Năng lực chung:

- Năng lực tự chủ và tự học trong tìm tòi khám phá

- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm

- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu được định nghĩa các tứ giác đã học.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng

hợp, khái quát hóa,

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu, phiếu

bài tập.

2. Học sinh: vở ghi, thước thẳng, thước, bảng nhóm

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

Tổng hợp kiến thức cần nhớ: Giáo viên ôn tập kiến thức cần thiết cho học sinh

Giáo viên tổ chức cho hs hoàn thành sơ đồ tư duy theo hình thức hoạt động nhóm

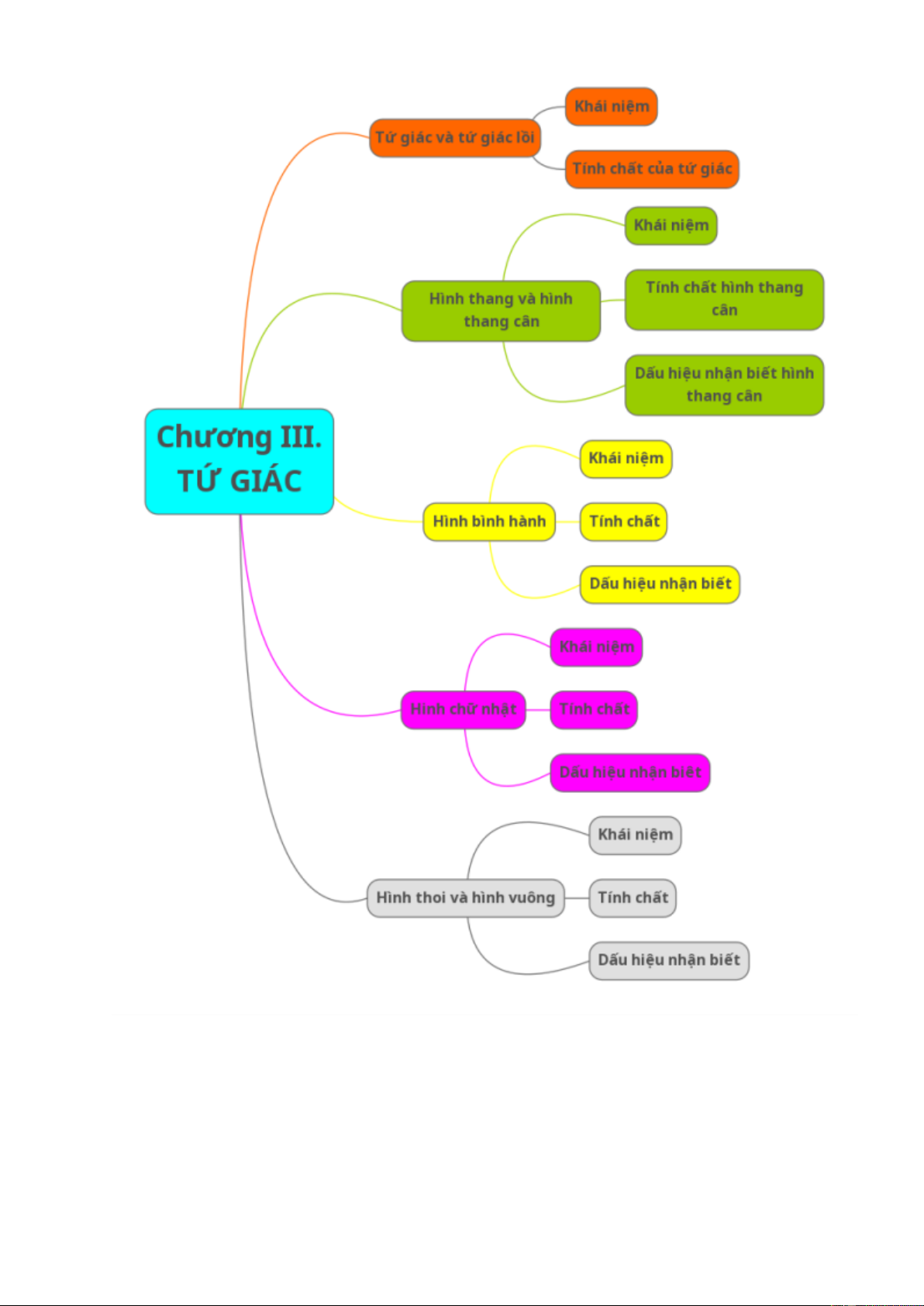
Trang 112

Trang 113

2. BÀI TẬP

Hoạt động của giáo viên

Nội dung

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài

toán trắc nghiệm 1

HS tìm hiểu bài toán 1

Hoặc nhận nhiệm vụ GV giao

Dạng 1: BÀI TẬP TRẮC NGHIỆM

Câu 1: Tứ giác

ABCD

có :

µ µ

0 0 0

0 0 0 0

65 ; 117 ; 71 . ?

.1 19 . 107 . 63 . 126

B C Thì C

A B C D

A = = ==

Câu 2: Chọn câu đúng trong các câu sau:

A.Hình thang có 3 góc tù, 1 góc nhọn.

B.Hình thang có 3 góc vuông, 1 góc nhọn

C.Hình thang có 3 góc nhọn, 1 góc tù.

D.Hình thang có nhiều nhất 2 góc tù, nhiều

nhất 2 góc nhọn

Câu 3: Hãy điền chữ “Đ” hoặc chữ “S”

vào mỗi câu khẳng định sau:

A.Tứ giác có hai cạnh bên bằng nhau là

hình thang cân

B.Hình thang cân có hai cạnh bên bằng

nhau.

C.Hình thang cân có hai góc kề với cạnh

đáy bù nhau.

D.Hình thang cân có hai góc kề với cạnh

đáy bằng nhau.

Câu 4 : Khẳng định nào sau đây đúng

A. Hình bình hành là tứ giác có hai cạnh

song song.

B. Hình bình hành là tứ giác có các góc

bằng nhau .

C. Hình bình hành là tứ giác có các cạnh

đối song song.

D. Hình bình hành là hình thang có hai

cạnh bên bằng nhau

Câu 5. Khẳng định nào sau đây đúng?

A.Hình chữ nhật là tứ giác có 4 cạnh bằng

nhau

B.Hình chữ nhật là tứ giác có 4 góc vuông

Bài 1: Bài tập trắc nghiệm

Câu 1: B

Câu 2: D

Câu 3: Hãy điền chữ “Đ” hoặc chữ “S”

vào mỗi câu khẳng định sau:

A. Tứ giác có hai cạnh bên bằng nhau là

hình thang cân S

B. Hình thang cân có hai cạnh bên bằng

nhau. Đ

C. Hình thang cân có hai góc kề với cạnh

đáy bù nhau. S

D .Hình thang cân có hai góc kề với cạnh

đáy bằng nhau. Đ

Câu 4: C

Câu 5: B

Câu 6: A

Câu 7: A

Câu 8: B

Câu 9: D

Câu 10: C

Trang 114

C.Hình chữ nhật là tứ giác có hai góc

vuông

D.Hình thang có một góc vuông là hình chữ

nhật.

Câu 6 Trong các khẳng định sau, khẳng

định nào sai đối với hình thoi.

A. Hai đường chéo bằng nhau.

B. Hai đường chéo vuông góc với nhau

và là các tia phân giác của các góc của hình

thoi

C. Hai đường chéo cắt nhau tại trung

điểm của mỗi đường.

D. Đường chéo là phân giác của các

góc của hình thoi

Câu 7. Trong các khẳng định sau, khẳng

định nào đúng.

A. Hình vuông là tứ giác có bốn góc vuông

và bốn cạnh bằng nhau.

B. Hình vuông là tứ gíac có bốn góc bằng

nhau.

C. Hình vuông là tứ giác có bốn cạnh bằng

nhau.

D. Hình vuông là tứ giác có hai cạnh kề

bằng nhau

Câu 8: Hình thang có hai cạnh đáy bằng

nhau là:

A. hình thang cân.

B. hình bình hành.

C. hình chữ nhật.

D. hình thoi.

Câu 9: Hình bình hành có hai đường chéo

bằng nhau và vuông góc với nhau là:

A. hình thang cân.

B. hình chữ nhật.

C. hình thoi.

D. hình vuông.

Câu 10: Hình vuông có diện tích bằng

2

1()cm

thì hình vuông đó có chu vi là:

A.

1( )cm

.

B.

2( )cm

.

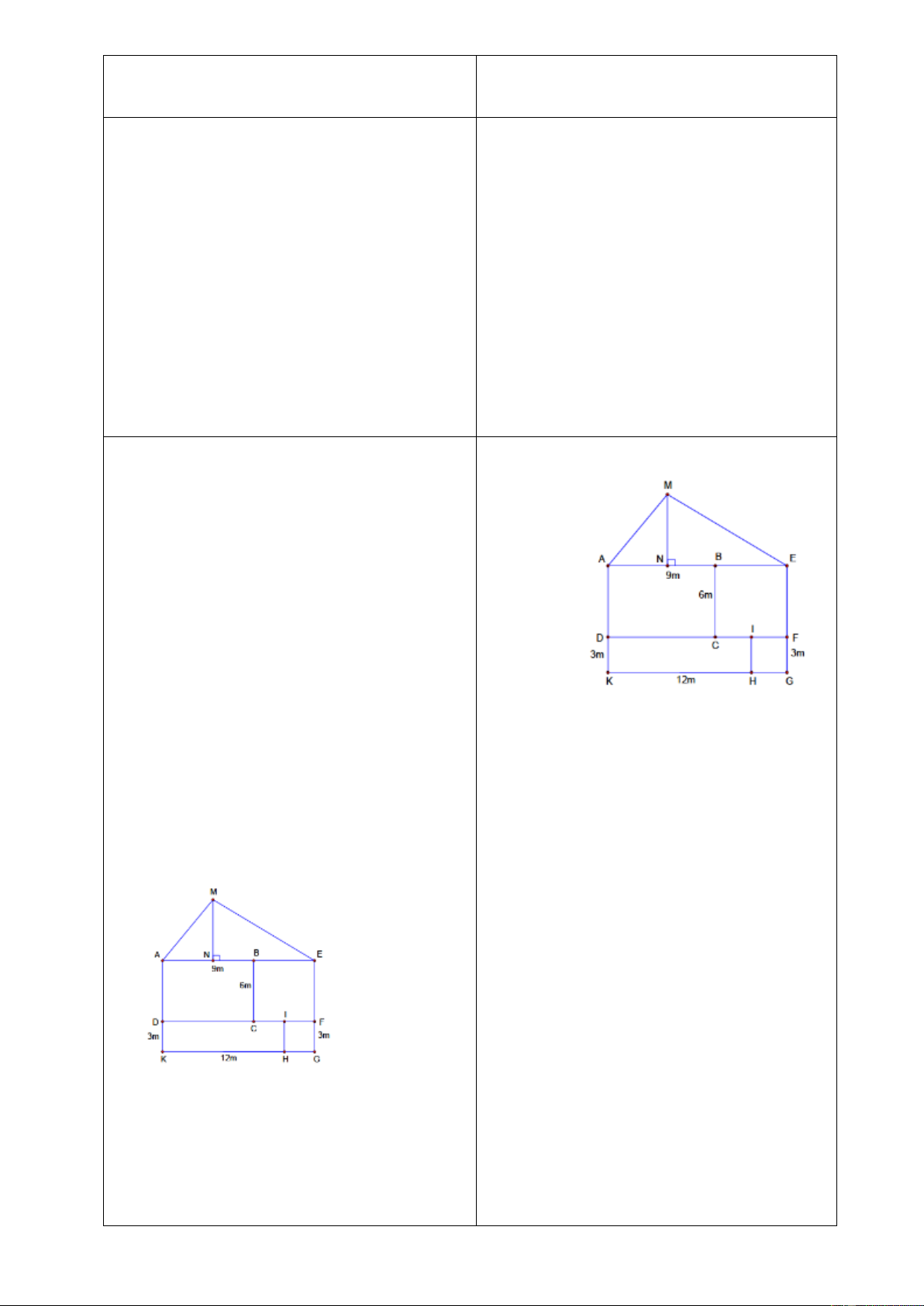
Trang 115

C.

4( )cm

.

D. Kết quả khác

*Thực hiện nhiệm vụ

- Giáo viên tổ chức cho học sinh làm trên

phiếu cá nhân trong thời gian 10 phút.

- Giáo viên chữa bài và cho hs đổi bài chấm

chéo kết quả.

- HS làm bài trên phiếu bài tập

*Kết luận, nhận định:

GV khai thác các câu hỏi theo các hướng

khác nhau (nếu được)

Bài 1:

Ông An muốn xây nhà trên miếng đất có

diện tích

2

160m

. Hình bên là sơ đồ tầng trệt

của căn nhà.

Phòng khách là hình chữ nhật

ABCD

.

Phòng ăn và nhà bếp là hình vuông

BEFC

.

Phòng vệ sinh là hình vuông

.FGHI

Sảnh

trước là hình chữ nhật

DIHK

. Kho chứa là

tam giác

AME

.

a. Tính diện tích kho chứa.

b. Khi xây dựng để đảm bảo an toàn ngôi

nhà.

Ông An phải thiết kế thêm đường giằng

MN

như hình vẽ. Tính độ dài đường giằng

.MN

(Kết quả làm tròn đến chữ số thập

phân thứ hai)

* Giao nhiệm

vụ

GV cho hs đọc

bài

- hs tìm lời giải

*Thực hiện nhiệm vụ

- Quan sát và phân tích đầu bài chỉ ra

hướng làm bài

*Kết luận, nhận định:

- Gv chữa bài cho hs

DẠNG 2: BÀI TOÁN THỰC TẾ

Bài 1

a)Tính được độ dài cạnh

12 3 15( )AE m= + =

6 3 9( )AK m= + =

Diện tích hình chữ nhật

AEGK

là :

2

135( )m

Diện tích kho chứa

AME

là:

2

160 135 25( )m−=

b) Độ dài đoạn

MN

là:

25.2:15 3,33( )m

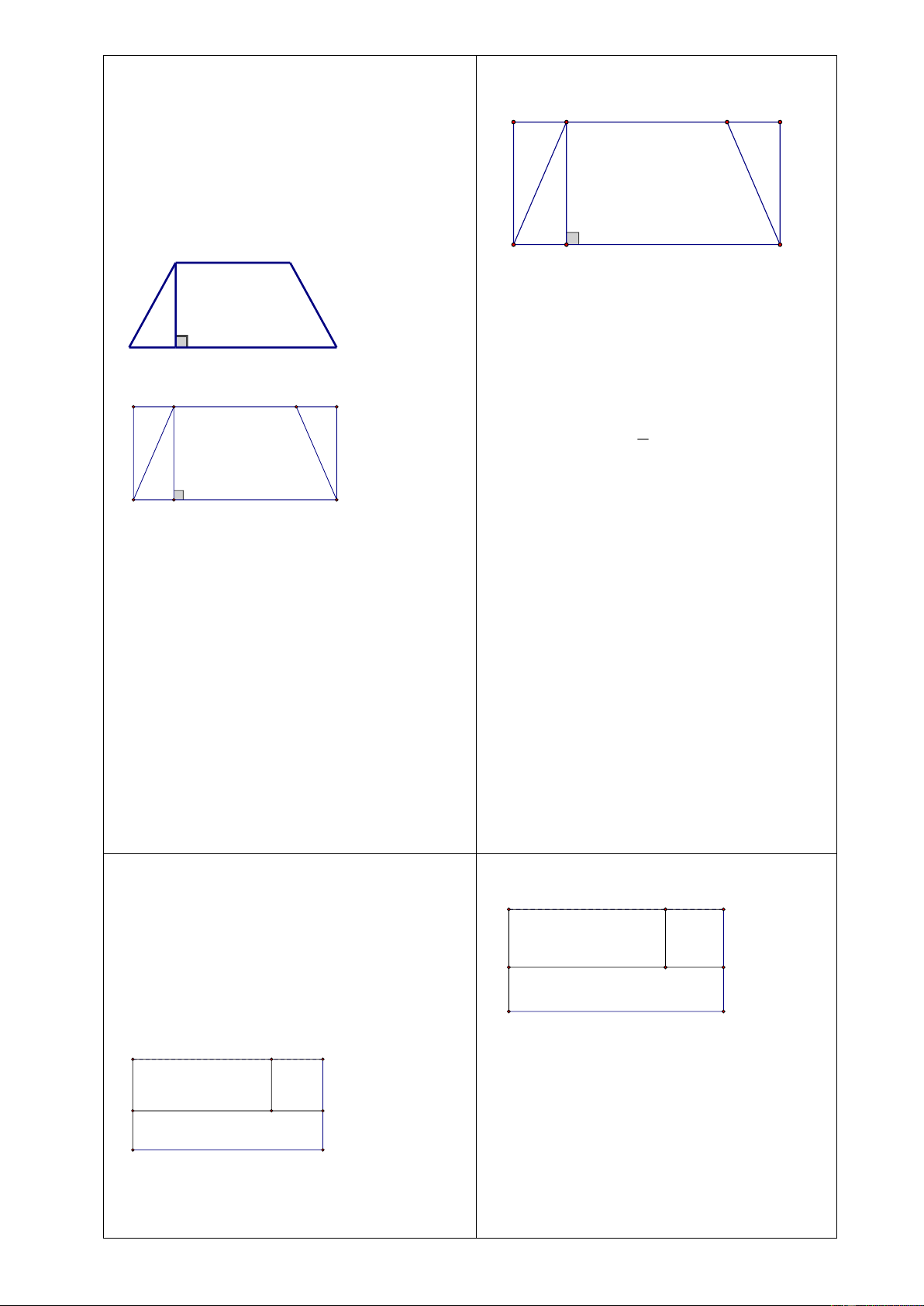
Trang 116

Bài 2. Bác Ngọc có một miếng đất hình

thang cân với diện tích là

2

1500(m )

(như

hình vẽ). Bác mua thêm hai miếng đất nữa

để đất của bác trở thành hình chữ nhật. Hỏi

diện tích đất mà bác mua thêm là bao

nhiêu?

* Giao nhiệm vụ

GV cho hs đọc bài

- hs tìm lời giải

*Thực hiện nhiệm vụ

- Quan sát và phân tích đầu bài chỉ ra

hướng làm bài

- Hs tìm lời giải và trình bày vào bài làm

*Kết luận, nhận định:

- Gv chữa bài cho hs

Bài 2:

Ta có:

 

(4 6 ).30 :2 1500xx+=

10 .30 3000x =

10x =

Diện tích

2

1

30.10 150( )

2

 = =ADH m

Hai miếng đất mua thêm có tổng diện tích

để mảnh vườn hình chữ nhật là:

2

2.150 300( )= m

Bài 3. Một miếng đất hình chữ nhật ABCD

được chia làm 3 phần như hình vẽ: phần

nhà ở là hình chữ nhật, phần vườn hoa là

hình vuông có cạnh 4m, phần trồng rau là

hình chữ nhật có diện tích

2

70( )m

và chiều

rộng là

3,5( )m

. Tính diện tích phần nhà ở?

* Giao nhiệm vụ

Bài 3

Tính DC:

70:3,5 20( )m=

20( )AB CD m = =

Chiều dài phần nhà ở là:

20 4 16( )m−=

Diện tích phần nhà ở là:

2

16.4 64( )m=

30(m)

4x (m)

6x (m)

4x (m)

30(m)

D

H

C

F

B

A

E

D

H

C

B

A

30(m)

6x(m)

4x(m)

H

F

E

B

D

C

A

30(m)

6x(m)

4x(m)

H

F

E

B

D

C

A

Vườn hoa

Trồng rau

nhà ở

70m

2

3,5m

4m

B

D

C

A

Vườn hoa

Trồng rau

nhà ở

70m

2

3,5m

4m

B

D

C

A

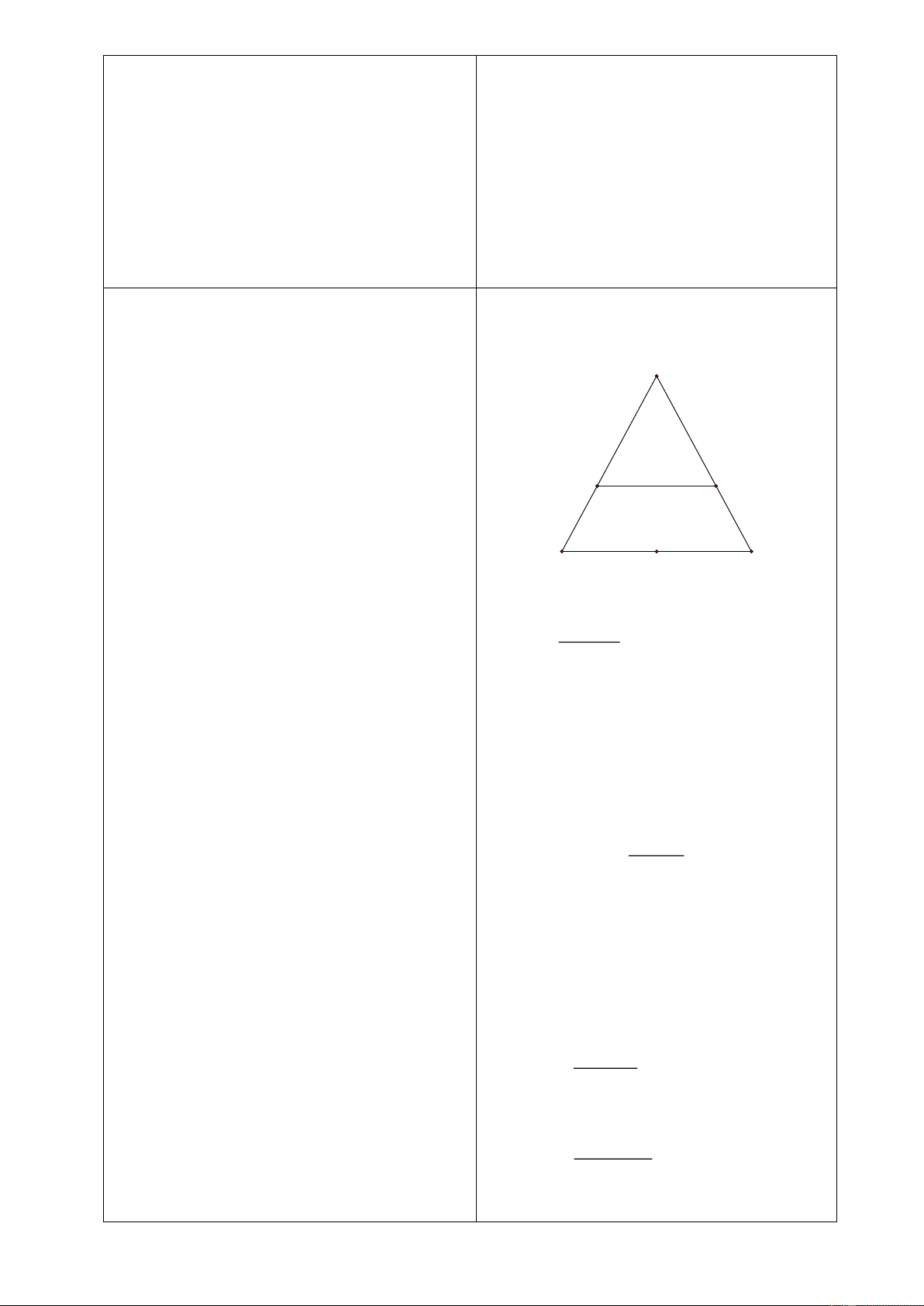
Trang 117

GV cho hs đọc bài

- hs tìm lời giải

*Thực hiện nhiệm vụ

- Quan sát và phân tích đầu bài chỉ ra

hướng làm bài

- Hs tìm lời giải và trình bày vào bài làm

*Kết luận, nhận định:

- Gv chữa bài cho hs

Bài 1:

Cho tam giác ABC cân tại A. Trên các cạnh

bên AB, AC lấy các điểm M, N sao cho

BM CN=

.

a) Tứ giác BMNC là hình gì?

b) Tính các góc của tứ giác BMNC

µ

0

40A =

.

GV cho hs đọc đề bài và cho lên vẽ hình.

*Thực hiện nhiệm vụ

- HS đọc đề bài và lên bảng vẽ hình.

* GV gợi ý chứng minh:

- HS nêu định nghĩa và dấu hiệu nhận biết

hình thang cân:

- Hình thang cân có tính chất gì?

- GV tổ chức hoạt động, hướng dẫn HS tìm

hiểu bài toán 2 (Đề bài)

+ a) Ta chứng minh tứ giác BMNC là hình

thang có 2 góc kề 1 đáy bằng nhau

=> hình thang cân.

+ * Hình thang cân:

. Định nghĩa: Hình thang cân là hình thang

có 2 góc kề 1 đáy bằng nhau.

+ Tính chất:

+ Trong hình thang cân, 2 cạnh bằng nhau.

+ Trong hình thang cân, 2 đường chéo bằng

nhau.

+ + Hình thang có 2 đường chéo bằng nhau

là hình thang cân.

*Kết luận, nhận định: GV gợi ý hs tìm

cách giải. Gọi 2 hs lên bảng thực hiện. Hs

DẠNG 3: BÀI TẬP TỔNG HỢP

Bài 1: Hướng dẫn giải

a) Vì ABC cân tại A nên

0

180 - A

B = C =

2

(1)

Mặt khác ta có:

()AB AC gt=

()MB NC gt=

AM AN=

AMN

cân tại A



0

180 -A

AMN=ANM=

2

(2)

Từ (1) và (2) suy ra:

B = AMN

//MN BC



Tứ giác

BMNC là hình thang(đ/n) .

Mà

B = C

nên là hình thang cân(dhnb).

b) Tứ giác

BMNC

là hình thang cân



µ

0

180

2

A

BC

−

==

Mà

µ

0

40A =



µ

00

0

180 40

70

2

BC

−

= = =

·

0 0 0

360 2.70 110BMC CNM= = − =

N

B

C

A

M

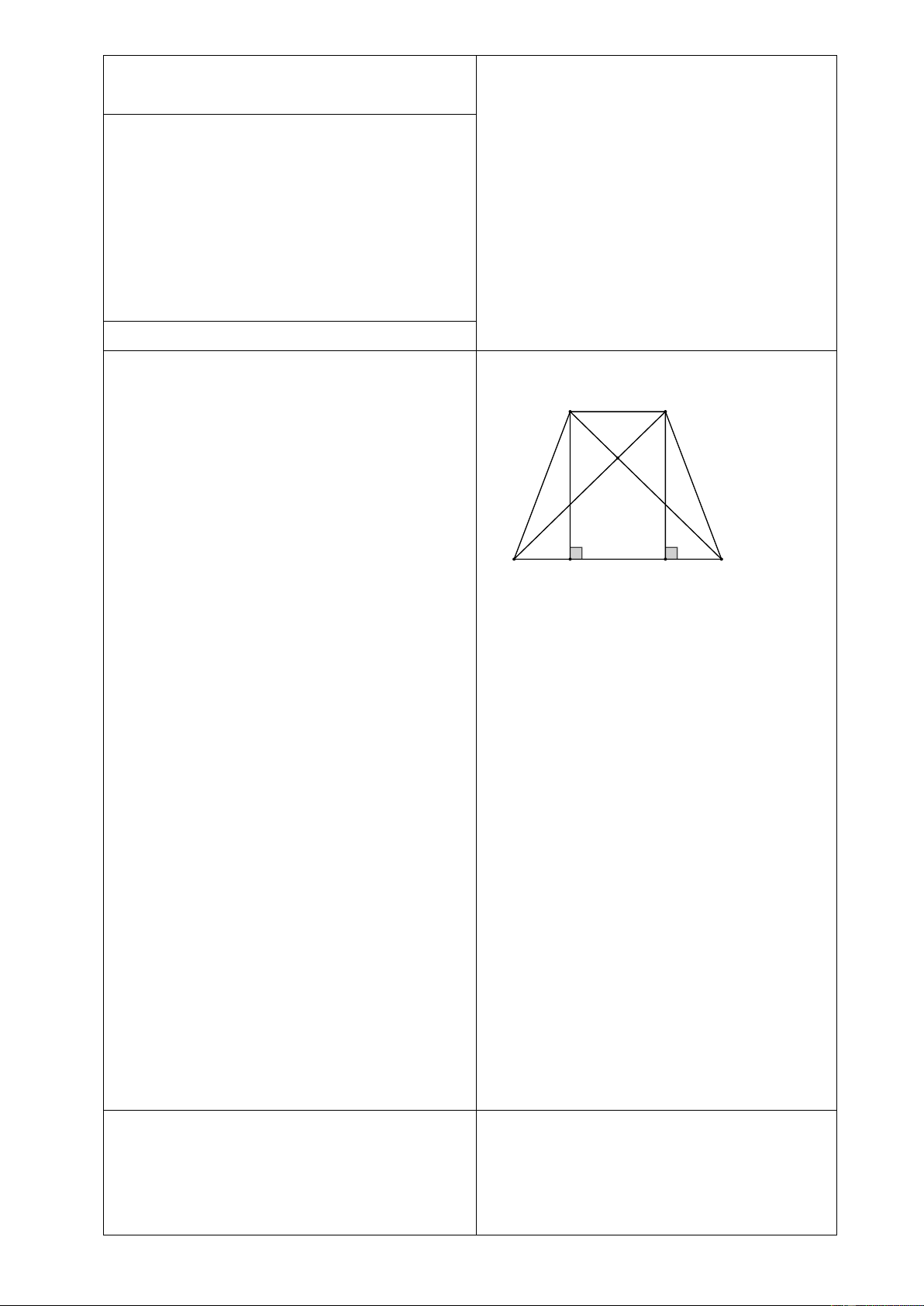
Trang 118

làm bài vào vở sau đó chuyển bài chấm

chéo

- Giáo viên có thể hướng dẫn học sinh khai

thác vận dụng cao trong bài toán trên: Tìm

vị trí của điểm M và N để

BM MN NC==

. Khi đó hướng dẫn học

sinh đưa về tìm vị trí của M và N là giao

điểm các đường phân giác tại góc B và C

tương ứng cắt cạnh AB và AC

Bài 2: Cho hình thang cân

( )

//ABCD AB CD

và

AB

là đáy nhỏ. Gọi

O là giao điểm của hai đường chéo. Chứng

minh rằng:

a.

CAD DBC=

b.

= , OA OB OC OD=

c. Kẻ các đường cao AH và BK. Chứng

minh

DH KC=

* Giao nhiệm vụ

- GV cho hs đọc đề bài và lên bảng vẽ hình

- GV tổ chức hs làm hoạt động cá nhân tìm

lời giải

*Thực hiện nhiệm vụ

- HS tìm hiểu bài toán và vẽ hình

(hình vẽ)

GV gọi hs lên bảng làm phần a

- Em có nhận xét gì về ODC và OAB

, cách cm OA OB OC OD = =

GV gọi hai

hs lên bảng hoàn thành phần b

*Kết luận, nhận định:

Gv hướng cho học sinh phát triển các ý tiếp

theo của bài toán và yêu cầu hs về nhà

chứng minh

Bài 2:

a.

( )

..CAD DBC c g c = 



CAD DBC=

b.

OAB

cân tại O

OA OB=

ODC

cân tại O

OD OC=

c.

( )

DAH CBK ch gn

DH CK

 =  −

=

Bài 3: Cho ∆ABC nhọn

( )

AB AC

. Kẻ

đường cao AH. Gọi M là trung điểm của

AB, trên tia HM lấy điểm N sao cho

MN MH=

.

Bài 3

O

K

B

H

D

C

A

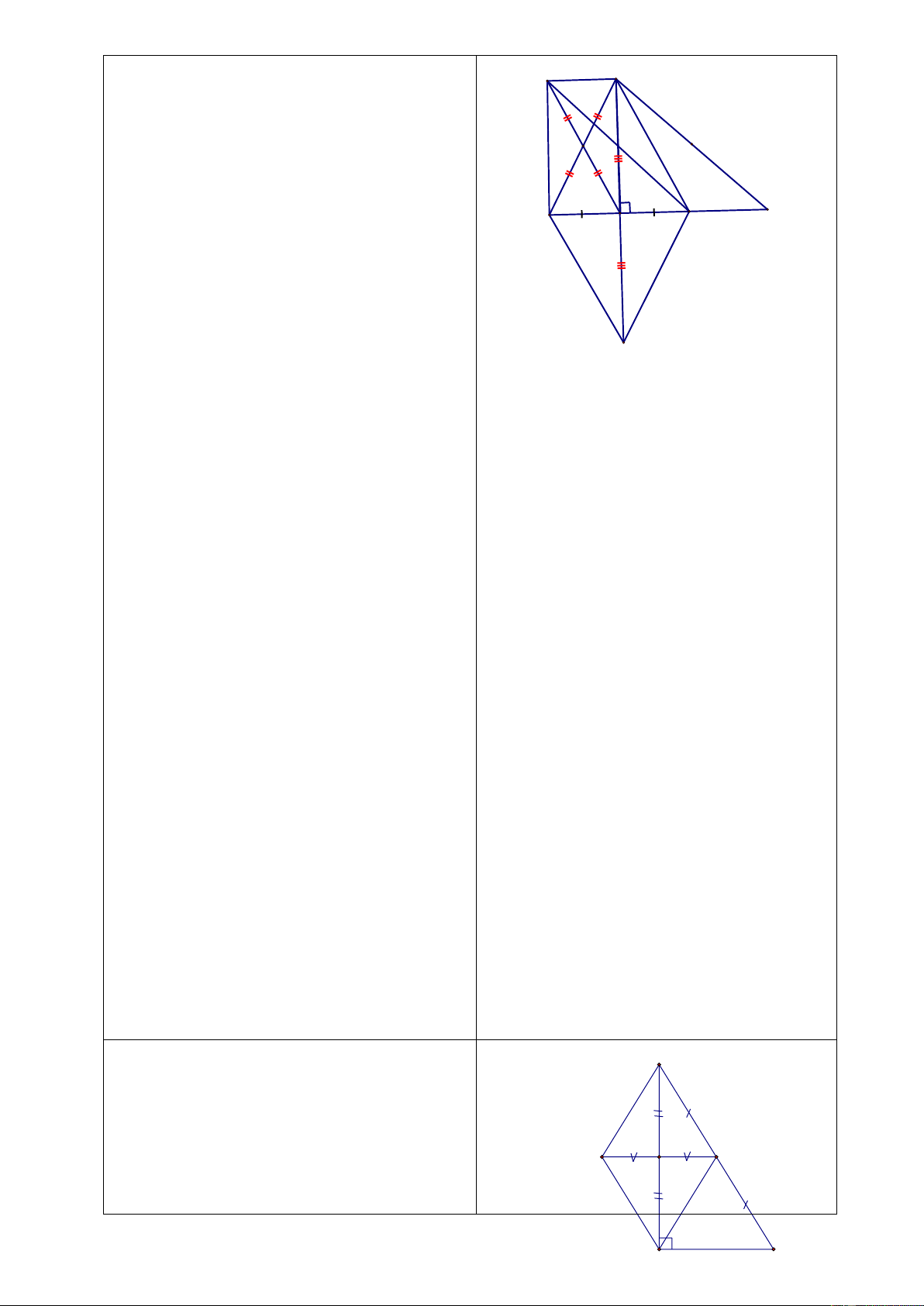
Trang 119

Q

P

M

A

C

B

a. Chứng minh: Tứ giác ANBH là hình chữ

nhật.

b. Trên tia đối của tia HB lấy điểm E sao

cho H là trung điểm của BE. Trên tia AH

lấy điểm F sao cho

AH HF=

. Chứng minh:

Tứ giác ABFE là hình thoi.

c. Gọi I là giao điểm của AH và NE. Chứng

minh:

/ / .MI BC

d. Gọi J là trung điểm của AC, chứng minh

: 3 điểm J, I, M thẳng hàng.

* Giao nhiệm vụ

- GV cho hs đọc đề bài và lên bảng vẽ hình

- GV tổ chức hs làm hoạt động cá nhân tìm

lời giải sau đó chấm chéo bài của nhau

*Thực hiện nhiệm vụ

- Hs vẽ hình ghi gt – kl bài toán

GV gọi hs lên bảng làm phần a

- Em sử dụng dấu hiệu nào để chứng minh

tứ giác là hình chữ nhật, hình thoi, chứng

minh 3 điểm thẳng hàng.

- - HS trình bày bài

- Nhận xét bài làm

- HS trả lời câu hỏi, làm bài vào vở

*Kết luận, nhận định:

Gv hướng cho học sinh phát triển các ý tiếp

theo của bài toán và yêu cầu hs về nhà

chứng

a) M là trung điểm AB và M là trung

điểm HN

Tứ giác ANBH là hình bình hành

Có góc

·

0

() 90AHB AH BC=⊥

Vậy tứ giác ANBH là hình chữ nhật

b) H là trung điểm BE và H là trung điểm

AF



Tứ giác ABFE là hình bình hành

Có

AF BE⊥

Kết luận tứgiác ABFE là hình thoi

c) tứ giác AHBN là hình chữ nhật



MH MA=

MAH

cân tại M mà MI là đường trung

tuyến

Suy ra MI là đường cao của

MAH

MI AH⊥

mà

BC AH⊥

//MI BC

d) chứng minh tương tự được

//JI BC

mà

//MI BC



MI và MJ trùng nhau



J, I, M thẳng hàng

Bài 4. Cho tam giác ABC vuông tại A,

đường trung tuyến AM. Gọi P là trung điểm

của AB, Q là điểm đối xứng với M qua P.

a) Chứng minh: Tứ giác AQBM là hình

thoi.

b) Tính diện tích tam giác ABC, biết

Bài 4

I

F

B

C

H

E

N

M

A



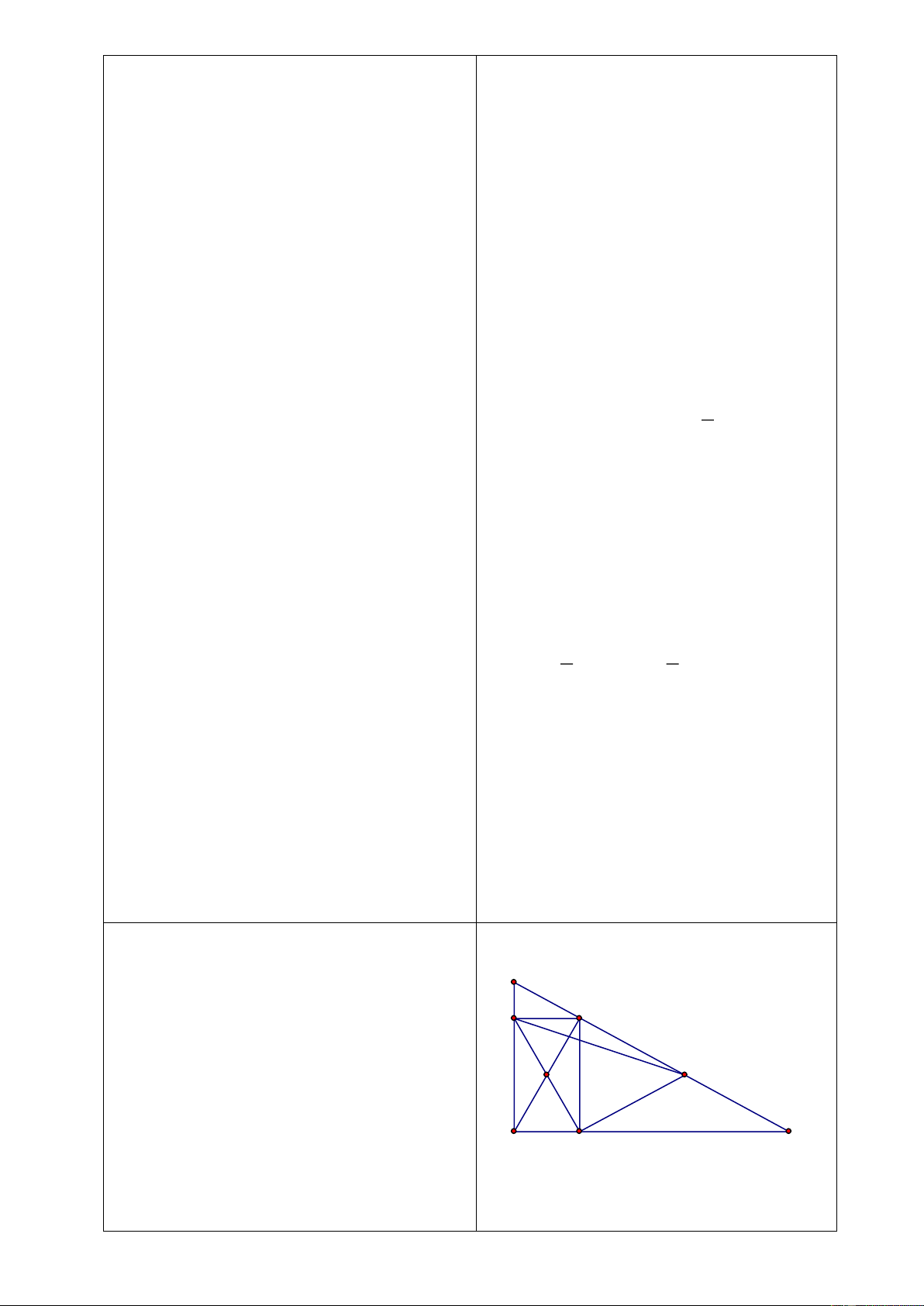
Trang 120

10( ), 6( ).AB cm AC cm==

c) Tam giác ABC cần điều kiện gì thì tứ

giác

AQBM

là hình vuông ?

* Giao nhiệm vụ

GV cho hs đọc bài và vẽ hình ghi gt – kl.

- hs tìm lời giải

*Thực hiện nhiệm vụ

- Hs vẽ hình ghi gt, kl

- Quan sát và phân tích đầu bài chỉ ra

hướng chứng minh

- Hãy cho biết các dấu hiệu nhận biết hình

thoi?

Trong bài ta sử dụng dấu hiệu nào?

- Nêu công thức tính diện tích tam giác

vuông?

- Với tam giác ABC đã đủ yếu tố để tính

diện tích chưa?

- Để tứ giác AQBM là hình vuông thì cần

thêm điều kiện gì ?

- Hs lên bảng trình bày chứng minh

- HS nhận xét bài làm của bạn

*Kết luận, nhận định:

- Gv chữa bài cho hs

GV khai thác các câu hỏi theo các hướng

khác nhau (nếu được)

a) Chứng minh Tứ giác

AQBM

là hình

thoi:

Ta có:

( ) ( )

AP BP gt và PM PQ gt==

 tứ giác

AQBM

là hình bình hành

(dhnb)

Mặt khác vì

1

AM MB BC

2



==





(t/c đường trung tuyến ứng với cạnh

huyền của tam giác vuông )

Vậy tứ giác

AQBM

là hình thoi.

b) Tính diện tích tam giác ABC biết

10( ), 6( ).AB cm AC cm==

Tam giác

ABC

vuông tại

A

nên:

. . .

ABC

11

S AB AC 10 6

22

==

( )

2

ABC

S 30 cm=

c) Tam giác ABC cần điều kiện gì thì tứ

giác AQBM là hình vuông ?

Tứ giác AQBM là hình vuông

·

00

90 45QBM MBP ==

ABC

là tam giác vuông cân tại A.

Bài 5.

Cho tam giác MNP vuông tại M, đường cao

MH. Gọi D,E lần lượt là chân các đường

vuông góc hạ từ H xuống MN và MP.

a) Chứng minh tứ giác MDHE là hình chữ

nhật.

b) Gọi A là trung điểm của HP. Chứng

minh tam giác DEA vuông.

c) Tam giác MNP cần có thêm điều kiện gì

để

2.DE EA=

Bài 5.

a) Tứ giác

MDHE

có

2

1

O

N

M

P

H

E

D

A

Trang 121

O

J

I

M

N

F

E

B

D

C

A

* Giao nhiệm vụ

GV cho hs đọc bài và vẽ hình ghi gt – kl.

- hs tìm lời giải

*Thực hiện nhiệm vụ

- Hs đọc bài

Hs vẽ hình và giải bài

- Quan sát và phân tích đầu bài chỉ ra

hướng chứng minh

- Hãy cho biết các dấu hiệu nhận biết hình

thoi?

Trong bài ta sử dụng dấu hiệu nào?

- Nêu công thức tính diện tích tam giác

vuông?

- Với tam giác ABC đã đủ yếu tố để tính

diện tích chưa?

- Để tứ giác AQBM là hình vuông thì cần

thêm điều kiện gì ?

*Kết luận, nhận định:

- Gv chữa bài cho hs

GV khai thác các câu hỏi theo các hướng

khác nhau (nếu được)

MDH MEH DME 90= = =

 Tứ giác MDHE là hình chữ nhật

b) Gọi

O

là giao điểm của

MH

và

DE

MDHE

là hình chữ nhật

MH DE =

và

O

là trung điểm của



11

OH OE MH DE

22

= = =

+)

EHP

vuông tại E có A là trung điểm

PH suy ra:

1

AE AH HP

2

==

+)

OHA OEA = 

(c-c-c)



OHA OEA 90==

hay



DEA vuông tại E.

c)

2DE EA OE EA=  =

OEA

vuông cân

0

EOA 45=

HOE 90=

HM DE⊥

tại O

MDHE

là hình vuông

MH

là tia phân giác của

DME

mà

MH NP⊥

(vì

MH

là đường cao

NMP

Suy ra

NMP

vuông cân tại M

Bài 6. Cho hình bình hành ABCD, E và F

lần lượt là trung điểm của AB, CD. Gọi M,

N lần lượt là giao điểm của AF, CE với BD.

a) Chứng minh: Tứ giác AECF là

hình bình hành.

b) Giả sử

DM MN BN==

Chứng

minh: MENF là hình bình hành.

c) AN cắt BC ở I, CM cắt AD ở J.

Chứng minh IJ, MN, EF đồng quy.

* Giao nhiệm vụ

GV cho hs đọc bài và vẽ hình ghi gt – kl.

- hs tìm lời giải

*Thực hiện nhiệm vụ

- Hs đọc bài và vẽ hình

Bài 6

a) Ta có ABCD là hình bình hành nên

/ / , AB CD AB CD=

E

là trung điểm

, AB F

là trung điểm

CD

mà

( )

AB CD cmt AE EB CF DF=  = = =

Trang 122

- Quan sát và phân tích đầu bài chỉ ra

hướng chứng minh

- Hs hoàn thành bài vào vở

*Kết luận, nhận định:

- Gv chữa bài cho hs

GV khai thác các câu hỏi theo các hướng

khác nhau (nếu được)

Xét tứ giác

AECF

có

( )

AE FC cmt=

( )

/ / / /AE FC vì AB CD



tứ giác

AECF

là hình bình

hành(dhnb)

b) Ta có

DM MN BN==

(gt)

DM MN MN NB hay DN BM + = + =

Xét

CDN

và

ABM

có :

( )

DN BM cmt=

CDN ABM=

(so le trong của

//AB CD

)

( )

CD AB cmt=

( )

..CDN ABM c g c  = 

CN AM=

(hai cạnh tương ứng)

Chứng minh được

NE MF=

Xét tứ giác

MENF

có

( )

/ / / /MF NE vì AF CE

( )

MF NE cmt MENF=

là hình bình

hành(đpcm)

c) Xét tứ giác

( ) ( )

/ / / / ; ANCM có AM CN vì AF CE AM CN cmt=

ANCM

là hình bình hành(dhnb)

( )

/ / AN CM đinh nghia

//AI CJ

//AN CM

(định nghĩa)

//AI CJ

Xét tứ giác

( )

/ / / /AICJ có AJ CI vì AD CB

( )

//AI CJ cmt AICJ

là hình bình

hành(dhnb).

Gọi

O

là giao

AC

và

DB



IJ

giao với

AC

tại

O

trung điểm mỗi

đg(t/c)

Ta lại có

MN

giao

AC

tại

O

trung điểm

mỗi đg( vì

MENF

là hình bình hành)



AC

,

MN

,

IJ

đồng quy tại

O

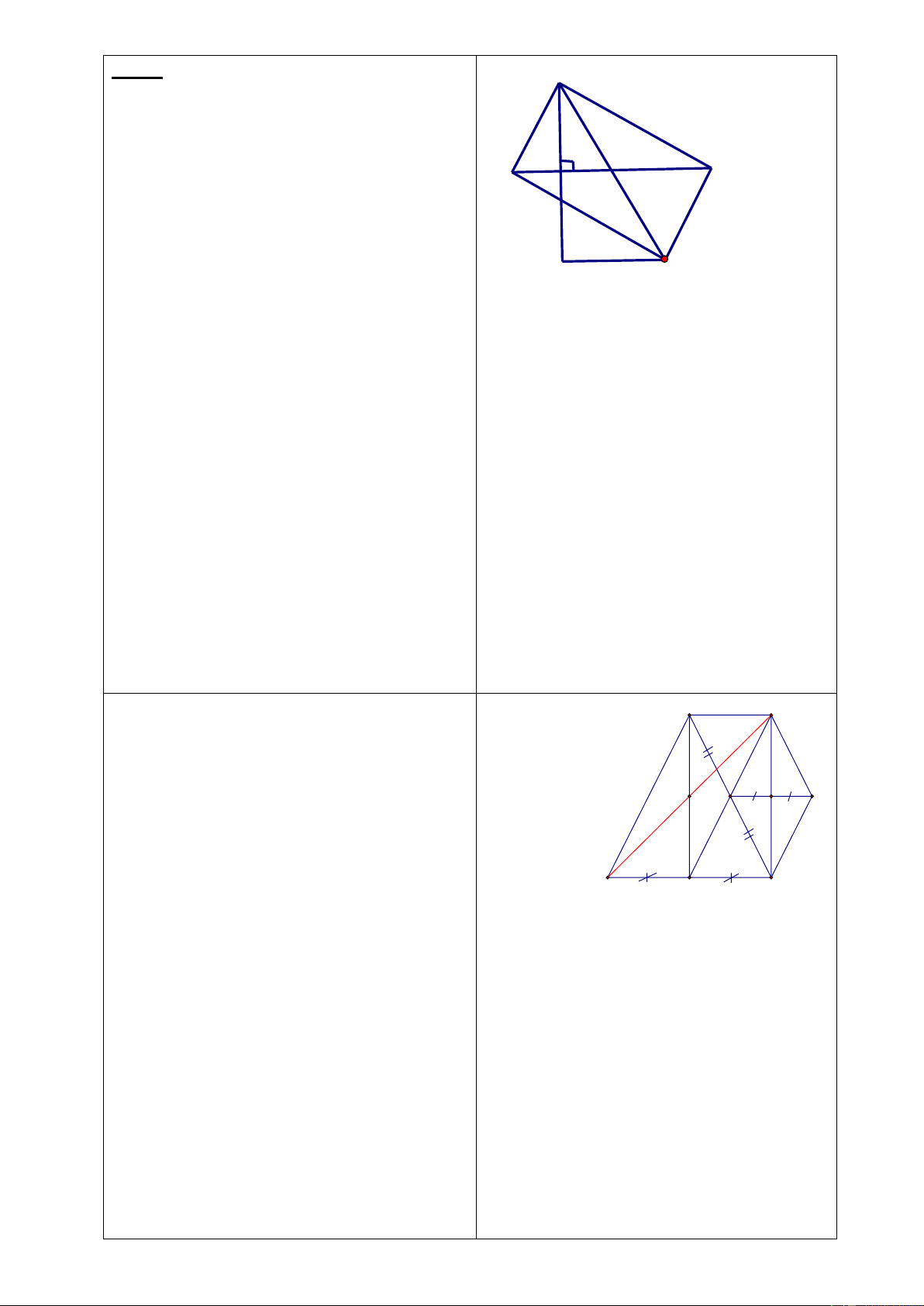
Trang 123

Q

H

K

I

M

B

C

A

Bài 7. Cho tam giác ABC vuông tại A (AB

< AC). M là trung điểm của BC. Lấy điểm

D sao cho M là trung điểm của AD.

a) Chứng minh ABDC là hình chữ nhật.

b) Kẻ AH vuông góc với BC. Trên tia AH

lấy điểm E sao cho

AH HE=

. Chứng minh

AE ED⊥

c) Tứ giác BCDE là hình gì ? Vì sao ?

* Giao nhiệm vụ

GV cho hs đọc bài và vẽ hình ghi gt – kl.

- hs tìm lời giải

*Thực hiện nhiệm vụ

- Hs đọc bài và vẽ hình

- Quan sát và phân tích đầu bài chỉ ra

hướng chứng minh

- Hs hoàn thành bài vào vở

*Kết luận, nhận định:

- Gv chữa bài cho hs

GV khai thác các câu hỏi theo các hướng

khác nhau (nếu được)

a) Tứ giác

ABDC

là hình chữ nhật( dấu

hiệu hình bình hành có 1 góc vuông)

b) AE cắt BC tại H

H là trung điểm của AE (gt).

Mà M là trung điểm của AD (vì M là

giao2 đg chéo hình chữ nhật ABDC)

Do đó

/ / / / .DE HM hay DE BC

Vậy

AE DE⊥

c) Chứng minh

EBC DCB( ABC)==

Hình thang

BCDE

( )

//DE BC

có

EBC DCB=

nên

BCDE

là hình thang cân.

Bài 8. Cho tam giác ABC cân tại A. Gọi I

và M theo thứ tự là trung điểm của

AC

và

BC

.

a) Trên tia

MI

lấy điểm K sao cho

MI IK=

. Chứng minh MAKC là hình chữ

nhật.

b) Chứng minh tứ giác

ABMK

là hình bình

hành.

c) Chứng minh

AIMB

là hình thang.

d) Gọi Q là trung điểm của AM. Chứng

minh B, Q, K thẳng hàng.

e) Lấy điểm H trên tia kẻ qua I và vuông

góc với KC sao cho CK là trung trực của

IH. Chứng minh HI là tia phân giác của

·

CHK

f) Tam giác ABC cần thêm điều kiện gì để

tứ giác

AMCK

là hình vuông?

* Giao nhiệm vụ

Bài 8

a) +/ Xét tứ giác

AMCK

là có

( )

IA IC gt=

( )

IM IK gt=

Nên tứ giác

AMCK

là hbh(dhnb)

+/

ABC

cân tại

A

nên trung tuyến AM

đồng thời là đường cao, nên

0

90AMC =

+/ Hình bình hành

AMCK

có

0

90AMC =

nên là hình chữ nhật (dhnb)

M

H

E

D

C

B

A

Trang 124

GV cho hs đọc bài và vẽ hình ghi gt – kl.

- hs tìm lời giải

*Thực hiện nhiệm vụ

- Hs đọc bài và vẽ hình

- Quan sát và phân tích đầu bài chỉ ra

hướng chứng minh

- Hs hoàn thành bài vào vở

*Kết luận, nhận định:

- Gv chữa bài cho hs

GV khai thác các câu hỏi theo các hướng

khác nhau (nếu được)

b)

AMCK

là hình chữ nhật

; / /AK MC AK MC=

Mà

MC MB=

(M là trung điểm của BC)

; / /AK MB AK MB=

Suy ra tứ giác

ABMK

là hình bình hành.

c) vì

/ / ( )AK BC cmt

·

()AKM KMC slt=

Mà

·

AKM ABM=

do tứ giác

ABMK

là hình bình hành

·

ABM KMC=

mà hai góc ở vị trí đồng

vị

//MI AB

Nên tứ giác

AIMB

là hình thang (định

nghĩa)

d) +/ Tứ giác

ABMK

là hình bình hành

(cmt)

Suy ra

AM và BK

cắt nhau tại trung

điểm của mỗi đường.

Mà

Q

là trung điểm của

AM

, nên

Q

cũng là trung điểm của

BK

, hay

,,B Q K

thẳng hàng.

e) c/m

HI

là tia phân giác của

·

CHK

f) lập luận ra được điều kiện là

ABC

vuông cân tại A

Củng cố và giao nhiệm vụ về nhà

- Ôn lại bài và xem bài đã chữa

- Hoàn thành bài trong phiếu.

- Học thuộc khái niệm, tính chất, dấu hiệu nhận biết của hình thang cân, hình

bình hành, hình chữ nhật, hình thoi và hình vuông.

Trang 125

PHIẾU BÀI TẬP

I. PHẦN TRẮC NGHIỆM

Câu 1: Tứ giác

ABCD

có :

µ µ

0 0 0

0 0 0 0

65 ; 117 ; 71 . ?

.1 19 . 107 . 63 . 126

B C Thì C

A B C D

A = = ==

Câu 2: Chọn câu đúng trong các câu sau:

A.Hình thang có 3 góc tù, 1 góc nhọn.

B.Hình thang có 3 góc vuông, 1 góc nhọn

C.Hình thang có 3 góc nhọn, 1 góc tù.

D.Hình thang có nhiều nhất 2 góc tù, nhiều nhất 2 góc nhọn

Câu 3: Hãy điền chữ “Đ” hoặc chữ “S” vào mỗi câu khẳng định sau:

A.Tứ giác có hai cạnh bên bằng nhau làn hình thang cân

B.Hình thang cân có hai cạnh bên bằng nhau.

C.Hình thang cân có hai góc kề với cạnh đáy bù nhau.

D.Hình thang cân có hai góc kề với cạnh đáy bằng nhau.

Câu 4 : Khẳng định nào sau đây đúng

A. Hình bình hành là tứ giác có hai cạnh song song.

B. Hình bình hành là tứ giác có các góc bằng nhau .

C. Hình bình hành là tứ giác có các cạnh đối song song.

D.Hình bình hành là hình thang có hai cạnh bên bằng nhau

Câu 5. Hãy khoanh tròn vào phương án mà em cho là đúng nhất

A.Hình chữ nhật là tứ giác có 4 cạnh bằng nhau

B.Hình chữ nhật là tứ giác có 4 góc vuông

C.Hình chữ nhật là tứ giác có hai góc vuông

D.Hình thang có một góc vuông là hình chữ nhật.

Câu 6 Trong các khẳng định sau, khẳng định nào sai đối với hình thoi.

A. Hai đường chéo bằng nhau.

B. Hai đường chéo vuông góc với nhau và là các tia phân giác của các góc của hình

thoi

C. Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

D. Đường chéo là phân giác của các góc của hình thoi

Câu 7. Hãy khoanh tròn vào phương án mà em cho là đúng.

A. Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

B. Hình vuông là tứ gíac có bốn góc bằng nhau.

C. Hình vuôgn là tứ giác có bốn cạnh bằng nhau.

D. Hình vuông là tứ giác có hai cạnh kề bằng nhau

Câu 8: Hình thang có hai cạnh đáy bằng nhau là:

A. hình thang cân.

B. hình bình hành.

C. hình chữ nhật.

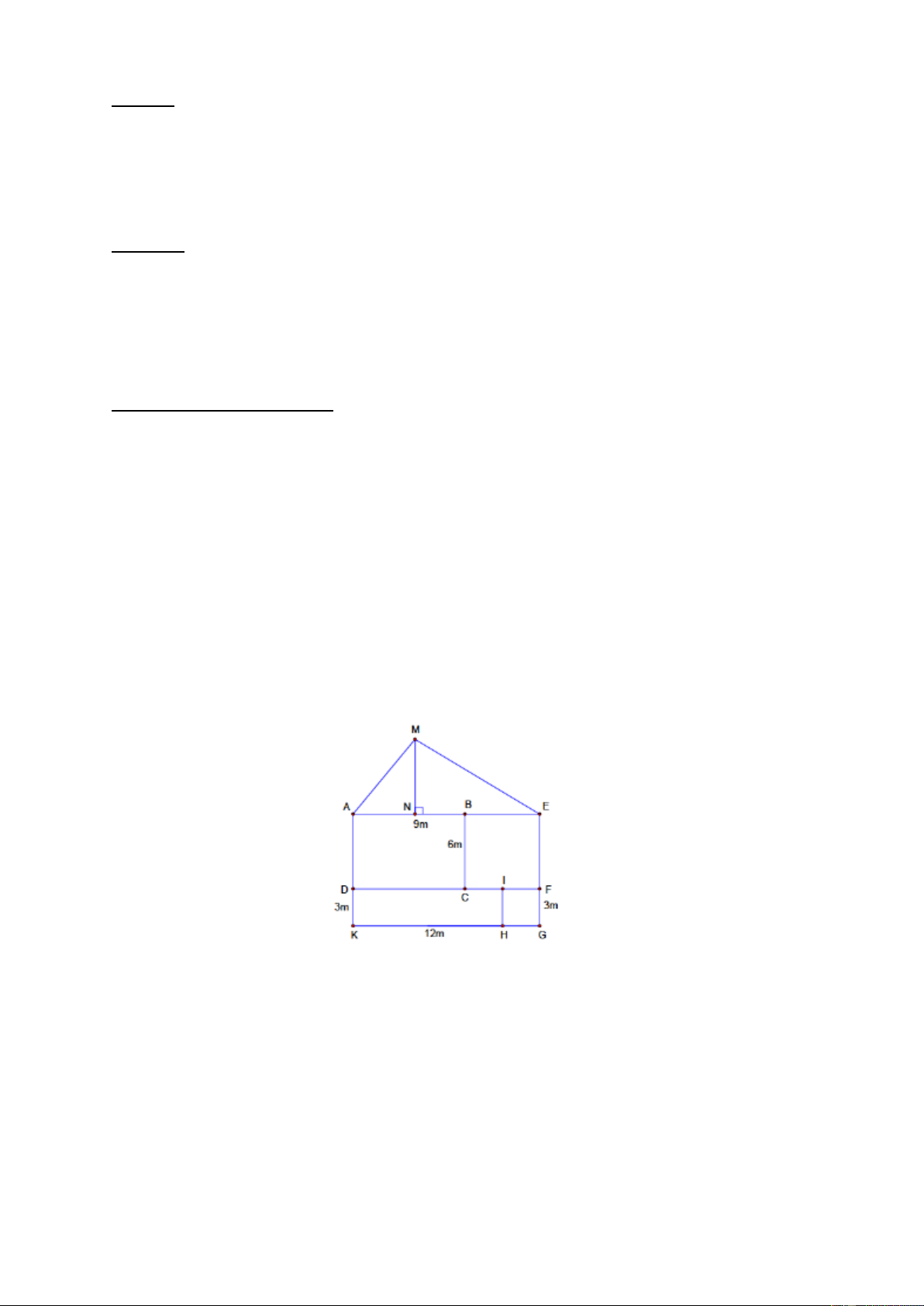
Trang 126

D. hình thoi.

Câu 9: Hình bình hành có hai đường chéo bằng nhau và vuông góc với nhau là:

A. hình thang cân.

B. hình chữ nhật.

C. hình thoi.

D. hình vuông.

Câu 10: Hình vuông có diện tích bằng

2

1cm

thì hình vuông đó có chu vi là:

A.

1cm

.

B.

2cm

.

C.

4cm

.

D. Kết quả khác

II. BÀI TOÁN THỰC TẾ

Bài 1:

Ông An muốn xây nhà trên miếng đất có diện tích

2

160m

. Hình bên là sơ đồ tầng trệt

của căn nhà.

Phòng khách là hình chữ nhật

ABCD

. Phòng ăn và nhà bếp là hình vuông

BEFC

.

Phòng vệ sinh là hình vuông

.FGHI

Sảnh trươc là hình chữ nhật

DIHK

. Kho chứa là

tam giác

AME

.

a. Tính diện tích kho chứa.

b. Khi xây dựng để đảm bảo an toàn ngôi nhà.

Ông An phải thiết kế thêm đường giằng

MN

như hình vẽ. Tính độ dài đường giằng

.MN

Bài 2. Bác Ngọc có một miếng đất hình thang cân với diện tích là

2

1500m

. Bác mua

thêm hai miếng đất nữa để đất của bác trở thành hình chữ nhật. Hỏi diện tích đất mà

bác mua thêm là bao nhiêu?

Trang 127

Bài 3. Một miếng đất hình chữ nhật ABCD được chia làm 3 phần như hình vẽ: phần

nhà ở là hình chữ nhật, phần vườn hoa là hình vuông có cạnh 4m, phần trồng rau là

hình chữ nhật có diện tích 70m

2

và chiều rộng là 3,5m. Tính diện tích phần nhà ở?

III. BÀI TẬP TỔNG HỢP

Bài 1:

Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho

BM = CN.

a) Tứ giác BMNC là hình gì?

b) Tính các góc của tứ giác BMNC biết góc A = 40

0

Bài 2: Cho hình thang cân ABCD (AB//CD) và AB là đáy nhỏ.Gọi O là giao điểm

của hai đường chéo. Chứng minh rằng:

a.

CAD DBC=

b. OA = OB, OC = OD

c. Kẻ các đường cao AH và BK. Chứng minh DH = KC

Bài 3: Cho ∆ABC nhọn (AB <AC). Kẻ đường cao AH. Gọi M là trung điểm của AB,

trên tia HM lấy điểm N sao cho

MN MH=

.

a. Chứng minh: Tứ giác ANBH là hình chữ nhật.

b. Trên tia đối của tia HB lấy điểm E sao cho H là trung điểm của BE. Trên tia AH lấy

điểm F sao cho

AH HF=

. Chứng minh: Tứ giác ABFE là hình thoi.

c. Gọi I là giao điểm của AH và NE. Chứng minh: MI // BC.

d. Gọi J là trung điểm của AC, chứng minh : 3 điểm J, I, M thẳng hàng.

Bài 4. Cho tam giác ABC vuông tại A, đường trung tuyến AM . Gọi P là trung điểm

của AB, Q là điểm đối xứng với M qua P.

a) Chứng minh : Tứ giác AQBM là hình thoi.

b) Tính diện tích tam giác ABC, biết

AB = 10cm, AC = 6cm.

c) Tam giác ABC cần điều kiện gì thì tứ giác AQBM là hình vuông?

30(m)

4x (m)

6x (m)

4x (m)

30(m)

D

H

C

F

B

A

E

D

H

C

B

A

30(m)

6x(m)

4x(m)

F

E

H

B

D

C

A

Vườn hoa

Trồng rau

nhà ở

70m

2

3,5m

4m

B

D

C

A

Trang 128

Bài 5. Cho tam giác MNP vuông tại M, đường cao MH. Gọi D,E lần lượt là chân các

đường vuông góc hạ từ H xuống MN và MP.

a) Chứng minh tứ giác MDHE là hình chữ nhật.

b) Gọi A là trung điểm của HP. Chứng minh tam giác DEA vuông.

c) Tam giác MNP cần có thêm điều kiện gì để DE = 2EA

Bài 6. Cho hình bình hành ABCD, E và F lần lượt là trung điểm của AB, CD. Gọi M,

N lần lượt là giao điểm của AF, CE với BD.

a) Chứng minh: Tứ giác AECF là hình bình hành.

b) Giả sử

DM MN BN==

Chứng minh: MENF là hình bình hành.

c) AN cắt BC ở I, CM cắt AD ở J. Chứng minh IJ, MN, EF đồng quy.

Bài 7. Cho tam giác ABC vuông tại A (AB < AC). M là trung điểm của BC. Lấy điểm

D sao cho M là trung điểm của AD.

a) Chứng minh ABDC là hình chữ nhật.

b) Kẻ AH vuông góc với BC. Trên tia AH lấy điểm E sao cho

AH HE=

. Chứng minh

AE ED⊥

c) Tứ giác BCDE là hình gì ? Vì sao ?

Bài 8. Cho tam giác ABC cân tại A. Gọi I và M theo thứ tự là trung điểm của

AC

và

BC

.

a) Trên tia

MI

lấy điểm K sao cho

MI IK=

. Chứng minh MAKC là hình chữ nhật.

b) Chứng minh tứ giác

ABMK

là hình bình hành.

c) Chứng minh

AIMB

là hình thang.

d) Gọi Q là trung điểm của AM. Chứng minh B, Q, K thẳng hàng.

e) Lấy điểm H trên tia kẻ qua I và vuông góc với KC sao cho CK là trung trực của IH.

Chứng minh HI là tia phân giác của

·

CHK

f) Tam giác ABC cần thêm điều kiện gì để tứ giác

AMCK

là hình vuông?

Trang 129

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ 12

1. TRẮC NGHIỆM

Câu 1: Tứ giác

ABCD

có

0

ˆˆ

ˆ

65 ; 117 ; 71.A B C



= = =

Thì

ˆ

?D =

A.

119



. B.

107



. C.

0

63

. D.

126



.

Câu 2: Hình bình hành có một góc vuông là hình gì?

A. Hình thang cân. B. Hình vuông.

C. Hình chữ nhật. D. Hình thang vuông.

Câu 3: Cho

HIK

vuông tại

H

có

M

là trung diểm

IK

, biết

6HM cm=

. Độ dài

đoạn thẳng

IK

là

A.

12cm

. B.

3cm

. C.

6cm

. D.

9cm

.

Câu 4: Cho hình thoi

ABCD

có cạnh

8cmAB =

, biết

AC BD=

. Diện tích hình thoi

ABCD

là

A.

2

32cm

. B.

2

16cm

. C.

2

8cm

. D.

2

64cm

.

Câu 5: Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi

đường thì tứ giác là

A. hình thang cân. B. hình bình hành. C. hình chữ nhật. D. hình

thoi.

Câu 6: Hình bình hành có hai góc kề một cạnh bằng nhau là hình:

A. hình thang cân. B. hình thoi. C. hình chữ nhật. D. hình

vuông.

Câu 7: Cho

ABC

vuông tại

A

có

,AH AM

theo thứ tự là đường cao, dường trung

tuyến của

( , )ABC H M BC

. Biết tích

AH

.

2

24AM cm=

thì diện tích của

ABC

bằng:

A.

2

48cm

. B.

2

24cm

. C.

2

12cm

. D.

2

8cm

.

Câu 8: Hình thoi

ABCD

có

ˆ

130A



=

thì

ˆ

B

bằng:

A.

130



. B.

50



. C.

70



. D.

130



.

Câu 9:

ABC

vuông tại

A

có

6 , 8 , 10AB cm AC cm BC cm= = =

thì độ dài đường cao

AH

là:

A.

4,8cm

. B.

3,6cm

. C.

5cm

. D.

10cm

.

Câu 10: Hình chữ nhật có hai kích thước là

6cm

và

10cm

thì có diện tích là:

A.

2

16cm

. B.

2

32cm

. C.

2

30cm

. D.

2

60cm

.

2. TỰ LUẬN

Bài 1: Tìm số đo x trong các hình sau:

50

0

x

D

C

B

A

4x

3x

2x

x

Q

P

N

M

x

2x

D

C

B

A

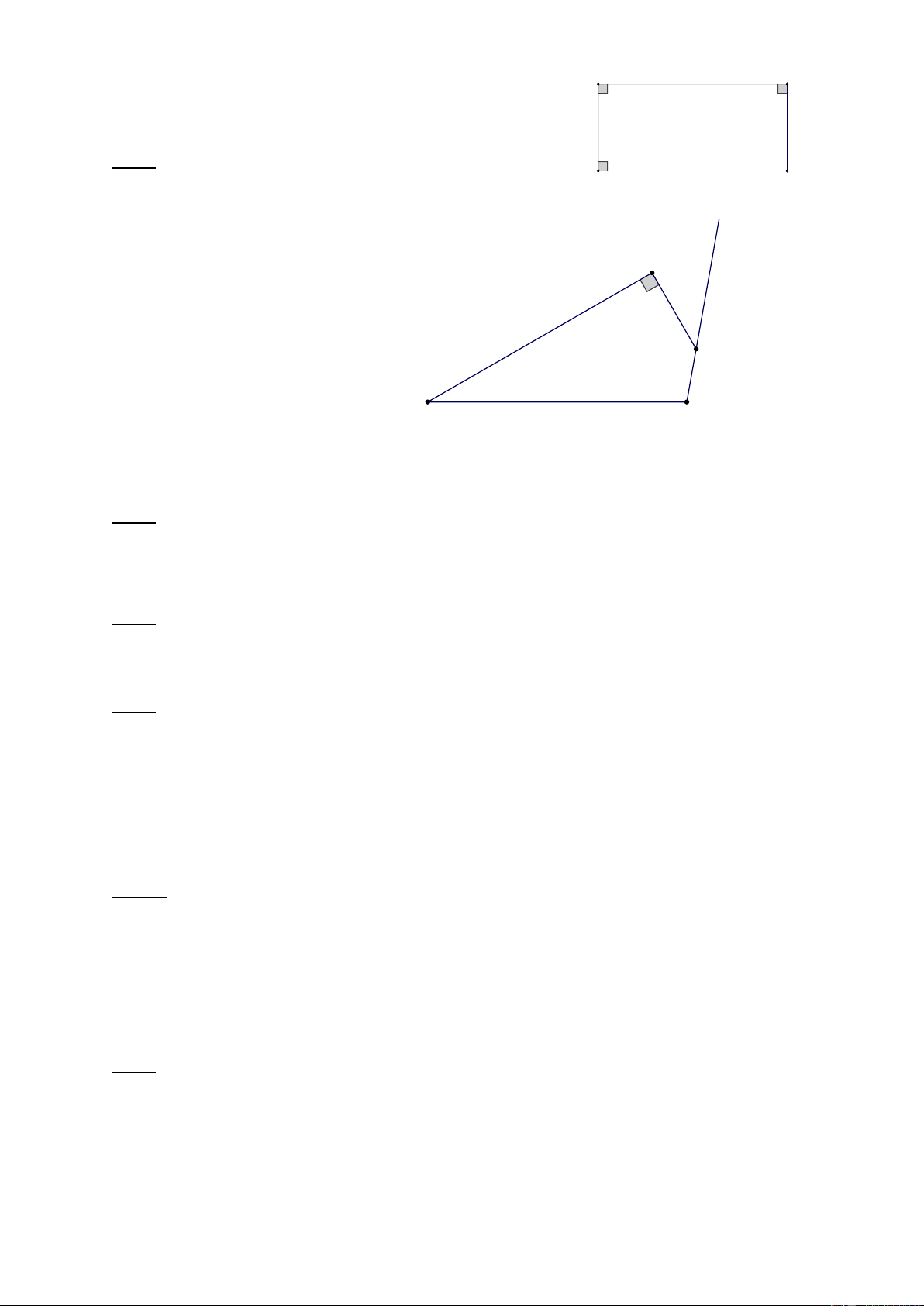
Trang 130

Bài 2: Cho tứ giác ABCD có

0 0 0

A 30 ,B 90 ,D 100= = =

. Tính góc

C

và góc ngoài tại C

của tứ giác.

Bài 3: Cho tứ giác ABCD có

AB AD,CB CD==

,

00

C 70 ,A 110==

.

a, Chứng minh AC là trung trực của BD.

b, Tính góc

B,D

.

Bài 4: Cho tứ giác ABCD có

0

B D 180+=

,

CB CD=

. Trên tia đối của tia DA lấy điểm

E sao cho

DE AB=

. Chứng minh:

a,

ABC EDC = 

.

Bài 5 : Cho hình thang ABCD có AB // CD và

CD AD BC=+

. Gọi K là điểm thuộc

đáy CD sao cho

KD AD=

. Chứng minh rằng :

a, AK là phân giác góc

A

.

b,

KC BC=

.

c, BK là tia phân giác của góc

B

.

b, AC là phân giác góc

A

.

Bài 6: Cho hình thang cân ABCD có AB // CD và

AB CD

. Gọi O là giao điểm của

AD và BC. E là giao điểm của AC và BD. Chứng minh :

a,

AOB

cân tại O.

b,

ABD BAC = 

.

c,

EC ED=

.

d, OE là trung trực của hai đáy AB và CD.

Bài 7: Cho

ABC

nhọn có

AB AC

. Các đường cao BE, CF cắt nhau tại H, Gọi M là

trung điểm của BC, kẻ Bx, Cy lần lượt vuông góc với AB, AC chúng cắt nhau tại K.

a, Chứng minh tứ giác BHCK là hình bình hành và H, M, K thẳng hàng.

b, Lấy điểm I sao cho

IH BC⊥

tại O và

HO IO=

. Chứng minh tứ giác BIKC

là hình thang cân.

x

C

B

D

A

100

0

30

0

D

C

B

A

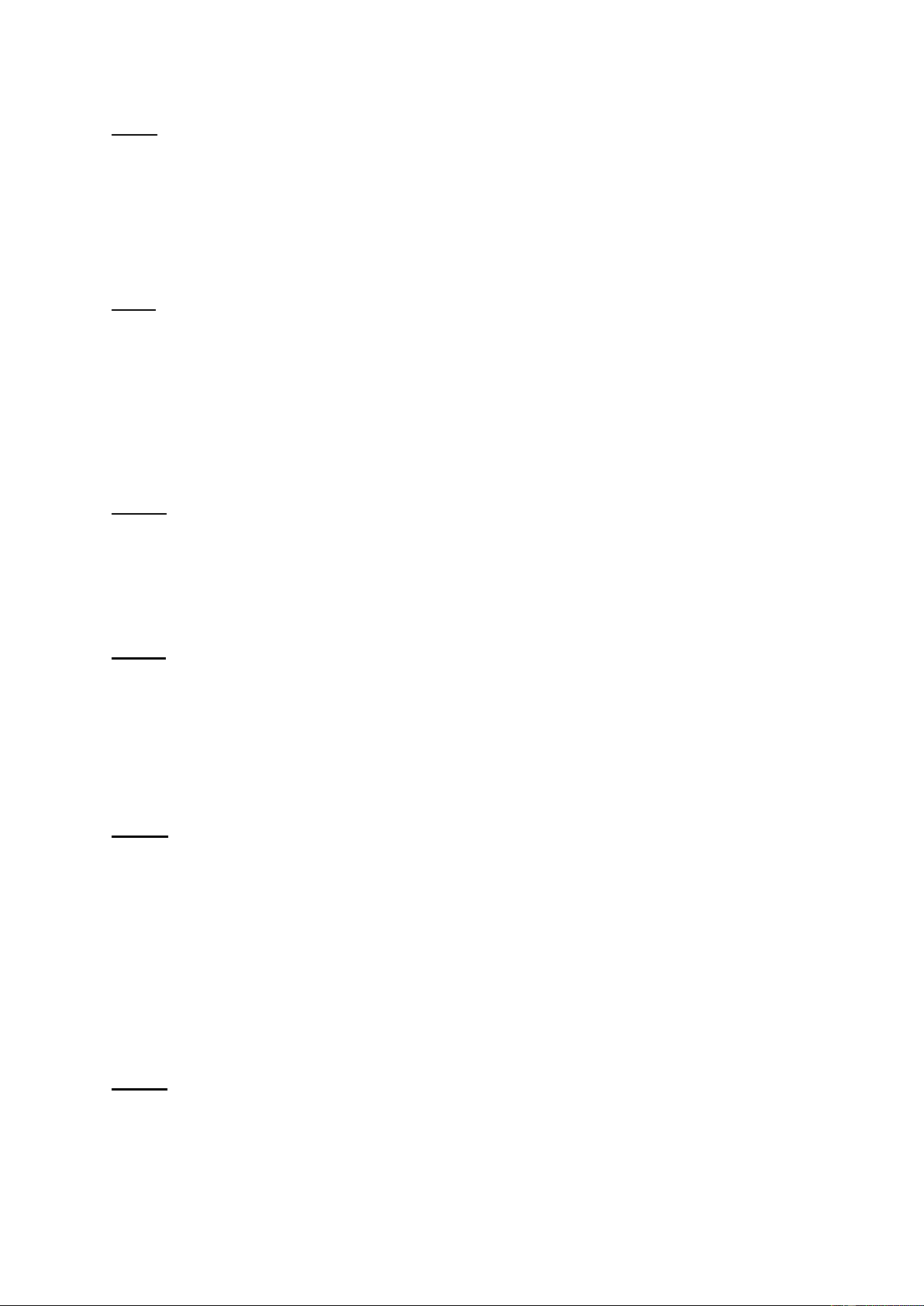
Trang 131

c, Gọi G là giao điểm của BK và HI,

ABC

phải có thêm điều kiện gì để tứ

giác GHCK là hình thang cân.

Bài 8: Cho

ABC

nhọn. các đường trung tuyến AM và BN cắt nhau tại G. Trên tia

BN lấy điểm E sao cho N là trung điểm của EG.

a, Chứng minh tứ giác AGCE là hình bình hành.

b, Trên tia AM lấy điểm F ( K khác A) sao cho

AG GF=

.

Chứng minh rằng:

MG MF=

và BF // AE.

c, Để tứ giác AECF là hình thang cân thì

ABC

cần điều kiện gì

Bài 9: Cho

ABC

vuông cân tại A. Trên đoạn thẳng AB lấy điểm E, Trên tia đối của

tia CA lấy điểm F sao cho

BE CF=

. Vẽ hình bình hành BEFD. Gọi I là giao điểm của

EF và BC. Qua E kẻ đường thẳng vuông góc với AB cắt BI tại K.

a, Chứng minh tứ giác EKFC là hình bình hành.

b, Qua I kẻ đường thẳng vuông góc với AF cắt BD tại M. Chứng minh

AI BM=

.

c, Tìm vị trí của E trên AB để A, I, D thẳng hàng.

Bài 10: Cho hình bình hành ABCD. Gọi O là giao điểm của AC và BD. Trên AB lấy

điểm E, trên CD lấy điểm F sao cho AE = CF

a) Chứng minh: Tam giác AEO bằng tam giác CFO

B) Từ E dựng Ex // AC cắt BC tại I, dựng Fy // AC cắt AD tại K.

Chứng minh: Tứ giác KEIF là hình bình hành

Bài 11: Cho

ABC

vuông tại A. Từ một điểm M trên cạnh BC. Kẻ

MH AB⊥

tại H.

Kẻ

MK AC⊥

tại K.

a, Chứng minh: Tứ giác AHMK là hình chữ nhật.

b, Tìm vị trí của M trên cạnh BC để AHMK là hình vuông.

c, Kẻ

AI BC⊥

tại I. So sánh AM với AI rồi tìm vị trí của M để

AM HK+

nhỏ

nhất.

Bài 12: Cho hình thoi ABCD ( góc

B

tù). Từ B hạ

BM AD,BN CD⊥⊥

. Từ D hạ

DP AB,DQ BC⊥⊥

. Gọi H là giao điểm của MB và PD, K là giao điểm của BN và

DQ. O là giao điểm của AC và BD. Chứng minh:

a, H là trực tâm

ABD

.

b, A, H, K, C thẳng hàng.

c,

PDQ MBN=

.

d,

PHM QKN=

.

e, Tứ giác BHDK là hình thoi

Bài 13: Cho đoạn thẳng AB và một điểm M thay đổi trên đoạn AB (M không trùng

với A và B) Vẽ các hình vuông AMCD và BMEF thuộc cùng một nửa mặt phẳng với

bờ AB.

a, Chứng minh

AE BC=

và

AE BC⊥

.b, Gọi G, I, N, K lần lượt là trung điểm của AB,

AC, CE, EB. Tứ giác GINK là hình gì? Vì sao?

c, Chứng minh DF luôn đi qua 1 điểm cố định khi M di chuyển trên AB.

Trang 132

d, Chứng minh rằng trung điểm Q của IK luôn nằm trên một đường cố định khi M di

chuyển trên AB.

Bài 14: Cho hình vuông ABCD. Qua A vẽ hai đường thẳng vuông góc với nhau lần

lượt cắt BC tại P và R. Cắt CD tại Q và S.

a, Chứng minh

AQR

và

APS

là các tam giác cân.

b, QR cắt PS tại H. Hai điểm M, N lần lượt là trung điểm của QR và PS.

Chứng minh tứ giác AMHN là hình chữ nhật.

c, Chứng minh P là trực tâm

SQR

.

d, Chứng minh MN là đường trung trực của AC.

e. Chứng minh bốn điểm M, B, N, D thẳng hàng.

Bài 15: Cho

ABC

vuông tại A,

AB 4cm,AC 8cm==

. Gọi E là trung điểm của AC,

M là trung điểm của BC.

a, Tính EM.

b, Vẽ tia Bx // AC sao cho Bx cắt EM tại D. Chứng minh rằng tứ giác ABDE là hình

vuông.

c, Gọi I là giao điểm của BE và AD. Gọi K là giao điểm của BE với AM. Chứng minh

rằng tứ giác BDCE là hình bình hành và

DC 6.IK=

.

Tuần 12

Tiết 31; 32; 33

Ngày soạn 01/11/2023

Lớp

8A

8B

Ngày dạy:

ÔN TẬP TỔNG VÀ HIỆU HAI LẬP PHƯƠNG

I. MỤC TIÊU

1. Về kiến thức:

- Mô tả được các hằng đẳng thức: tổng và hiệu hai lập phương.

2. Về năng lực:

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được các hằng đẳng thức tổng

và hiệu hai lập phương.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng

Trang 133

hợp, khái quát hóa. Vận dụng được hai hằng đẳng thức này để viết đa thức dưới dạng

tích, viết các biểu thức dưới dạng tổng hay hiệu hai lập phương; rút gọn biểu thức; tìm

x; tính nhanh.

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

Tổng hợp kiến thức cần nhớ:

Tổng hai lập phương:

3 3 2 2

( )( )A B A B A AB B+ = + - +

Hiệu hai lập phương :

3 3 2 2

( )( )A B A B A AB B- = - + +

2. BÀI TẬP

Hoạt động của giáo viên và học

sinh

Nội dung

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời

nhanh bài toán trắc nghiệm 1

Dạng 1: Viết đa thức dưới dạng tích hoặc tổng

hay hiệu hai lập phương

Bài 1: Bài tập trắc nghiệm

Bài 1: Trắc nghiệm

Chọn đáp án đúng cho mỗi câu sau

Câu 1: Đa thức

( )

3

5 1x -

viết dưới dạng tích là

A.

( )

2

5 1 25 5 1x x x- - +

B.

( )

2

5 1 25 5 1x x x- + +

C.

( )

2

5 1 5 5 1 x x x- + +

D.

( )

2

5 1 25 5 1x x x+ - +

Câu 2: Biểu thức

( )

2

3 3 9 x x x+ - +

viết dưới dạng tổng hay hiệu hai lập phương là

A.

33

3x -

B.

( )

3

3x -

C.

33

3x +

D .

( )

3

3x +

Câu 3: Điền biểu thức thích hợp vào chỗ trống

( )

2 3 3

3 ........ 3 27x y xy y x y+ - + = +

A .

9x

B .

2

6x

C .

2

9x

D.

9xy

*Thực hiện nhiệm vụ

- GV sử dụng máy chiếu tổ chức

cho HS trả lời từng câu hỏi.

- Yêu cầu HS xem lại các hằng

đẳng thức đã học để trả lời.

- HS hoạt động cá nhân nhớ lại

kiến thức cũ và trả lời các câu hỏi.

Trả lời

Bài 1

Câu 1: B

Câu 2: C

Câu 3: C

Trang 134

- HS tích cực tham gia trả lời các

câu hỏi. Trả lời bổ sung khi có bạn

trả lời sai.

*Kết luận, nhận định:

- GV kết luận:

+ Khẳng định các kết quả đúng.

Lưu ý: Để trả lời tốt các câu hỏi

trên cần nắm vững hai hằng đẳng

thức sau:

3 3 2 2

( )( )A B A B A AB B+ = + - +

3 3 2 2

( )( )A B A B A AB B- = - + +

+ Nhận xét thái độ học tập của cả

lớp.

- HS chốt được kiến thức. Rút kinh

nghiệm các hạn chế mà GV nêu,

khắc phục trong các buổi học sau.

* Giao nhiệm vụ

- GV yêu cầu HS hoạt động cá

nhân lần lượt làm các bài tập 2, 3.

Bài 2, 3

Bài 2: Viết các đa thức sau dưới dạng tích.

a)

3

1x +

b)

3

27 8x+

c)

3

1 x-

d)

3

27 8x -

Bài 3: Viết các biểu thức sau dưới dạng tổng hay hiệu hai lập phương.

a)

( )

2

2 2 4x x x+ - +

b)

( )

2

3 3 9x x x- + +

c)

( )

22

3 3 9x y x xy y- + +

d)

( )

4 2 2

3 9 3x x x+ + -

e)

( )

2

2 – 1 1 2 4x x x++

*Thực hiện nhiệm vụ

- Giáo viên yêu cầu HS đọc kĩ

từng bài và làm.

- HS tự làm vào vở.

- GV gọi HS lên bảng làm.

- GV tổ chức cho HS nhận xét,

đánh giá, giải thích kĩ từng bài.

*Kết luận, nhận định:

- GV kết luận:

1. Để làm tốt bài 1, 2 cần chú ý

+ Nhận diện đúng hằng đẳng thức

áp dụng.

+ Nhận diện đúng A, B trong các

Trả lời

Bài 2:

a)

( )

3 3 3 2

1 1 1 1x x x x x+ = + = + - +

b)

( ) ( )

( )

23

3

2 27 3 2 3 9 6 48 x x xx x= + = - ++ +

c)

( )

3 3 23

1 1 1 1x x xx x= - = + +- -

d)

( ) ( )

( )

3

323

42 8 3 2 3 2 9 67 xx x x x- = - = - + +

Bài 3:

a)

( )

2 3 3 3

2 2 4 2 8x x x x x+ - + = + = +

Trang 135

hằng đẳng thức

3 3 2 2

( )( )A B A B A AB B+ = + - +

3 3 2 2

( )( )A B A B A AB B- = - + +

2. Cách trình bày bài làm.

b)

( )

2 3 3 3

3 3 9 3 27x x x x x- + + = - = -

c)

( )

3

2 2 3 3 3

3 3 9 3 27x y x xy y x y x y- + + = - = -

d)

( )

( ) ( )

( )

4 2 2 2 4 2

3 9 3 3 3 9x x x x x x+ + - = - + +

( )

3

2 3 6

3 27xx= - = -

e)

( )

22

2 – 1 1 2 4 2 – 1 4 2 1x x x x x x+ + = + +

( )

3

33

2 – 1 8 – 1xx==

* Giao nhiệm vụ

- GV tổ chức cho HS hoạt động

nhóm 4 (theo bàn) làm các bài tập

1, 2, 3 của dạng 2.

Dạng 2: Rút gọn biểu thức

Bài 1: Rút gọn biểu thức

a)

( )

2 2 2 2

A x y x xy y x y x xy y= - + + - + - +

b)

( )( )

2 2 4 4 3 2 2 3

5 5 25 125B a b a a b a b a a= - + + +

c)

( )

2 2 3 3

2 3 4 6 9 7 26C x y x xy y x y= + - + - -

d)

( )

32

2 2 2 4D y y y y= - + + + - +

Bài 2: Chứng tỏ các biểu thức sau có giá trị không phụ thuộc vào biến x.

a)

( )

22

1 1 1 1A x x x x x x= + - + - - + +

b)

( )

23

2 6 4 12 36 8 10B x x x x= + - + - +

c)

( ) ( )

( )

3

2

1 3 3 9 3 1C x x x x x x= - - - + + - -

Bài 3: Rút gọn rồi tính giá trị của các biểu thức sau.

a)

( ) ( )( ) ( )

( )

3

2

1 4 1 1 3 1 1A x x x x x x x= - - + - + - + +

với

2x =

.

b)

( )( )

22

1 2 1 4 2B x x x x x x= - + + + - +

với

1

2

x =-

.

*Thực hiện nhiệm vụ

- Giáo viên chia nhóm, hướng dẫn

HS cách hoạt động nhóm. Yêu cầu

HS:

+ Với mỗi bài được giao cần đọc

kĩ đề bài, xác định rõ câu hỏi của

bài từ đó xác định cách làm.

+ Xác định rõ hằng đẳng thức sử

dụng trong từng ý của mỗi bài.

Trả lời

Bài 1: Rút gọn biểu thức

a)

( )

2 2 2 2

A x y x xy y x y x xy y= - + + - + - +

( ) ( )

3 3 3 3

x y x y= - - +

3

2y=-

b)

( )( )

2 2 4 4 3 2 2 3

5 5 25 125B a b a a b a b a a= - + + +

( )

3

2 2 3

5 125a b a a= - +

6 6 3 3

125 125a b a a= - +

Trang 136

- HS hoạt động nhóm, thảo luận

trả lời các câu hỏi GV giao.

- GV tổ chức cho HS báo cáo kết

quả hoạt động nhóm, các nhóm

khác nhận xét, bổ sung.

*Kết luận, nhận định:

- GV kết luận:

1. Cách làm dạng toán này

- Khai triển các hằng đẳng thức có

trong biểu thức.

- Rút gọn các đơn thức đồng dạng.

2. Cách trình bày bài làm.

66

ab=

c)

( )

2 2 3 3

2 3 4 6 9 7 26C x y x xy y x y= + - + - -

( ) ( )

33

2 3 7 26x y x y= + - -

3 3 3 3

8 27 7 26x y x y= + - -

33

xy=+

d)

( )

32

2 2 2 4D y y y y= - + + + - +

3 3 3

22yy= - + + +

33

28yy= - + + +

10=

Bài 2: Chứng tỏ các biểu thức sau có giá trị không phụ

thuộc vào biến x.

a)

( )

22

1 1 1 1A x x x x x x= + - + - - + +

( ) ( )

33

11xx= + - -

33

11xx= + - +

2=

b)

( )

23

2 6 4 12 36 8 10B x x x x= + - + - +

( )

3

33

2 6 8 10xx= + - +

226=

c)

( ) ( )

( )

3

2

1 3 3 9 3 1C x x x x x x= - - - + + - -

( ) ( )

3 2 3 2

3 3 1 27 3 3x x x x x x= - + - - - - +

3 2 3 2

3 3 1 27 3 3x x x x x x= - + - - + - +

26=

Bài 3: Rút gọn rồi tính giá trị của các biểu thức sau.

a) Ta có

( ) ( )( ) ( )

( )

3

2

1 4 1 1 3 1 1A x x x x x x x= - - + - + - + +

( ) ( )

3 2 2 3

3 3 1 4 1 3 1x x x x x x= - + - - - + -

3 2 3 3

3 3 1 4 4 3 3x x x x x x= - + - - + + -

2

3 7 4xx= - + -

Thay

2x =

vào biểu thức A ta có

2

3.2 7.2 4 12 14 4 2A = - + - = - + - = -

Vậy với

2x =

thì

2A =-

b) Ta có

( )( )

22

1 2 1 4 2B x x x x x x= - + + + - +

( )

22

1 1 . 2 2 4x x x x x x

é ù é ù

= - + + + - +

ê ú ê ú

ë û ë û

( )( )

3 3 3 3

12xx= - +

Trang 137

Thay

1

2

x =-

vào biểu thức B ta có

33

1 1 1 1

1 2 1 8

2 2 8 8

B

é ùé ù

æ ö æ ö æ öæ ö

--

ê úê ú

÷ ÷ ÷ ÷

ç ç ç ç

÷ ÷ ÷ ÷

= - - - + = - +

ç ç ç ç

ê úê ú

÷ ÷ ÷ ÷

ç ç ç ç

÷ ÷ ÷ ÷

ç ç ç ç

è ø è ø è øè ø

ê úê ú

ë ûë û

9 63 567

.

8 8 64

--

==

Vậy với

1

2

x =-

thì

567

64

B

-

=

* Giao nhiệm vụ

- GV yêu cầu HS hoạt động cá

nhân lần lượt làm các bài tập 1, 2

của dạng 3.

Dạng 3: Tìm x

Bài 1: Tìm x, biết:

a)

( )

( )( )

2

2 2 4 3 3 26x x x x x x+ - + - + - =

b)

( )

( )( )

2

3 3 9 4 4 21x x x x x x- + + - - + =

c)

( )

( ) ( )

22

2 1 4 2 1 ) 4 2 3 23x x x x x- + + - - =

Bài 2: Tìm x, biết:

a)

( ) ( )

3

22

1 3 3 9 3 4 2x x x x x- - + - + + - =

b)

( )

22

1 1 1 1 7x x x x x x+ + + - - + =

*Thực hiện nhiệm vụ

- Giáo viên yêu cầu HS đọc kĩ

từng bài và làm.

- HS tự làm vào vở.

- GV gọi HS lên bảng làm.

- GV tổ chức cho HS nhận xét,

đánh giá, giải thích kĩ từng bài.

*Kết luận, nhận định:

- GV kết luận:

+ Cách làm của dạng bài tập này.

Sử dụng các hằng đẳng thức đáng

nhớ, rút gọn vế trái rồi dựa vào

quan hệ giữa các phép tính để tìm

x

+ Cách trình bày bài làm.

Trả lời

Bài 1: Tìm x, biết:

a)

( )

( )( )

2

2 2 4 3 3 26x x x x x x+ - + - + - =

( ) ( )

32

8 9 26x x x+ - - =

33

8 9 26x x x+ - + =

9 18x =

2x =

b)

( )

( )( )

2

3 3 9 4 4 21x x x x x x- + + - - + =

( ) ( )

32

27 16 21x x x- - - =

33

27 16 21x x x- - + =

16 48x =

3x =

c)

( )

( ) ( )

22

2 1 4 2 1 4 2 3 23x x x x x- + + - - =

33

8 1 8 12 23x x x- - + =

12 24x =

2x =

Bài 2: Tìm x, biết:

Trang 138

a)

( ) ( )

3

22

1 3 3 9 3 4 2x x x x x- - + - + + - =

( )

3 2 3 3 2

3 3 1 3 3 12 2x x x x x- + - - + + - =

3 2 3 2

3 3 1 27 3 12 2x x x x x- + - - - + - =

3 40 2x -=

3 42x =

14x =

b)

( )

22

1 1 1 1 63x x x x x x+ + + - - + =

( )

22

1 1 . 1 1 63x x x x x x

é ù é ù

+ - + - + + =

ê ú ê ú

ë û ë û

( )( )

33

1 1 63xx+ - =

6

1 63x -=

6

64x =

66

2x =

2xÞ=

hoặc

2x =-

* Giao nhiệm vụ

- GV yêu cầu HS hoạt động cá

nhân lần lượt làm các bài tập 1, 2

của dạng 4.

Dạng 4: Tính nhanh

Bài 1: Tính nhanh.

a)

3

2

2023 1

2023 2022

A

+

=

-

b)

3

2

2023 1

2023 2024

B

-

=

+

Bài 2: Tính nhanh.

a)

33

23 27

23.27

50

C

+

=-

d)

33

52.38

52 38

14

D =+

-

*Thực hiện nhiệm vụ

- Giáo viên yêu cầu HS đọc kĩ

từng bài và làm.

- HS tự làm vào vở.

- GV gọi HS lên bảng làm.

- GV tổ chức cho HS nhận xét,

đánh giá, giải thích kĩ từng bài.

*Kết luận, nhận định:

- GV kết luận:

+ Cách làm của dạng bài tập này.

- Xem biểu thức bài cho có hằng

đẳng thức nào (Có thể phải thêm,

bớt, tách để biểu thức đã cho xuất

hiện hằng đẳng thức).

Bài 1: Tính nhanh.

a)

( )

2

3

22

2023 1 2023 2023 1

2023 1

2023 2022 2023 2023 1

A

+ × - +

+

==

- - +

2024=

b)

( )

2

3

22

2023 1 2023 2023 1

2023 1

2023 2024 2023 2023 1

B

- × + +

-

==

+ + +

2022=

Bài 2: Tính nhanh.

a)

33

23 27

23.27

50

C

+

=-

( )

22

23 27 23 23.27 27

23.27

50

+ - +

=-

Trang 139

- Áp dụng hằng đẳng thức để tính.

+ Cách trình bày bài làm.

- GV chốt phương pháp giải của 4

dạng toán và một số lưu ý khi làm

bài.

22

23 23.27 27 23.27= - + -

22

23 2.23.27 27= - +

( )

2

23 27=-

16=

b)

33

52.38

52 38

14

D =+

-

( )

22

52 52.38 38

52.38

52 38

14

++

=

-

+

22

52 52.38 38 52.38= + + +

22

52 2.52.38 38= + +

( )

2

52 38=+

2

90=

8100=

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ ….

1. TRẮC NGHIỆM

Câu 1: Đa thức

3

125x +

viết dưới dạng tích là

A.

( )

22

125 125 125x x x+ - +

B.

( )

22

125 125 125x x x-++

C.

( )

2

5 5 25x x x+ - +

D.

( )

2

5 5 25x x x-++

Câu 2: Đa thức

3

18x-

viết dưới dạng tích là

A.

( )

2

1 8 1 8 8x x x- - +

B.

( )

2

1 2 1 2 4x x x- - +

C.

( )

2

1 8 1 8 8x x x- + +

D.

( )

2

1 2 1 2 4x x x- + +

Câu 3: Biểu thức

( )

2

2 2 4 x x x+ - +

viết dưới dạng tổng hay hiệu hai lập phương

là

A.

33

2x -

B.

( )

3

2x -

C.

33

2x +

D .

( )

3

2x +

Câu 4: Biểu thức

( )

2

1 3 1 3 9 x x x- + +

viết dưới dạng tổng hay hiệu hai lập

phương là

A.

33

1 3x-

B.

( )

3

1 3x+

C.

( )

3

1 3x-

D .

( )

3

13x+

Câu 5: Điền biểu thức thích hợp vào chỗ trống

( )

2

2 3 4 6 9 ..... 27x x x+ - + = +

A .

8x

B .

3

8x

C .

3

2x

D.

3

x

Trang 140

Câu 6: Điền biểu thức thích hợp vào chỗ trống

( )

2 2 3 3

3 ..... 9 27y x y x y x- + + = +

A .

3xy

B .

xy

C .

2

3xy

D.

2

3xy

2. TỰ LUẬN

Bài 1: Nối mỗi ý ở cột A với một ý ở cột B để được đáp án đúng

A

B

1)

( )( )

x y x y+-

a)

33

xy+

2)

22

2x xy y-+

b)

22

2x x y y++

3)

( )

2

xy+

c)

22

xy-

4)

( )

22

()x y x xy y+ - +

d)

( )

2

xy-

e)

22

xy+

Bài 2: Viết các đa thức sau dưới dạng tích.

a)

3

1

27

x +

b)

3

8 27x-

c)

33

125 8

yx

-

d)

3

0,00164x +

e)

333

64x yz-

Bài 3: Viết các biểu thức sau dưới dạng tổng hay hiệu hai lập phương.

a)

( )

2

2 2 4x x x+ - +

b)

( )

2

3 3 9x x x- + +

c)

( )

22

3 3 9x y x xy y- + +

d)

( )

4 2 2

3 9 3x x x+ + -

Bài 4: Chứng tỏ các biểu thức sau có giá trị không phụ thuộc vào biến x.

a)

( )

23

5 5 25 2A x x x x= - + + - +

b)

( )

( ) ( )

22

2 3 4x 6 9 8 2 16 5B x x x x x= + - + - + + +

Bài 5: Tìm x biết:

a)

( ) ( )

( )

32

2

3 3 3 9 9 1 15x x x x x- - - + + + + =

b)

( )( ) ( )

( )

2

5 5 2 2 4 17x x x x x x- + - - + + = -

c)

( )

( )( )

2

1 1 2 2 5x x x x x x- + + - + - =

Bài 6: Chứng tỏ các biểu thức sau không phụ thuộc vào biến x.

a)

( )

( ) ( )

23

2 3 4 6 9 2 4 1x x x x+ - + - -

b)

( )

32

8 5 2 1 4x 2x 1xx- - + - +

Bài 7: Chứng minh:

Trang 141

a)

( ) ( )

3

33

3x y x y xy x y+ = + - +

b)

( ) ( )

3

33

3x y x y x y x y- = - + -

Bài 8:

a) Cho

1xy+=

và

1xy =-

. Chứng minh rằng:

33

4xy+=

b) Cho

1xy-=

và

6xy =

. Chứng minh rằng:

33

19xy-=

Bài 9:

a) Cho

3xy+=

và

22

5xy+=

. Tính

33

xy+

b) Cho

5xy-=

và

22

15xy+=

. Tính

33

xy-

ĐS: a) 2 b) - 5

Bài 10: Rút gọn rồi tính giá trị của các biểu thức sau.

a)

( ) ( )

( )

( )( )

3

2

1 2 2 4 3 4 4P x x x x x x= - - + - + + - +

với

5x =-

b)

( )

2

27 3 3 9Q x x x= + - + +

với

3x =-

Bài 11: Chứng minh rằng

3 3 3 3

1 2 3 ... 100A = + + + +

chia hết cho

1 2 3 ... 100B = + + + +

.

Hướng dẫn:

Ta có

1 2 3 ... 100B = + + + +

( ) ( ) ( ) ( )

1 100 2 99 3 98 ... 50 51= + + + + + + + +

101 101 101 ... 101= + + + +

(

50

số hạng

101

)

101.50=

Để chứng minh

A

chia hết cho

B

ta chứng minh

A

chia hết cho

50

và

101

.

* Ta có

3 3 3 3

1 2 3 ... 100A = + + + +

( ) ( ) ( )

3 3 3 3 3 3

1 100 2 99 ... 50 51= + + + + + +

( )

2 2 2 2 2 2

1 100 1 1.100 100 2 99 2 2.99 99 ... 50 51 50 50.51 51= + - + + + - + + + + - +

( ) ( ) ( )

2 2 2 2 2 2

101. 1 1.100 100 101. 2 2.99 99 ... 101. 50 50.51 51= - + + - + + + - +

( )

2 2 2 2

101. 1 2 3 ... 100 1.100 2.99 3.98 ... 50.51

éù

= + + + + - + + + +

êú

ëû

Do đó

A

chia hết cho

101

(1)

* Lại có

3 3 3 3

1 2 3 ... 100A = + + + +

( ) ( ) ( )

3 3 3 3 3 3

1 99 2 98 ... 50 100= + + + + + +

Mỗi biểu thức trong ngoặc đều chia hết cho

50

nên

A

chia hết cho

50

(2)

Trang 142

(Chú ý: Với mọi số nguyên a, b và số tự nhiên n thì

2 1 2 1nn

ab

++

+

chia hết cho

ab+

)

Từ (1) và (2) suy ra

A

chia hết cho

101

và

50

nên

A

chia hết cho

B

.

Tuần 13

Tiết 34; 35; 36

Ngày soạn 01/11/2023

Lớp

8A

8B

Ngày dạy:

ÔN TẬP ĐỊNH LÍ THALÈS TRONG TAM GIÁC

I. MỤC TIÊU

1. Về kiến thức:

- Củng cố các khái niệm tỉ số của hai đoạn thẳng và đoạn thẳng tỉ lệ.

- Củng cố định lí Thalès và định lí Thalès đảo trong một tam giác.

2. Về năng lực:

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà

và tại lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết

hỗ trợ nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn

thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được tỉ số của hai đoạn

thẳng và các cặp đoạn thẳng tỉ lệ, nội dung định lí Thalès và định lí Thalès đảo.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học,

năng lực mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh,

phân tích, tổng hợp, khái quát hóa, …để tính được độ dài các đoạn thẳng bằng

cách sử dụng định lí Thalès và giải quyết được một số vấn đề thực tiễn gắn với

việc vận dụng định lí Thalès.

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và

theo nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

1.1. Tỉ số của 2 đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

Trang 143

1.2. Đoạn thẳng tỉ lệ: Hai đoạn thẳng

AB

và

CD

gọi là tỉ lệ với hai đoạn thẳng

''AB

và

''CD

nếu có tỉ lệ thức:

''

AB A B

CD C D

=

hay

' ' ' '

AB CD

A B C D

=

1.3. Định lí Thalès trong tam giác:

a) Định lí Thalès: Nếu một đường thẳng song song với hai cạnh của một tam

giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng

tương ứng tỉ lệ.

b) Định lí Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và

định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó

song song với cạnh còn lại của tam giác.

2. BÀI TẬP

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ:

- GV tổ chức hoạt động, trả lời nhanh

bài toán trắc nghiệm

Dạng 1: Tính tỉ số của hai đoạn thẳng.

Chia đoạn thẳng theo tỉ số cho trước.

Bài 1: Bài tập trắc nghiệm

Câu 1. Cho

6AB cm=

và

18AC cm=

. Tỉ số của hai đoạn thẳng

AB

và

AC

là bao

nhiêu?

A.

1

2

B.

2

C.

1

3

D.

3

Câu 2. Cho

3MN cm=

và

12DE dm=

. Tỉ số của hai đoạn thẳng

DE

và

MN

là bao

nhiêu?

A.

1

3

B.

4

C.

1

30

D.

40

Câu 3. Cho các đoạn thẳng

6AB cm=

,

4CD cm=

,

8PQ cm=

,

10EF cm=

,

2,5MN cm=

,

1,5RS cm=

. Hãy chọn phát biểu đúng trong các phát biểu sau:

A. Hai đoạn thẳng

AB

và

PQ

tỉ lệ với hai đoạn thẳng

EF

và

RS

.

B. Hai đoạn thẳng

AB

và

CD

tỉ lệ với hai đoạn thẳng

PQ

và

EF

.

C. Hai đoạn thẳng

AB

và

RS

tỉ lệ với hai đoạn thẳng

EF

và

MN

.

D. Cả 3 phát biểu đều sai.

*Thực hiện nhiệm vụ:

- GV mời ba HS trả lời miệng.

- Ba HS trả lời miệng, cả lớp theo dõi

nhận xét bài bạn.

- HS chốt được kiến thức về cách tìm tỉ

Trả lời:

Câu

1

2

3

Đáp án

C

D

C

Hướng dẫn giải:

Trang 144

số của 2 đoạn thẳng và cách kiểm tra các

cặp đoạn thẳng có tỉ lệ với nhau hay

không.

*Kết luận, nhận định:

- Muốn tìm tỉ số của 2 đoạn thẳng ta chia

độ dài của chúng theo cùng một đơn vị

đo.

- Các cặp đoạn thẳng tỉ lệ với nhau khi tỉ

số của mỗi cặp đoạn thẳng đó bằng

nhau.

Câu 1.

61

18 3

AB

AC

==

.

Câu 2. Đổi

12 120DE dm cm==

.

120

40

3

DE

MN

==

.

Câu 3.

63

84

AB

PQ

==

và

10 20

1,5 3

EF

RS

==



AB EF

PQ RS



.

63

42

AB

CD

==

và

84

10 5

PQ

EF

==



AB PQ

CD EF



.

6

4

1,5

AB

RS

==

và

10

4

2,5

EF

MN

==



AB EF

RS MN

=

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 2: Tính tỉ số của hai đoạn

thẳng sau:

a)

1,2AB m=

và

3,8CD m=

.

b)

0,5MN cm=

và

4,1KP km=

.

HS tìm hiểu bài 2 và trình bày bài làm

vào vở.

*Thực hiện nhiệm vụ:

- GV cho HS hoạt động cá nhân làm bài.

- HS hoạt động cá nhân làm bài.

- Học sinh đọc đề bài và làm bài tập

- Một học sinh lên bảng làm bài

- Học sinh đối chiếu kết quả và nhận xét

bài làm của bạn.

*Kết luận, nhận định:

- Muốn tìm tỉ số của 2 đoạn thẳng ta chia

độ dài của chúng theo cùng một đơn vị

đo.

Bài 2: Tính tỉ số của hai đoạn thẳng sau:

a)

1,2AB m=

và

3,8CD m=

.

b)

0,5MN cm=

và

4,1KP km=

.

Lời giải:

a) Ta có:

1,2 6

3,8 19

AB

CD

==

.

b) Đổi

4,1 410000KP km cm==

.

Ta có:

0,5 1

410000 820000

MN

KP

==

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

Bài 3: Cho hình vẽ:

Trang 145

tìm hiểu Bài 3: Cho hình vẽ:

a) Hai đoạn thẳng

AE

và

AC

có tỉ lệ với

hai đoạn thẳng

AD

và

AB

không? Vì

sao?

b) Hai đoạn thẳng

HI

và

IF

có tỉ lệ

với hai đoạn thẳng

HJ

và

JG

không?

Vì sao?

*Thực hiện nhiệm vụ:

- GV cho HS hoạt động nhóm đôi làm

bài.

- HS hoạt động nhóm đôi làm bài.

- GV: Trước tiên ta phải tìm các độ dài

AD

,

AC

. Ta tính độ dài

AD

,

AC

như

thế nào?

- HS: Ta có:

AD AB DB=−

7 2 5cm=−=

.

AC AE EC=+

4 4 8cm= + =

.

*Kết luận, nhận định:

- Các cặp đoạn thẳng tỉ lệ với nhau khi tỉ

số của mỗi cặp đoạn thẳng đó bằng

nhau.

a) Hai đoạn thẳng

AE

và

AC

có tỉ lệ với

hai đoạn thẳng

AD

và

AB

không? Vì

sao?

b) Hai đoạn thẳng

HI

và

IF

có tỉ lệ với

hai đoạn thẳng

HJ

và

JG

không? Vì

sao?

Hướng dẫn giải:

a) Ta có:

7 2 5AD AB DB cm= − = − =

.

4 4 8AC AE EC cm= + = + =

.

41

82

AE

AC

==

và

5

7

AD

AB

=



AE AD

AC AB



.

Vậy: Hai đoạn thẳng

AE

và

AC

không

tỉ lệ với hai đoạn thẳng

AD

và

AB

.

b) Ta có:

2,7 3

1,8 2

HI

IF

==

và

2,1 3

1,4 2

HJ

JG

==



HI HJ

IF JG

=

.

Vậy: Hai đoạn thẳng

HI

và

IF

có tỉ lệ

với hai đoạn thẳng

HJ

và

JG

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

Bài 4: Điểm

C

thuộc đoạn thẳng

AB

và

7 cm

4 cm

2 cm

E

B

C

A

D

1,4 cm

2,1 cm

2,7 cm

1,8 cm

I

G

H

F

J

7 cm

4 cm

2 cm

E

B

C

A

D

1,4 cm

2,1 cm

2,7 cm

1,8 cm

I

G

H

F

J

Trang 146

tìm hiểu Bài 4 Điểm

C

thuộc đoạn

thẳng

AB

và chia

AB

theo tỉ số

4

5

. Hãy

tính các tỉ số:

;

AB AB

AC CB

.

*Thực hiện nhiệm vụ:

- GV: Một điểm

C

thuộc đoạn thẳng

AB

(hoặc đường thẳng

AB

), được gọi là

chia đoạn thẳng

AB

theo tỉ số

m

n

(

m

,

n

là các số dương) nếu ta có:

AC m

CB n

=

.

- GV: Nếu ta chia đoạn thẳng

AB

thành

4 5 9+=

phần bằng nhau thì đoạn thẳng

AC

chiếm 4 phần và

CB

chiếm 5 phần.

- GV vẽ hình minh họa:

- Học sinh đọc đề bài và làm bài tập

- Một học sinh lên bảng làm bài

- Học sinh đối chiếu kết quả và nhận xét

bài làm của bạn.

- GV: Giả sử mỗi phần có độ dài là

b

.

Hãy tính

AB

,

AC

,

CB

theo

b

.

- HS:

9AB b=

;

4AC b=

;

5CB b=

.

*Kết luận, nhận định:

- Điểm

C

chia

AB

theo tỉ số

4

5

nghĩa là

4

5

AC

CB

=

. Từ đó tính được:

4AC b=

;

5CB b=

với

0b 

.

chia

AB

theo tỉ số

4

5

. Hãy tính các tỉ số:

;

AB AB

AC CB

.

Hướng dẫn giải:

Vì điểm

C

chia đoạn thẳng

AB

theo tỉ

số

4

5

nên:

4

5

AC

CB

=



4

( 0)

5

AC b

b

CB b

=







=



.

Do đó:

9AB AC CB b= + =

.

Vậy:

99

44

AB b

AC b

==

và

99

55

AB b

CB b

==

.

Nhận xét:

- Trong lời giải trên ta đã sử dụng kĩ thuật

đại số hóa hình học:

Nếu ta có

AC m

CB n

=

thì

( 0)

AC mb

b

CB nb

=







=



.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 5: Cho đoạn thẳng

20AB cm=

.

Bài 5: Cho đoạn thẳng

20AB cm=

.

a) Trên đoạn thẳng

AB

lấy điểm

C

sao

cho

3

2

CA

CB

=

. Tính độ dài

CB

.

9

4

5

A

B

C

Trang 147

a) Trên đoạn thẳng

AB

lấy điểm

C

sao

cho

3

2

CA

CB

=

. Tính độ dài

CB

.

b) Trên tia đối của tia

BA

lấy điểm

D

sao cho

3

2

CA

CB

=

. Tính độ dài

CD

.

*Thực hiện nhiệm vụ:

- GV cho HS hoạt động cá nhân làm bài.

- HS hoạt động cá nhân làm bài.

- GV gợi ý: sử dụng kĩ thuật đại số hóa

hình học.

- Học sinh đọc đề bài và làm bài tập

- Hai học sinh lên bảng làm bài

- Học sinh đối chiếu kết quả và nhận xét

bài làm của bạn.

*Kết luận, nhận định:

- Ta có thể giải bài toán chia đoạn thẳng

theo tỉ số cho trước bằng nhiều cách

khác nhau, chẳng hạn:

Cách 1:

3

2

CA

CB

=



3

2

CA b

CB b

=





=



với

0b 

Cách 2:

3

2

CA

CB

=



32

CA CB

=

(Tính chất

của tỉ lệ thức).

Cách 3: Đặt

CB x=

thì

20CA x=−

.

b) Trên tia đối của tia

BA

lấy điểm

D

sao cho

3

2

CA

CB

=

. Tính độ dài

CD

.

Hướng dẫn giải:

a) Cách 1: Từ giả thiết:

3

2

CA

CB

=



3

2

CA b

CB b

=





=



với

0b 

Nên

20 5AB cm CA CB b= = + =



4b cm=

.

Vậy:

8CB cm=

.

Cách 2: Từ giả thiết:

3

2

CA

CB

=



32

CA CB

=

.

Theo tính chất của dãy tỉ số bằng nhau ta

có:

3 2 3 2

CA CB CA CB+

==

+

20

4.

55

AB

= = =

Vậy:

8CB cm=

.

Cách 3: Đặt

CB x=

thì

20CA x=−

.

Từ giả thiết và tính chất cơ bản của tỉ lệ

thức ta có

23CA CB=

hay

2(20 ) 3xx−=



8x cm=

.

Vậy:

8CB cm=

.

b) Từ giả thiết:

3

2

DA

DB

=



3

2

DA b

DB b

=





=



với

0b 

.

Mặt khác

D

thuộc tia đối của tia

BA

nên

DA DB

.

Do đó:

20 3 2AB cm DA DB b b= = − = −



20b cm=

. Suy ra

40DB cm=

.

A

B

C

D

Trang 148

Vậy:

40 8 48CD DB CB cm= + = + =

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, trả lời nhanh

bài toán trắc nghiệm

Dạng 2: Tính độ dài đoạn thẳng.

Bài 1: Bài tập trắc nghiệm

Câu 1. Cho các đoạn thẳng

8AB cm=

,

6AC cm=

,

12MN cm=

,

PQ x cm=

. Tìm

x

để

AB

và

AC

tỉ lệ với

MN

và

PQ

.

A.

6x cm=

B.

7x cm=

C.

8x cm=

D.

9x cm=

Câu 2. Cho tam giác

ABC

có

10AB cm=

và

20AC cm=

. Trên cạnh

AB

lấy điểm

M

sao cho

4AM cm=

. Qua

M

kẻ đường thẳng song song với

BC

cắt

AC

tại

N

. Tính

độ dài đoạn thẳng

AN

.

A.

8AN cm=

B.

10AN cm=

C.

12AN cm=

D.

6AN cm=

Câu 3. Cho hình vẽ :

Độ dài

x

phải bằng bao nhiêu để

DE

song song với

BC

?

A.

6,5x =

B.

7,5x =

C.

8,5x =

D.

12,5x =

*Thực hiện nhiệm vụ:

+ 3 HS quan sát và trả lời theo yêu cầu

của GV.

+ GV: quan sát và trợ giúp HS.

*Kết luận, nhận định:

GV nhận xét, đánh giá quá trình học của

HS, tổng quát lại các kiến thức về đoạn

thẳng tỉ lệ, định lí Thalès và định lí

Thalès đảo.

Trả lời:

Câu

1

2

3

Đáp án

D

A

B

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 2: Tìm độ dài y trong mỗi

Bài 2: Tìm độ dài y trong mỗi hình vẽ

sau (làm tròn kết quả đến chữ số thập

phân thứ nhất).

x

4,5

5

3

E

B

C

A

D

Trang 149

hình vẽ sau (làm tròn kết quả đến chữ số

thập phân thứ nhất).

- HS tìm hiểu bài 2 và vẽ hình

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès để tính độ dài y.

+ GV hướng dẫn HS tìm y trong hình 1:

GV: Tam giác

ABC

có

//DE BC

.

Trong phát biểu của định lí Thalès thì

các đoạn thẳng

AB

,

AD

,

DB

tương ứng

với các đoạn thẳng nào?

HS: Các đoạn thẳng

AB

,

AD

,

DB

tương ứng với các đoạn thẳng

AC

,

AE

,

EC

.

GV: Các đoạn thẳng tương ứng tỉ lệ nên

ta có đẳng thức nào để tìm y?

Giải

- Hình 1: Xét tam giác

ABC

có

//DE BC

nên theo định lí Thalès, ta có:

AD AE

DB EC

=

hay

3

6

y

=



2

18y =



18 4,2y =

(vì

0y 

) .

Vậy:

4,2y 

.

- Hình 2: Vì

()FGN GNP gt=

mà 2 góc

này là 2 góc so le trong của

GH

và

NP

nên

//GH NP

.

Xét tam giác

MNP

có

//GH NP

nên theo

định lí Thalès, ta có:

MG MH

GN HP

=

hay

11 7

3 y

=



7.3

1,9

11

y =

Vậy:

1,9y 

.

- Hình 3:

Ta có:

5,2 3,3 8,5QE QH HE= + = + =

Hình 1 . DE // BC

y

6

3

E

B

C

A

D

Hình 2

y

11

7

3

H

N

P

M

G

F

Hình 3.

y

5,2

3

3,3

R

Q

E

P

H

Hình 1 . DE // BC

y

6

3

E

B

C

A

D

Hình 2

y

11

7

3

H

N

P

M

G

F

Hình 3.

y

5,2

3

3,3

R

Q

E

P

H

Trang 150

HS: Ta có:

AD AE

DB EC

=

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý.

- Ở hình 2 và hình 3 để vận dụng định lí

Thalès thì trước tiên ta phải chứng minh

//GH NP

và

//RH PE

.

Vì

()QHR QEP gt=

mà 2 góc này là 2

góc đồng vị của

RH

và

PE

nên

//RH PE

.

Xét tam giác

QPE

có

//RH PE

nên theo

định lí Thalès, ta có:

QR QH

QP QE

=

hay

3 5,2

8,5y

=



3.8,5

4,9

5,2

y =

Vậy:

4,9y 

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 3: Cho tam giác

ABC

có

12AB cm=

và

21AC cm=

. Gọi

G

là

trọng tâm và

AM

là đường trung tuyến

của tam giác

ABC

. Đường thẳng đi qua

trọng tâm

G

và song song với

BC

cắt

AB

,

AC

lần lượt tại

N

,

P

. Tính

AN

,

NB

,

AP

,

PC

.

- HS tìm hiểu bài 3 và vẽ hình

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès để tính các độ dài

AN

,

NB

,

AP

,

PC

.

+ GV: Vì

G

là trọng tâm của tam giác

ABC nên ta có điều gì?

+ HS: Ta có :

2

3

AG

AM

=

.

+ GV: Vì

//NP BC

nên theo định lí

Thalès, ta có điều gì ?

HS: Ta có:

AG AN AP

AM AB AC

==

.

Bài 3: Cho tam giác

ABC

có

12AB cm=

và

21AC cm=

. Gọi

G

là trọng tâm và

AM

là đường trung tuyến của tam giác

ABC

. Đường thẳng đi qua trọng tâm

G

và song song với

BC

cắt

AB

,

AC

lần

lượt tại

N

,

P

. Tính

AN

,

NB

,

AP

,

PC

.

Giải

Vì

G

là trọng tâm của tam giác

ABC

nên

ta có :

2

3

AG

AM

=

.

Vì

//NP BC

nên theo định lí Thalès, ta

có:

AG AN AP

AM AB AC

==



2

3

AN AP

AB AC

==

hay

2

12 21 3

AN AP

==



8AN cm=

và

14AP cm=

N

P

G

M

C

B

A

Trang 151

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý.



12 8 4NB cm= − =

và

21 14 7PC cm= − =

Vậy:

8AN cm=

,

14AP cm=

,

4NB cm=

,

7PC cm=

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 1: Tìm các đường thẳng

song song trong hình vẽ và giải thích vì

sao chúng song song với nhau.

HS tìm hiểu bài 1 và vẽ hình

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès đảo để tìm ra các

đường thẳng song song.

*Kết luận, nhận định:

Dạng 3: Chứng minh hai đường thẳng

song song.

Bài 1: Tìm các đường thẳng song song

trong hình vẽ và giải thích vì sao chúng

song song với nhau.

Giải

- Hình 1a: Vì

5 6,25

3 3,75

=

hay

DB EB

DC EA

=

nên theo định lí Thalès đảo, ta có

//DE AC

.

- Hình 1b:

Vì

3 6 10

2 4 5

=

hay

QK QM PN

KP MR NR

=

nên

theo định lí Thalès đảo, ta có

//KM PR

Hình 1a.

3

5

6,25

3,75

D

B

C

A

E

2

3

Hình 1b.

4

6

10

5

M

Q

R

P

K

N

Hình 1a.

3

5

6,25

3,75

D

B

C

A

E

2

3

Hình 1b.

4

6

10

5

M

Q

R

P

K

N

Trang 152

GV chốt phương pháp giải của dạng toán

và một số lưu ý

và

MN

không song song với

QP

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 2: Cho tam giác

ABC

có

4BC cm=

. Trên cạnh

BC

,

CA

lần lượt

lấy các điểm

P

,

Q

sao cho

3CP cm=

,

4AC AQ=

. Chứng minh rằng

//PQ AB

.

- HS tìm hiểu bài 2 và vẽ hình

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès đảo để chứng minh

//PQ AB

.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Bài 2: Cho tam giác

ABC

có

4BC cm=

.

Trên cạnh

BC

,

CA

lần lượt lấy các điểm

P

,

Q

sao cho

3CP cm=

,

4AC AQ=

.

Chứng minh rằng

//PQ AB

.

Giải

Ta có:

4 3 1BP BC CP cm= − = − =



4

BC

BP

=

.

Vì

4AC AQ=

nên

4

AC

AQ

=

.

Do đó:

AC BC

AQ BP

=

.

Theo định lí Thalès đảo, ta có

//PQ AB

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 3: Cho tứ giác

ABCD

và

điểm

F

nằm trên

AC

. Kẻ

//FE CD

và

//FG CB

(

E AD

và

G AB

). Chứng

minh rằng

//EG DB

.

- HS tìm hiểu bài 3 và vẽ hình

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

Bài 3: Cho tứ giác

ABCD

và điểm

F

nằm trên

AC

.Kẻ

//FE CD

và

//FG CB

(

E AD

và

G AB

). Chứng minh rằng

//EG DB

.

Giải

4 cm

3 cm

Q

P

C

B

A

Trang 153

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès đảo để chứng minh

//EG DB



AE AG

AD AB

=



AE AF

AD AC

=

và

AG AF

AB AC

=

- Một học sinh lên bảng làm bài

- Học sinh đối chiếu kết quả và nhận xét

bài làm của bạn.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Vì

//FE CD

nên theo định lí Thalès, ta

có:

AE AF

AD AC

=

.

Vì

//FG CB

nên theo định lí Thalès, ta

có:

AG AF

AB AC

=

.

Do đó:

AE AG

AD AB

=

.

Theo định lí Thalès đảo, ta có

//EG DB

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 4: Cho hình thang

ABCD

(

//AB CD

). Gọi

G

và

K

lần lượt là trọng

tâm của tam giác

ACD

và

BCD

. Chứng

minh rằng

//GK CD

.

- HS tìm hiểu bài 4 và vẽ hình

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès đảo để chứng minh

//GK CD



//GK AB

Bài 4: Cho hình thang

ABCD

(

//AB CD

).

Gọi

G

và

K

lần lượt là trọng tâm của

tam giác

ACD

và

BCD

. Chứng minh rằng

//GK CD

.

Giải

Gọi

M

là trung điểm của

CD

.

Vì

G

là trọng tâm của tam giác

ACD

nên

ta có :

2

3

AG

AM

=

.

Vì

K

là trọng tâm của tam giác

BCD

nên

ta có :

2

3

BK

BM

=

.

G

E

A

C

D

B

F

K

G

M

A

C

D

B

Trang 154



AG BK

AM BM

=



2

3

AG

AM

=

và

2

3

BK

BM

=

.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Do đó:

AG BK

AM BM

=

.

Theo định lí Thalès đảo, ta có

//GK AB

.

Mà

//AB CD

nên

//GK CD

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 1: Cho tam giác

ABC

và

hai điểm

D

,

M

đều nằm trên cạnh

BC

.

Kẻ

//DE AC

và

//DF AB

(

E AB

và

F AC

). Kẻ

//MN AC

và

//MK AB

(

N AB

và

K AC

). Chứng minh rằng:

AE AF AN AK

AB AC AB AC

+ = +

.

- HS tìm hiểu bài 1 và vẽ hình.

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès để chứng minh hệ

thức

AE AF AN AK

AB AC AB AC

+ = +

.

+ GV: Theo định lí Thalès, ta có hai tỉ

số

AE

AB

và

AF

AC

lần lượt bằng hai tỉ số

nào?

+ HS:

AE DC

AB BC

=

và

AF DB

AB BC

=

.

+ GV: Tổng

?

DC DB

BC BC

+=

+ HS:

1

DC DB

BC BC

+=

.

Dạng 4: Chứng minh các hệ thức hình

học.

Bài 1: Cho tam giác

ABC

và hai điểm

D

,

M

đều nằm trên cạnh

BC

. Kẻ

//DE AC

và

//DF AB

(

E AB

và

F AC

).

Kẻ

//MN AC

và

//MK AB

(

N AB

và

K AC

). Chứng minh rằng:

AE AF AN AK

AB AC AB AC

+ = +

.

Giải

Vì

//DE AC

nên theo định lí Thalès, ta

có:

AE DC

AB BC

=

.

Vì

//DF AB

nên theo định lí Thalès, ta

có:

AF DB

AB BC

=

.

Do đó:

1

AE AF DC DB

AB AC BC BC

+ = + =

.

K

N

F

E

B

C

A

D

M

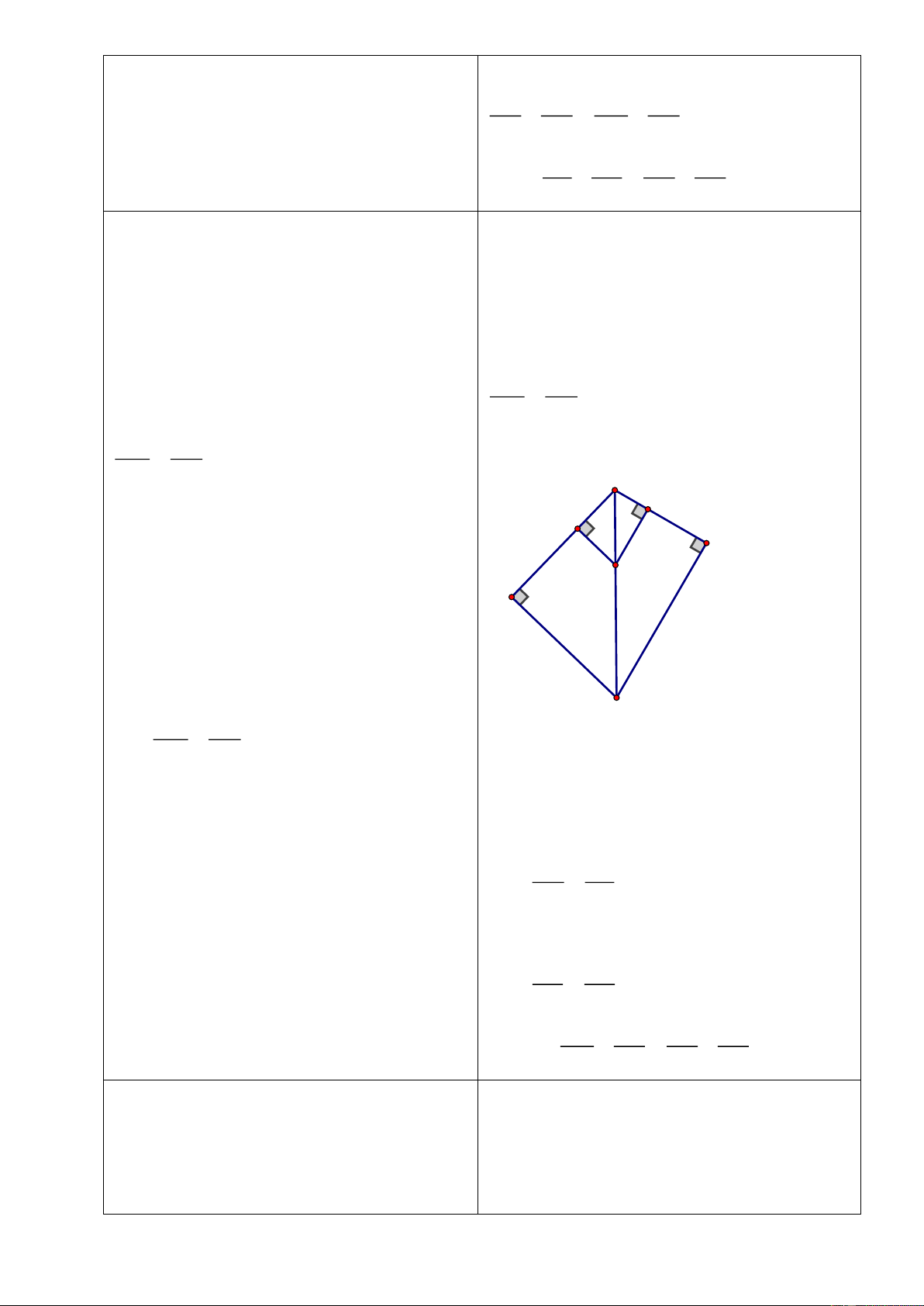
Trang 155

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Tương tự, ta cũng chứng minh được :

1

AN AK MC MB

AB AC BC BC

+ = + =

.

Vậy:

AE AF AN AK

AB AC AB AC

+ = +

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 2: Cho tứ giác

ABCD

có

góc

B

và góc

D

đều là góc vuông. Trên

đường chéo

AC

lấy điểm

P

. Kẻ

PH AB⊥

và

PE AD⊥

(

H AB

và

E AD

). Chứng minh rằng:

1

AH DE

AB DA

+=

.

- HS tìm hiểu bài 2 và vẽ hình.

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès để chứng minh hệ

thức

1

AH DE

AB DA

+=

.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

Bài 2: Cho tứ giác

ABCD

có góc

B

và

góc

D

đều là góc vuông. Trên đường

chéo

AC

lấy điểm

P

. Kẻ

PH AB⊥

và

PE AD⊥

(

H AB

và

E AD

). Chứng

minh rằng:

1

AH DE

AB DA

+=

.

Giải

Vì

PH AB⊥

và

BC AB⊥

nên

//PH BC

.

Vì

PE AD⊥

và

CD AD⊥

nên

//PE CD

.

Vì

//PH BC

nên theo định lí Thalès, ta

có:

AH AP

AB AC

=

.

Vì

//PE CD

nên theo định lí Thalès, ta

có:

DE PC

DA AC

=

.

Do đó:

1

AH DE AP PC

AB DA AC AC

+ = + =

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 3:

Cho hình thang

ABCD

(

//AB CD

). Một

Bài 3: Cho hình thang

ABCD

(

//AB CD

).

Một đường thẳng song song với hai đáy,

cắt

các cạnh bên

AD

và

BC

theo thứ tự ở

M

E

H

D

C

A

B

P

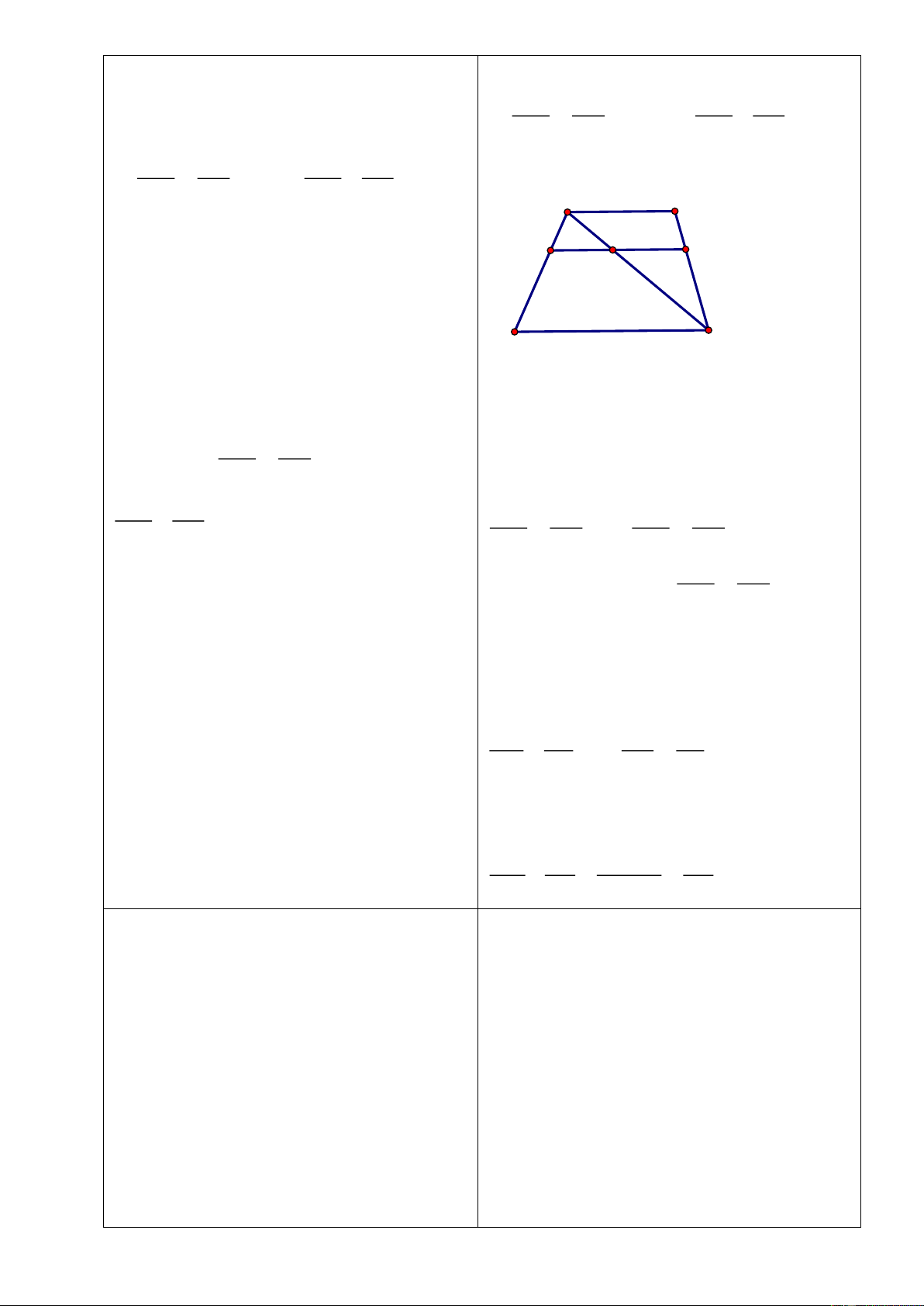
Trang 156

đường thẳng song song với hai đáy, cắt

các cạnh bên

AD

và

BC

theo thứ tự ở

M

và

N

. Chứng minh rằng:

a)

AM BN

MD NC

=

b)

1

AM CN

AD CB

+=

- HS tìm hiểu bài 3 và vẽ hình.

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès để chứng minh các

hệ thức: a)

AM BN

MD NC

=

b)

1

AM CN

AD CB

+=

.

+ GV: Trong hình ban đầu không có

hình tam giác. Vậy để sử dụng được

định lí Thalès ta phải làm gì?

+ HS: Nối

AC

và gọi

I

là giao điểm của

đường chéo

AC

với

MN

.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý

và

N

. Chứng minh rằng:

a)

AM BN

MD NC

=

b)

1

AM CN

AD CB

+=

Giải

a) Gọi

I

là giao điểm của đường chéo

AC

với

MN

.

Áp dụng định lí Thalès vào hai tam giác

ACD

và

ACB

có

//MI CD

,

//IN AB

ta

được:

AM BN

MD NC

=

(1);

AM BN

MD NC

=

(2).

Từ (1) và (2) suy ra:

AM BN

MD NC

=

.

b) Áp dụng định lí Thalès vào hai tam

giác

ACD

và

ACB

có

//MI CD

,

//IN AB

ta được:

AM AI

AD AC

=

(3);

CN CI

CB CA

=

(4).

Cộng theo vế các đẳng thức (3) và (4),

thu được:

1

AM CN AI CI AC

AD CB AC AC

+

+ = = =

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 4:

Cho hình bình hành

ABCD

có

M

và

N

lần lượt là trung điểm của AB và CD .

Gọi

P

và

Q

theo thứ tự là giao điểm

của

AM

và

CN

với đường chéo

BD

.

Chứng minh rằng:

DP PQ QB==

.

- HS tìm hiểu bài 4 và vẽ hình.

Bài 4: Cho hình bình hành

ABCD

có

M

và

N

lần lượt là trung điểm của AB và

CD . Gọi

P

và

Q

theo thứ tự là giao

điểm của

AM

và

CN

với đường chéo

BD

.

Chứng minh rằng:

DP PQ QB==

.

Giải

N

M

D

C

A

B

I

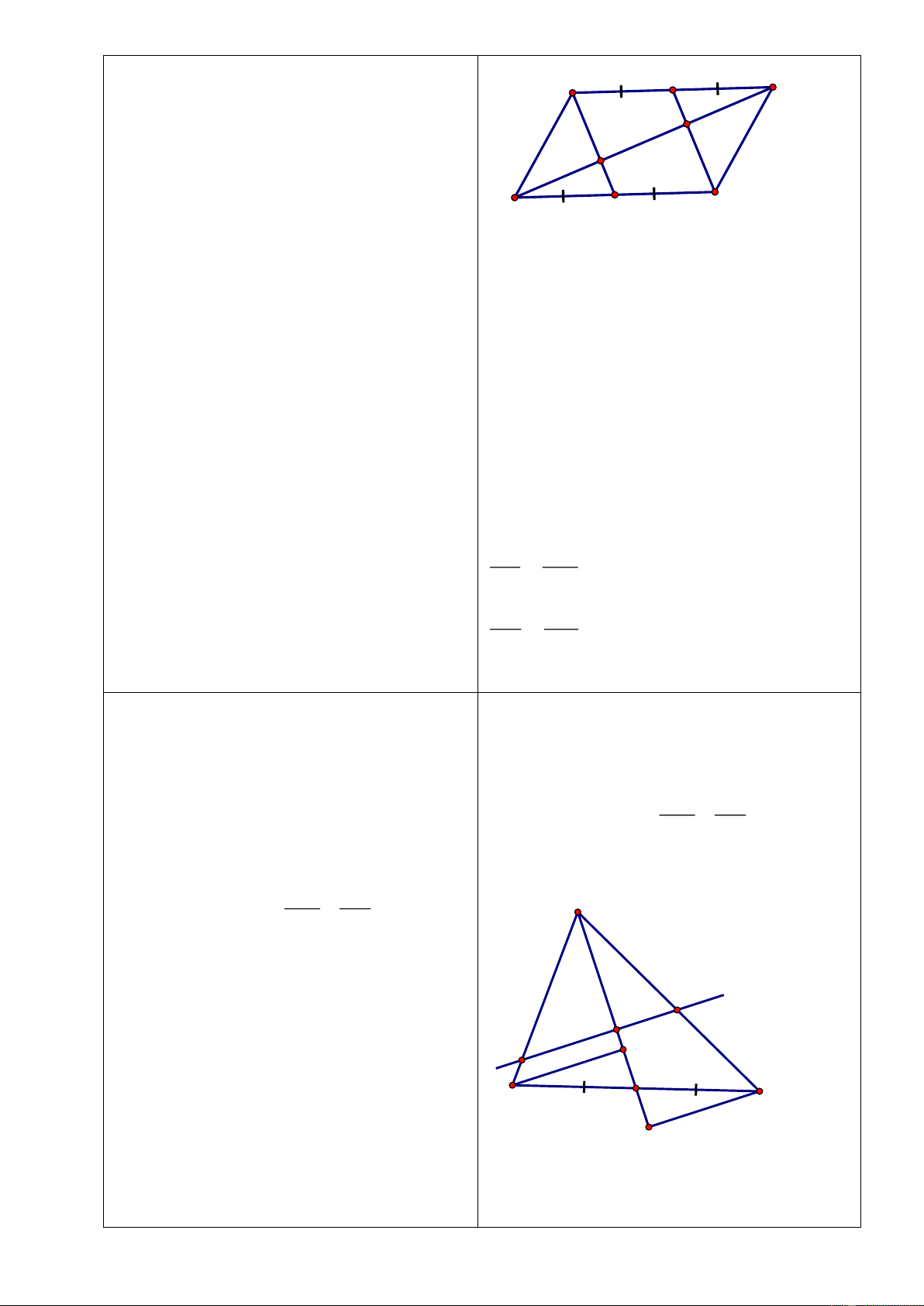
Trang 157

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès để chứng minh hệ

thức:

DP PQ QB==

.

+ GV: Nêu cách chứng minh

//MQ AP

,

//PN QC

?

+ HS: Chứng minh tứ giác

AMCN

là

hình bình hành để suy ra

//MC AN

.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý.

Áp dụng định nghĩa và giả thiết vào hình

bình hành

ABCD

, ta được:

AM NC=

,

//AM NC

.

Tứ giác

AMCN

có hai cạnh đối song

song và bằng nhau nên nó là hình bình

hành, do đó

//MC AN

, suy ra:

//MQ AP

,

//PN QC

.

Áp dụng định lí Thalès vào hai tam giác

APB

và

DQC

có

//MQ AP

,

//PN QC

,

ta được:

1

BQ BM

QP MA

==



BQ QP=

(1).

1

DP DN

PQ NC

==



DP PQ=

(2).

Từ (1) và (2) ta có:

DP PQ QB==

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 5:

Cho tam giác

ABC

có

G

là trọng tâm,

d

là một đường thẳng đi qua

G

và cắt

AB

và

AC

theo thứ tự tại

M

và

N

.

Chứng minh rằng:

3

AB AC

AM AN

+=

.

- HS tìm hiểu bài 5 và vẽ hình.

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès để chứng minh hệ

Bài 5: Cho tam giác

ABC

có

G

là trọng

tâm,

d

là một đường thẳng đi qua

G

và

cắt

AB

và

AC

theo thứ tự tại

M

và

N

.

Chứng minh rằng:

3

AB AC

AM AN

+=

.

Giải

Gọi

D

là trung điểm của cạnh

BC

. Ta

có:

Q

P

N

M

B

D

C

A

d

F

E

N

G

D

B

C

A

M

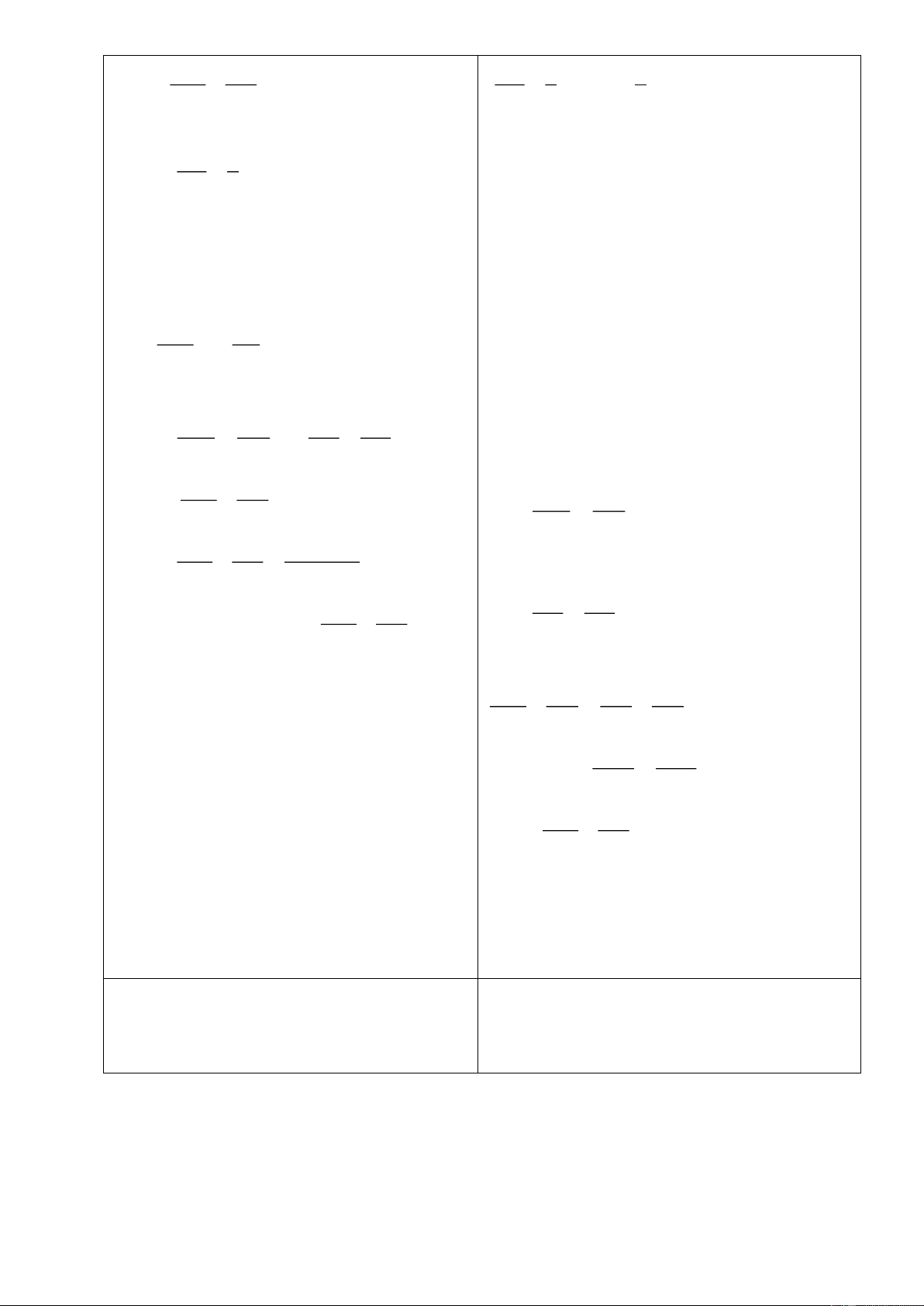
Trang 158

thức:

3

AB AC

AM AN

+=

.

+ GV: Trọng tâm G có tính chất gì?

+ HS:

3

2

AD

AG

=

.

+ GV:

//BF d

và

//CE d



?

+ HS:

//BF CE

.

+ GV: Sử dụng định lí Thalès, ta có các

tỉ số

AB

AM

và

AC

AN

lần lượt bằng các tỉ số

nào?

+ HS:

AB AF

AM AG

=

và

AC AE

AN AG

=

.

+ GV:

?

AB AC

AM AN

+=

+ HS:

AB AC AF AE

AM AN AG

+

+=

+ GV: Để chứng minh

3

AB AC

AM AN

+=

ta

phải chứng minh điều gì?

+ HS: Ta phải chứng minh:

32AF AE AG AD+ = =

+ GV : Chứng minh

2?AF AE AD+=

+ HS : Ta chứng minh

DE DF=

bằng

cách chứng minh

( . . )DBF DCE g c g = 

.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý.

3

2

AD

AG

=



3

2

AD AG=

.

Kẻ

//BF d

và

//CE d

(

,F E AD

).



//BF CE

.

Xét tam giác

DBF

và

DCE

, ta có:

DB DC=

(do

D

là trung điểm của

BC

)

DBF DCE=

(2 góc SLT của

//BF CE

)

BDF CDE=

(2 góc đối đỉnh).

Suy ra:

( . . )DBF DCE g c g = 

.



DE DF=

(2 cạnh tương ứng).



2AF AE AD+=

.

Vì

//MG BF

nên theo định lí Thalès, ta

có:

AB AF

AM AG

=

.

Vì

//NG CE

nên theo định lí Thalès, ta

có:

AC AE

AN AG

=

.

Do đó:

AB AC AF AE

AM AN AG AG

+ = +

.

23

3

AD AG

AG AG

= = =

.

Vậy:

3

AB AC

AM AN

+=

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 1:

Dạng 5: Bài toán thực tế.

Bài 1:

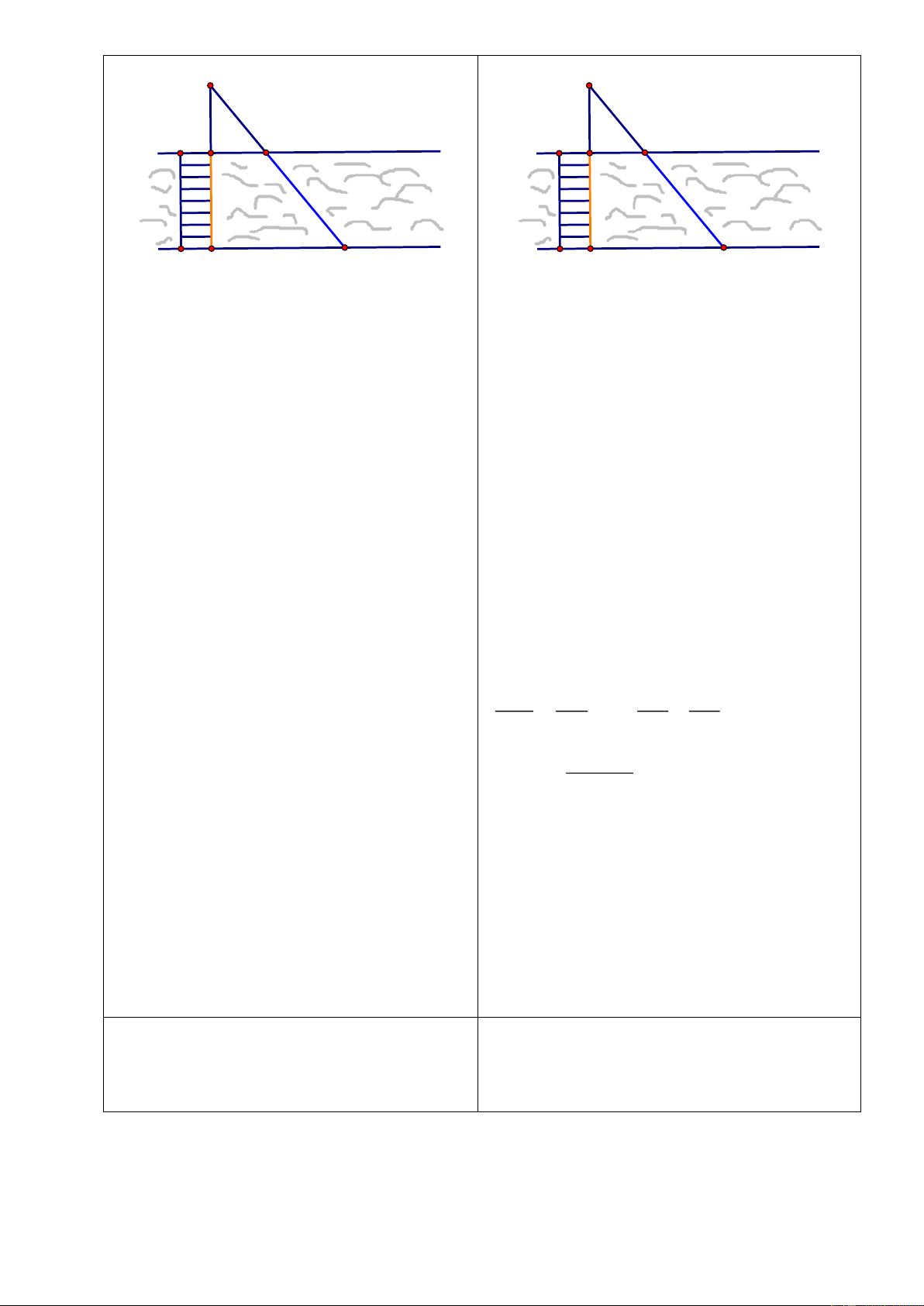
Trang 159

Cây cầu MN bắc qua một con sông có

chiều rộng

280m

. Để đo khoảng cách

giữa hai điểm

E

và

K

nằm trên hai bờ

sông, bác Toàn chọn một điểm

T

trên

đường thẳng

MN

sao cho ba điểm

T

,

E

,

K

thẳng hàng (hình vẽ). Trên mặt đất,

bác Toàn đo được

160TN m=

và

220TE m=

. Em hãy giúp bác Toàn tìm

khoảng cách giữa

E

và

K

.

- HS tìm hiểu bài 1 và vẽ hình.

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès để tìm khoảng cách

giữa

E

và

K

.

- Một học sinh lên bảng làm bài

- Học sinh đối chiếu kết quả và nhận xét

bài làm của bạn.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý.

Cây cầu MN bắc qua một con sông có

chiều rộng

280m

. Để đo khoảng cách

giữa hai điểm

E

và

K

nằm trên hai bờ

sông, bác Toàn chọn một điểm

T

trên

đường thẳng

MN

sao cho ba điểm

T

,

E

,

K

thẳng hàng (hình vẽ). Trên mặt đất,

bác Toàn đo được

160TN m=

và

220TE m=

. Em hãy giúp bác Toàn tìm

khoảng cách giữa

E

và

K

.

Giải

Xét tam giác

TMK

có

//NE MK

nên theo

định lí Thalès, ta có:

TN TE

NM EK

=

hay

160 220

280 EK

=



280.220

385

160

EK m==

Vậy: Khoảng cách giữa

E

và

K

là

385m

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 2:

Bài 2:

160

220

280

E

M

N

T

K

160

220

280

E

M

N

T

K

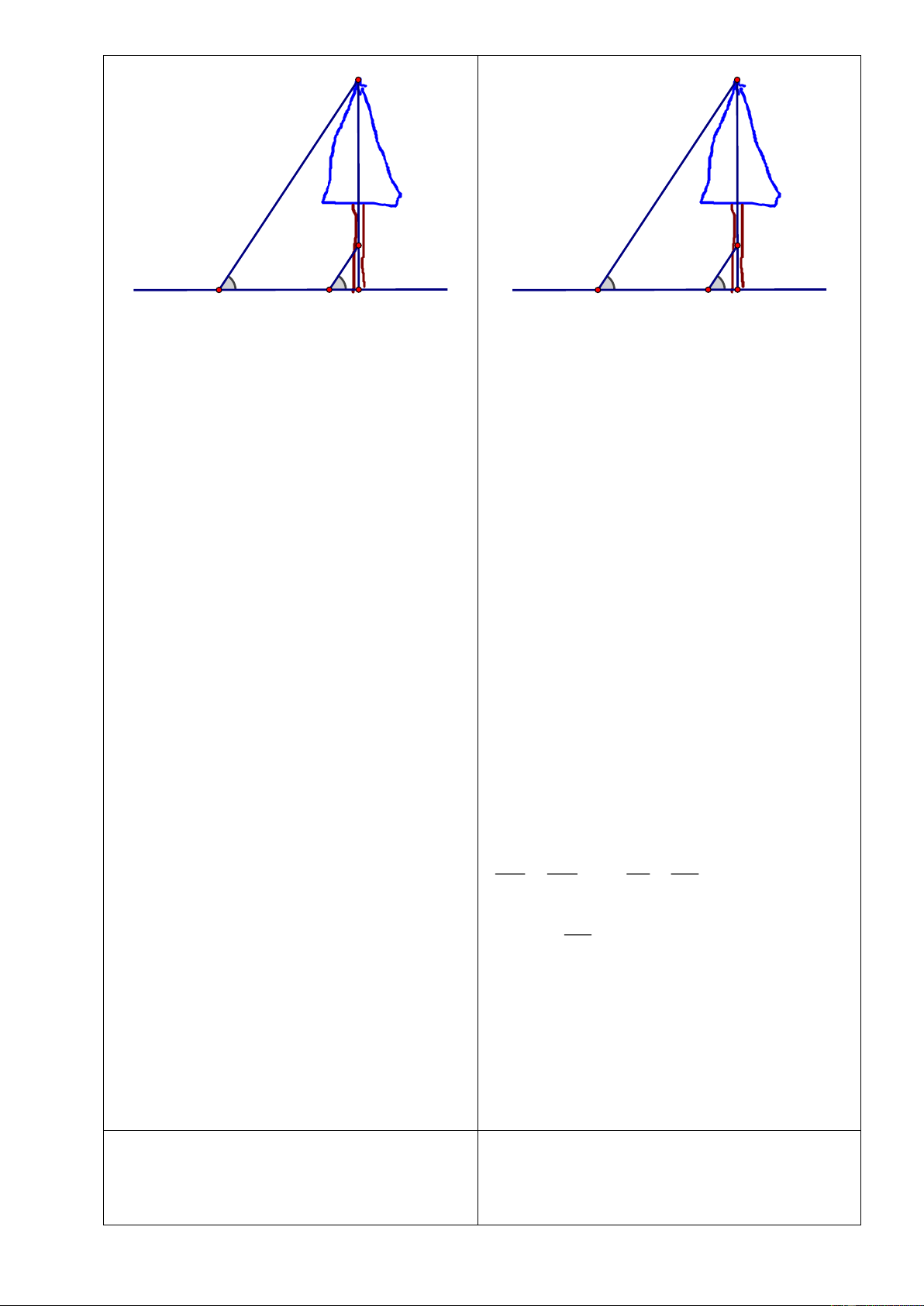
Trang 160

Để đo chiều cao

AB

của cây trong vườn,

bác Thái chọn các vị trí

C

,

D

,

E

sao

cho ba vị trí

A

,

D

,

B

thẳng hàng; ba vị

trí

C

,

E

,

B

thẳng hàng và

BCA BED=

(hình vẽ). Bác Thái đo được

2DB m=

,

1,8BE m=

,

5,2EC m=

. Em hãy giúp bác

Thái tìm ra chiều cao

AB

của cây (làm

tròn kết quả đến chữ số thập phân thứ

nhất).

- HS tìm hiểu bài 2 và vẽ hình.

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng định lí Thalès để tìm ra chiều cao

AB

của cây (làm tròn kết quả đến chữ

số thập phân thứ nhất).

- Một học sinh lên bảng làm bài

- Học sinh đối chiếu kết quả và nhận xét

bài làm của bạn.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý.

Để đo chiều cao

AB

của cây trong vườn,

bác Thái chọn các vị trí

C

,

D

,

E

sao

cho ba vị trí

A

,

D

,

B

thẳng hàng; ba vị

trí

C

,

E

,

B

thẳng hàng và

BCA BED=

(hình vẽ). Bác Thái đo được

2DB m=

,

1,8BE m=

,

5,2EC m=

. Em hãy giúp bác

Thái tìm ra chiều cao

AB

của cây (làm

tròn kết quả đến chữ số thập phân thứ

nhất).

Giải

Ta có:

1,8 5,2 7BC BE EC m= + = + =

.

Vì

BCA BED=

và 2 góc này là 2 góc đồng

vị của

DE

và

AC

nên

//DE AC

.

Xét tam giác

ABC

có

//DE AC

nên theo

định lí Thalès, ta có:

BE BD

BC AB

=

hay

1,8 2

7 AB

=



2.7

7,8

1,8

AB m=

Vậy: Chiều cao của cây xấp xỉ là

7,8m

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 1: Chứng minh rằng: Nếu

Dạng 6: Hệ quả của định lí Thalès.

Bài 1: Chứng minh rằng: Nếu một

đường thẳng cắt hai cạnh của một tam

2

5,2

1,8

E

B

A

D

C

2

5,2

1,8

E

B

A

D

C

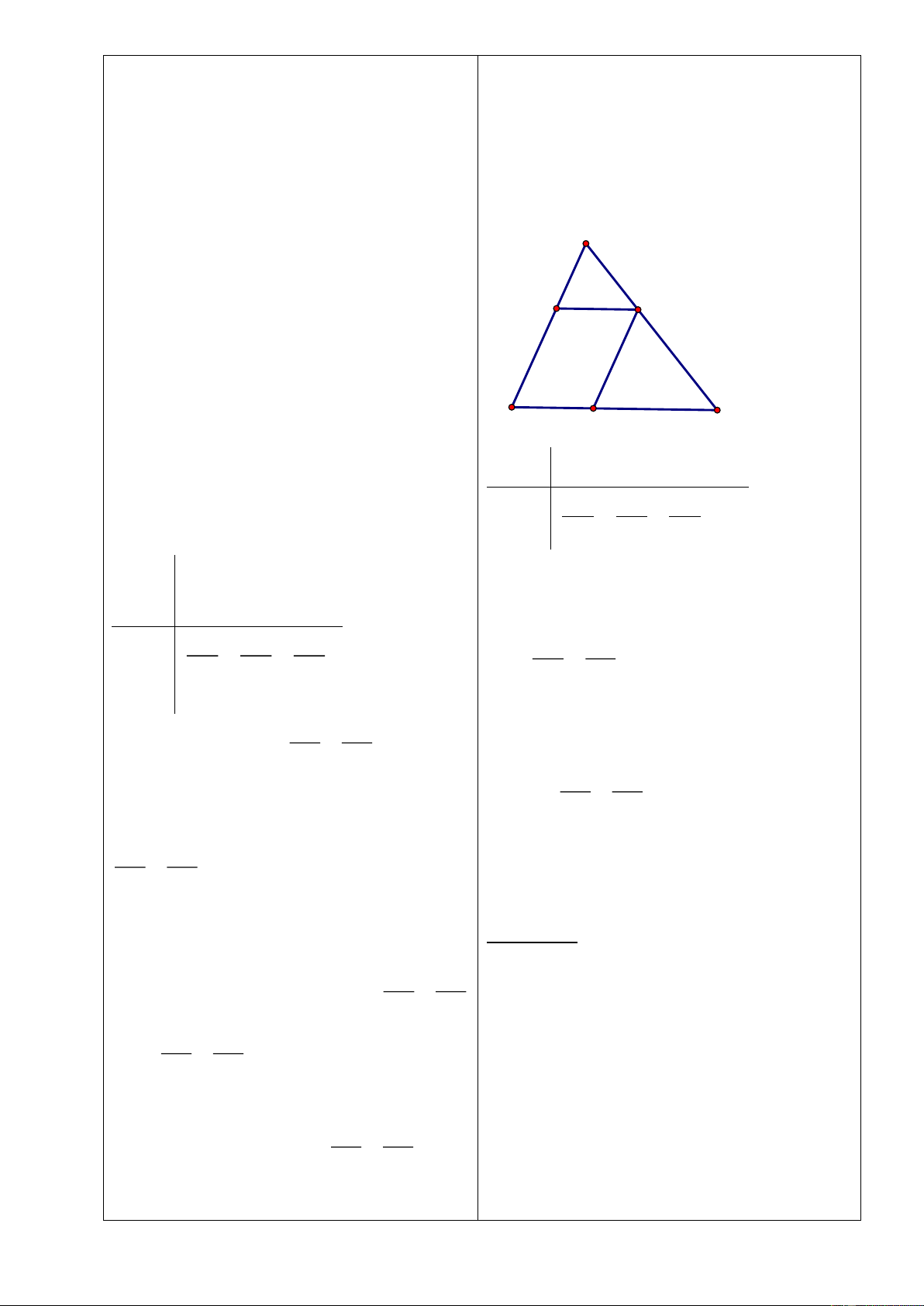
Trang 161

một đường thẳng cắt hai cạnh của một

tam giác và song song với cạnh còn lại

thì nó tạo thành một tam giác mới có ba

cạnh tương ứng tỉ lệ với ba cạnh của tam

giác đã cho (Hệ quả của định lí Thalès).

- HS tìm hiểu bài 1 và vẽ hình, ghi GT,

KL.

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS viết GT,

KL và vận dụng định lí Thalès để chứng

minh.

+ GV: Hãy viết GT, KL của bài toán.

+ HS:

GT

ABC

,

//DE BC

KL

AD AE DE

AB AC BC

==

.

+ GV: Kết quả

AD AE

AB AC

=

ta đã có

chưa?

+ HS: Theo định lí Thalès ta có ngay

AD AE

AB AC

=

.

+ GV: Tiếp theo ta cần chứng minh điều

gì?

+ HS: Ta cần chứng minh

AD DE

AB BC

=

hoặc

AE DE

AC BC

=

.

+ GV: Làm thế nào vận dụng được định

lí Thalès để chứng minh

AE DE

AC BC

=

?

+ HS: Kẻ

//EF AB

(

F BC

).

giác và song song với cạnh còn lại thì nó

tạo thành một tam giác mới có ba cạnh

tương ứng tỉ lệ với ba cạnh của tam giác

đã cho (Hệ quả của định lí Thalès).

Giải

GT

ABC

,

//DE BC

KL

AD AE DE

AB AC BC

==

.

Kẻ

//EF AB

(

F BC

).

Vì

//EF AB

nên theo định lí Thalès, ta

có:

AE BF

AC BC

=

.

Mà:

//DE BC

và

//EF AB

nên

DBFE

là

hình bình hành



DE BF=

.

Do đó:

AE DE

AC BC

=

.

Nhận xét:

1) Hệ quả của định lí Thalès:

Nếu một đường thẳng cắt hai cạnh của

một tam giác và song song với cạnh còn

lại thì nó tạo thành một tam giác mới có

ba cạnh tương ứng tỉ lệ với ba cạnh của

tam giác đã cho.

F

E

B

C

A

D

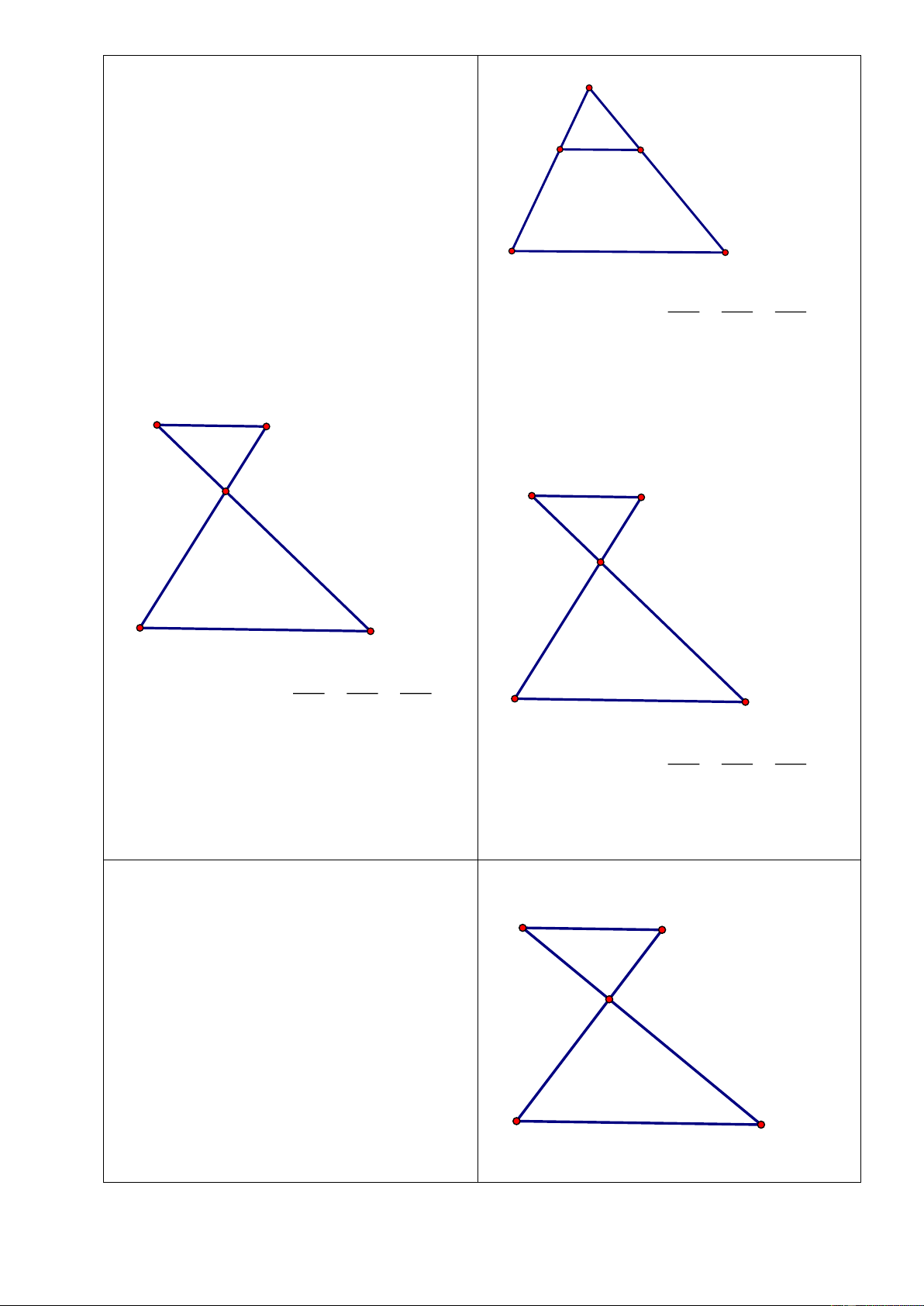
Trang 162

*Kết luận, nhận định:

- GV: Kết quả của Bài 1 được suy ra từ

định lí Thalès nên được gọi là hệ quả của

định lí Thalès. Hệ quả của định lí Thalès

thường được vận dụng để giải nhiều

dạng toán.

- Chú ý: Hệ quả trên vẫn đúng trong

trường hợp đường thẳng song song với

một cạnh của tam giác và cắt phần kéo

dài của hai cạnh còn lại.

ABC

,

//DE BC



AD AE DE

AB AC BC

==

.

ABC

,

//DE BC



AD AE DE

AB AC BC

==

.

2) Chú ý: Hệ quả trên vẫn đúng trong

trường hợp đường thẳng song song với

một cạnh của tam giác và cắt phần kéo

dài của hai cạnh còn lại.

ABC

,

//DE BC



AD AE DE

AB AC BC

==

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 2: Tìm số đo

x

trên mỗi

hình vẽ sau:

Bài 2: Tìm số đo

x

trên mỗi hình vẽ sau:

E

B

C

A

D

E

B

C

A

D

E

B

C

A

D

2

3

5

x

Hình 1. DE // BC.

E

B

C

A

D

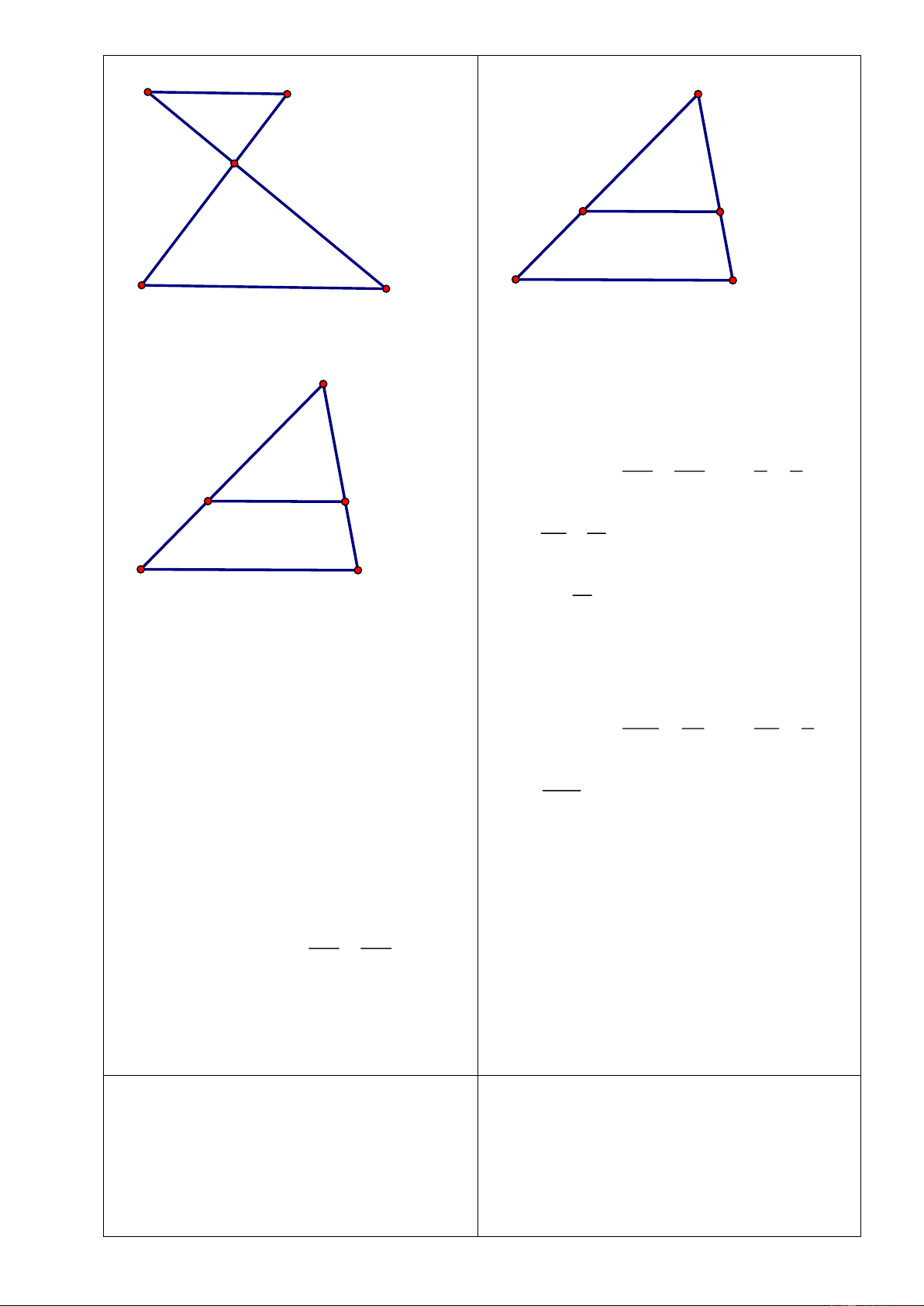
Trang 163

- HS tìm hiểu bài 2 và vẽ hình

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng Hệ quả của định lí Thalès để tìm

x

.

+ GV: Theo hệ quả của định lí Thalès,

ta có điều gì?

+ HS: Vì

//DE BC

nên theo hệ quả của

định lí Thalès, ta có:

DE AD

BC AB

=

.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý.

Giải

- Hình 1:

Vì

//DE BC

nên theo hệ quả của định lí

Thalès, ta có:

DE AD

BC AB

=

hay

2

53

x

=



2.5 10

33

x ==

.

Vậy:

10

3

x =

.

- Hình 2: Ta có:

2 1 3IJ IL LJ= + = + =

.

Vì

//LM JK

nên theo hệ quả của định lí

Thalès, ta có:

LM IL

JK IJ

=

hay

1,8 2

3x

=



1,8.3

2,7

2

x ==

.

Vậy:

2,7x =

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 3: Cho tam giác

ABC

.

Trên cạnh

AB

lấy điểm

D

sao cho

4AD cm=

và

8DB cm=

. Tính tỉ số

Bài 3: Cho tam giác

ABC

. Trên cạnh

AB

lấy điểm

D

sao cho

4AD cm=

và

8DB cm=

. Tính tỉ số khoảng cách từ các

điểm

D

và

B

đến cạnh

AC

.

2

3

5

x

Hình 1. DE // BC.

E

B

C

A

D

1,8

2

1

x

Hình 2. LM // JK.

M

J

K

I

L

1,8

2

1

x

Hình 2. LM // JK.

M

J

K

I

L

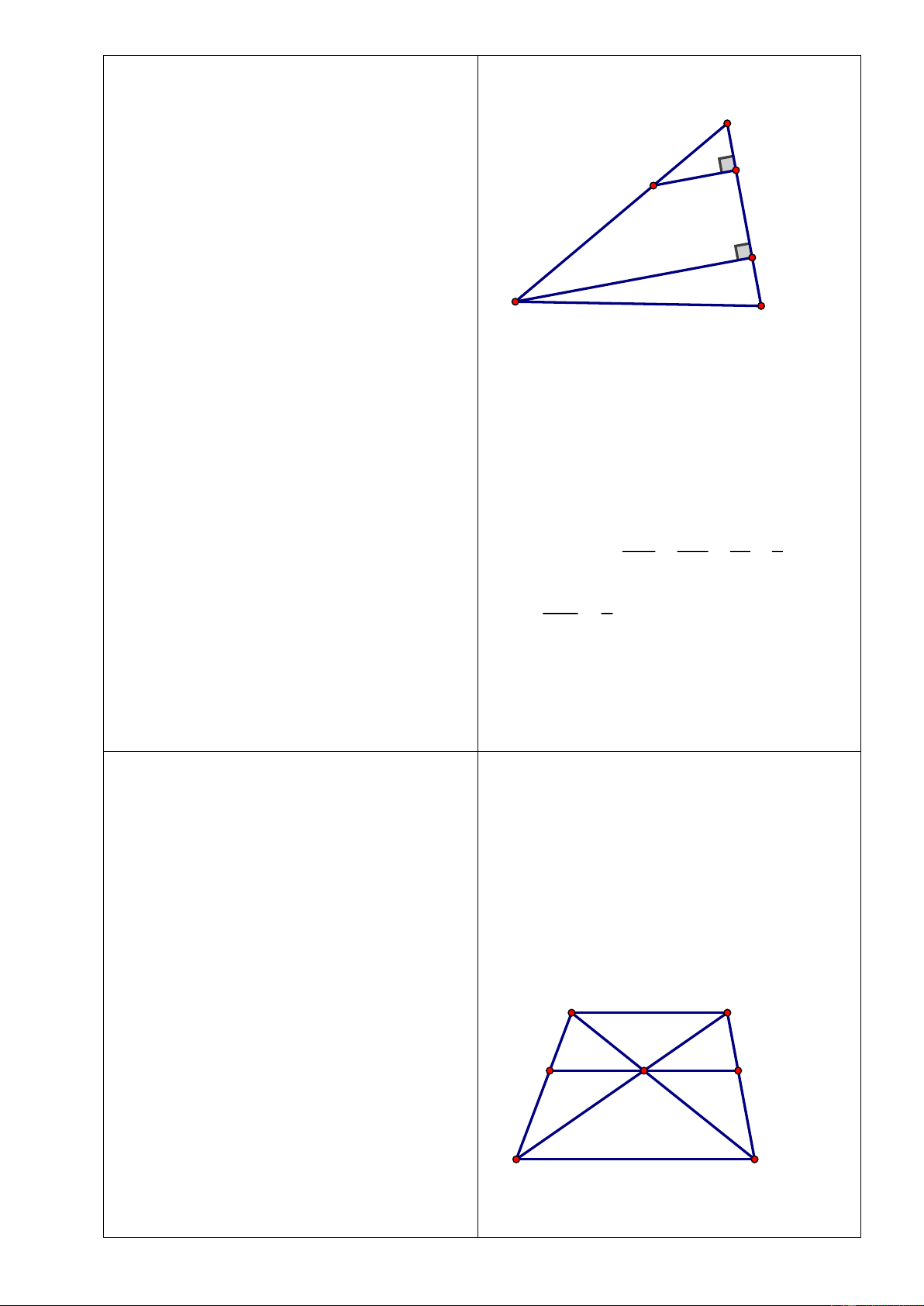
Trang 164

khoảng cách từ các điểm

D

và

B

đến

cạnh

AC

.

- HS tìm hiểu bài 3 và vẽ hình

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

dụng Hệ quả của định lí Thalès để tìm tỉ

số khoảng cách từ các điểm

D

và

B

đến

cạnh

AC

.

+ GV: Khoảng cách từ các điểm

D

và

B

đến cạnh

AC

là các độ dài nào?

+ HS: Là

DK

và

BH

.

+ GV: Vì sao

//BH DK

?

+ HS: Vì

BH AC⊥

và

DK AC⊥

.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý.

- Hai đường thẳng phân biệt cùng vuông

góc với một đường thẳng thứ ba thì

chúng song song với nhau.

Giải

Kẻ

BH AC⊥

và

DK AC⊥

(

,H K AC

).



//BH DK

.

Ta có:

AB AD DB=+

4 8 12cm= + =

.

Vì

//BH DK

nên theo hệ quả của định lí

Thalès, ta có:

41

12 3

DK AD

BH AB

= = =

.

Vậy:

1

3

DK

BH

=

.

* Giao nhiệm vụ:

- GV tổ chức hoạt động, hướng dẫn HS

tìm hiểu Bài 4:

Cho hình thang

ABCD

(

//AB CD

) có

O

là giao điểm của hai đường chéo. Một

đường thẳng qua

O

song song với hai

đáy cắt các cạnh bên

AD

và

BC

lần lượt

ở

M

và

N

. Chứng minh rằng:

OM ON=

.

- HS tìm hiểu bài 4 và vẽ hình.

*Thực hiện nhiệm vụ:

+ HS quan sát và trả lời theo yêu cầu của

GV.

+ GV: quan sát, hướng dẫn HS vận

Bài 4: Cho hình thang

ABCD

(

//AB CD

)

có

O

là giao điểm của hai đường chéo.

Một đường thẳng qua

O

song song với

hai đáy cắt các cạnh bên

AD

và

BC

lần

lượt ở

M

và

N

. Chứng minh rằng:

OM ON=

.

Giải

Vì

//MN CD

và

//AB CD

nên theo hệ

8 cm

4 cm

H

K

B

C

A

D

N

M

O

D

C

A

B

Trang 165

dụng Hệ quả của định lí Thalès để chứng

minh

OM ON=

.

+ GV: Làm thế nào để chứng minh

OM ON=

?

+ HS: Ta chứng minh

OM ON

CD CD

=

.

+ GV: Các tỉ số

;

OM ON

CD CD

lần lượt bằng

các tỉ số nào ?

+ HS: Ta có:

OM AO

CD AC

=

và

ON BO

CD BD

=

.

*Kết luận, nhận định:

GV chốt phương pháp giải của dạng toán

và một số lưu ý.

quả của định lí Thalès, ta có:

OM AO

CD AC

ON BO

CD BD

AO BO

AC BD



=



=





=







OM ON

CD CD

=



OM ON=

.

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ 13.

1. TRẮC NGHIỆM

(5 đến 10 câu)

Câu 1. Cho hình vẽ, trong đó

//DE BC

,

12AD =

,

18DB =

,

30CE =

. Độ dài

AC

bằng bao nhiêu?

A.

20AC =

B.

18

25

AC =

C.

50AC =

D.

45AC =

Câu 2. Tìm giá trị của

x

trên hình vẽ:

12

18

30

D

C

B

A

E

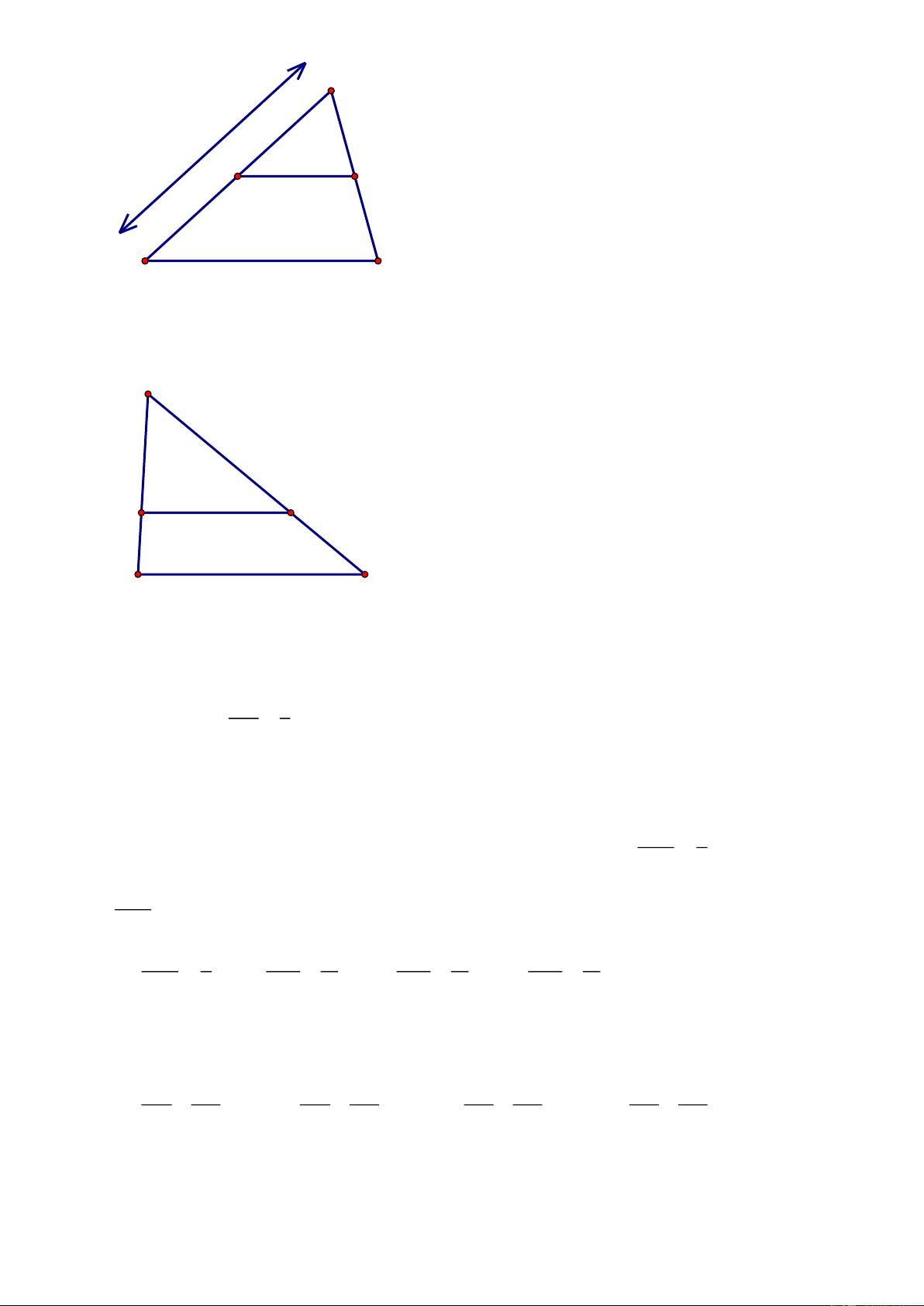
Trang 166

A.

3x =

B.

2,5x =

C.

1x =

D.

3,5x =

Câu 3. Cho hình vẽ. Hai đường thẳng nào dưới đây song song với nhau?

A.

//AD EC

B.

//DE AC

C.

//DE BC

D.

//BE AC

Câu 4. Cho hình thang

ABCD

(

//AB CD

) có

15BC cm=

. Điểm E thuộc cạnh

AD sao cho

1

3

AE

AD

=

. Qua

E

kẻ đường thẳng song song với

CD

, cắt

BC

tại

F

.

Tính độ dài

BF

.

A.

15BF cm=

B.

5BF cm=

C.

10BF cm=

D.

7BF cm=

Câu 5. Cho biết điểm

M

thuộc đoạn thẳng

AB

thỏa mãn

3

8

AM

MB

=

. Tính tỉ số

AM

AB

.

A.

5

8

AM

AB

=

B.

5

11

AM

AB

=

C.

3

11

AM

AB

=

D.

8

11

AM

AB

=

Câu 6. Cho hình thang

ABCD

(

//AB CD

). Một đường thẳng song song với

AB

cắt các cạnh bên

AD

,

BC

theo thứ tự ở

E

,

F

. Đẳng thức nào sau đây là đúng?

A.

1

ED BF

AD BC

+=

B.

1

AE BF

AD BC

+=

C.

1

AE BF

ED FC

+=

D.

1

AE FC

ED BF

+=

3,5x

4

x

6

M

K

H

S

N

10

4

2

5

E

A

C

B

D

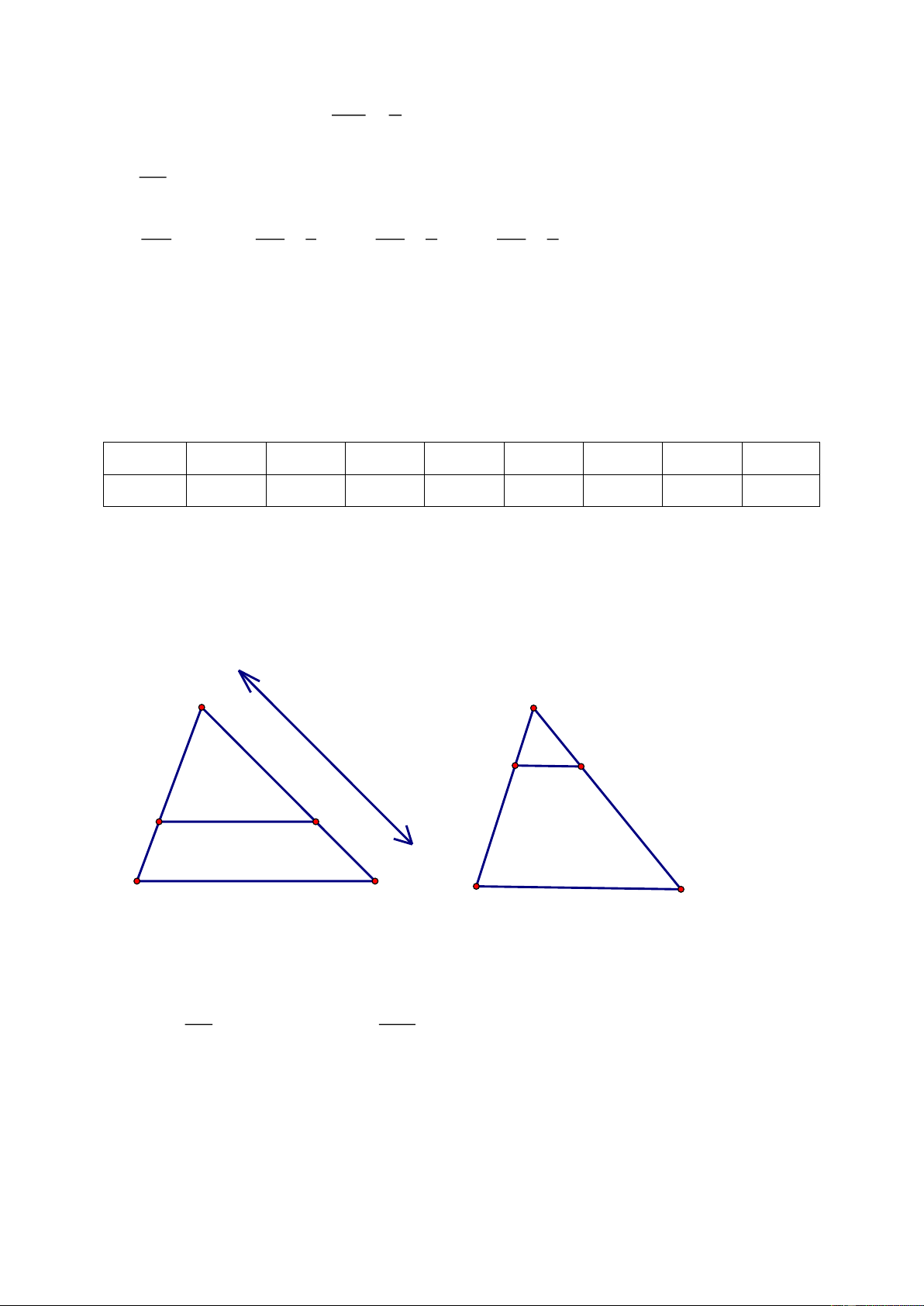
Trang 167

Câu 7. Cho tam giác

ABC

có

AD

là đường trung tuyến. Gọi

K

là điểm thuộc

đoạn thẳng

AD

sao cho

1

2

AK

KD

=

. Gọi

E

là giao điểm của

BK

và

AC

. Tính tỉ

số

AE

EC

.

A.

4

AE

EC

=

B.

1

3

AE

EC

=

C.

1

2

AE

EC

=

D.

1

4

AE

EC

=

Câu 8. Cho tam giác nhọn

ABC

có

AC AB

,

45AC cm=

, đường cao

AH

.

Đường trung trực của

BC

cắt

AC

tại

N

. Biết

15HB cm=

,

27HC cm=

. Tính

CN

.

A.

21CN cm=

B.

27CN cm=

C.

35CN cm=

D.

45CN cm=

Trả lời:

Câu

1

2

3

4

5

6

7

8

Đáp án

C

A

B

C

A

D

C

2. TỰ LUẬN

(5 bài trở lên – ko cần đáp án)

Bài 1. Tính

x

trên hình vẽ sau. Biết rằng các số ghi trên hình có cùng đơn vị đo

là

cm

.

Bài 2. Cho tam giác

ABC

, các đường trung tuyến

AM

,

BN

,

CK

cắt nhau tại

G.

a) Tính

AN

AC

. b) Tính

AG

GM

. c) Kể tên hai cặp đoạn thẳng tỉ lệ với

AG

và

GM

.

Bài 3. Cho hình thang

ABCD

(

//AB CD

). Gọi

K

,

Q

,

P

lần lượt là trung điểm

của

AD

,

AC

,

BC

. Chứng minh rằng: a)

//KQ CD

. b)

//KP CD

.

b) IJ // GH

a) DE // BC

x

9

11,5

4

5

8,5

x

4

J

E

B

C

A

G

H

F

D

I

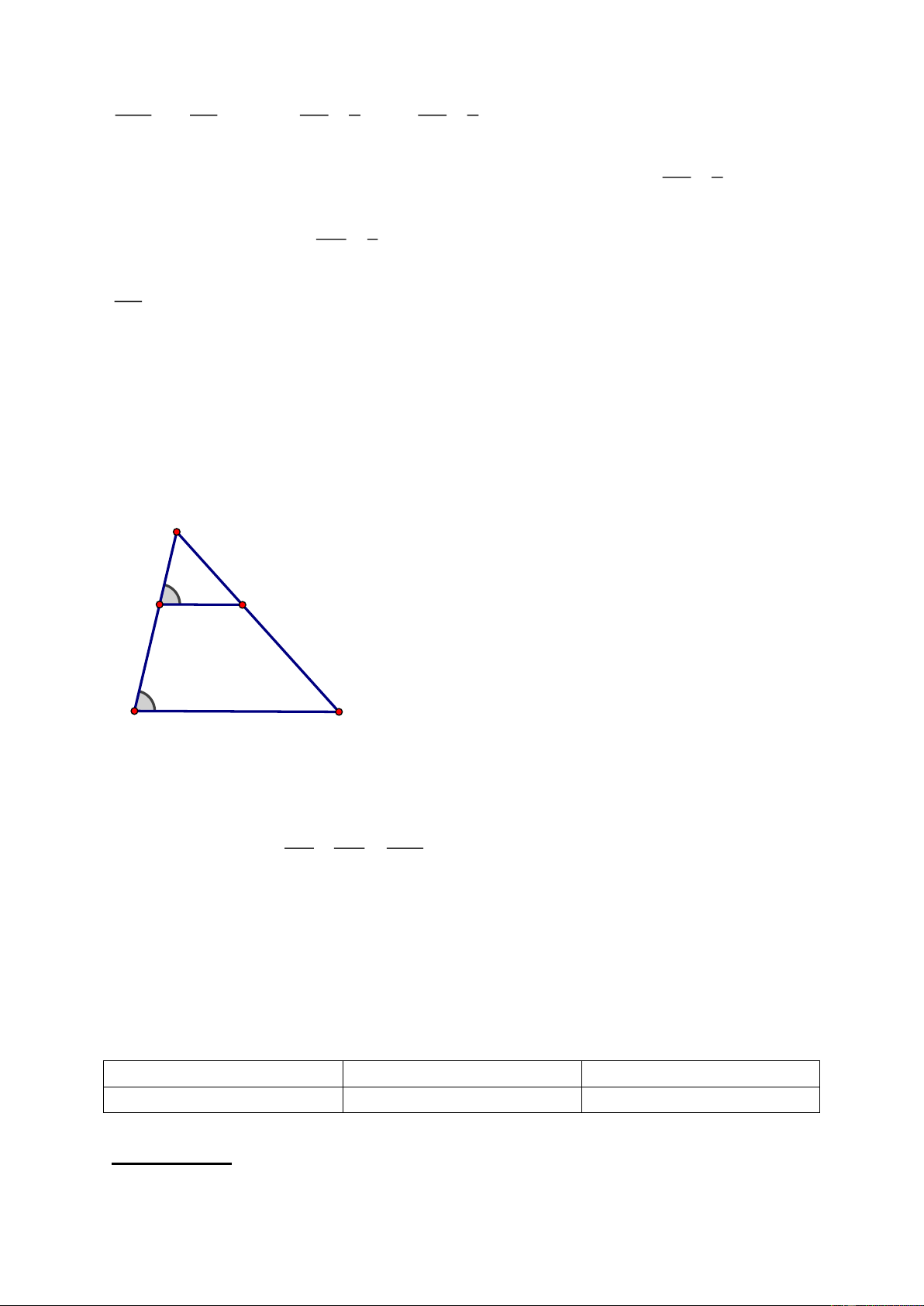
Trang 168

Bài 4. Cho đoạn thẳng

AH

,

H

là một điểm trên đoạn thẳng

AB

. Tính các tỉ số

AH

AB

và

HB

AB

nếu: a)

1

2

HA

HB

=

. b)

7

4

HA

HB

=

.

Bài 5. Cho tam giác

ABC

và điểm

D

trên cạnh

BC

sao cho

3

4

BD

BC

=

, điểm

E

trên cạnh

AD

sao cho

1

3

AE

AD

=

. Gọi

K

là giao điểm của

BE

và

AC

. Tính tỉ số

AK

KC

.

Bài 6. Cho góc nhọn

xOy

. Trên

Ox

lấy hai điểm

D

và

E

, một đường thẳng

a

qua

D

cắt

Oy

tại

F

. Đường thẳng

b

qua

E

song song với

DE

cắt

Oy

tại

G

. Đường thẳng

c

qua

G

song song với

EF

cắt

Ox

tại

H

. Chứng minh rằng:

2

.OE ODOH=

.

Bài 7. Tính

x

trên hình vẽ sau.

Bài 8. Cho hình thang

ABCD

(

//AB CD

) có

O

là giao điểm của hai đường chéo.

Một đường thẳng qua

O

song song với hai đáy cắt

BC

tại

M

.

Chứng minh rằng:

1 1 1

AB CD OM

+=

.

Tuần 14

Tiết 37; 38; 39

Ngày soạn 01/11/2023

Lớp

8A

8B

Ngày dạy:

ÔN TẬP PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ

I. MỤC TIÊU

1. Về kiến thức:

3,3

8,8

x

3

L

I

J

H

K

Trang 169

- Nhận biết phân tích đa thức thành nhân tử và ba phương pháp phân tích đa thức

thành nhân tử: đặt nhân tử chung, sử dụng hằng đẳng thức, nhóm các hạng tử.

2. Về năng lực:

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu được các các phân tích đa thức thành

nhân tử. Sử dụng ngôn từ toán học hợp lí.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng

hợp, khái quát hóa dựa trên các bài toán phân tích đa thức thành nhân tử và các yếu tố

liên quan.

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm, ôn tập 7 hẳng đẳng thức đáng nhớ, phép

tính đa thức nhiều biến

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

Phương pháp đặt nhân tử chung:

Bước 1: Chỉ ra nhân tử chung của các hạng tử trong đa thức.

VD: Đa thức:

2

24xx−

Nhận xét: các hạng tử có nhân tử chung là

2x

Bước 2: Đặt Nhân tử chung ra ngoài ngoặc khi đó trong ngoặc là tổng các các nhân

tử còn lại của các hạng tử.

( )

2

2 4 2 . 2 .2 2 2x x x x x x x− = − = −

Chú ý:

+ Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử.

+ Tính chất đổi dấu hạng tử:

( )

AA= − −

;

( )

2

AA=−

Phương pháp dùng hằng đẳng thức

Trang 170

Nếu đa thức là một vế của hằng đẳng thức đáng nhớ nào đó thì có thể dùng hằng đẳng

thức đó để biểu diễn đa thức này thành tích các đa thức.

Cho A và B là các biểu thức. Ta có một số hằng đẳng thức đáng nhớ sau:

HẰNG ĐẲNG THỨC VIẾT DẠNG

TỔNG

HẰNG ĐẲNG THỨC VIẾT DẠNG

TÍCH

* Bình phương của tổng

( )

2

22

2A B A AB B+ = + +

* Bình phương của hiệu

( )

2

22

2A B A AB B− = − +

* Lập phương của tổng

( )

3

3 2 2 3

33A B A A B AB B+ = + + +

* Lập phương của hiệu

( )

3

3 2 2 3

33A B A A B AB B− = − + −

* Hiệu hai bình phương

( )( )

22

A B A B A B− = − +

* Tổng hai lập phương

( )

3 3 2 2

A B A B A AB B+ = + − +

* Hiệu hai lập phương

( )

3 3 2 2

A B A B A AB B− = − + +

Phương pháp nhóm các hạng tử

Bước 1: Chọn và nhóm 2 hoặc 3, … hạng tử thành một nhóm sao cho mỗi nhóm sau

khi phân tích thành nhân tử thì các nhóm này có thừa số chung, hoặc liên hệ các nhóm

là hằng đẳng thức.

Bước 2:

+ Nếu các nhóm có thừa số chung: Đặt thừa số chung của các nhóm làm Nhân tử

chung ra ngoài ngoặc khi đó trong ngoặc là tổng các các thừa số còn lại của các

nhóm.

+ Nếu liên hệ các nhóm tạo thành hằng đẳng thức thì vận dụng hằng đẳng thức.

2. BÀI TẬP

Hoạt động của giáo viên và học

sinh

Nội dung

* Giao nhiệm vụ

- GV trình chiếu từng câu trắc

nghiệm lên máy chiếu, HS có 60s

vừa đọc vừa đưa ra câu trả lời cho

1 câu hỏi

HS tìm hiểu bài tập trắc nghiệm

HS áp dụng kiến thức cần nhớ về

3 phương pháp phân tích đa thức

Dạng 1. Phân tích đa thức thành nhân tử

Trắc nghiệm

Câu 1. B.

Đặt thừa số chung

Câu 2. B.

Dùng hằng đẳng thức

Câu 3. D.

Trang 171

thành nhân tử để linh hoạt khi làm

bài.

Nhóm các hạng tử

Bài 1: Trắc nghiệm

Câu 1. Phân tích đa thức

42

6aa−

thành nhân tử ta được

A.

( )

2

6aa+

. B.

( )

22

6aa−

.

C.

( )

2

6aa−

. D.

( )

2

3a −

.

Câu 2. Phân tích đa thức

( )

2

22

9 36aa+−

thành nhân tử ta được

A.

( )

4

3a +

. B.

( ) ( )

22

33aa−+

.

C.

( )( )

22

36 9 36 9a a a a+ + − +

. D.

( )

2

9a +

.

Câu 3. Phân tích đa thức

32

2 2 5 5x x x− − +

thành nhân tử ta được

A.

( )( )

2 5 1xx−−

. B.

( )

2

2 5 1xx+−

.

C.

( )( )

2 5 1xx+−

. D.

( )

2

2 5 1xx−−

.

GV đặt câu hỏi về sựa lựa chọn

các cách phân tích tùy theo từng

câu

Câu 1: Có thừa số chung giống

nhau

Câu 2 có dạng hằng đẳng thức

22

AB−

Câu 3: 4 hạng tử, có các hệ số

giống nhau. Ta nhóm

*Kết luận, nhận định:

GV chốt đáp án từng câu.

Chú ý phân tích triệt để.

Câu 1.

( )

4 2 2 2

66a a a a− = −

Câu 2.

( )

2

22

9 36aa+−

=

( ) ( )

22

33aa−+

Câu 3.

32

2 2 5 5x x x− − +

( ) ( )

2

2 1 5 1x x x= − − −

( )

2

2 5 1xx= − −

* Giao nhiệm vụ

Bài 2: Phân tích các đa thức

sau thành nhân tử

a)

( ) ( )

2

2x x 3 x x 3− − −

b)

( ) ( )

3 6 2x y x y y x− − −

Gợi ý: Phương pháp đặt nhân tử

chung

c) 8x

6

+ 12x

4

y + 6x

2

y

2

+ y

3

d)

33

125xy−

Gợi ý: Phương pháp dùng hằng

đẳng thức

BÀI TẬP TỰ LUẬN

Bài 2:

a)

( ) ( )

2

2x x 3 x x 3− − −

( )( )

x x 3 2x 1= − −

b)

( ) ( )

3 6 2x y x y y x− − −

( ) ( )

3 2 2x y x y x y= − + −

( )( )

32x y x y= + −

c) 8x

6

+ 12x

4

y + 6x

2

y

2

+ y

3

=

( )

3

2

2xy+

d)

33

125xy−

Trang 172

e)

43

1x x x+ + +

f)

( )

22

6 3 6 9x x x− + − −

Gợi ý: Phương pháp nhóm các

hạng tử

Bài 3: Phân tích các đa thức

sau thành nhân tử

a)

2 3 2

3 6 9x y x y xy−+

b)

( ) ( )

5 3 15 3x y x x y+ − +

c)

( ) ( )

35x y x y x− − −

d)

( ) ( ) ( )

32

2 1 2 1 1x x x− − − − −

Bài 4: Phân tích các đa thức

sau thành nhân tử

a)

22

4 4 9x xy y+ + −

b)

66

xy+

*Thực hiện nhiệm vụ

HS thực hiện theo gợi ý đề bài.

* Kết luận, nhận định:

GV chốt đáp án.

( )

22

5 5 25x y x xy y= − + +

e)

43

1x x x+ + +

( ) ( )

3

11x x x= + + +

( )

3

11xx= + +

( )

2

11x x x= + − +

f)

( )

22

6 6 9 6 9x x x− + − −

( )

22

9 6 6 6 9x x x



= − − + +



( )( ) ( )

2

3 3 6 3x x x= − + − +

( )( )

3 5 21xx= + − −

Bài 3:

a)

2 3 2

3 6 9x y x y xy−+

( )

2

3 2 3xy x x y= − +

b)

( ) ( )

5 3 15 3x y x x y+ − +

( )( )

5 3 1 3x y x= + −

c)

( ) ( )

35x y x y x− − −

( ) ( )

35x y x x y= − + −

( )( )

35x y x= − +

d)

( ) ( ) ( )

32

2 1 2 1 1x x x− − − − −

( ) ( ) ( )

32

2 1 2 1 1x x x= − + − − −

( )

2

1 2 3 5x x x= − − +

Bài 4:

a)

22

4 4 9x xy y+ + −

( )

2

23xy= + −

( )( )

2 3 2 3x y x y= + − + +

b)

66

xy+

( ) ( )

33

22

xy=+

Trang 173

( )( )

2 2 4 2 2 4

x y x x y y= + − +

* Giao nhiệm vụ

Thực hiện 3 câu trắc nghiệm.

Bài 2: Tìm

x

, biết:

a)

( ) ( )

22

2 1 3 0xx− − + =

b)

3

1

0

4

xx−=

c)

32

3 3 9 0x x x+ + + =

d)

32

9 9 4 4 0x x x+ − − =

Bài 3: Tìm

x

, biết:

a)

( )

22

6 3 6 9 0x x x− + − − =

b)

( ) ( )

2

2x x 3 x x 3 0− − − =

*Thực hiện nhiệm vụ

- Thực hiện phân tích vế trái

thành nhân tử.

- Chia thành các Trường hợp nhỏ

để tìm x

*Kết luận, nhận định:

Chốt đáp án và phương pháp làm

Phương pháp

( ) ( ) ( )

( )

0

. . ... 0

0

...

Ax

Bx

A x B x C x

Cx

=





=



=



=





Dạng 2: Toán Tìm x

Bài 1: Trắc nghiệm

Câu 1. Tổng các nghiệm của đa thức

42

6aa−

bằng:

A. 6.

B. 0.

C. 36.

D. 3.

Câu 2. Đa thức

( )

2

22

9 36aa+−

có nghiệm thỏa mãn

A.

4a −

.

B.

4a −

.

C.

3a 

.

D.

0a =

.

Câu 3. Tìm

x

nguyên biết.

32

2 2 5 5 0x x x− − + =

A. 2.

B. 5.

C. 0.

D. 1.

Đáp án:

Câu 1. B.

Câu 2. B.

Câu 3. D.

Bài 2:

a)

( ) ( )

22

2 1 3 0xx− − + =

( )( )

2 1 3 2 1 3 0x x x x − − − − + + =

( )( )

4 3 2 0xx − + =

4

2

3

x

=









=



Vậy

2

4;

3

x









b)

3

1

0

4

xx−=

2

1

0

4

xx



 − =





Trang 174

2

0

1

4

x

=









=



0

1

2

1

2

x





=



=



−



=



Vậy

11

0; ;

22

x

−









c)

32

3 3 9 0x x x+ + + =

( )

3

18x + = −

12x + = −

3x = −

Vậy

3x =−

d)

32

9 9 4 0xx+ − =

( ) ( )

2

9 1 4 1 0x x x + − + =

( )

2

9 4 1 0xx − + =

2

3

2

3

1

x



=



−



=



=−





Vậy

22

; ; 1

33

x

−



−





Bài 3:

a)

( )

22

6 3 6 9 0x x x− + − − =

( )

22

9 6 6 6 9 0x x x



= − − + + =



( )( ) ( )

2

3 3 6 3 0x x x − + − + =

( )( )

3 5 21 0xx + − − =

3

21

5

x

=−







−



=



Trang 175

Vậy

21

3;

5

x

−



−





b)

( ) ( )

2

2x x 3 x x 3 0− − − =

( )( )

3 2 1 0x x x − − =

1

0;3;

2

x









Vậy

1

0; ; 3

2

x



−





* Giao nhiệm vụ

Bài 1: Chứng minh: 2

9

- 1 chia

hết cho 73

Bài 2: Chứng minh: (n + 3)

2

– (n

– 1)

2

chia hết cho 8 với mọi số

nguyên n.

Bài 3: Với

n

là số lẻ, chứng

minh

32

33n n n+ − −

chia hết cho

48

*Thực hiện nhiệm vụ

Học sinh phân tích biểu thức

thành nhân tử để xuất hiện thừa số

chia hết hoặc là ước của số đề bài

yêu cầu chứng minh.

* Kết luận:

Phương pháp: Dùng phép toán

lũy thừa (đã học Lớp 6) và

phương pháp Đặt Nhân Tử Chung

để phân tích biểu thức lũy thừa

thành nhân tử trong đó có một

nhân tử là số a, suy ra Biểu thức

đã cho chia hết cho số a

DẠNG 3: Chứng minh một biểu thức lũy thừa chia

hết cho số a

Bài 1:

Tacó

( )( )

9 3 6 3

2 1 2 1 2 2 1− = − + +

( )

3

2 1 .73 73=−

Bài 2:

Tacó

( ) ( ) ( )

22

3 1 4. 2 2n n n+ − − = +

( )

4.2. 2 8n=+

Bài 3:

32

33n n n+ − −

32

3 3 1 4 4n n n n= + + + − −

( ) ( )

( )( )( )

3

1 1 4

1 3 1

nn

n n n

= + − +

= + + −

Với n là số lẻ thì

1; 1; 3n n n− + +

là ba số chẵn liên tiếp.

Ta đặt

12

1 2 2

3 2 4;

nk

n k k N

−=

+ = +

+ = + 

Do vậy

( )( )( )

( )( )

1 1 3

8 1 2

n n n

k k k

− + +

= + +

Tính ba số tự nhiên liên tiếp luôn chia hết cho 6, do vậy

Trang 176

tích trên chia hết cho 48.

* Giao nhiệm vụ

Bài 1: Tìm các cặp số nguyên (x,

y) thoả mãn một trong các đẳng

thức sau: x

2

– y

2

= 21

Bài 2: Tìm các cặp số nguyên (x,

y) thoả mãn một trong các đẳng

thức sau:

7

2x

y

−=

Bài 3: Tìm các cặp số nguyên (x,

y) thoả mãn một trong các đẳng

thức sau:

32x xy y− + =

*Thực hiện nhiệm vụ

HS phân tích vế trái thành nhân

tử, sau đó sử dụng kiến thức ước

và bội để chia trường hợp.

* Kết luận:

Phương pháp:

* Phân tích một vế của đẳng thức

thành tích của hai thừa số, vế còn

lại là một số nguyên n.

* Phân tích số nguyên n thành

tích hai thừa số bằng tất cả các

cách, từ đó tìm ra số nguyên x, y.

DẠNG 4: Tìm cặp số nguyên (x, y) thỏa mãn đẳng

thức.

Bài 1: Tìm các cặp số nguyên (x, y) thoả mãn một trong

các đẳng thức sau: x

2

– y

2

= 21

Lời giải

Ta có

( )( )

21x y x y− + =

Do

,xy

là số nguyên, nên

;x y x y−+

là ước của của 21. Do vậy ta có bảng

x-y

1

21

-1

-21

3

7

-3

-7

x+y

21

1

-21

-1

7

3

-7

-3

x

11

-11

5

-5

y

10

-10

10

2

-2

2

Đối

chiếu

TM

KL

Bài 2: Tìm các cặp số nguyên (x, y) thoả mãn một trong

các đẳng thức sau:

7

2x

y

−=

Lời giải

Ta có

( )

7

2 7 2 2 7x xy y y x

y

− =  − =  − =

Với

*

y

,

x

ta có các trường hợp sau

y

1

7

-1

-7

2x −

7

1

-7

-1

x

9

3

-5

1

Đối chiếu

TM

Bài 3: Tìm các cặp số nguyên (x, y) thoả mãn một trong

các đẳng thức sau:

32x xy y− + =

Lời giải

Ta có

( ) ( ) ( )( )

3 2 3 3 1 3 1 1x xy y x y y y x− + =  − − − = −  − − = −

Ta có bảng

Trang 177

3 y−

1

-1

1x −

-1

1

y

2

4

x

0

2

Đối chiếu

TM

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ ….

1. TRẮC NGHIỆM

Câu 1. Kết quả phân tích đa thức

2

5 4 5 4x x xy y− + −

thành nhân tử là

A.

( )( )

54x x y−−

. B.

( )( )

54x x y+−

. C.

( )( )

54x x y++

. D.

( )( )

54x x y−+

.

Câu 2. Đa thức

22

21x x y− + −

được phân tích thành nhân tử là

A.

( )( )

11x y x y− − − +

. B.

( )( )

11x y x y+ + − −

.

C.

( )( )

11x y x y− + + −

. D.

( )( )

11x y x y− − + −

.

Câu 3. Phân tích đa thức

22

49 6 9y x x− + −

ta được

A.

( )( )

7 3 7 3y x y x− + + −

. B.

( )( )

7 3 7 3y x y x− − + −

.

C.

( )( )

7 3 7 3y x y x− + + +

. D.

( )( )

7 3 7 3y x y x− − − +

.

Câu 4. Giá trị của biểu thức

22

3 3 2x y x y xy+ − − +

khi x và y là hai số đối nhau là

A. 0. B. 1. C. 2. D. 3.

Câu 5. Các giá trị của

x

thỏa mãn phương trình

32

2 4 2 4 0x x x− − + =

là

A.

 

1;1; 2x − −

. B.

 

1;2x−

. C.

 

1;1x−

. D.

 

1;1;2x−

.

Câu 6. Giá trị của biểu thức

2 2 2

40 25 35 80.25+ − +

là

A.

1000

. B.

2000

. C.

3000

. D.

4000

.

2. TỰ LUẬN

Bài 1. Phân tích đa thức thành nhân tử:

a)

77xy+

b)

22

26x y xy−

c)

( ) ( )

2

3 1 7 1x x x x− + −

d)

( ) ( )

35x x a a a x− + −

Bài 2. Phân tích đa thức thành nhân tử:

a)

43

69xx−

b)

10 6

5 15yy+

c)

2 2 2 2

9 15 21x y x y xy+−

d)

2 2 2 2 2 2

x y z xy z x yz++

Bài 3. Phân tích đa thức thành nhân tử:

a)

22

69x xy y−+

b)

3 2 2 3

6 12 8x x y xy y+ + +

c)

3

64x −

d)

36

125xy+

e)

( )

3

0,125 1 1.a +−

Bài 4. Phân tích đa thức thành nhân tử:

a)

( ) ( )

2 1 2 1x x x+ + +

b)

( )

2 2 2

y x y zx zy+ − −

c)

( ) ( )

4 2 8 2x x y y y x− + −

d)

( ) ( ) ( )

2

3 1 5 1 7 1x x x x x+ − + + +

Trang 178

Bài 5. Phân tích đa thức thành nhân tử:

a)

( ) ( )

22

2 1 1xx+ − −

b)

( ) ( )

22

9 5 7xx+ − −

c)

( ) ( )

22

25 16x y x y− − +

d)

( ) ( )

22

49 4 9 2yy− − +

Bài 6. Phân tích đa thức thành nhân tử:

a)

43

1x x x+ + +

b)

43

1x x x− − +

c)

22

x y xy x y+ − −

d)

22

77ax a y x y+ − −

e)

22

ax ay bx by+ − −

f)

( ) ( ) ( )

22

1 5 5 1x x x x x+ + − − +

Bài 7. Phân tích đa thức thành nhân tử:

a)

22

3 12xy−

b)

22

5 10 5xy xyz xz−+

c)

3 2 3

3 3 1 27 .x x x z+ + + −

Bài 9. Phân tích đa thức thành nhân tử:

a)

2

6xx−−

b)

2

45xx+−

c)

3

19 30xx−−

d)

42

1xx++

Bài 10. Tính giá trị biểu thức

a)

( ) ( )

22

43 11

36.5 27.5

−

b)

33

97 83

97.83

180

+

−

c)

( ) ( )

22A x x y z y x= − − −

với

1,2; 1,4;z 1,8.xy= = =

d)

( ) ( ) ( )

2

1 4 1 4 1B x x x x x= − − − + −

với

3.x =

Bài 11. Tìm x biết:

a)

( )

2

2 1 25 0x − − =

b)

3

8 50 0xx−=

c)

( )

( ) ( )

( )

22

2 2 7 2 4 5 2 0x x x x x− + + + − − − =

Bài 12. Tìm x biết:

a)

( )

3 1 1 0x x x− + − =

b)

( )

2

2 3 3 0x x x+ − − =

c)

( )( )

2

4 25 2 5 2 7 0x x x− − − + =

d)

( )( )

3

27 3 9 0x x x+ + + − =

Bài 13. Chứng minh rằng với n lẻ thì:

a)

2

43nn++

chia hết cho 8.

b)

32

33n n n+ − −

chia hết cho 48.

Bài 14. Tìm các cặp số nguyên

( )

,xy

thoả mãn một trong các đẳng thức sau:

a)

( )

2 3 6 1y x x− + − =

b)

3 2 7 0xy x y+ − − =

c)

5 7 0xy x y− + − =

Bài 15. Cho

0,abc+ + =

Chứng minh các đẳng thức sau:

a)

3 3 3

3a b c abc+ + =

b)

( ) ( )

5 5 5 2 2 2

25a b c abc a b c+ + = + +

c)

( ) ( )

2

2 2 2 4 4 4

2.a b c a b c+ + = + +

Bìa 16. Cho 3 số

,,abc

thoả mãn

1abc+ + =

và

3 3 3

1abc+ + =

. Chứng minh

2005 2005 2005

1.abc+ + =

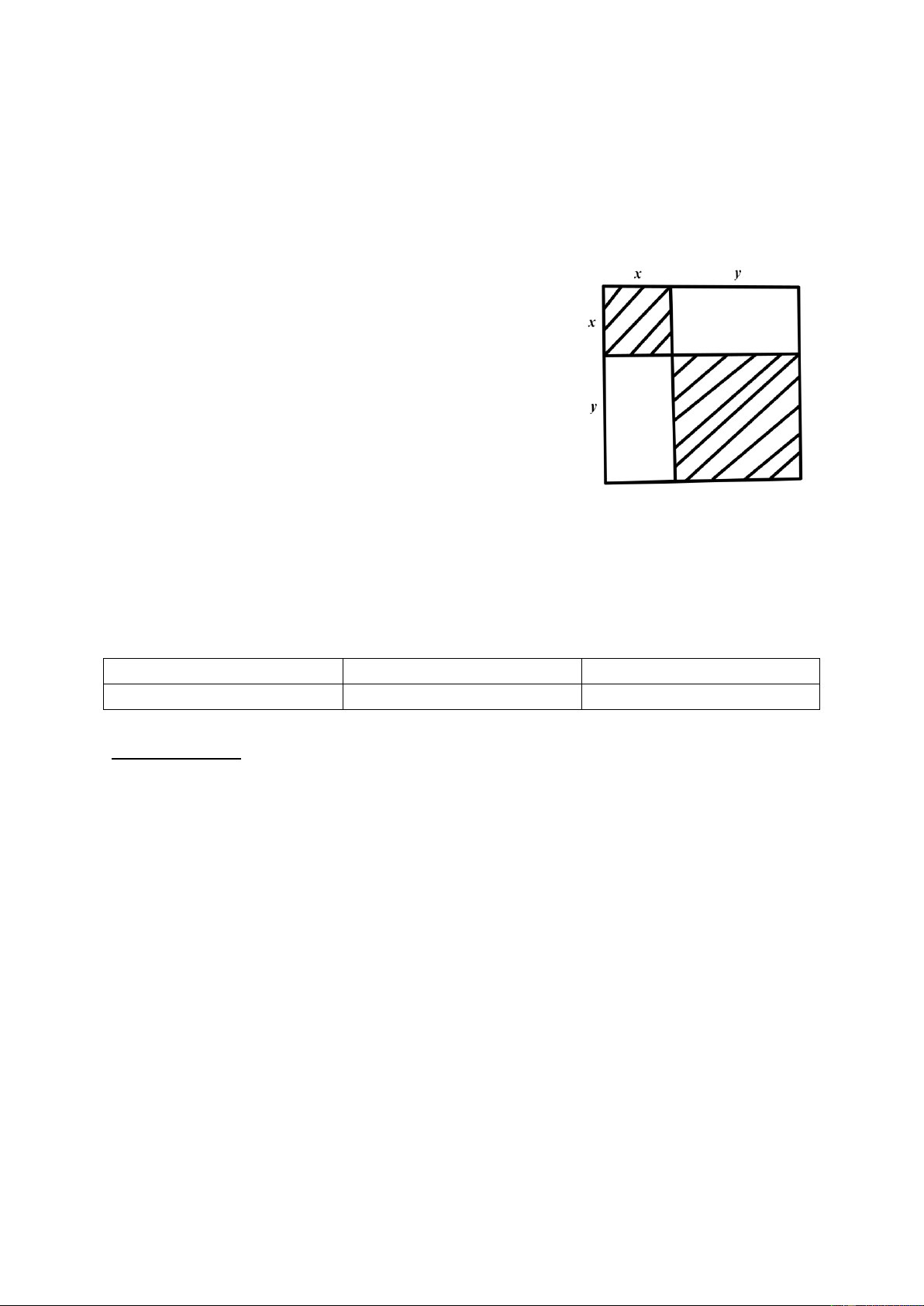
Trang 179

Bài 17. Cho

,,abc

là 3 cạnh tam giác. Chứng minh rằng:

a)

( ) ( ) ( )

3 3 3 2 2 2

2a b c abc a b c b c a c a b+ + +  + + + + +

b)

( )

2

9a b c bc+ + 

c)

2 2 2 2 2 2 4 4 4

2 2 2 0a b b c c a a b c+ + − − − 

d)

( )

2

2 2 2 2 2

4a b a b c + −

Bài 18. Tìm

n Î ¥

để biểu thức

2 2 2

( 10) 36A n n= + -

có giá trị là một số nguyên tố.

Bài 19. Chia một hình vuông thành các hình vuông và

hình chữ nhật (hình vẽ). Tính diện tích mỗi hình

vuông và mỗi hình chữ nhật được chia theo x và y rồi

tính tổng của chúng và phân tích kết quả vừa tìm được

thành nhân tử.

Tuần 15

Tiết 40; 41; 42

Ngày soạn 01/11/2023

Lớp

8A

8B

Ngày dạy:

ÔN TẬP ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC

I. MỤC TIÊU

1. Về kiến thức:

- Học sinh ghi nhớ được định nghĩa, định lí về đường trung bình của tam giác và

hình thang, cách vẽ đường trung bình.

- Sử dụng định nghĩa, định lí đường trung bình của tam giác và hình thang có

tìm độ dài các đoạn thẳng.

- Vận dụng định lí đường trung bình của tam giác, của hình thang làm số bài tập

chứng hai đoạn thẳng song song và chứng minh tỉ số bằng nhau, giải quyết một

số bài toán thực tế.

2. Về năng lực:

* Năng lực chung:

- Năng lực tự chủ và tự học: Học sinh đọc tài liệu, tự chiếm lĩnh kiến thức, tự

hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết

hỗ trợ nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn

thành nhiệm vụ.

- Năng lực giải quyết vấn đề và sáng tạo: Giải quyết các câu hỏi, bài tập.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được định nghĩa, định lí

đường trung bình tam giác và hình thang thông qua các bài tập.

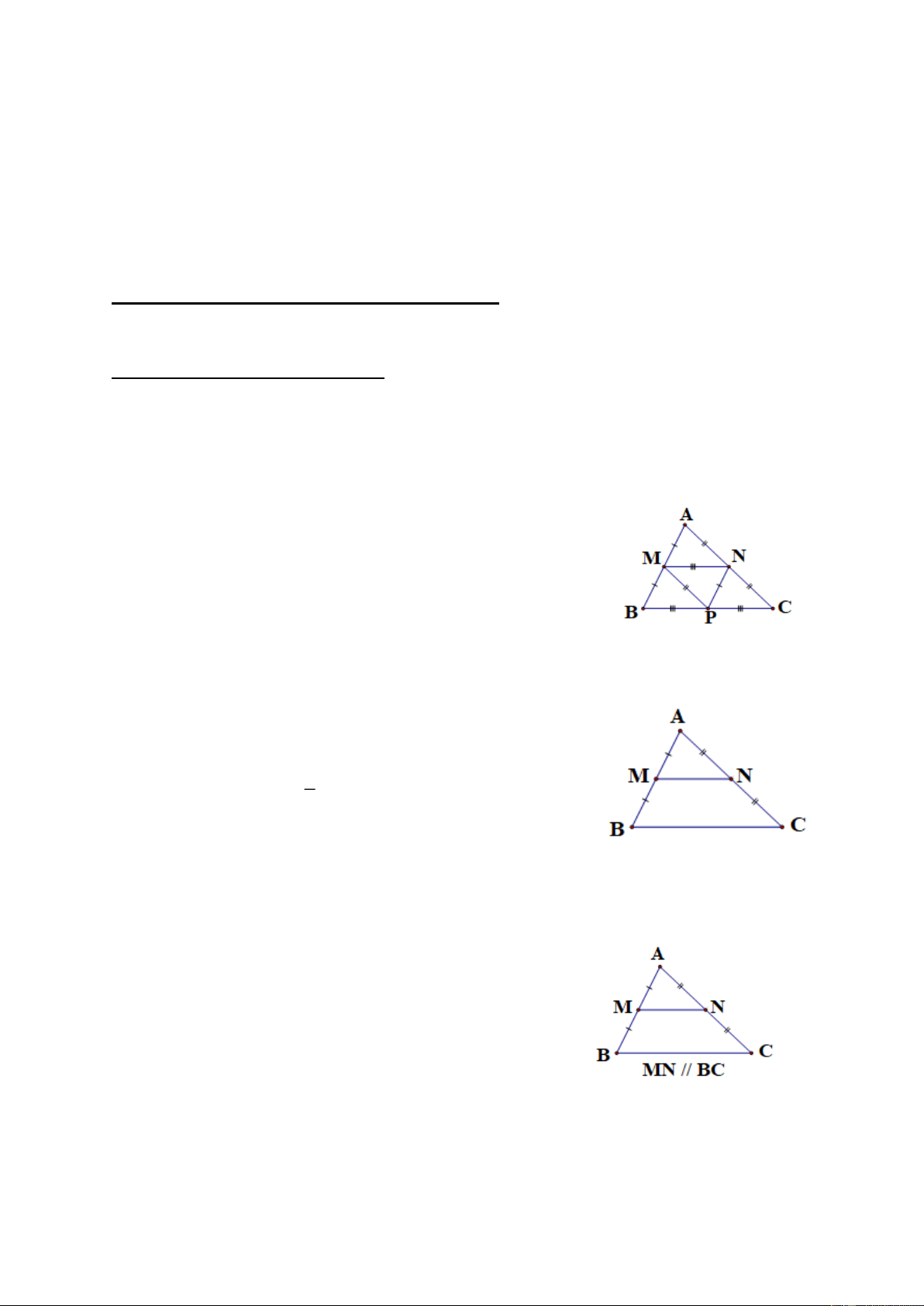
Trang 180

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học,

năng lực mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh,

phân tích, tổng hợp, khái quát hóa tìm ra đô dài các đoạn thẳng, chứng minh

song song, giải quyết các vấn đè thực tế.

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và

theo nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

I. KIẾN THỨC CẦN NHỚ

1. Đường trung bình của tam giác

a. Định nghĩa

*Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam

giác

ABCD

có

( )

MA=MB M ABÎ

và

NA=NC

( )

ACN Î

,

MNÞ

là đường trung bình của

ABCD

*Mỗi tam giác có ba đường trung bình.

b. Tính chất

*Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng một nửa

cạnh ấy.

MN

là đường trung bình của

//

1

.

2

MN BC

ABC

MN BC

ì

ï

í

ï

î

DÛ

=

c.Định lý đường trung bình của tam giác

*Trong một tam giác, nếu một đường thẳng đi qua trung điểm của một cạnh và

song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba của tam giác

đó.

( )

//

ABC

MA MB M AB NA NC

MN B

c

CN

ó

AC

ü

ï

ý

ï

þ

D

= Î Û =

Î

2. Đường trung bình của hình thang.

a. Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm

hai cạnh bên của hình thang

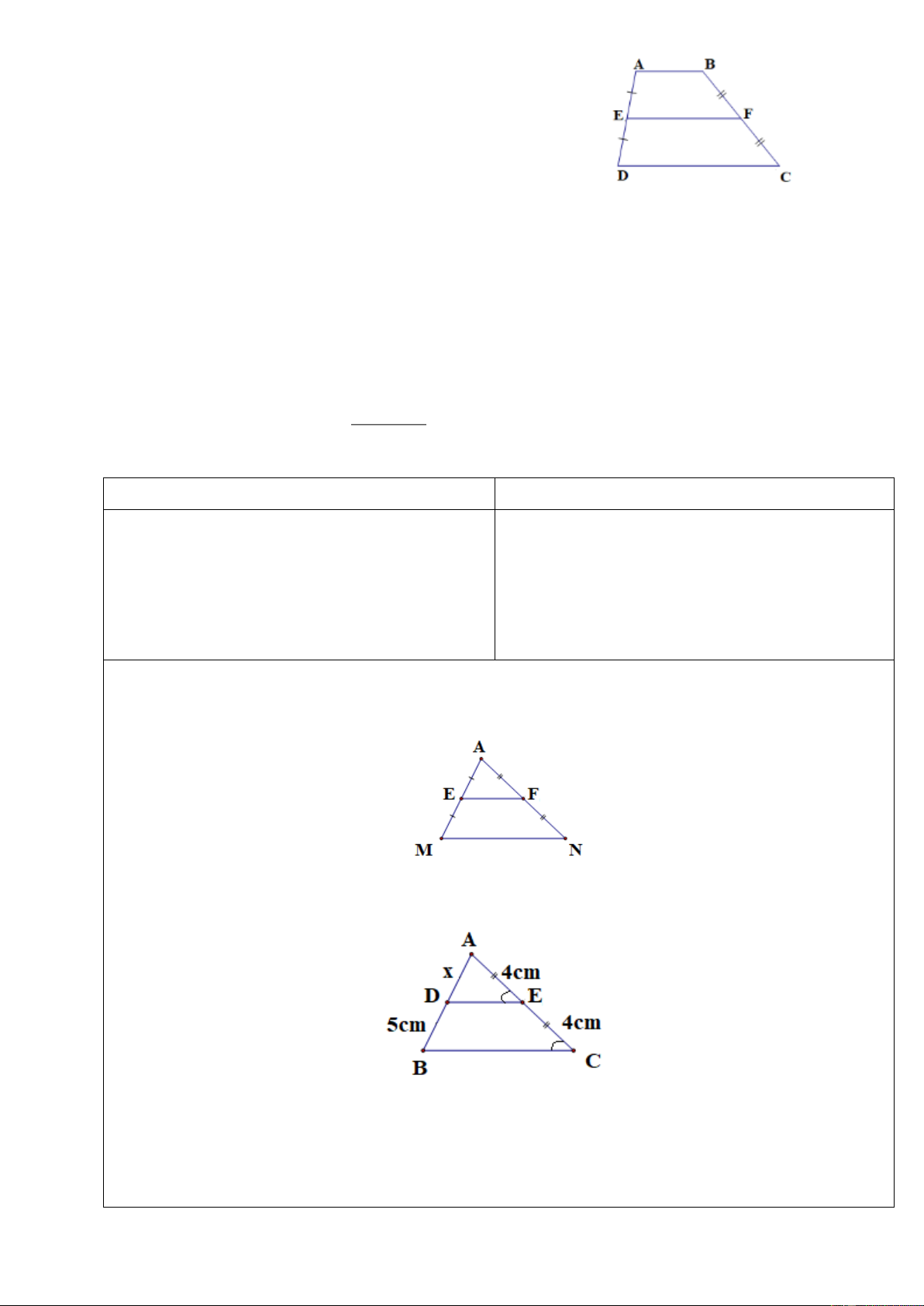
Trang 181

Hình thang

ABCD

( )

( / / ),AB CD AE ED E AD=

và

( )

BF FC F BC= Î Þ

là đường trung bình của hình

thang

b. Các định lý

* Định lý 1: Đường thẳng đi qua trung điểm 1 cạnh bên của hình thang và song

song với hai đáy thì đi qua trung điểm của cạnh bên thứ hai.

Hình thang

ABCD

( )

//AB CD

có

( )

EA ED E AD=

và

/ / / /EF AB DC

FB FC=

*Định lý 2: Đường trung bình của hình thang thì song song với hai đáy và bằng

nửa tổng độ dài hai đáy.

Hình thang

ABCD

( )

//AB CD

có

( ) ( )

,EA ED E AD FB FC F BC=  = 

/ / , / / , .

2

AB CD

EF AB EF CD EF

+

=

2. BÀI TẬP

Hoạt động của giáo viên và học sinh

Nội dung

- GV tổ chức hoạt động, trả lời nhanh bài

toán trắc nghiệm 1 .

Dạng 1: Sử dụng định nghĩa, định lí của

đường trung tam giác, của hình thang

bình hình thang để tính độ dài đoạn

thẳng.

Bài 1: Bài tập trắc nghiệm.

Bài 1: Bài tập trắc nghiệm

Câu 1. Cho

AMN

như hình vẽ dưới đây. Biết

, , 9 AE EM AF FN EF cm= = =

. Độ dài

đoạn thẳng

MN

là?

A. .

12 cmx =

B.

16 cmx =

. C.

18 cmx =

. D.

4,5 cmx =

.

Câu 2. Cho hình vẽ dưới đây. Tìm

x

.

A.

5 cmx =

B.

4 cmx =

. C.

8 cmx =

. D.

10 cmx =

.

Câu 3. Một hình thang có độ dài hai đáy là

4 cm

và

6 cm

. Độ dài đường trung bình của

hình thang là

A.

4 cm

. B.

5 cm

. C.

6 cm

. D.

10 cm

.

Câu 4. Giá trị

x

trong hình thang sau là?

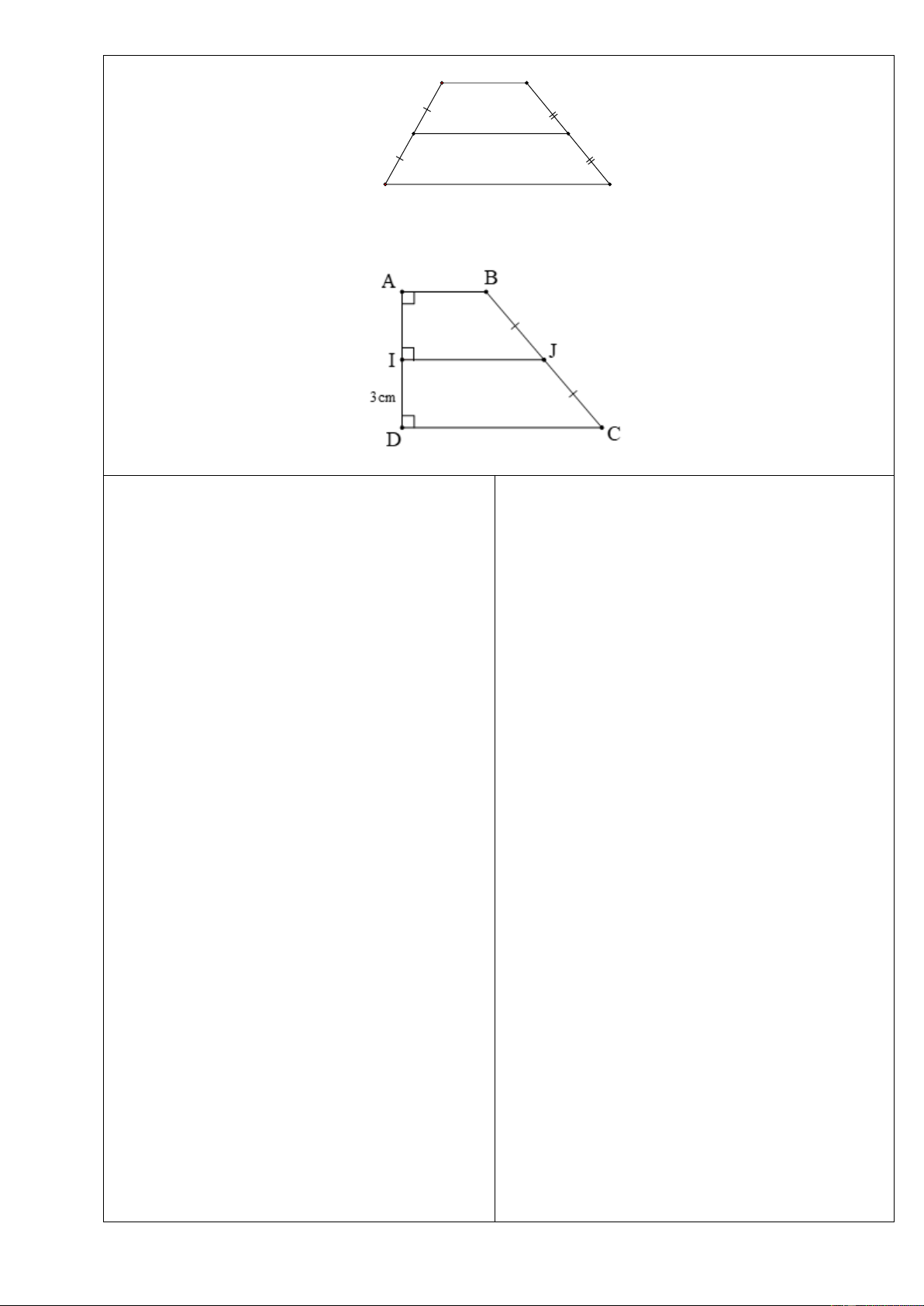
Trang 182

A.

2 cm

. B.

3 cm

C.

5 cm

. D.

7 cm

.

Câu 5. Cho hình vẽ sau .Độ dài

AI

là?

A.

6 cm

. B.

5 cm

. C.

4 cm

. D.

3 cm

.

*Thực hiện nhiệm vụ

GV gợi ý

Câu 1. Đoạn

EF

gọi là gì của

ABC

?

Cách tính?

Câu 2.

ABC

có

EF=

và

E

là trung điểm

của

AC

ta suy ra điều gì?

D

được gọi là

gì của

AB

? Cách tính

AD

?

Câu 3. Nêu cách tính độ dài đường trung

bình hình thang khi biết độ dài hai đáy

theo định lí đường trung bình của hình

thang?

Câu 4.

FG

gọi là của hình thang

ABCD

nêu

tìm

FG

?

Câu 5. Ta có

0

90A I D= = =

thì các đoạn

, , AD IJ DC

có mối quan hệ gì? .Hình

thang

ABCD

có

/ / / /AB IJ DC

và

J

là trung

điểm của

BC

thì

I

được gọi là gì của

AD

?

Hs trả lời miệng.

Câu 1. Vì

,AE EM AF FN==

nên

FE

là

đường trung bình của tam giác

.AMN

Do đó:

2 2.9 18 cmMN EF= = =

..

Câu 2. Ta có

4 cmAE EC==

( )

1

Đường thẳng

AC

cắt hai đoạn thẳng

DE

,

BC

tạo thành hai góc đồng vị:

50AED ECB= = 

.

Suy ra

//DE BC

.

( )

2

Câu 1. Chọn C.

Vì

,AE EM AF FN==

nên

FE

là đường

trung bình của tam giá

.AMN

Do đó:

2 2.9 18 cmMN EF= = =

.

Câu 2. Chọn A.

Ta có

4 cmAE EC==

( )

1

Đường thẳng

AC

cắt hai đoạn thẳng

DE

,

BC

tạo thành hai góc đồng vị:

50AED ECB= = 

x

7 cm

5 cm

G

F

A

D

B

C

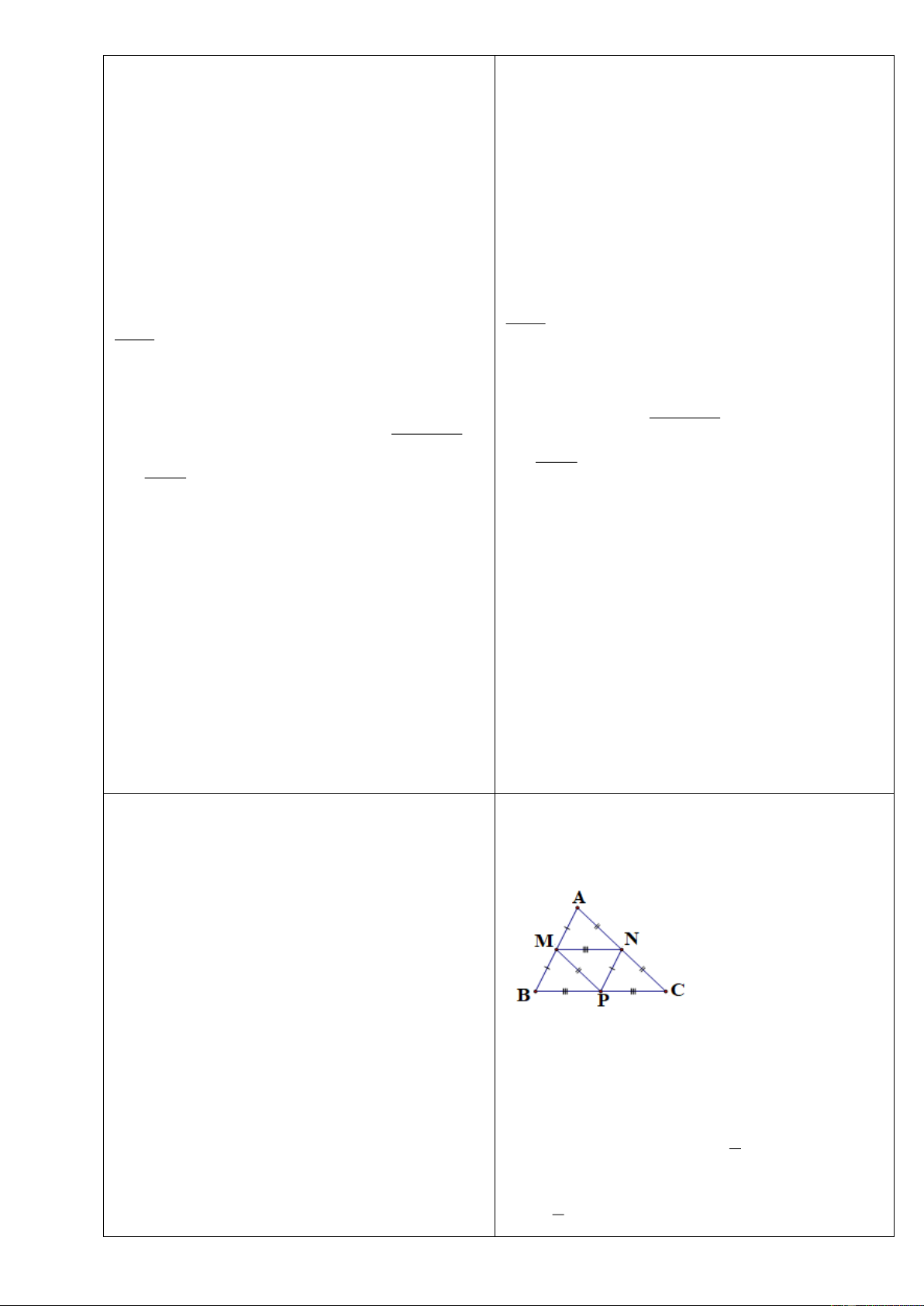
Trang 183

Từ

( )

1

và

( )

2

ta thấy

DE

đi qua trung

điểm một cạnh của tam giác và song song

với cạnh thứ hai nên

DE

đi qua trung

điểm của cạnh thứ ba.

Do đó

5AD BD cm==

hay

5x cm=

Câu 3.

Độ dài đường trung bình của hình thang

là:

5

4+6

cm

2

=

Câu 4. Chọn B.

FG

là đường trung bình

của hình thang

ABCD

nên

2

AB CD

FG

+

=

.

7

5

2

x +

=

hay

3x =

.

Câu 5.

Xét hình thang

ABCD

( vì

,AB AD CD AD⊥⊥

nên

AB CD//

)

có

JB JC=

(gt) và

IJ AB CD// //

(do

IJ AD⊥

)

Suy ra

I

là trung điểm của

AD

.

Vậy

3IA =

cm

*Kết luận, nhận định:

GV

Suy ra

//DE BC

( )

2

Từ

( )

1

và

( )

2

ta thấy

DE

đi qua trung điểm

một cạnh của tam giác và song song với

cạnh thứ hai nên

DE

đi qua trung điểm của

cạnh thứ ba.

Do đó

5AD BD cm==

hay

5x cm=

Câu 3. Chọn B.

Độ dài đường trung bình của hình thang là:

5

4+6

cm

2

=

Câu 4. Chọn B.

FG

là đường trung bình của hình thang

ABCD

nên

2

AB CD

FG

+

=

.

7

5

2

x +

=

10 7x=+

3x =

Câu 5. Chọn D

Xét hình thang

ABCD

( vì .

,AB AD CD AD⊥⊥

.

nên

AB CD//

) có:

JB JC=

(gt) và

IJ AB CD// //

( do

IJ AD⊥

).

Suy ra

I

là trung điểm của

AD

.

Vậy

3IA cm=

.

* Giao nhiệm vụ

- GV tổ chức hoạt động cá nhân HS tìm

hiểu.

Bài 2: Cho tam giác

ABC

có

6,AB cm=

7 , 10MN cm AC cm==

. Gọi

,,M N P

lần lượt

là trung điểm của

,,AB AC BC

. Tính độ dài

các đoạn

,,BC NP MP

và chu vi

NMP

.

*Thực hiện nhiệm vụ

GV gợi ý

ABC

có

,,M N P

theo thứ tự là trung điểm

của

,,AB AC BC

thì

, , MN NP MP

là được

gọi là gì của

ABC

? Tìm các đoạn

,,BC NP MP

như thế nào?

HS đọc đề bài, quan sát hình vẽ vẽ hình

Bài 2:

Lời giải.

ABC

có

,,M N P

theo thứ tự là trung điểm

của

,,AB AC BC

.

, , MN NP MP

là các đường trung bình

của

ABC

. Do đó

1

2

MN BC=

. Hay

2 14BC MN cm==

1

3

2

NP AB cm==

.

Trang 184

vào vở làm bài tập theo gợi các câu hỏi gợi

ý

Hs

ABC

có

,,M N P

theo thứ tự là trung

điểm của

,,AB AC BC

thì

, , MN NP MP

là

các đường trung bình của

ABC

nên

2BC MN=

,

1

2

NP AB=

.

1

2

MP AC=

*Kết luận, nhận định:

GV nhấn mạnh: Trong tam giác độ dài

đường trung bình bằng nửa độ dài cạnh

song song với đường trung bình.Từ đó suy

ra độ dài cạnh song song với đường trung

bình gấp đôi đường trung bình.

* Giao nhiệm vụ

- GV tổ chức hoạt động cá nhân HS tìm

hiểu. Bài 2: Cho hình vẽ sau.

Biết

EF/ // / / GHAB CD

.Tìm

,.xy

*Thực hiện nhiệm vụ

Gv gợi ý

Ta có

EF/ // / / GHAB CD

và

AC CE EG==

,

BD DF FH==

thì các

,CD EF

lần lượt được gọi là gì ? Cách tính

,xy

?

HS quan sát vẽ và làm vào vở theo hướng

dẫn trả lời các câu hỏi.

Hs

,CD EF

lần lượt là các đường trung

bình của các hình thang

ABFE

và

CDHG

nên

( )

:2CD AB EF=+

( )

:2EF CD GH=+

2GH EF CD = −

HS Một hs lên bảng trình bày.

*Kết luận, nhận định:

GV nhấn mạnh: Trong hình thang độ dài

đường trung bình bằng nửa tổng độ dài hai

đáy. Nên suy ra cách tính độ dài một cạnh

đáy chưa biết bằng hiệu hai lần độ dài

đường trung bình với độ dài cạnh đáy đã

1

5

2

MP AC cm==

.

Chu vi

NMP

là:

7 3 5 15MN NP MP cm+ + = + + =

.

Bài 2:

Lời giải

Ta có

EF/ // / / GHAB CD

và

AC CE EG==

,

BD DF FH==

nên các

,CD EF

lần lượt là

các đường trung bình của các hình thang

ABFE

và

CDHG

nên

( )

:2CD AB EF=+

.

(8 16):2 12 .cm= + =

Hay

12 .x cm=

( )

:2.EF CD GH=+

2.GH EF CD = −

2.16 12 20 .cm= − =

20 .y cm=

Bài 3:

Lời giải

Ta có:

/ / / / / /AB EF GH CD

và

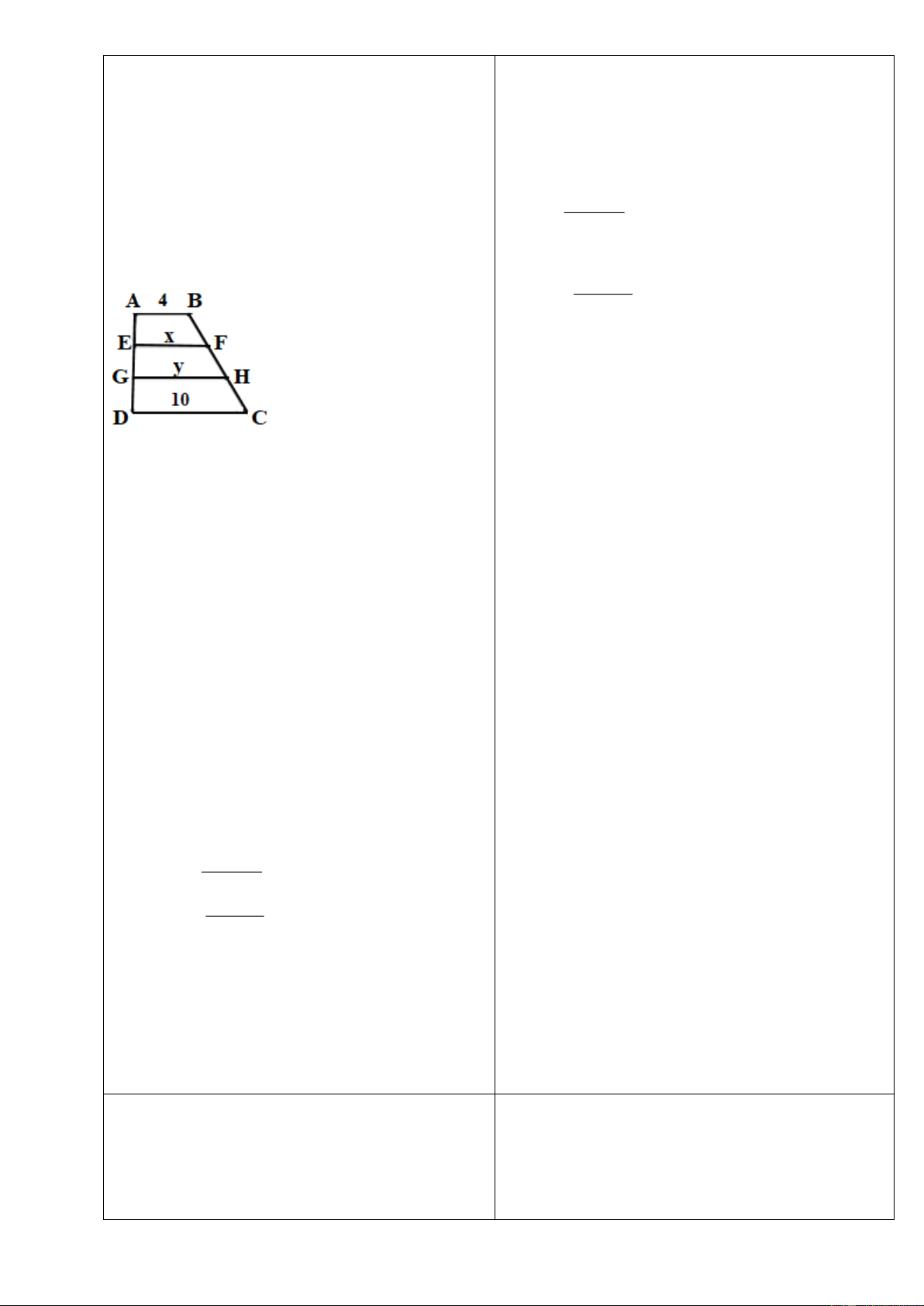
Trang 185

biết.

* Giao nhiệm vụ

- GV tổ chức hoạt động cá nhân, HS tìm

hiểu.

Bài 3: Tính các độ dài x và y trên hình.

Biết

/ / / / / /AB EF GH CD

AE EG GD==

,

4 ,AB cm=

10 CD cm=

.

*Thực hiện nhiệm vụ

HS đọc tìm hiểu đề bài, quan sát vẽ hình

nêu cách làm.

Gv gợi ý

Trên hình các đoạn

,EF GH

là trung bình

của những hình thang nào? Hãy biểu diễn

y

theo

x

từ đó rút ra một biểu thức chỉ

chứa toàn

x

để tìm

x

sau đó tìm

y

?

HS quan sát vẽ và làm vào vở theo hướng

dẫn trả lời các câu hỏi.

Ta có

/ / / / / /AB EF GH CD

và

AE EG GD==

nên các

,EF GH

lần lượt

là các đường trung bình của các hình thang

ABHG

và

EFCD

. Do đó

24yx=−

và

10

2

x

y

+

=

10

24

2

x

+

 − =

Hs lên bảng trình bày.

*Kết luận, nhận định:

GV phương pháp sử dụng định lí tính chất

đường trung bình hình thang để tính độ dài

đoạn thẳng.

AE EG GD==

nên các

,EF GH

lần lượt là

các đường trung bình của các hình thang.

ABHG

và

EFCD

.

Do đó

24xy=+

Hay

24yx=−

(1)

và

10

2

x

y

+

=

(2)

Từ (1) và (2) suy ra:

10

24

2

x

+

−=

4 8 10xx− = +

4 10 8xx− = +

3 18x =

6x =

8y =

* Giao nhiệm vụ

- GV tổ chức hoạt động cá nhân làm.

Dạng 2: Sử dụng định nghĩa, định lí

đường trung bình tam, chứng minh hai

đoạn thẳng song song, chứng minh hai số

tỉ số bằng nhau.

Bài 1:

Trang 186

Bài 1: Cho tam giác

ABC

, kẻ trung tuyến

AM

. Trên cạnh

AC

lấy điểm

,DE

sao

cho

AD DE EC==

.

a). Chứng minh rằng:

//ME BD

.

b). Gọi

I

là giao điểm của

,AM BD

.

Chứng minh:

AI IM=

.

c). Chứng minh:

1

4

ID

BD

=

.

*Thực hiện nhiệm vụ

HS Đọc tìm hiểu đề bài, vẽ hình nêu cách

làm và làm vào vở.

GV gợi ý

a) Các đoạn

ME

và

BD

cùng thuộc tam

giác nào? Các điểm

,ME

còn được gọi là

gì của các đoạn

DC

và

BC

?

ME

gọi là gì

của

BCD

và có tính chất gì?

b). Điểm

I

thuộc cạnh tam giác nào? Trên

tam giác đó còn có gì đặc biệt giúp liên

tưởng đến định lí nào?

c). Gợi ý so sánh

ME

và

BD

, so sánh

ME

và

ID

?

Hs trả lời các câu hỏi gợi ý

a). Điểm

E

là trung điểm của

DC

và

M

là

trung điểm của

BC

nên

ME

là đường

trung bình của

BCD

//ME BD

b).

AME

có

I

thuộc

AM

và

D

là trung

điểm của

AE

và

//ID ME

là định lí về

đường trung bình tam giác

c).

2BD EM=

và

2ME ID=

Hs lên bảng trình bày.

*Kết luận, nhận định:

Gv phương pháp chứng minh song song:

Sử dụng định lí tính chất đường trung bình

của tam giác.

* Giao nhiệm vụ

- GV tổ chức hoạt động nhóm làm.

Bài 2: Cho tam giác

ABC

. Điểm

D

thuộc

tia đối của tia

BA

sao cho

BD BA=

,

M

là

trung điểm của

BC

. Gọi

K

là giao điểm

của

DM

và

AC

, từ

B

kẻ

//BN DM

(

N

Lời giải:

a).

BCD

có

E

là trung điểm của

DC

và

M

là trung điểm của

BC

nên

ME

là đường

trung bình của

BCD

.

//ME BD

b). Xét

AME

có

D

là trung điểm của

AE

và

//ID ME

IA IM=

c).

BCD

có

ME

là đường trung bình nên

1

2

EM DB=

hay

2BD EM=

(1)

AME

có

ID

là đường trung bình nên

1

2

ID ME=

Hay

2ME ID=

(2)

Từ (1) và (2) suy ra

4BD DI=

1

4

DI BD=

1

4

ID

BD

=

Bài 2:

Lời giải

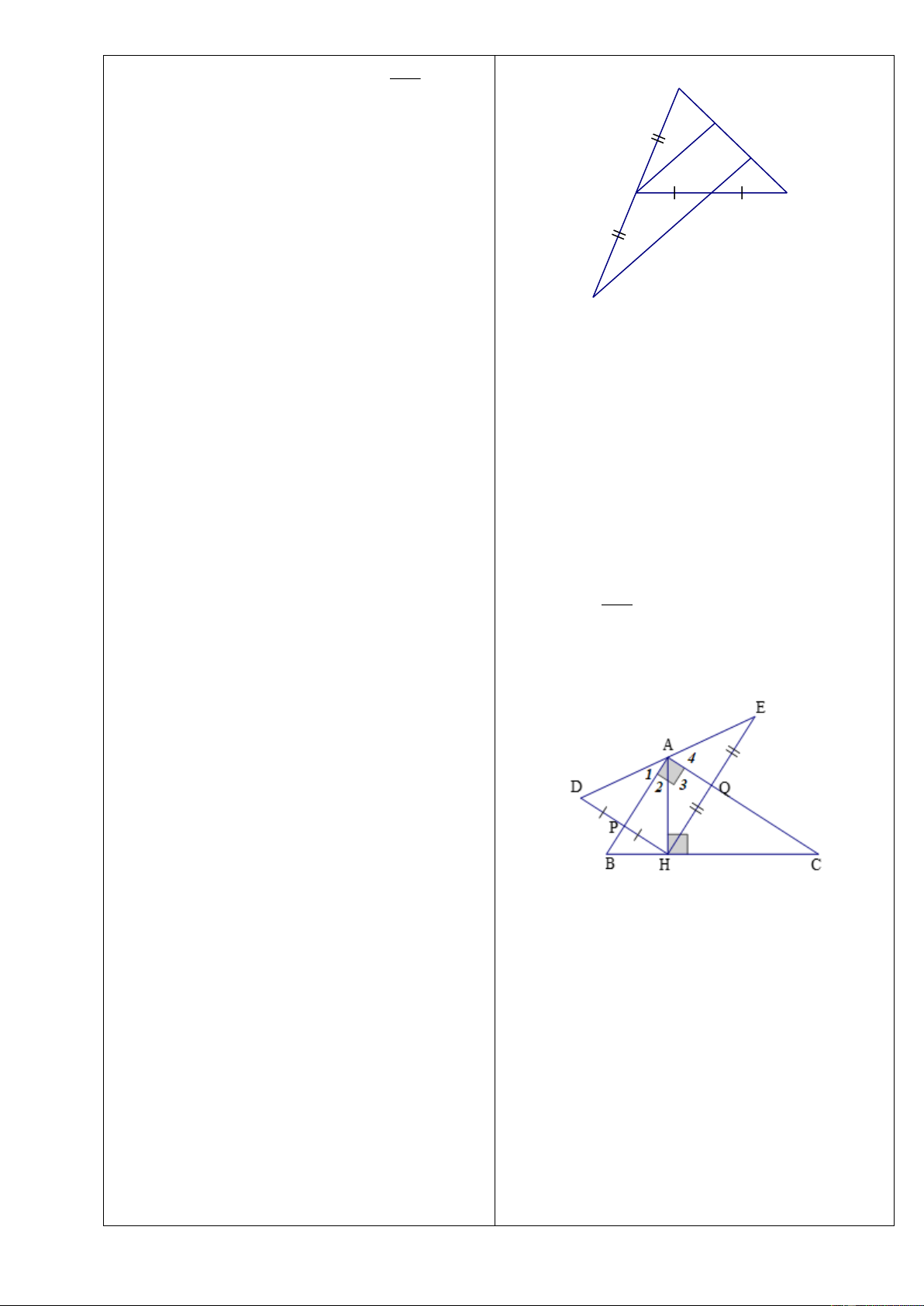
Trang 187

thuộc

AC

). Chứng minh rằng:

2

AK

KC

=

.

*Thực hiện nhiệm vụ

HS đọc tìm hiểu đề bài vẽ hình thảo luận

cách làm và làm vào bảng nhóm.

Gv gợi ý

So sánh

AK

với

NK

và

NK

với

KC

từ đó

suy ra điều cần chứng minh?

Hs

2AK NK=

do

BN

là đường trung bình

của

ADK

,

NK KC=

vì

K

là trung điểm

của

NC

.

Hs đại diện nhóm trình bày.

*Kết luận, nhận định:

GV phương pháp chứng minh hai tỉ số

bằng nhau: Sử dụng định lí đường trung

bình tam giác chỉ ra mối quan hệ giữa các

đoạn thẳng từ đó lập luận để có tỉ số cần

chứng minh.

* Giao nhiệm vụ

- GV tổ chức hoạt động nhóm làm .

Bài 3: Cho

ABC

vuông tại

A

, kẻ

đường cao

AH

. Từ

H

kẻ

Hx AB⊥

tại

P

,

trên

Hx

lấy điểm

D

sao cho

P

là trung

điểm của

HD

. Từ

H

kẻ

Hy

vuông góc

với

AC

tại

Q

và trên

Hy

lấy điểm

E

sao

cho

Q

là trung điểm của

HE

a). Chứng minh ba điểm

,,A D E

thẳng

hàng

b). Chứng minh :

//PQ DE

c). Chứng minh :

PQ AH=

.

*Thực hiện nhiệm vụ

HS Đọc tìm hiểu đề bài vẽ hình thảo luận

cách làm và làm vào bảng nhóm.

Gv gợi ý

a). Chứng minh

0

1 2 3 4

180A A A A+ + + =

,PQ

thuộc tam giác nào và còn có điều gì

đặc biệt giúp chứng minh song song?

b). Các đoạn

AH

và

PQ

thuộc tứ giác nào

và tứ giác đó là hình gì?

Xét

ADK

có

, / /AB DB BN DK=

nên

N

là

trung điểm của

AK

.

BN

là đường trung bình của

ADK

.

2AK NK=

(1)

Tương tự

BNC

có

K

là trung điểm của

NC

nên

NK KC=

. (2)

Từ (1) và (2) suy ra:

2AK KC=

.

Hay

2

AK

KC

=

(đpcm)

Bài 3:

Lời giải

a)

ADH

cân vì có

DH AB⊥

tại

P

và

P

là trung điểm của

HD

nên

AP

đồng

thời là đường phân giác. Do đó

12

AA=

(1)

Tương tự với

AHE

ta có :

34

AA=

(2)

Mà

0

34

90A A BAC+ = =

(3)

0

1 2 3 4

180A A A A=+ + +

Từ (1), (2), (3) suy ra:

,,A D E

thẳng hàng (đpcm).

b).

HDE

có

P

là trung điểm của

DH

và

Q

D

B

M

C

K

N

A

Trang 188

c). Các đoạn

AH

và

PQ

thuộc tứ giác nào

và tứ giác đó là hình gì?

Hs trả lời

a). Chứng minh

12

AA=

và

34

AA=

kết hợp

với

0

34

90BACAA==+

0

1 2 3 4

180A A A A=+ + +

b).

PQ

thuộc

HDE

đồng thời là đường

trung bình của tam giác đó.

c). Các đoạn

AH

và

PQ

là các đường chéo

thuộc hình chữ nhật

APHQ

.

hs đại diện nhóm báo cáo kết quả, các

nhóm khác quan sát nhận xét.

*Kết luận, nhận định:

GV phương pháp chứng minh ba điểm

thẳng hàng. Áp dụng tính chất góc bẹt .

là trung điểm của

AH

nên

PQ

là đường

trung bình của .

//PQ ED

c).Tứ giác

APHQ

là hình chữ nhật vì.

0

90A H P Q= = = =

PQ AH=

(tính chất hai đường chéo)

* Giao nhiệm vụ

- GV tổ chức hoạt động cá nhân làm

Bài 1: Khi thiết kế một cái thang gấp, để

đảm bảo an toàn người thợ đã làm thêm

một thanh ngang để giữ cố định ở chính

giữa hai bên thang (như hình vẽ bên) sao

cho hai chân thang rộng một khoảng là

80cm

. Hỏi người thợ đã làm thanh ngang

đó dài bao nhiêu

cm

.

*Thực hiện nhiệm vụ.

HS đọc tìm hiểu đề bài vẽ hình nêu cách

làm, và làm vào vở

Gv gợi ý

Khi nối hai chân thang bởi một đoạn

BC

và hai thanh bên thang cắt nhau ở điểm

A

Dạng 3: Bài toán thực tế liên quan

đường trung bình tam giác.

Bài 1:

Lời giải

Gọi

MN

là thanh ngang,

BC

l à độ rộng

giữa hai bên thang.

MN

nằm chính giữa thang nên

M

,

N

là

trung điểm

AB

và

AC

.

Suy ra

MN

là đường trung bình của tam

giác

ABC

.

Suy ra

11

.80 40( )

22

MN BC cm= = =

.

Vậy người thợ đã làm thanh ngang đó dài

40cm

.

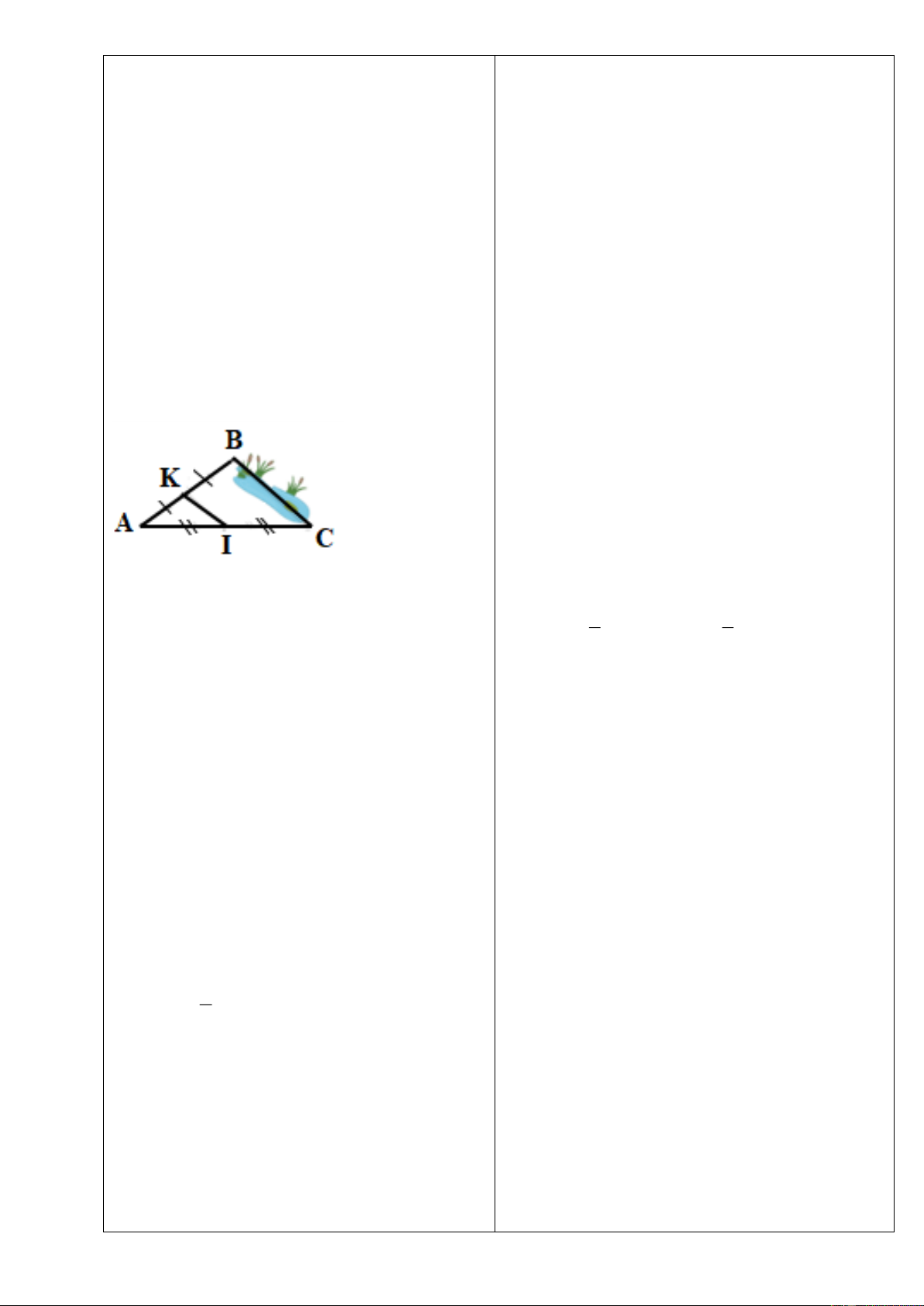
Trang 189

thì đoạn thẳng nối hai điểm để giữ cố định

ở chính giữa hai bên thang được gọi là gì?

Hs trả lời

- Hai điểm chính giữa bên thang là hai

trung điểm nên đoạn thẳng đó là đường

trung bình của tam giác

ABC

.

*Kết luận, nhận định:

GV gọi hs nhân xét, gv chốt kiến thức

phương pháp giải của dạng toán và một số

lưu ý

Bài 2: Cho hình vẽ tính. Biết

KA KB=

và

, 25AI IC KI cm==

.

a). Chứng minh:

//KI BC

.

b). Giữa hai điểm

B

và

C

là một khoảng

đất trống trong khuôn viên vườn . Người

ta muốn trồng hoa theo đoạn đường từ

B

đến

C

. Biết rằng

1m

đất cần

100000đ

để

mua hoa. Vậy muốn trồng hoa trên đoạn

đường

BC

thì phải tốn hết bao nhiêu tiền

mua hoa?

*Thực hiện nhiệm vụ

Gv gợi ý

Vị trí của

K

và

I

có gì đặc biệt

KI

được

gọi tam giác

ABC

? Hai đoạn

KI

và

BC

có

quan hệ như thế nào? Số tiền mua hoa

được tính như thế nào?

Hs

AB

là đường trung bình của

MCD

nên

1

2

AB DC=

.

60AB=

(bước chân)

Khoảng cách từ

A

đến

B

bằng số bước

chân nhân với độ dài 1 bước.

Hs lên bảng trình bày.

*Kết luận, nhận định:

GV gọi hs nhân xét, gv chốt kiến thức

phương pháp giải của dạng toán và một số

Bài 2:

Lời giải

a). Xét

ABC

có

K

là trung điểm

AB

và

I

là trung điểm

AC

.

KI

là đường trung bình của tam giác

ABC

.

//KI BC

.

b) Theo a) ta có

KI

là đường trung bình của

tam giác

ABC

.

Nên

1

2

KI BC=

Hay

1

25 .

2

BC=

.

( )

50BC m=

.

Số tiền hoa trồng quãng đường

BC

là:

50.100000 5000000=

(đồng).

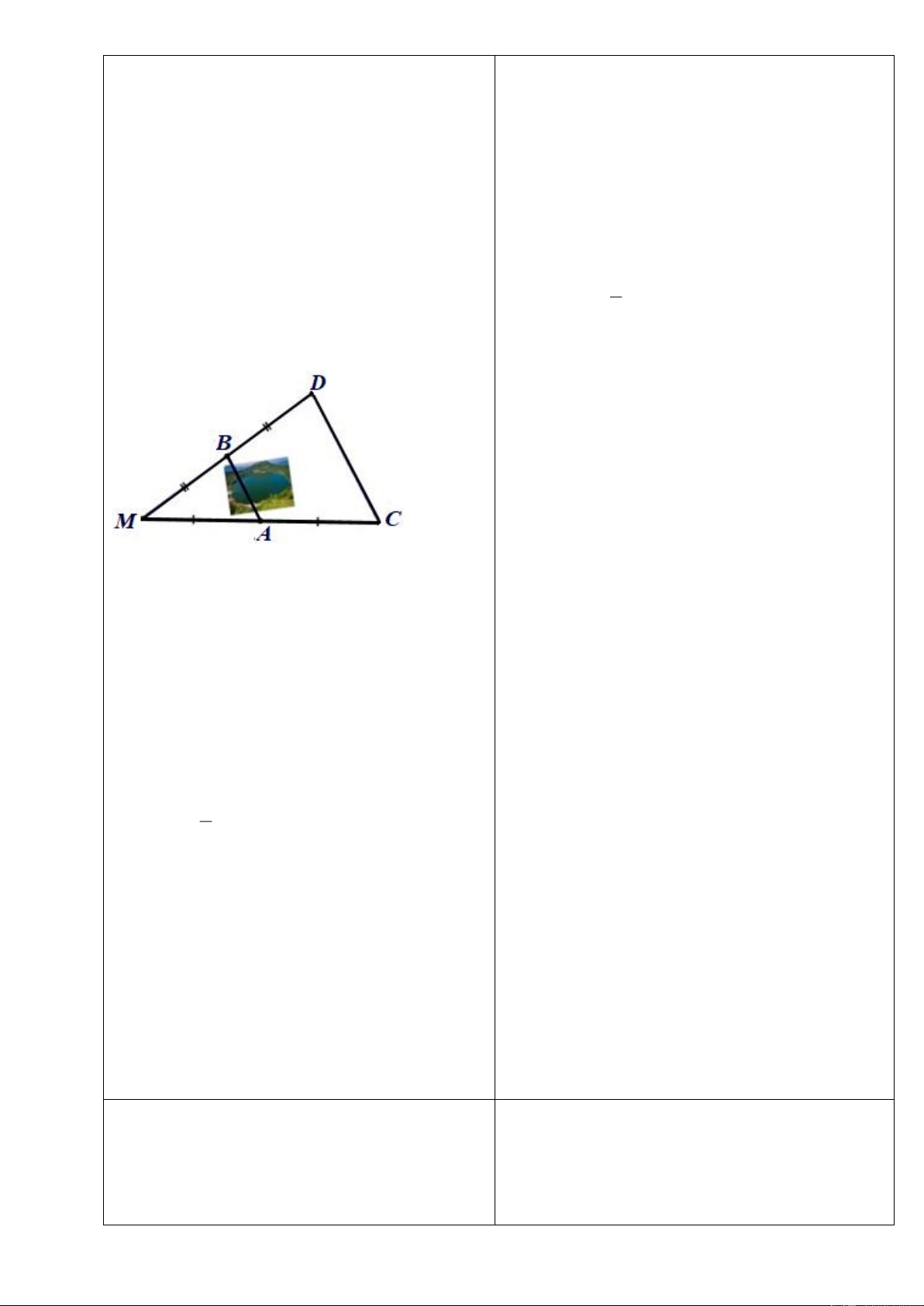
Trang 190

lưu ý.

* Giao nhiệm vụ

- GV tổ chức hoạt động cá nhân làm

Bài 3: Giữa 2 điểm

A

và

B

là một hồ

nước. Biết điểm

A

,

B

lần lượt là trung

điểm của

MB

MC

và

MD

(như hình vẽ).

Bạn Mai đi từ

C

đến

D

hết

120

bước

chân, trung bình mỗi bước chân của Mai

đi được

4dm

.Hỏi khoảng cách từ

A

đến

B

là bao nhiêu mét?

*Thực hiện nhiệm vụ

HS đọc tìm hiểu đề bài vẽ hình nêu cách

làm, và làm vào vở

GV gợi ý

Khoảng cách từ

AB

là bao nhiêu bước

chân? Một bước chân

4dm

vậy đoạn

AB

dài bao nhiêu mét ?

Hs

AB

là đường trung bình của

MCD

nên

1

2

AB DC=

60AB=

(bước chân)

Khoảng cách từ

A

đến

B

bằng số bước

chân nhân với độ dài 1 bước.

Hs lên bảng trình bày

*Kết luận, nhận định:

GV gọi hs nhân xét, gv chốt kiến thức

phương pháp giải của dạng toán và một số

lưu ý.

Bài 3.

Lời giải

AB

là đường trung bình củ

MCD

.

Nên

1

.

2

AB DC=

60AB=

(bước chân).

Khoảng cách từ

A

đến

B

là:

( ) ( )

60 . 4 240 24 .dm m==

* Giao nhiệm vụ

- GV tổ chức hoạt động cá nhân làm

Dạng 4: Sử dụng tính chất đường trung

bình của tam giác để chứng minh tứ giác

là các hình đặc biệt (hình thoi, hình bình

hành, hình chữ nhật, hình vuông)

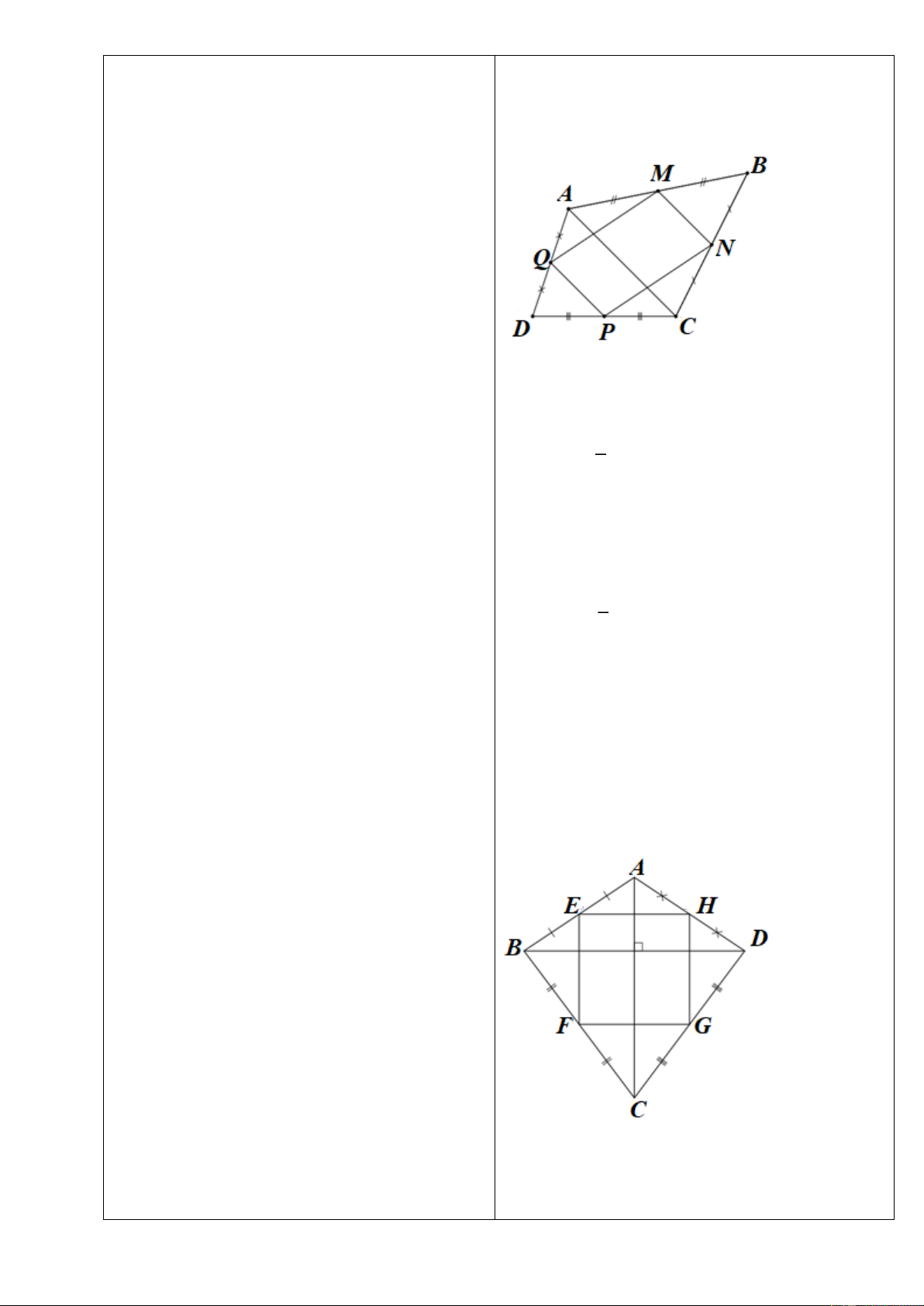
Trang 191

Bài 1: Cho tứ giác

ABCD

. Gọi

,MN

,

N

,

P

,

Q

lần lượt là trung điểm của các

cạnh

AB

,

BC

,

CD

,

DA

. Chứng minh tứ

giác

MNPQ

là hình bình hành.

*Thực hiện nhiệm vụ

HS đọc tìm hiểu đề bài vẽ hình nêu cách

làm, và làm vào vở.

Gv gợi ý

Kẻ các đường chéo

AC

(hoặc

BD

) thì các

cạnh

,MN PQ

có quan hệ gì với

AC

? Tứ

giác

MNPQ

là hình gì?

Hs lên bảng trình bày.

*Kết luận, nhận định:

GV nhấn mạnh: Sử dụng định lí tính chất

đường trung bình của tam giác để chứng

minh hai đoạn thẳng song song và các dấu

hiệu nhận biết hình bình hành để chứng

minh một tứ giác là hình bình hành.

* Giao nhiệm vụ

- GV tổ chức hoạt động cá nhân làm.

Bài 2: Cho tứ giác

ABCD

có hai đường

chéo vuông góc với nhau. Gọi

,,E F G

theo thứ tự là trung điểm của các cạnh

,,AB BC DA

. Chứng minh tứ giác

HEFG

là

hình chữ nhật.

*Thực hiện nhiệm vụ:

HS đọc tìm hiểu đề bài vẽ hình nêu cách

làm, và làm vào vở.

Gv gợi ý

Vẽ hình có thể vẽ hai đường chéo vuông

góc với nhau trước.

Tứ giác

EFGH

là hình gì? Hình bình hành

Bài 1:

Lời giải

Xét

DACD

có

PQ

là đường trung bình.

//

(1)

1

.

2

PQ AC

ì

ï

í

ï

î

Þ

=

Xét tam giác

BAC

có

MN

là đường trung

bình

//

(2)

1

.

2

MN AC

ì

ï

í

ï

î

Þ

=

Từ

( )

1

và

( )

2

suy ra

//

.

MN PQ

ì

ï

í

ï

î

=

Þ

Tứ giác

MNPQ

là hình bình hành.

Bài 2:

Lời giải

Xét

ABD

có

EH

là đường trung bình.

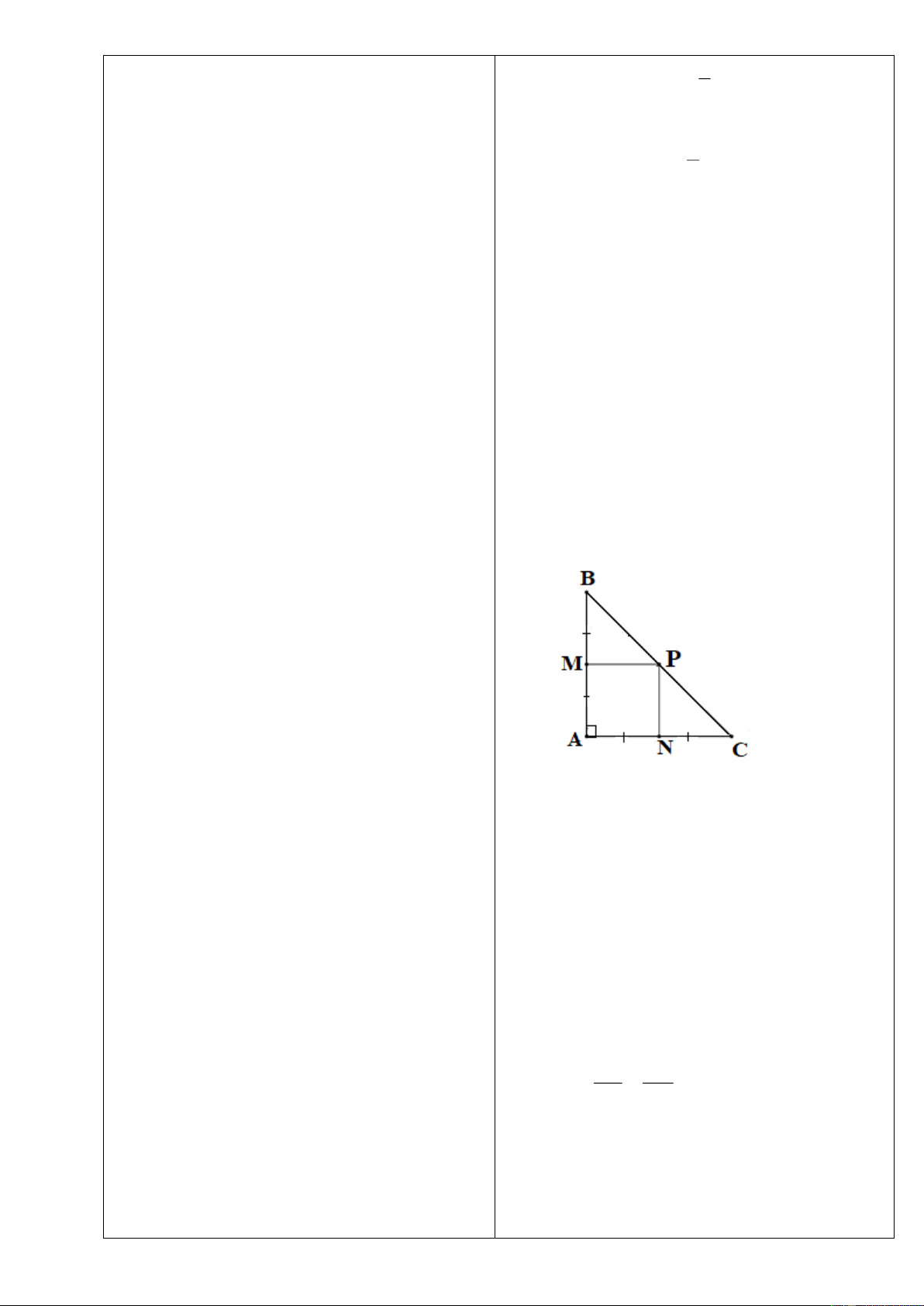
Trang 192

cần thêm điều kiện gì về góc để trở thành

hình chữ nhật ? Cách chứng minh

EF FG⊥

?

Hs trả lời các gợi ý và làm vào vở.

Các

,MN PQ

cùng song song và bằng một

nửa

AC

nên tứ giác

MNPQ

là hình bình

hành.

Hs lên bảng trình bày.

*Kết luận, nhận định :

GV nhấn mạnh : Áp dụng định lí đường

trung bình của tam giác, chứng minh tứ

giác là hình bình hành và các dấu hiệu

nhận biết hình chữ nhật để chứng minh tứ

giác là hình chữ nhật.

* Giao nhiệm vụ

- GV tổ chức hoạt động cá nhân làm.

Bài 3: Cho tam giác

ABC

vuông cân tại

A

. Gọi

M

,

N

là trung điểm

AB

,

AC

.

Qua

M

kẻ đường thẳng song song

AC

và

cắt

BC

tại

P

. Chứng minh rằng

AMPN

là hình vuông.

*Thực hiện nhiệm vụ :

Gv gợi ý

Có thể chứng tứ giác

AMPN

là hình bình

hành được không?

ABC

có

M

là trung

điểm của

AB

,

//MP AC

thì

P

gọi là gì

của

BC

? Các

MP

,

NP

được gọi là gì của

ABC

? Hình bình hành có một góc vuông

thì cần chứng minh thêm điều kiện gì về

cạnh nữa để trở thành hình vuông?

Hs chứng tứ giác

AMPN

là hình bình

hành.

ABC

có

M

là trung điểm của

AB

,

//MP AC

thì

P

gọi là trung điểm của

BC

và các

,MP NP

là đường trung bình của

ABC

nên từ đó suy ra tứ giác

AMPN

là

hình bình hành có một góc vuông cần

thêm

AM AN=

để trở thành hình vuông.

//EH BD

và

1

2

EH BD=

. (1)

Xét

CBD

có

FG

là đường trung bình.

//FG BD

và

1

2

FG BD=

. (2)

Từ (1) và (2) suy ra:

EFGH

là hình bình hành. (3)

Xét

BAC

có

EF

là đường trung bình.

//EF AC

.

Mà

AC BD⊥

và

//BD FG

.

EF FG⊥

. (4)

Từ (3) và (4)

EFGH

là hình chữ nhật.

Bài 3:

Lời giải

Ta có

M

là trung điểm của

AB

,

//MP AC

.

P

là trung điểm của

BC

.

MP

là đường trung bình của

ABC

.

Mà

N

là trung điểm của

AC

NP

là đường trung bình của

ABC

//NP AB

AMPN

là hình bình hành.

Mà

90MAN



=

AMPN

là hình chữ nhật.

Mà

22

AB AC

AM AN= = =

AMPN

là hình vuông.

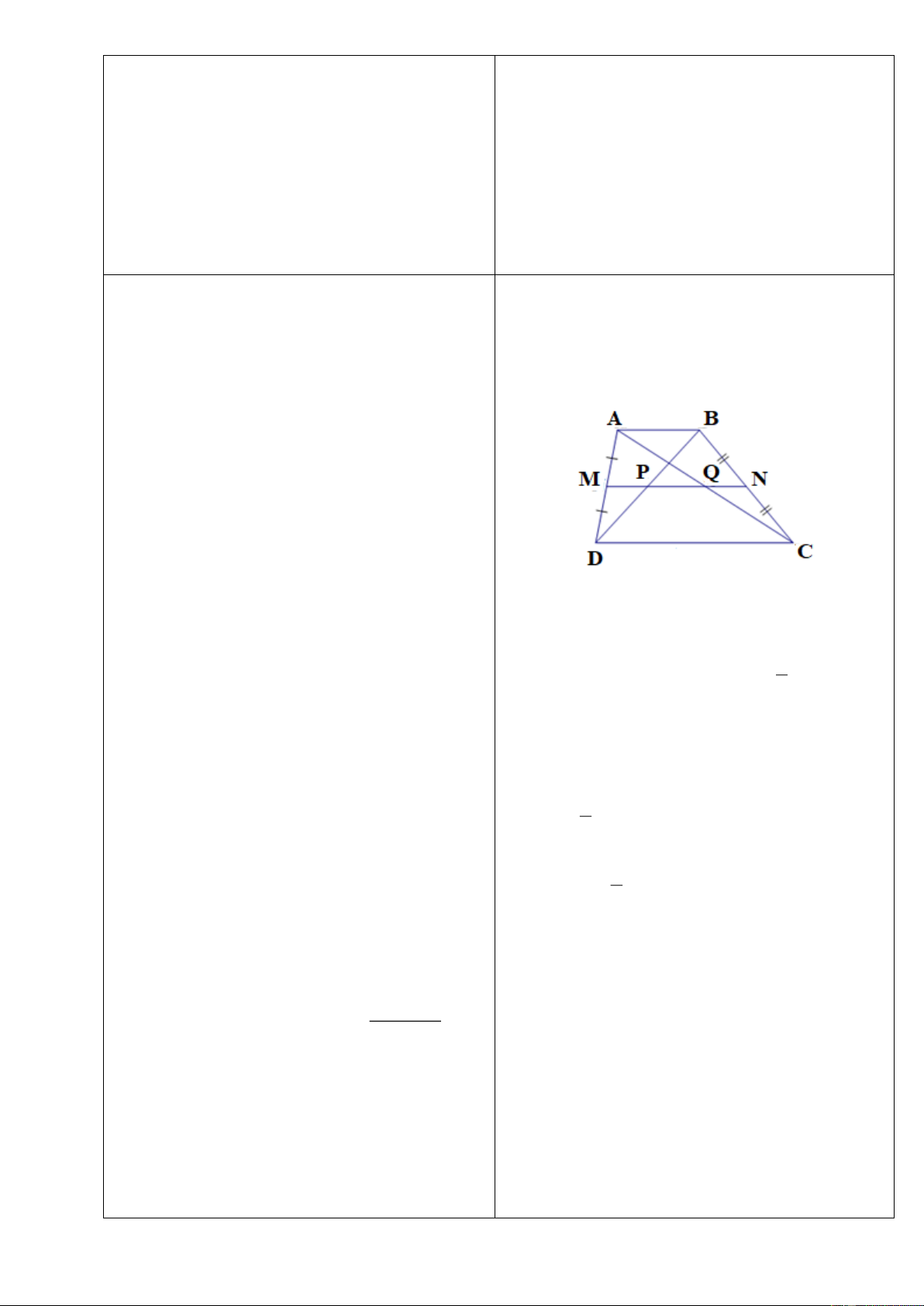
Trang 193

Hs lên bảng trình bày.

*Kết luận, nhận định:

GV nhấn mạnh : Áp sử dụng định lí

đường trung bình của tam giác chứng

minh tứ giác là hình bình hành và các dấu

hiệu nhận biết của hình vuông để chứng

minh hình bình hành là hình vuông .

Giao nhiệm vụ

- GV tổ chức hoạt động cá nhân, HS tìm

hiểu.

Bài 1: Cho hình thang

( )

//ABCD AB CD

,

M

là trung điểm của

AD

,

N

là trung điểm

của

BC

. Gọi

,PQ

theo thứ tự là giao

điểm của

MN

với

BD

và

AC

. Biết

8CD cm=

và

6MN cm=

.

a). Chứng minh:

//MN AB

và tính

AB

.

b). Tính

,,MP PQ QN

.

*Thực hiện nhiệm vụ

Gv gợi ý

a).

M

là trung điểm của

AD

,

N

là trung

điểm của

MN

thì

MN

được gọi là gì của

hình thang

ABCD

? Nêu cách tính

AB

?

b). Đoạn

MP

thuộc tam giác nào ? Tam

giác đó có gì đặc biệt? Hãy tính

,MP

,PQ

QN

?

Hs trả lời các gợi ý và làm bài vào vở.

a). Chứng minh

FE

là đường trung bình

của hình thang

ABCD

cần chứng minh

E

là trung điểm của

AD

hay chính là xét

ABD

.

b). Chứng minh

BHKI

là hình thang chỉ

ra

//IK BH

từ đó suy ra

2

BH IK

MN

+

=

.

Chứng minh

2BH IK=

xét

BDH

.

Hs lên bảng trình bày.

*Kết luận, nhận định:

GV phương pháp giải, sử dụng định lí tính

chất đường trung bình của tam giác và

hình thang tìm độ dài đoạn thẳng.

* Giao nhiệm vụ

Dạng 5: Sử dụng phối hợp đường trung

bình của hình thang và tam giác để tìm

độ dài đoạn thẳng và chứng minh hai tỉ

số bằng nhau.

Bài 1:

a). Xét hình thang

ABCD

có

M

là trung

điểm

AD

,

N

là trung điểm của

BC

.

MN

là đường trung bình của hình thang

ABCD

nên

//MN AB

và

1

()

2

MN AB CD=+

24AB MN CD cm = − =

b). Ta có

MP

thuộc

ABD

và

M

là trung

điểm của

AD

,

//MP AB

nên

P

là trung

điểm của

BD

hay

MP

là đường trung bình

1

2.

2

MP AB cm = =

*Chứng minh tương tự với

ABC

.

Ta có

1

2.

2

NQ AB cm==

.

Mà

MN MP PQ QN= + +

.

6.PQ MN MP QP cm = − − =

.

Vậy

6.PQ cm=

Bài 2:

Lời giải

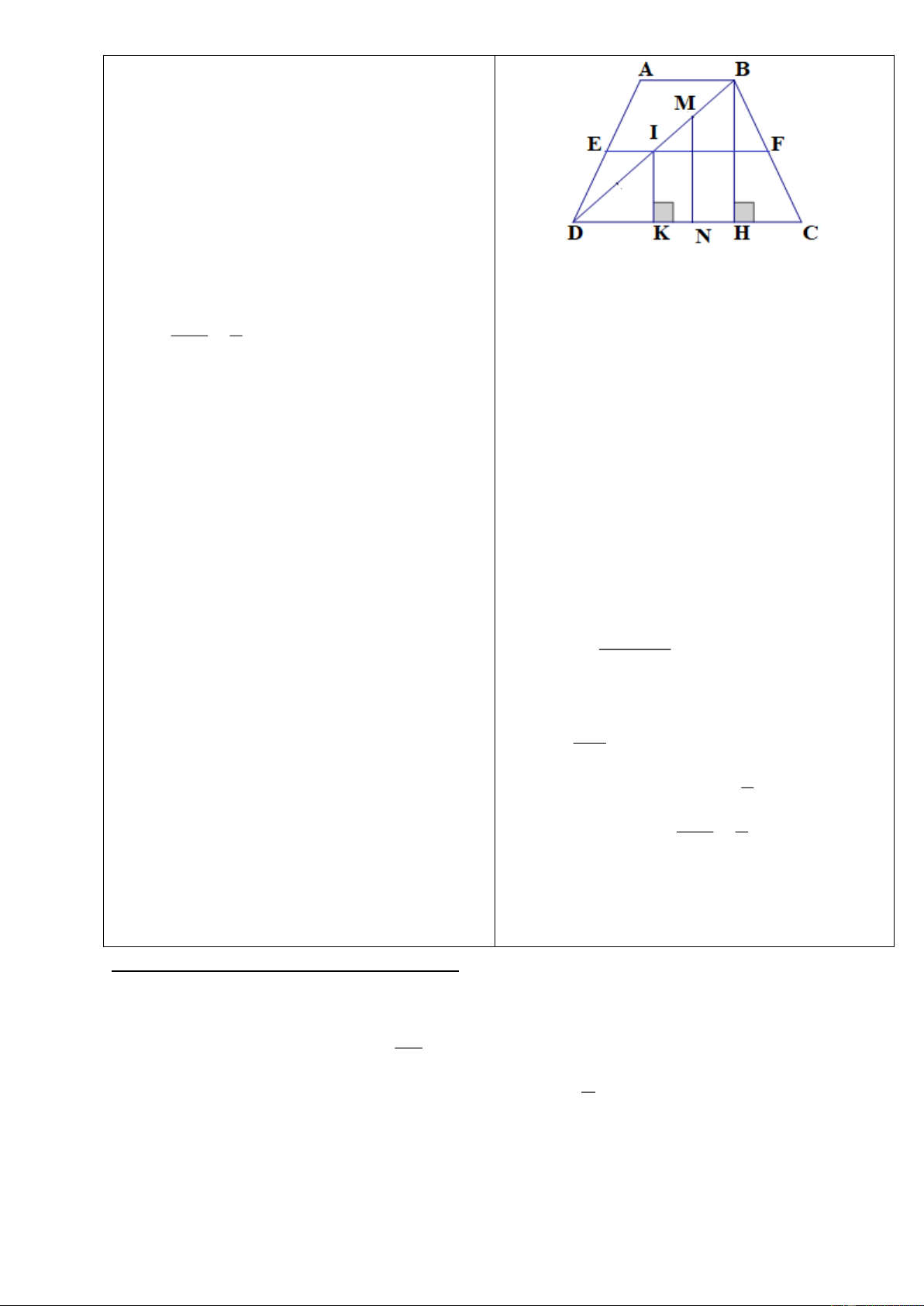
Trang 194

- GV tổ chức hoạt động cá nhân .

Bài 2: Hình thang cân

ABCD

( )

//AB CD

có đường cao

HB

và

I

là trung điểm của

BD

. Qua

I

kẻ

EF

song song với

AB

cắt

AD

tại

E

và cắt

BC

tại

F

.

a). Chứng minh

( )

:2EF AB CD=+

.

b). Từ

I

kẻ

( )

IK DC K DC⊥

. Trên các

đoạn

IB

,

KH

lần lượt hai điểm

M

và

N

sao cho

MI MB=

và

KN NH=

. Chứng

minh:

3

2

MN

IK

=

.

*Thực hiện nhiệm vụ

Gv gợi ý

a). Chứng minh

FE

là đường trung bình

của hình thang

ABCD

?

b). Chứng minh

BHKI

là hình thang và viết

biểu thức tính

MN

? Chứng minh

2BH IK=

từ đó suy ra điều cần chứng

minh?

Hs có thể chứng tứ giác

AMPN

là hình

bình hành.

ABC

có

M

là trung điểm của

AB

,

//MP AC

thì

P

gọi là trung điểm của

BC

và các

,MP NP

là đường trung bình

của

ABC

nên từ đó suy ra tứ giác

AMPN

là hình bình hành có một góc vuông cần

thêm

AM AN=

để trở thành hình vuông.

*Kết luận, nhận định:

GV phương pháp chứng minh hai tỉ số

bằng nhau. Dựa vào đinh lí tính chất

đường trung bình của tam giác, của hình

thang để chỉ ra mối quan hệ giữa các đoạn

thẳng từ đó lập luận để có tỉ số cần chứng

minh.

a). Xét

ABD

có

( )

BI ID I BD=

và

//EI AB

nên

E

là trung điểm của

AD

.

Hình thang

ABCD

có

E

là trung điểm của

AD

.

và

/ / / /FE AB CD

.

Nên

FE

là đường trung bình.

( )

:2EF AB CD = +

b). Ta có

KI DC⊥

và

BH DC⊥

.

//KI BH

nên tứ giác

BHKI

là hình

thang.

Hình thang

BHKI

có

M

là trung điểm của

BI

và

N

là trung điểm của

HK

. Do đó

MN

là đường trung bình của hình thang

BHKI

.

Hay

2

BH IK

MN

+

=

. (1)

Xét

BDH

có

I

là trung điểm của

BD

và

//KI BH

nên

MN

là đường trung bình.

2

BH

IK=

2Hay BH IK=

(2)

Từ (1) và (2) suy ra

3

2

MN IK=

.

Vậy

3

2

MN

IK

=

.

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ 14

1. TRẮC NGHIỆM

Câu 1. Cho tam giác

ABC

. Trên cạnh

,AB AC

lần lượt lấy các điểm

,EF

sao

cho

,AE BE=

AF FC=

. Khi đó

BC

EF

bằng ?

A.

2

. B.

1

. C.

1

2

. D.

3

.

Câu 2. Cho tam giác

ABC

vuông tại

A

như hình vẽ dưới đây: Biết

6cm, 8 cmAB AC==

. Độ dài đường trung bình ứng với cạnh

BC

là.

A.

10 cm

. B.

5 cm

. C.

20 cm

. D.

7 cm

.

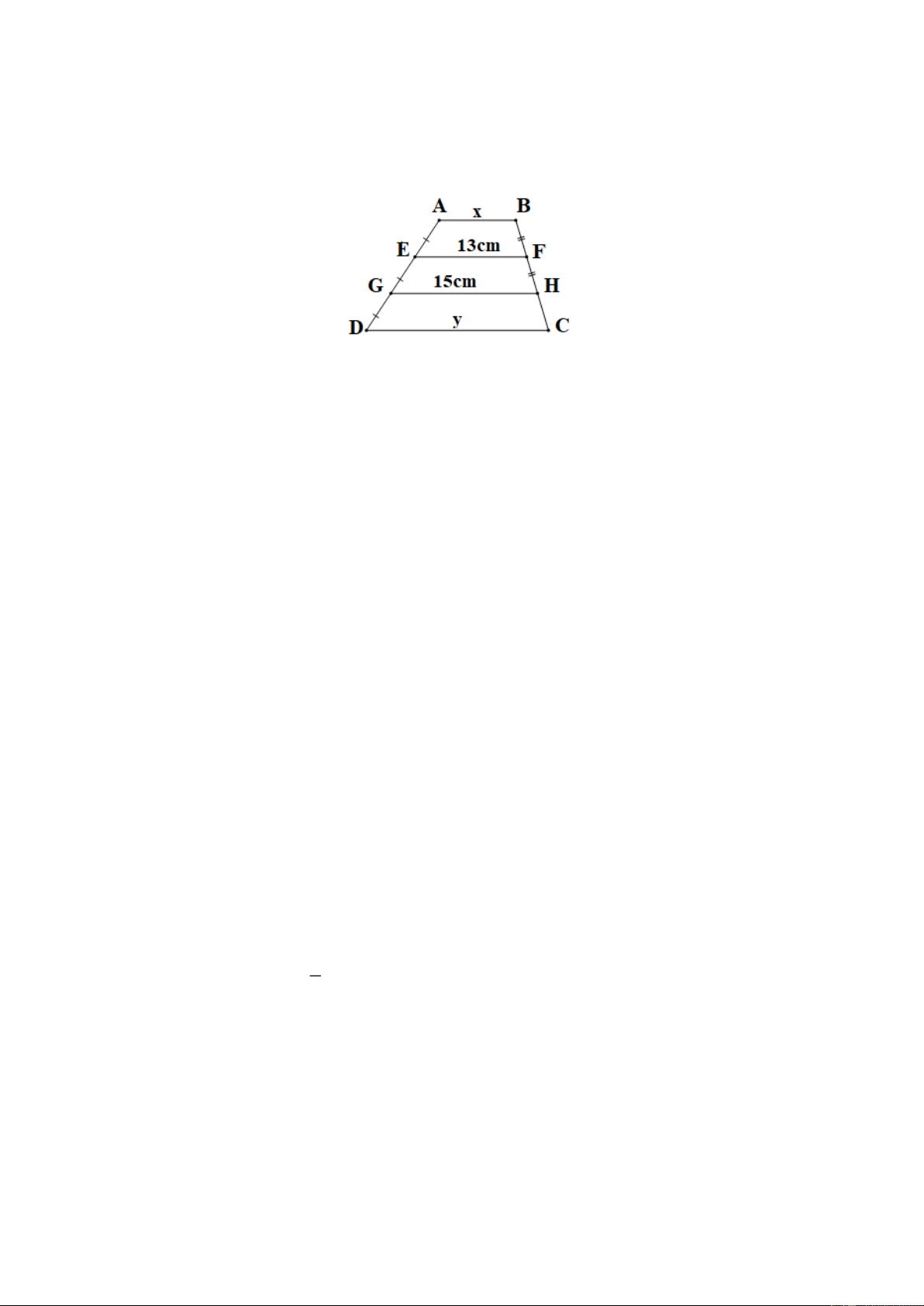
Trang 195

Câu 3. Cho tam giác đều

ABC

có chu vi bằng

60 cm

. Độ dài đường trung bình

ứng với cạnh

AB

là?

A.

20 cm

. B.

10 cm

. C.

30 cm

. D.

40cm

.

Câu 4. Cho hình vẽ sau, biết

AB EF GH DC// // //

. Giá trị của

,xy

lần lượt là?

A.

15 cm; 17 cm

. B.

11 cm; 17 cm

.

C.

12 cm; 16 cm

. D.

17 cm; 11 cm

.

Câu 5. Cho

ABC

đều cạnh

3cm

có

,MN

lần lượt là trung điểm của

,AB AC

.

Độ dài đường trung bình của hình thang

MNCB

là?

A.

1,5 cm

. B.

4,5 cm

. C.

2,25 cm

. D.

2 cm

.

Câu 6. Một hình thang có đáy lớn là

10 cm

, đáy nhỏ ngắn hơn đáy lớn

2 cm

. Độ

dài đường trung bình của hình thang là?

A.

5 cm

. B.

6 cm

. C.

9 cm

. D.

18 cm

.

Câu 7. Độ dài đường trung bình của hình thang là

16 cm

, hai đáy lần lượt tỉ lệ

với

3

và

5

. Khi đó, hai đáy có độ dài lần lượt là?

A.

12 cm; 20 cm

. B.

3 cm; 5 cm

. C.

6 cm; 10 cm

. D.

9 cm; 15 cm

.

2. TỰ LUẬN

Bài 1: Cho

ABC

trung tuyến

AM

, Trên

AC

lấy

E

và

F

sao cho

AE EF FC==

,

BE

cắt

AM

tại

O

.

a). Tứ giác

OEFM

là hình gì? Vì sao? b). Chứng minh

BO 3.OE=

.

Bài 2: Cho tam giác

MNP

,

K

là trung điểm

NP

,

Q

là một điểm nằm trên

cạnh

MN

sao cho

2NQ QM=

. Gọi

I

là giao điểm của

PQ

và

MK

. Chứng

minh

I

là trung điểm của

MK

.

Bài 3: Cho tam giác

ABC

, trung tuyến

AM

. Gọi

I

là trung điểm

AM

,

D

là

giao điểm của

BI

và

AC

.

a) Chứng minh

1

2

AD DC=

. b) So sánh độ dài

BD

và

ID

.

Bài 4: Cho tam giác

ABC

, hai đường trung tuyến

BM

và

CN

cắt nhau tại

G

.

Gọi

D

và

E

lần lượt là trung điểm của

GB

và

GC

. Chứng minh rằng.

a).

//MN DE

. b).

//ND ME

.

Bài 5: Để làm cây thông noel, người thợ sẽ dùng một cái khung sắt hình tam

giác cân như hình vẽ bên, sau đó gắn mô hình cây thông lên. Cho biết thanh

120 .BC cm=

Tính độ dài các thanh

, , .GF HE ID

Trang 196

Bài 6: Toán thực tế đường trung bình: Nhà tâm lý học Abraham Maslow (1908

– 1970) được xem như một trong những người tiên phong trong trường phái

Tâm lý học nhân văn. Năm 1943, ông đã phát triển Lý thuyết về Thang bậc nhu

cầu của con người (như hình vẽ bên). Trong đó,

6BK cm=

. Hãy tính đoạn thẳng

, CJ EH

?

Bài 7: Cho tam giác

ABC

có

A

là trung điểm của

,BD B

là trung điểm của

EC

.

AC

và

DE

cắt nhau tại

I

. Qua

B

kẻ đường thẳng

//BJ CI

cắt

ED

tại

J

.

Chứng minh rằng:

3

DE

DI =

Tuần 16

Tiết 43; 44; 45

Ngày soạn 01/11/2023

Lớp

8A

8B

Ngày dạy:

ÔN TẬP CUỐI CHƯƠNG II

I. MỤC TIÊU

1. Kiến thức:

- Tổng hợp, kết nối các kiến thức của nhiều bài học nhằm giúp HS ôn tập toàn bộ kiến

thức của chương: bảy hằng đẳng thức, các phương pháp phân tích đa thức thành nhân

tử.

Trang 197

- Giúp HS củng cố, khắc sâu những kiến thức đã học.

2. Năng lực

* Năng lực chung:

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu, vận dụng được các hằng đẳng thức, các

phương pháp phân tích đa thức thành nhân tử để tính nhẩm, tính nhanh một cách hợp

lí.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: Thực hiện được các thao tác tư duy so sánh, phân tích, tổng

hợp, khái quát hóa giải quyết được một số bài toán thực tiễn dùng hằng đẳng thức.

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: Thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: Hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

Tổng hợp kiến thức cần nhớ:

Cho A và B là các biểu thức. Ta có một số hằng đẳng thức đáng nhớ sau:

HẰNG ĐẲNG THỨC VIẾT

DẠNG TỔNG

HẰNG ĐẲNG THỨC VIẾT

DẠNG TÍCH

* Bình phương của tổng

( )

2

22

2 A B A AB B+ = + +

* Bình phương của hiệu

( )

2

22

– – 2 A B A AB B=+

* Lập phương của tổng

( )

3

3 2 2 3

3 3 A B A A B AB B+ = + + +

* Lập phương của hiệu

( )

3

3 2 2 3

3 3 A B A A B AB B− = − + −

* Hiệu hai bình phương

( )( )

22

– – A B A B A B=+

* Tổng hai lập phương

( )

3 3 2 2

– A B A B A AB B+ = + +

* Hiệu hai lập phương

( )

3 3 2 2

A B A B A AB B− = − + +

*Chú ý: Các hằng đẳng thức mở rộng

( )

2

2 2 2

2 2 2A B C A B C AB BC AC+ + = + + + + +

Trang 198

( )

2

2 2 2

– – 2 – 2 2A B C A B C AB BC AC+ = + + +

( )

2

2 2 2

– – – 2 2 – 2A B C A B C AB BC AC= + + +

( ) ( )

2

2 2 2

– 2 – A B C A B C AB AC BC+ = + + + −

( ) ( )( )( )

³ ³ ³ ³ 3 A B C A B C A B A C B C+ + = + + + + + +

( )

4 4 3 2 2 3

A B A B A A B AB B+ = + − + −

( )

4 4 3 2 2 3

A B A B A A B AB B− = − + + +

2. BÀI TẬP

Hoạt động của giáo viên

và học sinh

Nội dung

* Giao nhiệm vụ 1

GV tổ chức hoạt động, trả

lời nhanh bài toán trắc

nghiệm 1

Dạng 1: Khai triển biểu thức. Đưa biểu thức về dạng

hằng đẳng thức.

Phương pháp:

- Nhận diện số A và số B trong hằng đẳng thức.

- Viết khai triển theo đúng công thức của hằng đẳng thức

đã học.

Bài 1. Trắc nghiệm

Câu 1.

( )

2

2xy−

bằng :

A.

2

2xy−

. B.

2

2xy+

.

C.

( )( )

22x y x y−+

. D.

( )( )

22x y x y++

.

Câu 2.

32

11

3 27

x x x− + −

bằng :

A.

3

1

3

x −

. B.

3

1

3

x



−





. C.

3

1

3

x



+





. D.

3

1

3

x



−





.

Câu 3.

( )

2

7x −

bằng :

A.

( )

2

7 x−

. B.

2

14 49xx−+

. C.

2

2 49xx−+

. D.

2

14 7xx−+

.

*Thực hiện nhiệm vụ

HS thực hiện nhiệm vụ.

HS nào không chọn đúng

thì gv hướng dẫn theo các

bước.

GV yêu cầu nhận dạng

HĐT nào?

Trả lời

Câu 1. C

Câu 2. B

Câu 3. B

Trang 199

Đâu là biểu thức A ?

Đâu là biểu thức B?

Dự đoán biểu thức và khai

triển thử.

HS trả lời các câu hỏi

được GV đề xuất hoặc nêu

cách giải 1 bài toán

*Kết luận, nhận định:

GV khai thác các câu hỏi

theo các hướng khác nhau

ra được đáp án.

Rút ra phương pháp :

- Nhận diện số A và số B

trong hằng đẳng thức.

- Viết khai triển theo đúng

công thức của hằng đẳng

thức đã học

* Giao nhiệm vụ 2

- GV: yêu cầu hs hoạt

động cá nhân.

GV có thể hướng dẫn nếu

HS gặp khó khăn.

Đếm số hạng tử? quan sát

dấu của các hạng tử?

Dự đoán hằng đẳng thức

để áp dụng

Đâu là biểu thức A ? Đâu

là B ?

*Thực hiện nhiệm vụ 2

- HS: đọc đề, quan sát và

thục hiện nhiệm vụ

- HS thực hiện nhiệm vụ,

báo cáo kết quả:

*Báo cáo kết quả

- Yêu cầu đại diện học

sinh trả lời các câu hỏi

- HS thực hiện nhiệm vụ,

đại diện trả lời các câu

hỏi:

*Đánh giá kết quả

- Yêu cầu học sinh nhận

Bài 2: Viết các biểu thức sau dưới dạng bình phương

của một tổng hoặc một hiệu.

a)

2

44xx-+

b)

2

10 25xx-+

c)

2

1

4

x

x-+

d)

( ) ( )

2

9 1 6 1 1xx+ - + +

e)

( )

2

22

2 8 2 16x y x xy x- - - +

Lời giải

a)

( )

2

4 4 2x x x- + = -

;

b)

( )

2

10 25 5x x x- + = -

;

c)

2

11

42

xx

x

æö

÷

ç

÷

- + = -

ç

÷

ç

÷

ç

èø

;

d)

( ) ( )

2

9 1 6 1 1xx+ - + +

( ) ( )

2

3 1 1 3 2xx

éù

= + - = -

êú

ëû

e)

( )

2

22

2 8 2 16x y x xy x- - - +

( ) ( ) ( )

22

2 2.4 2 4x y x x y x= - - - +

( ) ( )

22

2 4 3 2x y x x y= - - = +

Trang 200

xét câu trả lời của bạn

- HS Nhận xét, đánh giá

câu trả lời của bạn

- GV nhận xét và nhấn

mạnh sau đó chốt lại thành

nội dung.

Rút ra phương pháp :

- Nhận diện số A và số B

trong hằng đẳng thức.

- Viết khai triển theo đúng

công thức của hằng đẳng

thức đã học

* Giao nhiệm vụ 3

- GV: yêu cầu hs hoạt

động cá nhân.

*Thực hiện nhiệm vụ3

- HS: đọc đề, quan sát và

thục hiện nhiệm vụ theo

như bài tập trong nhiệm

vụ 2.

- HS thực hiện nhiệm vụ,

báo cáo kết quả:

*Báo cáo kết quả

- Yêu cầu đại diện học

sinh trả lời các câu hỏi

- HS thực hiện nhiệm vụ,

đại diện trả lời các câu

hỏi:

*Đánh giá kết quả

- Yêu cầu học sinh nhận

xét câu trả lời của bạn

- HS Nhận xét, đánh giá

câu trả lời của bạn

- GV nhận xét và nhấn

mạnh sau đó chốt lại thành

nội dung.

Bài 3: Viết các biểu thức sau dưới dạng lập phương của

một tổng hoặc một hiệu:

a)

32

6 12 8x x x+ + +

b)

23

8 12 6x x x- + -

c)

3 2 2 4 6

8 12 6x x y xy y- + -

d)

32

6 12 8x x x- + - +

.

Lời giải

a)

3

( 2)x +

b)

3

(2 )x-

c)

23

(2 )xy-

d)

3

( 2)x-+

.

* Giao nhiệm vụ 1

GV tổ chức hoạt động, trả

lời nhanh bài toán trắc

nghiệm 1

Dạng 2: Rút gọn biểu thức

Phương pháp:

- Khai triển các hằng đẳng thức có trong biểu

thức.

- Rút gọn các đơn thức đồng dạng.

Trang 201

Bài 1. Trắc nghiệm

Câu 1. Rút gọn biểu thức

( ) ( )

22

a b a b+ − −

được kết quả là

A.

4ab

. B.

4ab−

. C.

0

. D.

2

2b

.

Câu 2.

( )

2

3 3 9x x x+ − +

bằng

A.

33

3x −

. B.

3

27x +

. C.

9x −

. D.

( )

3

3x +

.

Câu 3. Điền đơn thức vào chỗ trống:

( )

2 3 3

3 ....... 3 27x y xy y x y+ − + = +

A.

9x

. B.

2

6x

. C.

9xy

. D.

2

9x

.

*Thực hiện nhiệm vụ

HS thực hiện nhiệm vụ.

HS nào không chọn đúng

thì gv hướng dẫn theo các

bước.

GV yêu cầu nhận dạng và

vận dụng HĐT nào?

*Kết luận, nhận định:

GV khai thác các câu hỏi

theo các hướng khác nhau

ra được đáp án.

Rút ra phương pháp:

- Khai triển các

hằng đẳng thức có trong

biểu thức.

- Rút gọn các đơn

thức đồng dạng.

Đáp án

Câu 1. A

Câu 2. B

Câu 3. D

* Giao nhiệm vụ 2

- GV: yêu cầu hs hoạt

động cá nhân.

GV có thể hướng dẫn nếu

HS gặp khó khăn.

Nhận diện những HĐT có

trong đề bài?

Khai triển HĐT đó ra.

Thu gọn các đơn thức

đồng dạng.

Lưu ý :

Dự đoán hằng đẳng thức

Bài 2: Rút gọn biểu thức:

a)

( ) ( )

22

A x y x y= - + +

b)

( ) ( )

22

2 1 2 2 3 4B x x= - - - +

c)

( ) ( )( ) ( )

22

1 2 1 3 3C x x x x= - - - - + -

Lời giải

a)

( ) ( )

22

A x y x y= - + +

2 2 2 2

22x xy y x xy y= - + + + +

22

22xy=+

;

b)

( ) ( )

22

2 1 2 2 3 4B x x= - - - +

( )

22

4 4 1 2. 4 12 9 4x x x x= - + - - + +

Trang 202

để áp dụng

Đâu là biểu thức A ? Đâu

là B ?

Quy tắc phá ngoặc trước

có dấu trừ

*Thực hiện nhiệm vụ 2

- HS: đọc đề, quan sát và

thục hiện nhiệm vụ

- HS thực hiện nhiệm vụ,

báo cáo kết quả:

*Báo cáo kết quả

- Yêu cầu đại diện học

sinh trả lời các câu hỏi

- HS thực hiện nhiệm vụ,

đại diện trả lời các câu

hỏi:

*Đánh giá kết quả

- Yêu cầu học sinh nhận

xét câu trả lời của bạn

- HS Nhận xét, đánh giá

câu trả lời của bạn

- GV nhận xét và nhấn

mạnh sau đó chốt lại thành

nội dung ghi chép

Rút ra phương pháp:

- Khai triển các

hằng đẳng thức có trong

biểu thức.

- Rút gọn các đơn

thức đồng dạng.

22

4 4 1 8 24 18 4x x x x= - + - + - +

2

4 20 13xx= - + -

c)

( ) ( )( ) ( )

22

1 2 1 3 3C x x x x= - - - - + -

( ) ( )

2

1 3 2 4xx

éù

= - - - = =

êú

ëû

* Giao nhiệm vụ 3

- GV: yêu cầu hs hoạt

động cá nhân.

*Thực hiện nhiệm vụ3

- HS: đọc đề, quan sát và

thục hiện nhiệm vụ

- HS thực hiện nhiệm vụ,

báo cáo kết quả:

*Báo cáo kết quả

- Yêu cầu đại diện học

sinh trả lời các câu hỏi

- HS thực hiện nhiệm vụ,

Bài 3: Rút gọn các biểu thức sau:

a)

3

( 2 ) 6 ( 2 )x y xy x y+ - +

;

b)

( ) ( )

33

3

2a b a b a- + + -

;

c)

3 3 3

( 2) ( 2) 3 ( 2)( 2)x x x x x x+ + - + - + -

Lời giải

a)

3

( 2 ) 6 ( 2 )x y xy x y+ - +

3 2 2 3 2 2 3 3

6 12 8 6 12 8x x y xy y x y xy x y= + + + - - = +

b)

( ) ( )

33

3

2a b a b a- + + -

3 2 2 3 3 2 2 3 3

3 3 3 3 2a a b ab b a a b ab b a= - + - + + + + -

3 2 3 2

2 6 2 6a ab a ab= + - =

.

c)

3 3 3

( 2) ( 2) 3 ( 2)( 2)x x x x x x+ + - + - + -

Trang 203

đại diện trả lời các câu

hỏi:

*Đánh giá kết quả

- Yêu cầu học sinh nhận

xét câu trả lời của bạn

- HS Nhận xét, đánh giá

câu trả lời của bạn

- GV nhận xét và nhấn

mạnh sau đó chốt lại thành

nội dung ghi chép

3 2 3 2 3 3

6 12 8 6 12 8 3 12x x x x x x x x x= + + + + - + - + - +

36x=

.

* Giao nhiệm vụ 4

- GV: yêu cầu hs hoạt

động cá nhân.

GV: hướng dẫn hs tính

nhẩm

Vận dụng đưa về hằng

đẳng thức nào?

Vận dụng HDT sao cho

phù hợp và có thể nhẩm

được

*Thực hiện nhiệm vụ 4

- HS: đọc đề, quan sát và

thục hiện nhiệm vụ

- HS thực hiện nhiệm vụ,

báo cáo kết quả:

*Báo cáo kết quả

- Yêu cầu đại diện học

sinh trả lời các câu hỏi

- HS thực hiện nhiệm vụ,

đại diện trả lời các câu

hỏi:

*Đánh giá kết quả

- Yêu cầu học sinh nhận

xét câu trả lời của bạn

- HS Nhận xét, đánh giá

câu trả lời của bạn

- GV nhận xét và nhấn

mạnh sau đó chốt lại thành

nội dung ghi chép

Bài 4. Tính nhanh

a)

2

49

b)

22

23 21-

c)

22

89 11 22.89++

Lời giải

a)

( )

2

22

49 50 1 50 100 1 2401= - = - + =

.

b)

( )( )

22

23 21 23 21 23 21 44.2 88- = - + = =

c)

22

89 11 22.89++

22

89 2.98.11 11= + +

22

(89 11) 100 10000= + = =

* Giao nhiệm vụ 5

Bài 5: Chứng minh các giá trị của biểu thức sau không

Trang 204

- GV: yêu cầu hs hoạt

động cá nhân.

HS

*Thực hiện nhiệm vụ 5

- HS: đọc đề, quan sát và

thục hiện nhiệm vụ.

- HS có thể làm theo 2

hướng vận dụng hằng

đẳng thức hoặc nhân đa

thức.

- HS thực hiện nhiệm vụ,

báo cáo kết quả:

*Báo cáo kết quả

- Yêu cầu đại diện học

sinh trả lời các câu hỏi

- HS thực hiện nhiệm vụ,

đại diện trả lời các câu

hỏi:

*Đánh giá kết quả

- Yêu cầu học sinh nhận

xét câu trả lời của bạn

- HS Nhận xét, đánh giá

câu trả lời của bạn

- GV nhận xét và nhấn

mạnh sau đó chốt lại thành

nội dung ghi chép

phụ thuộc vào biến

a)

( )

23

6 2 2 4 6 2A x x x x= + - + - -

b)

( )

23

2 3 1 9 3 1 54B x x x x= + - + -

c)

( ) ( ) ( )

( )

22

2

2 2 1 3 3 9 1C x x x x x x= - + + + + + - + -

Lời giải

a)

( )

23

6 2 2 4 6 2A x x x x= + - + - -

( )

33

6 8 6 2A x x= + - -

33

6 48 6 2A x x= + - -

46A =

b)

( )

23

2 3 1 9 3 1 54B x x x x= + - + -

( )

33

2 27 1 54B x x= + -

33

54 2 54B x x= + -

2B =

c)

( ) ( ) ( )

( )

22

2

2 2 1 3 3 9 1C x x x x x x= - + + + + + - + -

( )

2 2 3

4 4 4 4 1 27 1C x x x x x x= - + + + + + + + -

3 2 2 3

4 4 4 4 1 27 1C x x x x x x= - - - + + + + + -

27C =

* Giao nhiệm vụ 1

GV tổ chức hoạt động, trả

lời nhanh bài toán trắc

nghiệm 1

DẠNG 3: Toán tìm x

Dùng phương pháp đặt nhân tử chung, đưa về dạng tích

A(x).B(x).... 0=

(vế trái là tích các đa thức

và mỗi đa thức là một thừa số)

A(x) 0 x

B(x) 0 x

....... ...

==





 =  =





Bài 1: Trắc nghiệm

Câu 1. Tìm x biết

( )

( 1) 6 0xx+ − =

.

A.

1; 6xx= = −

. B.

1; 6xx==

. C.

1; 6xx= − =

. D.

1; 6xx= − = −

Câu 2. Tìm x biết

( ) ( )

7 2 7 0x x x− − − =

.

A.

2; 7xx==

. B.

2; 7xx= = −

. C.

2; 7xx= − =

. D.

2; 7xx= − = −

Trang 205

Câu 3. Tìm x biết

2

9 4 0x −=

.

A.

2

3

x =

. B.

2

3

x =

. C.

3

2

x =

. D.

2

3

x =−

*Thực hiện nhiệm vụ

HS thực hiện nhiệm vụ.

HS nào không chọn đúng

thì gv hướng dẫn theo các

bước.

GV: yêu cầu nhận dạng

và vận dụng phương pháp

phân tích thành nhân tử.

*Kết luận, nhận định:

GV khai thác các câu hỏi

theo các hướng khác nhau

ra được đáp án.

Rút ra phương pháp:

Dùng phương pháp đặt

nhân tử chung, đưa về

dạng tích

A(x).B(x).... 0=

(vế

trái là tích các đa thức và

mỗi đa thức là một thừa

số)

A(x) 0 x

B(x) 0 x

....... ...

==





 =  =





Đáp án

Câu 1. C Câu 2. B Câu 3. B

* Giao nhiệm vụ 2

- GV: yêu cầu hs hoạt

động cá nhân.

GV: yêu cầu nhận dạng

và vận dụng phương pháp

phân tích thành nhân tử.

*Thực hiện nhiệm vụ 2

- HS: đọc đề, quan sát và

thục hiện nhiệm vụ

- HS thực hiện nhiệm vụ,

báo cáo kết quả:

*Báo cáo kết quả

- Yêu cầu đại diện học

sinh trả lời các câu hỏi

Bài 2: Tìm x.

a)

2

9 – 6 – 3 0xx =

b)

32

9 27 19 0x x x+ + + =

c)

( )( ) ( )

( )

2

5 – 5 – 2 – 2 4 3x x x x x x+ + + =

Lời giải

a)

2

9 – 6 – 3 0xx =

2

9 – 2.3 .1 1 – 4 0xx + =

( )

2

3 – 1 – 4 0x =

(Hiệu của hai bình phương)

( )( )

3 – 1 2 3 – 1 – 2 0xx+=

( )( )

3 1 3 – 3 0xx+=

Trang 206

- HS thực hiện nhiệm vụ,

đại diện trả lời các câu

hỏi:

*Đánh giá kết quả

- Yêu cầu học sinh nhận

xét câu trả lời của bạn

- HS Nhận xét, đánh giá

câu trả lời của bạn

- GV nhận xét và nhấn

mạnh sau đó chốt lại thành

nội dung ghi chép

Rút ra phương pháp:

Dùng phương pháp đặt

nhân tử chung, đưa về

dạng tích

A(x).B(x).... 0=

(vế trái là tích các đa thức

và mỗi đa thức là một

thừa số)

A(x) 0 x

B(x) 0 x

....... ...

==





 =  =





1

3 1 0 3 1

3

3 3 0 3 3

1

xx

x

xx

x



+ = = −

=−





  





− = =



=



Vậy

1

;1

3

x





−







b)

32

9 27 19 0x x x+ + + =

3 2 2 3

3. .3 3. .3 3 – 8 0x x x + + + =

( )

3

3 – 8 0x +=

( )

3

3 – 2 0x +=

(Hiệu của hai lập phương)

( ) ( ) ( )

2

3 – 2 3 2 3 4 0x x x







++



+ + + =

( )

2

1 6 9 2 6 4 0x x x x + + + + + + =

( )

2

1 8 19 0x x x+ + + =

( )

2

1 2.4 16 3 0x x x+ + +





+=

( ) ( )

2

1 4 3 0xx







+ + + =

( )

2

1 0 4 3 0x Vì x + = + + 

với mọi giá trị của

biến x.

1x = −

Vậy

1x =−

c)

( )( ) ( )

( )

2

5 – 5 – 2 – 2 4 3x x x x x x+ + + =

( ) ( )

23

– 25 – 8 – 3 0x x x + =

33

– 25 – – 8 – 3 0x x x=

(Thu gọn đồng dạng)

25 11x − =

11

25

x = −

Vậy

11

25

x =−

* Giao nhiệm vụ 3

- GV: yêu cầu hs hoạt

động cá nhân.

*Thực hiện nhiệm vụ 3

- HS: đọc đề, quan sát và

thục hiện nhiệm vụ

- HS thực hiện nhiệm vụ,

báo cáo kết quả:

Bài 3: Tìm x, biết:

a)

( )

2 7 5 35 0x x x- + - =

b)

( )

3 7 21 0.x x x- - + =

c)

32

2 2 0x x x- + - =

d)

32

5 5 0x x x- - + =

Lời giải

a)

( )

2 7 5 35 0x x x- + - =

Trang 207

*Báo cáo kết quả

- Yêu cầu đại diện học

sinh trả lời các câu hỏi

- HS thực hiện nhiệm vụ,

đại diện trả lời các câu

hỏi:

*Đánh giá kết quả

- Yêu cầu học sinh nhận

xét câu trả lời của bạn

- HS Nhận xét, đánh giá

câu trả lời của bạn

- GV nhận xét và nhấn

mạnh sau đó chốt lại thành

nội dung.

Lưu ý : cách trình bày

dạng toán này và kết luận

bài toán

( ) ( )

2 7 5 7 0x x xÞ - + - =

( )( )

7 2 5 0xxÞ - + =

7xÞ=

hoặc

5

2

x

-

=

Vậy

5

;7

2

x





−







b)

( )( )

3 7 0xxÞ - - =

3x =

hoặc

7x =

Vậy





3;7x

c)

( )

2

2 1 0 2xx x- = Þ =+

Vậy

2x =

d)

( )

2

5 0 5; 1;1 1x x x x xÞ - = =- Þ = = -

Vậy





1;1;5x−

* Giao nhiệm vụ 4

- GV: yêu cầu hs hoạt

động cá nhân.

- GV : Gợi ý với những

bài toán 2 biến thường đưa

về dạng

22

0

A

AB

B

ì

ï

=

ï

+ = Û

í

ï

=

ï

î

*Thực hiện nhiệm vụ 4

- HS: đọc đề, quan sát và

thục hiện nhiệm vụ

- HS thực hiện nhiệm vụ,

báo cáo kết quả:

*Báo cáo kết quả

- Yêu cầu đại diện học

sinh trả lời các câu hỏi

- HS thực hiện nhiệm vụ,

đại diện trả lời các câu

hỏi:

*Đánh giá kết quả

- Yêu cầu học sinh nhận

xét câu trả lời của bạn

Bài 4: Tìm

,xy

biết:

a)

22

2 4 5 0x y x y+ - + + =

b)

22

4 6 12 18 0x y x y+ + - + =

c)

22

5 9 12 6 9 0x y x y x+ - - + =

Gợi ý: Đưa về dạng

22

0

A

AB

B

ì

ï

=

ï

+ = Û

í

ï

=

ï

î

Lời giải

a)

22

( 1) (y 2) 0x - + + =

Để đẳng thức trên thỏa mãn thì:

10

1; 2

20

x

xy

y

ü

ï

-=

ï

Þ Þ = = -

ý

ï

+=

ï

þ

Vậy

1; 2xy= = -

b)

22

( 3) (2y 3) 0x - + - =

Để đẳng thức trên thỏa mãn thì:

30

3

3;

2 3 0

2

x

xy

y

ü

ï

-=

ï

Þ = =

ý

ï

-=

ï

þ

Vậy

3

3;

2

xy==

c)

22

( 3) (3y 2 ) 0xx- + - =

Để đẳng thức trên thỏa mãn thì:

Trang 208

- HS Nhận xét, đánh giá

câu trả lời của bạn

- GV nhận xét và nhấn

mạnh sau đó chốt lại thành

nội dung ghi chép

30

3; 2

3 2 0

x

xy

yx

ü

ï

-=

ï

Þ = =

ý

ï

-=

ï

þ

Vậy

3; 2xy==

DẠNG 4: Chứng minh một biểu thức lũy thừa chia

hết cho số a

Dùng phép toán lũy thừa (đã học Lớp 6) và phương pháp

Đặt Nhân Tử Chung để phân tích biểu thức lũy thừa

thành nhân tử trong đó có một nhân tử là số a

Vậy biểu thức đã cho chia hết cho số a

* Giao nhiệm vụ 1

- GV: yêu cầu hs hoạt

động cá nhân.

- GV Hướng dẫn: Dùng

phép toán lũy thừa (đã

học Lớp 6) và phương

pháp Đặt Nhân Tử Chung

để phân tích biểu thức lũy

thừa thành nhân tử trong

đó có một nhân tử là số a

Vậy biểu thức đã cho chia

hết cho số a

*Thực hiện nhiệm vụ 1

- HS: đọc đề, quan sát và

thục hiện nhiệm vụ

- HS thực hiện nhiệm vụ,

báo cáo kết quả:

*Báo cáo kết quả

- Yêu cầu đại diện học

sinh trả lời các câu hỏi

- HS thực hiện nhiệm vụ,

đại diện trả lời các câu

hỏi:

*Đánh giá kết quả

- Yêu cầu học sinh nhận

xét câu trả lời của bạn

- HS Nhận xét, đánh giá

câu trả lời của bạn

- GV nhận xét và nhấn

mạnh sau đó chốt lại thành

nội dung.

Bài 1: Chứng minh

a)

( ) ( )

22

7 2 2 7nn- - -

chia hết cho

5

( )

nZÎ

b)

( ) ( )

22

5 2 2 5nn- - -

chia hết cho

21

( )

nZÎ

Lời giải

a) Ta có:

( ) ( )

22

7 2 2 7nn- - -

( ) ( ) ( ) ( )

7 2 2 7 7 2 2 7n n n n

é ùé ù

= - + - - - -

ê úê ú

ë ûë û

( )( ) ( ) ( )

9 9 5 5 9 1 .5. 1n n n n= - + = - +

( )

2

45 1 5n=-M

b) Ta có:

( ) ( )

22

5 2 2 5nn- - -

( ) ( ) ( ) ( )

5 2 2 5 5 2 2 5n n n n

é ùé ù

= - + - - - -

ê úê ú

ë ûë û

( ) ( ) ( ) ( )

7 7 . 3 3 7. 1 .3. 1n n n n= - + = - +

( )

2

21 1 21n=-M

* Giao nhiệm vụ 2

Bài 2 : Chứng minh

Trang 209

- GV: yêu cầu hs hoạt

động cá nhân.

*Thực hiện nhiệm vụ 1

- HS: đọc đề, quan sát và

thục hiện nhiệm vụ

- HS thực hiện nhiệm vụ,

báo cáo kết quả:

*Báo cáo kết quả

- Yêu cầu đại diện học

sinh trả lời các câu hỏi

- HS thực hiện nhiệm vụ,

đại diện trả lời các câu

hỏi:

*Đánh giá kết quả

- Yêu cầu học sinh nhận

xét câu trả lời của bạn

- HS Nhận xét, đánh giá

câu trả lời của bạn

- GV nhận xét và nhấn

mạnh sau đó chốt lại thành

nội dung.

a)

( )

2

100 7 3n-+

chia hết cho 7

( )

nZÎ

b)

( ) ( )

2

1 2 1n n n n- - -

chia hết cho

21

( )

nZÎ

Lời giải

a) Ta có:

( )

2

100 7 3n-+

( ) ( )

10 7 3 10 7 3nn

é ùé ù

= + + - +

ê úê ú

ë ûë û

13 7 7 7nn

é ùé ù

= + -

ê úê ú

ë ûë û

7 13 7 1 7nn

é ùé ù

= + -

ê úê ú

ë ûë û

M

b) Ta có:

( ) ( )

2

1 2 1n n n n- - -

3 2 2

22n n n n= - - +

2

( 3 2)n n n= - +

( 1)( 2)n n n= - -

Do tích của ba số nguyên liên tiếp nên tích của chúng

chia hết cho 6

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ ….

1. TRẮC NGHIỆM

Câu 1.

2

1x −

bằng:

A.

( )( )

11xx−+

. B.

( )( )

11xx++

.

C.

2

21xx++

. D.

2

21xx+−

.

Câu 3. Đa thức

33

1mn m n− + −

được phân tích thành nhân tử là

A.

( )

2

11n n m+−

. B.

( )( )

2

11n n m+−

.

C.

( )

2

11nm++

. D.

( )

3

11nm+−

.

Câu 4. Đa thức

44xy xz y z− − +

được phân tích thành nhân tử là

A.

( )( )

41x y z+−

. B.

( )( )

41x y z−−

.

C.

( )( )

41x y z−+

. D.

( )( )

41x x y z+ + +

.

Câu 5. Đa thức

32

2x x x−+

được phân tích thành nhân tử là

A.

( )

2

1xx−

. B.

( )

2

1xx−

.

C.

( )

2

1xx−

. D.

( )

2

1xx+

.

2. TỰ LUẬN

Trang 210

Bài 1: Rút gọn biểu thức:

a)

( ) ( ) ( )( )

22

1 1 3 1 1 ;a a a a+ − − − + −

b)

( ) ( ) ( )( )

22

3 2 2 3

1 3 2 3 1 .m m m m m m− + + − − − − +

c)

( ) ( )( )

3

2 4 2 2

1 1 1 ;a a a a− − + + −

d)

( )( ) ( )

3

4 2 2 2

3 9 3 3 .a a a a− + + − +

Bài 2: Chứng minh rằng giá trị của các biểu thức sau không phụ thuộc vào biến

x

:

a)

( ) ( ) ( )

2 3 1 6 1 3 8x x x x x- - + - -

b)

( ) ( )

1 2 2

0,2 5 1 4 3

2 3 3

x x x

æö

÷

ç

÷

- - + + -

ç

÷

ç

÷

ç

èø

Bài 3: Phân tích biểu thức thành nhân tử rồi tính giá trị biểu thức.

a)

2

11

xx

2 16

++

tại

49,75x =

b)

22

– – 2 – 1 x y y

tại

93; 6xy==

c)

3 2 2 3

27 – 27 9 – y y x yx x+

tại

28; 9xy==

Bài 4: Phân tích các đa thức sau thành nhân tử:

( )

2

22

) 5 2 2 ;a a b ab+ − − +

( ) ( )

22

) 4 3 18 4 3 ;b a a a a− − − +

( )

2

) 2 3 4 ;c x x− + + −

33

)1 25 27 .d a b−

Bài 5: Chứng minh rằng:

a)

9

21−

chia hết cho 73

b)

64

5 10−

chia hết cho 9.

Tuần 17

Tiết 46; 47; 48

Ngày soạn 01/11/2023

Lớp

8A

8B

Ngày dạy:

ÔN TẬP PHÂN TÍCH SỐ LIỆU THỐNG KÊ DỰA VÀO BIỂU ĐỒ

I. MỤC TIÊU

1. Về kiến thức:

- Phát hiện được vấn đề hoặc quy luật đơn giản dựa trên phân tích các số liệu.

- Nhận ra tính hợp lí của dữ liệu được biểu diễn.

- Phát hiện mối liên hệ giữa thống kê với các kiến thức kĩ năng trong môn học.

2. Về năng lực:

* Năng lực chung:

Trang 211

- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại

lớp.

- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ

nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.

* Năng lực đặc thù:

- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được vấn đề khi phân biểu đồ.

- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực

mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích biểu đồ.

3. Về phẩm chất:

- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.

- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo

nhóm, trong đánh giá và tự đánh giá.

- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.

II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU

1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.

2. Học sinh: SGK, thước thẳng, bảng nhóm.

III. TIẾN TRÌNH DẠY HỌC

1. KIẾN THỨC CẦN NHỚ

Tổng hợp kiến thức cần nhớ:

* Lưu ý khi đọc biểu đồ:

+ Trong biểu đồ cột khi gốc của trục đứng khác

0

thì tỉ lệ chiều cao giữa các cột

không bằng tỉ lệ số liệu mà chúng biểu diễn.

+ Trong biểu đồ đoạn thẳng khi các điểm quan sát trên trục ngang không đều nhau ta

không thể dựa và độ dốc để kết luận về độ tăng hay giảm của đại lượng được biểu

diễn.

* Đọc biểu đồ:

+ Khi phân tích số liệu ta có thể kết hợp thông tin từ hai hay nhiều biểu đồ.

+ Để so sánh sự thay đổi của hai hay nhiều đại lượng theo thời gian, người ta thường

biểu diễn cùng một biểu đồ.

2. BÀI TẬP

Hoạt động của giáo viên và học sinh

Nội dung

* Giao nhiệm vụ

- GV tổ chức hoạt động, trả lời nhanh bài

toán trắc nghiệm

Phần I: Bài tập trắc nghiệm

Câu hỏi trắc nghiệm

Câu 1: Cho biểu đồ:

Trang 212

Khẳng định nào sau đây là đúng?

A. Số HS giỏi lớp 6A gấp đôi số HS Giỏi lớp 6B.

B. Số HS giỏi lớp 6C gấp bốn lần số HS Giỏi lớp 6B.

C. Số HS giỏi lớp 6C gấp đôi số HS Giỏi lớp 6B.

D. Số HS giỏi lớp 6C gấp đôi số HS Giỏi lớp 6A.

Câu 2: Cho biểu đồ:

Bạn An khẳng định thu nhập của của người công nhân trong năm

2020

tăng đột biến. khẳng

định đó đúng hay sai?

A. Đúng.

B. Sai.

Câu 3: Cho hai biểu đồ:

(a)

(b)

Bạn Bình khẳng định: hai biểu đồ trên biểu diễn cùng một dữ liệu là đúng hay sai?

A. Đúng.

4

6

8

10

12

14

16

18

6A 6B 6C

Số học sinh giỏi lớp 6

6A 6B 6C

0

50

100

150

2002 2004 2006 2020

Thu nhập của một công

nhân theo từng năm

(triệu đồng)

Thu nhập(triệu đồng)

35

37

43

32

30

35

40

45

3 4 5 6

Số lượng máy tính

bán được trong tháng

35

37

43

32

0

20

40

60

3 4 5 6

Số lượng máy tính

bán được trong tháng

Trang 213

B. Sai.

Câu 4: Trong tháng

2

, cửa hàng thứ nhất bán được ít hơn cửa hàng thứ hai bao nhiêu đôi

giày thể thao?

A.

5

B.

10

C.

12

D.

14

Câu 5: Cho biểu đồ:

Năm

2020

thu nhập bình quân đầu người của Singapore bằng khoảng bao nhiêu lần thu

nhập bình quân đầu người của Việt Nam?

A. Khoảng

18

lần

B. Khoảng

22

lần

C. Khoảng

25

lần

D. Khoảng

30

lần

Câu 6: Từ năm 2018 đến năm 2019 năng lượng than đã tăng bao nhiêu phần trăm?

A.

1,71%

B.

3,27%

C.

3,73%

D.

4,74%

Câu 7: Trong tháng mấy tốc độ gió ở Nha Trang và Hà Nội chênh lệch lớn nhất?

Trang 214

A. Tháng

1

B. Tháng

2

C. Tháng

11

D. Tháng

12

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện.

Câu 1: Lưu ý gốc của trục đứng khác

0

nên tỉ lệ chiều cao giữa các cột không bằng

tỉ lệ số học sinh giỏi của các lớp.

- HS trả lời các câu hỏi được GV đề xuất

Câu 1: chọn A

- Tỉ lệ chiều cao giữa các cột không bằng tỉ

lệ số học sinh giỏi của các lớp.

Câu 2: Lưu ý các mốc trên trục ngang

khoảng cách không đều nhau nên không thể

căn cứ vào độ dốc của đoạn thẳng để nhận

xét.

Câu 2: Chọn Sai (đáp án B)

các mốc trên trục ngang khoảng cách không

đều nhau nên không thể căn cứ vào độ dốc

của đoạn thẳng để nhận xét.

Câu 3: Nhìn vào số liệu trên hai biểu đồ ta

nhận thấy hai biểu đồ này biểu diễn cùng

một dãy dữ liệu.

Câu 3. Chọn Đúng

(đáp án A)

Câu 4: Chọn đúng mốc thời gian là tháng

2

và tính sự chênh lệch của hai của hàng.

Câu 4: chọn đáp án D

Câu 5: Chọn đúng năm 2020 và tính tỉ số

giữa thu nhập bình quân đầu người của

Singapore và Việt Nam.

Câu 5: Chọn B

Tỉ số giữa thu nhập bình quân đầu người

Trả lời

Câu 1: C

Câu 2: B

Câu 3: A

Câu 4: D

Câu 5: B

Câu 6: B

Câu 7: D

Trang 215

của Singapore và Việt Nam năm

2020

là

59798

22

2779



lần

Câu 6: trước hết cần đổi số liệu ở biểu đồ

năm

2019

sang dạng phần trăm.

Câu 6: Tỉ lệ năng lượng từ than năm

2019

là:

26408,48

47,74

55322,28



Năng lượng từ than đã tăng

47,74 45,02 2,72%−=

Câu 7: Thực hiện tính sự chênh lệch trong

tháng

1

, tháng

2

, tháng

11

, tháng

12

và so

sánh

Câu 7:

Tốc độ gió chênh lệch là:

tháng

1

:

6,7

tháng

2

:

3,7

tháng

11

:

6,8

Tháng

12

:

8,6

* Giao nhiệm vụ

Bài tập 1: Cho hai biểu đồ (a) và (b)

(a)

(b)

Phần II: Bài tập tự luận

Bài tập 1:

a. - Hai biểu đồ này cùng biểu diễn một dãy

dữ liệu.

- Bảng thống kê

năm

2017

2018

2019

2020

Sản

lượng

34

38

42.9

47.5

b. Tỉ lệ chiều cao và tỉ lệ giữa số liệu trong

biểu đồ (a) bằng nhau và bằng

35.5

0.93

38

=

Trong biểu đồ (b) tỉ lệ chiều cao không bằng

tỉ lệ giữa số liệu trong biểu đồ.

Nguyên nhân vì ở biểu đồ (b) gốc của trục

đứng không phải là số

0

.

34

38

42.9

47.5

0

10

20

30

40

50

2017 2018 2019 2020

năm

Sản lượng (triệu tấn)

34

38

42.9

47.5

30

40

50

2017 2018 2019 2020

năm

Sản lượng (triệu tấn)

Trang 216

a. hai biểu đồ trên có biểu diễn cùng một

tập dữ liệu không? Lập bảng thống kê cho

tập dữ liệu đó.

b. So sánh tỉ lệ chiều cao và tỉ lệ giữa số

liệu trong năm

2017

và năm

2018

.

- HS quan sát hai biểu đồ, so sánh phân tích

số liệu thu được từ hai biểu đồ này và đưa

ra nhận xét.

*Thực hiện nhiệm vụ

- Giáo viên hướng dẫn HS thực hiện

- Lưu ý sự khác nhau về điểm gốc giữa trục

đứng của hai biểu đồ.

*Chốt kiến thức

+ Trong biểu đồ cột khi gốc của trục đứng

khác

0

thì tỉ lệ chiều cao giữa các cột

không bằng tỉ lệ số liệu mà chúng biểu

diễn.

* Giao nhiệm vụ

Bài tập 2: Cho hai biểu đồ

a. so sánh độ dốc của hai đoạn thẳng cuối

cùng trong hai biểu đồ trên.

b. Có thể nhận định năm

2020

GDP của

Việt Nam tăng đột biến hay không? Vì sao?

*Thực hiện nhiệm vụ

Lưu ý các điểm quan sát trên trục ngang

được chia tỉ lệ đã đều nhau chưa?

- HS quan sát biểu đồ đưa ra nhận xét.

Dự kiến câu trả lời của HS: ở biểu đồ bên

trái đoạn thẳng cuối cùng có độ dốc cao

hơn.

- Không thể nhận định GDP của Việt Nam

tăng đột biến vì đoạn thẳng này nối từ năm

2016

đến năm

2020

.

* Chốt kiến thức:

+ Trong biểu đồ đoạn thẳng khi các điểm

quan sát trên trục ngang không đều nhau ta

không thể dựa và độ dốc để kết luận về độ

Bài tập 2:

a. ở biểu đồ bên trái đoạn thẳng cuối cùng có

độ dốc cao hơn.

b. Không thể nhận định trong năm

2020

GDP

của Việt Nam tăng đột biến vì trục ngang của

biểu đồ chia tỉ lệ không đều giữa các đoạn

thẳng.

Trang 217

tăng hay giảm của đại lượng được biểu

diễn.

* Giao nhiệm vụ

Bài tập 3: Biểu đồ sau biểu diễn kế hoạch

chi tiêu của một gia đình.

a. Em hãy cho biết khoản chi tiêu nào là lớn

nhất?

b. Số tiền dành cho Chi phí sinh hoạt gấp

bao nhiêu lần tiền tiết kiệm?

c. Giả sử mỗi tháng thu nhập của gia đình là

60

triệu thì khoản tiết kiệm được là bao

nhiêu?

*Thực hiện nhiệm vụ

- Hướng dẫn:

Cách tính tiền tiết kiệm:

Tiền tiết kiệm bằng tổng thu nhập nhân với

phần trăm tương ứng.

Học sinh quan sát biểu đồ và trả lời các câu

hỏi

Dự kiến câu trả lời

+ Khoản chi tiêu cho ăn uống là lớn nhất.

+ Số tiền dành cho sinh hoạt gấp

1,5

lần

tiền tiết kiệm.

+ Nếu thu nhập là

60

triệu đồng thì tiết

kiệm được

12

triệu đồng mỗi tháng.

Bài tập 3:

a. Khoản chi tiêu cho ăn uống là lớn nhất.

b. vì

30

1,5

20

=

nên

số tiền dành cho sinh hoạt gấp

1,5

lần tiền

tiết kiệm.

c. số tiền tiết kiệm được là

60.20% 12=

triệu đồng

Vậy nếu tổng thu nhập là

60

triệu đồng thì

tiết kiệm được

12

triệu đồng mỗi tháng.

* Giao nhiệm vụ

Bài tập 4: Cho bảng thống kê các môn thể

thao yêu thích của các bạn học sinh lớp 8A

a. Tính tổng số học sinh lớp 8A.

b. Môn thể thao nào có chênh lệch nam, nữ

Bài tập 4:

a. Tổng số học sinh lớp 8A là:

17 3 1 4 4 2 7 4 42+ + + + + + + =

Vậy lớp 8A có

42

học sinh.

b. Môn bóng đá là môn có chênh lệch nam

nữ chọn cao nhất. (số bạn nam yêu thích

nhiều hơn số bạn nữ yêu thích là

13

bạn)

Trang 218

chọn lớn nhất?

*Thực hiện nhiệm vụ

HS phân tích bảng số liệu tính toán và đưa

ra câu trả lời.

Dự kiến câu trả lời

+ Tổng số

42

.

+ Môn thể thao chênh lệch lớn nhất là bóng

đá.

*Kết luận, nhận định:

Một số lưu ý khi thực hiện dạng toán này.

+ Trong biểu đồ cột khi gốc của trục đứng khác

0

thì tỉ lệ chiều cao giữa các cột không

bằng tỉ lệ số liệu mà chúng biểu diễn.

+ Trong biểu đồ đoạn thẳng khi các điểm quan sát trên trục ngang không đều nhau ta không

thể dựa và độ dốc để kết luận về độ tăng hay giảm của đại lượng được biểu diễn.

* Giao nhiệm vụ

Bài tập 5: Biểu đồ cơ cấu năng lượng sản

xuất năm

2018

và

2019

a. Lập bảng thống kê cơ cấu năng lượng sản

xuất (theo tỉ lệ %) năm

2019

.

b. nhận xét về sự thay đổi cơ cấu năng

lượng được khai thác, sản xuất năm

2019

so với năm

2018

*Thực hiện nhiệm vụ

* Hướng dẫn:

+ Để lập bảng thống kê cơ cấu năng lượng

ta cần đổi từ đơn vị số lượng sang đơn vị

phần trăm.

+ HS hoàn thành bảng thống kê.

+ Dự kiến câu trả lời của học sinh.

Năng lượng từ than tăng lên.

Bài tập 5:

a.

Năng

lượng

Than

Dầu

mỏ

Khí ..

Nhiên

liệu ..

Tỉ lệ

47.7

20.4

16.8

15.3

b. Năng lượng từ than và Nhiên liệu sinh học

tăng lên.

Năng lượng từ dầu thô và khí thiên nhiên

giảm đi.

* Giao nhiệm vụ

Bài tập 6: Cho biểu đồ

Bài tập 6:

Giải

a. Tỉ lệ diện tích đất rừng trên tổng diện tích

đất của Indonesia cao hơn Việt Nam.

b. Tỉ lệ diện tích đất rừng trên tổng diện tích

đất của Việt Nam có xu thế tăng dần,

Indonesia có xu thế giảm dần.

Trang 219

a. So sánh tỉ lệ diện tích đất rừng trên tổng

diện tích đất của hai nước.

b. Cho biết xu thế tăng, giảm của tỉ lệ diện

tích đất rừng trên tổng diện tích đất của mỗi

nước.

c. Lập bảng thống kê về tỉ lệ diện tích đất

rừng của Việt Nam trên tổng diện tích đất

qua các năm.

d. Tổng diện tích đất của Việt Nam,

Indonesia tương ứng là

2

331690km

;

2

1826440km

. Tính diện tích đất rừng của

mỗi nước trong năm

2017

.

*Thực hiện nhiệm vụ

* Hướng dẫn:

Diện tích đất rừng bằng Tổng diện tích đất

nhân với phần trăm tương ứng.

HS tìm hiểu bài toán và trả lời các câu hỏi.

* dự kiến câu trả lời của học sinh.

+ Tỉ lệ diện tích đất rừng của Việt Nam

tăng dần, Indonesia giảm dần.

+ HS hoàn thành bảng thống kê.

+ Tính diện tích đất rừng của mỗi nước.

c. Bảng thống kê

Năm

2013

2014

2015

2016

2017

Tỉ lệ

44,5

44,9

45,4

46,4

46,5

d. Diện tích đất rừng của Việt Nam năm

2017

là

2

331690.46,5% 154235,85km=

Diện tích đất

rừng của Indonesia năm

2017

là

2

1826440.50% 913220km=

* Giao nhiệm vụ

Bài tập 7: Cho biểu đồ:

a. nhận xét về xu thế của thị phần xuất khẩu

gạo của Thái Lan trong các năm từ

2007

đến năm

2020

.

b. Lập bảng thống kê thị phần xuất khẩu

gạo của Việt Nam trong giai đoạn này.

*Thực hiện nhiệm vụ

HS tìm hiểu và trả lời các câu hỏi trong bài

tập 8.

Dự kiến câu trả lời của học sinh.

+ Thị phần xuất khẩu gạo của Thái Lan có

Bài tập 7:

a. Thị phần xuất khẩu gạo của Thái Lan có

xu hướng giảm dần.

b. Bảng thống kê.

Năm

2017

2018

2019

2020

Thị

phần

12

13

15

14

Trang 220

xu hướng giảm dần.

Hoàn thành bảng thống kê

* Những lưu ý rút ra:

Khi phân tích số liệu ta có thể kết hợp thông tin từ hai biểu đồ.

+ Để so sánh sự biến đổi theo thời gian của hai hay nhiều đại lượng ta nên biểu diễn chúng

trên cùng một biểu đồ.

IV. PHIẾU BÀI TẬP BỔ TRỢ SỐ

1. TRẮC NGHIỆM

Câu 1: Cho biểu đồ

Môn thể thao được các bạn học sinh khối

8

yêu thích nhất là

A. Bóng đá B. Bóng chuyền C. Bóng bàn D. Cầu lông

Câu 2: Cho cho biểu đồ.

Khẳng định “Số tiền bán phế liệu của bạn Tuyết gấp đôi của bạn Khánh” là đúng hay

sai?

A. Đúng B. Sai

Câu 3: Cho biểu đồ biểu diễn lương cơ bản của công nhân A

0

2

4

6

8

2015 2016 2017 2023

Lương cơ bản (Triệu đồng)

Trang 221

Ta có thể khẳng định năm

2023

lương của công nhân tăng đột biến hay không?

A. Có. B. Không.

Câu 4: Cho biểu đồ

Tháng

10

bạn nào có điểm kiểm tra môn Khoa học tự nhiên cao nhất

A. Mai B. Lan C. Đào D. Hùng

Câu 5: Cho biểu đồ

Số xe màu xanh dương bán được nhiều gấp mấy lần số xe màu đỏ ?

A.

6

B.

5

C.

4

D.

3

2. TỰ LUẬN

Bài 1: Cho Biểu đồ

a. Số hoa điểm tốt của bạn Dũng có gấp đôi số hoa điểm tốt của bạn Chinh không? Vì

sao khi xem biểu đồ này ta lại dễ nhầm lẫn?

b. Những bạn được ít nhất

10

hoa điểm tốt sẽ được thưởng. Hỏi trong số các bạn trên

có những bạn nào được thưởng?

4

5

6

7

8

9

10

11

12

13

An Bằng Chinh

Cường

Dũng

Số hoa điểm tốt

Trang 222

Bài 2: Cho biểu đồ

a. Doanh thu của nhà máy trong biểu đồ (a) có tăng nhanh hơn trong biểu đồ (b)

không?

b. Hai biểu đồ này có cùng biểu diễn một dãy dữ liệu không?

c. Vì sao độ dốc trong hai biểu đồ này lại khác nhau?

Bài 3: Cho biểu đồ

a. Trong tháng

6

của hàng bán được loại máy nào nhiều hơn?

b. Phân tích xu thế bán mỗi loại máy và giải thích vì sao lại có xu thế như vậy?

Bài 4. Cho biểu đồ

Trang 223

Em hãy tính tỉ lệ phần trăm thấm nước của mỗi loại đồng hồ từ đó đưa ra nhận định

xem loại đồng hồ nào chống thấm nước tốt nhất.

Bài 5. Cho biểu đồ biểu diễn thị trường xuất khẩu rau quả của Việt Nam năm

2020

.

a. Thị trường chính của Việt Nam trong năm

2020

là khu vực nào?

b. Biết rằng tổng kim ngạch xuất khẩu rau quả của Việt Nam năm

2020

là

3,27

tỉ

USD. Tính số tiền thu được khi xuất khẩu rau quả sang thị trường EU.

ĐÁP ÁN PHIẾU BÀI TẬP BỔ TRỢ

1. Trắc nghiệm

Câu

1

2

3

4

5

Đáp Án

A

B

C

2. Tự luận

Bài 1:

a) Số hoa điểm tốt của bạn Dũng không gấp đôi số hoa điểm tốt của bạn Chinh.

Trang 224

Biểu đồ này có gốc của trục đứng khác

0

nên tỉ lệ giữa chiều cao giữa các cột

không bằng tỉ lệ giữa số hoa điểm tốt của hai bạn.

b) Bạn Dũng được

10

hoa điểm tốt bạn Cường được

12

hoa điểm tốt nên hai bạn này

sẽ được thưởng.

Bài 2:

a) Doanh thu của nhà máy trong biểu đồ a không tăng nhanh hơn doanh thu của nhà

máy trong biểu đồ b

b) Hai biểu đồ này cùng biểu diễn một dãy dữ liệu.

c) Vì gốc của trục đứng trong hai biểu đồ khác nhau và tỉ lệ chia mỗi vạch trong hai

biểu đồ khác nhau nên độ dốc của biểu đồ a lớn hơn độ dốc của biểu đồ b.

Bài 3:

a. Trong tháng

6

máy điều hoà bán được nhiều hơn máy sưởi.

b. Trong sáu tháng đầu năm tháng 1 và tháng 2 trời còn rét nên máy sưởi bán được

nhiều và máy điều hoà bán được ít.

Bắt đầu từ tháng 3 đến tháng 6. Nhiệt độ tăng dần nên máy điều hoà bán được tăng lên

còn máy sưởi giảm đi. đến tháng 6 trời nắng nóng nên lượng máy sưởi bán được rất ít.

Bài 4.

Tỉ lệ thấm nước của mỗi loại đồng hồ

Loại A:

40

.100 20%

200

=

Loại B:

40

.100 26,7%

150

=

Loại C:

25

.100 12,5%

200

=

Loại D:

40

.100 40%

100

=

Loại E:

40

.100 13,3%

300

=

Vậy đồng hồ loại C là chống thấm nước tốt nhất.

Bài 5:

a) Thị trường chính của Việt Nam trong năm

2020

là Trung Quốc.

b) Số tiền thu được khi xuất khẩu rau quả sang thị trường EU là

3,27.4,5% 0,14715=

tỉ USD

Giáo án Toán 8 HK1 Kết nối tri thức

Thông tin :

Tài liệu liên quan:

Đề thi toán Bài 1 - 1. Textbook-Marketing An Introduction - global 13th - Tài liệu tham khảo

Bài 19: Biểu diễn dữ liệu bằng bảng, biểu đồ | Bài giảng PowerPoint Toán 8 | Kết nối tri thức

Bài 4: Phép nhân đa thức (tiết 1) | Bài giảng PowerPoint Toán 8 | Kết nối tri thức

Bài 35: Định lí Pythagore và ứng dụng | Bài giảng PowerPoint Toán 8 | Kết nối tri thức

Bài 29: Hệ số góc của đường thẳng | Bài giảng PowerPoint Toán 8 | Kết nối tri thức