
























































































Preview text:
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 1 ÔN TẬP CÔNG THỨC LƯỢNG GIÁC . I.Mục tiêu:
Củng có các công thức cộng, công thức nhân đôi và công thức biến đổi tích tổng, tổng thành tích .
Chuẩn bị kiến thức cho các bài học sau II.Phương pháp:
+Gợi mở vấn đáp kết hợp với thảo luận nhóm.
III.Tiến trình bài học: 1.Ổn định lớp 2.Kiểm tra bài cũ 3.Bài mới T/g Hoạt động của GV Hoạt động của HS Nội dung ghi bảng - Cho học sinh nêu ý
- Học sinh nêu ý tưởng. 2
7’ tưởng trình bày lời giải. Ta có:sin2a+cos2a =1
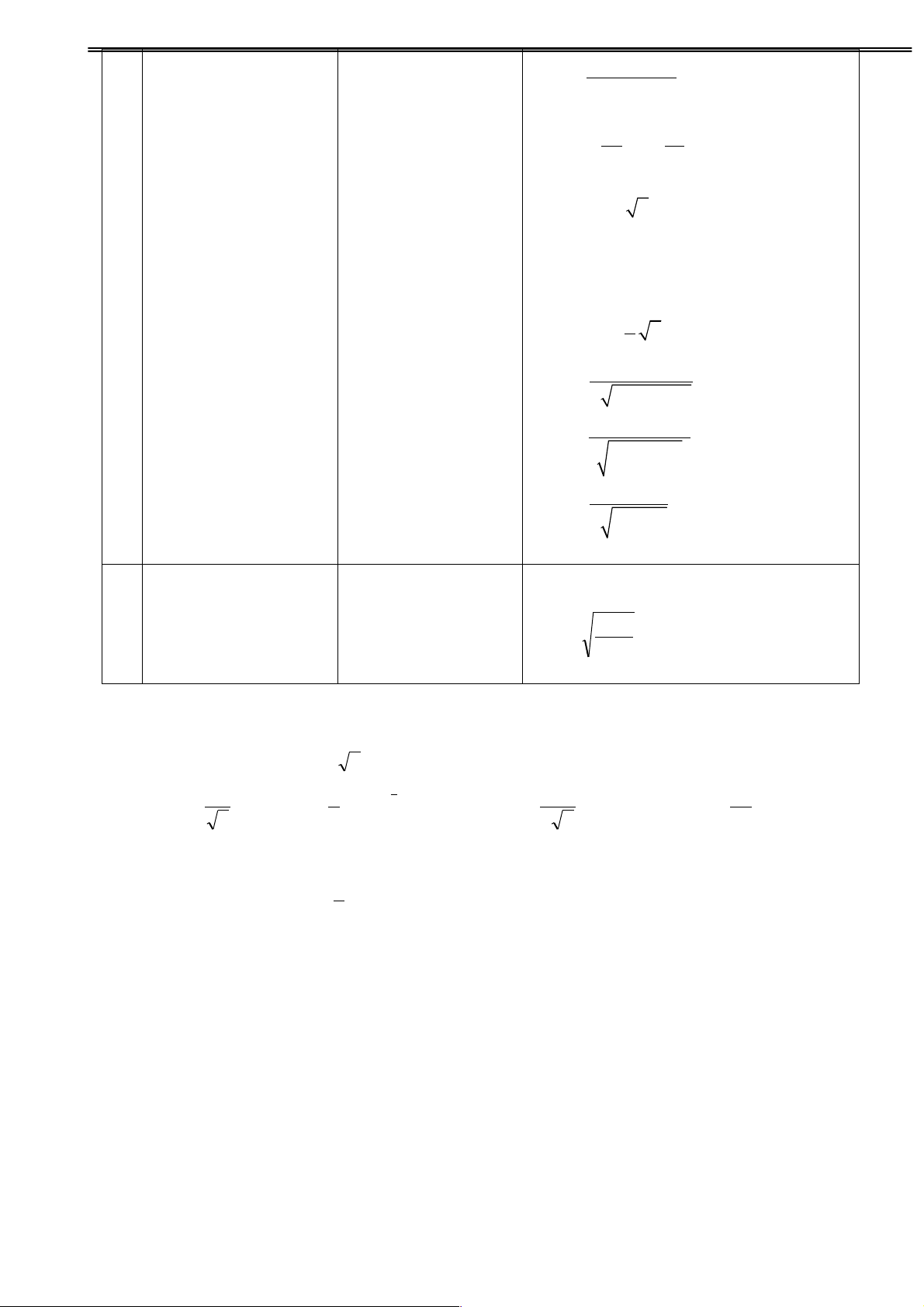
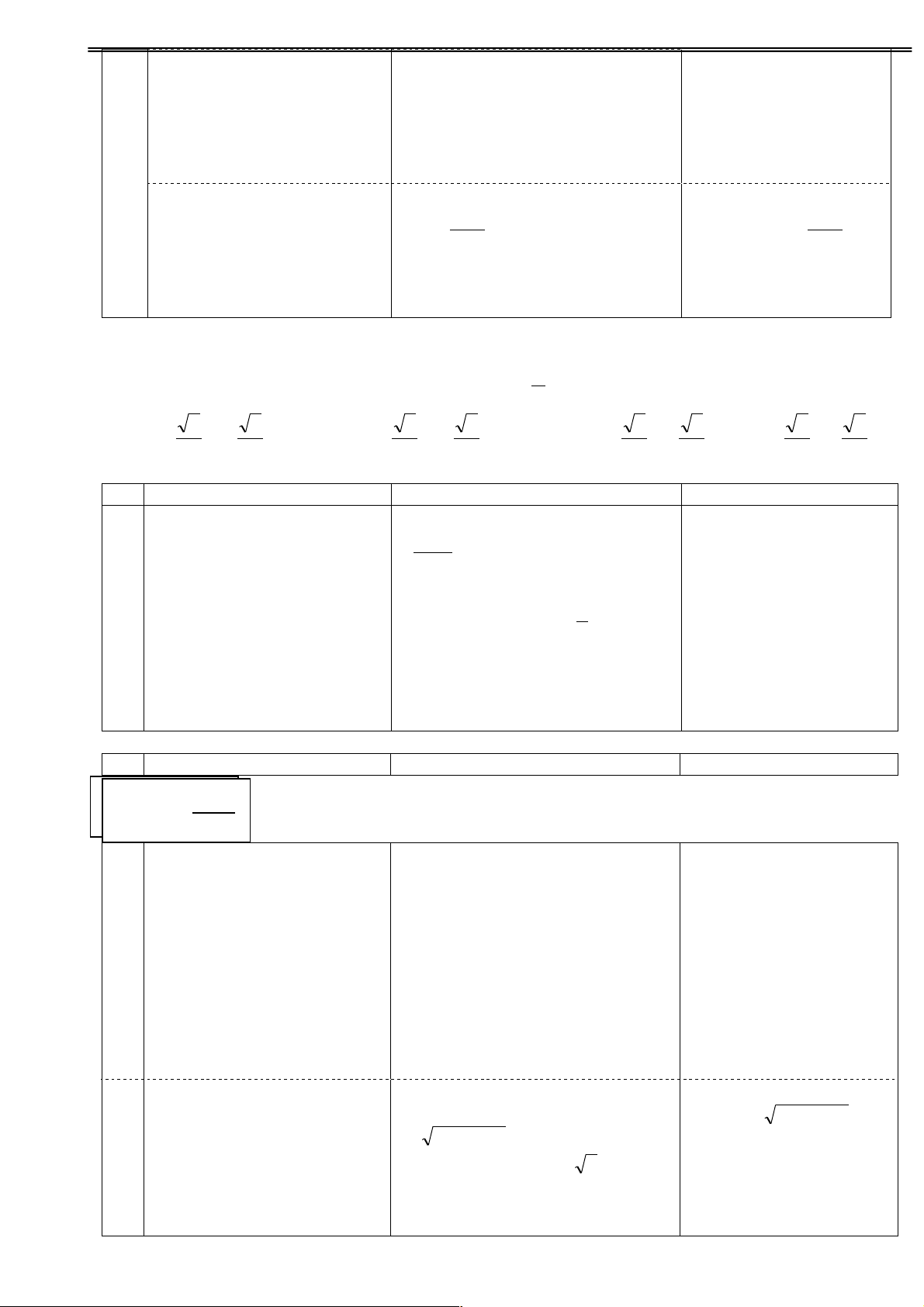
Bài 1:Tính sina nếu cosa= - và 3 2 Û sin a= ± 1-cos a p - GV cho học sinh khác < a < p nhận xét lời giải. 7 2 = ± . - Gợi ý: 3 7 ĐS:sina= . - Áp dụng công thức p 7 3 sin2a+cos2a =1 Vì
< a < p nên sina=
. Bài 2:Tính sin2a, cos2a, tan2a biết 2 3
10’ -Sử dụng công thức nhân 3p 3p
đôi tìm các giá trị sin2a, +Do p < a < nên cosa
Sina= -0,6 và p < a < . 2 cos2a, tan2a 2 ĐS:cosa= -0,8. Suy ra: <0, suy ra: cosa= -0,8.
sin2a=0,96; cos2a= 0,28; tan2a »3,43
- Áp dụng công thức nhân
đôi tìm được: sin2a=0,96; cos2a= 0,28; tan2a » 3,43
Học sinh làm việc theo nhóm
và đại diện nêu ý tưởng. - Yêu cầu học sinh làm - Ta có: việc theo nhóm.
Bài 3:Rút gọn biểu thức: - Gợi ý học sinh nhận (sinx+sin5x)+sin3x A= sinx+sin3x+sin5x 10’ x + 5x ( osx+c c os5x)+cos3x A= xét: = 3x . osx+c c os3x+cos5x 2 sin3x(2cosx+1) =
= tan 3x ĐS: A= tan3x. os3x( c 2cosx+1) +Ta có:
- Gợi ý:Học sinh áp dụng cos công thức cộng. p p 1 7’ 2
Bài 4: Rút gọn biểu thức: ( + a) os( c - a) + sin a 4 4 2 p p 1 - Giáo viên hướng dẫn B= cos 2 ( + a) os( c - a) + sin a = để học sinh làm đúng 4 4 2 hướng. 2 2 1 ( osa c -sina) ( osa c +sina) ĐS: B= 2 os c a . 2 2 2 - Yêu cầu học sinh làm việc theo nhóm. 1 1 2 2 + sin a = os c a .
- Gợi ý học sinh nhận xét
Bài 5:Chứng minh các đồng nhất thức: 2 2 7’ vế trái và vế phải. 1- osx+c c os2x a/ = cotx.
- Bài 5a/ biến đổi vế trái: sin 2x - sinx
đưa tất cả các cung về - Học sinh làm việc theo cung x.
nhóm và đại diện nêu ý
- Bài 5b/ đưa tất cả các
tưởng để giải bài toán. cung về cung x/2. 2 x os c x-cosx +5a/.VT= sinx+sin x 2sin . x osx c - sinx b/ 2 = tan . =cotx. x 2 1+cosx+cos 2 1
Giáo án Đại số 11 – Chương trình chuẩn x x sin (2 os c +1) +5b/.VT= 2 2 x x cos (2 os c +1) 2 2 x =tan 2 4. Củng cố:(5/) 2
Giáo án Đại số 11 – Chương trình chuẩn
CHƯƠNG I : HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Tiết: 2,3,4 BÀI 1: HÀM SỐ LƯỢNG GIÁC. I - MỤC TIÊU: * Về kiến thức:
-Học sinh nắm được định nghĩa hàm số: sin; cos; tang; cotang.
- Nắm được tính toàn hoàn, chu kỳ của các hàm số trên. * Về kỹ năng:
+ Tìm tập xác định; tập giá trị.
+ Khảo sát sự biến thiên và vẽ đồ thị các hàm số.
* Về tư duy và thái độ:
+ Rèn luyện tư duy logic, biến đổi toán học.
+ Rèn luyện tư duy phân tích, tổng hợp và đánh giá.
+ Phát huy tính tích cực học tập của học sinh.
II - CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
* Giáo viên:
- Soạn và chuẩn bị bài đầy đủ.
- Bảng phụ về đường tròn lượng giác . * Học sinh:
- kiến thức về các hàm số lượng giác
- Có đầy đủ dụng cụ học tập. III- PHƯƠNG PHÁP: -
Dùng phương pháp gợi mở, nêu vấn đề. - Hoạt động nhóm
IV- TIẾN HÀNH BÀI HỌC:
Tiết 1: Mục I, II. Tiết 2: Mục 1,2 - III. Tiết 3: Còn lại 1- Kiểm tra bài cũ
* Hoạt động 1:
Câu hỏi: nhắc lại giá trị lượng giác của các cung đặc biệt; vẽ đường tròn lượng giác; nhắc lại các trục sin,cos,tang, cotang. 2- Bài mới:
* Hoạt động 2: chiếm lĩnh các kiến thức về định nghĩa các hàm số
Hoạt động của học Hoạt động của Tg Ghi bảng sinh giáo viên - Vẽ đường tròn lg
CH1:Hãy vẽ đường tròn I/ Hàm số sin, cosin -Lấy điểm M bất kì LG; vẽ hệ trục Oxy?
a/ Hàm số sin:Hình vẽ 1a,b sgk 10 - CH2: xác định điểm M phút : ! sd AM =x? -M(x;sinx)
CH3:Xđ toạ độ điểm M? CH4:Quy tắc đặt tương
-Dựa vào đ/n được ứng trên gọi là gì? Đ/n:sin: R ® R
học 10, đn nghĩa CH5: hãy đn hàm số x! y=sinx.
tương tự cho hàm số trên? sin *TXĐ :D=R
các hoạt động tương CH6: tìm TXĐ?
b. Hàm số côsin: Hình vẽ 2a,b sgk. tự ở trên.
*Các câu hỏi tương tự ở trên. đ/n:cos: R ® R +Sử dụng Đ/n ở lớp x ! y=cosx 10, tanx= sinx/cosx. + ở lớp 10, tanx=? *TXĐ :D=R + Đ/n hàm số tan bởi
2.Hàm số tang và hàm số cotang
+ Căn cứ ĐK mẫu của công thức? a. Hàm số tang HS. +Hàm số tang xđ khi
Hàm số cho bởi công thức suy ra cosx khác nào? sinx không. y = ;( osx c ¹ 0)
+Xđ tính chẵn, lẽ của các cosx hs trên? kí hiệu: y=tanx 3
Giáo án Đại số 11 – Chương trình chuẩn ìp ü
*TXĐ: D = R / í + kp ,k Î Z ý î 2 þ b. Hàm số côtang
Hàm số cho bởi công thức cosx y = ;(sin x ¹ 0) sinx kí hiệu: y=cotx
*TXĐ: D = R /{kP,k Î Z}
* Nhận xét: hàm số sin là hs lẽ, h/s côsin là hs
chẵn; hs tang; cotang là hs lẻ.
• Hoạt động 3: xét tính tuần hoàn và chu kì của các hàm số lượng giác
Hoạt động của học
Hoạt động của giáo Tg Ghi bảng sinh viên
II. Tính tuần hoàn của các hàm số lượng
+Sử dụng sin(x+k2p ) +TìmT :f(x+T)=f(x) giác 10 =sinx thoả:a. f(x)=sinx Đ/n: phút suy ra T=2p ;4p ... b.f(x)=tanx
*Hàm số y=sinx,y=cox là hàm số tuần hoàn + MinT=2p
Sau đó tìm số T dương với chu kì 2p nhỏ nhất?
*Hàm số y=tanx ,y=cotx là hàm số tuần hoàn + tìm chu kì của hs? với chu kì p .
Ví dụ : hàm số y=cos2x là hs tuần hoàn với chu kỳ p .
• Hoạt động 4: xét tính biến thiên và đồ thị của càc hàm số lượng giác Tg
Hoạt động của học sinh Hoạt động của giáo viên Ghi bảng
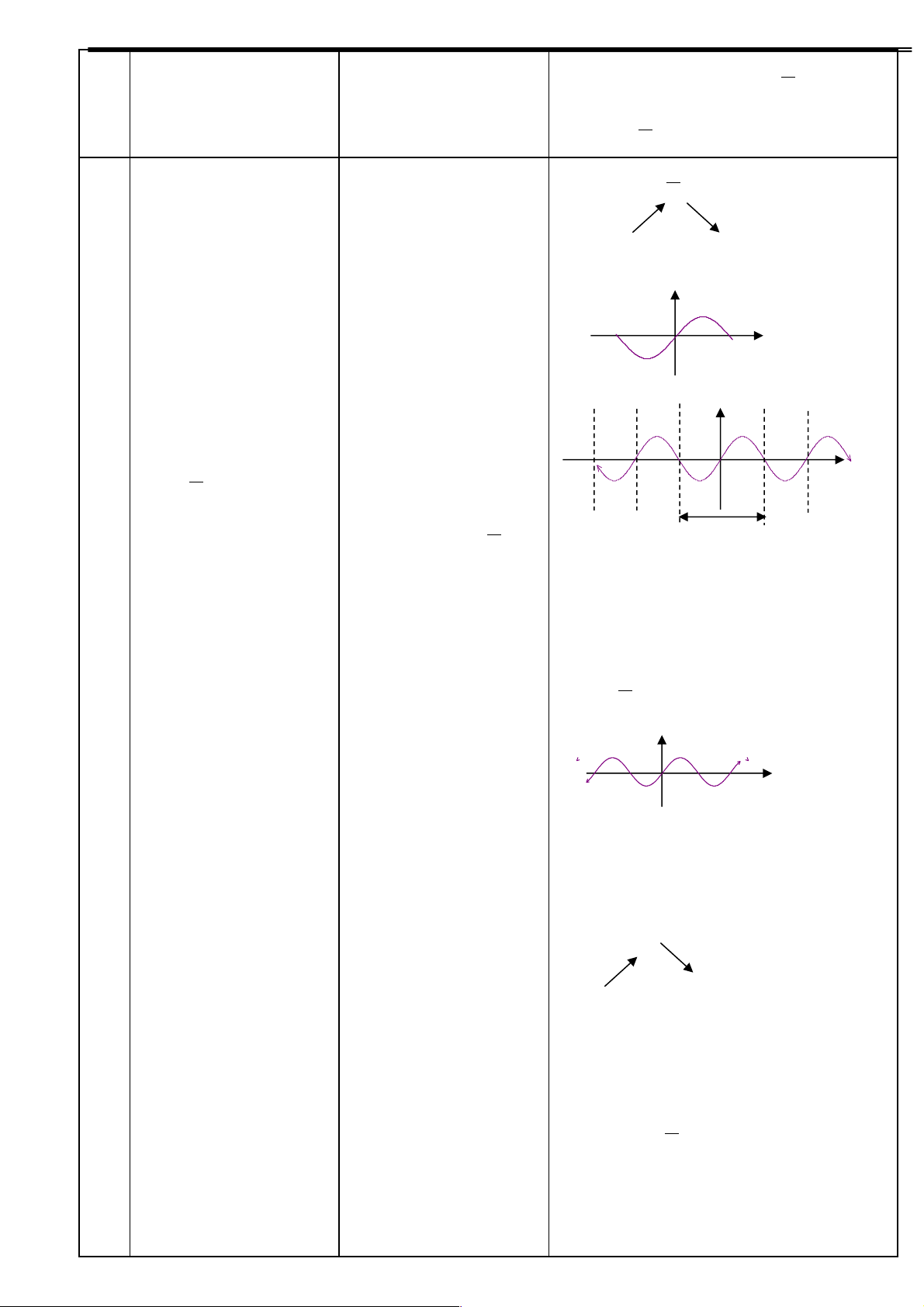
III.Sự biến thiên và đồ thị của các hàm số lượng giác 10 1.Hàm số y=sinx phút
+ sử dụng các mục học ở + Nhắc lại tính chẳn +BBT :Hàm số y=sinx trên để nhắc lại.
lẽ,TXĐ, chu kì của hs +TXĐ D=R sin? +Hàm số lẻ +Hoạt động nhóm:
+Hàm số tuần hoàn chu ki 2p é p ù
+Xét tính BT của hs trên a.Sự biến thiên và đồ thị của hàm số trên - Lấy x1,x2 Î 0; êë 2 ú é p ù ép ù [0;p ]: û 0; và ;p ? ê ú ê ú
-Dựa vào ĐTLG suy ra ë 2 û ë 2 û Hv3 sgk: sinx1 -Suy ra hàm số đb. Sin B y Sinx1 Sinx1 Sinx2 Sinx2 A’ O O A x1 x2 x B’ 4
Giáo án Đại số 11 – Chương trình chuẩn é p ù
+Hàm số đồng biến trên 0; và nghịch ê 2 ú ë û ép ù biến trên ;p ê 2 ú ë û +Vẽ BBT? p p X 0 2 y=sinx 1
+ Dựa vào tính lẽ vẽ đồ
thị đối xứng qua gốc O +ĐT của hs trên [ p - ;0] 0 0 được vẽ ntn? chú ý : hv4 SGK +Dựa vào chu ki + Trên R, hãy nêu cách
+sử dụng phép tịnh tiến. vẽ ĐT? +Dựa vào ĐT tìm được O x T. + Tìm TGT?
+ Sử dụng các mục học ở
b.Đồ thị hs y=sinx trên R.Hình 5 sgk. trên để nhắc lại. + Nhắc lại tính chẳn y lẽ,TXĐ, chu kì của hs cos? p O x sin(x+ ) = sinx 2 p
+So sánh sin(x+ ) và c.Tập giá trị của hàm số y=sinx 2 sinx? T=[ 1; - ] 1 +Nêu cách vẽ ĐT? 2.Hàm số y=cosx +TXĐ D=R +Hàm số chẵn.
+Hàm số tuần hoàn chu ki 2p p +sin(x+ )=cosx. 2 + Tìm TGT? Hv 6 sgk y + Nhắc lại tính chẵn O x
lẻ,TXĐ, chu kì của hs +Hàm số đồng biến trên [ p - ;0] và nghịch tanx? biến trên [0;p ] +BBT X -p 0 p y=cosx 1 -1 -1
Tập giá trị của hàm số T=[ 1; - ] 1
*Đồ thi hs y=sinx, y=cosx gọi là các đường hình sin. 3.Hàm số y=tanx ìp ü
+TXĐ D=R\ í + kp ,k Î Z ý î 2 þ +Hàm số lẻ.
+Hàm số tuần hoàn chu kỳ 2p
a.Sự biến thiên và đồ thị của hàm số trên [0;p ]. Hv7 sgk: 5
Giáo án Đại số 11 – Chương trình chuẩn tang tanx y 1 T1 B tanx2 T M1 2 M2 A’ O A x O x2 x1 B’ é p ù
+Hàm số đồng biến trên 0; và nghịch ê 2 ú ë û ép ù biến trên ;p . ê 2 ú ë û
+Hàm số tuần hoàn với chu kỳ p
+ Thảo luận nhóm như Sự bT và ĐT của hs trên + Hàm số lẻ. 10 hoạt động ở trên. é p ö é p ö phút 0; ? ê ÷
a.Sự bT và ĐT của hs trên 0; ë 2 ø ê ÷ ë 2 ø p x 0 p / 2 4 +¥ y=tanx 1 +Vẽ BBT? 0 y
b.SBT và Đồ thị hs y=cotx trên (0;p ) +BBT p x 0 p O 2 x y=cotx +¥ 0 -¥ y
c. Đồ thị hs y=cotx trên D. Hv11: O x +TGT T=R. 3- Củng cố: (3 phút)
- Cho học sinh nêu lại tính chất của các hàm số trên
- Chú ý các dạng đồ thị của các hàm số
4- Bài tập về nhà: (2 phút)
Câu1: Tìm chu kì của các hàm số sau : y=sin2x, y=cos3x Câu 2. Vẽ ĐTHS y= tan2x * các BT trong SGK
--------------Hết------------- 6
Giáo án Đại số 11 – Chương trình chuẩn Tiết 5 BÀI TẬP. I. Mục tiêu:
-K/t : Nắm vững các đồ thị hàm số sin, cos, tang, cotang
-K/n : + sử dụng các phép suy đồ thị
+ Tìm chu kì của hàm số
+ Giải bài toán tim Min, Max
II. Phương pháp: Vấn đáp , thảo luận nhóm
III.Các bước tiến hành
Tiết 1: Bài 1 à 4. Tiết 2: Bài 5 à8 1.Ổn định lớp 2. Kiểm tra bài cũ
Hđ1: Câu 1. Nêu các tính chất của các hàm số sin, cos, tang, cotang
Câu 2. Tìm TXĐ của các hàm số 1 a. y = sinx b. y = sinx +1 osx c
Thời Hoạt động của HS Hoạt động của GV Nội dung ghi bảng gian
+ Nhận xét câu trả lời Câu 1 . Gv chỉnh sửa và Câu 2 . a.
+Sử dụng điều kiện có nhắc lại chính xác p ¹ Þ ¹ + p nghĩa của mẫu Câu 2 . sinx 1 x -
k ; k Î Z 2 suy ra sinx +1 khác + Hàm số XĐ khi nào? b. không +Tìm x, ghi TXĐ D? + tương tự cosx > 0 3. Bài tập
HĐ 2 : Giải các bài tập SGK Tg Hoạt động của HS Hoạt động của GV Nội dung ghi bảng
+Dựa vào đồ thị tìm x. hoặc
+Nêu các bước giải bài é 3p ù sử dụng ĐTLG. toán? Bài 1.tìm x Î p - ; ê 2 ú ë û é 3p ù + kết quả? + chọn x Î p - ; a. t anx=0 Þ x=kp ê ú ë 2 û Vậy x Î{ p - ;0;p} + tương tự như trên p b. t anx=1Þ x= +kp 4 + tương tự như trên ì 3 p 5 ü
Vậy x Î í- p; ; p ý î 4 4 4 þ c. t anx>0 Vậy +Nêu cách giải bài æ p ö æ p ö æ 3p ö toán? x Î p - ;- È 0; È p; ç ÷ ç ÷ ç ÷ è 2 ø è 2 ø è 2 ø d.Tương tự câu c
Bài 2 . Tìm TXĐ của hàm số 1+ osx c a. y = sinx +Nêu ĐK để hàm số ĐK : sinx ¹ 0 Û x ¹ kp + Phân tích ĐK mẫu xác định ?
Vậy D = R \{kp ,k Î Z}
+tìm x để sinx khác không + tìm x để sinx khác không? 1+ osx c b. y = +kêt luận 1-cosx +Nêu ĐK để hàm số 1+ osx c ³ 0 p + xác định ? ĐK : cosx ¹ 0 Û x ¹ + kp 1- osx c ³ 0 + Giải thích vì sao chỉ 2 cần 1-cosx khác không? 7
Giáo án Đại số 11 – Chương trình chuẩn
+phân tích tương tự như ìp ü trên.
Vậy D = R \ í + kp ,k Î Z ý î 2 þ p c. tan(x - ) 3 ĐK: + Vẽ ĐT y=sinx
+ Nêu các bước vẽ đồ p 5p os( c x- ) ¹ 0 Û x ¹ + kp
+Giữ nguyên phần đồ thị ứng thị? 3 6 với sinx>0 ì5p ü
+Lấy đối xứng phần đồ thị có Vậy D = R \ í
+ kp ,k Î Z ý î 6 þ
sinx+ sin 2(x + kp ) = ?
Bài 3 . VĐT hàm số y = sinx
+ Nêu các bước vẽ đồ +Sử dụng thị? s ì inx,sinx>0 Ta có : sinx = í
sin 2(x + kp ) = sin(2x + k2p ) +Nêu cách tìm x? î-sinx,sinx<0
+đường thẳng y=1/2 cắt é p ù ĐTHS y=cosx tại các +Vẽ đồ thị trên 0; ê ú điểm có hoành độ ntn? ë 2 û +Lấy ĐX qua gốc O
+Tịnh tiến song song với Ox
một khoảng có độ dài p +Dựa vào đồ thị, hàm
Bài 4 . CM sin 2(x + kp ) = sin 2x
số nhận giá trị dương +Sử dụng đồ thị : Ta có khi nào? -Vẽ y=1/2 (d)
sin 2(x + kp ) = sin(2x + k2p ) -Vẽ y= cosx (C) = sin 2x
+Tìm giao điểm của (d) và (C ) Bài 5 . Tìm x : cosx=1/2
Ta có đường thẳng y=1/2 cắt +Sử dụng đồ thị
ĐTHS y=cosx tại các điểm có p p hoành độ + kp;- + kp
Hoạt động tương tự như 3 3 trên p p Vậy x =
+ kp; x = - + kp 3 3 HĐ3 Củng cố
-Nắm vững và vẽ thành thạo các ĐTHS TRẮC NGHIỆM
Câu 1. Chu kỳ của hàm số y = tanx là: p A. 2p B. C. kp , kÎZ D. p 4 1- sin x
Câu 2: Điều kiện xác định của hàm số y = là 2cos x p p p A. x ¹ + k2p B. x ¹
+ kp C. x ¹ - + k2p
D. x ¹ kp 2 2 2 1- 3cos x
Câu 3: Tập xác định của hàm số y = là sin x ì p ü ì p k ü
A. íx Î R x ¹ + p
k ý B. íx Î R x ¹
ý C. {x Î R x ¹ k p 2 }
D. {x Î R x ¹ p k } î 2 þ î 2 þ
Câu 4: Chọn phát biểu sai
A. Hàm số y = sin x , y = os
c x , y = t anx , y = ot
c x là hàm số lẻ
B. Hàm số y = sin x , y = os
c x tuần hoàn với chu kì 2p
C. Hàm số y = t anx , y = ot
c x tuần hoàn với chu kì p
D. Hàm số y = sin x , y = os
c x có tập giá trị là [ 1; - ] 1 8
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 6,7,8 BÀI 2. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN I. Mục têu
- KT : +Nắm được điều kiện của a để các phương trình sinx=a, cosx=a, tanx=a, cotx=a có nghiệm
+Biết cách viết công thức nghiệm của các PTLG cơ bản
+Biết cách sử dụng các kí hiệu arcsin, arccos, arctan, arccot - KN : Giải PTLG cơ bản
II. Phương pháp: Gởi mở-Vấn đáp , thảo luận nhóm
III.Các bước tiến hành
Tiết 1: PT sinx =a; Tiết 2: PT cosx = a; Tiết 3: còn lại 1.Ổn định lớp 2. Kiểm tra bài cũ
Hđ1: Tìm x thoả : a. sinx - 2 =0 b. 2sinx =1 TG Hoạt động của HS Hoạt động của GV Nội dung ghi bảng
+ sinx=2 dự vào đồ thị
+ gọi học sinh lên bảng
a. phương trình vô nghiệm KL : PTVN trình bày,theo dõi và b. sinx=1/2 +sinx=1/2 dựa vào đồ chỉnh sửa kết quả. é p x = + k 2p thị KL : x= ê 6 Û ê 5 ê p x = - + k 2p êë 6 3. Bài mới
HĐ2 : Từ HĐ1 và cách biểu diễn trên ĐTLG tìm nghiệm cho phương trình sinx=a. TG Hoạt động của HS HĐ của GV Nội dung ghi bảng 9
Giáo án Đại số 11 – Chương trình chuẩn + Sử dụng HĐ1 hình
+ Nêu cách tìm nghiệm 1.Phương trình sinx=a: dung được công thức cho Pt? Cách giải: nghiệm
+ a > 1 :Pt như thế +TH1: a > 1 : PTVN + Kiểm tra công thức nào? tổng quát dựa vào
+TH2 : a £ 1 PT có nghiệm dạng ĐTLG. + a £ 1 : nêu công éx = a + k2p thức nghiệm tổng quát? Û , k Î Z ê
ëx = p - a + k2p a ì = sdAM Trong đó í +Giới thiệu cách viết si î na = a trong trường hợp ì p p ì p p ï- £ a £ * Thảo luận nhóm : ï- £ a £ -Nếu í 2 2 í 2 2 si ïî na = a 3 p ï + = î a sin sin = a
thì ta viết a = arcsin a lúc đó 2 3 p
éx = arcsina + k2p +sin3x=1/2=sin +Hãy giải các Pt? sinx = a Û , k Î Z ê 6 +theo dõi kết quả hoạt
ëx = p - arcsina + k2p
+Ghi dưới dạng arcsin. động nhóm của học
Ví dụ: giải các phương trình: +sin(x+15o)=sin45o sinh. 3 +Họi học sinh lên bảng . a sinx= 2
trình bày, chỉnh sửa kết - =
+ sử dụng tổng quát từ quả . b sin 3x 5 / 4 0 Pt sinx=sinbo +PT sinf(x)=sing(x) có . c sinx+3/4=0 +Đổi ra đơn vị độ nghiệm ntn? 2 +Từ vd(d) học sinh ghi o +sinx=sin o b công thức d.sin(x+15 ) = được công thức 2 nghiệm được ghi ntn? *chú ý : nghiệm. + Trong cùng một pt có a.PT sinf(x)=sing(x) cho phép dùng đồng
é f (x) = g(x) + k2p thời hai đơn vị không? Û , k Î Z ê +Viết công thức
ë f (x) = p - g(x) + k2p nghiệm cho các trường hợp đặc biệt ? b. + Chú ý các đầu cung o
éx = b + k360o trùng nhau để ghi công sinx=sin o b Û ê , k Î Z thức nghiệm. o o
êëx = p - b + k360
c. Trong cùng một công thức nghiệm
không dùng đồng thời hai đơn vị độ và radian.
d.Các trường hợp đặc biệt + sinx=1 + sinx=-1 + sinx=0
HĐ3 : Tìm x : cosx-1/2=0 ; cosx+2 =0 . Tìm công thức nghiệm cho Pt cosx=a Tg Hoạt động của HS Hoạt động của GV Nội dung ghi bảng
* Hoạt động tương tự * Hoạt động tương
2.Phương trình cosx=a: như trên. tự như trên. Cách giải : +TH1: a > 1 : PTVN
+TH2 : a £ 1 PT có nghiệm dạng éx = a + k2p Û , k Î Z ê ëx = a - + k2p a = sdAM Trong đó os c a = a 10
Giáo án Đại số 11 – Chương trình chuẩn ì0 £ a £ p -Nếu í î os c a = a
thì ta viết a = arccosa lúc đó cosx= a
éx = arccosa + k2p Û , k Î Z ê
ëx = -arccosa + k2p
Ví dụ :giải các phương trình: 3 . a osx= c 2 . b os3 c x - 5 / 4 = 0 . c osx+3/ c 4=0 o 2 d.cos(x+15 ) = 2
*chú ý : a.PT cosf(x)=cosg(x)
é f (x) = g(x) + k2p Û , k Î Z ê
ë f (x) = -g(x) + k2p o
éx = b + k360o b.cosx=cos o b Û ê , k Î Z o
êëx = -b + k360o
c. Trong cùng một công thức nghiệm
không dùng đồng thời hai đơn vị độ và radian.
d.Các trường hợp đặc biệt +cosx=1 +cosx=-1 +cosx=0
HĐ4 : Tìm công thức nghiệm cho PT tanx=a
Thời Hoạt động của HS Hoạt động của GV Nội dung ghi bảng gian + Vẽ đồ thị y=a và y=
+ Nêu công thức nghiệm 3.Phương trình tanx=a: tana cho pt tanx=a? Cách giải : + Tìm hoành độ giao + GV hướng dẫn cách điểm ghi công thức nhgiệm PT có nghiệm dạng + Ghi công thức dạng arctan
Û x = a + kp ,k Î Z nghiệm tổng quát a = sdAM Trong đó tana = a ì p p ï- < a < -Nếu í 2 2 ïîtana = a
thì ta viết a = arctana lúc đó tanx = +Hãy giải các pt? a Þ x = arctana+kp * Thảo luận nhóm
Ví dụ : Giải các phương trình: +tan2x=tan3x
+theo dỏi kết quả hoạt . a tan x-tan3x=0 +tan3x=5/4
động nhòm của học sinh - = +Họi học sinh lên bảng .t b an 3x 5 / 4 0 + tan( 15o ) tan 30o x + =
trình bày, chỉnh sửa kết . c tan x+3/4=0 quả 3 o +PT tanf(x)=tang(x) có d.tan(x+15 ) = 3 nghiệm ntn? *chú ý : +tanx=tan o b công thức a.PT tanf(x)=tang(x) nhiệm được ghi ntn?
Þ f (x) = g(x) + kp , k Î Z + Trong cùng một pt có b. tanx=tan o b 11
Giáo án Đại số 11 – Chương trình chuẩn
cho phép dùng đồng thời Þ o = b + 180o x k , k Î Z hai đơn vị không?
c. Trong cùng một công thức
nghiệm không dùng đồng thời hai đơn vị độ và radian.
HĐ4 : Tìm công thức nghiệm cho PT cotx=a Tg Hoạt động của GV Hoạt động của HS Nội dung ghi bảng
10/ + Nêu công thức nghiệm + Vẽ đồ thị y=a và y=cotx
4.Phương trình cotx=a: cho pt cotx=a?
+ Tìm hoành độ giao điểm Cách giải : + GV hướng dẫn cách + Ghi công thức nghiệm PT có nghiệm dạng: ghi công thức nhgiệm tổng quát
pt Û x = a + kp , k Î Z dạng arccotan a = sdAM Trong đó cota = a ì < a < p 0 -Nếu í îcota = a
thì ta viết a = arccota lúc đó cotx = a Þ x = arccota+kp
Ví dụ : Giải các phương trình: 10/ +Hãy giải các pt? * Thảo luận nhóm . a cot 2x-tan3x=0 .
b cot 3x - 5 / 4 = 0
+theo dỏi kết quả hoạt
động nhòm của học sinh . c cot x+3/4=0 +Họi học sinh lên bảng 3 o
trình bày, chỉnh sửa kết d.cot(x+15 ) = 3 quả *Chú ý : +PT cotf(x)=cot(x) có a.PT cot(x)=cot(x) nghiệm ntn?
Þ f (x) = g(x) + kp , k Î Z +cotx = cot o b công b. cotx = cot o b thức nhiệm được ghi o o ntn? Þ x = b + 180 k , k Î Z + Trong cùng một pt có
c. Trong cùng một công thức nghiệm cho phép dùng đồng
không dùng đồng thời hai đơn vị độ và thời hai đơn vị không? radian 4. Củng cố
- Nắm vững công thức nghiệm
- Chú ý đơn vị trong công thức nghiệm
- Đối với các giá trị của a có trong bảng gia trị lượng giác của các cung đặc biệt thì không ghi dưới dạng arcsin, arccos ... TRẮC NGHIỆM
Câu 1: Chọn đáp án đúng trong các câu sau: A. B. C. D.
Câu 2: Chọn đáp án đúng trong các câu sau: A. B. C. D.
Câu 3: Chọn đáp án đúng trong các câu sau: A. B. C. D.
Câu 4: Phương trình tanx = 1 có nghiệm là 12
Giáo án Đại số 11 – Chương trình chuẩn A. p p p x = kp
B. x = + kp
C. x = + k2p
D. x = + kp 4 2 2
Câu 5: Phương trình 2sin x = 0 có nghiệm là : p p
A. x = k2p
B. x = kp C. x = + kp D. x = + k2p 2 2
Câu 6. Pt 2cosx=m có nghiệm khi a.m>2 b.m<-2 c. m £ 2 c.m=-3 13
Giáo án Đại số 11 – Chương trình chuẩn Tiết 9,10,11 BÀI TẬP I. Mục tiêu
-KT : Nắm vững cách giải PTLG cơ bản
-KN : Biến đổi Ptlg, giải thành thạo PTLG cơ bản
II. Phương pháp: Vấn đáp , thảo luận nhóm
III.Các bườc tiến hành
Tiết 1: Bài 1 à 3; Tiết 2: Bài 4 à5; Tiết 3: Bài 6 à7 1.Ổn định lớp 2.Kiểm tra bài cũ
Hđ1: Câu 1. Nêu công thức nghiệm của các PTLG cơ bản Câu 2. Giải các pt sau a. sinx.cosx=1 b. tan 2x - 3 = 0
Thời Hoạt động của HS Hoạt động của GV Nội dung ghi bảng gian
+ Nhận xét câu trả lời Câu 1 . Gv chỉnh sửa và
Câu 2 . a. sin2x=2 Þ PTVN
+Giải bài tập ,nhận xét nhắc lại chính xác 1 kp cách trình bày Câu 2 .
b. tan 2x = 3 Þ x = arctan3+ 2 2 trên bảng + Gọi HS lên bảng +chỉnh sủa kết quả 3. Bài tập
HĐ 2 : Giải các bài tập SGK
Thời Hoạt động của HS Hoạt động của GV Nội dung ghi bảng gian
+ Theo dỏi cách giải, + Gọi học sinh lên
Bài 1 . Giải phương trình NXkết quả bảng giải .
a sin(x + 2) = 1/ 3 +chỉnh sủa kết quả éx = arcsin1/2-3+k2p Û ê
ëx = p - arcsin1/2-3+k2p 2x p - = . c sin( ) 0 3 3 p k3p Û x = + 2 2 o 3 sin(2x + 20 ) = - 2
d. Û sin(2x + 20o ) = sin( 60o - ) o o + Dựa vào đồ thị giá éx = 40 - + 180 k Û ê , k Î Z trị hai hàm số bằng
êëx = 110o + 180o k
nhau khi : sin3x=sinx + Giá trị của hai hàm Bài 2 . Tìm x để các giá tri y=sin3x bằng + Giải pt
số bằng nhau khi nào y=sinx +x=...... ? éx = kp + nêu PT lập được? ê Ta có : sin3x=sinx Û kp êx = p / 4 + ë 2 + Sử dụng cách ghi
Bài 3 .Giải phương trình
nghiệm của PTLG cơ + Gọi học sinh lên 2 bản, biến đổi tim bảng giải a. os( c x-1)= 3 x=......... +chỉnh sửa kết quả éx =1+ arcsin2/3+k2p Û ê ëx =1- arcsin2/3+k2p b. cos3x=cos12o 14
Giáo án Đại số 11 – Chương trình chuẩn
éx = 4o + 120o k Û ê o o êëx = 4 - + 120 k 3x p os( c - ) = 1 - / 2 2 4 é 11p c. x = + k4p / 3 ê +Sử dụng công thức 18 Û ê , k Î Z nào? 5 - ê p x = + k4p / 3 êë 18 2 os c x = 1/ 4 1+ os2x c d. Û = 1/ 4 +sin2x-1 khác không 2 +giải pt cos2x=0 +Nêu cách giải ? é p x = + kp Kiểm tra ĐK và +ĐK? ê 6 Û chon x=...... +giải pt cos2x=0? ê ê p Kiểm tra ĐK và chon x = - + kp êë 6 x?
Bài 4 . Giải phương trình 2 os2x c = 0 *Các hoạt động như 1-sin2x trên p
DK : sin 2x ¹ 1 Û x ¹ + kp 4 *Các hoạt động như é p trên x = + kp (L) ê 4 pt Û os2x=0 c Û ê p
êx = - + kp(T) * Các hoạt động như êë 4 trên
Bài 5 . Giải phương trình o 3 a. tan(x -15 ) = 2 o ¹ os( c x-15 ) 0
+Biến đổi để đưa về
+ ĐK : pt Û x -15o = 30o + 180o k pt đã học?
Û x = 45o + 180o k (T ) c.cos2x.tanx=0 p osx c ¹ 0 Û x ¹ + kp 2 ĐK : é p +Nêu ĐK? é os2x=0 c x = + kp (T ) pt ê Û Û ê 4 +giải pt? tanx=0 ê ë
ëx = kp (T ) d.cos3x.cotx=0 +Còn cách giải nào ĐK : khác? sinx ¹ 0 Û x ¹ mp
éx = kp / 3(k ¹ 3m) ésin3x=0 pt ê Û Û ê p ëcotx=0
êx = + kp (T) ë 2
Bài 7 . Giải phương trình 15
Giáo án Đại số 11 – Chương trình chuẩn sin 3x = os5x c p a.sin3x=cos5x Û sin3x=sin( - 5x) 2 é p x = +kp / 4 ê Û 16 ê ëx = p - / 4 + kp b. tan3x.tanx=1 Đk : os3x c ¹ 0,cosx ¹ 0 C1. tan3x=cotx p
Û tan 3x = tan( - x) 2 p kp Û x = + (T ) 8 4 C2. sin3x.sinx=cos3x.cosx Û cos4x=0. HĐ3 : Củng cố
- Chú ý cách biến đổi pt để đưa về pt cơ bản
- Khi giải pt có điều kiện cần kiểm tra ĐK TRẮC NGHIỆM
Câu 1: Phương trình lượng giác .tan x = - 3 có nghiệm là : p p p p A. x = + kp B. x = - + k2p C. x = + kp D. x = - + kp 3 3 6 3 x 3
Câu 2: Giải phương trình lượng giác : cos = - có nghiệm là 2 2 5p p p p A. x = ± + 5
k2p B. x = ± + 5 k2p C. x = ± + 5 k4p D. x = ± + k4p 3 6 6 3 æ 2x p ö
Câu 3: Phương trình : sin - = 0 có nhghiệm là : ç ÷ è 3 3 ø 5p k3p p p k p A. x = ± +
B. x = kp C. x = + 3 kp D. x = + 2 2 3 2 2 1
Câu 4: Phương trình lượng giác: cot x = có nghiệm là: 3 p p p A. x = + kp B. x = + kp C. x = + k2p D.Vô nghiệm 6 3 3
Câu 5 :Số nghiệm Pt sinx=1/2 trong [ p - ;p ] là A. 0 B. 1 C .2 D. 3 1 æ p ö
Câu 6: Cho phương trình: cos 2x = - , số nghiệm của pt thuộc khoảng ç ; o ÷ là: 2 è 2 ø A. 1 B. 2 C. 3 D. 4
Câu 7: Nghiệm của phương trình sinx = 1 thỏa điều kiện: 0 < x < p A. p p x = B. x = p C. x = 0 D. x = - 2 2 16
Giáo án Đại số 11 – Chương trình chuẩn
Câu 8: Giải phương trình : 2
tan x = 3 có nghiệm là : p p p A. x = ± + p k B. x = ± + kp C. vô nghiệm D. x = + kp 3 6 6
Câu 9: Phương trình lượng giác : 0
cos3x = cos12 có nghiệm là : p p p p - p p p A. k k2 k2 x = ± + 2 k2p B. x = ± + C. x = + D. x = + 15 45 3 45 3 45 3 17
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 12 – 14. Bài 3. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP I/ MỤC TIÊU:
*Về kiến thức: Giúp học sinh nắm vững cách giải một phương trình bậc nhất, bậc hai đối với một hàm số
lượng giác,phương trình bậc nhất đối với sin và cos.
*Về kỹ năng: + Giúp học sinh nhận biết và giải thành thạo một phương trình bậc nhất, bậc hai đối với một hàm số lượng giác.
+ Biến đổi phương trình đưa về dạng đã gặp
*Về tư duyvà thái độ: Rèn luyện tư duy logic, tính chính xác , khoa học.
II/ CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH: GV: Phiếu học tập
HS: Kiến thức phương trình lượng giác cơ bản, bảng phụ của mỗi nhóm. III/ Phương pháp:
+Phát vấn, hoạt động nhóm. IV/ Tiến trình bài dạy:
Tiết 12: Mục I, tiết 13: Mục II; tiết 14: Mục III 1/ Kiểm tra bài cũ: *Hoạt động 1:
Tgian Hoạt động của Học Sinh
Hoạt động của GV Ghi bảng
GV đặt câu hỏi kiểm tra 1 H1: Gpt sin3x= - 2 H2: Gpt 2cosx - 3 =0
H3: Gpt (sinx -1)(sinx + 2) =0
3 hs lên bảng giải phương Gọi 3 HS trình bày bảng trình
Cả lớp theo dõi nhận xét
Gv hiệu chỉnh và dẫn dắt học sinh vào bài mới 2/ Bài mới:
*Hoạt động 2: Hình thành kỹ năng nhận biết và giải phương trình bậc nhất đối với một hàm số lượng giác.
Tgian Hoạt động của Học
Hoạt động của GV Ghi bảng Sinh
I/ Phương trình bậc nhất, đối với một
H1: Hs cho ví dụ về hàm số lượng giác.
HS cho 2 ví dụ về phương trình bậc nhất đối 1.ĐN: pt at + b = 0 (1)
phương trình bậc với một hàm số lượng t là một hàm số lượng giác
nhất đối với một hàm giác. 2.Cách giải số lượng giác. (1) Û t = -b/a : PTLGCB
H2: Gọi Hs chỉ ra hướng VD: Gpt: Đưa về ptlg cơ bản giải và giải a/ 3sinx+5=0 Cả lớp theo dõi và b/ 3cosx-2=0 nhận xét
GV nhận xét và hiệu c/ 2tan3x+2 =0 -Hs đọc đề và tìm chỉnh d.3sin(x+15o)+ 3 =0 hướng giải
3.Phương trình đưa về phương trình bậc
-không có dạng quen HDTP1:Giới thiệu ví dụ 1 nhất đối với một hàm LG thuộc Gợi ý Ví dụ1: Giải pt - Công thức hạ bậc CH1 Pt trên thuộc dạng Hs1: giải nào? Hs2: nhận xét
Ch2-Làm thế nào để đưa về dạng quen thuộc Gọi hs1 giải Hs2 nhận xét Gv:Kiểm tra ,nhận xét, 18
Giáo án Đại số 11 – Chương trình chuẩn hoàn chỉnh lời gải 2 osx+si c n2x=0 HDTP2:Yêu cầu hs Û 2cosx(1+sinx)=0 nghiên cứu vdụ2 Đọc đề nghiên cứu Câu hỏi gợi ý é p x= + kp é ê
đề trả lời các câu hỏi 1) có nên khai triển vế cosx=0 2 Û Û ê ê (1) của gv trái ?vì sao ësinx=-1 p ê + p x=- k2
2) có thể rút gọn 2vế cho êë 2 1+sinx không? p
GV nhận xét các câu trả Û x= + kp
hs1:trình bày cách lời của hs và giải thích 2 giải Giải Gọi hs1 giải ) 1 ( Û 1/ (cos 2 7x + cos3x) = Hs2 nhận xét 1/ (cos 2 7x + cos x) Û cos3x = cos x Gv hoàn chỉnh lời giải éx = p k
é3x = x + k2p ê Û Û ê p k
3x = -x + k2p ê ë x = ë 2 Ví dụ 2 Giải pt 1 ( + sin x 1 )( - cos x 2 ) = cos x (1) Giải ) 1 ( Û 1 ( + sin x 1
)( - cos x) = 1- sin 2 x Û 1
( + sin x)(sin x - cos x) = 0 ésin x = -1 ê Û ê p
sin x = cos x = sin( + x) ë 2 é p êx = - + k p 2 ê 2 ê p Û x x k p ê = - + 2 2 ê ê p x = x + + k p 2 (vn) êë 2 é -p êx = + k p 2 Û ê 2 ê p x p ê = + k ë 4
*Hoạt động3: Hình thành kỹ năng nhận biết và giải phương trình bậc hai đối với một hàm số lượng giác. Tgian Hoạt động của
Hoạt động của GV Ghi bảng Học Sinh 19
Giáo án Đại số 11 – Chương trình chuẩn
HĐTP1: Giải phương II/ Phương trình bậc hai đối với một hàm số
trình bậc hai đối với một lượng giác. hàm số lượng giác. 1. ĐN : Pt có dạng
H1: Hs nhận dạng phương at2 + bt + c = 0 ( a ¹ 0 )
trình bậc hai đối với một t là một trong các hàm lượng giác
Dạng tổng quát và hàm số lượng giác và Chẳng hạn
phương pháp đặt hướng giải cho mỗi pht * asin2x + bsinx + c = 0 ẩn phụ * acos2x + bcosx + c = 0 * atan2x + btanx + c = 0
H2: Có điều kiện ràng * acot2x + bcotx + c = 0 ĐK:
buộc cho ẩn phụ t không? 2.Cách giải sinx £ 1, osx c £1
+Đặt t = một trong các hàm LG .ĐK t £ 1
H3:Yêu cầu học sinh giải +Đưa về PT bậc hai theo t HS trình bày lời vd1 + Giải PT theo t, tìm t giải, lớp theo dõi + Thay t tìm x nhận xét. GV nhận xét chung và hiệu chỉnh. Vd1: Gpt: a)2cos2x – 5cosx + 3 = 0 b) 2cot2x – 5cotx +2 = 0 HĐTP2: Pht quy về
phương trình bậc hai đối
với một hàm số lượng Vd2: Gpt: giác. cos2x + sinx + 1 =0
Không phải là GV đưa vd2 và hỏi có phải 2
Û 1- sin x + sinx +1 =0
phương trình bậc là một phương trình bậc 2
hai đối với một hai đối với một hàm số Û sin x - sinx - 2 =0
hàm số lượng lượng giác không?
Đặt t = sinx Đk: t £ 1 giác. pht thành: t2 – t – 2 =0 H: Tìm cách đưa về ét = 1 -
phương trình bậc hai đối Û ê ët = 2(loai)
TL: Dùng công với một hàm số lượng thức cos2x = 1 – giác. Û sin x = -1 sin2x p Û x = - + k2p
Không phải là Gv ghi bảng nội dung trả 2
phương trình bậc lời của HS Vd1: Gpt: hai đối với một cos2x - sinx + 1 =0 hàm số lượng
<=>-sin2x - sinx + 2 =0 giác.
+PTcó phải là một phương Đặt t = sinx Đk: t £ 1
trình bậc hai đối với một pht thành: -t2 – t + 2 =0
hàm số lượng giác không? ét = 1 + Kiểm tra cosx=o Û ê ët = 2( - loai) và cosx khác không + Giải PT theo t với t=1 ta có + Tìm x=..... p x = + 2kp 2 20
Giáo án Đại số 11 – Chương trình chuẩn
HS hoạt động theo HĐTP3: Củng cố việc giải
nhóm và trình bày một phương trình bậc hai
lời giải trên bảng đối với một hàm số lượng phụ giác.
GV phát phiếu học tập cho
từng nhóm và yêu cầu hs gbiải trong 5 phút
HS thuyết trình lời Gv quan sát hiệu chỉnh
giải trên bảng phụ, cho từng nhóm. Chú ý
các nhóm khác hiệu chỉnh cho phiếu 3,
theo dõi và nhận phiếu 4. xét. Gv cho học sinh thuyết
trình lời giải của nhóm
trên bảng phụ và đưa ra lời giải chính xác Phiếu học tập Tg: 5 phút
Phiếu học tập 1: (5') Gpt: 2tan22x +5tan2x – 3 =0
Phiếu học tập 2: (5') Gpt : 4sin2x – 2 (1+ 2)sinx + 2 = 0
Phiếu học tập 3: (5') Gpt: 2cos2x + 2cosx - 2 = 0
Phiếu học tập4: (5') Gpt: 5tanx – 3cotx -3 = 0
*Hoạt động 4: Giải phương trình sinx+cosx=1 Tg
Hoạt động của GV Ghi bảng
Hoạt động của HS
H3:Biến đổi biểu thức HS:Biến đổi sinx + cosx thành tích? sinx+cosx=1 æ p ö æ p ö sinx+cosx= 2 sin x + ç ÷ è 4 ø Û 2 sin x+ =1 ç ÷ è 4 ø HS:giải PT H4:Giải PT æ p æ p ö 1 æ p ö 1 ö 1 sin x+ = Û sin x + = sin x+ = ç ÷ ç ÷ ç ÷ è 4 ø 2 è 4 ø 2 è 4 ø 2 æ p ö p Û sin x + = sin ç ÷ è 4 ø 4 é x = k2p ê Û p êx = + k2p ë 2
*Hoạt động 5: Giải phương trình 3 sinx-cosx=1(2) Tg
Hoạt động của HS
Hoạt động của GV Ghi bảng HS:Biến đổi H5:Biến đổi 3 sinx-cosx 3 sinx-cosx 3 sinx-cosx thành Ta có : 3 1 tích? =2( sinx- osx) c 3 1 =2( sinx- osx) c 2 2 2 2 H6: Nhận xét quan hệ HS: 2 2 2 æ ö 2 æ 3 æ 1 ö 3 ö æ 1 ö ç ÷ + - ç ÷ ç ÷ ç ÷ + - = 1 ç ÷ ç ÷ 2 è ø è 2 ø 2 è ø è 2 ø H7: Giải phương trình p 2sin(x - ) = 1 6 21
Giáo án Đại số 11 – Chương trình chuẩn 3 p p p = os c = 2(sinxcos - sin osx) c 6 6 HS: Thay 2 6 1 p p = sin =2sin(x- ) 2 6 6 HS: p 1 p (2) Û sin(x - ) = 3 sinx-cosx=2sin(x- ) 6 2 6 é p HS: x = + k2p ê Û 3 p 1 ê sin(x - ) = ë x = p + k2p 6 2
*Hoạt động 6: Giải phương trình 2 2
a sinx+bcosx=c(dk: a +b ¹ 0) Tg
Hoạt động của HS
Hoạt động của GV Ghi bảng HS: HĐTP1: Hình thành
III. Phương trình bậc nhất đối phương pháp giải với sin và cos 2 2 Giới thiệu khái niệm asinx+bcosx=c(3) æ a ö æ b ö ç ÷ + ç
÷ =1 dạng phương trình bậc * Cách giải : ç ÷ ç ÷ 2 2 2 2 è a + b ø è a + b ø
nhất đối với sinx, cosx Chia hai vế pt cho HS: Biến đổi H8: Biến đổi 2 2 a + b asinx+bcosx=
a sinx+bcosx về dạng 2 2 a b Đặt a + b ( sinx+ osx) c d sin(x+a ) hoặc 2 2 2 2 a + b a + b a os( dc x+a ) = os c a 2 2 H9: Nhận xét a + b HS:Đặt 2 2 b a æ ö æ ö Þ = a = a b sin os c a ç ÷ + ç ÷ = ? 2 2 + 2 2 a b a + b 2 2 2 2 è a + b ø è a + b ø c b (3) Û sin ( x + a ) = *Chú ý: Þ = sina GV: Hệ thống lại 2 2 a + b 2 2 a + b
phương pháp giải pt dạng (3) có nghiệm 2 2 2
Û a + b ³ c HS: a sinx+bcosx=c a sinx+bcosx=c GV: Pt(*) có nghiệm c (*) khi nào? Û sin(x+a) = 2 2 a + b c £ 1 HS: 2 2 a + b 2 2 2
Û a + b ³ c HĐTP2: Rèn luyện và củng phương pháp giải GV đưa vd củng cố, yêu Vd 1Gpt:
cầu học sinh giải và trình 2sin 3x + 5 os3x= c - 3 bày bảng
Vd2: Với giá trị nào của m thì
HS giải và trình bày bảng pt: 2sin 2x + 5 os2x = c m có
dưới hướng dẫn của GV HD vd2: Đk nào pt có nghiệm? nghiệm?
3/ Củng cố: (3ph)+Nắm vững cách giải phương trình bậc nhất, bậc hai đối với một hàm số lượng giác.
+Nhắc lại phương pháp giải pt bậc nhất đối với sinx và cosx TRẮC NGHIỆM
Câu 1: Phương trình lượng giác: 2cot x - 3 = 0 có nghiệm là: 22
Giáo án Đại số 11 – Chương trình chuẩn é p x = + k2p ê 3 p p A. 6 ê B. x = arc cot
+ kp C. x = + kp D. x = + kp p - ê 2 6 3 x = + k2p êë 6
Câu 2: Phương trình sin x + 3 cos x = 0 có nghiệm dương nhỏ nhất bằng: p 2p p 5p A. B. C. D. 3 3 6 6 3
Câu 3: Phương trình : 2
cos 2x + cos 2x - = 0 có nghiệm là : 4 2p p p p A. x = ± + kp
B. x = ± + kp
C. x = ± + kp
D. x = ± + k2p 3 3 6 6
Câu 4: Nghiệm của phương trình : sin x + cos x = 1 là : é p éx = k2p = + p p x k2 ê
A. x = k2p B. ê p C. x = + k2p D. 4 ê ê x = + k2p 4 p ë ê 2 x = - + k2p êë 4
Câu 5: Phương trình sin x = 3 cos x - 2 có các nghiệm là: p p p
A. x = - + k2p B. x =
+ kp C. x = + kp D. x = k2p 3 4 4
Câu 6: Cho phương trình: 2sin 2 3x = 1, nghiệm của pt là: p p p
A. x = k , k Î Z B. x = k , k Î Z C. x = k , k Î Z D. Đáp số 2 3 4 khác
Câu 7: Giải phương trình ( x+ 0 2cos 3 15 ) - 3 = 0 0 0 éx = 25 + k.120 0 0 éx = 5 + k.120 0 0 éx = 25 + k.120 0 0 éx = 5 + k.120 A. ê B. ê C. ê D. ê 0 0 êëx = 15 - + k.120 0 0
êëx = 15 + k.120 0 0
êëx = 15 + k.120 0 0 êëx = 15 - + k.120
Câu 8: Cho phương trình: cos 2x = 2cos x -1, nghiệm của pt là: p p p A. x =
+ kp; x = k2p , k Î Z B. x = k , k Î Z C. x = ± + kp , k Î Z D. Vô 2 2 2 ngiệm 23
Giáo án Đại số 11 – Chương trình chuẩn
Tiết: 15,16,17 BÀI TẬP I, Mục tiêu
-kt :+Giải một số phương trình lượng giác thường gặp
+Biết cách viết công thức nghiệm của các PTLG cơ bản
-KN : Biến đổi PT để đưa về giải PTLG cơ bản
II. Phương pháp: Vấn đáp , thảo luận nhóm III.Các bước tiến hành
Tiết 15: Bài 1, 2; Tiết 16: 3, 4; Tiết 17: 5-6 1.Ổn định lớp 2.Kiểm tra bài cũ
Hđ1: Tìm x thoả : a. 2sinx - 1 =0 b.sin2x-cosx =1 TG Hoạt động của HS Hoạt động của GV Nội dung ghi bảng +Trình bày bài toán + gọi học sinh lên +Nhận xét bảng trình bày,theo Giải pt: dỏi và chỉnh sửa kết sin2x - cosx =-1 quả 2 Û 1- os c x - osx +1 = c 0 2 Û - os c x - osx+2 = c 0
Đặt t = sinx Đk: t £ 1 pht thành: -t2 – t + 2 =0 ét = 1(T ) Û ê ët = 2( - loai) Û osx = c
1 Û x = k2p (k Î Z ) 3. Bài tập SGK Tg HĐ của HS HĐ của GV Nội dung ghi bảng + Đặt sinx làm thừa +Nêu cách giải bài 1.GPT sin2x-sinx =0 chung toán? ósinx(sinx-1)=0 éx = kp ésinx=0 ê Û Û ê p ësinx=1 êx = + k2p ë 2 + Pt bầc hai đối với + PT đã cho có dạng
2. Giải các phương trình một hàm số cos nào đã học? a.2cos2x - 3cosx+1 =0
+ Đặt ẩn phụ rồi giải +Nêu cách giải bài
Đặt t = cosx Đk: t £ 1 toán? pht thành: 2t2 – 3t + 1 =0 ét = 1(T ) Û ê ët = 1/ 2(T )
t =1Þ x = k2p + Với t=1/2 ta có cosx=1/2 é p x = + k2p ê 3 Û ê ê p x = - + k2p ê ë 3
b. 2sin 2x + 2 sin 4x = 0
+ sin4x= sin2x.cos2x + PT đã cho có dạng + Đặt sin2x thừa nào đã học? chung +Nêu cách biến đổi toán? 24
Giáo án Đại số 11 – Chương trình chuẩn +sin2x/2=1-cos2x/2 é + Pt bầc hai đối với êx = kp / 2 một hàm số cos ê 3p
+ Đặt ẩn phụ rồi giải + PT đã cho có dạng ê Û x = - + kp ê nào quen thuộc đã 8 ê học không ? 3p êx = - + kp +Nêu cách biến đổi ë 8 toán?
3. Giải các phương trình a.sin2x/2-2cosx/2+2 =0 + PT đãcho có dạng tđ cos2x/2+2cosx/2-3 =0 nào quen thuộc đã é x học không ? os c = 0(T ) ê 2 +Nêu cách biến Û ê Û x = k4p x ê os c = 3 - (L) ê đổi toán? ë 2 b.8cos2x +2sinx-7 =0 tđ -8sin2x+sinx+1 =0
Đặt t = sinx Đk: t £ 1 pht thành: -8t2 +t + 1 =0 é p x = + k2p ê 6 ê 5 ê p x = + k2p ê 6 Û , k Î Z ê 1 ê = + p x arcsin(- ) k2 ê 4 ê 1
êx = p - arcsin(- ) + k2p ë 4 d. tanx-2cotx+1=0 + Tìm ĐK ? ĐK : sinx ¹ 0 , cosx ¹ 0 +Nêu cách biến 2 Pttđ: tanx - +1=0 t anx đổi toán? Đặt t = tanx ét = 1(T ) pht thành: t2 +t-2 =0 Û ê ët = 2( - T ) + Với t=1 và t=-2 ta có é p x = + kp ê Û 4 ê
ëx = arctan(-2) + kp
4. Giải các phương trình + PT đã cho có dạng a. 2sin2x+sinx.cosx-3cos2x=0 nào quen thuộc đã
Giải : +Nếu cosx=0 không thoả phương trình. học không ?
+ Nếu cosx khác không, chia hai vế PT cho +Nêu cách biến đổi cos2x ta đươc pt toán? 2 tan2x+tanx-3=0 é p = + p ét anx=1 x k ê 4 Û Û ê ê , k Î Z ëtanx=-3/2 3
êx = arctan(- ) + kp êë 2 b. 3sin2x-4sinx.cosx+5cos2x=2
Giải : +Nếu cosx=0 không thoả phương trình. 25
Giáo án Đại số 11 – Chương trình chuẩn
+ Nếu cosx khác không, chia hai vế PT cho cos2x ta đươc pt tan2x-4tanx+3=0
d. 2cos2x- 3 3 sin2x-4sin2x=-4 Û6cos2x- 6 3 sinx.cosx=0 Giải: pt Û cosx(cosx- 3 sinx)=0 é p écosx=0 x = + k ê p 2 Û ê Û ê ,k Î Z cosx- 3sinx=0 ë ê p x = + kp êë 6
5. Giải các phương trình a.cos x - 3 sin x = 2
Û 1/ 2cos x - 3 / 2sin x = 2 / 2 π Û 2cos(x + ) = 2 3 é p x = - + k2 ê p 12 Û ê ,k Î Z 7 ê p x = - + k2p êë 12 b.3sin x3 -4cos x3 = 5 Û 3/ 5sin x 3 - c 3 os x 3 = 1 Û sin( x 3 - α) = 1
Với sin α =4/5 ; cos α =4/5 α π k π Vậy PT có nghiệm x = + + 2 3 6 3 c.2sin x + 2c x os - 2 = 0 Û 2 2 cos x + sin x = 2 / 2 2 2 π Û 2 2 cos(x - ) = 2 4 π Û cos(x - ) = 1/ 2 4
6. Giải các phương trình a. tan(2x+1).tan(3x-1) =1
ĐK : sin(2x+1) ¹ 0 ; cos(3x-1) ¹ 0 Þ tan(2x + ) 1 = cot( x 3 - ) 1 π pt Þ tan(2x + ) 1 = tan( - x 3 + ) 1 2 π kπ Þ x = + 10 5 4. Củng cố :
- Chú ý các cách giải PT 26
Giáo án Đại số 11 – Chương trình chuẩn
- Giải thêm các bài tập trong sách bài tập TRẮC NGHIỆM p
Câu 1: Cho phương trình: sin(2x - ) +1 = 0 , nghiệm của pt là: 6 p p p p A. x =
+ kp , k Î Z B. x = - + kp , k Î Z C. x =
+ kp , k Î Z D. x = - + kp , k Î Z 4 2 6 6
Câu 2: Cho phương trình: 2cos 2x + 2 = 0 , nghiệm của pt là: p 3p 3p p A. x = ±
+ kp , k Î Z B. x =
+ k2p , k Î Z C. x = ±
+ kp , k Î Z D. x = - + kp , k Î Z 4 8 8 6
Câu 3: Cho phương trình: 2sin 2x + sin x = 0 , pt có 1 họ nghiệm là: p 1 A. x =
+ kp , k Î Z B. x = kp , k Î Z C. x = ± + kp , k Î Z D. x = p + k2p , k Î Z 4 4
Câu 4: Cho phương trình: sin 2x - 2cos x = 0 , nghiệm của pt là: p 3p p A. x =
+ kp , k Î Z B. x =
+ k2p , k Î Z C. x =
+ kp , k Î Z D. 8 4 2 p x = - + kp , k Î Z 6
Câu 5: Phương trình : 2 sin x - m = 0 vô nghiệm khi m là: A. m > 1
B. m <-2 hoặc m >2 C. m < 1 - D. 2 - £ m £ 2
Câu 6: Nghiệm của phương trình 2
2cos x + sin x +1 = 0 (với k Î ! ) là p p
A. x = - + k2p B. x = + k2p
C. x = kp
D. x = k2p 2 2
Câu 7: Phương trình sin x + cos x = 2 sin 5x (với k Î ! ) có nghiệm là: p p p p π π π π p p p p p p p p A.
+ k , + k B. + k , + k C. + k , + k D. + k , + k 16 2 8 3 4 2 6 3 12 2 24 3 18 2 9 3
Câu 8: Nghiệm của phương trình 2
2cos x - 3cos x +1 = 0 (với k Î ! ) là p p p
A. x = k2p B. x = k2p , x = ± + k2p C. x = - + k2p D. x = + k2p 3 3 3 27
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 18,19 ÔN TẬP CHƯƠNG I I, Mục tiêu
- KT :+ Hệ thống các kiến thức về HSLG
+ Giải các phương trình lượng giác - KN : Giải PTLG cơ bản
II. Phương pháp: Gởi mở-Vấn đáp
III.Các bước tiến hành
Tiết 1: Ôn lý thuyết; Tiết 2: Bài tập 1.Ổn định lớp 2.Kiểm tra bài cũ 3.Ôn chương
A. Hệ thống các kiến thức
-Các HSLG, Tập xác định, chu kì , tuần hoàn
-Sự biến thiên và đồ thị của các HSLG
-Nêu các cách giải phương trình :
+Phương trình bậc nhất đối với một hàm số lượng giác
+Phương trình bậc hai đối với một hàm số lượng giác
+Phương trình bậc nhất đối với sin và cos
Thời Hoạt động của HS Hoạt động của GV Nội dung ghi bảng gian
+Hệ thống lại cáckiến + cho HS nhắc lại thức trên +chỉnh sửa B. Giải bài tập SGK Tg Hoạt động của HS Hoạt động của GV Nội dung ghi bảng Bài 1. - Sử dụng định nghĩa CH1: Nêu phương pháp a.y=cos3x của hsố chẵn lẻ. giải bài toán? Vì f(-x)=cos(-3x)=cos3x=f(x) Vậy hàm số chẵn - Tính f(-x). CH2: Tính f(-x)? b. y=tan(x+p / 5 ) - So sánh f(-x), f(x) CH3: KL.
Vì f(-x) ¹ f(x) Nên hàm số không phải là hàm số lẻ. - Vẽ đồ thị é p 3 ù y =sinx và y = -1
CH4: Dựa vào đồ thị tìm Bài 2 . Tìm x trên - ; p 2 để y=sinx ê ú ë 2 û
- Tìm giao điểm của hai x thỏa các điều kiện câu
a. Nhận giá trị bằng -1 đồ thị. a, b? x Î{- p / 3 ; 2 p / } - Tìm x thỏa 2 é p 3 ù b. Nhận giá trị âm - ; p 2 ê ú x Î (- p 0 ; )È (p ; p 2 ) ë 2 û
Bài 3: Tìm GTLN của hàm số: - Sử dụng ĐTLG hoặc đồ thị. a. y = 1 ( 2 + cos x) +1 Tacó: 1+ cosx £ 2 CH5: Tập giá của hàm + cos x £ 1 số cosx? à 1 ( 2 + cos x) +1 £ 3 Vậy maxy = 3 khi x = k2p . - Trả lời.
CH6: Đánh giá biểu thức p
b. y = 3sin(x - ) - 2 1+ cosx và bt 6 1 ( 2 + cos x) +1 p Tacó: 3sin(x - ) £ 3 6 * Hoạt động tương tự * Hoạt động tương tự p à 3sin(x - ) - 2 £ 1 câu a. câu a. 6 28
Giáo án Đại số 11 – Chương trình chuẩn 2p p Vậy maxy = 1 khi x =
+ k2 , k Î Z 3 Bài 4: Giải các pt: - PT cơ bản. 2 CH7: Nêu dạng pt? a. sin(x +1) = . 3 é 2
êx = p -1- arcsin + k p 2 Gọi học sinh lên bảng ê 3 giải. êx = -1+ 2 arcsin + k p 2 êë 3
- Sử dụng công thức hạ b. bậc. CH8: Nêu cách giải câu 1
- Hoặc lấy căn bậc hai. b? sin 2 2x = + Gợi ý C2: 2 Û 1- cos 4x = 1 2 Û cos 4x = 0 - Lấy căn bậc hai. sin 2x = ± 2 p p
Û x = ± + k , k Î Z 8 4 CH9: Nêu P2 giải? - Lên bảng giải. x 1 c. cot 2 = 2 3
- Gọi học sinh lên bảng x trình bày. ĐK: sin ¹ 0 2 p 2 - ĐK mẫu. PT có nghiệm: x = ± + k p 2 3 p - Lên bảng giải. d. tan( +12x) = - 3 CH10: Nêu ĐK? 12 ĐK: p cos( +12x) ¹ 0 12 PT có nghiệm: 5p p x = - + k (thỏa ĐK) - Phương trình bậc hai 144 12 đối một hàm số LG. CH11: Nêu dạng pt và Bài 5: Giải PT sau: 2 cách giải?
a. 2cos x - 3cos x +1 = 0 - Lên bảng giải. écos x =1 éx = k2p ê ê Û 1 Û p ê = ê = ± + p cos x x k2 ë 2 ë 3 b. 25sin2x+15sin2x+9cos2x=25. - Phương trình thuần Giải:
nhất bậc hai đối hàm sin
+Khi cosx=0 thoả phương trình. Nên pt và cos. có nghiệm: CH12: Nêu dạng pt và x = k p 2 - Lên bảng giải. cách giải?
+ Khi cosx ¹ 0 , chia hai vế PT cho cos2x ta đươc pt 30tanx - 16 = 0 8 Þ tan x = 15 8 Þ x = arctan + p k 15
- Phương trình bậc nhất c. 2sinx + cosx = 1 đối sin và cosx. 29
Giáo án Đại số 11 – Chương trình chuẩn 2 1 1 - Lên bảng giải. Û sin x + cos x = 5 5 5 CH13: Nêu dạng pt và Û sin(x + a) = sina cách giải? éx = k p 2 Û ê ëx = p - a 2 + k p 2 1 2 Với sina = và cosa = 5 5 d. sin x + 5 . 1 cot x = 0 ĐK: sin x ¹ 0 Pt trở thành:
2sin 2 x - 3cos x = 2 CH14: Nêu dạng pt và
Û 2cos2 x - 3cos x - 2 = 0 cách giải? écos x = ( 2 l) ê Û ê x = - 1 cos (t) ë 2 1 p 2 cos x = - Û x = ± + k p 2 2 3 C. Củng cố
-Nắm vững toàn bộ kiến thức trên
-Giải các bài tập trắc nghiệm SGK TRẮC NGHIỆM 1
Câu 1: Tập xác định của hàm số y = là cos x ìp ü ìp ü ì p ü
A. D = R \ í + kp ý B. D = R \ í + k2p ý C. D = R \ í- + k2p ý D. D = R \{kp} î 2 þ î 2 þ î 2 þ 1- cos x
Câu 2: Tập xác định của hàm số y = là sin 2x ìp ü ìkp ü
A. D = R \ í + kp ý B. D = R \{k2p}
C. D = R \ í
ý D. D = R \{kp} î 2 þ î 2 þ 2sin x
Câu 3: Tập xác định của hàm số y = là 1- cos x ìp ü ìp ü
A. D = R \ í + kp ý B. D = R \{k2p}
C. D = R \ í + k2p ý D. D = R \{kp} î 2 þ î 2 þ æ p ö
Câu 4: Điều kiện xác định của hàm số y = tan 2x - là ç ÷ è 3 ø 5p p p p kp p A. x ¹ + 5 k B. x ¹ + kp C. x ¹ + D. x ¹ + kp 12 2 12 6 2 2 x
Câu 5: Giải phương trình lượng giác : 2cos = - 3 có nghiệm là 2 5p p p p A. x = ± + 5 k4p B. x = ± + 5 k4p C. x = ± + 5 k2p D. x = ± + k2p 6 3 6 3
Câu 6: Nghiệm của phương trình lượng giác : 2
sin x + 4sin x = 0 có nghiệm là : 30
Giáo án Đại số 11 – Chương trình chuẩn p p
A. x = kp
B. x = k2p C. x = + kp D. x = + k2p 2 2
Câu 7: Phương trình lượng giác : tan x + 3 = 0 có nghiệm là : p p p p A. x = + kp B. x = - + kp C. x = + kp D. x = - + k2p 3 3 6 3
Câu 8: Phương trình : sin 2x - m = 0 vô nghiệm khi m là: A. 1 - £ m £ 1 B. m < 1 - C. m > 1 D. m > 1
Câu 9: Phương trình nào sau đây vô nghiệm:
A. 3sin x – 2 = 0 B. 2
2cos x - cos x -1 = 0 C. sin x = 3 D. tan x + 3 = 0 æ 2x ö
Câu 10: Phương trình 0 sin - 60 = 0 có nghiệm là : ç ÷ è 3 ø p k3p p k p p A. x = + 5 3 B. x = ± + C. x = + kp
D. x = kp 2 2 2 2 3
Câu 11: Các nghiệm của phương trình 2
2sin x - 5cos x +1 = 0 là: p p
A. x = ± + k2p
B. x = ± + k2p ; x = ± arccos ( 3 - ) + k2p 6 3 p p
C. x = ± + k2p
D. x = ± + k2p ; x = ± arccos ( 3 - ) + k2p 3 6
Câu 12: Phương trình 3 sin x - cos x = 1
- tương đương với phương trình nào sau đây : æ p ö 1 æ p ö 1 æ p ö 1 æ p ö p A. sin x + = - B. sin x + = C. sin x - = - D. ç ÷ ç ÷ ç ÷ sin x- = - ç ÷ è 6 ø 2 è 6 ø 2 è 6 ø 2 è 6 ø 6
Câu 13: Điều kiện để phương trình 3sin x + m cos x = 5 vô nghiệm là
A. m ³ 4 hoặc m £ 4 - B. m > 4 C. m < 4 - D. 4 - < m < 4
Câu 14: Giải phương trình 1 - 5sinx + 2cos2x = 0. p p p A. x = ± + 2 2 k p B. x = + k2p, x = + k2p 6 3 3 p 5p p C. x = + k2p, x = + k2p D. x = ± + 2 k p 6 6 3 31
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 20 KIỂM TRA 1 TIẾT ( TẬP TRUNG)
Tiết 21 QUY TẮC ĐẾM I.Mục tiêu:
- Nắm được qui tắc cộng và qui tắc nhân ,hiểu được các ví dụ trình bày trong sách giáo khoa,bước đầu biết
cách áp dụng vào giải toán.
II.Phương pháp: thuyết trình, đàm thoại, trực quan
III.Chuẩn bị của giáo viên và học sinh.
1. Giáo viên : Lập các phiếu học tập.
2.Học sinh : Chuẩn bị đọc trước bài học tại nhà. IV.Tiến trình bài học. Tg
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng Làm HĐ1:
Ví dụ1 nhằm dẫn đến qui tắc I.Qui tắc cộng: Tính n(A) =6,n(B)= 3 cộng Ví dụ1: A ! B = Æ
- HĐ1: kí hiệu A,B lần lượt là
-Các quả cầu là có đánh số khác
tập hợp các quả cầu trắng,đen
nhau nên mỗi lần lấy ra một quả cầu
n(A ! B) = n( )
A + n(B) = 6 + 3 = 9 là một cách chọn.
-Chọn quả cầu trắng có 6 cách chọn
- Chọn quả cầu đen có 3 cách chọn.
-Do đó số cách chọn một trong các quả cầu là 6+3 = 9.
*Nếu A và B là các tập hợp hữu hạn không giao nhau thì
n(A ! B) = n( ) A + n(B) Ví dụ 2:
Ví dụ 2:Giúphọc sinh cần phân Kí hiệu A là tập hợp hình vuông
biệt được rõ số lượng các hình
cạnh 1cm, kí hiệu B là tập hợp hình
vuông cạnh 1cm và cạnh 2cm. vuông cạnh 2cm.Thì n(A) =
-Nêu số phần tử của tập hợp 10,n(B)= 4 hai loại hình vuông. 32
Giáo án Đại số 11 – Chương trình chuẩn - A ! B = Æ
Hình thành khái niệm qui tắc cộng:
n(A ! B) = n( )
A + n(B) = 10 + 4 = 14
*Phát biểu qui tắc cộng:
*Nhấn mạnh nội dung qui tắc -Nội dung ( SGK ).
Từ đó có tất cả là 14 hình
để nhận biết qui tắc cộng. vuông
*Nêu nhận xét bài tập1.
- Công việc đặt ra có bao nhiêu *Luyện tập: hành động Bài tập:
*Rèn luyện cũng cố qui tắc
- Các hành động này khi thực cộng:
hiện có độc lập với nhau
Trong một cuộc thi tìm hiểu về đất
- Đưa thêm các ví dụ để học không?
nước việt nam.Ban tổ chức công bố sinh tự giải.
* Có thể nêu lên nhận xét về
danh sách các đề tài bao gồm :8 đề
- Học sinh thảo luận nhóm và qui tắc cộng cho công việc với
tài lịch sử,7 đề tài về thiên nhiên,10
tự đưa ra các ví dụ,sau đó cả nhiều phương án.
đề tài về con người và 6 đề tài về
lớp cùng đánh giá xem xét
văn hóa.Mỗi thí sinh được chọn một
các ví dụ được đưa ra.
đề tài.Hỏi mỗi thí sinh có bao nhiêu
khả năng lựa chọn đề tài.
-Đưa ra hình ảnh trực quan Nêu nhận xét ví dụ 3: II.Qui tắc nhân:
về số cách chọn một bộ áo
-Công việc đặt ra là chọn một Ví dụ3.Nội dung (SGK) quần,để học sinh hi 1 ểu đượ a1 c ý
bộ áo quần từ 2 áo và 3 quần đã nghĩa bài a toán.
-Hai áo được ghi chữ a,b. cho 2 a2
- Ba quần được đánh số 1,2,3.
-Để thực hiện được công việc
phải có 2 hành động nối tiếp
- Để chọn được một bộ áo quần ta 3 a3
nhau.Mỗi hành động nầy gắn
phải thực hiện liên tiếp hai hành động
liền với số cách chọn của hành b1 1 +Hành động1:chọn áo động tiếp theo. b
Có 2 cách chọn (chọn a,hoặc b) 2 b2 +Hành động2:chọn quần
+ Ứng với mỗi cách chọn áo có 3 3 b3 cách chọn quần
Vậy số cách chọn một bộ quần áo
*Học sinh cần phải nêu được là:2.3= 6(cách) tập hợp mô tả nầy: *Nêu lên qui tắc nhân. a1, a2, a3, a4 b1, b2, b3, b4
*Mô tả tập hợp các cách đi từ Qui tắc:(phát biểu SGK) c1, c2, c3, c4 A đến C qua B.? H Đ2
*Học sinh phải hiểu được
Kí hiệu a,b,c là tên ba con đường từ
cách giải ví dụ 4 theo qui tắc
A đến B;1,2,3,4 là tên bốn con nhân đường từ B đến C.
- có bao nhiêu cách chọn chữ số đầu tiên? *Nhận xét ví dụ 4.
Kết luận có tất cảlà:3.4=12 cách đi
- Tương tự cho cách chọn các a)Vì mỗi số điện thoại có 6 chữ từ A đến C qua B. chữ số tiếp theo.
số nên để thành lập số điện Ví dụ 4
-Áp dụng qui tắc nhân để có
thoại ta thực hiện 6 hành động
Có bao nhiêu số điện thoại gồm: kết quả.
lựa chọn liên tiếp các chữ số đó
từ 10 chữ số:0,1,2,3,4,5,6,7,8,9. a)Sáu chữ số bất kì b)Sáu chữ số lẽ. V.Cũng cố:
* Nhắc lại hai qui tắc đếm đã học đồng thời nhấn mạnh các hoạt đông1,hoạt động2 đã làm.
* Về nhà làm các bài tập từ bài1 đến bài4 ở SGK. *Bài tập làm thêm:
Bài1:Có bao nhiêu số tự nhiên có hai chữ số mà hai chữ số của nó đều chẵn. 33
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 22 HOÁN VỊ - CHỈNH HỢP – TỔ HỢP I/ MỤC TIÊU: +Về kiến thức :
- Hình thành các khái niệm hoán vị. Xây dựng các công thức tính số hoán vị
-Học sinh cần hiểu các khái niệm đó
II/ CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH :
+ Giáo viên : - Phiếu học tập, bảng phụ
+ Học sinh : - Kiến thức cũ ( Bài quy tắc đếm ), máy tính bỏ túi III/ PHƯƠNG PHÁP :
Tiếp cận, gợi mở, vấn đáp đan xen hoạt động nhóm
IV/ TIẾN TRÌNH BÀI HỌC : Kiểm tra bài cũ: Hoạt động
Câu hỏi 1: Từ các chữ số 1;2;3 và 4 có thể lập được tất cả bao nhiêu số tự nhiên có 4 chữ số?
Câu hỏi 2: Trong đó có bao nhiêu số có 4 chữ số khác nhau? (GV gợi ý)
Tg Hoạt động của học sinh
Hoạt động của Giáo viên GHI BẢNG
- HS từng nhóm đọc kết quả sắp -Mỗi kết quả của việc sắp 1.Định nghĩa:
thứ tự bằng ba cách khác nhau
thứ tự tên của năm cầu thủ Ví dụ1.(SGK) tên của năm cầu thủ.
đã được chọn được gọi là
Kí hiệu tên của năm cầu thủ là
- HS trả lời số hoán vị của HĐ1. một hoán vị tên của năm cầu A,B,C,D,E. thủ.
Có thể sắp xếp ba cách tổ chức đá luân lưu như sau: - HS làm HĐ1 Cách1: ABCDE Các số tìm được là: Cách2 :ABCED 123; 132;213;231;312;321. Cách3: ACBDE
-Nêu nhận xét: hai hoán vị Định nghĩa ( SGK)
của n phần tử chỉ khác nhau HĐ1( SGK) ở thứ tự sắp xếp.
-Từng HS lên bảng ghi các chữ
2.Số các hoán vị.
cái A,B,C,D vào các ô vuông Ví dụ 2 (SGK) kẻ sẵn A B C D Cách1: liệt kê.
- Đếm số các cách ghi được.
*Kết quả ta có 24 cách ghi, mỗi
*Có bao nhiêu cách sắp vào vị
- Cho ví dụ ghi tên HS vào
cách cho ta một hoán vị của bốn trí đầu tiên? các ô vuông (liệt kê) bạn và ngược lại.
Tương tự cho các câu hỏi Khác. * Hướng dẫn học sinh làm
Cách 2:Dùng qui tắc nhân.
- Một công việc thực hiện liên
ví dụ 2 theo qui tắc nhân.
-Đếm số cách chọn vào từng vị
tiếp qua 4 hành động thì áp
trí, lần lượt sắp vào bốn ô. dụng qui tắc gì ? - Dùng qui tắc nhân: 4.3.2.1 = 24 (cách). Định lý: ( SGK) * Hướng dẫn chứng minh
định lý cho học sinh bằng qui tắc nhân. *Chú ý: Kí hiệu
n(n-1)…..2.1 là n! (đọc là n giai thừa )
*HS thảo luận nhóm có thể
* Gợi ý học sinh thảo luận 3.Bài tập
dùng cách liệt kê đếm số cách
nhóm làm các bài tập câu Bài tập1(SGK)
chọn phần tử sắp vào các vị trí.
a,câub của bài tập1 SGK.
a)Mỗi số gồm sáu chữ số khác 34
Giáo án Đại số 11 – Chương trình chuẩn
* Đại diện nhóm lên bảng trình
* Các chữ số là khác nhau
nhau là một hoán vị của sáu chữ
bày cách giải lần lượt các bài
nên các vị trí trong số tự số đó.Vậy có 6! số.
toán ở câu a;câu b. Sau đó để nhiên là sắp thứ tự
b)- Chọn chữ số chẵn cho hàng
HS tự nhận xét ,cuối cùng GV
a) Là môt hoán vị của 6 số
đơn vị có 3 cách chọn. kết luận.
b) lập luận chữ số hàng đơn - 5 chữ số còn lại được sắp theo
vị phải là số chẵn nên phải
thứ tự sẽ tạo nên một hoán vị
ưu tiên chọn chữ số hàng
của 5 phần tử.Có 5! Cách chọn đơn vị trước.
-Vậy theo qui tắc nhân có 3´5!
= 360 cách.Hay 360 số chẵn được thành lập.
Tương tự số các số lẽ là 360 số V.Cũng cố.
- Nhắc lại định nghĩa hoán vị và cách tính số hoán vị của n phần tử.
- Xem trước bài chỉnh hợp - làm bài tập1câu c SGK. 35
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 23 HOÁN VỊ - CHỈNH HỢP – TỔ HỢP I/ MỤC TIÊU: +Về kiến thức :
- Hình thành chỉnh hợp. Xây dựng các công thức tính số chỉnh hợp.
-Học sinh cần hiểu các khái niệm đó, phân biệt sự khác và giống nhau giữa chỉnh hợp và hoán vị biết cách vận dụng.
II/ CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH :
+ Giáo viên : - Phiếu học tập, bảng phụ
+ Học sinh : - Kiến thức cũ :Hoán vị, Bài quy tắc đếm , máy tính bỏ túi III/ PHƯƠNG PHÁP :
Tiếp cận, gợi mở, vấn đáp đan xen hoạt động nhóm
IV/ TIẾN TRÌNH BÀI HỌC :
Tg Hoạt động của học sinh
Hoạt động của Giáo viên Ghi Bảng
*Chọn 5 học sinh của lớp và *Trình bày bảng phân
1.Định nghĩa: (SGK) chọn từng nhóm 3em trong
công của ví dụ3 để dẫn dắt Ví dụ3 (SGK).
số 5em.Kết luận mỗi nhóm
học sinh đến khái niệm
3 em là một chỉnh hợp chập chỉnh hợp 3 của 5 em.
* Hai chỉnh hợp chập k
Quét nhà Lau bảng Sắp bàn
-Sử dụng phương pháp liệt
của n phần tử đã cho ghế kê bằng bảng.
khác nhau ở chỗ: A -Sử dụng qui tắc nhân.
- Hoặc có phần tử ở A
chỉnh hợp này không ở C
chỉnh hợp kia. … C
- Hoặc thứ tự sắp xếp của D
các phần tử trong chúng B khác nhau. … D C E … * HĐ3
Dùng phương pháp liệt kê để ghi ra các véc tơ khác
véc tơ-không tạo thành từ 4 điểm A,B,C,D đã cho. -HS nghe hiểu
- Hình thành chứng minh 2.Số các chỉnh hợp
- Hoạt động làm ví dụ 4.
định lý cho học sinh bằng Kí hiệu k
A là số các chỉnh hợp
cách sắp k phần tử vào k n £
vị trí .Áp dụng qui tắc
chập k của n phần tử (1 k £ n) .Ta nhân để có kết quả. có công thức sau đây. Định lý.
- Học sinh tham giải bằng
Nêu nhận dạng về bài toán
cách khác,như đếm số cách chỉnh hợp vì:
chọn các số tự nhiên lần
Mỗi số tự nhiên có năm
lượt sắp vào năm vị trí.
chữ số khác nhau được lập Ví dụ 4 (SGK)
bằng cách lấy năm chữ số
Mỗi số tự nhiên gồm năm chữ số
khác nhau từ chín chữ số là một chỉnh hợp chập 5 của 9.Vậy khác nhau và sắp chúng số các số đó là
theo một thứ tự nhất định . 5 A = 5 . 6 . 7 . 8 . 9 = 15120
* Bài toán về chỉnh hợp 9 Chú ý.
có thể giải theo hai
a)Với qui ước 0! = 1,ta có hướng : Cách thứ nhất:
- Lấy ra tập con k phần tử của n phần tử đó
- Sắp xếp k phần tử đó 36
Giáo án Đại số 11 – Chương trình chuẩn theo thứ tự.
b) mỗi hoán vị của n phần tử cũng Cách thứ hai:
chính là một chỉnh hợp chập n của
- Lấy lần lượt k phần tử n phần tử đó.Vì vậy
của tập n phần tử đó và
sắp xếp theo trình tự của quá trình lấy.
- Đại diện nhóm trình bày
- Hướng dẫn cho học sinh Bài tập áp dụng cách giải.
hoạt động nhóm và trình
Có bao nhiêu cách chọn ra năm bày lời giải.
cầu thủ trong số 11 cầu thủ để đá luân lưu 11m. Số cách chọn là 5 ! 11 ! 11 A = = = 11 (11- 5) 11 . 10 . 9 . 8 . 7 ! ! 6 V.Cũng cố
- Đọc thật kỹ các ví dụ và hoạt động trong SGK để nắm thật chắc khái niệm về chỉnh hợp.
- Học thuộc công thức trong định lý và hai chú ý.
- Bài tập về nhà: 2,3,4,5a 37
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 24,25 LUYỆN TẬP I.Mục tiêu:
1.Về kiến thức: Hiểu rõ hoán vị,chỉnh hợp
2.Về kỹ năng:Biết vận dụng qui tắc đếm,hoán vị,chỉnh hợp.
II.Chuẩn bị của g.v và hs:
Gv: Soạn giáo án, hệ thống câu hỏi, bài tập ra thêm.
Hs: Học lý thuyết, chuẩnbị bài tập sgk. III.Phương pháp: Trực quan, đối thoại.
IV.Tiến trình bài giảng.
Tiết1: Bài tập hoán vị.
Tg Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng. Bài tập1C.(SGK) * nghe,hiểu, tham gia xây
*Hướng dẫn các trường hợp Xét các trường hợp xảy ra:
dựng bài ở các trường hợp cụ có thể có để thành lập các
*Chọn chữ số hàng trăm nghìn thể số.
nhỏ hơn 4: có 3 cách chọn.Các * Cho ví dụ minh họa
* Bài toán được áp dụng cả
chữ số còn lại có 5! Cách chọn.
hai qui tắc nhân và cộng.
Vậy số các số tự nhiên là: 3.5! = 360 số.
* Chữ số hàng trăm nghìn bằng
4.Chọn chữ số hàng chục nghìn
nhỏ hơn 3,có 2 cách chọn,các
chữ số còn lại có 4! Cách
chọn.Vậy có 2.4! = 48 số.
*Chữ số hàng trăm nghìn bằng
4,chữ số hàng chục nghìn bằng
3,chọn chữ số hàng nghìn nhỏ
hơn 2 có 1 cách chọn .Chọn các
chữ số còn lại có 3!Cách chọn .Vậy có 1.3! = 6 số.
Theo qui tắc cộng ta được: 360 + 48 + 6 = 414 số. Bài tập2 (SGK).
Mỗi cách sắp xếp của 10 người *Thông qua trực quan hình
khách theo một hàng ngang cho
thành tư duy giải quyết vấn *Thông qua kí hiệu tên
một hoán vị của 10 và ngược lại.
đề.Gọi một số học sinh cho A,B,C,D,…10 tên cho 10
Vậy có 10! Cách sắp xếp. ví dụ cụ thể.
người,và 10 ô trên bảng.
Liệt kê một số trường hợp Bài tập3.(SGK) vào các ô.
Vì bảy bông hoa là khác nhau và
ba lọ hoa cũng khác nhau,nên
*Học sinh tích cực hoạt động
mỗi lần chọn ba bông hoa để
cho các ví dụ cụ thể ứng với
cắm vào ba lọ ta có một chỉnh
cách đặt tên cho các bông
*Tổ chức cho học sinh tham hợp chập 3 của 7 phần tử.Vậy số hoa và các lọ hoa.
gia hoạt động theo từng cá cách cắm hoa là 3 A = 210
nhân hoặc theo nhóm,trình 7 cách. bày các phương án giải quyết vấn đề. Tiết 2 *
* Theo dỏi HS trình bày lời Bài tập 4.(SGK)
Cách lập luận giống bài tập
giải.Đánh số cho các bóng
Mỗi cách chọn ra bốn bóng đèn
3,HS hoạt động giải quyết đèn là 1,2,3,4,5,6.
khác nhau trong số sáu bóng đèn bài toán.
để mắc nối tiếp là một chỉnh hợp
chập 4 của 6.Vậy số cách mắc
bóng đèn bằng số chỉnh hợp chập
4 của 6 ,do đó kết quả cần tìm là : 4 A = 360 cách . 6 38
Giáo án Đại số 11 – Chương trình chuẩn a) Vì ba bông hoa là khác
a)Đánh số ba bông hoa là Bài tập5 (SGK)
nhau,nên khi thay đổi các
1,2,3.Từ đó chọn ra ba lọ
a)Mỗi cách cắm là một chỉnh
bông hoa thì ta có các lọ hoa trong số 5 lọ để cắm hoa.
hợp chập3 của 5.Vậy số cách khác nhau cắm là 3 A = 60 cách. 5
* Chia lớp ra các nhóm để
*Xét trường hợp nữ xếp ở
Bài 6 ( bài tập làm thêm)
HS hoạt động tìm đáp án và
vị trí lẻ có3!cách,nam xếp ở Tổ 1 của lớp 11 có 8 học sinh trình bày lời giải.
vị trí chẵn có 5!cách.Theo
trong đó có 3 nữ ,8 học sinh qui tắc nhân ta có 3!.5!
được xếp một hàng dài.Hỏi có
*Tương tự xếp nam ở vị trí
mấy cách sắp xếp biết các nữ
lẻ và nữ ở vị trí chẵn có
sinh đứng cạnh nhau và nam sinh 5!.3! cách. đứng cạnh nhau. Vậy có tất cả : A) 1480 B) 1440 (3!.5!)´2 = 1440 cách C) 1460 D) 1420. ĐA: B.
* Đây là bài tập khó đòi hỏi x=
Bài 7 ( bài tập làm thêm)
phải lập luận chặt chẽ.Chia ìa, ,... b Î{ T , 1 , 0 , 3 , 2
} ừ các chữ số 0,1,2,3,4,5. Có thể 5 , 4
lớp ra bốn nhóm,trong mỗi ï
lập được bao nhiêu số tự nhiên
nhóm có ít nhất một em học abcd í . a ¹ , 0 a ¹ ,... b
có bốn chữ số khác nhau và chia
khá để các em tự thảo ï hết cho5. îx!5
luận,tìm kiếm lời giải và đi đến phương án đúng. A) 108 B) 104
Trường hợp1: x = abc0 C) 98 D) 112. có 3
A cách chọn abc .Nên 5 ĐA: A có 3 A số. 5
Trường hợp2 : x = abc5 * a ¹ , 0 a ¹ 5 có 4 cách chọn a *Có 2
A cách chọn bc 4 Vậy có 4. 2 A số . 4 Kết luận : 3 A + 4. 2 A = 5 4 108 số. V.Cũng cố
- Xem thật kĩ các bài tập đã giải ở nhà,rút ra được những kinh nghiệm riêng cho mình.
- Xem trước bài học tổ hợp. - Bài tập làm thêm:
Bài1. Có bao nhiêu số tự nhiên chẵn gồm 4 chữ số đôi một khác nhau:
A) 3086. B) 2296 C)2806 D) 2606. ĐA: D.
Bài 2.Từ các chữ số 1;2;3;4;5;6;7 có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau và
nhất thiết phải có mặt chữ số 2. A) 440 B) 480 C) 520 D) 560. Đ A: B. 39
Giáo án Đại số 11 – Chương trình chuẩn
TIẾT 26 TỔ HỢP- BÀI TẬP I/ MỤC TIÊU: +Về kiến thức :
- Hình thành khái niệm tổ hợp. Xây dựng công thức tính tổ hợp.
-Học sinh cần hiểu khái niệm tổ hợp,phân biệt sự khác và giống nhau giữa chỉnh hợp và tổ hợp. +Về kỹ năng :
- Cần biết khi nào dùng tổ hợp, khi nào dùng chỉnh hợp và phối hợp chúng với nhau để giải toán.
II/ CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH :
+ Giáo viên : - Phiếu học tập, bảng phụ
+ Học sinh : - Kiến thức cũ ( Bài quy tắc đếm ,hoán vị,chỉnh hợp), máy tính bỏ túi . III/ PHƯƠNG PHÁP :
Tiếp cận, gợi mở, vấn đáp đan xen hoạt động nhóm
IV/ TIẾN TRÌNH BÀI HỌC : Kiểm tra bài cũ :
-Xem lại bài tập số 5 sách giáo khoa. Đặt vấn đề giải quyết câu b của bài toán. Tg Hoạt động của HS
Hoạt động của Giáo Viên Ghi bảng. 1.Định nghĩa: -Kể tên các tam giác
- Chọn ba điểm trong số 4 điểm đã Ví dụ 5.(SGK)
được thành lập trong ví cho ta có được một tam giác.
*Giả sử tập A có n phần tử (n dụ3. ³ )
1 .Mỗi tập con gồm k phần
tử của A được gọi là một tổ hợp -Phát biểu định nghĩa. chập k của n phần tử. Chú ý: (SGK)
* Tổ hợp chập 0 của n phần tử là tập * 1 £ k £ n
* Giải thích rõ sự khác rỗng.
nhau giữa khái niệm
HĐ4 :(SGK)
chỉnh hợp và tổ hợp,để * Ghi ra các tổ hợp chập3,chập4 của
áp dụng vào giải toán. 5 phần tử của A.
* Hướng dẫn phương pháp chứng minh định lý.
2.Số các tổ hợp: k A n! k n k *HS làm HĐ4: C = =
Kí hiệu C là số các tổ hợp n k !
k !(n - k)! n - Học sinh hoạt động chập k của n phần tử £ £ Î
nhóm ghi ra các tổ hợp (0 k n ,k N )
(0 £ k £ n) .Ta có định lý . *HS nghe hiểu,trả lời Ví dụ 6. (SGK) các câu hỏi. a) 10 C = 252
*Kết hợp giữa tổ hợp và qui tắc 5 3 nhân. b) C . 2 C = 142 6 4 HĐ 5 Số các trận đấu là 2 C = 120 -Thảo luận theo nhóm 16 Trận đấu.
và cử đại diện trả lời. -Các nhóm khác nhận xét. k
* Phát vấn để HS cho các ví dụ tự
3.Các tính chất của số C n kiểm tra. a) Tính chất1 £ k £ n) (0 40
Giáo án Đại số 11 – Chương trình chuẩn b) Tính chất 2 k n-k C = C n n
* Tổ chức các nhóm cho học sinh làm ví dụ7 Ví dụ7(SGK)
* Nếu ba bông hoa là như nhau thì
mỗi cách cắm là một tổ hợp chập3 Bài tâp 5b (SGK): của 5 lọ.
Ta có số cách cắm ba bông hoa * Đại diện các nhóm vào 5 lọ là : 3 C = 10 cách. làm ví dụ7 5 Bài tập 6.(SGK) +Giống ví dụ5. *Tổ chức cho học sinh Bài tập7(SGK) tham gia giải các bài
*Chú ý bài tập7 kết hợp giữa qui tắc Sốhình chữ nhật thành lập được tập trong SGK theo nhân và tổ hợp. 2 từng cá nhân. là : C . 2 C = . 60 4 5 V.Cũng cố.
+ Phân biệt tổ hợp và chỉnh hợp sự khác nhau giữa hai loại bài tập nầy để áp dụng giải toán chính xác.
+ Bài tập làm thêm :Cho đa giác lồi có 15 đỉnh .Hỏi tứ giác nầy có mấy đường chéo. 41
Giáo án Đại số 11 – Chương trình chuẩn
TIẾT 27,28 NHỊ THỨC NIUTƠN I/ Mục tiêu.
-Nắm được công thức nhị thức Niutơn.
-Nắm được quy tắc thiết lập hàng thức n +1 của tam giác Pascal khi đã biết hàng thứ n.
II/ Chuẩn bị của giáo viên và học sinh. Giáo viên: Bảng phụ
Học sinh: Có kiến thức về tổ hợp và máy tính bỏ túi. III/ Phương pháp.
Gọi mở, vấn đáp và kết hợp tổ chức hoạt động nhóm.
IV/ Tiến trình bài học.
1/: Kiểm tra bài cũ. + Nêu định nghĩa và các tính chất của tổ hợp + Tính 0 1 2
C + C + C , 0 1 2 3
C + C + C + C 2 2 2 3 3 3 3
Không tính , hãy dự đoán kết quả : 0 1 2 3 4
C + C + C + C + C 4 4 4 4 4
2/ Bài mới : Công thức nhị thức Niutơn.
Tg Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng
*Hoc sinh quan sát theo dỏi bài *Từ các kết quả của kiểm tra
I.Công thức nhị thức Niu – giảng. bài cũ ta thấy Tơn. 0 1 2
C + C + C = (1+1)2 2 2 2 * Nắm công thức : 0 1 2 3
C + C + C + C =(1+1)3 *Công thức (SGK) n 3 3 3 3 n k n-k k
(a + b) = åC a b
* Đặt vấn đề: Khai triển (a +b)2 n *Hệ quả: k =0 ; (a +b)3
xét hai trường hợp đặc biệt.
*Tái hiện các công thức đã học *Ghi sẵn công thức nhị thức - với a = b =1 Niu-Tơn trên bảng phụ - Với a = 1;b=-1. * HS làm HĐ1
*Lưu ý công thức thu gọn cho *Chú ý: (SGK) HS.
*Ví dụ1.Khai triển biểu thức (x +y)6
* Ví dụ 2. Khai triển biểu thức
*Nhấn mạnh ba chú ý cho học (2x – 3)4.
*Các ví dụ 1,2 thực hiện từng sinh.
* Ví dụ3. Chứng tỏ rằng với cá nhân. n ³ 4 ,ta có
Ví dụ3 thực hiện theo nhóm. 0 2 4
* Gọi học sinh thực hiện các ví
C + C + C + ... n n n dụ. 1 3 n 1
= C + C + ... 2 - = n n n n k n-k k
(a + b) = åC a b
*Công thức (1) có thể viết gọn n k =0 là:
*Hướng dẫn chi tiết ví dụ3,từ
ví dụ nầy cho thấy có thể áp
dụng công thức (1) để chứng (2)
minh các đẳng thức khác nhau liên quan đến tổ hợp.
* Nghe ,hiểu tham gia trả lời * Trình bày tam giác PA- II.Tam giác PA-XCAN nhận xét
XCAN cho học sinh quan sát.
Trong công thức nhị thức Niu-
* Cho ví dụ cụ thể làm rõ nhận
Tơn ở mụcI,và xếp các hệ số
*Học sinh hoạt động nhóm làm xét.
thành dòng,ta được tam giác gọi HĐ2 là tam giác PA-XCAN. * Nhận xét (SGK) 42
Giáo án Đại số 11 – Chương trình chuẩn
* Nhiệm vụ chú ý nghe giảng
* Gợi ý phương pháp giải quyết III.Bài tập nắm bắt phương pháp
bài tập2,dựa vào công thức (2) Bài tập2. Hệ số của x3 là 2 1 C =12 6 Bài tập3
* trên cở bài tập2 dùng phương Đáp số n = 5.
pháp đồng nhất hệ số giải
*bài tập4 ghi ra hạng tử tổng Bài tập4 phương trình tìm n quát. 8 C = k Hạng tử tìm được là 28. 6 - æ 1 ö C (x3 ç ÷ 8 )8 k k è x ø k 24-4k = C x 8
Vì hạng tử không chứa x nên 24-4k =0,hay k= 6 V.Cũng cố.
- Nắm vững hai công thức của nhị thức Niu-Tơn.
- Nghiên cứu thật kĩ phương pháp giải các bài toán trong ba ví dụ đã cho và bốn bài tập đã giải.
Bài tập về nhà: Làm các bài tập số5,số6 SGK Bài tập làm thêm 1.Cho k +6 C = k C .Tính 4 C 20 20 k A) 35 B) 30 C) 45 D) 40
2.Đặt T= C k + 2 k 1 - k -2 C + C ;( ,
n k Î N;n ³ k ³ ) 2 n n n
Khẳng định nào sau đây là đúng? A) T = k C B) 1 + T = k C C) T = k C D) T= k 1+ C n+2 n+2 n 1 + n 1 + ĐA: A 43
Giáo án Đại số 11 – Chương trình chuẩn Tiết 29
PHÉP THỬ VÀ BIẾN CỐ I.Mục tiêu:
- Hiểu được khái niệm phép thử ngẫu nhiên.
- nắm được các ví dụ về phép thử và không gian mẫu.
- Nắm thật vững khái niệm biến cố và mối liên hệ giữa biến cố với không gian mẫu của một phép thử.
- Hiểu được các khái niệm lôgic của các phép toán trên các biến cố. II.Phương pháp
- Đàm thoại,kết hợp trực quan.
III.Chuẩn bị của giáo viên và học sinh.
-Giáo viên : bảng phụ , một số dụng cụ trực quan:con xúc sắt, đồng tiền,bộ bài…
- Học sinh : đọc thật kĩ bài học trước ở nhà
IV.Tiến trình bài giảng.
1.Giới thiệu bài giảng : trình bày một số phép thử ngẫu nhiên 2.Bài giảng
Tg Hoạt động của học sinh Hoạt động của G.V Ghi bảng *Nghe nội dung bài
* Giới thiệu một số phép I.Phép thử,không gian mẫu
giảng,tham gia cho các ví dụ
thử và các kết quả có thể 1.Phép thử về phép thử
xuất hiện của các phép
Phép thử ngẫu nhiên là phép thử mà thử đó.
ta không đoán trước được kết quả của
nó,mặc dù đã biết tập hợp tất cả các kết
quả có thể có của phép thử đó. 2.không gian mẫu
Tập hợp các kết quả có thể xảy ra của
một phép thử được gọi là không gian
mẫu của phép thử và kí hiệu là W
Ví du1.Gieo một đồng tiền thì
* Kết quả của một phép thử
* HĐ1:hướng dẫn ghi ra W= {S.N}
được viết dưới dạng tập hợp. các kết quả.
Ví dụ 2 . Gieo một đồng tiền hai lần thì
Tập hợp mô tả phép thử
W= {SS,SN, NS, NN} là { ; 1 ; 3 ; 2 } 6 ; 5 ; 4
Ví dụ 3.Gieo một con súc sắc hai lần thì không gian mẫu là
({i, j)/i, j = ,1 }
*Làm các ví dụ tại lớp. W = 6 ,.. 2
- Ví dụ3 mô tả không gian *Hướng dẫn HS ghi ra
mẫu bằng bảng ô vuông. các không gian mẫu trong các ví dụ. 1 2 3 4 5 6 1 2 3 4 5 6
* Phát biểu bằng lời các biến
* Hướng dẫn ghi tập các II.Biến cố. cố. biến cố. Ví dụ 4 (SGK)
W= {SS,SN, NS, NN}
*Biến cố A xảy ra trong một * Khi nói các biến A= {SS, NN}
phép thử nào đó khi và chỉ khi A,B,… mà không nói gì
{SN, NS, NN}
kết quả của phép thử đó là một thêm thì ta hiểu chúng B=
phần tử của A (hay thuận lợi cùng liên quan đến một C= {SS, SN} cho A). phép thử.
*Biến cố là tập con của không gian mẫu.
* Tập rỗng được gọi là biến cố không
thể(gọi tắt là biến cố không).Còn tập 44
Giáo án Đại số 11 – Chương trình chuẩn
W được gọi là biến cố chắc chắn.
* A xảy ra khi và chỉ
III.Các phép toán trên biến cố khi A không xảy ra
-Giả sử A là biến cố liên quan đến một
* phát biểu các biến cố Kí hiệu Ngôn ngữ phép thử.
B,C trong ví dụ4. A Ì W A là biến
Tập W \ A được gọi là biến cố đối của cố A,kí hiệu là A A= Æ A là biến
-Giả sử A và B là hai biến cố liên quan cố không
đến một phép thử.Ta có định nghĩa sau. A= W A là biến
Tập A ! B : hợp các biến cố. cố chắc chắn
Tập A ! B : Giao các biến cố.
C= A! B C là biến
Nếu A! B = Æ thì ta nói A và B xung cố A hoặc B khắc. * Xem sách ví dụ 5. C= A! B C là biến cố A và B A ! B = Æ A và B là biến cố xung khắc B = A A và B đối nhau V.Cũng cố.
- Bài học có nhiều khái niệm khó cần phải hiểu đúng các khái niệm :Không gian mẫu, biến cố,Các phép toán trên biến cố.
- Làm các bài tập SGK từ bài1 đến bài7 45
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 30 BÀI TẬP PHÉP THỬ. I.Mục Tiêu
- Lập được không gian mẫu W của một phép thử.
- Xác định tập các biến cố của không gian mẫu W
- Xác định được các phép toán trên biến cố. II.Phương pháp
- Đàm thoại đan xen hoạt động nhóm
III. Chuẩn bị của thầy và trò. Giáo viên :
- Chuẩn bị hệ thống các dạng bài tập - Các phiếu học tập IV.Tiến trình bài giảng
Tg Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng Bài tập1.(SGK)
ìSSS, SSN, NSS, SNS, ü a) W = í ý
* Gọi 4 học sinh lên bảng
* Gọi học sinh làm bài tập theo
îNNS, NSN, SNN, NNN þ trình bày lời giải. từng cá nhân. b)
A= {SSS, SSN, SNS, SNN}
B= {NNS, NSN, SNN} C= W \ {SSS}
a) Tính số phần tử của a) thực chất tính 2 C4 Bài tâp3.(SGK)
không gian mẫu,sau đó liệt ì , 1 ( ); 2 ); 3 , 1 ( ; 1 ( ), 4 ü a) W = í ý kê các phần tử của W î( ); 3 , 2 ( , 2 ); 4 , 3 ( ) 4 þ
* Tập chuyển từ ngôn ngữ b) A = { ); 3 , 1 ( ( , 2 } ) 4
sang kí hiệu ở các biến cố c) B = W \ { }) 3 , 1 ( A,B.
* Học sinh hoạt động nhóm
* Luyện tập thật kĩ học sinh Bài4. làm bài tập 4.
chuyển tải ngôn ngữ chính xác a)
sang kí hiệu với các phép toán A = A Ç A 1 2 trên các biến cố. B = 1 A Ç 2 A
C = (A Ç A ) È (A Ç A ) 1 2 1 2 D = 1 A È 2 A
b) D : // cả hai người đều bắn trượt//
Như vậy D = A Ç A = A 1 2
*Hoạt động tìm không gian
* Tổ chức cho học sinh hoạt Bài tâp5
mẫu,tìm các biến cố thỏa
động làm bài tập,theo cá nhân a) Không gian mẫu W là mãn điều kiện hoặc nhóm. W = { , 1 } 10 ,... 3 , 2 b) A= { , 1 , 3 , 2 : } 5 , 4 là biến cố //lấy được thẻ màu đỏ//. B= { } 10 , 9 , 8 , 7 : là biến cố // lấy được thẻ màu vàng// C= { , 2 } 10 , 8 , 6 , 4 : là biến cố // lấy
được thẻ ghi số chẵn//. HS hoạt động tìm kiếm
Thực hành trực quan gieo thử và Bài tập6 không gian mẫu.
giải thích về phép thử của bài a)không gian mẫu toán đặt ra.
W = {S,NS,NNS,NNNS,NNNN}
b) .A = {S, NS, NNS}
B= {NNNS, NNNN}
Ôn tập về chỉnh hợp chập k
Thực chất số phần tử của không Bài tập7 của n phần tử.
gian mẫu là tính số chỉnh hợp a)Không gian mẫu 46
Giáo án Đại số 11 – Chương trình chuẩn chập2 của 5 số. ì , 12 , 14 , 31 , 13 , 21 , 51 , 15 , 41 ü ï ï W = ï , 32 , 23 , 24 , 42 52 , 25 ï í ý ï , 34 53 , 35 , 43 ï ï 54 , 45 ï î þ b) HS tự giải. V.Cũng cố.
Bài luyện tập chủ yếu là tìm không mẫu của phép thử và tập hợp các biến cố xảy ra của các phép thử
đó.Chuyển tải được từ ngôn ngữ sang kí hiệu. Bài tập về nhà.
Bài1.Gieo một con súc sắc cân đối,đồng chất và quan sát các số chấm xuất hiện a)Mô tả không gian mẫu
b)Xác định các biến cố sau:
A: // Xuất hiện mặt chẵn chấm//
B: //Xuất hiện mặt lẻ chấm//
C: // Xuất hiện mặt có số chấm không nhỏ hơn3”
c) trong các biến cố trên hãy tìm biến cố xung khắc. ( ĐA. A Ç B = Æ ) 47
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 31 XÁC SUẤT CỦA BIẾN CỐ I.Mục tiêu.
- Hình thành khái niệm xác suất của biến cố
- Hiểu và sử dụng được định nghĩa cổ điển của xác suất.
- Biết cách tính xác suất của biến cố trong các bài toán cụ thể,hiểu ý nghĩa của nó. II.Phương pháp
Đàm thoại ,trực quan và đan xen hoạt động nhóm III.Chuẩn bị
Giáo viên : Chuẩn bị các đồ dùng liên quan đến nội dung các hoạt động, phiếu học tập
Học Sinh : chuẩn bị trước bài học ở nhà, xem kĩ nội dung các hoạt động tại lớp.
IV.Tiến trình bài giảng *Kiểm tra bài cũ:
- Giáo viên Giới thiệu ví dụ1 SGK rồi chuyển sang nội dung bài học.(không kiểm tra) Tg
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng. * Học sinh làm HĐ1: *Dẫn dắt ví dụ1.
I.Định nghĩa cổ điển của sác xuất
- Gợi ý học sinh phải trả lời 1 1 1 3 1 1.Định nghĩa. được ý : + + = = Ví dụ1.(SGK)
+ Khả năng xảy ra của biến cố 6 6 6 6 2
* Phát biểu Định nghĩa. ( SGK). B,C là như nhau.
Số này được gọi là sác n( ) A
+ Khả năng xảy ra của biến cố xuất của biến cố A. P (A ) = n W
A gấp đôi khả năng xảy ra của ( ) biến cố B hoặc C. Trong đó:
+ P(A) là sác xuất của biến cố A
+ n(A) : Số phần tử của biến cố
A,hay cũng là số các kết quả thuận lợi cho A.
+ n( W ) : Số các kết quả có thể xảy ra của phép thử.
Ví dụ2 (SGK ): Không gian mẫu
W = {SS, SN, NS, NN} N( W ) = 4 a) A= {SS } Þ n(A) = 1
+ Học sinh nghe giảng ví dụ2 1
+ Tổ chức hoạt động ví dụ3 P(A) =
theo cá nhân hoặc theo nhóm. + trình bày các bước 4 {SN, NS}
trình tự để tính xác suất b) B=
theo các biến cố đặt ra. Þ n(B) = 2 2 1 P(B) = = 4 2
c) C = {SS, SN, NS } Þ n(C) = 3
+ Hoạt động tại lớp trình bày +Tổ chức cho HS làm ví 3 P(C ) =
cùng lúc hai ví dụ3,ví dụ4.
dụ3,ví dụ4 đồng thời. 4 Ví dụ3(SGK)
* Nghe giảng và trình bày cách *HĐ2:
II.Tính chất của xác suất. chứng minh HĐ2. a) vì 1.Định lí
n( Æ) = 0 Þ P(Æ) = 0 a) P( Æ) = 0 ,P( W) = 1 b) Vì :
b) 0 £ P(A) £ 1,với mọi biến cố A.
c) Nếu A và B xung khắc,thì 48
Giáo án Đại số 11 – Chương trình chuẩn 0 £ n( ) A £ n(W) P(A È B) = P( )
A + P(B) (công thức
+ Không gian mẫu bằng số tổ Þ 0 £ P( ) A £ 1 cộng xác suất). hợp chập2 của5. Hệ quả.
+ Ta thấy B = A vì sao?
Với mọi biến cố A ta có: + Tính n(A) ,n(B)? c) P( ) A = 1- P( ) A . * Ví dụ 6 . Hs SGK
n( A È B) = n( ) A + n(B) 2.Ví dụ
Þ P(A È B) = P( ) A + P(B V ) í dụ5:(SGK) Ví dụ6:(SGK) + Ví dụ5 : Tính n( W) 2 = C = 10 5 + Kí hiệu A:“ hai quả khác màu” ,B:// hai quả cùng màu”. * Hướng dẫn tóm tắt xác suất xảy ra hay
III.Các biến cố độc lập,công thức ví dụ 7 .HS xem SGK thông không xảy ra của biến nhân xác suất
qua ví dụ7 để thấy rõ công này không ảnh hưởng ví dụ7. thức:
đến xác suất xảy ra hay
A và B là hai biến cố độc lập khi và
không xảy ra của biến cố chỉ khi
kia gọi là hai biến cố độc lập V.Cũng cố
- Học thuộc định nghĩa về xác suất của biến cố,
- Xem kĩ các ví dụ để hiểu rõ tính chất của xác suất,biến cố độc lập, công thức nhân xác suất.
- Bài tập về nhà: bài1 đến bài7. 49
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 32,33 BÀI TẬP I. Mục tiêu:
- Nắm được các khái niệm cơ bản: phép thử, không gian mẫu, biến cố liên quan đến phép thử, tập hợp mô tả biến cố.
- Nắm được định nghĩa cổ điển của xác suất
-quy tắc cộng và quy tắc nhân xác suất
-Vận dụng các quy tắc cộng và quy tắc nhân để giải các bài toán xác suất.
II. Chuẩn bị của giáo viên và học sinh:
Giáo viên: Phiếu học tập, bảng phụ
Học sinh: Kiến thức đã học về Tổ hợp, máy tính bỏ túi. III. Phương pháp:
Gợi mở, vấn đáp. Hoạt động nhóm (Chia lớp học thành 6 nhóm).
IV. Tiến trình bài dạy: Tg Hoạt động của HS Hoạt động của GV Ghi bảng
- Ghi ra phần tử của không -Gợi ý HS xem ví dụ 4 (SGK) Bài1. gian mẫu a) W = (
{ i, j) 1£ i, j £ } 6 = 36
-dùng phương pháp liệt kê ghi
ra phần tử của biến cố A. (ì4,6),(6,4),(5,6),(6,5),ü ï ï
- Hoạt động nhóm tìm tập các b)A= í ý (ï5,5 î ),(6,6) ï
- Ghi ra tập hợp các biến biến cố. þ cố A , biến cố B. (ì1,5 ï
),(2,5),(3,5),(4,5),(5,5),(6,5)ü B= ï í ý - Tính P(A),P(B). (ï5, î )1,(5,2),(5,3),(5,4),(5,6) ïþ 6 1 C) P(A) = = , 36 6 11 P(B) = 36
- Tính số tổ hợp chập3
- Số phần tử của không gian Bài2
của4 và ghi ra các phần tử
mẫu là không xét đến thứ
a)Số phần tử của không gian mẫu không gian mẫu
tự,nên đây là bài toán tổ hợp là 3 C = 4
- ghi ra tập hợp các biến cố - Hoạt động nhóm tìm tập các 4 W = (
{ 1,2,3),(1,2,4),(1,3,4),(2,3,4,) } A , biến cố B. biến cố.
b) A = 1,3,4 ,B = 1,2,3 , 2,3,4 ({ )} ({ ) ( )} 1 c) P( ) A = 2 1 , P(B) = = 4 4 2
Bài toán cho ta tính số tổ
Một đôi giày gồm hai chiếc Bài3.Ta có 2
n(W) = C = 28 phần hợp hay chỉnh hợp ?
giày khác nhau,nên bốn đôi 8 tử. Tính n( W ),n(A) ?
giày khác cỡ cho ta 8 chiếc giày khác nhau.
Gọi A là biến cố chọn hai chiếc để
trở thành một đôi thì n(A) = 4
- Phát phiếu học tập tính n(W),n( ) A ,P(A) 4 1 P( ) A = = 28 7 50
Giáo án Đại số 11 – Chương trình chuẩn
Hướng đến giải bất phương Tìm điều kiện để phương trình Bài4. trình b2 -8 ³ 0 x2 + bx +2 =0 có nghiệm? Không gian mẫu
Từ đó ghi ra tập biến cố A
Xác định tập biến cố A, tính W = {1,2,3,4,5, } 6 * Tính n(A),P(A)? n(A) ? Þ n(W) = 6
a)Gọi A là biến cố xuất hiện mặt b chấm để phương trình x2 + bx +2 =0 có nghiệm A = {3,4,5, } 6 Þ n( ) A = 4 4 2 P(A) = =
b) Biến cố B là biến cố đối của 6 3 biến cố A vì sao ?
b) GọiB là biến cố xuất hiện mặt b
chấm để phương trình vô nghiệm thì B = A 1
P(B) = P(A) =1- P( ) A = c) 3
c) Bằng cách thử hãy tìm c) Hãy tìm tập C?, n(C) ?
Gọi C là biến cố phương trình có
số thích hợp để phương nghiệm nguyên trình có nghiệm nguyên. C = { } 3 Þ n(C) =1 1 P(C) = 6 * Hoạt động nhóm Tìm
*Nêu vấn đề tính tổ hợp chập 4 Bài5. n(A)?, n(B)?, n(C) ? của 52 a)Ta có n( W )= 4 C = 270725 . 52
*Tính số cách chọn cho biến
Kí hiệu A là biến cố rút ra được cả cốA
bốn con đều là át thì ta có n(A) = 4 C =1,nên P(A) = 4 1 » 0000037 , 0 270752
* Phát biểu biến cố đối của * Dẫn dắt học sinh tính xác
b) Gọi B là biến cố rút được ít nhất biến cố B?
suất biến cố đối của biến cố B, một con át trong bốn con bài được tức là tính P( B )
rút ra.Thì “ B là biến cố trong bốn
con bài rút ra không có con át nào ’’. n( B ) = 4 C = 194580 48 194580 P( B ) = » 7187 , 0 270725
Ta suy ra P(B) = 1- P( B ) = » 0, 2813
c) Gọi C là biến cố rút được hai
con át và hai con K,thì n(C) =
* Áp dụng bài toán tổ hợp và 36 2 2
qui tắc nhân để tính n(C) C .C = 36, à v P(C) = 4 4 270725 » 0,000133 V.Cũng cố.
* Xem kĩ các bài tập đã giải
* Làm các bài tập còn lại trong sách giáo khoa : Bài tập 6, Bài tập 7.
* Làm bài tập ôn chương II. 51
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 34,35 ÔN TẬP CHƯƠNG II I.Mục tiêu:
Ôn tập cho học sinh nắm vững định nghĩa qui tắc cộng,qui tắc nhân.Phân biệt được hai qui tắc.
Nắm được các khái niệm hoán vị,chỉnh hợp,tổ hợp,nhị thức Niu – Tơn.
Nắm được khái niệm phép thử,không gian mẫu,hiểu được định nghĩa xác suất cổ điển,tính chất tính chất của xác suất.
II.Phương pháp: thuyết trình, đàm thoại, trực quan
III.Chuẩn bị của giáo viên và học sinh. 1. Giáo viên
Lập các phiếu học tập.
2.Học sinh : Chẩn bị đọc trước bài học tại nhà. IV.Tiến trình bài học. Tg Hoạt động của HS Hoạt động của GV Ghi bảng.
a) Đại diện nhóm trình bày
a)Phát phiếu học tập cho 8 Bài tập 4.
trước lớp kết quả đáp án của nhóm,mỗi dãy hai nhóm.Trình a) Gọi số phải tìm là nhóm mình.
bày kết quả số các số tự nhiên abcd . tìm được. Chọn d có 4 cách chọn.
b) Nêu sự khác nhau giữa
b) Lưu ý với bài toán chọn số tự hai bài toán
nhiên mà các chữ số khác nhau Chọn a có 6 cách chọn
thì đưa đến bài toán chỉnh hợp.
Trình bày hướng giải quyết Chọn b có 7 cách chọn
vấn đề theo từng cá nhân
Tiếp tục cho HS hoạt động nhóm Chọn c có 7 cách chọn sau khi thảo luận nhóm. giải quyết bài toán.
Nên theo qui tắc nhân ta có: 6.7.7.4 = 1176 số
b) Chia ra hai trường hợp: Trường hợp1: d= 0
Thì cách chọn ba chữ số abc là 3 A =120 á
c ch .Nên có 120 cách 6
chọn số mà chữ số hàng đơn vị bằng 0.
Trường hợp2: d ¹ 0 Chọn d có 3 cách chọn Chọn a có 5 cách chọn Chọn bc 2 A = 20 á c ch 5
Theo qui tắc nhân có 3.5.20 = 300
số.Vậy theo qui tắc cộng,số các số
chẵn có bốn chữ số khác nhau là: 120 + 300 = 420 số. 52
Giáo án Đại số 11 – Chương trình chuẩn
Để dễ hình dung ta đánh số 1 2 3 4 5 6 Bài tập 5. ghế như hình vẽ . Xét hai trường hợp Ta có n( W) = 6!
Quan sát hình vẽ hãy nêu số Trường hợp1:
a)Kí hiệu A là biến cố
cách sắp xếp chỗ ngồi.
Nam ngồi ở vị trí lẻ và nữ ngồi ở “ nam và nữ ngồi xen kẽ nhau ’’ vị trí chẵn.
-Xếp nam ngồi ở vị trí lẻ và nữ Trường hợp2:
ngồi ở vị trí chẵn ta có: 3!.3! cách.
Nam ngồi ở vị trí chẵn và nữ
- Xếp nữ ngồi ở vị lẻ và nam ngồi ngồi ở vị trí lẻ.
ở vị trí chẵn ta có 3!.3! cách. Vậy ta có n(A) = 2(3!)2 Nên ( )2 2 3! 1 P(A) = = = 0,1. 6! 10
b) Kí hiệu B là biến cố “nam ngồi cạnh nhau’’.
b) Tích cực làm việc theo
- Trước tiên xếp chỗ cho 3 bạn
hướng dẫn của GV.Thảo
b) Sử dụng qui tắc đếm, xét
nam,vì ba bạn nam ngồi cạnh nhau
luận nhóm về các khả năng
riêng từng trường hợp xếp chỗ
nên chỉ có thể ngồi ở các ghế sắp xếp.
ngồi cho ba bạn nam trước hoặc
(1,2,3), (2,3,4),(3,4,5),(4,5,6). Vì ba bạn nữ trước.
ba bạn nam có thể đổi chỗ cho
Cho học sinh thảo luận theo
nhau nên có tất cả là :4.3! cách sắp
nhóm cử đại diện trả lời. xếp.
- Sau khi đã sắp ba bạn nam.Ta có 3! Cách sắp ba bạn nữ.
Theo qui tắc nhân số cách sắp xếp
thỏa mãn đầu bài là : 4.3!.3! Vậy n(B ) = 4.3!.3! P(B) P(B) = = 0, 2. n(W) Bài6. n( 4 W) = C = 210. 10
a)Kí hiệu A là biến cố:
“ Bốn quả lấy ra cùng màu ’’. ta a)Xét hai khả năng: có:
- Bốn quả cùng màu trắng. n(A) = 4 4 C + C = 16 . 6 4
Học sinh tích cực hoạt động - Bốn quả cùng màu đen n( ) A 8
theo sự dẫn dắt của GV. Suy ra cách tính n(A), P(A) P(A) = =
b) Đưa bài toán về sử dụng biến W n(W) 105
-Tính n( ) ? đây là bài toán chỉnh hợp hay tổ hợp?
cố đối ta có kết quả nhanh chóng b) Kí hiệu B là biến cố hơn. a)Tính n(A)?
“ trong 4 quả lấy ra có ít nhất một P(A) ? quả màu trắng’’. b) Tính n( B ) ?
Khi đó B là biến cố:
“cả 4 quả lấy ra màu đen’’. Tính P( B ) ? n( B ) = 1. 1 Nên P( B ) = 210 1 209 Vậy P(B) = 1- = 210 210 53
Giáo án Đại số 11 – Chương trình chuẩn
* HS tích cực làm việc theo * xét không gian mẫu theo qui Bài7. Không gian mẫu sự gợi ý của GV. tắc nhân. n( W) = {a, , b c /1 £ a, , b c £ } 6
Vậy theo qui tắc nhân ta có n( W) = 63 = 216
Gọi A là biến cố “ xuất hiện ít nhất
một lần mặt 6 chấm’’.
Thì A là biến cố
“ không lần nào xuất hiện mặt 6 chấm’’. n( A ) = 53 3 5 Þ P( ) A = 3 6
- Phát biểu biến cố A ?
Để bài toán được đơn giản hơn mà P( ) A = 1- P(A)
trong cách giải đôi khi ta phải - Tính n( A ) ?
xét biến cố đối,và tính xác suất 3 5 P(A) = 1- P( ) A = 1- - Tính P( A ) ?
của biến cố nầy rồi suy ra xác 3 6 - Tính P(A) ?
suất của biến cố cần tính. = 0,4213 Bài8. Không gian mẫu là 2 *HS hoạt động theo nhóm
Hai thẻ gắn hai tên rút được n( W) = C = 15 . 6
tính số phần tử không gian
tương ứng với một cạnh, một
a)Gọi A là biến cố “ hai thẻ rút mẫu.
đường chéo của hình lục giác.
được là tên của hai đầu mút của
Tính được xác suất của các
một cạnh một hình lục giác ‘’ biến cố theo đầu bài. n(A) = 6. Þ n( ) A 6 2 P(A) = = = n(W) 15 5
b) Gọi B là biến cố “ hai thẻ rút
được tên của hai đầu mút của một
đường chéo hình chữ nhật ’’ n(B) = 2 C - 6 = 9 6 9 3 Vậy P(B) = = 15 5
c) tương tự cách gọi như hai câu trên thì 3 1 P(C) = = 15 5 54
Giáo án Đại số 11 – Chương trình chuẩn
Vì các mặt xuất hiện là
*Tổ chức cho HS hoạt động theo Bài9
đồng khả năng nên yêu cầu nhóm theo từng ý riêng: W = (
{ i; j)/1£ i; j £ } 6 HS tính n( W )? - Tính n( W )? Þ n(W) = 36 - Tính n(A) ?
a)Gọi A là biến cố “Hai con súc - Tính n(B) ?
sắc đều xuất hiện mặt chẵn’’thì A = (
{ i; j)/i, j = 2,4, } 6 ê n n n(A) =9
HS liệt kê số phần tử của 9 1 Vậy P(A) = biến cố B. 36 4 Tính n(B) ? b) Gọi B là biến cố:
“ Tích các số chấm trên hai con súc sắc là lẽ ’’ Thì n(B) = 9. Vậy P(B) = 1/4
HS hoạt động nhóm làm các Giải thích các đáp án cho HS.
Các Bài tập trắc nghiệm. bài tập trắc nghiệm. 10(B); 11(D); 12(B); 13(A); 14(C); 15(C). V. Cũng cố:
- Xem kĩ các bài tập đã giải trong ôn tập chương và toàn bộ các bài tập đã giải trong chương.
- làm các bài tập còn lại trong các bài học trước ở trong chương chưa được giải. 55
Giáo án Đại số 11 – Chương trình chuẩn Tiết 37-38
PHƯƠNG PHÁP QUI NẠP TOÁN HỌC + BÀI TẬP I.Mục tiêu :
+Về kiến thức : Hiểu và nắm được phương pháp qui nạp toán học
+ Về kĩ năng :Hs vận dụng được phương pháp qui nạp toán học để chứng minh một số bài toán đơn giản, cụ thể. +Về tư duy thái độ :
- Nghiêm túc, tích cực hoạt động.
- Hs chủ động tiếp nhận kiến thức mới.
- Rèn luyện khả năng phân tích và tổng quát hoá một bài toán.
II.Chuẩn bị: GV : Giáo án, phiếu học tập.
HS : đọc bài trước ở nhà, sgk.
III.Phương pháp : Gợi mở, vấn đáp.Hoạt động nhóm.
IV.Tiến trình bài dạy :
Tết 1: phương pháp quy nạp
Tiết 2: Luyện tập phương pháp quy nạp.
Hoạt động 1 :Tiếp cận phương pháp qui nạp. Tg Hoạt động của HS Hoạt động của Gv Ghi bảng 20
HĐTP1 : Đưa ra bài toán
I.Phương pháp qui nạp
Xét hai mệnh đề chứa biến toán học : P(n): “3n < n + 100”
Các bước để cm một bài toán
Q(n): “2n > n” với n ÎN* qui nạp: (sgk)
HS thảo luận và đưa ra câu a) Với n = 1, 2, 3, 4, 5 thì P(n) và trả lời. Q(n) đúng hay sai? P(1),P(2), P(3), P(4),
b) Với mọi nÎN* thì P(n) và Q(n) Q(1),…, Q(5) :đúng đúng hay sai? P(5): sai.
HĐTP2 : Hình thành phương pháp qui nạp toán học.
Hoạt động 2 :Củng cố phương pháp qui nạp Tg HĐ của HS HĐ của Gv Ghi bảng 56
Giáo án Đại số 11 – Chương trình chuẩn 20 Cmr : 2.Các ví dụ n - 2 2 (4 2 2 ) 1 Ví dụ 1 : 1 + n 3 + ... + (2n - ) 1 = 2 3 n - 2 2 2 (4 ) 1 Hs trả lời 1 + n 3 + ... + (2n - ) 1 = 3 * n " Î N Ch1: B1 ta làm gì? * " CH2 :B2 ta làm gì ? n Î N Bài giải. *
HS thảo luận và lên bảng
Ví dụ 2: CMR n " Î N thì: giải.
Bước 1: n = 1 thì VT = 1 = VP:
1 + 3 + 5 + ... + (2n-1) = n2 (*) đúng Giải:
Bước 2: Giả sử (*) đúng với n = ³
k 1, nghĩa là: 1 + 3 + 5 + ...+ (2k – 1) = k2
Ta phải chứng minh rằng (*) cũng
đúng với n = k+1, tức là:
1 + 3 +5 + ...+(2k – 1)+[2(k + 1)- 1]= (k + 1)2 Ví dụ 3:CMR: * n " Î N thì: HS thảo luận theo nhóm Thật vậy, ta có: n(n + ) 1 1+2+3+...+n=
và cho kq đúng, trình bày
1+3+5+...+(2k–1)+[2(k+1)-1]=k2 2 lên bảng. +[2(k+1)-1] =(k+1)2 Vậy (*) đúng với * n " Î N .
HD HS thảo luận VD 3 và gọi lên bảng giải. Chú ý: sgk 4. Củng cố: (5)
Giáo viên nhắc lại các bước chứng minh bằng phương pháp quy nạp. Tiết 2:
Hoạt động 3 :Luyện tập phương pháp qui nạp Tg HĐ của HS HĐ của Gv Ghi bảng 10 HS thảo luận theo nhóm
GV hướng dẫn từng bước cho Bài tập 1: CMR và cho kq đúng. HS thảo luận và giải. n 3 ( n + ) 1 a) 2+5+8+...+3n-1= 2 b) n n + + 2 2 2 2 ( )( 1 2 ) 1 1 + n 2 + 3 + ... + n = 6
Hoạt động 4 : Hoạt động nhóm n 1 1 1 2 -1 Tổ 1,3 :Cmr + + ... + = với n * Î N n n 2 4 2 2 Tổ 2,4 :Cmr u *
n = 4n + 15n -1 ! 9, với n Î N Tg HĐ của Hs HĐ của Gv Ghi bảng 15
Hs thảo luận, trình bày vào Gv phát phiếu học tập.
Nội dung phiếu học tập. phiếu.
Gọi 1hs nhóm1 và 1 hs nhóm 2
Đại diện nhóm trình bày.
trình bày lời giải.Hai nhóm còn lại nhận xét.
Gv nhận xét và hoàn thiện bài giải.
Hoạt động 5: Giải bài tập 3 sgk Tg HĐ của Hs HĐ của Gv Ghi bảng 57
Giáo án Đại số 11 – Chương trình chuẩn Hs thảo luận, trình bày
Bài 3: CMR với mọi số tự nhiên 15
Đại diện nhóm trình bày.
Gọi 1hs nhóm1 và 1 hs nhóm 2 n ³ 2, ta có các bất đẳng thức: A, Cho n = 2: bđt đúng.
trình bày lời giải.Hai nhóm còn a. 3n > 3n + 1
Giả sử bđt đúng với n = k lại nhận xét. b. 2n+1 > 2n + 3 ³ 2, tức là:
Gv nhận xét và hoàn thiện bài 3k > 3k + 1(*). giải.
Ta cần CM bđt đúng tới n = k + 1, thât vậy: Nhân 2 vế (*) cho 3 ta được: 3k+1 > 9k + 3 Û 3k+1 > 3k + 4 + 6k -1 Û 3k+1 > 3k + 4 Û 3k+1 > 3(k+1)+1
Vậy 3n > 3n + 1với mọi số tự nhiên n ³ 2,
V.Củng cố toàn bài,dặn dò:(5’)-Gv yêu cầu hs nêu lại các bước cm một mệnh đề chứa biến bằng phương pháp qui nạp toán học. VI. Bài tập về nhà:
Bài 1: CM các đẳng thức sau:( * n " Î N ) n 3 ( n + ) 1
a. 2 + 5 + 8 + ... + (3n – 1 ) = 2 n - 2 2 2 4 2 2 1 b. 1 + n 3 + 5 + ... + (2n - ) ( ) 1 = 3 1 1 1 1 Bài 2: Cho tổng S = + + + ... + 5 . 1 9 . 5 13 . 9 (4n - ) 3 (4n + ) 1 a. Tính S1, S2, S3, S4 .
b, Dự đoán công thức tính Sn và chứng minh bằng phương pháp quy nạp. Bài 3: CMR * n " Î N , ta có:
A, 11 n+1 + 122n-1 chia hết cho 133
B, 2n3 – 3n2 +n chia hết cho 6. 58
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 39-40 DÃY SỐ I. Mục tiêu:
+ Về kiến thức: Qua bài học này, học sinh cần nắm vững được: - Định nghĩa dãy số.
- Các cách cho một dãy số ( cho dãy số bới công thức của số hạng tổng quát, cho dãy số
bởi hệ thức truy hồi, diễn đạt bằng lời).
- Các tính chất tăng, giảm, bị chặn của dãy số.
+ Về kỹ năng: Học sinh cần rèn luyện các kỹ năng sau:
- Kỹ năng cho một dãy số.
- Kỹ năng nhận biết dãy số tăng, dãy số giảm, dãy số bị chặn.
- Kỹ năng giải các bài tập về dãy số như: tìm số hạng tổng quát, xét tính tăng, giảm và bị chặn của dãy số.
+ Về tư duy và thái độ:
- Xây dựng cho học sinh có tư duy logic, linh hoạt; biết quy lạ về quen.
- Cẩn thận chính xác trong tính toán, lập luận.
II. Chuẩn bị của giáo viên và học sinh:
+ Giáo viên: Các phiếu học tập.
+ Học sinh: Kiến thức về hàm số đối với số tự nhiên; đọc qua nội dung bài mới. III. Phương pháp: - Gợi mở, vấn đáp.
- Phát hiện và giải quyết vấn đề.
- Tổ chức hoạt động nhóm.
IV. Tiến trình bài dạy: 1. Ổn định lớp 2. Kiểm tra bài cũ 3. Bài mới:
Hoạt động 1: Tìm hiểu về định nghĩa về dãy số và ví dụ về dãy số.
T Hoạt động của học sinh Hoạt động của giáo viên Ghi bảng g
10 - Học sinh quan sát và * Cho hàm
số: I. Định nghĩa : tính. f(n)= 1 ,n * Î N .
Tính - ĐN: Sgk 2n -1 - Ví dụ 1: f(1), f(2),f(3),f(4),f(5).
a) Dãy số các số tự nhiên lẻ
1, 3, 5, 7, 9,...có số hạng đầu là
u1 = 1, u2 = 2,..., un = 2n -1. b) Dãy các số chính
phương 1, 4, 9, 16, ... có số hạng đầu là
- Mỗi học sinh độc lập u1 = 1,.. ,un = n2 . suy nghĩ và trả lời. - Ký hiệu:
+ Ký hiệu dãy số là (un)
+ Ký hiệu số hạng tổng quát của dãy số là un.
2, Định nghĩa dãy số hữu
* GV đưa ra ký hiệu dãy hạn: 59
Giáo án Đại số 11 – Chương trình chuẩn
số, ký hiệu số hạng tổng ĐN: sgk quát.
* GV tiếp tục phân tích Ví
dụ 2 để học sinh hiểu rõ
hơn khái niệm dãy số hữu Ví dụ 2: Hàm số u(n) = n3; hạn.
xác định trên tập hợp M = {1;2;3;4; } 5 , là một dãy
số hữu hạn. Dãy số này gồm có 5 số hạng: n 1 2 3 4 5 un 1 8 27 64 125
Hoạt động 2: Củng cố định nghĩa dãy số
T Hoạt động của học sinh Hoạt động của giáo viên Ghi bảng g
5 - Học sinh độc lập suy * GV giao phiếu học tập nghĩ và hoàn thành
số 1 cho học sinh và yêu cầu học sinh hoàn thành * GV kiểm tra, nhận xét
Hoạt động 3: Tìm hiểu các cách cho một dãy số
T Hoạt động của học sinh Hoạt động của giáo viên Ghi bảng g
10 - Học sinh quan sát và * GV phân tích ví dụ, II.Các cách cho một dãy số: ghi nhớ.
giúp học sinh hiểu cách 1. Dãy số cho bằng công thức
cho một dãy số theo công của số hạng tổng quát. thức tổng quát.
Ví dụ 2: Cho dãy số (un) với n+1 u (- ) 1 n = .Tìm số hạng u5 và 2 n - Học sinh độc lập suy u14 của dãy số trên? nghĩ và trả lời
* GV yêu cầu học sinh Giải
trả lời câu hỏi . u 1
* GV kiểm tra và nhận 5 = 25 xét U 1 14 = - 196
- Học sinh lĩnh hội kiến * GV phân tích ví dụ , 2.Dãy số cho bằng phương thức
giúp học sinh biết cách pháp mô tả: cho dãy số bằng
Ví dụ 3: Số p là số thập phân phương pháp mô tả.
vô hạn không tuần hoàn. p = 3,141 592 653 589...
Nếu lập dãy số (un) với un là
giá trị gần đúng thiếu của số
p với sai số tuyệt đối là 10-n thì:
u1 = 3,1; u2 = 3,14; u3 =3,141; ...;
3.Dãy số cho bằng công thức
* GV phân tích ví dụ , truy hồi. 60
Giáo án Đại số 11 – Chương trình chuẩn
giúp học sinh biết cách Ví dụ 4 : Xét dãy số (un) xác cho dãy số bằng định bởi công thức: công thức truy hồi u ì = 1 1 số hạng thứ hai u í 2 có liên u = 2.u +1, n " ³ 2 î n n 1 -
quan như thế nào đến số Tìm số hạng thứ 2 và số hạng hạng thứ nhất u1 ? thứ 3?
+ số hạng thứ ba có liên u2 = 2.u1 + 1 = 3
quan như thế nào đến số u3 = 2.u2 + 1 = 7 hạng thứ hai u2 ?
Ví dụ 5: Xét dãy số (vn) xác
định bởi: v1 = -1, v2 = 2 và
- Học sinh trả lời: vn-1 * GV hướng dẫn cho học n
" ³ 3 v = v + 2v . - - Tìm số n n 1 n 2 và vn-2 sinh trả lời Ví dụ 5. hạng thứ 4 ? + Theo công thức của vn,
- Học sinh trả lời: v.3 và ta muồn tìm vn thì ta cần GiảiTa có: v3 = v2+2v1 = 0 v2 tính điều gì?
- Học sinh trả lời: thông + Từ dó, muốn tìm v v 4 4 = v3 + 2v2 = 4 qua v1 và v2 đã cho. như thế nào?
- Học sinh độc lập suy + Muốn tìm v
* Cách cho dãy số bằng 3 bằng cách nghĩ trả lời nào?
phương pháp truy hồi: a) Cho
số hạng đầu ( hay vài số hạng
* Gv giới thiệu dãy Phi đầu) bô na xi
b) Cho hệ thức truy hồi. * GV lưu ý thêm về cách
cho dãy số để học sinh tiếp tục ghi nhớ.
Hoạt động 4: Củng cố ( Cách cho một dãy số)
Tg Hoạt động của học sinh Hoạt động của giáo viên Ghi bảng
5 - Mỗi học sinh độc lập * Giao phiếu học tập số 2 Số hạng tổng quát un của dãy
suy nghĩ, tiến hành thực cho học sinh và yêu cầu ì 1 ï = hiện bài giải.
học sinh làm bài tập trong u1 í 3 đó. * u ï = 4u + 7, n " Î N î n 1+ n * GV theo dõi nhận xét 2n 1 2 + - 7 đánh giá. là u = n 3
Hoạt động 5: Biểu diễn hình học của dãy số.
Tg Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng 5 u1 = 2,
GV cho HS tìm u1, u2, u3, III. Biểu diễn hình học của u 3 4 u4… dãy số: 2 = , u3 = , 2 3
GV treo bảng phụ, học sinh Ví dụ: Dãy (u n +1 theo dõi và trả lời. n ) với un = n 5
có biểu diễn hình học : u4 = 4
Tiết 40: Dãy số tăng, dãy số giảm và dãy số bị chặn.
Hoạt động 6: Khái niệm dãy số tăng, dãy số giảm
Tg Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng 61
Giáo án Đại số 11 – Chương trình chuẩn
10 - Học sinh so sánh un và * GV đưa ra một dãy số III. Dãy số tăng, dãy số giảm,
un+1 bằng cách xét hiệu (un) với un = 2n-1, sau đó và dãy số bị chặn u un+1
yêu cầu học sinh so sánh un 1 .Dãy số tăng, dãy số giảm: n+1 – un hay tỉ số un
và un+1. Từ đó đưa ra định
nghĩa dãy số tăng cũng như - ĐN: Sgk dãy số giảm.
- Ví dụ 7: Dãy số (u 1 *GV cho học sinh dựa vào n) với un = là n + 4
định nghĩa để nhận biết:
một dãy số giảm, vì n " Î N ta Dãy số (u 1 luôn có: n) với un= n + 4 1 1 u = > = u
là dãy số tăng hãy dãy số n n 1 n + 4 n + 5 + giảm?
- Ví dụ 8: Dãy số (un) với *Chia nhóm học tập u n n = dãy số giảm. +GV yêu cầu mỗi nhóm n 3
học sinh tự cho một dãy số Thật vậy, * n " Î N , vì un 0 nên
tăng, một dãy số giảm, dãy ta xét tỉ số: un+1 . Ta có:
số không tăng không giảm. un
+ GV theo dõi và yêu cầu u n +1 n n +1 n+1 = : = < 1 suy
đại diện nhóm phát biểu, u n 1 + n 3 3 n 3 n nhóm còn lại nhận xét. ra: + GV nhận xét đánh giá u n+1 < un
* Chú ý:sgk trang 90
Hoạt động 7: Khái niệm dãy số bị chặn
Tg Hoạt động của học sinh Hoạt động của giáo viên Ghi bảng
10 - Học sinh đọc định * GV cho học sinh đọc 2. Dãy số bị chặn:
nghĩa và trả lời câu hỏi định nghĩa trong sgk, sau - ĐN: Sgk trang 90 của giáo viên. đó đưa ra câu hỏi:
+ Em hiểu như thế nào là dãy số bị chặn trên?
+ Em hiểu như thế nào là
dãy số bị chặn dưới?
* Gv yêu cầu học sinh - Ví dụ 7:
- Học sinh dựa vào đ/n dựa vào định nghĩa để xét a) Dãy số (un) với un = n2 là để trả lời.
tính bị chặn của các dãy dãy số bị chặn dưới, vì n " Î N số sau:
ta luôn có u ³1. Tuy nhiên n a) un = n2, với mọi n.
dãy số này không bị chặn trên. b) u 2n -1 2n -1 n = với mọi n. b) Dãy số (un) với un = n +1 n +1 c) u n
là một dãy số bị chặn trên, vi n = 2 n +1 n
" Î N ta luôn có u £ 1
* Gv theo dõi và nhận xét n c) Dãy số (u n n) với un = 2 n +1
bị chặn vì: 0< n < 1 2 n +1 2
Hoạt động 8: Luyện tập .
Tg Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng 62
Giáo án Đại số 11 – Chương trình chuẩn 10
HĐTP1: Yêu cầu 1 học sinh giải Bài 1 : Viết 5 số hạng đầu • Giải câu a trên câu a.
của dãy số cho bởi công bảng.
Cho các học sinh nhận xét n thức: a) u 2 -1 • n = .
Nhận xét bài giải bài giải 2n +1 của bạn
HĐTP2: Tiếp cận lời giải câu b. b) u 1 n = (1 + )n
*Cho hs suy nghĩ, thảo luận n cách giải. Giải: •
*Yêu cầu một hs lên bảng Trả lời câu hỏi a) u 1 3 7 1 = ; u2 = ; u3 = ; của giáo viên giải câu b. 3 5 9 •
*Cho hs nhận xét lời giải và Trình bày lời giải u 15 31 4 = ; u5 = chính xác hoá bài giải. 17 33 • 9 64 Nhận xét bài làm b)u1 =2; u2 = ; u3 = ; 4 27 625 u4 = ; u5 = 256
Gv cho HS thảo luận nhóm Bài 2: Cho dãy số (un) với 10 và trình bày lên bảng. un = - 1, un+1= un + 3 với HS thảo luận theo nhóm n ³ 1 và trình bày lên bảng.
a) Viết 5 số hạng đầu tiên a) -1;2;5;8;11. của dãy số. b) n=1 thì (*) đúng b) Chứng minh bằng
Giả sử (*)đúng với n = HD: Xét hiệu: u phương pháp quy nạp: u k (k ³ 1), tức là: u n+1-un n= k = 3k– n +1-1 n -1 3n – 4.(*) 4 b) un+1-un = - n +1+1 n +1 Cần chứng minh (*) n n -1
Bài 4: Xét tính tăng giảm đúng với n = k + 1. = - n + 2 n +1
của các dãy số (un) biết: Thật vậy: 2 2
n + n - n - n + 2 1 U = a) u k+1= uk+3=3k-4+3 n= -2 10 (n + )( 1 n + ) 2 n = 3(k+1)-4. n - 2 1 Bài 4: = >0 b) un= (n + )( 1 n + ) 2 n +1 1 1 a) u n+1-un=
-2-( -2) Vậy dãy số đã cho là dãy số n +1 n tăng 1 1 = - n +1 n
Gv yêu cầu hs thảo luận. 1 1 Vì < nên:
Gọi hs lên bảng. Đánh giá, n +1 n
Bài 5: Trong các dãy số (u u cho điểm n) n+1-un<0 10
sau, dãy số nào bị chặn Vậy dãy số đã cho là
dưới, bị chặn trên và bị chặn dãy số giảm. ? a. u n = 2n2 – 1. 1 b. un = n n + ( ) 2 a.u n = 2n2 – 1 ³ 1 với 1 mọi c. un = n(n + ) 2 n Î N*. Vậy dãy số bị
chặn dưới mà không bị
d. - 2 £ sinn +cosn £ 2 d. un = sinn +cosn. chặn trên. với 63
Giáo án Đại số 11 – Chương trình chuẩn b. Dãy bị chặn vì
"n Î N*. Vậy dãy số bị 0< un £ 1/3. chặn. c. 0 < un £ 1.Dãy bị chặn
4. Củng cố: ( 5 phút)
Giáo viên yêu cầu học sinh cần thực hiện một số công việc sau:
- Phát biểu đ/n về dãy số.
- Phát biểu đ/n dãy số tăng, giảm, bị chặn
- Nêu các cách cho một dãy số. 5. Bài tập về nhà:
Giáo viên yêu cầu học sinh về nhà làm bài tập trong sách sgk phần còn lại.
Phiếu học tập số 1:
Em hãy cho một dãy số bất kỳ, sau đó xác định số hạng thứ 5 và số hạng thứ 55.
Phiếu học tập số 2: (Câu hỏi trắc nghiệm)
Cho dãy số (un) bởi công thức truy hồi sau: ì 1 u ï = 1 í 3 * u ï = 4u + 7, n " Î N î n 1+ n
Hỏi số hạng tổng quát un có dạng như thế nào? 2n 1 + n 1 + 2n 1 + A) 2n +1 2 - 7 2 - 7 2 u = u = u = u = n B) n C) n D) n 3 3 3 3 64
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 41 CẤP SỐ CỘNG I. Mục tiêu 1.
Về kiến thức: Giúp học sinh
- Nắm vững khái niệm cấp số cộng
- Nắm được tích chất về ba số hạng liên tiếp của cấp số cộng
- Nắm vững công thức xác định số hạng tổng quát và công thức tính tổng n số
hạng đầu tiên của một cấp số cộng. 2.
Về kỹ năng: Giúp học sinh
- Biết dựa vào định nghĩa để nhận biết một cấp số cộng
- Biết cách tìm số hạng tổng quát và cách tính tổng n số hạng đầu tiên của một
cấp số cộng trong các trường hợp không phức tạp
- Biết cách vận dụng các kết quả lý thuyết đã học trong bài để giải quyết các bài
toán đơn giản liên quan đến cấp số công ở các môn học khác, cũng như trong thực tế cuộc sống. 3.
Tư duy và thái độ:
- Xây dựng tư duy logic, linh hoạt, quy lạ về quen
- Cẩn thận, chính xác trong tính toán, lập luận
II.Phương pháp: Gợi mở, phát vấn, hoạt động nhóm
III.Tiến trình bài học 1. Ổn định 2.Kiểm tra bài cũ :(5')
Hoạt động 1:Câu hỏi 1: Cho dãy số ( un) với un = 3n - 1. Hãy viết lại dãy số theo cách liệt kê các số hạng của dãy.
Câu hỏi 2: Từ kết quả trên, em có nhận xét gì về các số hạng liên tiếp của dãy số trên.
3.Bài mới: Tg Hoạt động của HS
Hoạt động của giáo viên Ghi bảng 10
Tiếp cận và nêu định nghĩa:
1. ĐN cấp số cộng:
GV nhấn mạnh: dãy số trên thoả a. ĐN: sgk/ 110
mỗi số hạng sau bằng số hạng đứng
kề trước cộng với một hằng số d = un= un-1 + d, "n Î N*
3. từ đó giáo viên hướng dẫn học
sinh đưa ra khái niệm cấp số cộng. b. VD:
Hs thực hiện yêu cầu - Củng cố định nghĩa VD1:cấp số cộng: 1; 3; của giáo viên
-Cho cấp số cộng: 1; 3; 5;..., 2n-1; 5;..., 2n-1;...có công sai Áp dụng định nghĩa ... d = 2 tính công sai
Tìm công sai của cấp số cộng đó VD2: Cho các dãy số,
dãy nào là cấp số cộng,
Học sinh làm việc Cho nhóm 1, 4 làm câu a; nhóm 2, vì sao?
theo nhóm và các 5 làm câu b và nhóm 3, 6 làm câu a. -6; -1; 4; 9; 14. nhóm 1, 2, 3 trả lời c b. 10; 7; 4; 1; -2; -5; -8. câu hỏi. Các nhóm c. 4; 6; 9; 13; 18. còn lại nhận xét.
Hoạt động 3: Công thức tổng quát của cấp số cộng Tg Hoạt động của HS
Hoạt động của giáo viên Ghi bảng 65
Giáo án Đại số 11 – Chương trình chuẩn 10 - Tiếp cận định lý
II.Số hạng tổng quát :
CH1: Cho CSC có số hạng đầu a. Định lý1 : sgk/ 94
HS sử dụng định là u1 và công sai d. Tính u2; u3; nghĩa tính u4; u5 theo u1 và d. un = u1 +(n- 1)d u2 = u1 + d
CH2: Từ đó hãy dự đoán công
u3 = u2 + d = u 1 +2d thức tính un theo u1 và d. ..... -Nêu định lý và cm b. Ví dụ: Cho CSC có u1 =
Hs nêu lại ý nghĩa Cho HS về nhà chứng minh 13 và công sai d = -3. Tính CT và tính u31; u12
định lý 1 theo phương pháp quy u31; u12. nạp u31 = 13 + 32(-3)
HS áp dụng định lý - Củng cố định lý u12 = 13 + 11(-3) 1 và làm H3. Cho HS làm H3
Hoạt động 4: Tính chất các số hạng của cấp số cộng Tg Hoạt động của HS
Hoạt động của giáo viên Ghi bảng 10
-Tiếp cận và lĩnh hội định lý 1
III. Tính chất các số hạng CH1:
của cấp số cộng: Học sinh
nhận Với cấp số cộng: 10; 7; 4; 1; -2; - a. Định lý 2: sgk/95 nhiệm vụ và trả lời 5; -8; ...
Hãy nhận xét mối quan hệ giữa u + u k 1 - k 1 +
bộ ba số hạng liên tiếp trong dãy; u = k ³ 2 k 2
Ví dụ: 10; 7; 4 hay 7; 4; 1 ... Cm: sgk/95
CH2: Từng bộ 3 số có một quy
tắc chung, đó là quy tắc gì?
GV hướng dẫn học sinh hình
HS thực hiện yêu thành định lý cầu
- Hình thành và chứng minh định b. Ví dụ: Cho cấp số cộng
lý: yêu cầu học sinh áp dụng định (un)có
nghĩa để chứng minh định lý
u1= - 1; u3 = 3. Tìm u2 và u4 u + u - Củng cố định lý u 1 3 = ĐS: u2 =1; u4 = 5 2
CH1: Có u1; u3, tính u2 bằng công 2 u thức nào? 4= u3 + d d = u CH2: Muốn tính u 2 - u1 4 ta cần có dữ u + u kiện gì? u 2 4 =
Yêu cầu HS lên bảng trình bày. 3 2
Hoạt động 5: Tổng n số hạng đầu tiên của cấp số cộng Tg Hoạt động của HS
Hoạt động của giáo viên Ghi bảng 66
Giáo án Đại số 11 – Chương trình chuẩn 10
HĐ1: Tiếp cận định lý
IV. Tổng n số hạng đầu
GV treo bảng phụ: Cho CSC tiên của cấp số cộng: gồm 7 số hạng
Nghe hiểu nhiệm vụ và 1 3 5 7 9 11 13 a. Định lý 3: sgk/96 trả lời
Yêu cầu HS viết các số hạng n(u + u ) 1 n
của cấp số đó vào dòng dưới S = n 2
theo thứ tự ngược lại. b. Chú ý: n " ³ 1,
CH1: hãy nhận xét về tổng của vì un = u1 +(n- 1)d nên
các số hạng ở mỗi cột n(n - ) 1
CH2: Tính tổng các số hạng S = nu + d n 1 2 của cấp số cộng.
GV treo bảng phụ: Cho CSC c. Ví dụ: sgk / 96
gồm n số hạng đầu tiên u1 u2 u3 .... un
Các câu hỏi tương tự như trên
và tính tổng n số hạng đầu tiên
phát hiện định lý và trả - Nêu định lý lời
- hình thành công thức tính tổng khác
CH: Từ định lý 3 ta có thể tính Sn theo u1 và d? - Củng cố định lý
GV hd cho học sinh làm VD 3 trang 96. 4.Củng cố
-Cho học sinh lấy các ví dụ thực tế về cấp số cộng
-Từ định nghĩa: un = un-1 +d.
-Học sinh biểu diễn trên rục toạ độ. Rút ra nhận xét: các điểm đó cách đều nhau
-Các số hạng của cấp số cộng liên tiếp thì cách đều nhau. 5.Bài tập về nhà:
Làm các bài tập:1-5/97,98(sgk) 67
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 42 LUYỆN TẬP CẤP SỐ CỘNG I. Mục tiêu :
+ Về kiến thức:- Ôn tập kiến thức cơ bản về cấp số cộng. Hiểu và vận dụng được các
định nghĩa, định lí, tính chất có trong bài cấp số cộng.
+ Về kỹ năng:- Biết cách tìm một trong các yếu tố còn lại khi cho một số yếu tố d, un , n, Sn .
- Rèn luyện kỹ năng tổng hợp các kiến thức đã biết.
II. Chuẩn bị :Giáo viên: Phiếu học tập, bảng phụ.
Học sinh: Kiến thức đã học về CSC, bài tập về nhà.
III. Phương pháp:Gợi mở, vấn đáp. Hoạt động nhóm .
IV. Tiến trình bài dạy:
1. Ổn định, Kiểm tra bài cũ 2. Bài mới Tg
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng 10 Chia thành từng nhóm .
Gọi HS lên bảng giải, theo Bài 1: trong các dãy số
dõi và cho nhận xét, kết sau, dãy số nào là CSC? a) un+1 - un = -2 " nÎN*. quả đúng. a) un = 5 - 2n.
Vậy dãy số là CSC với u1 = 3 PP chung:xét hiệu:H = và d = -2. u n n+1 - un b) un = - 1 2 b) tương tự a.( là CSC).
. Nếu H là hằng số thì dãy số là CSC c) un = 3n . c) un+1 - un = 2.3n .
. Nếu H = f(n) thì dãy số 7 - 3n
Vậy dãy số không phải là d) un = . 2 không phải là CSC CSC.
Hd HS làm bài tập, gọi HS Bài 2:a) Giải hệ:
lên bảng, theo dõi, nhận Bài 2: Tìm số hạng đầu 10 xét .
ìu - u - 2d + u + 4d = 10 í 1 1 1 và công sai của các CSC
îu + u + 5d = 17 1 1 Sử dụng công thức: sau biết : ìu + 2d = 10
ìu - u + u = 10 1 3 5 Hay: í 1 un = u1 + (n - 1)d. a) í î2u + 5d = 17 îu + u = 17 1 6 1 Suy ra: u ìu - u = 8 1= 16, d = -3 b) í 7 3 éu = , 3 d = 2 Suy ra: ê 1 îu .u = 75 2 7
ìu + 6d - u - 2d = 8 u = - , 17 d = 2 b) ë í 1 1 1
(u + d)(u + 6d) = 75 î 1 1 68
Giáo án Đại số 11 – Chương trình chuẩn
Hoạt động 2: (10) Hướng dẫn học sinh giải bài tập 3/97 u1 d un n Sn -2 3 55 20 530 36 -4 -20 15 120 3 4/27 7 28 140 -5 2 17 12 72 2 -5 10 -43 -205
Hoạt động 3: Hướng dẫn học sinh giải bài tập 4,5/98
10 Bài 4: Học sinh thảo luận H.Viết công thức để tìm độ Bài 4:Mặt sàn tầng một tìm mối liên kết.
cao của một bậc tuỳ ý so của một ngôi nhà cao hơn với mặt sân ? mặt sân 0,5m. Cầu thang
Gọi chiều cao của bậc thứ n
đi từ tầng một lên tầng hai
so với mặt sân là hn, ta có: hn = 0,5 + n.0,18
gồm 21 bậc, mỗi bậc cao 18 cm.
hn= 0,5 + 21.0,18 =4,28(cm) H. mặt sàn tầng so với mặt
sân cách nhau bao nhiêu a) Viết công thức để tìm b) h = 0,5+ 21. 0,18 = 4,2 bậc?
độ cao của một bậc tuỳ ý. Bài 5:
H. nêu công thức tính tổng b) Tính độ cao của sàn của CSC? 1 + 2 + ...+12 =78
tầng hai so với mặt sân. Bài 5:Từ 0 giờ đến 12
trưa, đồng hồ đánh bao nhiêu tiếng. 3. Củng cố(5) 4. Bài tập về nhà 69
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 43 CẤP SỐ NHÂN I/ Mục tiêu: + Về kiến thức:
Học sinh nắm chắc khái niệm, tính chất và các yếu tố liên quan của cấp số nhân.
Học sinh nắm chắc công thức SHTQ, công thức tính tổng n số hạng đầu tiên của một CSN. + Về kỹ năng:
Học sinh biết vận dụng định nghĩa để nhận biết được CSN, tìm được số hạng đầu và công bội;
Biết vận dụng tính chất để giải các ví dụ đơn giản,
Biết tìm các yếu tố còn lại khi biết 2 trong 4 yếu tố: u , u , q, S 1 n n
Biết vận dụng CSN vào giải các bài toán liên quan ở môn học khác và các bài toán thực tế.
+ Về tư duy và thái độ:
Học sinh tích cực tìm tòi lĩnh hội kiến thức;
Rèn luyện tư duy lôgic, tính cẩn thận.
II Phương pháp: Gợi mở, vấn đáp.
III Tiến trình bài dạy: 1. Ổn định
2. Kiểm tra bài cũ: (5’) ìu = -2 1
HĐ 1: Câu hỏi: Cho dãy số: í îu = . 3 u , n ³ 2 n n-1
a/ Tìm u ,u ,u 2 3 5 ;
b/ Nhận xét về mối liên hệ giữa hai số hạng liên tiếp của dãy số đã cho, từ đó tính u10 .
HS Thực hiện các yêu cầu trên;
GV Nhấn mạnh đặc điểm của dãy số đã cho. 3. Bài mới:
HĐ 2: Tiếp cận định nghĩa CSN: 1: Bài toán mở đầu: Tg Hoạt động của HS Hoạt động của GV Nội dung ghi bảng Đọc đề Nêu yêu cầu : * Bài toán mở 5
Tìm cách tính số thóc từ ô thứ
Gọi u , lập công thức tính đầu: SGK/98 n
nhất đến ô thứ 6 của bàn cờ;(1, u theo u 2,4, 8, 16, 32) n n 1 -
Nhấn mạnh đặc điểm của
Thiết lập công thức u sau khi n ( u ) => ĐN n được gợi ý
Nhận xét về dãy số u n
2: Khắc sâu định nghĩa: 5 Phát biểu ĐN Nhấn mạnh công bội và 1/ Định nghĩa: số hạng đầu, SGK tr 98 ?1 Một CSN được xác un+1 = un q với nÎN* Trả lời ?1
định nếu ta biết những Đặc biệt : Cho ví dụ CSN và chỉ ra yếu tố nào? . Khiq = 0 CSN có dạng u1. 70
Giáo án Đại số 11 – Chương trình chuẩn SH đầu và công bội 0,0, 0, … Làm vd 1 trang 99 . Khiq = 1 CSN có dạng u1, Giải:Vì:
Yêu cầu HS giải thích cụ u1,u1,u1, … 1 1 1 thể
. Khi u1 = 0 CSN có dạng 0,0, 1 = ( 4) - (- );- =1.(- ); 4 4 4 0, … 1 1 1
Chú ý : q là số không đổi. = (- ).(- ); 16 4 4
Ví dụ 1 : Chứng minh dãy số 1 1 1 - = .(- )
hữu hạn sau là một cấp số 64 16 4 nhân :
Nên dãy số trên là cấp số -4,1,- 1 1 1 , , - . 4 16 64
nhân với công bội q = - 1 4 HĐ 3: Công thức SHTQ:
Ta có số hạt thóc 6 ô đầu: Hãy cho biết ô thứ 11 3/ Số hạng tổng quát: 10 1, 2, 22, 23, 24,25.
của bàn cờ ở Hoạt động a. Định lí 1:SGK tr 99 Phát biểu định lí 1 1 có bao nhiêu thóc? un = u1.qn-1 (n ³ 2) HS thảo luận làm vd 2.
Gv nhận xét số hạt thóc u1 : số hạng đầu a) u7 = u1.q6 =
ở 6 ô đầu để đưa ra số q : công bội. 6 æ 1 ö 3
hạt thóc ở ô thứ 11: 210. Ví dụ 2 : Cho CSN (u 3. - = n) với ç ÷ HD HS làm vd 2 è 2 ø 64 u 1 1 = 3, q= - b) Vì: 2 n 1 - a)Tính u7. æ 1 ö 3 u = 3. - = 3 n ç ÷ è 2 ø 256 b) Hỏi là số hạng thứ 256 n 1 - 8 æ 1 ö 1 æ 1 ö mấy ? Û - = = - ç ÷ ç ÷ è 2 ø 256 è 2 ø Suy ra n- 1 = 8 hay n = 9
Vậy số 3 là số hạng thứ 256 9
HĐ 4: Phát hiện tính chất của CSN:
Tính các tích u .u ,u .u
Cho CSN (un) với u1 = - III/ Tính chất các số hạng của 1 3 2 4
5 So sánh tích đầu với 2 u và 1 2 2 và q = - . cấp số nhân: tích sau với 2 2 u a/ Định lí 2:SGK tr 101 3
a) Viết 5 số hạng đầu u 2 k = uk-1.uk+1 với k ³ 2 của nó.
(hay u = u .u k k - k + ) 1 1 Thực hiện yêu cầu b) So sánh u 2 2 với tích
Phát hiện và phát biểu định CM: SGK/101 u 2 1.u3 và u3 với tích lí u2.u4. Cho HS nhận xét .
HĐ 5: Tổng n số hạng đầu tiên: 71
Giáo án Đại số 11 – Chương trình chuẩn
10 HS thảo luận, tìm ra đáp
VD: Tính tổng số các hạt IV/ Tổng n số hạng đầu tiên án.
thóc ở 11 ô đầu của bàn của một CSN: S = 1+ 2+ 22+...+210. cờ ở HĐ1.
a. Định lí 3:Cho CSN (un) với công bội q ¹ 1. Đặt: CSN có công bội q có Sn = u1 +u2 +...+ un.
HS lắng nghe và ghi chép. thể được viết dưới dạng: Khi đó: u u1(1- qn ) 1, u1q, u1q2,...,u1qn-1,... S Khi đó: S n= n = u1+u2+...+un 1- q
Giải: Theo giả thiết, u1=2, = u1+ u1q
u =18. Ta có: u = u1q2 +u1q2+...+u1qn-1 3 3 * Chú ý: sgk Þ . 2 2 18 = q Þ q = 3 ± Từ đó GV đưa ra công
Vậy có hai trường hợp: thức của định lý.
Ví dụ 4: Cho CSN(un), biết q = 3:
Cho hs HĐ nhóm, gọi hs u1=2, 10 lên bảng giải, gv nhận 2(1- 3 )
u =18. Tính tổng của 10 số S 3 10 = = . 59048 xét và cho kết quả. 1- 3 hạng đầu tiên. q = -3: (21-(- )310) S10 = = 29524 - 1- (- ) 3 4.Củng cố (5) 5. Bài tập về nhà Bài 1: Cho CSN ( 5 u u = 10;u = n ) có 1 4
thì giá trị SH thứ 6 của CSN đó là: 4 a. 320 ; b. 5/16 ; c.5/24 ; d.5/32
Bài 2: CSN (u ) có u = 24
- ;u = 48 thì tổng bốn số hạng đầu tiên của nó sẽ là: n 3 4 A. -30 ; B. 30 ; C. -90 ; D. 90 ;
Bài 3: CSN (u ) có u = 2;u =18 thì S sẽ bằng: n 1 3 10 A. 59048; B. 29548; C. 29524;
D.C ả A v à C đ ều đ úng 72
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 44 LUYỆN TẬP CẤP SỐ NHÂN I/ Mục tiêu:
+ Về kiến thức:- Ôn tập kiến thức cơ bản về cấp số nhân. Hiểu và vận dụng được các định
nghĩa, định lí, tính chất có trong bài cấp số nhân.
+ Về kỹ năng:- Biết cách tìm một trong các yếu tố còn lại khi cho một số yếu tố q, un , n, Sn .
- Rèn luyện kỹ năng tổng hợp các kiến thức đã biết.
II Phương pháp: Gợi mở, vấn đáp.
III Tiến trình bài dạy: 1. Ổn định 2. Kiểm tra bài cũ
Câu 1) Nêu công thức số hạng tổng quát của CSN. Áp dụng:Cho CSN (u 1 1 n) : 1, , ,... .Tìm 3 9 u8.
Câu 2) Tìm công bội q của CSN hữu hạn biết số hạng đầu u1 = 2 và số hạng cuối u11 = 64. 3. Bài mới
Tg Hoạt động của giáo viên Hoạt động của học Ghi bảng sinh
10 HS thảo luận, tìm ra đáp Gv HD HS tìm ra câu
Bài 1: CM dãy số æ 3 n ö ç 2 . ÷ là án. trả lời. è 5 ø Để CM một dãy số là Bài 1:a) un+1 = un.2 CSN.
CSN ta cần cm dãy số đó b)u 1 Giải: có u n+1 = un. n+1 = un.q. 2 un 1+ Ta có: = c)u 1 n+1 = un. (- ) un 2 æ 3 1 3 n+ ö æ n ö 10 ç 2 . ÷ : ç 2 . ÷ =2 è 5 ø è 5 ø Vậy: u " Î n+1 = un.2 n N*. Bài 2: a) u 1 = 2, u6 = 486. q = 3 9 10 b) u1= 7
- Cho hs lên bảng giải và
-Lên bảng giải bài tập c) n = 7 sửa bài giải
Bài 3:Áp dụng công thức tổng quát un =u1.qn-1 , ta có: 10 u3= 3 = u1.q2 và u5= 27 =
Cho hs thảo luận giải trắc Thảo luận giải bài tập u1.q4 nghiệm trắc nghiệm Suy ra q = ± 3 Bài Tn1 Cho CSN c ó u = 5 - ;u =135 3 6 , công thức SHTQ của CSN đó là: a. (- )n n-3 1 15 . ; b. (- ) 1 n 3 . n-3 5 . ; 73
Giáo án Đại số 11 – Chương trình chuẩn 5 c. n 1 .3 - ; 9 5 n 1- d. - 3 . 9
B ài 2: Cho CSN c ó q = 2 v à 2
u + 1 = u + q 10 1 . Giá trị 9
số h ạng đầu tiên của CSN đó là: a. -1 ; b. -2 ; c. -3 ; d. - 4 ; 4. Củng cố (5)
5. Bài tập về nhà Từ bài 1 đến bài 19 SGK tr 107
Chuẩn bị luyện tập và ôn tập chương III. 74
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 45 ÔN TẬP CHƯƠNG III I. Mục tiêu Qua bài học, HS cần: + Về kiến thức:
+/ Hiểu được mạch kiến thức cơ bản trong chương III, Dãy số. Cấp số cộng. Cấp số nhân.
Hiểu và vận dụng được các định nghĩa, tính chất, định lí có trong chương. + Về kĩ năng:
- Biết cách chứng minh một mệnh đề bằng qui nạp
- Biết cách cho dãy số; biết cách xét tính tăng, giảm, bị chặn của dãy số.
- Biết cách tìm các yếu tố còn lại của cấp số cộng (hoặc cấp số nhân) khi cho trước một
số yếu tố xác định chúng, như: u1, d (q), un, n, Sn.
+Về tư duy và thái độ:
+/ Biết khái quát hoá, đặc biệt hoá, tương tự. Biết quy lạ về quen
+/ Tích cực hoạt động, trả lời câu hỏi.
B. Chuẩn bị của GV và HS
+ GV: Câu hỏi trắc nghiệm, các Slide, computer và projecter .
+ Học sinh : Ôn tập và làm bài tập trước ở nhà. ( Ôn tập tổng kết kiến thức của
chương, bài tập số .....) C. Phương pháp dạy học
Về cơ bản là gợi mở, vấn đáp đan xen hoạt động nhóm D. tiến trình bài học Hoạt động của HS Hoạt động của GV Ghi bảng (Trình chiếu)
HĐ1: Ôn tập kiến thức lí thuyết
I. bảng tổng kết Kiến thức cơ bản HĐ 1 : 5 phỳt chương iii - Nghe hiểu nhiệm vụ
- Em hãy nhắc lại những kiến thức 1. Mạch kiến thức cơ bản trong - Trả lời các câu hỏi chương
đã được học của chương III
BẢNG TỔNG KẾT CHƯƠNG III:
- Nêu cách hiểu của em về phương
DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN pháp quy nạp toán học ?
- Nêu lại kiến thức cơ bản đã học CẤP SỐ PP QUY NẠP DÃY SỐ CẤP SỐ CỘNG NHÂN TOÁN HỌC về dãy số -Chứng minh - Định nghĩa - Định nghĩa - Định nghĩa
- Nêu lại kiến thức cơ bản đã học những mệnh - DãyHH, VH - Số hạng TQ - Số hạng
- Nhận xét câu trả lời đề liên quan - Cách cho DS -Tính chất TQ đến số tự - DS tăng -Tổng của - Tính chất của bạn về cấp số cộng nhiên - DS giảm n số hạng -Tổng của
- Nêu lại kiến thức cơ bản đã học -Bước 1: - DS bị chặn đầu tiên n số hạng Bước 2: đầu tiên về cấp số nhân
- Nhận xét phần trả lời của bạn ?
- Gợi ý để HS nêu được như slide - Ghi nhận mạch trình chiếu kiến thức cơ bản đã
2.Bảng tổng kết chương III : học
HĐ2 : Tổng kết kiến thức cơ bản (Xem bảng phụ ở phần cuối của giáo trong chương án)
- Nhận xét, chính xác hoá, đi đến
bảng tổng kết kiến thức chương
III. (như Slide được chiếu) 75
Giáo án Đại số 11 – Chương trình chuẩn
HĐ 2 : Luyện tập và củng cố kiến II. luyện tập
thức đã học
1. Khi nào thì CSC là dãy số
HĐTP 1 : Củng cố lại kiến thức về tăng , dãy số giảm? chứng minh quy nạp
- Thảo luận theo - Yêu cầu HS trình bày rõ : cách
nhóm và cử đại diện hiểu bài toán (GT cho gì ? yêu cầu báo cáo
gì ? đã biết những gì, có bài toán
- Theo dõi câu trả nào tương tự không ?...); xây dựng
lời và nhận xét, chương trình giải (bước 1, bước chỉnh sửa chỗ sai
2,...) ; trình bày lời giải ; nghiên
cứu kết quả bài toán (bài tập tương tự ; dạng toán,...)
- GV nhận xét lời giải, chính xác hoá. 2.
- Nhấn mạnh lại về chứng minh
Bài toán 2: Hãy điền vào ô trống
qui nạp. Điều quan trọng nhất của
việc dùng qui nạp toán học để
để hoàn thiện bảng sau đây về dãy số
chứng minh là việc khai thác gtqn.
Chú ý hai bước không được bỏ
Cách cho SH TQ của Dãy số đã Dãy số đã Dãy số đã qua bước nào DS
dãy số đó cho là dãy cho là dãy cho là dãy tăng giảm bị chặn - Ra bài tập tương tự Cho bằng
HĐTP 2 : Củng cố lại kiến thức về công thức dãy số Cho bằng
- Chiếu đề bài tập yêu cầu các PP mô tả
nhóm thảo luận và phát biểu cách Cho bằng - Thảo luận theo làm. PP truy hồi
nhóm và cử đại diện - GV nhận xét lời giải, chính xác báo cáo hoá.
- Theo dõi câu trả - Yêu cầu HS trình bày rõ : cách
lời và nhận xét, hiểu bài toán (GT cho gì ? yêu cầu chỉnh sửa chỗ sai
gì ? đã biết những gì, có bài toán 3.
nào tương tự không ?...); xây dựng
chương trình giải (bước 1, bước
Bài toán 3: Hãy điền vào ô trống
2,...) ; trình bày lời giải ; nghiên
để hoàn thiện bảng CSC sau đây
cứu kết quả bài toán (bài tập tương tự ; dạng toán,...) u d u n Sn - Ra bài tập tương tự 1 n
HĐTP 3 : Củng cố lại kiến thức về -2 55 20 cấp số cộng
- Chiếu đề bài tập yêu cầu các - 4 15 120
- Thảo luận theo nhóm thảo luận và phát biểu cách
nhóm và cử đại diện làm. 17 12 72 báo cáo
- GV nhận xét lời giải, chính xác - Theo dõi câu trả hoá.
lời và nhận xét, - Yêu cầu HS trình bày rõ : cách chỉnh sửa chỗ sai
hiểu bài toán (GT cho gì ? yêu cầu
gì ? đã biết những gì, có bài toán
nào tương tự không ?...); xây dựng 76
chương trình giải (bước 1, bước
2,...) ; trình bày lời giải ; nghiên
cứu kết quả bài toán (bài tập tương
Giáo án Đại số 11 – Chương trình chuẩn Tiết 49,50
§1: GIỚI HẠN CỦA DÃY SỐ.
I.Mục tiêu bài học:
Về kiến thức: Giúp học sinh
- Nắm được định nghĩa giới hạn của dãy số .
- Ghi nhớ một số dãy số có giới hạn thường gặp. Về kỹ năng:
- Biết vận dụng định lí và các kết quả để chứng minh một dãy số có giới hạn . Tư duy – thái độ:
- Cẩn thận, chính xác và linh hoạt. II. Phương pháp:
Sử dụng phương pháp gợi mở, vấn đáp, nêu vấn đề kết hợp với giải quyết vấn đề.
III. Tiến trình bài dạy:
1. Ổn định tổ chức:
Ổn định lớp và kiểm tra sĩ số vắng
2. Kiểm tra bài cũ:
Kết hợp trong quá trình giảng dạy. 3. Bài mới: Tg HĐ của GV HĐ của HS Nội dung ghi bảng 77
Giáo án Đại số 11 – Chương trình chuẩn Tiết 1
I. Giới hạn hữu hạn của dãy số:
HĐ1: Hình thành đ\n dãy số 1.Định nghĩa:
15/ có giới hạn 0.
+ H\s theo dõi và trả lời 1 =
+ G\v hướng dẫn h\s xét một câu hỏi gợi ý của G\v.
Xét dãy số(un) với u , tức là dãy n n
dãy số cụ thể (un) với số 1; 1/2;1/3;... 1 = 1 u có giới hạn 0. n + Khoảng
cách Khoảng cách u = từ điểm un đến n n n + G\v : hình 4.1. 1
u = từ điểm u điểm 0 trở nên nhỏ bao nhiêu cũng
H: Em có nhận xét gì về n n n
được miễn là n đủ lớn.
khoảng cách từ điểm un đến đến điểm 0 càng nhỏ
Như vậy mọi số hạng của dãy số đã cho,
điểm 0 thay đổi như thế nào khi n càng lớn.
kể từ số hạng nào đó trở đi, đều có giá khi n đủ lớn?
+ H\s đứng tại chỗ thực
trị tuyệt đối nhỏ hơn một số dương nhỏ hiện hđ1 SGK. æ 1 ö
tùy ý cho trước.Ta nói rằng dãy số ç ÷
+ G\v cho h\s thực hiện hđ1 + H\s phát biểu đ\n dãy è n ø SGK. số có giới hạn . có giới hạn 0. 15/ Định nghĩa 1: SGK Định nghĩa 2:
+Tổng quát hoá đi đến đ\n
Limun = a Û lim(un - a) = 0. dãy có giơi hạn . 3n + 2 Vd: CMR lim = 3 n®+¥ n
2. Một vài giới hạn đặc biệt: 5/ 1 = 1 a. lim 0 ; lim = 0 k n n
b. limqn = 0 nếu q < 1
HĐ2: Chiếm lĩnh tri thức về + H\s phát biểu các kết
một số dãy số có giới hạn 0 quả trong SGK. c. lim C = C.
và vận dụng các đlí vào bài tập. + h\s nghe và hiểu cách c\m định lí.
+G\v đặt vấn đề: để c\m một
dãy số có giới hạn 0 bằng đ\n + PP: tìm dãy (v n) có
là khá phức tạp, đlí 1 sẽ cho giới hạn 0 sao cho | u n |
ta một phương pháp thường £ v n với mọi n
dùng để c\m một dãy số có giới hạn 0. + H\s thảo luận theo
H: Từ đlí 1, nêu phương nhóm và cử đại diện pháp để c\m dãy số (u n) có trình bày. giới hạn 0? + H\s phát biểu đlí 2
+ Áp dụng đlí 1 giải các vd. trong SGK.
+ G\v cho h\s thực hiện hđ 2 theo nhóm đã phân công + H\s thảo luận theo nhóm và cử đại diện
+ Từ đlí 1, ta có thể c\m trình bày.
được kết quả sau thể hiện trong đlí 2.
+ G\v cho h\s thực hiện hđ 3
10/ theo nhóm đã phân công
II.Định lý về giới hạn hữu hạn của HĐ 3:Tiếp cân định lý - Tiếp nhận tri thức dãy số -Phát biểu định lý Định lý 1: ( SGK) - Học sinh nhân xét Ví dụ : Tìm 2 2 2n - 3n +1 2 - 3/ n +1/ n lim = lim = 2 - 2 4 - n 4 / n -1 Tiết 2 78
HĐ4: Xây dựng tổng vô hạn
III. Tổng của cấp số nhân lùi vô hạn:
15/ của cấp số nhân lùi vô hạn Xét hai cấp số nhân
Giáo án Đại số 11 – Chương trình chuẩn
4.Củng cố và bài tập về nhà (5/)
BTVN: Bài 1, 2, 3, 4 SGK trang 130 Tiết 51,52
LUYỆN TẬP - GIỚI HẠN CỦA DÃY SỐ
I.Mục tiêu bài học:
+ Về kiến thức: Giúp HS củng cố lại kiến thức đã học về giới hạn của dãy số.
+ Về kỹ năng: Rèn luyện kĩ năng tính giới hạn của các dãy số, vận dụng vào giải được các bài tập cơ
bản trong sách giáo khoa và các bài tập nâng cao trong sách bài tập.
+ Về tư duy và thái độ: Tích cực hoạt động, có tinh thần hợp tác.
II. Chuẩn bị của giáo viên và học sinh:
+ Giáo viên: Giáo án, phiếu học tập, bảng phụ.
+ Học sinh: Ôn bài, làm bài tập. III. Phương pháp:
Gợi mở, vấn đáp, hoạt động nhóm. (Chia lớp thành 12 nhóm)
IV. Tiến trình bài dạy:
1. Kiểm tra bài cũ: Kết hợp với giải bài tập
Hoạt động 1: Ôn tập lại kiến thức về giới hạn.
H1: Phát biểu các ĐL về giới hạn hữu hạn và nêu các quy tắc tìm giới hạn vô cực.
H2: Cho biết kết quả của các giới hạn sau: limnk với kÎ *
Z , lim qn với |q| <1 và với q >1. + n lim với a Î Z, a>1 n a Thời gian
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng 7’
+ HS trả lời lần lượt các câu hỏi . + Giao nhiệm vụ:
Nêu lần lượt các câu hỏi 1, 2 limnk = với kÎ * Z +
sau khi HS trả lời xong mỗi câu.
lim qn = 0 với |q| <1 và + Các HS khác nhận xét.
+ Yêu cầu HS dưới lớp nhận xét lim qn = +¥ với q >1.
sau mỗi câu trả lời của bạn. n + Treo bảng KQ câu H2. lim =0 với a Î Z, n
+ Nhận xét và cho điểm. a a>1 2. Bài tập:
Hoạt động 2: Bài tập 1 Thời gian
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng 10’
Nhận nhiệm vụ và thảo luận Giao nhiệm vụ cho HS theo 2 n + 4n - 5
theo nhóm. Trình bày lời giải nhóm. a) lim = 0 3 2 3n + n + 7 vào bảng phụ. Nhóm 1, 2, 3: câu a, c 5 4 Nhóm 4, 5, 6: câu b, d
n + n - 3n - 2 b) lim =
Đại diện nhóm lên bảng treo Yêu cầu đại diện nhóm lên bảng 3 2 4n + 6n + 9
bảng lời giải và trình bày.
treo bảng lời giải và trình bày. + ¥
Cho các nhóm khác nhận xét. 4 2n + 3n - 2 Các nhóm khác nhận xét
Chính xác hoá bài giải của HS và c) lim = 2 2n - n + 3 cho điểm. 3n - 2.5n 2 d) lim = - 7 + 3.5n 3
Hoạt động 3: Bài tập 2 Thời gian
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng 79
Giáo án Đại số 11 – Chương trình chuẩn 10’
Nhận nhiệm vụ và thảo luận Giao nhiệm vụ cho HS theo b) lim 4 2
2n - n + n + 2 =
theo nhóm. Trình bày lời nhóm. + ¥ giải vào bảng phụ. Nhóm 1, 2: câu d Nhóm 3, 4: câu b
Đại diện nhóm lên bảng treo Nhóm 5, 6: câu c c) lim 3 3
1+ 2n - n = - ¥
bảng lời giải và trình bày.
Yêu cầu đại diện nhóm lên bảng d) lim 2.3n - n + 2 =
treo bảng lời giải và trình bày. Các nhóm khác nhận xét
Cho các nhóm khác nhận xét. n n lim ( ) 2 3 . 2 - + =
Chính xác hoá bài giải của HS 3n 3n và cho điểm. + ¥
Hoạt động 4: Củng cố.
Phiếu học tập 1: (Thời gian: 8 phút)
Ghép mỗi giới hạn ở cột bên trái tương ứng với kết quả đúng ở cột bên phải: Giới hạn Kết quả 3 2n - n +1 a) -1 1. lim 3 2 b) - ¥ 3n + n - 2 3 2 2 2n + n -1 c) 2. lim 2 3 3n - n + 2 d) + ¥ 2 n - n +1 3. lim 4 2 -n + n - 2 e) 0 3n + 5( 2n - ) - 4n 4. lim 4n + ( 10)n Thời
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng gian 8’
Nhận nhiệm vụ và thảo luận Giao nhiệm vụ cho HS theo nhóm. 1-c theo nhóm.
Yêu cầu đại diện nhóm trả lời 2-d
Đại diện nhóm trình bày.
Cho các nhóm khác nhận xét. 3-e Các nhóm khác nhận xét Đánh giá và cho điểm. 4-a
Phiếu học tập 2: (Thời gian: 10 phút) 1 1 1
Tìm giới hạn của dãy số (un) với un = + + ...+ 1 2 n Thời
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng gian 10’
* Gợi ý thông qua các câu Tìm giới hạn của dãy số (un) với 1 1 1 1 hỏi:+ So sánh số với các un = + + ...+ n 1 2 n 1 1 1 Trả lời câu hỏi. số: 1, , …, Ta có: là số nhỏ nhất trong 2 n n
+ Nếu un > vn mà lim vn = 1 1 n số: 1, , …, + ¥ thì limun = ? 2 n
Nhận nhiệm vụ và thảo luận Giao nhiệm vụ cho HS theo Do đó:
theo nhóm. Trình bày lời giải nhóm. 1 1 1 vào bảng phụ. un ³ 1 + +…+ = n. n n n n
Đại diện nhóm lên bảng treo Yêu cầu đại diện nhóm lên
bảng lời giải và trình bày.
bảng treo bảng lời giải và = n " n Các nhóm khác nhận xét trình bày. vì lim n = + ¥
Cho các nhóm khác nhận xét. nên lim u ¥
Chính xác hoá bài giải của n = + HS và cho điểm. Tiết 2: 80
Giáo án Đại số 11 – Chương trình chuẩn
Hoạt động 1: Bài tập 1 Thời
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng gian
10’ Nhận nhiệm vụ và thảo luận Giao nhiệm vụ cho HS theo 2
theo nhóm. Trình bày lời giải nhóm, lần lượt mỗi nhóm giải 1 a) lim ( n + n - 1 1 - n) = 2 vào bảng phụ.
câu: a, b, c, d, e, f theo hướng 1 dẫn ở sgk. b) lim = + ¥
Đại diện nhóm lên bảng treo Yêu cầu đại diện nhóm lên bảng n + 2 - n +1
bảng lời giải và trình bày.
treo bảng lời giải và trình bày c) lim( 2
n + n + 2 - n +1 ) =
câu a, c; còn lại chỉ yêu cầu nêu 1 1 1 1 cách giải và kết quả. lim n( 1+ + - + ) 2 2 Các nhóm khác nhận xét
Cho các nhóm khác nhận xét. n n n n Đánh giá và cho điểm. = + ¥
* Nhấn mạnh lại phương pháp 1 d) lim = 0
nhân với biểu thức liên hợp: 3n + 2 - 2n +1
A ± B , A ± B
e) lim ( n +1 - n )n = + ¥ 2 n +1 - n +1 1 f) lim = 3n + 2 3
Hoạt động 2: Ôn tập về cấp số nhân lùi vô hạn Thời
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng gian
10’ Đứng tai chỗ nhắc lại các Yêu cầu HS nhắc lại các công 1 n - q 1 công thức.
thức tính liên quan đến CSN lùi Sn = u1. ; S = 1- q 1- q vô hạn: Sn, S. Ghi kết quả lên bảng. ì u 5 1 =
Yêu cầu HS áp dụng vào BT 19 1 ïï -q 3
2 HS lên bảng trình bày lời sgk và BT 36 SBT. Bài 2: í 3 u (1- q ) 39 giải
Gọi 2 HS lên bảng giải. ï 1 = ïî - 1 q 25 => u1=1, q=2/5
Cho các HS khác nhận xét. ì u1 Các HS khác nhận xét
Chính xác hoá bài giải của HS và = 12 1 ïï - q cho điểm. Bài 3: í (u1>0) 3 u ï (1- q) = 1 ïî 4 => u1=3, q=3/4
Hoạt động 3: Bài tập 8 sgk Thời
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng gian 10’
Cho hai dãy (un) và (vn) có
Đứng tại chỗ trả lời.
- Gọi học sinh nêu phương pháp limun = 3; limvn = + ¥
Sử dụng tính chất các phép giải câu a 3u -1 n toán về giới hạn a. lim u +1 n lim(3u -1) 3.3 -1 - Lên bảng trình bày - GV nhận xét, đánh giá = n = lim(u +1) 3 +1 n
.- Gọi học sinh nêu phương pháp = 2
Đứng tại chỗ trả lời. giải câu b v + 2 b. lim n
Sử dụng các giới hạn đặc biệt 2 v -1 n 1 2 + 2 v v 0 = lim n n = = 0 1 1- 1 2 v n 81
Giáo án Đại số 11 – Chương trình chuẩn
Hoạt động 4: Củng cố.
Phiếu học tập 1: (Thời gian: 7 phút)
Chọn phương án đúng trong các phương án sau: 2 2 n - n 2sin n 1 Câu 1. lim ( + ) Câu 2. lim 2 1- 2n n 2 n + n - n
Câu 3: Trong các giới hạn sau, giới hạn nào là + ¥ : 3 1- n n 1 2 + + 3n a. lim b. lim
c. lim n( n + 2 - n) d. lim( 2
2n + n -1 - n - 2 ) 2 n + 2 n 1 3 + + 5n Thời
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng gian
7’ Nhận nhiệm vụ và thảo luận theo Giao nhiệm vụ cho HS theo 1-c nhóm. nhóm. 2-b
Đại diện nhóm trình bày.
Yêu cầu đại diện nhóm trả lời 3-d Các nhóm khác nhận xét
Cho các nhóm khác nhận xét. Đánh giá và cho điểm.
Phiếu học tập 2: (Thời gian: 8 phút) u ì = 3 Cho dãy số (u 1 n) xác định bởi: í
. Gọi (vn) là dãy số xác định bởi vn = un – 1 2u = u +1 î n 1+ n a. CMR (vn) là một CSN.
b. Gọi Sn là tổng n số hạng đầu tiên của dãy số (un). Tìm lim un? Thời
Hoạt động của học sinh
Hoạt động của giáo viên Ghi bảng gian
8’ Nhận nhiệm vụ và thảo luận theo Giao nhiệm vụ cho HS thảo luận u +1 n
nhóm. Trình bày lời giải vào theo nhóm. a. vn+1= un+1 -1 = = 2 bảng phụ. 1
Đại diện nhóm treo bảng và trình Yêu cầu đại diện nhóm trình bày vn 2 bày. trên bảng phụ. 1 Các nhóm khác nhận xét
Cho các nhóm khác nhận xét. Vậy (vn) là CSN có q = Đánh giá và cho điểm. 2 b. Sn = u1+u2+…+un = (v ’ 1+v2+…+vn) + n = Sn +n v với lim S ’ 1 n = = 4 1- q Vậy lim S ’ n = lim(Sn +n) =+ ¥
3. Dặn dò, bài tập: Làm bài tập còn lại trong sách giáo khoa và sách bài tập
Xem trước bài: Định nghĩa và một số địng lí về giới hạn của hàm số. 82
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 53,54,5 GIỚI HẠN HÀM SỐ I Mục tiêu: Kiến thức:
Giúp HS nắm được định nghĩa giới hạn của hàm số tại một điểm, giới hạn của hàm số tại vô cực,các định lí
về giới hạn của hàm số. Kĩ năng:
-Học sinh biết định nghĩa giới hạn của hàm số để tìm giới hạn của một hàm số
-Biết vận dụng các định lí về giới hạn để tìm giới hạn của một hàm số II. Phương pháp:
Gợi mở-vấn đáp, đang xen hoạt động nhóm
III. Tiến trình bài dạy: 1. Ổn định lớp
2. Kiểmtra bài cũ: ( 5’)
Tính các giới hạn sau : 2 2n + 3n +1 a. lim b. 2 lim( n +1 - n) n +1 3. Bài mới:
HĐ 1: Hình thành định nghĩa giới hạn hữu hạn Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng Với x ¹1, rút gọn f(x) HS xem đề bài toán
I.Giới hạn của hàm số tại 1 điểm 1.Giới hạn hữu hạn a. Bài toán: . Với x 2 n ¹1, f(xn) = ? . Trả lời câu hỏi 2x - 2x ChoHS f(x)= và một x -1 10’
dãy số thực bất kì x1, . Tính limf(xn)
x2,…xn,…(xn¹1) và limxn = 1 Tính f(xn), limf(xn)
Ta nói rằng hàm số f(x) có
giới hạn là 2 khi x dần đến 1
. HS phát biểu định nghĩa . Cho HS khái quát thành định nghĩa Định nghĩa : SGK
HĐ 2: Ví dụ - củng cố định nghĩa Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng Yêu cầu HS thảo luận . Tập trung thảo luận Ví dụ 1: Tìm x + 2
Đại diện nhóm trình bày lời giải, a. lim = 1 - x 1 ®- 2x +1
các HS khác nhận xét, bổ sung 2 x + 3x + 2 10’ b. lim =1 x 1 ®- x +1 3 x - 8 c. lim =12 x®2 x - 2 * Nhận xét: lim c = c x®xo
HĐ 3: Định lý về giới hạn hữu hạn Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng 83
Giáo án Đại số 11 – Chương trình chuẩn
Nhắc lại định lý giới hạn -Học sinh nhắc lại kiến thức
2.Định lý về giới hạn hữu hạn hữu hạn của dãy số ? Định lý 1: (SGK)
Tương tự giới hạn của hàm -Tiếp thu kiến thức mới số Ví dụ :Tính 10’ 2 x - x - 6 lim = 5 - x 2 ®- x + 2
HĐ 4: Củng cố tiết 1 (10’) (Giải toán nhanh theo nhóm) 2 x - 5x - 6 x + 5 - 3 3 2 - x +1 Tính a. lim b. lim c. lim x® 1 - x +1 x®4 x - 4 x®7 x - 7 Tiết :
HĐ 1:Hình thành định nghĩa giới hạn một bên của hàm số Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng Tính lim x -1 3.Giới hạn một bên : x 1 ® Định nghĩa : (SGK)
Nếu lấy dãy (xn) sao cho
- Chỉ có thể lấy dãy xn >1 xn 1 và xn < 1 ? -Tiếp nhạn kiến thức
15’ Hình thành định nghĩa Nêu định lý 2 Định lý 2:
lim f (x) = L Û lim f (x) = lim f (x) = L x x + - ® 0 x®x ® 0 x x0
HĐ 2: Ví dụ củng cố định nghĩa TG Hoạt động của Gv Hoạt động của Hs Ghi bảng
Phân nhóm cho học sinh - Học sinh thảo luận theo Ví dụ :Cho hàm số thảo luận yêu cầu của giáo viên 2 ì2x + 3x -1 nêu x ³1 f (x) = í î4 - 2x nêu x < 1 Tính 15’
lim f (x) , lim f (x) và lim f (x) (nếu x 1+ x 1- ® ® x 1 ® có )
HĐ 3: Hình thành khái niệm hữu hạn của hàm số tại vô cực Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng
10/ - Học sinh quan sát hình 52 - quan sát và trả lời các câu II.Giới hạn hữu hạn của hàm số tại vô
trang 127 SGK và trả ời các hỏi cực câu hỏi Định nghĩa 3: SGK - Hình thành khái niệm - Tiếp thu tri thức 10’ 2x -1
- Cho học sinh thảo luận -Học sinh giải ví dụ
Ví dụ : Cho hàm số f (x) = 3 - 4x nhóm để giải ví dụ Tìm lim f (x) , lim f (x) x®+¥ x®-¥ Giải : lim f (x) = lim f (x) = -1/2 x®+¥ x®-¥ HĐ 4: Củng cố Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng 84
Giáo án Đại số 11 – Chương trình chuẩn
1. Tính các giới hạn sau :
-Phân bài tập cho các nhóm -Học sinh thảo luận theo 2 3x - 2x - 2 5’ học sinh nhóm để giải bài tập a. lim 2 x®+¥ x +1 2 + + x x 2 b. lim 3 2 x®-¥ x - x c. 2 lim ( x + x +1 + x) x®-¥
-Gọi đại diện nhóm lên trình - Học sinh đại diện nhóm 2. Tìm m để hàm số sau có giới hạn bày trình bài khi x dần về 2 2 ì4 - x ï nêu x > 2 f (x) = í x - 2 ïî2x + 4m nêu x £ 2 Tiết
HĐ 1: Khái niệm giới hạn vô cực của hàm số Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng
Xây dựng định nghĩa tương -Liên hệ định nghĩa 1,2,3 để III. Giới hạn vô cực của hàm số
tự định nghĩa 1,2,,3 chỉ khác tiếp cận khái niệm 1. Định nghĩa 4: (SGK) ở chổ f(x) ±¥ 15’ Nhận xét :
lim f (x) = +¥ Û lim (-f (x)) = -¥ -Cho hs nhận xét tìm x®+¥ x®+¥ k lim x = ? (k nguyên) x®+¥
-Hs suy nghĩ dự đoán trả lời
2.Một vài giới hạn đặc biệt: k lim x = ? (k lẻ ) k lim x = +¥ (k nguyên) x®-¥ x®+¥ k lim x = ? (k chẵn) k lim x = -¥ (k lẻ ) x®-¥ x®-¥ k lim x = +¥ (k chẵn) x®-¥
HĐ 2: Các quy tắc về giới hạn vô cực Tg Hoạt động của HS Hoạt động của GV Ghi bảng 85
Giáo án Đại số 11 – Chương trình chuẩn
Định lý về giới hạn chỉ áp
3.Các quy tắc về giới hạn vô cực
dụng cho hàm số có giới hạn
a.Quy tắc tìm giới hạn của tích hữu hạn lim f (x) lim g(x)
20’ Nêu hai cột để Hs lên bảng - Suy nghĩ để điền vào cột 3 x®x ® 0 x x0 điền cột thứ 3 .Tiếp nhận kiến thức lim f (x).g(x) x®x 0 L > 0 +¥ +¥ -¥ -¥ L < 0 +¥ -¥
Phân công cho các nhóm -Thảo luận giải bài tập lên -¥ +¥
thảo luận giải bài tập ví dụ bảng trình bài Sửa chữa Ví dụ: Tính a. 5 3 lim (x - 2x +1) = -¥ x®-¥ b. 2 lim ( x + x +1 + x) = +¥
Nêu 3 cột để Hs lên bảng -thực hiện theo yêu cầu của x®+¥ điền cột thứ tư gv
b.Quy tắc tìm giới hạn của thương lim f (x) lim g(x) Dấu x®x ® 0 x x0 f (x) g(x) lim
Phân công cho các nhóm -Thảo luận giải bài tập lên x®x0 g(x)
thảo luận giải bài tập ví dụ bảng trình bài L ±¥ Tùy 0 L > 0 0 + +¥ - -¥ L < 0 + -¥ - +¥
Ví dụ: Tính các giới hạn 2x + 3 a. lim = +¥ 2 x 1 ® (x -1) 2x +10 b. lim = +¥ x 2- ® x - 2
4: Củng cố toàn bài (10’)
1. Gọi HS trình bày các định nghĩa và định lí
2. GV khắc sâu các nhận xét để áp dụng giải toán Tiết 56,57
BÀI TẬP GIỚI HẠN HÀM SỐ I Mục tiêu: Kiến thức:
Củng cố kiến thức giới hạn của hàm số tại một điểm, giới hạn của hàm số tại vô cực,các định lí về giới hạn
của hàm số, các quy tắc tính giới hạn Kĩ năng:
-Biết vận dụng các định lí về giới hạn để tìm giới hạn của một hàm số
-Khử được các dạng vô định II. Phương pháp:
Gợi mở-vấn đáp, đang xen hoạt động nhóm
III. Tiến trình bài dạy: 1.Ổn định lớp 2.Kiểmtra bài cũ: ( 5’)
Tính các giới hạn sau : 86
Giáo án Đại số 11 – Chương trình chuẩn 2 2x + 3x +1 a. lim b. 2 lim ( x + x +1 - x) x 1 ®- x +1 x®+¥ 3.Bài mới:
Hđ 1: Ôn lại quy tắc giới hạn vô cực Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng
-Cho hs nhắc lại kiến thức
*Quy tắc tìm giới hạn của tích về giới hạn vô cực
- Hs ôn lại kiến thức cũ
lim f (x) lim g(x) lim f (x).g(x)
- Cho hs điền vào các chổ điền vào chỗ trống x®x ® ® 0 x x0 x x0 còn thiếu trong bảng L > 0 +¥ +¥ Cột 3 ,4 -¥ -¥ L < 0 10’ +¥ -¥ -¥ +¥
*Quy tắc tìm giới hạn của thương lim f (x) lim g(x) Dấu x®x ® 0 x x0 f (x) g(x) lim x®x0 g(x) L ±¥ Tùy 0 L > 0 0 + +¥ - -¥ L < 0 + -¥ - +¥ Hđ 2: giải bài tập 3 Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng Bài 3:Tính giới hạn
Ghi các bài tập lên bảng Thảo luận giải bài tập 2 x -1 Cho hs thảo luận
Lên bảng trình trành lời a. lim = 4 - x 3 ®- x +1
Gọi hs lên bảng giải bài giải 2 tập 4 - x b. lim = lim (2 - x) = 4 Cho hs nhận xét sửa x 2 ®- x 2 x + 2 ®-
15’ chữa cách trình1 bài x + 3 - 3 x + 3 - 9 1 c. lim = lim = x®6 x®6 x - 6 (x - 6)( x + 3 + 3) 6
Phân loại các dạng ở các Câu a hàmsố xác định tại -3 2x - 6 bài tập trên ?
Câu b,c dạng vô định 0/0 d. lim = 2 - Câu d, f dạng vô định x®+¥ 4 - x ¥ / ¥ 2 2x - + x -1 f. lim = -¥ x®+¥ x + 3 Hđ 2: giải bài tập 4 Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng Bài 4 :Tính giới hạn Cho hs thảo luận nhóm
Thảo luận giải bài tập 3x - 5
Lên bảng trình bài lời giải a. lim = +¥ 2 x®2 (x - 2) 2x - 7 b. lim = +¥ - x 1 ® x -1 10’ 2x - 7 c. lim = -¥ x 1+ ® x -1
Hđ 3:Củng cố và bài tập về nhà (5/) Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng 87
Giáo án Đại số 11 – Chương trình chuẩn Chon phương án đúng
Thảo luận giải bài tập 3 x -1 Câu 1: Tính lim x 1 ® x -1 Cho hs thảo luận nhóm A. 0 B. 3 C. +¥ D. -¥ 5’ Trả lời đáp án 2 x +1 Câu 2: lim x®+¥ 1- x A. 1 B. 2 C. +¥ D. -¥ Câu 3: 2 lim ( x + x + x) x®-¥ A. 0 B. 2 C. +¥ D. -¥ Tiết 2 6 Hđ 4: Giải bài 5 Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng Học sinh thảo luận theo Bài 5: 4
nhóm quan sát đồ thị Thảo luận quan sát đồ thị
hàm số nhận xét f(x) dần 2 về đâu khi : 20’ x -¥ Trả lời đáp án -3 x -3 X -5 3 f(x) 5 x 3 M Yêu cầu hs tính x + 2 -2 1) lim 2 x®-¥ x - 9
- Hs tính các giới hạn để x + 2 x + 2 2) lim -4 lim = 0 - 2
kiểm tra lại kết quả từ việc 1) 2 x®3 x - 9 x®-¥ x - 9
nhận định giới hạn từ đồ x + 2 x + 2 3) lim thị 2) lim = -¥ -6 + 2 - 2 x 3 ®- x - 9 x®3 x - 9 x + 2 3) lim = +¥ + 2 x 3 ®- x - 9 Hđ 6: giải bài tập 4 Tg Hoạt động của Gv Hoạt động của Hs Ghi bảng Bài 6 :Tính giới hạn Cho hs thảo luận nhóm
Thảo luận giải bài tập a. 4 2 lim (x - x + x -1) = +¥
Lên bảng trình bài lời giải x®+¥
Gọi hs lên bảng giải bài b. 2 lim x - 2x + 5 = +¥ 15’ tập x®-¥ 2 x +1 + x Chú ý 2 x = x c. lim = 1 - x®+¥ 5 - 2x Bài 7:
- Lên bảng rút ra d/ từ CT. 1 1 1 a) + = suy ra / - Gọi HS nêu phương d d f pháp giải. fd
- Tính các giới hạn và nêu d/ =
được ý nghĩa trong từng d - f trường hợp. b) lim j(d) = +¥ + d ® f - Theo dõi HS trả lời. lim j(d) = -¥ - Đánh giá. d ® f lim j(d) = f d ®+¥
3. Củng cố và bài tập về nhà(10/)
- Trình bài cách khử các dạng vô định , các quy tắc tính giới hạn
Bài 1:Bài tập trắc nghiệm Câu 1: Tính giới hạn 88
Giáo án Đại số 11 – Chương trình chuẩn 2 x - x - 6 1- x -1 (2x - 3)(3 - 4x) 3 3 x - 6 a. lim b. lim , c. lim ,d, lim x 3 ® x - 3 x®0 x 2 x®¥ x - 9 x®0 x - 8 e. lim( x2 - x + - x2 1 + x +1) Bài 2 (Bài tập về nhà) 2 ì x - 4 ï , khi x > 2 - Cho hàm số y = í x + 2
. Tìm a để hàm số có giới hạn khi x dần về -2 5 ïî x +a,khix £ 2 - BÀI TẬP THÊM: BT1: Cho hàm số x2 - 2x + 3 nếu x £ 2 f (x) =
4x – 3 nếu x > 2. Tính lim f (x); lim f (x); lim f (x) (nếu có) x 2- x 2+ ® ® x®2 BT2: Cho hàm số 2 x - 2x - 3 nếu x > -1 x +1 f(x) = 3x - 1 nếu x £ 1
- . Tính lim f (x); lim f (x);lim f (x) (nếu có) x 1- ® x 1+ ® x 1 ®
BT3:Tçm caïc giåïi haûn sau : 3 1- x - 3x 3 x -1 4 x -16 1- x + x -1 A = lim B = lim C = lim D = lim 2 x 2 ®- 2x + x - 3 x 1 ® x -1 2 x® 2 - x + 6x + 8 x 1- ® 2 3 x - x Tiết 58,59
HÀM SỐ LIÊN TỤC 89
Giáo án Đại số 11 – Chương trình chuẩn I. Mục tiêu: Về kiến thức:
-Biết khái niệm hàm số liên tục tại một điểm, trên một khoảng và trên một đoạn.
-Biết đặc trưng "liên kết" của đồ thị của hàm số liên tục trên một khoảng, trên một đoạn
-Dựa vào tính liên tục chứng minh phương trình có nghiệm Về kỹ năng
- Biết xét tính liên tục của hàm số tại một điểm. Kết luận được điểm gián đoạn (nếu có) của một hàm số
-Biết cách phân biệt các khái niệm: hàm số liên tục trên một khoảng, trên một đoạn, trên các nửa khoảng.
-Nắm được đặc trưng của đồ thị của hàm số liên tục trên một khoảng là một "đường liền" trên khoảng đó. Về tư duy - thái độ
-Tích cực tham gia vào bài học. Có tinh thần hợp tác
-Biết quy lạ về quen. Rèn luyện tư duy lôgic
II. Phương pháp dạy học
Về cơ bản sử dụng PPDH gợi mở vấn đáp, đan xen hoạt động nhóm
III.Tiến trình bài học 1. Ổn định lớp 2. Kiểm tra bài cũ 3. Bài mới
Hoạt động 1: Ôn lại kiến thức cũ Tg HĐ của HS HĐ của GV Ghi bảng 5 - Nghe hiểu nhiệm vụ
- Nêu định nghĩa tập xác định của hàm số y = f(x) ?
- Hồi tưởng kiến thức cũ và - Cách tìm giá trị của hàm số y = f(x) tại Ghi tóm tắt kết quả trả lời câu hỏi
một điểm thuộc miền xác định của hàm số đó ?
- Giả sử lim f (x) = M và lim g(x) = N x®x ® 0 x x0
Khi đó giới hạn của các hàm số f (x)
- Nhận xét câu trả lời của bạn f(x) + g(x),f(x).g(x),
khi x ®x0 được g(x) tính thế nào?
- Nhận xét và chính xác hoá các câu trả lời
Hoạt động 2: Chiếm lĩnh tri thức về khái niệm hàm số liên tục tại một điểm (ĐN 1 - Trang 136 SGK)
(GV cho học sinh hoạt động nhóm để trả lời)
Phát phiếu học tập cho các nhóm (GV chuẩn bị sẵn bảng phụ để đại diện các nhóm lên trình bày sau này) Phiếu HĐ (nhóm 1) Phiếu HĐ (nhóm 2)
Cho hàm số f(x) = x2 ì2x -1, nêu x ³1 g(x) = í a. Tính f(-2), f(l), f(3) î2 ,nêu x < 1
b. Tính lim f(x), lim f(x), lim f(x) a. Tính g(-2) , g(1)
b. Tính lim g(x), lim g(x)
c. Có nhận xét gì về lim f(x) và f(l)
c. Có nhận xét gì về lim g(x) và g(1) Phiếu HĐ (nhóm 3) Phiếu HĐ (nhóm 4)
+ Vẽ đồ thị hàm số f(x) = x2 ì2x -1, nêu x ³1
+Vẽ đồ thi hàm số g(x) = í
+ Đồ thị là đường có "liền nét" không? î2 ,nêu x < 1
+ Đồ thị là đường có "liền nét" không? Tg HĐ của HS HĐ của GV Ghi bảng 90
Giáo án Đại số 11 – Chương trình chuẩn 4 20 - Các nhóm làm việc
HĐTP1: Chiếm lĩnh tri thức về Đồ thị : 4 - Cử đạ 2
i diện của nhóm trình ĐN1 (SGK, trang 136) bày
+ Cho đại diện nhóm 1 và 2 lên 2 -5 5
- Nhận xét vè kết quả của trình bày (trên bảng phụ) nhóm khá -2 c
+ Cho đại diện nhóm 3 và 4 lên -5 5
trình bày (trên bảng phụ) -4 -2
+ Cho HS các nhóm khác nhận xét
+ Nhận xét các câu trả lời của HS,
chính xác hoá nội dung và đi đến
phát biểu "Ta nói rằng y = f(x) là
hàm số liên tục tại diểm x = 1, còn
hàm y = g(x) là hàm số không liên
tục tại điểm x = 1 (còn nói g(x) gián I.Hàm số liên tục tại điểm đoạn tại x = 1) Định nghĩa 1: (SGK)
- Phát biểu ĐN1, trang 136 Đi vào ĐN1 (trang 136 SGK) SGK
Yêu cầu HS đọc SGK trang 136, -Tiếp thu định nghĩa phần ĐN1
HĐTP2: Củng cố kiến thức - Nghe hiểu nhiệm vụ
+ Hỏi: Để xét tính liên tục của hàm - Trả lời câu hỏi
số y = f(x) tại x0, ta cần thực hiện VD1 (trang 136 - SGK) những điều gì?
Hoạt động 3: Chiếm lĩnh tri thức về khái niệm hàm số liên tục trên một khoảng:
Định nghĩa 2 (SGK trang 136) Tg HĐ của HS HĐ của GV Ghi bảng 15
HĐTP1: Chiếm lĩnh tri thức về II Hàm số liên tục trên một ĐN2 (SGK trang 136) khoảng - Nghe hiểu nhiệm vụ
Từ kết quả dã có, kết luận được
hàm số f(x) = x2 liên tục tại các - Trả lời câu hỏi điểm nào?
- Phát biểu điều nhận xét
- Nhận xét các trả lời của HS, được chính xác hoá nội dung
Dẫn dắt để đi đến khái quát và phát
biểu: hàm số liên tục trên khoảng Định nghĩa 2 (SGK)
( - ¥;+¥ ) (hay là trên toàn tập số thực R) Hình thành định nghĩa
Hàm số liên tục trên (a,b) có đồ thị 5
là đường liền trên khoảng đó
HĐTP 2: Củng cố tri thức về ĐN2 (trang 136 SGK) Phiếu HĐ (nhóm 1) Phiếu HĐ (nhóm 2)
Hoàn chỉnh mệnh đề sau: Hàm số y = f(x) liên tục Hoàn chỉnh mệnh đề sau: Hàm số y = f(x) liên tục trên nửa khoảng [a; b) nếu trên nửa khoảng (a; b] nếu
...........................................
........................................... 91
Giáo án Đại số 11 – Chương trình chuẩn Phiếu HĐ (nhóm 3) Phiếu HĐ (nhóm 4)
Hoàn chỉnh mệnh đề sau: Hàm số y = f(x) liên tục Hoàn chỉnh mệnh đề sau: Hàm số y = f(x) liên tục
trên nửa khoảng [a; + ¥ ) nếu.............
trên nửa khoảng ( - ¥ ; a] nếu............ Tiết 2
Hoạt động 4:Hình thành định lý 1,2 Tg HĐ của HS HĐ của GV Ghi bảng 10
Cho hs thảo luận tham khảo nội III. Một số định lý cơ bản:
dung định lý 1 và 2 cho ví dụ: Định lý 1: SGK
Thảo luận theo yêu cầu của -Một hàm đa thức , một hàm hữu tỉ giáo viên kiểm chứng định lý
-Cho hai hàm số liên tục tại x = 1 và g(1) khác 0
-Kiểm tra tính liên tục các hàm Định lý 2: SGK tổng hiệu tích thương
Hoạt động 4:Củng cố định lý 1,2 Tg HĐ của HS HĐ của GV Ghi bảng
10 Trả lời câu hỏi của gv Tìm tập xác định ? Ví dụ: Cho hàm số
x ¹ 1 hàm số liên tục không ? 2 ìx - 4x + 3 ï nêu x ¹ 1
x =1 hàm số liên tục không ? y = í x -1 ïî2 nêu x = 1
Thảo luận giải bài tập ví dụ Thảo luận nhóm xét tính liên tục đại diện trình bày của hàm số tại x = 1
Xét tính liên tục của hàm số trên Sửa chữa trình bày bài tập xác định
Hoạt động 5: hình thành định lý 5 ứng dụng chứng minh pt có nghiệm Tg HĐ của HS HĐ của GV Ghi bảng
Nhắc lại tính chất đồ thị hàm liên
10 Trả lời câu hỏi của gv
tục trên môt đoạn [a,b] ?
Trưc quan đồ thị hàm số y = f(x) Định lý 3: Nếu hàm số y = f(x)
liên tục trên môt đoạn [a,b] và có
liên tục trên môt đoạn [a,b] và
f(a).f(b)<0 . Từ đồ thị kết luận pt có f(a).f(b)<0 thì có ít nhất một f(x) =0 có nghiệm ntn ?
điểm cÎ(a,b) sao cho f(c)=0 - Từ đó có định lý
* Phát biểu định lý dưới dạng khác (SGK)
Hoạt động 6:Củng cố định lý 3 Tg HĐ của HS HĐ của GV Ghi bảng 10
Ví dụ: Chứng minh phương 3
trình x + 2x - 5 = 0 có ít nhất một nghiệm trên (0,2)
Cho hs thảo luận nhóm giải ví dụ 3
Giải Hàm số f (x) = x + 2x - 5
liên tục trên [0,2] và có f(0) = -
Thảo luận nhóm đại diện
5, f(2)=7 do đó f(0).f(2)<0 nhóm lên bảng trình bày
Phương trình f(x) =0 có ít nhất
một nghiệm thuộc khoảng (0,2) 4: Củng cố (5)
5. Bài tập về nhà : 1,2,3, 6 trang 141,142 SGK 92
Giáo án Đại số 11 – Chương trình chuẩn Tiết 60,61 ÔN CHƯƠNG IV I Mục tiêu:
1.Kiến thức: Giúp HS củng cố lý thuyết toàn chương về:
- Định nghĩa giới hạn của: dãy số, hàm số; hàm số tại một điểm.
- Các định lí về giới hạn hữu hạn dãy số, của hàm số; các định lý về hàm số liên tục tại 1 điểm, liên tục trên khoảng.
- Giới hạn một bên, giới hạn tại vô cực. 2. Kĩ năng:
-Học sinh biết dùng các định nghĩa giới hạn của hàm số để tìm giới hạn của một: dãy số, hàm số một cách thành thạo.
-Biết vận dụng các định lí về giới hạn để tìm giới hạn của một: hàm số, dãy số và giải các bài toán liên quan.
3. Tư duy- thái độ:
- Rèn luyện tư duy khái quát hóa.
- Thái độ tích cực hoạt động. II. Chuẩn bị:
-GV: giáo án, SGK, SBT, thước kẻ, phấn màu, phiếu học tập.
-HS: Kiến thức về chương IV - giới hạn của dãy số, hàm số... III. Phương pháp:
Gợi mở-vấn đáp, đang xen hoạt động nhóm.
IV. Tiến trình bài dạy:
1. Ổn định lớp. Nắm sĩ số.
2. Kiểm tra bài cũ: Không.
3. Củng cố lý thuyết:( 10’) * lim u = 0 n n®+¥
Hay u ® 0 khi n ® +¥ n
* Cho khoảng K chứa điểm xo và hàm số y = f(x) xác định trên K hoặc trên K\ {x0}
Ta nói hs y = f(x) có giới hạn là số L khi x0 nếu với dãy số (xn) bất kỳ, xnÎK\ {xo} và xn ® xo, ta có f(xn) ®L.
Kí hiệu: lim f (x) = L hay f(x) ®L khi xn ®xo x® 0 x
*Điều kiện để hàm số tồn tại giới hạn tại điểm xo: lim f (x) = lim f (x) = L x + ® + ® o x x o x
* Điều kiện để hàm số liên tục tại điểm xo: lim f (x) = f (x ) o x® o x * Các định lý: 4. Bài tập: Tg
Hoạt động của GV
Hoạt động của HS Ghi bảng 93
Giáo án Đại số 11 – Chương trình chuẩn 10’
A. Giới hạn của dãy số: Bài 3: SGK * Gọi học sinh KTBC.
- Lên bảng giải tìm giới Tên của HS là mã số 1530 hạn của 4 dãy.
Cho 4 giới hạn ứng với từng kí tự hãy tìm tên của HS đó? 3n -1 A = lim = 3 n +1
( 2n +2n-n) H = lim
* Nhận xét đánh giá bài - Lên bảng giải tìm giới 2 2
n + 2n - n làm của Hs hạn của 4 dãy. = lim 2
n + 2n + n 2n = lim = 1 2
n + 2n + n n - 2 N = lim = 0 3n + 7 æ 3 n ö - 5 3n 5.4n ç ÷ - è 4 ø O = lim = lim = 5 1- 4n n æ 1 ö -1 ç ÷ è 4 ø - Thảo luận nhóm. Vậy 1530 là HOAN
* Chia lớp thành các - Cử đại diện lên bảng Bài tập 1: 5’ nhóm 04 HS/ nhóm. trình bày. a) Tính tổng: * Hướng dẫn HS thảo
S = 1 +0.1 + (0.1)2 + (0.1)3 +... luận.
b) Tìm u1 của CSN lùi vô hạn. Biết S = 4 và q = 1/2 10’ B. Giới hạn hàm:
a) Thay cận vào tìm được Bài 5: SGK - Gọi học sinh nêu KQ x + 3 1 phương pháp giải. a) lim = 2
x®2 x + x + 4 2
b) Đặt nhân tử chung để 2 x + 5x + 6 1
* Sử các định lý đã học rút gọn khử dạng vô định. b) lim = 2
và các cách khử dạng vô x 3 ®- x + 3x 3 định. c); d)Chia tử và mẫu cho 2x - 5 c) lim = +¥ x x 4- ® x - 4 2
x - 2x + 4 - x 2 - Bài 6 trong SGK học f) lim = - x®-¥ 3x -1 3
sinh đã chuẩn bị ở nhà Bài 6: ĐA 10’ rồi. - Lên bảng trình bày.
a) lim f (x) = +¥
- Gọi HS lên bảng giải. x®0 lim g(x) = +¥ x®0 lim f (x) = 1 - x®+¥
- Dựa vào các giới hạn lim g(x) = +¥
vưa tính được suy ra đồ x®+¥
thị của các hàm f(x) và b) Nhận xét: Đường cong a) là đồ thị của g(x)
f(x), đường cong b) là đồ thị của g(x) 94
Giáo án Đại số 11 – Chương trình chuẩn Bài tập 2: 20’ Tiết 2 2 x x ® ® 1 2 x®1 2x + 3x -1 x®+¥ a) lim có giá trị là : 3
x®+¥ x - 3x - 2 A. +¥ B. -1 C.-¥ D.2 - Thảo luận nhóm. * Chia lớp thành các
b) Trong 4 giới hạn sau, giới hạn nào có nhóm 04 HS/ nhóm.
- Nêu kết quả của nhóm giá trị bằng 4/3? mình. 2 x - 3x - 4 A. lim x -1 2 x - 4
- Cử đại diện lên bảng B. lim x - 2
* Hướng dẫn HS thảo trình bày. 2 2x - 2 luận. C. lim x 1 ® 3x - 3 3 2x - 2 D. lim x®+¥ x -1 x - x + 2 c) Tính lim lim x®2 4x +1 - 3 ĐA: 9/8 15’ * Chia lớp thành các
C. Hàm số liên tục: nhóm 04 HS/ nhóm. - Thảo luận nhóm.
Bài tập 3: Cho hàm số 2 ì x + 2x - 3
- Nêu kết quả của nhóm ï khi x < 1 f(x)= í x -1 mình. ïî ³ a +1 khi x 1
Xét tính liên tục của hs tại x = 1 * Hướng dẫn HS thảo Giải: luận.
- Cử đại diện lên bảng lim f (x) = 4 - trình bày. x 1 ® = +
lim f (x) a 1 x 1+ ® f(1) = a + 1
Gọi học sinh nêu phương
* Nếu a = 3 thì hs liên tục tại 1 pháp giải.
* Nếu a ¹ 3 thì hs không liên tục(gián đoạn) tại 1
* Sử các định lý đã học Bài 7: SGK
và các cách khử dạng vô
Hàm số liên tục tại 2. Suy ra hs liên tục định. trên R. - Bài 7, 8 trong SGK học Bài 8: SGK
sinh đã chuẩn bị ở nhà CM phương trình: rồi.
x5 - 3x4 + 5x - 2 = 0 có ít nhất 03 nghiệm
- Gọi HS lên bảng giải. - Lên bảng trình bày. thuộc khoảng (-2; 5) Củng cố: (10’) ì 2 x - 4x + 3
Câu 1Tìm m để hàm số f(x) = ï (x < ) 1 2 liên tục tại x0 = 1 í x - x
ïîmx + m + 4 (x ³ )1 4 + 7 +10 +13 + ... + 3 ( n + ) 1 Câu 2: Tính lim 2 1+ 2n - 3n 2x - 3x +1 Câu 3: Tính lim 2 x 1 ® x -1 95
Giáo án Đại số 11 – Chương trình chuẩn
lim ( x2 +1 - x2 - 4x ) Câu 4: Tính x®-¥ ì 2 ï x - 6x + 9 khi x < 3
Câu 5: Cho f (x) = í 9 - 2 x ï îax + 3 khi x ³ 3
Tìm a để hàm số liên tục tại x = 3. Tiết 62 KIỂM TRA 1 TIẾT.
CHƯƠNG V ĐẠO HÀM Tiết 63,64
§ 1 ĐỊNH NGHĨA VÀ Ý NGHĨA CỦA ĐẠO HÀM I) Mục tiêu
1) Kiến thức: Nắm được định nghĩa và quy tắc tính đạo hàm bằng định nghĩa, nắm mối quan hệ
giữa tính liên tục và sự tồn tại của đạo hàm.
2) Kỹ năng: Vận dụng quy tắc tính đạo hàm của hàm số tại một điểm
- Nắm vững cách viết PTTT của đồ thị hàm số tại một điểm cho trước thuộc đồ thị hoặc có hệ số góc cho trước
3) Tư duy và thái độ: Cẩn thận, chính xác, tích cực hoạt động nhóm II) Chuẩn bị:
GV: Giáo án, sgk, phiếu học tập. 0
HS: Xem lại cách tính giới hạn hàm số dạng vô định , chuẩn bị bài mới ở nhà. 0
III) Phương pháp: Thuyết trình, vấn đáp, hoạt động nhóm
IV) Tiến trình bài giảng 1) Kiểm tra bài cũ 0
Hoạt động 1: Ôn lại phương pháp khử dạng vô định 0 2 CH: Tính các giới hạn I x - 5x + 6 x +1 - 2 1 = ; I2 = lim lim 2 x®2 x - 2 x 1 ® x -1 Thời Hoạt động GV Hoạt động HS Ghi bảng gian
- GV nêu bài tập và yêu - Làm bài tập Bài tập KTBC 5’ cầu HS nêu cách giải
- Nhớ lại kiến thức cũ
- GV nhắc lại phương pháp khử 0 dạng vô định 0 2Bài mới
Hoạt động 2: Khái niệm đạo hàm thông qua bài toán mở đầu: 96
Giáo án Đại số 11 – Chương trình chuẩn
s(t) - s(t ) 0
được gọi là vân tốc tức thời của chuyển động tại thời điểm t0 lim - t®t t t 0 0
Q(t) - Q(t ) 0
được gọi là cường độ tức thời của dòng điện tại thời điểm t0 lim - t®t t t 0 0 Tg Hoạt động GV Hoạt động HS Ghi bảng
- Vẽ hình và nêu bài toán mở
I. Đạo hàm tại một điểm: đầu
1) Các bài toán dẫn đến định
- Yêu cầu HS tính vận tốc trung
- Trả lời câu hỏi và xác nghĩa: (Sgk)
7’ bình của viên bi trong khoảng thời
s(t) - s(t )
a. Bài toán tìm vận tốc tức thời: định V 0 tt = gian từ t
b. Bài toán tìm cường độ tức t - t 0 đến t1 0 - Nhận xét khi t thời: 1 dần đến t0 thì Vtb
- Nghe, hiểu và ghi nhận
càng dần đến vận tốc tức thời của
viên bi tại thời điểm t0
- Giới thiệu còn có nhiều bài toán
thực tế dần đến giới hạn dạng
s(x) - s(x ) 0 và giới thiệu khái lim - x® t t 0 x 0 niệm đạo hàm
Hoạt động 3: Hình thành định nghĩa đạo hàm và quy tắc tính đạo hàm Tg Hoạt động GV Hoạt động HS Ghi bảng
2) Đạo hàm của hàm số tại 1 điểm - Ghi nhận định nghĩa
a) Khái niệm đạo hàm tại 1 - Nêu định nghĩa đạo điểm: (Sgk) hàm, lưu ý x0Î TXĐ
- Nắm chú ý để tính đạo hàm bằng - định nghĩa.
f (x) f (x ) 0 f '(x ) = lim 0 x® x x - x 0 0 b) Chú ý:
Đặt Dx = x - x0: số gia của biến số tại x0 Dy = f(x) - f(x0) 15’ x D ) - HS làm Vd1 = f(x0 + - f(x0): số gia - Phát hiện PP tính
của hàm số ứng với số gia của
- Hiểu được quy tắc tính x D tại x0 - Làm Vd2 y D
Khi đó: f '(x ) = 0 lim x D ®0 x D
Vd1: Cho hàm số y = 2x - 3
Tính số gia của hàm số ứng với
số gia của biến số tại x0 = 1 và suy ra f ' ) 1 ( = ?
3. Quy tắc tính đạo hàm của
hàm số tại điểm x0: (Sgk)
Vd2: Tính đạo hàm của hàm số 2
y = x tại x = 3 Tg Hoạt động GV Hoạt động HS Ghi bảng - Chia lớp thành 6 nhóm,
- HS thảo luận theo nhóm
4. Quan hệ giữa sự tồn tại của phân công nhóm 1-2 làm để giải bài tập
đạo hàm và tính liên tục của
PHT1; nhóm 3-4 làm PHT2; - Đại diện nhóm lên trình bày, hàm số: 7’ nhóm 5-6 làm PHT3
các HS khác theo dõi nhận xét
- Hàm số có đạo hàm tại x0 thì liên
- Gọi đại diện nhóm trình bày tục tại đó 97
Giáo án Đại số 11 – Chương trình chuẩn
lời giải; HS dưới lớp nhận
- Chiều ngược lại có đúng không? xét, GV chỉnh sửa
- Nghe, hiểu và xem đây là bài (Bài Tập)
- Nxét về mối quan hệ giữa tập về nhà
tính liên tục và tính có đạo hàm tại một điểm
Hoạt động 4: Củng cố quy tắc tính đạo hàm 3) Củng cố:
- Khắc sâu lại định nghĩa và quy tắc tính đạo hàm tại một điểm
- Quan hệ giữa tính liên tục và tính có đạo hàm tại một điểm
4) Bài tập về nhà: - Xem và làm Vd1/149-Sgk
- Làm các bài tập: Sách bài tập PHT1 PHT2 PHT3
Cho hàm số y = x2 + 3x 1 y = 3 - x Cho hàm số y = Cho hàm số a) Tìm TXĐ 2x -1 a) Tìm TXĐ
b) Tính số gia của hàm số ứng a) Tìm TXĐ
b) Tính số gia của hàm số ứng với với số gia x
D của biến số tại b) Tính số gia của hàm số số gia x
D của biến số tại x0 = 2 x0 = 1 ứng với số gia x D của biến c) Tính f '( ) 2 bằng định nghĩa c) Tính f ' ) 1 ( bằng định số tại x0 = -1 nghĩa c) Tính f '(- ) 1 bằng định nghĩa Tiết 2.
1) Kiểm tra bài cũ:
CH: + Nêu định nghĩa và quy tắc tính đạo hàm tại một điểm + Tính f ' ) 1
( với f (x) = x2 - 2x
Hoạt động 1: Ôn lại phương pháp tính đạo hàm của hàm số tại 1 điểm bằng định nghĩa Tg Hoạt động GV Hoạt động HS Ghi bảng
+ Nêu CH và gọi HS lên bảng + HS trả lời
Ghi lại kết quả để phục vụ cho bài trả lời + HS khác nhận xét giảng 5’
+ GV nhận xét, chỉnh sửa, cho điểm 2) Bài mới
Hoạt động 2: Hình thành ý nghĩa hình học của đạo hàm Tg Hoạt động GV Hoạt động HS Ghi bảng * HĐTP1:
+ Nhớ lại kiến thức cũ và
3) Ý nghĩa hình học của đạo hàm
+ Ôn tập về đường thẳng trả lời câu hỏi
a) Tiếp tuyến cong của đường thẳng
10’ + Gọi lại HS nhắc lại hệ số
+ Cho đường thẳng (D) : y = ax + b . hệ góc của đường thẳng
số góc của đường thẳng (D) là
+ Nhắc lại HS cách viết ®
PTTT qua M(x0;y0) và có hệ
k = tan(D; 0x) = a số góc k
+ Đường thẳng đi qua M(x + Nghe, hiểu 0;y0) và có hệ
số góc k có phương trình là: - = - y y k(x ) 0 x0 98
Giáo án Đại số 11 – Chương trình chuẩn * HĐTP2:
+ GV dùng bảng phụ, giới + T
Hsg rảt2 l ời câu hỏi phát hiện b) Ý nghĩa nghĩa hình học của đạo
thiệu các khái niệm cát tuyến đượ M0T c công thức tính hàm
M0M, tiếp tuyến M0T, hệ số
f (x ) - f (x (Sgk) M 0 ) góc của các tuyến K K = M M x - x Cát tuyến M M M M 0 ¾ ¾ ® ¾ ¾ ®t2M T
+Yêu cầu HS đưa công thức M 0 0 0 tính K M + Khi
x ® x (M ® ) thì K M M 0 M0 + HS trả lời câu hỏi tiến về đâu?
+ Yêu cầu HS đưa ra công
thức tính Hsg của tiếp tuyến 10’
+ HS phát hiện công thức tại M0 Vậy:
+GV phát biểu lại ý nghĩa
+ HS hiểu ý nghĩa hình học Đạo hàm của hàm số y = f (x) tại x hình học của đạo hàm 0 là của đạo hàm
hệ số góc của tiếp tuyến của đồ thị hàm
số y = f (x) tại M0(x0;fx0))
Yêu cầu HS đưa ra công thức + HS trả lời câu hỏi
c) Phương trình tiếp tuyến: PTTT của hàm số Định lý 3:
y = f (x) tại M0(x0;fx0))
PTTT của đồ thị hàm số y = f (x) tại + Nêu Vd1 M0(x0;fx0)) là:
+ Gọi HS trả lời trên cơ sở
y = f '(x )(x - x ) + f (x ) 0 0 0
dựa vào kết quả của phần + HS làm Vd1
Vd3: Lập PTTT của đồ thị hàm số kiểm tra bài cũ 2 + Cho HS làm H2-Sgk, gọi + HS làm H2-Sgk
y = x - 2x tại M có hoành độ x = 1 0
HS trả lời, GV nhận xét, Vd4: (H5-Sgk) chỉnh sửa
Hoạt động 3: Hình thành ý nghĩa cơ học của đạo hàm Tg Hoạt động GV Hoạt động HS Ghi bảng 5’
+ Trên cơ sở của bài toán mở
+ Hs xem lại bài toán mở
4) Ý nghĩa vật lý của đạo hàm
đầu, GV hướng đến công thức đầu, nghe, hiểu
a. Vận tốc tức thời: (Sgk)
tính vận tốc tức thời của viên bi
Phương trình chuyển động của chất tại thời điểm t0
điểm s = s(t) + HD HS đọc mục 5. b-Sgk
+ Tự đọc, hiểu nội dung
+ GV tóm tắt ý nghĩa cơ học của mục 4-Sgk
Khi đó vận tốc tức thời của chất đạo hàm
điểm tại thời điểm t0 là: + Cho HS làm H3-Sgk, lưu ý
v(t ) = s'( ) 0 t0 trên kết quả Vd1/150-Sgk + HS trả lời câu hỏi
b. Cường độ tức thời:
Cường độ của dòng điện thay đổi có pt: Q = Q(t)
Q(t0) = Q'(t0) được gọi là cường độ
tức thời của dòng điện tại thời điểm t0
Hoạt động 4(5’): Củng cố quy tắc tính đạo hàm của hàm số tại 1 điểm - ý nghĩa hình học của đạo hàm
Vd5: Cho hàm số y = x3 + x , M0 là điểm thuộc đồ thị hàm số có hoành độ x0 (x0 là số thực cho trước)
a) Tính f '(x ) theo x0 0
b) Giả sử tiếp tuyến của đồ thị hàm số tại M0 có hệ số góc k = 3 . Xác định tọa độ của M0
c) Viết PTTT của đồ thị hàm số tại M0 Tg Hoạt động GV Hoạt động HS Ghi bảng Hoạt động 5 99
Giáo án Đại số 11 – Chương trình chuẩn 5’
- Giới thiệu khái niệm đạo hàm của - HS theo dõi, nghe, hiểu
II. Đạo hàm của hàm số trên hàm số trên 1 khoảng một khoảng - Cho HS làm Vd1 - HS làm Vd1
a) Khái niệm: (Sgk)
- Gọi HS đứng tại chỗ trả lời theo từng bước
- HS trả lời các câu hỏi theo
Vd1: Tìm đạo hàm của hàm + B1: Lấy x " Î R tính y D sự gợi ý của GV số y = x2 trên R y D + B2: Tính + B3: Kết luận lim x D ®0 x D Tg Hoạt động GV Hoạt động HS Ghi bảng
- Chia lớp thành 6 nhóm, phát
- HS thảo luận theo nhóm để
b) Đạo hàm của hàm số
phiếu học tập (3 loại phiếu) làm bài tập thường gặp
- Gọi đại diện nhóm lên trình bày
- Đại diện nhóm trình bày lời Định lý: (Sgk) lời giải
giải, các nhóm khác nhận xét
- Hàm số hằng y = c có đạo
- GV nhận xét, chỉnh sửa
- HS nghe, hiểu các kết quả hàm trên R và y’ = 0 5’
- Từ các kết quả của nhóm GV nêu - HS trả lời câu hỏi
- Hàm số y = x có đạo hàm
công thức cho phần a, b, d của định trên R và y’ = 1 lý - Hàm số y = xn ( nÎ N ,
- Từ các kết quả của Vd1- Vd3/189 n ³ )
2 có đạo hàm trên R và y’
- Sgk GV gọi HS dự đoán công n 1 - nx
thức đạo hàm của hàm số y = xn ( = nÎ N , n ³ ) 2
- Hàm số y = x có đạo hàm
- Gợi ý HS xem phần chứng minh trên ( ; 0 +¥) và y’ = trong Sgk 1
- Gọi HS trả lời câu hỏi, hướng HS HS làm Vd2, cần phát hiện 2 2 x đến 2 PP tính y’(2)
PP tính y’(2) và y’(-1) không + C1: Dùng định nghĩa
tồn tại vì hàm số không xác
Vd2: Cho hàm số y = x
+ C2: Tính y’(x), suy ra y’(2) định tại x = 1 - Tính y’(2) và y’(-1) 3) Củng cố:
+ Khắc sâu ý nghĩa hình học của đạo hàm
+ Khắc sâu quy tắc tính đạo hàm bằng định nghĩa
4) Bài tập về nhà: 5; 6/156-Sgk 100
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 65 Bài tập ĐỊNH NGHĨA VÀ Ý NGHĨA CỦA ĐẠO HÀM I) Mục tiêu
Kiến thức: - Nắm được định nghĩa đạo hàm của hàm số trên khoảng.
- Công thức tính đạo hàm của một số hàm số thường gặp.
Kỹ năng: Vận dụng thành thạo công thức tính đạo hàm của một số hàm số thường gặp
Tư duy và thái độ: Rèn luyện tính chính xác, cẩn thận, tinh thần tập thể II) Chuẩn bị
Thầy: Phiếu học tập; bảng phụ Trò: Sgk
III) Phương pháp: Thuyết trình, vấn đáp, hoạt động nhóm
IV) Tiến trình bài giảng
2) Kiểm tra bài cũ (5’)
CH1: Ý nghĩa hình học của đạo hàm; công thức PTTT của đồ thị hàm số y = f(x) tại M(x0,f(x0)) 1
CH2: Lập PTTT của đồ thị hàm số y = tại điểm M có hoành độ x0 = -2 x
Hoạt động 1: Kiểm tra kiến thức về ý nghĩa hình học của đạo hàm Tg Hoạt động GV Hoạt động HS Ghi bảng
- Gọi HS lên bảng trả lời các câu
- HS1: lên bảng trả lời, hỏi các HS khác theo dõi bài 5’ - Gọi HS nhận xét làm
- GV nhận xét, chỉnh sửa, cho - HS2: Nhận xét bài làm điểm 2) Bài mới Tg Hoạt động GV Hoạt động HS Ghi bảng 7’
- Giới thiệu khái niệm đạo hàm của - HS theo dõi, nghe, hiểu
II. Đạo hàm của hàm hàm số trên 1 khoảng
số trên một khoảng - Cho HS làm Vd1 - HS làm Vd1
a) Khái niệm: (Sgk)
- Gọi HS đứng tại chỗ trả lời theo từng bước
- HS trả lời các câu hỏi theo Vd1: Tìm đạo hàm + B1: Lấy x " Î R tính y D sự gợi ý của GV của hàm số y = x2 trên R y D + B2: Tính lim x D ®0 x D + B3: Kết luận
Hoạt động 2: Giới thiệu khái niệm đạo hàm của hàm số trên một khoảng Tg Hoạt động GV Hoạt động HS Ghi bảng
- Chia lớp thành 6 nhóm, phát
- HS thảo luận theo nhóm để
b) Đạo hàm của hàm số
phiếu học tập (3 loại phiếu) làm bài tập thường gặp
- Gọi đại diện nhóm lên trình bày
- Đại diện nhóm trình bày lời Định lý: (Sgk) lời giải
giải, các nhóm khác nhận xét
- Hàm số hằng y = c có đạo
- GV nhận xét, chỉnh sửa
- HS nghe, hiểu các kết quả hàm trên R và y’ = 0
15’ - Từ các kết quả của nhóm GV nêu - HS trả lời câu hỏi
- Hàm số y = x có đạo hàm
công thức cho phần a, b, d của định trên R và y’ = 1 lý - Hàm số y = xn ( nÎ N ,
- Từ các kết quả của Vd1- Vd3/189 n ³ ) 2 có đạo hàm trên R và
- Sgk GV gọi HS dự đoán công 101
Giáo án Đại số 11 – Chương trình chuẩn
thức đạo hàm của hàm số y = xn ( y’ = n 1 - nx nÎ N , n ³ ) 2
- Hàm số y = x có đạo
- Gợi ý HS xem phần chứng minh ( ;0+¥) trong Sgk hàm trên - Cho HS làm Vd2
HS làm Vd2, cần phát hiện 2 1 và y’ =
- Gọi HS trả lời câu hỏi, hướng HS PP tính y’(2) và y’(-1) không 2 x đến 2 PP tính y’(2)
tồn tại vì hàm số không xác + C1: Dùng định nghĩa định tại x = 1 - Vd2: Cho hàm số
+ C2: Tính y’(x), suy ra y’(2)
y = x Tính y’(2) và y’(- 1)
Hoạt động 3: Rèn luyện cách tính niệm đạo hàm của hàm số trên một khoảng - Hình thành CT
Hoạt động 4: Củng cố cách vận dụng công thức tính đạo hàm của hàm số thường gặp - Viết PTTT Tg Hoạt động GV Hoạt động HS Ghi bảng 8’ - Nêu Vd3 Vd3: Cho hàm số y = x4
- Gọi HS trình bày ở bảng HS làm Vd3
a) Lập PTTT của đồ thị hàm số tại M có hoành độ
- GV nhận xét, chỉnh sửa xM= -2
b) Lập PTTT của đồ thị biết tiếp tuyến có hệ số góc k = -4
Hoạt động 5: Củng cố ( thông qua bảng phụ ) Tg Hoạt động GV Hoạt động HS Ghi bảng
5’ - GV dùng bảng phụ trình bày
các câu hỏi trắc nghiệm
- HS trả lời các câu hỏi
- GV nhận xét, chỉnh sửa
3) Củng cố và dặn dò: (3’)
- Cách tính y’(x) bằng 2 cách
- Ý nghĩa hình học và cơ học của đạo hàm
- Chứng minh: Hàm số y = |x| liên tục tại x = 0 nhưng không có đạo hàm tại x = 0
- Làm các bài tập trang 156 - 157 Sgk PHT1 PHT2 PHT3 CMR: Hàm số hằng y = c
CMR: Hàm số y = x có đạo hàm trên R và CMR: Hàm số y = x có
(cÎ R) có đạo hàm trên R và y'= 1 đạo hàm trên ( ; 0 +¥) và y'= 0 1 y’ = 2 x Bảng phụ Câu 1: Tìm kết luận sai
Câu 2: Hệ số góc tiếp tuyến của đồ Câu 3: Phương trình nào sau đây
a) Hàm số y = 3 có y’ = 0
thị hàm số y = x3 tại điểm có hoành là PTTT của đồ thị hàm số y =
b) Hàm số y = x10 có đạo hàm độ x0 = -1 có giá trị là:
x tại điểm có hoành độ x0 = 1? trên R và y’ = 10x9 a) -1 a) y = x + 1
c) Hàm số y = x có đạo b) 1 b) y = -x + 1 c) -3 1 -1 1 hàm trên R và y’ = d) 3 c) y = x - 2 x 2 2
d) Hàm số y = x có đạo hàm 1 1 d) y = x + trên R và y’ = 1 2 2 3) Củng cố: 102
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 66,67 QUY TẮC TÍNH ĐẠO HÀM. I. MỤC TIÊU 1. Kiến thức
- Giúp học sinh hiểu cách chứng minh quy tắc tính đạo hàm của tổng, hiệu, tích và thương các hàm số.
- Nhớ lại hai bảng tóm tắt về đạo hàm của một số hàm số thường gặp và các quy tắc tính đạo hàm
của tổng, hiệu, tích, thương các hàm số. 2. Kỹ năng
- Giúp học sinh vận dụng thành thạo quy tắc tính đạo hàm và hai công thức tính đạo hàm của hàm số hợp y u n =
(x) và y = u(x) . II. CHUẨN BỊ : 1. Giáo viên: + Phiếu học tập.
+ Chuẩn bị bảng tóm tắt quy tắc tính đạo hàm trên một tờ giấy khổ lớn.
2. Học sinh: Ôn tập
+ Quy tắc tính đạo hàm theo định nghĩa.
+ Đạo hàm của một số hàm số thường gặp. III PHƯƠNG PHÁP.
- Kết hợp các phương pháp nêu vấn đề, đàm thoại ,hoạt động nhóm.
IV. TIẾN TRÌNH BÀI DẠY Tiết 1:
1.Kiểm tra bài cũ.(10 phút)
Cho hàm số f (x = x2 ) + x
Dùng định nghĩa để tính đạo hàm của hàm số trên tại x. 2. Bài mới. 1
Hoạt động 1: Tìm hiểu đạo hàm của tổng hay hiệu của hai hàm số. / / y = ( x) = 2 x T/g
Hoạt động của hs
Hoạt động của gv Ghi bảng HĐTP1: CÁC QUY TẮC TÍNH
- Việc dùng định nghĩa để tính ĐẠO HÀM (xn)/ = n.xn-1
đạo hàm thường rất phức tạp.Bài I. Đạo hàm một số hàm số thường gặp:
này sẽ cung cấp cho chúng ta 1. Định lý 1: quy tắc tính đạo hàm.
+ Hàm số y = xn có đạo hàm trên R. - Đọc hiểu và nhận
- Ngoài việc dùng định nghĩa để + xét.
tính đạo hàm của hàm số f (x = x2 )
+ x tại x ta còn có Chứng minh: SGK 10’
một số quy tắc để tính đạo hàm. 2. Định lý 2: - Ghi nhớ công thức
+ Hàm số y = x có đạo hàm với mọi x dưới dạng thu gọn.
-Hướng dẫn học sinh chứng dương minh định lý 1 +
-Hướng dẫn học sinh chứng - Đọc hiểu và nhận minh định lý 3
II. Đạo hàm của tổng, hiệu, tích, xét.
thương hai hàm số:
a) Đạo hàm của tổng, hiệu hai hàm
- Ghi nhớ công thức -Mở rộng định lý 3 cho tổng hay số: dưới dạng thu gọn.
hiệu của nhiều hàm số - Định lý 3(SGK tr 159) (Ý 1 và 2) 103
Giáo án Đại số 11 – Chương trình chuẩn - Ghi chú:
(u ± v)'= u'±v'
Nhận xét: Nếu các hàm số u,v,….,w có
đạo hàm trên D thì trên D có:
(u ± v ±....± w)'= u'±v' .... ± ± ' w HĐTP2:
- Gọi một học sinh lên bảng.
+ Ví dụ 1: Tìm đạo hàm của hàm số:
- Cho một học sinh dưới lớp f (x) 5
= x - x +1 trên khoảng - Học sinh lên bảng nhận xét ( ;0+¥)
(sử dụng định lý 1). - Chỉnh sửa, hoàn chỉnh
- Gọi một học sinh trả lời.
+ Ví dụ 2: Tính đạo hàm của hàm số: 5 3 2 - Giáo viên giải thích
f (x) = x + x - x + 2 tại x = - 1 A. 10. B. 6 - Trả lời. C. -6 D. -10
Hoạt động 2: Tìm hiểu đạo hàm của tích hai hàm số. HĐTP1:
- Đạo hàm của tổng hay hiệu
b)Đạo hàm của tích hai hàm số:
hai hàm số bằng tổng hay hiệu - Định lý 3(SGK tr 159)
các đạo hàm của hai hàm số đó. (Ý 3 và 4)
Liệu điều tương tự đó có xảy ra + (uv)’=u’v + uv’
với tích của hai hàm số không? / / / æ u ö u v - uv
- Giới thiệu định lý 3 ý 3 và 4 + = ç ÷ 2
20’ - Học sinh tiếp cận định - Hướng dẫn học sinh chứng è v ø v lý minh định lý (u+v)’=u’+v’ HĐTP1: (uv)’=?
- Đạo hàm của tổng hai hàm số Chứng minh (SGK) - Học sinh đọc hiểu
bằng tổng các đạo hàm của 2
định lý và ghi nhớ công hàm số đó.Vậy đạo hàm của thức thu gọn.
thương hai hàm số có bằng
thương của hai đạo hàm không? Ghi chú:
Định lý 3 sẽ trả lời điều đó.
+ (uv)’=u’v + uv’
- Giới thiệu CT tính đạo hàm
+ (ku)’=ku’ với k là hằng số hàm thương / / / æ u ö u v - uv =
- Sử dụng CT tính đạo hàm hàm + ç ÷ 2 è v ø v
tích để chứng minh công thức: ' æ 1 ö 1
- Học sinh chứng minh. ç ÷ = - với x ¹ 0 2 è x ø x ' æ 1 ö v'(x) = -
với v(x) ¹ 0 * Hệ quả: çç è v(x) ÷÷ 2 ø v (x) / / æ 1 ö v = - ; v = v(x) ¹ 0 ç ÷ 2 è v ø v 5’ HĐTP2:
Ví dụ: Tìm đạo hàm của hàm số sau:
- Gọi học sinh lên bảng
f (x) = x7 - 4x5 + 2 x - Hs 1 trình bày. - Cho học sinh nhận xét f (x) = (5 3 x - ) 1 (x + ) 1 - Hs 2 trình bày. - Hoàn chỉnh
(Sử dụng định lý 2)
- Mở rộng định lý 3 cho tích 3 Ghi chú:
hàm số (hướng dẫn học sinh
(uvw)’=u’vw+uv’w+uvw’ chứng minh) Tiết 2: 104
Giáo án Đại số 11 – Chương trình chuẩn
Hoạt động 3: Củng cố đạo hàm tích. Phiếu học tập 1: Cho hai hàm số:
- Phát phiếu học tập cho 6 nhóm 2 x
10’ Học sinh hoạt động học sinh f (x) = và 2 x + 2x + 2 nhóm và cử đại diện
- Cho các nhóm nhận xét chéo ( 2 x + ) 1 nhóm lên bảng trình - Hoàn chỉnh. g(x) = 2 bày. x + 2x + 2
Biết rằng hai hàm số này có đạo hàm
trên R. Chứng minh rằng với mọi xÎ R , ta có: f’(x)= - g’(x) Phiếu học tập 2:
- Tính đạo hàm của hàm số: f (x) 2 = x 1 ( - x)(x + ) 2 tại x= - 2 10’ HĐTP 3
- Gọi học sinh lên bảng.
+ Ví dụ 1: Tìm đạo hàm của hàm số:
- Học sinh lên bảng (áp - Học sinh nhận xét. 5x + 2 dụng định lý 3). - Chỉnh sửa. f (x) = , a là hằng số. x - 2a
+ Ví dụ 2: Viết phương trình tiếp
tuyến của đồ thị hàm số: Học sinh lên bảng :
- Gọi học sinh lên bảng. 1 + Tính y’(1). - Học sinh nhận xét. y = tại x=1 + Viết phương trình. - Chỉnh sửa. x x
Hoạt động 4: Củng cố đạo hàm thương: HĐTP 4
Phiếu học tập số 1.
Giáo viên phát phiếu học Cho hàm số: tập cho 6 nhóm. 2 x - mx +1 f (x) = với m là tham số. 2x -1 - Học sinh hoạt - Cho học sinh các nhóm 1
10’ động nhóm và cử nhận xét chéo.
Với giá trị nào của m thì f’(x)>0 với mọi x ¹ đại diện nhóm lên
- Chính xác hóa nội dung. 2 bảng trình bày. Phiếu học tập 2:
- Chọn kết quả đúng trong các kết quả cho sau đây: Đạo hàm của hàm số: 10’ 2 x - 3x +1 f (x) = 2x -1 3’ HĐTP 5 - Giáo viên giới thiệu Ghi nhớ:
bảng ghi nhớ (trang 203) a). Đạo hàm của một số hàm thường gặp (SGK - Xem bảng ghi
đã chuẩn bị sẵn trên tờ trang 203). nhớ. giấy khổ rộng.
b). Các quy tắc tính đạo hàm (SGK trang 203) Dặn dò(2’)
- Học sinh học thuộc các công thức
- Hướng dẫn về nhà làm các bài tập SGK trang 162 - 163 (bài 1 - 5)
- Học thuộc lòng các quy tắc tính đạo hàm đã học. - Làm bài tập SBT 105
Giáo án Đại số 11 – Chương trình chuẩn Tiết 68 BÀI TẬP. I.Mục tiêu :
* Về kiến thức :
- Các quy tắc tính đạo hàm (tổng, hiệu, tích, thương).
- Rèn luyện vận dụng các quy tắc tính đạo hàm .
- Củng cố cách viết phương trình tiếp tuyến với đồ thị hàm số tại 1 điểm cho trước.
* Về kỹ năng :
-Vận dụng các quy tắc tính đạo hàm.
-Viết được phương trình tiếp tuyến của đồ thị hàm số bất kỳ tại một điểm cho trước.
*Về tư duy- thái độ :
-Tập trung, tích cực, hợp tác.
II. Chuẩn bị của giáo viên và học sinh:
* Giáo viên : -Bảng phụ.- Phiếu học tập.
* Học sinh : -Làm trước bài tập. III/ Phương pháp :
- Nêu vấn đề, đàm thoại, hoạt động nhóm.
IV/ Tiến trình bài học :
1- Hoạt động 1: (Nêu vấn đề, đàm thoại) : Kiểm tra bài cũ.(7 phút)
- Nêu các quy tắc tính đạo hàm (tổng, hiệu, tích, thương).
- Tìm đạo hàm của hàm số: f (x) = ( 2 x + x)( 2 5 - 3x ) Tg Hoạt động của GV Hoạt động của HS Ghi bảng
Bài 2: Tìm đạo hàm của các hàm số sau: a) y = 5 3 2
f (x) = x - 4x + 2x - 3
- Gọi học sinh lên bảng - Đã chuẩn bị Bài tập 4 3 2 giải. ở nhà. x 2x 4x b) y = f (x) = - + -1 4 3 5 c) y = 5 2
f (x) = 3x (8 - 3x ) - Theo dõi nhận xét và
- 03 học sinh lên bảng ĐA: sửa chữa. giải. a) y/ = 4 2
5x -12x + 4x 8x - Đánh giá. b) y/ = 3 2 x - 2x + 5 6 4 c) y/ = 63 - x +120x - Hướng dẫn học sinh - Chia lớp thành
Bài 3: Tìm đạo hàm của các hàm số sau: 7 2 3 thảo luận nhóm. nhóm 04 học sinh.
a) y = (x - 5x ) 3 - 5x d) y = - Tổ 1: 3a) 2 x - x +1 - Tổ 2: 3d) 3 æ n
- Gọi học sinh lên bảng - Tổ 3: 3e) ö e) y = m + ç 2 ÷ giải. - Tổ 4: 4a) è x ø ĐA: a) / 5 5 2 5
y = 3x (x - 5) (7x -10) 106
Giáo án Đại số 11 – Chương trình chuẩn - Theo dõi nhận xét và 2 5x - 6x - 2 sửa chữa. d) y/ = (x - x+ )2 2 * Cử đại diện nhóm 1 - Đánh giá. lên bảng trình bày. 2 6n æ n ö e) / y = - m + 3 ç 2 ÷ x è x ø - Chia lớp thành
Bài 4: Tìm đạo hàm của các hàm số sau: nhóm 04 học sinh. a) 2
y = x - x x +1 b) - Theo dõi học thảo - Tổ 1,2: 4b) c) luận. - Tổ 3, 4: 4c) d) Giải: 3 / * Cử đại diện nhóm a) y = 2x - x 2 - Nhận xét bài làm của lên bảng trình bày. 2 - x - 5 HS. 4b) 4c) b) / y = 2 - Dưới lớp vừa theo 2 2 - 5x - x dõi 4b) 4c) và thảo 2 2 2
x (3a - 2x ) / = luận câu 4d) c) y (a - x )3 2 3 3 - x / d) y = 3 2 (1- x) CH: Nêu phương pháp Bài tập thêm: giải bài 1a)
1) Tính đạo hàm của hàm số sau : x - 2 a) y = 2
b) Bài 2.1 - 2.11/ trang 197 SBT *Củng cố:
- Các quy tắc tính đạo hàm (tổng, hiệu, tích, thương).
- Thông qua các câu hỏi trắc nghiệm ở phiếu học tập:
Câu 1: Hàm số y = x3 + x có đạo hàm bằng : 1 - 2 1 2 1 1 1 a. 3x + b. 4 2 x + x c. 3x + d. 3 2 x + 2x x 4 2 x 2
Câu 2: Hàm số y = x3 +2x2 có đạo hàm tại x0 = 1 là : a.3 b.6 c.-7 d.7 3 5
Câu 3: Hàm số y = x - x2 + 2x .Các giá trị x để y’> 0 là : 2 a.-1< x <2/3 b.x >1 c.x <2/3 d.2/3 < x <1 107
Giáo án Đại số 11 – Chương trình chuẩn
Tiết 69,70 ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC I. MỤC TIÊU: *Về kiến thức:
- Hiểu và nắm được các công thức tính đạo hàm các hàm số lượng giác. *Về kỹ năng:
- Áp dụng thành thạo các quy tắc tính đạo hàm để tính đạo hàm các hàm số lượng giác. sin x
- Áp dụng công thức Lim
= 1 để tính các giới hạn liên quan đến hàm số lượng giác. x®0 x *Về tư duy thái độ:
+ Biết quy lạ về quen, biết khái quát hoá và ứng dụng giải các bài toán liên quan.
+ Tích cực hoạt động, có tiinh thần hợp tác. II. CHUẨN BỊ .
* Giáo viên:Phiếu học tập, giáo án, bảng phụ.
* Học sinh : Nắm được định nghĩa đạo hàm, các quy tắc tính đạo hàm.
III.PHƯƠNG PHÁP: Chủ yếu gợi mở - Vấn đáp – Đan xen hoạt động nhóm. IV.TIẾN TRÌNH BÀI HỌC .
Tiết 1: HĐ1: Kiểm tra bài cũ: TG Hoạt động của trò Hoạt động của thầy Ghi bảng
-Nghe hiểu và thực hiện nhiệm
HĐTP1: Nêu các bước tính đạo - Ghi lại 2 bước tính vụ. hàm bằng định nghĩa? đạo hàm bằng địmh
-Nhận xét câu trả lời của bạn và - Yêu cầu các học sinh khác nhận nghĩa. bổ sung (nếu cần). xét.
-Nghe hiểu và thực hiện.
HĐTP2: Nêu các quy tắc tính đạo hàm?
10’ -Nhận xét câu trả lời của bạn và -Yêu cầu các học sinh khác nhận bổ sung ( nếu cần). xét.
-Nghe hiểu và thực hiện.
HĐTP3: Biến đổi thành tích biểu thức sau: Sin(x + D x) – Sinx
-Nhận xét kết quả và bổ sung
-Yêu cầu các học sinh khác nhận
-Lời giải của học sinh (nếu cần). xét.
đã được bổ sung nếu có.
2.HĐ2:Chiếm lĩnh kiến thức mới (ĐL1). TG Hoạt động của trò Hoạt động của thầy Ghi bảng sinx lim t anx =1 x®0 lim x = 1 x®0 x
-Phát biểu điều nhận xét được HĐTP1: Học sinh xem bảng giá trị sin x
trong SGK trang 163 và nêu nhận 1.Giới hạn của . x sin x a.ĐL1:(SGK trang 164) xét giá trị của khi x càng nhỏ x (dần về 0). b.Chú ý: 108
Giáo án Đại số 11 – Chương trình chuẩn sinx lim t anx =1 x®0 lim x = 1 x®0 x
HĐTP2: Xem các ví dụ trong SGK c.Các ví dụ: (SGK trang
10’ -Giải thích kết quả
trang 163 và giải thích kết quả. 164) -Gv bổ sung.
-Nghe hiểu và thực hiện HĐTP3: Tìm Lim( . x cot x) x®0
-Nhận xét và bổ sung (nếu
-Yêu cầu các học sinh khác nhận xét -Nội dung bài giải được có).
-Chỉnh sửa nội dung bài giải. chỉnh sửa. 1 sin *Chú ý : Không áp dụng x -Nhận xét của học sinh HĐTP4: Nhận xét Lim ? x®0
được ĐL1 đối với giới 1 x 1 sin
-Chỉnh sửa lời nhận xét của học sinh hạn: x Lim . x®0 1 x
3.HĐ3: Chiếm lĩnh kiến thức mới (ĐL2) TG Hoạt động của trò Hoạt động của thầy Ghi bảng
-Nghe, hiểu và thực hiện
HĐTP1: Tính đạo hàm của hàm số
2. Đạo hàm của hàm số
y = sinx bằng định nghĩa? y = sinx.
- Biến đổi D y thành tích.
-Sử dụng kết quả ở bài cũ. y D
-Dùng ĐL1 để tính Lim . x D ®0 x D
-HS trình bày kết quả của đạo -Chỉnh sửa bổ sung nếu có. a. ĐL2: (SGK trang 164) hàm.
-Tìm đạo hàm của hàm số (sinx)/ = cosx
y = sin[u(x)], ( u(x) là hàm số theo
-HS trình bày kết quả của đạo x). * Chú ý: 10’ hàm.
-Chính xác hoá và đưa ra ĐL2. (sinu)/ = u/.cosu -Xem ĐL2 SGK.
-Cả lớp cùng thực hiện. HĐTP2:Tính đạo b.Ví dụ: Tính đạo
-Một HS trình bày lời giải. hàm:y=sin( 4 2 x - x - 2 ). hàm:y=sin( 4 2 x - x - 2 ).
-Nhận xét và bổ sung nếu có.
-Yêu cầu HS khác nhận xét.
-Chính xác hóa nội dung bài giải. -Nội dung bài giải đã
-Hướng dẫn HS về tính đạo hàm được chỉnh sửa.
của hám số: y=sin x .
4.HĐ4:Chiếm lĩnh kiến thức mới (ĐL3). TG Hoạt động của trò Hoạt động của thầy Ghi bảng
* Thực hiện hoạt động 2/
HĐTP1: Xây dựng đạo hàm hàm số 3. Đạo hàm của hàm số SGK tr 165 y= cosx từ ĐL2. y = cosx.
-Gợi ý: Đưa cos về sin và dùng -Nghe và thực hiện. ĐL2. a.ĐL3(SGK trang 165)
-Chính xác hoá và đưa ra ĐL3. (cosx)/ = - sinx -HS nêu kết quả. *Chú ý: (cosu)/ = -u/.sinu 10’ 109
Giáo án Đại số 11 – Chương trình chuẩn -Nghe và thực hiện.
HĐTP2: Tinh đạo hàm của hàm số b.VD1: Tính đạo hàm y= cos2 2x . y= cos2 2x . -HS trình bày lời giải. -Gợi ý: Đặt u=cos2x.
-Các HS còn lại nhận xét và bổ sung (nếu có).
-Chính xác hoá lời giải -Nội dung bài giải. -Nghe và thực hiện.
HĐTP3: Tính đạo hàm của hàm số c.VD2: Tính đạo hàm x +1 x +1 -Hs trình bày bài giải. y= cos . hàm số y = cos . x x
-Các HS khác nhận xét và bổ sung (nếu có).
-Chính xác hoá nội dung bài giải. -Nội dung bài giải đã được chỉnh sửa. 5.Củng cố: (5’)
Câu hỏi1: Em hãy cho biết tiết học này có những nội dung chính nào? p
Câu hỏi2:Cho hàm số y = sin(cosx). Giá trị của y’(- ) là: 4 2 2 2 2 2 2 2 2 A. - Cos . B. Cos . C. - Sin . D. Sin . 2 2 2 2 2 2 2 2
TIẾT 2: 1.HĐ1:Kiểm tra bài cũ. TG Hoạt động của trò Hoạt động của thầy Ghi bảng
HĐTP:Tính đạo hàm của hàm số: y
* Thực hiện hoạt động 3/ SGK sin x tr166 = . cos x -Gợi ý: 5’ -HS trình bày lời giải. -Nội dung bài giải đã u
-Các HS khác nhận xét và bổ Dùng quy tắc đạo hàm . được chỉnh sửa. v sung (nếu có). -Chính xác hoá nội dung.
-HS tìm công thức đạo hàm
-HS kết luận công thức đạo y = tanx. hàm của y = tanx.
-Chính xác hoá và vào bài mới.
2.HĐ2:Chiếm lĩnh kiến thức mới(ĐL4). TG Hoạt động của trò Hoạt động của thầy Ghi bảng ( / x ( u tan)/ 1 tan =/ u) = 2 os c x 2 os c u
4. Đạo hàm của hàm số y = tanx. a. ĐL4:(SGK trang 166). -Nghe và thực hiện. HĐTP1:HS xem ĐL4 SGK trang
- Ghi nhớ Công thức tính đạo 166. hàm tan * Chú ý:
HĐTP2: Áp dụng các công thức đạo b.Ví dụ:Tính đạo hàm của
hàm tính đạo hàm của hàm số
hàm sốy= 1+ 2 tan x
10’ -Nghe và thực hiện. y= 1+ 2 tan x -HS trình bày lời giải.
-Gợi ý: Dùng đạo hàm u và đạo
-Các HS khác nhận xét và bổ sung (nếu có). hàm của tanx.
-Chính xác hoá nội dung bài giải
-Nội dung bài giải đã được chỉnh sửa.
3.HĐ3:Chiếm lĩnh kiến thức mới: (ĐL5) 110
Giáo án Đại số 11 – Chương trình chuẩn TG Hoạt động của trò Hoạt động của thầy Ghi bảng ( x)/ 1 cot = - / / u cot u = - 2 ( ) sin2 x sin u
* Thực hiện hoạt động 4/
HĐTP1:Tương tự như đạo hàm y = 5. Đạo hàm của hàm SGK tr167.
tanx, hãy tìm đạo hàm của hàm số y = cotx. y= cotx. a. ĐL5: (SGK trang 167)
-HS nêu cách giải và kết quả.
-Hỏi xem còn cách nào khác -HS trả lời (nếu có). không? * Chú ý: 7’ -Xem ĐL5 SGK trang 210.
-Chính xác hoá và nêu ĐL5. -Nghe và thực hiện.
HĐTP2: Tính đạo hàm của hàm số
b.Ví dụ:Tính đạo hàm của y=Cot( x x )
hàm số y=Cot( x x ).
-Các HS còn lại nhận xét và
-Một HS lên bảng trình bày. bổ sung (nếu có). -Chính xác hoá -Nội dung bài giải đã được chỉnh sửa.
4.HĐ4: Câu hỏi và bài tập. TG Hoạt động của trò Hoạt động của thầy Ghi bảng
HĐTP1:Củng cố kiến thức. Bài1) Tính đạo hàm các -Nghe và thực hiện. -Chia lớp thành 6 nhóm: hàm số sau:
Nhóm 1,2 làm bài 1;nhóm 3, 4 làm 1.y = 2sin3x.cos5x.
bài 2; nhóm 5, 6 làm bài 3. sin x + cos x 11’
-Đại diện nhóm lên trình bày. 2.y = sin x - cos x
-HS các nhóm khác nhận xét
-Cho HS nhóm khác nhận xét. 3.y = tan3x + cot2x. và bổ sung .
-Nhận xét và chính xác hoá nội - Dùng bảng phụ. dung các bài giải. HĐTP2: Bài2)CMR hàm số
-Gợi ý:Biến đổi đưa được y là hàm y=sin6x+cos6x+3sin2xcos2x -Nghe và thực hiện. hằng. có đạo hàm bằng 0. 4’ -Trình bày lời giải.
-Các HS còn lại nhận xét và
-Chính xác hoá nội dung bài giải bổ sung .
-Nội dung bài giải đã được chỉnh sửa .
5.Củng cố toàn bài : (3’)
Bảng đạo hàm tr 168 SGK. / u
( Un)/ = n.un-1.u/ ( u )/ = 2 u / u / u - (Tanu)/ = (cotu)/ = 2 cos u 2 sin u
Câu hỏi 1) Em hãy cho biết bài học này có những nội dung chính nào?
Câu hỏi 2) Bài tập về nhà: x.sin x
Bài1) Tính đạo hàm của các hàm số sau: a. y= . b. y=Cot 3 2 1+ x . 1+ tan x Tiết 71
LUYỆN TẬP ĐẠO HÀM CÁC HÀM SỐ LƯỢNG GIÁC. I. MỤC TIÊU: • Về kiến thức:
- Hiểu được mạch kiến thức cơ bản trong bài đạo hàm các hàm số lượng giác.
- Hiểu và vận dụng được các định lý trong bài. • Về kỹ năng:
- Vận dụng thành thạo các quy tắc tìm đạo hàm của các hàm số lượng giác.
- Củng cố kỹ năng vận dụng các công thức tìm đạo hàm của các hàm số thường gặp. 111
Giáo án Đại số 11 – Chương trình chuẩn • Về tư duy thái độ:
- Biết khái quát hoá, đặc biệt hoá, tương tự. Biết quy lạ về quen.
- Tích cực hoạt động, có tinh thần hợp tác. II. CHUẨN BỊ:
• Giáo viên:Phiếu học tập, giáo án, bảng phụ.
• Học sinh : Các công thức tính đạo hàm các hàm số lương giác.
III. PHƯƠNG PHÁP: Chủ yếu gợi mở - Vấn đáp – Đan xen hoạt động nhóm. IV.TIẾN TRÌNH BÀI DẠY: 1.H Đ1: Kiểm tra bài cũ: TG Hoạt động của trò Hoạt động của thầy Ghi bảng
HĐTP1: -Nêu các công thức đạo
hàm các hàm số lượng giác?
-Cho hàm số y = tan(sinx) . Tính y’(0). 5’
-Gọi một HS lên bảng trình bày. -Nội dung bài giải đã -Nghe và thực hiện.
-Chính xác hoá nội dung bài giải được chỉnh sửa
-HS cả lớp nhận xét và bổ sung (nếu có). 2.HĐ2:Luyện tập. TG Hoạt động của trò Hoạt động của thầy Ghi bảng
HĐTP1:Chia lớp thành 6 nhóm: Bài1) Tính đạo hàm các - Nhóm 1, 2 làm bài 1. hàm số sau: -Nghe và thực hiện. - Nhóm 3, 4 làm bài 2. sin 2 x - Nhóm 5, 6 làm bài 3. 1. y= . 1+ tan 2x
-Đại diện nhóm lên trình bày. sin x x
15’ -HS thực hiện yêu cầu.
-Cho HS các nhóm cón lại nhận 2. y= + . xét. x sin x
-HS các nhóm nhận xét và bổ
-Chính xác hoá nội dung bài
3. y= x sin 3x . sung (nếu có). giải . -Dùng bảng phụ. TG Hoạt động của trò Hoạt động của thầy Ghi bảng -Xem BT 2 SGK trang 168. HĐTP2:BT 5 SGK trang 169. Bài2) BT 2b SGK trang -Gợi ý:Tính f/(x); / j (x) 168.
-Gọi HS lên bảng trình bày. 5’
-Chính xác hoá nội dung bài -Nghe và thực hiện. giải.
-Các HS còn lại nhận xét và bổ
-Nội dung bài giải đã được sung (nếu có). chỉnh sửa . HĐTP3:BT 6a SGK trang 169 Bài3) BT 6a SGK trang 169 -Gợi ý: . + Tính y/ + CM y/ không chứa x
-Gọi một HS lên bảng trình bày. 6’
-Chính xác hoá nội dung bài giải . -Nghe và thực hiện.
-Các HS còn lại nhận xét và bổ
-Nội dung bài giải đã được sung .
chỉnh sửa hoặc dùng bảng phụ. 112
Giáo án Đại số 11 – Chương trình chuẩn HĐTP5: BT 7 SGK trang 169 Bài4) BT 7SGK trang 169 Gợi ý: -Nghe và thực hiện.
-Gợi ý:Giải phương trình: asinx + bcosx = c .
-Chia lớp thành hai nhóm theo
-GV trình bày bài giải theo 5’
hai dãy bàn, nhóm nào làm xong cách trình bày HS.
-Đại diện nhóm làm trước báo
sẽ trình bày bài giải trước. cáo kết quả.
-Có thể chỉnh sửa lại lời giải
-Nhóm còn lại nhận xét và bổ
-Gọi HS lên bảng trình bày. trên. sung .
-Chính xác hoá nội dung bài giải.
HĐTP6:HS lựa chọn đáp án Bài5) Cho hàm số:
-Trình bày lời giải và đáp án đúng. sin 2 x - cos2 x đúng.
-Chia lớp thành hai nhóm theo y= . Giá trị sin x cos x
-Nhóm còn lại nhận xét và bổ
hai dãy bàn, nhóm nào làm xong p 3’ sung (nếu có).
sẽ trình bày bài giải trước. của y’( ) là: 6 8 8 A. ; B. - . 3 3 16 16 C. ; D. - . 3 3 1’ -Xem BT 8 SGK trang 169
HĐTP7: Hướng dẫn BT 8 SGK trang 169. 3. Củng cố: (3’)
Câu hỏi) Em có nhận xét gì về phương pháp tính đạo hàm các hàm số lương giác và ứng dụng của đạo hàm. Lưu ý:
a. Về kiến thức :Nắm vững các công thức tính đạo hàm của các hàm số lượng giác.
b. Về kỹ năng: Kết hợp với các quy tắc tính đạo hàm đã biết để tính đạo hàm các hàm số lượng giác.
c. Về tư duy thái độ :Biết quy lạ về quen, tích cực tham gia học tập, có tinh thần hợp tác.
* Dặn dò: - Làm các BT còn lại SGK + BT 3.3 - 3.18 SBT trang 201 Tiết 72
KIỂM TRA GIỮA CHƯƠNG V I. MỤC TIÊU:
- Đánh giá khả năng tiếp nhận kiến thức về đạo hàm của HS
- Hiểu và thuộc công thức tính đạo hàm, vận dụng vào giải các bài toán thực tế II. ĐỀ
Câu 1: (2đ) Tìm đạo hàm của hàm số 1 y = 2 x 1 - Câu 2: (2đ) Cho hàm số 3 tan x y p = Tính y'( ) 2 6 3 2
Câu 3: (2đ) Cho hàm số f (x) = mx - mx + 3
( - m)x - 2 (m là tham số). 3 2 113
Giáo án Đại số 11 – Chương trình chuẩn
Tìm m để phương trình f '(x) = 0 có 2 nghiệm trái dấu. 2 Câu 4 (4đ) Cho hàm số x -x+ y =
a có đồ thị (Ca), a là tham số. x 1 -
a) Tìm a để đường thẳng y=3x - 2 tiếp xúc với Ca tại điểm có hoành độ x = 0
b) Tìm a để bất phương trìn Tiết 73 § 4 VI PHÂN. I) Mục tiêu:
1)Về kiến thức: Giúp học sinh
- Hiểu được định nghĩa vi phân.
- Nắm được công thức tính gần đúng nhờ vi phân.
2) Về kỹ năng: Giúp học sinh
- Hiểu cách tính vi phân của một số hàm số thường gặp.
- Hiểu được ứng dụng của vi phân trong tính gần đúng.
3) Về tư duy và thái độ:
- Tích cực tham gia vào bài học, có tinh thần hợp tác.
- Biết được toán học có ứng dụng trong thực tiễn. II) Chuẩn bị:
Giáo viên: Dụng cụ dạy học.
Học sinh: Kiến thức về đạo hàm.
III) Phương pháp: Gợi mở và vấn đáp thông qua các hoạt động.
IV) Tiến trình bài học: A) Kiểm tra bài cũ: p
CH1: Tính đạo hàm của hàm số y = f(x) = cosx tại x0 = 3
CH2: Tính đạo hàm của hàm số y = f(x) = x3- 4x+2
Hoạt động 1: Tiến trình kiểm tra bài cũ Tg Hoạt động HS Hoạt động GV Ghi bảng
CH1:Ta có: y' = - sin x p p
+ Nhớ lại công thức tính đạo
+ Giao nhiệm vụ: Nắm rõ quy Þ y '( ) =-sin( ) hàm
tắc, công thức tính đạo hàm để 3 3
+ Dự kiến trả lời câu hỏi
thực hiện hai câu hỏi trên = - 3 5’ + Nhận xét, cho điểm 2 CH2:Ta có: y' =( 3 x - 4x + )' 2 = 3x2- 4 B) Bài mới
Hoạt động 2: Vi phân của hàm số : 1) Hình thành kiến thức mới Thời Hoạt động HS Hoạt động GV Ghi bảng gian
HS xung phong trả lời câu hỏi
CH1: Nhắc lại công thức tính 1) Định nghĩa:
đạo hàm bằng định nghĩa Sgk trang 170 114
Giáo án Đại số 11 – Chương trình chuẩn
+ Nắm được công thức tính vi
+ Từ định nghĩa của đạo hàm
phân của hàm số y = f(x)
GV dẫn dắt tới công thức dy = df(x) = f/(x) x D y
D » f '(x ). x D 0 7’
+ Thấy được muốn làm tốt bài
+ Đưa ra khái niệm vi phân * Chú ý:
toán vi phân trước hết phải làm
của hàm số tại 1 điểm + y = x. Ta có: tốt bài toán đạo hàm
+ Chính xác hóa và đưa ra dx = d(x) = (x)/ x D = x D công thức trong Sgk + Do đó: dy = df(x) = f/(x) x D
Hoạt động 3: Củng cố vi phân của hàm số: T`g Hoạt động HS Hoạt động GV Ghi bảng
Nhắc lại về khái niệm vi phân của hàm số (Sgk trang 170 + Nghe, hiểu nhiệm vụ Giao nhiệm vụ:
Ví dụ: Tính vi phân của hàm số y + Trả lời câu hỏi
+ Tính vi phân của hàm số = f(x) = x3 - 4x + 2
+ Nhận xét câu trả lời của y = f(x) = x3 - 4x + 2 bạn
+ Gọi 1 HS đứng tại chỗ LG: trả lời
df (x) = (x3 - 4x + )' 2 dx 18’ = 3 ( x2 - ) 4 dx Ví dụ: BT 1 SGK tr 171
2) Mở rộng kiến thức: Thời Hoạt động HS Hoạt động GV Ghi bảng gian + Nghe, hiểu nhiệm vụ Giao nhiệm vụ:
VD: Tính vi phân của hàm số y
+ Đưa vào công thức để đưa ra + Tính vi phân của hàm số p kết quả nhanh nhất = f(x) = cosx tại x p = 0 3 y = cosx tại điểm x0 = 3 LGiải:
+ Gọi HS1 đứng tại chỗ trả 5’ p p 3 lời
df ( ) = - sin( ). x D = - . x D 3 3 2
+ Thấy rõ được rằng df(x0)
CH: Cho nhận xét về kết quả
không phải là một số không p đổi
của df ( ); df (x ) 3 0
+ Khi cố định df(x0) là một đại
lượng phụ thuộc tuyến tính vào x D
Hoạt động 4: Ứng dụng của vi phân vào phép tính gần đúng:
1) Tiếp cận kiến thức Tg Hoạt động HS Hoạt động GV Ghi bảng
+ Củng cố phần 1, đưa ra công thức Giao nhiệm vụ: y
D » f '(x ). x D
+ Từ phần một ta đã có công 0
+ Nhớ lại công thức tính số gia thức gì? 5’ y D của hàm số
+ Nhắc lại công thức tính số gia y D
+ Rút ra được điều gì? 115
Giáo án Đại số 11 – Chương trình chuẩn
2) Hình thành kiến thức mới Tg Hoạt động HS Hoạt động GV Ghi bảng Nắm công thức
Chính xác hóa và đưa ra công 2) Ứng dụng của vi phân vào tính gần thức đúng + Ta có y
D » f '(x ). x D (1) 0 3’ + Mà y D = f(x0+ x D ) - f(x0) (2) Từ (1) và (2) ta có: f(x0+ x
D ) = f(x0) + f '(x ). x D 0 (*)
3) Củng cố kiến thức Tg Hoạt động HS Hoạt động GV Ghi bảng + Nghe, hiểu nhiệm vụ Giao nhiệm vụ:
Vdụ: Cho hàm số y = f (x) = x . + Xung phong lên bảng + Cho hàm số
a) Tính: f(4) và f '( ) 4 + Cả lớp nhận xét
y = f (x) = x . Tính: f(4) và f '( ) 4 LG
+ Cho HS xung phong và gọi + Ta có: f ( ) 4 = 4 = 2 HS2 lên bảng 1 1 1
+ Nhận xét lời giải của HS f '(x) = Þ f '( ) 4 = = 2 x 2 4 4 Nghe, hiểu nhiệm vụ Giao nhiệm vụ: b) Tính f(4.01) + Tính f(4.01) C1: Dùng máy tính + Cho cả lớp tự làm f ( ) 01 . 4 = 01 . 4 » 0024 . 2 + Áp dụng công thức (*)
+ Không dùng máy tính, áp
C2: Áp dụng công thức (*) 12’ để tính 01 . 4
theo sự gợi dụng công thức (*) các em
Do 4.01=4+0.01 nên ta xét hàm số ý của GV tính 01 . 4 ?
y = f (x) = x tại x0 = 4 và số gia
+ GV gợi ý cho HS sử dụng x D = 0.01 + Cho ra kết quả câu a Ta có:
+ Gọi HS3 đứng tại chỗ trình f (4 + ) 01 . 0 » f ( ) 4 + f '( ) 4 * 01 . 0 bày lời giải 1
+ So sánh kết quả ở hai cách Û 01 . 4 » 2 + * 01 . 0 » 0025 . 2 + Đưa ra nhận xét
+ GV chốt lại: dùng công thức 4
(*) kết quả chính xác hơn
Nghe, hiểu và trả lời theo
CH: Qua ví dụ trên, còn cách
Chọn f (x) = 4 + x ; x0 = 0; yêu cầu của GV
nào khác để chọn f(x), x0, Dx = 01 . 0 và lời giải x D ?
+ Có nhiều cách chọn f(x), x0, x D nhưng cần chọn sao cho
f(x0), f '(x ) dễ tính nhất. 0 * Củng cố: dy = f/(x) .dx f(x + x
D ) » f(x ) + f/( x ). x D 0 0 0
Hoạt động 5: Bài tập về nhà
Làm bài tập 1, 2 trang 171-Sgk 116
Giáo án Đại số 11 – Chương trình chuẩn Tiết 74 ĐẠO HÀM CẤP HAI. I.Mục tiêu : *Về kiến thức :
-Giúp hs nắm được khái niệm đạo hàm cấp hai, cách tính đạo hàm cấp hai bằng định nghĩa .
-Hiểu được ý nghĩa cơ học của đạo hàm cấp hai, cách tính gia tốc của một chuyển động bằng đạo hàm
cấp hai của quãng đường đi của nó.
-Nắm được khái niệm đạo hàm cấp n của một hàm số.
*Về kĩ năng : Tính đạo hàm cấp hai trở lên của một hàm số. *Về tư duy, thái độ :
-Rèn luyện cho hs tính suy nghĩ chính xác, tư duy logic. -Cẩn thận ,chính xác. II.Chuẩn bị : - GV : Phiếu học tập.
- HS : Nắm vững các công thức tính đạo hàm và đạo hàm của các hàm số đặc biệt.
III.Phương pháp : Nêu vấn đề ,gợi mở, vấn đáp.
IV.Tiến trình bài dạy :
1.Kiểm tra bài cũ : (5’)
Hoạt động 1: Cho hàm số y = x3 – 2x2 +5x –1 a.Tính y’
b.Tính đạo hàm của y’. Tg HĐ của HS HĐ của GV Ghi bảng Hs lên bảng giải bài
HĐTP1: Thông qua kiểm tra bài
I.Định nghĩa(Đạo hàm cấphai) tập. f’’=(f’)’
cũ,GV giúp HS tiếp cậnkhái Đn : (sgk)
niệm đạo hàm cấp hai của hàm số. Hs trả lời CH1.
CH1: yêu cầu hs rút ra định nghĩa đạo hàm cấp hai. Hs làm vd1,vd2.
HĐTP2: GV củng cố lại định
Vd1.Tính y’’ của các hàm số sau : 15’ nghĩa. a.y = x4 + 3x2 –1
GV nhận xét, sửa chữa (nếu cần). b.y = sin2x p Vd2.Cho hàm số
GV : y’’ ( ) được gọi là đạo y = cotx 3
hàm cấp hai của hàm số y = cotx a.Tính y’’. p p tại x = . b.Tính y’’ ( ) . 3 3
Hoạt động 2 : Chú ý khái niệm đạo hàm cấp cao: Tg HĐ của HS Hđ Của GV Ghi bảng / (n) (n 1 - ) f (x) = é f (x)ù ë û H s theo dõi Gv lập luận
* Chú ý: (Đạo hàm cấp cao)
(y’)’= y’’: đạo hàm cấp hai
(y’’)’= y’’’: đạo hàm cấp 3 12’
Suy ra đạo hàm cấp ncủa hs. Nêu định nghĩa đạo
Gv :yêu cầu hs rút ra đnđạo hàm Vd4 :a.Cho hàm số hàm cấp cao. cấp cao của hàm số?
a.y = x3 + 3x +1 .Tính y(3), y(n). Gv lấy vd minh hoạ b.Cho y = sinx
Nhận xét hàm đa thức bậc n thì b1)Tínhy’, y’’, y(3).
đạo hàm cấp n + 1 bằng 0. p n Hs làm vd4 Hs giải câu i) b2)y(n) = sin(x + ) đúng hay 2 Từ i) Þ ii) sai? 117
Giáo án Đại số 11 – Chương trình chuẩn
Hoạt động 3: Ý nghĩa cơ học của đạo hàm cấp hai của hàm số. Tg HĐ của HS HĐ của Gv Ghi bảng
10’ Hs nhắc lại đạo hàm y’ CH1: Nhắc lại ý nghĩa cơ học
II. Ý nghĩa cơ học của đạo hàm cấp
của một chuyển động là của đạo hàm? hai :
vận tốc tức thời tại thời Gv nêu ý nghĩa cơ học của đạo 1. Đn: (sgk) điểm t0.
hàm cấp hai của một phương 2.Vd:
1) PT chuyển động của một vật: s(t) = Asin(wt +j ) (A, w;j là hằng số ) Khi đó
gọi v(t) là vận tốc tức thời thì PT v(t) = Hs trình bày ví dụ. [s(t)]/ v(t) = Aw cos(wt +j )
gọi a(t) là vận tốc tức thời thì PT a(t) =
Trình chuyển động của chất điểm tại t [v(t)]/ 0 là gia tốc tức thời 2 tại điểm đó. a(t) = -Aw sin(wt +j ) p
2)Phương trình của một chuyển động
Qua vd2, ta thấy y’’ ( ) chính của một chất điểm là 3
là gia tốc tức thời của chuyển
S(t) = 5t – 3t2 (s tính bằng m; t tính
động có phương trình y = cotx bằng giây).Tính gia tốc của chuyển
động tại thời điểm t = 4s. p tại x = . 3
V.Củng cố,dặn dò : (3’)Yêu cầu HS:
- Nhắc lại khái niệm đạo hàm cấp hai, ý nghĩa đạo hàm cấp hai, đạo hàm cấp n
- Làm các bài tập 1, 2 trang 174 SGK. 118




