Giao thoa ánh sáng | Bài giảng môn Vật lý đại cương 3 | Trường Đại học Bách Khoa Hà Nội
Giao thoa ánh sáng | Bài giảng môn Vật lý đại cương 3 | Trường Đại học Bách Khoa Hà Nội. Tài liệu gồm 21 trang giúp bạn tham khảo ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem.
Preview text:
Bμi gi¶ng VËt lý ®¹i c−¬ng
T¸c gi¶: PGS. TS §ç Ngäc UÊn ViÖn VËt lý kü thuËt
Tr−êng §H B¸ch khoa Hμ néi VËt lý ®¹i c−¬ng Quang häc sãng Ch−¬ng 3 Giao thoa ¸nh s¸ng 1. C¸c kh¸i niÖm c¬ së
1.1 Quang lé: Quang lé L gi÷a hai
®iÓm A, B (AB=d) lμ ®o¹n ®−êng ¸nh s¸ng
truyÒn ®−îc trong ch©n kh«ng trong
kho¶ng thêi gian t, trong ®ã t lμ kho¶ng
thêi gian mμ ¸nh s¸ng ®i ®−îc ®o¹n AB trong m«i tr−êng. A d B = d t ⇒ L = ct L= nd. v c n = chiÕt suÊt m«i tr−êng v n d 2 2 NÕu ¸nh s¸ng ®i qua n d n d 1 1 3 3 nhiÒu m«i tr−êng: L=n d +n d +...+n d = ∑n d 1 1 2 2 n n i i i
1.2. §Þnh lý Malus (Maluýt):
Quang lé gi÷a hai mÆt trùc giao cña mét
chïm s¸ng th× b»ng nhau hai mÆt trùc giao hai mÆt trùc giao
Quang lé L gi÷a A ,A vμ L gi÷a B ,B : 1 1 3 2 1 3 L = n A I +n I A +n A A B1 1 1 1 1 2 1 2 2 2 3 B L = n B B +n B I +n I B 2 2 1 1 2 1 2 2 2 2 3 A1 i1 i n n sini = n sini 1 1 I I 2 1 1 2 2 1 i A 2 I A 2 1 2 i n B I 2 2 B 2 2 sini = 3 sini = 1 2 A I I 3 I I 1 2 1 2 n B I n I A 1 2 2 n sini = 2 1 2 n sini = 1 1 2 2 I I I I 1 2 1 2 Suy ra n B I = n I A vμ L =L 1 2 2 2 1 2 1 2
2. C¬ së cña quang häc sãng
2.1. Hμm sãng cña ¸nh s¸ng:
¸nh s¸ng lμ mét lo¹i sãng ®iÖn tõ: Tõ
tr−êng vμ ®iÖn tr−êng biÕn thiªn trong kh«ng gian. rE rv rH
ChØ cã thμnh phÇn ®iÖn tr−êng t¸c dông
vμo m¾t míi g©y c¶m gi¸c s¸ng r
→ Dao ®éng cña E lμ dao ®éng s¸ng: r 2πL O x = a cos( t ω − ) λ
x = a.cosωt -dao ®éng t¹i gèc O. 0 T¹i r:(τ thêi gian trÔ) x= acos ω(t -τ) = 2π L 2πL a cos( t ω − ) = a cos( t ω − ) T c λ 2. 2. c−êng ®é s¸ng:
C−êng ®é s¸ng t¹i mét ®iÓm lμ mét ®¹i l−îng cã
trÞ sè b»ng n¨ng l−îng truyÒn qua mét ®¬n vÞ
diÖn tÝch ®Æt vu«ng gãc víi ph−¬ng truyÒn s¸ng
trong mét ®¬n vÞ thêi gian:
I = ka2, k lμ hÖ sè tû lÖ. LÊy k = 1 cã: I = a2. 2.3. Nguyªn lý chång chÊt:
Khi hai hay nhiÒu ¸nh s¸ng gÆp nhau th× tõng
sãng riªng biÖt kh«ng bÞ c¸c sãng kh¸c lμm
nhiÔu lo¹n. Sau khi gÆp nhau, c¸c sãng ¸nh s¸ng
vÉn truyÒn ®i nh− cò, Cßn t¹i nh÷ng ®iÓm gÆp
nhau dao ®éng s¸ng b»ng tæng c¸c dao ®éng thμnh phÇn. 2.4. Nguyªn lý Huyghen:
Nh÷ng sãng tõ nguån O truyÒn ra ngoμi mÆt kÝn
bÊt k× S bao quang nguån O, cã tÝnh chÊt gièng
hÖt nh÷ng sãng mμ ta sÏ cã, nÕu ta bá nguån O
®i vμ thay b»ng nh÷ng nguån phô (thø cÊp) thÝch hîp ph©n phèi trªn mÆt S.
3. Giao thoa ¸nh s¸ng bëi 2 nguån kÕt hîp
3.1. T¹o hai nguån s¸ng kÕt hîp: Hai
sãng kÕt hîp cã hiÖu pha kh«ng ®æi.
Hai nguån s¸ng kh¸c nhau kh«ng ®¸p øng ®iÒu kiÖn ®ã. khe Young hay g−¬ng Frenen: S r1 r y 2 O D 1 l O1 O2 O2 O O lμ 2 nguån 1 2 O O lμ 2 nguån kÕt hîp 1 2 kÕt hîp (thø cÊp) (¶o)
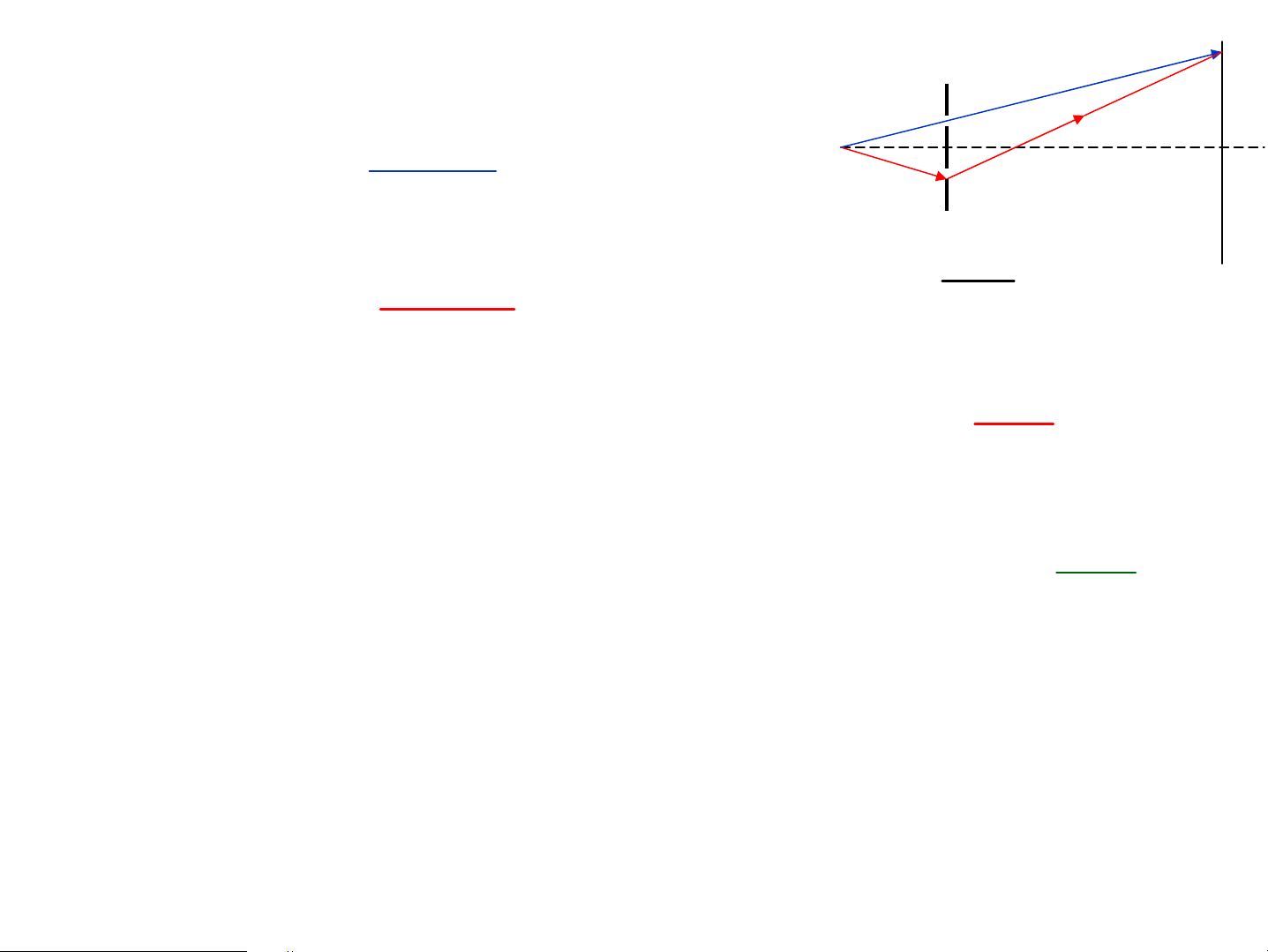
3.2. Kh¶o s¸t hiÖn t−îng giao thoa: r1 y 2πL r2 O D 1 x = a cos( t 1 ω − ) l 1 λ O2 HiÖu pha 2π 2πL Δϕ = (L − L x = ) a cos( t 2 ω − ) 1 2 2 λ λλD y = k L -L =r -r =kλ V©n s¸ng 1 2 1 2 l L -L =r -r =(2k+1)λ/2 1 2 1 2 λD y = (2k + 1) V©n tèi 2l
Kho¶ng c¸ch 2 v©n s¸ng liªn tiÕp i= λD/l
C¸c v©n giao thoa cã d¹ng hypecbol ®èi xøng qua v©n gi÷a. V©n gi÷a lμ v©n s¸ng
• Giao thoa ¸nh s¸ng tr¾ng 0,4μm ≤ λ ≤ 0,76μm
3.3. HiÖn t−îng giao thoa do ph¶n x¹
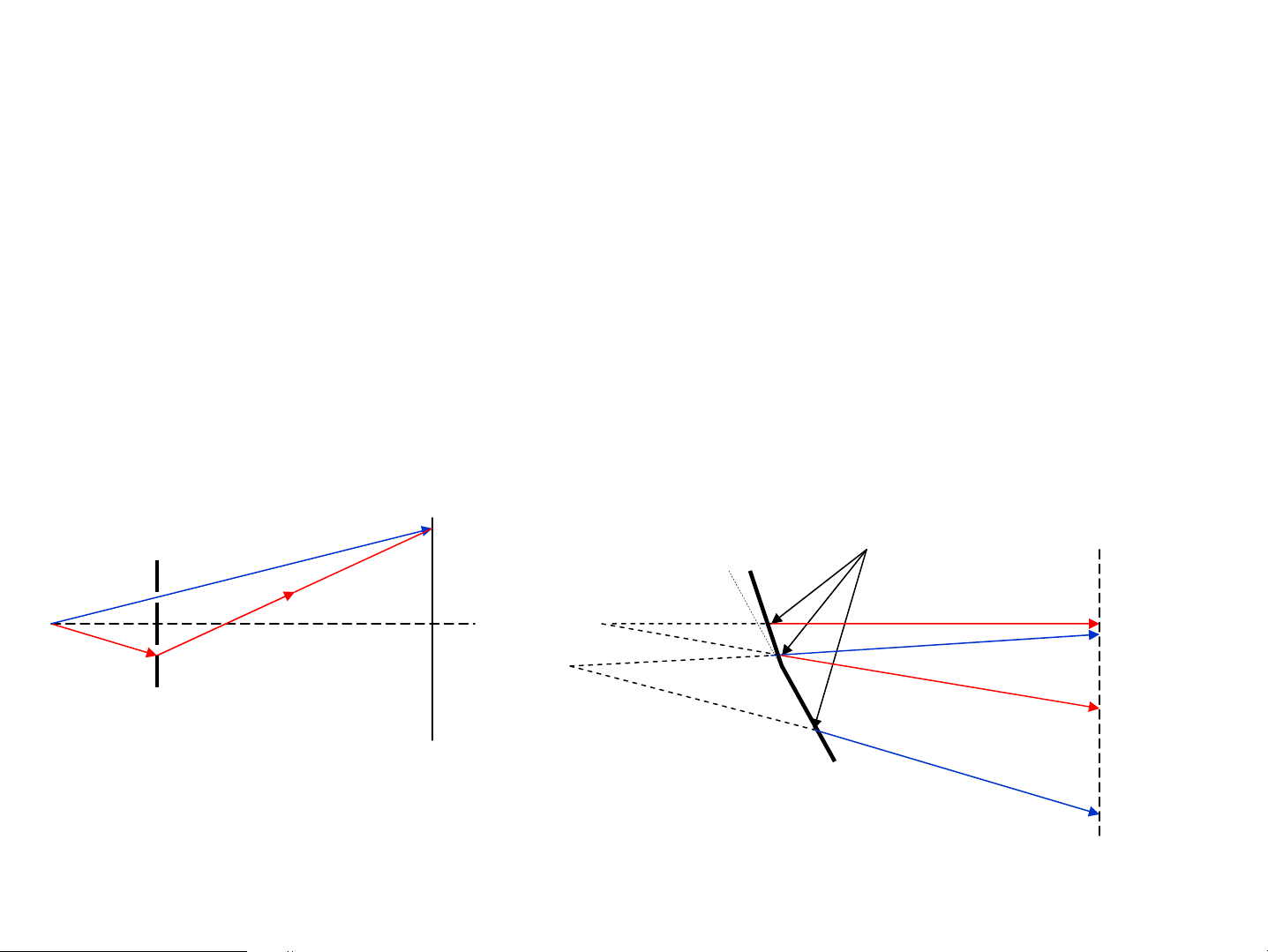
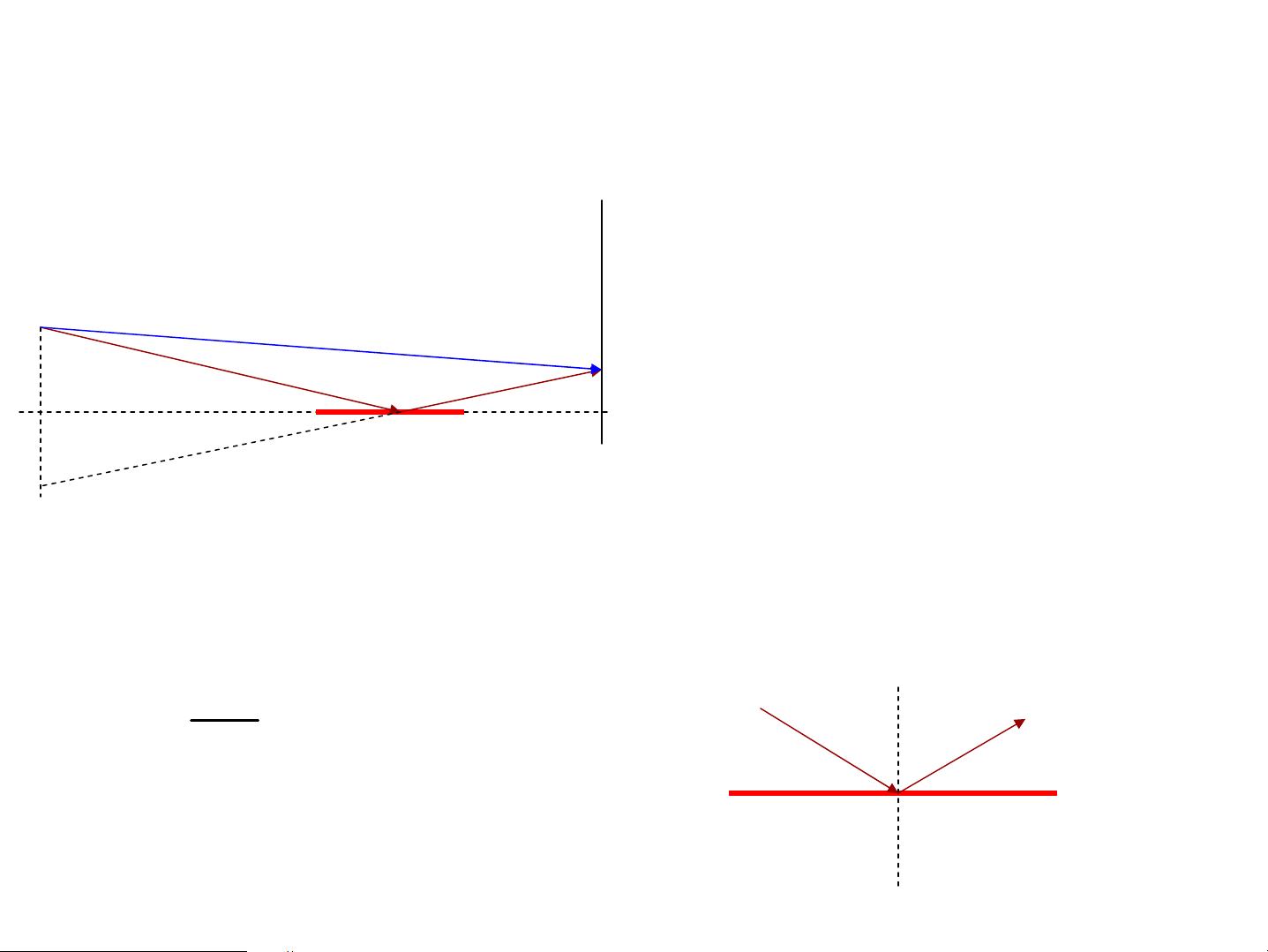
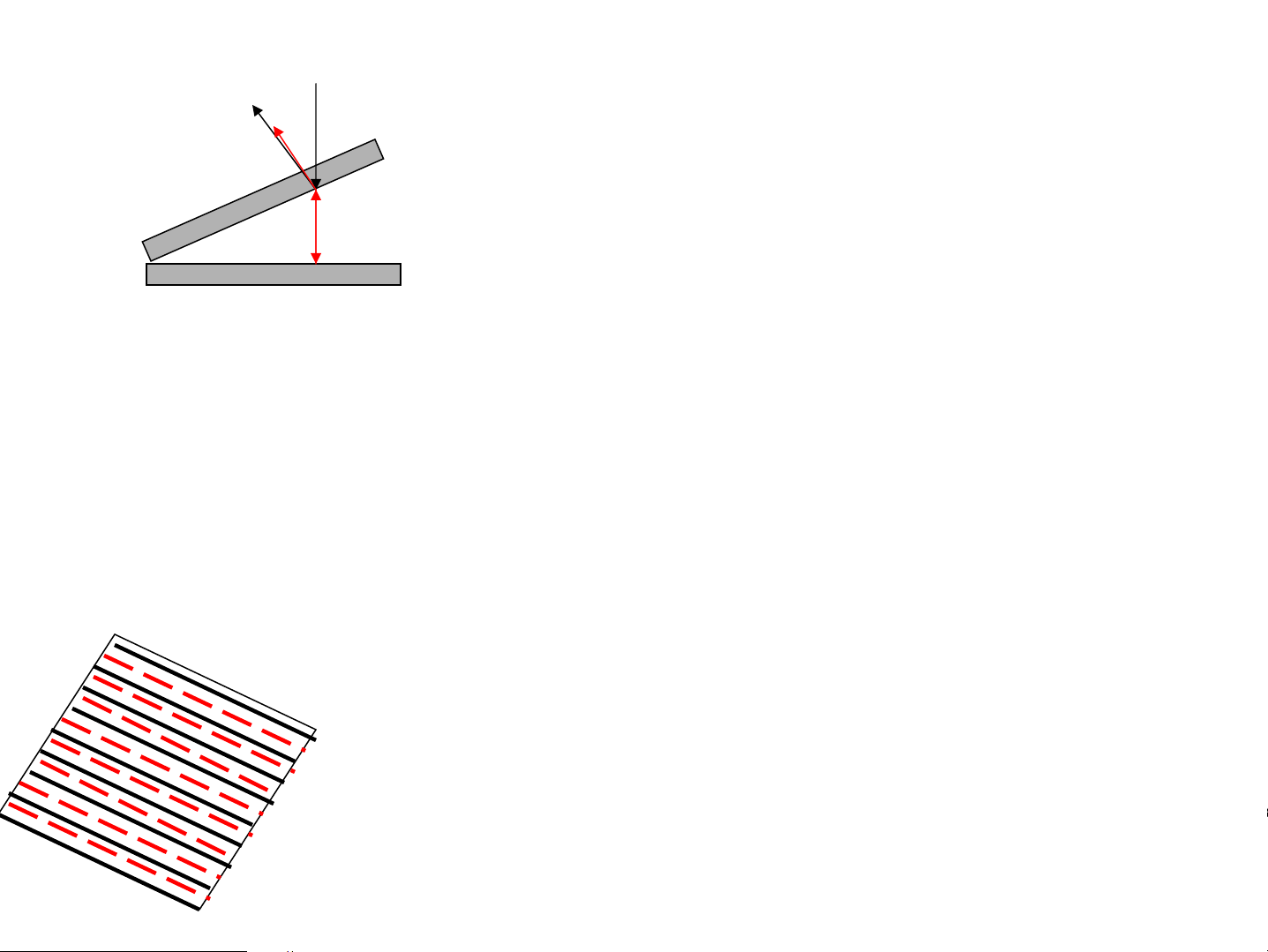
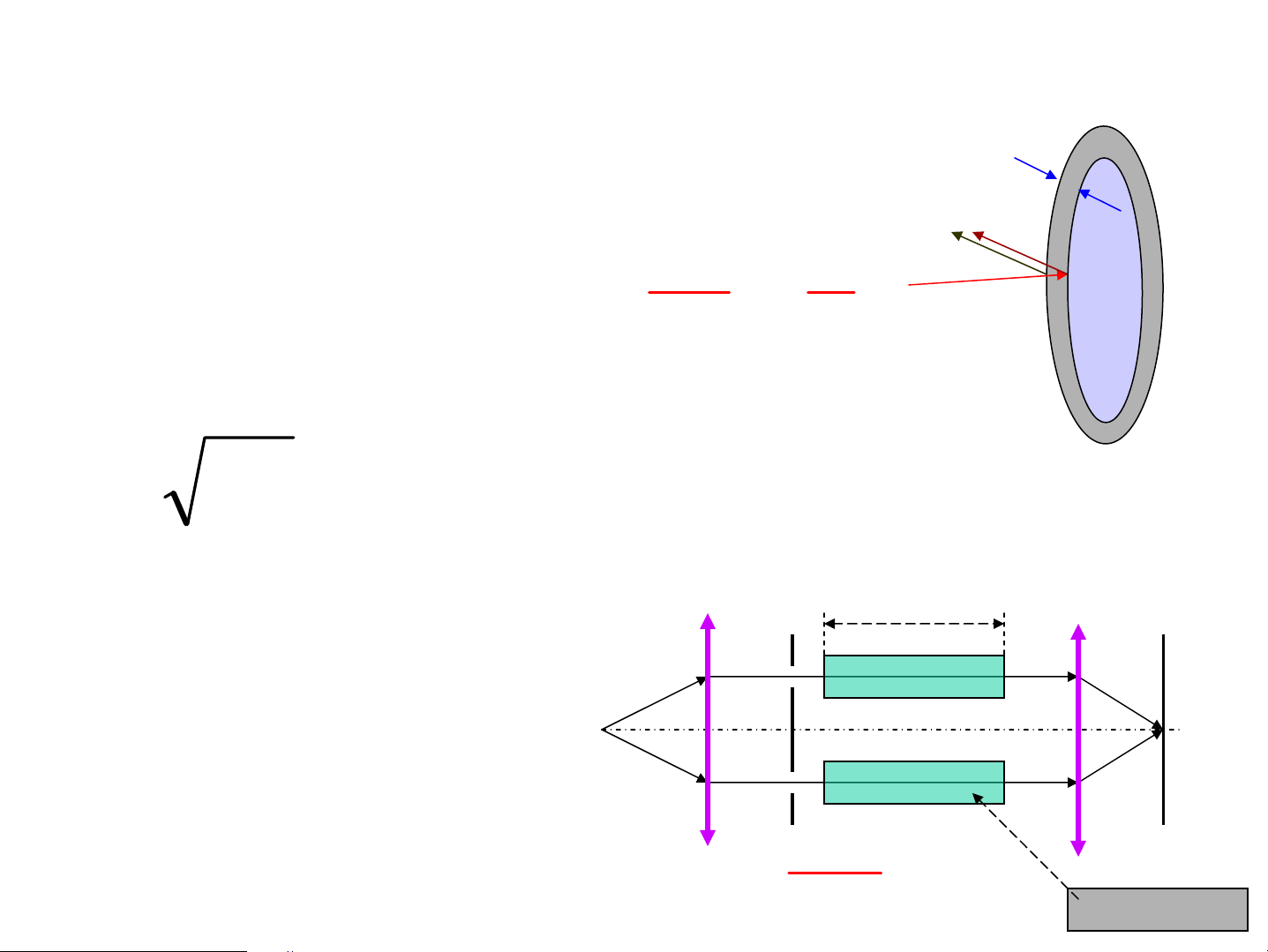
• ThÝ nghiÖm cña L«i (Lloyd) Theo lý thuyÕt V©n s¸ng O M L -L =OI+IM-OM =kλ 1 2 I V©n tèi L -L =OI+IM-OM=(2k+1)λ/2 1 2
Thùc tÕ ng−îc l¹i → Sau ph¶n x¹ ®¶o pha 2π Δϕ = (L − L ) + π λ 1 2 n1 L cña tia ph¶n x¹ 1 n dμi thªm λ/2 2 ChØ khi n > n 2 1
4. Giao thoa g©y bëi c¸c b¶n máng 4.1. B¶n máng cã bÒ dÇy
thay ®æi -V©n cïng ®é dμy O
Tia lã cña tia ph¶n x¹ tõ ®¸y i
d−íi (®á) giao thoa víi tia 1 i R
ph¶n x¹ tõ mÆt trªn (xanh) 1 M B cña tÊm HiÖu quang lé: d n i C L -L =OB+n(BC+CM)-(OM+λ/2) 1 2 2 = n(BC+CM)-RM-λ/2 RM=BM.sini =2d.tgi .sini BC = CM = d/cosi 1 2 1 2 2d λ ΔL = L − L = n − 2 . d tgi sin i − 1 2 cos i 2 1 2 2 sin i1 = n sin i 1 2 2 2 cos i = n − sin i 2 1 sin i n sin i 1 = 2 n 2d 2 . d tgi sin i = (n2 − sin2 i ) 2 1 n cos i 1 2 λ ΔL = 2d (n2 − sin2 i ) − 1 2
V©n s¸ng: L -L =kλ V©n tèi: L -L =(2k+1)λ/2 1 2 1 2
Gãc nh×n x¸c ®Þnh => i x¸c ®Þnh 1
=>Mçi v©n øng víi mét ®é dÇy d x¸c ®Þnh => V©n cïng ®é dÇy • Nªm kh«ng khÝ
Tia lã cña tia ph¶n x¹ tõ ®¸y d−íi (®en) tÊm trªn giao d
thoa víi tia ph¶n x¹ tõ mÆt trªn (®á) cña tÊm d−íi HiÖu quang lé L -L =2d+ λ/2 1 2
V©n s¸ng: L -L =2d+ λ/2=k λ 1 2 d = (2k-1)λ/4 d =k.λ/2 S T
V©n tèi: L -L =2d+λ/2=(2k+1) λ/2 1 2
øng dông: KiÓm tra ®é ph¼ng
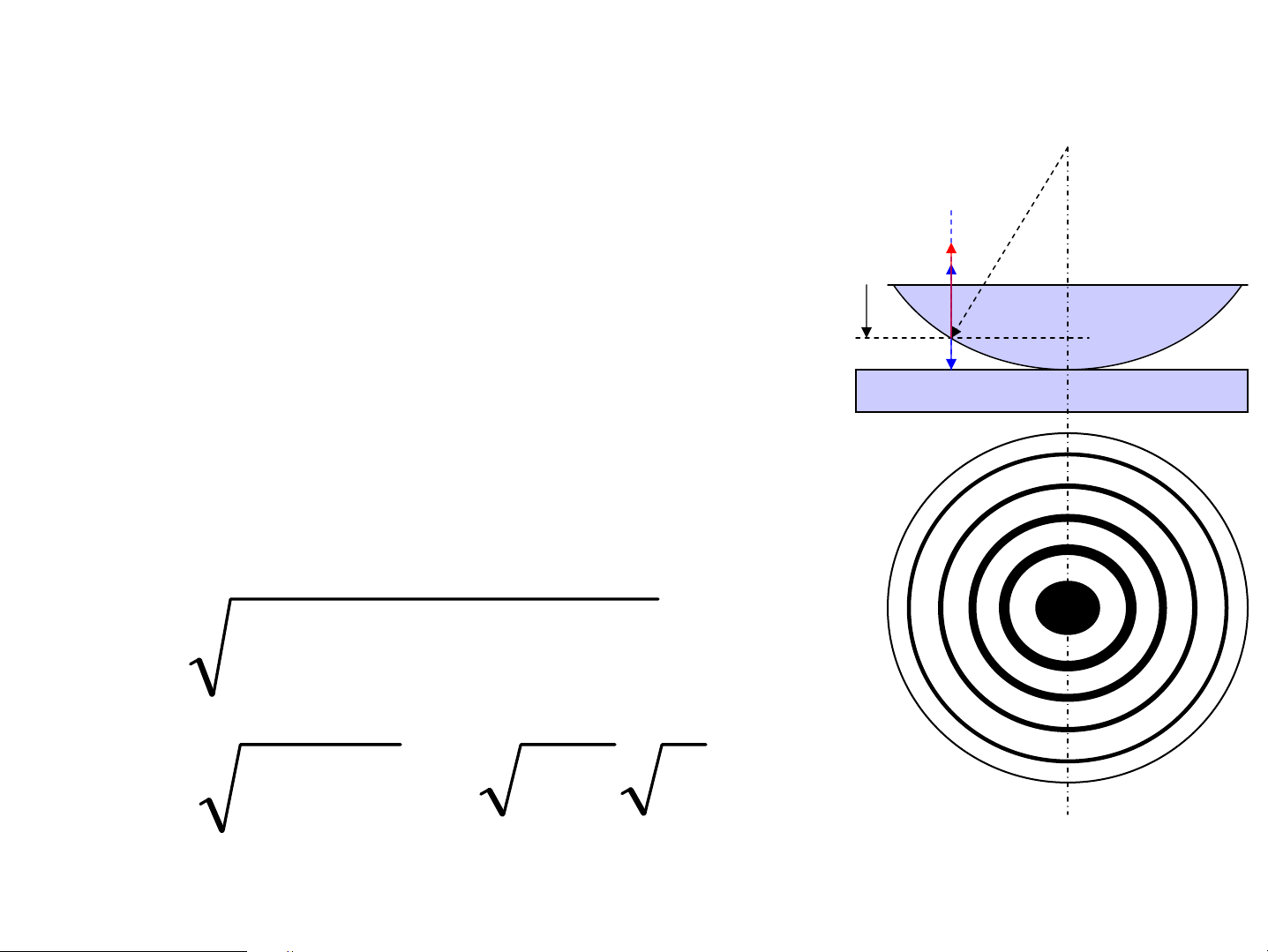
cña kÝnh sai sè 0,03-0,003 μm • V©n trßn Niut¬n Tia ph¶n x¹ tõ tÊm ph¼ng R
(xanh) vμ Tia ph¶n x¹ tõ mÆt r
cong cÇu (®á) giao thoa víi k dk nhau: V©n tèi : d =k. λ/2 k B¸n kÝnh v©n: 2 2 r = R − (R − d ) k k r ≈ 2Rd = Rλ k k k V©n s¸ng : d =(2k-1). λ/4 k
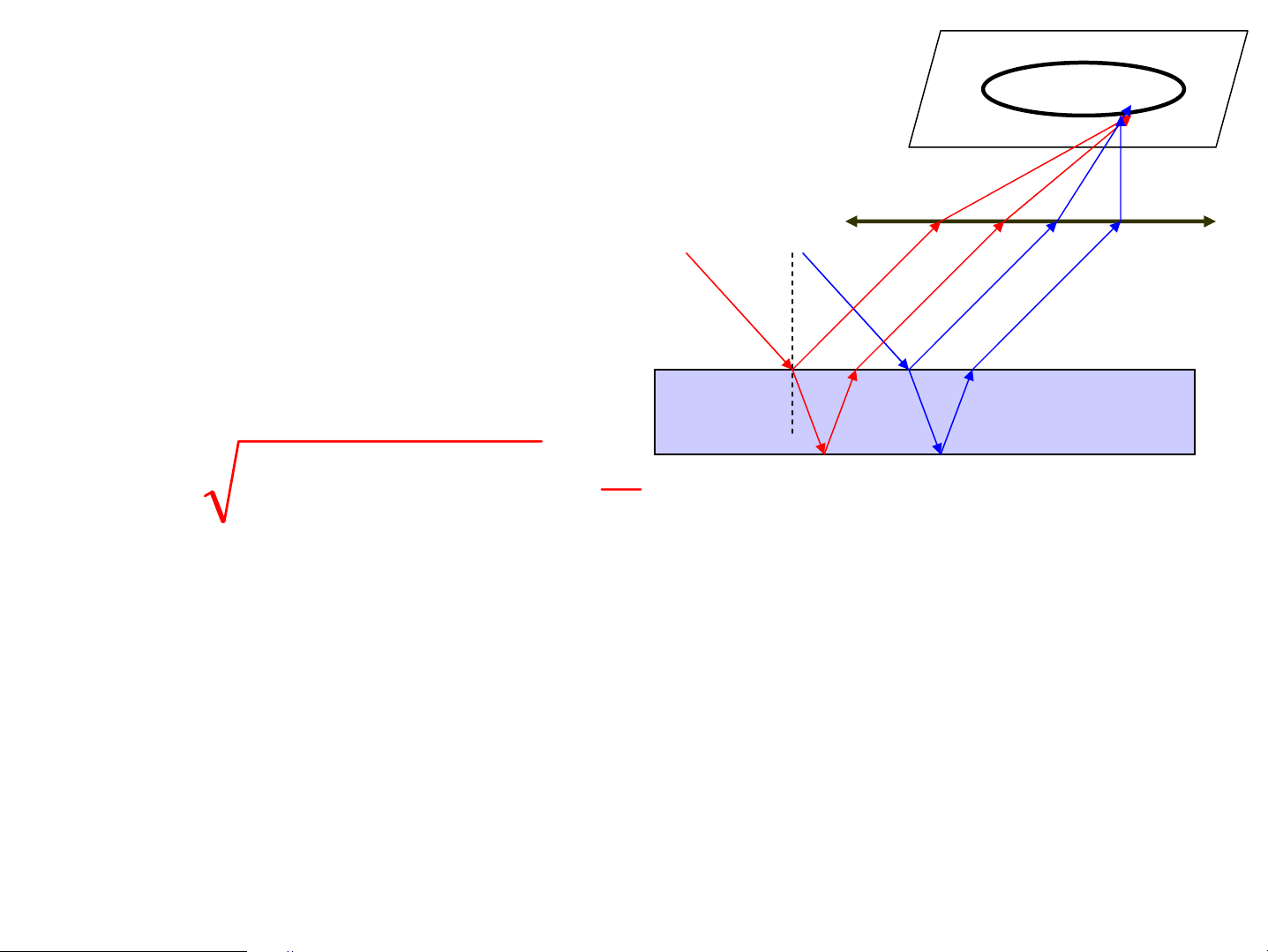
4.2. B¶n máng cã bÒ dÇy kh«ng
®æi - V©n cïng ®é nghiªng M Tia lã cña tia ph¶n x¹ tõ
®¸y d−íi giao thoa víi tia i1 ph¶n x¹ tõ mÆt trªn cña tÊm d, n λ ΔL = 2d (n2 − sin2 i ) − 1 2 ΔL=kλ S¸ng ΔL=(2k+1)λ/2 Tèi
C¸c v©n giao thoa s¸ng tèi lμ c¸c vßng trßn ®ång t©m.
d=const → v©n tuú thuéc vμo i → V©n cïng ®é 1 nghiªng
4.3. øng dông hiÖn t−îng giao thoa
• Khö ph¶n x¹ c¸c mÆt kÝnh d n > n > 1 tk Δ λ λ L=2dn=λ /2 = = 0 d 0 ntk 4n 4 λ n
trong ch©n kh«ng, λ trong líp phñ 0 n = n λ tk
=0,555μm ¸nh s¸ng nh¹y nhÊt 0
• §o chiÕt suÊt chÊt láng vμ chÊt khÝ - Giao thoa d kÕ Rª l©y (Rayleigh) n0 2 èng ®Òu ®ùng chuÈn Thay b»ng chÊt cÇn ®o n dÞch ®i m kho¶ng v©n mλ 0 n = + n n mλ = (n-n )d 0 0 d
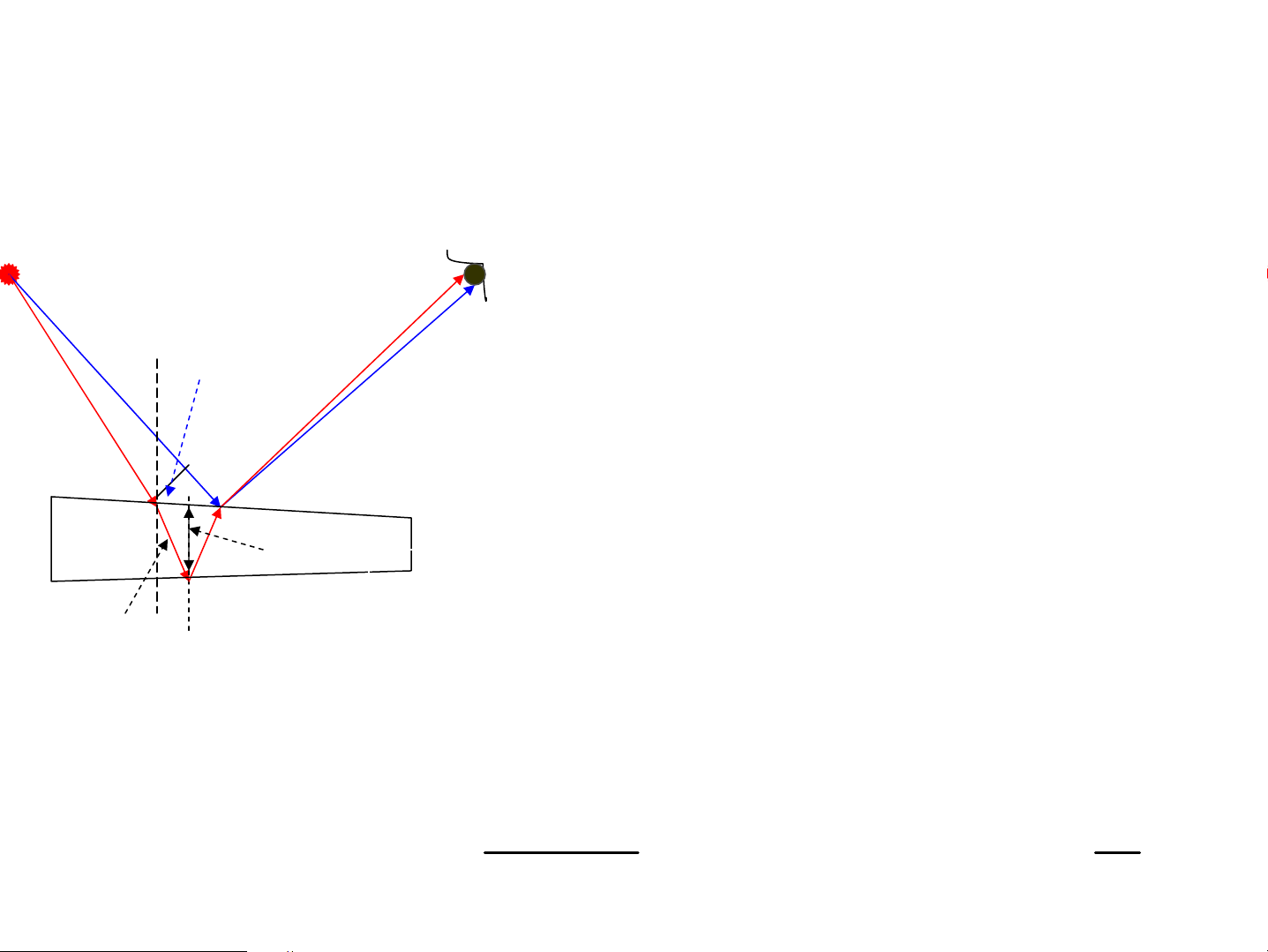
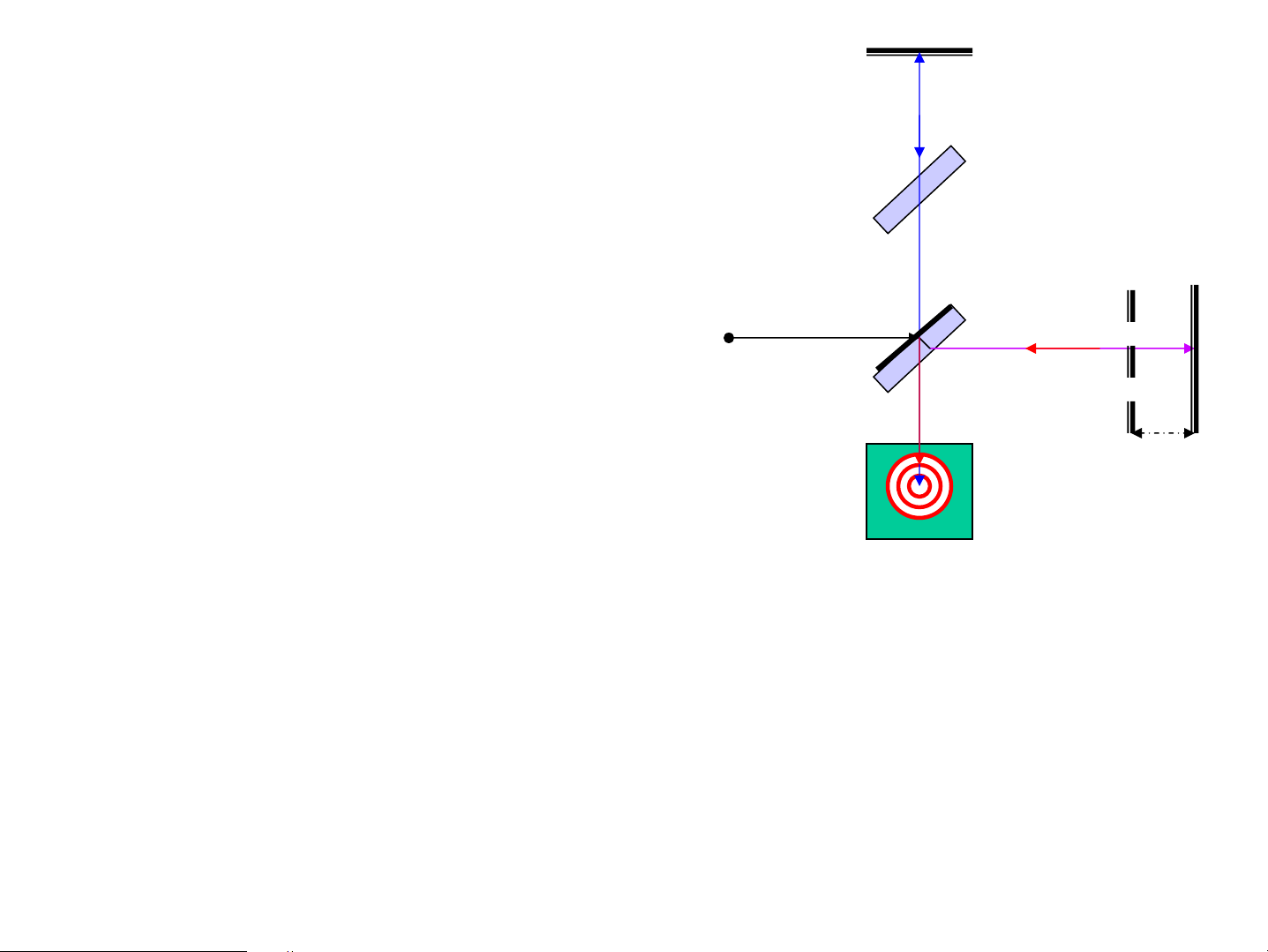
• §o chiÒu dμi - Giao thoa kÕ M G1 Maikenx¬n Micheson 1 P’ ΔL=0 V©n trung t©m s¸ng M’ M 2 2 DÞch ®i m kho¶ng v©n O A P 2l = mλ l = mλ/2 l
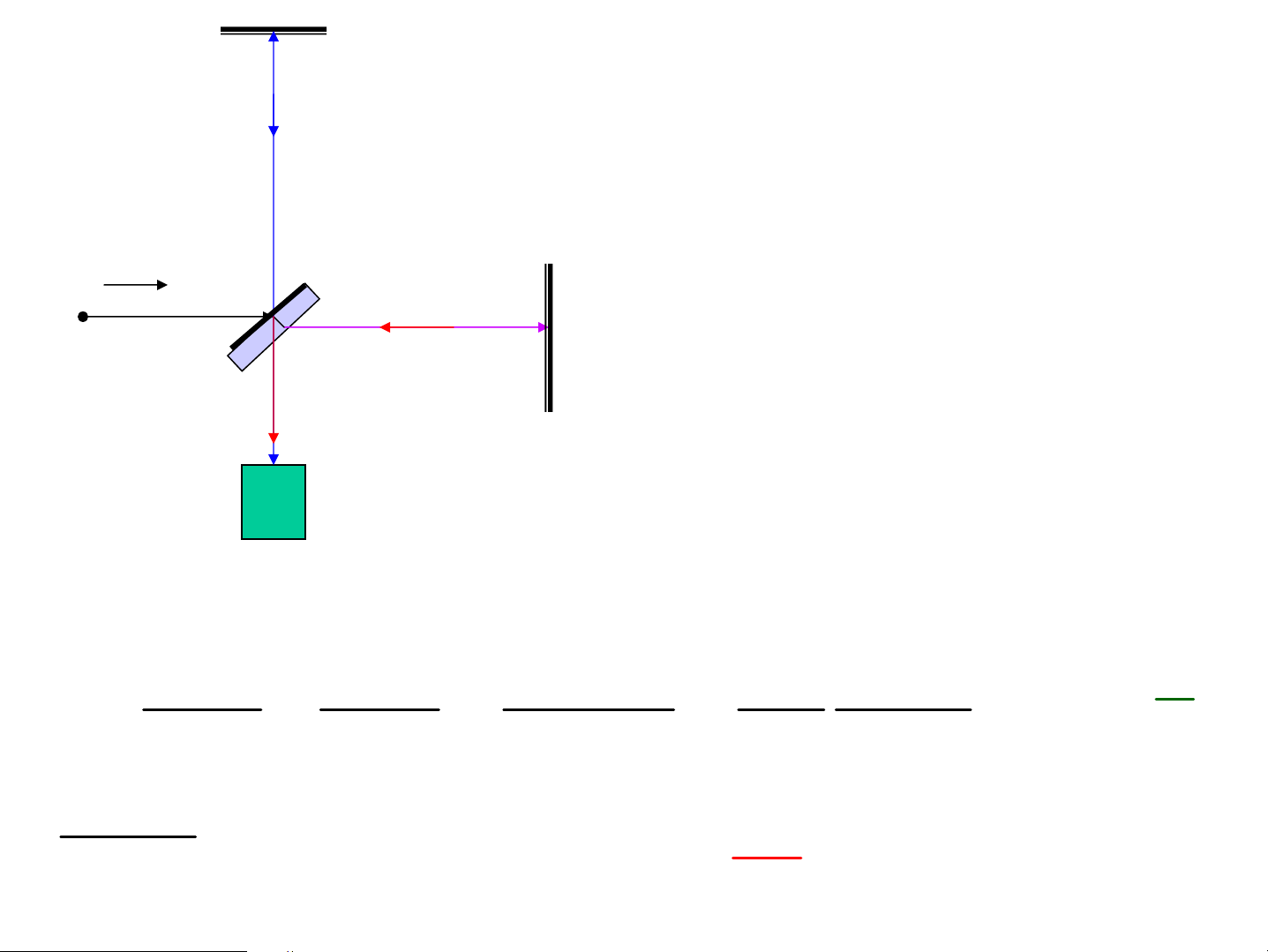
• ThÝ nghiÖm Maikenx¬n G2
Chøng minh tiªn ®Ò Anhxtanh vÒ vËn tèc AS
Gi¶ thiÕt: Tr¸i ®Êt quay quanh mÆt trêi víi vËn
tèc v. Theo c¬ häc cæ ®iÓn vËn tèc AS :
däc theo ph−¬ng ch®éng cña tr¸i ®Êt: c = c±v //
Vu«ng gãc víi ph−¬ng c® cña tr¸i ®Êt: c⊥ = c M G1 1 AM =AM = 1 2 l AM // ph−¬ng ch®éng 2 M2 tr¸i ®Êt O A AM ⊥ ph−¬ng ch®éng 1 P tr¸i ®Êt G2
t thêi gian ®i AM , t thêi gian ®i AM 1 1 2 2 l l 2lc 2lc 1 v t = + = = β = 2 2 2 2 2 c − v c + v c − v c 1 − β c 1 2 ≈ 1 + β 2 2 2 = l + β 1 − β t 1 ( ) 2 c