Giao Thoa Ánh Sáng: Chương 1 - Định Lý Malus & Thí Nghiệm môn Vật lý đại cương 2 | Trường Đại học Bách Khoa Hà Nội

ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT Chương 1 GIAO THOA ÁNH SÁNG
------------------------------------------------------------------------------------------------------------------------
§1.1 QUANG LỘ. ĐỊNH LÝ MALUS. HÀM SÓNG ÁNH SÁNG VÀ CƯỜNG ĐỘ SÁNG
§1.2 GIAO THOA TRONG THÍ NGHIỆM HAI KHE CỦA YOUNG
§1.3 GIAO THOA DO PHẢN XẠ. THÍ NGHIỆM VỚI GƯƠNG LLOYD
§1.4 GIAO THOA TỪ CÁC BẢN MỎNG. VÂN CÙNG ĐỘ DÀY
§1.5 GIAO THOA KẾ MICHELSON
-----------------------------------------------------------------------------------------------------------------------
Ánh sáng là gì? Câu hỏi này đã làm nhiều nhà khoa học lớn bận tâm. Newton cho rằng ánh
sáng là một dòng hạt, mặc dầu ông thừa nhận điều đó không chắc chắn lắm. Ông đã giải
thích được nhiều hiệu ứng quang học bằng cách dùng lý thuyết hạt của ánh sáng. Christian
Huygens (1629 - 1695), người cùng thời với Newton, lại tin rằng ánh sáng được tạo từ các
sóng. Ông đã khởi xướng ra lý thuyết sóng của ánh sáng, song lý thuyết của ông đã không
thành công, một phần vì ông giả thiết rằng các sóng ánh sáng là sóng dọc. Vào năm 1864,
James Clerk Maxwell đã đưa ra được bằng chứng lý thuyết có sức thuyết phục khẳng định
rằng ánh sáng là một sóng ngang trong điện trường và từ trường. Tính chất sóng của ánh
sáng đã được xác lập bằng thực nghiệm vào năm 1800 bởi Thomas Young (1773 - 1829).
Các thí nghiệm của Young với ánh sáng đã cho t
hấy các hiệu ứng chỉ có thể được giải thích
bằng giao thoa, hiệu ứng mà chỉ các sóng mới có.
§1.1 QUANG LỘ. ĐỊNH LÝ MALUS. HÀM SÓNG ÁNH SÁNG VÀ CƯỜNG ĐỘ SÁNG 1. Quang lộ
Thời gian ánh sáng đi được quãng đường d (giữa hai điểm A và B), trong môi trường c ó chiết suất n là d t = (1.1) v
trong đó v là vận tốc ánh sáng.
Trong thời gian t đó, ánh sáng đi được quãng đường L trong chân không. L có giá trị là d L = ct = c = nd v L = nd (1.2)
L được gọi là quang lộ giữa hai điểm A và B.
“Quang lộ giữa hai điểm A, B là quãng đường ánh sáng đi được
trong chân không tương ứng với thời gian ánh sáng đi được quãng
đường AB trong môi trường.”
Nếu ánh sáng truyền qua nhiều môi trường có chiết suất khác
nhau thì quang lộ L được xác định bởi L = n1d1 + n2d2 + … + nndn (1.3) ĐÀO TUẤN ĐẠT 1
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
Nếu ánh sáng đi trong môi trường có chiết suất biến đổi liên tục từ điểm này sang điểm khác thì B L = nds (1.4) A
trong đó ds mà đoạn trường trên đó chiết suất của môi trường xem như không đổi.
2. Định lý Malus
Mặt trực giao: Là mặt vuông góc với các tia sáng của một chùm sáng.
Mặt trực giao của chùm sáng đồng quy là những mặt cầu đồng tâm với tâm là điểm đồng quy.
Mặt trực giao của chùm sáng song song là những mặt phẳng song song.
Định lý Malus: “Quang lộ của các tia sáng giữa hai mặt trực giao của một chùm sáng bằng nhau.”
Chứng minh định lý Malus: trang 14-15, Tập 3 - Phần 1.
3. Hàm sóng ánh sáng
Theo thuyết điện từ ánh sáng là sóng điện từ được đặc trưng bởi vector điện trường E và vector
cường độ từ trường H vuông góc với nhau và vuông góc với phương truyền sóng. Nhưng thực tế
cho thấy các hiện tượng quang học xảy ra là do tác dụng của điện trường. Chỉ có thành phần E mới
gây cảm giác sáng nên người ta gọi dao động của vector E được g
ọi là dao động sáng. Và để đặc
trưng cho sóng ánh sáng, chỉ cần dùng vector E.
Giả sử sóng ánh sáng phát ra từ nguồn S được biểu diễn bởi phương trình ES = E0cos(ωt + φ) (1.5)
Nếu v là vận tốc ánh sáng trong môi trường chiết suất n, thì tại điểm M cách nguồn một khoảng
d, dao động sáng E có phương trình là E = E d 0cos[ω(t - )t + φ] v E = E d 0cos(ωt - ω + φ) v E = E 2 dn 0cos(ωt - + φ) T c E = E 2 0cos(ωt - L + φ) (1.6) 
trong đó λ = cT là bước sóng ánh sáng trong chân không L = nd là quang lộ của ánh sáng trên đoạn , SM.
(1.6) được gọi là phương trình sóng của ánh sáng. ĐÀO TUẤN ĐẠT 2
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
Nếu ánh sáng truyền theo chiều ngược lại thì phương trình sóng của ánh sáng là E = E 2 0cos(ωt + L + φ) (1.7) 
4. Cường độ sáng
Cường độ sáng là đại lượng đặc trưng cho độ sáng tại một điểm.
Cường độ sáng tại một điểm có trị số bằng năng lượng truyền qua một đơn vị diện tích đặt
vuông góc với phương truyền sóng, trong một đơn vị thời gian.
Cường độ sáng tại một điểm tỷ lệ với bình phương của biên độ dao động sáng tại điểm đó I k 20 E
trong đó k là hệ số tỷ lệ. Khi nghiên cứu hiện tượng giao thoa chỉ cần so sánh cường độ sáng tại
các điểm khác nhau mà không cần tính cụ thể giá trị của cường độ sáng nên có thể quy ước k = 1. Thế nên I = 2 0 E (1.8)
Đơn vị của cường độ sáng là W/m2.
§1.2 GIAO THOA TRONG THÍ NGHIỆM HAI KHE CỦA YOUNG
(Nguồn sáng điểm - vân không định xứ)
1. Thí nghiệm hai khe của Young
Thí nghiệm hai khe của Young cho ta một cách chứng minh đơn giản về bản chất sóng của ánh sáng.
Trên hình vẽ, ánh sáng đơn sắc đi qua khe chuẩn trực rồi sau đó qua hai khe song song S1 và S2
trước khi đập vào màn quan sát. Bức tranh của ánh sáng trên màn gồm một dãy các miền sáng hơn
xen kẽ với các miền tối hơn. Các miền sáng tối xen kẽ nhau này được gọi là các vân giao thoa. Đặt
màn quan sát ở bất cứ vị trí nào trong vùng giao thoa cũng quan sát được các vân giao thoa nên gọi
loại vân này là vân giao thoa không định xứ.
Giả sử ta che một trong hai khe, chẳng hạn S1 sao
cho chỉ có ánh sáng đi qua S2 chiếu sáng màn quan sát. Khi
đó chúng ta thấy các vân đều biến mất và ánh sáng ở gần tâm màn gần như đồn g
đều. Xét một điểm cụ thể nào đó trên màn ứng với
tâm của một vân tối khi cả hai khe đều mở, điểm
P chẳng hạn. Cường độ sáng ở điểm này trên màn về cơ bản
bằng không khi cả hai khe đều mở.
Tuy nhiên, nếu một trong hai khe bị che kín thì khi đó cường độ ở P lại không bằng không nữa.
Sao lại có thể xẩy ra chuyện ánh sáng tới được một điểm trên màn khi chỉ một khe được mở,
thế mà khi hai khe đều mở (ánh sáng đi qua chúng phải tăng gấp đôi) lại không có ánh sáng nào tới ĐÀO TUẤN ĐẠT 3
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
được điểm này? Ta có thể hiểu được kết quả này bằng cách giả thiết rằng ánh sáng bao gồm các
sóng. Ở vị trí của các vân tối, các sóng đi từ S
1 tới ngược pha với các sóng tới từ S 2. Khi hai sóng có
cùng cường độ đi tới mà ngược pha ở một điểm thì chúng sẽ giao thoa theo cách khử nhau và sóng
tổng cộng bằng không. Như vậ
y các vân tối là hệ quả của sự giao thoa huỷ nhau giữa các sóng sáng
đi từ S1 và các sóng đi từ S2. Ở vị trí của các vân sáng, các sóng đi từ S1 tới cùng pha với các sóng
tới từ S2 Kết quả là chúng sẽ giao thoa theo cách tăng cường nhau và sóng tổng cộng . khác không.
2. Nguồn kết hợp và sóng kết hợp
Chúng ta chỉ có thể quan sát thấy hiệu ứng giao thoa như trường hợp thí nghiệm hai khe của
Young ở trên khi các sóng tới là các sóng kết hợp. Hai sóng kết hợp có cùng tần số và độ lệch pha
không đổi theo thời gian. Các sóng này được tạo ra từ các nguồn kết hợp.
Có cách nào để tạo ra hai sóng kết hợp? Ánh sáng do các nguyên tử của nguồn sáng phát ra.
Chúng phát ra thành từng đoàn sóng riêng rẽ nối đuôi nhau. Biên độ và pha của các đoàn sóng do
một nguyên tử phát ra ở những thời điểm khác nhau; cũng như do các nguyên tử khác nhau phát ra
ở cùng một thời điểm có thể rất khác nhau. Chúng không có liên hệ gì với nhau, nên pha ban đầu
của chúng luôn thay đổi theo thời gian và có mọi giá trị bất kỳ. Tại điểm M nào đó nhận được các
cặp đoàn sóng do hai nguồn riêng biệt gửi tới, mỗi cặp đoàn sóng sẽ có một độ lệch pha nào đó. Độ
lệch pha này thay đổi hỗn loạn theo thời gian nên không phải
là các sóng kết hợp. Nếu bằng cách
nào đó, ta tách sóng phát ra từ một nguồn duy nhất, sau đó lại cho chúng gặp nhau thì độ lệch pha của hai sóng sẽ khôn
g còn phụ thuộc thời gian nữa, lúc đó ta có hai sóng kết hợp. Thí nghiệm hai
khe của Young thành công là bởi vì đã thực hiện theo cách này. Các khe S1 và S2 được chiếu sáng
từ cùng một nguồn điểm S nên các sóng do chúng tạo ra là các sóng kết hợp.
3. Hình dạng và vị trí của vân giao thoa trong thí nghiệm Young
Điều kiện để có cực đại và cực tiểu của cường độ sáng
Giả sử hai nguồn sáng kết hợp cùng pha S1 và S2 có phương trình là E1 = E01cosωt E2 = E02cosωt
Phương trình của các sóng ánh sáng tại điểm M là 2 E  1M = E01 cos(ωt - L  1) 2 E  2M = E02 cos(ωt - L  2)
Biên độ của dao động tổng hợp tại M là 2 2 2
E  E  E  2E E cos(  ) 0 01 02 01 02 1 2 2 2   với φ1 = - L L  1 và φ2 = -  2 2(L  L )
Biên độ này phụ thuộc độ lệch pha    2 1 hay hiệu quang lộ   L L  .  2 1 * Nếu  2
 k  (k = 0, ±1, ±2, …), hay   L  2 1L k  
hai sóng tới cùng pha, chúng tăng cường lẫn nhau và tại M cường độ sáng đạt cực đại 2 I (E E ) max 01 02 * Nếu   (2k 1
 )  (k = 0, ±1, ±2, …), hay   L     2 1 L (2k 1) 2
hai sóng tới ngược pha, chúng hủy nhau và tại M cường độ sáng đạt cực tiểu 2 I (E E ) min 01 02 ĐÀO TUẤN ĐẠT 4
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
Hình dạng và vị trí vân giao thoa
Xét trường hợp ánh sáng truyền trong chân không hoặc không khí. Lúc đó
Vị trí các cực đại được xác định bởi:  = d2 d – 1 = k (1.9)
Vị trí các cực tiểu được xác định bởi:   = d2 d – 1 = (2k 1  ) 2 (1.10) với (k = 0, ±1, ±2, …).
Quỹ tích những điểm sáng là một họ hypeboloit tròn xoay. Quỹ tích những điểm tối cũng như vậy.
Tọa độ của vân sáng, vân tối và khoảng vân:  SD x  k a (1.11)  tD x (2  k 1) 2a (1.12)  D ia (1.13)
4. Giao thoa của ánh sáng trắng
Nếu nguồn S phát ánh sáng trắng, gồm mọi ánh sáng có
bước sóng từ 0,38 µm - 0,76 µm thì
hình ảnh giao thoa sẽ phức tạp hơn nhiều.
- Mỗi bức xạ đơn sắc sẽ cho một hệ vân riêng. Tất cả các hệ vân này đều có vân sáng chính giữa
tại nên tại đây là một vân trắng. D Khoảng vân ia
sẽ khác nhau với các bước sóng λ
khác nhau. Sóng có bước sóng λ càng dài thì i càng lớn.
- Hai bên vân trắng là hai vân tối hoàn toàn, vì cực tiểu thứ nhất của mọi hệ vân đều trùng nhau tại đó.
- Tiếp theo là vân sáng thứ nhất của tất cả các hệ, đều không hoàn toàn trùng nhau, chúng tạo
thành một vân sáng mép ở trong viền tím, mép ở ngoài vân đỏ
và gọi là vân màu bậc một.
- Ngoài hai vân tối đầu tiên không có vân tối nào khác vì rằng tại chỗ có vân tối ứng với bước
sóng này lại có một vân sáng ứng với một số bước sóng khác chồng lên.
- Vân màu bậc hai cũng tương tự như vân màu bậc một nhưng rộng gấp đôi và màu nhạt hơn.
Phần cuối của vân màu bậc hai chồng lên phần đầu tiên của vân màu bậc ba. Các vân bậc càng cao
chồng lên nhau càng nhiều, do đó có màu bàng bạc và ranh giới không rõ rệt. ĐÀO TUẤN ĐẠT 5
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
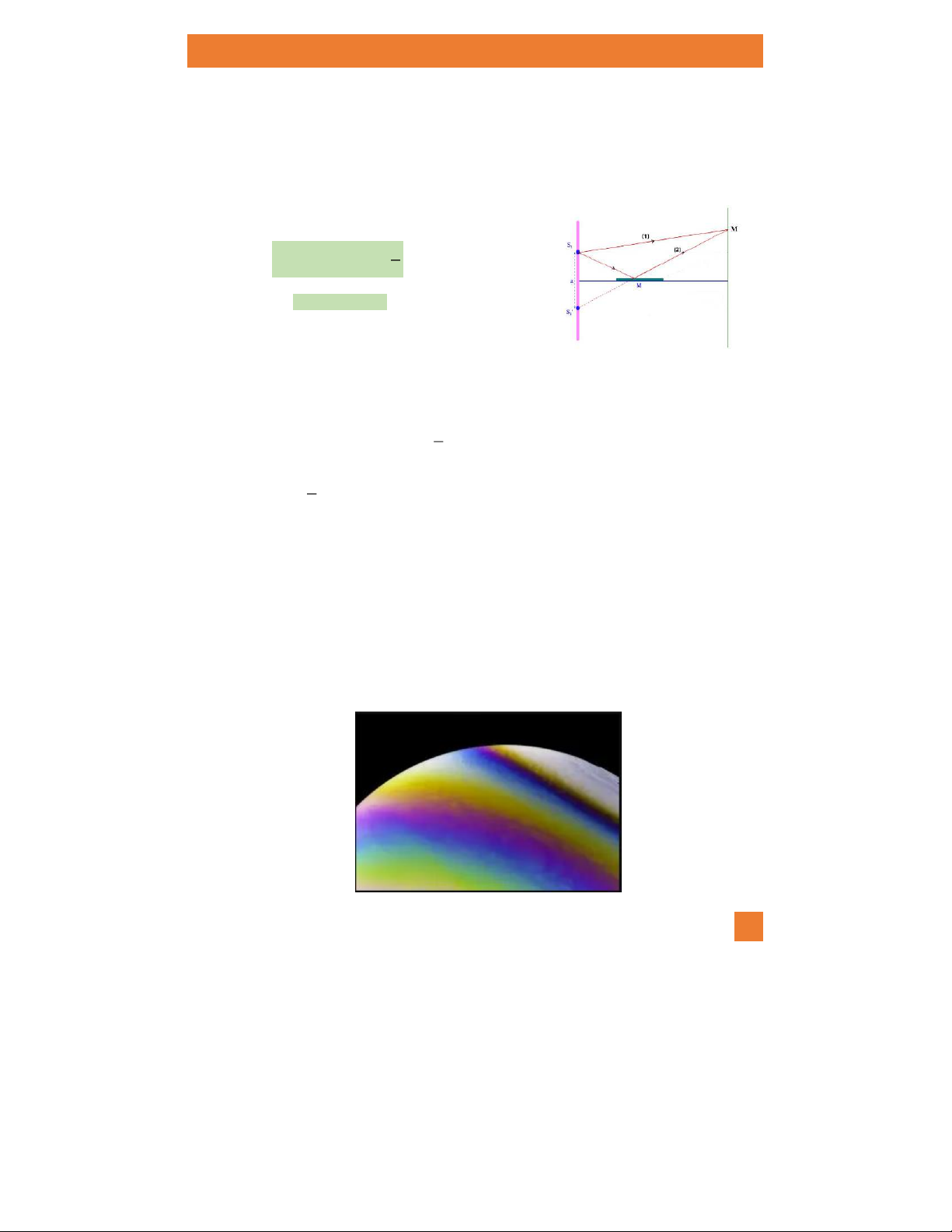
§1.3 GIAO THOA DO PHẢN XẠ. THÍ NGHIỆM VỚI GƯƠNG LLOYD
Một hình ảnh giao thoa giống
như giao thoa của hai khe Young có thể được tạo ra bằng cách
dùng gương Lloyd. Sự giao thoa là do chồng chất của chùm tia tới trực tiếp từ nguồn sáng điểm S
(1) và chùm tia phản xạ trên mặt gương phẳng (2). Chùm tia phản xạ dường như xuất phát từ S’ là
ảnh của S qua gương. S và S’ được coi là hai nguồn kết hợp.
Trên màn quan sát, điểm M là một cực đại (tâm vân sáng) ứng với điều kiện  = d2 - d1 = (2k 1  ) 2 (1.14)
và là một cực tiểu ứng với điều kiện = d2 - d1 = k (1.15)
trong đó k = 0, ±1, ±2, …
Điều này chứng tỏ S và S’ là hai nguồn kết hợp ngược pha nhau và trái với suy nghĩ ban đầu của
chúng ta S và S’ là hai nguồn cùng pha (khi
đó (1) là điều kiện để M là cực tiểu và (2) để M là một cực đại).
Như vậy so với trường hợp hai nguồn cùng pha hiệu số pha đã thay đổi một lượng là π tương 
ứng với hiệu quang lộ thay đổi một lượng . 2
Vì rằng tia (1) truyền trực tiếp từ S không có gì thay đổi nên kết luận tia phản xạ trên mặt gương 
thay đổi một lượng (tương ứng với pha từ S’ thay đổi một lượng là π). 2
Kết luận này cũng đúng cho trường hợp ánh sáng phản xạ trên môi trường có chiết suất lớn hơn
môi trường ánh sáng tới. Trong trường hợp ánh sáng phản xạ trên môi trường có chiết suất nhỏ hơn
pha dao động và do đó quang lộ không thay đổi, hai nguồn S và S’ cùng pha.
§1.4 GIAO THOA TỪ CÁC BẢN MỎNG. VÂN CÙNG ĐỘ DÀY
(Nguồn sáng rộng - vân định xứ)
Một hiệu ứng giao thoa quan sát được dễ dàng là hiệu ứng do phản xạ từ các màng mỏng trong
suốt như các màng xà phòng hay các màng dầu. Các mầu sắc lóng lánh mà bạn thường nhìn thấy
được phản xạ từ các màng như thế là do hiện tượng giao thoa tạo ra. ĐÀO TUẤN ĐẠT 6
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
1. Giao thoa từ bản mỏng. Vân cùng độ dày
Sự định xứ của vân
Xét một bản mỏng có bề dày d thay
đổi làm bằng chất có chiết suất n. Hai mặt của bản làm với
nhau một góc bé cỡ hàng phút.
Ta quan sát sự giao thoa khi bản mỏng được chiếu sáng bởi một nguồn sáng rộng. Chúng ta biết
rằng trong thực tế nguồn điểm khó thực hiện, trong nhiều trường hợp không thực hiện được. Hơn
nữa trong thiên nhiên hiện tượng giao thoa trên bản mỏng thường xảy ra với nguồn rộng. Từ điểm S của nguồn:
- Tia SA tới mặt bản bị khúc xạ tại A, phản xạ tại B và ló ra theo phương CR1.
- Ðồng thời từ S, tia SC sau khi phản xạ tại điểm C ở mặt trên của bản cho tia CR2.
Các tia sáng có hiệu quang lộ xác định nên giao thoa với nhau tại C và ta quan sát thấy vân giao
thoa ở ngay mặt bản. Thấu kính L
để chiếu ảnh giao thoa lên màn E. dùng
Thí nghiệm cho thấy hình ảnh giao thoa quan sát được rõ nhất chỉ trong một miền không gian
rất hẹp gần mặt bản mỏng và ra khỏi miền
đó vân sẽ nhanh chóng biến mất. Vì vậy người ta gọi loại
vân giao thoa này là vân giao thoa định xứ. Tuỳ thuộc vào độ dày, dạng hình học của bản mỏng;
cũng như điều kiện chiếu sáng mà miền định xứ của hệ vân rộng hay hẹp và nằm gần mặt bản nhiều hay ít.
Tính hiệu quang lộ
Ta đi tính hiệu quang lộ của hai tia SABCR1 và SCR2. Chú ý rằng tại C, sóng phản xạ bị đảo 
pha π, quang lộ của tia phản xạ dài thêm . Ta có 2 
∆L = L1 – L2 = SA + N(AB + BC) ( – SC + ) 2 Sau khi biến đổi ta có  ∆L = L 2 2 1 – L2 = 2d  n i sin - 2
Vì con ngươi của mắt nhỏ nên mắt chỉ nhìn được các tia nghiêng ít với nhau. Mặt khác nguồn ở
rất xa nên các điểm sáng S’ ≠ S
đến C có góc tới i không khác nhau bao nhiêu nên trong công thức
trên coi i không đổi. Vậy hiệu quang lộ ∆L chỉ còn phụ thuộc bề dày d của bản. ĐÀO TUẤN ĐẠT 7
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT Vị trí của vân
+ Vị trí vân sáng: Đó là những điểm có bề dày d thỏa mãn L1 – L2 = kλ (1.17)
+ Vị trí của vân tối: Đó là những điểm có bề dày d thỏa mãn  L1 – L2 = (2k + 1) (1.18) 2
Các vân ứng với cùng một giá trị xác định của d được gọi là các vân cùng độ dày.
Nếu chiếu bản mỏng bằng ánh sáng trắng thì mỗi ánh sáng đơn sắc sẽ cho một hệ vân màu
riêng. Trên bản mỏng sẽ quan sát được các vân nhiều màu sắc. Đó là màu của bản mỏng.
Giữa hai bản trong suốt đặt chồng lên nhau bao giờ cũng tồn tại một lớp không khí mỏng, nói
chung có độ dày thay đổi từ điểm này đến điểm khác. Lớp không khí này có thể cho ta vân giao
thoa cùng độ dày. Ta sẽ khảo sát hai ví dụ đơn giản sau
2. Vân của nêm không khí
+ Nêm không khí là một lớp không khí hình nêm, giới hạn bởi hai bản thủy tinh đặt nghiêng góc
với nhau một góc nhỏ. Giao tuyến của hai mặt nêm là cạnh nêm.
+ Rọi một chùm sáng đơn sắc, song song, vuông góc với mặt G2. Tia SA tới mặt nêm tách thành 2 tia:
- Tia phản xạ AR tại A (tia SAR).
- Tia truyền qua nêm không khí, phản xạ trên mặt G2, trở về A theo phương cũ và ló ra ngoài tới S (tia SAMAS). Như vậy tại A có
sự gặp nhau của hai tia phản xạ từ mặt trên và mặt dưới của lớp không khí. Vì
từ một tia tách ra, nên hai tia ló là hai tia kết hợp. Kết quả là trên mặt G1 của nêm sẽ quan sát được các vân giao thoa. + Tính hiệu quang lộ  ∆L = L1 – L2 = 2d + 2 
Phần là do phản xạ trên mặt G2 gây ra. 2 + Vị trí vân
Vị trí của vân tối: Những điểm tối thỏa mãn   L1 – L2 = 2d + = (2k + 1) 2 2  d = k (1.19) 2 ĐÀO TUẤN ĐẠT 8
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
Các điểm có cùng bề dày d là các đoạn thẳng song song với cạnh nêm, do đó các vân tối là
những đoạn thẳng song song với cạnh nêm. Ngay tại cạnh nêm (d = 0) là một vân tối.
Vị trí của vân sáng: Những điểm sáng thỏa mãn  L1 – L2 = 2d + = kλ 2  d = (2k - 1) (1.20) 4
Các vân sáng cũng là các đoạn thẳng song song với cạnh nêm và xen kẽ với vân tối.
Tốt hơn nếu quan sát thêm hình sau 3. Vân tròn Newton
Các vân giao thoa cùng độ dày có thể quan sát từ lớp
không khí mỏng nằm giữa mặt cong của thấu kính phẳng -
lồi và bản thủy tinh phẳng. Bán kính chính khúc R của thấu
kính lớn vài mét đến chục mét.
Rọi lên thấu kính một chùm sáng đơn sắc song song,
vuông góc với bản thủy tinh. Tương tự như nêm không khí,
tại mặt cong của thấu kính sẽ có sự gặp nhau của các tia
phản xạ và xảy ra giao thoa. ĐÀO TUẤN ĐẠT 9
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
Do tính chất đối xứng của bản mỏng xung quanh trục IO nên các vân giao thoa là các vòng tròn
đồng tâm, có tâm tại O. Các vân đó được gọi là các vân tròn Newton. Càng ra xa tâm các vân tròn càng sít nhau. + Vị trí vân Vị trí của vân tối:  d = k (1.21) 2 Vị trí của vân sáng:  d = (2k - 1) (1.22) 4
+ Tính bán kính của vân tối thứ k
Gọi rk là bán kính vân tối thứ k, dk là bề dày của lớp không khí tại vân tối thứ k. Tam giác IMH 2 2 2 2 2 2 r R   R d  R  R  R d d k ( ) k 2 k k Vì R>>dk nên r2Rd k 2 k 
M là vân tối thứ k, ta có dk = k , do đó 2  2 r = 2R.k = kRλ k 2 rk = kR (1.23) ĐÀO TUẤN ĐẠT 10
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
§1.5 GIAO THOA KẾ MICHELSON
Dụng cụ dùng các hiệu ứng giao thoa sóng để thực hiện các phép đo được gọi là giao thoa kế.
Vì bước sóng của ánh sáng nhìn thấy là rất bé, các giao thoa kế quang học có thể được dùng để o đ
khoảng cách với độ chính xác cao. Giao thoa kế Michelson, (A.A Michelson, 1852-1931) là một
trong số các dụng cụ đơn giản và quan trọng về mặt lịch sử.
Hình sau trình bầy các đặc điểm chính của giao thoa kế Michelson.
Chùm ánh sáng đơn sắc từ nguồn đập vào gương bán mạ M1/2 dưới góc tới 45 độ. Lớp bạc phủ
trên mặt gương có độ dầy vừa đún để cho nó phản g
xạ một nửa chùm tới về phía gương di động M1
(chùm 1), còn nửa kia truyền qua M1/2 và hướng tới gương cố định M2 (chùm 2). Các gương M1 và
M2 sau đó phản xạ các chùm quay về M1/2, ở đó một nửa của mỗi chùm lại được phản xạ và truyền
qua tạo thành tổ hợp truyền tới detector.
Chùm 1 đi quãng đường 2L1 và chùm 2 đi qãng đường 2L
2. Hiệu quang lộ của hai chùm là ∆L = 2L1 – 2L2
Vì các chùm 1 và 2 là các chùm kết hợp nên giao thoa với nhau. Hai chùm sẽ giao thoa tăng 
cường nhau nếu ∆L = 2L1 2L –
2 = kλ và giao thoa hủy nhau nếu ∆L = 2L1 2L – 2 = (2k + 1) . (Để 2 cho M
đơn giản ta bỏ qua bề dầy của
1/2). Như thế, cường độ của ánh sáng được đo ở detector phụ
thuộc vào hiệu quãng đường đi này.
Gương M1 có thể dịch chuyển dễ dàng trên các khoảng cách nhỏ dọc theo phương của chùm 1
bằng cách vặn một đinh ốc có ren tinh xảo. Cường độ ánh sáng được đo bằng detectơ có thể được
làm thay đổi từ cực đại sang cực tiểu bằng cách dịch chuyển M1 một khoảng bằng λ/4. Còn khi M1
dịch chuyển λ/2 sẽ có thay đổi cường độ tương ứng với một khoảng vân. V
ới một detector nhậy, các
khoảng cách nhỏ cỡ một phần trăm bước sóng (khoảng 5nm) là có thể dễ dàng phát hiện được.
Để đo chiều dài một vật ta dịch chuyển gương M1 từ đầu này tới đầu kia của vật. Nếu số vân
dịch chuyển là N thì chiều dài của vật là  L = N (1.24) 2
Vào lúc mà Michelson đã phát triển giao thoa kế của mình, chuẩn độ dài là mét, được xác định
là khoảng cách giữa hai vạch mảnh trên một thanh bạch kim - iridi đặt ở Sevres, nước Pháp. Dùng
giao thoa kế của mình, Michelson đã có thể o
đ được bước sóng của vạch phát xạ từ nguồn sáng
cadimi với độ chính xác một phần một trăm triệu. Khả năng này cuối cùng đã dẫn đến định nghĩa
mét theo bước sóng của một vạch phổ phát ra từ nguyên tố kripton.
BÀI TẬP ĐỊNH HƯỚNG
1.2, 3, 4, 5, 14, 19, 21, 22, 24, 25, 27, 28, 30, 32, 34, 35 ĐÀO TUẤN ĐẠT 11
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT Chương 2
NHIỄU XẠ ÁNH SÁNG
------------------------------------------------------------------------------------------------------------------------
§2.1 NGUYÊN LÝ HUYGENS - FRESNEL
§2.2 NHIỄU XẠ ÁNH SÁNG CHO BỞI SÓNG CẦU
§2.3 NHIỄU XẠ ÁNH SÁNG CHO BỞI SÓNG PHẲNG §2.4 NHIỄU XẠ TIA X
-----------------------------------------------------------------------------------------------------------------------
§2.1 NGUYÊN LÝ HUYGENS - FRESNEL
Cũng giống như hiện tượng giao thoa ánh sáng, sự nhiễu xạ ánh sáng là một bằng chứng chứng
tỏ bản chất sóng của ánh sáng.
1. Hiện tượng nhiễu xạ
Chúng ta đã làm quen với khái niệm ánh sáng được xem là truyền thẳng trong một môi trường
đồng tính về mặt quang hình học. Theo đó một vùng bóng tối hình học được tạo ra bởi một vật chắn sáng nào đó.
Tuy thế, trong rất nhiều trường hợp, chúng ta có thể quan sát thấy các vân sáng trong vùng bóng
tối này và các vân tối xuất hiện trong vùng ánh sáng hình học.
Đó là bởi vì đã có sự uốn cong của các tia sáng xung quanh mép của màn chắn. Hiện tượng này gọi là nhiễu xạ. ĐÀO TUẤN ĐẠT 12
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
Mức độ nhiễu xạ phụ thuộc vào bước sóng, bước sóng càng lớn sự uốn cong của tia sáng càng
đáng kể. Giả thiết cho rằng ánh sáng đi theo đường thẳng vẫn thường đúng vì ánh sáng có ướ b c
sóng rất nhỏ. Nếu ta không nhìn thật gần, nhiễu xạ có thể bị bỏ qua.
Một ví dụ đáng chú ý về hiện tượng nhiễu xạ, được xem là “khác thường” lúc đó là chấm sáng
Arago (đôi khi cũng được gọi là “chấm Poisson”). Một vật có hình đĩa, như một đồng penny chẳng
hạn, được chiếu bằng ánh sáng đơn sắc phát ra từ một nguồn điểm, một chấm sáng sẽ xuất hiện ở
tâm của vùng tối. Chấm sáng Arago đóng một vai trò lý thú trong việc phát triển quang học sóng.
Năm 1819, A.J. Fresnel (1788 - 1827) đã đưa ra một lý thuyết sóng của ánh sáng để giải thích
hiện tượng nhiễu xạ. Fresnel tiên đoán sẽ có chấm sáng ở tâm của vùng tối. Hoài nghi lý thuyết này,
S.D.Poisson (1781 - 1840) đã chứng minh “lý thuyết của Fresnel cho một kết quả khó tin”. Ông cho
rằng kết quả này đã hạ
thấp giá trị của lý thuyết sóng. Song sự phát hiện sau đó về chấm sáng của
D.E.J.Arago (1786 - 1853) đã cho ta một xác nhận đầy ấn tượng về bản chất sóng của ánh sáng.
Nghiên cứu về nhiễu xạ được chia thành 2 loại
- Nhiễu xạ Fresnel: Khoảng cách từ màn chắn đến màn quan sát có thể gần. Các sóng đập vào màn
chắn và màn quan sát là sóng cầu.
- Nhiễu xạ Fraunhofer: Nguồn và màn quan sát ở xa màn chắn vô cùng sao cho các sóng đập vào
màn chắn và màn quan sát là các sóng phẳng (trường hợp riêng của nhiễu xạ Fresnel). 2. Nguyên lý Huygens F – resnel Theo Huygens:
“Mỗi điểm ánh sáng truyền tới đều trở thành nguồn sáng thứ cấp phát ánh sáng về phía trước nó.” ĐÀO TUẤN ĐẠT 13
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
Để tính điện trường tại điểm P nào đó, ta tưởng tượng có một mặt sáng thứ cấp và cường độ
sáng tại P do các nguồn điểm trên mặt thứ cấp đó gửi tới. Muốn vậy phải biết biên độ và pha của
các nguồn thứ cấp. Nguyên lý Huygens chưa đề cập đến vấn đề này, do đó Fresnel đã bổ sung thêm nguyên lý:
“Biên độ và pha của nguồn thứ cấp là biên độ và pha do nguồn thực gây ra tại nguồn thứ cấp này.”
Fresnel đã đưa ra một phương pháp để có thể tính được thành phần điện trường tại điểm P thông
qua mặt sáng thứ cấp này. Đó là phương pháp đới cầu Fresnel.
3. Phương pháp đới cầu Fresnel
Xét một nguồn sáng điểm O và điểm được chiếu sáng P.
Vẽ mặt cầu ∑ có tâm O và bán kính R << OP.
Đặt BP = b, từ điểm P vẽ các mặt cầu với bán kính tương ứng: … b b+ b+2 …
Các mặt , , ... chia mặt ∑ thành các đới cầu
gọi là các đới Fresnel. Với cách chia như vậy các đới Fresnel có đặc điểm:
+ Diện tích của các đới cầu đều bằng nhau là sRb  dR b  (2.1)  ĐÀO TUẤN ĐẠT 14
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
+ Bán kính của đới cầu thứ n là nRb r n   (n = 1, 2, 3…) (2.2) R b
Theo nguyên lý Huygens xem mỗi đới là một nguồn thứ cấp gửi ánh sáng tới điểm P. Do có
diện tích bằng nhau nên cường độ sáng của mỗi đới là như nhau. Các đới này là các nguồn kết hợp
do đó có sự giao thoa. Điện trường E tại P là tổng hợp các thành phần điện trường do từng đới gửi tới P. Gọi
là biên độ của dao động sáng do đới thứ n gửi tới P. Khi n tăng, các đới cầu càng xa P, góc θ tăng và biên độ giảm dần. > > …
Tuy nhiên vì khoảng cách từ các đới đến P và góc θ tăng rất chậm nên các biên độ cũng giảm chậm và có thể coi E0,nE1 0,n 1 E0n2    (2.3)
Ngoài ra, các đới cầu đều nằm trên cùng mặt sóng cầu ∑ nên có cùng pha dao động. Khoảng
cách từ hai đới liên tiếp đến P khác nhau
nên hai đới liên tiếp sẽ gây ra tại P các dao động sóng có hiệu pha là: 2  ∆φ = 2 L1 L – 2) = =    2
Vậy hai dao động sáng do hai đới liên tiếp gửi tới P ngược pha nhau. Biên độ sóng tổng hợp tại P là: … (2.4)
§2.2 NHIỄU XẠ ÁNH SÁNG CHO BỞI SÓNG CẦU
Bây giờ chúng ta sẽ vận dụng các kết quả ở trên để nghiên cứu nhiễu xạ qua một lỗ tròn và qua một đĩa tròn.
1. Nhiễu xạ qua một lỗ tròn Xét sự truyền ánh sáng
từ nguồn điểm O tới một điểm P qua lỗ tròn AB khoét trên một màn
chắn. Giả sử số đới cầu Fresnel là n (lỗ chứa n đới). Biên độ của điện trường tại P là: …
Lấy dấu (+) nếu số đới là lẻ.
Lấy dấu (-) nếu số đới là chẵn. ĐÀO TUẤN ĐẠT 15
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
Ta sắp xếp biểu thức trên +… +
Một số kết luận
+ Khi không có màn chắn hoặc lỗ có kích thước lớn, n = ∞, thì
, cường độ sáng tại P là
+ Nếu lỗ chứa số lẻ đới I = >
> Điểm P sáng hơn so với khi không có màn chắn.
Đặc biệt khi chỉ có 1 đới = = 4
> Độ sáng tại P gấp 4 lần cường độ sáng khi không có màn chắn.
+ Nếu lỗ chứa số chẵn đới I = <
> Điểm P tối hơn so với khi không có màn chắn.
Đặc biệt khi n = 2 thì do  P tối.
2. Nhiễu xạ qua một đĩa tròn ĐÀO TUẤN ĐẠT 16
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
Giữa O và P đặt một đĩa chắn sáng bán kính . Giả sử đĩa che mất m đới đầu tiên. Khi đó … +….
Các biểu thức trong dấu ngoặc bằng 0 và số đới lại tiến tới vô cùng nên
Như vậy, dù bị che khuất nhưng tại P vẫn sáng.
Một số kết luận
+ Nếu đĩa tròn nhỏ, m nhỏ, thì không khác
bao nhiêu nên cường độ sáng tại P gần
bằng cường độ sáng khi không có đĩa che.
+ Nếu đĩa tròn lớn, tức m lớn, thì
0 và cường độ sáng tại P thực tế bằng 0.
§2.3 NHIỄU XẠ CỦA SÓNG PHẲNG
1. Nhiễu xạ qua một khe hẹp
Chúng ta mô tả hình ảnh nhiễu xạ do một chùm sáng song song tới khe hẹp có bề rộng AB = a.
Khoảng cách từ nguồn và từ màn chắn tới khe lớn hơn rất nhiều độ rộng a của khe. ĐÀO TUẤN ĐẠT 17
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
Khi đi qua khe các tia sáng bị nhiễu xạ theo nhiều phương khác nhau. Các tia nhiễu xạ theo
phương được xác định bởi góc φ nào đó sẽ song song với nhau nên gặp nhau ở vô cùng hay tại một
điểm P nằm trên mặt phẳng tiêu của thấu kính hội tụ L.
Tùy vào giá trị của φ mà điểm P có thể sáng hoặc tối khi thỏa mãn những điều kiện nhất định.
Bây giờ ta đi tìm sự phân bố cường độ sáng trên màn E.
Điều kiện của các cực đại và cực tiểu Vẽ các mặt phẳng , , … vuông
góc với chùm tia nhiễu xạ và cách nhau một nửa bước
sóng. Các mặt này chia mặt khe thành các khe sơ cấp gọi là các dải, bề rộng mỗi dải là Số dải trên khe là n = =
Vì quang lộ từ hai dải kế tiếp đến điểm P khác nhau do
đó hai dao động sáng do hai dải kế
tiếp gây ra tại P ngược pha nhau và chúng khử lẫn nhau. Kết quả là:
+ Nếu khe chứa một số chẵn dải (n = 2m) thì các sóng do 2 dải liên tiếp truyền tới P sẽ khử nhau và
P là một điểm tối. Vậy điều kiện của điểm tối là: (cực tiểu nhiễu xạ)
+ Trường hợp khe chứa số lẻ dải (n = 2m+1) thì sóng do hai dải liên tiếp tại P sẽ khử nhau, nhưng
sóng do dải lẻ thứ 2m+1 gây ra thì không bị khử, do đó P là điểm sáng. Vậy điều kiện để có điểm sáng là: (cực đại nhiễu xạ)
Với các tia nhiễu xạ đi theo phương = 0, các tia tới tâm màn F’ đều có cùng một khoảng cách,
do đó các sóng cùng pha với nhau và giao thoa được tăng cường tạo ra một cực đại gọi là cực đại giữa. Tóm lại ta có:
 Vị trí của cực đại giữa: ĐÀO TUẤN ĐẠT 18
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
 Vị trí của các cực tiểu:
 Vị trí của các cực đại:
Sự phân bố cường độ sáng
Giả sử sóng ánh sáng tới mặt khe là E =
Có thể tính được biên độ của sóng nhiễu xạ
theo phương gửi tới P là: = α =
Do đó cường độ sáng theo phương nhiễu xạ là =
Cường độ sáng phụ thuộc vào góc nhiễu xạ
, tức là phụ thuộc vào vị trí của điểm quan sát P.
Từ đây ta tìm lại được các công thức xác định vị trí các cực đại và cực tiểu.
Đồ thị biểu diễn sự phụ thuộc của cường độ sáng vào góc nhiễu xạ như hình vẽ. Từ đồ thị ta thấy:
+ Phần lớn năng lượng ánh sáng đi qua khe đều tập trung ở cực đại giữa (cực đại chính).
+ Năng lượng của các cực đại phụ không đáng kể và giảm nhanh khi xa tâm. Ví dụ: . ĐÀO TUẤN ĐẠT 19
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 3 - PH1131 - ĐÀO TUẤN ĐẠT
2. Nhiễu xạ qua nhiều khe
Khi khảo sát sự nhiễu xạ của sóng phẳng qua một khe ta thấy rằng sự phân bố cường độ sáng
chỉ phụ thuộc vào phương của chùm nhiễu xạ. Điều đó cho thấy, nếu dịch chuyển khe song song
với chính nó trong mặt phẳng chứa khe không làm thay đổi hình ảnh nhiễu xạ. Vì vậy nếu ta đặt
thêm khe thứ 2, thứ 3 có bề rộng a, song song với khe thứ nhất thì ảnh nhiễu xạ của từng khe riêng
rẽ sẽ hoàn toàn trùng nhau. Tuy nhiên ở đây ngoài sự nhiễu xạ của từng khe riêng rẽ còn có sự giao
thoa gây bởi các khe, nên có sự phân b
ố lại cường độ sáng, làm cho ảnh nhiễu xạ trở nên phức tạp hơn.
Giả sử có N khe hẹp giống nhau, song song và nằm trong cùng một mặt phẳng. Bề rộng của 1
khe là a và khoảng cách giữa các khe là d.
Khi rọi một chùm tia đơn sắc song song lên các khe, các khe được coi là nguồn kết hợp nên các
chùm nhiễu xạ sẽ giao thoa với nhau. Sự giao thoa của các chùm kết hợp này cho cường độ sáng tại điểm P là: I = = =
là cường độ sáng do 1 khe gây nên, ứng với = 0.
Kể đến sự nhiễu xạ qua mỗi khe nữa thì sự phân bố cường độ sáng trên màn quan sát là I = (*)
Điều kiện cho các cực đại, cực tiểu
Khảo sát (*) ta có các kết quả sau đây
+ = 0: xác định vị trí của cực đại giữa. + sin =
: xác định vị trí của cực tiểu chính.
Xét hai tia sáng xuất phát từ hai khe kế tiếp.
Hiệu quang lộ của hai tia là: + Nếu
thì tại P là một điểm sáng. Vị trí của các cực đại chính thỏa mãn sin =
Vì d > a do đó giữa 2 cực tiểu chính có thể có nhiều cực đại chính. ĐÀO TUẤN ĐẠT 20