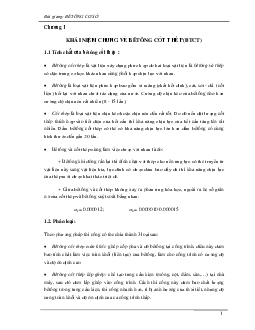




Preview text:
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM Chương 3
THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM
Ví dụ 3.1: Xét thanh thẳng chịu lực như trên hình 3.4. 3 P = 40KN 2 P = 80KN 1 P = 30KN 3 2 1 A D 3 C 2 B 1 1 NZ P = 30KN 1 a) 2 P2 = 80KN NZ P1 = 30KN b) 3 P3 = 40KN P2 = 80KN NZ P1 = 30KN c) 30KN + 30KN NZ - - 10KN 50KN 50KN
Hình 3.4. Cách vẽ biểu đồ lực dọc
Ta xét từ bên phải qua vì đầu bên phải là đầu tự do, không
cần xác định phản lực.
Đoạn AB: xét cân bằng tại mặt cắt 1-1 (hình 3.4a), ta được:
∑ Z = 0 ⇒ N1 − P = 0 ⇒ N1 = P = k 30 N z 1 z 1
Đoạn BC: xét cân bằng tại mặt cắt 2-2 (hình 3.4b), ta được: 2 2
N + P − P = 0 ⇒
N = P − P = 30 − 80 = 50 − KN < 0 Z 2 1 Z 1 2
Đoạn CD: xét cân bằng tại mặt cắt 3-3 (hình 3.4c), ta được: 3
N + P − P − P = 0 Z 2 3 1 3
⇒ N = P + P − P = 30 + 40 − 80 = 10 − KN < 0 Z 1 3 2
Biểu đồ lực dọc như trên hình 3.4. 83
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM
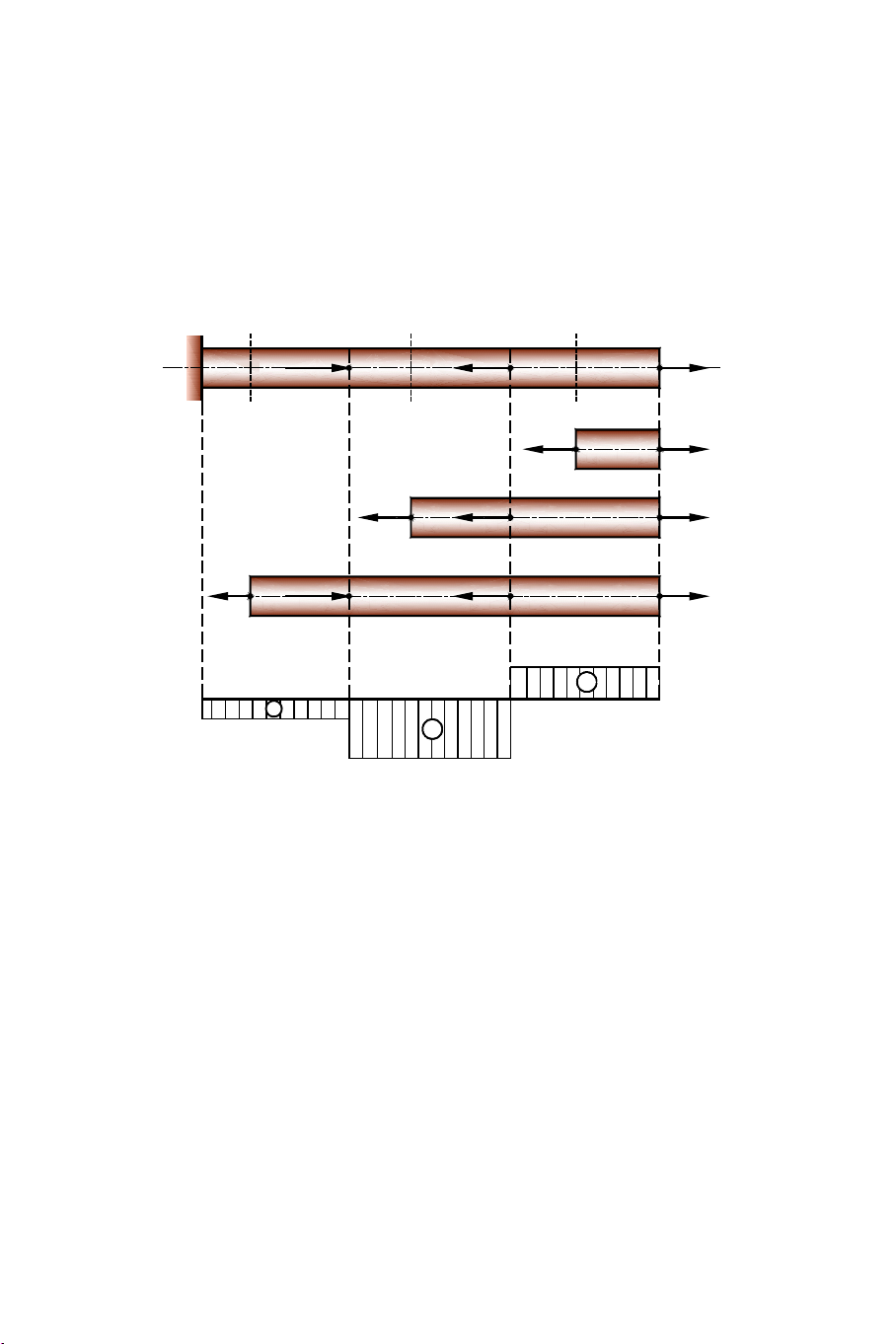
Ví dụ 3.2: Cho thanh có sơ đồ chịu lực như hình vẽ 3.11. A2 A1 P = 90KN 2 P = 40KN 1 C A B 1,5m 1,5m Hình 3.11
1. Vẽ biểu đồ lực dọc ?
2. Xác định trị số ứng suất pháp lớn nhất ?
3. Xác định chuyển vị theo phương dọc trục của trọng tâm tiết
diện tại C. Biết: A1 = 5cm2; A2 = 10cm2; E = 2.104 (KN/ cm2. Giải:
1. Dùng phương pháp mặt cắt xác định lực dọc:
Đoạn BC: N = P = 40KN > 0 BC 1
Đoạn AB: N = P − P = 40 − 90 = 50 − KN < 0 AB 1 2
Biểu đồ nội lực được vẽ trong hình 3.12. 2 P = 90KN 1 2 P = 40KN 1 C A 2 B 1 N 1 P = 40KN BC 1 a) C 1 2 P = 90KN N 2 P = 40KN AB 1 b) C 2 B + 40KN 50KN 40KN NZ _ 50KN Hình 3.12 84
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM
2. Xác định trị số ứng suất pháp lớn nhất N 40 BC 2 σ = = = 8 KN / cm BC A 5 1 N 50 AB 2 σ − = = = 5 − KN / cm AB A 10 2 2 ⇒ σ = 8 KN / cm max
3. Chuyển vị của điểm C
Chuyển vị của điểm C được tính so với gốc là đầu ngàm A N L N L BC BC AB AB y = y = y + y = + C CA CB BA EA EA 1 2 2 2 40.1,5.10 50.1 − ,5.10 ⇒ y = +
= 0,0225 cm > 0 Thanh dãn ra C 4 4 ( ) 2.10 .5 2.10 .10
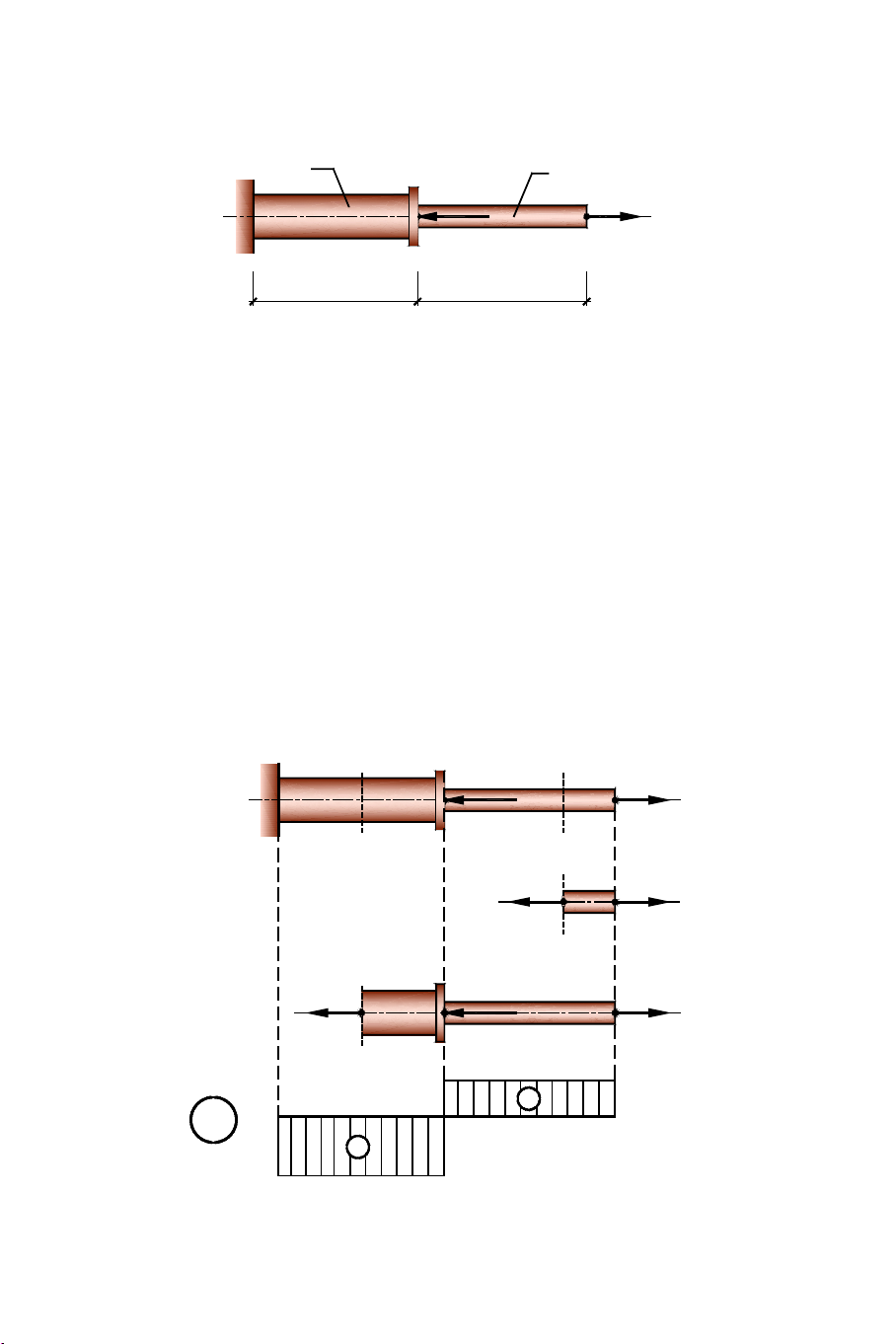
Ví dụ 3.3: Cho thanh tiết diện thay đổi, chịu tải trọng dọc trục như
hình 3.13. Vẽ biểu đồ lực dọc và tính ứng suất, chuyển vị của
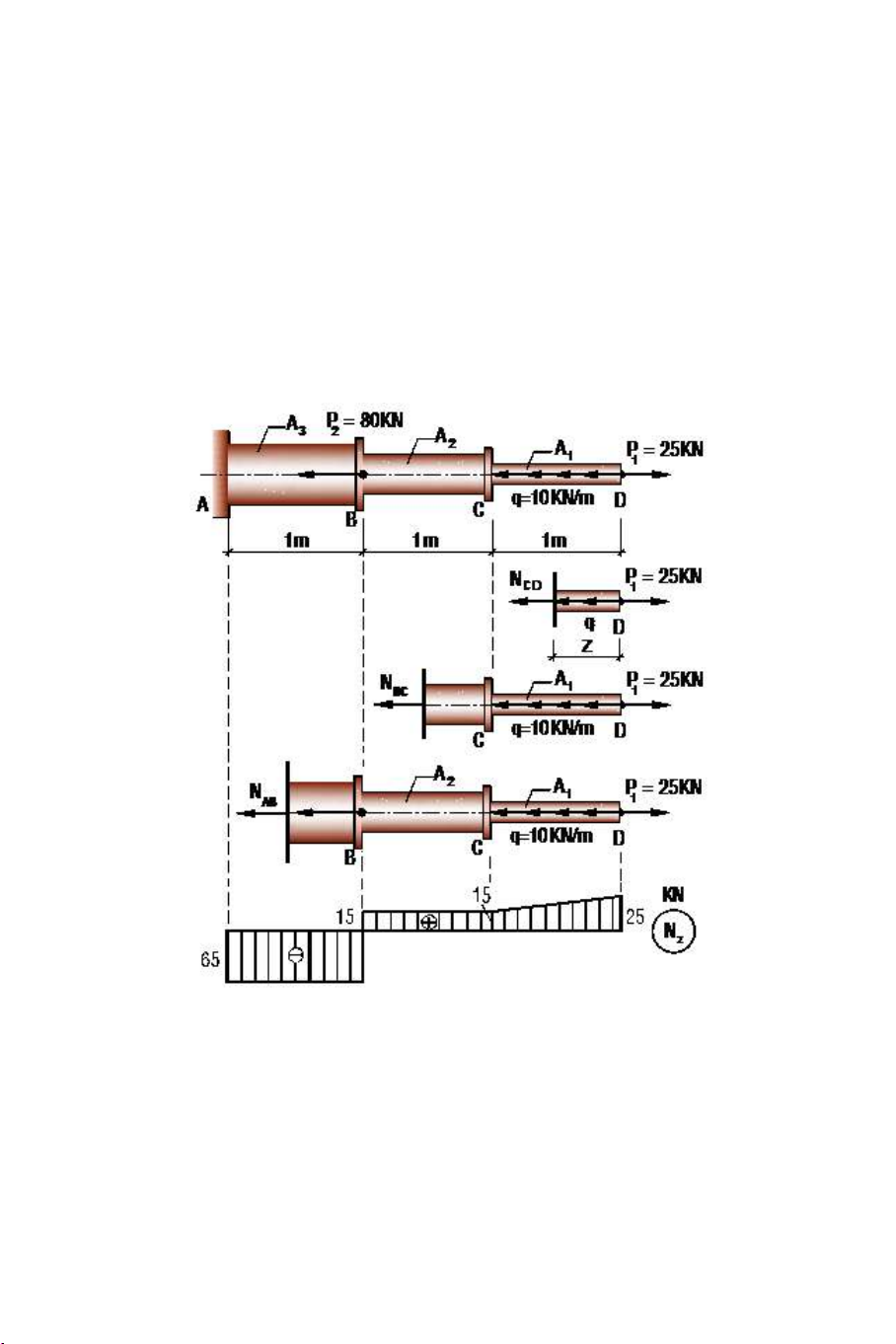
thanh. Biết: A3 = 1,5 A2 = 2A1 = 15cm2; E = 2.104 (kN/ cm2) P = 80KN A 3 2 A 2 A1 P = 25KN 1 A q=10KN/m D C B 1m 1m 1m Hình 3.13 Giải:
1. Nội lực các đoạn thanh
Ta xét từ bên phải qua vì đầu bên phải là đầu tự do, không
cần xác định phản lực.
Đoạn CD: ( 0 ≤ z ≤1m ):
∑ Z = 0 ⇒ N = P − qz = 25 −10z CD 1 85
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM
z = 0 ⇒ N = P = 25KN CD 1 ⇒ z = 1 ⇒ N
= P − q = 25 −10 = 15KN CD 1 Đoạn BC: ∑ Z = 0 ⇒ N
= P − q.1 = 25 −10.1 = k 15 N BC 1 Đoạn AB: ∑ Z = 0 ⇒ N
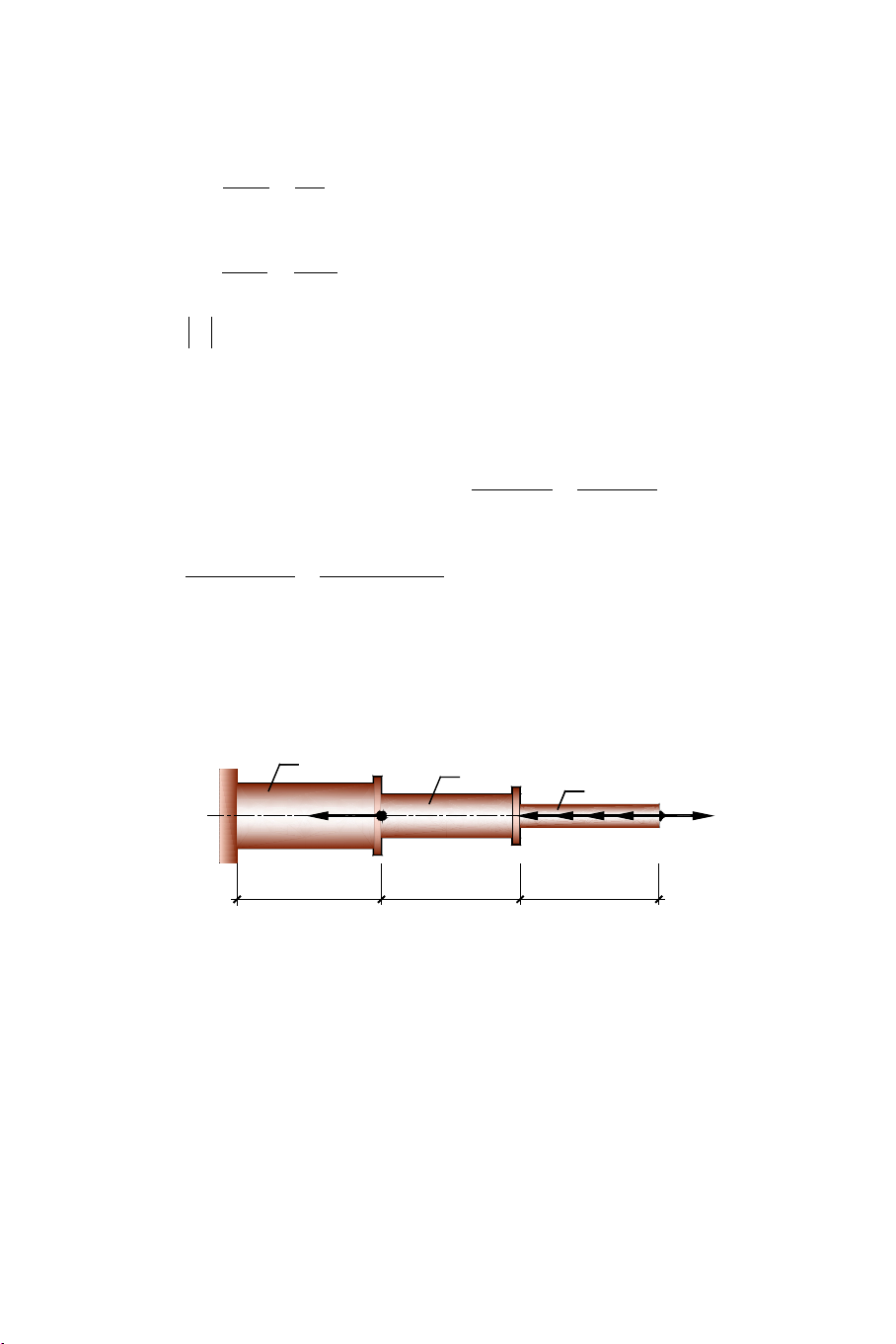
= P − q.1− P = 25 −10.1− 80 = − k 65 N AB 1 2 Hình 3.14
2. Giá trị ứng suất trên các đoạn:
Đoạn CD: ( 0 ≤ z ≤1m ) 86
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM N 25 CD 2 z = 0 ⇒ σ = = = 3,33 KN / cm CD A 7,5 1 ⇒ N 15 CD 2 z = 1 ⇒ σ = = = 2 KN / cm CD A 7,5 1 Đoạn BC: N 15 BC 2 σ = = = 1,5 KN / cm BC A 10 2 Đoạn AB: N 65 AB 2 σ − = = = 4 − ,3 KN / cm AB A 15 3
3. Chuyển vị tại các đoạn thanh:
Biểu đồ biến dạng của thanh diễn tả sự biến dạng của mặt cắt
ngang theo vị trí của chúng đối với một góc cố định nào đó. Ở đây gốc là đầu ngàm
Đoạn AB: ( 0 ≤ z ≤100cm) NAB , E, A3 = const 100 N 65 − z AB AB 4 y = y + dz = 0 + = 2 − ,2.10− .z cm ∫ AB A 4 AB ( ) EA 2.10 .15 0 3
Tại z = 0 ⇒ y = y = 0 AB A Tại z = 100cm 2 y y 2, 2.10− ⇒ = = − cm AB B
Đoạn BC: (0 ≤ z ≤100cm) NBC , E, A2 = const 100 N − z BC 2 15 y = y + dz = 2 − ,2.10 BC + ∫ BC B 4 EA 2.10 .10 0 3 2 − 4 2, 2.10 0,8.10− = − + .z cm BC ( ) Tại z = 0 2 y y 2, 2.10− ⇒ = = − cm BC B Tại z = 100cm 2 y y 1, 4.10− ⇒ = = − cm BC C
Đoạn CD: ( 0 ≤ z ' ≤100cm ) 87
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM 100 100 NCD 2 − 1 y = y + dz = 1 − ,4.10 + − z dz ∫ ∫ CD C (25 10 CD ) EA EA 0 1 1 0 2 − 2 − 25z 5z = 1 − ,4.10 CD CD + 4 2.10 .7,5 Tại z’ = 0 2 y y 1, 4.10− ⇒ = = − cm CD D Tại z’ = 100cm 2 y y 1, 4.10− ⇒ = = − cm CD C
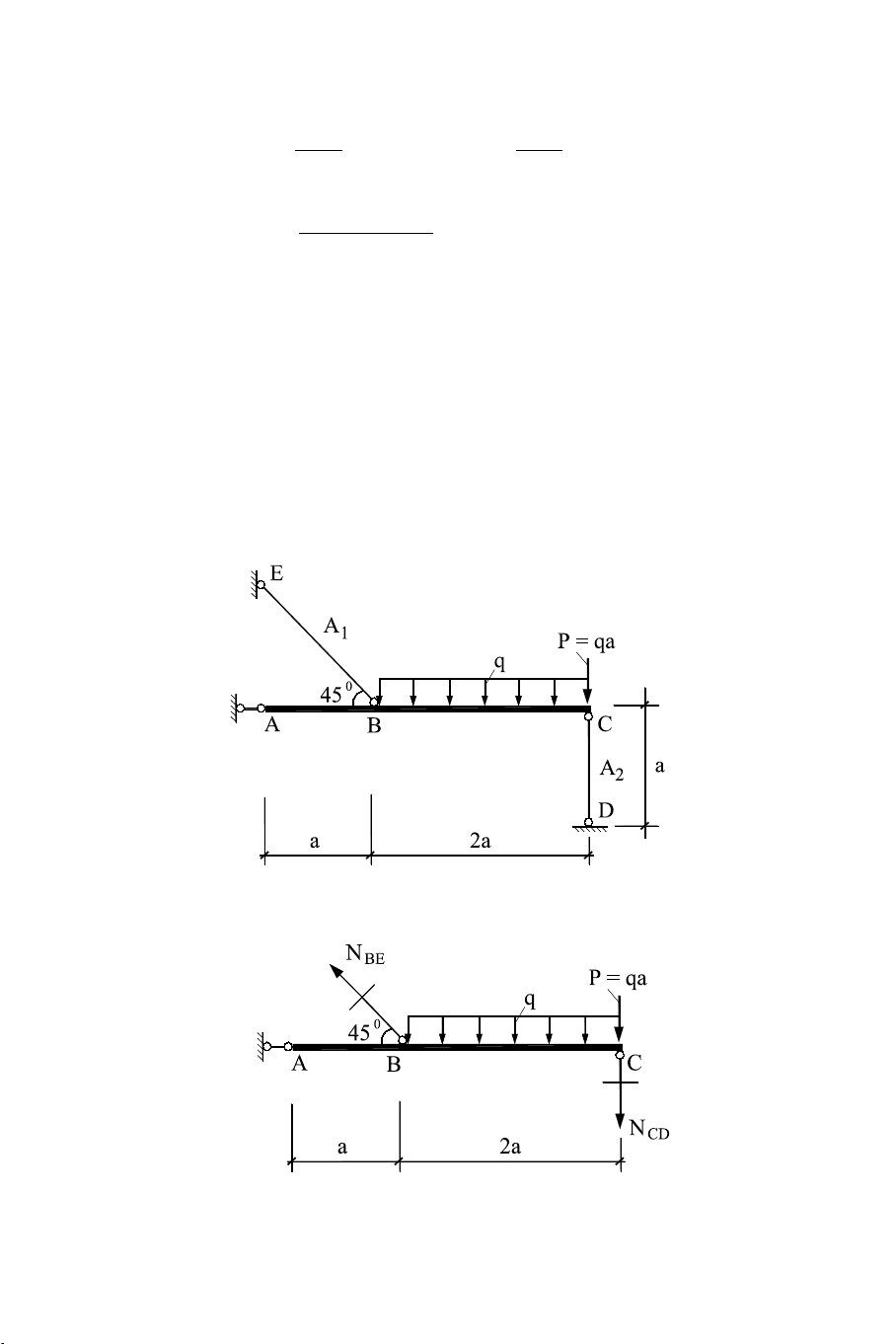
Ví dụ 3.4 Cho hệ kết cấu chịu lực như hình 3.23, trong đó thanh
ABC được xem là tuyệt đối cứng. Yêu cầu: Xác định tải trọng cho
phép [q] tác dụng lên hệ từ điều kiện bền của hệ ? Biết a = 1 m, A1
= 18 cm2, A2 = 6 cm2, thanh BE và CD cùng làm bằng một loại vật
liệu có [σ]k = 3 kN/cm2, [σ]n = 10 kN/cm2. Hình 3.23 Hình 3.24 88
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM
Giải. Trước hết ta tính nội lực trong các thanh BE và CD (hình 3.22):
∑Y = NBE.sin45o - NCD - qa - q.2a = 0
∑M/B = NCD .2a + qa.2a + q.2a.a = 0
⇒ NBE = 2 qa (kéo)
NCD = -2qa (nén)
Xác định [q] từ đk bền: Thanh BE: |N [σ] BE| = 2 qa ≤ k .A1 [σ ] → .A . 3 18 1 ( q k ≤ = = = 1) 0,38 k N / cm 38kN / m 2a 2.100
Thanh CD: |N | = 2qa ≤ [σ] CD n .A2 [σ ] → .A 10.6 2 ( q n ≤ = = = 2) 0,3 k N / cm 30kN / m 2a 2.100
Chọn [q] = min(q(1),q(2)) = 0,3 kN/cm = 30 kN/m
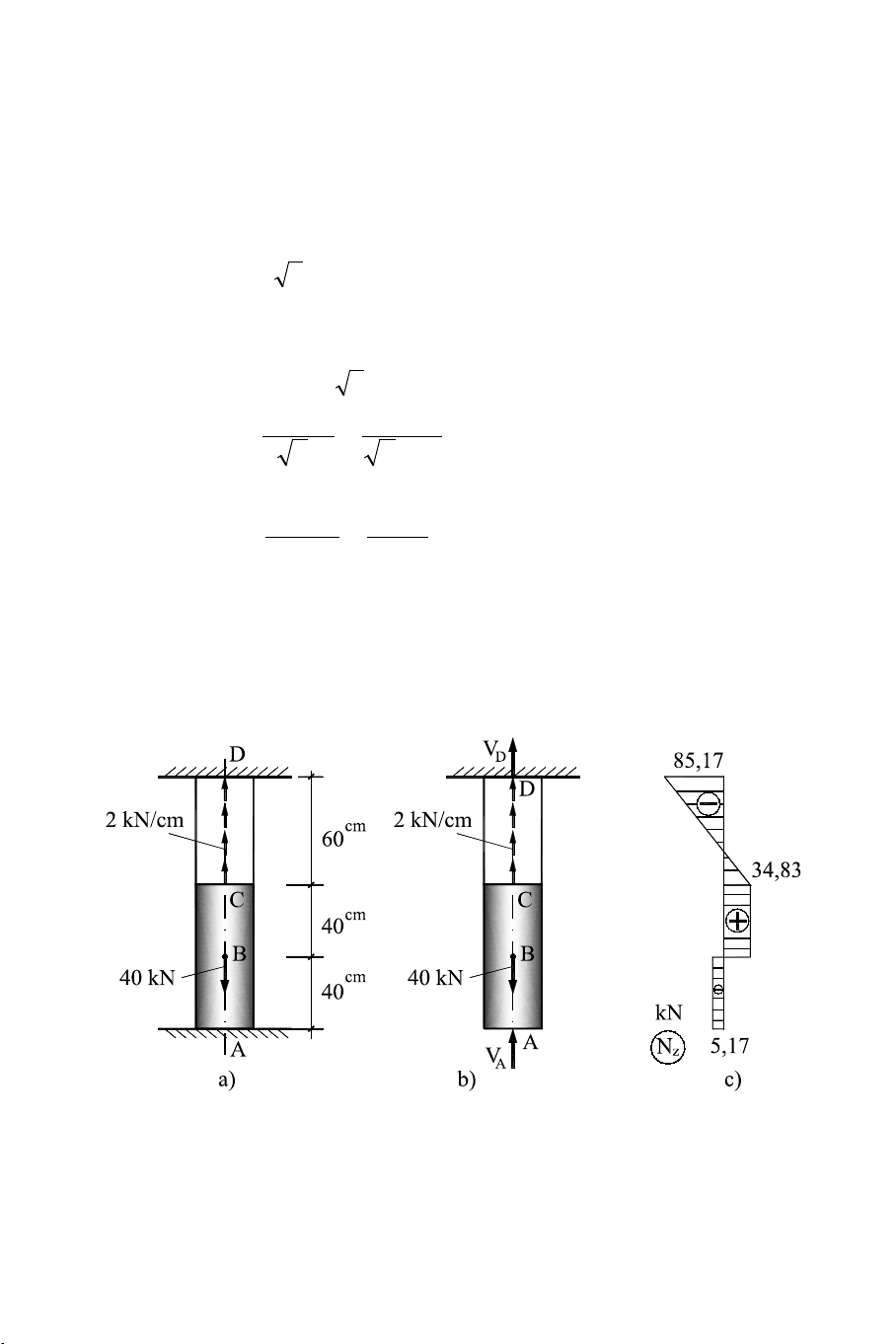
Ví dụ 3.5 Cho một thanh có sơ đồ chịu lực như hình 3.25a. Xác
định các phản lực liên kết và vẽ biểu đồ nội lực của thanh ? Hình 3.25 Giải. 89
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM
Ở hai ngàm có hai phản lực VA và VD. Ta có phương trình cân bằng: VA + VD +80 kN = 0 (a)
Ta thấy bài toán có hai ẩn nhưng chỉ có một phương trình cân
bằng, như vậy đây là bài toán siêu tĩnh. Muốn giải được ta phải tìm
thêm phương trình mô tả điều kiện biến dạng của thanh.
Tưởng tượng bỏ ngàm A để đưa về bài toán tĩnh định và thay
thế bằng phản lực VA (hình 3.23b). Khi đó, điều kiện biến dạng của hệ là: ∆ = 0 → L ∆ + L ∆ + L ∆ = 0 A AB BC CD 60 → N L . N L . N AB AB + BC BC + CD = 0 ∫ (b) EA EA EA AB BC 0 CD
Dùng phương pháp mặt cắt để xác định lực dọc trong các đoạn thanh AB ; BC và CD:
NAB = −VA; NBC = − VA + 40 ; NCD = − VA + 40 -2.z Thay vào (b) ta được: ( −V ) 40 . A (−V + 40 A ) 40 60 . (−V + 40 − 2 A ) → + + = 0 ∫ z . π (c) .42 / 4 π 42 . / 4 2 0 4
Giải hệ phương trình (a), (c) ta được: V = 5, k 17 N ;V = 85 − , k 17 N A D
Từ đó, suy ra: NAB = −5.17 kN; NBC = 34,83 kN; NCD = 34,83 -2.z (kN).
Biểu đồ lực dọc được vẽ trên hình 3.23c.
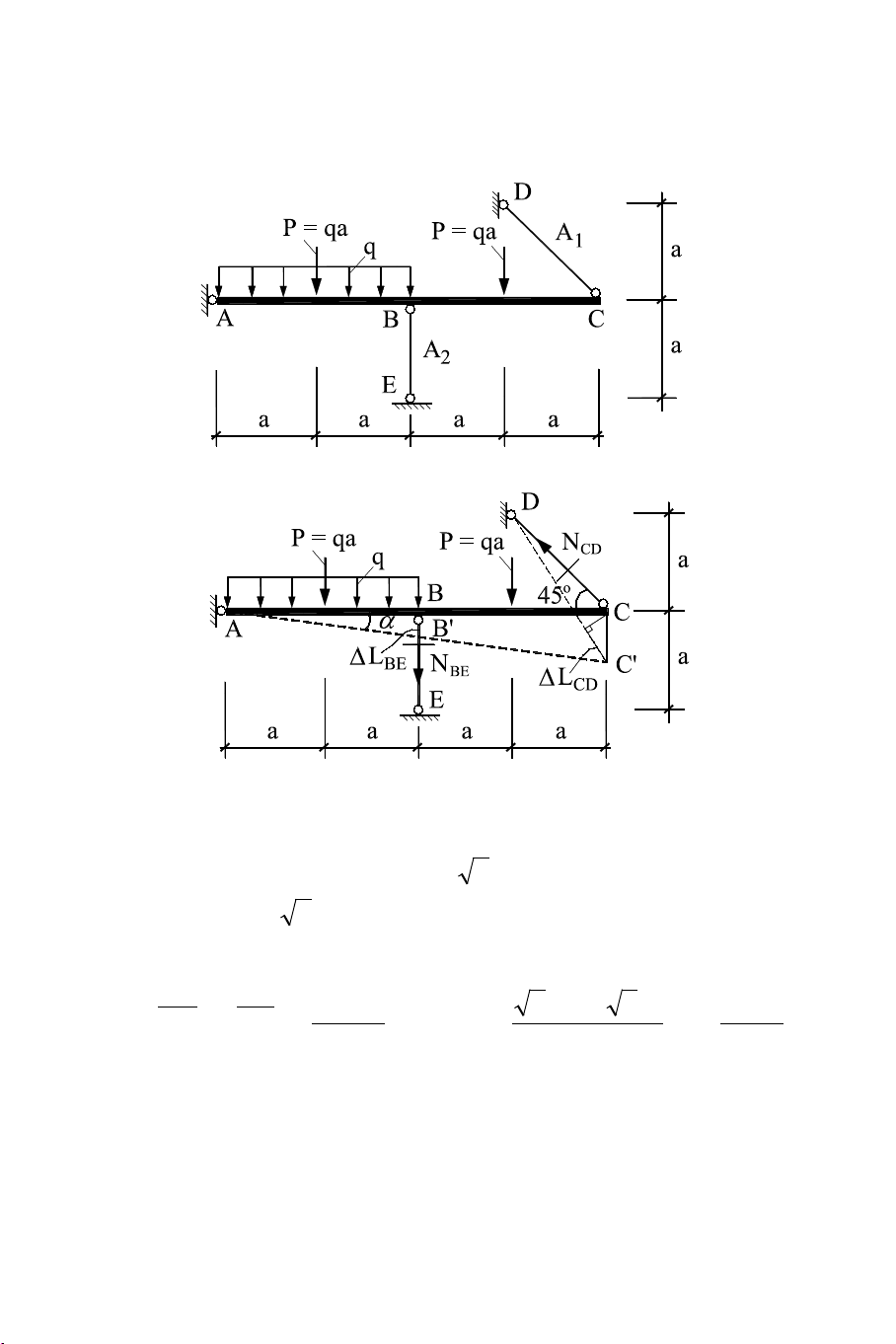
Ví dụ 3.6 Cho hệ kết cấu chịu lực như hình 3.26, trong đó thanh
ABC được xem là tuyệt đối cứng. Cho biết: a = 1 m, A1 = 8 cm2, A2
= 6 cm2, vật liệu các thanh có [σ]k = 3 kN/cm2, [σ]n = 10 kN/cm2 và E = 104 kN/cm2. Yêu cầu:
1. Xác định tải trọng cho phép [q] tác dụng lên hệ từ điều kiện bền của hệ ? 90
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM
2. Tính góc nghiêng của thanh ABC so với phương ngang với [q] đã chọn ở trên ? Hình 3.26 Hình 3.27
Giải. Đây là bài toán siêu tĩnh. Ta có phương trình cân bằng :
∑ M / A = 0 → N 2 . a − N 4 . . a 2 / 2 + qa 3 . a + . qa q + q 2 . . a a = 0 BE CD → 2N − N = qa 3 (1) CD BE
Ta cần tìm thêm phương trình biến dạng của hệ (hình 3.25): L ∆ 2N .( 2a ) N a . C ' C = 2 ' BB CD → = 2 L CD ∆ → = 2 BE − sin 45o BE EA EA 1 2 → 3N = 4 − N (2) CD BE
Giải hệ phương trình (1), (2) ta được: NCD = 1,386qa (kéo), NBE = -1,04qa (nén).
1. Chọn [q] từ điều kiện bền : 91
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM σ . 8 . 3 N = 386 , 1 qa ≤ σ . 1 → ≤ = = 173 , 0 / CD [ ] [ ] A A q k kN cm k 1 386 , 1 a 100 . 386 , 1 σ . 6 . 10 | N |= , 1 04qa ≤ σ . 2 → ≤ = = 577 , 0 / BE [ ] [ ] A A q n kN cm n 2 04 , 1 a 100 . 04 , 1
Chọn [q] = 0,173 kN/cm = 17,3 kN/m.
2. Tính góc nghiêng của thanh ABC : C ' C 2. L ∆ 2 N . . 2a N tan CD CD CD α = = = = = 4a 4a 4a EA . 2EA 1 1 , 1 . 386 0, . 173 100 = = , 1 . −4 o 5 10 → α = 0 ' 0 ' 30 ' . 2 104.8 92
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM CÂU HỎI ÔN TẬP
3.a Định nghĩa thanh chịu kéo hoặc nén đúng tâm ? Nêu các ví dụ
thực tế về thanh chịu kéo hoặc nén đúng tâm ?
3.b Các giả thiết khi tính toán thanh chịu kéo hoặc nén đúng tâm ?
3.c Công thức tính ứng suất pháp của thanh chịu kéo hoặc nén
đúng tâm ? Giải thích ý nghĩa và thứ nguyên của các đại lượng trong công thức đó ?
3.d Khái niệm biến dạng dài dọc trục và biến dạng dài ngang trục
của thanh chịu kéo hoặc nén đúng tâm ? Công thức tính các biến dạng này ?
3.e Dựa vào cơ sở nào để phân loại vật liệu dẻo và vật liệu giòn ?
Nêu một số loại vật liệu dẻo và giòn phổ biến trong kết cấu công trình ?
3.g Nêu các thí nghiệm kéo – nén cơ bản ? Từ các thí nghiệm đó ta
có thể xác định được những đặc trưng cơ học nào của vật liệu ?
Nhận xét về kết quả của các thí nghiệm đó ?
3.h Nêu quan điểm tính toán độ bền của vật liệu theo ứng suất cho
phép ? Biểu thức điều kiện bền của thanh chịu kéo hoặc nén đúng tâm ?
3.i Nêu ba bài toán cơ bản của thanh chịu kéo hoặc nén đúng tâm ?
3.k Thế nào gọi là bài toán siêu tĩnh và phương pháp giải như thế nào ?
3.l Khái niệm hiện tượng biến cứng nguội và hiện tượng lưu biến ? 93
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM BÀI TẬP CHƯƠNG 3
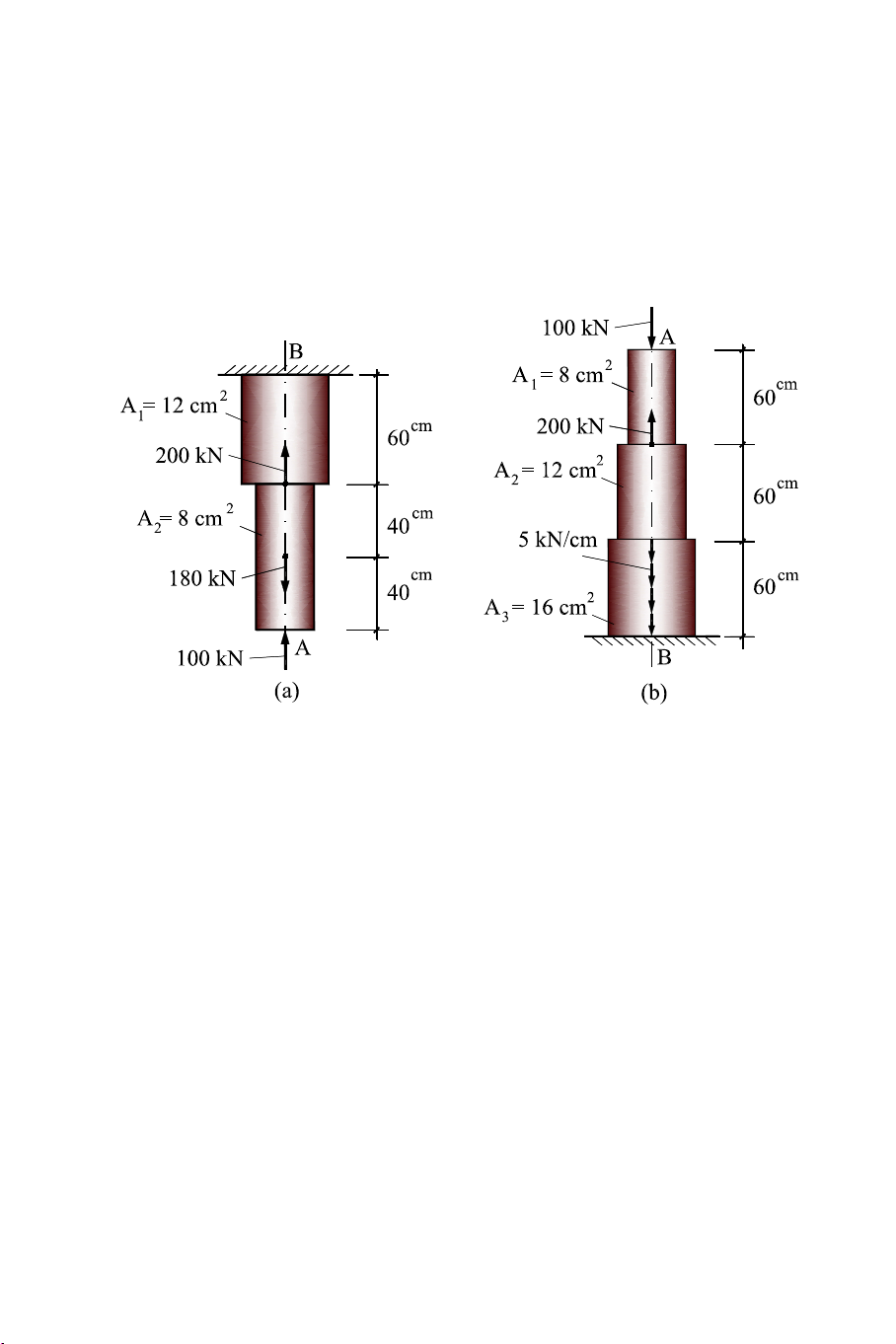
3.1 Cho thanh có sơ đồ chịu lực như hình 3.30. Vật liệu thanh có E = 104 kN/cm2. Yêu cầu:
1. Vẽ biểu đồ lực dọc và ứng suất của thanh ?
2. Tính chuyển vị của điểm A ? Hình 3.30
3.2 Cho hệ thanh liên kết như hình 3.31 trong đó thanh ABC được
xem là tuyệt đối cứng. Cho biết: Diện tích tiết diện thanh BE là A σ
1 = 5 cm2 và thanh CD là A2 = 3 cm2. Vật liệu thanh có: [ ] = 16
kN/cm2; E = 2.104 kN/cm2. Yêu cầu:
1. Tính lực dọc trong các thanh BE và CD (theo q và a) ?
2. Xác định tải trọng cho phép [q] tác dụng lên hệ trên ? Biết a = 1m.
3. Với tải trọng đã chọn ở trên, hãy tính biến dạng dọc của các thanh BE và CD? 94
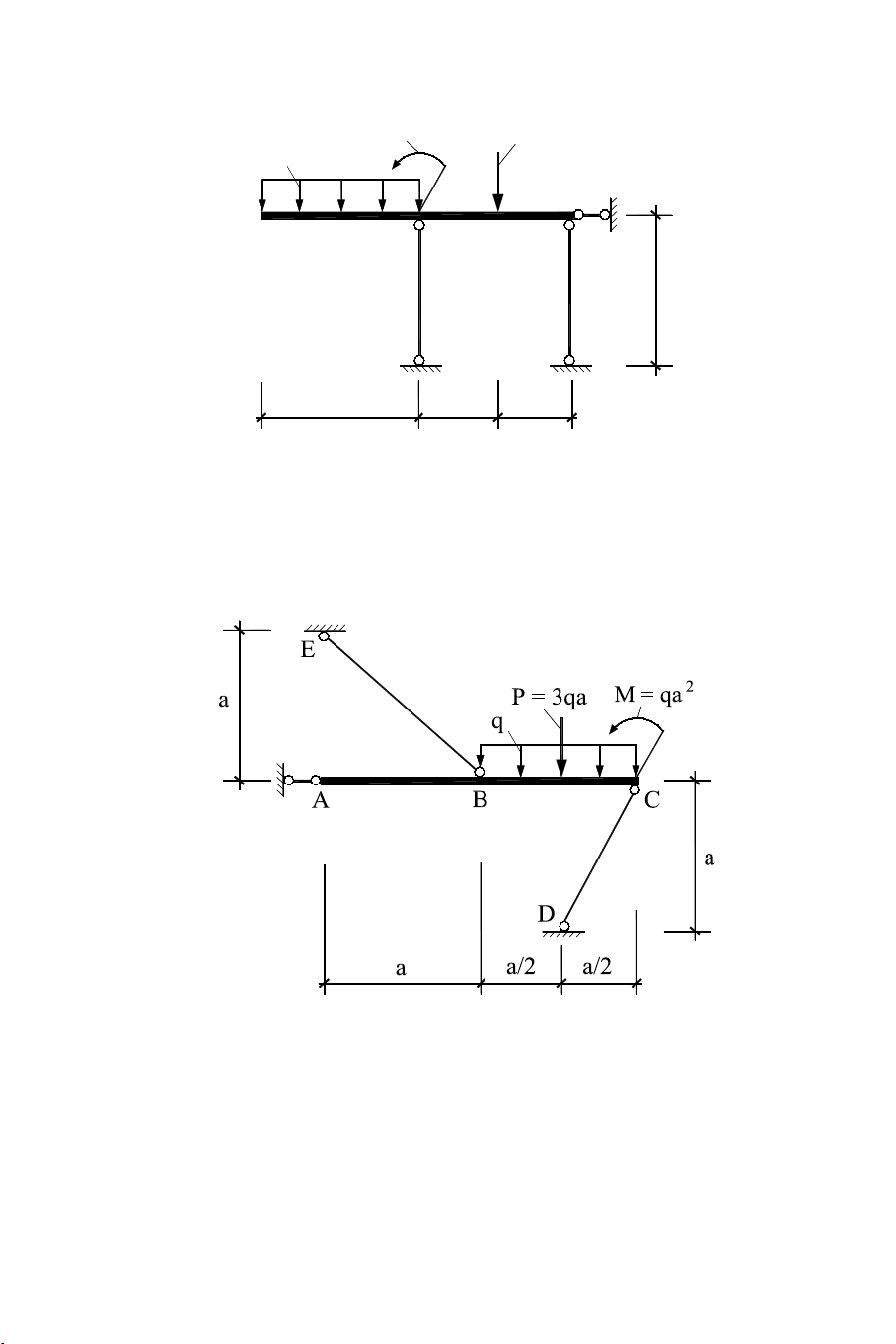
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM M = 2qa2 P = qa q A B C a E D a a/2 a/2 Hình 3.31
3.3 Cho hệ thanh liên kết như hình 3.32 trong đó thanh ABC được
xem là tuyệt đối cứng. Biết diện tích tiết diện thanh BE là A1 = 5 cm2 và thanh CD là A σ
2 = 2 cm2. Vật liệu các thanh có: [ ] k = 3
kN/cm2; [σ]n = 9 kN/cm2; E = 2.107 N/cm2. Hình 3.32 Yêu cầu:
1. Tính lực dọc trong các thanh BE và CD (theo q và a) ?
2. Xác định tải trọng cho phép [q] tác dụng lên hệ trên? Biết a=1 m. 95
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM
3. Với tải trọng đã chọn ở trên, hãy tính biến dạng dọc trục của các thanh BE và CD ?
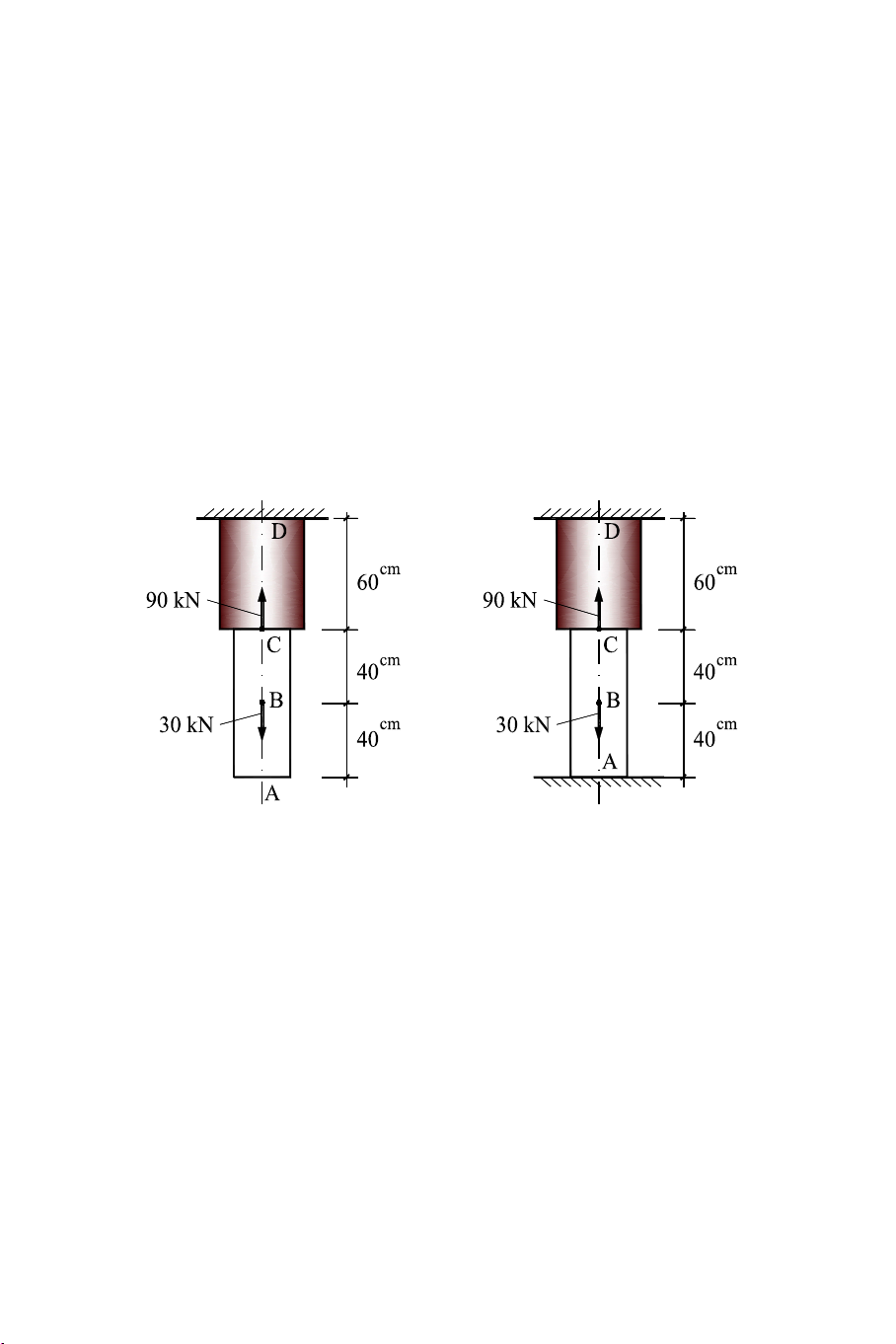
3.4 Cho một thanh có sơ đồ chịu lực như hình 3.33a. Biết đoạn
thanh AC có tiết diện tròn đường kính d = 6 cm còn đoạn thanh CD
có tiết diện vuông cạnh a = 4 cm. Các đoạn thanh đều làm bằng một
ại vật liệu như nhau có môđun đàn hồi E. Yêu cầu:
1. Vẽ biểu đồ lực dọc trong thanh ?
2. Thêm liên kết ngàm tại A (hình 3.33b), hãy vẽ lại biểu đồ lực dọc trong thanh ? a) b) Hình 3.33
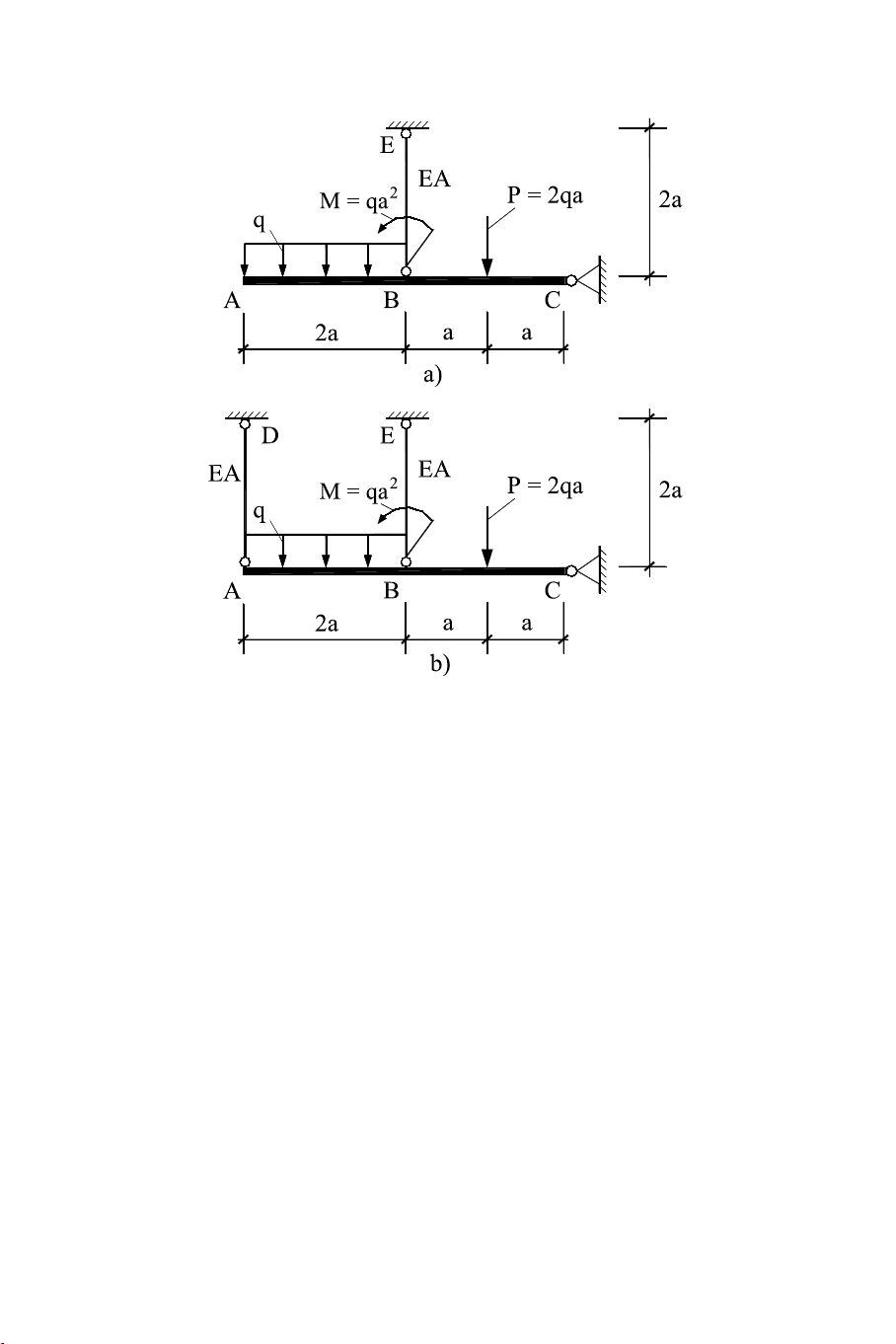
3.5 Cho hệ thanh liên kết như hình 3.34a trong đó thanh ABC được
xem là tuyệt đối cứng. Biết thanh BE có diện tích tiết diện là A = 4
cm2 và làm bằng vật liệu có: [σ] = 16 kN/cm2; E = 2.104 kN/cm2. 96
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM Yêu cầu: Hình 3.34
1. Tính lực dọc trong thanh BE (theo q và a) ?
2. Xác định tải trọng cho phép [q] tác dụng lên hệ trên từ điều kiện
bền của thanh BE? Biết a = 1 m.
3. Với tải trọng đã chọn ở trên, hãy tính chuyển vị đứng của điểm A?
4. Lắp thêm thanh treo AD vào hệ như hình 3.34b. Hãy tính lại nội
lực trong hai thanh AD và BE ? Biết hai thanh đều có độ cứng như nhau là EA.
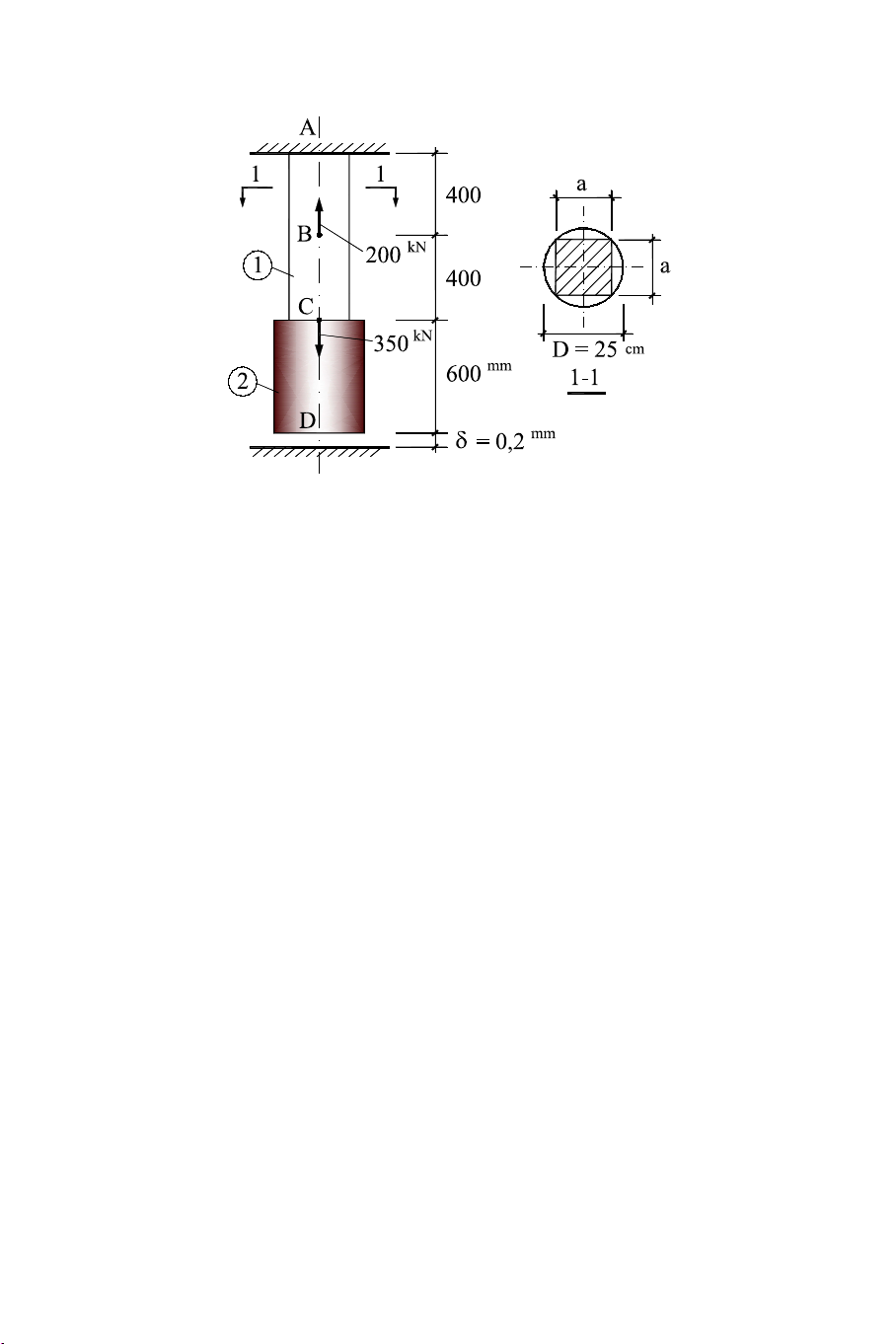
3.6 Cho thanh chịu lực như hình 3.35, trong đó đoạn (1) có mặt cắt
ngang hình vuông cạnh là a, đoạn (2) có mặt cắt ngang hình tròn
đường kính D = 25 cm (xem mặt cắt 1-1). Cho biết vật liệu thanh có E = 2,4.103 kN/cm2.
Yêu cầu: Vẽ biểu đồ nội lực và ứng suất trong thanh. 97
CHƯƠNG 3: THANH CHỊU KÉO HOẶC NÉN ĐÚNG TÂM Hình 3.35 98 Document Outline