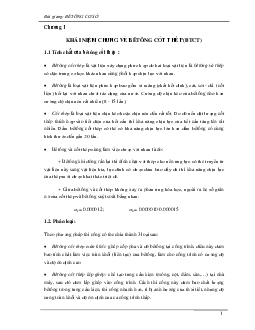

Preview text:
lOMoARcPSD|36477180
Chương 3+4 : TRẠNG THÁI ỨNG SUẤT – CÁC THUYẾT BỀN Chương 4
TR¹NG TH¸I øng suÊt - CÁC THUYẾT BỀN
4.1. Tóm tắt lý thuyết
1. Khái niệm về trạng thái ứng suất tại một điểm
- Nội lực: phân bố trên mặt cắt thuộc vật thể chịu lực.
- Ứng lực: Hợp lực của nội lực trên mặt cắt ngang.
- Ứng suất: tại một điểm trên một mặt cắt
- Trạng thái ứng suất: tại một điểm
- Định nghĩa trạng thái ứng suất tại một điểm: là tập hợp tất cả những thành
phần ứng suất trên tất cả các mặt đi qua điểm đó.
- Nghiên cứu trạng thái ứng suất tại một điểm: tách phân tố lập phương vô
cùng bé chứa điểm đang xét, biểu diễn các thành phần ứng suất trên tất cả các
mặt vuông góc với ba trục toạ độ x, y, z. Trên mỗi mặt ứng suất toàn phần có
phương, chiều bất kỳ được phân tích thành ba thành phần: 1 thành phần ứng suất
pháp vuông góc với mặt cắt và 2 thành phần ứng suất tiếp nằm trong mặt cắt.
Ký hiệu ứng suất: chỉ số 1 – phương pháp tuyến; chỉ số 2 – phương của ứng suất y y yx yz xy zy x zx z x z xz
Chín thành phần ứng suất tác dụng trên 3 cặp mặt vuông góc với ba trục tạo
thành một ten-xơ hạng hai gọi là ten-xơ ứng suất x xy xz T (4.1) yx y yz zx zy z
Tóm tắt lý thuyết và đề bài tập 1
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
Chương 4 – TRẠNG THÁI ỨNG SUẤT – CÁC THUYẾT BỀN
Lý thuyết đàn hồi đã chứng minh rằng: trạng thái ứng suất tại một điểm
hoàn toàn xác định nếu biết được ten-xơ ứng suất T tại điểm đó.
2. Mặt chính, phương chính, ứng suất chính
a) Mặt chính: Là mặt không có tác dụng của ứng suất tiếp.
b) Phương chính: là phương pháp tuyến của mặt chính.
c) Ứng suất chính: là ứng suất pháp tác dụng trên mặt chính.
d) Qui ước gọi tên các ứng suất chính:
Lý thuyết đàn hồi đã chứng minh rằng: tại 1 điểm luôn tồn tại ba mặt chính
vuông góc với nhau với ba ứng suất chính tương ứng ký hiệu là , , . Theo 1 2 3 qui ước: 1 2 3
3. Định luật đối ứng của ứng suất tiếp: Ứng suất tiếp trên hai mặt bất kỳ
vuông góc với nhau tại một điểm có giá trị bằng nhau, có chiều cùng hướng vào
cạnh chung hoặc cùng đi ra khỏi cạnh chung.
; ; (4.2) xy yx xz zx yz zy
4. Trạng thái ứng suất phẳng
Các thành phần ứng suất trên mặt cắt song song với trục z (z là
phương chính) và có pháp tuyến u hợp với trục x một góc
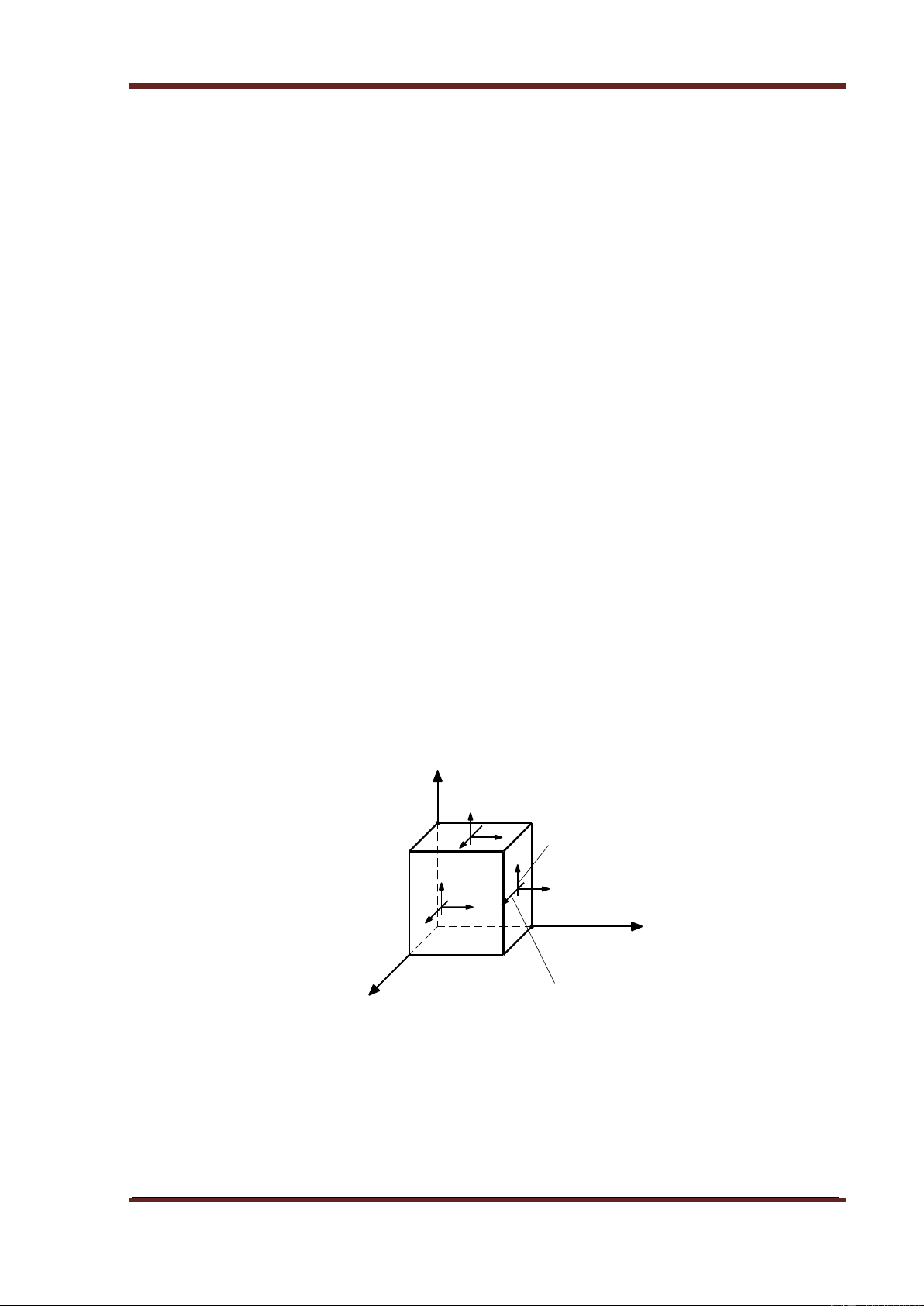
Qui ước dấu (như hình vẽ dưới đây):
- Ứng suất pháp dương khi có chiều đi ra khỏi phân tố
- Ứng suất tiếp có chiều dương khi đi vòng quanh phân tố theo chiều kim đồng hồ
- Góc dương khi quay từ trục x đến trục u theo chiều ngược chiều kim đồng hồ y y u yx u x x xy uv xy x yx y
Tóm tắt lý thuyết và đề bài tập 2
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
Chương 4 – TRẠNG THÁI ỨNG SUẤT – CÁC THUYẾT BỀN x y x y
cos2 - sin 2 u 2 2 xy x y
sin2 cos2 (4.3) uv 2 xy
Ứng suất pháp cực trị là các ứng suất chính 2 x y x y 2 (4.4) max, min 1,2(3) 2 2 xy
Các phương chính: Hai phương chính vuông góc với nhau 2 1 2 tg2 xy => 0 trong đó xy (4.5) arctg 1,2 0 90 0 2 x y 0 x y
Ứng suất tiếp cực trị: mặt có ứng suất tiếp cực trị hợp với mặt chính góc 450 2 x y 2 (4.6) max,min 2 xy
Bất biến của trạng thái ứng suất phẳng: tổng các ứng suất pháp trên
hai mặt bất kỳ vuông góc với nhau tại một điểm có giá trị không đổi
const (4.7) x y u v
Chú ý: Ngoài các công thức giải tích đã kể trên, người ta còn dùng đồ thị
để biểu diễn trạng thái ứng suất (vòng tròn Mohr ứng suất).
5. Quan hệ ứng suất - biến dạng -Định luật Hooke
a. Quan hệ ứng suất pháp – biến dạng dài 1 x x y z E 1 y y x z (4.8) E 1 z z x y E
b. Quan hệ ứng suất tiếp – biến dạng góc xy ; xz ; yz (4.9) xy G xz G yz G
với E, , G là mô đun đàn hồi kéo (nén), hệ số Poisson, mô đun đàn hồi
trượt, liên hệ với nhau bởi công thức: E G (4.10) 21
Tóm tắt lý thuyết và đề bài tập 3
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
Chương 4 – TRẠNG THÁI ỨNG SUẤT – CÁC THUYẾT BỀN
c. Quan hệ ứng suất pháp – biến dạng thể tích 12 (4.11) x y z x y z E
6. Các điều kiện bền theo các thuyết bền
+ Thuyết bền 1 (thuyết bền ứng suất pháp lớn nhất) 1 k (4.12) 3 n
+ Thuyết bền 2 (thuyết bền biến dạng dài lớn nhất)
(4.13) t 2 1 2 3 k
+ Thuyết bền 3 (thuyết bền ứng suất tiếp lớn nhất)
(4.14) t 3 1 3 k
+ Thuyết bền 4 (thuyết bền thế năng biến đổi hình dáng) 2 2 2
(4.15) t 4 1 2 3 1 2 1 3 2 3 k
+ Thuyết bền 5 (Thuyết bền Mohr) k (4.16) t 5 1 3 k n
Phạm vi sử dụng các thuyết bền: Hiện chỉ sử dụng các thuyết bền 3, 4, 5
- Thuyết bền 5 chỉ thích hợp với vật liệu giòn
- Thuyết bền 3, 4 chỉ thích hợp với vật liệu dẻo.
4.2. Bài tập tự giải
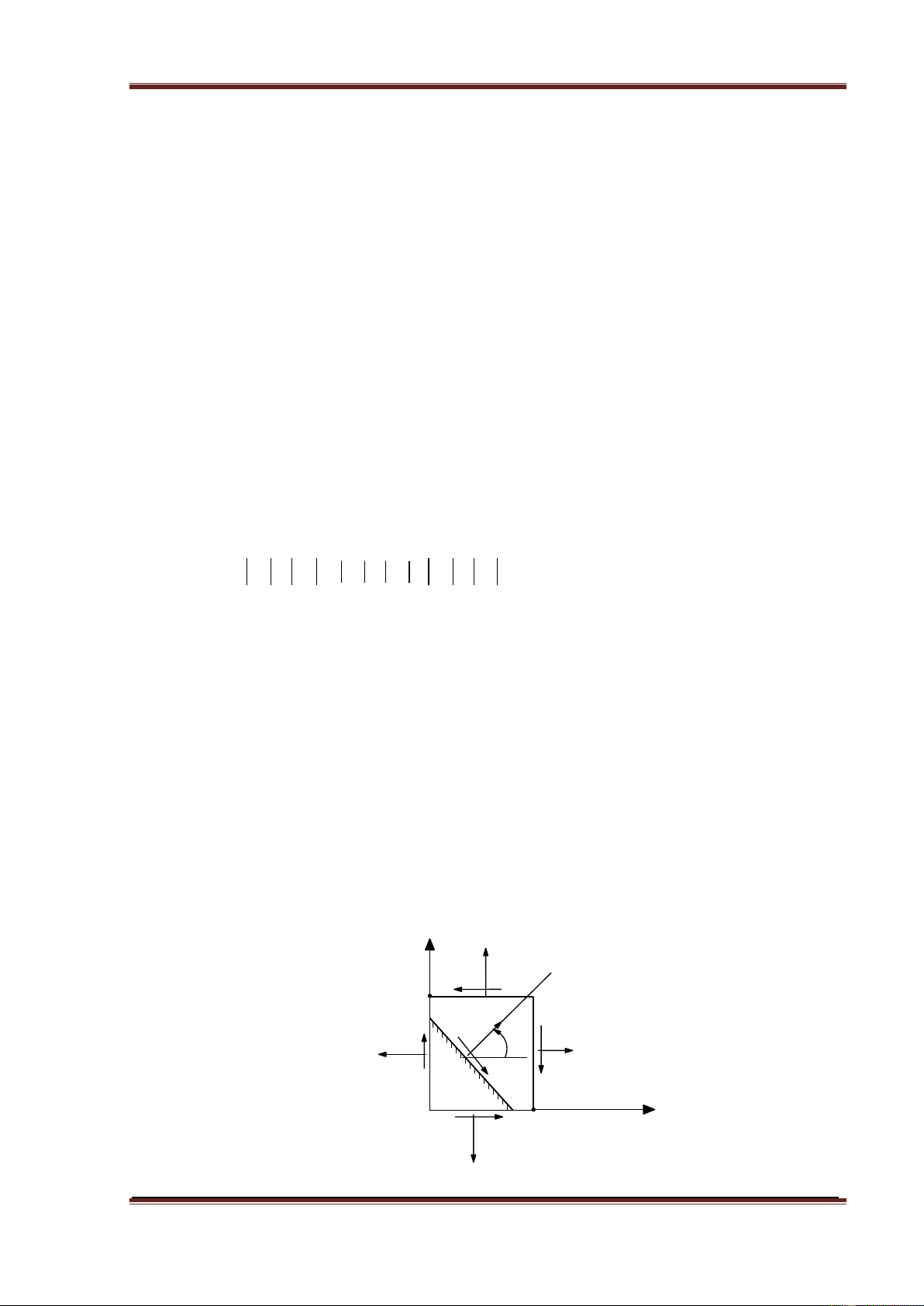
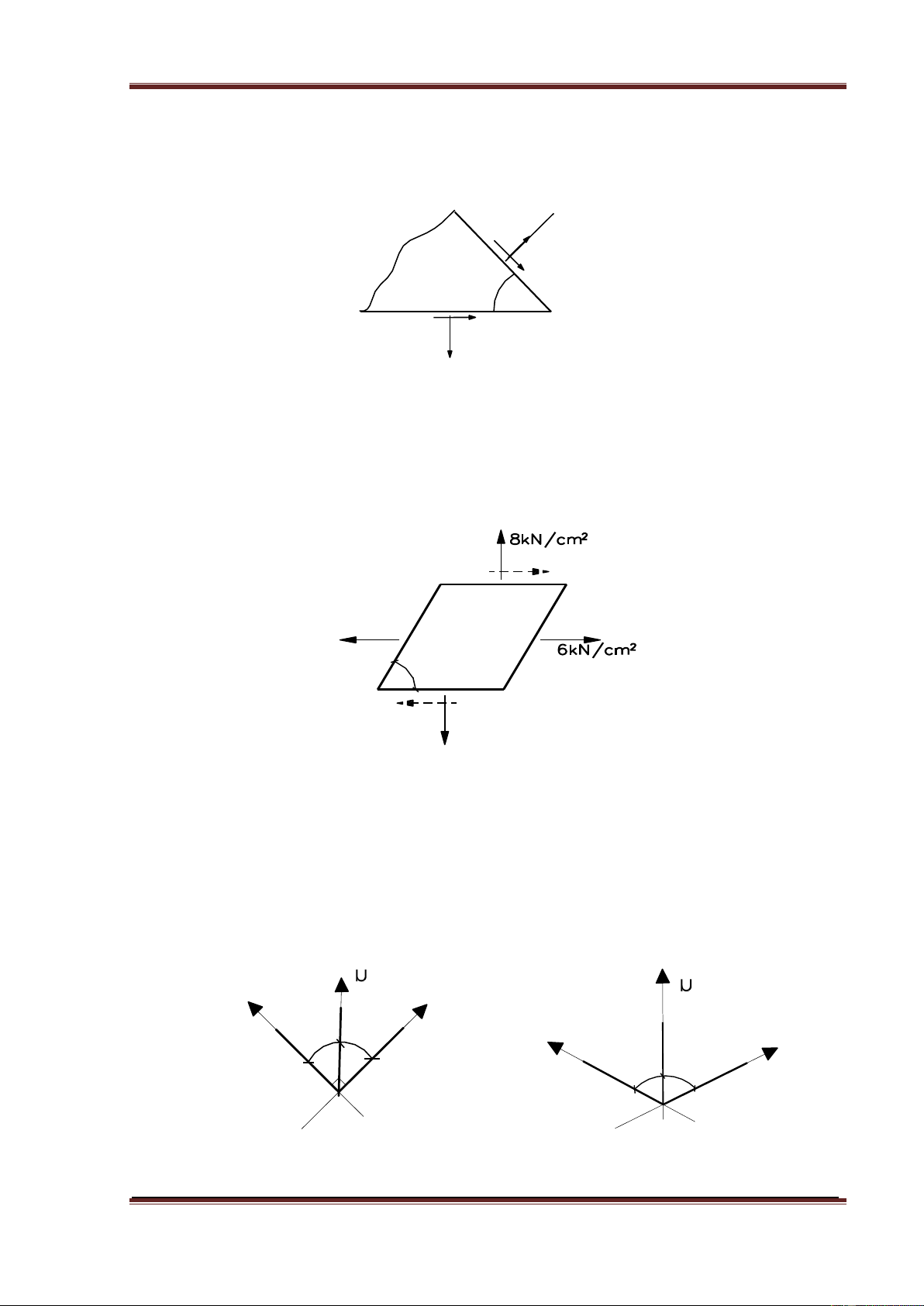
4.2.1. Ứng suất toàn phần trên mặt cắt m-n đi qua một điểm của vật thể ở trạng
thái ứng suất phẳng p=3kN/cm2 có phương tạo thành một góc 0 60 với
mặt cắt. Trên mặt vuông góc với mặt này chỉ có ứng suất tiếp. Tính ứng
suất pháp và ứng suất tiếp trên mặt cắt hợp với mặt m-n góc 450. Tính ứng suất pháp cực trị. m 600 p 0 45 n
Tóm tắt lý thuyết và đề bài tập 4
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
Chương 4 – TRẠNG THÁI ỨNG SUẤT – CÁC THUYẾT BỀN
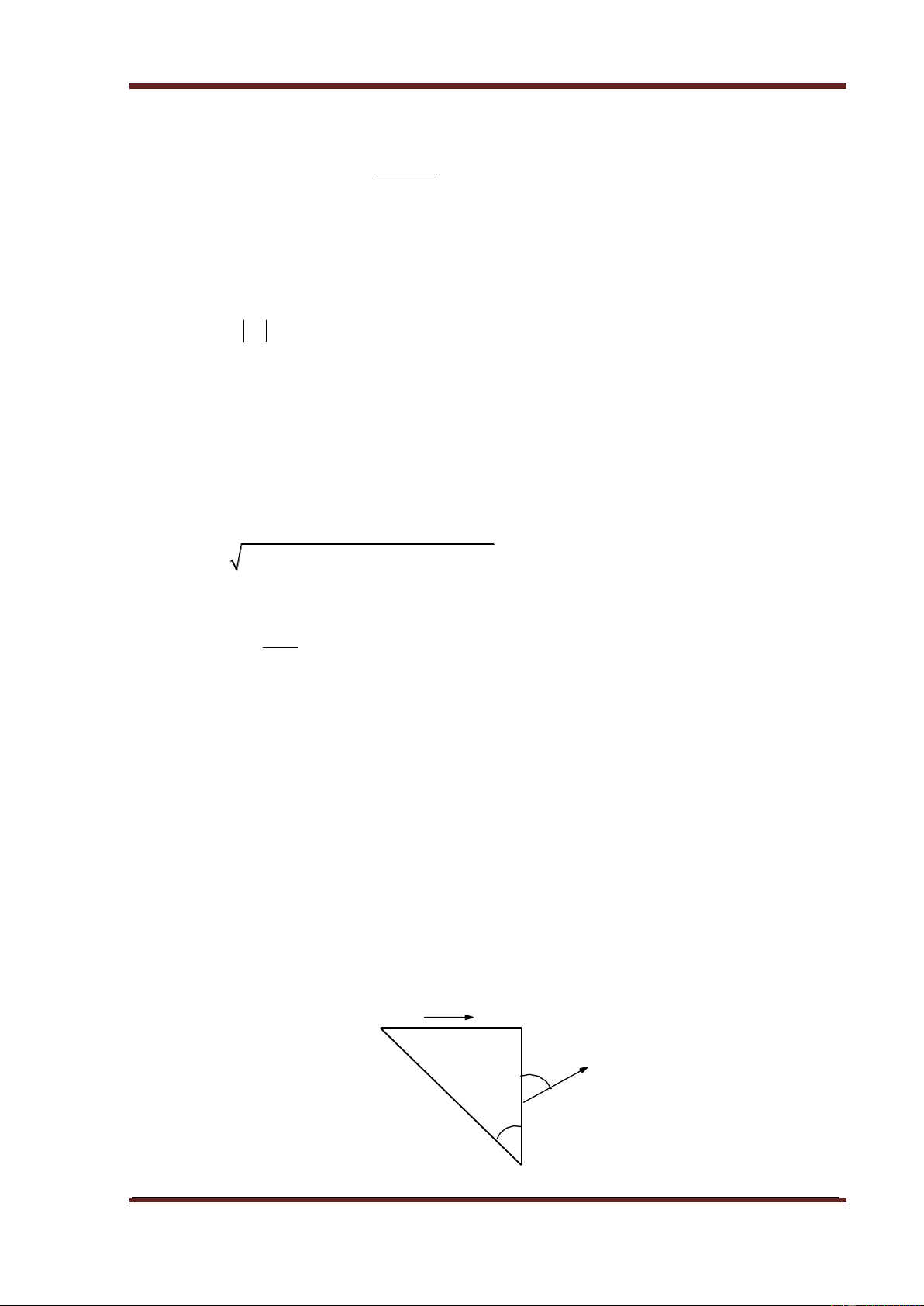
4.2.2. Trên hai mặt tạo với nhau góc 600 đi qua một điểm ở trạng thái ứng suất
phẳng có các thành phần ứng suất như trên hình vẽ. Hãy tính ứng suất
chính tại điểm đó, ứng suất pháp và biến dạng tương đối theo phương u. u 6 kN/cm2 600 5 kN/cm2 3 kN/cm2
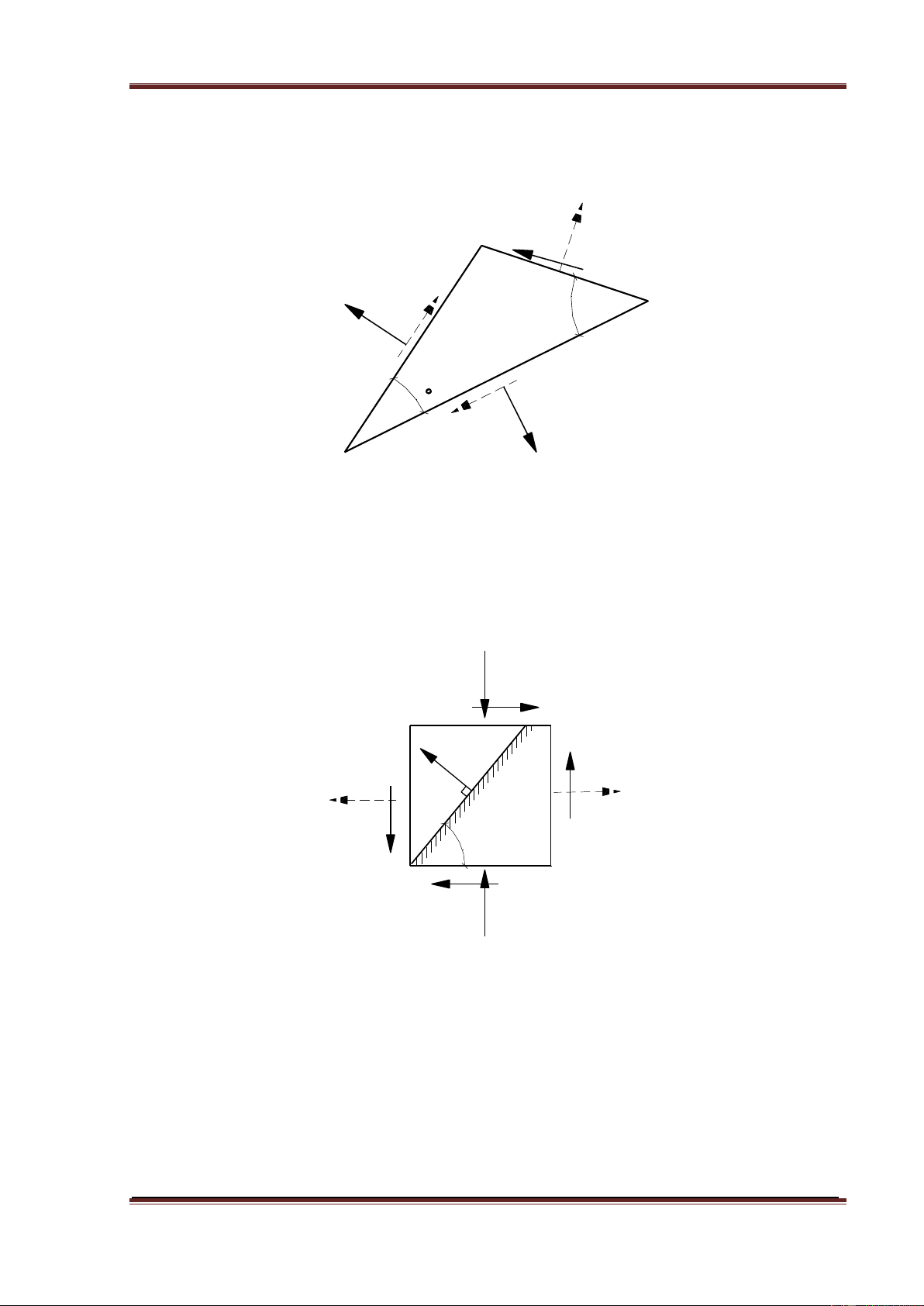
4.2.3. Một phân tố hình hộp xiên tách ra từ một vật thể chịu lực ở trạnh thái ứng
suất phẳng có các thành phần ứng suất tác động trên các mặt như hình vẽ.
Tìm các ứng suất chính và phương chính của trạng thái ứng suất tại điểm này (β=600)
4.2.4. T¹i mét ®iÓm thuéc tr¹ng th¸i øng suÊt ph¼ng ng- êi ta ®o ®- îc c¸c biÕn
d¹ng dµi t- ¬ng ®èi theo c¸c ph- ¬ng m, n, vµ u .TÝnh c¸c gi¸ trÞ øng suÊt
chÝnh vµ c¸c ph- ¬ng chÝnh t¹i ®iÓm nµy .
BiÕt vËt liÖu cã E=2104 kN/cm2 ; =0,3 ; =2,8110-4 ; =-2.8110-4 ; m n
=1,62510-4 . u n m 0 0 n m 45 45 0 0 60 60 (a) (b)
Tóm tắt lý thuyết và đề bài tập 5
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
Chương 4 – TRẠNG THÁI ỨNG SUẤT – CÁC THUYẾT BỀN
4.2.5. Trên các mặt cắt đi qua một điểm của vật thể ở trạng thái ứng suất phẳng
có các thành phần ứng suất như trên hình vẽ. Xác định các ứng suất chính
và các phương chính tại điểm này. 2kN/cm2 2 5kN/cm 45 C 30 6kN/cm2 A
4.2.6. Trªn c¸c mÆt c¾t ®i qua mét ®iÓm cña vËt thÓ ë tr¹ng th¸i øng suÊt ph¼ng cã
c¸c thµnh phÇn øng suÊt nh- h×nh vÏ .
1.X¸c ®Þnh c¸c øng suÊt chÝnh vµ c¸c ph- ¬ng chÝnh t¹i ®iÓm nµy
2.TÝnh biÕn d¹ng dµi t- ¬ng ®èi theo c¸c ph- ¬ng chÝnh.
BiÕt E=2x104 kN/cm2 ; =0,3 . =600 . 8kN/cm2 A 6kN/cm2 2kN/cm2 B
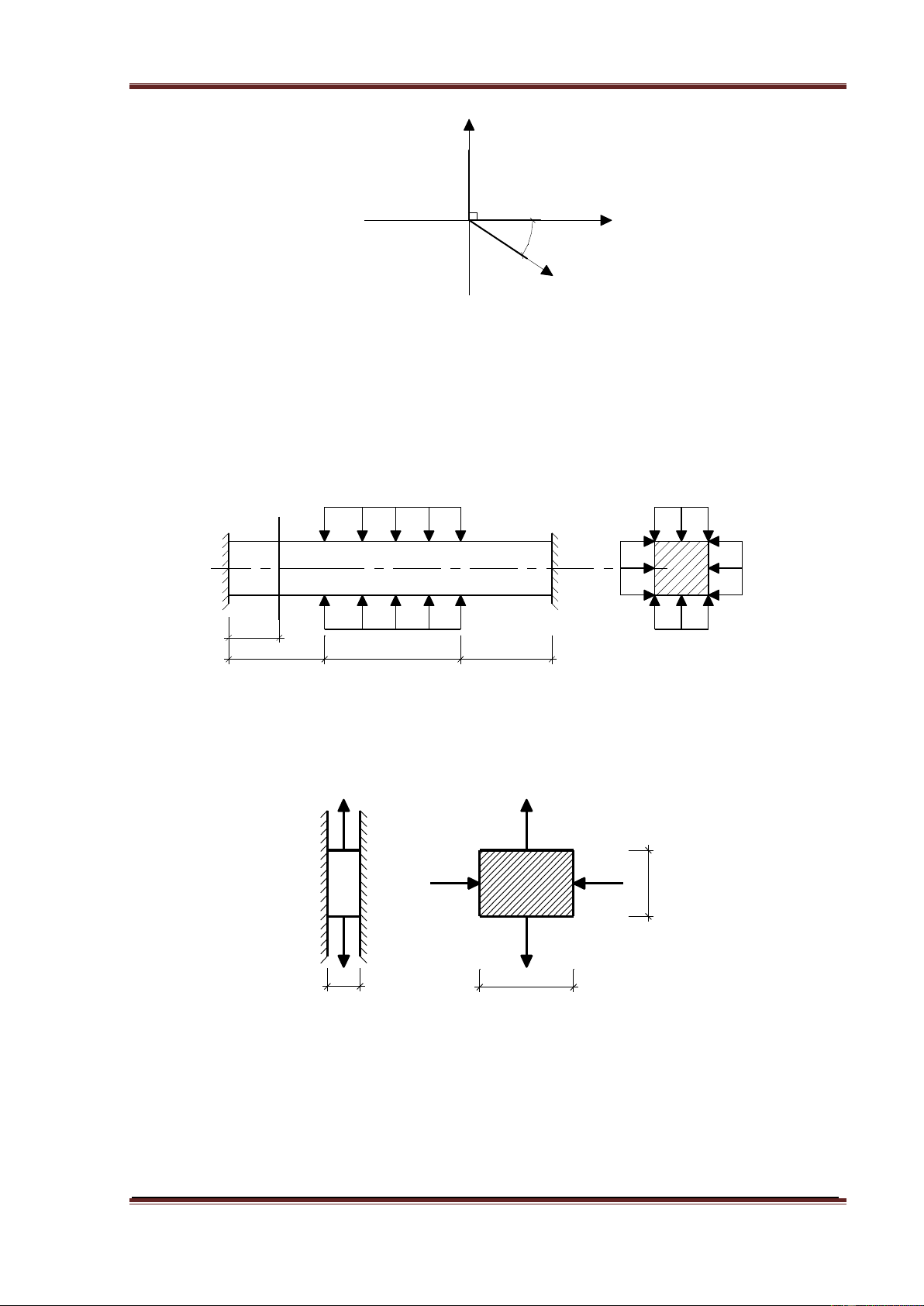
4.2.7. T¹i mét ®iÓm thuéc tr¹ng th¸i øng suÊt ph¼ng ng- êi ta ®o ®- îc c¸c biÕn
d¹ng dµi t- ¬ng ®èi theo c¸c ph- ¬ng u, v, vµ t .TÝnh c¸c gi¸ trÞ øng suÊt
chÝnh vµ c¸c ph- ¬ng chÝnh t¹i ®iÓm nµy .
BiÕt vËt liÖu cã E=2x104 kN/cm2 ; =0,25 ; =2x10-4 ; =2x10-4 ; =10-4 ; u v t =300 .
Tóm tắt lý thuyết và đề bài tập 6
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
Chương 4 – TRẠNG THÁI ỨNG SUẤT – CÁC THUYẾT BỀN v u t
4.2.8. Mét thanh thÐp BC cã mÆt c¾t h×nh vu«ng ®- îc ngµm chÆt t¹i hai ®Çu vµ
chÞu ¸p lùc trªn c¸c mÆt bªn trªn mét ®o¹n cã chiÒu dµi b nh- h×nh vÏ.
1. X¸c ®Þnh ph¶n lùc ngµm theo ph- ¬ng trôc thanh .
2. X¸c ®Þnh chuyÓn vÞ cña tiÕt diÖn 1-1 theo ph- ¬ng trôc thanh .
BiÕt L=1 m ; E=104 kN/cm2 ; =0,3; p=10 kN/cm2 ; diÖn tÝch tiÕt diÖn
thanh lµ a a=4 4 cm2 . 2p 2p 1 B C p p 1 0,5L 2p L 2L L 2p
4.2.9. Một tấm hình chữ nhật bề dày đặt sát giữa hai vách thẳng đứng song
song không biến dạng như hình vẽ. Tấm chịu lực kéo F và lực nén Q. Cho
hệ số Poisson ; chiều dài a, b. Hãy xác định áp lực nén của tấm vào vách (bỏ qua lực ma sát) F F Q Q a F F b
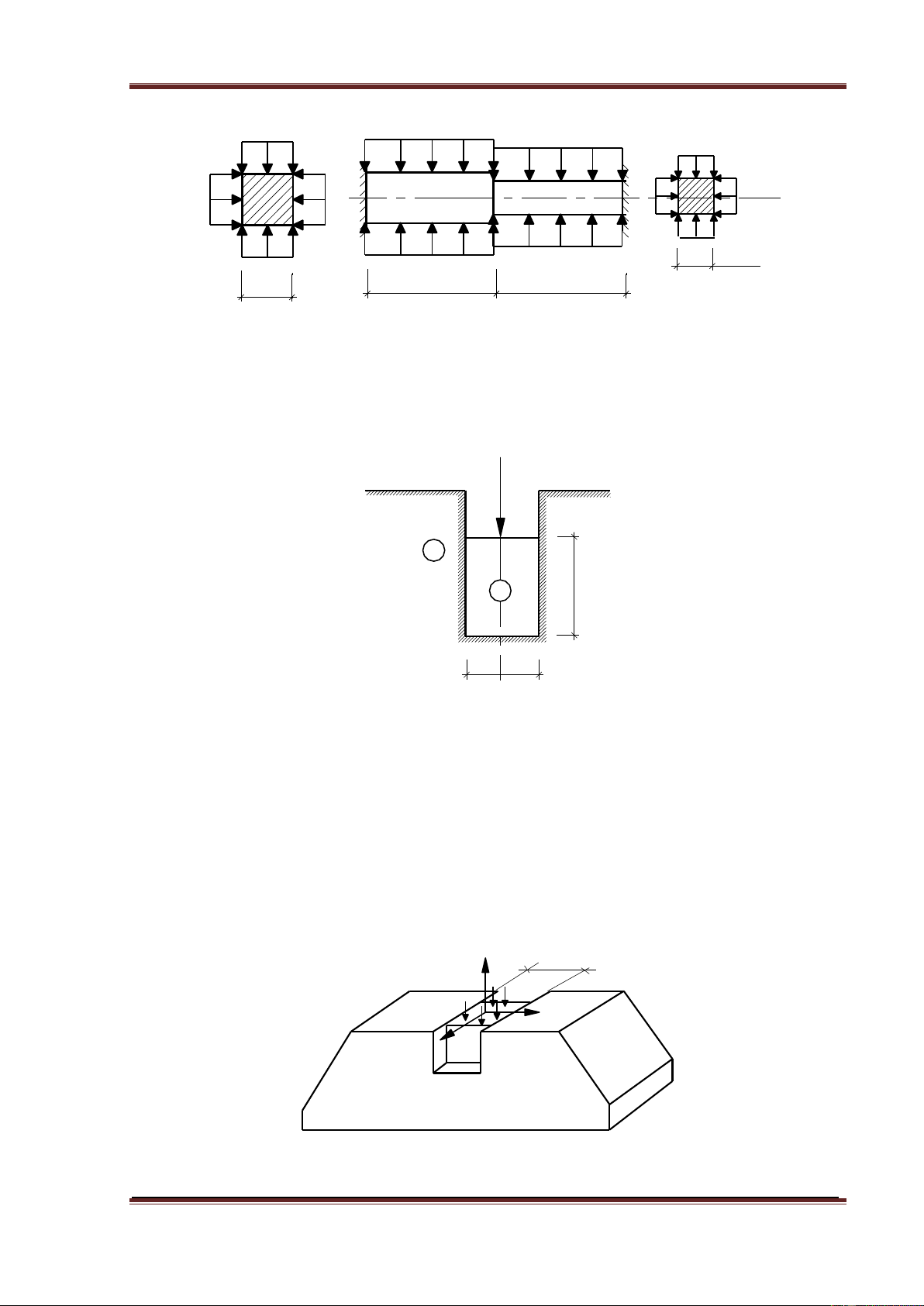
4.2.10. Một thanh thép mặt cắt ngang hình vuông gồm hai đoạn, đoạn AB có
cạnh là 4cm, đoạn BC có cạnh là 2cm. Thanh ngàm hai đầu và chịu áp lực
p phân bố đều như trên hình vẽ. Xác định giá trị cho phép của [p] sao cho
ứng suất pháp dọc trục lớn nhất của thanh không vượt quá 10kN/cm2.
Biết=0,3; E=2104 kN/cm2
Tóm tắt lý thuyết và đề bài tập 7
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
Chương 4 – TRẠNG THÁI ỨNG SUẤT – CÁC THUYẾT BỀN p p p p p B C D p p p p p p 2cm L L 4cm
4.2.11. Một khối trụ tròn A được nhét khít vào một lỗ khoét của một vật cứng
tuyệt đối B và chịu lực nén P=50 kN. Xác định áp lực nén vào vách lỗ
khoét, các biến dạng h và V của khối đồng. Biết d=4cm; =0,31; E=1,1104 kN/cm2. P B h A d
4.2.12. Một khối thép hình lập phương cạnh a=5cm đặt khít trong rãnh của một
khối thép lớn (coi như tuyệt đối cứng). Khối thép chịu áp lực p= 120 MN/m2.
Xác định áp lực nén vào vách rãnh và độ biến dạng thể tích tuyệt đối. Kiểm
tra độ bền của khối thép theo thuyết bền ứng suất tiếp cực đại và thuyết
bền thế năng biến đổi hình dáng biết [σ]=140 MN/m2. =0.3; Bỏ qua lực
ma sát giữa các mặt tiếp xúc của hai khối. E=2104 kN/cm2 y a p x z
Tóm tắt lý thuyết và đề bài tập 8
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com)