
lOMoARcPSD| 35883770
BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC CẦN THƠ
KHOA KHOA HỌC TỰ NHIÊN
GIÁO TRÌNH
ĐẠI SỐ TUYẾN TÍNH
VÀ HÌNH HỌC
(TN012)
(IN LẦN THỨ BẢY CÓ CHỈNH LÝ)
Chủ biên
GS.TS TRẦN PHƯỚC ĐƯỜNG. Đại học Cần Thơ
Cố vấn khoa học
Prof.Dr HENK PIJLS. The University of Amsterdam. Hà lan.
Gs. Ts NGUYỄN HỮU ANH. Đại học Khoa học Tự nhiên. TP HCM.
Biên soạn: Th.S HỒ HỮU LỘC
– LƯU HÀNH NỘI BỘ –
CẤM SAO CHÉP DƯỚI MỌI HÌNH THỨC
– 2017 –

lOMoARcPSD| 35883770
GIỚI THIỆU
Bộ giáo trình này gồm bài giảng các môn Toán, Lý, Hóa, Sinh và Tin học của hai
năm đầu khoa học cơ bản ở bậc đại học. Các bài giảng được biên soạn căn cứ vào đề
cương chi tiết do Bộ Giáo dục và Đào tạo ban hành cùng với 20% cải đổi được phép để
phù hợp với chuyên ngành đào tạo và thực tiễn ở địa phương.
Bộ giáo trình này là một phần của chương trình cải tiến phương pháp dạy và học ở
cấp đại học của Trường Đại học Cần thơ. Giáo trình được biên soạn với hai chủ đích:
– Cung cấp cho giáo viên nội dung chuẩn để biên soạn bài giảng.
– Cung cấp cho sinh viên kiến thức tối thiểu cần có của môn học.
Bài giảng, ngoài phần lý thuyết, giới thiệu phần đọc thêm, những ứng dụng vào
thực tiễn, bài tập v.v..., giúp sinh viên phát triển khả năng tự học, quen dần thói quen ứng
dụng kiến thức vào thực tiễn và, như vậy, dần dần hình thành tư duy sáng tạo và thực tế.
Bộ giáo trình này được thực hiện với sự hợp tác của các giáo sư nhiều kinh nghiệm
trong nước và các giáo sư Hà Lan. Bài giảng được hiệu chỉnh sau nhiều lượt góp ý của các
giáo viên trực tiếp đứng lớp và nhiều hội thảo. Cuối cùng ban Giám hiệu Trường Đại học
Cần thơ tổ chức nghệm thu thông qua hội đồng gồm nhiều thành viên phản biện là các
thầy, cô giáo trong và ngoài trường.
Bộ giáo trình xuất bản lần này tuy đã được thực hiện khá công phu và nghiêm túc
nhưng cũng không tránh khỏi một số thiếu sót. Chúng tôi rất mong nhận được sự đóng góp
của đọc giả để lần xuất bản sau hoàn chỉnh hơn.
Chúng tôi chân thành cảm ơn chính phủ Hà Lan (Nuffic) và Bộ Giáo dục và Đào
tạo đã tài trợ và tạo điều kiện thuận lợi cho công tác biên soạn bộ giáo trình này. Cám ơn
các giáo sư Hà Lan, các giáo sư trong nước và tất cả các cá nhân đã góp phần tích cực vào
công tác biên soạn và ấn hành bộ giáo trình này.
Cần thơ, tháng 1 năm 1999
Chủ biên
NGND Gs. Ts. TRẦN PHƯỚC ĐƯỜNG
2

lOMoARcPSD| 35883770
LỜI NÓI ĐẦU
GIÁO TRÌNH ĐẠI SỐ TUYẾN TÍNH và HÌNH HỌC là sự kết hợp của Giáo trình
đại số tuyến tính và Giáo trình hình học giải tích trước đây, biên soạn lại theo hướng tinh
giản hơn, phù hợp với quy trình đào tạo theo học chế tín chỉ và phù họp với khung chương
trình cải cách do bộ Giáo dục và Đào tạo quy định. Giáo trình này sử dụng chủ yếu cho
đối tượng là sinh viên các ngành thuộc Khối Kĩ thuật nên chú trọng khai thác nhiều đến
các ứng dụng, các thuật toán giải mà không đi sâu trình bày cơ sở lý thuyết của vấn đề.
Đặc biệt, các ví dụ được trình bày khá chi tiết, tỷ mỉ nhằm đáp ứng tốt nhu cầu tự đọc hiểu
của sinh viên trong quá trình tự học.
Nội dung giáo trình bao gồm 7 chương. Ba chương đầu là: Hệ phương trình tuyến
tính, Ma trận và Định thức được trình bày đan xen các kiến thức với nhau, xung quanh
điểm xuất phát ban đầu là hệ phương trình tuyến tính, để từ đó dẫn đến khái niệm ma trận
và định thức cùng với các phép toán trên chúng một cách tự nhiên, dễ hiểu. Ở đây, các lý
thuyết sơ cấp về ma trận được giới thiệu khá chi tiết với dụng ý sử dụng ma trận như một
công cụ cơ bản, xuyên suốt cả giáo trình này. Chương 4 trình bày những khái niệm cơ bản
nhất, có tính chất lý thuyết của môn Đại số tuyến tính, đó là Không gian vectơ và ánh xạ
tuyến tính. Chương 5 và 6 trình bày các vấn đề có nhiều ứng dụng và thiên về kỹ năng thực
hành, đó là Vectơ riêng–giá trị riêng; Chéo hóa; Ma trận đối xứng và Dạng toàn phương.
Sau mỗi mục của từng chương đều có một số bài tập, (sẽ được in riêng), nhằm củng cố
kiến thức lý thuyết, rèn kỹ năng tính toán và bổ sung thêm các vấn đề có tính chất lý thuyết
nâng cao, chưa có điều kiện trình bày trong bài giảng.
Hiện nay công cụ tính toán đang có sự chuyển đổi lớn theo hướng bỏ dần tính toán
“bằng tay”, thay vào đó là sử dụng máy vi tính. Nhằm thích ứng với những thay đổi đó,
chúng tôi đã mạnh dạn đưa vào giáo trình những cải tiến mới về thuật toán tính toán (chủ
yếu trên ma trận) để sinh viên dễ tiếp cận và sử dụng có hiệu quả hơn máy vi tính của
mình.
Do hướng tới mục tiêu viết để sinh viên tự đọc hiểu dễ dàng, nên giáo trình này có
phần chi tiết hơn so với những giáo trình về đại số tuyến tính đã từng có. Tuy nhiên, vì đây
là giáo trình giảng dạy ở bậc Đại học nên không nhất thiết phải được giảng dạy đầy đủ và
tuân thủ theo đúng thứ tự các chương mục đã trình bày. Tác giả chỉ mong muốn rằng giáo
trình này sẽ thực sự giúp ích cho sinh viên trong quá trình tự học và tiện lợi cho đồng
nghiệp trong công tác giảng dạy của mình.
Trong quá trình biên soạn, chúng tôi xin cảm ơn sự giúp đỡ qúy báu của giáo sư
tiến sĩ Trần Phước Đường, nguyên hiệu trưởng trường Đại học Cần thơ, là chủ biên. Rất
biết ơn công sức đóng góp lớn lao của nhóm cố vấn gồm: Giáo sư tiến sĩ Henk. Pijls, The
University of Amsterdam; Giáo sư tiến sĩ Nguyễn Hữu Anh và TS Nguyễn Ngọc Hội, khoa
Toán Đại học Khoa học Tự nhiên, Đại học Quốc gia thành phố Hồ Chí Minh. Xin chân
thành cảm ơn những nhận xét qúy báu của các đồng nghiệp thuộc bộ môn Toán thuộc hai
khoa: Khoa Khoa học và Khoa Sư phạm, trường Đại học Cần thơ. Đặc biệt xin cảm ơn
thầy giáo Nguyễn Xuân Tranh, tổ Toán, khoa Khoa học và thầy giáo Nguyễn Thanh Bình,
tổ Toán, Khoa Sư phạm, đã đọc lại toàn bộ bản thảo và cho nhiều ý kiến có giá trị.
Tuy đã hết sức cố gắng, nhưng vẫn không thể tránh hết những sai sót. Rất mong
nhận được nhiều ý kiến đóng góp của các đồng nghiệp và của các em sinh viên. Những ý
kiến đóng góp xin gửi về tổ Toán, khoa Khoa học, Trường Đại học Cần thơ.
Tác giả

lOMoARcPSD| 35883770
MỤC LỤC
Chương 1: HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
I. Mở đầu về hệ phương trình tuyến tính.
1
II. Khái niệm ma trận. Phép toán hàng và dạng bậc thang của ma trận
6
III. Giải hệ tuyến tính tổng quát. Phương pháp Gauss.
13
Chương 2: MA TRẬN
I. Các phép toán trên ma trận.
20
II. Ma trận khả nghịch.
27
III. Ma trận khối (Đọc thêm).
32
Chương 3: ĐỊNH THỨC
I. Khái niệm định thức.
36
II. Tính chất của định thức.
42
III. Ứng dụng của định thức.
46
Chương 4: KHÔNG GIAN VECTƠ
I. Không gian vector và không gian con.
49
II. Độc lập tuyến tính và phụ thuộc tuyến tính. Cơ sở của không gian vecơ.
60
III. Tọa độ đối với cơ sở.
76
IV. Tính trực giao và Không gian Euclide thực E
n
.
83
Chương 5: ÁNH XẠ TUYẾN TÍNH
I. Khái niệm ánh xạ tuyến tính.
99
II. Ảnh và nghịch ảnh. Nhân và ảnh của ánh xạ tuyến tính.
104
III. Tính đẳng cấu của các không gian vectơ và hạng của ánh xạ tuyến tính.
109
IV. Biểu diễn ma trận của ánh xạ tuyến tính.
113
Chương 6: VECTƠ RIÊNG, CHÉO HÓAVÀ DẠNG TOÀN PHƯƠNG
I. Giá trị riêng và véc tơ riêng.
122
II. Chéo hóa .
128
III. Chéo hóa trực giao ma trận đối xứng.
138
IV. Dạng toàn phương.
143
Chương 7: ĐƯỜNG BẬC HAI PHẲNG VÀ MẶT BẬC HAI
I. Đường bậc hai tổng quát và đồ thị của nó .
154
II. Mặt bậc hai cho bởi phương trình chính tắc.
163

lOMoARcPSD| 35883770
I.
GIỚI THIỆU VỀ HỆ TUYẾN TÍNH
Chương 1
HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
1. Giới thiệu hệ tuyến tính.
2. Khái niệm ma trận, phép toán hàng và dạng bậc thang của ma
trận.
3. Giải hệ tuyến tính tổng quát.
Hệ phương trình tuyến tính (còn gọi là hệ tuyến tính) được coi là điểm khởi đầu của
môn Đại số tuyến tính. Nhờ nghiên cứu hệ tuyến tính mà các khái niệm như định thức, ma
trận được ra đời. Phương pháp giải hệ tuyến tính bằng phép thế dẫn đến sự xuất hiện các
khái niệm: phép toán hàng, ma trận dạng bậc thang, ma trận dạng bậc thang rút gọn,...
Đặc biệt, từ khi có khái niệm hạng của ma trận, rồi định lý Kronecker–Kapelli về sự tồn
tại nghiệm ra đời, lý thuyết đầy đủ về hệ tuyến tính xem như đã được hoàn thiện vào cuối
thế kỷ 19. Ngày nay do sự xuất hiện và phát triển nhanh của máy tính mà công cụ để giải
hệ tuyến tính đã được thay đổi một cách căn bản. Do vậy, việc trình bày lý thuyết về hệ
tuyến tính cũng phải được thay đổi một cách tương ứng sao cho người học có thể sử dụng
tối ưu nhất một công cụ tính toán mạnh đó là máy tính (chứ không phải tính bằng tay với
viết chì và giấy nháp!). Với định hướng đó giáo trình đại số tuyến tính này sẽ bắt đầu bằng
việc trình bày hệ tuyến tính đan xen với khái niệm ma trận, mà nội dung xuyên suốt là
phương pháp rút gọn hàng.
I. GIỚI THIỆU HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
1. CÁC ĐỊNH NGHĨA
Định nghiã 1. Cho các số nguyên dương m và n, ta gọi hệ tuyến tính tổng quát là một
hệ gồm m phương trình, n ẩn dạng:
a
11
x
1
a x
+
a
12
x
2
+
a x
+
...
+
+
...
+
a
1n
x
n
a x
=
b
1
=
b
21 1 22 2 2n n
2
(1)
a
m1
x
1
+
a
m 2
x
2
+
...
+
a
mn
x
n
=
b
m
trong đó a
ij
, b
i
(i = 1..m; j = 1..n) là các số đã cho trước còn x
j
(j = 1..n) là các ẩn số cần
tìm. Các số a
ij
(i = 1..m; j = 1..n) được gọi là các hệ số (của ẩn), còn các số b
i
ở vế phải
(i = 1..m) được gọi là hệ số tự do.
(Do phạm vi chương trình mà ta chỉ xét các hệ tuyến tính có mọi hệ số đều là số
thực).
Nghiệm (hay lời giải) của hệ (1) là bộ gồm n số (c
1
; c
2
; ...; c
n
) mà khi thế tương ứng
vào các ẩn x
1
, x
2
, ..., x
n
thì tất cả các phương trình trong (1) trở thành đẳng thức đúng.
Giải hệ (1) nghĩa là tìm tập nghiệm của nó.
Định nghiã 2. Hai hệ tuyến tính được gọi là tương đương với nhau nếu chúng có cùng
số ẩn và có cùng tập nghiệm.
1

lOMoARcPSD| 35883770
n
đương.
Chương 1. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
Lưu ý rằng, hai hệ tuyến tính vô nghiệm (có cùng số ẩn) cũng là hai hệ tương
Định nghiã 3. Hệ tuyến tính có mọi hệ số vế phải đều bằng 0 được gọi là hệ tuyến tính
thuần nhất, hay đơn giản là hệ thuần nhất.
Như vậy, hệ thuần nhất là hệ có dạng:
a
11
x
1
a x
+
a
12
x
2
+
a x
+
...
+
+
...
+
a
1n
x
n
=
0
a x
=
0
21 1 22 2 2n n
(2)
a
m1
x
1
+
a
m 2
x
2
+
...
+
a
mn
x
n
=
0
Để thuận tiện, đôi khi ta còn viết hệ tuyến tính (1), (2) dưới dạng gọn như sau:
a
ij
x
j
= b
i
; i = 1..
m
(1)
j =1
n
a
ij
x
j
=
0
j=1
; i = 1..m (2)
2. VÍ DỤ VỀ GIẢI HỆ PHƯƠNG TRÌNH TUYẾN TÍNH – KHÁI NIỆM PHÉP
TOÁN HÀNG
Thuật toán cơ bản để giải hệ tuyến tính là thay thế hệ cần giải bằng hệ mới tương
đương nhưng dễ tìm nghiệm hơn. Cụ thể là thực hiện phép khử dần từng ẩn như sau:
– Dùng hạng tử chứa ẩn x
1
ở phương trình đầu để khử ẩn x
1
ở các phương trình
đứng sau nó. (Nếu phương trình đầu không chứa ẩn x
1
, hãy thực hiện một phép đổi hàng
thích hợp).
– Dùng hạng tử chứa ẩn x
2
ở phương trình thứ 2 để khử ẩn x
2
trong các phương
trình đứng sau nó. (Nếu phương trình thứ 2 không chứa ẩn x
2
, hãy thực hiện một phép đổi
hàng thích hợp).
– ...
– Cứ tiếp tục qúa trình như vậy, cuối cùng ta được một hệ đơn giản, dễ tìm nghiệm
hơn. Quy tắc giải được mô tả bởi ví dụ sau đây:
Ví dụ 1. Giải hệ:
x
1
2x
+
x
2
+
3x
+
x
3
+
x
= 2 (1)
= 3 (2)
(a)
1 2 3
x
1
−
x
2
− 2x
3
= − 6 (3)
Để thuận tiện cho việc theo dõi, ta ghi tất cả các hệ số của ẩn và hệ số tự do trong hệ (a)
thành một bảng như sau:
A* =
1
1
1 1
3 1
−
1
−
2
2
− 6
Bảng A* này được gọi là ma trận đầy đủ của hệ (a).
Bắt đầu khử ẩn x
1
trong tất cả các phương trình đứng sau phương trình (1) bằng
cách thay phương trình (2) bởi phương trình (2) cộng với 2 lần phương trình (1), thay
2
2
3

lOMoARcPSD| 35883770
−
0
I. GIỚI THIỆU VỀ HỆ TUYẾN TÍNH
phương trình (3) bởi phương trình (3) cộng với (–1) lần phương trình (1), thu được hệ mới
(b), mô tả như sau:
h2
→
h2
−
2h1
x
1
+ x
2
+ x
3
= 2 (1')
(a)
⎯
h
⎯
3
→
⎯
h3
−
⎯
h1
→
x − x = −1 (2 ')
(b).
2 3
−2x − 3x
= −8 (3')
2 3
1 1 1 2
Hệ (b) có ma trận đầy đủ là: B* =
0
1
−
1
− 2 − 3
−
1
− 8
Bước thực hiện này có hai tính chất quan trọng sau:
*) Thứ nhất, nếu (x
1
; x
2
; x
3
) thỏa mãn phương trình (2) (hoặc (3) của hệ (a) thì cũng
thỏa mãn phương trình (2’) (hoặc (3’) của hệ (b) vì nó dựa trên quy tắc số học là nếu A = B
và C = D thì A+C = B+D. Điều đó chứng tỏ nếu (x
1
; x
2
; x
3
) là nghiệm của hệ (a) thì nó
cũng là nghiệm của hệ (b).
*) Thứ hai, phép khử trên có phép khử ngược: Để trở lại phương trình (2) trong hệ
(a) ban đầu, chỉ cần thay phương trình (2’) bởi phương trình (2’) cộng với (–2) lần phương
trình (1’), thay phương trình (3’) bởi phương trình (3’) cộng với phương trình (1’). Điều đó
chứng tỏ nếu (x
1
; x
2
; x
3
) là nghiệm của hệ (b) thì cũng là nghiệm của hệ (a).Vậy hai hệ trên
thực sự là tương đương.
Tiếp theo, ta lại dùng hạng tử chứa ẩn x
2
ở phương trình (2') để khử ẩn x
2
có trong
các phương trình đứng sau nó:
x
1
+ x
2
+ x
3
= 2
(b)
⎯
h
⎯
3→
⎯
h 3
⎯
+2
⎯
h 2
→
x − x = −1
(c)
2 3
5x
3
= −10
1 1 1 2
Hệ (c) có ma trận đầy đủ là C* =
0 1
−
1
−
1
.
0
0
−
5
−
10
Lý luận tương tự như trên thì bước biến đổi này cũng không làm thay đổi tập nghiệm. Sau
2 bước thực hiện khử ẩn, ta thu được hệ (c) có phương trình sau cùng chỉ còn lại 1 ẩn x
3
.
Để tìm x
3
, ta thay phương trình thứ 3 trong hệ (c) bởi (–1/5) lần chính nó, được hệ mới
tương đương là:
h 3
→
−
1
h 3
5
x
1
+ x
2
+ x
3
= 2
(c) ⎯⎯⎯⎯→
x
2
− x
3
= −1 (d)
Hệ (d) có ma trận đầy đủ D* =
1 1
1
0 0
1 2
−
1
−
1
.
1 2
x
3
= 2
Qua các phép biến đổi trên, ta đã chuyển được việc giải hệ (a) về việc giải hệ (d) tương
đương với (a). Để giải hệ (d), ta chỉ cần dùng “phép thế ngược” sau:
– Từ phương trình cuối của (d), có x
3
= 2.
– Thế x
3
vào phương trình giữa, thu được x
2
= 1.
– Thế x
2
, x
3
vào phương trình đầu, thu được x
1
= –1.
Nghiệm của (a) là (2; 1; –1).
Việc khử dần từng ẩn như trên đã giúp tìm được tập nghiệm của hệ. Tuy nhiên để
có các ẩn x
1,
x
2
ta phải tiến hành các phép thế ngược (mà đôi khi khá cồng kềnh!). Để tránh
tình huống này, tiếp tục biến đổi thêm như sau:
3
0

lOMoARcPSD| 35883770
0
Chương 1. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
Dùng hạng tử chứa x
3
ở phương trình cuối của hệ (d) để khử các hạng tử chứa ẩn x
3
trong các phương trình trên nó:
x
1
+ x
2
+ x
3
= 2
h 2→h 2+h 3
x
1
+ x
2
= 0
x − x = −1
⎯
h
⎯
1→
⎯
h 1
⎯
−
⎯
h 3
→
x
= 1 (e)
2 3
x
3
= 2
2
x
3
= 2
Trong hệ (e), ta lại dùng hạng tử chứa ẩn x
2
ở phương trình giữa để khử ẩn x
2
ở
phương trình đầu:
x
1
+ x
2
= 0
x
1
= −1
x
2
= 1
x
3
= 2
⎯
h
⎯
1→
⎯
h 1
⎯
−
⎯
h 2
→
x
2
= 1
x
3
= 2
(g)
Rõ ràng hệ (g) cho biết ngay nghiệm của hệ (a) là (–1; 1; 2). Hơn nữa hệ (g) có ma trận
đầy đủ ở dạng rất đặc biệt là G* =
1 0 0
1 0
0 0 1
−
1
1
, nó cho phép dễ dàng đọc ra nghiệm mà
2
không cần thực hiện bất cứ một “phép thế ngược” nào.
Cách giải hệ vừa nêu trên là một ví dụ đơn giản, tuy nhiên nó cũng chỉ ra các phép
toán cần thực hiện trên các phương trình của hệ, (mà sau đây ta gọi tắt là các phép toán
hàng), để chuyển hệ đã cho về hệ mới tương đương với hệ ban đầu nhưng dễ tìm nghiệm
hơn. Đó là ba phép toán sau:
1) Phép thay thế phương trình thứ i (hay hàng i) bằng tổng của chính nó với một
bội lần phương trình thứ j (hay hàng j) khác, gọi là phép thay thế hàng. Ký hiệu bởi h
i
→ h
i
+.h
j
.
2) Phép nhân tất cả các số hạng của phương trình thứ i (hay hàng i) với cùng một
hằng số
0, gọi là phép tỷ lệ hóa. Ký hiệu bởi: h
i
→ .h
i
.
3) Phép đổi chỗ hai phương trình thứ i và thứ j (hay hai hàng i và j) cho nhau, gọi
là phép đổi hàng (hay đổi chỗ). Ký hiệu: h
i
h
j
.
Chú ý rằng trong phép tỷ lệ hóa, h
i
→.h
i
, điều kiện 0 là không thể bỏ qua
được.
Định nghiã 4. Ba phép toán trên hệ tuyến tính gồm: phép thay thế hàng, phép tỷ lệ
hóa, phép đổi hàng được gọi là các phép toán sơ cấp trên hàng (hay các phép toán
hàng) đối với hệ phương trình tuyến tính.
Cả ba phép toán hàng trên hệ tuyến tính đều có phép toán hàng ngược. Thật vậy:
Thực hiện phép thay thế hàng h
i
→ h
i
+.h
j
, hàng thứ i nhận giá trị mới là (h
i
+.h
j
).
Tiếp tục thực hiện phép thay thế hàng h
i
→ h
i
– .h
j
, thì hàng mới đó biến thành hàng có
giá trị bằng (h
i
+.h
j
) – .h
j
= h
i
, tức trở lại bằng giá trị của hàng cũ ban đầu. Vậy h
i
→
h
i
+.h
j
có phép toán hàng ngược là h
i
→ h
i
– .h
j
.
Thực hiện phép tỷ lệ hóa h
i
→ h
i
, 0, hàng thứ i nhận được giá trị mới là .h
i
.
Tiếp tục thực hiện phép tỷ lệ hóa h
i
→
1
.h
i
, thì hàng mới đó được nhân thêm với
1
nên
4

lOMoARcPSD| 35883770
I.
GIỚI THIỆU VỀ HỆ TUYẾN TÍNH
trở lại bằng giá trị của hàng cũ ban đầu. Vậy h
i
→ .h
i
có phép toán hàng ngược là h
i
→
1
.h
i
.
Thực hiện phép đổi hàng h
i
h
j
, hàng i được đổi cho hàng j, nếu ta tiếp tục thực
hiện thêm phép đổi hàng h
i
h
j
, hàng i mới lại được đổi ngược cho hàng j lần nữa, kết
qủa là cả 2 hàng đều trở lại vị trí cũ. Vậy h
i
h
j
có phép toán hàng ngược là chính nó: h
i
h
j
.
Từ các tính chất vừa nêu trên của phép toán hàng trên hệ tuyến tính mà có định lý
sau:
Định lý 1. Thực hiện các phép toán hàng trên hệ tuyến tính, sẽ thu được hệ tuyến tính
mới tương đương.
Hiển nhiên rằng, nếu thực hiện một phép toán hàng nào đó lên hệ tuyến tính (a) để
thu được hệ (b) thì mọi nghiệm của (a) đều là nghiệm của (b). Do mọi phép toán hàng đều
có phép toán ngược nên ta lại quy được (b) về (a) nhờ các phép toán hàng khác, điều đó
chứng tỏ mọi nghiệm của (b) lại là nghiệm của (a). Lý luận này còn đúng khi tập nghiệm
của (a) là , vì vậy hai hệ (a) và (b) là tương đương.
Qua trên ta thấy rằng, để giải hệ tuyến tính, phương pháp chung là cần thực hiện
phép toán hàng đối với hệ để chuyển hệ cần giải về hệ mới tương đương, nhưng có ma trận
đầy đủ ở dạng đặc biệt, mà nhờ nó ta dễ dàng lấy ra nghiệm. Ma trận dạng bậc thang mà ta
sẽ trình bày trong mục II. sau đây là loại ma trận thỏa mãn được yêu cầu đó.
5

lOMoARcPSD| 35883770
21 22
m1
a
m2
...
a
2n
mn
.
II.
KHÁI NIỆM MA TRẬN – PHÉP TOÁN HÀNG VÀ DẠNG BẬC
THANG CỦA MA TRẬN
3. KHÁI NIỆM MA TRẬN
Phương pháp giải hệ tuyến tính bằng phép khử dần từng ẩn như trên thực chất là
thực hiện các phép khử dần các hệ số ứng với các ẩn trong ma trận đầy đủ A* của hệ,
tức là thực hiện các phép biến đổi trên bảng ghi các hệ số thành các hàng và các cột, mà
sau đây chúng được định nghĩa là ma trận.
Định nghiã 5. Cho các số tự nhiên m, n. Ta gọi ma trận cỡ mn là một tập hợp gồm
m.n phần tử, được xếp thành bảng hình chữ nhật gồm m hàng và n cột, dạng:
a
11
a
12
a
a
A =
...
a
1n
...
a
Phần tử a
ij
gọi là phần tử (i,j) của ma trận A, ký hiệu a
ij
= [A]
ij
. Các chỉ số i, j
cho biết phần tử a
ij
đứng ở hàng thứ i và cột thứ j trong A.
Hàng thứ i trong A bao gồm các phần tử có chỉ số thứ nhất bằng i, kí hiệu h
i
A =
a
i1
a
i 2
....
a
in
.
a
j1
a
jm
Cột thứ j trong A bao gồm các phần tử có chỉ số thứ hai bằng j, kí hiệu c
j
A =
Tập hợp tất cả các ma trận cỡ mn được kí hiệu bởi M(m,n). Ma trận A
M(m,n) còn được viết là A
m
n
. Do phạm vi chương trình, ta chỉ xét những ma trận có
các phần tử a
ij
R.
Định nghiã 6. Hai ma trận A và B được gọi là bằng nhau nếu chúng có cùng cỡ và
mọi phần tử đứng ở vị trí tương ứng đều bằng nhau. Kí hiệu: A = B.
A = B
A,
B
M
(m,
n)
.
[A]
=
[B] , i
=
1..m; j
=
1..n
ij ij
4. CÁC MA TRẬN THƯỜNG GẶP
Ma trận cỡ n n, gồm n hàng và n cột, gọi là ma trận vuông cấp n. Trong ma trận
vuông A cấp n, tập hợp các phần tử [A]
ii,
i = 1..n, được gọi là các phần tử đường chéo,
hay đơn giản là đường chéo của ma trận.
Ma trận cỡ m 1 gồm m hàng và 1 cột gọi là ma trận cột.
Ma trận cỡ 1 n gồm 1 hàng và n cột gọi là ma trận hàng.
Ma trận cỡ 11 gồm chỉ 1 phần tử, ta đồng nhất nó với số là phần tử của nó.
Ma trận vuông cấp n được gọi là ma trận có dạng tam giác (hay ma trận tam giác)
nếu mọi phần tử đứng ở một phía của đường chéo đều bằng 0. Ma trận tam giác A có
[A]
ij
= 0 với mọi i > j thì A được gọi là ma trận tam giác trên. Ma trận tam giácB có[B]
ij
= 0 với mọi i < j thì B được gọi là ma trận tam giác dưới.
6
a

lOMoARcPSD| 35883770
0
0
*
*
0
*
0
0
0
0
d
II.
MA TRẬN, DẠNG BẬC THANG CỦA MA TRẬN
* *
Ví dụ 2. A =
*
0 0
0
* *
* 0
*
là ma trận tam giác trên, B =
*
* *
* *
0 *
* *
0 0
0
là ma trận
* 0
*
tam giác dưới. (Phần tử ký hiệu bởi "*" nhận giá trị bất kỳ, có thể bằng hoặc khác 0).
Ma trận vuông có mọi phần tử nằm ngoài đường chéo đều bằng 0 gọi là ma trận
đường chéo (hay gọi tắt là ma trận chéo). Ma trận chéo thường được kí hiệu bởi D, có
dạng D =
d
11
0 …
d
22
…
0
0
. Từ định nghĩa trên suy ra, ma trận chéo cũng là ma trận
⁝ ⁝
⋱ 0
nn
tam giác nhưng điều ngược lại không đúng.
Ma trận chéo có mọi phần tử đường chéo đều bằng 1 được gọi là ma trận đơn vị.
1
Ma trận đơn vị cấp n được kí hiệu là I
n
=
⁝
0
1
⁝
...
... 0
...
.
⁝ ⁝
5. PHÉP TOÁN HÀNG TRÊN MA TRẬN
Tương tự như các phép toán hàng trên hệ tuyến tính, ta cũng có 3 loại phép toán
hàng trên ma trận, đó là:
1. Phép thay thế hàng: Thay hàng i bởi tổng của chính nó với một bội lần của
hàng j khác, kí hiệu: h
i
→ h
i
+.h
j
.
2. Phép tỷ lệ hóa: Nhân tất cả các hạng tử của hàng i với cùng một hằng số 0,
kí hiệu: h
i
→.h
i
.
3. Phép đổi hàng: Đổi chỗ 2 hàng i, j bất kỳ cho nhau, kí hiệu: h
i
h
j
.
Định nghiã 7. Ba phép toán hàng gồm: phép thay thế, phép tỷ lệ hóa và phép đổi
hàng được gọi là ba phép toán hàng của ma trận.
Nếu thực hiện các phép toán hàng trên ma trận A để thu được ma trận B thì B
được gọi là tương đương hàng với A. Kí hiệu B ~A.
Vì các phép toán hàng đều có phép toán ngược nên nếu B ~ A thì A~ B. Do vậy
ta nói A và B tương đương hàng với nhau. Dễ thấy nếu A ~ B và B ~ C thì A ~ C.
6. MA TRẬN DẠNG BẬC THANG
Định nghiã 8. Trong ma trận A:
a)
Hàng có chứa ít nhất 1 phần tử khác 0 được gọi là hàng khác 0, còn hàng chứa
tất cả các phần tử đều bằng 0 gọi là hàng 0.
b)
Phần tử khác 0 đầu tiên (tính từ trái qua phải) của một hàng, gọi là phần tử
chính của hàng đó.
7
0
0
0
1
0

lOMoARcPSD| 35883770
0
Chương 1. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
0 0 9
Ví dụ 3. Cho A =
0 0
0 7 5
1 3 0
8
thì: h
2
A là hàng 0, h
1
A, h
3
A, h
4
A là hàng khác
1
0. Phần tử chính của h
1
A là “9”, của h
3
A là “7”, của h
4
A là “1”.
Định nghiã 9. Ma trận A được gọi là có dạng bậc thang (hay ma trận bậc thang)
nếu A thoả mãn 2 tính chất:
a)
Hàng 0 (nếu có) ở phía dưới hàng khác 0.
b)
Phần tử chính của hàng dưới, luôn đứng trong cột ở về phía phải so với cột
chứa phần tử chính của những hàng phía trên nó.
1 1
−2 4
1 1 0 4
Ví dụ, ma trận A =
0 2 −1 −1
có dạng bậc thang, ma trận B =
0 0 0 −1
chưa có dạng bậc thang.
0
0
0
3
0
0
1
3
Định nghiã 10. Ma trận bậc thang có thêm hai tính chất sau được gọi là ma trận
dạng bậc thang rút gọn (hay đơn giản là ma trận dạng rút gọn):
a)
Mọi phần tử chính đều bằng 1.
b)
Trong cột có chứa phần tử chính (bằng 1) thì 1 là phần tử khác không duy nhất
của cột.
1 1 0 4
1 1 0 4
Ví dụ, ma trận B =
0 0 1 −1
có dạng rút gọn còn ma trận C =
0 0 1 −1
chưa có dạng rút gọn.
Định nghiã 11.
0
0
0
0
0
0
0
3
a)
Nếu A ~ B và B có dạng bậc thang (hay dạng rút gọn), thì ta nói B là dạng bậc
thang (hay dạng rút gọn) của A.
b)
Qúa trình thực hiện các phép toán hàng để quy ma trận A về dạng bậc thang,
được gọi là qúa trình rút gọn hàng.
Ví dụ 4. A =
1
0
1 − 2
0 − 1
−
1
− 1
4
− 1
1
⎯
h
⎯
2
⎯
h 3
→
0
0
1 − 2
−
1
− 1
0 − 1
4
−
1
1
= B, do B có dạng
bậc thang và A~B nên B là dạng bậc thang của A.
7. THUẬT TOÁN QUY MA TRẬN VỀ DẠNG BẬC THANG
Do yêu cầu của dạng bậc thang, phần tử chính của hàng dưới, luôn đứng trong cột ở
về phía phải so với cột chứa phần tử chính của những hàng phía trên nó, mà trong ma
trận sẽ có những vị trí mà phần tử chính của hàng trưóc đang đứng ở đó, sẽ có tác dụng
như là các “vị trí mốc” mà phần tử chính của những hàng sau phải dựa vào đó mà sắp
xếp theo. Việc phát hiện ra các vị trí như vậy sẽ là chià khóa thành công cho thuật toán
quy ma trận về dạng bậc thang. Sau đây là ví dụ mô tả chi tiết cách phát hiện các “vị trí
mốc” và các phép toán hàng cần thực hiện để thu được dạng bậc thang của một ma trận.
8
0
7
0
1

lOMoARcPSD| 35883770
II. MA TRẬN, DẠNG BẬC THANG CỦA MA TRẬN
1 2 1 −3 1
0 4 8 12 −4
Ví dụ 5. Quy ma trận A =
về dạng bậc thang.
2 3 0 −3 1
−1 −1 1 0 −8
Bắt đầu bằng việc xét cột khác 0 (tức cột có chứa ít nhất một phần tử khác 0) đầu
tiên tính từ trái sang phải, trong trường hợp này là c
1
A. Phần tử (1,1) đứng ở đỉnh cột là
phần tử khác 0 nên nó là phần tử chính của hàng thứ nhất. Theo yêu cầu của dạng bậc
thang thì các phần tử chính của các hàng từ hàng thứ 2 trở về sau phải đứng lệch sang
phải so với cột 1. Do vậy cần phải thực hiện phép thay thế hàng để biến các phần tử
đứng phía dưới của phần tử (1,1)) thành phần tử 0. Lúc này, vị trí (1,1) là “vị trí mốc”,
căn cứ vào đó mà các phần tử chính của hàng sau phải đứng lệch sang phải. Hơn nữa,
giá trị của phần tử (1,1) đóng vai trò quan trọng trong việc phát hiện ra các phép thay
thế hàng cần phải thực hiện, vì vậy phần tử (1,1) đang đứng ở “vị trí mốc” được gọi là
phần tử chốt hay phần tử cơ sở (thứ nhất) của A. Các phép toán hàng cần thực hiện để
biến các phần tử đứng phiá dưới phần tử cơ sở thành phần tử 0 như sau:
1 2 1 −3 1
1 2 1 −3 1
0 4 8 12 −4
h3→h3−2.h1
0 4 8 12 −4
A
=
⎯
h
⎯
4→
⎯
h 4
⎯
+h
⎯
1
→
= B
2 3 0 −3 1
0 −1 −2 3 −1
−1 −1 1 0 −8
0 1 2 −3 −7
Trong ma trận B phần tử chính của hàng 2 là phần tử (2,2) bằng “4”. Cũng do yêu cầu
của dạng bậc thang, các phần tử đứng phía dưới phần tử (2,2) phải được quy về phần tử
0. Lúc này, phần tử “4” đứng ở vị trí (2,2) cũng đóng vai trò giống như phần tử cơ sở
thứ nhất ở trên, vì vậy nó lại được gọi là phần tử cơ sở (thứ hai) của A. Nhờ phần tử cơ
sở (thứ 2) mà phát hiện phép toán hàng cần thực hiện ở bước thứ hai như sau:
1 2 1 −3 1
1 2 1 −3 1
0 4 8 12 −4
h3→h3+(1/ 4).h 2
0 4 8 12 −4
B =
⎯
h
⎯
4→
⎯
h 4
⎯
−(1/
⎯
4).
⎯
h 2
→
= C
0 −1 −2 3 −1
0 0 0 6 −2
0 1 2 −3 −7
0 0 0 −6 −6
Trong ma trận C, phát hiện phần tử chính của hàng 3 trong C là phần tử (3,4) bằng “6”,
đóng vai trò là phần tử cơ sở (thứ 3) của A. Nhờ phần tử này ta phát hiện ra phép thay
thế hàng cần thực hiện trong bước thứ ba như sau:
1 2 1 −3 1
1 2 1 −3 1
0 4 8 12 −4
h 4
→
h 4
+
h3
0 4 8 12 −4
C =
⎯⎯⎯ ⎯→
= D
0 0 0 6 −2
0 0 0 6 −2
0 0 0 −6 −6
0 0 0 0 -8
Trong D, phát hiện phần tử chính của hàng thứ tư là phần tử (4,5) bằng “–8”, đóng vai
trò phần tử cơ sở (thứ 4) của A. Do phía dưới của phần tử cơ sở này không còn phần tử
nào khác cần biến thành 0 nên không cần thực hiện thêm phép toán hàng nào nữa. Ma
trận D chính là dạng bậc thang của A.
Vai trò quan trọng của phần tử cơ sở là ở chỗ: nó là “mốc” để dựa vào đó mà
sắp xếp các phần tử chính của những hàng sau, đồng thời nó còn được dùng để phát
hiện ra các phép toán hàng cần thiết phải thực hiện. Phần tử cơ sở có “hiệu qủa” nhất là
phần tử cơ sở bằng 1. Để có phần tử cơ sở là 1, có thể thực hiện phép tỷ lệ hóa, phép
9

lOMoARcPSD| 35883770
Chương 1. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
đổi hàng hoặc một phép thay thế hàng thích hợp. Thực tế cho thấy việc chọn đúng phần
tử cơ sở có thể làm giảm bớt khối lượng công việc và giảm bớt các lỗi gặp phải trong
quá trình thực hiện các phép toán hàng để quy ma trận về dạng bậc thang.
Qua ví dụ vừa trình bày ở trên, ta rút ra thuật toán gồm 3 bước như sau, gọi là
thuật toán rút gọn hàng, để quy được ma trận bất kỳ về dạng bậc thang:
Bước 1: Dùng phép đổi hàng (nếu cần) để có phần tử ở đỉnh của cột khác 0 đầu
tiên (tính từ trái sang phải) của ma trận là phần tử khác 0. Phần tử này gọi là phần tử
cơ sở thứ nhất của ma trận.
Bước 2: Dựa vào phần tử cơ sở thứ nhất, phát hiện các phép toán hàng cần
thực hiện để biến tất cả các phần tử, đứng phía dưới phần tử cơ sở thứ nhất (trong cùng
một cột), thành phần tử 0 và thực hiện các phép toán hàng này.
Bước 3: Lặp lại 2 bước trên đối với ma trận con thu được từ ma trận ban đầu
bằng cách bỏ đi hàng và cột chứa phần tử cơ sở thứ nhất, và cứ tiếp tục như vậy cho
đến phần tử cơ sở cuối cùng.
Ví dụ 6. Áp dụng thuật toán rút gọn hàng để quy ma trận sau về dạng bậc thang:
0
−
3
6
−
6
−
4
5
A =
− 3 9 −12 9
−
6
−15
−
3
7
−
8
5
−
8
−
9
Bước 1. Xét cột khác 0 đứng phiá trái nhất, đó là c
1
A, phần tử ở đỉnh là phần tử
0, cần phải thực hiện phép đổi hàng để có phần tử ở đỉnh của cột là phần tử khác 0. Sau
khi đổi hàng, phần tử khác 0 đứng ở đỉnh của cột là “–3”, chính là phần tử cơ sở thứ
nhất.
-3
9 −12 9 −6 −15
A
⎯
h
⎯
1
⎯
h2
⎯→
0
−
3
6
−
6
−
4
5
= B
−
3
7
−
8
5
−
8
9
Bước 2. Trong B, nhờ phần tử cơ sở thứ nhất, phát hiện phép thay thế hàng để
biến phần tử đứng phía dưới thành 0 như sau:
-3
9 −12 9
−6 −15
-3 9
−12 9
−6 −15
B =
0
−3 6
−6 −4 5
⎯
h
⎯
3→
⎯
h3−
⎯
.h1
→
0
−3 6 −6 −4 5
= D
−
3
7
−8 5
−8 9
0
−2 4
−4 −2 6
Bước 3. Trong D, phát hiện phần tử cơ sở thứ 2 là phần tử (2,2) bằng “–3”.
Trước hết, cần đơn vị hoá phần tử cơ sở để phép toán hàng tiếp theo là dễ thực hiện.
Muốn vậy, ta có thể thực hiện phép thay thế hàng trong D như sau:
-3 9
−12 9
−6 −15
-3 9
−12 9
−6 −15
D =
0
-3
6 −6 −4 5
⎯
h
⎯
2→
⎯
.h 2
⎯
−
⎯
h3
→
0 -1
2 −2 −2
−1
= E
0
−2 4
−4 −2 6
0
−2 4
−4 −2 6
Khi có phần tử cơ sở là phần tử (2,2) bằng “–1”, ta dễ phát hiện phép thay thế để biến
phần tử đứng dưới thành phần tử 0 như sau:
-3 9
−12 9 −6 −15
-3 9 −12 9
−6 −15
E =
0 -1
2 −2 −2
−1
⎯
h
⎯
3→
⎯
.h3
⎯
−2
⎯
h 2
→
0
-1
2
−2 −2 −1
= G
0
−2 4
−4 −2 6
0 0 0 0 2 8
Trong G, phát hiện phần tử cơ sở thứ 3 là phần tử (3,5) bằng “2”, do dưới phần tử cơ sở
này không còn phần tử nào khác cần biến thành phần tử 0, nên thuật toán được kết thúc
và G chính là dạng bậc thang của A.
10

lOMoARcPSD| 35883770
II.
MA TRẬN, DẠNG BẬC THANG CỦA MA TRẬN
Thuật toán rút gọn hàng luôn quy được ma trận A về dạng bậc thang, nhưng
trong thực tế, ta thường cần đến dạng rút gọn hơn. Phương pháp chung để quy dạng bậc
thang về dạng rút gọn là phương pháp “khử ngược’’ sau đây:
-
Trong dạng bậc thang của A, bắt đầu từ phần tử cơ sở cuối cùng (cũng là phần
tử chính của hàng cuối cùng trong dạng bậc thang) đơn vị hóa nó, rối phát hiện ra phép
thay thế hàng cần thiết để biến các phần tử đứng phía trên nó (trong cùng một cột)
thành phần tử 0.
-
Lặp lại quy trình trên cho từng cột có chứa phần tử cơ sở tiếp theo ở phía trên
cho đến hết.
Ví dụ 7. Quy ma trận G ở ví dụ trên về dạng rút gọn.
Phần tử cơ sở cuối cùng trong G là phần tử (3,5) bằng “2”, đơn vị hoá nó nhờ phép
tỷ lệ hoá:
−3 9
−12 9
−6 −15
1
−3 9
−12 9
−6 −15
G =
0
−1 2 −2 −2
−1
h3→ .h3
2
0 −1 2
−2 −2
−1
= H
⎯⎯⎯⎯→
0 0 0 0 2 8
0 0 0 0 1 4
Thực hiện phép toán hàng, biến tất cả các phần tử đứng phía trên phần tử cơ sở cuối
cùng, thành phần tử 0:
−3 9
−12 9
−6 −15
h 2→h 2+2.h3
−3 9
−12 9 0 9
H =
0
−1 2 −2 −2
−
1
⎯
h
⎯
1→
⎯
h1+
⎯
6.h3
⎯→
0
−1 2
−2 0 7
= K
0 0 0 0 1 4
0 0 0 0
1
4
Xét phần tử cơ sở tiếp theo, đó là phần tử (2,2) bằng “–1”. Đơn vị hóa nó và
biến các phần tử đứng phía trên, thành phần tử 0:
−3 9
−12 9 0 9
h 2→−h 2
−3 0 6
−9 0 72
K =
0 -1 2
−2 0 7
⎯
h
⎯
1→
⎯
h1+
⎯
9h 2
⎯→
0
1 −2 2 0
−7
= L
0 0 0 0 1 4
0 0 0 0 1 4
Xét phần tử cơ sở tiếp theo, đó là phần tử (1,1) bằng “–3”. Đơn vị hóa nó nhờ
phép tỷ lệ hoá:
-3 0 6
−9 0 72
1
1 0
−2 3 0 24
L =
0
1 −2 2 0
−7
h1→− h1
3
0 1
−2 2 0
−7
= U.
⎯⎯⎯⎯→
0 0 0 0 1 4
0
0
0
0
1
4
Ma trận U thu được sau cùng là dạng rút gọn của A.
Chú ý rằng, một ma trận, tùy theo phép toán hàng áp dụng cho nó, mà có thể quy
được về nhiều dạng bậc thang khác nhau.Tuy nhiên nếu quy về dạng rút gọn thì ma trận
thu được là duy nhất. Ta công nhận định lý sau đây phản ánh kết quả đó:
Định lý 2. (Định lý về tính duy nhất của dạng bậc thang rút gọn) Ma trận bất kỳ A
luôn quy được về dạng rút gọn nhờ qúa trình rút gọn hàng và dạng rút gọn của A là
duy nhất.
8. HẠNG CỦA MA TRẬN
Định nghiã 12. Hạng của ma trận A là số các hàng khác hàng 0 có trong dạng rút
gọn của A. Ký hiệu r(A).
11

lOMoARcPSD| 35883770
0
1
0
Chương 1. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
Vì trong dạng rút gọn của A, mỗi hàng khác hàng 0 đều có đúng một phần tử
chính, đó là phần tử cơ sở mà ta đã phát hiện trong quá trình quy A về dạng bậc thang.
Hơn nữa, trong suốt quá trình quy từ dạng bậc thang về dạng rút gọn bằng “phương
pháp khử ngược” thì các vị trí của những phần tử chính là không bao giờ thay đổi và vị
trí của phần tử chính cũng là vị trí mà các phần tử cơ sở đứng. Nhờ nhận xét trên, ta còn
tìm được hạng của ma trận qua các kết luận sau:
r(A) = Số hàng khác hàng 0 có trong bất kỳ dạng bậc thang nào của A.
= Số phần tử chính có trong bất kỳ dạng bậc thang nào của A.
= Số các cột có chứa phần tử cơ sở của A.
Nếu A cỡ mn thì từ nhận xét trên, suy ra r(A) m, r(A) n, nghĩa là r(A) min{m,
n}.
Ví dụ 8. Tìm hạng của ma trận A =
1 0
3
0 0
0 4
− 1 7
. Vì A đã có dạng bậc thang
0
7
nên hạng của A bằng số hàng khác hàng 0 có trong A, tức là r(A) = 3.
Ví dụ 9. Tìm hạng của ma trận A =
thang, quy A về dạng bậc thang:
1 1 − 2
3
−
1
2
1
−
5
4
7
. Vì A chưa có dạng bậc
7
1 1 − 2 4
h 2→h 2−h1;
1 1
− 2 4
1 1
−2 4
1 3
−
1
7
⎯
h
⎯
3→
⎯
h3−
⎯
2.h
⎯
1
→
0
2
1
3
⎯
h
⎯
2
⎯
h3
⎯→
0
−1 −1
−1
⎯
h
⎯
3→
⎯
h3+
⎯
2.h
⎯
2
→
2
1
1
−
5
1 − 2
7
4
0 − 1
−
1
− 1
0
2
1
3
−
1
− 1
0 0 − 1
−
1
1
= B.
Từ ma trận dạng bậc thang B, suy ra r(A) = 3.
12

lOMoARcPSD| 35883770
21 22
m1
a
m2
...
a
2n
mn
1
III.
GIẢI HỆ TUYẾN TÍNH TỔNG QUÁT
PHƯƠNG PHÁP GAUSS
a
11
x
1
a x
+
a
12
x
2
+
a x
+
...
+
+
...
+
a
1n
x
n
a x
=
b
1
=
b
Cho hệ tuyến tính:
21 1 22 2 2n n
2
(1)
a
m1
x
1
+
a
m 2
x
2
+
...
+
a
mn
x
n
=
b
m
Ma trận lập bởi các hệ số a
ij
: A =
a
11
a
12
a
a
...
...
a
1n
a
được gọi là ma trận hệ số. Ma
trận hệ số có bổ sung thêm cột cuối cùng là cột các hệ số vế phải, gọi là ma trận đầy đủ
A*, ký hiệu:
A* = [A|b] =
Mỗi cột trong ma trận hệ số A tương ứng với chỉ một ẩn. Khi A được quy về
dạng bậc thang, ẩn của hệ ứng với cột có chứa phần tử chính được gọi là ẩn chính, các
ẩn còn lại (không ứng với cột có chứa phần tử chính) gọi là ẩn tự do. Tùy từng trường
hợp mà hệ tuyến tính chỉ có ẩn chính hoặc có cả ẩn chính lẫn ẩn tự do.
1. ĐIỀU KIỆN CÓ NGHIỆM CỦA HỆ TUYẾN TÍNH TỔNG QUÁT
Định lý 3. Hai hệ tuyến tính có ma trận đầy đủ tương đương hàng với nhau là hai
hệ tương đương.
Do tính chất mọi phép toán hàng đều có phép toán hàng ngược và định nghiã
của hai ma trận tương đương hàng mà định lý trên là hiển nhiên. Vai trò quan trọng của
định lý là ở chỗ nó là cơ sở cho phương pháp giải hệ tuyến tính bằng quá trình rút gọn
hàng trên ma trận đầy đủ (mà sau này gọi là phương pháp Gauss). Nội dung cơ bản của
phương pháp là quy ma trận đầy đủ của hệ về dạng rút gọn, để từ đó tìm ra nghiệm.
x
1
+ x
2
− 2x
3
= 4
Ví dụ 10. Giải hệ:
x + 3x − x = 7
1 2 3
2x + x
− 5x
= 7
1 2 3
Lập ma trận đầy đủ A* =
1 1 − 2
3
−
1
2
1
−
5
4
7
.
7
Quy ma trận A* về dạng rút gọn:
13
a
11
a
21
a
a
12
22
...
a
a
1n
2 n
b
b
1
a
2
m1
a
m2
a
mn
b
m
a

lOMoARcPSD| 35883770
Chương 1. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
1 1 − 2 4
h 2→h 2−h1
1 1
− 2 4
1 1
− 2 4
1 3
−
1
7
⎯
h
⎯
3
→
⎯
h3
⎯
−
2
⎯
h1
→
0
2
1
3
⎯
h
⎯
2
⎯
h3
⎯→
0
−
1
−
1
− 1
2
1
−
5
7
0 − 1
−
1
− 1
0 2 1
3
1 1
−2 4
h3→(−1).h3
h 2→h 2−h3
1 1 0 2
h 2→−h 2
1 0 0 0
0 0 −2
⎯⎯⎯⎯→
0 1
2
−
1
Do A* ~ U nên hệ đã cho tương đương với hệ nhận U là ma trận đầu đủ:
x
1
+ 0x
2
+ 0x
3
= 0
x
1
= 0
0x
+ x
+ 0x
= 2
x = 2 .
1 2 3
2
0x + 0x − x = 1
x
= −1
1 2 3 3
Vậy hệ có nghiệm là (0; 2; –1).
Khi xét các ví dụ về giải hệ tuyến tính bằng thuật toán rút gọn hàng trên ma trận
đầy đủ, ta thấy một hệ tuyến tính bất kỳ có thể có nghiệm hoặc không có nghiệm. Vấn
đề tự nhiên đặt ra là cần phải có những dấu hiệu nào đó cho phép nhận biết được hệ nào
là có nghiệm, hệ nào không. Thật may mắn, thuật toán rút gọn hàng luôn quy được ma
trận đầy đủ A* của hệ về dạng bậc thang, và trên ma trận dạng bậc thang, lại áp dụng
được dấu hiệu khá thuận tiện cho bởi định lý sau đây:
Định lý 4. Giả sử hệ (1) có [S | c] là dạng bậc thang của ma trận đầy đủ A* =
[A|b]. Khi đó:
1) Hệ có nghiệm khi và chỉ khi ma trận [S |c] không chứa hàng dạng:
[0 0 .... 0 | ] với 0. (*)
2) Khi hệ có nghiệm, chỉ có 2 khả năng xẩy ra:
a) Nếu số ẩn chính bằng số ẩn (của cả hệ) thì hệ có nghiệm duy nhất.
b) Nếu số ẩn chính ít hơn số ẩn thì hệ có vô số nghiệm.
Chứng minh
1) Giả sử hệ có nghiệm, cần chứng minh hệ không chứa hàng dạng (*). Thật
vậy, giả sử trái lại, [S|c] có chứa hàng [0 0 .... 0 | ] với 0 thì rõ ràng hệ là vô
nghiệm vì không thể có bộ số (x
1
; x
2
; ...; x
n
) nào thỏa mãn được phương trình 0x
1
+ 0x
2
+...+ 0x
n
= 0, trái giả thiết hệ có nghiệm.
Ngược lại, do giả thiết, [S|c] không chứa hàng nào có dạng (*) nên mỗi hàng
của [S | c] phải có, hoặc dạng [0 0 .... 0 | 0], hoặc có phần tử chính là phần tử thuộc S.
Khi đó, bỏ qua các hàng dạng [0 0 .... 0 | 0], (vì nó ứng với phương trình 0x
1
+ 0x
2
+...+
0x
n
= 0, thỏa với mọi bộ số (x
1
; x
2
; ...; x
n
) và chỉ giữ lại các hàng có chứa phần tử chính,
để được hệ tuyến tính mới. Ta gán cho các ẩn tự do những giá trị hoàn toàn tuỳ ý, và
giải ra được các ẩn chính bằng phép thế ngược.Vì vậy hệ là có nghiệm.
2) Giả sử hệ là có nghiệm. Hiển nhiên rằng số các ẩn chính không thể lớn hơn số
các cột của ma trận hệ số A. Xét 2 khả năng sau:
Nếu xẩy ra số các ẩn chính bằng số các cột của A thì mọi ẩn đều là ẩn chính và
nó được giải ra một cách duy nhất nhờ phép thế ngược đối với hệ có ma trận đầy đủ là
[S | c].
Ngược lại, nếu số ẩn chính ít hơn số cột, sẽ có một số ẩn là ẩn tự do, giá trị của
nó được chọn hoàn toàn tùy ý nên ẩn chính nhận vô số giá trị, tùy thuộc vào việc gán trị
cho các ẩn tự do.Vậy hệ có vô số nghiệm.
14
⎯
h
⎯
3→
⎯
h3+
⎯
2.
h
⎯
2
→
−1 −1
−
1
⎯
h
⎯
1→
⎯
h1−
⎯
2.h3
⎯→
0
−
1
h1→
h1+h 2
0
= U.
0
0 −1
1
0
0
1 −1
0 0
1

lOMoARcPSD| 35883770
0
0
III. PHƯƠNG PHÁP GAUSS
x
1
+ 2x
2
− x
3
= 4
Ví dụ 11. Xét tính chất nghiệm của hệ:
2x + 5x + x = 10 .
1 2 3
4x + 9x − 3x
= 19
1 2 3
Cần quy ma trận đầy đủ về dạng bậc thang:
1 2
−
1
4
h 2→h 2−2.h1
1 2
−
1
4
1 2
−
1
4
A* =
2 5 1 10
⎯
h
⎯
3→
⎯
h3−
⎯
4
⎯
.h1
→
0
1
3
2
⎯⎯
h3→
⎯
h3−
⎯
h 2
→
0
1
3 2
= [S|c]
4
9
−
3
19
0 1 1
3
0 0
−
2
1
Kết luận ngay được hệ có nghiệm vì [S|c] có dạng bậc thang và không chứa hàng nào có
dạng [0 0 ...0 | ], 0. Hơn nữa, hệ có nghiệm duy nhất vì cả 3 ẩn của hệ đều là 3 ẩn
chính.
x
1
− 2x
3
+ x
4
+ x
5
=
−
5
x + 6x − 3x − 2x
=
7
Ví dụ 12. Xét tính chất nghiệm của hệ:
2 3 4 5
.
x
+
x
=
−
5
1 0 − 2
Lập A* = [A|b] =
1 6
0 0 0
0 0
1 1
− 3 − 2
1 1
0 1
4 5
x
5
=
0
− 5
.
− 5
Do A* đã có dạng bậc thang và trong A* không có hàng dạng [0 ...0 | ], 0 nên
hệ có nghiệm. Hơn nữa, trong ma trận A có 4 cột chứa phần tử chính theo thứ tự là c
1
A,
c
2
A, c
4
A, c
5
A nên hệ có 4 ẩn chính là x
1
, x
2
, x
4
, x
5
. Tổng số ẩn của hệ là 5 nên hệ có 1
ẩn tự do. Ẩn tự do là x
3
ứng với cột 3, (là cột không chứa phần tử chính). Áp dụng định
lý trên, suy ra hệ có vô số nghiệm.
Định lý 5. (Định lý Kronecker–Capelli) Cho hệ tuyến tính:
a
11
x
1
a x
+
a
12
x
2
+
a x
+
...
+
+
...
+
a
1n
x
n
a x
=
b
1
=
b
21 1 22 2 2n n
2
(1)
a
m1
x
1
+
a
m 2
x
2
+
...
+
a
mn
x
n
=
b
m
có A = [a
ij
]
m
n
là ma trận hệ số và A* =[A| b]
m
(n+1)
là ma trận đầy đủ.
Khi đó:
1)
Hệ (1) là hệ có nghiệm khi và chỉ khi hạng của ma trận hệ số A bằng hạng của
ma trận đầy đủ A*: r(A) = r(A*).
2)
Khi hệ (1) là hệ có nghiệm, có 2 khả năng:
a) Nếu r(A) = n thì hệ có nghiệm duy nhất.
b) Nếu r(A) < n, hệ có vô số nghiệm phụ thuộc n – r(A) tham số.
Chứng minh
1)
Trước hết nhận xét rằng dạng rút gọn của A chính là ma trận tạo bởi n cột đầu
tiên trong dạng rút gọn của A*, suy ra r(A*) r(A) (a). Hệ (1) vô nghiệm trong
dạng bậc thang rút gọn của A* có chứa hàng dạng [0 0 ...0 | ] với 0 r(A*) >
r(A). Vậy hệ (1) có nghiệm khi và chỉ khi r(A*) r(A) (b). Kết hợp (a) với (b) suy ra
(1)
có nghiệm khi và chỉ khi r(A) = r(A*).
2)
suy ra từ định lý 4 ở trên.
15
7
0

lOMoARcPSD| 35883770
0
0
Chương 1. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
Ví dụ 13. Xét tính chất nghiệm của hệ có ma trận đầy đủ là:
1
A* =
1
1 1
2 − 1
0 3
1 4
1
− 1
.
3
Quy A* về dạng bậc thang như sau:
h 2→h 2−h1
1 1 1 1
h3→h3+h 2
1 1 1 1
h3→h3−h1
A*
⎯
h
⎯
4→
⎯
h 4
⎯
−2
⎯
h1
→
0
1 − 2
− 1 2
− 1 − 2
− 2
2
− 2
⎯
h
⎯
4→
⎯
h 4
⎯
−
⎯
h 2
→
0 1 − 2
0 0 0
0 0
− 2
.
0
Do r(A*) = r(A) = 2, nên hệ có nghiệm và có vô số nghiệm vì r(A) < n = 3.
x
1
+ x
2
= 1
Ví dụ 14. Xét tính chất nghiệm của hệ:
x + x = 2
2 3
x + 2x + x
= −2
1 2 3
Quy ma trận đầy đủ về dạng bậc thang để tìm hạng:
A* =
1 1 0
1 1
1 2 1
1
− 2
1 1 0
⎯
h
⎯
3→
⎯
h3−
⎯
h1
→
0
1
1
0 1 1
1
− 3
1 1 0
⎯
h
⎯
3→
⎯
h3−
⎯
h2
⎯→
0
1
1
0
0
0
1
2
.
−
5
Do r(A*) = 3 > r(A) = 2, hệ vô nghiệm.
2. GIẢI HỆ TUYẾN TÍNH BẰNG PHƯƠNG PHÁP GAUSS
Giải hệ tuyến tính bằng cách quy hệ đã cho về hệ tương đương đơn giản hơn nhờ
thực hiện phép rút gọn hàng trên ma trận đầy đủ gọi là phương pháp Gauss. Để thuận
tiện trong thực hành, phương pháp Gauss thường được tiến hành theo lược đồ gồm 4
bước sau:
Bước 1. Viết ra ma trận đầy đủ A* của hệ tuyến tính.
Bước 2. Dùng thuật toán rút gọn hàng, quy ma trận đầy đủ A* về dạng bậc
thang. Khẳng định hệ có nghiệm hay không, nếu hệ có nghiệm, thực hiện bước tiếp
theo.
Bước 3. Quy dạng bậc thang của A* về dạng rút gọn.
Bước 4. Từ dạng rút gọn, viết ra nghiệm của hệ.
x
1
+ 2x
2
+ 5x
3
= −9
Ví dụ 15. Giải hệ:
x − x + 3x = 2
1 2 3
3x − 6x
− x
= 25
1 2 3
1 2 5 − 9
Bước 1. Lập ma trận đầy đủ A* =
1 − 1 3
3 − 6 − 1
25
Bước 2. Quy ma trận A* về dạng bậc thang:
h 2→h 2−h1
1 2
5 − 9
1 2
5 − 9
A*
⎯
h
⎯
3→
⎯
h3−
⎯
3
⎯
h1
→
0
0
− 3
− 12
− 2
− 16
11
52
⎯
h
⎯
3→
⎯
h3−
⎯
4
⎯
h 2
→
0
0
− 3 − 2
0 − 8
11
8
= B*.
Từ B suy ra r(A*) = r(A) nên hệ có nghiệm.
16
1
2
4
0
0
2
2
2
0

lOMoARcPSD| 35883770
0
0
2
2
2
0
III. PHƯƠNG PHÁP GAUSS
Bước 3. Tiếp tục quy A* về dạng rút gọn (từ B*):
h3
→
−
1
.h3
8
1 2
5 − 9
h 2→h 2+2.h3
h1→h1−5.h3
1 2
0 − 4
B*
⎯⎯⎯⎯→
0
0
− 3 − 2
0 1
11
− 1
⎯⎯⎯⎯⎯→
0
0
− 3 0
0 1
9
−
1
h 2
→−
1
.h 2
3
1 2 0
− 4
h1→h1−2h 2
1 0 0 2
⎯⎯⎯⎯→
0 1 0
0 0 1
−
3
−
1
⎯⎯⎯⎯⎯→
0
1
0
0 0 1
x
1
= 2
− 3
−
1
= U.
Bước 4. Từ dạng rút gọn U, viết ra nghiệm:
x
= −3 .
2
x
3
= −1
x
1
− 5x
2
− 8x
3
+ x
4
=
3
3x + x − 3x − 5x = 1
Ví dụ 16. Giải hệ:
1 2 3 4
x − 7x + 2x
=
−
5
1 3 4
11
x
2
+
20
x
3
−
9
x
4
=
2
Khi đã thành thạo các bước của phương pháp Gauss, ta có thể trình bày ngắn gọn lời
giải như sau:
1
3
h 2→h 2−3h1
1 − 5 − 8 1
0 16 21 − 8
3
− 8
h 2→h 2−3h3
A* =
1
⎯
h
⎯
3→
⎯
h3−
⎯
h
⎯
1
→
0 5
11
1 1
20 − 9
⎯⎯⎯⎯⎯→
− 8
1 − 5
0 1
− 8 1
18 − 11
3
16
h3→h3−5h 2
1 − 5
0 1
− 8 1
18 − 11
3
16
h 4→h 4−2h3
⎯
h
⎯
4→
⎯
h 4
⎯
−11
⎯
h 2
→
⎯⎯⎯⎯⎯→
0 5 1
11 20
1
0
1 − 8
− 9
.
0 0
89
178
56
112
− 88
− 174
Hệ vô nghiệm vì r(A*) = 4 > r(A) = 3.
2x
1
+ 2x
3
+ 7x
4
= −2
x − x + 2x = −1
Ví dụ 17. Giải hệ:
1 2 3
.
−
x
+
2x
−
3x
+
4x
=
1
1 2 3 4
2x
1
−
x
2
+
3x
3
+
3x
4
=
−
2
2 0 2 7
−2
1 −1 2 0
−1
−1
1 −1 2 0 −1
h1h 2
2 0 2 7 −2
0
A* =
−1 2
−3 4
⎯⎯⎯⎯→
1
−1 2
−3 4
→
1
0
−1 3 3 −2
−1 3 3
−2
17
0
2
0
0
0
0
− 5
− 8
1
3
1
− 3
− 5
1
0
− 7
2
− 5
11
20
− 9
2
− 5
− 8
1
3
1
18
− 11
16
0
89
56
− 88
0
0
0
2
1
−1
2
0
0
2
−2
7
0
1
−1
4
0
1
−1
3

lOMoARcPSD| 35883770
0
0
0
0
Chương 1. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
1 −1 2 0 −1
1 −1 2 0 −1
1 −1 2 0 −1
h 2h3
0 1 −1 4 0
0 1 −1 4 0
0 1 −1 4 0
⎯⎯⎯⎯→
0 2
0 1
−2 7
−1 3
→
0
0 0 0
0 0 0
−1 0
−1
→
→
0 0 0 1 0
0 0 0 0
1 −1 2 0
−1
1 0 1 0
−1
0 1 −1 0
0 1
→
−1 0
= U
0 0 0 1 0
0 0 0 0
0 0 0 1 0
0 0 0 0
Từ ma trận dạng rút gọn U, phát hiện ẩn x
3
ứng với cột 3 là cột không chứa phần
tử chính nên x
3
là ẩn tự do, còn x
1
, x
2
, x
4
là các ẩn chính. Đặt ẩn tự do x
3
= t R, ta có
x
1
=
−
1
−
t
x = t
nghiệm:
2
, hay viết ngắn gọn nghiệm là: (–1–t; t; t; 0), t R
x
=
t
R
3
x
4
=
0
CHÚ Ý VỀ PHƯƠNG PHÁP GAUSS
Khi thực hiện thuật toán rút gọn hàng trên ma trận, ta gặp điều bất lợi là phải viết lại
ma trận nhiều lần; do đó cần phải kết hợp một lúc nhiều phép toán cho một lần đổi
ma trận (như các ví dụ trên đã trình bày).
Ngày nay việc giải hệ tuyến tính được thực hiện trên máy tính đang ngày càng phổ
biến do tính hiệu quả của nó. Tuy nhiên, tính chính xác của nghiệm do máy tìm được,
đôi khi lại là điều băn khoăn lớn của chúng ta. Hãy xem ví dụ sau như là một minh họa:
Ví dụ 18. Cho hệ:
0,1000x
1
+ 0, 9990x
2
= 1, 000
0,1000
x
+
1, 000
x
=
1, 006
1 2
Các hệ số được cho với 4 chữ số có nghĩa, kết qủa nghiệm do máy tìm được là:
x
1
= −49, 94
x
=
6, 000
2
Giả sử rằng các hệ số được làm tròn với 3 chữ số có nghĩa, hệ trở thành hệ mới “gần”
như hệ cũ:
0,100x
1
+ 0, 999x
2
= 1, 00
0,100
x
+
1, 00
x
=
1, 01
2 2
nhưng khi đó nghiệm lại là:
x
1
= −89, 9
.
x = 10
2
Qua trên ta thấy, chỉ cần một thay đổi nhỏ trong hệ số ở vế phải của hệ, nghiệm
tìm được đã khác rất nhiều so với nghiệm ban đầu. Về mặt hình học, nghiệm của hệ
trên chính là tọa độ giao điểm của hai đường thẳng "gần song song", chỉ cần thay đổi
một chút về vị trí của một trong hai đường thẳng là tức khắc tạo ra sự dịch chuyển lớn
về giao điểm của chúng. Nguyên nhân là ở chỗ: số thực được biểu diễn trên máy tính
chỉ với một số hữu hạn các chữ số nên việc làm tròn số hay cắt đi một số chữ số, tất yếu
sẽ dẫn đến sai số. Khi làm việc với một số lớn các phép tính số học, các sai số này được
gia tăng thêm và chúng gây nên sự khác biệt lớn giữa nghiệm tìm được và nghiệm
đúng. Việc giải quyết vấn đề này thuộc phạm vi các giáo trình phương pháp tính, còn ở
đây ta chỉ cần ý thức được nguồn gốc của những sai số gặp phải khi tìm nghiệm của hệ
tuyến tính bằng máy để có được những giải pháp hợp lý khi thực hành cụ thể.
18
0
0
0

lOMoARcPSD| 35883770
3
1
III.
PHƯƠNG PHÁP GAUSS
3. HỆ TUYẾN TÍNH THUẦN NHẤT
Việc giải hệ thuần nhất không cần thêm công cụ và kỹ thuật mới. Tuy nhiên do
ma trận đầy đủ A* của hệ có cột cuối cùng là cột 0, sẽ không có gì thay đổi qua các
phép toán hàng. Vì vậy khi giải hệ thuần nhất, ta chỉ cần biến đổi trên ma trận hệ số A
là đủ. Mặt khác, luôn có r(A*) = r(A) nên hệ thuần nhất luôn có nghiệm. Định lý sau
đây là hiển nhiên:
Định lý 6. Cho hệ thuần nhất:
[a
ij
]
m
n
. Khi đó:
a
ij
x
j
=
0
; i = 1..m. (2) với ma trận hệ số A =
j=1
a)
Hệ thuần nhất (2) luôn có nghiệm (x
1
; x
2
; ...; x
n
) = (0; 0; ...; 0) gọi là nghiệm
tầm thường.
b)
Hệ thuần nhất (2) có nghiệm duy nhất là nghiệm tầm thường khi và chỉ khi r(A)
= n. Nếu r(A) n thì hệ có vô số nghiệm, phụ thuộc n–r(A) tham số.
Nghiệm phụ thuộc vào tham số của hệ thuần nhất thường được gọi là nghiệm tổng
quát.
x
1
+ 2x
2
+ 2x
3
+ x
4
+ 4x
5
= 0
Ví dụ 19. Giải hệ:
3x
1
+ 7x
2
+ 7x
3
+ 3x
4
+13x
5
= 0
2x + 5x + 5x + 2x + 9x = 0
1 2 3 4 5
Quy ma trận hệ số về dạng rút gọn:
1 2 2 1 4
h 2→h 2−3h1
1 2 2 1 4
h1→h1−2h 2
1 0 0 1 2
A =
7 7
2
5
5
3 13
2 9
⎯
h
⎯
3→
⎯
h3−
⎯
2
⎯
h1
→
0
1
0 1
1 0
1 0 1
⎯
h
⎯
3→
⎯
h 2−
⎯
h
⎯
2
→
0 1 1 0
0 0 0 0
= U
0
Từ U, có 3 ẩn tự do là x
3
, x
4
và x
5
. Đặt x
3
= t R
,
x
4
= u R, x
5
= v R thì
x
1
= −u − 2v
x
=
−
t
−
v
2
nghiệm tổng quát của hệ là:
x
3
= t R .
x
=
u
R
4
x
5
=
v
R
Nghiệm tổng quát còn được viết ở dạng:
x = (–u–2v; –t –v; t; u; v) = (0; –1; 1; 0; 0).t + (–1; 0; 0; 1; 0).u + (–2; –1; 0; 0; 1).v.
Cho lần lượt các giá trị của tham số:
t = 1, u = v = 0, có 1 nghiệm là (0; –1; 1; 0; 0).
t = 0, u = 1, v = 0, có 1 nghiệm là (–1; 0; 0; 1; 0).
t = 0, u =0, v = 1, có 1 nghiệm là (–2; –1; 0; 0; 1).
Tập gồm 3 nghiệm {(0; –1; 1; 0; 0), (–1; 0; 0; 1; 0), (–2; –1; 0; 0; 1)} gọi là tập
nghiệm cơ bản của hệ thuần nhất. Sau này, khi học đến không gian vectơ, tập nghiệm
cơ bản chính là cơ sở của không gian nghiệm của hệ thuần nhất đã cho.
19
n
1

lOMoARcPSD| 35883770
I.
CÁC PHÉP TOÁN TRÊN MA TRẬN
Chương 2
MA TRẬN
1. Các phép toán đại số trên ma trận.
2. Ma trận khả nghịch.
3. Ma trận chuyển vị, ma trận khối.
Khi giải hệ phương trình tuyến tính ta đã gặp khái niệm ma trận và sử dụng ma trận
như một công cụ đầy hiệu quả. Chưa hết, ma trận còn là một công cụ mạnh không những
của đại số tuyến tính mà còn của nhiều bộ môn toán học khác. Để sử dụng đầy đủ sức
mạnh của công cụ đó, chương này ta sẽ nghiên cứu ma trận như một khái niệm độc lập,
tách khỏi hệ phương trình tuyến tính, nhằm hiểu sâu thêm cả về lí thuyết lẫn ứng dụng của
nó.
I. CÁC PHÉP TOÁN ĐẠI SỐ TRÊN MA TRẬN
1. PHÉP CỘNG VÀ NHÂN MA TRẬN VỚI MỘT SỐ
Cho ma trận A = M(m,n), Khi đó:
– Phần tử (i,j) của A là a
ij
, kí hiệu [A]
ij
= a
ij
.
a
1 j
– Cột thứ j của A là c
j
A =
2 j
. Coi mỗi phần tử là một cột, ma trận A được viết
a
mj
thành dạng ma trận hàng của các cột: A = [c
1
A c
2
A... c
n
A].
– Hàng thứ i của là h
i
A = [a
i1
a
i2
... a
in
]. Coi mỗi phần tử là một hàng, ma trận A
h
1
A
h
A
được viết thành dạng ma trận cột của các hàng: A =
2
.
h A
m
Định nghiã 1. Cho A, B M(m,n) và R. Tổng của ma trận A và B, kí hiệu A+B,
tích của số với ma trận A, kí hiệu A, là các ma trận có phần tử xác định lần lượt
như sau:
[A+B]
ij
= [A]
ij
+ [B
ij
], i = 1..m, j = 1..n
[A]
ij
= [A]
ij
, i = 1..m, j = 1..n.
Tổng A + (–1)B gọi là hiệu của ma trận A và ma trận B, kí hiệu là A – B. Rõ ràng
tổng 2 ma trận xác định khi và chỉ khi chúng có cùng cỡ, tích của số với ma trận luôn
luôn xác định.
20
a
11
a
m1
a
mn
a
1n
a

lOMoARcPSD| 35883770
8
1
0
1
2 0
8
0
y
1
8
=
Chương 2: MA TRẬN
Ví dụ 1. Cho A =
4
5 7
, B =
x 1
y
và C =
3
4
thì:
−
7 0
0 2
x y
A+B =
4
5
7
+
x
1
y
=
x + 4
6
y + 7
.
−
7 0 8
0 2
x y
−
7 2
x
y + 8
2.C = 2.
3
4
6 8
2A–3B = 2
4
5 7
– 3
x 1 y
=
8 − 3x
7
14 − 3 y
−
7 0 8
0 2
x y
−
14
−6x 16 − 3 y
Định lý 1. Nếu A, B, C M(m,n) và , R thì:
1. A + B = B + A.
2. A + (B + C) = (A + B) + C.
3. Tồn tại duy nhất một ma trận trong M(m,n), ký hiệu là O sao cho A + O = A A
M(m,n).
4. Với mỗi A M(m,n), có duy nhất một ma trận trong M(m,n), ký hiệu là –A sao cho
A + (–A) = O.
5. (+)A = A + A.
6. (A + B) = A + B.
7. (A) = ()A.
8. 1.A = A.
9. A = O
= 0
A
=
O
.
Việc chứng minh các tính chất trên là tương tự nhau. Để làm ví dụ, ta chứng minh tính
chất kết hợp của phép cộng ma trận: A + (B + C) = (A + B) + C (*)
-
Trước hết, theo định nghĩa phép cộng thì hai ma trận ở vế phải và vế trái của (*) có
cùng cỡ.
-
Xét phần tử (i,j) ở vế trái của (*): [A+(B+C)]
ij
= [A]
ij
+[B+C]
ij
= [A]
ij
+([B]
ij
+[C]
ij
)
= ([A]
ij
+[B]
ij
)+[C]
ij
= [A+B]
ij
+[C
ij
] = [(A+B)+C]
ij
là phần tử (i,j) ở vế phải.
Ví dụ 2. Cho A =
4
−
7
5 7
, B =
x 1
0
2x
y
, C =
1 0
2
− 3
tìm D = {–A+(B–
3(B–2A+2C)}–{4(A–B)+3B–5C}.
Trước hết, biến đổi rút gọn D như sau:
D = {–A+(B–3B+6A–6C)}–{4A–4B+3B–5C} = {–A–2B+6A–6C}–{4A–B–5C}
= –A–2B+6A–6C–4A+B+5C = A–B–C.
Thay A, B, C vào biểu thức của D ta có : D = A–B–C =
4
5 7
–
x
1
y
–
1 0
− 3
=
3-x 4 10
−
y
.
−
7 0
0 2
x y
1 2 0
−
8
−2x − 2 8 − y
2. PHÉP NHÂN HAI MA TRẬN
Trước hết ta đưa ra khái niệm tích của ma trận hàng và ma trận cột như sau:
21
0
0
.

lOMoARcPSD| 35883770
4
4
b
0
5
I.
CÁC PHÉP TOÁN TRÊN MA TRẬN
b
1
Định nghiã 2. Cho A =
a
1
a
n
M
(1,n) và B =
b
n
M(n,1) thì tích của A và
B là ma trận cỡ 11 được cho bởi : AB = [a
1
b
1
+ a
2
b
2
+ ... + a
n
b
n
].
0
Ví dụ 3.
Ví dụ với A =
1
2
3
, B =
−
2
, C =
2
0
2
thì:
AB =
1 2 3
−2
= [1.0 + 2(–2) + 3.2] = [2].
2
AC =
1 2 3
2
là không tồn tại vì cỡ của A và C là không thích hợp để lấy tích
theo định nghiã.
Tích của ma trận hàng với ma trận cột còn gọi là tích vô hướng của vectơ hàng với
vectơ cột vì quy tắc tính tích này cũng giống như quy tắc tính tích vô hướng của 2 vectơ
trong hình học.
Định nghiã 3. Cho A M(m,n) và B M(n,p), tích của ma trận A với ma trận B là
ma trận AB M(m,p ) có phần tử (i,j) xác định bởi tích của hàng i trong A với cột j
trong B :
[AB]
ij
= h
i
A.c
j
B, i = 1..m, j = 1..p.
Từ định nghiã suy ra tích AB được xác định khi và chỉ khi số phần tử có trong hàng của
A phải bằng số phần tử có trong cột của B, tức là số cột của ma trận đứng trước phải bằng
số hàng của ma trận đứng sau. Xét cụ thể phần tử (i,j) của tích AB ta có :
b
1
j
b
n
[AB]
ij
= h
i
A.c
j
B =
a a a
.
2 j
= a
i1
b
1j
+a
i2
b
2j
+...+a
in
b
nj
=
a
b
.
i1
i 2
in
nj
k =1
ik kj
Nếu A là ma trận vuông cấp n thì các tích: AA ; AAA; ... luôn tồn tại và khi đó ta viết:
A
2
=
A.A
,
A
3
=
A.A.A,
..., A
–
.A
.......
.A
k
2
= A
k
.
3 0 1
3 1
1 2
Ví dụ 4. Tính tích AB với A =
− 1 2
và B =
.
2 3
Lần lượt tính các phần tử của tích AB theo công thức (*) ta có:
3
1
[AB]
11
= h
1
A
.
c
1
B =
2
3 0 1
= 2.3+3.1+0.2+1.0 = 9.
2
0
1
2
[AB]
12
= h
1
A
.
c
2
B =
2
3 0 1
= 2.1+3.2+0.3+1.5 = 13.
3
5
22
4
1

lOMoARcPSD| 35883770
3
9
21
=
=
Chương 2: MA TRẬN
3
1
[AB]
21
= h
2
A
.
c
1
B =
4
− 1 2 1
= 4.3–1.1+2.2.–1.0 = 15.
2
0
1
2
[AB]
22
= h
2
A
.
c
2
B =
4
− 1 2 1
= 4.1–1.2+2.3–1.5 = 3.
3
5
Từ đó AB =
9
15
13
.
2
− 1
− 5 0
3 − 4
4 − 6
Ví dụ 5. Cho
A =
, B =
7
1
. Không tính toàn bộ tích AB, hãy
6 − 8 7
− 3 0
3
2
tìm: [AB]
32
, h
2
(AB) và c
1
(AB).
- Có: [AB]
32
= h
3
A.c
2
B = 6 − 8
−
6
−
7
1
= 6(–6)+(–8)1+(–7).2 = –58.
2
- Có h
2
(AB) = [ h
2
A.c
1
B h
2
A.c
2
B] = [5 1].
vì:
h
2
A
.
c
1
B =
−
1
3
4
−
4
7
=
5.
h
2
A
.
c
2
B =
−
1
3
−
6
−
4
1
= 1.
[AB]
11
3
h
1
A.c
1
B
− 27
2
[AB]
h A.c B
5
- Có c
1
(AB) =
=
=
.
[AB]
31
h
3
A.c
1
B
− 11
[AB]
41
h
4
A.c
1
B
15
Định lý 2. Nếu A M(m,n) còn B Mn,p) thì:
1. c
j
(AB) = A.(c
j
B).
2. h
i
(AB) = (h
i
A).B.
3. AB = [A.c
1
B A.c
2
B ... A.c
p
B].
(h
1
A).B
(h
A).B
4. AB =
2
.
(h A).B
m
Chứng minh
[AB]
1j
h
1
A.c
j
B
h
1
A
[AB]
h A.c B
h A
1. c
j
(AB) =
⁝ ⁝
2
⁝
.c
j
B = A.c
j
B.
h
A.c B
[AB]
nj
n
j
h
n
A
23
2 j
2 j
2 1
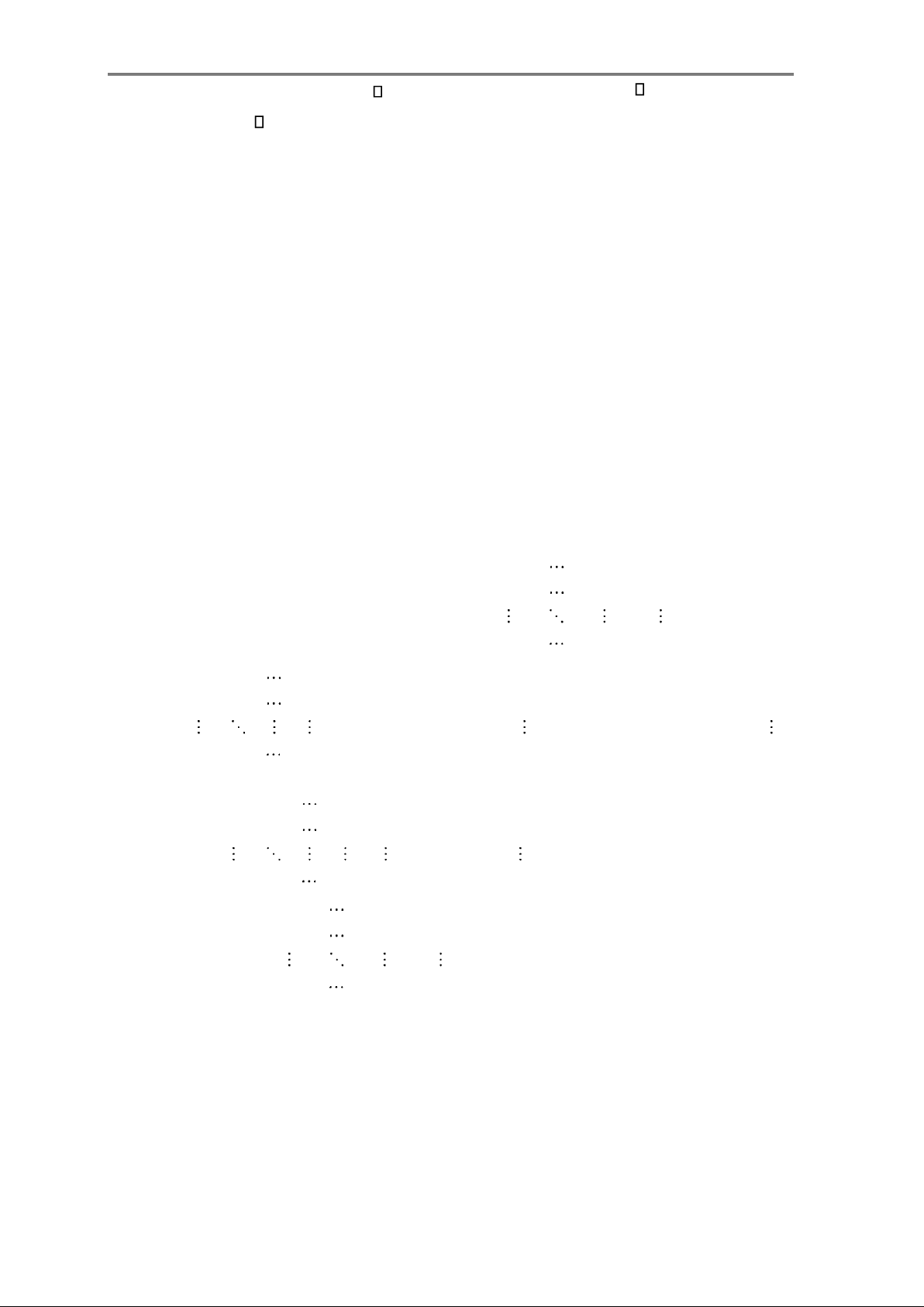
lOMoARcPSD| 35883770
1
2
I.
CÁC PHÉP TOÁN TRÊN MA TRẬN
2. h
i
(AB) = [AB]
[AB]
[AB]
= h A.c B h A.c B h A.c B
= h
i
A.
c B c B
2
i1 i2 in
c
p
B = h
i
A.B.
i 1 i 2 i p
3. và 4. là hệ quả của 1. và 2.
0 1 0
1 −1
Ví dụ 6. Cho A =
1 0 0
, B =
0 2
. C =
1 1 2
. Không tìm toàn bộ
−
2 1 0
0
0
−1
3
−
2
ma trận tích mà chỉ tìm hàng hay cột đã chỉ ra: c
2
(AB), h
3
(AB), h
1
(AB)C.
- c
2
(AB) = A.c
2
B =
0 1 0
1 0 0
−
1
2
=
−
1
.
0
0
−
1
−
2
2
1 −1
- h
3
(AB) = h
3
A.B =
0 0 −1
0 2
=
−
3
2
.
3
−
2
1 −1
-
h
1
(AB)C = h
1
(AB).C = ((h
1
A).B).C = (
0
1
0
.
0
2
).C =
0 2
1
1
2
=
−2 1 0
−
4
1
0
.
Ví dụ 7. Dạng ma trận của hệ tuyến tính:
3
−
2
.
x
1
b
1
x
b
Gọi A =
là ma trận hệ số , X =
2
là ma trận cột các ẩn , B =
2
x
b
là ma trận các hệ số tự do thì có:
n m
a
11
a
12
a
1n
x
1
a
11
x
1
+ a
12
x
2
+ ... + a
1n
x
n
a a a
x
a x
+ a x
+ ... + a x
AX =
21 22 2n
2
=
21 1 22 2 2 n n
.
a a a
x
a x
+ a x
+ ... + a x
m1 m2 mn n
m1 1
m2 2
mn n
a
11
x
1
+ +a
1n
x
n
= b
1
a x + +a x = b
AX = B
21 1 2n n 2
a
m1
x
1
+ +a
mn
x
n
= b
m
Do vậy, phương trình ma trận AX = B là cách viết của hệ tuyến tính dưới dạng ma
trận nên nó được gọi là dạng ma trận của hệ tuyến tính. Từ đây, ta sẽ viết hệ tuyến tính
dưới dạng này cho gọn.
3. TÍNH CHẤT CỦA PHÉP NHÂN HAI MA TRẬN
24
a
11
x
1
+
a
+a
1n
x
n
21 1
x +
+a x
2n n
= b
1
= b
2
a
m1
x
1
+
+a
mn
x
n
= b
m
a
11
a
21
a
a
12
22
a
1n
a
a
2n
m1
a
m2
a
mn

lOMoARcPSD| 35883770
Chương 2: MA TRẬN
Định lý 3. Cho A, B, C là các ma trận với cỡ thích hợp để phép toán là có nghiã còn
R. Khi đó:
1. (AB)C = A(BC).
2. A(B+C) = AB +AC.
3. (A+B)C = AC + BC.
4. (A)B = (AB) = A(B).
5. I
m
A = AI
n
A M(m,n)
Chứng minh. Các chứng minh được tiến hành tương tự, ở đây ta chứng minh tính chất 1):
(AB)C = A(BC) như là một ví dụ minh họa.
Giả sử A cỡ mn, B cỡ np còn C cỡ pq, thì AB cỡ mp nên (AB)C cỡ mq. Mặt
khác, A cỡ mn còn BC cỡ nq nên A(BC) cỡ mq. Chứng tỏ các ma trận (AB)C ở vế trái
và A(BC) ở vế phải 1) có cùng cỡ mq.
Xét phần tử [(AB)C]
ij
ở vế trái và phần tử [A(BC]
ij
ở vế phải với mọi i = 1..m, j =
1..q, ta có:
p p
n
[(A
B)C]
ij
=
[AB]
ih
[C]
hj
=
[A]
ik
[B]
kh
[C]
hj
. (*)
h=1
h=1 k=1
Do tổng hữu hạn các số thực có tính chất phân phối đối với phép nhân nên:
p
n
n
p
n
[A]
ik
[B]
kh
[C]
hj
=
[A]
ik
[B]
kh
[C]
hj
=
[A]
ik
[BC]
kj
= [
A(BC)]
ij
(**)
h=1 k=1
k
=
1
h=1
k=1
So sánh (*) và (**) thì [(AB)C]
ij
= [A(BC)]
ij
đúng với mọi i = 1..m, j = 1..q.
Chú ý rằng, khác với phép nhân các số, phép nhân các ma trận không có một số
tính chất thông thường mà phép nhân với số vốn có. Cụ thể như sau:
1. Phép nhân 2 ma trận không có tính chất giao hoán: AB BA.
2. Phép nhân ma trận không có luật giản ước: AB = AC và A O không suy ra được
B = C.
3. Nếu tích AB = O thì không thể kết luận hoặc A = O hoặc B = O. (Khi đó ta nói
phép nhân 2 ma trận không có ước của O).
Ví dụ 8. Cho A, B M(n,n) thì (A+B)
2
= (A+B)(A+B) = A
2
+ AB + BA + B
2
. Nếu
có thêm tính giao hoán AB = BA thì có (A+B)
2
= A
2
+ 2AB + B
2
, tức là hằng đẳng
thức về bình phương của tổng 2 số sẽ không còn đúng với bình phương của tổng 2 ma
trận vuông bất kỳ.
Mặc dù phép nhân 2 ma trận không có luật giản ước, nhưng trong trường hợp đặc biệt
ta vẫn có quy tắc giản ước sau đây, rất có lợi cho một số áp dụng về sau:
Định lý 4. Nếu A, B M(m,n) thoả mãn AX = BX với mọi ma trận cột X M(n,1) thì A
= B.
Chứng minh. Vì AX = BX đúng với mọi ma trận cột X =
x
1
, nên với ma trận cột X = e
1
x
n
1
0
1
0
1
0
=
ta sẽ có A
= B
c
1
A = c
1
B.
⁝
0
⁝
0
⁝
0
25

lOMoARcPSD| 35883770
I.
CÁC PHÉP TOÁN TRÊN MA TRẬN
Lý luận tương tự với X = e
i
thì có c
i
A = c
i
B với mọi i = 1..n. A = B vì chúng có
các cột tương ứng bằng nhau.
4. MA TRẬN CHUYỂN VỊ
Định nghiã 4. Cho ma trận A, ta gọi ma trận chuyển vị của ma trận A là ma trận A
T
,
thu được từ A bằng cách chuyển các hàng (hay cột) trong A thành các cột (hay hàng)
tương ứng trong A
T
.
Phép đổi một ma trận thành ma trận chuyển vị của nó được gọi là phép chuyển vị.
Từ định nghĩa suy ra nếu A M(m,n) thì A
T
M(n,m).
Định lý 5.
1)
(A
T
)
T
= A với bất kỳ ma trận A.
2)
(A+B)
T
= A
T
+B
T
với bất kỳ hai ma trận A, B cộng được.
3)
(A)
T
= A
T
với bất kỳ ma trận A và bất kỳ số .
4)
(AB)
T
= B
T
A
T
nếu tích AB xác định.
Chứng minh.
1)
Nếu A M(m,n) thì A
T
M(n,m) và (A
T
)
T
M(m,n). Mặt khác [(A
T
)
T
]
ij
= [A
T
]
ji
= [A]
ij
. Vậy (A
T
)
T
và A có cùng cỡ và mọi phần tử tương ứng đều bằng nhau nên
bằng nhau.
2)
Tự chứng minh.
3)
Tự chứng minh.
4)
Giả sử A M(m,n), B M(n,p) thì AB M(m,p), (AB)
T
M(p,m). Do A
T
M(n,m), B
T
M(p,n) nên B
T
A
T
M(pm). Xét phần tử (i,j) của (AB)
T
thì:
[(AB)
T
]
ij
= [AB]
ji
=
[A]
jk
[B]
ki
k
=
1
=
[A
T
]
kj
[B
T
]
ik
=
k
=
1
[B
T
]
ik
[A
T
]
kj
k
=
1
= [B
T
A
T
]
ij
.
Chứng tỏ (AB)
T
và B
T
A
T
có cùng cỡ, và mọi phần tử tương ứng đều bằng nhau.
Định nghiã 5. Ma trận A M(n,n) được gọi là ma trận đối xứng (hoặc phản đối xứng)
nếu A
T
= A (hoặc A
T
= –A).
Từ định nghiã suy ra:
a. A đối xứng thì [A]
ij
= [A]
ji
i, j = 1..n..
b. A chéo đối xứng thì [A]
ij
= – [A]
ji
,i, j = 1..n.
c. A, B M(n,n) và A, B đối xứng thì A+B và A là các ma trận đối xứng.
Ví dụ 9. Chứng minh rằng với A M(m,n) thì AA
T
và A+A
T
là các ma trận đối
xứng.
Thật vậy, có (AA
T
)
T
= (A
T
)
T
.A
T
= A.A
T
AA
T
là ma trận đối xứng vì (AA
T
)
T
= AA
T
.
Có (A+A
T
)
T
= A
T
+(A
T
)
T
= A
T
+A= A+A
T
A+A
T
là ma trận đối xứng vì (A+A
T
)
T
=
A+A
T
.
26
n
n
n

lOMoARcPSD| 35883770
− 1
1
c
d
=
=
1
2
1
2
1
0
1
1
2
1
2
II.
MA TRẬN KHẢ NGHỊCH
II. MA TRẬN KHẢ NGHỊCH
Trong mục này ta chỉ xét với ma trận vuông cấp n và nghiên cứu tính chất khả nghịch
của ma trận vuông, tương tự như tính chất khả nghịch của số thực khác 0, đóng vai trò
quan trọng trong các phép toán trên ma trận.
1. KHÁI NIỆM MA TRẬN KHẢ NGHỊCH
Định nghiã 6. Ma trận A M(n,n) được gọi là ma trận khả nghịch nếu tồn tại ma trận
B M(n,n) sao cho AB = I
n
= BA và khi đó ma trận B gọi là ma trận nghịch đảo của
A, kí hiệu là B = A
–1
.
Từ định nghiã suy ra:
-
Nếu A khả nghịch thì: AA
–1
= A
–1
A = I
n
.
-
Ma trận nghịch đảo A
–1
của A (khả nghịch) là duy nhất vì nếu A có 2 ma trận
nghịch đảo là B và C thì: BA = I
n
= AB và CA = I
n
= AC nên:
B = BI
n
= B(AC) = (BA)C = I
n
C = C.
Ví dụ 10. Cho A =
2
−
1
. Chứng tỏ rằng A khả nghịch và tìm A
–1
.
A khả nghịch Tồn tại B sao cho AB = I
2
= BA. Dễ thấy B là ma trận vuông cấp 2 nên
gọi B =
a
b
thì:
AB = I
2
2
− 1
− 1
a
b
1
c
d
1 0
0 1
2a − c
−a + c
2b − d
−b + d
1 0
0 1
2a − c = 1
2b − d = 0
−a + c = 0
−b + d = 1
a = 1
b = 1
c = 1
d
=
1
B =
1 1
Với B =
1
1
, có BA =
1
1
2
− 1
− 1
=
1
0
= I
2
.
Do tồn tại B =
1
1
để AB = I
2
= BA nên A là khả nghịch và A
–1
= B =
1
1
.
2. CÁC TÍNH CHẤT ĐƠN GIẢN CỦA MA TRẬN KHẢ NGHỊCH
Định lý 6. Nếu A, B M(n,n), A, B khả nghịch và 0 R thì:
a)
A
–1
khả nghịch và (A
–1
)
–1
= A
b)
A khả nghịch và ( A)
–1
=
1
A
–1
.
c)
AB khả nghịch và (AB)
–1
= B
–1
A
–1
.
d)
A
T
khả nghịch và (A
T
)
–1
= (A
–1
)
T
Chứng minh.
27
2
1
.

lOMoARcPSD| 35883770
Chương 2: MA TRẬN
a. A
–1
khả nghịch tồn tại C sao cho: A
–1
C = I
n
= CA
–1
. Dễ thấy ở đây C = A
thoả mãn phương trình, suy ra A
–1
là khả nghịch và nghịch đảo của A
–1
chính là A.
b. Vì giả thiết A khả nghịch nên tồn tại A
–1
và AA
–1
= A
–1
A = I. Xét:
(A).(
1
A
–1
) = (.
1
).(A.A
–1
) = 1.I = I.
(
1
A
–1
).(A) = (
1
.).(A
–1
.A) = 1.I = I.
Chứng tỏ A khả nghịch và nghịch đảo của A là
1
A
–1
.
c. Hiển nhiên có: (B
–1
A
–1
)(AB) = B
–1
(A
–1
A)B = B
–1
IB = B
–1
B = I. Tương tự có:
(AB)(B
–1
A
–1
) = A(B B
–1
)A
–1
= AI A
–1
= A A
–1
= I. Chứng tỏ AB khả nghịch và (AB)
–1
= B
–1
A
–1
.
d. Do A A
–1
= I (A A
–1
)
T
= I
T
= I (A
–1
)
T
A
T
= I. Xét tương tự ta có: A
T
(A
–1
)
T
=
I.
Nghiã là A
T
khả nghịch và (A
T
)
–1
= (A
–1
)
T
.
3. THUẬT TOÁN TÌM MA TRẬN NGHỊCH ĐẢO.
Ví dụ 1 vừa nêu đã gợi ý cách tìm ma trận nghịch đảo của ma trận vuông A nhờ
việc giải hệ tuyến tính AX = B. Nếu A M(n,n) là khả nghịch thì hệ tuyến tính AX = B
luôn có nghiệm duy nhất với mọi B M(n,1). Thật vậy, từ AX = B, nhân trái 2 vế với A
–1
ta có X = A
–1
B, là một nghiệm. Ngược lại, giả sử X
0
là một nghiệm nào đó của phương
trình thì AX
0
= B. Khi đó:
X
0
= I
n
X
0
= (A
–1
A)X
0
= A
–1
(AX
0
) = A
–1
B.
Nghiệm duy nhất X
0
hoàn toàn tìm được nhờ phương phápGauss, quy ma trận đầy đủ về
dạng rút gọn:
A* = [A | B] → [I
n
| X
0
].
Nhờ ý tưởng trên, ta có thể áp dụng thuật toán rút gọn hàng để tìm A
–1
(nếu có) như sau:
Giả sử A khả nghịch, gọi A
–1
là ma trận cần tìm thì A
–1
thoả mãn:
AA
–1
= I
n
c
j
(AA
–1
) = c
j
(I
n
) j = 1..n.
Xét phương trình đối với cột thứ j ở 2 vế:
c
j
(AA
–1
) = c
j
(I
n
) A.c
j
(A
–1
) = c
j
(I
n
).
Phương trình trên chứng tỏ c
j
(A
–1
) là nghiệm của AX = c
j
(I
n
). Thực hiện thuật toán rút gọn
hàng trên ma trận đầy đủ:
[A | c
j
(I
n
)] → [I
n
| c
j
(A
–1
)]
Mỗi lần giải hệ như vậy sẽ tìm được 1 cột của A
–1
. Thay vì giải riêng lẻ từng hệ, ta ghép
giải chung một lượt cho n cột của A
–1
. Thuật toán rút gọn hàng mô tả như sau:
[A | c
1
(I
n
) c
2
(I
n
) ... c
n
(I
n
)] → [ I
n
| c
1
(A
–1
) c
2
(A
–1
) ... c
n
(A
–1
)]
[A | I
n
] → {I
n
| A
–1
].
Như vậy, dãy các phép toán hàng quy A về I
n
sẽ quy I
n
về A
–1
. Nghịch đảo của A nhờ đó
tìm được theo thuật toán gồm các bước sau:
Bước 1. Lập ma trận gồm 2 khối: [A | I
n
].
Bước 2. Áp dụng thuật toán rút gọn hàng, quy khối trái về I
n
. Khi đó, khối phải là
A
–1
cần tìm.
Chú ý rằng thuật toán vừa nêu trên chỉ mới khẳng định trong trường hợp A quy
được về I
n
(tức A tương đương hàng với I
n
) thì A
–1
là khối phải. Trong trường hợp ngược
lại nếu không quy được A về I
n
(tức A không tương đương hàng với I
n
) thì định lý ở mục
sau sẽ chứng minh được A là không khả nghịch, tức không tồn tại A
–1
.
28

lOMoARcPSD| 35883770
0
0
1
0
0
1
1
0
0
0
II.
MA TRẬN KHẢ NGHỊCH
1 1
Ví dụ 11. Tìm ma trận nghịch đảo của A =
1 2
2
4
2
2
.
3
1 1
2 1 0 0
h 2→h 2−h1
1 1 2
1 0 0
[A | I
3
] =
1
2 2 0 1
0
⎯
h
⎯
3→
⎯
h3−
⎯
2.h
⎯
1
→
0
1
0
−1 1 0
⎯
h
⎯
3
→
⎯
h3
−
⎯
2.h
⎯
2
→
2
4
3 0 0
1
0 2
−1 −2 0 1
1 1 2
1 0 0
1 0 0 2
−5 2
2 − 5 2
0 1 0
−
1
1
0
⎯⎯→
0
1
0
−1 1
0
A
–1
=
−
1
1 0
.
0
0
−
1
0
−
2
1
0
0
1
0
2
−1
0
2
−
1
4. MA TRẬN SƠ CẤP VÀ TÍNH KHẢ NGHỊCH CỦA MA TRẬN
Định nghiã 7. Ma trận E được gọi là ma trận sơ cấp nếu nó là ma trận thu được bằng
cách thực hiện đúng một lần bởi một phép toán hàng trên ma trận đơn I
n
.
Do có 3 loại phép toán hàng nên sẽ có 3 loại ma trận sơ cấp tương ứng, đó là: ma
trận sơ cấp ứng với phép thay thế hàng, ma trận sơ cấp ứng với phép đổi hàng, ma trận sơ
cấp ứng với phép tỷ lệ hóa.
Ví dụ 12. Cho các ma trận sau, nếu là ma trận sơ cấp, hãy tìm phép toán hàng tương
ứng:
a)
E =
1 0
1
0 0
0
. E là ma trận sơ cấp, phép toán hàng tương ứng là: h
1
→ h
1
+.h
3
1
vì nếu ta thực hiện trên I
3
phép toán hàng tương ứng đó thì thu được E. Cụ thể:
I
3
=
1 0
1
0 0
0
1
1 0
⎯
h
⎯
1
→
⎯
h1
+
⎯
⎯
h3
→
0
1
0 0
1
= E.
b)
F =
0
1
. F là ma trận sơ cấp, phép toán hàng tương ứng là: h
1
h
2
vì nếu ta
thực hiện trên I
2
phép toán hàng tương ứng đó thì thu được F. Cụ thể: I
2
=
1 0
⎯
h
⎯
1
⎯
h
2
→
0
1
= F.
c)
G =
2
0
0 3
1 0
. G không phải là ma trận sơ cấp vì I
3
=
0
1
1 0
1
0 0
0
1
⎯
h
⎯
1
→
⎯
2
⎯
h
1
→
2 0
1
0 0
0
1
⎯
h
⎯
1
→
⎯
h1
+
⎯
3
⎯
h3
→
2
0
0 3
1 0
= G. Có nghĩa là để thu được G từ I
3
ta cần thực hiện
0
1
nhiều hơn 1 phép toán hàng.
29
0
0
0
0
0
0

lOMoARcPSD| 35883770
k
Chương 2: MA TRẬN
Định lý 7. Nếu A M(m,n) và E là ma trận sơ cấp ứng với phép toán hàng h, thì tích
EA là ma trận thu được do thực hiện chính phép toán hàng h đó trên A.
I
m
⎯
h
⎯→
E thì
A
⎯
h
⎯→
EA.
Chứng minh.
Xét hàng thứ i của EA ta có h
i
(EA) = (h
i
E).A. Mặt khác, theo định nghiã của ma
trận sơ cấp thì E và I
m
chỉ khác nhau duy nhất một hàng (ứng với phép thay thế hàng hay
phép tỷ lệ hoá) hoặc khác nhau đúng 2 hàng (ứng với phép đổi hàng). Gọi k là chỉ số mà
h
k
E = h
k
(I
m
) thì:
h
k
(EA) = (h
k
E).A = (h
k
I
m
).A = h
k
(I
m
A) = h
k
A
Chứng tỏ với chỉ số k này, hàng k trong EA và hàng k tương ứng trong A là hoàn toàn
giống nhau. Các hàng còn lại trong EA và trong A phụ thuộc vào loại của ma trận sơ cấp
E. Giả sử xét hàng thứ i k và E là ma trận sơ cấp ứng với phép thay thế hàng: h
i
→ h
i
+h
j
, nghiã là có h
i
E = .h
i
I
m
+ h
j
I
m
. Khi đó:
h
i
(EA) = (h
i
E).A = (.h
i
I
m
+ h
j
I
m
).A = (.h
i
I
m
)A + (h
j
I
m
).A = . h
i
(I
m
A) + h
j
(I
m
A)
= .h
i
A + h
j
A.
Điều này chứng tỏ hàng i trong EA là hàng thu được do thực hiện phép thay thế
hàng h
i
→ h
i
+h
j
trên A. Vậy, mọi hàng trong EA đều giống với hàng tương ứng trong ma
trận thu được từ A nhờ thực hiện phép thay thế hàng. Đối với 2 phép toán hàng còn lại
được chứng minh tương tự.
Định lý 8. Với bất kỳ ma trận A M(m,n), luôn tồn tại một dãy hữu hạn các ma trận
sơ cấp E
1
,E
2
,...,E
k
sao cho tích E
k
E
k–1
...E
1
.A đúng bằng ma trận dạng rút gọn của A.
Chứng minh. Cho trước ma trận A thì luôn tồn tại một dãy hữu hạn các phép toán
hàng để sau khi thực hiện nó, ma trận A được quy về dạng rút gọn U. Gọi E
1
là ma trận sơ
cấp ứng với phép toán hàng thứ nhất, E
2
là ma trận sơ cấp ứng với phép toán hàng thứ 2,...
và E
k
là ma trận sơ cấp ứng với phép toán hàng cuối cùng. Áp dụng định lý trên, suy ra
ngay tích E
k
E
k–1
...E
1
.A = U là rút gọn của A.
Định lý 9. Ma trận sơ cấp là ma trận khả nghịch, hơn nữa nghịch đảo của ma trận sơ
cấp cũng là ma trận sơ cấp.
Chứng minh. Vì mỗi phép toán hàng đều có phép toán ngược, nên nếu thực hiện
một phép toán hàng nào đó trên I, đổi I thành ma trận sơ cấp E, thì cũng có một phép toán
hàng cùng loại, thực hiện trên E để đổi E thành I. Nghĩa là có một ma trận sơ cấp F sao
cho FE = I (*). Vì E và F tương ứng với hai phép toán hàng ngược nhau nên EF = I (**).
Từ (*) và (**) suy ra E khả nghịch và E
–1
= F cũng là ma trận sơ cấp.
Định lý 10. Ma trận A M(n,n) khả nghịch khi và chỉ khi A I
n.
Khi A khả nghịch,
tích của dãy các ma trận sơ cấp ứng với dãy các phép toán hàng tương ứng khi quy A
về I
n
, đúng bằng A
–1
.
Chứng minh.
1)
Giả sử A khả nghịch, phương trình AX = B có nghiệm duy nhất với mọi ma trận
cột B M(n,1). Điều đó có nghĩa là trong dạng rút gọn U của A, tất cả các cột đều phải
chứa phần tử chính bằng 1, tức U = I
n
. Vậy dạng rút gọn U của A là I
n
hay A I
n
. Ngược
lại, giả sử A I
n.
, tồn tại dãy các ma trận sơ cấp E
1
,E
2
,...,E
k
sao cho: E
k
E
k–1
...E
1
A = I
n
(*). Vì mỗi E
i
là ma trận sơ cấp nên nó khả nghịch, suy ra tồn tại E
i
–1
(với mọi i = 1..k).
Nhân trái cả 2 vế của (*) với E
–1
ta có:
E
k
–1
(E
k
E
k–1
...E
1
A) = E
k
–1
I
n
(E
k
–1
E
k
)E
k–1
...E
1
A = E
k
–1
E
k–1
...E
1
A = E
k
–1
(**).
30

lOMoARcPSD| 35883770
1
2 k 1 2 k k k–1 1
II.
MA TRẬN KHẢ NGHỊCH
Lại nhân cả 2 vế của (**) với (E
k–1
)
–1
,..., tiếp tục qúa trình trên cho đến bước thứ k, nhân
hai vế của phương trình thu được ở bước thứ k–1, với E
–1
thì có:
E
–1
(E A)= E
–1
(E
–1
.... E
–1
)I hay A = E
–1
E
–1
.... E
–1
.
1 1 1 2 k n 1 2 k
Vì A bằng tích các ma trận E
i
–1
, i = 1..k, khả nghịch nên A khả nghịch.
2) Do A = E
1
–1
E
–1
.... E
–1
A
–1
= (E
–1
E
–1
.... E
–1
)
–1
= E E ........ E .
Định lý 11. Giả sử A, B M(m,n) thì A ~ B khi và chỉ khi tồn tại ma trận khả nghịch
P M(m,m) sao cho B = PA.
Chứng minh. Do A ~ B nên tồn tại dãy các ma trận sơ cấp E
1
, E
2
, ..., E
k
sao cho
E
k
...E
2
.E
1
.A = B. Đặt P = E
k
...E
2
.E
1
thì P là tích các ma trận sơ cấp nên P khả nghịch và B
= PA. Ngược lại, nếu B = PA với P khả nghịch thì do P khả nghịch nên P là tích của dãy
các ma trận sơ cấp nên B phân tích thành B = E
k ..
E
2
.E
1
.A, tức là A ~ B.
Tổng kết lại các kết quả đã trình bày, ta có định lí sau đây nêu rõ các tính chất của ma
trận khả nghịch.
Định lý 12. Với A M(n,n), các mệnh đề sau là tương đương:
1)
A khả nghịch.
2) r(A) = n .
3)
A là tích của một số hữu hạn các ma trận sơ cấp.
4)
Hệ thuần nhất AX = O có nghiệm duy nhất là nghiệm tầm thường.
5)
Hệ tuyến tính AX = B có nghiệm duy nhất với mọi ma trận cột B M(n,1).
6)
Tồn tại B M(n,n) sao cho AB = I
n
.
7)
Tồn tại C M(n,n) sao cho CA = I
n
.
8)
A
T
khả nghịch.
Chứng minh
-
Đã có các chứng minh (1) (2) do định lý 10,
-
(1) (3) vì (3) (1) là hiển nhiên do các ma trận sơ cấp là các ma trận khả
nghịch. Ngược lại, (1) (3) do của định lý 10.
-
(2) (4) và (2) (5) do định lý Kronecker– Capelli.
-
Chứng minh (1) (6). Hiển nhiên có (1) (6). Cần chứng minh thêm (6) (1)
Thật vậy, do AB = I
n
nên B khả nghịch (vì giả sử B ngược lại, B không khả nghịch Hệ
thuần nhất BX = O có nghiệm không tầm thường, nghĩa là tồn tại X
0
M(n,1), X
0
O
sao cho BX
0
= O A(BX
0
) = O (AB)X
0
= O I
n
X
0
= O X
0
= O: vô lý). Do B khả
nghịch nên A = I
n
B
–1
là tích 2 ma trận khả nghịch, sẽ khả nghịch.
-
(1) (7) vì (1) (7) là hiển nhiên do định nghiã, ngược lại, (7) (1) vì nếu CA
= I
n
thì áp dụng (6) suy ra A khả nghịch.
-
(1) (8) vì (1) (8) do định lý 1. Ngược lại, nếu A
T
khả nghịch thì (A
T
)
T
= A
khả nghịch.
31

lOMoARcPSD| 35883770
III.
MA TRẬN KHỐI
A
11
A
p1
A
1q
A
pq
=
A
4
0
− 3
1
− 1
III.
MA TRẬN KHỐI (ĐỌC THÊM)
1. KHÁI NIỆM MA TRẬN KHỐI
Khi xét tích hai ma trận AB ta thấy rằng mỗi phần tử của ma trận AB chính là
tích của ma trận hàng (còn gọi là véc tơ hàng) trong A với ma trận cột (còn gọi là véc tơ
cột) trong B. Như vậy ta đã coi các phần tử của A và B như là các ma trận con nằm trong
chúng. Chính quan điểm coi ma trận cỡ lớn được tạo thành bởi các "phần tử " là các ma
trận con, cỡ nhỏ hơn nằm trong nó, đã làm giảm đi cỡ của ma trận. Một số bài toán ứng
dụng hiện nay (nhất là các bài toán quy hoạch), do xuất hiện nhiều tham số, nên các phép
toán phải thực hiện trên các ma trận cỡ lớn, làm tràn bộ nhớ của máy tính. Một giải pháp
hợp lí là chia ma trận lớn thành các ma trận con, coi các ma trận con đó như những phần tử
của ma trận lớn. Kết quả là ta được ma trận cỡ nhỏ hơn. Dựa trên ý tưởng này mà khái
niệm ma trận khối xuất hiện.
Định nghiã 8. Cho ma trận A, dùng các đường thẳng nằm ngang và thẳng đứng để
tách A thành các ô hình chữ nhật, mà mỗi ô đó là một ma trận cỡ nhỏ hơn cỡ của A.
Ma trận A sau khi chia ra như vậy được gọi là ma trận chia khối, hay gọi tắt là ma trận
khối. Mỗi phần tử của ma trận khối là một ma trận con cỡ nhỏ hơn, được chứa trong
nó.
Ví dụ 13. Cho ma trận
1 2 3 4
− 2 5 4 0
− 8 6 3 1
5 6
− 3 1
7 4
7
− 1
, ta có thể chia nó bởi các
0
đường thẳng nằm ngang và thẳng đứng để được ma trận khối như sau:
1 2 3 4
A =
− 2 5 4 0
8 6 3 1
5 6
− 3 1
7 4
7
− 1
0
Khi đó A được viết thành ma trận cỡ 23 : A =
A
11
A
12
A
13
, trong đó các
21
A
22
A
23
phần tử là những ma trận con: A
11
=
1 2
−
2 5
3
, A
12
=
4
5
; A
13
=
6
7
; A
21
=
8
6
3
;
A
22
=
1
7
;
A
33
=
4
0.
2. CÁC PHÉP TOÁN TRÊN MA TRẬN KHỐI
Các phép toán chủ yếu trên ma trận khối như: cộng, nhân với một vô hướng, nhân
hai ma trận khối được thực hiện theo quy tắc giống hệt như quy tắc đối với các phép toán
tương ứng trên ma trận thông thường. Cụ thể như sau:
a)
Phép cộng 2 ma trận khối: Cho A, B là các ma trận mn, được chia thành ma trận khối
cỡ pp với phần tử là các ma trận con A
ij
, B
ij
cỡ m
i
n
j
gồm m
i
hàng và n
j
cột, m
i
= 1..p, n
j
= 1..p.
A =
32
m
1
n
1
m
1
n
q
m
p
n
1
m
p
n
q
lOMoARcPSD| 35883770
III.
MA TRẬN KHỐI
= .
=
1
A
B
A
7
2
A
11
B =
A
1q
B
11
B
1q
A
11
+ B
11
A
1q
B
1q
thì C = A+B =
+
=
là ma trận
A
p1
A
pq
B
p1
B
pq
A
p1
B
p1
A
pq
B
pq
khối cùng cỡ pq với phần tử (i,j) là [C]
ij
= A
ij
+ B
ij
.
A
11
A
1q
A
11
A
1q
b)
Phép nhân ma trận khối với 1 số: A =
A
p1
A
pq
A
p1
A
pq
c)
Phép nhân 2 ma trận khối: Cho A M(m,n) và B M(n,p). Chia A thành ma trận khối
cỡ rq còn B được chia thành ma trận khối cỡ qs:
A=
, B =
trong đó A
ik
cỡ m
i
n
k
còn B
kj
cỡ n
k
p
j
, i = 1.. r; j=1..s và m
1
+m
2
+...+m
r
= m;
n
1
+n
2
+....+n
q
= n; p
1
+p
2
+...+p
s
= p. Phần tử (i,j) của tích AB cũng được tính bởi tích của
hàng thứ i trong ma trận khối A với cột thứ j trong ma trận khối B như sơ đồ sau:
C
11
C
1s
q
Nếu kí hiệu C = AB =
⁝ ⁝
⁝
thì C
ij
=
A
ik
B
kj
.
C
r1
A
rs
2 − 3 1
k
=
1
0 − 4
A
11
A
12
6 4
− 2
B
1
Ví dụ 14. Cho A =
1 5
− 2 3 − 1
=
A
và B =
A
− 3 7
=
B
0 − 4 − 2 7 − 1
21 22
−
1
2
2
2
thì: AB =
A
11
A
12
B
1
=
A
11
B
1
+ A
12
B
2
, trong đó:
21
22 2
21
B
1
+ A
22
B
2
A B =
2 − 3
6
1
− 2
4
1
=
15
12
; A
B =
0
− 4
− 1
3
=
− 20
− 8
.
11 1
5
− 2
−
3
7
− 5
12 2
−
1
−
8
A B + A
B =
15
12
+
− 20
− 8
=
− 4 4
.
11 1
12 2
−
5
−
8
−
6
33
B
11
B
p1
B
1q
B
pq
=
.
3
1
2
3
5
2
2
7
A
m
1
n
1
m
1
n
q
m
p
n
1
m
p
n
q
A
1
1
A
1
q
⁝
⋱
⁝
A
r
1
A
rq
B
1
1
B
1
s
⁝
⋱
⁝
B
q
1
B
qs
m
i
n
1
m
i
n
q
n
1
p
j
⋱
⁝
⋱
n
q
p
j
m
i
p
j

lOMoARcPSD| 35883770
III.
MA TRẬN KHỐI
22 2
5
2
0
D
0
C 0
1
0
0
0
1
0
0 4
0 0
x
,
0
2
A
21
B
1
=
0
− 4
6
2
−
2
−
3
4
7
= 14
−
18
;
A
B
=
7
−
1
−
1
− 5
3
=
−
12
4
19
A
21
B
1
+ A
22
B
2
=
14
−
18
+
−
12
19
=
2
1. Vậy AB =
− 6 2
.
2
1
Ví dụ 15. Cho A, B M(m,m) và C, D M(n,n) ta lập được các ma trận khối có
dạng chéo cỡ (m+n)(m+n) là:
A
0
B
0
, trong đó O ở góc trên bên phải là
ma trận O cỡ mn còn O ở góc dưới bên trái là ma trận O cỡ nm. Khi đó ta có tích 2
ma trận khối này là:
A 0
B
0
=
AB
00
=
AB 0
00 CD
CD
Chẳng hạn, cần tính AB với A =
0 1 0
0 0
0 0 1
0 0
0 0 0
0 0
0
0 0
, B =
2
0 3
1
0
0
2 0 0
3 0 0
0 1 0
0 0 1
0 1 0
0
1
. Ta chia A và B
1
thành các ma trận khối và tính như sau:
A.B =
0 1 0
0 0
0 0 1
0 0
0 0 0
0 0
1
0 0
0
2
0 3
0
2 0 0
3 0 0
0 1 0
0 0 1
0 1 0
0
1
1
4
=
0
0
3 0 0
2 0 0
0 1 0
0 0 2
0 3 0
0
1
.
3
Phép tính trên ma trận khối này cho phép ta tính tích AB tiện lợi hơn.
Ví dụ 16. Sử dụng các phép toán trên ma trận khối, ta có thể viết được tích AX
dưới dạng một tổ hợp tuyến tính của các cột trong A với các hệ số là các tọa độ của
x
1
véc tơ cột X. Thật vậy, giả sử xét với ma trận A cỡ 33 ta có và X =
a
11
a
12
a
13
x
1
a
11
x
1
+ a
12
x
2
+ a
13
x
3
a
11
x
1
a
12
x
2
x
3
a
13
x
3
AX =
a a
a
x
=
a
x
+
a
x
+ a
x
=
a
x
+
a
x
+
a
x
21 22 33
2
21 1 22 2 23 3
21
1
22 2
23 3
a
31
a
32
a
33
x
3
a
31
x
1
+ a
32
x
2
+ a
33
x
3
a
31
x
1
a
32
x
2
a
33
x
3
a
11
a
12
a
13
= x
1
a
21
+ x
2
a
22
+ x
3
a
23
= x
1
.c
1
A + x
2
.c
2
A + x
3
.c
3
A.
a
31
a
32
a
33
Cách viết này còn được sử dụng nhiều lần ở các phần tiếp theo vì tính tiện lợi của nó.
34
1
C
0
D
4
0
0
0
0
0
1
0
0
0
.
0

lOMoARcPSD| 35883770
III.
MA TRẬN KHỐI
B
B
12
0
A
0
A
3. NGHỊCH ĐẢO CỦA MA TRẬN KHỐI
Nhiều bài toán được tìm thấy trong ứng dụng của đại số ma trận là tìm nghịch đảo
của ma trận với cỡ khá lớn, vượt qúa khả năng tính toán của máy tính hiện có. Một giải
pháp có hiệu quả là sử dụng tính chất của ma trận khối. Sau đây ta sẽ xét ví dụ về tìm ma
trận nghịch đảo của của các ma trận khối cỡ 22, dạng đơn giản. Đó là ma trận khối tam
giác trên và ma trận khối tam giác dưới.
Ví dụ 17. Giả sử cho A =
A
11
A
12
là ma trận khối tam giác trên khả nghịch;
22
trong đó A
11
cỡ pp ; A
22
cỡ qq. Hãy tìm công thức tính cho A
–1
?.
Giải: Gọi A
–1
= B =
B
11
B
12
. Khi đó cần tìm B sao cho:
21
B
22
A
11
B
11
+ A
12
B
21
= I
p
(1)
A
11
A
12
B
11
B
12
=
I
p
0
11
B
12
+ A
12
B
22
= 0
(2)
22 21
B
22
q
22
B
21
= 0
(3)
A
22
B
22
= I
q
(4)
(A
22
)
–1
.
Từ (4) suy ra A
22
khả nghịch (vì A
22
là ma trận vuông thỏa định lý 12) và B
22
=
Từ (3) suy ra B
21
= (A
22
)
–1
O = O. Thế vào (1) có A
11
B
11
= Ip. Chứng tỏ A
11
khả
nghịch và B
11
= (A
11
)
–1
.
Từ (2) có A
11
B
12
= – A
12
B
22
= – A
12
(A
22
)
–1
. Nhân trái hai vế của phương trình này
với (A
11
)
–1
ta có:
B
12
= – (A
11
)
–1
A
12
(A
22
)
–1
Vậy:
A
–1
=
A
11
A
−1
=
(A
11
)
−1
− (A
11
)
−1
A
12
(A
22
)
−1
(5)
0 A
22
0
(A
22
)
−1
Ngược lại nếu A
11
, A
22
đều khả nghịch, dễ dàng kiểm tra được ma trận cho bởi
công thức (5) chính là ma trận nghịch đảo của A.
Kết luận:
Ma trận khối tam giác trên A khả nghịch khi và chỉ khi các phần tử đường chéo
A
11
và A
22
đều khả nghịch.Khi đó A
–1
được tính theo công thức (5).
Tương tự, ma trận khối đường chéo dạng B =
B
11
0
0
là khả nghịch khi và chỉ
B
22
khi các ma trận nằm trên đường chéo là B
11
và B
22
đều khả nghịch.
35
A
0
I
A

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 3. ĐỊNH THỨC
Chương 3
ĐỊNH THỨC
1. Khái niệm định thức
2. Tính chất của định thức
3. Các ứng dụng của định thức
Khoảng 160 năm trước khi lí thuyết về ma trận phát triển thì định thức đã được
nghiên cứu đến. Năm 1683 nhà toán học Nhật bản là Seki Takakazu và năm 1693 nhà
toán học người Đức là Gottfried Leibnitz đã độc lập nghiên cứu về định thức, coi định
thức như một số được gắn cho một bảng vuông chứa các số được sắp thành hàng, cột
(mà ngày nay ta gọi nó là ma trận vuông). Sau đó khoảng 120 năm, người ta nghiên cứu
định thức chủ yếu để giải hệ phương trình tuyến tính, có dạng như:
a
1
x + b
1
y + c
1
z = 0
a x + b y + c z = 0 (*)
2 2 2
a
3
x + b
3
y + c
3
z = 0
(Mỗi phương trình thể hiện tính vuông góc của hai véc tơ nào đó).
Đến năm 1812, Augustin–Louis–Cauchy cho đăng bài báo, trong đó ông đã
dùng định thức như là công cụ để đưa ra công thức tính thể tích của khối đa diện.
Cauchy cũng chỉ ra rằng, thể tích của hình hộp bằng giá trị tuyệt đối của định thức liên
kết với hệ phương trình tuyến tính (*) ở trên. Phương pháp sử dụng định thức của
Cauchy trong hình học giải tích đã thu hút mạnh mẽ các nhà toán học vào nghiên cứu
các ứng dụng của định thức. Ở thời Cauchy, khi cuộc sống còn đơn giản, cỡ của ma trận
xuất hiện trong toán học còn nhỏ, thì định thức chỉ đóng vai trò quan trọng trong hình
học giải tích. Ngày nay, khi ma trận xuất hiện với cỡ lớn, định thức không chỉ dừng lại
ở vị trí là công cụ của hình học giải tích mà nó còn cung cấp những thông tin quan trọng
về các ma trận, là công cụ để giải hệ phương trình tuyến tính; đồng thời các kiến thức về
định thức cũng có lợi trong các ứng dụng của các ngành toán ứng dụng khác.
I. KHÁI NIỆM ĐỊNH THỨC
1. ĐỊNH NGHIÃ ĐỊNH THỨC
Định nghiã 1. Cho ma trận vuông A =[a
ij
] cấp n, ma trận con của A cấp n–1, có
được từ A bằng cách bỏ đi hàng i và cột j, được gọi là ma trận bù của phần tử a
ij
, kí
hiệu là M
ij
.
a
11
...
a
1( j −1)
a
1 ( j +1)
...
a
1n
M =
a
(i−1) 1
...
a
(i
−
1)( j
−
1)
a
( i −1)( j +1)
... a
( i −1 ) n
.
ij
a
... a a
... a
(i
+
1) 1
(i+1)( j −1)
( i
+
1)(
j
+
1) ( i
+
1) n
a
n1
...
a
n ( j
−
1)
a
n ( j +1)
...
a
nn
36

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
8
c d
2
6
I. KHÁI NIỆM ĐỊNH THỨC
1 2
5 6
3 4
7 8
2 3 4
1 2 3
Ví dụ 1. Cho A =
thì M
21
=
9 8
1
, M
34
=
5
6
7
, ....
0 9
8 1
4
3
4 8
2
3 4
Định nghiã 2. Định thức của ma trận A M(n,n) là một số, ký hiệu bởi detA, được
định nghĩa theo phương pháp quy nạp như sau:
a. Nếu A =
a b
thì detA = ad–bc.
b. Với n 3 và định thức đã được định nghiã đến cấp (n–1), thì với A = [a
ij
]
M(n,n), detA xác định bởi:
det A =
(−1)
1+
j
a
1j
.det( M
1j
)
j=1
(1).
Để cho gọn ta thường kí hiệu D
ij
= det(M
ij
) và C
ij
= (–1)
i+j
D
ij
(D
ij
và C
ij
gọi lần
lượt là phần phụ và phần phụ đại số của phần tử a
ij
trong ma trận A). Khi đó (1) có
dạng:
n n
det
A
=
(
−
1)
1
+
j
a
1j
.D
1j
=
a
1j
C
1j
. (2).
j=1 j=1
Công thức (1), hoặc (2) gọi là công thức khai triển Laplace của định thức cấp n theo
hàng thứ nhất.
Nhận xét. Ta đã định nghĩa định thức theo phương pháp quy nạp. Nghiã là từ
định nghĩa của định thức cấp 2 đã biết, ta định nghĩa được định thức cấp 3. Có định
thức cấp 3, ta định nghĩa được định thức cấp 4,. Cứ như vậy ta định nghĩa được định
thức cấp n bất kỳ qua định thức cấp (n–1) đã biết trước đó, theo quy tắc cho bởi công
thức (5). Tất nhiên ta coi định thức của ma trận A = [a] cỡ 11 là detA = a.
1 0 2
Ví dụ 2. Dùng định nghĩa, tính detA với A =
3 1
0 2 1
3 1
4
− 3
− 1
Áp dụng công thức (1):
3 1 − 3
2 3 − 3
2 3 1
detA = (−1)
1+1
.1. 2 1 − 1 + 0 + (−1)
1+3
.2. 0 2 − 1 + (−1)
1+4
.4. 0 2 1
3 1 0 6 3 0 6 3 1
Cũng theo (1), ta tính được các định thức cấp 3 như sau:
3 1 − 3
2 1
−
1
= 3
1
−1
– 1.
2 −1
– 3
2 1
= 3 (0+1) – 1(0+3) – 3(2–3) = 3.
3 1 0
1 0
2 3 − 3
3 0 3 1
0 2
−
1
= 2
2
−1
– 3
0 −1
– 3
0 2
= 2(0+3) – 3(0+6) – 3(0 – 12) = 24.
6 3 0
3 0 6 0 6 3
2 3 1
0 2 1
6 3 1
= 2
2 1
3 1
– 3
0 1
6 1
+1.
0 2
6 3
= 2(2–3) – 3(0–6) +1(0 – 12) = 4.
Cuối cùng ta có: detA = 3 – 0 + 2.24 – 4.4 = 35.
37
n
2
0
3

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
0
Chương 3. ĐỊNH THỨC
Công thức (1) còn gọi là công thức khai triển định thức cấp n theo hàng thứ
nhất. Ngoài ra ta còn có định lý sau đây, chứng tỏ định thức có thể khai triển theo hàng
thứ i hay cột thứ j bất kỳ:
2. Công thỨc khAi triỂn đỊnh thỨc theo hàng hoẶc cỘt
Định lý 1. Định thức của ma trận vuông A cấp n có thể khai triển theo hàng thứ i
bất kỳ bởi công thức:
detA =
(
−
1)
i
+
j
a
ij
.D
ij
j=1
=
a
ij
C
ij
j=1
(3)
Hoặc khai triển theo cột thứ j bất kì bởi công thức:
detA =
(
−
1)
i
+
j
a
ij
.D
ij
j=1
=
a
ij
C
ij
i=1
(4)
Ta công nhận mà không chứng minh định lí này.
Công thức (3), (4) cũng được gọi là công thức khai triển Laplace của định thức cấp
n theo hàng thứ i hoặc theo cột thứ j.
Ví dụ 3. Tính detA với A =
1 2
1
0 0
0
0 0
3 4
−
1
3
5 7
0 3
0 1
5
2
.
1
Vì hàng 5 có chứa nhiều phần tử 0 nên ta khai triển định thức của A theo hàng 5
như sau:
1 2 3 5 1 2 3 4
detA = (–1)
5+4
.1.
0 1 − 1 1
+ (–1)
5+5
.1.
0 1
− 1 3
.
0 0 5 2
0 0 0 1
0 0 5 7
0 0 0 3
Lại khai triển các định thức theo hàng cuối cùng, (có nhiều phần tử 0) ta có:
1 2
= (–1)
4+4
.1. 0 1
0 0
3
− 1 = 1.(–1)
3+3
.5
1
5
0
2
= 5(1 – 0) = 5.
1
1 2
= 3. 0 1
0 0
3
−
1
= 3.5.
1
5
0
2
= 3.5.1 = 15.
1
detA = –5 + 15 = 10.
Chú ý. Công thức (3), (4) thực sự có lợi khi trong ma trận A có hàng nào đó có
chứa nhiều phần tử bằng 0. Từ cách giải ví dụ trên, dễ dàng suy ra hệ quả:
Hệ qủa. Định thức của ma trận tam giác bằng tích các phần tử đường chéo.
Thật vậy, khai triển theo cột 1 trong từng dịnh thức, ta có:
38
n
n
n
n
1
1
1
2
3
5
0
1
− 1
1
0
0
5
2
0
0
0
1
1
0
2
1
3
− 1
4
3
0
0
5
7
0
0
0
3

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
a
22
0
a
23
a
33
...
...
a
2n
a
3n
0 ... 0
a
nn
1
⁝
⁝
⁝
⁝
⁝
⁝
n
I. KHÁI NIỆM ĐỊNH THỨC
= a
11
. = a
11
a
22
.
= ... = a
11
.a
22 ........
a
(n–1),(n–1)
. a
nn
.
3. Khai triỂn đỊnh thỨc theo ma trẬn phỤ hỢp
Cho ma trận A = [a
ij
] M(n,n), phần phụ đại số của phần tử a
ij
là C
ij
không phải
là một ma trận, nó chính là một số. Nếu ta lập ma trận gồm các phần tử C
ij,
thì được ma
trận mới, gọi là ma trận phụ hợp của ma trận A. Kí hiệu bởi Cof(A):
C
11 ...
C
1j
...
C
1n
Cof(A) = [C
ij
] =
C
i1
...
C
ij
...
C
in
= C
C
n1
...
C
nj
...
C
nn
Sử dụng kí hiệu h
i
A = [a
i1
a
i2
... a
in
] là hàng i trong A; h
i
C = [C
i1
C
i2 ......
C
in
)] là hàng i
trong Cof(A) = C và gọi tích vô hướng của vectơ hàng h
i
A với vectơ hàng h
i
C là số:
<h
i
A .h
i
C> = a
i1
.C
i1
+ a
i2
.C
i2
+ .... + a
in
.C
in
thì từ (4) ta có ngay:
detA =
a
ij
C
ij
= <h
i
A
.h
i
C> (5)
j=1
Công thức (5) có nghiã là định thức của ma trận A bằng tích vô hướng của véc tơ hàng
thứ i trong A, với véc tơ hàng thứ i trong Cof(A). Vì vậy, ta gọi (5) là công thức khai
triển định thức theo ma trận phụ hợp, hay công thức tính định thức nhờ ma trận phụ
hợp.
0
Ví dụ 4. Cho A=
1
2
2 1
− 1 1
, viết ra ma trận phụ hợp Cof(A) rồi tính detA nhờ
3 1
khai triển theo ma trận phụ hợp.
C
= (–1)
1+1
−
1
1
= –4; C
= (–1)
1+2
1 1
= 1; C = (–1)
1+3
1
−
1
= 5.
11
3 1
12
2 1
13
2 3
C
21
= (–1)
2+1
2
3
1
= 1; C
22
= (–1)
2+2
0
1 2
1
= –2; C
23
= (–1)
2+3
0
1 2
2
= 4;
3
C
31
= (–1)
3+1
2
−
1
1
= 3; C
32
= (–1)
2+3
0
1 1
1
= 1; C
33
= (–1)
3+3
0
1 1
2
= –2.
−
1
Suy ra C = Cof(A) =
−
4
1
−
2
3 1
5
4
.
−
2
Khai triển detA theo ma trận phụ hợp ta có: detA = <h
1
A.h
1
C> = 0.(–4)+2.1+1.5 = 8 =
<h
2
A.h
2
C> = <h
3
A.h
3
C>.
4. NHẬN XÉT VỀ ĐỊNH NGHĨA ĐỊNH THỨC
Theo công thức khai triển Laplace của định thức thì với A M(n,n), có:
39
a
11
0
0
a
12
a
22
0
...
...
a
33
...
...
...
a
1n
a
2n
a
3n
0 0 0 ...
a
nn
a
33
...
a
3n
0 ...
a
nn

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
1
1 2
a
22
a
2n
Chương 3. ĐỊNH THỨC
detA = a
11
.det
– a
12
.det + .... +
a
n
2
a
nn
a
21
a
2,n
−
1
+ (–1)
1+n
.a
1n
.det
. (6)
a
n
2
a
n,n
−
1
Mỗi hạng tử trong khai triển trên đều có dạng:
a
1k
.det(M) , 1 k
1
n.
trong đó det(M) là định thức của của ma trận vuông M cấp (n–1)(n–1), có hàng của M
thu được từ hàng thứ 2 trở đi của A và M không chứa cột thứ k
1
của A.
Tiếp tục khai triển vế phải của (6) theo hàng thứ nhất, ta biểu diễn được detA
thành tổng của n(n–1) số hạng dạng :
a
1k
.a
2k
det(M) , 1 k
2
n, k
2
k
1
trong đó ta lại kí hiệu det(M) là định thức của ma trận vuông M cấp (n–2)(n–2), có
hàng của M thu được từ hàng thứ 3 trở đi của A và M không chứa cột thứ k
1
và cột thứ
k
2
của A. Cứ tiếp tục khai triển theo cách trên, ta có:
detA=
a
1k
1
.a
2k
2
....a
nk
n
(7)
trong đó (k
1
, k
2
, , k
n
) là một hoán vị bất kì trong số n! hoán vị của n phần tử {1, 2, 3,
..., n} còn dấu trong tổng tuỳ thuộc tính chất của hoán vị (k
1
, k
2
, , k
n
).
Như vậy, (7) cho thấy định thức của ma trận vuông A cấp n là tổng (có kèm theo
dấu “+” hoặc “–“) của n! số hạng, mỗi số hạng bằng tích của n phần tử trong A sao
cho không có 2 phần tử nào đứng trong cùng 1 hàng và cùng 1 cột. Do nhận xét vừa
nêu mà định thức của ma trận vuông, ngoài định nghĩa theo lối quy nạp như trên, còn
được định nghĩa theo “ngôn ngữ phép thế” mà độc giả có thể bắt gặp trong nhiều giáo
trình đại số tuyến tính truyền thống khác.
5. CÁC TÍNH CHẤT ĐƠN GIẢN CỦA ĐỊNH THỨC
Trong các phát biểu sau đây, ta luôn giả thiết A M(n,n).
Tính chất 1. Nếu A có chứa hàng 0 (hay cột 0) thì detA = 0.
Tính chất này là hiển nhiên.
Tính chất 2. Nếu A có chứa 2 hàng (hay 2 cột) giống nhau thì detA = 0.
Chứng minh. Giả sử ma trận A có 2 hàng giống nhau và thực hiện chứng minh bằng
phép quy nạp theo cấp n của ma trận.
Với n = 2 hiển nhiên có detA = 0: mệnh đề đúng.
Giả sử mệnh đề đúng đối với bất kỳ ma trận có cấp n–1, ta cần chứng minh
mệnh đề đúng đối với ma trận A có cấp n. Thật vậy hãy khai triển detA theo một hàng
nào đó, loại trừ 2 hàng giống nhau, thì được một tổng trong đó mỗi hạng tử đều bằng
tích của một phần tử thuộc hàng đó với định thức của ma trận bù tương ứng. Do định
thức của tất cả các ma trận bù đều là định thức của ma trận vuông cấp n–1, có 2 hàng
giống nhau, theo giả thiết quy nạp, chúng đều bằng 0, do đó detA = 0.
Tính chất 3. Định thức của ma trận A không thay đổi khi ta thực hiện phép chuyển vị:
detA
T
= detA.
40
a
21
a
n1
a
23
a
2n
a
n3
a
nn

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
1j 1j
1j 1j
1j j1
I. KHÁI NIỆM ĐỊNH THỨC
Chứng minh. Với n = 2 hiển nhiên mệnh đề đúng. Giả sử mệnh đề đúng với bất kỳ ma
trận vuông cấp n–1, ta cần chứng minh định lí đúng với ma trận vuông A cấp n. Thật
vậy, khai triển detA theo hàng thứ nhất thì có:
n
detA=
(−1)
1+
j
[A] .det(M )
j=1
trong đó M
1j
là ma trận bù của phần tử a
1j
, cấp n–1. Do tính chất của ma trận chuyển vị
nên:
[A]
1j
= [A
T
]
j1
(*).
Theo giả thiết quy nạp thì det(M
1j
) = det(M
T
) kết hợp với (*) suy ra:
1j ,
n n
detA =
(−1)
1+
j
[A] .det(M ) =
(−1)
1+
j
[A] .det(M
T
)
j=1
n
j=1
=
(−1)
1+
j
[A
T
]
j1
.det(M
T
j1
) = det(A
T
) (khai triển của theo cột 1)
j=1
Đó là điều phải chứng minh.
Nhận xét. Do tính chất 3, một mệnh đề nào đó của định thức, nếu đã đúng đối với hàng,
thì nó vẫn còn đúng đối với cột. Vì vậy, từ đây ta chỉ phát biểu và chứng minh các mệnh
đề của định thức cho hàng, và cần hiểu rằng mệnh đó vẫn còn đúng cho cột. .
41

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
II. TÍNH CHẤT CỦA ĐỊNH THỨC
1. ẢNH HƯỞNG CỦA PHÉP TOÁN HÀNG LÊN ĐỊNH THỨC
Nhắc lại rằng các phép toán hàng trên ma trận bao gồm: phép thay thế, phép đổi
hàng và phép tỷ lệ hóa. Các phép toán hàng này đã được ứng dụng rất có hiệu qủa trong
việc giải hệ tuyến tính, tìm hạng của ma trận, đồng thời phép toán hàng cũng không làm
thay đổi hạng của ma trận. Mục này sẽ tìm hiểu thêm ảnh hưởng của phép toán hàng lên
định thức để từ đó có thể ứng dụng các ảnh hưởng này để tính định thức của ma trận dễ
dàng hơn.
Định lý 2. Cho A M(n,n).
1)
Thực hiện phép đổi hàng hi hj, i j trên ma trận A để thu được ma trận B thì
detB = – detA.
2)
Thực hiện phép phép tỷ lệ hoá hi → hi trên ma trận A để thu được ma trận B
thì detB = detA.
3)
Thực hiện phép phép thay thế hàng hi → hi+hj, i j trên ma trận A để thu
được ma trận B thì detB = detA.
Chứng minh
1)
Giả sử A
⎯
h
⎯
i
⎯
hj
→
B. Sử dụng phép chứng minh quy nạp theo cấp của ma trận
A.
Với n = 2, A =
a
11
a
12
B =
a
21
a
22
. Dễ kiểm tra được det
a
11
a
12
= –
a a
a a
a a
21 22 11 12 21 22
det
a
21
a
22
deB = – detA: định lí đúng.
a a
11 12
Giả sử định lí đúng đối với bất kỳ ma trận cấp n–1, ta cần chứng minh định lí đúng
đối với ma trận A có cấp n. Do trong A, ta đổi hàng i cho hàng j (j i) để được B, nên
h
i
A = h
j
B, h
p
A = h
p
B p i, p j. Khai triển cả A và B theo hàng p bất kỳ, (p i, p
j), ta có:
detB =
a
pk
.(
−
1)
p
+
k
det(B
pk
)
k
=
1
detA =
a
pk
.(
−
1)
p
+
k
.det(A
pk
)
k
=
1
(*)
(**)
Trong đó B
pk
là ma trận bù của phần tử (p,k) trong B, còn A
pk
là ma trận bù của phần tử
(p,k) trong A. Cả hai ma trận này đều có cùng cấp n–1,và B
pk
là ma trận thu được từ A
pk
bằng chính phép đổi hàng i cho hàng j. Theo giả thiết quy nạp thì det(B
pk
) = –det(A
pk
).
Thế kết quả này vào (*) và (**) ta có detB = – detA: điều phải chứng minh.
2)
Giả sử A
⎯
h
⎯
i
→
⎯
hj
⎯→
B, khi đó h
i
B = .h
i
A,
h
p
B = h
p
A
p i.
G
ọi Cof
(A),
Cof(B) là ma trận phụ hợp của A và của B thì h
i
(Cof(B)) = h
i
(Cof(A)). Khai triển detB
theo hàng i ta có:
detB = <h
i
B.h
i
(Cof(B))> = <(.h
i
A).h
i
(Cof(A))> = .<h
i
A.h
i
(Cof(A))> = .detA.
3)
Giả sử A
⎯
h
⎯
i
→
⎯
hi
+
⎯
hj
→
B, i j, khi đó có h
i
B = h
i
A
+ .h
j
A,
h
p
B = h
p
A
p i.
Gọi Cof(A), Cof(B) là ma trận phụ hợp của A và của B thì h
i
(Cof(B)) = h
i
(Cof(A)).
Khai triển detB theo hàng i ta có:
42
n
n
lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
II. TÍNH CHẤT CỦA ĐỊNH THỨC
detB = <h
i
B.h
i
(Cof(B))> = <(h
i
A + .h
j
A).h
i
(Cof(A))>
= <h
i
A.h
i
(Cof(A))> + <(.h
j
A).h
i
(Cof(A))>
= detA + .<h
j
A).h
i
(Cof(A))>.
Đánh giá tích vô hướng <h
j
A).h
i
(Cof(A))> như sau:
Gọi C là ma trận thu được từ A nhờ lấy ra hàng i và thay vào đó là hàng j, tức là C có 2
hàng giống nhau: h
i
C = h
j
A = h
j
C suy ra các ma trận bù của các phần tử thuộc hàng i
của C hoàn toàn giống với các ma trận bù của phần tử thuộc hàng i của A, nghiã là
h
i
(Cof(C) = h
i
(Cof(A)). Khai triển detC theo hàng thứ i ta có:
detC = <h
i
C. h
i
(Cof(C))> = <h
j
A. h
i
(Cof(A))>
Do C có 2 hàng giống nhau nên detC = 0 <h
j
A.h
i
(Cof(A))> = 0. Thay vào trên ta có
điều phải chứng minh:
detB = detA + .<h
j
A).h
i
(Cof(A))> = detA + 0 = detA
Một tổng dạng
i
.h
i
A
i=1
với
i
R còn h
i
A là hàng thứ i trong A, được gọi là
một tổ hợp tuyến tính của các hàng trong ma trận A. Với cách gọi như vậy, ta có hệ qủa
sau:
Hệ qủa. Nếu ta cộng vào một hàng, một tổ hợp tuyến tính của các hàng khác, thì
định thức không thay đổi.
Nhờ định lí nói về ảnh hưởng của các phép toán hàng đối với định thức như vừa
nêu trên mà ta có phương pháp mới để tính định thức của các ma trận vuông với cỡ khá
lớn, đó là sử dụng phép toán hàng để quy ma trận vuông A về dạng có một hàng hay
một cột chỉ còn lại duy nhất một phần tử khác 0 hoặc dạng tam giác. Sau đây sẽ trình
bày vài ví dụ mô tả phương pháp đó.
Ví dụ 5. Tính detA với A =
2
0
− 2
5 − 7
1 2
3 6
− 5 4
3
− 1
2
− 2
Giải. Cách1: Dùng phép rút gọn hàng để quy A về dạng bậc thang (dạng bậc thang của
ma trận vuông sẽ là ma trận tam giác) thì có:
2
detA =
0
5 − 7
1 2
3
− 1
h 4 → h 4 + h1
2 5 − 7
0 1 2
3
− 1
h3 → h3 − 3h 2
2 5 − 7
0 1 2
0 0 0
0 0 − 3
3
− 1
h3
h 4
5
1
2 5 − 7
−
0 1 2
0 0 − 3
0 0 0
3
− 1
= –(2.1.(–3).5) = 30.
1
5
Cách 2: Chọn hàng hay cột có chứa nhiều phần tử 0, thực hiện các phép toán
hàng trên ma trận để quy hàng hay cột đó về dạng chỉ chứa duy nhất một phần tử khác 0
rồi áp dụng công thức khai triển định thức theo hàng hay cột:
43
n
0
0
3
6
2
0
3
6
2
− 2
− 5
4
− 2
0
0
− 3
1
lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 3. ĐỊNH THỨC
2 5
detA =
0 1
1 2
− 7 3
2 − 1
−
1
2 5 − 7
0 1 2
h 4 → h 4 + h1
3
1
− 1
= 2. 3
0
2
−
1
6 2
−
3
1
h 2 → h 2 − 3h1
2. 0 0
0
−
3
5 = 2.1.
0
−
3
1
5
= 2.(0+15) = 30.
1
Ví dụ 6. Tính định thức: D = .
Giải: Nhận xét rằng mọi hàng trong định thức đều có tổng các phần tử là giống nhau
nên cộng 3 cột đầu tiên vào cho cột cuối ta có:
x +1 2 3 4 x +1 2 3 x +10
D =
1
x + 2 3 4
1
c4
→
c4
+
c1
+
c2
+
c3
x + 2 3
x +10
.
1 2 x + 3 4 1 2 x + 3 x +10
c4→
1
c4
(x+10).
x+10).
x+10
2. ĐỊNH THỨC CỦA MA TRẬN TÍCH
Trước hết, xét định thức của tích ma trận sơ cấp E với ma trận A M(n,n). Tuỳ theo
phép toán hàng đã thực hiện trên I
n
mà thu được các ma trận sơ cấp khác nhau, định
thức của chúng dễ tính được:
-
Nếu I
n
-
Nếu I
n
-
Nếu I
n
⎯
h
⎯
i
⎯
hj
→
E
1
thì detE
1
= – det
I
n
= –1.
⎯
h
⎯
i
→
⎯
hi
⎯→
E
2
thì detE
2
= .det
I
n
= .
⎯
h
⎯
i
→
⎯
hi
+
⎯
hj
→
E
3
thì detE
3
= det
I
n
= 1.
Từ đó
su
y ra với h là phép toán hàng bất kỳ và E là ma trận
s
ơ cấp ứng với h thì
A
⎯
h
⎯→
EA và det(EA) = detE.detA. Nghiã là nếu E là ma trận sơ cấp thì:
det(EA) = detE.detA
Sau đây sẽ đưa ra kết qủa tương tự đối với định thức của tích 2 ma trận vuông cùng cấp
bất kỳ.
Định lý 3. Nếu A, B M(n,n) thì det(AB) = (detA)(detB).
Chứng minh. Xét 2 trường hợp đối với A:
Nếu A khả nghịch, sẽ tồn tại dãy các ma trận sơ cấp E
1
, E
2
,.., E
k
sao cho A = E
k
E
k–
1
...E
1
. Khi đó áp dụng nhận xét vừa nêu, ta có:
detA = det(E
k
E
k–1
...E
1
) = det(E
k
). det(E
k–1
...E
1
) = det(E
k
). det(E
k–1
).det(E
k–2
...E
1
)
= ... = det(E
k
). det(E
k–1
).det(E
k–2
) ...det(E
1
) .
44
0
3
6
2
0
3
6
2
− 2
− 5
4
− 2
0
0
− 3
1
x +1
2
3
4
1
x + 2
3
4
1
2
x + 3
4
1
2
3
x + 4
1
2
3
x + 4
1
2
3
x +10
x +1
2
3
1
x
0
0
1
1
1
x + 2
2
3
x + 3
1
1
c1→c1−c4
c2→c2−2.c4
c3→c3−3.c4
(x+10).
0
0
x
0
0
x
1
=
1
x
3
(
1
2
3
1
0
0
0
1

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
II.
TÍNH CHẤT CỦA ĐỊNH THỨC
det(AB) = det(E
k
E
k–1
...E
1
B) = det(E
k
). det(E
k–1
...E
1
B) = det(E
k
). det(E
k–1
).
det(E
k–2
... E
1
B) = ... = det(E
k
). det(E
k–1
).det(E
k–2
) ...det(E
1
). detB = detA.detB.
Nếu A không khả nghịch, gọi U là dạng rút gọn của A thì U sẽ có chứa ít nhất 1
hàng 0 nên detU = 0. Mặt khác do U ~ A nên tồn tại ma trận P khả nghịch để A = PU
(định lý 11) và detA = detP.detU = 0 detA.detB = 0.detB = 0.
Xét det(AB) = det(PU.B) = detP.det(UB), (vì P khả nghịch). Do U có hàng 0 nên
UB có hàng 0 det(UB) = 0 det(AB) = detP.0 = 0 = detA.detB.
Định lý 4. A M(n,n) khả nghịch khi và chỉ khi detA 0. Nếu A khả nghịch thì
detA
–1
=
1
.
det A
Chứng minh
Nếu A khả nghịch thì I
n
= AA
–1
1 = detA.detA
–1
detA 0, detA
–1
=
1
.
det A
Ngược lại nếu detA 0 thì A là khả nghịch vì nếu A không khả nghịch, áp dụng
cách chứng minh của định lý 3.3 ở trên thì detA = 0: trái giả thiết..
1 1 1 1
1 2 3 4
Ví dụ 7. Xác định p để A =
1 4 9 16
1 8 27 p
khả nghịch.
Giải: Tính detA nhờ quy detA về dạng tam giác:
detA =
= 1.1.2.(p–58).
A khả nghịch detA = p – 58 0 p 58. .
45
1
1
1
2
1
3
1
4
h 2→h 2−h1
h3→h3−h1
h 4→h 4−h1
1
0
1
1
1
2
1
3
h3→h3−3.h 2
h 4→h 4−7.h 2
1
0
1
1
1
2
1
3
1
4
9
16
0
3
8
15
0
0
2
6
1
8
27
p
0
7
26
p −1
0
0
12
p − 22
1
1
1
1
h 4→h 4−6.h3
0
1
2
3
0
0
2
6
0
0
0
p − 58

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
n
c
d
0
0
Chương 3. ĐỊNH THỨC
III.
ỨNG DỤNG CỦA ĐỊNH THỨC
1. CÔNG THỨC TÌM MA TRẬN NGHỊCH ĐẢO
Dùng phép rút gọn hàng để tìm ma trận nghịch đảo, nói chung có hiệu quả hơn
so với phương pháp dùng định thức sẽ được trình bày sau đây. Tuy nhiên trong một số
ứng dụng có tính chất lí thuyết hoặc khi A là ma trận vuông cỡ nhỏ, công thức tính A
–1
qua các phần tử của ma trận A tỏ ra có lợi hơn.
Định lý 5. Nếu A M(n,n) thì A.[Cof(A)]
T
= detA.I
n
.=[Cof(A)]
T
A. Đặc biệt khi A
khả nghịch thì:
A
–1
=
1
.[Cof(A)]
T
det A
Chứng minh
a
11
a
12
a a
... a
1n
... a
C
11
C
12
C C
... C
1n
... C
Cho A =
21 22 2n
, C = Cof(A) =
21 22
2n
. Khi đó:
⁝ ⁝ ⁝
a a ... a
C C ... C
n1 n 2
nn
n1 n 2 nn
h
1
A.h
1
C h
1
A.h
2
C
T
h A.h C h A.h C
...
...
h
1
A.h
n
C
h A.h C
A.[Cof(A)] =
... ... ... ...
h A.h C h A.h C ... h A.h C
n 1 n 2 n n
Nhờ kết qủa chứng minh 3) của định lý 2 ta có <h A.h C> =
det A khi i = j
. Suy ra:
j
i
khi i j
det A 0 ... 0
A.[Cof(A)]
T
=
0
⁝
det A
⁝
...
0
= (detA).I .
⁝
... det A
Nếu A là khả nghịch thì detA 0 A.[
1
.(Cof(A))
T
] = I
n
. Suy ra:
det A
A
–1
=
1
.[Cof(A)]
T
(1)
det A
Phương pháp tính A
–1
bằng công thức (1) trên đây được gọi là phương pháp ma
trận nghịch đảo nhờ định thức.
Đặc biệt, nếu A =
a b
là ma trận vuông cấp hai, khả nghịch thì có công thức
tính ma trận nghịch đảo khá thuận tiện sau đây:
A
–1
=
1
d −b
=
1
d −b
det A
−c a
ad − bc
−c a
Ví dụ 8.
46
2 n
2 1 2 2

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
3 4
1
III. ỨNG DỤNG CỦA ĐỊNH THỨC
a.
Cho A =
1
2
thì có ngay A
–1
=
1
4
−2
.
−2
−3 1
2 1 3
b. Tìm ma trận nghịch đảo của ma trận A =
thức.
1
−
1
4 − 2
bằng phương pháp định
Công thức: A
–1
=
1
[Cof(A)]
T
.
det A
−
1
C
11
= +
4
1
= –2. C
12
− 2
= −
1
1
1
=
3
.
− 2
C
13
= +
1
1
−1
= 5 .
4
C
21
= −
1
4
3
=
14
.
C
22
= +
2
− 2 1
3
= −7 .
− 2
C
23
=
−
2
1
1
=
−
7
.
4
C
31
= +
1
3
= 4. C
32
=–
2
3
=1. C
33
=
2
1
= –3.
−
1
Cof(A) =
1
−
2
3
14
−
7
4 1
1 1
5
−
7
.
−
3
1
−
1
detA = 2.C
11
+ 1.C
12
+ 3.C
13
= 2(–2) + 1.3 + 3.5 = 14.
Suy ra: A
–1
=
1
[Cof(A)]
T
=
det A
− 2 14
1
3 − 7
14
5 − 7
4
1
.
−
3
2. GIẢI HỆ TUYẾN TÍNH BẰNG QUY TẮC CRAMER
Đối với hệ phương trình tuyến tính AX = B, trong đó A là ma trận vuông cỡ nhỏ
thì việc giải hệ bằng quy tắc Cramer là khá thuận tiện, hơn nữa công thức nghiệm do
phương pháp Cramer đưa ra rất ngắn gọn nên dễ dàng trình bày cho các phép tính có
tính chất lí thuyết. Với những lợi thế đó, ta sẽ trình bày thêm quy tắc Cramer ngoài
phương pháp Gauss đã biết, để giải những hệ tuyến tính có ma trận hệ số khả nghịch.
Định nghiã 3. Hệ tuyến tính AX = B được gọi là hệ Cramer nếu ma trận hệ số A
là ma trận vuông khả nghịch.
Định lý 6. (Quy tắc Cramer) Cho hệ Cramer AX = B với A M(n,n) và B M(n,1).
Gọi A
j
là ma trận thu được từ A nhờ thế cột B vào thay cho cột j trong A. Khi đó hệ
AX = B có nghiệm duy nhất X = [x
1
x
2
... x
n
]
T
, trong đó x
j
được tính bởi:
Chứng minh
b
1
x
1
x
j
=
det( A
j
)
, j = 1..n
det A
Gọi B =
, X =
. Do A khả nghịch nên AX = B X = A
–1
B =
1
b
n
.[Cof(A)]
T
.B. Suy ra:
x
n
det A
47
1

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
det A
3
b
2
Chương 3. ĐỊNH THỨC
x
j
= (X)
j1
= (
1
.[Cof(A)]
T
.B)
j1
=
det A
1
.([Cof(A)]
T
.B)
j1
=
det A
1
.[h
j
(Cof(A)]
T
).B]
det A
1
n
=
C
kj
b
k
k
=
1
n n
Áp dụng công thức khai triển theo cột j của det(A
j
), có det(A
j
) =
b
k
C
kj
=
C
kj
b
k
k
=
1
n
1
k
=
1
. Thay
C
kj
b
k
= det(
A
j
)
vào trên, thu được công thức: x
j
=
k
=
1
det A
.det(A
j
).
x
1
+ 2x
2
+ 3x
3
= −1
Ví dụ 9. Tìm ẩn x
3
của hệ
3x + x + 2x = 0 .
1 2 3
2x + x + 3x = 2
1 2 3
1 2
- Có A =
3 1
2
1
3
1 2
2
, detA =
3
1
3
2 1
3
2 = –6.
3
1 2
−
1
-
Thay cột 3 trong A bởi cột tự do B, có A
3
=
1
2
1
0
, det(A
3
) = – 11.
2
-
Áp dụng công thức: x
3
=
det( A
3
)
det A
= –
11
.
6
1 0 1
1
a
Ví dụ 10. Giải hệ: AX = B với A =
−1 1 0
với B =
2
, B =
với a,b,
c là các tham số thực.
1 0 1
0 −1 1
3
c
Do detA = −1 1 0 = 2 A khả nghịch X = A
–1
B.
0 −1 1
1 −1
−1
- Có A
–1
=
1
.[Cof(A)]
T
=
1
1 1
−
1
.
det A
1
1 −1
2
1 1 1
−1
1
−
4
−2
-
Với B =
2
X =
1
1 1
−1
2
=
1
0
=
0
.
3
2
1
1
1
3
2
6
3
a
1 −1
−1
a
a
−
b
−
c
-
Với B =
b
X =
1
1 1
−
1
b
=
1
a
+
b
−
c
.
c
1
1
1
c
2
a
+
b
+
c
48

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
I.
KHÔNG GIAN VÉCTƠ VÀ KHÔNG GIAN CON
Chương 4
KHÔNG GIAN VÉC TƠ
1. Không gian véc tơ và không gian con.
2. Tính độc lập tuyến tính, cơ sở và số chiều.
3. Tọa độ của vectơ đối với cơ sở.
4. Không gian hàng, hạng và tính khả nghịch của ma trận.
5. Tính trực giao và không gian Euclide.
Chương này ta sẽ nghiên cứu một trong những vấn đề trọng tâm nhất của đại số
tuyến tính, đó là cấu trúc không gian véc tơ, mà vai trò của chúng xuất hiện trong hầu
hết các lĩnh vực toán học. Mô hình của không gian véc tơ không những gặp trong các
ngành toán lý thuyết mà còn gặp trong các lĩnh vực ứng dụng như Vật lý, Kinh tế và
một số ngành khoa học khác.
I. KHÔNG GIAN VÉC TƠ VÀ KHÔNG GIAN CON
1. ĐỊNH NGHĨA KHÔNG GIAN VÉC TƠ
Cho V là tập khác bất kỳ, ánh xạ đặt tương ứng cặp phần tử (u, v) với u, v V
với phần tử, kí hiệu là u+v V được gọi là phép cộng trên V, còn ánh xạ đặt tương
ứng cặp phần tử (, v) với R, v V với phần tử ký hiệu v V được gọi là phép
nhân phần tử của V với một vô hướng, hay đơn giản là phép nhân với vô hướng.
Định nghiã 1. Ta gọi tập V , cùng với hai phép toán: cộng và nhân với một vô
hướng lập thành một không gian véc tơ trên R nếu 8 tiên đề sau đây được thỏa mãn:
1. (V
1
) Phép cộng có tính chất kết hợp: (u+v)+w = u+(v+w) u, v, wV.
2. (V
2
) Phép cộng có tính chất giao hoán: u+v = v+u u, v V.
3. (V
3
) Trong V có phần tử O (gọi là véc tơ không) sao cho: v+O = v vV.
4. (V
4
) Với mỗi phần tử vV, tồn tại phần tử – v, (gọi là phần tử đối của v) sao
cho:
v+(–v) = O v V.
5. (V
5
) Phép nhân véc tơ với vô hướng có tính chất phân phối đối với phépcộng véc
tơ: (v+w) = v+ w v, wV, R.
6. (V
6
) (+) v = v+ v , R và vV.
7. (V
7
) ( v) = ( )v , R và v V.
8. (V
8
) 1v = v v V.
Mỗi phần tử của không gian véc tơ được gọi là một véc tơ. Phép cộng trên V còn gọi
là phép cộng véc tơ, còn phép nhân với vô hướng gọi là phép nhân ngoài hay phép nhân
véc tơ với một vô hướng. Tổng v + ( − w) còn viết là v − w và gọi là hiệu của v và w.
Từ các tiên đề trên, dễ suy ra không gian véc tơ có một số tính chất đơn giản sau:
49

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
v = 0
Chương 4. KHÔNG GIAN VÉC TƠ
1. Véc tơ O của không gian véc tơ V là duy nhất.
Thật vậy giả sử trong V có 2 véc tơ không là O và O', theo (V
2
) ta có O + O' = O' +
O, theo (V
3
) thì có O + O' = O và O' + O = O', suy ra O = O'.
2. Với mỗi véc tơ vV tồn tại duy nhất một véc tơ đối − vV.
Thật vậy, giả sử v có 2 véc tơ đối là v
1
và v
2
thì:
v
1
= v
1
+ O = v
1
+ (v + v
2
) = (v
1
+ v) + v
2
= O + v
2
= v
2
v
1
= v
2
.
Hiển nhiên − (− v) = v.
3. Trong V, phép cộng véc tơ có luật giản ước: v + u = w + u v = w.
Thật vậy, từ v + u = w + u có (v + u) − u = (w + u) − u v + (u − u) = w + (u − u)
v + O = w + O v = w.
4. Với bất kỳ R ta đều có O = O.
Thật vậy, v = (v + O) = v + O O = v − v = O.
5. Với bất kỳ véc tơ vV ta có Ov = O.
Vì 0v = (0 + 0)v = 0v + 0v 0v = O (do luật giản ước của phép cộng).
6. Với R, vV thì v = O kéo theo hoặc = 0, hoặc v = O.
Thật vậy, giả sử v = O và 0 thì tồn tại
–1
và khi đó:
v = 1v = (
–1
)v =
–1
(v) =
–1
O = O.
Kết hợp 4), 5), và 6) ta có: v = O
= 0
.
7. − (v) =( − )v, R và vV. Đặc biệt − v = ( − 1)v.
Thật vậy, có:
v + [− (v)] = O = 0.v = ( − )v = v + ( − )v.
Áp dụng luật giản ước của phép cộng, suy ra: − (v) = ( − )v.
Từ (7) dễ dàng rút ra quy tắc:
8. ( − )v = v − v; ,R và vV.
9. (v − w) = v − w; R và v, wV
2. CÁC VÍ DỤ VỀ KHÔNG GIAN VÉC TƠ
Ví dụ 1. Không gian véc tơ các tọa độ R
n
.
Với n 1, ta định nghĩa:
R
n
= {(x
1
; x
2
; ...; x
n
), x
i
R, i = 1..n}.
Hai phần tử x = (x
1
; x
2
; ...; x
n
), y = (y
1
; y
2
; ...; y
n
) được gọi là bằng nhau nếu
các thành phần tương ứng của chúng đều bằng nhau:
x = y x
i
= y
i
, i = 1..n
Trên R
n
, trang bị hai phép toán:
Phép cộng: (x
1
; x
2
; ...; x
n
) + (y
1
; y
2
;...; y
n
) = (x
1
+y
1
; x
2
+y
2
; ...; x
n
+y
n
); (x
1
; x
2
;
...; x
n
), (y
1
; y
2
; ...; y
n
) R
n
.
Phép nhân ngoài: (x
1
; x
2
; ...; x
n
) = (x
1
; x
2
; ...; x
n
); R và (x
1
; x
2
; ...;
x
n
) R
n
.
Dễ thử được R
n
cùng với hai phép toán trên là không gian véc tơ, trong đó véc
tơ không là O = (0; 0; ...; 0); véc tơ đối của véc tơ x = (x
1
; x
2
; ...; x
n
) là – x = (−x
1
; −x
2
;
...; −x
n
). Mỗi véc tơ là một bộ gồm n số thực có thứ tự.
Ví dụ 2. Không gian véc tơ vật lý thông thường. Cho V = {Các đoạn thẳng định
hướng trong không gian 3 chiều thông thường}.
Coi hai đoạn thẳng định hướng là bằng nhau khi và chỉ khi chúng có cùng độ dài và
chỉ cùng một hướng. Phép cộng hai đoạn thẳng định hướng được thực hiện theo quy tắc
hình bình hành. Phép nhân đoạn thẳng định hướng với một vô hướng được một đoạn
50

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
I.
KHÔNG GIAN VÉCTƠ VÀ KHÔNG GIAN CON
thẳng định hướng có độ dài bằng || lần độ dài đoạn thẳng định hướng ban đầu và cùng
hướng nếu 0, hướng ngược lại nếu <0.
Dễ dàng nghiệm được rằng tập V và với hai phép toán trên, V là một không
gian véc tơ, trong đó véc tơ không là đoạn thẳng định hướng có độ dài bằng 0 (tức là 1
điểm), véc tơ đối của véc tơ x là véc tơ (−1)x. Mỗi véc tơ trong trường hợp này chính là
một đoạn thẳng định hướng. Trong Vật lý, không gian véc tơ V được coi là mô hình
chung của không gian các lực biến thiên trong không gian 3 chiều.
Ví dụ 3. Không gian véc tơ M(m,n) các ma trận cỡ mn.
Cho M(m, n) = {A = [a
ij
]
m
n;
a
ij
R, i = 1..m, j = 1..n} là tập hợp tất cả các ma trận
cỡ mn với các phần tử số. Hai phép toán trên M(m, n) là phép cộng và phép nhân ma
trận với một số như định nghĩa thông thường. Dễ kiểm tra được M(m, n) với hai phép
toán trên là một không gian véc tơ, trong đó véc tơ không là O = [0]
m
n,
véc tơ đối của
véc tơ A = [a
ij
]
m
n
là véc tơ −A = [−a
ij
]
m
n
.
Chú ý rằng : Mỗi vectơ x = (x
1
; x
2
; ...; x
n
) R
n
đặt tương ứng 1–1 với một ma trận
x
1
cột [x] =
, vì vậy ta còn gọi ma trận cột [x] là vectơ cột của vectơ x R
n
. Khi đó ta
x
n
dễ dàng suy ra mối quan hệ giữa các vectơ của R
n
với các vectơ cột của nó như sau:
- x = y [x] = [y].
- z = x + y [z] = [x] + [y].
- y = x [y] = [x]
Đặc biệt, vectơ cột của vectơ O = (0 ; 0 ; … ; 0) R
n
là [O] đôi khi còn được viết
đơn giản là O. Tập hợp tất cả các vectơ cột của vectơ x R
n
được kí hiệu là [R]
n
:
[R]
n
= { [x] / x R
n
}
Ví dụ 4. Hiển nhiên [R]
n
= M(n,1) là không gian véc tơ với 2 phép toán cộng và
nhân ma trận với số.
Ví dụ 5. Không gian véc tơ P
n
(x) các đa thức bậc không quá n.
Cho P
n
(x) là tập hợp tất cả các đa thức một biến x với hệ số thực, có bậc không
vượt quá n:
P
n
(x) ={p = a
o
.1 + a
1
x + .... + a
n
x
n
; a
i
R, i = 0..n}
Hai đa thức p = a
o
.1 + a
1
x +.... + a
n
x
n
và q = b
o
.1 + b
1
x + .... + b
n
x
n
được gọi là bằng
nhau khi và chỉ khi p(x) = q(x) x R a
i
= b
i
i = 0..n.
Phép cộng và phép nhân ngoài trên P
n
(x) được định nghiã là phép cộng và phép
nhân đa thức với số thông thường, nghĩa là:
Phép cộng: Với bất kỳ p, qP
n
(x): p = a
o
.1 + a
1
x +.... + a
n
x
n
,
q = b
o
.1 + b
1
x +....
+ b
n
x
n
thì tổng của p + q là đa thức xác định bởi:
p + q = (a
o
+ b
0
).1 + (a
1
+ b
1
)x + ... + (a
n
+ b
n
)x
n
Phép nhân ngoài: Với mọi R và pP
n
(x), tích p là đa thức xác định bởi:
p = a
o
.1 + a
1
x + ..... + a
n
x
n
Từ định nghiã phép cộng đa thức và nhân đa thức với một số như trên ta dễ thấy giá
trị của đa thức tổng và đa thức tích lấy tại x
0
là:
(p+q)(x
0
) = p(x
0
) + q(x
0
)
(p)(x
0
) = .p(x
0
)
51

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 4. KHÔNG GIAN VÉC TƠ
Dễ dàng kiểm tra được 2 phép toán trên thỏa mọi tiên đề của không gian véc tơ nên
P
n
(x) là một không gian véc tơ, với véc tơ không là đa thức không O = 0.1 + 0.x + +
0.x
n
; vectơ đối của p là: − p = (−a
o
).1 + (−a
1
)x +....+ (−a
n
)x
n
. Ta gọi P
n
(x) là không
gian véc tơ các đa thức bậc không qúa n.
Ví dụ 6. Không gian véc tơ F các hàm số xác định trên tập D R.
Cho tập F = {f: D → R, x f(x)} là tập hợp tất cả các hàm một biến số thực, xác
định trên tập D R. Hai hàm f F và g F được gọi là bằng nhau khi và chỉ khi f(x) =
g(x) x D. Phép cộng và phép nhân ngoài trên F được định nghiã là phép cộng hai
hàm số và phép nhân hàm số với 1 số thông thường, nghĩa là với f , g F thì:
f + g : D → R
,
(f+g)(x) = f(x) + g(x)
f : D → R
,
(f)(x) = .f(x)
Dễ dàng kiểm tra được F cùng 2 phép toán vừa định nghiã, thỏa mãn mọi tiên đề của
không gian véc tơ nên F là một không gian véc tơ. Véc tơ không là hàm đồng nhất bằng
0, véc tơ đối của f là –f = (−1)f. Ta gọi F là không gian véc tơ của các hàm thực xác
định trên tập D.
3. KHÔNG GIAN CON
Định nghiã 2. Cho V là không gian véc tơ, ta gọi không gian véc tơ con của không
gian véc tơ V là một tập E , E V sao cho E cùng với hai phép toán trên V
cũng là một không gian véc tơ.
Từ định nghĩa trên suy ra V là không gian con của chính nó, tập {O} gồm chỉ một
phần tử OV cũng là không gian con của V. Ta gọi V và {O} là các không gian con
tầm thường của V. Dễ thấy {O} là không gian con nhỏ nhất còn V là không gian con
lớn nhất (theo nghiã tập hợp) của V.
Chú ý rằng, khi nói “E là không gian con của V” thì ta hiểu rằng E, V đều là các
không gian véc tơ, trong đó E V.
Định lý 1. (Tiêu chuẩn không gian con) Cho tập E và E V. Khi đó E là
không gian con của V khi và chỉ khi E thỏa mãn hai tiêu chuẩn sau:
a)
(S
1
) u, v E thì u+v E.
b) (S
2
) u E, R thì u E.
Chứng minh
) Nếu E là không gian con của V thì hiển nhiên (S
1
) và (S
2
) thỏa mãn.
) Giả sử E , thỏa mãn cả (S
1
) và (S
2
), ta cần chứng tỏ E là không gian véc tơ.
Thử trực tiếp các tiên đề của không gian véc tơ ta có:
-
Các tiên đề (V
1
), (V
2
), (V
5
), (V
6
), (V
7
), (V
8
) là hiển nhiên thỏa mãn trên E vì
chúng đã thỏa mãn trên V E.
-
(V
3
) thỏa mãn vì từ (S
2
) chọn = 0 thì 0u = O E.
-
(V
4
) thỏa mãn vì với mọi u E, theo (S
2
) thì (−1).uE −u = (−1)u E.
Vậy E chính là không gian véc tơ. Để thuận tiện, nhiều khi ta còn thay thế định lý
trên đây bởi định lý sau:
Định lý 2. Cho tập tập E , E V. Khi đó, E là không gian con u, v E,
, R ta có ( u+ v) E.
Dễ chứng minh được 2 định lý vừa nêu là hoàn toàn tương đương với nhau.
52

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
I.
KHÔNG GIAN VÉCTƠ VÀ KHÔNG GIAN CON
Nhận xét. Nếu E là không gian con của V thì E phải chứa 0
V
. Thật vậy, với u E
thì 0.u E. Do 0.u = 0
V
nên 0
V
E. Suy ra nếu 0
V
E thì E không thể là không gian
con của V.
Ví dụ 7. Cho P = {(x; y; 0)
;
x, y R} R
3
. Hãy chứng tỏ rằng P là không gian con
của R
3
.
Theo tiêu chuẩn của không gian con, ta cần chứng tỏ P và P thỏa mãn các điều
kiện (S
1
) và (S
2
). Thật vậy:
- P vì có (0; 0; 0) P. (1)
- Với bất kỳ u = (x
1
; y
1
; 0) P, v = (x
2
; y
2
; 0) P thì có ngay u+v = (x
1
+x
2
;
y
1
+y
2
; 0). Đặt x = x
1
+x
2
và y = y
1
+y
2
thì u+v = (x ; y ; 0) P. (2).
- Với R ta có u = (x
1
; y
1
; 0) = (x
1
; y
1
; 0). Đặt x = x
1
; y = y
1
thì có
ngay u = (x ; y ; 0) P. (3)
Từ (1), (2) và (3) suy ra P là không gian con của R
3
.
Dễ thấy P đóng vai trò như một mặt phẳng trong không gian. Do P chứa véc tơ O =
(0; 0; 0) nên P là mặt phẳng đi qua gốc tọa độ. Sau này ta còn chứng tỏ được điều
ngược lại: mọi mặt phẳng đi qua gốc tọa độ đều là không gian con của R
3
. Tất cả chúng
được gọi là không gian con 2 chiều.
Tương tự, ta chứng minh được D = {(x; 0; 0)
;
x R} cũng là không gian con của
R
3
, đó là đường thẳng Ox đi qua gốc tọa độ. Ngược lại, mọi đường thẳng đi qua gốc tọa
độ đều là không gian con của R
3
và chúng được gọi là không gian con 1 chiều.
Tuy nhiên hãy cảnh giác rằng R, R
2
không phải là không gian con của R
3
vì R, R
2
đều không phải là các tập con của R
3
.
Ví dụ 8. Cho E = {(3t; 5t+2); tR}. Xác định xem E có phải là không gian con của
R
2
hay không ?
Dễ thấy O = (0; 0) E vì không tồn tại tR để
không gian con của R
2
vì O E .
3
t
=
0
5t + 2 = 0
. Suy ra E không là
Ví dụ 9. A M(n,n) được gọi là ma trận đối xứng nếu A = A
T
. Gọi S(n,n) = {A
M(n,n) / A = A
T
} là tập hợp tất cả các ma trận đối xứng cấp n. Chứng minh rằng S(n,n)
là không gian con của M(n,n).
Cần kiểm tra tiêu chuẩn không gian con đối với S(n,n).
-
S(n, n) vì ma trận không OM(n,n) thỏa O
T
= O, nên OS(n,n).
-
Với bất kỳ A, B S(n,n), , R ta cần chứng minh (A+B) S(n,n).
Thật vậy: do A, B S(n,n) nên A
T
= A, B
T
= B, khi đó có ngay:
(A+ B)
T
= (A)
T
+ (B)
T
= (A
T
) + (B)
T
= A
T
+B
T
= A+B (A+B)
S(n,n).
4. KHÔNG GIAN CON SINH BỞI TẬP HỢP
Cho không gian véc tơ V và tập gồm p vectơ S = {v
1
, v
2
, ..., v
p
} V. Khi đó ta cần
vài khái niệm sau:
-
Tổng bất kỳ dạng:
1
v
1
+
2
v
2
+ .... +
p
v
p
, (
i
R, i = 1..p) được gọi là một tổ
hợp tuyến tính của các véc tơ v
1
, v
2
, ..., v
p
với các hệ số
1
,
2
,...,
p
.
-
Nếu véc tơ v có sự biểu diễn qua các vectơ của S dưới dạng: v =
1
v
1
+
2
v
2
+
.... +
p
v
p
, thì véc tơ v được gọi là biểu thị tuyến tính được qua các véc tơ v
1
, v
2
,
53

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
p
Chương 4. KHÔNG GIAN VÉC TƠ
..., v
p
của S, hay véc tơ v là tổ hợp tuyến tính của các véc tơ thuộc S với các hệ
số
1
,
2
, ...,
p
.
Định nghiã 3. Cho E là không gian con của V, tập gồm p vectơ S = {v
1
, v
2
,..., v
p
}
E được gọi là tập sinh của không gian véc tơ E nếu mọi véc tơ của E đều biểu thị
tuyến tính được qua các véc tơ của tập S. Khi đó ta viết E = Sp(S) với ý nghiã E là
không gian vectơ sinh ra bởi S.
E =
S
p{v
1
, v
2
,..., v
p
} v E v =
i
v
i
,
i
R, v
i
S
E, i = 1, 2, ..., p.
i
=
1
Từ định nghĩa suy ra một không gian véc tơ hoàn toàn được xác định qua tập sinh
của nó vì bất kỳ véc tơ nào của không gian cũng đều biểu diễn được qua các véc tơ
thuộc tập sinh.
Định lý 3. Với S = {v
1
, v
2
,..., v
p
} V thì tập hợp tất cả các tổ hợp tuyến tính có thể
có của các véc tơ thuộc S lập nên không gian con của V và được gọi là không gian con
của V sinh bởi S. Kí hiệu Sp(S) hay Sp{ v
1
, v
2
, ..., v
p
}. Khi đó S là tập sinh của Sp(S).
p
Sp(S) = {v =
i
v
i
,
i
R, v
i
S, i = 1..p}
i
=
1
Chứng minh
-
Hiển nhiên Sp(S) V và Sp(S) vì có O = 0v
1
+0v
2
+...+0v
p
Sp(S).
-
Lấy bất kỳ u, v Sp(S) thì có:
u =
1
v
1
+
2
v
2
+...+
p
v
p
, (
i
R, i = 1..p)
v =
1
v
1
+
2
v
2
+ ...+
p
v
p
, (
i
R, i = 1..p).
Khi đó:
u+v = (
1
v
1
+
2
v
2
+...+
p
v
p
) + (
1
v
1
+
2
v
2
+...+
p
v
p
) = (
1
+
1
)v
1
+
(
2
+
2
)v
2
+...+(
p
+
p
)v
p
.
Đặt
i
=
i
+
i
thì u+v =
1
v
1
+
2
v
2
+...+
p
v
p
là một tổ hợp tuyến tính của các
vectơ trong S nên u+v Sp(S).
- Tương tự, với bất kỳ R, u Sp(S) thì u = (
1
v
1
+
2
v
2
+...+
p
v
p
) = (
1
) v
1
+ (
2
)v
2
+...+ (
p
)v
p
lại là một tổ hợp tuyến tính của các vectơ trong S nên u
Sp(S).
Vậy Sp(S) là không gian con của V do nó thoả mãn tiêu chuẩn của không gian con.
Định lý 4. Nếu S là tập con khác rỗng của V thì Sp(S) là không gian véc tơ con nhỏ
nhất trong tất cả các không gian con của V có chứa S (theo nghĩa nếu U là không gian
con bất kỳ có chứa S thì phải có Sp(S) U).
Thật vậy, tính nhỏ nhất của Sp(S) thể hiện ở chỗ: Với bất kỳ uSp(S) thì u có sự
biểu diễn: u =
1
v
1
+
2
v
2
+...+
p
v
p
, (
i
R, i = 1..p). Do U là không gian véc tơ chứa S =
{v
1
, v
2
, ...., v
p
} nên U cũng chứa tổ hợp tuyến tính
1
v
1
+
2
v
2
+...+
p
v
p
= u, tức là uU,
chứng tỏ Sp(S) U.
Ví dụ 10. Cho u = (1; –2; –5), v = (2; 5; 6).Hãy chứng tỏ w = (7; 4; –3) Sp{u,
v}.
Theo định nghĩa thì w Sp{u, v} , R sao cho u+v = w. Viết dưới dạng
véc tơ cột (để dễ thấy) ta có:
1
2
7
+ 2 = 7
.
− 2
+ .
5
=
4
− 2 = 5 = 4 .
− 5
6
− 3
− 5 + 6
54
= − 3

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
2
I.
KHÔNG GIAN VÉCTƠ VÀ KHÔNG GIAN CON
Giải hệ trên ta được =3; = 2 w Sp{u, v}.
Ví dụ 11. Cho x = (3; 2; 1), kiểm tra xem x Sp{(1; 2; 1), (–1; 1; 2)} hay không.
Có x Sp{(1; 2; 1), (–1; 1; 2)} Phương trình (1; 2; 1) + (−1; 1; 2) = x (*)có
nghiệm đối với , . Viết ở dạng vectơ cột:
1
−
1
3
1 − 1
3
.
2
+
.
1
=
2
2
1
=
2
(**)
1
−
1
1
2
3
1
1 2
1
Đặt A =
2 1
, [x] =
2
thì (*) là hệ tuyến tính AX = [x]. Quy ma trận đầy đủ
1 2
1
A* của hệ (*) về dạng bậc thang:
A* =
1
1
−
1
3
1
2
1
1
→
0
0
−
1
3
3 − 4
3 − 2
1
→
0
0
−
1
3
3 − 4
0 2
Dễ thấy hệ (**) vô nghiệm nên (*) vô nghiệm x Sp{(1; 2; 1), (–1; 1; 2)}.
Ví dụ 12. Cho các đa thức p = x+1, q = 2x
2
– 2x +3. Xác định xem r = 6x
2
– 10x +5
có thuộc không gian sinh bởi p và q hay không?.
Có r Sp{p, q} , / r = p + q hay r Sp{p, q} Phương trình p + q
= r có nghiệm đối với và . Thật vậy, xét:
r = p + q 6x
2
– 10x +5 = (x+1) + (2x
2
– 2x +3) x R 6x
2
– 10x +5 =
2
=
6
=
−
4
2x
2
+(–2)x + +3 x R
− 2 = −10
= 3
.
+
3
=
5
Do phương trình có nghiệm nên: r Sp{p, q}.
Ví dụ 13. Cho E = {(2c−3d; d−2c; c; d)
;
c, dR} R
4
. Hãy chứng tỏ E là không
gian con của R
4
nhờ chứng minh E được sinh ra bởi tập hợp.
Lấy bất kỳ w E w = (2c−3d; d−2c; c; d) = (2c; −2c; c; 0) + (−3d; d; 0; d) = c(2;
−2; 1; 0) + d(−3; 1; 0; 1) = cu + dv, với u = (2; −2; 1; 0) và v = (−3; 1; 0; 1). Do bất kỳ
w E đều là tổ hợp tuyến tính của 2 véc tơ {u, v} E Sp{u, v}.
Ngược lại, với bất kỳ w Sp{u, v} thì có sự phân tích w = cu +dv = c(2; −2; 1;
0) + d(−3; 1; 0; 1) = (2c−3d; d−2c; c; d) với c, d R. w E, tức là có Sp{u, v}
E.
Kết hợp E Sp{u, v} và Sp{u, v} E có E = Sp{u, v} là không gian con của
R
4
, được sinh bởi tập gồm 2 véc tơ {(2; −2; 1; 0), (−3; 1; 0; 1)}.
Nhận xét: Ví dụ vừa nêu trên đã cung cấp một phương pháp thường dùng để tìm
tập sinh của không gian con E, đó là hãy phân tích phần tử bất kỳ của E thành dạng tổ
hợp tuyến tính của các véc tơ nào đó (chú ý các vectơ này phải thuộc E). Tập các véc tơ
tìm được sau quá trình phân tích chính là tập sinh cần tìm.
5. KHÔNG GIAN CỘT VÀ KHÔNG GIAN HÀNG CỦA MA TRẬN
Định nghiã 4. Cho A M(m,n), không gian sinh ra bởi tập các véc tơ ứng với các
cột (hay các hàng) của A được gọi là không gian cột (hay không gian hàng) của ma
trận A, kí hiệu bởi ColA ( hay RowA).
55
2

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 4. KHÔNG GIAN VÉC TƠ
ColA = Sp{c
1
A, c
2
A, ..., c
n
A}.
RowA = Sp{h
1
A, h
2
A, ..., h
n
A}
Do tính chất của không gian con sinh bởi tập hợp mà ColA là không gian con của
R
m
còn RowA là không gian con của R
n
. Tất nhiên ColA = Row(A
T
).
Ví dụ 14. Cho W = {w = (c−d; c+d; −3c)/ c, dR}. Chứng minh W là không gian
con của R
3
bằng cách chỉ ra một ma trận A sao cho RowA = W.
Ma trận A thỏa mãn RowA = W phải có tập các hàng là tập các vec tơ lấy từ tập
sinh của W. Với bất kỳ w W, có sự phân tích:
w = (c−d; c+d; −3c) = c.((1 ; 1 ; −3) + d.(−1 ; 1 ; 0). (*)
Lập A là ma trận có 2 hàng là 2 vectơ trong (*): A =
1 1
−3
thì do sự phân tích
−
1 1 0
(*) nên có w Sp{h
1
A, h
2
A} = RowA W RowA. Ngược lại, nếu w RowA thì có
ngay (*) w W. Cuối cùng, do W = RowA nên W là không gian con của R
3
.
Định lý 5. Với A M(m,n), hệ tuyến tính AX = [B] có nghiệm khi và chỉ khi B
ColA.
Chứng minh
x
1
Giả sử hệ AX = [B] có nghiệm là véc tơ cột [x] =
x
n
thì có: [B] = A[x] = [c
1
A ...
c
n
A]
x
1
x
n
= x
1
.c
1
A +...+ x
n
c
n
A, chứng tỏ [B] là tổ hợp tuyến tính của các cột trong A
B Sp{c
1
A, c
2
A, ..., c
n
A} = ColA.
Ngược lại, giả sử véc tơ B ColA = Sp{c
1
A, ..., c
n
A} thì tồn tại
1
, ...,
n
R
để [B] có sự phân tích:
1
[B] =
1
.c
1
A +...+
n
.c
n
A = [c
1
A ... c
n
A]
n
1
n
1
tức là phương trình AX = [B] có nghiệm [x] =
.
n
6. KHÔNG GIAN TRIỆT CỦA MA TRẬN
Cho hệ phương trình tuyến tính thuần nhất AX = O (1) với A M(m,n). Tập
hợp tất cả các véc tơ x R
n
sao cho A[x] = O vẫn thường gọi là tập nghiệm của hệ (1).
Để thấy rõ hơn mối liên kết giữa tập nghiệm này với ma trận hệ số A, ta xét khái niệm
không gian triệt của ma trận A như định nghĩa sau đây:
56
= A

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
5
3
1
I.
KHÔNG GIAN VÉCTƠ VÀ KHÔNG GIAN CON
Định nghiã 5. Cho ma trận A M(m,n), ta gọi không gian triệt của ma trận A là
tập hợp tất cả các nghiệm của hệ phương trình tuyến tính thuần nhất AX = O, kí
hiệu NulA.
NulA = {
x
R
n
/ A[
x
] =
O
}
Ví dụ 15. Cho A =
1 0
1
0 0
2 0 4
3 0
0 1 6
và x = (–2; –3; 1; 0; 0), y = (0; –5; 0; –6; 1).
Hãy xác định xem x và y có phải là phần tử của NulA không ?
1 0
− 2
2 0 4
− 3
0
Có A[x] =
0 1 3 0
0 0 0 1
5
1
6
0
=
0
0
x NulA.
1 0
0
0
2 0 4
−5
4
0
Có A[y] =
0 1
0 0
3 0 5
0
0 1 6
−
6
1
=
0
0
0
y NulA.
0
Định lý 6. Nếu A M(m,n) thì NulA là không gian con của R
n
.
Định lý này là hiển nhiên do tính chất nghiệm của hệ thuần nhất, theo đó NulA đóng
kín đối với hai phép toán là cộng và nhân ngoài của R
n
.
Nhờ kết quả của định lí vừa nêu mà ta có: Tập nghiệm của hệ thuần nhất AX = O
lập thành không gian con của R
n
. Chú ý rằng, tính thuần nhất của hệ là quan trọng, nếu
bỏ giả thiết thuần nhất, tập nghiệm của hệ tuyến tính tùy ý AX = [B] không lập nên
không gian con của R
n
. Chẳng hạn xét hệ:
x
1
+ x
2
+ 3x
3
+ x
4
= 6
3x
1
+ x
2
+ −5x
3
+ x
4
= 0
là hệ không thuần nhất với ma trận hệ số A =
1 1
1
3 1
−
5
M(2,4). Hiển nhiên tập
nghiệm của hệ trên không là không gian con của R
4
vì O = (0; 0; 0; 0) không là nghiệm,
a
Ví dụ 16. Cho W =
w =
b
/ a − 3b − c = 0
. Hãy chứng minh W là không gian con
c
của [R]
3
bằng các cách khác nhau.
Cách 1: Xét hệ thuần nhất gồm 1 phương trình và 3 ẩn x
1
–3x
2
–x
3
= 0 (*) với
ma trận hệ số là A =
1
−
3
−
1
M
(1,3). Rõ ràng
W
là tập nghiệm của hệ (*), nên
W
là không gian con của [R]
3
.
57

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
1 0
2
2
2
2
0
0
1
0
0
t
R
Chương 4. KHÔNG GIAN VÉC TƠ
a
Cách 2: Lấy phần tử bất kì w =
b
c
W . Do a–3b–c = 0 a = 3b+c nên có sự
a
3b + c
3
1
phân tích: w =
b
=
b
= b.
1
+ c.
0
.(*)
c
c
0
1
Lập ma trận A =
3 1
0
1
M(3,2) thì do sự phân tích (*), suy ra W = ColA nên W
là không gian con của [R]
3
.
Cách 3: Chứng minh nhờ áp dụng trực tiếp tiêu chuẩn của không gian con (hãy tự
giải).
7. CÁCH TÌM TẬP SINH CHO KHÔNG GIAN TRIỆT CỦA MA TRẬN
Từ định nghĩa của không gian triệt NulA, ta chưa biết một thông tin gì về các phần
tử của NulA mặc dù ma trận A hoàn toàn đã biết. Một vấn đề rất tự nhiên đặt ra là làm
sao có được sự biểu diễn rõ ràng của các phần tử thuộc NulA? Ví dụ sau đây mô tả qúa
trình đi tìm sự biểu diễn đó thông qua việc tìm tập sinh.
1 − 2
Ví dụ 17. Tìm tập sinh của NulA với A =
− 3
3 − 5
−1 1
1 −1
4 − 3
5 − 4
− 3
- Quy A về dạng rút gọn.
1 − 2
A =
− 3
3 − 5
−1 1
1 −1
1 − 2
4 − 3
→
1
5 − 4
0 1
− 3
− 1
1 − 1
1 0 5
2 − 1
1 2
→
2 − 1
0 0 0
− 2
0 0
− 3
− 1
0
- Nghiệm tổng quát của hệ AX = O (nhờ phương pháp Gauss):
−
5t
1
+
3t
2
−2t + t
[x] =
1 2
t
1
R
2
-
Phân tích vectơ nghiệm [x] thành tổ hợp tuyến tính của các véc tơ cột theo quy
tắc mô tả như sau (chú ý các ẩn tự do được chọn làm các hệ số trong sự phân
tích):
−5t
1
+ 3t
2
− 5
3
−2t + t
− 2
1
[x] =
1 2
= t
1
.
+ t
2
.
= t
1
[u] + t
2
[v], với u = (–5 ; –2 ; 1 ; 0), v = (3 ;
t
1
R
1
0
t
R
0
1
2
1 ; 0 ; 1). (*)
58
0

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
I.
KHÔNG GIAN VÉCTƠ VÀ KHÔNG GIAN CON
Do (*) suy ra x NulA thì x = t
1
.u + t
2
.v Sp{u, v} NulA Sp{u, v}. Ngược
lại, dễ thấy Sp{u, v} NulA nên NulA = Sp{u, v} S = {u, v}là tập sinh của NulA.
Bằng phương pháp phân tích như trên, ta rút ra các bước tìm tập sinh cho NulA như
sau :
-
Bước 1: Quy A về dạng rút gọn, viết ra nghiệm tổng quát của hệ AX = O.
-
Bước 2: Bằng cách lấy các ẩn tự do làm hệ số, phân tích nghiệm tổng quát thành
tổ hợp tuyến tính của các vectơ nào đó. Các vectơ xuất hiện trong sự phân tích
này lập nên tập sinh cho NulA.
Như vậy, số véc tơ tìm được trong tập sinh của NulA bằng số ẩn tự do mà hệ AX =
O có. Sau này ta sẽ chứng minh được rằng số véc tơ ít nhất phải có trong mỗi tập sinh
của NulA, đúng bằng số ẩn tự do của hệ thuần nhất tương ứng.
59

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 4. KHÔNG GIAN VÉC TƠ
II.
TÍNH ĐỘC LẬP TUYẾN TÍNH VÀ PHỤ THUỘC TUYẾN TÍNH.
CƠ SỞ VÀ SỐ CHIỀU CỦA KHÔNG GIAN VÉC TƠ
1. TẬP VÉC TƠ ĐỘC LẬP TUYẾN TÍNH VÀ PHỤ THUỘC TUYẾN TÍNH
Định nghiã 6. Cho V là không gian véc tơ.
a)
Tập S = {v
1
, v
2
, ..., v
p
} V được gọi là phụ thuộc tuyến tính nếu vectơ Ov biểu
thị tuyến tính được qua các vectơ của S với ít nhất một hệ số
i
0, i = 1..p.
b)
Tập S không phụ thuộc tuyến tính được gọi là tập độc lập tuyến tính.
Từ định nghiã, suy ra:
S = {v
1
, v
2
, ..., v
p
} phụ thuộc tuyến tính Tồn tại các số
1,
2
, ...,
p
không đồng
thời bằng 0 sao cho
1
v
1
+
2
v
2
+...+
p
v
p
= O
V
.
S = {v
1
, v
2
, ..., v
p
} độc lập tuyến tính Hệ thức
1
v
1
+
2
v
2
+...+
p
v
p
= O
V
chỉ
đúng khi
1
=
2
= ... =
p
= 0.
Nếu ta gọi tổ hợp tuyến tính dạng: 0.v
1
+ 0.v
2
+...+ 0v
p
(với tất cả các hệ số đều bằng
0) là tổ hợp tuyến tính tầm thường thì:
S = {v
1
, v
2
, ..., v
p
} là độc lập tuyến tính Mọi tổ hợp tuyến tính của vectơ O
V
theo
các vectơ của S đều là tổ hợp tuyến tính tầm thường.
S = {v
1
, v
2
, ..., v
p
} là phụ thuộc tuyến tính Tồn tại ít nhất một tổ hợp tuyến
tính của vectơ O
V
theo các vectơ của S, là tổ hợp tuyến tính không tầm thường.
Ví dụ 18. Tập gồm chỉ 1 véc tơ {v} V là độc lập tuyến tính khi và chỉ khi v O.
Tập gồm 2 véc tơ là phụ thuộc tuyến tính khi và chỉ khi 2 véc tơ đó tỷ lệ (hiểu theo
nghĩa, trong 2 véc tơ, có 1 véc tơ bằng một vô hướng nhân với véc tơ kia). Hai véc tơ
phụ thuộc tuyến tính còn gọi là hai véc tơ cùng phương.
Ví dụ 19. Trong R
n
, tập B
0
= {e
1
= (1; 0; ..., 0), e
2
= (0; 1; 0; ...; 0), ..., e
n
= (0; ...,
0; 1)} là độc lập tuyến tính, vì:
1
1
e
1
+...+
n
e
n
= O
1
[e
1
] +...+
n
[e
n
] = O I
n
.
n
0
0
1
= 0
.
n
= 0
Ví dụ 20. Trong P
n
(x), tập tập gồm n+1 đa thức: B = {1, x, x
2
, ..., x
n
}là độc lập
tuyến tính.
Thật vậy, xét một tổ hợp tuyến tính bất kỳ của vectơ O P
n
(x) ta có:
0
1+
1
x+
2
x
2
+...+
n
x
n
= O (*)
0
1+
1
x+
2
x
2
+...+
n
x
n
= 0.1 + 0.x + 0.x
2
+...+0.x
n
0
=
1
= ... =
n
= 0.
Do (*) chỉ đúng khi
0
=
1
=...=
n
= 0 nên tổ hợp tuyến tính đang xét là tổ hợp
tuyến tính tầm thường, theo định nghiã, B là độc lập tuyến tính.
Ví dụ 21. Cho các đa thức p = x
2
+1, q = 3x–1, r = – 4x+1 là các véc tơ của không
gian véc tơ P
2
(x). Chứng minh rằng tập {p, q, r} là độc lập tuyến tính.
Xét tổ hợp tuyến tính bất kỳ của OP
2
(x):
60
=

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
2
II. TÍNH ĐỘC LẬP TUYẾN TÍNH, CƠ SỞ VÀ SỐ CHIỀU
1
p +
2
q +
3
r = O
1
(x
2
+1) +
2
(3x–1) +
3
(–4x+1) = 0+0x+0x
2
1
–
2
+a
3
1
−
2
+
3
=
0
1
= 0
+ (3
2
–4a
3
)x +
1
x
2
= 0+0x+0x
2
3 − 4 = 0
= 0 .
2 3
1
= 0
3
=
0
Do
1
=
2
=
3
= 0 là nghiện duy nhất nên tổ hợp tuyến tính đang xét là tổ hợp
tuyến tính tầm thường, theo định nghiã, tập {p, q, r} là độc lập tuyến tính.
Định lý 7. Tập S = {v
1
, v
2
,..., v
p
} V gồm p 2 véc tơ là phụ thuộc tuyến tính khi
và chỉ khi v
i
S, i = 1, 2, ..., p, là tổ hợp tuyến tính của các véc tơ còn lại.
Chứng minh. Giả sử S là phụ thuộc tuyến tính. Theo định nghĩa, tồn tại bộ p số (
1
;
2
;...;
p
), trong đó có ít nhất một số
i
0, i = 1..p sao cho:
1
v
1
+ ... +
i
v
i
+...+
p
v
p
= O
i
v
i
= −(
1
v
1
+ ... +
i–1
v
i–1
+
i+1
v
i+1
+...+
p
v
p
)
Do
i
0 nên: v
i
= −
1
i
(
1
v
1
+ ... +
i–1
v
i–1
+
i+1
v
i+1
+...+
p
v
p
), tức v
i
là tổ hợp
tuyến tính của các véc tơ còn lại.
Ngược lại, giả sử v
i
, i = 1..p là tổ hợp tuyến tính của các véc tơ còn lại, nghiã là:
v
i
=
1
v
1
+ ... +
i–1
v
i–1
+
i+1
v
i+1
+...+
p
v
p
1
v
1
+ ... +
i–1
v
i–1
− v
i
+
i+1
v
i+1
+...+
p
v
p
= O. (*). Hệ số thứ i trong hệ thức (*) là
i
= −1 0, theo định nghĩa ta có tập
S phụ thuộc tuyến tính.
Chú ý rằng định lí trên thường được áp dụng ở dạng thuận lợi hơn như sau: Tập
không ít hơn 2 véc tơ {v
1
, v
2
, ..., v
p
} (p 2) với v
1
O, là phụ thuộc tuyến tính khi và chỉ
khi trong tập có véc tơ v
i
nào đó (i 2) là tổ hợp tuyến tính của các véc tơ đứng trước
nó: v
1
, v
2
,..., v
i–1
. Hơn nưã, ta có thể chọn để tập hợp các véc tơ đứng trước véc tơ v
i
là
độc lập tuyến tính.
Áp dụng định lí, dễ dàng chứng minh các tính chất sau đây:
1)
Nếu tập S có chứa véc tơ O thì S phụ thuộc tuyến tính.
2)
Nếu tập có một bộ phận con phụ thuộc tuyến tính thì tập phụ thuộc tuyến tính.
Từ đó suy ra nếu một tập đã phụ thuộc tuyến tính thì thêm vào tập đó bao nhiêu véc
tơ đi nữa, ta vẫn được tập mới phụ thuộc tuyến tính.
3)
Nếu tập đã cho là độc lập tuyến tính thì mọi tập con (khác rỗng) của nó cũng
độc lập tuyến tính.
4)
S là tập độc lập tuyến tính trong V thì với bất kỳ v V, tập S {v} là độc lập
tuyến tính khi và chỉ khi v Sp(S).
2.XÉT TÍNH ĐỘC LẬP TUYẾN TÍNH, PHỤ THUỘC TUYẾN TÍNH TRONG R
n
NHỜ MA TRẬN
Phương pháp kiểm tra tập véc tơ S = {v
i
}
1,p
độc lập tuyến tính hay phụ thuộc tuyến
tính thường được bắt đầu bằng việc xét tổ hợp tuyến tính bất kỳ của véc tơ O
V
theo các
vectơ của S:
1
v
1
+
2
v
2
+...+
p
v
p
= O
V
(1)
Điều khác nhau cơ bản giữa phương trình (1) được xét trong không gian véc tơ tổng
quát và xét trong không gian véc tơ R
n
là trong R
n
phương trình (1) có thể viết được
dưới dạng hệ phương trình tuyến tính thuần nhất AX = O, với A = [[v
1
] [v
2
] ... [v
p
]] còn
trong các không gian khác, không có được khả năng như vậy. Nhờ tính chất đặc biệt đó,
ta có cách xét thuận lợi sau đây:
61

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
0
1
0
1
1
1
0
Chương 4. KHÔNG GIAN VÉC TƠ
Cho S ={v
1
, v
2
, ..., v
p
} R
n
thì tổ hợp tuyến tính bất kỳ của OR
n
, luôn viết
được ở dạng:
1
v
1
+
2
v
2
+...+
p
v
p
= O
1
[v
1
] +
2
[v
2
] +...+
p
[v
p
] = O
1
0
[[v
1
] [v
2
] ... [v
p
]]
2
=
(2)
⁝
n
Đặt A = [[v
1
] [v
2
] ... [v
p
]] thì (2) chứng tỏ (
1
,
2
, ...,
n
) là nghiệm của hệ thuần
nhất AX = O. Nếu (2) có duy nhất nghiệm là nghiệm tầm thường (0; 0; ...; 0) thì mọi tổ
hợp tuyến tính của vectơ O theo các vectơ thuộc S đều là tổ hợp tuyến tính tầm thường,
nên S là độc lập tuyến tính. Nếu ngược lại, S sẽ phụ thuộc tuyến tính. Từ đó có định lí
sau là cơ sở cho phương pháp xét tính độc lập tuyến tính của tập các véc tơ trong R
n
:
Định lý 8. Tập S = {v
1
, v
2
, ..., v
p
} của R
n
là tập độc lập tuyến tính khi và chỉ khi ma
trận A = [[v
1
] [v
2
] ... [v
p
]] tạo bởi các véc tơ cột của vectơ v
i
S, có hạng đúng bằng
số véc tơ có trong S.
Ví dụ 22. Xét tính độc lập tuyến tính của tập các véc tơ: S = {(3; 2; 2; 1); (1; 0; 1;
1); (1; 1; 1; 0)} trong R
4
.
Lập ma trận A bao gồm các cột là các vectơ cột của véc tơ trong S rồi quy A về
dạng bậc thang:
3
A =
2
1 1
1
0
→
1 1
0
1
1 0
1
− 2
→
− 1 1
0
− 2
1 0
− 1
0 − 1
0
r(A) = 3.
Do r(A) = 3 (bằng số véc tơ có trong S) nên S là độc lập tuyến tính.
Từ phương pháp xét tính độc lập tuyến tính của các véc tơ thuộc R
n
vừa nêu trên, ta
có kết qủa sau:
Định lý 9. Trong R
n
thì:
1)
Tập gồm đúng n véc tơ là độc lập tuyến tính khi và chỉ khi tập các véc tơ cột của
chúng lập nên ma trận khả nghịch.
2)
Mọi tập chứa nhiều hơn n véc tơ đều phụ thuộc tuyến tính.
Chứng minh:
Giả sử S = {v
1
, v
2
, ..., v
p
} R
n
. Lập A = [[v
1
] [v
2
] ... [v
p
]] M(n,p). Khi đó:
-
1) là hiển nhiên vì khi p = n thì A M(n,n) khả nghịch r(A) = n.
-
Nếu p > n thì A = [[v
1
] [v
2
] ... [v
p
]] M(n,p), nên có r(A) n <p, suy ra S phụ
thuộc tuyến tính.
3. CƠ SỞ CỦA KHÔNG GIAN VÉC TƠ
Định nghiã 7. Tập B = {v
1
, v
2
, ..., v
n
} V, gồm n véc tơ có thứ tự, được gọi là cơ sở
của không gian véc tơ V nếu B độc lập tuyến tính và B là tập sinh của V.
Hay nói ngắn gọn hơn: Cơ sở của không gian véc tơ là một tập sinh có thứ tự và độc
lập tuyến tính. Thông thường, tính có thứ tự của tập sinh được thể hiện qua cách viết,
nên từ đây về sau ta không nói đến tính có thứ tự của cơ sở nữa.
62
2
1
0
0
0
0

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
0
0
0
0
1
0
0
1
2
1
0
0
II. TÍNH ĐỘC LẬP TUYẾN TÍNH, CƠ SỞ VÀ SỐ CHIỀU
Ví dụ 23. Tập B
0
= {e
1
= (1; 0; ..., 0), e
2
= (0; 1; 0; ...; 0), ..., e
n
= (0; ..., 0; 1)} lập
nên cơ sở của R
n
và gọi là cơ sở chính tắc.
Thật vậy:
-
Tập {e
1
, e
2
, ..., e
n
} độc lập tuyến tính (xem ví dụ 1 ở trên).
-
{e
1
, e
2
, ..., e
n
} là tập sinh của R
n
vì với bất kỳ x = (x
1
; x
2
; ...; x
n
) R
n
ta đều có sự
phân tích x = (x
1
; x
2
; ...; x
n
) = x
1
(1; 0; ...; 0) + x
2
(0; 1; 0; ...; 0) + ... + x
n
(0; ...; 0; 1) =
x
1
e
1
+ x
2
e
2
...+ x
n
e
n
.
Ví dụ 24. Tập B
0
= {1, x, x
2
, ..., x
n
} P
n
(x) lập nên cơ sở của P
n
(x) và gọi là cơ sở
chính tắc của P
n
(x).
Thật vậy:
-
Tập {1, x, x
2
, ..., x
n
} là độc lập tuyến tính (xem ví dụ 2 ở trên).
-
Tập {1, x, x
2
, ..., x
n
} là tập sinh của P
n
(x) vì với bất kỳ p = a
0
1+a
1
x+a
2
x
2
+...+a
n
x
n
P
n
(x) đều là tổ hợp tuyến của các véc tơ thuộc B
0
: p = a
0
.1 +a
1
x+a
2
x
2
+...+a
n
x
n
, a
i
R,
i = 0..n.
Ví dụ 25. Tập B
0
= {E
ij
/ [E
ij
]
kl
=
1
khi k = i,l = j
} lập nên cơ sở của M(m,n) và
khi k
i,l
j
gọi là cơ sở chính tắc của M(m,n). ).Chẳng hạn, M(2,2) có cơ sở chính tắc gồm 4 vectơ
là:
B
0
= {E
11
=
1
0
, E
12
=
0
1
, E
21
=
0
0
, E
22
=
0
0
}
Ví dụ 26. Tập S = {(1; 2; –1; 1), (0; 1; 3; 1), (2; 5; 1; 3)} có phải là cơ sở của Sp(S)
hay không?
S là tập sinh của Sp(S) nên S là cơ sở của Sp(S) khi S độc lập tuyến tính. Lập ma
trận A gồm các cột là các vectơ cột của vectơ trong S rồi quy A về dạng bậc thang:
1 0
A =
1
− 1 3
1
2
1 0
→
1
0 3
1
2
1 0
→
3
0 0
0
2
r(A) = 2.
0
Vì r(A) = 2, nhỏ hơn số véc tơ (bằng 3) của S, nên S phụ thuộc tuyến tính, và vì
vậy, S không là cơ sở của Sp(S).
Ví dụ 27. Tập gồm 3 véc tơ B ={u = (1; 2; −1), v = (2; −1; 0), w = (3; 0; 1)} R
3
có
phải là cơ sở của R
3
không?
- Kiểm tra tính độc lập tuyến tính của B:
1 2 3
1 2 3
1 2 3
1 2 3
A = [[u] [v] [w]] =
2
−
1
0
→
0
5
6
→
0
−1 −4
→
0 1 4
.
−
3 0 1
0
6
10
0
3
5
0
0
−
7
Vì r(A) = 3 nên B là độc lập tuyến tính.
- Kiểm tra B là tập sinh của R
3
. Lập A = [[u] [v] [w]] thì R
3
= Sp(B) Hệ AX
= [x] có nghiệm với mọi x = (x
1
; x
2
; x
3
) R
3
. Tuy nhiên, từ trên ta đã có r(A) = 3 nên
hệ có nghiệm là hiển nhiên.
63
5
3
0
1
1
0
1
0
1
1

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 4. KHÔNG GIAN VÉC TƠ
Kết luận: B vừa là tập sinh của R
3
, vừa độc lập tuyến tính nên là cơ sở của R
3
.
Định lý 10. Trong R
n
mọi tập gồm n véc tơ độc lập tuyến tính đều là cơ sở.
Chứng minh
Giả sử S = {v
1
, v
2
, ..., v
n
} R
n
là tập gồm n véc tơ độc lập tuyến tính. Để chứng
minh S là cơ sở, chỉ cần chứng minh thêm S là tập sinh. Thật vậy, đặt A = [[v
1
] [v
2
] ...
[v
n
]]
n
n
là ma trận tạo bởi các véc tơ cột của vectơ trong S, thì với mọi b R
n
, phương
trình AX = [b] luôn có nghiệm (do A khả nghịch) R
n
= Sp{v
1
, v
2
, ..., v
n
}.
4. ĐỊNH LÍ VỀ TẬP SINH. PHƯƠNG PHÁP TÌM CƠ SỞ TỪ TẬP SINH
Ta hiểu tập sinh tối tiểu là tập sinh mà nếu loại bỏ khỏi nó một véc tơ nào đó, thì tập
còn lại không còn là tập sinh nữa. Định lý sau đây cho ta biết tập sinh tối tiểu chính là
cơ sở, đồng thời còn cho biết cách xây dựng cơ sở từ một tập sinh đã có.
Định lý 11. (Định lý về tập sinh) Cho không gian véc tơ V và E là không gian con
của V sinh bởi S = {v
1
, v
2
, ..., v
p
} V. Khi đó:
1)
Nếu trong S có một véc tơ nào đó, giả sử v
k
, k = 1..p, là tổ hợp tuyến tính của
các véc tơ còn lại thì tập S\{v
k
} vẫn còn là tập sinh của E.
2)
Nếu E {O
V
} thì E luôn có ít nhất một cơ sở là tập con của S.
Chứng minh
1) Sắp lại thứ tự, ta luôn giả thiết được véc tơ đứng cuối cùng trong S là tổ hợp
tuyến tính của các véc tơ còn lại:
p−1
v
p
=
1
v
1
+
2
v
2
+...+
p–1
v
p
−
1
=
i
v
i
;
i
R.
i=1
Lấy bất kỳ v E = Sp(S) thì do S là tập sinh, tồn tại các hệ số
i
, i = 1..p, sao cho:
p−1
v =
1
v
1
+
2
v
2
+...+
p–1
v
p–1
+
p
v
p
=
1
v
1
+
2
v
2
+...+
p
−
1
v
p
−
1
+
p
(
i
v
i
)
i=1
= '
1
v
1
+ '
2
v
2
+...+ '
p–1
v
p–1
(*).
(*) chứng tỏ bất kỳ v E đều biểu thị tuyến tính được qua các vectơ thuộc S
1
=
S\{v
p
} = {v
1
, v
2
..., v
p
−
1
} nên S
1
là tập sinh mới của E.
2) Nếu S là độc lập tuyến tính thì hiển nhiên S là cơ sở của E = Sp(S). Ngược lại nếu
S là phụ thuộc tuyến tính thì sẽ có một véc tơ nào đó (không giảm tính tổng quát, ta giả
sử đó là v
p
) là tổ hợp tuyến tính của các véc tơ còn lại. Khi đó loại bỏ v
p
ra khỏi S ta
được S
1
= {v
1
, v
2
..., v
p
−
1
} là tập sinh mới của E. Nếu S
1
là độc lập tuyến tính thì nó là cơ
sở của E, nếu nó vẫn còn phụ thuộc tuyến tính thì ta lặp lại qúa trình như trên đối với
S
1
, thu được tập sinh mới S
2
của E, …. Cứ tiếp tục như vậy, nhiều nhất là đến bước thứ
p − 1, tập sinh S
p
−
1
chỉ còn lại đúng 1 véc tơ, giả sử đó là S
p
−
1
= {v
1
}. Do giả thiết E
{O
V
} nên v
1
O
V
, suy ra S
p
−
1
là độc lập tuyến tính và nó là cơ sở của E. Vậy ta đã
chứng minh được trong S có một tập con là cơ sở của E.
Nhận xét
- Nhờ định lý về tập sinh, ta có khả năng xây dựng cơ sở cho không gian véc tơ V từ
một tập sinh bất kỳ nào đó bằng cách rút bỏ những véc tơ biểu thị tuyến tính được qua
64

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
1
3
0
0
0
0
.1
+
.0
1
0
II. TÍNH ĐỘC LẬP TUYẾN TÍNH, CƠ SỞ VÀ SỐ CHIỀU
các véc tơ còn lại. Hiển nhiên, những vectơ ứng với hệ số khác 0 trong tổ hợp tuyến tính
của vectơ O là các vectơ biểu thị được qua các vectơ còn lại. Ngoài ra, còn một phương
pháp khác nữa để xây dựng cơ sở, đó là mở rộng dần một tập độc lập tuyến tính nào đó
đã có trong V, sẽ được trình bày ở phần sau.
- Từ phương pháp xây dựng cơ sở cho không gian véc tơ như đã trình bày ở trên, ta
thấy rằng việc loại bỏ các véc tơ trong tập sinh phải dừng lại khi tập sinh thu được là
độc lập tuyến tính, (kí hiệu bởi B). Nếu ta tiếp tục loại bỏ thêm một véc tơ nào đó nữa,
giả sử là w, ra khỏi B thì do w không thể là tổ hợp tuyến tính của các véc tơ còn lại nên
tập B \{w} không thể là tập sinh được (vì w không thể biểu thị tuyến tính được qua các
véc tơ của tập này). Vậy cơ sở là tập sinh tối tiểu. Mặt khác, cơ sở B là tập độc lập
tuyến tính có số véc tơ nhiều nhất (hay còn gọi là tập độc lập tuyến tính tối đại), vì giả
sử ta thêm một véc tơ v nào đó vào cho B thì {B; v} không còn là độc lập tuyến tính nữa
(do v là tổ hợp tuyến tính của các véc tơ trong B).
Tóm lại: Cơ sở của không gian véc tơ là tập độc lập tuyến tính tối đại, và là tập sinh
tối tiểu của không gian véc tơ đó.
Ví dụ 28. Cho S = {u = (1; 2; −1; 1); v = (0; 1; 3; 1); w = (2; 5; 1; 3)}. Hãy tìm một
cơ sở của Sp(S).
Để tìm cơ sở của Sp(S) ta cần loại bỏ khỏi S các véc tơ biểu thị tuyến tính được qua
các véc tơ còn lại. Muốn vậy, trước hết cần xác định tính độc lập tuyến tính của S. Lập
ma trận bao gồm các cột là các véc tơ cột của u, v, w; sau đó quy gọn về dạng bậc
thang, ta có:
1 0 2
2 1 5
1 0 2
0 1 0
1 0 2
0 1 1
A = [[u] [v] [w]] =
→
→
= B r(A) = 2.
− 1 3 1
1
0 3 0
0 0 0
Do r(A) = 2 < 3 (là số véc tơ), nên S là phụ thuộc tuyến tính. Mặt khác, từ ma trận
bậc thang B suy ra phương trình:
x
1
x
1
=
−
2x
3
x
1
[u] + x
2
[v] + x
3
[w] = O A
x
= O có nghiệm
x
= − x .
2
2 3
x
3
x
3
=
x
3
R
Cho x
3
= −1 ta có một quan hệ phụ thuộc tuyến tính giữa u, v, w là: 2u + v − w = O
w = 2u + v. Loại bỏ w ra khỏi S ta có S
1
= {u, v} vẫn còn là tập sinh và dễ thấy nó
độc lập tuyến tính (nhờ xét các cột tương ứng trong ma trận bậc thang B), nên S
1
là cơ
sở của Sp(S). (Có thể nhận ra ngay cơ sở cần tìm là các vectơ của S, ứng với các cột có
chứa phần tử chính trong dạng bậc thang B, tức là ứng với các cột cơ sở của A).
Ví dụ 29. Tìm cơ sở của E = Sp{1, sin
2
x, cos2x, cos
2
x}.
Gọi S = {1, sin
2
x, cos2x, cos
2
x}. Vì 1 = sin
2
x + cos
2
x; cos2x = cos
2
x − sin
2
x nên sau
khi loại bỏ 1 và cos2x ra khỏi S, được tập S’ = {sin
2
x, cos
2
x} vẫn còn là tập sinh của E.
Mặt khác S’ là độc lập tuyến tính vì với bất kì , R thì:
sin
2
x + cos
2
x = O
E
sin
2
x + cos
2
x = 0 x R.
Cho lần lượt x = 0; x = /2 ta có :
.0 + .1 =
=
0
0
=
0
.
= 0
Vậy, S’= {sin
2
x, cos
2
x} là cơ sở cần tìm cho E.
65

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
1
Chương 4. KHÔNG GIAN VÉC TƠ
5.CƠ SỞ CỦA KHÔNG GIAN TRIỆT, KHÔNG GIAN CỘT VÀ KHÔNG GIAN
HÀNG
a. Cơ sở của không gian triệt NulA
Ta đã hoàn toàn biết phương pháp tìm tập sinh cho NulA. Rất may mắn là tập sinh
tìm được (theo phương pháp đã trình bày) tự nó đã là tập độc lập tuyến tính (dễ dàng
chứng minh được điều này), nên nó cũng đóng vai trò là cơ sở cho NulA. Vậy lược đồ
tìm cơ sở cho NulA có thể tóm tắt như sau:
Bước 1: Tìm NulA, tức là tìm nghiệm tổng quát của hệ thuần nhất AX = O.
Bước 2: Phân tích nghiệm tổng quát thành tổ hợp tuyến tính của các véc tơ, với các
ẩn tự do đóng vai trò là các hệ số trong sự phân tích đó.
Các véc tơ xuất hiện trong tổ hợp tuyến tính tìm được chính là các véc tơ lập nên cơ
sở của NulA.
Ví dụ 30. Tìm cơ sở của NulA với A =
2
− 2
3
4 − 2
− 5 7
7 − 8
1
3
.
6
Bước 1. Tìm NulA. Quy A về dạng rút gọn ta có:
1 2 − 1
1
1 0
9
17
1 0 9 0
A → 0 − 1 5
2
→
0 −
2
→
0 1
− 5 0
= B
4
− 5
9
2
1 5 4
0 0
17
2
0 0
0 1
Từ B, thấy ngay NulA = {x = (–9t; 5t; t; 0), t R}
Bước 2. Với x NulA x = (–9t; 5t; t; 0) = t.(–9; 5; 1; 0), tR.
Vậy, cơ sở của NulA chỉ gồm một véc tơ: B = {(–9; 5; 1; 0)}.
Nhận xét. Số véc tơ có trong cơ sở của NulA đúng bằng số ẩn tự do có trong hệ
thuần nhất AX = O và chúng được gọi là tập nghiệm cơ bản của hệ. Vì vậy, việc tìm cơ
sở cho NulA chính là việc tìm tập nghiệm cơ bản của hệ thuần nhất AX = O. Một khi đã
biết nghiệm tổng quát, ta có thể tìm được tập nghiệm cơ bản bằng cách lần lượt cho
từng ẩn tự do nhận giá trị bằng 1, các ẩn tự do còn lại nhận giá trị bằng 0. Trong ví dụ
trên, để có tập nghiệm cơ bản, ta chỉ cần thế t = 1 vào biểu thức nghiệm tổng quát để
được {(−9; 5; 1; 0)} là tập nghiệm cơ bản.
x
1
+ 2x
2
+ x
3
− x
4
=
0
Ví dụ 31. Tìm tập nghiệm cơ bản của hệ thuần nhất:
2x + 5x + 3x + x
=
0
1 2 3 4
3x + 7x + 4x
=
0
1 2 3
Thực hiện phép rút gọn hàng trên ma trận hệ số A ta có:
66
0

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
1
t
=
1
0
0
0
0
II. TÍNH ĐỘC LẬP TUYẾN TÍNH, CƠ SỞ VÀ SỐ CHIỀU
1 2 1
−
1
h 2→h 2−2h1
1 2 1
− 1
h1→h1−2h 2
1 0
− 1 − 7
2 5 3
1
⎯⎯
h3→
⎯
h3−
⎯
3
⎯
h1
→
0 1 1
3
⎯
h
⎯
3→
⎯
h3−
⎯
h
⎯
2
→
0 1 1 3
3
7
4
0
0 1 1
3
0 0 0
0
Rút ra nghiệm tổng quát của hệ là:
t
1
+ 7t
2
1
7
−
t
−
3t
−
1
−3
[x] =
1
2
= t
1
.
+ t
2
.
, t
1,
t
2
R.
t
1
t
2
1
0
Cho lần lượt các tham số
t
1
= 1
và
t
2
= 0
t
1
= 0
, ta được tập nghiệm cơ bản gồm 2 véc tơ:
2
(1;
−
1;1;0), (7;
−
3;0;1)
.
b. Cơ sở của không gian cột ColA
- Nếu A là ma trận dạng rút gọn
Nếu A M(m,n) có dạng rút gọn thì tập các cột cơ sở của A là tập độc lập tuyến
tính (vì nó là một tập con của tập các véc tơ thuộc cơ sở chính tắc của R
m
) và những cột
không phải là cột cơ sở, luôn biểu thị tuyến tính được qua tập các cột cơ sở. Theo định
lý về tập sinh, sau khi loại bỏ tất cả các cột không là cột cơ sở, tập các cột cơ sở còn lại
vẫn là tập sinh của ColA, nên chúng là cơ sở của ColA. Vậy, nếu A có dạng rút gọn thì
tập các cột cơ sở tạo nên cơ sở của ColA.
1 4 0
Ví dụ 32. Tìm cơ sở của ColA với: A =
0 1
0 0 0
0 0
2 0
− 1
0 1
0
Do ma trận A là ma trận dạng rút gọn nên phát hiện các cột cơ sở của A là c
1
A, c
3
A
và c
5
A. Cơ sở của ColA là tập gồm 3 véc tơ ứng với 3 cột cơ sở của A: {(1; 0; 0; 0),
(0; 1; 0; 0), (0; 0; 1; 0)}.
- Nếu A là ma trận dạng bất kỳ
Ta có mệnh đề: Các phép toán hàng trên ma trận không làm thay đổi quan hệ phụ
thuộc tuyến tính hay độc lập tuyến tính giữa các cột của ma trận.
Thật vậy, một quan hệ phụ thuộc tuyến tính hay độc lập tuyến tính nào đó giữa các
cột của A = [c
1
A c
2
A ... c
n
A], hoàn toàn được xác định bởi các hệ số
1
,
2
, ...,
n
trong
hệ phương trình:
1
1
.c
1
A +
2
.c
2
A + ... +
n
.c
n
A = O A
⁝
= O (*)
n
67

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
1
3
0
0
0
Chương 4. KHÔNG GIAN VÉC TƠ
Do các phép toán hàng không làm thay đổi tập nghiệm của hệ phương trình AX = O,
tức không làm thay đổi các hệ số
1
,
2
, ...,
n
, nên cũng không làm thay đổi quan hệ
phụ thuộc tuyến tính hay độc lập tuyến tính giữa các cột.
Nhờ mệnh đề trên, để tìm cơ sở của ColA ta chỉ cần quy A về dạng bậc thang nhờ
các phép toán hàng rồi áp dụng định lí sau:
Định lý 12. Tập hợp các véc tơ ứng với các cột cơ sở của ma trận A tạo nên cơ sở
của không gian cột ColA.
Chứng minh
Giả sử A M(m,n) và U là dạng rút gọn của A. Gọi S là tập hợp tất cả các cột cơ sở
của U thì S là độc lập tuyến tính (vì S là tập con của tập các véc tơ thuộc cơ sở chính tắc
của R
m
). Mặt khác do mệnh đề trên, một quan hệ độc lập tuyến tính (hay phụ thuộc
tuyến tính) nào đó giữa các cột trong ma trận A cũng chính là quan hệ độc lập tuyến
tính (hay phụ thuộc tuyến tính) giữa các cột tương ứng trong ma trận U, nên tập các cột
cơ sở của A là độc lập tuyến tính, còn tập các cột của A vì có chứa cột không là cột cơ
sở, sẽ phụ thuộc tuyến tính. Nhờ định lí về tập sinh, ta loại bỏ tất cả các cột không phải
là cột cơ sở, để được tập sinh mới là tập các cột cơ sở. Vậy, tập các cột cơ sở của A là
cơ sở của ColA.
Ví dụ 33. Tìm cơ sở của ColA với A =
Quy ma trận A về dạng bậc thang:
1 0 2
.
− 1 3 1
1
1 0
A →
1
0 3
1
2
1 0
→
3
0 0
0
2
= B.
0
Từ B phát hiện các cột cơ sở (cột có chứa phần tử cơ sở) là cột 1 và cột 2. Suy ra cơ
sở của ColA là: {(1; 2; –1; 1), (0; 1; 3; 1)}.
Nhận xét. Sẽ gặp sai lầm nếu lấy tập các véc tơ ứng với các cột cơ sở trong ma trận
B (là ma trận dạng bậc thang của A) làm cơ sở của ColA vì tập các véc tơ ứng với các
cột cơ sở của B không thể là tập sinh của ColA. Ví dụ cột 1 và cột 2 trong B có hai phần
tử đứng cuối cùng bằng 0, còn cột của A có mọi phần tử đều khác 0 nên không thể là tổ
hợp tuyến tính nào đó của các cột trong B được. Vì vậy, tác dụng của ma trận bậc thang
B chỉ là xác định rõ cột nào là cột cơ sở trong A.
c. Cơ sở của không gian hàng RowA
Cho ma trận A M(m,n) thì hàng thứ i của A được kí hiệu là: h
i
A = [a
i1
a
12
... a
in
].
Như thường lệ, ta vẫn kí hiệu véc tơ ứng hàng của A là h
i
A = (a
i1
; a
12
; ...; a
in
) trùng với
kí hiệu hàng của ma trận A.
68
2
5
1
1
0
1
0
1
1

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Định lý 13.
II.
TÍNH ĐỘC LẬP TUYẾN TÍNH, CƠ SỞ VÀ SỐ CHIỀU
1)
Nếu 2 ma trận tương đương hàng với nhau thì không gian hàng của chúng trùng
nhau: A B RowA = RowB.
2)
Nếu B là ma trận dạng bậc thang thì tập hợp các véc tơ ứng với các hàng khác
0 của B tạo nên cơ sở của RowB.
Chứng minh
1).
Vì B thu được từ A bởi qúa trình rút gọn hàng nên mỗi hàng của B phải là một tổ
hợp tuyến tính của các hàng trong A. Do đó, một tổ hợp tuyến tính giữa các hàng trong
B cũng là một tổ hợp tuyến tính giữa các hàng trong A, nghiã là RowB RowA (*).
Mặt khác, do các phép toán hàng luôn có phép toán ngược nên lý luận tương tự như
trên ta có RowA RowB (**). Kết hợp (*) và (**) ta được RowA RowB.
2).
Nếu B là ma trận dạng bậc thang thì tập hợp các véc tơ ứng với các hàng khác 0
trong B phải độc lập tuyến tính (dễ dàng chứng minh). Áp dụng định lý về tập sinh ta
kết luận được chúng là cơ sở của RowB.
Ví dụ 34. Tìm cơ sở của RowA với A =
Quy A về dạng bậc thang:
1 − 4 9
−
1
2 − 4
5 − 6 10
− 7
7
1
A →
0
−4 9
−2 5
−7
−6
1
→
0
−4 9
−2 5
−7
−6
= B.
0
14
−
35
42
0 0 0 0
Ma trận dạng bậc thang B có tập hợp các hàng khác 0 là {h
1
B, h
2
B}, nên cơ sở của
RowB, cũng là cơ sở của RowA, là {(1; –4; 9; –7), (0; –2; 5; –6)}.
Chú ý. Tuy các phép toán hàng trên ma trận bảo toàn quan hệ độc lập tuyến tính
(hay phụ thuộc tuyến tính) giữa tập các cột của ma trận, nhưng lại hoàn toàn không
bảo toàn những quan hệ đó giữa tập các hàng. Chẳng hạn trong ví dụ trên đây, h
1
A và
h
3
A là độc lập tuyến tính (dễ thấy do chúng không tỷ lệ) nhưng h
1
B và h
3
B lại phụ
thuộc tuyến tính.
6. SỐ CHIỀU CỦA KHÔNG GIAN VÉC TƠ
Định lý 14. Nếu không gian véc tơ V có một cơ sở gồm n véc tơ thì:
a. Mọi tập con của V, có chứa nhiều hơn n véc tơ, đều phụ thuộc tuyến tính.
b. Mọi tập con độc lập tuyến tính của V đều có không qúa n véc tơ.
Chứng minh
a. Giả sử cơ sở của V là B = {v
1
, v
2
,..., v
n
} còn S = {u
1
, u
2
,...,u
k
}, (k > n) là tập con
tùy ý của V có chứa nhiều hơn n vectơ, cần chứng tỏ S là phụ thuộc tuyến tính. Xét tổ
hợp tuyến tính bất kỳ của O
V
theo các vectơ của S:
1
u
1
+
2
u
2
+ ...+
k
u
k
= O
V
.(*)
Do B là cơ sở nên các vectơ u
j
S, j = 1..k được phân tích một cách duy nhất qua
các vectơ thuộc B:
Thay u
j
vào (*) ta có:
u
j
= t
1j
v
1
+ t
2j
v
2
+
...+ t
nj
v
n
, j = 1..k
69
1

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 4. KHÔNG GIAN VÉC TƠ
1
(t
11
v
1
+ t
21
v
2
+ ...+ t
n1
v
n
) +
2
(t
12
v
1
+ t
22
v
2
+ ...+ t
n2
v
n
) + ...+
k
(t
1k
v
1
+ t
2k
v
2
+ ...+
t
nk
v
n
) = O
V
.
(t
11
1
+ t
12
.
2
+ ....+ t
1k
.
k
)v
1
+ (t
21
1
+ t
22
.
2
+ ....+ t
2k
.
k
)v
2
+ .... + (t
n1
1
+
t
n2
.
2
+ ....+ t
nk
.
k
)v
n
= O
V
. Do {v
1
, v
2
,..., v
n
} độc lập tuyến tính nên có hệ:
t
11
1
+ t
12
2
+ ..... + t
1k
k
= 0
t + t + .... + t = 0
21 1 22 2 2k k
t
n1
1
+ t
n 2
2
+ .... + t
nk
k
= 0
(**)
Hệ thuần nhất (**) có ma trận hệ số A = [t
ij
] M(n,k) với k > n nên sẽ có nghiệm
không tầm thường, tức là (*) xẩy ra với ít nhất 1 hệ số
i
nào đó khác 0. Do vậy, S phụ
thuộc tuyến tính.
b. 2) là hệ quả của 1).
Định lý 15. Nếu không gian véc tơ V có một cơ sở gồm n véc tơ thì mọi cơ sở khác
của V cũng có đúng n véc tơ.
Chứng minh. Giả sử V có hai cơ sở khác nhau là B = {v
1
, v
2
,..., v
n
} và B’ = {w
1
,
w
2
,..., w
m
}. Theo hệ quả trên, do B là cơ sở nên phải có m n, mặt khác do B’ là cơ sở
nên cũng có n m, suy ra m = n.
Định nghiã 8. Cho V là không gian véc tơ.
a)
Nếu V có cơ sở gồm n (hữu hạn) véc tơ thì V gọi là không gian hữu hạn chiều
và n gọi là số chiều của V, kí hiệu dimV = n.
b)
Ngược là, không gian V không hữu hạn chiều được gọi là không gian vô hạn
chiều, kí hiệu dimV = .
Ta thường dùng kí hiệu V
n
để chỉ không gian véc tơ V có số chiều bằng n. Không
gian con {O
V
} không có cơ sở, ta quy ước nó cũng là không gian hữu hạn chiều và có
số chiều bằng 0. Do phạm vi chương trình, ta chỉ nghiên cứu các không gian véc tơ hữu
hạn chiều.
Ví dụ 35.
a)
dimR
n
= n vì R
n
có cơ sở chính tắc B
0
= {e
1
, e
2
, ..., e
n
} gồm n véc tơ.
b)
dimP
n
(x) = n+1 vì P
n
(x) có cơ sở chính tắc là B
0
= {1, x, x
2
, ..., x
n
} gồm (n+1)
véc tơ.
c)
dimM(m,n) = m.n vì M(m,n) có cơ sở chính tắc B
0
= {E
ij
, I = 1..m, j = 1..n} gồm
m.n vectơ.
Ví dụ 36. Tìm dimE với E = {x = (a+2b+c+d; a–b–2c+5d; –2a+b+3c+3d)/ a, b, c,
d R} là không gian con của R
3
.
- Tìm tập sinh của E. Lấy bất kỳ x E, viết ở dạng vectơ cột, có sự phân tích:
a + 2b + c + d
1
2
1
1
[
x
]=
a − b − 2c + 5d
= a
1
+ b
−
1
+ c
−
2
+ d
5
= a[v
1
]+b[v
2
]+c[v
3
]+d[v
4
],
−
2a
+
b
+
3c
+
3d
−
2
1
3
3
với v
1
= (1; 1; –2) E, v
1
= (1; 1; –2) E, v
2
= (2; –1; 1) E, v
3
= (1; –2; 3) E, v
4
=
(1; 5; 3) E (*).
Do sự phân tích (*) nên E có tập sinh là:
S = {(1; 1; –2), (2; –1; 1), (1; –2; 3), (1; 5; 3)}.
70

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
II. TÍNH ĐỘC LẬP TUYẾN TÍNH, CƠ SỞ VÀ SỐ CHIỀU
- Xét tính độc lập tuyến tính của S: Lập ma trận A có các cột là các vectơ cột của
vectơ thuộc S, rồi quy A về dạng bậc thang:
1 2 1 1
1 2 1 1
1 2 1 1
A =
1 −1 −2 5
→
0 −3 −3 4
→
0
1 1 1
= B.
−
2
1
3
3
0
5
5
5
0
0
0
7
- Từ B suy ra 3 vectơ ứng với c
1
A, c
2
A, c
4
A là 3 vectơ độc lập tuyến tính nên cơ sở
của E gồm 3 véc tơ {(1; 1; –2), (2; –1; 1), (1; 5; 3)} dimE = 3.
Định lý 16. Giả sử A M(m,n) thì:
a)
dimColA = dimRowA = r(A).
b)
dimNulA = n – r(A).
Định lý là hiển nhiên, được suy ra từ cách tìm cơ sở của ColA, RowA và NulA .
1 − 2
Ví dụ 37. Tìm dimNulA, với A =
2 − 4
−
3
6
2 3
5 8
−
1
1
− 1
− 4
.
−
7
Quy A về dạng bậc thang:
1 −2 2 3
−1
1 −2 2 3
−1
A →
0 0 1 2 −2
→
0 0 1 2
−
2
.
0
0
5
10
−
10
0
0
0
0
0
dim(NulA) = 5 – r(A) = 5–2 = 3 dimNulA = 3.
7. CƠ SỞ VÀ SỐ CHIỀU CỦA KHÔNG GIAN CON
Định lý 17. Giả sử V là không gian véc tơ hữu hạn chiều còn E là không gian con
của V. Khi đó:
a)
Bất kỳ tập độc lập tuyến tính S E đều có thể mở rộng thành một cơ sở của E.
b)
dimE dimV. Đặc biệt khi dimE = dimV thì E V.
Chứng minh. Xét 2 trường hợp đối với không gian con E
-
Trường hợp E = {O} thì trong E không có tập con độc lập tuyến tính nên a) không
xẩy ra, tuy nhiên do E = {O} nên dimE = 0 dimV và b) được chứng minh.
-
Trường hợp E {O} thì do E {O} nên tồn tại S = {v
1
, v
2
,..., v
k
} E là tập độc
lập tuyến tính. Có các khả năng xẩy ra như sau:
i) Nếu S là tập sinh của E thì S là cơ sở của E.
ii) Nếu S không là tập sinh của E (E Sp(S)) thì tồn tại véc tơ v
k+1
E nhưng
v
k+1
Sp(S). Khi đó tập S
1
= {v
1
, v
2
,..., v
k,
v
k+1
} là độc lập tuyến tính trong E. Nếu S
1
sinh ra E thì S
1
là cơ sở của E, nếu xẩy ra trường hợp ngược lại: E Sp(S
1
), thì tồn tại
v
k+2
{E\Sp(S
1
)} và ta có được tập độc lập tuyến tính mới là S
2
= {v
1
, v
2
, ..., v
k+1
, v
k+2
}
E, ... Tiếp tục quá trình như vậy để mở rộng dần tập S. Quá trình đó phải dừng lại ở
bước thứ q nào đó vì số véc tơ độc lập tuyến tính của S
q
= {v
1
, v
2
,..v
k+1
, v
k+2
, ... v
k+q
}
không thể vượt qúa dimV. Tại đây ta có S
q
là tập sinh độc lập tuyến tính của E, tức S
q
là
cơ sở của E, và hiển nhiên dimE dimV vì số vectơ độc lập tuyến tính trong S
q
không
thể vượt quá số vectơ có trong cơ sở của V.
- Đặc biệt khi dimE = dimV xẩy ra thì cơ sở của E cũng là cơ sở của V nên suy ra
E V.
71

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 4. KHÔNG GIAN VÉC TƠ
Nhận xét. Bên cạnh phương pháp xây dựng cơ sở bằng cách rút gọn dần một tập
sinh phụ thuộc tuyến tính (xem định lý về tập sinh), nhờ cách chứng minh định lý trên,
ta còn có phương pháp xây dựng cơ sở mới, đó là phương pháp mở rộng dần một tập
độc lập tuyến tính bất kỳ trong không gian véc tơ. Ví dụ sau sẽ minh họa cụ thể phương
pháp này.
Ví dụ 38. Cho mặt phẳng P trong R
3
: P = {(x
1
; x
2
; x
3
)/ x
1
+ 2x
2
− x
3
= 0} là mặt
phẳng đi qua gốc tọa độ nên nó là không gian con của R
3
. Hãy chọn một cơ sở của P
sau đó mở rộng thành cơ sở của R
3
.
- Chọn cơ sở của P
Cơ sở của P chính là cơ sở của NulA với A = [1 2 –1]. Dùng phương pháp tìm cơ
sở cho NulA, tìm được cơ sở của P là {v
1
= ( −2; 1; 0), v
2
= (1; 0; 1}.
- Mở rộng cơ sở {v
1
, v
2
} của P thành cơ sở của R
3
.
Lấy thêm một véc tơ v
3
R
3
sao cho v
3
P = Sp{v
1
, v
2
}, (tức các tọa độ của v
3
không
thỏa mãn phương trình mặt phẳng), chẳng hạn chọn v
3
= (0; 0; 1). Khi đó tập B = {v
1
,
v
2
, v
3
} sẽ độc lập tuyến tính trong R
3
và có đúng 3 véc tơ nên B là cơ sở của R
3
.
Định lý 18. Giả sử S = {v
1
, v
2
,...,v
n
} là tập gồm đúng n véc tơ của không gian n
chiều V
n
. Hai mệnh đề sau là tương đương:
a)
S độc lập tuyến tính trong V
n
.
b)
S là tập sinh của V
n
.
Chứng minh
a) b): Hiển nhiên có Sp(S) V
n
. Giả sử có v V
n
nhưng v Sp(S) = Sp{v
1
,
v
2
,...,v
n
} thế thì tập gồm n+1 vectơ {v
1
, v
2
,...,v
n
, v} là tập độc lập tuyến tính, đó là điều
vô lí (vì dimV
n
= n) nên buộc phải có v Sp(S), suy ra V
n
Sp(S). Kết hợp với Sp(S)
V
n
ta có b).
b) a): Nếu S là tập sinh của V
n
thì sẽ có tập con của S là S' tạo thành cơ sở cho V
n
(do định lý về tập sinh). Vì dimV
n
= n nên số véc tơ có trong S' là n, cũng bằng số véc
tơ mà S có. Chứng tỏ S S' là độc lập tuyến tính.
Ý nghĩa thực tiễn của định lý là ở chỗ khi biết số chiều n của không gian véc tơ V
n
thì việc tìm cơ sở cho V
n
được quy về việc tìm một tập sinh hay một tập độc lập tuyến
tính có đúng n véc tơ là đủ. Đặc biệt điều này thực sự có lợi đối với các bài toán áp
dụng liên quan đến phương trình vi phân hay phương trình sai phân, ở đó việc kiểm tra
một tập là tập độc lập tuyến tính đơn giản hơn nhiều so với kiểm tra tập đó là tập sinh.
8. HẠNG MA TRẬN VÀ CÁC KHÔNG GIAN LIÊN QUAN ĐẾN MA TRẬN
Hạng của ma trận đã được định nghĩa từ chương ma trận, là số cột cơ sở có trong ma
trận đó. Nay nhờ có thêm kiến thức về không gian véc tơ, hạng của ma trận giúp ta hiểu
sâu thêm các tính chất cũng như các mối quan hệ thú vị có bên trong mỗi ma trận mà
chúng đang bị che khuất bởi các hàng và các cột. Hãy lần lượt làm sáng tỏ các vấn đề
bằng việc xét mối quan hệ giữa hạng của ma trận với các không gian véc tơ có được từ
ma trận như ColA, RowA và NulA.
Định lý 19. Với A M(n,n), các mệnh đề sau đây là tương đương:
1).
A khả nghịch.
2).
Tập các véc tơ ứng với các cột của A là cơ sở của R
n
.
3). ColA = R
n
.
4).
NulA = {O}.
5).
dim(NulA) = 0.
72

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
II. TÍNH ĐỘC LẬP TUYẾN TÍNH, CƠ SỞ VÀ SỐ CHIỀU
Chứng minh. Từ (1) r(A) = n Tập n cột của A là độc lập tuyến tính
Tập n véc tơ ứng với n cột của A tạo thành cơ sở của R
n
(tức là có (2)) ColA = R
n
(tức là có (3)), dimNulA = n − r(A) = n − n = 0 (tức là có (5)) NulA = O (tức là
có (4)). Vậy ta đã chứng minh được các mệnh đề trên theo sơ đồ: (1) (2) (3)
(5) (4).
Xét chiều ngược lại, từ (4) dim(NulA) = 0 (tức là có (5)) dimColA = n −
dim(NulA) = n − 0 = n ColA = R
n
(tức là có (3)) Tập các véc tơ ứng với các cột
cơ sở của A là cơ sở của R
n
(tức là có (2)) A khả nghịch (tức là có (1)).
Định lý 20. Nếu A M(m,n) và P M(m,m) là khả nghịch thì :
1)
Row(PA) = RowA.
2)
Nul(PA) = NulA
3) r(PA) = r(A).
Chứng minh
1)
Do P khả nghịch nên phân tích được P thành tích của 1 dãy các ma trận sơ cấp:
P = E
k
.....E
1
PA = E
k
...E
1
.A ~ A Row(PA) = RowA.
2)
Do PA ~ A nên các hệ thuần nhất (PA)X = O và AX = O có cùng tập nghiệm
Nul(PA) = NulA.
3)
Do 1) nên có dimRow(PA) = dimRowA r(PA) = r(A).
Định lý 21. Nếu A M(m,n) và Q M(n,n) là khả nghịch thì :
1) Col(AQ) = ColA.
2) r(AQ) = r(A).
Chứng minh
1)
Xét cột thứ j bất kỳ của AQ thì c
j
(AQ) = A.c
j
Q là một tổ hợp tuyến tính của các
cột trong A nên véc tơ ứng với c
j
(AQ) sẽ thuộc ColA Col(AQ) ColA (*). Ngược
lại, do Q khả nghịch nên (AQ).Q
–1
= A. Vì ma trận Q
–1
là khả nghịch, lý luận tương tự,
ta lại có Col(AQQ
–1
) Col(AQ) hay ColA Col(AQ) (**). Kết hợp (*) và (**) ta có
Col(AQ) = ColA.
2)
Do 1) nên 2) là hiển nhiên.
Định lý 22. Giả sử A M(m,n), P M(m,m), Q M(n,n). Nếu P, Q khả nghịch thì
các ma trận A, PA, QA và PAQ có cùng hạng:
r(A) = r(PA) = r(AQ) = r(PAQ)
Định lí là kết qủa do định lí 20 và định lí 21 vừa nêu trên kết hợp lại.
9.SỐ CHIỀU CỦA KHÔNG GIAN TỔNG VÀ KHÔNG GIAN GIAO (ĐỌC
THÊM)
Định nghiã 9. Cho H và K là hai không gian con của V, ta gọi:
a)
Giao của 2 không gian con H và K là tập gồm tất cả các véc tơ trong V vừa
thuộc H vừa thuộc K. Ký hiệu: HK = { v V/ v H và v K}.
b)
Tổng của 2 không gian con H và K là tập hợp tất cả các véc tơ có dạng u+v với
uH và vK. Ký hiệu: H+K = {u+v / uH và vK}
Dễ kiểm tra được tổng và giao của 2 không gian con của V lại là không gian con của
V.
Đặc biệt khi HK = {O
v
} thì tổng H+K được gọi là tổng trực tiếp của 2 không gian
con H và K, ký hiệu bởi HK.
73

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
2
2
2
2
3
Chương 4. KHÔNG GIAN VÉC TƠ
Định lý 23. Nếu V là không gian véc tơ hữu hạn chiều thì với 2 không gian con bất
kỳ H và K của V ta luôn có:
a)
dim(H+K) = dimH + dimK − dim(HK).
b)
H+K là tổng trực tiếp khi và chỉ khi mỗi phần tử v của H+K đều biểu thị một
cách duy nhất dưới dạng w = u + v với u H và v K.
c)
Nếu H+K là tổng trực tiếp thì hợp của hai cơ sở của H và của K là cơ sở của
HK và dim(HK) = dimH + dimK.
Việc chứng minh định lý này được bỏ qua, độc giả có thể tham khảo thêm ở các tài
liệu tham khảo.
Ví dụ 39. Trong R
4
cho các véc tơ u
1
= (1; 0; 2; 2), u
2
= (2; 1; 3; 4), u
3
= (1; 1; 1; 3)
và v
1
= (3; 1; 5; 6), v
2
= (0; 1; 4; 0), v
3
= (1; 2; 3; 2). Gọi H = Sp{u
1
, u
2
, u
3
}, K = Sp{v
1
,
v
2
, v
3
}. Tìm cơ sở và số chiều của H+K và HK.
- Tìm cơ sở và số chiều của H+K:
Hiển nhiên tập sinh S của H+K là hợp của tập sinh H với tập sinh K: S = {u
1
, u
2
,
u
3
} { v
1
, v
2
, v
3
}. Tìm cơ sở cho H+K từ tập sinh S:
1 1
A = [[u
1
] [u
2
] [u
3
] [v
1
] [v
2
] [v
3
]] =
→
2 3
1 2
0 − 1
1 3 0
1 1 1
− 1 − 1 4
1 0 0
1
1
→
1
0
2 1 3 0
1 1 1 1
0 0 0 5
0 1 0 0
1
1
→
3
0
2 1 3 0 1
1 1 1 1
.
0 1 0 0 0
0 0 0 5
Tập các cột cơ sở của A là {c
1
A, c
2
A, c
3
A, c
5
A}, nên cơ sở của H+K là B = {u
1
=
(1; 0; 2; 2), u
2
= (2; 1; 3; 4), u
3
= (1; 1; 1; 3), v
2
= (0; 1; 4; 0)} dim(H+K) = 3.
- Tìm cơ sở và số chiều của HK:
Lấy bất kỳ u HK thì do u H = Sp{u
1
, u
2
, u
3
} nên u có sự phân tích u = x
1
u
1
+ x
2
u
2
+ x
3
u
3
, hay viết ở dạng véc tơ cột ta có:
1
2
1
x
1
+ 2x
2
+ x
3
0
1
1
2
x
+
x
[u] = x
1
+ x
2
+ x
3
=
2 3
.
2
3
1
2x
1
+ 3x
2
+ x
3
2
4
3
2x
1
+ 4x
2
+ 3x
3
Mặt khác, do u K = Sp{v
1
, v
2
, v
3
} nên tập 4 vectơ {v
1
, v
2
, v
3
, u} phải phụ thuộc
tuyến tính. Lập ma trận A có các cột là các véc tơ cột lấy từ {v
1
, v
2
, v
3
, u} và quy về
dạng bậc thang ta có:
3 0 1
x
1
+ 2x
2
+ x
3
1 1 2 2
x
2
+
x
3
1 1 2 2
x
+
x
0
−
3
−
5
x − 4x − 2x
A =
2 3
→
1 2 3
5 4 3
2x
1
+ 3x
2
+ x
3
0
−
1
−
7
2x
1
− 7x
2
− 4x
3
6 0 2
2x + 4x + 3x
0
−
6
−
10
2x − 8x − 3x
1 2 3
1 2 3
74
0
0
2
0
0
0
2
0
0
0
1
0
2
1
3
0
1
1
1
1
3
1
5
4
4
3
6
0

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
II.
TÍNH ĐỘC LẬP TUYẾN TÍNH, CƠ SỞ VÀ SỐ CHIỀU
1 1 2 2
x
2
+
x
3
1 1 2 2
x
2
+
x
3
0
−
3
−
5
x − 4x − 2x
0
−
1
−
7
2x − 7x − 4x
→
1 2 3
→
1 2 3
.
0
−
1
−
7
2x
1
− 7x
2
− 4x
3
0 0 16
−
5
x
1
+
17
x
2
+
10
x
3
0 0 0
x
3
0 0 0
x
3
Do {v
1
, v
2
, v
3
, u} phụ thuộc tuyến tính nên r(A) < 4 x
3
= 0. u = x
1
u
1
+ x
2
u
2
+
x
3
u
3
= x
1
u
1
+x
2
u
2
. Vì bất kỳ u HK đều phân tích được ở dạng u = x
1
u
1
+x
2
u
2
nên
HK = Sp{u
1
, u
2
}. Kiểm ta được {u
1
, u
2
} độc lập tuyến tính nên nó là cơ sở của HK
và dim(HK) = 2.
75

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
⁝
⁝
⁝
⁝
Chương 4. KHÔNG GIAN VÉC TƠ
III.
TỌA ĐỘ ĐỐI VỚI CƠ SỞ
1. TỌA ĐỘ CỦA VÉC TƠ ĐỐI VỚI CƠ SỞ
Nếu trong không gian véc tơ V
n
đã chỉ ra được một cơ sở B = {v
1
, v
2
, ..., v
n
} nào đó
thì bất kỳ véc tơ vV
n
đều phân tích được qua các véc tơ thuộc cơ sở B, dạng:
v =
1
v
1
+
2
v
2
+...+
n
v
n
,
1
,
2
,...,
n
R. (1)
Mục này sẽ chỉ ra rằng sự phân tích (1) là duy nhất, tức là mỗi vectơ v V
n
tương
ứng duy nhất với 1 bộ gồm n số thực thuộc R
n
, tức là thiết lập được sự tương ứng 1
1 giữa V
n
với [R]
n
từ đó dẫn đến khả năng “số hoá” cho mọi vectơ v V
n
.
Định lý 24. Giả sử V là không gian véc tơ và B = {v
1
, v
2
, ..., v
n
} V. Khi đó:
a. Nếu B là cơ sở của V thì mọi véc tơ vV đều phân tích một cách duy nhất qua
các véc tơ của B:
v =
1
v
1
+
2
v
2
+...+
n
v
n
,
i
R, i = 1..n (1)
b. Ngược lại, nếu mọi vV đều phân tích một cách duy nhất qua các véc tơ của B
thì B là cơ sở của V.
Chứng minh
Trước hết, B là cơ sở nên nó là tập sinh của V, suy ra vV luôn tồn tại sự biểu
diễn véc tơ v thành tổ hợp tuyến tính của các véc tơ trong B:
v =
1
v
1
+
2
v
2
+ ... +
n
v
n
(1)
Giả sử v còn có sự biểu diễn khác:
v =
1
v
1
+
2
v
2
+...+
n
v
n
(2),
thì từ (1) và (2) có:
v – v = O
V
= (
1
−
1
)v
1
+ (
2
−
2
)v
2
+...+ (
n
−
n
)v
n
(*).
Do B độc lập tuyến tính nên từ (*) suy ra:
1
−
1
= 0
1
=
1
; chứng tỏ (1) là duy nhất.
n
−
n
= 0
n
=
n
Ngược lại, nếu bất kỳ véc tơ v V đều biểu thị một cách duy nhất qua các véc tơ
thuộc B dướïi dạng (1) thì B là cơ sở của V. Thật vậy, B hiển nhiên là tập sinh của V,
chỉ cần chứng minh thêm B độc lập tuyến tính. Xét một tổ hợp tuyến tính của vectơ O
v
theo các vectơ của B:
1
v
1
+
2
v
2
+ ... +
n
v
n
= O
V
,
i
R, i = 1..n (**).
Do véc tơ O
V
được biểu thị một cách duy nhất dưới dạng: O
V
= 0v
1
+0v
2
+...+0v
n
nên
trong (**) phải có
1
=
2
= ... =
n
= 0, tức là B độc lập tuyến tính.
Từ định lí vừa nêu, ta có khái niệm tọa độ của vectơ đối với cơ sở như sau:
Định nghiã 10. Cho V là không gian véc tơ có cơ sở B = {v
1
, v
2
, ..., v
n
}. Toạ độ của
v V là bộ gồm n số
1
,
2
, ...,
n
thoả mãn sự phân tích:
v =
1
v
1
+
2
v
2
+...+
n
v
n
.
1
Ký hiệu [v]
B
=
, hay (v)
B
= (
1
; ..;
n
) khi ta muốn viết chúng thành hàng.
n
76

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
III. TỌA ĐỘ ĐỐI VỚI CƠ SỞ
Tọa độ của vectơ v đối với cơ sở B còn gọi là B−tọa độ của v. Định lý trên chứng tỏ
rằng B–tọa độ của véc tơ v là duy nhất. Nếu v V
n
thì [v]
B
[R]
n
.
Ví dụ 40. Trong R
2
cho cơ sở B = {v
1
= (1; 0), v
2
= (1; 1)}. Hãy xác định B − tọa độ
của các véc tơ x = (3; 2) và y = (1; −2).
- Gọi [x]
=
1
thì x = v
+ v
[
x
]
=
3
= [
v
] + [
v
]
1
+
B
1 1 2 2
2
1 1 2 2 1
0
2
2
1
=
3
1
+
2
= 3
1
= 1
[x]
=
1
.
1
2
= 2
= 2
B
2
2 2
- Tương tự, nếu đặt [y]
=
1
thì y = v + v [y] =
1
= [v ] +
B
1 1 2 2
− 2
1 1
2
[v ]
1
+
1
=
1
1
+
2
=
1
1
=
3
[y]
=
3
.
2 2 1
0
2
1
− 2
= − 2
= − 2
B
− 2
2 2
Ví dụ 41. Cho B = {(x+1)
3
, (x+1)
2
, x+1, 1} là cơ sở của P
3
(x). Hãy tìm B − tọa
độ của véc tơ p = x
3
+ x
2
− x − 1.
1
Gọi [
p
]
B
=
2
3
p = x
3
+ x
2
− x − 1 =
1
(x+1)
3
+
2
(x+1)
2
+
3
(x+1) +
4
1
4
=
1
(x
3
+3x
2
+3x+1) +
2
(x
2
+2x+1) +
3
(x+1) +
4
1 =
=
1
x
3
+ (3
1
+
2
)x
2
+ (3
1
+2
2
+
3
)x + (
1
+
2
+
3
+
4
)1
1
3 +
= 1
1
= 1
= 1
= − 2
1
−
2
1 2
2
[p]
B
=
.
3 + 2 +
= − 1
= 0
0
1 2 3
3
1
+
2
+
3
+
4
= − 1
4
= 0
0
B− tọa độ của véc tơ p cho ta biết sự phân tích đa thức p theo các lũy thừa của
(x+1) là:
có:
p = x
3
+ x
2
− x − 1 = 1.(x+1)
3
– 2.(x+1)
2
.
Định lý 25. Nếu B là cơ sở của không gian véc tơ V
n
thì v, w V, R ta đều
a) [v+w]
B
= [v]
B
+ [w]
B
b) [v]
B
= [v]
B
.
Chứng minh. Giả sử B = {v
1
, v
2
, ..., v
n
} là cơ sở cho V
n
và [v]
B
=
1
n
1
, [w]
B
=
n
77
.

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
→
Chương 4. KHÔNG GIAN VÉC TƠ
a)
Theo định nghiã tọa độ, ta có v =
1
v
1
+...+
n
v
n
; w =
1
v
1
+ ... +
n
v
n
. Suy ra v
+ w = (
1
+
1
)v
1
+ ... + (
n
+
n
)v
n
. Từ đó:
1
+
1
[v+w]
B
=
=
n
+
n
1
n
1
n
= [v]
B
+ [w]
B
.
1
1
b) v = (
1
v
1
+...+
n
v
n
) =
1
v
1
+...+
n
v
n
[v]
B
=
[v]
B
.
n
n
Mở rộng định lý cho trường hợp tổng của một số hữu hạn gồm k 3 véc tơ:
[
1
v
1
+
2
v
2
+...+
k
v
k
]
B
=
1
[v
1
]
B
+
2
[v
2
]
B
+...+
k
[v
k
]
B
Định lý 26. Trong không gian vectơ V
n
với cơ sở B, tập gồm k vectơ {u
1
, u
2
, ..., u
k
}
V là độc lập tuyến tính trong V
n
khi và chỉ khi khi và chỉ khi tập gồm k vectơ toạ độ
của chúng {[u
1
]
B
, [u
2
]
B
, ..., [u
k
]
B
} là độc lập tuyến tính trong [R]
n
.
Chứng minh
-
Giả sử {u
1
, u
2
, ..., u
k
} là độc lập tuyến tính trong V, cần chứng minh {[u
1
]
B
,
[u
2
]
B
, ..., [u
k
]
B
} là độc lập tuyến tính trong [R]
n
. Xét
1
[u
1
]
B
+
2
[u
2
]
B
+ ...+
k
[u
k
]
B
= O
[
1
u
1
]
B
+ [
2
u
2
]
B
+ ...+ [
k
u
k
]
B
= O [
1
u
1
+
2
u
2
+ ... +
k
u
k
]
B
= O
1
u
1
+
2
u
2
+ ... +
k
u
k
= 0v
1
+ 0v
2
+ ... +0v
n
= O
V
. Do {u, u
2
, ..., u
k
} là độc lập tuyến tính nên
từ
1
u
1
+
2
u
2
+ ... +
k
u
k
= O
V
ta phải có
1
=
2
= ... =
k
= 0, tức là {[u
1
]
B
, [u
2
]
B
, ...,
[u
k
]
B
} độc lập tuyến tính.
-
Ngược lại, giả sử {[u
1
]
B
, [u
2
]
B
, ..., [u
k
]
B
} là độc lập tuyến tính trong [R]
n
, cần
chứng minh {u
1
, u
2
, ..., u
k
} là độc lập tuyến tính trong V. Xét tổ hợp tuyến tính của
vectơ O
V
theo các vectơ u
i
:
1
u
1
+
2
u
2
+ ... +
k
u
k
= O
V
[
1
u
1
+
2
u
2
+... +
k
u
k
]
B
= [O
V
]
B
1
[u
1
]
B
+
2
[u
2
]
B
+ ...+
k
[u
k
]
B
= O
1
=
2
= ... =
k
= 0 (do {[u
1
]
B
, [u
2
]
B
, ..., [u
k
]
B
} là độc
lập tuyến tính trong [R]
n
) {u
1
, u
2
, ..., u
k
} là độc lập tuyến tính trong V.
Nhận xét: Ý nghĩa quan trọng của định lý là ở chỗ nó phép chuyển việc xét tính độc
lập tuyến tính, phụ thuộc tuyến tính của tập vectơ trong không gian vectơ tổng quát V
n
,
về việc xét các tính chất đó của tập vectơ trong không gian vectơ quen thuộc [R]
n
, nơi
mà công cụ ma trận tỏ ra rất có hiệu quả.
Ví dụ 42. Xét tính độc lập tuyến tính của S = {u = x
2
−3x+2, v = 3x
2
+5x−4, w =
7x
2
+21x −16} trong P
2
(x).
Chọn cơ sở trong P
2
(x) là cơ sở chính tắc B = {1, x, x
2
} thì có: [u]
B
= [x
2
−3x+2]
B
=
2
− 3
, [v]
B
= [3x
2
+5x − 4]
B
=
−
4
5
, [w]
B
= [7x
2
+21x − 16]
B
=
−
16
21
. Để xét tính độc
1
3
7
lập tuyến tính của S, ta cần xét tính độc lập tuyến tính của tập các vectơ toạ độ {[u]
B
,
[v]
B
, [w]
B
} trong [R]
3
. Lập ma trận A = [[u]
B
[v]
B
[w]
B
] và quy về dạng bậc thang:
2
−
4
A =
− 3 5
−16
21
1 3
→
0
14
7
1
42
3 7
1 3
= B.
1 3 7
0
−
10
78
−
30
0 0
0
+
=
0
=

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
1
III. TỌA ĐỘ ĐỐI VỚI CƠ SỞ
Từ B suy ra r(A) = 2 < số vectơ, nên {[u]
B
, [v]
B
, [w]
B
}là phụ thuộc tuyến tính trong
[R]
3
, kéo theo S là phụ thuộc tuyến tính trong P
2
(x).
2. CÔNG THỨC TÌM B − TỌA ĐỘ TRONG R
n
Giả sử B = {v
1
, v
2
, ..., v
n
}là một cơ sở nào đó của R
n
. Với bất kỳ x R
n
, gọi [x]
B
=
1
n
1
x =
1
v
1
+... +
n
v
n
[x] =
1
[v
1
] +... +
n
[v
n
] = [[v
1
] ... [v
n
]].
. Đặt P
n
= [[v
1
] ... [v
n
]] là ma trận được lập bởi các véc tơ cột của các vectơ thuộc B thì đẳng
thức trên có dạng: [x] = P[x]
B
. Do P là khả nghịch nên nhân trái 2 vế với P
−
1
ta có:
[x]
B
= P
−
1
[x] (3)
Đây là công thức tìm B –tọa độ của bất kỳ véc tơ xR
n
.
Ví dụ 43. Trong R
3
cho cơ sở B = {(1; 2; −3); (2; −1; 0); (3; 0; 1)}. Hãy tìm B −
tọa độ của các véc tơ: x = (− 2; − 4; 6); y = (4; 5; 6); z = (2; 3; 4).
Lập ma trận P gồm các vectơ cột của các vectơ thuộc cơ sở B:
1 2 3
1 2
− 3
P =
2 − 1 0
, và tìm được P
–1
=
1
2
− 10
− 6
.
−
3
0
1
14
3 6
5
Áp dụng công thức (3) ta có:
1 2
−
3
−
2
− 2
[x]
B
= P
−
1
[x] =
1
2
−
10
− 6
− 4
=
0
;
14
3
6
5
6
0
1 2
−
3
4
− 4
[y]
B
= P
−
1
[y] =
1
2
−
10
− 6
5
=
1
− 78
;
14
14
3
6
5
6
72
1
[z]
B
= P
−
1
[z] =
1
2
2
− 10
−
3
2
−
6
3
− 4
=
1
−
52
.
14
14
3
6
5
4
44
Nhận xét: Công thức (3) [x]
B
= P
−
1
[x] đôi khi tỏ ra bất lợi do phải tìm P
−
1
. Để tránh
tình huống này, có thể tìm [x]
B
nhờ việc giải hệ tuyến tính P[x]
B
= [x] bằng phương
pháp Gauss. Sau đây là ví dụ minh họa:
Ví dụ 44. Tìm tọa độ của véc tơ x = (1; 2; −2) đối với cơ sở B = {(1; 1; 1); (1; 2; 0);
(1; 0; 1)} trong R
3
.
Ví dụ 45. Lập ma trận P có các cột là các véc tơ cột của vectơ thuộc B: P =
1 1
2
1 0
1
0
. Giải hệ tuyến tính P[x]
B
= [x] , bằng phương pháp Gauss như sau:
1
79

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
1
0
1
0
Chương 4. KHÔNG GIAN VÉC TƠ
A* =
1 1 1
2 0
1 0 1
1
− 2
1
→
0
0
1 1
1
−
1
−
1
0
1
− 3
1 0
1
0 0
2 0
− 1
− 1 − 2
1 0 0
1 0
0 0 1
− 4
2
Từ đó suy ra [x]
B
=
− 4
3
.
2
3.MA TRẬN CHUYỂN TOẠ ĐỘ VÀ TOẠ ĐỘ CỦA VÉC TƠ ĐỐI VỚI CÁC CƠ
SỞ KHÁC NHAU
Giả sử trong không gian véc tơ V đã cho 2 cơ sở B và C. Vấn đề xét ở đây là tìm
mối quan hệ giữa các tọa độ [v]
B
và [v]
C
của cùng một véc tơ v V đối với 2 cơ sở khác
nhau đang xét.
Định lý 27. Trong không gian véc tơ V cho 2 cơ sở là B = {v
1
, v
2
,..., v
n
} và C = {w
1
,
w
2
,..., w
n
} thì với bất kỳ v V, luôn tồn tại duy nhất một ma trận vuông cấp n, khả
nghịch P
B
,C
sao cho:
[v]
C
= P
B
,C
[v]
B
(4)
Khi đó ma trận P
B,C
được gọi là ma trận chuyển tọa độ từ tọa độ đối với cơ sở B
sang tọa độ đối với cơ sở C.
Chứng minh
Với bất kỳ v V, gọi [v]
B
=
vectơ v ta có:
1
n
v =
1
v
1
+ ... +
n
v
n
. Lấy C − tọa độ cho
1
[v]
C
= [
1
v
1
+ ... +
n
v
n
]
C
=
1
[v
1
]
C
+ ...+
n
[v
n
]
C
= [[v
1
]
C
.....
[
v
n
]
C
].
.
n
Đặt:
thì có ngay:
P
B,C
= [[v
1
]
C
[v
2
]
C
..... [v
n
]
C
] (5)
[v]
C
= P
B,C
.[v]
B
(4)
Hiển nhiên P
B,C
vuông cấp n và khả nghịch vì tập các véc tơ {v
1
, v
2
,..., v
n
} là độc lập
tuyến tính. P
B,C
là duy nhất do tính duy nhất của C − toạ độ của các véc tơ v
1
, v
2
, ..., v
n
.
Nhận xét. Do P
B,C
khả nghịch nên từ (4) suy ra: [v]
B
= (P
B,C
)
−
1
[v]
C
. Chứng tỏ
(P
B,C
)
−
1
chính là ma trận chuyển tọa độ từ cơ sở C sang cơ sở B, tức là:
P
C,B
= (P
B,C
)
−
1
. (6)
Ví dụ 46. Trong P
2
(x) cho 2 cơ sở là B = {x
2
, x, 1} và C = {x
2
−x, 2x
2
−2x+1, x
2
−
2x}. Hãy tìm:
a)
Tìm ma trận chuyển tọa độ từ C sang B.
b)
Tìm ma trận chuyển tọa độ từ B sang C.
c)
Tìm tọa độ của véc tơ p = 2x
2
+3x −1 đối với cơ sở C.
80
2
1
3
→
→

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Giải
III.
TỌA ĐỘ ĐỐI VỚI CƠ SỞ
1 2 1
a) Áp dụng (5) thì P
C,B
= [[x
2
−x]
B
[2x
2
−2x+1]
B
[x
2
−2x]
B
] =
−1 − 2
0 1
− 2
.
0
b)
Áp dụng (6) thì: P
= (P
1
2
)
−
1
=
− 1 − 2
1
−
1
−
2
2
=
0
1 − 2
0 1
.
B,C C,B
0
1
0
−
1
−
1
0
2
c)
Áp dụng (4) ta có: [p]
C
= P
B,C
.[p]
B
= P
B,C
3
2
=
0
1 − 2
2
0 1
3
9
=
−
1
.
−
1
−
1
−
1
0
−
1
−
5
Ý nghiã của véc tơ [p]
C
là ở chỗ nó cho biết sự phân tích đa thức p = 2x
2
+3x−1 theo
các đa thức có trong cơ sở C như sau:
2x
2
+3x−1 = 9.(x
2
−x) −1.(2x
2
−2x+1) − 5(x
2
−2x).
4. THUẬT TOÁN TÌM MA TRẬN CHUYỂN TỌA ĐỘ TRONG R
n
Giả sử trong R
n
cho trước cơ sở B = {v
1
, v
2
, ..., v
n
} (gọi là cơ sở cũ) và lấy thêm
một cơ sở mới bất kỳ C = {w
1
, w
2
,..., w
n
}. Đặt P
B
= [[v
1
] [v
2
] ... [v
n
]] (ma trận gồm
các cột là các véc tơ cột của vectơ thuộc cơ sở B) và P
C
= [[w
1
] [w
2
] ... [v
n
]] (ma trận
gồm các cột là các véc tơ cột của các vectơ thuộc cơ sở C). Theo công thức tìm B – tọa
độ của vectơ trong R
n
thì:
[v
1
]
C
= (P
C
)
−
1
.[v
1
]; [v
2
]
C
= (P
C
)
−
1
.[v
2
]; .... ; [v
n
]
C
= (P
C
)
−
1
.[v
n
].
Thế vào (2) ta có:
P
B,C
= [[v
1
]
C
[v
2
]
C
..... [v
n
]
C
] = [P
C
−
1
.[v
1
] (P
C
−
1
.[v
2
] ... P
C
−
1
.[v
n
]]
= P
C
−
1
.[[v
1
] [v
2
] ... [v
n
]] = P
C
−
1
.P
B
Gọi ẩn là ma trận X = P
B,C
= [X
1
X
2
... X
n
] thì có: X = P
C
−
1
.P
B
hay nhân trái 2 vế
với P
C
ta có:
P
C
X
1
P
C
X = P
B
[P
C
X
1
P
C
X
2
... P
C
X
n
] = [[v
1
] [v
2
] ... [v
n
]]
P
C
X
n
=
[
v
1
]
= [v
n
]
(*).
Để tìm X, cần giải (*) với mỗi phương trình là một hệ phương trình tuyến tính có ma
trận hệ số là P
C
. Ví dụ, giải hệ P
C
X
1
= [v
1
] bằng cách quy ma trận đầy đủ [P
C
| [v
1
]] về
dạng rút gọn [I
n
| [v’
1
]], rút ra nghiệm X
1
= [v’
1
] là cột đầu tiên của X, ... và cứ tiếp tục
như vậy cho đến khi tìm đủ n cột cho ma trận X.
Tuy nhiên, để có kết qủa nhanh hơn, thay vì giải riêng lẻ từng hệ, ta kết hợp giải
đồng thời n hệ bằng cách lập ma trận đầy đủ chung là ma trận khối [P
B
|[v
1
] [v
2
] ... [v
n
]],
rồi dùng phép toán hàng quy nó về dạng [I
n
| [v’
1
] [v’
2
] ... [v’
n
]]. Ma trận thu được từ
khối bên phải là ma trận X cần tìm. Tóm lại, ta có thể tìm ma trận chuyển tọa độ trong
R
n
theo lược đồ gồm 2 bước sau:
Bước 1. Lập ma trận khối có khối bên trái là cột các véc tơ có trong cơ sở mới còn
khối bên phải là cột các véc tơ có trong cơ sở cũ:
[[w
1
] [w
2
] ... [w
n
] | [v
1
] [v
2
] ... [v
n
]]
[ cơ sở mới | cơ sở cũ ]
(7)
81

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
1
1
)
–1
=
1
1
I
n
:
Chương 4. KHÔNG GIAN VÉC TƠ
Bước 2. Dùng phép toán hàng, quy ma trận khối bên trái của (7) về ma trận đơn vị
[[w
1
] [w
2
] ... [w
n
] | [v
1
] [v
2
] ... [v
n
]] → [ I
n
| B]
khi đó ma trận B ở khối bên phải chính là ma trận chuyển tọa độ P
B,C
cần tìm.
Ví dụ 47. Trong R
3
cho 2 cơ sở là B = {(1; 1; 0); (2; 0; 1); (1; –1; 0)} và B
0
= {(1;
0; 0); (0; 1; 0); (0; 0; 1)} là cơ sở chính tắc. Tìm ma trận chuyển tọa độ từ cơ sở B
0
sang cơ sở B và B − tọa độ của v = (2; 3; 4).
- Tìm P
B0,B
Cách 1. Sử dụng thuật toán gồm 2 bước:
Bước 1. Lập ma trận khối theo công thức (7) ta có:
1 2
0
0 1
1 1
−
1
0
0 0
0 0
1 0
.
0
1
Bước 2. Thực hiện phép rút gọn hàng quy khối bên trái về I
3
:
1 2 1 1 0 0
1 2 1 1 0 0
1 0 1
1 0 − 2
1 0 − 1 0 1 0
→
0 − 2 − 2
− 1 1
0
→
0 1 0 0 0 1
0 1 0
0 0 1
1 1
0 1
0 0 0
1
1
0
1
0 − 2
− 1 1
2
1 0 0
2 2
− 1
2 2
− 1
→
0 1 0 0 0 1
, suy ra P
B0,B
=
0 0 1
.
0 0 1 −
2 2
− 1
−
2 2
− 1
Cách 2. Áp dụng công thức (6). Vì B
0
là cơ sở chính tắc nên dễ thấy ngay sự phân
tích của các véc tơ thuộc cơ sở B qua cơ sở B
0
. Nghĩa là áp dụng định nghiã, có ngay:
Áp dụng (6) thì:
1 2
P
B,B0
=
1 0
0 1
1
−
1
.
0
P
B0,B
= (P
B, B0
1
2
0
0
1
1
−
1
− 1
=
0
1
1
0
2
1
1 − 2
0 2
.
−
1
−
2
- Tìm [v]
B
: Áp dụng công thức (4): [v]
B
= P
B0,B
[v]
B0
ta có:
[v]
B
= P
B0,B
[v]
B0
=
1 1
1
0 0
− 2
2
=
−
3
1
2
.
2
2
1
−
1
−
2
9
82
1
1

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
x
2
+ x
2
+ ... + x
2
1 2
n
IV.
TÍNH TRỰC GIAO VÀ KHÔNG GIAN EUCLIDE
IV. TÍNH TRỰC GIAO VÀ KHÔNG GIAN EUCLIDE THỰC
(ĐỌC THÊM)
Mục này sẽ phát triển một số khái niệm mang tính chất hình học quan trọng như tính
vuông góc, độ dài, góc và khoảng cách của 2 véc vơ ..., từ mặt phẳng hay trong không
gian (đó là những không gian 2 hay 3 chiều), vào không gian véc tơ n chiều R
n
. Nhờ bổ
sung vào không gian véc tơ R
n
phép toán mới là tích vô hướng mà ta có khái niệm
không gian Euclide n chiều E
n
, trong đó sẽ xây dựng được các cơ sở trực giao và cơ sở
trực chuẩn, rất thuận lợi trong các ứng dụng có tính chất tính toán.
1. KHÁI NIỆM TÍCH VÔ HƯỚNG VÀ KHÔNG GIAN EUCLIDE THỰC
Định nghiã 11. Cho các véc tơ x = (x
1
; x
2
; ...;x
n
), y = (y
1
; y
2
; ...;y
n
) R
n
, tích vô
hướng của hai véc tơ x và y, ký hiệu <x.y>, là số xác định bởi:
<x.y> = x
1
y
1
+ x
2
y
2
+...+ x
n
y
n
.
Coi x =
x
1
y
1
x
n
là ma trận hàng ứng với vectơ
x
= (x
1
; x
2
; ...; x
n
), còn [
y
] =
y
n
là vectơ cột của y = (y
1
; y
2
; ...; y
n
) R
n
thì tích vô hướng được viết ở dạng tích
hai ma trận:
<x.y> = x
1
y
1
+ ... + x
n
y
n
=
x
1
y
1
y
n
= x.[y]
Từ định nghiã, dễ dàng suy ra tích vô hướng có các tính chất cơ bản sau:
Tính chất. Với bất bỳ các véc tơ x, y, z R
n
và R ta đều có:
1)
<x.y> = <y.x> (Tính giao hoán).
2)
<(x+y).z> = <x.z > + <y.z> (Tính phân phối đối với phép cộng véc tơ).
3)
<(x).y> = <x.y> (Tính kết hợp đối với phép nhân với vô hướng).
4)
<x.x> 0 ;< x.x> = 0 x = 0. (Tính xác định dương).
Định nghiã 12. Không gian véc tơ R
n
trên đó có xác định tích vô hướng của 2 vectơ
được gọi là không gian Euclide n chiều, ký hiệu E
n
.
Trong không gian Euclide E
n
, nhờ có thêm khái niệm tích vô hướng mà ta có thêm
khái niệm độ dài và góc giữa các véc tơ như sau:
Định nghiã 13. Ta gọi độ dài (hay chuẩn) của véc tơ x = (x
1
; x
2
;...; x
n
) E
n
là số
x , được xác định bởi công thức: x = .
Từ định nghiã ta cũng có các tính chất sau đây:
Định lý 28. Với bất kỳ hai véc tơ x, yE
n
và bất kỳ R ta đều có:
1. x
2.
x
=
= ||. x .
<x.x> = x
2
3. x.y
x . y .
83
x
n
x.x

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
x.y
x . y
x.y
x . y
4. x + y
x + y
Chương 4. KHÔNG GIAN VÉC TƠ
(Bất đẳng thức tam giác).
Chứng minh
-
1) và 2) là hiển nhiên.
-
3) Giả sử x = (x
1
; x
2
; ...; x
n
) và y = (y
1
; y
2
; ...; y
n
) thì theo bất đẳng thức
Bunhiakovski :
|<x.y>| =
x
1
y
1
+x
2
y
2
+...+x
n
y
n
= x . y
-
4) Xét hiệu:
x + y
2
– ( x + y )
2
= <(x+y).(x+y)> –( x
2
+2
x
.
y
+
y
2
)
(3))
= <x.x> + 2<x.y> + <y.y> –
x
2
–2
x
.
y
–
y
2
= 2[<x.y> –
x
.
y
] 0 (do
x + y
2
( x + y
)
2
hay x + y x + y .
Định nghiã 14. Ta gọi khoảng cách giữa 2 véc tơ x và y thuộc E
n
, là độ dài của véc
tơ hiệu y− x. Ký hiệu bởi d(x,y) = y - x .
Nếu x = (x
1
; x
2
; ...; x
n
), y = (y
1
; y
2
; ...; y
n
) thì:
d(x,y) = y - x =
Định nghiã 15. Góc giữa hai véc tơ khác không x và y trong E
n
là góc xác định
bởi:
cos = ; 0 .
Nếu = 0 hoặc = thì hai véc tơ x và y được gọi là cùng phương, kí hiệu: x//y.
Chú ý rằng công thức xác định cos trong định nghĩa là hợp lý vì theo tính chất ở
trên thì |<x.y>| < x . y –1 1 nên tồn tại duy nhất góc [0; ] để cos
= . Góc giữa véc tơ O với véc tơ x là góc tùy chọn thuộc đoạn [0; ]. Khi biết
cos ta có thể tính tích vô hướng theo công thức quen thuộc: <x.y> =
x
.
y
cos.
Dễ thấy nếu là góc giữa x và y thì góc giữa y và x cũng là (do tính giao hoán của
tích vô hướng), nên ta không cần quan tâm tới thứ tự của các véc tơ khi ta nói về góc
giữa chúng.
2. TÍNH TRỰC GIAO
Định nghiã 16.
a)
Hai véc tơ x, y E
n
được gọi là vuông góc (hay trực giao) với nhau nếu <x.y> =
0, kí hiệu x⊥y.
b)
Tập các véc tơ {v
1
, v
2
, ..., v
k
} E
n
được gọi là tập trực giao nếu bất kỳ hai véc
tơ khác nhau đều vuông góc với nhau.
c)
Cơ sở B của không gian E
n
được gọi là cơ sở trực giao nếu B đồng thời là tập
trực giao.
Từ định nghĩa suy ra:
84
x
2
+
x
2
+
...
+
x
2
y
2
+
y
2
+
...
+
y
2
1 2
n 1 2
n
( y - x )
2
+ ( y - x )
2
+... + ( y - x )
2
1 1
2 2
n n
x.y
x . y

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
2
2
IV. TÍNH TRỰC GIAO VÀ KHÔNG GIAN EUCLIDE
{v
1
, v
2
, ..., v
k
} là tập trực giao <v
i
.v
j
> = 0 i j =1 .. k.
Ví dụ 48. Tập S = {v
1
= (1; 1; 1; 1); v
2
= (1; −1; 1; −1); v
3
= (−1; 0; 1; 0)} là tập
trực giao trong E
4
vì có:
<v
1
.v
2
> = 1.1+1.(−1)+1.1+1.(−1) = 0 = <v
2
.v
1
>.
<v
1
.v
3
> = 1.(−1)+1.0+1.1+1.0 = 0 = <v
3
.v
1
>.
<v
2
.v
3
> = 1.(−1)+(–1).0+1.1+(−1).0 = 0 = <v
3
.v
2
>.
Định lý 29. (Định lý Pythagore) Véc tơ x⊥y khi và chỉ khi x + y
2
=
x
2
+
y
2
.
Chứng minh
Luôn có
x + y
2
= <x+y>.<x+y> = <x.x> + 2<x.y> + <y.y> =
x
2
+
y
2
+ 2<x.y>.
Nên x⊥y <x.y> = 0
x + y
2
=
x
2
+
y
2
+ 2<x.y> =
x
2
+
y
2
.
Định lý 30. Mọi tập trực giao S = {v
1
, v
2
, ..., v
k
} E
n
không chứa véc tơ O đều là
tập độc lập tuyến tính, và do đó, nó là cơ sở trực giao của không gian con sinh bởi S.
Chứng minh. Xét tổ hợp tuyến tính bất kỳ của vec tơ không:
1
v
1
+
2
v
2
+...+
k
v
k
=
O;
i
R ; i = 1..k. Nhân vô hướng hai vế với véc tơ v
i
, i = 1..k, ta có: <
1
v
1
+
2
v
2
+ ...
+
k
v
k
>.v
i
= <O.v
i
>
1
<v
1
.v
i
> +
2
<v
2
.v
i
> +...+
i
<v
i
.v
i
> +...+
k
<v
i
.v
k
> = 0
i
<v
i
.v
i
> = 0 (do <v
i
.v
j
> = 0 i j)
i
= 0 i = 1..k. (do v
i
O nên <v
i
.v
i
> 0).
Chứng tỏ {v
1
, v
2
, ..., v
k
} là độc lập tuyến tính.
3. CƠ SỞ TRỰC CHUẨN
Định nghiã 17.
a)
Tập S = {u
1
, u
2
, ..., u
k
} E
n
được gọi là tập trực chuẩn nếu S là tập trực giao và
mọi véc tơ của S đều là véc tơ đơn vị.
b)
Cơ sở B của không gian E
n
được gọi là cơ sở trực chuẩn nếu B là tập trực
chuẩn.
Từ định nghĩa suy ra:
{
u
,
u
, ...,
u
} là tập trực chuẩn
<
u
.
u >
=
1
khi i = j
1 2 k
i
j
0
khi
i j
Ví dụ 49. Tập sau có phải là cơ sở trực chuẩn của E
4
không?
B = {
u
1
= (
1
;
1
;
1
;
1
),
u
2
= (
1
; −
1
;
1
; −
1
),
u
3
= (−
1
; 0;
1
; 0),
u
4
= (0;
2 2 2 2
1
; 0; −
1
)}.
2 2 2 2
Chỉ cần kiểm tra B là tập trực chuẩn (vì tập trực chuẩn B gồm 4 vectơ sẽ độc lập
tuyến tính trong E
4
nên là cơ sở của E
4
), tức là kiểm tra <u .u > =
1 khi i = j
.
Thật vậy:
i
j
0
khi
i j
<u
1
.u
1
> =
1
.
1
+
1
.
1
+
1
.
1
+
1
.
1
= 1. Tương tự, <u
2
.u
2
> = <u
3
.u
3
> = <u
4
.u
4
> = 1.
2 2 2 2 2 2 2 2
<u
1
.u
2
> =
1
.
1
−
1
.
1
+
1
.
1
−
1
.
1
= 0. Tương tự: <u
1
.u
3
> = <u
1
.u
4
> =0; <u
2
.u
3
> =
2 2 2 2 2 2 2 2
<u
2
.u
4
> = 0; <u
3
.u
4
> = 0.
85
2
2

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
x
v
i
n
Chương 4. KHÔNG GIAN VÉC TƠ
Do tích vô hướng có tính chất giao hoán nên ta không cần thử các tích còn lại.
Định lý 31. Nếu B = {v
1
, v
2
, ..., v
n
} là cơ sở trực giao của E
n
, thì với bất kỳ véc tơ
x
E
n
, thành phần tọa độ thứ i của [
x
]
B
là:
x
i
=
x.v
i
; i = 1..n.
2
i
x
1
x
Chứng minh. Gọi B −tọa độ của véc tơ x là [x]
B
=
2
thì: x = x
1
v
1
+ x
2
v
2
+...+ x
n
v
n
.
n
Nhân vô hướng hai vế với véc tơ v
i
(i = 1..n), đồng thời chú ý <v
i
.v
j
> = 0 ij, ta có:
<x.v
i
> = <(x
1
v
1
+ x
2
v
2
+...+ x
n
v
n
).v
i
> = x
i
<v
i
.v
i
> x
i
=
x.v
i
=
x.v
i
.
v
i
.v
i
2
(<v
i
.v
i
> 0 vì v
i
O).
Ví dụ 50. Trong E
3
cho v
1
= (3; 1; 1); v
2
= (−1; 2; 1) ; v
3
= (
− 1
; −2;
2
7
). Chứng tỏ
2
tập {v
1
, v
2
, v
3
} là cơ sở trực giao của E
3
và biểu diễn véc tơ x = (6; 1; −8) dưới dạng tổ
hợp tuyến tính của các véc tơ v
1
, v
2
, v
3
.
Tập {v
1
, v
2
, v
3
} là trực giao vì:
<v
1
.v
2
> = 3.(−1) + 1.2 + 1.1 = 0 = <v
2
.v
1
>
<v
1
.v
3
> = 3.(
− 1
) + 1.(−2) + 1.(
7
) = 0 = <v
3
.v
1
>
2
<v
2
.v
3
> = (−1).(
2
− 1
) +2.(−2) + 1.(
2
7
) = 0 = <v
3
.v
2
>
2
Do {v
1
, v
2
, v
3
} là tập trực giao và không chứa véc tơ O nên nó độc lập tuyến tính và
trở thành cơ sở của E
3
. Phân tích véc tơ x qua cơ sở này ta có:
x =
x.v
1
v
1
+
|| v
1
||
2
x.v
2
v
2
+
||
v
2
||
2
x.v
3
v
3
= v
1
−2v
2
−2v
3
.
||
v
3
||
2
Hệ quả: Nếu B = {u
1
, u
2
, ..., u
n
} là cơ sở trực chuẩn của E
n
thì tọa độ thứ i của
véc tơ x đối với cơ sở B là x
i
= x.u
i
. Khi đó véc tơ x có sự biểu diễn đơn giản qua các
véc tơ của cơ sở B như sau:
x = <x.u
1
>u
1
+ <x.u
2
>u
2
+ ... + <x.u
n
>u
n
Hay tương đương:
Nếu B = {u
1
, u
2
, ..., u
n
} là cơ sở trực chuẩn của E
n
thì với x E
n
ta có :
x.u
1
x.u
[x]
B
=
2
x.u
Hệ qủa trên cho thấy ý nghĩa quan trọng của việc chọn cơ sở trực chuẩn là ở chỗ: sử
dụng cơ sở trực chuẩn thực sự có lợi hơn so với sử dụng bất kỳ một cơ sở nào khác cả
về tính trực quan cũng như tính đơn giản của công thức biểu diễn.
86
v

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
2
2
2
−
2
4
IV. TÍNH TRỰC GIAO VÀ KHÔNG GIAN EUCLIDE
Ví dụ 51. Tìm B −tọa độ của véc tơ x = (1; 2; 3; 4) đối với cơ sở:
B = {u
1
= (
1
;
1
;
1
;
1
), u
2
= (
1
; −
1
;
1
; −
1
), u
3
= (−
1
; 0;
1
; 0), u
4
= (0;
2 2 2 2
1
; 0; −
1
)}.
2 2 2 2
Vì B là cơ sở trực chuẩn của E
4
(xem ví dụ 24 ở trên) nên ta có ngay:
x.u
1
5
x.u
− 1
[x]
B
=
=
.
x.u
3
x.u
4. TRỰC GIAO HOÁ GRAM−SCHMIDT
Trực giao hóa Gram−Schmitdt là quy trình xây dựng một tập trực giao {w
1
, w
2
, ...,
w
k
} từ tập các vectơ độc lập tuyến tính cho trước {v
1
, v
2
, ..., v
k
} E
n
sao cho Sp{w
1
,
w
2
, ..., w
k
} = Sp{v
1
, v
2
, ..., v
k
}. Từ đó suy ra cách xây dựng một cơ sở trực giao (hay
trực chuẩn) từ một cơ sở bất kỳ đã biết của không gian con W E
n
.
Giả sử S = {v
1
, v
2
, ..., v
k
} là tập gồm k 2 vectơ độc lập tuyến tính của E
n
, tiến
hành xây dựng tập trực giao {w
1
, w
2
, ..., w
k
} như sau:
1. Đặt w
1
= v
1
. (1)
2. Tìm w
2
sao cho w
2
⊥ w
1
và Sp{w
1
, w
2
} = Sp{v
1
, v
2
}. Để thỏa mãn điều kiện
Sp{w
1
, w
2
} = Sp{v
1
, v
2
} thì w
2
Sp{v
1
, v
2
}, nghiã là w
2
=
1
v
1
+
2
v
2
=
1
w
1
+
2
v
2
.
Do w
2
⊥ w
1
nên 0 = <w
2
.w
1
> = <(
1
w
1
+
2
v
2
).w
1
> =
1
||w
1
||
2
+
2
<v
2
.w
1
> =
1
||w
1
||
2
+
2
<v
2
.v
1
>. Đây là phương trình bậc nhất đối với 2 ẩn
1
và
2
, có vô số nghiệm.
Chọn
2
= 1, tìm được
1
= −
v
2
.v
1
, từ đó có:
|| w
1
||
2
w
2
=
1
w
1
+
2
v
2
=
−
v
2
.v
1
w
1
+ v
2
. (2)
|| w
1
||
2
Tập {w
1
, w
2
} vừa chọn là tập trực giao (do dễ kiểm tra được <w
1
.w
2
> = 0). Do (1)
và (2) thì w
1
, w
2
là tổ hợp tuyến tính của 2 vectơ v
1
, v
2
nên Sp{w
1
, w
2
} Sp{v
1
, v
2
}.
Mặt khác do (1) và (2) suy ra v
1
, v
2
lại là tổ hợp tuyến tính của 2 vectơ w
1
, w
2
nên
Sp{v
1
, v
2
} Sp{w
1
, w
2
}. Từ đó có Sp{v
1
, v
2
} = Sp{w
1
, w
2
}.
3. Tiếp tục tìm w
3
sao cho w
3
⊥ w
1
, w
3
⊥w
2
và Sp{w
1
, w
2
, w
3
} = Sp{v
1
, v
2
, v
3
}. Do
Sp{v
1
, v
2
} = Sp{w
1
, w
2
} nên Sp{v
1
, v
2
, v
3
} = Sp{w
1
, w
2
, v
3
}. Để thỏa mãn điều kiện
Sp{w
1
, w
2
, w
3
} = Sp{w
1
, w
2
, v
3
} thì w
3
Sp{w
1
, w
2
, v
3
}, nghiã là w
3
=
1
w
1
+
2
w
2
+
3
v
3
. Do w
3
⊥ w
1
, w
3
⊥ w
2
nên đồng thời có:
0 = <w
3
.w
1
> = <(
1
w
1
+
2
w
2
+
3
v
3
).w
1
> =
1
<w
1
.w
1
> +
2
<w
2
.w
1
> +
3
<v
3
.w
1
>
=
1
<w
1
.w
1
> +
3
<v
3
.w
1
>.
0 = <w
3
.w
2
> = <(
1
w
1
+
2
w
2
+
3
v
3
).w
2
> =
1
<w
1
.w
2
> +
2
<w
2
.w
2
> +
3
<v
3
.w
2
>
=
2
<w
2
.w
2
> +
3
<v
3
.w
2
>.
Đây là hệ 2 phương trình bậc nhất đối với 3 ẩn
1
,
2
và
3
, có vô số nghiệm. Chọn
3
= 1, tìm được
1
= −
v
3
.w
1
,
2
= −
v
3
.w
2
, từ đó tìm được:
|| w
1
||
2
|| w
2
||
2
87
2
2
2

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
6
6
6
6
2
1
Chương 4. KHÔNG GIAN VÉC TƠ
w
3
=
1
w
1
+
2
w
2
+
3
v
3
=
−
v
3
.w
1
w
1
−
v
3
.w
2
w
2
+ v
3
(3)
|| w
1
||
2
|| w
2
||
2
Lí luận tương tự như trên thì tập {w
1
, w
2
, w
3
} vừa lập được là tập trực giao và
Sp{w
1
, w
2
, w
3
} = Sp{w
1
, w
2
, v
3
}= Sp{v
1
, v
2
, v
3
}.
4. Tiếp tục quá trình trên đến bước k−1, ta thu được tập gồm k−1 vectơ trực giao
{w
1
, w
2
, ..., w
k
−
1
} thỏa mãn Sp{w
1
, w
2
, ..., w
k
−
1
} = Sp{v
1
, v
2
, ..., v
k
−
1
}. Chọn vectơ thứ
k là:
w
k
=
−
v
k
.w
1
w
1
−
v
k
.w
2
w
2
− ... −
v
k
.w
k−1
w
k–1
+ v
k
(4)
||
w
1
||
2
|| w
2
||
2
|| w
k−1
||
2
Tập k vectơ tìm được {w
1
, w
2
, ..., w
k
} là tập trực giao vì với bất kỳ i k thì:
k−1
v
k
.w
j
v
k
.w
i
<w
k
.w
i
> =
−
2
w
j
+ v
k
w
i
=
−
2
.<w
i
.w
i
> + <v
k
.w
i
> = − <v
k
.w
i
>
+ <v
k
.w
i
> = 0.
j=1
|| w
j
||
|| w
i
||
Hơn nữa, do (4) thì w
k
Sp{w
1
, w
2
, ..., w
k
−
1
, v
k
} và v
k
Sp{w
1
, w
2
, ..., w
k
−
1
, w
k
}
nên Sp{w
1
, w
2
, ..., w
k
−
1
, w
k
} = Sp{w
1
, w
2
, ..., w
k
−
1
, v
k
}= Sp{v
1
, v
2
, ..., v
k
−
1
, v
k
}.
Từ quy trình trực giao hóa Gram–Schmidt, ta có định lí sau đây:
Định lý 32. Mọi không gian con khác không gian tầm thường {O} của E
n
luôn có ít
nhất một cơ sở trực giao, và vì vậy, luôn có ít nhất một cơ sở trực chuẩn.
Ví dụ 52. Tìm một cơ sở trực giao và một cơ sở trực chuẩn cho W = Sp{v
1
= (2; 1;
0; −1), v
2
= (3; 2; 1; −4), v
3
= (2; 2; −4; 0)}.
Các vectơ này là độc lập tuyến tính nên nó là cơ sở (nhưng không là cơ sở trực giao)
của W. Áp dụng quá trình trực giao hoá Gram–Schmidt để xây dựng cơ sở trực giao
như sau:
Đặt w
1
= v
1
= (2; 1; 0; −1).
w = v
−
v
2
.v
1
w
= (3; 2; 1; −4) −
3.2 + 2.1 + 1.0 + (−4)(−1)
2
2
+ 1
2
+ 0
2
+ (−1)
2
.(2; 1; 0; −1) =
2
2
|| w ||
2
1
(3; 2; 1; −4) − 2.(2; 1; 0; −1) = (−1; 0; 1; −2).
6 6
w
3
= v
3
−
v
3
.w
1
w
1
|| w
1
||
2
1; −2) = (−1; 1; −3; −1).
Một cơ sở trực giao là:
−
v
3
.w
2
w
2
= (2; 2; −4; 0)−
6
(2; 1; 0; −1) −
6
(−1; 0;
|| w
2
||
2
B = {w
1
= (2; 1; 0; −1), w
2
= (−1; 0; 1; −2), w
3
= (−1; 1; −3; −1)}.
Để tìm cơ sở trực chuẩn, ta chỉ cần đơn vị hoá các véc của B.
Chọn u
1
=
w
1
=
|| w
1
||
1
(2; 1; 0; −1); u
2
=
w
2
|| w
2
||
=
1
(−1; 0; 1; −2); u
3
=
w
3
=
|| w
3
||
(−1; 1; −3; −1).
Cơ sở:
E = {u
1
=
1
(2; 1; 0; −1), u
2
=
1
(−1; 0; 1; −2), u
3
=
1
(−1; 1; −3; −1)}
2
là cơ sở trực chuẩn của W.
88
1
2 2
lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Proj
y
(x) =
|| y ||
2
IV. TÍNH TRỰC GIAO VÀ KHÔNG GIAN EUCLIDE
5. PHÉP CHẾU TRỰC GIAO
Xét x và y là 2 vectơ khác O trong E
3
và gọi W = Sp{y} thì W là đường thẳng trong
không gian đi qua gốc O. Chiếu vuông góc vectơ x lên W ta được duy nhất một vectơ
trên W, gọi là hình chiếu của vectơ x trên W, kí hiệu là Proj
y
(x). Tuỳ theo góc giữa x và
y là nhọn hay tù mà Proj
y
x là vectơ cùng hướng hay ngược hướng với vectơ y. Gọi là
góc giữa x và y thì độ lớn của hình chiếu là:
||Proj
y
(x)|| = ||x||.|cos|| =
|| x || . || y || .cos
=
|| y ||
| x.y |
|| y ||
Mặt khác, khi [0; /2] thì <x.y> 0 và Proj
y
x là vectơ cùng hướng với vectơ y
nên:
Proj
y
(x) = ||Proj
y
(x)||.
y
=
|| y ||
| x.y |
|| y ||
y
=
|| y ||
x.y
|| y ||
y
=
|| y ||
x.y
.y
|| y ||
2
Khi [/2; ] thì <x.y> 0 và vectơ Proj
y
(x) ngược hướng với y nên:
Proj
y
(x) = ||Proj
y
(x)||.( −
y
) =
| x.y |
(−
y
) = (−
x.y
)(−
y
) =
x.y
.y
|| y || || y || || y || || y || || y ||
|| y ||
2
Vì vậy trong mọi trường hợp ta luôn có:
Proj
y
(x) =
x.y
.y
|| y ||
2
Định nghiã 18. Cho x, y E
n
thì hình chiếu của vectơ x lên vectơ y là vectơ:
x.y
.y
khi
y O
0 khi y = O
Ví dụ 53. Tìm hình chiếu của x = (2; 3; 4) lên y = (1; 2; 3).
Áp dụng Proj
y
(x) =
x.y
.y
=
2 + 6 + 12
y =
20
y =
10
(1; 2; 3) = (
10
;
20
;
30
).
|| y ||
2
1 + 4 + 9 14 7
7 7 7
Định nghiã 19. Ta gọi véc tơ x E
n
là vuông góc với không gian con W E
n
nếu x
vuông góc với mọi véc tơ thuộc W. Tập hợp tất cả các véc tơ của E
n
cùng vuông góc
với không gian con W lập nên tập gọi là phần bù trực giao của không gian con W.
Ký hiệu: W
⊥
.
W
⊥
= {
x
E
n
:
x
⊥
W
}.
Ví dụ 54. Cho P là mặt phẳng có phương trình x + y−z = 0 thì P là không gian con
của E
3
. Tập tất cả các véc tơ vuông góc với P là tập tất cả các véc tơ cùng phương với
véc tơ pháp tuyến n = (1; 1; −1), suy ra P
⊥
= Sp(n).
Ví dụ 55. Xét hai không gian con đặc biệt của E
n
là {O} và E
n
thì x E
n
ta có
<x.O> = 0 nên {O}
⊥
= E
n
. Tương tự, y (E
n
)
⊥
thì <y.x> = 0 xE
n
, đặc biệt khi x =
y thì <y.y> = 0 y = O. Chứng tỏ (E
n
)
⊥
= {O}.
Định lý 33. Cho W = Sp{v
1
, v
2
,..., v
k
} E
n
. Khi đó:
a) Véc tơ xW
⊥
khi và chỉ khi x vuông góc với tập sinh của W.
b) W
⊥
là không gian con của E
n
.
Chứng minh.
89

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
3
3
3
0
0
→
Chương 4. KHÔNG GIAN VÉC TƠ
a) Tập sinh của W là: S = {v
1
, v
2
, ..., v
k
}. Nếu x W
⊥
thì x ⊥S là hiển nhiên do định
nghiã. Ngược lại, giả sử x⊥S = {v
1
, v
2
, ..., v
k
} x ⊥v
i
, i = 1..k. Lấy bất kỳ vW, v =
1
v
1
+
2
v
2
+...+
k
v
k
. Nhân vô hướng 2 vế với x thì:
<x.v> = <x.(
1
v
1
+
2
v
2
+...+
k
v
k
)> =
1
<x.v
1
> +
2
<x.v
2
> +...+
k
<x.v
k
> =
1
.0 +
2
.0 +...+
k
.0 = 0. x⊥v, vW x⊥W hay xW
⊥
.
b) Hiển nhiên O W
⊥
. Với bất kì x, yW
⊥
và , R ta có <(x+y).w> =
<x.w> + <y.w> = 0, w W. Chứng tỏ (x+y) W
⊥
. Từ 2 khẳng định trên, W
⊥
là
không gian con của E
n
.
Định lý 34. Nếu W = Sp{v
1
, v
2
,..., v
k
} E
n
. Lập ma trận A =
v
1
⁝
gồm các hàng là
các vectơ v
i
,( i = 1..k). Khi đó ta có W
⊥
= Nul(A).
Chứng minh
v
k
Có ngay A cỡ kn và W = RowA, ta sẽ chứng minh W
⊥
= Nul(A). Thật vậy, với bất
kỳ x W
⊥
, thì x vuông góc với tập sinh của W nên ta có: <v
i
.x> = 0, i = 1..k, hay viết
dưới dạng ma trận:
v
1
.x
0
v
1
.[
x
]
0
v
1
<v
i
.x> = v
i
.[x] = 0, i = 1..k
⁝
=
⁝
=
⁝
⁝
.[x] =
0
⁝
A.[x] = O x Nul(A).
v
k
.
x
0
v
k
.[
x
]
0
v
k
0
Nhận xét. Từ cách chứng minh định lý trên ta có một phương pháp tìm phần bù trực
giao W
⊥
của không gian con W E
n
bằng cách tìm không gian triệt của ma trận lập
bởi các hàng là các véc tơ thuộc tập sinh của W.
Ví dụ 56. Cho W = Sp{(1; 2; 2; 1), (3; 4; 2; 3)}. Hãy tìm W
⊥
và chỉ ra một cơ sở
của nó.
Lập ma trận A bao gồm các hàng là các véc tơ thuộc tập sinh của W: A =
1 2
2 1
. Quy A về dạng rút gọn:
2
1 2
A =
4
2 1
2
→
1
2 2
− 2 − 4
1
1 0
− 2 1
= U.
2
Từ U dễ dàng suy ra W
⊥
= NulA là tập các phần tử có dạng:
W
⊥
= {(2s−t; −2s; s; t) ; s, t R}= Sp{(2; −2; 1; 0), (−1; 0; 0; 1)}
Dễ tìm được cơ sở của W
⊥
là B = {(2; −2; 1; 0), (−1; 0; 0; 1)}.
Định lý 35. Nếu W
⊥
là phần bù trực giao của không gian con W E
n
thì:
a)
dim W
⊥
= n − dim W hay dimW
⊥
+ dimW = n.
b) W
⊥
W = {O}.
c) (W
⊥
)
⊥
= W.
Chứng minh
90
3
0
0
4
1

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
W
W
.
IV. TÍNH TRỰC GIAO VÀ KHÔNG GIAN EUCLIDE
a) và b) là hiển nhiên, được suy ra từ định lý về hạng của ma trận.
c) Do mọi véc tơ của W đều vuông góc với W
⊥
nên W (W
⊥
)
⊥
(*), (do định
nghiã). Mặt khác, theo a) thì dim (W
⊥
)
⊥
= n − dim(W)
⊥
= n − (n − dim W) = dimW
(**). Từ (*) và (**) suy ra (W
⊥
)
⊥
= W.
Định lý 36. Nếu W là không gian con của E
n
thì E
n
= WW
⊥
Chứng minh. Do W
⊥
W = {O} nên chỉ cần chứng minh E
n
= W+W
⊥
.
Xét trường hợp đặc biệt nếu W ={O} thì W
⊥
= E
n
thì bất kỳ x E
n
= W
⊥
ta đều có
x = O + x, tức là E
n
= O + E
n
= W + W
⊥
.
Xét trường hợp W O. Gọi {v
1
, v
2
, ..., v
k
} là cơ sở trực giao (gồm k véc tơ) của W
còn {v
k+1
, v
k+2
, ..., v
n
} là cơ sở trực giao của W
⊥
(do định lý ở trên, nên cơ sở của W
⊥
gồm n−k véc tơ). Hợp của hai cơ sở trên là tập gồm n véc tơ trực giao, không chứa
vectơ không: B = {v
1
, v
2
, ..., v
k
, v
k+1
, v
k+2
, ..., v
n
}, nên là cơ sở trực giao của E
n
. Khi đó
với mọi x E
n
, đều có sự phân tích duy nhất:
x = d
1
v
1
+ d
2
v
2
+...+ d
k
v
k
+ d
k+1
v
k+1
+...+ d
n
v
n
.
Đặt x* = d
1
v
1
+ d
2
v
2
+...+ d
k
v
k
, z = d
k+1
v
k+1
+...+ d
n
v
n
thì hiển nhiên x* W, z W
⊥
và x được phân tích dưới dạng: x = x*+ z trong đó x* W còn z W
⊥
, tức là E
n
= W +
W
⊥
.
Định nghiã 20. Với W là không gian con của E
n
thì bất kỳ véc tơ xE
n
đều phân
tích được một cách duy nhất dưới dạng: x = x*+z trong đó x*W còn zW
⊥
. Khi
đó, ta gọi x* là hình chiếu trực giao của véc tơ x lên không gian con W và được ký
hiệu là: x* = Proj
W
(x).
Do (W
⊥
)
⊥
= W và x = z + x* với z W
⊥
và x
*
(W
⊥
)
⊥
. Theo định nghiã thì lại
có z = Proj
⊥
(x), suy ra:
x = Proj
W
(x) + Proj
⊥
(x), x E
n
Ví dụ 57. Tìm hình chiếu trực giao của véc tơ x = (3; −1; 2) lên W là mặt phẳng x +
y + z = 0 trong E
3
.
Dễ nhận ra mọi vectơ trong W đều vuông góc với vectơ pháp tuyến n = (1; 1; 1) của
mặt phẳng, nên W
⊥
= Sp(n) và:
Proj
⊥
(x) =
x.n
n =
3 -1+ 2
n =
4
n = (
4
;
4
;
4
).
W
|| n ||
2
1+1+1
3
3 3 3
Áp dụng công thức cho bởi định nghiã, suy ra:
Proj
W
(x) = x − Proj
⊥
(x) = (3; −1; 2) −(
4
;
4
;
4
) = (
5
; −
7
;
2
).
W
3 3 3
3 3 3
Ví dụ 58. Tìm hình chiếu trực giao của véc tơ x = (2; 1; 5) lên không gian con W =
Sp{(1; 2; 1), (2; 1; −1)}.
Áp dụng định nghiã, cần phân tích x = x* + z sao cho x* W, z W
⊥
từ đó suy ra
Proj
W
(x) = x*. Để có sự phân tích của x, ta cần tìm cho E
3
một cơ sở trực giao bao gồm
cơ sở trực giao của W hợp với cơ sở trực giao của W
⊥
91

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
1
w
w
v
v
Chương 4. KHÔNG GIAN VÉC TƠ
- Tìm cơ sở trực giao cho W. Vì {v
1
= (1; 2; 1), v
2
= (2; 1; −1)} là tập độc lập
tuyến tính nên nó là cơ sở cho W. Đặt w
1
= v
1
= (1; 2; 1), w
2
= v
2
−
v
2
.v
1
v
1
= (2;
|| v
1
||
2
1; −1) −
3
(1; 2; 1) = (
3
; 0; −
3
). Cơ sở trực giao của W là {w
1
= (1; 2; 1), w
2
= (
3
; 0;
6 2 2 2
−
3
)}.
2
- Tìm cơ sở cho W
⊥
bằng cách tìm cơ sở cho NulA với A =
1 2 1
. Quy
3 / 2
0
− 3 / 2
A về dạng rút gọn: A→
1 0
1
− 1
, có NulA = {(t; − t; t); t R}= Sp{(1; −1; 1)}, chọn
một cơ sở cho NulA là {w
3
= (1; −1; 1)}.
- Cơ sở trực giao của E
3
là hợp của 2 cơ sở vừa tìm:
B = {w
1
= (1; 2; 1), w
2
= (3/2; 0; −3/2), w
3
= (1; −1; 1)}.
Phân tích x = (2; 1; 5) theo cơ sở B ta có:
x =
x.w
1
w
1
+
x.w
2
w
2
+
x.w
3
w
3
=
3
w
1
−1.w
2
+ 2.w
3
.
2 2 2
2
1 2 3
Trong sự phân tích trên, (
3
.w
1
− w
2
) W còn 2w
3
W
⊥
, suy ra:
2
x* = Proj
W
(x) =
3
w
1
− w
2
=
3
.(1; 2; 1) − (
3
; 0; −
3
) = (0; 3; 3).
2 2 2 2
Nhận xét. Áp dụng cách chứng minh định lý ở trên, suy ra nếu {v
1
, v
2
, ..., v
k
} là cơ
sở trực giao của W thì với bất kỳ xE
n
hình chiếu trực giao của x trên không gian con
W được tính bởi công thức:
Proj
W
(x) =
x.v
1
v
1
+
x.v
2
v
2
+ ... +
x.v
k
v
k
(*).
2 2 2
1 2 k
Đặc biệt, nếu {u
1
, u
2
,..., u
k
} là cơ sở trực chuẩn của W thì:
Proj
W
(x) = <x.u
1
>u
1
+ <x.u
2
>u
2
+...+ <x.u
k
>u
k
(**).
Công thức (*) và (**) cho phép tìm được hình chiếu của bất kỳ véc tơ x E
n
lên
không gian con W một cách đơn giản, nếu biết được một cơ sở trực giao hay trực
chuẩn nào đó của W.
Về mặt hình học, x* = Proj
W
(x) là véc tơ nằm trong W, “gần” với véc tơ x nhất theo
nghĩa d(x,x*) d(x,w), wW. Vì vậy x* được gọi là xấp xỉ tốt nhất của x đối với
mọi phần tử trong W. Thật vậy, w W ta có:
[d(x,w)]
2
=
w)] >
x - w
2
= <(x − w).(x − w)> = <[(x − x*)+(x* − w)}.{(x − x*)+(x* −
= <(x − x*).(x – x*)> + 2.<(x − x*).(x* − w)> + <(x* − w).(x* − w)>.
Do (x − x*)W
⊥
còn (x* − w)W nên <(x − x*).(x* − w)> = 0, dẫn đến:
[d(x,w)]
2
= <(x − x*).(x − x*)> + <(x* − w).(x* − w)> = x - x *
2
+ x * -w
2
x - x *
2
= [d(x,x*)]
2
. Hay d(x,w) d(x,x*). Dấu ‘’=’’ xẩy ra hi và chỉ khi w = x*.
6. MA TRẬN TRỰC GIAO
92
w
v

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
B,C
j
IV. TÍNH TRỰC GIAO VÀ KHÔNG GIAN EUCLIDE
Cho ma trận A M(n,n), nếu A khả nghịch thì tập các véc tơ ứng với các cột của A
lập nên cơ sở cho không gian cột ColA. Mục này sẽ xét trường hợp đặc biệt khi cơ sở
của ColA là cơ sở trực chuẩn để từ đó phát hiện thêm các tính chất đặc biệt của ma trận
tương ứng.
Định nghiã 21. Ma trận A M(n,n) được gọi là ma trận trực giao nếu tập các véc
tơ ứng với tập các cột của A là tập trực chuẩn.
Từ định nghiã, suy ra nếu A trực giao thì <c A.c A> =
1 khi i
=
j
h A
T
.c A =
i j
0 khi i
j
i j
1 khi i
=
j
0 khi i
j
là hiển nhiên:
[A
T
A]
ij
=
1 khi i
=
j
0 khi i
j
A
T
A = I
n
. Vì vậy, ta có các tính chất sau
a) A M(n,n) là trực giao A
T
A = I
n
.
b) A M(n,n) là trực giao A
–1
= A
T
.
c) A M(n,n) là trực giao A
–1
trực giao.
Định lý 37. Nếu W là không gian con của E
n
và B = {u
1
, u
2
, ..., u
k
}, C = {w
1
, w
2
,
..., w
k
} là các cơ sở trực chuẩn của W thì ma trận chuyển tọa độ P
B
,
C
là ma trận trực
giao.
u
i
.w
1
u .w
Chứng minh. Có P
B,C
= [[u
1
]
C
[u
2
]
C
... [u
k
]
C
], trong đó [u
i
]
C
=
i 2
⁝
nên phần
u .w
i k
tử (i,j) của ma trận P
B,C
là [P
B,C
]
ij
= <u
i
.w
j
>. Tương tự, P
C,B
= [[w
1
]
B
[w
2
]
B
... [w
k
]
B
],
w
i
.
u
1
w .u
trong đó [w
i
]
B
=
i 2
⁝
nên phần tử (i,j) của ma trận P
C,B
là [P
C,B
]
ij
= <w
i
.u
j
> Do
w .u
i k
tính giao hoán của tích vô hướng mà có [P
B,C
]
ij
= <u
i
.w
j
> = <w
i
.u
j
> = [P
C,B
]
ij
). Đẳng
thức này đúng với mọi i, j = 0..k nên P
B,C
= P
C,B
= P
−
1
P
B,C
trực giao.
Nhờ ma trận trực giao mà ta có thể tìm thấy mối quan hệ giữa cơ sở trực giao và cơ
sở trực chuẩn tương ứng như phân tích sau đây. Gọi {v
1
, v
2
, ..., v
p
} là tập gồm p vectơ
độc lập tuyến tính của E
n
, đặt A = [[v
1
] [v
2
] ... [v
p
]] M(n,p). Nhờ qúa trình trực giao
hóa Gram–Schmidt, xây dựng được tập trực giao {w
1
, w
2
, ..., w
p
} sao cho Sp{v
1
, v
2
, ...,
v } = Sp{w , w , ..., w } k = 1..p. Với mỗi j = 1..p, đặt u =
w
j
thì {u , u , ..., u }
k 1 2 k
j
|| w ||
1 2 p
gọi là tập các vectơ trực chuẩn ứng với tập trực giao {w
1
, w
2
, ..., w
p
}. Khi đó, với mỗi k
= 1..p–1, ta có mối quan hệ cho bởi quy trình trực giao hoá Gram–Schmidt:
w
k+1
= ||w
k+1
||u
k+1
= v
k+1
– Proj
W
k
(v
k+1
) với W
k
= Sp{v
1
, v
2
, ..., v
k
}.
Do {u
1
, u
2
, ..., u
k
} là cơ sở trực chuẩn của W
k
= Sp{v
1
, v
2
, ..., v
k
} nên có
Proj
W
k
(v
k+1
) = <v
k+1
.u
1
>u
1
+ <v
k+1
.u
2
>u
2
+ ... + <v
k+1
.u
k
>u
k
và :
w
k+1
= ||w
k+1
||u
k+1
= v
k+1
– <v
k+1
.u
1
>u
1
− <v
k+1
.u
2
>u
2
− ... − <v
k+1
.u
k
>u
k
.
v
k+1
= <v
k+1
.u
1
>u
1
+ <v
k+1
.u
2
>u
2
+ ... + <v
k+1
.u
k
>u
k
+ ||w
k+1
||u
k+1
.
Cụ thể:
93

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
⁝
0
2
⁝
0
0
⋱
0
⁝
v
1
= ||w
1
||.u
1
.
Chương 4. KHÔNG GIAN VÉC TƠ
v
2
= <v
2
.u
1
>u
1
+ ||w
2
||.u
2
.
v
3
= <v
3
.u
1
>u
1
+ <v
3
.u
2
>u
2
+ ||w
3
||.u
3
.
⁝
v
p
= <v
p
.u
1
>u
1
+ <v
p
.u
2
>u
2
+ ... + <v
p
.u
p–1
>u
p–1
+ ||w
p
||u
p
. (*)
Đặt Q = [[u
1
] [u
2
].... [u
p
]] là ma trận lập bởi các vectơ cột [u
1
], [u
2
], ..., [u
p
] thì (*)
chứng tỏ mỗi cột trong A là tổ hợp tuyến tính của các cột trong Q, tức là có sự phân
tích :
v
k
.u
1
v
k
.u
k
−
1
v
k
= <v
k
.u
1
>u
1
+ <v
k
.u
2
>u
2
+ ...+ <v
k
.u
k–1
>u
k–1
+ ||w
k
||u
k
= [u
1
u
2
.... u
p
]
||
w
||
k
Lập ma trận:
|| w
1
|| v
2
.u
1
v
3
.u
1
0
⁝
0
v
p
.u
1
|| w ||
v
3
.u
2
v
p
.u
2
R =
0
0
||
w
3
||
v
p
.u
3
||
w
p
||
thì R M(p,p) là ma trận tam giác trên, khả nghịch và có sự phân tích: A = QR. Từ kết
qủa trên ta có định lý sau :
Định lý 38. Nếu A M(n,p) có tập các cột độc lập tuyến tính thì tồn tại ma trận Q
M(n,p) với tập các cột trực chuẩn và ma trận tam giác trên khả nghịch R M(p,p)
sao cho A = QR. Đặc biệt nếu A vuông thì Q là ma trận trực giao.
Việc phân tích A = QR với Q là ma trận có tập các cột trực chuẩn còn R là ma trận
tam giác trên, khả nghịch gọi là nhân tử hóa dạng QR đối với ma trận A. Nếu A là ma
trận có tập các cột độc lập tuyến tính thì theo định lý trên, A luôn nhân tử hóa dạng QR
được.
1
1
Ví dụ 59. Nhân tử hoá dạng QR với A = [v
1
v
2
] =
− 1
− 1
.
1
Áp dụng quy trình trực giao hoá Gram–Schmidt:
−
1
1
−
1
−
1
v .w
1
− 2
1
1
3
Đặt w
1
= v
1
và w
2
= v
2
−
2
1
w
1
=
–
=
.
|| w
1
||
1
4
− 1
2
1
−
1
1
−
1
94
1
1

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
3
3
−
1
0
2
−
IV. TÍNH TRỰC GIAO VÀ KHÔNG GIAN EUCLIDE
1
−
1
1
1
Có ||w
1
|| = 2, ||w
2
|| = , đơn vị hoá w
1
, và w
2
ta có u
1
= w
1
=
=
|| w
1
||
2
1
− 1/ 2
1/ 2
1 1 1
−
1
1
− 1/ 2 3
1/ 2
1
; u
2
=
w
2
=
=
. Lập Q = [u
1
u
2
] và R =
1/ 2
|| w
2
||
2
1
1/ 2 3
− 1/ 2
−
− 1/ 2 3
1
|| w
1
||
v
2
.u
1
=
2
−
1
ta có sự phân tích :
|| w ||
1 − 1
1 1
1/ 2
1/ 2
− 1/ 2
1/ 2
3
2
− 1
A =
=
.
− 1 1
− 1/ 2
1/ 2
3
0 3
1
1/ 2
− 1/ 2
3
Một trong những ứng dụng thường thấy của nhân tử hóa dạng QR là tìm ma trận
nghịch đảo của A. Nếu A khả nghịch thì A = QR với Q là ma trận trực giao nên:
A
–1
= R
–1
Q
–1
= R
–1
Q
T
.
Từ đó việc tìm A
–1
được quy về tìm nghịch đảo của ma trận tam giác trên R, thực sự
dễ hơn.
7. PHƯƠNG PHÁP BÌNH PHƯƠNG NHỎ NHẤT
Trong vật lý và trong các ngành khoa học xã hội thường gặp bài toán tìm hệ thức
quan hệ giữa các đại lượng đo được qua thí nghiệm hoặc qua thực nghiệm (để từ đó
phát hiện dáng điệu trong tương lai của chuỗi dữ liệu này). Bài toán đơn giản nhất được
phát biểu như sau: Cho trước n điểm (x
1
; y
1
); (x
2
; y
2
), ..., (x
n
; y
n
) trên mặt phẳng (gọi là
các điểm dữ liệu), cần tìm đa thức bậc nhất f(x) = a+bx sao cho f(x
k
) được ‘’xấp xỉ tốt
nhất’’với y
k
với mọi k = 1..n. Về mặt hình học, bài toán vừa nêu có nghiã là cần tìm một
đường thẳng
«
đi gần sát nhất’’ với tất cả các điểm đã cho. Tính ‘’xấp xỉ tốt nhất’’ giữa
f(x
k
) với y
k
được đặc trưng bởi độ lớn của hiệu |y
k
−f(x
k
)|, do đó ta cần tìm f(x) = a+bx
n n
sao cho tổng
| y
k
− f( x
k
)| đạt nhỏ nhất, hay tương đương, tổng
[y
k
− f (x
k
)]
2
đạt
k
=
1
k
=
1
n
nhỏ nhất. Việc chọn hàm f sao cho tổng
[y
k
− f (x
k
)]
2
k
=
1
đạt nhỏ nhất thường gọi là
phương pháp bình phương nhỏ nhất. Hàm f tìm được gọi là hàm bình phương nhỏ nhất.
Đồ thị của hàm f là một đường thẳng, được gọi là đường thẳng bình phương nhỏ nhất
của các điểm dữ liệu đã cho.
Phương pháp bình phương nhỏ nhất thường được thực hiện bằng công cụ ma trận
y
1
1
x
1
a
như sau. Đặt Y =
, A =
và Z =
thì:
b
y
n
1 x
n
95
3
3
0
3

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
b
W
n
Chương 4. KHÔNG GIAN VÉC TƠ
n n
[y
k
− f (x
k
)]
2
=
[y
k
− (a + bx
k
)]
2
= ||Y−AZ||
2
.
k
=
1 k
=
1
Tổng
[y
k
− f (x
k
)]
2
đạt nhỏ nhất ||Y−AZ|| đạt nhỏ nhất khi vectơ cột Z thay
k
=
1
đổi trên [R]
2
. Gọi W = {w = AZ / Z [R]
2
} = ColA là không gian con của [R]
n
và
min{||Y−AZ||/ Z[R]
2
} = min{||Y − w||/ wW}. Áp dụng ý nghiã hình học của hình
chiếu trực giao thì trong W tồn tại duy nhất một vectơ ‘’gần’’ với Y nhất, cụ thể là
Proj
W
(Y), tức là min{||Y − w||/ wW} đạt tại w
0
= AZ
0
= Proj
W
(Y). Nghiệm Z
0
cần tìm
chính là nghiệm của phương trình:
AZ = Proj
W
(Y) (*) với W = {AZ / Z R
2
} = ColA.
Phương trình (*) ở trên luôn có nghiệm vì vế phải là vectơ Proj
W
(Y) ColA. Để
phương trình (*) có nghiệm duy nhất thì tập các cột trong A phải độc lập tuyến tính,
điều này xẩy ra khi và chỉ khi có ít nhất 2 trong các giá trị x
1
, x
2
, ..., x
n
là khác nhau.
Định lý sau sẽ đưa ra lời giải cho phương pháp bình phương nhỏ nhất.
Định lý 39. Nếu (x
k
; y
k
), k = 1..n là n điểm dữ liệu đã cho, trong đó có ít nhất 2
trong n giá trị x
1
, x
2
, ..., x
n
là khác nhau thì tồn tại duy nhất cặp số (a
0
, b
0
) sao cho:
n n
[y
k
− (a
0
+ b
0
x
k
)]
2
[y
k
− (a + bx
k
)]
2
với mọi (a, b) R
2
. Hơn nữa a
0
,, b
0
được tìm
k
=
1
k
=
1
1
x
1
từ Z
0
=
a
0
là nghiệm của hệ tuyến tính AZ = Proj (Y), trong đó A =
, Z =
b
W
0
1 x
y
1
a
, Y =
và W = ColA.
n
b
y
n
Áp dụng định lý, để tìm Z
0
=
a
0
, cần tìm Proj
W
(Y) rồi giải hệ tuyến tính AZ =
0
Proj
W
(Y). Tuy nhiên, có thể thay thế quy trình trên nhờ phép giải trực tiếp sau.
Do Y – AZ
0
= Y − Proj
W
(Y) = Proj
⊥
(Y) W
⊥
từ đó với AZ W thì:
0 = <AZ.(Y−AZ
0
)> = (AZ)
T
(Y−AZ
0
) = Z
T
(A
T
Y – A
T
AZ
0
) = <Z.(A
T
Y – A
T
AZ
0
)>
chứng tỏ vectơ A
T
Y – A
T
AZ
0
vuông góc với bất kỳ vectơ cột Z [R]
2
nên phải có:
A
T
Y – A
T
AZ
0
= O (A
T
A)Z
0
= A
T
Y
Người ta chứng minh được nếu A có tập các cột độc lập tuyến tính thì A
T
A là ma
trận khả nghịch, từ đó rút ra công thức tìm Z
0
:
Z
0
= (A
T
A)
−
1
A
T
Y
Ví dụ 60. Tìm đường thẳng để tổng các khoảng cách từ 4 điểm M
1
(−3 ; 8), M
2
(−1 ;
5), M
3
(1 ; 3), M
4
(3 ; 0) đến đường thẳng đó là nhỏ nhất.
Gọi đường thẳng cần tìm có phương trình y = a+bx, đó là đường thẳng ‘’bình
phương nhỏ nhất’’.
1 − 3
1 − 1
8
5
a
Lập A =
, Y=
, Z =
.
1 1
3
b
1 3
0
96

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
1 1
1
1
IV. TÍNH TRỰC GIAO VÀ KHÔNG GIAN EUCLIDE
T
1
1
1 1 1
1
−
3
−
1
4 0
T −1
1
20
0
1/ 4
0
Có A .A=
=
(A .A) =
=
Áp dụng:
− 3 − 1 1
3
1
1
1
0
20
8
80
0
4
0
1/ 20
T −1 T
1/ 4
0
1
1 1 1
5
1/ 4
0
16
4
Z = (A A) A Y =
=
=
.
0 1/ 20
−
3
− 1 1
3
3
0
0
1/ 20
−
26
13 / 10
Đường thẳng cần tìm: y = 4+
13
x.
10
Ví dụ 61. Doanh thu của một nhà máy trong 4 tháng đầu năm cho bởi bảng sau:
Tháng
1
2
3
4
Doanh thu (tỷ đồng)
2,5
3,0
3,8
4,5
Áp dụng phưong pháp bình phương nhỏ nhất để dự đoán doanh thu của nhà máy
trong tháng thứ 5.
Gọi đường thẳng bình phương nhỏ nhất có phương trình y = a + bx.
1 1
1 2
2,5
3
a
T
1 1 1
1 1
1
1 2
4
10
Lập A =
, Y=
, Z =
. Có A .A =
=
1 3
3,8
b
1 2
3 4
1 3
10
30
1 4
4,5
1 4
(A.A
T
)
−
1
=
1
30
− 10
=
3 / 2
− 1/ 2
.
20
− 10
4
− 1/ 2 1/ 5
Áp dụng công thức:
2,5
T −1 T
3 / 2
− 1/ 2
1 1
1
1
3
3 / 2
− 1/ 2
13,8
1,75
Z=(A A) A Y =
=
=
.
− 1/ 2 1/ 5
1 2
3 4
3,8
4,5
− 1/ 2 1/ 5
37,9
0,68
Rút ra đường thẳng cần tìm có phương trình: y = 1,75+0,68x. Thế x = 5 y(5) =
5,15, nghiã là doanh thu của nhà máy trong tháng thứ 5 được dự đoán là 5,15 tỷ đồng.
Các nghiên cứu lý thuyết cũng chỉ ra rằng, đôi khi đường cong, chứ không phải là
đường thẳng, mới là đường phù hợp với phương pháp bình phương nhỏ nhất. Chẳng
hạn, trong kinh tế, đường cho bởi phương trình đa thức bậc 3 là đường bình phương nhỏ
nhất của các điểm dữ liệu biểu thị mối quan hệ giữa tổng giá và tổng sản phẩm hàng
hoá; trong sinh học, đường cho bởi hàm mũ, hàm logarit lại là đường bình phương nhỏ
nhất của các điểm dữ liệu biểu thị mối quan hệ giữa sự tăng trưởng về số lượng của một
loài với các yếu tố như bệnh dịch, kẻ săn mồi, nạn đói, ...
Giả sử đường bình phương nhỏ nhất của các điểm dữ liệu (x
1
, y
1
), (x
2
; y
2
), ..., (x
n;
y
n
)
là đồ thị của hàm đa thức bậc q: y = f(x) = a
0
+a
1
x+ ... + a
q
x
q
. Với cách giải tương tự như
trường hợp đường bình phương nhỏ nhất là đường thẳng, bằng cách đặt:
y
1 x
x
2
...
x
q
a
0
Y =
, A =
và Z =
y
1
x x
2
...
x
q
a
n
n n n q
97
3

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
64
1
thì:
n
Chương 4. KHÔNG GIAN VÉC TƠ
n
[y
k
− f (x
k
)]
2
=
[y
k
− (a
0
+ a
1
x + ...a
q
x
q
)]
2
= ||Y − AZ||
2
.
k
=
1
n
k
=
1
Tổng
[y
k
− f (x
k
)]
2
đạt nhỏ nhất ||Y−AZ|| đạt nhỏ nhất vectơ cột Z là
k
=
1
nghiệm của:
(A
T
A)Z = A
T
Y
Nếu A có tập các cột độc lập tuyến tính thì phương trình trên có nghiệm duy nhất:
Z
0
= (A
T
A)
−
1
A
T
Y
Ví dụ 62. Quan sát quan hệ giữa giá bán và tải trọng của con tàu, số liệu thu được
cho bởi bảng sau:
Tải trọng (ngàn tấn)
2
4
5
8
Giá (ngàn USD)
1,0
3,0
5,0
12,0
Hãy tìm đường bình phương nhỏ nhất ở dạng đường parabol rồi dự đoán giá bán của
tàu có tải trọng 10.000 tấn.
Gọi đường bình phương nhỏ nhất có phương trình y = a
0
+ a
1
x +a
2
x
2
.
1 2
1 4
4
16
1,0
3,0
a
0
Lập A =
, Y=
, Z =
a
1
.
1 5 25
5,0
a
2
1 8
1
T
64
1 1
12,0
1
1 2
1 4
4
16
4
19 109
Có A .A =
2 4 5
4 16 25
8
5
1 8
25
64
=
19
109
109
709
709
.
4993
1 1 1
1
1,0
21
T
3,0
A Y =
2 4 5 8
=
135
.
4 16 25 64
5,0
945
12,0
4 19
109
a
0
21
0,207
Giải hệ (A
T
A)Z = A
T
Y
19 109
709
a
=
135
Z
0
=
0,010
.
1
109
709
4993
a
2
945
0,183
Rút ra đường bình phương nhỏ nhất cần tìm có phương trình: y =
0,27+0,010x+0,183x
2
. Thế x=10 y(10) = 18,67, nghiã là giá bán của tàu có tải trọng
10.00 tấn vào khoảng 18,67 ngàn USD.
98

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
I. KHÁI NIỆM ÁNH XẠ TUYẾN TÍNH
Chương 5
ÁNH XẠ TUYẾN TÍNH
1. Khái niệm ánh xạ tuyến tính
2. Nhân và ảnh của ánh xạ tuyến tính
3. Tính đẳng cấu của không gian véc tơ và hạng của ánh xạ
tuyến tính .
4. Biểu diễn ma trận của ánh xạ tuyến tính.
I. KHÁI NIỆM ÁNH XẠ TUYẾN TÍNH
1. ĐỊNH NGHĨA VÀ VÍ DỤ
Định nghiã 1. Ánh xạ f: V→ W từ không gian véc tơ V vào không gian véc tơ W
được gọi là ánh xạ tuyến tính, nếu f thỏa mãn:
1) f(u+v) = f(u)+f(v) u, v V.
2) f( u) = f(u) R và uV.
Các tính chất 1) và 2), tương ứng gọi là tính bảo toàn phép cộng và tính bảo toàn
phép nhân với vô hướng của f.
Nếu V W thì ánh xạ tuyến tính f: V→V được gọi là phép biến đổi tuyến tính hay
toán tử tuyến tính trên V.
Từ định nghiã ở trên, dễ dàng suy ra các tính chất đơn giản sau đây của ánh xạ tuyến
tính f: V→ W:
1) f(0
V
) = 0
W
.
2) f(–v) = – f(v) v V.
3) f
k
i
v
i
=
i
f(
v
i
)
,
v
i
V
và
i
R
, i = 1..k; (k
2).
i
=
1
i
=
1
Ví dụ 1. Chứng minh ánh xạ f: R
2
→ R
2
, f(x; y) = (2x; x+y) là ánh xạ tuyến tính.
Với hai phần tử bất kỳ của R
2
: u = (x
1
; y
1
), v = (x
2
; y
2
) và bất kỳ R ta có: u+v =
(x
1
+ x
2
; y
1
+y
2
), .u = (x
1
; y
1
), f(u) = f(x
1
; y
1
) = (2x
1
; x
1
+y
1
), f(v) = f(x
2
; y
2
) = (2x
2
;
x
2
+y
2
). Khi đó:
-
Tính bảo toàn phép cộng thỏa mãn vì f(u+v) = f(x
1
+x
2
; y
1
+y
2
) = (2x
1
+2x
2
;
x
1
+x
2
+y
1
+y
2
) = (2x
1
; x
1
+y
1
) + (2x
2
; x
2
+y
2
) = f(u) + f(v).
-
Tính bảo toàn phép nhân với vô hướng thỏa mãn vì f(u) = f(x
1
; y
1
) = (2x
1
;
x
1
+y
1
) = .(2x
1
; x
1
+y
1
) = .f(u).
Áp dụng định nghĩa, f bảo toàn phép cộng và phép nhân với vô hướng nên f là ánh xạ
tuyến tính.
Định lý sau là tương đương với định nghĩa 1:
Định lý 1. Ánh xạ f: V→ W là tuyến tính u, vV; , R ta đều có
f(u+v) = f(u) + f(v).
99
k

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
x
2
Chương 5: ÁNH XẠ TUYẾN TÍNH
Ta thường hay sử dụng định lý trên thay cho định nghĩa khi cần chứng minh một
ánh xạ f nào đó là ánh xạ tuyến tính.
Ví dụ 2. Chứng minh rằng ánh xạ f: P
2
(x) → P
2
(x), f(ax
2
+bx+c) = (a+b)x + c là ánh
xạ tuyến tính.
Áp dụng định lý, cần chứng minh với bất kỳ p, q P
2
(x) và , R, ta có:
f(p+q) = f(p) + f(q). Thật vậy :
Với p, q P
2
(x) p = ax
2
+bx+c, q = a’x
2
+b’x+c’, p+q = (a+a’)x
2
+ (b+b’)x +
c+c’, f(p) = (a+b)x +c, f(q) = (a’+b’)x +c’. Khi đó:
f(p+q) = f[(a+a’)x
2
+(b+b’)x+c+c’)] = (a+a’+b+b’)x+c+c’ =
[(a+b)x +c] + [(a’+b’)x+c’] = [(a+b)x +c] + [(a’+b’)x+c’] = f(p) + f(q).
Ví dụ 3. Gọi V là không gian véc tơ các hàm số f khả vi đến cấp 1 trên [a, b], còn W
là không gian véc tơ các hàm xác định trên [a, b]. Gọi D: V → W, D(f) = f ' là ánh xạ
đặt f tương ứng với đạo hàm của nó. Nhờ quy tắc lấy đạo hàm, ta có:
D(f+g) = (f+g) ‘ = f ‘ + g ‘ = D(f) + D(g) f, gV.
D(f) = (f)’= .f ‘ = .D(f) R và fV.
Chứng tỏ D bảo toàn phép cộng và phép nhân với vô hướng, nên D là ánh xạ tuyến tính.
2. ÁNH XẠ TUYẾN TÍNH TỪ R
n
VÀO R
m
Ánh xạ tuyến tính có một trường hợp riêng rất quan trọng, đó là ánh xạ tuyến tính từ
không gian véc tơ R
n
vào không gian véc tơ R
m
. Với mục này, ta sẽ chỉ ra rằng, quy luật
xác định ảnh của một véc tơ qua ánh xạ tuyến tính từ R
n
vào R
m
được tìm thuận lợi nhờ
quy tắc nhân ma trận, đồng thời cũng vạch ra sự tương ứng 1–1 giữa tập ánh xạ tuyến
tính từ R
n
vào R
m
với tập các ma trận cỡ mn đã xét ở chương 2.
Định nghiã 2. Cho ma trận A M(m,n), ánh xạ T: R
n
→ R
m
, đặt mỗi vectơ x R
n
với vectơ T(x) R
m
sao cho [T(x)] = A[x] được gọi là ánh xạ ma trận, ứng với ma
trận A, Kí hiệu: [T(x)] = A[x].
1 0 0
Ví dụ 4. Cho A =
0 1 0
thì ánh xạ ma trận T: R
3
→ R
3
ứng với ma trận A có
0
0
0
1 0
0
x
1
x
1
ảnh của x = (x
1
; x
2
; x
3
) là T(x) cho bởi [T(x)] = A[x] =
0 1
0
x
=
2
0
0
0
x
3
0
Định lý 2.
-
Mỗi ánh xạ ma trận ứng với ma trận A M(m,n) là một ánh xạ tuyến tính từ R
n
vào R
m
.
-
Ngược lại, với bất kỳ ánh xạ tuyến tính T: R
n
→ R
m
, luôn tồn tại duy nhất một
ma trận A M(m,n) sao cho [T(x)] = A[x] với mọi x R
n
nên T lại là ánh xạ ma trận.
Khi đó ma trận A gọi là ma trận chính tắc của T.
Chứng minh
1. Gọi T: R
n
→R
m
là ánh xạ ma trận ứng với ma trận A M(m,n) thì với bất kỳ x, y
R
n
và bất kỳ , R, ta đều có:
100
.

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
0
1
0 1 0
x
I. KHÁI NIỆM ÁNH XẠ TUYẾN TÍNH
[T(x+y)] = A[x+y] = A[x] + A[y] = A[x] + A[y] = [T(x)] + [T(y)]. Chứng
tỏ T là ánh xạ tuyến tính.
2. Với bất kỳ x R
n
ta đều có sự phân tích duy nhất qua cơ sở chính tắc B
0
= {e
1
,
e
2,
... e
n
} của R
n
: x = x
1
e
1
+ ... + x
n
e
n
. Do T là ánh xạ tuyến tính nên:
[T(x)] = [T(x
1
e
1
+ ... + x
n
e
n
)] = [x
1
T(e
1
) +...+ x
n
T(e
n
)] = [x
1
T(e
1
)] +...+ [x
n
T(e
n
)] =
x
1
x
1
[T(e
1
)] +...+ x
n
[T(e
n
)] = [[T(e
1
)] ... [T(e
n
)]].
.
x
n
Đặt A = [[T(e
1
)] ... [T(e
n
)]] M(m,n) thì có [T (x)] = A[x]. Sự tồn tại của A được chứng
minh.
Tính duy nhất của A là hiển nhiên vì nếu tồn tại B để [T(x)] = B[x] x R
n
thì
do A[x] = B[x], x R
n
suy ra A = B.
Nhờ cách chứng minh định lý trên mà ta có ngay ma trận chính tắc của ánh xạ
tuyến tính từ R
n
vào R
m
được cho bởi:
A = [[T(e
1
)] ... [T(e
n
)]]
với {e
1
, ...e
n
} là cơ sở chính tắc của R
n
.
Ví dụ 5. Cho T: R
3
→ R
2
, T(x
1
, x
2
, x
3
) = (x
1
; x
2
) là ánh xạ tuyến tính. Hãy tìm ma
trận chính tắc của T.
Cơ sở chính tắc của R
3
là {e
1
= (1; 0; 0), e
2
= (0; 1; 0), e
3
= (0; 0; 1)}. Tính
được:
[T(e
1
)] = [T(1; 0; 0)] = [(1; 0)] =
1
, [T(e
2
)] = [(0; 1)] =
0
, [T(e
3
)] = [(0; 0)] =
0
. Ma trận chính tắc của T là :
A = [[T (e
1
)] [T(e
2
)] [T(e
3
)]] =
1 0 0
.
Ví dụ 6. Chứng minh rằng ánh xạ f : R
2
→ R
3
, f(x
1
; x
2
) = (3x
1
–x
2
; x
1
; x
1
+x
2
) là ánh
xạ tuyến tính bằng cách chỉ ra f là ánh xạ ma trận.
x
3x
1
−
x
2
Với x = (x
1
; x
2
) R
2
[x] =
1
. Có [f(x)] = [(3x
1
–x
2
; x
1
; x
1
+x
2
)] =
x
1
2
x + x
3x
1
−
x
2
3
−
1
3 −1
x
3 −1
1 2
x
+
0
=
x
1
.
1
+ x
2
.
0
=
1
0
1
= A[x], với A =
1 0
.
1
x
x
x
1
1
1 1
2
1 1
1 2
Do [f(x)] = A[x], nên f là ánh xạ ma trận, suy ra f là ánh xạ tuyến tính.
3. ĐỊNH LÍ VỀ SỰ XÁC ĐỊNH CỦA ÁNH XẠ TUYẾN TÍNH
Định lý 3. Cho không gian véc tơ n chiều V
n
, có cơ sở B = {v
1
, v
2
, ..., v
n
} và {w
1
, w
2
,
..., w
n
} là tập gồm n véc tơ nào đó của không gian véc tơ W. Khi đó tồn tại duy nhất
một ánh xạ tuyến tính f:
V
n
→
W
sao cho f(
v
i
) =
w
i
i = 1..n.
101
=

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
2
3
0
2
3
0
1
Chương 5: ÁNH XẠ TUYẾN TÍNH
Hay nói ngắn gọn hơn, ánh xạ tuyến tính hoàn toàn được xác định bởi ảnh của
một cơ sở nào đó.
Chứng minh
- Sự tồn tại: Lấy bất kì véc tơ vV
n
, biểu thị v qua cơ sở B:
v =
1
v
1
+
2
v
2
+...+
n
v
n
.
Trong W, lấy véc tơ w =
1
w
1
+
2
w
2
+...+
n
w
n
và lập ánh xạ f: V
n
→ W, f(v) = w thì f
thỏa mãn:
f(v
i
) = w
i
, i = 1..n, ví dụ f(v
1
) = f(1.v
1
+0.v
2
+...+ 0.v
n
) = 1.w
1
+ 0.w
2
+ ... +0.w
n
=
w
1
.
f là ánh xạ tuyến tính vì , R; u = c
1
v
1
+c
2
v
2
+...+c
n
v
n
V
n
, v = d
1
v
1
+ d
2
v
2
+...+ d
n
v
n
V
n
, c
i
, d
i
R , ta đều có:
u+v = (c
1
v
1
+c
2
v
2
+...+c
n
v
n
) + .(d
1
v
1
+ d
2
v
2
+...+ d
n
v
n
)
= (c
1
v
1
+c
2
v
2
+...+c
n
v
n
) + (d
1
v
1
+d
2
v
2
+...+d
n
v
n
)
= (c
1
+d
1
)v
1
+(c
2
+d
2
)v
2
+...+(c
n
+d
n
)v
n
f(u+v) = f{(c
1
+d
1
)v
1
+(c
2
+d
2
)v
2
+...+(c
n
+d
n
)v
n
}
= (c
1
+d
1
)w
1
+(c
2
+d
2
)w
2
+...+(c
n
+d
n
)w
n
= (c
1
)w
1
+(c
2
)w
2
+...+(c
n
)w
n
+ (d
1
)w
1
+(d
2
)w
2
+...+(d
n
)w
n
= (c
1
w
1
+c
2
w
2
+...+c
n
w
n
) + (d
1
w
1
+d
2
w
2
+...+d
n
w
n
)
= f(u) + f(v).
- Tính duy nhất: Giả sử còn có thêm ánh xạ tuyến tính g: V
n
→ W thỏa mãn g(v
i
)
= w
i
; (i = 1..n). Khi đó với bất kì v =
1
v
1
+
2
v
2
+...+
n
v
n
V
n
, ta đều có:
g(v) = g(
1
v
1
+
2
v
2
+...+
n
v
n
) =
1
g(v
1
)+
2
g(v
2
)+...+
n
g(v
n
) =
1
w
1
+
2
w
2
+...+
n
w
n
=
f(v). Vậy, f(v) = g(v) v V
n
nên f = g, tức f là duy nhất.
Ví dụ 7. Cho ánh xạ tuyến tính T: [R]
3
→ [R]
2
, xác định bởi :
1
−
1
3
6
T
0
=
1
, T
1
=
−
2
, T
2
=
−
1
. Hãy tìm T(x), x =
1
.
2
1
−
1
2
1
−1
3
Gọi B =
0
,
1
,
2
là cơ sở gồm 3 vectơ mà giả thiết đã cho ảnh của nó qua T.
2
1
−1
Phân tích x theo các vectơ của B ta có :
6
1
−1
3
x =
1
= 2.
0
–1.
1
+1.
2
.
Do T là ánh xạ tuyến tính nên :
2
2
1
−
1
6
1
−
1
3
T(x) = T
1
= 2.T
0
– 1.T
1
+1.T
2
= 2.
1
–1.
−
2
+1.
−
1
=
3
.
2
2
1
−
1
102

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
II. NHÂN VÀ ẢNH CỦA ÁNH XẠ TUYẾN TINH
II. ẢNH VÀ NGHỊCH ẢNH CỦA KHÔNG GIAN CON
NHÂN VÀ ẢNH CỦA ÁNH XẠ TUYẾN TÍNH
1. ẢNH VÀ NGHỊCH ẢNH CỦA KHÔNG GIAN CON
Nhắc lại khái niệm ảnh và nghịch ảnh (hay tạo ảnh) của một tập qua ánh xạ như sau:
Giả sử f: X→ Y là ánh xạ bất kỳ từ tập X vào tập Y. Khi đó:
a)
Với E X thì tập f(E) = {y Y / y = f(x) với x E} được gọi là ảnh của tập E
qua ánh xạ f.
b)
Với F Y thì tập f
–1
(F) = {x X / f(x) F} được gọi là nghịch ảnh (hay tạo
ảnh) của tập F qua ánh xạ f.
Định lý 4. Cho ánh xạ tuyến tính f: V → W.
a)
Nếu E là không gian con của V thì f(E) là không gian con của W.
b)
Nếu S là tập sinh của E thì f
–
(S) là tập sinh của f(E).
c)
Nếu F là không gian con của W thì f
–1
(F) là không gian con của V.
Chứng minh.
a)
Giả sử E là không gian con của V, cần chứng minh f(E) là không gian con của
W. Thật vậy:
*) f(E) do 0
V
E f(0
V
) = 0
W
f(E).
*) Lấy bất kỳ w
1
, w
2
f(E) cần chứng minh (w
1
+w
2
) f(E) , R.
Do w
1
, w
2
f(E) nên tồn tại v
1
, v
2
E sao cho f(v
1
) = w
1
và f(v
2
) = w
2
.
Do f là ánh xạ tuyến tính nên có w
1
+w
2
= f(v
1
)+f(v
2
) = f(v
1
)+f(v
2
) =
f(v
1
+v
2
)
Do E là không gian con của V nên v
1
+v
2
E suy ra f(v
1
+v
2
) f(E), hay
(w
1
+w
2
) f(E).
b)
Giả sử S = {v
1
, ..., v
p
} là tập sinh của E và gọi f(S) = {f(v
1
), ..., f(v
p
)} thì hiển
nhiên f(S) f(E). Ta cần chứng minh f(E) = Sp{f(v
1
), ..., f(v
p
)}, tức là chứng minh mọi
vectơ thuộc f(E) đều là tổ hợp tuyến tính của các vectơ thuộc f(S) = {f(v
1
), ..., f(v
p
)}.
Thật vậy, bất kỳ w f(E) thì tồn tại vE sao cho w = f(v). Do v E = Sp{v
1
, ..., v
p
}
nên:
p
p
p
v =
i
v
i
f(v) =
f
i
v
i
=
i
f (v
i
)
.
i=1
p
i=1
i=1
Đẳng thức f
(
v
) =
i
f (v
i
)
i=1
chứng tỏ f(v) là tổ hợp tuyến tính của các vectơ thuộc f(S).
c)
Chứng minh tương tự a).
2. NHÂN VÀ ẢNH CỦA ÁNH XẠ TUYẾN TÍNH
Định nghiã 3. Cho ánh xạ tuyến tính f: V→ W.
a)
Tập hợp tất cảc vectơ vV sao cho f(v) = 0
W
được gọi là nhân của ánh xạ f, kí
hiệu bởi Kerf.
Kerf = {vV/ f(v) = 0
W
} = f
–1
(0
W
).
b)
Tập hợp f(V) gồm tất cả các ảnh của vV qua f, được gọi là ảnh của f, kí hiệu
bởi Imf.
Imf = {wW/ w = f(v), vV}.
103

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 5: ÁNH XẠ TUYẾN TÍNH
Định lý 5. Nếu ánh xạ f: V→ W là ánh xạ tuyến tính thì:
a)
Imf là không gian con của W.
b)
Kerf là không gian con của V.
Định lý là hệ qủa hiển nhiên của định lý 4 vừa nêu ở trên.
Ví dụ 8. Cho ánh xạ f : P
3
(x) → P
2
(x), f(a
0
1+a
1
x+a
2
x
2
+a
3
x
3
) = −a
0
1+ a
3
x
2
.
a)
Chứng minh rằng f là ánh xạ tuyến tính.
b)
Tìm Kerf và Imf.
Giải
a)
Với bất kỳ , R và bất kỳ p = a
0
1+a
1
x+a
2
x
2
+a
3
x
3
, q = b
0
1+b
1
x+b
2
x
2
+b
3
x
3
P
3
(x), ta có: f(p) = − a
0
1+ a
3
x
2
, f(q) = − b
0
1+ b
3
x
2
, p + q = (a
0
+b
0
)1+ (a
1
+b
1
) x
+ (a
2
+ b
2
) x
2
+ (a
3
+ b
3
) x
3
. Khi đó:
f(p + q) = −( a
0
+b
0
)1 + (a
3
+ b
3
)x
2
(do định nghiã ánh xạ f).
= (−a
0
1 +a
3
x
2
) + (−b
0
1 +b
3
x
2
) (do thực hiện phép toán trên P
2
(x)).
= (−a
0
1+ a
3
x
2
) + (− b
0
1+ b
3
x
2
) = f(p) + f(q).
Do f(p + q) = f(p) + f(q) nên f là ánh xạ tuyến tính.
b)
Tìm Kerf và Imf.
- Kerf = { p P
3
(x) / f(p) = O} = {p = a
0
1+a
1
x+a
2
x
2
+a
3
x
3
/ − a
0
1+ a
3
x
2
= O} =
{p = a
0
1+a
1
x+a
2
x
2
+a
3
x
3
/ a
0
= 0, a
3
= 0} = {p = a
1
x+a
2
x
2
, a
1
, a
2
R}= Sp{x, x
2
}.
- Im f = {p P
2
(x) / tồn tại r P
3
(x) để f(r) = p}.
Gọi p = b
0
1 + b
1
x + b
2
x
2
P
2
(x) và r = a
0
1+a
1
x+a
2
x
2
+a
3
x
3
P
3
(x) thì:
Phương trình f(r) = p có nghiệm đối với r.
Phương trình f(a
0
1+a
1
x+a
2
x
2
+a
3
x
3
) = b
0
1 + b
1
x + b
2
x
2
có nghiệm đối với a
0,
a
1
, a
2
, a
3
.
Phương trình −a
0
1 + a
3
x
2
= b
0
1 + b
1
x + b
2
x
2
có nghiệm đối với a
0,
a
1
, a
2
, a
3
.
−a
0
= b
0
Hệ phương trình
0 = b có nghiệm đối với các ẩn a
0,
a
1
, a
2
, a
3
.
1
b
1
= 0 .
a
3
= b
2
Imf = {q = b
0
.1+ b
2
x
2
, b
0
, b
2
R}= Sp{1, x
2
} là tập các đa thức chẵn, bậc không
quá 2.
Nhận xét
Có thể tìm Imf nhanh hơn nhờ áp dụng tính chất ánh xạ tuyến tính f sẽ biến tập sinh
của P
3
(x) thành tập sinh của Imf . Chọn tập sinh của P
3
(x) là {1, x, x
2
, x
3
} thì có:
Imf = Sp{f(1), f(x), f(x
2
), f(x
3
)} = Sp{–1, O, O, x
2
} = Sp{–1, x
2
}.
Ví dụ 9. Cho ánh xạ tuyến tính T: M(2,2) → M(2,2), T(A) = A − A
T
. Tìm tập sinh
của ImT và KerT.
Giải
- Tìm tập sinh của ImT bằng cách tìm ảnh của một tập sinh của M(2,2).
104

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0 0
0 0
1 0
0 1
0 0
0 0
0 0
0 0
1 0
1 0
0 0
1 0
0 1
0 1
0 0
0 0
1 0
c d
b d
b d
0 0
1 0
0 1
0 0 1 0 0 1
0 0 1 0 0 1
1
n
II. NHÂN VÀ ẢNH CỦA ÁNH XẠ TUYẾN TINH
Chọn tập sinh của M(2,2) là cơ sở chính tắc B = {E
11
=
1 0
; E
12
=
0 1
, E
21
=
0 0
, E
22
=
0 0
} thì ImT = Sp{T(B)}= Sp{T(E
11
), T(E
12
), T(E
21
), T(E
22
)}.
T(E
11
) = E
11
– E
11
T
=
1 0
–
1 0
=
0 0
.
T(E
12
) = E
12
– E
12
T
=
0 1
–
0 0
=
0 1
.
−
1 0
T(E ) = E
– E
T
=
0 0
–
0 1
=
0
−1
.
21 21 21
T(E
11
) = E
22
– E
22
T
=
0 0
–
0 0
=
0 0
.
Tập sinh của Im
T
là
S
=
0
0
,
0 1
,
0
−
1
- Tìm tập sinh của KerT
−
1 0
Có KerT = {A M(2,2) / A = A
T
} =
A
=
a
b
/
a b
=
a
c
=
c d
c d
b
d
A
=
a
b
/
c
=
b;
a,b,
d
R
=
A
=
a
b
,
a,b,
d
R
.
Lấy bất kỳ A KerT thì A =
a b
= a
1 0
+ b
0 1
+ d
0 0
KerT =
Sp
1
0
,
0
1
,
0
0
, hay tập sinh của Ker
T
là
1
0
,
0
1
,
0
0
.
Định lý 6. Nếu T: R
n
→ R
m
,[T(x)] = A[x] là ánh xạ ma trận ứng với ma trận A
M(m,n) thì:
a)
KerT = NulA.
b)
ImT = ColA.
Chứng minh
a)
Với x R
n
thì [T(x)] = A[x] nên KerT = {xR
n
/A[x] = O} = NulA.
b)
Có ImT = {yR
m
/ [y] = A[x], x R
n
} = {y R
m
/ [y] =
c A
= {y
R
m
/ [y
] =
x
i
.
c
i
A } = ColA.
i=1
x
1
x
n
x
1
x
1
+
2x
2
+
3x
3
Ví dụ 10. Cho ánh xạ T: [R]
3
→ [R]
3
, T
x
=
−x + x
.
2
2 3
a)
Chứng minh T là ánh xạ tuyến tính.
b)
Tìm KerT và ImT
x
3
x
1
+ x
2
+ 4x
3
105
c
n
A

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Giải
x
1
Chương 5: ÁNH XẠ TUYẾN TÍNH
x
1
+
2x
2
+
3x
3
1
2
3
a)
Với x =
x
ta có : T(x)
=
−x
2
+ x
3
= x
1
.
0
+
x
2
.
−
1
+ x
3
.
1
=
x
3
1 2
3
x
1
x
1
+ x
2
+ 4x
3
1
1
4
0
−
1
1
x
= Ax, chứng tỏ T là ánh xạ ma trận nên T là ánh xạ tuyến tính.
2
1
1
4
x
3
b)
Quy A về dạng rút gọn ta có:
1 2 3
1 2 3
1 2 3
1 0 5
0 −1 1
→
0 −1 1
→
0 −1 1
→
0 1 −1
.
1
1
4
0
−
1
1
0
0
0
0
0
0
−5t
−5
- KerT = NulA =
x =
t
,t R
= Sp
1
.
t
1
1
2
- ImT = ColA.= Sp{c
1
A, c
2
A} = Sp
0
,
−1
.
1
1
3. ÁNH XẠ ĐƠN CẤU, TOÀN CẤU VÀ ĐẲNG CẤU
Nhắc lại rằng:
a)
Ánh xạ f: V→ W được gọi là đơn ánh nếu 2 tạo ảnh khác nhau: v
1
v
2
thì 2 ảnh
tương ứng sẽ khác nhau: f(v
1
) f(v
2
) hay tương đương, nếu f(v
1
) = f(v
2
) thì v
1
= v
2
. Ánh
xạ đơn ánh f: V→ W còn gọi là ánh xạ 1–1 từ V vào W
b)
Ánh xạ f: V→ W được gọi là toàn ánh nếu f(V) = W.
c)
Ánh xạ vừa đơn ánh vừa toàn ánh được gọi là song ánh.
Định nghiã 4. Ánh xạ tuyến tính f: V→ W được gọi là ánh xạ đơn cấu (toàn cấu,
đẳng cấu) nếu f là đơn ánh (toàn ánh, song ánh).
Như vậy, f là đẳng cấu nếu nó vừa đơn cấu, vừa toàn cấu. Một đẳng cấu từ V lên
chính nó còn gọi là một tự đẳng cấu trên V.
Định lý 7. Cho ánh xạ tuyến tính f: V→ W. Khi đó:
a)
f là đơn cấu khi và chỉ khi Kerf = {O
V
}.
b)
f là toàn cấu khi và chỉ khi Imf = W.
Chứng minh
a)
Giả sử f là đơn cấu thì phương trình f(v) = O
W
có duy nhất một nghiệm. Mặt khác
do f(O
V
) = O
W
nên nghiệm duy nhất đó chính là O
V
, tức Kerf = {O
V
}. Ngược lại, nếu
có Kerf = O
V
ta cần chứng minh f đơn ánh. Thật vậy, lấy u, v V, giả sử f(u) = f(v)
f(u) − f(v) = O
W
f(u − v) = O
W
u − v Kerf = {O
V
} u − v = O
V
u = v f
là đơn ánh.
106
2

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
II. NHÂN VÀ ẢNH CỦA ÁNH XẠ TUYẾN TINH
b)
là hiển nhiên do định nghiã toàn ánh.
Định lý 8. Cho f: V → W là ánh xạ tuyến tính. Khi đó:
a)
f là đơn cấu khi và chỉ khi f biến bất kỳ tập độc lập tuyến tính trong V thành tập
độc lập tuyến tính trong W.
b)
f là toàn cấu khi và chỉ khi f biến tập sinh của V thành tập sinh của W.
c)
f là đẳng cấu khi và chỉ khi f biến cơ sở của V thành cơ sở của W.
Chứng minh
a)
Giả thiết f là đơn cấu và S = {v
1
, v
2
, ..., v
k
} là độc lập tuyến tính, cần chứng
minh tập {f(v
1
), f(v
2
), ..., f(v
k
)} độc lập tuyến tính. Thật vậy, do f là tuyến tính nên:
k k k
i
f(
v
i
)
= O
f(
i
v
i
)
= O
i
v
i
Kerf
i=1 i=1
k
i=1
Vì Kerf = {O}, (do f đơn cấu), nên phải có
k
i
v
i
= O
i
= 0, i = 1..k, (do
S
độc
i=1
lập tuyến tính). Vậy từ
i
f(
v
i
)
= O , suy ra được
i
= 0, i = 1..k, nên {f
(
v
1
),
f
(
v
2
),
i=1
..., f(v
k
)} là độc lập tuyến tính.
Ngược lại, giả sử f biến tập độc lập tuyến tính thành tập độc lập tuyến tính, cần
chứng minh f là đơn cấu, hay tương đương chứng minh Kerf = {O
V
}. Thật vật, nếu
Kerf {O
V
} thì sẽ vKerf, với v O
V
. Khi đó, tập gồm một phần tử {v} là tập độc lập
tuyến tính, kéo theo tập {f(v)} cũng độc lập tuyến tính, suy ra f(v) O
W
. Đó là điều vô
lí vì v Kerf thì phải có f(v) = {O
W
}. Mâu thuẫn đó chứng tỏ Kerf = {O
V
}.
b)
Gọi S là một tập sinh của V, tức V = Sp(S). Khi đó do f tuyến tính nên f(S) là tập
sinh của f(V), nghĩa là f(V) = Imf = Sp(f(S)). Với giả thiết f toàn ánh thì W = Imf, suy ra
W = Sp(f(S)), hay f(S) là một tập sinh của W.
Ngược lại, giả sử f biến S là tập sinh của V thành f(S) là tập sinh của W, tức là W =
Sp(f(S)), ta cần chứng minh f là toàn cấu, tức chứng minh f(V) = W. Thật vậy, do f là
tuyến tính nên f(S) là tập sinh của f(V), nghiã là f(V) = Sp(f(S) = W.
c)
là hệ qủa của a) và b).
Hệ quả: Nếu f: V → W là đơn cấu thì f sẽ biến cơ sở của V thành cơ sở của Imf.
107

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
0
1
Chương 5: ÁNH XẠ TUYẾN TÍNH
III. TÍNH ĐẲNG CẤU CỦA CÁC KHÔNG GIAN VÉC TƠ
VÀ HẠNG CỦA ÁNH XẠ TUYẾN TÍNH
1. TÍNH ĐẲNG CẤU CỦA CÁC KHÔNG GIAN VÉC TƠ
Định nghiã 5. Không gian véc tơ V được gọi là đẳng cấu với không gian véc tơ W
nếu tồn tại một ánh xạ đẳng cấu f: V→ W từ V vào W. Kí hiệu V W.
Từ định nghiã suy ra:
-
Nếu V W thì W V (nên ta gọi V và W là 2 không gian véc tơ đẳng cấu với
nhau).
-
Nếu U V, V W thì U W.
Nếu f: V→ W là ánh xạ đẳng cấu thì mỗi vectơ v V tương ứng duy nhất với vectơ
f(v) W và ngược lại. Hơn nữa do f là tuyến tính nên tổ hợp tuyến tính
1
v
1
+...+
p
v
p
của các vectơ {v
1
,..., v
p
} trong V tương ứng duy nhất với tổ hợp tuyến tính
1
f(v
1
)+...+
p
f(v
p
) của các vectơ {f(v
1
) ,..., f(v
p
)} trong W. Dẫn đến hai không gian véc
tơ đẳng cấu với nhau là đồng nhất với nhau về mặt cấu trúc đại số, cho dù bản chất phần
tử của mỗi không gian có thể khác nhau. Vì vậy một phương pháp giải toán có hiệu qủa
là, khi gặp bài toán cho trên không gian véc tơ không quen thuộc, ta hãy chuyển bài
toán đó về bài toán tương ứng trên không gian véc tơ quen thuộc, đẳng cấu với nó. Định
lý sau đây giúp ta phát hiện một lớp các không gian véc tơ đẳng cấu với không gian véc
tơ quen thuộc [R]
n
, nơi mà công cụ ma trận tỏ ra cực kì có hiệu quả.
Định lý 9. Nếu B = {v
1
, v
2
, ..., v
n
} là cơ sở của V
n
thì ánh xạ T
B
: V → [R]
n
, T
B
(v) =
[v]
B
đặt mỗi vectơ v V với B–tọa độ của nó, là một đẳng cấu từ V lên [R]
n
.
Ánh xạ đẳng cấu T
B
: V → [R]
n
, T
B
(v) = [v]
B
được gọi là đẳng cấu B– tọa độ.
Chứng minh
Xét ảnh của cơ sở B qua ánh xạ T
B
ta có:
1
0
0
1
0
T
B
(v
1
) =
= [e
1
], T
B
(v
2
) =
= [e
2
], ..., T
B
(v
n
) =
= [e
n
].
0
Chứng tỏ T
B
biến cơ sở B của V thành cơ sở chính tắc của [R]
n
nên T
B
là đẳng cấu.
Định lý 10.
a)
Mọi không gian véc tơ n chiều V
n
đều đẳng cấu với [R]
n
.
b)
Cần và đủ để 2 không gian véc tơ đẳng cấu là chúng có cùng số chiều.
Chứng minh
a)
Gọi B = {v
1
, v
2
, ..., v
n
} là cơ sở của V
n
thì với bất kỳ v V
n
, lập ánh xạ T
B
: V
n
→
[R]
n
, T
B
(v) = [v]
B
thì T
B
là đẳng cấu từ V
n
lên [R]
n
nên V
n
[R]
n
.
108

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
III. TÍNH ĐẲNG CẤU VÀ HẠNG CỦA ÁNH XẠ TUYẾN TINH
b)
Hiển nhiên, nếu hai không gian véc tơ đẳng cấu với nhau thì chúng phải có cùng
số chiều. Ngược lại, nếu hai không gian véc tơ có cùng số chiều là n 1, thì chúng cùng
đẳng cấu với [R]
n,
nên chúng đẳng cấu với nhau. Nếu hai không gian cùng số chiều
bằng 0 thì chúng là các không gian gồm chỉ 1 vectơ là vectơ không, đẳng cấu với nhau
là hiển nhiên.
Chú ý rằng, khi chứng minh mệnh đề b), ta không xét trường hợp số chiều của
không gian véc tơ là vô hạn, song mệnh đề vẫn đúng trong trường hợp này.
Ví dụ 11. Các không gian véc tơ sau là đẳng cấu với nhau nhờ các đẳng cấu tọa độ
tương ứng:[R]
n
R
n
; P
n
(x) R
n+1
; M(m, n) R
m.n
.
Ví dụ 12. Trong P
2
(x), hãy tìm cơ sở cho không gian con E sinh bởi tập các đa thức:
{p
1
= 2−3x+x
2
; p
2
= −4+5x+3x
2
; p
3
= −16+21x+7x
2
}.
Giải
Gọi B = {1, x, x
2
} là cơ sở chính tắc của P
2
(x) và T
B
: P
2
(x) → [R]
3
là đẳng cấu tọa
độ thì E Sp{[p
1
]
B
, [p
2
]
B
, [p
3
]
B
}. Cơ sở của E được tìm gián tiếp qua cơ sở của
Sp{[p
1
]
B
, [p
2
]
B
, [p
3
]
B
} như sau đây.
2
−4
−16
[p
1
]
B
= [x
2
−3x+2]
B
=
−3
, [p
2
]
B
= [3x
2
+5x−4]
B
=
5
, [p
3
]
B
= [7x
2
+21x−16]
B
=
21
1
3
7
Xét ma trận gồm các cột là các véc tơ B–toạ độ của p
1
, p
2
, p
3
:
2 −4 −16
1 3 7
1 3 7
[[p
1
]
B
[p
2
]
B
[p
3
]
B
] =
−3 5 21
→
0 14 42
→
0 1 3
= B
1 3 7
0 −10 −30
0 0 0
Từ ma trận bậc thang B, rút ra cơ sở của Sp{[p
1
]
B
, [p
2
]
B
, [p
3
]
B
} là {[p
1
]
B
, [p
2
]
B
}nên cơ
sở cho E là {p
1
= 2−3x+x
2
; p
2
= −4+5x+3x
2
}.
2. HẠNG CỦA ÁNH XẠ TUYẾN TÍNH
Định nghiã 6. Ta gọi hạng của ánh xạ tuyến tính f là số chiều của không gian ảnh
Imf. Kí hiệu: r(f) = dim(Imf).
Từ định nghĩa suy ra nếu f: R
n
→ R
m
, f(x) = A[x] là ánh xạ ma trận ứng với ma trận
A thì r(f) = r(A).
Định lý 11. (Định lý về hạng của ánh xạ tuyến tính) Nếu V
n
và W
m
là các không
gian véc tơ hữu hạn chiều và f: V
n
→ W
m
là ánh xạ tuyến tính thì:
r(f) + dim(Kerf) = dimV
n
= n.
Chứng minh. Trước hết, xét trường hợp Kerf {O}. Giả sử dim(Kerf) = k, (k 1) thì
trong Kerf tồn tại ít nhất một cơ sở gồm k véc tơ là B’ = {v
1
, v
2
, ..., v
k
}. Mở rộng cơ sở
của Kerf thành cơ sở của V
n
bằng cách thêm vào B’ tất cả (n−k) véc tơ: u
k+1
, u
k+2
, ..., u
n
V
n
để có:
B = {v
1
, v
2
, ..., v
k
, u
k+1
, u
k+2
, ..., u
n
}
Lấy bất kỳ w Imf thì tồn tại v V
n
sao cho w = f(v). Do v V
n
nên v biểu diễn được
qua cơ sở B với các hệ số c
i
như sau:
v = c
1
v
1
+ c
2
v
2
+...+ c
k
v
k
+ c
k+1
u
k+1
+ ... + c
n
u
n
109

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
c d
Lấy ảnh của v qua f ta có:
Chương 5: ÁNH XẠ TUYẾN TÍNH
w = f(v) = f(c
1
v
1
+ c
2
v
2
+ ... + c
k
v
k
+ c
k+1
u
k+1
+ ... + c
n
u
n
) = c
1
f(v
1
) + c
2
f(v
2
) +...+
c
k
f(v
k
) + c
k+1
f(u
k+1
) + ... + c
n
f(u
n
) = c
k+1
f(u
k+1
) +...+ c
n
f(u
n
), (do v
1
, v
2
, ..., v
k
Kerf
nên f(v
1
) = f(v
2
)... = f(v
k
) = O).
Bất kỳ w = f(v) Imf đều biểu thị tuyến tính được qua tập các véc tơ {f(u
k+1
), ...,
f(u
n
)}nên {f(u
k+1
), ..., f(u
n
)}là tập sinh của Imf. Ta chỉ cần kiểm tra thêm tính độc lập
tuyến tính của tập sinh này. Thật vật, xét một tổ hợp tuyến tính bất kỳ của vectơ O và
nhờ tính tuyến tính của f:
1
f(u
k+1
) + ... +
n–k
f(u
n
) = O f(
1
u
k+1
+ ...+
n–k
u
n
) = O (
1
u
k+1
+ ... +
n–
k
u
n
) Kerf . Biểu thị vectơ (
1
u
k+1
+ ... +
n–k
u
n
) Kerf qua cơ sở B’ của Kerf ta có:
1
u
k+1
+ ... +
n–k
u
n
=
1
v
1
+ ... +
k
v
k
1
v
1
+ ... +
k
v
k
−
1
u
k+1
− ... −
n–k
u
n
= O
(**). Do tính độc lập tuyến tính của B = {v
1
, v
2
, ..., v
k
, u
k+1
, u
k+2
, ..., u
n
} nên từ (**)
phải có
1
= ... =
k
= 0, nghĩa là tập {f(u
k+1
), ...,f(u
n
)} độc lập tuyến tính.
Như vậy, ta đã chứng tỏ được tập {f(u
k+1
), ...,f(u
n
)} gồm n−k vectơ là cơ sở của Imf
nên r(f) = dim(Imf) = n−k r(f) + dim(Kerf) = (n−k) + k = n = dimV
n
.
Trường hợp Kerf = {O} thì ánh xạ f là đơn cấu, biến cơ sở của V
n
thành cơ sở của
Imf. Do vậy, dimV = dim(Imf) và đẳng thức dim(Imf) + dimKerf = dimV
n
được thỏa
mãn.
Từ định lý về hạng của ánh xạ tuyến tính, trực tiếp suy ra được các hệ qủa sau:
Hệ qủa 1: Nếu f: V
n
→ W
m
là ánh xạ tuyến tính thì:
1. f là đơn cấu r(f) = n.
2. f là toàn cấu r(f) = m.
3. f là đẳng cấu r(f) = n = m.
a b
a
+
b
Ví dụ 13. Cho ánh xạ f: M(2,2) → [R]
3
, f
=
b + c
.
c d
a)
Chứng minh rằng f là ánh xạ tuyến tính.
c
+
d
b)
Tìm r(f), từ đó xác định f có là ánh xạ đơn cấu, toàn cấu không.
Giải
a)
Tự chứng minh.
b)
Tìm r(f)
- Kerf = {A M(2,2) / f(A) = O}.
a = −b
a b
a
+
b
0
a
+
b
=
0
c = −b
Gọi A =
thì f(A) = O
b
+
c
=
0
b + c = 0
c
+
d
0
c + d = 0
d = −c = b
b R
Ker
f =
A
=
−
b
b
,b
R
=
A
=
b.
−
1
1
,b
R
=
S
p
−
1
1
b
−b
1
−
1
1
−1
Dễ thấy
−
1
1
là độc lập tuyến tính nên nó là
cơ
sở
của
Kerf
dim
Ker
f = 1.
1 −1
- r(f) = dimM(2,2) – dimKerf = 4 – 1 = 3.
110

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
III. TÍNH ĐẲNG CẤU VÀ HẠNG CỦA ÁNH XẠ TUYẾN TINH
-
Do
K
e
r
f =
S
p
−
1
1
{O
}
nên f không là đơn cấu.
1 −1
-
Do r(f) = 3 = dim [R]
3
nên f là toàn cấu.
Trong trường hợp n = m, hệ qủa sau đây là kết quả trực tiếp của hệ qủa 1:
Hệ qủa 2: Nếu f: V
n
→ W
n
là ánh xạ tuyến tính giữa hai không gian có số chiều
bằng nhau thì các phát biểu sau là tương đương:
a)
f là đơn cấu.
b)
f là toàn cấu.
c)
f là đẳng cấu.
Đặc biệt, đối với phép biến đổi tuyến tính f: V
n
→ V
n
, các tính đơn cấu, toàn cấu và
đẳng cấu là luôn đồng thời xẩy ra.
Hệ qủa 3: Cho f: V
n
→ W
m
là ánh xạ tuyến tính. Khi đó thì:
a)
Nếu n < m thì f không thể là toàn cấu.
b)
Nếu n > m thì f không thể là đơn cấu.
c)
Nếu n = m thì f là toàn cấu khi và chỉ khi f là đơn cấu.
Thật vậy:
a)
Do r(f) + dim(Kerf) = n nên r(f) n. Nếu n < m thì r(f) = dim(Imf) < m = dimW
m
,
chứng tỏ Imf là không gian con thực sự của W
m
, f không thể là toàn cấu.
b)
Vì Imf là không gian con của W
m
nên r(f) m. Nếu n > m thì dimKerf = n – r(f) >
0, f không thể là đơn cấu.
c)
Nếu f là toàn cấu thì r(f) = m = n nên dimKerf = 0, f là đơn cấu. Ngược lại, f là
đơn cấu thì dimKerf = 0 r(f) = n = m nên Imf = W
m
, f là toàn cấu. .
111

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 5: ÁNH XẠ TUYẾN TÍNH
IV. BIỂU DIỄN MA TRẬN CỦA ÁNH XẠ TUYẾN TÍNH
1. MA TRẬN CỦA ÁNH XẠ TUYẾN TÍNH ĐỐI VỚI CẶP CƠ SỞ
Trong phần trước ta đã đưa ra khái niệm ma trận chính tắc của ánh xạ tuyến tính T:
R
n
→R
m
, đó là ma trận A = [[T(e
1
)] [T(e
2
)] ... [T(e
n
)]] M(m,n). Mỗi ánh xạ tuyến
tính từ R
n
vào R
m
đều được xác định duy nhất bởi ma trận chính tắc A của nó và ngược
lại, nghĩa là đã có sự tương ứng 1–1 giữa tập các ánh xạ tuyến tính T: R
n
→ R
m
với tập
các ma trận A M(m,n). Nhằm tổng quát hóa tính chất vừa nêu trên, mục này ta sẽ xét
xem có hay không một tương ứng 1–1 giữa tập các ánh xạ tuyến tính f: V
n
→ W
m
từ
không gian véc tơ n chiều V
n
vào không gian véc tơ m chiều W
m
với tập các ma trận A
M(m,n).
Định lý 12. Cho B = {v
1
, v
2
,..., v
n
} là cơ sở của V
n
và C = {w
1
, w
2
, ..., w
m
} là cơ sở
của W
m
. Khi đó:
a)
Với mỗi ánh xạ tuyến tính f: V
n
→ W
m
luôn tồn tại duy nhất một ma trận A
M(m,n) sao cho:
[f(v)]
C
= A[v]
B
v V
n
(1)
b)
Ngược lại, với mỗi ma trận A M(m,n), luôn tồn tại ánh xạ tuyến tính f: V
n
→
W
m
biến véc tơ v V
n
thành véc tơ f(v) W
m
sao cho (1) thỏa mãn.
Chứng minh
a)
Chứng minh sự tồn tại của ma trận A.
1
Lấy bất kỳ vV
n
, gọi [v]
B
=
v =
1
v
1
+...+
n
v
n
. Do f tuyến tính, ta có:
n
f(v) = f(
1
v
1
+...+
n
v
n
) =
1
f(v
1
) +...+
n
f(v
n
).
Lấy C–tọa độ vào 2 vế:
[f(v)]
C
= [
1
f(v
1
) +...+
n
f(v
n
)]
C
=
1
[f(v
1
)]
C
+ ...+
n
[f(v
n
)]
C
1
= [[f(v
1
)]
C
... [f(v
n
)]
C
].
= A.[v]
B
với A = [[f(v
1
)]
C
... [f(v
n
)]
C
]
n
Sự tồn tại của ma trận A thỏa (1) đã được chứng minh.
Chứng minh tính duy nhất của A.
Giả sử tồn tại ma trận B thỏa mãn [f(v)]
C
= B[v]
B
v V
n
thì do (1) và do tính chất
duy nhất của [f(v)]
C
mà có A[v]
B
= B[v]
B
, [v]
B
[R]
n
. Suy ra A = B.
b)
Giả sử cho ma trận A = [a
ij
] M(m,n), cần chứng minh tồn tại ánh xạ tuyến tính
f: V
n
→ W
m
sao cho (1) thỏa mãn. Muốn vậy, trong W
m
lấy n véc tơ:
a
11
w’
1
= a
11
w
1
+ a
21
w
2
+. ..+ a
m1
w
m
tức [w
1
]
C
=
a
m1
112

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
IV. BIỂU DIỄN MA TRẬN CỦA ÁNH XẠ TUYẾN TINH
a
12
w’
2
= a
12
w
1
+ a
22
w
2
+. ..+ a
m2
w
m
tức [w’
2
]
C
=
.
a
m
2
⁝
a
1n
w’
n
= a
1n
w
1
+ a
2n
w
2
+. ..+ a
mn
w
m
tức [w’
n
]
C
=
.
a
mn
Khi đó, theo định lí về sự xác định của ánh xạ tuyến tính thì sẽ tồn tại (và duy nhất)
ánh xạ tuyến tính f: V
n
→ W
m
sao cho f(v
i
) = w’
i
i = 1..n và hiển nhiên (1) được thỏa
mãn vì với mọi v V
n
ta có:
[f(v)]
C
= [
1
f(v
1
) +
2
f(v
2
) +...+
n
f(v
n
)]
C
=
1
[f(v
1
)]
C
+
2
[f(v
2
)]
C
+...+
n
[f(v
n
)]
C
=
1
[w’
1
]
C
+
2
[w’
2
]
C
+...+
n
[w’
n
]
C
a
11
a
12
a
1n
a
11
a
1n
1
=
1
.
+
1
+ ... +
n
=
= A[v]
B
.
a
m1
a
m
2
a
mn
a
m1
a
mn
n
Nhờ sự tồn tại và duy nhất của ma trận A vừa nêu mà ta có khái niệm ma trận của
ánh xạ tuyến tính đối với cặp cơ sở như sau đây:
Định nghiã 7. Cho V
n
, W
m
là các không gian véc tơ lần lượt có cơ sở B = {v
1
,..., v
n
}
và C = {w
1
,..., w
m
} và f: V
n
→ W
m
là ánh xạ tuyến tính thì ma trận:
[[f(v
1
)]
C
[f(v
2
)]
C
. .. [f(v
n
)]
C
]. (2)
được gọi là ma trận biểu diễn (hay gọi tắt là ma trận) của ánh xạ tuyến tính f đối với
cặp cơ sở B và C.
Kí hiệu:
[f]
B,C
= [[f(v
1
)]
C
[f(v
2
)]
C .....
[f(v
n
)]
C
].
Đặc biệt khi V
n
W
m
, ánh xạ tuyến tính f:V
n
→ V
n
trở thành phép biến đổi tuyến
tính. Khi đó, chọn hai cơ sở B và C là trùng nhau thì ma trận A ở (2) có dạng:
[[f(v
1
)]
B
[f(v
2
)]
B
...[f(v
n
)]
B
] (3)
Theo định nghiã thì ma trận ở (3) có tên gọi là ma trận của ánh xạ tuyến tính f đối
với cặp cơ sở (B, B). Để cho gọn, ta có định nghiã sau đây:
Định nghiã 8. Cho T: V
n
→ V
n
là phép biến đổi tuyến tính từ không gian véc tơ n
chiều V
n
vào chính nó. Với bất kỳ cơ sở B = {v
1
,. . , v
n
} của V
n
, ma trận:
[T]
B
= [[T(v
1
)]
B
[T(v
2
)]
B
.
.. [T(v
n
)]
B
] (4)
được gọi là ma trận của phép biến đổi tuyến tính T đối với cơ sở B hay B− ma trận của
T.
Hiển nhiên khi cho biết ma trận [T]
B
của T đối với cơ sở B nào đó thì B –tọa độ của
véc tơ ảnh T(v), vV
n
được tính theo công thức suy ra từ (1):
[T(v)]
B
= [T]
B
[v]
B
(5).
113

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
3
9
27
Chương 5: ÁNH XẠ TUYẾN TÍNH
p(−3)
Ví dụ 14. Cho f: P
3
(x) → [R]
4
p(−1)
xác định bởi f(p) = , p P
3
(x).
p(1)
p(3)
a)
Chứng minh rằng f là ánh xạ tuyến tính.
b)
Tìm [f]
B,
E
với B = {1, x, x
2
, x
3
} và E = {[e
1
], [e
2
], [e
3
], [e
4
]} là cơ sở chính tắc
của P
3
(x) và [R]
4
.
Giải
p(−3)
p(−1)
q(−3)
q(−1)
a) , R, p, q P
3
(x) ta có: f(p) =
, f(q) =
và
(p + q)(−3)
(p + q)(−1)
f(p+q) =
p(1)
p(3)
.p(−3) + .q(−3)
.p(−1) + .q(−1)
=
q(1)
q(3)
.p(−3)
.q(−3)
.p(−1)
.q(−1)
= +
(p + q)(1)
(p + q)(3)
.p(1) + .q(1)
.p(3) + .q(3)
.p(1)
.q(1)
.p(3)
.q(3)
p
(
−
3)
p(−1)
q(−3)
q(−1)
= .
+.
= .f(p)+ .f(q). Suy ra f là ánh xạ tuyến tính.
p(1)
p(3)
q(1)
q(3)
b) Có: [f]
B,E
= [[f(1)]
E
[f(x)]
E
[f(x
2
)]
E
[f(x
3
)
E
]].
Tính được:
1
1
−3
−1
2
9
2
1
[f(1)]
E
= f(1) =
, [f(x)]
E
= f(x) =
; [f(
x
)]
E
= f(
x
) =
;
1
1
1
1
27
3 3
1
1 −3 9 27
1 −1 1 1
[f(x )]
E
= f(x ) =
1
[f]
B,E
=
.
Ví dụ 15. Gọi D là phép lấy đạo hàm và xét D: P
2
(x) → P
2
(x), D(p) = p’. Hãy tìm
ma trận của D đối với cơ sở B = {1, 1+2x, 1+x
2
}, rồi áp dụng ma trận đó để tìm sự phân
tích đạo hàm của q = −2 − 4x + x
2
thành tổ hợp tuyến tính của các vectơ trong B.
Giải
0
2
Có: D(1) = 0 [D(1)]
B
=
0
; D(1+2
x
) =
2
[D(1+2
x
)]
B
=
0
; D(
1
+
x
2
) = 2
x
0
0
114
1
1
1
1
1
3
9
27

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
IV. BIỂU DIỄN MA TRẬN CỦA ÁNH XẠ TUYẾN TINH
−1
0 2
−1
[D(1+x
2
)]
B
=
1
[D]
B
=
0
0 1
.
0
0
0
0
Phân tích q’= D(q) thành tổ hợp tuyến tính của các vectơ trong B:
Áp dụng công thức (5) ta có:
0 2 −1
−1
−5
[q’]
B
= [D(q)]
B
= [D]
B
[q]
B
=
0 0
1
.
−
2
=
1
q’= −5.1 + 1.(1+2x) +0.(1+x
2
).
0
0
0
1
0
Định lý 13. Cho V
n
, W
m
thứ tự là các không gian hữu hạn chiều, có cơ sở tương ứng
là B, C và f: V
n
→ W
m
là ánh xạ tuyến tính thì:
a) dimKerf = dimNul([f]
B
,C
).
b) r(f) = r(([f]
B
,C
)
Chứng minh. Trước hết ta chỉ ra T
B
(Kerf) = Nul([f]
BC
).
Gọi B , C là cơ sở của V , W và T
B
: V
n
→ [R]
n
, T
B
(v) = [v]
B
là đẳng cấu B –toạ độ
thì:
T
B
(Kerf) = {T
B
(v) / v Kerf } = {[v]
B
/ f(v) = O
W
, v V
n
}, (do định nghiã Kerf)
= {[v]
B
/[f(v)]
C
= O, v V
n
}, (do [f(v)]
C
= 0 f(v) = 0)
= {[v]
B
/ [f]
BC
. [v]
B
= O, v V
n
}, (do công thức (1)).
= {[x] = [v]
B
[R]
n
/ [f]
BC
.[x] = O}, (do T
B
là đẳng cấu tọa độ nên [R]
n
=
T
B
(V
n
)).
= Nul([f]
BC
), (do định nghiã không gian triệt của ma trận)
a)
Do T
B
(Kerf) = Nul([f]
B,C
) và T
B
là đẳng cấu Kerf Nul([f]
BC
) dimKerf =
dimNul([f]
B,C
).
b)
Do định lý về hạng của ánh xạ tuyến tính:
r(f) = n – dimKerf
= n − dimNul([f]
B,C
).
= r([f]
B,C
).
Nhờ áp dụng kết quả cho bởi định lý vừa nêu mà ta có thể xét tính đơn cấu, toàn cấu
và đẳng cấu của ánh xạ f: V
n
→ W
m
nhờ xét hạng của ma trận [f]
B,C
, cụ thể là:
Hệ quả. Cho f: V
n
→ W
m
là ánh xạ tuyến tính và V
n
, W
m
có cơ sở tương ứng là B, C
thì:
a) f đơn cấu r([f]
B
C
) = n.
a)
f toàn cấu r([f]
B
C
) = m.
b)
f đẳng cấu r([f]
B
C
) = n = m.
2. MA TRẬN BIỂU DIỄN CỦA ÁNH XẠ TỔNG, ÁNH XẠ TÍCH VÀ ÁNH
XẠ NGƯỢC.
Trước hết, ta xét các tính chất của ánh xạ tổng, tích và ánh xạ ngược của ánh xạ
tuyến tính cho bởi định lí sau:
Định lý 14.
115

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 5: ÁNH XẠ TUYẾN TÍNH
a)
Tổng của hai ánh xạ tuyến tính là ánh xạ tuyến tính.
b)
Tích của ánh xạ tuyến tính với một vô hướng là ánh xạ tuyến tính.
c)
Tích của hai ánh xạ tuyến tính cũng là ánh xạ tuyến tính.
d)
Ánh xạ ngược (nếu có) của ánh xạ tuyến tính cũng là ánh xạ tuyến tính.
Chứng minh
a)
Giả sử V, W là các không gian véc tơ còn f: V → W, g: V → W là các ánh xạ
tuyến tính thì ánh xạ tổng f+g: V → W, (f+g)(v) = f(v) + g(v). Lấy bất kỳ v
1
, v
2
V; bất
kỳ , R, ta có:
(f+g)(v
1
+v
2
) = f(v
1
+v
2
) + g(v
1
+v
2
) (do định nghĩa ánh xạ tổng)
= {f(v
1
)+f(v
2
)}+{g(v
1
)+g(v
2
)} (do tính tuyến tính của f và g)
= {f(v
1
)+g(v
1
)}+{f(v
2
)+g(v
2
)} = .(f+g)(v
1
)+.(f+g)(v
2
)
Chứng tỏ f +g là ánh xạ tuyến tính.
b)
và c) được chứng minhtương tự a) .
d) Giả sử ánh xạ tuyến tính f: V→W là song ánh thì có ánh xạ ngược f
–1
: W → V,
xác định bởi f
–1
(w) = v f(v) = w. Cần chứng minh f
–1
cũng là ánh xạ tuyến tính. Thật
vậy, lấy bất kỳ w
1
, w
2
W = f(V), và gọi v
1
= f
–1
(w
1
) V, v
2
= f
–1
(w
2
) V. Do định
nghiã ánh xạ ngược, có f(v
1
) = w
1
, f(v
2
) = w
2
. Khi đó: w
1
+w
2
= f(v
1
)+f(v
2
) = f(v
1
+v
2
)
v
1
+v
2
= f
–
1
(w
1
+w
2
). Vậy có f
–1
(v
1
+ v
2
) = v
1
+v
2
= f
–
1
(w
1
) + f
–1
(w
2
): f
–1
bảo toàn phép
cộng trên W.
Với R ta cũng có w
1
= f(v
1
) = f(v
1
) v
1
= f
–
1
(w
1
). Vậy có f
–
1
(w
1
) =
v
1
= f
–
1
(w
1
): f
–1
bảo toàn phép nhân với vô hướng.
Nhận xét. Do các mệnh đề a), b) của định lí, suy ra tập tất cả các ánh xạ tuyến tính
từ V vào W lập thành không gian véc tơ đối với phép cộng và phép nhân ánh xạ với một
vô hướng, kí hiệu là L(V,W).
L(V,W) = {f : V → W / f là ánh xạ tuyến tính}
Định lý 15. Cho V, W thứ tự là các không gian hữu hạn chiều, có cơ sở tương ứng
là B, C ; còn f, g L(V,W). Khi đó:
a)
[f+g]
B
,C
= [ f]
B
,C
+[g]
B
,C
b) [ f]
B
,C
= [ f]
B
,C
.
Chứng minh. Tự chứng minh như bài tập.
Định lý 16. Cho U, V, W là các không gian véc tơ hữu hạn chiều với cơ sở tương
ứng là B, C, D. và f L(U,V), g L(V,W) là các ánh xạ tuyến tính thì:
[g
o
f]
B,
D
= [g]
C,
D
.[f]
B,
C
Đặc biệt khi U = V = W thì: [g
o
f]
B
= [g]
B
.[f]
B
Chứng minh. Với u U thì:
[(g
o
f)(u)]
D
= [g(f(u))]
D
= [g]
C,D
[f(u)]
C
= [g]
C,D
([f]
B,C
.[u]
B
) = ([g]
C,D
[f]
B,C
)[u]
B
.
[g]
C,D
[f]
B,C
= [g
o
f]
B,D
.
Ví dụ 16. Cho D:P
3
(x) → P
3
(x), D(p) = p’là ánh xạ đạo hàm (nên là phép biến đổi
tuyến tính) trên P
3
(x). Gọi B = {1, x, x
2
, x
3
} là cơ sở chính tắc của P
3
(x). Hãy:
a)
Tìm ma trận của D
2
= D
o
D đối với cơ sở B.
116

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
0
0
0
0
B
B
IV. BIỂU DIỄN MA TRẬN CỦA ÁNH XẠ TUYẾN TINH
b)
Chứng minh rằng [D
4
]
B
= 0.
a) Có [D]
B
= [[D(1)]
B
[D(x)]
B
[D(x
2
)]
B
[D(x
3
)]
B
]. Tính được:
0
0
1
0
2 2
[D(1)]
B
= [(1)’]
B
=
0
; [D(x)]
B
= [(x)’]
B
= [1]
B
=
0
0
;
[D(
x
)]
B
=
[(
x
)’]
B
= [2
x
]
=
0
2
3 3 2
0
; [D(
x
)]
B
= [(
x
)’]
B
= [3
x
]
B
=
.
0
0 1 0 0
0 0 2 0
3
2
0 1 0 0
2
2
0 0 2 0
0 0 2 0
0 0 0 6
[D]
B
=
0 0 0 3
0 0 0 0
[D ]
B
= ([D]
B
)
=
0 0 0 3
0 0 0 0
=
0 0 0 0
0 0 0 0
b) Có [D]
B
4
là ma trận đối với cơ sở B của ánh xạ tích D
4
vì [D
4
]
B
= [D]
4
Với bất kỳ p P
3
(x) ta có:
D
4
(p) = D
3
(D(p)) = D
3
(p’) = D
2
(D(p’)) = D
2
(p’’) = D(D(p’’)) = D(p’’’) = p
(4)
= 0.
D
4
là ánh xạ không nên ma trận của nó đối với cơ sở bất kỳ là ma trận không, hay
[D]
4
= 0.
Định lý 17. Cho V, W là các không gian véc tơ n chiều với các cơ sở tương ứng B,
C và f L(V,W), thì:
a) f là đẳng cấu khi và chỉ khi [f]
B
,
C
là ma trận khả nghịch.
b) Hơn nữa, [f
–1
]
C
,
B
= ( [f]
B
,
C
)
–1
.
Chứng minh
a)
Ma trận [f]
B
,
C
có tập các cột là tập các vectơ C–tọa độ của các vectơ là ảnh qua f
của các vectơ thuộc cơ sở B. Do ánh xạ tọa độ và ánh xạ f đều là các đẳng cấu nên tập
các cột của ma trận [f]
B
,
C
là độc lập tuyến tính trong [R]
n
, vì vậy nó khả nghịch.
b)
Với w W, gọi f
–1
(w) = v V thì f(v) = w [f(v)]
C
= [w]
C
= [f]
B
,
C
.[v]
B
.
Nhân trái 2 vế với [f]
B
,
C
)
–1
thì có [v]
B
= ([f]
B
,
C
)
–1
.[w]
C
( [f]
B,C
)
–1
= [f
–1
]
C,B
.
Ví dụ 17. Cho ánh xạ tuyến tính f: P
2
(x) → P
2
(x), f(p) = p’+2p.
1) Chứng minh rằng f là đẳng cấu.
2) Cho p = 1+2x+4x
2
, tìm q = f
–1
(p).
Giải
1) Gọi B = {1, x, x
2
} là cơ sở chính tắc của P
2
(x) thì [f]
B
= [[f(1)]
B
[f(x)]
B
[f(x
2
)]
B
].
2
1
0
[f(1)]
B
= [0+2.1]
B
=
0
, [f(
x
)]
B
= [
1
+2
x
]
B
=
2
, [f(
x
2
)]
B
= [2
x
+2.
x
2
]
B
=
2
.
0
0
2
117

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
Chương 5: ÁNH XẠ TUYẾN TÍNH
2 1 0
[f]
B
=
0 2 2
. Dễ thấy [f]
B
là khả nghịch (do det[f]
B
= 8 0) nên f là đẳng cấu.
0
0
2
2) Tìm q = f
–1
(p).
2 1 0
−
1
1
2 −1 1
1
Có [q]
B
= [f
–1
(p)]
B
= [f
–1
]
B
[p]
B
= [f]
B
–1
[p]
B
=
0 2 2
.
2
=
1
0 2
−
2
.
2
4
=
1
−4
1
=
−1
q = 1 – x + 2x
2
.
0
0
2
4
4
0 0 2
4
4
8
2
(Dễ kiểm tra lại f(q) = q’+2q = −1+4x + 2(1 – x + 2x
2
) = 1+2x + 4x
2
= p).
3. MA TRẬN CỦA ÁNH XẠ TUYẾN TÍNH ĐỐI VỚI CÁC CẶP CƠ SỞ
KHÁC NHAU
Cho V
n
và W
m
là các không gian véc tơ hữu hạn chiều. Giả sử trong V
n
có cơ sở B
= {v
i
; i = 1..n}, chọn thêm cơ sở mới B‘ = {v
i
’; i = 1..n} và ma trận chuyển tọa độ từ B
sang B’ là P
B,B'
= [[v
1
]
B'
[v
2
]
B'
... [v
n
]
B'
]. Trong W
m
, có cơ sở C = {w
i
; i = 1..m}, chọn
thêm cơ sở mới C’ = {w
i
’; i = 1..m} và ma trận chuyển tọa độ từ C sang C’ là P
C,C’
=
[[w
1
]
C’
[w
2
]
C’
... [w
m
]
C’
]. Gọi A = [f]
B,C
, A’ = [f]
B’,
C’
thứ tự là ma trận của f đối với các
cặp cơ sở (B,C) và (B‘,C‘). Cần tìm quan hệ giữa A’ với A.
Lấy bất kỳ vV
n
thì: [f(v)]
C‘
= A’[v]
B
‘
= A’(P
B,
B
‘
[v]
B
) = (A’P
B,
B
‘
)[v]
B
(*).
Mặt khác ta lại có: [f(v)]
C‘
= P
C,C‘
[f(v)]
C
= P
C,C’
(A[v]
B
) = (P
C,C’
A)[v]
B
(**).
Từ (*) và (**) ta có: (A’P
B,
B
‘
)[v]
B
= (P
C,C’
A)[v]
B
[v]
B
[R]
n
, suy ra: A’P
B,
B
‘
= P
C,C’
A
,
hay:
A’= P
C,C’
A (P
B, B ‘
)
–1
[f]
B’, C’
= P
C,C’
.[f]
B,C
.(P
B, B ‘
)
–1
(5).
(5) chính là mối quan hệ cần tìm.
Đặc biệt nếu T: V
n
→ V
n
là phép biến đổi tuyến tính còn B, C là 2 cơ sở nào đó
của V
n
thì có:
[T]
C
= P
B,C
[T]
B
(P
B,C
)
–1
(6)
Ví dụ 18. Cho ánh xạ tuyến tính f : R
3
→ R
2
, f(x
1
; x
2
; x
3
) = (x
1
–2x
2
+3x
3
; 2x
1
+x
2
–x
3
)
và các cơ sở B = {(0 ; 0 ; 1), (0 ; 1 ; 1), (1 ; 1 ; 1), C = (1 ; 1), (–1 ; 1). Tìm [f]
B,C
bằng
các cách khác nhau.
Giải
Cách 1. Áp dụng định nghiã
[f]
B,C
= [[f(0 ; 0 ; 1)]
C
[f(0 ; 1 ; 1)]
C
[f(1 ; 1 ; 1)]
C
] = [[(3 ; –1)]
C
[(1, 0)]
C
[(2 ;
2)]
C
].
Thay vì tìm riêng lẻ từng cột trong ma trận [f]
B,C
ta có thể tìm chúng đồng thời nhờ
giải hệ tuyến tính bằng phương pháp Gauss như sau:
Lập ma trận khối có khối trái là cột các vec tơ của C, khối phải là vec tơ cột của ảnh
qua f của các vectơ thuộc cơ sở B:
1
−
1
3 1 2
→
1
−
1
3 1 2
→
1 −1
3 1 2
1 1
−
1 0 2
1 1
−
1 0 2
0 2
−
4
−
1 0
118

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
IV. BIỂU DIỄN MA TRẬN CỦA ÁNH XẠ TUYẾN TINH
→
1 0
1
1/ 2
2
[f]
=
1 1/ 2 2
cần tìm.
0 1
−
2
−1/ 2
0
B,C
−
2
−1/ 2
0
Cách 2. Áp dụng công thức (5): Gọi B
0
, C
0
lần lượt là cơ sở chính tắc của R
3
và R
2
thì:
[f]
B, C
= P
C0,C
.[f]
B0,C0
.(P
B0,B
)
–1
= (P
C, C0
)
–1
[f]
B0,C0
.P
B,B0
1
−
1
−
1
1
−2 3
0 0 1
1
1 1
3 1 2
1
2 1 4
=
0 1 1
=
=
1 1
2 1
−1
1 1
1
2
−
1 1
−
1 0 2
2
−
4
−
1 0
4. PHÉP BIẾN ĐỔI TUYẾN TÍNH VÀ SỰ ĐỒNG DẠNG CỦA CÁC MA
TRẬN BIỂU DIỄN
Định nghiã 9. Cho A, B M(n,n), ma trận A được gọi là đồng dạng với ma trận B
nếu tồn tại ma trận khả nghịch P sao cho B = P
–1
AP, kí hiệu A B.
Từ định nghiã ruy ra:
Nếu A B thì B A. (vì A B B = P
–1
AP A = PBP
–1
= (P
–1
)
–1
BP
–1
B
A).
Nếu A B và B C thì A C. Thật vậy, do A B B = P
–1
AP, do B C nên
C = Q
–1
BQ = Q
–1
(P
–1
AP) Q = (Q
–1
P
–1
)A(PQ) = (PQ)
–1
A(PQ) A C.
Định lý 18. Cho V
n
là không gian véc tơ n chiều.
a)
Nếu T: V
n
→ V
n
là phép biến đổi tuyến tính thì ma trận của T đối với hai cơ sở
nào đó trong V
n
là hai ma trận đồng dạng.
b)
Ngược lại, hai ma trận vuông cấp n đồng dạng cho trước sẽ là hai ma trận biểu
diễn của phép biến đổi tuyến tính T đối với hai cơ sở trong V
n
.
Chứng minh
a)
Gọi B, C là hai cơ sở bất kỳ của V
n
thì [T]
B
và [T]
C
là 2 ma trận vuông cấp n,
thoả mãn:
[T]
C
= P
B,C
[T]
B
(P
B,C
)
–1
= (P
C,
B
)
–1
[T]
B
P
B,C
[T]
B
[T]
C
.
b)
Ngược lại, giả sử cho A = [a
ij
] M(n,n), A’ M(n,n) và A A’. Gọi B = {v
1
, v
2,
..., v
n
} là 1 cơ sở nào đó của V
n
. Giả sử T: V
n
→ V
n
là ánh xạ tuyến tính xác định bởi
ảnh của các vectơ thuộc cơ sở B: T(v
i
) = a
1i
v
1
+ a
2i
v
2
+ ...+ a
ni
v
n
. với mọi i = 1..n. Dễ
thấy [T]
B
= A. Do A’ A nên tồn tại ma trận vuông P cấp n, khả nghịch sao cho A’ = P
–
1
AP. Gọi C là cơ sở thu được do thực hiện phép chuyển cơ sở xác định bởi ma trận
chuyển tọa độ P
B,C
= P
–1
. Khi đó ma trận của T đối với cơ sở C sẽ là:
[T]
C
= P
B,C
[T]
B
(P
B,C
)
–1
= P
–1
A (P
–1
)
–1
= P
–1
AP = A’.
Như vậy, A, A’ là ma trận của chính ánh xạ tuyến tính T đối với 2 cơ sở B và C trong
V
n
.
Chú ý. Trong thực hành, việc tìm ma trận [T]
C
khi biết ma trận của nó đối với cơ
sở cũ [T]
B
nhờ công thức [T]
C
= P
B,C
[T]
B
(P
B,C
)
–1
đôi khi khá cồng kềnh do phải tìm
119

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
→
Chương 5: ÁNH XẠ TUYẾN TÍNH
(P
B,C
)
–1
. Để tránh tình trạng đó, ta có thể tính [T]
C
mà không cần phải tìm ma trận
nghịch đảo (P
B,C
)
–1
, nhờ thực hiện phép rút gọn hàng trên ma trận như sau:
Trước hết, gọi P = (P
B,C
)
–1
= P
C,
B
, A = [T]
B
. thì [T]
C
= P
–1
AP P[T]
C
= AP chứng
tỏ [T]
C
là nghiệm của hệ tuyến tính có ma trận đầy đủ A
*
= [P|AP]. Áp dụng phương
pháp Gauss như sau:
-
Tính tích AP = [T]
B
P
C,
B
rồi lập ma trận khối A
*
= [P|AP].
-
Dùng phép toán hàng quy khối bên trái về ma trận đơn vị I:
[ P| AP ] → ... → [ I| P
–1
AP ]
-
Khối bên phải của ma trận thu được sẽ là ma trận [T]
C
= P
–1
AP cần tìm.
Ví dụ 19. Cho T: R
3
→ R
3
, T(x
1
; x
2
; x
3
) = (x
1
+x
2
+x
3
; x
1
+x
2
; x
3
). Tìm ma trận của T
đối với cơ sở B = {(1; 1; 0), (1; 0; 1), (0; 1; 1)}.
Giải
Gọi E={e
1
= (1 ; 0 ; 0), e
2
= (0 ; 1 ; 0), e
3
= (0 ; 0 ; 1)} là cơ sở chính tắc của R
3
thì ta
có ngay: [T]
B
= P
E,B
[T]
E
(P
E,B
)
–1
= (P
B,E
)
–1
[T]
E
(P
B,E
) (P
B,E
) [T]
B
= [T]
E
(P
B,E
)
Lập ma trận khối (tương tự lập ma khối A* trong phương pháp Gauss):
[[T]
E
.P
B,E
| P
B,E
]
Có [T]
E
=
2 2 2
1 1 1
1 1 0
0
0
1
và P
B,E
=
1 1 0
1 0 1
0
1
1
[T]
E
P
B,E
=
1 1 1
1 1 0
1 1 0
1 0 1
=
0
0
1
0
1
1
2 1 1
. Thay vào ma trận khối:
0
1
1
1 1 0
2 2 2
1 1 0
2 2 2
[[T]
E
.P
B,E
| P
B,E
] =
1 0 1 2 1 1
−1 1 0
−1 −1
→
0 1 1 0 1 1
0 1 1 0 1 1
1 0 1 2 1 1
1 0 0
2 1 1
0 1 −1 0 1 1
→
0 1 0
0 1
1
.
0
0
2
0
0
0
0
0
1
0
0
0
2 1 1
[T]
B
=
0
1
1
.
0
0
0
120
0

lOMoARcPSD| 35883770
0
1
1
0
2 1 2
1
0
2
1
2
1
I.
GIÁ TRỊ RIÊNG VÀ VÉCTƠ RIÊNG
Chương 6
VÉC TƠ RIÊNG, CHÉO HÓA
VÀ DẠNG TOÀN PHƯƠNG
1. Giá trị riêng và vectơ riêng
2. Chéo hoá
3. Dạng toàn phương và ứng dụng
I. GIÁ TRỊ RIÊNG VÀ VÉC TƠ RIÊNG
1. KHÁI NIỆM GIÁ TRỊ RIÊNG VÀ VÉC TƠ RIÊNG CỦA MA TRẬN
Cho ma trận vuông A cấp n thì qua ánh xạ ma trận [T(x)] = A[x], véc tơ x R
n
có
khả năng biến thành những véc tơ ảnh với hướng khác nhau, tuy nhiên vẫn có những
véc tơ đặc biệt nào đó mà ảnh của nó là véc tơ khá “đơn giản”, là véc tơ cùng phương
với chính nó. Ví dụ, qua ánh xạ ma trận T: [R
2
] → [R
2
], T(x) = Ax với A =
3
− 2
thì
ảnh của các véc tơ x =
−
1
và
y
=
2
lần lượt là:
T(x) = Ax =
3
−
2
−
1
=
−
5
−
1
T(y) = Ay =
3
− 2
2
=
4
= 2
2
= 2y
Rõ ràng trong hai véc tơ ảnh ở trên thì T(x) hoàn toàn khác phương với x, trong khi
đó T(y) lại cùng phương với y.
Mục đích của phần này là tìm các véc tơ đặc biệt, mà qua phép biến đổi tuyến tính,
nó được biến thành véc tơ cùng phương với chính nó.
Định nghiã 1. Cho A M(n,n), số được gọi là giá trị riêng của A nếu tồn tại véc
tơ x [R]
n
, x O, sao cho Ax = x. Khi đó, véc tơ x được gọi là véc tơ riêng của
ma trận A ứng với giá trị riêng .
Chú ý rằng điều kiện véc tơ x O là quan trọng vì ta không muốn xét trường hợp
tầm thường véc tơ O là véc tơ riêng của mọi ma trận vuông.
121
2

lOMoARcPSD| 35883770
1
3
= = 2
= .
Chương 6. VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
Ví dụ 1. Cho A =
17
20
−15
. Xác định véc tơ nào trong các véc tơ sau là véc tơ
−18
riêng của A, khi đó hãy tìm giá trị riêng tương ứng: a) x =
1
. b)
y
=
1
.
Giải
a)
Xét Ax =
17
20
−15
1
2
1
−18
1
2
1
= 2x. Chứng tỏ x là véc tơ riêng, tương ứng
với giá trị riêng
1
= 2.
b)
Xét Ay =
17
20
−15
1
−28
1
−18
3
−34
3
R. Chứng tỏ y không phải là véc tơ
riêng của A.
Từ định nghĩa dễ dàng suy ra:
1)
Nếu x là véc tơ riêng ứng với giá trị riêng thì là duy nhất. Vì nếu có Ax = x
= ‘x thì ( − ‘)x = O −‘ = 0 = ‘.
2)
Ngược lại, một giá trị riêng có thể ứng với nhiều véc tơ riêng khác nhau. Ví
dụ, nếu x là véc tơ riêng của A ứng với thì x, ≠ 0, cũng là véc tơ riêng của
A ứng với vì A(x) = (Ax) = (x) = (x).
3)
Nếu biết x là véc tơ riêng của A ứng với giá trị riêng thì việc tính tích A
k
x thực
sự đơn giản vì A
k
x = A
k
−
1
(Ax) = A
k
−
1
(x) = A
k
−
2
(Ax) = A
k
−
2
(x) =
2
A
k
−
2
x
= ... =
k
x.
2.ĐA THỨC ĐẶC TRƯNG VÀ CÁCH TÌM GIÁ TRỊ RIÊNG, VÉC TƠ RIÊNG
TƯƠNG ỨNG
Với A = [a
ij
] M(n,n) thì là giá trị riêng của A Ax = x, x O, x [R]
n
Hệ (A−I)X = O có nghiệm không tầm thường det(A−I) = 0
a
11
−
a
21
a
n1
a
12
a
22
−
a
n2
...
...
...
a
1n
a
2n
a
nn
−
= 0 (3)
Khai triển vế trái của (3) ta được một đa thức bậc n đối với , dạng:
p() = a
n
n
+ a
n
−
1
n
−
1
+ ... + a
o
.
Từ đó có định nghiã sau:
122

lOMoARcPSD| 35883770
I. GIÁ TRỊ RIÊNG VÀ VÉCTƠ RIÊNG
Định nghiã 2. Với A M(n,n), đa thức p() = det(A−I) gọi là đa thức đặc trưng
của ma trận A, còn phương trình p( )= 0 gọi là phương trình đặc trưng của A.
Do det(A−I) là tổng (có kèm theo dấu “+” hoặc “−“) của n! hạng tử, mỗi hạng tử
bằng tích của n phần tử trong A−I, sao cho không có 2 phần tử nào cùng đứng trong
cùng một hàng và cùng một cột, nên hạng tử có bậc cao nhất đối với là hạng tử gồm
tích các phần tử đường chéo: (a
11
− )(a
22
− )...(a
nn
− ), có bậc n đối với . Khai triển
chi tiết det(A−I), đa thức đặc trưng của ma trận A có dạng:
p() = (−1)
n
n
+ (−1)
n
−
1
(a
11
+a
22
+...+a
nn
)
n
−
1
+ ... + a
o
Phương trình đặc trưng p() = 0 là phương trình bậc n nên sẽ có không quá n
nghiệm. Hơn nữa do p(0) = det(A−0I) = detA nên trong p(), có a
0
= detA, nghiã là:
p() = (−1)
n
n
+ (−1)
n
−
1
(a
11
+a
22
+...+a
nn
)
n
−
1
+ ... + detA
Định lý sau là hiển nhiên:
Định lý 1. Cho A M(n,n)
a)
Số là giá trị riêng của A khi và chỉ khi là nghiệm của phương trình đặc
trưng:
p() = det(A−I) = 0 (4)
b)
Nếu
k
là một giá trị riêng của A thì véc tơ riêng x ứng với
k
, là nghiệm khác O
của hệ thuần nhất:
(A−
k
I)X = O (5)
Định lí đã nêu rõ qúa trình tìm véc tơ riêng của ma trận vuông A. Đó là bắt đầu
bằng việc giải phương trình đặc trưng (4) để tìm tất cả các giá trị riêng. Với mỗi giá trị
riêng vừa tìm được, thế vào (5) để tìm véc tơ riêng tương ứng.
Có thể xẩy ra trường hợp phương trình đặc trưng (4) có nghiệm phức, nghĩa là A có
giá trị riêng phức, nhưng do phạm vi chương trình, ta không xét trường hợp này.
2 1 0
Ví dụ 2. Tìm giá trị riêng và véc tơ riêng tương ứng của ma trận A =
−1 0 1
.
1
3
1
- Tìm giá trị riêng:
2
−
1 0
2
−
1 0
det(A−I) = 0 −1 − 1 = 0 0 − 1
2
−
1 0
1 3
1
−
1
= 2
2
−
3
1
−
0 −
1 = 0 (2−)(
2
−−2) = 0
= −1.
2
0 2
1
−
3
= 2
123
c1→c1+c3
h3→h3−h1

lOMoARcPSD| 35883770
0
Chương 6. VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
A có 2 giá trị riêng khác nhau là
1
= 2 và
2
= −1. Do nghiệm
1
=
3
= 2 là nghiệm
kép nên ta gọi
1
= 2 là giá trị riêng bội 2.
- Tìm véc tơ riêng tương ứng
Với
1
= 2, véc tơ riêng tương ứng là nghiệm khác O của hệ thuần nhất (A−
1
I)X =
O (A−2I)X = O. Quy ma trận hệ số A−2I về dạng rút gọn:
0 1 0
1 3 −1
1 0 −1
A−2I =
−1 −2 1
→
0 1
0
→
0
1
0
.
1
3
−
1
0
1
0
0
0
0
Véc tơ riêng tương ứng là x =
t
t
1
= t.
0
1
với 0 t R.
Với
2
= −1. Quy A−
2
I = A+I về dạng rút gọn:
3 1 0
1 −1 −1
1 0
−
1/ 4
A+I =
−1 1 1
→
0 4 3
→
0 1
3 / 4
.
1
3
3
0
4
4
0
0
0
t / 4
1
Véc tơ riêng tương ứng là y =
−
3t / 4
=
t
−3
4
với 0 t R
t
4
Chú ý rằng, đôi khi để ngắn gọn trong cách viết, ta vẫn thường ghi véc tơ riêng thay
vì ở dạng véc tơ cột, lại ghi ở dạng véc tơ hàng. Khi đó, tập các giá trị riêng và véc tơ
riêng tương ứng của A được ghi gọn là:
{
1
= 2, x = (1; 0; 1).t, t 0} {
2
= −1, y = (1/4; −3/4; 1).s, s 0}.
Từ định lý trên dễ dàng suy ra các hệ qủa sau đây:
Hệ quả. Nếu A là ma trận dạng tam giác thì các giá trị riêng của A là các phần tử
đường chéo.
Ví dụ, ma trận A =
3 0 0
2 1 0
0
4
0
có tập giá trị riêng là {
1
= 3;
2
= 1;
3
= 0}.
3. MỘT SỐ TÍNH CHẤT CỦA TRỊ RIÊNG VÀ VÉC TƠ RIÊNG
Định lý 2. Ma trận A khả nghịch khi và chỉ khi A không có giá trị riêng nào bằng
không.
Chứng minh. Giả sử ngược lại, A có giá trị riêng = 0 AX = 0X = O có nghiệm
không tầm thường detA = 0 A không khả nghịch.(Trái giả thiết).
124

lOMoARcPSD| 35883770
I. GIÁ TRỊ RIÊNG VÀ VÉCTƠ RIÊNG
Định lý 3. Hai ma trận đồng dạng có chung tập các giá trị riêng.
Chứng minh. Giả sử A B, theo định nghĩa, tồn tại P khả nghịch sao cho B =
P
−
1
AP. Khi đó:
det(B−I) = det(P
−
1
AP−I) = det(P
−
1
AP−(P
−
1
P)) = det{P
−
1
(AP−P)} =
det{P
−
1
(A−I)P}= (detP
−
1
).det(A−I).(detP) = (detP).(detP
−
1
).{det(A−I)} = det(A−I).
Chứng tỏ A và B có chung đa thức đặc trưng, nên có chung tập các giá trị riêng.
Định lý 4. Với là giá trị riêng của A M(n,n) thì tập hợp gồm véc tơ O và tất cả
các véc tơ riêng ứng với , lập thành một không gian con của [R]
n
, gọi là không
gian riêng của ma trận A ứng với giá trị riêng kí hiệu là E
.
E
= {x [R]
n
/ (A−I)x = O}
Định lý là hiển nhiên vì E
= {x [R]
n
/ (A−I)x = O} = Nul(A−I) là không gian
con của [R]
n
.
Nhận xét rằng nếu
1
,
2
là 2 giá trị riêng phân biệt của A M(n,n) thì giao của 2
không gian riêng tương ứng bằng {O}, tức là E
1
E
2
= {O}. Thật vậy, nếu x E
1
E
2
thì
1
x = Ax =
2
x (
1
−
2
)x = O x = O (vì
1
2
).
Nhờ nhận xét trên mà ta chứng minh được định lý nói về tính độc lập tuyến tính của
các vectơ riêng ứng với các giá trị riêng phân biệt, như sau đây:
Định lý 5. Giả sử A M(n,n) có 2 giá trị riêng phân biệt
1
,
2
. Gọi B
1
= {v
1
, v
2
, ..,
v
k
} là tập gồm k véc tơ riêng độc lập tuyến tính có trong E
1
, và B
2
= {w
1
, w
2
, .., w
p
}
là tập gồm p véc tơ riêng độc lập tuyến tính có trong E
2
. Khi đó tập B
1
B
2
là tập
các véc tơ riêng độc lập tuyến tính của A.
Chứng minh
Xét tổ hợp tuyến tính bất kì của O qua các véc tơ của B
1
B
2
:
1
v
1
+ ...+
k
v
k
+
1
w
1
+ ..+
p
w
p
= O
Đặt v =
1
v
1
+ ...+
k
v
k
E
1
, w =
1
w
1
+ ..+
p
w
p
E
2
thì có v + w = O
v = − w E E = {O}
v = 0
1
v
1
+
...
+
k
v
v
=
0
1
=
...
=
k
=
0
w = 0
w + ... + w = 0
= ... = = 0
B
1
B
2
độc lập tuyến tính.
1 1 p p
1 p
Bằng cách chứng minh tương tự, ta có định lý sau:
Định lý 6. Giả sử A M(n,n) có k, (1 k n) giá trị riêng phân biệt:
1
,
2
,...,
k
.
Gọi B
j
là tập các vectơ riêng độc lập tuyến tính của E
j
, thì B = B
j
, 1 j k, là
tập độc lập tuyến tính.
Đặc biệt nếu A có đủ n giá trị riêng phân biệt thì tập gồm n véc tơ riêng tương ứng
lập nên cơ sở cho [R]
n
.
125

lOMoARcPSD| 35883770
Chương 6. VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
4. GIÁ TRỊ RIÊNG VÀ VÉC TƠ RIÊNG CỦA PHÉP BIẾN ĐỔI TUYẾN TÍNH
Giả sử T: R
n
→ R
n
là phép biến đổi tuyến tính cho bởi ma trận chính tắc A, nghĩa là
[T(x)] = A[x], x R
n
. Nếu v là véc tơ riêng ứng với giá trị riêng của ma trận A, thì
Av = v, kéo theo T(v) = v. Trong trường hợp này ta cũng gọi v là véc tơ riêng của
phép biến đổi tuyến tính T ứng với giá trị riêng . Tổng quát hóa ta có định nghiã sau
đây:
Định nghiã 3. Cho T: V → V là phép biến đổi tuyến tính trên V. Số được gọi là
giá trị riêng của T nếu tồn tại véc tơ v V, v O, sao cho T(v) =v. Khi đó, véc tơ v
gọi là véc tơ riêng của T ứng với giá trị riêng . và E
= { v V / T(v) = v} gọi là
không gian riêng của T ứng với giá trị riêng .
Từ định nghiã suy ra phép biến đổi tuyến tính T biến véc tơ riêng v của nó, thành
véc tơ mới v, cùng phương với v còn không gian riêng E
là không gian con của V.
Ví dụ 3. Cho T: R
2
→ R
2
, T(x
1
; x
2
) = (3x
1
+x
2
; x
1
+3x
2
) là phép biến đổi tuyến tính
trên R
2
. Tìm giá trị riêng và véc tơ riêng tương ứng của T.
- Tìm tập giá trị riêng. Gọi x = (x
1
; x
2
) là véc tơ riêng của T ứng với giá trị riêng
thì T(x) = x (3x +x ; x +3x ) = (x ; x )
3x
1
+ x
2
= x
1
(3 − x
1
) + x
2
= 0
.
1 2 1 2
1 2
x
+ 3x
= x
x + (3 − )x = 0
1 2 2 1 2
Do véc tơ riêng x O nên hệ phải có nghiệm không tầm thường, suy ra
3
−
1
= 0
1
= 4
.
= 2
1
3
−
2
- Tìm tập vectơ riêng tương ứng
Với
1
= 4, véc tơ riêng tương ứng với x thỏa mãn T(x) = 4x (3x
1
+x
2
; x
1
+3x
2
) =
4(x ; x )
3x
1
+ x
2
= 4x
1
−x
1
+ x
2
= 0
x
1
= t
x = (1; 1).t, 0 t R.
1 2
x
+ 3x = 4x
x − x = 0
x = t R
1 2 2 1 2 2
Với
2
= 2, bằng cách tương tự, tìm được véc tơ riêng tương ứng là y = (−1; 1).t, 0
t R.
Nếu T: R
n
→ R
n
, T(x) → A[x] là ánh xạ ma trận ứng với ma trận A thì dễ thấy giá
trị riêng và véc tơ riêng tương ứng của T cũng chính là giá trị riêng và véc tơ riêng
tương ứng của ma trận A. Việc tìm giá trị riêng và véc tơ riêng tương ứng của phép
biến đổi tuyến tính T: V
n
→ V
n
tổng quát được thực hiện như sau:
Giả sử T: V
n
→ V
n
là phép biến đổi tuyến tính. Gọi B là cơ sở nào đó của V
n
và A =
[T]
B
là ma trận của T đối với cơ sở B. Khi đó véc tơ v O là véc tơ riêng của T ứng với
giá trị riêng khi và chỉ khi T(v) = v [T(v)]
B
= [v]
B
A[v]
B
= [v]
B
. Điều đó
chứng tỏ:
Định lý 7. Giả sử T: V
n
→ V
n
là phép biến đổi tuyến tính và B là cơ sở nào đó của
V
n
. Khi đó:
126

lOMoARcPSD| 35883770
0
0
I.
GIÁ TRỊ RIÊNG VÀ VÉCTƠ RIÊNG
a)
là giá trị riêng của T khi và chỉ khi là giá trị riêng của ma trận A = [T]
B
.
b)
v O là véc tơ riêng của T ứng với giá trị riêng khi và chỉ khi [v]
B
là véc tơ
riêng ứng với giá trị riêng của ma trận A = [T]
B
.
Ví dụ 4. Tìm giá trị riêng và véc tơ riêng tương ứng của T: P
2
(x) → P
2
(x),
T(a
0
1+a
1
x+a
2
x
2
) = 2a
0
1+ a
1
x + (a
1
+a
2
)x
2
.
Giải.
2 0 0
Gọi B = {1, x, x
2
} là cơ sở chính tắc của P
2
(x) thì có A = [T]
B
=
0 1
0
.
0
1
1
-
Tập giá trị riêng của T là tập giá trị riêng của A = [T]
B
, dễ tìm được là
1
= 2,
2
=
3
= 1 (do A là ma trận tam giác).
-
Ứng với
1
= 2, véc tơ riêng tương ứng của A tìm được là x =
t
t
0
, 0 t R.
0
Gọi v
1
là véc tơ riêng của T ứng với
1
thì [v
1
]
B
= x =
với 0 t R.
0
v
1
= t.1 + 0.x + 0.x
2
= t.1 ,
0
-
Ứng với
2
=
3
= 1, véc tơ riêng tương ứng của A tìm được là y =
0
0
, 0 s
s
R. Gọi v
2
là véc tơ riêng của T ứng với
2
thì [v
2
]
B
= y =
s.x
2
, với 0 s R.
s
v
2
= 0.1 + 0.x + s.x
2
=
Tóm lại, tập giá trị riêng và véc tơ riêng tương ứng của T là: {
1
= 2, v
1
= t.1, 0
t R } {
2
= 1, v
2
= s.x
2
, 0 s R }.
127

lOMoARcPSD| 35883770
Chương 6. VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
II. CHÉO HÓA
1. CHÉO HÓA MA TRẬN
Nhắc lại rằng ma trận chéo là ma trận vuông có tất cả các phần tử nằm ngoài đường
chéo đều bằng 0. Khi D là ma trận chéo thì việc tính lũy thừa D
k
thực sự đơn giản. Ví
2 0 0
dụ với D =
0 −1 0
thì có:
0
0
3
2 0 0
2 0 0
2
2
0 0
D
2
= DD =
0 −1 0
0 −1 0
=
0 (−1)
2
0
.
0
0
3
0
0
3
0 0
3
2
2
2
0 0
2 0 0
2
3
0 0
D
3
= D
2
D =
0 (−1)
2
0
0 −1 0
=
0 (−1)
3
0
.
0
0
3
2
0
0
3
0 0
3
3
...
Nhờ phương pháp quy nạp,chứng minh được D
k
=
2
k
0 0
0 (−1)
k
0
0 0
3
k
Mặt khác, nếu ma trận vuông A phân tích được dưới dạng A = PDP
−
1
với P khả
nghịch và D là ma trận chéo thì việc tính A
k
cũng sẽ thực hiện được một cách đơn giản
như sau:
A
2
= AA = (PDP
−
1
).( PDP
−
1
) = PD(P
−
1
P)DP
−
1
= PD
2
P
−
1
.
A
3
= A
2
A = (PD
2
P
−
1
)( PDP
−
1
) = (P.D
2
.(P
−
1
P)DP
−
1
= PD
3
P
−
1
.
⁝
A
k
= A
k
−
1
.A = (PD
k
−
1
P
−
1
)( PDP
−
1
) = PD
k
P
−
1
trong đó D
k
là lũy thừa bậc k của ma trận chéo, dễ dàng tính được như vừa trình bày ở
trên.
Nội dung của mục này là giúp nhận biết khả năng và cung cấp phương pháp để
phân tích ma trận vuông A thành dạng PDP
−
1
, nhằm đáp ứng nhu cầu tính nhanh các lũy
thừa A
k
xuất hiện trong nhiều bài toán ứng dụng.
128

lOMoARcPSD| 35883770
2
0 0
n
0 0
n
2
II. CHÉO HOÁ
Định nghiã 4. Ma trận vuông A gọi là chéo hóa được nếu tồn tại ma trận P khả
nghịch sao cho P
−
1
AP = D là ma trận chéo. Khi đó ta nói P chéo hóa được A, hay A
được chéo hóa bởi P, còn D gọi là dạng chéo của A.
Từ định nghiã suy ra: A chéo hóa được Tồn tại ma trận P khả nghịch và ma trận
chéo D, sao cho A có sự phân tích A = PDP
−
1
Tồn tại ma trận P khả nghịch và ma
trận chéo D, sao cho D = P
−
1
AP A D. Do vậy, A chéo hóa được nếu A đồng dạng
với ma trận chéo D .
Khi nói “chéo hóa ma trận A” có nghĩa là tìm ma trận P khả nghịch và ma trận chéo
D để cho A có sự phân tích A = PDP
−
1
.
2. ĐIỀU KIỆN CHÉO HÓA ĐƯỢC CỦA MA TRẬN
Chú ý rằng không phải ma trận vuông nào, thậm chí kể cả ma trận khả nghịch, cũng
đều chéo hóa được. Định lí sau đây đưa ra một điều kiện mạnh, cho phép khẳng định
tính chéo hóa được của ma trận vuông bất kỳ.
Định lý 8. A M(n,n) chéo hóa được khi và chỉ khi A có đủ n véc tơ riêng độc lập
tuyến tính.
Chứng minh. Giả sử A chéo hóa được, tức là A viết được dưới dạng A = PDP
−
1
,
1
0 ... 0
trong đó: P = [v
1
v
2
... v
n
] là ma trận khả nghịch và D =
chéo. Biến đổi ma trận A ta có:
... 0
là ma trận
1
0 ... 0
A = PDP
−
1
0
AP = PD (1) A[v
1
v
2
... v
n
] = [v
1
v
2
... v
n
]
... 0
Av
1
Av
=
1
v
1
= v
[Av
1
Av
2
... Av
n
] = [
1
v
1
2
v
2
...
n
v
n
] (2)
2 2 2
(3)
Av
n
=
n
v
n
Do P khả nghịch nên tập các véc tơ cột {v
i
, i = 1..n}là độc lập tuyến tính, dẫn đến v
i
O i = 1..n. Do v
i
O và (3), suy ra {
1
,
2
, ...,
n
} là tập các giá trị riêng còn {v
1
,
v
2
, ..., v
n
} là tập n véc tơ riêng tương ứng của A.
Ngược lại, giả sử A có n véc tơ riêng độc lập tuyến tính {v
1
, v
2
, ..., v
n
} và các giá trị
riêng tương ứng là {
1
,
2
, ...,
n
}, (những giá trị riêng này có thể trùng nhau). Lập các
ma trận:
129
0

lOMoARcPSD| 35883770
2
0 0
n
Chương 6. VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
1
0 ... 0
0
P = [v
1
v
2
... v
n
] và D =
... 0
thì có ngay ma trận P là khả nghịch do tập n cột trong P là tập các vectơ {v
i
, i = 1..n}
độc lập tuyến tính. Do Av
i
=
i
v
i
i = 1..n, nên có (3), suy ra có (2) và có (1), nghiã là
A chéo hóa được.
Ví dụ 5. Xác định tính chéo hóa được của A =
2 1 0
−1 0 1
.
1
3
1
- Tìm tập giá trị riêng của A:
2
−
1 0
= −1
det(A−I) = 0 1 − 1
= 0 −(+1)(−2)
2
= 0
1
.
1 3
1
−
2
=
3
= 2
- Tìm tập các véc tơ riêng độc lập tuyến tính của A.
1
Với
1
= 1, có E
1
= Nul(A−
1
I) = {
−1
.t, t R} và véc tơ riêng tương ứng là v
1
=
1
1
−1
.t; 0 t R. Tập các véc tơ riêng độc lập tuyến tính tương ứng với
1
= 1 nhiều
1
nhất chỉ gồm 1 vectơ, vì không gian riêng E
1
có số chiều bằng 1.
1
Với
2
= −2, có E
2
= Nul(A−
2
I) = {
0
.t, t R} và véc tơ riêng tương ứng là v
2
=
1
1
0
.t; 0 t R. Tập các véc tơ riêng độc lập tuyến tính tương ứng với
2
= − 2 nhiều
1
nhất chỉ gồm 1 vectơ, vì không gian riêng E
2
có số chiều bằng 1.
Tập các vectơ riêng độc lập tuyến tính nhiều nhất của A chỉ gồm 2 vectơ nên A
3x3
không chéo hóa được.
Hệ quả 1. Nếu A M(n,n), có đúng n giá trị riêng phân biệt thì A chéo hóa được.
Hệ qủa này là hiển nhiên vì khi A M(n,n) có n giá trị riêng phân biệt thì A có đủ n
véc tơ riêng tương ứng độc lập tuyến tính.
130

lOMoARcPSD| 35883770
II. CHÉO HOÁ
Hệ quả 2. Khi A chéo hóa được thì ma trận P chéo hóa được A là ma trận có các
cột là các véc tơ riêng độc lập tuyến tính của A và dạng chéo của A là ma trận chéo D
có các phần tử trên đường chéo là các giá trị riêng tương ứng.
1 0 0
Ví dụ 6. Hãy tìm ma trận P chéo hóa được ma trận A =
−8 4 −6
và dạng chéo
tương ứng của A.
- Tìm tập các giá trị riêng của A:
8 1 9
1 − 0 0
|A−I| = 0
1
= 1
= 6 .
−8 4 − −6
8 1 9 −
= (1−)(
2
−13+42) = (1−)(−6)(−7) = 0
2
3
= 7
- Lập ma trận P chéo hóa được A và dạng chéo tương ứng:
0 0 0
1
1/ 8
1
1
0
15 /16
Với
1
= 1 A−
1
I = A−I =
−8 3
−
6
→
0
4
2
→
0
1
1/ 2
. Vectơ
8
1
8
0
0
0
0
0
0
−
15 /16
15
riêng tương ứng là
v
=
−
1/ 2
.t, t 0. Chọn
v
1
=
8
.
1
−
16
−5 0 0
1 0 0
1 0 0
Với
2
= 6 A−
2
I = A−6I =
−8 −2
−
6
→
0
−2 −6
→
0
1 3
. Vectơ
0
8
1 3
0
0
1
3
0
0
0
riêng tương ứng là v =
−3
.t, t 0. Chọn v
2
=
−3
.
1
−6 0 0
1
1 0 0
1 0 0
Với
3
= 7 A−7I =
−8 −3 −6
→
0 −3 −6
→
0 1 2
. Véc tơ riêng
0
8
1 2
0
0
1
2
0
0
0
tương ứng là v =
−
2
.t, t 0. Chọn
v
3
=
−
2
.
1
1
15 0 0
1 0 0
Lập P = [v
1
v
2
v
3
] =
8 −3 −2
thì dạng chéo tương ứng là D =
0 6
0
.
−
16
1
1
0
0
7
131

lOMoARcPSD| 35883770
k
Chương 6. VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
Để kiểm tra lại ma trận P có thực sự chéo hóa được A và dạng chéo tương ứng là D
hay không (tránh khả năng tính sai hoặc lập ma trận D không phù hợp), cần kiểm tra
đẳng thức P
−
1
AP = D AP = PD. Thật vậy, có:
1 0 0
15 0 0
15 0 0
AP =
−8 4 −6
8 −3 −2
=
8 −18 −14
8
1
9
−
16
1
1
−
16
6
7
15 0 0
1 0 0
15 0 0
PD =
8 −3 −2
0 6 0
=
8 −18 −14
AP = PD.
−
16
1
1
0
0
7
−
16
6
7
Nhận xét. Rõ ràng ma trận P chéo hóa được A và dạng chéo tương ứng của A tìm
được là không duy nhất vì chúng phụ thuộc vào việc chọn tập vectơ riêng độc lập tuyến
tính và việc sắp các vec tơ đó thành các cột của A.
Chú ý rằng khi A M(n,n) nhưng có ít hơn n giá trị riêng phân biệt thì không thể
kết luận rằng A không chéo hóa được. Sau đây ta sẽ đưa ra định lí cho phép khẳng định
tính chéo hóa được của ma trận A, khi A M(n,n) nhưng lại có ít hơn n giá trị riêng
phân biệt.
Định lý 9.
Giả sử A
M
(n,n) có k
n giá trị riêng phân biệt:
1
,
2
,...,
k
. Gọi B
i
là
cơ sở của không gian riêng E
i
, i = 1..k, và B = B
1
B
2
... B
k
. Khi đó, A chéo
hóa được khi và chỉ khi B chứa đúng n véc tơ, hay tương đương
dim
E
i
= n.
i=1
Chứng minh. Theo tính chất của vectơ riêng (Định lý 6) thì B là tập các vectơ riêng
độc lập tuyến tính của A nên A chéo hoá được A có đủ n vectơ riêng độc lập tuyến
tính B có đủ n vectơ.
Ví dụ 7. Xác định tính chéo hóa được của A =
0 3
−2 5
−2
−
2
.
−
2
3
0
- Tìm tập giá trị riêng của A:
− 3 −2 − + 2 3 −2
Có |A−I| = 0
−2
5
−
−2
= 0
⎯
c
⎯
1→
⎯
c1−c
⎯
3
→
0
5
−
−2 = 0
− + 2 3
−2 3 −
−2
−
2
+
3 −
⎯
h
⎯
3→
⎯
h3+
⎯
h1
→
0
5
−
−2 = 0 (2−)(
2
−3+2) = 0
1
= 1;
2
= 2 (bội 2).
0 6 −2 −
- Tìm tổng số chiều của các không gian riêng.
132

lOMoARcPSD| 35883770
II. CHÉO HOÁ
Với
1
=1 A−
1
I = A−I =
−1 3
−2 4
−2
−2
1
→
0
−3 2
−2 2
1 0
→
0
1
−1
−1
dimE
1
= 1.
Với
2
= 2 A−
2
I = A−2I =
−
2
3
−
1
0
−
3
3
0
0
0
−2 3 −2
2 −3 2
−2 3 −2
→
0 0 0
dimE
2
= 2.
−
2
3
−
2
0
0
0
Tổng số chiều của các không gian riêng E
1
và E
2
bằng 3, nên A
3x3
chéo hoá được.
Ví dụ 8. Xác định tính chéo hóa được của A =
−1 7
−4 11
−5
−6
.
−
4
8
−
3
- Tìm tập giá trị riêng của A:
Có |A−I| = 0
1 −
−4
7
11 −
−5
−6 = 0 −(−1)(−3)
2
= 0
1
= 1;
2
= 3
−4
8
−3 −
(bội 2).
Với
1
= 1 A−
1
I =
−2 7
−4 10
−5
−6
→
1 0
0 1
−1
−1
, suy ra dimE
1
= 1.
−
4
8
−
4
0
0
0
−4 7
−5
4 0
−2
Với
2
= 3 A−
2
I =
−4 8
−
6
→
0
1 −1
, suy ra dimE
2
= 1.
−
4
8
−
6
0
0
0
- Tổng số chiều của các không gian riêng dimE
1
+dimE
2
= 2 < 3 nên A
3x3
không
chéo hoá được.
Định nghiã 5. Nghiệm x= được gọi là nghiệm bội m của đa thức p(x) bậc n nếu
có sự phân tích p(x) = (x−)
m
.q(x), trong đó q(x) là đa thức bậc n−m và q() 0.
Với khái niệm nghiệm bội của đa thức vừa nêu, người ta chứng minh được kết quả
“Nếu ma trận A M(n,n) có giá trị riêng bội m thì số chiều của không gian riêng
tương ứng E
i
không vượt quá m: dimE
i
m.” từ đó có định lý sau:
Định lý 10. Giả sử A M(n,n) có k giá trị riêng phân biệt:
1
,
2
,...,
k
.(1 k n)
với bội tương ứng là m
1
, m
2
, ..., m
k
thì A chéo hóa được khi và chỉ khi m
1
+ m
2
+ ...
+ m
k
= n và dimE
i
= m
i
i =1..k.
Ta công nhận mà không chứng minh định lý này.
133

lOMoARcPSD| 35883770
Chương 6. VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
2 1 1
Ví dụ 9. Xét tính chéo hóa được của A =
1 2 1
.
1
1
2
2
−
1 1
= = 1
- Tìm tập giá trị riêng |A−I| = 0 1
2
−
1 = 0
1 2
.
1 1
2
−
3
= 4
- Với
1
= 1 (bội 2) A−
2
I = A−I =
bội của
1
.
1 1 1
1 1 1
1 1 1
1 1 1
→
0 0 0
0
0
0
dim E
2
= 2 =
- Với
3
= 4 có bội 1, hiển nhiên dimE
3
=1 = bội của
3
.
A là chéo hoá được vì có tổng các bội của giá trị riêng bằng 3 và tất cả các giá trị
riêng đều có bội đúng bằng số chiều của không gian riêng tương ứng.
3. THUẬT TOÁN CHÉO HÓA MA TRẬN
Cho A M(n,n), chéo hóa ma trận A có nghĩa là tìm ma trận vuông P khả nghịch,
và ma trận chéo D sao cho có sự phân tích A = PDP
−
1
. Khi A chéo hoá được, ma trận P
chéo hóa được A và dạng chéo tương ứng D cho bởi công thức:
A=
v
1
v
2
v
n
, D =
trong đó v
1
, v
2
, ..., v
n
là n vectơ riêng độc lập tuyến tính của A còn
1
,
2
, ...,
n
là
các giá trị riêng tương ứng.
Để thực hiện việc chéo hóa ma trận A, ta có thể áp dụng lược đồ gồm các bước sau:
Bước 1. Tìm tập giá trị riêng và xác định tính chéo hóa được của A.
Bước 2. Nếu A chéo hóa được, tìm tập n véc tơ riêng độc lập tuyến tính.
Bước 3. Lập ma trận P chéo hóa được A và dạng chéo D tương ứng của A (chú ý
cần thử lại AP = PD để đảm bảo các phép tính là thực hiện chính xác và việc lập các
ma trận P, D là phù hợp).
1
Ví dụ 10. Chéo hóa ma trận A =
0
−3 3
−5 6
(nếu có thể được).
0
−
3
4
Bước 1. Tìm tập giá trị riêng và xác định tính chéo hóa được của A.
134
1
0
0
0
2
0
0
0
n

lOMoARcPSD| 35883770
II. CHÉO HOÁ
0 −3 3
0 1 −1
- Với
1
= 1 (bội 2), có A−I =
0 −6 6
→
0 0 0
dimE
1
= 2.
0
−
3
3
0
0
0
3
- Với
2
= −2 (bội 1), có A+2I =
0
−3 3
−3 6
3 0
→
0
1
−3
−
2
dimE
2
= 1.
0
−
3
6
0
0
0
Do dimE
1
+ dimE
2
= 3 nên A
3x3
là chéo hóa được.
Bưóc 2. Tìm tập 3 véc tơ riêng độc lập tuyến tính:
0
1
- Với
1
= 1, vectơ riêng tương ứng là v =
1
s +
1
0
t; s
2
+ t
2
0. Do dimE
1
=
0
0
1
2 nên số véc tơ riêng độc lập tuyến tính nhiều nhất là 2 vectơ. Chọn v
1
=
1
, v
2
=
0
.
1
1
0
- Với
3
= −2, vectơ riêng tương ứng là v =
2
.t; t 0. Do dimE
3
= 1 nên số
1
1
véc tơ riêng độc lập tuyến tính nhiều nhất là 1 véc tơ. Chọn v
3
=
2
.
1
Bước 3. Tìm ma trận P chéo hóa được A và dạng chéo của A.
0 1 1
1
0 0
1 0 0
Lập P =
v
1
v
2
v
3
=
1
0
2
,
D =
0
1
0
=
0 1 0
.
1
0
1
0 0
3
0
0
−
2
Thử lại sự phân tích A = PDP
−
1
AP = PD:
1
AP =
0
−3 3
0 1 1
−5 6
1 0 2
0 1
=
1 0
−2
−4
. PD =
0 1 1
1 0 0
1 0 2
0 1 0
=
0 1
−2
0
−
3
4
1
0
1
1 0
−
2
1
0
1
0
0
−
2
1 0 −4
nên AP = PD thỏa.
1
0
−
2
135
- |A−I| = 0
1
−
−3
0
−
5
−
3
6 = 0 (1−)(
2
+−2) = 0
1
= = 1
2
0
−3
4
−
3
= −2

lOMoARcPSD| 35883770
2
0 ... 0
n
0
n
Chương 6. VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
0 1 1
Đáp số: A = PDP
-1
với P =
1 0
2
,
D =
1 0 0
0 1 0
.
1
0
1
0
0
−
2
4. CHÉO HÓA PHÉP BIẾN ĐỔI TUYẾN TÍNH
Định nghiã 6. Phép biến đổi tuyến tính T: V
n
→ V
n
gọi là chéo hóa được nếu trong
V
n
tồn tại một cơ sở B sao cho [T]
B
có dạng chéo.
Điều kiện về tính chéo hóa được của phép biến đổi tuyến tính cho bởi định lý sau:
Định lý 11. Phép biến đổi tuyến tính T: V
n
→ V
n
từ không gian n chiều V
n
vào
chính nó là chéo hóa được khi và chỉ khi trong V
n
tồn tại một cơ sở bao gồm các véc
tơ riêng của T.
Chứng minh
- Giả sử T là chéo hóa được thì trong V
n
tồn tại cơ sở B = {v
1
, v
2
, ..., v
n
} sao cho
1
0 ... 0
[T]
B
= [[T(v
1
)]
B
[T(v
2
)]
B
... [T(v
n
)]
B
] =
... 0
là ma trận chéo. Cần
chứng minh các véc tơ trong cơ sở B là các véc tơ riêng của T. Thật vật, xét cột thứ nhất
1
0
trong [T]
B
ta có [T(v
1
)]
B
=
T(v
1
) =
1
v
1
+ 0.v
2
+ ...+ 0.v
n
T(v
1
) =
1
v
1
v
1
là véc tơ riêng của T. Bằng lý luận tương tự, suy ra được tất cả các véc tơ v
i
B, i =
1..n, đều là các véc tơ riêng của T.
- Ngược lại, giả sử trong V
n
tồn tại cơ sở B = {v
1
, v
2
, ..., v
n
} bao gồm n véc tơ
riêng của T, cần chứng minh [T]
B
là ma trận chéo. Thật vậy, gọi
i
là giá trị riêng của T
ứng với vectơ riêng v
i
thì:
0
T(v
i
) =
i
v
i
, i = 1..n. [T(vi)]
B
= [
i
v
i
]
B
, i = 1..n. [T(vi)]
B
=
i
0
(
i
ở hàng thứ
i). Lập ma trận của T đối với cơ sở B ta có:
1
0 ... 0
0
[T]
B
= [[T(v
1
)]
B
[T(v
2
)]
B
... [T(v
n
)]
B
] =
... 0
2
, là ma trận chéo.
0 ... 0
136
0

lOMoARcPSD| 35883770
2
0 ... 0
n
B
0
1
1
2
n
n
II. CHÉO HOÁ
Từ kết quả chứng minh định lý trên ta rút ra:
Định lý 12. Với B là cơ sở của V
n
thì phép biến đổi tuyến tính T: V
n
→ V
n
là chéo
hóa được khi và chỉ khi [T]
B
là chéo hoá được.
Chứng minh
- Nếu T là chéo hóa được thì trong V
n
tồn tại cơ sở B = {v
1
, v
2
, ..., v
n
} sao cho
1
0 ... 0
[T] =
... 0
= D là ma trận chéo. Hiển nhiên [T]
B
= D là chéo hoá được vì
D = I
n
DI
n
−
1
với I là ma trận đơn vị cấp n.
- Ngược lại, giả sử [T]
B
= [[T(v
1
)]
B
[T(v
2
)]
B
... [T(v
n
)]
B
] là chéo hoá
được, tức là có sự phân tích [T]
B
= PDP
−
1
với P =
p
là ma trận khả nghịch
1
0
còn D =
là ma trận chéo. Khi đó, cột thứ k trong P là vectơ riêng của [T]
B
n
ứng giá trị riêng
k
, k = 1..n. Vì giá trị riêng
k
của [T]
B
cũng là giá trị riêng của T nên
vectơ riêng w
k
của T ứng với giá trị riêng
k
là vectơ thỏa [w
k
]
B
= p
k
. Do P khả nghịch
nên {p
k
, k = 1..n} độc lập tuyến tính trong [R]
n
, suy ra {w
k
, k = 1..n} là độc lập tuyến
tính trong V
n
. Vậy, trong V
n
tồn tại {w
k
, k =1..n}là tập gồm n vectơ riêng độc lập tuyến
tính của T nên T là chéo hoá được.
Nhận xét
-
Ma trận của T đối với cơ sở gồm các véc tơ riêng là ma trận chéo có các phần
tử đường chéo là các giá trị riêng tương ứng của T.
-
Nếu trong V
n
đã biết cơ sở bao gồm n véc tơ riêng của T là B = {v
1
, v
2
, ..., v
n
}
thì việc tính giá trị của T
k
(k 2 là số tự nhiên) tại bất kỳ vV
n
sẽ thực sự đơn giản.
Cụ thể là nếu
i
là giá trị riêng ứng với v
i
thì với mọi v V
n
, v =
1
v
1
+
2
v
2
+ ... +
n
v
n
, ta có:
T
k
(v) =
1
.
k
.v + .
k
.v + ... + .
k
.v .
Ví dụ 11. Gọi B = {1, x, x
2
} là cơ sở của P
2
(x) và phép biến đổi tuyến tính T : P
2
(x)
→ P
2
(x) xác định bởi: T(1) = 3 + 2x + x
2
, T(x) = 2, T(x
2
) = 2x
2
.
a)
Tìm cho P
2
(x) một cơ sở để ma trận của T đối với cơ sở đó là ma trận chéo.
b)
Tìm T
4
(2+x).
Giải
a) Cơ sở cần tìm là cơ sở bao gồm 3 véc tơ riêng độc lập tuyến tính của T.
-
Gọi [T]
B
là ma trận của T đối với B thì có:
137
p
n
0
1
2
2
n

lOMoARcPSD| 35883770
Chương 6. VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
3 2 0
[T]
B
= [[T(1)]
B
[T(x)]
B
[T(x
2
)]
B
] =
2 0 0
= A
1
0
2
- Tập giá trị riêng của A:
3
−
2 0
= 2
|A−I|=0 2 − 0 = 0 (2−)(
2
−3−4) = 0
= −1 .
1 0
2
−
1 2 0
1 0 0
=
4
- Với = 2, A−2I =
2 −2 0
→
0 1 0
. Véc tơ riêng tương ứng của A là x
0
1
0
0
0
0
0
=
0
.t, t 0 Véc tơ riêng tương ứng của T là v = 0.1+0.x+t.x
2
, t 0. Chọn 1 vectơ
1
riêng cho T: v
1
= x
2
.
4 2 0
1 0 3
- Với = −1, A – (–I) =
2 1 0
→
0 1 −6
. Véc tơ riêng tương ứng của A
−3
1
0
3
0
0
0
là y =
6
.t, t 0 Véc tơ riêng tương ứng của T là v = (−3t).1+6t.x+t.x
2
, t 0. Chọn
1
1 vectơ riêng cho T : v
2
= −3 + 6x + x
2
.
−1 2 0
1 0
−2
- Với = 4, A−4I =
2 −4 0
→
0 1 −1
. Véc tơ riêng tương ứng của A
2
1
0
−
2
0
0
0
là z =
1
.t, t 0. Véc tơ riêng tương ứng của T là v = (2t).1+t.x+t.x
2
, t 0. Chọn 1
1
vectơ riêng cho T : v
3
= 2 + x + x
2
.
Cơ sở cần tìm gồm 3 vectơ riêng độc lập tuyến tính của T là:
C = {v
1
= x
2
, v
2
= − 3 + 6x + x
2
, v
3
= 2 + x + x
2
}
2) Tìm T
4
(2+x).
Trước hết, cần tìm sự phân tích của p = 2 + x qua cơ sở C, tức là tìm [p]
C
. Dễ thấy
có sự phân tích:
nên có [p]
C
=
p = 2 + x = 0.(− 3 + 6x + x
2
) + (−1).(x
2
) + 1.(2 + x + x
2
)
0
−1
. Áp dụng công thức tìm T
k
(v) đã cho ở trên:
1
T
4
(2+x) = 0.
4
.p + (−1).
4
.p + 1.
4
.p = O + (−1).2
2
.(x
2
) + 1.4
4
.(2 + x + x
2
) =
1 1
512 + 256x + 240x
2
.
2 2 3 3
138

lOMoARcPSD| 35883770
0
n
II.
CHÉO HOÁ
III.
CHÉO HÓA TRỰC GIAO MA TRẬN ĐỐI XỨNG
(ĐỌC THÊM)
Lý thuyết về ma trận đối xứng rất phong phú, tuy nhiên với mục này, ta chỉ đề cập
tới vấn đề chéo hóa trực giao đối với ma trận đối xứng. Để thuận tiện cho đọc phần này,
cần đọc thêm tính trực giao và không gian Euclide thực được trình bày ở chương không
gian véc tơ.
1. KHÁI NIỆM MA TRẬN TRỰC GIAO
Giả sử A M(n,n), ký hiệu h
i
A là ma trận hàng i của A còn h
i
A
T
= c
i
A [R]
n
, i =
1..n. Theo quy tắc nhân ma trận ta có tích:
h
1
A
T
.c
1
A h
1
A
T
.c
2
A
h A
T
.c A h A
T
.c A
...
...
h
1
A
T
.c
n
A
h A
T
.c A
A
T
A=
2 1 2 2 2 n
.
h
n
A
T
.c
1
A h
n
A
T
.c
2
A
...
h
n
A
T
.c
n
A
Nếu tập các cột của A là tập trực chuẩn, tức h
i
A
T
.c
j
A = <c
i
A.c
j
A> =
1 khi
khi
i = j
i j
thì có ngay:
A
T
A =
1 0 ... 0
0 1 ... 0
= I .
0 ... 0 1
Ma trận A với đặc điểm như vậy, có tên gọi là ma trận trực giao, nó đóng vai trò
quan trọng trong nhiều bài toán ứng dụng của đại số tuyến tính. Vì vậy ta có định nghiã
sau:
Định nghiã 7. Ma trận A M(n,n) được gọi là ma trận trực giao nếu A
T
A = I.
Từ định nghiã, ta dễ dàng chứng minh được các điều kiện sau là tương đương với
nhau:
Định lý 13. Cho A M(n,n), các mệnh đề sau là tương đương:
1)
A trực giao.
2)
A khả nghịch và A
−
1
= A
T
.
3)
Tập các véc tơ ứng với hàng của A tạo nên cơ sở trực chuẩn của E
n
.
4)
Tập các véc tơ ứng với cột của A tạo nên cơ sở trực chuẩn của E
n
.
Định lý 14. Cho A M(n,n) là ma trận trực giao và x, y E
n
. Khi đó:
1) <(A[x].A[y] = < x.y>
139

lOMoARcPSD| 35883770
k
Chương 6. VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
2) ||A[x]|| = ||x||
Chứng minh
1) <(A[x].A[y] = (A[x])
T
(A[y]) = ([x]
T
A
T
)(A[y]) = [x]
T
(A
T
A)[y] = [x]
T
I[y] =
[x]
T
[y] = <x.y>.
2) Do 1) ta có ||A[x]||
2
= <A[x].A[x]> = <x.x> = ||x||
2
.
2. GIÁ TRỊ RIÊNG, VÉC TƠ RIÊNG CỦA MA TRẬN ĐỐI XỨNG
Định lý 15. Nếu A M(n,n) đối xứng thì A chéo hóa được.
Ta công nhận mà không chứng minh định lý này.
Định lý 16. Nếu A M(n,n) đối xứng thì hai véc tơ riêng ứng với hai giá trị riêng
phân biệt luôn vuông góc với nhau.
Chứng minh. Giả sử v
1
, v
2
là 2 véc tơ riêng nào đó của A, ứng với 2 giá trị riêng
phân biệt
1
2
. Xét tích vô hướng
1
<v
1
.v
2
> = <(
1
v
1
).v
2
> = <Av
1
.v
2
> = (Av
1
)
T
v
2
=
(v
1
T
A
T
)v
2
= v
1
T
(A
T
v
2
) = v
1
T
(Av
2
) = <v
1
.Av
2
> = <v
1
.(
2
v
2
)> =
2
<v
1
.v
2
>. Do đó
1
<v
1
.v
2
> =
2
<v
1
.v
2
> (
1
−
2
)<v
1
.v
2
> = 0 <v
1
.v
2
> = 0 (vì
1
2
).
3. CHÉO HÓA TRỰC GIAO MA TRẬN ĐỐI XỨNG
Nhắc lại rằng, ma trận A M(n,n) là đối xứng A
T
= A. Ma trận A gọi là chéo
hóa được nếu tồn tại ma trận khả nghịch P và ma trận chéo D sao cho A = PDP
−
1
. Khi A
được chéo hóa bởi ma trận trực giao P thì A gọi là chéo hóa trực giao được (bởi P).
Vậy, ta có định nghĩa sau:
Định nghiã 8. Ma trận A M(n,n) gọi là chéo hóa trực giao được nếu tồn tại ma
trận trực giao P và ma trận chéo D sao cho A = PDP
T
.
Định lý sau đây sẽ trình bày tính chất quan trọng nhất của ma trận đối xứng, đó là
mọi ma trận đối xứng đều chéo hóa trực giao được và ngược lại.
Định lý 17. Nếu A M(n,n) thì các phát biểu sau là tương đương:
1)
A là đối xứng.
2)
Có một cơ sở trực chuẩn của [E
n
] bao gồm các vectơ riêng của A.
3)
Có một ma trận trực giao P và một ma trận chéo D sao cho P
T
AP = D.
Chứng minh
- Chứng minh 1) 2).
Giả sử tập các giá trị riêng phân biệt của A là {
1
,
2
, ...,
k
} với bội tương ứng là
m
1
,
m
2
, ,,,
m
k
.
V
ì
A
đối xứng nên chéo hóa được
m
i
= n và dimE
i
=
m
i
, i = 1..k.
i=1
140

lOMoARcPSD| 35883770
II. CHÉO HOÁ
trực giao với nhau nên B là cơ sở trực chuẩn của [E
n
].
- Chứng minh 2) 3).
Giả sử B = {u
1
, u
2
, ..., u
n
} là cơ sở trực chuẩn bao gồm các vectơ riêng của [E
n
],
tương ứng với các giá trị riêng
1
,
2
, ...,
n
thì ma trận
P
=
[u
1
]
là trực giao
và P
T
AP = P
−
1
AP = = D là ma trận chéo.
-
Chứng minh 3) 1).
Nếu P là ma trận trực giao, D là ma trận chéo và P
T
AP = D thì A = (P
T
)
−
1
DP
−
1
=
PDP
T
A
T
= (PDP
T
)
T
= PD
T
P
T
= PDP
T
= A, tức A là ma trận đối xứng.
5 −4 −2
Ví dụ 12. Ví dụ. Cho A =
−4 5 −2
−
2
−
2
8
1)
Chứng minh rằng A là chéo hóa trực giao được.
2)
Chéo hóa trực giao ma trận A.
Giải
1)
A là ma trận đối xứng nên A chéo hóa trực giao được.
2)
Chéo hóa trực giao ma trận A.
Cần tìm ma trận trực giao P và ma trận chéo D sao cho A = PDP
T
. Ma trận trực giao
P có tập các cột là tập trực chuẩn bao gồm các véc tơ riêng của A. Việc tìm được tóm tắt
như sau:
- det(A−I) = −
3
+18
2
−81 = −(−9)
2
= 0
1
= 0;
2
=
3
= 9.
2
-
Với
1
= 0, chọn được véc tơ riêng
v
1
=
2
.
1
−1
−1
-
Với
2
= 9, chọn được 2 véc tơ riêng
v
2
=
1
,
v
3
=
0
.
0
2
Tập gồm 3 véc tơ riêng {v
1
, v
2
, v
3
} là cơ sở của [E]
3
, tuy nhiên nó chưa là cơ sở trực
chuẩn nên chưa lấy chúng để lập các cột cho P được.
Áp dụng thuật toán trực giao hoá Gram−Schmidt ta sẽ xây dựng cơ sở trực giao từ
cơ sở {v
1
, v
2
, v
3
}. Hiển nhiên đã có v
1
⊥ {v
2
, v
3
}.
141
k
Gọi B
i
là cơ sở trực chuẩn của E
i
và B = B
i
thì do các vec tơ của B
i
và B
j
, i j, là
i=1
[
u
n
]
1
0
0
n

lOMoARcPSD| 35883770
2
2
3
2
−4
3
2
3
Chương 6. VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
−1
Đặt
a
1
=
v
2
=
1
.
0
a .v
−
1
1
−1
−
1/ 2
a
2
= v
3
− (
1
3
)
a
1
=
0
−
1
=
−
1/ 2
.
a
1
.a
1
2
2
0
2
Chọn a’
2
= −2a
2
=
2
−1
1
1
1
, ta có cơ sở trực giao gồm 3 vectơ:
−
4
v =
2
, a
=
1
, a '
=
1
. Đơn vị hóa các véc tơ thuộc cơ sở trực giao để được cơ
1
1
1
0
2
−4
2 / 3
−1/ 2
1/ 3
sở trực chuẩn:
=
2 / 3
,u
= u = 1/ 3 . Ma trận P lập bởi các cột {u ,
u
1
2
1/ 2
,
3
1
1/ 3
0
−4 / 3 2
u
2
, u
3
} là ma trận chéo hóa trực giao được A.
2
−1 1
0 0 0
- Đáp số: A = PDP
T
với P =
2
1
1
, D =
3 2
0
0 9
0
.
0
0
9
142
2
1
2
3
3

lOMoARcPSD| 35883770
2 j
x
j
1 1
x
n n
Chương 6: VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
IV. DẠNG TOÀN PHƯƠNG
1. KHÁI NIỆM DẠNG TOÀN PHƯƠNG
Một đa thức bậc 2 của 2 biến x
1
, x
2
có dạng:
P(x
1
, x
2
) = a x
2
+ a
2
x
1
x
2
+ a
3
x
2
2
+ b
1
x
1
+ b
2
x
2
+ c
Nếu chỉ xét các hạng tử bậc hai, ta được đa thức đẳng cấp bậc 2:
Q(x
1
, x
2
) = a
1
x
1
2
+ a
2
x
1
x
2
+ a
3
x
2
2
. (*)
gọi là dạng toàn phương của 2 biến x
1
và x
2
. Đồ thị của phương trình Q(x
1
,x
2
) = d, d R là
đường bậc hai trong mặt phẳng (còn gọi là đường mức của Q).
Định nghiã 1. Ta gọi dạng toàn phương trên R
n
là một hàm Q: R
n
→ R mà giá trị của
nó tại véc tơ x = (x
1
; x
2
; ..., x
n
) R
n
cho bởi tổng dạng:
Q(
x
1
; x
2
; ..., x
n
) =
a
ij
x
i
x
j
, a
ij
R
, i = 1..n, j = 1..n.
i
=
1
j
=
1
x
1
2 n
a
11
21
a
12
a
22
...
...
a
1n
2 n
Ký hiệu vectơ cột của x là X =
[R]
và đặt A =
thì:
x
a a ... a
n
n1 n2 nn
n
a
1
j
x
j
a a ...
a
x
j
=
1
11 12 1n
n
T
a
21
a
22 ...
a
2n
x
2
a
X
AX
=
x
1
x
2
x
n
.
=
x
1
x
2
j
=
1
a a ... a x
n1 n2
nn
n
n
a
nj
x
j
j
=
1
n n n n n
=
a
1 j
x
1
x
j +
a
2
j
x
2
x
j
+ ... +
a
nj
x
n
x
j
=
a
ij
x
i
x
j
.
j
=
1
j
=
1
j
=
1
i=1
j
=
1
Điều đó có nghiã là:
Q(x
1
; x
2
; ..., x
n
) =
a
ij
x
i
x
j
i
=
1 j
=
1
= X
T
AX = Q(X)
143
n n
x
n
a
a
1

lOMoARcPSD| 35883770
0
0 a
nn
x
3
2
+ a x
x
2
IV. DẠNG TOÀN PHƯƠNG
Dạng toàn phương Q(X) = X
T
AX trên R
n
còn có tên gọi là dạng toàn phương của các
biến x
1
, x
2
, ..., x
n
. Hạng tử chứa x
i
2
gọi là hạng tử bình phương, còn hạng tử chứa tích x
i
x
j
với i j gọi là hạng tử chéo. Với i j hạng tử chéo chứa tích x
i
x
j
là (a
ij
+ a
ji
)x
i
x
j
. Có nhiều
cách chọn a
ij
và a
ji
để tổng (a
ij
+ a
ji
) không đổi, tuy nhiên nếu chọn a
ij
= a
ji
thì có ma trận
A= [a
ij
] M(n,n) là ma trận đối xứng và khi đó nó được gọi là ma trận của dạng toàn
phương Q(X) vì nó là ma trận đối xứng duy nhất, nhờ đó tính được giá trị của dạng toàn
phương.
Ví dụ 1. Cho Q(X) = 3x
1
2
+5x
2
2
+2x
3
2
−2x
1
x
2
+8x
1
x
3
. Hãy tìm ma trận của dạng toàn
phương Q(X) rồi viết Q(X) dưới dạng X
T
AX.
Ma trận A = [a
ij
] M(3,3) của dạng toàn phương là ma trận đối xứng, được thành lập
theo quy tắc:
-
Phần tử đường chéo a
ii
là các hệ số của hạng tử bình phương x
i
2
: a
11
= 3; a
22
= 5;
a
33
= 2.
-
Phần tử nằm ngoài đường chéo: a
ij
= a
ji
, (i j) là phân nửa hệ số của hạng tử chéo
chứa x
i
x
j
tương ứng: a
12
= a
21
= −2/2 = −1; a
13
= a
31
= 8/2 = 4; a
23
= a
32
= 0. Vậy:
3 −1 4
3
−
1
4
x
1
A =
−1 5 0
. Khi đó, Q(X) =X
T
AX. = [x
1
x
2
x
3
]
−1 5
0
x
.
2
4
0
2
4
0
2
x
3
5
−
1/ 2
0
Ví dụ 2. Cho Q(X) = X
T
AX, A =
−
1/ 2
3 4
. Hãy viết biểu thức của Q(X) dưới
0
4
2
dạng đa thức đối với các biến x
1
, x
2
, x
3
.
x
1
5
−
1/ 2 0
x
1
Với X =
2
thì Q(X) = X
T
AX = [x
1
x
2
x
3
]
−
1/ 2
3
4
x
=
x
3
5x
1
2
+3x
2
2
+2x
2
−x
1
x
2
+8x
2
x
3
.
0
4
2
x
3
Định nghiã 2. Dạng toàn phương Q(X) =X
T
AX được gọi là có dạng chính tắc nếu ma
trận A của nó có dạng chéo.
Từ định nghiã suy ra dạng toàn phương Q(X) có dạng chính tắc khi và chỉ khi Q(X)
viết được dưới dạng:
a
11
0 ...
0
x
1
Q(X) =
x
1
x
2
0
x
n
.
a
22
...
0
x
= a
11
x
1
2
2
22 2
+...+ a
nn
x
n
2
n
không chứa bất kì hạng tử chéo nào.
144

lOMoARcPSD| 35883770
0
0
n
2
2 1
1
1
1
1
2
0 0
Chương 6: VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
2. QUY DẠNG TOÀN PHƯƠNG VỀ DẠNG CHÍNH TẮC
Cho dạng toàn phương Q(X) =X
T
AX với A M(n,n) là ma trận đối xứng. Do A đối
xứng nên A chéo hoá trực giao được, nghiã là trong [R]
n
tồn tại 1 cơ sở trực chuẩn bao
gồm các vectơ riêng của A: B = {u
1
, u
2
, ..., u
n
}. Gọi
i
là vectơ riêng ứng với u
i
, i = 1..n,
(tức là
A
u
i
=
i
u
i
) v
à
P
=
u
1
u
2
thì:
1
0 ... 0
P
T
AP =
... 0
Đặt Y = [X]
B
thì X = [X]
E
= P
B
E
[X]
B
= PY (E là cơ sở chính tắc), khi đó:
1
0 ... 0
T T T T
T
0 ... 0
Q(X) = X AX = (PY) APY = Y (P AP)Y = Y
Y =
1
y
1
2
+
2
y
2
2
+...+
n
y
n
2
.
n
Biểu thức trên biểu thị giá trị của dạng toàn phương Q(X) theo tọa độ của vectơ X đối
với cơ sở B. Rõ ràng sự biểu thị này đơn giản hơn nhiều so với sự biểu thị của Q(X) theo
tọa độ của X đối với cơ sở E ban đầu.
Với lý luận như trên, ta khẳng định rằng bất kỳ dạng toàn phương nào cũng đưa được
về dạng chính tắc nhờ thực hiện chéo hoá trực giao ma trận của nó. Quá trình đưa dạng
toàn phương về dạng chính tắc còn gọi là chéo hóa dạng toàn phương.
Ví dụ 3. Chéo hóa dạng toàn phương Q(X) = x
1
2
+ 4x
1
x
2
+x
2
2
.
-
Lập ma trận của dạng toàn phương: A=
1 2
.
-
Tìm tập giá trị riêng của A:
1
= 3,
2
= −1.
-
Với
1
= 3 E
1
=
S
p
1
, cơ
s
ở của E
: {v
1
=
1
}.
-
Với
2
= 2, E
2
=
S
p
−
1
, cơ
s
ở của E
: {v
2
=
−1
}.
-
Cơ sở {v
1
, v
2
}là trực giao, nhưng chưa trực chuẩn, đơn vị hoá v
1
, v
2
ta được cơ sở
trực chuẩn bao gồm các vectơ riêng là B = {u
1
=
1/ 2
=
−1/ 2
}. Đặt P =
1/
145
2
u
n
1/ 2
0
, u
1
2
2

lOMoARcPSD| 35883770
6
1/
3
1/
3
0 1
0 1
u
1
u
2
thì: P
T
AP =
IV.
DẠNG TOÀN PHƯƠNG
3 0
. Đổi qua cơ sở B nhờ đặt Y = P
−
1
X X = PY thì Q(X) sẽ có
dạng chéo :
Q(X) = Y
T
3 0
Y = 3y
1
2
– y
2
2
.
Về mặt hình học, đường mức của Q: (C) = {M(x
1
, x
2
) R
2
/ Q(X) = d} là đường bậc hai
cho bởi phương trình x
1
2
+ 4x
1
x
2
+x
2
2
= d. Khi chuyển về hệ toạ độ mới, xác định bởi cơ sở
B = {u
1
, u
2
}, thì phương trình (C) có dạng 3y
1
2
– y
2
2
= d, dễ nhận ra nó là đường hypebol
khi d 0 và là cặp đường thẳng cắt nhau khi d = 0.
Ví dụ 4. Chéo hóa dạng toàn phương Q(X) = 2x
1
2
+2x
2
2
+2x
3
2
+2x
1
x
2
+2x
1
x
3
+2x
2
x
3
.
-
Ma trận của dạng toàn phương: A =
2 1 1
1 2 1
.
1
1
2
-
Tập các giá trị riêng của A: {
1
= 1 (bội 2);
2
= 4}.
−1
−1
−
1
−1
-
Với
1
= 0,
E
1
= Sp
0
,
1
, cơ sở của
E
1
: {
v
1
=
0
,
v
2
=
1
}.
1
0
1
0
1
1
-
Với
2
=
,
E
2
= Sp
1
, cơ sở của
E
2
:{
v
3
=
1
}.
1
1
Cơ sở {v
1
, v
2
, v
3
} vừa tìm được chưa là cơ sở trực giao vì cơ sở của E
1
chưa trực giao.
Thực hiện thuật toán Gram−Schmidt cho {v
1
, v
2
}, đặt w
1
= v
1
và:
v .w
−
1
−
1
1
−
1/ 2
w
2
= v
2
−
2 1
w
1
=
1
−
0
=
1
.
|| w
1
||
2
0
2
1
−
1/
2
Cơ sở trực giao bao gồm các vectơ riêng là {v
1
, w
1
, w
2
}. Đơn vị hóa chúng, thu được
cơ sở trực chuẩn:
−
1/
2
−
1/
6
B = { u
1
=
0
,
u
2
=
2 /
,
u
3
=
1/
3
}.
−
1/
2
−
1/
6
146
2

lOMoARcPSD| 35883770
6
3
x
2
1
0
Chương 6: VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
−1/
−1/
1/
3
1 0 0
Đặt P = [u u
u ] =
0
2 /
1/ 3
thì P
T
AP =
0 1 0
. Đổi qua cơ sở B
1 2 3
−1/
−1/
1/
3
0
0
4
nhờ đặt Y = P
−
1
X X = PY. Khi đó, dạng toàn phương sẽ có dạng chéo:
1 0 0
Q(X) = X
T
AX = Y
T
0 1 0
Y = y
1
2
+y
2
2
+4y
2
.
3
0
0
4
Về mặt hình học, mặt mức của Q: (S) = {M(x
1
, x
2
; x
3
) R
3
/ Q(X) = d} là mặt bậc hai
cho bởi phương trình : 2x
1
2
+2x
2
2
+2x
2
+2x
1
x
2
+2x
1
x
3
+2x
2
x
3
= d. Khi chuyển về hệ toạ độ
mới, xác định bởi cơ sở B = {u
1
, u
2
, u
3
}, thì phương trình (S) có dạng: y
1
2
+y
2
2
+4y
3
2
= d, dễ
nhận ra nó là mặt Elipxoit khi d > 0, là tập rỗng khi d < 0, là tập gồm 1 điểm khi d = 0.
3. DẠNG TOÀN PHƯƠNG XÁC ĐỊNH DẤU
Cho A M(n,n) và dạng toàn phương Q(X) = X
T
AX, X [R]
n
. Hiển nhiên khi X =
[0]
thì Q(X) = 0, khi X = X
0
[0] thì t R ta có :
Q(tX
0
) = (tX
0
)
T
A(tX
0
) = t
2
(X
0
T
AX
0
) = t
2
Q(X
0
).
Do vậy, Q(X) và Q(X
0
) luôn cùng dấu với nhau tại mọi X Sp{X
0
}, X [O], hoặc là
Q(X) đồng nhất bằng 0 trên Sp{X
0
}.
Định nghiã 3. Giả sử Q là dạng toàn phương trên R
n
.
1. Nếu Q(X) > 0 (hoặc Q(X) < 0) X [O], X [R]
n
thì Q được gọi là dạng toàn
phương xác định dương (hoặc dạng toàn phương xác định âm).
2. Nếu Q(X) 0 (hoặc Q(X) 0) X [R]
n
thì Q được gọi là dạng toàn phương nửa
xác định dương (hoặc dạng toàn phương nửa xác định âm).
3. Nếu Q(X) nhận cả giá trị dương lẫn giá trị âm thì Q(X) được gọi là dạng toàn
phương không xác định dấu.
Ví dụ 5.
1. Dạng toàn phương Q(X) = x
1
2
−6x
1
x
2
+9x
2
2
là nửa xác định dương vì Q(X) = (x
1
–3x
2
)
2
0 với mọi X =
x
1
. Q(X) không là xác định dương vì Q(X) = 0 trên đường thẳng x
1
=
3x
2
.
2
2. Dạng toàn phương Q(X) = x
1
2
−2x
1
x
2
−3x
2
là không xác định dấu vì Q(X) sẽ thay đổi
dấu tuỳ theo X, ví dụ với X =
0
thì Q(X) = −3 <0, với X =
1
thì Q(X) = 1 > 0.
147
2
6
2
6

lOMoARcPSD| 35883770
3
1
1
2
2
n
n
0 0
IV. DẠNG TOÀN PHƯƠNG
3. Dạng toàn phương Q(X) = 3x
1
2
+x
2
2
+9x
2
là xác định dương vì Q(X) > 0 với mọi X
[O].
Định lý 1. Nếu A M(n,n) là ma trận đối xứng, có giá trị riêng
1
,
2
, ...,
n
và Q(X)
= X
T
AX thì Q là:
1)
Xác định dương (xác định âm) khi và chỉ khi
i
>0 (
i
< 0) i = 1.n.
2)
Nửa xác định dương (nửa xác định âm) khi và chỉ khi
i
0 (
i
0) i = 1.n.
3)
Không xác định dấu khi và chỉ khi tồn tại ít nhất một giá trị riêng dương và một giá
trị riêng âm.
Chứng minh
Gọi B = {u
1
, u
2
, ..., u
n
} là cơ sở trực chuẩn bao gồm các vectơ riêng đơn vị của A, Au
i
=
i
u
i
i = 1..n. Đặt
P
=
u
1
u
2
= P
B,
E
và X = PY thì:
1
0 ... 0
T T
0
... 0
2 2 2
Q(X) = X AX = Y
Y =
1
y
1
+
2
y
2
+...+
n
y
n
(*)
n
trong đó
1
,
2
, ...,
n
là các giá trị riêng (có thể trùng nhau) của A.
1). Nếu
i
> 0 i = 1..n, thì y
2
+ y
2
+...+ y
2
>0 Y [O]. Hơn nữa, do X [O]
Y [O] (vì X = PY, P khả nghịch) nên Q(X) là xác định dương.
Ngược lại, nếu Q(X) là xác định dương, thì :
0 < Q(u
i
) = u
i
T
Au
i
= u
i
T
(
i
u
i
) =
i
||u
i
||
2
=
i
, i = 1..n.
Vậy, 1) đã được chứng minh, còn 2) và 3) hãy tự chứng minh.
3 0 −1
Ví dụ 6. Cho dạng toàn phương Q(X) = X
T
AX, A =
xác định dương hay xác định âm của Q.
Giải
0 4 0
. Hãy xác định tính
−
1
0
3
3
−
0 −1
- det(A−
i
) = 0
0
4
−
0 = 0 (4−)(
2
−6+8) = 0
1
=
2
=4,
3
=1.
−1 0
3
−
- Q là xác định dương vì mọi giá trị riêng của A đều dương
148
2
u
n

lOMoARcPSD| 35883770
b
c
0
b c
0
a 0
a 0
1 1
Chương 6: VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
Việc xác định tính xác định dương (âm) của dạng toàn phương nhờ định lý trên phụ
thuộc việc tìm giá trị riêng của ma trận, đôi khi tỏ ra không hiệu quả vì phải giải phương
trình đặc trưng bậc cao. Tuy nhiên, ta có cách tiếp cận khác nhờ xuất phát từ nhận xét với
dạng toàn phương đơn giản nhất Q(X) = X
T
AX, A =
a b
M(2,2) như sau:
Giả sử đa thức đặc trưng của A: p() = det(A−I) = (−
1
)( −
2
) p(0) = detA =
1
.
2
. Như vậy, nếu detA > 0 thì
1
và
2
cùng dấu dương hoặc cùng dấu âm. Mặt khác với
1
X =
thì Q(X) =
1 0
a
b
1
= a, nên:
-
Q(X) xác định dương
1
,
2
> 0
1
.
2
0
-
Q(X) xác định âm
1
,
2
< 0
1
.
2
0
.
-
Q(X) không xác định dấu detA < 0.
Như vậy, tính xác định dấu của dạng toàn phương ứng với ma trận đối xứng cấp 2 hoàn
toàn được xác định qua dấu của detA và dấu của phần tử a
11
. Một cách tổng quát, ta công
nhận kết quả cho bởi định lý sau:
Định lý 2. (Định lý Sylvester) Cho dạng toàn phương Q(X) = X
T
AX với A là ma trận
a
11
a
1k
đối xứng cấp n. Gọi A
k
=
là ma trận vuông lấy từ k hàng và k cột đầu
tiên của A. Khi đó:
a
k1
a
kk
1)
Q xác định dương det(A
k
) > 0 k = 1..n.
2)
Q xác định âm (−1)
k
det(A
k
) > 0 k = 1..n.
Ví dụ 7. Cho Q(X) = 2x
1
2
+ 2x
1
x
2
+ x
2
2
+ 2x
2
x
3
+ 3x
3
2
thì có :
2 1 0
A =
1 1 1
, A
1
= [2], A
2
=
0
1
3
2 1
, A
3
= A. Do detA
1
= 2 > 0, detA
2
= 1 > 0 và
detA
3
= 1 > 0 nên Q là xác định dương.
149

lOMoARcPSD| 35883770
x
0
x
0
0
IV. DẠNG TOÀN PHƯƠNG
−4 0 −2 0
T
0 −2 0 1
Ví dụ 8. Cho Q(X) = X AX, A =
, thì :
−2 0 −3 1
0 1 1 −2
- A
1
= [−4] detA
1
= −4 < 0.
- A =
−4 0
detA
= 8 > 0.
2
0 −2
2
−4 0 −2
- A
3
=
0 −2 0
detA
3
= −16 < 0.
−
2
0
−
3
- A
4
= A, detA = 16 > 0.
Q là xác định âm theo 2) của định lý.
4. ỨNG DỤNG VÀO BÀI TOÁN TÌM CỰC TRỊ.
Với bài toán tìm cực trị tự do của hàm 2 biến (tương tự cho hàm nhiều biến) trong lân
cận của điểm O, dạng toàn phương sẽ cung cấp công cụ hữu hiệu.
Ví dụ 9. Tìm giá trị nhỏ nhất (nếu có) của biểu thức Q(x
1
, x
2
) = 5x
1
2
−4x
1
x
2
+2x
2
2
.
Giải
Dễ thấy Q(x , x ) là dạng toàn phương Q(X) = X
T
AX ứng với ma trận A =
5
−
2
và X =
1 2
x
1
.
−
2 2
2
-
Tìm tập giá trị riêng của A:
|A− I| = 0
5 − −2
−
2
2 −
= 0
2
−7+6 = 0
1
= 1;
2
= 6.
-
Do mọi giá trị riêng của A đều dương nên Q(X) là dạng toàn phương xác định
dương, tức Q(X) > 0, X =
x
1
0
. Do Q(X) = 0 khi X =
0
, suy ra Q(X) đạt giá trị
nhỏ nhất bằng 0, tại X =
2
0
.
Nhiều bài toán thực tiễn yêu cầu phải tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của
dạng toàn phương Q(X) khi véc tơ X [R]
n
biến thiên trên một tập nào đó đã được chỉ ra,
150

lOMoARcPSD| 35883770
n
0
1 1
0
Chương 6: VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
thường là trên mặt cầu đơn vị (S) = {X [R]
n
/ ||X|| 1}. Người ta chứng minh được rằng,
với bất kỳ ma trận đối xứng A M(n,n), thì tập hợp tất cả các giá trị có thể có của dạng
toàn phương Q(X) = X
T
AX lấy trên mặt cầu đơn vị, là một khoảng đóng nào đó trên trục
thực. Hơn nữa với là một giá trị riêng nào đó của A, thì có:
m = min{X
T
AX/ ||X|| = 1} M = max{{X
T
AX/ ||X|| = 1}
Các định lý sau đây sẽ cho ta vài dấu hiệu để tìm giá trị lớn nhất, nhỏ nhất của dạng
toàn phương trên tập các véc tơ đơn vị (tức trên mặt cầu đơn vị). Chú ý rằng, điều kiện
ràng buộc để véc tơ X [R]
n
là véc tơ đơn vị thường được cho bởi một trong các điều kiện
tương đương sau:
||X|| = 1 ||X||
2
= 1 x
1
2
+ x
2
2
+ ... + x
2
= 1 X
T
X = 1.
Định lý 3. Giả sử A là ma trận đối xứng cấp n của dạng toàn phương Q(X), có n giá
trị riêng
1
,
2
, ... ,
n
(chúng có thể trùng nhau) được sắp xếp theo thứ tự nhỏ dần:
1
2
.....
n
. Khi đó:
1)
Giá trị lớn nhất của Q(X) trên mặt cầu đơn vị đúng bằng
1
, đạt được tại véc tơ
riêng đơn vị ứng với giá trị riêng lớn nhất
1
.
2)
Giá trị nhỏ nhất của Q(X) trên mặt cầu đơn vị đúng bằng
n
, đạt được tại véc tơ
riêng đơn vị ứng với giá trị riêng nhỏ nhất
n
.
Chứng minh
1. Gọi u
i
là véc tơ riêng đơn vị của A ứng với
i
(i = 1..n) thì ma trận chéo hóa trực
giao được A là P =
u
1
u
2
u
n
.
Thực
hiện
phép
đổi
biến
X
=
PY
thì
dạng
toàn
phương Q(X) = X
T
AX được quy về dạng chính tắc:
1
0 ... 0
T T
0
... 0
n
Q(X) = X
AX
=
Y
Y
=
i
y
i
Do ||X|| = ||PY|| = ||Y|| y
1
2
+ y
2
2
+...+ y
n
2
= 1, nên:
i=1
Q(X) =
2
=
1
y
1
2
+
2
y
2
2
+...+
n
y
n
2
1
(y
1
2
+ y
2
2
+...+ y
n
2
) =
1
.
i=1
1
Nhưng do tại X = P[e ], [e ] =
thì:
151
n
2
2
0 ... 0
n
y
i i

lOMoARcPSD| 35883770
0 ... 0
n
1/
3
1/
3
0
0
IV. DẠNG TOÀN PHƯƠNG
1
0 ... 0
1
Q(X) = X
T
AX =
1
0
2
... 0
0
=
1
.
nên max{Q(X)}=
1
, đạt tại X = P[e
1
] = u
1
là véc tơ riêng đơn vị ứng với giá trị riêng
1
.
2) được chứng minh tương tự 1).
Ví dụ 10. Tìm giá trị lớn nhất và nhỏ nhất của dạng toàn phương Q(X) = X
T
AX , A =
3 2 1
2 3 1
, với điều kiện X
T
X= 1. Xác định véc tơ đơn vị để tại đó dạng toàn phương
1
1
4
đạt giá trị lớn nhất.
-
Tìm tập giá trị riêng của A.
3 − 2 1
=
1
|(A−I| = 0
2 3 −
1
= 0
=
3
.
1 1 4 −
=
6
-
Áp dụng định lý, suy ra:
max{Q(X) / X
T
X= 1} = 6, đạt tại X = u
1
là vectơ riêng đơn vị ứng với = 6.
min{Q(X) / X
T
X = 1} = 1, đạt tại X = u
2
là vectơ riêng ơn vị ứng với = 1.
-
Để tìm véc tơ riêng đơn vị mà tại đó dạng toàn phương đạt giá trị lớn nhất, ta cần
tìm véc tơ riêng ứng với = 6 rồi đơn vị hoá nó. Cụ thể:
−3 2 1
1 1 −2
1 0
−1
A−6I =
2 −3
1
→
0
−5 5
→
0 1 −1
1
1
1
1
−
2
0
5
−
5
0
0
0
v
1
=
1
là 1 vectơ riêng. Đơn vị hóa v
1
, ta có u
1
=
1/
3
là véc tơ tại đó Q(X) đạt
giá trị lớn nhất với điều kiện X
T
X = 1.
Trong một số ứng dụng, véc tơ X không những bị ràng buộc bởi điều kiện đơn vị mà
còn cần thỏa mãn thêm những điều kiện khác, chẳng hạn, X phải vuông góc với véc tơ
riêng v
1
. Khi đó, ta có kết qủa sau:
152
0

lOMoARcPSD| 35883770
1
2 n 2 n 1
n n 2 2 n 2
2 2
Chương 6: VÉC TƠ RIÊNG, CHÉO HÓA VÀ DẠNG TOÀN PHƯƠNG
Định lý 4. Giả sử A là ma trận đối xứng cấp n của dạng toàn phương Q(X), có n giá
trị riêng
1
,
2
, ... ,
n
(chúng có thể trùng nhau) được sắp xếp theo thứ tự nhỏ dần:
1
2
. ...
n
, và các véc tơ riêng đơn vị tương ứng là u
1
, u
2
, ..., u
n
. Khi đó, giá trị
T
X
T
X
=
1
lớn nhất của Q(X
)
= X AX với điều kiện ràng buộc:
X
T
u
=
0
đúng bằng
2
, đạt được
có:
tại véc tơ riêng đơn vị ứng với
2
.
Chứng minh. Thực hiện chứng minh tương tự với cách chứng minh định lý 3 ở trên ta
Q(X) =
i
y
i
i
=
1
=
1
y
1
2
+
2
y
2
+...+
n
y
n
Véc tơ riêng đơn vị của A, ứng với giá trị riêng
1
là u
1
= P[e
1
], nên điều kiện X
T
u
1
= 0
tương đương với:
(PY)
T
(P[e
1
]) = 0 Y
T
(P
T
P)[e
1
] = 0 Y
T
[e
1
] = 0 y
1
= 0,
và từ điều kiện X
T
X = 1 suy ra được:
||X||
2
= 1 ||Y|| = 1 y
1
2
+ y
2
+ ...+ y
2
= 1 y
2
+ ...+ y
2
= 1, (do y = 0).
Do vậy:
Q(X) =
2
y
2
2
+ ...+ y
2
(y
2
+ ...+ y
2
) = .
Dấu bằng xẩy ra khi X = P[e
2
] = u
2
là véc tơ riêng đơn vị ứng với giá trị riêng
2
.
Chứng tỏ Q(X) đạt giá trị lớn nhất bằng
2
tại u
2
.
Mở rộng định lý 5, ta có kết qủa sau, mà cách chứng minh hoàn toàn tương tự như cách
chứng minh trên, nên được bỏ qua:
Định lý 5. Giả sử A là ma trận đối xứng cấp n của dạng toàn phương Q(X), có n giá
trị riêng
1
,
2
, ... ,
n
(chúng có thể trùng nhau) được sắp xếp theo thứ tự nhỏ dần:
1
2
. ...
n
, và các véc tơ riêng đơn vị tương ứng là
u
1
,
u
2
, ...,
u
n
. Khi đó, với k = 2,
3,..., n; giá trị lớn nhất của Q(X) = X
T
AX với điều kiện ràng buộc:
X
T
X
=
1
X
T
u = 0
1
X
T
u
k-1
= 0
Có giá trị đúng bằng
k
, đạt được tại véc tơ riêng đơn vị ứng với
k
.
153
n
2

lOMoARcPSD| 35883770
I. ĐƯỜNG BẬC HAI TỔNG QUÁT
Chương 7
ĐƯỜNG BẬC HAI PHẲNG VÀ MẶT BẬC HAI
1. Đường bậc hai tổng quát trong mặt phẳng
2. Mặt bậc hai cho bởi phương trình chính tắc
Trong chương này, nhờ công cụ là dạng toàn phương, ta sẽ nghiên cứu sâu thêm về
đường bậc hai trong mặt phẳng và mặt bậc hai trong không gian mà chúng đã được giới
thiệu ở bậc học phổ thông với một vài trường hợp đặc biệt như đường tròn, đường elip,
đường hypebol, đường parabol hay mặt cầu, mặt trụ.
I. ĐƯỜNG BẬC HAI TỔNG QUÁT VÀ ĐỒ THỊ CỦA NÓ
1. GIỚI THIỆU
Trong mặt phẳng, đồ thị của phương trình bậc hai đối với 2 biến x, y dạng:
ax
2
+ 2bxy + cy
2
+ 2dx + 2ey + f = 0, a
2
+b
2
+c
2
>0 (1)
được gọi là đường bậc hai tổng quát và phương trình (1) được gọi là phương trình tổng
quát của đường bậc hai. Hạng tử chứa tích xy trong (1) được gọi là hạng tử chéo.
Dễ dàng nhận ra rằng phương trình dạng chính tắc của các đường conic (elip,
hypebol, parabol) không bao giờ có chứa hạng tử chéo, vì vậy ta dễ dàng nhận dạng đồ
thị qua phương trình chính tắc của chúng. Ngược lại, nếu phương trình đường bậc hai
có chứa hạng tử chéo, cho dù ở dạng đơn giản nhất, ta vẫn rất khó để nhận ra ngay hình
dạng đồ thị của nó, chẳng hạn, đồ thị của phương trình: 2xy + x – 1 = 0, muốn nhận biết
được là hypebol, cần phải biến đổi và khảo sát hàm phân thức y =
− x + 1
.
2x
Trong mục này, nhờ sử dụng công dạng toàn phương mà ta có thể quy được phương
trình đường bậc hai từ dạng tổng quát về dạng chính tắc, rồi từ đó nhận ra ngay hình
dạng đồ thị của đường bậc hai đang xét.
2.PHƯƠNG PHÁP KHỬ HẠNG TỬ CHÉO NHỜ PHÉP QUAY HỆ TRỤC
TỌA ĐỘ
Cho đường bậc hai tổng quát có phương trình:
ax
2
+ 2bxy + cy
2
+ 2dx + 2ey + f = 0, a
2
+b
2
+c
2
>0 (C)
Xét các hạng tử bậc hai, ta có dạng toàn phương tương ứng:
Q(X) = ax
2
+ 2bxy + cy
2
154

lOMoARcPSD| 35883770
3
y
b
c
y '
0
y
y
'
= 1/ 2
Chương 7. ĐƯỜNG BẬC HAI PHẲNG VÀ MẶT BẬC HAI
trong đó X =
x
và A =
a b
là ma trận của dạng toàn phương Q.
Chéo hóa trực giao
A
bởi ma trận trực giao
P
=
u
1
u
2
,
A
u
1
=
1
,
A
u
2
=
2
u
2
và
đặt X = PY, Y =
x '
thì Q(X) được quy dạng về không còn hạng tử chéo:
Q(X) = Y
T
1
0
Y = x’
2
+ y’
2
1 2
2
Chú ý rằng, phương trình:
X = PY
x
=
u
1
u
2
x '
là phương trình của phép quay hệ trục tọa độ Oxy xung quanh gốc O, biến vec tơ chỉ
hướng đơn vị e
1
của trục Ox thành vec tơ u
1
và vec tơ chỉ hướng đơn vị e
2
của trục Oy
thành u
2
. Góc quay của phép quay được xác định bởi cos = <e
1
.u
1
>. Qua phép quay,
ta thu được hệ trục tọa độ mới Ox’y’ mà trong hệ trục đó, đường cong (C) có phương
trình không còn hạng tử chéo. Từ lý luận trên, ta có định lý sau:
Định lý 1. Trong mặt phẳng tọa độ Oxy luôn tồn tại hệ tọa độ mới Ox’Wy’ sao cho
đường cong (1) có phương trình đối với hệ tọa độ đó không còn chứa hạng tử chéo
nữa.
Ví dụ 1. Hãy quy phương trình đường bậc hai (C): 2x
2
+ xy+y
2
–10 = 0 về dạng
không còn hạng tử chéo và xác định phép quay hệ trục tọa độ tương ứng.
Giải
- Quy phương trình đường bậc hai về dạng không còn hạng tử chéo
Ma trận của dạng toàn phương Q(X) = 2x
2
+
xy+y
2
là A =
3 / 2
1
Tập trị riêng của A: |A–I| = 0
2 − 3 / 2
= 0
2
– 3 +
5
= 0
3 / 2 1 −
4
1
= 5 / 2
. Suy ra phương trình không còn hạng tử chéo:
2
5
x '
2
+
1
y '
2
−10 = 0 .
2 2
- Xác định phép quay hệ trục tọa độ tương ứng
155
3
2
3 / 2
.

lOMoARcPSD| 35883770
2
2
2
2
1 0
I. ĐƯỜNG BẬC HAI TỔNG QUÁT
Với
=
5
, A – I = A –
5
I =
−1/ 2 3 / 2
→
1
− 3
Véc tơ riêng tương
1
2
1
2
3 / 2
−3 / 2
0 0
ứng là v =
3
. Với
=
1
, A – I = A –
1
I =
3 / 2 3 / 2
→
1 1/ 3
Véc
1
1
2
2
2
2
3 / 2 1/ 2
0 0
tơ riêng tương ứng là v
=
−1 / 3
. Đơn vị hóa các vec tơ v , v , thu được cơ sở gồm
2
1
1 2
các vec tơ riêng đơn vị B =
u
=
3 / 2
, u
=
−
1/
2
. Ma trận chéo hóa trực giao được
1
1/ 2
2
3 / 2
A là P =
u
1
u
2
, suy ra phép quay hệ trục tọa độ có phương trình:
x =
3
x '−
1
y '
X = PY =
3 / 2
−1/ 2
Y
2 2
.
1/
2
3
/
2
y =
1
x '+
3
y '
2 2
Về mặt hình học, phép quay trên sẽ biến vec tơ e
=
1
thành vec tơ u =
3 / 2
.
1
0
1
1/ 2
Góc quay là góc giữa 2 vec tơ e
1
, u
1
, thoả mãn cos = <e
1
.u
1
> =
3
2
= /6. Do
vậy đây là phép quay hệ trục tọa độ Oxy xung quanh gốc O với góc quay = /6, theo
chiều dương (chiều ngược kim đồng hồ trên mặt phẳng).
Ví dụ 2. Quy phương trình đường bậc hai (C): 2xy +
hạng tử chéo.
Giải
- Ma trận của dạng toàn phương Q(X) = 2xy là A =
x –1 = 0 về dạng không còn
0 1
. Tập trị riêng của A:
|A–I| = 0
−
1
1
−
= 0
2
– 1 = 0
1
= 1
= −1
. Dạng toàn phương Q(X) = 2xy
2
được quy về dạng không còn hạng tử chéo là x’
2
– y’
2
nhờ thực hiện phép quay hệ trục
tọa độ X = PY với P là ma trận chéo hóa trực giao được A.
- Cần biểu thị hạng tử bậc nhất x trong phương trình của (C) qua hệ trục mới.
Sau khi tìm các véc tơ riêng và đơn vị hóa chúng, ta thu được ma trận chéo hóa trực
giao được A là P =
1/ −1/ 2
. Phương trình phép quay X = PY có dạng:
1/
1/
156
2
lOMoARcPSD| 35883770
2
2
1
2
Chương 7. ĐƯỜNG BẬC HAI PHẲNG VÀ MẶT BẬC HAI
x =
2
x '−
2
y '
X = PY
2 2
, suy ra
2x
=
2( x '
−
y ') = x '− y ' .
y =
2
x '+
2
y '
2 2
2 2
- Phương trình dạng không còn hạng tử chéo của (C) là: x’
2
– y’
2
+ x’ – y’ – 1 = 0.
3. PHÂN LOẠI ĐỒ THỊ CỦA ĐƯỜNG BẬC HAI TỔNG QUÁT
Vì mọi phương trình bậc hai tổng quát dạng (1) luôn quy được về dạng không còn
hạng tử chéo nên không giảm tính tổng quát, ta luôn giả thiết đường bậc hai (C) có
phương trình dạng:
(C):
1
x’
2
+
2
y’
2
+ 2d’x’+ 2e’y’+ F = 0 (1’)
Có các trường hợp xẩy ra sau đây:
- Trường hợp 1: Nếu
1
.
2
0 thì: (1’)
1
(x’
2
+2
d '
x’) +
2
(y’
2
+2
d '
y’) + F = 0
(x’+
d '
)
2
+ (y’+
d '
)
2
+ F –
e '
2
–
d '
2
1
2
= 0.
1
2
1
2
x ''
=
x '
+
d '
Thực hiện phép tịnh tiến hệ trục tọa độ:
y ''
=
y '
+
1
e '
2
và đặt F’=
e '
2
1
+
d '
2
2
– F, thì
trong hệ tọa độ mới O’x”y”, phương trình của (C) có dạng:
1
x’’
2
+
2
y’’
2
= F’ (2)
Các khả năng xẩy ra đối với (6) như sau:
Khả năng 1: Nếu
1
và
2
cùng dấu (chỉ cần xét
1
> 0,
2
> 0 còn
1
< 0,
2
< 0
được xét tương tự) thì có các tình huống sau xẩy ra:
-
Với
1
> 0,
2
> 0; F’>0, chia 2 vế của (2) cho F’ và đặt
F'
1
= a
2
;
F'
2
= b
2
. Khi
đó (2) có dạng:
x ''
2
+
y ''
2
= . Đường cong (C) là elip.
a
2
b
2
1
157
lOMoARcPSD| 35883770
1
I. ĐƯỜNG BẬC HAI TỔNG QUÁT
-
Với
1
> 0,
2
> 0; F’<0, chia 2 vế của (2) cho F’ và đặt –
F'
1
= a
2
; –
F'
2
= b
2
. Khi
đó (2) có dạng:
x ''
2
+
y ''
2
= − . (C) là tập rỗng (hay còn gọi là elip ảo).
a
2
b
2
1
-
Với
> 0, > 0; F’= 0 thì (2) quy được về dạng:
x ''
2
+
y ''
2
= . Phương trình
1 2
a
2
b
2
0
này xác định một điểm duy nhất, (C) là elip suy biến thành elip điểm.
Khả năng 2: Nếu
1
và
2
trái dấu (chỉ cần xét
1
> 0,
2
< 0 còn
1
< 0,
2
> 0
được xét tương tự) thì có các tình huống sau xẩy ra:
- Với
1
> 0,
2
< 0; F’>0, chia 2 vế của (2) cho F’ và đặt
F'
1
= a
2
; –
F'
2
= b
2
. Khi
đó (2) có dạng:
x ''
2
−
y ''
2
= . (C) là đường hypebol.
a
2
b
2
1
- Với
1
> 0,
2
< 0; F’<0, chia 2 vế của (2) cho F’ và đặt –
F'
1
= a
2
;
F'
2
= b
2
. Khi
đó (2) có dạng:
−
x ''
2
+
y ''
2
= , (C) cũng là hypebol.
a
2
b
2
1
- Với
> 0, < 0; F’= 0, (2) quy được về dạng:
x ''
2
−
y ''
2
= . Phương trình này
1 2
a
2
b
2
0
xác định cặp đường thẳng
cặp đường cắt nhau.
x"
+
y "
= 0 ,
a b
x"
−
y "
= 0
a b
cắt nhau tại gốc tọa độ O' nên (C) là
Trường hợp 2: Nếu
1
.
2
= 0 (chỉ cần xét với
1
0,
2
= 0 còn trường hợp
1
= 0,
2
0 được xét tương tự) thì:
Khả năng 1: Nếu
1
0,
2
= 0 và e’ 0 thì viết lại (1’): (1’)
1
(x’
2
+2
d '
x’) +
1
2e’(y’+
F
) = 0 (x’+
d '
)
2
+ 2e’(y’+
f
–
d '
2
) = 0. (3)
2e '
1
2e '
2
1
e '
Thực hiện phép tịnh tiến hệ tọa độ:
x" = x '+
d '
1
F d '
2
thì (3) có dạng:
y" = y '+ −
2e ' 2
1
e '
1
x”
2
+ 2e’y” = 0 (4)
Các tình huống có thể xẩy ra đối với (4) là:
158

lOMoARcPSD| 35883770
x" = −a
x" = 0
b
c
1
Chương 7. ĐƯỜNG BẬC HAI PHẲNG VÀ MẶT BẬC HAI
- Với
1
e’ < 0, chia 2 vế (4) cho
1
, chuyển vế và đặt –
e '
1
= p >0 ta được x”
2
=
2py”, p > 0. Đường cong (C) là parabol.
- Với
1
e’ > 0 thì chia 2 vế cho
1
, chuyển vế và đặt
2py”, p > 0. Đường cong (C) cũng là parabol.
Khả năng 2: Nếu
1
0,
2
= 0 và e’= 0 thì viết lại (1’):
e '
1
= p > 0 ta được x”
2
= –
2
(1’) (x‘+
d '
)
2
+ F –
d '
= 0. (5)
1
1
x" = x '+
d '
d '
2
Thực hiện phép tịnh tiến hệ tọa độ:
1
Y = y '
thì (5)
1
x”
2
+ F –
1
= 0. Đặt
F’ =
F
1
–
d '
2
1
2
thì (5) có dạng:
x”
2
+ F’ = 0 (6).
Các tình huống xẩy ra đối với (6) là:
- Nếu F’ < 0, đặt –F’ = a
2
ta có x"
2
= a
2
x" = a
. (C) là cặp đường thẳng song
song.
-
Nếu F’ = 0 thì (6) có dạng x"
2
= 0
x" = 0
. (C) là cặp đường thẳng trùng nhau.
-
Nếu F’ > 0 thì (6) không biểu diễn điểm nào cả. Đường cong (C) là tập rỗng.
Tóm lại, qua các trường hợp đã xét trên đây, ta đi đến kết luận rằng:
Định lý 2. Cho đường bậc hai (C) có phương trình (1), gọi A =
a b
của dạng toàn phương tương ứng và
1
,
2
là các trị riêng của A. Khi đó :
là ma trận
1)
Nếu
1
.
2
= 0 thì (C) là đường dạng parabol (bao gồm parabol và parabol bị
suy biến thành cặp đường thẳng cùng phương).
2)
Nếu
1
.
2
> 0 thì (C) là đường dạng elip (bao gồm elip và elip bị suy biến thành
elip điểm hoặc là tập rỗng).
3)
Nếu
1
.
2
< 0 thì (C) là đường dạng hypebol (bao gồm hypebol và hypebol bị
suy biến thành cặp đường thẳng cắt nhau).
159

lOMoARcPSD| 35883770
b
c
Nhận xét. Do det
a b
I. ĐƯỜNG BẬC HAI TỔNG QUÁT
= ac – b
2
=
1
2
nên nếu đặt = – detA = b
2
– ac = –
1
2
thì từ định lý trên, ta có dấu hiệu để nhận biết đường bậc 2 khá thuận tiện sau:
Dấu hiệu. Cho đường bậc hai (C): ax
2
+ 2bxy + cy
2
+ 2dx + 2ey + f = 0, a
2
+b
2
+c
2
>0. Gọi = b
2
– ac là biệt thức của (C). Khi đó:
1)
Nếu < 0 thì (C) là đường dạng elip (bao gồm elip và elip bị suy biến thành
elip điểm hoặc là tập rỗng).
2)
Nếu = 0 thì (C) là đường dạng parabol (bao gồm parabol và parabol bị suy
biến thành cặp đường thẳng cùng phương).
3)
Nếu > 0 thì (C) là đường dạng hypebol (bao gồm hypebol và hypebol bị suy
biến thành cặp đường thẳng cắt nhau).
Coi nhánh có thể kéo dài đến vô cùng của đồ thị đường bậc hai là nhánh vô tận thì
hypebol là đường có 2 nhánh vô tận, parabol có 1 nhánh vô tận còn elip không có nhánh
vô tận nào. Dấu hiệu vừa nêu trên hoàn toàn tương tự với dấu hiệu về số nghiệm của
phương trình bậc 2 thông thường, ví dụ nếu > 0 thì đường bậc hai sẽ có hai nhánh vô
tận nên là đường dạng hyebol.
Ví dụ 3. Nhận dạng các đường bậc hai sau:
a) (C
1
): 3x
2
–6xy+3y
2
+2x–7 = 0, = b
2
–ac = 3
2
–3.3 = 0 (C
1
) là đường dạng
parabol.
b) (C
2
): x
2
+xy+y
2
–1 = 0, = b
2
–ac = (1/2)
2
–1.1 = –3/4 < 0 (C
2
) là đường dạng
elip.
c) (C
3
): xy–y
2
–5y+1 = 0, = b
2
–ac = (1/2)
2
+0.(–1) = 1/4 > 0 (C
3
) là đường dạng
hypebol.
4.QUY PHƯƠNG TRÌNH ĐƯỜNG BẬC HAI TỔNG QUÁT VỀ DẠNG CHÍNH
TẮC VÀ DỰNG ĐỒ THỊ.
Để dựng được đồ thị, cần quy phương trình tổng quát về dạng chính tắc. Muốn có
được phương trình ở dạng chính tắc, ta cần chọn hệ tọa độ sao cho gốc tọa độ trùng với
tâm đối xứng, các trục tọa độ trùng với các trục đối xứng của đường cong. Muốn vậy, từ
hệ trục Oxy ban đầu ta cần thực hiện:
Bước 1. Khử hạng tử chéo. Thực chất của bước này là thực hiện phép quay hệ tọa độ
Oxy xung quanh gốc O để thu được hệ tọa độ mới Ox’y’ có vec tơ chỉ hướng của Ox’,
Oy’ là các vec tơ riêng đơn vị của ma trận của dạng toàn phương tương ứng.
Bước 2. Tiếp tục tịnh tiến hệ tọa độ Ox’y’ sao cho gốc O đến trùng với tâm đối xứng
I của đường cong. Khi đó thu được hệ tọa độ mới Ix”y” mà đối với nó, phương trình
đường bậc 2 đang xét sẽ có dạng chính tắc.
160

lOMoARcPSD| 35883770
5
5
5
5
5
1
5
5
1
Chương 7. ĐƯỜNG BẬC HAI PHẲNG VÀ MẶT BẬC HAI
Bước 3. Vẽ đồ thị đường bậc hai cho bởi phương trình chính tắc trong hệ trục tọa độ
sau cùng.
Ví dụ 4. Quy phương trình đường bậc hai (C): 4x
2
–4xy+y
2
–2x–14y+7 = 0 về dạng
chính tắc và dựng đồ thị của nó.
Bước 1. Khử hạng tử chéo
Ma trận của dạng toàn phương tương ứng là A =
4 −2
. Tập trị riêng của A là
−
2 1
1
= 0
. Với = 0, véc tơ riêng tương ứng v =
1 / 2
. Với
= 5 véc tơ riêng tương
= 5
1
1
1
2
2
ứng v
=
−2
. Đơn vị hóa các vec tơ v , v
để được các véc tơ viêng đơn vị. Từ đó lập
2
1 2
ma trận chéo hóa trực giao được A là P =
1/ −2 / 5
. Phương trình phép quay: X
x =
1
x '−
2
y '
2
/
1/
= PY
y =
5 5
2
x '+
1
. Phương trình dạng không chứa hạng tử chéo:
y '
(C): 0.x’
2
–5y’
2
–2(
y’ + 7 = 0.
x’ – y’) – 14( x’+ y’) + 7 = 0 5y’
2
– x’ –
Bước 2. Quy phương trình không chứa hạng tử chéo về dạng chính tắc
Biến đổi phương trình không chứa hạng tử chéo theo hướng thêm bớt số hạng để đề
xuất bình phương cho các ẩn bậc hai:
5y’
2
– x’ – y’ + 7 = 0 5(y’
2
– 2.
y’+
1
) –
5
x’ + 7 – 1 = 0 5(y’ –
)
2
= x’ – 6 (y’ – )
2
= (x’ – ).
Đặt
x" = x '−
1
5
y "
=
y '
−
1
thì phương trình (C) có dạng: y”
2
=
x”. Đây là phương trình
chính tắc.
Bước 3. Dựng đồ thị (C):
161
1
5
2
5
2
5
1
5
30
5
10
5
30
5
10
5
1
5
30
5
1
5
30
5
1
5
6
5
6
5
lOMoARcPSD| 35883770
2 / 5
5
5
1
5
1
5
5
5
I. ĐƯỜNG BẬC HAI TỔNG QUÁT
Dựng hệ trục Ox’y’ với vec tơ chỉ hướng của
Ox’, Oy’ lần lượt là u =
1/ 5
, u =
−2 / 5
.
1
2
1/
- Dựng hệ trục Ix’’y’’ nhờ phép tịnh tiến
x" = x '−
1
5
y "
=
y '
−
1
với gốc I( ; ).
- Trong hệ trục Ix’’y’’ dựng đồ thị có phương trình chính tắc: y’’
2
=
đường parabol
6
x’’, đó là
Parabol y’’
2
=
6
x’’.
162
y
x’
y’
u
2
u
1

lOMoARcPSD| 35883770
II.
MẶT BẬC HAI CHO BỞI PHƯƠNG TRÌNH CHÍNH TẮC
1. GIỚI THIỆU VỀ MẶT VÀ ĐƯỜNG TRONG KHÔNG GIAN
a)
Mặt trong không gian
Trong không gian, cho hệ tọa độ Descartes Oxyz. Mặt trong không gian được định
nghĩa là đồ thị của phương trình 3 biến x, y, z dạng: F(x;y;z) = 0. Khi đó phương trình:
F(x;y;z) = 0 (1)
được gọi là phương trình tổng quát của mặt trong không gian.
Ví dụ, phương trình x
2
+y
2
+z
2
+2ax+2by+2cz+d = 0, a
2
+b
2
+c
2
> 0 là phương trình
tổng quát của mặt cầu, phương trình x
2
+y
2
–4 = 0 là phương trình mặt trụ, phương trình
2x+y+z–1 = 0 là phương trình mặt phẳng.
b)
Đường trong không gian
Đường trong không gian được định nghĩa là giao tuyến của 2 mặt. Giả sử cho 2 mặt
(S
1
): F
1
(x; y; z) = 0 và (S
2
): F
2
(x; y; z) = 0 thì giao tuyến của (S
1
) và (S
2
) là một đường
cong mà tọa độ của điểm nằm trên nó phải đồng thời thỏa mãn hệ:
F
1
(x; y; z) = 0
F (x; y; z) = 0
(3)
2
Khi đó hệ (3) được gọi là phương trình tổng quát của đường cong trong không gian.
x
2
+ y
2
+ z
2
= 1
Ví dụ, hệ phương trình:
x + z = 0
biểu diễn giao tuyến giữa mặt cầu và mặt
phẳng, nên là phương trình tổng quát của đường tròn trong không gian, phương trình
tổng quát của đường thẳng trong không gian có dạng
Ax + By + Cz + D = 0
với điều
A x + B y + C z + D = 0
1 1 1 1
kiện (A:B:C) ((A
1
:B
1
:C
1
).
c)
Mặt bậc hai tổng quát
Trong không gian, đồ thị của phương trình bậc hai đối với 3 biến x, y, z dạng:
ax
2
+ by
2
+ cz
2
+ 2d.xy + 2e.xz + 2g.yz + p.x + q.y + rz + s = 0 (1)
với điều kiện trong 6 hệ số của hạng tử bậc hai là a, b, c, d, e, g phải có ít nhất một hệ số
khác không, được gọi là mặt bậc hai tổng quát.
Phương trình (1) được gọi là phương trình tổng quát của mặt bậc hai. Hạng tử chứa
một trong các tích xy, xz, yz trong (1) được gọi là hạng tử chéo.
Xét tổng các hạng tử bậc hai trong (1) ta có dạng toàn phương, gọi là dạng toàn
phương tương ứng của phương trình (1):
163

lOMoARcPSD| 35883770
Chương 7: ĐƯỜNG BẬC HAI PHẲNG VÀ MẶT BẬC HAI
Q(X) = ax
2
+ by
2
+ cz
2
+ 2d.xy + 2e.xz + 2g.yz
Gọi A =
a
d
e
d b
g
e
g
c
là ma trận của dạng toàn phương Q và
1
,
2
,
3
là các trị riêng
của A. Bằng phương pháp tương tự như đối với đường bậc hai tổng quát trong mặt
phẳng, ta có thể chéo hóa dạng toàn phương Q để khử hạng tử chéo trong (1). Khi đó,
người ta phân loại mặt bậc 2 trong không gian tùy theo tập giá trị riêng của A như sau:
Giá trị riêng của A
Tên gọi mặt tương ứng
1)
Tất cả 3 các giá trị riêng đều cùng dấu
Elipxoit
2)
Hai giá trị riêng cùng dấu, giá trị riêng
còn lại trái dấu
Mặt nón elip, hoặc Mặt hypeboloit 1
hay 2 tầng
3)
Hai giá trị riêng cùng dấu, trị riêng còn
lại bằng 0.
Mặt paraboloit eliptic hoặc trụ elip.
4)
Hai giá trị riêng trái dấu, giá trị riêng còn
lại bằng 0.
Mặt paraboloit , hypebotic hoặc trụ
hypebol.
5)
Hai giá trị riêng bằng 0, giá trị riêng còn
lại khác 0.
Mặt parabolol , hoặc hai mặt phẳng
cùng phương.
Sau khi khử hạng tử chéo, thực hiện phép tịnh tiến trong không gian, ta quy được
phương trình tổng quát về dạng chính tắc và sẽ nghiên cứu chúng ở dạng chính tắc. Sau
đây, ta chỉ xét các mặt bậc hai cho bởi phương trình chính tắc.
2. MẶT ELIPXOIT
Định nghiã 1. Mặt bậc hai trong không gian mà phương trình của nó có thể quy
được về dạng:
x
2
+
y
2
+
z
2
=
a
2
b
2
c
2
1 ; a, b, c > 0 (2)
được gọi là mặt elipxoit.
Phương trình (2) gọi là phương trình chính tắc
của elipxoit, các hằng số dương a, b, c gọi là các
bán trục. Nếu có a = b = c thì elipxoit là mặt cầu.
Nếu có hai trong ba bán trục bằng nhau thì elipxoit
là mặt tròn xoay, sinh ra do đường elip quay xung
quanh một trục đối xứng của nó.
Mặt elipxoit (2) nhận các mặt phẳng tọa độ làm
164

lOMoARcPSD| 35883770
II. MẶT BẬC HAI CHO BỞI PHƯƠNG TRÌNH CHÍNH TẮC
mặt phẳng đối xứng vì trong phương trình của (2) nếu thay x bởi –x; y bởi –y; z bởi –z,
phương trình vẫn không đổi. Do các mặt phẳng tọa độ là mặt phẳng đối xứng nên giao
của các mặt phẳng tọa độ (tức các trục tọa độ) sẽ là trục đối xứng và giao các trục tọa độ
(là gốc tọa độ O) sẽ là tâm đối xứng của elipxoit.
Các trục tọa độ Ox, Oy, Oz cắt elipxoit (2) lần lượt tại các cặp điểm A
1,2
( a; 0; 0),
B
1,2
(0; b; 0), C
1,2
(0; 0; c), gọi là các đỉnh của elipxoit. Đoạn nối 2 đỉnh trên 1 trục gọi
là trục, vì lý do vậy nên các độ dài a, b, c gọi là các bán trục của elipxoit.
Cắt elipxoit (2) bởi mặt phẳng {z = h} (h là hằng số) thì giao tuyến thu được là
đường có phương trình:
x
2
+
y
2
+
z
2
=
x
2
+
y
2
=
−
h
2
a
2
b
2
c
2
1
a
2
b
2
1
c
2
(E)
z = h
z = h
Nếu |h| > c thì giao tuyến (E) là tập rỗng.
Nếu |h| = c thì giao tuyến (E) là elip điểm.
Nếu |h| < c thì giao tuyến (E) là đường elip nằm trong mặt phẳng {z = h}, có các bán
trục song song với Ox và Oy, độ dài tương ứng là a' = a. ; b' = b. . Các
bán trục này lớn dần khi |h| tiến dần về 0. Khi h = 0, giao tuyến giữa elipxoit với mặt
x
2
+
y
2
=
phẳng {z = 0} là elip:
a
2
b
2
1
nằm trong mặt phẳng Oxy, có các bán trục lớn nhất
z = 0
bằng a và b.
Cũng lí luận tương tự như trên, giao tuyến giữa elipxoit với các mặt phẳng {x = h}
hay {y = h} (nếu tồn tại) đều là các đường elip.
3. MẶT TRỤ VÀ MẶT NÓN BẬC HAI
a. Mặt trụ bậc hai
Định nghiã 2. Mặt bậc hai trong không gian mà phương trình của nó có thể quy
được về một trong các dạng:
x
2
+
y
2
= ; a, b > 0, (3)
a
2
b
2
1
x
2
−
y
2
= , a, b > 0, (4)
a
2
b
2
1
x
2
= 2py, p>0 (5)
165
1
−
h
2
c
2
1
−
h
2
c
2

lOMoARcPSD| 35883770
Chương 7: ĐƯỜNG BẬC HAI PHẲNG VÀ MẶT BẬC HAI
thứ tự được gọi là mặt trụ elip, trụ hypebol và trụ parabol.
Các phương trình (3), (4), (5) gọi là phương trình chính tắc. Đặc trưng của phương
trình chính tắc mặt trụ là sự vắng mặt của ẩn z và vì vậy, các mặt trụ (3), (4), (5) đều là
mặt được sinh ra do 1 đường thẳng song song với trục Oz chuyển động luôn giữ
phương không đổi (gọi là đường sinh) và luôn tựa trên một đường cônic cố định trong
mặt phẳng Oxy (gọi là đường chuẩn). Tùy theo đường chuẩn là elip, hypebol hay
parabol mà ta có tên của mặt trụ tương ứng là trụ elip, trụ hypebol, hay trụ parabol. Cụ
thể hóa một vài chi tiết như sau đây:
x
2
y
2
a. Mặt trụ có phương trình
+ = 1
a
2
b
2
(3)
là mặt trụ
elip, đường sinh song song với trục Oz và đường chuẩn là
x
2
+
y
2
=
đường elip (E):
a
2
b
2
1
, nằm trong mặt phẳng Oxy. Khi
z = 0
a = b thì đường chuẩn (E) là đường tròn
x
2
+
y
2
=
a
2
nên
mặt trụ còn có tên là mặt trụ tròn xoay, trục quay Oz.
z
=
0
Tương tự elipxoit, mặt trụ elip (3) nhận các mặt phẳng tọa độ làm mặt phẳng đối
xứng, nhận các trục tọa độ làm trục đối xứng và gốc O sẽ là tâm đối xứng. Cắt trụ bởi
mặt phẳng vuông góc với trục Oz, giao tuyến là các elip. Cắt trụ bởi mặt phẳng vuông
góc với Ox hoặc Oy thì giao tuyến (nếu có) sẽ là cặp đường thẳng cùng phương.
Chú ý rằng, nếu hóan vị tên của trục tọa độ trong phương trình chính tắc, ta sẽ
có các phương trình mặt trụ với đường sinh song song với trục Ox, Oy. Ví dụ phương
trình
y
2
+
z
2
= biểu diễn mặt trụ có đường sinh song song với trục Ox, đường chuẩn là
a
2
b
2
1
y
2
+
z
2
=
elip:
2 2
1
, nằm trong mặt phẳng tọa độ Oyz.
a b
x = 0
b. Phương trình
x
2
−
y
2
= (4) là phương trình của mặt trụ hypebol có đường sinh
a
2
b
2
1
song song với Oz và đường chuẩn là hypebol:
x
2
−
y
2
=
2 2
1
, nằm trong mặt phẳng Oxy.
a b
z = 0
Tương tự trụ elip, mặt trụ hypebol (4) nhận các
mặt phẳng tọa độ làm mặt phẳng đối xứng, nhận
các trục tọa độ làm trục đối xứng và gốc O sẽ là
tâm đối xứng. Cắt trụ bởi mặt phẳng vuông góc với
trục Oz, giao tuyến là hypebol. Cắt trụ bởi mặt
166
lOMoARcPSD| 35883770
II. MẶT BẬC HAI CHO BỞI PHƯƠNG TRÌNH CHÍNH TẮC
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
phẳng vuông góc với Ox hoặc Oy thì giao tuyến (nếu có) sẽ là cặp đường thẳng song
song với Oz.
c. Phương trình x
2
= 2py (5) là phương trình mặt trụ parabol, đường sinh song
song với Oz và đường chuẩn là parabol (P):
x
2
=
2
py
, nằm trong mặt phẳng
O
xy.
z
=
0
Mặt trụ parabol (5) nhận các mặt phẳng tọa
độ Oxy, Oyz làm mặt phẳng đối xứng, nhận
trục Oy làm trục đối xứng. Cắt trụ bởi mặt
phẳng vuông góc với trục Oz, giao tuyến là
parabol. Cắt trụ bởi mặt phẳng vuông góc với
Ox, hoặc Oy, giao tuyến (nếu có) là đường
thẳng cùng phương với Oz.
b. Mặt nón elip
Định nghiã 3. Mặt bậc hai trong không gian mà phương trình của nó có thể quy
được về dạng:
x
2
+
y
2
−
z
2
=
a
2
b
2
c
2
0 ; a, b, c> 0 (6)
được gọi là mặt nón elip.
Nếu có a = b thì mặt nón (6) là mặt nón tròn xoay, được
sinh ra do đường thẳng:
ax = cy
quay xung quanh trục Oz.
y
=
0
Mặt nón elip (6) nhận các mặt phẳng tọa độ làm mặt phẳng
đối xứng, nhận các trục tọa độ làm trục đối xứng và nhận gốc
tọa độ O làm tâm đối xứng.
Cắt mặt nón (6) bởi mặt phẳng tọa độ {x = 0}, được giao tuyến là cặp đường thẳng
cắt nhau tại gốc tọa độ:
y
2
=
z
2
z =
c
y
b
2
c
2
b
.
x = 0
x = 0
Cắt mặt nón (6) bởi mặt phẳng tọa độ {z = 0}, được giao tuyến là điểm (0; 0; 0). Cắt
mặt nón (6) bởi mặt phẳng {z = h, h 0}, được giao tuyến là elip có phương trình:
167

lOMoARcPSD| 35883770
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
+
+
2
c
2
c
2
Chương 7: ĐƯỜNG BẬC HAI PHẲNG VÀ MẶT BẬC HAI
x
2
y
2
h
2
x
2
+
y
2
=
2 2
=
2
a
2
(h
2
/ c
2
)
b
2
(h
2
/ c
2
)
1
.
a b c
z = h
z = h
Ngoài ra nếu cắt mặt nón (6) bởi những mặt phẳng bất kỳ khác thì tuỳ theo phương
của mặt cắt mà giao tuyến có thể là elip, hypebol hay parabol. Chính vì lý do này mà
các đường elip, hypebol hay parabol còn có tên gọi là các đường conic với ý nghiã nó là
giao tuyến thu được khi cắt mặt nón bởi những mặt phẳng.
4. CÁC MẶT HYPEBOLOIT
a. Mặt hypeboloit một tầng
Định nghiã 4. Mặt bậc hai trong không gian mà phương trình của nó có thể quy
được về dạng:
x
2
+
y
2
−
z
2
=
a
2
b
2
c
2
1 ; a, b, c > 0 (7)
được gọi là mặt hypeboloit một tầng.
Nếu có b = c hoặc a = c thì hypeboloit một tầng là mặt tròn xoay, được sinh ra do
một đường hypebol quay xung quanh trục ảo của nó.
Cũng tương tự như mặt nón elip, hypeboloit một tầng (7) nhận các mặt phẳng tọa
độ làm mặt phẳng đối xứng, nhận các trục tọa độ làm trục đối xứng và nhận gốc tọa độ
O làm tâm đối xứng.
Hypeboloit một tầng (7) không cắt trục Oz, nhưng lại cắt cả
hai trục tọa độ Ox, Oy lần lượt tại các cặp điểm A
1,2
( a; 0; 0),
B
1,2
(0; b; 0).
Cắt hypeboloit một tầng (7) bởi mặt phẳng {z = h}, được
giao tuyến có phương trình:
x
2
y
2
x
2
h
2
2
+
y
= 1
2
2 2 = 1+
2
a
2
1+
h
b
2
1+
h
.
a b c
z = h
z
=
h
Đây là phương trình của đường elip nằm trong mặt phẳng {z = h}, có các bán trục a'
= a. , b' = b.
. Khi h → thì các bán trục a', b' → . Khi h = 0, giao
168
1 +
h
2
c
2
1
+
h
2
c
2

lOMoARcPSD| 35883770
II. MẶT BẬC HAI CHO BỞI PHƯƠNG TRÌNH CHÍNH TẮC
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
a
b
−
− =
x
2
+
y
2
=
tuyến là elip (E):
a
2
b
2
1
z = 0
nằm trong mặt phẳng Oxy, có các bán trục nhỏ nhất,
(bằng a, bằng b) nên có tên gọi là elip thắt. Cắt hypeboloit một tầng (7) bởi mặt phẳng
x
2
−
z
2
=
−
h
2
mặt phẳng {y = h}, được giao tuyến là đường có phương trình:
a
2
c
2
1
b
2
(H).
y = h
Khi |h| < b, giao tuyến (H) là hypebol nằm trong mặt phẳng {y = h}, có trục thực
song song với trục tọa độ Ox. Khi |h| = b, chẳng hạn h = b, giao tuyến (H) có phương
trình:
x
2
z
2
x
+
z
= 0
2 2
= 0
y
=
b
a c
y = b
x
z
0
a
b
y = b
Đây là phương trình của cặp đường thẳng cắt nhau tại điểm (0; b; 0). Khi |h| > b,
giao tuyến (H) là hypebol, nằm trong mặt phẳng {y = h}, có trục thực song song với trục
tọa độ Oz.
b. Mặt hypeboloit hai tầng
Định nghiã 5. Mặt bậc hai trong không gian mà phương trình của nó có thể quy
được về dạng:
x
2
−
y
2
−
z
2
=
a
2
b
2
c
2
1 ; a, b, c >0 (8)
được gọi là mặt hypeboloit hai tầng.
Trong (8) nếu có a = b hoặc a = c thì hypeboloit hai
tầng là mặt tròn xoay, được sinh ra do một đường
hypebol quay xung quanh trục thực của nó. Dễ nhận
thấy rằng hypeboloit hai tầng có tính chất đối xứng
giống với tính chất đối xứng của hypeboloit một tầng.
Nếu cắt hypeboloit hai tầng (8) bởi mặt phẳng {z = h},
luôn được giao tuyến là đường hypebol:
169

lOMoARcPSD| 35883770
Chương 7: ĐƯỜNG BẬC HAI PHẲNG VÀ MẶT BẬC HAI
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
−
b
2
y
2
2
h
c
2
c
2
x
2
y
2
x
2
h
2
2
−
y
= 1
2
2 2 = 1+
2
a
2
1+
h
b
2
1+
h
a b c
z = h
z
=
h
Đây là hypebol nằm trong mặt phẳng {z = h}, trục thực song song với trục tọa độ
Ox. Nếu cắt hypeboloit hai tầng (8) bởi mặt phẳng {x = h}, được giao tuyến có phương
trình:
y
2
+
z
2
=
h
2
−
(E):
b
2
c
2
a
2
1
x = h
Nếu |h| < a thì (E) = . Nếu |h| = a, thì (E) là elip điểm. Nếu |h| > a thì (E) là elip:
y
2
+
z
2
=
h
2
c
2
2
−1
c
c
2
1
−1
x
=
h
Đây là elip nằm trong mặt phẳng {x = h}, các trục song song với các trục tọa độ Oy
và Oz. Khi |h| → thì các bán trục của elíp này tăng dần đến .
5. CÁC MẶT PARABOLOIT
a. Mặt paraboloit eliptic
Định nghiã 6. Mặt bậc hai trong không gian mà phương trình của nó có thể quy
được về dạng:
2 2
+ = 2z ; p, q > 0 (9)
p q
được gọi là mặt paraboloit eliptic.
Nếu có p = q thì (9) là mặt paraboloit eliptic tròn xoay,
được sinh ra do một parabol quay xung quanh trục đối xứng
của nó.
Mặt paraboloit eliptic (9) nhận các mặt phẳng tọa độ Oyz,
Oxz làm mặt phẳng đối xứng, nhận trục Oz làm trục đối xứng.
Nếu cắt paraboloit eliptic (9) bởi mặt phẳng {z = h}, giao
170
x

lOMoARcPSD| 35883770
II. MẶT BẬC HAI CHO BỞI PHƯƠNG TRÌNH CHÍNH TẮC
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
p q
y
tuyến có phương trình: (E):
x
2
+
y
2
=
2h
. Với h > 0, phương trình của giao tuyến (E)
x
2
+
y
2
=
z = h
có dạng:
2 ph
2qh
z = h
1
nên (E) là đường elip nằm trong mặt phẳng {z = h}, các bán
trục song song với các trục tọa độ Ox và Oy. Với h = 0, giao tuyến (E) là elip điểm. Với
h < 0, giao tuyến (E) là tập rỗng, điều đó chứng tỏ mặt paraboloit eliptic (9) là mặt nằm
hoàn toàn ở nửa trên của mặt phẳng Oxy.
Nếu cắt paraboloit eliptic (9) bởi mặt phẳng {y = h}, giao tuyến thu được có phương
trình:
x
2
+
y
2
=
x
2
=
−
h
2
2
=
h
2
p q
2z
p
2z
q
x 2 p
z −
2q
y = h
y = h
y = h
Đây là phương trình của đường parabol nằm trong mặt phẳng {y = h}, trục đối xứng
song song với Oz, hướng lõm quay về chiều dương. Tương tự, giao tuyến giữa
paraboloit eliptic (9) với mặt phẳng {x = h} cũng là đường parabol.
b. Mặt paraboloit eliptic
Định nghiã 7. Mặt bậc hai trong không gian mà phương trình của nó có thể quy
được về dạng:
2 2
− = 2z ; p, q > 0 (10)
p q
được gọi là mặt paraboloit hypebolic.
Mặt paraboloit hypebolic (10) nhận các mặt phẳng tọa độ Oyz, Oxz làm các mặt
phẳng đối xứng, nhận trục Oz làm trục đối xứng.
Nếu cắt paraboloit hypebolic (10) bởi mặt phẳng {z = h}, giao tuyến có phương
x
2
−
y
2
=
trình: (H):
p q
2h
. Với
h
>
0,
phương
trình
z = h
x
2
−
y
2
=
của giao tuyến (H) có dạng:
2 ph
2qh
z = h
1
nên (H)
là đường hypebol nằm trong mặt phẳng {z = h}, có
trục thực song song với trục tọa độ Ox còn trục ảo
171
x

lOMoARcPSD| 35883770
Chương 7: ĐƯỜNG BẬC HAI PHẲNG VÀ MẶT BẬC HAI
Downloaded by thu hoan nguyen (hoanmiu98@gmail.com)
song song với Oy. Với h = 0, giao tuyến (H) là cặp đường thẳng cắt nhau tại gốc tọa độ.
Với h < 0, giao tuyến (H) là hypebol nằm trong mặt phẳng {z = h}, có trục thực song
song với trục tọa độ Oy còn trục ảo song song với Ox.
Nếu cắt paraboloit hypebolic (10) bởi mặt phẳng {y = h}, giao tuyến thu được có
phương trình:
x
2
−
y
2
=
x
2
=
+
h
2
2
=
h
2
p q
2z
p
2z
q
x 2 p
z +
2q
y = h
y = h
y = h
Đây là phương trình của đường parabol nằm trong mặt phẳng {y = h}, trục đối xứng
song song với Oz, hướng lõm quay về chiều dương. Tương tự, giao tuyến giữa
paraboloit hypebolic (10) với mặt phẳng {x = h} cũng là đường parabol.
Từ việc khảo sát các thiết diện giữa paraboloit hypebolic (10) với các mặt phẳng
song song với các mặt phẳng tọa độ, ta có thể dung hình dạng của nó được vạch nên
y
2
= −2qz
khi cho Parabol (P
1
):
x = 0
trượt tịnh tiến với phương của mặt phẳng chứa nó
x
2
= 2 pz
không đổi, còn đỉnh luôn tựa trên parabol (P
2
):
y = 0
. Vì hình dáng của nó, mặt
paraboloit hypebolic còn có tên là mặt yên ngựa.
– HẾT –
172
Bấm Tải xuống để xem toàn bộ.




