Giáo trình Môn Hóa đại cương | Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58675420
BÀI GIẢNG HÓA ĐẠI CƯƠNG GV. TS LÊ MINH TÂM TP.HCM, 2018
Chương II. CẤU TẠO NGUYÊN TỬ
I. NGUYÊN TỬ VÀ QUANG PHỔ NGUYÊN TỬ
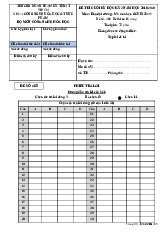
1. Nguyên tử và các hạt cơ bản
- Nguyên tử là hạt cấu tạo nên vật chất. Chúng
có khối lượng, kích thước rất nhỏ bé nhưng có cấu tạo rất tinh vi.
- Cấu tạo nguyên tử :
• Hạt nhân : tích điện dương (+)
• Lớp vỏ điện tử : tích điện âm (–)
* nguyên tử trung hòa về điện
- Các hạt căn bản của nguyên tử: Khối lượng Ký Điện tích Tên hiệu kg đvC culomb đve –1,60219.10-19 Eletron 9,1095.10-31 0,000549 – 1 e Proton +1,60219.10-19 1,6726.10-27 p 1,007276 + 1 Neutron n 1,6745.10-27 1,008665 0 0
2. Quang phổ nguyên tử
• Quang phổ của ánh sáng là quang phổ liên tục.
Hình: Phổ bức xạ điện từ của ánh sáng
Quang phổ nguyên tử là quang phổ vạch. Mỗi vạch ứng với một bước sóng xác
định, đặc trưng cho nguyên tử đó.
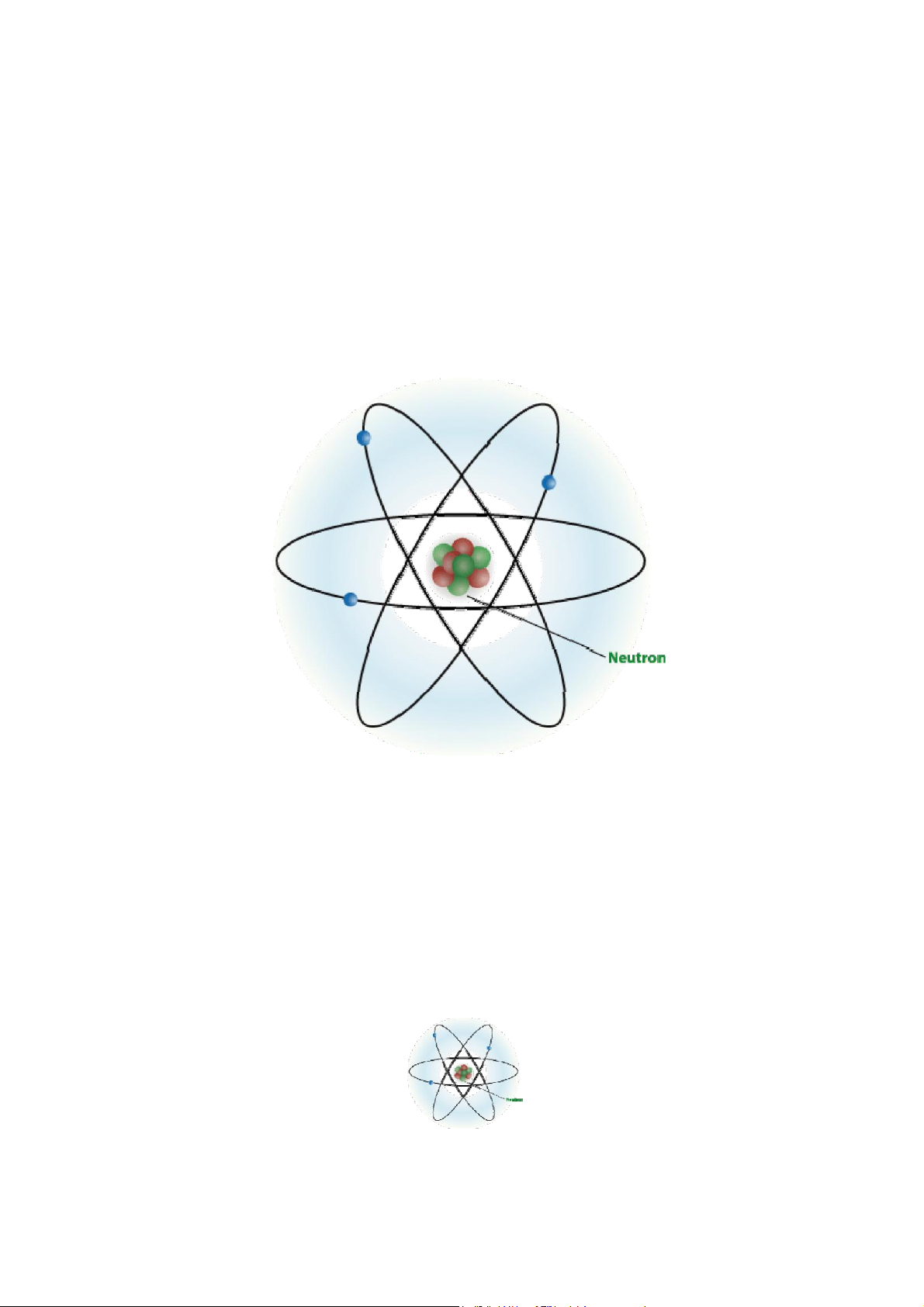
Ví dụ: phổ hydro trong vùng khả kiến gồm 4 vạch
Hình: Quang phổ vạch của nguyên tử hydro
• Sóng tương ứng với các tia bức xạ được đặc trưng bở biên độ sóng (a), bước sóng (λ), tần số (ν)
Hình: Các thông số sóng
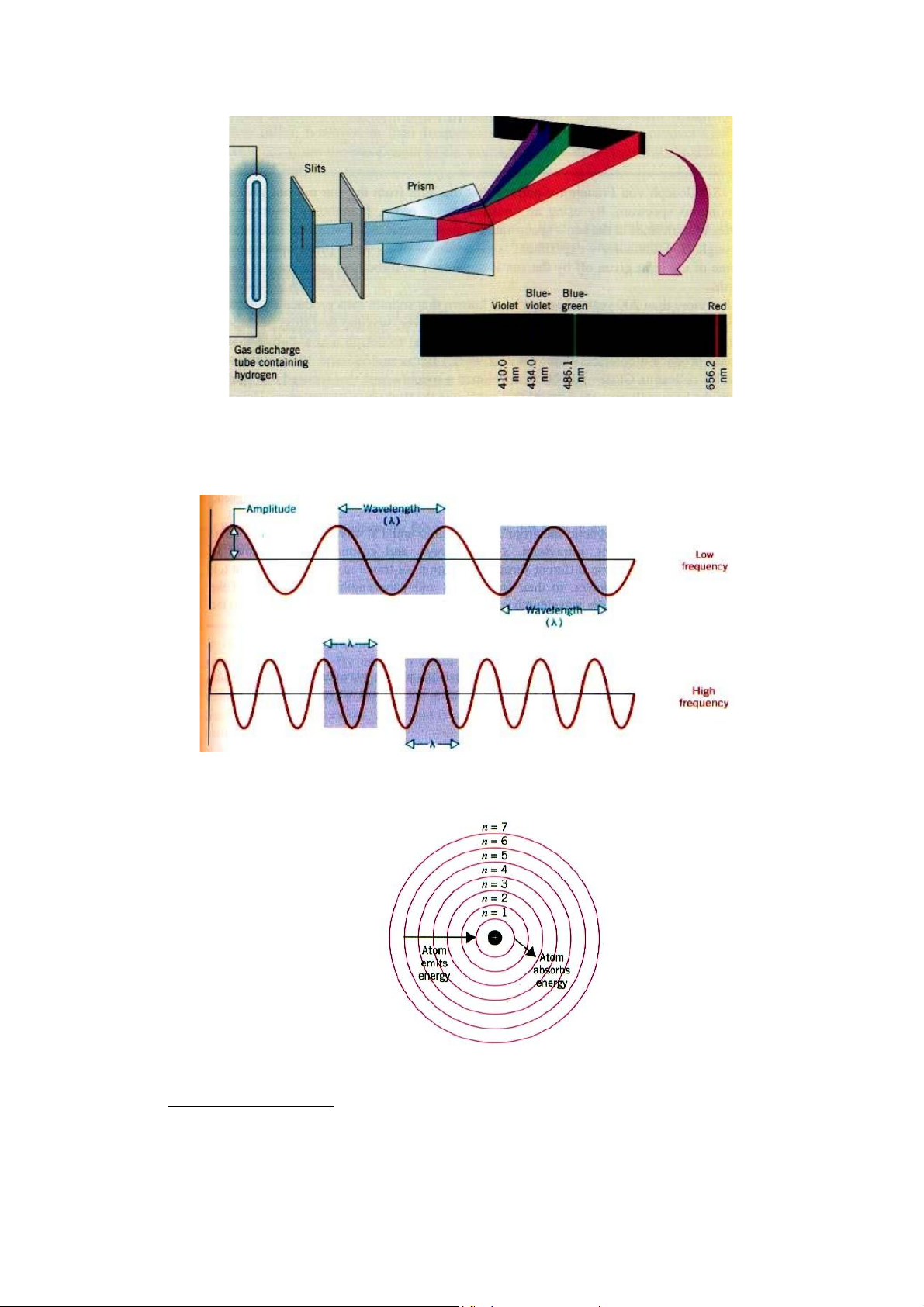
II. THUYẾT CẤU TẠO NGUYÊN TỬ CỦA BOHR
Hình: Mô hình hành tinh nguyên tử của Bohr
Ba định đề của Bohr:
• Định đề 1: electron quay quanh nhân trên những quỹ đạo tròn đồng tâm xác định gọi là quỹ đạo bền
• Định đề 2: Khi electron quay trên quỹ đạo bền không phát ra năng lượng điện từ.
• Định đề 3: Năng lượng sẽ được phát xạ hay hấp thu khi electron chuyển từ quỹ đạo
bền này sang quỹ đạo bền khác ΔE = Eđ – Ec = hν
Hình: sự thay đổi trạng thái của e
III. CẤU TẠO NGUYÊN TỬ THEO CƠ HỌC LƯỢNG TỬ
1. Tính sóng hạt của các hạt vi mô
- Cơ học lượng tử quan niệm rằng các hạt vi mô có cả tính chất hạt và tính chất sóng.
• Bản chất hạt: các hạt vi mô đều có khối lượng m, kích thước r và chuyển động
với một tốc độ v xác định.
• Bản chất sóng: khi hạt vi mô chuyển động sẽ tạo ra một sóng, truyền đi với bước
sóng λ. Được nghiên cứu qua hiện tượng giao thoa và nhiễu xạ.
- Quan hệ giữa tính sóng hạt của các hạt vi mô được thể hiện qua hệ thức: h λ= (L. de Broglie) mv
h - hằng số Plank = 6,625.10-27erg.s - Ví dụ:
• Đối với electron: m = 9,1.10-31kg, chuyển động với tốc độ v = 106cm/s sẽ tạo nên
sóng với bước sóng λ = 7,3.10-10m. CÓ thể dùng mạng tinh thể chất rắn làm mạng
nhiễu xạ để phát hiện sóng này:
Đối với hạt vĩ mô: m = 1g, chuyển động với tốc độ v = 1cm/s sẽ tạo nên sóng
6,6.10-29m. bước sóng quá bé, không phát hiện được.
2. Nguyên lý bất định Heisenberg
• Bản chất sóng - hạt đưa tới hệ quả quan trọng về sự chuyển động của hạt vi mô,
thể hiện trong nguyên tắc do Heisenberg đưa ra năm 1927: không thể đồng thời
xác định chính xác cả vị trí và tốc độ của hạt vi mô.  h
Δx.Δv≥ = m 2πm
o Δx - độ bất định về vị trí o
Δv - độ bất định về tốc độ 
*Đối với hạt vi mô xác định là hằng số nên
khi tốc độ của hạt càng được xác m
định chính xác (Δv càng bé) thì tọa độ của nó sẽ được xác định càng kém chính xác (Δx
càng lớn)và ngược lại.
Đối với hạt vi mô, khi xác định tương đối chính xác tốc độ chuyển động của electron
chúng ta không thể nói đến đường đi chính xác của nó, mà chỉ có thể nói đến xác suất
có mặt của nó ở chỗ nào đó trong không gian.
3. Khái niệm đám mây electron
• Không thể dùng khái niệm quỹ đạo để mô tả sự chuyển động của electron.
• Cơ học lượng tử quan niệm: khi chuyển động xung quanh hạt nhân nguyên tử,
electron đã tạo ra một vùng không gian bao quanh hạt nhân mà nó có thể có mặt
ở thời điểm bất kỳ với xác suất có mặt khác nhau.
• Vùng không gian này có thể hình dung như một đám mây electron. Nơi nào
electron thường hay xuất hiện hơn thì đám mây dày đặc hơn, nghĩa là mật độ của
đám mây tỷ lệ thuận với xác suất có mặt của electron.
• Theo tính toán của cơ học lượng tử thì đám mây electron là vô cùng vì electron
có thể tiến lại rất gần hạt nhân, cũng có thể ra xa vô cùng. Quy ước: đám mây
electron là vùng không gian gần hạt nhân trong đó chứa khoảng 90% xác suất có
mặt của electron. Hình dạng của đám mây được biểu diễn bằng bề mặt giới hạn vùng không gian đó.
4. Phương trình sóng Schrödinger và 4 số lượng tử
a. Phương trình sóng Schrödinger
• Phương trình sóng Schrödinger được xem là định luật cơ học lượng tử về sự
chuyển động của các hạt vi mô, tương tự như các định luật của Newton trong cơ học cổ điển.
• Theo cơ học lượng tử, việc nghiên cứu cấu trúc của các hệ vi mô là việc giải
phương trình sóng Schrödinger đối với hệ vi mô đó.
Phương trình sóng Schrödinger cơ bản mô tả sự chuyển động của hạt vi mô trong
trường thế năng đối với trường hợp trạng thái của hệ không thay đổi theo thời gian (trạng thái dừng):
∂2Ψ ∂2Ψ ∂2Ψ 8π2m ( 2 + 2 + 2 + 2 E−V)Ψ= 0 ∂x ∂y ∂z h Trong đó:
o ∂ - vi phân riêng phần o m - khối lượng hạt vi mô o h – hằng số Plank
o E – năng lượng toàn phần của hạt vi mô (tổng động năng và thế năng)
o V - thế năng của hạt vi mô, phụ thuộc vào toạ độ x, y, z
o Ψ - hàm sóng đối với các biến x, y, z mô tả sự chuyển động của hạt vi
mô ở điểm có tọa độ x, y, z.
- Sau khi có hàm Ψ, người ta bình phương hàm Ψ thì thu được hàm Ψ2
Ψ2 – mật độ xác suất có mặt của hạt vi mô tại điểm có tọa độ x, y, z. - Xét trong không gian dV
Ψ2dV – xác suất có mặt của e trong vùng không gian dV
• Giải phương trình sóng Schrödinger để tìm các hàm sóng Ψ thích hợp thỏa mãn
phương trình sóng và các giá trị năng lượng E tương ứng.
• Phương trình sóng Schrödinger chỉ giải được chính xác cho trường hợp hệ H.
Đối với các hệ vi mô phức tạp hơn phải giải gần đúng.
• Khi giải phương trình sóng Schrödinger cho các hệ nguyên tử khác nhau người
ta thấy xuất hiện 4 đại lượng không thứ nguyên nhưng lại xác định trạng thái của
electron trong nguyên tử. Đó là 4 số lượng tử.
5. Bốn số lượng tử
a. Số lượng tử chính n và các mức năng lượng • Xác định:
+ Trạng thái năng lượng của electron + Kích
thước trung bình của đám mây electron. Ví dụ: đối với H: 2 2 me4 2 −18 Z Z E=− 2 2 2 Z =−2,18.10
2 J =−13.6 2 eV 8ε0n h n n a0n2 ⎧ 1⎡ l(l +1)⎤⎫ r =
⎨1+ ⎢⎣1− n2 ⎥⎦⎬⎭ Z ⎩ 2
n càng tăng thì E và r càng tăng
• Giá trị: n = 1, 2, 3, …, ∞
• Trạng thái năng lượng của electron tương ứng với mỗi giá trị của n được gọi
là một mức năng lượng. n 1 2 3 … ∞ Các mức năng lượng E1 E2 E3 … E∞
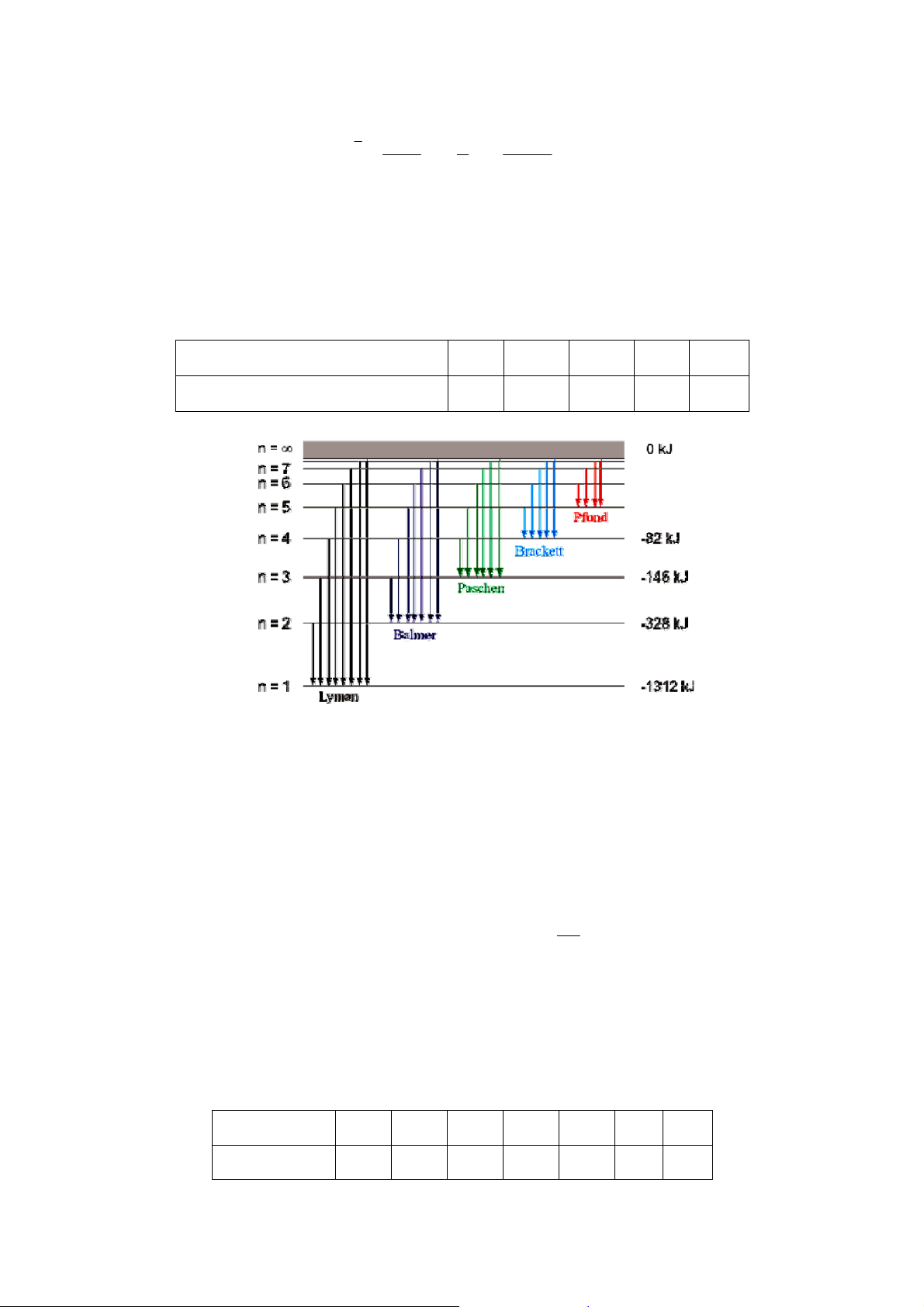
• Giải thích quang phổ vạch của nguyên tử hydro:
Hình: Các mức năng lượng và dãy quang phổ nguyên tử hydro o Ở điều
kiện bình thường electron ở mức năng lượng thấp nhất (mức bền nhất): mức cơ bản.
o Khi hấp thu năng lượng, electron sẽ chuyển lên mức cao hơn: mức kích thích,
kém bền hơn → electron sẽ nhanh chóng chuyển về mức cơ bản, phát ra năng
lượng đã hấp thụ dưới dạng các sóng ánh sáng: hc
ΔE = Ekt − Ecb = λ
o E là các giá trị rời rạc → λ là các giá trị rời rạc → quang phổ của các nguyên tử là quang phổ vạch.
o Đối với mỗi nguyên tố: ΔE là đặc trưng → λ là đặc trưng → quang phổ của
mỗi nguyên tử là đặc trưng
• Các electron nằm trên cùng một mức năng lượng họp thành một lớp electron. n 1 2 3 4 5 6 7 lớp electron K L M N O P Q
b. Số lượng tử orbital (phụ) l và hình dạng đám mây electron • Xác định:
o Năng lượng của đám mây trong nguyên tử nhiều electron
o Trong nguyên tử nhiều electron: các mức năng lượng có thể bị tách ra
thành nhiều phân mức năng lượng. Mỗi phân mức năng lượng được đặc
trưng bởi một số lượng tử orbital l. l càng tăng, năng lượng của các phân mức càng lớn.
o Hình dạng đám mây electron
• Giá trị: l = 0, 1, …, (n – 1) o Lớp n có n giá trị của l
• Những electron có cùng giá trị n và l tạo thành một phân lớp electron. Số lượng tử orbital l 0 1 2 3 Tên phân lớp electron s p d f
→ Ký hiệu phân lớp: 1s, 2s, 2p, 3s, 3p, 3d…
c. Số lượng tử từ ml và các orbital nguyên tử
• Xác định: o Sự định hướng của đám mây trong từ tường o Mỗi giá trị của ml
ứng với một cách định hướng của đám mây electron.
• Giá trị: ml = 0, ±1, …, ±l. Như vậy, mỗi giá trị của l có (2l + 1) giá trị của ml.
• Đám mây electron được xác định bởi ba số lượng tử n, l, ml được gọi là orbitan nguyên tử (AO).
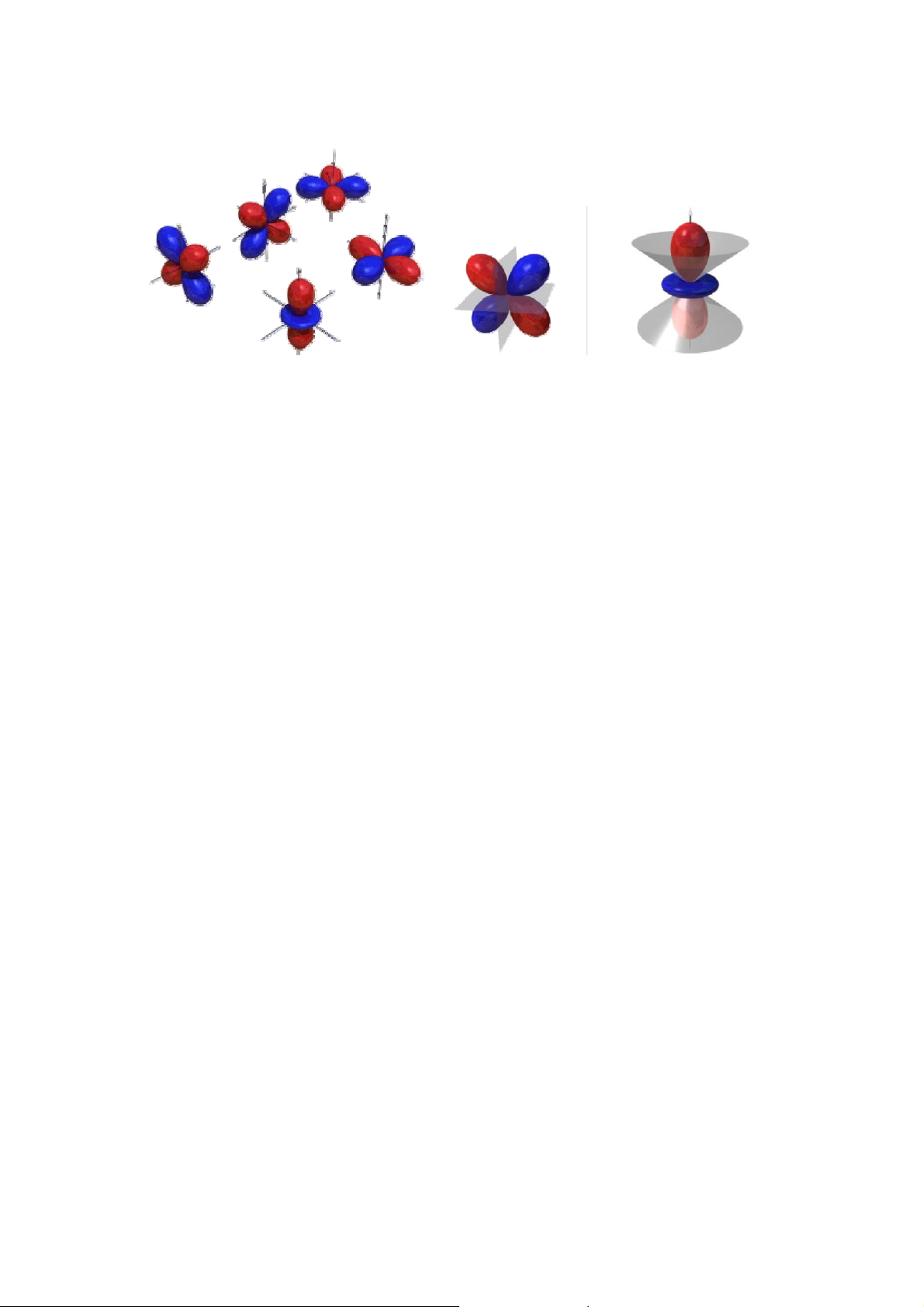
Hình: hình dạng AO s, p
Hình: Hình dạng AO d
d. Số lượng tử spin ms
• Xác định: trạng thái chuyển động riêng của electron, tức là sự tự quay quanh trục của electron.
• Giá trị: ms = ± ½ ứng với hai chiều quay thuận và nghịch với chiều quay của kim đồng hồ.
• Mỗi tổ hợp n, l, ml, ms tương ứng một electron trong nguyên tử.
IV. NGUYÊN TỬ NHIỀU ELECTRON
1. Trạng thái năng lượng của electron trong nguyên tử nhiều electron.
• Giống e trong nguyên tử 1e:
o Cũng được xác định bằng 4 số lượng tử n, l, ml, ms o
Hình dạng, độ lớn, phân bố, định hướng của các AO
• Khác nhau giữa nguyên tử 1e và nhiều e: o Năng lượng:
phụ thuộc vào cả n và l o Lực tương tác:
+ lực hút hạt nhân – electron + lực đẩy e – e.
→ Xuất hiện hiệu ứng chắn và hiệu ứng xâm nhập
• Hiệu ứng chắn: các lớp electron bên trong biến thành màn chắn làm yếu lực
hút của hạt nhân đối với các electron bên ngoài.
- Hiệu ứng chắn tăng khi: + số lớp electron tăng + số electron tăng
• Hiệu ứng xâm nhập: ngược lại với hiệu ứng chắn.
- Khả năng xâm nhập giảm khi n và l tăng
→ Thứ tự năng lượng của các phân lớp trong nguyên tử nhiều e:
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s < 5f ≈ 6d
2. Các quy luật phân bố electron vào nguyên tử nhiều e.
a. Nguyên lý ngoại trừ Pauli:
Trong phạm vi một nguyên tử không thể có hai electron có cùng 4 số lượng tử.
→ Một AO chứa tối đa 2e có spin ngược dấu.
b. Nguyên lý vững bền:
Trong điều kiện bình thường nguyên tử phải ở trạng thái có năng lượng thấp nhất -
trạng thái cơ bản, những trạng thái có năng lượng cao hơn là trạng thái kích thích.
c. Quy tắc Klechcowski:
• Trong một nguyên tử nhiều electron, trật tự điền các electron vào các phân lớp
(đặc trưng bởi n và l) sao cho tổng (n + l) tăng dần.
• Khi hai phân lớp khác nhau có cùng giá trị (n + l) thì electron được xếp vào phân
mức có n tăng dần. Phân mức:
1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s 5f 6d (n + l)
1 2 3 3 4 4 5 5 5 6 6 6 7 7 7 7 8 8
d. Quy tắc Hund:
Khi electron không đủ để bão hòa một phân mức thì trạng thái năng lượng thấp nhất
ứng với trường hợp khi các orbital được sử dụng tối đa, spin của các cặp electron không
cặp đôi phải song song. + Ví dụ: O 1s22s22p4
+ Quy ước: Điền electron có spin dương trước, âm sau
3. Công thức electron nguyên tử. Ví dụ: N 1s22s22p3
- các số 1, 2… - giá trị của số lượng tử chính
- các chữ s, p… - ký hiệu của số lượng tử orbital
- các số mũ – cho biết số electron có trên phân mức
Chương III. HỆ THỐNG TUẦN HOÀN
I. ĐỊNH LUẬT TUẦN HOÀN VÀ ĐIỆN TÍCH HẠT NHÂN NGUYÊN TỬ
Mendeleev: “tính chất các đơn chất cũng như dạng và tính chất các hợp chất củanhững
nguyên tố hóa học phụ thuộc tuần hoàn vào trọng lượng nguyên tử của các nguyên tố”.
Theo quan niệm hiện đại: “Tính chất các đơn chất cũng như dạng và tính chất của các
hợp chất phụ thuộc tuần hoàn vào chiều tăng điện tích hạt nhân nguyên tử của các nguyên tố”. II.
CẤU TRÚC ELECTRON NGUYÊN TỬ VÀ HỆ THỐNG TUẦN HOÀN CÁC
NGUYÊN TỐ HÓA HỌC
1. Các họ nguyên tố s, p, d, f
a. Các nguyên tố họ s:
Là các nguyên tố có electron cuối cùng điền vào phân lớp s của lớp ngoài cùng • ns1: kim loại kiềm
• ns2: kim loại kiềm thổ
b. Các nguyên tố họ p:
Là các nguyên tố có electron cuối cùng điền vào phân lớp p của lớp ngoài cùng np1 np2 np3 np4 np5 np6
B – Al C – Si N – P O – S halogen khí trơ
c. Các nguyên tố họ d:
Là các nguyên tố có electron cuối cùng điền vào phân lớp d của lớp trước ngoài cùng
• (n – 1)d1 – 10: 10 nguyên tố chuyển tiếp (kim loại chuyển tiếp)
d. Các nguyên tố họ f:
Là các nguyên tố có electron cuối cùng điền vào phân lớp f của hai phân lớp trước ngoài cùng.
(n – 2)f1 – 14: các nguyên tố đất hiếm • 4f1 – 14: lantanoit • 5f1 – 14: actinoit 2. Chu kỳ
• Là dãy các nguyên tố viết theo hàng ngang, bắt đầu bằng các nguyên tố họ s, kết thúc
bằng các nguyên tố họ p, ở giữa có thể có (có thể không có) các nguyên tố họ d, f.
• Trong một chu kỳ, tính chất các nguyên tố biến đổi một cách tuần hoàn
• Số thứ tự chu kỳ bằng số lượng tử chính của lớp electron ngoài cùng o Chu kỳ I: chu
kỳ đặc biệt: chỉ có 2 nguyên tố họ s
o Chu kỳ II, III: 2 chu kỳ nhỏ: mỗi chu kỳ có 8 nguyên tố, gồm 2 nguyên tố họ s và 6 nguyên tố họ p
o Chu kỳ IV, V: 2 chu kỳ lớn: mỗi chu kỳ có 18 nguyên tố, gồm 2 nguyên tố họ s,
10 nguyên tố họ d và 6 nguyên tố họ p o Chu kỳ VI: chu kỳ hoàn hảo: có 32
nguyên tố, gồm 2 nguyên tố họ s, 14 nguyên tố họ f, 10 nguyên tố họ d và 6 nguyên tố họ p
o Chu kỳ VII: chu kỳ dở dang: có 2 nguyên tố dọ s, 14 nguyên tố dọ f và một số nguyên tố họ d
3. Nhóm: là cột dọc các nguyên tố có số electronở lớp ngoài cùng hoặc các phân lớp
ngoài cùng giống nhau và bằng số thứ tự của nhóm.
• Mỗi nhóm thường được chia thành 2 phân nhóm. Các nguyên tố trong cùng một
phân nhóm có cấu trúc electron hóa trị giống nhau nên tính chất hóa học tương tự nhau.
a. Phân nhóm chính A
• Gồm các nguyên tố s và p điển hình: IA IIA IIIA IVA VA VIA VIIA VIIIA ns1 ns2 ns2np1 ns2np2 ns2np3 ns2np4 ns2np5 ns2np6
• Mỗi phân nhóm chính có 6 – 7 nguyên tố, tạo cột dọc dài hơn
• Bắt đầu từ chu kỳ II
• Số thứ tự PNC = tổng số electron ở lớp ngoài cùng
b. Phân nhóm phụ B
• Gồm các nguyên tố họ d, f o Nhóm IIIB: ns2(n – 1)d1 o Nhóm IVB: ns2(n – 1)d2 o Nhóm VB: ns2(n – 1)d3 o Nhóm VIB: ns2(n – 1)d4 → ns1(n- 1)d5 (bán bão hòa sớm)
o Nhóm VIIB: ns2(n – 1)d5 o Nhóm VIIIB: ns2(n – 1)d6,7,8
o Nhóm IB: ns2(n – 1)d9 →
ns1(n – 1)d10 (bão hòa sớm) o Nhóm IIB: ns2(n – 1)d10
• Mỗi phân nhóm phụ có 3 – 4 nguyên tố, tạo cột dọc ngắn hơn phân nhòm chính o
Riêng PNP VIIIB có 9 ngtố o PNP IIIB có 14 PNP thứ cấp (PNP loại 2):  6s24f1 – 14: lantanoit  7s25f1 – 14: actinoit
• Số thứ tự PNP = tổng số electron ở lớp ngoài cùng và phân lớp ngoài cùng (ngoại trừ PNP IB, IIB, VIIB)
4. Mối liên quan giữa công thức electron nguyên tử và vị trí của nguyên tố trong bảng HTTH
a. Biết vị trí nguyên tố trong HTTH → công thức e nguyên tử của nguyên tố Ví dụ: Se: STT = 34 → Z = 34 Chu kỳ 4 → n = 4 Nhóm VIA → 4s24p4
→ công thức electron nguyên tử: 1s22s22p63s23p64s23d104p4
b. Biết công thức e nguyên tử → vị trí nguyên tố trong HTTH Ví dụ:
1s22s22p63s23p64s23d104p65s14d10 Z = Σe = 47
Electron hóa trị: 5s14d10 → X ở chu kỳ 5, PNP IB → nguyên tố là Ag
II. SỰ THAY ĐỔI TÍNH CHẤT CỦA CÁC NGUYÊN TỐ TRONG HTTH 1. Tổng quan:
• Tính chất các nguyên tố hóa học trong HTTH thay đổi một cách tuần hoàn theo 3
chiều: ngang, dọc và đường chéo (không quan trọng):
• Trong một phân nhóm: cấu trúc electron hóa trị tương tự nhau → tính chất hóa học
tương tự nhau. Từ trên xuống dưới, do số lớp electron tăng → lực hút của hạt nhân
đối với e ngoài cùng giảm: o
tính kim loại tăng, tính phi kim
giảm o tính khử tăng, tính oxi hóa giảm
• Trong một chu kỳ: từ trái sang phải, số lớp e không thay đổi, tổng số e lớp ngoài cùng
tăng → lực hút của hạt nhân đối với e ngoài cùng tăng o
tính kim loại giảm, tính phi kim
tăng o tính khử giảm, tính oxi hóa tăng
2. Bán kính nguyên tử và ion
• Coi nguyên tử hay ion như những hình cầu, hợp chất là các hình cầu tiếp xúc nhau.
Bán kính nguyên tử hay ion được xác định dựa trên khoảng cách giữa các hạt nhân
nguyên tử tạo nên đơn chất hay hợp chất tương ứng (bán kính hiệu dụng r)
• Bán kính hiệu dụng phụ thuộc: o
bản chất nguyên tử o đặc trưng liên
kết o trạng thái tập hợp
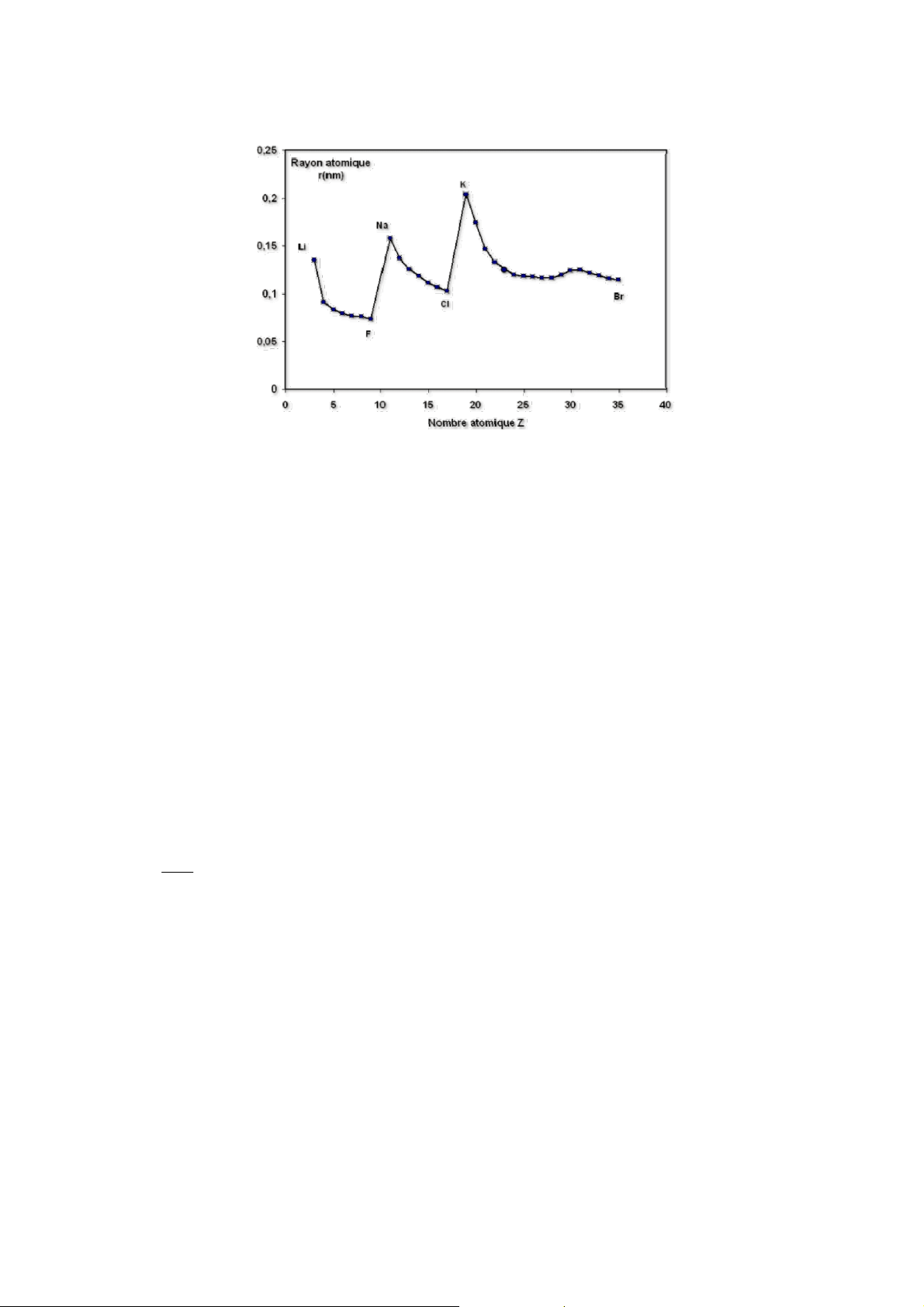
a. Bán kính nguyên tử
• Trong một chu kỳ khi đi từ trái sang phải bán kính nguyên tử giảm do Z tăng o
trong chu kỳ nhỏ r giảm rõ rệt
o trong chu kỳ lớn do e điền vào lớp kế ngoài cùng (n – 1)d làm tăng hiệu ứng chắn
→ r giảm chậm và đều đặn hơn
• Trong một phân nhóm chính, khi đi từ trên xuống số lớp e tăng → hiệu ứng chắn tăng → r tăng.
• Trong một phân nhóm phụ, khi đi từ trên xuống, xu hướng chung: r tăng nhưng
không đều đặn như ở PNC:
o Từ dãy 1 xuống dãy 2: r tăng do tăng thêm một lớp e
o Từ dãy 2 xuống dãy 3: r hầu như không tăng do hiện tượng co lantanit b. Bán kính ion:
• r ↑ khi lực hút của hạt nhân đối với e ngoài cùng ↓ • Mà: lực hút đối với 1e ∼ Z . Nên: ∑e
o r cation < r nguyên tử; r anion > r nguyên tử;
o Đối với cation của cùng một nguyên tố: r giảm theo chiều tăng điện tích ion o
Đối với các ion trong cùng phân nhóm có điện tích ion giống nhau (cấu trúc e
tương tự nhau) r tăng theo chiều tăng Z nguyên tử o Đối với các ion đẳng e (cấu
trúc e giống nhau) theo chiều tăng Z, r ion sẽ giảm
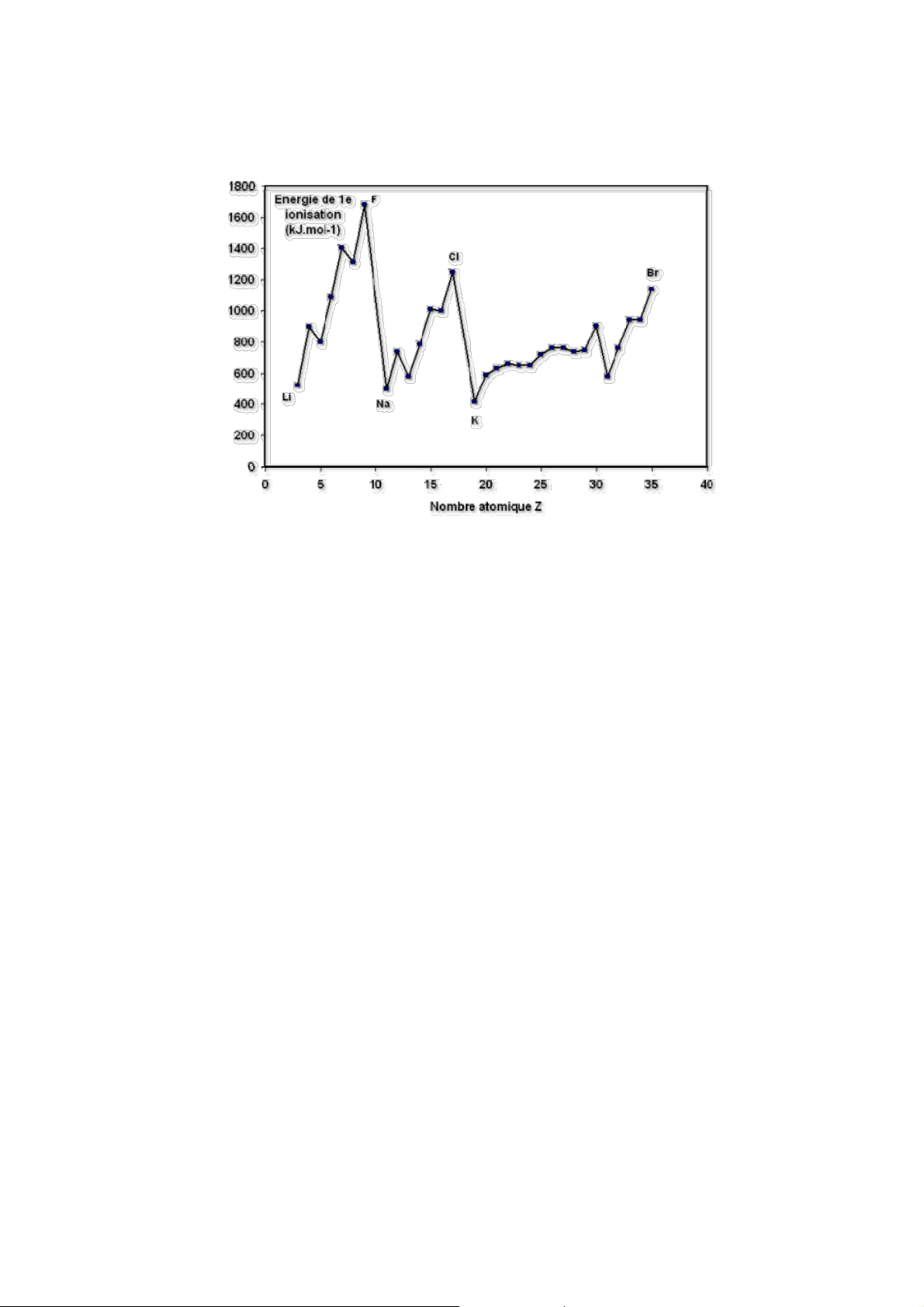
2. Năng lượng ion hóa I: đặc trưng cho khả năng nhường e của nguyên tử.
• Năng lượng ion hóa I là năng lượng cần tiêu tốn để tách một e ra khỏi nguyên tử ở
thể khí và không bị kích thích. X(k) = X+(k) + e I = ΔH
• I càng nhỏ nguyên tử càng dễ nhường e, do đó tính kim loại và tính khử càng mạnh.
• Trong một chu kỳ từ trái sang phải nhìn chung I tăng dần do Z tăng dần.
• Trong một phân nhóm chính khi đi từ trên xuống I giảm do số lớp e tăng → tăng hiệu ứng chắn.
• Trong phân nhóm phụ khi đi từ trên xuống, I tăng.
Giải thích: PNP có đặc điểm: e được điền vào phân lớp d của lớp kế ngoài cùng, còn e lớp
ngoài cùng ns2 không thay đổi. Do đó:
• Z tăng rất nhanh → tăng lực hút hạt nhân đến e ns2 ở lớp ngoài cùng
• Các AO (n – 1)d có tính đối xứng khác hẳn AO ns nên hiệu ứng chắn hầu như không
tăng → tăng hiệu ứng xâm nhập của các e s của lớp ngoài cùng.
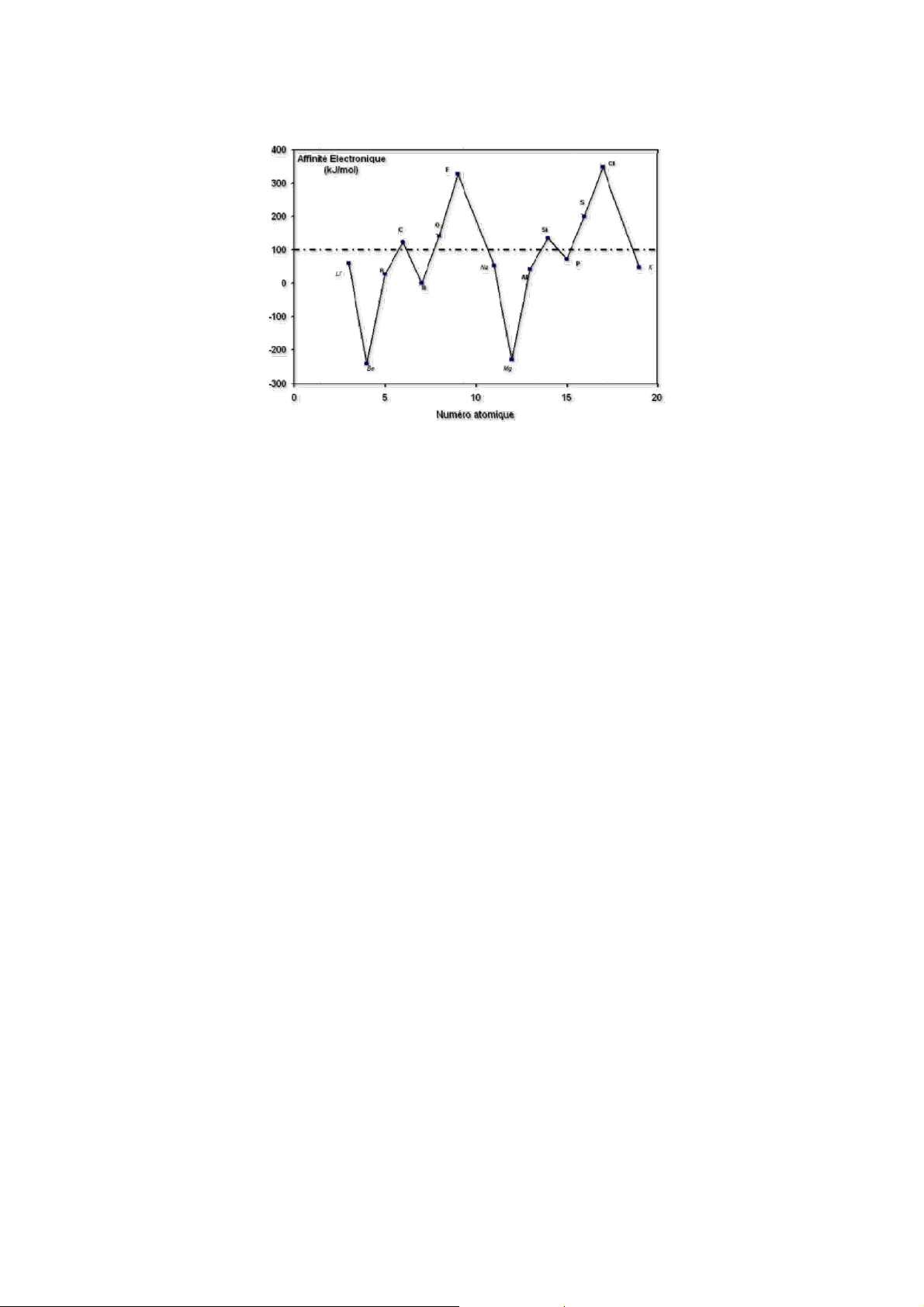
3. Ái lực electron F: đặc trưng cho khả năng nhận e của nguyên tố.
• Ái lực e F là năng lượng phát ra hay thu vào khi kết hợp một e vào nguyên tử ở thể
khí không bị kích thích. X(k) + e = X-(k), F = ΔH
• F có giá trị càng âm thì nguyên tử càng dễ nhận e, do đó tính phi kim và tính oxi hóa
của nguyên tố càng mạnh.
• Ái lực e của X = năng lượng ion hóa của X- nhưng ngược dấu: FX =−IX−
4. Độ âm điện χ: đặc trưng cho khả năng hút mật độ e về phía mình khi tạo liên kết với
nguyên tử của nguyên tố khác.
• Nguyên tử của nguyên tố có độ âm điện lớn hơn sẽ hút e về phía mình khi tương tác
với nguyên tử của nguyên tố khác có độ âm điện nhỏ hơn
• Có nhiều cách khác nhau để xác định độ âm điện
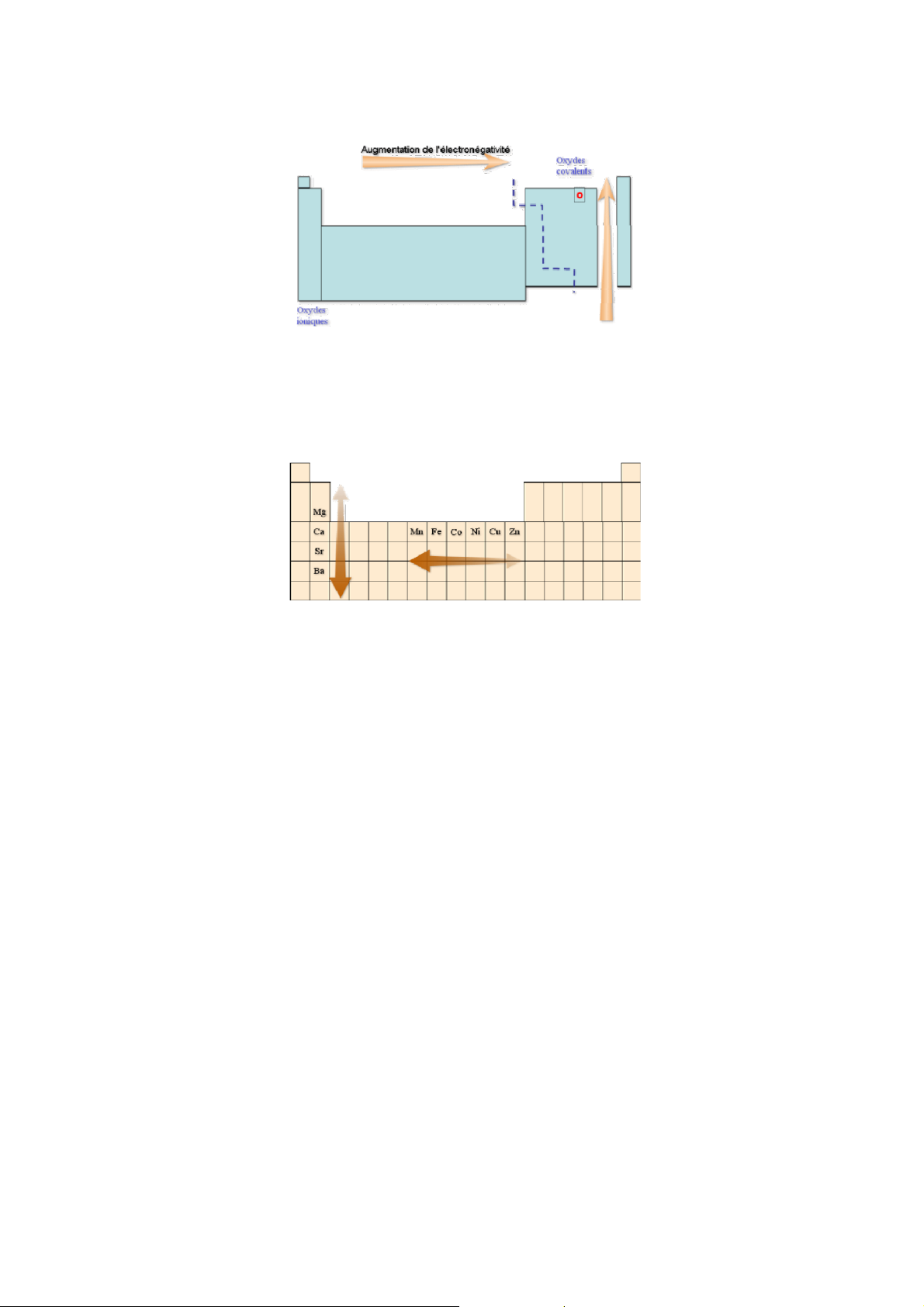
• Trong mỗi chu kỳ khi đi từ trái sang phải, nhìn chung độ âm điện tăng lên.
• Trong mỗi nhóm khi đi từ trên xuống, độ âm điện giảm.
* Chú ý: độ âm điện không phải là đại lượng cố định của một nguyên tố vì nó được xác định
trong sự phụ thuộc vào thành phần cụ thể của hợp chất. 5. Số oxi hóa
• Hóa trị: của một nguyên tố bằng số liên kết hóa học mà một nguyên tử của nguyên
tố đó tạo nên trong phân tử.
• Số oxi hóa: là điện tích dương hay âm của nguyên tố trong hợp chất được tính với
giả thiết rằng hợp chất được tạo thành từ các ion
o Số oxi hóa dương cao nhất của các nguyên tố = số thứ tự của nhóm o
Số oxi hóa âm thấp nhất của phi kim = 8 - số thứ tự nhóm