Giáo trình môn sức bền vật liệu chương 2: Nội lực | Trường Đại học sư phạm kỹ thuật TP Hồ Chí Minh

Phương pháp mặt cắt xác định nội lực : giả sử ta có 1 vật thể cân bằng dưới tác dụng của ngoại lực. để xác định nội lực trên mặt cắt ngang .Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

34 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: sức bền vật liệu 1

Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

Thông tin:

34 trang 3 tháng trước

Tác giả:

Profile Lê Kim Dung
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 1 05/2012
Chöông 02
NOÄI LÖÏC
I) TOÙM TAÉT LYÙ THUYEÁT
1.1.
Caùc thaønh phaàn noäi löïc treân maët caét ngang
Phöông phaùp maët caét xaùc ñònh noäi löïc: giaû söû ta coù moät vaät theå caân baèng döôùi taùc duïng
cuûa ngoaïi löïc
i
P
. Ñeå xaùc ñònh noäi löïc treân maët caét ngang chöùa ñieåm
C
thuoäc vaät theå ta
töôûng töôïng coù moät maët phaúng
qua ñieåm
C
vaø caét vaät theå thaønh hai phaàn
A
vaø
B
nhö hình 2.1. Xeùt söï caân baèng cuûa moät phaàn, ví duï phaàn
A
. Phaàn
A
ñöôïc caân baèng nhôø
noäi löïc cuûa phaàn
B
taùc duïng leân phaàn
A
. Noäi löïc naøy phaân boá baát kì treân maët caét vaø
hôïp löïc cuûa noäi löïc naøy caân baèng vôùi ngoaïi löïc taùc duïng leân phaàn
A
ñang xeùt. Töông töï
neáu ta xeùt söï caân baèng cuûa phaàn
B
thì phaàn
A
cuõng taùc duïng leân phaàn
B
caùc noäi löïc
töông töï nhöng ngöôïc chieàu nhö hình 2.1.
Thu goïn heä noäi löïc veà taâm maët caét ta ñöôïc moät veùc tô chính noäi löïc
R
vaø moät moâ men
chính noäi löïc
M
nhö hình 2.2.
Hình 2.2
. Hôïp cuûa noäi löïc treân maët caét
a)
1
P
2
P
3
P
M
A
4
P
1n
P
n
P
M
C
B
I
Hình 2.1.
Phöông phaùp maët caét vaø noäi löïc.
C
II
1
P
2
P
3
P
4
P
1n
P
n
P
1
P
2
P
3
P
4
P
1n
P
n
P
A
B
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 2 05/2012
Xeùt baøi toaùn thanh: ñaët heä truïc toaï ñoä taïi troïng taâm maët caét, truïc
z
truøng vôùi phaùp
tuyeán cuûa maët caét, caùc truïc
,x y
cuøng vôùi truïc
z
taïo thaønh moät tam dieän thuaän.
Chieáu veùc tô chính noäi löïc
R
vaø moâ men chính noäi löïc
M
leân caùc truïc toïa ñoä ta ñöôïc
saùu thaønh phaàn noäi löïc nhö hình 2.3:
Löïc doïc
z
N
laøm thanh chòu keùo_neùn ñuùng taâm.
Löïc caét
,
x y
Q Q
laøm thanh chòu caét.
Moâ men uoán
,
x y
M M
laøm thanh chòu uoán.
Moâ men xoaén
z
M
laøm thanh chòu xoaén.
1.2.
Xaùc ñònh caùc thaønh phaàn noäi löïc treân maët caét ngang
Khi ñaët saùu thaønh phaàn noäi löïc vaøo maët caét thì phaàn
A
trôû neân caân baèng (ngoaïi löïc taùc
duïng leân phaàn
A
caân baèng vôùi saùu thaønh phaàn noäi löïc ñaët treân maët caét). Söû duïng saùu
phöông trình caân baèng tónh hoïc ta coù theå xaùc ñònh ñöôïc trò soá, chieàu cuûa saùu thaønh phaàn noäi
löïc naøy:
1
1
1
1
1
0
0
0
0
0
n
z i
x
i
n
y i
y
i
n
x i
x
i
n
x x i
i
n
y y i
i
N P
Q P
Q P
M m P
M m P
(2.1)
Hình 2.3.
Caùc thaønh phaàn noäi löïc
1
P
2
P
n
P
y
x
z
z
N
y
Q
x
Q
x
M
z
M
y
M
A
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 3 05/2012
1
0
n
z z i
i
M m P
1.3.
Quan heä giöõa caùc thaønh phaàn noäi löïc vôùi caùc thaønh phaàn öùng suaát
Löïc doïc:
z z
F
N dF
(2.2)
Löïc caét :
x zx
F
y zy
F
Q dF
Q dF
(2.3)
Moâmen uoán:
x z
F
y z
F
M ydF
M xdF
(2.4)
Moâmen xoaén:
z zx zy
F
M y x dF
(2.5)
Hình 2.4.
Caùc thaønh phaàn noäi löïc
1
P
2
P
3
P
y
x
z
z
N
y
Q
x
Q
x
M
z
M
y
M
A
x
z
zy
zx
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 4 05/2012
1.4.
Qui öôùc daáu cuûa caùc thaønh phaàn noäi löïc
Nhö hình 2.6
Löïc doïc :
z
N
höôùng ra maët caét (keùo) laø döông.
Löïc caét:
,
x y
Q Q
coù xu höôùng laøm cho phaàn ñang xeùt quay cuøng chieàu kim ñoàng
hoà laø döông.
Moâmen uoán:
,
x y
M M
laøm caêng (keùo) phaàn beân döôùi laø döông.
Moâmen xoaén: khi nhìn vaøo maët caét thaáy
z
M
quay cuøng chieàu kim ñoàng hoà laø
döông.
Ví duï 1: Xaùc ñònh caùc thaønh phaàn noäi löïc treân maët caét ngang taïi
B
cuûa daàm chòu löïc
nhö hình 2.6 a.
Böôùc 1 xaùc ñònh phaûn löïc lieân keát taïi ngaøm
A
: ñaët caùc phaûn löïc lieân keát taïi
A
nhö hình 2.6 b, söû duïng ñieàu kieän caân baèng tónh hoïc ñeå xaùc ñònh caùc thaønh phaàn
phaûn löïc naøy.
Hình 2.5.
Chieàu döông cuûa noäi löïc.
0
z
N
0
y
Q
0
x
M
0
z
M
a
2a
A
B
C
Hình 2.6
q
2
M qa
a
2a
A
B
C
q
2
M qa
A
Y
A
M
A
A
Y
A
M
x
M
y
Q
a
2a
B
C
q
2
M qa
y
Q
x
M
)a
)b
)c
)d
1
1
z
y
A
Z
B
z
N
z
N
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 5 05/2012
2 2
0 .2 .2 0 5
0 .2 0 2
0 0
A A A
y A A
z A
m M q a a qa M qa
F Y q a Y qa
F Z
Böôùc 2 duøng maët caét
1 1
qua
B
caét daàm thaønh hai phaàn
AB
vaø
BC
. Giaû söû
daàm chòu löïc trong maët phaúng
yz
, ñaët caùc thaønh phaàn noäi löïc töông öùng vaøo hai
phaàn nhö hình 2.6 c vaø 2.6 d. Xeùt moät trong hai phaàn, giaû söû xeùt phaàn beân traùi nhö
hình 2.6 c. Söû duïng ñieàu kieän caân baèng tónh hoïc ñeå xaùc ñònh caùc thaønh phaàn noäi
löïc naøy:
2
0 0 2
0 0
0 . 0 3
y A y y A
z z
B A A x x
F Y Q Q Y qa
F N
m M Y a M M qa
Neáu xeùt phaàn beân phaûi nhö hình 2.6 d ta ñöôïc:
2 2
0 .2 0 2
0 0
0 .2 . 0 3
y y y
z z
B x x
F Q q a Q qa
F N
m M q a a qa M qa
Ví duï 2: Cho coät
AB
coù kích thöôùc, lieân keát vaø chòu löïc nhö hình 2.7a. Xaùc ñònh caùc
thaønh phaàn noäi löïc treân maët caét taïi
A
cuûa coät.
Ñaët caùc thaønh phaàn noäi löïc vaøo maët caét taïi
A
nhö hình 2.7 b. Söû duïng ñieàu kieän caân
baèng tónh hoïc ñeå xaùc ñònh caùc thaønh phaàn phaûn löïc naøy.
Hình 2.7
0,5m
2
100 /q kN m
1
50 /q kN m
A
B
0,5m
A
B
x
M
y
Q
z
N
1
R
2
R
0,5
3
m
0,5
2
m
1
2
50.0,5 25
1
100 50 .0,5 12,5
2
R kN
R kN
1
50 /q kN m
2
100 /q kN m
)a
)b
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 6 05/2012
1 2 1 2
1 2
0 0 25 12,5 37,5
0 0
0,5 0,5 25
0 . . 0 .
2 3 3
y y y
z z
A x x
F Q R R Q R R kN
F N
m M R R M kN m
Ví duï 3: Cho khung
ABCDE
coù kích thöôùc, lieân keát vaø chòu löïc nhö hình 2.8a. Xaùc
ñònh caùc thaønh phaàn noäi löïc treân caùc maët caét
1 1,2 2,3 3, 4 4
.
Böôùc 1 xaùc ñònh phaûn löïc lieân keát taïi ngaøm
A
: ñaët caùc phaûn löïc lieân keát taïi
A
nhö hình 2.8 b, söû duïng ñieàu kieän caân baèng tónh hoïc ñeå xaùc ñònh caùc thaønh phaàn
phaûn löïc naøy.
2 2
1
0 3 . 2 .2 . . 0
2 2
0 3 . 0 4
0 2 0 2
A A A
y A A
x A A
a
m M qa a qa qa a q a M qa
F Y qa q a Y qa
F X qa X qa
C
Hình 2.8
q
2
M qa
A
3P qa
a
)a
)c
)d
B
D
E
2P qa
a
a
a
C
q
2
M qa
A
3P qa
a
)b
B
D
E
2P qa
a
a
a
A
M
1
1
2
2
3
3
4
4
2
z
1
z
3
z
4
z
A
X
A
Y
A
Y
1
y
Q
1
x
M
1
z
N
A
X
1
z
A
M
1
1
C
2
M qa
3P qa
2
x
M
2
y
Q
2
z
2
q
D
E
2P qa
3
3
z
3
y
Q
3
x
M
a
q
E
4
4
z
4
y
Q
4
x
M
)e
)f
3
Z
N
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 7 05/2012
Böôùc 2 duøng maët caét
1 1
caét khung thaønh hai phaàn, xeùt phaàn beân döôùi. Ñaët caùc
thaønh phaàn noäi löïc töông öùng vaøo maët caét
1 1
nhö hình 2.8 c. Söû duïng ñieàu kieän
caân baèng tónh hoïc ñeå xaùc ñònh caùc thaønh phaàn noäi löïc naøy:
1 1
1 1
1 1
2
1 1 1 1
0 0 2
0 0 4
1
0 . 0 2 .
2
y A y y A
z A z z A
A A x x
F X Q Q X qa
F Y N N Y qa
m M X z M M qa qa z
Töông töï cho caùc maët caét khaùc nhö hình 2.8d,e,f, ta coù ñöôïc caùc thaønh phaàn noäi
löïc:
2 2
3 3 3
4 4
2
2
2
3
2
4 4
3 ; 3 .
1
2 ; ; 2 .
2
1
. ; .
2
y x
y z x
y x
Q qa M qa qa z
Q qa N qa M qa z qa
Q q z M q z
Ví duï 4: Moùc chöõ
U
coù kích thöôùc vaø chòu löïc nhö . Xaùc ñònh caùc thaønh phaàn hình 2.9 a
noäi löïc treân maët caét
A A
.
Duøng maët caét
A A
caét chi tieát thaønh hai phaàn, xeùt phaàn döôùi. Ñaët heä truïc toïa ñoä vaø caùc
thaønh phaàn noäi löïc töông öùng nhö hình Söû duïng ñieàu kieän caân baèng tónh hoïc ñeå xaùc 2.9 b.
ñònh caùc thaønh phaàn phaûn löïc naøy.
0 0
0 0
0 .6 0 6
x x
z z z
y y y
F Q
F N P N P
m M P b M Pb
z
x
x
y
z
N
y
M
C
P
b
b
2b
4b
A
A
AA
Hình 2.9
)a
)b
x
Q
q
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 8 05/2012
Ví duï 5: Truïc
AE
ñöôïc ñôû treân hai oå laên taïi
,A E
, lieân keát, chòu löïc nhö hình 2.10a.
Xaùc ñònh caùc thaønh phaàn noäi löïc treân maët caét taïi
O
.
Böôùc 1: vì truïc ñoái xöùng neân
2
A E
Y Y P
.
Böôùc 2: Duøng maët caét taïi
O
caét truïc laøm hai phaàn, xeùt phaàn beân traùi. Ñaët heä truïc
toïa ñoä vaø caùc thaønh phaàn noäi löïc vaøo maët caét taïi
O
nhö hình 2.10c. söû duïng caùc
phöông trình caân baèng ta xaùc ñònh ñöôïc caùc thaønh phaàn noäi löïc:
0 2 0
0 0
0 2 . 0 2
y y y
z z z
x x x
F P P Q Q P
m M M M M
m P z P z a M M Pz P z a
Ví duï 6: Truïc
AB
ngaøm taïi
A
, ñaàu
B
ñöôïc haøn vuoâng goùc vôùi thanh
BC
vaø chòu löïc
nhö hình 2.11a. Xaùc ñònh caùc thaønh phaàn noäi löïc treân maët caét taïi
A
.
Xeùt maët caét taïi
A
, ñaët heä truïc toïa ñoä vaø caùc thaønh phaàn noäi löïc vaøo maët caét taïi
A
nhö
hình 2.11b. söû duïng caùc phöông trình caân baèng ta xaùc ñònh ñöôïc caùc thaønh phaàn noäi löïc:
1m
0,3m
A
B
C
150P kN
1m
0,3m
A
B
C
150P kN
z
x
y
Q
z
M
x
M
Hình 2.11
)a
)b
z
y
x
z
M
x
M
A
y
Q
150P kN
B
C
1m
0,3m
Hình 2.10
M
2M
M
a
2a
2a
a
P
2P
P
A
B
C
D
E
z
O
M
2M
M
a
2a
2a
a
P
2P
P
A
B
C
D
E
z
O
A
Y
E
Y
M
P
A
B
z
O
2
A
Y P
x
z
y
x
M
z
M
y
Q
)a
)b
)c
a
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 9 05/2012
0 150 0 150
0 150.0,3 0 45 .
0 150.1 0 150 .
y y y
z z z
x x x
F Q Q kN
m M M kN m
m M M kN m
1.5.
Bieåu ñoà noäi löïc
1.5.1.
Ñònh nghóa
Bieåu ñoà noäi löïc laø ñoà thò moâ taû qui luaät phaân boá noäi löïc doïc theo truïc thanh.
Ñoaïn chòu löïc: laø ñoaïn maø treân ñoù haøm soá xaùc ñònh noäi löïc laø moät haøm lieân tuïc.
Caùch chia ñoaïn chòu löïc: khi coù söï thay ñoåi veà löïc, lieân keát ta phaûi tieán haønh chia ñoaïn
chòu löïc môùi.
1.5.2.
Veõ bieåu ñoà noäi löïc baèng phöông phaùp maët caét bieán thieân
Trong moãi ñoaïn chòu löïc ta söû duïng moät maët caét ñeå thieát laäp caùc haøm noäi löïc cho töøng ñoaïn,
sau ñoù veõ caùc haøm soá naøy leân heä truïc ta ñöôïc söï phaân boá noäi löïc doïc theo truïc thanh.
Ví duï 7: Veõ bieåu ñoà noäi löïc phaùt sinh trong daàm nhö hình 2.13 a.
Böôùc 1 giaûi phoùng lieân keát taïi
,A B
vaø ñaët caùc phaûn löïc lieân keát töông öùng nhö
hình 2.12 b.
2
2
3
0 .2 . 2 .2 .3 0
2
3
0 .2 .2 . 2 . 0
2
A B B
B A A
m q a a qa Y a qa a Y qa
m Y a q a a qa qa a Y qa
Böôùc 2 thieát laäp bieåu thöùc tính noäi löïc trong hai ñoaïn
,
AB BC
Duøng maët caét
1 1
caét daàm laøm hai phaàn, xeùt phaàn beân traùi vaø ñaët caùc thaønh phaàn noäi
löïc töông öùng nhö hình 2.12 c.
2
2
M qa
q
A
B
P qa
C
2a
a
2
2
M qa
q
A
B
P qa
C
2a
a
B
Y
q
A
1
1
z
A
Y
y
Q
x
M
P qa
2
y
Q
x
M
C
3
2
qa
1
2
qa
qa
2
9
8
qa
2
qa
2
qa
y
Q
x
M
)a
)b
)c
)d
Hình 2.12
1
1
2
2
1
0 2z a
2
0
z a
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 10 05/2012
1 1
2
1 1
1 1 1 1
3
0 . 0 .
2
3
0 . . . 0 .
2 2 2
y A y y
A x x
F Y q z Q Q qa q z
z z
m Y z q z M M qa z q
Ta thaáy treân ñoaïn
AB
y
Q
laø haøm baäc nhaát, theá
1
0
z
vaø
1
2z a
ta veõ ñöôïc bieåu ñoà
y
Q
treân ñoaïn
AB
. Haøm
x
M
laø haøm baäc hai neân ñi tìm cöïc trò vaø khaûo saùt söï loài, loõm
cuûa ñoà thò
1 1
1
3 3
0
2 2
x
M
qa qz z a
z
, taïi
1
3
2
z a
haøm
x
M
ñaït cöïc trò.
2
2
1
0
x
M
q
z
haøm
x
M
loài.
Töông töï duøng maët caét
2 2
caét daàm laøm hai phaàn, xeùt phaàn beân phaûi vaø ñaët caùc
thaønh phaàn noäi löïc töông öùng nhö hình 2.10 d.
2 2 2
0 0
0 . 0 .
y y y
x x
F Q P Q qa
m M P z M qa z
Ta thaáy treân ñoaïn
BC
y
Q
laø haøm haèng soá,
x
M
laø haøm baäc nhaát neân theá theá
2
0
z
vaø
2
z a
ta veõ ñöôïc ñoà thò
y
Q
,
x
M
treân ñoaïn
BC
nhö hình veõ.
Ví duï 8: Veõ bieåu ñoà noäi löïc phaùt sinh trong coät chòu löïc nhö hình 2.13 a.
Böôùc 1: giaûi phoùng lieân keát taïi ngaøm
A
vaø ñaët phaûn löïc lieân keát töông öùng nhö
hình 2.13 b.
0 3 2 .4 0 9
z A A
F qa qa q a N N qa
.
P qa
3P
P
q
3a
a
A
B
C
Hình 2.13
3qa
4qa
6qa
9qa
z
N
3P
P
q
3a
a
A
B
C
A
N
P qa
1
1
1
z
2
2
2
z
A
A
N
1
1
1
z
q
1
z
N
C
3P
2
2
2
z
q
2
z
N
)a
)b
)c
)d
)e
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 11 05/2012
Böôùc 2: thieát laäp bieåu thöùc tính noäi löïc trong hai ñoaïn
,
AB BC
: treân ñoaïn
AB
duøng maët caét
1 1
caùch
A
moät ñoaïn
1
z
caét coät laøm hai phaàn, xeùt phaàn döôùi nhö
hình 2.13c vaø ñaët noäi löïc töông öùng vaøo maët caét. Töông töï, treân ñoaïn
BC
duøng
maët caét
2 2
caùch
C
moät ñoaïn
2
z
caét coät laøm hai phaàn, xeùt phaàn treân nhö hình
2.13d vaø ñaët noäi löïc töông öùng vaøo maët caét. Söû duïng caùc phöông trình caân baèng ta
xaùc ñònh ñöôïc:
1
1 1
9 (0 3 )
Z
N qz qa z a
,
1
Z
N
laø haøm baäc nhaát.
2
2 2
3 (0 )
Z
N qa qz z a
,
2
Z
N
laø haøm baäc nhaát.
Ví duï9: Veõ bieåu ñoà noäi löïc phaùt sinh trong truïc chòu löïc nhö hình 2.14 a.
Böôùc 1: giaûi phoùng lieân keát taïi ngaøm
A
vaø ñaët phaûn löïc lieân keát töông öùng nhö
hình 2.14 b.
0 6 .2 0 3
z A A
m M ma m a ma M ma
.
Böôùc 2: thieát laäp bieåu thöùc tính noäi löïc trong hai ñoaïn
,
AB BC
: treân ñoaïn
AB
duøng maët caét
1 1
caùch
A
moät ñoaïn
1
z
caét truïc laøm hai phaàn, xeùt phaàn beân traùi
nhö hình 2.14c vaø ñaët noäi löïc töông öùng vaøo maët caét. Töông töï, treân ñoaïn
BC
duøng maët caét
2 2
caùch
C
moät ñoaïn
2
z
caét coät laøm hai phaàn, xeùt phaàn beân phaûi
nhö hình 2.14d vaø ñaët noäi löïc töông öùng vaøo maët caét. Söû duïng caùc phöông trình
caân baèng ta xaùc ñònh ñöôïc:
1
1
3 (0 )
Z
M ma z a
,
1
Z
M
haèng soá treân ñoaïn
AB
.
2
2 2
(0 2 )
Z
M ma mz z a
, laø haøm baäc nhaát
2
Z
M
.
M ma
2a
6M
A
B
C
m
M ma
2a
6M
A
B
C
m
A
M
ma
3ma
3ma
z
M
Hình 2.14
a
a
)a
)b
)e
A
M
1
Z
M
1
z
A
1
C
m
M ma
2
Z
M
2
z
2
)c
)d
1
1
2
2
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 12 05/2012
1.5.3.
Veõ bieåu ñoà noäi löïc baèng phöông phaùp veõ nhanh.
Lieân heä vi phaân giöõa moâmen uoán, löïc caét vaø taûi troïng ngang phaân boá
Xeùt daàm chòu uoán phaúng trong maët phaúng
yz
vôùi taûi troïng laø caùc löïc taäp trung, löïc phaân
boá vaø ngaãu löïc taäp trung nhö hình 2.15. Duøng hai maët caét
1 1
vaø
2 2
taùch töø ñoaïn chòu
löïc phaân boá
BC
moät phaân toá chieàu daøi
dz
vaø ñaët caùc thaønh phaàn noäi löïc töông öùng vaøo hai
maët caét nhö hình 2.16a.
0 0 ( )
y
y y y y
dQ
F Q Q dQ qdz q z
dz
(2.6)
Nhaän xeùt 1: ñoà löïc caét hôn bieåu ñoà taûi troïng phaân boá moät baäc bieåu .
Tích phaân hai veá bieåu thöùc (2.6):
C
C
C B
y y y q
B
B
dQ qdz Q Q S
(2.7)
Nhaän xeùt 2: khi ñi töø traùi qua phaûi, löïc caét cuoái ñoaïn baèng löïc caét ñaàu ñoaïn coäng
hôïp löïc phaân boá treân ñoaïn ñoù (hôïp löïc phaân boá höôùng leân döông, höôùng xuoáng aâm).
2
2 x x x y
.( )
0 M - (M dM ) Q dz 0
2
q dz
m
, boû qua ñaïi löôïng voâ cuøng beù
baäc cao
2
( )dz
ta ñöôïc:
y
x
Q
dz
dM
(2.8)
Nhaän xeùt 3: bieåu ñoà moâ men uoán hôn bieåu ñoà löïc caét moät baäc. Neáu trong nhöõng
ñoaïn moâ men uoán coù baäc hai, moâ men uoán ñaït cöïc trò taïi nhöõng ñieåm coù
0
y
Q
.
Tích phaân hai veá bieåu thöùc (2.8):
y
C
C
C B
x y x x Q
B
B
dM Q dz M M S
(2.9)
Nhaän xeùt 4: khi ñi töø traùi qua phaûi, moâ men uoán cuoái ñoaïn baèng moâ men uoán ñaàu
ñoaïn coäng dieän tích bieåu ñoà löïc caét treân ñoaïn ñoù.
Lieân heä giöõa moâmen uoán, löïc caét vaø taûi troïng ngang taäp trung
Hình 2.15 Daàm chòu löïc
dz
dz
1
1
2
2
3
3
4
4
q z
M
P
z
y
B
C
D
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 13 05/2012
Duøng hai maët caét
3 3
vaø
4 4
taùch töø daàm ôû hai beân
D
moät phaân toá chieàu daøi
dz
vaø ñaët
caùc thaønh phaàn noäi löïc töông öùng vaøo hai maët caét nhö hình 2.16b.
0 0
t p p t
y y y y y
F Q P Q Q Q P
(2.10)
Nhaän xeùt 5: khi ñi töø traùi qua phaûi neáu treân sô ñoà tính coù löïc taäp trung bieåu ñoà löïc
caét coù böôùc nhaûy, giaù trò buôùc nhaûy baèng giaù trò löïc taäp trung, chieàu böôùc nhaûy cuøng
chieàu vôùi löïc taäp trung.
0 . . 0
2 2
t t p p
D y x y x
dz dz
m Q M M Q M
, boû qua thaønh phaàn voâ cuøng beù baäc cao
ta ñöôïc:
p t
x x
M M M
(2.11)
Nhaän xeùt 6: khi ñi töø traùi qua phaûi neáu treân sô ñoà tính coù ngaãu löïc taäp trung bieåu ñoà
moâ men uoán coù böôùc nhaûy, giaù trò buôùc nhaûy baèng giaù trò ngaãu löïc taäp trung, nhaûy
xuoáng khi ngaãu löïc quay cuøng chieàu kim ñoàng hoà, nhaûy leân cho tröôøng hôïp ngöôïc laïi.
Lieân heä giöõa löïc doïc vaø caùc taûi troïng doïc.
Duøng hai maët caét
1 1
vaø
2 2
taùch töø ñoaïn chòu löïc phaân boá
BC
moät phaân toá chieàu daøi
dz
vaø ñaët caùc thaønh phaàn noäi löïc töông öùng vaøo hai maët caét nhö hình 2.17b.
0 . 0
z
z z z z
dN
F N q dz N dN q
dz
(2.12)
Nhaän xeùt 7: bieåu ñoà löïc doïc hôn bieåu ñoà taûi troïng phaân boá moät baäc.
Hình 2.16 Lieân heä giöõa taûi troïng ngang vaø noäi löïc
dz
q
y
Q
x
M
y y
Q dQ
x x
M dM
1
1
2
2
)a
3
3
4
4
t
y
Q
t
x
M
p
y
Q
p
x
M
)b
D
M
P
dz
Hình
2.17: Lieân heä giöõa taûi troïng doïc vaø noäi löïc.
2
2
1
1
q z
q
P
z
N
z z
N dN
1
1
2
2
B
C
D
)a
)b
t
z
N
p
z
N
dz
3
3
4
4
)c
P
D
3
3
4
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 14 05/2012
Tích phaân hai veá bieåu thöùc (2.12):
C
C
C B
z z z q
B
B
dN qdz N N S
(2.13)
Nhaän xeùt 8: löïc doïc cuoái ñoaïn baèng löïc doïc ñaàu ñoaïn coäng hôïp löïc phaân boá treân
ñoaïn ñoù (hôïp löïc phaân boá gaây keùo döông, gaây neùn aâm).
Duøng hai maët caét
3 3
vaø
4 4
taùch töø thanh ôû hai beân
D
moät phaân toá chieàu daøi
dz
vaø ñaët
caùc thaønh phaàn noäi löïc töông öùng vaøo hai maët caét nhö hình 2.17c.
0 0
t p p t
z z z z z
F N P N N N P
(2.14)
Nhaän xeùt 9: neáu treân sô ñoà tính coù löïc taäp trung bieåu ñoà löïc doïc coù böôùc nhaûy, giaù
trò böôùc nhaûy baèng giaù trò löïc taäp trung, nhaûy veà phía döông khi löïc gaây keùo, nhaûy veà
phía aâm khi löïc gaây neùn.
Lieân heä giöõa moâmen xoaén vaø caùc taûi troïng moâmen xoaén.
Duøng hai maët caét
1 1
vaø
2 2
taùch töø ñoaïn chòu taûi phaân boá
BC
moät phaân toá chieàu daøi
dz
vaø ñaët caùc thaønh phaàn noäi löïc töông öùng vaøo hai maët caét nhö hình 2.18b.
0 . 0
z
z z z z
dM
m M dM m dz M m
dz
(2.15)
Nhaän xeùt 10: bieåu ñoà moâ men xoaén hôn bieåu ñoà taûi troïng phaân boá moät baäc.
Tích phaân hai veá bieåu thöùc (2.15):
C
C
C B
z z z m
B
B
dM mdz M M S
(2.16)
Nhaän xeùt 11:moâ men xoaén cuoái ñoaïn baèng moâ men xoaén ñaàu ñoaïn coäng hôïp ngaãu
löïc phaân boá treân ñoaïn ñoù (hôïp moâ men xoaén löïc phaân boá cuøng chieàu kim ñoàng hoà
döông, ngöôïc chieàu kim ñoàng hoà aâm).
Duøng hai maët caét
3 3
vaø
4 4
taùch töø thanh ôû hai beân
D
moät phaân toá chieàu daøi
dz
vaø ñaët
caùc thaønh phaàn noäi löïc töông öùng vaøo hai maët caét nhö hình 2.18c.
0 0
t p p t
z z z z z
m M M M M M M
(2.14)
Nhaän xeùt 12: neáu treân sô ñoà tính coù moâ men xoaén taäp trung bieåu ñoà moâ men xoaén
coù böôùc nhaûy, giaù trò böôùc nhaûy baèng giaù trò ngaãu löïc taäp trung, nhaûy veà phía döông
khi ngaãu löïc cuøng chieàu kim ñoàng hoà, nhaûy veà phía aâm khi ngaãu löïc quay ngöôïc chieàu
kim ñoàng hoà.
Hình 2.18 Lieân heä giöõa moâmen taûi troïng vaø noäi löïc. :
2
2
1
1
z z
M dM
z
M
m z
m
1
1
2
2
p
z
M
1
1
2
2
dz
t
z
M
3
3
4
4
B
C
D
M
M
D
)a
)c
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 15 05/2012
Ví duï 10: Veõ bieåu ñoà noäi löïc phaùt sinh trong coät chòu neùn ñuùng taâm nhö hình 2.20.
Phaûn löïc lieân keát taïi ngaøm
A
:
0 .4 2 3 0 9
z A A
F N q a qa qa N qa
Taïi
C
coù löïc taäp trung
3 3P qa
gaây neùn neân bieåu ñoà
z
N
coù böôùc nhaûy veà phía
aâm (beân traùi) moät ñoaïn baèng
3qa
töø vò trí khoâng thuoäc ñöôøng chuaån.
Noäi löïc ôû phía treân cuûa maët caét taïi
B
. 3 4
B C
z z
tren
N N q a qa qa qa
Taïi
B
coù löïc taäp trung
2 2P qa
gaây neùn neân bieåu ñoà
z
N
coù böôùc nhaûy veà phía
aâm (beân traùi) moät ñoaïn baèng
2qa
töø giaù trò
4qa
neân
z
N
phía döôùi maët caét taïi
B
coù giaù trò
4 2 6qa qa qa
.
Noäi löïc ôû phía treân cuûa maët caét taïi
A
:
.3 6 3 9
A B
z z
tren duoi
N N q a qa qa qa
Taïi
A
coù löïc taäp trung
9
A
N qa
gaây keùo neân bieåu ñoà
z
N
coù böôùc nhaûy veà phía
döông (beân phaûi) moät ñoaïn baèng
9qa
töø giaù trò
9qa
neân
z
N
phía döôùi maët caét
taïi
A
coù giaù trò
9 9 0
qa qa
.
Ví duï11: Veõ bieåu ñoà noäi löïc phaùt sinh trong coät chòu neùn ñuùng taâm nhö hình 2.20.
P qa
3P
P
q
3a
a
A
B
C
Hình 2.19
3qa
4qa
6qa
9qa
z
N
3P
P
q
3a
a
A
B
C
A
N
P qa
Caùch veõ bieåu ñoà noäi löïc trong thanh chòu keùo-neùn ñuùng taâm: (vẽ từ đầu tự do)
Bieåu ñoà löïc doïc hôn bieåu ñoà taûi troïng phaân boá moät baäc.
Neáu treân sô ñoà tính coù löïc taäp trung bieåu ñoà löïc doïc coù böôùc nhaûy, giaù trò
böôùc nhaûy baèng giaù trò löïc taäp trung, nhaûy veà phía döông khi löïc gaây keùo, nhaûy
veà phía aâm khi löïc gaây neùn.
Löïc doïc cuoái ñoaïn baèng löïc doïc ñaàu ñoaïn coäng hôïp löïc phaân boá treân ñoaïn
ñoù (hôïp löïc phaân boá gaây keùo döông, gaây neùn aâm).
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 16 05/2012
Phaûn löïc lieân keát taïi ngaøm
A
:
0 .3 5 0
z A A
F N q a qa qa N qa
Taïi
C
coù löïc taäp trung
P qa
gaây neùn neân bieåu ñoà
z
N
coù böôùc nhaûy veà phía aâm
(beân traùi) moät ñoaïn baèng
qa
töø vò trí “0” thuoäc ñöôøng chuaån.
Noäi löïc ôû phía treân cuûa maët caét taïi
B
0
B C C
z z z
tren duoi duoi
N N N qa
(ñoaïn
BC
khoâng coù taûi phaân boá neân
z
N
haèng soá).
Taïi
B
coù löïc taäp trung
5 5P qa
gaây keùo neân bieåu ñoà
z
N
coù böôùc nhaûy veà phía
döông (beân phaûi) moät ñoaïn baèng
5qa
töø giaù trò
qa
neân
z
N
phía döôùi maët caét
taïi
B
coù giaù trò
5 4qa qa qa
.
Noäi löïc ôû phía treân cuûa maët caét taïi
A
:
.3 4 3
A B
z z
tren duoi
N N q a qa qa qa
Taïi
A
coù löïc taäp trung
A
N qa
gaây neùn neân bieåu ñoà
z
N
coù böôùc nhaûy veà phía
aâm (beân traùi) moät ñoaïn baèng
qa
töø giaù trò
qa
neân
z
N
phía döôùi maët caét taïi
A
coù
giaù trò
0
qa qa
.
Caùch veõ bieåu ñoà noäi löïc trong truïc chòu xoaén: (Vẽ bắt đầu từ hướng nhìn qua)
Bieåu ñoà moâmen xoaén hôn bieåu ñoà taûi troïng phaân boá moät baäc.
Neáu treân sô ñoà tính coù ngaãu löïc taäp trung bieåu ñoà moâmen xoaén coù böôùc nhaûy,
giaù trò böôùc nhaûy baèng giaù trò ngaãu löïc taäp trung, nhaûy veà phía döông khi nhìn vaøo
maët caét thaáy ngaãu löïc quay cuøng chieàu kim ñoàng hoà, nhaûy veà phía aâm cho tröôøng
hôïp ngöôïc laïi.
Moâmen xoaén cuoái ñoaïn baèng moâmen xoaén ñaàu ñoaïn coäng hôïp ngaãu löïc phaân
boá treân ñoaïn ñoù (hôïp ngaãu löïc phaân boá quay cuøng chieàu kim ñoàng hoà döông,
ngöôïc laïi laø aâm).
Hình 2.20
P qa
q
3a
a
A
B
C
A
N
P qa
q
3a
a
A
B
C
2,5P
2,5P
2,5P
2,5P
qa
4qa
z
N
4qa
qa
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 17 05/2012
Ví duï 12: Veõ bieåu ñoà noäi löïc phaùt sinh trong truïc chòu xoaén nhö hình 2.21 a.
Phaûn löïc lieân keát taïi ngaøm
A
: ñaët phaûn löïc lieân keát taïi ngaøm
A
nhö hình 2.21 b
0 6 .2 0 3
z A A
m M ma m a ma M ma
Taïi
C
coù ngaãu löïc taäp trung
M ma
cuøng chieàu kim ñoàng hoà neân bieåu ñoà
z
M
coù
böôùc nhaûy veà phía döông (beân treân) moät ñoaïn baèng
qa
töø vò trí “0” thuoäc ñöôøng
chuaån.
Noäi löïc ôû phía beân phaûi cuûa maët caét taïi
B
:
.2 2 3
B C
z z
phai
M M m a ma ma ma
Taïi
B
coù ngaãu löïc taäp trung
6 6M ma
ngöôïc chieàu kim ñoàng hoà neân bieåu ñoà
z
M
coù böôùc nhaûy veà phía aâm (beân döôùi) moät ñoaïn baèng
6ma
töø giaù trò
3ma
neân
z
M
beân traùi maët caét taïi
B
coù giaù trò
3 6 3ma ma ma
.
Noäi löïc ôû phía beân phaûi cuûa maët caét taïi
A
:
0 3
A B B
z z z
phai trai trai
M M M ma
(treân ñoaïn
BA
khoâng coù taûi phaân boá neân
z
M
haèng soá).
Taïi
A
coù ngaãu löïc taäp trung
3
A
M ma
cuøng chieàu kim ñoàng hoà neân bieåu ñoà
z
M
coù böôùc nhaûy veà phía döông (beân treân) moät ñoaïn baèng
3qa
töø giaù trò
3ma
neân
z
M
phía traùi maët caét taïi
A
coù giaù trò
3 3 0
ma ma
.
Ví duï 13: Veõ bieåu ñoà noäi löïc phaùt sinh trong truïc chòu xoaén nhö hình 2.22a.
Phaûn löïc lieân keát taïi ngaøm
A
:
M ma
2a
6M
A
B
C
m
M ma
2a
6M
A
B
C
m
A
M
ma
3ma
3ma
z
M
Hình 2.21
a
a
)a
)b
)c
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 18 05/2012
0 4 0 3
z A A
m M M M M M
Taïi
C
coù ngaãu löïc taäp trung
M
cuøng chieàu kim ñoàng hoà neân bieåu ñoà
z
M
coù böôùc
nhaûy veà phía döông (beân treân) moät ñoaïn baèng
M
töø vò trí “0” thuoäc ñöôøng
chuaån.
Noäi löïc ôû phía beân phaûi cuûa maët caét taïi
B
: 0
B C C
z z z
phai
M M M M
(treân
ñoaïn
CB
khoâng coù taûi phaân boá neân
z
M
haèng soá).
Taïi
B
coù ngaãu löïc taäp trung
4M
ngöôïc chieàu kim ñoàng hoà neân bieåu ñoà
z
M
coù
böôùc nhaûy veà phía aâm (beân döôùi) moät ñoaïn baèng
4M
töø giaù trò
M
neân
z
M
beân
traùi maët caét taïi
B
coù giaù trò
4 3M M M
.
Noäi löïc ôû phía beân phaûi cuûa maët caét taïi
A
:
0 3
A B B
z z z
phai trai trai
M M M M
(treân ñoaïn
BA
khoâng coù taûi phaân boá neân
z
M
haèng soá).
Taïi
A
coù ngaãu löïc taäp trung
3
A
M M
cuøng chieàu kim ñoàng hoà neân bieåu ñoà
z
M
coù böôùc nhaûy veà phía döông (beân treân) moät ñoaïn baèng
3M
töø giaù trò
3M
neân
z
M
phía trí maët caét taïi
A
coù giaù trò
3 3 0
M M
.
M
2a
4M
A
B
C
M
2a
A
B
C
A
M
M
3M
z
M
a
4M
a
Hình 2.22
)a
)b
)c
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 19 05/2012
Ví duï14: Veõ bieåu ñoà noäi löïc phaùt sinh trong daàm chòu uoán phaúng nhö hình 2.23 a.
Phaûn löïc lieân keát taïi caùc goái
,A B
: ñaët caùc phaûn löïc lieân keát töông öùng taïi
,A B
nhö hình 2.23 b.
0 3 .2 .3 0
2
0 .2 3 . 0
2
A B B
B A A
P
m Pa Pa Y a P a Y
P
m Pa Y a Pa P a Y
Veõ bieåu ñoà löïc caét
y
Q
: treân ñoaïn
,
AB BC
khoâng coù löïc phaân boá neân bieåu ñoà löïc caét
y
Q
coù
daïng haèng soá.
Taïi
A
coù löïc taäp trung
/ 2
A
Y P
höôùng leân neân bieåu ñoà
y
Q
coù böôùc nhaûy höôùng
leân moät ñoaïn baèng
/ 2P
töø vò trí “0” thuoäc ñöôøng chuaån.
Löïc caét beân traùi cuûa maët caét taïi
B
:
0 / 2
B A A
y y y
trai
Q Q Q P
(treân ñoaïn
AB
khoâng coù taûi phaân boá neân
y
Q
haèng soá).
Taïi
B
coù löïc taäp trung
/ 2
B
Y P
höôùng leân neân bieåu ñoà
y
Q
coù böôùc nhaûy höôùng
leân moät ñoaïn baèng
/ 2P
töø giaù trò
/ 2P
neân
y
Q
beân phaûi maët caét taïi
B
coù giaù
trò
/ 2 / 2
P P P
.
Löïc caét beân traùi cuûa maët caét taïi
C
: 0
C B B
y y y
trai phai phai
Q Q Q P
(treân ñoaïn
BC
khoâng coù taûi phaân boá neân
y
Q
haèng soá).
Caùch veõ bieåu ñoà noäi löïc trong daàm chòu uoán phaúng: (vẽ từ trái sang phải)
Bieåu ñoà löïc caét:
Bieåu ñoà löïc caét hôn bieåu ñoà taûi troïng phaân boá moät baäc.
Khi ñi töø traùi qua phaûi, neáu treân sô ñoà tính coù löïc taäp trung bieåu ñoà löïc caét coù
böôùc nhaûy, giaù trò böôùc nhaûy baèng giaù trò löïc taäp trung, chieàu böôùc nhaûy cuøng
chieàu vôùi löïc taäp trung.
Khi ñi töø traùi qua phaûi, löïc caét cuoái ñoaïn baèng löïc caét ñaàu ñoaïn coäng hôïp löïc
phaân boá treân ñoaïn ñoù (hôïp löïc phaân boá höôùng leân döông, höôùng xuoáng aâm).
Bieåu ñoà moâmen uoán:
Bieåu ñoà moâmen uoán hôn bieåu ñoà löïc caét moät baäc.
Khi ñi töø traùi qua phaûi, neáu treân sô ñoà tính coù ngaãu löïc taäp trung bieåu ñoà
moâmen uoán coù böôùc nhaûy, giaù trò böôùc nhaûy baèng giaù trò ngaãu löïc taäp trung, nhaûy
xuoáng khi ngaãu löïc quay cuøng chieàu kim ñoàng hoà, nhaûy leân khi ngaãu löïc quay
ngöôïc chieàu kim ñoàng hoà.
Khi ñi töø traùi qua phaûi, moâmen uoán cuoái ñoaïn baèng moâmen uoán ñaàu ñoaïn
coäng dieän tích löïc caét treân ñoaïn ñoù (Neáu treân ñoaïn ñoù moâmen uoán laø haøm baäc hai,
moâmen uoán seõ ñaït cöïc trò taïi vò trí löïc caét baèng khoâng).
Noäi löïc Khoa Xaây Döïng
Baøi taäp söùc beàn vaät lieäu trang 20 05/2012
Taïi
C
coù löïc taäp trung
P
höôùng xuoáng neân bieåu ñoà
y
Q
coù böôùc nhaûy höôùng
xuoáng moät ñoaïn baèng
P
töø giaù trò
P
neân
y
Q
beân phaûi maët caét taïi
C
coù giaù trò
0
P P
.
Veõ bieåu ñoà moâ men uoán
x
M
: (Bieåu ñoà moâ men uoán treân aâm döôùi döông) ta ñaõ bieát bieåu
ñoà moâmen uoán
x
M
hôn bieåu ñoà löïc caét
y
Q
moät baäc neân treân ñoaïn
,
AB BC
bieåu ñoà moâmen
uoán
x
M
coù daïng baäc nhaát.
Taïi
A
coù ngaãu löïc taäp trung
M Pa
cuøng chieàu kim ñoàng hoà neân bieåu ñoà
x
M
coù
böôùc nhaûy höôùng xuoáng moät ñoaïn baèng
Pa
töø vò trí “0” thuoäc ñöôøng chuaån.
Moâmen uoán beân traùi cuûa maët caét taïi
B
:
1
.2 2
2
y
AB
B A
x x Q
trai phai
M M S Pa P a Pa
.
Taïi
B
coù ngaãu löïc taäp trung
3M Pa
ngöôïc chieàu kim ñoàng hoà neân bieåu ñoà
x
M
coù böôùc nhaûy höôùng leân moät ñoaïn baèng
3Pa
töø giaù trò
2Pa
neân
x
M
beân phaûi
maët caét taïi
B
coù giaù trò
2 3
Pa Pa Pa
.
Moâmen uoán beân traùi cuûa maët caét taïi
C
:
. 0
y
BCC B
x x Q
trai phai
M M S Pa P a
.
a
2a
P
3M
A
C
a
2a
P
3M Pa
A
C
A
Y
B
Y
M Pa
P
1
2
P
Pa
2Pa
Pa
y
Q
x
M
Hình 2.23
M Pa
)a
)b
)c
)d
| 1/34
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Noäi löïc Khoa Xaây Döïng Chöông 02 NOÄI LÖÏC I) TOÙM TAÉT LYÙ THUYEÁT
1.1. Caùc thaønh phaàn noäi löïc treân maët caét ngang
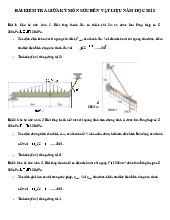
Phöông phaùp maët caét xaùc ñònh noäi löïc: giaû söû ta coù moät vaät theå caân baèng döôùi taùc duïng 
cuûa ngoaïi löïc  P . Ñeå xaùc ñònh noäi löïc treân maët caét ngang chöùa ñieåm C thuoäc vaät theå ta i 
töôûng töôïng coù moät maët phaúng   qua ñieåm C vaø caét vaät theå thaønh hai phaàn A vaø B
nhö hình 2.1. Xeùt söï caân baèng cuûa moät phaàn, ví duï phaàn A. Phaàn  A ñöôïc caân baèng nhôø
noäi löïc cuûa phaàn B taùc duïng leân phaàn A. Noäi löïc naøy phaân boá baát kì treân maët caét vaø
hôïp löïc cuûa noäi löïc naøy caân baèng vôùi ngoaïi löïc taùc duïng leân phaàn A ñang xeùt. Töông töï
neáu ta xeùt söï caân baèng cuûa phaàn B thì phaàn A cuõng taùc duïng leân phaàn B caùc noäi löïc
töông töï nhöng ngöôïc chieàu nhö hình 2.1.
Thu goïn heä noäi löïc veà taâm maët caét ta ñöôïc moät veùc tô chính noäi löïc R vaø moät moâ men
chính noäi löïc M nhö hình 2.2.  P3 P P 3 4 I P C 4 P   A 2 P II P n1 P 2 B P n 1  1 P1 P P n n
Hình 2.1. Phöông phaùp maët caét vaø noäi löïc. a) P3 M R P4 C P2  P A C n1 R B P1 M P
Hình 2.2. Hôïp cuûa noäi löïc treân maët caét n
Baøi taäp söùc beàn vaät lieäu trang 1 05/2012 Noäi löïc Khoa Xaây Döïng
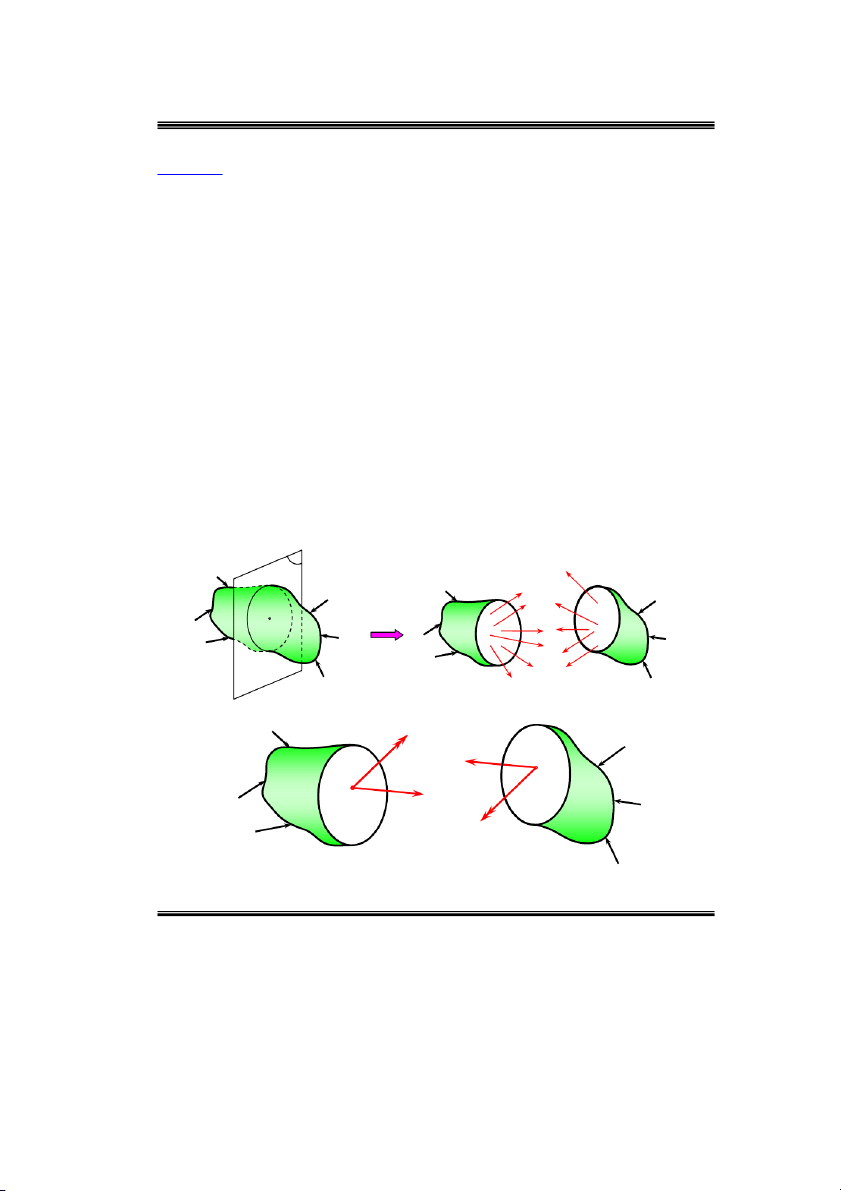
Xeùt baøi toaùn thanh: ñaët heä truïc toaï ñoä taïi troïng taâm maët caét, truïc z  truøng vôùi phaùp
tuyeán cuûa maët caét, caùc truïc x, y cuøng vôùi truïc z taïo thaønh moät tam dieän thuaän.
Chieáu veùc tô chính noäi löïc R vaø moâ men chính noäi löïc M leân caùc truïc toïa ñoä ta ñöôïc
saùu thaønh phaàn noäi löïc nhö hình 2.3:
 Löïc doïc N  laøm thanh chòu keùo_neùn ñuùng taâm. z
 Löïc caét Q ,Q  laøm thanh chòu caét. x y
 Moâ men uoán M , M  laøm thanh chòu uoán. x y
 Moâ men xoaén M  laøm thanh chòu xoaén. z Pn Mz A M x N C z P z 2 x Q My x Q P y 1 y
Hình 2.3. Caùc thaønh phaàn noäi löïc
1.2. Xaùc ñònh caùc thaønh phaàn noäi löïc treân maët caét ngang
Khi ñaët saùu thaønh phaàn noäi löïc vaøo maët caét thì phaàn A trôû neân caân baèng (ngoaïi löïc taùc
duïng leân phaàn A caân baèng vôùi saùu thaønh phaàn noäi löïc ñaët treân maët caét). Söû duïng saùu
phöông trình caân baèng tónh hoïc ta coù theå xaùc ñònh ñöôïc trò soá, chieàu cuûa saùu thaønh phaàn noäi löïc naøy: n N  P  0   z i x i 1   n Q  P  0   y i y i 1   n  Q   P  0 (2.1) x i x i 1   n  M   m P  x x  i  0 i1   n M   m P  y y  i  0  i1
Baøi taäp söùc beàn vaät lieäu trang 2 05/2012 Noäi löïc Khoa Xaây Döïng n  M  m P  z z  i  0  i1
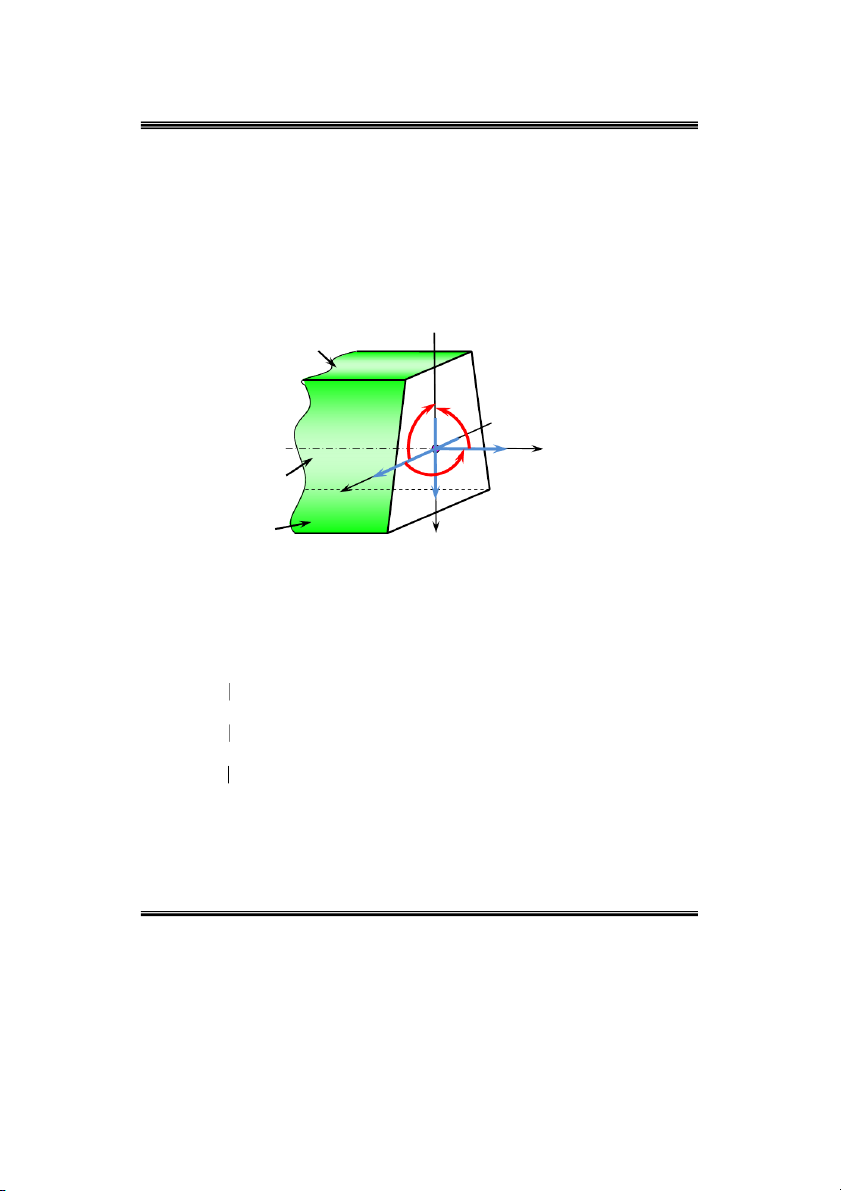
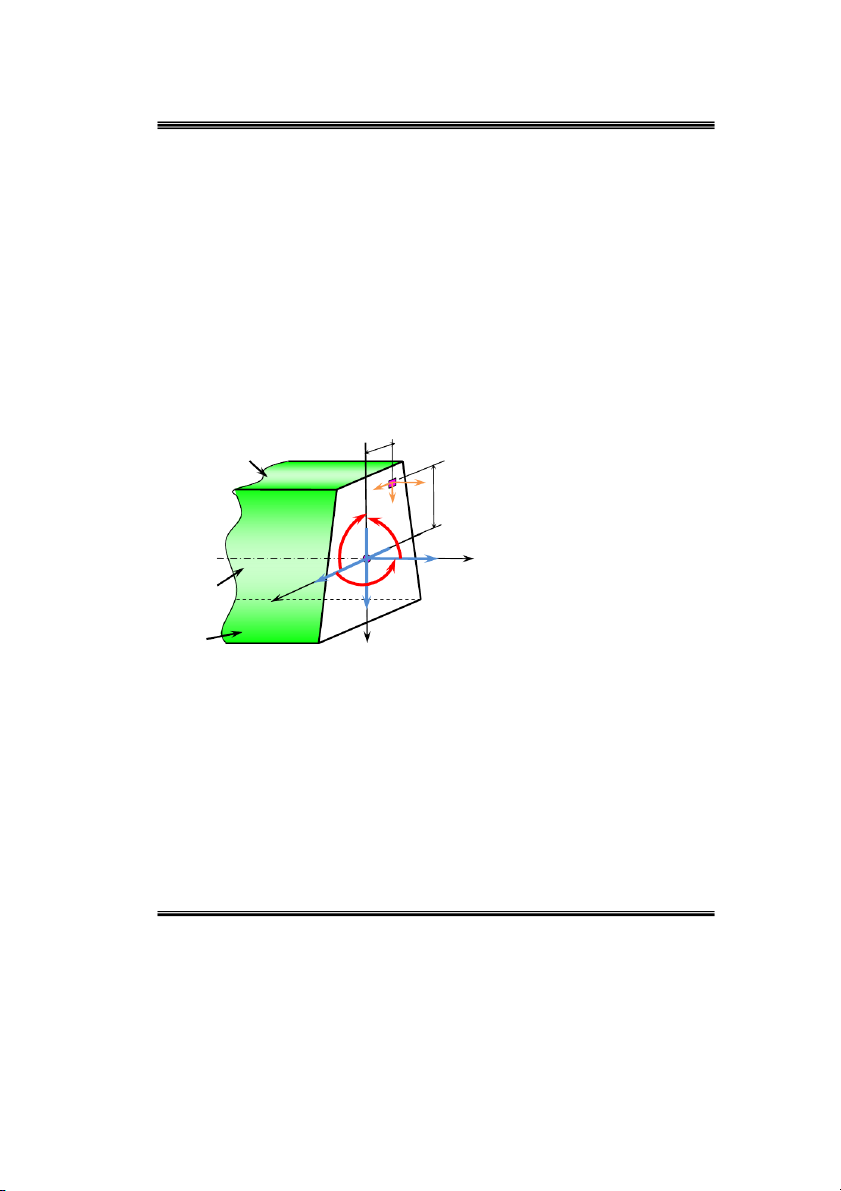
1.3. Quan heä giöõa caùc thaønh phaàn noäi löïc vôùi caùc thaønh phaàn öùng suaát  Löïc doïc: N   dF  (2.2) z z F Q    dF  x zx   Löïc caét : F  (2.3) Q    dF  y zy  F M    ydF  x z   Moâmen uoán: F  (2.4) M    xdF  y z  F
 Moâmen xoaén: M   y  x dF  (2.5) z  zx zy  F x P3   z y M zx  z  zy A M x N z P z 2 Qx M y x Qy P1 y
Hình 2.4. Caùc thaønh phaàn noäi löïc
Baøi taäp söùc beàn vaät lieäu trang 3 05/2012 Noäi löïc Khoa Xaây Döïng N  0 z Q  0 y M  0 x M  0 z
Hình 2.5. Chieàu döông cuûa noäi löïc.
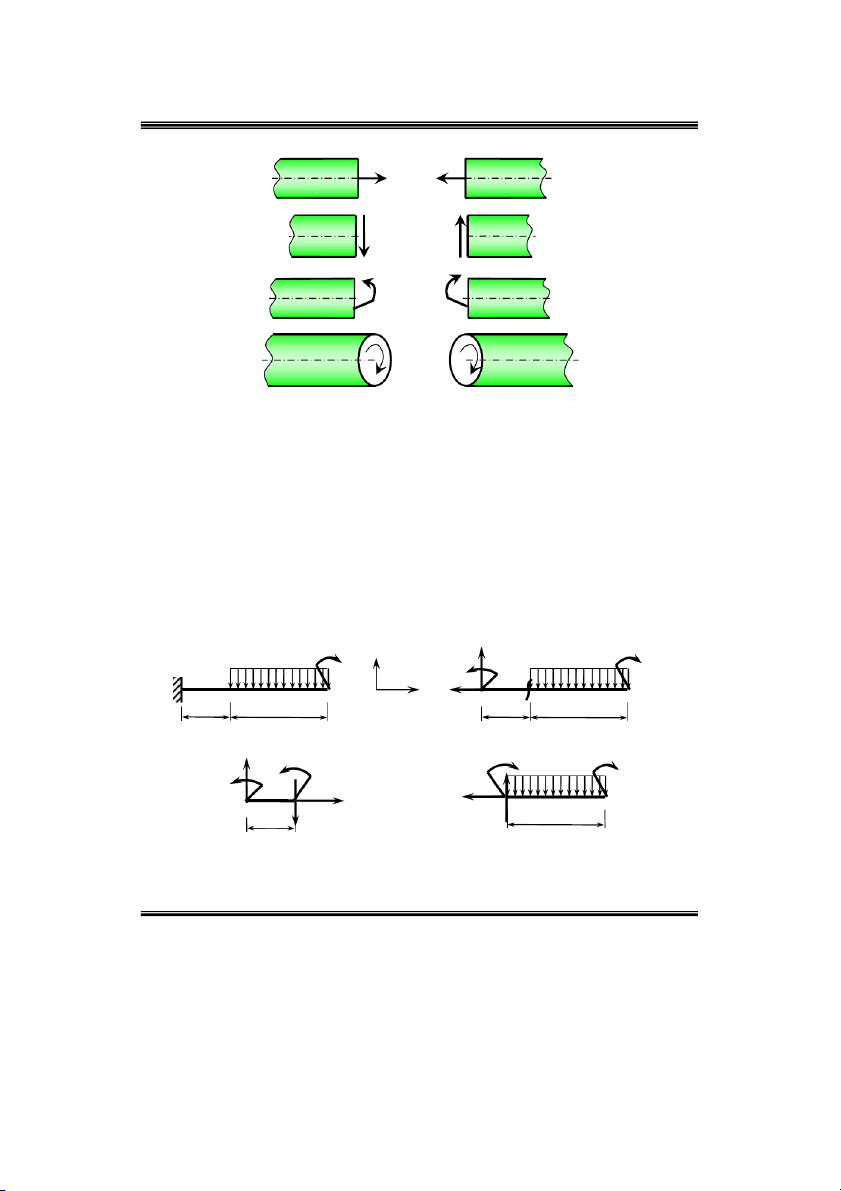
1.4. Qui öôùc daáu cuûa caùc thaønh phaàn noäi löïc Nhö hình 2.6
 Löïc doïc : N höôùng ra maët caét (keùo) laø döông. z
 Löïc caét: Q , Q coù xu höôùng laøm cho phaàn ñang xeùt quay cuøng chieàu kim ñoàng x y hoà laø döông.
 Moâmen uoán: M , M laøm caêng (keùo) phaàn beân döôùi laø döông. x y
 Moâmen xoaén: khi nhìn vaøo maët caét thaáy M quay cuøng chieàu kim ñoàng hoà laø z döông. 
Ví duï 1: Xaùc ñònh caùc thaønh phaàn noäi löïc treân maët caét ngang taïi B cuûa daàm chòu löïc nhö hình 2.6 a. 2 M q  a 2 ) b Y Mqa A ) a q q y M A 1 z A B C Z A 1 B C a 2a A a 2a 2 c) Y d ) M M q  a A x q M x M A N N A z B Q z B C y a Hình 2.6 Q 2a y
 Böôùc 1 xaùc ñònh phaûn löïc lieân keát taïi ngaøm A : ñaët caùc phaûn löïc lieân keát taïi A
nhö hình 2.6 b, söû duïng ñieàu kieän caân baèng tónh hoïc ñeå xaùc ñònh caùc thaønh phaàn phaûn löïc naøy.
Baøi taäp söùc beàn vaät lieäu trang 4 05/2012 Noäi löïc Khoa Xaây Döïng 2 2
m  0  M  .q2 .a2a  qa  0  M  5qa A A A   F  0  Y  . q 2a 0  Y  2qa y A A  F  0  Z   0  z A
 Böôùc 2 duøng maët caét 11 qua B caét daàm thaønh hai phaàn AB vaø BC . Giaû söû
daàm chòu löïc trong maët phaúng yz , ñaët caùc thaønh phaàn noäi löïc töông öùng vaøo hai
phaàn nhö hình 2.6 c vaø 2.6 d. Xeùt moät trong hai phaàn, giaû söû xeùt phaàn beân traùi nhö
hình 2.6 c. Söû duïng ñieàu kieän caân baèng tónh hoïc ñeå xaùc ñònh caùc thaønh phaàn noäi löïc naøy:
 F  0 Y  Q  0  Q  Y  2qa y A y y A   F  0  N  0 z z  2
 m  0   M  Y .a  M  0  M  3qa  B A A x x
Neáu xeùt phaàn beân phaûi nhö hình 2.6 d ta ñöôïc:  F
  0 Q  .q2a 0 Q  2qa y y y   F  0  N  0 z z  2 2  m  0  M  . q 2 .
a a  qa  0  M  3qa  B x x 
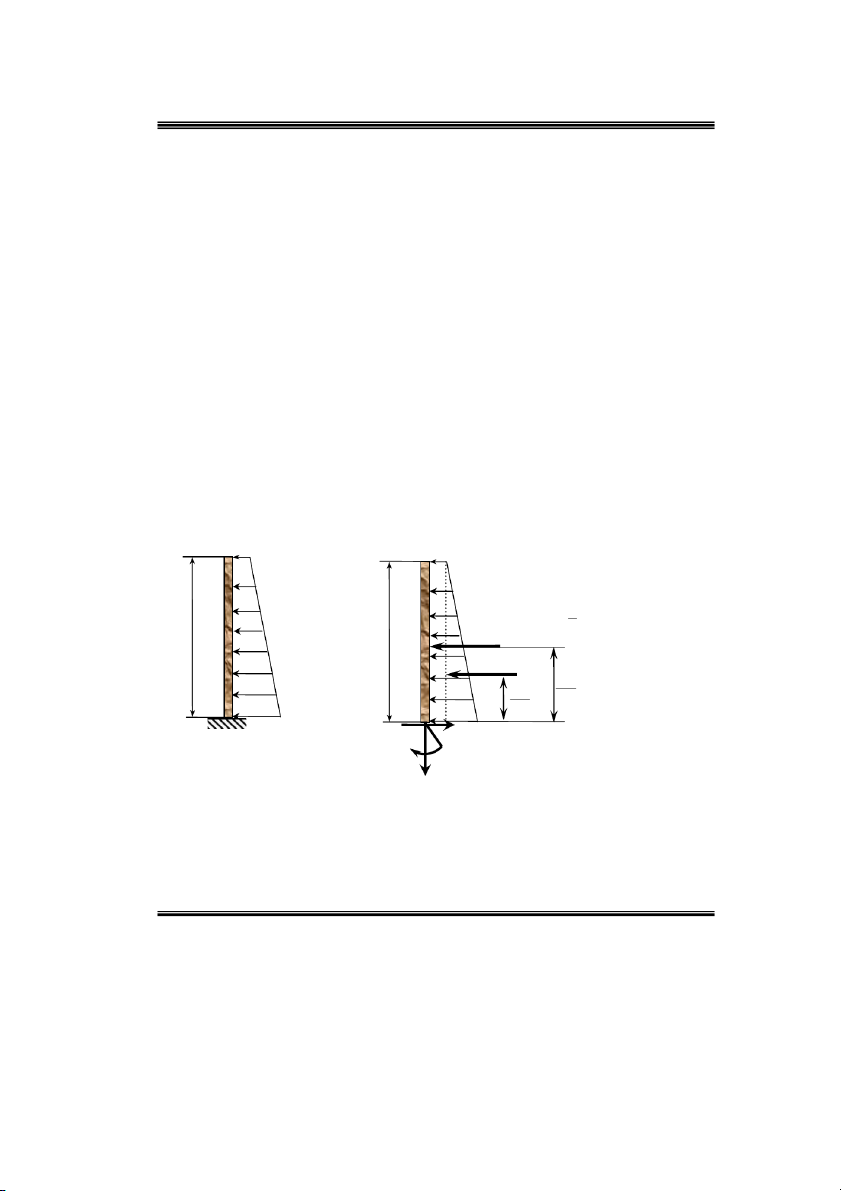
Ví duï 2: Cho coät AB coù kích thöôùc, lieân keát vaø chòu löïc nhö hình 2.7a. Xaùc ñònh caùc
thaønh phaàn noäi löïc treân maët caét taïi A cuûa coät. a ) B q  50kN / m b ) B 1 q  50kN / m 1 R  50.0,5 25kN 1   1 R  100 50 .0,5 12,5kN  2    2 0,5m 0,5m R1 R2 0,5 0,5 m m 2 A A 3 q  100kN / m 2 Q q  100kN / m M y 2 x Hình 2.7 N z
Ñaët caùc thaønh phaàn noäi löïc vaøo maët caét taïi A nhö hình 2.7 b. Söû duïng ñieàu kieän caân
baèng tónh hoïc ñeå xaùc ñònh caùc thaønh phaàn phaûn löïc naøy.
Baøi taäp söùc beàn vaät lieäu trang 5 05/2012 Noäi löïc Khoa Xaây Döïng 
F  0  Q R R  0  Q  R R  25 12,5  37,5kN y y 1 2 y 1 2  F  0 N  0 z z  0,5 0,5 25 m  0 M R .  R .  0  M  kN .m A x 1 2  2 3 x 3 
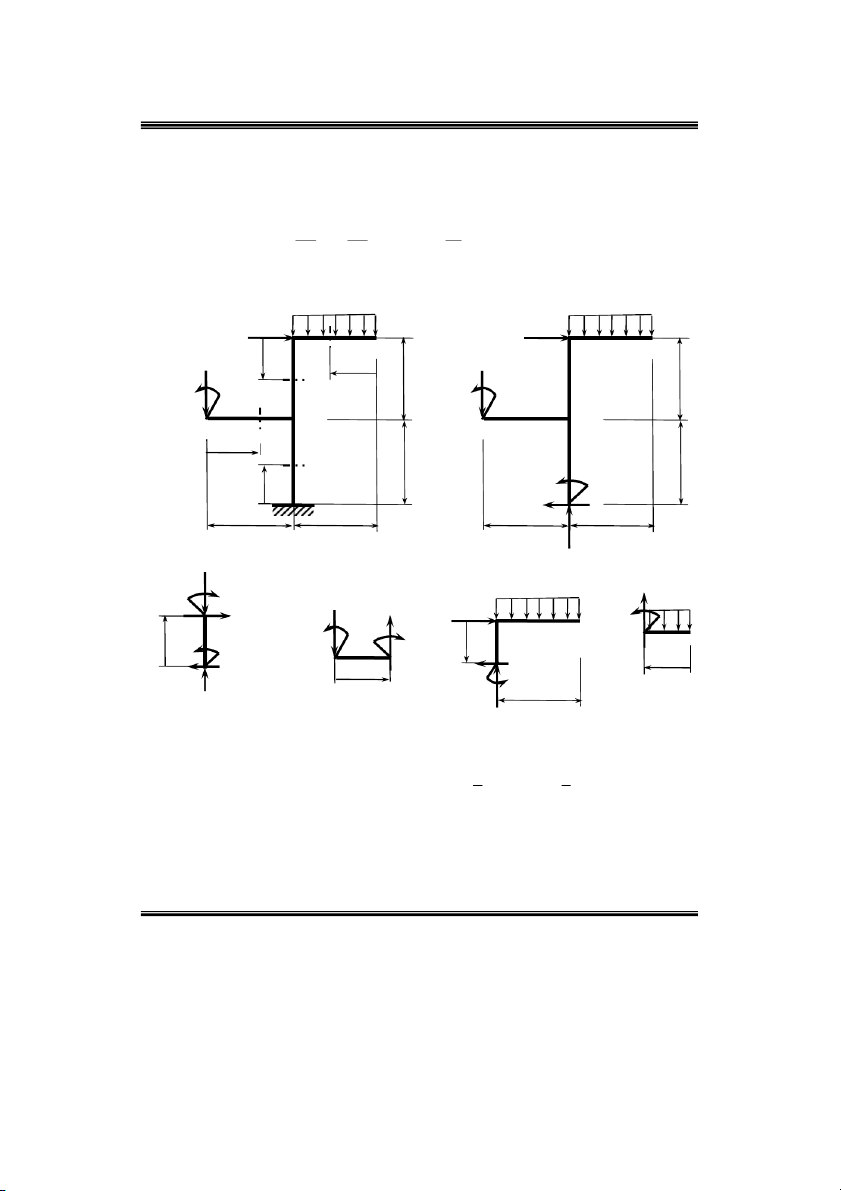
Ví duï 3: Cho khung ABCDE coù kích thöôùc, lieân keát vaø chòu löïc nhö hình 2.8a. Xaùc
ñònh caùc thaønh phaàn noäi löïc treân caùc maët caét 11,2  2,3  3,4  4 . q q 4 P  2qa ) b P  2qa ) a D E D E 4 z P  3qa 3 z4  a P 3qa a 3 3 2 M q  a 2 2 M q  a B B C C 2 z2 a a 1 1 M A z1 A X A a a A a a YA Hình 2.8 Nz1 d ) e) f ) Q c) M q 4 y 1 x P  3qa Q q Q  2 y P 2qa M 1 y 1 1 x4 D E E z 2 M Mqa z 1 M 2 x 4 3 A 3 C z4 X z 2 2 Q A 3 y M Y 3 x A N a Z 3
 Böôùc 1 xaùc ñònh phaûn löïc lieân keát taïi ngaøm A : ñaët caùc phaûn löïc lieân keát taïi A
nhö hình 2.8 b, söû duïng ñieàu kieän caân baèng tónh hoïc ñeå xaùc ñònh caùc thaønh phaàn phaûn löïc naøy.  a 1 2 2 m
  0 M  3qa.a  qa  2qa.2a q.a.  0 M  qa A A A  2 2  
F  0  Y  3qa  q.a  0  Y  4qa  y A A
 F  0  X 2qa 0  X  2qa  x A A 
Baøi taäp söùc beàn vaät lieäu trang 6 05/2012 Noäi löïc Khoa Xaây Döïng
 Böôùc 2 duøng maët caét 11 caét khung thaønh hai phaàn, xeùt phaàn beân döôùi. Ñaët caùc
thaønh phaàn noäi löïc töông öùng vaøo maët caét 11 nhö hình 2.8 c. Söû duïng ñieàu kieän
caân baèng tónh hoïc ñeå xaùc ñònh caùc thaønh phaàn noäi löïc naøy: 
 F  0   X  Q  0  Q  X  2qa y A y 1 y 1 A 
 F  0  Y  N  0  N  Y  4 qa z A 1 z z1 A  1 2  m 
 0  M  X .z  M  0  M  qa  2qa.z 1 1  A A 1 1 x 1 x 1  2
Töông töï cho caùc maët caét khaùc nhö hình 2.8d,e,f, ta coù ñöôïc caùc thaønh phaàn noäi löïc:  2  Q  3 ; qa M  qa  3 . qa z 2 y 2 x 2   1 2
Q  2qa; N  qa; M  2qa.z  qa y 3 z 3 x3 3 2   1 2 Q  q.z ; M  q.z  y4 4 x 4 4  2 
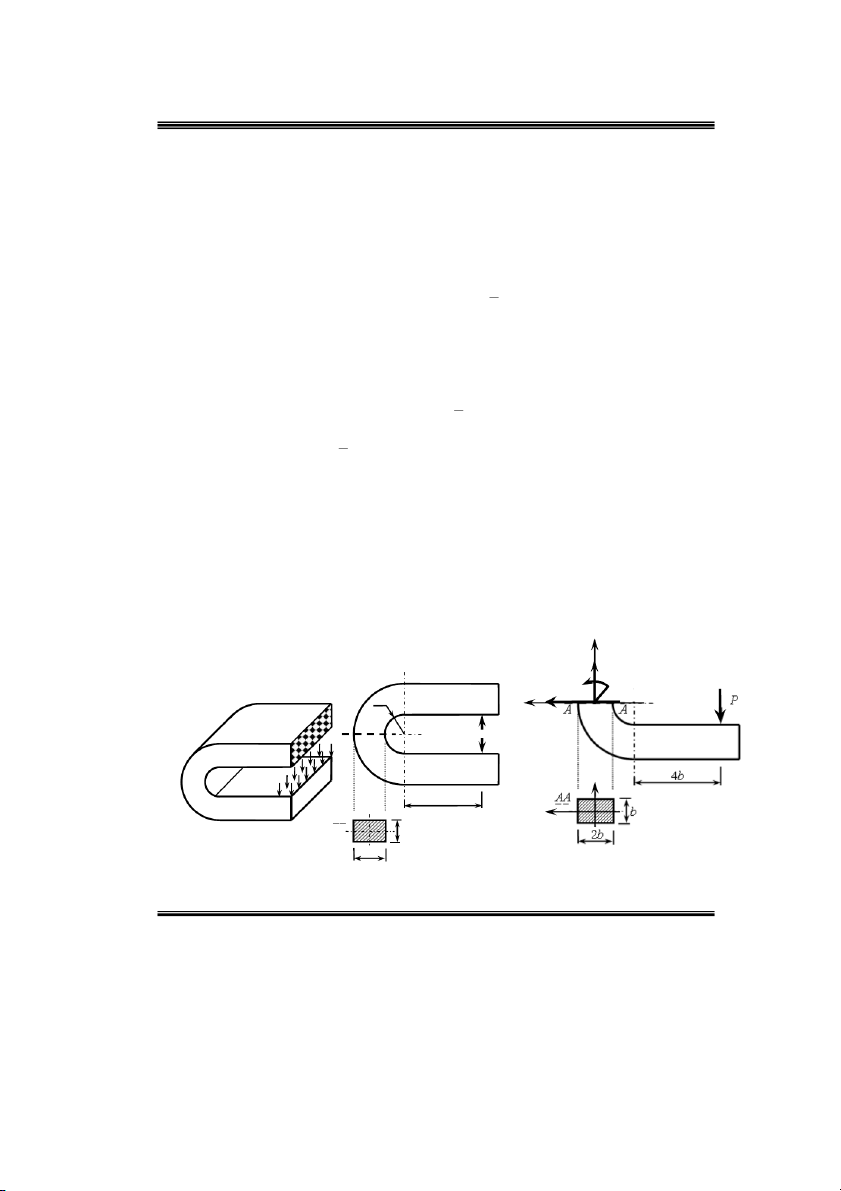
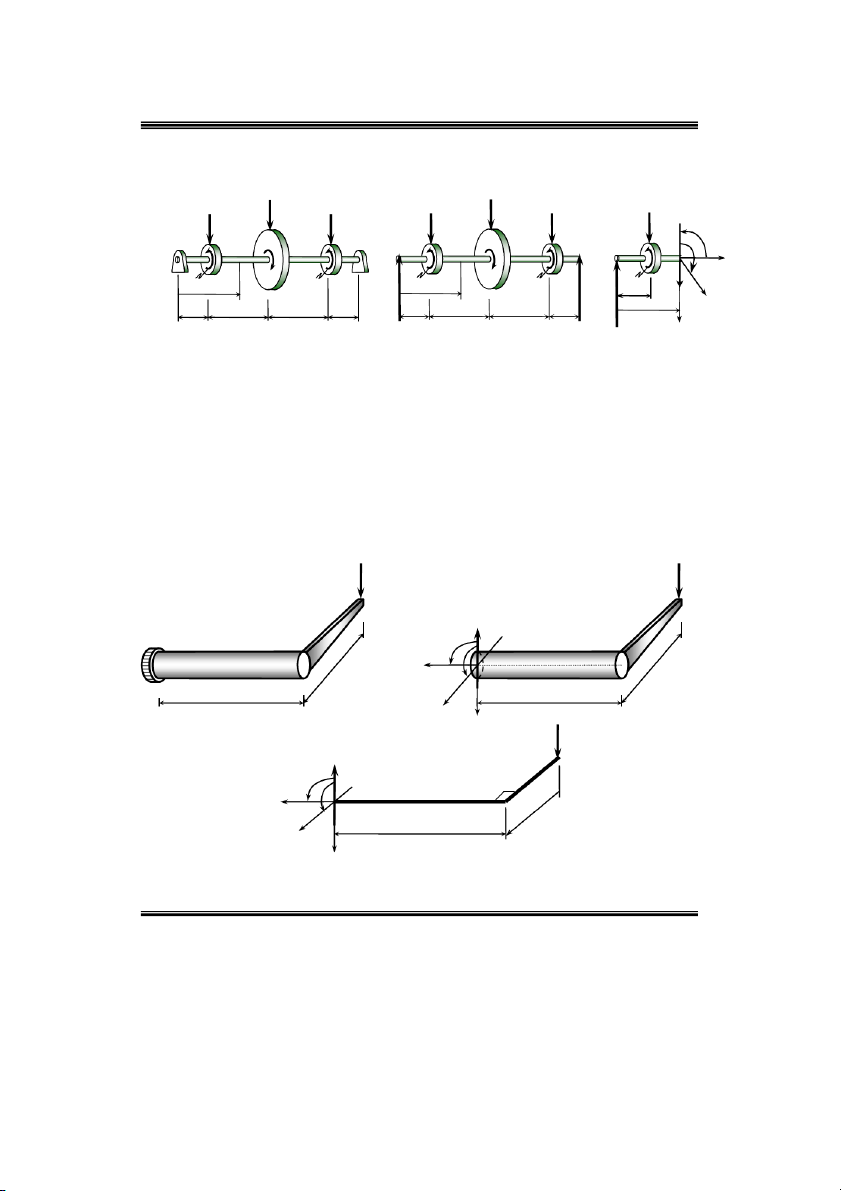
Ví duï 4: Moùc chöõ U coù kích thöôùc vaø chòu löïc nhö hình 2.9 a. Xaùc ñònh caùc thaønh phaàn
noäi löïc treân maët caét A  A.
Duøng maët caét A  A caét chi tieát thaønh hai phaàn, xeùt phaàn döôùi. Ñaët heä truïc toïa ñoä vaø caùc
thaønh phaàn noäi löïc töông öùng nhö hình 2.9 b. Söû duïng ñieàu kieän caân baèng tónh hoïc ñeå xaùc
ñònh caùc thaønh phaàn phaûn löïc naøy.  F  0  Q  0 x x 
 F  0  N  P  0  N  P z z z
m 0 M P.6b 0  M   6Pb  y y y z b) Nz a) My Qx b x C P A A q y 4b AA x b Hình 2.9 2b
Baøi taäp söùc beàn vaät lieäu trang 7 05/2012 Noäi löïc Khoa Xaây Döïng 
Ví duï 5: Truïc AE ñöôïc ñôû treân hai oå laên taïi ,
A E , lieân keát, chòu löïc nhö hình 2.10a.
Xaùc ñònh caùc thaønh phaàn noäi löïc treân maët caét taïi O. ) a 2P 2P P P ) b P P c) P M x O C D O A O C D E E A A z B B B M M 2M M M 2M M M z z z Qy a x a 2a 2a a Y Y z A a 2a 2a a E y Y  2P Hình 2.10 A
 Böôùc 1: vì truïc ñoái xöùng neân Y  Y 2 P . A E
 Böôùc 2: Duøng maët caét taïi O caét truïc laøm hai phaàn, xeùt phaàn beân traùi. Ñaët heä truïc
toïa ñoä vaø caùc thaønh phaàn noäi löïc vaøo maët caét taïi O nhö hình 2.10c. söû duïng caùc
phöông trình caân baèng ta xaùc ñònh ñöôïc caùc thaønh phaàn noäi löïc:
 F  0  2P P Q  0 Q  P y y y 
 m  0  M  M  0  M  M z z z   m  0  2 . P z  P z  a  M   M  Pz  P z  a  x   0 2 x x   
Ví duï 6: Truïc AB ngaøm taïi A , ñaàu B ñöôïc haøn vuoâng goùc vôùi thanh BC vaø chòu löïc
nhö hình 2.11a. Xaùc ñònh caùc thaønh phaàn noäi löïc treân maët caét taïi A . P  150kN P  150kN ) a ) b C C Qy A B A B Mx 0,3m 0,3m z M z 1m 1m x y Hình 2.11 P  150kN Qy C M x z A B M z 0,3m 1m x y
Xeùt maët caét taïi A , ñaët heä truïc toïa ñoä vaø caùc thaønh phaàn noäi löïc vaøo maët caét taïi A nhö
hình 2.11b. söû duïng caùc phöông trình caân baèng ta xaùc ñònh ñöôïc caùc thaønh phaàn noäi löïc:
Baøi taäp söùc beàn vaät lieäu trang 8 05/2012 Noäi löïc Khoa Xaây Döïng
 F  0  150Q  0 Q  150kN y y y  m 0 M 150.  0,3 0  M 45k . N m z z z
m  0 M 150.1 0  M   150kN .m  x x x
1.5. Bieåu ñoà noäi löïc 1.5.1. Ñònh nghóa 
Bieåu ñoà noäi löïc laø ñoà thò moâ taû qui luaät phaân boá noäi löïc doïc theo truïc thanh. 
Ñoaïn chòu löïc: laø ñoaïn maø treân ñoù haøm soá xaùc ñònh noäi löïc laø moät haøm lieân tuïc. 
Caùch chia ñoaïn chòu löïc: khi coù söï thay ñoåi veà löïc, lieân keát ta phaûi tieán haønh chia ñoaïn chòu löïc môùi.
1.5.2. Veõ bieåu ñoà noäi löïc baèng phöông phaùp maët caét bieán thieân
Trong moãi ñoaïn chòu löïc ta söû duïng moät maët caét ñeå thieát laäp caùc haøm noäi löïc cho töøng ñoaïn,
sau ñoù veõ caùc haøm soá naøy leân heä truïc ta ñöôïc söï phaân boá noäi löïc doïc theo truïc thanh. 
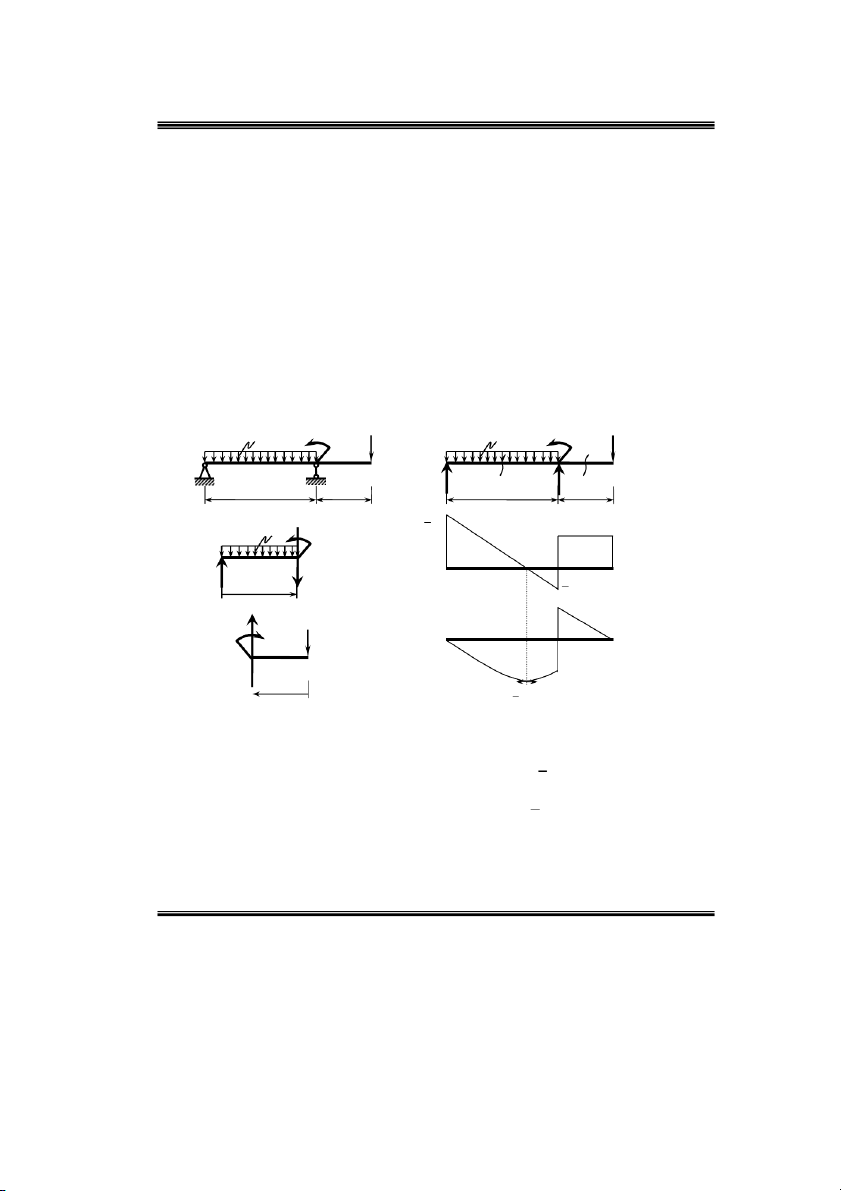
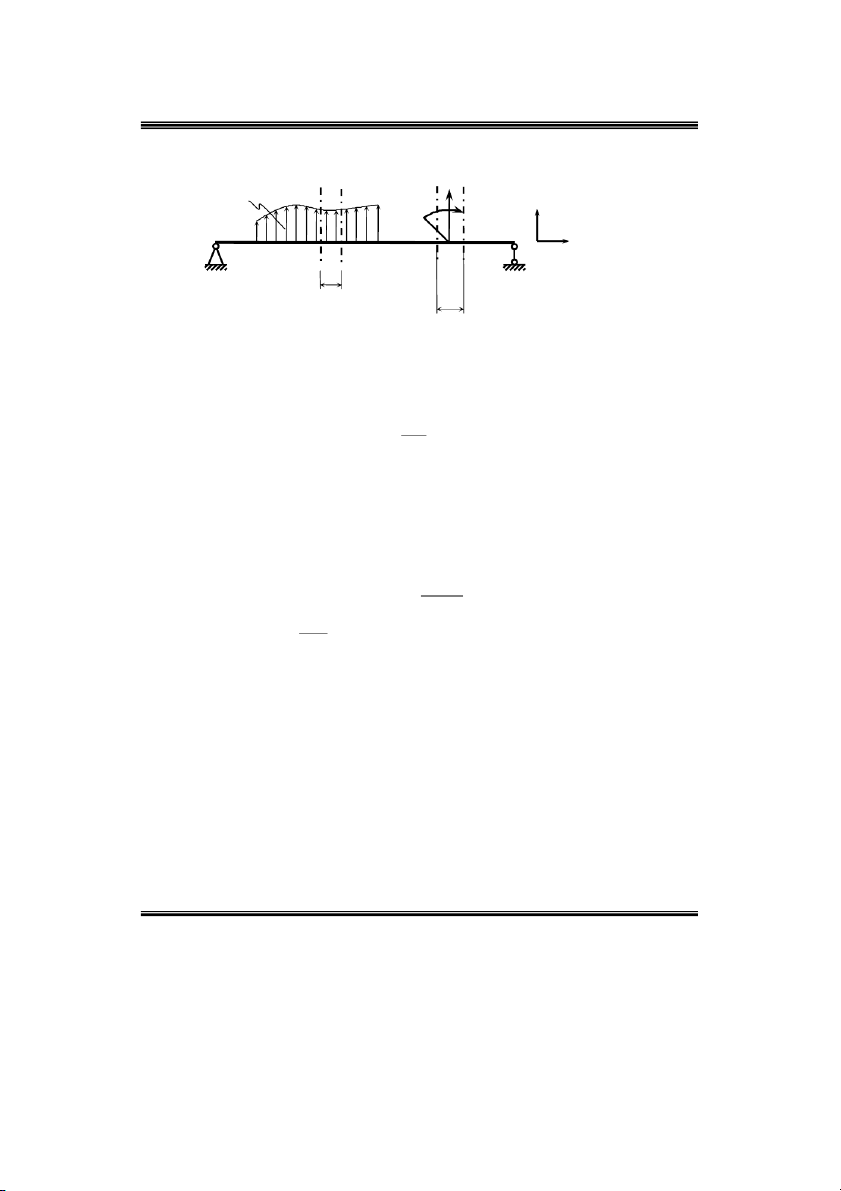
Ví duï 7: Veõ bieåu ñoà noäi löïc phaùt sinh trong daàm nhö hình 2.13 a. 2 M 2qa P  qa 2 M  2qa P  qa ) a q ) b q 1 2 A B C A B C 1 2 Y Y 2a a A 2a B a 3 qa q 2 qa M     x ) c A 1 0  z  2a 1 Qy   Y Q 1 A z y qa 1 2 2 qa Qy  P  qa d) M x  M 0   x z a C 2   2 2 qa z Hình 2.12 2 9 2 qa 8
 Böôùc 1 giaûi phoùng lieân keát taïi ,
A B vaø ñaët caùc phaûn löïc lieân keát töông öùng nhö hình 2.12 b.  3 2 m   0  .2 q . a a  2qa  Y .2a  .3 qa a  0  Y  qa A B B  2  3 2  m  0  Y .2a  .2 q . a a  2qa  . qa a  0  Y  qa  B A A  2
 Böôùc 2 thieát laäp bieåu thöùc tính noäi löïc trong hai ñoaïn AB, BC
Duøng maët caét 11 caét daàm laøm hai phaàn, xeùt phaàn beân traùi vaø ñaët caùc thaønh phaàn noäi
löïc töông öùng nhö hình 2.12 c.
Baøi taäp söùc beàn vaät lieäu trang 9 05/2012 Noäi löïc Khoa Xaây Döïng  3  F  0 Y 
q .z Q  0  Q  qa q.z  y A 1 y y 1  2  2 z 3 z  1 1 m  0 Y .z  q.z .
 M  0  M  qa.z  q  1 A 1 1 x x 1  2 2 2
Ta thaáy treân ñoaïn AB Q laø haøm baäc nhaát, theá z 0 vaø z  2a ta veõ ñöôïc bieåu ñoà y 1 1
Q treân ñoaïn AB . Haøm M laø haøm baäc hai neân ñi tìm cöïc trò vaø khaûo saùt söï loài, loõm y x cuûa ñoà thò M  3 3 3
x  qa  qz  0  z  a , taïi z  a haøm M ñaït cöïc trò. 1 1  1 x z 2 2 2 1 2
 Mx  q  0  haøm M loài. 2  x z1
Töông töï duøng maët caét 2  2 caét daàm laøm hai phaàn, xeùt phaàn beân phaûi vaø ñaët caùc
thaønh phaàn noäi löïc töông öùng nhö hình 2.10 d.  F 
 0 Q  P  0  Q  qa y y y 
 m 0 M  .Pz  0  M  . qa z  2 x 2 x 2
Ta thaáy treân ñoaïn BC Q laø haøm haèng soá, M laø haøm baäc nhaát neân theá theá z  0 y x 2
vaø z  a ta veõ ñöôïc ñoà thò Q , M treân ñoaïn BC nhö hình veõ. 2 y x 
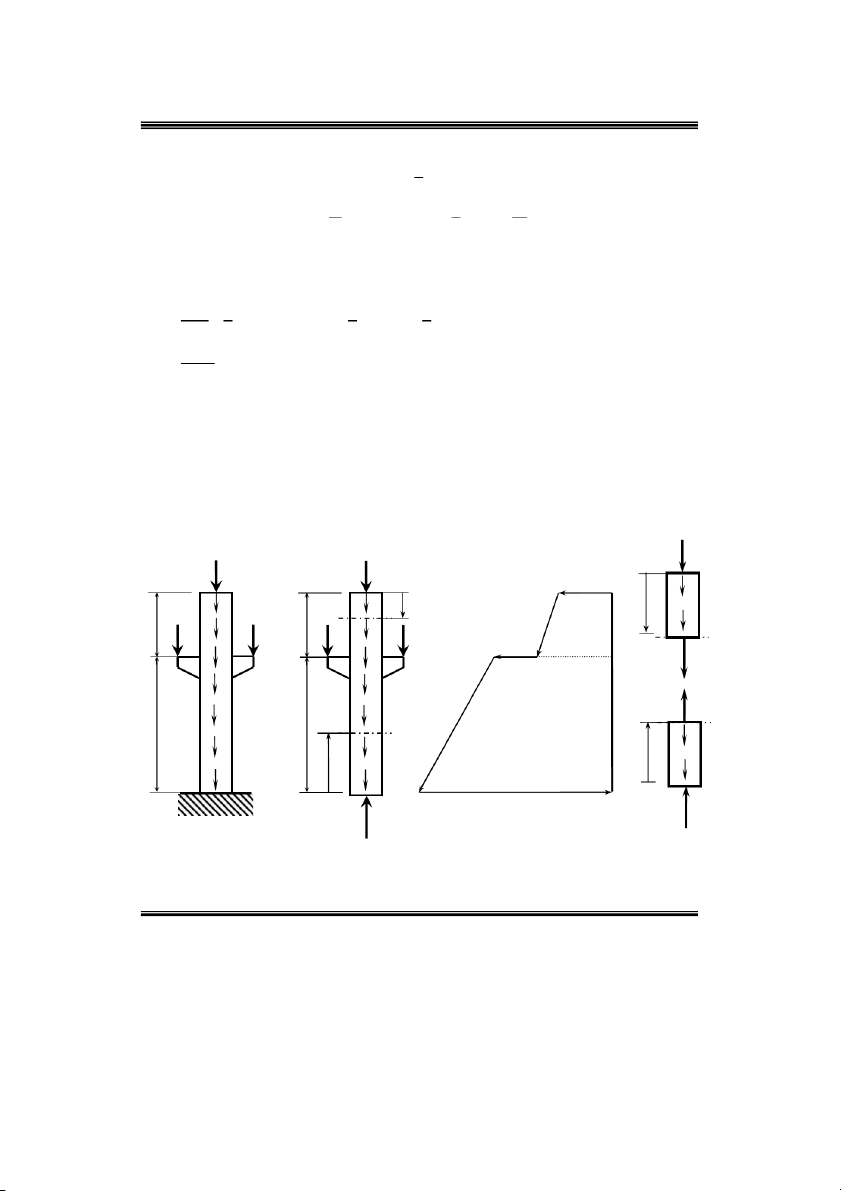
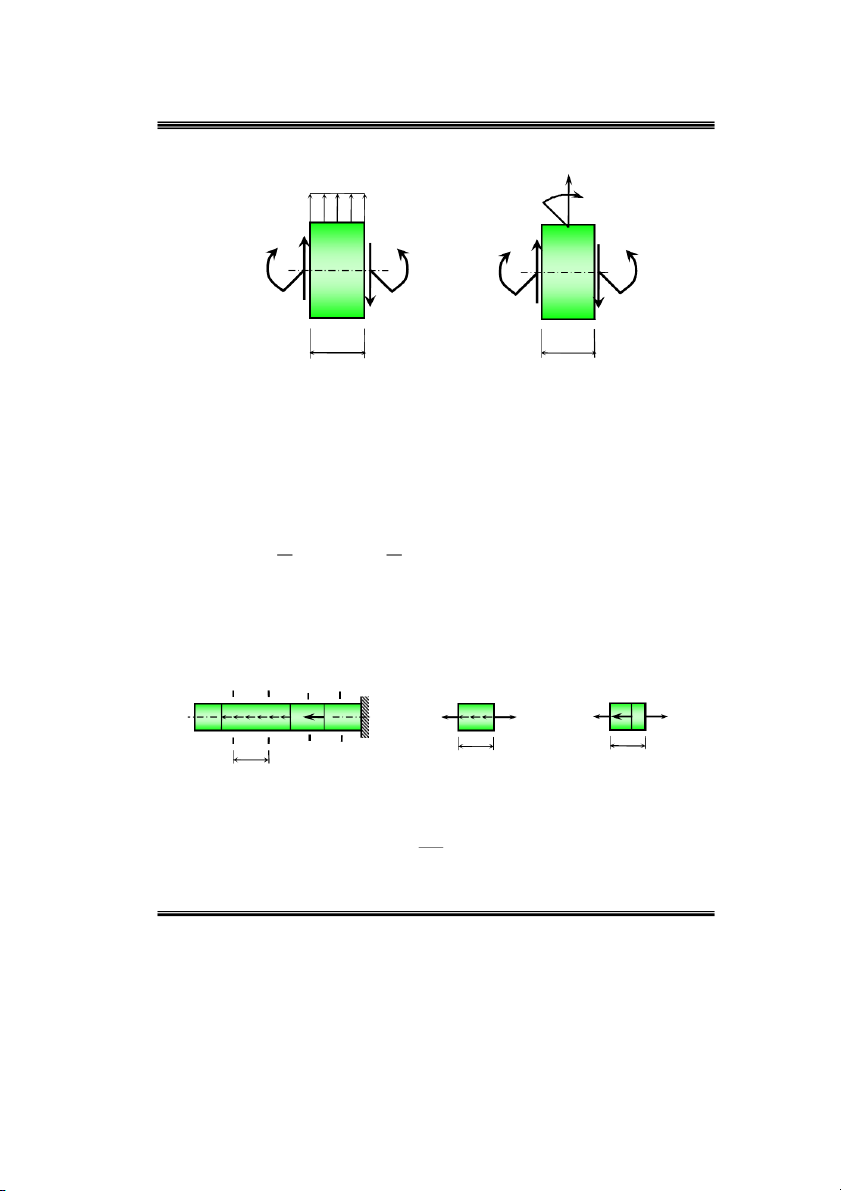
Ví duï 8: Veõ bieåu ñoà noäi löïc phaùt sinh trong coät chòu löïc nhö hình 2.13 a. d ) 3P a ) b ) e) 3P 3P C 3  qa C C z z 2 2 2 2 q P P qa   a a P P qa 2 2 B B 4  qa 6  qa Nz2 c ) Nz1 q q 3a 3a 1 1  1 1  z1 z q 1 A A A 9  qa Nz N N A A Hình 2.13
 Böôùc 1: giaûi phoùng lieân keát taïi ngaøm A vaø ñaët phaûn löïc lieân keát töông öùng nhö
hình 2.13 b.  F 0 3qa 2qa q.4a N 0 N 9qa . z A A
Baøi taäp söùc beàn vaät lieäu trang 10 05/2012 Noäi löïc Khoa Xaây Döïng
 Böôùc 2: thieát laäp bieåu thöùc tính noäi löïc trong hai ñoaïn AB, BC : treân ñoaïn AB
duøng maët caét 11 caùch A moät ñoaïn z caét coät laøm hai phaàn, xeùt phaàn döôùi nhö 1
hình 2.13c vaø ñaët noäi löïc töông öùng vaøo maët caét. Töông töï, treân ñoaïn BC duøng
maët caét 2  2 caùch C moät ñoaïn z caét coät laøm hai phaàn, xeùt phaàn treân nhö hình 2
2.13d vaø ñaët noäi löïc töông öùng vaøo maët caét. Söû duïng caùc phöông trình caân baèng ta xaùc ñònh ñöôïc: N
qz  9qa (0  z  3a ) , N laø haøm baäc nhaát. 1 Z 1 1 1 Z N
 3qa  qz (0  z  a) , N laø haøm baäc nhaát. Z 2 2 2 Z 2 
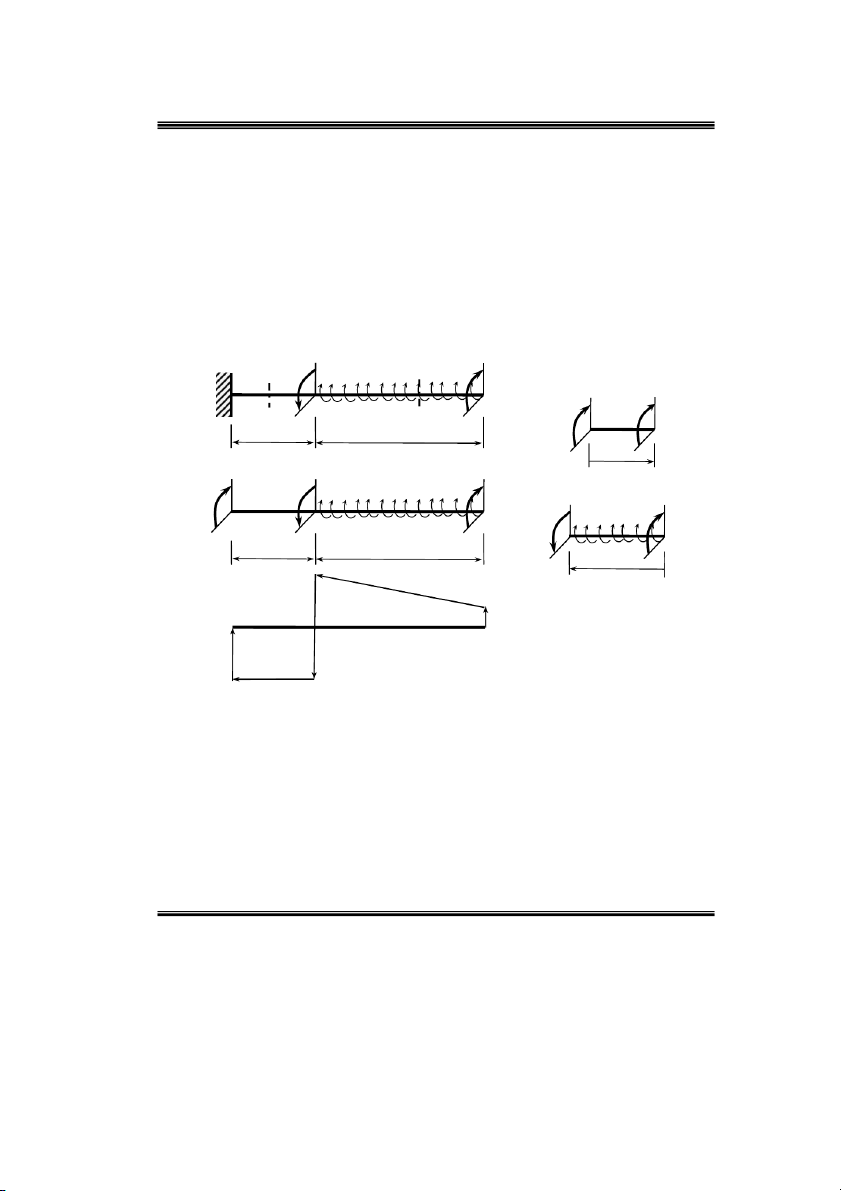
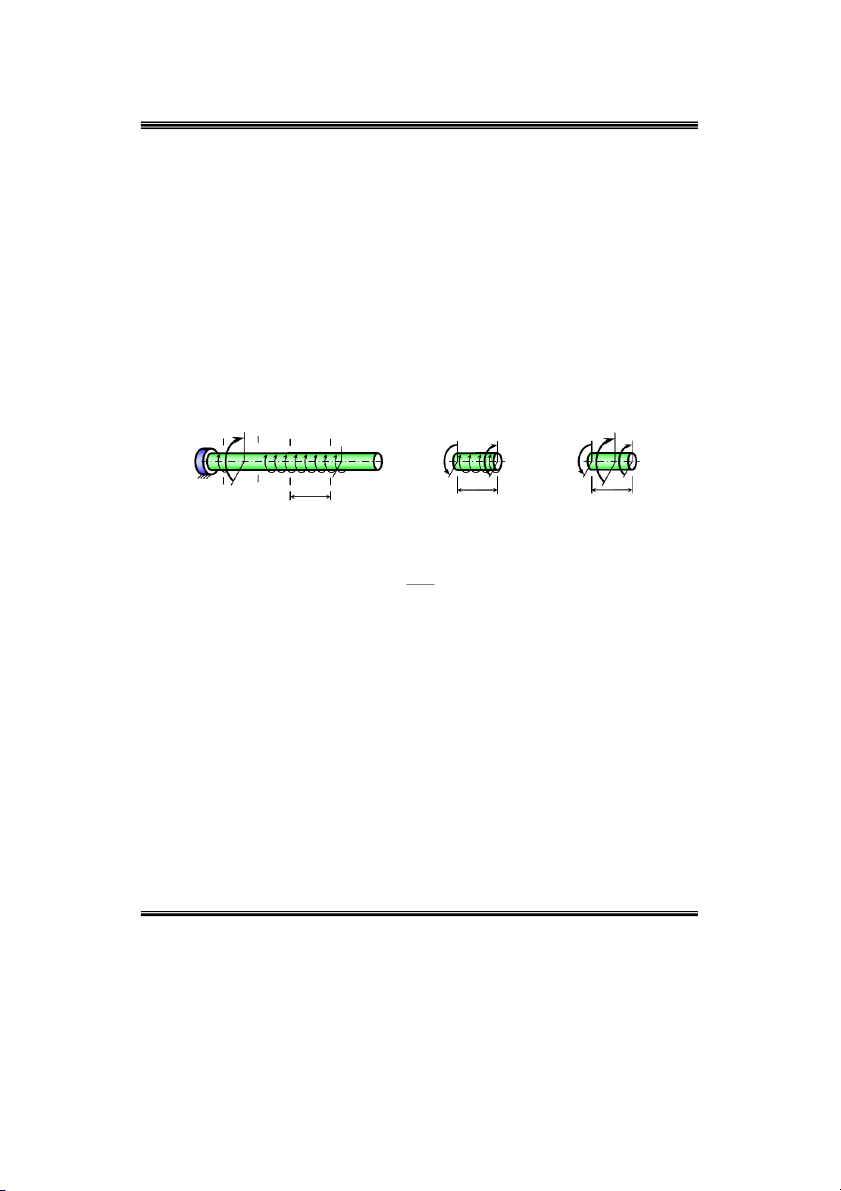
Ví duï9: Veõ bieåu ñoà noäi löïc phaùt sinh trong truïc chòu löïc nhö hình 2.14 a. M  ma 6M m 1 2 a) c) M A C A M 1 B 2 1 Z 1 a 2a A z1 M  ma M 6M A m b) M  ma d ) A C m B M 2Z 2 C a 2a z 2 3ma ma   e) Mz   Hình 2.14 3  ma
 Böôùc 1: giaûi phoùng lieân keát taïi ngaøm A vaø ñaët phaûn löïc lieân keát töông öùng nhö hình 2.14 b. m  0  M  6ma  .
m 2a  ma  0  M  3ma  . z A A
 Böôùc 2: thieát laäp bieåu thöùc tính noäi löïc trong hai ñoaïn AB, BC : treân ñoaïn AB
duøng maët caét 11 caùch A moät ñoaïn z caét truïc laøm hai phaàn, xeùt phaàn beân traùi 1
nhö hình 2.14c vaø ñaët noäi löïc töông öùng vaøo maët caét. Töông töï, treân ñoaïn BC
duøng maët caét 2  2 caùch C moät ñoaïn z caét coät laøm hai phaàn, xeùt phaàn beân phaûi 2
nhö hình 2.14d vaø ñaët noäi löïc töông öùng vaøo maët caét. Söû duïng caùc phöông trình
caân baèng ta xaùc ñònh ñöôïc: M
 3ma (0  z  a) , M haèng soá treân ñoaïn AB . Z1 1 1 Z M
 ma  mz (0  z 2a) , laø haøm baäc nhaát M . Z2 2 2 2 Z
Baøi taäp söùc beàn vaät lieäu trang 11 05/2012 Noäi löïc Khoa Xaây Döïng
1.5.3. Veõ bieåu ñoà noäi löïc baèng phöông phaùp veõ nhanh. P 1 2 3 4 q z M y z B C D 1 2 3 4 dz Hình 2.15 Daàm chòu löïc dz 
Lieân heä vi phaân giöõa moâmen uoán, löïc caét vaø taûi troïng ngang phaân boá
Xeùt daàm chòu uoán phaúng trong maët phaúng yz  vôùi taûi troïng laø caùc löïc taäp trung, löïc phaân
boá vaø ngaãu löïc taäp trung nhö hình 2.15. Duøng hai maët caét 11 vaø 2  2 taùch töø ñoaïn chòu
löïc phaân boá BC moät phaân toá chieàu daøi dz vaø ñaët caùc thaønh phaàn noäi löïc töông öùng vaøo hai maët caét nhö hình 2.16a. dQ
F 0 Q  Q dQ qdz    q z (2.6) y y  y y  0 y ( ) dz
Nhaän xeùt 1: bieåu ñoà löïc caét hôn bieåu ñoà taûi troïng phaân boá moät baäc. C
Tích phaân hai veá bieåu thöùc (2.6): C C B dQ  qdz  Q  Q  S   (2.7) y y y q B B
Nhaän xeùt 2: khi ñi töø traùi qua phaûi, löïc caét cuoái ñoaïn baèng löïc caét ñaàu ñoaïn coäng
hôïp löïc phaân boá treân ñoaïn ñoù (hôïp löïc phaân boá höôùng leân döông, höôùng xuoáng aâm). 2 .( q ) dz
 m 0 M - (M  dM )  Q dz 
 0 , boû qua ñaïi löôïng voâ cuøng beù 2 x x x y 2 baäc cao dM 2 (dz) ta ñöôïc: x  Q (2.8) y dz
Nhaän xeùt 3: bieåu ñoà moâ men uoán hôn bieåu ñoà löïc caét moät baäc. Neáu trong nhöõng
ñoaïn moâ men uoán coù baäc hai, moâ men uoán ñaït cöïc trò taïi nhöõng ñieåm coù Q  0 . y C
Tích phaân hai veá bieåu thöùc (2.8): C C B dM  Q dz  M  M S   (2.9) x y x x y Q B B
Nhaän xeùt 4: khi ñi töø traùi qua phaûi, moâ men uoán cuoái ñoaïn baèng moâ men uoán ñaàu
ñoaïn coäng dieän tích bieåu ñoà löïc caét treân ñoaïn ñoù. 
Lieân heä giöõa moâmen uoán, löïc caét vaø taûi troïng ngang taäp trung
Baøi taäp söùc beàn vaät lieäu trang 12 05/2012 Noäi löïc Khoa Xaây Döïng P q a) b) M 1 2 3 4 Q t y M M  dM t Q x x x y M x p M x Q  dQ p Q y y y 1 2 3 D 4 dz dz
Hình 2.16 Lieân heä giöõa taûi troïng ngang vaø noäi löïc
Duøng hai maët caét 3 3 vaø 4  4 taùch töø daàm ôû hai beân D moät phaân toá chieàu daøi dz vaø ñaët
caùc thaønh phaàn noäi löïc töông öùng vaøo hai maët caét nhö hình 2.16b. F  0 t p  Q  P  Q  0 p t Q   Q  P (2.10) y y y y y
Nhaän xeùt 5: khi ñi töø traùi qua phaûi neáu treân sô ñoà tính coù löïc taäp trung bieåu ñoà löïc
caét coù böôùc nhaûy, giaù trò buôùc nhaûy baèng giaù trò löïc taäp trung, chieàu böôùc nhaûy cuøng
chieàu vôùi löïc taäp trung. dz dz m  0 t  Q . t  M  M  Q .p p  M  0 
, boû qua thaønh phaàn voâ cuøng beù baäc cao D y x y x 2 2 ta ñöôïc: p t M  M  M (2.11) x x
Nhaän xeùt 6: khi ñi töø traùi qua phaûi neáu treân sô ñoà tính coù ngaãu löïc taäp trung bieåu ñoà
moâ men uoán coù böôùc nhaûy, giaù trò buôùc nhaûy baèng giaù trò ngaãu löïc taäp trung, nhaûy
xuoáng khi ngaãu löïc quay cuøng chieàu kim ñoàng hoà, nhaûy leân cho tröôøng hôïp ngöôïc laïi. 
Lieân heä giöõa löïc doïc vaø caùc taûi troïng doïc. 1 2 a) 3 4 b) 1 c) 3 D q z q 2 4 P N t N P z N  dN p z N z z z 1 2 3 4 B 1 C 3 D 4 2 dz dz dz
Hình 2.17: Lieân heä giöõa taûi troïng doïc vaø noäi löïc.
Duøng hai maët caét 11 vaø 2  2 taùch töø ñoaïn chòu löïc phaân boá BC moät phaân toá chieàu daøi dz
vaø ñaët caùc thaønh phaàn noäi löïc töông öùng vaøo hai maët caét nhö hình 2.17b. dN
F  0  N q.dz  N dN  0 z   q (2.12) z z z z dz
Nhaän xeùt 7: bieåu ñoà löïc doïc hôn bieåu ñoà taûi troïng phaân boá moät baäc.
Baøi taäp söùc beàn vaät lieäu trang 13 05/2012 Noäi löïc Khoa Xaây Döïng C
Tích phaân hai veá bieåu thöùc (2.12): C C B dN  qdz  N  N  S   (2.13) z z z q B B
Nhaän xeùt 8: löïc doïc cuoái ñoaïn baèng löïc doïc ñaàu ñoaïn coäng hôïp löïc phaân boá treân
ñoaïn ñoù (hôïp löïc phaân boá gaây keùo döông, gaây neùn aâm).
Duøng hai maët caét 3 3 vaø 4  4 taùch töø thanh ôû hai beân D moät phaân toá chieàu daøi dz vaø ñaët
caùc thaønh phaàn noäi löïc töông öùng vaøo hai maët caét nhö hình 2.17c.  F  0 t p  N  P  N  0 p t N   N  P (2.14) z z z z z
Nhaän xeùt 9: neáu treân sô ñoà tính coù löïc taäp trung bieåu ñoà löïc doïc coù böôùc nhaûy, giaù
trò böôùc nhaûy baèng giaù trò löïc taäp trung, nhaûy veà phía döông khi löïc gaây keùo, nhaûy veà
phía aâm khi löïc gaây neùn. 
Lieân heä giöõa moâmen xoaén vaø caùc taûi troïng moâmen xoaén. M M t M a) 3 4 1 2 b) M c) z z m z 1 2 1 2 D M  dM 2 p M 2 z z D 1 m z 1 3 4 C 1 2 B dz dz dz
Hình 2.18: Lieân heä giöõa moâmen taûi troïng vaø noäi löïc.
Duøng hai maët caét 11 vaø 2  2 taùch töø ñoaïn chòu taûi phaân boá BC moät phaân toá chieàu daøi dz
vaø ñaët caùc thaønh phaàn noäi löïc töông öùng vaøo hai maët caét nhö hình 2.18b. dM m 0  M dM  . m dz  M  0 z   m (2.15) z z z z dz
Nhaän xeùt 10: bieåu ñoà moâ men xoaén hôn bieåu ñoà taûi troïng phaân boá moät baäc. C
Tích phaân hai veá bieåu thöùc (2.15): C C B dM  mdz  M  M  S   (2.16) z z z m B B
Nhaän xeùt 11:moâ men xoaén cuoái ñoaïn baèng moâ men xoaén ñaàu ñoaïn coäng hôïp ngaãu
löïc phaân boá treân ñoaïn ñoù (hôïp moâ men xoaén löïc phaân boá cuøng chieàu kim ñoàng hoà
döông, ngöôïc chieàu kim ñoàng hoà aâm).
Duøng hai maët caét 3 3 vaø 4  4 taùch töø thanh ôû hai beân D moät phaân toá chieàu daøi dz vaø ñaët
caùc thaønh phaàn noäi löïc töông öùng vaøo hai maët caét nhö hình 2.18c.  m 0 t p  M  M  M  0 p t M   M  M (2.14) z z z z z
Nhaän xeùt 12: neáu treân sô ñoà tính coù moâ men xoaén taäp trung bieåu ñoà moâ men xoaén
coù böôùc nhaûy, giaù trò böôùc nhaûy baèng giaù trò ngaãu löïc taäp trung, nhaûy veà phía döông
khi ngaãu löïc cuøng chieàu kim ñoàng hoà, nhaûy veà phía aâm khi ngaãu löïc quay ngöôïc chieàu kim ñoàng hoà.
Baøi taäp söùc beàn vaät lieäu trang 14 05/2012 Noäi löïc Khoa Xaây Döïng
Caùch veõ bieåu ñoà noäi löïc trong thanh chòu keùo-neùn ñuùng taâm: (vẽ từ đầu tự do)
 Bieåu ñoà löïc doïc hôn bieåu ñoà taûi troïng phaân boá moät baäc.
 Neáu treân sô ñoà tính coù löïc taäp trung bieåu ñoà löïc doïc coù böôùc nhaûy, giaù trò
böôùc nhaûy baèng giaù trò löïc taäp trung, nhaûy veà phía döông khi löïc gaây keùo, nhaûy
veà phía aâm khi löïc gaây neùn.
 Löïc doïc cuoái ñoaïn baèng löïc doïc ñaàu ñoaïn coäng hôïp löïc phaân boá treân ñoaïn
ñoù (hôïp löïc phaân boá gaây keùo döông, gaây neùn aâm). 
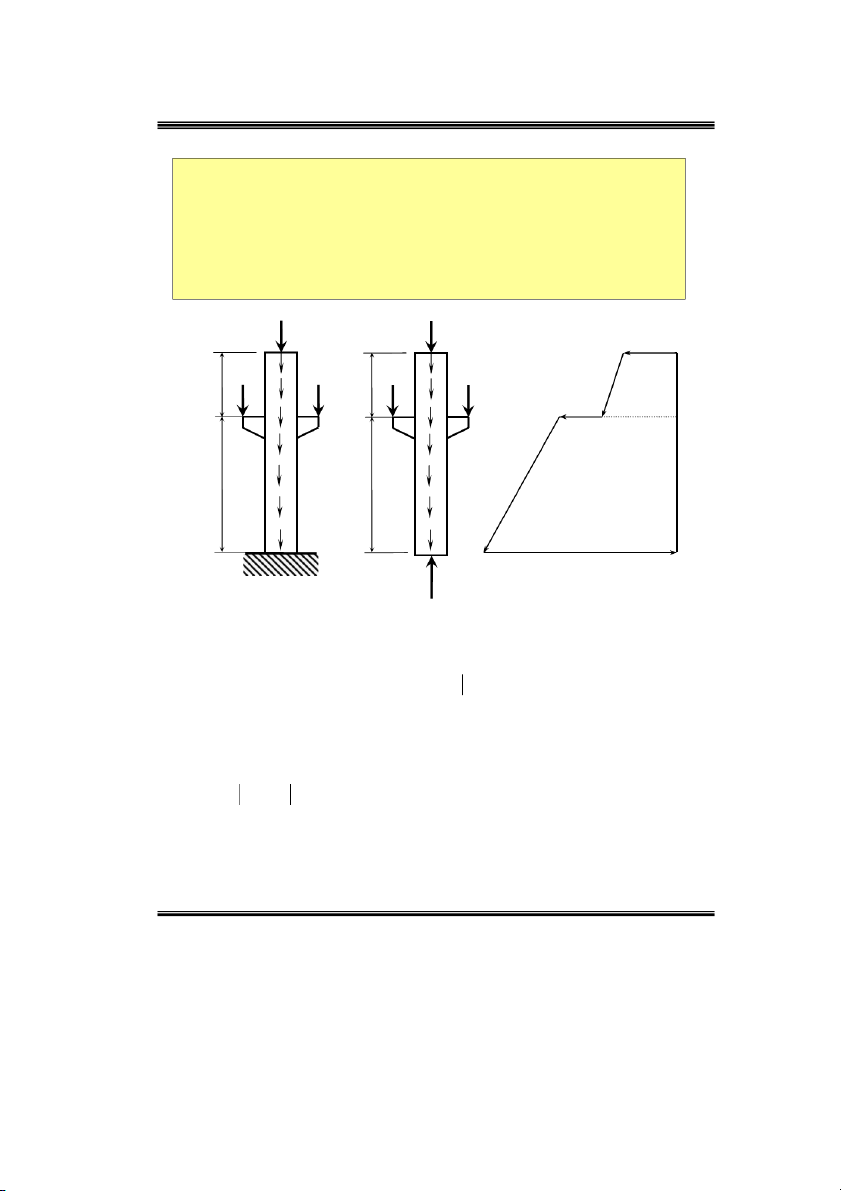
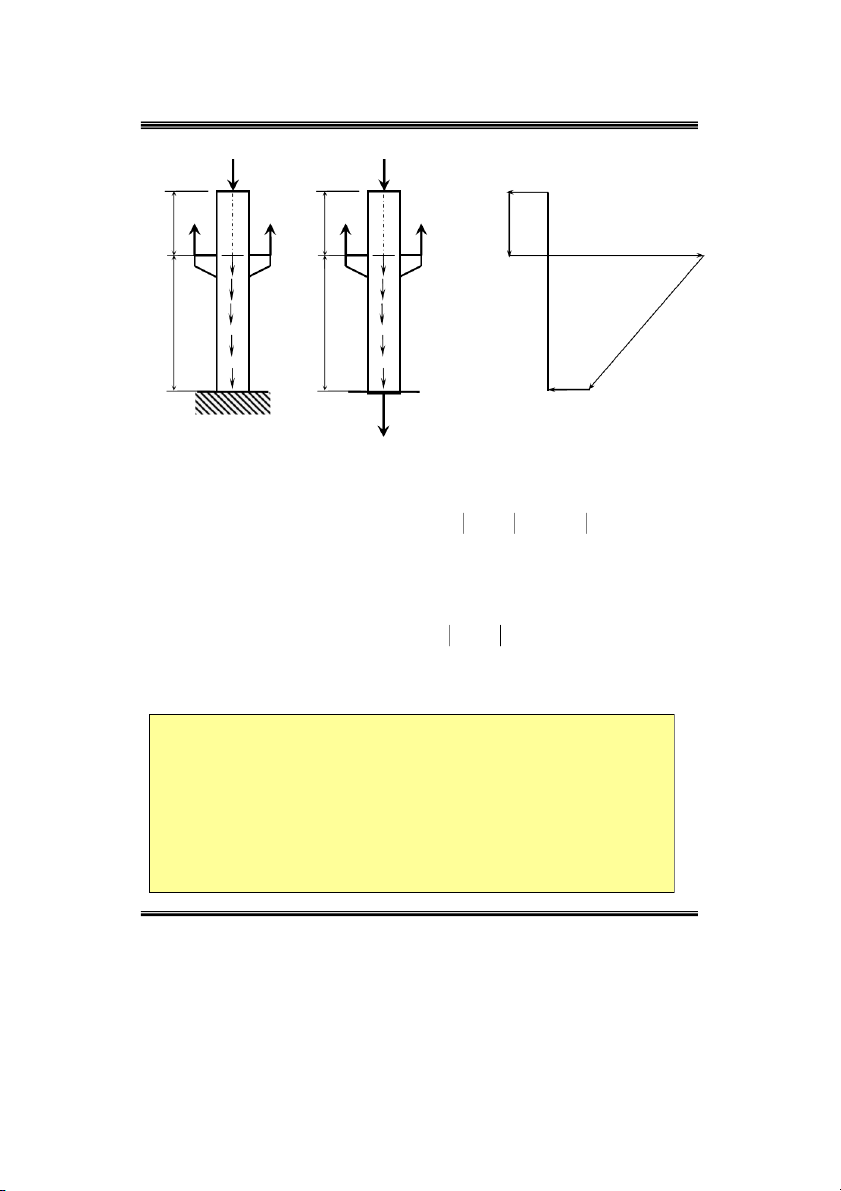
Ví duï 10: Veõ bieåu ñoà noäi löïc phaùt sinh trong coät chòu neùn ñuùng taâm nhö hình 2.20. 3P 3P 3  qa C C P P qa P P qa   a a B B 4  qa 6  qa q q 3a 3a  A A 9  qa Nz  Hình 2.19 NA
 Phaûn löïc lieân keát taïi ngaøm A :
F  0  N  q.4a  2qa  3qa  0 N    9qa z A A
 Taïi C coù löïc taäp trung 3P  3qa gaây neùn neân bieåu ñoà N coù böôùc nhaûy veà phía z
aâm (beân traùi) moät ñoaïn baèng 3qa töø vò trí khoâng thuoäc ñöôøng chuaån.
 Noäi löïc ôû phía treân cuûa maët caét taïi B B C N  N  q
 a   qa qa   qa z z  .  3 4 tren
 Taïi B coù löïc taäp trung 2P  2qa gaây neùn neân bieåu ñoà N coù böôùc nhaûy veà phía z
aâm (beân traùi) moät ñoaïn baèng 2qa töø giaù trò 4qa neân N phía döôùi maët caét taïiB z coù giaù trò 4  qa  2qa  6  qa .
 Noäi löïc ôû phía treân cuûa maët caét taïi A: A B N  N
 q a   qa  qa   qa z z  .3  6 3 9 tren duoi
 Taïi A coù löïc taäp trung N 9qa gaây keùo neân bieåu ñoà N coù böôùc nhaûy veà phía A z
döông (beân phaûi) moät ñoaïn baèng 9qa töø giaù trò 9qa neân N phía döôùi maët caét z
taïi A coù giaù trò 9qa  9qa  0 . 
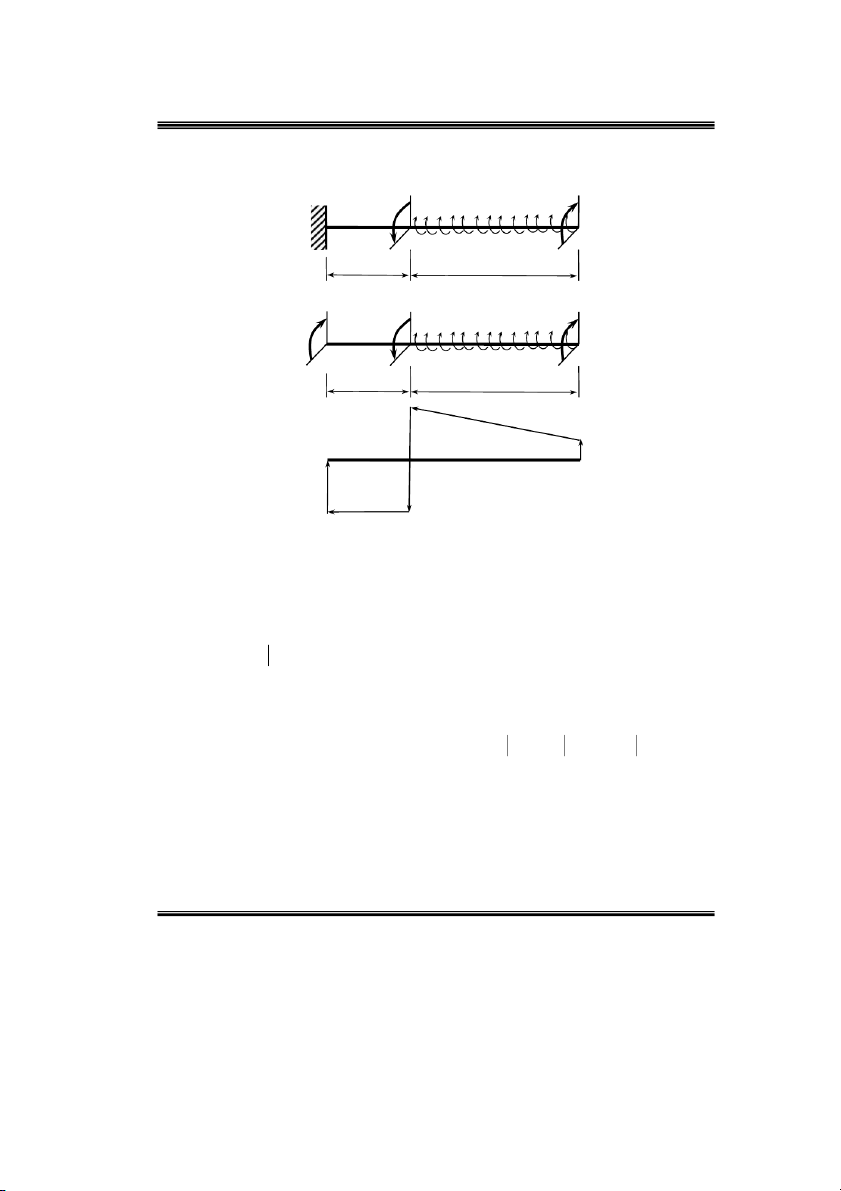
Ví duï11: Veõ bieåu ñoà noäi löïc phaùt sinh trong coät chòu neùn ñuùng taâm nhö hình 2.20.
Baøi taäp söùc beàn vaät lieäu trang 15 05/2012 Noäi löïc Khoa Xaây Döïng P qa P qa C C q  a 2,5P 2,5P 2,5P 2,5P  a a 4qa B B 4  qa q q 3a 3a  A A N qa z  Hình 2.20 NA
 Phaûn löïc lieân keát taïi ngaøm A : F  0 N  q.3a  5qa  qa  0 N   qa z A A
 Taïi C coù löïc taäp trung P  qa gaây neùn neân bieåu ñoà N coù böôùc nhaûy veà phía aâm z
(beân traùi) moät ñoaïn baèng qa töø vò trí “0” thuoäc ñöôøng chuaån.
 Noäi löïc ôû phía treân cuûa maët caét taïi B B C N  N  0 C  N  qa (ñoaïn z z z tren duoi duoi
BC khoâng coù taûi phaân boá neân N haèng soá). z
 Taïi B coù löïc taäp trung 5P  5qa gaây keùo neân bieåu ñoà N coù böôùc nhaûy veà phía z
döông (beân phaûi) moät ñoaïn baèng 5qa töø giaù trò qa neân N phía döôùi maët caét z
taïiB coù giaù trò qa  5qa  4qa .
 Noäi löïc ôû phía treân cuûa maët caét taïi A : A B N  N
 q a  qa  qa  qa z z  .3  4 3 tren duoi
 Taïi A coù löïc taäp trung N  qa gaây neùn neân bieåu ñoà N coù böôùc nhaûy veà phía A z
aâm (beân traùi) moät ñoaïn baèng qa töø giaù trò qa neân N phía döôùi maët caét taïi A coù z giaù trò qa qa  0 .
Caùch veõ bieåu ñoà noäi löïc trong truïc chòu xoaén: (Vẽ bắt đầu từ hướng nhìn qua)
 Bieåu ñoà moâmen xoaén hôn bieåu ñoà taûi troïng phaân boá moät baäc.
 Neáu treân sô ñoà tính coù ngaãu löïc taäp trung bieåu ñoà moâmen xoaén coù böôùc nhaûy,
giaù trò böôùc nhaûy baèng giaù trò ngaãu löïc taäp trung, nhaûy veà phía döông khi nhìn vaøo
maët caét thaáy ngaãu löïc quay cuøng chieàu kim ñoàng hoà, nhaûy veà phía aâm cho tröôøng hôïp ngöôïc laïi.
 Moâmen xoaén cuoái ñoaïn baèng moâmen xoaén ñaàu ñoaïn coäng hôïp ngaãu löïc phaân
boá treân ñoaïn ñoù (hôïp ngaãu löïc phaân boá quay cuøng chieàu kim ñoàng hoà döông, ngöôïc laïi laø aâm).
Baøi taäp söùc beàn vaät lieäu trang 16 05/2012 Noäi löïc Khoa Xaây Döïng 
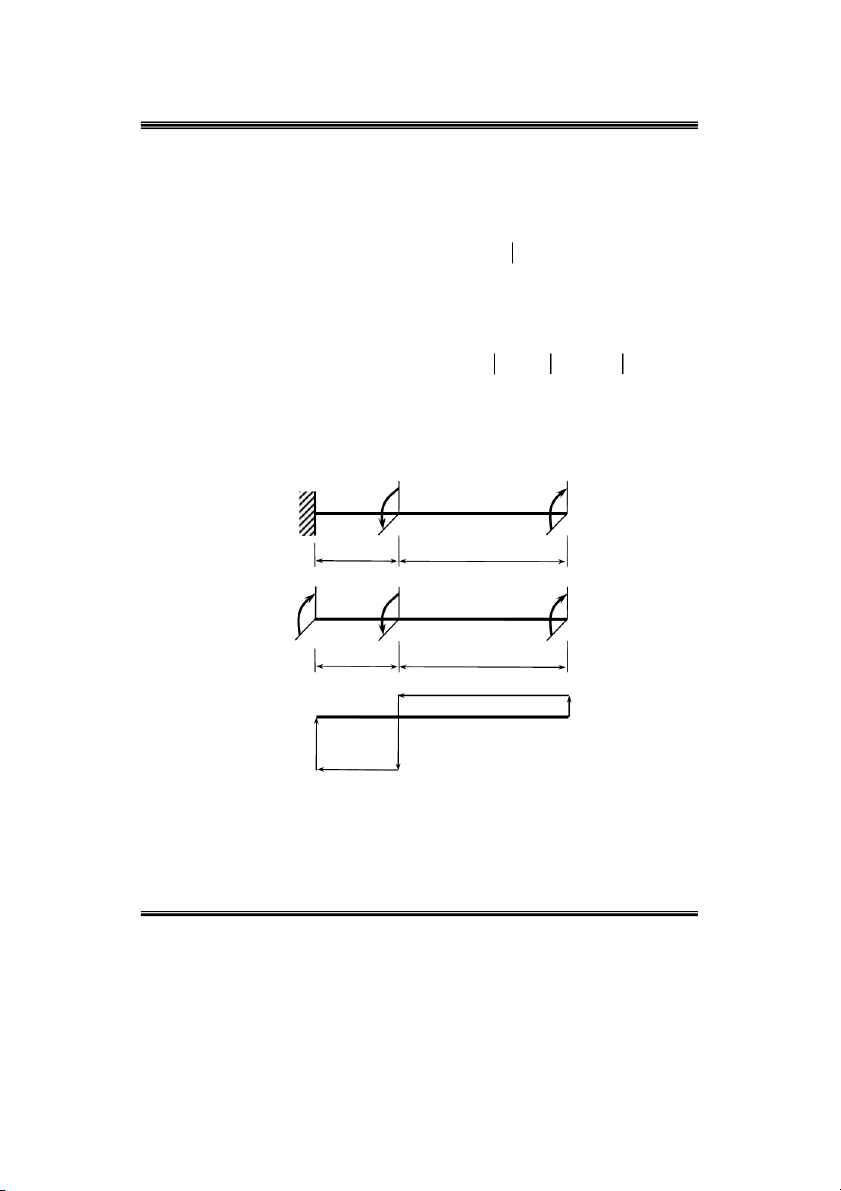
Ví duï 12: Veõ bieåu ñoà noäi löïc phaùt sinh trong truïc chòu xoaén nhö hình 2.21 a. M  ma 6M m a) A C B a 2a M  ma M 6M A m b) A C B a 2a 3ma ma   c) Mz   Hình 2.21 3  ma
 Phaûn löïc lieân keát taïi ngaøm A : ñaët phaûn löïc lieân keát taïi ngaøm A nhö hình 2.21 b  m  0 M  6ma .
m 2a  ma  0 M  3ma z A A
 Taïi C coù ngaãu löïc taäp trung M  ma cuøng chieàu kim ñoàng hoà neân bieåu ñoà M coù z
böôùc nhaûy veà phía döông (beân treân) moät ñoaïn baèng qa töø vò trí “0” thuoäc ñöôøng chuaån.
 Noäi löïc ôû phía beân phaûi cuûa maët caét taïi B : B C M M m  .2a ma 2ma  3ma z z phai
 Taïi B coù ngaãu löïc taäp trung 6M  6ma ngöôïc chieàu kim ñoàng hoà neân bieåu ñoà
M coù böôùc nhaûy veà phía aâm (beân döôùi) moät ñoaïn baèng 6ma töø giaù trò 3ma z
neân M beân traùi maët caét taïi B coù giaù trò 3ma  6ma  3  ma . z
 Noäi löïc ôû phía beân phaûi cuûa maët caét taïi A: A B M  M  0 B  M  3  ma z z z phai trai trai
(treân ñoaïn BA khoâng coù taûi phaân boá neân M haèng soá). z
 Taïi A coù ngaãu löïc taäp trung M  3ma cuøng chieàu kim ñoàng hoà neân bieåu ñoà M A z
coù böôùc nhaûy veà phía döông (beân treân) moät ñoaïn baèng 3qa töø giaù trò 3ma neân
M phía traùi maët caét taïi A coù giaù trò 3ma  3ma  0 . z 
Ví duï 13: Veõ bieåu ñoà noäi löïc phaùt sinh trong truïc chòu xoaén nhö hình 2.22a.
 Phaûn löïc lieân keát taïi ngaøm A :
Baøi taäp söùc beàn vaät lieäu trang 17 05/2012 Noäi löïc Khoa Xaây Döïng
m  0 M  4M  M  0M  3M z A A
 Taïi C coù ngaãu löïc taäp trung M cuøng chieàu kim ñoàng hoà neân bieåu ñoà M coù böôùc z
nhaûy veà phía döông (beân treân) moät ñoaïn baèng M töø vò trí “0” thuoäc ñöôøng chuaån.
 Noäi löïc ôû phía beân phaûi cuûa maët caét taïi B : B C M  M  0 C  M  M (treân z z z phai
ñoaïn CB khoâng coù taûi phaân boá neân M haèng soá). z
 Taïi B coù ngaãu löïc taäp trung 4M ngöôïc chieàu kim ñoàng hoà neân bieåu ñoà M coù z
böôùc nhaûy veà phía aâm (beân döôùi) moät ñoaïn baèng 4M töø giaù trò M neân M beân z
traùi maët caét taïiB coù giaù trò M  4M  3  M .
 Noäi löïc ôû phía beân phaûi cuûa maët caét taïi A : A B M  M  0 B  M  3  M z z z phai trai trai
(treân ñoaïn BA khoâng coù taûi phaân boá neân M haèng soá). z
 Taïi A coù ngaãu löïc taäp trung M 3M cuøng chieàu kim ñoàng hoà neân bieåu ñoà M A z
coù böôùc nhaûy veà phía döông (beân treân) moät ñoaïn baèng 3M töø giaù trò 3  M neân
M phía trí maët caét taïi A coù giaù trò 3M  3M  0 . z M 4M a) A C B a 2a M M A 4M b) A C B a 2a M   c) Mz   Hình 2.22 3  M
Baøi taäp söùc beàn vaät lieäu trang 18 05/2012 Noäi löïc Khoa Xaây Döïng
Caùch veõ bieåu ñoà noäi löïc trong daàm chòu uoán phaúng: (vẽ từ trái sang phải)  Bieåu ñoà löïc caét:
 Bieåu ñoà löïc caét hôn bieåu ñoà taûi troïng phaân boá moät baäc.
 Khi ñi töø traùi qua phaûi, neáu treân sô ñoà tính coù löïc taäp trung bieåu ñoà löïc caét coù
böôùc nhaûy, giaù trò böôùc nhaûy baèng giaù trò löïc taäp trung, chieàu böôùc nhaûy cuøng
chieàu vôùi löïc taäp trung.
 Khi ñi töø traùi qua phaûi, löïc caét cuoái ñoaïn baèng löïc caét ñaàu ñoaïn coäng hôïp löïc
phaân boá treân ñoaïn ñoù (hôïp löïc phaân boá höôùng leân döông, höôùng xuoáng aâm).  Bieåu ñoà moâmen uoán:
 Bieåu ñoà moâmen uoán hôn bieåu ñoà löïc caét moät baäc.
 Khi ñi töø traùi qua phaûi, neáu treân sô ñoà tính coù ngaãu löïc taäp trung bieåu ñoà
moâmen uoán coù böôùc nhaûy, giaù trò böôùc nhaûy baèng giaù trò ngaãu löïc taäp trung, nhaûy
xuoáng khi ngaãu löïc quay cuøng chieàu kim ñoàng hoà, nhaûy leân khi ngaãu löïc quay
ngöôïc chieàu kim ñoàng hoà.
 Khi ñi töø traùi qua phaûi, moâmen uoán cuoái ñoaïn baèng moâmen uoán ñaàu ñoaïn
coäng dieän tích löïc caét treân ñoaïn ñoù (Neáu treân ñoaïn ñoù moâmen uoán laø haøm baäc hai,
moâmen uoán seõ ñaït cöïc trò taïi vò trí löïc caét baèng khoâng). 
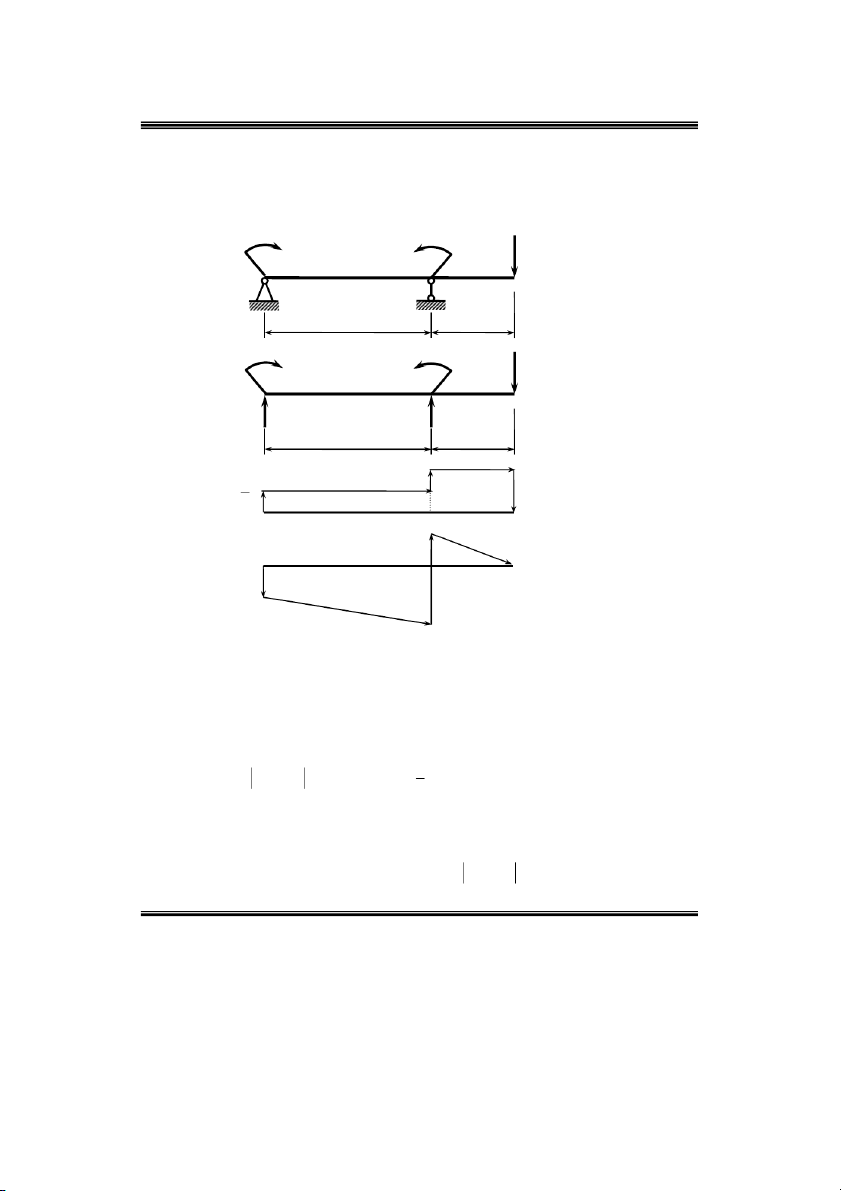
Ví duï14: Veõ bieåu ñoà noäi löïc phaùt sinh trong daàm chòu uoán phaúng nhö hình 2.23 a.
 Phaûn löïc lieân keát taïi caùc goái ,
A B : ñaët caùc phaûn löïc lieân keát töông öùng taïi , A B nhö hình 2.23 b.  P
 m  0  Pa 3PaY .2a  .3 P a  0 Y    A B B  2  P
 m  0 PaY .2a3Pa .Pa  0 Y   B A A  2
Veõ bieåu ñoà löïc caét Q : treân ñoaïn AB, BC khoâng coù löïc phaân boá neân bieåu ñoà löïc caét Q coù y y daïng haèng soá.
 Taïi A coù löïc taäp trung Y  P / 2 höôùng leân neân bieåu ñoà Q coù böôùc nhaûy höôùng A y
leân moät ñoaïn baèng P / 2 töø vò trí “0” thuoäc ñöôøng chuaån.
 Löïc caét beân traùi cuûa maët caét taïi B : B A Q  Q 0 A
 Q  P / 2 (treân ñoaïn AB y y y trai
khoâng coù taûi phaân boá neân Q haèng soá). y
 Taïi B coù löïc taäp trung Y  P / 2 höôùng leân neân bieåu ñoà Q coù böôùc nhaûy höôùng B y
leân moät ñoaïn baèng P / 2 töø giaù trò P / 2 neân Q beân phaûi maët caét taïi B coù giaù y
trò P / 2 P / 2  P .
 Löïc caét beân traùi cuûa maët caét taïi C : C B Q  Q  0 B  Q  P (treân ñoaïn y y y trai phai phai
BC khoâng coù taûi phaân boá neân Q haèng soá). y
Baøi taäp söùc beàn vaät lieäu trang 19 05/2012 Noäi löïc Khoa Xaây Döïng
 Taïi C coù löïc taäp trung P höôùng xuoáng neân bieåu ñoà Q coù böôùc nhaûy höôùng y
xuoáng moät ñoaïn baèng P töø giaù trò P neân Q beân phaûi maët caét taïiC coù giaù trò y P  P  0 . M  Pa 3M P a) A B C 2a a M  Pa M  3Pa P b) A B C Y Y A B 2a a P 1 P c)  2  Qy  Pa  d ) Mx   Pa Hình 2.23 2Pa
Veõ bieåu ñoà moâ men uoán M : (Bieåu ñoà moâ men uoán treân aâm döôùi döông) ta ñaõ bieát bieåu x
ñoà moâmen uoán M hôn bieåu ñoà löïc caét Q moät baäc neân treân ñoaïn AB, BC bieåu ñoà moâmen x y
uoán M coù daïng baäc nhaát. x
 Taïi A coù ngaãu löïc taäp trung M  Pa cuøng chieàu kim ñoàng hoà neân bieåu ñoà M coù x
böôùc nhaûy höôùng xuoáng moät ñoaïn baèng Pa töø vò trí “0” thuoäc ñöôøng chuaån.
 Moâmen uoán beân traùi cuûa maët caét taïi B : B A  A  B 1 M  M  S  Pa  . P 2a  2  Pa . x x y Q trai phai 2
 Taïi B coù ngaãu löïc taäp trung M  3Pa ngöôïc chieàu kim ñoàng hoà neân bieåu ñoà M x
coù böôùc nhaûy höôùng leân moät ñoaïn baèng 3Pa töø giaù trò 2  Pa neân M beân phaûi x
maët caét taïiB coù giaù trò 2Pa 3Pa  Pa .
 Moâmen uoán beân traùi cuûa maët caét taïi C : C B  B  C M  M  S  Pa  . P a  0 . x x Qy trai phai
Baøi taäp söùc beàn vaät lieäu trang 20 05/2012