Giáo trình vật lý đại cương | Trường Đại học Sư phạm, Đại học Đà Nẵng

BÀI MỞ ĐẦU
I. Mục đích và đối tượng nghiên cứu của Vật lý
Mục đích của môn khoa học tự nhiên là nghiên cứu thế giới tự nhiên để hiểu biết và
chinh phục nó. Nhưng thế giới tự nhiên vận động không ngừng, cho nên nghiên cứu nó chính
là nghiên cứu các dạng vận động của nó, từ đó nắm bắt được các quy luật, định luật vận động,
cũng như bản chất của sự vận động của thế giới tự nhiên
Trong các môn học của khoa học tự nhiên thì Vật lý học được coi là môn học cơ bản
nhất, vì các từ kiến thức của Vật lý có thể suy ra những tính chất đơn giản cũng như tổng quát
nhất của thế giới vật chất. Nó là cơ sở để học các môn học khác của khoa học tự nhiên
Vật lý có mối quan hệ với ngành khoa học khác như toán học, thiên văn, triết học...
Thực tiễn đã và đang chứng tỏ rằng những phát minh mới, những khái niệm, giả thiết và định
luật mới của vật lý đã làm phong phú thêm, chính xác thêm quan điểm của triết học, đồng thời
làm phong phú hơn và chính xác hơn trí thức của con người đối với thế giới vô cùng vô tận
Đối tượng nghiên cứu của vật lý học bao gồm các dạng vận động sau:
Vận động cơ: Là sự chuyển động và tương tác của các vật thể vĩ mô trong không gian và thời gian
Vận động nhiệt: Là sự chuyển động và tương tác của các phân tử và nguyên tử
Vận động điện từ: Là sự chuyển động và tương tác của các hạt mang điện và phôtôn
Vận động nguyên tử: Là sự tương tác giữa các hạt bên trong hạt nhân, giữa các Nucleon
II. Phương pháp nghiên cứu của Vật lý
Vật lý là môn khoa học thực nghiệm, nên phương pháp nghiên cứu nó tuân theo con
đường mà lí luận triết học đã nêu: Thực tiễn – lý luận - Thực tiễn
Quan sát hiện tượng: bằng giác quan hoặc dụng cụ, máy móc
Tiến hành thí nghiệm: Lặp lại hiện tượng quan sát ở những điều kiện xác định
Rút ra các định luật và nguyên lý dựa trên cơ sở quan sát và thí nghiệm. Định luật nêu
lên thuộc tính của một hiện tượng, còn nguyên lý là những định luật đóng vai trò cơ sở cho một lý thuyết
Đề xuất những giả thiết: để giải thích các tính chất các định luật
Xây dựng lý thuyết: bằng cách tập hợp các giả thiết, các định luật, các hệ quả của định
luật. Như vậy lý thuyết vật lý thông thường được xây dựng bằng con đường thực nghiệm
Ứng dụng các kết quả của vật lý: đây là bước cuối cùng của con đường nhận thức để
trở về với thực tiễn
III. Đại lượng Vật lý, đơn vị và thứ nguyên 1
Mỗi thuộc tính của một hiện tượng hay đối tượng vật lý đều được đặc trưng nhờ một
hay vài đại lượng vật lý
Các đại lượng vật lý có thể là vô hướng (như: Khối lượng, điện tích…) hoặc hữu
hướng (như: Lực, vận tốc…). Đại lượng vô hướng được biểu diễn bằng giá trị số có thể
dương, âm hoặc bằng không. Do đó, xác định đại lượng vô hướng nghĩa là xác định số trị của
nó. Đại lượng hữu hướng được biểu diễn bằng một vectơ. Vậy, xác định một đại lượng hữu
hướng là xác định phương chiều, môđun và điểm đặt của vectơ biểu diễn đại lượng đó
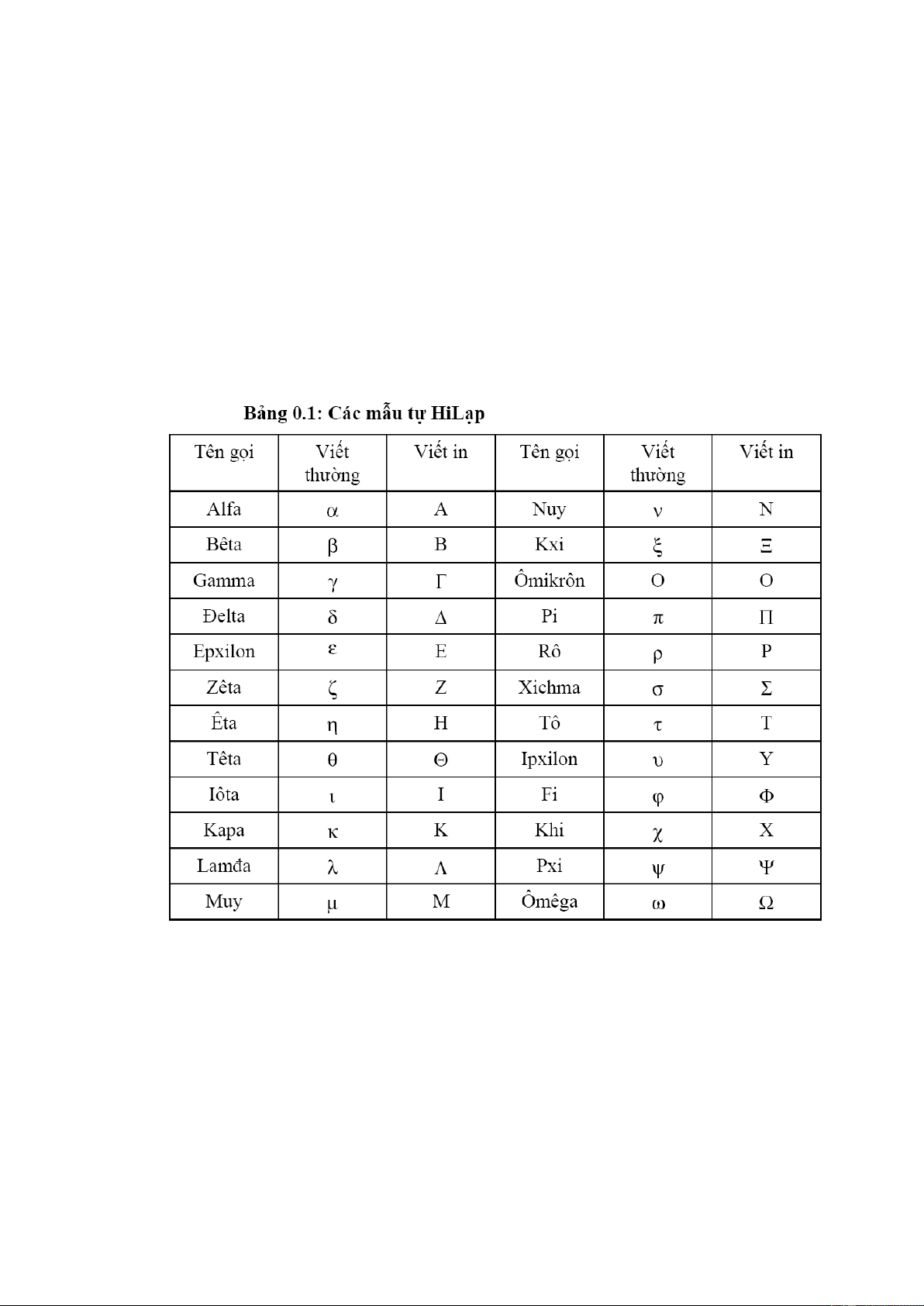
Mỗi đại lượng vật lý được kí hiệu bởi một hay nhiều kí tự La Tinh hoặc kí tự Hi Lạp ( xem bảng 0.1)
Để đo một đại lượng vật lý ta chọn một đại lượng cùng loại làm mẫu được gọi là đơn vị
Giá trị đo đại lượng đó bằng tỉ số đo trên đại lượng đơn vị
Các đơn vị được chọn trước làm mẫu được gọi là đơn vị cơ bản. Các đơn vị khác được
suy ra từ đơn vị cơ bản gọi là đơn vị dẫn xuất. Tập hợp các đơn vị cơ bản và đơn vị dẫn xuất
tương ứng tạo thành một hệ đơn vị đo
Hệ đo lường hợp pháp của nước ta ban hành năm 1965 dựa trên cơ sở SI (System
International). Trong SI có 7 đơn vị cơ bản:
+ Đơn vị chiều dài: mét (m) 2
+ Đơn vị khối lượng: kilôgam (kg)
+ Đơn vị thời gian: giây (s)
+ Đơn vị cường độ dòng điện: Ampe (A)
+ Đơn vị nhiệt độ: kelvin (K)
+ Đơn vị cường độ sáng: Candela (Cd)
+ Đơn vị lượng chất: mol (mol)
Ngoài 7 đơn vị cơ bản nói trên còn có đơn vị phụ: đơn vị đo góc phẳng là radian (rad);
góc khối là steradian ( sterad). Các đơn vị này không có thứ nguyên
Thứ nguyên: Từ các đơn vị cơ bản ta định nghĩa các đơn vị dẫn xuất. Việc định nghĩa
này dựa vào một khái niệm thứ nguyên. Thứ nguyên của một đại lượng là quy luật biểu diễn
sự phụ thuộc đơn vị đo đại lượng đó vào các đơn vị cơ bản.
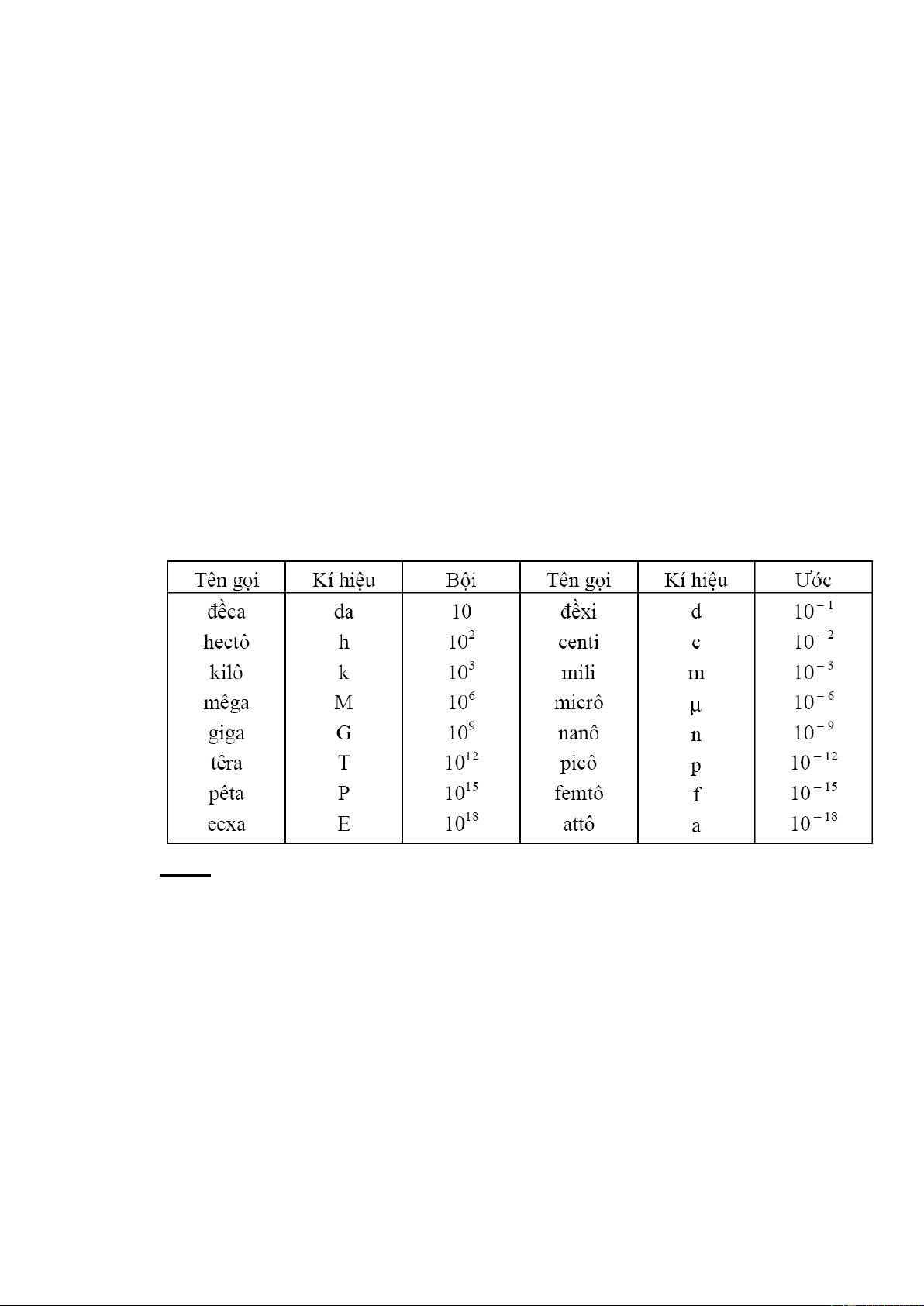
Ngoài các đơn vị chuẩn, người ta còn dùng các tiếp đầu ngữ để chỉ ước và bội của đơn vị ( xem bảng 0.2)
Bảng 0.2: Tiếp đầu ngữ chỉ ước và bội của đơn vị
Thí dụ: Thể tích hộp chữ nhật: V = a.b.c
Thể tích khối trụ thẳng: V = R2h
Nếu bỏ qua các hệ số ta có: Thể tích = độ dài*độ dài*độ dài. Vậy [Thể tích]= (chiều dài)3
Nếu ta kí hiệu các thứ nguyên của các đại lượng là:
[chiều dài] = L; [khối lượng] = M; [Thời gian] = T , thì:
[Thể tích] = L3; [Vận tốc] = L/T = L.T-1; [Gia tốc] = L/T2 = L.T-2; [Lực] = M.L/T2 = MLT-2
Ngoài ra một số nước còn dùng hệ đơn vị CGS (hệ Gauss) : trong đó đơn vị chiều dài
(cm), khối lượng (g). vận tốc (cm/s), gia tốc(cm/s2), lực trong hệ này: dyn(1dyn = 1g.cm/s2) 3 PHẦN THỨ NHẤT CƠ HỌC
Cơ học nghiên cứu các dạng vận động đơn giản nhất của vật chất, tức là dịch chuyển
các vật hay các phần của vật đối với nhau.
Cơ học gồm những phần sau: -
Động học: Nghiên cứu các đặc trưng của chuyển động và các dạng chuyển
động khác nhau mà không chú ý tới nguyên nhân gây ra chuyển động đó -
Động lực học: Nghiên cứu chuyển động của vật trong mối liên hệ với tương
tác dẫn đến sự thay đổi trạng thái chuyển động của vật
CHƯƠNG 1: ĐỘNG HỌC CHẤT ĐIỂM
§1.1 - NHỮNG KHÁI CƠ BẢN VỀ CHUYỂN ĐỘNG
I. Chuyển động và hệ quy chiếu
Chuyển động là một khái niệm cơ bản của cơ học. Chuyển động cơ học là sự thay đổi
vị trí của vật thể trong không gian theo thời gian
Hệ vật trong không gian được quy ước đứng yên dùng làm mốc để xác định vị trí các
vật khác được gọi là hệ quy chiếu
Vật chuyển động hay đứng yên là có tính tương đối tuỳ thuộc vào hệ quy chiếu mà ta chọn
Vì chuyển động xảy ra trong không gian và theo thời gian nên để mô tả chuyển
động trước tiên phải tìm cách định vị vật trong không gian. Muốn vậy ta phải đưa thêm
vào hệ quy chiếu một hệ toạ độ. Trong Vật lý người ta sử dụng nhiều hệ toạ độ khác
nhau. Ở đây, sẽ giới thiệu hai hệ toạ độ hay dùng đó là hệ toạ độ Đề-các (Descartes) và hệ toạ cầu
1. Hệ tọa độ Descartes
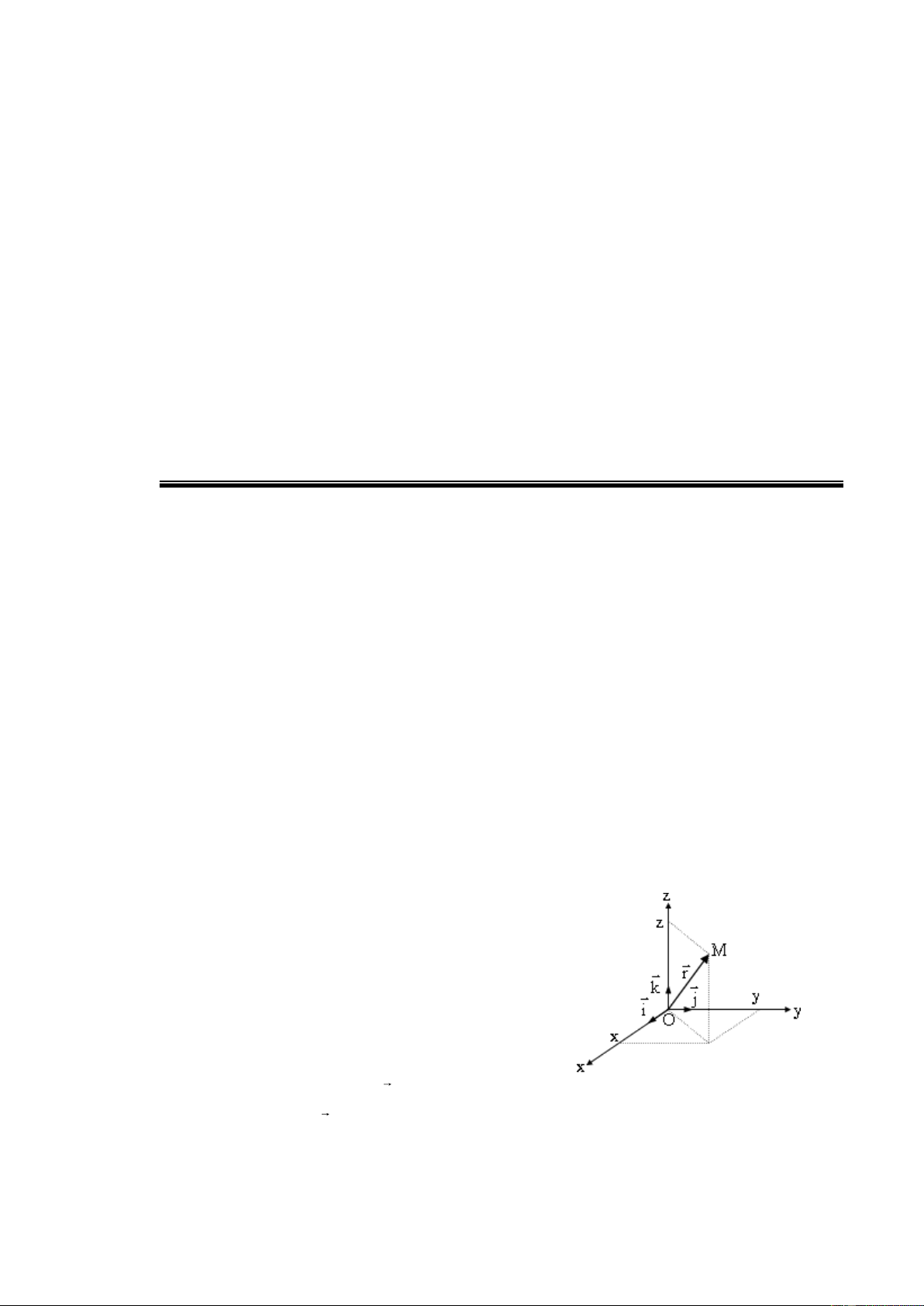
Hệ toạ độ Descartes gồm 3 trục Ox, Oy, Oz
tương ứng vuông góc với nhau từng đôi một, chúng
tạo thành một tam diện thuận. Điểm O gọi là gốc
toạ độ. Vị trí của một điểm M bất kỳ được hoàn
toàn xác định bởi bán kính vectơ r , hay bởi tập hợp
Hệ tọa độ Decartes
của 3 số (x,y,z) trong đó r là hình chiếu của điểm
mút M của vectơ lên các trục Ox, Oy, Oz tương
ứng, được gọi là 3 toạ độ của điểm M trong hệ toạ độ Descartes. 4
2. Hệ tọa độ cầu
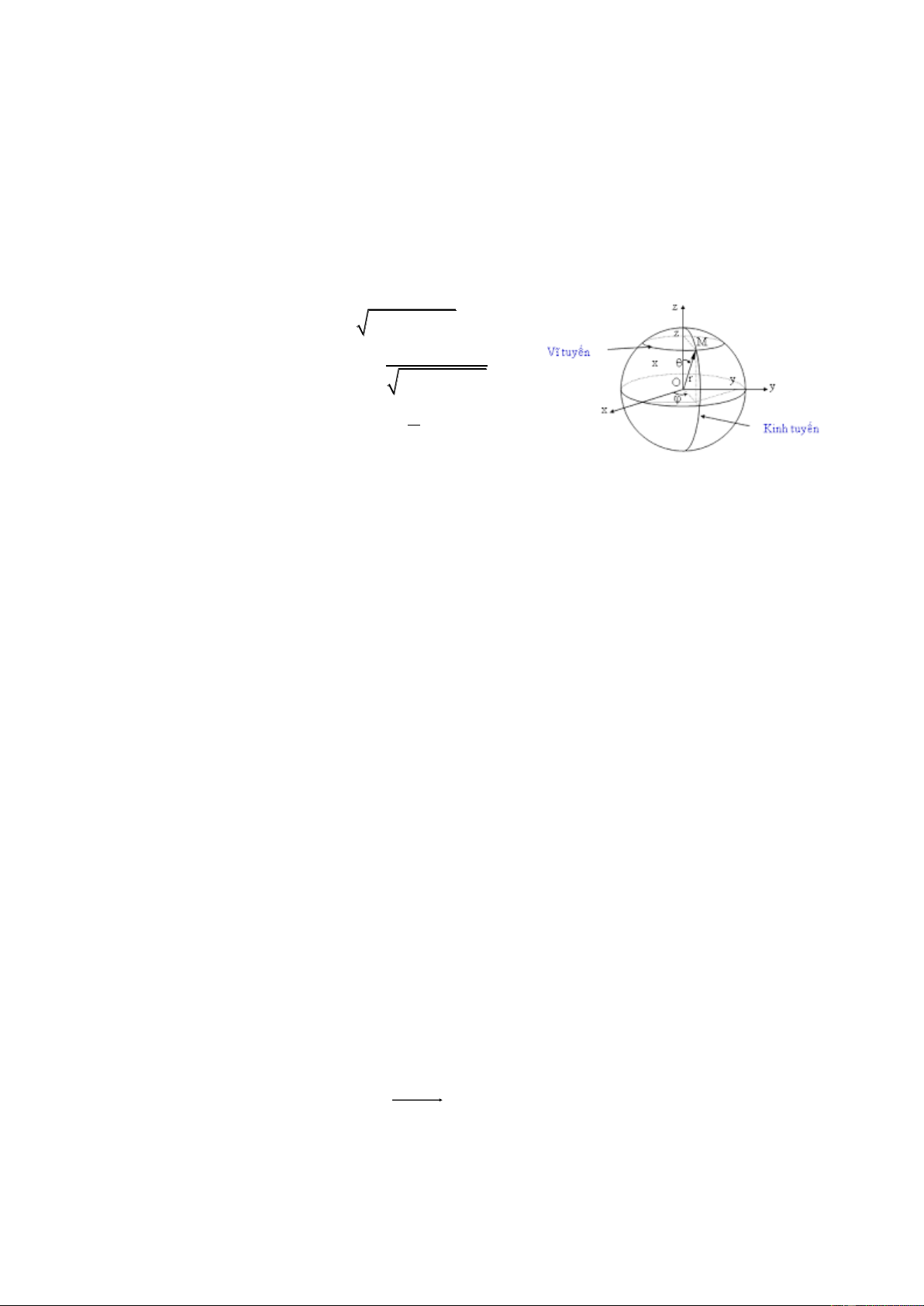
Trong hệ toạ độ cầu, vị trí của một điểm M bất kỳ được xác định bởi 3 toạ độ r,
θ, φ. Trong đó, r là độ dài bán kính vectơ, θ là góc giữa trục Oz và rr , còn φ là góc trục
Ox và tia hình chiếu của t trong mặt phẳng xOy. Biết ba toạ độ cầu của điểm M, ta có
thể tính được toạ độ Descartes của điểm M theo công thức sau:   2 2 2     r x y z
x  r.sin. os c     z
y  r.sin.sin hay cos   2 2 2 
x  y  z z  r. os c    y    arctan  x
Hệ tọa độ cầu
Trong hệ toạ độ cầu: 0 ≤ θ ≤ 1800 và 0 ≤ φ ≤ 3600. Các đường tròn ứng với cùng
một giá trị của e gọi là Các đường vĩ tuyến, còn các đường tròn ứng với cùng một giá
trị của φ gọi là các đường kinh tuyến. Hệ toạ độ cầu rất thuận tiện khi định vị các địa điểm trên quả đất.
II. Chất điểm và hệ chất điểm
Mọi vật đều có kích thước xác định, tuy nhiên nếu kích thước của vật quá nhỏ bé so
với khoảng cách mà ta khảo sát thì vật đó được coi là một chất điểm. Vậy, chất điểm là một
vật có kích thước nhỏ không đáng kể so với khoảng cách, kích thước mà ta đã khảo sát. Chất
điểm là một khái niệm trừu tượng, không có trong thực tế nhưng rất thuận tiện cho việc
nghiên cứu chuyển động của các vật. Do đó khái niệm chất điểm mang tính chất tương đối
Tập hợp các chất điểm được gọi là hệ chất điểm. Vật rắn là một hệ chất điểm trong đó
khoảng cách tương tác giữa các chất điểm của hệ là không đổi
III. Quỹ đạo, quãng đường và độ dời
Qũy đạo của chất điểm là tập hợp các vị trí của chất điểm trong quá trình chuyển
động. Nói một cách khác, khi chất điểm chuyển động, nó sẽ vạch ra trong không gian một
đường gọi là quỹ đạo. Căn cứ vào hình dạng của quỹ đạo, ta có thể phân chia chuyển động
của chất điểm là thẳng, cong hoặc tròn.
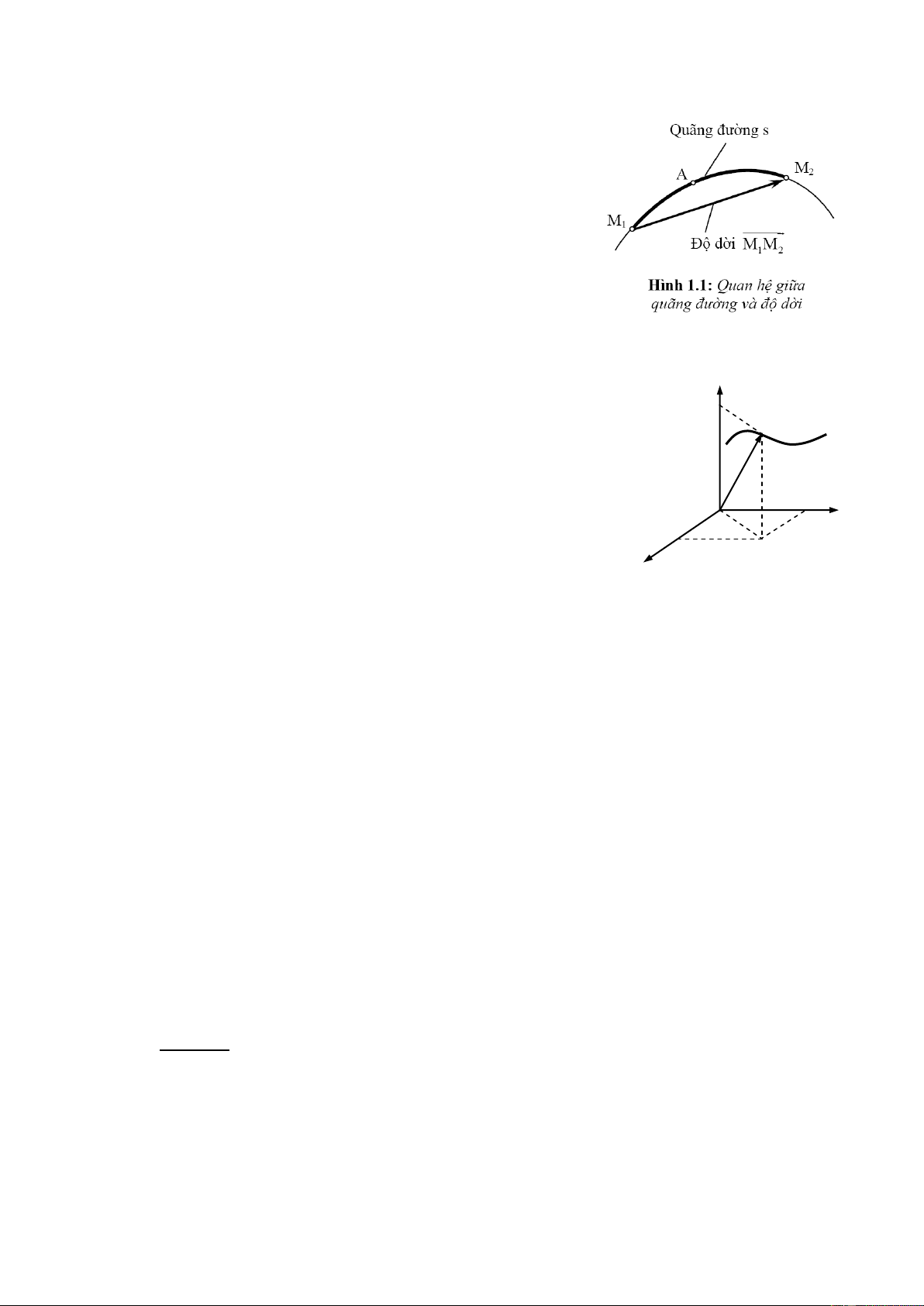
Xét một chất điểm M chuyển động trên quỹ đạo cong bất kỳ từ vị trí M1 qua điểm A 
đến M2 ( hình 1.1). Ta gọi độ dài của cung M M A
là quãng đường vật đi từ M 1 2 1 đến M2 và
được kí hiệu là s. Và ta gọi véc tơ M M là véc tơ độ dời của chất điểm từ điểm M 1 2 1 đến điểm M2 5
Như vậy quãng đường s là một đại lượng vô hướng
luôn dương; còn độ dời là một vectơ. Nếu vật chuyển động
trên đường cong kín hoặc đổi chiều chuyển động sao cho
vị trí đầu và cuối trùng nhau thì độ dời sẽ triệt tiêu nhưng
quãng đường là khác không. Khi vật chuyển động trên
đường thẳng theo một chiều duy nhất thì quãng đường vật
đi được bằng độ lớn của vectơ độ dời.
IV. Phương trình chuyển động và phương trình quỹ đạo của c hất điểm
Để xác định chuyển động của một chất điểm người ta
thường gắn vào hệ quy chiếu một hệ toạ độ. Hệ toạ độ y M
Descartes gồm 3 trục Ox, Oy, Oz vuông góc với nhau từng đôi
một lập thành một tam diện thuận Oxyz. O là gốc toạ độ
Vị trí của chất điểm M trong không gian được xác định O   x bởi véctơ M O
 r . Nếu gọi các véc tơ đơn vị trên ba trục là     z
i , j, k thì r được biểu diễn hình chiếu trên các trục x, y, z là:
Hình 1.2: Vị trí chất điểm M
trong hệ tọa độ Descartes     r  x i
.  y. j  z k . (1.1) 
Khi M chuyển động thì r thay đổi theo thời gian. Hàm số biểu diễn sự phụ thuộc của
r theo thời gian t được gọi là phương trình chuyển động:  
r  r (t) (1.2)
x  x(t) 
y  y(t) (1.3) 
z  z(t)
Quỹ đạo chuyển động là đường tạo bởi tập hợp tất cả các vị trí mà chất điểm đi qua.
Phương trình toán học mô tả quỹ đạo chính là phương trình biểu diễn mối liên hệ giữa các toạ
độ không gian của chất điểm.
Để tìm phương trình quỹ đạo, ta cần khử tham số thời gian từ phương trình (1.3)
Như vậy: Phương trình chuyển động cho phép ta xác định được vị trí của chất điểm ở
một thời điểm t bất kì; Phương trình quỹ đạo cho biết hình dạng quỹ đạo của vật
Ví dụ 1.1: Cho phương trình chuyển động của chất điểm có dạng: x t ( )  a.sin t
 ; y t()  a.cos t  Giải
Khử tham số t phương trình trên bằng cách bình phương hai vế mỗi phương trình x2 t ( )  a2 2 .sin t
 ; y2 t()  a2 2 .cos t  6
cộng hai phương trình lại vế theo vế ta được: 2 2 2
x  y  a (cos2 t  sin2 t)
Vì cos2 t  sin2 t  1nên: 2 2 2
x  y  a
Như vậy quỹ đạo chuyển động của chất điểm là một đường tròn có bán kính là a.
-----------------------------------------------------------------------------
§1.2 - TỐC ĐỘ VÀ VẬN TỐC
Vận tốc là đại lượng vật lý mô tả cả mức độ nhanh chậm lẫn phương, chiều của
chuyển động. Vận tốc ở đây được hiểu là vận tốc dài hay vận tốc tuyến tính, phân biệt với vận
tốc góc. Trong vật lý, vận tốc được biểu diễn bởi vectơ (có thể hiểu là "đoạn thẳng có
hướng"). Độ dài của vectơ vận tốc cho biết tốc độ nhanh chậm của chuyển động, và chiều của
vectơ biểu thị chiều của chuyển động. Do đó, vận tốc là một đại lượng hữu hướng, khác với
tốc độ, một đại lượng vô hướng đơn thuần mô tả đặc tính nhanh chậm của chuyển động.
I. Tốc độ trung bình và vận tốc trung bình
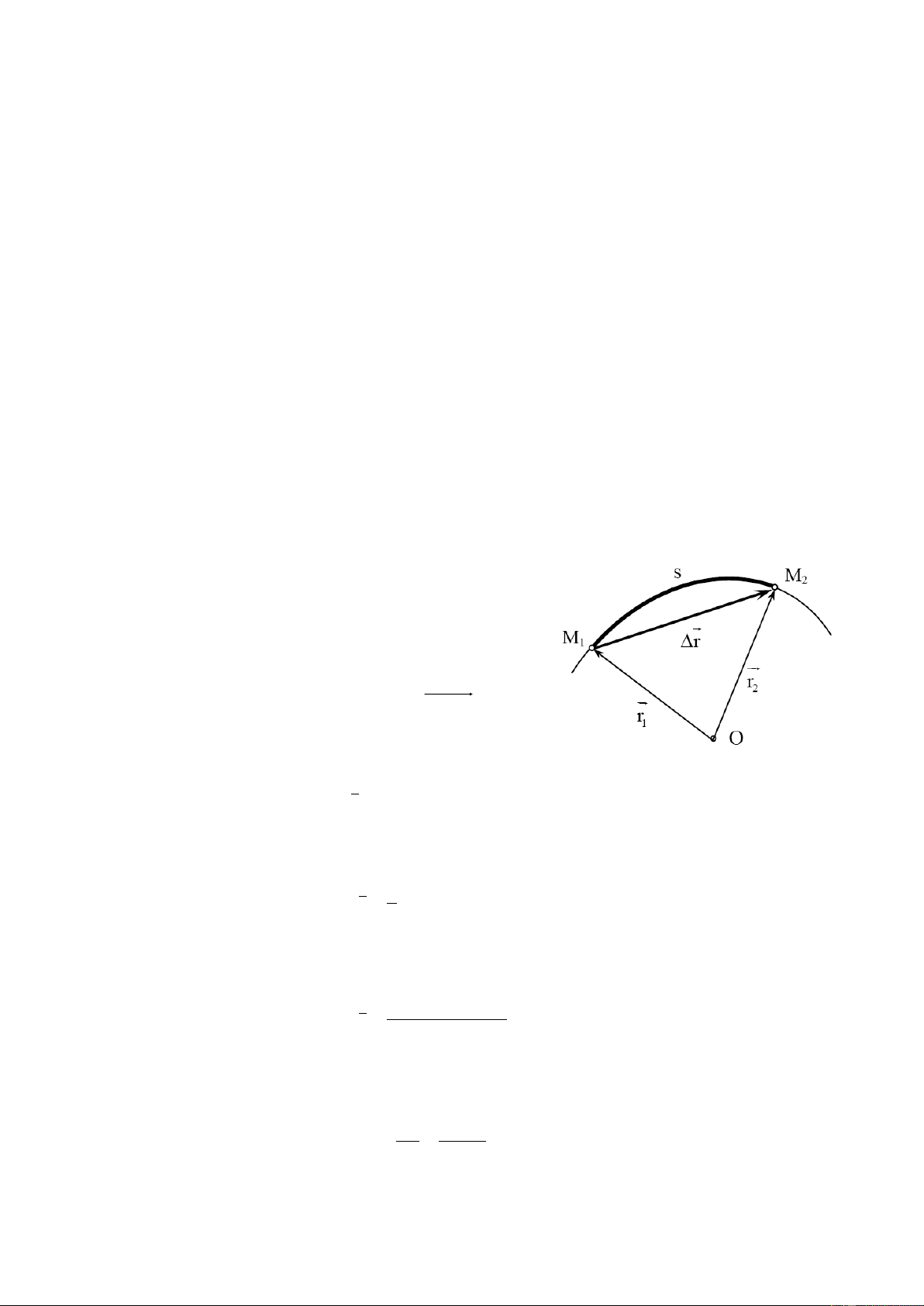
- Xét chất điểm M chuyển động trên quỹ đạo
cong bất kỳ. Giả sử tại thời điểm t1 chất điểm ở M1 
được xác định bởi vectơ vị trí r , tại thời điểm t 1 2 chất 
điểm ở M2 được xác định bởi vectơ vị trí r . Gọi s là 2   
quãng đường vật đã đi được và r
  M M  r  r 1 2 2 1
là độ rời từ M1 đến M2. Ta định nghĩa tốc độ trung
bình và vận tốc trung bình của chất điểm như sau:
Hình 1.3. Vận tốc trung bình
Tốc độ trung bình v trên một đoạn đường
nhất định của chất điểm chuyển động là đại lượng đo bằng thương số giữa quãng đường s mà
chất điểm đi được với khoảng thời gian t để chất điểm đi hết quãng đường đó. s v  (1.4) t
- Nếu quãng đường s gồm nhiều quãng đường nhỏ s1, s2…., sn và thời gian tương ứng
để vật đi hết các quãng đường đó là t1, t2,…,tn thì (1.4) được viết dưới dạng:
s  s  .....  s 1 2 n v  (1.5)
t  t  ...  t 1 2 n
Vận tốc trung bình của một chất điểm chuyển động trong khoảng thời gian từ t1 đến t2
là đại lượng đo bằng thương số giữa vectơ độ dời và khoảng thời gian đó     r  r  r 2 2 v   (1.6) tb t  t  t 2 1 7
Như vậy, Tốc độ trung bình là một đại lượng vô hướng, không âm, đặc trưng cho mức
độ nhanh chậm của chuyển động trên một đoạn đường nhất định; còn vận tốc trung bình là
một đại lượng vectơ đặc trưng cho sự thay đổi của vectơ độ dời trong một khoảng thời gian
nhất định. Khi vật chuyển động liên tục trên đường thẳng theo một chiều duy nhất thì tốc độ
trung bình bằng với độ lớn của vectơ vận tốc trung bình
- Cần nhấn mạnh sự khác biệt của các công thức định nghĩa (1.4) và (1.6) là: Đối với
tốc độ trung bình, ta quan tâm đến quãng đường s mà chất điểm đã đi và thời gian t mà chất
điểm dùng để đi hết quãng đường đó, không quan tâm đến thời gian nghỉ; còn đối với vận tốc
trung bình, ta quan tâm đến vị trí và thời điểm đầu và cuối, không quan tâm đến quá trình diễn biến của chuyển động
Ví dụ 1.2: Một ô tô dự định đi từ A đến B với tốc độ 30km/h, nhưng sau khi đi được 1/3 đoạn
đường, ô tô bị chết máy. Tài xế phải dừng 30 phút để sửa xe, sau đó đi tiếp với tốc độ 40km/h
và đến B đúng quy định. Tính tốc độ trung bình của ô tô trên đoạn đường AB và thời gian dự
định ban đầu. Có thể tính được độ lớn của vectơ vận tốc trung bình trong khoảng thời gian từ A đến B hay không Giải
Giả sử ô tô chết máy tại C. Gọi t1, t2 là
thời gian ô tô chuyển động trên các đoạn AC,
CB. Tốc độ trung bình của ô tô trên đoạn đường AB là:
Vì ô tô đến B đúng giờ quy định nên thời gian dự định đúng bằng thời gian thực tế
Vậy thời gian dự định ban đầu là: AB 90 t    ( 3 h) v 30 1
Với giả thiết của bài toán trên, ta không thể tính được độ lớn của vectơ vận tốc trung
bình, vì không biết quỹ đạo từ A đến B là thẳng hay cong. Nếu quỹ đạo là đường thẳng thì   r  AB v  
 30m/ s . Nếu quỹ đạo là đường cong thì chưa đủ dữ kiện để tính vận tốc tb t  t  t B A trung bình
Ví dụ 1.3: Một ô tô đi từ A đến B với tốc độ 30km/h, rồi quay về A với tốc độ v2= 50km/h.
Tính tốc độ trung bình và vận tốc trung bình trên lộ trình đi – về 8 Giải
Tốc độ trung bình trên lộ trình đi – về
Vận tốc trung bình trên lộ trình đi – về
II. Tốc độ tức thời và vận tốc tức thời
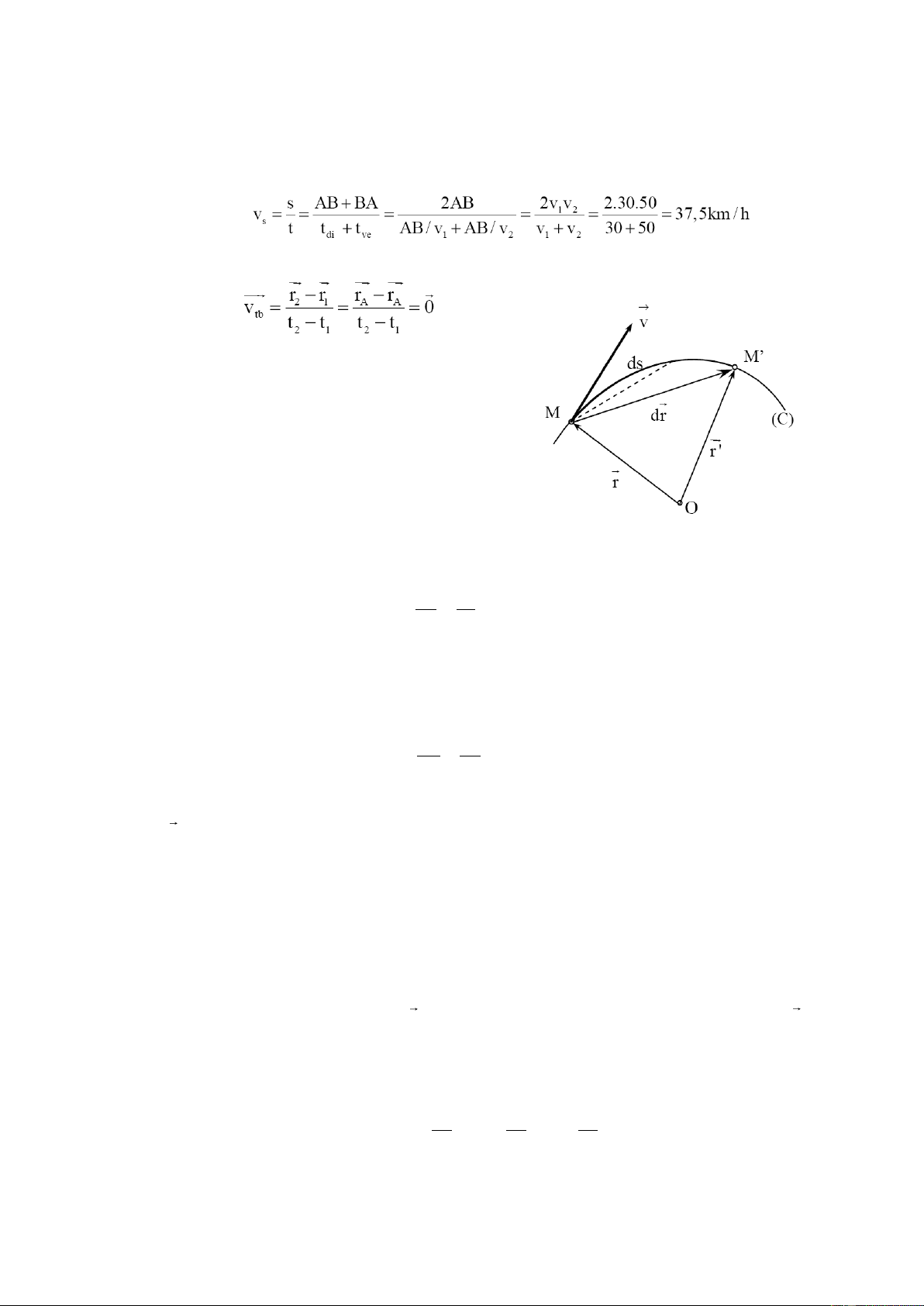
Để đặc trưng cho tính nhanh, chậm của
chuyển động ở từng thời điểm trên quỹ đạo, ta
dùng khái niệm tốc độ tức thời. Tốc độ tức thời tại
một điển đã cho trên quỹ đạo là đại lượng đo bằng
thương số giữa quãng đường đi rất nhỏ tính từ
điểm đã cho và khoảng thời gian rất
Hình 1.4. Véctơ vận tốc nhỏ để vật đi hết quãng đường đó s  ds v  lim  (1.7) t  0 t  dt
Tốc độ tức thời của chất điểm chuyển động bằng đạo hàm theo thời gian của quãng
đường mà chất điểm đi qua.
Tương tự, Vận tốc tức thời bằng đạo hàm véctơ độ dời theo thời gian.    r  r d v  lim  (1.8) t  0 t  dt
Vậy véctơ vận tốc bằng đạo hàm theo thời gian của bán kính véctơ. Véctơ vận tốc tức
thời v có đặc điểm:
- Phương: là tiếp tuyến với qũi đạo tại điểm khảo sát.
- Chiều: là chiều chuyển động.
- Độ lớn: bằng đạo hàm của quãng đường đối với thời gian.
- Điểm đặt: tại điểm khảo sát.
Thứ nguyên của vận tốc: [vận tốc] = LT-1 do đó đơn vị đo là (m/s)
Trong hệ tọa độ Descartes , vì r được biểu diễn theo (1.1) nên tương tự ta biểu diễn v :     v  v i
.  v . j  v k . (1.9) x y z 
Từ (1.6) và (1.1) ta có các thành phần của v trên ba trục: dx dy dz v  ; v  ; v  x dt y dt z dt
Độ lớn của vận tốc tức thời: 9 2 2 2 v  
v  v  v  v (1.10) x y z
Ví dụ 1.4 :Xét một chất điểm chuyển động theo phương trình S =3t2 + 4t +2; Trong đó s đo
bằng đơn vị mét(m) và t đo bằng đơn vị giây(s). Tính tốc độ trung bình trong 2s đầu và tốc độ
tức thời tại thời điểm t = 2s Giải
Quãng đường chất điểm đi được trong 2 giây: S = S(t = 2) – S(t = 0) = 20(m) S  20
Tốc độ trung bình: v    ( 10 m / s) t  2
Tốc độ tức thời tại thời điểm t = 2s: dS v   6t  4  2 . 6  4  ( 16 m / s) tt dt x 15t
Ví dụ 1.5 :Vật chuyển động trong mặt phẳng oxy với phương trình:  (SI ) . Tính y  5 2 t
quãng đường vật đã đi được kể từ lúc t = 0 đến t = 2s Giải
---------------------------------------------------------
§1.3 – VÉCTƠ GIA TỐC
Gia tốc là đại lượng vật lý đặc trưng cho sự thay đổi về phương, chiều và độ lớn của
véctơ vận tốc, cũng chính là đặc trưng cho trạng thái chuyển động I. Véc tơ gia tốc 
Giả sử tại thời điểm t chất điểm ở vị trí M có véc tơ vận tốc v , tại thời điểm t + t  
chất điểm ở vị trí M’ có vận tốc v  v
 . Trong khoảng thời gian t, véctơ vận tốc chất điểm 
biến thiên một lượng v
 . Gia tốc được định nghĩa là tỉ số giữa độ biến thiên vận tốc và thời
gian để có độ biến thiên đó.
Véc tơ gia tốc trung bình:   v  a  (1.11) t  10
Khi thời gian t đủ bé thì v cũng đủ bé nên theo định nghĩa đạo hàm ta có vectơ gia tốc tức thời:    v  v d a  lim  (1.12) t  0 t  dt    
Trong hệ toạ độ Descartes: a  a i.  a . j  a k . x y z
Trong đó ba thành phần trên ba trục là: 2 dv d x 2 dv d y 2 dv d z a x   ; a y   ; a z   x 2 dt dt y 2 dt dt z 2 dt dt
Độ lớn của gia tốc là: 2 2 2 a   a 
a  a  a (1.13) x y z
Đơn vị của gia tốc là m/s2
Ví dụ 1.5 : Một chất điểm chuyển động trong mặt phẳng oxy với phương trình:  2 4 x  3 3 t  t  3 (SI ) y  8t
a, Xác định véc tơ gia tốc tại thời điểm t = 3s
b, Có thời điểm nào gia tốc triệt tiêu hay không? Giải
II. Gia tốc tiếp tuyến và pháp tuyến 
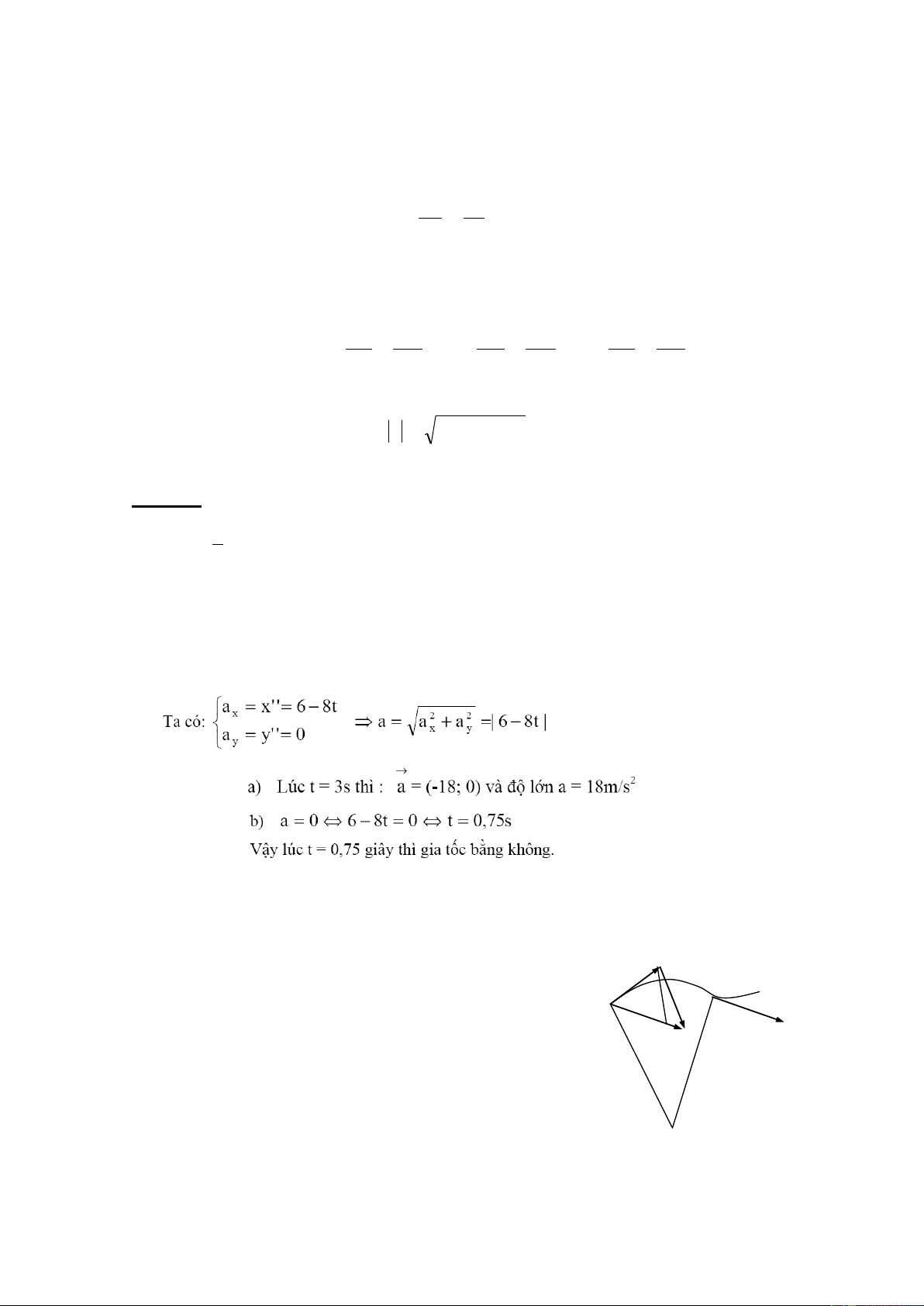
Trong chuyển động cong bất kỳ, gia tốc a
tại một điểm bất kì trên quỹ đạo được biểu diễn A
bằng tổng của hai thành phần.  v  M’  
Thật vậy, giả sử tại M chất điểm có vận tốc M v v ' A’   B A
M  v sau thời gian t chất điểm ở M’ có vận tốc C     M ' '
A  v' , với v và v ' khác nhau về cả độ lớn và   hướng. Từ M vẽ C
M song song và bằng M ' ' A , lấy trên MC một đ O oạn MB = v. Khi đó
Hình 1.5. Gia tốc tiếp tuyến và pháp tuyến 11             C M  A M  C A suy ra C A  C M  A
M  v' v   v  mà C A  B A  C B    Nên v   B A  C B     
Từ định nghĩa gia tốc: v B A C B a  lim  lim  lim t  0 t t   0 t t   0 t 
1. Gia tốc pháp tuyến      Ta kí hiệu B A a  lim
thì phương của a là phương của B
A khi t  0. Vậy a n n n t  0 t  có:
+ Phương: vuông góc với tiếp tuyến quỹ đạo tai M ( nên được gọi là gia tốc pháp tuyến)  + Chiều: theo chiều B
A tức là quay về phía lõm của quỹ đạo tại M ( gia tốc hướng tâm) 2 + Độ lớn: v a  (1.14) n R
Rõ ràng ta thấy với một giá trị vận tốc, R càng bé (phương của vận tốc thay đổi càng
nhiều) thì a càng lớn  Gia tốc pháp tuyến đặc trưng cho sự thay đổi phương của véc tơ n vận tốc
2. Gia tốc tiếp tuyến      Ta kí hiệu C B a  lim
thì phương của a là phương của A
M khi t  0 . Vậy a t t t t  0 t  có:
+ Phương: trùng với tiếp tuyến quỹ đạo tại M (được gọi là gia tốc tiếp tuyến)  
+ Chiều: theo chiều chuyển động nếu v tăng và ngược chiều chuyển động nếu v giảm + Độ lớn: dv a  (1.15) t dt
Vậy gia tốc tiếp tuyến bằng đạo hàm của vận tốc theo thời a
gian, đặc trưng cho sự thay đổi về độ lớn của M t véc tơ vận tốc Như vậy ta có:   
a  a  a   n t a n a  
Hình 1.6. Gia tốc toàn phần
Vì a  a nên: n t 2 2 a  a  a (1.16) n t 12
Ví dụ 1.6 :Một chất điểm chuyển động trong mặt phẳng oxy với phương trình
x 10  50t :  (SI )
y  40t  5 2 t
a, Dạng quỹ đạo của chuyển động?
b, Xác định tung độ lớn nhất mà vật đạt được
c, Xác định các thành phần và độ lớn của vectơ vận tốc, gia tốc tại thời điểm t = 2s. Tính
gia tốc tiếp tuyến, gia tốc pháp tuyến và bán kính chính khúc của quỹ đạo lúc đó Giải
-----------------------------------------------------------------------------
§1.4 - HAI DẠNG CƠ BẢN CỦA CHUYỂN ĐỘNG
I. Chuyển động thẳng biến đổi đều
Là chuyển động dọc theo một trục nào đó với gia tốc không đổi 13 dv Vì a  
n = 0; at = a = const, do đó từ a a
ta tính được vận tốc ở thời điểm t nếu t dt v t
biết vận tốc ban đầu là v0, ta biến đổi dv = a.dt lấy tích phân hai vế:  dv   a dt . sẽ được v0 0 v = v0 + a.t (1.17)
Từ biểu thức trên ta nhận thấy:
+ Khi a > 0 (v > v0): chuyển động nhanh dần đều
+ Khi a < 0 (v < v0): chuyển động chậm dần đều
+ Khi a = 0 (v = v0): chuyển động thẳng đều
Tương tự từ biểu thức ds v 
ta cũng tính được quãng đường đi được sau t giây, nếu dt
biết quãng đường ban đầu là s0 2 at
s  s  v .t  (1.18) 0 0 2
Từ công thức (1.17) và (1.18) ta có mối liên hệ như sau:
v2  v2  a 2 s . (1.19) 0
II. Chuyển động tròn
Chuyển động tròn là chuyển động của chất điểm theo một quỹ đạo tròn bán kính R. Để
đặc trưng cho chuyển động, ngoài gia tốc pháp tuyến và tiếp tuyến người ta còn đưa ra khái
niệm vận tốc góc và gia tốc góc.
a, Vận tốc góc
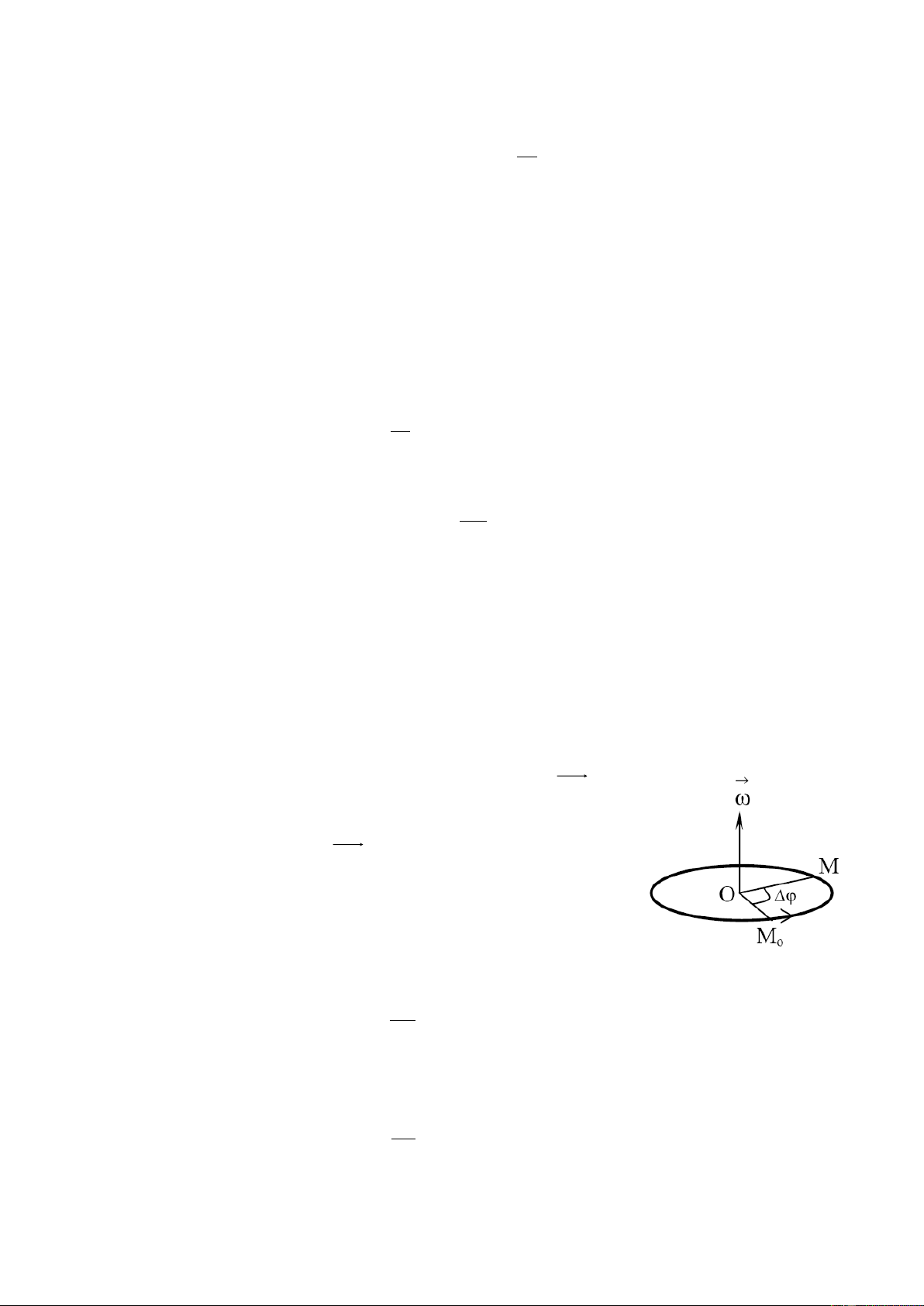
Khi chất điểm chuyển động tròn, vectơ bán kính OM sẽ
quay theo và quét được một góc  nào đó. Đặc trưng cho sự
quét nhanh hay chậm của OM , ta dùng khái niệm vận tốc góc.
Vận tốc góc là đại lượng đặc trưng cho sự quay nhanh hay
chậm của chất điểm, có giá trị bằng góc quay mà nó quay được
trong một đơn vị thời gian
Hình 1.7. Véctơ vận tốc góc Vận tốc góc trung bình:    (1.20) t 
Khi cho t 0 và lấy giới hạn tỉ số trên thì theo định nghĩa ta tìm được vận tốc góc tức thời:   d   (1.21) dt
Véc tơ vận tốc góc có: 14
+ Phương: là phương của trục vòng tròn (đi qua tâm vuông góc với mặt phẳng quỹ đạo)
+ Chiều: thuận với chiều quay ( theo quay tắc cái đinh ốc) d + Độ lớn:   dt + Đơn vị: Rad/s
Khi chất điểm chuyển động tròn đều (  không đổi) người ta định nghĩa chu kì là thời
gian chất điểm chuyển động hết một vòng:  2 T   (1.22)
T được gọi là chu kì, đơn vị (s). Nghịch đảo của chu kỳ quay là tần số (đơn vị Hz) 1 f  (1.23) T
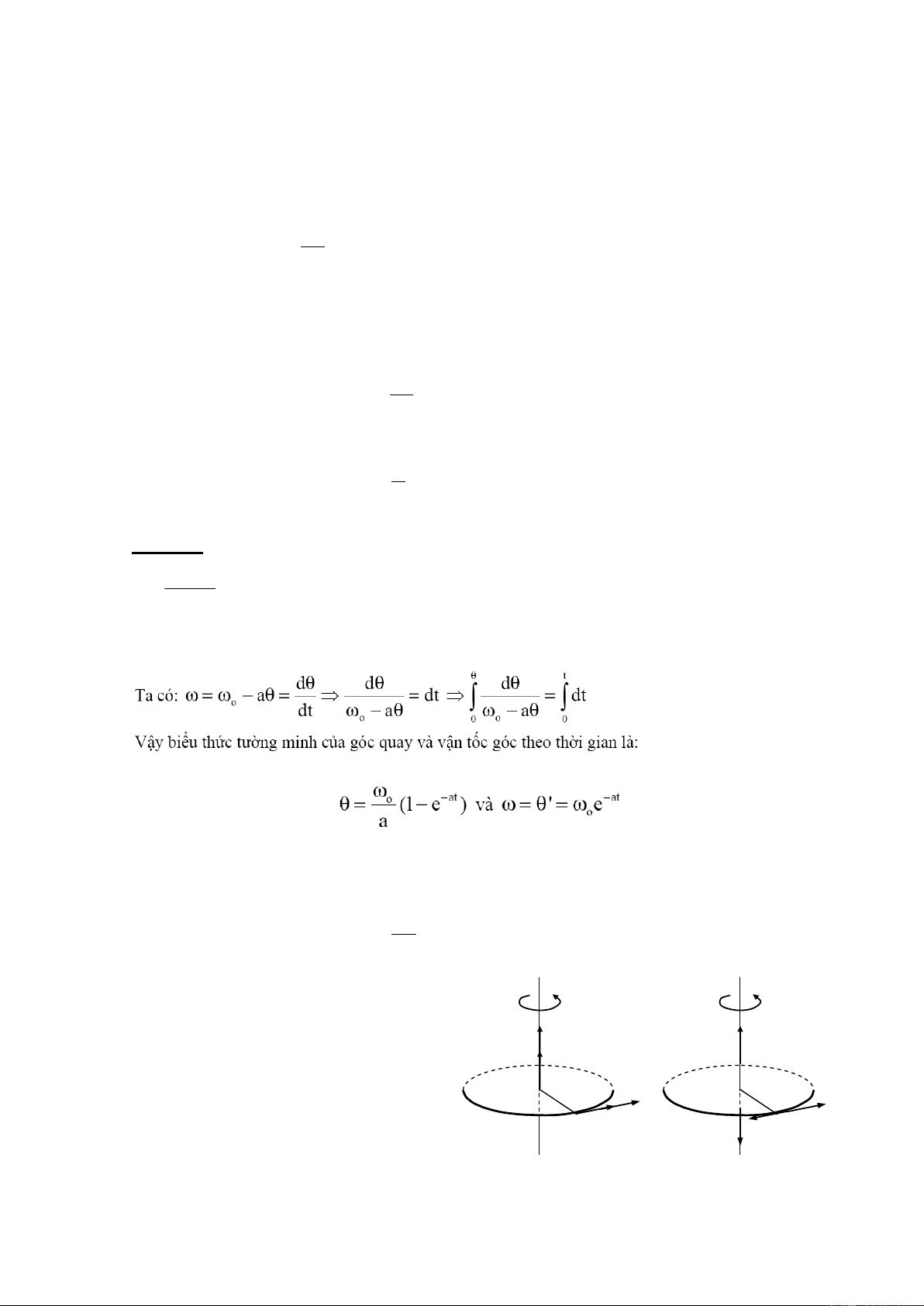
Ví dụ 1.7 : Một vật chuyển động tròn quanh điểm O với góc quay  là hàm của vận tốc góc  0   
. Trong đó 0 , a là các hằng số dương. Lúc t = 0 thì  = 0. Tìm (t) và (t) a Giải
b, Gia tốc góc 
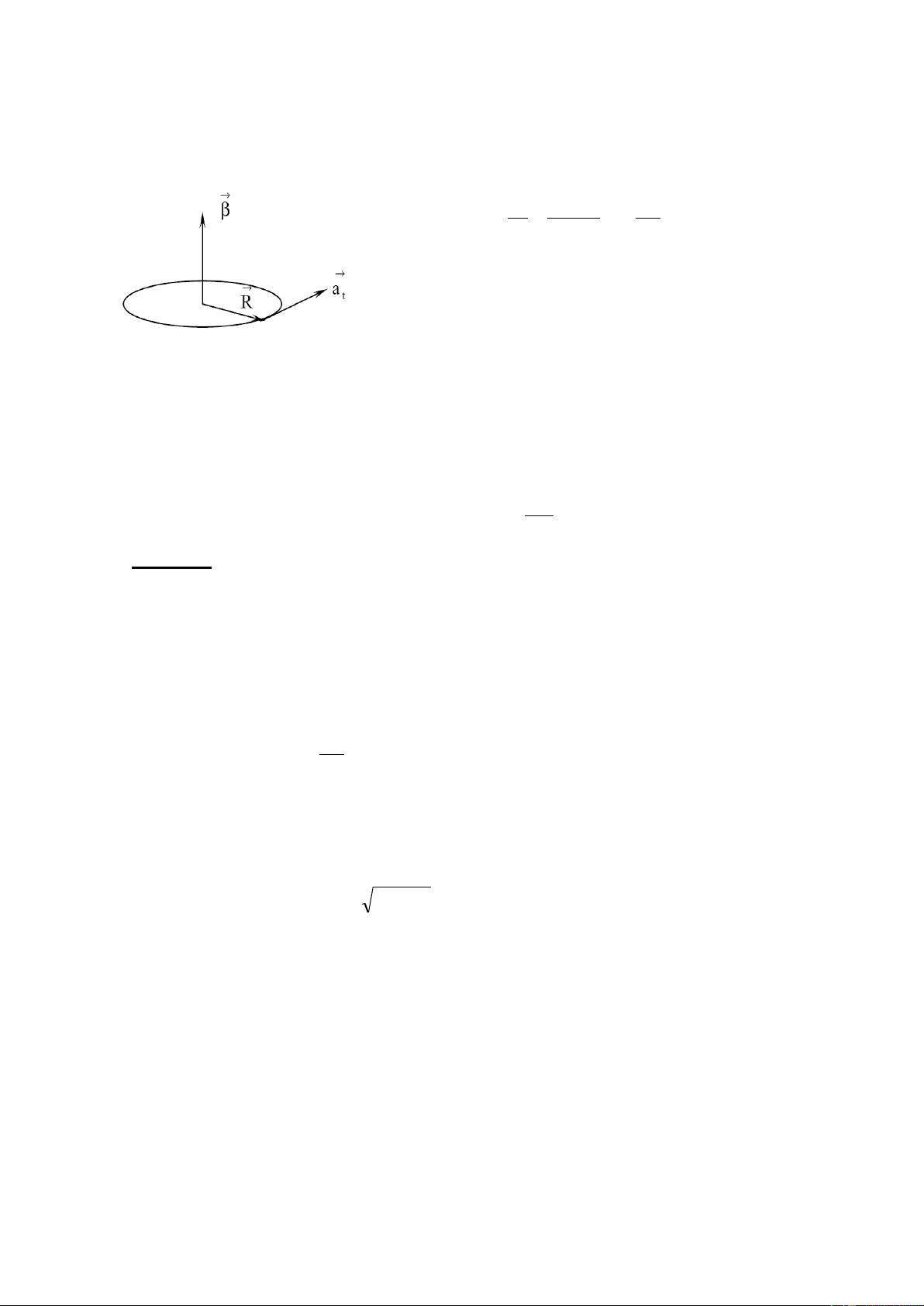
Véc tơ gia tốc góc  bằng đạo hàm theo thời gian của vận tốc góc:   d   (1.24) dt Véc tơ gia tốc góc có:
+ Phương: trùng với phương vận
tốc góc ( tức là trùng vớ   i trục đường   tròn quỹ đạo)
+ Chiều: cùng chiều  nếu  O M’  O M’  v    v tăng, ngược chiều  a nếu  giảm M t M a  t
Hình 1.8. Véctơ gia tốc góc 15 + Độ lớn: d   dt + Đơn vị: Rad/s2
Ví dụ 1.8 : Một chất điểm quay tròn quanh một trục cố định. Phương trình chuyển động có dạng: 3
  bt  ct với b = 6rad/s; c = 2rad/s3. Hãy xác định vận tốc góc, gia tốc góc lúc t = 0
và lúc chất điểm dừng lại. Tính giá trị trung bình của vận tốc góc, gia tốc góc trong khoảng thời gian đó Giải
c, Các công thức liên hệ
 Liên hệ giữa vận tốc dài và vận tốc góc ds d Vì ds = Rd nên  R Vậy: dt dt v = R. (1.25)  
Nếu để ý đến chiều của ba véc tơ v, , R  ta viết được:   
v    R
Hình 1.9: Quan hệ giữa vận tốc dài và vận tốc góc
 Liên hệ giữa gia tốc pháp tuyến và vận tốc góc 2 2  Từ v (R ) a   n R R an = R.2 (1.26)     Hay dạng véc tơ: a 2  
 R ( vì R ngược chiều với a ) n n 16
 Liên hệ giữa gia tốc tiếp tuyến và gia tốc góc dv d (R) d - Từ a    R t dt dt dt at = R. (1.27)   
- Nếu để ý đến chiều của ba véc tơ a , , R  ta viết t   
được: a    R t
Hình 1.10: Quan hệ giữa gia tiếp tuyến và gia tốc góc
 Các công thức chuyển động:      t. (1.28) 0 2 t
     t  (1.29) 0 0 2
Ví dụ 1.10: Một bánh xe bán kính r =10cm bắt đầu quay có gia tốc sao cho tần số quay tăng
thêm ½ vòng sau mỗi giây. Tìm vận tốc góc, gia tốc góc, vận tốc dài, gia tốc tiếp tuyến, gia
tốc pháp tuyến và gia tốc toàn phần của một điểm trên vành bánh xe tại giây thứ hai. Giải:
Tần số quay của bánh xe là: f = ½.t
Vận tốc góc:  = 2.f = .t = 3,14.2 = 6,28(rad/s) 
Gia tốc góc:   d   = 3,14(rad/s2) dt
Vận tốc dài: v = .R = .t.R = 3,14.2.0,1 =0,628(m/s)
Gia tốc pháp tuyến: an = 2.R = 2.t2.R = (3,14)2.22.0,1 = 3,944(m/s2)
Gia tốc tiếp tuyến: at = .R = .R = 3,14.0,1 = 0,314(m/s2) Gia tốc toàn phần: 2 2 a 
a  a = 3,965(m/s2) t n
III. Bài toán áp dụng
1. Bài toán ném xiên:
Một hòn đá được ném lên với vận tốc ban đầu v0 và nghiêng với mặt phẳng nằm
ngang một góc , hãy xác định:
a, Dạng quỹ đạo của hòn đá
b, Độ cao lớn nhất mà hòn đá đạt được
c, Tầm xa của hòn đá
d, Độ lớn và hướng của vận tốc ở điểm rơi. bỏ qua sức cản của không khí Giải: 17
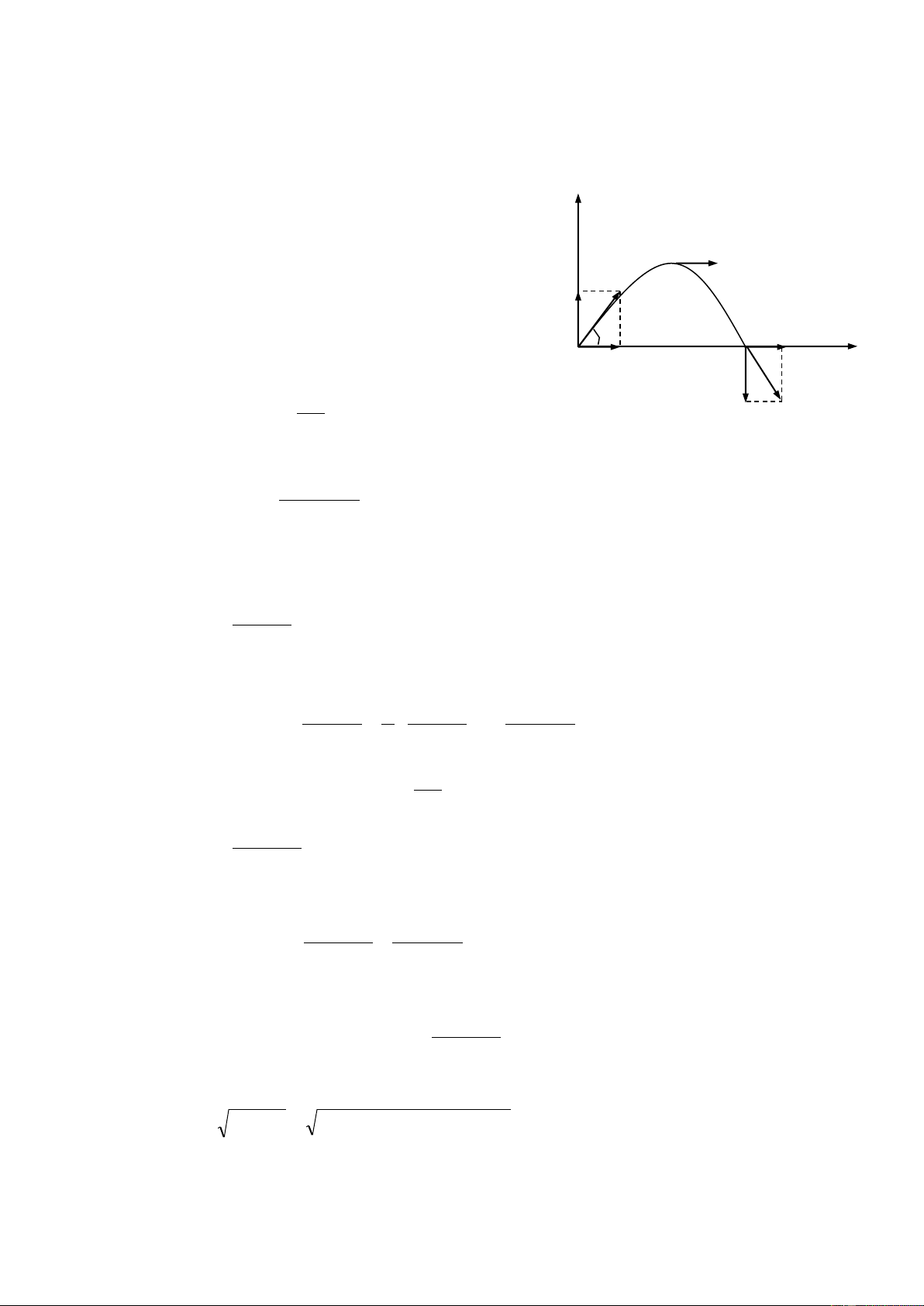
Chọn hệ quy chiếu O tại mặt đất và ngay điểm ném, gắn hai trục Ox, Oy như hình vẽ
Các thành phần gia tốc trên hai trục là:
a(a  ,o a  g) y x y
Các thành phần vận tốc ở thời điểm t bất kì: A
vx = vox + axt = v0x = v0.cos
vy = voy + ayt = v0.sin - gt v v o oy
Phương trình chuyển động của hòn đá: vox B v x = v ox x x 0.cos.t vy 2 gt VB y = v0.sin.t - 2
Khử t từ phương trình chuyển động ta có phương trình quỹ đạo: g 2 y  . x tg  x 2 2 2v cos  0
ta nhận thấy quỹ đạo là đường Parabol
Ở điểm cao nhất A thì vy = 0 nên v0.sin - gt = 0, suy ra thời gian đến độ cao cực đại là v sin  t 0  OA g
Thay vào phương trình chuyển động ta tính được độ cao cực đại: 2 v sin 
g  v sin   v 2 sin 2  y  v sin 0 0 0    max 0   g 2  g  2g 2
Ở điểm rơi B thì y = 0 hay v gt 0.sin.t -
= 0, suy ra thời gian tương ứng là: 2 v 2 sin  t 0  OB g
Thay vào phương trình ta tính được tầm xa: v 2 sin  v 2 sin  x  v cos 2 0 0  max 0 g g
Các thành phần vận tốc tại B: vx = v0cos 2v sin  v v sin  0    y = v0sin - gtOB = g v sin  0 0 g
Độ lớn của vận tốc tại B là: 2 2 2 2
v  v  v  (v cos  )  ( v  sin)  v x y 0 0 0
2. Bài toán ném ngang: 18
Từ một đỉnh tháp cao h ta ném một hòn đá theo phương nằm ngang với vận tốc v0. Xác định:
a, Quỹ đạo của hòn đá
b, Thời gian chuyển động của hòn đá (từ lúc ném đến lúc chạm đất)
c, Khoảng cách từ chân tháp đến điểm hòn đá chạm đất ( tầm xa)
d, Vận tốc, gia tốc toàn phần, gia tốc tiếp tuyến và gia tốc pháp tuyến của hòn đá tại
điểm nó chạm đất
e, Bán kính cong của quỹ đạo tại điểm bắt đầu ném và điểm chạm đất. Bỏ qua sức cản của không khí Giải:
Hòn đá tham gia đồng thời hai chuyển động: chuyển động đều theo phương nằm
ngang với vận tốc v0 và chuyển động rơi tự do theo phương thẳng đứng.
Chọn hệ trục toạ độ Oxy như hình vẽ, gốc O trùng với điểm hòn đá bắt đầu chuyển
động. Chọn gốc thời gian lúc bắt đầu ném đá
Gọi x, y là toạ độ của hòn đá tại thời điểm t. Phương trình chuyển động của hòn đá theo hai trục: x = v0.t 1 y = 2 gt 2
Khử t trong các phương trình chuyển động ta được phương trình quỹ đạo: g 2 y  x 2 2v0
Quỹ đạo là một nhánh Parabol
Khi hòn đá chạm đất: y = h. Gọi t’ là thời gian chuyển động của hòn đá, ta có: 2h t'  g
Khoảng cách L từ chân tháp đến điểm hòn đá rơi ( tầm xa) chính là hoành độ của hòn đá ứng
với thời gian chuyển động t = t’ L = v0.t’
Vận tốc lúc hòn đá cham đất (t = t’) 2 2  dx   dy  2 v     
  v  gt' t ' 0  2  dt   dt 
Gia tốc toàn phần của hòn đá: 19  2 2 d 2 x   d 2 y  a  
 0  g 2  g  2    2    dt   dt   
Góc  hợp bởi v và v được xác định: x v y sin   v
Gia tốc tiếp tuyến và pháp tuyến lần lượt là: at = a.sin = gsin an = a.cos = gcos 2 v
Bán kính cong quỹ đạo bằng v R 
. Tại điểm bắt đầu ném đá v = v 0 0, an = g nên: R  a 0 g n 2
tại điểm hòn đá chạm đất v = v v '
t’, an = g.cos nên: R t  g. cos 
--------------------------------------------------------------- Bài tập chương 1 A. Bài tập ví dụ
Bài 1. Một ôtô chuyển động nhanh dần đều trên một đoạn đường thẳng Ox. Ô tô đi qua hai
điểm A, B cách nhau 20m trong khoảng 2s. Vận tốc ô tô qua B là 12m/s. Xác định:
a, Gia tốc của ô tô và vận tốc của ô tô tại điểm A
b, Quãng đường mà ô tô đi được từ điểm khởi hành O đến A Giải
Chọn gốc tọa độ và thời gian tại điểm khởi hành O: t0 = 0, x0 = 0, v0 = 0    Áp dụng công thức: v v v v v B A B A a   
suy ra v  v   . a (1) t  t  t  B A B A
Mặt khác theo công thức: 2 2 v  v  . 2 .
a S hay: (v  v ).(v  v )  . 2 . a S (2) B A 2 B A B A 2 Lấy . 2 S
(2) chia cho (1) vế theo vế ta được: 2 v  v  B A  . 2 S 20 . 2 Suy ra 2 v   v  12  ( 8 m / s) A B  2
Bài 2. Một vật rơi tự do tại nơi có g = 10m/s2. Trong 2 giây cuối vật rơi được 180m.
a, Tính thời gian rơi
b, Độ cao nơi buông vật Giải
Chọn trục Oy có phương thẳng đứng chiều dương hướng xuống, gốc O tại vị trí thả vật 20