Giới thiệu thuật toán xấp xỉ và các bài toán áp dụng - Công nghệ thông tin | Trường Đại học Quy Nhơn

Thuật toán xấp xỉ MỤC LỤC
CHƯƠNG 1: MỘT SỐ KIẾN THỨC CƠ BẢN 5
VỀ THUẬT TOÁN VÀ ĐỘ PHỨC TẠP CỦA THUẬT TOÁN 7
1. Thuật toán....................................................................................................................7
1.1 Khái niệm bài toán.........................................................................................................................................7
1.2. Khái niệm thuật toán....................................................................................................................................7
1.3. Các yêu cầu của thuật toán.......................................................................................................................7
1.4 Các phương pháp mô tả thuật toán........................................................................................................8
2. Độ phức tạp của thuật toán.........................................................................................8
2.1. Đánh giá thời gian thực hiện thuật toán.............................................................................................8
2.2. Chi phí phải trả cho một quá trình tính toán..................................................................................10
2.3. Thời gian thực hiện giải thuật................................................................................................................11
2.4. Độ phức tạp của thuật toán.....................................................................................................................11
2.5. Các qui tắc xác định độ phức tạp thuật toán..................................................................................13
3. Vấn đề phân lớp các bài toán....................................................................................14
CHƯƠNG 2: MỘT SỐ THUẬT TOÁN XẤP XỈ 17
1...................................................................................... Khái niệm về thuật toán xấp xỉ
.............................................................................................................................................. 17
2. Một số bài toán minh họa..........................................................................................18
2.1. Bài toán phủ đỉnh đồ thị...........................................................................................................................18
2.2. Bài toán Người du lịch..............................................................................................................................19
2.2.1. Thuật toán láng giềng gần nhất (Nearest-neighbor algorithm).........................................20
2.2.2. Thuật toán phân mảnh (Multifragment-heuristic algorithm)..............................................21
2.2.3. Thuật toán vòng quanh cây 2 lần (Twice-around-the-tree algorithm)............................21
2.3. Bài toán KNAPSACK - Bài toán xếp ba lô.....................................................................................23 1 1
Thuật toán xấp xỉ
2.3.1 Phát biểu bài toán....................................................................................................................................24
2.3.2 Các hướng tiếp cận giải bài toán......................................................................................................26
2.3.2.1 Tiếp cận hướng kỹ thuật Quay lui – Vét cạn...........................................................................26
2.3.2.2 Tiếp cận hướng kỹ thuật Quy hoạch động.................................................................................30
2.3.2.3 Tiếp cận hướng kỹ thuật Nhánh – cận.........................................................................................34
2.3.2.4 Tiếp cận hướng kỹ thuật Tham lam...............................................................................................40
2.3.2.5 Tiếp cận hướng kỹ thuật Di truyền................................................................................................45
Một số bài tập áp dụng.......................................................................................................................................63 2 2
Thuật toán xấp xỉ 3 3
Thuật toán xấp xỉ PHẦN MỞ ĐẦU
1. Lý do chọn đề tài
Như chúng ta đã biết, để giải quyết được một bài toán, chúng ta cần tìm ra
đưuọc thuật toán. Khi có nhiều thuật toán, ta cần lựa chọn thuạt toán “tôt nhất”. Để
đánh giá thuật toán “tôt”, có thể có nhiều tiêu chí. Tuy nhiên, thường thì ta xét đến hai
tiêu chí chính là độ phức tạp về không gian và độ phức tạp về thời gian. Với khoa học
công nghệ phát triển như hiện nay, không gian nhớ hầu như không còn là vấn đề. Hiện
nay có khá nhiều phương pháp hữu hiệu với chi phí khá thấp về thời gian tính toán để tìm
được lời giải. Tuy nhiên, với những bài toán trong thực tế có dữ liệu vào rất lớn hoặc những
bài toán không tồn tại thuật toán giải tối ưu đề tìm nghiệm chính xác thì ta cần sử dụng
phương pháp giải – thuật toán xấp xỉ để tìm nghiệm với tỉ lệ xấp xỉ chấp nhận được. Phương
pháp này đã được ứng dụng rộng rãi để giải các bài toán mà không yêu cầu đòi hỏi phải
tìm được nghiệm chính xác, bởi ngay từ dữ liệu đầu vào của bài toán có thể đã là dữ liệu xấp
xỉ. Vì vậy, tìm được thuật toán xấp xỉ giải bài toán có chi phí thời gian tính toán thấp mà vẫn
đảm bảo độ chính xác theo yêu cầu là mục tiêu của bài báo cáo này cần đạt được. Theo cách
tiếp cận này, chúng tôi xây dựng được thuật toán có độ phức tạp về thời gian tính toán là đa
thức khi bài toán được xét trong không gian Euclide và nghiệm tìm được có độ chính xác chấp nhận được.
Trong bài báo cáo này, chúng tôi giới thiệu một số kiến thức về thuật toán nói chung
và thuật toán xấp xỉ. Từ đó, đề xuất một thuật toán xấp xỉ để tìm lời giải cho bài toán Phủ
đỉnh đồ thị, Người du lịch, Xếp ba lô. 2. M
ục đích nghiên cứu
- Đưa ra cơ sở lí thuyết về thuật toán, độ phức tạp thuật toán; thuật toán xấp xỉ.
- Trình bày hướng giải quyết bằng thuật toán xấp xỉ cho bài toán: Phủ đỉnh đồ thị,
Người du lịch, Xếp ba lô. 3. Đ
ối tượng và phạm vi nghiên cứu
3.1. Đối tượng nghiên cứu: Thuật toán xáp xỉ. 4 4
Thuật toán xấp xỉ
3.2. Phạm vi nghiên cứu: Lý thuyết về thuật toán, thuật toán xấp xỉ và ứng dụng
4. Phương pháp nghiên cứu
Phương pháp sử dụng: Nghiên cứu lý thuyết
- Nghiên cứu tài liệu về thuật toán, phân tích và đánh giá độ phức tạp thuật toán.
- Nghiên cứu, phân tích và đề xuất hướng giải quyết bằng thuật toán xấp xỉ cho
bài toán: Phủ đỉnh đồ thị, Người du lịch, Xếp ba lô. 5 5
Thuật toán xấp xỉ
CHƯƠNG 1: MỘT SỐ KIẾN THỨC CƠ BẢN
VỀ THUẬT TOÁN VÀ ĐỘ PHỨC TẠP CỦA THUẬT TOÁN 1. Thuật toán 1.1 Khái niệm bài toán
Một bài toán trong tin học là một bài toán thỏa mãn: xuất phát từ bộ INPUT đầu
vào, chúng ta phải thu được bộ OUTPUT đầu ra.
Một số vấn đề cần quan tâm:
+ Bài toán được giải bằng máy tính điện tử
+ Cần làm rõ: dữ liệu cần được đưa vào máy tính (Input) là gì và cần lấy ra (Output) thông tin gì?
+ Làm thế nào để từ Input ta có được Output? (Thuật toán giải)
Hiển nhiên đối với bài toán tin học là nghiên cứu thuật toán giải bài toán tương ứng.
1.2. Khái niệm thuật toán
Định nghĩa 1: Thuật toán là một dãy hữu hạn các thao tác được sắp xếp theo một
trình tự nhất định để sau khi thực hiện dãy các thao tác đó, từ input ta có output cần tìm [1].
Trong lý thuyết thuật toán, cụm từ “thuật toán” đôi khi người ta dùng bằng một từ
khác là “giải thuật”.
1.3. Các yêu cầu của thuật toán
Thuật toán phải đảm bảo được các yêu cầu sau đây:
- Tính tổng quan: thuật toán phải đúng đối với mọi bộ dữ liệu đầu vào.
- Tính xác định: Các bước của thuật toán phải được trình bày rõ ràng, mạch lạc, đảm
bảo cho người đọc chỉ hiểu theo một nghĩa duy nhất.
- Tính khả thi: Thuật toán phải thực hiện được, nghĩa là ta có thể sử dụng máy tính kết
hợp giữa các ngôn ngữ lập trình để thể hiện thuật toán trong thời gian hữu hạn.
- Tính dừng: Nếu dữ liệu vào thỏa mãn điều kiện đầu vào thì thuật toán phải kết thúc
và cho ra kết quả sau một số hữu hạn bước. 6 6
Thuật toán xấp xỉ
- Tính chính xác (tính đúng đắn): Thuật toán phải cho kết quả chính xác và thể hiện
đúng đắn trên cơ sở toán học.
- Tính tối ưu: Thuật toán phải có chi phí về không gian bộ nhớ ít nhất và chạy trong thời gian nhanh nhất.
1.4 Các phương pháp mô tả thuật toán
Thuật toán được thể hiện bằng một trong các cách sau:
Phương pháp liệt kê:
Liệt kê lần lượt các bước để thực hiện thuật toán, tại mỗi bước ta sử dụng các ký hiệu
toán học kết hợp với ngôn ngữ tự nhiên.
Phương pháp sử dụng sơ đồ khối
Sử dụng các loại hình khối để thể hiện là: hình elip chỉ điểm bắt đầu hay kết thúc, hình
thoi chỉ khối kiểm tra và hình chữ nhật chỉ khối tính toán. Có một cung định hướng để chỉ
hướng đi của thuật toán.
Khối bắt đầu (kết thúc) Khối kiểm tra Khối tính toán Cung định hướng
Ta kết hợp ba loại hình khối và cung định hướng này để biểu diễn thuật toán.
Mô tả thuật toán bằng các chương trình
Sử dụng ngôn ngữ lập trình để thể hiện thuật toán, cấu trúc chặt chẽ của các ngôn ngữ
lập trình cho phép chúng ta thể hiện thuật toán một cách rõ ràng và dễ hiểu. Phương pháp này
được áp dụng rộng rãi nhất.
2. Độ phức tạp của thuật toán
2.1. Đánh giá thời gian thực hiện thuật toán - Tính độc lập
Tốc độ thực hiện một chương trình là khoảng thời gian từ INPUT có được OUTPUT
của bài toán. Tuy nhiên tốc độ thực hiện một chương trình phụ thuộc vào ngôn ngữ lập trình,
chương trình dịch, hệ điều hành, phần cứng của máy… Mặt khác, phải lập trình mới đo được
thời gian thực hiện của thuật toán.
Cần đánh giá thời thực hiện sao cho: 7 7
Thuật toán xấp xỉ
+ Không phụ thuộc máy, ngôn ngữ lập trình, chương trình biên dịch;
+ Không cần phải triển khai chương trình thực hiện thuật toán;
+ Chỉ dựa vào bản thân thuật toán.
Trong 2 thuật toán, ta đã tính thời gian thực hiện thuật toán bằng số phép tính cần tiến
hành. Đây chính là cách làm đáp ứng nhu cầu trên.
- Các phép toán sơ cấp
Các phép toán sơ cấp là những phép toán mà thời gian thực hiện nó đủ ngắn, hay nói
đúng hơn là không vượt quá một hằng số nào đó. Các phép toán sau đây có thể coi là sơ cấp: + Các phép tính số học; + Các phép tính logic;
+ Các phép chuyển chỗ, phép gán;
+ Lời gọi các thủ tục.
- Kích thước dữ liệu đầu vào
Cho một thuật toán ta hoàn toàn ước lượng được tổng số các phép toán sơ cấp cần thiết
để thực hiện thuật toán đó. Một điều hiển nhiên là tổng số phép toán sơ cấp để giải một bài
toán phụ thuộc vào kích thước của bài toán. Dùng cùng một thuật toán, tính một định thức
cấp 5 rõ ràng cần ít phép tính hơn định thức cấp 10. Tổng số mục dữ liệu đầu vào là đặc trưng
cho kích thước của bài toán. Người ta thường dùng một số nguyên dương n để thể hiện kích thước này.
Như vậy, một thuật toán T áp dụng để giải bài toán có kích thước n sẽ cần một tổng số
T(n) các phép toán sơ cấp. T(n) là một hàm của tham số n. Hàm số T(n) là đặc trưng cho hiệu quả của thuật toán T.
- Tình trạng dữ liệu đầu vào
Không chỉ có số lượng dữ liệu đầu vào quyết định thời gian thực hiện giải thuật mà
tình trạng dữ liệu cũng ảnh hưởng đến việc thuật toán thực hiện nhanh hay chậm.
Xét bài toán sắp xếp đơn điệu một dãy số. Rõ ràng là nếu dãy đã có sẵn thứ tự mong
muốn hoặc gần thư thế thì công việc phải làm ít hơn trường hợp một dãy bất kỳ.
Hoặc bài toán tìm kiếm tuần tự trong một dãy số cho sẵn như tìm vị trí của phần tử k
trong mảng a[1.. n] (nếu k ở vị trí đầu tiên hoặc k không tồn tại trong mảng a)
+ Trường hợp mới bắt đầu tìm kiếm gặp ngay phần từ k thì đây là trường hợp tốt nhất (best case) T(n) = 1. 8 8
Thuật toán xấp xỉ
+ Trường hợp tìm kiếm mà không có k trong mảng hay k nằm ở cuối mảng thì đây là
trường hợp xấu nhất, phải duyệt qua tất cả các phần tử của mảng a[1..n] (worst case). T(n) = n.
+ Trường hợp trung bình T(n) = 0, 5. p(n + 1) + n(1 – p).
Tùy theo tình trạng dữ liệu đầu vào mà ta có các trường hợp:
+ Thời gian tốt nhất T(n) là thời gian thực hiện nhanh nhất của thuật toán với một bộ
dữ liệu nào đó, ta ký hiệu là Tmin (best case).
+ Thời gian tồi nhất T(n) là thời gian thực hiện chậm nhất của thuật toán với một bộ
dữ liệu nào đó, ta ký hiệu là Tmax (worst case).
+ Thời gian tính trung bình T(n) là trung bình cộng của các thời gian thực hiện thuật
toán với các bộ dữ liệu khác nhau nào đó, ta ký hiệu là Taver (average case).
Trong thực tế ta thường dùng thời gian thực hiện trung bình Taver để so sánh đánh giá
thuật toán. Nếu việc tính thời gian thực hiện trung bình quá khó khăn, có thể đánh giá căn cứ
vào trường hợp xấu nhất, tức là dùng Tmax. Đôi khi, nhiều bài toán thời gian thực đòi hỏi thời
gian trả lời phải không vượt quá một giới hạn cho phép nào đó (ví dụ như bài toán dự báo
thời tiết). Trong trường hợp này, chỉ có thể dùng ước lượng trong trường hợp xấu nhất, nghĩa là Tmax mà thôi.
2.2. Chi phí phải trả cho một quá trình tính toán
Xét một quá trình tính toán, chi phí phải trả cho một quá trình tính toán bao gồm:
+ Chi phí về không gian: bộ nhớ - số ô nhớ cần sử dụng trong quá trình tính toán.
+ Chi phí về thời gian: thời gian cần sử dụng cho một quá trình tính toán.
+ Nếu cho một thuật toán A. Thuật toán này thực hiện trên bộ dữ liệu e. Khi đó, thuật toán A
phải trả 2 giá: giá về không gian là LA(e), giá về thời gian là TA(e), với e là bộ dữ liệu vào.
Nhận xét: cùng một thuật toán A mà xác định thực hiện trên các bộ dữ liêu khác nhau
sẽ trả các giá khác nhau. Khi đó ta có các khái niệm về chi phí phải trả trong các trường hợp như sau:
+ Chi phí phải trả trong trường hợp xấu nhất ứng với bộ dữ liệu xấu nhất so với Output.
+ Chi phí phải trả trung bình: là tổng số các chi phí khác nhau ứng với các bộ số liệu
chia cho tổng số số bộ số liệu. 9 9
Thuật toán xấp xỉ
+ Chi phí phải trả tiệm cận: Đó là biểu thức biểu diễn tốc độ tăng của chi phí thực tế
phải trả. Nó có giá trị tiệm cận với chi phí thực tế.
Ngày nay do sự phát triển không ngừng của khoa học công nghệ kỹ thuật điện tử nên
chi phí về bộ nhớ không còn là vấn đề cần thiết phải bàn tới mà ta chỉ quan tâm tới chi phí
phải trả về thời gian thực hiện giải thuật. Từ đây ta chỉ xét đến thời gian thực hiện giải thuật
T(n), hay đó chính là độ phức tạp của thuật toán.
2.3. Thời gian thực hiện giải thuật
Với một bài toán, không chỉ có một giải thuật. Chọn một giải thuật đưa tới kết quả
nhanh là một đòi hỏi thực tế. Nhưng căn cứ vào đâu để có thể nói được giải thuật này nhanh hơn giải thuật kia?
Có thể thấy ngay: thời gian thực hiện một giải thuật (hay chương trình thể hiện một
giải thuật đó) phụ thuộc vào rất nhiều yếu tố. Một yếu tố cần chú ý trước tiên đó là kích thước
của dữ liệu đưa vào. Chẳng hạn thời gian sắp xếp một dãy số phải chịu ảnh hưởng của số
lượng các số thuộc dãy số đó. Nếu gọi n là số lượng này (kích thước của dữ liệu vào) thì thời
gian thực hiện T của một giải thuật phải được biểu diễn như một hàm của n: T(n).
Các kiểu lệnh và tốc độ xử lý của máy tính, ngôn ngữ viết chương trình và chương
trình dịch ngôn ngữ ấy đều ảnh hưởng tới thời gian thực hiện; nhưng những yếu tố này không
đồng đều với mọi loại máy trên đó cài đặt giải thuật, vì vậy không thể đưa chúng vào khi xác
lập T(n). Điều đó có nghĩa là T(n) không thể được biểu diễn thành đơn vị thời gian bằng giây,
bằng phút được. Tuy nhiên, không phải vì thế mà không thể so sánh được các giải thuật về
mặt tốc độ. Nếu như thời gian thực hiện của một giải thuật là T1(n) = c.n^2 và thời gian thực
hiện một giải thuật khác là T2(n) = k.n (với c và k là một hằng số nào đó), thì khi n khá lớn,
thời gian thực hiện giải thuật T2 rõ ràng ít hơn so với thời gian thực hiện giải thuật T1. Như
vậy, nếu nói thời gian thực hiện giải thuật bằng T(n) tỉ lệ với n^2 hay tỉ lệ với n cũng cho ta ý
niệm về tốc độ thực hiện giải thuật đó khi n khá lớn (với n nhỏ thì việc xét T(n) không có ý
nghĩa). Cách đánh giá thời gian thực hiện giải thuật độc lập với máy tính và các yếu tố liên
quan với máy như vậy sẽ dẫn tới khái niệm về cấp độ lớn của thời gian thực hiện giải thuật
hay còn gọi là độ phức tạp tính toán của giải thuật.
2.4. Độ phức tạp của thuật toán
Định nghĩa 2: Một hàm f(n) được xác định là O(g(n)), kí hiệu f(n) = O(g(n)) nếu tồn
tại các hằng số C và số nguyên n0 sao cho f(n) ≤ C.g(n) với mọi n ≥ n0 10 1 0
Thuật toán xấp xỉ
Ví dụ: Chứng minh hàm t( ) = 100 n + 5 n O(n^2).
- Giả sử ta chọn số c và n0 tương ứng trong trường hợp này là 101 và 5. - Ta có: 100 + 5 < 100 n n + n ( ≥ 5) = 101 n ≤ 101n^2 n
Một cách khác để kiểm tra hàm t( )
n có thuộc lớp hàm O(g(n)) đó là ta sử dụng giới hạn hàm số:
nếu c là một hằng số thì t(n) O(g(n)).
Ví dụ: chứng minh hàm t(n) = ½ n(n-1) O( 2). n^
Suy ra hàm t(n) = ½ n(n-1) O(n^2).
Thông thường các hàm thể hiện độ phức tạp tính toán của giải thuật có dạng: O(log2n), O(n), O(nlog n), 2
O(n^2), O(n^3), O(2^n), O(n!), O(n^n). Các hàm như 2^n, n^n được gọi là
hàm loại mũ. Các dạng như n^3, n^2, nlog n, 2 log n
2 được gọi là các hàm loại đa thức. Giải
thuật với thời gian thực hiện có cấp hàm đa thức thì thường hiệu quả và chấp nhận được. 11 1 1
Thuật toán xấp xỉ
Một số lớp hàm thông dụng trong phân tích thuật toán
Nhìn vào bảng trên ta nhận thấy rằng thời gian máy tính thực hiện dùng bởi một thuật
toán phụ thuộc rất lớn vào thuật toán và dữ liệu đầu vào áp dụng đối với thuật toán đó, điều
này giúp chúng ta trong việc lựa chọn thuật toán phù hợp đáp ứng nhu cầu thực tiễn và tính khả thi của nó.
2.5. Các qui tắc xác định độ phức tạp thuật toán
Quy tắc tổng và lấy max: Giả sử T1(n) và T2(n) là thời gian thực hiện của 2 đoạn
chương trình P1 và P2 kế tiếp nhau, T1(n) = O(f(n)); T2(n) = O(g(n)) thì thời gian thực hiện
P1 rồi P2 tiếp theo sẽ là: T1(n) + T2(n) = O(max(f(n), g(n))).
Tính chất này cho ta biết tình huống sau: nếu thuật toán thực hiện hai phần liên tiếp
nhau, độ phức tạp của thuật toán chính là độ phức tạp của phần có bậc cao hơn. Ví dụ, để
kiểm tra một mảng có các phần tử bằng nhau hay không? Ta có thể thiết kế thuật toán thành
hai phần: phần thứ nhất sắp xếp mảng tăng dần, phần thứ hai kiểm tra các phần tử kề nhau có bằng nhau không?
Độ phức tạp của phần sắp xếp mảng là O( 2)
n^ và độ phức tạp của phần kiểm tra phần
tử liền kề có bằng nhau hay không là O( ), vậy độ phức tạp c n
ủa thuật toán trên là O(max{n^2, n}) = O(n^2)
Quy tắc nhân: Nếu thời gian thực hiện tương ứng với P1 và P2 là T1(n)=O(f(n));
T2(n) = O(g(n)) thì thời gian thực hiện P1 và P2 lồng nhau sẽ là: T1(n).T2(n) = O(f(n).g(n)).
Chú ý: Trong các ngôn ngữ lập trình, chúng ta có thể đánh giá:
+ Thời gian thực hiện mỗi câu lệnh Gán, đọc, ghi dữ liệu là O(1).
+ Thời gian thực hiện mỗi chuỗi tuần tự các câu lệnh được tính theo quy tắc cộng. 12 1 2
Thuật toán xấp xỉ
+ Thời gian thực hiện cấu trúc if (điều kiện) ... được tính bằng thời gian thực hiện câu
lệnh sau điều kiện hoặc sau else. Còn câu lệnh điều kiện thường là O(1).
+ Thời gian thực hiện vòng lặp được tính là tổng trên tất cả số lần lặp thời gian thực
hiện thân vòng lặp. Nếu thời gian thực hiện thân vòng lặp là hằng số thì thời gian thực hiện
vòng lặp là tích của số lần lặp với thời gian thực hiện thân vòng lặp.
3. Vấn đề phân lớp các bài toán.
Xét một bài toán tin học bất kì, chúng ta quan tâm đến các bài toán có lời giải. Vì độ
phức tạp giải thuật đối với mỗi bài toán là khác nhau, trên cơ sở đó các bài toán cũng được
phân chia thành các lớp thông qua độ phức tạp thuật toán giải chúng. Chúng ta xét các khái niệm sau:
- Lớp bài toán P (Lớp P-Polynomial time): là lớp các bài toán có thể giải được bằng
thuật toán đơn định đa thức có độ phức tạp đa thức.
Những bài toán thuộc lớp này có độ phức tạp là O(nk) với k là hằng số trong đó do vậy
O(logn); O(n); O(n.logn); O(n2) thuộc lớp này.
- Lớp bài toán NP (Lớp NP - Nondeterministic Polynomial ): là lớp các bài toán có thể
giải được bằng các thuật toán không đơn định đa thức.
Lớp bài toán có độ phức tạp không đa thức thường có độ phức tạp là O(an) hoặc O(n!),
những bài toán này chỉ giải được với độ lớn bộ dữ liệu đầu vào nhất định.
Cách phát biểu khác: Ta gọi NP là lớp các bài toán quyết định mà để xác nhận câu trả
lời ‘yes’ của nó ta có thể đưa ra bằng chứng ngắn gọn dễ kiểm tra.
Ví dụ: Cho một tập hợp các số nguyên, bài toán yêu cầu tìm một tập hợp con khác rỗng có tổng bằng 0.
+ INPUT: {−2, −3, 15, 14, 7, −10}
+ OUTPUT: {−2, −3, −10, 15}
Ta có thể được kiểm chứng dễ dàng bằng cách cộng các số đó lại. Tuy nhiên, hiện
chưa có thuật toán nào để tìm ra một tập hợp như thế trong thời gian đa thức (có một thuật
toán đơn giản thực thi là kiểm tra tất cả 2 -1 n
tập hợp con khác rỗng). Như vậy, bài toán này
nằm trong NP (kiểm chứng nhanh chóng) nhưng chưa biết có nằm trong P (giải nhanh chóng) hay không.
- Lớp Co-NP: Ta gọi Co-NP là lớp các bài toán quyết định mà để xác nhận câu trả lời
‘no’ của nó ta có thể đưa ra bằng chứng ngắn gọn dễ kiểm tra.
Một ngôn ngữ nằm trong Co-NP khi và chỉ khi phần bù của nó nằm trong NP. 13 1 3
Thuật toán xấp xỉ
Quan hệ giữa lớp P và NP có thể nhìn thấy một cách trực quan P NP, nhưng chúng
ta chưa biết P = NP hay không?
Lời giải của bài toán P = NP sẽ cho biết liệu tất cả các bài toán trong NP đều có thuật
toán thực thi trong thời gian đa thức hay không? Hầu hết các nghiên cứu cho thấy P ≠
NP việc xem xét quan hệ giữa P và NP dẫn đến chúng ta đi nghiên cứu lớp NP- đầy đủ.
- Lớp bài toán NP - đầy đủ (NP - Completeness): Một bài toán quyết định A được gọi
là NP-đầy đủ (NPC) nếu như:
+ A là một bài toán trong NP.
+ Mọi bài toán trong NP đều có thể quy dẫn về A.
Ta nói bài toán A quy dẫn được về bài toán B nếu bất kì thuật toán nào giải được B thì
cũng có thể được dùng để giải A (kí hiệu A α B).
Điểm then chốt của việc quyết định P thực tế có bằng NP hay không? được dựa trên
các định lý NPC sau đây:
Định lý 1: Ta có một phép dẫn thời gian đa thức từ bài toán A về bài toán B
i) Nếu bài toán A NPC, bài toán B NP thì B NPC
ii) Nếu bài toán B P thì bài toán A P
Định lý 2: Nếu một bài toán NPC
bất kỳ giải được trong thời gian đa thức thì P=NP,
ngược lại nếu một bài toán NP bất kỳ không giải được trong thời gian đa thức thì tất cả các
bài toán NPC đều không giải được trong thời gian đa thức.
Bằng việc sử dụng kỹ thuật dẫn bài toán A về bài toán B với một phép dẫn thích hợp
giúp chúng ta có thể biến đổi mỗi dữ kiện của bài toán A thành dữ kiện tương ứng của bài
toán B nhờ đó mà có thể chuyển thuật toán giải quyết bài toán B thành thuật toán tương ứng
giải quyết bài toán A
Định lí Cook-Levin: Nếu tồn tại một thuật toán thời gian đa thức để giải bài toán thỏa
mãn mạch logic thì mọi bài toán trong lớp NP đều có thể giải được trong thời gian đa thức.
Rõ ràng có những bài toán đã biết thuộc vào lớp NP nhưng không rõ có thuộc vào
lớp P hay không? tức là chúng ta có thể giải chúng trên một máy không đơn định nhưng chưa
tìm được lời giải hữu hiệu chạy trên máy thông thường để giải chúng. Hơn nữa những bài
toán NP này lại có thêm một tính chất nữa là “Nếu bất kì một trong những bài toán này có thể
giải được trong thời gian đa thức thì tất cả những bài toán thuộc lớp NP cũng sẽ giải được
trong thời gian đa thức trên một máy đơn định”. Những bài toán như vậy thuộc vào lớp bài
toán NP-đầy đủ - NPC. 14 1 4
Thuật toán xấp xỉ
Để chứng minh một bài toán A thuộc lớp NPC ta cần thực hiện 4 bước sau đây:
Bước 1: Chứng minh A NP
Bước 2: Lựa chọn bài toán A’ NPC
Bước 3: Xây dựng hàm biến đổi f từ A’ sang A
Bước 4: Chứng minh rằng f là một biến đổi đa thức
Ví dụ: bài toán A tìm chu tình Hamilton.
Cho đồ thị G vô hướng. Hỏi có tồn tại một chu trình qua tất cả các đỉnh của đồ thị?
Ta lựa chọn bài toán A’ sau: Cho tập hữu hạn các thành phố C={c1, c2, c3, ... cn}.
Khoảng cách giữa thành phố ci và cj là d(i,j) > 0 và một số B >0. Hỏi có tồn tại hay không
một đường đi qua tất cả các thành phố trong C mà có tổng độ dài không lớn hơn B.
Phép dẫn f biến đổi đồ thị G thành đồ thị G’ trong đó G’ được xây dựng bằng cách bổ
sung tất cả các cạnh của G để trở thành đồ thị đầy đủ G’ gán các trọng số của G’ như sau:
Trọng số các cạnh cũ của G gán bằng 1, trọng số các cạnh mới bổ sung gán bằng 2 và chọn
số B=n là số đỉnh của đồ thị.
Như vậy chu trình Hamilton trong G chính là đường đi qua tất cả các thành phố
trong G’ mà có tổng độ dài không lớn hơn n.
- Lớp bài toán NP- khó (NP-Hard): Một cách ngắn gọn có thể hiểu bài toán NP-khó là
bài toán mà không có thuật toán thời gian tính đa thức để giải nó trừ khi P = NP, mà chỉ có
các thuật toán giải trong thời gian hàm mũ. Sau đây là định nghĩa chính thức của bài toán NP- khó.
Định nghĩa. Một bài toán A được gọi là NP- (NP-har khó
d) nếu như sự tồn tại thuật
toán đa thức để giải nó kéo theo sự tồn tại thuật toán đa thức để giải mọi bài toán trong NP.
Bức tranh phân lớp các bài toán. 15 1 5
Thuật toán xấp xỉ
CHƯƠNG 2: MỘT SỐ THUẬT TOÁN XẤP XỈ
1. Khái niệm về thuật toán xấp xỉ
Nhiều bài toán có ý nghĩa rất quan trọng trong thực tiễn lại là NP đầy đủ. Nếu là
một bài toán NP đầy đủ, ta không thể tìm một thuật toán thời gian đa thức để giải nó chính
xác. Có hai cách tiếp cận để khắc phục tính đầy đủ NP.
Thứ nhất: nếu các đầu vào thực tế là nhỏ, một thuật toán có thời gian thực hiện hàm
mũ có thể hoàn toàn chấp nhận được
Thứ hai: vẫn có thể tìm các giải pháp gần tối ưu trong thời gian đa thức (hoặc
trong trường hợp xấu nhất hoặc tính trung bình). Trong thực tế để tính gần tối ưu thường là
đủ. Một thuật toán trả về các giải pháp gần tối ưu được gọi là một thuật toán xấp xỉ.
Xét một bài toán tối ưu hóa, ở đó mỗi giải pháp có thể đưa ra có một mức hao phí
dương, và ta muốn tìm giải pháp gần tối ưu. Tùy thuộc vào bài toán, một giải pháp gần tối
ưu có thể được định nghĩa là một giải pháp có mức hao phí khả dĩ cực đại hoặc một giải
pháp có mức hao phí khả dĩ cực tiểu, bài toán có thể là bài toán cực đại hóa hoặc cực tiểu hóa.
Một số thuật toán xấp xỉ cho bài toán có một cận tỷ số P(n) nếu với bất kỳ đầu vào
có kích cỡ n, mức hao phí C của giải pháp mà thuật toán xấp xỉ tạo sẽ nằm trong một thừa
số p(n) của mức hao phí C* của một giải pháp tối ưu:
Định nghĩa này áp dụng cả bài toán cực đại hóa lẫn cực tiểu hóa. Với một bài toán
cực đại hóa, 0 < C ≤ C* , và tỷ số cho ra thừa số qua đó mức hao phí của một giải pháp tối
ưu lớn hơn mức hao phí của một giải pháp xấp xỉ. Cũng vậy, với
một bài toán cực tiểu hóa,
0hao phí của một giải pháp tối ưu.
Cận tỷ số của một thuật toán xấp xỉ không bao giờ nhỏ hơn 1 bởi >= 1.
Tuy nhiên vấn đề ở đây là chúng ta không thể xác định được chính xác giá trị của C * .
Do đó chứng ta cần xác định một tỷ lệ hiệu suất xấp xỉ (gọi là p) và tất nhiên p>=1. Một thuật
toán có hiệu suất xấp xỉ là p(n) được gọi là thuật toán xấp xỉ -p(n). Khi p = 1 ta sẽ nhận được
nghiệm của thuật toán xấp xỉ chính là nghiệm tối ưu.
Như vậy một thuật toán xấp xỉ là chấp nhận được khi max(,)<=p. 16 1 6
Thuật toán xấp xỉ
Sau đây chúng ta sẽ nghiên cứu một số phương pháp thiết kế các thuật toán xấp xỉ
điển hình trong việc giải quyết các bài toán thuộc lớp NP.
2. Một số bài toán minh họa
2.1. Bài toán phủ đỉnh đồ thị (Vertex cover)
Phát biểu bài toán. Cho đồ thị vô hướng G=(V,E). Phủ đỉnh của G là một tập con
V’⸦V sao cho nếu (u,v) là một cạnh của G thì u V’ hoặc v V’. Kích thước của phủ đỉnh là
số lượng các đỉnh ở trong nó.
Cần xác định phủ các đỉnh có kích thước nhỏ nhất?
Bài toán quyết định phủ các đỉnh là bài toán thuộc lớp NP-C
Với một k cho trước, có tồn tại phủ các đỉnh V’ của đồ thị G sao cho |V’|<=k hay không?
Rất phức tạp để tìm giải pháp tối ưu.
Thuật toán xấp xỉ thì đơn giản
void Phucacdinh-xapxi(G=(V,E) { C=∅; U=E; while (U ∅) {
(u,v) là một cạnh bất kì thuộc U C=C (u,v)
Xóa trong U tất cả các cạnh nối đến u hoặc v } return C }
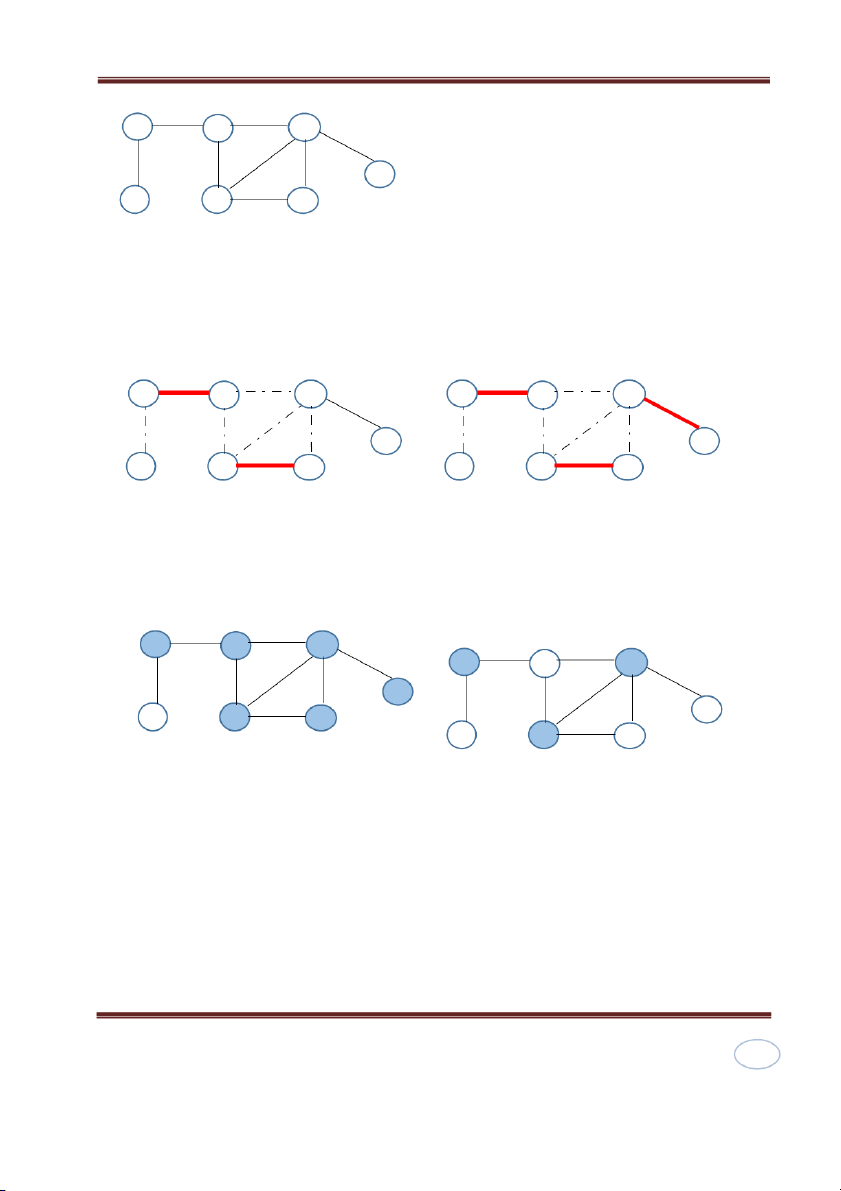
Thuật toán có độ phức tạp là hàm tuyến tính Minh họa b c d 17 1 g 7 f
Thuật toán xấp xỉ b c d g a e f C=∅ C={b,c} b c d b c d g g a e f a e f C={b,c, e,f} C={b,c, e,f,d,g} b c d b c d g a e g f a e f
Giái pháp xấp xỉ: b, c, e, f, d, g Giái pháp tối ưu: b, e, d
Thuật toán Phucacdinh-xapxi là thuật toán xấp xỉ - 2 Chứng minh
Gọi A là tập các cạnh (u,v) được chọn bởi thuật toán. Theo cách xây dựng A thì không
có hai cạnh bất kì trong A có chung đỉnh (do bước xóa tất cả các cạnh đến u và v) 18 1 8
Thuật toán xấp xỉ
Vậy, mỗi bước lặp sẽ thêm vào C hai đỉnh u và v mới và |C|=2|A| (*)
Gọi C* là phủ các đỉnh với kích thước nhỏ nhất.
Vì hai cạnh của A không có đỉnh chung, nên mỗi đỉnh của C *chỉ nối đến nhiều nhất một cạnh của A.
Theo định nghĩa phủ các đỉnh thì C* phải chứa ít nhất một đỉnh của mỗi cạnh thuộc A. Vậy |C*|>=A (**)
Từ (*) và (**) ta có |C|<=2|C |*
2.2. Bài toán Người du lịch
Phát biểu bài toán. Cho đồ thị liên thông hoàn toàn G=(V,E), nghĩa là giữa hai đỉnh
bất kì luôn có một đường nối giữa chúng. Mỗi cạnh (u,v) có một trọng sô c(u,v)>0. Tìm chu
trình Halminton có tổng trọng số nhỏ nhất.
Các thuật toán xấp xỉ đơn giản nhất cho bài toán Người du lịch là dựa trên kỹ thuật tham lam.
2.2.1. Thuật toán láng giềng gần nhất (Nearest-neighbor algorithm)
Thuật toán láng giềng gần nhất được xây dựng dựa trên ý tưởng: Luôn đi đến đỉnh gần
với đỉnh vừa thăm nhất mà nó chưa được thăm. Thuật toán
Bước 1: Chọn một thành phố bất kì để bắt đầu.
Bước 2: Lặp lại thao tác sau cho đến khi tất cả các thành phố đã được thăm: đi đến
thành phố chưa được thăm gần nhất với thành phố vừa được thăm
Bước 3: Trở lại thành phố xuất phát
Ví dụ: Cho đồ thị như sau: 19 1 9
Thuật toán xấp xỉ
Giả sử đầu tiên ta chọn a làm đỉnh xuất phát, ta sẽ có chu trình sau: a-b-c-d-a với tổng
chi phí là 10. Ta có thể thấy rằng chu trình tối ưu là a-b-d-c-a có tổng chi phí là 8.
Như vậy tỉ lệ xâp xỉ trong trường hợp này là: 10/8=1.25
Độ phức tạp của thuật toán này là O(n2). Tỷ lệ xấp xỉ:
+ Gọi H* là chu trình tối ưu, C(H ) là trọng số của chu tr * ình H*.
+ Gọi H là chu trình xây dựng được từ thuật toán trên, C(H) là trọng số của chu trình H.
+ Theo cách xây dựng chu trình H, gọi C(H’) là trọng số sau khi thăm n đỉnh (n-1 cạnh).
Để tạo thành chu trình H ta cần nối đỉnh cuối và đỉnh đầu của chu trình, gọi trọng số cạnh cuối là w. Ta có, C(H)= C(H’)+w.
+ Tỷ lệ xấp xỉ của thuật toán p(n)==. Khi w có độ lớn tùy ý thì p(n)~=
2.2.2. Thuật toán đa phân mảnh (Multifragment-heuristic algorithm)
Ý tưởng của thuật toán này là tìm tập hợp các cạnh có trọng số nhỏ nhất tạo thành chu
trình sao cho thỏa mãn tất cả các đỉnh đều bậc 2. Thuật toán
Bước 1. Sắp xếp tăng dần theo trọng số các cạnh
Bước 2. Lặp lại thao tác sau n lần: Nếu cạnh tiếp theo trong danh sách thỏa mãn điều
kiện: khi bổ sung vào nghiệm nó không tạo ra bất kì đỉnh nào có bậc 3 hoặc một chu trình có
độ dài nhỏ hơn n; nếu không thỏa mãn điều kiện thì bỏ qua nó và xét cạnh tiếp theo.
Bước 3. Trả lại kết quả.
Trong đồ thị trên, sau khi sắp xếp ta sẽ có thứ tự các cạnh: (a,b), (c,d), (b,c), (b,d), (c,a), (a,d)
Khi thực hiện theo thuật toán trên ta sẽ có tập các cạnh được lựa chọn như sau: (a,b),
(c,d), (b,c), (a,d). Tổng chi phí cho phương án này là 10
Cũng như phương án láng giềng gần nhất, tỉ lệ xấp xỉ trong trường hợp này là 10/8=1.25 20 2 0