Hàm số lũy thừa – mũ và logarit -Trần Sĩ Tùng

Tài liệu gồm 35 trang với phần tóm tắt lý thuyết và bài tập trắc nghiệm. Chuyên đề trắc nghiệm hàm số lũy thừa, mũ và logarit. Hàm số lũy thừa – mũ và logarit -Trần Sĩ Tùng

85 43 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

28 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
TRAÀN SÓ TUØNG
---- ›š & ›š ----
BAØI TAÄP GIAÛI TÍCH 12
TAÄP 2
OÂN THI TOÁT NGHIEÄP THPT & ÑAÏI HOÏC
Naêm 2009
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 51
1. Ñònh nghóa luyõ thöøa
Soá muõ a Cô soá a
Luyõ thöøa
a
a
*
Nn Î=
a
a
Î
R
.......
n
aaaaa
a
== (n thöøa soá a)
0
=
a
0
¹
a
1
0
== aa
a
)(
*
Nnn Î-=
a
0
¹
a
n
n
a
aa
1
==
-
a
),(
*
NnZm
n
m
ÎÎ=
a
0
>
a
)( abbaaaa
n
n
n m
n
m
=Û===
a
),(lim
*
NnQrr
nn
ÎÎ=
a
0
>
a
n
r
aa lim=
a
2. Tính chaát cuûa luyõ thöøa
· Vôùi moïi a > 0, b > 0 ta coù:
a
a
a
aaabababa
b
a
baba
b
a
b
a
baabaaa
a
a
aaa =
÷
ø
ö
ç
è
æ
====
-+
;.)(;)(;;.
.
· a > 1 : aa
>Û>
ab
ab
; 0 < a < 1 : aa
>Û<
ab
ab
· Vôùi 0 < a < b ta coù:
0
mm
abm
<Û>
;
0
mm
abm
>Û<
Chuù yù: + Khi xeùt luyõ thöøa vôùi soá muõ 0 vaø soá muõ nguyeân aâm thì cô soá a phaûi khaùc 0.
+ Khi xeùt luyõ thöøa vôùi soá muõ khoâng nguyeân thì cô soá a phaûi döông.
3. Ñònh nghóa vaø tính chaát cuûa caên thöùc
· Caên baäc n cuûa a laø soá b sao cho
n
ba
=
.
· Vôùi a, b
³
0, m, n
Î
N*, p, q
Î
Z ta coù:
.
nnn
abab
= ;
(0)
n
n
n
aa
b
b
b
=>
;
( )
(0)
p
n
pn
aaa
=>
;
m
nmn
aa
=
(0)
nm
pq
pq
Neáuthìaaa
nm
==>
; Ñaëc bieät
mn
nm
aa
=
· Neáu n laø soá nguyeân döông leû vaø a < b thì
nn
ab
< .
Neáu n laø soá nguyeân döông chaün vaø 0 < a < b thì
nn
ab
< .
Chuù yù:
+ Khi n leû, moãi soá thöïc a chæ coù moät caên baäc n. Kí hieäu
n
a
.
+ Khi n chaün, moãi soá thöïc döông a coù ñuùng hai caên baäc n laø hai soá ñoái nhau.
4. Coâng thöùc laõi keùp
Goïi A laø soá tieàn göûi, r laø laõi suaát moãi kì, N laø soá kì.
Soá tieàn thu ñöôïc (caû voán laãn laõi) laø:
(1)
N
CAr
=+
CHÖÔNG II
HAØM SOÁ LUYÕ THÖØA – HAØM SOÁ MUÕ – HAØM SOÁ LOGARIT
I. LUYÕ THÖØA
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 52
Baøi 1. Thöïc hieän caùc pheùp tính sau::
a)
( ) ( )
32
3
727
1..7.
8714
A
æöæöæö
=-----
ç÷ç÷ç÷
èøèøèø
b)
( ) ( )
( ) ( )
26
4
64
2
3.15.8
9.5.6
B
--
=
--
c)
32
23
48
C
=+
d)
( )
2
3
5
2
32D
-
=
e)
( ) ( )
( ) ( ) ( )
73
4
452
18.2.50
25.4.27
E
--
=
---
f)
( ) ( )
( )
33
6
4
2
3
125.16.2
255
F
--
=
éù
-
êú
ëû
g)
( )
( ) ( )
2
31342
03
322
2.25.50,01.10
10:100,25100,01
G
-
---
-
---
+-
=
-+
h)
(
)
(
)
11111
33333
4102525
H=-++
i)
4
3
54
3
4.64.2
32
I
æö
ç÷
èø
= k)
55
5
2
3
5
81.3.9.12
3.1827.6
K=
æö
ç÷
èø
Baøi 2. Vieát caùc bieåu thöùc sau döôùi daïng luyõ thöøa vôùi soá muõ höõu tæ:
a)
( )
4
2
3
,0
xxx
³
b)
( )
5
3
,,0
ba
ab
ab
¹
c)
5
3
222
d)
3
3
232
323
e)
4
3
8
a
f)
5
2
3
bb
bb
Baøi 3. Ñôn giaûn caùc bieåu thöùc sau:
a)
1,51,5
0,50,5
0,5
0,50,5
0,50,5
2
ab
ab
b
ab
ab
ab
+
-
+
+
-
+
b)
0,50,50,5
0,50,5
221
.
1
21
aaa
a
aaa
æö
+-+
-
ç÷
ç÷
-
++
èø
c)
111131
222222
1111
2222
2
.
xyxyxyy
xyxy
xyxyxyxy
æö
ç÷
-+
+-
ç÷
+-
ç÷
+-
èø
d)
111111
222222
2
11
22
33
.
2
xyxyxy
xy
xy
æö
ç÷
+--
+
ç÷
-
ç÷
æö
ç÷
ç÷
-
èø
èø
e)
(
)
(
)
122124
333333
..
abaabb
-++ f)
(
)
(
)
(
)
111111
444422
..
ababab
-++
g)
( )
( )
( )
1
1
222
2
1
1
.1.
2
abc
bca
abc
bc
abc
-
-
-
-
-
æö
++
+-
+++
ç÷
ç÷
-+
èø
h)
111
222
11
22
22(1)
.
1
21
aaa
a
aaa
æö
ç÷
+-+
-
ç÷
-
ç÷
ç÷
++
èø
Baøi 4. Ñôn giaûn caùc bieåu thöùc sau:
a)
33
66
ab
ab
-
-
b)
4
:
ababb
ab
ab
aab
æö
-
-
ç÷
-
+
èø
c)
4
2
4
2
4
2
axxa
axax
axax
æö
+
-++
ç÷
ç÷
+
èø
d)
33
22
3333
2222
3
6
66
2
axaxax
axaaxx
x
ax
+-
+
--+
-
-
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 53
e)
3
44
33
44
11
11
xxx
xx
xx
xx
éù
-
êú
æöæö
êú
-+
ç÷ç÷
--
êú
ç÷ç÷
-+
êú
èøèø
ëû
f)
333
2222
33
3
33
3
2
3
2
:
aaabababab
a
ab
aab
éù
-+-
êú
+
êú
-
-
ëû
g)
( )
33
22
1
666
3333
2222
3
.
2
ababab
aba
aabbab
-
éù
-+
êú
--+
êú
-+-
ëû
Baøi 5. So saùnh caùc caëp soá sau:
a)
( )
( )
2
2
0,01vaø10
--
b)
26
vaø
44
æöæö
ç÷ç÷
èøèø
pp
c)
2332
5vaø5
--
d)
300200
5vaø8
e)
( )
0,3
3
0,001vaø100
-
f)
( )
2
2
4vaø0,125
-
g)
( ) ( )
35
22
vaø
--
h)
45
45
54
vaø
-
æöæö
ç÷ç÷
èøèø
i)
1011
0,0250
vaø
-
k)
( ) ( )
12
42
3131vaø-- l)
22
32
vaø
52
--
æöæö
ç÷ç÷
èøèø
m)
510
23
vaø
22
æöæö
ç÷ç÷
èøèø
pp
Baøi 6. So saùnh hai soá m, n neáu:
a)
3,23,2
mn
< b)
( ) ( )
22
mn
> c)
11
99
mn
æöæö
>
ç÷ç÷
èøèø
d)
33
22
mn
æöæö
>
ç÷ç÷
èøèø
e)
( ) ( )
5151
mn
-<- f)
( ) ( )
2121
mn
-<-
Baøi 7. Coù theå keát luaän gì veà soá a neáu:
a)
( ) ( )
21
33
11
aa
--
-<- b)
( ) ( )
31
2121
aa
--
+>+ c)
0,2
2
1
a
a
-
æö
<
ç÷
èø
d)
( ) ( )
11
32
11
aa
--
->- e)
( ) ( )
3
2
4
22
aa
->- f)
11
22
11
aa
-
æöæö
>
ç÷ç÷
èøèø
g)
37
aa
< h)
11
178
aa
--
< i)
0,253
aa
--
<
Baøi 8. Giaûi caùc phöông trình sau:
a)
5
41024
x
= b)
1
528
25125
x+
æö
=
ç÷
èø
c)
13
1
8
32
x-
=
d)
( )
2
2
1
33
9
x
x
-
æö
=
ç÷
èø
e)
2827
.
92764
xx-
æöæö
=
ç÷
ç÷
èø
èø
f)
2
56
3
1
2
xx-+
æö
=
ç÷
èø
g)
28
10,25
.32
0,125
8
x
x
-
-
æö
=
ç÷
èø
h)
0,20,008
x
= i)
3773
97
493
xx
--
æöæö
=
ç÷
ç÷
èø
èø
k)
5.20,001
xx
= l)
( ) ( )
1
12.3
6
xx
=
m)
11
1
7.4
28
xx--
=
Baøi 9. Giaûi caùc baát phöông trình sau:
a)
0,1100
x
> b)
3
1
0,04
5
x
æö
>
ç÷
èø
c)
100
0,3
9
x
>
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 54
d)
2
7.49343
x+
³ e)
2
11
9
327
x+
æö
<
ç÷
èø
f)
1
3
93
x
<
g)
( )
1
3.3
27
x
> h)
1
1
27.3
3
xx-
<
i)
3
1
.21
64
x
æö
>
ç÷
èø
Baøi 10. Giaûi caùc phöông trình sau:
a)
2
2220
xx+
+=
b)
1
3312
xx+
+=
c)
1
5530
xx-
+=
d)
11
44484
xxx-+
++=
e)
2
424.41280
xx
-+=
f)
121
4248
xx++
+=
g)
3.92.950
xx-
-+=
h)
2
56
31
xx-+
=
i)
1
42240
xx+
+-=
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 55
1. Ñònh nghóa
· Vôùi a > 0, a
¹
1, b > 0 ta coù:
log
a
bab
=Û=
a
a
Chuù yù:
log
a
b
coù nghóa khi
0,1
0
aa
b
ì
>¹
í
>
î
· Logarit thaäp phaân:
10
lgloglog
bbb
==
· Logarit töï nhieân (logarit Nepe):
lnlog
e
bb
=
(vôùi
1
lim12,718281
n
e
n
æö
=+»
ç÷
èø
)
2. Tính chaát
·
log10
a
=
;
log1
a
a
=
; log
b
a
ab
=
;
log
(0)
a
b
abb
=>
· Cho a > 0, a
¹
1, b, c > 0. Khi ñoù:
+ Neáu a > 1 thì loglog
aa
bcbc
>Û>
+ Neáu 0 < a < 1 thì loglog
aa
bcbc
>Û<
3. Caùc qui taéc tính logarit
Vôùi a > 0, a
¹
1, b, c > 0, ta coù:
·
log()loglog
aaa
bcbc
=+ ·
logloglog
aaa
b
bc
c
æö
=-
ç÷
èø
·
loglog
aa
bb
=
a
a
4. Ñoåi cô soá
Vôùi a, b, c > 0 vaø a, b
¹
1, ta coù:
·
log
log
log
a
b
a
c
c
b
= hay
log.loglog
aba
bcc
=
·
1
log
log
a
b
b
a
= ·
1
loglog(0)
a
a
cc
=¹
a
a
a
Baøi 1. Thöïc hieän caùc pheùp tính sau:
a)
21
4
log4.log2
b)
527
1
log.log9
25
c)
3
log
a
a
d)
3
2
log2
log3
49+ e)
22
log8
f)
9 8
log2
log27
274+
g)
34
1/3
7
1
log.log
log
aa
a
aa
a
h)
386
log6.log9.log2
i)
381
2log2 4log5
9
+
k)
99
3
log364log7
log5
81273
++
l)
57
log6log8
2549+ m)
5
32log4
5
-
n)
68
11
log3log2
94+ o)
9 2125
1log4
2log3log27
345
+ -
++
p)
3
6
log3.log36
q)
000
lg(tan1)lg(tan2)...lg(tan89)
+++
r)
842234
loglog(log16).loglog(log64)
éùéù
ëûëû
II. LOGARIT
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 56
Baøi 2. Cho a > 0, a
¹
1. Chöùng minh:
1
log(1)log(2)
aa
aa
+
+>+
HD: Xeùt A =
111
11
log(2)loglog(2)
log.log(2)
log(1)2
aaa
aa
a
aaa
aa
a
+++
++
+++
=+£
+
=
=
2
11
log(2)log(1)
1
22
aa
aaa
++
++
<=
Baøi 3. So saùnh caùc caëp soá sau:
a)
34
1
log4 vaø log
3
b)
3
0,10,2
log2 vaø log0,34
c)
35
42
23
log vaø log
54
d)
11
32
11
loglog
80
152
vaø
+
e)
1317
log150log290
vaø f)
6
6
1
log
log3
2
2 vaø 3
g)
711
log10log13
vaø h)
23
log3log4
vaø i)
910
log10log11
vaø
HD: d) Chöùng minh:
11
32
11
log4log
80
152
<<
+
e) Chöùng minh:
1317
log1502log290
<<
g) Xeùt A =
777
711
7
log10.log11log13
log10log13
log11
-
-=
=
777
7
110.11.71011
loglog.log
log117.7.1377
æö
+
ç÷
èø
> 0
h, i) Söû duïng baøi 2.
Baøi 4. Tính giaù trò cuûa bieåu thöùc logarit theo caùc bieåu thöùc ñaõ cho:
a) Cho
2
log14
a
=
. Tính
49
log32
theo a.
b) Cho
15
log3
a
=
. Tính
25
log15
theo a.
c) Cho
lg30,477
=
. Tính
lg9000
;
lg0,000027
;
81
1
log100
.
d) Cho
7
log2
a
=
. Tính
1
2
log28
theo a.
Baøi 5. Tính giaù trò cuûa bieåu thöùc logarit theo caùc bieåu thöùc ñaõ cho:
a) Cho
25
log7
a
=
;
2
log5
b
=
. Tính
3
5
49
log
8
theo a, b.
b) Cho
30
log3
a
=
;
30
log5
b
=
. Tính
30
log1350
theo a, b.
c) Cho
14
log7
a
=
;
14
log5
b
=
. Tính
35
log28
theo a, b.
d) Cho
2
log3
a
=
;
3
log5
b
=
;
7
log2
c
=
. Tính
140
log63
theo a, b, c.
Baøi 6. Chöùng minh caùc ñaúng thöùc sau (vôùi giaû thieát caùc bieåu thöùc ñaõ cho coù nghóa):
a)
loglog
aa
cb
bc= b)
loglog
log()
1log
aa
ax
a
bx
bx
x
+
=
+
c)
log
1log
log
a
a
ab
c
b
c
=+
d)
1
log(loglog)
32
ccc
ab
ab
+
=+, vôùi
22
7
abab
+= .
e)
1
log(2)2log2(loglog)
2
aaaa
xyxy
+-=+, vôùi
22
412
xyxy
+= .
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 57
f) loglog2log.log
bccbcbcb
aaaa
+-+-
+= , vôùi
222
abc
+=
.
g)
234
11111(1)
...
logloglogloglog2log
k
aa
aaaa
kk
xxxxxx
+
+++++= .
h)
log.log.log
log.loglog.loglog.log
log
abc
abbcca
abc
NNN
NNNNNN
N
++= .
i)
1
1lg
10
z
x
-
= , neáu
11
1lg1lg
1010
xy
yvaøz
--
==.
k)
2320092009!
1111
...
loglogloglog
NNNN
+++= .
l)
logloglog
logloglog
aba
bcc
NNN
NNN
-
=
-
, vôùi caùc soá a, b, c laäp thaønh moät caáp soá nhaân.
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 58
1. Khaùi nieäm
a) Haøm soá luyõ thöøa
yx
=
a
(a laø haèng soá)
Soá muõ a
Haøm soá
yx
=
a
Taäp xaùc ñònh D
a = n (n nguyeân döông)
n
yx
=
D = R
a = n (n nguyeân aâm hoaëc n = 0)
n
yx
=
D = R \ {0}
a laø soá thöïc khoâng nguyeân
yx
=
a
D = (0; +¥)
Chuù yù: Haøm soá
1
n
yx
= khoâng ñoàng nhaát vôùi haøm soá
(*)
n
yxnN
=Î.
b) Haøm soá muõ
x
ya
=
(a > 0, a
¹
1).
· Taäp xaùc ñònh: D = R.
· Taäp giaù trò: T = (0; +¥).
· Khi a > 1 haøm soá ñoàng bieán, khi 0 < a < 1 haøm soá nghòch bieán.
· Nhaän truïc hoaønh laøm tieäm caän ngang.
· Ñoà thò:
c) Haøm soá logarit
log
a
yx
= (a > 0, a
¹
1)
· Taäp xaùc ñònh: D = (0; +¥).
· Taäp giaù trò: T = R.
· Khi a > 1 haøm soá ñoàng bieán, khi 0 < a < 1 haøm soá nghòch bieán.
· Nhaän truïc tung laøm tieäm caän ñöùng.
· Ñoà thò:
0<a<1
y=log
a
x
1
x
y
O
a>1
y=log
a
x
1
y
x
O
0<a<1
y=a
x
y
x
1
a>1
y=a
x
y
x
1
III. HAØM SOÁ LUYÕ THÖØA
HAØM SOÁ MUÕ – HAØM SOÁ LOGARIT
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 59
2. Giôùi haïn ñaëc bieät
·
1
0
1
lim(1)lim1
x
x
xx
xe
x
®®±¥
æö
+=+=
ç÷
èø
·
0
ln(1)
lim1
x
x
x
®
+
=
·
0
1
lim1
x
x
e
x
®
-
=
3. Ñaïo haøm
·
( )
1
(0)
xxx
-
¢
=>
aa
a
;
( )
1
.
uuu
-
¢
¢
=
aa
a
Chuù yù:
( )
1
1
0
0
n
n
n
vôùixneáunchaün
x
vôùixneáunleû
nx
-
¢
æö
>
=
ç÷
<
èø
.
( )
1
n
n
n
u
u
nu
-
¢
¢
=
·
( )
ln
xx
aaa
¢
=
;
( )
ln.
uu
aaau
¢
=¢
()
xx
ee
¢
=
;
( )
.
uu
eeu
¢
=¢
·
( )
1
log
ln
a
x
xa
¢
=
;
( )
log
ln
a
u
u
ua
¢
¢
=
()
1
ln x
x
¢
=
(x > 0);
( )
ln
u
u
u
¢
¢
=
Baøi 1. Tính caùc giôùi haïn sau:
a) lim
1
x
x
x
x
®+¥
æö
ç÷
+
èø
b)
1
1
lim1
x
x
x
x
+
®+¥
æö
+
ç÷
èø
c)
21
1
lim
2
x
x
x
x
-
®+¥
æö
+
ç÷
-
èø
d)
1
3
34
lim
32
x
x
x
x
+
®+¥
æö
-
ç÷
+
èø
e)
1
lim
21
x
x
x
x
®+¥
æö
+
ç÷
-
èø
f)
21
lim
1
x
x
x
x
®+¥
æö
+
ç÷
-
èø
g)
ln1
lim
xe
x
xe
®
-
-
h)
2
0
1
lim
3
x
x
e
x
®
-
i)
1
lim
1
x
x
ee
x
®
-
-
k)
0
lim
sin
xx
x
ee
x
-
®
-
l)
sin2sin
0
lim
xx
x
ee
x
®
-
m)
(
)
1
lim1
x
x
xe
®+¥
-
Baøi 2. Tính ñaïo haøm cuûa caùc haøm soá sau:
a)
3
2
1
yxx
=++
b)
4
1
1
x
y
x
+
=
-
c)
2
5
2
2
1
xx
y
x
+-
=
+
d)
3
sin(21)
yx
=+
e)
3
2
cot1
yx
=+
f)
3
3
12
12
x
y
x
-
=
+
g)
3
3
sin
4
x
y
+
= h)
11
5
9
96
yx
=+ i)
2
4
2
1
1
xx
y
xx
++
=
-+
Baøi 3. Tính ñaïo haøm cuûa caùc haøm soá sau:
a)
(
)
2
22
x
yxxe
=-+ b)
(
)
2
2
x
yxxe
-
=+ c)
2
.sin
x
yex
-
=
d)
2
2
xx
ye
+
= e)
1
3
.
xx
yxe
-
= f)
2
2
xx
xx
ee
y
ee
+
=
-
g)
cos
2.
xx
ye= h)
2
3
1
x
y
xx
=
-+
i) cos.
cotx
yxe
=
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 60
Baøi 4. Tính ñaïo haøm cuûa caùc haøm soá sau:
a)
(
)
2
ln23
yxx
=++
b)
(
)
2
logcos
yx
= c)
(
)
.lncos
x
yex
=
d)
(
)
(
)
2
21ln3
yxxx
=-+
e)
(
)
3
1
2
logcos
yxx
=- f)
(
)
3
logcos
yx
=
g)
(
)
ln21
21
x
y
x
+
=
+
h)
(
)
ln21
1
x
y
x
+
=
+
i)
(
)
2
ln1
yxx
=++
Baøi 5. Chöùng minh haøm soá ñaõ cho thoaû maõn heä thöùc ñöôïc chæ ra:
a)
( )
2
2
2
.;1
x
yxexyxy
-
=¢=- b)
(
)
1;
xx
yxeyye
=+¢-=
c)
4
2;13120
xx
yeeyyy
-
¢¢¢
=+-¢-=
d)
2
..;320
xx
yaebeyyy
--
¢¢
=++¢+=
g)
.sin;220
x
yexyyy
-
¢¢¢
=++=
h)
(
)
4
.cos;40
x
yexyy
-
=+=
i)
sin
;cossin
x
yeyxyxy
=¢--¢¢=0
k)
2
.sin5;4290
x
yexyyy
=¢¢-¢+=
l)
2
1
.;2
2
xx
yxeyyye
=¢¢-¢+=
m)
4
2;13120
xx
yeeyyy
-
¢¢¢
=+-¢-=
n)
(
)
(
)
(
)
22
2
2
12010;1
1
xx
xy
yxeyex
x
=++¢=++
+
Baøi 6. Chöùng minh haøm soá ñaõ cho thoaû maõn heä thöùc ñöôïc chæ ra:
a)
1
ln;1
1
y
yxye
x
æö
=¢+=
ç÷
+
èø
b)
1
;ln1
1ln
yxyyyx
xx
éù
=¢=-
ëû
++
c)
(
)
(
)
2
sinlncosln;0
yxxyxyxy
=++¢+¢¢=
d)
( )
(
)
222
1ln
;21
1ln
x
yxyxy
xx
+
=¢=+
-
e)
2
22
1
1ln1;2 ln
22
x
yxxxxyxyy
=+++++=¢+¢
Baøi 7. Giaûi phöông trình, baát phöông trình sau vôùi haøm soá ñöôïc chæ ra:
a)
(
)
2
'()2();()31
x
fxfxfxexx
==++
b)
3
1
'()()0;()ln
fxfxfxxx
x
+==
c)
2112
'()0;()2.75
xx
fxfxeex
--
==++-
d)
'()'();()ln(5);()ln(1)
fxgxfxxxgxx
>=+-=-
e)
21
1
'()'();().5;()54ln5
2
xx
fxgxfxgxx
+
<==+
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 61
1. Phöông trình muõ cô baûn
Vôùi a > 0, a ¹ 1:
0
log
x
a
b
ab
xb
ì
>
=Û
í
=
î
2. Moät soá phöông phaùp giaûi phöông trình muõ
a) Ñöa veà cuøng cô soá
Vôùi a > 0, a ¹ 1:
()()
()()
fxgx
aafxgx
=Û=
Chuù yù: Trong tröôøng hôïp cô soá coù chöùa aån soá thì:
(1)()0
MN
aaaMN
=Û--=
b) Logarit hoaù
(
)
()()
()log.()
=Û=
fxgx
a
abfxbgx
c) Ñaët aån phuï
· Daïng 1:
()
()0
fx
Pa
=
Û
()
,0
()0
fx
tat
Pt
ì
=>
í
=
î
, trong ñoù P(t) laø ña thöùc theo t.
· Daïng 2:
2()()2()
()0
fxfxfx
aabb
++=
abg
Chia 2 veá cho
2()
fx
b , roài ñaët aån phuï
()
fx
a
t
b
æö
=
ç÷
èø
· Daïng 3:
()()fxfx
abm
+=
, vôùi
1
ab
=
. Ñaët
()()
1
fxfx
tab
t
=Þ=
d) Söû duïng tính ñôn ñieäu cuûa haøm soá
Xeùt phöông trình: f(x) = g(x) (1)
· Ñoaùn nhaän x
0
laø moät nghieäm cuûa (1).
· Döïa vaøo tính ñoàng bieán, nghòch bieán cuûa f(x) vaø g(x) ñeå keát luaän x
0
laø nghieäm duy
nhaát:
() ñoàng bieán vaø () nghòch bieán (hoaë
c ñoàng bieán nhöng nghieâm ngaët).
() ñôn ñieäu vaø () haèng soá
fxgx
fxgxc
é
ê
=
ë
· Neáu f(x) ñoàng bieán (hoaëc nghòch bieán) thì
()()
fufvuv
=Û=
e) Ñöa veà phöông trình caùc phöông trình ñaëc bieät
· Phöông trình tích A.B = 0 Û
0
0
A
B
é
=
ê
=
ë
· Phöông trình
22
0
0
0
A
AB
B
ì
=
+=Û
í
=
î
f) Phöông phaùp ñoái laäp
Xeùt phöông trình: f(x) = g(x) (1)
Neáu ta chöùng minh ñöôïc:
()
()
fxM
gxM
ì
³
í
£
î
thì (1)
()
()
fxM
gxM
ì
=
Û
í
=
î
Baøi 1. Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc logarit hoaù):
a)
3182
93
xx
--
= b)
105
1015
160,125.8
xx
xx
++
--
=
c)
222
3265237
4441
xxxxxx-+--++
+=+
d)
22
575.357.350
xxxx
--+=
e)
2222
121
2233
xxxx
-+-
+=+
f)
2
4
525
xx-+
=
IV. PHÖÔNG TRÌNH MUÕ
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 62
g)
2
2
43
1
2
2
x
x
-
-
æö
=
ç÷
èø
h)
712
11
.2
22
xx+-
æöæö
=
ç÷ç÷
èøèø
i)
( )
2
322322
x
-=+ k)
( ) ( )
1
1
1
5252
x
x
x
-
-
+
+=-
l)
1
3.272
xx+
=
m)
1-1
5 6. 5–3. 552
xxx+
+=
Baøi 2. Giaûi caùc phöông trình sau (ñaët aån phuï daïng 1):
a)
1
4280
xx+
+-=
b)
11
46.280
xx++
-+=
c)
4825
34.3270
xx++
-+=
d)
1617.4160
xx
-+=
e)
1
49780
xx+
+-=
f)
22
2
223.
xxxx-+-
-=
g)
(
)
(
)
743236
xx
+++=
h)
2
cos2cos
443
xx
+=
i)
251
336.390
xx++
-+=
k)
22
221
328.390
xxxx+++
-+=
l)
22
22
49.280
xx++
-+=
m)
211
3.52.50,2
xx--
-=
Baøi 3. Giaûi caùc phöông trình sau (ñaët aån phuï daïng 1):
a)
252(3).5270
xx
xx
--+-=
b)
22
3.25(310).530
xx
xx
--
+-+-=
c)
3.4(310).230
xx
xx
+-+-=
d)
92(2).3250
xx
xx
+-+-=
e)
22
3.25(310).530
xx
xx
--
+-+-=
f)
212
4332.3.26
xxx
xxx
+
++=++
g)
(
)
4+–82+12–20
xx
xx
=
h)
(
)
(
)
4.95.310
xx
xx
+-++=
i)
22
22
4(7).21240
xx
xx
+-+-=
k)
9(2).32(4)0
xx
xx
--
-+-+=
Baøi 4. Giaûi caùc phöông trình sau (ñaët aån phuï daïng 2):
a)
64.984.1227.160
xxx
-+=
b)
111
469
xxx
---
+= c)
3.162.815.36
xxx
+=
d)
21
25102
xxx
+
+= e)
xxx
8.21227 =+ f) 04.66.139.6
111
=+-
xxx
g)
22
6.313.66.20
xxx
-+=
h)
3.162.815.36
xxx
+= i)
111
2.469
xxx
+=
k)
(752)(25)(322)3(12)120.
xxx
++-++++-=
Baøi 5. Giaûi caùc phöông trình sau (ñaët aån phuïdaïng 3):
a)
(23)(23)14
xx
-++=
b)
23234
xx
æöæö
++-=
ç÷ç÷
èøèø
c)
(23)(743)(23)4(23)
xx
+++-=+ d)
3
(521)7(521)2
xxx
+
-++=
e)
( ) ( )
52452410
xx
++-=
f)
735735
78
22
xx
æöæö
+-
+=
ç÷ç÷
ç÷ç÷
èøèø
g)
(
)
(
)
63563512
-++=
xx
h)
(
)
(
)
22
(1)21
4
2323
23
---
++-=
-
xxx
i)
(
)
(
)
3
3516352
+
++-=
xx
x
k)
(
)
(
)
35357.20
++--=
xx
x
l)
(743)3(23)20
xx
+--+=
m)
33
38386.
xx
æöæö
++-=
ç÷ç÷
èøèø
Baøi 6. Giaûi caùc phöông trình sau (söû duïng tính ñôn ñieäu):
a)
(23)(23)4
xxx
-++= b)
(32)(32)(5)
xxx
-++=
c)
( ) ( )
3223226
++-=
xx
x
d)
( ) ( )
3
3516.352
xx
x
+
++-=
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 63
e)
37
2
55
æö
+=
ç÷
èø
x
x
f)
(
)
(
)
23232
++-=
xx
x
g)
23510
xxxx
++=
h)
235
xxx
+=
i)
2
12
22(1)
xxx
x
--
-=-
k)
352
x
x
=-
l) 23
x
x
=-
m)
1
241
xx
x
+
-=-
n)
2
231
x
x
=+
o) 2974 +=+ x
xx
p) 0155
312
=+--
+
x
xx
q)
xxxx
7483 +=+ r)
xxxx
3526 +=+ s)
xxxx
1410159 +=+
Baøi 7. Giaûi caùc phöông trình sau (ñöa veà phöông trình tích):
a)
8.33.2246
xxx
+=+
b)
1
12.33.15520
xxx+
+-=
c)
3
8.2 2 0
xx
xx
-
-+-=
d)
xxx
6132 +=+
e)
1
4
4
4
73.25623
222
+
=
+
+++++- xxxxxx
f)
( )
1
2
2
4
2
22
11
+
=
+
+-+ xxxx
g)
222
.33(127)81912
xx
xxxxx
+-=-+-+
h)
211
.3(32)2(23)
xxxxx
xx
--
+-=-
i)
sin1sin
42cos()20
y
xx
xy
+
-+=
k)
2222
2()12()1
222.210
xxxxxx+-+-
+--=
Baøi 8. Giaûi caùc phöông trình sau (phöông phaùp ñoái laäp):
a)
4
2cos,
x
x
= vôùi x ³ 0 b)
2
6102
366
xx
xx
-+
=-+-
c)
sin
3cos
x
x
=
d)
3
2
2.cos33
2
xx
xx
-
æö
-
=+
ç÷
èø
e) x
x
cos
sin
=
p
f)
x
x
xx
1
2
2
2
2
+
=
-
g) x
x
2cos3
2
= h)
2
5cos3
x
x
=
Baøi 9. Tìm m ñeå caùc phöông trình sau coù nghieäm:
a)
930
xx
m
++=
b)
9310
xx
m
+-=
c)
1
42
xx
m
+
-=
d)
2
32.3(3).20
xxx
m
+-+=
e)
2(1).20
xx
mm
-
+++=
f)
252.520
xx
m
---=
g)
2
16(1).210
xx
mm
--+-=
h)
25.5120
xx
mm
++-=
i)
22
sinos
8181
xcx
m
+=
k)
22
422
32.3230
xx
m
--
-+-=
l)
1 3 1 3
414.28
xxxx
m
++-++-
-+=
m)
22
11
98.34
xxxx
m
+-+-
-+=
n)
22
1111
9(2).3210
tt
mm
+-+-
-+++=
Baøi 10. Tìm m ñeå caùc phöông trình sau coù nghieäm duy nhaát:
a)
.2250
xx
m
-
+-=
b)
.162.815.36
xxx
m+=
c)
( ) ( )
51512
xx
x
m
++-=
d)
735735
8
22
xx
m
æöæö
+-
+=
ç÷ç÷
èøèø
e)
3
423
xx
m
+
-+=
f)
9310
xx
m
++=
Baøi 11. Tìm m ñeå caùc phöông trình sau coù 2 nghieäm traùi daáu:
a)
1
(1).4(32).2310
+
++--+=
xx
mmm b)
2
49(1).720
+-+-=
xx
mmm
c)
93(1).3520
+--+=
xx
mm d)
(3).16(21).410
++-++=
xx
mmm
e)
(
)
421.2+380
xx
mm
-+-=
f) 42 6
xx
m
-+=
Baøi 12. Tìm m ñeå caùc phöông trình sau:
a)
.162.815.36
+=
xxx
m coù 2 nghieäm döông phaân bieät.
b)
16.8(21).4.2
xxxx
mmm
-+-= coù 3 nghieäm phaân bieät.
c)
22
2
426
xx
m
+
-+=
coù 3 nghieäm phaân bieät.
d)
22
94.38
xx
m
-+=
coù 3 nghieäm phaân bieät.
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 64
1. Phöông trình logarit cô baûn
Vôùi a > 0, a ¹ 1: log
b
a
xbxa
=Û=
2. Moät soá phöông phaùp giaûi phöông trình logarit
a) Ñöa veà cuøng cô soá
Vôùi a > 0, a ¹ 1:
()()
log()log()
()0(()0)
aa
fxgx
fxgx
fxhoaëcgx
ì
=
=Û
í
>>
î
b) Muõ hoaù
Vôùi a > 0, a ¹ 1:
log()
log()
a
fx
b
a
fxbaa
=Û=
c) Ñaët aån phuï
d) Söû duïng tính ñôn ñieäu cuûa haøm soá
e) Ñöa veà phöông trình ñaëc bieät
f) Phöông phaùp ñoái laäp
Chuù yù:
·
Khi giaûi phöông trình logarit caàn chuù yù ñieàu kieän ñeå bieåu thöùc coù nghóa.
·
Vôùi a, b, c > 0 vaø a, b, c
¹
1:
loglog
bb
ca
ac=
Baøi 1. Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc muõ hoaù):
a)
2
log(1)1
xx
éù
-=
ëû
b)
22
loglog(1)1
xx
+-=
c)
21/8
log(2)6.log352
xx
---=
d)
22
log(3)log(1)3
xx
-+-=
e)
444
log(3)log(1)2log8
xx+--=- f)
lg(2)lg(3)1lg5
xx
-+-=-
g)
88
2
2log(2)log(3)
3
xx
---=
h)
lg54lg12lg0,18
xx-++=+
i)
2
33
log(6)log(2)1
xx
-=-+
k)
225
log(3)log(1)1/log2
xx++-=
l)
44
loglog(10)2
xx
+-=
m)
51/5
log(1)log(2)0
xx
--+=
n)
222
log(1)log(3)log101
xx
-++=-
o)
93
log(8)log(26)20
xx
+-++=
Baøi 2. Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc muõ hoaù):
a)
31/3
3
logloglog6
xxx
++=
b)
22
1lg(21)lg(1)2lg(1)
xxxx
+-+-+=-
c)
41/168
logloglog5
xxx
++=
d)
22
2lg(441)lg(19)2lg(12)
xxxx
+-+-+=-
e)
248
logloglog11
xxx
++=
f)
1/21/2
1/2
log(1)log(1)1log(7)
xxx
-++=+-
g)
2233
loglogloglog
xx
= h)
2332
loglogloglog
xx
=
i)
233233
loglogloglogloglog
xxx
+= k)
234432
loglogloglogloglog
xx
=
Baøi 3. Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc muõ hoaù):
a)
2
log(92)3
x
x
-=-
b)
3
log(38)2
x
x
-=-
c)
7
log(67)1
x
x
-
+=+
d)
1
3
log(4.31)21
x
x
-
-=-
e)
5
log(3)
2
log(92)5
x
x
-
-= f)
2
log(3.21)210
x
x
---=
V. PHÖÔNG TRÌNH LOGARIT
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 65
g)
2
log(122)5
x
x
-=-
h)
5
log(263)2
x
-=
i)
1
2
log(525)2
xx+
-=
k)
1
4
log(3.25)
x
x
+
-=
l)
1
1
6
log(525)2
xx+
-=-
m)
1
1
5
log(636)2
xx+
-=-
Baøi 4. Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc muõ hoaù):
a)
2
5
log(265)2
x
xx
-
-+=
b)
2
1
log(45)1
x
xx
-
-+=
c)
2
log(583)2
x
xx
-+=
d)
32
1
log(2231)3
x
xxx
+
+-+=
e)
3
log(1)2
x
x
-
-=
f)
log(2)2
x
x
+=
g)
2
2
log(56)2
x
xx
-+=
h)
2
3
log()1
x
xx
+
-=
i)
2
log(2712)2
x
xx
-+=
k)
2
log(234)2
x
xx
--=
l)
2
2
log(56)2
x
xx
-+=
m)
2
log(2)1
x
x
-=
n)
2
3 5
log(982)2
x
xx
+
++=
o)
2
2 4
log(1)1
x
x
+
+=
p)
15
log2
12
x
x
=-
-
q)
2
log(32)1
x
x
-=
r)
2
3
log(3)1
xx
x
+
+=
s)
2
log(254)2
x
xx
-+=
Baøi 5. Giaûi caùc phöông trình sau (ñaët aån phuï):
a)
22
33
loglog150
xx
++-=
b)
2
21/2
2
log3loglog2
xxx
++=
c)
4
7
log2log0
6
x
x
-+=
d)
2
2
12
2
log4log8
8
x
x
+=
e)
2
21/2
2
log3loglog0
xxx
++=
f)
2
2
log16log643
x
x
+=
g)
5
1
loglog2
5
x
x
-=
h)
7
1
loglog2
7
x
x
-=
i)
5
1
2log2log
5
x
x-= k)
22
3 loglog40
xx
-=
l)
33
3loglog310
xx
--=
m)
3
3
22
loglog4/3
xx+=
n)
3
3
22
loglog2/3
xx-=- o)
2
24
1
log2log0
x
x
+=
p)
2
21/4
log(2)8log(2)5
xx
---=
q)
2
525
log4log550
xx
+-=
r)
2
9
log5log5log5
4
xxx
x+=+ s)
2
9
log3log1
x
x
+=
t)
12
1
4lg2lgxx
+=
-+
u)
13
1
5lg3lgxx
+=
-+
v)
23
2164
log14log40log0
xxx
xxx
-+=
Baøi 6. Giaûi caùc phöông trình sau (ñaët aån phuï):
a)
2
3
3
log(12)log110
xxxx
+-+-=
b)
2
22
loglog6
6.96.13.
x
xx+=
c)
2
22
.log2(1).log40
xxxx
-++=
d) xxxx 26log)1(log
2
2
2
-=-+
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 66
e)
2
33
(2)log(1)4(1)log(1)160
xxxx
+++++-=
f)
2
2
log(2)log2
x
x
xx
-
++=
g)
2
33
log(1)(5)log(1)260
xxxx
++-+-+=
h)
33
4log1log4
xx
--=
i)
22
222
log(32)log(712)3log3
xxxx+++++=+
Baøi 7. Giaûi caùc phöông trình sau (ñaët aån phuï):
a)
73
loglog(2)
xx
=+
b)
23
log(3)log(2)2
xx
-+-=
c)
(
)
(
)
35
log1log212
xx
+++=
d)
(
)
6
log
26
log3log
x
xx
+=
e)
(
)
7
log3
4
x
x
+
=
f)
(
)
23
log1log
xx
+=
g)
222
log9loglog3
2
.3
x
xxx=-
h)
22
3723
log(9124)log(62321)4
xx
xxxx
++
+++++=
i)
(
)
(
)
(
)
222
236
log1.log1log1
xxxxxx
--+-=--
Baøi 8. Giaûi caùc phöông trình sau (söû duïng tính ñôn ñieäu):
a)
22
log3log5
(0)
xxxx
+=>
b)
22
loglog
2
35
xx
x+=
c)
5
log(3)3
xx
+=-
d)
2
log(3)
xx
-=
e)
2
22
log(6)log(2)4
xxxx
--+=++
f)
2
log
2.33
x
x
+=
g)
23
4(2)log(3)log(2)15(1)
xxxx
éù
--+-=+
ëû
Baøi 9. Giaûi caùc phöông trình sau (ñöa veà phöông trình tích):
a)
2727
log2.log2log.log
xxxx
+=+ b)
2332
log.log33.loglog
xxxx
+=+
c)
( )
(
)
2
933
2loglog.log211
xxx
=+-
Baøi 10. Giaûi caùc phöông trình sau (phöông phaùp ñoái laäp):
a)
23
ln(sin)1sin0
xx
-+=
b)
(
)
22
2
log11
xxx
+-=-
c)
2132
2
3
8
22
log(444)
xx
xx
+-
+=
-+
Baøi 11. Tìm m ñeå caùc phöông trình sau coù nghieäm duy nhaát:
a)
2
2323
log2(1)log(22)0
xmxxm
+-
éù
-+++-=
ëû
b)
(
)
(
)
2
2
log2log
xmx
-=
c)
(
)
2
5252
log1log0
xmxmx
+-
++++=
d)
(
)
()
lg
2
lg1
mx
x
=
+
e)
2
33
log(4)log(221)
xmxxm
+=--
f)
2
227227
log(1)log()0
xmmxx
+-
-++-=
Baøi 12. Tìm m ñeå caùc phöông trình sau:
a)
(
)
2
log41
-=+
x
mx
coù 2 nghieäm phaân bieät.
b)
2
33
log(2).log310
xmxm
-++-=
coù 2 nghieäm x
1
, x
2
thoaû x
1
.x
2
= 27.
c)
2222
42
2log(224)log(2)
-+-=+-
xxmmxmxm
coù 2 nghieäm x
1
, x
2
thoaû
22
12
1
xx
+>
.
d)
22
33
loglog1210
xxm
++--=
coù ít nhaát moät nghieäm thuoäc ñoaïn
3
1;3
éù
ëû
.
e)
( )
2
22
4loglog0
xxm
++=
coù nghieäm thuoäc khoaûng (0; 1).
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 67
Khi giaûi heä phöông trình muõ vaø logarit, ta cuõng duøng caùc phöông phaùp giaûi heä phöông trình
ñaõ hoïc nhö:
· Phöông phaùp theá.
· Phöông phaùp coäng ñaïi soá.
· Phöông phaùp ñaët aån phuï.
· …….
Baøi 1. Giaûi caùc heä phöông trình sau:
a)
25
21
y
y
x
x
ì
ï
+=
í
-=
ï
î
b)
24
432
x
x
y
y
ì
ï
=
í
=
ï
î
c)
2
31
319
y
y
x
x
ì
ï
-=
í
+=
ï
î
d)
1
26
8
4
y
y
x
x
-
-
ì
ï
=
í
=
ï
î
e)
î
í
ì
=+
=+
1
322
yx
yx
f)
2.936
3.436
xy
xy
ì
ï
=
í
=
ï
î
f)
.
2520
5.250
xy
xy
ì
ï
=
í
=
ï
î
g)
2.312
3.218
xy
xy
ì
ï
=
í
=
ï
î
h)
( )
2
710
1
8 x0
yy
x
xy
-+
ì
ï
=
í
+=>
ï
î
i)
( )
22
16
1
2 x0
xy
x
xy
--
ì
ï
=
í
-=>
ï
î
Baøi 2. Giaûi caùc heä phöông trình sau:
a)
437
4.3144
xy
xy
ì
ï
-=
í
=
ï
î
b)
2317
3.22.36
xy
xy
ì
ï
+=
í
-=
ï
î
c)
1
22.356
3.2387
xxy
xxy
+
++
ì
ï
+=
í
+=
ï
î
d)
2222
1
3217
2.33.28
xy
xy
++
+
ì
ï
+=
í
+=
ï
î
e)
1
11
324
321
xy
xy
+
++
ì
ï
-=-
í
-=-
ï
î
f)
22
2
2(1)12
21.
44.4.221
23.4.24
xxyy
yxy
--
-
ì
ï
-+=
í
-=
ï
î
g)
2
cot3
cos2
y
y
x
x
ì
ï
=
í
=
ï
î
h)
2
2
2
2
()21
9()6
yx
xy
xy
xy
-
-
ì
ï
+=
í
+=
ï
î
i)
2
3277
327
xy
xy
ì
ï
-=
í
-=
ï
î
k)
22
22()(2)
2
xy
yxxy
xy
ì
ï
-=-+
í
+=
ï
î
Baøi 3. Giaûi caùc heä phöông trình sau:
a)
321
321
x
y
y
x
ì
ï
=+
í
=+
ï
î
b)
3211
3211
x
y
xy
yx
ì
ï
+=+
í
+=+
ï
î
c)
22
22
3
xy
yx
xxyy
ì
ï
-=-
í
++=
ï
î
d)
1
1
765
765
-
-
ì
=-
ï
í
=-
ï
î
x
y
y
x
VI. HEÄ PHÖÔNG TRÌNH
MUÕ VAØ LOGARIT
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 68
Baøi 4. Giaûi caùc heä phöông trình sau:
a)
22
6
loglog3
xy
xy
ì
+=
í
+=
î
b)
loglog2
6
yx
yx
xy
ì
+=
í
+=
î
c)
2
2
log4
2log2
xy
xy
ì
+=
í
-=
î
d)
( ) ( )
22
35
3
loglog1
xy
xyxy
ì
ï
-=
í
+--=
ï
î
e)
32
log4
y
xy
x
ì
=
í
=
î
f)
2
3
log
log23
9
y
y
x
x
ì
ï
+=
í
=
ï
î
g)
î
í
ì
=
=+
8
5)log(log2
xy
yx
xy
h)
23
93
121
3log(9)log3
xy
xy
ì
-+-=
ï
í
-=
ï
î
i)
2
33
3
2
1
loglog0
2
20
xy
xyy
ì
-=
ï
í
ï
+-=
î
k)
3
12
log1
3
y
yx
x
ì
-=
í
=
î
Baøi 5. Giaûi caùc heä phöông trình sau:
a)
(
)
( )
log322
log232
x
y
xy
xy
ì
+=
ï
í
+=
ï
î
b)
log(64)2
log(64)2
x
y
xy
yx
ì
+=
ï
í
+=
ï
î
c)
22
33
22
log12log
loglog4
x
y
y
xy
ì
æö
-=-
ï
ç÷
ï
èø
í
+=
ï
ï
î
d)
2
2
44
loglog1
loglog1
y
xy
xy
ì
-=
ï
í
-=
ï
î
e)
(
)
22
2
33
log64
loglog1
xy
xy
ì
++=
ï
í
+=
ï
î
f)
22
22
loglog
16
loglog2
yx
xy
xy
ì
ï
+=
í
-=
ï
î
g)
î
í
ì
=-
=+
1loglog
27.2
33
loglog
33
xy
yx
xy
h)
22
2
42
loglog
3.2.10
loglog2
yx
xy
xy
ì
ï
+=
í
+=
ï
î
i)
(
)
( )
log222
log222
x
y
xy
yx
ì
+-=
ï
í
+-=
ï
î
k)
(
)
2
2
log4
log2
xy
x
y
ì
=
ï
æö
í
=
ç÷
ï
èø
î
l)
222
2
lglglg()
lg()lg.lg0
xyxy
xyxy
ì
ï
=+
í
-+=
ï
î
m)
22
6
5
loglog
2
log()1
yy
xx
xy
ì
+=
ï
í
ï
+=
î
n)
(
)
(
)
22
log5log
lglg4
1
lglg3
xyxy
x
y
ì
-=-+
ï
-
í
=-
ï
-
î
o)
(
)
( )( )
22
lg1lg8
lglglg3
xy
xyxy
ì
+=+
ï
í
+--=
ï
î
p)
( )
1
log2
log233
x
x
y
y
+
ì
=
ï
í
+=
ï
î
q)
( )
2
2
loglog1
log1
xyy
y
x
x
yx
ì
-=
ï
í
ï
-=
î
Baøi 6. Giaûi caùc heä phöông trình sau:
a)
lg
lglg4
1000
y
xy
x
ì
+=
í
=
î
b)
( )
2
6
36
42log9
xy
x
xyx
-
ì
ï
=
í
-+=
ï
î
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 69
c)
5
5
()3
27
3log()
yx
xy
xyxy
-
ì
ï
+=
í
ï
+=-
î
d)
lglg
lg4lg3
34
(4)(3)
xy
xy
ì
ï
=
í
=
ï
î
e)
2
1
2
2log2log50
32
x
y
xy
xy
ì
æö
-+=
ï
ç÷
í
èø
ï
=
î
Baøi 7. Giaûi caùc heä phöông trình sau:
a)
244
399
41616
logloglog2
logloglog2
logloglog2
xyz
yzx
zxy
ì
++=
ï
++=
í
ï
++=
î
b)
222
333
3
log3loglog
2
2
log12loglog
3
x
xyy
y
xxy
ì
+=+
ï
í
ï
+=+
î
c)
22
11
11
log(12)log(12)4
log(12)log(12)2
xy
xy
yyxx
xx
+-
+-
ì
-++++=
ï
í
+++=
ï
î
d)
23
23
log13sinlog(3cos)
log13coslog(3sin)
xy
yx
ì
+=
ï
í
+=
ï
î
e)
(
)
( )
( )
( )
22
23
22
23
log131log12
log131log12
xy
yx
ì
+-=-+
ï
í
ï
+-=-+
î
f)
2
32
32
2log(632)log(69)6
log(5)log(2)1
xy
xy
yxyxxx
yx
--
--
ì
-+-+-+=
ï
í
--+=
ï
î
Baøi 8. Giaûi caùc heä phöông trình sau:
a)
2
log
4
22
2
loglog1
x
y
xy
ì
ï
=
í
-=
ï
î
b)
( )
( ) ( )
2
22
1
3
3
loglog4
xy
xy
xyxy
-
-
ì
æö
ï
=
ç÷
í
èø
ï
++-=
î
c)
88
loglog
44
4
loglog1
yx
xy
xy
ì
ï
+=
í
-=
ï
î
d)
( )
1
3
3.218
log1
xy
xy
ì
=
ï
í
+=-
ï
î
e)
( )
ï
î
ï
í
ì
=-++
÷
ø
ö
ç
è
æ
=
-
-
4)(log)(log
3
1
3
22
2
yxyx
yx
yx
f)
( ) ( )
33
432
log1log
xy
yx
xyxy
+
ì
ï
=
í
ï
-=-+
î
g)
( )
3
3.2972
log2
xy
xy
ì
=
ï
í
-=
ï
î
h)
( )
5
3.21152
log2
xy
xy
-
ì
=
ï
í
+=
ï
î
i)
( ) ( )
22
loglog1
xy
xyxy
xy
ì
ï
+=-
í
-=
ï
î
k)
33
loglog2
22
42()
3312
xy
xy
xyxy
ì
ï
=+
í
+--=
ï
î
l)
33
loglog
33
227
loglog1
yx
xy
yx
ì
ï
+=
í
-=
ï
î
m)
2
2log
loglog
43
y
xy
x
xyx
yy
ì
=
ï
í
=+
ï
î
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 70
· Khi giaûi caùc baát phöông trình muõ ta caàn chuù yù tính ñôn ñieäu cuûa haøm soá muõ.
()()
1
()()
01
()()
fxgx
a
fxgx
aa
a
fxgx
é
ì
>
í
ê
>
î
>Û
ê
ì
<<
ê
í
ê
<
î
ë
· Ta cuõng thöôøng söû duïng caùc phöông phaùp giaûi töông töï nhö ñoái vôùi phöông trình muõ:
– Ñöa veà cuøng cô soá.
– Ñaët aån phuï.
– ….
Chuù yù: Trong tröôøng hôïp cô soá a coù chöùa aån soá thì:
(1)()0
MN
aaaMN
>Û-->
Baøi 1. Giaûi caùc baát phöông trình sau (ñöa veà cuøng cô soá):
a)
2
1
2
1
3
3
xx
xx
--
-
æö
³
ç÷
èø
b)
63
211
11
22
xxx
-+-
æöæö
<
ç÷ç÷
èøèø
c)
23412
22255
xxxxx
+++++
-->-
d)
12
33311
xxx--
+-<
e)
22
3232
960
xxxx-+-+
-<
f)
13732
3.26
-++
<
xxx
g)
222
212
4.23.2.2812
xxx
xxxx
+
++>++
h) 93.3.23.3.6
212
++<++
+
xxxx
xxx
i)
1212
999444
xxxxxx
++++
++<++ k)
1342
7.3535
xxxx
++++
+£+
l)
212
2525
xxxx
+++
+<+
m)
1 2
2.3 36
xx-+
>
n)
( ) ( )
31
13
103103
xx
xx
-+
-+
+<- o)
( ) ( )
1
1
2121
x
x
x
+
-
+³-
p)
2
1
2
1
2
2
x
xx
-
-
£ q)
1
1
21
31
22
x
x
-
+
³
Baøi 2. Giaûi caùc baát phöông trình sau (ñaët aån phuï):
a)
2.143.4940
xxx
+-³
b)
11
12
4230
xx
--
--£
c)
2
(2)
2(1)
3
42852
x
xx
-
-
-+>
d)
44
1
8.399
xxxx
++
+>
e)
25.210525
xxx
-+>
f)
211
56305.30
xxxx
++
+>+
g)
62.33.260
xxx
--+³
h)
27122.8
xxx
+>
i)
111
493525
xxx
-£ k)
121
2
32120
x
xx++
--<
l)
222
21212
25934.25
xxxxxx
-+-+-
+³ m) 09.93.83
442
>--
+++ xxxx
o)
1 1 1
45.2160
xxxx+-+-+
-+³
p)
( ) ( )
32322
x
x
++-£
r)
21
1
11
312
33
xx
+
æöæö
+>
ç÷ç÷
èøèø
s)
31
11
1280
48
xx-
æöæö
--³
ç÷ç÷
èøèø
t)
11
12
229
xx
+-
+<
u)
(
)
22 1
29.24.230
xx
xx
+
-++-³
VII. BAÁT PHÖÔNG TRÌNH MUÕ
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 71
Baøi 3. Giaûi caùc baát phöông trình sau (söû duïng tính ñôn ñieäu):
a)
2
231
x
x
<+
b) 0
1
2
122
1
£
-
+-
-
x
xx
c) 1
2
3
23.2
2
£
-
-
+
xx
xx
d)
424
3213
xx++
+>
e)
2
332
0
42
x
x
x
-
+-
³
-
f)
2
34
0
6
x
x
xx
+-
>
--
g)
( )
2
22x
3x522x3.2x3x522x3
x
xx--++>--++
Baøi 4. Tìm m ñeå caùc baát phöông trình sau coù nghieäm:
a)
4.230
xx
mm
-++£
b)
9.330
xx
mm
-++£
c) 2722
xx
m
++-£
d)
( ) ( )
22
1
21210
xx
m
-
++-+=
Baøi 5. Tìm m ñeå caùc baát phöông trình sau nghieäm ñuùng vôùi:
a)
(31).12(2).630
xxx
mm
++-+<
, "x > 0. b)
1
(1)4210
xx
mm
+
-+++>
, "x.
c)
( )
.9216.40
xxx
mmm
-++£
, "x Î [0; 1]. d)
2
.9(1).310
xx
mmm
+
+-+->
, "x.
e)
( )
coscos
2
42212430
xx
mm
+++-<
, "x. f)
1
43.20
xx
m
+
--³
, "x.
g)
420
xx
m
--³
, "x Î (0; 1) h) 3353
xx
m
++-£
, "x.
i)
2.25(21).10(2).40
xxx
mm
-+++³
, "x ³ 0. k)
1
4.(21)0
xx
m
-
-+>
, "x.
Baøi 6. Tìm m ñeå moïi nghieäm cuûa (1) ñeàu laø nghieäm cuûa baát phöông trình (2):
a)
( ) ( )
21
1
2
2
11
312(1)
33
23610(2)
xx
mxmxm
+
ì
æöæö
ï
ï
+>
ç÷ç÷
í
èøèø
ï
-----<
ï
î
b)
21
1
22
228(1)
42(1)0(2)
xx
xmxm
+
ì
ï
->
í
ï
---<
î
c)
21
2
29.240(1)
(1)(3)10(2)
xx
mxmx
+
ì
ï
-+£
í
++++>
ï
î
d)
( )
21
2
2
11
9.12(1)
33
22230(2)
xx
xmxm
+
ì
æöæö
ï
ï
+>
ç÷ç÷
í
èøèø
ï
+++-<
ï
î
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 72
· Khi giaûi caùc baát phöông trình logarit ta caàn chuù yù tính ñôn ñieäu cuûa haøm soá logarit.
1
()()0
log()log()
01
0()()
aa
a
fxgx
fxgx
a
fxgx
é
ì
>
í
ê
>>
î
>Û
ê
ì
<<
ê
í
ê
<<
î
ë
· Ta cuõng thöôøng söû duïng caùc phöông phaùp giaûi töông töï nhö ñoái vôùi phöông trình
logarit:
– Ñöa veà cuøng cô soá.
– Ñaët aån phuï.
– ….
Chuù yù: Trong tröôøng hôïp cô soá a coù chöùa aån soá thì:
log0(1)(1)0
a
BaB
>Û-->
;
log
0(1)(1)0
log
a
a
A
AB
B
>Û-->
Baøi 1. Giaûi caùc baát phöông trình sau (ñöa veà cuøng cô soá):
a) )1(log1)21(log
5
5
++<- xx b)
(
)
29
log12log1
x
-<
c)
( )
11
33
log5log3
xx
-<-
d)
215
3
logloglog0
x
>
e)
0)
1
21
(loglog
2
3
1
>
+
+
x
x
f)
(
)
2
1
2
4log0
xx
->
g)
(
)
2
14
3
loglog50
x
éù
->
ëû
h)
2
66
loglog
612
xx
x
+£
i)
(
)
(
)
22
log31log1
xx
+³+-
k)
( )
2
2
2
log
log
2
x
x
x+
l)
31
2
loglog0
x
æö
³
ç÷
èø
m)
81
8
2
2log(2)log(3)
3
xx
-+->
n)
(
)
(
)
22
1531
35
loglog1loglog1
xxxx
éùéù
++>+-
ëû
êú
êú
ëû
Baøi 2. Giaûi caùc baát phöông trình sau:
a)
(
)
( )
2
lg1
1
lg1
x
x
-
<
-
b)
( ) ( )
23
23
2
log1log1
0
34
xx
xx
+-+
>
--
c)
(
)
2
lg32
2
lglg2
xx
x
-+
>
+
d)
2
2
5log2log
log
180
x
x
x
xx
-
+-<
e)
0
1
13
log
2
>
+
-
x
x
x
f)
2
3232
log.logloglog
4
x
xxx<+
g)
4
log(log(24))1
x
x
-£
h)
2
3
log(3)1
xx
x
-
->
i)
(
)
2
5
log8160
x
xx
-+³
k)
(
)
2
2
log561
x
xx
-+<
VIII. BAÁT PHÖÔNG TRÌNH LOGARIT
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 73
l)
62
3
1
loglog0
2
x
x
x
+
æö
-
>
ç÷
+
èø
m)
(
)
(
)
2
1
1
log1log1
x
x
xx
-
-
+>+
n)
2
3
(4167).log(3)0
xxx
-+->
o)
2
(412.232).log(21)0
xx
x
-+-£
Baøi 3. Giaûi caùc baát phöông trình sau (ñaët aån phuï):
a)
2
log2log430
x
x
+-£
b)
(
)
(
)
5
5
log121log1
xx
-<++
c)
5
2loglog1251
x
x
-<
d)
2
2
log64log163
x
x
+³
e)
22
log2.log2.log41
xx
x
>
f)
22
11
24
loglog0
xx
+<
g)
42
2
222
loglog2
1log1log1log
xx
xxx
+>
-+-
h) 1
log2
2
log4
1
22
£
-
+
+ xx
i) 08log6log
2
2
2
1
£+- xx k)
2
333
log4log92log3
xxx
-+³-
l) )243(log1)243(log
2
3
2
9
++>+++ xxxx m)
55
12
1
5log1logxx
+<
-+
n)
2
11
88
19log14log
xx
->- o)
100
1
log100log0
2
x
x
->
p)
2
3
3
1log
1
1log
x
x
+
>
+
q)
2
16
1
log2.log2
log6
xx
x
>
-
Baøi 4. Giaûi caùc baát phöông trình sau (söû duïng tính ñôn ñieäu):
a)
2
0,50,5
( x 1)log(25)log60
xxx
++++³
b) 2)24(log)12(log
32
£+++
xx
c)
( ) ( )
23
32
log1log1
xx
>
++
d)
5
lg
5
0
231
x
x
x
x
+
-
<
-+
Baøi 5. Tìm m ñeå caùc baát phöông trình sau coù nghieäm:
a)
(
)
2
1/2
log23
xxm
-+>-
b)
1
log100log1000
2
xm
->
c)
12
1
5log1log
mm
xx
+<
-+
d)
2
1log
1
1log
m
m
x
x
+
>
+
e)
22
loglog
xmx
+> f)
22
log(1)log(2)
xmxm
xxx
--
->+-
Baøi 6. Tìm m ñeå caùc baát phöông trình sau nghieäm ñuùng vôùi:
a)
(
)
(
)
22
22
log77log4
xmxxm
+³++, "x
b)
(
)
(
)
52log42log
2
2
2
2
£+-++- mxxmxx , "x Î[0; 2]
c)
22
55
1log(1)log(4)
xmxxm
++³++
, "x.
d)
2
111
222
2log21log21log0
111
mmm
xx
mmm
æöæöæö
--+-+>
ç÷ç÷ç÷
ç÷ç÷ç÷
+++
èøèøèø
, "x
Baøi 7. Giaûi baát phöông trình, bieát x = a laø moät nghieäm cuûa baát phöông trình:
a)
(
)
(
)
22
log2log23;9/4
mm
xxxxa-->-++=.
b).
22
log(23)log(3);1
mm
xxxxa
++£-=
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 74
Baøi 8. Tìm m ñeå moïi nghieäm cuûa (1) ñeàu laø nghieäm cuûa baát phöông trình (2):
a)
22
11
24
22
loglog0(1)
60(2)
xx
xmxmm
ì
+<
ï
í
ï
+++<
î
b)
2
24
log(583)2(1)
210(2)
x
xx
xxm
ì
-+>
ï
í
-+->
ï
î
Baøi 9. Giaûi caùc heä baát phöông trình sau:
a)
2
2
4
0
1664
lg7lg(5)2lg2
x
xx
xx
ì
+
>
ï
í
-+
ï
+>--
î
b)
( )
(
)
(
)
()
1
1lg2lg21lg7.212
log22
xx
x
x
x
+
ì
-++<+
ï
í
+>
ï
î
c)
(
)
()
2
4
log20
log220
x
y
y
x
-
-
ì
->
ï
í
->
ï
î
d)
1
2
log(5)0
log(4)0
x
y
y
x
-
+
ì
+<
ï
í
-<
ï
î
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 75
Baøi 1. Giaûi caùc phöông trình sau:
a)
211
1
2.4
64
8
xx
x
-+
-
=
b)
3182
93
xx
--
=
c)
0,5
0,2(0,04)
25
5
xx
+
= d)
2
12119
595
.
3253
xxx++-
æöæöæö
=
ç÷ç÷ç÷
èøèøèø
e)
211
1
7.714.72.748
7
xxxx++-
--+=
f)
(
)
2
7,23,9
393lg(7)0
xx
x
-+
--=
g)
2
1
1
3
2
2(2)4
x
x
x
-
+
æö
ç÷
=
èø
h)
1
5.8500
x
xx-
=
i)
2
1
1lg
3
3
1
100
x
x
-
= k)
lg2
1000
x
xx
=
l)
lg5
5lg
3
10
x
x
x
+
+
= m)
( )
3
log1
3
x
x
-
=
Baøi 2. Giaûi caùc phöông trình sau:
a)
22
22
49.280
xx++
-+=
b)
22
515
412.280
xxxx-----
-+=
c)
64.984.1227.160
xxx
-+=
d)
13
3
642120
xx
+
-+=
e)
22
13
936.330
xx--
-+=
f)
4825
2
34.3282log2
xx++
-+=
g)
2122(1)
3316.33
xxxx
+++
=+-+ h)
( ) ( )
52452410
xx
++-=
i)
33
1log1log
932100
xx++
--=
k)
2
lg1lglg2
462.30
xxx++
--=
l)
22
sincos
24.26
xx
+=
m)
lg(tan)lg(cot)1
32.31
xx+
-=
Baøi 3. Giaûi caùc baát phöông trình sau:
a)
65
25
225
54
x
x
-
+
æö
<
ç÷
èø
b)
1
1
21
2
21
x
x
-
+
-
<
+
c)
22
.550
xx
x
+
-<
d)
2
lg3lg1
1000
xx
x
-+
>
e)
424
2
1
x
x
x
+-
£
-
f)
2
32
8.1
3
32
x
x
xx
-
æö
>+
ç÷
èø
-
g)
23412
22255
xxxxx
+++++
-->-
h)
2
2
log(1)
1
1
2
x -
æö
>
ç÷
èø
i)
2
2
1
9
3
x
x
+
-
æö
>
ç÷
èø
k)
12
2
11
3
27
x
x
+-
æö
>
ç÷
èø
l)
21
3
1
11
55
x
x
+
-
-
æöæö
>
ç÷ç÷
èøèø
m)
72
11
3..1
33
xx
æöæö
>
ç÷ç÷
èøèø
IX. OÂN TAÄP HAØM SOÁ
LUYÕ THÖØA
–
MUÕ
–
LOGARIT
Haøm soá luyõ thöøa – muõ –logarit Traàn Só Tuøng
Trang 76
Baøi 4. Giaûi caùc baát phöông trình sau:
a)
2
42.5100
xxx
-->
b)
1
25550
xx--+
-³
c)
111
9.45.64.9
xxx
---
+< d)
2
lg2lg5
332
xx++
<-
e)
1
4
4162log8
xx+
-< f)
23
21
1
221.20
2
x
x
+
+
æö
-+³
ç÷
èø
g)
2(2)
2(1)
3
42852
x
xx
-
-
-+>
h)
23
43
1
335.60
3
x
x
-
-
æö
-+³
ç÷
èø
i)
2
9339
xxx+
->-
k)
93293
xxx
+-³-
Baøi 5. Giaûi caùc phöông trình sau:
a)
3
log(38)2
x
x
-=-
b)
2
5
log(265)2
x
xx
-
-+=
c)
77
log(21)log(27)1
xx
-+-=
d)
33
log(1log(27))1
x
+-=
e)
3
loglg
2
3lglg30
x
xx
-+-=
f)
3
log(12)
2
955
x
x
-
=-
g)
1lg
10
x
xx
+
= h)
( )
5
log1
5
x
x
-
=
i)
22
lglg2
lg
lg
2
xx
x
x
+-
æö
=
ç÷
èø
k)
lg7
lg1
4
10
x
x
x
+
+
=
l)
39
1
loglog92
2
x
xx
æö
++=
ç÷
èø
m)
33
33
2log1log
71
xx
xx
--
+=
--
Baøi 6. Giaûi caùc phöông trình sau:
a)
( )
2
2log53log510
xx
-+=
b)
1/31/3
log3log20
xx
-+=
c)
2
22
log2log20
xx
+-=
d)
13
32log32log(1)
x
x
+
+=+
e)
(
)
22
3
log9.log4
x
xx
=
f)
(
)
2
31/21/2
loglog3log52
xx
-+=
g)
222
lg(100)lg(10)lg6
xxx
-+=
h)
22
222
9
log(2).log(16)log
2
xxx
=
i)
33
log(99)log(282.3)
xx
x+=+- k)
1
222
log(44)log2log(23)
xxx+
+=+-
l)
33
22
log(251)2log(51)
xx++
-=++
m)
lg(6.525.20)lg25
xx
x+=+
Baøi 7. Giaûi caùc baát phöông trình sau:
a)
2
0,5
log(56)1
xx
-+>-
b)
7
26
log0
21
x
x
-
>
-
c)
33
loglog30
xx
--<
d)
1/3
23
log1
x
x
-
³-
e)
1/41/4
2
log(2)log
1
x
x
->
+
f)
2
1/34
loglog(5)0
x
éù
->
ëû
g)
2
2
1/2
4
0
log(1)
x
x
-
<
-
h)
2
log(1)
0
1
x
x
+
>
-
i)
9
loglog(39)1
x
x
éù
-<
ëû
k)
2
23
log1
x
x
+
<
l)
2
2
log(815)
21
x
xx
-
++
<
m)
1/3
2
5
log
3
(0,5)1
x
x
+
+
>
Traàn Só Tuøng Haøm soá luyõ thöøa – muõ –logarit
Trang 77
Baøi 8. Giaûi caùc heä phöông trình sau:
a)
2
()1
41
5125
xy
xy
--
+
ì
ï
=
í
=
ï
î
b)
323
4128
51
xy
xy
+
--
ì
ï
=
í
=
ï
î
c)
2212
5
xy
xy
ì
+=
í
+=
î
d)
3.22.32,75
230,75
xx
xy
ì
ï
+=
í
-=-
ï
î
e)
7160
4490
x
x
y
y
ì
ï
-=
í
-=
ï
î
f)
3
3.2972
log()2
xy
xy
ì
ï=
í
-=
ï
î
g)
5
43.416
2128
xyx
yy
xy
-
ì
ï
-=
í
ï
-=-
î
h)
2
/2
3277
327
xy
xy
ì
ï
-=
í
-=
ï
î
i)
(
)
( )
2
2
2
2
21
96
yx
xy
xy
xy
-
-
ì
+=
ï
í
+=
ï
î
Baøi 9. Giaûi caùc heä phöông trình sau:
a)
42
22
loglog0
540
xy
xy
ì
-=
í
-+=
î
b)
3
4
log()2
7
loglog
6
x
xy
xy
ì
-=
ï
í
-=
ï
î
c)
lg
2
20
y
x
xy
ì
=
í
=
î
d)
22
24
log2log3
16
xy
xy
ì
+=
í
+=
î
e)
333
112
15
loglog1log5
xy
xy
ì
-=
ï
í
ï
+=+
î
f)
5
7
log2
log
log3
log
3
2
x
y
y
x
y
x
ì
ï
=
í
=
ï
î
g)
22
lg()1lg13
lg()lg()3lg2
xy
xyxy
ì
+-=
í
+--=
î
h)
22
2
2
9
8
loglog3
xy
yx
xy
ì
+=
ï
í
ï
+=
î
i)
( )
8
2loglog5
yx
xy
xy
ì
=
ï
í
+=
ï
î
k)
2
1
22
2log315
3.log2log3
y
yy
x
xx
+
ì
-=
ï
í
=+
ï
î
l)
33
432
log()1log()
xy
yx
xyxy
+
ì
ï
=
í
ï
-=-+
î
m)
2
3.2576
log()4
xy
yx
ì
ï=
í
-=
ï
î
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRAÀN SÓ TUØNG ---- ›š & ›š ----
BAØI TAÄP GIAÛI TÍCH 12 TAÄP 2
OÂN THI TOÁT NGHIEÄP THPT & ÑAÏI HOÏC Naêm 2009
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit CHÖÔNG II
HAØM SOÁ LUYÕ THÖØA – HAØM SOÁ MUÕ – HAØM SOÁ LOGARIT I. LUYÕ THÖØA
1. Ñònh nghóa luyõ thöøa Soá muõ a Cô soá a
Luyõ thöøa aa *
a = n Î N a Î R a n a = a = . a ...... a a (n thöøa soá a) a = 0 a ¹ 0 0
aa = a = 1 a a - 1 = -n ( * n Î N ) a ¹ 0 n a = a = n a m a = m (m Î Z, * n Î N ) a > 0 a n n m n n n
a = a = a ( a = b Û b = a)
a = lim r (r Î Q, * n Î N ) a > a n r n n 0 a = lim a
2. Tính chaát cuûa luyõ thöøa
· Vôùi moïi a > 0, b > 0 ta coù: a a a a b a +b a a -b a b a .b a a a æ a ö a a a . = a ; = a ; (a ) = a ; (ab) = a b . ; ç ÷ = b a a è b ø b
· a > 1 : aa > ab Û a > b ; 0 < a < 1 : aa > ab Û a < b
· Vôùi 0 < a < b ta coù: m m
a < b Û m > 0 ; m m
a > b Û m < 0
Chuù yù: + Khi xeùt luyõ thöøa vôùi soá muõ 0 vaø soá muõ nguyeân aâm thì cô soá a phaûi khaùc 0.
+ Khi xeùt luyõ thöøa vôùi soá muõ khoâng nguyeân thì cô soá a phaûi döông.
3. Ñònh nghóa vaø tính chaát cuûa caên thöùc
· Caên baäc n cuûa a laø soá b sao cho n b = a .
· Vôùi a, b ³ 0, m, n Î N*, p, q Î Z ta coù: n p n n a a = .n ab a b ; n = (b > 0) ; n p = (n a
a ) (a > 0) ; m n mn a = a n b b p q n p m q Neáu =
thì a = a (a > 0); Ñaëc bieät n mn m a = a n m
· Neáu n laø soá nguyeân döông leû vaø a < b thì n n a < b .
Neáu n laø soá nguyeân döông chaün vaø 0 < a < b thì n n a < b . Chuù yù:
+ Khi n leû, moãi soá thöïc a chæ coù moät caên baäc n. Kí hieäu n a .
+ Khi n chaün, moãi soá thöïc döông a coù ñuùng hai caên baäc n laø hai soá ñoái nhau.
4. Coâng thöùc laõi keùp
Goïi A laø soá tieàn göûi, r laø laõi suaát moãi kì, N laø soá kì.
Soá tieàn thu ñöôïc (caû voán laãn laõi) laø: = (1+ )N C A r Trang 51
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng
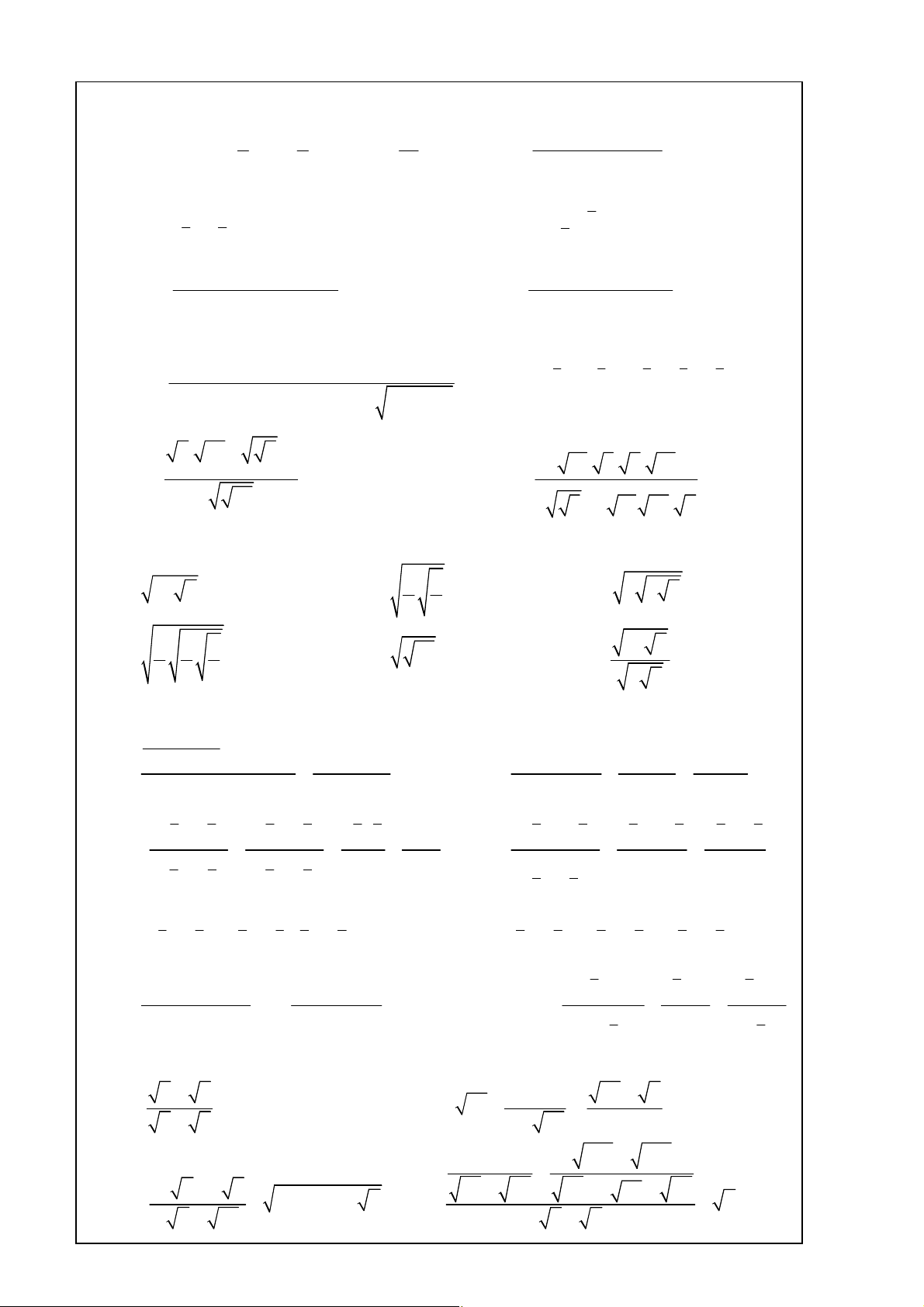
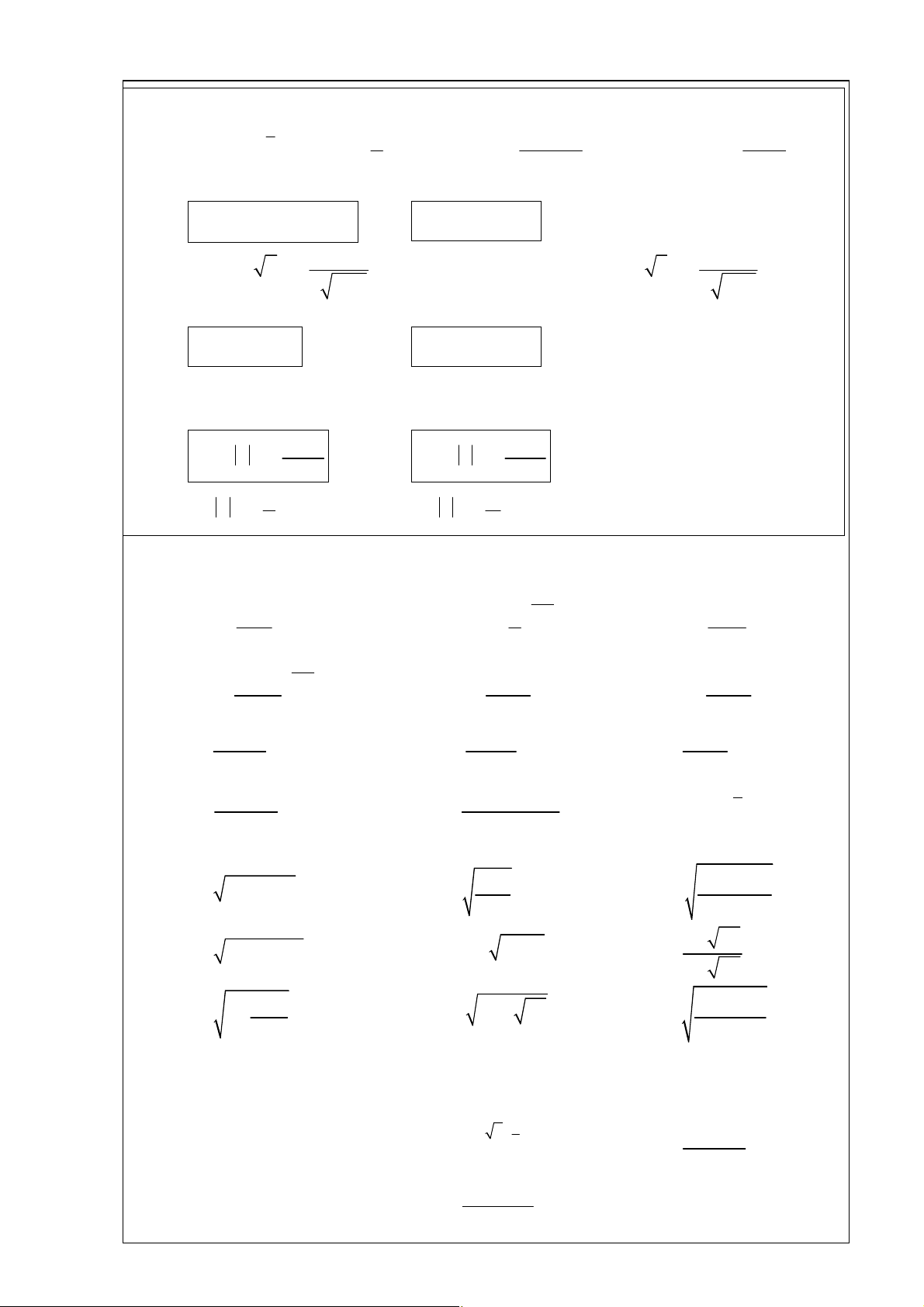
Baøi 1. Thöïc hieän caùc pheùp tính sau:: 3 2 2 6 æ ö æ ö æ ö ( 3 - ) .(-15) 4 .8 a) A = (- )3 7 2 - - ÷ ç ÷ (- ) 7 1 . . 7 . - ç b) B = 8 7 ç 14 ÷ è ø è ø è ø 9 .( 5 - )6 .(-6)4 2 3 2 - D = ( 2 32 ) 2 3 5 c) 2 3 C = 4 + 8 d) ( 1 - 8)7 .2 .(-50)3 4 125 .(-16)3 .(-2)3 6 e) E = f) F = ( 2 - 5)4 .( 4 - )5 .( 27 - )2 25 é( 5) 4 2 3 ù - ê ú ë û 2 .2 + 5 .5 - (0,0 ) 2 3 1 3 4 - - - -2 H = ( 1 1 1 - + )( 1 1 3 3 3 3 3 4 10 25 2 + 5 ) g) 1 .10 G = h)
10- :10- - (0,25)0 +10- (0, )-3 3 2 2 01 4 5 4 æ 3 4. 64. 2 ö ç ÷ 5 5 5 i) I è ø 81. 3. 9. 12 = k) K = 3 32 2 æ 3 ö 5 ç 3 ÷ . 18 27. 6 è ø
Baøi 2. Vieát caùc bieåu thöùc sau döôùi daïng luyõ thöøa vôùi soá muõ höõu tæ: a) 4 2 3 x x , ( x b a ³ 0) b) 5 3 , ( , a b ¹ 0) c) 5 3 2 2 2 a b 5 2 d) 3 2 3 3 2 e) 4 3 8 a f) b b 3 2 3 3 b b
Baøi 3. Ñôn giaûn caùc bieåu thöùc sau: 1,5 1,5 a + b 0,5 0,5 - a b 0,5 0,5 0,5 0,5 0,5 0,5 æ ö a) a + b 2b a + 2 a - 2 a +1 + b) ç - ÷. 0,5 0,5 a - b a + b ç 0,5 ÷ 0,5 è a + 2a +1 a -1 ø a 1 1 1 1 3 1 æ ö 1 1 1 1 1 1 æ ö ç 2 2 2 2 - + ÷ 2 2 x y x y x y 2y ç 2 2 2 2 + - ÷ 2 2 c) x 3y x 3y x - y ç + ÷. - d) ç + ÷. 1 1 1 1
x + y x - y ç ÷ 2 ç 1 1 x - y 2 æ ö ÷ 2 2 2 2
è xy + x y xy - x y ø ç ç 2 2 è è x y ÷ ÷ - ø ø ( 1 2 ( 1 1 a - b ) ( 1 1 a + b ) ( 1 1 4 4 4 4 2 2 . . a + b ) a - b ) ( 2 1 2 4 3 3 3 3 3 3
. a + a .b + b ) e) f) 1 1 1 æ ö
a + (b + c) 1 1 - - 2 2 2 æ ö ç 2 2 + - ÷ 2 a 2 a 2 (a +1) g)
.ç1 b + c - a +
÷.(a + b + c) 2 - h)ç - ÷. ( ) 1 1 - - ç 2bc a b c ÷ - + 1 1 è ø a -1 ç ÷ ç 2 ÷ 2 a + 2a +1 a è ø
Baøi 4. Ñôn giaûn caùc bieåu thöùc sau: 3 3 4 æ ö a) a - b b) ab - : ab - b ab 6 6 ç ÷ a - b è a + ab a - b ø 3 2 3 2 a + x ax - a x 4 + 2 æ 4 ö 3 2 3 2 3 2 3 3 2 c) a x + x a 2 ç
- a + x + 2a x ÷ a - x
a - 2 ax + x 6 ç d) - x 4 è a x ax ÷ + ø 6 6 a - x Trang 52
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit 3 é ù é 3 3 3 2 2 3 2 3 2 ù e) x x - x
a a - 2a b + a b a b - ab ê ú f) 3 ê + ú : a êæ 4 3 öæ 4 3 ê 3 3 3 x -1 x +1 öú 2 3 ë a - ab a - b ú ç û ê - x ÷ç - x ÷ú ç 4 ÷ç 4 êëè x 1 øè x 1 ÷ - + øúû é 3 2 3 2 ù 1 - g) a b - ab a + b ê - ú.(6 6 a - b ) 6 + a ê 3 2 3 3 2 3 2 3 2 ë a 2 ab b a b ú - + - û
Baøi 5. So saùnh caùc caëp soá sau: 2 6 æ p ö æ p ö a) ( )- 2 0,01 vaø (10)- 2 b) ç ÷ vaø c) 2 - 3 3 - 2 5 vaø 5 4 ç 4 ÷ è ø è ø d) 300 200 5 vaø 8 e) ( ) 0-,3 3 0,001 vaø 100 f) ( ) 2 2 4 vaø 0,125 - 3 - -5 4 - 5 æ ö æ ö g) ( 2 ) vaø ( 2 ) h) 4 5 ç ÷ vaø i) 1 - 0 11 0,02 vaø 50 5 ç 4 ÷ è ø è ø 1 2 - 2 - 2 5 10 æ ö æ ö æ p ö æ p ö k) ( 3 2 2 3 - )4 vaø ( - ) 2 3 1 3 1 l) ç ÷ vaø ç ÷ m) ç ÷ vaø ç ÷ è 5 ø è 2 ø è 2 ø è 2 ø
Baøi 6. So saùnh hai soá m, n neáu: m n m n æ ö æ ö a) 3,2m 3,2n < b) ( 2 ) > ( 2 ) c) 1 1 ç ÷ > 9 ç 9÷ è ø è ø m n æ ö æ ö m n m n d) 3 3 ç ÷ > ç ÷ e) ( 5 - ) 1 < ( 5 - ) 1 f) ( 2 - ) 1 < ( 2 - ) 1 è 2 ø è 2 ø
Baøi 7. Coù theå keát luaän gì veà soá a neáu: 2 1 0 - ,2 æ ö a) (a ) 1 - - 1 - 3 - -1 3 < (a - ) 1 3 b) (2a + ) 1 > (2a + ) 1 c) 2 ç ÷ < a è a ø 1 1 1 1 3 - æ ö æ ö d) (1 a)- - 1 2 1 2 - 2 3 > (1- a) 2
e) (2 - a)4 > (2 - a) f) ç ÷ > a ç a ÷ è ø è ø 1 1 - - g) 3 7 a < a h) 17 8 a < a i) 0 - ,25 - 3 a < a
Baøi 8. Giaûi caùc phöông trình sau: x 1 + æ ö a) x 5 4 5 2 8 = 1024 b) ç ÷ = c) 1 - 3x 1 8 = 2 è 5 ø 125 32 x 2 x - æ ö x -x æ ö æ ö x -5x+6 æ ö d) ( ) 2 2 1 3 3 3 = ç e) 2 8 27 ç ÷ .ç ÷ = f) ç ÷ = 1 9 ÷ è ø è 9 ø è 27 ø 64 è 2 ø -x æ ö 3x-7 7x-3 æ ö æ ö g) 1 2x-8 0,25 .32 9 7 = h) 0,2x = 0,008 i) ç ÷ = 0,125 ç ÷ ç ÷ è 8 ø è 49 ø è 3 ø x x
k) 5x.2x = 0,001 l) ( ) ( ) 1 12 . 3 = m) 1-x 1-x 1 7 .4 = 6 28
Baøi 9. Giaûi caùc baát phöông trình sau: x æ ö a) 0,1x 1 > 100 b) 3 ç ÷ > 0,04 c) x 100 0,3 > è 5 ø 9 Trang 53
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng x+2 æ ö d) x+2 7 . 49 1 1 ³ 343 e) ç ÷ < 9 f) x 1 3 < è 3 ø 27 9 3 x x æ ö g) ( ) 1 3 .3 1 > h) x 1-x 1 27 .3 < i) 3 ç ÷ . 2 > 1 27 3 è 64 ø
Baøi 10. Giaûi caùc phöông trình sau: a) x x+2 2 + 2 = 20 b) x x 1 3 3 + + = 12 c) x x 1 5 5 - + = 30 d) x 1 - x x 1 4 4 4 + + + = 84 e) 2 4 x 24.4x - +128 = 0 f) x 1 + 2x 1 4 2 + + = 48
g) 3.9x - 2.9-x + 5 = 0 h) 2x-5x+6 3 = 1 i) x x 1 4 2 + + - 24 = 0 Trang 54
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit II. LOGARIT 1. Ñònh nghóa
· Vôùi a > 0, a ¹ 1, b > 0 ta coù: log a
a b = a Û a = b Chuù yù: log ìa > a ¹ a b coù nghóa khi 0, 1 í îb > 0 · Logarit thaäp phaân:
lg b = log b = l 10 og b n æ ö
· Logarit töï nhieân (logarit Nepe):
ln b = loge b (vôùi 1
e = lim ç1+ ÷ » 2,718281) è n ø 2. Tính chaát · log 1 0 b a a = ; log 1 a a = ; log b a a = b ; log a = b (b > 0)
· Cho a > 0, a ¹ 1, b, c > 0. Khi ñoù:
+ Neáu a > 1 thì log b > log a
a c Û b > c
+ Neáu 0 < a < 1 thì log b > log a
a c Û b < c
3. Caùc qui taéc tính logarit
Vôùi a > 0, a ¹ 1, b, c > 0, ta coù: æ ö b
· log (bc) = log b + log a a a a c
· log ç ÷ = log b - log a a
a c · log b = a log b è c ø a a 4. Ñoåi cô soá
Vôùi a, b, c > 0 vaø a, b ¹ 1, ta coù: log c · log a b c = hay log .
b log c = log c log a b a a b · 1 loga b = · 1 log a a c = log c ( ¹ 0) log a a b a a
Baøi 1. Thöïc hieän caùc pheùp tính sau: a) log 1 2 4.log 1 2 b) log5 .log27 9 c) 3 log 25 a a 4 d) log 3 log 2 log 2 log 27 2 3 4 + 9 e) log 8 f) 9 8 27 + 4 2 2 1/3 log . a log a g) 3 4 a a h) log 6.log 9.log 2 i) 2log 2 4log 5 3 81 9 + 7 log 3 8 6 1 a a k) log 5 log 36 4log 7 log 6 log 8 3 2 log 4 3 9 9 81 + 27 + 3 l) 5 7 25 + 49 m) 5 5 - 1 1 n) log 3 log 2 1+log 4 2-log 3 log 27 6 8 9 + 4 o) 9 2 125 3 + 4 + 5 p) log 3.log 36 6 3 q) 0 0 0
lg(tan1 ) + lg(tan 2 ) + ... + lg(tan89 )
r) log8 élog4(log216)ù.log2 élog3(log4 64)ù ë û ë û Trang 55
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng
Baøi 2. Cho a > 0, a ¹ 1. Chöùng minh: log (a +1) > log 1(a + 2) a a + log (a + 2) log a + log (a + 2) HD: Xeùt A = a 1 + a 1 + a 1 = log + a 1 . a log = + a 1(a + 2) £ log (a +1) + 2 a 2 log (
a a + 2) log (a +1) = a 1 + a 1 + < = 1 2 2
Baøi 3. So saùnh caùc caëp soá sau: a) 1 log 2 3 3 4 vaø log4 b) 3 log 2 vaø log 0,34 c) log vaø log 3 0,1 0,2 3 5 5 4 4 2 1 log d) 1 1 log log 3 2 1 vaø log1
e) log 150 vaø log 290 f) 6 6 2 vaø 3 80 15 + 2 13 17 3 2 g) log710 vaø lo 11 g 13 h) log2 3 vaø log3 4 i) log910 vaø lo 10 g 11 HD: d) Chöùng minh: 1 1 log1 < 4 80 15 + 2 3 2 e) Chöùng minh: lo 1 g 3150< 2 g 290 log 10.log 11- log 13 g) Xeùt A = 7 7 7 log710 -lo 11 g 13 = log711 æ ö = 1 10.11.7 10 11 ç log7 + log7 .log7 > 0 log ÷ 7 11 è 7.7.13 7 7 ø
h, i) Söû duïng baøi 2.
Baøi 4. Tính giaù trò cuûa bieåu thöùc logarit theo caùc bieåu thöùc ñaõ cho:
a) Cho log214 = a . Tính log49 32 theo a. b) Cho lo 15
g 3 = a . Tính log2515 theo a. c) Cho lg3 1
= 0,477 . Tính lg 9000 ; lg 0,000027 ; . log81100
d) Cho log7 2 = a . Tính log1 28 theo a. 2
Baøi 5. Tính giaù trò cuûa bieåu thöùc logarit theo caùc bieåu thöùc ñaõ cho: a) Cho log 49
25 7 = a ; log2 5 = b . Tính log theo a, b. 3 5 8
b) Cho log30 3 = a ; log30 5 = b . Tính log301350 theo a, b. c) Cho lo 14 g 7 = a ; lo 14
g 5 = b . Tính log35 28 theo a, b.
d) Cho log2 3 = a ; log3 5 = b; log7 2 = c . Tính lo 1 g 40 63 theo a, b, c.
Baøi 6. Chöùng minh caùc ñaúng thöùc sau (vôùi giaû thieát caùc bieåu thöùc ñaõ cho coù nghóa): log b + log x log c a) log c log b a a b = c b) log (bx) a a a ax = c) = 1+ log b 1+ log a a x logab c d) a + b 1 log
= (log a + log b) c , vôùi 2 2
a + b = 7ab . 3 2 c c e) 1
log (x + 2y) - 2 log 2 = (log x + log y) a a , vôùi 2 2
x + 4y = 12xy . 2 a a Trang 56
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit f) log a + log a = 2 log . a log b c c b c b c b a , vôùi 2 2 2
a + b = c . + - + - g) 1 1 1 1 1 k(k +1) + + + + ...+ = .
log x log x log x log x log x x k 2 log 2 3 4 a a a a a a
log N.log N.log N
h) log N.log N + log N.log N + log N.log a b c a b b c c a N = . logabc N 1 1 1 i) 1 lg 10 z x - = , neáu 1-lg x 1-lg = 10 = 10 y y vaø z . k) 1 1 1 1 + + ...+ = . log2 N log3 N
log2009 N log2009! N
log N - log N log N l) a b a =
, vôùi caùc soá a, b, c laäp thaønh moät caáp soá nhaân. log N - log N log b c c N Trang 57
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng
III. HAØM SOÁ LUYÕ THÖØA
HAØM SOÁ MUÕ – HAØM SOÁ LOGARIT 1. Khaùi nieäm
a) Haøm soá luyõ thöøa y = xa (a laø haèng soá) Soá muõ a
Haøm soá y = xa Taäp xaùc ñònh D a = n (n nguyeân döông) n y = x D = R
a = n (n nguyeân aâm hoaëc n = 0) n y = x D = R \ {0}
a laø soá thöïc khoâng nguyeân y = xa D = (0; +¥) 1
Chuù yù: Haøm soá n
y = x khoâng ñoàng nhaát vôùi haøm soá n
y = x (nÎ N*) . b) Haøm soá muõ x
y = a (a > 0, a ¹ 1). · Taäp xaùc ñònh: D = R. · Taäp giaù trò: T = (0; +¥).
· Khi a > 1 haøm soá ñoàng bieán, khi 0 < a < 1 haøm soá nghòch bieán.
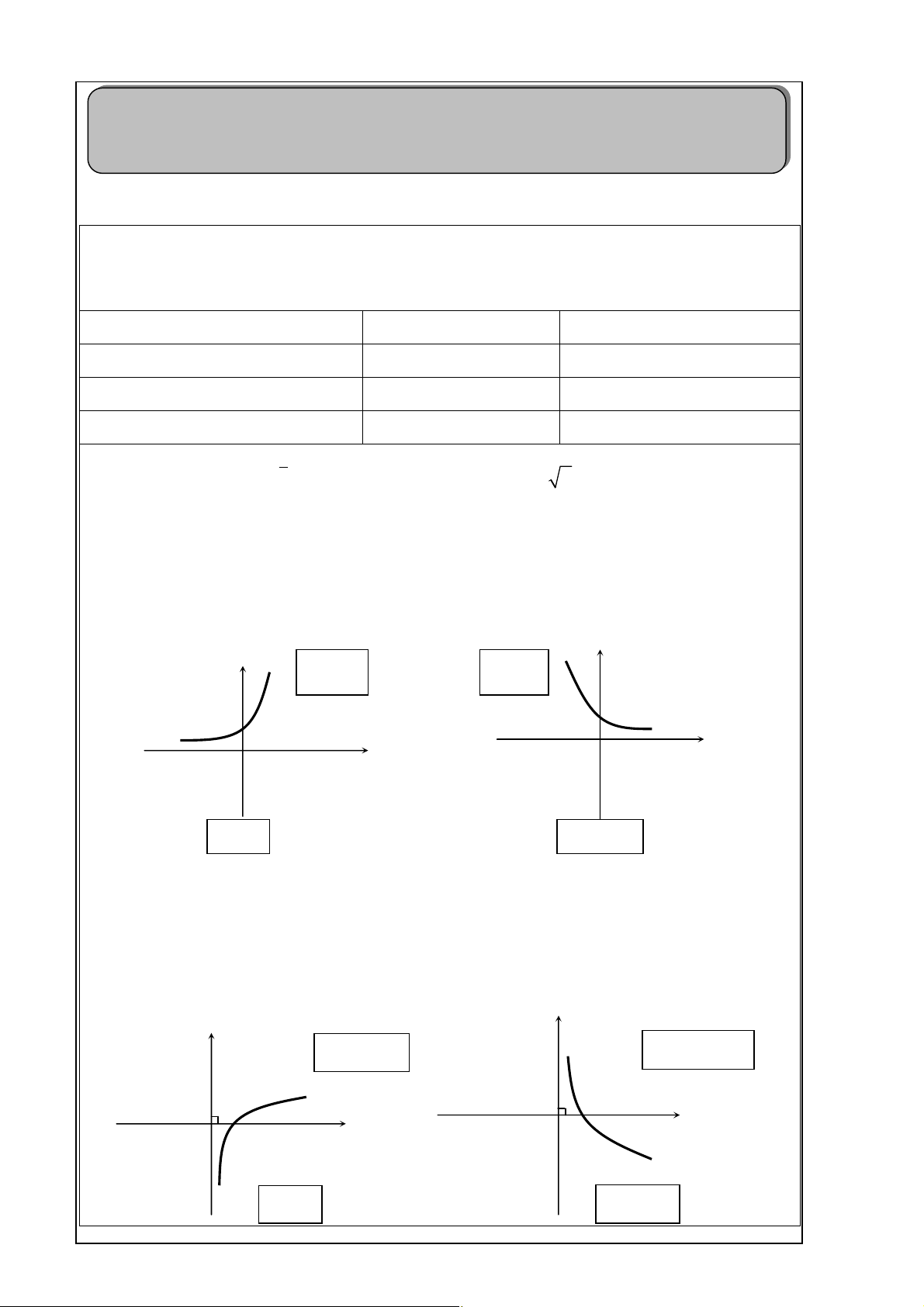
· Nhaän truïc hoaønh laøm tieäm caän ngang. · Ñoà thò: y y y=ax y=ax 1 x 1 x a>1 0
c) Haøm soá logarit y = loga x (a > 0, a ¹ 1) · Taäp xaùc ñònh: D = (0; +¥). · Taäp giaù trò: T = R.
· Khi a > 1 haøm soá ñoàng bieán, khi 0 < a < 1 haøm soá nghòch bieán.
· Nhaän truïc tung laøm tieäm caän ñöùng. · Ñoà thò: y y y=log y=logax ax 1 x x O O 1 a>1 0 Trang 58
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit
2. Giôùi haïn ñaëc bieät 1 x æ ö x 1 ln(1+ x) e -1
· lim (1+ x)x = lim ç1+ ÷ = e · lim = 1 · lim = 1 x®0 x®±¥ è x ø x®0 x x®0 x 3. Ñaïo haøm a ¢ a ¢ · ( x ) a 1
= a x - (x > 0) ; (u ) a 1 = au - .u¢ Chuù yù: (n )¢ 1
æ vôùi x > 0 neáu n chaün x ö ¢ u¢ = . (n u) = n ç ÷
n 1 è vôùi x < 0 neáu n leû n x - ø n n 1 n u - ¢ ¢ · ( x ) x a = a ln a ; ( u) u a = a ln . a u¢ ( x )¢ x e ¢ = e ; ( u) u e = e .u¢ ¢ u¢ · ( ¢ a x ) 1 log = ; (loga u ) = x ln a u ln a ( )¢ 1 ln x ¢ u¢ = (x > 0); (ln u ) = x u
Baøi 1. Tính caùc giôùi haïn sau: x x 1 + æ ö æ ö 2x 1 - æ + ö a) lim x 1 x x 1 ç ÷ b) lim ç1+ ÷ c) lim ç ÷
x®+¥ è 1+ x ø x®+¥ è x ø
x®+¥ è x - 2 ø x 1 + æ - ö x æ + ö x æ + ö d) 3x 4 3 lim x x ç ÷ e) 1 lim ç ÷ f) 2 1 lim ç ÷
x®+¥ è 3x + 2 ø
x®+¥ è 2x -1 ø
x®+¥ è x -1 ø 2x x g) ln x -1 lim h) e -1 lim i) lim e - e x e ® x - e x®0 3x x 1 ® x -1 x -x sin2x sin x x ( 1 lim x e - ) k) lim e - e l) lim e - e m) 1 x®0 sin x x®0 x x®+¥
Baøi 2. Tính ñaïo haøm cuûa caùc haøm soá sau: 2 a) 3 2 y x +1 x + x - 2 = x + x +1 b) 4 y = c) y = 5 x -1 2 x +1 3 d) 3 y 1- 2x = sin(2x +1) e) 3 2 y = cot 1+ x f) y = 3 1+ 2x 2 g) x + 3 x + x +1 3 y = sin h) 11 5 9 y = 9 + 6 x i) y = 4 4 2 x - x +1
Baøi 3. Tính ñaïo haøm cuûa caùc haøm soá sau: a) = ( 2 -2 +2) x y x x e b) ( 2 2 ) x y x x e- = + c) 2 - x y = e .sin x 1 x - x 2x x d) 2 2x x y e + e + e = e) 3 y = x.e f) y = 2x x e - e x g) x cos 3 = 2 . x y e h) y = i) = cos . cotx y x e 2 x - x +1 Trang 59
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng
Baøi 4. Tính ñaïo haøm cuûa caùc haøm soá sau: a) y = ( 2 ln 2x + x + 3) b) y = log x 2 (cos x )
c) y = e .ln (cos x)
d) y = ( x - ) ( 2 2 1 ln 3x + x) e) y = log ( 3 1 x - cos x )
f) y = log3 (cos x) 2 ln(2x + ) 1 ln(2x + ) 1 g) y = h) y = i) y = ( 2 ln x + 1+ x ) 2x +1 x +1
Baøi 5. Chöùng minh haøm soá ñaõ cho thoaû maõn heä thöùc ñöôïc chæ ra: 2 x - a) 2 y = x.e ; xy¢ = ( 2 1- x )y b) = ( + ) 1 x; x y x e
y¢ - y = e c) 4x = + 2 -x y e e ;
y¢¢¢ -13y¢ -12y = 0 d) -x 2 = . + . - x y a e b e
; y¢¢ + 3y¢ + 2y = 0 g) -x y = e .sin ; x
y¢ + 2y¢ + 2y = 0 h) -x (4)
y = e .cos x; y + 4y = 0 i) sin x y = e ;
y¢cos x - y sin x - y¢¢ = 0 k) 2x y = e .sin 5 ;
x y¢¢ - 4y¢ + 29y = 0 l) 1 2 = . x; ¢¢ - 2 x y x e y
y¢ + y = e m) 4x = + 2 -x y e
e ; y¢¢¢ -13y¢ -12y = 0 2 n) y = ( 2 x + )( xe + ) 2 1 2010 ; xy x y¢ = + e ( 2 x +1 2 ) x +1
Baøi 6. Chöùng minh haøm soá ñaõ cho thoaû maõn heä thöùc ñöôïc chæ ra: æ ö a) 1 = ln ; ¢ +1 y y xy = e ç b) 1 y =
; xy¢ = y éy ln x -1ù ë û è 1 x ÷ + ø 1+ x + ln x c) y 1+ ln x = ( x)+ ( x) 2 sin ln
cos ln ; y + xy¢ + x y¢¢ = 0 d) 2 2 2 y = ¢ = +
x ( - x); 2x y (x y )1 1 ln 2 e) x 1 2 2 y =
+ x x +1 + ln x + x +1;
2y = xy¢ + ln y¢ 2 2
Baøi 7. Giaûi phöông trình, baát phöông trình sau vôùi haøm soá ñöôïc chæ ra: a) x f x = f x f x = e ( 2 '( ) 2 ( ); ( ) x + 3x + )1 b) 1 3
f '(x) + f (x) = 0;
f (x) = x ln x x c) 2x 1 - 1-2 '( ) = 0; ( ) = + 2. x f x f x e e + 7x - 5
d) f '(x) > g'(x); f (x) = x + ln(x - 5);g(x) = ln(x -1) e) 1 2x 1 '( ) '( ); ( ) .5 + < = ; ( ) = 5x f x g x f x g x + 4x ln 5 2 Trang 60
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit
IV. PHÖÔNG TRÌNH MUÕ
1. Phöông trình muõ cô baûn Vôùi a > 0, a ìb ¹ 1: x > 0 a = b Û í x = log î a b
2. Moät soá phöông phaùp giaûi phöông trình muõ
a) Ñöa veà cuøng cô soá Vôùi a > 0, a ¹ 1: f (x) g(x) a = a
Û f (x) = g(x)
Chuù yù: Trong tröôøng hôïp cô soá coù chöùa aån soá thì: M N
a = a Û (a -1)(M - N) = 0 b) Logarit hoaù f ( x) g (x) a = b
Û f (x) = (log b g x a ). ( ) c) Ñaët aån phuï f (x) ì · Daïng 1: f (x) P(a ) = 0 Û t = a , t > 0 í
, trong ñoù P(t) laø ña thöùc theo t. îP(t) = 0 · Daïng 2: 2 f (x) f (x) 2 f (x) aa + b(ab) + g b = 0 f (x) æ ö Chia 2 veá cho a 2 f ( x) b
, roài ñaët aån phuï t = ç b ÷ è ø
· Daïng 3: f (x) f (x) a + b
= m , vôùi ab = 1. Ñaët f (x) f (x) 1 t = a Þ b = t
d) Söû duïng tính ñôn ñieäu cuûa haøm soá Xeùt phöông trình: f(x) = g(x) (1)
· Ñoaùn nhaän x0 laø moät nghieäm cuûa (1).
· Döïa vaøo tính ñoàng bieán, nghòch bieán cuûa f(x) vaø g(x) ñeå keát luaän x0 laø nghieäm duy nhaát:
é f (x) ñoàng bieán vaø g(x) nghòch bieán (hoaëc ñoàng bieán nhöng nghieâm ngaët). ê
ë f (x) ñôn ñieäu vaø g(x) = c haèng soá
· Neáu f(x) ñoàng bieán (hoaëc nghòch bieán) thì f (u) = f (v) Û u = v
e) Ñöa veà phöông trình caùc phöông trình ñaëc bieät
· Phöông trình tích A.B = 0 Û éA = 0 ìA = ê · Phöông trình 2 2 0 A + B = 0 Û í ëB = 0 îB = 0
f) Phöông phaùp ñoái laäp Xeùt phöông trình: f(x) = g(x) (1)
Neáu ta chöùng minh ñöôïc: ì f (x) ³ M ì f x = M í thì (1) ( ) Û í î ( g x) £ M î ( g x) = M
Baøi 1. Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc logarit hoaù): x 1 + 0 x+5 a) 3x 1 - 8x-2 9 = 3 b) x 1 - 0 x 15 16 0,125.8 - = c) 2 2 2 x 3 - x+2 x -6x-5 2x +3x+7 4 + 4 = 4 +1 d) 2x x 2 5 7 5 x.35 7x - - + .35 = 0 e) 2 2 2 2 x 1 - x +2 x x 1 2 2 3 3 - + = + 2 f) x- x +4 5 = 25 Trang 61
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng 2 x -2 æ ö x+7 1-2x æ ö æ ö g) 1 1 1 4-3 = 2 x ç . = 2 2 ÷ h) ç ÷ ç ÷ è ø è 2 ø è 2 ø x x 1 x 1 - - i) ( - )2 3 2 2 = 3 + 2 2 k) ( ) ( )x 1 5 2 5 2 + + = - l) x x 1 3 .2 + = 72 m) x 1 + x x-1 5 + 6. 5 – 3. 5 = 52
Baøi 2. Giaûi caùc phöông trình sau (ñaët aån phuï daïng 1): a) x x 1 4 2 + + - 8 = 0 b) x 1 + x 1 4 6.2 + - + 8 = 0 c) 4x+8 2x+5 3 - 4.3 + 27 = 0 d) 16x 17.4x - +16 = 0 e) x x 1 49 7 + + - 8 = 0 f) 2 2 x -x 2 2 - 2 +x-x = 3. x x
g) (7+ 4 3) +(2+ 3) = 6 h) 2 cos2x cos 4 4 x + = 3 i) 2x+5 x 1 3 36.3 + - + 9 = 0 k) 2 2 2x +2x 1 3
+ - 28.3x +x + 9 = 0 l) 2 2 x +2 x +2 4 - 9.2 + 8 = 0 m) 2x 1 - x 1 3.5 2.5 - - = 0,2
Baøi 3. Giaûi caùc phöông trình sau (ñaët aån phuï daïng 1):
a) 25x - 2(3 - ).5x x + 2x - 7 = 0 b) x-2 x-2 3.25 + (3x -10).5 + 3 - x = 0
c) 3.4x + (3 -10).2x x + 3- x = 0
d) 9x + 2( - 2).3x x + 2x - 5 = 0 e) x-2 x-2 3.25 + (3x -10).5 + 3- x = 0 f) 2 x 1+ x x 2 4x + 3 + 3
= 2.3 .x + 2x + 6
g) 4x +( – 8)2x x +12 – 2x = 0
h) ( + 4).9x -( + 5).3x x x +1 = 0 i) 2 2 x 2 x 2
4 + (x - 7).2 +12 - 4x = 0
k) 9-x - ( + 2).3-x x - 2(x + 4) = 0
Baøi 4. Giaûi caùc phöông trình sau (ñaët aån phuï daïng 2): 1 1 1 - - -
a) 64.9x 84.12x 27.16x - +
= 0 b) 4 x + 6 x = 9 x
c) 3.16x 2.81x 5.36x + = 1 1 1 d) x x 2x 1 25 10 2 + + = e) x x x 27 +12 = 8 . 2 f) 9 . 6 x - 6 . 13 x + 4 . 6 x = 0 1 1 1 g) 2x x 2 6.3 13.6 6.2 x - + = 0
h) 3.16x 2.81x 5.36x + =
i) 2.4x 6x 9x + =
k) (7 5 2)x ( 2 5)(3 2 2)x 3(1 2)x + + - + + + +1- 2 = 0.
Baøi 5. Giaûi caùc phöông trình sau (ñaët aån phuïdaïng 3): x x a) (2 3)x (2 3)x - + + = 14 b) æç 2 3 ö æ ÷ ç 2 3 ö + + - ÷ = 4 è ø è ø c) (2 3)x (7 4 3)(2 3)x + + + - = 4(2 + 3) d) x x x+3 (5 - 21) + 7(5 + 21) = 2 x x x x æ + ö æ - ö
e) (5 + 24 ) + (5 - 24 ) = 10 f) 7 3 5 7 3 5 ç ÷ + 7ç ÷ = 8 ç 2 ÷ ç 2 ÷ è ø è ø x x 2 2 x- x - x- g) ( ( 1) 2 1 4 6 - 35 ) +( 6+ 35 ) =12 h) (2+ 3) + (2- 3) = 2 - 3 i) ( )x ( )x x x x 3 3 5 16 3 5 2 + + + - =
k) (3+ 5) +(3- 5) -7.2x = 0 x x l) (7 4 3)x 3(2 3)x + - - + 2 = 0 m) æ 3 ö æ 3 ç 3 8 ÷ ç 3 8 ö + + - ÷ = 6. è ø è ø
Baøi 6. Giaûi caùc phöông trình sau (söû duïng tính ñôn ñieäu): a)(2 3)x (2 3)x 4x - + + = b) ( 3 2)x ( 3 2)x ( 5)x - + + = x x x x
c) (3+ 2 2 ) + (3 - 2 2 ) = 6x d) ( + ) + ( - ) x+3 3 5 16. 3 5 = 2 Trang 62
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit x x x e) æ 3 ö 7 + = 2 ç ÷ x
f) ( 2 + 3 ) + ( 2 - 3 ) = 2x è 5 ø 5
g) 2x 3x 5x 10x + + =
h) 2x 3x 5x + = i) 2 x 1 - x -x 2 2 - 2 = (x -1)
k) 3x = 5 - 2x l) 2x = 3 - x m) x 1 2 + - 4x = x -1 x n) x 2 2 = 3 +1
o) 4x + 7x = 9x + 2
p) 52x 1+ - 53x - x +1 = 0 q) x x x x 3 + 8 = 4 + 7 r) x x x x 6 + 2 = 5 + 3 s) x x x x 9 +15 = 10 +14
Baøi 7. Giaûi caùc phöông trình sau (ñöa veà phöông trình tích):
a) 8.3x 3.2x 24 6x + = + b) x x x 1 12.3 3.15 5 + + - = 20 c) x 3 8 - .2 + 2 -x x - x = 0 d) x x x 2 + 3 = 1+ 6
e) 4 2x-3x+2 + 4 2x+6x+5 = 4 .2 2x+3x+7 +1 f) 2 2 x + x 1-x (x 1 + ) 4 + 2 = 2 2 +1 g) 2 x x 2 2
x .3 + 3 (12 - 7x) = -x + 8x -19x +12 h) 2 x 1 - x x x x 1 x .3 x(3 2 ) 2(2 3 - + - = - ) i) sin x 1+sin 4 - 2
x cos(xy)+ 2 y = 0 k) 2 2 2 2 2(x +x) 1-x 2(x +x) 1 2 + 2 - 2 .2 -x -1 = 0
Baøi 8. Giaûi caùc phöông trình sau (phöông phaùp ñoái laäp): a) x 4
2 = cos x , vôùi x ³ 0 b) 2x-6x 1 + 0 2 3
= - x + 6x - 6 c) sin 3 x = cos x 3 æ ö 2 d) 2 2.cos x - x ç
÷ = 3x + 3-x e) 2 2 - +1 x x x sin x p = cos x f) 2 = è 2 ø x 2 g) x 3 2 = cos 2x h) 5x = cos3x
Baøi 9. Tìm m ñeå caùc phöông trình sau coù nghieäm:
a) 9x + 3x + m = 0 b) 9x + 3x m -1 = 0 c) x x+ 1 4 - 2 = m d) 2
3 x + 2.3x - ( + 3).2x m = 0
e) 2x + ( +1).2-x m
+ m = 0 f) 25x - 2.5x - m - 2 = 0 g) x 2 16 - ( -1).2 x m
+ m -1 = 0 h) 25x + .5x m +1- 2m = 0 i) 2 2 sin x cos 81 + 81 x = m k) 2 2 4-2x 2 3
- 2.3 -x + 2m - 3 = 0 l) x + 1 + 3 - x x + 1 + 3 4 -14.2 - x +8 = m m) 2 2 x+ 1-x x+ 1 9 - 8.3 -x + 4 = m n) 2 2 1+ 1-t 1+ 1 9 - ( + 2).3 -t m + 2m +1 = 0
Baøi 10. Tìm m ñeå caùc phöông trình sau coù nghieäm duy nhaát: a) .2x 2 x m - + - 5 = 0
b) .16x 2.81x 5.36x m + = x x x x æ ö æ ö c) ( 5 + - + ) 1 + ( 5 - ) 1 = 2x m d) 7 3 5 7 3 5 ç ÷ + mç ÷ = 8 è 2 ø è 2 ø e) x x+ 3 4 - 2 + 3 = m f) 9x + 3x m +1 = 0
Baøi 11. Tìm m ñeå caùc phöông trình sau coù 2 nghieäm traùi daáu: a) x x 1 (m 1).4 (3m 2).2 + + + - - 3m +1 = 0 b) x x 2
49 + (m -1).7 + m - 2m = 0
c) 9x + 3( -1).3x m - 5m + 2 = 0
d) ( + 3).16x + (2 -1).4x m m + m +1 = 0 e) 4x - 2( + ) 1 .2x m +3m - 8 = 0
f) 4x - 2x + 6 = m
Baøi 12. Tìm m ñeå caùc phöông trình sau:
a) .16x + 2.81x = 5.36x m
coù 2 nghieäm döông phaân bieät.
b) 16x - .8x + (2 -1).4x = .2x m m m
coù 3 nghieäm phaân bieät. c) 2 2 x x +2 4 - 2
+ 6 = m coù 3 nghieäm phaân bieät. 2 2
d) 9x - 4.3x + 8 = m coù 3 nghieäm phaân bieät. Trang 63
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng
V. PHÖÔNG TRÌNH LOGARIT
1. Phöông trình logarit cô baûn Vôùi a > 0, a ¹ 1: log b
a x = b Û x = a
2. Moät soá phöông phaùp giaûi phöông trình logarit
a) Ñöa veà cuøng cô soá Vôùi a > 0, a ¹ 1:
ì f (x) = g(x)
log f (x) = log g(x) a a
Û íîf(x) > 0 (hoaëcg(x)> 0) b) Muõ hoaù Vôùi a > 0, a ¹ 1: log f (x) log ( ) a b
a f x = b Û a = a c) Ñaët aån phuï
d) Söû duïng tính ñôn ñieäu cuûa haøm soá
e) Ñöa veà phöông trình ñaëc bieät
f) Phöông phaùp ñoái laäp Chuù yù:
· Khi giaûi phöông trình logarit caàn chuù yù ñieàu kieän ñeå bieåu thöùc coù nghóa.
· Vôùi a, b, c > 0 vaø a, b, c ¹ 1: log c log a b b a = c
Baøi 1. Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc muõ hoaù):
a) log2 éx(x -1)ù =1 ë û
b) log2 x + log2(x -1) =1 c) log2(x -2)- 6.lo 1 g /8 3x - 5 = 2
d) log2(x -3)+ log2(x -1) = 3
e) log4(x + 3)- log4(x -1) = 2 - log4 8 f) lg(x - 2)+ lg(x -3) =1- lg5 g) 2
2 log8(x - 2)- log8(x -3) =
h) lg 5x - 4 + lg x +1 = 2 + lg 0,18 3 i) 2
log3(x -6) = log3(x - 2)+1
k) log2(x +3)+ log2(x -1) =1/ log5 2
l) log4 x + log4(10 - x) = 2 m) log5(x -1)- lo 1 g /5(x + 2) = 0
n) log2(x -1)+ log2(x + 3) = log210 -1 o) log9(x +8)- log3(x + 26)+ 2 = 0
Baøi 2. Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc muõ hoaù):
a) log3 x + log x + log x = 6 b) 2 2
1+ lg(x - 2x +1) - lg(x +1) = 2 lg(1- x) 3 1/3 c) log4 x + lo 1
g /16 x + log8 x = 5 d) 2 2
2 + lg(4x - 4x +1) - lg(x +19) = 2 lg(1- 2x)
e) log2 x + log4 x + log8 x =11 f) lo 1 g /2(x -1)+ lo 1 g /2(x +1) =1+ log (7 - x) 1/ 2
g) log2 log2 x = log3 log3 x
h) log2 log3 x = log3 log2 x
i) log2 log3 x + log3 log2 x = log3 log3 x k) log2 log3 log4 x = log4 log3 log2 x
Baøi 3. Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc muõ hoaù): a) log x x 2 (9 - 2 ) = 3 - x b) log3(3 -8) = 2 - x c) log -x x- 7(6 + 7 ) = 1+ x d) 1 log3(4.3 -1) = 2x -1 e) x log (3- ) 5 log x 2 (9 - 2 ) = 5 x
f) log2(3.2 -1)- 2x -1= 0 Trang 64
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit g) log x x 2 (12 - 2 ) = 5 - x h) log5(26 -3 ) = 2 i) x+ 1 log x x+ 2 (5 - 25 ) = 2 k) 1 log4(3.2 - 5) = x l) x+ 1 log x x+ x 1 (5 - 25 ) = 2 - m) 1 log 1 (6 - 36 ) = -2 6 5
Baøi 4. Giaûi caùc phöông trình sau (ñöa veà cuøng cô soá hoaëc muõ hoaù): a) 2 log5 ( 2 65) 2 x x x log
(x - 4x + 5) = 1 - - + = b) 2 x - 1 c) 2 log (5 - 8 + 3) = 2 x x x d) 3 2 log 1(2 2 3 1) 3 x x x x + + - + = e) log 3( 1) 2 x x - - = f) log ( 2) 2 x x + = g) 2 log2 ( -5 + 6) = 2 x x x h) 2 log 3( ) 1 x x x + - = i) 2 log (2 - 7 +12) = 2 x x x k) 2 log (2 - 3 - 4) = 2 x x x l) 2 log2 ( -5 + 6) = 2 x x x m) 2 log ( 2) 1 x x - = n) 2 log3 5(9 8 2) 2 x x x log (x +1) = 1 + + + = o) 2 2x + 4 p) 15 log = 2 x - q) log (3 - 2x) = 1 1- 2x 2 x r) log (x + 3) = 1 s) 2 log (2 - 5 + 4) = 2 2 x + 3x x x x
Baøi 5. Giaûi caùc phöông trình sau (ñaët aån phuï): a) 2 2
log3 x + log3 x +1 -5 = 0 b) 2
log x + 3log x + log x = 2 2 2 1/2 2 c) 7 log 2 x - log 2 x 4 x + = 0 d) log 4x + log = 8 6 1 2 8 2 e) 2
log x + 3log x + log x = 0 f) log 16 + log 64 = 3 2 2 1/2 2 x 2x g) 1 log 1 5 x - log = 2 x h) log x - log = 2 5 7 x 7 i) 1
2 log5 x -2 = logx
k) 3 log x - log 4x = 0 5 2 2
l) 3 log3 x - log3 3x -1 = 0 m) 3 3
log2 x + log2 x = 4 / 3 n) 3 1 3
log2 x - log2 x = 2 - / 3 o) 2 log2 x + 2log4 = 0 x p) 2 log2(2 - x)-8lo 1 g /4(2 - x) = 5 q) 2
log5 x + 4log25 5x - 5 = 0 r) 9 2 log 5 + log 5x = + log 5 x x s) log 3 + log x = 1 4 x 2 x 9 t) 1 2 + = 1 u) 1 3 + = 1
4 - lg x 2 + lg x
5 - lg x 3 + lg x v) 2 3 log2 x -14lo 1
g 6 x + 40log4 x = 0 x x x
Baøi 6. Giaûi caùc phöông trình sau (ñaët aån phuï): a) 2
log x + (x -12) log x +11- x = 0 b) log x 2 2 log2 6 6.9 + 6.x =13.x 3 3 c) 2 . x log d) 2
2 x - 2(x +1).log2 x + 4 = 0 log x + (x - ) 1 log x = 6 - 2x 2 2 Trang 65
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng e) 2
(x + 2) log (x +1) + 4(x +1) log (x + 1) -16 = 0 f) log (2 + x) + log x = 2 3 3 2 x 2-x g) 2
log3(x +1)+ (x - 5)log3(x +1)- 2x + 6 = 0 h) 4 log3 x -1 - log3 x = 4 i) 2 2
log2(x +3x + 2)+ log2(x + 7x +12) = 3+ log2 3
Baøi 7. Giaûi caùc phöông trình sau (ñaët aån phuï): a) log
7 x = log3( x + 2)
b) log2(x -3)+ log3(x - 2) = 2 c) log log x 6 3 ( x + ) 1 + log5 (2x + ) 1 = 2 d) log2 (x +3 )=log6 x e) log +3 7( ) 4 x = x f) log (1+ x ) 2 = log3 x g) log 9 2 log log 3 2 2 2 = .3 x x x - x h) 2 2 log3
+7(9 + 12x + 4x ) + log2 +3(6x + 23x + 21) = 4 x x i) log ( 2 x - x -1).log ( 2
x + x -1) = log ( 2 x - x -1) 2 3 6
Baøi 8. Giaûi caùc phöông trình sau (söû duïng tính ñôn ñieäu): a) log 3 log 5 2 log x log x 2 2 x + x = x (x > 0) b) 2 2 x + 3 = 5
c) log5(x +3) = 3- x
d) log2(3- x) = x e) 2 log log x
2 (x - x - 6) + x = log2 (x + 2) + 4 f) 2 x +2.3 = 3 g) 4(x - 2) élog ë
2 (x - 3) + log3(x - 2)ù = 15(x + 1) û
Baøi 9. Giaûi caùc phöông trình sau (ñöa veà phöông trình tích):
a) log2 x + 2.log7 x = 2 + log2 x.log7 x
b) log2 x.log3 x +3 = 3.log3 x + log2 x c) 2(log x)2 9
= log3 x.log3 ( 2x +1 - )1
Baøi 10. Giaûi caùc phöông trình sau (phöông phaùp ñoái laäp): a) 2 3
ln(sin x) -1+ sin x = 0 b) log ( 2 x + x - ) 2 2 1 = 1- x c) 2x 1 + 3-2x 8 2 + 2 = 2
log3(4x - 4x + 4)
Baøi 11. Tìm m ñeå caùc phöông trình sau coù nghieäm duy nhaát: a) 2 log
éëx 2(m 1)xù - + û + log
(2x + m - 2) = 0 b) log (x - 2) = log 2 ( mx) 2+ 3 2- 3 2 lg(mx) c) log ( 2
x + mx + m + ) 1 + log x = 0 d) = 2 5+2 5-2 lg(x + ) 1 e) 2
log3(x + 4mx) = log3(2x - 2m -1) f) 2 log (x - m +1) + log (mx - x ) = 0 2 2+ 7 2 2- 7
Baøi 12. Tìm m ñeå caùc phöông trình sau: a) log (4x - m)
coù 2 nghieäm phaân bieät. 2 = x +1 b) 2 log coù 2 nghieäm x
3 x - (m + 2).log3 x + 3m -1 = 0
1, x2 thoaû x1.x2 = 27. c) 2 2 2 2
2log (2x - x + 2m - 4m ) = log (x + mx - 2m ) coù 2 nghieäm x
x + x > 1. 4 2 1, x2 thoaû 2 2 1 2 d) 2 2 log é ù
3 x + log3 x +1 - 2m -1 = 0 coù ít nhaát moät nghieäm thuoäc ñoaïn 3 1 ë ;3 û . e) 4(log x )2 2
+ log2 x + m = 0 coù nghieäm thuoäc khoaûng (0; 1). Trang 66
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit
VI. HEÄ PHÖÔNG TRÌNH MUÕ VAØ LOGARIT
Khi giaûi heä phöông trình muõ vaø logarit, ta cuõng duøng caùc phöông phaùp giaûi heä phöông trình ñaõ hoïc nhö: · Phöông phaùp theá.
· Phöông phaùp coäng ñaïi soá.
· Phöông phaùp ñaët aån phuï. · …….
Baøi 1. Giaûi caùc heä phöông trình sau: ì y ì x a) ïx + 2 = 5 ï = y í b) 2 4 í ï x îx - 2y = 1 ïî4 = 32y ì y ì y 1 - c) ïx - 3 = 1 ïx = 8 í 2 d) í ï 2y-6 îx + 3y = 19 ïîx = 4 ì2x + 2y = ì x y e) 3 ï = í f) 2 .9 36 í îx + y = 1 3x ïî .4y = 36 ì x. y ì x y f) ï2 5 = 20 ï = í g) 2 .3 12 í ïî5x.2y = 50 3x ïî .2y =18 2 ì y -7y 10 + 2 2 ì x -y 16 - h) ïx = 1 ïx = 1 í i) x + y = 8 í ïî (x > 0) x - y = 2 ïî (x > 0)
Baøi 2. Giaûi caùc heä phöông trình sau: ì x y ì x y a) ï4 - 3 = 7 ï + = í b) 2 3 17 í ï x y î4x.3y = 144 3. ïî 2 - 2.3 = 6 ì x x + y ì 2x+2 2y+2 c) ï2 + 2.3 = 56 3 ï + 2 = 17 í d) x x + y + 1 í 3. ïî 2 + 3 = 87 x 1 ïî2.3 + + 3.2y = 8 ì x 1 + y 2 2 ì 2(x 1 - ) x 1 - y 2y e) 3 ï - 2 = -4 ï4 - 4.4 .2 + 2 = 1 í f) í x 1 + y 1 3 2 ï 2y x 1. - y î - 2 + = 1 - ïî2 -3.4 .2 = 4 ì 2 y 2 ì 2 y-x g) ïcot x = 3 ( ï x + y)2 = 1 í h) í ï 2 îcos x = 2y 2
ïî9(x + y) = 6x -y ì 2x y ì x y i) 3 ï - 2 = 77
ï2 - 2 = (y - x)(xy + 2) í k) í 3x ïî - 2y = 7 2 2 ïîx + y = 2
Baøi 3. Giaûi caùc heä phöông trình sau: ì x ì x a) 3 ï = 2y +1 ï + x = y + í b) 3 2 11 í 3y ï y î = 2x +1 3
ïî + 2y = x +11 ì x y x 1 - ì
c) ï2 - 2 = y - x ï7 = 6y - 5 í d) 2 2 í
ïîx + xy + y = 3 y 1 ïî7 - = 6x - 5 Trang 67
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng
Baøi 4. Giaûi caùc heä phöông trình sau: ìlog + log x = 2 a) ìx + y = 6 í x y y log b) í î 2 x + log2 y = 3 îx + y = 6 ìx + log y = 4 ì 2 2 c) 2 ïx - y = 3 í d) 2x - log í î log
ïî 3 (x + y) - log5 (x - y) 2 y = 2 = 1 ìxy = 32 ì log2 y e) ïlog x + 2 = 3 ílog x 3 = 4 f) í î y y ïîx = 9 ì (log 2 x + log y) = 5 ì g)
ï x -1 + 2 - y = 1 í y x h) í îxy = 8 2 3 3 ï log î
9(9x ) - log3 y = 3 ì1 2
log x - log y = 0 ìy - log x = 1 i) ï 3 3 í2 k) 3 í 3 y 12 2
ï x + y - 2y = 0 îx = 3 î
Baøi 5. Giaûi caùc heä phöông trình sau:
ìïlog (3x + 2y) = 2
ìïlog (6x + 4y) = 2 a) x í b) x
log (2x + 3y) = 2 í ïî
log (6y + 4x) = 2 y ïî y ì æ ö ïlog x 2 1- = 2 - log ç ÷ 2 y ì 2 c) ï è y ø ïlog - log y = 1 í d) y x 2 log x + log y = 4 í ï
ïlog x - log y = 1 3 3 î 4 4 ïî 2 2 ìïlog ( 2 2 ì log y log x 2 x + y + 6) = 4 e) ïx + y = 16 í f) 2 2 í ïlog î
ïlog x - log y = 2 3 x + log3 y = 1 î 2 2 ì log ì log y log x 3 x y + . 2 log3 y x = 2 2 g) 27 3 ï .x + 2.y = 10 í h) í
îlog y - log x = 1 2
ïlog x + log y = 2 3 3 î 4 2 ì ìlog2 (xy) = 4
ïlogx (2x + y - 2) = 2 i) ï í k) log í æ x ö ïî
y (2y + x - 2) = 2 log ï 2 = 2 ç î è y ÷ø ì 2 2 2 ì 5
ïlog x + log x =
l) ïlg x = lg y + lg (xy) í m) y y 2 í 2
ïîlg (x - y) + lg x.lg y = 0 2 2 ïlog î 6 (x + y ) = 1
ìlog2 (x - y) = 5- log2 (x + y) ìï ( 2 2
lg x + y ) =1+ lg8 n) ïílg x - lg4 o) = -1 í ï ïlg
î ( x + y) - lg( x - y) = lg3 î lg y - lg3 ì ì y ïlog y = 2 2 ïlog - log x = 1 p) x í q) xy y log í x ïî x 1 + ( y + 23) = 3 ïlog î 2 ( y - x ) = 1
Baøi 6. Giaûi caùc heä phöông trình sau:
ìlg x + lg y = 4 ì x-2y a) ïx = 36 í lgy b) í îx = 1000 4
ïî (x - 2y) + log6 x = 9 Trang 68
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit ì y-x 5 ì lg x lg y c) ( ï x + y)3 = 3 ï = 4 í 27 d) í lg4 lg3 3 ï log ( ïî 4x) = (3y) î
5(x + y) = x - y
ì2æ log x - 2 log y ö + 5 = 0 2 1 x e) ï ç ÷ í è y ø ï 2 îxy = 32
Baøi 7. Giaûi caùc heä phöông trình sau: ìlog ì 3x
2 x + log4 y + log4 z = 2 x log ï
2 3 + log2 y = y + log2 a) ïílog 2
3 y + log9 z + log9 x = 2 b) í ï 2y log î
ïx log 12 + log x = y + log 4 z + lo 1 g 6 x + lo 16 g y = 2 3 3 3 î 3 2 2
ìïlog (1-2y + y )+ log (1+ 2x + x ) = 4
ìïlog 1+ 3sin x = log (3cos y) c) 1+x 1-y í d) 2 3 lo í ïî 1 g (1+ 2x) + lo +x 1 g (1+ 2x) = 2 -y ïlog î
2 1+ 3 cos y = log3(3sin x) ì ïlog ( 2 1+ 3 1- x ) = log ( 2 1- y ) + 2 e) 2 í ïlog î 2 (1+ 3 1- y ) 3 2 = log ( 2 1- x ) 3 + 2 2 ì
f) ï2 log3 (6 - 3y + xy - 2x) + log -x
2 (x - 6x + 9) = 6 -y í log ïî 3 (5 - y) - log -x 2 (x + 2) = 1 -y
Baøi 8. Giaûi caùc heä phöông trình sau: ì x - 2y log x ì 4 ( x - y æ ö ï 3) 1 a) ï 2 2 = y í b) = ç 3÷ í è ø ïlog î 2 x - log2 y = 1
ïlog (x + y)+ log (x - y) î 2 2 = 4 x y log y log x ì 3 ì .2 =18 c) ï 8 8 x + y = 4 ï í
d) ílog (x + y) = -1 ïlog î 1 4 x - log4 y = 1 ïî 3
(ì x y æ1öx-2y - x y ì ï 3) + e) = ç ÷ ï í y x è 3 ø f) í4 = 32 ï ïlog î
3 ( x - y) = 1- log3 ( x + y)
îlog (x + y) + log (x - y) = 4 2 2 ì x y ì -x y g) 3 ï .2 = 972 3 ï .2 = 1152 í h) log í ï (x - y) = 2 log ï (x + y) î = 2 3 î 5 x y ì ì log xy log 2 i) (
ï x + y) = (x - y) ï4 = 2 + (xy) í k) 3 3 í ïlog 2 2 î 2 x - log2 y = 1
ïîx + y - 3x - 3y = 12 log y log x ì 2
ìïlog xy = log x l) ï 3 3 x + 2y = 27 í m) x y í ï log î 2log x 3 y - log3 x = 1 y ïîy = 4y + 3 Trang 69
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng
VII. BAÁT PHÖÔNG TRÌNH MUÕ
· Khi giaûi caùc baát phöông trình muõ ta caàn chuù yù tính ñôn ñieäu cuûa haøm soá muõ. éìa >1 êí f (x) g(x)
î f (x) > g(x) a > a Û ê ì ê 0 < a < 1 í
êëî f (x) < g(x)
· Ta cuõng thöôøng söû duïng caùc phöông phaùp giaûi töông töï nhö ñoái vôùi phöông trình muõ:
– Ñöa veà cuøng cô soá. – Ñaët aån phuï. – ….
Chuù yù: Trong tröôøng hôïp cô soá a coù chöùa aån soá thì: M N
a > a Û (a -1)(M - N) > 0
Baøi 1. Giaûi caùc baát phöông trình sau (ñöa veà cuøng cô soá): x - x - 1 6 3 æ ö x -2x 1 + 1 - x æ ö æ ö a) 2 x - 2x 1 3 1 1 ³ ç b) ç ÷ < 3 ÷ ç ÷ è ø è 2 ø è 2 ø c) x + 2 x + 3 x + 4 x + 1 x + 2 2 - 2 - 2 > 5 - 5 d) x x - 1 x - 2 3 + 3 - 3 < 11 e) 2 2 x 3 - x+2 x -3x+2 9 - 6 < 0 f) 2x+3 x+7 3x 1 6 < 2 3 . - g) 2 2 2 2 x + 1 x 2 4 + .2 + 3.2 > .2x x x x + 8x +12 h) . 6 2
x + 3 x.x + 31+ x < 3 . 2 x . 2 x + 3x + 9 i) x x 1 + x+2 x x 1 + x+2 9 + 9 + 9 < 4 + 4 + 4 k) x 1+ x+3 x+4 x+2 7.3 + 5 £ 3 + 5 l) x 2 + x+1 x x+2 2 + 5 < 2 + 5 m) x 1 - x+ 2 2 .3 > 36 x-3 x 1 + 1 x x+ n) ( + ) x 1 - < ( - )x+3 10 3 10 3 o) ( ) ( )x 1 2 1 2 1 - + ³ - 1 1 p) 1 x 1 £ 2 - q) 2x 1 - 3x 1 2 2 + ³ 2 x -2 2 x
Baøi 2. Giaûi caùc baát phöông trình sau (ñaët aån phuï): 1 1 - 1 - 2
a) 2.14x 3.49x 4x + - ³ 0 b) 4 x - 2 x - 3 £ 0 2(x - 2) c) x 2(x - 1) 3 4 - 2 + 8 > 52 d) 4 4 x + x 1 8.3
+ 9 + x > 9 x
e) 25.2x 10x 5x - + > 25 f) 2x + 1 x + 1 5 + 6
> 30 + 5x.30x
g) 6x 2.3x 3.2x - - + 6 ³ 0
h) 27x 12x 2.8x + > 1 1 1 x
i) 49x 35x 25x - £ k) x 1 + 2x 1 + 2 3 - 2 -12 < 0 l) 2 2 2 2x-x 1 + 2x-x 1 + 2 25 + 9 ³ 34.25 x-x m) 32x - 3 . 8 x+ x+4 - 9 . 9 x+4 > 0 x x o) x + x - 1 x + x - 1 + 1 4 - 5.2 +16 ³ 0 p) ( 3 + 2 ) + ( 3 - 2 ) £ 2 2 1 + 1 æ ö æ ö 3x x - 1 æ ö æ ö r) 1 x 1 1 1 ç ÷ + 3 x ç ÷ > 12 s) ç ÷ - ç ÷ -128 ³ 0 è 3 ø è 3 ø è 4 ø è 8 ø 1 1 + 1 2 - t) 2 x + 2 x < 9 u) ( 2x + 1 2 - 9.2x + 4) 2
. x + 2x - 3 ³ 0 Trang 70
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit
Baøi 3. Giaûi caùc baát phöông trình sau (söû duïng tính ñôn ñieäu): x -x x a) x 2 2 - + < 3 +1 21 2 1 b) £ 0 2x -1 x x+2 c) 2 3 . - 2 £ 1 d) x+4 2x+4 3 + 2 > 13 3x - 2x 2-x x e) 3 + 3 - 2x 3 + x - 4 ³ 0 f) > 0 4x - 2 2 x - x - 6 g) x - - x + + > - - x + + ( )2 2 2 x 3x 5 2 2x 3 .2x 3x 5 2 2x 3
Baøi 4. Tìm m ñeå caùc baát phöông trình sau coù nghieäm: a) 4x - .2x m + m + 3 £ 0 b) 9x - .3x m + m + 3 £ 0 2 2 x x 1 -
c) 2x + 7 + 2x - 2 £ m d) ( 2 + ) 1 + ( 2 - ) 1 + m = 0
Baøi 5. Tìm m ñeå caùc baát phöông trình sau nghieäm ñuùng vôùi:
a) (3 +1).12x + (2 - ).6x + 3x m m < 0 , "x > 0. b) x x 1 (m 1)4 2 + - + + m +1 > 0 , "x. c) .9x - (2 + ) 1 6x + .4x m m m £ 0 , "x Î [0; 1]. d) x x+2 . m 9 + (m -1).3 + m -1 > 0 , "x.
e) cosx + ( m + ) cosx 2 4 2 2 1 2
+ 4m - 3 < 0 , "x. f) x x 1 4 3.2 + - - m ³ 0 , "x.
g) 4x - 2x - m ³ 0 , "x Î (0; 1)
h) 3x + 3 + 5 - 3x £ m , "x.
i) 2.25x - (2 +1).10x + ( + 2).4x m m ³ 0 , "x ³ 0. k) x 1 4 - - .(2x m +1) > 0 , "x.
Baøi 6. Tìm m ñeå moïi nghieäm cuûa (1) ñeàu laø nghieäm cuûa baát phöông trình (2): 2 1 ì + 1 æ ï 1 öx æ 1 öx 2 1 ì 1 + a) ïç ÷ + 3ç ÷ > 12 (1) ï í x x è 3 ø è 3 ø b) 2 - 2 > 8 (1) í 2 2 ( ï
ïî4x -2mx -(m -1) < 0 (2) ïî m - 2)2 2
x - 3(m - 6) x - m -1 < 0 (2) 2 1 ì +2 ì 2x 1 + x æ ï 1 öx æ 1 öx c) ï2 - 9.2 + 4 £ 0 (1) ï + 9. > 12 (1) í d) ç ÷ ç ÷ 2 í ( è 3 ø è 3
ïî m +1)x + m(x + 3)+1 > 0 (2) ø ï 2 ï2x + î
(m+2)x +2-3m < 0 (2) Trang 71
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng
VIII. BAÁT PHÖÔNG TRÌNH LOGARIT
· Khi giaûi caùc baát phöông trình logarit ta caàn chuù yù tính ñôn ñieäu cuûa haøm soá logarit. éìa > 1 êí
î f (x) > g(x) > 0
log f (x) > log g(x) a a Û êìê0 < a<1 í
êëî0 < f (x) < g(x)
· Ta cuõng thöôøng söû duïng caùc phöông phaùp giaûi töông töï nhö ñoái vôùi phöông trình logarit:
– Ñöa veà cuøng cô soá. – Ñaët aån phuï. – ….
Chuù yù: Trong tröôøng hôïp cô soá a coù chöùa aån soá thì: log A log > 0 Û ( -1)( -1) > 0 a a B a B ;
> 0 Û (A -1)(B -1) > 0 loga B
Baøi 1. Giaûi caùc baát phöông trình sau (ñöa veà cuøng cô soá): a) log 1
( - 2x) < 1+ log (x + ) 1
b) log2 (1-2log9 x) <1 5 5 c) log
5 - x < log (3 - x) 1 1
d) log2 log1 log5 x > 0 3 3 3 + e) 1 2x log (log ) > 0 f) ( 2
x - 4)log x > 0 1 2 1+ x 1 3 2 2 g) log élog ( 2 x - 5)ù log x log x 6 6 1 ë 4 > 0 û h) 6 + x £ 12 3 i) log (log )2 2 log2
2 ( x + 3) ³ 1+ log2 ( x - ) 1 k) 2 x x + x l) 2
log3 ælog1 x ö ³ 0
m) 2 log (x - 2) + log (x - 3) > ç ÷ 8 1 3 è 2 ø 8 n) é ù é ù log log ( 2
x +1 + x) > log log ( 2 x +1 - x) 1 ë 5 û 3 ê 1 ú 3 êë 5 úû
Baøi 2. Giaûi caùc baát phöông trình sau: ( 2 2 3 lg x - ) log ( x + ) 1 - log ( x + ) 1 a) 1 2 3 ( < b) > 0 - x) 1 lg 1 2 x - 3x - 4 ( 2 lg x - 3x + 2) c) > 2 d) log x 5log 2 log x 2 x 2 x x - + -18 < 0 lg x + lg 2 e) 3x -1 x log > 0 f) 2
log x.log x < log x + log x 2 x +1 3 2 3 2 4 g) log (log x x 4 (2 - 4)) £ 1 h) log (3 - x) > 1 2 3x-x i) log ( 2 - 8 +16) ³ 0 2 x x x k) log ( - 5 + 6) 2 < 1 x x x 5 Trang 72
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit æ - ö l) x 1 log x m) logx - ( x + ) 1 > log x +1 2 1 x 1 - ( ) +6 log ç 2 > 0 è x 2 ÷ + 3 ø n) 2
(4x -16x + 7).log x x 3(x - 3) > 0
o) (4 -12.2 + 32).log2(2x -1) £ 0
Baøi 3. Giaûi caùc baát phöông trình sau (ñaët aån phuï):
a) log2 x + 2log 4 -3 £ 0 x
b) log (1- 2x) < 1+ log ( x + ) 5 1 5
c) 2 log5 x - log 125 <1 x
d) log 64 + log 16 ³ 3 2 2x x
e) log 2.log2 2.log2 4 1 x x x > f) 2 2
log1 x + log1 x < 0 2 4 g) 2 log x log x 1 2 4 2 + > h) + £ 1 2
1- log x 1+ log x 1- log x 4 + log x 2 - log x 2 2 2 2 2
i) log2 x - 6log x + 8 £ 0 k) 2
log x - 4 log x + 9 ³ 2 log x - 3 1 2 3 3 3 2 l) 1 2 log 3 ( 2 x + 4x + ) 2 +1 > log 3 ( 2 x + 4x + ) 2 m) + < 1 9 3
5 - log5 x 1+ log5 x n) 2 1 1
- 9 log1 x >1- 4log1 x o) log 100 - lo x 1 g 00 x > 0 2 8 8 2 1+ log x p) 3 1 > 1 q) log 2.log 2 > 1+ log x x 3 x log2 x -6 16
Baøi 4. Giaûi caùc baát phöông trình sau (söû duïng tính ñôn ñieäu): a) 2 ( x + 1)log x x
0,5x + (2x + 5) log0,5 x + 6 ³ 0 b) log (2 + ) 1 + log (4 + ) 2 £ 2 2 3 5 lg + x c) 3 2 > d) 5 - x < 0 log x +1 log x +1 x 2 ( ) 3 ( ) 2 - 3x +1
Baøi 5. Tìm m ñeå caùc baát phöông trình sau coù nghieäm: a) log ( 2
x - 2x + m) 1/2 > -3 b) 1 log 100 - log 100 > 0 x 2 m 2 c) 1 2 1+ log x + < 1 d) m > 1 5 - log x 1+ log m m x 1+ logm x
e) log2 x + m > log2 x f) 2 2 log (x -1) > log (x + x - 2) x -m x-m
Baøi 6. Tìm m ñeå caùc baát phöông trình sau nghieäm ñuùng vôùi: a) log ( 2 7x + 7) ³ log ( 2
mx + 4x + m) 2 2 , "x b) log
x - x + m +
x - x + m £ , "x Î[0; 2] 2 ( 2 2 ) 4 log2( 2 2 ) 5 c) 2 2
1+ log5(x +1) ³ log5(mx + 4x + m) , "x. æ ö æ ö æ ö d) m 2 2 - log m m ç 1 x - 2 1+ log ÷ ç 1 x - 2 1+ log ÷ ç 1 > 0 , "x 1+ m 1+ m 1+ m ÷ ç ÷ ç ÷ ç ÷ è 2 ø è 2 ø è 2 ø
Baøi 7. Giaûi baát phöông trình, bieát x = a laø moät nghieäm cuûa baát phöông trình: a) ( 2 x - x - ) > ( 2 log 2
log -x + 2x + 3); a = 9 / 4 m m . b). 2 2
log (2x + x + 3) £ log (3x - x); a = 1 m m Trang 73
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng
Baøi 8. Tìm m ñeå moïi nghieäm cuûa (1) ñeàu laø nghieäm cuûa baát phöông trình (2): 2 2 ìlog ï
1 x + log 1 x < 0 (1) 2 ì a) ïlog (5 - 8 + 3) > 2 (1) í x x x 2 4 b) í ï 2 4 2 2
ïîx - 2x +1- m > 0 (2)
îx + mx + m + 6m < 0 (2)
Baøi 9. Giaûi caùc heä baát phöông trình sau: 2 ì x + 4
(ìïx - ) + ( x 1
1 lg 2 lg 2 + + )1 < lg(7.2x +12) a) ï > 0 2 í x -16x + 64 b) í ï ïlog î
x ( x + 2) > 2
îlg x + 7 > lg(x - 5) - 2 lg 2
ìïlog2-x (2 - y) > 0 ìïlog (y + 5) < 0 c) í d) x 1 - log í ï log (4 - x) < 0 î
4-y (2x - 2) > 0 ïî y+2 Trang 74
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit
IX. OÂN TAÄP HAØM SOÁ
LUYÕ THÖØA – MUÕ – LOGARIT
Baøi 1. Giaûi caùc phöông trình sau: 2x 1 - x 1 + a) 2 .4 = 64 b) 3x 1 - 8x-2 9 = 3 x 1 8 - x 2 +0,5 x x 1 + x +2x 1 - 1 9 æ ö æ ö æ ö c) 0,2 (0,04) 5 9 5 = d) ç ÷ .ç ÷ = ç ÷ 5 25 è 3 ø è 25 ø è 3 ø e) x+2 1 x 1 + x 1 7 .7 14.7 - - - + 2.7x = 48 f) ( 2x-7,2x+3,9 3 - 9 3) lg(7 - x) = 0 7 2 1 æ ö x 1 - g) ç x +3 2 x x è 2(2 ) x ÷ø = 4 h) x 1 5 . 8 - = 500 1 2 1- lg x i) 3 1 x = k) lgx 2 x = 1000x 3 100 lg x+5 log x 1 - l) 3 5+lg = 10 x x m) ( x ) 3 = 3
Baøi 2. Giaûi caùc phöông trình sau: a) 2 2 x +2 x +2 4 - 9.2 + 8 = 0 b) 2 2 x- x -5 x 1 - - x -5 4 -12.2 + 8 = 0 1 3 3+
c) 64.9x 84.12x 27.16x - + = 0
d) 64x - 2 x +12 = 0 e) 2 2 x 1 - x -3 9 - 36.3 + 3 = 0 f) 4x+8 2x+5 3 - 4.3 + 28 = 2 log2 2 x x g) 2x 1 + x+2 x 2(x 1) 3 3 1 6.3 3 + = + - +
h) ( 5 + 24 ) + ( 5 - 24 ) = 10 i) 1+log x 1+log x 3 3 9 - 3 - 210 = 0 k) 2 lg x 1 + lg x lg x +2 4 - 6 - 2.3 = 0 l) 2 2 sin x cos 2 4.2 x + = 6 m) lg(tan x) lg(cot x) 1 3 2.3 + - = 1
Baøi 3. Giaûi caùc baát phöông trình sau: 6-5x æ ö x 1 - a) 2 2+5x 25 2 -1 ç ÷ < b) < 2 è 5 ø 4 x 1 2 + +1 c) 2 x 2 .5 5 x x + - < 0 d) 2 lg x 3lg x 1 x - + >1000 x -2 x x æ ö e) 4 + 2x - 4 3 2 £ 2 f) 8. > 1+ x ç ÷ -1 3x - 2x è 3 ø 2 log (x 1) - 2 æ ö g) x+2 x+3 x+4 x 1 + x+2 2 1 - 2 - 2 > 5 - 5 h) ç ÷ > 1 è 2 ø x+2 1 2 æ ö x+ - æ ö i) 1 2- x 1 2 x 1 ç ÷ > 9 k) ç ÷ > è 3 ø è 3 ø 27 2x 1 + 3 - æ ö æ ö x x æ ö æ ö l) 1 1-x 1 ç ÷ > m) 72 1 1 3 .ç ÷ .ç ÷ >1 5 ç 5÷ è ø è ø è 3 ø è 3 ø Trang 75
Haøm soá luyõ thöøa – muõ –logarit
Traàn Só Tuøng
Baøi 4. Giaûi caùc baát phöông trình sau: a) x 2 4 2.5 x 10x - - > 0 b) -x -x 1 25 5 + - ³ 50 1 1 1 - - -
c) 9.4 x + 5.6 x < 4.9 x d) 2 lg x+2 lg x +5 3 < 3 - 2 2x+3 ö e) x 1 4 + -16x < 2 log 2x 1 + æ 1 4 8 f) 2 - 21.ç ÷ + 2 ³ 0 è 2 ø 2(x-2) 2-3x æ ö g) x 2(x 1) - 3 4 - 2 + 8 > 52 h) 4-3x 1 3 - 35.ç ÷ + 6 ³ 0 è 3 ø i) x x+2 9 - 3 > 3x - 9
k) 9x 3x 2 9 3x + - ³ -
Baøi 5. Giaûi caùc phöông trình sau: a) log x 3(3 - 8) = 2 - x b) 2 log5 ( 2 65) 2 x x x - - + = c) log x x x 7(2 -1) + log7(2 - 7) = 1 d) log3(1+ log3(2 -7)) =1 e) log lg x log (1-2x) 3 2 3
- lg x + lg x - 3 = 0 f) 3 2 9 = 5x - 5 log x 1 - g) 1+lgx x = 10x h) ( x ) 5 = 5 2 2 lg x+lg x -2 æ ö lg x+7 i) lg x ç ÷ = lg x k) 4 lg x 1 x 10 + = è 2 ø æ ö l) 1 log x x - 3 x - 3 3 ç log9 x + + 9 ÷ = 2x m) 2 log +1 = log è 2 ø 3 3 x - 7 x -1
Baøi 6. Giaûi caùc phöông trình sau: a) ( )2 2 log 5 - 3log 5 +1 = 0 x x b) lo 1 g /3 x -3 lo 1 g /3 x + 2 = 0 c) 2
log2 x + 2log2 x -2 = 0 d) 3 + 2 log 13 = 2log3( +1) x x + e) log ( 2 9 ) 2 .log 2 3 4 x x x = f) log3 (lo 1 g /2 x -3lo 1 g /2 x +5) = 2 g) 2 2 2 lg (100x) 9
- lg (10x) + lg x = 6 h) 2 2
log2(2x ).log2(16x) = log2 x 2 i) log x x x x x+
3(9 + 9) = x + log3(28 - 2.3 ) k) 1
log2(4 + 4) = log2 2 + log2(2 -3) l) x+3 x+3 log x x 2 (25 -1) = 2 + log2(5 +1)
m) lg(6.5 + 25.20 ) = x + lg25
Baøi 7. Giaûi caùc baát phöông trình sau: a) 2 log 2x - 6
0,5(x - 5x + 6) > 1 - b) log7 > 0 2x -1 c) log 2 - 3x
3 x - log3 x - 3 < 0 d) lo 1 g /3 ³ 1 - x e) 2 lo é ù 1 g /4(2 - x) > l 1 og /4 f) 2 log log (x - 5) > 0 x +1 1/3 ë 4 û 2 log (x +1) g) x - 4 < 0 h) 2 > 0 2 lo x -1 1 g /2(x -1) i) log élog x ù x ë 9(3 - 9) < 1 û k) 2 log2 3 1 x x + < x+5 2 log
l) log (x +8x 15) + 2 2 - x < 1 m) 1/3 2 x +3 (0,5) > 1 Trang 76
Traàn Só Tuøng
Haøm soá luyõ thöøa – muõ –logarit
Baøi 8. Giaûi caùc heä phöông trình sau: 2 ì (x-y) 1 - ì x+y x y ì a) ï4 = 1 ï 4 = 128 í b) í c) 2 + 2 = 12 í ï 3x-2y-3 î 5x+y = 125 ïî5 = 1 î x + y = 5 ì x x ì x x y ì d) 3. ï 2 + 2.3 = 2,75 ï - y = ï 3 .2 = 972 í e) 7 16 0 í f) í ïî 2x - 3y = -0,75 ïî4x - 49y = 0 log (x - y) = 2 ïî 3 x 5y ì -x ì 2x y (ì 2 ï x + y) 2 y-x g) ï 3 ï - 2 = 77 2 = 1
í4 y - 3.4 y = 16 h) í i) í 2 ï x y/2 ï 9 î
( 2x + y) x -y x - 2y = 12 - 8 3 ïî - 2 = 7 = 6 î
Baøi 9. Giaûi caùc heä phöông trình sau:
ìlog x - log y = 0
ìlog (x - y) = 2 3 lg y ì a) 4 2 ï í b) c) x = 2 2 2 í 7 í
î x - 5y + 4 = 0 ïlog î xy = 20 4 x - logx y = î 6
ìlog x + 2 log y = 3 ì1 1 2 log 2 ì log y d) 2 2 ï - = 3 x ï = y í e) f) 5 2 4 í x y 15 í î x + y = 16 log 3 ï y log x log 7 ïî2 = x î
3 x + log3 y = 1+ log3 5 ì x y 9 2 2 ì + = ï ìï xy = 8 g)
lg(x + y ) -1 = lg13 í h) 2 2 í y x 8 i) í
îlg(x + y) - lg(x - y) = 3lg 2 2 ïî (log x + log y x y) = 5 ïlog2 x + log y = 3 î 2 ì x y ì
ï2 log x - 3y = 15 + x y ì k) 2 ï ï 3 .2 = 576 í l) í 4y x = 32 m) y y 1 í 3 ï .log + log (y - x) = 4 î
2 x = 2 log2 x + 3 ïlog î ï
3(x - y) = 1- log3(x + y) î 2 Trang 77