Hàm tăng và hàm giảm Cực trị tương đối Tính lõm và điểm uốn Vẽ đồ thị hàm số - Môn Toán cho các nhà kinh tế | Đại học Kinh Tế Quốc Dân

KHOATOÁNKINHTẾ
BỘMÔNTOÁNCƠBẢN Bài giảng
TOÁNCHOCÁCNHÀKINHTẾ
Chương 3:MỘTSỐỨNGDỤNGCỦA ĐẠOHÀM
Bài 1+2+3:Hàm tăng và hàm giảm
Cực trị tương đối
Tính lõm và điểm uốn
Vẽ đồ thị hàm số
Mục tiêu bài học
 Tìm hiểu về hàm tăng và hàm giảm.
 Tìm các điểm tới hạn và cực trị tương đối.
 Sử dụng đạo hàm cấp một để tìm ự
c c trị tương đối và vẽ đồ thị hàm số.
 Tìm hiểu về tính lõm và điểm uốn.
 Sử dụng dấu của đạo hàm cấp hai để tìm các khoảng lõm và điểm uốn.
 Sử dụng đạo hàm cấp hai để kiểm tra cực trị tương đối.
 Xác định các tiệm cận đứng và tiệm cận ngang của đồ thị.
 Đưa ra một quy trình chung để vẽ đồ thị hàm số.  Bài tập yêu cầu:
 Mục 3.1: 5, 7, 15, 17, 29, 47, 51, 53, 55, 57, 6, 8, 30, 48, 56.
 Mục 3.2: 1, 5, 11, 19, 23, 27, 47, 55, 57, 63, 16, 60.
 Mục 3.3: 11, 25, 33, 35, 41, 43, 45, 47, 49, 51, 56, 64. 2
1.Hàm tăng và hàm giảm
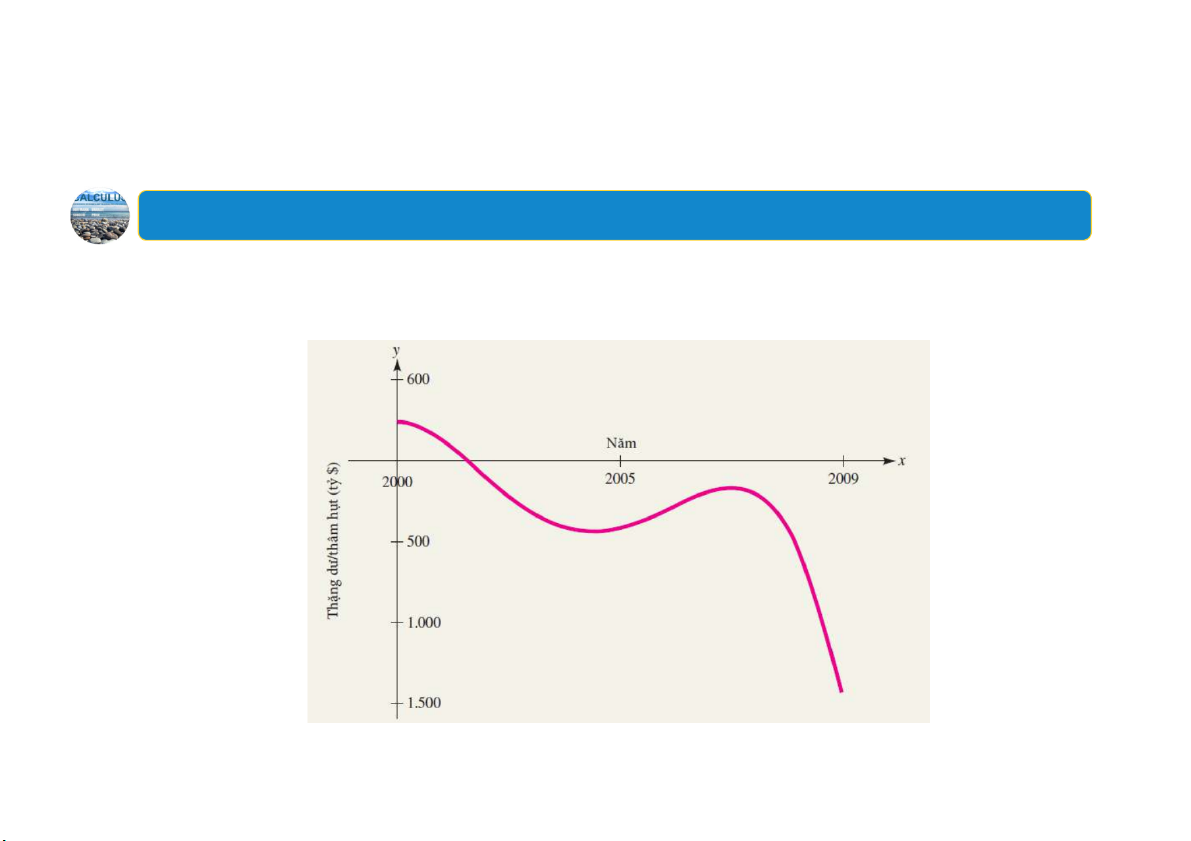
Đồ thị dưới đây mô tả sự thay đổi ngân sách liên bang ở Hoa Kỳ (thặng
dư hoặc thâm hụt) theo thời gian trong các năm từ 2000 đến 2009. 3
1.Hàm tăng và hàm giảm
Địnhnghĩa:
Giả sử hàm số 𝑓󰇛𝑥󰇜 xác định trên khoảng 󰇛𝑎, 𝑏󰇜, 𝑥 và 𝑥 là hai số bất kỳ
trên khoảng này. Khi đó 𝑓󰇛𝑥󰇜 được gọi là:
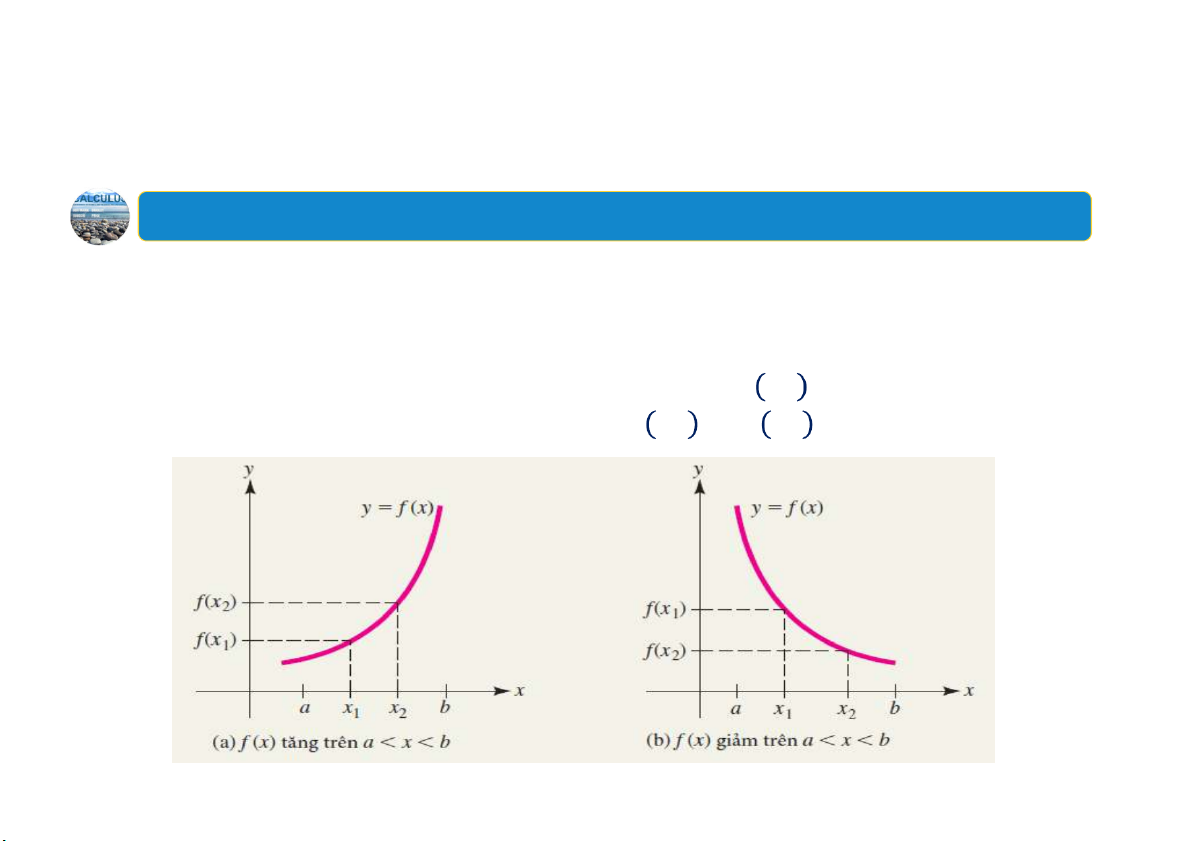
 Hàm tăng trên khoảng 󰇛𝑎, 𝑏󰇜 nếu: 𝑓󰇛𝑥󰇜  𝑓 𝑥 với mọi 𝑥  𝑥.
 Hàm giảm trên khoảng 󰇛𝑎, 𝑏󰇜 nếu: 𝑓 𝑥 𝑥 
 𝑓  với mọi 𝑥  𝑥. 4
1.Hàmtăn  g vàhà  m giảm
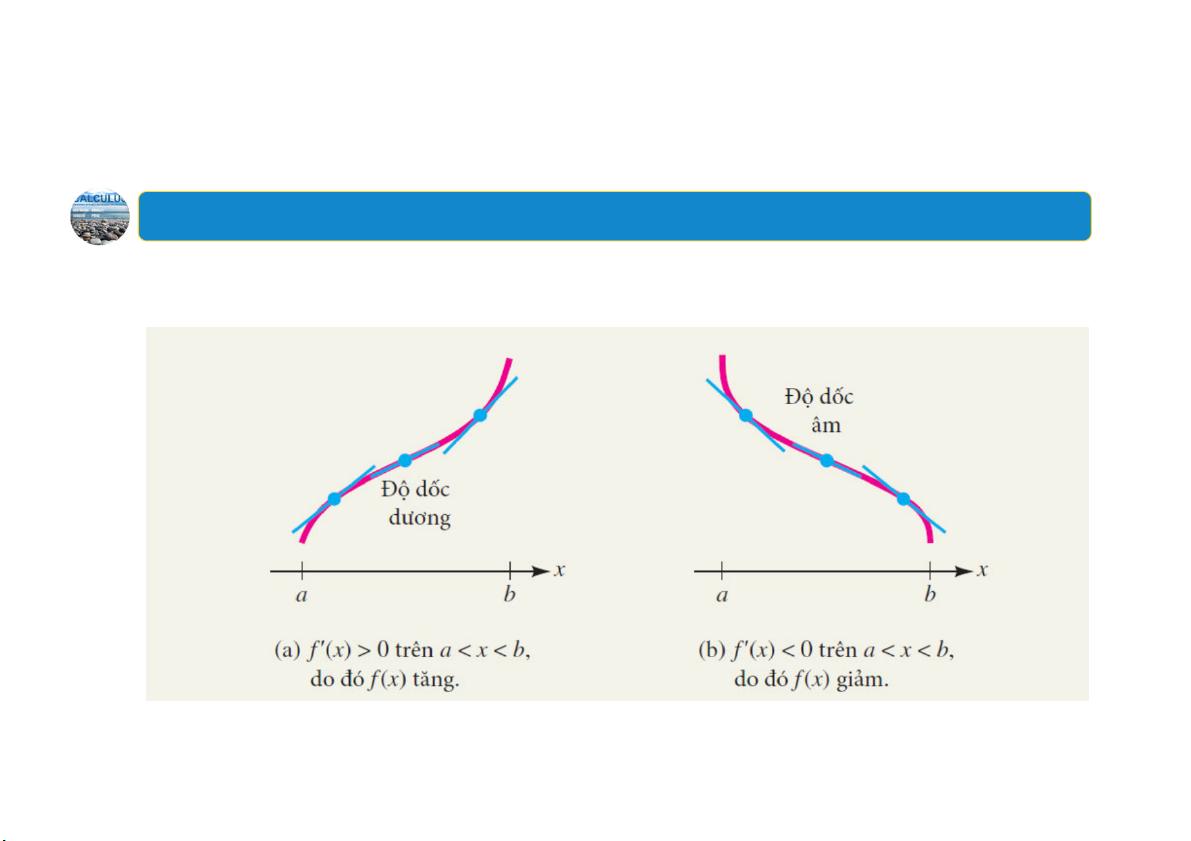
Đạo hàm của các hàm số tăng và giảm: 5
1.Hàmtăn  g vàhà  m giảm
Quy trình sử dụng đạo hàm để tìm các khoản 
g tăng ,g ả
i m của hàm số 𝒇:
Bước 1. Tìm tất cả các giá trị của 𝑥 thỏa mãn 𝑓󰆒 𝑥  0 hoặc 𝑓󰆒 𝑥 không tồn
tại. Đánh dấu các giá trị trên trục số theo thứ tự tăng ầ d n.
Bước 2. Trong mỗi khoảng con 𝑎  𝑥  𝑏 được xác định ở Bước 1, chọn số 𝑐
bất kỳ trong khoảng đó và tính 𝑓’󰇛𝑐󰇜. Khi đó:
 Nếu 𝑓’󰇛𝑐󰇜  0 thì hàm số 𝑓󰇛𝑥󰇜 tăng (đồ thị đi lên) trong khoảng 𝑎  𝑥  𝑏.
 Nếu 𝑓’ 𝑐  0 thì hàm số 𝑓󰇛𝑥󰇜 giảm (đồ thị đi xuống) trong
khoảng 𝑎  𝑥  𝑏. 6
2.Cực trị tươngđối
Địnhnghĩa:
 Hàm số 𝑓󰇛𝑥󰇜 được gọi là có một cực đại tương đối tại 𝑥  𝑐 nếu
𝑓󰇛𝑐󰇜  𝑓󰇛𝑥󰇜 với mọi 𝑥 thuộc một khoảng 𝑎  𝑥  𝑏 chứa c.
 Hàm số 𝑓󰇛𝑥󰇜 được gọi là có một cực tiểu tương đối tại 𝑥  𝑐 nếu
𝑓󰇛𝑐󰇜  𝑓󰇛𝑥󰇜 với mọi 𝑥 thuộc một khoảng 𝑎  𝑥  𝑏 chứa c .
 Cực đại tương đối và cực tiểu tương đối của 𝑓 được chung gọi là cực
trị tương đối.
 Một số 𝑐 trong miền xác định của hàm 𝑓󰇛𝑥󰇜 được gọi là một số tới
hạn nếu 𝑓′ 𝑐  0 hoặc 𝑓′󰇛𝑐󰇜 không tồn tại. Điểm tương ứng
󰇛𝑐, 𝑓󰇛𝑐󰇜󰇜 trên đồ thị của 𝑓󰇛𝑥󰇜 được gọi là một điểm tới hạn của 𝑓󰇛𝑥󰇜. 7
2.Cựctrịtươngđ i ố Chú ý:
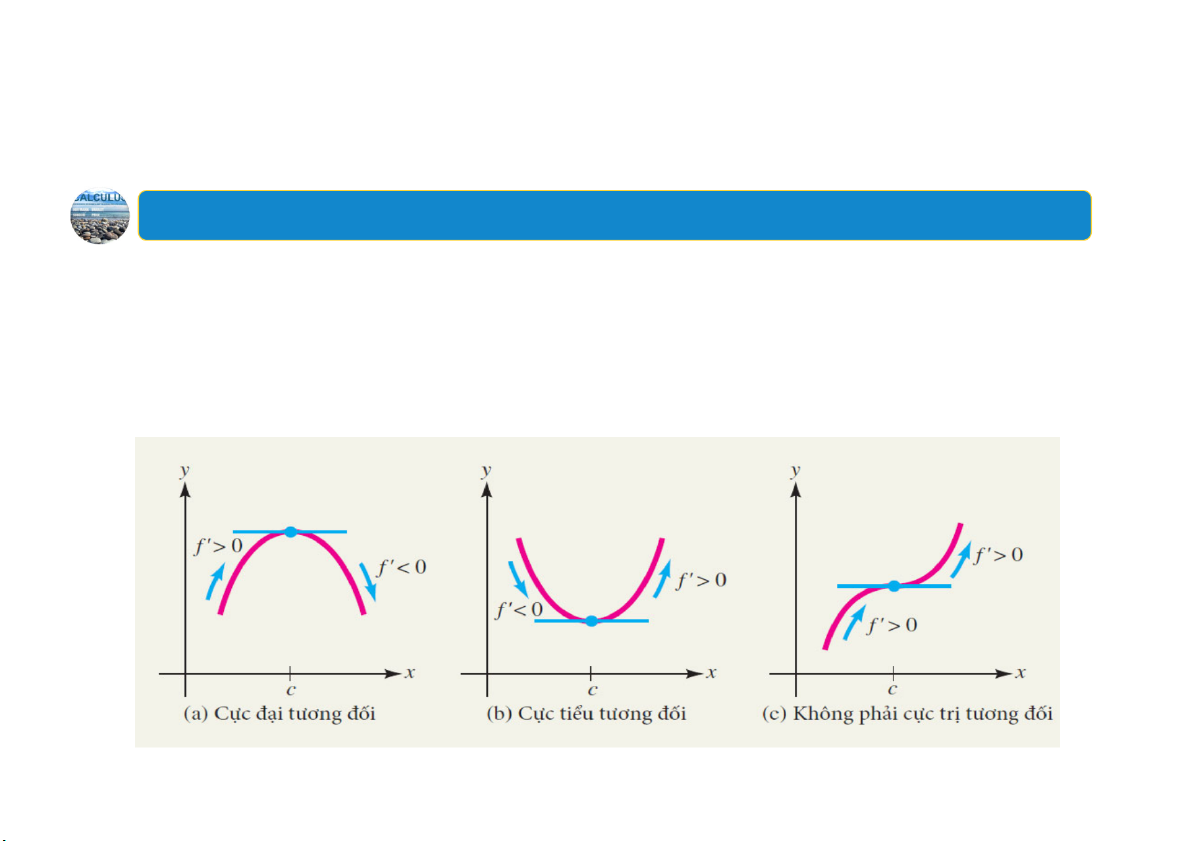
Cực trị tương đối chỉ có thể xảy ra tại các điểm tới hạn, n ư h ng không
phải tất cả các điểm tới hạn đều tương ứng với cực trị tương đối.
Bađiểm tới hạn 󰇛𝒄, 𝒇󰇛𝒄󰇜󰇜 ởđó 𝒇’󰇛𝒄󰇜  𝟎. 8
2.Cực trị tươngđối Chúý:
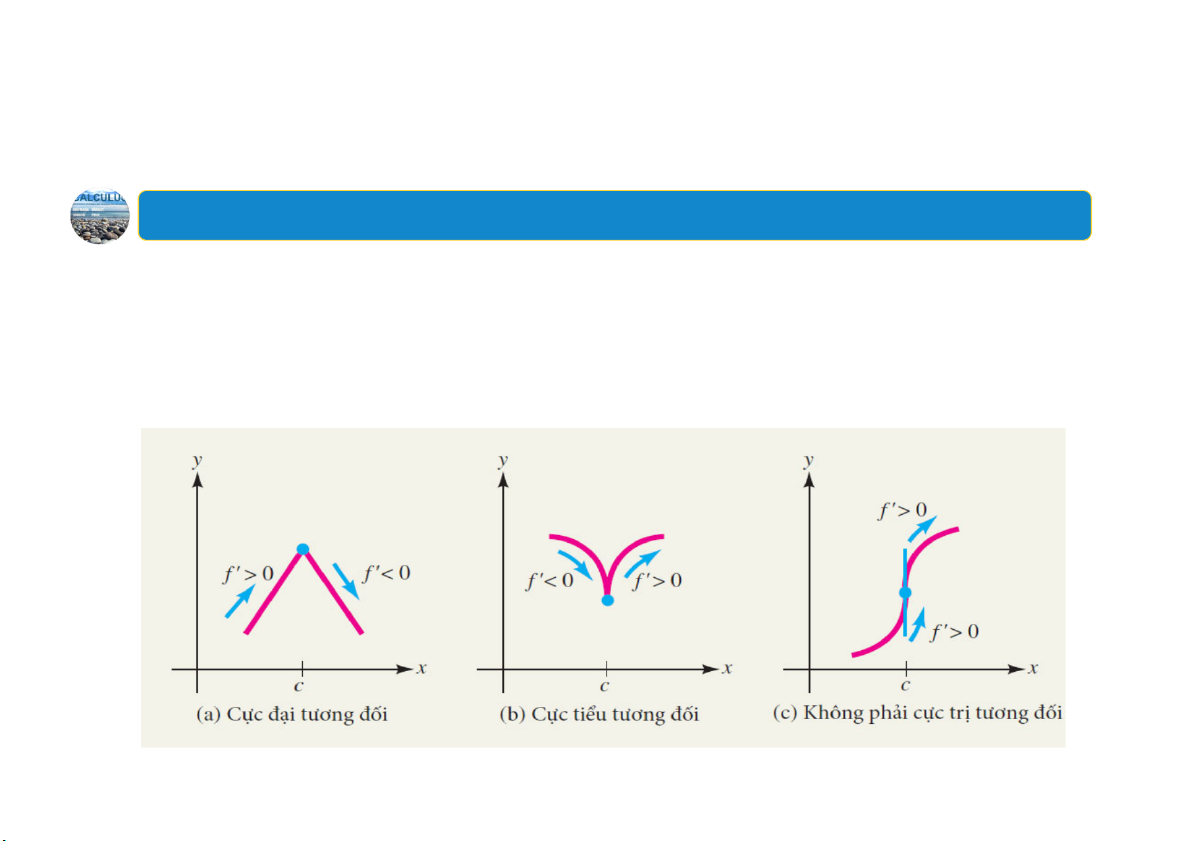
Cực trị tương đối chỉ có thể xảy ra tại các điểm tới hạn, nhưng không
phải tất cả các điểm tới hạn đều tương ứng với cực trị tương đối.
Bađiểm tới hạn 󰇛𝒄, 𝒇󰇛𝒄󰇜󰇜 ởđó 𝒇’󰇛𝒄󰇜 không xác định. 9
2.Cựctrịtươngđ i ố
Sử dụng đạo hàm cấp một để kiểm tracực trị tươngđối:
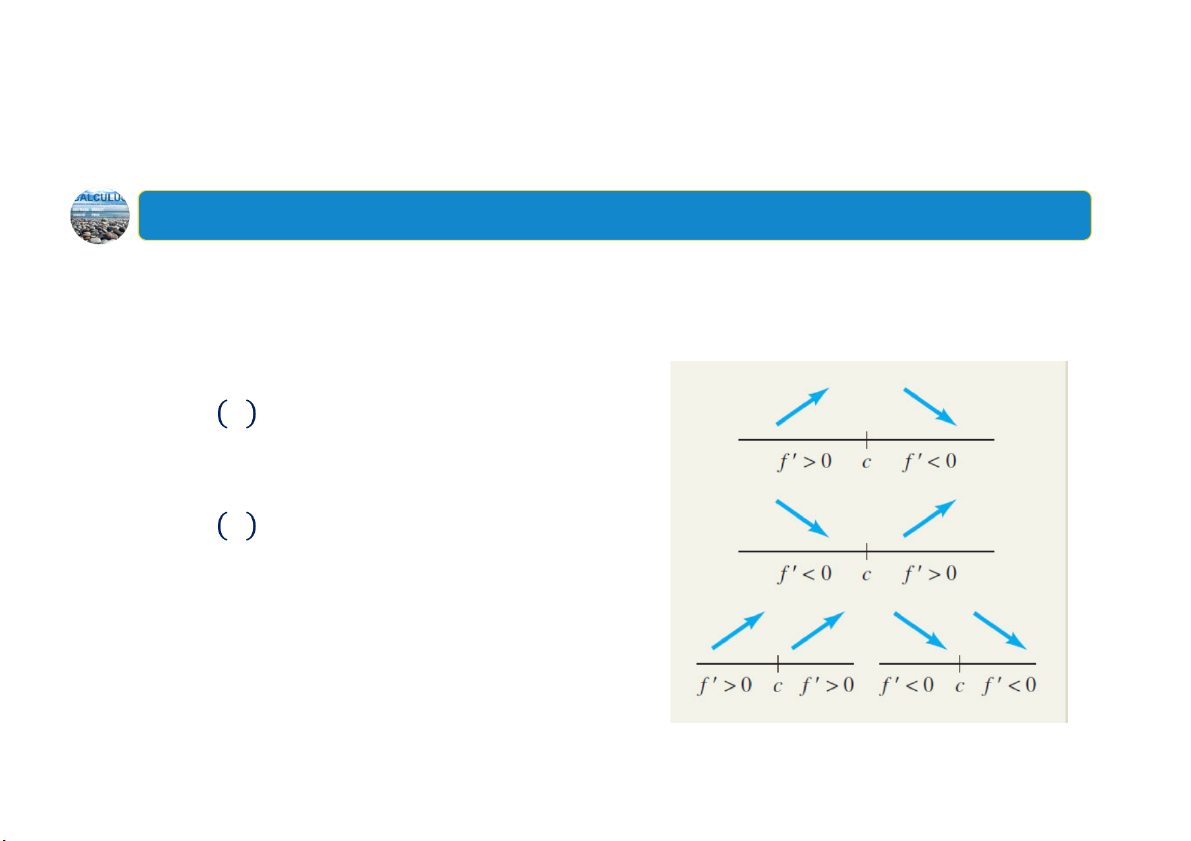
Cho 𝑐 là một số tới hạn của 𝑓󰇛𝑥󰇜 . Khi đó, điểm tới hạn 󰇛𝑐, 𝑓󰇛𝑐󰇜󰇜 là:
 Một cực đại tương đối nếu qua 𝑐
𝑓’ 𝑥 đổi dấu từ  sang 
 Một cực tiểu tương đối nếu qua 𝑐
𝑓’ 𝑥 đổi dấu từ  sang 
 Không phải là cực trị tương đối
nếu 𝑓’󰇛𝑥󰇜 có cùng một dấu ở cả hai phía của 𝑐. 10
3.Phác họa đồ thị của hàm số
Quy trình phác họa đồ thị của hàm 𝒇󰇛𝒙󰇜 liên tục trên miền xác
định sử dụng đạo hàm 𝒇’ 𝒙 :
Bước 1. Tìm miền xác định của 𝑓󰇛𝑥󰇜.
Bước 2. Tính 𝑓’󰇛𝑥󰇜, tìm các số tới hạn của 𝑓󰇛𝑥󰇜 và xác định các khoảng tăng, g ả
i m của 𝑓󰇛𝑥󰇜 trong miền xác định của nó.
Bước 3. Biểu diễn các điểm tới hạn 󰇛𝑐, 𝑓󰇛𝑐󰇜󰇜 trên mặt phẳng tọa độ với hình "chóp mũ“
nếu nó là cực đại tương đối và hình "đáy cốc"
nếu nó là cực tiểu tương đối, tìm các giao điểm với các
trục tọa độ và một số điểm đặc biệt khác.
Bước 4. Phác họa đồ thị của 𝑓 là một đường cong trơn nối các điểm tới
hạn, sao cho đồ thị đi lên nếu 𝑓󰆒 𝑥  0, đi xuống nếu 𝑓󰆒 𝑥 
0 và có tiếp tuyến nằm ngang tại các điểm mà 𝑓󰆒 𝑥  0. 11
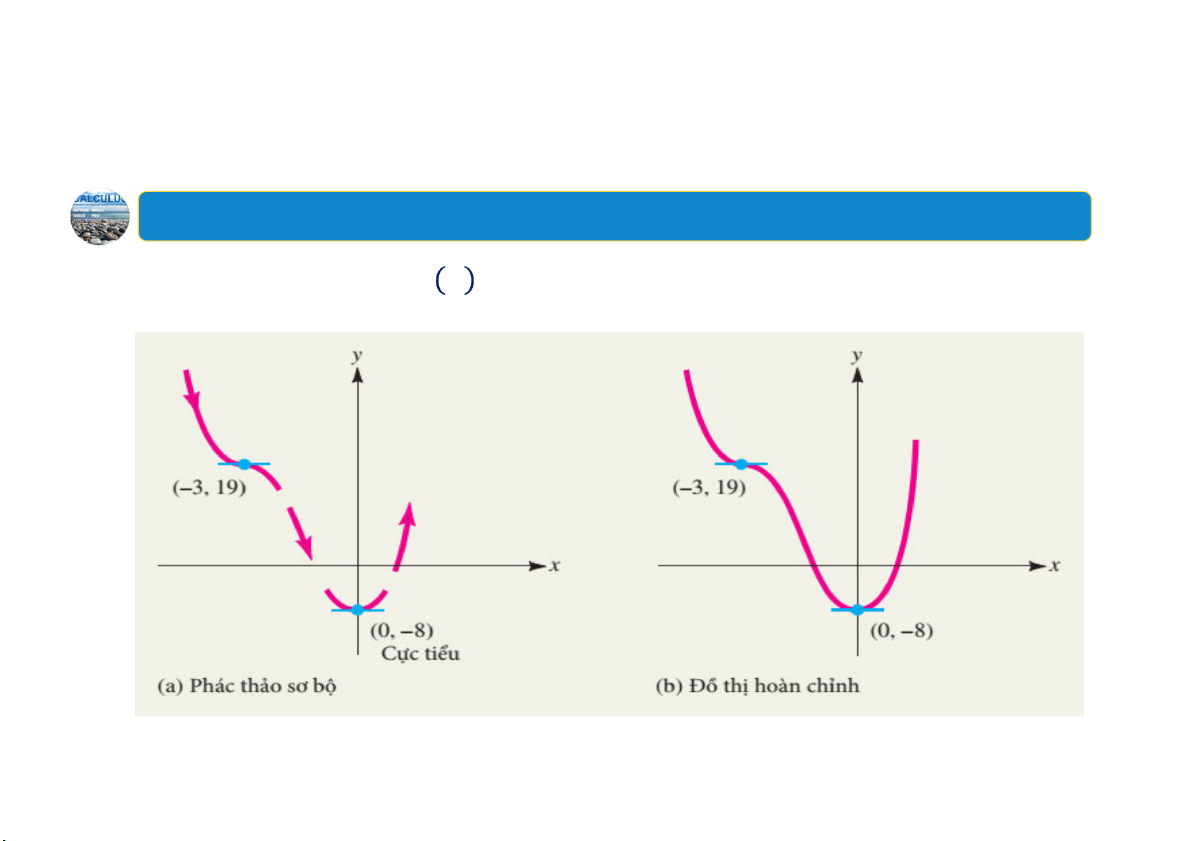
Ví dụ:Sử dụng đạo hàm để vẽ đồ thị
Vẽđồ thị của hàm số 𝑓 𝑥  𝑥   8𝑥  18𝑥  8. 12
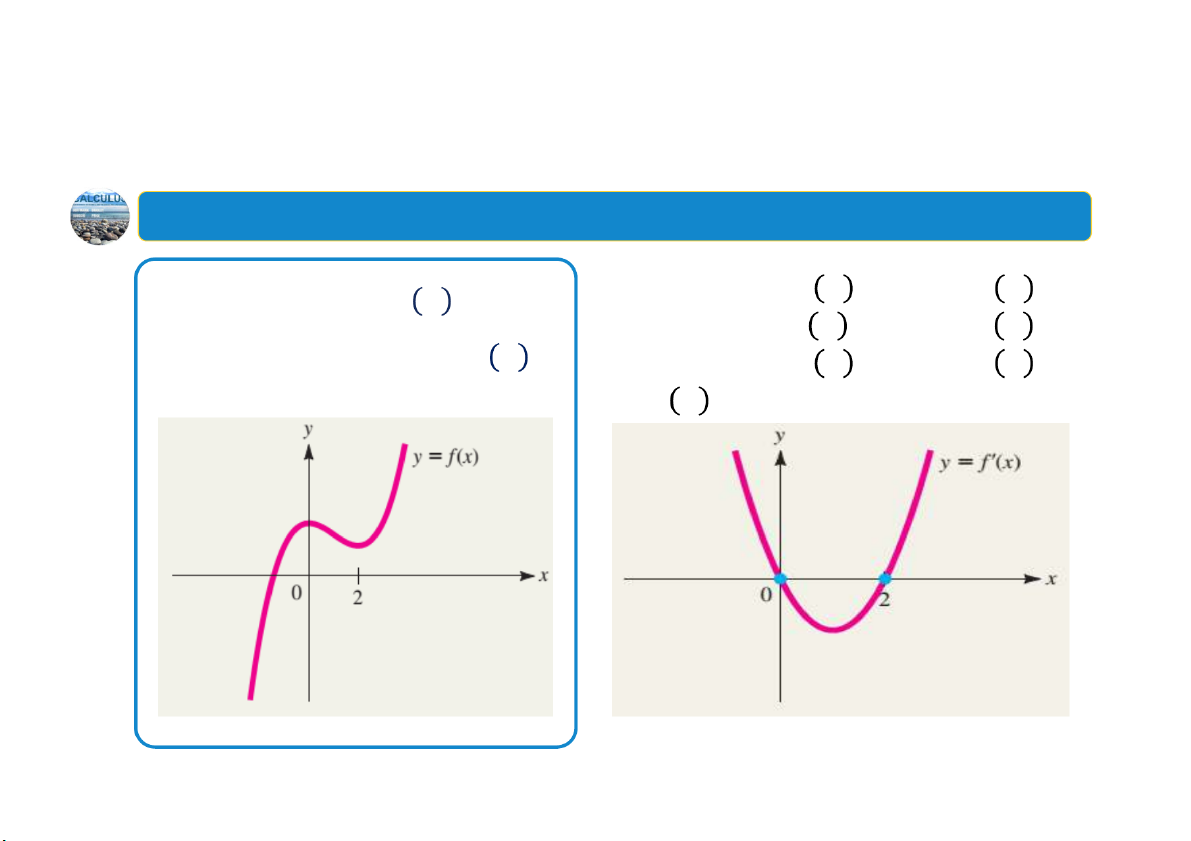
Ví dụ:Sử dụng đồ thị của fđể vẽ đồ thị của f’  ă
Cho đồ thị của 𝑓 𝑥 . Hãy vẽ • 𝑥  0:
𝑓 𝑥 t ng =>𝑓󰆒 𝑥  0
• 0  𝑥  2:𝑓 𝑥 giảm=>𝑓󰆒 𝑥  0
một đồ thị có thể có của 𝑓󰆒 𝑥 .
• 𝑥  2:𝑓 𝑥 tăng =>𝑓󰆒 𝑥  0
• 𝑓󰆒 𝑥  0 khi𝑥  0 hoặc𝑥  2. 13 4.Tính lõm
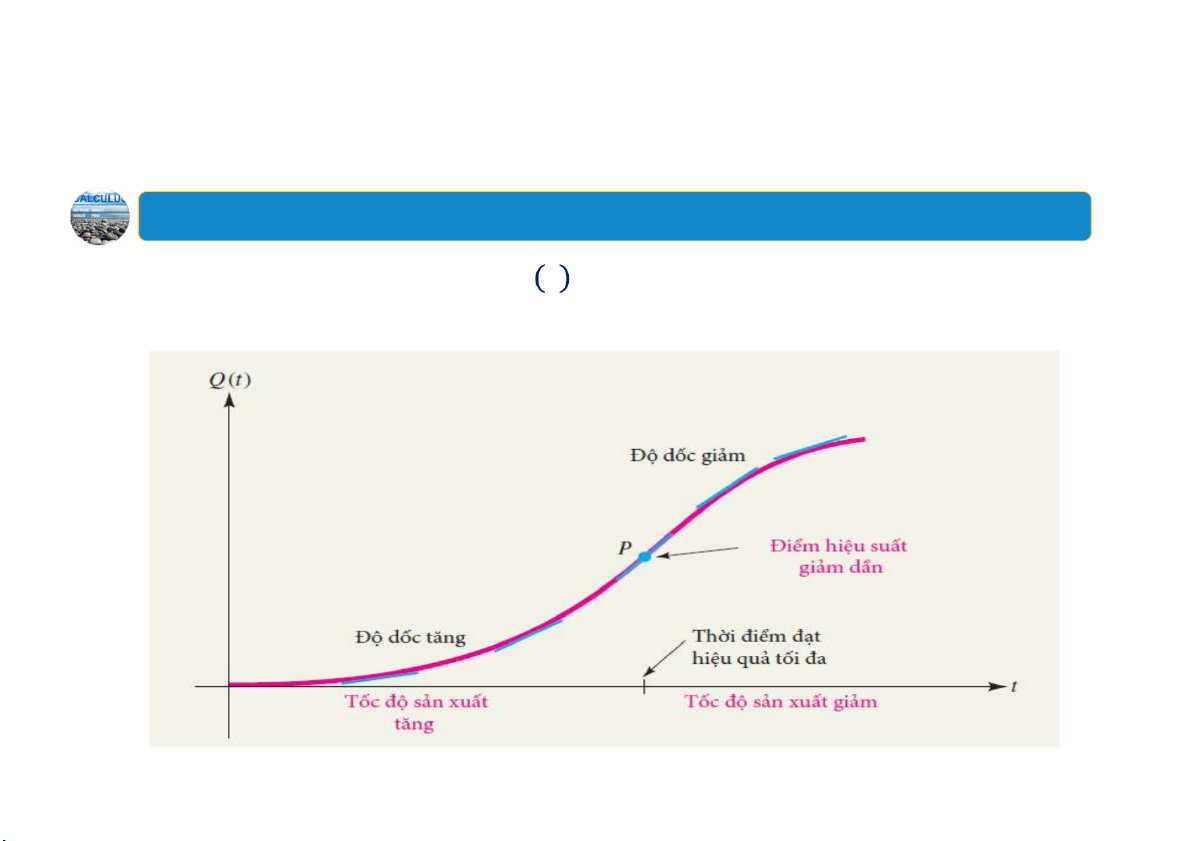
Đồ thị sau mô tả sản lượng 𝑄 𝑡 của lao động trong 𝑡 giờ làm việc. Điểm
𝑃 được gọi là điểm hiệu suất giảm dần. 14 4.Tính lõm
Địnhnghĩa:
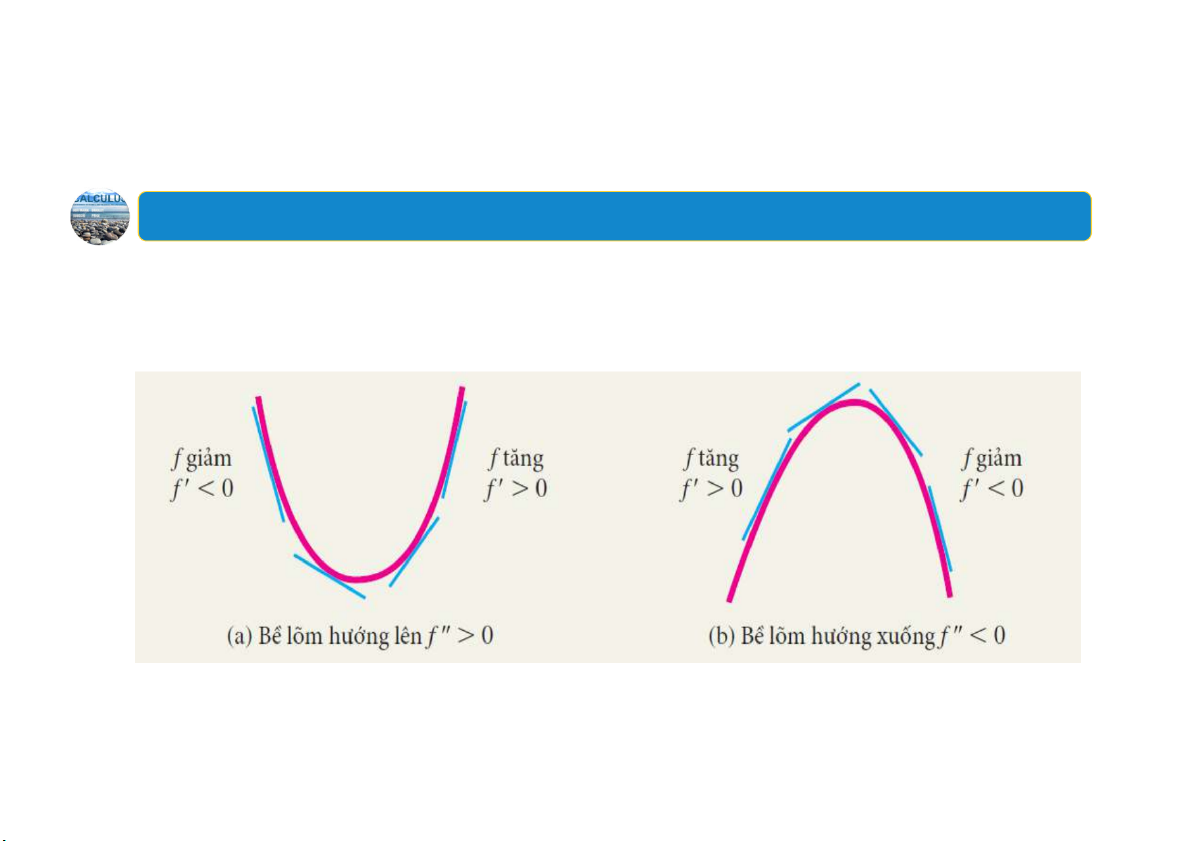
Nếu hàm 𝑓 𝑥 khả vi trên khoảng 𝑎  𝑥  𝑏 thì đồ thị của 𝑓 được gọi là:
 Có bề lõm hướng lên trong khoảng 𝑎  𝑥  𝑏 nếu 𝑓′ 𝑥 tăng trong khoảng đó.
 Có bề lõm hướng xuống trong khoảng 𝑎  𝑥  𝑏 nếu 𝑓′ 𝑥 giảm trong khoảng đó. 15 4.Tính lõm
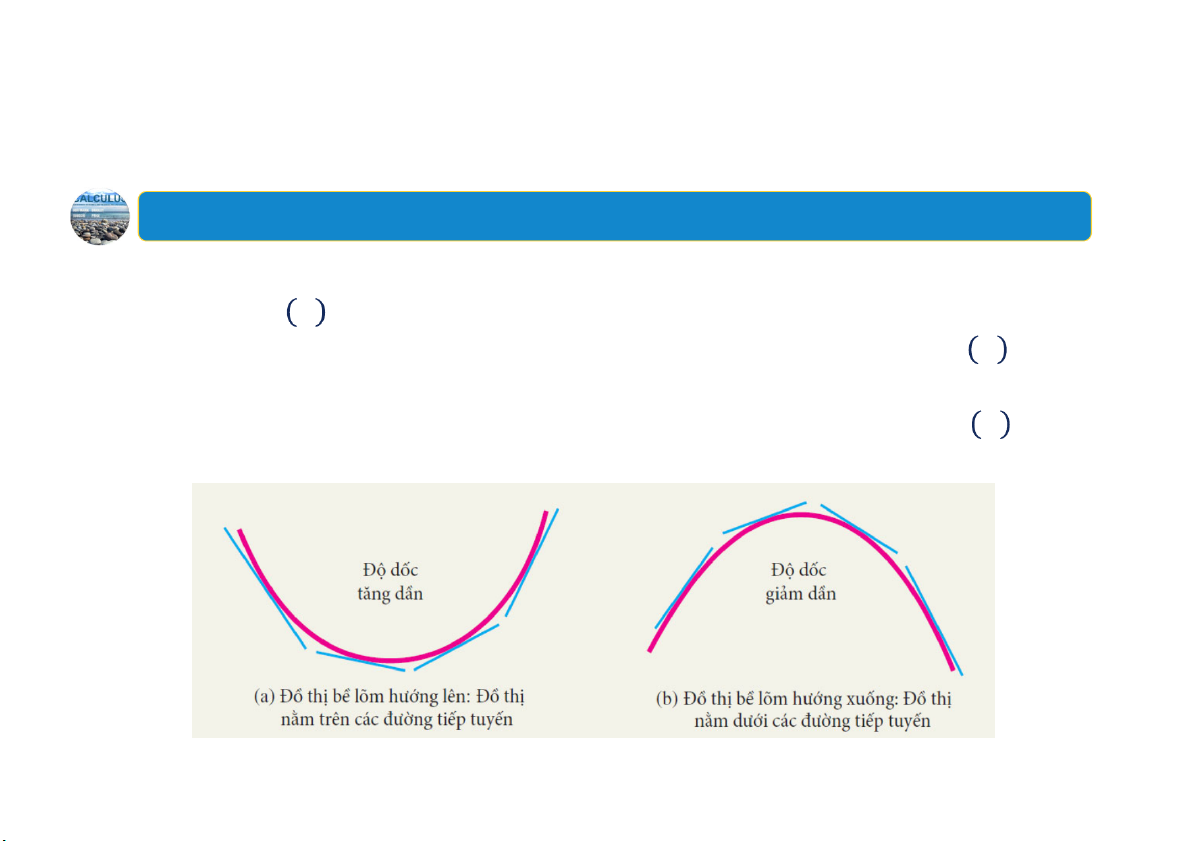
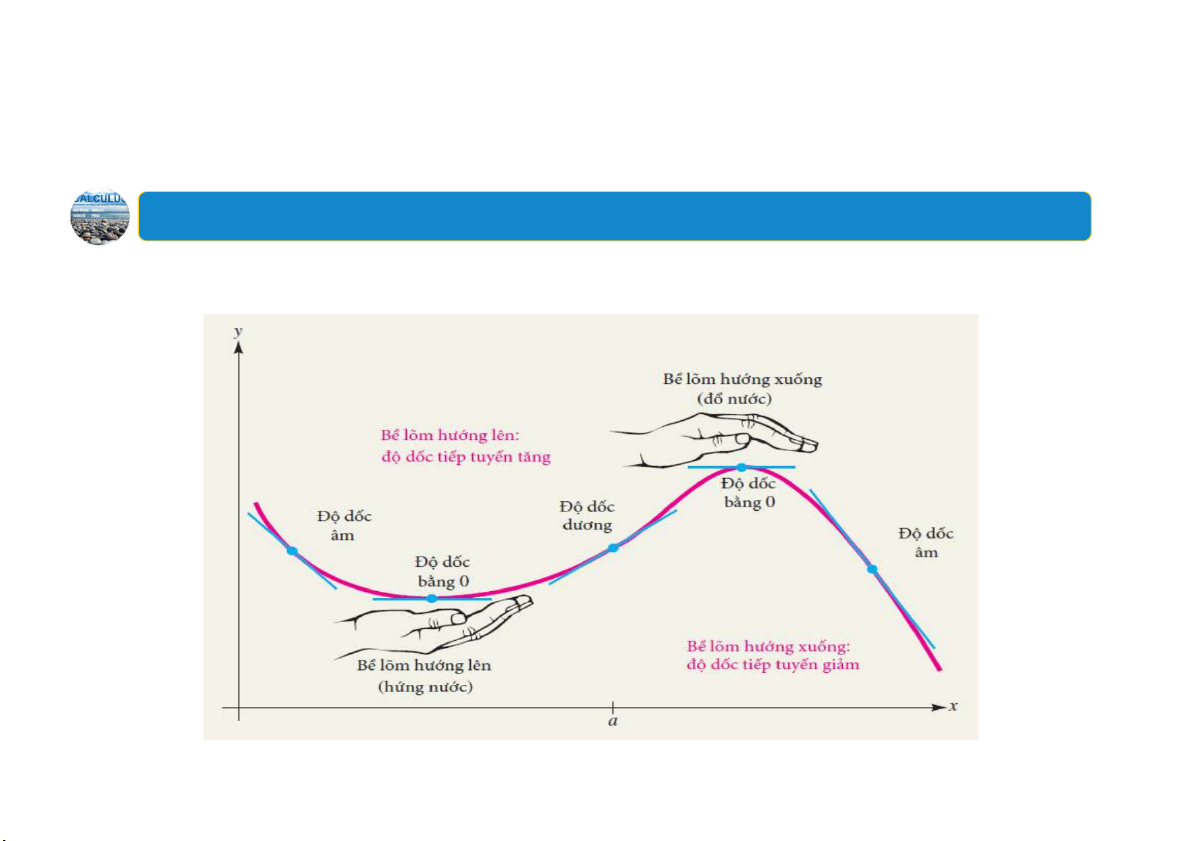
Minhhọa tính lõm và độ dốc của tiếp tuyến: 16 4.Tính lõm
Quy trình sử dụng đạo hàm cấp hai để xác định các khoảng lõm của
đồ thị hàm 𝒇:
Bước 1. Tìm tất cả các giá trị của 𝑥 sao cho 𝑓’’󰇛𝑥󰇜  0 hoặc 𝑓’’󰇛𝑥󰇜 không
tồn tại và đánh dấu các giá trị này trên trục số.
Bước 2. Trên mỗi khoảng 𝑎  𝑥  𝑏 tìm được trong Bước 1, chọn một số
𝑐 bất kỳ và tính 𝑓’’󰇛𝑐󰇜. Khi đó:
 Nếu 𝑓’’ 𝑐  0 thì đồ thị của 𝑓 𝑥 có bề lõm hướng lên
trong khoảng 𝑎  𝑥  𝑏.
 Nếu 𝑓’’ 𝑐  0 thì đồ thị của 𝑓 𝑥 có bề lõm hướng xuống
dưới trong khoảng 𝑎  𝑥  𝑏. 17 4.Tính lõm Chú ý:
Cần phânbiệt giữa tính lõm và tính tăng – g ả
i m của đồ thị. 18 5. i Đ ểm uốn Định nghĩa:
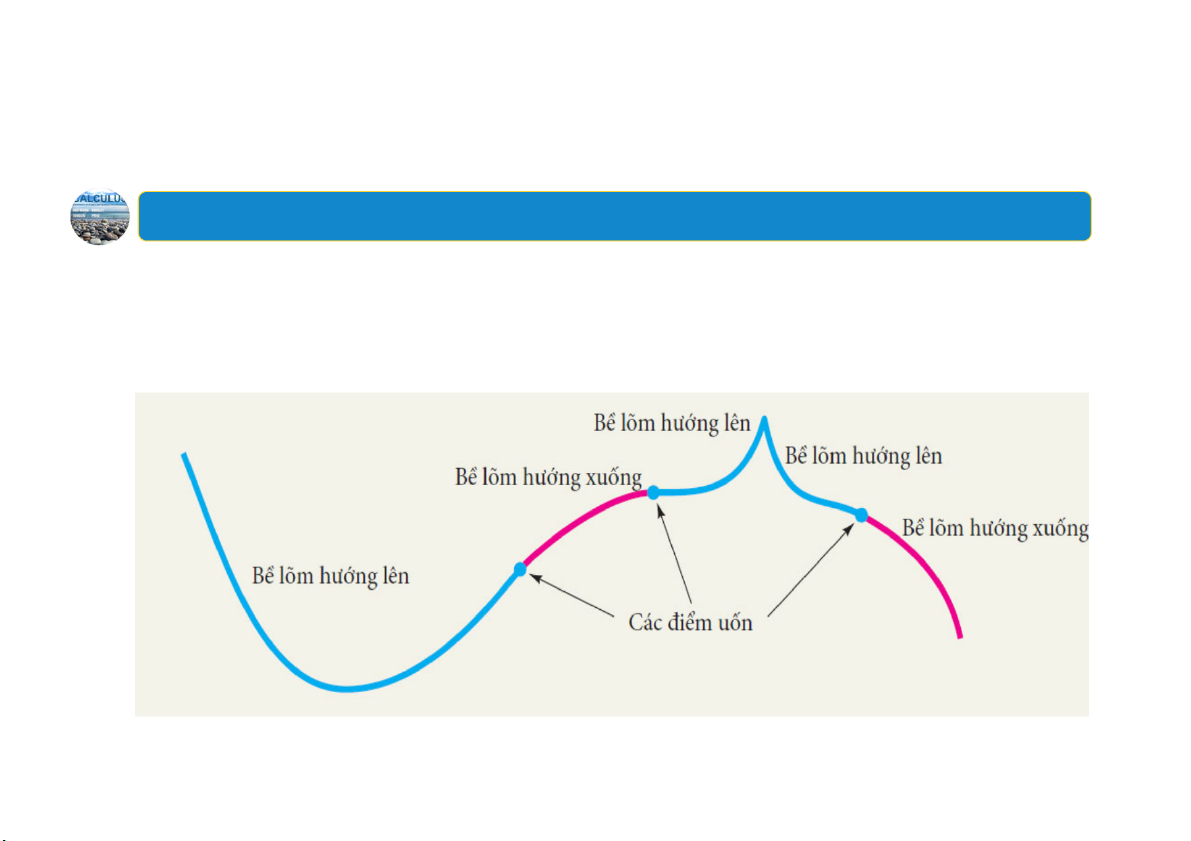
Điểm uốn của hàm 𝑓 là điểm 󰇛𝑐, 𝑓󰇛𝑐󰇜󰇜 trên đồ thị của 𝑓 mà tại đó 𝑓
liên tục và thay đổi hướng lõm. 19 5. i Đ ểm uốn
Quytrình xác định các điểm uốn của đồ thị hàm 𝒇:
Bước 1. Tính 𝑓󰇛𝑥󰇜 và tìm tất cả các điểm 𝑐 thuộc miền xác định của 𝑓 sao
cho 𝑓’’󰇛𝑐󰇜  0 hoặc 𝑓’’󰇛𝑐󰇜 không tồn tại.
Bước 2. Với mỗi số 𝑐 tìm được trong Bước 1, nếu qua 𝑐 mà 𝑓”󰇛𝑥󰇜 đổi dấu
thì 󰇛𝑐, 𝑓󰇛𝑐󰇜󰇜 là một điểm uốn của 𝑓. 20
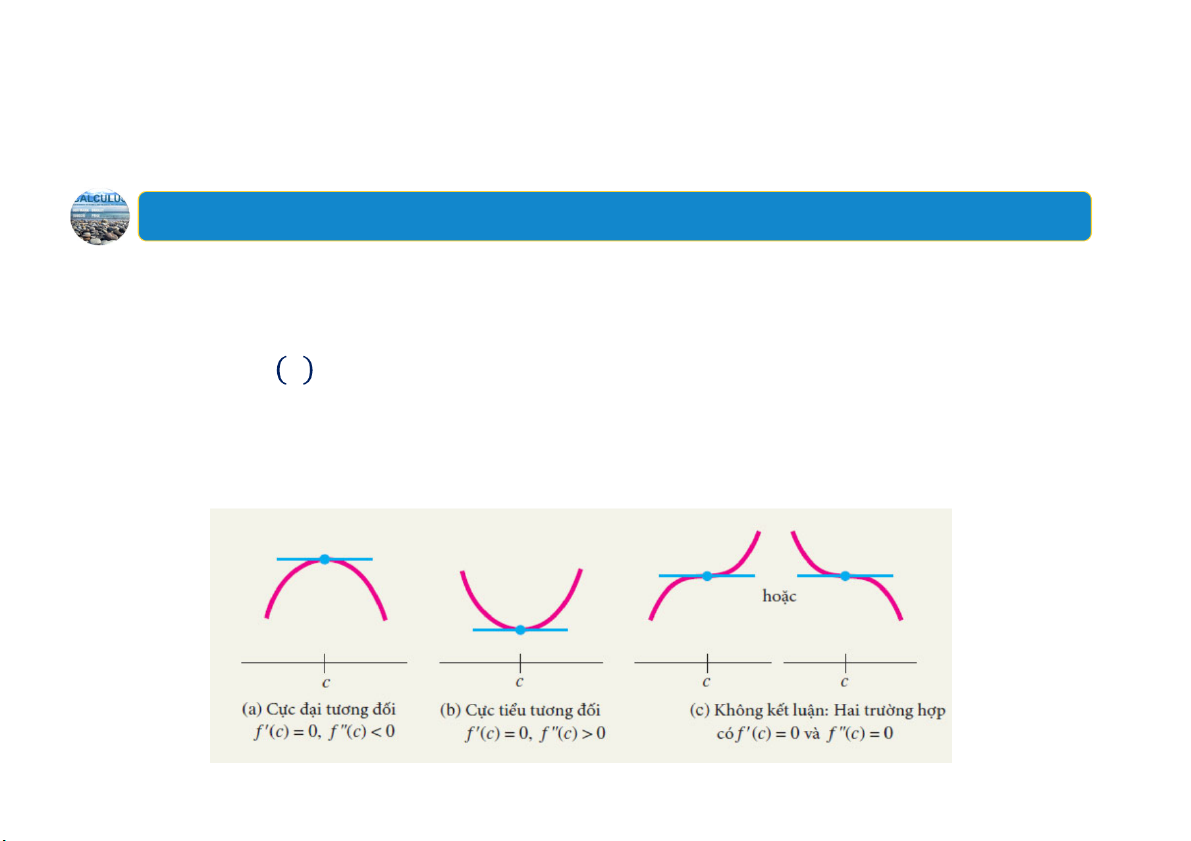
6.Sử dụng đạo hàm cấp hai để kiểm tra cực trị tương đối
Giả sử 𝑓󰇛𝑥󰇜 xác định trên một khoảng mở chứa 𝑥  𝑐 và 𝑓’󰇛𝑐󰇜  0.
 Nếu 𝑓’’󰇛𝑐󰇜  0 thì 𝑓 có một cực tiểu tương đối tại 𝑥  𝑐.
 Nếu 𝑓’’ 𝑐  0 thì 𝑓 có một cực đại tương đối tại 𝑥  𝑐.
 Nếu 𝑓’’󰇛𝑐󰇜  0 hoặc 𝑓’’󰇛𝑐󰇜 không tồn tại thì chưa kết luận được. Khi
đó, 𝑓 có thể đạt cực đại, cực tiểu hoặc có thể không đạt cực trị tương đối tại 𝑥  𝑐. 21
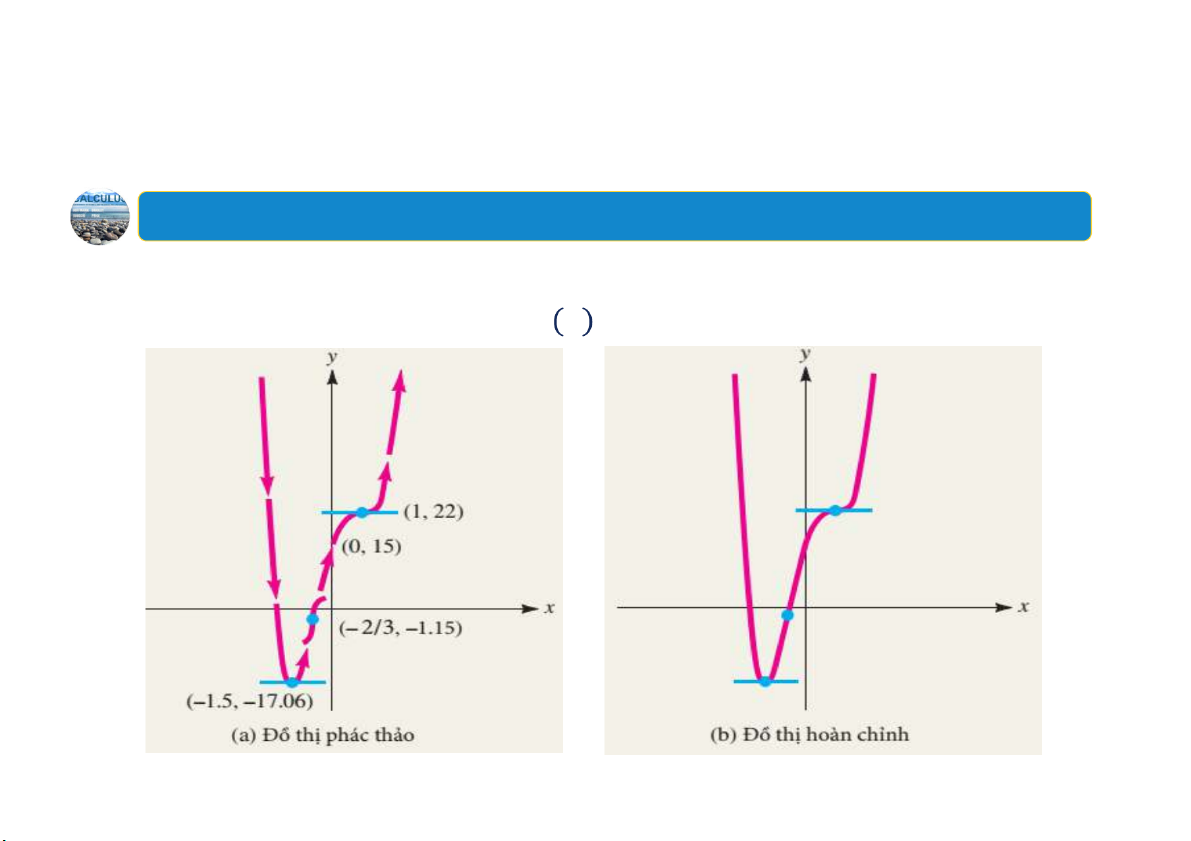
Ví dụ:Sử dụng tính lõm để vẽ đồ thị
Tìm các khoảng tăng – giảm, các khoảng lõm, các cực trị tương đối, các
điểm uốn và vẽ đồ thị hàm số: 𝑓 𝑥  3𝑥  2𝑥  12𝑥  18𝑥  15. 22
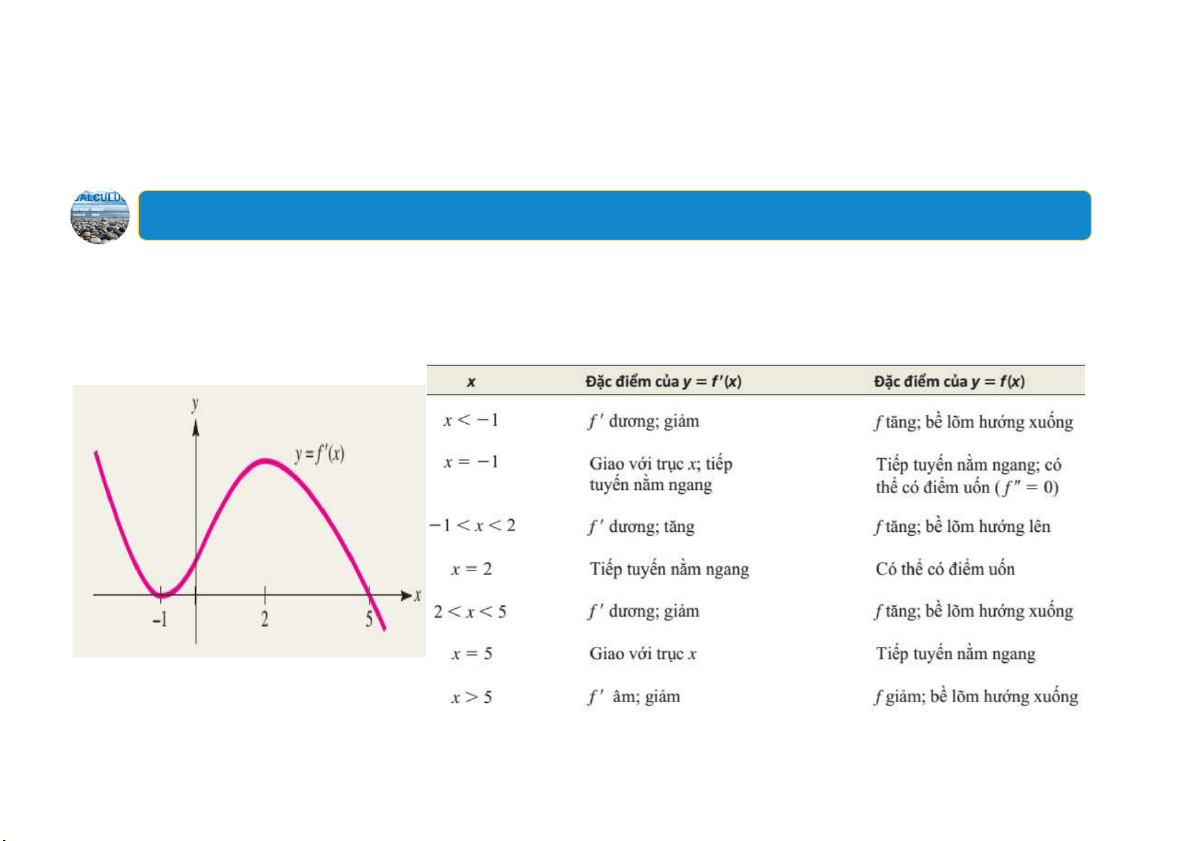
Ví dụ:Sử dụng đồ thị của f’để vẽ đồ thị của f
Cho đồ thị của hàm đạo hàm 𝑓′󰇛𝑥󰇜 trong hình vẽ dưới đây. Hãy xác định các khoảng ă t ng – g ả
i m, các khoảng lõm, các cực trị tương đối, các
điểm uốn và vẽ một đường cong 𝑓󰇛𝑥󰇜 có tất cả các đặc điểm đó. 23
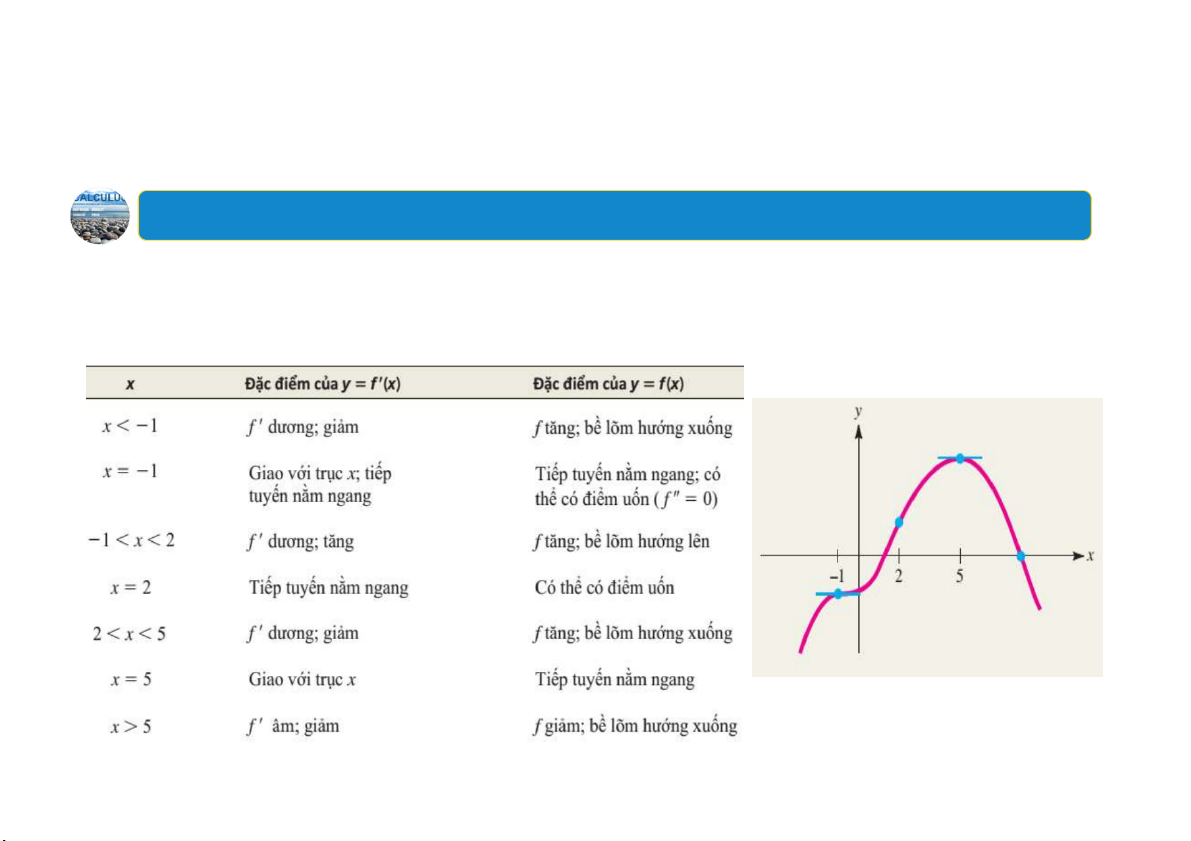
Ví dụ:Sử dụng đồ thị của f’để vẽ đồ thị của f
Cho đồ thị của hàm đạo hàm 𝑓′󰇛𝑥󰇜 trong hình vẽ dưới đây. Hãy xác định các khoảng ă t ng – g ả
i m, các khoảng lõm, các cực trị tương đối, các
điểm uốn và vẽ một đường cong 𝑓󰇛𝑥󰇜 có tất cả các đặc điểm đó. 24
Ví dụ:Sử dụng đạo hàm cấp 2để kiểm tra cực trị tương đối
Tìm các điểm tới hạn của
• 𝑓󰆒 𝑥  6𝑥  6𝑥  12 hàm số:
• 𝑓󰆒󰆒 𝑥  12𝑥  6
𝑓 𝑥  2𝑥  3𝑥  12𝑥  7
• 𝑓󰆒 𝑥  0 khi 𝑥  2 hoặc 𝑥  1
Sử dụng đạo hàm cấp 2 để
• 𝑓󰆒󰆒 2  18  0 nên điểm tới
hạn 2, 13 là một điểm cực đại
phân loại và kết luận về các tương đối. điểm tới hạn đó.
• 𝑓󰆒󰆒 1  18  0 nên điểm tới hạn 1, 14 là một điểm cực tiểu tương đối. 25
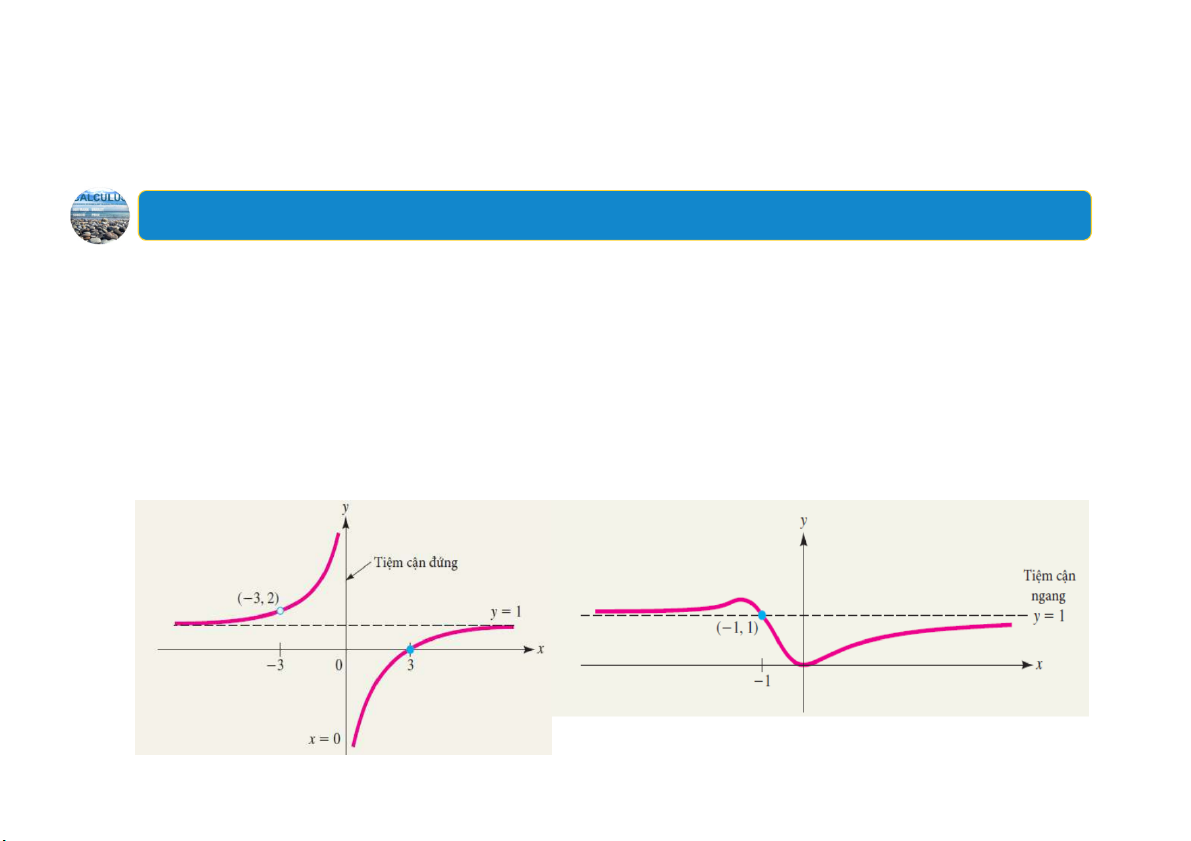
7.Tiệm cận đứng và tiệm cận ngang Định nghĩa:
 Đường thẳng 𝑥  𝑐 được gọi là một tiệm cận đứng của đồ thị hàm
số 𝑓󰇛𝑥󰇜 nếu: 𝑙𝑖𝑚 𝑓󰇛𝑥󰇜  ∞ hoặc 𝑙𝑖𝑚 𝑓󰇛𝑥󰇜  ∞. → →
 Đường thẳng 𝑦  𝑏 được gọi là một tiệm cận ngang của đồ thị hàm
số 𝑓󰇛𝑥󰇜 nếu: 𝑙𝑖𝑚 𝑓󰇛𝑥󰇜  𝑏 hoặc
𝑙𝑖𝑚 𝑓󰇛𝑥󰇜  𝑏. → → 26
8.Vẽ đồ thị hàm số
Quy trình chung để vẽ đồ thị của hàm số 𝒇󰇛𝒙󰇜:
Bước 1. Tìm miền xác định của 𝑓󰇛𝑥󰇜.
Bước 2. Tìm và định vị các hệ số chặn.
Bước 3. Tìm tất cả các tiệm cận đứng và t ệ
i m cận ngang của đồ thị rồi vẽ chúng
trên cùng một hệ trục tọa độ.
Bước 4. Tính 𝑓′󰇛𝑥󰇜 và xác định các số tới hạn, các kh ả o ng ă t ng, g ả i m của 𝑓󰇛𝑥󰇜.
Bước 5. Tìm tọa độ các điểm cực trị tương đối của hàm số. Vẽ một chóp mũ tại
điểm cực đại tương đối và một đáy cốc tại điểm cực tiểu tương đối.
Bước 6. Tính 𝑓′′󰇛𝑥󰇜 và tìm các khoảng lõm và điểm uốn của đồ thị hàm số. Vẽ
tại vị trí điểm uốn một "đường xoắn" để định dạng của đồ thị tại
những điểm gần điểm uốn.
Bước 7. Vẽ đồ thị hàm số. 27
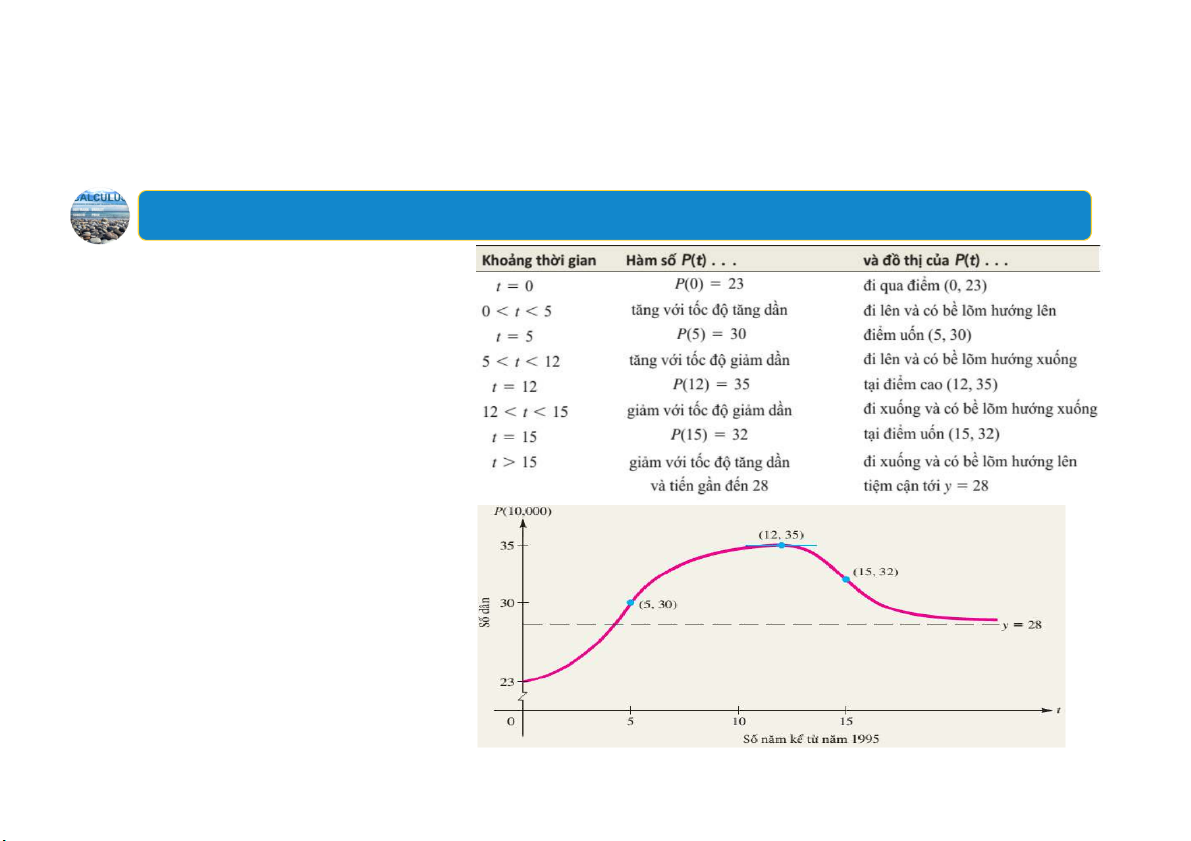
Ví dụ:Biểu diễn dân số dưới dạng đồ thị
Dân số của một địa phương năm 1995 là 230,000 người
và tăng trưởng với tốc độ tăng dần trong 5 năm, lên mức 300,000 vào năm 2000.
Sau đó dân số tiếp tục tăng
lên nhưng tốc độ tăng g ả i m
dần cho đến khi đạt đỉnh là
350,000 người vào năm 2007.
Sau đó dân số bắt đầu giảm
với tốc độ giảm dần trong 3 năm xuống còn 320,000
người, rồi tốc độ tăng ầ d n và
tiến gần đến 280,000 người trong dài hạn. Biểu diễn các thông tin dưới dạng đồ thị. 28
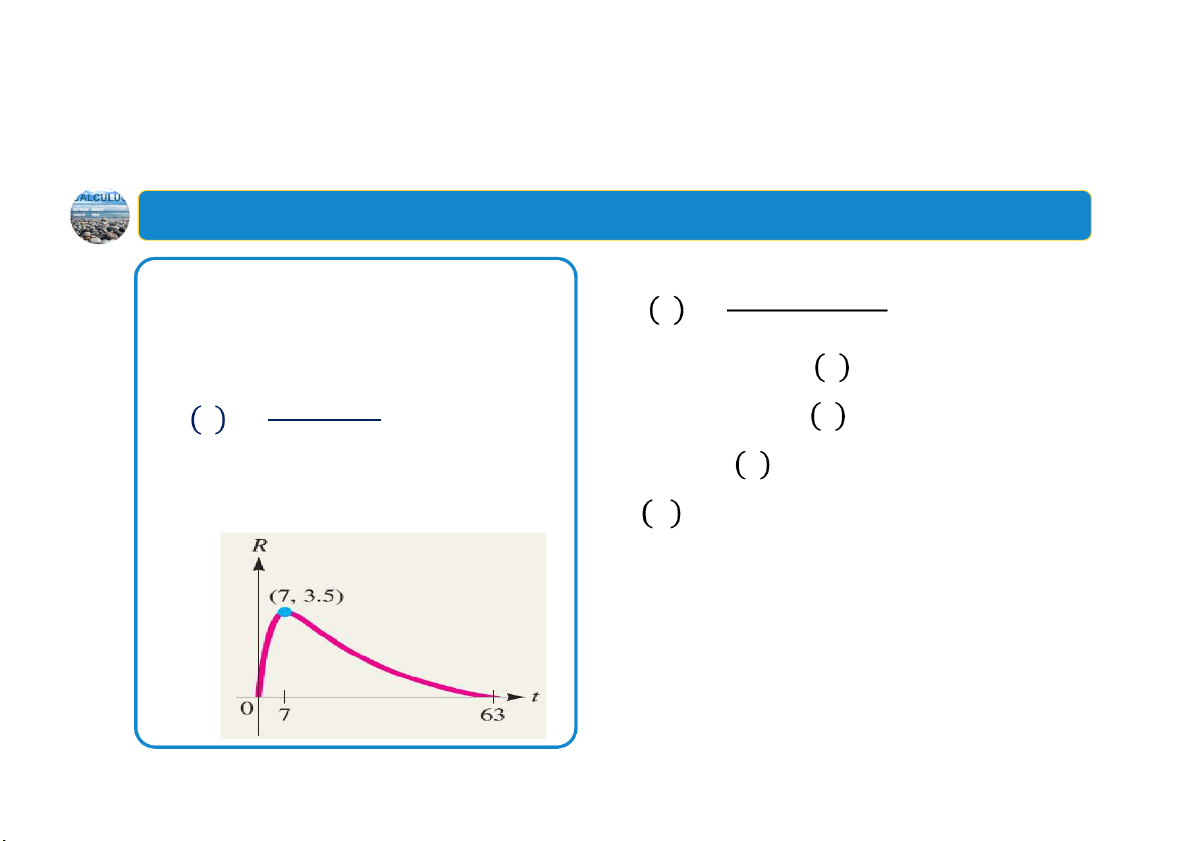
Ví dụ:Tìm doanh thu tối đa
Doanh thu từ việc bán một loại ván
󰇛󰇜󰇛󰇜
trượt gắn động cơ mới sau 𝑡 tuần kể • 𝑅′ 𝑡  󰇛󰇜
từ khi được đưa ra thị trường là:
• 0  t  7:𝑅󰆒 𝑡  0 63𝑡  𝑡 𝑅 𝑡  ; 0  t  63
• 7  t  63:𝑅󰆒 𝑡  0 𝑡  63
(triệu đô‐la). Thời điểm nào doanh
• t  7:𝑅󰆒 𝑡  0 và𝑅󰇛𝑡󰇜 đạt cực đại
thu đạt tối đa? Tính doanh thu tối
• 𝑅 7  3.5 (triệu đô la). đa.
(Sản phẩm có doanh thu tăng mạnh
ngay sau khi ra mắt và giảm về 0 trong
một khoảng thời gian sau đó được gọi
là mốt nhất thời). 29
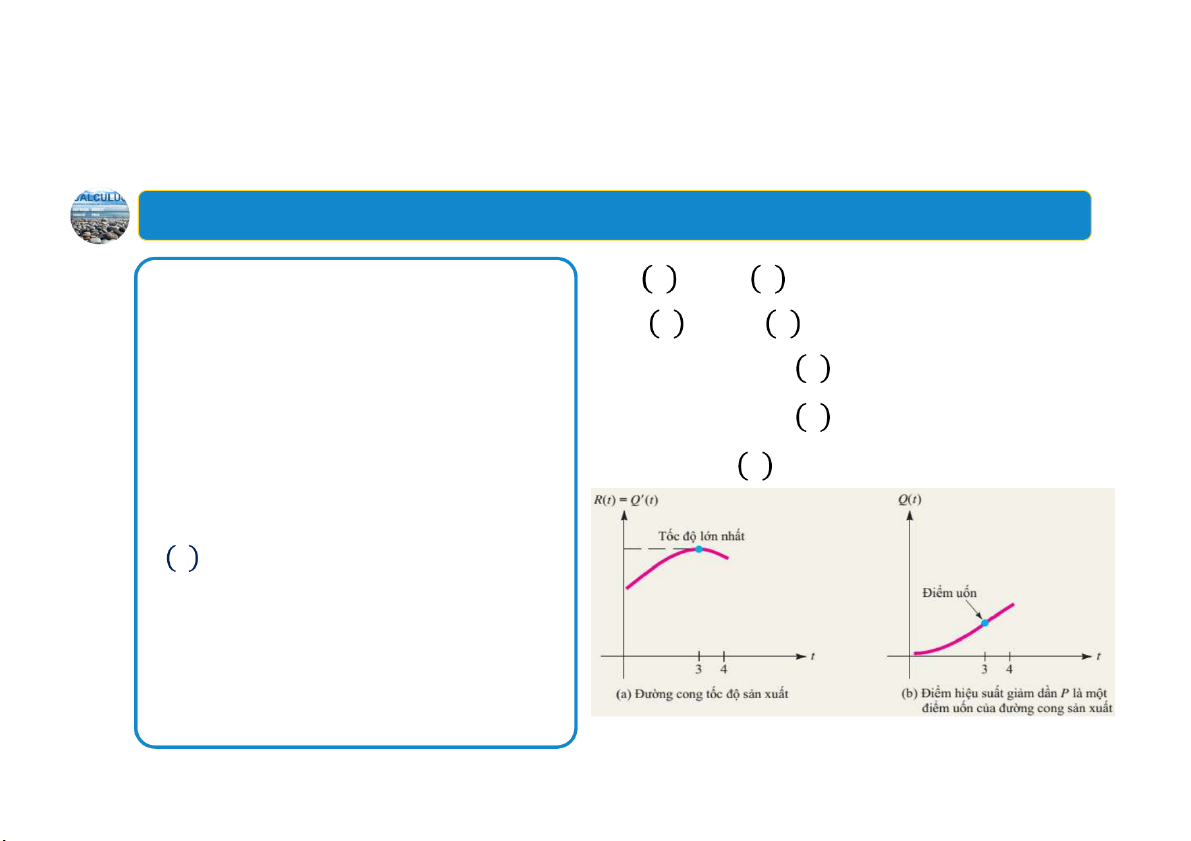
Ví dụ:Tìm điểm hiệusuất giảm dần trong sản xuất
Anish là một chuyên gia phân tích
• 𝑅 𝑡  𝑄′ 𝑡  3𝑡  18𝑡  12
hiệu quả của một hãng sản xuất
• 𝑅′ 𝑡  𝑄′′ 𝑡  6𝑡  18
hàng điện tử. Anh tiến hành một
nghiên cứu về ca làm việc buổi sáng
• 0  𝑡  3:𝑅󰆒 𝑡  0
(8 giờ sáng đến 12 giờ trưa) tại một
• 3  𝑡  4:𝑅󰆒 𝑡  0
nhà máy của hãng và thấy rằng,
• 𝑡  3:𝑅󰆒 𝑡  0 (lúc 11giờ sáng)
trung bình một công nhân đến làm
việc lúc 8 giờ sáng sẽ sản xuất được 𝑄 𝑡  𝑡   9𝑡  12𝑡 đơn vị
sản phẩm trong t giờ sau đó.
Anish xác định sản xuất của công
nhân đạt tới điểm hiệu suất giảm
dần vào thời điểm nào trong ca làm việc buổi sáng? 30
Bài tập thảo luận:Ch itiêu của chính p ủ h
Trong thời kì suy thoái, chính phủ ra quyết đị
• 𝑅 𝑡  𝑁′ 𝑡  3𝑡  90𝑡  408
nh kích thích nền kinh tế bằng cách cung cấp
vốn để thuê các công nhân làm việc cho các dự
• 𝑅󰆒 𝑡  0 khi 𝑡  34
án của chính phủ. Giả sử rằng t tháng sau khi
chương trình kích thích bắt đầu, có 𝑁 𝑡 
• 𝑅′ 𝑡  𝑁′′ 𝑡  6𝑡  90
 𝑡  45𝑡  408𝑡  3,078 nghìn người
• 𝑅󰆒 𝑡  0 khi 𝑡  15 thất nghiệp.
a) Số người thất nghiệp tối đa là bao nhiêu?
a) 𝑡  34: Số người thất nghiệp đạt tối
Thời điểm nào số người thất nghiệp đạt
đa (𝑁 34  29,666 nghìn người). mức tối đa?
b) Để ngăn ngừa việc bơm tiền quá mức vào
b) 𝑡  15 : chính phủ nên dừng
nền kinh tế (dẫn đến lạm phát cao), chính
chương trình hỗ trợ (𝑁 15  15,948
phủ sẽ kết thúc chương trình ngay khi tốc
độ thất nghiệp bắt đầu giảm. Hãy tìm thời nghìn người).
điểm chính phủ nên dừng chương trình hỗ
trợ và tính số người thất nghiệp khi đó. 31 Th T ất bại chỉ là l à l một nơi để đ ể đ ng n h g ỉ ng n ơi. i  Đó là cơ hội để đ ể đ bạn bắt đầ đ u lại th t e h o e o các á h c h th t ô h n ô g n g mi m n i h n h hơn. n He H n e r n yFo F rd 32