Hệ thống bài tập trắc nghiệm vận dụng cao, phân loại hàm số mũ, logarit

Tài liệu gồm 21 trang được biên soạn bởi thầy giáo Lương Tuấn Đức (Giang Sơn), tuyển tập hệ thống bài tập trắc nghiệm vận dụng cao, phân loại hàm số mũ, hàm số logarit thuộc chương trình Toán 12

51 26 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

21 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
1
THÂN TẶNG QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TOÀN QUỐC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ,
LOGARIT LỚP 12 THPT
LỚP BÀI TOÁN PT, BPT, HPT
PHẦN 1 – 10
CREATED BY GIANG SƠN
TP.THÁI BÌNH; THÁNG 4/2020
_____________________________________________________________________________________________________________
1, 0
x
e x x
2
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 1)
__________________________________________________
C
C
â
â
u
u
1
1
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2 2
3 2 6 5 2 3 7
4 4 4 1
x x x x x x
c
c
ó
ó
b
b
ố
ố
n
n
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
, , ,
a b c d
t
t
h
h
e
e
o
o
t
t
h
h
ứ
ứ
t
t
ự
ự
t
t
ă
ă
n
n
g
g
d
d
ầ
ầ
n
n
.
.
T
T
í
í
n
n
h
h
g
g
i
i
á
á
t
t
r
r
ị
ị
b
b
i
i
ể
ể
u
u
t
t
h
h
ứ
ứ
c
c
2 3 4
.
.
A
A
.
.
1
1
0
0
B
B
.
.
3
3
C
C
.
.
4
4
D
D
.
.
5
5
C
C
â
â
u
u
2
2
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
n
n
h
h
ỏ
ỏ
h
h
ơ
ơ
n
n
1
1
0
0
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
b
b
a
a
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
2 1 2 2
27 .3 2 5 .3 5
x x x
m m m m m
.
.
A
A
.
.
6
6
B
B
.
.
5
5
C
C
.
.
4
4
D
D
.
.
7
7
C
C
â
â
u
u
3
3
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
b
b
a
a
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
2 2
125 4 .25 4 5 .5 2 10 0
x x x
m m m m m
.
.
A
A
.
.
6
6
B
B
.
.
5
5
C
C
.
.
3
3
D
D
.
.
7
7
C
C
â
â
u
u
4
4
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2
3 3
log 1 log 2
x x x x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
2
2
B
B
.
.
1
1
C
C
.
.
3
3
D
D
.
.
4
4
C
C
â
â
u
u
5
5
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
n
n
h
h
ỏ
ỏ
h
h
ơ
ơ
n
n
1
1
0
0
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
?
?
12 3.6 1 .2 3 3 0
x x x
m m
.
.
A
A
.
.
4
4
B
B
.
.
1
1
0
0
C
C
.
.
6
6
D
D
.
.
7
7
C
C
â
â
u
u
6
6
.
.
T
T
ì
ì
m
m
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
6 3 .2 0
x x
m m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
u
u
ộ
ộ
c
c
k
k
h
h
o
o
ả
ả
n
n
g
g
(
(
0
0
;
;
1
1
)
)
.
.
A
A
.
.
(
(
–
–
4
4
;
;
–
–
2
2
)
)
B
B
.
.
[
[
–
–
4
4
;
;
–
–
3
3
]
]
C
C
.
.
[
[
–
–
4
4
;
;
–
–
2
2
]
]
D
D
.
.
(
(
–
–
4
4
;
;
–
–
1
1
)
)
C
C
â
â
u
u
7
7
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 1 1
3 3 3 7 2
x x
x x
c
c
ó
ó
m
m
ộ
ộ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
h
h
ệ
ệ
q
q
u
u
ả
ả
l
l
à
à
A
A
.
.
3 3 6
x
x
B
B
.
.
3 4 7
x
x
C
C
.
.
3 2 5
x
x
D
D
.
.
3 3
x
C
C
â
â
u
u
8
8
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
1 1 1
3 4 5
2 3 4
x x x
x x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
2
2
B
B
.
.
1
1
C
C
.
.
3
3
D
D
.
.
4
4
C
C
â
â
u
u
9
9
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3 2
log sin log sin
x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
t
t
r
r
o
o
n
n
g
g
k
k
h
h
o
o
ả
ả
n
n
g
g
(
(
–
–
5
5
;
;
5
5
)
)
?
?
A
A
.
.
2
2
B
B
.
.
1
1
C
C
.
.
4
4
D
D
.
.
3
3
C
C
â
â
u
u
1
1
0
0
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
3 3
2 log 1 4 1 log 1 16
x x x x
c
c
ó
ó
t
t
ổ
ổ
n
n
g
g
c
c
á
á
c
c
n
n
g
g
h
h
i
i
ệ
ệ
m
m
b
b
ằ
ằ
n
n
g
g
A
A
.
.
1
1
B
B
.
.
82
81
C
C
.
.
2
2
D
D
.
.
11
81
C
C
â
â
u
u
1
1
1
1
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
b
b
a
a
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
2 2
27 5 .18 6 2 .12 3 6 .8 0
x x x x
m m m m m
.
.
A
A
.
.
6
6
B
B
.
.
5
5
C
C
.
.
0
0
D
D
.
.
7
7
C
C
â
â
u
u
1
1
2
2
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
b
b
a
a
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
2 2
2.8 5 .4 2 6 2 6
x x x
m m m m m
.
.
A
A
.
.
6
6
B
B
.
.
5
5
C
C
.
.
3
3
D
D
.
.
7
7
C
C
â
â
u
u
1
1
3
3
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
2
2
2
1
log 3 2
2 4 3
x x
x x
x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
3
3
B
B
.
.
1
1
C
C
.
.
4
4
D
D
.
.
2
2
C
C
â
â
u
u
1
1
4
4
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
3
3 3 8
x x
x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
3
3
B
B
.
.
2
2
C
C
.
.
4
4
D
D
.
.
1
1
3
C
C
â
â
u
u
1
1
5
5
.
.
T
T
í
í
n
n
h
h
t
t
ổ
ổ
n
n
g
g
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3 2
3
2
2
3 3 5
log 1 6 7
1
x x x
x x x
x
l
l
à
à
A
A
.
.
0
0
B
B
.
.
–
–
2
2
C
C
.
.
2 3
D
D
.
.
2 3
C
C
â
â
u
u
1
1
6
6
.
.
T
T
ổ
ổ
n
n
g
g
c
c
á
á
c
c
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
x
x
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3 3 3
4 2 2 4 4 2 6
x x x x
l
l
à
à
A
A
.
.
2
2
,
,
5
5
B
B
.
.
1
1
,
,
7
7
5
5
C
C
.
.
3
3
,
,
5
5
D
D
.
.
1
1
,
,
5
5
C
C
â
â
u
u
1
1
7
7
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2
3
3.2019 3.2019 8 4 1
x x
x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
3
3
B
B
.
.
2
2
C
C
.
.
4
4
D
D
.
.
1
1
C
C
â
â
u
u
1
1
8
8
.
.
C
C
h
h
o
o
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
0,5 2
log 6 log 3 2 0
m x x x
,
,
m
m
l
l
à
à
t
t
h
h
a
a
m
m
s
s
ố
ố
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
c
c
ủ
ủ
a
a
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
.
.
A
A
.
.
1
1
5
5
B
B
.
.
1
1
8
8
C
C
.
.
1
1
3
3
D
D
.
.
1
1
7
7
C
C
â
â
u
u
1
1
9
9
.
.
T
T
ì
ì
m
m
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
2 2
4log 2log 3 0
x x m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
u
u
ộ
ộ
c
c
đ
đ
o
o
ạ
ạ
n
n
1
;4
2
.
.
A
A
.
.
[
[
2
2
;
;
3
3
]
]
B
B
.
.
[
[
2
2
;
;
6
6
]
]
C
C
.
.
11
;15
4
D
D
.
.
11
;9
4
C
C
â
â
u
u
2
2
0
0
.
.
T
T
ì
ì
m
m
đ
đ
i
i
ề
ề
u
u
k
k
i
i
ệ
ệ
n
n
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
b
b
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
5 4
12 log 3
x
x x x m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
.
.
A
A
.
.
2 3
m
B
B
.
.
3
12log 5
m
C
C
.
.
3
2 12log 5
m
D
D
.
.
2 3
m
C
C
â
â
u
u
2
2
1
1
.
.
T
T
ì
ì
m
m
đ
đ
i
i
ề
ề
u
u
k
k
i
i
ệ
ệ
n
n
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
3 1
3
log 1 log 4 0
x x m
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
.
.
A
A
.
.
21
5
4
m
B
B
.
.
1
2
4
m
C
C
.
.
21
5
4
m
D
D
.
.
1
0
4
m
C
C
â
â
u
u
2
2
2
2
.
.
T
T
ì
ì
m
m
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
b
b
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
3 1
3
log 3 log 1
x x m x
c
c
ó
ó
t
t
ậ
ậ
p
p
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
h
h
ứ
ứ
a
a
k
k
h
h
o
o
ả
ả
n
n
g
g
1;

.
.
A
A
.
.
3;

B
B
.
.
2;

C
C
.
.
;0

D
D
.
.
;1

C
C
â
â
u
u
2
2
3
3
.
.
T
T
ì
ì
m
m
đ
đ
i
i
ề
ề
u
u
k
k
i
i
ệ
ệ
n
n
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2
log 4 3 log 1
x x m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
.
.
A
A
.
.
4
m
B
B
.
.
2 3
m
C
C
.
.
0 2
m
D
D
.
.
2
m
C
C
â
â
u
u
2
2
4
4
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
3 3
log 3log 2 7 0
x x m
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
1 2
3 3 72
x x
.
.
G
G
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
t
t
h
h
u
u
đ
đ
ư
ư
ợ
ợ
c
c
t
t
h
h
u
u
ộ
ộ
c
c
k
k
h
h
o
o
ả
ả
n
n
g
g
n
n
à
à
o
o
s
s
a
a
u
u
đ
đ
â
â
y
y
?
?
A
A
.
.
7
0;
2
B
B
.
.
7
;0
2
C
C
.
.
21
7;
2
D
D
.
.
7
;7
2
C
C
â
â
u
u
2
2
5
5
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
n
n
h
h
ỏ
ỏ
h
h
ơ
ơ
n
n
1
1
2
2
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
b
b
a
a
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
2 2 3
27 4 .36 3 5 .48 5 .4 0
x x x x
m m m m m
.
.
A
A
.
.
6
6
B
B
.
.
5
5
C
C
.
.
4
4
D
D
.
.
7
7
C
C
â
â
u
u
2
2
6
6
.
.
T
T
ì
ì
m
m
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2 .4 8 0
x x x
m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
u
u
ộ
ộ
c
c
k
k
h
h
o
o
ả
ả
n
n
g
g
(
(
0
0
;
;
1
1
)
)
.
.
A
A
.
.
7
2;
2
B
B
.
.
7
1;
2
C
C
.
.
7
1;
2
D
D
.
.
7
2;
2
C
C
â
â
u
u
2
2
7
7
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
1 2
4 .2 2 5
x x
m m
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
1
1
B
B
.
.
5
5
C
C
.
.
2
2
D
D
.
.
4
4
_________________________________
4
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 2)
__________________________________________________
C
C
â
â
u
u
1
1
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3 2
2log cot log cos
x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
d
d
ư
ư
ơ
ơ
n
n
g
g
n
n
h
h
ỏ
ỏ
h
h
ơ
ơ
n
n
2
2
0
0
?
?
A
A
.
.
5
5
B
B
.
.
6
6
C
C
.
.
3
3
D
D
.
.
4
4
C
C
â
â
u
u
2
2
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
n
n
h
h
ỏ
ỏ
h
h
ơ
ơ
n
n
1
1
0
0
c
c
ủ
ủ
a
a
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
2
3 3 2 5
x x
x x m
.
.
A
A
.
.
6
6
B
B
.
.
7
7
C
C
.
.
9
9
D
D
.
.
8
8
C
C
â
â
u
u
3
3
.
.
T
T
ậ
ậ
p
p
h
h
ợ
ợ
p
p
[
[
a
a
;
;
b
b
]
]
g
g
ồ
ồ
m
m
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
sin
2
x
x x m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
.
.
T
T
í
í
n
n
h
h
g
g
i
i
á
á
t
t
r
r
ị
ị
b
b
i
i
ể
ể
u
u
t
t
h
h
ứ
ứ
c
c
2
4
a b
.
.
A
A
.
.
6
6
,
,
5
5
B
B
.
.
7
7
C
C
.
.
8
8
,
,
5
5
D
D
.
.
5
5
,
,
2
2
5
5
C
C
â
â
u
u
4
4
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
.
.
2
2 2
2
log 1 log log 2 7
x x x x m
.
.
A
A
.
.
4
4
g
g
i
i
á
á
t
t
r
r
ị
ị
B
B
.
.
3
3
g
g
i
i
á
á
t
t
r
r
ị
ị
C
C
.
.
1
1
0
0
g
g
i
i
á
á
t
t
r
r
ị
ị
D
D
.
.
8
8
g
g
i
i
á
á
t
t
r
r
ị
ị
.
.
C
C
â
â
u
u
5
5
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
n
n
h
h
ỏ
ỏ
h
h
ơ
ơ
n
n
1
1
0
0
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 3 2
4 4 5 2 5 5 25 0
x x
m m m m m
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
đ
đ
ề
ề
u
u
l
l
ớ
ớ
n
n
h
h
ơ
ơ
n
n
2
2
?
?
A
A
.
.
6
6
B
B
.
.
8
8
C
C
.
.
7
7
D
D
.
.
9
9
C
C
â
â
u
u
6
6
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
6
log
2 6
log 3 log
x
x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
2
2
B
B
.
.
1
1
C
C
.
.
4
4
D
D
.
.
3
3
C
C
â
â
u
u
7
7
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
h
h
ệ
ệ
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
2 2
2 2
2 1 3 2
log 2 1 4 log 4 0
1
x y x y
x y m x m
e e x y
A
A
.
.
3
3
B
B
.
.
4
4
C
C
.
.
5
5
D
D
.
.
6
6
C
C
â
â
u
u
8
8
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2
5 6 1 6 5
2 2 2.2 1
x x x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
d
d
ư
ư
ơ
ơ
n
n
g
g
?
?
A
A
.
.
2
2
B
B
.
.
1
1
C
C
.
.
3
3
D
D
.
.
4
4
C
C
â
â
u
u
9
9
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
.
.
7
7
2log cos sin 6 log 3sin 2cos 1
x x x x m
.
.
A
A
.
.
4
4
g
g
i
i
á
á
t
t
r
r
ị
ị
B
B
.
.
9
9
g
g
i
i
á
á
t
t
r
r
ị
ị
C
C
.
.
1
1
0
0
g
g
i
i
á
á
t
t
r
r
ị
ị
D
D
.
.
8
8
g
g
i
i
á
á
t
t
r
r
ị
ị
.
.
C
C
â
â
u
u
1
1
0
0
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
2
2cos 2 2
6
x x
x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
k
k
h
h
ô
ô
n
n
g
g
â
â
m
m
?
?
A
A
.
.
3
3
B
B
.
.
1
1
C
C
.
.
2
2
D
D
.
.
4
4
C
C
â
â
u
u
1
1
1
1
.
.
T
T
í
í
n
n
h
h
t
t
ổ
ổ
n
n
g
g
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
1
5 3
ln 5 5.3 30 10 0
6 2
x x
x x
x
x
.
.
A
A
.
.
1
1
B
B
.
.
2
2
C
C
.
.
–
–
1
1
D
D
.
.
3
3
C
C
â
â
u
u
1
1
2
2
.
.
B
B
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2
log 2 log 2 3
a a
x x x x
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
9
4
x
.
.
G
G
i
i
ả
ả
s
s
ử
ử
;
S p q
l
l
à
à
t
t
ậ
ậ
p
p
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
b
b
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
đ
đ
ã
ã
c
c
h
h
o
o
.
.
T
T
ì
ì
m
m
2 5
p q
.
.
A
A
.
.
1
1
4
4
B
B
.
.
1
1
2
2
C
C
.
.
1
1
3
3
D
D
.
.
1
1
0
0
C
C
â
â
u
u
1
1
3
3
.
.
K
K
ý
ý
h
h
i
i
ệ
ệ
u
u
;
S a b
l
l
à
à
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3
3
log 9 9
x
m x
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
.
.
T
T
í
í
n
n
h
h
g
g
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
b
b
i
i
ể
ể
u
u
t
t
h
h
ứ
ứ
c
c
3
72
a b
.
.
5
A
A
.
.
4
4
B
B
.
.
2
2
C
C
.
.
1
1
D
D
.
.
5
5
C
C
â
â
u
u
1
1
4
4
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3
3
3 27 3 27.2 2
x x
m m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
V
V
ô
ô
s
s
ố
ố
B
B
.
.
4
4
C
C
.
.
8
8
D
D
.
.
6
6
C
C
â
â
u
u
1
1
5
5
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
ln 2sin ln 3sin sin
m x m x x
.
.
A
A
.
.
3
3
B
B
.
.
4
4
C
C
.
.
5
5
D
D
.
.
6
6
C
C
â
â
u
u
1
1
6
6
.
.
C
C
h
h
o
o
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 1 sin
cos sin
2 sin cos
x
m x x
e e x m x
v
v
ớ
ớ
i
i
m
m
l
l
à
à
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
h
h
ự
ự
c
c
.
.
G
G
ọ
ọ
i
i
S
S
l
l
à
à
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
.
.
K
K
h
h
i
i
đ
đ
ó
ó
S
S
c
c
ó
ó
d
d
ạ
ạ
n
n
g
g
; ;a b
 
,
,
t
t
í
í
n
n
h
h
10 20
T a b
.
.
A
A
.
.
1
1
B
B
.
.
0
0
C
C
.
.
10 3
D
D
.
.
3 10
C
C
â
â
u
u
1
1
7
7
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
k
k
h
h
i
i
m
m
t
t
h
h
u
u
ộ
ộ
c
c
đ
đ
o
o
ạ
ạ
n
n
[
[
a
a
;
;
b
b
]
]
.
.
T
T
í
í
n
n
h
h
8 16
a b
.
.
sin cos sin 2 3 1
sin 2 sin cos 4 1
x x m x m
e e x x x m
.
.
A
A
.
.
1
1
0
0
B
B
.
.
9 2 2
C
C
.
.
10 3 2
D
D
.
.
4 2
C
C
â
â
u
u
1
1
8
8
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
l
l
ớ
ớ
n
n
h
h
ơ
ơ
n
n
–
–
1
1
0
0
đ
đ
ể
ể
b
b
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
đ
đ
ú
ú
n
n
g
g
v
v
ớ
ớ
i
i
m
m
ọ
ọ
i
i
g
g
i
i
á
á
t
t
r
r
ị
ị
x
x
sin 4 cos
cos sin 4
x x m
e e x x m
.
.
A
A
.
.
1
1
3
3
B
B
.
.
1
1
4
4
C
C
.
.
1
1
5
5
D
D
.
.
1
1
2
2
C
C
â
â
u
u
1
1
9
9
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
15;15
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3
3 log
x
m x m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
?
?
A
A
.
.
1
1
6
6
B
B
.
.
9
9
C
C
.
.
1
1
4
4
D
D
.
.
1
1
5
5
C
C
â
â
u
u
2
2
0
0
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2
2 2 3 6 2 3
2 2 9 3 .8 3 6 .8
x x x x
x x x x x x
.
.
A
A
.
.
1
1
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
4
4
C
C
â
â
u
u
2
2
1
1
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
25; 25
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
7
7 log
x
m x m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
?
?
A
A
.
.
2
2
5
5
B
B
.
.
9
9
C
C
.
.
2
2
4
4
D
D
.
.
2
2
6
6
C
C
â
â
u
u
2
2
2
2
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2
log 2 log 4 3
x
x
c
c
ó
ó
t
t
ổ
ổ
n
n
g
g
c
c
á
á
c
c
n
n
g
g
h
h
i
i
ệ
ệ
m
m
b
b
ằ
ằ
n
n
g
g
A
A
.
.
5
5
B
B
.
.
6
6
C
C
.
.
3
3
D
D
.
.
4
4
C
C
â
â
u
u
2
2
3
3
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
30;30
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
4 4 4
x x
x m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
A
A
.
.
2
2
B
B
.
.
1
1
C
C
.
.
4
4
D
D
.
.
3
3
C
C
â
â
u
u
2
2
4
4
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
2 2 2
sin cos cos
2
5 6 7 log
x x x
m
.
.
A
A
.
.
6
6
2
2
B
B
.
.
6
6
3
3
C
C
.
.
6
6
4
4
D
D
.
.
6
6
C
C
â
â
u
u
2
2
5
5
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
m
m
đ
đ
ể
ể
b
b
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2 2
cos sin sin
3 2 .3
x x x
m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
.
.
A
A
.
.
1
1
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
4
4
C
C
â
â
u
u
2
2
6
6
.
.
C
C
h
h
o
o
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
.4 sin 4 4
x x
a x
;
;
a
a
l
l
à
à
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
h
h
ự
ự
c
c
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
d
d
u
u
y
y
n
n
h
h
ấ
ấ
t
t
g
g
i
i
á
á
t
t
r
r
ị
ị
0
a a
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
d
d
u
u
y
y
n
n
h
h
ấ
ấ
t
t
.
.
T
T
í
í
n
n
h
h
g
g
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
2 0
log
a
.
.
A
A
.
.
B
B
.
.
1
C
C
.
.
2
2
D
D
.
.
2 1
C
C
â
â
u
u
2
2
7
7
.
.
C
C
h
h
o
o
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
6 .6 cos 1296
x x
a x
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
d
d
u
u
y
y
n
n
h
h
ấ
ấ
t
t
m
m
ộ
ộ
t
t
g
g
i
i
á
á
t
t
r
r
ị
ị
a
a
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
d
d
u
u
y
y
n
n
h
h
ấ
ấ
t
t
0
x
.
.
N
N
g
g
h
h
i
i
ệ
ệ
m
m
0
x
n
n
ằ
ằ
m
m
t
t
r
r
o
o
n
n
g
g
k
k
h
h
o
o
ả
ả
n
n
g
g
n
n
à
à
o
o
?
?
A
A
.
.
(
(
1
1
;
;
2
2
)
)
B
B
.
.
(
(
1
1
;
;
4
4
)
)
C
C
.
.
(
(
4
4
;
;
7
7
)
)
D
D
.
.
(
(
3
3
;
;
5
5
)
)
_________________________________
6
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 3)
__________________________________________________
C
C
â
â
u
u
1
1
.
.
B
B
i
i
ế
ế
t
t
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
b
b
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2 2
sin cos cos
4 5 .7
x x x
m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
l
l
à
à
n
n
ử
ử
a
a
k
k
h
h
o
o
ả
ả
n
n
g
g
;
a
b

v
v
ớ
ớ
i
i
a
a
,
,
b
b
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
v
v
à
à
p
p
h
h
â
â
n
n
s
s
ố
ố
a
b
t
t
ố
ố
i
i
g
g
i
i
ả
ả
n
n
.
.
T
T
í
í
n
n
h
h
g
g
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
S a b
.
.
A
A
.
.
13
S
B
B
.
.
15
S
C
C
.
.
9
S
D
D
.
.
11
S
C
C
â
â
u
u
2
2
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
2 2
sin cos cos 2
3
3 13 8.7 log
x x x
m
.
.
A
A
.
.
1
1
8
8
B
B
.
.
1
1
4
4
C
C
.
.
4
4
5
5
D
D
.
.
6
6
0
0
C
C
â
â
u
u
3
3
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3
3
3 3.4 4
x x
m m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
V
V
ô
ô
s
s
ố
ố
B
B
.
.
4
4
C
C
.
.
8
8
D
D
.
.
6
6
C
C
â
â
u
u
4
4
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
n
n
h
h
ỏ
ỏ
h
h
ơ
ơ
n
n
1
1
0
0
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
x x
m m e e
.
.
A
A
.
.
1
1
0
0
B
B
.
.
9
9
C
C
.
.
7
7
D
D
.
.
6
6
C
C
â
â
u
u
5
5
.
.
C
C
h
h
o
o
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
ẩ
ẩ
n
n
x
x
:
:
4 4
6 .6 cos 36
x x
a x
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
a
a
t
t
h
h
u
u
ộ
ộ
c
c
đ
đ
o
o
ạ
ạ
n
n
[
[
–
–
2
2
0
0
1
1
8
8
;
;
2
2
0
0
1
1
8
8
]
]
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ó
ó
đ
đ
ú
ú
n
n
g
g
m
m
ộ
ộ
t
t
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
2
2
0
0
1
1
8
8
C
C
â
â
u
u
6
6
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
2
2 2
2
sin 2
ln sin cos 1 0
3 cos
x
x x m
m x
.
.
A
A
.
.
7
7
B
B
.
.
6
6
C
C
.
.
5
5
D
D
.
.
3
3
C
C
â
â
u
u
7
7
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
d
d
u
u
y
y
n
n
h
h
ấ
ấ
t
t
m
m
ộ
ộ
t
t
g
g
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
9 2 .6 .4 0
x x x
m m
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
1 2
,
x x
c
c
ó
ó
t
t
ổ
ổ
n
n
g
g
b
b
ằ
ằ
n
n
g
g
2
2
.
.
G
G
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
t
t
h
h
u
u
đ
đ
ư
ư
ợ
ợ
c
c
n
n
ằ
ằ
m
m
t
t
r
r
o
o
n
n
g
g
k
k
h
h
o
o
ả
ả
n
n
g
g
n
n
à
à
o
o
?
?
A
A
.
.
(
(
2
2
;
;
3
3
)
)
B
B
.
.
17 5
;
16 4
C
C
.
.
8 17
;
9 16
D
D
.
.
11
;2
8
C
C
â
â
u
u
8
8
.
.
T
T
ì
ì
m
m
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3 4 2 .5 0
x x x
m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
t
t
h
h
u
u
ộ
ộ
c
c
k
k
h
h
o
o
ả
ả
n
n
g
g
(
(
0
0
;
;
2
2
)
)
.
.
A
A
.
.
[
[
3
3
;
;
4
4
]
]
B
B
.
.
[
[
2
2
;
;
4
4
]
]
C
C
.
.
(
(
2
2
;
;
4
4
)
)
D
D
.
.
(
(
3
3
;
;
4
4
)
)
C
C
â
â
u
u
9
9
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
l
l
ớ
ớ
n
n
h
h
ơ
ơ
n
n
5
5
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
sin cos 2
ln sin 2 6 sin cos
sin 2 4
x x
x m x x
x m
.
.
A
A
.
.
2
2
B
B
.
.
6
6
C
C
.
.
5
5
D
D
.
.
3
3
C
C
â
â
u
u
1
1
0
0
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
2 2 3 5 8 3
5 2 8 3 .8 3 5 .8
x x x
x x x x x
.
.
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
2
2
C
C
â
â
u
u
1
1
1
1
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
5 5 5
sin 3cos 2cos sin 2 2sin cos
x x m x x m x x m
.
.
A
A
.
.
4
4
B
B
.
.
6
6
C
C
.
.
5
5
D
D
.
.
7
7
C
C
â
â
u
u
1
1
2
2
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 3 2
2 2
3 2 log 1 log
x x x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
7
A
A
.
.
3
3
B
B
.
.
1
1
C
C
.
.
4
4
D
D
.
.
2
2
C
C
â
â
u
u
1
1
2
2
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
3 3
log 2 log 3 1 0
x m x m
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ó
ó
t
t
í
í
c
c
h
h
b
b
ằ
ằ
n
n
g
g
2
2
7
7
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
d
d
ư
ư
ớ
ớ
i
i
đ
đ
â
â
y
y
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
2; 1
m
B
B
.
.
0;2
m
C
C
.
.
K
K
h
h
ô
ô
n
n
g
g
t
t
ồ
ồ
n
n
t
t
ạ
ạ
i
i
m
m
.
.
D
D
.
.
2;4
m
C
C
â
â
u
u
1
1
3
3
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
1 2 3
5.3 3.4 3.5
20 30 40
x x x
x x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
2
2
B
B
.
.
1
1
C
C
.
.
3
3
D
D
.
.
4
4
C
C
â
â
u
u
1
1
4
4
.
.
T
T
ì
ì
m
m
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3 .2 2 0
x x
m m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
u
u
ộ
ộ
c
c
k
k
h
h
o
o
ả
ả
n
n
g
g
(
(
0
0
;
;
2
2
)
)
.
.
A
A
.
.
1 7
;
2 5
B
B
.
.
1 7
;
2 5
C
C
.
.
1 7
;
3 5
D
D
.
.
1 7
;
3 5
C
C
â
â
u
u
1
1
5
5
.
.
G
G
ọ
ọ
i
i
S
S
l
l
à
à
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
b
b
a
a
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
3 2
1
2
2
log 6 2log 14 29 2 0
mx x x x
S
S
ố
ố
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
S
S
l
l
à
à
A
A
.
.
2
2
0
0
B
B
.
.
3
3
0
0
C
C
.
.
0
0
D
D
.
.
V
V
ô
ô
s
s
ố
ố
C
C
â
â
u
u
1
1
6
6
.
.
T
T
ì
ì
m
m
đ
đ
i
i
ề
ề
u
u
k
k
i
i
ệ
ệ
n
n
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
3 1
3
log 1 log 4 0
x x m
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
.
.
A
A
.
.
21
5
4
m
B
B
.
.
1
2
4
m
C
C
.
.
21
5
4
m
D
D
.
.
1
0
4
m
C
C
â
â
u
u
1
1
7
7
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
3 5 6
2 3
x x x
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
1 2 1 2
,
x x x x
.
.
L
L
ự
ự
a
a
c
c
h
h
ọ
ọ
n
n
p
p
h
h
á
á
t
t
b
b
i
i
ể
ể
u
u
đ
đ
ú
ú
n
n
g
g
A
A
.
.
1 2 3
3 2 log 8
x x
B
B
.
.
1 2 3
2 3 log 8
x x
C
C
.
.
1 2 3
2 3 log 54
x x
D
D
.
.
1 2 3
3 2 log 54
x x
C
C
â
â
u
u
1
1
8
8
.
.
T
T
ì
ì
m
m
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
m
m
đ
đ
ể
ể
b
b
ấ
ấ
t
t
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
2 2
log 2 2 1 log 2 0
x m x
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
u
u
ộ
ộ
c
c
k
k
h
h
o
o
ả
ả
n
n
g
g
2;

.
.
A
A
.
.
;0

B
B
.
.
3
;0
4
C
C
.
.
3
;
4

D
D
.
.
0;

C
C
â
â
u
u
1
1
9
9
.
.
T
T
ì
ì
m
m
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
g
g
i
i
á
á
t
t
r
r
ị
ị
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
2 1
2
4 log log 0
x x m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
u
u
ộ
ộ
c
c
k
k
h
h
o
o
ả
ả
n
n
g
g
(
(
0
0
;
;
1
1
)
)
.
.
A
A
.
.
1
0;
4
B
B
.
.
1
;
4

C
C
.
.
1
;
4

D
D
.
.
;0

C
C
â
â
u
u
2
2
0
0
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
l
l
ớ
ớ
n
n
h
h
ơ
ơ
n
n
–
–
5
5
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
d
d
u
u
y
y
n
n
h
h
ấ
ấ
t
t
5 1 . 5 1 2
x x
x
m
A
A
.
.
0
0
B
B
.
.
5
5
C
C
.
.
2
2
D
D
.
.
3
3
C
C
â
â
u
u
2
2
1
1
.
.
T
T
ì
ì
m
m
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
ự
ự
c
c
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
u
u
ộ
ộ
c
c
n
n
ử
ử
a
a
k
k
h
h
o
o
ả
ả
n
n
g
g
1;

.
.
2 4
log 5 1 log 2.5 2
x x
m
.
.
A
A
.
.
1;

B
B
.
.
6;

C
C
.
.
3;

D
D
.
.
1
;
4

C
C
â
â
u
u
2
2
2
2
.
.
T
T
ì
ì
m
m
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
g
g
i
i
á
á
t
t
r
r
ị
ị
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
6 2 .3 0
x x
m m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
t
t
h
h
u
u
ộ
ộ
c
c
k
k
h
h
o
o
ả
ả
n
n
g
g
(
(
0
0
;
;
1
1
)
)
.
.
A
A
.
.
3 27
;
2 5
B
B
.
.
3
;3
2
C
C
.
.
3 27
;
2 5
D
D
.
.
3
;3
2
________________________________
8
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 4)
__________________________________________________
C
C
â
â
u
u
1
1
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
2018 2019
2
6f x x mx
x
x
á
á
c
c
đ
đ
ị
ị
n
n
h
h
t
t
r
r
ê
ê
n
n
R
R
?
?
A
A
.
.
6
6
B
B
.
.
7
7
C
C
.
.
9
9
D
D
.
.
1
1
0
0
C
C
â
â
u
u
2
2
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3 722 3 2018 1296
x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
n
n
g
g
u
u
y
y
ê
ê
n
n
?
?
A
A
.
.
2
2
B
B
.
.
1
1
C
C
.
.
3
3
D
D
.
.
4
4
Câu 3. Tìm tập hợp tất cả các giá trị m để hàm số
8 .2 1
x x
y m
đồng biến trên
.
A.
;1

B.
;0
 C.
1
;5
3
D.
5;

C
C
â
â
u
u
4
4
.
.
H
H
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
l
l
à
à
h
h
a
a
i
i
đ
đ
ồ
ồ
t
t
h
h
ị
ị
1 2
: log ; :
x
b
C y x C y a
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
a
a
>
>
1
1
;
;
b
b
>
>
1
1
.
.
B
B
.
.
0
0
<
<
a
a
<
<
1
1
,
,
0
0
<
<
b
b
<
<
1
1
.
.
C
C
.
.
0
0
<
<
a
a
<
<
1
1
<
<
b
b
.
.
D
D
.
.
0
0
<
<
b
b
<
<
1
1
<
<
a
a
.
.
C
C
â
â
u
u
5
5
.
.
Tìm giá trị nhỏ nhất của tham số m để hàm số
2
3
log 2 1
y x mx m
xác định trên [1;2].
A. 0,25 B. 0,5 C. 0,75 D. 1
C
C
â
â
u
u
6
6
.
.
Phương trình
2
2 1 2 2 2
x x
x x y
có bao nhiêu cặp nghiệm (x;y) ?
A. 2 B. 3 C. 1 D. Vô nghiệm
Câu 7. Tìm điều kiện tham số
m
để hàm số
3
1 1
1972
1973
x x
e m e
y
đồng biến trên khoảng (1;2).
A.
3 4
3 1 3 1
e m e
B.
2 3
3 1 3 1
e m e
C.
4
3 1
m e
D.
2
3 1
m e
Câu 8. Tồn tại bao nhiêu số nguyên m lớn hơn – 10 để hàm số
2
ln 1 1
y x mx
đồng biến trên
.
A. 5 B. 7 C. 9 D. 10
C
C
â
â
u
u
9
9
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 2
log 3 log 7
2
x x x
.
.
A
A
.
.
3
3
B
B
.
.
1
1
C
C
.
.
2
2
D
D
.
.
4
4
C
C
â
â
u
u
1
1
0
0
.
.
C
C
h
h
o
o
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
a
a
<
<
c
c
<
<
b
b
B
B
.
.
a
a
<
<
b
b
<
<
c
c
C
C
.
.
b
b
<
<
c
c
<
<
a
a
D
D
.
.
c
c
<
<
a
a
<
<
b
b
C
C
â
â
u
u
1
1
1
1
.
.
T
T
í
í
n
n
h
h
t
t
r
r
u
u
n
n
g
g
b
b
ì
ì
n
n
h
h
c
c
ộ
ộ
n
n
g
g
c
c
á
á
c
c
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
8 2
2 2 8 2
x x x
x x
.
.
A
A
.
.
2
2
B
B
.
.
1
1
C
C
.
.
3
3
D
D
.
.
1
1
,
,
5
5
C
C
â
â
u
u
1
1
2
2
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
t
t
h
h
u
u
ộ
ộ
c
c
[
[
–
–
2
2
0
0
;
;
2
2
0
0
]
]
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
2
1
2 ln 4 6
x
y
x m x x m
x
x
á
á
c
c
đ
đ
ị
ị
n
n
h
h
t
t
r
r
ê
ê
n
n
m
m
i
i
ề
ề
n
n
1;

?
?
9
A
A
.
.
2
2
1
1
B
B
.
.
2
2
0
0
C
C
.
.
4
4
D
D
.
.
3
3
C
C
â
â
u
u
1
1
3
3
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
16
mx
x m
y e
n
n
g
g
h
h
ị
ị
c
c
h
h
b
b
i
i
ế
ế
n
n
t
t
r
r
ê
ê
n
n
2;

?
?
A
A
.
.
6
6
B
B
.
.
5
5
C
C
.
.
7
7
D
D
.
.
9
9
C
C
â
â
u
u
1
1
4
4
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 1
3 .5 15
x
x
x
c
c
ó
ó
m
m
ộ
ộ
t
t
n
n
g
g
h
h
i
i
ệ
ệ
m
m
log 1 8,1 8; ,
a
x b a b a b
.
.
T
T
í
í
n
n
h
h
a
a
+
+
b
b
.
.
A
A
.
.
1
1
0
0
B
B
.
.
8
8
C
C
.
.
1
1
3
3
D
D
.
.
5
5
C
C
â
â
u
u
1
1
5
5
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
sin
5
x
y
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
5cos ln 5
y x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
r
r
o
o
n
n
g
g
k
k
h
h
o
o
ả
ả
n
n
g
g
(
(
0
0
;
;
1
1
0
0
)
)
?
?
A
A
.
.
1
1
B
B
.
.
3
3
C
C
.
.
4
4
D
D
.
.
2
2
C
C
â
â
u
u
1
1
6
6
.
.
T
T
ì
ì
m
m
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
h
h
ỏ
ỏ
n
n
h
h
ấ
ấ
t
t
c
c
ủ
ủ
a
a
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3
3 3x x
e m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
0;2
x
.
.
A
A
.
.
m
m
=
=
2
2
e
e
B
B
.
.
m
m
=
=
3
3
e
e
C
C
.
.
m
m
=
=
e
e
D
D
.
.
m
m
=
=
1
e
C
C
â
â
u
u
1
1
7
7
.
.
Ký hiệu S là tập hợp tất cả các giá trị thực m để phương trình
2 2
2 2
log 4 log 2 0
x x m m
có hai
nghiệm phân biệt
1 2
,
x x
thỏa mãn
2 2
1 2
68
x x
. Tính tổng bình phương các phần tử của S.
A. 15 B. 10 C. 18 D. 26
C
C
â
â
u
u
1
1
8
8
.
.
C
C
h
h
o
o
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
a
a
>
>
b
b
>
>
1
1
B
B
.
.
1
1
>
>
a
a
>
>
b
b
C
C
.
.
b
b
>
>
a
a
>
>
1
1
D
D
.
.
a
a
>
>
1
1
>
>
b
b
C
C
â
â
u
u
1
1
9
9
.
.
Có bao nhiêu số nguyên m < 2018 để phương trình
6 4
log 2018 log 1009
x m x
có nghiệm.
A. 2019 B. 2018 C. 2017 D. 2020
C
C
â
â
u
u
2
2
0
0
.
.
Tìm tập hợp tất cả các giá trị m để phương trình
2
2 2
log log
2
3 2 3 3 3 0
x x
m m
có hai nghiệm
phân biệt mà tích của chúng lớn hơn 2.
A.
1; \ 0

B.
1;

C.
0;

D.
\ 1;1
C
C
â
â
u
u
2
2
1
1
.
.
Tồn tại bao nhiêu số nguyên m trong khoảng (– 5;15) để bất phương trình sau nghiệm đúng với mọi số
thực x:
2 2
5 5
1 log 1 log 4
x mx x m
.
A. 2 B. 1 C. 3 D. 11
C
C
â
â
u
u
2
2
2
2
.
.
C
C
h
h
o
o
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
0
0
<
<
c
c
<
<
1
1
<
<
a
a
<
<
b
b
.
.
B
B
.
.
0
0
<
<
a
a
<
<
b
b
<
<
1
1
<
<
c
c
.
.
C
C
.
.
0
0
<
<
c
c
<
<
a
a
<
<
1
1
<
<
b
b
.
.
D
D
.
.
0
0
<
<
c
c
<
<
1
1
<
<
b
b
<
<
a
a
.
.
Câu 23. Cho hàm số
81
81 9
x
x
g x
. Với mọi số thực x, phần nguyên của x được ký hiệu [x], tức là số nguyên
lớn nhất không vượt quá x. Tìm phần nguyên của số
1 2 2016
... 3
2017 2017 2017
Q g g g g
.
A.
112
Q B.
113
Q C.
115
Q D.
120
Q
_________________________________
10
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 5)
__________________________________________________
C
C
â
â
u
u
1
1
.
.
H
H
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
l
l
à
à
đ
đ
ồ
ồ
t
t
h
h
ị
ị
c
c
á
á
c
c
h
h
à
à
m
m
s
s
ố
ố
; ;
x x x
y a y c y b
.
.
N
N
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
x x x
a c b
l
l
à
à
A
A
.
.
x
x
=
=
0
0
B
B
.
.
x
x
=
=
2
2
C
C
.
.
x
x
=
=
1
1
D
D
.
.
x
x
=
=
3
3
Câu 2. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
ln 2sin ln 7sin 5sin
m x m x x
.
A. 35 B. 141 C. 52 D. 66
Câu 3. Có bao nhiêu số nguyên dương m để hàm số
2
8ln 1
y x x m
đồng biến trên tập xác định của nó
A. 2 B. 1 C. 3 D. 4
Câu 4. Phương trình
sin 1 sin
4 2 cos 2 0
y
x x
xy
có nghiệm
0 0
;
x y
. Tính tổng các giá trị
0 0
,
x y
khi
0 0
10
x y
.
A.
4
B.
2
C.
3
D.
6
Câu 5. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình sau có nghiệm thực
x x
m m e e
.
A. 10 B. 9 C. 7 D. 6
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
s
s
a
a
u
u
đ
đ
â
â
y
y
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
a
a
>
>
1
1
;
;
0
0
<
<
b
b
<
<
1
1
.
.
B
B
.
.
1
1
>
>
a
a
>
>
0
0
;
;
b
b
>
>
1
1
.
.
C
C
.
.
0
0
<
<
a
a
<
<
1
1
;
;
b
b
<
<
1
1
.
.
D
D
.
.
a
a
>
>
1
1
;
;
b
b
>
>
1
1
.
.
Câu 7. Cho hàm số
2016
2016 2016
x
x
f x
. Tìm số nguyên dương n lớn nhất sao cho
1 2 2015 2016
3 ...
2017 2017 2017 2017
n
f f f f
.
A.
4
n
B.
5
n
C.
6
n
D.
7
n
Câu 8. Cho hàm số
2 2
1 1
1
1
x
x
f x e
. Biết rằng
1 . 2 ... 2017
m
n
f f f e
với
m
n
là phân số tối giản. Tính
giá trị của biểu thức
2
m n
.
A. 2018 B. 1 C. – 2018 D. – 1
Câu 9. Tập hợp
;
S a b
bao gồm tất cả các giá trị m để phương trình sau có nghiệm thực
sin 4 cos 2 3sin cos 5
4 cos 3 sin 2 5
m x x m x m x
e e m x m x m
Tính
20
a b
.
A. 4 B. 2 C. 5 D. 3
11
Câu 10. Có bao nhiêu giá trị nguyên m thuộc (– 2018;2018) để hàm số
4 2
2 . 2 1
ln 4 ln 2
x x
y m m x
đồng
biến trên khoảng
;
 
?
A. 2018 B. 2019 C. 2020 D. 4034
C
C
â
â
u
u
1
1
1
1
.
.
C
C
h
h
o
o
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
s
s
a
a
u
u
đ
đ
â
â
y
y
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
b
b
<
<
c
c
<
<
a
a
.
.
B
B
.
.
c
c
<
<
a
a
<
<
b
b
C
C
.
.
a
a
<
<
b
b
<
<
c
c
D
D
.
.
b
b
<
<
a
a
<
<
c
c
Câu 12. Tính tích các nghiệm của phương trình
8.3 3.2 24 6
x x x
.
A. 3 B. 2 C. 4 D. 6
Câu 13. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực ?
2
2
4
sin
cos
5
5 5 5cos 2
m
x
x m
e e x m
.
A. 12 B. 10 C. 11 D. 15
Câu 14. Phương trình
2 2
log log
2
3 1 3 1 1
x x
x x
có bao nhiêu nghiệm thực ?
A. 2 B. 1 C. 3 D. 0
Câu 15. Tìm giá trị lớn nhất của tham số m để phương trình
ln ln cos cos
m m x x
có nghiệm thực ?
A. 1 B. e C.
1
2
e
D. e – 1
C
C
â
â
u
u
1
1
6
6
.
.
C
C
h
h
o
o
0 , , 1
a b c
v
v
à
à
b
b
a
a
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
s
s
a
a
u
u
đ
đ
â
â
y
y
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
1
1
<
<
c
c
<
<
a
a
<
<
b
b
B
B
.
.
c
c
<
<
a
a
<
<
b
b
<
<
1
1
C
C
.
.
c
c
<
<
1
1
<
<
b
b
<
<
a
a
D
D
.
.
c
c
<
<
1
1
<
<
a
a
<
<
b
b
Câu 17. Có bao nhiêu giá trị nguyên
18;18
m
để phương trình
2
2 log
x
m x m
có nghiệm ?
A. 19 B. 9 C. 17 D. 18
Câu 18. Tính tổng các nghiệm của phương trình
2 2
3 2 2 2 3
2 9 6 4 3 5
x x x x x x
x x
.
A. 6 B. 7 C. 8 D. 4
Câu 19. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để phương trình sau có nghiệm
2
3 cos 2
x
x m
.
A. 10 B. 12 C. 15 D. 14
Câu 20. Phương trình
8
4 4
log 3 1 1 3 6 log
x y y x
có bao nhiêu cặp nghiệm thực (x;y) ?
A. 3 B. 2 C. 1 D. 4
Câu 21. Tìm tất cả các giá trị m để phương trình
3
2
log 1
x m
x
có hai nghiệm phân biệt.
A.
1 0
m
B. m > – 1 C. Không tồn tại m D. – 1 < m < 0
_________________________________
12
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 6)
__________________________________________________
C
C
â
â
u
u
1
1
.
.
Đ
Đ
ố
ố
i
i
v
v
ớ
ớ
i
i
g
g
ó
ó
c
c
p
p
h
h
ầ
ầ
n
n
t
t
ư
ư
t
t
h
h
ứ
ứ
n
n
h
h
ấ
ấ
t
t
,
,
t
t
h
h
e
e
o
o
t
t
h
h
ứ
ứ
t
t
ự
ự
t
t
ừ
ừ
t
t
r
r
á
á
i
i
s
s
a
a
n
n
g
g
p
p
h
h
ả
ả
i
i
t
t
r
r
o
o
n
n
g
g
h
h
ì
ì
n
n
h
h
b
b
ê
ê
n
n
l
l
à
à
đ
đ
ồ
ồ
t
t
h
h
ị
ị
c
c
á
á
c
c
h
h
à
à
m
m
s
s
ố
ố
; ;
x x x
y a y c y b
.
.
N
N
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
x x x
a c b
l
l
à
à
A
A
.
.
x
x
=
=
0
0
B
B
.
.
x
x
=
=
1
1
C
C
.
.
x
x
=
=
2
2
D
D
.
.
x
x
=
=
3
3
C
C
â
â
u
u
2
2
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
2
3
2 2
log
6 sin 2 cos
x mx m
f x
x x
x
x
á
á
c
c
đ
đ
ị
ị
n
n
h
h
t
t
r
r
ê
ê
n
n
?
?
A
A
.
.
3
3
B
B
.
.
2
2
C
C
.
.
1
1
D
D
.
.
4
4
C
C
â
â
u
u
3
3
.
.
T
T
ì
ì
m
m
g
g
i
i
á
á
t
t
r
r
ị
ị
b
b
é
é
n
n
h
h
ấ
ấ
t
t
c
c
ủ
ủ
a
a
m
m
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
2
ln 16 1 1 2
y x m x m
n
n
g
g
h
h
ị
ị
c
c
h
h
b
b
i
i
ế
ế
n
n
t
t
r
r
ê
ê
n
n
?
?
A
A
.
.
m
m
=
=
2
2
B
B
.
.
m
m
=
=
4
4
C
C
.
.
m
m
=
=
5
5
D
D
.
.
m
m
=
=
3
3
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
v
v
ớ
ớ
i
i
c
c
á
á
c
c
đ
đ
ồ
ồ
t
t
h
h
ị
ị
h
h
à
à
m
m
s
s
ố
ố
; log ; log
x
b c
y a y x y x
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
s
s
a
a
u
u
đ
đ
â
â
y
y
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
c
c
>
>
b
b
>
>
a
a
B
B
.
.
b
b
>
>
a
a
>
>
c
c
C
C
.
.
a
a
>
>
b
b
>
>
c
c
D
D
.
.
b
b
>
>
c
c
>
>
a
a
C
C
â
â
u
u
5
5
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
2
3 3
log log 1
x x x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
l
l
ớ
ớ
n
n
h
h
ơ
ơ
n
n
1
1
,
,
5
5
?
?
A
A
.
.
3
3
B
B
.
.
4
4
C
C
.
.
2
2
D
D
.
.
1
1
C
C
â
â
u
u
6
6
.
.
Đ
Đ
ồ
ồ
t
t
h
h
ị
ị
h
h
à
à
m
m
s
s
ố
ố
y
y
=
=
g
g
(
(
x
x
)
)
đ
đ
ố
ố
i
i
x
x
ứ
ứ
n
n
g
g
v
v
ớ
ớ
i
i
đ
đ
ồ
ồ
t
t
h
h
ị
ị
c
c
ủ
ủ
a
a
h
h
à
à
m
m
s
s
ố
ố
1, 0
x
y a a a
q
q
u
u
a
a
đ
đ
i
i
ể
ể
m
m
I
I
(
(
1
1
;
;
1
1
)
)
.
.
T
T
í
í
n
n
h
h
g
g
i
i
á
á
t
t
r
r
ị
ị
b
b
i
i
ể
ể
u
u
t
t
h
h
ứ
ứ
c
c
1
2 log
2018
a
g
.
.
A
A
.
.
2
2
0
0
1
1
6
6
B
B
.
.
–
–
2
2
0
0
2
2
0
0
C
C
.
.
2
2
0
0
2
2
0
0
D
D
.
.
–
–
2
2
0
0
1
1
6
6
C
C
â
â
u
u
7
7
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
3 2
1
2 3 5
3
2019
x mx m x
f x e
đ
đ
ồ
ồ
n
n
g
g
b
b
i
i
ế
ế
n
n
t
t
r
r
ê
ê
n
n
?
?
A
A
.
.
1
1
0
0
B
B
.
.
4
4
C
C
.
.
1
1
2
2
D
D
.
.
5
5
C
C
â
â
u
u
8
8
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
m
m
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
2
4
x x
f x e e m
c
c
ó
ó
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
h
h
ỏ
ỏ
n
n
h
h
ấ
ấ
t
t
t
t
r
r
ê
ê
n
n
đ
đ
o
o
ạ
ạ
n
n
[
[
0
0
;
;
l
l
n
n
4
4
]
]
b
b
ằ
ằ
n
n
g
g
6
6
.
.
A
A
.
.
3
3
B
B
.
.
4
4
C
C
.
.
1
1
D
D
.
.
2
2
C
C
â
â
u
u
9
9
.
.
C
C
h
h
o
o
d
d
ã
ã
y
y
s
s
ố
ố
n
u
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
18 18
1 1
4 4
5
u u
u u
e e e e
v
v
à
à
1
3
n n
u u
v
v
ớ
ớ
i
i
n
n
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
.
.
G
G
i
i
á
á
t
t
r
r
ị
ị
l
l
ớ
ớ
n
n
n
n
h
h
ấ
ấ
t
t
c
c
ủ
ủ
a
a
n
n
đ
đ
ể
ể
3
log ln 2018
n
u
b
b
ằ
ằ
n
n
g
g
A
A
.
.
1
1
4
4
2
2
0
0
B
B
.
.
1
1
4
4
1
1
9
9
C
C
.
.
1
1
4
4
1
1
7
7
D
D
.
.
1
1
4
4
1
1
8
8
C
C
â
â
u
u
1
1
0
0
.
.
T
T
í
í
n
n
h
h
t
t
ổ
ổ
n
n
g
g
c
c
á
á
c
c
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 5 1
1 1
2 5 1
x x
e e
x x
.
.
A
A
.
.
5
5
B
B
.
.
6
6
C
C
.
.
7
7
D
D
.
.
4
4
13
C
C
â
â
u
u
1
1
1
1
.
.
C
C
h
h
o
o
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
s
s
a
a
u
u
đ
đ
â
â
y
y
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
c
c
>
>
b
b
>
>
a
a
B
B
.
.
b
b
>
>
a
a
>
>
c
c
C
C
.
.
a
a
>
>
b
b
>
>
c
c
D
D
.
.
b
b
>
>
c
c
>
>
a
a
C
C
â
â
u
u
1
1
2
2
.
.
T
T
ì
ì
m
m
g
g
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
h
h
a
a
i
i
đ
đ
ư
ư
ờ
ờ
n
n
g
g
c
c
o
o
n
n
g
g
s
s
a
a
u
u
t
t
i
i
ế
ế
p
p
x
x
ú
ú
c
c
n
n
h
h
a
a
u
u
2
1 2
: 3 3 2 3 ; : 3 1
x x x
C y m m m C y
.
.
A
A
.
.
5 2 10
3
B
B
.
.
5 2 10
3
C
C
.
.
5 2 2
3
D
D
.
.
5 3 2
3
C
C
â
â
u
u
1
1
3
3
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 1 3 2
2
3
8
2 2
log 4 4 4
x x
x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
3
3
B
B
.
.
2
2
C
C
.
.
1
1
D
D
.
.
V
V
ô
ô
n
n
g
g
h
h
i
i
ệ
ệ
m
m
C
C
â
â
u
u
1
1
4
4
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
2 2
sin cos cos 2
3
4 15 9.6 log 1
x x x
m
.
.
A
A
.
.
6
6
9
9
B
B
.
.
9
9
0
0
C
C
.
.
4
4
2
2
D
D
.
.
1
1
1
1
2
2
C
C
â
â
u
u
1
1
5
5
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
ln 6
ln 2
x
y
x m
.
.
G
G
ọ
ọ
i
i
S
S
l
l
à
à
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
c
c
ủ
ủ
a
a
m
m
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
đ
đ
ã
ã
c
c
h
h
o
o
đ
đ
ồ
ồ
n
n
g
g
b
b
i
i
ế
ế
n
n
t
t
r
r
ê
ê
n
n
k
k
h
h
o
o
ả
ả
n
n
g
g
(
(
1
1
;
;
e
e
)
)
.
.
T
T
ì
ì
m
m
s
s
ố
ố
p
p
h
h
ầ
ầ
n
n
t
t
ử
ử
c
c
ủ
ủ
a
a
S
S
.
.
A
A
.
.
1
1
B
B
.
.
2
2
C
C
.
.
4
4
D
D
.
.
3
3
C
C
â
â
u
u
1
1
6
6
.
.
C
C
h
h
o
o
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
3 .3 cos 9
x x
a x
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
a
a
t
t
h
h
u
u
ộ
ộ
c
c
đ
đ
o
o
ạ
ạ
n
n
[
[
–
–
2
2
0
0
1
1
8
8
;
;
2
2
0
0
1
1
8
8
]
]
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ó
ó
đ
đ
ú
ú
n
n
g
g
m
m
ộ
ộ
t
t
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
2
2
0
0
1
1
8
8
C
C
â
â
u
u
1
1
7
7
.
.
C
C
h
h
o
o
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
4 4
6 .6 cos 36
x x
a x
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
t
t
h
h
ự
ự
c
c
a
a
t
t
h
h
u
u
ộ
ộ
c
c
đ
đ
o
o
ạ
ạ
n
n
[
[
–
–
2
2
0
0
1
1
8
8
;
;
2
2
0
0
1
1
8
8
]
]
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
đ
đ
ã
ã
c
c
h
h
o
o
c
c
ó
ó
đ
đ
ú
ú
n
n
g
g
m
m
ộ
ộ
t
t
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
2
2
0
0
1
1
8
8
C
C
â
â
u
u
1
1
8
8
.
.
G
G
ọ
ọ
i
i
S
S
l
l
à
à
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
h
h
ự
ự
c
c
m
m
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
2
ln 2
y x x m
đ
đ
ồ
ồ
n
n
g
g
b
b
i
i
ế
ế
n
n
t
t
r
r
ê
ê
n
n
t
t
ậ
ậ
p
p
x
x
á
á
c
c
đ
đ
ị
ị
n
n
h
h
c
c
ủ
ủ
a
a
n
n
ó
ó
.
.
B
B
i
i
ế
ế
t
t
;
S a b

,
,
t
t
í
í
n
n
h
h
t
t
ổ
ổ
n
n
g
g
K a b
.
.
A
A
.
.
5
K
B
B
.
.
5
K
C
C
.
.
0
K
D
D
.
.
2
K
C
C
â
â
u
u
1
1
9
9
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
2 2
sin cos cos 2
2
2 9 4 log
x x x
m
.
.
A
A
.
.
4
4
0
0
9
9
6
6
B
B
.
.
4
4
0
0
9
9
1
1
C
C
.
.
1
1
3
3
0
0
0
0
D
D
.
.
1
1
2
2
5
5
0
0
C
C
â
â
u
u
2
2
0
0
.
.
C
C
h
h
o
o
h
h
a
a
i
i
s
s
ố
ố
t
t
h
h
ự
ự
c
c
d
d
ư
ư
ơ
ơ
n
n
g
g
x
x
,
,
y
y
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
9 6 4
log log log
x y x y
.
.
K
K
h
h
i
i
đ
đ
ó
ó
2
x a b
y
,
,
a
a
v
v
à
à
b
b
đ
đ
ề
ề
u
u
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
.
.
T
T
í
í
n
n
h
h
a
a
+
+
b
b
.
.
A
A
.
.
a
a
+
+
b
b
=
=
1
1
1
1
B
B
.
.
a
a
+
+
b
b
=
=
4
4
C
C
.
.
a
a
+
+
b
b
=
=
6
6
D
D
.
.
a
a
+
+
b
b
=
=
8
8
C
C
â
â
u
u
2
2
1
1
.
.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
20;20
m
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
2
3 3
1
log 4log 3
y
m x x m
x
x
á
á
c
c
đ
đ
ị
ị
n
n
h
h
v
v
ớ
ớ
i
i
x
x
>
>
0
0
.
.
A
A
.
.
3
3
5
5
B
B
.
.
2
2
0
0
C
C
.
.
1
1
6
6
D
D
.
.
3
3
8
8
_________________________________
14
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 7)
__________________________________________________
Câu 1. Cho hình vẽ bên với các đồ thị hàm số
; ; log
x x
c
y a y b y x
Mệnh đề nào sau đây đúng ?
A
A
.
.
a
a
<
<
b
b
=
=
c
c
B
B
.
.
b
b
>
>
a
a
>
>
c
c
C
C
.
.
a
a
>
>
c
c
>
>
b
b
D
D
.
.
b
b
>
>
c
c
>
>
a
a
C
C
â
â
u
u
2
2
.
.
Hệ phương trình
log log
log 7 log 5
5 7 ,
7 5
x y
x y
có nghiệm duy nhất (x;y). Tính P = 7x – 5y + 1.
A. P = 3 B. P = 2 C. P = 13 D. P = 6
Câu 3. Cho dãy số
n
u
thỏa mãn
3 2
1 1 1
log 2log log 2 0
u u u
và
1
2 10
n n
u u
, n nguyên dương. Tìm
giá trị nhỏ nhất của n sao cho
100
10 10
n
u
.
A. 226 B. 325 C. 225 D. 326
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
log ; log
a b
y x y x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Đ
Đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
x
x
=
=
7
7
c
c
ắ
ắ
t
t
t
t
r
r
ụ
ụ
c
c
h
h
o
o
à
à
n
n
h
h
v
v
à
à
c
c
á
á
c
c
đ
đ
ồ
ồ
t
t
h
h
ị
ị
h
h
à
à
m
m
s
s
ố
ố
log ; log
a b
y x y x
l
l
ầ
ầ
n
n
l
l
ư
ư
ợ
ợ
t
t
t
t
ạ
ạ
i
i
H
H
,
,
M
M
,
,
N
N
.
.
B
B
i
i
ế
ế
t
t
r
r
ằ
ằ
n
n
g
g
2
2
H
H
M
M
=
=
H
H
N
N
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
s
s
a
a
u
u
đ
đ
â
â
y
y
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
a
a
=
=
7
7
b
b
B
B
.
.
2
a b
C
C
.
.
a
a
=
=
2
2
b
b
D
D
.
.
7
a b
C
C
â
â
u
u
5
5
.
.
Hệ phương trình
2
3
2 3 log 5
4
3 5 ,
4 1 3 8.
x x
y
y y y
có hai nghiệm
0 0
;
x y
. Tính
0 0
2 3
x y
.
A. 5 B. 7 C. 6 D. 4
Câu 6. Có bao nhiêu số nguyên m nhỏ hơn 10 để phương trình
x x
m m e e
có nghiệm thực ?
A. 10 B. 9 C. 7 D. 6
Câu 7. Cho dãy số
n
u
thỏa mãn
2
1 1
log log 6 0
u u
và
1
5
n n
u u
, n nguyên dương. Giá trị lớn nhất của
n để
500
n
u
bằng bao nhiêu ?
A. 80 B. 100 C. 99 D. 82
Câu 8. Cho dãy số
n
u
thỏa mãn
3 2
1 1
;
n n
u e u u
, k là số tự nhiên thỏa mãn
765
1 2
...
k
u u u e
. Giá trị của k là
A. 6 B. 7 C. 8 D. 9
C
C
â
â
u
u
9
9
.
.
Tìm điều kiện tham số m để phương trình
2
4 1
log
4 1
x
x
m
có nghiệm.
A. – 1 < m < 1 B. m < 0 C. – 1 < m < 0 D.
1
m
Câu 10. Cho dãy số
n
u
thỏa mãn
5 2 5 2
log 2 log 2 1 log 2log 1
u u u u
và
1
3
n n
u u
, n nguyên
dương. Giá trị lớn nhất của n để
100
7
n
u bằng
A. 192 B. 191 C. 176 D. 177
Câu 11. Có bao nhiêu số nguyên
m
[– 2018;2018] để hàm số
1 ln 2
f x x x m x
đồng biến trên
15
khoảng
2
0;
e
.
A. 2022 B. 2014 C. 2023 D. 2016
Câu 12. Giá trị
,m a b a b
là giá trị nhỏ nhất của tham số m để phương trình sau có nghiệm
3
1
3
2.2 4 3.2 2
x x x
m m
.
Tính giá trị biểu thức
2 7
a b
.
A. 10 B. 15 C. 18 D. 12
C
C
â
â
u
u
1
1
3
3
.
.
C
C
h
h
o
o
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
.5 sin 5 5
x x
a x
;
;
a
a
l
l
à
à
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
h
h
ự
ự
c
c
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
đ
đ
ã
ã
c
c
h
h
o
o
t
t
ồ
ồ
n
n
t
t
ạ
ạ
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
d
d
u
u
y
y
n
n
h
h
ấ
ấ
t
t
0
x
.
.
T
T
í
í
n
n
h
h
0 0 0
sin cos sin
2
x x x
.
.
A
A
.
.
1
1
B
B
.
.
2
2
C
C
.
.
4
4
D
D
.
.
3
3
Câu 14. Phương trình
2 2
3.25 3 10 .5 3
x x
x x
có tổng các nghiệm gần nhất với giá trị nào
A. 8 B. 3 C. 10 D. 12
C
C
â
â
u
u
1
1
5
5
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
2 1
6
f x f x
g e
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
A
A
.
.
3
3
B
B
.
.
6
6
C
C
.
.
4
4
D
D
.
.
5
5
Câu 16. Phương trình
3
4 2
5 125 5
log 3 3 log 4 log 1
x x x m x x
có ba nghiệm thực phân biệt khi
m thuộc khoảng (a;b). Mệnh đề nào sau đây đúng ?
A.
4
ab
B.
1
a b
C.
2 6
b a
D.
2
5
a
b
Câu 17. Tồn tại bao nhiêu số nguyên m < 100 để hệ
2 1 2 1
2
7 7 2012 2012,
( 2) 2 3 0.
x x x
x
x m x m
có nghiệm ?
A. 100 B. 105 C. 102 D. 90
Câu 18. Phương trình
2
3
3 ln( 1) 4 0
2
x
x x
có bao nhiêu nghiệm thực ?
A. 3 B. 2 C. 1 D. 4
Câu 19. Có bao nhiêu số nguyên a thuộc (– 200;200) để phương trình
ln( ) ln( 1)
x x a
e e x a x a
có
nghiệm thực duy nhất.
A. 399 B. 199 C. 200 D. 398
C
C
â
â
u
u
2
2
0
0
.
.
C
C
h
h
o
o
c
c
á
á
c
c
s
s
ố
ố
t
t
h
h
ự
ự
c
c
d
d
ư
ư
ơ
ơ
n
n
g
g
a
a
,
,
b
b
k
k
h
h
á
á
c
c
1
1
.
.
B
B
i
i
ế
ế
t
t
r
r
ằ
ằ
n
n
g
g
b
b
ấ
ấ
t
t
k
k
ỳ
ỳ
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
n
n
à
à
o
o
s
s
o
o
n
n
g
g
s
s
o
o
n
n
g
g
v
v
ớ
ớ
i
i
t
t
r
r
ụ
ụ
c
c
h
h
o
o
à
à
n
n
h
h
m
m
à
à
c
c
ắ
ắ
t
t
c
c
á
á
c
c
đ
đ
ư
ư
ờ
ờ
n
n
g
g
t
t
h
h
ẳ
ẳ
n
n
g
g
;
x x
y a y b
,
,
t
t
r
r
ụ
ụ
c
c
t
t
u
u
n
n
g
g
l
l
ầ
ầ
n
n
l
l
ư
ư
ợ
ợ
t
t
t
t
ạ
ạ
i
i
M
M
,
,
N
N
v
v
à
à
A
A
t
t
h
h
ì
ì
t
t
a
a
l
l
u
u
ô
ô
n
n
c
c
ó
ó
A
A
N
N
=
=
2
2
A
A
M
M
(
(
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
)
)
.
.
M
M
ệ
ệ
n
n
h
h
đ
đ
ề
ề
n
n
à
à
o
o
s
s
a
a
u
u
đ
đ
â
â
y
y
đ
đ
ú
ú
n
n
g
g
?
?
A
A
.
.
2
2
a
a
=
=
b
b
B
B
.
.
2
1
ab
C
C
.
.
2
a b
D
D
.
.
2
2
a
a
b
b
=
=
1
1
_________________________________
16
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 8)
__________________________________________________
Câu 1. Biết rằng a là số thực dương để 9 1,
x
a x x
. Mệnh đề nào sau đây đúng ?
A.
3 4
10 ;10
a
B.
2 3
10 ;10
a
C.
2
0;10
a
D.
4
10 ;a

Câu 2. Có bao nhiêu số nguyên m < 10 để hàm số
2
ln 1
y x mx
đồng biến trên
0;

?
A. 10 B. 11 C. 8 D. 9
Câu 3. Cho dãy số
n
u
thỏa mãn
2018 1 2018 1
log 2017 2018 2log log 2log
u u u u
và
1
1
2
n n
u u
, n là số
nguyên dương. Tìm giá trị lớn nhất của n để
1917
5
n
u
.
A. 232 B. 233 C. 234 D. 235
Câu 4. Tính tổng các nghiệm của phương trình
2
3 3
log 12 log 11
x x x x
.
A. 18 B. 10 C. 12 D. 6
Câu 5. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để phương trình sau có nghiệm
2
2
65.13 4cos 3 3 1
x x
x m
.
A. 10 B. 11 C. 13 D. 12
Câu 6. Gọi a là giá trị nhỏ nhất của hàm số
3 3 3 3 *
log 2 log 3 log 4 ... log
; , 2
9
n
n
f n n n
. Có bao
nhiêu số tự nhiên n để f (n) = a ?
A. 2 B. 4 C. 1 D. Vô số
Câu 7. Biết a là số thực dương sao cho bất đẳng thức
3 6 9
x x x x
a
đúng với mọi số thực x. Mệnh đề nào
sau đây đúng ?
A.
a
(10;12] B.
a
(16;18] C.
a
(14;16] D.
a
(12;14]
Câu 8. Tính tổng các nghiệm của phương trình
7
7 1 6log 6 1
x
x
.
A. 2 B. 3 C. 1 D. 0
Câu 9. Cho hàm số
2
1
ln 1f x
x
thỏa mãn
2 3 ... 2018 ln ln ln ln
f f f a b c d
, trong
đó a, b, c, d là các số nguyên dương tăng dần, a, c, d đều là số nguyên tố. Tính P = a + b + c + d.
A. 1986 B. 1698 C. 1689 D. 1968
Câu 10. Giả sử a, b là các số thực sao cho
3 3 3 2
.10 .10
z z
x y a b
đúng với mọi số thực dương x, y, z thỏa
mãn điều kiện
2 2
log ;log 1
x y z x y z
. Giá trị của a + b là
A. 15,5 B. 14,5 C. – 15,5 D. – 12,5
Câu 11. Tồn tại bao nhiêu giá trị nguyên m để phương trình sau có 4 nghiệm thực phân biệt ?
2 2
3
3
2
6
log 2.6 5 3.6
x x
m m x
.
A. 4 B. 3 C. 1 D. 2
Câu 12. Biết hệ phương trình
2 2
2 2
2 2
log 1 log ,
3 81.
x xy y
x y xy
có hai nghiệm
; ; , ; ;
x y a b c d a c
.
Tính b + 2d.
A. b + 2d = 4 B. b + 2d = 3 C. b + 2d = 2 D. b + 2d = 5
17
Câu 13. Gọi a là số thực lớn nhất sao cho
2 2
2 ln 1 0,x x a x x x
. Mệnh đề nào đúng ?
A.
a
(2;3] B.
a
8;

C.
a
(6;7] D.
a
(– 6;– 5]
Câu 14. Tìm điều kiện tham số m để hàm số
2
ln 1 ln
y x x m x
đồng biến trên khoảng (0;4).
A.
2
1
3
m B.
2
1
3
m
C.
28
13
m
D.
0
m
Câu 15. Tìm điều kiện tham số m để hàm số
2
2018
log 2018
2
x
x
y x m
xác định với mọi x không âm.
A. m > 9 B. m < 1 C. 0 < m < 1 D. m < 2
Câu 16. Có bao nhiêu số nguyên m để phương trình sau có hai nghiệm phân biệt
1 2
,
x x
với tổng bình phương
các nghiệm bằng 3:
2 2 2 2
2 5
5 2
log 2 4 2 log 2 0
x x m m x mx m
.
A. 1 B. 0 C. 3 D. 2
Câu 17. Cho dãy số
n
u
thỏa mãn
1 1 10 10
log 2 log 2log 2 log
u u u u
và
1
2
n n
u u
, n nguyên dương.
Giá trị lớn nhất của n để
100
5
n
u
bằng
A. 248 B. 246 C. 247 D. 290
Câu 18. Tìm điều kiện tham số m để phương trình
4 2 4 3 2 1
x x m x
có hai nghiệm phân biệt.
A.
3
1 log 4
m
B.
3
1 log 4
m
C.
4
log 3 1
m
D.
4
log 3 2
m
Câu 19. Có bao nhiêu số nguyên dương khác 1 của m để phương trình sau có nghiệm x lớn hơn 2
2 2 2
2 5
log 1 .log 1 log 1
m
x x x x x x
A. Vô số B. 3 C. 2 D. 1
Câu 20. Biết rằng a là số thực dương để
2018 1,
x
a x x
. Hỏi log(a) gần nhất với giá trị nào ?
A. 2018 B. 876 C. 1010 D. 502
Câu 21. Tập hợp
;
S a b
bao gồm tất cả các giá trị m để phương trình sau có nghiệm thực
sin 4 cos 2 3sin cos 5
4 cos 3 sin 2 5
m x x m x m x
e e m x m x m
Tính
20
a b
.
A. 4 B. 2 C. 5 D. 3
Câu 22. Tìm điều kiện tham số m để hàm số
2
2
log 2
log
m
y x
x m
đồng biến trên đoạn
1
;100
10
.
A.
3
2
m
B.
1
2
m
m
C.
2
m
D.
2
m
Câu 23. Tính tích các nghiệm của phương trình
2 2
3 2
log 2 1 log 2
x x x x
.
A. – 2 B. 1 C. – 1 D. 4
Câu 24. Cho dãy số
n
u
có số hạng đầu
1
1
u
và thỏa mãn
2 2 2 2
2 1 2 2 2 2
log 5 log 7 log 5 log 7
u u
.Biết
1
7
n n
u u
với
1
n
. Giá trị nhỏ nhất của n để
1111111
n
u
bằng
A. 11 B. 8 C. 9 D. 10
Câu 25. Có bao nhiêu số nguyên m lớn hơn – 40 để hàm số
2
2
log 2
log 1
m x
y
x m
nghịch biến với mọi x > 4 ?
A. 37 B. 20 C. 16 D. 32
_________________________________
18
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 9)
__________________________________________________
Câu 1. Giả sử a là số thực dương sao cho
4.5 2 20 15 ,
x x x x
a x
. Khi đó số nghiệm thực của
phương trình
3
2018
x x a
là
A. 3 B. 2 C. 1 D. Vô số
Câu 2. Cho hàm số
2
1 2
log
2 1
x
f x
x
. Ký hiệu
1 2 3 2016
...
2017 2017 2017 2017
M f f f f
.
Biết rằng M là một số tự nhiên, hỏi M có bao nhiêu ước nguyên dương ?
A. 10 B. 12 C. 8 D. 30
Câu 3. Có bao nhiêu số nguyên m để phương trình
2
2
2
3
2
1
log 8 7
x
x m
x
có nghiệm ?
A. 6 B. 3 C. 2 D. 2
Câu 4. Tồn tại bao nhiêu số nguyên m để hàm số
2
4
log 3 5
m
y mx m
xác định với mọi
3
2
x
?
A. 5 B. 4 C. 3 D. 2
Câu 5. Giả sử a là số thực dương để
4
2 10 39,
x
a x x
. Giá trị log(a) gần nhất với
A. 4,3 B. 6,1 C. 3,2 D. 2,5
Câu 6. Trong tất cả các cặp số (x;y) thỏa mãn
2 2
2
log 4 4 4 1
x y
x y
. Tìm giá trị của tham số m thỏa mãn
đẳng thức
2 2
2 2 2 0
x y x y m
.
A. m = 4 B. m =
10 2
C. m =
7 1
D.
10 2
m
Câu 7. Có bao nhiêu số nguyên m nhỏ hơn 8 để phương trình sau có nghiệm duy nhất
2
3 2 2 3 2 2
log 1 log 0
x m mx x
.
A. 5 B. 4 C. 6 D. 7
Câu 8. Tính tổng các nghiệm của phương trình
2
3
2
2 1
log 3 8 5
3 1
x
x x
x
.
A. 4 B.
8
3
C.
11
7
D.
2
3
Câu 9. Biết rằng phương trình
2
2 2
1
2
2
4 log 2 3 2 log 2 2 0
x m x m
x x
x x
có nghiệm khi và chỉ khi m > a
hoặc m < b. Tính a + b.
A. a + b = 2 B. a + b = 4 C. a + b = 5 D. a + b = 2,5
Câu 10. Phương trình
2
2
1 1
2 2
1
1 log 2 4 5 log 4 4 0
2
m x m m
x
có nghiệm thực trong đoạn
5
;4
4
khi m thuộc đoạn [p;q]. Tính p + 3q.
A. p + 3q = 5 B. p + 3q = 4 C. p + 3q = 8 D. p + 3q = 10
Câu 11. Tìm tất cả các giá trị của tham số m để phương trình
2 1
x
mx
có hai nghiệm phân biệt.
A.
0 ln 2
m
B. Mọi giá trị m C.
ln 2
m
D. 0 < m < ln2
Câu 12. Tìm điều kiện tham số m để hàm số
2
2 .
x
f x mx x e
đồng biến trên khoảng (1;2).
A.
5
8
m
B.
4
3
m
C.
5
8
m
D.
4
3
m
19
Câu 13. Hệ phương trình
2 2
2
2
3 2
2017
2016 ,
2017
3log 2 6 2 log 2 1.
y x
x
y
x y x y
có bao nhiêu nghiệm thực
A. 3 B. 2 C. 1 D. 0
Câu 14. Tìm số nghiệm nguyên của bất phương trình
2 2
2 15 100 10 50 2
2 2 25 150 0
x x x x
x x
.
A. 6 B. 4 C. 5 D. 3
Câu 15. Phương trình
2
2
7
4 4 1
log 4 1 6
2
x x
x x
x
có hai nghiệm
1 2
,
x x
thỏa mãn
1 2
1
2
4
x x a b
, trong
đó a và b là hai số nguyên dương. Tính a + b.
A. 16 B. 11 C. 14 D. 13
Câu 16. Có bao nhiêu giá trị nguyên m để phương trình
1 1 2 2
4 4 1 2 2 16 8
x x x x
m m
có nghiệm
thuộc đoạn [0;1].
A. 2 B. 5 C. 4 D. 3
Câu 17. Cho hai số thực a, b thỏa mãn
2017 2 2018
ln 1 sin 2
f x a x x bx x
. Biết
log 6
5 6
c
f
, tính giá
trị của biểu thức
log 5
6
c
P f với
0 1
c
.
A. P = – 2 B. P = 6 C. P = 4 D. P = 2
Câu 18. Phương trình
2 1 1 3 1 1
2 0, 25 1 0,5 2 2 1
x x
x x
có tổng các nghiệm bằng
A. 4 B. 8 C. 3 D. 6
Câu 19. Giả sử có hệ thức
2 2
11
a b ab
(a và b là hai số dương khác nhau). Khẳng định nào sau đây đúng ?
A.
2 2 2
2log log log
3
a b
a b
B.
2 2 2
1
log log log
2 3
a b
a b
C.
2 2 2
2log log log
3
a b
a b
D.
2 2 2
2 log log log
a b a b
Câu 20. Cho các số thực x, y, z thỏa mãn
2017
3 5 15
z
x y
x y
. Ký hiệu S = xy + yz + xz. Chọn mệnh đề đúng
A. 1 < S < 2016 B. 0 < S < 2017 C. 2016 < S < 2017 D. 0 < S < 2018
Câu 21. Có bao nhiêu số nguyên âm m để phương trình
3 2
log 3 8 14 log 1
x x x m x
có hai nghiệm
phân biệt ?
A. 1 B. 0 C. 2 D. 3
Câu 22. Có bao nhiêu số nguyên m để bất đẳng thức
2 2
ln 5 ln 1 ln 4
x mx x m
đúng với mọi m ?
A. 3 B. 4 C. 1 D. 2
Câu 23. Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình sau nghiệm đúng với mọi x thuộc
khoảng (2;4):
2 2 3 2
4 2
log 1 log 2 0
x m x m m m
.
A. 0 B. 2 C. 1 D. 3
Câu 24. Tính tích tất cả các nghiệm của phương trình
2 2
1 3 3
2
2 1 3 2 2 3 1
x x x x
x x
.
A. – 3 B. – 1 C. 2 D. 4
Câu 25. Tìm tất cả các giá trị thực của m để hàm số
2
1
log
2
x
y m x
đồng biến trên nửa khoảng (0;2].
A.
ln 2
m
e
B.
2ln 2
m
e
C.
ln 2
m
e
D.
2ln 2
m
e
20
______________________
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 10)
__________________________________________________
Câu 1. Có bao nhiêu số nguyên m lớn hơn – 12 để hàm số
2
2 5
log 2sin 3cos
m m
y x x m
xác định với
mọi x ?
A. 7 B. 8 C. 6 D. 5
Câu 2. Cho hàm số
sin
x
y e x
. Lựa chọn mệnh đề đúng
A.
2 2 0
y y y
B.
2 0
y y y
C.
2 2 0
y y y
D.
3 0
y y y
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình
3
3
3 27 3 27.2 2
x x
m m
có nghiệm thực ?
A. Vô số B. 4 C. 8 D. 6
Câu 4. Tồn tại giá trị
0
m m
để phương trình
2 2
1 log 4 2 log
m x m x m
có nghiệm duy nhất.
Mệnh đề nào sau đây đúng ?
A.
0
m
[3;5] B.
0
m
[6;9] C.
0
m
(0;3) D.
0
10
m
Câu 5. Tồn tại duy nhất giá trị m = a để phương trình
2
2 3
log 2 1 1 log 4 4
x m m x x
có nghiệm
duy nhất. Giá trị a thuộc khoảng nào sau đây ?
A. (0;4) B. (4;6) C. (6;9) D. (9;14)
Câu 6. Tính tổng các số tự nhiên m để phương trình
2
3 3
log 3 log (3 ) 2 2 1 0
x m x m m
có hai nghiệm phân
biệt mà tổng hai nghiệm không nhỏ hơn
10
3
.
A. 6 B. 1 C. 0 D. 10
Câu 7. Tồn tại bao nhiêu số nguyên m thuộc khoảng (– 10;10) để hàm số
2
2 6
ln
10 sin 2 3cos 2
mx mx m
y
x x
xác định
với mọi x.
A. 15 B. 8 C. 9 D. 10
Câu 8. Cho hàm số
4
2
x x
y e e
. Tính
13 5
y y y
theo y.
A. 6y B. 5y C. 7y D. 8y
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình
2
3 3
log 4 log 3 0
x x m
có hai nghiệm phân biệt
1 2
x x
thỏa mãn điều kiện
2 1
81
x x
.
A. 4 B. 5 C. 3 D. 6
Câu 10. Tồn tại bao nhiêu số nguyên a < 50 để bất phương trình
2
60 10 2
x x x x
a
nghiệm đúng với mọi số
thực x ?
A. 46 B. 49 C. 30 D. 27
Câu 11. Tồn tại bao nhiêu số nguyên m thuộc [– 2020;2020] để bất phương trình sau nghiệm đúng với mọi x
thuộc [0;4]:
2
2
2
2
2
log 4 3
1
x x m
x x m
x x
.
A. 2023 B. 1 C. 2 D. 2012
Câu 12. Hàm số y = f (x) thỏa mãn
( ) 2
2019 2019
f x
x x . Có tất cả bao nhiêu giá trị nguyên m thỏa mãn
điều kiện
(log ) (log 2019)
m
f m f
?
A. 66 B. 65 C. 63 D. 64
21
Câu 13. Hàm số
2018
1
logy
x
có đồ thị (H), hàm số y = f (x) có đồ thị (H’). Hai đồ thị trên đối xứng nhau gốc tọa
độ. Khi đó hàm số
( )
y f x
nghịch biến trên khoảng
A.
( ; 1)

B. (– 1;0) C. (0;1) D.
(1; )

Câu 14. Kết quả đạo hàm cấp 2018 của hàm số
10 20
( )
x
f x e
là
A. 200
( )
f x
B. 10!
( )
f x
C. 10
2018
20
1009
( )
f x
D. 10
2018
( )
f x
Câu 15. Có tất cả bao nhiêu số nguyên dương m để phương trình
2
2 2
(4 log log 5) 4 0
x
x x m
có đúng
hai nghiệm phân biệt ?
A. 14 B. 15 C. Vô số D. 16
Câu 16. Tiếp tuyến của đồ thị của hàm số
x
y x
tại điểm có hoành độ bằng 2 cắt trục tung tại điểm M. Tung độ
điểm M gần nhất giá trị nào ?
A. – 9,54 B. – 10,51 C. – 7,56 D. – 2,75
Câu 17. Có bao nhiêu số nguyên m > – 20 để phương trình
2
3 3
log ( 4) ( 5)log ( 4) 2 1 0
x m x m
có hai
nghiệm phân biệt a, b thỏa mãn
4( ) 65
ab a b
.
A. 10 B. 12 C. 20 D. 21
Câu 18. Tổng các nghiệm phương trình
1
5 .8 500
x
x
x
gần nhất với giá trị nào ?
A. 2,56 B. 2,89 C. 3,54 D. 4,23
Câu 19. Có bao nhiêu số nguyên dương m để phương trình
1
5 .8
x
x
x
m
có tổng các nghiệm lớn hơn
1
2020
?
A. 8 B. 7 C. 6 D. 10
Câu 20. Tồn tại bao nhiêu số nguyên m để phương trình
2
2 2
2 2
log ( .4 9) 2 3 log 3
x x
m x x
có hai
nghiệm phân biệt ?
A. 12 B. 11 C. 4 D. 13
Câu 21. Cho hàm số
3
( ) 2
m
f x x x
. Tồn tại bao nhiêu số nguyên m để phương trình
( ( ))
f f x x
có
nghiệm trên [1;2].
A. 0 B. 4 C. 2 D. 3
Câu 22. Tồn tại bao nhiêu giá trị nguyên dương m để phương trình
2 1
3 .5
x
x
x
m
có hai nghiệm phân biệt a, b
thỏa mãn điều kiện
ln( ) 3
a b ab
.
A. 5 B. 6 C. 18 D. 10
Câu 23. Tồn tại bao nhiêu số nguyên m để hàm số
16
3
8 4 2020
mx
x m
y e x
nghịch biến trên
(2; )

?
A. 7 B. 6 C. 5 D. 9
Câu 24. Tồn tại bao nhiêu số nguyên m thuộc [– 100;100] để phương trình sau có đúng hai nghiệm phân biệt
2
2 2
(log 3log 2) 9 ( 1).3 0
x x
x x m m
.
A. 103 B. 102 C. 101 D. 100
Câu 25. Tìm điều kiện tham số m để bất phương trình sau có nghiệm
2 2
3 3
2log (sin ) 4log sin 2sin cos 2 2 1 0
x m x x x m
.
A.
2; 2
m
B.
1
4
m
C. Không tồn tại m. D. m = 0
_________________________________
| 1/21
| | Tải xuống

Có thể bạn quan tâm:

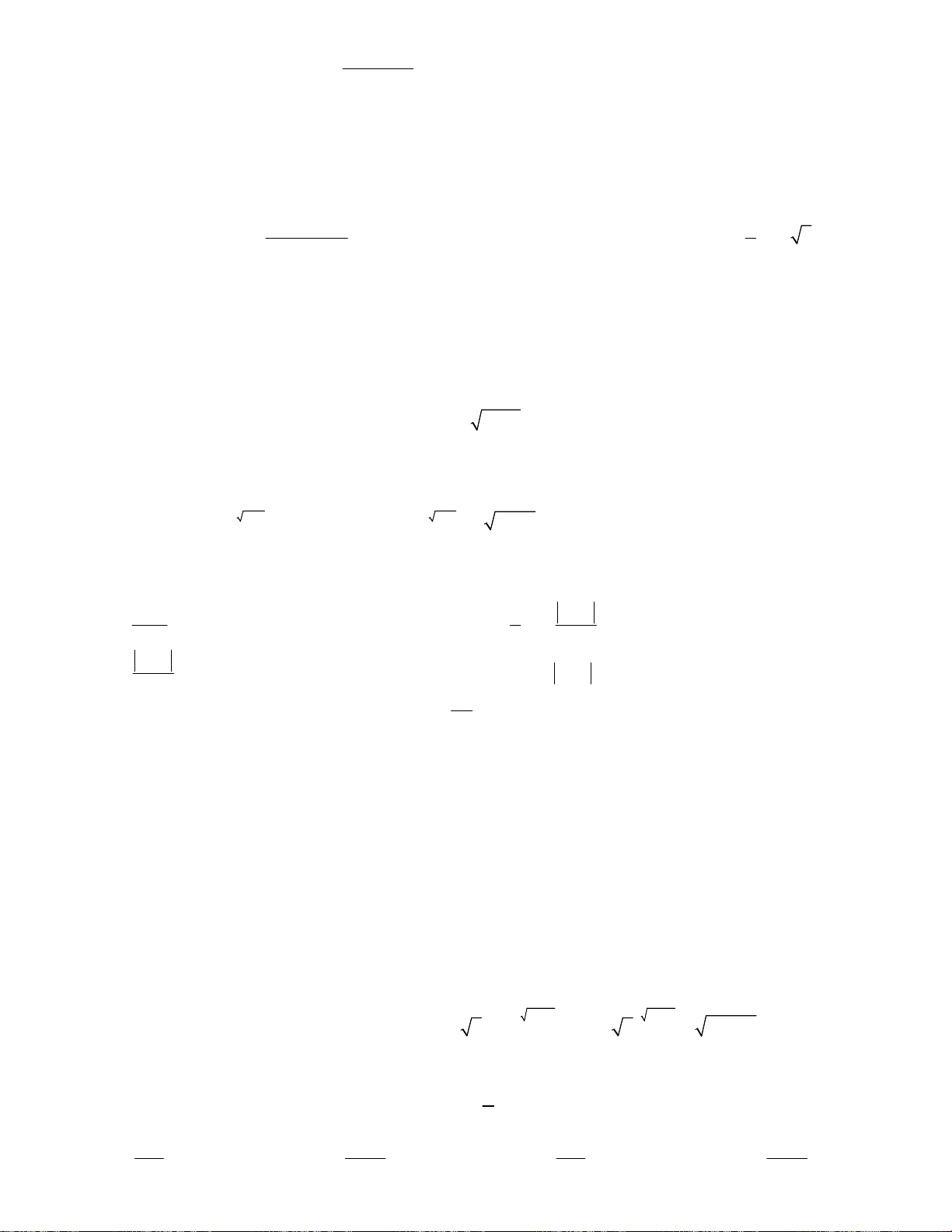
Preview text:


THÂN TẶNG QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TOÀN QUỐC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, LOGARIT LỚP 12 THPT LỚP BÀI TOÁN PT, BPT, HPT PHẦN 1 – 10 CREATED BY GIANG SƠN TP.THÁI BÌNH; THÁNG 4/2020
_____________________________________________________________________________________________________________ x e  x 1, x   0 1
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 1)
__________________________________________________ Câu 1. Phương trình 2 2 2 x 3x2 x 6 x5 2 x 3x7 4  4  4
1có bốn nghiệm phân biệt a,b,c,d theo thứ tự tăng dần.
Tính giá trị biểu thức a  2b  3c  4d . A. 10 B. 3 C. 4 D. 5
Câu 2. Tồn tại bao nhiêu giá trị nguyên m nhỏ hơn 10 để phương trình sau có ba nghiệm phân biệt x 2 x 1 m     2 m  m   x 2 27 .3 2 5 .3  m  5m . A. 6 B. 5 C. 4 D. 7
Câu 3. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có ba nghiệm phân biệt x x  m   2 m  m   x 2 125 4 .25 4 5 .5  2m 10m  0 . A. 6 B. 5 C. 3 D. 7
Câu 4. Phương trình log  2 x  x   2
1  log x  2x  x có bao nhiêu nghiệm thực ? 3 3 A. 2 B. 1 C. 3 D. 4
Câu 5. Tồn tại bao nhiêu số nguyên m nhỏ hơn 10 để phương trình có hai nghiệm phân biệt ? 12x  3.6x     1 .2x m  3m  3  0 . A. 4 B. 10 C. 6 D. 7
Câu 6. Tìm tất cả các giá trị m để phương trình 6x    3.2x m
 m  0 có nghiệm thuộc khoảng (0;1). A. (– 4;– 2) B. [– 4;– 3] C. [– 4;– 2] D. (– 4;– 1) Câu 7. Phương trình 2x 1  x 1 3 3  
3x 7  2  x có một phương trình hệ quả là A. 3x  3x  6 B. 3x  4x  7 C. 3x  2x  5 D. 3x  3 x x x 1 1 1
Câu 8. Phương trình 3  4  5   
có bao nhiêu nghiệm thực ? 2x 3x 4x A. 2 B. 1 C. 3 D. 4
Câu 9. Phương trình log sin x  log sin x có bao nhiêu nghiệm thực trong khoảng (– 5;5) ? 3   2   A. 2 B. 1 C. 4 D. 3
Câu 10. Phương trình  x  2 2
log x 1  4 x 1 log x 1  16 có tổng các nghiệm bằng 3     3   82 11 A. 1 B. C. 2 D. 81 81
Câu 11. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có ba nghiệm phân biệt x x 
  2    x   2 27 5 .18 6 2 .12 3  6 .8x m m m m m  0 . A. 6 B. 5 C. 0 D. 7
Câu 12. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có ba nghiệm phân biệt x x  m   2 m  m   x 2 2.8 5 .4 2 6 2  m  6m . A. 6 B. 5 C. 3 D. 7 2 x  x 1 Câu 13. Phương trình 2 log
 x  3x  2 có bao nhiêu nghiệm thực ? 2 2 2x  4x  3 A. 3 B. 1 C. 4 D. 2 Câu 14. Phương trình x  x 3 2
3  3  8  x có bao nhiêu nghiệm thực ? A. 3 B. 2 C. 4 D. 1 2 3 2 x  3x  3x  5
Câu 15. Tính tổng tất cả các nghiệm của phương trình log  x  3 2 1  x  6x  7 là 2 x 1 A. 0 B. – 2 C. 2  3 D. 2  3 3 3 3
Câu 16. Tổng các nghiệm thực x của phương trình 4x 2 2x 4 4x 2x       6 là A. 2,5 B. 1,75 C. 3,5 D. 1,5 Câu 17. Phương trình x  x 3 2 2
3.2019  3.2019  8  x  4 1 x có bao nhiêu nghiệm thực ? A. 3 B. 2 C. 4 D. 1
Câu 18. Cho phương trình log m  6x  log  2
3  2x  x  0 , m là tham số. Có bao nhiêu giá trị nguyên 0,5 2 
dương của m để phương trình có nghiệm thực. A. 15 B. 18 C. 13 D. 17
Câu 19. Tìm tất cả các giá trị thực của tham số m để phương trình 2
4log x  2log x  3  m  0 có nghiệm 2 2 1  thuộc đoạn ;4  . 2    11  11  A. [2;3] B. [2;6] C. ;15  D. ;9 4     4   
Câu 20. Tìm điều kiện tham số m để bất phương trình x x  x 12  mlog 3 có nghiệm. 5 4x A. m  2 3 B.m  12log 5 C. 2  m  12log 5 D. m  2 3 3 3
Câu 21. Tìm điều kiện m để phương trình log  2
1 x  log x  m  4  0 có hai nghiệm thực phân biệt. 3  1   3 21 1 21 1 A. 5  m  B.   m  2 C. 5  m  D.   m  0 4 4 4 4
Câu 22. Tìm tập hợp tất cả các giá trị tham số m để bất phương trình log  2
x  3x  m  log x 1 có tập 3  1   3
nghiệm chứa khoảng 1; . A. 3; B. 2; C.  ;  0 D. ;  1
Câu 23. Tìm điều kiện tham số m để phương trình log 4x  3  log x 1  m có nghiệm. 2   2   A. m  4 B. 2  m  3 C. 0  m  2 D. m  2 Câu 24. Phương trình 2
log x  3log x  2m  7  0 có hai nghiệm thực thỏa mãn  x  3 x  3  72 . Giá trị 1  2  3 3
tham số m thu được thuộc khoảng nào sau đây ?  7   7   21  7  A. 0;   B.  ;0   C. 7;   D. ;7    2   2   2   2 
Câu 25. Tồn tại bao nhiêu giá trị nguyên m nhỏ hơn 12 để phương trình sau có ba nghiệm phân biệt x x 
  2    x   2   3 27 4 .36 3 5 .48 5 .4 x m m m m m  0 . A. 6 B. 5 C. 4 D. 7
Câu 26. Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình 2x  2  .4x  8x m  0 có nghiệm thuộc khoảng (0;1).  7   7   7   7  A. 2;  B. 1; C. 1;   D. 2;   2     2    2   2 
Câu 27. Có bao nhiêu giá trị nguyên m để phương trình x x 1  2 4  . m 2
 2m  5 có hai nghiệm thực ? A. 1 B. 5 C. 2 D. 4
_________________________________ 3
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 2)
__________________________________________________
Câu 1. Phương trình 2log cot x  log cos x có bao nhiêu nghiệm dương nhỏ hơn 20 ? 3   2   A. 5 B. 6 C. 3 D. 4
Câu 2. Tồn tại bao nhiêu giá trị nguyên dương nhỏ hơn 10 của m để phương trình sau có nghiệm thực x  x 2
3  3  x  2x  m  5 . A. 6 B. 7 C. 9 D. 8 2 
Câu 3. Tập hợp [a;b] gồm tất cả các giá trị m để phương trình sin x  
 x  x  m có nghiệm. Tính giá 2 trị biểu thức 2 a  4b . A. 6,5 B. 7 C. 8,5 D. 5,25
Câu 4. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình có hai nghiệm thực phân biệt. log  x   1  log x  log 2x  7x  m . 2  2 2 2  A. 4 giá trị B. 3 giá trị C. 10 giá trị D. 8 giá trị.
Câu 5. Có bao nhiêu số nguyên m nhỏ hơn 10 để phương trình x   2 m  m   x 3 2 4 4
5 2  5m  5m  25m  0 có
hai nghiệm phân biệt đều lớn hơn 2 ? A. 6 B. 8 C. 7 D. 9 Câu 6. Phương trình log  3 x x
 log x có bao nhiêu nghiệm thực ? 2  log6  6 A. 2 B. 1 C. 4 D. 3
Câu 7. Tồn tại bao nhiêu giá trị nguyên của tham số m để hệ phương trình sau có nghiệm 2 log 2x  y   1  m  4 2 log x  m  4  0 2 2  2 x y 1  3x2 y e  e  x  y 1 A. 3 B. 4 C. 5 D. 6 Câu 8. Phương trình 2 2 x 5x6 1x 65 2  2
 2.2 x 1có bao nhiêu nghiệm dương ? A. 2 B. 1 C. 3 D. 4
Câu 9. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực.
2log cos x  sin x  6  log
3sin x  2cos x  m 1 . 7     7 A. 4 giá trị B. 9 giá trị C. 10 giá trị D. 8 giá trị. 2 x  x Câu 10. Phương trình 2 2cos
 2x  2x có bao nhiêu nghiệm không âm ? 6 A. 3 B. 1 C. 2 D. 4  5x  3x 
Câu 11. Tính tổng tất cả các nghiệm của phương trình x 1 ln
 5   5.3x  30x 10  0   . 6x  2   A. 1 B. 2 C. – 1 D. 3 9
Câu 12. Bất phương trình  2x  x     2 log 2
log x  2x  3 có nghiệm x  . Giả sử S   p;q là tập a a  4
nghiệm của bất phương trình đã cho. Tìm p  2q  5 . A. 14 B. 12 C. 13 D. 10
Câu 13. Ký hiệuS  a;b là tập hợp tất cả các giá trị m để phương trình log  x 3
9  9m  x có hai nghiệm thực 3 
phân biệt. Tính giá trị của biểu thức 3 a  72b . 4 A. 4 B. 2 C. 1 D. 5
Câu 14. Có bao nhiêu số nguyên m để phương trình 3 3 3  27 3  27.2x  2x m m có nghiệm thực ? A. Vô số B. 4 C. 8 D. 6
Câu 15. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
ln m  2sin x  lnm  3sin x  sin x . A. 3 B. 4 C. 5 D. 6
Câu 16. Cho phương trình mcos xsin x 21sin x e  e
 2  sin x  mcos x với m là tham số thực. Gọi S là tập hợp tất
cả các giá trị của m để phương trình có nghiệm. Khi đó S có dạng ;a ;
b  , tính T  10a  20b . A. 1 B. 0 C. 10 3 D. 3 10
Câu 17. Phương trình sau có nghiệm thực khi m thuộc đoạn [a;b]. Tính 8a 16b . sin xcos xm sin 2 x3m 1 e e  
 sin 2x  sin x  cos x  4m 1. A. 10 B. 9  2 2 C. 10  3 2 D. 4 2
Câu 18. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để bất phương trình sau nghiệm đúng với mọi giá trị x sin x4 cos xm e  e
 cos x  sin x  m  4 . A. 13 B. 14 C. 15 D. 12
Câu 19. Có bao nhiêu giá trị nguyên m  1
 5;15 để phương trình 3x  m  log x  m có nghiệm ? 3   A. 16 B. 9 C. 14 D. 15
Câu 20. Tìm số nghiệm của phương trình x  x   x  x   2x x  x  x   2 2 2 3 6 2 x x3 2 2 9 3 .8 3 6 .8 . A. 1 B. 3 C. 2 D. 4
Câu 21. Có bao nhiêu giá trị nguyên m  2
 5;25 để phương trình 7x  m  log x  m có nghiệm ? 7   A. 25 B. 9 C. 24 D. 26
Câu 22. Phương trình log 2  log 4x  3 có tổng các nghiệm bằng 2 2 x A. 5 B. 6 C. 3 D. 4
Câu 23. Tồn tại bao nhiêu số nguyên m  3
 0;30 để phương trình x  x    x  m2 4 4 4 có nghiệm A. 2 B. 1 C. 4 D. 3
Câu 24. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực 2 2 2 sin x cos x cos 5  6  7 x log m . 2 A. 62 B. 63 C. 64 D. 6
Câu 25. Có bao nhiêu giá trị nguyên dương m để bất phương trình 2 2 2 cos x sin x sin 3  2  .3 x m có nghiệm. A. 1 B. 3 C. 2 D. 4 Câu 26. Cho phương trình .4x sin 4 4x a x   
; a là tham số thực. Tồn tại duy nhất giá trị a  a để phương 0
trình đã cho có nghiệm thực duy nhất. Tính giá trị của log a . 2 0 A.  B.  1 C. 2 D. 2 1
Câu 27. Cho phương trình 6x  .6x a
cos x 1296 . Tồn tại duy nhất một giá trị a để phương trình đã cho có
nghiệm duy nhất x . Nghiệm x nằm trong khoảng nào ? 0 0 A. (1;2) B. (1;4) C. (4;7) D. (3;5)
_________________________________ 5
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 3)
__________________________________________________
Câu 1. Biết tập hợp tất cả các giá trị của tham số m để bất phương trình 2 2 2 sin x cos x cos 4  5  .7 x m có nghiệm là a  a nửa khoảng ; 
 với a, b nguyên dương và phân số tối giản. Tính giá trị của S  a  b . b  b A. S  13 B. S  15 C. S  9 D. S  11
Câu 2. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực 2 2 sin x cos x cos 2 3 13  8.7 x log m . 3 A. 18 B. 14 C. 45 D. 60
Câu 3. Tồn tại bao nhiêu giá trị nguyên m để phương trình 3 3  3  3.4x  4x m m có nghiệm thực ? A. Vô số B. 4 C. 8 D. 6
Câu 4. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình sau có nghiệm thực x x m  m  e  e . A. 10 B. 9 C. 7 D. 6
Câu 5. Cho phương trình ẩn x: 4x 4 6  .6 x a
cos x  36 . Tồn tại bao nhiêu giá trị thực của tham số a thuộc
đoạn [– 2018;2018] để phương trình đã cho có đúng một nghiệm thực ? A. 2 B. 3 C. 1 D. 2018
Câu 6. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực 2 sin x  2 2 2 ln
 sin x  cos x  m 1  0 . 2 m  3  cos x A. 7 B. 6 C. 5 D. 3
Câu 7. Tồn tại duy nhất một giá trị thực của m để phương trình 9x  2 .6x  .4x m m
 0 có hai nghiệm thực phân
biệt x , x có tổng bằng 2. Giá trị tham số m thu được nằm trong khoảng nào ? 1 2 17 5   8 17  11  A. (2;3) B. ;   C. ;   D. ;2   16 4   9 16   8 
Câu 8. Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình 3x  4x  2  .5x m  0 có nghiệm
thực thuộc khoảng (0;2). A. [3;4] B. [2;4] C. (2;4) D. (3;4)
Câu 9. Tồn tại bao nhiêu giá trị nguyên lớn hơn 5 của tham số m để phương trình sau có nghiệm thực sin x  cos x  2 ln
 sin 2x  m  6  sin x  cos x . sin 2x  m  4 A. 2 B. 6 C. 5 D. 3
Câu 10. Tìm số nghiệm của phương trình x  x   x  x   x   x   2 2 2 3 5 x 8x3 5 2 8 3 .8 3 5 .8 . A. 4 B. 3 C. 1 D. 2
Câu 11. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực  x  x  m5   x  x  m5   x  x  m5 sin 3cos 2cos sin 2 2sin cos . A. 4 B. 6 C. 5 D. 7 Câu 12. Phương trình 2 3 3x  2x  log  2
x 1  log x có bao nhiêu nghiệm thực ? 2  2 6 A. 3 B. 1 C. 4 D. 2 Câu 12. Phương trình 2
log x  m  2 log x  3m 1  0 có hai nghiệm thực có tích bằng 27. Mệnh đề nào 3   3 dưới đây đúng ? A. m  2  ;  1 B. m 0;2 C. Không tồn tại m. D. m  2;4 x x x 1 2 3
Câu 13. Phương trình 5.3  3.4  3.5   
có bao nhiêu nghiệm thực ? 20x 30x 40x A. 2 B. 1 C. 3 D. 4
Câu 14. Tìm tập hợp tất cả các giá trị m để phương trình 3x  .2x m
 m  2  0 có nghiệm thuộc khoảng (0;2).  1 7   1 7   1 7  1 7  A.  ;   B.  ; C. ;   D. ;  2 5   2 5    3 5  3 5  
Câu 15. Gọi S là tập hợp các giá trị tham số m để phương trình sau có ba nghiệm phân biệt log
mx  6x  2log 14x  29x  2  0 2  3   2 1  2
Số các giá trị nguyên của S là A. 20 B. 30 C. 0 D. Vô số
Câu 16. Tìm điều kiện m để phương trình log  2
1 x  log x  m  4  0 có hai nghiệm thực phân biệt. 3  1   3 21 1 21 1 A. 5  m  B.   m  2 C. 5  m  D.   m  0 4 4 4 4 Câu 17. Phương trình 2 x3 x 5 x6 2  3
có hai nghiệm x , x x  x . Lựa chọn phát biểu đúng 1 2  1 2  A. 3x  2x  log 8 B. 2x  3x  log 8 1 2 3 1 2 3 C. 2x  3x  log 54 D. 3x  2x  log 54 1 2 3 1 2 3
Câu 18. Tìm tất cả các giá trị m để bất phương trình 2
log 2x  2 m 1 log x  2  0 có nghiệm thuộc khoảng 2   2  2;.  3   3  A.  ;  0 B.  ;0   C.  ;   D. 0;  4   4 
Câu 19. Tìm tập hợp giá trị m để phương trình 4log x 2  log x  m  0 có nghiệm thuộc khoảng (0;1). 2 1 2  1  1   1  A. 0;  B. ;   C.  ;   D.  ;  0 4   4  4  
Câu 20. Tồn tại bao nhiêu số nguyên của tham số m lớn hơn – 5 để phương trình sau có nghiệm duy nhất  x x 5   1  . 5   1  2x m A. 0 B. 5 C. 2 D. 3
Câu 21. Tìm tập hợp tất cả các giá trị thực m để phương trình có nghiệm thuộc nửa khoảng 1; .
log 5x 1 log 2.5x  2  m . 2   4  1  A. 1; B. 6; C. 3; D. ;    4 
Câu 22. Tìm tập hợp giá trị m để phương trình 6x  2  .3x m
 m  0 có nghiệm thực thuộc khoảng (0;1).  3 27   3  3 27   3  A. ;   B. ;3   C. ; D. ;3  2 5   2  2 5     2   
________________________________ 7
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 4)
__________________________________________________ 
Câu 1. Có bao nhiêu số nguyên m để hàm số f x  x  mx   2018 2019 2 6 xác định trên R ? A. 6 B. 7 C. 9 D. 10 Câu 2. Phương trình 3x 722 3x  
 2018 1296 có bao nhiêu nghiệm nguyên ? A. 2 B. 1 C. 3 D. 4
Câu 3. Tìm tập hợp tất cả các giá trị m để hàm số  8x  .2x y m
1đồng biến trên  . 1  A.  ;   1 B.  ;  0 C. ;5   D. 5; 3 
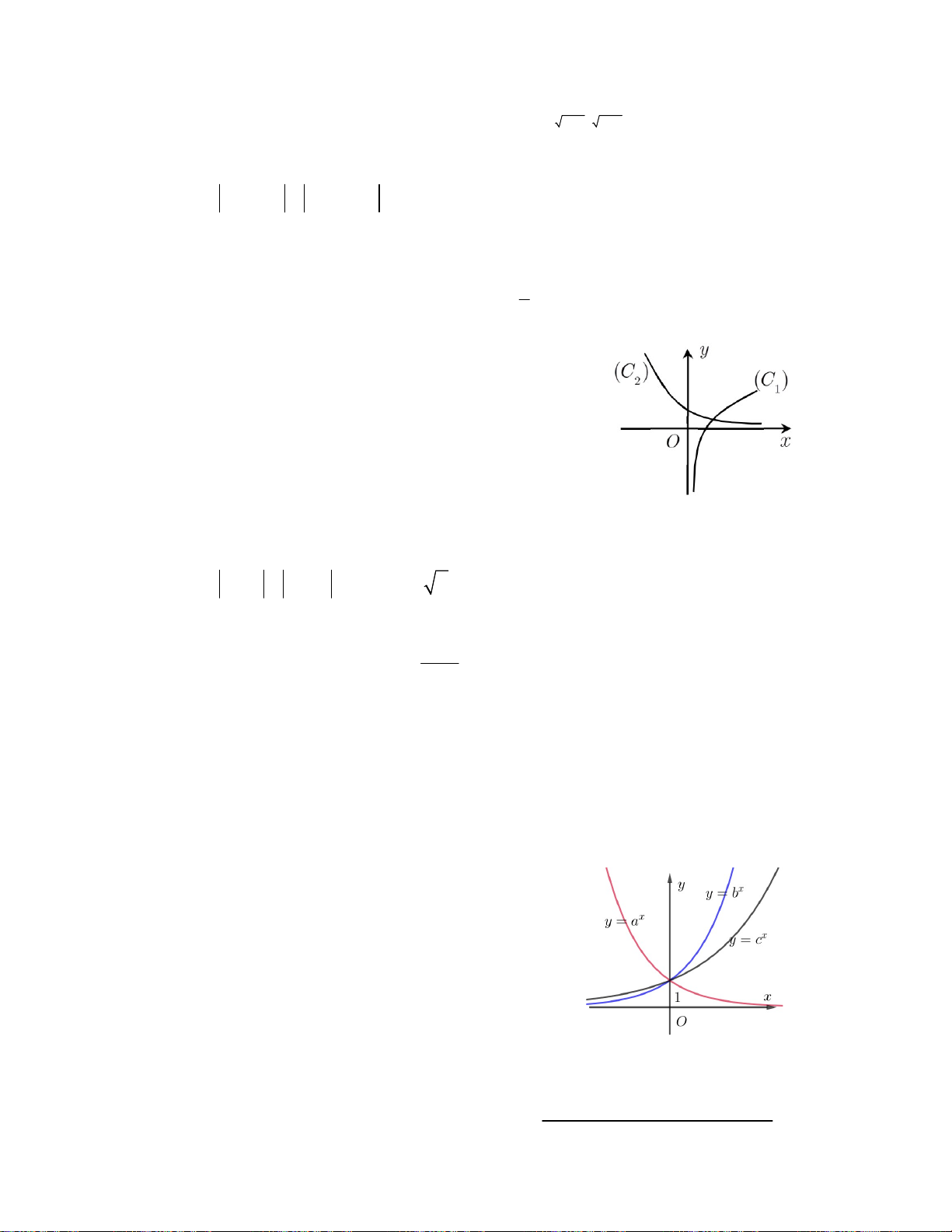
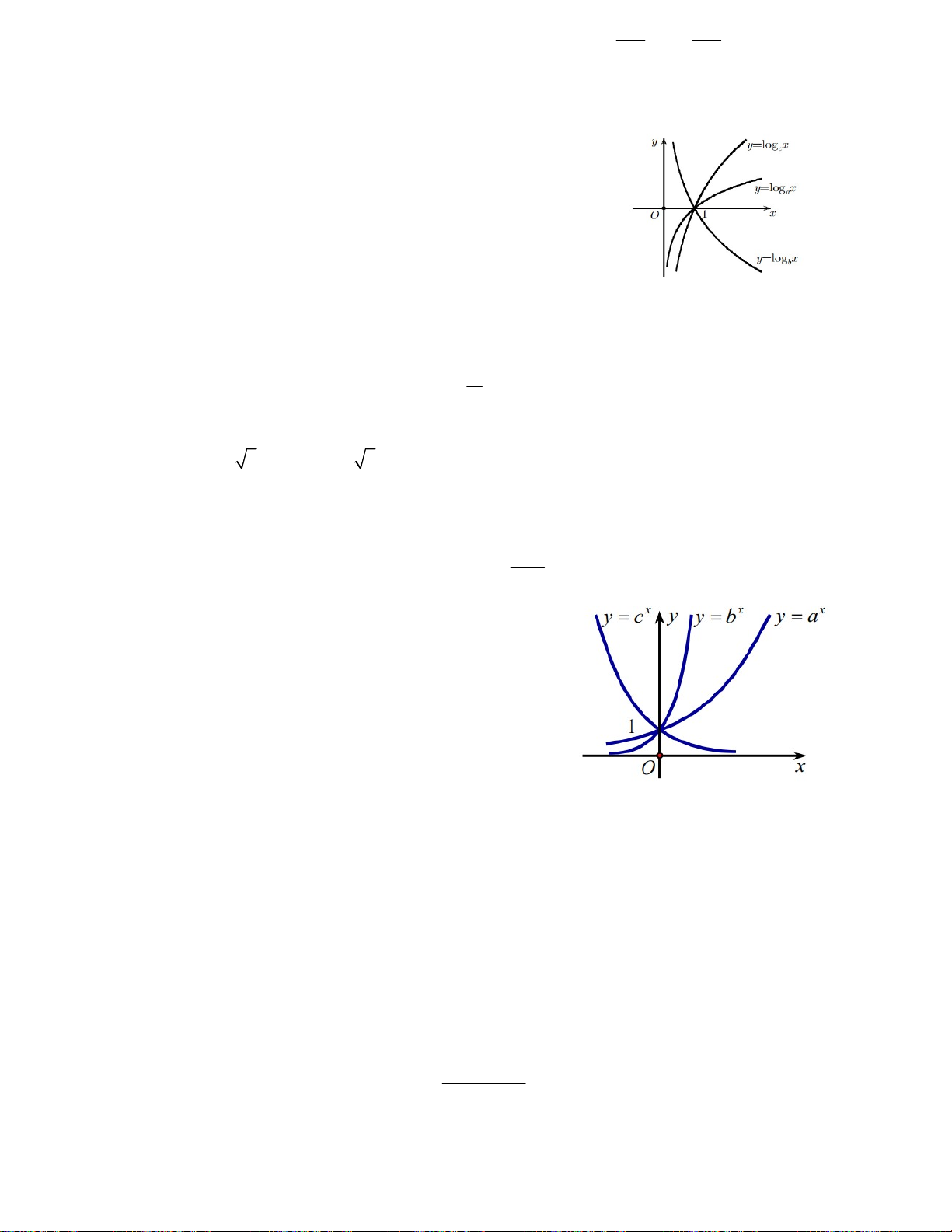
Câu 4. Hình vẽ bên là hai đồ thị C : y  log ; x C : x y  a . 1  b  2 Mệnh đề nào đúng ?
A. a > 1; b > 1. B. 0 < a < 1, 0 < b < 1.
C. 0 < a < 1 < b. D. 0 < b < 1 < a.
Câu 5. Tìm giá trị nhỏ nhất của tham số m để hàm số y  log  2
x  mx  2m 1 xác định trên [1;2]. 3  A. 0,25 B. 0,5 C. 0,75 D. 1 Câu 6. Phương trình x x 2
2 1  2  2  x  2x  y có bao nhiêu cặp nghiệm (x;y) ? A. 2 B. 3 C. 1 D. Vô nghiệm 3 x    1 x e m e 1 1972   
Câu 7. Tìm điều kiện tham số m để hàm số y   
đồng biến trên khoảng (1;2).  1973  A. 3 4 3e 1  m  3e 1 B. 2 3 3e 1  m  3e 1 C. 4 m  3e 1 D. 2 m  3e 1
Câu 8. Tồn tại bao nhiêu số nguyên m lớn hơn – 10 để hàm số y   2 ln x  
1  mx 1đồng biến trên  . A. 5 B. 7 C. 9 D. 10
Câu 9. Tìm số nghiệm thực của phương trình log2 3 log2 7 x  x  x  2 . A. 3 B. 1 C. 2 D. 4
Câu 10. Cho hình vẽ bên. Mệnh đề nào đúng ?
A. a < c < b B. a < b < c
C. b < c < a D. c < a < b
Câu 11. Tính trung bình cộng các nghiệm thực của phương trình 2xx x8 2 2  2  8  2x  x . A. 2 B. 1 C. 3 D. 1,5 x 1
Câu 12. Có bao nhiêu số nguyên m thuộc [– 20;20] để hàm số y   xác định trên x  m  2ln  2 x  4x  6  m miền 1; ? 8 A. 21 B. 20 C. 4 D. 3 mx 1  6
Câu 13. Có bao nhiêu số nguyên m để hàm số xm y  e
nghịch biến trên 2; ? A. 6 B. 5 C. 7 D. 9 2 x 1 
Câu 14. Phương trình 3 .x5 x  15 có một nghiệm x  log b 1  a  8,1  b  8;a,b   . Tính a + b. a  A. 10 B. 8 C. 13 D. 5 Câu 15. Cho hàm số sin 5 x y 
. Phương trình y  5cos x ln 5 có bao nhiêu nghiệm trong khoảng (0;10) ? A. 1 B. 3 C. 4 D. 2
Câu 16. Tìm giá trị nhỏ nhất của m để phương trình 3x3x3 e
 m có nghiệm x 0;2. 1 A. m = 2e B. m = 3e C. m = e D. m = e
Câu 17. Ký hiệu S là tập hợp tất cả các giá trị thực m để phương trình 2 2
log x  4log x  m  2m  0 có hai 2 2
nghiệm phân biệt x , x thỏa mãn 2 2
x  x  68 . Tính tổng bình phương các phần tử của S. 1 2 1 2 A. 15 B. 10 C. 18 D. 26
Câu 18. Cho hình vẽ bên. Mệnh đề nào đúng ?
A. a > b > 1 B. 1 > a > b
C. b > a > 1 D. a > 1 > b
Câu 19. Có bao nhiêu số nguyên m < 2018 để phương trình log 2018x  m  log 1009x có nghiệm. 6   4   A. 2019 B. 2018 C. 2017 D. 2020 2
Câu 20. Tìm tập hợp tất cả các giá trị m để phương trình log2 x  m   log2 x 2 3 2 3 3
 m  3  0 có hai nghiệm
phân biệt mà tích của chúng lớn hơn 2. A. 1; \   0 B. 1; C. 0; D.  \ 1  ;  1
Câu 21. Tồn tại bao nhiêu số nguyên m trong khoảng (– 5;15) để bất phương trình sau nghiệm đúng với mọi số thực x: 1 log  2 x   1  log  2 mx  4x  m . 5 5  A. 2 B. 1 C. 3 D. 11
Câu 22. Cho hình vẽ bên. Mệnh đề nào đúng ?
A. 0 < c < 1 < a < b. B. 0 < a < b < 1 < c.
C. 0 < c < a < 1 < b. D. 0 < c < 1 < b < a. x
Câu 23. Cho hàm số g  x 81 
. Với mọi số thực x, phần nguyên của x được ký hiệu [x], tức là số nguyên 81x  9
lớn nhất không vượt quá x. Tìm phần nguyên của số  1   2   2016  Q  g  g  ...  g  g        3.  2017   2017   2017  A. Q  112 B. Q  113 C. Q  115 D. Q  120
_________________________________ 9
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 5)
__________________________________________________
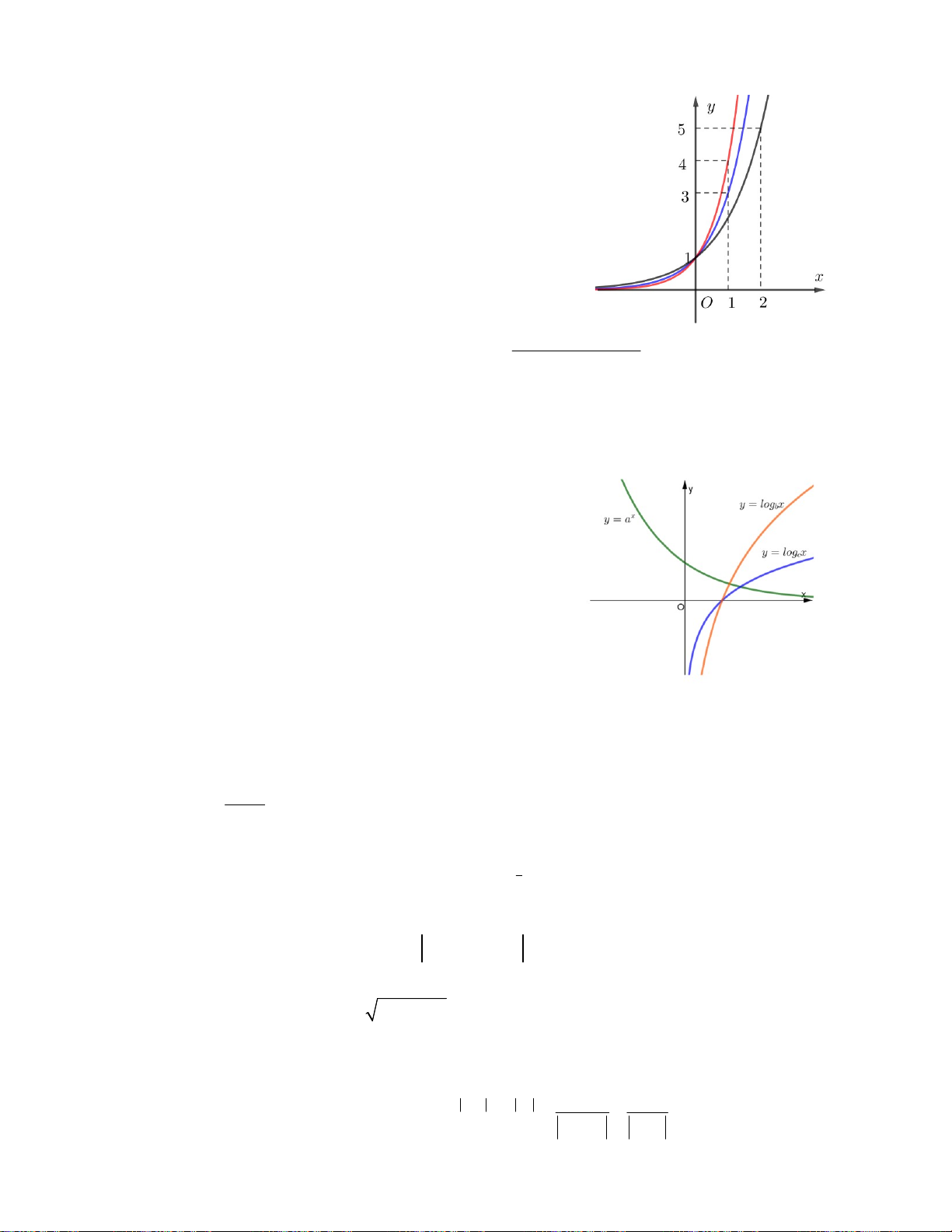
Câu 1. Hình vẽ bên là đồ thị các hàm số x  ; x  ; x y a y c y  b .
Nghiệm của phương trình x x x a  c  b là A. x = 0 B. x = 2 C. x = 1 D. x = 3
Câu 2. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
ln m  2sin x  lnm  7sin x  5sin x . A. 35 B. 141 C. 52 D. 66
Câu 3. Có bao nhiêu số nguyên dương m để hàm số 2
y  x  8ln  x  m  
1 đồng biến trên tập xác định của nó A. 2 B. 1 C. 3 D. 4 Câu 4. Phương trình sin x 1sin 4  2
x cos xy  2 y  0 có nghiệm  x ; y . Tính tổng các giá trị x , y khi 0 0  0 0 x  y  10 . 0 0 A. 4 B. 2 C. 3 D. 6
Câu 5. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình sau có nghiệm thực x x m  m  e  e . A. 10 B. 9 C. 7 D. 6
Câu 6. Cho hình vẽ bên. Mệnh đề nào sau đây đúng ?
A. a > 1; 0 < b < 1. B. 1 > a > 0; b > 1.
C. 0 < a < 1; b < 1. D. a > 1; b > 1. x
Câu 7. Cho hàm số f  x 2016 
. Tìm số nguyên dương n lớn nhất sao cho 2016x  2016 n  1   2   2015   2016  3  f  f  ...  f  f         .  2017   2017   2017   2017  A. n  4 B. n  5 C. n  6 D. n  7 1 1 1  m 2 2 m
Câu 8. Cho hàm số f  x x x  1  e . Biết rằng   1 . 2... 2017 n f f f
 e với là phân số tối giản. Tính n
giá trị của biểu thức 2 m  n . A. 2018 B. 1 C. – 2018 D. – 1
Câu 9. Tập hợp S  a;b bao gồm tất cả các giá trị m để phương trình sau có nghiệm thực m sin x4 cos x2m 3sin xm cos x5 e  e
 m  4cos x  3  msin x  2m  5 Tính a  b  20 . A. 4 B. 2 C. 5 D. 3 10 4x 2x
Câu 10. Có bao nhiêu giá trị nguyên m thuộc (– 2018;2018) để hàm số y   2 . m
 m  2 x 1đồng ln 4 ln 2 biến trên khoảng  ;   ? A. 2018 B. 2019 C. 2020 D. 4034
Câu 11. Cho hình vẽ bên. Mệnh đề nào sau đây đúng ?
A. b < c < a. B. c < a < b
C. a < b < c D. b < a < c
Câu 12. Tính tích các nghiệm của phương trình 8.3x 3.2x 24 6x    . A. 3 B. 2 C. 4 D. 6
Câu 13. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực ? 2 4m 2 sin  cos x xm 5 5e  5e  5cos2x  m . A. 12 B. 10 C. 11 D. 15 log x log x
Câu 14. Phương trình    2  x   2 2 3 1 3 1
 1 x có bao nhiêu nghiệm thực ? A. 2 B. 1 C. 3 D. 0
Câu 15. Tìm giá trị lớn nhất của tham số m để phương trình ln m  ln  m  cos x  cos x  có nghiệm thực ? e 1 A. 1 B. e C. D. e – 1 2
Câu 16. Cho 0  a,b,c  1 và ba đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ?
A. 1 < c < a < b B. c < a < b < 1
C. c < 1 < b < a D. c < 1 < a < b
Câu 17. Có bao nhiêu giá trị nguyên m  1
 8;18 để phương trình 2x  m  log x  m có nghiệm ? 2   A. 19 B. 9 C. 17 D. 18
Câu 18. Tính tổng các nghiệm của phương trình 2 2 x x 32 x 2 2x3 2  9   6  4  3xx x  5x . A. 6 B. 7 C. 8 D. 4
Câu 19. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để phương trình sau có nghiệm 2 3x  cos 2x  m . A. 10 B. 12 C. 15 D. 14
Câu 20. Phương trình log  8
3x 1  y 1 y  3  6log x có bao nhiêu cặp nghiệm thực (x;y) ? 4     4 A. 3 B. 2 C. 1 D. 4 2
Câu 21. Tìm tất cả các giá trị m để phương trình x 
 m có hai nghiệm phân biệt. log x 1 3   A. 1  m  0 B. m > – 1 C. Không tồn tại m D. – 1 < m < 0
_________________________________ 11
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 6)
__________________________________________________
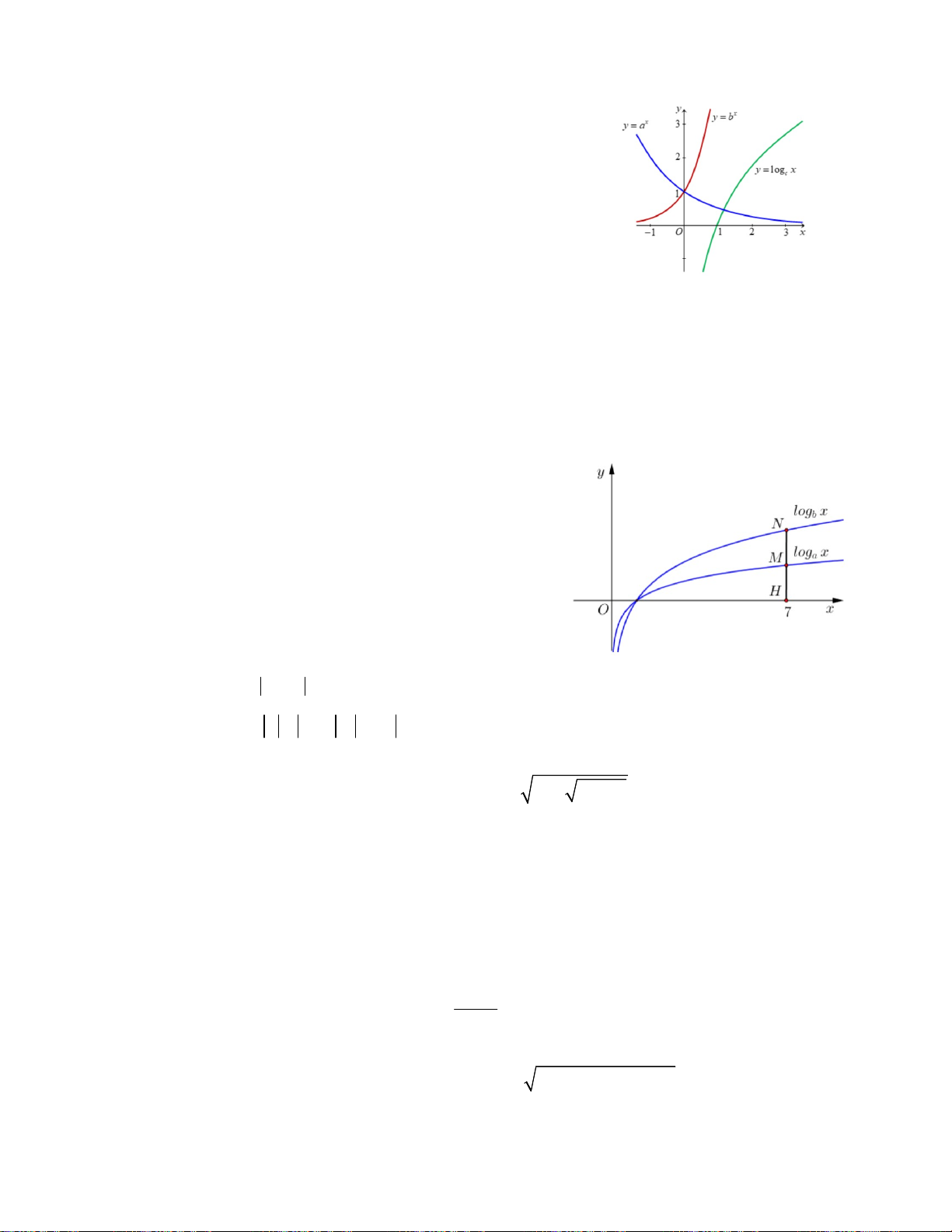
Câu 1. Đối với góc phần tư thứ nhất, theo thứ tự từ trái sang phải
trong hình bên là đồ thị các hàm số x  ; x  ; x y a y c y  b .
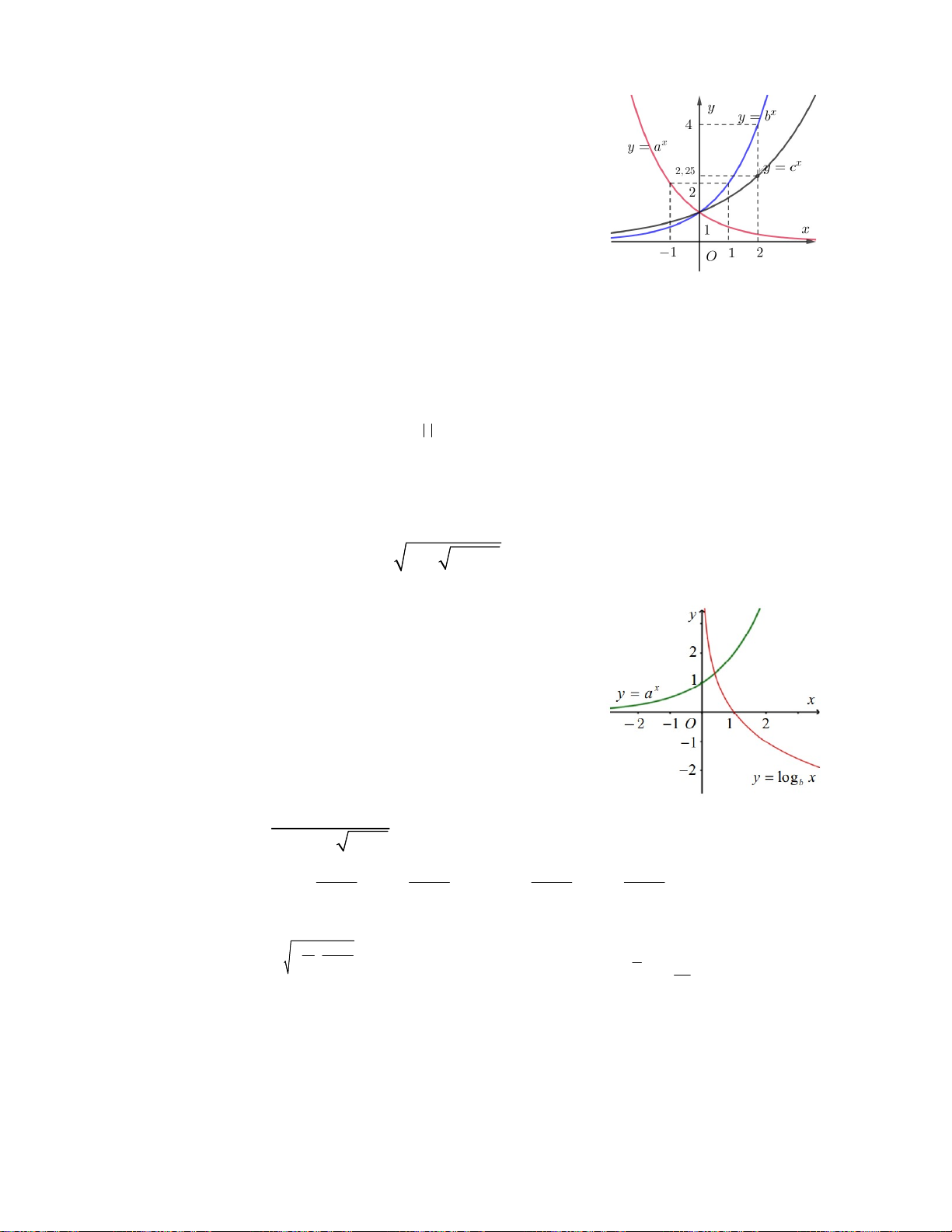
Nghiệm của phương trình x x 2 x a  c  b là A. x = 0 B. x = 1 C. x = 2 D. x = 3 2 x  2mx  m  2
Câu 2. Có bao nhiêu giá trị nguyên m để hàm số f x  log xác định trên  ? 3 6  sin x  2cos x A. 3 B. 2 C. 1 D. 4
Câu 3. Tìm giá trị bé nhất của m để hàm số y   2 ln 16x   1  m  
1 x  m  2 nghịch biến trên  ? A. m = 2 B. m = 4 C. m = 5 D. m = 3
Câu 4. Cho hình vẽ bên với các đồ thị hàm số x
y  a ; y  log x; y  log x . Mệnh đề nào sau đây đúng ? b c
A. c > b > a B. b > a > c
C. a > b > c D. b > c > a
Câu 5. Phương trình x log x  log x  2 2
1  x có bao nhiêu nghiệm thực lớn hơn 1,5 ? 3 3 A. 3 B. 4 C. 2 D. 1
Câu 6. Đồ thị hàm số y = g (x) đối xứng với đồ thị của hàm số x
y  a a  1,a  0 qua điểm I (1;1). Tính giá trị  1  biểu thức g 2  log  . a   2018  A. 2016 B. – 2020 C. 2020 D. – 2016 1 3 2 x mx  2m3 x5
Câu 7. Tồn tại bao nhiêu giá trị nguyên m để hàm số f  x   3  e
 2019 đồng biến trên  ? A. 10 B. 4 C. 12 D. 5
Câu 8. Có bao nhiêu giá trị m để hàm số   2 x   4 x f x e
e  m có giá trị nhỏ nhất trên đoạn [0;ln4] bằng 6. A. 3 B. 4 C. 1 D. 2
Câu 9. Cho dãy số u thỏa mãn 1u8 1 u 8 4 1 u 4 1  5 u e e  e
 e và u  u  3 với n nguyên dương. Giá trị lớn nhất n  n 1  n
của n để log u  ln 2018 bằng 3 n A. 1420 B. 1419 C. 1417 D. 1418
Câu 10. Tính tổng các nghiệm thực của phương trình 2x5 x 1  1 1 e  e   . 2x  5 x 1 A. 5 B. 6 C. 7 D. 4 12
Câu 11. Cho hình vẽ bên. Mệnh đề nào sau đây đúng ?
A. c > b > a B. b > a > c
C. a > b > c D. b > c > a
Câu 12. Tìm giá trị tham số m để hai đường cong sau tiếp xúc nhau
 :  3x 3x   2 2   3 ; :  3x C y m m m C y 1. 1  2  5  2 10 5  2 10 5  2 2 5  3 2 A. B. C. D. 3 3 3 3 x  x 8 Câu 13. Phương trình 2 1 3 2 2  2 
có bao nhiêu nghiệm thực ? log  2 4x  4x  4 3  A. 3 B. 2 C. 1 D. Vô nghiệm
Câu 14. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực 2 2 sin x cos x cos 2 4 15  9.6 x log m 1 . 3  A. 69 B. 90 C. 42 D. 112 ln x  6 Câu 15. Cho hàm số y 
. Gọi S là tập hợp tất cả các giá trị nguyên dương của m để hàm số đã cho ln x  2m
đồng biến trên khoảng (1;e). Tìm số phần tử của S. A. 1 B. 2 C. 4 D. 3
Câu 16. Cho phương trình 3x  .3x a
cos x  9 . Có bao nhiêu giá trị thực của tham số a thuộc đoạn [–
2018;2018] để phương trình đã cho có đúng một nghiệm thực ? A. 2 B. 3 C. 1 D. 2018
Câu 17. Cho phương trình 4x 4 6  .6 x a
cos x  36 . Có bao nhiêu giá trị thực a thuộc đoạn [– 2018;2018] để
phương trình đã cho có đúng một nghiệm thực ? A. 2 B. 3 C. 1 D. 2018
Câu 18. Gọi S là tập hợp các giá trị của tham số thực m để hàm số 2
y  x  ln  x  m  2 đồng biến trên tập
xác định của nó. Biết S   ;
 a  b  , tính tổng K  a  b . A. K  5  B. K  5 C. K  0 D. K  2
Câu 19. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực 2 2 sin x cos x cos 2 2  9  4 x log m . 2 A. 4096 B. 4091 C. 1300 D. 1250 x a  b
Câu 20. Cho hai số thực dương x, y thỏa mãn log x  log y  log x  y . Khi đó  , a và b đều 9 6 4   y 2 nguyên dương. Tính a + b. A. a + b = 11 B. a + b = 4 C. a + b = 6 D. a + b = 8 1
Câu 21. Có bao nhiêu số nguyên m  2
 0;20 để hàm số y  xác định với x > 0. 2 m log x  4log x  m  3 3 3 A. 35 B. 20 C. 16 D. 38
_________________________________ 13
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 7)
__________________________________________________
Câu 1. Cho hình vẽ bên với các đồ thị hàm số x y  a ; x y  b ; y  log x c
Mệnh đề nào sau đây đúng ?
A. a < b = c B. b > a > c
C. a > c > b D. b > c > a log x log 5   7 y,  Câu 2. Hệ phương trình
có nghiệm duy nhất (x;y). Tính P = 7x – 5y + 1.    7x  log7  5ylog5 A. P = 3 B. P = 2 C. P = 13 D. P = 6
Câu 3. Cho dãy số u thỏa mãn 3 2
log u  2log u  log u  2  0 và u
 2u 10, n nguyên dương. Tìm n  1 1 1 n 1  n
giá trị nhỏ nhất của n sao cho 100 u  10 10 . n A. 226 B. 325 C. 225 D. 326
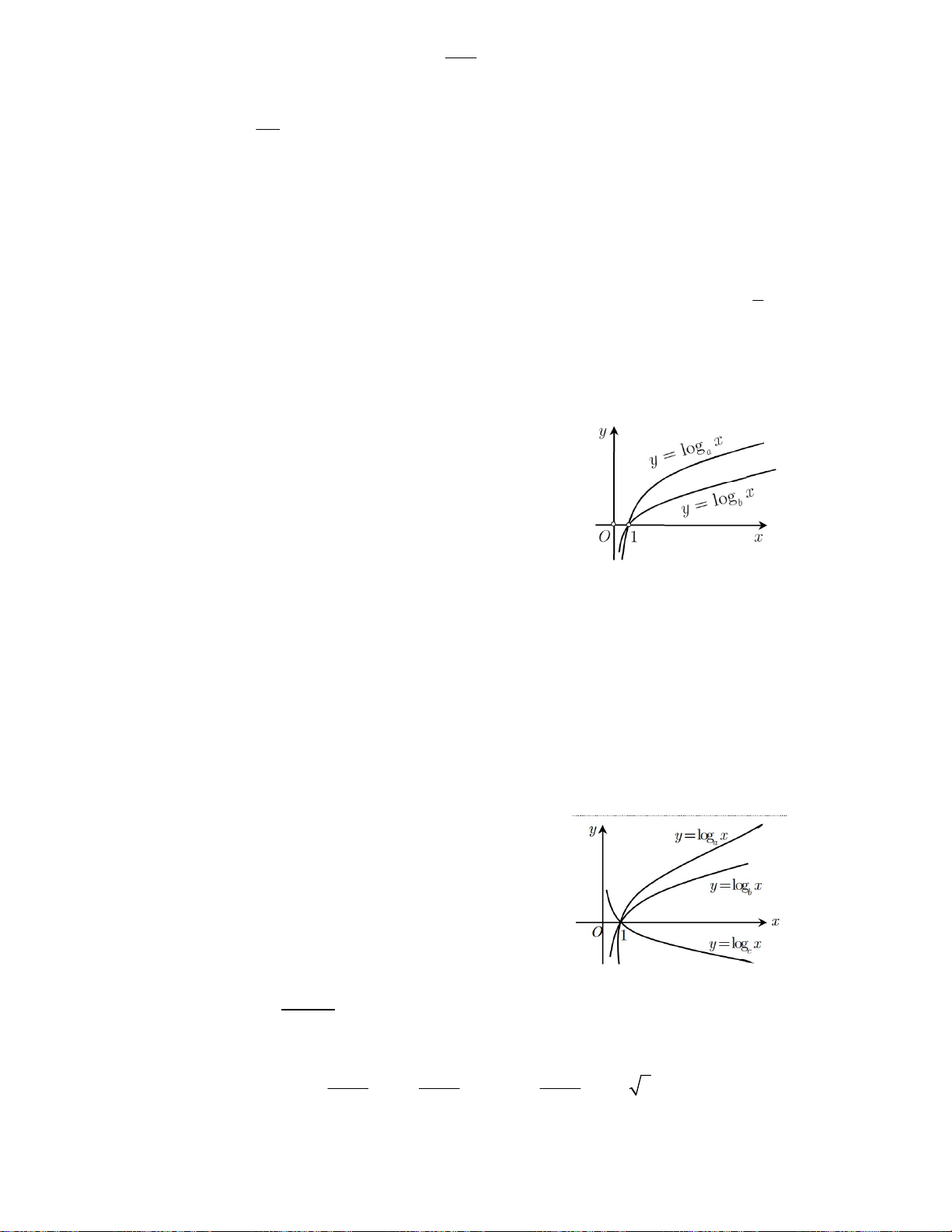
Câu 4. Cho hàm số y  log x; y  log x có đồ thị như hình vẽ a b
bên. Đường thẳng x = 7 cắt trục hoành và các đồ thị hàm số
y  log x; y  log x lần lượt tại H, M, N. Biết rằng 2HM = HN. a b
Mệnh đề nào sau đây đúng ? A. a = 7b B. 2 a  b C. a = 2b D. 7 a  b 2 x 2 x3 log  3 5  y4 3   5 ,
Câu 5. Hệ phương trình 
có hai nghiệm  x ; y . Tính 2 x  3 y . 0 0  0 0
4 y  y 1  y  3  8.  A. 5 B. 7 C. 6 D. 4
Câu 6. Có bao nhiêu số nguyên m nhỏ hơn 10 để phương trình x x
m  m  e  e có nghiệm thực ? A. 10 B. 9 C. 7 D. 6
Câu 7. Cho dãy số u thỏa mãn 2
log u  logu  6  0 và u
 u  5, n nguyên dương. Giá trị lớn nhất của n  1 1 n 1  n
n để u  500 bằng bao nhiêu ? n A. 80 B. 100 C. 99 D. 82
Câu 8. Cho dãy số u thỏa mãn 3 2 u  e ;u
 u , k là số tự nhiên thỏa mãn 765
u u ...u  e . Giá trị của k là n  1 n 1  n 1 2 k A. 6 B. 7 C. 8 D. 9 4x 1
Câu 9. Tìm điều kiện tham số m để phương trình log  m có nghiệm. 2 4x 1 A. – 1 < m < 1 B. m < 0 C. – 1 < m < 0 D. m  1
Câu 10. Cho dãy số u thỏa mãn logu  2logu  2 1 logu  2logu 1 và u  3u , n nguyên 5 2  5 2  n  n n 1 
dương. Giá trị lớn nhất của n để 100 u  7 bằng n A. 192 B. 191 C. 176 D. 177
Câu 11. Có bao nhiêu số nguyên m [– 2018;2018] để hàm số f  x   x  
1 ln x  2  m x đồng biến trên 14 khoảng  2 0;e  . A. 2022 B. 2014 C. 2023 D. 2016
Câu 12. Giá trị m  a b a,b  là giá trị nhỏ nhất của tham số m để phương trình sau có nghiệm 3 x 3 x 1 2.2 4 3.2 2x m m      .
Tính giá trị biểu thức a  2b  7 . A. 10 B. 15 C. 18 D. 12 Câu 13. Cho phương trình .5x sin 5 5x a x   
; a là tham số thực. Phương trình đã cho tồn tại nghiệm duy   
nhất x . Tính sin x  cos x  sin x  . 0 0 0  0   2  A. 1 B. 2 C. 4 D. 3 Câu 14. Phương trình x2   x   x2 3.25 3 10 .5
 3  xcó tổng các nghiệm gần nhất với giá trị nào A. 8 B. 3 C. 10 D. 12
Câu 15. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Hàm số 2 f  x 1 f  x g e    6
có bao nhiêu điểm cực trị ? A. 3 B. 6 C. 4 D. 5
Câu 16. Phương trình log x  3x  3x  m  log 4  x3 4 2
 log x 1 có ba nghiệm thực phân biệt khi 5 125 5  
m thuộc khoảng (a;b). Mệnh đề nào sau đây đúng ? a 2 A. ab  4 B. a  b  1 C. b  2a  6 D.  b 5 2 x x 1  2 x 1 7 7     2012x  2012,
Câu 17. Tồn tại bao nhiêu số nguyên m < 100 để hệ  có nghiệm ? 2
x  (m  2)x  2m  3  0. A. 100 B. 105 C. 102 D. 90 2 x Câu 18. Phương trình 3
 3x  ln(x 1)  4  0 có bao nhiêu nghiệm thực ? 2 A. 3 B. 2 C. 1 D. 4
Câu 19. Có bao nhiêu số nguyên a thuộc (– 200;200) để phương trình x xa e  e
 ln(x  a)  ln(x  a 1) có nghiệm thực duy nhất. A. 399 B. 199 C. 200 D. 398
Câu 20. Cho các số thực dương a, b khác 1. Biết rằng bất kỳ
đường thẳng nào song song với trục hoành mà cắt các đường thẳng x  ; x
y a y  b , trục tung lần lượt tại M, N và A thì ta luôn có
AN = 2AM (hình vẽ bên). Mệnh đề nào sau đây đúng ? A. 2a = b B. 2 ab  1 C. 2 a  b D. 2ab = 1
_________________________________ 15
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 8)
__________________________________________________
Câu 1. Biết rằng a là số thực dương để x a  9x 1, x
   . Mệnh đề nào sau đây đúng ? A. a   3 4 10 ;10  4  B. a   2 3 10 ;10  C. a   2 0;10  D. a  1  0 ;  
Câu 2. Có bao nhiêu số nguyên m < 10 để hàm số y   2 ln x  mx  
1 đồng biến trên 0; ? A. 10 B. 11 C. 8 D. 9 1
Câu 3. Cho dãy số u thỏa mãn logu
 2017 2018  2logu  logu
 2logu và u  u , n là số n  2018 1 2018 1 n 1  2 n
nguyên dương. Tìm giá trị lớn nhất của n để 1917 u  5 . n A. 232 B. 233 C. 234 D. 235
Câu 4. Tính tổng các nghiệm của phương trình 2
log x  x 12 log x 11  x . 3   3 A. 18 B. 10 C. 12 D. 6
Câu 5. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để phương trình sau có nghiệm 2 x 2 65.13
x  4cos3x  3  m 1. A. 10 B. 11 C. 13 D. 12 log 2 log 3 log 4 ... log n
Câu 6. Gọi a là giá trị nhỏ nhất của hàm số f n  3
 3  3   3  *  ;n   ,n  2. Có bao 9n
nhiêu số tự nhiên n để f (n) = a ? A. 2 B. 4 C. 1 D. Vô số
Câu 7. Biết a là số thực dương sao cho bất đẳng thức 3x x   6x  9x a
đúng với mọi số thực x. Mệnh đề nào sau đây đúng ? A. a (10;12] B. a (16;18] C. a (14;16] D. a (12;14]
Câu 8. Tính tổng các nghiệm của phương trình 7x  1 6log 6x 1 . 7   A. 2 B. 3 C. 1 D. 0  1 
Câu 9. Cho hàm số f x  ln 1 
thỏa mãn f 2  f 3  ...  f 2018  ln a  ln b  ln c  ln d , trong 2   x 
đó a, b, c, d là các số nguyên dương tăng dần, a, c, d đều là số nguyên tố. Tính P = a + b + c + d. A. 1986 B. 1698 C. 1689 D. 1968
Câu 10. Giả sử a, b là các số thực sao cho 3 3 3z 2   .10  .10 z x y a b
đúng với mọi số thực dương x, y, z thỏa mãn điều kiện x  y  z  2 2 log
;log x  y   z 1. Giá trị của a + b là A. 15,5 B. 14,5 C. – 15,5 D. – 12,5
Câu 11. Tồn tại bao nhiêu giá trị nguyên m để phương trình sau có 4 nghiệm thực phân biệt ? 2 2 3 x 3 x 2 log
m  2.6  5 m  3.6  x . 6 A. 4 B. 3 C. 1 D. 2 log   2 2 x  y  1 log xy , 2  2  
Câu 12. Biết hệ phương trình  có hai nghiệm  ; x y  a;b, ; c d ;a  c . 2 2 3x xyy   81. Tính b + 2d. A. b + 2d = 4 B. b + 2d = 3 C. b + 2d = 2 D. b + 2d = 5 16
Câu 13. Gọi a là số thực lớn nhất sao cho 2 x  x   a  2 2 ln x  x   1  0, x
   . Mệnh đề nào đúng ? A. a (2;3] B. a  8; C. a (6;7] D. a (– 6;– 5]
Câu 14. Tìm điều kiện tham số m để hàm số y   2 ln x  x  
1  mln x đồng biến trên khoảng (0;4). 2 2 28 A. m  1 B. m  1 C. m   D. m  0 3 3 13 2  
Câu 15. Tìm điều kiện tham số m để hàm số  log 2018x x y  x 
 m xác định với mọi x không âm. 2018   2   A. m > 9 B. m < 1 C. 0 < m < 1 D. m < 2
Câu 16. Có bao nhiêu số nguyên m để phương trình sau có hai nghiệm phân biệt x , x với tổng bình phương 1 2 các nghiệm bằng 3: log        .   2 2 2x x 4m 2m 2 2 log x mx 2m 0 2 5 52 A. 1 B. 0 C. 3 D. 2
Câu 17. Cho dãy số u thỏa mãn logu  2  logu  2logu  2logu và u  2u , n nguyên dương. n  1 1 10 10 n 1  n
Giá trị lớn nhất của n để 100 u  5 bằng n A. 248 B. 246 C. 247 D. 290
Câu 18. Tìm điều kiện tham số m để phương trình 4x 2x 4 3m 2x     
1 có hai nghiệm phân biệt. A. 1  m  log 4 B. 1  m  log 4 C. log 3  m  1 D. log 3  m  2 3 3 4 4
Câu 19. Có bao nhiêu số nguyên dương khác 1 của m để phương trình sau có nghiệm x lớn hơn 2 log  2 x  x 1.log  2
x  x 1  log x  x  m  2 1 2 5  A. Vô số B. 3 C. 2 D. 1
Câu 20. Biết rằng a là số thực dương để x a  2018x 1, x
   . Hỏi log(a) gần nhất với giá trị nào ? A. 2018 B. 876 C. 1010 D. 502
Câu 21. Tập hợp S  a;b bao gồm tất cả các giá trị m để phương trình sau có nghiệm thực m sin x4 cos x2m 3sin xm cos x5 e  e
 m  4cos x  3  msin x  2m  5 Tính a  b  20 . A. 4 B. 2 C. 5 D. 3 2 m  2  1 
Câu 22. Tìm điều kiện tham số m để hàm số y  log x  2  đồng biến trên đoạn ;100 . log x  m 10    3 m  1 A. m   B. C. m  2 D. m  2 2  m  2
Câu 23. Tính tích các nghiệm của phương trình log  2 x  2x   1  log  2 x  2x . 3 2  A. – 2 B. 1 C. – 1 D. 4
Câu 24. Cho dãy số u có số hạng đầu u  1và thỏa mãn 2
log 5u  log 7u  log 5  log 7 .Biết 2  1  2 2  2  2 2 n  1 2 2 u
 7u với n  1. Giá trị nhỏ nhất của n để u  1111111bằng n 1  n n A. 11 B. 8 C. 9 D. 10 mlog x  2
Câu 25. Có bao nhiêu số nguyên m lớn hơn – 40 để hàm số 2 y 
nghịch biến với mọi x > 4 ? log x  m 1 2 A. 37 B. 20 C. 16 D. 32
_________________________________ 17
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 9)
__________________________________________________
Câu 1. Giả sử a là số thực dương sao cho x  4.5x  220x 15x a , x
   . Khi đó số nghiệm thực của phương trình 3 x  2018x  a là A. 3 B. 2 C. 1 D. Vô số 1 2x  1   2   3   2016 
Câu 2. Cho hàm số f  x  log . Ký hiệu M  f  f  f  ...  f . 2         2 1 x  2017   2017   2017   2017 
Biết rằng M là một số tự nhiên, hỏi M có bao nhiêu ước nguyên dương ? A. 10 B. 12 C. 8 D. 30 x  2 1
Câu 3. Có bao nhiêu số nguyên m để phương trình log  8  7x  m 2 2 3 có nghiệm ? 2 x A. 6 B. 3 C. 2 D. 2 3
Câu 4. Tồn tại bao nhiêu số nguyên m để hàm số y  log
mx  3m  5 xác định với mọi x  ? 2   m 4 2 A. 5 B. 4 C. 3 D. 2
Câu 5. Giả sử a là số thực dương để a  x4 2  10x  39, x
   . Giá trị log(a) gần nhất với A. 4,3 B. 6,1 C. 3,2 D. 2,5
Câu 6. Trong tất cả các cặp số (x;y) thỏa mãn log
4x  4 y  4  1. Tìm giá trị của tham số m thỏa mãn 2 2   x  y 2 đẳng thức 2 2
x  y  2x  2 y  2  m  0 . A. m = 4 B. m = 10  2 C. m = 7 1 D. m  10  2
Câu 7. Có bao nhiêu số nguyên m nhỏ hơn 8 để phương trình sau có nghiệm duy nhất log x  m   1  log   .    2 mx x 0 3 2 2 3 2 2  A. 5 B. 4 C. 6 D. 7 
Câu 8. Tính tổng các nghiệm của phương trình 2x 1 2 log  3x  8x  5 . 3 3x  2 1 8 11 2 A. 4 B. C. D. 3 7 3
Câu 9. Biết rằng phương trình 4 xm log  2  3  2x  x x x
log 2 xm  2  0 có nghiệm khi và chỉ khi m > a 2   2 2 2 1   2 hoặc m < b. Tính a + b. A. a + b = 2 B. a + b = 4 C. a + b = 5 D. a + b = 2,5 Câu 10. Phương trình    m   1 log  x  22 1 2  4 m  5 log
 4m  4  0 có nghiệm thực trong đoạn 5 ;4 1   1 x2 4    2 2
khi m thuộc đoạn [p;q]. Tính p + 3q. A. p + 3q = 5 B. p + 3q = 4 C. p + 3q = 8 D. p + 3q = 10
Câu 11. Tìm tất cả các giá trị của tham số m để phương trình 2x  mx 1 có hai nghiệm phân biệt. A. 0  m  ln 2 B. Mọi giá trị m C. m  ln 2 D. 0 < m < ln2
Câu 12. Tìm điều kiện tham số m để hàm số     2   2. x f x mx x
e đồng biến trên khoảng (1;2). 5 4 5 4 A. m   B. m   C. m   D. m   8 3 8 3 18 2  2 2  x  y x 2017 2016  ,  Câu 13. Hệ phương trình 2  y  2017
có bao nhiêu nghiệm thực 3
 log x  2y  6  2log x  y  2 1.  3   2   A. 3 B. 2 C. 1 D. 0
Câu 14. Tìm số nghiệm nguyên của bất phương trình 2 2 2 x 1  5x 1  00 x 1  0 x50 2 2  2  x  25x 150  0 . A. 6 B. 4 C. 5 D. 3 2 4x  4x 1 Câu 15. Phương trình 1 2 log
 4x 1  6x có hai nghiệm x , x thỏa mãn x  2x  a  b , trong 1 2   7 2x 1 2 4
đó a và b là hai số nguyên dương. Tính a + b. A. 16 B. 11 C. 14 D. 13
Câu 16. Có bao nhiêu giá trị nguyên m để phương trình 1x 1x      2x 2 4 4 1 2  2 x m 168mcó nghiệm thuộc đoạn [0;1]. A. 2 B. 5 C. 4 D. 3
Câu 17. Cho hai số thực a, b thỏa mãn f x 2017  a  2x  x 2018 ln 1  bxsin x  2 . Biết  log 6 5 c f   6, tính giá
trị của biểu thức   log 5 6 c P f   với 0  c 1. A. P = – 2 B. P = 6 C. P = 4 D. P = 2
Câu 18. Phương trình 2x 1 1 x   3x 1 1 2 0, 25 1 0,5 2    
 2x 1 có tổng các nghiệm bằng A. 4 B. 8 C. 3 D. 6
Câu 19. Giả sử có hệ thức 2 2
a  b  11ab (a và b là hai số dương khác nhau). Khẳng định nào sau đây đúng ? a  b 1 a  b A. 2log  log a  log b B. log  log a  log b 2 2 2 3 2 2 2 2 3 a  b C. 2log  log a  log b
D. 2log a  b  log a  log b 2 2 2 3 2 2 2 2017 z
Câu 20. Cho các số thực x, y, z thỏa mãn 3x  5y 15 xy . Ký hiệu S = xy + yz + xz. Chọn mệnh đề đúng A. 1 < S < 2016 B. 0 < S < 2017 C. 2016 < S < 2017 D. 0 < S < 2018
Câu 21. Có bao nhiêu số nguyên âm m để phương trình  3 2
log x  3x  8x 14  m  log x   1 có hai nghiệm phân biệt ? A. 1 B. 0 C. 2 D. 3
Câu 22. Có bao nhiêu số nguyên m để bất đẳng thức   2 x     2 ln 5 ln 1
ln mx  4x  m đúng với mọi m ? A. 3 B. 4 C. 1 D. 2
Câu 23. Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình sau nghiệm đúng với mọi x thuộc khoảng (2;4): 2 log x   2 m   3 2
1 log x  m  2m  m  0 . 4 2 A. 0 B. 2 C. 1 D. 3 2 2 1 x 3x x 3x
Câu 24. Tính tích tất cả các nghiệm của phương trình        2 2 1 3 2 2  x  3x 1. A. – 3 B. – 1 C. 2 D. 4  1 x 
Câu 25. Tìm tất cả các giá trị thực của m để hàm số y   mlog x  
đồng biến trên nửa khoảng (0;2]. 2  2  ln 2 2ln 2 ln 2 2ln 2 A. m   B. m   C. m   D. m   e e e e 19 ______________________
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 10)
__________________________________________________
Câu 1. Có bao nhiêu số nguyên m lớn hơn – 12 để hàm số y  log
2sin x  3cos x  m xác định với 2   m 2m5 mọi x ? A. 7 B. 8 C. 6 D. 5 Câu 2. Cho hàm số  x
y  e sin x . Lựa chọn mệnh đề đúng
A. y  2y  2y  0 B. y  2y  y  0
C. y  2y  2y  0 D. y  y  3y  0
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình 3 3 3  27 3  27.2x  2x m m có nghiệm thực ? A. Vô số B. 4 C. 8 D. 6
Câu 4. Tồn tại giá trị m  m để phương trình 1 m  log x  4m  2  log x  m có nghiệm duy nhất. 0 2 2
Mệnh đề nào sau đây đúng ? A. m [3;5] B. m [6;9] C. m (0;3) D. m  10 0 0 0 0
Câu 5. Tồn tại duy nhất giá trị m = a để phương trình log  2x 1  m 1 log  2 m  4x  4x có nghiệm 2 3 
duy nhất. Giá trị a thuộc khoảng nào sau đây ? A. (0;4) B. (4;6) C. (6;9) D. (9;14)
Câu 6. Tính tổng các số tự nhiên m để phương trình 2
log x  3mlog (3x)  2m  2m 1  0có hai nghiệm phân 3 3 10
biệt mà tổng hai nghiệm không nhỏ hơn . 3 A. 6 B. 1 C. 0 D. 10 2 mx  2mx  m  6
Câu 7. Tồn tại bao nhiêu số nguyên m thuộc khoảng (– 10;10) để hàm số y  ln xác định 10  sin 2x  3cos 2x với mọi x. A. 15 B. 8 C. 9 D. 10 Câu 8. Cho hàm số 4 x 2 x y e e  
. Tính y  13y  5y theo y. A. 6y B. 5y C. 7y D. 8y
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình 2
log x  4log x  m  3  0 có hai nghiệm phân biệt 3 3
x  x thỏa mãn điều kiện x  81x . 1 2 2 1 A. 4 B. 5 C. 3 D. 6
Câu 10. Tồn tại bao nhiêu số nguyên a < 50 để bất phương trình 2x 60x 10x 2x a  
 nghiệm đúng với mọi số thực x ? A. 46 B. 49 C. 30 D. 27
Câu 11. Tồn tại bao nhiêu số nguyên m thuộc [– 2020;2020] để bất phương trình sau nghiệm đúng với mọi x 2 x  2x  m thuộc [0;4]: 2 log  x  4x  3  m . 2 2 x  x 1 A. 2023 B. 1 C. 2 D. 2012
Câu 12. Hàm số y = f (x) thỏa mãn f ( x) 2 2019
 x  x  2019 . Có tất cả bao nhiêu giá trị nguyên m thỏa mãn
điều kiện f (log m)  f (log 2019) ? m A. 66 B. 65 C. 63 D. 64 20 1 Câu 13. Hàm số y  log
có đồ thị (H), hàm số y = f (x) có đồ thị (H’). Hai đồ thị trên đối xứng nhau gốc tọa 2018 x
độ. Khi đó hàm số y  f (x) nghịch biến trên khoảng A. ( ;  1  ) B. (– 1;0) C. (0;1) D. (1;)
Câu 14. Kết quả đạo hàm cấp 2018 của hàm số 10 20 ( ) x f x e   là A. 200 f (x) B. 10! f (x) C. 102018201009 f (x) D. 102018 f (x)
Câu 15. Có tất cả bao nhiêu số nguyên dương m để phương trình 2 (4log  log  5) 4x x x  m  0 có đúng 2 2 hai nghiệm phân biệt ? A. 14 B. 15 C. Vô số D. 16
Câu 16. Tiếp tuyến của đồ thị của hàm số x
y  x tại điểm có hoành độ bằng 2 cắt trục tung tại điểm M. Tung độ
điểm M gần nhất giá trị nào ? A. – 9,54 B. – 10,51 C. – 7,56 D. – 2,75
Câu 17. Có bao nhiêu số nguyên m > – 20 để phương trình 2
log (x  4)  (m  5)log (x  4)  2m 1  0 có hai 3 3
nghiệm phân biệt a, b thỏa mãn ab  4(a  b)  65. A. 10 B. 12 C. 20 D. 21 x 1 
Câu 18. Tổng các nghiệm phương trình 5x.8 x  500 gần nhất với giá trị nào ? A. 2,56 B. 2,89 C. 3,54 D. 4,23 x 1  1
Câu 19. Có bao nhiêu số nguyên dương m để phương trình 5x.8 x  m có tổng các nghiệm lớn hơn ? 2020 A. 8 B. 7 C. 6 D. 10
Câu 20. Tồn tại bao nhiêu số nguyên m để phương trình 2 x 2 x 2 log ( . m 4
 9)  x  2x  3  log 3 có hai 2 2 nghiệm phân biệt ? A. 12 B. 11 C. 4 D. 13 Câu 21. Cho hàm số 3 ( )    2m f x x x
. Tồn tại bao nhiêu số nguyên m để phương trình f ( f (x))  x có nghiệm trên [1;2]. A. 0 B. 4 C. 2 D. 3 2 x 1 
Câu 22. Tồn tại bao nhiêu giá trị nguyên dương m để phương trình 3 .x5 x  m có hai nghiệm phân biệt a, b
thỏa mãn điều kiện ln(a  b  ab)  3 . A. 5 B. 6 C. 18 D. 10 mx 1  6
Câu 23. Tồn tại bao nhiêu số nguyên m để hàm số  3  8 x m y e
 4 x  2020nghịch biến trên (2;) ? A. 7 B. 6 C. 5 D. 9
Câu 24. Tồn tại bao nhiêu số nguyên m thuộc [– 100;100] để phương trình sau có đúng hai nghiệm phân biệt 2 (log  3log  2) 9x  ( 1).3x x x m  m  0 . 2 2 A. 103 B. 102 C. 101 D. 100
Câu 25. Tìm điều kiện tham số m để bất phương trình sau có nghiệm 2 2
2log (sin x  m )  4log sin x  2sin x  cos 2x  2m 1  0 . 3 3 1 A. m   2; 2   B. m   C. Không tồn tại m. D. m = 0 4
_________________________________ 21