

























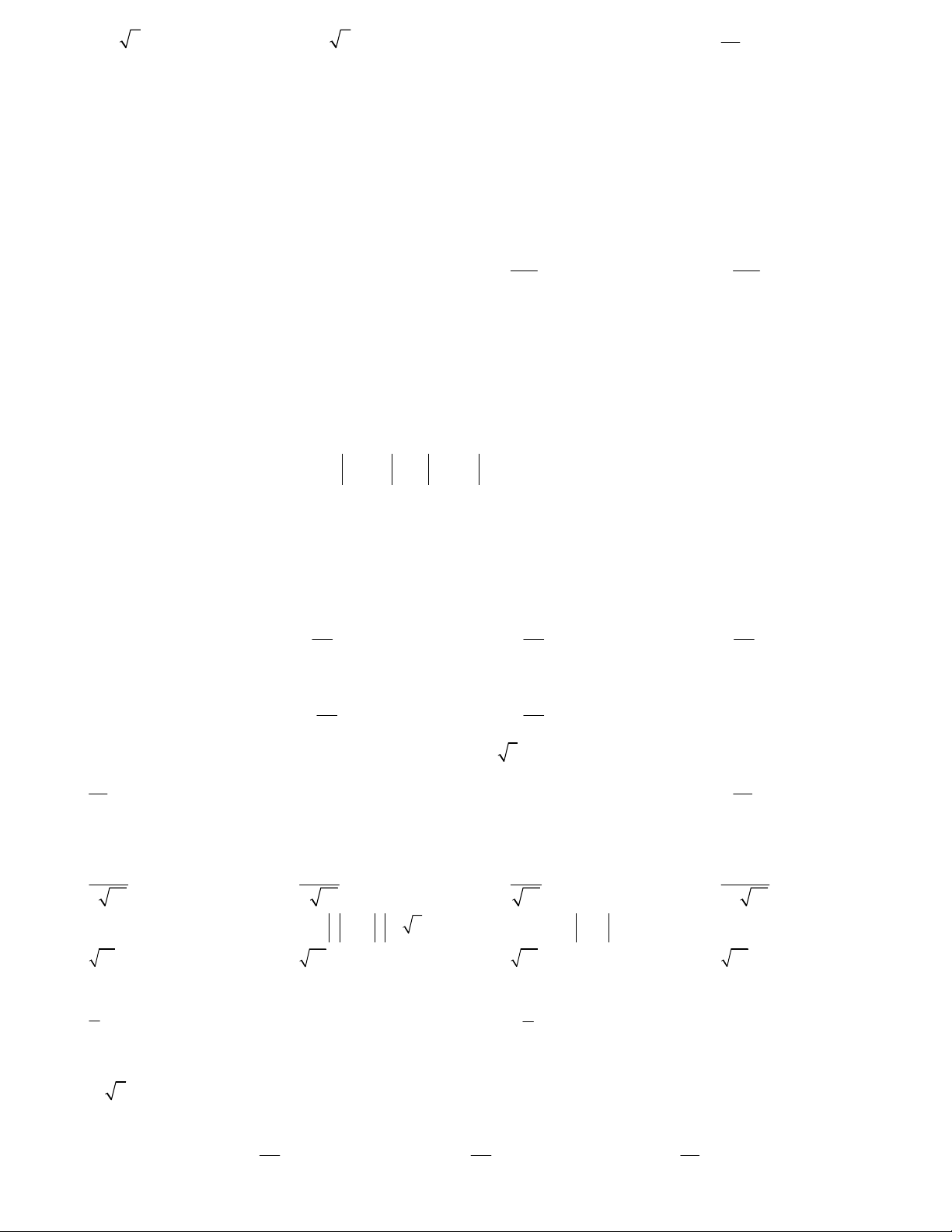
Preview text:
TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
--------------------------------------------------------------------------------------------
CHUYÊN ĐỀ VECTOR CƠ BẢN
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM VECTOR CƠ BẢN
CƠ BẢN TỔNG, HIỆU, PHÂN TÍCH VECTOR (P1 – P6)
CƠ BẢN ĐỘ DÀI VECTOR (P1 – P6)
CƠ BẢN TÍCH VÔ HƯỚNG VECTOR (P1 – P6)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
GACMA1431988@GMAIL.COM (GMAIL); TEL 0333275320
THÀNH PHỐ THÁI BÌNH – THÁNG 10/2022 1
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, TÍCH, PHÂN TÍCH VECTOR P1)
_________________________________________________
Câu 1. Cho ba điểm A, B, C phân biệt, điều kiện cần và đủ để A nằm giữa B và C là A. k
0; AB k AC B. k
0; AB k AC C. AB = AC D. AB AC
Câu 2. Trên đoạn thẳng AB lấy M, N sao cho AM = MN = NB. Có bao nhiêu vec tơ bằng vec tơ MA A.2 B. 1 C. 3 D. 4
Câu 3. Trên đoạn thẳng AB = 6 lấy M, N sao cho AM = MN = NB. Tính độ dài vec tơ MA MN AB . A. 3 B. 6 C. 1 D. 4
Câu 4. Cho tứ giác ABCD, có bao nhiêu vec tơ khác véc tơ không có điểm đầu và điểm cuối là 2 trong số 4 đỉnh của tứ giác A.4 B. 8 C. 6 D. 10
Câu 5. Hình vẽ sau có bao nhiêu cặp vec tơ bằng nhau A. 3 B. 1 C. 0 D. 2
Câu 6. Cho hình vuông ABCD. Tính AB AD . A. 0 B. AC C. AO D. DA
Câu 7. Cho tam giác ABC có trọng tâm G, D đối xứng với G qua trung điểm M của BC. Tính GB GC . A. GA B. GD C. 2GA D. 2GD MB MA
Câu 8. Cho hình bình hành ABCD. Tính . MD MC A.2 B. – 1 C. 1 D. – 2
Câu 9. Cho đường tròn tâm O bán kính R. Lấy hai điểm A, B trên đường tròn sao cho OA OB 0 . Có bao
nhiêu cặp điểm A, B thỏa mãn A.2 B. 3 C. 4 D. Vô số
Câu 10. Cho 3 điểm M , N , P tùy ý khi đó
A. MN NP PM
B. MN NP MP
C. NM NP MP
D. MN NP MP
Câu 11. Cho tam giác ABC ,để: MA MB MC 0 thì vị trí điểm M thỏa:
A. AMBC là hình bình hành
B. CBAM là hình bình hành
C. MACB là hình bình hành
D. MABC là hình bình hành
Câu 12. Cho tứ giác ABCD . Khẳng định nào sau đây đúng ?
A. AC BA BC
B. AB AD BD
C. BC BD CD
D. AD DB AB
Câu 13. Cho tam giác ABC có M; N; P lần lượt là trung điểm AB , AC , BC . Vectơ NM bằng 1 1 A. CP B. BC C. CP D. CB 2 2
Câu 14. Cho 3 điểm M , N , P thẳng hàng ; P nằm giữa M và N . Cặp vectơ nào sau đây ngược hướng với nhau ? A. MN; NP B. MN ; MP C. M ; P PN D. NM ; NP
2
Câu 15. Cho tam giác ABC có D là trung điểm của BC . Xác định vị trí của điểm G biết GA AD 0 3 2 1
A. G nằm trên đoạn AD và AG AD
B. G nằm trên đoạn AD và AG AD 3 3 1
C. G nằm trên đoạn AD và GD 2GA
D. G nằm trên đoạn AD và GA GD 3
Câu 16. Cho hình vuông ABCD . Gọi M , N lần lượt là trung điểm của AD , BC . Các vectơ bằng AM là:
A. MD, M , A BN
B. MD, BN , NC
C. MD, NB, NC
D. DM , BN , NC
Câu 17. Cho hình vuông ABCD . Khẳng định nào sau đây đúng ? 2
A. AD AB DB
B. BA BC BD
C. CA CB CD
D. DA DB BC
Câu 18. Cho tam giác ABC , M là điểm tùy ý. Tìm khẳng định đúng:
A. MA BC MC BA
B. MA BC MC BA
C. AC BM AM BC
D. AB CM AM BC
Câu 19. Gọi AD là trung tuyến của tam giác ABC , gọi E là trung điểm của AD . Khi đó 2EA EB EC bằng: 5 A. 2EA B. 0 C. 4EA D. EA 2
Câu 20. Cho hình thoi ABCD có M là trung điểm của cạnh AB, N là trung điểm cạnh CD.
MA MC MN MC MD Tính
. MC MD MA MC MN A.2 B. 3,5 C. 1 D. – 2
Câu 21. Điều kiện cần và đủ để MN PQ là chúng:
A. Cùng phương, cùng độ dài. B. Cùng hướng.
C. Cùng hướng, cùng độ dài. D. Cùng độ dài.
Câu 22. Cho A
BC và điểm K thỏa mãn KA KB KC 0 . Khẳng định nào sau đây đúng ?
A. ABKC là hình bình hành
B. K là trung điểm AB
C. ABCK là hình bình hành
D. K là trung điểm BC
Câu 22. Cho tam giác ABC , gọi M , N là trung điểm của AB và AC . Khi đó A. 2MN BC
B. - 2MN BC
C. 2MN BC D. MN BC CO OB
Câu 23. Cho hình bình hành ABCD tâm O. Tính . BA A.2 B. – 2 C. 1 D. – 1
Câu 24. Cho hình bình hành ABCD tâm O . Quy tắc nào sau đây là quy tắc hình bình hành?
A. OA OB 0
B. AB BC AC
C. CB CD CA
D. OA OB BA
Câu 25. Cho đoạn thẳng AB , gọi M là trung điểm và O là điểm tùy ý. Khẳng định nào sau đây sai: 1
A. MO ( AO BO)
B. AM BM 0
C. MB MA AB
D. OA OB 2OM 2
Câu 26. Cho tam giác ABC . Điểm M thỏa MA MB 2MC 0 , N là trung điểm AB . Khi đó
A. M thuộc CN sao cho CM 2NM
B. M thuộc CN sao cho CN 3NM
C. M nằm ngoại đoạn CN
D. M là trung điểm CN .
Câu 27. Cho 4 điểm bất kỳ A , B , C , D . Đẳng thức nào sau đây là đúng:
A. AB DB DA DC
B. DA AC DB BA
C. AD BC AC DB
D. AB CB AC BC
Câu 28. Cho tam giác ABC vuông tại C có cạnh AC 4 cm, BC 3cm. Tính độ dài AB A. 7cm B. 6cm C. 4cm D. 5cm
Câu 29. Cho tam giác ABC . Trên đoạn AB lấy điểm H sao cho AH = 2HB . Qua H dựng đường thẳng
song song với BC cắt AC tại I . Khi đó: 1 1 2 2 A. HI BC B. HI BC C. HI BC D. HI BC 3 3 3 3
Câu 30. Cho tứ giác ABCD . Khi đó:
A. BA CD BC AD
B. AD CB AC BD
C. AB CD AC BD
D. AB DC AC BD
Câu 31. Cho tam giác ABC . Xác định điểm M thỏa đẳng thức sau:. MA 2MB CB
A. Điểm M là trung điểm của AC
B. Điểm M là trọng tâm của tam giác ABC
C. Điểm M đối xứng với C qua B
D. Điểm M là một đỉnh của hình bình hành ABMC
Câu 32. Cho tứ giác ABCD . Gọi I , J lần lượt là trung điểm AC và BD . Gọi E là trung điểm IJ . Tìm đẳng thức vectơ đúng: 1
A. . EA EB 2EJ 0 B. . IJ ( AC BD)
C. EA EB EC ED 0 D. . AB DC 2IJ 2
Câu 33. Cho tam giác ABC . Gọi M , D lần lượt là trung điểm cạnh BC và AM , I là điểm tùy ý. Ta có
A. 2 AI IB IC 3ID
B. 2IA IB IC 4ID
C. 2IA IB IC 3ID
D. 2IA IB IC 4ID
_________________________________ 3
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, TÍCH, PHÂN TÍCH VECTOR P2)
_________________________________________________
Câu 1. Hai vectơ cùng hướng và cùng độ dài là hai vectơ A. Bằng nhau B. Đối nhau C. Ngược hướng D. Song song
Câu 2. Cho M là một điểm thuộc đoạn thẳng AB sao cho AB = 3AM . Hãy tìm khẳng định sai? 1 A. MB 2 MA B. MA 2 MB C. BA 3 AM D. AM BM 2
Câu 3. Cho hình bình hành ABCD , vectơ nào sau đây bằng CD ? A. DC B. BD C. AD D. BA
Câu 4. Cho hình bình hành ABCD tâm O . AD AB ? A. DB B. AC C. BD D. BC
Câu 5. Cho hình vuông ABCD tâm O . Véctơ bằng DO là: A. OC B. OA C. BO D. OB
Câu 6. Cho hình bình hành ABCD . Hai vec tơ nào ngược hướng? A. AB và AC B. AB và DC C. AB và DB D. AB và CD
Câu 7. Hai vectơ cùng phương thì chúng A. Cùng hướng B. Ngược hướng
C. Có giá song song hoặc trùng nhau D. Song song
Câu 8. Nếu I là trung điểm đoạn thằng AB thì với mọi điểm H ta luôn có
A. HA HB 2HI
B. AH BH 2HI
C. HA HB 2IH
D. AH BH 2IH
Câu 9. Chọn khẳng định đúng trong các hệ thức sau:
A. MP NM NP
B. AB AC BC
C. CA BA CB
D. AA AB BA
Câu 10. Cho hình bình hành ABCD . Khi đó đẳng thức nào sau đây đúng:
A. AB BC CD
B. AB AD BD
C. AB AD AC
D. AB AD CA
Câu 11. Cho tam giác ABC với trung tuyến AM và trọng tâm G .Khi đó GA =? 2 1 2 A. 2GM B. GM C. AM D. AM 3 2 3
Câu 12. Gọi I là trung điểm AB , M là điểm tùy ý. Đẳng thức nào đúng? 1 1
1 A. MI (MA MB) B. MI (MA MB)
C. 2IM (MA MB) D. MI (MA MB) 2 2 3
Câu 13. Cho đoạn thẳng AB . Gọi I là điểm đối xứng của A qua B . Gọi M là điểm tùy ý. Đẳng thức nào sau đây đúng:
A. IA IB 0
B. AI BI 0
C. MA MB 2MI
D. BA BI 0
A. AB CD AC BD
B. AB CD DA BC
C. AB CD AD BC
D. AB CD AD CB
Câu 14. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Khi đó:
A. AB AD BD
B. AB OA BO
C. AB BD 0
D. AB CD 0
Câu 15. Cho ba điểm A , B , C thẳng hàng và B là trung điểm AC . Tổng BA BC bằng A. 2 AC B. AC C. 0 D. 2CA Câu 16. Cho A
BC , M là điểm trên cạnh AB sao cho MB=3MA. Đẳng thức vectơ nào sau đây đúng? 1 5 1 5 1 1 1 A. MC CB CA B. MC CB 3CA C. MC CA CB D. MC CA CB 4 4 4 4 4 2 6
Câu 17. Cho 4 điểm A , B , C , D . khi đó
A. AB CD AC DB
B. AB CD AC DB
C. AB CD AC DB
D. AB CD AD DB 2
Câu 18. Cho tứ giác ABCD . Gọi I là trung điểm của cạnh AC , K là điểm thỏa. AK
AD Phân tích CK 3
theo CA và ID 2 2 2 2 2 2 2 2 A. CK CA ID B. CK CA ID C. CK CA ID D. CK CA ID 3 3 3 3 3 3 3 3
Câu 19. Cho hình bình hành ABCD . Đẳng thức nào sau đây đúng?
A. AB AC AD 2AB
B. AB AC AD 2 AC
C. AB AC AD 2 AD
D. AB AC AD 2BD 4
Câu 20. Cho 4 điểm A , B , C , D tùy ý. Chọn đẳng thức đúng
A. BA BC DA DC
B. BC BA DA DC
C. BA BC DC DA
D. BA BC DA DB
Câu 21. Cho hình bình hành ABCD . Khi đó CA CB CD bằng: A. 2 AC B. 2BD C. 2 AC D. 2BD
Câu 22. Cho hình thoi ABCD. Có bao nhiêu véc tơ có điểm đầu là 2 trong 4 đỉnh đồng thời bằng véc tơ AB A.2 B. 1 C. 3 D. Vô số
Câu 23. Cho tam giác ABC có trọng tâm G . Gọi I là điểm đối xứng của B qua G . Vectơ AI được phân tích
theo AB và AC là:
1 1
1 1 2 1 2 1 A. AI AC AB B. AI AC AB C. AI AC AB D. AI AC AB 3 3 3 3 3 3 3 3 Câu 24. Cho A
BC có trọng tâm G , I là điểm đối xứng của B qua G , M là trung điểm BC , đẳng thức nào đúng? 2 1
1 2 2 1
1 1 A. AI AC AB B. AI AC AB C. AI AC AB D. AI AC AB 3 3 3 3 3 3 3 3
Câu 25. Cho điểm B nằm giữa hai điểm A và C , AB 2 cm, AC 6 cm. Đẳng thức nào sau đây đúng? A. CB 2AB B. BC 2 BA C. AC 2BC D. AC 3 AB
Câu 26. Cho tứ giác ABCD , Gọi M ,N lần lượt là trung điểm của AB và DC , gọi I là trung điểm của MN , O
là một điểm tùy ý. Khi đó OB OC OD OA bằng: A. 4OI B. 4ON C. 0 D. 4OM
Câu 27. Cho ba điểm M , N , P bất kỳ. Khi đó đẳng thức nào sau đây đúng:
A. MN MP NP
B. MP NP MN
C. MN NP MP
D. MN PN MP
Câu 28. Cho tam giác ABC điểm I thoả:. IA 2IB Chọn mệnh đề đúng: CA 2CB CA 2CB AC 2CB A. CI B. CI C A 2CB C. CI D. CI 3 3 3 AB AF
Câu 29. Cho lúc giác đều ABCDEF. Tính . AD 1 A.2 B. 0,5 C. 0,25 D. 3
Câu 30. Cho tam giác ABC có trung tuyến AM . Gọi I là trung điểm của AM . Ta có:
A. IA IB 2IC 0
B. 2IA IB IC 0
C. IA IB IC 0
D. 2IA IB IC 4IA Câu 31. Cho AB
C có trọng tâm G , I là trung điểm của đoạn thẳng AG . Đẳng thức nào sau đây là đúng ?
1
A. GB GC GA
B. GB GC 2 AI C. IG IA D. GA 2GI 3
Câu 32. Cho tứ giác ABCD có E , H , I lần lượt là trung điểm của AB , CD , EH và M là một điểm tùy ý.
Tổng MA MB MC MD bằng: A. 0 B. 4ME C. 4MI D. 4MH
Câu 33. Cho bốn điểm A ; B ; C ; D tuỳ ý. Đẳng thức vectơ nào dưới đây đúng?
A. AB CD AD CB
B. AB CD AD DB
C. CA AB AD DB
D. CA AB AD CB
Câu 34. Cho tam giác ABC có điểm O thỏa mãn OA OB 2OC OA OB . Khi đó A. Tam giác ABC đều B. Tam giác ABC cân tại C
C. Tam giác ABC vuông tại C D. Tam giác ABC cân tại B
Câu 35. Hình bình hành ABCD có điểm M thỏa mãn 4 AM AB AD AC . Khi đó A. M là trung điểm AC B. M trùng với điểm C C. M là trung điểm AB D. M là trung điểm AD
Câu 36. Cho tam giác ABC và điểm M tùy ý. Tìm điểm D sao cho MA MB 2MC CD
A. D là điểm thứ tư của hình bình hành ABCD
B. D là điểm thứ tư của hình bình hành ACBD
C. D là trọng tâm tam giác ABC
D. D là trực tâm tam giác ABC Câu 37. Cho A
BC có trung tuyến AM ; I là trung điểm của AM . Tổng 2IA IB IC bằng: A. AM B. 0 C. 4IA D. 4IM 5
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, TÍCH, PHÂN TÍCH VECTOR – P3)
_________________________________________________
Câu 1. Cho hình bình hành ABCD. Tính OA OB OC OD . A. BA B. CB C. 0 D. 2OD IB IC
Câu 2. Cho tam giác ABC, M là trung điểm của BC, I là trung điểm AM. Tính AI A.2 B. 3 C. 1 D. 4
Câu 3. Cho hình bình hành ABCD có M là trung điểm của CD, điểm N thuộc đoạn BM sao cho BN = 2MN. Tính 2 AB BD giá trị của tỉ số . AC A.2 B. 1 C. 3 D. 4
MA MB MC
Câu 4. Cho tam giác ABC, G là trọng tâm. Với điểm M bất kỳ, tỉ số thuộc miền nào MG A.(0;1) B. [2;3] C. (3;5) D. [5;7) IA IC
Câu 5. Tứ giác lồi ABCD có M, N lần lượt là trung điểm AD, BC, I thỏa mãn IM IN 0 . Tính IB ID A.1 B. – 1 C. 2 D. – 2 MA MC MA MB
Câu 6. Cho hình bình hành ABCD. Với điểm M bất kỳ, tính
MB MD MC MD A.4 B. 2 C. 1 D. 2,5 AB AC
Câu 7. Cho tam giác ABC với trọng tâm G. Tính . AG A.3 B. 4 C. 2,5 D. 2
Câu 8. Cho hình bình hành ABCD có M là trung điểm của CD, điểm N thuộc đoạn BM sao cho BN = 2MN. Tính
a + b biết rằng AN a AB bBD . A.2 B. 3 C. 1 D. 1,5 DO AO
Câu 9. Cho hình bình hành ABCD. Tính . AB DC A.0,5 B. 1 C. 2 D. 2,5
Câu 10. Cho tam giác ABC có M, N lần lượt thuộc hai cạnh AB, AC sao cho AM = MB, NC = 2AN. Gọi K là trung 1 1 điểm của MN. Tính AB AC . 4 6 1 A.2 AK B. AK C. 3 AK D. AK 2
EA EB 2EC
Câu 11. Cho hình bình hành ABCD, E là trung điểm đoạn AD, tính . AB A.3 B. 2 C. 4 D. 1
Câu 12. Cho hình bình hành ABCD, M là trung điểm CD. Hệ thức nào sau đây đúng 1
1 A. AM AC AB
B. 2 AM AC AB 2 2 1 1
C. AM 2 AC AB D. AM AC AB 2 2
2OA OB OC
Câu 13. Cho tam giác ABC, M là trung điểm của BC, I là trung điểm AM. Tính OI A.3 B. 4 C. 2 D. 2,5 6 AC BD 2EF
Câu 14. Cho tứ giác lồi ABCD, E và F lần lượt là trung điểm của AB, CD. Tính EF AD BC A.3 B. 4 C. 2,5 D. 1
Câu 15. Cho hình bình hành ABCD, E là trung điểm đoạn AD. Tính EB 2EB 4ED . A. EC B. 2 EC C. 3 EC D. – EC
AB AC AD
Câu 16. Tứ giác lồi ABCD có E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tính AI A.3 B. 4 C. 2 D. 5
Câu 17. Cho tam giác ABC, trên hai cạnh AB, AC lần lượt lấy hai điểm D, E sao cho AD 2DB,CE EA . Gọi
M là trung điểm của DE và I là trung điểm của BC. Tính 6a + 8b biết MI a AB b AC . A.3 B. 5 C. 4 D. 2
Câu 18. Cho hình bình hành ABCD có H, K lần lượt thuộc hai cạnh AB, AC sao cho 3AH = 2AB, 3AK = AC. Trên
cạnh BC lấy điểm M sao cho 4BM = 3MC. Khi đó 1 1 9 9 A. BM AK AH B. BM AK AH 4 7 7 14 9 9 3 5 C. BM AK AH D. BM AK AH 7 14 7 14
Câu 19. Cho hình bình hành ABCD có M là trung điểm của BC, G là trọng tâm tam giác ACD. Tính a + b biết
rằng a, b thỏa mãn MG a AB b AD . A.0,5 B. – 0,5 C. 1 D. – 1
Câu 20. Cho tam giác ABC có M, N, P lần lượt là trung điểm của AB, BC, CA. Gọi G là trọng tâm tam giác ABC.
Tính tổng vecto AM BN CP . 1 1 1 A. 0 B. AB C. CB D. AC 2 2 2
Câu 21. Cho hình bình hành ABCD có I là trung điểm BC, G là trọng tâm tam giác CDI. Khi đó đặt các véc tơ AB ;
a AD b thì véc tơ AG được biểu thị là 2 5 2 5 2 1 1 5 A. a b B. a b C. a b D. a b 3 6 3 6 3 6 3 6
Câu 22. Cho tam giác ABC có M, N lần lượt thuộc hai cạnh AB, AC sao cho AM = MB, NC = 2AN. Gọi K, P lần
lượt là trung điểm của MN, BC. Mệnh đề nào sau đây đúng 1 1 1 1 A. KP AB AC B. KP AB AC 4 6 6 8 1 1 1 2 C. KP AB AC D. KP AB AC 4 3 4 3
Câu 23. Cho hình bình hành ABCD có M là trung điểm của CD, điểm N thuộc đoạn BM sao cho BN = 2MN. Tính 3AB 4CD
giá trị của biểu thức .
CM ND MN A.2 B. 3 C. 4 D. 1
Câu 24. Cho tam giác ABC, trên hai cạnh AB, AC lần lượt lấy hai điểm D, E sao cho AD 2DB,CE EA . Gọi
M là trung điểm của DE và I là trung điểm của BC. Tính 3a + 8b biết AM a AB b AC . A.3 B. 5 C. 1 D. 2
Câu 25. Cho tam giác ABC có trọng tâm G, H là điểm đối xứng với B qua G, M là trung điểm của BC. Khi đó 1 5 1 5 A. MH AC AB B. MH AC AB 3 6 3 6 1 5 1 1 C. MH AC AB D. MH AC AB 6 6 4 6
Câu 26. Cho tam giác ABC có I, J, K lần lượt là trung điểm của AB, BC, CA. Điểm D thuộc đoạn BC sao cho
3DB = 2BC, M là trung điểm của đoạn AD. Tính a + b biết 6BM a AC b AB . A.2 B. – 2 C. – 3 D. – 1 7
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, TÍCH, PHÂN TÍCH VECTOR – P4)
_________________________________________________
Câu 1. Cho hình bình hành ABCD . Khẳng định nào sau đây đúng? A. AD BC B. AB AC C. AC DB D. AB CD
Câu 2. Cho hình bình hành ABCD . Đẳng thức vectơ nào sau đây đúng:
A. DA DC DB
B. BA BD BC
C. DA DB DC
D. AB AC AD
Câu 3. Cho hình bình hành ABCD . Đẳng thức vectơ nào sau đây đúng?
A. AD AC AB
B. AB AD BD
C. AB AC AD
D. AB AD AC
Câu 4. Cho tam giác ABC có trọng tâm G và M là trung điểm của AB . Đẳng thức nào sau đây sai?
A. GA GB GC 0
B. GA GB 2GM
C. MA MB MC 0
D. MA MB MC 3MG 1
Câu 5. Cho tam giác ABC . N là trung điểm AB , M là điểm thoả đẳng thức MN
AB AC . Kết luận nào 2 dứơi đây đúng:
A. M đối xứng với C qua A ;
B. A đối xứng với M qua C ;
C. C đối xứng với A qua M
D. M là điểm tuỳ ý.
Câu 6. Cho tam giác ABC , trên hai cạnh AB , AC lấy hai điểm D và E sao cho AD 2DB , AE 3EA . Gọi
M là trung điểm của DE và I là trung điểm của BC . Đẳng thức vectơ nào sau đây đúng? 1 3 1 3 1 3 1 3 A. MI AB AC B. MI AB AC C. MI AB AC D. MI AB AC 6 8 6 8 6 8 6 8
Câu 7. Tìm x để hai vec tơ u (x 1) AB 4 AC; v 3AB 2 AC cùng hướng. A.x = 5 B. x = 1 C. x = 3 D. x = 2
Câu 8. Cho tam giác ABC, M là trung điểm của cạnh AB, N thuộc cạnh AC sao cho NC = 2AN. Gọi H, K lần lượt
là trung điểm của MN, BC. Tính 4m + 12n biết HK m AB n AC . A.7 B. 8 C. 5 D. 6
BA BC BD
Câu 9. Cho hình bình hành ABCD tâm O. Tính . OD A.4 B. 3 C. 2 D. 6
Câu 10. Cho tam giác ABC, các điểm M, N, P thỏa mãn MB 3MC, NA 3CN , PA PB 0 . Tính giá trị tổng
m + n biết rằng PN m AB n AC . A.1 B. 0,25 C. 0,5 D. 2
OA OB OC OD
Câu 11. Cho tứ giác ABCD. Gọi M, N, I lần lượt là trung điểm của AC, BD, MN. Tính OI A.3 B. 4 C. 6 D. 8
Câu 12. Cho tứ giác ABCD, các điểm M, N lần lượt thuộc các cạnh AB, CD sao cho MB = 2MA, NC = 2DN. Tính
tổng 6a + 3b biết rằng MN p AD qBC . A.4 B. 5 C. 6 D. 8 2
Câu 13. Cho tam giác ABC, điểm D thỏa mãn BD
BC , I là trung điểm của AD, M là điểm thỏa mãn 3 2 AM
AC . Mệnh đề nào sau đây đúng 5 1 1 1 1 A. BI BA BC B. BI BA BC 2 3 2 3 1 1 1 1 C. BI BA BC D. BI BA BC 2 6 4 6
Câu 14. Cho tam giác ABC với AD là đường phân giác trong. Biết AB = 5, BC = 5, AC = 7. Khi đó 5 7 7 5 A. AD AB AC B. AD AB AC 12 12 12 12 7 5 5 7 C. AD AB AC D. AD AB AC 12 12 12 12 8
Câu 15. Cho hình bình hành ABCD tâm O, xác định vị trí điểm K thỏa mãn KA KB KC 3KD 0
A.K là trung điểm của đoạn OD
B. K là trọng tâm tam giác ACD
C.K là trọng tâm tam giác ABD
D. K là trọng tâm tam giác ABC
Câu 16. Tam giác ABC có hai trung tuyến AK, BM. Khi đó 2 2 A. AB
AK BM B. AB
AK BM 3 3 1 3 C. AB
AK BM D. AB
AK BM 3 2
Câu 17. Cho tam giác ABC có u 2 AB 3BC AC . Khi đó
A. u 2 AB 3AC
B. u AB 3AC
C. u 2 AB 4 AC
D. u AB 2 AC
Câu 18. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 2a; AC 3a . Khi đó 9 4 4 5 A. AH AB AC B. AH AB AC 13 13 9 9 9 4 2 3 C. AH AB AC D. AH AB AC 13 13 5 5
Câu 19. Cho tam giác ABC có trọng tâm G, điểm M thỏa mãn MA MB 4MC 0 . Khi đó
A. M là trọng tâm tam giác ABG B. M là trung điểm CG C. MGAC là hình bình hành D. ABCM là hình bình hành
Câu 20. Cho tam giác ABC, các trung tuyến AM, BN, CP. Khi đó 4 2 4 2 A. AB AN CP B. AB AN CP 3 3 3 3 4 2 2 4 C. AB AN CP D. AB AN CP 3 3 3 3
Câu 21. Cho tam giác ABC có AB = 3a, AC = 2a, phân giác trong AD. Khi đó tính a + 2b với AD a AB b AC A.1,6 B. 2,4 C. 1,8 D. 2,6
Câu 22. Cho tam giác ABC có trọng tâm G, D là trung điểm của BG. Tính 3a + 12b với AD a AB b AC . A.4 B. 6 C. 5 D. 3
Câu 27. Cho tam giác ABC, M là trung điểm của BC, N là trung điểm của AM. Đường thẳng BN cắt AC tại P. Khi
đó tìm x để AC xCP 4 5 3 2 A. x B. x C. x D. x 3 3 2 3 AB AD
Câu 28. Cho hình bình hành ABCD, trên đường chéo BD lấy G, H sao cho DG = GH = HB. Tính AG AH A.1 B. 2 C. 1,5 D. 3
Câu 29. Cho hình bình hành ABCD, M và N tương ứng là trung điểm BC, CD. Tính AM AN : AC A.1,5 B. 2 C. 1 D. 3
Câu 30. Cho hai tam giác ABC, A’B’C’ có trọng tâm lần lượt là G, G’. Điều kiện hai tam giác có cùng trọng tâm là
A. A A B B C C 0 B. A A B B C C AG
C. AA B B C C AB D. A A B B C C BC
Câu 31. Cho tam giác ABC có trọng tâm G, EA 2EB,3FA 2FC 0 . Khi đó 1 2
A. EF 2 AB AC
B. EF 2 AB AC 2 5 1 3
C. EF 3AB AC
D. EF 4 AB AC 4 4
Câu 32. Cho tam giác ABC, điểm M thỏa mãn 4BM 3MC . Tính 12a + 12b biết AM a AB b AC . A.12 B. 10 C. 8 D. 6
_________________________________ 9
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, TÍCH, PHÂN TÍCH VECTOR – P5)
_________________________________________________
Câu 1. Cho ba điểm A , B , C phân biệt. Đẳng thức nào sau đây là đẳng thức đúng?
A. AB BC CA .
B. CA AB CB .
C. BA AC CB .
D. AB CB AC .
Câu 2. Cho hình bình hành ABCD . Khẳng đinh nào sau đây sai?
A. AD BC 0 .
B. AB CD 0 .
C. AB AD AC .
D. AB AC CB .
Câu 3. Cho hình bình hành ABCD có tâm O . Khẳng định nào sau đây là đúng?
A. AB AC DA . B. AO AC . BO
C. AO BO CD .
D. AO BO D B .
Câu 4. Ta có MN QP RN PN QR MN QP QR PN RN MN RP PR MN .Cho hình
bình hành ABCD . Đẳng thức nào sau đây đúng?
A. BA BC DC CB .
B. BA BC DC BC .
C. BA BC DC AD .
D. BA BC DC CA.
Câu 5. Cho tam giác ABC . Gọi D, E, F lần lượt là trung điểm của các cạnh BC,C ,
A AB . Đẳng thức nào sau đây đúng?
A. AD BE CF AF CE BD .
B. AD BE CF AB AC BC .
C. AD BE CF AE AB CD .
D. AD BE CF BA BC AC .
Câu 6. Cho bốn điểm A ; B ; C ; D tuỳ ý. Đẳng thức vectơ nào dưới đây đúng?
A. AC AD BD BC
B. CA DB AD BC
C. AC BD DA CB
D. AC BD AD BC
Câu 7. Cho ba điểm A , B , C phân biệt. Mệnh đề nào dưới đây đúng? A. AB AC
B. Nếu AB BC thì AB BC
C. Nếu AB = BC thì AB BC D. AB BA Câu 8. Cho A
BC với M , N , P lần lượt là trung điểm của AB , BC , CA . Đẳng thức vectơ nào sau đây đúng 1
1 1 A. MN AC
B. AM BN CP 0 C. MA BN D. MP CP 2 2 2
Câu 9. Vectơ tổng MN PQ RN QR NP bằng? A. MN B. MP C. PR D. MR
Câu 10. Cho tam giác ABC có trung tuyến AI , D là trung điểm của AI . Đẳng thức nào sau đây đúng
A. DA DB DI
B. DA DB DC 0
C. AB AC AI
D. DA DB DC
Câu 11. Cho hình bình hành ABCD tâm O . Vectơ AD bằng vectơ nào sau đây? A. BC B. CB C. AB D. DC
Câu 12. Gọi G là trọng tâm của tam giác ABC , M tùy ý khi đó
A. MA MB MC 2MG
B. GA GB GC 3GM
C. MA MB MC 3MG
D. MA MB MC MG
Câu 13. Cho hình bình hành ABCD . Đẳng thức nào sau đây đúng: A. AB CD B. DA BC C. AD BC D. AD CB
Câu 14. Tam giác ABC có điểm I thỏa mãn IA 3IB . Đẳng thức nào sau đây đúng 3 1
A. CI CA 3CB B. CI CA CB 2 2 1 C. CI CA 3CB
D. CI 3CA CB 2
Câu 15. Gọi M, N lần lượt là trung điểm của các cạnh AB và CD của tứ giác ABCD. Mệnh đề nào sau đây đúng
A. AC BD BC AD 4MN
B. AC BD 4MN
C. BC AD 4MN
D. AC BD BC AD MN
Câu 16. Cho hình bình hành ABCD , M là điểm tùy ý. Đẳng thức vectơ nào sau đây đúng?
A. MB MC MD MA 0
B. MB MC MD MA
C. MA MC MB MD
D. MD MC MB MA Câu 17. Cho A
BC có trung tuyến AI , D là trung điểm AI . Đẳng thức nào sau đây đúng mọi điểm O? 10
A. OA OB OC 3OI
B. 2OA OB OC 0
C. OA OB OC 0
D. 2OA OB OC 4OD
Câu 18. Cho tam giác ABC , gọi E là trung điểm của AC . Một điểm N thỏa: NA NC 2BN . Đẳng thức vectơ nào sau đây đúng?
A. N là trung điểm BC
B. N là trung điểm AC
C. N là trọng tâm tam giác ABC
D. N là trung điểm BE
Câu 19. Cho tam giác ABC và điểm I thỏa mãn IA 2BI . Tính m + n biết rằng CI mCA nCB . A.1 B. 2 C. 3 D. – 3 AC BD
Câu 20. Cho hình bình hành ABCD. Tính . 2 A. AB B. AD C. CB D. DC Câu 21. Cho A
BC có D thuộc cạnh AC sao cho AD 2DC . Gọi E , H và I lần lượt là trung điểm của
AB , BC và ED . Đẳng thức vectơ nào sau đây đúng? 2 1 2 1 2 1 2 1 A. AI AH AB B. AI AH AB C. AI AH AB D. AI AH AB 3 2 3 12 3 12 3 2
Câu 22. Khẳng định nào sau đây là đúng?
A. Hai vectơ a, ka luôn cùng hướng
B. Hai vectơ a, ka luôn cùng phương
C. Hai vectơ a, ka bằng độ dài
D. Hai vectơ a, ka luôn ngược hướng Câu 23. Cho A
BC , N là điểm trên cạnh AB sao cho AN 2NB . Biểu diễn CN theo AB và AC là: 2
1 2 1 2 A. CN AB AC B. CN AB AC C. CN
AB AC D. CN AB AC 3 3 3 2 3
Câu 24. Cho hình bình hành ABCD . Tổng CB CD bằng: A. BD B. AC C. CA D. DB
Câu 25. Cho hình bình hành ABCD tâm O . Đẳng thức vectơ nào dưới đây đúng?
A. OA OB CO DO
B. OA OD OB OC
C. OA BO OC DO
D. OA OB OC OD
Câu 26. Cho tam giác ABC có trung tuyến AB . Xác định điểm I sao cho 2IA 3IB IC 1 1 A. MI 4CB B. MI CB C. MI 4BC D. MI BC 4 4
Câu 27. Điểm M thuộc cạnh BC của tam giác ABC sao cho BC 3BM . Khi đó AM a AB b AC , tính giá trị biểu thức 3a + 6b. A.3a + 6b = 7 B. 3a + 6b = 10 C. 3a + 6b = 4 D. 3a + 6b = 2
Câu 28. Cho tam giác ABC , có trung tuyến AM và trọng tâm G . Khẳng định nào sau đây là đúng
2
A. AM AB AC B. AG
AB AC 3
C. 3MG MA MB MC D. AM 3MG
Câu 29. Cho hình chữ nhật ABCD tâm O, điểm M bất kỳ. Tìm số thực m sao cho MB MC MD MA mMO . A.m = 4 B. m = 5 C. m = 2 D. m = 3
Câu 30. Cho 4 điểm A , B , C , D phân biệt. Đẳng thức vectơ nào sau đây sai:
A. AB BD AD
B. DA AB DB
C. BA AC BC
D. DA BD AB
Câu 31. Cho tam giác ABC có trọng tâm G . Gọi I là trung điểm của AG . Đẳng thức vectơ nào sau đây đúng? 1 1 2 1
1 1 1 1
A. CI CA CB B. CI CA CB C. CI CA CB
D. CI CA CB 3 6 3 6 3 6 3 6
Câu 32. Cho tam giác ABC có trọng tâm G, giả sử CG xCA yCB . Tính 6x + 9y. A. 1 B. 5 C. – 1 D. – 2
Câu 33. Cho tam giác ABC . Gọi G là trọng tâm, M là trung điểm của BC và D là điểm đối xứng với B qua
G . Đẳng thức vectơ nào sau đây đúng? 3 5
1 2 1 5 1 5 A. MD AC AB B. MD AC AB C. MD AC AB D. MD AC AB 4 4 3 3 6 6 2 2
_________________________________ 11
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, PHÂN TÍCH VECTOR P6)
___________________________________________
Câu 1. Tam giác ABC có điểm M thuộc cạnh BC sao cho BM = 3MC. Tính 16a + 60b khi AM a AB b AC . A.30 B. 25 C. 49 D. 40
Câu 2. Cho tam giác ABC . Gọi M và N lần lượt là trung điểm của AB và AC . Ta có:
A. BA AC 2NM 0
B. BC NM 0
C. AB BC CM 0
D. BC NM 0
Câu 3. Cho 4 điểm A , B , C , D tùy ý. Nếu AB CD thì A. AC DB B. CD AD C. AC BD D. CA BD Câu 4. Cho A
BC có M , N , P lần lượt là trung điểm của AB , BC , CA . Hãy chọn đẳng thức vectơ đúng:
A. NA NB NC NP 4NM
B. AP BM CN 0
C. AN BP CM 0
D. PA PB 2PN 0
Câu 5. Cho hình bình hành ABCD có tâm O . Khẳng định nào sau đây là đúng ?
A. AO BO AB
B. AO BO AD
C. AO BO BD
D. AO BO BA
Câu 6. Cho hình bình hành ABCD . Đẳng thức nào sau đây là đúng ?
A. AB AD AC
B. AC BD 2CD
C. AC BC AB
D. AC AD CD
Câu 7. Cho tam giác ABC có G là trọng tâm. Đẳng thức nào sau đây là sai?
A. MA MB MC 0, M
B. AG BG CG 0
C. GA GB GC 0
D. MA MB MC 3MG, M
Câu 8. Với ba điểm M , N , P tùy ý. Ta luôn có
A. MN NP MP
B. MN PN MP
C. MN NP PM
D. MN PN PM
Câu 9. Cho hình bình hành ABCD . Đẳng thức nào sao đây là đúng?
A. DA DB DC 0
B. DA DB BA 0
C. DA DB DC 0
D. DA DB DC 0
Câu 10. Cho ba điểm A , B , C thẳng hàng, trong đó điểm B nằm giữa hai điểm A và C . Khi đó các cặp vecto
nào sau đây cùng hướng? A. CB và AB B. AB và AC C. AB và CB D. BA và BC Câu 11. Cho A
BC có trọng tâm G , I là điểm thỏa bởi IA 2.IB . Đẳng thức vectơ nào dưới đây đúng? 5 1 5 1 5 1 5 1 A. IG AB AC B. IG AB AC C. IG AB AC D. IG AB AC 3 3 3 3 3 3 3 3
Câu 12. Cho hình bình hành ABCD , khi đó
A. AB AD BD
B. AB AD CA
C. AB AD AC
D. AB AD DB
Câu 13. Cho hình bình hành ABCD . Mệnh đề nào dưới đây đúng? A. Hai vectơ A ; B BC cùng phương B. Hai vectơ A ; B CD cùng phương C. Hai vectơ A ; B CD cùng hướng D. Hai vectơ A ;
B DC ngược hướng
Câu 14. Cho tam giác ABC . Gọi M là trung điểm cạnh BC . Chọn đẳng thức đúng
A. AB AC AM 0
B. AB AC 2 AM 0
C. AB AC AM 0
D. AB AC 2 AM 0
Câu 15. Cho ba điểm A , B , C phân biệt. Tổng CB AC bằng: A. BA B. 0 C. AB D. AB Câu 16. Cho A
BC có trung tuyến AI và trọng tâm G . Khẳng định nào sau đây sai ?
A. GB GC 2GI
B. IA IB IC 3IG
C. GA GB GC 0
D. AB AC AI
Câu 17. Cho hình chữ nhật ABCD có AB 3 và AD 4 . Khẳng định nào sau đây đúng ? A. CD BC B. AC AB C. AC BD D. BD =7
Câu 18. Khẳng định nào sau đây là khẳng định sai?
A. Tích của một số với một vecto là một số.
B. Tích của một số với một vecto là một vectơ
C. Nếu k 0 thì vecto ka cùng hướng với vecto a
D. Nếu k 0 thì vecto ka ngược hướng với vecto a
Câu 19. Cho hình bình hành ABCD tâm O . Khẳng định nào sau đây sai?
A. OA OD BA
B. AB AD DB C. OC OD
D. AB AD AC
Câu 20. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Khẳng định nào sau đây sai:
A. AC BA AD
B. AO OD DC
C. DA DB DC 0
D. CO OB BA
Câu 21. Cho hình bình hành ABCD , tâm I . Số các vectơ cùng hướng với vectơ AC là: 12 A. 6 B. 3 C. 5 D. 4
Câu 22. Cho tứ giác ABCD có I, J, K lần lượt là trung điểm của AB, CD, IJ. Tìm k để CA CB CD kCK . A.k = 1 B. k = 4 C. k = 2 D. k = 3
Câu 23. Cho hình bình hành ABCD tâm O, I là trung điểm của cạnh BC. Tính m + n biết rằng AI m AD n AB . A.1 B. 3,5 C. 2,5 D. 4,5
Câu 24. Chọn khẳng định đúng:
A. Hai vectơ cùng phương thì chúng cùng hướng
B. Hai vectơ cùng phương thì giá của chúng song song hoặc trùng nhau
C. Hai vectơ có giá vuông góc thì cùng phương
D. Hai vectơ ngược hướng với 1 vectơ thứ ba thì cùng phương
Câu 25. Cho hình bình hành ABCD tâm O . Các véctơ ngược hướng với OB là:
A. BD, OD
B. DB, OD, OB C. DB, DO
D. BD, OD, BO
Câu 26. Cho tam giác ABC . Hãy xác định điểm M thỏa mãn: 2MA 3MB 0 .
A. M thuộc cạnh AB và AM 2MB
B. M không thuộc AB
C. M là trung điểm của AB
D. M trên AB và ngoài đoạn AB
Câu 27. Cho ba điểm phân biệt A , B , C . Đẳng thức nào sau đây là đúng ?
A. CA BA BC
B. AB AC BC
C. AB BC CA
D. AB CA CB
Câu 28. Cho hình bình hành ABCD tâm O . Vectơ AB cùng hướng với vectơ nào sau đây? A. AD B. DC C. CD D. BC
Câu 29. Cho tam giác ABC, điểm M thuộc cạnh BC sao cho AM x AB y AC . Tính x y . 2 1 A.1 B. – 1 C. D. 3 3
Câu 30. Cho tam giác ABC có điểm I thuộc cạnh AC sao cho AC 4IC . Tính m + 2n biết BI m AC n AB . A.2,5 B. 2,75 C. – 1,5 D. – 1,25
Câu 31. Cho hình bình hành ABCD tâm O . OA AB ? A. BO B. AC C. OB D. BA
Câu 32. Cho tam giác ABC, I là trung điểm AB và M là trung điểm CI. Mệnh đề nào sau đây đúng
A. MA MB 2MC 0
B. MA MB MC 0
C. MA 2MB MC 0
D. 2MA MB MC 0
Câu 33. Hình bình hành ABCD có M là trung điểm của CD, N là trung điểm của BM. Tính giá trị p + b biết rằng
AN p AB q AD . A.1 B. 1,25 C. 2,5 D. 2
Câu 34. Cho hình bình hành ABCD; M , N lần lượt là trung điểm của AB; CD; Đẳng thức vectơ nào dưới đây sai?
A. NA MB CN DM 0
B. MA MB CN DN
C. NA MB MC ND
D. NA BN CM MD 0
Câu 35. Cho tứ giác ABCD, I và J lần lượt là trung điểm BC và AD. Tìm k biết rằng AB AI JA DA k DB . A.k = 1 B. k = 2,5 C. k = 3 D. k = 1,5
Câu 36. Cho tam giác ABC, I là trung điểm của AB. Tìm điểm M thỏa mãn MA MB 2MC 0
A. M là trung điểm của BC
B. M là trung điểm của IC
C. M là điểm thuộc đoạn IC sao cho IM = 2MC
D. M là trung điểm của IA
Câu 37. Cho tứ giác ABCD có điểm E thỏa mãn AE EB 3EC . Tính m n p biết rằng
DE mDA nDB pDC . 17 A.1 B. 2 C. 1,25 D. 15
Câu 38. Cho 3 điểm A , B , C không thẳng hàng. Tìm khẳng định đúng
A. AB CA BC
B. AB BC CA 0
C. AB BC AB BC
D. AB BC AC
Câu 39. Cho tứ giác ABCD, điểm M tùy ý, tồn tại a, b sao cho MA 4MB 3MC a AB bBC . Tính a + b. A.2,5 B. 4 C. 5 D. 2
_________________________________ 13
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P1)
_________________________________________________
Câu 1. Cho đoạn thẳng AB = a và điểm M thỏa mãn MA 3MB . Tính MB 2 A.0,5a B. 0,25a C. a D. 0,75a 3
Câu 2. Cho đoạn thẳng AB = 6a và điểm M thỏa mãn MA 5MB . Tính MB 2 A.a B. 0,25a C. a D. 0,75a 3
Câu 3. Cho tam giác đều ABC cạnh a. Tính độ dài vec tơ AB BC 4 AC A.2a B. a C. 5a D. 2a 3
Câu 4. Cho hình vuông ABCD tâm O, cạnh a. Tính AB DC . A.2a B. a 5 C. a 2 D. 0
Câu 5. Cho hình vuông ABCD tâm O, cạnh a. Tính AB 2DC . A.2a B. a 5 C. a 2 D. 3a
Câu 6. Cho hình vuông ABCD tâm O, cạnh a. Tính 4 AB 3DC 2CD . A.3a B. a 5 C. a 2 D. 5a
Câu 7. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ AB BC 4 AO . A. 3a 2 B. a 5 C. 6a 2 D. 4a 3
Câu 8. Cho tam giác đều ABC cạnh a. Tính độ dài vec tơ AB AC A.2a B. a C. a 3 D. 2a 3
Câu 9. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ AB AD . A.2a B. a 5 C. a 2 D. a 3
Câu 10. Cho tam giác đều ABC cạnh a, trọng tâm G, đường cao AH. Tính độ dài vec tơ AG 2GH 3AH 10a 3 8a 3 A. B. C. a 3 D. 2a 3 3 3
Câu 11. Cho hình thang vuông ABCD tại A, D có AB = AD = a, DC = 2a. Tính AB DC A.3a B. 4a C. a D. a 5
Câu 12. Cho hình thang vuông ABCD tại A, D có AB = AD = a, DC = 2a. Tính 2 AB 5CD A.3a B. 4a C. a D. a 5
Câu 13. Cho tam giác ABC đều cạnh a, trọng tâm G. Tính GA GC 4 1 A. 2a 3 B. a 3 C. a 3 D. a 3 3 3
Câu 14. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài véc tơ AB AC . A.2a B. a 5 C. a 2 D. a 3
Câu 15. Cho tam giác đều ABC cạnh a, trọng tâm G. Tính độ dài vec tơ AB AC 2 AG 5a 3 A. B. a C. a 3 D. 2a 3 3
Câu 16. Cho hình thang vuông ABCD tại A, D có AB = AD = a, DC = 2a. Tính AD AC A.3a B. 2a 2 C. a D. a 5
Câu 17. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ AB AD 2 AC . 14 3a 2 A. a 5 B. 3a 2 C. a 3 D. 2
Câu 18. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ 3AB 4 AO . A. a 5 B. a 29 C. a 3 D. 2a 17
Câu 19. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a. Tính AB 3AD . A. a 97 B. a 29 C. 5a 13 D. 2a 17
Câu 20. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a. Tính AB 4 AD . A. a 97 B. a 29 C. 4a 10 D. 2a 17
Câu 21. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a. Tính AB CA . A. a 97 B. a 29 C. 4a 10 D. a 73
Câu 22. Cho tam giác ABC đều cạnh a, trọng tâm G. Tính 2BG GA GC 4 3a 2 A. 2a 3 B. a 3 C. a 3 D. 3 2
Câu 23. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ AB 2 AD . 3a 2 A. a 5 B. 3a 2 C. a 3 D. 2
Câu 24. Cho tam giác đều ABC cạnh a. Tính độ dài vec tơ GA GC 16GB A.6a B. 7a 3 C. 5a 3 D. 2a 3
Câu 25. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a. Tính AB 4 AC . A. a 97 B. 5a 29 C. 4a 10 D. 4a 34
Câu 26. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a. Tính AB 4 AC . A. 8a 5 B. a 29 C. 4a 10 D. 16 2
Câu 27. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ AB 2 AC . A. a 5 B. 3a 2 C. a 3 D. a 13
Câu 28. Cho tam giác ABC đều cạnh a, trọng tâm G, đường cao AH. Tính AH AC a 13 A. B. a 5 C. a 13 D. a 3 2
Câu 29. Cho tam giác đều ABC cạnh a, trọng tâm G, đường cao AH. Tính độ dài vec tơ AG 2CH a 6 2a 6 A. B. C. a 3 D. 2a 3 3 3
Câu 30. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ AB 3AO . a 34 3a 2 A. a 5 B. C. a 3 D. 2 2
Câu 31. Cho tam giác đều ABC cạnh a. Tính độ dài vec tơ GA AC 2GB A.2a B. a C. a 3 D. 2a 3
Câu 32. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ AC BD 7BC . A. a 5 B. 9a C. a 3 D. 10a
Câu 33. Cho tam giác đều ABC cạnh a. Tính độ dài vec tơ GA 2GC 3GB A.2a B. a C. a 3 D. 2a 3
_________________________________ 15
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P2) _____________________________
Câu 1. Cho hình chữ nhật ABCD có AB = 3 , BC = 4 . Độ dài của AC là: A. 5 B. 6 C. 9 D. 7
Câu 2. Cho hình vuông ABCD cạnh a . Khi đó độ dài của AC bằng: a 3 a 2 A. a 2 B. a 3 C. D. 2 2
Câu 3. Cho ABCD là hình vuông cạnh bằng 1. Khi đó độ dài của AC bằng A. 1 B. 2 C. 2 D. 3
Câu 4. Cho tam giác ABC là tam giác vuông tại A , cạnh AB 2a , ACB 30
. Tính AB AC A. a 3 B. a C. 2a 3 D. 4a
Câu 5. Cho tam giác đều ABC cạnh a. Tính độ dài vec tơ GA 2GC 4GB a 93 A.2a B. C. a 3 D. 2a 17 3
Câu 6. Cho ba lực F , F , F cùng tác động vào một vật tại điểm O và vật đứng yên. Cường độ của F , F đều là 1 2 3 1 2
120N và AOB 120 . Tìm cường độ của lực F . 3 A. 120N B. 100N C. 150N D. 100 3N
Câu 7. Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc 10km/h. Một chiếc ca nô chuyển động từ
phía đông sang phía tây với vận tốc 40km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông. A.10 7 km/h B. 20km/h C. 30km/h D. 20 3 km/h
Câu 8. Điểm M nằm trên đường tròn ngoại tiếp hình vuông ABCD cạnh a. Tính MA MC A. 3a 2 B. a 5 C. 6a 2 D. a 2
Câu 9. Điểm M nằm trên đường tròn ngoại tiếp hình vuông ABCD cạnh a. Tính MA MB MC MD A. 3a 2 B. 2a 2 C. 6a 2 D. a 2
Câu 10. Có hai lực F , F có cường độ tương ứng 5N và 8N cùng tác động vào một vật đứng yên tại O. Giả sử 1 2
hai lực vuông góc với nhau. Cường độ lực tổng hợp tác dụng lên vật là A. 89N B. 40N C. 2 13N D. 13N
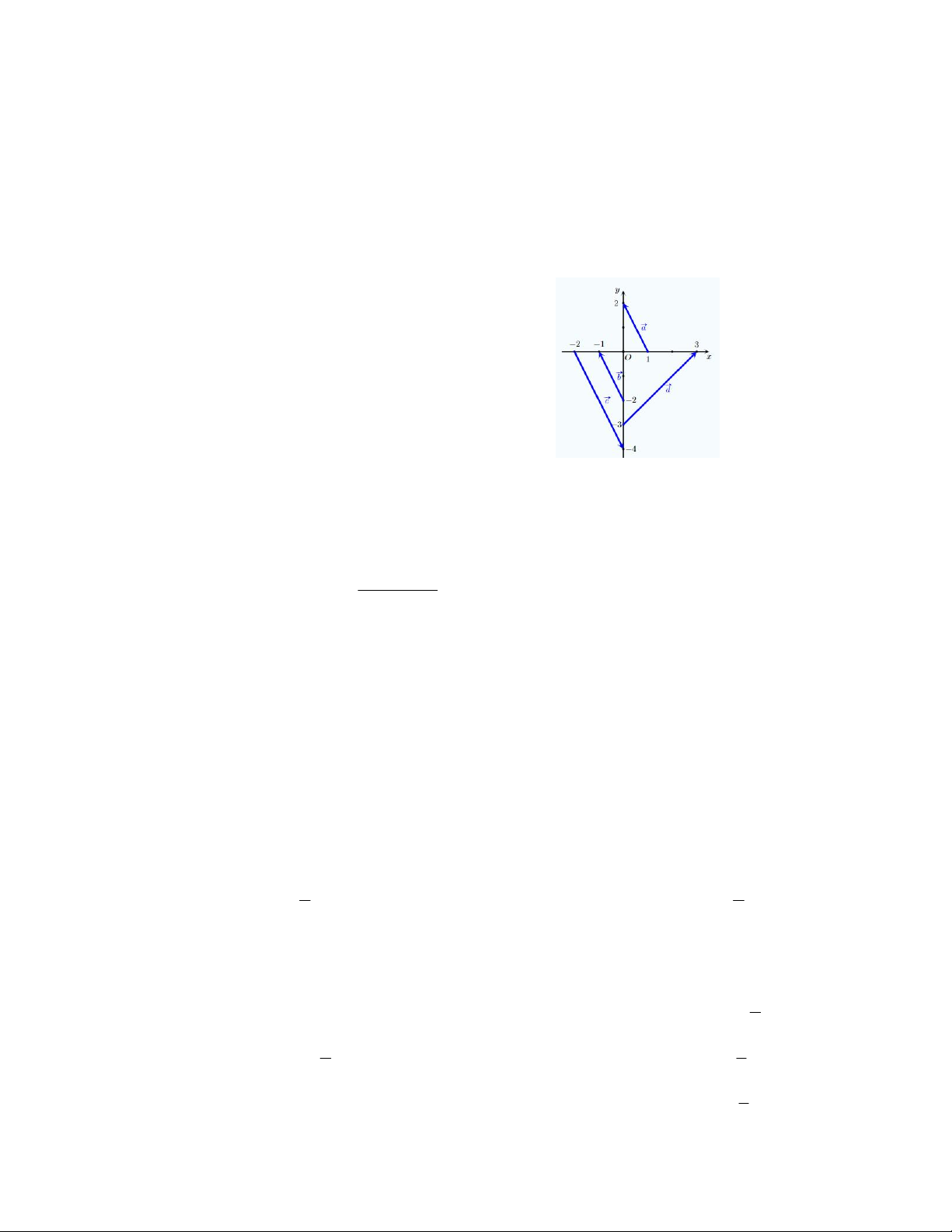
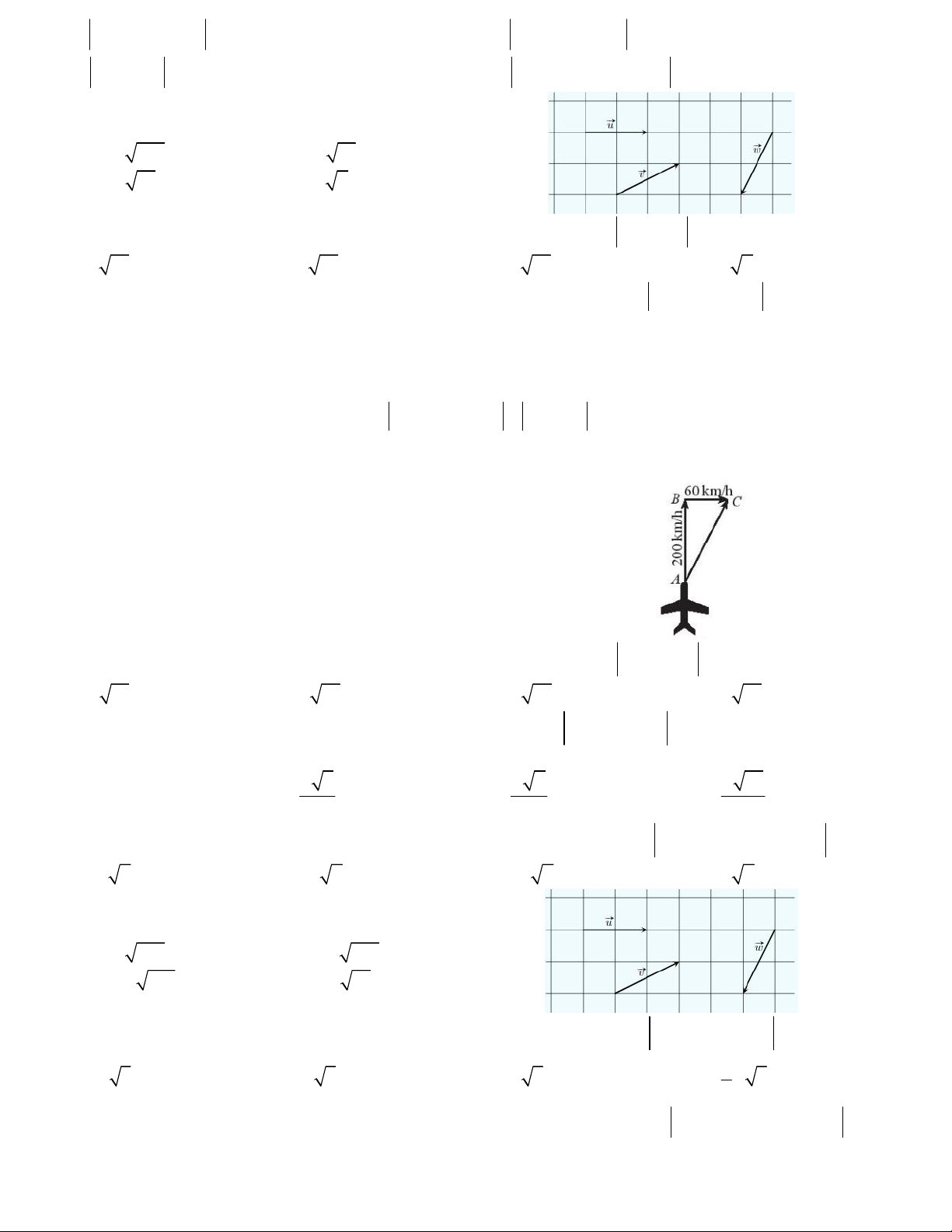
Câu 11. Mỗi ô vuông trong hình vẽ có kích thước 1.1,
tính độ dài của véc tơ u v w . A. 5 C. 13 B. 10 D. 17
Câu 12. Có hai lực F , F có cường độ đều là 50N và hợp với nhau góc 60 . Hỏi vật đó phải chịu một lực tổng 1 2
hợp có cường độ là bao nhiêu A.100N B. 200N C. 50 3N D. 100 3N
Câu 13. Điểm M nằm trên đường tròn ngoại tiếp tam giác ABC đều cạnh a, tính MA MB MC . 4 1 A. 2a 3 B. a 3 C. a 3 D. a 3 3 3
Câu 14. Điểm M nằm trên đường tròn nội tiếp tam giác ABC đều cạnh a, tính MA MB MC . 1 4 1 A. a 3 B. a 3 C. a 3 D. a 3 2 3 3
Câu 15. Cho tam giác ABC vuông tại A, AB = 2a, AC = a. Tính AB 3AC 4BC 16 A.5a B. a 132 C. a 101 D. a 13
Câu 16. Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc 10km/h. Một chiếc ca nô chuyển động từ
phía đông sang phía tây với vận tốc 45km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông. A.10 7 km/h B. 5 85 km/h C. 45km/h D. 20 3 km/h
Câu 17. Cho tam giác ABC vuông tại A, AB = 2a, AC = a. Tính MA 2MB 3MC với M bất kỳ. A. a 5 B. 2a 2 C. 5a D. a 13
Câu 18. Cho hình vuông ABCD cạnh a. Tính 3MA MB 2MC với M bất kỳ. A. a 26 B. a 13 C. a 5 D. a 29
Câu 19. Một máy bay di chuyển theo hướng bắc như hình vẽ, vận
tốc máy bay là 200km/h, vận tốc gió theo hướng đông là 60km/h.
Nếu máy bay tăng vận tốc gấp đôi thì máy bay sẽ bay theo hướng
đông bắc với vận tốc khoảng A. 404km/h B. 500km/h C. 420km/h D. 450km/h
Câu 20. Cho hình thang ABCD vuông tại A, D có AB = AD = a, DC = 2a. Tính AB AC . a 10 3a 2 A. a 5 B. 3a 2 C. D. 2 2
Câu 21. Cho hình thoi ABCD cạnh a, BAC 30 . Tính AB AC . a 10 a 13 3a 2 A.2a B. C. D. 2 2 2
Câu 22. Có hai lực F , F có cường độ tương ứng 300N xuất phát từ 1 2
điểm gốc M như hình vẽ. Tính cường độ tổng hợp lực. A.300N B. 320N C.350N D. 330N
Câu 23. Cho hình vuông ABCD có cạnh bằng a . Độ dài của CB CD bằng A. 2a B. a 2 C. 2 a 2 D. a
Câu 24. Cho hình chữ nhật ABCD tâm I , AB 3 cm, BC 4 cm. Khi đó BI là: 7 5 A. 7 B. 5 C. D. 2 2
Câu 25. Cho hình thoi ABCD cạnh a, BAC 30 . Tính AB 3AD . a 10 a 13 A.2a B. C. D. a 13 2 2
Câu 26. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a, M và N lần lượt là trung điểm của BC, CD. Tính độ dài
của véc tơ AM AN . A.7,75 B. 7,5 C. 2a 13 D. 4a 2
Câu 27. Cho hình thang ABCD vuông tại A, D có AB = AD = a, DC = 2a. Tính 2 AM ME MF với E, F lần
lượt là trung điểm của DC, BC. a 10 a 34 A. a 5 B. 3a 2 C. D. 2 2
_________________________________ 17
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P3) _____________________________
Câu 1. Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc 10km/h. Một chiếc ca nô chuyển động từ
phía đông sang phía tây với vận tốc 50km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông. A.10 7 km/h B. 10 26 km/h C. 45km/h D. 20 3 km/h
Câu 2. Có hai lực F , F có cường độ đều 50N cùng tác động vào một vật đứng yên tại O và hợp với nhau một 1 2
góc 60 . Cường độ lực tổng hợp tác dụng lên vật là A. 50 3N B. 100 3N N C. 2 13N D. 200N
Câu 3. Cho tam giác đều ABC có độ dài cạnh bằng a. Tính AB 2 AC . A.4a B. a 10 C. 2a 3 D. a 7
Câu 4. Ba lực F , F , F tác động vào một vật ở vị trí 1 2 3
cân bằng như hình vẽ. Tính F biết rằng 3
F 30N; F 40N . 1 2 A. 50N B. 70N C. 45 2 D. 35N
Câu 5. Có hai lực F , F có cường độ đều 50N cùng tác động vào một vật đứng yên tại O và hợp với nhau một 1 2
góc vuông. Tính tổng hợp lực tác dụng lên vật. A.100N B. 100 3N C. 50 2N D. 200N
Câu 6. Cho hình vuông ABCD có tâm I và độ dài cạnh bằng a. Tính AC DI . a 10 a 7 A.2a B. a 5 C. D. 2 2
Câu 7. Cho hình thoi ABCD tâm I có độ dài cạnh bằng a, BAC 30 . Tính 3AB IC . a 10 a 31 a 13 A.6a B. C. D. 2 2 2
Câu 8. Tam giác ABC cân tại A, BAC 120 . Gọi M là trung điểm cạnh BC. Tính BA CA MC . A.5a B. a 5 C. a 21 D. a 19
Câu 9. Có hai lực F ,3F cùng tác động vào một vật đứng yên tại O và hợp với nhau một góc 60 , trong đó 1 1
F có cường độ x (N). Tính tổng hợp lực tác dụng lên vật theo x. 1 A.4xN B. x 26N C. x 14N D. x 17N
Câu 10. Cho tam giác đều ABC có độ dài cạnh bằng a, tính 3AB 2 AC . A.5a B. a 5 C. a 21 D. a 19
Câu 11. Có hai lực F , F có cường độ tương ứng 6N và 8N cùng tác động vào một vật đứng yên tại O. Giả sử 1 2
hai lực vuông góc với nhau. Cường độ lực tổng hợp tác dụng lên vật là A. 10N B. 40N C. 2 13N D. 13N
Câu 12. Cho hình vuông ABCD tâm I và độ dài cạnh bằng 2a. Tính AC BD theo a. A.3a B. 4a C. 8a D. 7a 18
Câu 13. Cho tam giác đều ABC có đường cao AH, độ dài cạnh bằng a. Tính AB AH . a 34 a 7 A.2a B. C. a 5 D. 4 2
Câu 14. Có hai lực F , F có cường độ đều là 40N, hợp với nhau một góc 60 . cùng tác động vào một vật đứng 1 2
yên tại O, tổng hợp lực thu được là F . Giả sử tăng cường độ hai lực F , F lên lần lượt là 2 lần và 5 lần, chiều 1 2
của lực giữ nguyên như thế, ta thu được tổng hợp lực K . Hỏi cường độ của K gấp bao nhiêu lần cường độ của lực F . A.7 lần B. 10 lần C. 29 lần D. 13 lần
Câu 15. Cho hình vuông ABCD tâm I và có độ dài cạnh bằng a. Tính AB DI theo a. a 10 a 13 a 7 A.5a B. C. D. 2 2 2
Câu 16. Cho tam giác đều ABC có đường cao AH, độ dài cạnh bằng a. Tính AB CH . a 3 a 5 A.a B. 2a C. D. 2 2
Câu 17. Có hai lực F , F có cường độ đều là 10N, hợp với nhau một góc 30 . cùng tác động vào một vật đứng 1 2
yên tại O, tổng hợp lực thu được là F . Giả sử tăng cường độ hai lực F , F lên lần lượt là 3 lần và 4 lần, chiều 1 2
của lực giữ nguyên như thế, ta thu được tổng hợp lực K . Cường độ của K gấp x cường độ của lực F , hỏi x gần nhất giá trị nào A.2,7 lần B. 4,5 lần C. 5,4 lần D. 3,5 lần
Câu 18. Cho hình vuông ABCD tâm I, độ dài cạnh bằng a, gọi M là trung điểm cạnh CD, tính IC IM theo a. a 10 a 7 a 5 A.2a B. C. D. 2 2 2
Câu 19. Cho tam giác đều ABC có đường cao AH, độ dài cạnh bằng a. Tính 3AB BC theo a. A. a 13 B. a 17 C. a 21 D. a 19
Câu 20. Hình vuông ABCD tâm I, độ dài cạnh bằng a. Gọi M là trung điểm của cạnh CD, tính IA IM ID . a 10 a 7 a 5 A.2a B. C. D. 2 2 2
Câu 21. Có hai lực F , F có cường độ lần lượt là 5N và 7N, hợp với nhau một góc 45 . cùng tác động vào một 1 2
vật đứng yên tại O, tổng hợp lực thu được là F . Cường độ của lực F gần nhất giá trị nào A.11,11N B. 10,95N C. 12,25N D. 14,75N
Câu 22. Tam giác ABC có độ dài cạnh bên là a và góc ngoài tại đỉnh C là 160 . Khi đó 5AB 2 AC : a gần
nhất giá trị nào sau đây A.4,25 B. 3,69 C. 5,68 D. 2,73
Câu 23. Cho tam giác đều ABC cạnh a. Tính MA 2MB 3MC với M bất kỳ. 1 A. a 17 B. a 13 C. a 3 D. a 3 3
Câu 24. Cho tam giác đều ABC cạnh a. Tính 2MA 3MB 5MC với M bất kỳ. A. a 17 B. a 13 C. a 39 D. a 29
Câu 25. Tam giác ABC cân tại A có độ dài cạnh bên là a và ABC 40 . Khi đó 3AB 2 AC : a gần nhất giá trị nào sau đây A.7,2 B. 8,6 C. 3,3 D. 4,5 19
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P4)
______________________________
Câu 1. Cho tam giác ABC đều cạnh bằng 6cm. Tính AB CB bằng: A. 6 3 B. 12 3 C. 12 D. 3 3
Câu 2. Cho hình vuông ABCD tâm O , cạnh 2a . Độ dài vectơ DO bằng a 2 A. 2a 2 B. C. a 2 D. 2a 2 2
Câu 3. Cho ba lực F , F , F cùng tác động vào một vật tại điểm M như 1 2 3
hình vẽ với F MB, F M ,
A F MC , AMB 120 ; AMC 60 , với 1 2 3
cường độ tương ứng F F 300N; F 400N . Tính cường độ lực 1 2 3
tổng hợp tác động vào vật. D. 300N C. 100N E. 500N D. 700N
Câu 3. Cho tam giác ABC đều cạnh a , có AH là đường trung tuyến. Tính AC AH : a 13 a 3 A. a 3 B. 2a C. D. 4 2
Câu 4. Cho hình thang ABCD vuông tại A và D , có AD CD 4 , AB 8 . Tính BA AC ? A. 2 2 B. 2 10 C. 4 10 D. 4 2
Câu 5. Một máy bay khởi động theo hướng bắc dự kiến như hình
vẽ, vận tốc máy bay là 200km/h, vận tốc gió theo hướng đông là
60km/h. Khi đó máy bay sẽ bay theo hướng đông bắc với vận tốc khoảng B. 209km/h B. 215km/h F. 220km/h D. 230km/h
Câu 6. Cho tam giác đều ABC có độ dài cạnh bằng a. Tính AB AC . A.2a B. 3a C. a 3 D. a 5
Câu 7. Cho hình vuông ABCD có độ dài cạnh bằng a, I là giao điểm hai đường chéo. Tính IA IB . A.a B. 0,5a C. a 3 D. a 5
Câu 8. Có hai lực F , F có cường độ đều là 40N, hợp với nhau một góc 60 . cùng tác động vào một vật đứng 1 2
yên tại O, tổng hợp lực thu được là F . Giả sử tăng cường độ hai lực F , F lên lần lượt là 2 lần và 3 lần, chiều 1 2
của lực giữ nguyên như thế, ta thu được tổng hợp lực K . Hỏi cường độ của K gấp bao nhiêu lần cường độ của lực F . 19 23 A. lần B. 3 lần C. 6 lần D. lần 3 3
Câu 9. Khi máy bay nghiêng cánh một góc 45 , lực F của
không khí tác động vuông góc với cánh và bằng tổng của lực
nâng F và lực cản F . Biết F x 2N , cường độ của lực F là. 1 2 1 A. xN B. 0,5aN x 2 C. N D. 10000N 2 20
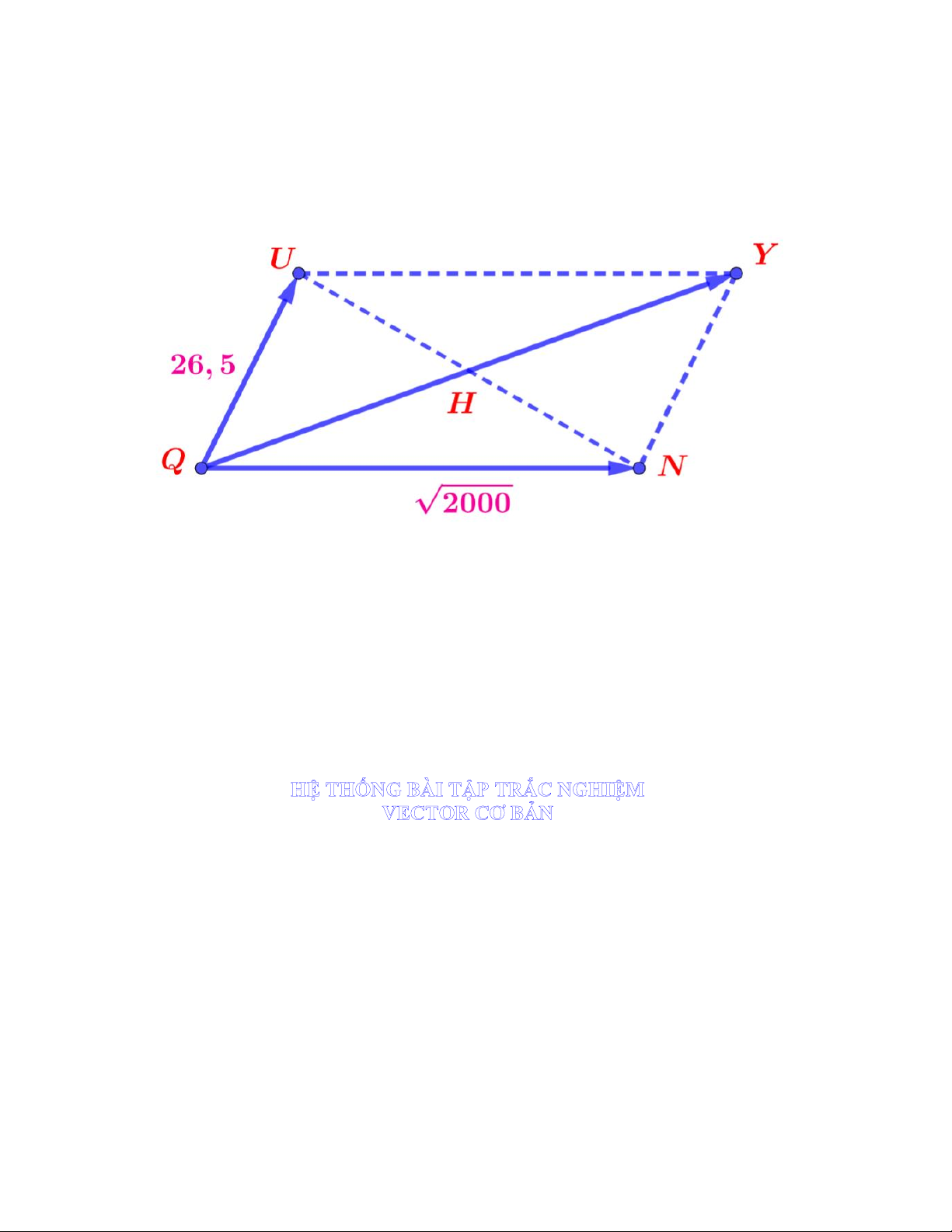
Câu 10. Cho ba lực F , F , F cùng tác động vào một vật tại điểm O và vật đứng yên. Cường độ của F , F đều 1 2 3 1 2
là 26,5N và AOB 120 . Tìm cường độ của lực F . 3 A. 26,5N B. 27N C. 30N D. 100 3N
Câu 11. Cho hình vuông ABCD tâm O và độ dài cạnh bằng 6a, Tính MN khi các điểm M, N xác định bởi:
MA MD 0, NB ND NC 0 . A. a 65 B. a 39 C. a 26 D. a 41
Câu 12. Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc 10km/h. Một chiếc ca nô chuyển động từ
phía đông sang phía tây với vận tốc 60km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông. A.10 7 km/h B. 10 37 km/h C. 30km/h D. 20 3 km/h
Câu 13. Cho hình vuông ABCD cạnh a. Tính 2MA 3MB 5MC với M bất kỳ. A. a 26 B. a 13 C. a 39 D. a 29
Câu 14. Điểm M nằm trên đường tròn nội tiếp hình vuông ABCD cạnh a. Tính MA MB MC MD A. 3a 2 B. 2a 2 C. 2a D. a 2
Câu 15. Cho hình thang vuông ABCD có hai đáy AB a ; CD 2a ; đường cao AD a . Đặt
u DA AB CD . Độ dài vectơ u bằng: a 2 A. 2a 2 B. C. a 2 D. 2 a 2 2
Câu 16. Ba lực F , F , F cùng tác động vào một vật tại điểm M như 1 2 3
hình vẽ với F MB, F M ,
A F MC , AMB 120 ; AMC 150 , 1 2 3
với cường độ tương ứng F F 300N; F 400N . Tính cường 1 2 3
độ lực tổng hợp tác động vào vật. Tính cường độ lực tổng hợp tác động vào vật. A. 300N C. 100N B. 500N D. 700N
Câu17. Cho hình thoi ABCD tâm O cạnh a, BAC 30 . Tính 2 AB 2 AD OB . a 13 A.2a B. 3,5a C. D. a 13 2
Câu 18. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a, M là trung điểm DC. Tính AC AM . A.2a B. 3a 2 C. 6a 2 D. a 13
Câu 19. Cho hình vuông ABCD cạnh a, K và H lần lượt là trung điểm của BC, DC. Tính AK AH a 10 a 13 3a 2 A.2a B. C. D. 2 2 2
Câu 20. Cho hình bình hành ABCD có DA 2; AB 4 và đường chéo BD 5 . Tính BA DA . A.2 B. 4 C. 5 D. 6
Câu 21. Cho hình thang ABCD có hay đáy AB a;CD 2a . Gọi M, N là trung điểm của AD, BC.
Tính MA MC MN . A.3a B. a C. 2a D. 0,5a
Câu 22. Cho hình vuông ABCD cạnh a, tâm O. Tính độ dài vector AB OD BC . a 2 3a 2 A. B. C. a 2 D. a 2 2
_________________________________ 21
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P5)
______________________________
Câu 1. Có hai lực F , F có cường độ tương ứng 6N và 8N cùng tác động vào một vật đứng yên tại O. Giả sử 1 2
hai lực tạo với nhau một góc 60 . Cường độ lực tổng hợp tác dụng lên vật là A. 89N B. 2 37 N C. 2 13N D. 10N
Câu 2. Cho hình vuông ABCD cạnh a, tính độ dài vector 2 AD AC . A. 3a B. a 10 C. a 11 D. a 13
Câu 3. Cho tam giác ABC có AB 3; AC 4; BC 5 . Điểm M nằm trên đường tròn ngoại tiếp tam giác ABC.
Tính độ dài vector MB MC . A.5 B. 6 C. 4 D. 3
Câu 4. Cho tam giác ABC đều cạnh a, trọng tâm G, tính độ dài vector GB 2GA 3GC . A.a B. 2a C. a 5 D. a 3
Câu 5. Cho ba lực F , F , F cùng tác động vào một vật tại điểm O và vật đứng yên. Cường độ của F , F đều là 1 2 3 1 2
150N và AOB 120 . Tìm cường độ của lực F . 3 A. 120N B. 100N C. 150N D. 100 3N
Câu 6. Tam giác ABC vuông tại A nội tiếp đường tròn đường kính BC = 10. Điểm M đối xứng với A qua đường
thẳng BC, tính độ dài vector MB MC . A.10 B. 6 C. 8 D. 12
Câu 7. Cho hình vuông ABCD cạnh a. Với điểm M bất kỳ, tính độ dài vector 4MA 3MB MC 2MD . A. 2a B. 2a 2 C. a 5 D. a 6
Câu 8. Cho hình chữ nhật ABCD có AD a; AB 2a , M và N lần lượt là trung điểm của AB và CD. Tính độ
dài của vector 2CM 3AN . A.2a B. a C. a 2 D. a 3
Câu 9. Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc 10km/h. Một chiếc ca nô chuyển động từ
phía đông sang phía tây với vận tốc 35km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông. A.10 7 km/h B. 20km/h C. 5 53 km/h D. 20 3 km/h
Câu 10. Điểm M nằm trên đường tròn ngoại tiếp hình vuông ABCD cạnh 6a. Tính MA MC A. 3a 2 B. a 5 C. 6a 2 D. a 2
Câu 11. Có hai lực F , F có cường độ tương ứng 6N và 8N cùng tác động vào một vật đứng yên tại O. Giả sử 1 2
hai lực vuông góc với nhau. Cường độ lực tổng hợp tác dụng lên vật là A. 89N B. 40N C. 2 13N D. 10N
Câu 12. Cho hình thang ABCD vuông tại A, D có AB = AD = a, DC = 3a. Tính BD BC . a 6 a 5 a 10 3a 2 A. B. C. D. 2 2 2 2
Câu 13. Cho hình thoi ABCD cạnh a, BAC 30 . Tính BD BC . a 3 a 5 3a 2 A.2a B. C. D. 2 2 2
Câu 14. Cho hình vuông ABCD cạnh a. Với điểm M bất kỳ, tính độ dài vector 2MA MB MC 2MD . A. 2a B. 2a 2 C. a 5 D. a 6
Câu 15. Có hai lực F , F có cường độ tương ứng 200N xuất phát từ 1 2
điểm gốc M như hình vẽ. Tính cường độ tổng hợp lực. A.200N B. 210N C.240N D. 250N 22
Câu 16. Cho hình thoi ABCD cạnh a, BAC 30 . Tính 2 AB 3AD . A.2a B. a 19 C. 3a 2 D. a 13
Câu 17. Tam giác ABC có AB 4; AC 5; BC
21 . Tính độ dài vector AB AC . 61 46 3 5 A. B. 3 2 C. D. 2 2 2
Câu 18. Cho hình vuông ABCD tâm O và độ dài cạnh bằng 6a, Tính NM NC khi các điểm M, N xác định
bởi: MA MD 0, NB ND NC 0 . A. a 5 B. a 7 C. a 26 D. a 6
Câu 19. Cho hình vuông ABCD cạnh a. Với điểm M bất kỳ, tính độ dài vector 3MA MB MC MD . A. 2a B. 2a 2 C. a 5 D. a 6
Câu 20. Có hai lực F , F có cường độ đều là 10N, hợp với nhau một góc 30 . cùng tác động vào một vật đứng 1 2
yên tại O, tổng hợp lực thu được là F . Giả sử tăng cường độ hai lực F , F lên lần lượt là 2 lần và 6 lần, chiều 1 2
của lực giữ nguyên như thế, ta thu được tổng hợp lực K . Cường độ của K gấp x cường độ của lực F , hỏi x gần nhất giá trị nào A.3,124 lần B. 4,123 lần C. 5,102 lần D. 4,035 lần
Câu 21. Cho hình vuông ABCD tâm O và độ dài cạnh bằng a. Điểm G thỏa mãn GA GC GD 0 . Tính độ
dài của vector GA GB . a 17 a 14 a 11 a 17 A. B. C. D. 3 3 3 2
Câu 22. Cho tam giác đều ABC cạnh a. Tính 5MA 2MB 7MC với M bất kỳ. A. a 17 B. a 39 C. a 26 D. a 41
Câu 23. Khi máy bay nghiêng cánh một góc 45 , lực F của
không khí tác động vuông góc với cánh và bằng tổng của lực
nâng F và lực cản F . Biết F 6x 2N , cường độ của lực 1 2 F là. 1 A. 6xN B. 0,5aN x 2 C. N D. 10000N 2
Câu 24. Cho hình thoi ABCD cạnh a, BAC 30 . Tính AC 2 AD . A. 2a B. a 13 C. a 5 D. a 6
Câu 25. Cho hình vuông ABCD cạnh a. Với điểm M bất kỳ, tính độ dài vector 4MA 5MB 2MC MD . A. a 57 B. 2a 2 C. a 58 D. 2a 15
Câu 26. Cho tam giác đều ABC cạnh a. Tính độ dài vector 0, 75MA 2,5MB với M là trung điểm cạnh BC. a 127 a 5 a 101 a 6 A. B. C. D. 8 3 3 2
Câu 27. Có hai lực F , F có cường độ tương ứng 6N và 8N cùng tác động vào một vật đứng yên tại O. Cường 1 2
độ lực tổng hợp tác dụng lên vật là 12N thì góc giữa hai vector lực gần nhất với A.65 độ B. 67 độ C. 62 độ D. 56 độ
Câu 28. Cho hình vuông ABCD cạnh a, tâm O, M là trung điểm cạnh AB. Tính độ dài vector AM AO CB . a 6 a 5 a 10 3a 2 A. B. C. D. 2 2 2 2
_________________________________ 23
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P6) _____________________________
Câu 1. Cho tam giác đều ABC có độ dài cạnh bằng a. Tính AB 2 AC . A. 4a B. 2a 3 C. a 7 D. a 10
Câu 2. Có hai lực F , F cùng tác động vào một vật đứng yên tại O. Biết hai lực F , F cùng có cường độ là 1 2 1 2
1000 N và chúng hợp với nhau một góc 60 . Hỏi vật đó phải chịu một lực tổng hợp có cường độ bao nhiêu ? A. 100 N B. 50 3 N C. 100 3 N D. 200 N AB GC
Câu 3. Cho tam giác ABC đều có độ dài cạnh là 2a, tính Z . a 3 2 7 4 A. Z = 1 B. Z = C. Z = D. Z = 3 3 3
Câu 4. Cho hình vuông ABCD cạnh a với M, N lần lượt là trung điểm của AB, BC. Tính độ dài vector AM CN . a 3 a 2 a 5 a 7 A. B. C. D. 2 2 2 2
Câu 5. Có hai lực F , F cùng tác động vào một vật đứng yên tại O. Biết hai lực F , F cùng có cường độ là 26 1 2 1 2
N và vuông góc với nhau. Tính tổng hợp lực tác dụng lên vật. A. 100 N B. 26 2 N C. 100 3 N D. 70,5 N
Câu 6. Cho hình thoi ABCD tâm I và có độ dài cạnh bằng a, BAC 30 . Tính 2 AB IC . a 10 a 31 a 13 A. 6a B. C. D. 2 2 2
Câu 7. Cho ba lực F AB, F AC, F AD cùng tác động vào một vật đặt tại điểm A như hình vẽ, vật đứng 1 2 3
yên. Giả định BAC 60 , F 60N , F 30N . Độ lớn lực F 1 2
3 thỏa mãn bất đẳng thức nào ? A. 50 < F3 < 60 B. 70 < F3 < 80 C. 80 < F3 < 90 D. 64 < F3 < 69
Câu 8. Cho hình vuông ABCD tâm I và có độ dài cạnh bằng a. Tính AB DI theo a. a 10 a 13 a 7 A. 5a B. C. D. 2 2 2
Câu 9. Cho tam giác ABC vuông tại A có độ dài cạnh huyền bằng 10. Tính AB AC . A.10 B. 8 C. 6 D. 12
Câu 10. Cho hình vuông ABCD cạnh a. Với điểm M bất kỳ, tính độ dài vector 4MA MB 4MC 7MD . A. 2a B. 2a 2 C. D. a 6
Câu 11. Có hai lực F , F có cường độ đều là 10N, hợp với nhau một góc 30 . cùng tác động vào một vật đứng 1 2
yên tại O, tổng hợp lực thu được là F . Giả sử tăng cường độ hai lực F , F lên lần lượt là 6 lần và 2 lần, chiều 1 2
của lực giữ nguyên như thế, ta thu được tổng hợp lực K . Cường độ của K gấp x cường độ của lực F , hỏi x gần nhất giá trị nào A.3,124 lần B. 4,123 lần C. 5,102 lần D. 4,035 lần
Câu 12. Cho hình chữ nhật ABCD có AB = a, AD = 2a. Lựa chọn mệnh đề đúng 24
A. AB BC CD 2a
B. AB BC CD 4a
C. AB AD 3a
D. AB BC CD DA 6a .
Câu 13. Mỗi ô vuông trong hình vẽ có kích thước 1.1,
tính độ dài của véc tơ 2u w . A. 109 C. 13 B. 10 D. 7
Câu 14. Cho hình thang ABCD vuông tại A và D, AD = CD = 4, AB = 8. Tính BA AC . A. 2 10 B. 3 10 C. 4 10 D. 5 2
Câu 15. Tam giác ABC vuông tại A có trọng tâm G và cạnh huyền BC = 12. Tính 4GA GB GC . A. 9 B. 12 C. 10 D. 8
Câu 16. Có hai lực F , F có cường độ tương ứng 6N và 8N cùng tác động vào một vật đứng yên tại O. Cường 1 2
độ lực tổng hợp tác dụng lên vật là 11N thì góc giữa hai vector lực gần nhất với A.65 độ B. 81 độ C. 77 độ D. 72 độ
Câu 17. Tam giác ABC có điểm O thỏa mãn OA OB 2OC OA OB . Khẳng định nào sau đây đúng ? A. Tam giác ABC đều B. Tam giác ABC cân tại C
C. Tam giác ABC vuông tại C D. Tam giác ABC cân tại B
Câu 18. Một máy bay di chuyển theo hướng bắc như hình vẽ, vận
tốc máy bay là 200km/h, vận tốc gió theo hướng đông là 60km/h.
Nếu máy bay tăng vận tốc gấp ba thì máy bay sẽ bay theo hướng
đông bắc với vận tốc khoảng C. 603km/h B. 610km/h G. 650km/h D. 620km/h
Câu 19. Cho tam giác đều ABC có đường cao AH, độ dài cạnh bằng a. Tính 3AB BC theo a. A. a 13 B. a 10 C. a 17 D. a 19
Câu 20. Cho hình vuông ABCD có tâm I, độ dài cạnh bằng a. Tính IA IM ID theo a biết M là trung điểm của CD. a 5 a 7 a 10 A. 2a B. C. D. 2 2 2
Câu 21. Điểm M nằm trên đường tròn ngoại tiếp hình vuông ABCD cạnh 3a. Tính MA MB MC MD A. 3a 2 B. 2a 2 C. 6a 2 D. a 2
Câu 22. Mỗi ô vuông trong hình vẽ có kích thước 1.1,
tính độ dài của véc tơ 2u 3v . A. 109 C. 130 H. 113 D. 91
Câu 23. Điểm M nằm trên đường tròn ngoại tiếp tam giác ABC đều cạnh 3a, tính MA MB MC . 1 A. 2a 3 B. 3a 3 C. a 3 D. a 3 3
Câu 24. Điểm M nằm trên đường tròn nội tiếp hình vuông ABCD cạnh bằng 26, tính MA MB MC MD . A.26 B. 13 C. 52 D. 40 25
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P1) _____________________________
Câu 1. Cho tam giác ABC cạnh a. Tính . AB AC . A. 2 0,5a B. 2 a C. 2 2a D. 2 3a
Câu 2. Cho hình vuông ABCD tâm O cạnh a. Tính . AB OC . A. 2 0,5a B. 2 a C. 2 2a D. 2 3a
Câu 3. Cho hình vuông ABCD tâm O cạnh a. Tính . AB BD . A. 2 0,5a B. 2 a C. 2 2a D. 2 3a
Câu 4. Cho tam giác đều ABC cạnh a, trực tâm H. Tính M .
AB AC AH.BC theo a. A. 0 B. 2 0,5a C. 2 2 a D. 2 a
Câu 4. Cho A, B, C thỏa mãn AB = 2, CB = 3, AC = 5. Tính C . A CB . A. 14 B. 13 C. 17 D. 15
Câu 5. Cho đường tròn tâm O đường kính AB = 2R. Gọi M, N là hai điểm phân biệt thuộc nửa đường tròn. Tính giá trị biểu thức 2 . MA MB 3N . A NB theo R. A. 0 B. 5R C. 6R2 D. 8R2 2
Câu 6. Cho a b 1và hai vector a ;
b a b vuông góc với nhau. Tính góc giữa hai vector a,b . 5 A. 100 độ B. 180 độ C. 120 độ D. 45 độ
Câu 7. Cho tam giác ABC có AB = c, BC = a, CA = b. Tính AB AC BC . 2 2 2
c b a A. 2 2 b c B. 2 2 c a C. 2 2 2c a D. 2
Câu 8. Cho hai vector a,b thỏa mãn a b 4, a b 2 . Tính . a b . A. – 2 B. – 3 C. – 5 D. 3
Câu 9. Cho tam giác ABC có AB = c, BC = a, CA = b, M là trung điểm cạnh BC. Tính AM .BC theo a, b, c. 2 2 b c A. B. 2 2 3 b c C. 2 2 2c a D. 2 2 c a 2
Câu 10. Cho hình vuông ABCD cạnh a. Tính AC.CD CA . AB AC theo a. A. 4 2 a B. – 2 2 a C. – 3 2 a D. – 6 2 a
Câu 11. Cho hình vuông ABCD cạnh a. Tính AB ACBC BD BAtheo a. A. 4 2 a B. – 2 2 a C. – 3 2 a D. – 6 2 a
Câu 12. Cho hình vuông ABCD cạnh a. Gọi E là điểm đối xứng với D qua C. Tính AE.AB theo a. A. 4 2 a B. 2 2 a C. 3 2 a D. 5 2 a
Câu 13. Cho a 5, b 12, a b 13. Tính cos của góc , là góc giữa hai vector a,b . 12 5 11 A. B. 0 C. D. 13 13 15
Câu 14. Tính cos a,b với a 3, b 4, a b 4. 1 3 2 A. 0,5 B. C. D. 2 8 5
Câu 15. Cho hình chữ nhật ABCD có AB = 3, AD = 4. Gọi M là điểm thỏa mãn điều kiện AM k AB . Xác định
k để hai đường thẳng AC, DM vuông góc với nhau. 9 16 4 3 A. k B. k C. k D. k 16 9 3 4
Câu 16. Cho hình vuông ABCD có độ dài cạnh bằng 1. Gọi M, N lần lượt là trung điểm của các cạnh BC, AB. 26
Tính giá trị biểu thức DM .NM . 2 3 A. 0,25 B. 0,5 C. D. 2 2 2
Câu 17. Cho điểm M thuộc nửa đường tròn tâm O đường kính AB = 2R. Tính MA M . A AB theo R. A. 3R B. 0 C. 4R2 D. 2R2
Câu 18. Cho tam giác đều ABC cạnh a, các đường cao AH, BK, kẻ HI vuông góc với AC. Mệnh đề nào đúng ?
A. 2 2 A . B AC a B. 2 AB AC BC a C. 2 8C . B CK a D. 2 . CB AK a
Câu 19. Cho tam giác ABC vuông tại A có AB = 3, AC = 5, đường cao AH. Tính H . B HC . 225 16 A. 34 B. C. – 4 D. 34 5
Câu 20. Cho hình vuông ABCD cạnh a. Mệnh đề nào sau đây sai A. . AB AD 0 B. 2 . AB AC a
C. 2 . AB CD a D. 2 AB CD BC AD a
Câu 21. Cho hình vuông ABCD có I là trung điểm của AD, tính cos AC, BI . 1 1 1 2 A. B. C. D. 3 10 5 10
Câu 22. Cho AB = 4, AC = 3, hỏi có mấy điểm C để . AB AC 12 ? A. 2 B. 0 C. 1 D. 3
Câu 23. Cho AB = 4, AC = 3, hỏi có mấy điểm C để . AB AC 8 ? A. 2 B. 0 C. 1 D. 3
Câu 24. Cho hình vuông ABCD cạnh a. Tính AC CD CAtheo a. A. – 1 B. 3 2 a C. – 3 2 a D. 2 2 a
Câu 25. Cho hai vector ,
m n khác 0, tính góc giữa hai vecto , m n nếu .
m n m . n . A. 0 độ B. 180 độ C. 90 độ D. 45 độ
Câu 26. Cho hình vuông ABCD cạnh a, E đối xứng với D qua C. Tính AE.AB . A. 2 2 a B. 3 2 a C. 5 2 a D. 5 2 a
Câu 27. Cho tam giác đều ABC cạnh bằng 1. Tính .
AB BC BC.CA C . A AB . 3 3 A. 1,5 B. – 1,5 C. D. – 2 2
Câu 28. Cho a,b 120 , a 3, b 5. Tính a b . A. 7 B. 4 C. 2 D. 19
Câu 29. Cho tam giác ABC có AB 3e 4e ; BC e 5e với e , e là các vector đơn vị. Độ dài AC là 1 2 1 2 1 2 A. 4e e B. 4 e e C. 5 D. 17 1 2 1 2
Câu 30. Cho tam giác ABC vuông tại A. Khẳng định nào sau đây sai ?
A. . AB AC . BA BC
B. AC.CB AC.BC
C. AC.BC . CA CB
D. AC.BC BC.AB
Câu 31. Cho a 3, b 5, 2a 3b 171 . Tính 5a 4b . A. 2 17 B. 6 C. 5 13 D. 7 2
Câu 32. Cho tam giác đều ABC cạnh a, đường cao AH, BK, kẻ HI vuông góc với AC tại I. Mệnh đề nào sai ? A. . BA BC 2B . A BH B. . CB CA 4 . CB CI
C. AC AB BC 2 . BA BC D. .
CB CA 4KC.CH 27
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P2) _____________________________
Câu 1. Cho hình vuông ABCD cạnh a, mệnh đề nào sau đây sai ? A. 2 D . A CB a B. 2 . AB CD a
C. 2 AB BC AC a D. . AB AD . CB CD 0
Câu 2. Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a, I là trung điểm
của cạnh AB. Tìm mệnh đề sai A. 2 . AB DC 8a B. . AB DC 0 C. . AB AD 0 D. D . A DB 0
Câu 3. Cho m 2;3, n 4;
1 . Tìm độ dài vector p biết . m p 4; . n p 2 . 61 21 13 A. 4 B. C. D. 7 17 5
Câu 4. Cho tam giác đều ABC cạnh a = 2. Hỏi mệnh đề nào sai ?
A. .
AB AC.BC 2BC
B. BC.CA 2
C. AB BC AC 4
D. AC BC BA 4
Câu 5. Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để OA OB AB 0 là A. Tam giác OAB đều B. Tam giác OAB cân tại O
C. Tam giác OAB vuông tại O
D. Tam giác OAB vuông cân tại O
Câu 6. Cho hai điểm A và B có AB = 4. Tập hợp những điểm M sao cho M . A MB 0 là
A. Đường thẳng vuông góc với AB
B. Đường tròn bán kính r = 2
C. Đường thẳng vuông góc với AB
D. Đường tròn bán kính r = 4
Câu 7. Cho AB = 2a và O là trung điểm của đoạn thẳng AB. Tập hợp những điểm M thỏa mãn 2 M . A MB a là
đường tròn có bán kính bằng A. a B. 2a C. a 2 D. a 3
Câu 8. Cho đoạn thẳng AB = a cố định. Tập hợp những điểm M mà 2
AM .AB a là
A. Đường tròn tâm A, bán kính r = a
B. Đường thẳng vuông góc với AB tại B
C. Đường trung trực của AB.
D. Đường tròn đường kính AB.
Câu 9. Tồn tại bao nhiêu điểm C trên trục tung sao cho tam giác ABC vuông tại C, với A (1;2), B (3;– 1) ? A. 2 B. 1 C. 3 D. 4 2
Câu 10. Cho điểm M nằm trên đường tròn đường kính AB. Tính F MA M . A AB . A. F = 7 B. F = 2 C. F = 1 D. F = 0 . AB AC
Câu 11. Cho tam giác đều ABC có cạnh bằng a. Tính giá trị biểu thức M . 2 a 3 A. M = 1 B. M = 0,5 C. M = 2 D. M = 2
Câu 12. Cho tam giác ABC cân tại A, AB = AC = 5, BAC 120 . Tính Q AC.BC . A. Q = 37,5 B. Q = 22,5 C. Q = 10 D. Q = 30,5 BM .DO
Câu 13. Hình vuông ABCD tâm O và có độ dài cạnh bằng a, M là trung điểm cạnh AB. Tính P . 2 a A. – 1 B. – 0,5 C. – 2 D. – 0,25
Câu 14. Cho hình vuông ABCD tâm O, độ dài cạnh bằng a. Tập hợp các điểm M thỏa mãn đẳng thức
2 M .
A MB MC.MD a là một đường tròn. Tìm bán kính R của đường tròn này. A. R = 1,5a B. R = 2a C. R = 3a D. R = a
Câu 15. Cho hình bình hành ABCD có độ dài các đường chéo AC = 6, BD = 8. Tính . AB AD . A. 5 B. – 7 C. 7 D. 25 MH.MA
Câu 16. Cho tam giác ABC có trực tâm H. Gọi M là trung điểm cạnh BC. Tính . 2 BC 28 2 1 A. 0,5 B. 0,25 C. D. 3 3
Câu 17. Cho tam giác ABC với ba trung tuyến AD, BE, CF. Tính .
AD BC BE.CA . AB CF . A. 3 B. 2 C. 0 D. 1
Câu 18. Tam giác ABC vuông tại A, AB = 3, AC = 4, đường cao AH. Tính tích vô hướng H . B HC . 144 144 A. B. – 25 C. 25 D. 25 25
Câu 19. Cho tam giác ABC cân tại A có BC = 6, H là hình chiếu vuông góc của A trên BC. Tính H . B AC . A. 9 B. 36 C. – 9 D. – 12
Câu 20. Cho hình vuông ABCD cạnh a, M và N lần lượt là trung điểm của AB, AD. Tính 4.MI.MA 2.IN.IC . 5 2 5 5 A. B. – 4 C. D. 25 25
10
Câu 21. hình vuông ABCD cạnh bằng 1, M là trung điểm BC, G là trọng tâm tam giác ABC. Tính 9GM .GD . A. – 3 B. – 2 C. – 1 D. 2
Câu 22. Cho tam giác đều ABC cạnh bằng 4. Tập hợp điểm M thỏa mãn (MA MB)(MA MC) 0 là đường
tròn (W), chu vi của đường tròn này bằng A. 2 B. 4 C. 6 D. 5
Câu 23. Cho hình vuông ABCD cạnh a, các điểm E, F theo thứ tự là trung điểm của AB, AD. Tính CE.CF . A. 2 2 a B. 2 a C. – 3 2 a D. 4 2 a
Câu 24. Cho tam giác đều ABC cạnh a, trực tâm H. Tính M .
AB AC AH.BC theo a. A. 0 B. 2 0,5a C. 2 2 a D. 2 a
Câu 25. Cho tam giác đều ABC cạnh a, trọng tâm G. Tính P G .
A GB AC.CG theo a. 2 1 2 A. 0 B. 2 a C. 2 a D. 2 a 3 2 5
Câu 26. Cho tam giác đều ABC có độ dài cạnh là 3a, trên các cạnh BC, CA lần lượt lấy các điểm M, N sao cho
BM = a, CN = 2a. Tính AM .BC theo a. A. 2 2 a B. – 1,5 2 a C. 3,5 2 a D. – 4 2 a 2
Câu 27. Cho điểm M thuộc nửa đường tròn tâm O đường kính AB = 2R. Tính MA M . A AB theo R. A. 3R B. 0 C. 4R2 D. 2R2
Câu 28. Cho AB = 4, AC = 3, hỏi có mấy điểm C để . AB AC 12 ? A. 2 B. 0 C. 1 D. 3
Câu 29. Cho hình vuông ABCD cạnh a. Tính AC.CD CA . AB AC theo a. A. 4 2 a B. – 2 2 a C. – 3 2 a D. – 6 2 a
Câu 30. Cho tam giác ABC vuông tại A có AB = c, AC = b, BC = a. Tính . BA BC theo a, b, c. A. 2a + b B. a + b + c C. 2 c D. 2 c + 2ab
Câu 31. Cho A, B, C thỏa mãn AB = 2, CB = 3, AC = 5. Tính C . A CB . A. 14 B. 13 C. 17 D. 15
Câu 32. Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để OA OB AB 0 là A. Tam giác OAB đều B. Tam giác OAB cân tại O
C. Tam giác OAB vuông tại O
D. Tam giác OAB vuông cân tại O
Câu 33. Cho tam giác đều ABC cạnh a, trọng tâm G. Tính P .
GA GB AC.CG theo a. 2 1 2 A. 0 B. 2 a C. 2 a D. 2 a 3 2 5
Câu 34. Cho tam giác ABC vuông tại A có AB = c, AC = b, BC = a. Tính . BA BC theo a, b, c. A. 2a + b B. a + b + c C. 2 c D. 2 c + 2ab
_________________________________ 29
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P3) _____________________________
Câu 1. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng? A. .
a b a . b . B. a.b 0 .
C. a.b 1 . D. .
a b a . b .
Câu 2. Cho tam giác đều ABC cạnh a = 2. Hỏi mệnh đề nào sau đây sai
A. A .
B AC.BC 2BC B. BC.CA 2
C. AB BC.AC 4
D. AC BC.BA 4
Câu 3. Cho hai vectơ a và b khác 0 . Xác định góc giữa hai vectơ a và b khi .
a b a . b . A. 0 180 . B. 0 0 . C. 0 90 . D. 0 45 .
Câu 4. Cho hình vuông ABCD cạnh a. M là trung điểm của AB. Tính . MA MC . A. 2 2a B. 0 C. 2 a D. 2 0, 25a
Câu 5. Cho hai vectơ a và b . Đẳng thức nào sau đây sai? 2 2 1 2 2 1 A. 2 2 a.b
a b a b . B. a.b a b a b . 2 2 2 2 1 2 2 1
C. a.b a b a b . D. a.b a b a b . 2 4
Câu 6. Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng AB.AC. 2 a 3 2 a 2 a A. 2
AB.AC 2a . B. . AB AC . C. AB.AC . D. AB.AC . 2 2 2
Câu 7. Cho tam giác đều ABC có cạnh bằng a và chiều cao AH . Mệnh đề nào sau đây là sai? 2 a 2 a
A. AH .BC 0. B. AB HA 0 , 150 . C. AB.AC . D. AC.CB . 2 2
Câu 8. Cho tam giác ABC vuông tại A và có AB c, AC . b Tính B . A BC. A. 2 B . A BC b . B. 2 B . A BC c . C. 2 2 B .
A BC b c . D. 2 2 B .
A BC b c .
Câu 9. Tính công sinh bởi một lực F có độ lớn 40N kéo vật dịch chuyển theo một vector d có độ lớn 50N và
góc giữa hai vector lực là 60 . A.1000J B. 1200J C. 900J D. 950J
Câu 10. Cho tam giác ABC có AB 2 cm, BC 3 cm, CA 5 cm. Tính C . A CB. A. C . A CB 13. B. C . A CB 15. C. C . A CB 17. D. C . A CB 19.
Câu 11. Cho ba điểm O, ,
A B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng OA OB.AB 0 là
A. tam giác OAB đều.
B. tam giác OAB cân tại O.
C. tam giác OAB vuông tại O.
D. tam giác OAB vuông cân tại O.
Câu 12. Cho M , N , P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?
A. MN NP PQ MN.NP MN.PQ .
B. MP.MN MN .MP .
C. MN.PQ PQ.MN . D. 2 2 MN PQ MN
PQ MN PQ .
Câu 13. Cho hình vuông ABCD có cạnh a, trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao
cho AM BN CP DQ x(0 x a) . Tính diện tích tứ giác MNPQ. A. 2 2
2x 2ax a B. 2 2
2x 2ax a C. 2 2
2x ax a D. 2 2
x 2ax a
Câu 14. Cho hình vuông ABCD cạnh a. Tính AB.AC. 2 1 A. 2
AB.AC a . B. 2
AB.AC a 2. C. 2 A . B AC a . D. 2 AB.AC a . 2 2 AC
Câu 15. Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho AM . Gọi N là 4
trung điểm của đoạn thẳng DC. Tính MB.MN .
A. MB.MN 4. B. MB.MN 0. C. MB.MN 4.
D. MB.MN 16.
Câu 16. Cho hình vuông ABCD có cạnh a, trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao
cho AM BN CP DQ x(0 x a) . Tính tích vô hướng PN.PQ . A. 2 AB B. 2 AC C. 2 AD
D. 0
Câu 17. Cho hình vuông ABCD cạnh a. M là trung điểm của AB, N là trung điểm của AD. Tính MN.MC . A. 2 2a B. 0 C. 2 a D. Kết quả khác 30
Câu 18. Cho hình vuông ABCD có cạnh a, trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao 2 a
cho AM BN CP DQ x(0 x a) . Nếu PM .DC thì giá trị x bằng 2 a a 3a A. B. C. D. a 4 2 4
Câu 19. Cho hình chữ nhật ABCD có AB 8, AD 5. Tích AB.BD.
A. AB.BD 62.
B. AB.BD 64.
C. AB.BD 62.
D. AB.BD 64.
Câu 20. Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng AB.BC. 2 a 3 2 a 2 a A. 2
AB.BC a . B. . AB BC . C. AB.BC . D. AB.BC . 2 2 2
Câu 21. Tính công sinh bởi một lực F có độ lớn 30N kéo vật dịch chuyển theo một vector d có độ lớn 60N và
góc giữa hai vector lực là 60 . A.900J B. 800J C. 700J D. 1000J
Câu 22. Cho hình vuông ABCD có cạnh a, trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao
cho AM BN CP DQ x(0 x a) . Tính PN.PM . A. 2 2
x (x a) B. 2 2
x (a 2x) C. 2 2
x (x a) D. 2 2
x (2a x)
Câu 23. Cho hình thoi ABCD có AC 8 và BD 6. Tính AB.AC.
A. AB.AC 24.
B. AB.AC 26.
C. AB.AC 28.
D. AB.AC 32.
Câu 24. Cho hình vuông ABCD cạnh a. M là trung điểm của AB. Tính MC.MD . A. 2 a B. 2 0, 25a C. 2 0, 75a D. Kết quả khác
Câu 25. Hình bình hành ABCD có AB 8 cm, AD 12 cm , góc
ABC nhọn và diện tích bằng 2 54 cm . Tính cosAB,BC. A. AB BC 2 7 cos , . B. AB BC 2 7 cos , . 16 16 C. AB BC 5 7 cos , . D. AB BC 5 7 cos , . 16 16
Câu 26. Cho hình chữ nhật ABCD có AB a và AD a 2 . Gọi K là trung điểm của cạnh A .
D Tính BK.AC.
A. BK .AC 0. B. 2 BK .AC a 2. C. 2
BK .AC a 2. D. 2
BK .AC 2a .
Câu 27. Tìm tập các hợp điểm M thỏa mãn MBMA MB MC 0 với ,
A B, C là ba đỉnh của tam giác. A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 28. Cho tam giác ABC vuông cân tại A và có AB AC .
a Tính AB.BC. 2 a 2 2 a 2 A. 2 AB.BC a . B. 2
AB.BC a . C. . AB BC . D. . AB BC . 2 2
Câu 29. Tính công sinh bởi một lực F có độ lớn 50N kéo vật dịch chuyển theo một vector d có độ lớn 50N và
góc giữa hai vector lực là 60 . A.1250J B. 1200J C. 900J D. 1300J
Câu 30. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn M . A BC 0 là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn. 2
Câu 31. Cho hai vectơ a và b thỏa mãn a b 1 và hai vectơ u a 3b và v a b vuông góc với nhau. 5
Xác định góc giữa hai vectơ a và b. A. 0 90 . B. 0 180 . C. 0 60 . D. 0 45 .
Câu 32. Cho tam giác ABC có BC ,
a CA b, AB c. Tính P AB AC.BC. 2 2 c b 2 2 2
c b a 2 2 2
c b a A. 2 2
P b c . B. P . C. P . D. P . 2 3 2
Câu 33. Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua C. Tính AE.AB. A. 2
AE.AB 2a . B. 2
AE.AB 3a . C. 2
AE.AB 5a . D. 2
AE.AB 5a .
Câu 34. Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a . Mệnh đề nào sau đây là sai? 1 1 2 a 1 A. 2 AB.AC a . B. 2
AC.CB a . C. G . A GB . D. 2 AB.AG a . 2 2 6 2 31
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P4) _____________________________
Câu 1. Cho tam giác OAB cân tại O có OA OB 26a ; có M là trung điểm đoạn thẳng AB. Tính tích vô hướng
OI.IA OI.IB . A.0 B. 2 C. 26 D. 52
Câu 2. Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng AB.AC. 2 a 3 2 a 2 a A. 2
AB.AC 2a . B. A . B AC . C. AB.AC . D. AB.AC . 2 2 2
Câu 3. Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng AB.BC. 2 a 3 2 a 2 a A. 2
AB.BC a . B. . AB BC . C. AB.BC . D. AB.BC . 2 2 2
Câu 4. Tam giác ABC có AB 3; AC 4; A 60 . M là trung điểm của cạnh BC. Tính . AB AE . A. 6 3 B. 3 3 C. 2 3 D. 4 3
Câu 5. Tam giác ABC có AB 3; AC 4; A 60 . M là trung điểm của cạnh BC. Tính AC.AD . A. 6 3 B. 3 3 C. 2 3 D. 4 3
Câu 6. Cho hai điểm M, N thỏa mãn MN.NM 4
. Tìm độ dài đoạn thẳng MN. A. MN 2 B. MN 4 C. MN 6 D. MN 8
Câu 7. Cho tam giác ABC vuông tại A có AB a , AC a 3 và AM là trung tuyến. Tính tích vô hướng . BA AM . 2 a 2 a A. 2 a . B. 2 a . C. . D. . 2 2
Câu 8. Cho tam giác ABC đều cạnh bằng a , trọng tâm G . Tích vô hướng của hai vectơ BC.CG bằng 2 a 2 a 2 a 2 a A. . B. . C. . D. . 2 2 2 2
Câu 9. Cho hình vuông ABCD , tâm O , cạnh bằng a . Tìm mệnh đề sai: 2 2 2 a a A. A . B AC a .
B. AC.BD 0 . C. A . B AO . D. A . B BO . 2 2 Câu 10. Cho AB
C vuông tại A , biết A .
B CB 4 , AC.BC 9 . Khi đó AB , AC , BC có độ dài là A. 2 ; 3 ; 13 . B. 3 ; 4 ; 5 . C. 2 ; 4 ; 2 5 . D. 4 ; 6 ; 2 13 .
Câu 11. Cho hình thang vuông ABCD có đáy lớn AB 4a , đáy nhỏ CD 2a , đường cao AD 3a ; I là trung
điểm của I . Khi đó I bằng 2 9a 2 9 a 2 A. . B. . C. 0 . D. 9a . 2 2
Câu 12. Cho a , b , c thỏa mãn: a 4 , b 1, c 5 và 5b a 3c 0 . Khi đó M a .b b .c c .a có giá trị là A. 29 . B. 33,5. C.18, 25 . D. 18, 25 .
Câu 13. Cho hình vuông ABCD có cạnh bằng1. Hai điểm M , N thay đổi lần lượt ở trên cạnh AB , AD sao
cho AM x 0 x
1 , DN y 0 y
1 . Tìm mối liên hệ giữa x và y sao cho CM BN
A. x y 0.
B. x y 2 0.
C. x y 1.
D. x y 3 0.
Câu 14. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng? A. .
a b a . b . B. a.b 0 .
C. a.b 1 . D. .
a b a . b .
Câu 15. Cho hai vectơ a và b khác 0 . Xác định góc giữa hai vectơ a và b khi .
a b a . b . A. 0 180 . B. 0 0 . C. 0 90 . D. 0 45 .
Câu 16. Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a . Mệnh đề nào sau đây là sai? 1 1 2 a 1 A. 2 AB.AC a . B. 2
AC.CB a . C. G . A GB . D. 2 AB.AG a . 2 2 6 2
Câu 17. Cho tam giác ABC vuông tại A và có AB c, AC . b Tính B . A BC. A. 2 B . A BC b . B. 2 B . A BC c . C. 2 2 B .
A BC b c . D. 2 2 B .
A BC b c .
Câu 18. Cho tam giác ABC có AB 2 cm, BC 3 cm, CA 5 cm. Tính C . A CB. A. C . A CB 13. B. C . A CB 15. C. C . A CB 17. D. C . A CB 19. 32
Câu 19. Cho hai vector a,b thỏa mãn 3a b 5, 3a b 4 . Tính . a b . A. – 1,2 B. – 3 C. – 0,75 D. 3
Câu 20. Cho tam giác ABC có BC ,
a CA b, AB c. Tính P AB AC.BC. 2 2 c b 2 2 2
c b a 2 2 2
c b a A. 2 2
P b c . B. P . C. P . D. P . 2 3 2
Câu 21. Cho hình vuông ABCD cạnh a, tâm O, M là trung điểm của BC. Tính AM .AO . 3 2 a A. 2 a . B. 2 a . C. 2 a . D. . 4 2
Câu 22. Cho tam giác ABC có BC a, CA b, AB c. Gọi M là trung điểm cạnh BC. Tính AM .BC. 2 2 b c 2 2 c b A. AM .BC . B. AM .BC . 2 2 2 2 2
c b a 2 2 2
c b a C. AM.BC . D. AM .BC . 3 2
Câu 23. Cho ba điểm O, ,
A B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng OA OB.AB 0 là
A. tam giác OAB đều.
B. tam giác OAB cân tại O.
C. tam giác OAB vuông tại O.
D. tam giác OAB vuông cân tại O.
Câu 24. Cho hai vector a,b thỏa mãn 2a b 5, 2a b 3 . Tính . a b . A. – 1,2 B. – 3 C. – 2 D. 3
Câu 25. Cho M , N , P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?
A. MN NP PQ MN.NP MN.PQ .
B. MP.MN MN .MP .
C. MN.PQ PQ.MN . D. 2 2 MN PQ MN
PQ MN PQ .
Câu 26. Cho hình vuông ABCD cạnh a. Tính AB.AC. 2 1 A. 2
AB.AC a . B. 2
AB.AC a 2. C. 2 . AB AC a . D. 2 AB.AC a . 2 2
Câu 27. Cho hình vuông ABCD cạnh a, tâm O, M là trung điểm của BC. Tính AM ( AB AC) . A. 2 2,5a B. 2 2a C. 2 3a D. 2 a
Câu 28. Cho hình vuông ABCD cạnh a . Tính P AC.CD CA. A. P 1. B. 2 P 3a . C. 2 P 3 a . D. 2 P 2a .
Câu 29. Hình bình hành ABCD có AB 8 cm, AD 12 cm , góc
ABC nhọn và diện tích bằng 2 54 cm . Tính cosAB,BC. A. AB BC 2 7 cos , . B. AB BC 2 7 cos , . C. AB BC 5 7 cos , . D. AB BC 5 7 cos , . 16 16 16 16
Câu 30. Cho hình chữ nhật ABCD có AB a và AD a 2 . Gọi K là trung điểm của cạnh A .
D Tính BK .AC.
A. BK .AC 0. B. 2 BK .AC a 2. C. 2
BK .AC a 2. D. 2
BK .AC 2a .
Câu 31. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn MAMB MC 0 là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 32. Cho hình vuông ABCD cạnh a, tâm O, M là trung điểm của BC. Tính AM .AB . 2 a A. B. 2 2a C. 2 3a D. 2 a 3
Câu 33. Tìm tập các hợp điểm M thỏa mãn MBMA MB MC 0 với ,
A B, C là ba đỉnh của tam giác. A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 34. Cho hai vector a,b thỏa mãn a b 3, a b 2 . Tính . a b . A. – 2 B. – 3 C. – 1,25 D. 3
_________________________________ 33
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P5) _____________________________
Câu 1. Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua C. Tính AE.AB. A. 2
AE.AB 2a . B. 2 AE.AB 3a . C. 2 AE.AB 5a . D. 2
AE.AB 5a .
Câu 2. Cho hình vuông ABCD cạnh a. Tính AB BC BDDA DB DC. A. 2 a B. 2 2a C. 2 3a D. 0
Câu 3. Tính công sinh bởi một lực F có độ lớn 20N kéo vật dịch chuyển theo một vector d có độ lớn 50N và
góc giữa hai vector lực là 60 . A.500J B. 300J C. 450J D. 540J
Câu 4. Cho hai vectơ a và b thỏa mãn a 3, b 2 và a.b 3. Xác định góc giữa hai vectơ a và b. A. 0 30 . B. 0 45 . C. 0 60 . D. 0 120 .
Câu 5. Cho hai vector a,b thỏa mãn 3a b 5, 3a b 4 . Tính . a b . A. – 1,2 B. – 3 C. – 0,75 D. 3 2
Câu 6. Cho hình vuông ABCD cạnh a. Tính A . B AC 25AB . A. 2 20a B. 2 26a C. 2 30a D. 2 18a 2
Câu 7. Cho hai vectơ a và b thỏa mãn a b 1 và hai vectơ u a 3b và v a b vuông góc với nhau. Xác 5
định góc giữa hai vectơ a và b. A. 0 90 . B. 0 180 . C. 0 60 . D. 0 45 .
Câu 8. Cho hình vuông ABCD cạnh a. Tính AB ADBD BC. A. 2 a B. 2 2a C. 2 3a D. 2 4a
Câu 9. Cho hai vectơ a và b . Đẳng thức nào sau đây sai? 2 2 1 2 2 1 A. 2 2 a.b
a b a b . B. a.b a b a b . 2 2 2 2 1 2 2 1
C. a.b a b a b . D. a.b a b a b . 2 4
Câu 10. Cho tam giác đều ABC có cạnh bằng a và chiều cao AH . Mệnh đề nào sau đây là sai? 2 a 2 a
A. AH .BC 0. B. AB HA 0 , 150 . C. AB.AC . D. AC.CB . 2 2
Câu 11. Cho tam giác ABC vuông cân tại A và có AB AC .
a Tính AB.BC. 2 a 2 2 a 2 A. 2 AB.BC a . B. 2
AB.BC a . C. . AB BC . D. . AB BC . 2 2
Câu 12. Tính công sinh bởi một lực F có độ lớn 30N kéo vật dịch chuyển theo một vector d có độ lớn 50N và
góc giữa hai vector lực là 60 . A.750J B. 300J C. 450J D. 650J
Câu 13. Cho hình vuông ABCD cạnh a. Tính P AB AC.BC BD BA. A. P 2 2 . a B. 2 P 2a . C. 2 P a . D. 2 P 2 a . AC
Câu 14. Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho AM . Gọi N là 4
trung điểm của đoạn thẳng DC. Tính MB.MN .
A. MB.MN 4. B. MB.MN 0. C. MB.MN 4.
D. MB.MN 16.
Câu 15. Cho tam giác ABC đều cạnh a, tính 3 . GA GB 6G .
A GC với G là trọng tâm tam giác. 2 a 2 a 3 2 a A. B. C. 2 a D. 2 3 2 2
Câu 16. Cho hình chữ nhật ABCD có AB 8, AD 5. Tích AB.BD.
A. AB.BD 62.
B. AB.BD 64.
C. AB.BD 62.
D. AB.BD 64.
Câu 17. Cho hình vuông ABCD cạnh a, tính AC AB2AD AB . A. 2 a B. 2 2a C. 2 3a D. 2 4a 34
Câu 18. Cho tam giác ABC vuông tại A có AB a; BC 2a , trọng tâm G. Tính .
BA BC BC.CA . 1 A. 2 2a B. 2 2a C. 2 3a D. 2 a 2
Câu 19. Cho hình vuông ABCD tâm O, điểm M nằm trên đường tròn ngoại tiếp hình vuông, N là điểm tùy ý trên
cạnh BC. Tính M .
A MB MC.MD . 1 1 A. 2 2 a B. 2 2a C. 2 a D. 2 a 2 2
Câu 20. Cho hai vector a,b thỏa mãn 3a b 8, 3a b 6 . Tính . a b . A. – 6 B. – 3 C. – 5,75 D. Kết quả khác
Câu 21. Cho hình vuông ABCD cạnh a, tâm O, điểm M thuộc đường tròn ngoại tiếp tam giác ABC. Tính giá trị
của M . B MD C . O BO . 2 a 2 a 2 a A. B. C. 2 a D. 2 3 2
Câu 22. Cho tam giác ABC đều cạnh a, tính G . A GB 2G .
A GC với G là trọng tâm tam giác. 2 a 2 a 2 a 2 a A. B. C. D. 2 3 3 2
Câu 23. Cho hai vector a,b thỏa mãn 4a b 5, 4a b 4 . Tính . a b . A. – 1,2 B. – 3 C. – 0,75 D. Kết quả khác
Câu 24. Cho hình vuông ABCD cạnh a. Tính AC AB AD . A. 2 2a B. 2 2 a C. 2 3a D. 2 4a
Câu 25. Cho hình vuông ABCD cạnh a. Tính AB ADBC BD . A. 2 a B. 2 2a C. 2 3a D. Kết quả khác
Câu 26. Cho hình thoi ABCD có AC 8 và BD 6. Tính AB.AC.
A. AB.AC 24.
B. AB.AC 26.
C. AB.AC 28.
D. AB.AC 32.
Câu 27. Cho hình vuông ABCD cạnh a. Tính AC AB2AD AB . A. 2 2a B. 2 2 a C. 2 3a D. 2 4a
Câu 28. Cho hình vuông ABCD cạnh a. Tính . OA AB . 2 a 2 2 a 3 2 a 2 a A. B. C. D. 2 2 2 2
Câu 29. Cho tam giác đều ABC có trọng tâm G và độ dài cạnh bằng a. Tính . AB AG . 2 a 3 2 3a 2 a 3 2 a A. B. C. D. 6 4 4 2
Câu 30. Cho tam giác ABC đều cạnh a, đường cao AH. Tính AC AC AB . 2 a 2 2 a 3 2 a 2 a A. B. C. D. 2 2 2 2
Câu 31. Cho hình thoi ABCD tâm O có cạnh bằng a 2 và ABD 60 . Điểm I thỏa mãn 2IC ID 0 . Tính . AO BI . 2 a 2 2 a 3 2 a 2 a 2 A. B. C. D. 2 2 2 6
Câu 32. Tam giác ABC vuông tại A có AB 3; AC 4 . Trên đoạn thẳng BC lấy điểm M sao cho MB 2MC .
Tính tích vô hướng AM .BC . 23 41 A.8 B. – 23 C. D. 3 3
_________________________ 35
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P6) _____________________________ 2
Câu 1. Cho hai vector a,b có a 4, b 5 và a,b 120 . Tính a b . A.21 B. 41 C. 50 D. 62
Câu 2. Cho hai vectơ a và b thỏa mãn a 3, b 2 và a.b 3. Xác định góc giữa hai vectơ a và b. A. 0 30 . B. 0 45 . C. 0 60 . D. 0 120 .
Câu 3. Cho hình vuông ABCD cạnh a, tâm O. M là trung điểm của BC. Tính OM .OD . 2 a 2 3a 2 2a A. B. 2 a C. D. 2 4 3
Câu 4. Cho tam giác ABC có BC ,
a CA b, AB c. Gọi M là trung điểm cạnh BC. Tính AM .BC. 2 2 b c 2 2 c b A. AM .BC . B. AM .BC . 2 2 2 2 2
c b a 2 2 2
c b a C. AM.BC . D. AM .BC . 3 2
Câu 5. Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính
A . B CD . BD BC A. 2 a B. 2 3a C. 2 2a D. Kết quả khác
Câu 6. Cho hình chữ nhật ABCD tâm I, cạnh AB = a, AD = b. Tính tích vô hướng A . B AC . A. 2 a B. ab C. 2 2a D. 2 2b
Câu 7. Cho tam giác đều ABC cạnh a, trọng tâm G. Tính GAGB GC. 2 a 2 a 2 a A. 2 2a B. C. D. 2 4 3
Câu 8. Cho hình chữ nhật ABCD tâm I, cạnh AB = a, AD = b. Tính AC AB AC AD . A. 2 a B. ab C. 2 2a D. 2 b
Câu 9. Cho hình vuông ABCD cạnh a . Tính P AC.CD CA. A. P 1. B. 2 P 3a . C. 2 P 3 a . D. 2 P 2a .
Câu 10. Cho hình chữ nhật ABCD tâm I, cạnh AB = a, AD = b. Tính 2 . MA MC .
MB MD với M là điểm nằm trên
đường tròn ngoại tiếp hình chữ nhật. A. 2 a B. ab C. 2 2a D. 0
Câu 11. Cho hình vuông ABCD cạnh a. Tính P AB AC.BC BD BA. A. P 2 2 . a B. 2 P 2a . C. 2 P a . D. 2 P 2 a .
Câu 12. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn MAMB MC 0 là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 13. Cho hình vuông ABCD cạnh a, M là trung điểm của AB, G là trọng tâm của tam giác ADM. Tính giá trị
của biểu thức CG CA DM . 21 11 9 2 a A. 2 a B. 2 a C. 2 a D. 4 4 4 4
Câu 14. Cho các vector a,b thỏa mãn a b 1; 2a 3b 7 . Tính cos a,b . 2 1 1 1 A. B. C. D. 4 4 2 3
Câu 15. Cho các vector a,b thỏa mãn a b 1và góc giữa hai vector bằng 60 . Xác định cosin giữa hai vector sau 1 1 1 1 A. B. C. D. 2 6 4 3
Câu 16. Cho hình thang vuông ABCD có đường cao AB a 3 , cạnh đáy AD ;
a BC 2a . Tính AC.BD . 36 2 a A. 2 (2 2)a B. 2 (2 2)a C. 2 3a D. 2
Câu 17. Cho hình vuông ABCD cạnh a, tính AB ADBD BC . A. 2 a B. 2 3a C. 2 2a D. 2 4a
Câu 18. Một lực F có độ lớn x (N) kéo vật dịch chuyển theo một vector d có độ lớn 50N và góc giữa hai vector
lực là 60 . Biết công sinh ra bởi lực F là 1200J. Giá trị của x bằng A.48N B. 30N C. 45N D. 50N.
Câu 19. Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a, I là trung điểm
đoạn thẳng AB. Tính IA IB ID . 2 3a 2 3a A.0 B. 2 9a C. D. 2 2
Câu 20. Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a. Tính . DA BC . A.0 B. 2 9a C. 2 15a D. 2 9 a
Câu 21. Cho hình vuông ABCD cạnh a, E là điểm đối xứng với C qua D. Tính AC.BE . A. 2 a B. 2 3a C. 2 2a D. 2 a
Câu 22. Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a. Câu nào sau đây sai A. 2 A . B DC 8a B. A . D CD 0 C. A . B AD 0 D. . DA DB 0
Câu 23. Cho hai vector a,b thỏa mãn 2a b 5, 2a b 6 . Tính . a b . A.1,375 B. 2 C. – 2,25 D. 1,25
Câu 24. Tính công sinh bởi một lực F có độ lớn 35N kéo vật dịch chuyển theo một vector d có độ lớn 50N và
góc giữa hai vector lực là 60 . A.875J B. 300J C. 450J D. 540J
Câu 25. Cho hình vuông ABCD cạnh a, tâm O. M là trung điểm của AD. Tính OM OB OC OA. 2 a 2 a 2 a A. 2 2a B. C. D. 2 4 8
Câu 26. Cho hình vuông ABCD cạnh a, điểm M bất kỳ, tính M . A MC . MB MD . 2 a 2 a A.0 B. C. D. 2 a 2 4
Câu 27. Cho tam giác ABC vuông tại A có AB ;
a AC a 3 và AM là trung tuyến. Tính . BA AM . 2 a 2 a A. . B. 2 a . C. 2 a . D. . 2 2
Câu 28. Cho hình vuông ABCD có cạnh bằng 3. Trên cạnh AB lấy điểm M sao cho BM = 1, trên cạnh CD lấy
điểm N sao cho DN = 1 và P là trung điểm của BC. Tính cos MNP . 13 13 13 13 A. B. C. D. 5 10 4 10 10 45 10
Câu 29. Cho hai vectơ a và b . Biết a 2, b 3 và a,b 30. Tính a b . A. 11 . B. 13 . C. 12 . D. 14 .
Câu 30. Cho hình bình hành ABCD , với AB 2 , AD 1, BAD 60 . Tích vô hướng . AB DA bằng 1 1 A. . B. 1. C. . D. 1 . 2 2
Câu 31. Cho hình vuông ABCD cạnh bằng 5. Tính AB AC.BC BD BA. A. 10 2. B. 50. C. 0. D. 75.
Câu 32. Cho hình vuông ABCD cạnh a, E là điểm đối xứng với C qua D, tính OC.OE . 2 a 2 a 2 a A. 2 2a B. C. D. 2 4 3 37




