


























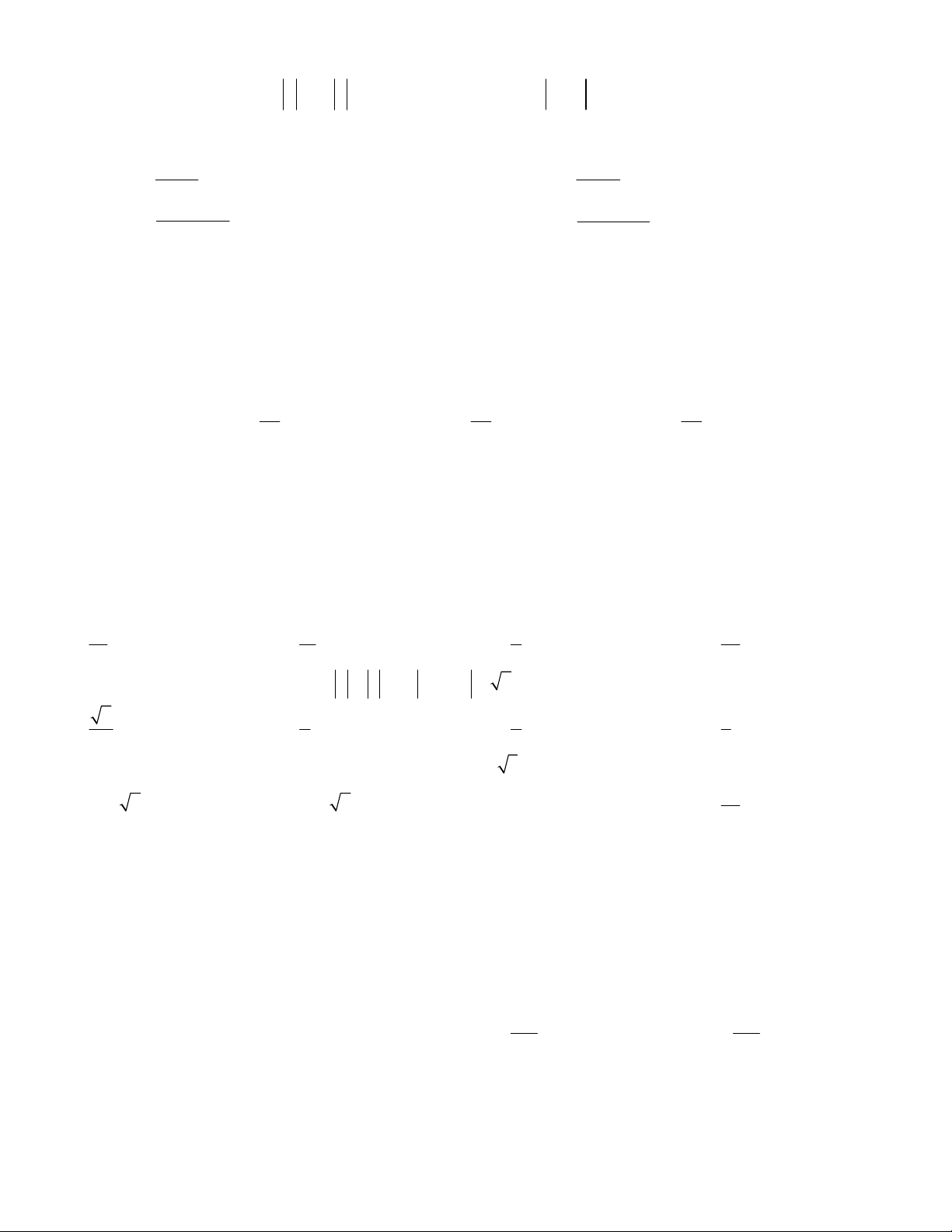
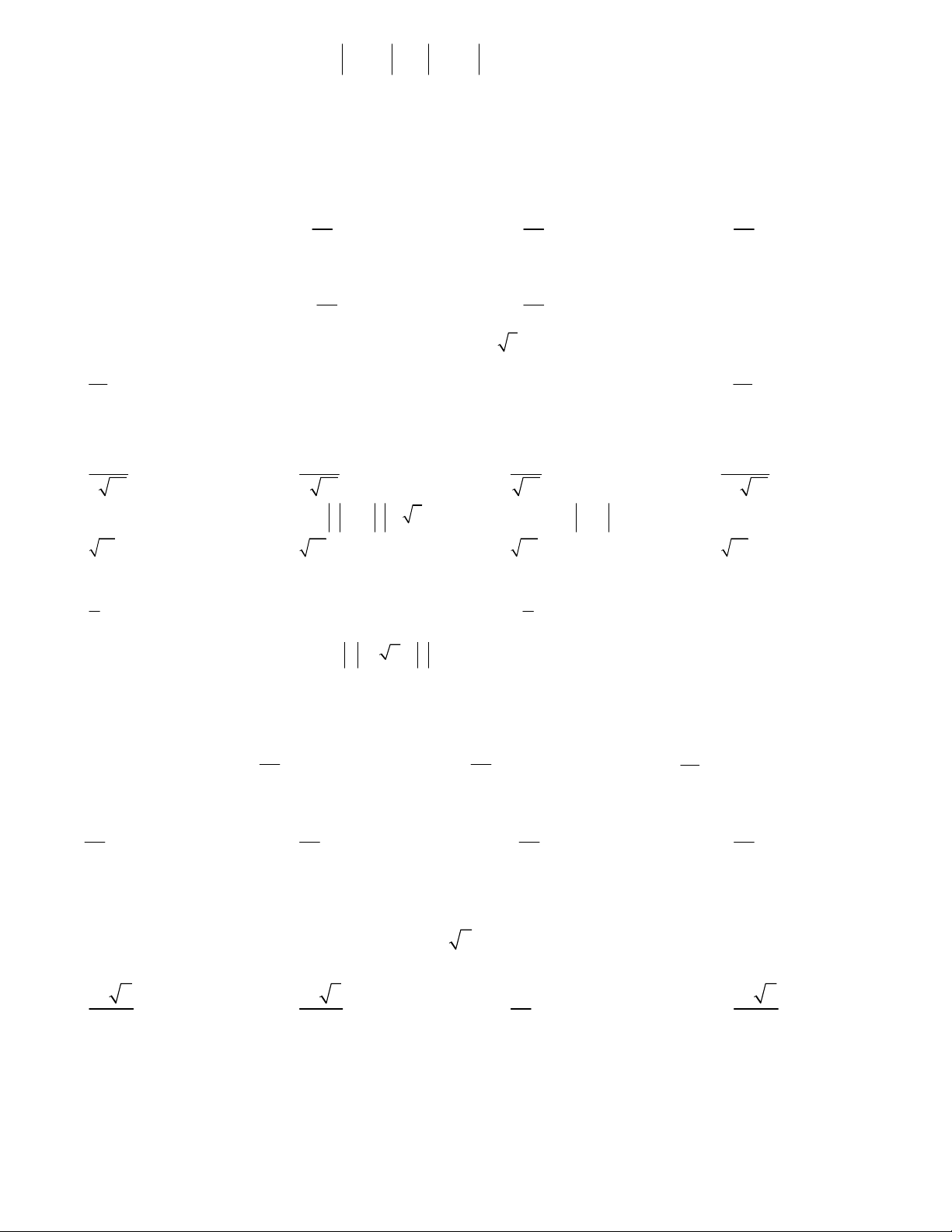







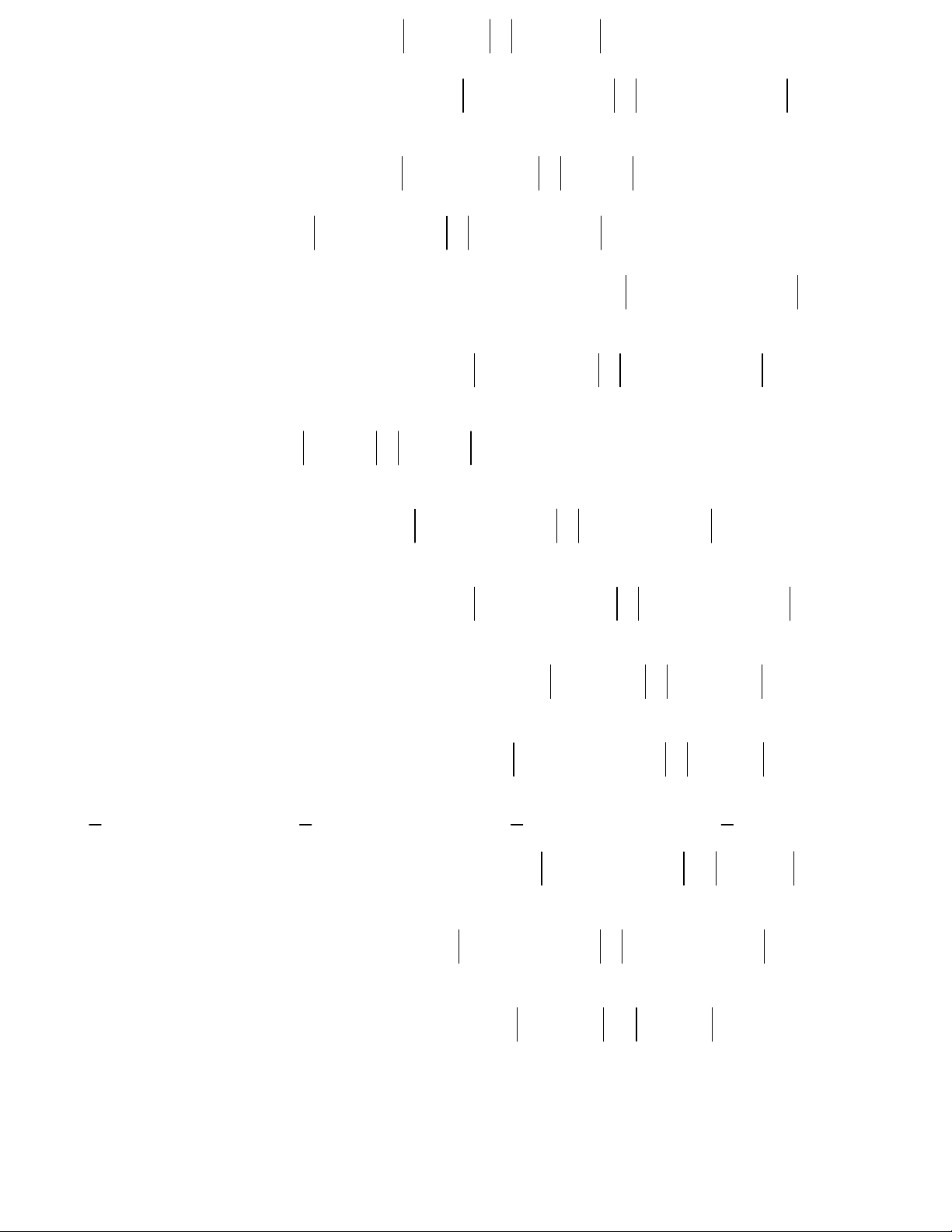





Preview text:
TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
--------------------------------------------------------------------------------------------
CHUYÊN ĐỀ VECTOR HÌNH HỌC PHẲNG
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM VECTOR HÌNH HỌC PHẲNG
CƠ BẢN – VẬN DỤNG – VẬN DỤNG CAO
CƠ BẢN TỔNG, HIỆU, TÍCH VECTOR VỚI 1 SỐ THỰC, PHÂN TÍCH VECTOR (P1 – P3)
VẬN DỤNG TỔNG, HIỆU, TÍCH VECTOR VỚI 1 SỐ THỰC, PHÂN TÍCH VECTOR (P1 – P3)
CƠ BẢN ĐỘ DÀI VECTOR (P1 – P3)
VẬN DỤNG ĐỘ DÀI VECTOR (P1 – P3)
CƠ BẢN TÍCH VÔ HƯỚNG VECTOR (P1 – P3)
VẬN DỤNG TÍCH VÔ HƯỚNG VECTOR (P1 – P3)
VẬN DỤNG CAO PHÂN TÍCH VECTOR, TỶ LỆ VECTOR, BA ĐIỂM THẲNG HÀNG (P1 – P3)
VẬN DỤNG CAO QUỸ TÍCH, TẬP HỢP ĐIỂM (P1 – P3)
VẬN DỤNG CAO CỰC TRỊ VÀ BÀI TOÁN THỰC TẾ VECTOR (P1 – P3)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
GACMA1431988@GMAIL.COM (GMAIL); TEL 0333275320
THÀNH PHỐ THÁI BÌNH – THÁNG 10/2023 1
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM TOÁN 10
VECTOR HÌNH HỌC PHẲNG
CƠ BẢN – VẬN DỤNG – VẬN DỤNG CAO
__________________________________________ DUNG NỘI DUNG BÀI TẬP LƯỢNG 3 FILE
CƠ BẢN TỔNG, HIỆU, TÍCH VECTOR VỚI 1 SỐ THỰC, PHÂN TÍCH VECTOR 3 FILE
VẬN DỤNG TỔNG, HIỆU, TÍCH VECTOR VỚI 1 SỐ THỰC, PHÂN TÍCH VECTOR 3 FILE
CƠ BẢN ĐỘ DÀI VECTOR TÍCH VÔ HƯỚNG, GÓC 3 FILE
VẬN DỤNG ĐỘ DÀI VECTOR 3 FILE
CƠ BẢN TÍCH VÔ HƯỚNG VECTOR 3 FILE
VẬN DỤNG TÍCH VÔ HƯỚNG VECTOR 3 FILE
VẬN DỤNG CAO PHÂN TÍCH VECTOR, TỶ LỆ VECTOR,
BA ĐIỂM THẲNG HÀNG 3 FILE
VẬN DỤNG CAO QUỸ TÍCH, TẬP HỢP ĐIỂM 3 FILE
VẬN DỤNG CAO CỰC TRỊ VÀ BÀI TOÁN THỰC TẾ VECTOR 2
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, TÍCH VECTOR VỚI 1 SỐ THỰC, PHÂN TÍCH VECTOR P1)
_________________________________________________
Câu 1. Cho ba điểm A, B, C phân biệt, điều kiện cần và đủ để A nằm giữa B và C là A. k
0; AB k AC B. k
0; AB k AC C. AB = AC D. AB AC
Câu 2. Trên đoạn thẳng AB lấy M, N sao cho AM = MN = NB. Có bao nhiêu vec tơ bằng vec tơ MA A.2 B. 1 C. 3 D. 4
Câu 3. Trên đoạn thẳng AB = 6 lấy M, N sao cho AM = MN = NB. Tính độ dài vec tơ MA MN AB . A. 3 B. 6 C. 1 D. 4
Câu 4. Cho tứ giác ABCD, có bao nhiêu vec tơ khác véc tơ không có điểm đầu và điểm cuối là 2 trong số 4 đỉnh của tứ giác A.4 B. 12 C. 6 D. 10
Câu 5. Hình vẽ sau có bao nhiêu cặp vec tơ bằng nhau A. 3 B. 1 C. 0 D. 2
Câu 6. Cho hình vuông ABCD. Tính AB AD . A. 0 B. AC C. AO D. DA
Câu 7. Cho tam giác ABC có trọng tâm G, D đối xứng với G qua trung điểm M của BC. Tính GB GC . A. GA B. GD C. 2GA D. 2GD
Câu 8. Cho hình bình hành ABCD. Điểm M thỏa mãn MB MA k MD MC . Giá trị của k bằng A.2 B. – 1 C. 1 D. – 2
Câu 9. Cho đường tròn tâm O bán kính R. Lấy hai điểm A, B trên đường tròn sao cho OA OB 0 . Có bao
nhiêu cặp điểm A, B thỏa mãn A.2 B. 3 C. 4 D. Vô số
Câu 10. Cho 3 điểm M , N , P tùy ý khi đó
A. MN NP PM
B. MN NP MP
C. NM NP MP
D. MN NP MP
Câu 11. Cho tam giác ABC ,để: MA MB MC 0 thì vị trí điểm M thỏa:
A. AMBC là hình bình hành
B. CBAM là hình bình hành
C. MACB là hình bình hành
D. MABC là hình bình hành
Câu 12. Cho tứ giác ABCD . Khẳng định nào sau đây đúng ?
A. AC BA BC
B. AB AD BD
C. BC BD CD
D. AD DB AB
Câu 13. Cho tam giác ABC có M; N; P lần lượt là trung điểm AB , AC , BC . Vectơ NM bằng 1 1 A. CP B. BC C. CP D. CB 2 2
Câu 14. Cho 3 điểm M , N , P thẳng hàng ; P nằm giữa M và N . Cặp vectơ nào sau đây ngược hướng với nhau ? A. MN; NP B. MN; MP C. M ; P PN D. NM ; NP
2
Câu 15. Cho tam giác ABC có D là trung điểm của BC . Xác định vị trí của điểm G biết GA AD 0 3 2 1
A. G nằm trên đoạn AD và AG AD
B. G nằm trên đoạn AD và AG AD 3 3 1
C. G nằm trên đoạn AD và GD 2GA
D. G nằm trên đoạn AD và GA GD 3
Câu 16. Cho hình vuông ABCD . Gọi M , N lần lượt là trung điểm của AD , BC . Các vectơ bằng AM là:
A. MD, , MA BN
B. MD, BN , NC
C. MD, NB, NC
D. DM , BN , NC
Câu 17. Cho hình vuông ABCD . Khẳng định nào sau đây đúng ?
A. AD AB DB
B. BA BC BD
C. CA CB CD
D. DA DB BC 3
Câu 18. Cho tam giác ABC , M là điểm tùy ý. Tìm khẳng định đúng:
A. MA BC MC BA
B. MA BC MC BA
C. AC BM AM BC
D. AB CM AM BC
Câu 19. Gọi AD là trung tuyến của tam giác ABC , gọi E là trung điểm của AD . Khi đó 2EA EB EC bằng: 5 A. 2EA B. 0 C. 4EA D. EA 2
Câu 21. Điều kiện cần và đủ để MN PQ là chúng:
A. Cùng phương, cùng độ dài. B. Cùng hướng.
C. Cùng hướng, cùng độ dài. D. Cùng độ dài.
Câu 22. Cho tam giác ABC , gọi M , N là trung điểm của AB và AC . Khi đó A. 2MN BC
B. - 2MN BC
C. 2MN BC D. MN BC
Câu 23. Cho hình bình hành ABCD tâm O. Tìm k sao cho CO OB k BA . A.2 B. – 2 C. 1 D. – 1
Câu 24. Cho hình bình hành ABCD tâm O . Quy tắc nào sau đây là quy tắc hình bình hành?
A. OA OB 0
B. AB BC AC
C. CB CD CA
D. OA OB BA
Câu 25. Cho đoạn thẳng AB , gọi M là trung điểm và O là điểm tùy ý. Khẳng định nào sau đây sai: 1
A. MO ( AO BO)
B. AM BM 0
C. MB MA AB
D. OA OB 2OM 2
Câu 26. Cho tam giác ABC . Điểm M thỏa MA MB 2MC 0 , N là trung điểm AB . Khi đó
A. M thuộc CN sao cho CM 2NM
B. M thuộc CN sao cho CN 3NM
C. M nằm ngoại đoạn CN
D. M là trung điểm CN .
Câu 27. Cho 4 điểm bất kỳ A , B , C , D . Đẳng thức nào sau đây là đúng:
A. AB DB DA DC
B. DA AC DB BA
C. AD BC AC DB
D. AB CB AC BC
Câu 28. Cho tam giác ABC vuông tại C có cạnh AC 4 cm, BC 3cm. Tính độ dài AB A. 7cm B. 6cm C. 4cm D. 5cm
Câu 29. Cho tam giác ABC . Trên đoạn AB lấy điểm H sao cho AH = 2HB . Qua H dựng đường thẳng
song song với BC cắt AC tại I . Khi đó: 1 1 2 2
A. HI BC B. HI BC C. HI BC D. HI BC 3 3 3 3
Câu 30. Cho tứ giác ABCD . Khi đó:
A. BA CD BC AD
B. AD CB AC BD
C. AB CD AC BD
D. AB DC AC BD
Câu 31. Cho tam giác ABC . Xác định điểm M thỏa đẳng thức sau:. MA 2MB CB
A. Điểm M là trung điểm của AC
B. Điểm M là trọng tâm của tam giác ABC
C. Điểm M đối xứng với C qua B
D. Điểm M là một đỉnh của hình bình hành ABMC
Câu 32. Cho tứ giác ABCD . Gọi I , J lần lượt là trung điểm AC và BD . Gọi E là trung điểm IJ . Tìm đẳng thức vectơ đúng: 1
A. . EA EB 2EJ 0 B. . IJ ( AC BD)
C. EA EB EC ED 0 D. . AB DC 2IJ 2
Câu 24. Chọn khẳng định đúng:
A. Hai vectơ cùng phương thì chúng cùng hướng
B. Hai vectơ cùng phương thì giá của chúng song song hoặc trùng nhau
C. Hai vectơ có giá vuông góc thì cùng phương
D. Hai vectơ ngược hướng với 1 vectơ thứ ba thì cùng phương
Câu 25. Cho hình bình hành ABCD tâm O . Các véctơ ngược hướng với OB là:
A. BD, OD
B. DB,OD,OB C. DB, DO
D. BD, OD, BO
Câu 26. Cho tam giác ABC . Hãy xác định điểm M thỏa mãn: 2MA 3MB 0 .
A. M thuộc cạnh AB và AM 2MB
B. M không thuộc AB
C. M là trung điểm của AB
D. M trên AB và ngoài đoạn AB
Câu 27. Cho ba điểm phân biệt A , B , C . Đẳng thức nào sau đây là đúng ?
A. CA BA BC
B. AB AC BC
C. AB BC CA
D. AB CA CB
Câu 28. Cho hình bình hành ABCD tâm O . Vectơ AB cùng hướng với vectơ nào sau đây? A. AD B. DC C. CD D. BC 4
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, TÍCH VECTOR VỚI 1 SỐ THỰC, PHÂN TÍCH VECTOR P2)
_________________________________________________
Câu 1. Hai vectơ cùng hướng và cùng độ dài là hai vectơ A. Bằng nhau B. Đối nhau C. Ngược hướng D. Song song
Câu 2. Cho M là một điểm thuộc đoạn thẳng AB sao cho AB = 3AM . Hãy tìm khẳng định sai? 1 A. MB 2 MA B. MA 2 MB C. BA 3 AM D. AM BM 2
Câu 3. Cho hình bình hành ABCD , vectơ nào sau đây bằng CD ? A. DC B. BD C. AD D. BA
Câu 4. Cho hình bình hành ABCD tâm O . AD AB ? A. DB B. AC C. BD D. BC
Câu 5. Cho hình vuông ABCD tâm O . Véctơ bằng DO là: A. OC B. OA C. BO D. OB
Câu 6. Cho hình bình hành ABCD . Hai vec tơ nào ngược hướng? A. AB và AC B. AB và DC C. AB và DB D. AB và CD
Câu 7. Hai vectơ cùng phương thì chúng A. Cùng hướng B. Ngược hướng
C. Có giá song song hoặc trùng nhau D. Song song
Câu 8. Nếu I là trung điểm đoạn thằng AB thì với mọi điểm H ta luôn có
A. HA HB 2HI
B. AH BH 2HI
C. HA HB 2IH
D. AH BH 2IH
Câu 9. Chọn khẳng định đúng trong các hệ thức sau:
A. MP NM NP
B. AB AC BC
C. CA BA CB
D. AA AB BA
Câu 10. Cho hình bình hành ABCD . Khi đó đẳng thức nào sau đây đúng:
A. AB BC CD
B. AB AD BD
C. AB AD AC
D. AB AD CA
Câu 11. Cho tam giác ABC với trung tuyến AM và trọng tâm G .Khi đó GA =? 2 1 2 A. 2GM B. GM C. AM D. AM 3 2 3
Câu 12. Gọi I là trung điểm AB , M là điểm tùy ý. Đẳng thức nào đúng? 1 1
1 A. MI (MA MB) B. MI (MA MB)
C. 2IM (MA MB) D. MI (MA MB) 2 2 3
Câu 13. Cho đoạn thẳng AB . Gọi I là điểm đối xứng của A qua B . Gọi M là điểm tùy ý. Đẳng thức nào sau đây đúng:
A. IA IB 0
B. AI BI 0
C. MA MB 2MI
D. BA BI 0
A. AB CD AC BD
B. AB CD DA BC
C. AB CD AD BC
D. AB CD AD CB
Câu 14. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Khi đó:
A. AB AD BD
B. AB OA BO
C. AB BD 0
D. AB CD 0
Câu 15. Cho ba điểm A , B , C thẳng hàng và B là trung điểm AC . Tổng BA BC bằng A. 2 AC B. AC C. 0 D. 2CA
Câu 16. Cho hình bình hành ABCD . Khẳng định nào sau đây đúng? A. AD BC B. AB AC C. AC DB D. AB CD
Câu 17. Cho hình bình hành ABCD . Đẳng thức vectơ nào sau đây đúng:
A. DA DC DB
B. BA BD BC
C. DA DB DC
D. AB AC AD
Câu 18. Cho hình bình hành ABCD . Đẳng thức vectơ nào sau đây đúng?
A. AD AC AB
B. AB AD BD
C. AB AC AD
D. AB AD AC
Câu 19. Cho tam giác ABC có trọng tâm G và M là trung điểm của AB . Đẳng thức nào sau đây sai?
A. GA GB GC 0
B. GA GB 2GM
C. MA MB MC 0
D. MA MB MC 3MG
Câu 20. Cho hình bình hành ABCD tâm O. Biết rằng BA BC BD kOD . Giá trị của k bằng A.4 B. 3 C. 2 D. 6
Câu 21. Cho 4 điểm A , B , C , D . khi đó
A. AB CD AC DB
B. AB CD AC DB 5
C. AB CD AC DB
D. AB CD AD DB 2
Câu 22. Cho tứ giác ABCD . Gọi I là trung điểm của cạnh AC , K là điểm thỏa. AK
AD Phân tích CK 3
theo CA và ID 2 2 2 2 2 2 2 2 A. CK CA ID B. CK CA ID C. CK CA ID D. CK CA ID 3 3 3 3 3 3 3 3
Câu 23. Cho hình bình hành ABCD . Đẳng thức nào sau đây đúng?
A. AB AC AD 2AB
B. AB AC AD 2 AC
C. AB AC AD 2 AD
D. AB AC AD 2BD
Câu 24. Cho 4 điểm A , B , C , D tùy ý. Chọn đẳng thức đúng
A. BA BC DA DC
B. BC BA DA DC
C. BA BC DC DA
D. BA BC DA DB
Câu 25. Cho hình bình hành ABCD . Khi đó CA CB CD bằng: A. 2 AC B. 2BD C. 2 AC D. 2BD
Câu 26. Cho hình thoi ABCD. Có bao nhiêu véc tơ có điểm đầu là 2 trong 4 đỉnh đồng thời bằng véc tơ AB A.2 B. 1 C. 3 D. Vô số
Câu 27. Cho điểm B nằm giữa hai điểm A và C , AB 2 cm, AC 6 cm. Đẳng thức nào sau đây đúng? A. CB 2AB
B. BC 2BA C. AC 2BC
D. AC 3AB
Câu 28. Cho tứ giác ABCD , Gọi M ,N lần lượt là trung điểm của AB và DC , gọi I là trung điểm của MN , O
là một điểm tùy ý. Khi đó OB OC OD OA bằng: A. 4OI B. 4ON C. 0 D. 4OM
Câu 29. Cho ba điểm M , N , P bất kỳ. Khi đó đẳng thức nào sau đây đúng:
A. MN MP NP
B. MP NP MN
C. MN NP MP
D. MN PN MP
Câu 30. Cho lúc giác đều ABCDEF. Tính k biết AB AF k AD . 1 A.2 B. 0,5 C. 0,25 D. 3
Câu 31. Cho tam giác ABC có trung tuyến AM . Gọi I là trung điểm của AM . Ta có:
A. IA IB 2IC 0
B. 2IA IB IC 0
C. IA IB IC 0
D. 2IA IB IC 4IA Câu 32. Cho A
BC có trọng tâm G , I là trung điểm của đoạn thẳng AG . Đẳng thức nào sau đây là đúng ?
1
A. GB GC GA
B. GB GC 2 AI C. IG IA D. GA 2GI 3
Câu 33. Cho ba điểm A , B , C phân biệt. Đẳng thức nào sau đây là đẳng thức đúng?
A. AB BC CA .
B. CA AB CB .
C. BA AC CB .
D. AB CB AC .
Câu 34. Cho hình bình hành ABCD . Khẳng đinh nào sau đây sai?
A. AD BC 0 .
B. AB CD 0 .
C. AB AD AC .
D. AB AC CB .
Câu 35. Cho hình bình hành ABCD có tâm O . Khẳng định nào sau đây là đúng?
A. AB AC DA . B. AO AC . BO
C. AO BO CD .
D. AO BO D B .
Câu 36. Cho bốn điểm A ; B ; C ; D tuỳ ý. Đẳng thức vectơ nào dưới đây đúng?
A. AC AD BD BC
B. CA DB AD BC
C. AC BD DA CB
D. AC BD AD BC
Câu 37. Cho ba điểm A , B , C phân biệt. Mệnh đề nào dưới đây đúng? A. AB AC
B. Nếu AB BC thì AB BC
C. Nếu AB = BC thì AB BC D. AB BA Câu 38. Cho A
BC với M , N , P lần lượt là trung điểm của AB , BC , CA . Đẳng thức vectơ nào sau đây đúng 1
1 1 A. MN AC
B. AM BN CP 0 C. MA BN D. MP CP 2 2 2
Câu 39. Vectơ tổng MN PQ RN QR NP bằng? A. MN B. MP C. PR D. MR
Câu 40. Cho tam giác ABC có trung tuyến AI , D là trung điểm của AI . Đẳng thức nào sau đây đúng
A. DA DB DI
B. DA DB DC 0
C. AB AC AI
D. DA DB DC 6
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, TÍCH VECTOR VỚI 1 SỐ THỰC, PHÂN TÍCH VECTOR – P3)
_________________________________________________
Câu 1. Cho AB AC , mệnh đề nào sau đây là đúng?
A. Tam giác ABC là tam giác cân.
B. Tam giác ABC là tam giác đều.
C. A là trung điểm của đoạn BC .
D. điểm B trùng với điểm C . Câu 2. Cho 4 điểm , A B, C, .
D không thẳng hàng Điều kiện nào là điều kiện cần và đủ để AB CD ?
A. ABCD là hình bình hành.
B. ABDC là hình bình hành.
C. AB và DC có cùng trung điểm. D. AB D C .
Câu 3. Cho tứ giác ABC .
D Gọi M , N , P, Q lần lượt là trung điểm của AB, BC, CD, D .
A Khẳng định nào sau đây là sai? A. MN QP . B. QP MN . C. MQ NP . D. MN AC .
Câu 4. Gọi M , N lần lượt là trung điểm của các cạnh AB, AC của tam giác đều ABC . Đẳng thức nào sau đây đúng? A. MA MB . B. AB AC . C. MN BC .
D. BC 2 MN .
Câu 5. Cho hình chữ nhật ABCD . Mệnh đề nào dưới đây SAI?
A. Độ dài hai véc tơ AC và BD bằng nhau.
B. Hai véc tơ AB và DC bằng nhau.
C. Hai véc tơ AB và AC cùng chiều.
D. Hai véc tơ AC và BD không cùng phương.
Câu 6. Cho tam giác ABC . Gọi M và N lần lượt là trung điểm của AB và AC . Ta có:
A. BA AC 2NM 0
B. BC NM 0
C. AB BC CM 0
D. BC NM 0
Câu 7. Cho 4 điểm A , B , C , D tùy ý. Nếu AB CD thì A. AC DB B. CD AD C. AC BD D. CA BD
Câu 8. Cho hình bình hành ABCD có tâm O . Khẳng định nào sau đây là đúng ?
A. AO BO AB
B. AO BO AD
C. AO BO BD
D. AO BO BA
Câu 9. Cho hình bình hành ABCD . Đẳng thức nào sau đây là đúng ?
A. AB AD AC
B. AC BD 2CD
C. AC BC AB
D. AC AD CD
Câu 10. Cho tam giác ABC có G là trọng tâm. Đẳng thức nào sau đây là sai?
A. MA MB MC 0, M
B. AG BG CG 0
C. GA GB GC 0
D. MA MB MC 3MG, M
Câu 11. Với ba điểm M , N , P tùy ý. Ta luôn có
A. MN NP MP
B. MN PN MP
C. MN NP PM
D. MN PN PM
Câu 12. Cho hình bình hành ABCD . Đẳng thức nào sao đây là đúng?
A. DA DB DC 0
B. DA DB BA 0
C. DA DB DC 0
D. DA DB DC 0
Câu 10. Cho ba điểm A , B , C thẳng hàng, trong đó điểm B nằm giữa hai điểm A và C . Khi đó các cặp vecto
nào sau đây cùng hướng? A. CB và AB B. AB và AC C. AB và CB D. BA và BC
Câu 12. Cho hình bình hành ABCD , khi đó
A. AB AD BD
B. AB AD CA
C. AB AD AC
D. AB AD DB
Câu 13. Cho hình bình hành ABCD . Mệnh đề nào dưới đây đúng? A. Hai vectơ A ; B BC cùng phương B. Hai vectơ A ; B CD cùng phương C. Hai vectơ A ; B CD cùng hướng D. Hai vectơ A ;
B DC ngược hướng
Câu 14. Cho tam giác ABC . Gọi M là trung điểm cạnh BC . Chọn đẳng thức đúng
A. AB AC AM 0
B. AB AC 2 AM 0
C. AB AC AM 0
D. AB AC 2 AM 0
Câu 15. Cho ba điểm A , B , C phân biệt. Tổng CB AC bằng: A. BA B. 0 C. AB D. AB 7 Câu 16. Cho A
BC có trung tuyến AI và trọng tâm G . Khẳng định nào sau đây sai ?
A. GB GC 2GI
B. IA IB IC 3IG
C. GA GB GC 0
D. AB AC AI
Câu 17. Cho hình chữ nhật ABCD có AB 3 và AD 4 . Khẳng định nào sau đây đúng ? A. CD BC B. AC AB C. AC BD D. BD =7
Câu 18. Khẳng định nào sau đây là khẳng định sai?
A. Tích của một số với một vecto là một số.
B. Tích của một số với một vecto là một vectơ
C. Nếu k 0 thì vecto ka cùng hướng với vecto a
D. Nếu k 0 thì vecto ka ngược hướng với vecto a AC BD
Câu 19. Cho hình bình hành ABCD. Tính . 2 A. AB B. AD C. CB D. DC
Câu 20. Cho hình bình hành ABCD tâm O . Khẳng định nào sau đây sai?
A. OA OD BA
B. AB AD DB C. OC OD
D. AB AD AC
Câu 21. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Khẳng định nào sau đây sai:
A. AC BA AD
B. AO OD DC
C. DA DB DC 0
D. CO OB BA
Câu 22. Cho hình bình hành ABCD , tâm I . Số các vectơ cùng hướng với vectơ AC là: A. 6 B. 3 C. 5 D. 4
Câu 23. Cho hình bình hành ABCD. Tính OA OB OC OD . A. BA B. CB C. 0 D. 2OD
Câu 24. Cho tam giác ABC, M là trung điểm của BC, I là trung điểm AM. Biết rằng IB IC k AI , giá trị của k bằng A.2 B. 3 C. 1 D. 4
Câu 25. Cho hình bình hành ABCD có M là trung điểm của CD, điểm N thuộc đoạn BM sao cho BN = 2MN. Biết
rằng 2 AB BD k AC . Giá trị của k bằng A.2 B. 1 C. 3 D. 4
Câu 27. Cho hình bình hành ABCD tâm O . Vectơ AD bằng vectơ nào sau đây? A. BC B. CB C. AB D. DC
Câu 28. Gọi G là trọng tâm của tam giác ABC , M tùy ý khi đó
A. MA MB MC 2MG
B. GA GB GC 3GM
C. MA MB MC 3MG
D. MA MB MC MG
Câu 29. Cho hình bình hành ABCD . Đẳng thức nào sau đây đúng: A. AB CD B. DA BC C. AD BC D. AD CB
Câu 30. Cho tứ giác ABCD có E , H , I lần lượt là trung điểm của AB , CD , EH và M là một điểm tùy ý.
Tổng MA MB MC MD bằng: A. 0 B. 4ME C. 4MI D. 4MH
Câu 31. Cho bốn điểm A ; B ; C ; D tuỳ ý. Đẳng thức vectơ nào dưới đây đúng?
A. AB CD AD CB
B. AB CD AD DB
C. CA AB AD DB
D. CA AB AD CB
Câu 32. Cho tam giác ABC . Gọi M , D lần lượt là trung điểm cạnh BC và AM , I là điểm tùy ý. Ta có
A. 2 AI IB IC 3 ID
B. 2IA IB IC 4 ID
C. 2IA IB IC 3ID
D. 2IA IB IC 4ID Câu 33. Cho A
BC có trung tuyến AM ; I là trung điểm của AM . Tổng 2IA IB IC bằng: A. AM B. 0 C. 4IA D. 4IM
Câu 34. Cho tam giác ABC có M, N, P lần lượt là trung điểm của AB, BC, CA. Gọi G là trọng tâm tam giác ABC.
Tính tổng vecto AM BN CP . 1 1 1 A. 0 B. AB C. CB D. AC 2 2 2
________________________ 8
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P1) _____________________________
Câu 1. Cho đoạn thẳng AB = a và điểm M thỏa mãn MA 3MB . Tính MB 2 A.0,5a B. 0,25a C. a D. 0,75a 3
Câu 2. Cho đoạn thẳng AB = 6a và điểm M thỏa mãn MA 5MB . Tính MB 2 A.a B. 0,25a C. a D. 0,75a 3
Câu 3. Cho hình vuông ABCD cạnh a . Tính AB . A. a 3 B. a C. 2a 3 D. 4a
Câu 4. Cho hình vuông ABCD cạnh a . Khi đó độ dài của AC bằng: a 3 a 2 A. a 2 B. a 3 C. D. 2 2
Câu 5. Cho ABCD là hình vuông cạnh bằng 1. Khi đó độ dài của AC bằng A. 1 B. 2 C. 2 D. 3
Câu 6. Cho hình chữ nhật ABCD có AB = 3 , BC = 4 . Độ dài của vector AC CB là: A. 3 B. 6 C. 9 D. 7
Câu 7. Cho hình chữ nhật ABCD có AB = 3 , BC = 4 . Độ dài của AC là: A. 5 B. 6 C. 9 D. 7
Câu 8. Cho tam giác đều ABC cạnh a. Tính độ dài vec tơ tổng AB AC A.2a B. a C. a 3 D. 2a 3
Câu 9. Cho hình vuông ABCD cạnh a . Tính độ dài vector tổng AB DC . A. a 3 B. a C. 2a 3 D. 2a
Câu 10. Cho hình vuông ABCD cạnh a . Tính độ dài vector tổng AB 3DC . A. a 3 B. a C. 2a 3 D. 4a
Câu 11. Cho hình vuông ABCD cạnh a , O là giao điểm hai đường chéo. Tính độ dài vector tổng OB OC . A. a 3 B. a C. 2a 3 D. 4a
Câu 12. Cho hình vuông ABCD cạnh a , O là giao điểm hai đường chéo. Tính độ dài vector tổng
OB OC OA. a 2 A. a 3 B. a C. 2a 3 D. 2
Câu 12. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ tổng AB AD . A.2a B. a 5 C. a 2 D. a 3
Câu 13. Cho hình vuông ABCD cạnh a , O là giao điểm hai đường chéo. Tính độ dài vector tổng
OA 2OB OC a 2 A. a 3 B. a C. a 2 D. 2
Câu 14. Cho tam giác đều ABC cạnh a. Tính độ dài vec tơ tổng AB BC 4 AC A.2a B. a C. 5a D. 2a 3
Câu 15. Cho hình vuông ABCD tâm O, cạnh a. Tính AB DC . A.2a B. a 5 C. a 2 D. 0
Câu 16. Cho tam giác ABC là tam giác vuông tại A , cạnh AB 2a , ACB 30
. Tính AB AC A. a 3 B. a C. 2a 3 D. 4a
Câu 17. Cho hình vuông ABCD có cạnh bằng a . Độ dài của vector hiệu CB CD bằng A. 2a B. a 2 C. 2 a 2 D. a 9
Câu 18. Cho hình chữ nhật ABCD tâm I , AB 3 cm, BC 4 cm. Khi đó BI là: 7 5 A. 7 B. 5 C. D. 2 2
Câu 19. Cho hình vuông ABCD tâm O, cạnh a. Tính AB 2DC . A.2a B. a 5 C. a 2 D. 3a
Câu 20. Cho hình vuông ABCD tâm O, cạnh a. Tính 4 AB 3DC 2CD . A.3a B. a 5 C. a 2 D. 5a
Câu 21. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ tổng AB BC 4 AO . A. 3a 2 B. a 5 C. 6a 2 D. 4a 3
Câu 22. Cho hình thang vuông ABCD tại A, D có AB = AD = a, DC = 2a. Tính AB DC A.3a B. 4a C. a D. a 5
Câu 23. Cho hình thang vuông ABCD tại A, D có AB = AD = a, DC = 2a. Tính 2 AB 5CD A.3a B. 4a C. a D. a 5
Câu 24. Cho tam giác ABC đều cạnh a, trọng tâm G. Tính GA GC 4 1 A. 2a 3 B. a 3 C. a 3 D. a 3 3 3
Câu 25. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài véc tơ tổng AB AC . A.2a B. a 5 C. a 2 D. a 3
Câu 26. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a. Tính AB CA . A. a 97 B. a 29 C. 4a 10 D. a 73
Câu 27. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ tổng AB 2 AD . 3a 2 A. a 5 B. 3a 2 C. a 3 D. 2
Câu 28. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a. Tính AB 4 AC . A. a 97 B. 5a 29 C. 4a 10 D. 4a 34
Câu 29. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a. Tính AB 4 AC . A. 8a 5 B. a 29 C. 4a 10 D. 16 2
Câu 30. Cho tam giác ABC đều cạnh a, trọng tâm G, tính độ dài vector tổng GB 2GA GC . a 2 a 3 A. B. C. a 5 D. a 3 2 3
Câu 31. Cho hình thoi ABCD tâm O , cạnh bằng a và 0
BAD 60 . Kết luận nào sau đây đúng? a 3 a 2 A. OA . B. OA a . C. OA OB . D. OA . 2 2
Câu 32. Cho tam giác ABC có đường cao AH . Biết AB 9cm, AC 12cm, BC 15cm . Tính AH ? 15 36 A. cm . B. 3cm . C. 6cm . D. cm . 2 5
Câu 33. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ AB 2 AC . A. a 5 B. 3a 2 C. a 3 D. a 13
_________________________________ 10
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P2) _____________________________
Câu 1. Cho tam giác ABC đều cạnh a . Tính AB AC . a 3
A. AB AC a 3 . B. AB AC .
C. AB AC 2a .
D. AB AC 2a 3 . 2
Câu 2. Cho hình vuông ABCD có cạnh bằng a . Độ dài AD AB bằng a 2 a 3 A. 2a B. . C. . D. a 2 . 2 2
Câu 3. Cho tam giác đều ABC cạnh a , mệnh đề nào sau đây đúng? A. AC BC . B. AC a . C. AB AC . D. AB a .
Câu 4. Cho AB khác 0 và cho điểm C .Có bao nhiêu điểm D thỏa AB CD ? A. Vô số. B. 1 điểm. C. 2 điểm. D. Không có điểm nào.
Câu 5. Chọn mệnh đề sai trong các mệnh đề sau đây:
A. 0 cùng hướng với mọi vectơ.
B. 0 cùng phương với mọi vectơ. C. AA 0 . D. AB 0 .
Câu 6. Có hai lực F , F cùng tác động vào một vật đứng tại điểm O , biết hai lực F , F đều có cường độ là 1 2 1 2
50 N và chúng hợp với nhau một góc 60 . Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu? A. 100 N . B. 50 3 N . C. 100 3 N . D. Đáp án khác.
Câu 7. Cho tứ giác ABCD có AB DC và AB BC . Khẳng định nào sau đây sai? A. AD BC .
B. ABCD là hình thoi. C. CD BC .
D. ABCD là hình thang cân.
Câu 8. Cho tam giác ABC vuông cân tại A có AB a . Tính AB AC . a 2
A. AB AC a 2 . B. AB AC .
C. AB AC 2a .
D. AB AC a . 2
Câu 9. Cho tam giác ABC đều cạnh a , có AH là đường trung tuyến. Tính AC AH . a 3 a 13 A. . B. 2a . C. . D. a 3 . 2 2
Câu 10. Cho tam giác ABC đều cạnh a, trọng tâm G. Tính 2BG GA GC 4 3a 2 A. 2a 3 B. a 3 C. a 3 D. 3 2
Câu 11. Cho hình vuông ABCD cạnh a, tâm O. Tính độ dài vector AB OD BC . a 2 3a 2 A. B. C. a 2 D. a 2 2
Câu 12. Cho tam giác đều ABC cạnh a, trọng tâm G, đường cao AH. Tính độ dài vec tơ AG 2CH a 6 2a 6 A. B. C. a 3 D. 2a 3 3 3
Câu 13. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ AB 3AO . a 34 3a 2 A. a 5 B. C. a 3 D. 2 2
Câu 14. Cho tam giác đều ABC cạnh a. Tính độ dài vec tơ GA AC 2GB A.2a B. a C. a 3 D. 2a 3 11
Câu 15. Cho tam giác đều ABC cạnh a, trọng tâm G. Tính độ dài vec tơ AB AC 2 AG 5a 3 A. B. a C. a 3 D. 2a 3 3
Câu 16. Cho hình thang vuông ABCD tại A, D có AB = AD = a, DC = 2a. Tính AD AC A.3a B. 2a 2 C. a D. a 5
Câu 17. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ AB AD 2 AC . 3a 2 A. a 5 B. 3a 2 C. a 3 D. 2
Câu 18. Có hai lực F , F có cường độ tương ứng 300N xuất phát từ 1 2
điểm gốc M như hình vẽ. Tính cường độ tổng hợp lực. A.300N B. 320N C.350N D. 330N
Câu 19. Cho tam giác ABC đều cạnh bằng 6cm. Tính AB CB bằng: A. 6 3 B. 12 3 C. 12 D. 3 3
Câu 20. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ 3AB 4 AO . A. a 5 B. a 29 C. a 3 D. 2a 17
Câu 21. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a. Tính AB 3AD . A. a 97 B. a 29 C. 5a 13 D. 2a 17
Câu 22. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a. Tính AB 4 AD . A. a 97 B. a 29 C. 4a 10 D. 2a 17
Câu 23. Cho hình vuông ABCD tâm O, cạnh a. Tính độ dài vec tơ AC BD 7BC . A. a 5 B. 9a C. a 3 D. 10a
Câu 24. Có hai lực F , F có cường độ đều 50N cùng tác động vào một vật đứng yên tại O và hợp với nhau một 1 2
góc 60 . Cường độ lực tổng hợp tác dụng lên vật là A. 50 3N B. 100 3N N C. 2 13N D. 200N
Câu 25. Có hai lực F , F có cường độ đều 50N cùng tác động vào một vật đứng yên tại O và hợp với nhau một 1 2
góc vuông. Tính tổng hợp lực tác dụng lên vật. A.100N B. 100 3N C. 50 2N D. 200N
Câu 26. Cho tam giác đều ABC cạnh a, trọng tâm G, đường cao AH. Tính độ dài vec tơ AG 2GH 3AH 10a 3 8a 3 A. B. C. a 3 D. 2a 3 3 3
Câu 27. Cho tam giác đều ABC có độ dài cạnh bằng a. Tính AB AC . A.2a B. 3a C. a 3 D. a 5
Câu 28. Cho hình vuông ABCD có độ dài cạnh bằng a, I là giao điểm hai đường chéo. Tính IA IB . A.a B. 0,5a C. a 3 D. a 5
Câu 29. Có hai lực F , F có cường độ tương ứng 6N và 8N cùng tác động vào một vật đứng yên tại O. Giả sử 1 2
hai lực vuông góc với nhau. Cường độ lực tổng hợp tác dụng lên vật là A. 10N B. 40N C. 2 13N D. 13N
Câu 30. Cho tam giác đều ABC cạnh a. Tính độ dài vec tơ GA 2GC 3GB A.2a B. a C. a 3 D. 2a 3 12
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P3) _____________________________
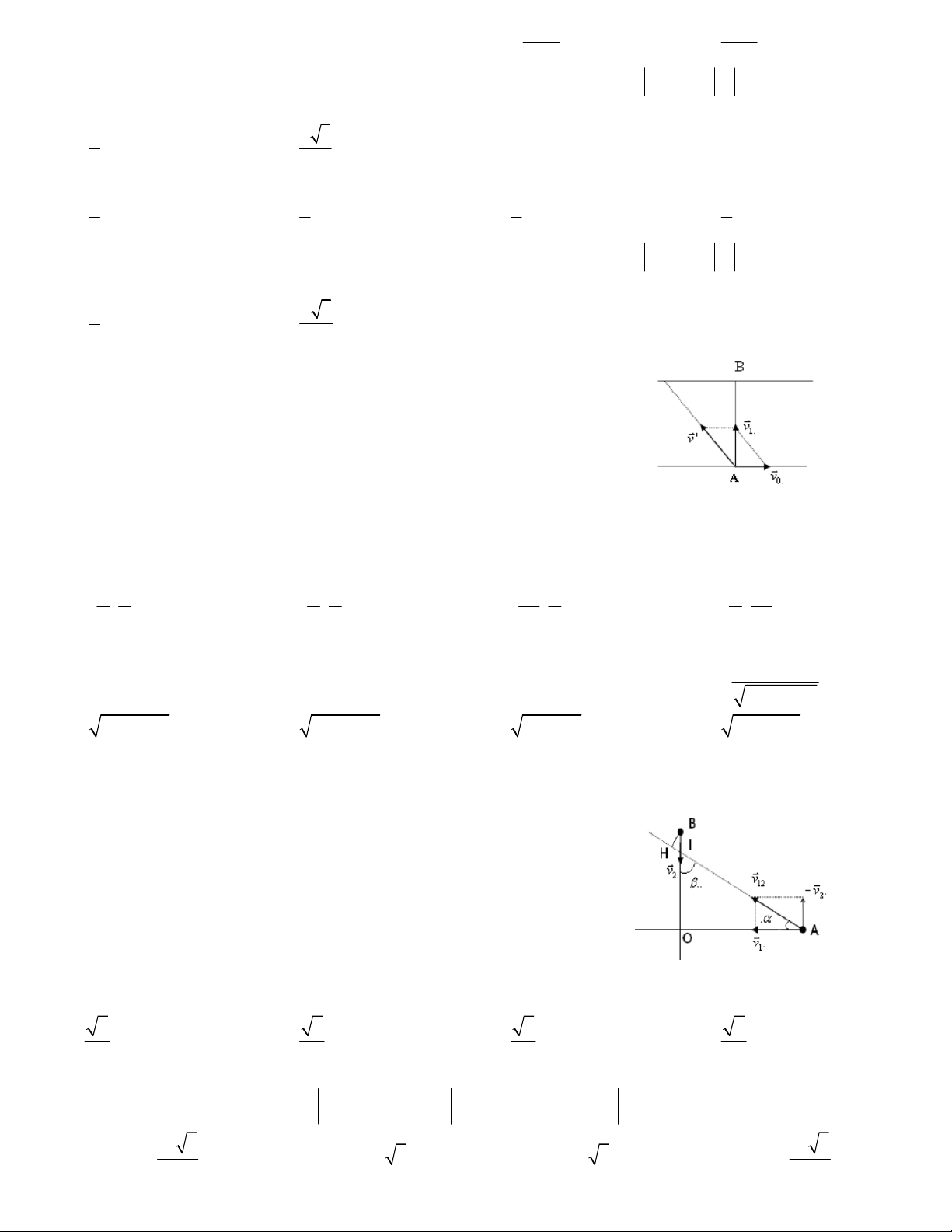
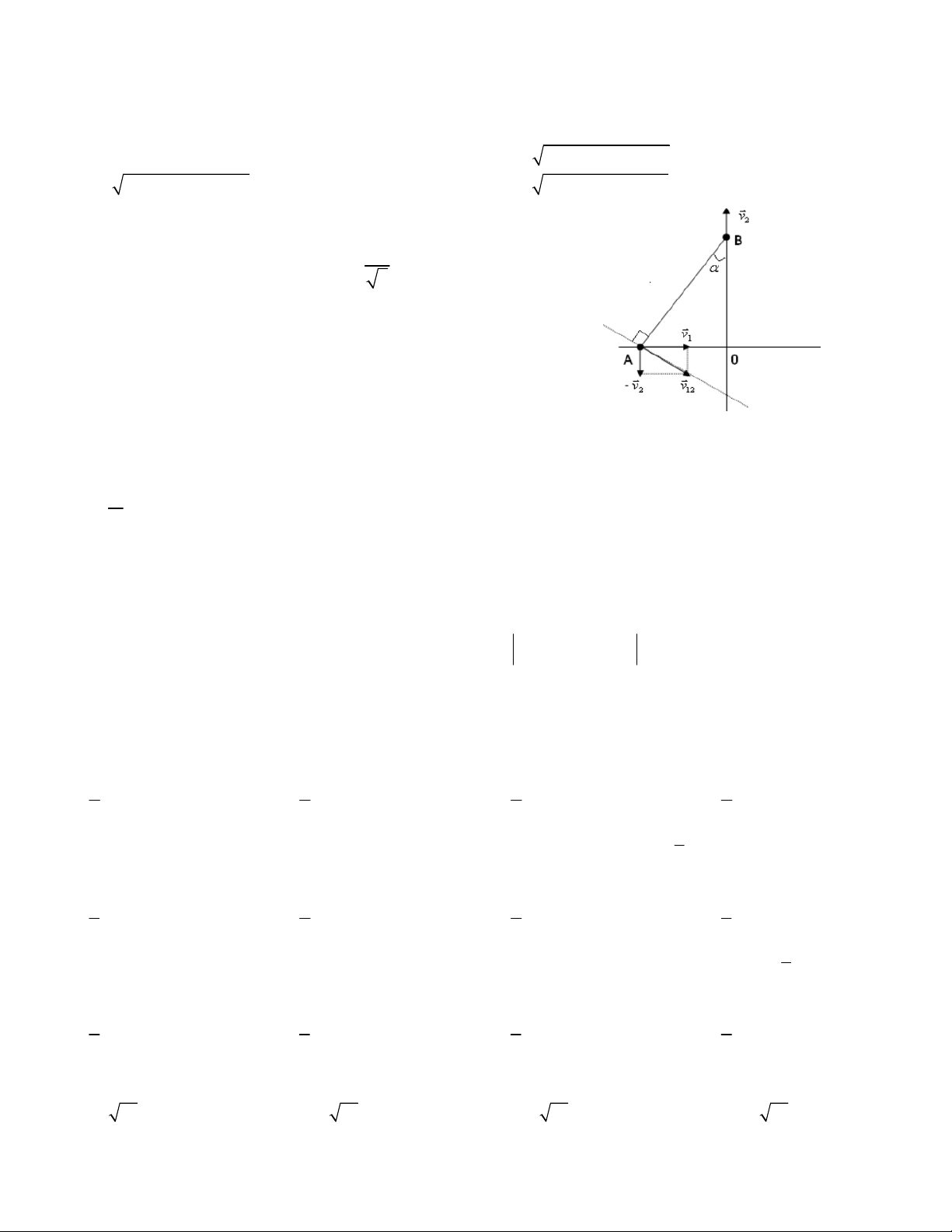
Câu 1. Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc 10km/h. Một chiếc ca nô chuyển động từ
phía đông sang phía tây với vận tốc 50km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông. A.10 7 km/h B. 10 26 km/h C. 45km/h D. 20 3 km/h
Câu 2. Cho tam giác đều ABC có độ dài cạnh bằng a. Tính AB 2 AC . A.4a B. a 10 C. 2a 3 D. a 7
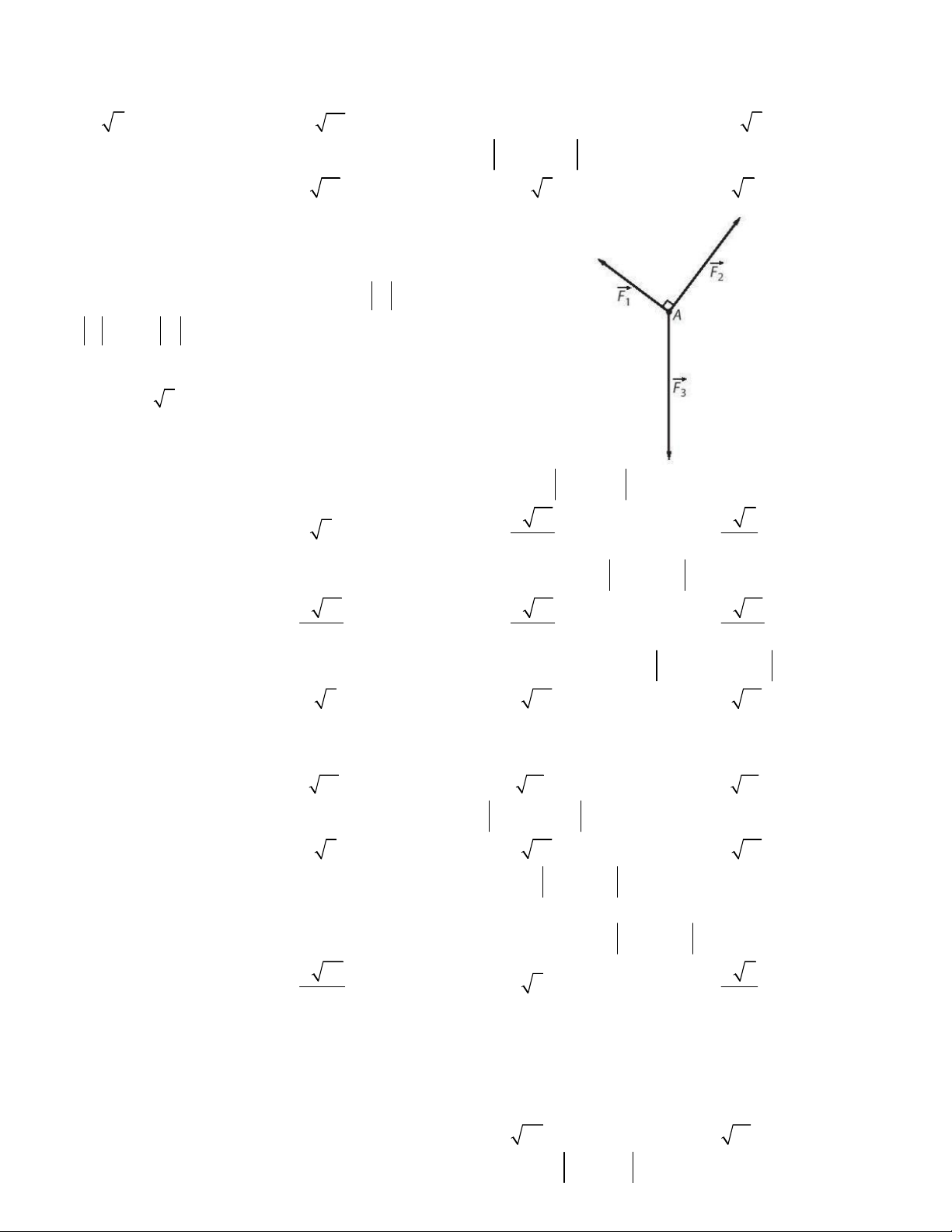
Câu 3. Ba lực F , F , F tác động vào một vật ở vị trí 1 2 3
cân bằng như hình vẽ. Tính F biết rằng 3
F 30N; F 40N . 1 2 A. 50N B. 70N C. 45 2 D. 35N
Câu 4. Cho hình vuông ABCD có tâm I và độ dài cạnh bằng a. Tính AC DI . a 10 a 7 A.2a B. a 5 C. D. 2 2
Câu 5. Cho hình thoi ABCD tâm I có độ dài cạnh bằng a, BAC 30 . Tính 3AB IC . a 10 a 31 a 13 A.6a B. C. D. 2 2 2
Câu 6. Tam giác ABC cân tại A, BAC 120 . Gọi M là trung điểm cạnh BC. Tính BA CA MC . A.5a B. a 5 C. a 21 D. a 19
Câu 7. Có hai lực F ,3F cùng tác động vào một vật đứng yên tại O và hợp với nhau một góc 60 , trong đó 1 1
F có cường độ x (N). Tính tổng hợp lực tác dụng lên vật theo x. 1 A.4xN B. x 26N C. x 14N D. x 17N
Câu 8. Cho tam giác đều ABC có độ dài cạnh bằng a, tính 3AB 2 AC . A.5a B. a 5 C. a 21 D. a 19
Câu 9. Cho hình vuông ABCD tâm I và độ dài cạnh bằng 2a. Tính AC BD theo a. A.3a B. 4a C. 8a D. 7a
Câu 10. Cho tam giác đều ABC có đường cao AH, độ dài cạnh bằng a. Tính AB AH . a 34 a 7 A.2a B. C. a 5 D. 4 2
Câu 11. Có hai lực F , F có cường độ đều là 40N, hợp với nhau một góc 60 . cùng tác động vào một vật đứng 1 2
yên tại O, tổng hợp lực thu được là F . Giả sử tăng cường độ hai lực F , F lên lần lượt là 2 lần và 5 lần, chiều 1 2
của lực giữ nguyên như thế, ta thu được tổng hợp lực K . Hỏi cường độ của K gấp bao nhiêu lần cường độ của lực F . A.7 lần B. 10 lần C. 29 lần D. 13 lần
Câu 12. Cho hình vuông ABCD tâm I và có độ dài cạnh bằng a. Tính AB DI theo a. 13 a 10 a 13 a 7 A.5a B. C. D. 2 2 2
Câu 13. Cho tam giác đều ABC có đường cao AH, độ dài cạnh bằng a. Tính AB CH . a 3 a 5 A.a B. 2a C. D. 2 2
Câu 14. Cho hình vuông ABCD tâm I, độ dài cạnh bằng a, gọi M là trung điểm cạnh CD, tính IC IM theo a. a 10 a 7 a 5 A.2a B. C. D. 2 2 2
Câu 15. Cho tam giác đều ABC có đường cao AH, độ dài cạnh bằng a. Tính 3AB BC theo a. A. a 13 B. a 17 C. a 21 D. a 19
Câu 16. Có hai lực F , F có cường độ tương ứng 6N và 8N cùng tác động vào một vật đứng yên tại O. Giả sử 1 2
hai lực tạo với nhau một góc 60 . Cường độ lực tổng hợp tác dụng lên vật là A. 89N B. 2 37 N C. 2 13N D. 10N
Câu 17. Có hai lực F , F có cường độ tương ứng 6N và 8N cùng tác động vào một vật đứng yên tại O. Giả sử 1 2
hai lực vuông góc với nhau. Cường độ lực tổng hợp tác dụng lên vật là A. 89N B. 40N C. 2 13N D. 10N
Câu 18. Cho hình vuông ABCD cạnh a, tính độ dài vector 2 AD AC . A. 3a B. a 10 C. a 11 D. a 13
Câu 19. Hình vuông ABCD tâm I, độ dài cạnh bằng a. Gọi M là trung điểm của cạnh CD, tính IA IM ID . a 10 a 7 a 5 A.2a B. C. D. 2 2 2
Câu 20. Có hai lực F , F có cường độ lần lượt là 5N và 7N, hợp với nhau một góc 45 . cùng tác động vào một 1 2
vật đứng yên tại O, tổng hợp lực thu được là F . Cường độ của lực F gần nhất giá trị nào A.11,11N B. 10,95N C. 12,25N D. 14,75N
Câu 21. Tam giác ABC có độ dài cạnh bên là a và góc ngoài tại đỉnh C là 160 . Khi đó 5AB 2 AC : a gần
nhất giá trị nào sau đây A.4,25 B. 3,69 C. 5,68 D. 2,73
Câu 22. Cho tam giác đều ABC cạnh a. Tính độ dài vec tơ GA GC 16GB A.6a B. 7a 3 C. 5a 3 D. 2a 3
Câu 23. Có hai lực F , F có cường độ tương ứng 200N xuất phát từ 1 2
điểm gốc M như hình vẽ. Tính cường độ tổng hợp lực. A.200N B. 210N C.240N D. 250N
Câu 24. Cho tam giác ABC đều cạnh a, trọng tâm G, đường cao AH. Tính AH AC a 13 A. B. a 5 C. a 13 D. a 3 2
Câu 25. Cho hình vuông ABCD tâm O , cạnh 2a . Độ dài vectơ DO bằng a 2 A. 2a 2 B. C. a 2 D. 2 a 2 2
Câu 26. Tam giác ABC cân tại A có độ dài cạnh bên là a và ABC 40 . Khi đó 3AB 2 AC : a gần nhất giá trị nào sau đây A.7,2 B. 8,6 C. 3,3 D. 4,5
CƠ BẢN VECTOR LỚP 10 THPT 14
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P1) _____________________________
Câu 1. Cho hai véctơ a và b đều khác véctơ 0 . Khẳng định nào sau đây đúng? A. .
a b a . b . B. .
a b a . b .cos a,b. C. . a b .
a b .cos a,b . D. .
a b a . b .sin a,b .
Câu 2. Cho tam giác đều ABC có cạnh bằng 4a .Tích vô hướng của hai vectơ AB và AC là A. 2 8a . B. 8a . C. 2 8 3a . D. 8 3a .
Câu 3. Cho hình vuông ABCD có cạnh a Tính A . B AD . 2
a A. A . B AD 0 . B. A . B AD a . C. A . B AD . D. 2 A . B AD a . 2
Câu 4. Cho hai véc tơ a và b . Đẳng thức nào sau đây sai? 2 2 2 1 A. .
a b a . b .cos , a b. B. . a b
a b a b . 2 2 2 2 2 2 2 1
C. a . b a.b . D. . a b
a b a b . 2 0 ˆ 0 ˆ
Câu 5. Cho tam giác ABC có A 90 , B 60 và AB a . Khi đó AC.CB bằng A. 2 2a . B. 2 2a . C. 2 3a . D. 2 3 a .
Câu 6. Cho tam giác ABC đều cạnh bằng a . Tính tích vô hướng A . B BC . 2 a 3 2 a 3 2 a 2 a A. . AB BC . B. . AB BC . C. . AB BC . D. A . B BC . 2 2 2 2
Câu 7. Cho tam giác ABC cạnh a. Tính . AB AC . A. 2 0,5a B. 2 a C. 2 2a D. 2 3a
Câu 8. Cho hình vuông ABCD tâm O cạnh a. Tính . AB OC . A. 2 0,5a B. 2 a C. 2 2a D. 2 3a
Câu 9. Cho hình vuông ABCD tâm O cạnh a. Tính . AB BD . A. 2 0,5a B. 2 a C. 2 2a D. 2 3a
Câu 10. Cho tam giác đều ABC cạnh a, trực tâm H. Tính M .
AB AC AH.BC theo a. A. 0 B. 2 0,5a C. 2 2 a D. 2 a
Câu 11. Cho hình bình hành ABCD , với AB 2 , AD 1, BAD 60 . Tích vô hướng A . B AD bằng 1 1 A. 1. B. 1. C. . D. . 2 2
Câu 12. Cho tam giác ABC vuông tại A có AB ;
a AC a 3 và AM là trung tuyến. Tính B . A AM 2 a 2 a A. . B. 2 a . C. 2 a . D. . 2 2
Câu 13. Cho hình bình hành ABCD , với AB 2 , AD 1, BAD 60 . Tích vô hướng B . A BC bằng 1 1 A. 1. B. C. 1. D. . 2 2
Câu 14. Cho ABC đều; AB 6 và M là trung điểm của BC . Tích vô hướng A . B MA bằng A. 18 . B. 27 . C. 18 . D. 27 .
Câu 15. Cho tam giác ABC vuông tại B , BC a 3 . Tính AC.CB . 2 a 3 2 a 3 A. 2 3a . B. . C. . D. 2 3 a . 2 2
Câu 16. Cho hình thang ABCD vuông tại A và D ; AB AD a,CD 2 .
a Khi đó tích vô hướng AC.BD bằng 2 3a 2 a A. 2 a . B. 0 . C. . D. . 2 2
Câu 17. Cho tam giác ABC vuông tại A có AB ;
a BC 2a . Tính tích vô hướng B . A BC . 15 2 a 2 a 3 A. 2 B . A BC a . B. . BA BC . C. 2 B . A BC 2a . D. B . A BC . 2 2
Câu 18. Cho tam giác ABC vuông tại A có AB 4 . Kết quả B . A BC bằng A. 16 . B. 0 . C. 4 2 . D. 4 .
Câu 19. Cho tam giác ABC vuông tại A có B 30 ,
AC 2 . Gọi M là trung điểm của BC . Tính giá trị của
biểu thức P AM . BM . A. P 2 . B. P 2 3 . C. P 2 . D. P 2 3 .
Câu 20. Cho hình chữ nhật ABCD có AB 8, AD 5 . Tích A . B BD A. A . B BD 62 . B. A . B BD 6 4 . C. A . B BD 6 2 . D. A . B BD 64 .
Câu 21. Cho A, B, C thỏa mãn AB = 2, CB = 3, AC = 5. Tính C . A CB . A. 14 B. 13 C. 17 D. 15
Câu 22. Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng AB.AC. 2 a 3 2 a 2 a A. 2
AB.AC 2a . B. . AB AC . C. AB.AC . D. AB.AC . 2 2 2
Câu 23. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng? A. .
a b a . b . B. a.b 0 .
C. a.b 1 . D. .
a b a . b .
Câu 24. Cho hai vectơ a và b khác 0 . Xác định góc giữa hai vectơ a và b khi .
a b a . b . A. 0 180 . B. 0 0 . C. 0 90 . D. 0 45 .
Câu 25. Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a . Mệnh đề nào sau đây là sai? 1 1 2 a 1 A. 2 AB.AC a . B. 2
AC.CB a . C. G . A GB . D. 2 AB.AG a . 2 2 6 2
Câu 26. Cho hình vuông ABCD cạnh a. Tính AC.CD CA . AB AC theo a. A. 4 2 a B. – 2 2 a C. – 3 2 a D. – 6 2 a
Câu 27. Tính công sinh bởi một lực F có độ lớn 20N kéo vật dịch chuyển theo một vector d có độ lớn 50N và
góc giữa hai vector lực là 60 . A.500J B. 300J C. 450J D. 540J 2
Câu 28. Cho hình vuông ABCD cạnh a. Tính A . B AC 25AB . A. 2 20a B. 2 26a C. 2 30a D. 2 18a
Câu 29. Cho hình vuông ABCD cạnh a. Tính AB ADBD BC. A. 2 a B. 2 2a C. 2 3a D. 2 4a
Câu 30. Cho hình chữ nhật ABCD tâm I, cạnh AB = a, AD = b. Tính AC AB AC AD . A. 2 a B. ab C. 2 2a D. 2 b
Câu 31. Cho hình vuông ABCD cạnh a . Tính P AC.CD CA. A. P 1. B. 2 P 3a . C. 2 P 3 a . D. 2 P 2a .
Câu 32. Cho hình vuông ABCD cạnh a. Tính P AB AC.BC BD BA. A. P 2 2 . a B. 2 P 2a . C. 2 P a . D. 2 P 2 a .
Câu 33. Cho hình vuông ABCD cạnh bằng 5. Tính AB AC.BC BD BA. A. 10 2. B. 50. C. 0. D. 75.
Câu 34. Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng AB.BC. 2 a 3 2 a 2 a A. 2
AB.BC a . B. A . B BC . C. AB.BC . D. AB.BC . 2 2 2
Câu 35. Tính công sinh bởi một lực F có độ lớn 30N kéo vật dịch chuyển theo một vector d có độ lớn 60N và
góc giữa hai vector lực là 60 . A.900J B. 800J C. 700J D. 1000J 16
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P2) _____________________________
Câu 1. Cho hai vectơ a và b thỏa mãn a 3, b 2 và a.b 3. Xác định góc giữa hai vectơ a và b. A. 0 30 . B. 0 45 . C. 0 60 . D. 0 120 .
Câu 2. Cho hình vuông ABCD cạnh a, tâm O. M là trung điểm của BC. Tính OM .OD . 2 a 2 3a 2 2a A. B. 2 a C. D. 2 4 3 2
Câu 3. Cho điểm M thuộc nửa đường tròn tâm O đường kính AB = 2R. Tính MA . MA AB theo R. A. 3R B. 0 C. 4R2 D. 2R2
Câu 4. Cho các vector a, b thỏa mãn a b 1và góc giữa hai vector bằng 60 . Xác định cosin giữa hai vector sau 1 1 1 1 A. B. C. D. 2 6 4 3 1
Câu 5. Cho hai vectơ a;b khác vectơ 0 thỏa mãn a.b
a . b . Khi đó góc giữa hai vectơ a; b là 2 A. 60 . B. 120. C. 150. D. 30 .
Câu 6. Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng AB.BC. 2 a 3 2 a 2 a A. 2
AB.BC a . B. . AB BC . C. AB.BC . D. AB.BC . 2 2 2
Câu 7. Cho hình vuông ABCD , tâm O , cạnh bằng a . Tìm mệnh đề sai: 2 2 2 a a A. A . B AC a .
B. AC.BD 0 . C. A . B AO . D. A . B BO . 2 2
Câu 8. Cho hình vuông ABCD cạnh a. Gọi E là điểm đối xứng với D qua C. Tính AE.AB theo a. A. 4 2 a B. 2 2 a C. 3 2 a D. 5 2 a
Câu 9. Cho hình vuông ABCD cạnh a. Mệnh đề nào sau đây sai A. . AB AD 0 B. 2 . AB AC a
C. 2 . AB CD a D. 2 AB CD BC AD a
Câu 10. Cho hình vuông ABCD có I là trung điểm của AD, tính cos AC, BI . 1 1 1 2 A. B. C. D. 3 10 5 10
Câu 11. Cho hình vuông ABCD cạnh a. Tính AC CD CAtheo a. A. – 1 B. 3 2 a C. – 3 2 a D. 2 2 a
Câu 12. Cho hai vector ,
m n khác 0, tính góc giữa hai vecto , m n nếu .
m n m . n . A. 0 độ B. 180 độ C. 90 độ D. 45 độ
Câu 13. Cho hình vuông ABCD cạnh a, E đối xứng với D qua C. Tính AE.AB . A. 2 2 a B. 3 2 a C. 5 2 a D. 5 2 a
Câu 14. Cho tam giác đều ABC cạnh bằng 1. Tính .
AB BC BC.CA C . A AB . 3 3 A. 1,5 B. – 1,5 C. D. – 2 2
Câu 15. Cho hình vuông ABCD cạnh a, mệnh đề nào sau đây sai ? A. 2 D . A CB a B. 2 . AB CD a
C. 2 AB BC AC a D. . AB AD . CB CD 0
Câu 16. Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a, I là trung điểm
của cạnh AB. Tìm mệnh đề sai A. 2 . AB DC 8a B. . AB DC 0 C. . AB AD 0 D. . DA DB 0 17
Câu 17. Cho hình vuông ABCD cạnh a. Tính AC AB AD . A. 2 2a B. 2 2 a C. 2 3a D. 2 4a
Câu 18. Cho hình vuông ABCD cạnh a. Tính AB ADBC BD . A. 2 a B. 2 2a C. 2 3a D. Kết quả khác
Câu 19. Cho hình vuông ABCD cạnh a. Tính .
OA AB với O là giao điểm hai đường chéo. 2 a 2 2 a 3 2 a 2 a A. B. C. D. 2 2 2 2
Câu 20. Cho tam giác đều ABC có trọng tâm G và độ dài cạnh bằng a. Tính . AB AG . 2 a 3 2 3a 2 a 3 2 a A. B. C. D. 6 4 4 2
Câu 21. Cho tam giác ABC đều cạnh a, đường cao AH. Tính AC AC AB . 2 a 2 2 a 3 2 a 2 a A. B. C. D. 2 2 2 2
Câu 22. Cho tam giác đều ABC cạnh a, trực tâm H. Tính M .
AB AC AH.BC theo a. A. 0 B. 2 0,5a C. 2 2 a D. 2 a
Câu 23. Cho tam giác đều ABC cạnh a, trọng tâm G. Tính P G .
A GB AC.CG theo a. 2 1 2 A. 0 B. 2 a C. 2 a D. 2 a 3 2 5
Câu 24. Cho AB = 4, AC = 3, hỏi có mấy điểm C để . AB AC 12 ? A. 2 B. 0 C. 1 D. 3
Câu 25. Cho hình vuông ABCD cạnh a. Tính AC.CD CA . AB AC theo a. A. 4 2 a B. – 2 2 a C. – 3 2 a D. – 6 2 a
Câu 26. Cho tam giác ABC vuông tại A có AB = c, AC = b, BC = a. Tính . BA BC theo a, b, c. A. 2a + b B. a + b + c C. 2 c D. 2 c + 2ab
Câu 27. Cho A, B, C thỏa mãn AB = 2, CB = 3, AC = 5. Tính C . A CB . A. 14 B. 13 C. 17 D. 15
Câu 28. Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để OA OB AB 0 là A. Tam giác OAB đều B. Tam giác OAB cân tại O
C. Tam giác OAB vuông tại O
D. Tam giác OAB vuông cân tại O
Câu 29. Cho tam giác đều ABC cạnh a, trọng tâm G. Tính P G .
A GB AC.CG theo a. 2 1 2 A. 0 B. 2 a C. 2 a D. 2 a 3 2 5
Câu 30. Cho tam giác ABC có BC ,
a CA b, AB c. Tính P AB AC.BC. 2 2 c b 2 2 2
c b a 2 2 2
c b a A. 2 2
P b c . B. P . C. P . D. P . 2 3 2
Câu 31. Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua C. Tính AE.AB. A. 2
AE.AB 2a . B. 2
AE.AB 3a . C. 2
AE.AB 5a . D. 2
AE.AB 5a .
Câu 32. Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a . Mệnh đề nào sau đây là sai? 1 1 2 a 1 A. 2 AB.AC a . B. 2
AC.CB a . C. G . A GB . D. 2 AB.AG a . 2 2 6 2
Câu 33. Cho tam giác ABC vuông tại A có AB = c, AC = b, BC = a. Tính . BA BC theo a, b, c. A. 2a + b B. a + b + c C. 2 c D. 2 c + 2ab
_________________________________ 18
CƠ BẢN VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P3) _____________________________
Câu 1. Cho tam giác đều ABC cạnh a = 2. Hỏi mệnh đề nào sai ?
A. .
AB AC.BC 2BC B. BC.CA 2
C. AB BC AC 4
D. AC BC BA 4
Câu 2. Cho tam giác đều ABC có độ dài cạnh là 3a, trên các cạnh BC, CA lần lượt lấy các điểm M, N sao cho
BM = a, CN = 2a. Tính AM .BC theo a. A. 2 2 a B. – 1,5 2 a C. 3,5 2 a D. – 4 2 a 2
Câu 3. Cho điểm M thuộc nửa đường tròn tâm O đường kính AB = 2R. Tính MA . MA AB theo R. A. 3R B. 0 C. 4R2 D. 2R2
Câu 4. Cho AB = 4, AC = 3, hỏi có mấy điểm C để . AB AC 12 ? A. 2 B. 0 C. 1 D. 3
Câu 5. Cho AB = 4, AC = 3, hỏi có mấy điểm C để . AB AC 8 ? A. 2 B. 0 C. 1 D. 3
Câu 6. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng? A. .
a b a . b . B. a.b 0 .
C. a.b 1 . D. .
a b a . b .
Câu 7. Cho tam giác đều ABC cạnh a = 2. Hỏi mệnh đề nào sau đây sai
A. A .
B AC.BC 2BC B. BC.CA 2
C. AB BC.AC 4
D. AC BC.BA 4
Câu 8. Cho hai vectơ a và b khác 0 . Xác định góc giữa hai vectơ a và b khi .
a b a . b . A. 0 180 . B. 0 0 . C. 0 90 . D. 0 45 .
Câu 9. Cho hình vuông ABCD cạnh a. M là trung điểm của AB. Tính . MA MC . A. 2 2a B. 0 C. 2 a D. 2 0, 25a
Câu 10. Cho hai vectơ a và b . Đẳng thức nào sau đây sai? 2 2 1 2 2 1 A. 2 2 a.b
a b a b . B. a.b a b a b . 2 2 2 2 1 2 2 1
C. a.b a b a b . D. a.b a b a b . 2 4
Câu 11. Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng AB.AC. 2 a 3 2 a 2 a A. 2
AB.AC 2a . B. A . B AC . C. AB.AC . D. AB.AC . 2 2 2
Câu 12. Cho tam giác đều ABC có cạnh bằng a và chiều cao AH . Mệnh đề nào sau đây là sai? 2 a 2 a
A. AH .BC 0. B. AB HA 0 , 150 . C. AB.AC . D. AC.CB . 2 2
Câu 13. Cho tam giác ABC vuông tại A và có AB c, AC . b Tính B . A BC. A. 2 B . A BC b . B. 2 B . A BC c . C. 2 2 B .
A BC b c . D. 2 2 B .
A BC b c .
Câu 14. Tính công sinh bởi một lực F có độ lớn 40N kéo vật dịch chuyển theo một vector d có độ lớn 50N và
góc giữa hai vector lực là 60 . A.1000J B. 1200J C. 900J D. 950J
Câu 15. Cho tam giác ABC có AB 2 cm, BC 3 cm, CA 5 cm. Tính C . A CB. A. C . A CB 13. B. C . A CB 15. C. C . A CB 17. D. C . A CB 19.
Câu 16. Cho ba điểm O, ,
A B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng OA OB.AB 0 là
A. tam giác OAB đều.
B. tam giác OAB cân tại O.
C. tam giác OAB vuông tại O.
D. tam giác OAB vuông cân tại O.
Câu 17. Cho M , N , P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?
A. MN NP PQ MN.NP MN.PQ .
B. MP.MN MN .MP .
C. MN.PQ PQ.MN . D. 2 2 MN PQ MN
PQ MN PQ . 19
Câu 18. Cho hình vuông ABCD có cạnh a, trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao
cho AM BN CP DQ x(0 x a) . Tính diện tích tứ giác MNPQ. A. 2 2
2x 2ax a B. 2 2
2x 2ax a C. 2 2
2x ax a D. 2 2
x 2ax a
Câu 19. Cho hình vuông ABCD cạnh a. Tính AB.AC. 2 1 A. 2
AB.AC a . B. 2
AB.AC a 2. C. 2 . AB AC a . D. 2 AB.AC a . 2 2 AC
Câu 20. Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho AM . Gọi N là 4
trung điểm của đoạn thẳng DC. Tính MB.MN .
A. MB.MN 4. B. MB.MN 0. C. MB.MN 4.
D. MB.MN 16.
Câu 21. Cho hình vuông ABCD cạnh a. M là trung điểm của AB, N là trung điểm của AD. Tính MN.MC . A. 2 2a B. 0 C. 2 a D. Kết quả khác
Câu 22. Cho hình chữ nhật ABCD có AB 8, AD 5. Tích AB.BD.
A. AB.BD 62.
B. AB.BD 64.
C. AB.BD 62.
D. AB.BD 64.
Câu 23. Cho hình thoi ABCD có AC 8 và BD 6. Tính AB.AC.
A. AB.AC 24.
B. AB.AC 26.
C. AB.AC 28.
D. AB.AC 32.
Câu 24. Cho hình vuông ABCD cạnh a. M là trung điểm của AB. Tính MC.MD . A. 2 a B. 2 0, 25a C. 2 0, 75a D. Kết quả khác
Câu 25. Hình bình hành ABCD có AB 8 cm, AD 12 cm , góc
ABC nhọn và diện tích bằng 2 54 cm . Tính cosAB,BC. A. AB BC 2 7 cos , . B. AB BC 2 7 cos , . 16 16 C. AB BC 5 7 cos , . D. AB BC 5 7 cos , . 16 16
Câu 26. Cho hình chữ nhật ABCD có AB a và AD a 2 . Gọi K là trung điểm của cạnh A .
D Tính BK.AC.
A. BK .AC 0. B. 2 BK .AC a 2. C. 2
BK .AC a 2. D. 2
BK .AC 2a .
Câu 27. Tìm tập các hợp điểm M thỏa mãn MBMA MB MC 0 với ,
A B, C là ba đỉnh của tam giác. A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 28. Cho tam giác ABC vuông cân tại A và có AB AC .
a Tính AB.BC. 2 a 2 2 a 2 A. 2 AB.BC a . B. 2
AB.BC a . C. . AB BC . D. . AB BC . 2 2
Câu 29. Tính công sinh bởi một lực F có độ lớn 50N kéo vật dịch chuyển theo một vector d có độ lớn 50N và
góc giữa hai vector lực là 60 . A.1250J B. 1200J C. 900J D. 1300J
Câu 30. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn M . A BC 0 là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 31. Cho tam giác ABC đều cạnh bằng a , trọng tâm G . Tích vô hướng của hai vectơ BC.CG bằng 2 a 2 a 2 a 2 a A. . B. . C. . D. . 2 2 2 2
Câu 32. Cho hình vuông ABCD cạnh a, tâm O, M là trung điểm của BC. Tính AM .AO . 3 2 a A. 2 a . B. 2 a . C. 2 a . D. . 4 2
Câu 33. Cho hình vuông ABCD cạnh a. Tính AB.AC. 2 1 A. 2
AB.AC a . B. 2
AB.AC a 2. C. 2 A . B AC a . D. 2 AB.AC a . 2 2
Câu 34. Cho hình vuông ABCD cạnh a, tâm O, M là trung điểm của BC. Tính AM ( AB AC) . A. 2 2,5a B. 2 2a C. 2 3a D. 2 a
Câu 35. Cho hình vuông ABCD cạnh a . Tính P AC.CD CA. A. P 1. B. 2 P 3a . C. 2 P 3 a . D. 2 P 2a . 20
VẬN DỤNG VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, TÍCH VECTOR VỚI 1 SỐ THỰC, PHÂN TÍCH VECTOR – P1)
_________________________________________________ 1
Câu 1. Cho tam giác ABC . N là trung điểm AB , M là điểm thoả đẳng thức MN
AB AC . Kết luận nào 2 dứơi đây đúng:
A. M đối xứng với C qua A ;
B. A đối xứng với M qua C ;
C. C đối xứng với A qua M
D. M là điểm tuỳ ý.
Câu 2. Cho tam giác ABC , trên hai cạnh AB , AC lấy hai điểm D và E sao cho AD 2DB , AE 3EA . Gọi
M là trung điểm của DE và I là trung điểm của BC . Đẳng thức vectơ nào sau đây đúng? 1 3 1 3 1 3 1 3 A. MI AB AC B. MI AB AC C. MI AB AC D. MI AB AC 6 8 6 8 6 8 6 8
Câu 3. Tìm x để hai vec tơ u (x 1) AB 4 AC; v 3AB 2 AC cùng hướng. A.x = 5 B. x = 1 C. x = 3 D. x = 2
Câu 4. Cho tam giác ABC, M là trung điểm của cạnh AB, N thuộc cạnh AC sao cho NC = 2AN. Gọi H, K lần lượt
là trung điểm của MN, BC. Tính 4m 12n biết HK m AB n AC . A.7 B. 8 C. 5 D. 6 Câu 5. Cho A
BC , M là điểm trên cạnh AB sao cho MB 3MA . Đẳng thức vectơ nào sau đây đúng? 1 5 1 5 1 1 1 A. MC CB CA B. MC CB 3CA C. MC CA CB D. MC CA CB 4 4 4 4 4 2 6
Câu 6. Cho tam giác ABC, các điểm M, N, P thỏa mãn MB 3MC, NA 3CN , PA PB 0 . Tính giá trị tổng
m + n biết rằng PN m AB n AC . A.1 B. 0,25 C. 0,5 D. 2
Câu 7. Cho tứ giác ABCD. Gọi M, N, I lần lượt là trung điểm của AC, BD, MN. Tìm giá trị của k biết rằng
OA OB OC OD kOI A. k 3 B. k 4 C. k 6 D. k 8
Câu 8. Cho tứ giác ABCD, các điểm M, N lần lượt thuộc các cạnh AB, CD sao cho MB = 2MA, NC = 2DN. Tính
tổng 6a + 3b biết rằng MN p AD qBC . A.4 B. 5 C. 6 D. 8 2
Câu 9. Cho tam giác ABC, điểm D thỏa mãn BD
BC , I là trung điểm của AD, M là điểm thỏa mãn 3 2 AM
AC . Mệnh đề nào sau đây đúng 5 1 1 1 1 A. BI BA BC B. BI BA BC 2 3 2 3 1 1 1 1 C. BI BA BC D. BI BA BC 2 6 4 6
Câu 10. Cho tam giác ABC với AD là đường phân giác trong. Biết AB = 5, BC = 5, AC = 7. Khi đó 5 7 7 5 A. AD AB AC B. AD AB AC 12 12 12 12 7 5 5 7 C. AD AB AC D. AD AB AC 12 12 12 12
Câu 11. Tam giác ABC có hai trung tuyến AK, BM. Khi đó 2 2 A. AB
AK BM B. AB
AK BM 3 3 1 3 C. AB
AK BM D. AB
AK BM 3 2
Câu 12. Cho tam giác ABC có u 2 AB 3BC AC . Khi đó
A. u 2 AB 3AC
B. u AB 3AC C. u 2 AB 4AC
D. u AB 2 AC
Câu 13. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 2a; AC 3a . Khi đó 21 9 4 4 5 A. AH AB AC B. AH AB AC 13 13 9 9 9 4 2 3 C. AH AB AC D. AH AB AC 13 13 5 5
Câu 14. Cho tam giác ABC có trọng tâm G, điểm M thỏa mãn MA MB 4MC 0 . Khi đó
A. M là trọng tâm tam giác ABG B. M là trung điểm CG C. MGAC là hình bình hành D. ABCM là hình bình hành
Câu 15. Cho tam giác ABC, các trung tuyến AM, BN, CP. Khi đó 4 2 4 2 A. AB AN CP B. AB AN CP 3 3 3 3 4 2 2 4 C. AB AN CP D. AB AN CP 3 3 3 3
Câu 16. Cho tam giác ABC có AB = 3a, AC = 2a, phân giác trong AD. Khi đó tính a + 2b với AD a AB b AC A.1,6 B. 2,4 C. 1,8 D. 2,6
Câu 17. Cho tam giác ABC có trọng tâm G, D là trung điểm của BG. Tính 3a + 12b với AD a AB b AC . A.4 B. 6 C. 5 D. 3
Câu 18. Cho tam giác ABC có trọng tâm G . Gọi I là điểm đối xứng của B qua G . Vectơ AI được phân tích
theo AB và AC là:
1 1
1 1 2 1 2 1 A. AI AC AB B. AI AC AB C. AI AC AB D. AI AC AB 3 3 3 3 3 3 3 3 Câu 19. Cho A
BC có trọng tâm G , I là điểm đối xứng của B qua G , M là trung điểm BC , đẳng thức nào đúng? 2 1
1 2 2 1
1 1 A. AI AC AB B. AI AC AB C. AI AC AB D. AI AC AB 3 3 3 3 3 3 3 3
Câu 20. Cho tam giác ABC điểm I thoả:. IA 2IB Chọn mệnh đề đúng: CA 2CB CA 2CB AC 2CB A. CI B. CI C A 2CB C. CI D. CI 3 3 3
Câu 21. Cho tam giác ABC, M là trung điểm của BC, N là trung điểm của AM. Đường thẳng BN cắt AC tại P. Khi
đó tìm x để AC xCP 4 5 3 2 A. x B. x C. x D. x 3 3 2 3
Câu 22. Cho hình bình hành ABCD, trên đường chéo BD lấy G, H sao cho DG GH HB . Biết rằng
AB AD k AG AH , giá trị của tham số k bằng A.1 B. 2 C. 1,5 D. 3
Câu 23. Cho hình bình hành ABCD, M và N tương ứng là trung điểm BC, CD. Tìm tham số k biết rằng
AM AN k AC A.1,5 B. 2 C. 1 D. 3
Câu 24. Cho hai tam giác ABC, A’B’C’ có trọng tâm lần lượt là G, G’. Điều kiện hai tam giác có cùng trọng tâm là
A. A A B B C C 0 B. A A B B C C AG
C. AA B B C C AB D. A A B B C C BC
Câu 25. Cho tam giác ABC, điểm E thỏa mãn EA 2EB,3FA 2FC 0 . Khi đó 1 2
A. EF 2 AB AC
B. EF 2 AB AC 2 5 1 3
C. EF 3AB AC
D. EF 4 AB AC 4 4
Câu 26. Cho hình bình hành ABCD tâm O, xác định vị trí điểm K thỏa mãn KA KB KC 3KD 0
A.K là trung điểm của đoạn OD
B. K là trọng tâm tam giác ACD
C.K là trọng tâm tam giác ABD
D. K là trọng tâm tam giác ABC
_________________________________ 22
VẬN DỤNG VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, TÍCH VECTOR VỚI 1 SỐ THỰC, PHÂN TÍCH VECTOR – P2)
_________________________________________________
Câu 1. Ta có MN QP RN PN QR MN QP QR PN RN MN RP PR MN .Cho hình
bình hành ABCD . Đẳng thức nào sau đây đúng?
A. BA BC DC CB .
B. BA BC DC BC .
C. BA BC DC AD .
D. BA BC DC CA .
Câu 2. Cho tam giác ABC . Gọi D, E, F lần lượt là trung điểm của các cạnh BC,C ,
A AB . Đẳng thức nào sau đây đúng?
A. AD BE CF AF CE BD .
B. AD BE CF AB AC BC .
C. AD BE CF AE AB CD .
D. AD BE CF BA BC AC .
Câu 3. Tam giác ABC có điểm I thỏa mãn IA 3IB . Đẳng thức nào sau đây đúng 3 1
A. CI CA 3CB B. CI CA CB 2 2 1 C. CI CA 3CB
D. CI 3CA CB 2
Câu 4. Gọi M, N lần lượt là trung điểm của các cạnh AB và CD của tứ giác ABCD. Mệnh đề nào sau đây đúng
A. AC BD BC AD 4MN
B. AC BD 4MN
C. BC AD 4MN
D. AC BD BC AD MN
Câu 5. Cho hình thoi ABCD có M là trung điểm của cạnh AB, N là trung điểm cạnh CD.
Biết rằng MA MC a MC MD, MN bMA MC, MC MD cMN . Tính a b c . A.2 B. 3,5 C. 1 D. – 2
Câu 6. Cho A
BC và điểm K thỏa mãn KA KB KC 0 . Khẳng định nào sau đây đúng ?
A. ABKC là hình bình hành
B. K là trung điểm AB
C. ABCK là hình bình hành
D. K là trung điểm BC
Câu 7. Cho hình bình hành ABCD , M là điểm tùy ý. Đẳng thức vectơ nào sau đây đúng?
A. MB MC MD MA 0
B. MB MC MD MA
C. MA MC MB MD
D. MD MC MB MA Câu 8. Cho A
BC có trung tuyến AI , D là trung điểm AI . Đẳng thức nào sau đây đúng mọi điểm O?
A. OA OB OC 3OI
B. 2OA OB OC 0
C. OA OB OC 0
D. 2OA OB OC 4OD
Câu 9. Cho tam giác ABC, điểm M thỏa mãn 4BM 3MC . Tính 12a + 12b biết AM a AB b AC . A.12 B. 10 C. 8 D. 6
Câu 10. Cho tam giác ABC , gọi E là trung điểm của AC . Một điểm N thỏa: NA NC 2BN . Đẳng thức vectơ nào sau đây đúng?
A. N là trung điểm BC
B. N là trung điểm AC
C. N là trọng tâm tam giác ABC
D. N là trung điểm BE
Câu 11. Cho tam giác ABC và điểm I thỏa mãn IA 2BI . Tính m + n biết rằng CI mCA nCB . A.1 B. 2 C. 3 D. – 3 Câu 12. Cho A
BC , M là điểm trên cạnh AB sao cho MB 3MA . Đẳng thức vectơ nào sau đây đúng? 1 5 1 5 1 1 1 A. MC CB CA B. MC CB 3CA C. MC CA CB D. MC CA CB 4 4 4 4 4 2 6 Câu 13. Cho A
BC có D thuộc cạnh AC sao cho AD 2DC . Gọi E , H và I lần lượt là trung điểm của
AB , BC và ED . Đẳng thức vectơ nào sau đây đúng? 2 1 2 1 2 1 2 1 A. AI AH AB B. AI AH AB C. AI AH AB D. AI AH AB 3 2 3 12 3 12 3 2
Câu 14. Khẳng định nào sau đây là đúng?
A. Hai vectơ a, ka luôn cùng hướng
B. Hai vectơ a, ka luôn cùng phương
C. Hai vectơ a, ka bằng độ dài
D. Hai vectơ a, ka luôn ngược hướng 23 Câu 15. Cho A
BC , N là điểm trên cạnh AB sao cho AN 2NB . Biểu diễn CN theo AB và AC là: 2
1 2 1 2 A. CN AB AC B. CN AB AC C. CN
AB AC D. CN AB AC 3 3 3 2 3
Câu 16. Cho tam giác ABC có trung tuyến AB . Xác định điểm I sao cho 2IA 3IB IC 1 1 A. MI 4CB B. MI CB C. MI 4BC D. MI BC 4 4
Câu 17. Điểm M thuộc cạnh BC của tam giác ABC sao cho BC 3BM . Khi đó AM a AB b AC , tính giá trị biểu thức 3a + 6b. A.3a + 6b = 7 B. 3a + 6b = 10 C. 3a + 6b = 4 D. 3a + 6b = 2
Câu 18. Cho tam giác ABC , có trung tuyến AM và trọng tâm G . Khẳng định nào sau đây là đúng
2
A. AM AB AC B. AG
AB AC 3
C. 3MG MA MB MC D. AM 3MG
Câu 18. Cho tam giác ABC có điểm O thỏa mãn OA OB 2OC OA OB . Khi đó A. Tam giác ABC đều B. Tam giác ABC cân tại C
C. Tam giác ABC vuông tại C D. Tam giác ABC cân tại B
Câu 19. Hình bình hành ABCD có điểm M thỏa mãn 4 AM AB AD AC . Khi đó A. M là trung điểm AC B. M trùng với điểm C C. M là trung điểm AB D. M là trung điểm AD
Câu 20. Cho tam giác ABC và điểm M tùy ý. Tìm điểm D sao cho MA MB 2MC CD
A. D là điểm thứ tư của hình bình hành ABCD
B. D là điểm thứ tư của hình bình hành ACBD
C. D là trọng tâm tam giác ABC
D. D là trực tâm tam giác ABC
Câu 21. Cho hình chữ nhật ABCD tâm O, điểm M bất kỳ. Tìm số thực m sao cho MB MC MD MA mMO . A.m = 4 B. m = 5 C. m = 2 D. m = 3
Câu 22. Cho 4 điểm A , B , C , D phân biệt. Đẳng thức vectơ nào sau đây sai:
A. AB BD AD
B. DA AB DB
C. BA AC BC
D. DA BD AB
Câu 23. Cho tam giác ABC có trọng tâm G . Gọi I là trung điểm của AG . Đẳng thức vectơ nào sau đây đúng? 1 1 2 1
1 1 1 1
A. CI CA CB B. CI CA CB C. CI CA CB
D. CI CA CB 3 6 3 6 3 6 3 6
Câu 24. Cho tam giác ABC có trọng tâm G, giả sử CG xCA yCB . Tính 6x + 9y. A. 1 B. 5 C. – 1 D. – 2
Câu 25. Cho tam giác ABC, trên hai cạnh AB, AC lần lượt lấy hai điểm D, E sao cho AD 2DB,CE EA . Gọi
M là trung điểm của DE và I là trung điểm của BC. Tính 6a + 8b biết MI a AB b AC . A.3 B. 5 C. 4 D. 2
Câu 26. Cho hình bình hành ABCD có H, K lần lượt thuộc hai cạnh AB, AC sao cho 3AH = 2AB, 3AK = AC. Trên
cạnh BC lấy điểm M sao cho 4BM = 3MC. Khi đó 1 1 9 9 A. BM AK AH B. BM AK AH 4 7 7 14 9 9 3 5 C. BM AK AH D. BM AK AH 7 14 7 14
Câu 27. Cho tam giác ABC có M, N lần lượt thuộc hai cạnh AB, AC sao cho AM = MB, NC = 2AN. Gọi K, P lần
lượt là trung điểm của MN, BC. Mệnh đề nào sau đây đúng 1 1 1 1 A. KP AB AC B. KP AB AC 4 6 6 8 1 1 1 2 C. KP AB AC D. KP AB AC 4 3 4 3
Câu 28. Cho tam giác ABC . Gọi G là trọng tâm, M là trung điểm của BC và D là điểm đối xứng với B qua
G . Đẳng thức vectơ nào sau đây đúng? 3 5
1 2 1 5 1 5 A. MD AC AB B. MD AC AB C. MD AC AB D. MD AC AB 4 4 3 3 6 6 2 2
_________________________________ 24
VẬN DỤNG VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TỔNG, HIỆU, TÍCH VECTOR VỚI 1 SỐ THỰC, PHÂN TÍCH VECTOR – P3)
_________________________________________________
Câu 1. Tam giác ABC có điểm M thuộc cạnh BC sao cho BM = 3MC. Tính 16a + 60b khi AM a AB b AC . A.30 B. 25 C. 49 D. 40 Câu 2. Cho A
BC có M , N , P lần lượt là trung điểm của AB , BC , CA . Hãy chọn đẳng thức vectơ đúng:
A. NA NB NC NP 4NM
B. AP BM CN 0
C. AN BP CM 0
D. PA PB 2PN 0 Câu 3. Cho A
BC có trọng tâm G , I là điểm thỏa bởi IA 2.IB . Đẳng thức vectơ nào dưới đây đúng? 5 1 5 1 5 1 5 1 A. IG AB AC B. IG AB AC C. IG AB AC D. IG AB AC 3 3 3 3 3 3 3 3
Câu 4. Cho tứ giác ABCD có I, J, K lần lượt là trung điểm của AB, CD, IJ. Tìm k để CA CB CD kCK . A.k = 1 B. k = 4 C. k = 2 D. k = 3
Câu 5. Cho hình bình hành ABCD tâm O, I là trung điểm của cạnh BC. Tính m + n biết rằng AI m AD n AB . A.1 B. 3,5 C. 2,5 D. 4,5
Câu 6. Cho tam giác ABC, điểm M thuộc cạnh BC sao cho AM x AB y AC . Tính x y . 2 1 A.1 B. – 1 C. D. 3 3
Câu 7. Cho tam giác ABC có điểm I thuộc cạnh AC sao cho AC 4IC . Tính m + 2n biết BI m AC n AB . A.2,5 B. 2,75 C. – 1,5 D. – 1,25
Câu 8. Cho hình bình hành ABCD tâm O . OA AB ? A. BO B. AC C. OB D. BA
Câu 9. Cho tam giác ABC, I là trung điểm AB và M là trung điểm CI. Mệnh đề nào sau đây đúng
A. MA MB 2MC 0
B. MA MB MC 0
C. MA 2MB MC 0
D. 2MA MB MC 0
Câu 10. Hình bình hành ABCD có M là trung điểm của CD, N là trung điểm của BM. Tính giá trị p + b biết rằng
AN p AB q AD . A.1 B. 1,25 C. 2,5 D. 2
Câu 11. Cho hình bình hành ABCD; M , N lần lượt là trung điểm của AB; CD; Đẳng thức vectơ nào dưới đây sai?
A. NA MB CN DM 0
B. MA MB CN DN
C. NA MB MC ND
D. NA BN CM MD 0
Câu 12. Cho hình bình hành ABCD có M là trung điểm của CD, điểm N thuộc đoạn BM sao cho BN = 2MN. Tính
a + b biết rằng AN a AB bBD . A.2 B. 3 C. 1 D. 1,5
Câu 13. Cho tam giác ABC có M, N lần lượt thuộc hai cạnh AB, AC sao cho AM = MB, NC = 2AN. Gọi K là trung 1 1 điểm của MN. Tính AB AC . 4 6 1 A.2 AK B. AK C. 3 AK D. AK 2
Câu 14. Cho hình bình hành ABCD, M là trung điểm CD. Hệ thức nào sau đây đúng 1
1 A. AM AC AB
B. 2 AM AC AB 2 2 1 1
C. AM 2 AC AB D. AM AC AB 2 2
Câu 15. Cho tứ giác ABCD, I và J lần lượt là trung điểm BC và AD. Tìm k biết rằng AB AI JA DA k DB . A.k = 1 B. k = 2,5 C. k = 3 D. k = 1,5
Câu 16. Cho tam giác ABC, I là trung điểm của AB. Tìm điểm M thỏa mãn MA MB 2MC 0
A. M là trung điểm của BC
B. M là trung điểm của IC
C. M là điểm thuộc đoạn IC sao cho IM = 2MC
D. M là trung điểm của IA
Câu 17. Cho tứ giác ABCD có điểm E thỏa mãn AE EB 3EC . Tính m n p biết rằng 25
DE mDA nDB pDC . 17 A.1 B. 2 C. 1,25 D. 15
Câu 18. Cho hình bình hành ABCD có I là trung điểm BC, G là trọng tâm tam giác CDI. Khi đó đặt các véc tơ
AB a; AD b thì véc tơ AG được biểu thị là 2 5 2 5 2 1 1 5 A. a b B. a b C. a b D. a b 3 6 3 6 3 6 3 6
Câu 19. Cho hình bình hành ABCD có M là trung điểm của CD, điểm N thuộc đoạn BM sao cho BN = 2MN. Biết
rằng 3AB 4CD k CM ND MN , giá trị của k bằng A.2 B. 3 C. 4 D. 1
Câu 20. Cho tam giác ABC, trên hai cạnh AB, AC lần lượt lấy hai điểm D, E sao cho AD 2DB,CE EA . Gọi
M là trung điểm của DE và I là trung điểm của BC. Tính 3a + 8b biết AM a AB b AC . A.3 B. 5 C. 1 D. 2
Câu 21. Cho tam giác ABC có trọng tâm G, H là điểm đối xứng với B qua G, M là trung điểm của BC. Khi đó 1 5 1 5 A. MH AC AB B. MH AC AB 3 6 3 6 1 5 1 1 C. MH AC AB D. MH AC AB 6 6 4 6
Câu 22. Cho tam giác ABC có I, J, K lần lượt là trung điểm của AB, BC, CA. Điểm D thuộc đoạn BC sao cho
3DB = 2BC, M là trung điểm của đoạn AD. Tính a + b biết 6BM a AC b AB . A.2 B. – 2 C. – 3 D. – 1
Câu 23. Cho 3 điểm A , B , C không thẳng hàng. Tìm khẳng định đúng
A. AB CA BC
B. AB BC CA 0
C. AB BC AB BC
D. AB BC AC
Câu 24. Cho tứ giác ABCD, điểm M tùy ý, tồn tại a, b sao cho MA 4MB 3MC a AB bBC . Tính a + b. A.2,5 B. 4 C. 5 D. 2
Câu 25. Cho tam giác ABC và một điểm M tùy ý. Hãy chọn hệ thức đúng:
A. 2MA MB 3MC AC 2BC
B. 2MA MB 3MC 2 AC BC
C. 2MA MB 3MC 2CA CB
D. 2MA MB 3MC 2CB CA
Câu 26. Cho tam giác ABC với H , O, G lần lượt là trực tâm, tâm đường tròn ngoại tiếp, trọng tâm của tam
giác. Hệ thức đúng là: 3 1 A. OH OG B. OH 3OG C. OG GH
D. 2GO 3OH 2 2
Câu 27. Ba trung tuyến AM , BN , CP của tam giác ABC đồng quy tại G . Hỏi vectơ AM BN CP bằng vectơ nào? 3
1 A.
GAGB CG
B. 3MG NG GP C.
AB BC AC D. 0 2 2
Câu 28. Cho hình bình hành ABCD có M là trung điểm của BC, G là trọng tâm tam giác ACD. Tính a + b biết
rằng a, b thỏa mãn MG a AB b AD . A.0,5 B. – 0,5 C. 1 D. – 1 Câu 29. Cho A
BC nhọn, có H là trực tâm. BHC nội tiếp I ,
R . Gọi M là trung điểm B .
C Khẳng định nào sau đây là đúng?
A. MB, MC cùng hướng. B. H , A IM cùng hướng.
C. MB, BC cùng hướng. D. Cả , A , B C đều sai. 1
Câu 30. Cho tam giác ABC vuông tại , A có AM
BC M BC . Dựng 2 đường phân giác của AM , B AMC 2 lần lượt cắt A ,
B AC tại D, E . Số các cặp vectơ cùng hướng là A. 36 . B. 30 . C. 18 . D. 27 .
_________________________________ 26
VẬN DỤNG VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P1)
______________________________
Câu 1. Cho tam giác đều ABC cạnh a, trọng tâm G. Tính độ dài vec tơ GA 2GC 4GB a 93 A.2a B. C. a 3 D. 2a 17 3
Câu 2. Cho ba lực F , F , F cùng tác động vào một vật tại điểm O và vật đứng yên. Cường độ của F , F đều là 1 2 3 1 2
120N và AOB 120 . Tìm cường độ của lực F . 3 A. 120N B. 100N C. 150N D. 100 3N
Câu 3. Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc 10km/h. Một chiếc ca nô chuyển động từ
phía đông sang phía tây với vận tốc 40km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông. A.10 7 km/h B. 20km/h C. 30km/h D. 20 3 km/h
Câu 4. Điểm M nằm trên đường tròn ngoại tiếp hình vuông ABCD cạnh a. Tính MA MC A. 3a 2 B. a 5 C. 6a 2 D. a 2
Câu 5. Điểm M nằm trên đường tròn ngoại tiếp hình vuông ABCD cạnh a. Tính MA MB MC MD A. 3a 2 B. 2a 2 C. 6a 2 D. a 2
Câu 6. Có hai lực F , F có cường độ tương ứng 5N và 8N cùng tác động vào một vật đứng yên tại O. Giả sử 1 2
hai lực vuông góc với nhau. Cường độ lực tổng hợp tác dụng lên vật là A. 89N B. 40N C. 2 13N D. 13N
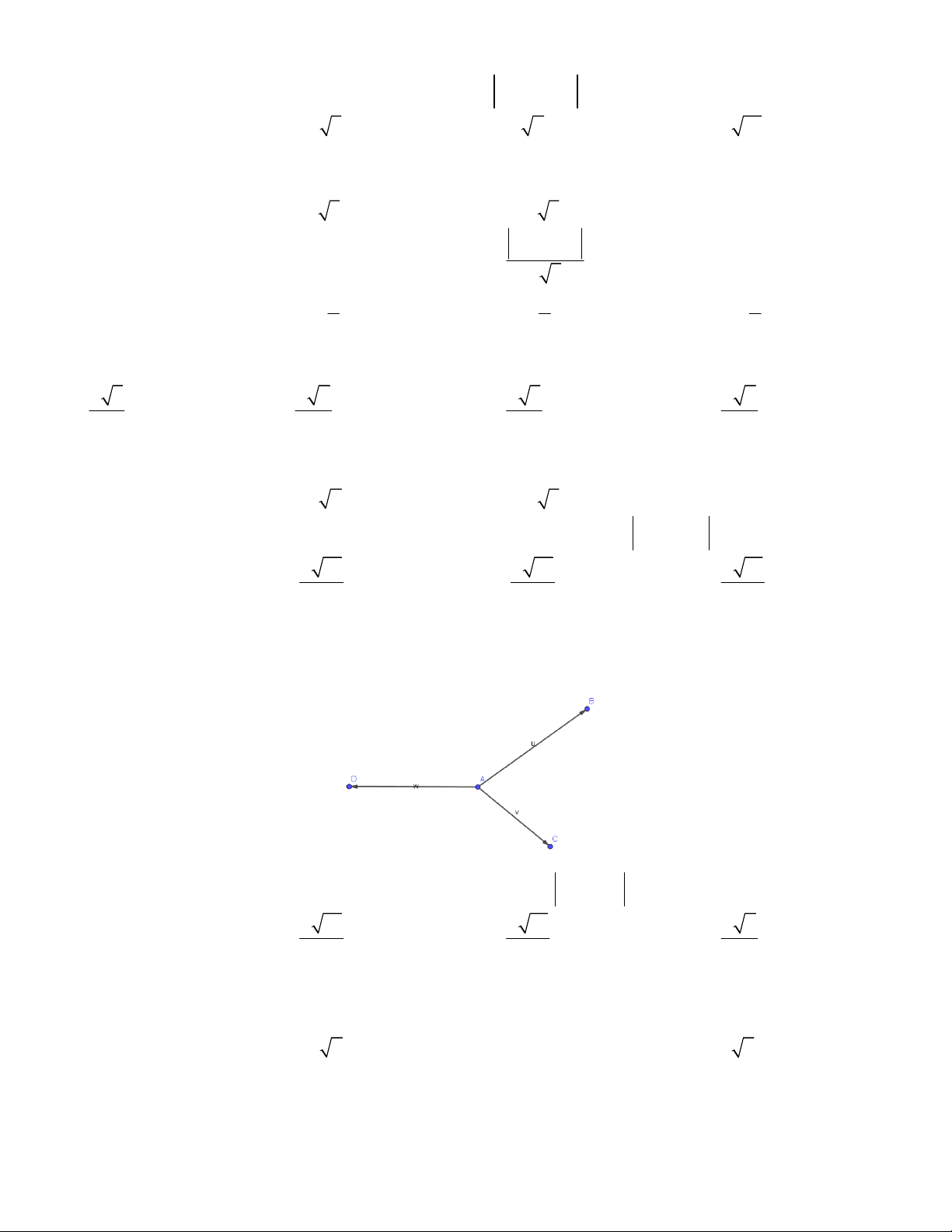
Câu 7. Mỗi ô vuông trong hình vẽ có kích thước 1.1,
tính độ dài của véc tơ u v w . E. 5 C. 13 F. 10 D. 17
Câu 8. Có hai lực F , F có cường độ đều là 50N và hợp với nhau góc 60 . Hỏi vật đó phải chịu một lực tổng 1 2
hợp có cường độ là bao nhiêu A.100N B. 200N C. 50 3N D. 100 3N
Câu 9. Điểm M nằm trên đường tròn ngoại tiếp tam giác ABC đều cạnh a, tính MA MB MC . 4 1 A. 2a 3 B. a 3 C. a 3 D. a 3 3 3
Câu 10. Điểm M nằm trên đường tròn nội tiếp tam giác ABC đều cạnh a, tính MA MB MC . 1 4 1 A. a 3 B. a 3 C. a 3 D. a 3 2 3 3
Câu 11. Cho tam giác ABC vuông tại A, AB = 2a, AC = a. Tính AB 3AC 4BC A.5a B. a 132 C. a 101 D. a 13
Câu 12. Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc 10km/h. Một chiếc ca nô chuyển động từ
phía đông sang phía tây với vận tốc 45km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông. A.10 7 km/h B. 5 85 km/h C. 45km/h D. 20 3 km/h
Câu 13. Cho tam giác ABC vuông tại A, AB = 2a, AC = a. Tính MA 2MB 3MC với M bất kỳ. A. a 5 B. 2a 2 C. 5a D. a 13
Câu 14. Cho hình vuông ABCD cạnh a. Tính 3MA MB 2MC với M bất kỳ. 27 A. a 26 B. a 13 C. a 5 D. a 29
Câu 15. Một máy bay di chuyển theo hướng bắc như hình vẽ, vận
tốc máy bay là 200km/h, vận tốc gió theo hướng đông là 60km/h.
Nếu máy bay tăng vận tốc gấp đôi thì máy bay sẽ bay theo hướng
đông bắc với vận tốc khoảng A. 404km/h B. 500km/h G. 420km/h D. 450km/h
Câu 16. Cho hình thang ABCD vuông tại A, D có AB = AD = a, DC = 2a. Tính AB AC . 3a 2 A. a 5 B. 3a 2 C. a 10 D. 2
Câu 17. Cho hình thoi ABCD cạnh a, BAC 30 . Tính AB AC . a 10 a 13 3a 2 A.2a B. C. D. 2 2 2
Câu 18. Cho hình thoi ABCD cạnh a, BAC 30 . Tính AB 3AD . a 10 a 13 A.2a B. C. D. a 13 2 2
Câu 19. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a, M và N lần lượt là trung điểm của BC, CD. Tính độ dài
của véc tơ AM AN . A.7,75 B. 7,5 C. 2a 13 D. 4a 2
Câu 20. Cho ba lực F , F , F cùng tác động vào một vật tại điểm M như 1 2 3
hình vẽ với F MB, F M ,
A F MC , AMB 120 ; AMC 60 , với 1 2 3
cường độ tương ứng F F 300N; F 400N . Tính cường độ lực 1 2 3
tổng hợp tác động vào vật. H. 300N C. 100N I. 500N D. 700N
Câu 21. Cho tam giác ABC đều cạnh a , có AH là đường trung tuyến. Tính AC AH : a 13 a 3 A. a 3 B. 2a C. D. 4 2
Câu 22. Khi máy bay nghiêng cánh một góc 45 , lực F của
không khí tác động vuông góc với cánh và bằng tổng của lực
nâng F và lực cản F . Biết F x 2N , cường độ của lực F là. 1 2 1 A. xN B. 0,5aN x 2 C. N D. 10000N 2
Câu 23. Cho hình chữ nhật ABCD có AB = 4a, AD = 3a, M là trung điểm DC. Tính AC AM . A.2a B. 3a 2 C. 6a 2 D. a 13
Câu 24. Cho hình thoi ABCD tâm O cạnh a, BAC 30 . Tính 2 AB 2 AD OB . a 13 A.2a B. 3,5a C. D. a 13 2
Câu 25. Cho hình thang ABCD vuông tại A và D , có AD CD 4 , AB 8 . Tính BA AC ? A. 2 2 B. 2 10 C. 4 10 D. 4 2 28
VẬN DỤNG VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P2)
______________________________
Câu 1. Cho tam giác ABC có AB 3; AC 4; BC 5 . Điểm M nằm trên đường tròn ngoại tiếp tam giác ABC.
Tính độ dài vector MB MC . A.5 B. 6 C. 4 D. 3
Câu 2. Cho tam giác ABC đều cạnh a, trọng tâm G, tính độ dài vector GB 2GA 3GC . A.a B. 2a C. a 5 D. a 3
Câu 3. Cho ba lực F , F , F cùng tác động vào một vật tại điểm O và vật đứng yên. Cường độ của F , F đều là 1 2 3 1 2
150N và AOB 120 . Tìm cường độ của lực F . 3 A. 120N B. 100N C. 150N D. 100 3N
Câu 4. Tam giác ABC vuông tại A nội tiếp đường tròn đường kính BC = 10. Điểm M đối xứng với A qua đường
thẳng BC, tính độ dài vector MB MC . A.10 B. 6 C. 8 D. 12
Câu 5. Cho hình vuông ABCD cạnh a. Với điểm M bất kỳ, tính độ dài vector 4MA 3MB MC 2MD . A. 2a B. 2a 2 C. a 5 D. a 6
Câu 6. Cho hình chữ nhật ABCD có AD a; AB 2a , M và N lần lượt là trung điểm của AB và CD. Tính độ
dài của vector 2CM 3AN . A.2a B. a C. a 2 D. a 3
Câu 7. Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc 10km/h. Một chiếc ca nô chuyển động từ
phía đông sang phía tây với vận tốc 35km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông. A.10 7 km/h B. 20km/h C. 5 53 km/h D. 20 3 km/h
Câu 8. Điểm M nằm trên đường tròn ngoại tiếp hình vuông ABCD cạnh 6a. Tính MA MC A. 3a 2 B. a 5 C. 6a 2 D. a 2
Câu 9. Cho hình thang ABCD vuông tại A, D có AB = AD = a, DC = 3a. Tính BD BC . a 6 a 5 a 10 3a 2 A. B. C. D. 2 2 2 2
Câu 10. Cho hình thoi ABCD cạnh a, BAC 30 . Tính BD BC . a 3 a 5 3a 2 A.2a B. C. D. 2 2 2
Câu 11. Cho hình vuông ABCD cạnh a. Với điểm M bất kỳ, tính độ dài vector 2MA MB MC 2MD . A. 2a B. 2a 2 C. a 5 D. a 6
Câu 12. Cho hình thoi ABCD cạnh a, BAC 30 . Tính 2 AB 3AD . A.2a B. a 19 C. 3a 2 D. a 13
Câu 13. Tam giác ABC có AB 4; AC 5; BC
21 . Tính độ dài vector AB AC . 61 46 3 5 A. B. 3 2 C. D. 2 2 2
Câu 14. Cho hình vuông ABCD tâm O và độ dài cạnh bằng 6a, Tính NM NC khi các điểm M, N xác định
bởi: MA MD 0, NB ND NC 0 . A. a 5 B. a 7 C. a 26 D. a 6
Câu 15. Cho hình vuông ABCD cạnh a. Với điểm M bất kỳ, tính độ dài vector 3MA MB MC MD . A. 2a B. 2a 2 C. a 5 D. a 6
Câu 16. Có hai lực F , F có cường độ đều là 10N, hợp với nhau một góc 30 . cùng tác động vào một vật đứng 1 2 29
yên tại O, tổng hợp lực thu được là F . Giả sử tăng cường độ hai lực F , F lên lần lượt là 2 lần và 6 lần, chiều 1 2
của lực giữ nguyên như thế, ta thu được tổng hợp lực K . Cường độ của K gấp x cường độ của lực F , hỏi x gần nhất giá trị nào A.3,124 lần B. 4,123 lần C. 5,102 lần D. 4,035 lần
Câu 17. Cho hình vuông ABCD tâm O và độ dài cạnh bằng a. Điểm G thỏa mãn GA GC GD 0 . Tính độ
dài của vector GA GB . a 17 a 14 a 11 a 17 A. B. C. D. 3 3 3 2
Câu 18. Cho tam giác đều ABC cạnh a. Tính 5MA 2MB 7MC với M bất kỳ. A. a 17 B. a 39 C. a 26 D. a 41
Câu 19. Khi máy bay nghiêng cánh một góc 45 , lực F của
không khí tác động vuông góc với cánh và bằng tổng của lực
nâng F và lực cản F . Biết F 6x 2N , cường độ của lực 1 2 F là. 1 A. 6xN B. 0,5aN x 2 C. N D. 10000N 2
Câu 20. Cho hình thoi ABCD cạnh a, BAC 30 . Tính AC 2 AD . A. 2a B. a 13 C. a 5 D. a 6
Câu 21. Cho hình vuông ABCD cạnh a. Với điểm M bất kỳ, tính độ dài vector 4MA 5MB 2MC MD . A. a 57 B. 2a 2 C. a 58 D. 2a 15
Câu 22. Cho tam giác đều ABC cạnh a. Tính độ dài vector 0, 75MA 2,5MB với M là trung điểm cạnh BC. a 127 a 5 a 101 a 6 A. B. C. D. 8 3 3 2
Câu 23. Có hai lực F , F có cường độ tương ứng 6N và 8N cùng tác động vào một vật đứng yên tại O. Cường 1 2
độ lực tổng hợp tác dụng lên vật là 12N thì góc giữa hai vector lực gần nhất với A.65 độ B. 67 độ C. 62 độ D. 56 độ
Câu 24. Cho hình vuông ABCD cạnh a, tâm O, M là trung điểm cạnh AB. Tính độ dài vector AM AO CB . a 6 a 5 a 10 3a 2 A. B. C. D. 2 2 2 2
Câu 25. Có hai lực F , F có cường độ đều là 10N, hợp với nhau một góc 30 . cùng tác động vào một vật đứng 1 2
yên tại O, tổng hợp lực thu được là F . Giả sử tăng cường độ hai lực F , F lên lần lượt là 3 lần và 4 lần, chiều 1 2
của lực giữ nguyên như thế, ta thu được tổng hợp lực K . Cường độ của K gấp x cường độ của lực F , hỏi x gần nhất giá trị nào A.2,7 lần B. 4,5 lần C. 5,4 lần D. 3,5 lần
Câu 26. Cho tam giác đều ABC cạnh a. Tính MA 2MB 3MC với M bất kỳ. 1 A. a 17 B. a 13 C. a 3 D. a 3 3
Câu 27. Cho tam giác đều ABC cạnh a. Tính 2MA 3MB 5MC với M bất kỳ. A. a 17 B. a 13 C. a 39 D. a 29
Câu 28. Cho hình vuông ABCD cạnh a, K và H lần lượt là trung điểm của BC, DC. Tính AK AH a 10 a 13 3a 2 A.2a B. C. D. 2 2 2 30
VẬN DỤNG VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN ĐỘ DÀI VECTOR P3) _____________________________
Câu 1. Cho tam giác đều ABC có độ dài cạnh bằng a. Tính AB 2 AC . A. 4a B. 2a 3 C. a 7 D. a 10
Câu 2. Có hai lực F , F cùng tác động vào một vật đứng yên tại O. Biết hai lực F , F cùng có cường độ là 1 2 1 2
1000 N và chúng hợp với nhau một góc 60 . Hỏi vật đó phải chịu một lực tổng hợp có cường độ bao nhiêu ? A. 100 N B. 50 3 N C. 100 3 N D. 200 N AB GC
Câu 3. Cho tam giác ABC đều có độ dài cạnh là 2a, tính Z . a 3 2 7 4 A. Z = 1 B. Z = C. Z = D. Z = 3 3 3
Câu 4. Cho hình vuông ABCD cạnh a với M, N lần lượt là trung điểm của AB, BC. Tính độ dài vector AM CN . a 3 a 2 a 5 a 7 A. B. C. D. 2 2 2 2
Câu 5. Có hai lực F , F cùng tác động vào một vật đứng yên tại O. Biết hai lực F , F cùng có cường độ là 26 1 2 1 2
N và vuông góc với nhau. Tính tổng hợp lực tác dụng lên vật. A. 100 N B. 26 2 N C. 100 3 N D. 70,5 N
Câu 6. Cho hình thoi ABCD tâm I và có độ dài cạnh bằng a, BAC 30 . Tính 2 AB IC . a 10 a 31 a 13 A. 6a B. C. D. 2 2 2
Câu 7. Cho ba lực F AB, F AC, F AD cùng tác động vào một vật đặt tại điểm A như hình vẽ, vật đứng 1 2 3
yên. Giả định BAC 60 , F 60N , F 30N . Độ lớn lực F 1 2
3 thỏa mãn bất đẳng thức nào ? A. 50 < F3 < 60 B. 70 < F3 < 80 C. 80 < F3 < 90 D. 64 < F3 < 69
Câu 8. Cho hình vuông ABCD tâm I và có độ dài cạnh bằng a. Tính AB DI theo a. a 10 a 13 a 7 A. 5a B. C. D. 2 2 2
Câu 9. Cho tam giác ABC vuông tại A có độ dài cạnh huyền bằng 10. Tính AB AC . A.10 B. 8 C. 6 D. 12
Câu 10. Cho hình vuông ABCD cạnh a. Với điểm M bất kỳ, tính độ dài vector 4MA MB 4MC 7MD . A. 2a B. 2a 2 C. D. a 6
Câu 11. Có hai lực F , F có cường độ đều là 10N, hợp với nhau một góc 30 . cùng tác động vào một vật đứng 1 2
yên tại O, tổng hợp lực thu được là F . Giả sử tăng cường độ hai lực F , F lên lần lượt là 6 lần và 2 lần, chiều 1 2
của lực giữ nguyên như thế, ta thu được tổng hợp lực K . Cường độ của K gấp x cường độ của lực F , hỏi x gần nhất giá trị nào A.3,124 lần B. 4,123 lần C. 5,102 lần D. 4,035 lần
Câu 12. Cho hình chữ nhật ABCD có AB = a, AD = 2a. Lựa chọn mệnh đề đúng 31
A. AB BC CD 2a
B. AB BC CD 4a
C. AB AD 3a
D. AB BC CD DA 6a .
Câu 13. Mỗi ô vuông trong hình vẽ có kích thước 1.1,
tính độ dài của véc tơ 2u w . A. 109 C. 13 B. 10 D. 7
Câu 14. Cho hình thang ABCD vuông tại A và D, AD = CD = 4, AB = 8. Tính BA AC . A. 2 10 B. 3 10 C. 4 10 D. 5 2
Câu 15. Tam giác ABC vuông tại A có trọng tâm G và cạnh huyền BC = 12. Tính 4GA GB GC . A. 9 B. 12 C. 10 D. 8
Câu 16. Có hai lực F , F có cường độ tương ứng 6N và 8N cùng tác động vào một vật đứng yên tại O. Cường 1 2
độ lực tổng hợp tác dụng lên vật là 11N thì góc giữa hai vector lực gần nhất với A.65 độ B. 81 độ C. 77 độ D. 72 độ
Câu 17. Tam giác ABC có điểm O thỏa mãn OA OB 2OC OA OB . Khẳng định nào sau đây đúng ? A. Tam giác ABC đều B. Tam giác ABC cân tại C
C. Tam giác ABC vuông tại C D. Tam giác ABC cân tại B
Câu 18. Một máy bay di chuyển theo hướng bắc như hình vẽ, vận
tốc máy bay là 200km/h, vận tốc gió theo hướng đông là 60km/h.
Nếu máy bay tăng vận tốc gấp ba thì máy bay sẽ bay theo hướng
đông bắc với vận tốc khoảng B. 603km/h B. 610km/h J. 650km/h D. 620km/h
Câu 19. Cho tam giác đều ABC có đường cao AH, độ dài cạnh bằng a. Tính 3AB BC theo a. A. a 13 B. a 10 C. a 17 D. a 19
Câu 20. Cho hình vuông ABCD có tâm I, độ dài cạnh bằng a. Tính IA IM ID theo a biết M là trung điểm của CD. a 5 a 7 a 10 A. 2a B. C. D. 2 2 2
Câu 21. Điểm M nằm trên đường tròn ngoại tiếp hình vuông ABCD cạnh 3a. Tính MA MB MC MD A. 3a 2 B. 2a 2 C. 6a 2 D. a 2
Câu 22. Mỗi ô vuông trong hình vẽ có kích thước 1.1,
tính độ dài của véc tơ 2u 3v . A. 109 C. 130 K. 113 D. 91
Câu 23. Điểm M nằm trên đường tròn ngoại tiếp tam giác ABC đều cạnh 3a, tính MA MB MC . 1 A. 2a 3 B. 3a 3 C. a 3 D. a 3 3
Câu 24. Điểm M nằm trên đường tròn nội tiếp hình vuông ABCD cạnh bằng 26, tính MA MB MC MD . A.26 B. 13 C. 52 D. 40 32
VẬN DỤNG VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P1) _____________________________
Câu 1. Cho các véc tơ a, b và c thỏa mãn các điều kiện a x, b y và z c và a b 3c 0 . Tính A . a b . b c . c a . 2 2 2
3x z y 2 2 2
3z x y 2 2 2
3y x z 2 2 2
3z x y A. A . B. A . C. A . D. A . 2 2 2 2
Câu 2. Cho hai vectơ a và b . Biết a 2, b 3 và a b 0 ,
30 . Tính a b . A. 11 . B. 13 . C. 12 . D. 14 . 2
Câu 3. Cho a b 1và hai vector a ;
b a b vuông góc với nhau. Tính góc giữa hai vector a,b . 5 A. 100 độ B. 180 độ C. 120 độ D. 45 độ
Câu 4. Cho tam giác ABC có AB = c, BC = a, CA = b. Tính AB AC BC . 2 2 2
c b a A. 2 2 b c B. 2 2 c a C. 2 2 2c a D. 2
Câu 5. Cho hai vector a,b thỏa mãn a b 4, a b 2 . Tính . a b . A. – 2 B. – 3 C. – 5 D. 3
Câu 6. Cho tam giác ABC có AB = c, BC = a, CA = b, M là trung điểm cạnh BC. Tính AM .BC theo a, b, c. 2 2 b c A. B. 2 2 3 b c C. 2 2 2c a D. 2 2 c a 2
Câu 7. Cho a 5, b 12, a b 13. Tính cos của góc , là góc giữa hai vector a,b . 12 5 11 A. B. 0 C. D. 13 13 15
Câu 8. Tính cos a,b với a 3, b 4, a b 4. 1 3 2 A. 0,5 B. C. D. 2 8 5
Câu 9. Cho hình chữ nhật ABCD có AB = 3, AD = 4. Gọi M là điểm thỏa mãn điều kiện AM k AB . Xác định k
để hai đường thẳng AC, DM vuông góc với nhau. 9 16 4 3 A. k B. k C. k D. k 16 9 3 4
Câu 10. Cho hình vuông ABCD có độ dài cạnh bằng 1. Gọi M, N lần lượt là trung điểm của các cạnh BC, AB.
Tính giá trị biểu thức DM .NM . 2 3 A. 0,25 B. 0,5 C. D. 2 2
Câu 11. Cho tam giác đều ABC cạnh a, các đường cao AH, BK, kẻ HI vuông góc với AC. Mệnh đề nào đúng ?
A. 2 2 A . B AC a B. 2 AB AC BC a C. 2 8C . B CK a D. 2 . CB AK a
Câu 12. Cho tam giác ABC vuông tại A có AB = 3, AC = 5, đường cao AH. Tính . HB HC . 225 16 A. 34 B. C. – 4 D. 34 5
Câu 13. Cho tam giác OAB cân tại O có OA OB 26a ; có M là trung điểm đoạn thẳng AB. Tính tích vô
hướng OI.IA OI.IB . A.0 B. 2 C. 26 D. 52
Câu 14. Tam giác ABC có AB 3; AC 4; A 60 . E là trung điểm của cạnh BC. Tính . AB AE . A. 6 3 B. 3 3 C. 2 3 D. 4 3 33
Câu 15. Tam giác ABC có AB 3; AC 4; A 60 . D là trung điểm của cạnh BC. Tính AC.AD . A. 6 3 B. 3 3 C. 2 3 D. 4 3
Câu 16. Cho hai điểm M, N thỏa mãn MN.NM 4
. Tìm độ dài đoạn thẳng MN. A. MN 2 B. MN 4 C. MN 6 D. MN 8
Câu 17. Cho tam giác ABC vuông tại A có AB a , AC a 3 và AM là trung tuyến. Tính tích vô hướng . BA AM . 2 a 2 a A. 2 a . B. 2 a . C. . D. . 2 2 Câu 18. Cho AB
C vuông tại A , biết A .
B CB 4 , AC.BC 9 . Khi đó AB , AC , BC có độ dài là A. 2 ; 3 ; 13 . B. 3 ; 4 ; 5 . C. 2 ; 4 ; 2 5 . D. 4 ; 6 ; 2 13 .
Câu 19. Cho hình thang vuông ABCD có đáy lớn AB 4a , đáy nhỏ CD 2a , đường cao AD 3a ; I là trung
điểm của I . Khi đó I bằng 2 9a 2 9 a 2 A. . B. . C. 0 . D. 9a . 2 2
Câu 20. Cho a , b , c thỏa mãn: a 4 , b 1, c 5 và 5b a 3c 0 . Khi đó M a .b b .c c .a có giá trị là A. 29 . B. 33,5. C.18, 25 . D. 18, 25 .
Câu 21. Cho tam giác ABC vuông tại A và có AB c, AC . b Tính B . A BC. A. 2 B . A BC b . B. 2 B . A BC c . C. 2 2 B .
A BC b c . D. 2 2 B .
A BC b c .
Câu 22. Cho tam giác ABC có AB 2 cm, BC 3 cm, CA 5 cm. Tính C . A CB. A. C . A CB 13. B. C . A CB 15. C. C . A CB 17. D. C . A CB 19.
Câu 23. Cho hai vector a,b thỏa mãn 3a b 5, 3a b 4 . Tính . a b . A. – 1,2 B. – 3 C. – 0,75 D. 3
Câu 24. Cho hình vuông ABCD có cạnh a, trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao
cho AM BN CP DQ x(0 x a) . Tính tích vô hướng PN.PQ . A. 2 AB B. 2 AC C. 2 AD D. 0
Câu 25. Cho hình vuông ABCD có cạnh a, trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao 2 a
cho AM BN CP DQ x(0 x a) . Nếu PM .DC thì giá trị x bằng 2 a a 3a A. B. C. D. a 4 2 4
Câu 26. Cho hình vuông ABCD có cạnh a, trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao
cho AM BN CP DQ x(0 x a) . Tính PN.PM . A. 2 2
x (x a) B. 2 2
x (a 2x) C. 2 2
x (x a) D. 2 2
x (2a x)
Câu 27. Cho tam giác ABC có BC a, CA b, AB c. Tính P AB AC.BC. 2 2 c b 2 2 2
c b a 2 2 2
c b a A. 2 2
P b c . B. P . C. P . D. P . 2 3 2
Câu 28. Cho tam giác ABC có BC ,
a CA b, AB c. Gọi M là trung điểm cạnh BC. Tính AM .BC. 2 2 b c 2 2 c b A. AM .BC . B. AM .BC . 2 2 2 2 2
c b a 2 2 2
c b a C. AM.BC . D. AM .BC . 3 2
Câu 29. Cho ba điểm O, ,
A B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng OA OB.AB 0 là
A. tam giác OAB đều.
B. tam giác OAB cân tại O.
C. tam giác OAB vuông tại O.
D. tam giác OAB vuông cân tại O.
Câu 30. Cho hai vector a,b thỏa mãn 2a b 5, 2a b 3 . Tính . a b . A. – 1,2 B. – 3 C. – 2 D. 3
_________________________________ 34
VẬN DỤNG VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P2) _____________________________
Câu 1. Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua C. Tính AE.AB. A. 2
AE.AB 2a . B. 2
AE.AB 3a . C. 2
AE.AB 5a . D. 2
AE.AB 5a .
Câu 2. Cho hình vuông ABCD cạnh a. Tính AB BC BDDA DB DC. A. 2 a B. 2 2a C. 2 3a D. 0
Câu 3. Cho hai vectơ a và b thỏa mãn a 3, b 2 và a.b 3. Xác định góc giữa hai vectơ a và b. A. 0 30 . B. 0 45 . C. 0 60 . D. 0 120 .
Câu 4. Cho hai vector a,b thỏa mãn 3a b 5, 3a b 4 . Tính . a b . A. – 1,2 B. – 3 C. – 0,75 D. 3 2
Câu 5. Cho hai vectơ a và b thỏa mãn a b 1 và hai vectơ u a 3b và v a b vuông góc với nhau. Xác 5
định góc giữa hai vectơ a và b. A. 0 90 . B. 0 180 . C. 0 60 . D. 0 45 .
Câu 6. Cho hai vectơ a và b . Đẳng thức nào sau đây sai? 2 2 1 2 2 1 A. 2 2 a.b
a b a b . B. a.b a b a b . 2 2 2 2 1 2 2 1
C. a.b a b a b . D. a.b a b a b . 2 4
Câu 7. Cho AB = 2a và O là trung điểm của đoạn thẳng AB. Tập hợp những điểm M thỏa mãn 2 M . A MB a là
đường tròn có bán kính bằng A. a B. 2a C. a 2 D. a 3
Câu 8. Cho đoạn thẳng AB = a cố định. Tập hợp những điểm M mà 2
AM .AB a là
A. Đường tròn tâm A, bán kính r = a
B. Đường thẳng vuông góc với AB tại B
C. Đường trung trực của AB.
D. Đường tròn đường kính AB. 2
Câu 9. Cho điểm M nằm trên đường tròn đường kính AB. Tính F MA M . A AB . A. F = 7 B. F = 2 C. F = 1 D. F = 0 . AB AC
Câu 10. Cho tam giác đều ABC có cạnh bằng a. Tính giá trị biểu thức M . 2 a 3 A. M = 1 B. M = 0,5 C. M = 2 D. M = 2
Câu 11. Cho tam giác ABC cân tại A, AB = AC = 5, BAC 120 . Tính Q AC.BC . A. Q = 37,5 B. Q = 22,5 C. Q = 10 D. Q = 30,5 BM .DO
Câu 12. Hình vuông ABCD tâm O và có độ dài cạnh bằng a, M là trung điểm cạnh AB. Tính P . 2 a A. – 1 B. – 0,5 C. – 2 D. – 0,25
Câu 13. Cho hình vuông ABCD tâm O, độ dài cạnh bằng a. Tập hợp các điểm M thỏa mãn đẳng thức
2 M .
A MB MC.MD a là một đường tròn. Tìm bán kính R của đường tròn này. A. R = 1,5a B. R = 2a C. R = 3a D. R = a
Câu 14. Cho hình bình hành ABCD có độ dài các đường chéo AC = 6, BD = 8. Tính . AB AD . A. 5 B. – 7 C. 7 D. 25 MH.MA
Câu 15. Cho tam giác ABC có trực tâm H. Gọi M là trung điểm cạnh BC. Tính . 2 BC 2 1 A. 0,5 B. 0,25 C. D. 3 3
Câu 16. Cho tam giác ABC với ba trung tuyến AD, BE, CF. Tính .
AD BC BE.CA . AB CF . A. 3 B. 2 C. 0 D. 1
Câu 17. Tam giác ABC vuông tại A, AB = 3, AC = 4, đường cao AH. Tính tích vô hướng H . B HC . 35 144 144 A. B. – 25 C. 25 D. 25 25
Câu 18. Cho tam giác đều ABC có cạnh bằng a và chiều cao AH . Mệnh đề nào sau đây là sai? 2 a 2 a
A. AH .BC 0. B. AB HA 0 , 150 . C. AB.AC . D. AC.CB . 2 2
Câu 19. Cho tam giác ABC vuông cân tại A và có AB AC .
a Tính AB.BC. 2 a 2 2 a 2 A. 2 AB.BC a . B. 2
AB.BC a . C. A . B BC . D. A . B BC . 2 2
Câu 20. Tính công sinh bởi một lực F có độ lớn 30N kéo vật dịch chuyển theo một vector d có độ lớn 50N và
góc giữa hai vector lực là 60 . A.750J B. 300J C. 450J D. 650J
Câu 21. Cho hình vuông ABCD cạnh a. Tính P AB AC.BC BD BA. A. P 2 2 . a B. 2 P 2a . C. 2 P a . D. 2 P 2 a . AC
Câu 22. Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho AM . Gọi N là 4
trung điểm của đoạn thẳng DC. Tính MB.MN .
A. MB.MN 4. B. MB.MN 0. C. MB.MN 4.
D. MB.MN 16.
Câu 23. Cho tam giác ABC đều cạnh a, tính 3 . GA GB 6G .
A GC với G là trọng tâm tam giác. 2 a 2 a 3 2 a A. B. C. 2 a D. 2 3 2 2
Câu 24. Cho hình chữ nhật ABCD có AB 8, AD 5. Tích AB.BD.
A. AB.BD 62.
B. AB.BD 64.
C. AB.BD 62.
D. AB.BD 64.
Câu 25. Cho hình vuông ABCD cạnh a, tính AC AB2AD AB . A. 2 a B. 2 2a C. 2 3a D. 2 4a
Câu 26. Cho tam giác ABC vuông tại A có AB a; BC 2a , trọng tâm G. Tính .
BA BC BC.CA . 1 A. 2 2 a B. 2 2a C. 2 3a D. 2 a 2
Câu 27. Cho hình vuông ABCD tâm O, điểm M nằm trên đường tròn ngoại tiếp hình vuông, N là điểm tùy ý trên
cạnh BC. Tính M .
A MB MC.MD . 1 1 A. 2 2a B. 2 2a C. 2 a D. 2 a 2 2
Câu 28. Cho hai vector a,b thỏa mãn 3a b 8, 3a b 6 . Tính . a b . A. – 6 B. – 3 C. – 5,75 D. Kết quả khác
Câu 29. Cho hình vuông ABCD cạnh a, tâm O, điểm M thuộc đường tròn ngoại tiếp tam giác ABC. Tính
M . B MD C . O BO . 2 a 2 a 2 a A. B. C. 2 a D. 2 3 2
Câu 30. Cho hai vector a,b thỏa mãn 4a b 5, 4a b 4 . Tính . a b . A. – 1,2 B. – 3 C. – 0,75 D. Kết quả khác
Câu 31. Cho a,b 120 , a 3, b 5. Tính a b . A. 7 B. 4 C. 2 D. 19
Câu 32. Cho tam giác ABC vuông tại A. Khẳng định nào sau đây sai ?
A. . AB AC . BA BC
B. AC.CB AC.BC
C. AC.BC . CA CB
D. AC.BC BC.AB
Câu 33. Cho a 3, b 5, 2a 3b 171 . Tính 5a 4b . A. 2 17 B. 6 C. 5 13 D. 7 2
_________________________ 36
VẬN DỤNG VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TÍCH VÔ HƯỚNG P3) _____________________________ 2
Câu 1. Cho hai vector a,b có a 4, b 5 và a,b 120 . Tính a b . A.21 B. 41 C. 50 D. 62
Câu 2. Cho tam giác ABC có BC ,
a CA b, AB c. Gọi M là trung điểm cạnh BC. Tính AM .BC. 2 2 b c 2 2 c b A. AM .BC . B. AM .BC . 2 2 2 2 2
c b a 2 2 2
c b a C. AM.BC . D. AM .BC . 3 2
Câu 3. Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính
A . B CD . BD BC A. 2 a B. 2 3a C. 2 2a D. Kết quả khác
Câu 4. Cho hình chữ nhật ABCD tâm I, cạnh AB = a, AD = b. Tính tích vô hướng A . B AC . A. 2 a B. ab C. 2 2a D. 2 2b
Câu 5. Cho tam giác đều ABC cạnh a, trọng tâm G. Tính GAGB GC. 2 a 2 a 2 a A. 2 2a B. C. D. 2 4 3
Câu 6. Cho hình chữ nhật ABCD tâm I, cạnh AB = a, AD = b. Tính 2M . A MC M .
B MD với M là điểm nằm trên
đường tròn ngoại tiếp hình chữ nhật. A. 2 a B. ab C. 2 2a D. 0
Câu 7. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn MAMB MC 0 là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 8. Cho hình vuông ABCD cạnh a, M là trung điểm của AB, G là trọng tâm của tam giác ADM. Tính giá trị
của biểu thức CG CA DM . 21 11 9 2 a A. 2 a B. 2 a C. 2 a D. 4 4 4 4
Câu 9. Cho các vector a, b thỏa mãn a b 1; 2a 3b
7 . Tính cos a,b . 2 1 1 1 A. B. C. D. 4 4 2 3
Câu 10. Cho hình thang vuông ABCD có đường cao AB a 3 , cạnh đáy AD ;
a BC 2a . Tính AC.BD . 2 a A. 2 (2 2)a B. 2 (2 2)a C. 2 3a D. 2
Câu 11. Cho hình vuông ABCD cạnh a, tính AB ADBD BC . A. 2 a B. 2 3a C. 2 2a D. 2 4a
Câu 12. Một lực F có độ lớn x (N) kéo vật dịch chuyển theo một vector d có độ lớn 50N và góc giữa hai vector
lực là 60 . Biết công sinh ra bởi lực F là 1200J. Giá trị của x bằng A.48N B. 30N C. 45N D. 50N.
Câu 13. Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a, I là trung điểm
đoạn thẳng AB. Tính IA IB ID . 2 3a 2 3a A.0 B. 2 9a C. D. 2 2
Câu 14. Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a. Tính . DA BC . A.0 B. 2 9a C. 2 15a D. 2 9 a
Câu 15. Cho hình vuông ABCD cạnh a, E là điểm đối xứng với C qua D. Tính AC.BE . A. 2 a B. 2 3a C. 2 2a D. 2 a
Câu 16. Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a. Câu nào sau đây sai 37 A. 2 A . B DC 8a B. A . D CD 0 C. A . B AD 0 D. . DA DB 0
Câu 17. Cho hai vector a,b thỏa mãn 2a b 5, 2a b 6 . Tính . a b . A.1,375 B. 2 C. – 2,25 D. 1,25
Câu 18. Tính công sinh bởi một lực F có độ lớn 35N kéo vật dịch chuyển theo một vector d có độ lớn 50N và
góc giữa hai vector lực là 60 . A.875J B. 300J C. 450J D. 540J
Câu 19. Cho hình vuông ABCD cạnh a, tâm O. M là trung điểm của AD. Tính OM OB OC OA. 2 a 2 a 2 a A. 2 2a B. C. D. 2 4 8
Câu 20. Cho hình vuông ABCD cạnh a, điểm M bất kỳ, tính M . A MC M . B MD . 2 a 2 a A.0 B. C. D. 2 a 2 4
Câu 21. Cho tam giác ABC vuông tại A có AB ;
a AC a 3 và AM là trung tuyến. Tính . BA AM . 2 a 2 a A. . B. 2 a . C. 2 a . D. . 2 2
Câu 22. Cho hình vuông ABCD có cạnh bằng 3. Trên cạnh AB lấy điểm M sao cho BM = 1, trên cạnh CD lấy
điểm N sao cho DN = 1 và P là trung điểm của BC. Tính cos MNP . 13 13 13 13 A. B. C. D. 5 10 4 10 10 45 10
Câu 23. Cho hai vectơ a và b . Biết a 2, b 3 và a,b 30. Tính a b . A. 11 . B. 13 . C. 12 . D. 14 .
Câu 24. Cho hình bình hành ABCD , với AB 2 , AD 1, BAD 60 . Tích vô hướng A . B DA bằng 1 1 A. . B. 1. C. . D. 1 . 2 2
Câu 25. Cho hai vecto a, b sao cho a
2 , b 2 và hai véc tơ x a b , y 2a b vuông góc với nhau.
Tính góc giữa hai véc tơ a và b . A. 120. B. 60 . C. 90 . D. 30 .
Câu 26. Cho hình vuông ABCD cạnh a, E là điểm đối xứng với C qua D, tính OC.OE . 2 a 2 a 2 a A. 2 2a B. C. D. 2 4 3
Câu 27. Cho tam giác ABC đều cạnh a, tính G . A GB 2G .
A GC với G là trọng tâm tam giác. 2 a 2 a 2 a 2 a A. B. C. D. 2 3 3 2
Câu 28. Cho hình vuông ABCD cạnh a. Tính AC AB2AD AB . A. 2 2a B. 2 2 a C. 2 3a D. 2 4a
Câu 29. Cho hình thoi ABCD tâm O có cạnh bằng a 2 và ABD 60 . Điểm I thỏa mãn 2IC ID 0 . Tính . AO BI . 2 a 2 2 a 3 2 a 2 a 2 A. B. C. D. 2 2 2 6
Câu 30. Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để OA OB AB 0 là A. Tam giác OAB đều B. Tam giác OAB cân tại O
C. Tam giác OAB vuông tại O
D. Tam giác OAB vuông cân tại O
Câu 31. Cho hai điểm A và B có AB = 4. Tập hợp những điểm M sao cho M . A MB 0 là
A. Đường thẳng vuông góc với AB
B. Đường tròn bán kính r = 2
C. Đường thẳng vuông góc với AB
D. Đường tròn bán kính r = 4 38
VẬN DỤNG CAO, PHÂN LOẠI VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN PHÂN TÍCH VECTOR, TỶ LỆ VECTOR, BA ĐIỂM THẲNG HÀNG – P1)
_______________________________________________________
Câu 1. Cho AD và BE là hai phân giác trong của tam giác ABC . Biết AB 4 , BC 5 và CA 6 . Khi đó DE bằng: 5 3 3 5 9 3 3 9 A. CA CB . B. CA CB . C. CA CB . D. CA CB . 9 5 5 9 5 5 5 5
Câu 2. Cho tam giác ABC biết AB 3,BC 4, AC 6 , I là tâm đường tròn nội tiếp tam giác ABC .Gọi , x , y z x y z
là các số thực dương thỏa mãn . x IA . y IB .
z IC 0 .Tính P y z x 3 41 23 2 A. P . B. P . C. P . D. P . 4 12 12 3
Câu 3. Cho hình bình hành ABCD . Gọi I là trung điểm của CD , G là trọng tâm tam giác BCI . Đặt
a AB, b AD . Hãy tìm đẳng thức đúng trong các đẳng thức sau? 5 2 5 5 4 2 A. AG a b . B. AG a b . C. AG a b . D. AG a b . 6 3 6 6 3 3
Câu 4. Cho tam giác ABC với các cạnh AB c, BC a, CA b . Gọi I là tâm đường tròn nội tiếp tam giác
ABC. Đẳng thức nào sau đây đúng.
A. aIA bIB cIC 0
B. bIA cIB aIC 0
C. cIA bIB aIC 0
D. cIA aIB bIC 0 0
Câu 5. Cho hình thang cân ABCD có CD là đáy lớn, ADC 30 . Biết DA = a, DC = b, hãy biểu diễn DB
theo hai vectơ DA và DC .
b a 3
A. DB DA DC. B. DB DA DC. b
b a C. DB DA DC.
D. DB bDA aDC. b
Câu 6. Cho tam giác ABC . Gọi M là điểm thuộc cạnh AB, N là điểm thuộc cạnh AC sao cho 1 3
AM AB, A
N AC . Gọi O là giao điểm của CM và BN. Trên đường thẳng BC lấy E . Đặt 3 4
BE xBC . Tìm x để A, O, E thẳng hàng. 2 8 9 8 A. B. C. D. 3 9 13 11
Câu 7. Cho tam giác ABC . Gọi I là trung điểm BC ; P là điểm đối xứng với A qua B ; R là điểm trên cạnh 2
AC sao cho AR
AC . Khi đó đường thẳng AR đi qua điểm nào trong các điểm sau đây? 5
A. Trọng tâm tam giác ABC .
B. Trọng tâm tam giác ABI . C. Trung điểm AI . D. Trung điểm BI .
Câu 8. Cho ABC có H là trung điểm của AB và G AC : GC 2 AG . Gọi F là giao điểm của CH và BG .
Tìm điểm I trên BC sao cho I , F , A thẳng hàng A. IC 2 I . B B. IB 2 IC. C. IB IC. D. IC 3 I . B
Câu 9. Cho tam giác ABC. I là trung điểm của BC. Gọi M, N, P lần lượt là các điểm xác định bởi AM m A ;
B AN n AI ; AP p AC , với mnp 0 . Tìm điều kiện của ,
m n, p để M, N, P thẳng hàng.
A. mp mn np
B. 2mp mn np
C. 2np mn mp
D. 2mn mp np
Câu 10. Cho tam giác ABC. Gọi G là trọng tâm của tam giác, I là trung điểm của BC, M và N là các điểm được 1
xác định bởi CN
BC; 3MA 4MB 0 . Gọi P là giao điểm của AC và MN. Tính tỉ số diện tích tam giác 2 ANP và tam giác CNP. 7 A.3 B. C. 4 D. 2 2 39 2 1
Câu 11. Cho tam giác ABC . Gọi ,
D E lần lượt là các điểm thỏa mãn: BD BC; AE AC . Điểm K trên 3 4 a a
AD thỏa mãn AK AD (với
là phân số tối giản) sao cho 3 điểm ,
B K, E thẳng hàng. Tính 2 2
P a b . b b A. P 10 . B. P 13 . C. P 29 . D. P 5 .
Câu 12. Cho hình bình hành ABCD , M là điểm thỏa mãn 5AM 2CA 0 . Trên các cạnh AB , BC lần lượt
lấy các điểm P, Q sao cho MP / B
/ C, MQ / A
/ B . Gọi N là giao điểm của AQ và CP . Giá trị của tổng AN CN bằng: AQ CP 21 24 23 25 A. B. C. D. 19 19 19 19
Câu 13. Cho tứ giác ABCD, M là điểm tùy ý. K là điểm cố định thỏa mãn đẳng thức
MA MB MC 3MD xMK . Tìm x : A.2. B.6. C.5. D.4.
Câu 14. Cho tam giác ABC , trên cạnh AC lấy điểm M , trên cạnh BC lấy điểm N sao cho AM 3MC ,
NC 2NB . Gọi O là giao điểm của AN và BM . Tính diện tích tam giác ABC biết diện tích tam giác OBN bằng 1. A. 24 . B. 20 . C. 30 . D. 45
Câu 15. Cho tam giác ABC , gọi I là điểm trên BC kéo dài sao cho IB 3IC . Gọi J , K lần lượt là những
điểm trên cạnh AC, AB sao cho JA 2JC; KB 3KA . Khi đó BC . m AI .
n JK . Tính tổng P m n ? A. P 34 . B. P 34 . C. P 14 . D. P 14 .
1 1
Câu 16. Cho hình bình hành ABCD, lấy M trên cạnh AB và N trên cạnh CD sao cho AM AB, DN DC . 3 2
Gọi I và J là các điểm thỏa mãn BI mBC, AJ n AI . Khi J là trọng tâm tam giác BMN thì tích m.n bằng bao nhiêu? 1 2 A. B. 3 C. D. 1 3 3
Câu 17. Cho tam giác ABC, trên cạnh AB lấ y điểm M, trên cạnh BC lấ y N sao cho AM = 3MB, NC = 2BN. Gọi
I là giao điểm của AN với CM. Tính diện tích tam giác ABC biết diện tích tam giác ICN bằng 2. 3 33 9 A. B. C. 11 D. 2 2 11
Câu 18. Cho tam giác ABC . Gọi A', B' ,C' là các điểm xác định bởi 2018A' B 2019 A'C 0 ,
2018B 'C 2019B ' A 0 , 2018C ' A 2019C ' B 0 . Khi đó , mệnh đề nào sau đây đúng?
A. ABC và A' B 'C ' có cùng trọng tâm.
B. ABC A' B 'C ' .
C. ABC A ' B 'C '.
D. ABC và A' B 'C ' có cùng trực tâm.
Câu 19. Cho ∆ABC có trọng tâm G và hai điểm M, N thỏa mãn: 3MA 2CM 0 , NA 2NB 0 . Chọn mệnh đề đúng. A. NG 4GM . B. NG 5GM . C. NG 6GM . D. NG 7GM . 1
Câu 20. Cho tam giác đều ABC cạnh a . Gọi điểm M là trung điểm BC . Tính độ dài của vec tơ AB 2AC 2 a 21 a 21 a 21 a 21 A. . B. . C. . D. . 3 2 4 7
Câu 21. Cho ABC có M là trung điểm của BC, H là trực tâm, O là tâm đường tròn ngoại tiếp. Tìm x để
HA HB HC xHO . A. x . 2 B. x 2 . C. x . 1 D. x 3.
Câu 22. Cho tam giác ABC có đường trung tuyến CM vuông góc với phân giác trong AL . Giả sử ngoài ra còn 2 a bk
có CM kAL . Biết cos A
. Tính a b c d . 2 c dk A.18 . B. 5 . C. 26 . D.17 .
_____________________________________ 40
VẬN DỤNG CAO, PHÂN LOẠI VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN PHÂN TÍCH VECTOR, TỶ LỆ VECTOR, BA ĐIỂM THẲNG HÀNG – P2)
_______________________________________________________
Câu 1. Cho hình thang ABCD ( AB / /CD) có hai đường chéo vuông góc với nhau. Biết AB CD 20c . m Tìm
AC BD . A. 40c . m . B. 20c . m . C. 30c . m . D. 10 . cm .
Câu 2. Cho tam giác ABC , M và N là hai điểm thỏa mãn: BM BC 2 AB , CN x AC BC . Xác định x để
A , M , N thẳng hàng. 1 1 A. 3. B. . C. 2. D. . 3 2
Câu 3. Cho tam giác ABC có G là trọng tâm, I là trung điểm AG , lấy K thuộc cạnh AC sao cho
AK kAC . Nếu B, I, K thẳng hàng thì giá trị của k nằm trong khoảng? 1 1 1 1 1 A. 0; B. 0; C. ; D. ;1 6 2 5 3 5
Câu 4. Cho tam giác ABC , M là điểm thuộc cạnh AC sao cho MA 2
.MC , N thuộc BM sao cho NB 3
NM , P là điểm thuộc BC . Biết rằng ba điểm ,
A N , P thẳng hàng khi PB k PC . Khẳng định nào sau đây là đúng? 5 5 1 1 A. k 3; . B. k ; 1 . C. 1 ; . D. ; 0 . 2 2 2 2
Câu 5. Cho tam giác ABC . Gọi M , N, P lần lượt nằm trên đường thẳng BC, CA , AB sao cho MB mMC , NC n ,
NA PA k PB . Tính tích mnk để M , N, P thẳng hàng? A.1 . B. 1 . C. 2 . D. 2 .
Câu 6. Cho hình bình hành ABCD gọi M là trung điểm của cạnh CD, N là điểm thuộc cạnh AD sao cho 1 m m AN
AD . Gọi G là trọng tâm của tam giác BMN, đường thẳng AG cắt BC tại K. Khi đó BK BC ( là 3 n n
tối giản) . Tính S m n A. S 16 . B. S 17 . C. S 18 . D. S 19 .
Câu 7. Cho hình thang ABCD có đáy AB , CD , CD 2 AB . M , N lần lượt là các điểm thuộc cạnh AD và
BC sao cho AM 5MD , 3BN 2NC . Gọi P là giao điểm của AC và MN ; Q là giao điểm của BD và PM QN a a MN ; Khi đó , với
là phân số tối giản. Khi đó a b bằng PN QM b b A. 386 . B. 385 . C. 287 . D. 288 .
Câu 8. Cho tam giác ABC, trên cạnh AC lấy điểm M, trên cạnh BC lấy điểm N sao cho AM = 3MC, NC = 2BN.
Gọi I là giao điểm của AN và BN. Tính diện tích tam giác ABC biết diện tích tam giác ABN bằng 4. A. S 110 . B. S 115 . C. S 125 . D. S 120 . ABC ABC ABC ABC
Câu 9. Cho tam giác ABC M thuộc cạnh AC sao cho MA M . 2
C , N thuộc BM sao cho NB . 3 NM , P thuộc
BC sao cho PB k PC .
. Tìm giá trị k để ba điểm A, N, P thẳng hàng. A. k 1 . B. k 2 . C. k 1 . D. k 2. 2 2
Câu 10. Cho tam giác ABC có AB 3; AC 4 .Gọi AD là đường phân giác trong của góc A .Biết
AD m AB n AC .Khi đó tổng m n có giá trị là: 1 1 A.1 B. 1 C. D. 7 7
Câu 11. Cho tam giác ABC bất kỳ, gọi M , N , P lần lượt là trung điểm các cạnh AB, BC, CA . H , H ' lần lượt là
trực tâm các tam giác ABC, MNP . Khẳng định nào đúng trong các khẳng định sau?
A. HA HB HC 3HH ' .
B. HA HB HC 2HH '.
C. HA HB HC 0 .
D. HM HN HP 3HH ' .
Câu 12. Cho tam giác đều ABC tâm O. M là một điểm bất kì bên trong tam giác. Gọi D, E, F lần lượt là hình
chiếu của M lên BC, CA, AB. Với giá trị nào của k ta có hệ thức: MD ME MF k MO 41 1 3 A. k . B. k 1. C. k . D. k 2 2 2
Câu 13. Cho tam giác đều A B C nội tiếp đường tròn tâm O , M là một điểm tùy ý nằm bên trong tam giác đã
cho; gọi A '; B '; C ' theo thứ tự là hình chiếu vuông góc của M lên các cạnh BC ; CA và A B . Khi đó ta có đẳng k
thức vectơ k MA ' MB ' MC ' l MO , k.l 0, là phân số tối giản. Tính 2 2 2k l . . l A. 2 2 2k l 1. B. 2 2
2k l 1. C. 2 2
2k l 14 . D. 2 2
2k l 5 .
Câu 14. Cho tam giác ABC , trên cạnh AC lấy điểm M , trên cạnh BC lấy điểm N sao cho: AM 3MC ,
NC 2NB , gọi O là giao điểm của AN và BM .Tính diện tích ABC
biết diện tích OBN bằng 1. A. 10 . B. 20 . C. 25 . D. 30 .
Câu 15. Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Chọn khẳng định đúng?
A. HA HB HC 4HO .
B. HA HB HC 2HO . 2
C. HA HB HC HO .
D. HA HB HC 3HO . 3
Câu 16. Cho tam giác ABC có D là trung điểm của BC , O là một điểm trên đoạn AD sao cho AO 4OD . Gọi
E CO AB ,F BO AC , M AD EF . Khẳng định nào sau đây đúng? 1 2 1 2 A. MO AD B. MO AD C. MO AD D. EM BC 7 15 8 7
Câu 17. Cho hình thang ABCD có AB //CD . Gọi M , N lần lượt là trung điểm của AC, BD . Kẻ
NH AD (H AD) và ME BC (E BC) . Gọi I ME NH , kẻ IK DC (K DC) . Khi đó trong tam
giác MNK hệ thức nào sau đây đúng?
A. MK.IN NK.IM MN.IK 0
B. IN. tan N IM .tan M IK.tan K 0
C. IN.cot N IM .cot M IK.cot K 0
D. IM IN IK 0
Câu 18. Cho ABC , điểm M thuộc cạnh BC sao cho 2018.S 2019.S
. Đẳng thức nào sau đây sai? ABM ACM A. 2018.S 4037.S .
B. 2018.BM 2019.CM 0 . ABC ACM 4037 2019 C. BC .BM D. S .S . 2018 ABM 4037 ABC
Câu 19. Cho tam giác ABC . M là điểm nằm trên cạnh BC sao cho S 3S
. Một đường thẳng cắt các ABC AMC AB AC AM cạnh A ,
B AM , AC lần lượt tại B ,
M ,C phân biệt. Biết rằng 2 k. . Tìm số k . AB AC AM 2 A. k 1. B. k 2 . C. k 3 . D. . 3
Câu 21. Cho hình vuông ABCD có cạnh bằng1. Hai điểm M , N thay đổi lần lượt ở trên cạnh AB , AD sao
cho AM x 0 x
1 , DN y 0 y
1 . Tìm mối liên hệ giữa x và y sao cho CM BN
A. x y 0.
B. x y 2 0.
C. x y 1.
D. x y 3 0.
Câu 22. Cho hai tam giác ABC và A B C ; gọi A , B ,C lần lượt là trọng tâm các tam giác 1 1 1 2 2 2 GG BCA , CA B , A
BC . Gọi G,G G ,
lần lượt là trọng tâm các tam giác ABC, A
B C , A B C . Tính tỉ số 1 1 1 1 1 2 1 1 1 2 2 2 GG2 ta được kết quả : 1 1 A. B. C. 3 D. 2 3 2
Câu 23. Cho tam giác ABC . Gọi M , N , P là các điểm lần lượt thỏa mãn MA M
3 B 0, AN 1 AC , 3
2PB 3PC 0 Gọi K là giao điểm của AP và MN . Trong các mệnh đề sau, mệnh đề nào đúng? A. 4KA KP 5 0. B. K 3 A KP 2 0 .
C. KA KP 0. D. KA KP .
_____________________________________ 42
VẬN DỤNG CAO, PHÂN LOẠI VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN PHÂN TÍCH VECTOR, TỶ LỆ VECTOR, BA ĐIỂM THẲNG HÀNG – P3)
_______________________________________________________
Câu 1. Cho n điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là A , A ,..., A . Bạn Bình kí hiệu chúng là 1 2 n
B , B ,..., B
A B ). Vectơ tổng A B A B ... A B bằng 1 2 n ( 1 n 1 1 2 2 n n A. 0 . B. A A . C. B B . D. A B . 1 n 1 n 1 n 2 1
Câu 2. Cho tam giác ABC. Gọi D, E lần lượt là các điểm thỏa mãn: BD BC, AE
AC . Điểm K trên AD sao 3 4 AK
cho 3 điểm B, K ,E thẳng hàng. Xác định tỷ số AD 1 1 1 1 A. B. C. D. 2 3 4 5
Câu 3. Cho tam giác ABC vuông tại C, có AC b, BC a , D là chân đường cao kẻ từ C. Khẳng định nào sau đây là đúng? 2 2 a b 2 2 a b A. CD CA CB . B. CD CA CB . 2 2 2 2 a b a b 2 2 2 2 a b a b 2 2 a b 2 2 a b C. CD AC BC D. CD AC BC . 2 2 2 2 a b a b 2 2 2 2 a b a b
Câu 4. Cho tam giác ABC có trọng tâm G. Gọi I là điểm xác định bởi 5IA 7IB IC 0. Gọi E là giao điểm của EA AI và BG. Tính tỷ số . EI 1 1 A. 2. B. . . 2 C. 3. D. 3
Câu 5. Cho 2 tia Ox, Oy vuông góc. Trên tia Ox lấy các điểm A,B sao cho OA = OB = 1. C là điểm thuộc đoạn
OA, N là một điểm thuộc đoạn OB và dựng hình vuông OCMN. Trên đoạn CM lấy điểm Q và dựng hình vuông 1
ACQP. Gọi S là giao điểm của AM và PN. Giả sử OC kOA , AS x AM , NS y NP , k 1 ; . 2 13 a Khi x + y = thì k =
, với a,b và a, b nguyên tố cùng nhau thì a.b bằng 10 b A. 7 B. 4 C. 5 D.12
Câu 6. Cho tam giác ABC . Giả sử điểm M nằm trên cạnh BC thỏa các tam giác MA ,
B MAC lần lượt có diện
tích là S , S . Khẳng định nào sau đây đúng? 1 2
A. S S AM S AB S AC.
B. S S AM S AB S AC. 1 2 1 2 2 1 1 2
C. S S AM S AB S AC.
D. S S AM S AB S AC. 2 1 2 1 2 1 1 2 1
Câu 7. Cho tam giác ABC có có M là trung điểm của BC, AI
MI . Điểm K thuộc cạnh AC sao cho B,I,K 2 m
thẳng hàng. Khi đó KA
CK . Tính S 25m 6n 2019 n A. S 2019 . B. S 2068 . C. S 2018 . D. S 2020 .
Câu 8. Cho tam giác ABC có trọng tâm G, lấy các điểm I, J sao cho IA 2IB và 3JA 2JC 0 và thỏa mãn đẳng
thức IJ kIG . Giá trị của biểu thức 2 2 500
P (25k 36)(k k 1) là: 5 6 A. P 1235 B. P 0 C. P D. P 6 5
Câu 9. Cho tam giác ABC . M là điểm nằm trên cạnh BC sao cho S S 3
. Một đường thẳng cắt các ABC AMC AB AC AM
cạnh AB, AM, AC lần lượt tại B ', M ' C , ' phân biệt. Biết m n
. Tính m n . AB ' AC ' AM ' A.2. B.5. C.3. D.4.
Câu 10. Cho tam giác ABC có D là trung điểm của BC , O là một điểm trên đoạn AD sao cho AO 4OD . Gọi
E CO AB ,F BO AC , M AD EF . Khẳng định nào sau đây đúng? 43 1 2 1 2 A. MO AD B. MO AD C. MO AD D. EM BC 7 15 8 7
Câu 11. Cho hình thang ABCD có AB//CD . Gọi M , N lần lượt là trung điểm của AC, BD . Kẻ
NH AD (H AD) và ME BC (E BC) . Gọi I ME NH , kẻ IK DC (K DC) . Khi đó trong tam
giác MNK hệ thức nào sau đây đúng?
A. MK.IN NK.IM MN.IK 0
B. IN. tan N IM .tan M IK.tan K 0
C. IN.cot N IM.cot M IK.cot K 0
D. IM IN IK 0
Câu 12. Cho hình bình hành ABCD . Gọi I là trung điểm của CD , G là trọng tâm tam giác BCI . Đặt
a AB, b AD . Hãy tìm đẳng thức đúng trong các đẳng thức sau? 5 2 5 5 4 2 A. AG a b . B. AG a b . C. AG a b . D. AG a b . 6 3 6 6 3 3
Câu 13. Một đường thẳng cắt các cạnh D ,
A DC và đường chéo DB của hình bình hành ABCD lần lượt tại
các điểm E, F và M . Biết DE . m , DA DF .
n DC (m, n 0). Khẳng định đúng là:
m n m A. DM DB . B. DM DB . . m n m n n . m n C. DM DB . D. DM DB . m n m n
Câu 14. Hình thang cân ABCD có độ dài đường cao AH ; a AB / /C ,
D AB a 3; AD a 2; AB DC
x y z
AC cắt BH tại I. Biết AI AC; ; x ;
y z; m N . Tính tổng T x y z m m A.20 B. 18 C.17 D.21
Câu 15. Cho hình thang ABCD với O là giao điểm của hai đường chéo AC và BD. Qua O vẽ đường thẳng song
song với đáy hình thang, đường thẳng này cắt các cạnh bên AD và BC theo thứ tự tại M và N. Với AB a ,
CD b , khi đó MN bằng: a .AB . b DC . b AB . a DC a .AB . b DC . b AB . a DC A. . B. . C. . D. . a b a b a b a b
Câu 16. Cho tam giác ABC đều tâm O ; điểm M thuộc miền trong tam giác OBC ; D , E , F lần lượt là hình
chiếu vuông góc của M trên BC , CA , AB . Khẳng định nào sau đây đúng?
1
A. MD ME MF MO .
B. MD ME MF MO . 2
3
C. MD ME MF 3MO .
D. MD ME MF MO . 2
Câu 17. Cho hình bình hành ABCD có các điểm M , I , N lần lượt thuộc các cạnh AB, BC,CD sao cho 1 1 AM ,
AB BI kBC, CN
CD . Gọi G là trọng tâm tam giác BMN . Xác định k để AI đi qua G . 3 2 1 9 6 12 A. . B. . C. . D. . 3 13 11 13
Câu 18. Cho ABC có AB 3 ; AC 4 . Phân giác trong AD của góc BAC cắt trung tuyến BM tại I . Tính tỉ AD số . AI AD 3 AD 10 AD 29 AD 7 A. . B. . C. . D. AI 2 AI 7 AI 20 AI 5
Câu 19. Cho tứ giác ABCD có hai đường chéo cắt nhau tại O thỏa mãn OC 3 , OA OD 4 OB . Qua trung CN
điểm M của AB dựng đường thẳng MO cắt CD tại N . Tính tỉ số . ND 3 1 2 1 A. . B. . C. . D. . 4 4 3 3
_____________________________________ 44
VẬN DỤNG CAO, PHÂN LOẠI VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TẬP HỢP ĐIỂM, QUỸ TÍCH – P1)
______________________________________________
Câu 1. Cho tam giác ABC. M là điểm di động thỏa mãn điều kiện MA MB MC 3 . Quỹ tích các điểm M là
đường tròn có bán kính bằng A. 1 B. 2 C. 3 D. 0,5
Câu 2. Cho tam giác ABC có trọng tâm G, I là trung điểm của BC. Quỹ tích các điểm N di động thỏa mãn đẳng
thức 2 NA NB NC 3 NB NC có dạng như thế nào ?
A. Đường trung trực của IG.
B. Đường thẳng qua F và vuông góc với IG.
C. Đường tròn tâm G, bán kính IG.
D. Đường tròn tâm G, bán kính BC:2.
Câu 3. Cho tam giác ABC. Tìm vị trí điểm M thỏa mãn đẳng thức MA MB MC 0 .
A. Trọng tâm tam giác ABC.
B. Tâm đường tròn ngoại tiếp tam giác ABC. C. Trực tâm tam giác ABC.
D. Tâm đường tròn nội tiếp tam giác ABC.
Câu 4. Cho tam giác ABC và điểm M thỏa mãn đẳng thức MA MB MC 0 . Tìm mệnh đề đúng.
A. M là trọng tâm tam giác ABC.
B. M là trung điểm của AC.
C. ABCM là hình bình hành.
D. ACBM là hình bình hành.
Câu 5. Cho tam giác ABC có trọng tâm G, tìm tập hợp điểm M thỏa mãn MB MC BC .
A. Đường tròn đường kính BC.
B. Đường tròn tâm C, bán kính BC.
C. Đường tròn tâm B, bán kính BC.
D. Đường tròn tâm A, bán kính BC.
Câu 6. Cho tam giác ABC, tập hợp điểm M thỏa mãn MA MB MB MC có dạng một đường thẳng. Tìm
tính chất của đường thẳng đó. A. Đường phân giác. B. Đường trung trực. C. Đường trung tuyến. D. Đường cao
Câu 7. Cho tam giác ABC, tập hợp điểm M thỏa mãn MA MB MA MC có dạng một đường thẳng. Tìm
tính chất của đường thẳng đó. A. Đường phân giác. B. Đường trung trực. C. Đường cao. D. Đường trung tuyến.
Câu 8. Cho tam giác ABC với AB = 2, tập hợp điểm M thỏa mãn MA MB MA MB là
A. Một đường trung trực.
B. Đường tròn có bán kính bằng 2.
C. Một đường tròn có đường kính bằng 2.
D. Một đường phân giác.
Câu 9. Cho tam giác ABC với BC = 6, M là di động thỏa mãn điều kiện MA MB MC AB AC . Quỹ tích
các điểm M là một đường tròn có bán kính bằng A. 2 B. 1 C. 3 D. 6
Câu 11. Cho hình chữ nhật ABCD tâm I, tìm tập hợp các điểm M thỏa mãn MA MB MC MD .
A. Trung trực của đoạn thẳng AB.
B. Trung trực của đoạn thẳng AD.
C. Đường tròn tâm I, bán kính 0,5AC.
D. Đường tròn tâm I, bán kính (AB + BC):2.
Câu 12. Cho tam giác ABC, điểm M di động thỏa mãn đẳng thức 2MA MB MA 2MB . Quỹ tích các
điểm M là một đường thẳng có tính chất nào ? A. Trung trực B. Đường cao C. Phân giác D. Trung tuyến.
3
Câu 13. Cho tam giác ABC, điểm M di động thỏa mãn đẳng thức MA MB MC
MB MC . Quỹ tích 2
các điểm M là một đường thẳng có tính chất nào ? A. Trung trực B. Đường cao C. Phân giác D. Trung tuyến.
Câu 14. Cho tam giác đều ABC cạnh a và điểm M thỏa mãn 2MA 3MB MC MB MA . Tập hợp các
điểm M là đường tròn cố định bán kính r. Tính ra theo a. a a a a A. B. C. D. 3 2 6 9
Câu 15. Cho ABC, M thỏa mãn 4MA MB MC 2MA MB MC . Tập hợp các điểm M có dạng A. Một đường tròn B. Một điểm. C. Một đường thẳng. D. Một đường elip. 45
Câu 16. Cho tam giác ABC. Điểm M thỏa mãn 2MA MB 4MB MC . Tập hợp các điểm M có dạng A. Một đường tròn B. Một điểm. C. Một đường thẳng. D. Một đường elip.
Câu 20. Cho tam giác ABC. Điểm M thỏa mãn hệ thức 2MA 5MB 3MC 3MA 5MB 2MC .
Tập hợp điểm M có dạng như thế nào ? A. Một đường tròn B. Một điểm. C. Một đường thẳng. D. Một đường elip.
Câu 17. Cho tam giác ABC. Điểm H thỏa mãn 3HA 2HB HC HA HB . Tập hợp các điểm H có dạng A. Một đường tròn B. Một điểm. C. Một đường thẳng. D. Một đường elip.
Câu 18. Cho ABC, M thỏa mãn 3MA MB MC 2MA MB MC . Tập hợp các điểm M có dạng A. Một đường tròn B. Một điểm. C. Một đường thẳng. D. Một đường elip.
Câu 19. Cho hình chữ nhật ABCD và số thực dương k. M là điểm thỏa mãn MA MB MC MD k . Tập
hợp điểm M có dạng như thế nào ? A. Một đường tròn B. Một điểm. C. Một đường thẳng. D. Một đường elip.
Câu 20. Cho tam giác ABC. Điểm M thỏa mãn hệ thức 2 MA MB MC MA 2MB 3MC .
Tập hợp điểm M có dạng như thế nào ? A. Một đường tròn B. Một điểm. C. Một đường thẳng. D. Một đường elip.
Câu 21. Cho tam giác ABC, biết AB AC AB AC . Xác định đặc điểm tam giác ABC. A. Tam giác vuông tại A B. Tam giác vuông tại B. C. Tam giác vuông tại C. D. Tam giác cân tại A.
Câu 22. Cho tam giác ABC. Điểm M thỏa mãn MA 3MB 2MC 2MA MB MC . Tập hợp điểm M có dạng như thế nào ? A. Một đường tròn B. Một đường thẳng C. Một điểm D. Không tồn tại.
Câu 23. Cho tam giác ABC. Điểm M thỏa mãn hệ thức 2 2MA MB 3MC 3MA 5MB 4MC .
Tập hợp điểm M có dạng như thế nào ? A. Một đường tròn B. Một điểm. C. Một đường thẳng. D. Một đường elip.
Câu 24. Cho tam giác ABC, điểm M di động thỏa mãn đẳng thức 4MA 3MB 3MA 4MB . Quỹ tích các
điểm M là một đường thẳng có tính chất nào ? A. Trung trực B. Đường cao C. Phân giác D. Trung tuyến.
Câu 25. Cho tam giác đều ABC cạnh a và điểm M thỏa mãn 2MA 3MB 4MC MB MA . Tập hợp các
điểm M là đường tròn cố định bán kính r. Tính ra theo a. a a a a A. B. C. D. 3 2 6 9
Câu 26. Cho tam giác ABC, điểm M di động thỏa mãn đẳng thức MA 2MB 3MC 3 MA MC . Quỹ tích
các điểm M là một đường thẳng có tính chất nào ? A. Trung trực B. Đường cao C. Phân giác D. Trung tuyến.
Câu 27. Cho tam giác ABC. Điểm M thỏa mãn hệ thức 5MA 7MB MC MA 4MB 3MC .
Tập hợp điểm M có dạng như thế nào ? A. Một đường tròn B. Một điểm. C. Một đường thẳng. D. Một đường elip.
Câu 28. Cho tam giác ABC. Tập hợp những điểm M thỏa mãn MA 2MB 6 MA MB là
A. Đường tròn tâm I, bán kính R = 2AB với I thuộc cạnh AB sao cho IA = 2IB.
B. M thuộc đường trung trực của BC.
C. M nằm trên đường tròn tâm I, bán kính R = 2AC với I nằm trên cạnh AB sao cho IA = 2IB.
D. M nằm trên đường thẳng qua trung điểm của AB và song song với BC.
_____________________________________ 46
VẬN DỤNG CAO, PHÂN LOẠI VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TẬP HỢP ĐIỂM, QUỸ TÍCH – P2)
______________________________________________
Câu 1. Cho tam giác ABC với BC = 18, M là di động thỏa mãn điều kiện MA MB MC AB AC . Quỹ
tích các điểm M là một đường tròn có bán kính bằng A. 2 B. 1 C. 3 D. 6 2
5a
Câu 2. Tam giác ABC đều cạnh a, tập hợp những điểm M thỏa mãn M . A MB M .
A MC MC.MA có 2
dạng đường tròn với bán kính bằng a 2 a 3 a A. a B. C. D. 6 5 3
Câu 3. Cho tam giác ABC có AB 10 , trọng tâm G. Tìm tập hợp các điểm M thỏa mãn
2 2 2
(MA MB MC BC) (MA MC 3MC) AB .
A.Đường tròn đường kính bằng 10
B. Đường tròn đường kính bằng 5.
C.Đường trung trực đoạn thẳng AB
D. Đường trung trực đoạn thẳng AG.
Câu 4. Cho đoạn thẳng AB
5 . Tập hợp điểm M thỏa mãn 2 2
MA MB 3M .
A MB là đường tròn có bán kính bằng bao nhiêu 5 3 A.1,5 B. 2,5 C. D. 2 2 26
Câu 5. Cho đoạn thẳng AB
. Tập hợp điểm M thỏa mãn 2 2 MA MB 4 .
MA MB là đường tròn có bán 5 kính bằng bao nhiêu 26 5 3 A. B. 2,5 C. D. 5 2 2
Câu 6. Cho đoạn thẳng AB x 0 . Tập hợp điểm M thỏa mãn 2 2
MA MB k M .
A MB, k 2 là đường tròn
có bán kính nhỏ nhất bằng bao nhiêu A.x B. 2x C. 1,5x D. 2,5x
Câu 7. Cho hình vuông ABCD tâm O cạnh bằng 1. Tập hợp các điểm M thỏa mãn 2 2 2 2
2MA MB 2MC MD 9 là một đường tròn có bán kính R. Khẳng định nào sau đây đúng 3 1 3
A. 0 R 1 B. R 2 C. R D. 1 R 2 2 2 2
Câu 8. Tam giác ABC có hai đỉnh B, C cố định với BC 2a . Gọi H là trực tâm của tam giác ABC và M là trung
điểm của đoạn BC. Nếu đỉnh A thay đổi nhưng luôn thỏa mãn 2 M .
A MH MA 4a thì điểm A luôn thuộc
đường tròn cố định có bán kính bằng A.2a B. a C. a 3 D. a 2
Câu 9. Cho tam giác ABC vuông tại A. Tập hợp điểm M sao cho 2 2 2
MB MC MA có dạng A.Đường thẳng B. Đường tròn C. Đoạn thẳng D. Một điểm
Câu 10. Cho hai điểm A, B cố định. Tìm điều kiện của tham số k 0 để tập hợp điểm M thỏa mãn điều kiện thỏa mãn 2 2
MA MB k là một đường tròn. 2 2 2 2 A. 2 k AB B. 2 k AB C. 2 k AB D. 2 k AB 3 3 3 3
Câu 11. Cho tam giác ABC. Điểm M thỏa mãn 3MA MB 2MC 26MA 5MB 19MC . Tập hợp điểm M có dạng như thế nào ? A.Một đường tròn B. Một đường thẳng C. Một elip D. Không tồn tại
Câu 12. Cho hình vuông ABCD tâm O cạnh bằng 1. Tập hợp các điểm M thỏa mãn 2 2 2 2
2MA 2MB MC MD 9 là một đường tròn có bán kính R. Khẳng định nào sau đây đúng 3 1 3
A. 0 R 1 B. R 2 C. R D. 1 R 2 2 2 2
Câu 13. Cho hình vuông ABCD tâm O cạnh bằng 1. Tập hợp các điểm M thỏa mãn 2 2 2 2
2MA MB MC 2MD 16,5 là một đường tròn có bán kính R. Khẳng định nào sau đây đúng 47 3 1 3
A. 0 R 1 B. R 2 C. R D. 1 R 2 2 2 2
Câu 14. Câu 22. Cho tam giác ABC. Điểm M thỏa mãn 3MA 4MB 2MC 2MA MB MC . Tập hợp
điểm M có dạng như thế nào ? A.Một đường tròn B. Một đường thẳng C. Một elip D. Không tồn tại
Câu 15. Cho tam giác ABC. Tập hợp điểm M thỏa mãn M .
A MB k với k 0 là đường tròn có bán kính bằng 2 AB 2 5AB 2 3AB 2 AB A. k B. k C. k D. k 4 4 4 4
Câu 16. Tam giác ABC vuông cân tại A có AB = 5cm, I là trung điểm của BC. (S) là tập hợp là các điểm M trong
mặt phẳng thỏa mãn M . A MB M .
A MC 25 . Mệnh đề nào sau đây đúng
A. (S) là đường trung trực của đoạn thẳng AI B. (S) là đoạn thẳng AI 5 10 5 2
C. (S) là đường tròn cố định bán kính R
D. (S) là đường tròn tâm I bán kính R . 4 4
Câu 17. Cho tam giác đều ABC cạnh a, tập hợp các điểm M thỏa mãn 2 2 2 2
4MA MB MC 2,5a nằm trên
một đường tròn (C) có bán kính là a a a 3 a A. B. C. D. 3 4 2 6
Câu 18. Cho tam giác đều ABC cạnh a, tập hợp các điểm M thỏa mãn 2 2 2 2
4MA MB MC 3,5a nằm trên
một đường tròn (C) có bán kính là a a a 3 a A. B. C. D. 3 4 2 6 2
a
Câu 19. Tam giác ABC đều cạnh a, tập hợp những điểm M thỏa mãn M . A MB M .
A MC MC.MA có 6
dạng đường tròn với bán kính bằng a 2 a 2 a 3 a A. B. C. D. 3 6 5 3
Câu 20. Cho hai điểm A, B cố định nằm trên trục hoành. Tập hợp điểm M thỏa mãn 2 2
MA MB k là đường thẳng có đặc điểm A.Song song với trục tung
B. Tạo với chiều dương trục hoành góc 60
C.Tạo với chiều âm trục hoành góc 45
D. Đi qua điểm 3;4 .
Câu 21. Cho tam giác đều ABC nội tiếp đường tròn tâm O, bán kính R. Đường thẳng bất kỳ đi qua O, tính
tổng bình phương khoảng cách từ các đỉnh của tam giác đến đường thẳng . 2 3R 2 5R A. 2 R B. C. D. 2 2R 2 2
Câu 22. Tam giác ABC có BC 4; AC 3; AB 5 . Đường tròn (C) là tập hợp điểm M thỏa mãn hệ thức
BM .CM 2CM .AM 2AM .BM 10 .
Bán kính của đường tròn này bằng A.10 B. 46 C. 3 3 D. 5 2
Câu 23. Tam giác ABC đều cạnh bằng 2. Tập hợp các điểm M thỏa mãn BM .CM 2 AM .AD 5 là đường tròn có bán kính bằng A. 3 B. 2 C. 5 D. 1
Câu 24. Cho tứ giác ABCD, điểm M bất kỳ thỏa mãn 2 2 2 2
MA MC MB MD . Định dạng của tứ giác ABCD là A.Hình thang cân B. Hình chữ nhật C. Hình vuông D. Hình thoi
Câu 25. Tứ giác ABCD thỏa mãn . AB AD . BA BC .
CB CD DC.DA 0 . Định dạng của tứ giác ABCD là A.Hình thang cân B. Hình chữ nhật C. Hình vuông D. Hình bình hành
_____________________________________ 48
VẬN DỤNG CAO, PHÂN LOẠI VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN TẬP HỢP ĐIỂM, QUỸ TÍCH – P3)
______________________________________________
2
Câu 1. Cho hai điểm ,
B C phân biệt. Tập hợp những điểm M thỏa mãn CM .CB CM là :
A. Đường tròn đường kính BC .
B. Đường tròn B; BC .
C. Đường tròn C;CB . D. Một đường khác.
Câu 2. Cho đoạn thẳng AB 4 . Tập hợp các điểm M thỏa mãn điều kiện 2 2
AM BM 10 là đường tròn có bán kính bằng A.1 B. 3 C. 4 D. 2
Câu 3. Cho ba điểm , A ,
B C phân biệt. Tập hợp những điểm M mà CM .CB C . A CB là :
A. Đường tròn đường kính AB .
B. Đường thẳng đi qua A và vuông góc với BC .
C. Đường thẳng đi qua B và vuông góc với AC .
D. Đường thẳng đi qua C và vuông góc với AB .
Câu 4. Cho tam giác ABC , điểm J thỏa mãn AK 3KJ , I là trung điểm của cạnh AB ,điểm K thỏa mãn
KA KB 2KC 0 . Một điểm M thay đổi nhưng luôn thỏa mãn 3MK AK .MA MB 2MC 0. Tập hợp
điểm M là đường nào trong các đường sau.
A. Đường tròn đường kính IJ .
B. Đường tròn đường kính IK .
C. Đường tròn đường kính JK .
D. Đường trung trực đoạn JK .
Câu 5. Cho tam giác ABC , có bao nhiêu điểm M thoả mãn: MA MB MC 1 A. 0 B. 1 C. 2 D. vô số
Câu 6. Cho đoạn thẳng AB 4 . Tập hợp các điểm M thỏa mãn điều kiện M .
A MB 4 là đường tròn có bán kính bằng A.2 B. 3 C. 2 2 D. 6
Câu 7. Cho tam giác ABC và một điểm M tùy ý. Chứng minh rằng vectơ v MA MB 2MC . Hãy xác định
vị trí của điểm D sao cho CD v .
A. D là điểm thứ tư của hình bình hành ABCD
B. D là điểm thứ tư của hình bình hành ACBD
C. D là trọng tâm của tam giác ABC
D. D là trực tâm của tam giác ABC
Câu 8. Cho tam giác ABC và đường thẳng d . Gọi O là điểm thỏa mãn hệ thức OA OB 2OC 0 . Tìm điểm
M trên đường thẳng d sao cho vectơ v MA MB 2MC có độ dài nhỏ nhất.
A. Điểm M là hình chiếu vuông góc của O trên d
B. Điểm M là hình chiếu vuông góc của A trên d
C. Điểm M là hình chiếu vuông góc của B trên d
D. Điểm M là giao điểm của AB và d
Câu 9. Cho tam giác ABC . Gọi M là trung điểm của AB và N thuộc cạnh AC sao cho NC 2NA . Hãy xác
định điểm K thỏa mãn: 3AB 2AC 12AK 0 và điểm D thỏa mãn: 3AB 4AC 12KD 0 .
A. K là trung điểm của MN và D là trung điểm của BC
B. K là trung điểm của BC và D là trung điểm của MN
C. K là trung điểm của MN và D là trung điểm của AB
D. K là trung điểm của MN và D là trung điểm của AC
Câu 10. Cho hình bình hành ABCD, điểm M thỏa 4 AM AB AC AD . Khi đó điểm M là: A. trung điểm AC B. điểm C C. trung điểm AB D. trung điểm AD
Câu 11. Cho hình chữ nhật ABCD . Tập hợp các điểm M thỏa mãn MA MB MC MD là:
A. Đường tròn đường kính AB .
B. Đường tròn đường kính BC .
C. Đường trung trực của cạnh AD . D. Đường trung trực của cạnh AB .
Câu 12. Cho hình bình hành ABCD . Tập hợp các điểm M thỏa mãn MA MC MB MD là: A. Một đường thẳng. B. Một đường tròn.
C. Toàn bộ mặt phẳng ABCD . D. Tập rỗng. 49
Câu 13. Cho tam giác ABC và điểm M thỏa 2 MA MB MC 3 MB MC . Tập hợp M là: A. Một đường tròn B. Một đường thẳng C. Một đoạn thẳng D. Nửa đường thẳng
Câu 14. Cho tam giác ABC. Có bao nhiêu điểm M thỏa MA MB MC 3 A. 1 B. 2 C. 3 D. Vô số
Câu 15. Cho tam giác ABC và điểm M thỏa 3MA 2MB MC MB MA . Tập hợp M là: A. Một đoạn thẳng B. Một đường tròn C. Nửa đường tròn D. Một đường thẳng
Câu 16. Cho hai điểm ,
A B cố định có độ dài bằng a , vectơ a khác 0 và số thực k cho trước. Tìm tập hợp 2
3a điểm M sao cho . MA MB
là đường tròn có bán kính bằng 4 4 1 A. a B. a 3 C. a 3 D. a 3 3 3
Câu 17. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn MAMB MC 0 là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 18. Tìm tập các hợp điểm M thỏa mãn MB MA MB MC 0 với , A ,
B C là ba đỉnh của tam giác. A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 19. Tam giác ABC đều cạnh a, tập hợp những điểm M thỏa mãn 2 2 2 2
MA MB MC 5a là đường tròn có bán kính bằng 1 A. a B. a 2 C. a 3 D. a 3 3
Câu 20. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn M . A BC 0 là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 21. Cho tam giác ABC có đường trung tuyến IB 4 , tập hợp điểm M thỏa mãn điều kiện
MB MA MC 4 là đường tròn có bán kính bằng A.2 B. 2 5 C. 4 2 D. 5 3
Câu 22. Cho hai điểm ,
A B cố định có khoảng cách bằng a . Tập hợp các điểm N thỏa mãn 2
AN.AB 2a là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 23. Tam đoạn thẳng AB 3a , tập hợp những điểm M thỏa mãn 2 2 2
MA 2MB 8a là đường tròn có bán kính bằng 1 A. a B. a 2 C. a 3 D. a 3 3
Câu 24. Cho hai điểm ,
A B cố định và AB 8. Tập hợp các điểm M thỏa mãn M . A MB 1 6 là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 25. Cho tam giác ABC đều cạnh bằng a . Tập hợp các điểm M thỏa mãn đẳng thức 2 5a 2 2 2
4MA MB MC
nằm trên một đường tròn C có bán kính R . Tính R . 2 a a a 3 a A. R . B. R . C. R . D. R . 3 4 2 6
Câu 26. Cho tam giác đều ABC cạnh 18 cm . Tìm tập hợp các điểm M thỏa mãn đẳng thức
2MA 3MB 4MC MA MB A. Tập rỗng.
B. Đường tròn cố định có bán kính R 2 cm .
C. Đường tròn cố định có bán kính R 3cm . D. Một đường thẳng.
Câu 27. Tam giác ABC đều cạnh a, tập hợp những điểm M thỏa mãn 2 M . A MB M .
A MC MC.MA 4a có
dạng đường tròn với bán kính bằng a 2 a 3 a A. a B. C. D. 2 5 3
_____________________________________ 50
VẬN DỤNG CAO – PHÂN LOẠI VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN CỰC TRỊ VECTOR VÀ BÀI TOÁN THỰC TẾ VECTOR P1)
_____________________________________________________
Câu 1. Cho hai điểm ,
A B (I;6) và M (I;3) , thỏa mãn : AIB 60 . Khi A, B , M thay đổi tìm giá trị nhỏ nhất
của biểu thức P MA 2MB ? A. 9 . B. 3 2 6 . C. 3 13 . D. 6 3 .
Câu 2. Cho tứ giác ABCD , M là điểm tùy ý và các điểm I, J, K cố định sao cho đẳng thức thỏa mãn với mọi
điểm M: MA MB MC 3MD k MK. Giá trị của k là A. k = 3 B. k = 4 C. k = 5 D. k = 6
Câu 3. Cho tam giác ABC vuông tại A. Gọi là góc giữa hai đường trung tuyến BD và CK. Giá trị nhỏ nhất của cos bằng 4 5 4 3 A. B. C. D. 5 4 3 4
Câu 4. Cho hai điểm cố định G và G ' là trọng tâm của tam giác ABC và tam giác A' B 'C '. Giá trị nhỏ nhất của
biểu thức P AA' BB ' CC ' bằng 1 A. GG ' B. 3GG ' C. 2GG ' D. GG ' 3
Câu 5. Hai chiếc tàu chuyển động cùng với vận tốc đều hướng đến O theo các quỹ đạo là những đường thẳng
hợp với nhau góc 60 . Xác định khoảng cách nhỏ nhất giữa các tàu biết ban đầu chúng cách O các khoảng
cách lần lượt là 20km, 30km. A. 5 3 km B. 6 3 km C. 10 3 km D. 12 3
Câu 6. Cho hình thang A B C D có 0
A B / /C D , A B 3a,C D 2a, D A B C B A 60 . Với mỗi điểm 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
G di động trên cạnh A B ta xác định điểm F sao cho G F G C G D . Tìm độ dài nhỏ nhất của G F . 1 1 1 1 1 1 1 1 1 1 1 1 3a 3 3a A. 2a . B. a 3 . C. . D. . 2 2
Câu 7. Cho ABC đều có cạnh bằng 2a . Gọi d là đường thẳng qua A và song song BC , điểm M di động
trên d . Tìm giá trị nhỏ nhất của MA 2MB MC . a 3 a 3 A. 2a 3 . B. a 3 . C. . D. . 4 2
Câu 8. Cho tam giác ABC vuông ở A, BC 2;CA ;
b AB c và điểm M di động. Tìm giá trị lớn nhất của 2 2 2 2 2 M 8
MA b MB c MC A. 4 B. 12 C. 16 D. 24
Câu 9. Trong mặt phẳng cho tam giác ABC và một điểm M bất kỳ. Đặt a BC, b C ,
A c AB . Tìm giá trị nhỏ MA MB MC
nhất của biểu thức T . a b c 3 3 A. 3 3 . B. 3 . C. . D. . 3 2
Câu 10. Cho tam giác ABC có trung tuyến ' AA CC' '
A BC, C' AB . Tìm giá trị nhỏ nhất của cos . B 4 2 1 A. . B. . C. 1. D. 5 5 2
Câu 11. Cho tam giác ABC có các cạnh AB = c, AC = b, BC = a. Tìm điểm M để vecto aMA bMB cMC có độ dài nhỏ nhất
A. M trùng với trọng tâm G của tam giác ABC.
B. M trùng với tâm đường tròn nội tiếp I của tam giác ABC.
C. M trùng với trực tâm H của tam giác ABC.
D. M trùng với tâm đường tròn ngoại tiếp I của tam giác ABC.
Câu 12. Cho tam giác ABC. Tìm giá trị nhỏ nhất của biểu thức cos 2 A cos 2B cos 2C . A.1 B. – 0,5 C. – 1,5 D. – 1
Câu 13. Cho ABC có AB 3 ; AC 4 . Phân giác trong AD của góc BAC cắt trung tuyến BM tại I . Biết 51 AD a a
, với a,b và
tối giãn. Tính S a 2b . AI b b A. S 10 . B. S 14 . C. S 24 . D. S 27 .
Câu 14. Cho tứ giác ABCD có AD và BC cùng vuông góc với AB , AB 8 , AD a , BC b . Gọi E là một
điểm thuộc cạnh CD . Biết AEB 90 , giá trị lớn nhất của T ab là A. 4 . B. 16 . C. 8 . D. 64 . 1
Câu 15. Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho BH HC . Điểm M di 3
động trên BC sao cho BM xBC . Tìm x sao cho MA GC đạt giá trị nhỏ nhất. 4 5 5 6 A. . B. . C. . D. . 5 4 6 5
Câu 16. Cho tam giác ABC đều cạnh 2 3 , d là đường thẳng qua B và tạo với AB một góc 0
60 C . Với
điểm M thuộc đường thẳng d, tìm giá trị nhỏ nhất của A MA MB 3MC ? 3 2 4 A. B. C. D. 2 5 5 5
Câu 17. Cho tam giác ABC đều cạnh 1 nội tiếp đường tròn ( )
O và điểm M thay đổi trên O . Gọi s , i lần lượt
là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức MA MB MC . Tính s i . 4 3 5 3
A. s i 3 . B. s i . C. s i .
D. s i 2 3 . 3 3
Câu 18. Cho lục giác đều ABCDEF cạnh a . Trên đường chéo AC , CE lấy hai điểm M , N sao cho AM CN
k 0 k 1 . Độ dài 2 2
BM BN đạt giá trị nhỏ nhất khi k bằng bao nhiêu ? AC CE 1 1 2 3 A. . B. . C. . D. . 2 4 3 4
Câu 19. Cho hình bình hành ABCD, M thuộc đường chéo AC, (M không trùng với các đỉnh A, C). Trên các
đường thẳng AB, BC, lấy các điểm P và Q sao cho MP // BC, MQ // AB. Gọi N là giao hai đường thẳng AQ và
CP. Giả sử DN mDA nDC . Tìm giá trị lớn nhất của m + n 4 3 1 A. B. C. D. 2 3 4 2
Câu 20. Cho tam giác ABC với các cạnh AB ,
x AC y ; x y 0 . Gọi AD là đường phân giác trong của
góc A . Biết biểu thị vectơ AD m AB n AC . Tính S m n . A. S 2 . B. S 0 . C. S 1 . D. S 2 .
Câu 21. Cho tam giác ABC và điểm O nằm trong tam giác. Gọi m, n, p lần lượt là khoảng cách từ O đến các
đỉnh A, B, C và x, y, z lần lượt là khoảng cách từ O đến các cạnh BC, ,
CA AB của tam giác ABC. Tìm giá trị nhỏ nhất của 2 2 2 250mnp 3m 3n 3 p Q . 2 2 2 xyz ( y z) (x z) (x y) A.2022 B. 2009 C. 2000 D. 1992 2 2 2
Câu 22. Tam giác ABC có bán kính đường tròn ngoại tiếp R 2 . Tìm giá trị lớn nhất của BC AB AC . A. 1. B. 2. C. 3. D. 4
Câu 23. Cho tam giác ABC có AB 5;CA 6; BC 7 . Gọi G là trọng tâm tam giác ABC, d là đường thẳng bất
kỳ đi qua G. Khi đó x, y, z tương ứng là khoảng cách từ A, B, C đến đường thẳng d. Tìm giá trị lớn nhất của
27 xy yz xz . A.580 B. 980 C. 722 D. 602
Câu 24. Cho tam giác ABC có trọng tâm G thỏa mãn 2 2 2
GA GB GC 26 . Với điểm M bất kỳ, tìm giá trị
nhỏ nhất của biểu thức 2 2 2
MA MB MC . A.26 B. 39 C. 26,5 D. 39,5
_________________________________ 52
VẬN DỤNG CAO – PHÂN LOẠI VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN CỰC TRỊ VÀ BÀI TOÁN THỰC TẾ VECTOR P2)
_________________________________________________
Câu 1. Cho hình chữ nhật ABCD có AD a , AB b . O và I lần lượt là trung điểm DB và DO . N là điểm
thỏa mãn 2NA 2NC AB AD 2 AD và NB lớn nhất. Tính NB . 2 2
2a 3 a b 2 2
a a b 2 2
2a 3 a b 2 2
2a a b A. B. C. D. . 2 2 4 4
Câu 2. Cho tam giác ABC, AB 3(cm), BC 4(cm), CA 5(cm). Điểm M thuộc đường tròn ngoại tiếp tam giác 2 2 2
ABC. Giá trị nhỏ nhất của biểu thức P MB MC MA là 5 97 5 97 5 97 A. 0 . B. 5 . C. 5 . D. 5 . 2 2 4 1
Câu 3. Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho BH HC . Điểm 3
M di động nằm trên BC sao cho BM xBC . Tìm x sao cho độ dài của vectơ MA GC đạt giá trị nhỏ nhất. 4 5 6 5 A. . . B. . C. . D. . 5 6 5 4
Câu 4. Hai vật chuyển động thẳng đều trên hai đường thẳng v
tạo với nhau một góc 30 với tốc độ 1 v và đang 2 3
hướng về phía giao điểm, tại thời điểm khoảng cách giữa hai ô
tô nếu chúng cách O các khoảng cách d 60k ; m d 40km . 1 2 A. 8,45m B. 5,65m C. 6,45m D. 4,64m
Câu 5. Cho hình thang ABCD có 2 AB DC , AC 8, BD 6 , góc tạo bởi hai véc tơ AC và BD bằng 120 .
Khi đó giá trị của (AD BC) bằng: 13 2 5 14 4 7 15 2 10 A. . B. . C. . D. 6 4 3 . 2 3 4
Câu 6. Cho hình thang ABCD có 2 AB DC , AC 9, BD 6 . Giá trị của biểu thức 2 2
(BC AD ) bằng: 80 A. 15 . B. . C. 12. D. 14. 3
Câu 7. Cho tam giác ABC có BAC 60 và AB, AC đã biết. Biểu thức P k.MA MB MC đạt giá trị nhỏ
nhất bằng (AB AC) với mọi giá trị thực k k . Giá trị của k nằm trong khoảng nào dưới đây ? 0 0 3 3 A. (0;1) . B. ( ; 2) . C. (1; ) . D. (2;3) . 2 2
Câu 8. Cho tam giác ABC có các cạnh AB = c, AC = b, BC = a. Tìm điểm M để vecto aMA bMB cMC có độ dài nhỏ nhất
A. M trùng với trọng tâm G của tam giác ABC.
B. M trùng với tâm đường tròn nội tiếp I của tam giác ABC.
C. M trùng với trực tâm H của tam giác ABC.
D. M trùng với tâm đường tròn ngoại tiếp I của tam giác ABC.
Câu 9. Cho tam giác ABC đều cạnh a và điểm M thay đổi. Giá trị nhỏ nhất của biểu thức 2 2 2
P 2MA 3MB 4MC là: 53 2 2 2 2 26a 26a A. 14a B. 14a C. D. 3 3
Câu 10. Cho đoạn thẳng AB có độ dài bằng a. Một điểm M di động sao cho MA MB MA MB . Gọi H
là hình chiếu của M lên AB . Tính độ dài lớn nhất của MH ? a a 3 A. . B. . C. a. D. 2 . a 2 2
Câu 11. Tam giác ABC có hai trung tuyến kẻ từ B và C vuông góc với nhau. Tính giá trị nhỏ nhất của cos A . 1 2 3 4 A. . B. . C. . D. . 2 3 4 5
Câu 12. Cho đoạn thẳng AB có độ dài bằng a. Một điểm M di động sao cho MA MB MA MB . Gọi H
là hình chiếu của M lên AB . Tính độ dài lớn nhất của MH ? a a 3 A. . B. . C. a. D. 2a. 2 2
Câu 13. Một ô tô chuyển động thẳng đều với vận tốc 54km/h. Một
hành khách cách ô tô đoạn a 400m và cách đường một đoạn
d 80m , muốn đón ô tô. Hỏi người ấy phải chạy theo hướng nào, với
vận tốc nhỏ nhất là bao nhiêu để đón được ô tô ? A.10,8km B. 11,2km C. 13,2km D. 14,5km
Câu 14. Một miếng gỗ có hình tam giác có diện tích là S điểm I , O lần lượt thỏa mãn IB IC 0 ;
OA OI 0 . Cắt miếng gỗ theo một đường thẳng qua O , đường thẳng này đi qua M , N lần lượt trên các
cạnh AB, AC . Khi đó diện tích miếng gỗ chứa điểm A thuộc đoạn: S S S S 3S S S 3S A. ; . B. ; . C. ; . D. ; 4 3 3 2 8 2 4 8
Câu 15. Cho đường tròn tâm O bán kính R. Gọi I là một điểm cố định sao cho OI d (0 d R) . Hai điểm A, . IA IB
B di động trên (O) sao cho IA vuông góc với IB. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của . 2 2 IA IB A. 2 2 2R d B. 2 2 4R d C. 2 2 R d D. 2 2 3R d
Câu 16. Cho tam giác ABC có các điểm M, N, P lần lượt trên các cạnh BC, CA, AB sao cho tam giác MNP có
các góc đều nhọn. Độ dài chiều cao ngắn nhất của tam giác ABC bằng 26, khi đó chiều cao dài nhất của tam giác MNP bằng A.13 B. 26 C. 20 D. 24
Câu 17. Hai xe chuyển động trên hai vuông góc với nhau, xe A đi về
hướng tây với tốc độ 50km/h, xe B đi về hướng Nam với tốc độ 30km/h.
Vào một thời điểm nào đó xe A và B còn cách giao điểm của hai đường
lần lượt 4,4km và 4km và đang tiến về phía giao điểm. Tìm khoảng cách ngắn nhất giữa hai xe. A. 1,265km B. 2,455km C. 4,125km D. 1,166km I . A I . B IC
Câu 18. Cho tam giác ABC có I là tâm đường tròn ngoại tiếp. Tìm giá trị lớn nhất của . 2 2 2
aIA bIB cIC 3 3 3 5 A. B. C. D. 2 9 4 2
Câu 19. Cho tam giác ABC là tam giác đều cạnh bằng a , M là điểm di động trên đường thẳng AC . Khi đó,
giá trị nhỏ nhất của biểu thức T MA MB MC 3 MA MB MC là: 2a 3 5a 3 A. MinT .
B. MinT 2a 3.
C. MinT a 3. D. MinT . 3 2 54
VẬN DỤNG CAO – PHÂN LOẠI VECTOR LỚP 10 THPT
(LỚP BÀI TOÁN CỰC TRỊ VÀ BÀI TOÁN THỰC TẾ VECTOR P3)
_________________________________________________
Câu 1. Cho tam giác ABC có BC , a AC ,
b AB c nội tiếp đường tròn tâm O, bán kính R. M là điểm thuộc
đường tròn (O). Gọi N, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2 2
P MA MB MC .
Khi đó giá trị của N n bằng A. 2 12R . B. 2 2 2 2
4R 9R a b c . C. 2 2 2 2
2R 9R a b c . D. 2 2 2 2
8R 9R a b c .
Câu 2. Hai vật chuyển động thẳng đều trên hai đường thẳng tạo với v
nhau một góc 30 với tốc độ 1 v và đang hướng về phía 2 3
giao điểm, tại thời điểm khoảng cách giữa hai ô tô nếu chúng cách
O các khoảng cách d 60 ; km d 40km . 1 2 A. 8,45m B. 5,65m C. 6,45m D. 4,64m
Câu 3. Cho đa giác đều A A A ...A tâm O. Tìm điểm M sao cho MA MA MA ... MA nhỏ nhất. 1 2 3 n 1 2 3 n A. M trùng tâm O B. M trùng đỉnh A C. M trùng đỉnh A D. M trùng đỉnh A 26 5 2000
Câu 4. Cho tam giác ABC có trọng tâm G, tâm đường tròn ngoại tiếp là O. Điểm M thỏa mãn A 2 cos
.MA MB MC đạt giá trị nhỏ nhất. Khi đó 2 A.M trùng đỉnh A B. M trùng trọng tâm G C.M trùng đỉnh B D. M trùng với tâm O
Câu 5. Cho tam giác ABC nội tiếp đường tròn (O) bán kính bằng 5. Tìm giá trị nhỏ nhất của 2 2 2
AB AC BC . A.25 B. 10 C. 20 D. 15
Câu 6. Cho hình bình hành ACBD trong đó tam giác ABC nhọn nội tiếp đường tròn (O) bán kính bằng 5 đồng
thời OD = 12. Tính tổng giá trị nhỏ nhất và giá trị lớn nhất của MA MB MC . A.26 B. 24 C. 30 D. 27
Câu 7. Cho tam giác ABC có CA CB 26 và góc C 126 . Giá trị nhỏ nhất của MA MB MC (với M là điểm M bất kỳ) là A.20 B. 28 C. 26 D. 13c
Câu 8. Tam giác ABC vuông tại A ; là góc giữa hai trung tuyến BD và CK . Giá trị nhỏ nhất của cos là:. 1 4 2 3 A. . B. . C. . D. . 2 5 3 4 1 Câu 9. Cho ABC
có trọng tâm G. Gọi H là chân đường cao kẻ từ A sao cho CH
HB . Điểm M di động trên 3 BC sao cho CM .
x CB . Tìm x sao cho độ dài vecto MA GB đạt giá trị nhỏ nhất. 8 5 6 5 A. . B. . C. . D. . 5 6 5 8 1
Câu 10. Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho BH HC . Điểm 3
M di động nằm trên BC sao cho BM xBC . Tìm x sao cho độ dài của vectơ MA GC đạt giá trị nhỏ nhất. 4 5 6 5 A. . B. . C. . D. . 5 6 5 4
Câu 11. Cho tam giác đều ABC nội tiếp đường tròn tâm O ,bán kính R , M là một điểm bất kì trên đường tròn.
Giá trị lớn nhất của biểu thức 2 2 2
S MA 2MB 3MC là A. 2 R 21 . B. 2 R 21 . C. 2 2R 21 . D. 2 2 R 21 .
Câu 12. Hai tam giác ABC, AB C
có trọng tâm lần lượt là G,G sao cho GG 26 . Tìm tổng giá trị lớn nhất,
giá trị nhỏ nhất của Q A A B B C C . A.156 B. 130 C. 182 D. 208 55
Câu 13. Từ một tấm ảnh chụp trên máy bay người ta thấy
đường ray xe lửa và những làn khói phát ra từ các đầu máy
chuyển động thẳng đều là những đoạn thẳng như hình vẽ. Đầu
máy I chạy với vận tốc 80km/h trên đường ray I, đầu máy II
chạy với vận tốc 60km/h trên đường ray II. Tìm vận tốc chuyển
động của đầu máy III trên đường ray III (Trong hình vẽ ta ký hiệu V
là vận tốc khói đối với đất, V
là vận tốc của xe đối KD DX 1
với đất trên đường ray I). A. 45km/h B. 50km/h C. 36km/h D. 28km/h
Câu 14. Cho hình thang ABCD có đáy CD gấp đôi đáy AB. Lấy một điểm E sao cho 3BC 2DE và đồng thời
thỏa mãn CA CE . Giá trị nhỏ nhất của góc ABC nằm trong khoảng nào dưới đây ? A. (95;100 ) . B. (100;106 ) . C. (106;115 ) . D. (115;120 ) .
Câu 15. Tứ giác ABCD nội tiếp đường tròn tâm O bán kính bằng 5. Tìm số thực k lớn nhất để 2 2 2 2 2 2
AB AC AD BC CD DB k . A. k = 20 B. k = – 30 C. k = – 100 D. k = – 150 Câu 16. Cho A BC và A
' B 'C ' có các trọng tâm G và G ' cố định và GG ' a . Khi đó giá trị nhỏ nhất của
T AA ' BB ' CC ' là: A. T a . B. T 2a . C. T 3a . D. T 4a .
Câu 17. Cho hình vuông ABCD có cạnh AB = 1. Trên cạnh AB lấy điểm P. Tổng giá trị lớn nhất, giá trị nhỏ nhất
của tổng độ dài PA PB gần nhất với số nào A.4,65 B. 4,82 C. 5,15 D. 3,75
Câu 18. Cho tam giác ABC có độ dài ba cạnh là 2, 6, 5. Tìm giá trị lớn nhất của biểu thức
24 cos 2 A 60 cos 2B 20 cos 2C A.65 B. 26 C. 62 D. 52
Câu 19. Cho tam giác đều ABC cạnh .
a Gọi M là điểm nằm trên cạnh .
AB Tính giá trị nhỏ nhất của biểu thức
MA 2MB MC theo . a a 3 a 3 a 3 2a 3 A. . B. . C. . D. . 4 2 8 3
Câu 20. Cho tam giác ABC. Giá trị nhỏ nhất của biểu thức 26 cos 2 A 5cos 2B 2000 cos 2C gần nhất với A.- 2650 B. – 5392 C. – 2022 D. – 2015
Câu 21. Cho tam giác có trọng tâm G , qua G dựng đường thẳng d cắt cách cạnh AB , AC lần lượt tại M , AM AN N . Đặt x ,
y , gọi m , M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của T x y . Tính m M . AB AC 10 17 11 5 A. . B. . C. . D. . 3 6 6 2
Câu 22. Tam giác ABC nội tiếp đường tròn tâm O bán kính R. Ký hiệu D, E, F là chân các đường cao kẻ từ O
đến các cạnh của tam giác ABC. Tìm giá trị nhỏ nhất của 2 2 2
OD OE OF . 2 3R 2 3R 2 5R 2 R A. B. C. D. 4 2 4 4 26
Câu 23. Cho tam giác ABC có diện tích S, bán kính đường tròn ngoại tiếp R thỏa mãn S . Tìm giá trị nhỏ R nhất của biểu thức 2 2 2
aMA bMB cMC với điểm M bất kỳ. A.104 B. 192 C. 86 D. 265
Câu 24. Tam giác ABC có đường thẳng d cố định đi qua điểm C và điểm I thỏa mãn 3IA 2IB 0 . Tìm vị trí điểm M sao cho 2 2
3MA 2MB đạt giá trị nhỏ nhất.
A.M là giao điểm của d với đường tròn đường kính IC
B.M là giao điểm của d với đường tròn đường kính IB.
C.M là giao điểm của d với đường tròn đường kính AB.
D.M là giao điểm của d với đường tròn đường kính IA. 26
Câu 25. Cho tam giác ABC. Tìm giá trị lớn nhất của biểu thức Q cos A
(cos B cos C) . 5 A.15,52 B. 14,52 C. 20,25 D. 25,5 56




