

Preview text:
lOMoAR cPSD| 58605085
International University, HCMC
School of IEM – LSCM Program Student Full name: Student ID: INVENTORY MANAGEMENT HOMEWORK 4 Problem 1:
Ceiling Drug is concerned about the inventory control of an important item.
Currently, they are using an (s,Q) system where Q is the EOQ and the safety factor
k is selected based on a B1 shortage-costing method. Relevant parameter values are estimated to be
D=2,500units/ year B1=$100 v=$ 10/unit
x^L=500units
A=$5 σL=100units r=0.25$/$/ year
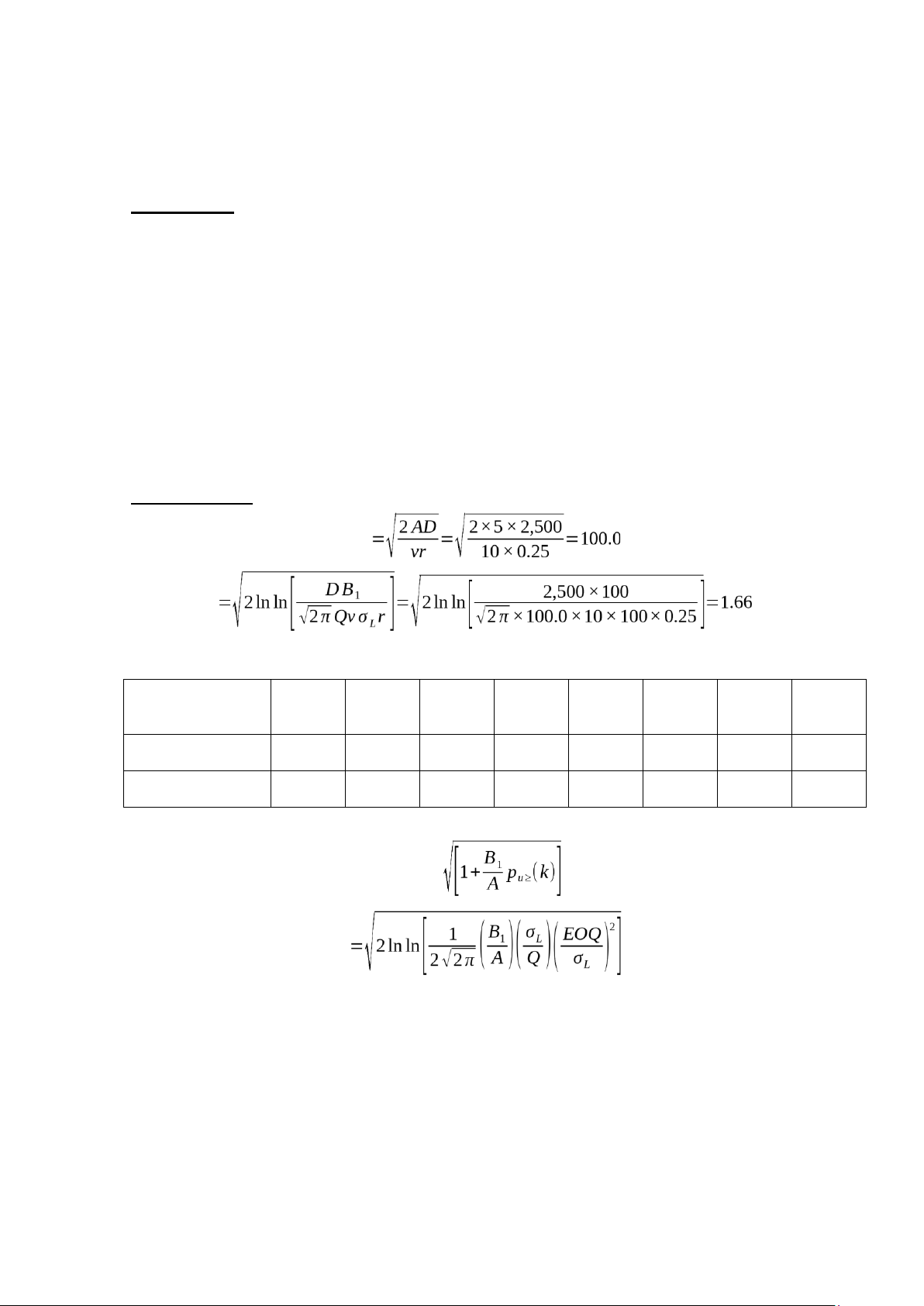
Determine the simultaneous best values of Q and s. SOLUTION: EOQ k
With the iterative procedure, we obtain: Iteration 1 2 3 4 5 6 7 8 Number Q
100.0 140.3 157.2 165.5 168.4 170.4 171.3 171.3 k 1.66 1.45 1.36 1.33 1.31 1.30 1.30 1.30
based on the following formulas: Q=EOQ k
pu≥(k )=1−NORM .S. DIST(k ,TRUE) Conclusion:
● The order quantity (Q) is: Q=171.3units≈171units
● The reorder point (s) is: s=x^L+kσL=500+1.30×100=630units lOMoAR cPSD| 58605085
International University, HCMC
School of IEM – LSCM Program Student Full name: Student ID: Problem 2:
A retail electronic-supply outlet is considering an (s,S) control system for one of
its products. Relevant given characteristics of the product include
D=2,000units/ year B1=$200 v=$ 7.5/unit
x^L=250units A=$10
σ L=75units r=0.25$/$/ year
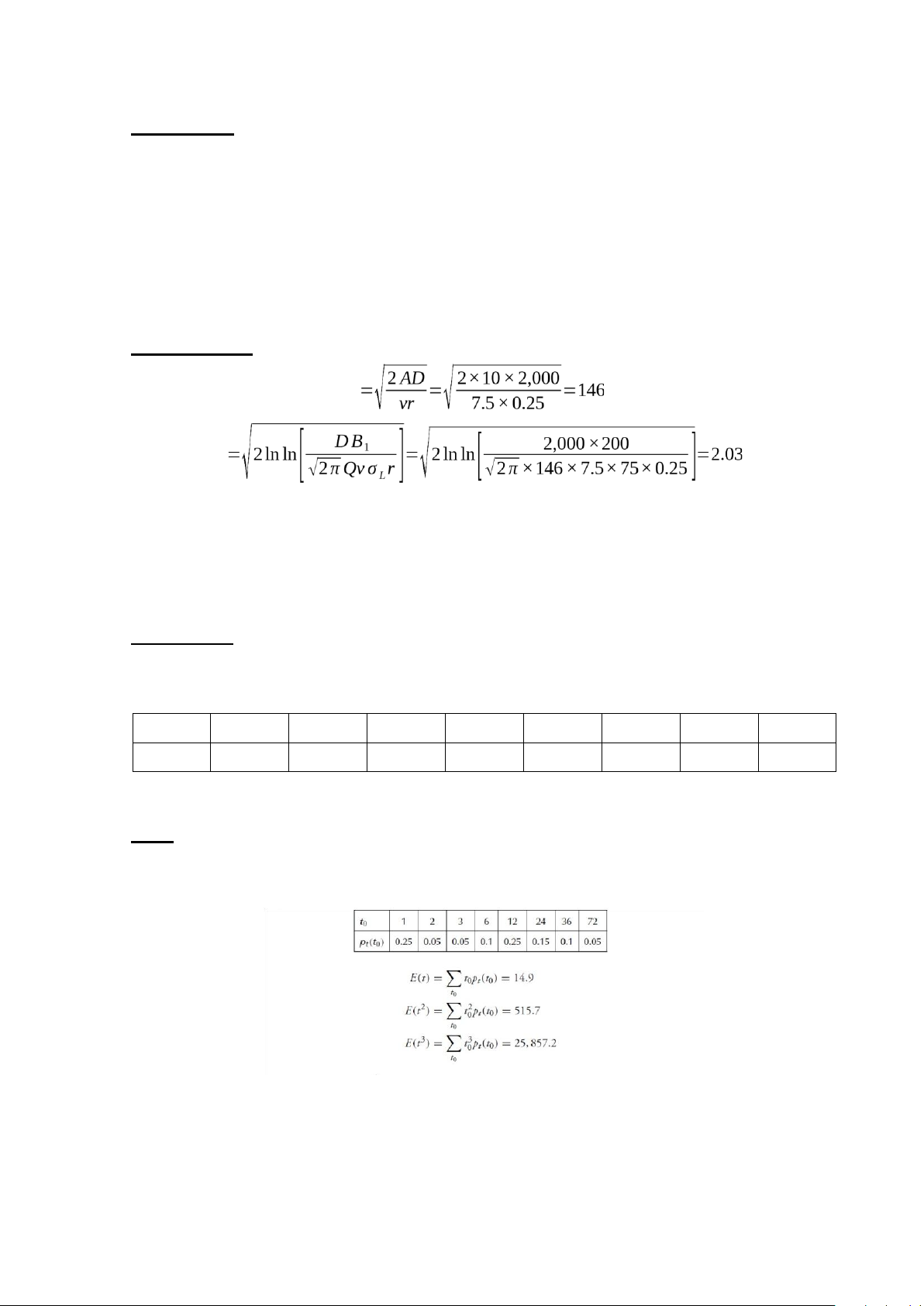
Find s and S of this inventory policy neglecting the undershoots. SOLUTION: EOQ units k
s=x^L+kσL=250+2.03×75=402units
S=s+Q=402+146=548units Problem 3:
Consider the same product in Question 2, the probability distribution of
transaction sizes is as follows: t 0 1 2 3 6 12 24 36 72 pt (t0) 0.15 0.05 0.05 0.3 0.15 0.05 0.1 0.15
Select s and S simultaneously using the undershoot distribution.
Note: For question 3, students will use Excel to solve the problem. After that,
students only need to write down some key results in their answer sheet. There is
an example in the following page. lOMoAR cPSD| 58605085
International University, HCMC
School of IEM – LSCM Program Student Full name: Student ID: SOLUTION: E (t )=19.6 E (t2)=969.2 E (t3)=61,669.9 ' 1 E(t2)
E (x )=E ( z)+E ( x )=2 [ E(t) −1]+x^L=24.22+250=274.22 ' 1 4 E (t3) E(t2) 2 2 2 { } var(x )=12
E(t) −3[ E (t ) ] −1 +σ L=437.42+75 =6,062.42 Step 1: Q=EOQ
(k)−E(z) lOMoAR cPSD| 58605085
International University, HCMC
School of IEM – LSCM Program Student Full name: Student ID: k Iteration 1 2 3 4 5 Number Q 146.1 156.8 159.1 159.9 159.9 k 1.93 1.9 1.89 1.89 1.89 The solution is: Q=160units k=1.89 Step 2: s units Step 3:
S=s+Q=421+160=581units



