Hướng dẫn giải 50 câu hỏi hay và khó trong đề thi thử Toán 2018 – Phạm Minh Tuấn

Tài liệu gồm 40 trang được biên soạn bởi tác giả Phạm Minh Tuấn hướng dẫn giải 50 câu hỏi hay và khó trong đề thi thử Toán 2018, các bài toán được chọn lọc với nhiều chủ đề kiến thức khác nhau, phân tích và giải chi tiết.

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

40 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
50 caâu hoûi hay vaø khoù
trong ñeà thi thöû 2018
Sưutâmvàbiênsoạn:PhạmMinhTuấn
ChúccácemđỗvàotrườngĐạiHọcmàmìnhmongmuốn<3
PMT
2810
1
Bài1.Chocấpsốcộng

n
u cócácsốhạngđềudương,sốhạngđầu
1
u1
vàtổngcủa100số
hạngđầutiênbằng
14950
.Tínhgiátrịcủatổng
2 1 1 2 3 2 2 3 2018 2017 2017 2018
11 1
...S
uu uu uu uu u u u u


A.
11
1
3
6052



B.
12
1
3
6052




B.
11
1
3
6052



D.
12
1
3
6052



Hướngdẫngiải
Tổngcủansốhạngđầucủacấpsốcộngđượcgọilàtổngriêngthứ
n
:

1
21
2
n
nu n d
S



Ápdụng:
100
100 2 99
14950 3
2
d
Sd


và
1 2018 1
, 2017 6052
nn
uudu u d

Tacó:


1
11 11 1
11
11 111
.
.
nn
nnnn nnn n n n
nn n n
uu
d
uuuu uuu u u u
uu u u








Khiđó:
1 2 2 3 2017 2018 1 2018
11 1 11 1 1 1 1 11 1
...
11
1
3
6052
S
dd d d
uu uu u u uu




 








Bài2.
Chocácsốphức
12
,zz
thỏamãn
12
1zz
,
12
1zz 
và
12
zz
.Tìmgiátrịnhỏ
nhấtcủabiểuthức
12 12
12 1 2
1
1
zz zz
P
zz z z




A.
1
B.
2
C.
3
2
 D.
4
Hướngdẫngiải
2
Đặt
12
12
1
zz
t
zz
,tacó:










121212 121212
12 12
12
12
12 1 2
11221122 2211 1122 22 11
12 1 2 12 1 2
.
1
1.
11.
0
11. 11.
zzzzzz zzzzzz
zz zz
zz
zz
zz z z
zzzzzzzz zzzz zzzz zz zz
zz z z zz z z
 



 

 
Suyratlàsốthực,khiđó
1
Pt
t

,khảosáthàmsốtađượcGTNNc ủaPlà2,đạt
đượckhi
1t 
Chúý:
0zzthìzlàsốthựcvà 0zzthìzlàsốthuầnảo
Bài3.
Chocácsốphức
12
,zz
thỏamãn
12
6, 2zz
.GọiM,Nlầnlượtlàđiểmbiểudiển
cácsốphức
12
,ziz
.Biết
0
60MON
.Tínhgiátrịcủabiểuthức
22
12
9Tz z
.
A.
24 3
B.
36 2
C.
36
 D.
36 3
Hướngdẫngiải
22
121 21 2
933
Tz z z izz iz OMOPOMOP
   
VớiPlàđiểmbiểudiễnsốphức
2
2
3
36
PON
iz
OP iz


Tacó:
0
60
OM OP
MON

OMP đều,gọiIlàtrung
điểmMP
63
2 . 2. .6 36 3
2
TOIPM
Bài4.
Chongẫunhiênhaisốthực
,0;1ab

.Tínhxácsuấtđểphươngtrình
32
30xaxb
cótốiđahainghiệm
A.
3
3
44
B.
3
1
44
C.
3
1
1
44
D.
3
3
1
44
Hướngdẫngiải
3
Xét
32
3yx ax b
;
2
ʹ 36yxax
;
0
ʹ 0
2
x
y
xa


Yêucầubàitoán


3
0. 2 0 4 0yya bba
‐
Nếu 00ba
‐
Nếu

3
04bba
Tacó:
3
3
1
41
4
aa
Xácsuấtcầntìmlàdiệntíchcủamiềnđượcgiới
hạnbởi:
3
4ya
,
1y
,
3
1
0,
4
aa
Vậyxácsuấtcầntìmlà

3
1
4
3
3
0
3
14
44
Pada
Bài5.
Chohàmsố
yfx
cóđồthịnhưhìnhvẽ.Cóbaonhiêugiátrịthựccủathamsốmđể
hàmsố
 
2
yfxfxm
cóđúng3điểm cựctrị. 
A.
1
4
m
 B.
1
4
m
C.
1m
 D.
1m
Hướngdẫngiải
Tacó
 
    
 
2
2
2
2
2
2 ʹʹ
ʹ
2
fx fx m fxfx fx
yfxfxmy
fx fxm











4



0
2
ʹ 01;3
1
ʹ 00
2
0 1
fx x x
yfx xx
fx fx m



Đặt

tfx
,từ(1)tađược:
2
0ttm
(*)
Tađãtìmra3điểmcựctrịlà
0
1; 3; 0xxxx
,nênđểhàmsốđãchocó đúng3
điểmcực trịthì

*
vônghiệmhoặccónghiệmkép
1
2
t 
,hay
1
14 0
4
mm
.
Thửlạitathấy
2
11 1
0
42 2
mt t

 


(thỏa)
Vậyđápsốlà
1
4
m
Bài6.
[CHUYÊNHẠLONG]Chohaihộpđựngbi,đựng2loạibịtrắngvàbiđen,tổng sốbi
tronghaihộplà20bivàhộpthứnhấtđựngítbihơnhộpthứhai.Lấyngẫunhiên
từmỗihộp1
bi.Chobiếtxácsuấtđểlấyđượchaiviênbiđenlà
55
84
,tínhxácsuấtđểlấyđược2viênbitrắng.
A.
1
28
B.
15
84
C.
11
84
 D.Đápánkhác
Hướngdẫngiải
Gọix,ylần lượtlàsốbiởhộpthứnhấtvàhộpthứhai,

,0;20xy
Vì
09
20
11 19
x
xy
y



(*).Lấyngẫunhiên2viênbibấtkỳtừ2hộp

.nxy
Gọim,nlầnlượtlàsốbiđenởhộpthứnhấtvàhộpthứhai,

0; , 0;mxny
GọiAlàbiếncố:“Lấyđượchaiviênbiđen”

.55 55
..
.84 84
mn
PA mn xy
xy

Mặtkhác

,.84mn xy

.Từđiềukiện(*)thìchỉcó
6; 14xy
thỏamãn
Suyra .555.11mn nên
5; 11mn
5
Gọic,dlầnl ượtlàsốbịtrắngởhộpthứnhấtvàhộpthứhai,khiđó
1
3
cxm
dyn


Vậyxácsuấtđểlấyđược2viênbitrắnglà
1.3 1
6.14 28
P 
Bài7.
TrongkhônggianvớihệtọađộOxyz,chobốnđiểm

7;2;3 , 1; 4; 3 , 1; 2; 6ABC

1; 2; 3D
vàđiểmMtùyý.TínhđộdàiđoạnOMkhibiểuthức
3PMAMBMC MD
đạtgiátrịnhỏnhất.
A.
14
OM
B.
26OM
C.
317
4
OM D.
321
4
OM
Hướngdẫngiải
 
6;0;0 , 0;2;0 , 0;0;3DA DB DC
  
nêntứdiệnABCDlàtứdiệnvuôngđỉnhD
Dựđoán MD nêntagiảsử

222
1; 2; 3
3
xyz
Mx y z MD x y z


Tacó:

2
22
666MA x y z x x
Tươngtự

2
22
222MB x y z y y
,

2
22
333MC x y z z z
Suyra
623 11Pxyzxyz
Dấu“=”xảyrakhivàchỉkhi
0xyz
hay
14
MD OM
BTTL
.TrongkhônggianvớihệtọađộOxyz,chobốnđiểm

2;2;2 , 0;2;2AB

2;0;2C
,

2;2;0D
vàđiểmMtùyý.TínhđộdàiđoạnOMkhibiểuthức
3PMAMBMCMD
đạtgiátrịnhỏnhất.
. 32
AOM
B.
23OM
C.
2
OM
D.
3OM
Bài8.
Chohàmsố

fx
liêntụctrên
vàcóđồthịnhưhìnhbêndưới
6
Gọihàm
 
gx f fx


.Phươngtrình

ʹ 0gx
cóbaonhiêunghiệmphânbiệt.
A.
8 B.10C.
14
 D.
12
Hướngdẫngiải
Tacó:
  
ʹʹ. ʹgx fxf fx


;




 



ʹ 0 1
0 2
ʹ 0
ʹ 02 3
ʹ 0
21 4
12 5
fx
fx
fx
gx fx
ffx
fx m m
fx n n





‐
Đồthihàmsố

yfx
có4điểmcực trịnên

1
có4nghiệmphânbiệt
‐
Đồthị

yfx
giaovớiOxtại3điểmnên

2
có3nghiệm,trongđócó2
nghiệmtrùngvới

1
.Suyra

2
có1nghiệmphânbiệt
‐
Đồthị

yfx
giaovới
2y
tại3điểmnên

3
có3nghiệmphânbiệt
‐
Đồthị

yfx
giaovới

21ym m
tại1điểmnên

3
có1nghiệm
phânbiệt
‐
Đồthị

yfx
giaovới

12yn m
tại3điểmnên

3
có3nghiệmphân
biệt
Vậytổngcócó
4131312
nghiệmphânbiệt
Bài9.
Chocấpsốnhân
123
,,,..,
n
uuu u
;trongđó
0, 1,2,...,
i
ui n
.Biếtrằng
123
... 2018
n
uuu u
,
123
111 1
... 2019
n
uuu u

và
123
1
. . ....
100
n
Puuu u
.Hỏisố
tựnhiênnhỏnhấtthỏamãnPlà:
A.
9295
B.
9296
C.
18592
D.
18591
7
Hướngdẫngiải
Tacó:

1
123
1
... 2018 2018
1
n
n
uq
uuu u
q

(1)
Và


1
1
123
1
11
1
1
111 1
... 2019 2019 2019
1
1
1
n
n
n
n
uq
q
uuu u
uq q
q








(2)
Từ(1)và(2)suyra



21
1
1
1
1
1
1
2019 2018
.
2018 2019
1
1
n
n
n
n
q
q
uq
uq q
uq

Tacó:
123
1
. . ....
100
n
uuu u




21
11 1 1
1
2
21
2
2
11
2018
2019
1
. . . . .... .
100
1 1 2018 1
100 100 2019 100
1
2log 18591,1 185 92
100
n
n
nn
n
nn
uuq uq uq
uq uq
nn






 


Bài10.
Cótấtcảbaonhiêugiátrịnguyêncủathamsốmđểphươngtrình
3
3
3
4sin sin sin 4sin 8 2xm x x xm
cónghiệmthực
A.
20 B.
21
C.
22
D.19
Hướngdẫngiải
Đặt
3
4sin
sin
axm
bx

.Phươngtrìnhtrởthành:


3
3
33 33
82 2 8 3 2 2 0
2
2
0
ab ab ab ab aba b
a
bVN
ab




8
TH1:
88
2sin 1 14 12
44
mm
ax m


TH2:
3
0sin4sin55ab m x x m
Vậycó20giátrịnguyênmthỏamãn
Bài11.
Cótấtcảbaonhiêugiátrịthựccủathamsốmđểgiátrịlớnnhấtcủahàmsố
2
ln 2yxxm
lànhỏnhấttrênđoạn
1; 2

A.
1
B.
2
C.
3
D.vôsố
Hướngdẫngiải
Xét
  
2
11
ln 2 ; ʹ 4;ʹ 0
2
gx x x g x xg x x
x

(loại)



12; 2 ln2 8 max max 2 ; ln2 8gg gxmmm hm
Đườngmàuxanh,tím,đenlầnlượtlàđồthị

2ym m
,

ln2 8ym m
và

hm
Phươngtrìnhhoànhđộgiaođiểm:
1
ln2 8 2 5 ln 2
2
mmm
Dựavàođồthịtathấy

hm
nhỏnhấtkhivàchỉkhi
1
5ln2
2
m 
Bài12.
[CHUYÊNĐẠIHỌCVINH‐LẦN1]Giảsử
12
,zz
làhaitrongsốcácsốphứczthỏa
mãn
21iz i
và
12
2zz
.Giátrịlớnnhấtcủa
12
zz
bằng:
A.
4
B.
23
C.
32
D.3
Hướngdẫngiải
9
Cách1:Đạisố
Tacó:
21 121iz i z i
Đặt
12
11
12
22
2
12
1
12
ww
wz i
ww
wz i






2222
12 12 1 2 12 12
22 0 0ww ww w w ww ww  

12 12
21 2 2 3zz i zz
Tacó:
22 2 2
12 1 2 12 12
22 1244Pz z z z zz zz
Cách2:Hìnhhọc
GọiA,Blầnlượtlàđiểmbiểudiễnsốphức
12
,zz
A,Bthuộcđườngtròn(C)tâm

1; 2I
,bánkính
1R
Khiđó,
12
2z z OA OB BA AB AB
  
làđườngkínhcủađườngtròn(C)
Và
12
22z z OA OB OI OI
 
,vớiIlàtrungđiểmAB
10
Ápdụngcôngthứcđườngtrung tuyến:
22 2 2 2
2222
2
2238
24 4 4
OA OB AB AB
OI OA OB OI




Tacó

22
12
22.84Pz z OAOB OAOB
BTTL1.
Giảsử
12
,zz
làhaisốphứcthỏamãn

1
12zi
và
21
ziz
.Giátrịnhỏnhấtcủa
12
zz
bằng:
A.
22 1
B.
22 1
C.
22 2
D.
22 2
BTTL2.
Giảsử
12
,zz
làhaisốphứcthỏamãn


11
1zi iz
và

22
34zz i
.Giátrị
nhỏnhấtcủa
12
zz
bằng:
A.
2
B.
33
2
10
C.
33
2
5
D.
22 1
BTTL3.
Giảsử
12
,
zz
làhaitrongsốcácsốphứczthỏamãn  34 2zivà

12
1zz
.Giá
trịnhỏnhấtcủa
22
12
zz
bằng:
A.
10B.
5
C.
625
D.
435
Bài13.
Chohàm số
yfx
liêntụctrên
,có

20f
vàđồthịhàmsố

fx
nhưhình
vẽbên.Khẳngđịnhnàosauđâylàkhẳngđịnh sai?
A.Hàmsố


2018
1yf x
nghịchbiếntrênkhoảng

 ;2
.
B.Hàmsố


2018
1yf x
cóhaicựctiểu.
11
C.Hàmsố


2018
1yf x
cóhaicựcđạivàmộtcựctiểu.
D.Hàmsố


2018
1yf x
đồngbiếntrênkhoảng

2;
.
Hướngdẫngiải
Từđồthìcủa

fx
tacóbảngbiếnthiênnhưsau:
Từgiảthiết

20f
và


2018 2018
111 0xfx
vớimọix.
Đặt

2018
1tx
,tacó:





   
2018 2018
2018 2018
0khi 2;1 3; 3
0khi ;2 2; ; 3 3;
t
ft t x
ft t x

Đặt



2018
1gx f x
,tacó:

 


2017
2
2018. . .
2
t
xftft
gx
ft
Dođó,tacóbảngbiếnthiêncủa

ygx
nhưsau:
VậychọnC.
Bài14.
Chocácsốphức
12
,zz
thỏamãn
112 2
, 2zrz r
và

22
1212
14iz i z r r
.Gọi
,, ,ABMN
lầnlượtlàđi ểmbiểudiễncácsốphức

1221
2, 22 , 1,iz iz iz iz
.Biết
làgóc
giữa
AM
và
BN
.Tìmgiátrịnhỏnhấtcủa
cos
.
12
A.

min
4
cos
5
 B.

min
3
cos
4
C.

min
3
cos
5
 D.

min
2
cos
3
Hướngdẫngiải
Từđềsuyra
12
2; 4OA r OB r
vàM,NlầnlượtlàtrungđiểmOBvàOA
Tacó:
 
22 22 22
1 2 12 1 2 12 12
1422124 24iz iz rr iz iz rr OAOBAB rr
 
Dođótamgiác
OAB
vuôngtạiO
Tacó:


2
.
.
.
cos
.4. 4.
AO BO AB BO AO AB
AO AB BO BA
AM BN
AM BN AM BN AM BN



     
   
 
Vì
2
2
2
.0cos
4. 2.
AB
AB
OA OB AO BO
AM BN AM BN


 
Lạicó:
 
22 2 22 2
22
2
22 2 2 22
2.
24 24
15
 
44
OA AB O B OB AB OA
AM BN AM BN
AB
OA OB AB do AB OA OB






Vậy
2
2
4
cos
5
5
4
AB
AB

Nhậnxét:
Ngoàicáchtrêntacóthểchuẩnhóa
1
r
bằngmộtsốdươngbấtkìrồiđưa
cos
vềhàmtheobiến
2
r
,khiđóviệctìmminsẽdễdànghơn.
13
Bài15.
Gọi
1
z
,
2
z
,
3
z
và
4
z
làcácnghiệmcủaphươngtrình
4
1 2018
2 i 2019
z
z



.Tínhgiátrịcủa
biểuthức

2222
1234
1111Pzzzz
.
A.


2
4.2019 2018 4.2019 2018.81
2018.16 2019

B.


2
4.2019 2018 4.2019 2018.81
2018.16 2019

C.


2
4.2019 2 01 8 4.2019 2018.81
2018.16 2019

D.


2
4.2019 2018 4.2019 2018.81
2018.16 2019

Hướngdẫngiải
Đặt

44
2018 2 i 2019 1fz z z

1234
2018.16 2019 zz zz zz zz
.



1234
44
1234
 2018.16 2019
 2018 2 i 2019 1 4.2019 2018
4.2019 2018
2018.16 2019
fi iz iz iz iz
ii
zizizizi








1234
4
4
1234
 2018.16 2019
 2018 2. i 2019 1 4.2019 2018.81
4.2019 2018.81
2018.16 2019
f i iz iz iz iz
ii
zizizizi
   


Mà

12341234
P z iz iz iz iz iz iz iz i



2
4.2019 2018 4.2019 2018.81
4.2019 2018 4.2019 2018.81
.
2018.16 2019 2018.16 2019
2018.16 2019






.
Bài16.
Chohàmsố

fx
khôngâmvàliêntụctrên
0;
thỏamãn:



0
1
2
0
2018 2 , 0
1009 1
x
fx ftdt x
fxdx e


Tínhtíchphân

1
0
x
fx
dx
e
A.

2018 1
e
 B.

1009 1
e

C.

2018 2e
D.

2018 2
e
14
Hướngdẫngiải
Tacó
 
00
2018 2 2018 2 0
xx
fx ftdt fx ftdt

(1)
Đặt
  
00
; gʹ
xx
ax ax
gx e ftdt b x e a ftdt f x ab






Từ(1)thựchiệnphépđồngnhấtsuyra
22
2018 1009
aa
ab b
 



Vậy

gʹ 0, 0xx
,tức

g x
nghịchbiếntrên
0;
 
2 2
00
1009 0 1009 2 2018 2018
xx
x x
eftdt gxg ftdt e

 




Vậy
 
1
22
0
2018 1009 1009
x
fx e fxdx e
Dấu“=”xảyrakhivàchỉkhi



1
2
0
2018 2018 1
x
x
fx
fx e dx e
e

Bài17.
Cho16phiếughicácsốthứtựtừ1đến16.Lấylầnlượt8phiếukhônghoànlại,gọi
i
a
làsốghitrênphiếuthứ
i
l ấyđược

18i
.Tínhxácsuất
P
để8phiếulấyđượcthỏamãn
12 8
...aa a

vàkhôngcóbấtkýhaiphiếunàocótổngcácsốbằng17.
A.
8
8
16
3
P
A
B.
8
8
16
2
P
A
C.
8
8
16
2
P
C
D.
8
8
16
3
P
C
Hướngdẫngiải
Tacó

8
16
A
.Do8phiếulấyđượcthỏamãnđiều kiện

12 8
...
aa a
,nêntacóthể
xem8phiếulấyđượcnhưlàmộttậpconcủatậpcó16phầntử.
Gọi

1,2,3,...16S
và
ES
thỏamãnyêucầubàitoán.Từ1đến16có8cặpsốcótổng
bằng17chiathànhhaitậptươngứnglà

1,2,...,8M
và

16,15,...,9N
.Nếu
E
có
k
phầntửthuộc
M
thìcó
8
k
C
cáchchọnvàkhiđó
E
sẽcótốiđa
8 k
phầntửthuộc
N
15
nêncó
8
2
k
cáchchọn,với

0,1,...,8k
.Vậysốtậphợp
E
thỏamãnyêucầubàitoánlà

08 17 80
88 8
.2 .2 ... .2 3
CC C
.vậy
8
8
16
3
P
A
.
Bài18.
Chocácsốphức
12
,zz
thỏamãn
12
1,zzr
.GọiM,N,Plầnlượtlàđiểmbiểu
diểncácsốphức
12 2
, ,4ziz iz
.Biết
90


o
NMP
MOP
.Khi
0
rr
thìgóc
làlớnnhất.Khẳng
địnhnàosauđâyđúng?
A.

1; 2r
 B.

0;1r
C.

2;3r
D.

3;4r
Hướngdẫngiải
Từđềsuyra
;44
1
NOPOP ON r
OM

Tacó:tan OMN r
Và

tan tan tan
tan 4
1 tan .tan 1 tan
OMN r OP
OMN r
OMN r OM





Suyra

2
2
333
tan max
4
41
24.1
r
r
r


đạtđượckhi
1
2
r
Bài19.Chohàmsố

fx
cóđạohàmkhác0vàliêntụcđếncấphaitrên
1; 2

thỏamãn
 

 

3
1
2
ln2 ʹ 111
ʹʹʹ
ʹ
2ln2
fx
ff
fx xf x
fx

,
1; 2x

16
Tínhtíchphân

2
1
Ixfxdx
A.
2
1
log 5 1
2ln2
I 
B.
2
3
3log 5 2
4ln2
I 

C.
2
3
log 5 2
ln2
I 
D.
2
3
2log 5 1
2ln2
I 
Hướngdẫngiải
Tacó:

 



 

2
3
2
1
2
ʹʹʹ 2 ʹ 2 ʹʹ
ʹʹ2ln2
2ln2
ʹ
fx
fx
fx xf x fx xf x
fx fx
fx










1
22
2ln2ʹʹ2ln2
ʹʹ
fx fx
xx
C
fx fx





Vì

1
ln2 ʹ 111 0ff C
Khiđó:

 




22
222
ʹ 2ln22 2 ʹ 22 2 log
fx fx fx
fx x x xdxxC fx xC 
Vì

2
11 1fC
,khiđó:


2
2
log 1fx x
Xét

2
2
2
1
log 1Ix x dx
,Đặt


2
2
2
2
2
log 1
1ln2
2
x
v
ux
x
dv xdx
x
v



Suyra

2
21
3
22
22
22
10
1
11 11
log 1 2log 5
2ln2 2ln2
11
xx
Ix x x
xx









2
2
2
2
22
1
1
11 1 3
2log 5 ln 1 2log 5 1
2 ln2 2 2 2ln2
x
x


 


BTTL.Chohàmsố

f
x
đồngbiếnvàcóđạohàmliêntụcđếncấphaitrên
0;1

thỏamãn
17
 
  


 
2
2
0 ʹ 01
ʹʹ ʹ 12 ʹ
ff
f
xfx f x x xfxf x




,
0;1x

Tínhdiệntíchcủahìnhphẳnggiới hạnbởiđườngcong


2
1yx fx ,haitrụctọađộvà
đưởngthẳng 1x
A.
47
12
B.
101
30
C.
3
9
20
ee
D.
3
1ee
Bài 20. Cho dãy số

n
u
thỏa mãn

35 4
log 2 63 2log 8 8
n
uun
,
*

.Đặt
12
...
nn
Suu u
.Tìmsốnguyêndươnglớnnhấtnthỏamãn
2
2
148
75
nn
nn
uS
uS
A.
16n
B.
17n
. C.
18n
D.
19n
Hướngdẫngiải
Xétvới
, 1nknk
:



35 4
35 4 1
log 2 63 2log 8 8
log 2 63 2log 8 1 8
k
k
uuk
uuk




441 1
log 8 8 log 8 1 8 8
kk kk
uk u k u u


Suyra

n
u
làmộtcấpsốcộngvớicôngsai

51 1
885132duu u
Mặckhácvới 1n :

3 5 41 3 1 41 1
log2 63 2log log2 1 2log 4
SHIFT SOLVE
uuuuu 


2
48 1 8 4
2.4 8 1 .
4
2
n
n
unn
nn
Sn





Tacó:


2
2
84.16
148
19
75
16 4 .4
nn
n
nn

.Vậysốnguyêndươnglớnnhấtlà 18n
Bài21.Trongmặtphẳngphức,xéthìnhbìnhhànhtạobởicácđiểm
1
0, ,z
z
và
1
z
z
.Biết
z
18
cóphầnthựcdươngvàdiệntíchhìnhbìnhhànhbằng
35
37
.Tìmgiátrịnhỏnhấtcủa
2
1
z
z

A.
53
37
B.
49
37
C.
43
37
D.
50
37
Hướngdẫngiải
GọiO,A,C,Blầnlượtlàđiểmbiểudiễncácsốphức
1
0, ,z
z
và
1
z
z
Suyra
1
,OA z OC AB
z

,
1
OB OA OC OB OB OA OC z
z

     
Diệntíchhìnhbìnhhành:
35 35 12
..sin sin cos
37 37 37
S OA AB OAB OAB OAB

Tacó:
22
2
22
1 1 12 50
2cos 2 . 2cos 2 2.
37 37
OC z OAB z OAB
zz

Bài22.TrongkhônggianvớihệtọađộOxyz,cho4đườngthẳng



:
1
y2
x2 z1
111
;

:
2
y1
x1 z
121
;

:
3
y2
xz1
11 1
;

:
4
ya
x5 zb
131
. Biết không tồn tại
đườngthẳngnàotrongkhônggianmàcắtđượcđồngthờicảbốnđườngthẳngtrên.Tínhgiátrị
củabiểuthức
Ta2b
A.
2
B.
3
C.
2
D.
3
Hướngdẫngiải
Tacó:

13
//
19
GọiPlàmặtphẳngchứa
1
và


3
:2 30Px yz
Gọi


2
0; 1;1IPI
Gọi





4
222324278
;;
666
ab b a b
JPJ





2 22 3 18 2 7 14
;;
66 6
ab b a b
IJ
Đểthỏamãnyêucầubàitoánthì

IJ
phảicùngphươngvới



1
1; 1; 1u
,hay:
 


2 22 3 18 2 7 14
22
666
ab b a b
ab
Bài 23. Cho cấp số cộng

n
u
có tất cả các số hạngđều dương thỏa mãn:

 ... ...
1 2 2018 1 2 1009
uu u 4uu u
.Giátrịnhỏnhấtcủa
log log log
222
32 35 314
Pu u u
A.
2
B.
3
C.
2
D.
3
Hướngdẫngiải
Tacó:



  ... ... .
1
1 2 2018 1 2 1009 1
2018 2u 2017d
u u u 4 u u u 2 1009 2u 1008d
2

 : ; ; ;...
1n
dd3d5d
uu
2222
Khiđó:

log l og log min
MODE 7222
333
3d 9d 27d
PP2
22 2
Bài 24. Cho dãy số

n
u
thỏa mãn:


 ln ln
22
12 1 2
uu10 2u6u
và

 ,
n2 n n1
uu2u1n1
.Giátrịnhỏnhấtcủanđể
n
u 5050

A.
100
B.
99
C.
101
D.
102
Hướngdẫngiải
Tacó:




ln ln
22
22
1
12 1 2 1 2
2
2
u1
uu10 2u6u u1 u3 0
u3
20
Mặtkhác:


n2 n n1 n2 n1 n1 n
uu2u1uuuu1
.Đặt

nn1n
vu u
Suyra

n1 n
vv1

n
v
làmộtdãyCSCcócôngsai d1
 
n1 21
v v n1u u n1n1
Khiđó




.................
21
32
n1 n
nn1
uu2
uu3
uun1
uu n
Cộngvếtheovếtađược::


  ... ...
n1
nn 1
uu 23 n123 n
2
Vậy:


nn 1
5050 n 100
2
,suyraGiátrịnhỏnhất
min
n 101
Bài25.Xétcácsốthứcdương
,,xyz
thayđổisaochotồntạicácsốthực
,,abc 1
vàthỏa
mãn

y
xz
abc a b c
.Tìmgiátrịnhỏnhấtcủabiểuthứcvà

2
Pxy2z

A.
42
B.
4
C.6 D.10
Hướngdẫngiải
Tacó:







log
log log log log log
log
2x
a
2y
babcabcabcabc
2z
c
2x abc
aabc
111
b abc 2y abc a b c abc 1
2x 2y 2z
cabc
2z abc
Suyra



1
z
111
2
10
12 4z
2z 2x 2y
1xy
2z x y 2z 1
Khiđó,

,
2
4z 1
P2zz
2z 1 2
.Khảosáthàmsốsuyra MinP 6
Chúý:BĐTCauchy–Schwarz:

11 4
abab
21
Bài26.Chosốphức
zxyi
với
,xy
thỏamãn
z1i 1
và
 z33i 5
.GọiM,
mlầnlượt làgiátrịnhỏnhấtvàgiátrịlớnnhấtcủabiểuthức
Px2y
.Tínhtỉsố
M
m
.
A.
9
4
B.
7
2
C.
5
4
D.
14
5
Hướngdẫngiải
Tacó:


22
z33i 5 x3 y3 5
(1)
Thế
xP2y
vào(1)tađược:


22
22
P2y3 y3 5 5y 232PyP 6P130
(*)
Vậy(*)cónghiệmvớimọi
,xy
khivàchỉkhi:



*
ʹ
2
2
M7
0 3 2P 5 P 6P 13 0 4 P 14
m2
Nhậnxét:Cáchđạisốđơngiảndễhiểuvàv ớicáchgiảiđóanhnhậnrarằngđềcho
thừadữkiện
z1i 1
.
Bài 27. Cho các số phức
,,
123
zzz
thỏa mãn
,,
123
z4z3z2
và

12 23 31
4z z 16z z 9z z 48
.Giátrịcủabiểuthức

123
Pzzz
bằng:
A.
2
B. 3 C.
4
D.
1
Hướngdẫngiải
Tacó:




1
11
222
33
3
z4
zz 16
z3 zz9
zz 4
z2
.Thayvào

12 23 31
4z z 16z z 9z z 48
tađược:
.. .
33 12 11 23 22 31 1 2 3 1 2 3
123 123 123
123
zz zz zzzz zz zz 48 z z z z z z 48
48
zzz 2 zzz 2 zzz 2
zzz

 
22
Bài28.Chohaisốphức
,
12
zz
thỏamãn  
11 2
5
z12iz33i2z1 i 17
2
.Tìmgiá
trịlớnnhấtcủabiểuthức

12 1
Pzz z2i
.
A.
17 2 29
B.
17 29
C.
217
D.
329
Hướngdẫngiải
GọiM,Nlầnlượtlàđiểmbiểu diễncácsốphức
,
12
zz
Tacó:

;, ;A12B33 AB 17
và



;
5
I1
2
làtrungđiểmAB
Mà

11
z 1 2i z 3 3i 17 MA MB AB
MthuộcđoạnAB
Nthuộcđườngtròn(C)cótâm



;
5
I1
2
,

17
R
2
ABlàđườngkínhcủa(C)
Tacó:

 
12 1
P z z z 2 i OM ON MD MN MD
,với

;
D21
Vì



MAB
NC
nên MN 2R và MD BD 
Vậy

P2RBD 17 29
.Dấu“=”xảyrakhivàchỉkhi
,MDNA
23
BTTL. Cho các số phức
12
z, z , z thỏa mãn
12
12 52 4ziz i
và
32 72 10zizi
.GọiM,mlầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủabiểu
thức
12
3Pzz z i
.Tính
TMm
A.
9226
B.
15 109
C.
8107
D.
11 110
Bài 29. Chohai số phức
,
12
zz
thỏa mãn
  ,
12
1
z34i1z34i
2
.Số phứcz cóphần
thực bằng a, phầnảo bằng b thỏa mãn 3a 2b 12. Tìm giá trị nhỏ nhất của biểu thức

12
P z z z 2z 2
.
A.
8845
15
B.
9945
13
C.
9091
12
D.
9667
17
Hướngdẫngiải
TâphợpđiểmbiểudiễnSP
,
12
zz
làđườngtròntâm

;
I34
cóbánkínhlầnlượtlà
,
1
1
2
GọiMlàđiểmbiểudiễnsốphức
z
Mthuộcđườngthẳng
3x 2y 12
Đặt

323
z2z z68i1
làđườngtròntâm

;J68
cóbánkính
R1
Tacó:
 
13
Pzz zz 2MI1MJ12MIMJ
GọiAlàđiểmđốixứngcủaJ qua




;
138 64
3x 2y 12 A
13 13
24
Khiđó, 
9945
PMIMAIA
13
.Dấu“=”xảyrakhivàchikhi
,,MIA
thẳnghàng
Bài30.Chohàmsố
fx
cóđạohàmliêntụctrênđoạn


1; 2
thỏamãn:
Tínhgiátrịcủatíchphân



2
2
1
fx dx
.
A.
15
 B.
18
C.
21
D.
25
Hướngdẫngiải
Từđề
  
 

 

222 2
22 2
22
111 1
ʹ 27 63f x dx f x dx x f x dx x dx
(1)
Xét



2
2
1
Ifxdx
.Đặt

 




2
2 ʹdu f x f x
ufx
vx
dv dx
    




22
2
2
1
11
2 ʹ 63 2 ʹ
I x f x xf x f x dx xf x f x dx
     




22 2 2
222
2
11 1 1
12ʹʹ0 ʹ 0f x dx xf x f x dx x f x dx f x xf x dx
Dođó
   
1
ʹ 0 ʹ 0fx xf x fx fx Cx
x




Tacó:





2
2
2
22 22 2
1
23273 21
Cx x C C x x C f x dx
Bài31.Cho
,xy
là2gócthỏamãn

,
2
xy kk
và

sin 2sinxxy
.GọiM,mlần
lượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủabiểuthức

tanPxy
.Tính
22
QM m

A.
2
5
 B.
1
 C.
2
3
 D.
3
5


 








22
22
22
22 1 63
, 1; 2
2 ʹ 27
ff
x
fx x f x x
25
Hướngdẫngiải
Tacó:


 
sin sin sin cos sin .cosx xy y xy y y xy
    
sin cos sin .cos 2sin tan cos sin 2tan
xy y y xy xy xy y y xy

sin
tan
cos 2
y
xy
y

Tacó:
sin
sin cos 2
cos 2
y
PyPy
y

Điềukiệncónghiệm:
2
112
14
3
33
PPQ
Bài32.Chosốphứczkhác0thayđổivàthỏamãnđiềukiện

2
1
2mzzziz
z




với
m
làsốthựcdương.Tìmgiátrịnhỏnhấtcủa
m
.
A.
22
B.
22
C.
12
D.
12
Hướngdẫngiải


 
22 2
2
2
2
22
24
11
221121
.
1
2112 11
i
mzzzizmz i z mi
z
zz
z
i
zmi z m
zz





Xét
222 22
3
44 4
11 1
23..3
zzz zz
zz z


Suyra
 

22
22
12
113 12
12
m
mm
mLoai




Vậygiátrịnhỏnhấtcủamlà
12
.Dấu“=”xảyrakhivàchỉkhi 1
z
Bài33
.Chohàmsố
fx
cóđạohàmliêntụctrên
0;1

thỏamãn:
26





11
22
2
00
1404
11
ʹ 4
3
xx
ef f
efx fxdxefxdx






Tính

1
0
Ifxdx
.
A.

41
e
I
e
B

31
e
I
e
  C.

22
e
I
e
D.

52
e
I
e

Hướngdẫngiải
Xét





11
22
2
00
11
ʹ 4
3
xx
Je fx fx dx efxdx





Đặt
   
ʹʹʹʹ
xxxx
ux efx u efx ef x ef x u u
Khiđó

11
22
2
00
ʹ 4 ʹ 2.ʹ 4J u u u udx u uu udx





,với

14, 01
uu
Tacó
1
1
2
0
0
15
. ʹ
22
u
uu dx
và
111
1
0
000
ʹ 4 ʹudx xu xu dx xu dx

Suyra

1
2
0
8
ʹ 4 ʹ
3
Juxudx




Chọn
m
saocho:

1111
22 2
0000
ʹ 20ʹ 4 ʹ 2 ʹ 20u x m dx u xu dx m u dx x m dx







2
84
6202
33
mm m m 
Vậy
 
1
2
0
ʹ 22 0 ʹ 22
xx
u x dx e f x e f x x





 

1
22
01
0
52
221
ʹ 22
f
x
xx
e
xxC xx
efx x fx fx fxdx
e
ee
 
 
27
Bài34
.Chocácsốphức
12
,zz
thỏamãn
1zi
và

11 2 2
23 3 zz zz
.Giátrịlớnnhất
Mcủabiểuthức
12
23Pz iz i
thuộckhoảngnàosauđây?
A.

4; 6M
 B.

5; 7M
 C.

6;8M
 D.

7;9M
Hướngdẫngiải
Từđềsuyra
12
1
zi zi 
ÁpdụngBĐTBunhiacopxki:
22
12 1 2
2322 3Pz iz i z i z i   
Tacó:

 
22
111111
222 24zizizizizz  
Và

 
22
222222
333 39zizizizizz 


22
12 1122
22313223136Pzizizzzz




Bài35
.Chohìnhđagiácđều
H
có24đỉnh,chọnngẫunhiên4đỉnhcủahình
.H
Tínhxácsuất
để4đỉnhchọnđượctạothànhmộthìnhchữnhậtkhôngphảilàhìnhvuông?
A.
10
1771
 B.
15
1771
 C.
20
1771
 D.
18
1771
Hướngdẫngiải
Sốphầntửcủakhônggianmẫulà
4
24
10626.
C
Đagiácđều24đỉnhcó12đườngchéoquatâm.Cứ2đườngchéoquatâmtươngứng
chotamộthìnhchữnhậthoặchìnhvuông.Sốhìnhchữnhậtvàhìnhvuôngđượctạo
thànhlà
2
12
.C
Giảsử
12 24
, ,...,AA A
là24đỉnhcủahìnhH.VìHlàđagiácđềunên24đỉnhnằmtrên1
đườngtròntâmO
Góc
0
0
1
360
15
24
ii
AOA

với
1,2,...,23i
Tathấy:
0
17 714 1421
90
AOA AOA A OA
,dođó
171421
AAA A
làmộthìnhvuông,xoay
hìnhvuôngnày
0
15
tađượchìnhvuông
281522
AAA A
,cứnhưvậytađược6hìnhvuông.
28
Sốhìnhchữnhậtkhônglàhìnhvuônglà:
2
12
6 60.C 
Vậyxácsuấtcầntínhlà:
4
24
60 10
.
1771
C

Bài 36
. Cho số phức z thỏa mãn
42 2
23 29zz z
. Giá trị nhỏ nhất của biểu thức
2
2
1Pz z
bằng:
A.
2
B.
1
 C.
23
D.
2
Hướngdẫngiải
Tacó
42 2 2 2 2 2
2
9
23 29 2 13 29 1 3
2
zz z z z z z
z
 
Cách1:
Tacó
2
2
2
99
133
2
2
z
z
z

22 2
22 2
99 9
3252.251
22 2
Pzz z
zz z


Cách2:
Đặt

2
2
2
442422
22 2
224244442tz t z zz z zz z z z z

  


Suyra
2
99
2322.51zt P t t
tt
  
Dấu“=”xảyrakhivàchỉkhi zi
Bài 37
. Cho hàm số

fx
d ương và cóđạo hàm liên tục trên
0;1


thỏa mãn

1
0
16
f
,

1
3
0
1
1 ʹ
8
xfxdx
và


3
1
2
0
1
64
ʹ
fx
dx
fx




.Tínhtíchphân

1
0
fxdx
.
29
A.
1
24
 B.
1
32
 C.
1
8

D.
1
4
Hướngdẫngiải
  
111
1
33 2 2
0
000
11
1 ʹ 131 1
816
xfxdxxfx xfx xfx 

ÁpdụngBĐTHoldertacó:









1
2
3
3
3
3
111
2 2
2
2 2
3 3
22
000
33
1
2
12
3
3
11
3
33
3
2
00
1
1 ʹ .1ʹ
16
ʹʹ
111
 .1ʹ .
64 8 1
ʹ
fx fx
xfxdx dx xfxdx
fx fx
fx
dx x f x dx
fx








 




 




 


 





















6
Dấu“=”xảyrakhivàchỉkhi



3
3
2
2
2
3
2
3
1 ʹ
ʹ
fx
kx fx
fx
















3
33
ʹ
1
1
fx
kx
fx





(1)
Tacó




 
33
11 1
3
23
00 0
1
11
64
. ʹ 1 ʹ
1
64 8
ʹʹ
8
fx fx
dx f x dx k x f x dx k
fx fx
 
 

 
 

(1)


ʹ
2
1
fx
x
fx





1
0
16
2
1
ln 2ln 1
16 1
f
fx x C fx
x


1
0
1
32
fxdx
Bài 38
. Cho hàm số

fx
liên tục và cóđạo hàm cấp 2 trên
0;
thỏa mãn

01f
,

ʹ 00f
,
  
ʹʹ 5 ʹ 60, 0;fx fx fx x
,

ln2
0
1
6
fxdx
.Tínhtíchphân

ln2
2
0
fxdx
30
A.
15
4
B.
35
17
C.
27
20
D.
24
7
Hướngdẫngiải
      
ʹʹ 5 ʹ 60ʹʹ 2 ʹ 3 ʹ 20f x fx fx f x fx fx fx



(1)
Đặt
  
ʹ 2gx f x fx
,từ(1)suyra
 
ʹ 30gx gx
Xéthàmsố
     
3333
ʹ 3 ʹʹ30
xxxx
hx egx hx egx egx e gx gx




Suyra

hx
đồngbiếntrên

0; 0 0 ʹ 020 2hx h g f f

  
32
2 ʹ 220
xx x
egx e fx fx e




Xéthàmsố
    
22
2 ʹʹ220
xx x x
kx e fx e k x e f x fx e




Suyra

kx
đồngbiếntrên

0; 0 0 2 3kx k f

  
ln2
223
0
1
23 3 2
6
xx xx
efx e fx e e fxdx

Dấu“=”xảyrakhivàchỉkhi
 
ln2
2
23
0
27
32
20
xx
fx e e fx dx



Bài39
.Chohaihộpbimỗihộpcó2viênbiđỏvà8bitrắng.Cácviênbichỉkhánhauvềmàu.
Chohai người l ấymỗingườimộthộpvàtừhộpcủamình,mỗing
ườilấyngẫunhiên3viênbi.
Tínhxácsuấtđểhaingườilấyđượcsốbiđỏnhưnhau.
A.
4
5
P
B.
2
9
P
C.
11
25
P
D.
1
5
P
Hướngdẫngiải
GọiAlàbiếncốlấy0biđỏ,3bitrắng

3
8
3
10
7
15
C
PA
C

A
1
làbiếncốngườithứnhấtlấyđược0biđỏ,3bitrắng

1
7
15
PA
A
2
làbiếncốngườithứhailấyđược0biđỏ,3bitrắng

2
7
15
PA
VìA
1
vàA
2
độclậpnênxácsuấtđểhaingườicùnglấyđược0 biđỏ,3bitrắng là:
31

2
12 1 2
7
.
15
PA A PA PA




GọiBlàbiếncốlấy1biđỏ,2bitrắng

12
28
3
10
7
15
CC
PB
C

B
1
làbiếncốngườithứnhấtlấyđược1biđỏ,2bitrắng

1
7
15
PB
B
2
làbiếncốngườithứhailấyđược1biđỏ,2bitrắng

2
7
15
PB
VìB
1
vàB
2
độclậpnênxácsuấtđểhaingườicùnglấyđược1 biđỏ,2bitrắng là:

2
12 1 2
7
.
15
PB B PB PB




GọiClàbiếncốlấy2biđỏ,1bitrắng

21
28
3
10
1
15
CC
PB
C

C
1
làbiếncốngườithứnhấtlấyđược2biđỏ,1bitrắng

1
7
15
PC
C
2
làbiếncốngườithứhailấyđược2biđỏ,1bitrắng

2
7
15
PC
VìC
1
vàC
2
độclậpnênxácsuấtđểhaingườicùnglấyđược 2biđỏ,1bitrắnglà:

2
12 1 2
1
.
15
PC C PC PC




Vậyxácsuấtđểhaingườilấyđượcsốbiđỏnhưnhaulà:
222
77111
15 15 15 25
P




Bài40
.Cho sốphứczthỏamãn
13 3 22 2zizizi
.Tìm giátrịlớnnh ấtcủabiểu
thức
1Pz i
.
A.
11
3
B.
46
5
C.
33
3
D.
35
5
Hướngdẫngiải
32
Tacó:
 
22 22
13 3 1 3 3 1zizix y x y
Và

22
22 2 2 2 2 2 1zi x y
ÁpdụngBĐTBunhiacopxki:
  
22 22 2222
13 3121331
xy xy xyxy

 


Suyra
 
22 2222
22 2 2 1 2 1 3 3 1
xy xyxy

  


Thựchiệnphépbìnhphươngvàrútgọntađược:

22
11 33
11 1
33
xy zi
Dấu“=”xảyrakhivàchỉkhi
55
66
55
66
zi
zi


Bài41
.Chohàmsố
yfx
cóđạohàmliêntụctrênđoạn
1; 2

thỏamãn:


 

3
2
2
7
1
3
, 1; 2
3
ʹ
ʹʹ
f
x
xfx
fx x
fx xfx x








Tính

2f
.
A.

77 1
2
3
f
B.

77 1
2
3
f
C.

27 1
2
3
f
D.

27 1
2
3
f
Hướngdẫngiải
Đề
     
23
3233
3 ʹʹʹ 3 ʹxfx f x x f x xf x x xfx f x x

 
 
 


 


3
3
3
ʹ
31ʹ
31
fx
xfx fx x
fx



Suyra


 

222
1
3
3
111
ʹ
31 3
3131
23 2
31
fx
dx xdx f x d f x
fx




   
2
222
333
1
13 3 7 7 1
.3 1 321 311 3 2
32 2 3
fx f f f
 

 
33
BTTL1:
Chohàmsố

fx
dươngvàcóđạohàmkhôngâm,liêntụctrênđoạn
0;1

thỏamãn:

 

2
2
2
01
, 0;1
. ʹ
1
x
f
x
fx f x
fx
e








Khẳngđịnhnàosauđâyđúng?
A.

5
13
2
f
B.

7
31
2
f
C.

5
21
2
f
D.

3
12
2
f
Bài42
.Chosốphứczkhôngphảilàsốthuầnảothỏamãn
2z
vàsốphức
4
1
z
w
z
làsố
thuầnảo.Biết

2
a
zz
b



,ab
,
a
b
làphânsốtốigiản.Tính
2
Taabb
A.
125
B.
125
C.
75
D.
75
Hướngdẫngiải
Vì
w
làsốthuầnảonên:
44
0
1
1
zz
z
z




44
44
32
32
2
2
110 ..0
.0. .0
1. . 0
z z z z zzzz zz
zzzzz z zzzzzzz zzz
zz zzz zzz





 









Vì
z
khôngphảilàsốthuẩnảonên

0zz
,suyra:

 
2
2
2
2
22
22
1. . 0 3. 1
147
31 3.4
44
zz z zz z z z z zz
zzz z zz











Bài43
.Chosốphứcz,wthỏamãn
53 3zi
và
42 2iw i
.Tìmgiátrịlớnnhấtcủabiểu
thức
32Pizw
A.
554 5
B.
578 13
C.
578 5
D.
554 13
Hướngdẫngiải
34
Đặt
1
1
2
2
3
3
2
2
z
z
ziz
i
zw
z
w




.Thayvàogiảthiếttađược:
1
1
22
53 3
15 9 9
3
844
.422
2
z
i
zi
i
zzi
ii







GọiA,Blầnlượtlàđiểmbiểudiễncácsốphức
12
,zz
SuyraAthuộcđườngtròntâm

9;15I
,bánkính
1
9R vàBthuộcđườngtròntâm

4; 8J
,bánkính
2
4R
Tacó:
12 1 2
554 13Pzz OAOBABIJRR 
 
Bài44
.Chosốphức
12
,,zz z
thỏamãn
12
45 11ziz
và
484ziz i
.Tính
12
zz
khi
12
Pzz zz 
đạt
giátrịnhỏnhất.
A.
41
B.
6
C.
25
D.
8
Hướngdẫngiải
*GọiAlàđiểmbiểudiễn
1
z
Athuộcđường
tròn

1
C
tâm

11
4;5 , 1JR
*GọiBlàđiểmbiểudiễn
2
z
Bthuộcđường
tròn

2
C
tâm

22
1;0 , 1JR
*

484 : 4ziz i dy x
Mthuộcđườngthẳng

d
,
zxyi
Tacó:
P OMOA OMOB MAMB
   
*Gọi

3
C
cótâm

33
4; 3 , 1JR

làđườngtròn
đốixứngcủa

2
C
qua

d
vàB’làđiểmđối
xứngcủaBqua

d
,khiđó

3
ʹBC
………………………………………………
………………………………………………
Khiđó:
13 1 3
ʹʹ 6PMAMBMAMB AB JJ R R 
Dấu“=”xảyrakhivàchỉkhi
13
,, ,ʹ,JAMBJ
thẳnghàng
Tacó

ʹ
331
ʹ
40
1
ʹʹ4; 2 2;0
1
8
3.8
8
B
B
x
JB JJ B B
y



 
35
Lạicó

113
40
1
4;4
1
8
5.8
8
A
A
x
JA JJ A
y



 
Vậy
12
44 2 25zz i
Bài 45
. Cho dãy số

n
u
thỏa mãn
2
11
1, 1, 1
nn
uu au n

,
1a
. Biết rằng

22 2
12
lim ... 2
n
uu u nb
.Giátrịcủabiểuthức
Tab
A.
1
B.
2
C.
1
D.
2
Hướngdẫngiải
Đề
22 2 2
11
11
1
11
nn n n
uau u au
aa






Đặt
2
1
1
1
nn n n
vu v av
a


n
v
làcấpsốcôngvớicôngb ội qa
Suyra
12 1 1 2 1
11
11
..
1111
nnnn
nn
aa
vva u a a ua
aa aa






Tacó:

2
1
2
22 2 1
2
12
21
1
11
1
.
1
... 1 ... .
11
11
.............................
1
.
11
n
n
n
n
a
u
aa
a
ua
a
uu u a a n
aa
aa
a
ua
aa



 




22 2
12
11
... . .
111
n
n
aa
uu u n
aa a


Thựchiệnphépđồngnhấttađược:
1
2
1
2
1
1
1
1
2
1
lim 2
lim .
1
11
1
2
n
n
a
a
T
aa
b
b
aa




















BTTL
. Cho dãy số

n
u
thỏa mãn
2
11
2
1, ,1
3
nn
uu uan

. Biết rằng

22 2
12
lim ... 2
n
uu u nb
.Giátrịcủabiểuthức
Tab
A.
1
B.
2
C.
1
D.
2
Hướngdẫngiải
36
Bài46
.Chodãysố

n
u
thỏamãn
12
21 3
2
331
8
22
1
log 4 4
4
uu
uu






và
1
2
nn
uu
vớimọi
1n
.Đặt
12
...
nn
Suu u
.Giátrịnhỏnhấtcủanđể
10
28
n
S
là:
A.
53
B.
51
C.
50
D.
52
Hướngdẫngiải
TheoGT,
1
2
nn
uu
nên

n
u
làmộtCSNvớicôngbội
1
21
1
31
2
2.2
4
n
n
uu
quu
uu

Xét
121 1
11
21 3
88
2 2 2.4 2 2.4 . 8
44
uuu u
uu


Và

2
22
3
331 333 3 3
8888
8
log 3
111
log 44log 4log 23
444
uu uu u





Dođódấu“=”xảyrakhivàchỉkhi
1
1
1
3
3
8
1
2.4
2
4
2
2
u
u
u
u
u



Khiđó

10 10
12min
12 2 1
. 28 log 2.28 1 49,07 50
12 2
nn
n
Su n n


Bài47
.Chohàmsố

fx
cóđạohàmliêntụctrênđoạn
0;1

thỏamãnđiềukiện:

2018 2017 2018fx fx
,
x

Giátrịtíchphân

1
2
0
f
xdx


bằng:
A.

2
4
ʹ 1
3
f


B.

2
5
ʹ 1
3
f


C.

2
7
ʹ 1
3
f


D.

2
8
ʹ 1
3
f


Hướngdẫngiải
Xét

2018 2017 2018fx fx
(*)
Đạohàm2vếcủa(*):

2018 ʹ 2018 2017 2018 ʹfx fx
37
Thay
x
bởi
2017
2018
x
,tađược:

2017 2018 1
ʹʹ ʹ
2018 2018
xx
fx f f
 



(1)
Tiếptụcthay x bởi
2017
2018
x
:

2
2
2017
2018 1
2018 1
2018
ʹʹ ʹ
2018
2018
x
x
fx f f











Thayđếnn lầnvàbằngquynạptachứngminhđược:

2018 1 1
ʹʹ ʹ 1
2018 2018 2018
n
nnn
xx
fx f f







Khi
n 
thì
 
ʹʹ1 ʹ 1fx f fx f xC 
(2)
Thay 1x  vàođềtađược
  
1 2018 1 1 0fff 
Thay 1x  vào(2)tađược
 
1 ʹ 10ʹ 1ffCfC 
Vậy
  
1
22
0
7
ʹ 11 ʹ 1
3
fx f x fx dx f



Bài48.TrongkhônggianOxyz,xétmặtphẳng


22
:2 1 1 10 0Pmxm ym z
và
điểm

2;11; 5A
.Biếtkhi
m
thayđổi,tồntạihaimặtcầucốđịnhtiếpxúcvớimặtphẳng

P
vàcùngđiqua
A
.Tínhtổngbánkínhcủahaimặtcầuđó.
A.
22
B.
52
C.
72
D.
12 2
Hướngdẫngiải
Gọi lầnlượtlàtâmvàbánkínhcủamặtcầu.Domặtcầutiếpxúcvới nênta
có
(
)
;; ,
abc r
()
P










22
2
22
21110
210
,
12 12
ma m b m c
bcm mabc
rdIP
mm
38
TH1:
Domthayđổivẫncómặtcầu cốđịnhtiếpxúcvới(P)nênyêucầubttrởthànhtìm
điềukiệnsaocho(1)khôngphụthuộcvàom.Dođó(1)luônđúngvớimọi
25
0
5
br
a
c




Suyra .
Lạicónênsuyra:
TH2:
làmtươngtựTH1(trườnghợpnàykhôngthỏa
đềbài)
Tómlại:Khi thayđổi,tồntạihaimặtcầucốđịnhtiếpxúcvớimặtphẳngvà
cùngđiquavàcótổng
bánkínhlà:suyrachọnD
Bài49.TrongkhônggianOxyz,chođiểm

1; 4; 3A
vàmặtphẳng

:2 0Pyz
.Biếtđiểm
Bthuộc

P
,điểmCthuộc

Oxy
saochochuvitamgiác ABC nhỏnhất.Hỏigiátrịnhỏnhất
đólà:
A.
45
B.
25
C.
5
D.
65
Hướngdẫngiải
Gọi
12
,AA
lầnlượtlàđiểmđốixứngcủaAqua

P
và

Oxy
.
Phươngtrìnhthamsố

1
1
:42 1;42;3
3
x
AA y t H t t
zt



với

1
HPAA
Vì

HP
nên

1
24 2 3 0 1 1;0;5tt t A






 

 
2
22
2
22 21001
21012
22 21002
bcr m mabcr
bcm mabc rm
bcr m mabcr


 
2
22 21001bcr m mabcr
,,abc
20
0
210 0
bcr
a
bcr
ì
ï
+- =
ï
ï
ï
=
í
ï
ï
ï
-- - =
ï
î





2
2
22
0;5 2; 5 : 5 2 5Ir Sxyr z r
()
A
SÎ


2
22
22
4115 2 122400
10 2
r
rrr r
r

 
2
22 2100bcr m mabcr
m
()
P
A
12 2
39
Tươngtựtatìmđược

2
1; 4; 3A
Dễthấy
1
AA B
cântạiBvà
2
AA C
cântạiCnên
1
2
AB A B
AC A C

.Vậychuvi
ABC
bằng:
1212
45
ABC
C ABBCCA ABBCAC AA

Dấu“=”xảyrakhivàchỉkhi
12
,,,ABCA
thẳnghàng
Bài50.Chohàmsố

fx
cóđạohàmliêntụctrênđoạn
0;1

thỏamãn:


   
11
0, 0;1
ln ʹ 1
f
fx x
fx fx xf x fx





Tínhtíchphân

1
0
f
xdx
.
A.

1
0
1
3
e
fxdx
B.

1
0
6
6
e
fxdx
C.

1
0
4fxdx
D.

1
0
1fxdx
Hướngdẫngiải
Đề
     



ʹ
ln ʹʹ ln . ʹ
fx
f
x f x x f x xf x f x f x x xf x
fx




    
11
11
00
00
ln ʹʹ ln ʹx f x xf x x f x xf x dx xf x f x dx

Suyra

1
0
11fxdx f
| 1/40
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PMT 2810 50 caâu hoûi hay vaø khoù trong ñeà thi thöû 2018
Sưu tâm và biên soạn: Phạm Minh Tuấn
Chúc các em đỗ vào trường Đại Học mà mình mong muốn <3 1
Bài 1. Cho cấp số cộng u có các số hạng đều dương, số hạng đầu u 1 n 1
và tổng của 100 số
hạng đầu tiên bằng 14950 . Tính giá trị của tổng 1 1 1 S    ...  u u u u u u u u u uu u 2 1 1 2 3 2 2 3 2018 2017 2017 2018 1  1  1  2  A. 1   B. 1   3  6052  3  6052  1  1  1  2  B. 1  D. 1   3  6052  3  6052  Hướng dẫn giải
Tổng của n số hạng đầu của cấp số cộng được gọi là tổng riêng thứ n:
n 2u n  1 d  1    S n 2 100 2  99d   Áp dụng : S
 14950  d  3 và u u d, u
u  2017d  6052 100 2 n1 n 2018 1    1 1 u u nn 1 1 1 Ta có:       u u u u       u u u u u u u u d u u n n n n . . n1 n n1 n  1 1 1 n1 n n1 n   n n1  Khi đó:         1 1 1 1 1 1 1 1 1 1 1 1 S          ...        d u
u d u u d u ud u u   1 2   2 3   2017 2018   1 2018  1  1   1  3  6052 
Bài 2. Cho các số phức z , z thỏa mãn z z  1 , z z  1 và z  z . Tìm giá trị nhỏ 1 2 1 2 1 2 1 2 z z 1  z z
nhất của biểu thức 1 2 1 2 P   1  z z z z 1 2 1 2 A. 1
B. 2 C. 3 2 D. 4 Hướng dẫn giải 2 z z Đặt 1 2 t  , ta có: 1  z z 1 2
z z z .z z z z z z z z    z z z z z 1 2 1 2  1 2  1 2 1 2  1 2  1 2 1 2   1  z z    1 2 1 z .z 1 z z 1 z .z 1 2  1 2   1 2 
z z z z z z z z z z z z
z z z z z z z z 1 1 2 2 1 1  2 2  2 2  1 1  1 1 2 2  2 2  1 1     0 1  z z 1  z .z 1  z z 1  z .z 1 2   1 2   1 2   1 2  1
Suy ra t là số thực, khi đó P t
, khảo sát hàm số ta được GTNN của P là 2, đạt t được khi t  1 
Chú ý: z z  0 thì z là số thực và z z  0 thì z là số thuần ảo
Bài 3. Cho các số phức z , z thỏa mãn z  6, z  2 . Gọi M, N lần lượt là điểm biểu diển 1 2 1 2
các số phức z , iz . Biết 0 MO
N  60 . Tính giá trị của biểu thức 2 2
T z  9z . 1 2 1 2 A. 24 3
B. 36 2 C. 36 D. 36 3 Hướng dẫn giải
    2 2
T z  9z z  3iz z  3iz OM OP OM OP 1 2 1 2 1 2 P   ON
Với P là điểm biểu diễn số phức 3iz   2 OP  3iz   6  2 OM   OP Ta có: 
 OMP đều, gọi I là trung 0  MON  60 6 3
điểm MP  T  2OI.PM  2. .6  36 3 2
Bài 4. Cho ngẫu nhiên hai số thực a,b  0;1 
. Tính xác suất để phương trình 3 2
x  3ax b  0
có tối đa hai nghiệm 3 1 1 3 A. B. C. 1  D. 1  3 4 4 3 4 4 3 4 4 3 4 4 Hướng dẫn giải 3 x  0 Xét 3 2
y x  3ax b ; 2
y ʹ  3x  6ax ; y ʹ  0   x   2a
Yêu cầu bài toán  y   y a   b 3 0 . 2 0
b  4a   0
‐ Nếu b  0  a  0
‐ Nếu b   b  3 0 4a 1 Ta có: 3
4a  1  a  3 4
Xác suất cần tìm là diện tích của miền được giới hạn bởi: 3 1
y  4a , y  1, a  0, a  3 4 1 3 4 3
Vậy xác suất cần tìm là P   3
1  4a da   3 0 4 4
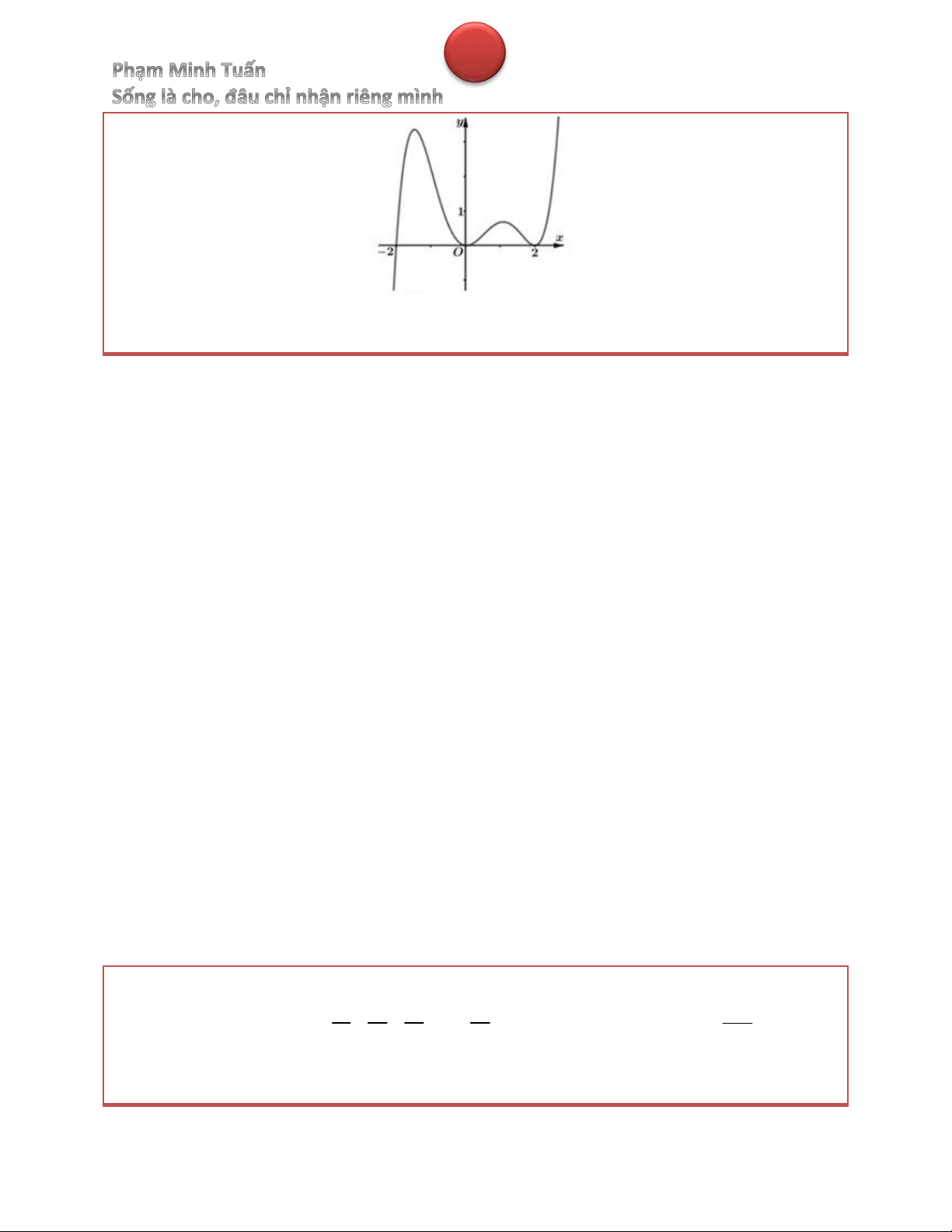
Bài 5. Cho hàm số y f x có đồ thị như hình vẽ. Có bao nhiêu giá trị thực của tham số m để hàm số 2
y f x  f x  m có đúng 3 điểm cực trị. 1 1 A. m B. m C. m  1 D. m  1 4 4 Hướng dẫn giải 2        2 f x f x
m 2 f ʹ x f x f ʹ x     Ta có 2
y   f x  f x          
m  yʹ    2  f
 x  f x 2 2  m 4
f ʹx  0  x  1; x  3  
y   f x 1 ʹ 0
   x x  0 0  2  2 f
 x  f x  m  0 1 
Đặt t f x , từ (1) ta được: 2
t t m  0 (*)
Ta đã tìm ra 3 điểm cực trị là x  1; x  3; x x  0 , nên để hàm số đã cho có đúng 3 0 1 1
điểm cực trị thì * vô nghiệm hoặc có nghiệm kép t   , hay   1 4m  0  m  . 2 4 2 1  1  1
Thử lại ta thấy m    t   0  t     (thỏa) 4  2  2 1
Vậy đáp số là m  4
Bài 6. [CHUYÊN HẠ LONG] Cho hai hộp đựng bi, đựng 2 loại bị trắng và bi đen, tổng số bi
trong hai hộp là 20 bi và hộp thứ nhất đựng ít bi hơn hộp thứ hai. Lấy ngẫu nhiên từ mỗi hộp 1 55
bi. Cho biết xác suất để lấy được hai viên bi đen là
, tính xác suất để lấy được 2 viên bi trắng. 84 1 15 11 A. B. C. D. Đáp án khác 28 84 84 Hướng dẫn giải
Gọi x, y lần lượt là số bi ở hộp thứ nhất và hộp thứ hai, x, y 0; 20 0  x  9
Vì x y  20  
(*). Lấy ngẫu nhiên 2 viên bi bất kỳ từ 2 hộp n  . x y 11  y   19
Gọi m, n lần lượt là số bi đen ở hộp thứ nhất và hộp thứ hai, m 0; x ,n0; ym n
Gọi A là biến cố: “Lấy được hai viên bi đen”  P A . 55 55    . m n  . x y . x y 84 84
Mặt khác m,n    .
x y84 . Từ điều kiện (*) thì chỉ có x  6; y  14 thỏa mãn Suy ra .
m n  55  5.11 nên m  5; n  11 5
c x m  1
Gọi c, d lần lượt là số bị trắng ở hộp thứ nhất và hộp thứ hai, khi đó 
d y n   3 1.3 1
Vậy xác suất để lấy được 2 viên bi trắng là P   6.14 28
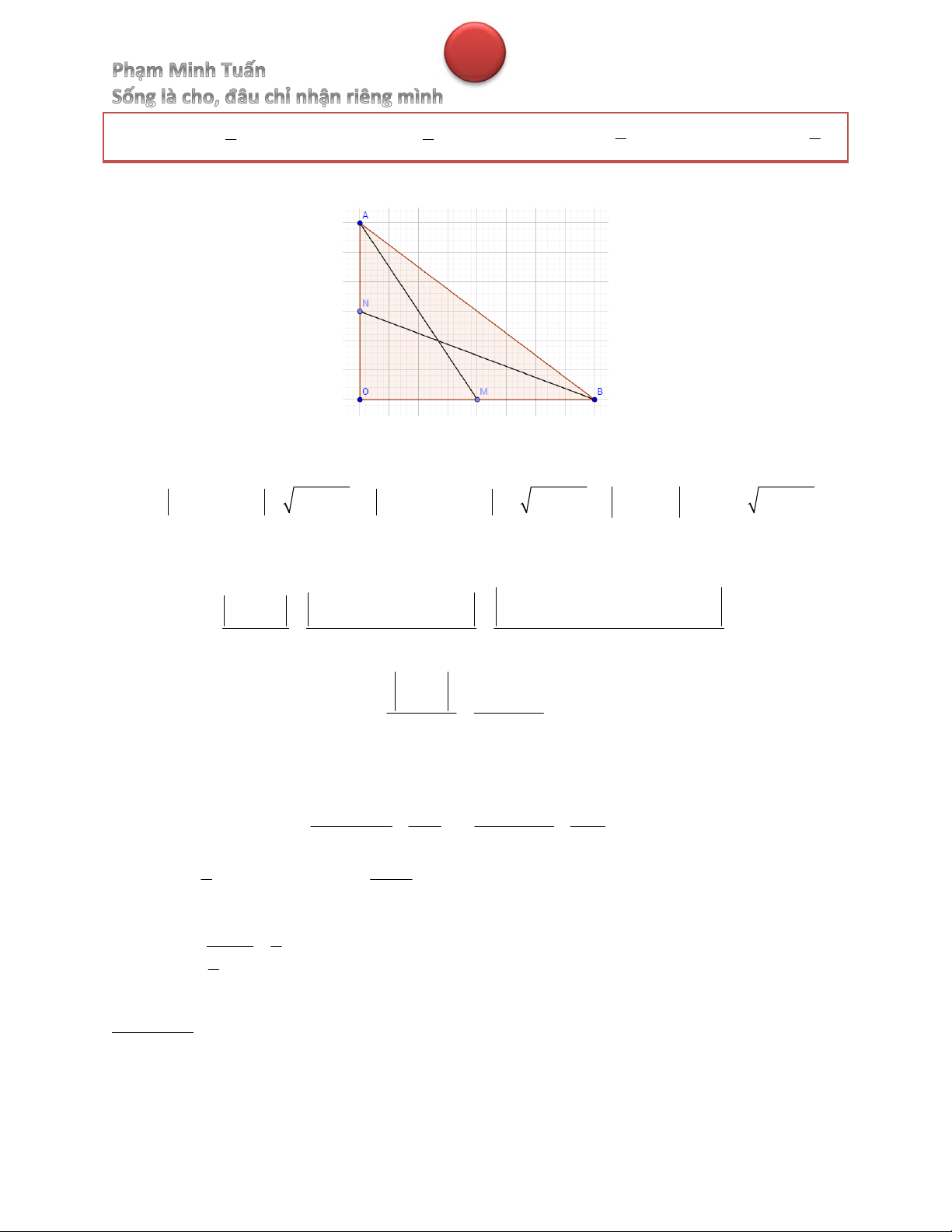
Bài 7. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A 7; 2; 3 , B1; 4; 3 , C 1; 2; 6
D 1; 2; 3 và điểm M tùy ý. Tính độ dài đoạn OM khi biểu thức P MA MB MC  3MD
đạt giá trị nhỏ nhất. 3 17 3 21
A. OM  14 B. OM  26 C. OM D. OM  4 4 Hướng dẫn giải   
DA  6; 0; 0 , DB  0; 2; 0 , DC  0; 0; 3 nên tứ diện ABCD là tứ diện vuông đỉnh D
x y z
Dự đoán M D nên ta giả sử M x y z   2 2 2 1; 2;
3  MD x y z  3
Ta có: MA  x  2 2 2
6  y z x  6  6  x
Tương tự MB x   y  2 2 2
2  z y  2  2  y , MC x y  z  2 2 2 3
z  3  3  z
Suy ra P  6  x  2  y  3  z x y z  11
Dấu “=” xảy ra khi và chỉ khi x y z  0 hay M D OM  14
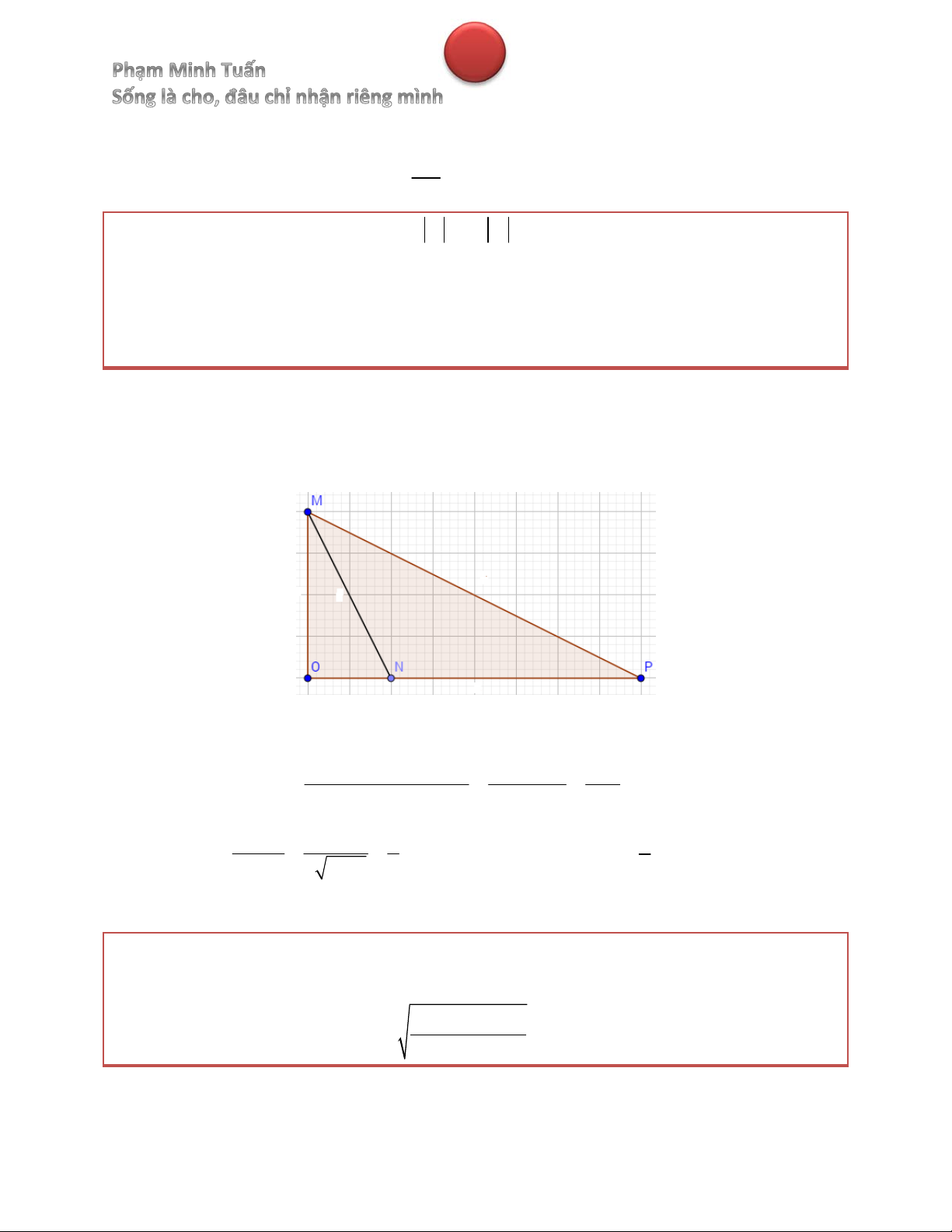
BTTL. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A 2; 2; 2 , B0; 2; 2 C 2; 0; 2 ,
D 2; 2; 0 và điểm M tùy ý. Tính độ dài đoạn OM khi biểu thức P  3MA MB MC MD
đạt giá trị nhỏ nhất. .
A OM  3 2 B. OM  2 3 C. OM  2 D. OM  3
Bài 8. Cho hàm số f x liên tục trên và có đồ thị như hình bên dưới 6
Gọi hàm g x  f f
 x . Phương trình gʹx  0 có bao nhiêu nghiệm phân biệt. A. 8
B. 10 C. 14 D. 12 Hướng dẫn giải
Ta có: g ʹx  f ʹx. f ʹ  f  x ;
f ʹx  0 1   f x   f ʹx   0 2   g x 0 ʹ  0    f x    f ʹ  f   x   2 3   0 
f x  m  2   m  1   4   f
 x  n 1  n  2 5
‐ Đồ thi hàm số y f x có 4 điểm cực trị nên 1 có 4 nghiệm phân biệt
‐ Đồ thị y f x giao với Ox tại 3 điểm nên 2 có 3 nghiệm, trong đó có 2
nghiệm trùng với 1 . Suy ra 2 có 1 nghiệm phân biệt
‐ Đồ thị y f x giao với y  2 tại 3 điểm nên 3 có 3 nghiệm phân biệt
‐ Đồ thị y f x giao với y m  2   m  1
  tại 1 điểm nên 3 có 1 nghiệm phân biệt
‐ Đồ thị y f x giao với y n 1  m  2 tại 3 điểm nên 3 có 3 nghiệm phân biệt
Vậy tổng có có 4  1  3  1  3  12 nghiệm phân biệt
Bài 9. Cho cấp số nhân u ,u ,u ,..,u ; trong đó u  0, i  1, 2,...,n . Biết rằng 1 2 3 n i 1 1 1 1 1
u u u  ...  u  2018 ,    ...
 2019 và P u .u .u ....u . Hỏi số 1 2 3 n u u u u 1 2 3 n 100 1 2 3 n
tự nhiên nhỏ nhất thỏa mãn P là:
A. 9295 B. 9296 C. 18592 D. 18591 7 Hướng dẫn giải n u q  1 1  
Ta có: u u u  ...  u  2018   2018 (1) 1 2 3 n q  1 n   1  1    1 n u  q    1   1 1 1 1 1 q  Và    ...  2019   2019   2019 (2) n1 u u u u 1 u q 1  q 1 2 3 n 1   1 q 1 nq q  1 2019 n 2018 Từ (1) và (2) suy ra .   u qn1 u q 1 nq u q 1 2018 2019 1   1  2 1 1 1
Ta có: u .u .u ....u  1 2 3 n 100
u u q  2 u q   n1 1 . . . . .... u .q  1 1 1 1  100  n n n1 1 n   n n 1 2018 1 2  u q   u q    1  1  2 2 1 2   100 100  2019  100  1   n  2log  18591,1  n    18592 2018  100  2019
Bài 10. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 3 3 3
4 sin x m  sin x  sin x  4 sin x m  8  2 có nghiệm thực
A. 20 B. 21 C. 22 D. 19 Hướng dẫn giải 3
a  4sin x m Đặt 
. Phương trình trở thành:
b  sin x
a b a b    a b  3 3 3 3 3 3 8 2 2
a b  8  3a ba  2b  2  0 a  2   b  2  VN a b   0 8 8  m 8  m
TH1: a  2  sin x   1  
 1  4  m  12 4 4 TH2: 3
a b  0  m  sin x  4sin x  5   m  5
Vậy có 20 giá trị nguyên m thỏa mãn
Bài 11. Có tất cả bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số 2
y  ln x  2x m
là nhỏ nhất trên đoạn 1; 2  
A. 1 B. 2 C. 3 D. vô số Hướng dẫn giải 1 1 Xét g x 2
 ln x  2x ; gʹx   4x; gʹx  0  x   (loại) x 2 g 1  2
 ; g2  ln 2  8  max gx  m  max m  2 ; m  ln2 8  hm
Đường màu xanh, tím, đen lần lượt là đồ thị y m  m  2 , y m  m  ln 2  8 và hm 1
Phương trình hoành độ giao điểm : m  ln 2  8  m  2  m  5  ln 2 2 1
Dựa vào đồ thị ta thấy h m nhỏ nhất khi và chỉ khi m  5  ln 2 2
Bài 12. [CHUYÊN ĐẠI HỌC VINH‐LẦN 1] Giả sử z , z là hai trong số các số phức z thỏa 1 2
mãn iz  2  i  1 và z z  2 . Giá trị lớn nhất của z z bằng: 1 2 1 2
A. 4 B. 2 3 C. 3 2 D. 3 Hướng dẫn giải 9 Cách 1: Đại số
Ta có: iz  2  i  1  z  1  i 2  1
w z 1i 2
 w w  2 Đặt 1 1 1 2   
w z 1 i 2
w w  1  1 2 2 2 2 2 2 2
w w w w  2 w  2 w w w  0  w w  0 1 2 1 2 1 2 1 2 1 2
z z  2 1 i 2  z z  2 3 1 2   1 2 2 2 2 2
Ta có: P z z  2 z  2 z
z z z z  12  4  4 1 2 1 2 1 2 1 2 Cách 2: Hình học
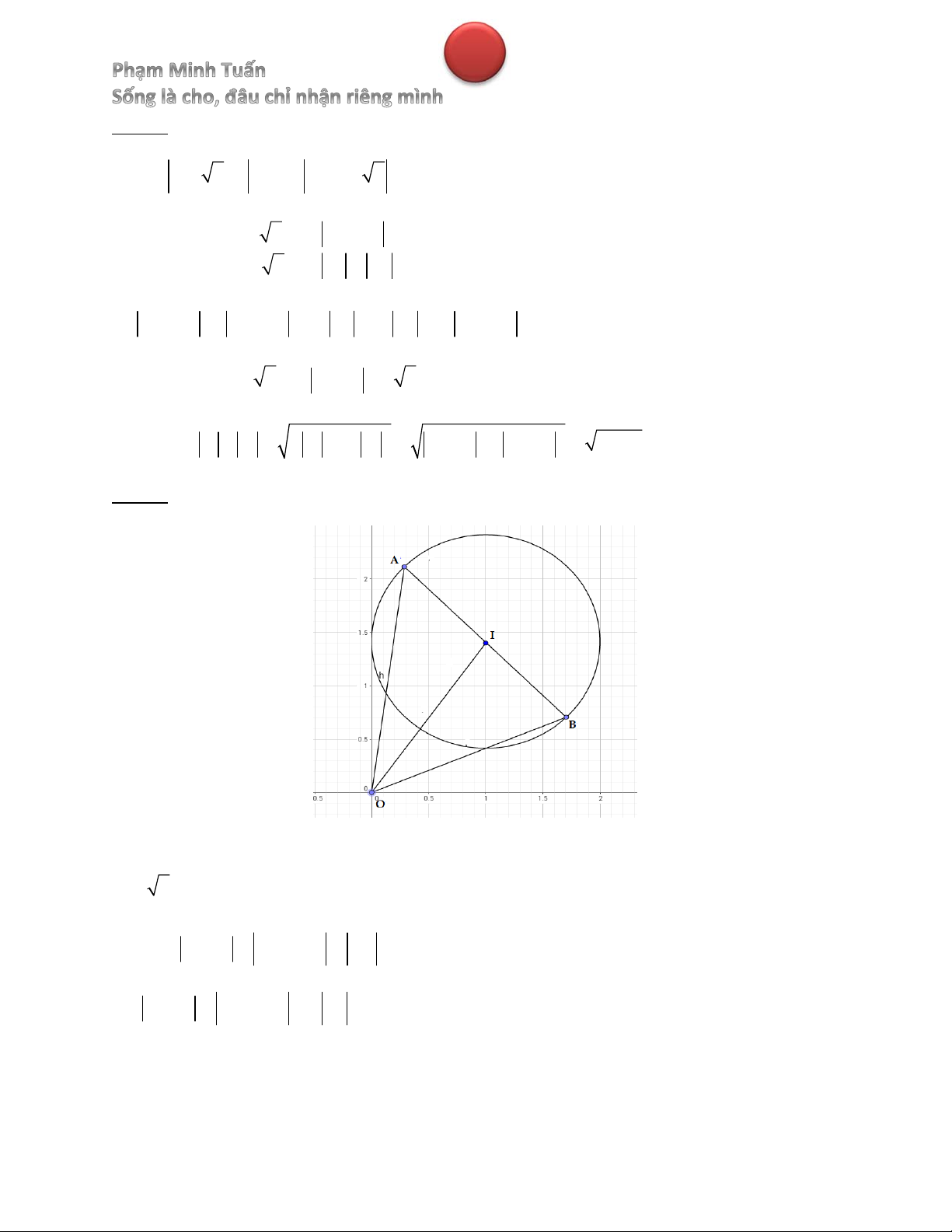
Gọi A, B lần lượt là điểm biểu diễn số phức z , z  A, B thuộc đường tròn (C) tâm 1 2
I 1; 2  , bán kính R  1   
Khi đó, z z OA OB BA AB  2  AB là đường kính của đường tròn (C) 1 2   
Và z z OA OB  2 OI  2OI , với I là trung điểm AB 1 2 10
Áp dụng công thức đường trung tuyến: 2 2 2 2 2      2 OA OB AB 2 2 2 AB 2 OI  
OA OB  2OI    2 3    8 2 4  4   4 
Ta có P z z OA OB  2  2 2 OA OB  2.8  4 1 2 
BTTL1. Giả sử z , z là hai số phức thỏa mãn z  1  i  2 và z iz . Giá trị nhỏ nhất của 1 2 1 2 1 z z bằng: 1 2
A. 2 2  1 B. 2 2  1 C. 2 2  2 D. 2 2  2
BTTL2. Giả sử z , z là hai số phức thỏa mãn z i  1 i z và z z  3  4i . Giá trị 1  1 2 1 2 2
nhỏ nhất của z z bằng: 1 2 33 33 A. 2 B.  2 C.  2 D. 2 2  1 10 5
BTTL3. Giả sử z , z là hai trong số các số phức z thỏa mãn z  3  4i  2 và z z  1 . Giá 1 2 1 2 2 2
trị nhỏ nhất của zz bằng: 1 2
A. 10 B. 5 C. 6  2 5 D. 4  3 5
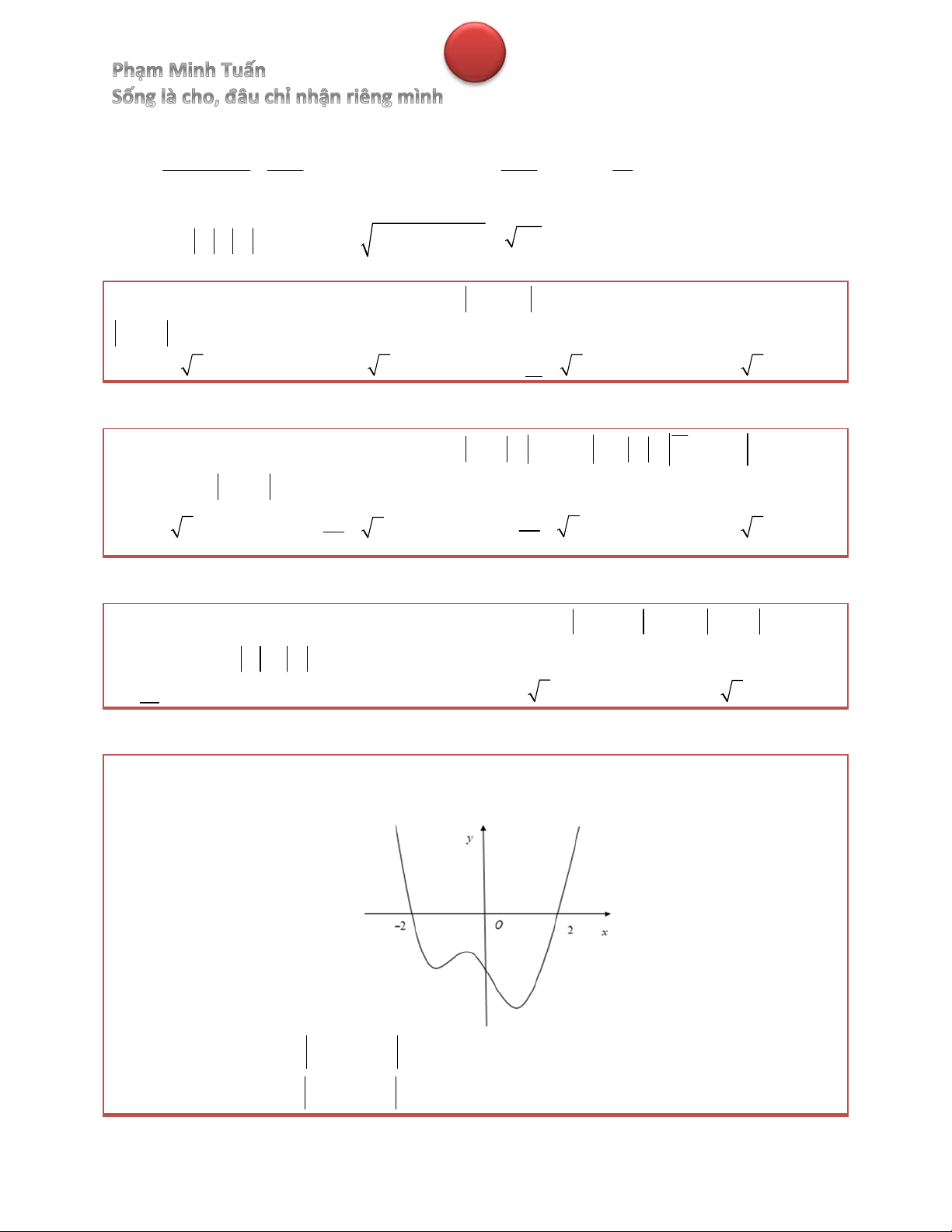
Bài 13. Cho hàm số y f x liên tục trên , có f 2  0 và đồ thị hàm số f x như hình
vẽ bên. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số y f   2018 1 x
nghịch biến trên khoảng ;2.
B. Hàm số y f   2018 1 x
có hai cực tiểu. 11
C. Hàm số y f   2018 1 x
có hai cực đại và một cực tiểu.
D. Hàm số y f   2018 1 x
đồng biến trên khoảng 2;. Hướng dẫn giải
Từ đồ thì của f x ta có bảng biến thiên như sau:
Từ giả thiết f 2  0 và  2018 x   f   2018 1 1 1 x 0 với mọi x.  ft t x
t    0 khi   2;  1  2018 2018  3; 3  Đặt t   2018 1 x , ta có: 
f t  0 khi t ;22;  x 2018 2018 
; 3 3; 2017 2018.x
. f t . f t
Đặt g x  f   2018 1 x
 , ta có: gxt       2 2 f t
Do đó, ta có bảng biến thiên của y g x như sau: Vậy chọn C.
Bài 14. Cho các số phức z ,z thỏa mãn z r , z  2r và iz  1  i z r  4r . Gọi 1   2 2 1 2 1 1 2 2 2 1 2
A,B, M,N lần lượt là điểm biểu diễn các số phức 2iz , 2  2i z , 1  i z , iz . Biết là góc 1   2   2 1
giữa AM và BN . Tìm giá trị nhỏ nhất của cos . 12 4 3 3 2 A. cos   B. cos 
C. cos   D. cos   min 5 min 4 min 5 min 3 Hướng dẫn giải
Từ đề suy ra OA  2r ; OB  4r và M ,N lần lượt là trung điểm OB và OA 1 2  
Ta có: iz  1  i 2 2
z r  4r  2iz  21  i 2 2 2 2
z  2 r  4r OA OB AB  2 r  4r 1 2 1 2 1 2 1 2 1 2
Do đó tam giác OAB vuông tại O      
      AM.BN
AOAB.BOBAAO BOABBOAO 2 .  AB Ta có: cos    AM.BN 4AM.BN 4AM.BN 2   2  AB 2 AB
Vì OA OB  .
AO BO  0  cos   4AM.BN 2AM.BN Lại có: 2 2 2 2 2 2       2 2 OA AB OB OB AB OA
2AM.BN AM BN          2 4   2 4  1
 OA OB  2 2 2 2 5ABAB   2 2 2
do AB OA OB  4 4 2 AB 4 Vậy cos   5 2 5 AB 4
Nhận xét: Ngoài cách trên ta có thể chuẩn hóa r bằng một số dương bất kì rồi đưa 1
cos về hàm theo biến r , khi đó việc tìm min sẽ dễ dàng hơn. 2 13 4  z 1  2018 Bài 15. Gọi  1 z , z2 , 3
z và z4 là các nghiệm của phương trình  
. Tính giá trị của  2z  i  2019
biểu thức P   2 z  1 2 z  1 2 z  1 2 z  1 . 1 2 3 4 
4.2019 20184.2019  2018.81
4.2019 20184.20192018.81 A. B. 2018.16  20192 2018.1620192
4.201920184.2019 2018.81
4.201920184.2019 2018.81 C. D. 2018.16  20192 2018.1620192 Hướng dẫn giải 4 4
Đặt f z  20182z  i  2019z  1  2018.16  2019z z z z z z z z . 1   2   3   4 
f i  2018.16  2019i z i z i z i z 1   2   3   4 
 2018 2i  i4  2019i  14  4.2019  2018   4.2019  2018
z i z i z i z i  1
 2  3  4  2018.162019
f i  2018.16  2019i z i z i z i z 1   2   3   4 
 2018 2.i  i4  2019i 14  4.2019  2018.81   4.2019  2018.81
z i z i z i z i  1
 2  3  4  2018.162019
Mà P  z i z i z i z i z i z i z i z i 1
 2  3  4  1  2  3  4 
 4.2019  2018   4.2019  2018.81  4.2019  20184.2019  2018.81  .      .
 2018.16  2019   2018.16  2019  2018.1620192
Bài 16. Cho hàm số f x không âm và liên tục trên 0;    thỏa mãn:     x
f x  2018  2 f
 tdt, x   0  0  1  f
 xdx 1009   2e 1 0 1 f xTính tích phân dx x e 0
A. 2018 e  1
B. 1009 e  1 C. 2018e  2 D. 2018e  2 14 Hướng dẫn giải x x
Ta có f x  2018  2 f
 tdt f x20182 f
 tdt  0 (1) 0 0 x x     Đặt   ax
     ; gʹ  ax g x e f t dt b
x e a f
 tdt f x ab      0   0  a  2  a  2 
Từ (1) thực hiện phép đồng nhất suy ra    ab  2018  b    1009
Vậy gʹx  0, x
  0 , tức g x nghịch biến trên 0;   x x   2  x
    1009     0  1009  2   2  2018  2018 x e f t dt g x g f t dt e    0  0 1 Vậy   2  2018 x f x e f  x 2
dx  1009e  1009 0 1 f x
Dấu “=” xảy ra khi và chỉ khi f x 2 x    2018e
dx  2018 e   x  1 e 0
Bài 17. Cho 16 phiếu ghi các số thứ tự từ 1 đến 16. Lấy lần lượt 8 phiếu không hoàn lại, gọi a i
là số ghi trên phiếu thứ i lấy được 1  i  8 . Tính xác suất P để 8 phiếu lấy được thỏa mãn
a a  ...  1 2 8
a và không có bất ký hai phiếu nào có tổng các số bằng 17. 8 3 8 2 8 2 8 3 A. P B. P C. P D. P  8 A 8 A 8 C 8 C 16 16 16 16 Hướng dẫn giải Ta có   8
A . Do 8 phiếu lấy được thỏa mãn điều kiện a a  ...  a , nên ta có thể 16 1 2 8
xem 8 phiếu lấy được như là một tập con của tập có 16 phần tử.
Gọi S  1,2,3,... 
16 và E S thỏa mãn yêu cầu bài toán. Từ 1 đến 16 có 8 cặp số có tổng
bằng 17 chia thành hai tập tương ứng là M  1,2,..., 
8 và N  16,15,...,  9 . Nếu E có
k phần tử thuộc M thì có k
C cách chọn và khi đó E sẽ có tối đa 8  k phần tử thuộc N 8 15 nên có 8
2 k cách chọn, với k 0,1,..., 
8 . Vậy số tập hợp E thỏa mãn yêu cầu bài toán là 8 0 8 3 C .2  1 7 C .2  ...  8 0
C .2  3 . vậy P  . 8 8 8 8 A16
Bài 18. Cho các số phức z , z thỏa mãn z  1, z r . Gọi M, N, P lần lượt là điểm biểu 1 2 1 2 NMP  
diển các số phức z , iz , 4iz . Biết
. Khi r r thì góc là lớn nhất. Khẳng 1 2 2
MOP  90o 0
định nào sau đây đúng?
A. r 1; 2
B. r 0;1
C. r 2; 3
D. r 3; 4 Hướng dẫn giải
N OP;OP  4ON  4r Từ đề suy ra  OM   1 Ta có: tan OMN r OMN   r   OP Và
OMN   tan tan tan tan     4r 1  tan OMN.tan 1  r tan OM 3r 3 3 1 Suy ra tan  
  max  đạt được khi r 2   2 4r  1 4 2 4r .1 2
Bài 19. Cho hàm số f x có đạo hàm khác 0 và liên tục đến cấp hai trên 1;  2   thỏa mãn
ln 2 f ʹ1  f 1  1   f x xf x , x   1;  2   f ʹx ʹ  ʹ   3  f x1 2  2 ln 2 16 2
Tính tích phân I xf  xdx 1 1 3 A. I  log 5 
 1 B. I  3log 5   2 2 2 ln 2 2 4 ln 2 3 3 C. I  log 5   2 D. I  2 log 5   1 2 ln 2 2 2 ln 2 Hướng dẫn giải
f ʹ x xf ʹʹ x
2 f ʹ x  2xf ʹʹ x
Ta có: f ʹx     f x 3   f ʹ   x   2     f x 2 ln 2 1 2 2 ln 2
f ʹx 2     f x 2x f x 2x  2 ln 2ʹ         x ʹ 2 ln 2 C f ʹ  f ʹ  x 1
Vì ln 2 f ʹ1  f 1  1  C  0 1 Khi đó:
f ʹxfxf x 2
ln 2  2x  2  f x 2 ʹ  2x  2
 2xdx x C f
x  log  2x C 2 2 2 
Vì f 1  1  C  1, khi đó: f x  log  2 x  1 2  2  2x v   2 u
  log  2x 1   2x 1 ln2 2  Xét I x log 
 2x 1 dx, Đặt    2  2   1 dv xdxx v   2 3 1 1 x 1 1  x  Suy ra 2 I x log  2 x  1   2log 5    x 2 2 2 1  2 2 2 2 ln 2 x  1 2 ln 2  x  1  1 1 0 2   1 1 x 1      x  2 2 2 3 2 log 5 ln 1   2 log 5   1 2 2 2 ln 2  2 2  2 ln 2 1 1  
BTTL. Cho hàm số f x đồng biến và có đạo hàm liên tục đến cấp hai trên 0;1   thỏa mãn 17
f 0  f ʹ0  1  , x   0;1  
f ʹʹxf x   f ʹ  x 2    2x1 
2xf xf ʹx
Tính diện tích của hình phẳng giới hạn bởi đường cong y   2
x  1 f x, hai trục tọa độ và
đưởng thẳng x  1 47 101 9 A. B. C. 3 e e D. 3 e e  1 12 30 20
Bài 20. Cho dãy số u thỏa mãn log 2u  63  2 log u  8n  8 , *   . Đặt 3  5  4  nn u S 148
S u u  ...  u . Tìm số nguyên dương lớn nhất n thỏa mãn n 2n n 1 2 n u S 75 2n n A. n  16 B. n  17 . C. n  18 D. n  19 Hướng dẫn giải
log 2u  63  2log u  8k  8  3  5  4  k
Xét với n k, n k  1: 
log 2u  63  2 log u  8 k  1   8 3  5  4   k1   
 log u  8k  8  log u  8 k  1  8  u u  8 4  k  4  k1    k1 k
Suy ra u là một cấp số cộng với công sai d  8  u u  8 5  1  u  32 5 1   n  1
Mặc khác với n  1 : log 2  63  2 log  log 2 1 SHIFT  2log SOLVE u u u u  u  4 3 5 4 1 3 1 4 1 1 u
  4  8 n   n n  1 8 4    2.4  8  n1.n  2 S    4n n  2 8n4 2 .16n 148 Ta có:    n
. Vậy số nguyên dương lớn nhất là n  18 16n  4 19 2 .4n 75 1 1
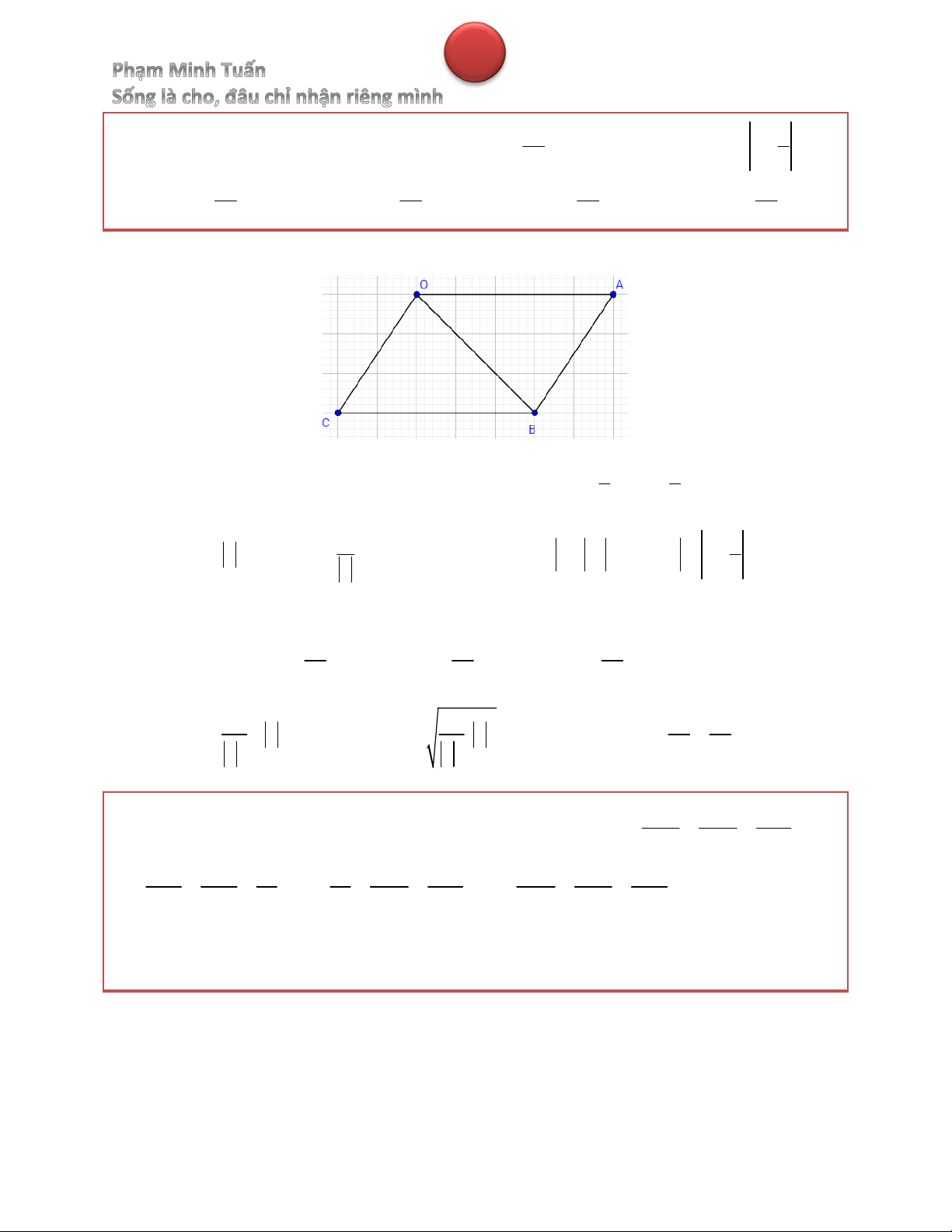
Bài 21. Trong mặt phẳng phức, xét hình bình hành tạo bởi các điểm 0, z, và z . Biết z z z 18 2 35 1
có phần thực dương và diện tích hình bình hành bằng
. Tìm giá trị nhỏ nhất của z 37 z 53 49 43 50 A. B. C. D. 37 37 37 37 Hướng dẫn giải 1 1
Gọi O, A, C, B lần lượt là điểm biểu diễn các số phức 0, z, và z z z 1
      1
Suy ra OA z ,OC AB
, OB OA OC OB OB OA OC z z z
Diện tích hình bình hành: 35 35 12 S O . A A . B sin OAB   sin OAB    cos OAB  37 37 37 1 2 1 2 12 50 Ta có: 2 OC   z  2cos OAB  2 . z  2 cos OAB  2  2.  2 2 37 37 z z x 2 y 2 z 1
Bài 22. Trong không gian với hệ tọa độ Oxyz, cho 4 đường thẳng  :   ; 1 111 x 1 y x y 2 z x 5 y a z   1 z 1 b :   ;  :   ;  :  
. Biết không tồn tại 2 1 21 31 1 1 4 1 3 1
đường thẳng nào trong không gian mà cắt được đồng thời cả bốn đường thẳng trên. Tính giá trị
của biểu thức T a 2b A. 2 B. 3 C. 2 D. 3 Hướng dẫn giải Ta có:  / / 1 3 19
Gọi P là mặt phẳng chứa  và   P : x 2y z 3 0 3       1
Gọi I    P  I 0; 1;1 2  2a b 22 3b 24 2a 7b 8 Gọi J P J ; ; 4                   6 6 6 
  2a b  22 3b 18 2a  7b 14   IJ   ; ;   6 6 6   
Để thỏa mãn yêu cầu bài toán thì IJ phải cùng phương với u  1; 1;    1 , hay: 1
2a b  22 3b  18 2a  7b   
14  a  2b  2 6 6 6
Bài 23. Cho cấp số cộng u có tất cả các số hạng đều dương thỏa mãn: n
u u  ...  u4 u u u
. Giá trị nhỏ nhất của P  log2 u  log2 u  log2 u 1 2 2018   ... 1 2 1009 3 2 3 5 3 14 A. 2 B. 3 C. 2 D. 3 Hướng dẫn giải
2018 2u 2017d
Ta có: u u  ...  u4 u u u 2 1009 2u 1008d 1 2 2018   ... 1 2 1009   1    .   12
d    d 3d 5d u u : ; ; ;... 1 n 2 2 2 2 3d 9d 27d Khi đó: P 222  MODE log log log
7 min P 2 3 3 3 2 2 2 Bài 24. Cho dãy số
u thỏa mãn: ln 2u 2u 10 2u 6u và 1 2   ln  1 2 n u
u 2u  ,
1 n 1. Giá trị nhỏ nhất của n để u 5050 n2 n n1 n A. 100 B. 99 C. 101 D. 102 Hướng dẫn giải 2 2 u 1 Ta có: ln  2 2 u u
10 ln2u 6u
u 1 u 3            0   1 1 2 1 2 1 2 2 u   3 2 20 Mặt khác: u
u 2u 1 u u u u 1. Đặt v u u n2 n n1 n2 n1 n1 n n n1 n Suy ra v
v 1  v là một dãy CSC có công sai d 1 n n1 n
v v n 1 u u n 1 n 1 n 1 2 1
u u 22 1
u u 3 Khi đó u
u n 13 2 n1 n  ................. u u   n n n1 n n 1
Cộng vế theo vế ta được: : u u 2 3 n 1 2 3 n n 1   ...        ...  2 nn   1 Vậy:
5050 n 100 , suy ra Giá trị nhỏ nhất n101 2 min
Bài 25. Xét các số thức dương x, y, z thay đổi sao cho tồn tại các số thực a,b,c 1 và thỏa mãn
x y z abc a b
c . Tìm giá trị nhỏ nhất của biểu thức và    2 P x y 2z A. 4 2 B. 4 C. 6 D. 10 Hướng dẫn giải Ta có:  2x a   abc 2x  log abc a     2y 1 1 1
b abc  2y  log abc a b c abc 1 b
     log log log  log abc abc abc abc     2x 2y 2z 2zc abc 2z    log abc c   z 11 1 12 Suy ra 1    0   2z 2x 2y
11 2 x y 4z2z x y 2z   1 4z 1 Khi đó, P   2 2z , z
. Khảo sát hàm số suy ra MinP 6 2z 1 2 1 1 4
Chú ý: BĐT Cauchy – Schwarz:   a b a b 21
Bài 26. Cho số phức z x yi với x, y   thỏa mãn z 1i 1 và z 3 3i 5 . Gọi M, M
m lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P x 2y . Tính tỉ số . m 9 7 5 14 A. B. C. D. 4 2 4 5 Hướng dẫn giải 2 2
Ta có: z 3 3i 5  x 3   y 3  5 (1)
Thế x P 2y vào (1) ta được:
   2   2   2      2 P 2y 3 y 3 5 5y
2 3 2P y P 6P 13 0 (*)
Vậy (*) có nghiệm với mọi x, y   khi và chỉ khi:  2 M 7
ʹ  0  3 2P  5 2
P 6P 13  0 4 P 14   * m 2
Nhận xét: Cách đại số đơn giản dễ hiểu và với cách giải đó anh nhận ra rằng đề cho
thừa dữ kiện z 1i 1. Bài 27. Cho các số phức
z , z , z thỏa mãn
z 4, z 3, z 2 và 1 2 3 1 2 3
4z z 16z z 9z z 48 . Giá trị của biểu thức P z z z bằng: 1 2 2 3 3 1 1 2 3 A. 2 B. 3 C. 4 D. 1 Hướng dẫn giải z   4 z z 161    1 1
Ta có:  z 3 z z
9 . Thay vào 4z z 16z z 9z z 48 ta được: 2     2 2 1 2 2 3 3 1 z 2 z z   4 3  3 3
z z .z z z z .z z z z .z z 48 z z z z z z 48 3 3 1 2 1 1 2 3 2 2 3 1 1 2 3 1 2 3 48
z z z
2 z z z 2 z z z 2 1 2 3 1 2 3 1 2 3 z z z 1 2 3 22 5
Bài 28. Cho hai số phức z , z thỏa mãn z 12i z 3 3i 2 z 1i 17 . Tìm giá 1 2 1 1 2 2
trị lớn nhất của biểu thức P z z z 2 i . 1 2 1 A. 17  2 29 B. 17  29 C. 2 17 D. 3 29 Hướng dẫn giải
Gọi M , N lần lượt là điểm biểu diễn các số phức z , z 1 25  Ta có : A  ; 1 2 , B ;
3 3  AB 17 và I  ; 1  là trung điểm AB  2
Mà z 12i z 3 3i 17 MA MB AB  M thuộc đoạn AB 1 15 17
N thuộc đường tròn (C) có tâm I  ; 1  , R
 AB là đường kính của (C)  2 2
 
Ta có: P z z z 2 i OM ON MD MN MD , với D  ; 2 1 1 2 1
M  AB    Vì 
nên MN 2R và MD BD N   C
Vậy P 2R BD 17 29 . Dấu “=” xảy ra khi và chỉ khi M D, N A 23 BTTL. Cho các số phức z, z , z       1 2 thỏa mãn z 1 2i z 5 2i 4 và 1 2
z  3  2i z  7  2i  10 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu
thức P z z z  3  i . Tính T M m 1 2 A. 9  2 26 B. 15  109 C. 8  107 D. 11  110 1
Bài 29. Cho hai số phức z , z thỏa mãn z 3 4i  ,
1 z 3 4i
. Số phức z có phần 1 2 1 2 2
thực bằng a, phần ảo bằng b thỏa mãn 3a 2b 12 . Tìm giá trị nhỏ nhất của biểu thức
P z z z 2z 2 . 1 2 8845 9945 9091 9667 A. B. C. D. 15 13 12 17 Hướng dẫn giải 1
Tâp hợp điểm biểu diễn SP z , z là đường tròn tâm I  ;
3 4 có bán kính lần lượt là , 1 1 2 2
Gọi M là điểm biểu diễn số phức z  M thuộc đường thẳng 3x 2y 12
Đặt z 2z z 6 8i 1 là đường tròn tâm J  ;
6 8 có bán kính R 1 3 2 3
Ta có: P z z z z 2 MI 1MJ 12 MI MJ 1 3138 64
Gọi A là điểm đối xứng của J qua 3x 2y 12 A  ;   13 13 24 Khi đó,     9945 P MI MA IA
. Dấu “=” xảy ra khi và chi khi M, I , A thẳng hàng 13
Bài 30. Cho hàm số f x có đạo hàm liên tục trên đoạn 1; 2   thỏa mãn:
2 f 22   f 12       63  ,  x  1; 2  2 2 2 2
2  f x  
x f ʹx         27x 2 2
Tính giá trị của tích phân   f x   dx . 1 A. 15 B. 18 C. 21 D. 25 Hướng dẫn giải 2 2 2 2 2 2 2 Từ đề  
f x dx 
f x dx 2x  
f ʹx dx  2 27x dx         63 (1) 1 1 1 1 2
u   f x 2  2   
du  2 f ʹxf x Xét I    
f x dx . Đặt    dv dxv x 1   2 2 2
I x f x2  2 xf ʹxf xdx  63    
2 xf ʹxf xdx 1 1 1 1 2 2 2 2  
f x2 dx2xf ʹxf xdxx  
f ʹx2 dx  0  
f x xf ʹx2 2 dx        0 1 1 1 1  1 
Do đó f x  xf ʹx  0 
f x ʹ  0  f x    Cx x  2 2 2
Ta có: 2 Cx  2 2 x C  2 2 3C x  2
27x C  3  
f x dx      21 1 
Bài 31. Cho x, y là 2 góc thỏa mãn x y   
k , k   và sin x  2 sin x y. Gọi M, m lần 2
lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P  tan x y. Tính 2 2
Q M m 2 2 3 A. B. 1 C. D. 5 3 5 25 Hướng dẫn giải
Ta có: sin x  sin  x y  y  sinx ycos y  sin .
y cosx y
 sinx ycos y  sin y.cosx y  2sinx y  tanx ycos y  sin y  2tanx y 
xy sin y tan  cosy 2 sin y Ta có: P
 sin y P cos y  2  cos y  2 Điều kiện có nghiệm: 2 1 1 2 1  P  4    P   Q  3 3 3  1 
Bài 32. Cho số phức z khác 0 thay đổi và thỏa mãn điều kiện  2
m  2 z z   z i    z với z
m là số thực dương. Tìm giá trị nhỏ nhất của m . A. 2  2 B. 2  2
C. 1  2 D. 1 2 Hướng dẫn giải      2  z  1 2 1 i m 2 z
z i z m  2 z
 1 i  1  2 z    2 m  1      i 2   z   . z zz iz   m   2 2 1 2
1 i  1  2 z    2 m  1  1 2 4 2 z z 2 1 2 2 1 2 2 1 Xét 2 z   z z   3  3 z . z . 3 4 4 4 z z z  2 2 m  1  2 Suy ra  2 m 1 1 3  2 m 1 2          m   1  2  Loai
Vậy giá trị nhỏ nhất của m là 1  2 . Dấu “=” xảy ra khi và chỉ khi z  1
Bài 33. Cho hàm số f x có đạo hàm liên tục trên 0;1   thỏa mãn: 26
ef 1  4 f 0  4 1  x    e
f x  f x 1 2 2 2 x dx e f  x 11 ʹ 4 dx     3 0 0 1 Tính I f  xdx . 0 4   1 3   1 2   2 5  2 A. e I B e I C. e I D. e I e e e e Hướng dẫn giải 1 1 2 2 x   x 11 Xét 2 J e
f ʹx  f x dx 4 e f
 xdx     3 0 0 Đặt   x     ʹ x    x  ʹ  x u x e f x u e f x
e f x e f ʹx  uʹ u 1 1 2 2 Khi đó J   uʹ u 2 u 4udx
 uʹ 2 .uuʹ 4u        dx      
 , với u1 4, u0 1 0 0 1 1 2 u 15 1 1 1 1 Ta có . u uʹ dx   
và udx xu xuʹ dx  4  xuʹ dx    2 2 0 0 0 0 0 0 1 2   8
Suy ra J   uʹ  4xuʹ dx    3 0
Chọn m  sao cho: 1 1 uʹ 2x m dx 0     uʹ 1 1 2 2 4xuʹ       
dx  2m uʹdx  
2xm2 dx  0   0 0 0 0 8 4 2
  6m m  2m   0  m  2 3 3 1 2 Vậy  ʹ 2  2  0 x      x u x dx
e f x e f ʹx  2x  2 0  
x x C     x x e x
e f xʹ  2x  2  f x 2 2 f  2 1 5 2 0 1   f x   f x dx   x   2 1 x     e e e 0 27
Bài 34. Cho các số phức z ,
z i và 2z z  3 z z  3 1 1   2 2
. Giá trị lớn nhất 1 z thỏa mãn 1 2
M của biểu thức P z  2  i z  3  1 2
i thuộc khoảng nào sau đây?
A. M 4;6
B. M 5;7
C. M 6;8
D. M 7;9 Hướng dẫn giải
Từ đề suy ra z i z i  1 1 2 2 2
Áp dụng BĐT Bunhiacopxki: P z  2  i z  3  i  2 z  2  i z  3  i 1 2  1 2  2 2
Ta có: z  2  i z  2  i z  2  i z i  2 z z  4 1  1  1  1  1 1 2 2
Và z  3  i z  3  i z  3  i z i  3 z z  9 2  2  2  2  2 2 2 2 P 2  z i z i 2 z z 3 z z 13            2 2  3  13  6 1 2   1 1  2 2    
Bài 35. Cho hình đa giác đều H có 24 đỉnh, chọn ngẫu nhiên 4 đỉnh của hình H. Tính xác suất
để 4 đỉnh chọn được tạo thành một hình chữ nhật không phải là hình vuông? 10 15 20 18 A. B. C. D. 1771 1771 1771 1771 Hướng dẫn giải
Số phần tử của không gian mẫu là 4
  C  10626. 24
Đa giác đều 24 đỉnh có 12 đường chéo qua tâm. Cứ 2 đường chéo qua tâm tương ứng
cho ta một hình chữ nhật hoặc hình vuông. Số hình chữ nhật và hình vuông được tạo thành là 2 C . 12
Giả sử A , A ,..., A là 24 đỉnh của hình H. Vì H là đa giác đều nên 24 đỉnh nằm trên 1 1 2 24
đường tròn tâm O  0 360 Góc 0 A OA
 15 với i  1,2,...,23 i i1 24    Ta thấy: 0
A OA A OA A OA  90 , do đó A A A A là một hình vuông, xoay 1 7 7 14 14 21 1 7 14 21 hình vuông này 0
15 ta được hình vuông A A A A , cứ như vậy ta được 6 hình vuông. 2 8 15 22 28
Số hình chữ nhật không là hình vuông là: 2
C  6  60. 12 60 10
Vậy xác suất cần tính là:  . 4 C 1771 24
Bài 36. Cho số phức z thỏa mãn 4 2 2
z z  2  3 z  2  9 . Giá trị nhỏ nhất của biểu thức 2 2
P z  1  z bằng: A. 2 B. 1
C. 2 3 D. 2 Hướng dẫn giải 9 Ta có 4 2 2 2 2 2 2
z z  2  3 z  2  9  z  2 z  1  3 z  2  9  z  1   3 2 z  2 Cách 1: 9 9 Ta có 2 z  1   3   3 2 2 z  2 z  2 9 2 9 2 9  P   3  z   z  2  5  2 . 2
z  2  5  1 2 2 2  z  2 z  2 z  2 Cách 2: Đặt 4 2 4   t z
t z   z z    z  z z 2 4 2
z   z z      2 2 2 2 2 2 4 2 4 4 4 4 z  22 2 2 9 9
Suy ra z t  2  P   3  t  2  2 .t  5  1 t t
Dấu “=” xảy ra khi và chỉ khi z  i
Bài 37. Cho hàm số f x dương và có đạo hàm liên tục trên 0;1 
thỏa mãn f   1 0  , 16 3 1 1  f  x   1 1
x  3 f x 1 1 ʹ dx    và dx  
. Tính tích phân f xdx. 8   64 0 f ʹ  x 2 0  0 29 1 1 1 A. B. C. 24 32 8 1 D. 4 Hướng dẫn giải
1 x  f xdx x  f x 1 
x   f x 1 1 3 3 2 1
   x  2 f x 1 1 ʹ 1 3 1 1     0 8 16 0 0 0
Áp dụng BĐT Holder ta có: 1 2 3 3         1 f x 3 3 1  f x      
x  1  f ʹ x dx      
dx .   x  1  f ʹ x   dx 2     2 1   1 2      2 2 2 2 3 3   16   0          f ʹ  x 3 0   f ʹ   x 3 0         1    f   x 2 3 1 2 3 1  1      1   1  1  dx . 
x  1 f ʹ x dx          .     2     3 3 3 3        64   8  16 0 f ʹ   x 0   3    f x 3 2 2    2
Dấu “=” xảy ra khi và chỉ khi 
  k x  1  f ʹ x   2      3    
f ʹx 3     
f ʹx 3   1   (1)  f  x 3  k x  13   f  x 3   f   x 3 1 1 1  1 3  1 1 Ta có 64 dx
. f ʹ x dx k x  1 f ʹ x dx   k       2 3           64 1 8 0 f ʹ  x 0 f ʹ   x 0   8 f ʹx 1  1 (1) 2    f  1 ln f x 0 1 16  2
 ln x  1  C 
f x 
f xdx   f xx  1 16x  12 32 0
Bài 38. Cho hàm số f x liên tục và có đạo hàm cấp 2 trên 0; 
thỏa mãn f 0 1, ln 2 1 ln 2
f ʹ0  0 , f ʹʹx  5 f ʹx  6 f x  0, x  0; 
, f xdx    . Tính tích phân 2
f xdx 6 0 0 30 15 35 27 24 A. B. C. D. 4 17 20 7 Hướng dẫn giải
f ʹʹx  5 f ʹx  6 f x  0  f ʹʹx  2 f ʹx  3  f ʹ
 x  2 f x  0  (1)
Đặt gx  f ʹx  2 f x , từ (1) suy ra gʹx  3gx  0 Xét hàm số   3  x       3  x     3x    3 ʹ 3 ʹ  x h x e g x h x e g x e g x egʹ
 x  3gx  0 
Suy ra hx đồng biến trên 0;  hx  h0  g0  f ʹ0  2 f 0  2   3  x    2  2  x    ʹ
    2    2 x e g x e f x f x e  0  Xét hàm số   2  x    x     2 2 ʹ  x   ʹ
    2    2 x k x e f x e k x e f x f x e  0 
Suy ra k x đồng biến trên 0;  
  kx  k0  f 0 2  3  x    x      ln 2 2 2 x 3x e f x e
f x e ef x 1 2 3 3 2 dx    6 0 ln 2 2 x x 27
Dấu “=” xảy ra khi và chỉ khi f x 2 3
 3e  2e   f
 x dx    20 0
Bài 39. Cho hai hộp bi mỗi hộp có 2 viên bi đỏ và 8 bi trắng. Các viên bi chỉ khá nhau về màu.
Cho hai người lấy mỗi người một hộp và từ hộp của mình, mỗi người lấy ngẫu nhiên 3 viên bi.
Tính xác suất để hai người lấy được số bi đỏ như nhau. 4 2 11 1 A. P B. P C. P D. P 5 9 25 5 Hướng dẫn giải C 7
Gọi A là biến cố lấy 0 bi đỏ, 3 bi trắng  PA 3 8   3 C 15 10 7
A1 là biến cố người thứ nhất lấy được 0 bi đỏ, 3 bi trắng  PA 1  15 7
A2 là biến cố người thứ hai lấy được 0 bi đỏ, 3 bi trắng  PA 2  15
Vì A1 và A2 độc lập nên xác suất để hai người cùng lấy được 0 bi đỏ, 3 bi trắng là: 31 2   P  7
A A P A .P A    1 2   1  2 15  C C 7
Gọi B là biến cố lấy 1 bi đỏ, 2 bi trắng  PB 1 2 2 8   3 C 15 10 7
B1 là biến cố người thứ nhất lấy được 1 bi đỏ, 2 bi trắng  PB 1  15 7
B2 là biến cố người thứ hai lấy được 1 bi đỏ, 2 bi trắng  PB 2  15
Vì B1 và B2 độc lập nên xác suất để hai người cùng lấy được 1 bi đỏ, 2 bi trắng là: 2   P  7
B B P B .P B    1 2   1  2 15  C C 1
Gọi C là biến cố lấy 2 bi đỏ, 1 bi trắng  PB 2 1 2 8   3 C 15 10 7
C1 là biến cố người thứ nhất lấy được 2 bi đỏ, 1 bi trắng  PC 1  15 7
C2 là biến cố người thứ hai lấy được 2 bi đỏ, 1 bi trắng  PC 2  15
Vì C1 và C2 độc lập nên xác suất để hai người cùng lấy được 2 bi đỏ, 1 bi trắng là: 2   P  1 C C
P C .P C    1 2   1  2 15
Vậy xác suất để hai người lấy được số bi đỏ như nhau là: 2 2 2  7   7   1  11 P            15   15   15  25
Bài 40. Cho số phức z thỏa mãn z  1  3i z  3  i  2 2z  2  i . Tìm giá trị lớn nhất của biểu
thức P z  1  i . 11 46 33 35 A. B. C. D. 3 5 3 5 Hướng dẫn giải 32 2 2 2 2
Ta có: z  1  3i z  3  i  x  1   y  3  x  3   y  1 2 2
Và 2 2z  2  i  2 2x  2  2y  1 Áp dụng BĐT Bunhiacopxki:
x 2 y 2 x 2 y 2
x 2 y 2 x 2 y 2 1 3 3 1 2 1 3 3 1                   2 2 2 2 2 2 Suy ra 2 2x 2 2y 1 2 x 1
y 3 x 3 y 1              
Thực hiện phép bình phương và rút gọn ta được:
x 2 y  2 11 33 1 1 
z  1 i  3 3  5 5 z   i  6 6
Dấu “=” xảy ra khi và chỉ khi  5 5 z    i  6 6
Bài 41. Cho hàm số y f x có đạo hàm liên tục trên đoạn 1;  2   thỏa mãn: f   7 1   3  3  x f x , x   1;  2 3   
f ʹ x x 2     f ʹ
  x  xf ʹ  x 2  x
Tính f 2 .     A. f   7 7 1 2  B. f   7 7 1 2  C. f   2 7 1 2  D. f   2 7 1 2  3 3 3 3 Hướng dẫn giải 2 3 Đề 3  
x f x   f
 x  x  f
  x  xf  x 2 3
x x f x   f    x 3 3 ʹ ʹ ʹ 3 ʹ   x   f xx 3 f
x1   f ʹ   x 3 ʹ 3      x
3 3 f x  1 2 f ʹx 2 2 1 3 1  3 Suy ra dx xdx   3 f    x 3  1 d
3f x1   3  2 3 2 1 3 f x 1 1 1 2 2 2 2 1 3 3 7 7  1
 . 3 f x 3  1   3 f 2 3
 1  3 f   3
1  1  3  f 2        3 2 2 3 1 33
BTTL1: Cho hàm số f x dương và có đạo hàm không âm, liên tục trên đoạn 0;1   thỏa mãn: f 0  1      
f xf x 2 , x 0;1 . ʹ       1   f x x    2 2   e
Khẳng định nào sau đây đúng? 5 3
A. f 1  3
B. f   7 3 1 
C. f   5 2 1 
D. f 1  2 2 2 2 2 z
Bài 42. Cho số phức z không phải là số thuần ảo thỏa mãn z  2 và số phức w là số 4 1  z a
thuần ảo. Biết   2 a z z
a,b , là phân số tối giản. Tính 2
T a ab b b b A. 125  B. 125 C. 75 D. 75  Hướng dẫn giải z z
Vì w là số thuần ảo nên:   0 4 4 1  z 1  z 4  
z1 z   z1 z  4 4 4
 0  z z  . z z  . z z  0   3    
z z  .
z z z z   0  z z  .
z z z z 2 3 2  z  .
z z z   0          z z 2 2 1  . z z z  .
z z z   0     
Vì z không phải là số thuẩn ảo nên z z  0 , suy ra: 2 2     2 1  . z zz  .
z z z   0  z z z2  3 .zz  1        
z z z2  z    z z2 2 2 1 47 3 1    3.4      4 4
Bài 43. Cho số phức z,w thỏa mãn z  5  3i  3 và iw  4  2i  2 . Tìm giá trị lớn nhất của biểu
thức P  3iz  2w A. 554  5 B. 578  13 C. 578  5 D. 554  13 Hướng dẫn giải 34 z1    3 z z iz  Đặt 1 3i   
. Thay vào giả thiết ta được: z  2  w z 2  2 w    2  z1   5  3i  3 3i
z  15i  9    9 1    z
z  8i  4    4 2  2 i.  4  2i  2  2 
Gọi A, B lần lượt là điểm biểu diễn các số phức z ,z 1 2
Suy ra A thuộc đường tròn tâm I 9;15 , bán kính R  9 và B thuộc đường tròn tâm 1 J 4; 8
  , bán kính R  4 2  
Ta có: P z z OA OB AB IJ R R  554  13 1 2 1 2
Bài 44. Cho số phức z,z ,z thỏa mãn z  4  5i z  1  1 và z  4i z  8  4i . Tính z z 1 2 1 2 1 2
khi P z z z z đạt giá trị nhỏ nhất. 1 2 A. 41 B. 6 C. 2 5 D. 8 Hướng dẫn giải
*Gọi A là điểm biểu diễn z  A thuộc đường 1
tròn C tâm J 4; 5 ,R  1 1   1  1
*Gọi B là điểm biểu diễn z  B thuộc đường 2
tròn C tâm J 1;0 ,R  1 2   2  2
* z  4i z  8  4i  d : y  4  x
 M thuộc đường thẳng d , z x yi    
Ta có: P OM OA OM OB MA MB
*Gọi C có tâm J 4; 3
 ,R  1 là đường tròn 3   3  3
đối xứng của C qua d và B’ là điểm đối 2 
xứng của B qua d , khi đó BʹC 3 
………………………………………………
………………………………………………
Khi đó: P MA MB MA MBʹ  ABʹ  J J R R  6 1 3 1 3
Dấu “=” xảy ra khi và chỉ khi J , A, M, Bʹ, J thẳng hàng 1 3 x  4  0   Bʹ 1 
Ta có J Bʹ  J J    Bʹ 4; 2   B 2;0 3 3 1 1     8 y  3   .8 Bʹ  8 35 x  4  0  1  A
Lại có J A J J    A 4;4 1 1 3 1   8 y  5    .8 A  8
Vậy z z  4  4i  2  2 5 1 2
Bài 45. Cho dãy số u thỏa mãn 2 u  1, uau  1, n
  1 , a  1. Biết rằng n  1 n1 n lim  2 2 2
u u  ...  u  2n b . Giá trị của biểu thức T ab 1 2 n A. 1  B. 2  C. 1 D. 2 Hướng dẫn giải 1  1  Đề 2 2 2 2
u au  1  u   a u    n1 n n1 1 na  1  a  1 Đặt 2 v u
v av  v là cấp số công với công bội q a n n n n 1 1 na    n 1 nna na 1 Suy ra 1 2 1 1 2 1 v v au aa .  u a .    n 1 1  1  a a  1 n a  1 1  a  2 a 1 u    1 a  1 1  a   2 a 1 u   . aa n 1 Ta có: 2 2 2 2  a  1 1  a
u u  ...  u
1  a  ...  a  .n 1 2 n  1  a  1 1  a ..
 ...........................   2 n1 a 1 u a .  n  a  1 1  a n  2 2 2 1 a 1 a
u u  ...  u  .n  . 1 2 n 1  a a  1 1  a
Thực hiện phép đồng nhất ta được:  1 a    2 1   2 n      1 a   1      1      T   n 1  a 1 a    2   b  lim .   b  lim  2  a  1 1    a  1       1    2     2
BTTL. Cho dãy số
u thỏa mãn 2 u  1, u
u a , n
  1 . Biết rằng n  1 n1 3 n lim  2 2 2
u u  ...  u  2n b . Giá trị của biểu thức T ab 1 2 n A. 1  B. 2  C. 1 D. 2 Hướng dẫn giải 36 u  u 8
Bài 46. Cho dãy số u thỏa mãn 2 1 3 1 2 2  2  và u  2u với mọi n    1  n 1 n 2 log u  4u   4 3 3 1   4 
n  1 .Đặt S u u  ...  u . Giá trị nhỏ nhất của n để 10 S  28 là: n 1 2 n n A. 53 B. 51 C. 50 D. 52 Hướng dẫn giải    u 2u Theo GT, u
 2u nên u là một CSN với công bội n 1 2 1
q  2  u u .2   n n1 n n 1 u  4u  3 1 Xét 2u 1 3u u 8 u 8 1 2 1 1 2  2  2.4   2 2.4 .  8 u u 1 1 4 4 8 8 8 8 Và     8  1   1   1  log u  4u  4 log u u  4 log u 22 2 2 log 3 3       3 3 3 1 3 3 3 3 3   4   4   4    u 8 1 1 2.4  u  
Do đó dấu “=” xảy ra khi và chỉ khi u 1 1  4   2 u   2 u   2  3  3 1  2n 2n  1 Khi đó 10 S u .   28  n  log    nn  10 2.28 1 49,07 50 1 2  min 1  2 2
Bài 47. Cho hàm số f x có đạo hàm liên tục trên đoạn 0;1 
thỏa mãn điều kiện:
f 2018x  2017  2018 f x, x    1 2
Giá trị tích phân f
 x dxbằng: 0 A. f    2 4 ʹ 1  B. f    2 5 ʹ 1  C. f    2 7 ʹ 1  D. f    2 8 ʹ 1  3 3 3 3 Hướng dẫn giải
Xét f 2018x  2017  2018 f x (*)
Đạo hàm 2 vế của (*) :
2018 f ʹ2018x  2017  2018 f ʹx37 x  2017 Thay x bởi , ta được: 2018        f xx 2017 x 2018 1 ʹ  f ʹ    f ʹ  (1)  2018   2018  x  2017
Tiếp tục thay x bởi : 2018  x  2017          f x 2018 1 2 x 2018 1 2018 ʹ  f ʹ   f ʹ  2  2018   2018     
Thay đến n lần và bằng quy nạp ta chứng minh được:       f xx 2018n 1 x 1 ʹ  f ʹ   f ʹ   1    2018n   2018n 2018n
Khi n   thì f ʹx  f ʹ 1
   f x  f ʹ 1
 x C (2) Thay x  1
 vào đề ta được f  1
   2018 f  1
   f 1  0 Thay x  1
 vào (2) ta được f  1
    f ʹ1 C  0  f ʹ 1    C 1 2 2 7
Vậy f x  f ʹ 1
 x 1   f
 x dx   f ʹ 1      3 0
Bài 48. Trong không gian Oxyz, xét mặt phẳng Pmx   2
m   y   2 : 2 1
m  1 z  10  0 và điểm A2;11; 5
  . Biết khi m thay đổi, tồn tại hai mặt cầu cố định tiếp xúc với mặt phẳng P
và cùng đi qua A . Tính tổng bán kính của hai mặt cầu đó. A. 2 2 B. 5 2 C. 7 2 D. 12 2 Hướng dẫn giải Gọi I (a; ;
b c), r lần lượt là tâm và bán kính của mặt cầu . Do mặt cầu tiếp xúc với (P) nên ta có 2 2 
2ma m  1 b m  1 c  10 bc 2 m ma b c r d I,P      2   10     2 m  1 2  2 m  1 2 38  2 b c r 2 m 2ma b c r 2 10 0 1 2 2   
        
bcm  2mabc 10  rm 1 2   2
b c r 2  m  2ma b c r 2  10   0 2
TH1: b c r  2
2 m  2ma b c r 2  10  0 1
Do m thay đổi vẫn có mặt cầu cố định tiếp xúc với (P) nên yêu cầu bt trở thành tìm điều kiện , a ,
b c sao cho (1) không phụ thuộc vào m. Do đó (1) luôn đúng với mọi ìï 
b + c - r 2 = 0 b r 2  5 ïï  ï  ía = 0  a  0 ïïï  b
ï - c - r 2 -10 = 0 î c  5   2 Suy ra I   r
   Sx y  r  z  2 2  2 0; 5 2; 5 : 5 2 5 r . 2 r 2 2
Lại có A Î(S) nên suy ra : 4  11 5 r 2        2 r  2
r  12 2r  40  0   r   10 2
TH2: b c r  2
2 m  2ma b c r 2  10  0 làm tương tự TH1 (trường hợp này không thỏa đề bài )
Tóm lại : Khi m thay đổi, tồn tại hai mặt cầu cố định tiếp xúc với mặt phẳng (P ) và
cùng đi qua A và có tổng bán kính là : 12 2 suy ra chọn D
Bài 49. Trong không gian Oxyz, cho điểm A1; 4; 3 và mặt phẳng P : 2y z  0 . Biết điểm
B thuộc P, điểm C thuộc Oxy sao cho chu vi tam giác ABC nhỏ nhất. Hỏi giá trị nhỏ nhất đó là :
A. 4 5
B. 2 5
C. 5
D. 6 5 Hướng dẫn giải
Gọi A , A lần lượt là điểm đối xứng của A qua P và Oxy . 1 2 Phương trình tham số x  1 
AA : y  4  2t H 1; 4  2t; 3  t với H  P  AA 1    1 z  3  t
Vì H P nên
2 4  2t  3  t  0  t  1   A 1;0; 5 1   39
Tương tự ta tìm được A 1; 4; 3  2   AB A B Dễ thấy AA
B cân tại B và AAC cân tại C nên 1 
. Vậy chu vi ABC bằng: 1 2 AC   A C 2 C
AB BC CA A B BC A C A A  4 5 ABC  1 2 1 2
Dấu “=” xảy ra khi và chỉ khi A , B,C, A thẳng hàng 1 2
Bài 50. Cho hàm số f x có đạo hàm liên tục trên đoạn 0;1   thỏa mãn: f 1  1
f x0 , x   0;1    f
 xln f x  xf ʹx  f   x 1 1
Tính tích phân f xdx. 0 1 e  1 1 e  6 1 1
A. f xdx  
B. f xdx   C. f
 xdx  4 D. f
 xdx 1 3 6 0 0 0 0 Hướng dẫn giải f ʹ x
Đề  f xln f x  xf ʹx  xf ʹxf x  ln f x    . xf xxf ʹx 1 1 1 1
 x ln f xʹ  xf ʹx  x ln f x  xf ʹ
 xdx xf x  f  xdx 0 0 0 0 1 Suy ra f
 xdx f 1 1 0