












Preview text:
1
ĐỖ ĐỨC THÁI (Tổng chủ biên kiêm chủ biên)
LÊ TUẤN ANH – ĐỖ TIẾN ĐẠT – NGUYỄN SƠN HÀ
NGUYỄN THỊ PHƯƠNG LOAN – PHẠM SỸ NAM – PHẠM ĐỨC QUANG TO T ÁN O 8TẬPMỘT Số học sinh 9 9 Nữ 8 8 8 Nam 24% 28% 6 6 6 26% 22% 5 5 4 4 4 O Khối 6 Khối 7 Khối 8 Khối 9 Khối
NHÀ XUẤT BẢN ĐẠI HỌC SƯ PHẠM MỤC LỤC
Chương 1. ĐA THỨC NHIỀU BIẾN 1
§1 – ĐƠN THỨC NHIỀU BIẾN.
ĐA THỨC NHIỀU BIẾN 1 A
ĐƠN THỨC NHIỀU BIẾN.................................................................................................................................................................................................1 B
ĐA THỨC NHIỀU BIẾN.........................................................................................................................................................................................................3 C
BÀI TẬP....................................................................................................................................................................................................................................................................5
§2 – CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN 7 A
CỘNG HAI ĐA THỨC NHIỀU BIẾN..........................................................................................................................................................7 B
TRỪ HAI ĐA THỨC NHIỀU BIẾN...................................................................................................................................................................7 C
NHÂN HAI ĐA THỨC NHIỀU BIẾN...........................................................................................................................................................8 D
CHIA ĐA THỨC CHO ĐƠN THỨC..............................................................................................................................................................9 E
BÀI TẬP................................................................................................................................................................................................................................................................10
§3 – HẰNG ĐẲNG THỨC ĐÁNG NHỚ 15 A
HẰNG ĐẲNG THỨC...................................................................................................................................................................................................................15 B
NHỮNG HẰNG ĐẲNG THỨC.................................................................................................................................................................................15 C
BÀI TẬP................................................................................................................................................................................................................................................................21
§4 – VẬN DỤNG HẰNG ĐẲNG THỨC VÀO PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ 23 A
PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ............................................................................................................................23 B
VẬN DỤNG HẰNG ĐẲNG THỨC VÀO PHÂN TÍCH ĐA THỨC THÀNH NHÂN
TỬ......................................................................................................................................................................................................................................................................................23 C
BÀI TẬP................................................................................................................................................................................................................................................................25
§5 – BÀI TẬP CUỐI CHƯƠNG I 28
Chương 2. PHÂN THỨC ĐẠI SỐ 32
§1 – PHÂN THỨC ĐẠI SỐ 32 A
KHÁI NIỆM VỀ PHÂN THỨC ĐẠI SỐ..............................................................................................................................................32 MỤC LỤC B
TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC...................................................................................................................................33 C
ĐIỀU KIỆN XÁC ĐỊNH VÀ GIÁ TRỊ CỦA PHÂN THỨC............................................................................36 D
BÀI TẬP................................................................................................................................................................................................................................................................38
§2 – PHÉP CỘNG, PHÉP TRỪ PHÂN THỨC ĐẠI SỐ 42 A
PHÉP CỘNG CÁC PHÂN THỨC ĐẠI SỐ...................................................................................................................................42 B
PHÉP TRỪ CÁC PHÂN THỨC ĐẠI SỐ............................................................................................................................................44 C
BÀI TẬP................................................................................................................................................................................................................................................................46
§3 – PHÉP NHÂN, CHIA PHÂN THỨC ĐẠI SỐ 52 A
PHÉP NHÂN CÁC PHÂN THỨC ĐẠI SỐ....................................................................................................................................52 B
PHÉP CHIA CÁC PHÂN THỨC ĐẠI SỐ.......................................................................................................................................54 C
BÀI TẬP................................................................................................................................................................................................................................................................56
§4 – BÀI TẬP CUỐI CHƯƠNG II 60
Chương 3. HÀM SỐ VÀ ĐỒ THỊ 64 §1 – HÀM SỐ 64 A
ĐỊNH NGHĨA.............................................................................................................................................................................................................................................64 B
GIÁ TRỊ CỦA HÀM SỐ.......................................................................................................................................................................................................65 C
BÀI TẬP................................................................................................................................................................................................................................................................65
§2 – MẶT PHẲNG TỌA ĐỘ. ĐỒ THỊ HÀM SỐ 68 A
MẶT PHẲNG TỌA ĐỘ.........................................................................................................................................................................................................68 B
TỌA ĐỘ MỘT ĐIỂM TRONG MẶT PHẲNG TỌA ĐỘ...................................................................................68 C
ĐỒ THỊ CỦA HÀM SỐ........................................................................................................................................................................................................69 D
BÀI TẬP................................................................................................................................................................................................................................................................70
§3 – HÀM SỐ BẬC NHẤT y = ax + b (a ̸= 0) 73 A
HÀM SỐ BẬC NHẤT................................................................................................................................................................................................................73 B
ỨNG DỤNG....................................................................................................................................................................................................................................................74 C
BÀI TẬP................................................................................................................................................................................................................................................................75
§4 – ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT y = ax + b(a ̸= 0) 78 A
ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT.........................................................................................................................................................78 B
VẼ ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT............................................................................................................................................79 C
HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG y = ax + b (a ̸= 0)......................................................................................80 D
ỨNG DỤNG CỦA HỆ SỐ GÓC...........................................................................................................................................................................81 Thầy Hóa - 0344.083.670 ii MỤC LỤC E
BÀI TẬP................................................................................................................................................................................................................................................................82
§5 – BÀI TẬP CUỐI CHƯƠNG III 85
Chương 4. HÌNH HỌC TRỰC QUAN 90
§1 – HÌNH CHÓP TAM GIÁC ĐỀU 90 A
HÌNH CHÓP TAM GIÁC ĐỀU.............................................................................................................................................................................90 B
DIỆN TÍCH XUNG QUANH CỦA HÌNH CHÓP TAM GIÁC ĐỀU...........................................90 C
THỂ TÍCH CỦA HÌNH CHÓP TAM GIÁC ĐỀU............................................................................................................91 D
BÀI TẬP................................................................................................................................................................................................................................................................91
§2 – HÌNH CHÓP TỨ GIÁC ĐỀU 94 A
HÌNH CHÓP TỨ GIÁC ĐỀU....................................................................................................................................................................................94 B
DIỆN TÍCH XUNG QUANH CỦA HÌNH CHÓP TỨ GIÁC ĐỀU..................................................94 C
THỂ TÍCH CỦA HÌNH CHÓP TỨ GIÁC ĐỀU...................................................................................................................95 D
BÀI TẬP................................................................................................................................................................................................................................................................96
§3 – BÀI TẬP CUỐI CHƯƠNG IV 98
Chương 5. TAM GIÁC. TỨ GIÁC 102
§1 – ĐỊNH LÍ PYTHAGORE 102 A
ĐỊNH LÝ PYTHAGORE...................................................................................................................................................................................................102 B
ĐỊNH LÝ PYTHAGORE ĐẢO..............................................................................................................................................................................102 C
BÀI TẬP............................................................................................................................................................................................................................................................104 §2 – TỨ GIÁC 108 A
TỨ GIÁC..........................................................................................................................................................................................................................................................108 B
TỔNG CÁC GÓC CỦA TỨ GIÁC...............................................................................................................................................................109 C
BÀI TẬP............................................................................................................................................................................................................................................................109
§3 – HÌNH THANG CÂN 112 A
ĐỊNH NGHĨA.........................................................................................................................................................................................................................................112 B
TÍNH CHẤT..............................................................................................................................................................................................................................................112 C
DẤU HIỆU NHẬN BIẾT..................................................................................................................................................................................................113 D
BÀI TẬP............................................................................................................................................................................................................................................................114
§4 – HÌNH BÌNH HÀNH 118 A
ĐỊNH NGHĨA.........................................................................................................................................................................................................................................118 Thầy Hóa - 0344.083.670 iii MỤC LỤC B
TÍNH CHẤT..............................................................................................................................................................................................................................................118 C
DẤU HIỆU NHẬN BIẾT..................................................................................................................................................................................................119 D
BÀI TẬP............................................................................................................................................................................................................................................................120
§5 – HÌNH CHỮ NHẬT − HÌNH VUÔNG 123 A
ĐỊNH NGHĨA.........................................................................................................................................................................................................................................123 B
TÍNH CHẤT..............................................................................................................................................................................................................................................123 C
DẤU HIỆU NHẬN BIẾT..................................................................................................................................................................................................124 D
BÀI TẬP............................................................................................................................................................................................................................................................126 §6 – HÌNH THOI 129 A
ĐỊNH NGHĨA.........................................................................................................................................................................................................................................129 B
TÍNH CHẤT..............................................................................................................................................................................................................................................129 C
DẤU HIỆU NHẬN BIẾT..................................................................................................................................................................................................130 D
BÀI TẬP............................................................................................................................................................................................................................................................131 §7 – HÌNH VUÔNG 134 A
Định nghĩa...................................................................................................................................................................................................................................................134 B
TÍNH CHẤT..............................................................................................................................................................................................................................................134 C
DẤU HIỆU NHẬN BIẾT..................................................................................................................................................................................................135 D
BÀI TẬP............................................................................................................................................................................................................................................................135
§8 – BÀI TẬP CUỐI CHƯƠNG V 137 Thầy Hóa - 0344.083.670 iv Chương 1. Đ Đ A A THỨ THỨ C C NHIỀU NHIỀU BIẾN BIẾN
Chủ đề 1. ĐƠN THỨC NHIỀU BIẾN.
ĐA THỨC NHIỀU BIẾN
A ĐƠN THỨC NHIỀU BIẾN 1 Định nghĩa
c Định nghĩa 1.1. Đơn thức nhiều biến (hay đơn thức) là biểu thức đại số chỉ gồm
một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Ví dụ 1. Trong các biểu thức sau, biểu thức nào là đơn thức? 1 1
; x; y; 2x + y; x2y; −3xy2z3; x2y2xz. 4 2 Lời giải. 1 1 Các biểu thức
; x; y; x2y; −3xy2z3;
x2y2xz là những đơn thức, còn biểu thức 2x + y không 4 2 phải là đơn thức. □
Luyện tập Trong các biểu thức sau, biểu thức nào là đơn thức? 1
5y; y + 3z; x3y2x2z. 2 Lời giải. 1 Các biểu thức 5y;
x3y2x2z là những đơn thức, còn biểu thức 2x + y không phải là đơn thức. 2 □ 2
Đơn thức thu gọn
c Định nghĩa 1.2. Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các
biến, mà mỗi biến đã được nâng lên lũy thừa với số mũ nguyên dương và chỉ được viết một lần.
Số nói trên gọi là hệ số, phần còn lại gọi là phần biến của đơn thức thu gọn. Ví dụ 2.
a) Trong những đơn thức sau, đơn thức nào là đơn thức thu gọn? √ 1
2; x; y; x2y3; −5x2y3z4; x2y2xz3. 4
b) Thu gọn đơn thức: 2x3y5z5z2. Lời giải.
1. ĐƠN THỨC NHIỀU BIẾN.ĐA THỨC NHIỀU BIẾN √ 1 a) Các đơn thức
2; x; y; x2y3; −5x2y3z4 là những đơn thức thu gọn, còn đơn thức x2y2xz3 4
không phải là đơn thức thu gọn.
b) Ta có 2x3y5z5z2 = 2x3y5 · (z5 · z2) = 2x3y5z7. □ 1
Luyện tập Thu gọn mỗi đơn thức sau: y3y2z; xy2x3z. 3 Lời giải.
y3y2z = y5z. 1 1 xy2x3z = x4y2z. 3 3 □ Chú ý
Ta cũng coi một số là đơn thức thu gọn.
Từ nay về sau, khi nói đến đơn thức mà không nói gì thêm thì ta hiểu đó là đơn thức thu gọn. 3
Đơn thức đồng dạng
c Định nghĩa 1.3. Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Ví dụ 3. Chỉ ra các đơn thức đồng dạng trong mỗi trường hợp sau 1
a) −x2y3z4 và − x2y3z4.
b) 0,5xy2 và 0,5x2y. 3 1 √ c)
x3y5; −6x3y5 và 3x3y5. 5 Lời giải. 1
a) Hai đơn thức −x2y3z4 và − x2y3z4 có hệ số khác 0 và có cùng phần biến nên chúng 3
là hai đơn thức đồng dạng.
b) Hai đơn thức 0,5xy2 và 0,5x2y không có cùng phần biến nên chúng không phải là hai đơn thức đồng dạng. 1 √ c) Những đơn thức
x3y5; −6x3y5 và
3x3y5 có hệ số khác 0 và có cùng phần biến nên 5
chúng là những đơn thức đồng dạng. □
Luyện tập Chỉ ra các đơn thức đồng dạng trong mỗi trường hợp sau: √
a) x2y4; −3x2y4 và 5x2y4.
b) −x2y2z2 và −2x2y2z3. Lời giải. √
a) Ba đơn thức x2y4; −3x2y4 và
5x2y4 có cùng phần biến nên ba đơn thức đã cho là ba đơn thức đồng dạng.
b) Hai đơn thức −x2y2z2 và −2x2y2z3 khác phần biến nên hai đơn thức đã cho là hai đơn thức không đồng dạng. □ Thầy Hóa - 0344.083.670 2
1. ĐƠN THỨC NHIỀU BIẾN.ĐA THỨC NHIỀU BIẾN 4
Cộng, trừ các đơn thức đồng dạng
c Định nghĩa 1.4. Để cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ)
các hệ số với nhau và giữ nguyên phần biến.
Ví dụ 4. Thực hiện phép tính:
a) 3x2y3 + 4x2y3.
b) 4x3y2 − 7x3y2. c) 8xy3 + xy3. Lời giải.
a) 3x2y3 + 4x2y3 = (3 + 4)x2y3 = 7x2y3.
b) 4x3y2 − 7x3y2 = (4 − 7)x3y2 = −3x3y2.
c) 8xy3 + xy3 = (8 + 1)xy3 = 9xy3. □
Luyện tập Thực hiện phép tính
a) 4x4y6 + 2x4y6.
b) 3x3y5 − 5x3y5. Lời giải.
a) 4x4y6 + 2x4y6 = (4 + 2)x4y6 = 6x4y6.
b) 3x3y5 − 5x3y5 = (3 − 5)x3y5 = −2x3y5. □
B ĐA THỨC NHIỀU BIẾN 1 Định nghĩa
c Định nghĩa 1.5. Đa thức nhiều biến (hay đa thức) là một tổng của những đơn thức. Chú ý
Mỗi đơn thức được coi là một đa thức.
Đa thức A = x2 − 2x + 3 của biến x, kí hiệu A(x).
Đa thức của hai biến x, y, kí hiệu P (x, y).
Đa thức Q = x3 + y3 + z3 − 3xyz của ba biến x, y, z, kí hiệu là Q(x, y, z).
Ví dụ 5. Trong những biểu thức sau, biểu thức nào là đa thức 1 x + y
2x + y + x2y; −3xy2z3 + x2y2z; . 2 x − y Lời giải. 1 x + y
Các biểu thức 2x + y + x2y; −3xy2z3 + x2y2z là đa thức, còn biểu thức không phải là 2 x − y đa thức. □ Thầy Hóa - 0344.083.670 3
1. ĐƠN THỨC NHIỀU BIẾN.ĐA THỨC NHIỀU BIẾN
Luyện tập Trong những biểu thức sau, biểu thức nào là đa thức 1 x2 + y2 y + 3z + y2z; . 2 x + y Lời giải. 1 x2 + y2
Biểu thức y + 3z +
y2z là đa thức, còn biểu thức không phải là đa thức. □ 2 x + y 2
Đa thức thu gọn
c Định nghĩa 1.6. Thu gọn đa thức nhiều biến là làm cho trong đa thức đó không
còn hai đơn thức nào đồng dạng.
Ví dụ 6. Thu gọn đa thức: Q = x2 + y2 + z2 + xy + xy + yz + yz + 2zx. Lời giải.
Ta có Q = x2 + y2 + z2 + xy + xy + yz + yz + 2zx □
= x2 + y2 + z2 + (xy + xy) + (yz + yz) + 2zx
= x2 + y2 + z2 + 2xy + 2yz + 2zx.
Luyện tập Thu gọn đa thức: R = x3 − 2x2y − x2y + 3xy2 − y3. Lời giải.
Ta có R = x3 − 2x2y − x2y + 3xy2 − y3 □
= x3 + −2x2y − x2y + 3xy2 − y3
= x3 − 3x2y + 3xy2 − y3. 3
Giá trị của đa thức
c Nhận xét 1.1. Để tính giá trị của một đa thức tại những giá trị cho trước của các biến,
ta thay những giá trị cho trước đó vào biểu thức xác định đa thức rồi thực hiện các phép tính.
Ví dụ 7. Tính giá trị của đa thức P = x2 − 2xy + y2 tại x = 1; y = 1. Lời giải.
Giá trị của đa thức P tại x = 1; y = 1 là
12 − 2 · 1 · 1 + 12 = 1 − 2 + 1 = 0. □
Luyện tập Tính giá trị của đa thức Q = x3 − 3x2y + 3xy2 − y3 tại x = 2; y = 1. Lời giải.
Giá trị của đa thức Q tại x = 2; y = 1 là
23 − 3 · 22 · 1 + 3 · 2 · 12 − 13 = 8 − 12 + 6 − 1 = 1. □ 4
Bậc của đơn thức, đa thức
Bậc của đơn thức (thu gọn) có hệ số khác 0 là tổng số mũ của tất cả các biến có trong đơn thức đó.
Bậc của đa thức là bậc cao nhất của các đơn thức trong dạng thu gọn của đa thức đó. Thầy Hóa - 0344.083.670 4
1. ĐƠN THỨC NHIỀU BIẾN.ĐA THỨC NHIỀU BIẾN Chú ý
Khi tìm bậc của đa thức, ta phải thu gọn đa thức đó.
Quy ước: số thực khác 0 là đa thức bậc không. Số 0 là đa thức không có bậc. C BÀI TẬP L Bài 1.
a) Trong những biểu thức sau, biểu thức nào là đơn thức? 1 3 1 xy2z3;
3 − 2x3y2z; − x4yxz2;
x2 y3 − z3 . 5 2 2
b) Trong những biểu thức sau, biểu thức nào là đa thức? 1 x − y 1
2 − x + y; −5x2yz3 +
xy2z + x + 1; ; + 2y − 3z. 3 xy2 x Lời giải. 1 3 a) Các biểu thức
xy2z3; − x4yxz2 là các đơn thức. 5 2 1
b) Các biểu thức 2 − x + y; −5x2yz3 +
xy2z + x + 1 là các đa thức. 3 □
L Bài 2. Thu gọn mỗi đơn thức sau: 1 a) x2yxy3.
b) 0,5x2yzxy3. 2 Lời giải. 1 1 a) x2yxy3 = x3y4.
b) 0,5x2yzxy3 = 0,5x3y4z. 2 2 □
L Bài 3. Chỉ ra các đơn thức đồng dạng trong mỗi trường hợp sau: 1 √
a) x3y5; − x3y5 và 3x3y5.
b) x2y3 và x2y7. 6 Lời giải. 1 √
a) Các đơn thức x3y5; − x3y5 và
3x3y5 là các đơn thức đồng dạng vì có cùng phần biến. 6
b) Các đơn thức x2y3 và x2y7 không phải là đơn thức đồng dạng vì khác phần biến. □
L Bài 4. Thực hiện phép tính:
a) 9x3y6 + 4x3y6 + 7x3y6.
b) 9x5y6 − 14x5y6 + 5x5y6. Thầy Hóa - 0344.083.670 5
1. ĐƠN THỨC NHIỀU BIẾN.ĐA THỨC NHIỀU BIẾN Lời giải.
a) 9x3y6 + 4x3y6 + 7x3y6 = (9 + 4 + 7)x3y6 = 20x3y6.
b) 9x5y6 − 14x5y6 + 5x5y6 = (9 − 14 + 5)x5y6 = 0. □
L Bài 5. Thu gọn mỗi đa thức sau:
a) A = 13x2y + 4 + 8xy − 6x2y − 9.
b) B = 4,4x2y − 40,6xy2 + 3,6xy2 − 1,4x2y − 26. Lời giải.
a) A = 13x2y + 4 + 8xy − 6x2y − 9.
= 13x2y − 6x2y + 4 + 8xy − 9
= 7x2y + 4 + 8xy − 9
b) B = 4,4x2y − 40,6xy2 + 3,6xy2 − 1,4x2y − 26
= 4,4x2y − 1,4x2y − 40,6xy2 + 3,6xy2 − 26
= 3x2y − 37xy2 − 26. □
L Bài 6. Tính giá trị của mỗi đa thức sau
a) P = x3y − 14y3 − 6xy2 + y + 2 tại x = −1; y = 0,5.
b) Q = 15x2y − 5xy2 + 7xy − 21 tại x = 0,2; y = −1,2. Lời giải.
a) Giá trị của đa thức P tại x = −1; y = 0,5 là
(−1)3 · 0,5 − 14 · (0,5)3 − 6 · (−1) · (0,5)2 + 0,5 + 2
= −0,5 − 1,75 + 1,5 + 2,5 = 1,25.
b) Giá trị của đa thức P tại x = 0,2; y = −1,2 là
15 · (0,2)2 · (−1,2) − 5 · 0,2 · (−1,2)2 + 7 · 0,2 · (−1,2) − 21
= −0,72 − 1,44 − 1,68 − 21 = −24,84. □ Thầy Hóa - 0344.083.670 6
2. CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN
Chủ đề 2. CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN
A CỘNG HAI ĐA THỨC NHIỀU BIẾN Chú ý
Để cộng hai đa thức theo hàng ngang, ta có thể làm như sau
Viết tổng hai đa thức theo hàng ngang;
Nhóm các đơn thức đồng dạng với nhau;
Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.
Ví dụ 8. Tính tổng của hai đa thức
P = x3 + 3x2y + 3xy2 + y3 và Q = x3 − 3x2y + 3xy2 − y3. Lời giải.
P + Q = x3 + 3x2y + 3xy2 + y3 + x3 − 3x2y + 3xy2 − y3 □
= x3 + x3 + 3x2y − 3x2y + 3xy2 + 3xy2 + y3 − y3
= 2x3 + 6xy2.
Ví dụ 9. Bác Huỳnh muốn sơn bề mặt của hai khối gỗ có dạng hình hộp chữ nhật. Hình
hộp chữ nhật thứ nhất có ba kích thước là x (cm), 2y (cm), z (cm). Hình hộp chữ nhật thứ
hai có ba kích thước là 2x (cm), 2y (cm), 3z (cm). Viết đa thức biểu thị tổng diện tích bề
mặt của hai khối gỗ mà bác Huỳnh cần sơn. Lời giải.
Tổng diện tích các mặt của hình hộp chữ nhật thứ nhất là
2 [x · 2y + x · z + 2y · z] = 4xy + 2xz + 4yz cm2 .
Tổng diện tích các mặt của hình hộp chữ nhật thứ hai là
2 [2x · 2y + 2x · 3z + 2y · 3z] = 8xy + 12xz + 12yz cm2 .
Đa thức biểu thị tổng diện tích bề mặt của hai khối gỗ mà bác Huỳnh cần phải sơn là
(4xy + 2xz + 4yz) + (8xy + 12xz + 12yz) = 4xy + 2xz + 4yz + 8xy + 12xz + 12yz
= (4xy + 8xy) + (2xz + 12xz) + (4yz + 12yz)
= 12xy + 14xz + 16yz cm2 . □
B TRỪ HAI ĐA THỨC NHIỀU BIẾN Chú ý
Để trừ đa thức P cho đa thức Q theo hàng ngang, ta có thể làm như sau
Viết hiệu P − Q theo hàng ngang, trong đó đa thức Q được đặt trong dấu ngoặc;
Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức Q, nhóm các đơn thức Thầy Hóa - 0344.083.670 7
2. CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN đồng dạng với nhau;
Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
Ví dụ 10. Cho ba đa thức: A = x2 − 2xy + y2; B = 2x2 − y2; C = x2 − 3xy. Tính: a) A − B. b) A − C. Lời giải.
a) Ta có A − B = x2 − 2xy + y2 − 2x2 − y2
= x2 − 2xy + y2 − 2x2 + y2
= x2 − 2x2 + y2 + y2 − 2xy
= −x2 + 2y2 − 2xy.
b) Ta có A − C = x2 − 2xy + y2 − x2 − 3xy
= x2 − 2xy + y2 − x2 + 3xy
= x2 − x2 + (−2xy + 3xy) + y2
= xy + y2. □
C NHÂN HAI ĐA THỨC NHIỀU BIẾN 1
Nhân hai đơn thức Chú ý
Tương tự như đối với đơn thức một biến, để nhân hai đơn thức nhiều biến ta có thể làm như sau:
Nhân các hệ số với nhau và nhân phần biến với nhau.
Thu gọn đơn thức nhận được ở tích.
Ví dụ 11. Tính tích
a) 3x2y3 · 8x4y6;
b) 3x2y3z · 9x3y3z2. Lời giải.
a) 3x2y3 · 8x4y6 = (3 · 8) (x2 · x4) (y3 · y6) = 24x6y9;
b) 3x2y3z · 9x3y3z2 = (3 · 9) (x2 · x3) (y3 · y3) (z · z2) = 27x5y6z3. □ 2
Nhân đơn thức với đa thức Chú ý
Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức đó với từng đơn thức của
đa thức rồi cộng các kết quả với nhau.
Ví dụ 12. Tính tích Thầy Hóa - 0344.083.670 8
2. CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN Å 1 ã
a) (xy2) (x + y + xy); b)
− xy (6x3 − 9xy + 3y3). 3 Lời giải.
a) (xy2) (x + y + xy) = xy2x + xy2y + xy2xy = x2y2 + xy3 + x2y3; Å 1 ã Å 1 ã Å 1 ã Å 1 ã b) − xy
6x3 − 9xy + 3y3 =
− xy · 6x3 − − xy · 9xy + − xy · 3y3 3 3 3 3 Å 1 ã Å 1 ã Å 1 ã = − · 6 xyx3 −
− · 9 (xyxy) + − · 3 xyy3 3 3 3
= −2x4y + 3x2y2 − xy4. □ 3
Nhân hai đa thức Chú ý
Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với
từng đơn thức của đa thức kia rồi cộng các kết quả với nhau.
Ví dụ 13. Tính tích a) (x + y)2;
b) (x + y) (x − y). Lời giải.
a) (x + y)2 = (x + y) (x + y) = x2 + xy + yx + y2 = x2 + 2xy + y2;
b) (x + y) (x − y) = x2 − xy + yx − y2 = x2 − y2. □
Ví dụ 14. Một mảnh vườn có dạng hình chữ nhật với độ dài hai cạnh là 2x + y (m) và 2x − y (m).
a) Viết đa thức biểu thị diện tích của mảnh vườn trên theo x và y.
b) Tính diện tích mảnh vườn khi x = 3; y = 2. Lời giải.
a) Đa thức biểu thị diện tích của mảnh vườn là
(2x + y) (2x − y) = 4x2 − 2xy + 2yx − y2 = 4x2 − y2 m2 .
b) Với x = 3 và y = 2, diện tích của mảnh vườn là
4 · 32 − 22 = 36 − 4 = 32 m2 . □
D CHIA ĐA THỨC CHO ĐƠN THỨC 1
Phép chia hết một đơn thức cho một đơn thức Thầy Hóa - 0344.083.670 9
2. CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN Chú ý
Tương tự như trường hợp một biến, ta nói đơn thức nhiều biến A là chia hết cho đơn
thức nhiều biến B (B ̸= 0) nếu tìm được đơn thức Q sao cho A = B · Q.
Đơn thức A chia hết cho đơn thức B (B ̸= 0) khi mỗi biến của B đều là biến của A với
số mũ không lớn hơn số mũ của nó trong A.
Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết B), ta có thể làm như sau:
Chia hệ số của đơn thức A cho hệ số của đơn thức B.
Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
Nhân các kết quả vừa tìm được với nhau.
Ví dụ 15. Tìm thương trong phép chia đơn thức 16x4y5z6 cho đơn thức 8x3y2. Lời giải. Ta có
(16x4y5z6) : (8x3y2) = (16 : 8) (x4 : x3) (y5 : y2) z6 = 2xy3z6.
Vậy thương trong phép chia đơn thức 16x4y5z6 cho đơn thức 8x3y2 là 2xy3z6. □ 2
Phép chia hết một đa thức cho một đơn thức Chú ý
Tương tự như trên, ta nói đa thức nhiều biến A là chia hết cho đơn thức nhiều biến B
(B ̸= 0) nếu tìm được đơn thức Q sao cho A = B · Q.
Đa thức A chia hết cho đơn thức B (B ̸= 0) khi mỗi đơn thức của A đều chia hết cho đơn thức B.
Muốn chia đa thức A cho đơn thức B (trường hợp A chia hết B), ta chia mỗi đơn thức
của A cho B rồi cộng các kết quả với nhau.
Ví dụ 16. Tìm thương trong phép chia đa thức 15x3y2 − 20x2y3 + 25x4y4 cho đơn thức 5x2y2. Lời giải. Ta có
15x3y2 − 20x2y3 + 25x4y4 : 5x2y2
= 15x3y2 : 5x2y2 − 20x2y3 : 5x2y2 + 25x4y4 : 5x2y2
= 3x − 4y + 5x2y2.
Vậy thương trong phép chia đa thức 15x3y2 − 20x2y3 + 25x4y4 cho đơn thức 5x2y2 là 3x −
4y + 5x2y2. □ E BÀI TẬP
L Bài 7. Thực hiện phép tính Å 1 ã
a) (−xy) (−2x2y + 3xy − 7x); b)
x2y2 (−0,3x2y − 0,4xy + 1); 6
c) (x + y) (x2 + 2xy + y2);
d) (x − y) (x2 − 2xy + y2). Lời giải. Thầy Hóa - 0344.083.670 10
2. CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN
a) (−xy) −2x2y + 3xy − 7x
= (−xy) −2x2y + (−xy) (3xy) − (−xy) (7x)
= 2x3y2 − 3x2y2 + 7x2y. Å 1 ã b) x2y2
−0,3x2y − 0,4xy + 1 6 Å 1 ã Å 1 ã Å 1 ã = x2y2
−0,3x2y −
x2y2 (0,4xy) + x2y2 6 6 6 −1 1 1 = x4y3 − x3y3 + x2y2. 20 15 6
c) (x + y) x2 + 2xy + y2
= x · x2 + x · 2xy + x · y2 + y · x2 + y · 2xy + y · y2
= x3 + 2x2y + xy2 + x2y + 2xy2 + y3
= x3 + 3x2y + 3xy2 + y3.
d) (x − y) x2 − 2xy + y2
= x · x2 − x · 2xy + x · y2 − y · x2 + y · 2xy − y · y2
= x3 − 2x2y + xy2 − x2y + 2xy2 − y3
= x3 − 3x2y + 3xy2y3. □
L Bài 8. Thực hiện phép tính Å 1 ã Å 1 ã
a) (39x5y7) : (13x2y); b) x2y2 +
x3y2 − x5y4 : x2y2 . 6 2 Lời giải.
a) (39x5y7) : (13x2y) = (39 : 13) (x5 : x2) (y7 : y) = 3x3y6; Å 1 ã Å 1 ã b) x2y2 +
x3y2 − x5y4 : x2y2 6 2 Å 1 ã Å 1 ã Å 1 ã Å 1 ã = x2y2 : x2y2 + x3y2 : x2y2 − x5y4 : x2y2 2 6 2 2 1 = 2 +
x − 2x3y2. 3 □
L Bài 9. Rút gọn biểu thức
a) (x − y) (x2 + xy + y2);
b) (x + y) (x2 − xy + y2); Å 4 ã
c) (4x − 1) (6y + 1) − 3x 8y + ;
d) (x + y) (x − y) + (xy4 − x3y2) : (xy2). 3 Lời giải.
a) (x − y) x2 + xy + y2
= x · x2 + x · xy + x · y2 − y · x2 − y · xy − y · y2
= x3 + x2y + xy2 − x2y − xy2 − y3
= x3 − y3. Thầy Hóa - 0344.083.670 11
2. CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN
b) (x + y) x2 − xy + y2
= x · x2 − x · xy + x · y2 + y · x2 − y · xy + y · y2
= x3 − x2y + xy2 + x2y − xy2 + y3
= x3 + y3. Å 4 ã
c) (4x − 1) (6y + 1) − 3x 8y + 3 4
= 4x · 6y + 4x · 1 − 6y · 1 − 1 · 1 − 3x · 8y − 3x · 3
= 24xy + 4x − 6y − 1 − 24xy − 4x = −6y − 1.
d) (x + y) (x − y) + xy4 − x3y2 : xy2
= x · x − x · y + x · y − y · y + xy4 : xy2 − x3y2 : xy2
= x2 − xy + xy − y2 + y2 − x2 = 0. □ L Bài 10.
a) Rút gọn rồi tính giá trị của biểu thức
P = 5x2 − 2xy + y2 − x2 + y2 − 4x2 − 5xy + 1
khi x = 1,2 và x + y = 6,2.
b) Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x:
x2 − 5x + 4 (2x + 3) − 2x2 − x − 10 (x − 3) . Lời giải.
a) Ta có P = 5x2 − 2xy + y2 − x2 + y2 − 4x2 − 5xy + 1
= 5x2 − 2xy + y2 − x2 − y2 − 4x2 + 5xy − 1
= 5x2 − x2 − 4x2 + (−2xy + 5xy) + y2 − y2 − 1 = 3xy − 1.
Với x = 1,2 và x + y = 6,2 suy ra y = 4, thay vào P ta được P = 3 · 1,2 · 4 − 1 = 13, 4. b)
x2 − 5x + 4 (2x + 3) − 2x2 − x − 10 (x − 3)
= 2x3 + 3x2 − 10x2 − 15x + 8x + 6 − 2x3 − 6x2 − x2 + 3x − 10x + 30
= 2x3 − 2x3 + 3x2 − 10x2 + 6x2 + x2 + (−15x + 8x − 3x + 10x) + (6 − 30) = −24.
Vậy giá trị của biểu thức trên không phụ thuộc vào giá trị của biến x. □ L Bài 11.
a) Chứng minh rằng biểu thức P = 5x (2 − x) − (x + 1) (x + 9) luôn nhận giá trị âm với
mọi giá trị của biến x. Thầy Hóa - 0344.083.670 12
2. CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN
b) Chứng minh rằng biểu thức Q = 3x2 + x (x − 4y) − 2x (6 − 2y) + 12x + 1 luôn nhận giá
trị dương với mọi giá trị của biến x. Lời giải.
a) P = 5x (2 − x) − (x + 1) (x + 9)
= 10x − 5x2 − x2 + 9x + x + 9
= 10x − 5x2 − x2 − 10x − 9 = −6x2 − 9.
Vì x2 ⩾ 0 nên −6x2 ⩽ 0 với mọi x. Do đó −6x2 − 9 < 0 với mọi giá trị của biến x.
Vậy biểu thức P luôn nhận giá trị âm với mọi giá trị của biến x.
b) Q = 3x2 + x (x − 4y) − 2x (6 − 2y) + 12x + 1
= 3x2 + x2 − 4xy − 12x + 4yx + 12x + 1 = 4x2 + 1.
Vì x2 ⩾ 0 nên 4x2 ⩾ 0 với mọi x. Do đó 4x2 + 1 > 0 với mọi giá trị của biến x.
Vậy biểu thức Q luôn nhận giá trị dương với mọi giá trị của biến x. □ L Bài 12.
Bạn Hạnh dự định cắt một miếng bìa có dạng tam giác
vuông với độ dài hai cạnh góc vuông lần lượt là 6 (cm), x (cm)
8 (cm). Sau khi xem xét lại, bạn Hạnh quyết định tăng
độ dài cạnh góc vuông 6 (cm) thêm x (cm) và tăng độ
dài cạnh góc vuông 8 (cm) thêm y (cm) (Hình 2). Viết đa 6 (cm)
thức biểu thị diện tích phần tăng thêm của miếng bìa theo x và y. 8 (cm) y (cm) Hình 2 Lời giải. 1
Diện tích tam giác vuông bạn Hạnh dự định cắt là · 8 · 6 = 24 (cm2). 2 1
Diện tích tam giác vuông bạn Hạnh cắt là
· (8 + y) · (6 + x) (cm2). 2
Diện tích của phần tăng thêm là 1 1
· (8 + y) · (6 + x) − 24 =
· (48 + 6y + 8x + xy) − 24 2 2 xy = 24 + 3y + 4x + − 24 2 xy = 3y + 4x + . 2 xy
Vậy đa thức biểu thị diện tích phần tăng thêm của miếng bìa theo x và y là 3y+4x+ (cm2). 2 □ L Bài 13. Thầy Hóa - 0344.083.670 13
2. CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN
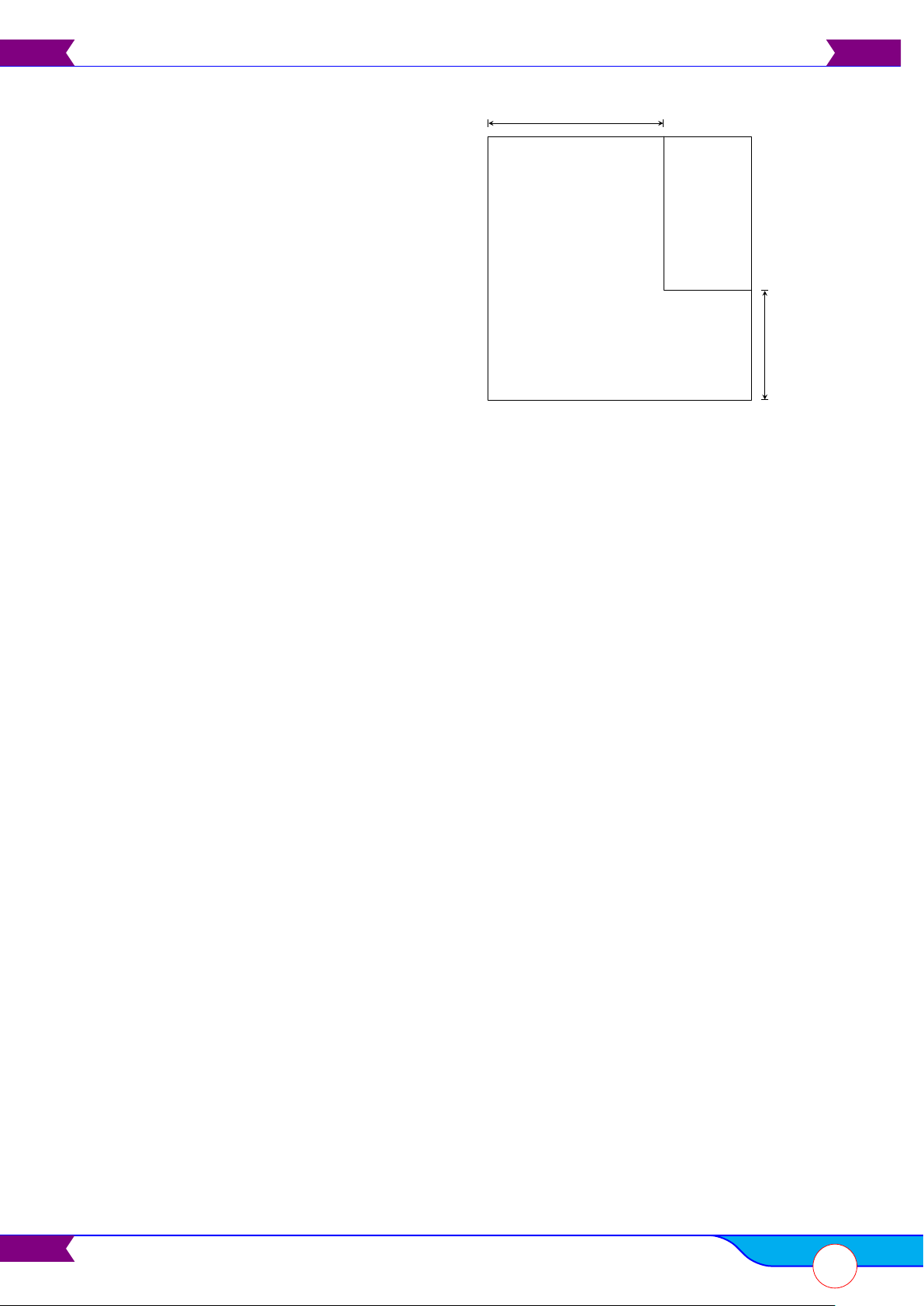
Khu vườn nhà bác Xuân có dạng hình vuông. 15 (m)
Bác Xuân muốn dành một mảnh đất có dạng
hình chữ nhật ở góc khu vườn để trồng rau Mảnh
(Hình 3). Biết diện tích của mảnh đất trồng rau
bằng 150 m2. Tính độ dài cạnh x (m) của khu đất vườn đó. trồng rau 10 (m) x (m) Hình 3 Lời giải.
Chiều dài của mảnh đất trồng rau là x − 10 (m).
Chiều rộng của mảnh đất trồng rau là x − 15 (m).
Vì diện tích của mảnh đất trồng rau là 150m2 nên (x − 10) (x − 15) = 150.
Ta có x2 − 10x − 15x + 150 = 150 x2 − 25x = 0 x (x − 25) = 0
⇒ x = 25 (vì x > 0).
Vậy độ dài cạnh của khu vườn là 25 (m). □ Thầy Hóa - 0344.083.670 14




