





Preview text:
lOMoAR cPSD| 44729304 •
CHAPTER 4: PARAMETER ESTIMATION POINT ESTIMATE
METHOD OF MOMENTS ESTIMATION
MAXIMUM LIKELIHOOD ESTIMATION
Population X: Discrete or Continuous Population : Discrete or Continuous
MoM Estimator θbof θ: biased or unbiased
MLE θ of θ: biased or unbiased
CONFIDENCE INTERVAL FOR POPULATION MEAN E[X] = µ
POPULATION X ∼ N(µ, σ2) (Normal Distribution) σ2: σ2: KNOWN UNKNOWN
Z−statistic: Z =
σ− µ√n ∼ N(0,1) X
T−statistic: T =
S− µ√n ∼ t(n − 1) X
• Two-sided confidence interval for µ with a
• Two-sided confidence interval for µ with a confidence level confidence level : S 1 − α: S where . where .
Error of confidence interval estimation:
Error of confidence interval estimation: . .
• One-sided confidence interval for µ with a
• One-sided confidence interval for µ with a
confidence level 1 − α:
confidence level 1 − α: Case 1: Lower interval Case 1: Lower interval Case 2: Upper interval Case 2: Upper interval
where Φ(zα) = P(Z < zα) = 1 − α.
where P(T > tα,n−1) = α.
POPULATION X is non-normal with E[X] = µ and Var(X) = σ2
Sample size n large enough: n ≥ 30 σ2: KNOWN σ2: UNKNOWN
Z−statistic: Z =
σ− µ√n ≈ N(0,1) X
Z−statistic: Z =
S− µ√n ≈ N(0,1) X
• Two-sided confidence interval for µ with a
• Two-sided confidence interval for µ with a confidence level : confidence level :
• One-sided confidence interval for µ with a
confidence level 1 − α: 1
Downloaded by C?m Tú ?ào (daocamtu22042002@gmail.com) lOMoAR cPSD| 44729304
• One-sided confidence interval for µ with a
confidence level 1 − α: Case 1: Lower interval Case 1: Lower interval Case 2: Upper interval Case 2: Upper interval
CONFIDENCE INTERVAL FOR POPULATION PROPORTION p
Let p be the population proportion. Let pbbe the sample
proportion. For n large enough (check npb≥ 5 and n(1 − pb) ≥ 5), we have
with a confidence level 1 − α:
Error of confidence interval estimation:
• One-sided confidence interval for p: Case 1: Lower interval Case 2: Upper interval
Problem 4.7. In a random sample of 500 families owning television sets in the city of Hamilton,
Canada, it is found that 340 families subscribe to HBO.
Find a 95% confidence interval for the actual proportion p of families with television sets in this city that subscribe to HBO. 2 lOMoAR cPSD| 44729304 •
CHAPTER 5: HYPOTHESIS TESTING
ONE SAMPLE: TEST ON A SINGLE MEAN σ2: KNOWN σ2: UNKNOWN
Any population X with E[X] = µ, Var(X) = σ2
Population X ∼ N(µ,σ2)
• Null and alternative hypotheses: X µ σ
Standardized test statistic: Z = − 0√n ≈ N(0,1)Test statistic:
when H0 is true.when H0 is true.
Rejection region for H0: Wα = (−∞,−z α2 ) ∪ (z α2 ,+∞)
W α = (−∞,−tα 2 ,n−1) ∪ (t α2 ,n−1,+∞) •
Null and alternative hypotheses: 0
Rejection region for H0: Wα = (−∞,−zα)W α = (−∞,−tα,n−1)
• Null and alternative hypotheses:
Rejection region for H0: Wα = (zα,+∞)
Wα = (tα,n−1,+∞) Sample size
n ≥ 30; Any population X Test statistic: when H0 is true.
ONE SAMPLE: TEST ON A SINGLE PROPORTION 3 lOMoAR cPSD| 44729304
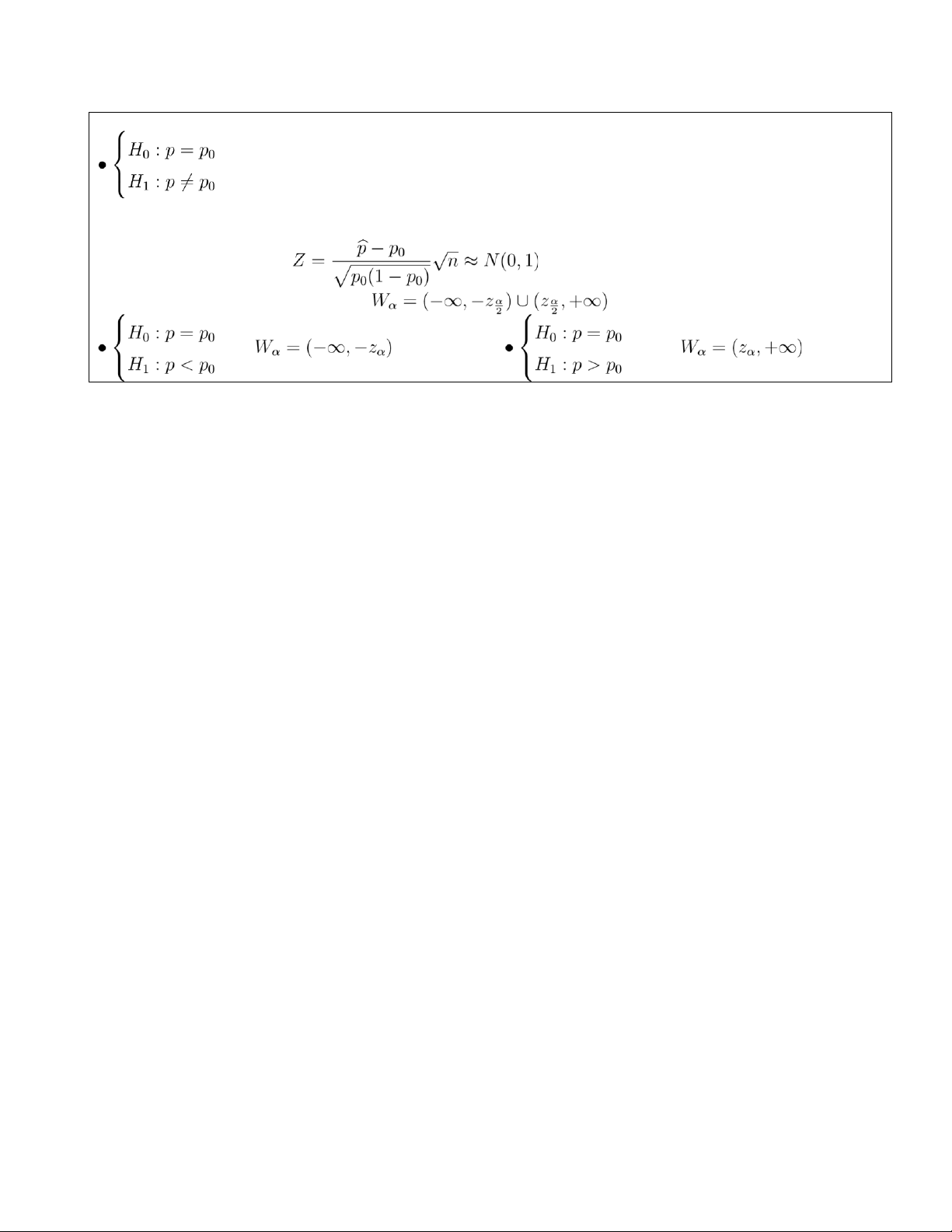
Let p be the population proportion. Let pbbe the sample proportion.
(Check: np0 ≥ 5 and n(1 − p0) ≥ 5) Standardized test statistic: when H0 is true. 4 lOMoAR cPSD| 44729304 •
TWO SAMPLES: TEST ON TWO MEANS TWO
POPULATIONS X,Y WITH MEANS µ1,µ2 and VARIANCES TWO VARIANCES : KNOWN
Any X,Y and n1 ≥ 30,n2 ≥ 30 Test statistic: when H0 is true. when H0 is true. 1 = µ2
Wα = (zα,+∞) 1 > µ2 TWO VARIANCES : UNKNOW N ; EQUAL VARIANCES
Any X,Y and n1 ≥ 30,n2 ≥ 30 Test statistic: when H0 is true.
Wα = (−∞,−zα) Wα = when H0 is true. (zα,+∞)
TWO SAMPLES: TEST ON TWO PROPORTIONS 5 lOMoAR cPSD| 44729304 •
Let p1,p2 be two population proportions. Let be two sample proportions. (Check:, and Standardized test statistic: when H0 is true. Here, . Rejection region: 6 lOMoAR cPSD| 44729304 •
Problem 5.11. A men’s softball league is experimenting with a yellow baseball that is easier to see
during night games. One way to judge the effectiveness is to count the number of errors. In a
preliminary experiment, the yellow baseball was used in 10 games and the traditional white
baseball was used in another 10 games. The number of errors in each game was recorded and is listed here Yellow 5 2 6 7 2 5 3 8 4 9 White 7 6 8 5 9 11 8 3 6 10
Can we infer that there are fewer errors on average when the yellow ball is used at the 0.05 level
of significance? Assume the two populations to be normally distributed with equal variances. 7




