Kế hoạch giáo dục Toán 11 cả năm

KẾ HOẠCH GIÁO DỤC MÔN HỌC - NĂM HỌC 2020-2021 MÔN: TOÁN KHỐI: 11 I. Thông tin: 1. Tổ trưởng:
2. Nhóm trưởng chuyên môn: …………………………………………………………….. II.
Kế hoạch cụ thể:
Cả năm: (35 tuần x … tiết/tuần) = 123 tiết.
Học kỳ I: (18 tuần x 4 tiết/tuần) = 72 tiết.
Học kỳ II: (17 tuần x 3 tiết/tuần) = 51 tiết.
PHẦN I. GIẢI TÍCH 11 Nội dung/Mạch
Hình thức tổ chức
Yêu cầu cần đạt Tuần Tiết
Tên chủ đề /Bài học kiến thức dạy học Ghi chú - Định nghĩa. Về kiến thức: - Dạy học theo -Tính tuần hoàn.
Hiểu khái niệm hàm số lượng nhóm kết hợp dạy - Sự biến thiên và
giác (của biến số thực). học cá nhân. đồ thị của hàm số Về kỹ năng. - Hình thức thảo lượng giác.
- Xác định được: tập xác định; luận. CHƯƠNG I.
tập giá trị; tính chất chẵn, lẻ; tính HÀM SỐ
tuần hoàn; chu kì; khoảng đồng LƯỢNG §1: Hàm
biến, nghịch biến của các hàm số GIÁC VÀ 1 1,2,3 số lượng
y = sinx: y = cosx; y = tanx; y = PHƯƠNG giác cotx. TRÌNH
- Vẽ được đồ thị của các hàm số LƯỢNG
y = sinx: y = cosx; y = tanx; y GIÁC = cotx. Trang 1
- Bt hàm số lượng Bài tập cần 4 giác làm (tr17): 1, 2, 3, 4, 5, 6, 7
- Các phương trình Về kiến thức: - Dạy học theo
lượng giác cơ bản. Biết các phương trình lượng giác nhóm kết hợp dạy - Mục I.3
sinx = a; cosx = a; cơ bản: sinx = a; cosx = a; tanx = học cá nhân. (trang 30) và - 2 tanx = a; a; và công thức nghiệm.
- Hình thức thảo Mục II.3 Về kỹ năng: luận. (trang 32 – 34) 5,6
Giải thành thạo phương trình (Khuyến khích
lượng giác cơ bản. Biết sử dụng học sinh tự
máy tính bỏ túi để giải phương đọc)
trình lượng giác cơ bản. §2.Phươn g trình cotx = a
Giải thành thạo phương trình - Dạy học theo lượng
lượng giác cotx = a nhóm kết hợp dạy giác cơ học cá nhân. 7 bản - Hình thức thảo CHƯƠNG I. luận. HÀM SỐ LƯỢNG 3
-Bài tập pt lượng Về kỹ năng: GIÁC VÀ giác cơ bản
Giải thành thạo phương trình PHƯƠNG
-Sử dụng máy tính lượng giác cơ bản. Biết sử dụng - Bài tập cần TRÌNH làm (trang 28): 8,9 cầm tay để giải pt
máy tính bỏ túi để giải phương LƯỢNG
trình lượng giác cơ bản. 1, 3, 4, 5 GIÁC 10
§3.Một số phương trình bậc Biết dạng và cách giải các - Dạy học theo 4 11,12 phương
nhất, bậc hai đối phương trình: bậc nhất, bậc hai nhóm kết hợp dạy Trang 2 trình
với một hàm số đối với một hàm số lượng giác; học cá nhân. lượng lượng giác; asinx+bcosx = c. - Hình thức thảo giác asinx+bcosx = c. Về kỹ năng: luận. thường
Giải thành thạo phương trình gặp + Bài
lượng giác cơ bản. Biết sử dụng tập ( có
máy tính bỏ túi để giải phương thực hành
trình lượng giác cơ bản. máy tính
Giải được phương trình thuộc cầm tay) dạng nêu trên.
Giải các phương Về kỹ năng:
trình bậc nhất, Giải thành thạo phương trình
bậc hai đối với lượng giác cơ bản. Biết sử dụng - Bài tập cần 5 13,14, 15 Bài tập
một hàm số lượng máy tính bỏ túi để giải phương làm (trang 36):
giác; asinx+bcosx trình lượng giác cơ bản. 1, 2a, 3c, 5 = c.
Giải được phương trình thuộc dạng nêu trên.
Ôn lại kiến thức lý Về kiến thức: - Dạy học theo
thuyết về hàm số - Tập xác định, TGT của các hàm nhóm kết hợp dạy Ôn tập lượng giác; các pt số lượng giác học cá nhân. chương I
lg cơ bản; các ptlg - Phương trình lượng giác cơ bản - Hình thức thảo - Câu hỏi ôn thường gặp
- Phương trình bậc nhất và bậc luận. tập
hai đối với một hàm số lượng chương. giác - Bài tập ôn 6 16,17, 18
- Phương trình đưa về bậc nhất, tập
bậc hai đối với một hàm số chương. lượng giác - Trắc
- Phương trình bậc nhất với sin nghiệm ôn tập và cos chương. Về kỹ năng:
- Giải các phương trình lượng giác cơ bản Trang 3
- Qui tắc cộng, qui Kiến thức: - Dạy học theo tắc nhân.
Biết: Quy tắc cộng và quy tắc nhóm kết hợp dạy §1. Quy nhân; học cá nhân. 19,20 tắc đếm - Kỹ năng: - Hình thức thảo Bài tập cần 7 Bài tập
Bước đầu vận dụng được quy tắc luận. làm : bài cộng và quy tắc nhân. 1,2,3,4 (trang 46) 21 -Hoán vị, Kiến thức: Ví dụ 2 trang - Chỉnh hợp,
Biết: Hoán vị, chỉnh hợp, tổ hợp 47 lặp lại hoạt CHƯƠNG -Tổ hợp
chập k của n phần tử; Công thức động 1 trang Nhị thức 47 - Khuyến II. TỔ HỢP – XÁC SUẤT Kỹ năng: khích học sinh
- Tính được số các hoán vị, chỉnh tự học
hợp, tổ hợp chập k của n phần tử - Không chứng §2. Hoán . minh các định vị - Chỉnh 8 22,23, 24
- Tính được số các hoán vị n lí trang 48, 50, hợp - Tổ
phần tử; chỉnh hợp, tổ hợp chập 52 - Khuyến hợp k của n phần tử. khích học sinh tự học - Mục III.3 - Tự học có hướng dẫn. Bài tập Bài 1, 2, 3, 6 25,26 9 (trang 54) 27
KIỂM TRA GIỮA KÌ I Trang 4
- Công thức nhị Về kiến thức:
- Dạy học theo - Ví dụ 3 trang thức Niu – tơn.
- Biết khai triển nhị thức
nhóm kết hợp dạy 56 - Tự học có
- Các ứng dụng - Biết biểu diễn hệ số của khai học cá nhân. hướng dẫn.
của Công thức nhị triển theo tam giác Pascal
- Hình thức thảo - HĐ 2 tr 57 - thức Niu – tơn.
- Biết tìm số hạng bất kì trong luận. Không dạy khai triển §3.Nhị Về kỹ năng: 28, 29 thức Niu
- Biết khai triển nhị thức Niu-tơn – tơn
với một số mũ cụ thể.
-Tìm được hệ số của xk trong
khai triển (ax + b)n thành đa thức. - Bài tập cần
tay hỗ trợ việc tính toán. làm: 1, 2, 5 10 (trang 57)
- Phép thử và biến Về kiến thức: - Dạy học theo cố.
Biết : Phép thử ngẫu nhiên; nhóm kết hợp dạy
không gian mẫu; biến cố liên học cá nhân.
quan đến phép thử ngẫu nhiên. - Hình thức thảo §4. Phép
Định nghĩa xác suất của biến cố. luận. thử và 30 Về kỹ năng: biến cố.
Xác định được: phép thử ngẫu Bài tập
nhiên; không gian mẫu; biến cố Bài tập cần
liên quan đến phép thử ngẫu làm: 2,4,6 nhiên (trang 63-64)
- Phép thử và biến Về kiến thức: cố.
Biết : Phép thử ngẫu nhiên;
không gian mẫu; biến cố liên §4. Phép
quan đến phép thử ngẫu nhiên. CHƯƠNG thử và
Định nghĩa xác suất của biến cố. 11 31 II. TỔ HỢP – biến cố. Về kỹ năng: XÁC SUẤT Bài
Xác định được: phép thử ngẫu Bài tập cần tập(TT)
nhiên; không gian mẫu; biến cố làm: 2,4,6
liên quan đến phép thử ngẫu (trang 63-64); nhiên Trang 5
- Xác suất của Về kiến thức: - Dạy học theo biến cố.
Biết : Định nghĩa xác suất của nhóm kết hợp dạy biến cố. học cá nhân. - Biết tính chất: - Hình thức thảo
P(Æ) = 0; P(W) =1; luận. 32,33 0 £ P( A) £1. §5. Xác
- Biết (không chứng minh) định lí suất của
cộng xác suất và định lí nhân xác biến cố suất. Về kỹ năng:
Xác định được: Biết dùng máy
tính bỏ túi hỗ trợ tính xác suất. Bài tập
Biết giải các dạng bt cơ bản - Hình thức thảo Bài tập cần 34
Thực hành giải toán trên MTCT luận nhóm. làm 1, 4, 5 (trang 74); Ôn tập các nd
Yêu cầu: hs biết vận dụng kiến - Dạy học theo
- Công thức nhị thức đã học vào giải các bài tập nhóm kết hợp dạy thức Niu – tơn. sgk học cá nhân. 12 - Các ứng dụng - Hình thức thảo Bài tập cần Ôn tập của Công thức nhị luận. làm 35,36
chương II thức Niu – tơn. 1,2,3,4,5,7 - Phép thử và biến (trang 76) cố. - Xác suất của biến cố.
-Phương pháp quy Về kiến thức: - Dạy học theo CHƯƠNG §1. nạp toán học.
- Hiểu được phương pháp quy nhóm kết hợp dạy III. DÃY SỐ Phương nạp toán học. học cá nhân. Làm các bài 13 37,38 - CẤP SỐ pháp quy Về kỹ năng: - Hình thức thảo tập 1; 4; 5 CỘNG VÀ nạp toán
- Biết cách chứng minh một số luận. CẤP SỐ học
mệnh đề đơn giản bằng quy nạp. NHÂN (12 §2. Dãy - Định nghĩa dãy Về kiến thức: - Dạy học theo 14 39 tiết) số. Bài số.
- Biết khái niệm dãy số; cách cho nhóm kết hợp dạy Trang 6 tập
-Cách cho dãy số. dãy số (bởi công thức tổng quát; học cá nhân. - Dãy số tăng,
bởi hệ thức truy hồi; mô tả); dãy - Hình thức thảo Mục II.2, III– giảm và bị chặn. số hữu hạn, vô hạn. luận. Học sinh tự
- Biết tính tăng, giảm, bị chặn học. 40 của một dãy số. Bài tập cần Về kỹ năng: làm: 1, 2a, 3a,
Chứng minh được tính tăng, 4a,b,c.
giảm, bị chặn của một dãy số đơn giản cho trước. - Định nghĩa Về kiến thức: - Dạy học theo - Số hạng tổng
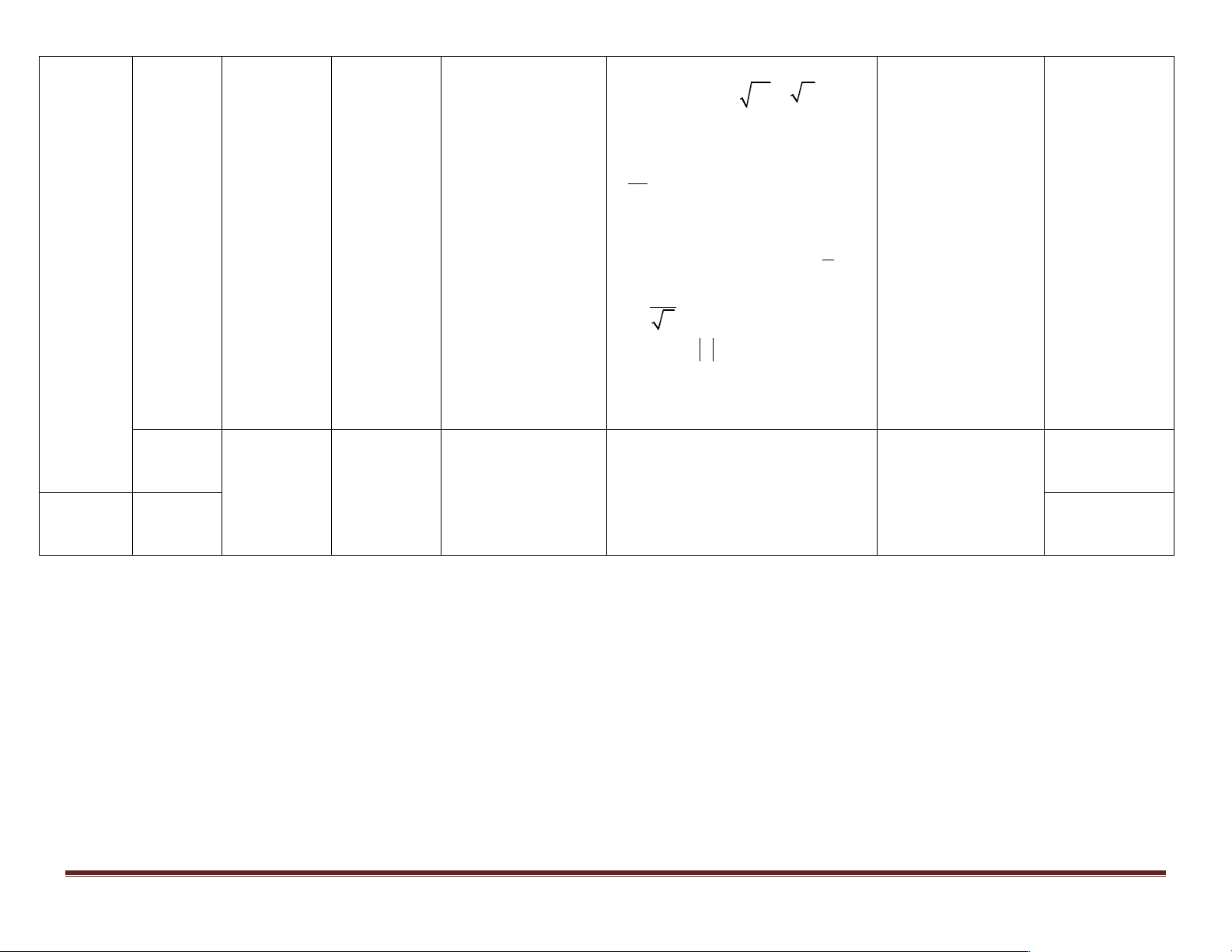
- Biết được: khái niệm cấp số nhóm kết hợp dạy Mục II. Định quát. cộng, tính chất học cá nhân. lý 1, III. Định - Tính chất của các u + u - Hình thức thảo k 1 - k 1 + lý 2 – GV định
số hạng của cấp số u = ; k ³ 2, số hạng k luận. 2 hướng phần §3. Cấp cộng. chứng minh - 15 41,42 số cộng.
tổng quát un, tổng của n số hạng - Công thức tính Học sinh tự Bài tập
đầu tiên của cấp số cộng Sn.
tổng n số hạng Về kỹ năng: học. đầu.
- Tìm được các yếu tố còn lại khi Bài tập cần
cho biết 3 trong 5 yếu tố u1, un,, làm: 1, 2, 3, 4, n, d, Sn. 5. Trang 7 - Định nghĩa Về kiến thức: - Dạy học theo - Số hạng tổng
Biết được: khái niệm cấp số nhóm kết hợp dạy quát. nhân, tính chất học cá nhân. - Tính chất của các 2 u = u .u
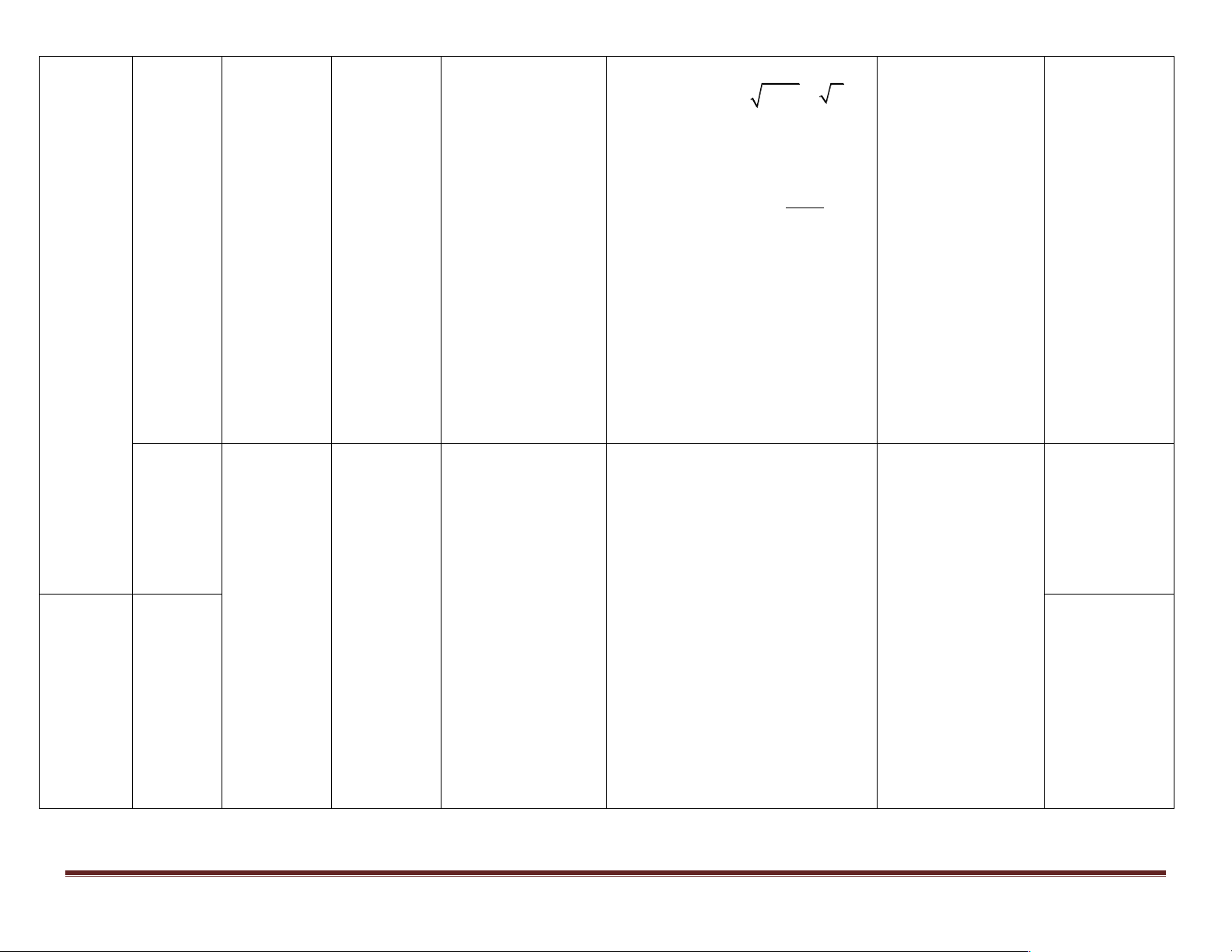
; k ³ 2 , số hạng - Hình thức thảo k k 1 - k 1 + Mục II.VD3 - số hạng của cấp số luận. tổng quát u Học sinh tự nhân. n, tổng của n số hạng
đầu tiên của cấp số nhân Sn. học Về kỹ năng: Mục II. Định
Tìm được các yếu tố còn lại khi lý 1, III. Định lý 2 - GV định §4. Cấp
cho biết 3 trong 5 yếu tố u1, un,, hướng phần 16 43,44 số nhân. n, q, Sn. chứng minh - Bài tập Học sinh tự học. Bài tập luyện tập: 1, 2, 3 (T103), bài 4 (T104) Về kiến thức: - Dạy học theo
- Hiểu được các kiến thức về dãy nhóm kết hợp dạy
số, cấp số cộng, cấp số nhân và học cá nhân.
mạch kiến thức của chương. - Hình thức thảo
- Hiểu và vận dụng được các định luận. Ôn tập
nghĩa, tính chất, định lý và công Bài tập cần chương thức trong chương. làm: 17 45,46 III đại số Về kỹ năng: 2,3,4,6a,8,9, và giải
- Biết cách cho một dãy số, xét 10,11,12. tích
tính tăng giảm của một dãy số.
- Xác định được các yếu tố còn
lại của cấp số cộng, cấp số nhân
khi biết một số yếu tố xác định cấp số đó. Trang 8 - Ôn tập học kỳ I Về kiến thức: - Dạy học theo Ôn tập
- Nắm được các kiến thức đã học nhóm kết hợp dạy cuối học trong học kỳ I. học cá nhân. 47 kì 1 đại 18 Về kỹ năng: - Hình thức thảo số và giải
- Tổng hợp các kỹ năng các chủ luận. tích
đề trong học kỳ I. 48 KIỂM TRA HỌC KỲ I Nội dung/Mạch
Hình thức tổ chức
Yêu cầu cần đạt Tuần Tiết
Tên chủ đề /Bài học kiến thức dạy học Ghi chú
-Giới hạn hữu hạn Về kiến thức: - Dạy học theo của dãy số nhóm kết hợp dạy CHƯƠNG
- Biết khái niệm giới hạn của dãy
§1.Giới hạn -Định lí về giới hạn học cá nhân. -Bài tập cần 19 49,50 IV. GIỚI
số (thông qua ví dụ cụ thể). của dãy số -Tổng của cấp số - Hình thức thảo làm 3, 4, 5, 7 HẠN
- Biết (không chứng minh): nhân lùi vô hạn
+/ Nếu limu = L , u luận.
-Giới hạn vô cực n ³ 0 với n Trang 9 mọi n
thì L ³ 0 và lim u = L n +/ Định lí về:
lim (un ± vn), lim (un .vn), lim æ u ö n . ç ÷ v è n ø Về kỹ năng : 51 Bài tập 1 20
- Biết vận dụng: lim = 0; n®¥ n 1 lim = 0; n®¥ n lim n
q = 0, q <1 tìm giới hạn
của một số dãy số đơn giản.
- Tìm được tổng của một cấp số nhân lùi vô hạn.
§2.Giới hạn - Giới hạn của hàm Về kiến thức : - Dạy học theo 52
của hàm số số tại một điểm.
- Biết khái niệm giới hạn của nhóm kết hợp dạy
- Giới hạn một bên hàm số. học cá nhân. của hàm số.
- Biết (không chứng minh): - Hình thức thảo 21 53,54
- Giới hạn của hàm +/ Nếu lim f (x) = L, f (x) ³ 0 luận. x®x0 Trang 10 số tại ±¥ . với x ¹ x0 thì L ³ 0 và lim
f (x) = L x®x0
+/ Định lí về giới hạn:
lim f (x) ± g(x) [ ] x®x0 f (x)
lim [ f (x).g(x)], lim . x®x ® 0 x x g(x) 0 Về kỹ năng:
Trong một số trường hợp đơn giản, tính được
- Giới hạn của hàm số tại một điểm.
- Giới hạn một bên của hàm số.
- Giới hạn của hàm số tại ±¥ . Bài tập Bài tập cần 22 55 làm 3, 4, 6 Về kiến thức: Biết - Dạy học theo
- Định nghĩa hàm số liên tục (tại nhóm kết hợp dạy 56
một điểm, trên một khoảng). học cá nhân.
- Định lí về tổng, hiệu, tích, - Hình thức thảo
thương của hai hàm số liên tục. luận.Bài tập cần
- Định lí: Nếu f(x) liên tục trên làm 1, 2, 3, 6 -Hàm số liên lục tại §3.Hàm số
một khoảng chứa hai điểm a, b và một điểm liên tục
f(a).f(b) < 0 thì tồn tại ít nhất một -Hàm số liên túc +bài tập
điểm c Î(a,b) sao cho f(c) = 0. trên một khoảng Về kỹ năng :
- Biết ứng dụng các định lí nói 23 57
trên xét tính liên tục của một hàm số đơn giản.
- Biết chứng minh một phương
trình có nghiệm dựa vào định lí
về hàm số liên tục. Trang 11 Về kiến thức: - Dạy học theo
- Nắm vững kiến thức về nhóm kết hợp dạy
giới hạn dãy số, hàm số học cá nhân. và hàm số liên tục. - Hình thức thảo
- Nắm vững cách dùng tính luận.
liên tục để chứng minh phương trình có nghiệm.
- Nắm vững tính liên tục 58
của hàm số để xét dấu. Về kỹ năng: - Ôn tập kiến thức Câu hỏi và bài tập ôn
- Tính giới hạn của dãy số, toàn chương.
chương IV giải tích
hàm số thường gặp một
cách thành thạo, xử lý tốt các dạng vô định.
- Xét sự liên tục của hàm
số tại một điểm và trên
một miền một cách thành thạo.
- Định tham số để hàm số 59 liên tục.
Chứng minh phương trình có nghiệm. 24 Về kiến thức: - Dạy học theo
- Biết định nghĩa đạo hàm (tại nhóm kết hợp dạy 60
một điểm, trên một khoảng). học cá nhân.
- Biết ý nghĩa cơ học và ý nghĩa - Hình thức thảo - Đạo hàm tại một §1.Định
hình học của đạo hàm. luận. CHƯƠNG điểm. nghĩa và ý Về kỹ năng: V. ĐẠO - Đạo hàm trên một - §1: Mục I.1 nghĩa của
- Tính được đạo hàm của hàm luỹ HĐ1: Hướng HÀM khoản. đạo hàm
thừa, hàm đa thức bậc 2 hoặc 3 dẫn học sinh 25 61,62 theo định nghĩa; tự đọc bài toán
- Viết được phương trình tiếp về cường độ
tuyến của đồ thị hàm số tại một tức thời điểm thuộc đồ thị Trang 12
- Biết tìm vận tốc tức thời tại một - Bài tập cần
thời điểm của một chuyển động làm bài 3,4,5,6 63
có phương trình S = f(t). trang 156 - Dạy học theo nhóm kết hợp dạy học cá nhân. - Hình thức thảo luận. 26
-Đạo hàm của một Về kiến thức: - Các định lí 64
số hàm số thường Biết quy tắc tính đạo hàm của gặp
tổng, hiệu, tích, thương các hàm 1,2,3 giáo viên
§2.Qui tắc - Đạo hàm của số; hàm hợp và đạo hàm của hàm chỉ nêu nội tính đạo tổng, hiệu, tích, hợp. dung định lí, hàm thương Về kỹ năng: phần chứng
- Đạo hàm của hàm Tính được đạo hàm của hàm số minh hướng hợp
được cho ở các dạng nói trên. dẫn học sịnh tự học 65 - Bài tập cần 27 làm bài 2,3,4,5 trang 163 66 28 67
KIỂM TRA GIỮA KÌ II Trang 13 - Dạy học theo nhóm kết hợp dạy học cá nhân. - Hình thức thảo luận. -Tính đạo hàm của 68 các hs lượng giác ĐẠO Về kiến thức: HÀM
- Biết (không chứng minh): CỦA sin x HÀM §3.Đạo lim = . 1 SỐ hàm của x®0 x LƯỢNG hàm số
- Biết đạo hàm của hàm số GIÁC lượng giác lượng giác. (Gồm Về kĩ năng: §3)
- Tính được đạo hàm của một số
hàm số lượng giác. 29 69 Bài tập Trang 14 Về kiến thức: - Dạy học theo
- Nắm vững kiến thức về nhóm kết hợp dạy
đạo hàm hàm số tại 1 học cá nhân. điểm. - Hình thức thảo -Đạo hàm bằng đn
- Nắm vững cách đạo hàm luận. Ôn tập -Qui tắc tính đạo
bằng các qui tắc tính đạo chương 70 hàm hàm. V giải -Đạo hàm các hàm
- Nắm vững cách đạo hàm tích số lượng giác
các hàm số lượng giác. Về kỹ năng:
Tính thành thạo các bài toán cơ
bản, biết sử dụng máy tính để tính đạo hàm - Dạy học theo nhóm kết hợp dạy học cá nhân. - Hình thức thảo Về kiến thức -Định nghĩa vi luận.
Nắm được định nghĩa vi phân. §4.Vi phân phân 30 71 Về kỹ năng .Bài tập
-Ứng dụng vi phân Tính được vi phân của các hàm vào tính gần đúng số đơn giản. Trang 15 - Dạy học theo nhóm kết hợp dạy Về kiến thức : học cá nhân.
Biết định nghĩa đạo hàm cấp - Hình thức thảo hai. luận. .-Định nghĩa Về kỹ năng : §5.Đạo
-Ý nghĩa cơ học Tính được 31 72 hàm cấp
của đạo hàm cấp - Đạo hàm cấp hai của một số hai .Bài tập hai hàm số. - Bài tập cần
- Gia tốc tức thời của một làm bài 1,2
chuyển động có phương trình S = trang 174 f(t) cho trước Về kiến thức : - Dạy học theo
Ôn tập về đạo hàm của các hàm nhóm kết hợp dạy
cơ bản, các qui tắc tính đạo hàm, học cá nhân. Ôn tập
tiếp tuyến của đường cong - Hình thức thảo - Bài tập cần chương 32 73 Về kỹ năng : luận. làm bài 1,2,3 V (giải Tính được trang 176 tích )
- Đạo hàm của hàm số
- Viết được phương trình tiếp tuyến Về kiến thức: - Dạy học theo
- Nắm được các kiến thức đã học nhóm kết hợp dạy - Ôn tập Ôn tập
Nội dung các bài trong học kỳ II. học cá nhân. 33 76 học II. cuối năm học trong HKII Về kỹ năng: - Hình thức thảo
- Tổng hợp các kỹ năng các chủ luận. đề trong học kỳ II Về kiến thức: - Dạy học theo
- Nắm được các kiến thức đã học nhóm kết hợp dạy - Ôn tập Ôn tập
Nội dung các bài trong học kỳ II. học cá nhân. 34 77 học II. cuối năm học trong HKII Về kỹ năng: - Hình thức thảo
- Tổng hợp các kỹ năng các chủ luận.
đề trong học kỳ II 35 78 KIỂM TRA CUỐI NĂM Trang 16 . HỌC KỲ I
Từ tuần 1 đến tuần 18 (thực học)
PHẦN II. HÌNH HỌC 11
Tuần Tiết Bài học
Nội dung/Mạch kiến
Yêu cầu cần đạt
Hình thức tổ chức dạy học Ghi chú thức 1 1 Phép biến hình
-Định nghĩa phép biến Về kiến thức:
Dạy học theo nhóm kết hợp Dạy gộp §1 với §2. Phép tịnh tiến - hình Biết được: dạy học cá nhân.
-Định nghĩa phép tịnh - Biết định nghĩa phép - Hình thức thảo luận. HĐ 1, HĐ 2: tự học tiến biến hình. có hướng dẫn -Các tính chất của - Định nghĩa của phép phép tịnh tiến tịnh tiến; -Biểu thức tọa độ
- Phép tịnh tiến có các
tính chất của phép dời hình;
- Biểu thức toạ độ của phép tịnh tiến. Về kỹ năng:
- Biết một quy tắc tương
ứng là phép biến hình. - -
Dựng được ảnh của một
điểm qua phép biến hình đã cho.
- Dựng được ảnh của một
điểm, một đoạn thẳng, một tam giác qua phép tịnh tiến 2 2 Bài tập phép tịnh Bài tập cần làm tiến 1,2,3,4 3 3 Phép quay - Bt
- Định nghĩa của phép Về kiến thức:
Dạy học theo nhóm kết hợp . Phép đối xứng trục quay; Biết được: dạy học cá nhân. . Phép đối xứng Trang 17 -Tính chất phép quay
- Định nghĩa của phép - Hình thức thảo luận. tâm(Tự học có hướng quay; dẫn) - Phép quay có các tính
chất của phép dời hình. Bài tập cần làm 1,2 Về kỹ năng : trang 19
Dựng được ảnh của một
điểm, một đoạn thẳng, một tam giác qua phép quay 4 4
Khái niệm về phép -Định nghĩa phép dời Về kiến thức:
-Dạy học theo nhóm kết hợp -HĐ 2, 3, 5: tự học có dời hình và hai hình Biết được: dạy học cá nhân. hướng dẫn hình bằng nhau – - Tính chất của phép
- Khái niệm về phép dời - Hình thức thảo luận. Bài tập dời hình hình; -Bài tập 2: Khuyến - Định nghĩa hai hình
- Phép tịnh tiến, đối xứng khích học sinh tự làm bằng nhau
trục, đối xứng tâm, phép quay là phép dời hình;
- Nếu thực hiện liên tiếp hai phép dời hình thì ta
được một phép dời hình;
- Phép dời hình: biến ba
điểm thẳng hàng thành ba
điểm thẳng hàng và thứ
tự giữa các điểm được bảo toàn; biến đường
thẳng thành đường thẳng; biến tia thành tia; biến
đoạn thẳng thành đoạn
thẳng bằng nó; biến tam giác thành tam giác bằng nó; biến góc thành góc
bằng nó; biến đường tròn
thành đường tròn có cùng bán kính; - Khái niệm hai hình bằng nhau. Về kỹ năng : - Bước đầu vận dụng Trang 18 phép dời hình trong bài tập đơn giản
- Nhận biết được hai tam giác, Hình tròn bằng nhau 5 5
Phép vị tự - Bài tập -Định nghĩa phép vị tự Về kiến thức:
-Dạy học theo nhóm kết hợp -Mục III. Tâm vị tự Biết được: dạy học cá nhân. của hai đường tròn: -Tính chất phép vị tự
- Định nghĩa phép vị tự - Hình thức thảo luận Khuyến khích học
(biến hai điểm M, N lần sinh tự đọc
lượt thành hai điểm M’, !!!!!!" !!!!" ìï M 'N ' = kM N N’ thì íM ï 'N ' = k M N î ); - Ảnh của một đường
tròn qua một phép vị tự. Về kỹ năng :
- Dựng được ảnh của một
điểm, một đoạn thẳng, một đường tròn,... qua một phép vị tự. - Bước đầu vận dụng
được tính chất của phép
vị tự để giải bài tập. 6 6 Phép đồng dạng - -Định nghĩa phép Về kiến thức:
- Dạy học theo nhóm kết hợp -HĐ 1, 2, 3, 4: tự học Bài tập đồng dạng Biết được : dạy học cá nhân. có hướng dẫn -Tính chất phép đồng
- Khái niệm phép đồng - Hình thức thảo luận. dạng dạng;
-Định nghĩa hình đồng - Phép đồng dạng: biến dạng
ba điểm thẳng hàng thành ba điểm thẳng hàng và
bảo toàn thứ tự giữa các
điểm; biến đường thẳng
thành đường thẳng; biến một tam giác thành tam
giác đồng đạng với nó; biến đường tròn thành Trang 19 đường tròn; - Khái niệm hai hình đồng dạng. Về kỹ năng: - Bước đầu vận dụng
được phép đồng dạng để giải bài tập.
- Nhận biết được hai tam giác đồng dạng. - Xác định được phép
đồng dạng biến một trong
hai đường tròn cho trước
thành đường tròn còn lại. 7 7 Ôn tập chương 1, -Phân biệt được phép
-Vẽ được ảnh của tam
Dạy học theo nhóm kết hợp Bài tập cần làm 1a,c bài tập biến hình ,phép dời
giác qua phép tịnh tiến và dạy học cá nhân. ,2a,d,3a,b hình, phép đồng dạng phép quay - Hình thức thảo luận. -Tìm được ảnh của
đường thẳng , đường tròn
qua một hoặc nhiều phép biến hình 8 8 Ôn tập chương 1,
Dạy học theo nhóm kết hợp Giaỉ bài tập trắc bài tập dạy học cá nhân. nghiệm chương 1 - Hình thức thảo luận. 9 9 Ôn tập kiểm tra giữa kì 10 10 . Đại cương về -Các khái niệm mở Về kiến thức:
Dạy học theo nhóm kết hợp Bài tập cần làm đường thẳng và đầu(mặt phẳng,điểm
- Biết các tính chất thừa dạy học cá nhân. 1,5,6,8,10
mặt phẳng - Bài tập thuộc mặt phẳng , hình nhận: - Hình thức thảo luận. biễu diễn của hình
+ Có một và chỉ một mặt không gian) phẳng đi qua ba điểm -Các tính chất thừa không thẳng hàng cho nhận trước - Cách xác định một
+ Nếu một đường thẳng Trang 20 mặt phẳng có hai điểm phân biệt -Hình chóp và tứ diện
thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó + Có bốn điểm không cùng thuộc một mặt phẳng + Nếu hai mặt phẳng
phân biệt có một điểm chung thì chúng có một điểm chung khác + Trên mỗi mặt phẳng,
các kết quả đã biết trong hình học phẳng đều đúng.
- Biết được ba cách xác định mặt phẳng (qua ba điểm không thẳng hàng;
qua một đường thẳng và
một điểm không thuộc đ- ường thẳng đó; qua hai
đường thẳng cắt nhau).
- Biết được khái niệm
hình chóp; hình tứ diện. Về kỹ năng :
- Vẽ được hình biểu diễn của một số hình không gian đơn giản.
- Xác định được: giao
tuyến của hai mặt phẳng; giao điểm của đường thẳng và mặt phẳng;
- Biết sử dụng giao tuyến
của hai mặt phẳng chứng minh ba điểm thẳng hàng trong không gian Trang 21
- Xác định được: đỉnh,
cạnh bên, cạnh đáy, mặt bên, mặt đáy của hình chóp
-Xác định được thiết diện
hình chóp với mặt phẳng 11 11 Đại cương về
Dạy học theo nhóm kết hợp đường thẳng và dạy học cá nhân. mặt phẳng - Bài tập - Hình thức thảo luận. 12 12 Đại cương về Bài tập
Dạy học theo nhóm kết hợp đường thẳng và dạy học cá nhân. mặt phẳng - Bài tập - Hình thức thảo luận. 13 13 Đại cương về Bài tập
Dạy học theo nhóm kết hợp đường thẳng và dạy học cá nhân. mặt phẳng - Bài tập - Hình thức thảo luận. 14
14,1 Hai đường thẳng
-Vị trí tương đối của Về kiến thức:
Dạy học theo nhóm kết hợp 5 chéo nhau và hai
hai đường thẳng trong - Hai đường thẳng chéo dạy học cá nhân. đường thẳng song không gian nhau - Hình thức thảo luận. song - Bài tập -Các tính chất
- Biết cách xác định giao
tuyến hai mặt phẳng phân biệt khi biết 1 điểm chung và phương giao tuyến. Về kỹ năng:
- Nắm được vị trí tương
đối của hai đường thẳng trong không gian. - Thực hiện được dang
bài tập tìm giao tuyến hai mặt phẳng. 15 16 Hai đường thẳng
Dạy học theo nhóm kết hợp -Bài tập cần làm 1,2 3 chéo nhau và hai Bài tập dạy học cá nhân. trang 59 Trang 22 đường thẳng song - Hình thức thảo luận. song - Bài tập Đường thẳng và mặt phẳng song 17 song - Bài tập
-Vị trí tương đối của Về kiến thức: đường thẳng và mặt
- Biết khái niệm và điều phẳng kiện đường thẳng song -Bài tập cần làm 1,2 3 -Các tính chất song với mặt phẳng. trang 63 - Biết (không chứng minh): các định lý Về kỹ năng :
- Xác định được vị trí
tương đối giữa đường thẳng và mặt phẳng.
- Biết cách vẽ hình biểu
diễn một đường thẳng song song với một mặt phẳng; chứng minh một đường thẳng song song với một mặt phẳng.
- Biết dựa vào các định lí
trên xác định giao tuyến
hai mặt phẳng, giao điểm
của đường thẳng và mặt phẳng trong một số trường hợp đơn giản. 16 18 Đường thẳng và
Dạy học theo nhóm kết hợp mặt phẳng song dạy học cá nhân. song - Bài tập - Hình thức thảo luận. Ôn tập chương 2 19 Ôn tập các kiến thức
đã học ở chương 2 ( vị -Chứng minh đường song Bài tập cần làm 1,2 Trang 23 trí tương đối của hai
song với đương , đường trang 77
đường , của đường với song song với mặt mặt, các định lý và
-Tìm được giao điểm của ttính chất thừa nhận) đường với mặt , giao
tuyến của hai mặt , thiết diện của hình chóp 17 20, Ôn tập học kỳ 1 - Ôn tập học kỳ I Về kiến thức:
Dạy học theo nhóm kết hợp
- Nắm được các kiến dạy học cá nhân. 21
thức đã học trong học kỳ - Hình thức thảo luận I. Về kỹ năng:
- Tổng hợp các kỹ năng
các bài học trong học kỳ I. 18 22 KIỂM TRA HỌC KIỂM TRA HỌC KỲ KỲ 1 1 HỌC KỲ II
Từ tuần 19 đến tuần 35 (thực học) Tuần Tiết Bài học
Nội dung/Mạch kiến
Yêu cầu cần đạt
Hình thức tổ chức dạy học Ghi chú thức 19 23
Hai mặt phẳng -Định nghĩa hai mặt Về kiến thức:
Dạy học theo nhóm kết hợp Bài tập cần làm 1,2 song song – phẳng song song Biết được: dạy học cá nhân. trang 71 bài tập -Các tính chất
- Khái niệm và điều kiện Trang 24 -Định lý TA-LET
hai mặt phẳng song song; - Hình thức thảo luận -Hình lăng trụ và hình
- Định lí Ta-lét (thuận và hộp đảo) trong không gian; -Hình chóp cụt - Khái niệm hình lăng trụ, hình hộp; - Khái niệm hình chóp cụt. Về kỹ năng : - Biết cách chứng minh hai mặt phẳng song song.
- Vẽ được hình biểu diễn
của hình hộp; hình lăng
trụ, hình chóp có đáy là tam giác, tứ giác.
- Vẽ được hình biểu diễn của hình chóp cụt với
đáy là tam giác, tứ giác. 20 24 Hai mặt phẳng Bài tập
Dạy học theo nhóm kết hợp Bài tập cần làm 2,3 song song – dạy học cá nhân. trang 71 bài tập - Hình thức thảo luận 21 25 Phép chiếu -Phép chiếu song song Về kiến thức:
Dạy học theo nhóm kết hợp HĐ 2, HĐ 6: Tự học có song song.
-Các tính chất của phép Biết được: dạy học cá nhân. hướng dẫn
Hình biểu diễn chiếu song song
- Khái niệm phép chiếu - Hình thức thảo luận của một hình
-Hình biễu diễn của một song song; trong không hình không gian trong
- Khái niệm hình biểu gian mặt phẳng
diễn của một hình không gian. Về kĩ năng :
- Xác định được: phương
chiếu; mặt phẳng chiếu trong một phép chiếu song song. Dựng được
ảnh của một điểm, một đoạn thẳng, một tam
giác, một đường tròn qua một phép chiếu song Trang 25 song.
- Vẽ được hình biểu diễn của một hình không gian 22 26 Ôn tập chương
-Chứng minh đường song Dạy học theo nhóm kết hợp 2 tiếp theo
song với đương , đường dạy học cá nhân.
Ôn tập các kiến thức đã song song với mặt - Hình thức thảo luận Bài tập cần làm 3 và
học ở chương 2 ( vị trí
-Tìm được giao điểm của câu hỏi trắc nghiệm
tương đối của hai đường đường với mặt , giao trang 77
, của đường với mặt, các tuyến của hai mặt , thiết diện của hình chóp
định lý và ttính chất thừa nhận) 23 27 Vectơ trong
-Định nghĩa và các phép Về kiến thức :
Dạy học theo nhóm kết hợp HĐ 2, 4, 6, 7: Tự học không gian - toán về véctơ trong Biết được : dạy học cá nhân. có hướng dẫn Bài tập không gian
- Quy tắc hình hộp để - Hình thức thảo luận cộng vectơ trong không
-Điều kiện đồng phẳng gian; của ba véctơ
- Khái niệm và điều kiện
đồng phẳng của ba vectơ - trong không gian. Về kỹ năng :
- Xác định được góc giữa hai vectơ trong không gian.
- Vận dụng được: phép
cộng, trừ; nhân vectơ với
một số, tích vô hướng của hai vectơ; sự bằng nhau của hai vectơ trong không gian.
- Biết cách xét sự đồng phẳng hoặc không đồng phẳng của ba vectơ trong không gian. Trang 26 24 28 Vectơ trong
Dạy học theo nhóm kết hợp Bài tập cần làm 2,4,7,9 không gian - dạy học cá nhân. trang 92 Bài tập - Hình thức thảo luận 25 29 Hai đường -Tích vô hướng của hai Về kiến thức:
Dạy học theo nhóm kết hợp HĐ 2,4 - Tự học có thẳng vuông véctơ trong không gian Biết được: dạy học cá nhân. hướng dẫn. góc - Bài tập
-Véc tơ chỉ phương của
- Khái niệm vectơ chỉ - Hình thức thảo luận + Học sinh cần làm các đường thẳng
phương của đường thẳng; bài tập : Bài tập 6,7: -Góc giữa hai đường
- Khái niệm góc giữa hai khuyến khích học sinh thẳng trong không gian đường thẳng; tự làm
-Hai đường thẳng vuông - Khái niệm và điều kiện góc hai đường thẳng vuông góc với nhau. Về kỹ năng :
- Xác định được vectơ
chỉ phương của đường thẳng; góc giữa hai đường thẳng. - Biết chứng minh hai đường thẳng vuông góc với nhau. 26 30 Hai đường Bài tập
Dạy học theo nhóm kết hợp Bài tập cần làm 1,4,8 thẳng vuông dạy học cá nhân. góc - Bài tập - Hình thức thảo luận 27 31 Ôn tập kiểm tra giữa kì. 28 32 Đường thẳng
-Định nghĩa đường thẳng Về kiến thức:
Dạy học theo nhóm kết hợp
vuông góc với vuông góc với mặt Biết được: dạy học cá nhân. HĐ 1, 2 Phần chứng mặt phẳng - phẳng
- Định nghĩa và điều kiện - Hình thức thảo luận minhcác định lí – Tự Bài tập
-Điều kiện để đường đường thẳng vuông góc học có hướng dẫn
thẳng vuông góc với mặt với mặt phẳng; phẳng - Khái niệm phép chiếu -Các tính chấ vuông góc; -Liên hệ giữa quan hệ - Khái niệm mặt phẳng song song và quan hệ
trung trực của một đoạn Trang 27 vuông góc của đường thẳng. thẳng và mặt phẳng Về kỹ năng : -Phép chiếu vuông góc - Biết cách chứng minh: và định lý ba đường
một đường thẳng vuông vuông góc
góc với mặt phẳng; một đường thẳng vuông góc
với một đường thẳng. - Xác định được hình
chiếu vuông góc của một
điểm, một đường thẳng lên một mặt phẳng. - Bước đầu vận dụng
được định lí ba đường vuông góc.
- Xác định được góc giữa đường thẳng và mặt phẳng.
- Biết xét mối liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng. 29 33 Đường thẳng
Dạy học theo nhóm kết hợp Học sinh cần làm các vuông góc với dạy học cá nhân.
bài tập : Bài tập 3, 4, 5 mặt phẳng - - Hình thức thảo luận Bài tập 6,7 tự học có Bài tập hướng dẫn 30
34,35 Hai mặt phẳng -Góc giữa hai mặt phẳng Về kiến thức:
Dạy học theo nhóm kết hợp vuông góc - -Hai mặt phẳng vuông Biết được : dạy học cá nhân. Bài tập góc
- Khái niệm góc giữa hai - Hình thức thảo luận HĐ 1,3– Tự học có -Hình lăng trụ đứng , mặt phẳng; hướng dẫn.
hình hộp chữ nhật , hình - Khái niệm và điều kiện Phần chứng minh Định lập phương hai mặt phẳng vuông lí 1, 2 – Tự học có -Hình chóp đều và hình góc; hướng dẫn chóp cụt đều
- Tính chất hình lăng trụ
đứng, lăng trụ đều, hình
hộp đứng, hình hộp chữ nhật, hình lập phương; Trang 28 - Khái niệm hình chóp
đều và chóp cụt đều. Về kỹ năng :
- Xác định được góc giữa hai mặt phẳng. - Biết chứng minh hai mặt phẳng vuông góc 31 36 Hai mặt phẳng
Dạy học theo nhóm kết hợp Bài tập cần làm : Bài vuông góc - dạy học cá nhân. tập 3, 5, 7, 10 Bài tập - Hình thức thảo luận Bài tập 4,11: Khuyến khích học sinh tự làm 37. HĐ 1, 2, 3, 4, 6: Tự học có hướng dẫn
Khoảng cách - -Khoảng cách từ một
Về kiến thức, kỹ năng: Bài tập
điểm đến một đường
Biết và xác định được: thẳng ,một mặt phẳng - Khoảng cách từ một -Khoảng cách giữa
điểm đến một đường đường thẳng và mặt thẳng; phẳng song song ,giữa - Khoảng cách từ một
hai mặt phẳng song song điểm đến một mặt phẳng; -Đường vuông góc - Khoảng cách giữa hai chung với khoảng cách đường thẳng; giữa hai đường thẳng - Khoảng cách giữa chéo nhau đường thẳng và mặt phẳng song song; - Khoảng cách giữa hai mặt phẳng song song; - Đường vuông góc chung của hai đường thẳng chéo nhau; - Khoảng cách giữa hai đường thẳng chéo nhau. 32 38,39 Khoảng cách -
Dạy học theo nhóm kết hợp Học sinh cần làm bài Trang 29 Bài tập dạy học cá nhân. tập :2,4,8. - Hình thức thảo luận Bài tập 1, 6: Khuyến khích học sinh tự làm 33
40,41 Ôn tập chương Hệ thống hóa các kiến -Chứng minh được các
Dạy học theo nhóm kết hợp Bài tập cần làm 4,7 3 thức lý thuyết trong đẳng thức véctơ dạy học cá nhân. trang 122 và các bài tập chương -Chứng minh được hai - Hình thức thảo luận trắc nghiệm
đường thẳng vuông góc , đường thẳng vuông góc
với mặt phẳng , hai mặt phẳng vuông góc và tính được khoảng cách trong các trường hợp 34
42,43 Ôn tập học kỳ Ôn tập học kỳ 2 Về kiến thức:
Dạy học theo nhóm kết hợp 2
- Nắm được các kiến dạy học cá nhân.
thức đã học trong học kỳ - Hình thức thảo luận 2. Về kỹ năng:
- Tổng hợp các kỹ năng
các bài học trong học kỳ 35 44 THI HỌC KỲ 2 Trang 30