

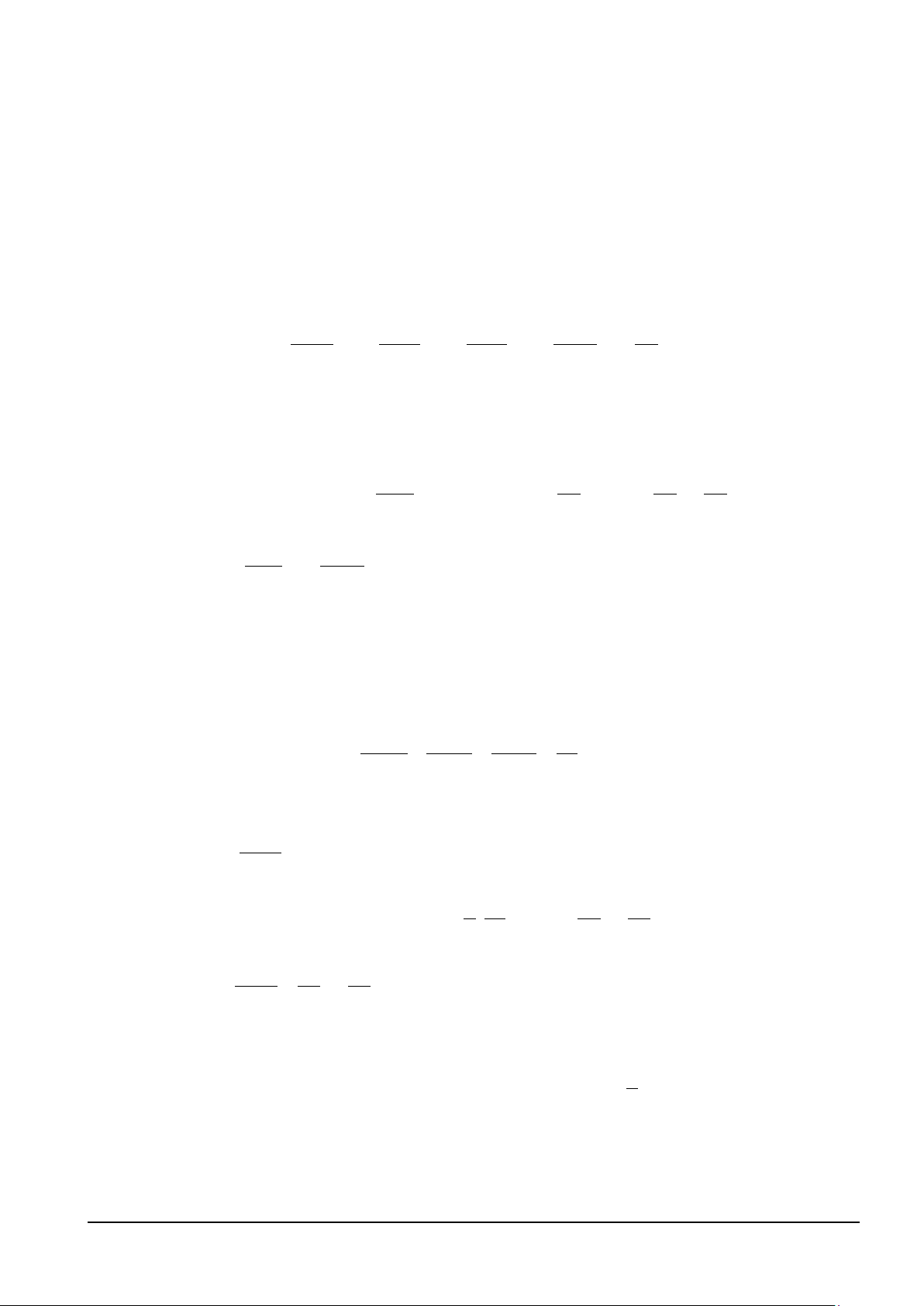

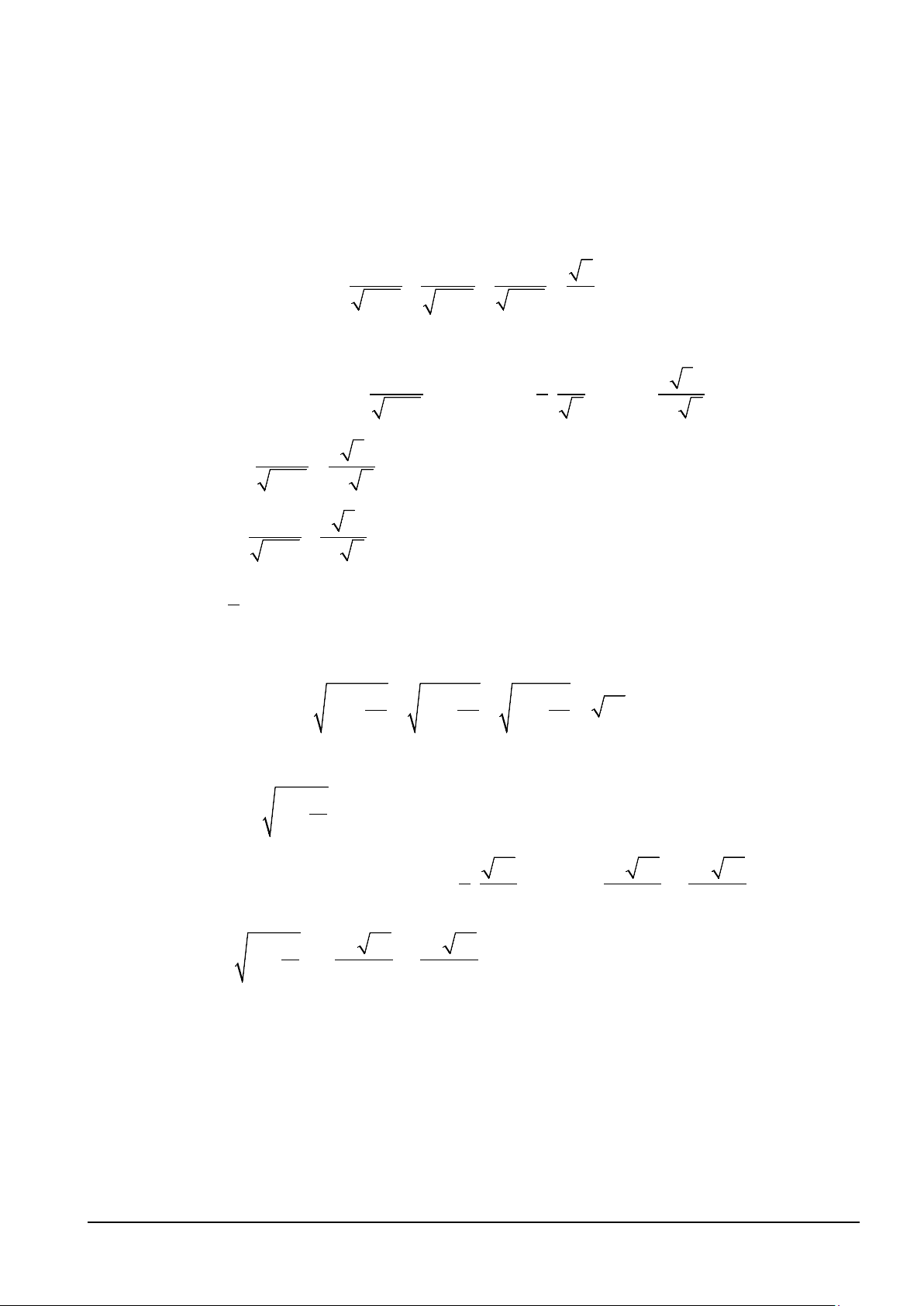
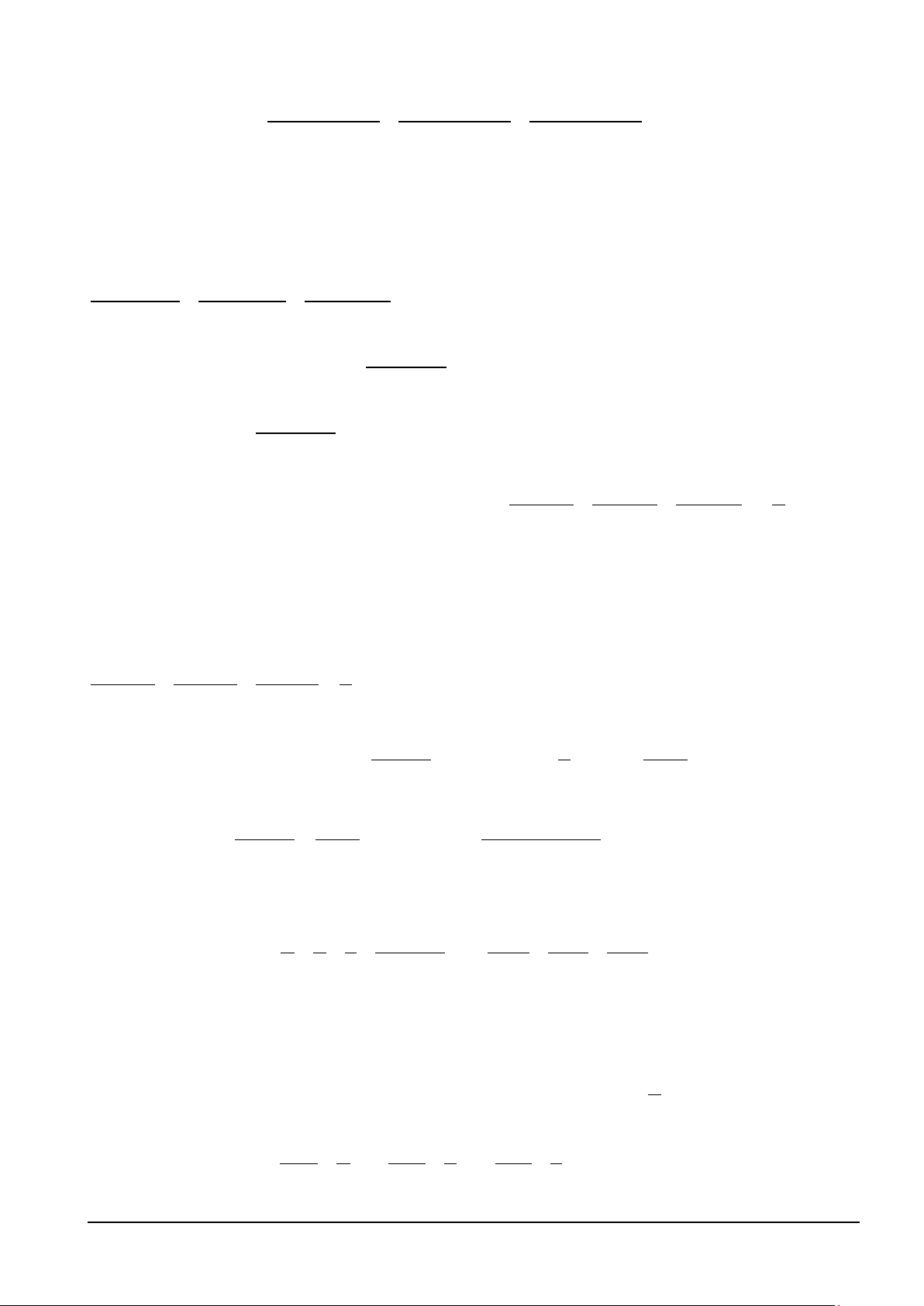

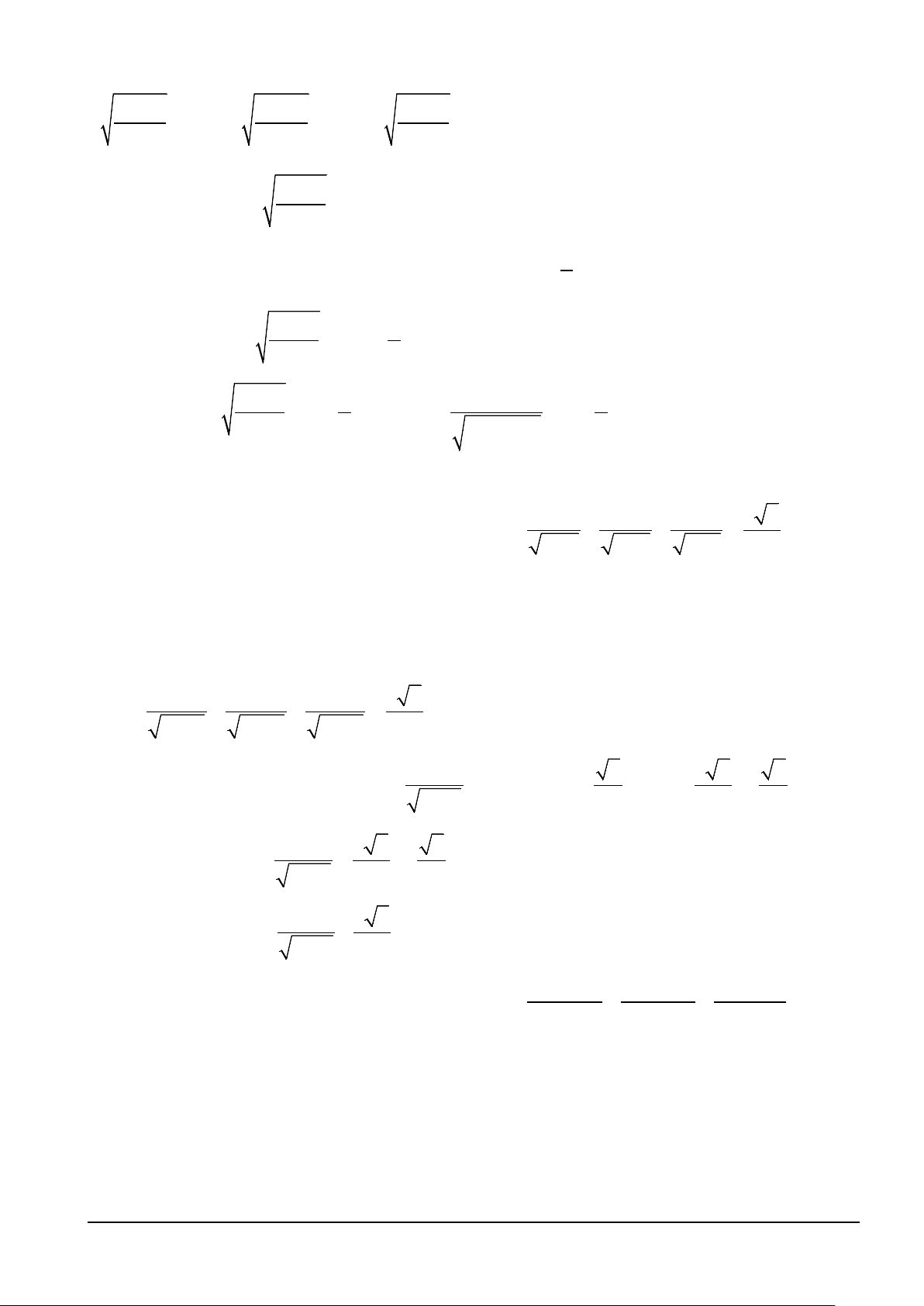


















Preview text:
CHUYÊN ĐỀ
KHAI THÁC HAI TÍNH CHẤT CỦA HÀM SỐ
TRONG CHỨNG MINH BẤT ĐẲNG THỨC
NGUYỄN TRƯỜNG SƠN
THPT CHUYÊN LƯƠNG VĂN TỤY - NINH BÌNH Page 1/26
Chương I. PHƯƠNG PHÁP TIẾP TUYẾN
Trong khuôn khổ sáng kiến, tôi chỉ đề cập đến một ứng dụng nhỏ của đạo hàm trong
việc chứng minh bất đẳng thức, đó chính là phương pháp tiếp tuyến. Ý tưởng chính của
phương pháp tiếp tuyến là sử dụng công thức phương trình tiếp tuyến của một đồ thị hàm số để
tìm một biểu thức trung gian trong các đánh giá bất đẳng thức.
1.1 Kiến thức chuẩn bị
Trước hết ta nhắc lại một bài toán sau: Cho hàm số f (t) liên tục và có đạo hàm trên
D . Khi đó, nếu tiếp tuyến tại một điểm t ∈ D (giả sử có phương trình y = a(t − t + b ) luôn 0 ) 0
nằm trên (nằm dưới) đồ thị hàm số f trên một lân cận D ⊂ D nào đó của t thì hiển nhiên ta 0 0
có f (t) ≤ a(t − t + b hay f t ≥ a t − t + b , t ∀ ∈ D . 0 ) ( ( ) ( 0) ) 0
Từ tính chất này ta thấy với mọi t ,t ,...,t ∈ D thì 1 2 n 0
f (t + f t +...+ f t ≤ a t + t + + t − nt + nb . n ... 1 ) ( 2) ( ) ( 1 2 n 0 )
Như vậy, nếu một bất đẳng thức có dạng “tổng hàm” như ở vế trái của bất đẳng thức
trên và có giả thiết t + t + ...+ t = nt với đẳng thức xảy ra khi tất cả các biến t đều bằng 1 2 n 0 i
nhau và bằng t thì ta có thể thử chứng minh nó bằng phương pháp tiếp tuyến, nghĩa là ta sẽ 0
tìm phương trình tiếp tuyến y = a(t − t + b tại điểm t của đồ thị hàm số y = f (t) , rồi sau 0 ) 0
đó tiến hành kiểm chứng BĐT f (t) ≤ a(t − t + b hay f t ≥ a t − t + b , t ∀ ∈ D . 0 ) ( ( ) ( 0) ) 0
1.2 Một số ví dụ minh họa
Ví dụ 1. Cho a,b,c,d ≥ 0 thỏa mãn a + b + c + d = 4 . Chứng minh a b c d 1 + + + ≤ . 2 2 2 2 5 + 3a 5 + 3b 5 + 3c 5 + 3d 2 Lời giải
+ Từ giả thiết suy ra a,b,c,d ∈[0;4]. Dấu đẳng thức xảy ra khi a = b = c = d =1.
+ PTTT của đồ thị hàm số ( ) t f t = tại điểm 1 M 1 1; là y = (t + 3). 2 5 + 3t 8 32 2 t 1 − t + 5 t −1 + Ta có − t + 3 = ≤ 0, t ∀ ∈ 0;4 (*) 2 ( ) ( )( ) 5 + 3t 32 32( 2 5 + 3t ) [ ]
+ Thay a,b,c,d vào t trong bất đẳng thức (*), cộng vế theo vế ta có đpcm.
Nhận xét: Page 2/26
- Khi xét hiệu f (t) − (a(t − t + b , ta thường tách được nghiệm kép t = t (điểm dấu 0 ) ) 0 đẳng thức xảy ra).
- Khi trình bày lời giải, có thể ta không cần viết ra các giai đoạn tìm tiếp tuyến mà đưa ra
luôn bất đẳng thức đặc trưng cho bài toán cần chứng minh.
Tương tự, ta yêu cầu học sinh lên trình bày Ví dụ 2 và Ví dụ 3.
Ví dụ 2. Cho a,b,c,d > 0 thỏa mãn a + b + c + d = 4 . Chứng minh rằng 3 3 3 3 a b c d 4 + + + ≥ . a 2 b 2 c 2 d 2 + + + + 27 Lời giải
+ Từ giả thiết suy ra a,b,c,d ∈(0;4) . Dấu đẳng thức xảy ra khi a = b = c = d =1. 3
+ PTTT của đồ thị hàm số ( ) t f t = tại điểm 1 M 1; là 2 1 y = t − . t 2 + 27 27 27 3
+ Ta chứng minh t 2t −1 ≥ , t ∀ ∈ 2
(0;4) (*) ⇔ (t − ) ( 2 2
1 t − 6t − 4) ≤ 0 t ∀ ∈(0;4) t + 2 27
(luôn đúng vì 2t − 6t − 4 = t (t − 4) − 2t − 4 < 0, t ∀ ∈(0;4) )
+ Thay a,b,c,d vào t trong bất đẳng thức (*), cộng vế theo vế ta có đpcm.
Ví dụ 3. Cho a,b,c > 0 thỏa mãn a + b + c = 1. Chứng minh rằng a b c 9 + + ≤ . 2 2 2 1+ a 1+ b 1+ c 10 Hướng dẫn + Xét hàm ( ) t f t = trên (0; ) 1 2 1+ t
+ PTTT của đồ thị hàm số f (t) tại điểm 1 3 M ; là 18 3 y = t + . 3 10 25 50 + Ta chứng minh t 18 3 ≤ t + , t ∀ ∈ 0;1 . 2 ( ) 1+ t 25 50
Ví dụ 4. Cho a,b,c,d > 0 thỏa mãn a + b + c + d = 1. Chứng minh ( 3 3 3 3
a + b + c + d ) 2 2 2 2 1 6
≥ a + b + c + d + . 8 Lời giải
+ Bất đẳng thức cần chứng minh có dạng Page 3/26 ( 3 2
a − a ) + ( 3 2
b − b ) + ( 3 2 c − c ) + ( 3 2 d − d ) 1 6 6 6 6 ≥ . 8
+ PTTT của đồ thị hàm số f (t) 3 2
= 6t − t tại điểm 1 1 M ; t là 5 1 y − = . 4 32 8 + Ta có ( 3 2 t −
− t ) 5t −1 1 6 − = (4t − )2 1 (3t + ) 1 ≥ 0, t ∀ ∈(0; )
1 ⇒ f (t) 5t 1 ≥ , t ∀ ∈(0; ) 1 (*). 8 8 8
+ Thay a,b,c,d vào t trong bất đẳng thức (*), cộng vế theo vế ta có đpcm.
Qua Ví dụ 4, yêu cầu học sinh tương tự làm Ví dụ 5.
Ví dụ 5. Cho a,b,c > 0 thỏa mãn a + b + c = 3. Chứng minh 2 2 2 a + 9 b + 9 c + 9 + + ≤ 5. 2
2a + (b + c)2 2
2b + (c + a)2 2
2c + (a + b)2 Hướng dẫn
+ Bất đẳng thức cần chứng minh tương đương với 2 2 2 a + 9 b + 9 c + 9 + + ≤ 5. 2 2a + (3− a)2 2 2b + (3− b)2 2 2c + (3− c)2 2
+ PTTT của đồ thị hàm số f (t) t + 9 = tại điểm 5 M t 1; là 4 y + = . 2 2 t + (3− t)2 3 3 2 + Ta đi chứng minh t + 9 t + 4 ≤ , t ∀ ∈ 0;3 2 2 ( ) 2t + (3− t) 3 2 2 Thật vậy t + 9 t + 9 1 2t + 6 1 2t + 6 t + 4 = = + ≤ + = . 2 2t + (3− t)2 2
3t − 6t + 9 3 3(t − )2 1 + 6 3 6 3
Nhận xét:
Qua các ví dụ trên ta thấy việc xác định dấu của biểu thức f (t) − (a(t − t + b trên D 0 ) ) có thể làm như sau:
- Dựa vào dấu của bất đẳng thức cần chứng minh.
- Dự đoán bằng cách thay một giá trị bất kì của t ∈ D vào biểu thức
f (t) − (a(t − t + b . 0 ) )
- Phân tích f (t) − (a(t − t ) + b) = (t − t )2 .h t và xác định dấu của h(t) trên D . 0 0 ( )
Trong các ví dụ trên ta đều sử dụng cách 3. Tuy nhiên trong một số bài toán việc phân
tích như trên gặp khó khăn vì bài toán chứa căn thức. Do đó, ta có thể gợi ý cho học sinh sử Page 4/26
dụng phương pháp hàm số, tận dụng luôn kết quả mà các em tính đạo hàm của hàm f (t) khi
lập phương trình tiếp tuyến và chú ý đạo hàm của hàm số f (t) − (a(t − t + b vẫn có nghiệm 0 ) )
t = t . Ta xét tiếp ví dụ sau: 0
Ví dụ 6. Cho các số thực dương x, y, z thỏa mãn x + y + z = 1. Chứng minh rằng x y z 6 + + ≥ 1− x 1− y 1− z 2 Hướng dẫn
+ PTTT của đồ thị hàm số ( ) x f x = tại điểm 1 1 M 3 ; là y = (15x − )1. 1− x 3 6 12 2 + Ta đi chứng minh x 3 ≥ (15x − )1, x ∀ ∈(0; ) 1 1− x 12 2
Xét hàm số g (x) x 3 = −
(15x − )1 trên (0; )1 1− x 12 2 g (x) 1 '
= 0 ⇔ x = . Từ bảng biến thiên ta có điều phải chứng minh. 3
Bài tập tương tự. Cho a,b,c > 0 thỏa mãn a + b + c =1. Chứng minh 2 1 2 1 2 1 a + + b + + c + ≥ 82 . 2 2 2 a b c Hướng dẫn + Xét hàm số ( ) 2 1
f t = t + trên (0; ) 1 . 2 t
+ PTTT của đồ thị hàm số f (t) tại điểm 1 82 M ; là 40 82 27 82 y = − t + . 3 3 41 41 + Ta chứng minh 2 1 40 82 27 82 t + ≥ − t + , t
∀ ∈ 0;1 (sử dụng bảng biến thiên). 2 ( ) t 41 41
Các ví dụ trên đều cần có giả thiết a + a + ...+ a = nα , để sử dụng phương pháp tiếp 1 2 n
tuyến. Tuy nhiên trong các bài toán, có sự đồng bậc của tử và mẫu trong từng số hạng hoặc
đồng bậc của hai vế bất đẳng thức cần chứng minh, ta vẫn có thể nghĩ đến phương pháp tiếp
tuyến nhờ việc chuẩn hóa bài toán. Ta xét ví dụ sau:
Ví dụ 7. Cho a,b,c > 0. Chứng minh Page 5/26
(2a + b + c)2 (2b + c + a)2 (2c + a + b)2 + + ≤ 8 . 2
2a + (b + c)2 2
2b + (c + a)2 2
2c + (a + b)2 Lời giải
+ Do mỗi số hạng có tử và mẫu là các biểu thức đẳng cấp nên không mất tính tổng quát ta giả
sử a + b + c = 3. Khi đó, bất đẳng thức cần chứng minh là 2 2 2
a + 6a + 9 b + 6b + 9 c + 6c + 9 + + ≤ 24. 2 2 2
a − 2a + 3 b − 2b + 3 c − 2c + 3 2
+ PTTT của đồ thị hàm số f (t) t + 6t + 9 =
tại điểm M (1;8) là y = 4t + 4 . 2 t − 2t + 3 2
+ Ta đi chứng minh t + 6t + 9 ≤ 4t + 4, t ∀ ∈ 0;3 . 2 ( ) t − 2t + 3 a b c 9
Ví dụ 8. Cho a,b,c > 0. Chứng minh (a + b + c) + + ≥ .
(b c)2 (c a)2 (a b)2 + + + 4 Lời giải
+ Do mỗi số hạng có tử và mẫu là các biểu thức đẳng cấp nên không mất tính tổng quát ta giả
sử a + b + c = 3. Khi đó, bất đẳng thức cần chứng minh có dạng a b c 3 + + ≥
(3− a)2 (3−b)2 (3− c)2 4
+ PTTT của đồ thị hàm số ( ) t f t = tại điểm 1 M t 1; là 2 1 y − = . ( − t)2 3 4 4 (t − )2 1 (9 − 2t) + Ta chứng minh t 2t −1 ≥ , t ∀ ∈ 0;3 ⇔ ≥ 0, t ∀ ∈ 0;3 (luôn đúng). 2 ( ) 2 ( ) (3−t) 4 4(3− t)
Ví dụ 9. Cho a,b,c là độ dài ba cạnh một tam giác. Chứng minh 1 1 1 9 1 1 1 4 + + + ≥ + + . a b c a b c a b b c c a + + + + + Lời giải
+ Vì vai trò của a,b,c như nhau và sự đồng bậc của hai vế nên không mất tính tổng quát ta giả
sử a + b + c =1. Mặt khác, a,b,c là ba cạnh tam giác nên 1
a,b,c 0; ∈ . Bất đẳng thức cần 2
chứng minh trở thành 4 1 4 1 4 1 − + − + − ≤ 9 .
1− a a 1− b b 1− c c Page 6/26
+ PTTT của đồ thị hàm số f (t) 4 1 = − tại điểm 1
M ;3 là y =18t −3. 1− t t 3 + Ta có 4
1 ( t ) ( t )2( t ) 1 18 3 3 1 2 1 0, t 0; − − − = − − ≤ ∀ ∈ (*). 1 t t 2 −
+ Thay a,b,c vào t trong bất đẳng thức (*), cộng vế theo vế ta có điều phải chứng minh. Bài tập tương tự: a(b + c) b(c + a) c(a + b)
1) Cho a,b,c > 0. Chứng minh 6 + + ≤ . (b + c)2 2 + a (c + a)2 2 + b (a + b)2 2 + c 5
(b + c − a)2 (c + a −b)2 (a + b − c)2
2) Cho a,b,c > 0. Chứng minh 3 + + ≥ (b + c)2 2 + a (c + a)2 2 + b (a + b)2 2 + c 5
Hướng dẫn: Nếu đem các số hạng của vế trái bất đẳng thức trừ đi 1 thì ta có được các
số hạng của bất đẳng thức ở bài 1.
3) Cho a,b,c > 0. Chứng minh a b c 3 + + ≥ .
b + c c + a a + b 2 Hướng dẫn
Bất đẳng thức trên có rất nhiều có cách chứng minh ngắn gọn. Tuy nhiên trong chuyên
đề này chúng ta hướng dẫn học sinh sử dụng phương pháp tiếp tuyến. Không mất tính
tổng quát ta chứng minh bất đẳng thức cho trường hợp a + b + c = 3. Khi đó, bất đẳng
thức cần chứng minh có dạng a b c 3 + + ≥ . Ta đi chứng minh
3 − a 3 − b 3 − c 2 t 3t −1 ≥ ,t ∈(0;3) . 3 − t 4
Việc sử dụng tính chất của logarit log bc = b +
c ( a,b,c > 0,a ≠ 1), ta có thể a ( ) loga loga
sử dụng phương pháp tiếp tuyến để chứng minh bài toán bất đẳng thức với giả thiết a .a ... n
a = α nhờ sử dụng ẩn phụ. 1 2 n
Ví dụ 10. Cho a,b,c > 0 thỏa mãn abc = 1. Chứng minh 2 2 2 a +1 b +1 c +1 + +
≤ a + b + c. 2 2 2 Lời giải
Ta có abc =1⇒ ln a + lnb + ln c = 0. Đặt x = ln a, y = lnb, z = ln c . Khi đó ta có bài toán
Cho các số thực x, y, z thỏa mãn x + y + z = 0. Chứng minh Page 7/26 2x 2 y 2 e 1 e +1 z + x y e +1 z − e + − e + − e ≤ 0 . 2 2 2 2t
+ Xét hàm số f (t) e +1 t = − e trên . 2
+ PTTT của đồ thị hàm số f (t) tại điểm O(0;0) là 1 y = − t 2 2t
+ Ta đi chứng minh e +1 t 1
− e ≤ − t, t ∀ ∈ . 2 2 2t 2t Xét hàm g (t) e +1 t 1 =
− e + t ⇒ g (t) e t 1 ' =
− e + = ⇔ t = . 2 2 ( 0 0 2t e + ) 2 2 1
Bài tập tương tự:
1) Cho a,b,c > 0 thỏa mãn abc =1. Chứng minh a b c 3 2 + + ≥ . 1+ a 1+ b 1+ c 2 Hướng dẫn
Đặt x = ln a, y = lnb, z = ln c . Ta có bài toán
Cho các số thực x, y, z thỏa mãn x + y + z = 0. Chứng minh x y z e e e 3 2 + + ≥ 1 x + e 1 y + e 1 z + e 2 t
PTTT của đồ thị hàm số ( ) e f t = tại điểm 2 M 0; là 3 2 2 y = t + 1 t + e 2 8 2 t Ta chứng minh e 3 2 2 ≥ t + , t ∀ ∈ 1 t + e 8 2 t Xét hàm g (t) e 3 2 = −
t , lập bảng biến thiên suy ra đpcm. 1 t + e 8
2) Cho a,b,c > 0 thỏa mãn abc =1. Chứng minh 1 1 1 + + ≥ 1. 2 2 2
a − a +1 b − b +1 c − c +1
Trong một số bài toán việc xét hiệu f (x) − a
( x − x + b 0 )
mặc dù tách được nghiệm
bội x − x , nhưng hiệu đó không giữ nguyên một dấu trên D . Trong trường hợp đó, ta có thể 0
chia trường hợp để chứng minh. Ta xét một số ví dụ sau:
Ví dụ 11. Cho a,b,c > 0 thỏa mãn a + b + c = 3. Chứng minh Page 8/26 1 1 1 2 2 2 + +
≥ a + b + c . 2 2 2 a b c Lời giải
Nhận xét: Nếu xét hàm số f (t) 1 2 =
− t trên (0;3) thì phương trình tiếp tuyến tại điểm 2 t
M (1;0) là y = 4 − t + 4 (t − )2 1 t + 2 −1 1+ 2 1 − t 2 ( )( ) Khi đó − t − 4 − t + 4 =
lúc âm, lúc dương trên (0;3). Do đó 2 ( ) 2 t t
ta cần chia khoảng giá trị cho các biến a,b,c . Lời giải Cách 1.
+ Nếu 3 > a ≥ 2,4 thì b + c ≤ 0,6 . Khi đó, 2 2 2
VP = a + b + c < (a + b + c)2 = 9 . 1 1 1 1 2 1 2 1 2 VT = + + ≥ + ≥ + ≥ + > 9 . 2 2 2 2 2 a b c 3
bc 9 b + c 9 (0,3)2 2
+ Ta chỉ xét các số a,b,c ∈(0;2,4) . Khi đó, sử dụng phương trình tiếp tuyến ta có (t − )2 1 t + 2 −1 1+ 2 1 − t 2 ( )( ) − t − 4 − t + 4 = ≥ 0, t ∀ ∈ 0;2,4 . 2 ( ) 2 ( ) t t Cách 2.
Ta thấy nếu có một số trong ba số a,b,c nhỏ hơn 1 khi đó 3 1 1 1 + +
> 9 = (a + b + c)2 2 2 2
≥ a + b + c , bất đẳng thức luôn đúng. 2 2 2 a b c Vậy ta chỉ xét 1
a,b,c ≥ . Vì 1 7 a b c 3
a,b,c ; + + = ⇒ ∈ . 3 3 3 (t − )2 1 2 − (t − )2 1 Khi đó 1 2 1 7 − t − 4 − t + 4 = ≥ 0, t ∀ ∈ ; . 2 ( ) 2 t t 3 3 2 2 2 a b c 3
Ví dụ 12. Cho a,b,c > 0. Chứng minh + + ≥ . 2
a + (b + c)2 2
b + (a + c)2 2
c + (b + a)2 5 Hướng dẫn Page 9/26
+ Không mất tính tổng quát ta giả sử a + b + c = 3. Khi đó, bất đẳng thức cần chứng minh có 2 2 2 dạng a b c 3 + + ≥ . 2 2 2
2a − 6a + 9 2b − 6b + 9 2c − 6c + 9 5 2
+ PTTT của đồ thị hàm số ( ) t f t = tại điểm 1 M t 1; là 12 7 y − = 2 2t − 6t + 9 5 25 t
12t − 7 3(t − )2 2 1 (21−8t) + Xét 21 0, t 0; − = ≥ ∀ ∈ (*) 2 2t 6t 9 25 25( 2 2t 6t 9) 8 − + − + + Vậy nếu 21
a,b,c 0; ∈
thì thay t lần lượt bởi a,b,c trong (*) và cộng các bất đẳng thức 8
theo vế ta có điều cần chứng minh.
+ Nếu có 1 số nào đó trong ba số a,b,c lớn hơn hoặc bằng 21 . Giả sử 21 a ≥ 8 8 2 Ta có a 1 1 49 3 = ≥ = > . 2 2 2a − 6a + 9 9 3 50 5 1 1 1 + + − 2 21 a (Vì 21 3 24 3 3 3 > a ≥ ⇒ 1 < ≤ ⇒ 0 < −1 ≤ ). 8 a 21 a 21
Trong các bài toán trên dấu đẳng thức chỉ xảy ra tại điểm các biến bằng nhau. Tuy
nhiên có những bài toán dấu bằng còn xảy ra tại những điểm khác nữa hoặc có một dấu bằng
nhưng không phải tại các biến bằng nhau, ta phải đánh giá như thế nào. Khi đó, phương pháp
tiếp tuyến có giải quyết được không ?
Những bài toán như vậy thường là những bài toán khó, việc sử dụng tiếp tuyến tưởng
như không thể. Tuy nhiên, trong một số trường hợp, ta vẫn có thể sử dụng phương pháp tiếp
tuyến theo từng trường hợp đẳng thức. Cụ thể ta xét ví dụ sau:
Ví dụ 13. Cho a,b,c ≥ 0 thỏa mãn a + b + c = 3. Chứng minh 2 2 2 a b c 1 + + ≤ . 2
5a + (b + c)2 2
5b + (c + a)2 2
5c + (a + b)2 3 Lời giải 2 2 2
+ Viết lại bất đẳng thức dưới dạng a b c + + ≤ 1 2 2 2
2a − 2a + 3 2b − 2b + 3 2c − 2c + 3
+ Ta thấy dấu đẳng thức xảy ra khi và chỉ khi a = b = c =1 hoặc 3
a = b = ,c = 0 (cùng các 2 hoán vị). Page 10/26 2
+ PTTT của đồ thị hàm số ( ) t f t = tại điểm 1 M t 1; là 4 1 y − = . 2 2t − 2t + 3 3 9 t
4t −1 (3 −8t)(t − )2 2 1 + Khi đó − = 2 2t − 2t + 3 9 9( 2 2t − 2t + 3) + Nếu cả ba số 3
a,b,c ≥ thì ta có điều phải chứng minh. 8
+ Nếu có 1 số nhỏ hơn 3 . Giả sử 3
c < thì điểm rơi của bài toán không còn là a = b = c =1 và 8 8 3
a = b = ,c = 0 mà chỉ còn 3
a = b = ,c = 0 . Do đó, rất tự nhiên ta nghĩ đến lập phương trình 2 2 2
tiếp tuyến của đồ thị hàm số ( ) t f t = tại điểm 3 1
M ; . Phương trình đó là 2 2t − 2t + 3 2 2 4t 3 y + = . 18 t 4t + 3 ( 2 − t − ) 1 (2t − 3)2 2 + Ta có − = ≤ 0, t ∀ ∈ 0;3 (*) 2 2t − 2t + 3 18 18( 2 2t − 2t + 3) ( ) 2 2 a b
(4a + 3) + (4b + 3)
+ Ta sử dụng (*) cho a,b ta có 2 + ≤ = 1 c − 2 2
2a − 2a + 3 2b − 2b + 3 18 9 2
+ Từ đây ta chỉ cần chứng minh c 2c ≤ ⇔ c( 2
4c −13c + 6 ≥ 0 . Bất đẳng thức này 2 ) 2c − 2c + 3 9 hiển nhiên đúng với 3 c < . 8
Ta đã biết có nhiều bất đẳng thức liên quan đến tổng các số dương. Ví dụ như 3
(a + b + c)2 ≤ ( 2 2 2
3 a + b + c ) hoặc a b c abc + + ≤
. Do đó, trong một số bài toán giả thiết 3
có thể không cho dưới dạng tổng a + b + c hay kết luận của bài toán các số hạng chứa đồng
thời các biến (nghĩa là chưa xác định được hàm đặc trưng cho bất đẳng thức) ta vẫn có thể sử
dụng phương pháp tiếp tuyến. Ta xét ví dụ sau:
Ví dụ 14. Cho a,b,c > 0 thỏa mãn 2 2 2
a + b + c =1. Chứng minh 1 1 1
+ + − (a + b + c) ≥ 2 3 . a b c Lời giải Page 11/26
+ PTTT của đồ thị hàm số ( ) 1
f t = − t tại điểm 1 2 3 M ; là y = 4 − t + 2 3 . t 3 3 1 ( t − )2 3 1 + Ta có − t ≥ 4 − t + 2 3, t ∀ ∈(0; ) 1 ⇔ ≥ 0, t ∀ ∈(0; ) 1 (luôn đúng). t t + Do đó, ta có 1 1 1
+ + − (a + b + c) ≥ 4
− (a + b + c) + 6 3 ≥ 2 3 a b c
(Vì (a + b + c)2 ≤ ( 2 2 2
3 a + b + c ) = 3 ⇒ −(a + b + c) ≥ − 3 ).
Ví dụ 15. Cho a,b,c > 0 thỏa mãn a + b + c = 1. Chứng minh a b c 9 + + ≥
1+ bc 1+ ac 1+ ab 10 Lời giải
Nhận xét: Trong bài toán trên dấu đẳng thức xảy ra khi 1
a = b = c = . Tuy nhiên trong kết 3
luận của bài toán ta chưa xác định được hàm đặc trưng. + Ta có a a a 4a ≥ = = 2 2 2 1+ bc b + c 1− a a − 2a + 5 1+ 1+ 2 2 + Ta đi chứng minh 4a 4b 4c 9 + + ≥ 2 2 2
a − 2a + 5 b − 2b + 5 c − 2c + 5 10
+ PTTT của đồ thị hàm số ( ) 4t f t = tại điểm 1 3 M t ; là 99 3 y − = . 2 t − 2t + 5 3 10 100 4t
99t − 3 (3t − )2 1 (15 −11t) + Ta có − = ≥ 0, t ∀ ∈ 0;1 (*). 2 t − 2t + 5 100
100( 2t − 2t + 5) ( )
+ Thay a,b,c bởi t trong (*) và cộng các bất đẳng thức theo vế ta có đpcm.
Bài tương tự: Cho a,b,c > 0 thỏa mãn a + b + c = 3. Chứng minh 1 1 1 3 + + ≤ .
9 − ab 9 − bc 9 − ca 8
Ví dụ 16. Cho các số dương a,b,c thỏa mãn 4 4 4
a + b + c = 3. Chứng minh 1 1 1 + + ≤ 1.
4 − ab 4 − bc 4 − ca Lời giải Page 12/26 + Ta có 1 2 ≤ 4 − ab 8 − ( 2 2 a + b ) + Tương tự, ta có 1 1 1 2 2 2 + + ≤ + +
4 − ab 4 − bc 4 − ca 8 − ( 2 2
a + b ) 8 − ( 2 2
b + c ) 8 − ( 2 2 c + a )
+ Để vận dụng giả thiết 4 4 4
a + b + c = 3, ta đặt x = (a + b )2 y = (b + c )2 z = (c + a )2 2 2 2 2 2 2 , , . Khi đó
x, y, z > 0
x + y + z =
(a +b )2 +(b +c )2 +(c + a )2 2 2 2 2 2 2 ≤ 2( 4 4 a + b ) + 2( 4 4 b + c ) + 2( 4 4 c + a ) = 12
⇒ x, y, z ∈(0;12) + Ta đi chứng minh 1 1 1 1 + + ≤
8 − x 8 − y 8 − z 2
+ Dự đoán dấu đẳng thức xảy ra tại x = y = z = 4.
+ PTTT của đồ thị hàm số f (t) 1 = tại điểm 1 M 4; là 1 5 y = t + . 8 − t 6 144 36 + Ta có 1 1 5 t ≤ + , t ∀ ∈ (0;12) (*). 8 − t 144 36
+ Thay x, y, z bởi t trong (*) và cộng các bất đẳng thức theo vế ta có đpcm.
Tuy nhiên trong bài toán sau (nhìn tương tự như Ví dụ 14) thì phương pháp tiếp tuyến
không giải quyết được.
Ví dụ 17. Cho a,b,c > 0 thỏa mãn 2 2 2
a + b + c = 3. Chứng minh 1 1 1 + + ≥ 3.
2 − a 2 − b 2 − c
Nhận xét: Ta thấy, phương pháp tiếp tuyến cũng chỉ là trường hợp riêng của bài toán sau:
Cho các số thực a ,a ,...,a ∈ D thỏa mãn điều kiện g (a + g a +...+ g a = ng α với 1 ) ( 2) ( n) ( ) 1 2 n
α ∈ D . Chứng minh f (a + f a +...+ f a ≥ nf α (≤ nf (α )) 1 ) ( 2) ( n) ( )
Để giải bài toán trên ta thường nghĩ đến một phương án là biểu diễn f (a qua g (a , i ) i )
nên ta xét hàm số h(t) = f (t) − .
m g (t) với t ∈ D. Ở đây, m là số được xác định sao cho α là
điểm cực tiểu (cực đại) của hàm số đồng thời h(α ) là giá trị nhỏ nhất (lớn nhất) của hàm số trên D . Page 13/26 f ' α
Vì α là điểm cực tiểu (cực đại) của hàm số nên h(α ) ( ) = 0 ⇒ m = g '(α )
Vì h(α ) là giá trị nhỏ nhất (lớn nhất) của hàm số trên D nên
h(t) = f (t) − .
m g (t) ≥ h(α )(≤ h(α )), t ∀ ∈ D (*)
Khi đó thay a ,a ,...,a vào t trong (*) và cộng theo vế các bất đẳng thức ta có điều 1 2 n phải chứng minh.
Ta giải bài toán theo phương pháp trên f '( ) 1 + Xét hàm ( ) 2
g t = t , f (t) 1 = . Chọn 1 m = = . 2 − t g '( ) 1 2
+ Xét hàm số h(t) 1 1 2 = − t trên (0; 3). 2 − t 2
+ Từ bảng biến thiên ta thấy h(t) 1 ≥ , t ∀ ∈(0; 3) (*). 2
+ Thay a,b,c vào t trong bất đẳng thức (*), cộng vế theo vế ta có điều phải chứng minh.
Yêu cầu học sinh thử giải lại các ví dụ theo phương pháp trên.
Không chỉ trong các bất đẳng thức đại số, mà ngay cả trong một số bất đẳng thức
lượng giác, phương pháp tiếp tuyến còn có nhiều áp dụng. Ta xét ví dụ sau:
Ví dụ 18. Chứng minh rằng 1) 3 3
sin A + sin B + sinC ≤ , ABC ∀∆ . 2 2) 3
cos A + cos B + cosC ≤ , ABC ∀∆ . 2
3) tan A + tan B + tanC ≥ 3 3, ABC ∀∆ nhọn. Lời giải 1)
Nhận xét: Đây là một trong những bất đẳng thức cơ bản của tam giác. Học sinh hoàn toàn có
thể giải quyết theo kiến thức lớp 11 nhờ sử dụng bất đẳng thức
sin x + sin y ≤ sin x+ y , x ∀ , y ∈(0;π ) . 2 2 Page 14/26 Khi đó, ta có π π C +
A + B + C + ( π + π A + B) A B 3 3 sin sin + sinC + sin ≤ 2sin + 2sin ≤ 4sin = 4sin 3 2 2 4 3 Vậy 3 3
sin A + sin B + sinC ≤ , ABC ∀∆ . 2
Tuy nhiên, trong phương pháp trên học sinh cần nhớ được bất đẳng phụ. Do đó,
phương pháp tiếp tuyến ta thấy tương đối dễ vận dụng đối với học sinh: π
+ PTTT của đồ thị hàm số π
f (t) = sint,t ∈(0;π ) tại điểm 3 M ; là 1 3 y = t − + . 3 2 2 3 2 π
+ Xét hàm số g (t) 1 3
= sint − t − + trên (0;π ) . 2 3 2 π Từ bảng biến thiên π g (t) g ⇒ ≤ = 0, t ∀ ∈ 1 3
(0;π ) ⇒ sint ≤ t − + , t ∀ ∈ (0;π ) (*). 3 2 3 2 + Thay ,
A B,C bởi t trong (*) và cộng các BĐT theo vế ta có đpcm. 2) π
+ PTTT của đồ thị hàm số π
f (t) = cost,t ∈(0;π ) tại 1 M ; là 3 1 y = − t − + . 3 2 2 3 2 π
+ Xét hàm số g (t) 3 1 = cost + t − − trên (0;π ) . 2 3 2 Từ bảng biến thiên π g (t) g ⇒ ≤ = 0, t ∀ ∈ (0;π ) 3 3 π 1 ⇒ cost ≤ − t − + , t ∀ ∈ (0;π ) (*). 2 3 2 + Thay ,
A B,C bởi t trong (*) và cộng các BĐT theo vế ta có đpcm. 3) Cách 1.
+ PTTT của đồ thị hàm số π π π
f (t) tant,t 0; = ∈
tại M ; 3 là y = 4 t − + 3 . 2 3 3 + Xét hàm số π π
g (t) tant 4 t = − − − 3 trên 0; . 3 2 Từ bảng biến thiên π π π π g (t) g 0, t 0; ⇒ ≥ = ∀ ∈
⇒ tant ≥ 4 t − + 3, t ∀ ∈ 0; (*). 3 2 3 2 Page 15/26 + Thay ,
A B,C bởi t trong (*) và cộng các BĐT theo vế ta có đpcm. Cách 2.
Áp dụng đẳng thức trong tam giác ta có
tan A + tan B + tanC = tan Atan B tanC, ABC ∀∆ nhọn.
Áp dụng bất đẳng thức TBC-TBN 3
tan A + tan B + tanC ≥ 3 tan Atan B tanC ⇒ tan Atan B tanC ≥ 3 3 ⇒đpcm. A B C
Ví dụ 19. Chứng minh 1 sin sin sin ≤ , ABC ∀∆ . 2 2 2 8 Lời giải Cách 1.
+ Viết lại bất đẳng thức cần chứng minh dưới dạng A B C 1
lnsin + lnsin + lnsin ≤ 3ln . 2 2 2 2
+ Phương trình tiếp tuyến của đồ thị hàm số ( ) π = lnsin t f t
,t ∈(0;π ) tại điểm 1 M ;ln là 2 3 2 3 π 1 y = t − + ln . 2 3 2 π
+ Xét hàm g (t) t 3 1 = lnsin − t − − ln trên (0;π ) . 2 2 3 2 + Từ bảng biến thiên π g (t) g ⇒ ≤ = 0, t ∀ ∈ (0;π ) (đpcm). 3 Cách 2.
+ Áp dụng đẳng thức cơ bản trong tam giác
cos + cos + cos =1+ 4sin A sin B sin C A B C 2 2 2
+ Theo chứng minh ở Ví dụ 18, ta có 3
cos A + cos B + cosC ≤ A B C 1 ⇒ sin sin sin ≤ . 2 2 2 2 8 Page 16/26
1.3 Bài tập tự luyện 1 1 1 2( 2 2 2
a + b + c )
1) Cho a,b,c > 0 và a + b + c = 3. Chứng minh + + + ≥ 5. 2 2 2 a b c 3
2) Cho a,b,c∈ thỏa mãn a + b + c = 6. Chứng minh 4 4 4
a + b + c ≥ ( 2 2 2
2 a + b + c ).
3) Cho a,b,c > 0 và a + b + c = 3. Chứng minh
( a + b + c) ≥ −( 2 2 2 2
9 a + b + c ).
4) Cho a,b,c > 0 và a + b + c = 3. Chứng minh 1 1 1 + + ≤ 1. 2 2 2
a + b + c b + c + a c + a + b
5) Cho a,b,c > 0 và a + b + c = 3. Chứng minh a + b + c ≥ ab + bc + ca .
6) Cho a,b,c,d > 0 và a + b + c + d ≤ 4 . Chứng minh 1 1 1 1 + + + ≥ 1.
(1+ a)2 (1+ b)2 (1+ c)2 (1+ d )2
7) Cho a,b,c ≥ 0 và a + b + c =1. Chứng minh ( 3 3 3
a + b + c ) − ( 5 5 5 10
9 a + b + c ) ≥1.
(b + c −3a)2
(c + a −3b)2
(a + b −3c)2
8) Cho a,b,c > 0. Chứng minh 1 + + ≥ . (b + c)2 2 + 2a (c + a)2 2 + 2b (a + b)2 2 + 2c 2 3 3 3
9) Cho a,b,c > 0. Chứng minh a b c + + ≥ 1. 3
a + (b + c)3 3
b + (a + c)3 3
c + (a + b)3
10) Cho a,b,c > 0. Chứng minh a b c 3 + + ≥
(a + b + c) . b + c a + c a + b 2
11) Cho a,b,c + + +
> 0. Chứng minh b c c a a b 4 a b c + + ≥ + + . a b c b c c a a b + + + Page 17/26 Chương II
KHAI THÁC TÍNH CHẤT CỦA HÀM SỐ Y = AX + B
TRONG CHỨNG MINH BẤT ĐẲNG THỨC
2.1 Kiến thức chuẩn bị
Cho hàm số y = f (x) = ax + b . Nếu xét trên đoạn [α;β ] thì đồ thị của nó là một đoạn
thẳng có hai đầu mút là hai điểm A(α; f (α )) và B(β; f (β )). Do đó, f (α ) ≥ f (x) ≥ x ∀ ∈[α β ] 0 0, ; ⇔ . f (β ) ≥ 0 f (α ) ≤ f (x) ≤ x ∀ ∈[α β ] 0 0, ; ⇔ . f (β ) ≤ 0
min f (x) = min{ f (α ); f (β )}. [α;β]
max f (x) = max{ f (α ); f (β )}. [α;β]
2.2 Một số ví dụ minh họa
Ví dụ 1. Cho a,b,c ∈[0;2]. Chứng minh 2(a + b + c) − (ab + bc + ca) ≤ 4. Lời giải
+ Ycbt ⇔ f (a) = (2 − b − c)a + 2(b + c) − bc − 4 ≤ 0, a ∀ ∈[0;2], b ∀ ,c ∈[0;2]. f (0) ≤ 0 ⇔ , b ∀ ,c ∈[0;2]. f (2) ≤ 0
+ Mà f (0) = −(2 − b)(2 − c) ≤ 0 ; f (2) = bc − ≤ 0 , b ∀ ,c ∈[0;2] .
Do đó, f (a) ≤ 0, a
∀ ,b,c ∈[0;2] (đpcm).
Ví dụ 2. Cho a,b,c ≥ 0 thỏa mãn a + b + c = 1. Chứng minh 7
ab + bc + ca − 2abc ≤ . 27 Lời giải
Bài toán trên đã xuất hiện nhiều trong các tài liệu và đều được giải theo phương pháp
ứng dụng đạo hàm.
Vì vai trò bình đẳng ngang nhau của các biến a,b,c nên việc chọn phần tử nhỏ nhất
(lớn nhất) có thể làm cho giả thiết của bài toán được sáng tỏ thêm hay như được cho thêm giả Page 18/26
thiết. Tuy nhiên, việc đánh giá để qui về một biến cũng không hề đơn giản. Ta xem lại cách giải sau: Cách 1.
+ Vì vai trò của a,b,c bình đẳng nên ta luôn có thể giả sử a = {a b } 1
min , ,c ⇒ 0 ≤ a ≤ . 3
+ Ta có VT = (ab + ca) + (bc − 2abc) = a(b + c) + bc(1− 2a) 2 (1 ) b + c a a ≤ − + (1−
2a) (vì 1− 2a < 0) 2 2 ( ) 1 1 − a a a = − + (1− 2a) 2 2 + Xét hàm ( ) ( ) 1 1 − a f a a a = − + (1− 2a) , với 1 a
∈ 0; . Lập bảng biến thiên, tìm GTLN 2 3
của hàm f (a) trên 1 0;
, ta có điều phải chứng minh. 3 Cách 2.
+ Ycbt ⇔ f (a) = (b + c − bc) 7 2 a + bc − ≤ 0, a ∀ ∈[0; ] 1 , b
∀ ,c ≥ 0,a + b + c =1 27 f ( ) 7 0 = bc − , b
∀ ,c ≥ 0,b + c =1 27 ⇔ . f ( ) 7
1 = b + c − bc − ≤ 0, b
∀ ,c ≥ 0,b + c = 0 27 2 + b
∀ ,c ≥ 0,b + c =1, f ( ) 7 b c 7 1 7 0 = bc + − ≤ − = − < 0 27 2 27 4 27 + b
∀ c ≥ b + c = ⇒ b = c = ⇒ f ( ) 7 , 0, 0 0 0 = − < 0 . 27
Ta có điều phải chứng minh.
Trong cách giải trên, khi quan sát bất đẳng thức cần chứng minh ta thấy có thể qui về
hàm số bậc cao nhất là 1, với biến a , tham số b,c . Khi đó, bài toán có hai tham số, mà việc
khai thác điều kiện cho hai tham số trong từng trường hợp tại a = 0 , hoặc tại a =1 không
phải học sinh nào cũng phát hiện được. Do đó, ta có thể hướng dẫn học sinh sử dụng những
biến đổi đại số cơ bản để đưa về hàm số chỉ còn chứa một tham số như Cách 3 sau đây: Cách 3.
+ Biến đổi bất đẳng thức cần chứng minh về dạng Page 19/26
a(b + c) + bc( − a) 7 1 2 −
≤ 0 ⇔ a( − a) + bc( − a) 7 1 1 2 − ≤ 0 . 27 27 2 b + c (1− a)2
+ Ycbt ⇔ f (u) = a( − a) + u( − a) 7 1 1 2 −
≤ 0 với 0 ≤ u = bc ≤ = , 27 2 4 a ∀ ∈[0; ] 1 . f (0) ≤ 0
⇔ (1− a)2 , a ∀ ∈[0; ] 1 . f ≤ 0 4
a + − a
+ Ta có f ( ) = a( − a) 7 ( ) 2 1 7 1 7 0 1 − ≤ − = − < 0, a ∀ ∈[0; ] 1 27 2 27 4 27 ( − a)2 1 f ≤ 0 , a ∀ ∈[0; ] 1 . 4
Ví dụ 3. Cho a,b,c ≥ 0 thỏa mãn a + b + c = 3. Chứng minh 2 2 2
a + b + c + abc ≥ 4. Lời giải Cách 1.
+ Không mất tính tổng quát, ta giả sử a = min{a,b, }
c ⇒ 0 ≤ a ≤1. + Khi đó, 2 2 2 2
a + b + c + abc = a + (b + c)2 + bc(a − 2) 2 2 (3 )2 b + c a a ≥ + − + (a −
2) (vì a − 2 < 0) 2 2 2 ( )2 3 3 − a a a = + − + (2 − a) 2 2
+ Ta đi tìm GTNN của hàm số ( ) 2 ( )2 3 3 − a f a a a = + − + (2 − a) trên [0; ] 1 2 Cách 2.
Biến đổi bất đẳng thức cần chứng minh về dạng 2 2 2 2
a + b + c + abc ≥ 4 ⇔ a + (b + c)2 − 2bc + abc ≥ 4 2
⇔ a + (3 − a)2 + bc(a − 2) − 4 ≥ 0 2 + Ycbt +
⇔ f (u) = (a − ) 2
2 u + 2a − 6a + 5 ≥ 0 với b c 1 0 ≤ u = bc ≤ = (3− a)2 , a ∀ ∈[0; ] 3 2 4 Page 20/26 f (0) ≥ 0 ⇔ 1 a ∀ ∈[0; ] 3 . f (3− a) , 2 ≥ 0 4 2 + Mà f ( ) 3 1 0 = 2 a − + > 1 2 1 2 0; f
(3− a) = (a − ) 1 (a + 2) ≥ 0 , a ∀ ∈[0; ] 3 . 2 5 4 4 Do đó, f (u) 1 0, u 0; (3 a)2 ≥ ∀ ∈ − điều phải chứng minh. 4
Ví dụ 4. Cho a,b,c ≥ 0 thỏa mãn a + b + c = 1. Chứng minh 3 3 3 1
a + b + c + 6abc ≥ . 4 Lời giải Cách 1.
+ Vì vai trò của a,b,c bình đẳng nên ta luôn có thể giả sử a = {a b } 1
min , ,c ⇒ 0 ≤ a ≤ 3 + Khi đó, 3 3 3 3
a + b + c + 6abc = a + (b + c)3 − 3bc(b + c) + 6abc 3
= a + (1− a)3 + 3bc(3a − ) 1 2 3
(1 )3 3. b + c a a ≥ + − + (3a − ) 1 (vì 3a −1≤ 0) 2 2 3 ( )3 1 1 3 − a a a = + − + (3a − ) 1 2 2 + Xét hàm số ( ) 3 ( )3 1 1 3 − a f a a a = + − + (3a − ) 1 , với 1 a ∈ 0; . Tìm GTNN của hàm 2 3
f (a) trên 1 0;
ta có điều phải chứng minh. 3 Cách 2.
+ Biến đổi bất đẳng thức cần chứng minh về dạng (a + b)3 − ab(a + b) 3 1 3 + c + 6abc ≥ 4
⇔ ( − c)3 − ab( − c) 3 1 1 3 1
+ c + 6abc ≥ ⇔ ab( c − ) 2 3
9 3 + 3c − 3c + ≥ 0 4 4 2 a + b (1− c)2
+ Ycbt ⇔ f (u) = ( c − ) 2 3
9 3 u + 3c − 3c + ≥ 0, với 0 ≤ u = ab ≤ = , c ∀ ∈ [0; ]1 4 2 4 2 (1− c)2 + Ta có f ( ) 1 0 3 c = − ≥ 3 0; f = c( 2 3c − 3c + ) 1 > 0 , c ∀ ∈[0; ] 1 ⇒đpcm. 2 4 4 Page 21/26
Ví dụ 5. Cho a,b,c,d ∈[0; ]
1 . Chứng minh (1− a)(1− b)(1− c)(1− d ) + a + b + c + d ≥1. Lời giải + Ycbt ⇔ f (a) = 1
− (1− b)(1− c)(1− d ) a + (1− b)(1− c)(1− d ) + b + c + d −1≥ 0, a ∀ ∈ [0; ]1,
b,c,d ∈[0; ] 1 . f (0) ≥ 0 ⇔ , b
∀ ,c,d ∈[0; ]. f ( ) 1 1 ≥ 0 + Mà f ( )
1 = b + c + d ≥ 0, b
∀ ,c,d ∈[0; ] 1 .
+ Ta cần chứng minh f (0) = (1− b)(1− c)(1− d ) + b + c + d −1≥ 0, b
∀ ,c,d ∈[0; ] 1 .
+ Ta xét bài toán: Chứng minh (1− b)(1− c)(1− d ) + b + c + d −1≥ 0, b
∀ ,c,d ∈[0; ] 1 (1).
Ta thấy bài toán (1) tương tự bài toán ban đầu, tuy nhiên đã giảm bớt đi một biến. Do
đó, tiếp tục cách làm trên ta có thể giải quyết triệt để được bài toán ban đầu.
Ycbt (1) ⇔ g (b) = 1
− (1− c)(1− d )b + (1− c)(1− d ) + c + d −1≥ 0, b ∀ ∈[0; ] 1 , c ∀ ,d ∈ [0; ]1 g (0) ≥ 0 ⇔ , c ∀ ,d ∈[0; ]. g ( ) 1 1 ≥ 0 + Mà g ( )
1 = c + d ≥ 0; g (0) = (1− c)(1− d ) + c + d −1 = cd ≥ 0 ⇒ g (b) ≥ 0 b
∀ ,c,d ∈[0; ] 1
Ta có điều phải chứng minh.
Một số bài toán, không phải lúc nào cũng có sẵn dạng hàm số y = ax + b . Tuy nhiên,
trong một số trường hợp, nhờ những biến đổi, đánh giá bất đẳng thức đại số thích hợp ta có
thể áp dụng tính chất hàm số y = ax + b trong chứng minh. Ta xét các ví dụ sau: a b c
Ví dụ 6. Chứng minh + +
+ (1− a)(1− b)(1− c) ≤1, a
∀ ,b,c ∈[0; ] 1
b + c +1 c + a +1 a + b +1 Lời giải
+ Không mất tính tổng quát ta giả sử a = max{a,b, } c . Khi đó a + b + c VT ≤
+ (1− a)(1− b)(1− c) b + c +1
+ Ta chứng minh ( ) a + b + c f a =
+ (1− a)(1− b)(1− c) −1≤ 0, a ∀ ∈[0; ] 1 , b ∀ ,c ∈[0; ] 1 . b + c +1 + b ∀ ,c ∈[0; ] 1 , ta có Page 22/26 b + c + − − b + c
bc(b + c) − (b + c ) − ( 2 2 2 2 b c ) 1 bc f ( ) bc (b c) bc 2 0 = + − + = ≤ ≤ 0 b + c +1 b + c +1 b + c +1 f ( ) 1 = 0
Ta có điều phải chứng minh.
Ví dụ 7. Cho a,b,c ∈[0; ] 1 . Chứng minh 2 2 2 2 2 2
a + b + c ≤ a b + b c + c a +1. Lời giải
+ Biến đổi bất đẳng thức về dạng (b − ) 2 2 2 2 2
1 a + c a + b c +1− b − c ≥ 0 + Vì a ∈[0; ] 1 nên 2
a ≥ a , suy ra (b − ) 2 2 2 2 2
a + c a + b c + − b − c ≥ (b − ) 2 2 2 2 2 2 1 1
1 a + c a + b c +1− b − c .
+ Ta đi chứng minh (b − ) 2 2 2 2 2 2
1 a + c a + b c +1− b − c ≥ 0, a
∀ ,b,c ∈[0; ] 1 . ⇔ f (u) = ( 2 b + c − ) 2 2 2
1 u + b c +1− b − c ≥ 0, với 2
0 ≤ u = a ≤1, b ∀ ,c ∈[0; ] 1 . f (0) ≥ 0 ⇔ , b ∀ ,c ∈[0; ]. f ( ) 1 1 ≥ 0 + Ta có f ( ) 2 2 2
= b c + − b − c = ( − c)c + ( 2 0 1 1 1− b ) ≥ 0 b ∀ ,c ∈[0; ] 1 f ( ) 2 = b c + ( 2 1
b − b ) ≥ 0 b ∀ ,c ∈[0; ] 1
Vậy f (u) ≥ 0, u ∀ ∈[0; ] 1 (đpcm).
Ví dụ 8. Cho x, y, z ≥ 0 và x + y + z = 1. Chứng minh 2 2 2 4
x y + y z + z x ≤ . 27 Lời giải
+ Không mất tính tổng quát ta giả sử x = {x y } 1
min ; ; z ⇒ 0 ≤ x ≤ . 3 Khi đó, 2 2 2 1 2 2 1 2 2
x y + y z + z x ≤ xy + y z + z x = y + z x + y z 3 3 + Ycbt f (x) 1 2 2 4 1 y z x y z , x 0; ⇔ = + + ≤ ∀ ∈ , y
∀ , z ≥ 0, x + y + z = 1 3 27 3 f ( ) 4 0 ≤ , y
∀ , z ≥ 0, y + z =1 27 ⇔ . 1 4 2 f ≤ , y
∀ , z ≥ 0, y + z = 3 27 3 Page 23/26 3 + Ta có f ( ) 2 1
1 2y + 2z 4
= y z = y y z ≤ = ( y + z)3 4 0 . .2 = , y
∀ , z ≥ 0, y + z =1. 2 2 3 27 27 1 1 1 2 2 f = y + z + y z . 3 3 3 Vì 1 x = thì 2 2
y + z = ⇒ z = − y nên 3 3 3 1 3 2 1 4 2 1 4 4 f = −
y + y − y +
= −y y − y + + ≤ 3 3 27 3 27 27
Vậy ta có điều phải chứng minh.
Ta đã biết, bất đẳng thức xuất hiện rất nhiều trong các bài toán (có thể trực tiếp hoặc
gián tiếp), và ở một số trường hợp nhất định việc khai thác tính chất của hàm số y = ax + b để
chứng minh bất đẳng thức vẫn còn hiệu quả trong việc giải quyết lớp bài toán đó. Ta xét một số ví dụ sau: Ví dụ 9.
1) Tìm m để hàm số y = ( m − ) x + ( m − ) 2 4 5 cos 2
3 x + m − 3m +1 nghịch biến trên .
2) Tìm m để hàm số y = x + msin x đồng biến trên . Lời giải 1)
+ Ycbt ⇔ y ' = (5 − 4m)sin x + (2m − 3) ≤ 0, x ∀ ∈
⇔ g (u) = (5 − 4m)u + (2m − 3) ≤ 0, x ∀ ∈[ 1; − ] 1 g (− ) 1 ≤ 0
+ Do đồ thị hàm số y = g (u),u ∈[ 1; − ]
1 là một đoạn thẳng nên ycbt ⇔ . g ( ) 1 ≤ 0
2) Học sinh trình bày tương tự.
Ví dụ 10. Tìm x để bất phương trình 2
x + 2x(sin y + cos y) +1≥ 0 đúng với mọi y ∈. Lời giải
+ Đặt u = sin y + cos y ⇒ u ∈ − 2; 2
+ Ycbt ⇔ Tìm x để f (u) 2 = 2 .
x u + x +1≥ 0, u ∀ ∈ − 2; 2 f (− 2 ) ≥ 0 2
x − 2 2x +1≥ 0 ⇔ ⇔ f ( 2 ) 2 ≥ 0
x + 2 2x +1≥ 0 Page 24/26
Ví dụ 11. Chứng minh với mọi m ≤ 2 − thì 2 x − (2m + )
1 x + 3m + 2 ≤ 0 , với mọi x ∈[ 4; − ] 1 . Lời giải + Ycbt 2
⇔ x − (2m + )
1 x + 3m + 2 ≤ 0, x ∀ ∈[ 4; − ] 1 , m ∀ ∈( ; −∞ 2 − ] .
⇔ f (m) = (− x + ) 2 2
3 m + x − x + 2 ≤ 0, m ∀ ∈( ; −∞ 2 − ], x ∀ ∈[ 4; − ] 1 (1).
+ Vì f (m) là hàm bậc nhất với hệ số góc 2
− x + 3 > 0, x ∀ ∈[ 4; − ] 1 nên ( ) ⇔ f (− ) ≤ x ∀ ∈[− ] 2 1 2 0,
4;1 ⇔ x + 3x − 4 ≤ 0, x ∀ ∈[ 4; − ]
1 (luôn đúng) ⇒Điều phải chứng minh.
2.3 Bài tập tự luyện
1) Cho a,b,c là ba cạnh của tam giác có chu vi bằng 1. Chứng minh 2 2 2
a + b + c + 2abc < 2.
2) Cho x, y, z ≥ 0 và x + y + z =1. Chứng minh 7(xy + yz + xz) ≤ 2 + 9xyz .
3) Cho x, y, z ≥ 0 và x + y + z =1. Chứng minh ( 2 2 2
x + y + z ) ≤ ( 3 3 3 5
6 x + y + z ) +1.
4) Cho 1≤ x, y, z ≤ 3 thỏa mãn x + y + z = 6. Chứng minh rằng 2 2 2
x + y + z ≤14 .
5) Cho 0 ≤ x, y, z ≤ 2 thỏa mãn x + y + z = 3. Chứng minh rằng 3 3 3
x + y + z ≤ 9 .
6) Cho a,b,c ≥ 0 thỏa mãn a + b + c =1. Chứng minh ( 3 3 3
4 a + b + c ) +15abc ≥1.
7) Chứng minh rằng với mọi m ≤1 thì 2 x − 2(3m − )
1 x + m + 3 ≥ 0, với mọi x ≥1. Page 25/26
TÀI LIỆU THAM KHẢO
[1] Đoàn Quỳnh (Chủ biên), Tài liệu chuyên toán Giải tích 12, NXBGD.
[2] Đoàn Quỳnh (Chủ biên), Tài liệu chuyên toán Bài tập Giải tích 12, NXBGD.
[3] Trần Lưu Cường, Toán Olympic cho sinh viên, NXBGD 1998.
[4] Trần Phương, Những viên kim cương trong bất đẳng thức toán học, NXB Tri Thức.
[5] Trần Phương, Tuyển chọn các chuyên đề luyện thi Đại học môn Toán Hàm số, NXBĐHQGHN.
[6] Phạm Kim Hùng, Sáng tạo bất đẳng thức, NXB Tri Thức.
[7] Tạp chí THTT, số 408, tháng 6/2011.
[8] Tuyển tập 30 năm tạp chí THTT, NXBGD 1998.
[9] Tuyển tập đề thi Olympic 30/4, lần XV, NXBGD 2009.
[10] Tuyển tập đề thi Olympic 30/4, lần XVI, NXBGD 2010.
[11] Tuyển tập đề thi Olympic 30/4, lần XVII, NXBGD 2011.
[12] Tuyển tập đề thi Olympic 30/4, lần XVIII, NXBGD 2012.
[13] Tài liệu trên mạng Internet. Page 26/26
Document Outline
- KHAI THÁC HAI TÍNH CHẤT CỦA HÀM SỐ
- TRONG CHỨNG MINH BẤT ĐẲNG THỨC




