Khảo sát hàm số và các bài toán liên quan – Nguyễn Thanh Tùng Toán 12

Khảo sát hàm số và các bài toán liên quan – Nguyễn Thanh Tùng Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

56 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
1
CHUYÊN ĐỀ
KHẢO SÁT HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
Mục Lục
Đề mục Trang
A. KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ……………………………………….
B. CÁC BÀI TOÁN LIÊN QUAN…………………………………………………
Bài toán 1: Các bài toán liên quan tới phương trình tiếp tuyến…………………………………….. 2
Bài toán 1.1………………………………………………………………………………………….. 2
Bài toán 1.2………………………………………………………………………………………….. 10
Bài toán 2: Các bài toán liên quan tới cực trị………………………………………………………… 15
Bài toán 2.1………………………………………………………………………………………….. 15
Bài toán 2.2………………………………………………………………………………………….. 19
Bài toán 2.3………………………………………………………………………………………….. 26
Bài toán 3: Bài toán giao điểm………………………………………………………………………… 28
Bài toán 3.1………………………………………………………………………………………….. 28
Bài toán 3.2………………………………………………………………………………………….. 41
Bài toán 3.3………………………………………………………………………………………….. 44
Bài toán 4: Bài toán tìm điểm…………………………………………………………………………. 49
Bài toán 5: Các bài toán về tính đơn điệu của hàm số……………………………………………….. 52
Bài toán 5.1………………………………………………………………………………………….. 52
Bài toán 5.2………………………………………………………………………………………….. 53
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
2
CHUYÊN ĐỀ 1: KHẢO SÁT HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
A. KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
B. CÁC BÀI TOÁN LIÊN QUAN
Bài toán 1: Các bài toán liên quan tới phương trình tiếp tuyến
Cơ sở lí thuyết:
* Cho hàm số
( )
y f x
có đồ thị (C), phương trình tiếp tuyến của (C) tại điểm
0 0 0
( , ) ( )
M x y C
là :
0 0 0
'( )( )
y f x x x y
(*) (
0
M
gọi là tiếp điểm).
* Hai đồ thị hàm số
( )
y f x
và
( )
y g x
tiếp xúc với nhau khi và chỉ khi hệ phương trình sau có nghiệm :
( ) ( )
'( ) '( )
f x g x
f x g x
(2*)
Nghiệm của (2*) là hoành độ tiếp điểm của hai đồ thị.
Nhận xét : Với kiến thức cơ bản trên, giúp ta giải quyết hai lớp câu hỏi liên quan tới việc viết phương trình
tiếp tuyến (tại điểm và đi qua điểm). Cụ thể :
+) Với câu hỏi tại điểm, để viết được phương trình (*) ta cần 3 yếu tố
0 0
,
x y
và
0
'( )
f x
. Ứng với điều này sẽ có
3 cách ra đề : cho biết
0
x
, cho biết
0
y
hoặc cho biết
0
'( )
f x
dưới các cách phát biểu khác nhau, và điều này sẽ
được diễn đạt thông qua Bài toán 1.1.
+) Với câu hỏi đi qua điểm sẽ được phát biểu qua Bài toán 1.2 .
Bài toán 1.1
Nội dung bài toán :
Cho hàm số
( )
y f x
có đồ thị là
( )
C
. Viết phương trình tiếp tuyến của đồ thị
( )
C
:
1. Tại điểm có hoành độ là
a
. 2. Tại điểm có tung độ là
b
.
3. Có hệ số góc là
k
. 4. Song song với đường thẳng
y ax b
.
5. Vuông góc với đường thẳng
y ax b
. 6. Tạo với trục hoành (
Ox
) một góc bằng
.
7. Cắt các trục
,
Ox Oy
lần lượt tại hai điểm
,
A B
sao cho
OB kOA
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
3
Cách giải chung:
Gọi
0 0 0
( ; )
M x y
là tiếp điểm của tiếp tuyến cần lập. Khi đó phương trình tiếp tuyến tại
0 0 0
( ; )
M x y
có dạng:
0 0 0
'( )( )
y f x x x y
(*)
1. Với
0
0
0
'( ) '( )
( )
f x f a
x a
y f a
, thay vào (*) ta được phương trình cần lập.
2. Với
0 0
( )
y b f x b
(2) . Giải phương trình (2) tìm
0
x
và suy ra
0
'( )
f x
. Sau đó thay các thông số tìm
được vào (*) ta được phương trình cần lập.
3. Tiếp tuyến có hệ số góc
k
, suy ra
0
'( )
f x k
(3). Giải phương trình (3) tìm
0
x
và suy ra
0
y
. Sau đó thay vào
(*) ta được phương trình cần lập.
4. Tiếp tuyến song song với đường thẳng
y ax b
, suy ra
0
'( )
f x a
(4).
Giải phương trình (4) tìm được
0
x
và suy ra
0
y
. Sau đó thay vào (*) ta được phương trình (kiểm tra lại tính
song song) và kết luận.
5. Tiếp tuyến vuông góc với đường thẳng
y ax b
, suy ra
0
1
'( )f x
a
(5).
Giải phương trình (5) tìm được
0
x
và suy ra
0
y
. Sau đó thay vào (*) ta được phương trình cần lập.
6. Tiếp tuyến tạo với trục hoành một góc
, suy ra
0
'( ) tan
f x
(6).
Giải phương trình (6) tìm được
0
x
và suy ra
0
y
. Sau đó thay vào (*) ta được phương trình cần lập.
7. Tiếp tuyến cắt trục
,
Ox Oy
lần lượt tại
,
A B
sao cho
OB kOA
, khi đó gọi
là góc tạo bởi
tiếp tuyến và trục hoành ta có: tan
OB
k
OA
Suy ra
0
'( ) tan
f x k
(7)
Giải phương trình (7) tìm được
0
x
và suy ra
0
y
.
Sau đó thay vào (*) ta được phương trình cần lập.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
4
Nhận xét:
*) Ngoài cách phát biểu tường minh như ý 1, 2 ta có thể gặp những câu hỏi tương tự như sau:
– Viết phương trình tiếp tuyến của đồ thị
( )
C
tại giao điểm của
( )
C
với trục hoành (với đường thẳng
y ax b
, với đường cong
( )
y g x
…).
– Viết phương trình tiếp tuyến của đồ thị
( )
C
tại điểm thoả mãn điều kiện cho trước.
*) Các ý 3, 4, 5, 6, 7 thực chất là dữ kiện cho biết
0
'( )
f x
nhưng được phát biểu dưới nhiều cách diễn đạt
khác nhau.
Ví dụ 1. Cho hàm số
3 2
( ) 6 9 1
y f x x x x
có đồ thị
( )
C
. Viết phương trình tiếp tuyến của đồ thị
( )
C
:
1. Tại điểm có hoành độ bằng
2
. 2. Tại điểm có tung độ bằng
15
.
3. Tại giao điểm của đồ thị
( )
C
với đường thẳng
4 1
y x
.
4. Tại điểm có hoành độ
0
x
, biết
0
''( ) 0
f x
và chứng minh rằng tiếp tuyến khi đó là tiếp tuyến của
( )
C
có
hệ số góc nhỏ nhất.
Giải: Ta có
2
' '( ) 3 12 9
y f x x x
. Gọi
0 0 0
( ; )
M x y
là tiếp điểm của tiếp tuyến cần lập.
1. Với
0
0
'(2) 3
2
(2) 3
f
x
y f
, suy ra phương trình tiếp tuyến cần lập:
3( 2) 3
y x
hay
3 9
y x
2. Với
3 2
0 0 0 0
15 6 9 1 15
y x x x
3 2
0 0 0
6 9 16 0
x x x
2
0 0 0 0
( 1)( 7 16) 0 1 '( 1) 24
x x x x f
Vậy phương trình tiếp tuyến cần lập là:
24 9
y x
3. Phương trình hoành độ giao điểm của
( )
C
với đường thẳng
4 1
y x
là:
3 2 2
0 1
6 9 1 4 1 ( 6 5) 0 1 5
5 21
x y
x x x x x x x x y
x y
+) Với
0
(0;1) '(0) 9
M f
, suy ra phương trình tiếp tuyến:
9 1
y x
+) Với
0
(1;5) '(1) 0
M f
, suy ra phương trình tiếp tuyến:
5
y
+) Với
0
(5;21) '(5) 24
M f
, suy ra phương trình tiếp tuyến:
24 99
y x
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
5
4. Ta có
'' ''( ) 6 12
y f x x
, khi đó
0 0 0
''( ) 0 6 12 0 2
f x x x
0
'(2) 3
(2) 3
f
y f
Suy ra phương trình tiếp tuyến cần lập:
3 9
y x
Hệ số góc tiếp tuyến của đồ thị
( )
C
tại điểm có hoành độ
x
bằng :
2 2
'( ) '( ) 3 12 9 3( 2) 3 3
y x f x x x x
, x
, suy ra
min
'( ) 3
y x
khi
0
2
x x
Vậy tiếp tuyến của
( )
C
tại điểm có hoành độ
0
x
thỏa mãn
0
''( ) 0
f x
có hệ số góc nhỏ nhất (đpcm).
Ví dụ 2. Cho hàm số
4 2
6
y x x
có đồ thị là
( )
C
. Viết phương trình tiếp tuyến của đồ thị
( )
C
:
1. Có hệ số góc là
6
. 2. Song song với đường thẳng
3 2 2 0
x y
.
3. Vuông góc với đường thẳng
1
3
6
y x
. 4. Tạo với trục hoành (
Ox
) một góc bằng
, biết
9
tan
16
5. Cắt các trục
,
Ox Oy
lần lượt tại hai điểm
,
A B
sao cho
36
OB OA
.
Giải:
Ta có
3
' 4 2
y x x
. Gọi
0 0 0
( ; )
M x y
là tiếp điểm của tiếp tuyến cần lập.
1. Tiếp tuyến có hệ số góc là
6
, suy ra:
3
0 0 0
'( ) 6 4 2 6
y x x x
2
0 0 0 0 0
( 1)(2 2 3) 0 1 ( 1) 4
x x x x y y
Vậy phương trình tiếp tuyến cần lập là:
6 10
y x
.
2. Đường thẳng
3 2 2 0
x y
được viết lại thành:
3
1
2
y x
Khi đó tiếp tuyến song song với đường thẳng
3
1
2
y x
, suy ra:
0
3
'( )
2
y x
3 3
0 0 0 0
3
4 2 8 4 3 0
2
x x x x
2
0 0 0 0 0
1 1 91
(2 1)(4 2 3) 0
2 2 16
x x x x y y
Tiếp tuyến cần lập là:
3 1 91
2 2 16
y x
hay
3 103
2 16
y x (thỏa mãn điều kiện song song).
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
6
3. Do tiếp tuyến vuông góc với đường thẳng
1
3
6
y x
, suy ra:
0
'( ) 6
y x
3 3
0 0 0 0
4 2 6 2 3 0
x x x x
2
0 0 0 0 0
( 1)(2 2 3) 0 1 (1) 4
x x x x y y
Khi đó phương trình tiếp tuyến:
6( 1) 4
y x
hay
6 10
y x
.
4. Do tiếp tuyến tạo với trục hoành (
Ox
) một góc bằng
, nên suy ra:
0
9
'( ) tan
16
y x
+) Với
3 3
0 0 0 0 0
9 9 9
'( ) 4 2 4 2 0
16 16 16
y x x x x x
0 0
1 1 1503
4 4 256
x y y
Tiếp tuyến cần lập :
9 1 1503
16 4 256
y x
hay
9 1539
16 256
y x
+) Với
3 3
0 0 0 0 0
9 9 9
'( ) 4 2 4 2 0
16 16 16
y x x x x x
0 0
1 1 1503
4 4 256
x y y
Tiếp tuyến cần lập :
9 1 1503
16 4 256
y x
hay
9 1539
16 256
y x
5. Gọi
là góc tạo bởi tiếp tuyến cần lập và trục hoành, khi đó tiếp tuyến cắt các trục
,
Ox Oy
lần lượt tại hai
điểm
,
A B
, ta được:
0
36
tan 36 '( ) tan 36
OB OA
y x
OA OA
+) Với
3 3
0 0 0 0 0
'( ) 36 4 2 36 4 2 36 0
y x x x x x
0 0
2 (2) 14
x y y
Tiếp tuyến cần lập :
36( 2) 14
y x
hay
36 58
y x
+) Với
3 3
0 0 0 0 0
'( ) 36 4 2 36 4 2 36 0
y x x x x x
0 0
2 ( 2) 14
x y y
Tiếp tuyến cần lập :
36( 2) 14
y x
hay
36 58
y x
.
Ví dụ 3. Cho hàm số
2
(3 1)
m x m m
y
x m
có đồ thị
( )
m
C
và
m
là tham số .
1. Với
1
m
, viết phương trình tiếp tuyến của
1
( )
C
song song với đường thẳng
4 16
y x
.
2. Tìm
m
để tiếp tuyến của
( )
m
C
tại giao điểm của đồ thị
( )
m
C
với trục hoành song song với đường thẳng
: 1
d y x
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
7
Giải:
1. Với
1
m
ta có
1
4
( ) :
1
x
C y
x
, suy ra
2
4
'
( 1)
y
x
Gọi
0 0 0
( ; )
M x y
là tiếp điểm của tiếp tuyến cần lập. Khi đó tiếp tuyến tại
0 0 0
( ; )
M x y
song song với đường
thẳng
4 16
y x
nên suy ra:
0 0
2
0 0
2
0 0
0
0 0
4
'( ) 4 4 ( 1) 1
2 8
( 1)
x y
y x x
x yx
+) Với
0
(0;0)
M , phương trình tiếp tuyến:
4
y x
(thỏa mãn)
+) Với
0
( 2;8)
M , phương trình tiếp tuyến:
4 16
y x
(loại).
Vậy phương trình tiếp tuyến cần lập là
4
y x
.
2. Ta có:
2
2
4
'
( )
m
y
x m
và
( )
m
C
cắt trục hoành tại điểm
2
;0
3 1
m m
M
m
. Do tiếp tuyến của
( )
m
C
tại
M
song
song với đường thẳng
: 1
d y x
nên:
2
2
3 1
' 1 1
3 1 2
m m m
y
m m
1
m
hoặc
1
5
m
.
+) Với
1 ( 1;0)
m M
, phương trình tiếp tuyến là:
1
y x
(loại).
+) Với
1 3
;0
5 5
m M
, phương trình tiếp tuyến là:
3
5
y x
(thỏa mãn)
Vậy
1
5
m
là giá trị cần tìm.
Nhận xét: Như vậy qua Ví dụ 3 ta nhận thấy, khi gặp dạng câu hỏi viết phương trình tiếp tuyến của đồ thị hàm
số
( )
y f x
song song với đường thẳng
y ax b
, việc sử dụng dữ kiện
0
'( )
f x a
chỉ là điều kiện cần nhưng
chưa đủ . Do đó sau khi giải ra kết quả ta cần có bước kiểm tra lại điều kiện song song.
Ví dụ 4. Cho hàm số
1
x
y
x
có đồ thị
( )
C
và gốc tọa độ
O
.
1. Viết phương trình tiếp tuyến của
( )
C
, biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân
biệt
,
A B
và tam giác
OAB
cân .
2. Tìm tọa độ điểm
M
thuộc (C), biết tiếp tuyến của (C) tại
M
cắt hai trục
Ox
,
Oy
lần lượt tại
,
A B
sao cho
tam giác
OAB
có diện tích bằng
1
8
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
8
Giải: Ta có
2
1
'
( 1)
y
x
1. Gọi
0 0 0
( ; )
M x y
là tiếp điểm của tiếp tuyến cần lập.
Do tam giác
OAB
cân và vuông tại
O
nên
OA OB
, suy ra:
0
'( ) 1
y x
Mà
0 0
2
0
1
'( ) 0, 1
( 1)
y x x
x
0
0
2
0
0
0
1
'( ) 1 1
2
( 1)
x
y x
xx
+) Với
0 0
0 (0) 0
x y y
(loại do
0
(0;0)
M O
)
+) Với
0 0
2 ( 2) 2
x y y
, suy ra phương trình tiếp tuyến:
1.( 2) 2
y x
hay
4
y x
(thỏa mãn).
Vậy tiếp tuyến cần lập là:
4
y x
.
2. Vì
( )
M C
nên ;
1
m
M m
m
. Phương trình tiếp tuyến của
( )
C
tại
M
là:
2
2 2 2
1 1
( )
( 1) 1 ( 1) ( 1)
m m
y x m y x
m m m m
( )
d
Do
d Ox A
tọa độ điểm
A
là nghiệm của hệ:
2
2
2
2 2
1
( ;0)
( 1) ( 1)
0
0
m
y x
x m
A m
m m
y
y
Do
d Oy B
tọa độ
B
là nghiệm của hệ:
2
2
2 2
2
2
2
0
1
0;
( 1) ( 1)
( 1)
0
( 1)
x
m
y x
m
B
m m
m
y
m
x
m
Theo giả thiết:
2
2
2 2
2
2
1 1 1 1
. .
8 4 ( 1) 4 1 2
OAB
m m
S OAOB m
m m
2
2
2 1 0
2 1 0
m m
m m
1
m
hoặc
1
2
m
1
1;
2
M
hoặc
1
; 1
2
M
Vậy có hai điểm
M
thỏa mãn yêu cầu bài toán là
1
1;
2
M
và
1
; 1
2
M
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
9
Ví dụ 5. Cho hàm số
3 2
3 3( 1) 1
y x mx m x
có đồ thị
( )
m
C
và
m
là tham số thực.
1. Tìm
m
biết tiếp tuyến của đồ thị
( )
m
C
tại điểm
K
song song với đường thẳng
3 0
x y
và
K
là điểm
thuộc đồ thị
( )
m
C
có hoành độ bằng
1
.
2. Với
2
m
. Tìm hai điểm phân biệt
,
M N
thuộc đồ thị
2
( )
C
sao cho tiếp tuyến của đồ thị
2
( )
C
tại
M
và
N
song song với nhau và thỏa mãn:
a. Độ dài
2 5
MN , đồng thời
,
M N
có tọa độ nguyên.
b. Đường thẳng
MN
vuông góc với đường thẳng
2015 0
x y
.
Giải:
1. Ta có
2
' 3 6 3( 1)
y x mx m
. Do
( )
m
K C
và có hoành độ bằng
1
, suy ra
( 1; 6 3)
K m
Khi đó tiếp tuyến tại
K
có phương trình:
'( 1)( 1) 6 3 (9 6) 3 3
y y x m y m x m
( )
Do
song song với đường thẳng
3 0
x y
(hay
3
y x
) khi và chỉ khi:
9 6 3
1
3 3 0
3
m
m
m
Vậy giá trị cần tìm là
1
3
m
.
2. Với
2
m
ta có đồ thị
3 2
2
( ): 6 9 1
C y x x x
, suy ra
2
' 3 12 9
y x x
Do
3 2
2
3 2
2
; 6 9 1
( )
( )
; 6 9 1
M a a a a
M C
N C
N b b b b
với
a b
Tiếp tuyến của đồ thị
2
( )
C
tại
M
và
N
song song với nhau nên suy ra:
2 2
'( ) '( ) 3 12 9 3 12 9
y a y b a a b b
( )( 4) 0 4
a b a b a b
(do
0
a b
)
Do đó
4
a b
ta có:
3 3 2 2
6( ) 9( )
N M
y y b a b a b a
2
( ) ( ) 6( ) 9 ( )(1 )
b a a b ab a b b a ab
Suy ra
;( )(1 )
MN b a b a ab
a. Với
2
2 5 20
MN MN
2 2 2
( ) ( ) (1 ) 20
b a b a ab
( kết hợp với
4
a b
)
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
10
2
2 2
( ) 1 1 20 (16 4 ) ( ) 2 2 20
a b ab ab ab ab
3 2
( ) 6( ) 10 3 0
ab ab ab
3
ab
(do ,a b
)
Khi đó ta có hệ:
3 1
4 3
ab a
a b b
hoặc
3
1
a
b
Vậy
(1;5), (3;1)
M N hoặc
(3;1), (1;5)
M N
b. Do
0
b a
nên
;( )(1 )
MN b a b a ab
cùng phương với vecto
(1;1 )
MN
u ab
Đường thẳng
: 2015 0
d x y
có vecto chỉ phương
(1; 1)
d
u
Do đó
0 4
. 0 1 1 0 0
0 4
MN d
a b
MN d u u ab ab
b a
Vậy
(0;1), (4;5)
M N hoặc
(4;5), (0;1)
M N .
Bài toán 1.2
Nội dung bài toán :
Cho hàm số
( )
y f x
có đồ thị là
( )
C
. Viết phương trình tiếp tuyến của đồ thị
( )
C
đi qua điểm
0 0 0
( ; )
M x y
.
Cách giải chung:
+) Đường thẳng
có hệ số góc
k
đi qua
0 0 0
( ; )
M x y
có phương trình :
0 0
( )
y k x x y
+)
là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm :
0 0
( ) ( ) (1)
'( ) (2)
f x k x x y
f x k
+) Thay
(2)
vào
(1)
ta được phương trình :
0 0
( ) '( )( )
f x f x x x y
(*)
Giải phương trình
(*)
ta tìm được
x
, sau đó thay vào (2) suy ra được
k
Khi đó ta viết được phương trình tiếp tuyến cần lập.
Chú ý :
Do các tiếp tuyến của các đồ thị hàm số trong chương trình phổ thông luôn có hệ số góc (trường hợp phương
trình tiếp tuyến không có hệ số góc là
x a
không có ), nên ta được phép gọi luôn phương trình có hệ số góc
k
như cách trình bày trên.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
11
Ví dụ 1. Cho hàm số
4 2
3
y x x
( )
C
. Viết phương trình tiếp tuyến của đồ thị
( )
C
đi qua điểm
(1; 1)
M
.
Giải:
+) Đường thẳng
có hệ số góc
k
đi qua
(1; 1)
M
có phương trình :
( 1) 1
y k x
+)
là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm :
4 2
3
3 ( 1) 1 (1)
4 2 (2)
x x k x
x x k
+) Thay
(2)
vào
(1)
ta được phương trình :
4 2 3
3 (4 2 )( 1) 1
x x x x x
4 3 2 2 2
3 4 2 2 0 ( 1) (3 2 2) 0 1
x x x x x x x x
Thay
1
x
vào
(2)
suy ra
6
k
. Vậy phương trình tiếp tuyến cần lập là
6 7
y x
.
Nhận xét :
Ở Bài toán 1.1 khi viết phương trình tiếp tuyến tại điểm thì điểm đó luôn thuộc đồ thị, trong khi Bài toán 1.2
thì điểm đi qua có thể thuộc hoặc không thuộc đồ thị . Ở ví dụ trên điểm mà tiếp tuyến cần lập đi qua
(1; 1)
M
khá đặc biệt khi
( )
M C
. Do đó trong trường hợp này rất nhiều bạn sẽ đi viết phương trình giống như Bài
toán 1.1 (nghĩa là chuyển về bài toán viết phương trình tiếp tuyến tại điểm
(1; 1)
M
) và cũng cho ra kết quả
tương tự. Song cách làm đó sẽ không được điểm tuyệt đối (nếu bạn không chứng minh thêm tính duy nhất của
tiếp tuyến). Vì vậy việc trình bày theo Bài toán 1.2 là sự lựa chọn hợp lí nhất. Để hiểu rõ hơn chúng ta chuyển
qua Ví dụ 2.
Ví dụ 2 (B – 2008). Cho hàm số
3 2
4 6 1
y x x
(1). Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết
rằng tiếp tuyến đó đi qua điểm
( 1; 9)
M
.
Giải:
+) Đường thẳng
có hệ số góc
k
đi qua
( 1; 9)
M
có phương trình :
( 1) 9
y k x
+)
là tiếp tuyến của đồ thị hàm số (1) khi và chỉ khi hệ sau có nghiệm :
3 2
2
4 6 1 ( 1) 9 (2)
12 12 (3)
x x k x
x x k
+) Thay
(3)
vào
(2)
ta được phương trình :
3 2 2
4 6 1 (12 12 )( 1) 9
x x x x x
3 2 2
1
4 3 6 5 0 ( 1) (4 5) 0
5
4
x
x x x x x
x
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
12
Với
1 24
x k
, phương trình tiếp tuyến là :
24 15
y x
Với
5 15
4 4
x k
, phương trình tiếp tuyến là :
15 21
4 4
y x
Nhận xét :
Trong Ví dụ 2 ta cũng nhận thấy điểm
M
thuộc đồ thị. Song nếu viết phương trình tiếp tuyến theo góc nhìn
của Bài toán 1.1 (viết phương trình tiếp tuyến tại điểm
M
) thì ta chỉ thu được phương trình
24 15
y x
và
thiếu đi một phương trình. Lí do là vì khi sử dụng Bài toán 1.1 thì tiếp tuyến luôn tiếp xúc với đồ thị tại điểm
M
, trong khi ở Bài toán 1.2 nếu
M
thuộc đồ thị thì tiếp tuyến có thể tiếp xúc hoặc không tiếp xúc với đồ thị tại
M
( do tiếp tuyến chỉ cần đi qua điểm
M
). Do đó ta được 2 phương trình tiếp tuyến như trên. Vì vậy khi câu
hỏi trong đề bài là viết phương trình tiếp tuyến đi qua điểm thì ta sẽ giải theo cách giải của Bài toán 1.2.
Ví dụ 3. Cho hàm số
3
3 2
y x x
có đồ thị là
( )
C
. Tìm các điểm
M
trên đường thẳng
4
y
, sao cho từ
M
kẻ được ba tiếp tuyến tới
( )
C
, trong đó có hai tiếp tuyến vuông góc với nhau.
Giải:
Gọi
( ;4)
M m thuộc được thẳng
4
y
Khi đó phương trình tiếp tuyến
( )
d
có hệ số góc
k
đi qua
M
có dạng:
( ) 4
y k x m
( )
d
là tiếp tuyến của
( )
C
khi hệ sau có nghiệm:
3
2
3 2 ( ) 4 (1)
3 3 (2)
x x k x m
x k
Thay (2) vào (1) ta được phương trình:
3 2
3 2 (3 3)( ) 4
x x x x m
3 2 2
2 3 3 2 0 ( 1) 2 (3 2) 3 2 0
x mx m x x m x m
2
1
( ) 2 (3 2) 3 2 0 (3)
x
h x x m x m
Để có ba tiếp tuyến kẻ từ
M
tới
( )
C
thì phương trình
(3)
phải có hai nghiệm phân biệt khác
1
, hay :
(3 2)(3 6) 0
2
; 2; \ 1
( 1) 6 6 0
3
a a
a
f a
 
(*)
Với
4
1
'( 1) 0
y
x
y
, suy ra phương trình tiếp tuyến là
4
y
. Do tiếp tuyến này không vuông góc với bất
kì một tiếp tuyến nào khác. Nên để có hai tiếp tuyến vuông góc với nhau thì phương trình
(3)
phải có hai
nghiệm phân biệt
1 2
,
x x
thỏa mãn:
2 2
1 2 1 2
'( ). '( ) 1 9( 1)( 1) 1 0
y x y x x x
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
13
2 2
1 2 1 2 1 2
9 ( ) ( ) 2 1 1 0
x x x x x x
(2*)
Thay
1 2 1 2
3 2
2
m
x x x x
vào
(2*)
ta có:
28
9(3 2 1) 1 0
27
m m , thỏa mãn điều kiện
(*)
Vậy
28
;4
27
M
là điểm cần tìm.
Ví dụ 4. Cho hàm số
3 2
3 3
y x x
có đồ thị là
( )
C
. Tìm trên đồ thị
( )
C
những điểm mà qua đó kẻ được
đúng một tiếp tuyến tới
( )
C
.
Giải:
Gọi
3 2
( ; 3 3) ( )
M m m m C
Khi đó phương trình tiếp tuyến
( )
d
có hệ số góc
k
đi qua
M
có dạng:
3 2
( ) 3 3
y k x m m m
( )
d
là tiếp tuyến của
( )
C
khi hệ sau có nghiệm:
3 2 3 2
2
3 3 ( ) 3 3 (1)
( ) 3 6 (2)
x x k x m m m
h x x x k
Thay (2) vào (1) ta được phương trình:
3 2 2 3 2
3 3 (3 6 )( ) 3 3
x x x x x m m m
2
( ) (2 3) 0
3
2
x m
x m x m
m
x
Để
( )
d
là tiếp tuyến duy nhất qua
M
của
( )
C
thì xảy ra các khả năng sau:
+) Khả năng 1:
3
1 (1;1)
2
m
m m M
+) Khả năng
2
:
3
( )
2
m
h m h
(*)
và hai tiếp tuyến trùng nhau.
Điều kiện
2
(*) 2 1 0 1 (1;1)
m m m M
Vậy
(1;1)
M là điểm cần tìm.
Ví dụ 5. Cho hàm số
4 2
2 3
y x x
có đồ thị là
( )
C
. Tìm các điểm thuộc trục tung mà từ đó kẻ được một
tiếp tuyến duy nhất đến
( )
C
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
14
Giải:
Gọi (0; )
M m Oy
Khi đó phương trình tiếp tuyến
( )
d
có hệ số góc
k
đi qua
M
có dạng :
y kx m
( )
d
là tiếp tuyến của
( )
C
khi hệ sau có nghiệm:
4 2
3
2 3 (1)
4 4 (2)
x x kx m
x x k
Thay
(2)
vào
(1)
ta được phương trình:
4 2
3 2 3 0
x x m
(3)
Đặt
2
t x
với
0
t
, lúc này
(3)
có dạng :
2
3 2 3 0
t t m
(4)
Nhận thấy với mỗi nghiệm
0
0
t t
của
(4)
cho ta nghiệm
0 0
x x t
. Suy ra
0 0
4( 1).
k t t
.
Do đó
( )
d
là tiếp tuyến duy nhất qua
M
khi
(4)
có duy nhất một nghiệm
0
t
thỏa mãn:
0
4( 1). 4( 1). ( 1). 0
1
t
t t t t t t
t
+) Với
0
t
, thay vào
(4)
ta được
3
m
, khi đó
(4)
có nghiệm
0
t
và
2
3
t
(loại)
+) Với
1
t
, thay vào
(4)
ta được
4
m
, khi đó
(4)
có nghiệm
1
t
và
1
3
t
(thỏa mãn yêu cầu)
Vậy
(0; 4)
M
là điểm cần tìm.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
15
Bài toán 2: Các bài toán liên quan tới cực trị
Bài toán 2.1
Nội dung bài toán :
Viết phương trình đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số
3 2
( , )
y f x m ax bx cx d
.
Cách giải chung:
Bước 1: Tính
2
' 3 2
y ax bx c
;
2
' 0 3 2 0
y ax bx c
(*)
Bước 2: Đồ thị hàm số có 2 điểm cực trị khi phương trình
(*)
có hai nghiệm phân biệt
1 2
,
x x
m D
.
+) Nếu nghiệm
1 2
,
x x
đẹp (
2 2
' 3
b ac u
: có dạng bình phương)
Ta có hai điểm cực trị
1 1 2 2
( ; ), ( ; )
A x y B x y
, suy ra phương trình
AB
.
+) Nếu nghiệm
1 2
,
x x
“không đẹp” , chia
y
cho
'
y
( làm nháp) và viết thành: ( ). '
y u x y px q
Gọi
1 1
2 2
( ; )
( ; )
A x y
B x y
là hai điểm cực trị
1 2
'( ) '( ) 0
y x y x
, khi đó
1 1 1 1 1
2 2 2 2 2
( ). '( )
( ). '( )
y u x y x px q px q
y u x y x px q px q
Suy ra phương trình :
AB y px q
.
Ví dụ 1 (A – 2002). Cho hàm số:
3 2 2 3 2
3 3(1 )
y x mx m x m m
(1) ( với
m
là tham số thực).
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số (1).
Giải: Ta có
2 2
' 3 6 3(1 )
y x mx m
Cách 1:
1
2 2
2
1
' 0 2 1 0
1
x m
y x mx m
x m
. Vì
1 2
x x
nên hàm số đạt cực trị tại
1 2
,
x x
.
Khi đó ta có hai điểm cực trị
1 1 2 2
( ; ), ( ; )
A x y B x y
với
2
2
1
2 2
2
( 1) 3 2
( 1; 3 2)
( 1) 3 2 ( 1; 3 2)
y y m m m
A m m m
y y m m m B m m m
(2;4)
AB
Suy ra phương trình đi qua hai điểm cực trị
,
A B
là:
2
2
1 3 2
2
2 4
x m y m m
y x m m
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
16
Cách 2: Với
2 2
' 0 2 1 0
y x mx m
có
2 2
' ( 1) 1 0
m m
Nên hàm số đạt cực trị tại
1 2
,
x x
. Ta có
1 2
'( ) '( ) 0
y x y x
Mặt khác:
3 2 2 3 2
3 3(1 )
y x mx m x m m
2 2 2
1
3 6 3 3 2
3
x m x mx m x m m
2
1 1
2
2
2 2
2
1
' 2
3
2
y x m m
x m y x m m
y x m m
Vậy phương trình đi qua hai điểm cực trị
1 1 2 2
( ; ), ( ; )
A x y B x y
là:
2
2
y x m m
Ví dụ 2. Cho hàm số
3 2
2 3( 1)
y x m x m
. Tìm
m
để đồ thị hàm số có điểm cực đại, cực tiểu
,
A B
sao
cho ba điểm
, , (3;1)
A B I
thẳng hàng.
Giải: Ta có
2
' 6 6( 1)
y x m x
. Khi đó
1
2
0
' 0 6 ( 1) 0
1
x
y x x m
x m
Hàm số có cực đại, cực tiểu khi và chỉ khi
1 2
0 1 1
x x m m
Cách 1: Ta có
1
3 2 3 2
2
(0)
(0; )
( 1) 3 2 1 ( 1; 3 2 1)
y y m
A m
y y m m m m B m m m m
Suy ra
3 2
(3;1 )
(4 ; 3 2 )
AI m
BI m m m m
. Do
, ,
A B I
thẳng hàng nên
,
AI BI
cùng phương, tương đương:
3 2
4 3 2
3 1
m m m m
m
(do
1
m
)
2
4
2
3
m
m m
2
3 7 4 0 1
m m m
(loại) hoặc
4
3
m
(thỏa mãn).
Cách 2: Ta có
2 2
1 1
6 6( 1) ( 1)
3 6
m
y x x m x m x m
2
1 1
' ( 1)
3 6
m
x y m x m
. Với
2
1 1
1 2
2
2 2
( 1)
'( ) '( ) 0
( 1)
y m x m
y x y x
y m x m
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
17
Khi đó phương trình đi qua hai điểm cực trị
1 1 2 2
( ; ), ( ; )
A x y B x y
là :
2
( 1)
y m x m
Do
, , (3;1)
A B I thẳng hàng nên
2
1 3( 1)
I AB m m
2
3 7 4 0
m m
1
m
(loại) hoặc
4
3
m
(thỏa mãn). Vậy
4
3
m
.
Ví dụ 3 (B – 2013). Cho hàm số
3 2
2 3( 1) 6
y x m x mx
(1). Tìm
m
để đồ thị hàm số (1) có hai điểm cực
trị
A
và
B
sao cho đường thẳng
AB
vuông góc với đường thẳng
2
y x
.
Giải: Ta có
2
' 6 6( 1) 6
y x m x m
;
1
2
2
1
' 0 ( 1) 0
x
y x m x m
x m
Hàm số có hai cực trị khi và chỉ khi
1 2
1
x x m
(*)
Cách 1: Ta có
1
3
3 2 3 2
2
(1) 3 1
(1;3 1)
( 1; ( 1) )
( ) 3 ( ; 3 )
y y m
A m
AB m m
y y m m m B m m m
Do
1
m
nên
AB
cùng phương với vecto
2
(1; ( 1) )
AB
u m
Đường thẳng
: 2 2 0
d y x x y
có vecto chỉ phương
(1;1)
d
u
Khi đó
2
0
. 0 1 ( 1) 0
2
d
m
AB d AB u m
m
(thỏa mãn
(*)
)
Cách 2: Ta có
3 2
2 3( 1) 6
y x m x mx
2 2
(2 1) ( 1) ( 1) ( 1)
x m x m x m m x m m
2
1
(2 1) ' ( 1) ( 1)
6
x m y m x m m
.
Với
2
1 1
1 2
2
2 2
( 1) ( 1)
'( ) '( ) 0
( 1) ( 1)
y m x m m
y x y x
y m x m m
Vậy phương trình đường thẳng đi qua hai điểm cực trị
1 1 2 2
( ; ), ( ; )
A x y B x y
là :
2
( 1) ( 1)
y m x m m
Do
AB
vuông góc với đường thẳng
2
y x
nên:
2
0
( 1) 1
2
m
m
m
(thỏa mãn điều kiện
(*)
)
Vậy giá trị
m
cần tìm là
0
m
hoặc
2
m
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
18
Ví dụ 4. Cho hàm số
3 2
3 2
y x x
có đồ thị là
( )
C
và đường tròn
( )
T
có phương trình:
2 2
( ) ( 1) 5
x m y m
. Tìm
m
để đường thẳng đi qua hai điểm cực trị của
( )
C
tiếp xúc với đường tròn
( )
T
Giải:
Ta có:
2
' 3 6
y x x
;
0 2
' 0 3 ( 2) 0
2 2
x y
y x x
x y
Vậy ta có hai điểm cực trị:
(0;2)
A và
(2; 2)
B
(2; 4) 2(1; 2)
AB
Khi đó phương trình đi qua 2 điểm cực trị là :
2
1 2
x y
hay
2 2 0
x y
( )
Đường tròn
( )
C
có tâm
( ; 1)
I m m
và bán kính
5
R
( )
tiếp xúc với
( )
C
khi và chỉ khi: ( ; )
d I R
2 2
2
2 1 2
5 3 1 5
4
2 1
3
m
m m
m
m
Vậy
2
m
hoặc
4
3
m
là đáp số của bài toán.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
19
Bài toán 2.2
Nội dung bài toán : Tìm
m
để hàm số
( , )
y f x m
có
n
cực trị thỏa mãn điều kiện
(*)
cho trước
Cách giải chung:
Trường hợp 1: Tìm
m
để hàm số bậc ba:
3 2
( , )
y f x m ax bx cx d
có
2
( 2)
n
cực trị thỏa mãn
điều kiện
(*)
cho trước.
Bước 1:
2 2
' 3 2
y ax bx c Ax Bx C
;
2
' 0 0
y Ax Bx C
(1)
Hàm số có 2 cực trị
(1)
có hai nghiệm phân biệt
0
0
A
m D
Bước 2: +) Gọi
1 1
2 2
( ; )
( ; )
M x y
N x y
là hai điểm cực trị với
1 2
1 2
B
x x
A
C
x x
A
(2)
(Nếu cần biểu diễn
1 2
,
y y
theo
m
thì sử dụng Bài toán 2.1 )
+) Cắt nghĩa điều kiện
(*)
(có thể sử dụng
(2)
hoặc kết hợp các kiến thức hình học phẳng…) thiết lập được :
( ) 0
g m
(hoặc ( ( ) 0, ( ) 0...)
m D
g m g m m

Kết luận.
Chú ý: Do số cực trị của hàm bậc ba chỉ có thể là 2 hoặc không có. Do đó nếu đề bài yêu cầu tìm
m
để hàm số
có cực trị, được hiểu là tìm
m
để hàm số có 2 cực trị (một cực đại và một cực tiểu).
Ví dụ 1 (D – 2012). Cho hàm số
3 2 2
2 2
2(3 1)
3 3
y x mx m x
( )
C
, m là tham số thực.
Tìm m để hàm số
( )
C
có hai điểm cực trị
1
x
và
2
x
sao cho
1 2 1 2
2( ) 1
x x x x
.
Giải:
+) Ta có
2 2
' 2 2 2(3 1) 0
y x mx m
;
2 2
' 0 3 1 0
y x mx m
(1)
Hàm số có hai cực trị
1 2
,
x x
(1)
có hai nghiệm phân biệt
1 2
,
x x
2
2 13
' 13 4 0
13
m m hoặc
2 13
13
m
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
20
+) Với
1 2
,
x x
là nghiệm của
(1)
nên
1 2
2
1 2
1 3
x x m
x x m
(2)
. Ta có:
1 2 1 2
2( ) 1
x x x x
(*)
.
Thay
(2)
vào
(*)
ta được:
2
1 3 2 1 (3 2) 0 0
m m m m m
(loại) hoặc
2
3
m
(thỏa mãn).
Vậy
2
3
m
là giá trị cần tìm.
Ví dụ 2 (B – 2012). Cho hàm số
3 2 3
3 3
y x mx m
( )
C
, m là tham số thực. Tìm m để đồ thị hàm số
( )
C
có
hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 48.
Giải: +) Ta có
2
' 3 6
y x mx
;
3
1 1
3
2 2
0 3
' 0 3 ( 2 ) 0
2
x y m
y x x m
x m y m
Đồ thị hàm số
( )
C
có hai điểm cực trị
1 2
0
x x m
+) Ta có hai điểm cực trị:
3
3
3
3
(0;3 )
(2 ; )
( , ) ( , ) 2
OA m
A m Oy
B m m
d B OA d B Oy m
Theo đề ra ta có:
4
1
48 . ( , ). 48 3 48 2
2
OAB
S d B OA OA m m
(thỏa mãn ) . Vậy
2
m
.
Ví dụ 3. Cho hàm số
3 2 2
(2 1) ( 3 2) 4
y x m x m m x
. Xác định m để đồ thị hàm số có các điểm cực
đại và cực tiểu nằm về hai phía của trục tung.
Giải: Ta có
2 2
' 3 2(2 1) ( 3 2)
y x m x m m
Suy ra
2 2
' 0 3 2(2 1) ( 3 2) 0
y x m x m m
(1)
+) Để đồ thị hàm số các các điểm cực đại, cực tiểu thì phương trình
(1)
phải có hai nghiệm phân biệt, khi đó:
2 2
' (2 1) 3( 3 2) 0
m m m
2
13 3 21
13 5 0
2
m m m
hoặc
13 3 21
2
m
(2)
+) Hàm số có hai điểm cực trị
1 1 2 2
( ; ), ( ; )
A x y B x y
với
1 2
,
x x
là nghiệm của
(1)
Khi đó hai điểm
1 1 2 2
( ; ), ( ; )
A x y B x y
nằm về hai phía của trục tung khi và chỉ khi:
2
1 2
0 3 2 0 1 2
x x m m m
, kết hợp với
(2)
ta được đáp số:
1 2
m
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
21
Chú ý: Việc cắt nghĩa điều kiện
(*)
khi hai điểm cực trị
1 1 2 2
( ; ), ( ; )
A x y B x y
:
+) cùng phía với trục tung (trục
Oy
) là:
1 2
0
x x
+) khác phía (nằm về hai phía) với trục tung (trục
Oy
) là:
1 2
0
x x
+) cùng phía với trục hoành (trục
Ox
) là:
1 2
0
y y
+) khác phía (nằm về hai phía) với trục hoành (trục
Ox
) là:
1 2
0
y y
.
Ví dụ 4. Cho hàm số
3 2 2
3 3
y x x m m
với
m
là tham số thực. Chứng minh hàm số luôn có cực đại, cực
tiểu với mọi
m
. Tìm
m
để các điểm cực đại, cực tiểu của đồ thị hàm số cách đều đường thẳng
: 5
y x
.
Giải: +) Có
2
' 3 6
y x x
;
2
2
0 3
' 0 3 ( 2) 0
2 3 4
x y m m
y x x
x y m m
Vậy với m
,
' 0
y
có hai nghiệm phân biệt nên hàm số đã cho luôn có cực đại, cực tiểu với mọi
m
.
+) Ta có
2 2
(0; 3 ), (2; 3 4)
A m m B m m
là hai điểm cực trị
Đường thẳng
: 5
y x
hay
5 0
x y
Theo đề ra ta có:
2 2
3 5 3 3
( , ) ( , )
2 2
m m m m
d A d B
2 2
2
2 2
3 5 3 3 1
3 4 0
4
3 5 3 3
m m m m m
m m
m
m m m m
Vậy
1
m
hoặc
4
m
là các giá trị cần tìm.
Ví dụ 5. Cho hàm số
3 2
3
y x x mx
có đồ thị là
( )
m
C
. Xác định m để
( )
m
C
có các điểm cực đại và cực tiểu
đối xứng nhau qua đường thẳng
2 5 0
x y
.
Giải:
+) Ta có:
2
' 3 6
y x x m
;
2
' 0 3 6 0
y x x m
(1)
Đồ thị
( )
m
C
có các điểm cực đại, cực tiểu khi và chỉ khi phương trình
(1)
có hai nghiệm phân biệt,
hay
' 9 3 0
m
3
m
(2)
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
22
+) Gọi
1 1 2 2
( ; ), ( ; )
A x y B x y
là hai điểm cực trị của
( )
m
C
với:
1 2
'( ) '( ) 0
y x y x
Ta có
2
1 1 2 6
(3 6 )
3 3 3 3
m m
y x x x m x
hay
1 1 2 6
. '
3 3 3 3
m m
y x y x
1 1 1 1 1
2 2 2 2 2
1 1 2 6 2 6
. '( )
3 3 3 3 3 3
1 1 2 6 2 6
. '( )
3 3 3 3 3 3
m m m m
y x y x x x
m m m m
y x y x x x
, suy ra phương trình
2 6
:
3 3
m m
AB y x
Đường thẳng
: 2 5 0
d x y
được viết lại:
1 5
2 2
y x
,
A B
đối xứng với nhau qua
d
thỏa mãn điều kiện cần là:
2 6 1
. 1 0
3 2
m
AB d m
(thỏa mãn
(2)
)
Với
0
m
hàm số có dạng
3 2
3
y x x
có hai điểm cực trị
(0;0), (2; 4)
A B
Khi đó trung điểm
AB
là (1; 2)
I d
(thỏa mãn điều kiện đủ)
Vậy giá trị
0
m
là đáp số của bài toán.
Ví dụ 6. Cho hàm số
3
( 3) 2 3
y m x mx
với
m
là tham số thực. Biện luận theo
m
số cực trị của hàm
số trên.
Giải:
Ta có
2
' 3( 3) 2
y m x m
, khi đó
2
' 0 3( 3) 2 0
y m x m
(*)
*) Với
3
m
phương trình
(*)
có dạng:
6 0
(vô nghiệm), nghĩa là hàm số không có cực trị với
3
m
.
*) Với
3
m
, suy ra :
24 ( 3)
m m
+) Nếu
0 24 ( 3) 0 0 3
m m m
thì phương trình
(*)
vô nghiệm hoặc có nghiệm kép hay
'
y
không đổi dấu. Suy ra hàm số không có cực trị.
+) Nếu
0
0 24 ( 3) 0
3
m
m m
m
Khi đó phương trình
(*)
có hai nghiệm phân biệt, hay hàm số có hai cực trị (một cực đại, một cực tiểu).
Kết luận: Với
0 3
m
: hàm số không có cực trị. Với
0
m
hoặc
3
m
: hàm số có hai cực trị.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
23
Chú ý: Các kiến thức hình học phẳng cơ bản cần nhớ để cắt nghĩa điều kiện
(*)
:
+)
2 2
2 1 2 1
1 1 2 2
1 2 1 2
( ) ( )
( ; ), ( ; )
; : Trung ®iÓm cña
2 2
AB x x y y
A x y B x y
x x y y
I AB
+)
1 1 2 2 3 3
( ; ), ( ; ), ( ; )
A x y B x y C x y
là ba đỉnh của tam giác khi đó
1 2 3 1 2 3
;
3 3
x x x y y y
G
: là trọng tâm của
tam giác
ABC
+)
0 0
( ; )
M x y
và
: 0
ax by c
0 0
2 2
( , )
ax by c
d M
a b
+)
1 1 1
2 2 2
:
:
d y k x m
d y k x m
, khi đó:
1 2 1 2
1 2 1 2 1 2
1
/ / ;
d d k k
d d k k m m
+)
0
1 1
90
. ( , ). . .
2 2
ABC ABC
A
S d A BC BC S AB AC
Trường hợp 2:
Tìm
m
để hàm số trùng phương :
4 2
y ax bx c
có
n
cực trị thỏa mãn điều kiện
(*)
cho trước.
Bước 1:
3
' 4 2
y ax bx
;
2
2
0
' 0 2 (2 ) 0
2 0 (1)
x
y x ax b
ax b
+) Hàm số có
1
cực trị
( 1)
n
(1)
thỏa mãn mãn
0
ab
.
+) Hàm số có
3
cực trị
( 3)
n
(1)
có hai nghiệm phân biệt 0 0
2
b
ab m D
a
.
Bước 2: (dành cho 3 cực trị )
+) Ta có 3 cực trị
1 1
2 2
(0; )
( ; )
( ; )
A c
B x y
C x y
với
1,2
1 1 2 2
2
( ); ( )
b
x
a
y y x y y x
(Tam giác
ABC
luôn cân tại
A
)
+) Cắt nghĩa điều kiện
(*)
, suy ra được phương trình: ( ) 0
m D
g m m

Kết luận.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
24
Ví dụ 1. Cho hàm số
4 2
1 5
2 2
m
y x mx
( )
m
C
, với
m
là tham số thực. Tìm
m
để hàm số
( )
m
C
có cực
tiểu mà không có cực đại.
Giải:
+) Ta có
3 2
' 2( 1) 2 2 ( 1)
y m x mx x m x m
, khi đó
2
0
' 0
( 1) 0 (1)
x
y
m x m
+) Hàm số
( )
m
C
có cực tiểu mà không có cực đại
' 0
y
có một nghiệm khi và chỉ khi phương trình
(1)
thỏa mãn:
( 1).( ) 0 ( 1) 0 1 0
m m m m m
Vậy
1 0
m
là đáp số của bài toán.
Ví dụ 2 (A – A1 – 2012). Cho hàm số
4 2 2
2( 1)
y x m x m
( )
m
C
, với
m
là tham số thực. Tìm
m
để đồ
thị của hàm số
( )
m
C
có ba cực trị tạo thành ba đỉnh của một tam giác vuông.
Giải:
+) Ta có
3 2
' 4 4( 1) 4 ( 1)
y x m x x x m
;
2
0
' 0
1 (1)
x
y
x m
+) Đồ thị hàm số có 3 cực trị khi
(1)
có hai nghiệm phân biệt khác
0
1 0 1
m m
(2)
+) Có 3 điểm cực trị :
2
2
2
(0; )
1; ( 1)
1; 2 1
1; ( 1)
1; 2 1
A m
AB m m
B m m
AC m m
C m m
Theo đề bài tam giác
ABC
vuông, mà tam giác
ABC
luôn cân tại
A
Suy ra
ABC
vuông tại
A
. 0
AB AC
4
( 1) ( 1) 0
m m
3
1
( 1) ( 1) 1 0
0
m
m m
m
Kết hợp với điều kiện
(2)
ta được đáp số
0
m
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
25
Ví dụ 3. Cho hàm số
4 2
2 4
y x mx
( )
m
C
,
m
là tham số thực.
Tìm các giá trị của
m
để tất cả các điểm cực trị của đồ thị
( )
m
C
đều nằm trên các trục tọa độ.
Giải: Ta có
3 2
' 4 4 4 ( )
y x mx x x m
;
2
0
' 0
x
y
x m
+) Với
0
m
thì đồ thị
( )
m
C
có một điểm cực trị (0; 4)
A Oy
+) Với
0
m
thì
0
' 0
x
y
x m
Suy ra
( )
m
C
có 3 điểm cực trị
2 2
(0; 4)
( ; 4) ; ( ; 4)
A Oy
B m m Oy C m m Oy
Để
, ,
A B C
nằm trên các trục tọa độ thì
2
0
2
4 0
m
B Ox
m
C Ox
m
Vậy
0
m
hoặc
2
m
là các giá trị cần tìm.
Ví dụ 4. Cho hàm số
4 2 2
2( 1) 1
y x m m x m
,
m
là tham số thực. Tìm
m
để đồ thị hàm số có
khoảng cách giữa hai điểm cực tiểu ngắn nhất.
Giải:
+) Ta có
3 2 2 2
' 4 4( 1) 4 ( 1)
y x m m x x x m m
, khi đó
2
0
' 0
1
x
y
x m m
+) Vậy với m
, đồ thị hàm số luôn có 3 điểm cực trị .
Mặt khác:
1 0
a
nên ta có hai điểm cực tiểu đối xứng nhau qua trục tung và có hoành độ
lần lượt là:
2 2
1 2
1; 1
x m m x m m
. Khi đó khoảng cách giữa hai điểm cực tiểu là:
2
2
2 1
1 3
2 1 2 3
2 4
d x x m m m
min
3
d khi
1
2
m
Vậy với
1
2
m
khoảng cách giữa hai điểm cực tiểu ngắn nhất.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
26
Ví dụ 5. Cho hàm số
4 2
1
(3 1) 2( 1)
4
y x m x m
( )
m
C
. Tìm
m
để đồ thị
( )
m
C
có ba điểm cực trị tạo
thành một tam giác có trọng tâm trùng với gốc tọa độ.
Giải:
Ta có
3 2
' 2(3 1) 2(3 1)
y x m x x x m
;
2
0
' 0
2(3 1)
x
y
x m
+) Hàm số có 3 cực trị khi và chỉ khi
' 0
y
có 3 nghiệm phân biệt
1
2(3 1) 0
3
m m
(*)
+) Khi đó đồ thị có 3 điểm cực trị:
(0;2 2)
A m
,
2
( 2(3 1); 9 4 1)
B m m m
,
2
( 2(3 1); 9 4 1)
C m m m
Suy ra
2
4
0; 6 2
3
G m m
là trọng tâm của
ABC
Do
2
4 2
6 2 0
3 3
G O m m m
hoặc
1
3
m
. Kết hợp với điều kiện
(*)
ta được
1
3
m
Bài toán 2.3
Nội dung bài toán : Cho hàm số
( , )
y f x m
. Tìm
m
để hàm số đạt cực đại (cực tiểu) tại
0
x x
.
Cách giải chung:
+) Điều kiện cần:
Hàm số đạt cực trị (cực đại hoặc cực tiểu ) tại
0
x x
khi
0 0
'( , ) 0
f x m m m
(ở đây
y
có đạo hàm tại
0
x
)
+) Điều kiện đủ: (kiểm tra giá trị
0
m m
)
Cách 1: Nếu
0 0
''( ; ) 0
f x m
thì hàm số đạt cực đại tại
0
x x
Nếu
0 0
''( ; ) 0
f x m
thì hàm số đạt cực tiểu tại
0
x x
.
Cách 2: Dùng bảng biến thiên để kiểm tra.
Ví dụ 1. Tìm
m
để hàm số
3 2 2
1
( 1) 12
3
y x m x mx
đạt cực đại tại
2
x
.
Giải: Ta có
2 2
' 2( 1) 12
y x m x m
và
2
'' 2 2( 1)
y x m
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
27
+) Điều kiện cần: Hàm số đạt cực đại tại
2
x
, suy ra :
2
1
'( 2) 0 4 12 8 0
2
m
y m m
m
+) Điều kiện đủ: Với
1 '' 2 4 ''( 2) 8 0
m y x y
(thỏa mãn)
Với
2 '' 2 10 ''( 2) 14 0
m y x y
(thỏa mãn)
Vậy với
1
m
hoặc
2
m
hàm số đạt cực đại tại
2
x
.
Nhận xét: +) Với bài toán trên ta có thể chỉ ra luôn
2
''( 2) 2 6 0
y m
, m
.
+) Với hàm số bậc ba. Cụ thể với ví dụ trên, ta có thể trình bày gọn bằng cách giải hệ:
'( 2) 0
''( 2) 0
y
y
Ví dụ 2. Tìm
m
để hàm số
4 2 2
( 1) 1
y mx m x m
có giá trị cực tiểu bằng
1
.
Giải: Ta có
3
' 4 2( 1)
y mx m x
và
2
'' 12 2( 1)
y mx m
Gọi
0
x x
là điểm cực tiểu của hàm số với
CT
1
y
. Khi đó ta có:
Điều kiện cần:
3
0 0 0
4 2 2
0
0 0
'( ) 0 4 2( 1) 0 (1)
( ) 1
( 1) 1 1 (2)
y x mx m x
y x
mx m x m
Từ
0
2
0 0
2
0
0
(1) 2 . 2 ( 1) 0
2 1
x
x mx m
mx m
*) Với
0
0
x
thay vào
(2)
ta được:
2
1 1
m m
Điều kiện đủ: Với
0
0
x x
và
1 '' 4 0
m y
(không thỏa mãn)
Với
0
0
x x
và
1 '' 0
m y
(chưa kết luận được)
Hàm số có dạng
4
y x
có
1 0
a
nên có cực đại là gốc tọa độ.
Vậy
0
0
x
không thỏa mãn.
*) Với
2 2
0 0
1
2 1
2
m
mx m x
m
(do
0
m
) thay vào
(2)
ta được:
3 2
3 2 2 2
0
4 6 1
1 4 2 1 0 ( 1)(4 3 1) 0 1 1
4
m m m
m m m m m m m x
m
Điều kiện đủ: Với
1
m
và
2 2
0
1 '' 8 0
x x y
(thỏa mãn).
Vậy với
1
m
thì hàm số có giá trị cực tiểu bằng
1
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
28
BÀI TOÁN 3: Bài toán giao điểm
Bài toán 3.1
Nội dung bài toán : Tìm
m
để đồ thị hàm số
( )
y g x
cắt đường thẳng
y px q
tại
n
điểm phân biệt thỏa
mãn điều kiện
(*)
(nếu có).
Cách giải chung:
Trường hợp 1:
( )
g x
là hàm bậc ba.
Bước 1: Phương trình hoành độ giao điểm :
3 2
( ) 0
g x px q ax bx cx d
(1)
Bước 2: Nhẩm nghiệm
0
x x
(bằng cách khử
m
) ta đưa
(1)
về dạng tích:
0
2
0 1 1
2
1 1
( )( ) 0
( ) 0 (2)
x x
x x ax b x c
f x ax b x c
Bước 3: ( Xét
a
không chứa tham số
m
- xem thêm Chú ý sau Ví dụ 2)
*) Nếu cắt tại một điểm
( 1)
n
thì
(1)
có một nghiệm
(2)
vô nghiệm hoặc có nghiệm kép
0
x x
1
0
0
0
( ) 0
m D
f x
*) Nếu cắt tại hai điểm phân biệt
( 2)
n
thì
(1)
có hai nghiệm
(2)
có nghiệm kép khác
0
x
hoặc có hai nghiệm phân biệt và có nghiệm
0
x
0
0
( ) 0
f x
hoặc
0
0
( ) 0
f x
2
m D
*) Nếu cắt tại ba điểm phân biệt
( 3)
n
thì
(1)
có ba nghiệm phân biệt
(2)
có hai nghiệm phân biệt khác
0
x
3
0
0
( ) 0
m D
f x
Bước 4 (nếu có
(*)
và xét với
3
n
):
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
29
*) Ta có ba giao điểm:
0 0
1 1
2 2
( ; )
( ; )
( ; )
A x px q
B x px q
C x px q
với
1
1 2
b
x x
a
và
1
1 2
c
x x
a
(3)
*) Cắt nghĩa
(*)
(sử dụng
(3)
hoặc kết hợp kiến thức hình học phẳng) ta được:
( ) 0
h m
(hoặc
3
( ) 0, ( ) 0...)
m D
h m h m m

Kết luận.
Ví dụ 1. Cho hàm số
3 2
3 1
y x x
( )
C
, m là tham số thực. Tìm m để đường thẳng
: (2 1) 4 1
d y m x m
cắt đồ thị hàm số
( )
C
tại hai điểm phân biệ
t.
Giải:
+) Phương trình hoành độ giao điểm của đồ thị
( )
C
và đường thẳng
d
là:
3 2 3 2
3 1 (2 1) 4 1 3 (2 1) 4 2 0
x x m x m x x m x m
(1)
2
2
2
( 2)( 2 1) 0
( ) 2 1 0 (2)
x
x x x m
f x x x m
+)
d
cắt
( )
C
tại hai điểm phân biệt khi và chỉ khi phương trình
(1)
có hai nghiệm phân biệt
(2)
có nghiệm
kép khác
2
hoặc có hai nghiệm phân biệt trong đó có một nghiệm bằng
2
, tương đương với điều kiện:
5 8 0
5
(2) 1 2 0
8
1
5 8 0
2
(2) 1 2 0
m
m
f m
m
m
f m
Vậy
5
8
m
hoặc
1
2
m
thì
d
cắt
( )
C
tại hai điểm phân biệt.
Ví dụ 2. (D – 2013). Cho hàm số
3 2
2 3 ( 1) 1
y x mx m x
( )
C
, m là tham số thực.
Tìm
m
để đường thẳng
1
y x
cắt đồ thị hàm số
( )
C
tại ba điểm phân biệt.
Giải:
+) Phương trình hoành độ giao điểm của
( )
C
và đường thẳng
1
y x
là:
3 2 3 2
2 3 ( 1) 1 1 2 3 0
x mx m x x x mx mx
(1)
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
30
2
2
0
(2 3 ) 0
( ) 2 3 0 (2)
x
x x mx m
f x x mx m
+) Yêu cầu bài toán
(1)
có ba nghiệm phân biệt
(2)
có hai nghiệm phân biệt khác
0
2
0
9 8 0
8
(0) 0
9
m
m m
m
f m
Vậy
0
m
hoặc
8
9
m
là đáp số của bài toán.
Chú ý: Trong cách giải chung
+) Ta đang đề cấp tới trường hợp
a
không chứa tham số
m
(
0
a
). Nếu
a
chứa tham số
m
, ta xét thêm
trường hợp
0
a
.
+) Trong trường hợp không nhẩm được nghiệm (nghiệm “xấu”) ta dùng định lí Viet cho hàm bậc ba hoặc sử
dụng yếu tố cực trị (khả năng này xuất hiện trong đề thi là rất thấp, tác giả không đề cập trong cuốn sách này –
sẽ được nói chi tiết trong cuốn sách “10 vấn đề trọng tâm trong khảo sát hàm số và ứng dụng” của tác giả).
Ví dụ 3. Tìm
m
để đồ thị hàm số
3 2
( 1) 3 (2 10) 12
y m x mx m x
cắt trục hoành tại một điểm duy nhấ
t.
Giải: +) Phương trình hoành độ giao điểm của đồ thị và trục hoành là:
3 2
( 1) 3 (2 10) 12 0
m x mx m x
2
( 2) ( 1) ( 2) 6 0
x m x m x
2
2
( ) ( 1) ( 2) 6 0 (*)
x
f x m x m x
+) Yêu cầu bài toán
(*)
vô nghiệm hoặc có một nghiệm bằng 2. Xét phương trình
(*)
:
Với
1
m
, phương trình
(*)
có dạng:
3 6 0 2
x x
(thỏa mãn)
Với
1
m
, ta có
2
20 28
m m
. Khi đó yêu cầu bài toán tương đương :
2
2
0 20 28 0
10 6 2 10 6 2
0
20 28 0
(2) 0
2 2 0
m m
m
m m
f
m
Vậy
1
m
hoặc
10 6 2 10 6 2
m là đáp số của bài toán.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
31
Ví dụ 4. Cho hàm số
3 2
2 ( 3) 4
y x mx m x
( )
m
C
, điểm
(1;3)
K và đường thẳng
( ): 4
d y x
. Tìm các
giá trị của
m
để
( )
d
cắt
( )
m
C
tại ba điểm phân biệt
(0;4), ,
A B C
sao cho tam giác
KBC
có diện tích bằng
4
.
Giải:
+) Phương trình hoành độ giao điểm của
( )
d
và
( )
m
C
:
3 2
2 ( 3) 4 4
x mx m x x
(1)
2
( 2 2) 0
x x mx m
2
0
( ) 2 2 0 (2)
x
f x x mx m
+)
( )
d
cắt
( )
m
C
tại ba điểm phân biệt
(1)
có ba nghiệm phân biệt
(2)
có hai nghiệm phân biệt khác
0
2
( ; 1) (2; )
' 2 0
2
(0) 2 0
m
m m
m
f m
 
(3)
+) Ta có
1 1
2 2
(0;4)
( ; 4)
( ; 4)
A
B x x
C x x
với
1 2
,
x x
là nghiệm của
(2)
nên
1 2
1 2
2
2
x x m
x x m
(4)
Ta có
2 2
2 1 2 1 2 1
( ) ( ) 2
BC x x x x x x
Phương trình
BC
(hay chính là phương trình
( )
d
) viết lại:
4 0
x y
Suy ra
1 3 4
( , ) 2
2
d K BC
+) Ta có :
2 1
1 1
4 . ( , ). 4 . 2. 2 4
2 2
KBC
S d K BC BC x x
2 2
2 1 1 2 1 2
( ) 16 ( ) 4 16
x x x x x x
(5)
Thay
(4)
vào
(5)
ta được:
2 2
2
4 4( 2) 16 6 0
3
m
m m m m
m
Kết hợp với điều kiện
(3)
ta được đáp số của bài toán là
3
m
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
32
Ví dụ 5. Cho hàm số
3
3 1
y x x
( )
m
C
, đường thẳng
( ): 3
d y mx m
.Tìm m để
( )
d
cắt
( )
m
C
tại ba
điểm phân biệt
( 1;3), ,
M N P
sao cho tiếp tuyến của
( )
m
C
tại
N
và
P
vuông góc với nhau.
Giải:
+) Phương trình hoành độ giao điểm của
( )
d
và
( )
m
C
:
3
3 1 3
x x mx m
3
( 3) 2 0
x m x m
2
( 1)( 2) 0
x x x m
2
1
( ) 2 0 (2)
x
f x x x m
+)
( )
d
cắt
( )
m
C
tại ba điểm phân biệt
(1)
có ba nghiệm phân biệt
(2)
có hai nghiệm phân biệt khác
1
9
4 9 0
4
( 1) 0
0
m
m
f m
m
(3)
+) Ta có
1 1
2 2
( 1;3)
( ; )
( ; )
M
N x y
P x y
với
1 2
,
x x
là nghiệm của
(2)
nên
1 2
1 2
1
2
x x
x x m
(4)
+) Tiếp tuyến của
( )
m
C
tại
N
và
P
vuông góc với nhau khi và chỉ khi:
2 2
1 2 1 2
'( ). '( ) 1 (3 3)(3 3) 1
y x y x x x
2 2 2
1 2 1 2
9 ( ) ( ) 1 1
x x x x
2 2
1 2 1 2 1 2
9 ( ) ( ) 2 1 1
x x x x x x
(5)
Thay
(4)
vào
(5)
ta được:
2
9 ( 2) 1 2( 2) 1 1
m m
2
3 2 2
9 18 1 0
3
m m m
Kết hợp điều kiện
(3)
ta được đáp số bài toán là
3 2 2
3
m
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
33
Trường hợp 2:
( )
g x
là hàm trùng phương và đường thẳng
y q
.
Bước 1: Phương trình hoành độ giao điểm :
4 2
( ) 0
g x q ax bx c
(1)
Bước 2: Đặt
2
t x
, khi đó
(1)
có dạng:
2
( ) 0
f t at bt c
(2)
Bước 3: (Biện luận số giao điểm – giả sử
a
không chứa tham số
( 0)
a
)
+) Nếu không cắt
( 0)
n
(1)
vô nghiệm
1 2
(2) v« nghiÖm
(2) cã nghiÖm 0
t t
0
hoặc
0
0; 0
b c
S P
a a
0
m D
+) Nếu cắt tại một điểm
( 1)
n
(1)
có một nghiệm
(2)
có hai nghiệm
1 2
0
t t
1
0; (0) 0
0
f
m D
b
S
a
+) Nếu cắt tại hai điểm phân biệt
( 2)
n
(1)
có hai nghiệm phân biệt
(2) cã hai nghiÖm tr¸i dÊu
(2) cã nghiÖm kÐp d¬ng
2
0
0
0
2
ac
m D
b
a
+) Nếu cắt tại ba điểm phân biệt
( 3)
n
(1)
có ba nghiệm phân biệt
(2)
có hai nghiệm
2 1
0
t t
3
0; (0) 0
0
f
m D
b
S
a
+) Nếu cắt bốn điểm phân biệt
( 4)
n
(1)
có bốn nghiệm phân biệt
(2)
có hai nghiệm
2 1
0
t t
4
0
0; 0
m D
b c
S P
a a
Bước 4: (Dành cho trường hợp
4
n
)
+) Ta có
1,2 1
3,4 2
x t
x t
với
1 2
b
t t
a
và
1 2
c
t t
a
(3)
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
34
+) Cắt nghĩa
(*)
(sử dụng
(3)
hoặc kết hợp kiến thức hình học phẳng) ta được:
( ) 0
h m
(hoặc
4
( ) 0, ( ) 0...)
m D
h m h m m

Kết luận.
Chú ý: Nếu
a
chứa tham số , ta xét thêm trường hợp
0
a
.
Ví dụ 1. Cho hàm số
4 2 3 2
2
y x mx m m
có đồ thị là
( )
m
C
, m là tham số. Tìm m để đồ thị hàm số
( )
m
C
không có điểm chung với trục hoành.
Giải:
+) Phương trình hoành độ giao điểm của
( )
m
C
và trục hoành là:
4 2 3 2
2 0
x mx m m
(1)
+) Đặt
2
t x
, khi đó
(1)
có dạng:
2 3 2
2 0
t mt m m
(2)
+)
( )
m
C
không có điểm chung với trục hoành khi và chỉ khi phương trình
(1)
vô nghiệm
(2)
vô nghiệm
hoặc có hai nghiệm âm
1 2
( 0)
t t
hay ta có điều kiện:
2 3
2 3
3 2
' 2 0
2
2
' 2 0
2
0
2 0
1
0
m m
m
m
m m
m
m
S m
m
P m m
Vậy đáp số của bài toán là
2
m
.
Ví dụ 2. Cho hàm số
4 2
1
y x mx m
có đồ thị
( )
m
C
, m là tham số thực.
Tìm
m
để
( )
m
C
cắt trục hoành tại bốn điểm phân biệt sao cho độ dài đoạn thẳng
1
AB
. Trong đó
,
A B
là
hai giao điểm có hoành độ dương của
( )
m
C
với trục hoành .
Giải: Phương trình hoành độ giao điểm của đồ thị
( )
m
C
và trục hoành:
4 2
1 0
x mx m
(1)
Đặt
2
t x
,
0
t
; khi đó
(1)
có dạng:
2
1 0
t mt m
1
1
t
t m
(2)
Đồ thị
( )
m
C
cắt trục hoành tại bốn điểm phân biệt, khi phương trình
(1)
có bốn nghiệm phân biệt, tương đương
(2)
có hai nghiệm phân biệt dương
1 1 2
1 0 1
m m
m m
(3)
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
35
Khi đó hai giao điểm có hoành độ dương của đồ thị
( )
m
C
và trục hoành là:
(1;0), ( 1;0)
A B m
.
Khi đó
2
1 1
AB AB
2
( 1 1) 1
m
1 1 1
1 1 1
m
m
1 2
1 0
m
m
5
1
m
m
Kết hợp với điều kiện
(3)
ta được giá trị
m
cần tìm là:
5
m
Ví dụ 3 (D – 2009). Cho hàm số
4 2
(3 2) 3
y x m x m
có đồ thị là
( )
m
C
, m là tham số.
Tìm m để đường thẳng
1
y
cắt đồ thị
( )
m
C
tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2.
Giải:
+) Phương trình hoành độ giao điểm của
( )
m
C
và đường thẳng
1
y
là:
4 2 4 2
(3 2) 3 1 (3 2) 3 1 0
x m x m x m x m
(1)
+) Đặt
2
t x
, khi đó
(1)
có dạng:
2
(3 2) 3 1 0
t m t m
1
3 1
t
t m
(2)
+) Đường thẳng
1
y
cắt đồ thị
( )
m
C
tại bốn điểm phân biệt đều có hoành độ nhỏ hơn 2 , khi và chỉ khi :
(1)
có bốn nghiệm phân biệt nhỏ hơn 2
(2)
có hai nghiệm dương phân biệt nhỏ hơn 4
3 1 1
0
0 1 4
1
1
0 3 1 4
3
m
m
m
m
Nhận xét: Ở ví dụ trên ta đã kết hợp đồng thời Bước 3 và Bước 4.
Ví dụ 4. Cho hàm số
4 2
2( 1) 2 1
y x m x m
( )
m
C
. Tìm m để đồ thị
( )
m
C
cắt trục hoành tại bốn điểm
phân biệt có hoành độ lập thành cấp số cộng.
Giải:
+) Phương trình hoành độ giao điểm của
( )
m
C
và trục hoành là:
4 2
2( 1) 2 1 0
x m x m
(1)
+) Đặt
2
t x
, khi đó
(1)
có dạng:
2
2( 1) 2 1 0
t m t m
(2)
+)
( )
m
C
cắt trục hoành tại bốn điểm phân biệt khi và chỉ khi phương trình
(1)
có bốn nghiệm phân biệt
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
36
(2)
có hai nghiệm dương phân biệt
2
' 0
0
2( 1) 0
1
2 1 0
2
m
m
S m
m
P m
(3)
+) Khi đó
(1)
có nghiệm
1 2 2 1 3 1 4 2
x t x t x t x t
Vì tính đối xứng nên
1 2 3 4
, , ,
x x x x
theo thứ tự là cấp số cộng khi :
2 4 3 1 2 1 2 1 2 1
2 2 3 9
x x x t t t t t t t
Kết hợp với
1 2
2( 1)
t t m
, suy ra:
1
1
5
m
t
và
2
9( 1)
5
m
t
. Khi đó :
1 2
2 1
t t m
1 9( 1)
. 2 1
5 5
m m
m
2
9 32 16 0
m m
4
m
hoặc
4
9
m
(thỏa mãn
(3)
)
Vậy
4
m
hoặc
4
9
m
là giá trị cần tìm.
Trường hợp 3:
( )
g x
là hàm phân thức
ax b
y
cx d
và
2
n
.
Bước 1: Phương trình hoành độ giao điểm của
ax b
y
cx d
và
y px q
:
2
1 1 1
( ) 0 (1)
d
x
ax b
px q
c
cx d
f x a x b x c
Bước 2: Hai đồ thị cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình
(1)
có hai nghiệm phân biệt khác
d
c
hay ta có điều kiện:
1
0; 0
0
a
m D
d
f
c
Bước 3: Ta có hai giao điểm
1 1
2 1
( ; )
( ; )
A x px q
B x px q
với
1
1 2
1
b
x x
a
;
1
1 2
1
c
x x
a
(2)
Cắt nghĩa
(*)
(sử dụng
(2)
hoặc kết hợp kiến thức hình học phẳng) ta được:
( ) 0
h m
(hoặc ( ) 0, ( ) 0...)
m D
h m h m m

Kết luận.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
37
Ví dụ 1. Cho hàm số
2 1
1
x
y
x
( )
C
. Tìm các giá trị m để đường thẳng
1
y mx m
cắt
( )
C
tại hai điểm
phân biệt
A
và
B
sao cho
OAB
là tam giác có trọng tâm thuộc đường thẳng
2 0
x y
(
O
là gốc tọa độ
).
Giải:
Phương trình hoành độ giao điểm của
( )
C
và
1
y mx m
là:
2
1
2 1
1
1
( ) 3 0 (1)
x
x
mx m
x
f x mx x m
Đường thẳng
1
y mx m
cắt
( )
C
tại hai điểm phân biệt
A
và
B
, khi và
chỉ khi phương trình
(1)
có hai nghiệm phân biệt, khác 1
2
0
9 4 0 0
(1) 3 0
m
m m
f
(2)
Hai giao điểm
1 1
( ; 1)
A x mx m
,
2 2
( ; 1)
B x mx m
với
1 2
3
x x
m
Suy ra trọng tâm
G
của tam giác
OAB
được xác định:
1 2
1 2
1
3
( ) 2 2
2 1
3 3
G
G
x x
x
m
m x x m m
y
1 2 1
;
3
m
G
m
Khi đó
OAB
là tam giác, có trọng tâm thuộc đường thẳng
: 2 0
d x y
khi và chỉ khi:
2
0 1
1
1 2 1
2 0
2 5 3 0
3
m
m
O AB
m
G d
m m
m
3
2
m
(thỏa mãn)
Vậy, giá trị cần tìm là:
3
2
m
Ví dụ 2. Cho hàm số
2 2
1
x
y
x
( )
C
. Tìm m để đường thẳng
( ):
d
2
y x m
cắt đồ thị hàm số
( )
C
tại 2
điểm phân biệt
,
A B
sao cho
5
AB .
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
38
Giải:
Phương trình hoành độ giao điểm của
( )
C
và
( )
d
là:
2
1
2 2
2
1
( ) 2 2 0 (1)
x
x
x m
x
f x x mx m
Đường thẳng
( )
d
cắt
( )
C
tại hai điểm phân biệt
A
và
B
, khi và chỉ khi phương trình
(1)
có hai nghiệm phân biệt, khác
1
2
8 16 0
4 4 2
( 1) 6 0
m m
m
f
hoặc
4 4 2
m
(2)
Hai giao điểm
1 1
( ;2 )
A x x m
,
2 2
( ;2 )
B x x m
Với
1 2
,
x x
là nghiệm của
(1)
nên ta có:
1 2
2
m
x x
và
1 2
2
2
m
x x
(3)
Theo đề ra:
2 2 2
2 1 2 1
5 5 ( ) 4( ) 5
AB AB x x x x
2 2
2 1 1 2 1 2
( ) 1 ( ) 4 1
x x x x x x
(*)
Thay
(3)
vào
(*)
ta được:
2
2
10
2( 2) 1 8 20 0
2
4
m
m
m m m
m
(thỏa mãn điều kiện
(2)
)
Vậy
10
m
hoặc
2
m
.
Ví dụ 3. Cho hàm số
2 3
1
mx
y
x
( )
m
C
,
m
là tham số thực.
Tìm m để đường thẳng
2 3
y x
cắt đồ thị hàm số
( )
m
C
tại hai điểm phân biệt
A
và
B
sao cho đườ
ng
thẳng trung trực của đoạn thẳng
AB
đi qua giao điểm hai đường tiệm cận của đồ thị hàm số
( )
m
C
.
Giải:
Phương trình hoành độ giao điểm của
( )
m
C
và đường thẳng
2 3
y x
là:
2
1
1
2 3
0
2 3
1
2 (2 1) 0
2 1
2
x
x
mx
x
x
x
x m x
m
x
(1)
Đường thẳng
2 3
y x
cắt đồ thị
( )
m
C
tại hai điểm phân biệt
A
và
B
, khi và chỉ khi
(1)
có hai nghiệm phân
biệt, khác
1
2 1 1
0
2 2
2 1 3
1
2 2
m
m
m
m
(2)
, khi đó
2 1
(0; 3), ;2 2
2
m
A B m
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
39
Tiệm cận tiệm cận đứng
1
x
; Tiệm cận ngang
2
y m
nên giao điểm hai tiệm cận là
( 1;2 )
I m
Cách 1:
I
thuộc đường trung trực của
AB
khi và chỉ khi :
2 2
IA IB IA IB
2
2 2
2 3
1 (2 3) 4 (2 3) 4
2
m
m m
2 3 2
2 3 2
m
m
1
2
m
hoặc
5
2
m
Kết hợp với với điều kiện
(2)
ta được
5
2
m
là giá trị cần tìm.
Cách 2: Gọi
M
là trung điểm của
AB
khi đó
2 1 2 5
;
4 2
m m
M
Đường thẳng trung trực
d
của
AB
đi qua
M
có véctơ pháp tuyến
(1;2)
d AB
n u
nên có phương trình:
2 1 2 5
2 0 4 8 10 19 0
4 2
m m
x y x y m
Có
5
4 8.2 10 19 0
2
I d m m m
, thỏa mãn điều kiện
(2)
)
Vậy
5
2
m
là giá trị cần tìm.
Ví dụ 4 (B – 2010). Cho hàm số
2 1
1
x
y
x
( )
C
. Tìm m để đường thẳng
2
y x m
cắt đồ thị hàm số
( )
C
tại hai điểm phân biệt
,
A B
sao cho tam giác
OAB
có diện tích bằng
3
.
Giải:
+) Phương trình hoành độ giao điểm:
2
1
2 1
2
1
( ) 2 ( 4) 1 0 (1)
x
x
x m
x
f x x m x m
+) Đường thẳng
2
y x m
cắt đồ thị
( )
C
tại hai điểm phân biệt, khi và chỉ khi:
2
8 0
( 1) 1 0
m
m
f
+) Ta có hai giao điểm
1 1 2 2
( ; 2 ), ( ; 2 )
A x x m B x x m
với
1 2
,
x x
là nghiệm của
(1)
nên ta có:
1 2
4
2
m
x x
và
1 2
1
2
m
x x
(2)
+) Đường thẳng
AB
viết lại thành:
2 0
x y m
( , )
5
m
d O AB
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
40
Với
(2)
ta có:
2
2 2 2
2 1 2 1 1 2 1 2
5( 8)
( ) 4( ) 5 ( ) 4
2
m
AB x x x x x x x x
Khi đó:
2
8
1
( , ).
2 4
OAB
m m
S d O AB AB
, suy ra:
2
4 2 2 2
8
3 8 48 0 ( 4)( 12) 0 2
4
m m
m m m m m
Vậy
2
m
.
Ví dụ 5 (A – 2011). Cho hàm số
1
2 1
x
y
x
( )
C
. Chứng minh rằng với mọi
m
đường thẳng
y x m
luôn
cắt đồ thị hàm số
( )
C
tại hai điểm phân biệt
A
và
B
. Gọi
1 2
,
k k
lần lượt là hệ số góc của các tiếp tuyến với
( )
C
tại
A
và
B
. Tìm
m
để tổng
1 2
k k
đạt giá trị lớn nhất.
Giải:
+) Phương trình hoành độ giao điểm:
2
1
1
2
2 1
( ) 2 2 ( 1) 0 (1)
x
x
x m
x
f x x mx m
+) Xét hệ:
2 2
2 2 ( 1) 1 0
1 1
0
2 2
m m m
f
, đúng với m
Suy ra
(1)
luôn có hai nghiệm phân biệt khác
1
2
hay với mọi
m
đường thẳng
y x m
luôn cắt đồ thị hàm số
( )
C
tại hai điểm phân biệt (đpcm).
+) Gọi
1 2
,
x x
lần lượt là hoành độ của hai giao điểm
,
A B
với
1 2
,
x x
là nghiệm của
(1)
thỏa mãn:
1 2
x x m
và
1 2
1
2
m
x x
Khi đó ta có:
1 2 1 1
'( ) '( )
k k y x y x
2 2
1 2
2
2 2
1 2
1 2
(2 1) (2 1)
1 1
(2 1) (2 1)
(2 1)(2 1)
x x
x x
x x
2
1 2 1 2 1 2
2
1 2 1 2
4( ) 8 4( ) 2
4 2( ) 1
x x x x x x
x x x x
2 2
4 8 6 4( 1) 2 2
m m m
Suy ra
1 2
k k
lớn nhất bằng
2
khi
1
m
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
41
Bài toán 3.2
Nội dung bài toán : Cho hàm số
( )
y f x
( )
C
.
1. Khảo sát và vẽ đồ thị
( )
C
của hàm số trên.
2. Biện luận theo
m
số nghiệm thực của phương trình:
( , ) 0
g x m
(*)
Cách giải chung:
1. Ta vẽ được đồ thị
( )
C
(xem lại phần khảo sát hàm số).
2. Ta thực hiện theo các bước sau:
+) Chuyển
(*)
về dạng :
( ) ( )
f x h m
(2*)
+) Khi đó số nghiệm của
(2*)
chính là số giao điểm của đồ thị hàm số
( )
C
với đường thẳng
( )
y h m
.
+) Trên cùng hệ trục tọa độ đã vẽ đồ thị
( )
C
(vẽ được ở câu 1), ta vẽ thêm đường thẳng
( )
y h m
có phương
vuông góc với trục
Oy
(song song hoặc trùng với
Ox
).
+) Từ số giao điểm chung của hai đồ thị, ta suy ra số nghiệm của
(*)
và đưa ra kết luận.
Ví dụ 1. Cho hàm số
4 2
4 1
y x x
( )
C
.
1. Khảo sát và vẽ đồ thị
( )
C
của hàm số trên.
2. Biện luận theo
m
số nghiệm thực của phương trình:
4 2
1
0
4
x x m
.
Giải:
1. Bạn đọc tự làm và ta được đồ thị
( )
C
như sau:
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
42
2. Ta có phương trình:
4 2 4 2
1
0 4 1 4 1
4
x x m x x m
(1)
Số nghiệm của phương trình
(1)
chính là số giao
điểm của đồ thị
( )
C
và đường thẳng
4 1
y m
(có phương vuông góc với
Oy
)
Do đó dựa vào đồ thị ta có:
+) Nếu
4 1 3 1
m m
thì phương trình vô nghiệm.
+) Nếu
4 1 3 1
m m
thì phương trình có 2 nghiệm phân biệt.
+) Nếu
3 4 1 1 1 0
m m
thì phương trình có 4 nghiệm phân biệt.
+)
4 1 1 0
m m
thì phương trình có 3 nghiệm phân biệt.
+)
4 1 1 0
m m
thì phương trình có 2 nghiệm phân biệt.
Vậy, ta có
1
m
: Phương trình vô nghiệm;
1
0
m
m
: Phương trình có 2 nghiệm phân biệt.
0
m
: Phương trình có 3 nghiệm phân biệt;
1 0
m
: Phương trình có 4 nghiệm phân biệt.
Nhận xét: Ngoài cách giải trên ta có thể giải theo Bài toán 3.1 ở Trường hợp 2.
Ví dụ 2 (A – 2002). Cho hàm số
3 2
3
y x x
( )
C
.
1. Khảo sát và vẽ đồ thị
( )
C
của hàm số trên.
2. Tìm
m
để phương trình:
3 2 3 2
3 3 0
x x m m
có 3 nghiệm phân biệt.
Giải: 1. Bạn đọc tự khảo sát và vẽ được đồ thị như sau:
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
43
2. Xét phương trình
3 2 3 2
3 3 0
x x m m
(1)
Cách 1: Ta có
3 2 3 2
(1) 3 3
x x m m
(2)
Số nghiệm của
(2)
chính là số giao điểm của đồ thị
( )
C
và đường thẳng
3 2
3
y m m
(có phương vuông góc với trục
Oy
)
Nên dựa vào đồ thị ta thấy phương trình
(1)
có 3 nghiệm khi và chỉ khi:
3 2
0 3 4
m m
(*)
Cách 1.1: Xét hàm
3 2
( ) 3
f m m m
có đồ thị giống
( )
C
(biến là
m
)
Do đó dựa vào đồ thị ta có :
1 3
(*) ( ) (0;4)
0; 2
m
f m
m m
Cách 1.2: Ta có
3 2 2
3 2 2
3 0 ( 3) 0
(*)
3 4 0 ( 1)( 2) 0
m m m m
m m m m
0 3 1 3
2 1 0; 2
m m
m m m
Cách 2: Ta có :
2 2
(1) ( ) ( 3) 3 0
x m x m x m m
2 2
( ) ( 3) 3 0 (2)
x m
f x x m x m m
(1)
có 3 nghiệm phân biệt khi và chỉ khi
(2)
có hai nghiệm phân biệt khác
m
2
2
3 3 9 0 1 3
0; 2
( ) 3 6 0
m m m
m m
f m m m
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
44
Bài toán 3.3
Nội dung bài toán : Dựa vào đồ thị hàm số
( )
y f x
( )
C
hãy suy ra đồ thị hàm số chứa trị tuyệt đối.
Cách giải chung:
Trường hợp 1: Dựa vào đồ thị hàm số
( )
y f x
( )
C
, hãy suy ra đồ thị hàm số
1
( ) ( )
y f x C
Cách vẽ:
1
( ) ( ) 0 (1)
( ): ( )
( ) ( ) 0 (2)
f x khi f x
C y f x
f x khi f x
. Do đó đồ thị
1
( )
C
gồm hai phần:
+) Phần
(1)
: là phần không nằm phía dưới trục hoành của đồ thị
( )
C
.
+) Phần
(2)
: là phần đối xứng của phần dưới trục hoành của
( )
C
qua trục
Ox
.
Trường hợp 2: Dựa vào đồ thị hàm số
( )
y f x
( )
C
, hãy suy ra đồ thị hàm số
2
( ) ( )
y f x C
Nhận xét :
2
( ): ( )
C y f x
là hàm số chẵn nên
2
( )
C
nhận
Oy
làm trục đối xứng.
Cách vẽ:
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
45
2
( ): ( )
C y f x
=
( ) 0 (1)
( ) 0 (2)
f x khi x
f x khi x
. Do đó đồ thị
2
( )
C
gồm hai phần
+) Phần
(1)
: Phần đồ thị
( )
C
nằm bên phải trục
Oy
.
+) Phần
(2)
: Phần đồ thị lấy đối xứng qua Oy của phần
(1)
.
Nhận xét: Ngoài 2 trường hợp trên chúng ta có thể gặp các dạng:
*) Dựa vào đồ thị hàm số
( ) ( ). ( )
y f x u x v x
( )
C
, suy ra đồ thị hàm số
3
( ) . ( ) ( )
y u x v x C
*) Dựa vào đồ thị hàm số
( ): ( )
C y f x
suy ra đồ thị các hàm số sau:
+)
4
( ): ( )
C y f x
(Trường hợp 4)
+)
5
( ) : ( )
C y f x
(Dựa vào Trường hợp 2 sau đó đến Trường hợp 1)
+)
6
( ) : ( )
C y f x
( Dựa vào Trường hợp 2 sau đó đến Trường hợp 4)
+)
7
( ) : ( )
C y f x
( Dựa vào TH2 sau đó đến TH1 và cuối cùng là TH4)”.
Song vì xác suất xuất hiện các dạng toán này trong đề thi là rất thấp, nên tác giả không đề cập trong
cuốn sách này.
Ví dụ 1. Cho hàm số
4 2
1 1
2
4 2
y x x
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Tìm m để phương trình
4 2
4 2
2 8
1
2 9
x x
m m
có đúng 5 nghiệm thực phân biệt.
Giải:
1. Bạn đọc tự làm câu này, ta được đồ thị của hàm số
4 2
1 1
2
4 2
y x x
:
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
46
2. Ta có:
4 2
4 2 4 2
4 2
2 8
1 2 8 2 9
2 9
x x
x x m m
m m
4 2
4 2
1 1 2 9
2
4 2 4
m m
x x
(*)
Ta có:
4 2
1 1
2
4 2
y x x
=
4 2
4 2
1 1
2 ( ) ( ) 0
4 2
1 1
2 ( ) ( ) 0
4 2
x x f x khi f x
x x f x khi f x
Do đó đồ thị hàm số sẽ được vẽ như sau:
Số nghiệm của
(*)
chính là số giao điểm của đồ thị hàm số
4 2
1 1
2
4 2
y x x
và
4 2
2 9
4
m m
y
có phương vuông góc với trục
Oy
. Nên để phương trình có đúng 5 nghiệm thực thì:
4 2
2 9
2
4
m m
(2*)
(2*)
4 2 2 2 2
2 1 0 ( 1) 0 1 1
m m m m m
. Vậy
1
m
là giá trị cần tìm.
Ví dụ 2 (B – 2009). Cho hàm số
4 2
2 4
y x x
( )
C
1. Khảo sát và vẽ đồ thị
( )
C
của hàm số trên.
2. Với giá trị nào của m, phương trình
2 2
2
x x m
có đúng 6 nghiệm thực phân biệt .
Giải: 1. Bạn đọc tự làm câu này, ta được đồ thị của hàm số
4 2
2 4
y x x
:
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
47
2. Ta có
2 2 4 2
2 2 4 2
x x m x x m
. Phương trình có đúng 6 nghiệm thực phân biệt khi và chỉ khi đường
thẳng
2
y m
(có phương vuông góc với trục
Oy
) cắt đồ thị hàm số
4 2
2 4
y x x
tại 6 điểm phân biệt.
Biến đổi
4 2
4 2
4 2
2 4 ( ) ( ) 0
2 4
2 4 ( ) ( ) 0
x x f x khi f x
y x x
x x f x khi f x
Do đó ta có đồ thị hàm hàm số
4 2
2 4
y x x
và đường thẳng
2
y m
:
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi và chỉ khi:
0 2 2 0 1
m m
.
Vậy giá trị
m
cần tìm là
0 1
m
.
Ví dụ 3 (A – 2006). Cho hàm số
3 2
2 9 12 4
y x x x
( )
C
.
1. Khảo sát và vẽ đồ thị
( )
C
của hàm số trên.
2. Tìm m để phương trình sau có 6 nghiệm phân biệt :
3
2
2 9 12
x x x m
.
Giải: 1. Bạn đọc tự làm câu này, ta được đồ thị của hàm số
3 2
2 9 12 4
y x x x
:
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
48
2. Ta có
3 3
2 2
2 9 12 2 9 12 4 4
x x x m x x x m
Phương trình có đúng 6 nghiệm thực phân biệt khi và chỉ khi đường thẳng
4
y m
(có phương vuông góc với
trục
Oy
) cắt đồ thị hàm số
3
2
2 9 12 4
y x x x
tại 6 điểm phân biệt.
Hàm số
3
2
2 9 12 4
y x x x
là hàm chẵn , nên đồ thị nhận
Oy
là trục đối xứng. Do đó từ đồ thị hàm số
( )
C
vẽ ở cầu 1, ta suy ra đồ thị hàm số :
3
2
2 9 12 4
y x x x
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi và chỉ khi:
0 4 1 4 5
m m
.
Vậy giá trị
m
cần tìm là
4 5
m
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
49
BÀI TOÁN 4: Bài toán tìm điểm thuộc đồ thị
Nội dung bài toán : Tìm điểm
M
thuộc đồ thị
( )
y f x
thỏa mãn điều kiện
(*)
cho trước.
Cách giải chung:
Bước 1: Do
M
thuộc đồ thị
( )
y f x
nên gọi
( ; ( ))
M m f m
.
Bước 2: Cắt nghĩa điều kiện
(*)
để thiết lập phương trình : ( ) 0g m m
tọa độ điểm
M
.
Ví dụ 1(A, A1 – 2014). Cho hàm số
2
1
x
y
x
( )
C
. Tìm tọa độ điểm
M
thuộc đồ thị
( )
C
sao cho khoảng
cách từ
M
đến đường thẳng
y x
bằng
2
.
Giải:
+) Do
( )
M C
nên gọi
2
;
1
m
M m
m
với
1
m
+) Đường thẳng
y x
được viết lại thành :
0
x y
( )
Khi đó
2
2
1
( , ) 2 2 2 2 1
2
m
m
m
d M m m
2
2
2 4 0 0 (0; 2)
2 ( 2;0)
2 0
m m m M
m M
m m
Vậy
(0; 2)
M
hoặc
( 2;0)
M
.
Ví dụ 2. Tìm trên đồ thị
2
( ):
3
x
C y
x
những điểm
M
sao cho khoảng cách từ
M
đến tiệm cận đứng bằng
1
5
khoảng cách từ
M
đến tiệm cận ngang.
Giải: +) Do
( )
M C
2
;
3
m
M m
m
với
3
m
.
Tiệm cận đứng có phương trình:
3
x
hay
3 0
x
1
( )
Tiệm cận ngang có phương trình:
1
y
hay
1 0
y
2
( )
+)
1 2
1 1 2
( , ) ( , ) 3 . 1
5 5 3
m
d M d M m
m
2
4 (4;6)
( 3) 1
2 (2; 4)
m M
m
m M
Vậy
(4;6)
M hoặc
(2; 4)
M
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
50
Ví dụ 3. Cho hàm số
2 1
1
x
y
x
có đồ thị
( )
C
. Tìm tọa độ hai điểm
,
A B
trên đồ thị
( )
C
sao cho tiếp tuyến
của đồ thị
( )
C
tại
A
và
B
song song với nhau và
8
AB .
Giải: Do
( ), ( )
A C B C
nên gọi
2 1
;
1
a
A a
a
và
2 1
;
1
b
B b
b
với
1; 1
a b
a b
.
Tiếp tuyến của đồ thị
( )
C
tại
A
và
B
song song nên suy ra:
2 2
1 1
'( ) '( )
( 1) ( 1)
y a y b
a b
(với
2
1
'
( 1)
y
x
)
2 2
( 1) ( 1)
a b a b
(loại) hoặc 2
b a
(1)
.
Mặt khác:
2
2 2
2 1 2 1
8 8 ( ) 8
1 1
a b
AB AB a b
a b
(2)
Thay
(2)
vào
(1)
ta được:
2 2
2
2 0
4
4( 1) 8 ( 1) 1
0 2
( 1)
a b
a a
a b
a
+) Với
2, 0 (2;3), (0;1)
a b A B
(thử lại thỏa mãn điều kiện song song).
+) Với
0, 2 (0;1), (2;3)
a b A B
(thử lại thỏa mãn điều kiện song song).
Vậy
(2;3), (0;1)
A B hoặc
(0;1), (2;3)
A B .
Ví dụ 4. (HSG – Hà Nội – 2013). Cho hàm số
3
3 4
y x x
có đồ thị
( )
C
. Tìm các điểm
,
M N
cùng
nằm trên
( )
C
sao cho điểm
1
;2
2
I
là trung điểm của đoạn thẳng
MN
.
Giải: Do
3
( ) ( ; 3 4)
M C M m m m
Ta có
I
là trung điểm của
MN
nên:
3
3 3
2 1
( 1 ; 3 )
2 4 ( 3 4) 3
N I M
N I M
x x x m
N m m m
y y y m m m m
Mặt khác :
3 3
( ) 3 ( 1 ) 3( 1 ) 4
N C m m m m
2
1 (1;2), ( 2;2)
2 0
2 ( 2;2), (1;2)
m M N
m m
m M N
Vậy
(1;2)
M
và
( 2;2)
N
hoặc
( 2;2)
M
và
(1;2)
N
.
Chú ý: Ngoài cách phát biểu trên, bài toán có thể hỏi theo cách diễn đạt sau:
“Tìm trên
( )
C
hai điểm
,
M N
đối xứng với nhau qua điểm
1
;2
2
I
”.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
51
Ví dụ 5. Cho hàm số
2 1
1
x
y
x
có đồ thị
( )
C
. Tìm các điểm
M
thuộc đồ thị
( )
C
sao cho khoảng cách từ
giao điểm
I
của hai đường tiệm cận của
( )
C
tới tiếp tuyến của
( )
C
tại
M
là lớn nhất.
Giải:
+) Tiệm cận đứng, ngang lần lượt của
( )
C
là
1
x
và
2 ( 1;2)
y I
+) Do
( )
M C
2 1
;
1
m
M m
m
với
1
m
. Khi đó phương trình tiếp tuyến của
( )
C
tại
M
là:
2 2
2
3 2 1
.( ) 3 ( 1) 2 2 1 0
( 1) 1
m
y x m x m y m m
m m
( )
+) Ta có:
2 2
4
3 2( 1) 2 2 1
( , )
9 ( 1)
m m m
d I
m
4
6 1
9 ( 1)
m
m
2
2
2
2
6 6
6
9
9
( 1)
2. .( 1)
( 1)
( 1)
m
m
m
m
max
( , ) 6
d M khi
2 2
2
1 3
9
( 1) ( 1) 3
( 1)
1 3
m
m m
m
m
Vậy
1 3;2 3
M
hoặc
1 3;2 3
M
thỏa mãn bài toán.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
52
BÀI TOÁN 5: Tính đơn điệu của hàm số
Bài toán 5.1
Nội dung bài toán : Tìm
m
để hàm số
( , )
y f x m
đồng biến (hoặc nghịch biến) trên
.
Cách giải chung:
Yêu cầu của bài toán
'( , ) 0
f x m
(hoặc
'( , ) 0
f x m
)
(*)
đúng x
. Khi đó có 2 cách giải quyết:
Cách 1: Nếu
2
'( , )
f x m ax bx c
thì
(*)
0
0
a
( hoặc
0
0
a
)
và xét thêm điều kiện
0
a
nếu
a
chứa
m
.
Cách 2: Nếu
(*)
( ) ( )
h m g x
(hoặc
( ) ( )
h m g x
) thì bài toán tương đương:
( ) ( )
x
h m max g x
( hoặc
( ) ( )
x
h m min g x
)
Ví dụ. Cho hàm số
3 2
1
( 1) ( 3) ( 5) 1
3
y m x m x m x
. Tìm
m
để hàm số đồng biến trên tập xác định.
Giải:
Tập xác định:
D
Yêu cầu của bài toán tương đương với:
2
' ( 1) 2( 3) 5 0
y m x m x m
với x
(*)
Cách 1:
+) Với
1
m
:
(*) 8 4 0
x
với x
(vô lí).
+) Với
1
m
:
1
1 0
1
(*)
1
' 12 4 0
3
3
m
a m
m
m
m
Cách 2: Ta có
2 2
(*) ( 1) 6 5
m x x x
với x
.
+) Với
1
x
ta được:
0 12
với x
(luôn đúng)
+) Với
1
x
thì
2
2
6 5
(*) ( )
( 1)
x x
m g x
x
với
1
x
( ;1) (1; )
max ( )
x
m g x
 
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
53
Xét
2
2
6 5
( )
( 1)
x x
g x
x
với
1
x
3
8( 2)
'( )
( 1)
x
g x
x
;
'( ) 0 2
g x x
lim ( ) 1
x
g x
và
1
lim ( )
x
g x
. Do đó ta có bảng biến thiên sau:
Khi đó ta có
( ;1) (1; )
1
max ( )
3
x
g x

1
3
m
Vậy
1
3
m
là giá trị cần tìm.
Nhận xét:
Ở ví dụ trên, cách giải 1 cho ta lời giải ngắn gọn song có một hạn chế nó chỉ sử dụng với dạng tam thức bậc
hai. Còn ở cách giải 2 tuy khá dài (cụ thể trong bài toán này) nhưng nó có thể giải quyết được cả dạng
'( , )
f x m
không phải là tam thức bậc 2, nhưng sẽ gặp “khó khăn” nếu tham số
m
không phải là bậc nhất. Như
vậy mỗi cách có những ưu và nhược điểm khác nhau. Tùy vào số liệu cụ thể của từng bài toán giúp ta chọn ra
cách giải tối ưu nhất.
Bài toán 5.2
Nội dung bài toán : Tìm
m
để hàm số
( , )
y f x m
đồng biến (hoặc nghịch biến) trên
( ; )
a b
( với
a
có thể

và
b
có thể
).
Cách giải chung:
Yêu cầu của bài toán
'( , ) 0
f x m
(hoặc
'( , ) 0
f x m
)
(*)
đúng
( ; )
x a b
. Ta có 2 cách giải quyết:
Cách 1: Nếu
(*)
( ) ( )
h m g x
(hoặc
( ) ( )
h m g x
) thì bài toán tương đương:
( ; )
( ) ( )
x a b
h m max g x
( hoặc
( ; )
( ) ( )
x a b
h m min g x
)
Cách 2: Nếu
2
'( , )
f x m ax bx c
thì ta sử dụng định lý thuận và đảo về dấu tam thức bậc 2
(xem thêm phần Chú ý).
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
54
Chú ý:
*) Vì trong chương trình chính khóa đang học, định lý đảo về dấu tam thức bậc
2
đã bị lược bỏ. Vì vậy ta hạn
chế sử dụng Cách 2 . Nếu muốn sử dụng chúng ta sẽ phải “lách” bằng cách chuyển về so sánh với số
0
hoặc
sử dụng công thức nghiệm trực tiếp (sẽ thấy rõ hơn qua các ví dụ minh họa ).
*) Với trường hợp hàm số dưới dạng phân thức
( )
( )
u x
y
v x
thì hàm số đồng biến (hay nghịch biến) trên
( ; )
a b
2
'( ). ( ) '( ). ( )
' 0
( )
u x v x v x u x
y
v x
( 0)
với
( ; )
x a b
( ) '( ). ( ) '( ). ( ) 0( 0) , ( ; )
( ) 0
h x u x v x v x u x x a b
v x
*) Nếu biểu thức định dấu của
'
y
không chứa x thì trong điều kiện
(*)
không có dấu
" "
.
*) Ưu và nhược điểm của Cách 1 và Cách 2:
+) Cách 1: Với
( , )
f x m
có dạng bất kì nhưng chỉ giải quyết “tốt” nếu m là bậc nhất.
+) Cách 2: Với m có bậc bất kì nhưng
( , )
f x m
phải là đa thức bậc 2 và giải quyết
“nhẹ nhàng” khi
(*)
đúng với
x R
.
+) Cách 1 thường sử dụng trong các bài toán phức tạp mà khó giải quyết với Cách 2
Ví dụ 1 (A,A1 – 2013). Cho hàm số
3 2
3 3 1
y x x mx
(1), với
m
là tham số thực.
Tìm
m
để hàm số (1) nghịch biến trên khoảng
(0; )

.
Giải: Yêu cầu của bài toán
2
' 3 6 3 0
y x x m
với
(0; )
x

2
( ) 2 0
f x x x m
với
(0; )
x

(*)
Cách 1:
(*)
2
2 ( )
m x x g x
với
(0; )
x

(0; )
( )
x
m min g x

Ta có
'( ) 2 2
g x x
;
( ) 0 1
g x x
. Ta có bảng biến thiên:
Khi đó
(0; )
( ) 1
x
m min g x

. Vậy
1
m
là đáp số của bài toán.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
55
Cách 2:
Đồ thị hàm số
2
( ) 2
f x x x m
là một parabol có
1 0
a
nên có bề lõm quay lên trên.
Vì vậy
(*)
xảy ra khi và chỉ khi :
Trường hợp 1:
( )
f x
nằm phía trên hoặc tiếp xúc với trục
Ox
(
( ) 0
f x
với x
)
Khi đó phương trình
( ) 0
f x
thỏa mãn:
1 0 1
m m
Trường hợp 1 Trường hợp 2
Trường hợp 2:
( )
f x
cắt trục
Ox
tại các điểm có hoành độ
1 2
,
x x
sao cho:
1 2
0
x x
( với
(0; )
x

thì
( ) 0
f x
)
Khi đó phương trình
( ) 0
f x
thỏa mãn:
1 0
2 0
0
m
S
P m
(vô nghiệm).
Vậy giá trị
m
thỏa mãn yêu cầu bài toán là
1
m
.
Nhận xét: Ta có thể nhận thấy ngay được ở Trường hợp 2 không thể xảy ra được vì đỉnh của parabol là:
(1; 1 )
I m
thuộc bên phải trục
Oy
.
Ví dụ 2. Cho hàm số
4
mx
y
x m
với
m
là tham số thực. Tìm
m
để hàm số :
1. đồng biến trên khoảng
(2; )

. 2. nghịch biến trên khoảng
( ;1)

.
Giải: Ta có
2
2
4
'
( )
m
y
x m
với
x m
. Dấu của
'
y
là dấu của
2
4
m
(không chứa
)
x
nên để hàm số:
1. đồng biến trên khoảng
(2; )

thì:
0, (2; )
y x

2
2
4
0, (2; )
( )
m
x
x m

2
2 2 2 2
4 0
2
2 2
(2; )
m m m m
m
m
m m
m

Vậy hàm số đồng biến trên
(2; )

khi
2
m
.
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
56
2. nghịch biến trên khoảng
( ;1)

thì:
2
2
4
0, ( ;1) 0, ( ;1)
( )
m
y x x
x m
 
.
2
2 2 2 2
4 0
2 1
1 1
( ;1)
m m
m
m
m m
m

Vậy hàm số nghịch biến trên
( ;1)

khi
2 1
m
.
Ví dụ 3. Cho hàm số
3 2 2
( 1) (2 3 2) 1
y x m x m m x
với
m
là tham số thực.
Tìm
m
để hàm số nghịch biến trên
(2; )

.
Giải: Yêu cầu bài toán
2 2
' 3 2( 1) 2 3 2 0, (2; )
y x m m m x

2 2
( ) 3 2( 1) (2 3 ) 0, (2; )
f x x m m m x

(*)
Ta có
2 2 2
' ( 1) 3(2 3 2) 7( 1) 0,m m m m m m
Suy ra
( ) 0
f x
luôn có hai nghiệm phân biệt
1 2
,
x x
với m
. Do đó:
1 2
(*) 2
x x
1 '
2
3
m
' 5
m
2 2
7( 1) ( 5)
5 0
m m m
m
2
6 3 18 0
5
m m
m
3
2
3
2
2
2
5
m
m
m
.
Vậy
3
2
2
m
là đáp số của bài toán.
Chuyên đề nhỏ này được trích sơ lược từ bản thảo cuốn sách của tác giả:
10 CHUYÊN ĐỀ BÁM SÁT ĐỀ THI TRUNG HỌC PHỔ THÔNG MÔN TOÁN
Mọi ý kiến, xây dựng góp ý các bạn gửi theo địa chỉ:
Nguyễn Thanh Tùng
Địa chỉ: Nhà số 9 – Ngõ 880 – Bạch Đằng – Hai Bà Trưng – Hà Nội
E-mail: giaidaptoancap3@yahoo.com
CẢM ƠN CÁC BẠN ĐÃ QUAN TÂM VÀ ĐỌC TÀI LIỆU !
| 1/56
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 CHUYÊN ĐỀ
KHẢO SÁT HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN Mục Lục Đề mục Trang
A. KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ……………………………………….
B. CÁC BÀI TOÁN LIÊN QUAN…………………………………………………
Bài toán 1: Các bài toán liên quan tới phương trình tiếp tuyến…………………………………….. 2
Bài toán 1.1………………………………………………………………………………………….. 2
Bài toán 1.2………………………………………………………………………………………….. 10
Bài toán 2: Các bài toán liên quan tới cực trị………………………………………………………… 15
Bài toán 2.1………………………………………………………………………………………….. 15
Bài toán 2.2………………………………………………………………………………………….. 19
Bài toán 2.3………………………………………………………………………………………….. 26
Bài toán 3: Bài toán giao điểm………………………………………………………………………… 28
Bài toán 3.1………………………………………………………………………………………….. 28
Bài toán 3.2………………………………………………………………………………………….. 41
Bài toán 3.3………………………………………………………………………………………….. 44
Bài toán 4: Bài toán tìm điểm…………………………………………………………………………. 49
Bài toán 5: Các bài toán về tính đơn điệu của hàm số……………………………………………….. 52
Bài toán 5.1………………………………………………………………………………………….. 52
Bài toán 5.2………………………………………………………………………………………….. 53 1
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
CHUYÊN ĐỀ 1: KHẢO SÁT HÀM SỐ VÀ CÁC BÀI TOÁN LIÊN QUAN
A. KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
B. CÁC BÀI TOÁN LIÊN QUAN
Bài toán 1: Các bài toán liên quan tới phương trình tiếp tuyến
Cơ sở lí thuyết:
* Cho hàm số y f ( x) có đồ thị (C), phương trình tiếp tuyến của (C) tại điểm M (x , y )  (C) là : 0 0 0
y f '(x )(x x )  y (*) ( M gọi là tiếp điểm). 0 0 0 0
* Hai đồ thị hàm số y f ( x) và y g (x) tiếp xúc với nhau khi và chỉ khi hệ phương trình sau có nghiệm :
f (x)  g(x)  (2*)
f '(x)  g '(x) 
Nghiệm của (2*) là hoành độ tiếp điểm của hai đồ thị.
Nhận xét : Với kiến thức cơ bản trên, giúp ta giải quyết hai lớp câu hỏi liên quan tới việc viết phương trình
tiếp tuyến (tại điểm và đi qua điểm). Cụ thể :
+) Với câu hỏi tại điểm, để viết được phương trình (*) ta cần 3 yếu tố x , y và f '(x ) . Ứng với điều này sẽ có 0 0 0
3 cách ra đề : cho biết x , cho biết y hoặc cho biết f '(x ) dưới các cách phát biểu khác nhau, và điều này sẽ 0 0 0
được diễn đạt thông qua Bài toán 1.1.
+) Với câu hỏi đi qua điểm sẽ được phát biểu qua Bài toán 1.2 . Bài toán 1.1
Nội dung bài toán :
Cho hàm số y f (x) có đồ thị là (C) . Viết phương trình tiếp tuyến của đồ thị (C) :
1. Tại điểm có hoành độ là a . 2. Tại điểm có tung độ là b .
3. Có hệ số góc là k . 4. Song song với đường thẳng y ax b .
5. Vuông góc với đường thẳng y ax b . 6. Tạo với trục hoành ( Ox ) một góc bằng .
7. Cắt các trục Ox, Oy lần lượt tại hai điểm ,
A B sao cho OB kOA . 2
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Cách giải chung:
Gọi M (x ; y ) là tiếp điểm của tiếp tuyến cần lập. Khi đó phương trình tiếp tuyến tại M (x ; y ) có dạng: 0 0 0 0 0 0
y f '(x )(x x )  y (*) 0 0 0
f '(x )  f '(a) 1. Với 0 x a
, thay vào (*) ta được phương trình cần lập. 0
y f (a)  0
2. Với y b f (x )  b (2) . Giải phương trình (2) tìm x và suy ra f '(x ) . Sau đó thay các thông số tìm 0 0 0 0
được vào (*) ta được phương trình cần lập.
3. Tiếp tuyến có hệ số góc k , suy ra f '(x )  k (3). Giải phương trình (3) tìm x và suy ra y . Sau đó thay vào 0 0 0
(*) ta được phương trình cần lập.
4. Tiếp tuyến song song với đường thẳng y ax b , suy ra f '(x )  a (4). 0
Giải phương trình (4) tìm được x và suy ra y . Sau đó thay vào (*) ta được phương trình (kiểm tra lại tính 0 0 song song) và kết luận. 1
5. Tiếp tuyến vuông góc với đường thẳng y ax b , suy ra f '( x )   (5). 0 a
Giải phương trình (5) tìm được x và suy ra y . Sau đó thay vào (*) ta được phương trình cần lập. 0 0
6. Tiếp tuyến tạo với trục hoành một góc , suy ra f '(x )   tan (6). 0
Giải phương trình (6) tìm được x và suy ra y . Sau đó thay vào (*) ta được phương trình cần lập. 0 0
7. Tiếp tuyến cắt trục Ox, Oy lần lượt tại , A B
sao cho OB kOA , khi đó gọi là góc tạo bởi OB
tiếp tuyến và trục hoành ta có: tan   k OA
Suy ra f '(x )   tan  k (7) 0
Giải phương trình (7) tìm được x và suy ra y . 0 0
Sau đó thay vào (*) ta được phương trình cần lập. 3
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 Nhận xét:
*) Ngoài cách phát biểu tường minh như ý 1, 2 ta có thể gặp những câu hỏi tương tự như sau:
– Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với trục hoành (với đường thẳng
y ax b , với đường cong y g(x) …).
– Viết phương trình tiếp tuyến của đồ thị (C) tại điểm thoả mãn điều kiện cho trước.
*) Các ý 3, 4, 5, 6, 7 thực chất là dữ kiện cho biết f '(x ) nhưng được phát biểu dưới nhiều cách diễn đạt 0 khác nhau.
Ví dụ 1. Cho hàm số 3 2
y f (x)  x  6x  9x 1 có đồ thị (C) . Viết phương trình tiếp tuyến của đồ thị (C) :
1. Tại điểm có hoành độ bằng 2 . 2. Tại điểm có tung độ bằng 1  5 .
3. Tại giao điểm của đồ thị (C) với đường thẳng y  4x 1.
4. Tại điểm có hoành độ x , biết f ' (x )  0 và chứng minh rằng tiếp tuyến khi đó là tiếp tuyến của (C) có 0 0 hệ số góc nhỏ nhất. Giải: Ta có 2
y '  f '(x)  3x 12x  9 . Gọi M (x ; y ) là tiếp điểm của tiếp tuyến cần lập. 0 0 0  f '(2)  3
1. Với x  2 
, suy ra phương trình tiếp tuyến cần lập: y  3(x  2)  3 hay y  3x  9 0
y f (2)  3  0 2. Với 3 2
y  15  x  6x  9x 1  15 3 2
x  6x  9x 16  0 0 0 0 0 0 0 0 2
 (x  1)(x  7x  16)  0  x  1  f '(1)  24 0 0 0 0
Vậy phương trình tiếp tuyến cần lập là: y  24x  9
3. Phương trình hoành độ giao điểm của (C) với đường thẳng y  4x 1 là:
x  0  y  1  3 2 2
x  6x  9x 1  4x 1  x(x  6x  5)  0  x  1  y  5 
x  5  y  21 
+) Với M (0;1)  f '(0)  9 , suy ra phương trình tiếp tuyến: y  9x  1 0
+) Với M (1;5)  f '(1)  0 , suy ra phương trình tiếp tuyến: y  5 0
+) Với M (5; 21)  f '(5)  24 , suy ra phương trình tiếp tuyến: y  24x  99 0 4
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3  f '(2)  3
4. Ta có y '  f ' (x)  6x 12 , khi đó f ' (x )  0  6x 12  0  x  2  0 0 0
y f (2)  3  0
Suy ra phương trình tiếp tuyến cần lập: y  3x  9
Hệ số góc tiếp tuyến của đồ thị (C) tại điểm có hoành độ x bằng : 2 2
y '(x)  f '( x)  3x 12x  9  3( x  2)  3  3  , x
   , suy ra y '(x)  3
 khi x  2  x min 0
Vậy tiếp tuyến của (C) tại điểm có hoành độ x thỏa mãn f ' (x )  0 có hệ số góc nhỏ nhất (đpcm). 0 0
Ví dụ 2. Cho hàm số 4 2
y  x x  6 có đồ thị là (C) . Viết phương trình tiếp tuyến của đồ thị (C) :
1. Có hệ số góc là 6 . 2. Song song với đường thẳng 3x  2 y  2  0 . 1 9
3. Vuông góc với đường thẳng y
x  3 . 4. Tạo với trục hoành ( Ox ) một góc bằng , biết tan 6 16
5. Cắt các trục Ox, Oy lần lượt tại hai điểm ,
A B sao cho OB  36OA . Giải: Ta có 3 y '  4
x  2x . Gọi M (x ; y ) là tiếp điểm của tiếp tuyến cần lập. 0 0 0
1. Tiếp tuyến có hệ số góc là 6 , suy ra: 3
y '(x )  6  4x  2x  6 0 0 0 2
 (x 1)(2x  2x  3)  0  x  1  y y(1)  4 0 0 0 0 0
Vậy phương trình tiếp tuyến cần lập là: y  6x  10 . 3
2. Đường thẳng 3x  2 y  2  0 được viết lại thành: y   x 1 2 3 3
Khi đó tiếp tuyến song song với đường thẳng y  
x 1, suy ra: y '(x )   2 0 2 3 1  1  91 3 3  4
x  2x  
 8x  4x  3  0 2
 (2x 1)(4x  2x  3)  0  x   y y  0 0 0 0   2 0 0 0 0 0 2  2  16 3  1  91 3 103
Tiếp tuyến cần lập là: y   x     hay y   x
(thỏa mãn điều kiện song song). 2  2  16 2 16 5
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 1
3. Do tiếp tuyến vuông góc với đường thẳng y
x  3 , suy ra: y '(x )  6 6 0 3 3
 4x  2x  6  2x x  3  0 2
 (x 1)(2x  2x  3)  0  x  1  y y(1)  4 0 0 0 0 0 0 0 0 0
Khi đó phương trình tiếp tuyến: y  6
 (x 1)  4 hay y  6  x 10 . 9
4. Do tiếp tuyến tạo với trục hoành ( Ox ) một góc bằng , nên suy ra: y '(x )   tan   0 16 9 9 9 1  1  1503 +) Với 3 3 y '(x )    4
x  2x  
 4x  2x   0  x   y y  0 0 0 0 0   16 16 16 0 0 4  4  256 9  1  1503 9 1539
Tiếp tuyến cần lập : y   x     hay y   x  16  4  256 16 256 9 9 9 1  1  1503 +) Với 3 3 y '(x ) 
 4x  2x
 4x  2x   0  x    y y   0 0 0 0 0   16 16 16 0 0 4  4  256 9  1  1503 9 1539
Tiếp tuyến cần lập : y x     hay y x  16  4  256 16 256
5. Gọi là góc tạo bởi tiếp tuyến cần lập và trục hoành, khi đó tiếp tuyến cắt các trục Ox, Oy lần lượt tại hai OB 36OA điểm ,
A B , ta được: tan  
 36  y '(x )   tan 3  6 0 OA OA +) Với 3 3 y '(x )  3
 6  4x  2x  36  4x  2x  36  0  x  2  y y(2)  14  0 0 0 0 0 0 0
Tiếp tuyến cần lập : y  3
 6(x  2) 14 hay y  36x  58 +) Với 3 3
y '(x )  36  4
x  2x  36  4x  2 x  36  0  x  2  y y( 2)   14  0 0 0 0 0 0 0
Tiếp tuyến cần lập : y  36(x  2) 14 hay y  36x  58 . 2
(3m 1)x m m
Ví dụ 3. Cho hàm số y
có đồ thị (C ) và m là tham số . x m m
1. Với m  1, viết phương trình tiếp tuyến của (C ) song song với đường thẳng y  4x  16 . 1
2. Tìm m để tiếp tuyến của (C ) tại giao điểm của đồ thị (C ) với trục hoành song song với đường thẳng m m
d : y x 1 . 6
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 Giải: 4x 4
1. Với m  1 ta có (C ) : y  , suy ra y '  1 x 1 2 (x 1)
Gọi M (x ; y ) là tiếp điểm của tiếp tuyến cần lập. Khi đó tiếp tuyến tại M (x ; y ) song song với đường 0 0 0 0 0 0 4
x  0  y  0
thẳng y  4x  16 nên suy ra: 2 0 0
y '(x )  4 
 4  (x 1)  1  0 2 0  (x 1) x  2   y  8 0  0 0
+) Với M (0; 0) , phương trình tiếp tuyến: y  4x (thỏa mãn) 0
+) Với M (2;8) , phương trình tiếp tuyến: y  4x  16 (loại). 0
Vậy phương trình tiếp tuyến cần lập là y  4x . 2 4m 2  m m
2. Ta có: y ' 
và (C ) cắt trục hoành tại điểm M
;0 . Do tiếp tuyến của (C ) tại M song 2   (x m) m 3m 1 m   2 2  m m   3m 1 1
song với đường thẳng d : y x 1 nên: y '  1   1     
m  1 hoặc m   . 3m 1    2m  5 +) Với m  1   M ( 1
 ;0) , phương trình tiếp tuyến là: y x 1 (loại). 1  3  3 +) Với m    M ; 0 
 , phương trình tiếp tuyến là: y x  (thỏa mãn) 5  5  5 1
Vậy m   là giá trị cần tìm. 5
Nhận xét: Như vậy qua Ví dụ 3 ta nhận thấy, khi gặp dạng câu hỏi viết phương trình tiếp tuyến của đồ thị hàm
số y f (x) song song với đường thẳng y ax b , việc sử dụng dữ kiện f '(x )  a chỉ là điều kiện cần nhưng 0
chưa đủ . Do đó sau khi giải ra kết quả ta cần có bước kiểm tra lại điều kiện song song. x
Ví dụ 4. Cho hàm số y
có đồ thị (C) và gốc tọa độ O . x  1
1. Viết phương trình tiếp tuyến của (C) , biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt ,
A B và tam giác OAB cân .
2. Tìm tọa độ điểm M thuộc (C), biết tiếp tuyến của (C) tại M cắt hai trục Ox , Oy lần lượt tại , A B sao cho 1
tam giác OAB có diện tích bằng . 8 7
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 1
Giải: Ta có y '  2 (x 1)
1. Gọi M (x ; y ) là tiếp điểm của tiếp tuyến cần lập. 0 0 0
Do tam giác OAB cân và vuông tại O nên OA OB , suy ra: y '(x )  1 0 1 1 x  0 Mà y '(x )   0, x   1 0
y '(x )  1   1  0 2 0  (x 1) 0 2 (x 1) x  2  0 0  0
+) Với x  0  y y(0)  0 (loại do M (0; 0)  O ) 0 0 0 +) Với x  2
  y y( 2) 
 2 , suy ra phương trình tiếp tuyến: y  1.(x  2)  2 hay y x  4 (thỏa mãn). 0 0
Vậy tiếp tuyến cần lập là: y x  4 .  m
2. Vì M  (C) nên M ; m
 . Phương trình tiếp tuyến của (C) tại M là:  m  1 2 1 m 1 m y  (x m)   y x  (d ) 2 2 2 (m 1) m 1 (m 1) (m 1) 2  1 m 2  y x  x  m
Do d Ox   
A  tọa độ điểm A là nghiệm của hệ: 2 2 2  (m 1) (m 1)    ( A m ; 0) y  0   y  0  2  1 mx  0 2  y x    m
Do d Oy   
B  tọa độ B là nghiệm của hệ: 2 2 2  (m 1) (m 1)   mB 0;  2  y  (m 1)   2   x  0 (m 1)   2 2 2 2 1 1 m 1  m   1  Theo giả thiết: 2 S   O . A OB   m .    OAB 2     8 4 (m 1) 4 m 1    2  2
2m m 1  0 1  1   1   
m  1 hoặc m    M 1;   hoặc M  ; 1    2
2m m 1  0  2  2   2   1   1 
Vậy có hai điểm M thỏa mãn yêu cầu bài toán là M 1;   và M  ; 1    .  2   2  8
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Ví dụ 5. Cho hàm số 3 2
y x  3mx  3(m  1)x 1 có đồ thị (C ) và m là tham số thực. m
1. Tìm m biết tiếp tuyến của đồ thị (C ) x y  và K là điểm m
tại điểm K song song với đường thẳng 3 0
thuộc đồ thị (C ) có hoành độ bằng 1. m
2. Với m  2 . Tìm hai điểm phân biệt M , N thuộc đồ thị (C ) sao cho tiếp tuyến của đồ thị (C ) tại M và 2 2
N song song với nhau và thỏa mãn:
a. Độ dài MN  2 5 , đồng thời M , N có tọa độ nguyên.
b. Đường thẳng MN vuông góc với đường thẳng x y  2015  0 . Giải: 1. Ta có 2
y '  3x  6mx  3(m 1) . Do K  (C ) và có hoành độ bằng 1, suy ra K (1; 6  m  3) m
Khi đó tiếp tuyến tại K có phương trình: y y '( 1
 )(x 1)  6m  3  y  (9m  6)x  3m  3 () 9  m  6  3 1
Do  song song với đường thẳng 3x y  0 (hay y  3x ) khi và chỉ khi:   m   3m  3  0 3  1
Vậy giá trị cần tìm là m   . 3
2. Với m  2 ta có đồ thị 3 2
(C ) : y x  6x  9x 1 , suy ra 2
y '  3x 12x  9 2 M    3 2
a; a  6a  9a M C    1 ( ) Do 2    với a b N  (C )  N  3 2 2
b;b  6b  9b   1 
Tiếp tuyến của đồ thị (C ) tại M và N song song với nhau nên suy ra: 2 2 2
y '(a)  y '(b)  3a 12a  9  3b 12b  9  (a b)(a b  4)  0  a b  4 (do a b  0 )
Do đó a b  4 ta có: 3 3 2 2 y y
b a  6(b a )  9(b a) N M 2
 (b a) (a b)  ab  6(a b)  9  (b a)(1 ab)   
Suy ra MN  b a;(b a)(1 ab) a. Với 2
MN  2 5  MN  20 2 2 2
 (b a)  (b a) (1 ab)  20 ( kết hợp với a b  4 ) 9
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3  a b     ab2 2 2 ( ) 1 1
  20  (16  4ab) (a ) b
 2ab  2  20     3 2
 (ab)  6(ab) 10ab  3  0  ab  3 (do a, b   ) ab  3 a  1 a  3 Khi đó ta có hệ:    hoặc  a b  4 b  3   b  1 
Vậy M (1;5), N (3;1) hoặc M (3;1), N (1;5)  
b. Do b a  0 nên MN  b a;(b a)(1 ab) cùng phương với vecto u  (1;1 ab) MN 
Đường thẳng d : x y  2015  0 có vecto chỉ phương u  (1; 1  ) d  
a  0  b  4
Do đó MN d u
.u  0  11 ab  0  ab  0  MN d
b  0  a  4 
Vậy M (0;1), N (4;5) hoặc M (4;5), N (0;1) . Bài toán 1.2 Nội dung bài toán :
Cho hàm số y f (x) có đồ thị là (C) . Viết phương trình tiếp tuyến của đồ thị (C) đi qua điểm M (x ; y ) . 0 0 0
Cách giải chung:
+) Đường thẳng  có hệ số góc k đi qua M (x ; y ) có phương trình : y k (x x )  y 0 0 0 0 0
f (x)  k(x x )  y (1)
+)  là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm : 0 0 
f '(x)  k (2) 
+) Thay (2) vào (1) ta được phương trình : f (x)  f '(x)(x x )  y (*) 0 0
Giải phương trình (*) ta tìm được x , sau đó thay vào (2) suy ra được k
Khi đó ta viết được phương trình tiếp tuyến cần lập. Chú ý :
Do các tiếp tuyến của các đồ thị hàm số trong chương trình phổ thông luôn có hệ số góc (trường hợp phương
trình tiếp tuyến không có hệ số góc là x a không có ), nên ta được phép gọi luôn phương trình có hệ số góc k
như cách trình bày trên. 10
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Ví dụ 1. Cho hàm số 4 2
y x x  3 (C) . Viết phương trình tiếp tuyến của đồ thị (C) đi qua điểm M (1; 1) . Giải:
+) Đường thẳng  có hệ số góc k đi qua M (1; 1) có phương trình : y k (x 1) 1 4 2 
x x  3  k(x 1) 1 (1)
+)  là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm :  3
4x  2x k (2) 
+) Thay (2) vào (1) ta được phương trình : 4 2 3
x x  3  (4x  2x)(x 1) 1 4 3 2 2 2
 3x  4x x  2x  2  0  (x 1) (3x  2x  2)  0  x  1
Thay x  1 vào (2) suy ra k  6 . Vậy phương trình tiếp tuyến cần lập là y  6x  7 . Nhận xét :
Ở Bài toán 1.1 khi viết phương trình tiếp tuyến tại điểm thì điểm đó luôn thuộc đồ thị, trong khi Bài toán 1.2
thì điểm đi qua có thể thuộc hoặc không thuộc đồ thị . Ở ví dụ trên điểm mà tiếp tuyến cần lập đi qua M (1; 1)
khá đặc biệt khi M  (C) . Do đó trong trường hợp này rất nhiều bạn sẽ đi viết phương trình giống như Bài
toán 1.1 (nghĩa là chuyển về bài toán viết phương trình tiếp tuyến tại điểm M (1; 1) ) và cũng cho ra kết quả
tương tự. Song cách làm đó sẽ không được điểm tuyệt đối (nếu bạn không chứng minh thêm tính duy nhất của
tiếp tuyến). Vì vậy việc trình bày theo Bài toán 1.2 là sự lựa chọn hợp lí nhất. Để hiểu rõ hơn chúng ta chuyển qua Ví dụ 2.
Ví dụ 2 (B – 2008). Cho hàm số 3 2
y  4x  6x 1 (1). Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết
rằng tiếp tuyến đó đi qua điểm M ( 1  ; 9) . Giải:
+) Đường thẳng  có hệ số góc k đi qua M ( 1
 ; 9) có phương trình : y k( x 1)  9 3 2 
4x  6x  1  k(x 1)  9 (2)
+)  là tiếp tuyến của đồ thị hàm số (1) khi và chỉ khi hệ sau có nghiệm :  2 1
 2x 12x k (3) 
+) Thay (3) vào (2) ta được phương trình : 3 2 2
4x  6x 1  (12x 12x)(x 1)  9  x  1 3 2 2 4x 3x 6x 5 0 (x 1) (4x 5) 0            5  x   4 11
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Với x  1  k  24 , phương trình tiếp tuyến là : y  24x  15 5 15 15 21 Với x   k
, phương trình tiếp tuyến là : y x  4 4 4 4 Nhận xét :
Trong Ví dụ 2 ta cũng nhận thấy điểm M thuộc đồ thị. Song nếu viết phương trình tiếp tuyến theo góc nhìn
của Bài toán 1.1 (viết phương trình tiếp tuyến tại điểm M ) thì ta chỉ thu được phương trình y  24x  15 và
thiếu đi một phương trình. Lí do là vì khi sử dụng Bài toán 1.1 thì tiếp tuyến luôn tiếp xúc với đồ thị tại điểm
M , trong khi ở Bài toán 1.2 nếu M thuộc đồ thị thì tiếp tuyến có thể tiếp xúc hoặc không tiếp xúc với đồ thị tại
M ( do tiếp tuyến chỉ cần đi qua điểm M ). Do đó ta được 2 phương trình tiếp tuyến như trên. Vì vậy khi câu
hỏi trong đề bài là viết phương trình tiếp tuyến đi qua điểm thì ta sẽ giải theo cách giải của Bài toán 1.2.
Ví dụ 3. Cho hàm số 3
y x  3x  2 có đồ thị là (C) . Tìm các điểm M trên đường thẳng y  4 , sao cho từ M
kẻ được ba tiếp tuyến tới (C) , trong đó có hai tiếp tuyến vuông góc với nhau. Giải: Gọi M ( ;
m 4) thuộc được thẳng y  4
Khi đó phương trình tiếp tuyến (d ) có hệ số góc k đi qua M có dạng: y k( x m)  4 3 
x  3x  2  k(x m)  4 (1)
(d ) là tiếp tuyến của (C) khi hệ sau có nghiệm:  2 3
x  3  k (2) 
Thay (2) vào (1) ta được phương trình: 3 2
x  3x  2  (3x  3)(x m)  4 3 2 2
 2x  3mx  3m  2  0  (x 1) 2x  (3m  2)x  3m  2  0    x  1    2
h(x)  2x  (3m  2)x  3m  2  0 (3) 
Để có ba tiếp tuyến kẻ từ M tới (C) thì phương trình (3) phải có hai nghiệm phân biệt khác 1, hay :
  (3a  2)(3a  6)  0  2    a   ;   
   2;  \   1 (*) f ( 1
 )  6a  6  0   3   y  4
Với x  1  
, suy ra phương trình tiếp tuyến là y  4 . Do tiếp tuyến này không vuông góc với bất y '( 1  )  0 
kì một tiếp tuyến nào khác. Nên để có hai tiếp tuyến vuông góc với nhau thì phương trình (3) phải có hai
nghiệm phân biệt x , x thỏa mãn: 2 2
y '(x ).y '(x )  1
  9( x 1)( x 1) 1  0 1 2 1 2 1 2 12
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 2 2
 9 (x x )  (x x )  2x x 1 1  0 1 2 1 2 1 2   (2*) 3m  2 28
Thay x x x x
vào (2*) ta có: 9(3m  2  1) 1  0  m  
, thỏa mãn điều kiện (*) 1 2 1 2 2 27  28  Vậy M  ; 4   là điểm cần tìm.  27 
Ví dụ 4. Cho hàm số 3 2
y x  3x  3 có đồ thị là (C) . Tìm trên đồ thị (C) những điểm mà qua đó kẻ được
đúng một tiếp tuyến tới (C) . Giải: Gọi 3 2 M ( ;
m m  3m  3)  (C)
Khi đó phương trình tiếp tuyến (d ) có hệ số góc k đi qua M có dạng: 3 2
y k (x m)  m  3m  3 3 2 3 2 
x  3x  3  k (x m)  m  3m  3 (1)
(d ) là tiếp tuyến của (C) khi hệ sau có nghiệm:  2
h(x)  3x  6x k (2) 
Thay (2) vào (1) ta được phương trình: 3 2 2 3 2
x  3x  3  (3x  6x)(x  )
m m  3m  3  x m 2 (x m) (2x m 3) 0        3  m x   2
Để (d ) là tiếp tuyến duy nhất qua M của (C) thì xảy ra các khả năng sau: 3  m +) Khả năng 1: m
m  1  M (1;1) 2  3  m
+) Khả năng 2 : h(m)  h
 (*) và hai tiếp tuyến trùng nhau.  2  Điều kiện 2
(*)  m  2m 1  0  m  1  M (1;1)
Vậy M (1;1) là điểm cần tìm.
Ví dụ 5. Cho hàm số 4 2
y x  2x  3 có đồ thị là (C) . Tìm các điểm thuộc trục tung mà từ đó kẻ được một
tiếp tuyến duy nhất đến (C) . 13
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 Giải:
Gọi M (0; m)  Oy
Khi đó phương trình tiếp tuyến (d ) có hệ số góc k đi qua M có dạng : y kx m 4 2 
x  2x  3  kx m (1)
(d ) là tiếp tuyến của (C) khi hệ sau có nghiệm:  3
4x  4x k (2) 
Thay (2) vào (1) ta được phương trình: 4 2
3x  2x m  3  0 (3) Đặt 2
t x với t  0 , lúc này (3) có dạng : 2
3t  2t m  3  0 (4)
Nhận thấy với mỗi nghiệm t t  0 của (4) cho ta nghiệm x x   t . Suy ra k  4
 (t 1). t . 0 0 0 0 0
Do đó (d ) là tiếp tuyến duy nhất qua M khi (4) có duy nhất một nghiệm t  0 thỏa mãn: t  0
4(t 1). t  4(t 1). t  (t 1). t  0   t  1  2
+) Với t  0 , thay vào (4) ta được m  3
 , khi đó (4) có nghiệm t  0 và t  (loại) 3 1
+) Với t  1, thay vào (4) ta được m  4
 , khi đó (4) có nghiệm t  1 và t   (thỏa mãn yêu cầu) 3
Vậy M (0; 4) là điểm cần tìm. 14
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Bài toán 2: Các bài toán liên quan tới cực trị Bài toán 2.1 Nội dung bài toán :
Viết phương trình đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số 3 2 y f ( ,
x m)  ax bx cx d .
Cách giải chung: Bước 1: Tính 2
y '  3ax  2bx c ; 2
y '  0  3ax  2bx c  0 (*)
Bước 2: Đồ thị hàm số có 2 điểm cực trị khi phương trình (*) có hai nghiệm phân biệt x , x m D . 1 2
+) Nếu nghiệm x , x đẹp ( 2 2
 '  b  3ac u : có dạng bình phương) 1 2
Ta có hai điểm cực trị (
A x ; y ), B(x ; y ) , suy ra phương trình AB . 1 1 2 2
+) Nếu nghiệm x , x “không đẹp” , chia y cho y ' ( làm nháp) và viết thành: y u(x).y ' px q 1 2  ( A x ; y )
y u(x ).y '(x )  px q px q Gọi 1 1 
là hai điểm cực trị  y '(x )  y '(x )  0 , khi đó 1 1 1 1 1  B(x ; y ) 1 2 
y u(x ).y '(x )  px q px q 2 2  2 2 2 2 2
Suy ra phương trình AB : y px q .
Ví dụ 1 (A – 2002). Cho hàm số: 3 2 2 3 2
y  x  3mx  3(1 m )x m m (1) ( với m là tham số thực).
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số (1).
Giải: Ta có 2 2 y '  3
x  6mx  3(1 m ) x m 1 Cách 1: 2 2 1
y '  0  x  2mx m 1  0  
. Vì x x nên hàm số đạt cực trị tại x , x . x m 1 1 2 1 2  2
Khi đó ta có hai điểm cực trị (
A x ; y ), B(x ; y ) với 1 1 2 2 2 2 
y y(m 1)  m  3m  2   (
A m 1; m  3m  2)  1     AB  (2; 4) 2 2
y y(m  1)  m  3m  2 
B(m 1; m  3m  2) 2  2 x m 1
y m  3m  2
Suy ra phương trình đi qua hai điểm cực trị , A B là: 2 
y  2x m m . 2 4 15
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 Cách 2: Với 2 2
y '  0  x  2mx m 1  0 có 2 2
 '  m  (m 1)  1  0
Nên hàm số đạt cực trị tại x , x . Ta có y '(x )  y '(x )  0 1 2 1 2 Mặt khác: 3 2 2 3 2
y  x  3mx  3(1 m )x m m 1 
x m 2 2
3x  6mx  3  3m  2
 2x m m 3 2 1 
y  2x m m   x m 2 1 1
y ' 2x m m   2 3
y  2x m m  2 2
Vậy phương trình đi qua hai điểm cực trị (
A x ; y ), B(x ; y ) là: 2
y  2x m m 1 1 2 2
Ví dụ 2. Cho hàm số 3 2
y  2x  3(m 1)x m . Tìm m để đồ thị hàm số có điểm cực đại, cực tiểu , A B sao cho ba điểm , A ,
B I (3;1) thẳng hàng. x  0
Giải: Ta có 2
y '  6x  6(m 1)x . Khi đó 1
y '  0  6x(x m 1)  0   x m 1  2
Hàm số có cực đại, cực tiểu khi và chỉ khi x x  0  m 1  m  1 1 2
y y(0)  m  ( A 0; m) 1 Cách 1: Ta có    3 2 3 2
y y(m 1)  m  3m  2m 1
B(m 1; m  3m  2m  1)  2   
AI  (3;1 m)   Suy ra  . Do ,
A B, I thẳng hàng nên AI , BI cùng phương, tương đương: 3 2 BI  (4  ;
m m  3m  2m)  3 2 4  m
m  3m  2m 4  m  (do m  1) 2   2m m 3 1 m 3 4 2
 3m  7m  4  0  m  1
 (loại) hoặc m  (thỏa mãn). 3  1 m 1  Cách 2: Ta có 2 2 y x
6x  6(m 1)x  (m 1) x m   3 6     2  1 m 1  
y  (m 1) x m 2  x
y ' (m 1) x m 1 1  
. Với y '(x )  y '(x )  0  1 2   3 6  2
y  (m 1) x m  2 2 16
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Khi đó phương trình đi qua hai điểm cực trị (
A x ; y ), B(x ; y ) là : 2
y  (m 1) x m 1 1 2 2 Do ,
A B, I (3;1) thẳng hàng nên 2
I AB  1  3
 (m 1)  m 2
 3m  7m  4  0 4 4  m  1
 (loại) hoặc m
(thỏa mãn). Vậy m  . 3 3
Ví dụ 3 (B – 2013). Cho hàm số 3 2
y  2x  3(m 1)x  6mx (1). Tìm m để đồ thị hàm số (1) có hai điểm cực
trị A và B sao cho đường thẳng AB vuông góc với đường thẳng y x  2 .  x  1
Giải: Ta có 2
y '  6x  6(m 1)x  6m ; 2 1
y '  0  x  (m 1)x m  0   x m  2
Hàm số có hai cực trị khi và chỉ khi x x m  1 (*) 1 2
y y(1)  3m 1  ( A 1;3m 1)  1 Cách 1: Ta có 3   
AB  (m 1; (m 1) ) 3 2 3 2 y y( )
m  m  3m B( ;
m m  3m )  2   
Do m  1 nên AB cùng phương với vecto 2 u  (1; (m 1) ) AB 
Đường thẳng d : y x  2  x y  2  0 có vecto chỉ phương u  (1;1) d   m  0 Khi đó 2
AB d A .
B u  0  1 (m 1)  0  (thỏa mãn (*) ) dm  2  Cách 2: Ta có 3 2
y  2x  3(m 1)x  6mx 2 2         (2x m 1) x (m 1)x
m  (m 1) x m(m  1)   1 2 
(2x m 1) y ' (m 1) x m(m 1) . 6 2 
y  (m 1) x m(m 1) Với 1 1
y '(x )  y '(x )  0  1 2  2
y  (m 1) x m(m  1)  2 2
Vậy phương trình đường thẳng đi qua hai điểm cực trị (
A x ; y ), B(x ; y ) là : 2
y  (m 1) x  ( m m 1) 1 1 2 2 m  0
Do AB vuông góc với đường thẳng y x  2 nên: 2 (m 1)  1   
(thỏa mãn điều kiện (*) ) m  2 
Vậy giá trị m cần tìm là m  0 hoặc m  2 . 17
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
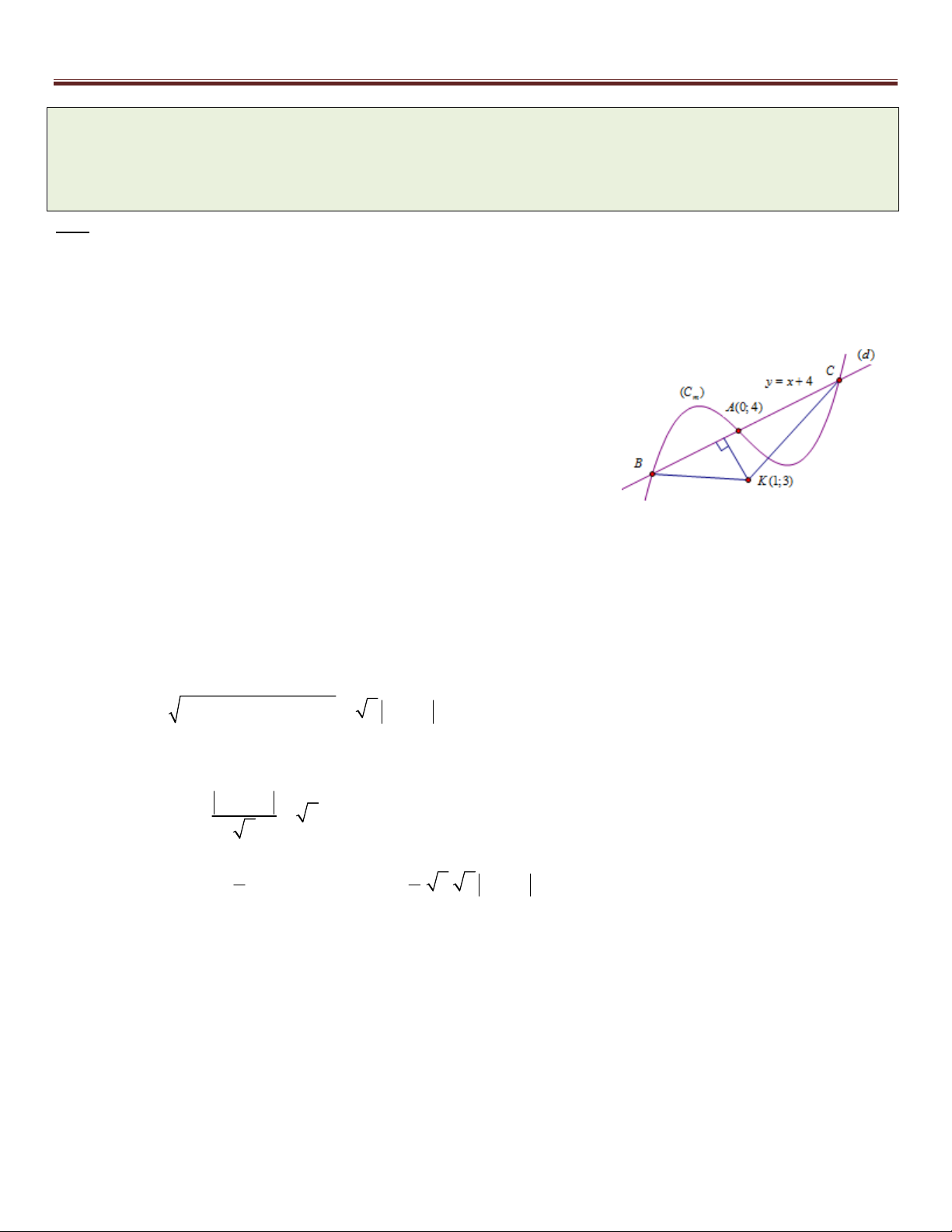
Ví dụ 4. Cho hàm số 3 2
y x  3x  2 có đồ thị là (C) và đường tròn (T ) có phương trình: 2 2
(x m)  ( y m 1)  5 . Tìm m để đường thẳng đi qua hai điểm cực trị của (C) tiếp xúc với đường tròn (T ) Giải:
x  0  y  2 Ta có: 2
y '  3x  6x ; y '  0  3x(x  2)  0  
x  2  y  2   
Vậy ta có hai điểm cực trị: (
A 0; 2) và B(2; 2)  AB  (2; 4)  2(1; 2) x y  2
Khi đó phương trình đi qua 2 điểm cực trị là : 
hay 2x y  2  0 () 1 2 
Đường tròn (C) có tâm I ( ;
m m 1) và bán kính R  5 m  2
2m m  1 2
() tiếp xúc với (C) khi và chỉ khi: d (I ; )  R 5 3m 1 5        4 2 2 2 1 m    3 4
Vậy m  2 hoặc m  
là đáp số của bài toán. 3 18
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 Bài toán 2.2
Nội dung bài toán : Tìm m để hàm số y f (x, m) có n cực trị thỏa mãn điều kiện (*) cho trước
Cách giải chung:
Trường hợp 1: Tìm m để hàm số bậc ba: 3 2 y f ( ,
x m)  ax bx cx d có 2 (n  2) cực trị thỏa mãn
điều kiện (*) cho trước. Bước 1: 2 2
y '  3ax  2bx c Ax Bx C ; 2
y '  0  Ax Bx C  0 (1) A  0
Hàm số có 2 cực trị  (1) có hai nghiệm phân biệt    m D   0   B x x  
M (x ; y ) 1 2   A Bước 2: +) Gọi 1 1 
là hai điểm cực trị với  (2)
N (x ; y )  C 2 2 x x  1 2   A
(Nếu cần biểu diễn y , y theo m thì sử dụng Bài toán 2.1 ) 1 2
+) Cắt nghĩa điều kiện (*) (có thể sử dụng (2) hoặc kết hợp các kiến thức hình học phẳng…) thiết lập được : m D
g(m)  0 (hoặc (g(m)  0, g(m)  0...)  m  Kết luận.
Chú ý: Do số cực trị của hàm bậc ba chỉ có thể là 2 hoặc không có. Do đó nếu đề bài yêu cầu tìm m để hàm số
có cực trị, được hiểu là tìm m để hàm số có 2 cực trị (một cực đại và một cực tiểu). 2 2
Ví dụ 1 (D – 2012). Cho hàm số 3 2 2 y
x mx  2(3m 1)x
(C) , m là tham số thực. 3 3
Tìm m để hàm số (C) có hai điểm cực trị x và x sao cho x x  2(x x )  1. 1 2 1 2 1 2 Giải: +) Ta có 2 2
y '  2x  2mx  2(3m 1)  0 ; 2 2
y '  0  x mx  3m 1  0 (1)
Hàm số có hai cực trị x , x  (1) có hai nghiệm phân biệt x , x 1 2 1 2 2 13 2 13 2
  '  13m  4  0  m  hoặc m   13 13 19
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
x x m 1 2
+) Với x , x là nghiệm của (1) nên
(2) . Ta có: x x  2(x x )  1 (*) . 1 2  2 1 2 1 2 x x  1 3m  1 2 2
Thay (2) vào (*) ta được: 2
1 3m  2m  1  (
m 3m  2)  0  m  0 (loại) hoặc m  (thỏa mãn). 3 2 Vậy m  là giá trị cần tìm. 3
Ví dụ 2 (B – 2012). Cho hàm số 3 2 3
y x  3mx  3m (C) , m là tham số thực. Tìm m để đồ thị hàm số (C) có
hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 48. 3
x  0  y  3m
Giải: +) Ta có 2
y '  3x  6mx ; 1 1
y '  0  3x(x  2m)  0   3
x  2m y  m  2 2
Đồ thị hàm số (C) có hai điểm cực trị  x x m  0 1 2 3 3   (
A 0;3m ) Oy OA  3 m
+) Ta có hai điểm cực trị:    3 B(2 ; m m ) 
d (B,O )
A d (B, Oy)  2 m  1 Theo đề ra ta có: 4 S  48 
.d (B, O )
A .OA  48  3m  48  m  2
 (thỏa mãn ) . Vậy m  2  . OAB 2
Ví dụ 3. Cho hàm số 3 2 2
y  x  (2m 1)x  (m  3m  2)x  4 . Xác định m để đồ thị hàm số có các điểm cực
đại và cực tiểu nằm về hai phía của trục tung.
Giải: Ta có 2 2 y '  3
x  2(2m 1)x  (m  3m  2) Suy ra 2 2
y '  0  3x  2(2m 1)x  (m  3m  2)  0 (1)
+) Để đồ thị hàm số các các điểm cực đại, cực tiểu thì phương trình (1) phải có hai nghiệm phân biệt, khi đó: 13  3 21 1  3  3 21 2 2
 '  (2m 1)  3(m  3m  2)  0 2
m 13m  5  0  m  hoặc m  (2) 2 2
+) Hàm số có hai điểm cực trị (
A x ; y ), B(x ; y ) với x , x là nghiệm của (1) 1 1 2 2 1 2 Khi đó hai điểm (
A x ; y ), B(x ; y ) nằm về hai phía của trục tung khi và chỉ khi: 1 1 2 2 2
x x  0  m  3m  2  0  1  m  2 , kết hợp với (2) ta được đáp số: 1  m  2 1 2 20
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Chú ý: Việc cắt nghĩa điều kiện (*) khi hai điểm cực trị (
A x ; y ), B(x ; y ) : 1 1 2 2
+) cùng phía với trục tung (trục Oy ) là: x x  0 1 2
+) khác phía (nằm về hai phía) với trục tung (trục Oy ) là: x x  0 1 2
+) cùng phía với trục hoành (trục Ox ) là: y y  0 1 2
+) khác phía (nằm về hai phía) với trục hoành (trục Ox ) là: y y  0 . 1 2
Ví dụ 4. Cho hàm số 3 2 2
y  x  3x m  3m với m là tham số thực. Chứng minh hàm số luôn có cực đại, cực
tiểu với mọi m . Tìm m để các điểm cực đại, cực tiểu của đồ thị hàm số cách đều đường thẳng  : y x  5 . 2
x  0  y m  3m
Giải: +) Có 2 y '  3
x  6x ; y '  0  3
x(x  2)  0   2
x  2  y m  3m  4  Vậy với m
   , y '  0 có hai nghiệm phân biệt nên hàm số đã cho luôn có cực đại, cực tiểu với mọi m . +) Ta có 2 2 (
A 0; m  3m), B(2; m  3m  4) là hai điểm cực trị
Đường thẳng  : y x  5 hay x y  5  0 2 2
m  3m  5
m  3m  3
Theo đề ra ta có: d ( ,
A )  d (B, )   2 2 2 2
m  3m  5  m  3m  3 m  1  2  
m  3m  4  0  2 2 
m  3m  5  m  3m  3 m  4  
Vậy m  1 hoặc m  4 là các giá trị cần tìm.
Ví dụ 5. Cho hàm số 3 2
y x  3x mx có đồ thị là (C ) . Xác định m để (C ) có các điểm cực đại và cực tiểu m m
đối xứng nhau qua đường thẳng x  2y  5  0 . Giải: +) Ta có: 2
y '  3x  6x m ; 2
y '  0  3x  6x m  0 (1)
Đồ thị (C ) có các điểm cực đại, cực tiểu khi và chỉ khi phương trình (1) có hai nghiệm phân biệt, m
hay  '  9  3m  0  m  3 (2) 21
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 +) Gọi (
A x ; y ), B(x ; y ) là hai điểm cực trị của (C ) với: y '(x )  y '(x )  0 1 1 2 2 m 1 2  1 1  2m  6 m  1 1  2m  6 m Ta có 2 y x
(3x  6x m)  x    hay y x  .y ' x     3 3  3 3  3 3  3 3   1 1  2m  6 m 2m  6 m y x  .y '(x )  x   x   1  1  1 1 1   3 3  3 3 3 3 2m  6 m  
, suy ra phương trình AB : y x   1 1  2m  6 m 2m  6 m  3 3 y x  .y '(x )  x   x  2  2  2 2 2    3 3  3 3 3 3 1 5
Đường thẳng d : x  2 y  5  0 được viết lại: y x  2 2 2m  6 1 ,
A B đối xứng với nhau qua d thỏa mãn điều kiện cần là: AB d  .  1
  m  0 (thỏa mãn (2) ) 3 2
Với m  0 hàm số có dạng 3 2
y x  3x có hai điểm cực trị ( A 0; 0), B(2; 4  )
Khi đó trung điểm AB là I (1; 2
 )  d (thỏa mãn điều kiện đủ)
Vậy giá trị m  0 là đáp số của bài toán.
Ví dụ 6. Cho hàm số 3
y  (m  3)x  2mx  3 với m là tham số thực. Biện luận theo m số cực trị của hàm số trên. Giải: Ta có 2
y '  3(m  3)x  2m , khi đó 2
y '  0  3(m  3)x  2m  0 (*)
*) Với m  3 phương trình (*) có dạng: 6
  0 (vô nghiệm), nghĩa là hàm số không có cực trị với m  3 .
*) Với m  3 , suy ra :   24m(m  3)
+) Nếu   0  24m(m  3)  0  0  m  3
thì phương trình (*) vô nghiệm hoặc có nghiệm kép hay y ' không đổi dấu. Suy ra hàm số không có cực trị. m  0
+) Nếu   0  24m(m  3)  0   m  3 
Khi đó phương trình (*) có hai nghiệm phân biệt, hay hàm số có hai cực trị (một cực đại, một cực tiểu).
Kết luận: Với 0  m  3 : hàm số không có cực trị. Với m  0 hoặc m  3 : hàm số có hai cực trị. 22
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Chú ý: Các kiến thức hình học phẳng cơ bản cần nhớ để cắt nghĩa điều kiện (*) : AB  (x  2 x )  (y  2 y )  2 1 2 1 +) (
A x ; y ), B(x ; y )  1 1 2 2
  x x y y   1 2 1 2 I  ;
 : Trung ®iÓm cña AB   2 2 
x x x
y y y  +) (
A x ; y ), B(x ; y ), C(x ; y ) là ba đỉnh của tam giác khi đó 1 2 3 1 2 3 G ; : là trọng tâm của 1 1 2 2 3 3    3 3  tam giác ABC
ax by c
+) M (x ; y ) và  : ax by c  0 0 0
d (M , )  0 0 2 2 a b
d : y k x m
d d k k  1  +) 1 1 1  , khi đó: 1 2 1 2 
d : y k x m
d / /d k k ; m m 2 2 2  1 2 1 2 1 2  1 0  1 +) A 90 S  .d ( ,
A BC).BC   S  .A . B AC ABC 2 ABC 2
Trường hợp 2:
Tìm m để hàm số trùng phương : 4 2
y ax bx c có n cực trị thỏa mãn điều kiện (*) cho trước. x  0 Bước 1: 3
y '  4ax  2bx ; 2
y '  0  2x(2ax b)  0   2 2ax b  0 (1) 
+) Hàm số có 1 cực trị (n  1)  (1) thỏa mãn mãn ab  0 . b
+) Hàm số có 3 cực trị (n  3)  (1) có hai nghiệm phân biệt 
 0  ab  0  m D . 2a
Bước 2: (dành cho 3 cực trị )  ( A 0; c)  b  x   
+) Ta có 3 cực trị B(x ; y ) với 1,2
(Tam giác ABC luôn cân tại A ) 1 1  2a C  (x ; y )  
y y(x );
y y(x ) 2 2  1 1 2 2 m D
+) Cắt nghĩa điều kiện (*) , suy ra được phương trình: g(m)  0  m  Kết luận. 23
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 m 1 5
Ví dụ 1. Cho hàm số 4 2 y x mx
(C ) , với m là tham số thực. Tìm m để hàm số (C ) có cực 2 2 m m
tiểu mà không có cực đại. Giải: x  0 +) Ta có 3 2
y '  2(m  1)x  2mx  2x (m  1)x m 
 , khi đó y '  0   2
(m 1)x m  0 (1) 
+) Hàm số (C ) có cực tiểu mà không có cực đại m
y '  0 có một nghiệm khi và chỉ khi phương trình (1) thỏa mãn:
(m  1).(m)  0  m(m 1)  0  1   m  0 Vậy 1
  m  0 là đáp số của bài toán.
Ví dụ 2 (A – A1 – 2012). Cho hàm số 4 2 2
y x  2(m  1)x m (C ) , với m là tham số thực. Tìm m để đồ m
thị của hàm số (C ) có ba cực trị tạo thành ba đỉnh của một tam giác vuông. m Giải:  x  0 +) Ta có 3 2
y '  4x  4(m  1)x  4x(x m 1) ; y '  0   2 x m 1 (1) 
+) Đồ thị hàm số có 3 cực trị khi (1) có hai nghiệm phân biệt khác 0  m 1  0  m  1 (2)  2 ( A 0; m )    AB     2
m 1; (m 1) 
+) Có 3 điểm cực trị : B  m 1;2m   1     AC   2
m  1; (m  1)   C   m 1; 2  m   1 
Theo đề bài tam giác ABC vuông, mà tam giác ABC luôn cân tại A   m  1 
Suy ra ABC vuông tại A  . AB AC  0 4
 (m 1)  (m 1)  0 3
 (m 1) (m  1) 1  0     m  0 
Kết hợp với điều kiện (2) ta được đáp số m  0 . 24
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Ví dụ 3. Cho hàm số 4 2
y  x  2mx  4 (C ) , m là tham số thực. m
Tìm các giá trị của m để tất cả các điểm cực trị của đồ thị (C ) đều nằm trên các trục tọa độ. mx  0 Giải: Ta có 3 2 y '  4
x  4mx  4
x(x m) ; y '  0   2 x m
+) Với m  0 thì đồ thị (C ) có một điểm cực trị ( A 0; 4  )  Oy mx  0
+) Với m  0 thì y '  0   x   m   ( A 0; 4  )  Oy
Suy ra (C ) có 3 điểm cực trị m  2 2
B( m; m  4)  Oy; C( m; m  4)  Oy  B Oxm  0 Để ,
A B, C nằm trên các trục tọa độ thì     m  2 2 C Oxm  4  0 
Vậy m  0 hoặc m  2 là các giá trị cần tìm.
Ví dụ 4. Cho hàm số 4 2 2
y x  2(m m  1)x m 1 , m là tham số thực. Tìm m để đồ thị hàm số có
khoảng cách giữa hai điểm cực tiểu ngắn nhất. Giải:  x  0 +) Ta có 3 2 2 2
y '  4x  4(m m 1) x  4x x  (m m  1) 
 , khi đó y '  0   2
x   m m  1  +) Vậy với m
   , đồ thị hàm số luôn có 3 điểm cực trị .
Mặt khác: a  1  0 nên ta có hai điểm cực tiểu đối xứng nhau qua trục tung và có hoành độ lần lượt là: 2 2
x   m m 1; x
m m 1 . Khi đó khoảng cách giữa hai điểm cực tiểu là: 1 2 2  1  3 1 2
d x x  2 m m 1  2 m    3  d  3 khi m  2 1   min  2  4 2 1 Vậy với m
khoảng cách giữa hai điểm cực tiểu ngắn nhất. 2 25
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 1
Ví dụ 5. Cho hàm số 4 2 y
x  (3m 1) x  2(m 1) (C ) . Tìm m để đồ thị (C ) có ba điểm cực trị tạo 4 m m
thành một tam giác có trọng tâm trùng với gốc tọa độ. Giải:  x  0 Ta có 3 2
y '  x  2(3m 1) x x x  2(3m 1)   ; y '  0   2 x  2(3m 1)  1
+) Hàm số có 3 cực trị khi và chỉ khi y '  0 có 3 nghiệm phân biệt  2(3m 1)  0  m   (*) 3
+) Khi đó đồ thị có 3 điểm cực trị: (
A 0; 2m  2) , 2
B( 2(3m 1); 9m  4m 1) , 2 C( 2(3m 1); 9
m  4m 1)  4  Suy ra 2 G 0; 6  m  2m  
 là trọng tâm của ABC  3  4 2 1 1 Do 2
G O  6m  2m   0  m   hoặc m
. Kết hợp với điều kiện (*) ta được m  3 3 3 3 Bài toán 2.3
Nội dung bài toán : Cho hàm số y f (x, m) . Tìm m để hàm số đạt cực đại (cực tiểu) tại x x . 0
Cách giải chung:
+) Điều kiện cần:
Hàm số đạt cực trị (cực đại hoặc cực tiểu ) tại x x khi f '(x , m)  0  m m (ở đây y có đạo hàm tại x ) 0 0 0 0
+) Điều kiện đủ: (kiểm tra giá trị m m ) 0
Cách 1: Nếu f ' (x ; m )  0 thì hàm số đạt cực đại tại x x 0 0 0
Nếu f ' (x ; m )  0 thì hàm số đạt cực tiểu tại x x . 0 0 0
Cách 2: Dùng bảng biến thiên để kiểm tra. 1
Ví dụ 1. Tìm m để hàm số 3 2 2 y
x  (m  1)x 12mx đạt cực đại tại x  2  . 3 Giải: Ta có 2 2
y '  x  2(m 1)x 12m và 2
y '  2x  2(m  1) 26
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 m  1
+) Điều kiện cần: Hàm số đạt cực đại tại x  2  , suy ra : 2 y '( 2) 
 0  4m 12m  8  0   m  2 
+) Điều kiện đủ: Với m  1  y '  2x  4  y ' ( 2
 )  8  0 (thỏa mãn)
Với m  2  y '  2x 10  y ' ( 2
 )  14  0 (thỏa mãn)
Vậy với m  1 hoặc m  2 hàm số đạt cực đại tại x  2  .
Nhận xét: +) Với bài toán trên ta có thể chỉ ra luôn 2 y ' ( 2)   2
m  6  0 , m    .y '( 2)   0
+) Với hàm số bậc ba. Cụ thể với ví dụ trên, ta có thể trình bày gọn bằng cách giải hệ: y ' ( 2)   0 
Ví dụ 2. Tìm m để hàm số 4 2 2
y mx  (m 1)x m 1 có giá trị cực tiểu bằng 1. Giải: Ta có 3
y '  4mx  2(m 1)x và 2
y '  12mx  2(m 1)
Gọi x x là điểm cực tiểu của hàm số với y  1. Khi đó ta có: 0 CT 3
y '(x )  0
4mx  2(m 1)x  0 (1) 
Điều kiện cần: 0 0 0    4 2 2 y(x )  1   0
mx  (m  1)x m 1  1  (2)  0 0  x  0 0 Từ 2
(1)  2x . 2mx  (m 1)  0  0 0    2 2mx m  1  0
*) Với x  0 thay vào (2) ta được: 2
m  1  m  1  0
Điều kiện đủ: Với x x  0 và m  1  y '  4
  0 (không thỏa mãn) 0
Với x x  0 và m  1
  y '  0 (chưa kết luận được) 0 Hàm số có dạng 4
y  x có a  1  0 nên có cực đại là gốc tọa độ.
Vậy x  0 không thỏa mãn. 0 m 1 *) Với 2 2
2mx m 1  x
(do m  0 ) thay vào (2) ta được: 0 0 2m 3 2
4m m  6m 1 3 2 2 2
 1  4m m  2m 1  0  (m 1)(4m  3m 1)  0  m  1  x  1 0 4m
Điều kiện đủ: Với m  1 và 2 2
x x  1  y '  8  0 (thỏa mãn). 0
Vậy với m  1 thì hàm số có giá trị cực tiểu bằng 1. 27
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
BÀI TOÁN 3: Bài toán giao điểm Bài toán 3.1
Nội dung bài toán : Tìm m để đồ thị hàm số y g(x) cắt đường thẳng y px q tại n điểm phân biệt thỏa
mãn điều kiện (*) (nếu có).
Cách giải chung:
Trường hợp 1: g(x) là hàm bậc ba.
Bước 1: Phương trình hoành độ giao điểm : 3 2
g(x)  px q ax bx cx d  0 (1)
Bước 2: Nhẩm nghiệm x x (bằng cách khử m ) ta đưa (1) về dạng tích: 0  x x0 2
(x x )(ax b x c )  0  0 1 1  2
f (x)  ax b x c  0 (2)  1 1
Bước 3: ( Xét a không chứa tham số m - xem thêm Chú ý sau Ví dụ 2)
*) Nếu cắt tại một điểm (n  1) thì (1) có một nghiệm   0 
 (2) vô nghiệm hoặc có nghiệm kép x x    0  m D 0 1   f (x )  0  0
*) Nếu cắt tại hai điểm phân biệt (n  2) thì (1) có hai nghiệm
 (2) có nghiệm kép khác x hoặc có hai nghiệm phân biệt và có nghiệm x 0 0   0   0   hoặc   m D f (x )  0 2  f (x )  0 0  0
*) Nếu cắt tại ba điểm phân biệt (n  3) thì (1) có ba nghiệm phân biệt   0
 (2) có hai nghiệm phân biệt khác x    m D 0 3 f (x )  0  0
Bước 4 (nếu có (*) và xét với n  3 ): 28
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3  (
A x ; px q) 0 0  b c
*) Ta có ba giao điểm: B(x ; px q) với 1 x x   và 1 x x   (3) 1 1 1 2 a 1 2 a C
 (x ; px q)  2 2
*) Cắt nghĩa (*) (sử dụng (3) hoặc kết hợp kiến thức hình học phẳng) ta được: m D
h(m)  0 (hoặc 3 ( h m)  0, h( )
m  0...)  m   Kết luận.
Ví dụ 1. Cho hàm số 3 2
y x  3x  1 (C) , m là tham số thực. Tìm m để đường thẳng
d : y  (2m 1)x  4m 1 cắt đồ thị hàm số (C) tại hai điểm phân biệt. Giải:
+) Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d là: 3 2 3 2
x  3x 1  (2m 1)x  4m 1  x  3x  (2m 1)x  4m  2  0 (1) x  2 2
 (x  2)(x x  2m 1)  0   2
f (x)  x x  2m 1  0 (2) 
+) d cắt (C) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt  (2) có nghiệm
kép khác 2 hoặc có hai nghiệm phân biệt trong đó có một nghiệm bằng 2 , tương đương với điều kiện:
  5  8m  0  5  m  
f (2)  1 2m  0   8  
  5  8m  0 1   m  
f (2)  1 2m  0  2  5 1
Vậy m   hoặc m
thì d cắt (C) tại hai điểm phân biệt. 8 2
Ví dụ 2. (D – 2013). Cho hàm số 3 2
y  2x  3mx  (m 1)x 1 (C) , m là tham số thực.
Tìm m để đường thẳng y  x 1 cắt đồ thị hàm số (C) tại ba điểm phân biệt. Giải:
+) Phương trình hoành độ giao điểm của (C) và đường thẳng y  x 1 là: 3 2 3 2
2x  3mx  (m 1)x 1  x 1  2x  3mx mx  0 (1) 29
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3  x  0 2
x(2x  3mx m)  0   2
f (x)  2x  3mx m  0 (2) 
+) Yêu cầu bài toán  (1) có ba nghiệm phân biệt  (2) có hai nghiệm phân biệt khác 0 m  0 2
  9m  8m  0     8
f (0)  m  0 m    9 8
Vậy m  0 hoặc m
là đáp số của bài toán. 9
Chú ý: Trong cách giải chung
+) Ta đang đề cấp tới trường hợp a không chứa tham số m ( a  0 ). Nếu a chứa tham số m , ta xét thêm
trường hợp a  0 .
+) Trong trường hợp không nhẩm được nghiệm (nghiệm “xấu”) ta dùng định lí Viet cho hàm bậc ba hoặc sử
dụng yếu tố cực trị (khả năng này xuất hiện trong đề thi là rất thấp, tác giả không đề cập trong cuốn sách này –
sẽ được nói chi tiết trong cuốn sách “10 vấn đề trọng tâm trong khảo sát hàm số và ứng dụng” của tác giả).
Ví dụ 3. Tìm m để đồ thị hàm số 3 2
y  (m  1)x  3mx  (2m 10)x 12
cắt trục hoành tại một điểm duy nhất.
Giải: +) Phương trình hoành độ giao điểm của đồ thị và trục hoành là: 3 2
(m  1)x  3mx  (2m 10)x 12  0 2
 (x  2) (m 1)x  (m  2)x  6  0    x  2   2
f (x)  (m 1)x  (m  2)x  6  0 (*) 
+) Yêu cầu bài toán  (*) vô nghiệm hoặc có một nghiệm bằng 2. Xét phương trình (*) :
Với m  1, phương trình (*) có dạng: 3x  6  0  x  2 (thỏa mãn) Với m  1  , ta có 2
  m  20m  28 . Khi đó yêu cầu bài toán tương đương : 2   0
m  20m  28  0   2   0   
m  20m  28  0  10   6 2  m  10   6 2    f (2)  0   2m  2  0 
Vậy m  1 hoặc 1
 0  6 2  m  10  6 2 là đáp số của bài toán. 30
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Ví dụ 4. Cho hàm số 3 2
y x  2mx  (m  3)x  4 (C ) , điểm K (1;3) và đường thẳng (d ) : y x  4 . Tìm các m
giá trị của m để (d ) cắt (C ) tại ba điểm phân biệt (
A 0; 4), B, C sao cho tam giác KBC có diện tích bằng 4 . m Giải:
+) Phương trình hoành độ giao điểm của (d ) và (C ) : m 3 2
x  2mx  (m  3)x  4  x  4 (1) 2
x(x  2mx m  2)  0  x  0   2
f (x)  x  2mx m  2  0 (2) 
+) (d ) cắt (C ) tại ba điểm phân biệt  (1) có ba nghiệm phân biệt m
 (2) có hai nghiệm phân biệt khác 0 2
 '  m m  2  0 m  ( ;  1  )  (2; )     (3)
f (0)  m  2  0 m  2     ( A 0; 4)  x x  2  m
+) Ta có B(x ; x  4) với x , x là nghiệm của (2) nên 1 2 (4) 1 1 1 2
x x m  2  C
 (x ; x  4) 1 2  2 2 Ta có 2 2
BC  (x x )  (x x )  2 x x 2 1 2 1 2 1
Phương trình BC (hay chính là phương trình (d ) ) viết lại: x y  4  0 1 3  4
Suy ra d (K, BC)   2 2 1 1 +) Ta có : S  4 
.d (K , BC).BC  4 
. 2. 2 x x  4 KBC 2 1 2 2 2 2
 (x x )  16  (x x )  4 x x  16 (5) 2 1 1 2 1 2 m  2 
Thay (4) vào (5) ta được: 2 2
4m  4(m  2)  16  m m  6  0   m  3 
Kết hợp với điều kiện (3) ta được đáp số của bài toán là m  3 . 31
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Ví dụ 5. Cho hàm số 3
y x  3x 1 (C ) , đường thẳng (d ) : y mx m  3 .Tìm m để (d ) cắt (C ) tại ba m m
điểm phân biệt M (1;3), N , P sao cho tiếp tuyến của (C ) tại N và P vuông góc với nhau. m Giải:
+) Phương trình hoành độ giao điểm của (d ) và (C ) : m 3
x  3x  1  mx m  3 3
x  (m  3)x m  2  0  x  1  2
 (x 1)(x x m  2)  0   2
f (x)  x x m  2  0 (2) 
+) (d ) cắt (C ) tại ba điểm phân biệt  (1) có ba nghiệm phân biệt m
 (2) có hai nghiệm phân biệt khác 1  9
  4m  9  0 m       4 (3) f ( 1  )  m  0  m  0  M ( 1  ;3)  x x  1
+) Ta có N (x ; y ) với x , x là nghiệm của (2) nên 1 2 (4) 1 1 1 2  
x x  m  2  P(x ; y ) 1 2  2 2
+) Tiếp tuyến của (C ) tại N và P vuông góc với nhau khi và chỉ khi: m 2 2
y '(x ).y '(x )  1
  (3x  3)(3x  3)  1 1 2 1 2 2 2 2
 9 (x x )  (x x ) 1  1  2 2
 9 ( x x )  (x x )  2x x  1  1  1 2 1 2   1 2 1 2 1 2   (5) 3   2 2
Thay (4) vào (5) ta được: 2
9 (m  2) 1 2(m  2) 1  1  2  
 9m  18m 1  0  m  3 3   2 2
Kết hợp điều kiện (3) ta được đáp số bài toán là m  3 32
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
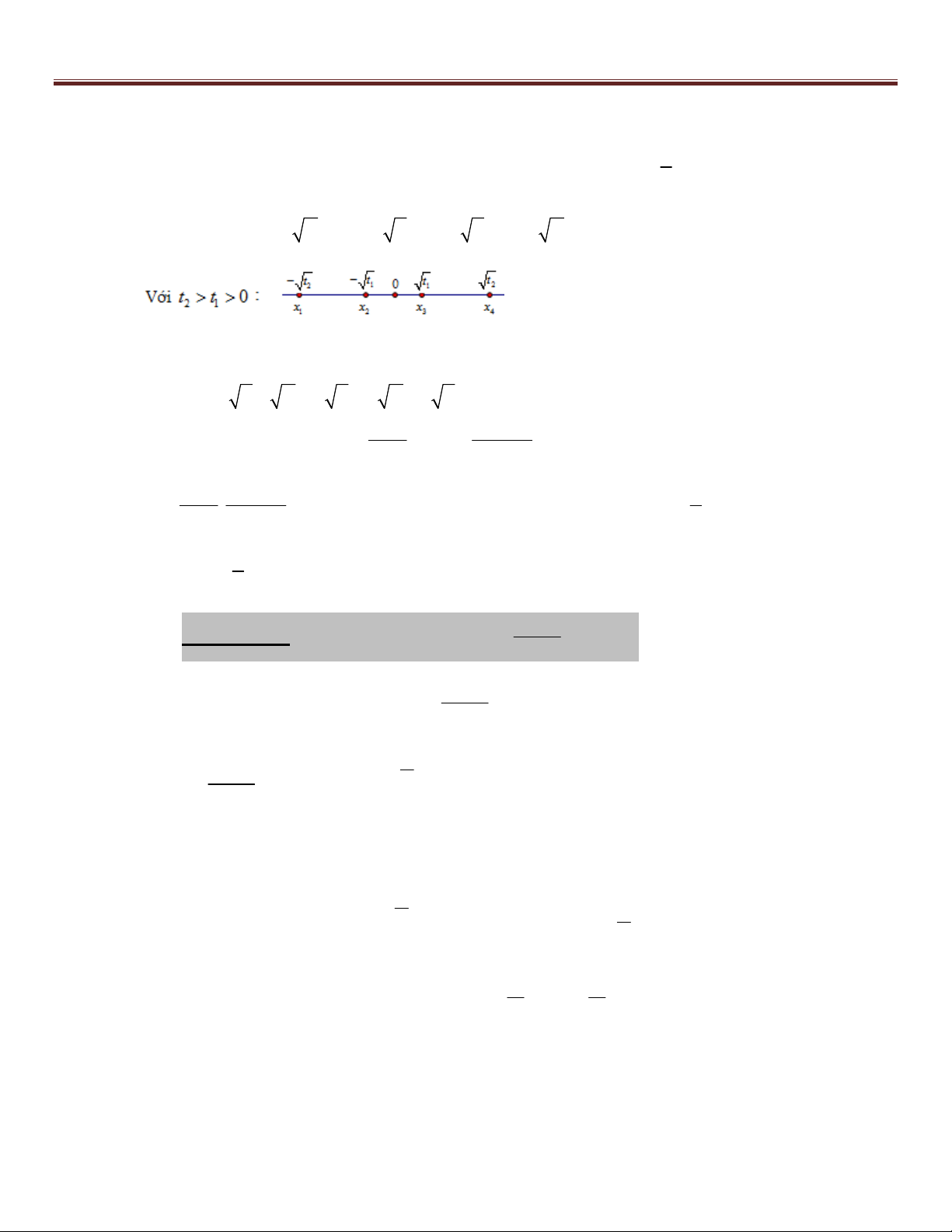
Trường hợp 2: g(x) là hàm trùng phương và đường thẳng y q .
Bước 1: Phương trình hoành độ giao điểm : 4 2
g(x)  q ax bx c  0 (1) Bước 2: Đặt 2
t x , khi đó (1) có dạng: 2
f (t)  at bt c  0 (2)
Bước 3: (Biện luận số giao điểm – giả sử a không chứa tham số (a  0) )
+) Nếu không cắt (n  0)  (1) vô nghiệm   0 (2) v« nghiÖm       0 hoặc  b cm D
(2) cã nghiÖm t t  0  0 S    0; P   0 1 2   a a
+) Nếu cắt tại một điểm (n  1)  (1) có một nghiệm   0; f (0)  0 
 (2) có hai nghiệm t t  0    m D 1 2 b 1 S    0   a
+) Nếu cắt tại hai điểm phân biệt (n  2)  (1) có hai nghiệm phân biệt ac  0 
(2) cã hai nghiÖm tr¸i dÊu   0       m D
(2) cã nghiÖm kÐp d­¬ng 2  b   0   2a
+) Nếu cắt tại ba điểm phân biệt (n  3)  (1) có ba nghiệm phân biệt   0; f (0)  0 
 (2) có hai nghiệm t t  0    m D 2 1 b 3 S    0   a
+) Nếu cắt bốn điểm phân biệt (n  4)  (1) có bốn nghiệm phân biệt   0 
 (2) có hai nghiệm t t  0    m D 2 1 b c 4 S    0; P   0   a a
Bước 4: (Dành cho trường hợp n  4 ) x   t  1,2 1 b c +) Ta có 
với t t   và t t  (3) 1 2 1 2 x   t a a 3,4 2  33
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
+) Cắt nghĩa (*) (sử dụng (3) hoặc kết hợp kiến thức hình học phẳng) ta được: m D
h(m)  0 (hoặc 4 ( h m)  0, h( )
m  0...)  m   Kết luận.
Chú ý: Nếu a chứa tham số , ta xét thêm trường hợp a  0 .
Ví dụ 1. Cho hàm số 4 2 3 2
y x  2mx m m có đồ thị là (C ) , m là tham số. Tìm m để đồ thị hàm số (C ) m m
không có điểm chung với trục hoành. Giải:
+) Phương trình hoành độ giao điểm của (C ) và trục hoành là: 4 2 3 2
x  2mx m m  0 (1) m +) Đặt 2
t x , khi đó (1) có dạng: 2 3 2
t  2mt m m  0 (2)
+) (C ) không có điểm chung với trục hoành khi và chỉ khi phương trình (1) vô nghiệm  (2) vô nghiệm m
hoặc có hai nghiệm âm (t t  0) hay ta có điều kiện: 1 2 2 3
 '  2m m  0 m  2   2 3 
  '  2m m  0 m  2      m  2 
S  2m  0 m  0    3 2       m  1 P m m 0  
Vậy đáp số của bài toán là m  2 .
Ví dụ 2. Cho hàm số 4 2
y x mx m 1 có đồ thị (C ) , m là tham số thực. m
Tìm m để (C ) cắt trục hoành tại bốn điểm phân biệt sao cho độ dài đoạn thẳng AB  1. Trong đó , A B là m
hai giao điểm có hoành độ dương của (C ) với trục hoành . m
Giải: Phương trình hoành độ giao điểm của đồ thị (C ) và trục hoành: 4 2
x mx m 1  0 m (1) t  1 Đặt 2
t x , t  0 ; khi đó (1) có dạng: 2
t mt m 1  0   (2) t m 1 
Đồ thị (C ) cắt trục hoành tại bốn điểm phân biệt, khi phương trình (1) có bốn nghiệm phân biệt, tương đương mm 1  1 m  2
(2) có hai nghiệm phân biệt dương     (3) m 1  0 m  1   34
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Khi đó hai giao điểm có hoành độ dương của đồ thị (C ) và trục hoành là: (
A 1; 0), B( m 1; 0) . mm 1 1  1  m 1  2 m  5 Khi đó 2
AB  1  AB  1 2
 ( m 1 1)  1        m 1 1  1    m 1  0  m  1 
Kết hợp với điều kiện (3) ta được giá trị m cần tìm là: m  5
Ví dụ 3 (D – 2009). Cho hàm số 4 2
y x  (3m  2)x  3m có đồ thị là (C ) , m là tham số. m
Tìm m để đường thẳng y  1
 cắt đồ thị (C ) tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2. m Giải:
+) Phương trình hoành độ giao điểm của (C ) và đường thẳng y  1  là: m 4 2 4 2
x  (3m  2)x  3m  1  x  (3m  2)x  3m  1  0 (1) t  1 +) Đặt 2
t x , khi đó (1) có dạng: 2
t  (3m  2)t  3m 1  0   (2) t  3m 1 
+) Đường thẳng y  1
 cắt đồ thị (C ) tại bốn điểm phân biệt đều có hoành độ nhỏ hơn 2 , khi và chỉ khi : m
(1) có bốn nghiệm phân biệt nhỏ hơn 2  (2) có hai nghiệm dương phân biệt nhỏ hơn 4 3m 1  1 m  0    0  1  4   1   m  1 0 3m 1 4       3
Nhận xét: Ở ví dụ trên ta đã kết hợp đồng thời Bước 3 và Bước 4.
Ví dụ 4. Cho hàm số 4 2
y x  2(m 1)x  2m 1 (C ) . Tìm m để đồ thị (C ) cắt trục hoành tại bốn điểm m m
phân biệt có hoành độ lập thành cấp số cộng. Giải:
+) Phương trình hoành độ giao điểm của (C ) và trục hoành là: 4 2
x  2(m  1)x  2m 1  0 (1) m +) Đặt 2
t x , khi đó (1) có dạng: 2
t  2(m 1)t  2m 1  0 (2)
+) (C ) cắt trục hoành tại bốn điểm phân biệt khi và chỉ khi phương trình (1) có bốn nghiệm phân biệt m 35
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 2  '  m  0 m  0  
 (2) có hai nghiệm dương phân biệt  S  2(m 1)  0   1 (3) m   P 2m 1 0      2 
+) Khi đó (1) có nghiệm x   t x   t x t x t 1 2 2 1 3 1 4 2
Vì tính đối xứng nên x , x , x , x theo thứ tự là cấp số cộng khi : 1 2 3 4
x x  2x   t t  2 t t  3 t t  9t 2 4 3 1 2 1 2 1 2 1 m 1 9(m 1)
Kết hợp với t t  2(m 1) , suy ra: t  và t  . Khi đó : 1 2 1 5 2 5 m 1 9(m 1) 4
t t  2m 1  .  2m 1 2
 9m  32m 16  0  m  4 hoặc m   (thỏa mãn (3) ) 1 2 5 5 9 4
Vậy m  4 hoặc m   là giá trị cần tìm. 9 ax b
Trường hợp 3: g(x) là hàm phân thức y và n  2 .
cx d ax b
Bước 1: Phương trình hoành độ giao điểm của y
và y px q : cx dd ax b x   
px q   c cx d 2
f (x)  a x b x c  0 (1)  1 1 1
Bước 2: Hai đồ thị cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình a  0;   0 1 d
(1) có hai nghiệm phân biệt khác 
hay ta có điều kiện:   dm Dc f   0      c   (
A x ; px q) b c
Bước 3: Ta có hai giao điểm 1 1  với 1 x x   ; 1 x x  (2)
B(x ; px q) 1 2 1 2  a a 2 1 1 1
Cắt nghĩa (*) (sử dụng (2) hoặc kết hợp kiến thức hình học phẳng) ta được: m D
h(m)  0 (hoặc (
h m)  0, h(m)  0...)  m  Kết luận. 36
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 2x 1
Ví dụ 1. Cho hàm số y
(C) . Tìm các giá trị m để đường thẳng y mx m 1 cắt (C) tại hai điểm x 1
phân biệt A và B sao cho OAB là tam giác có trọng tâm thuộc đường thẳng x y  2  0 (O là gốc tọa độ). Giải:
Phương trình hoành độ giao điểm của (C) và y mx m 1 là: 2x 1 x  1
mx m 1   2 x 1
f (x)  mx  3x m  0 (1) 
Đường thẳng y mx m 1 cắt (C) tại hai điểm phân biệt A và B , khi và m  0 
chỉ khi phương trình (1) có hai nghiệm phân biệt, khác 1 2
   9  4m  0  m  0 (2)  f (1)  3  0  3 Hai giao điểm (
A x ; mx m 1) , B(x ; mx m 1) với x x  1 1 2 2 1 2 m
Suy ra trọng tâm G của tam giác OAB được xác định:  x x 1 1 2 x   G   3 m  1 2m 1    G ;   (
m x x )  2m  2 2m  1  m 3 1 2   y   G   3 3
Khi đó OAB là tam giác, có trọng tâm thuộc đường thẳng d : x y  2  0 khi và chỉ khi: 0  m 1 O   AB  m  1 3    1 2m 1    m  (thỏa mãn) 2 G d   2  0 
2m  5m  3  0   2 m 3 3
Vậy, giá trị cần tìm là: m  2 2x  2
Ví dụ 2. Cho hàm số y
(C) . Tìm m để đường thẳng (d ) : y  2x m cắt đồ thị hàm số (C) tại 2 x 1 điểm phân biệt ,
A B sao cho AB  5 . 37
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 Giải: 2x  2 x  1 
Phương trình hoành độ giao điểm của (C) và (d ) là:
 2x m   2 x 1
f (x)  2x mx m  2  0 (1) 
Đường thẳng (d ) cắt (C) tại hai điểm phân biệt A và B , khi và chỉ khi phương trình (1) 2
  m  8m 16  0
có hai nghiệm phân biệt, khác 1  
m  4  4 2 hoặc m  4  4 2 (2) f (1)  6  0  Hai giao điểm (
A x ; 2x m) , B(x ; 2x m) 1 1 2 2 m m  2
Với x , x là nghiệm của (1) nên ta có: x x   và x x  (3) 1 2 1 2 2 1 2 2 Theo đề ra: 2 2 2
AB  5  AB  5  (x x )  4(x x )  5 2 2
 (x x )  1  (x x )  4x x  1 (*) 2 1 2 1 2 1 1 2 1 2 2 mm  10
Thay (3) vào (*) ta được: 2
 2(m  2)  1  m  8m  20  0  
(thỏa mãn điều kiện (2) ) 4 m  2  
Vậy m  10 hoặc m  2  . 2mx  3
Ví dụ 3. Cho hàm số y
(C ) , m là tham số thực. x 1 m
Tìm m để đường thẳng y  2x  3 cắt đồ thị hàm số (C ) tại hai điểm phân biệt A và B sao cho đường m
thẳng trung trực của đoạn thẳng AB đi qua giao điểm hai đường tiệm cận của đồ thị hàm số (C ) . m Giải:
Phương trình hoành độ giao điểm của (C ) và đường thẳng y  2x  3 m là: x  1   x  1  2mx 3 x  0  2x  3     (1) 2  x 1
2x  (2m 1)x  0  2m 1 x    2
Đường thẳng y  2x  3 cắt đồ thị (C ) tại hai điểm phân biệt A và B , khi và chỉ khi (1) có hai nghiệm phân m  2m 1  1  0 m    2    2  2m  1  biệt, khác 1     (2) , khi đó ( A 0; 3  ), B ; 2m  2   2m 1 3   2  1    m     2   2 38
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
Tiệm cận tiệm cận đứng x  1
 ; Tiệm cận ngang y  2m nên giao điểm hai tiệm cận là I (1; 2m)
Cách 1: I thuộc đường trung trực của AB khi và chỉ khi : 2 2
IA IB IA IB 2  2m  3 2m  3  2 1 5 2  2  1 (2m  3) 
 4  (2m  3)  4      m   hoặc m    2  2m  3  2   2 2 5
Kết hợp với với điều kiện (2) ta được m   là giá trị cần tìm. 2
 2m 1 2m  5 
Cách 2: Gọi M là trung điểm của AB khi đó M ;    4 2   
Đường thẳng trung trực d của AB đi qua M có véctơ pháp tuyến n u
 (1; 2) nên có phương trình: d AB  2m 1   2m  5  x   2 y
 0  4x  8 y 10m 19  0      4   2  5
Có I d  4
  8.2m 10m 19  0  m  
, thỏa mãn điều kiện (2) ) 2 5 Vậy m   là giá trị cần tìm. 2 2x 1
Ví dụ 4 (B – 2010). Cho hàm số y
(C) . Tìm m để đường thẳng y  2  x m C x 1
cắt đồ thị hàm số ( )
tại hai điểm phân biệt ,
A B sao cho tam giác OAB có diện tích bằng 3 . Giải: 2x 1 x  1 
+) Phương trình hoành độ giao điểm:
 2x m   2 x 1
f (x)  2x  (m  4)x 1 m  0 (1)  2
  m  8  0
+) Đường thẳng y  2  x m
cắt đồ thị (C) tại hai điểm phân biệt, khi và chỉ khi:   m f ( 1  )  1   0  +) Ta có hai giao điểm ( A x ; 2  x  )
m , B(x ; 2
x m) với x , x là nghiệm của (1) nên ta có: 1 1 2 2 1 2 m  4 1 m x x  và x x  (2) 1 2 2 1 2 2 m
+) Đường thẳng AB viết lại thành: 2x y m  0  d ( , O AB)  5 39
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 2 5(m  8) Với (2) ta có: 2 2 2
AB  (x x )  4(x x )  5 (x x )  4x x   2 1 2 1 1 2 1 2   2 2 1 m m  8 Khi đó: S
d (O, AB).AB  , suy ra: OAB 2 4 2 m m  8 4 2 2 2
 3  m  8m  48  0  (m  4)(m 12)  0  m  2  4 Vậy m  2  . x 1
Ví dụ 5 (A – 2011). Cho hàm số y
(C) . Chứng minh rằng với mọi m đường thẳng y x m luôn 2x 1
cắt đồ thị hàm số (C) tại hai điểm phân biệt A và B . Gọi k , k lần lượt là hệ số góc của các tiếp tuyến với 1 2
(C) tại A và B . Tìm m để tổng k k đạt giá trị lớn nhất. 1 2 Giải:  1  x 1 x
+) Phương trình hoành độ giao điểm:
x m   2 2x 1 2
f (x)  2x  2mx  (m 1)  0 (1)  2 2
  m  2m  2  (m 1) 1  0  +) Xét hệ:   1  1 , đúng với m    f    0      2  2 1
Suy ra (1) luôn có hai nghiệm phân biệt khác
hay với mọi m đường thẳng y x m luôn cắt đồ thị hàm số 2
(C) tại hai điểm phân biệt (đpcm).
+) Gọi x , x lần lượt là hoành độ của hai giao điểm ,
A B với x , x là nghiệm của (1) thỏa mãn: 1 2 1 2 m 1
x x  m và x x   1 2 1 2 2 2 2 1 1
(2x 1)  (2x 1)
Khi đó ta có: k k y '(x )  y '(x ) 1 2      1 2 1 1 2 2 (2x 1) (2x 1) 1 2
(2x 1)(2x 1) 1 2 2 2
4(x x )  8x x  4(x x )  2 1 2 1 2 1 2   2 2  4
m  8m  6  4(  m 1)  2  2 
4x x  2(x x )  2 1 1 2 1 2
Suy ra k k lớn nhất bằng 2 khi m  1. 1 2 40
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 Bài toán 3.2
Nội dung bài toán : Cho hàm số y f ( x) (C) .
1. Khảo sát và vẽ đồ thị (C) của hàm số trên.
2. Biện luận theo m số nghiệm thực của phương trình: g(x, m)  0 (*)
Cách giải chung:
1. Ta vẽ được đồ thị (C) (xem lại phần khảo sát hàm số).
2. Ta thực hiện theo các bước sau:
+) Chuyển (*) về dạng : f (x)  h(m) (2*)
+) Khi đó số nghiệm của (2*) chính là số giao điểm của đồ thị hàm số (C) với đường thẳng y h(m) .
+) Trên cùng hệ trục tọa độ đã vẽ đồ thị (C) (vẽ được ở câu 1), ta vẽ thêm đường thẳng y h(m) có phương
vuông góc với trục Oy (song song hoặc trùng với Ox ).
+) Từ số giao điểm chung của hai đồ thị, ta suy ra số nghiệm của (*) và đưa ra kết luận.
Ví dụ 1. Cho hàm số 4 2
y x  4x 1 (C) .
1. Khảo sát và vẽ đồ thị (C) của hàm số trên. 1
2. Biện luận theo m số nghiệm thực của phương trình: 4 2 
x x m  0 . 4 Giải:
1. Bạn đọc tự làm và ta được đồ thị (C) như sau: 41
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 1
2. Ta có phương trình: 4 2 4 2 
x x m  0  x  4x  1  4m 1 (1) 4
Số nghiệm của phương trình (1) chính là số giao
điểm của đồ thị (C) và đường thẳng y  4m 1
(có phương vuông góc với Oy )
Do đó dựa vào đồ thị ta có:
+) Nếu 4m 1  3  m  1
 thì phương trình vô nghiệm.
+) Nếu 4m 1  3  m  1
 thì phương trình có 2 nghiệm phân biệt. +) Nếu 3
  4m 1  1  1  m  0 thì phương trình có 4 nghiệm phân biệt.
+) 4m 1  1  m  0 thì phương trình có 3 nghiệm phân biệt.
+) 4m 1  1  m  0 thì phương trình có 2 nghiệm phân biệt. m  1 Vậy, ta có m  1
 : Phương trình vô nghiệm; 
: Phương trình có 2 nghiệm phân biệt. m  0 
m  0 : Phương trình có 3 nghiệm phân biệt; 1
  m  0 : Phương trình có 4 nghiệm phân biệt.
Nhận xét: Ngoài cách giải trên ta có thể giải theo Bài toán 3.1 ở Trường hợp 2.
Ví dụ 2 (A – 2002). Cho hàm số 3 2
y   x  3x (C) .
1. Khảo sát và vẽ đồ thị (C) của hàm số trên.
2. Tìm m để phương trình: 3 2 3 2
x  3x m  3m  0 có 3 nghiệm phân biệt.
Giải: 1. Bạn đọc tự khảo sát và vẽ được đồ thị như sau: 42
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
2. Xét phương trình 3 2 3 2
x  3x m  3m  0 (1) Cách 1: Ta có 3 2 3 2
(1)  x  3x  m  3m (2)
Số nghiệm của (2) chính là số giao điểm của đồ thị (C) và đường thẳng 3 2
y  m  3m
(có phương vuông góc với trục Oy )
Nên dựa vào đồ thị ta thấy phương trình (1) có 3 nghiệm khi và chỉ khi: 3 2
0  m  3m  4 (*) Cách 1.1: Xét hàm 3 2 f ( )
m  m  3m có đồ thị giống (C) (biến là m )  1   m  3
Do đó dựa vào đồ thị ta có : (*)  f ( ) m  (0; 4)   m  0; m  2  3 2 2 
m  3m  0 
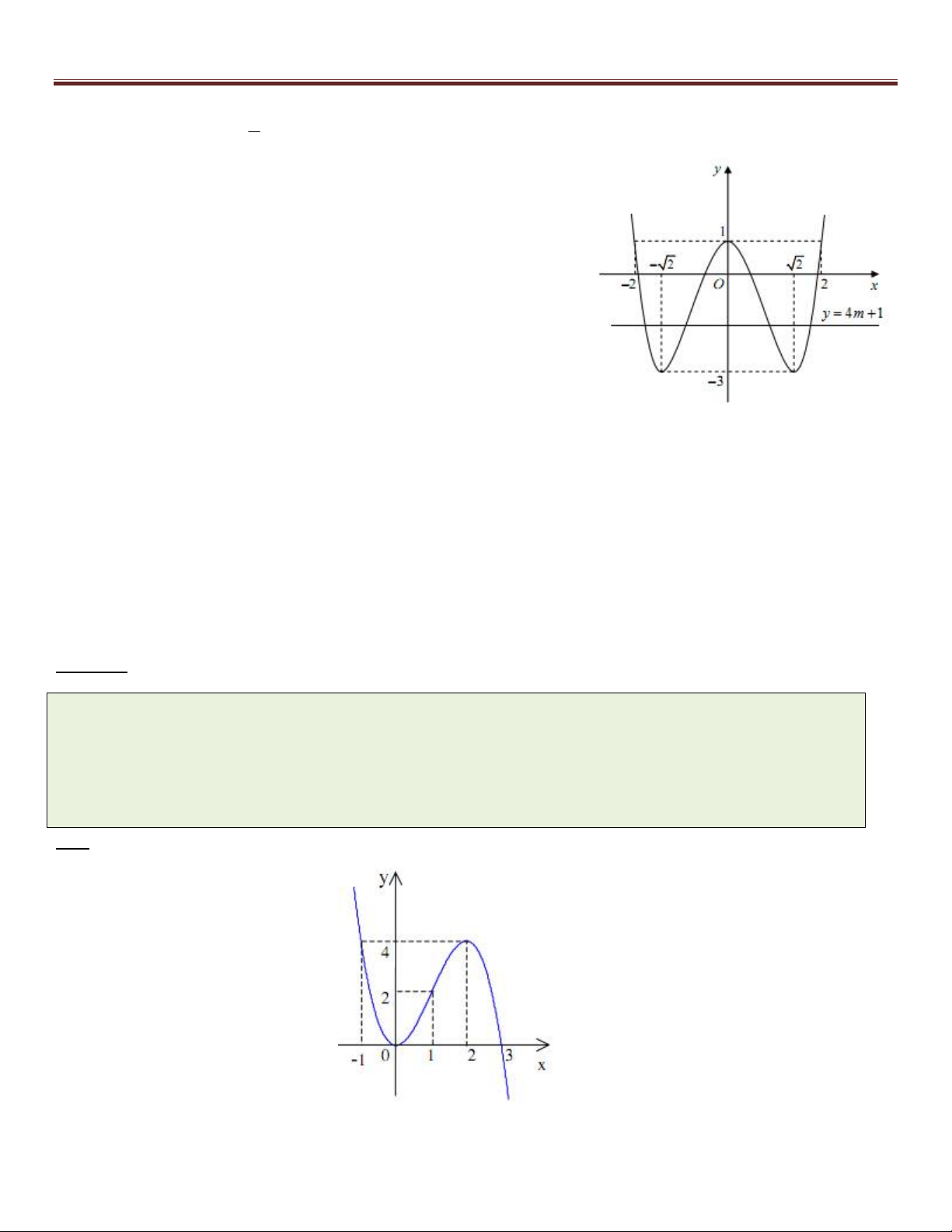
m (m  3)  0
Cách 1.2: Ta có (*)     3 2 2
m  3m  4  0 
(m 1)(m  2)  0  0  m  3 1  m  3     2  m  1  m  0; m  2  
Cách 2: Ta có : 2 2
(1)  ( x m) x  (m  3)x m  3m  0    x m   2 2
f (x)  x  (m  3)x m  3m  0 (2) 
(1) có 3 nghiệm phân biệt khi và chỉ khi (2) có hai nghiệm phân biệt khác m 2 
  3m  3m  9  0  1   m  3     2
f (m)  3m  6m  0 m  0; m  2   43
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 Bài toán 3.3
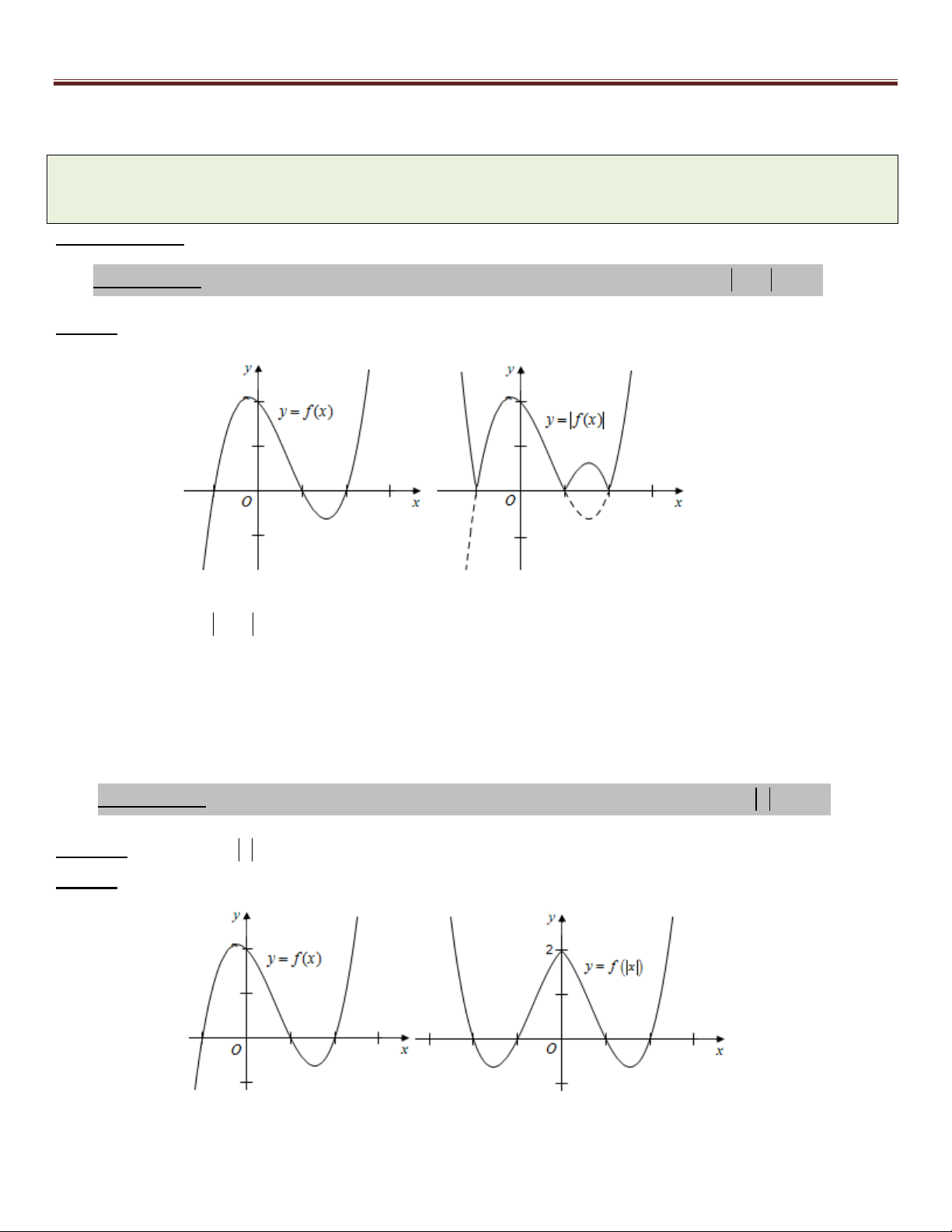
Nội dung bài toán : Dựa vào đồ thị hàm số y f ( x) (C) hãy suy ra đồ thị hàm số chứa trị tuyệt đối.
Cách giải chung:
Trường hợp 1: Dựa vào đồ thị hàm số y f ( x) (C) , hãy suy ra đồ thị hàm số y f (x) (C ) 1 Cách vẽ:  f (x) khi f (x)  0 (1) (C ) :
y f (x) 
. Do đó đồ thị (C ) gồm hai phần: 1
 f (x) khi f (x)  0 (2) 1 
+) Phần (1) : là phần không nằm phía dưới trục hoành của đồ thị (C) .
+) Phần (2) : là phần đối xứng của phần dưới trục hoành của (C) qua trục Ox .
Trường hợp 2: Dựa vào đồ thị hàm số y f ( x) (C) , hãy suy ra đồ thị hàm số y f ( x ) (C ) 2
Nhận xét : (C ) : y f ( x ) là hàm số chẵn nên (C ) nhận Oy làm trục đối xứng. 2 2
Cách vẽ: 44
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3  f (x) khi x  0 (1)
(C ) : y f ( x ) =
. Do đó đồ thị (C ) gồm hai phần 2
f (x) khi x  0 (2) 2 
+) Phần (1) : Phần đồ thị (C) nằm bên phải trục Oy .
+) Phần (2) : Phần đồ thị lấy đối xứng qua Oy của phần (1) .
Nhận xét: Ngoài 2 trường hợp trên chúng ta có thể gặp các dạng:
*) Dựa vào đồ thị hàm số y f (x)  u(x).v(x) (C) , suy ra đồ thị hàm số y u(x) .v(x) (C ) 3
*) Dựa vào đồ thị hàm số (C) : y f (x) suy ra đồ thị các hàm số sau:
+) (C ) : y f (x) (Trường hợp 4) 4
+) (C ) : y f ( x ) (Dựa vào Trường hợp 2 sau đó đến Trường hợp 1) 5
+) (C ) : y f ( x ) ( Dựa vào Trường hợp 2 sau đó đến Trường hợp 4) 6
+) (C ) : y f ( x ) ( Dựa vào TH2 sau đó đến TH1 và cuối cùng là TH4)”. 7
Song vì xác suất xuất hiện các dạng toán này trong đề thi là rất thấp, nên tác giả không đề cập trong cuốn sách này. 1 1
Ví dụ 1. Cho hàm số 4 2 y x x  2 4 2
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 4 2 x  2x  8
2. Tìm m để phương trình
 1 có đúng 5 nghiệm thực phân biệt. 4 2 m  2m  9 Giải: 1 1
1. Bạn đọc tự làm câu này, ta được đồ thị của hàm số 4 2 y x x  2 : 4 2 45
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 4 2 x  2x  8 4 2 1 1 m  2m  9 2. Ta có: 4 2 4 2
 1  x  2x  8  m  2m  9 4 2  x x  2  (*) 4 2 m  2m  9 4 2 4 1 1 4 2 x
x  2  f (x)  khi f (x)  0 1 1   4 2 Ta có: 4 2 y x x  2 =  4 2  1 1 4 2   x
x  2   f (x) khi f (x)  0      4 2 
Do đó đồ thị hàm số sẽ được vẽ như sau: 1 1 4 2 m  2m  9
Số nghiệm của (*) chính là số giao điểm của đồ thị hàm số 4 2 y x
x  2 và y  4 2 4 4 2 m  2m  9
có phương vuông góc với trục Oy . Nên để phương trình có đúng 5 nghiệm thực thì:  2 (2*) 4 (2*)  4 2 2 2 2
m  2m 1  0  (m 1)  0  m  1  m  1. Vậy m  1
 là giá trị cần tìm.
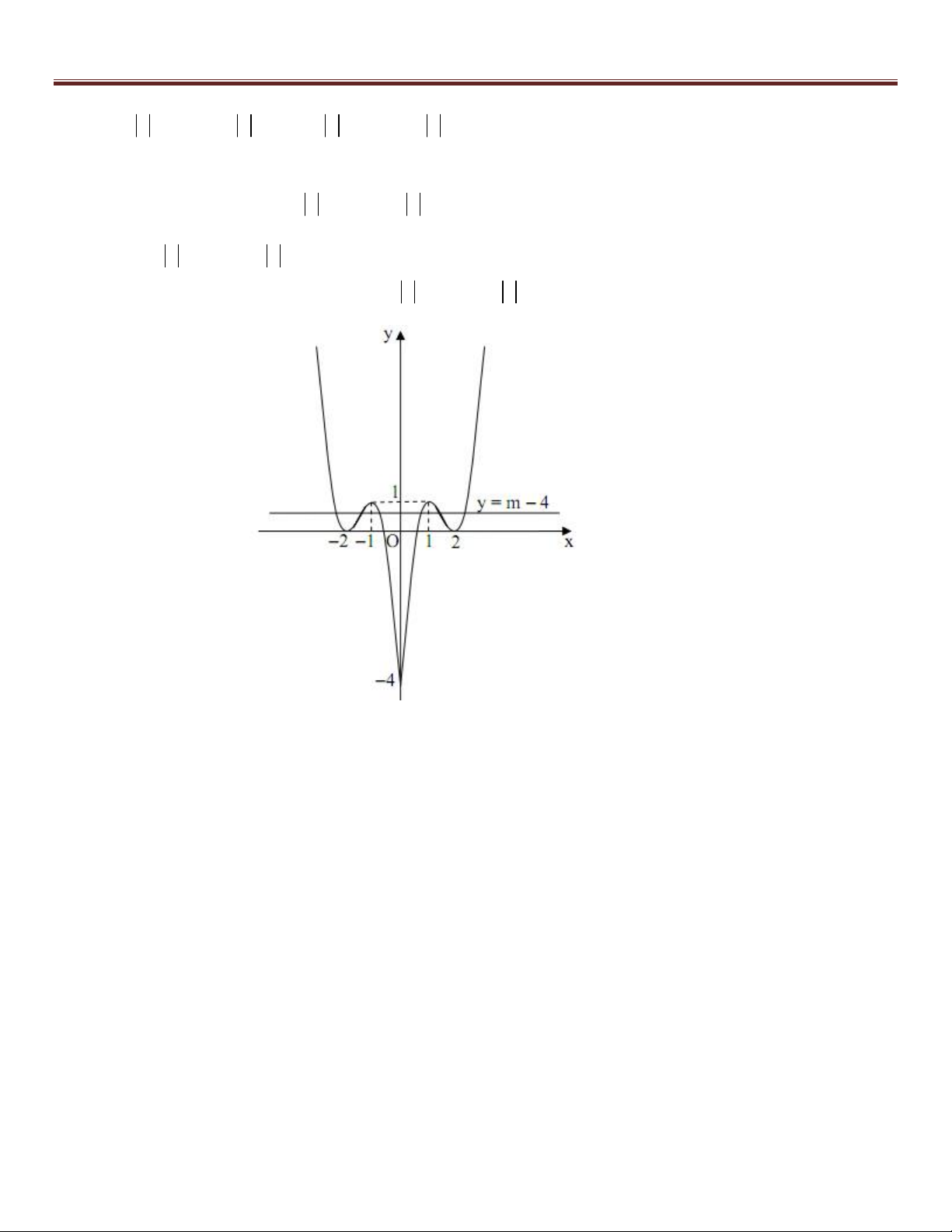
Ví dụ 2 (B – 2009). Cho hàm số 4 2
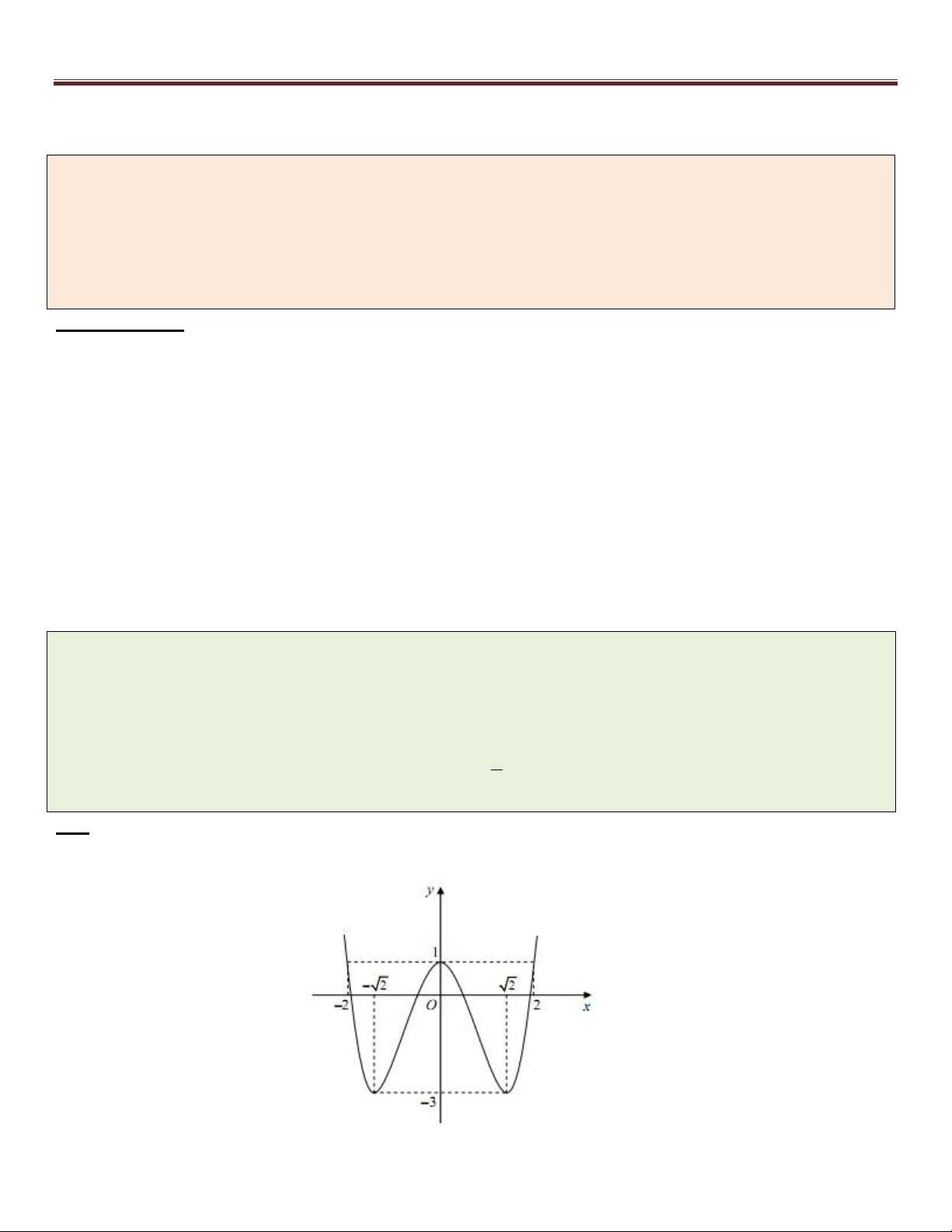
y  2x  4x (C)
1. Khảo sát và vẽ đồ thị (C) của hàm số trên.
2. Với giá trị nào của m, phương trình 2 2
x x  2  m có đúng 6 nghiệm thực phân biệt .
Giải: 1. Bạn đọc tự làm câu này, ta được đồ thị của hàm số 4 2
y  2x  4x : 46
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 2. Ta có 2 2 4 2
x x  2  m  2x  4x  2m . Phương trình có đúng 6 nghiệm thực phân biệt khi và chỉ khi đường
thẳng y  2m (có phương vuông góc với trục Oy ) cắt đồ thị hàm số 4 2
y  2x  4x tại 6 điểm phân biệt. 4 2
2x  4x f (x)  khi f (x)  0  Biến đổi 4 2
y  2x  4x      4 2
2x  4x    f (x) khi f (x)  0 
Do đó ta có đồ thị hàm hàm số 4 2
y  2x  4x và đường thẳng y  2m :
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi và chỉ khi: 0  2m  2  0  m  1.
Vậy giá trị m cần tìm là 0  m  1 .
Ví dụ 3 (A – 2006). Cho hàm số 3 2
y  2x  9x 12x  4 (C) .
1. Khảo sát và vẽ đồ thị (C) của hàm số trên. 3
2. Tìm m để phương trình sau có 6 nghiệm phân biệt : 2
2 x  9x 12 x m .
Giải: 1. Bạn đọc tự làm câu này, ta được đồ thị của hàm số 3 2
y  2x  9x 12x  4 : 47
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 3 3 2. Ta có 2 2
2 x  9x 12 x m  2 x  9x 12 x  4  m  4
Phương trình có đúng 6 nghiệm thực phân biệt khi và chỉ khi đường thẳng y m  4 (có phương vuông góc với 3
trục Oy ) cắt đồ thị hàm số 2
y  2 x  9x  12 x  4 tại 6 điểm phân biệt. 3 Hàm số 2
y  2 x  9x  12 x  4 là hàm chẵn , nên đồ thị nhận Oy là trục đối xứng. Do đó từ đồ thị hàm số 3
(C) vẽ ở cầu 1, ta suy ra đồ thị hàm số : 2
y  2 x  9x  12 x  4
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi và chỉ khi: 0  m  4  1  4  m  5 .
Vậy giá trị m cần tìm là 4  m  5 . 48
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
BÀI TOÁN 4: Bài toán tìm điểm thuộc đồ thị
Nội dung bài toán : Tìm điểm M thuộc đồ thị y f (x) thỏa mãn điều kiện (*) cho trước.
Cách giải chung:
Bước 1: Do M thuộc đồ thị y f (x) nên gọi M ( ; m f (m)) .
Bước 2: Cắt nghĩa điều kiện (*) để thiết lập phương trình : g(m)  0  m  tọa độ điểm M . x  2
Ví dụ 1(A, A1 – 2014). Cho hàm số y
(C) . Tìm tọa độ điểm M thuộc đồ thị (C) sao cho khoảng x 1
cách từ M đến đường thẳng y   x bằng 2 . Giải:  m  2 
+) Do M  (C) nên gọi M ; m   với m  1  m 1 
+) Đường thẳng y   x được viết lại thành : x y  0 () m  2 m  2 m 1
m  2m  4  0 m  0 M (0; 2  ) Khi đó 2 d (M , )  2 
 2  m  2  2 m 1       2 2 m  2m  0 m  2  M ( 2  ;0)   
Vậy M (0; 2) hoặc M ( 2  ; 0) . x  2
Ví dụ 2. Tìm trên đồ thị (C) : y
những điểm M sao cho khoảng cách từ M đến tiệm cận đứng bằng x  3
1 khoảng cách từ M đến tiệm cận ngang. 5  m  2 
Giải: +) Do M  (C)  M ; m   với m  3 .  m  3 
Tiệm cận đứng có phương trình: x  3 hay x  3  0 ( ) 1
Tiệm cận ngang có phương trình: y  1 hay y 1  0 ( ) 2 1 1 m  2 m  4 M (4;6)
+) d (M ,  ) 
d (M ,  )  m  3  . 1 2  (m  3)  1   1 2   5 5 m  3 m  2 M (2; 4)  
Vậy M (4; 6) hoặc M (2; 4) . 49
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 2x 1
Ví dụ 3. Cho hàm số y
có đồ thị (C) . Tìm tọa độ hai điểm ,
A B trên đồ thị (C) sao cho tiếp tuyến x 1
của đồ thị (C) tại A và B song song với nhau và AB  8 .  2a 1   2b 1  a b
Giải: Do A  (C), B  (C) nên gọi A a;   và B b;   với  .  a 1   b 1  a  1;b  1 
Tiếp tuyến của đồ thị (C) tại A và B song song nên suy ra: 1  1 1
y '(a)  y '(b)   (với y '  ) 2 2
 (a 1)  (b 1)  a b (loại) hoặc b  2  a (1) . 2 2 (a 1) (b 1) 2 (x 1) 2  2a 1 2b 1  Mặt khác: 2 2
AB  8  AB  8  (a b)    8   (2)  a 1 b 1  4
a  2  b  0
Thay (2) vào (1) ta được: 2 2 4(a 1) 
 8  (a 1)  1  2  (a 1)
a  0  b  2 
+) Với a  2, b  0  (
A 2;3), B(0;1) (thử lại thỏa mãn điều kiện song song).
+) Với a  0, b  2  (
A 0;1), B(2;3) (thử lại thỏa mãn điều kiện song song). Vậy (
A 2;3), B(0;1) hoặc (
A 0;1), B(2;3) .
Ví dụ 4. (HSG – Hà Nội – 2013). Cho hàm số 3
y x  3x  4 có đồ thị (C) . Tìm các điểm M , N cùng  1 
nằm trên (C) sao cho điểm I  ; 2 
 là trung điểm của đoạn thẳng MN .  2  Giải: Do 3
M  (C)  M ( ;
m m  3m  4)
x  2x x  1   mN I M
Ta có I là trung điểm của MN nên: 3 
N (1 m; m  3m) 3 3
y  2 y y
 4  (m  3m  4)  m  3mN I Mm  1
M (1; 2), N ( 2  ; 2) Mặt khác : 3 3
N  (C)  m  3m  ( 1   m)  3( 1   m)  4 2
m m  2  0     m  2 M ( 2  ; 2), N (1; 2)  
Vậy M (1; 2) và N ( 2  ; 2) hoặc M ( 2  ;2) và N(1; 2) .
Chú ý: Ngoài cách phát biểu trên, bài toán có thể hỏi theo cách diễn đạt sau:  1 
“Tìm trên (C) hai điểm M , N đối xứng với nhau qua điểm I  ;2   ”.  2  50
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 2x 1
Ví dụ 5. Cho hàm số y
có đồ thị (C) . Tìm các điểm M thuộc đồ thị (C) sao cho khoảng cách từ x 1
giao điểm I của hai đường tiệm cận của (C) tới tiếp tuyến của (C) tại M là lớn nhất. Giải:
+) Tiệm cận đứng, ngang lần lượt của (C) là x  1
 và y  2  I ( 1  ; 2)  2m 1 
+) Do M  (C)  M ; m   với m  1
 . Khi đó phương trình tiếp tuyến của (C) tại M là:  m 1  3 2m 1 2 2 y  .(x  ) m
 3x  (m 1) y  2m  2m 1  0 () 2 (m 1) m 1 2 2 3
  2(m 1)  2m  2m 1 6 m 1
+) Ta có: d (I , )   4 9  (m 1) 4 9  (m 1) 6 6    6 9 2 9 2  (m 1) 2 2. .(m 1) 2 (m 1) (m  1) 9 m  1   3  d (M , )  6 khi 2 2
 (m  1)  (m 1)  3   max 2 (m 1) m  1   3  Vậy M  1
  3; 2  3  hoặc M  1
  3; 2  3  thỏa mãn bài toán. 51
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3
BÀI TOÁN 5: Tính đơn điệu của hàm số Bài toán 5.1
Nội dung bài toán : Tìm m để hàm số y f (x, m) đồng biến (hoặc nghịch biến) trên  .
Cách giải chung:
Yêu cầu của bài toán f '(x, m)  0 (hoặc f '(x, m)  0 ) (*) đúng x
   . Khi đó có 2 cách giải quyết: a  0 a  0 Cách 1: Nếu 2 f '( ,
x m)  ax bx c thì (*)   ( hoặc   )   0    0 
và xét thêm điều kiện a  0 nếu a chứa m .
Cách 2: Nếu (*)  h(m)  g(x) (hoặc h(m)  g( x) ) thì bài toán tương đương:
h(m)  max g(x) ( hoặc h(m)  min g(x) ) x x 1
Ví dụ. Cho hàm số 3 2 y
(m 1)x  (m  3)x  (m  5)x 1. Tìm m để hàm số đồng biến trên tập xác định. 3 Giải:
Tập xác định: D  
Yêu cầu của bài toán tương đương với: 2
y '  (m  1)x  2(m  3)x m  5  0 với x    (*) Cách 1:
+) Với m  1: (*)  8x  4  0 với x
   (vô lí). m  1
a m 1  0  1 +) Với m  1  : (*)     1  m
 '  12m  4  0 m  3    3
Cách 2: Ta có 2 2 (*)  (
m x 1)  x  6x  5 với x    .
+) Với x  1 ta được: 0  1  2 với x    (luôn đúng) 2 x  6x  5
+) Với x  1 thì (*)  m  
g(x) với x
  1  m  max g(x) 2 (x 1) x (  ;1)(1;) 52
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 2 x  6x  5 8(x  2)
Xét g(x)  
với x  1  g '(x) 
; g '(x)  0  x  2  2 (x 1) 3 (x 1)
lim g(x)  1 và lim g(x)   . Do đó ta có bảng biến thiên sau: x x 1  1 1
Khi đó ta có max g(x)   m x (  ;1)(1;) 3 3 1 Vậy m  là giá trị cần tìm. 3 Nhận xét:
Ở ví dụ trên, cách giải 1 cho ta lời giải ngắn gọn song có một hạn chế nó chỉ sử dụng với dạng tam thức bậc
hai. Còn ở cách giải 2 tuy khá dài (cụ thể trong bài toán này) nhưng nó có thể giải quyết được cả dạng
f '(x, m) không phải là tam thức bậc 2, nhưng sẽ gặp “khó khăn” nếu tham số m không phải là bậc nhất. Như
vậy mỗi cách có những ưu và nhược điểm khác nhau. Tùy vào số liệu cụ thể của từng bài toán giúp ta chọn ra
cách giải tối ưu nhất. Bài toán 5.2
Nội dung bài toán : Tìm m để hàm số y f (x, m) đồng biến (hoặc nghịch biến) trên (a;b)
( với a có thể  và b có thể  ).
Cách giải chung:
Yêu cầu của bài toán f '(x, m)  0 (hoặc f '(x, m)  0 ) (*) đúng x
  (a;b) . Ta có 2 cách giải quyết:
Cách 1: Nếu (*)  h(m)  g(x) (hoặc h(m)  g( x) ) thì bài toán tương đương: (
h m)  max g(x) ( hoặc (
h m)  min g(x) ) x (  a;b) x (  a;b) Cách 2: Nếu 2 f '( ,
x m)  ax bx c thì ta sử dụng định lý thuận và đảo về dấu tam thức bậc 2
(xem thêm phần Chú ý). 53
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 Chú ý:
*) Vì trong chương trình chính khóa đang học, định lý đảo về dấu tam thức bậc 2 đã bị lược bỏ. Vì vậy ta hạn
chế sử dụng Cách 2 . Nếu muốn sử dụng chúng ta sẽ phải “lách” bằng cách chuyển về so sánh với số 0 hoặc
sử dụng công thức nghiệm trực tiếp (sẽ thấy rõ hơn qua các ví dụ minh họa ). u( x)
*) Với trường hợp hàm số dưới dạng phân thức y
thì hàm số đồng biến (hay nghịch biến) trên (a;b) v(x)
u '( x).v( x)  v '( x).u(x) y ' 
 0 ( 0) với x   (a;b) 2 v (x)
h(x)  u '(x).v(x)  v '(x).u(x)  0 ( 0) , x   (a;b)
 v(x)  0
*) Nếu biểu thức định dấu của y ' không chứa x thì trong điều kiện (*) không có dấu "  " .
*) Ưu và nhược điểm của Cách 1 và Cách 2:
+) Cách 1: Với f (x, m) có dạng bất kì nhưng chỉ giải quyết “tốt” nếu m là bậc nhất.
+) Cách 2: Với m có bậc bất kì nhưng f (x, m) phải là đa thức bậc 2 và giải quyết
“nhẹ nhàng” khi (*) đúng với x   R .
+) Cách 1 thường sử dụng trong các bài toán phức tạp mà khó giải quyết với Cách 2
Ví dụ 1 (A,A1 – 2013). Cho hàm số 3 2
y   x  3x  3mx 1 (1), với m là tham số thực.
Tìm m để hàm số (1) nghịch biến trên khoảng (0; ) .
Giải: Yêu cầu của bài toán 2  y '  3
x  6x  3m  0 với x   (0; ) 2
f (x)  x  2x m  0 với x   (0; ) (*) Cách 1: (*) 2
m x  2x g(x) với x
  (0; )  m min g(x) x (  0;)
Ta có g '(x)  2x  2 ; g(x)  0  x  1 . Ta có bảng biến thiên: Khi đó m min g( x)  1  . Vậy m  1
 là đáp số của bài toán. x (  0;) 54
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 Cách 2: Đồ thị hàm số 2
f (x)  x  2x m là một parabol có a  1  0 nên có bề lõm quay lên trên.
Vì vậy (*) xảy ra khi và chỉ khi :
Trường hợp 1: f (x) nằm phía trên hoặc tiếp xúc với trục Ox ( f (x)  0 với x    )
Khi đó phương trình f (x)  0 thỏa mãn:   1 m  0  m  1 
Trường hợp 1 Trường hợp 2 Trường hợp 2:
f (x) cắt trục Ox tại các điểm có hoành độ x , x sao cho: x x  0 ( với x
  (0; ) thì f (x)  0 ) 1 2 1 2   1 m  0 
Khi đó phương trình f (x)  0 thỏa mãn: S  2  0 (vô nghiệm).
P  m  0 
Vậy giá trị m thỏa mãn yêu cầu bài toán là m  1  .
Nhận xét: Ta có thể nhận thấy ngay được ở Trường hợp 2 không thể xảy ra được vì đỉnh của parabol là: I (1; 1
  m) thuộc bên phải trục Oy . mx  4
Ví dụ 2. Cho hàm số y
với m là tham số thực. Tìm m để hàm số : x m
1. đồng biến trên khoảng (2; ) . 2. nghịch biến trên khoảng ( ;  1) . 2 m  4
Giải: Ta có y ' 
với x  m . Dấu của y ' là dấu của 2
m  4 (không chứa x) nên để hàm số: 2 (x m) 2 m  4
1. đồng biến trên khoảng (2; ) thì: y  0, x   (2; )   0, x   (2; ) 2 (x m) 2 m  4  0
m  2  m  2
m  2  m  2        m  2 m  (2; ) m  2 m  2   
Vậy hàm số đồng biến trên (2; ) khi m  2 . 55
Nguyễn Thanh Tùng 0947141139 – 0925509968 htpp://www.facebook.com/giaidaptoancap3 2 m  4
2. nghịch biến trên khoảng ( ;
 1) thì: y  0,x  ( ;1  )   0, x   ( ;1  ) . 2 (x m) 2 m  4  0  2   m  2  2   m  2        2   m  1  m  ( ;  1) m  1 m  1    
Vậy hàm số nghịch biến trên ( ;  1) khi 2   m  1  .
Ví dụ 3. Cho hàm số 3 2 2
y  x  (m 1)x  (2m  3m  2)x 1 với m là tham số thực.
Tìm m để hàm số nghịch biến trên (2; ) .
Giải: Yêu cầu bài toán 2 2  y '  3
x  2(m 1)  2m  3m  2  0, x   (2; ) 2 2
f (x)  3x  2(m 1)  (2m  3m)  0, x   (2; ) (*) Ta có 2 2 2
 '  (m 1)  3(2m  3m  2)  7(m m  1)  0,m  
Suy ra f (x)  0 luôn có hai nghiệm phân biệt x , x với m
   . Do đó: (*)  x x  2 1 2 1 2 1 m   ' 
 2   '  m  5 3 2 2
7(m m 1)  (m  5) 2
6m  3m 18  0     m  5  0  m  5    3   m  2 3   2    m  2 . 2 m  5   3 Vậy 
m  2 là đáp số của bài toán. 2
Chuyên đề nhỏ này được trích sơ lược từ bản thảo cuốn sách của tác giả:
10 CHUYÊN ĐỀ BÁM SÁT ĐỀ THI TRUNG HỌC PHỔ THÔNG MÔN TOÁN
Mọi ý kiến, xây dựng góp ý các bạn gửi theo địa chỉ: Nguyễn Thanh Tùng
Địa chỉ: Nhà số 9 – Ngõ 880 – Bạch Đằng – Hai Bà Trưng – Hà Nội
E-mail: giaidaptoancap3@yahoo.com
CẢM ƠN CÁC BẠN ĐÃ QUAN TÂM VÀ ĐỌC TÀI LIỆU ! 56