KHOẢNG CÁCH TỪ ĐIỂM ĐẾN MẶT PHẲNG - PHẦN 1 BUỔI 1

KHOẢNG CÁCH TỪ ĐIỂM ĐẾN MẶT PHẲNG (BUỔI 1 DẠNG 1:
KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN “MẶT PHẲNG CHỨA ĐƯỜNG CAO”
Phương pháp xác định khoảng cách
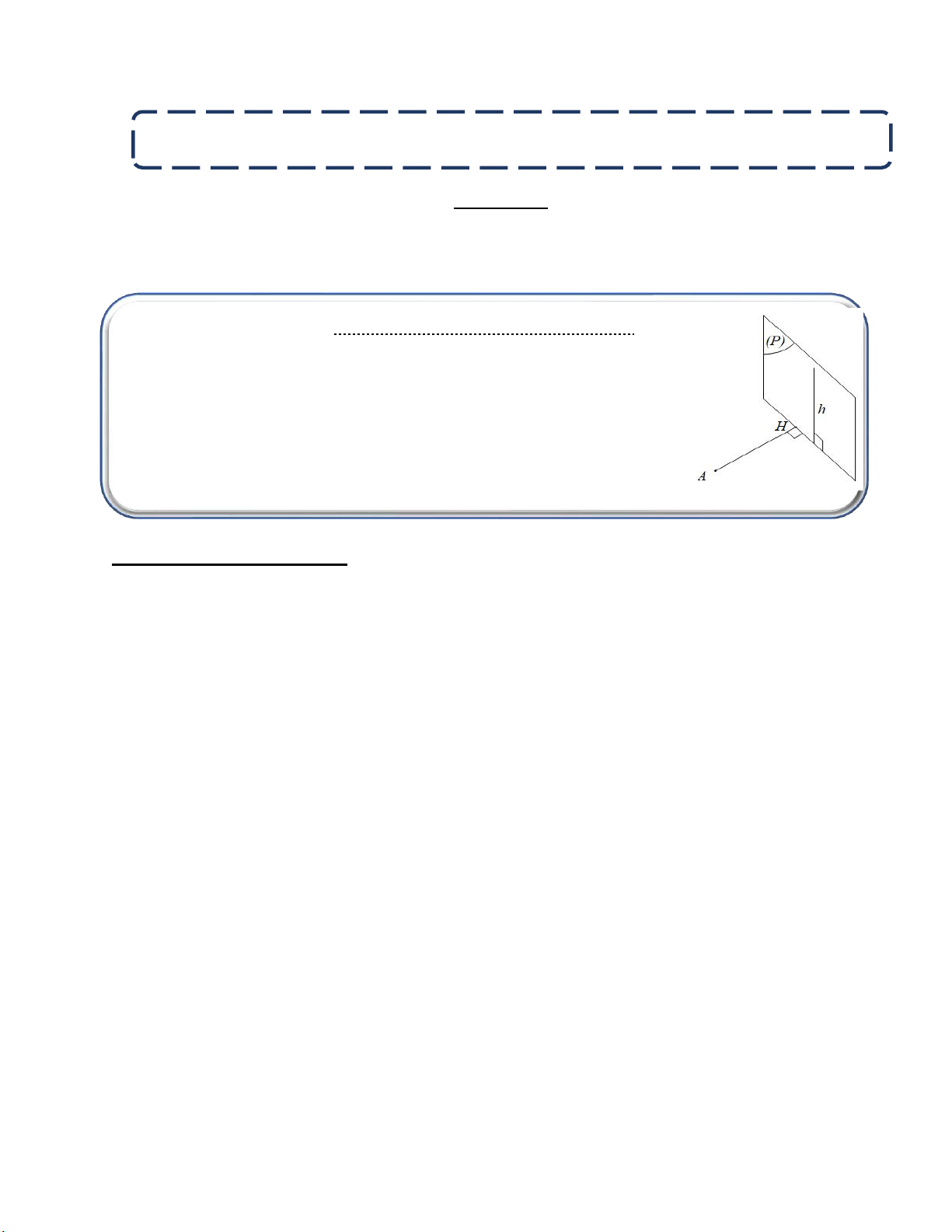
 Dựng khoảng cách từ A đến mặt phẳng P
Ta kẻ AH vuông góc với đường dưới đáy của mặt phẳng
 AH  P
 AH  d A;P
I. BÀI T숃⌀P MINH HỌA
Câu 1: Cho hình chóp S.ABC có SA  đáy. Tam giác ABC vuông cân tại B với AB  BC  a
a) Tính khoảng cách từ C tới (SAB)
b) Tính khoảng cách từ B tới (SAC)
Câu 2: Cho hình chóp S.ABCD có các cạnh bên SA  SB  SC  SD . Biết rằng đáy là hình chữ
nhật với AB  a, AD  2a . Tính khoảng cách từ điểm A đến mặt phẳng SBD
Câu 3: Cho hình lập phương ABCD.ABCD có cạnh bằng 3 . Tính khoảng cách từ B đến mặt phẳng ACCA
Câu 4: Cho hình lăng trụ đứng ABC.A'B'C ' có đáy ABC là tam giác đều với AB  4 . Khoảng
cách từ C đến mặt phẳng  ABB' A' bằng
Câu 5: Cho hình chóp S.ABCD, có SA  đáy. Đáy là hình chữ nhật cạnh tâm O, có
AB  a, BC  2a .
G là trọng tâm tam giác ABC
a) Tính khoảng cách từ O tới (SAD)
b) Tính khoảng cách từ G tới (SAB) DẠNG 2:
KHOẢNG CÁCH TỪ “ CHÂN VUÔNG GÓC ” ĐẾN MẶT PHẲNG BẤT KÌ
Phương pháp xác định khoảng cách
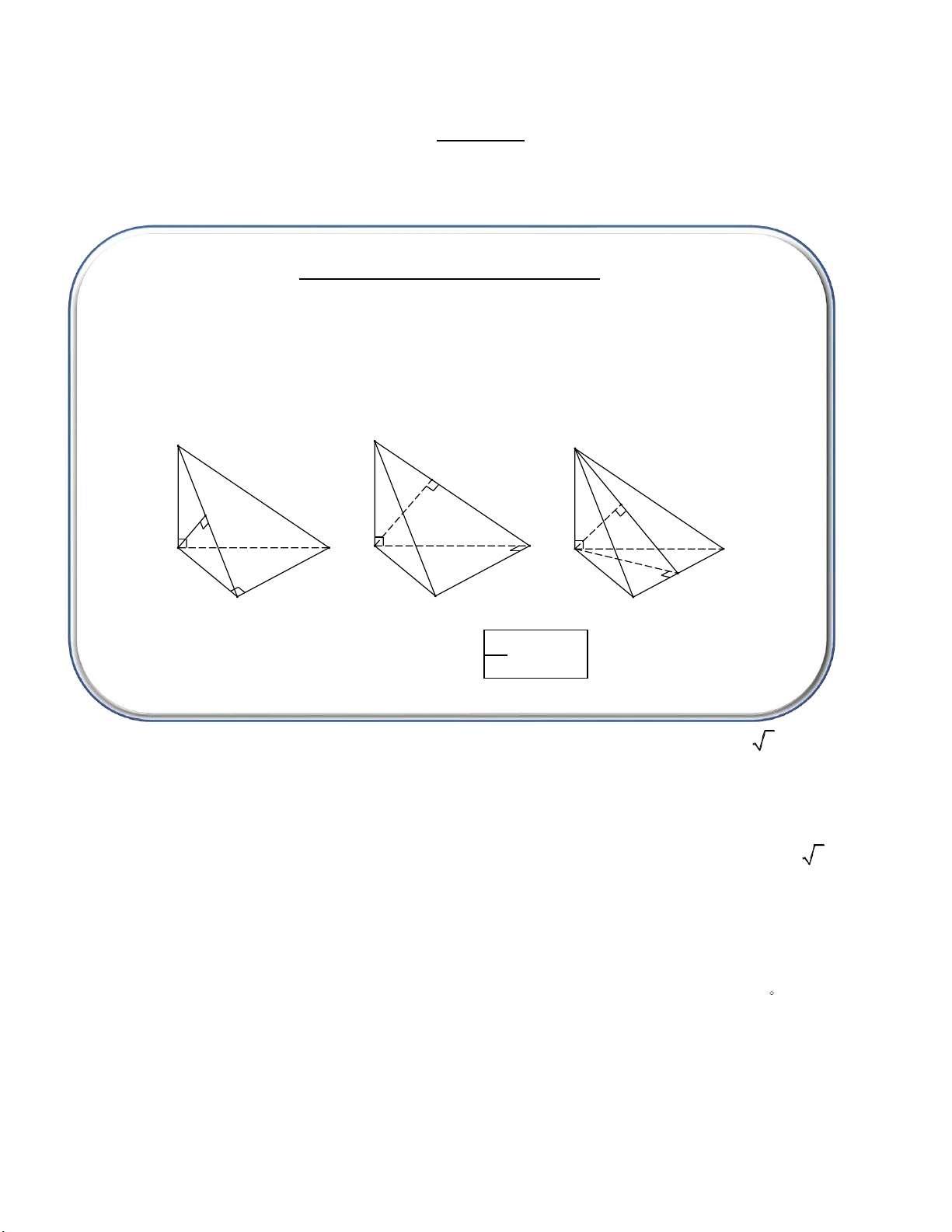
 Cho hình chóp S.ABC có SA   ABC
- Dựng d  A;SBC
- A: đại diện chân đường cao
- SBC: đại diện cho mặt phẳng bất kì S S S H H H A C A C A C M B B B
Ghi nhớ công thức: 1  1  1 h2 a2 b2
I. BÀI T숃⌀P MINH HỌA
Câu 1: Cho hình chóp S.ABCD có SA  đáy. Đáy là hình chữ nhật có AB  a, AD  a 3. Biết rằng SA  2a
a) Tính khoảng cách từ A tới (SCD)
b) Tính khoảng cách từ A tới (SBC)
Câu 2: Cho hình chóp S.ABC có SA  đáy. Đáy là tam giác vuông tại A với AB  a, AC  a 3 .
Cho cạnh bên SB  2a . Tính khoảng cách từ A tới (SBC)
Câu 3: Cho hình chóp đều S.ABCD có chiều cao a, AC  2a . Tính khoảng cách từ tâm O của đáy
đến mặt phẳng SCD
Câu 4: Cho hình chóp S.ABCD có SA  đáy. Đáy là hình thoi cạnh a với góc ABC  60 . Biết
SA  a . Tính khoảng cách từ A tới (SBC)
Câu 5: Cho hình chóp đều S.ABC có cạnh đáy bằng 2a . Biết góc giữa cạnh bên và đáy bằng 450
Tính khoảng cách từ tâm O của đáy tới (SBC)
Câu 6: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Tam giác SAB là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy. Gọi H là trung điểm của AB . Tính khoảng cách từ H đến mặt phẳng SBC ?
Câu 7: Cho hình chóp S.ABCD có hình chiếu của S lên đáy là trọng tâm H của tam giác ABC, cho
SH  2a . Đáy là hình vuông cạnh a tâm O
a) Tính khoảng cách từ H tới (SOA)
b) Tính khoảng cách từ H tới (SCD)
Document Outline

• I. BÀI T숃⌀P MINH HỌA
  • KHOẢNG CÁCH TỪ “ CHÂN VUÔNG GÓC ” ĐẾN MẶT PHẲNG BẤ