Kĩ năng sử dụng máy tính Casio trong giải toán – Bùi Thế Việt

Trong các dụng cụ học tập được phép mang vào phòng thi trong các kỳ thi đại học, kỳ thi THPT Quốc Gia thì máy tính cầm tay là dụng cụ không thể thiếu giúp chúng ta tính toán nhanh chóng. Tuy nhiên, máy tính cầm tay sẽ là trợ thủ đắc lực để giải toán. 

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

104 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
(Bùi Thế Việt – THPT Chuyên Thái Bình)
Trong các dụng cụ học tập được phép mang vào phòng thi trong các kỳ thi
đại học, kỳ thi THPT Quốc Gia thì máy tính cầm tay là dụng cụ không thể
thiếu giúp chúng ta tính toán nhanh chóng.
Tuy nhiên, máy tính cầm tay sẽ là trợ thủ đắc lực để giải toán, đặc biệt là
giải Phương Trình, Hệ Phương Trình, Bất Phương Trình, ... hay kể cả là Bất
Đẳng Thức.
Mình (tác giá - Bùi Thế Việt) là một người rất đam mê với những kỹ năng,
thủ thuật sử dụng máy tính cầm tay trong giải toán. Mình đã áp dụng nó
vào đề thi THPT Quốc Gia 2015. Chỉ trong 3 – 5 phút, mình đã đưa ra lời
giải chính xác cho câu Phương Trình Vô Tỷ và cũng chỉ gần 1 giờ, mình đã
hoàn thành xong bài làm với điểm số tuyệt đối, là 1 trong 85/671.149 người
được điểm tối đa.
Vậy sử dụng sao cho hiệu quả ? Hãy đến với chuyên đề Kỹ Năng Sử Dụng
CASIO Trong Giải Toán.
Chuyên đề này chưa phải là tất cả những Thủ Thuật mà mình đưa tới cho
bạn đọc. Tuy không nhiều nhưng các thủ thuật dưới đây sẽ mang tới sự kỳ
diệu mà chiếc máy tính CASIO có thể mang lại.
Chuyên đề sẽ giới thiệu 8 thủ thuật CASIO hay dùng trong việc giải toán :
Thủ thuật sử dụng CASIO để rút gọn biểu thức
Thủ thuật sử dụng CASIO để giải phương trình bậc 4
Thủ thuật sử dụng CASIO để tìm nghiệm phương trình
Thủ thuật sử dụng CASIO để phân tích đa thức thành nhân tử một ẩn
Thủ thuật sử dụng CASIO để phân tích đa thức thành nhân tử hai ẩn
Thủ thuật sử dụng CASIO để giải hệ phương trình
Thủ thuật sử dụng CASIO để tích nguyên hàm, tích phân
Thủ thuật sử dụng CASIO để giải bất đẳng thức
KỸ NĂNG SỬ DỤNG CASIO
TRONG GIẢI TOÁN
THỦ THUẬT 1 : THỦ THUẬT SỬ DỤNG CASIO
ĐỂ RÚT GỌN BIỂU THỨC
Bài 1: Giải Phương trình:
2
2 1 3 1 0x x x
(đề thi Đại Học khối D năm 2006)
Điều kiện xác định:



1
;
2
x
.
Thông thường với dạng toán này, ta sẽ bình phương hoặc đặt ẩn để đưa về
phương trình bậc 4.
Hướng 1 : Bình phương hai vế :
2
22
4 3 2
2 1 3 1 0
2 1 3 1 0
6 11 8 2 0
x x x
x ( x x )
x x x x
Hướng 2 : Đặt ẩn phụ : Đặt
2
1
2 1 0
2
t
t x x
ta được :
2
2
22
4
2
2 1 3 1 0
11
3 1 0
22
1
0
44
x x x
tt
t
t
tt

❓ Làm thế nào để rút gọn biểu thức một cách nhanh chóng :
2
2 2 4
2
1 1 1
31
2 2 4 4
t t t
t t t

Nếu bạn chưa biết Thủ Thuật Sử Dụng Casio Để Rút Gọn Biểu Thức,
chắc hẳn bạn sẽ phải kỳ công ngồi nháp. Và đôi khi bạn cũng sẽ gặp những
sai sót.
Tuy nhiên, nếu bạn sử dụng CASIO, mọi chuyện sẽ đơn giản hơn bạn nghĩ.
▶ Ý tưởng :
Ta sẽ xét biểu thức khi
1000x
. Dựa vào chữ số hàng đơn vị, hàng nghìn,
hàng triệu, hàng tỷ, ... ta sẽ tìm được hệ số tương ứng với hệ số tự do, hệ số
x
, hệ số
2
x
, hệ số
3
x
, ...
Ví dụ xét :
32
f(x) ax bx cx d
thì
9
(1000) 00 00 00 10f a b c d a
Suy ra
9
1000
10
f
a
.
❓ Làm thế nào để tính giá trị biểu thức khi
1000x
.
Cách nhanh nhất là sử dụng phím CALC để gán giá trị
Ví dụ khi ta nhập một biểu thức ẩn
X
, ta ấn CALC và cho
1000X
và ấn
“=” thì máy tính sẽ hiển thị kết quả của biểu thức khi
1000X
Để hiểu rõ hơn, vui lòng xem cách làm dưới đây.
▶ Thực hiện :
a) Ta muốn rút gọn biểu thức
22
2 1 3 1f(x) x ( x x )
, ta lần lượt
tính như sau:
Ta có :
11 12 4
4 9 3
4 3 6 2
4 3 2 3
4 3 2
4 3 2
1000 9 94010992 10 10
1000 5989007998 6 10 6
1000 6 10992002 11 10 11
1000 6 11 7998 8 10 8
1000 6 11 8 2
6 11 8 2
f , x
f x x
f x x x
f x x x x
f x x x x
f x x x x x
Vậy đáp số:
2
2 4 3 2
2 1 3 1 6 11 8 2x x x x x x x
.
b) Ta muốn rút gọn biểu thức
2
22
11
31
22
f x x
xx

, ta sẽ
nhân biểu thức trên với
4
để hệ số của
()fx
đều là số nguyên.
Ta có :
11
4
4
12 4
62
3
2
2
42
4
2
4
4 1000 9 99996004 10
4 1000 3996001
4 1000 4 3999
4 1000 4 4 1
1
44
10
4 10 4
4 10 4
4 4 4 1
f,
fx
f x x
f x x x
x
x
x
f x x x x
x
f xxx


Vậy đáp số:
2
2 2 4
2
1 1 1
31
2 2 4 4
xx
x
x
xx

.
▶ Phân tích hướng giải:
❓ Làm thế nào để giải quyết nốt bài toán trên ?
Hãy từ từ, đọc hết chuyên đề này rồi xem lại bài toán trên, chắc chắn bạn
đọc sẽ có cái nhìn hoàn toàn khác về những bài tập dạng này.
Hãy thử xem qua các lời giải sau :
▶ Cách 1 : Nhân liên hợp hoàn toàn:
Ta có :
2
2
2
2 1 3 1 0
1 2 2 1 1 0
2
1 2 0
2 1 1
2 1 1
1 1 0
2 1 1
2
1 1 0
2 1 1
x x x
x x x
xx
x
x
xx
x
x
x
















▶ Cách 2 : Nhân liên hợp không hoàn toàn:
Ta có :
2
2 1 3 1 0
1 2 2 1 1 0
1
2 1 1 2 1 1 2 2 1 1 0
2
1
2 1 1 2 1 1 2 2 0
2
1
2 1 1 2 1 1 1 2 1 1 0
2
12
2 1 1 1 2 1 1 0
2
2 1 1
1
2 1 1 1 2 1 1 2 2 1 1 2 0
2
x x x
x x x
x x x x
x x x
x x x x
x x x
x
x x x x




▶ Cách 3 : Phân tích thành nhân tử không hoàn toàn:
2
2 1 3 1 0
2 1 1 2 1 0
x x x
x x x x
▶ Cách 4 : Phân tích thành nhân tử hoàn toàn:
2
2
2 1 3 1 0
1
2 1 1 2 1 1 0
2
x x x
x x x
▶ Cách 5 : Bình phương hai vế:
2
2
2
2
2
2 1 3 1 0
2 1 3 1
4 2 1 0
x x x
x x x
x x x
▶ Cách 6 : Đặt ẩn phụ hoàn toàn:
Đặt
2
1
21
2
t
t x x
. Vậy ta có :
2
22
2
2
2
11
2 1 3 1 0 3 1 0
22
1
02 1 1
4
tt
x x x t
t t t

▶ Cách 7 : Đặt ẩn phụ không toàn toàn:
Đặt
21tx
. Vậy ta có :
2
22
2 1 3 1 0
10
x x x
x t x t
t x t x
▶ Cách 8 : Đặt ẩn phụ đưa về hệ phương trình:
Đặt
21yx
. Ta có hệ phương trình :
2
2
3 1 0
2 1 0
x x y
yx
Lấy
(1) (2)PT PT
ta được :
22
03 1 2 1
10
x x y y x
x y x y
8 cách làm trên tuy có khác nhau về cách trình bày nhưng về bản chất thì
giống nhau. Đó là cùng xuất phát từ một thứ gọi là “nhân tử”. Khi có nhân
tử, chúng ta biết được biểu thức nào cần nhóm để đặt ẩn phụ, nhân liên
hợp, phân tích nhân tử. Để hiểu rõ hơn, bạn đọc hãy đọc các thủ thuật tiếp
theo rồi quay lại xem bài toán này và thử làm những bài tập tương tự.
Một số bài tập tương tự :
1.
2
2 2 1 0x x x x
2.
2
2 15 2 6 11 2 1 x x x x
3.
2
24 35 4 2 7 2 x x x x
4.
2
4 13 14 4 2 3 2 x x x x
Bài 2: Giải phương trình:
2
3
4 6 3 13x x x
(đề thi thử Đại Học lần 3 khối B THPT Ngô Gia Tự – Bắc Ninh năm 2013)
Điều kiện xác định:

0,x
.
▶ Ý tưởng :
Tương tự bài 1, ta cũng sẽ sử dụng máy tính CASIO để rút gọn phương
trình bậc 4 sau :
2
2
3
4 13 36 3f x x x x


▶ Thực hiện :
Ta làm các bước như bài 1 :
Ta có :
11 12 4
4 10 9 3
4 3 6 2
4 3 2 3
4 3 2
432
1000 9 8006994 10 10
1000 1 993005999 10 20 10 20
1000 20 69940009 70 10 70
1000 20 70 59991 60 10 60
1000 20 70 60 9
1000 20 70 60 9
f , x
f x , x
f x x x
f x x x x
f x x x x
f x x x x
Kết luận :
2
2
3 4 3 2
4 13 36 3 20 70 60 9x x x x x x x


▶ Phân tích hướng giải :
Vậy bài toán đã cho chỉ đơn giản là việc giải phương trình bậc 4 :
432
20 70 60 9 0x x x x
Cách giải phương trình bậc 4 bằng máy tính cầm tay ở các thủ thuật tiếp
theo.
Ngoài ra có vô vàn cách giải khác tương tự như bài 1. Tuy nhiên chúng ta
nên để ý cách giải phương trình này bằng việc phân tích nhân tử vì đó là ý
tưởng ra đề của rất nhiều bài toán khó.
▶ Cách 1 : Bình phương hai vế:
Ta có :
2
2
3
2
3
432
2
4 13 36 3 0
20 70 60 9 0
13
4
16 0
3 13
3
6x
x x x
x x x x
x x x x
xx



▶ Cách 2 : Phân tích thành nhân tử:
Ta có :
2
2
22
4 6 3 13
3 4 3 2
x x x
x x x x
Một số bài tập tương tự :
1.
23
15 1 8 x x x x
2.
23
2 3 3 x x x x
3.
2
7
13 8 8 2 1 1 0
8
x
x x x
4.
2 2 2
4 6 1 4 1 2 x x x x x
Bài 3: Giải phương trình:
5 4 3 2
6 7 29 16 2 0x x x x x
Điều kiện xác định:
x
.
▶ Ý tưởng :
Thông thường những bài tập giải phương trình kiểu này thường có một
hướng giải nhanh gọn. Đó là “Phân Tích Thành Nhân Tử”.
Muốn phân tích được thì ta phải biết được nhân tử của bài toán.
❓ Làm thế nào để tìm ra nhân tử của bài toán ?
Bằng thủ thuật CASIO, ta dễ dàng tìm ra nhân tử của bài toán này là
2
62xx
. Nhưng để tìm được thì bạn đọc hãy đợi tới các thủ thuật sau.
Tóm lại là ta muốn tìm nhân tử còn lại của bài toán, hay chính là thương
của phép chia :
5 4 3 2
2
6 7 29 16 2
62
x x x x x
fx
xx

▶ Thực hiện:
Ta coi biểu thức
5 4 3 2
2
6 7 29 16 2
62
x x x x x
xx

chỉ là một đa thức ẩn
x
và
làm tương tự bài 1 :
93
33
3
1000 999995001 10
1000 4999 5 10 5
1000 5 1
fx
f x x
f x x
Vậy ta được :
5 4 3 2
3
2
6 7 29 16 2
51
62
x x x x x
xx
xx

▶ Phân tích hướng giải:
Sau khi chia đa thức, ta được :
5 4 3 2 3 2
6 7 29 16 2 5 1 6 2x x x x x x x x x
Để giải phương trình bậc 3 :
3
5 1 0xx
thì hãy đón xem thủ thuật giải
phương trình bậc 3 ở dưới
Vậy ta có lời giải như sau :
▶ Lời giải :
Ta có :
5 4 3 2
32
6 7 29 16 2 0
5 1 6 2 0
x x x x x
x x x x
Xét đa thức :
3
51g x x x
Vì
()gx
bậc 3 nên
( ) 0gx
có tối đa 3 nghiệm. Chỉ ra 3 nghiệm này là :
1
1 3 15
os arccos
35
2
15c
3 0








x
2
1 3 15 2
os arccos
35
2
15c
3 03






x
3
1 3 15 2
os arccos
35
2
15c
3 03






x
Bài toán được giải quyết hoàn toàn.
Hy vọng qua 3 bài toán cơ bản trên, bạn đọc hình dung được lợi ích của
việc sử dụng máy tính cầm tay trong việc rút gọn biểu thức khi giải toán.
Một số bài tập tương tự :
1.
4 3 2
2 6 2 0 x x x x
2.
5 4 2
3 2 0 x x x x
3.
5 4 3 2
2 2 5 2 4 2 0 x x x x x
4.
6 5 4 3 2
6 7 24 72 64 16 0 x x x x x x
THỦ THUẬT 2 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
TÌM NGHIỆM PHƯƠNG TRÌNH
Bài 1: Giải Bất Phương Trình:
2
300 40 2 10 1 3 10
0
1 1 2
x x x x
xx
(đề thi thử Đại Học lần 2 THPT Quỳnh Lưu 1 – Nghệ An năm 2013)
Điều kiện xác định:



13
; / 0
10 10
x
.
▶ Ý tưởng :
Ta luôn có :
13
1 1 2 1 1 2
10 10
x x x x x ;



Quan trọng nhất bây giờ là giải quyết bất phương trình :
2
300 40 2 10 1 3 10 0x x x x
Thông thường với dạng toán này, ta sẽ nhân liên hợp với nghiệm của bài
toán.
❓ Làm thế nào để tìm các nghiệm của phương trình :
2
300 40 2 10 1 3 10 0x x x x
Sử dụng phím SOLVE để tìm nghiệm, nhưng có lẽ với một số bạn, phím
SOLVE cho ta đúng một nghiệm của bài toán. Vậy với bài toán có nhiều
nghiệm thì sao ? Làm thế nào để biết bài toán chỉ có một nghiệm duy nhất ?
Để hiểu rõ hơn, bạn đọc hãy xem cách làm dưới đây :
▶ Thực hiện :
Ta viết biểu thức
2
300 40 2 10 1 3 10 0x x x x
lên máy
tính
Ấn SOLVE để tìm nghiệm, máy hỏi
?X
.
Nhập
1
10
để tìm nghiệm gần
1
10
nhất.
Máy cho nghiệm
1
0.2
5
x
Ấn SOLVE để tìm nghiệm, máy hỏi
?X
.
Nhập
3
10
để tìm nghiệm gần
3
10
nhất.
Máy cho nghiệm
1
0.2
5
x
Vậy ta có thể kết luận : Phương trình
2
300 40 2 10 1 3 10 0x x x x
có nghiệm duy nhất
1
5
x
.
▶ Phân tích hướng giải:
Khi biết
1
5
x
là nghiệm duy nhất của phương trình, ta chắc chắn sử dụng
được phương pháp nhân liên hợp. Ngoài ra, nếu bạn đọc thủ thuật giải
phương trình vô tỷ bằng CASIO, ta có thể có thêm những cách làm khác.
▶ Cách 1 : Nhân liên hợp hoàn toàn:
Ta có :
2
300 40 2 10 1 3 10 0
11
10 2 30 2 0
10 1 1 3 10 1
10 1 1
10 2 30 1 0
10 1 1 3 10 1
x x x x
xx
xx
x
xx
xx







▶ Cách 2 : Phân tích thành nhân tử:
Ta có :
2
2
300 40 2 10 1 3 10 0
300 40 3 3 10 10 1 1 0
1 3 10 30 3 10 30 3 10 1 1 0
30 3 10 30 3
1
10 2 0
1 3 10 10 1 1
30 3 10 30 2
10 1
10 2 0
1 3 10 10 1 1
2
2
1
x x x x
x x x x
x x x x
xx
x
xx
xx
x
x
x
x
x
x
x









Một số bài tập tương tự :
1.
2
2 2 2 2 1 2 0 x x x x
2.
3
2 7 2 3 3 2 5 0 x x x x
3.
2
11 12 3 2 4 1 11 2 0 x x x x x
4.
3 2 2
14 6 5 2 10 0 x x x x
Bài 2: Giải Phương Trình:
3
2 2 3 1x x x
(đề thi thử Đại Học lần 1 Khối D THPT Tuy Phước – Bình Định năm 2013)
Điều kiện xác định:

1,x
.
▶ Ý tưởng :
Tương tự bài 1, ta sẽ tìm nghiệm để nhân liên hợp thử xem.
▶ Thực hiện :
Ta viết biểu thức
3
2 2 3 1 0x x x
lên máy tính
Ấn SOLVE để tìm nghiệm, máy hỏi
?X
.
Nhập
1
để tìm nghiệm gần
1
nhất.
Máy cho nghiệm
0.541381265 x
Lưu nghiệm này vào A bằng cách ấn X + Shift STO + A
Tương tự tìm nghiệm gần
10
nhất
Máy cho nghiệm
.54138 655 12x
Lưu nghiệm này vào B bằng cách ấn X + Shift STO + B
Tương tự tìm nghiệm gần
2.5
nhất
Máy cho nghiệm
.54138 655 12x
Đây chính là nghiệm B
Vậy ta có thể kết luận : Phương trình
3
2 2 3 1 0x x x
có hai nghiệm
là
xA
và
xB
.
❓ Làm thế nào để viết nghiệm
,AB
dưới dạng vô tỷ ?
Đơn giản chỉ cần làm một trong hai cách sau :
Cách 1 : ta thấy
5
3
AB
AB


.
A,B
là nghiệm của phương trình :
2
5 3 0XX
Cách 2 : ta thấy
AB
nên ta luôn có :
2
5 37
22
A B A B
A

và
2
5 37
22
A B A B
B

Ta được 2 nghiệm của bài toán này là :
5 37
2
và
5 37
2
.
▶ Phân tích hướng giải:
❓ Làm thế nào để nhân liên hợp với nghiệm vô tỷ ?
Rất đơn giản, hãy xem cách làm dưới đây :
Ta thấy : khi
5 37
2
x
thì
3
1 86 14 37 7 37 2 2xx
Vậy ta chỉ cần nhân liên hợp
3
1 2 2xx
.
▶ Cách 1 : Nhân liên hợp hoàn toàn:
Ta có :
3
2
2
3
2
2
2
22
2 2 3 1
2 10 6 3 1 2 2
2 10 6 3 1 1 2 1
31
5 3 2 0
1 2 1
5 3 1 1 0
x x x
x x x x
x x x x x
x
xx
x
xxx
x x x xx




▶ Cách 2 : Phân tích thành nhân tử:
Ta có :
3
22
2 2 3 1
2 1 1 1 2 1 0
x x x
x x x x x x
Một số bài tập tương tự :
1.
23
16 14 2 1 0 x x x
2.
23
2 5 1 7 1 0 x x x
3.
2 4 2
5 1 1 0 x x x x
4.
4
8 4 3 3 4 3 1 0 x x x
Bài 3: Giải Phương Trình:
2
4 1 3 5 2 0x x x x
(đề thi thử Đại Học lần 1 Khối A + A1 THPT Tuy Phước – Bình Định năm 2013)
Điều kiện xác định:



5
;
2
x
.
▶ Ý tưởng :
Tương tự bài 1, ta vẫn sẽ tìm nghiệm để nhân liên hợp.
▶ Thực hiện :
Ta viết biểu thức
2
4 1 3 5 2 0x x x x
lên máy tính
Ấn SOLVE để tìm nghiệm, máy hỏi
?X
.
Nhập
10
để tìm nghiệm gần
10
nhất.
Máy cho nghiệm
0.895643923x
Lưu nghiệm này vào A bằng cách ấn X + Shift STO + A
Tương tự tìm nghiệm gần
2.5
nhất
Máy cho nghiệm
0.895643923x
Tương tự tìm nghiệm gần
6
nhất
Máy vẫn cho nghiệm
0.895643923x
Vậy ta có thể kết luận : Phương trình
2
4 1 3 5 2 0x x x x
chỉ có
nghiệm duy nhất là
xA
.
❓ Làm thế nào để viết nghiệm
A
dưới dạng vô tỷ ?
Tương tự bài 2, ta cũng sẽ tìm số vô tỷ
B
để thỏa mãn
AB
. Nhưng
B
sẽ không thỏa mãn phương trình ban đầu, mà thỏa mãn phương trình
khi đã đổi dấu trước căn. Tức
B
là nghiệm của phương trình :
2
4 1 3 5 2 0x x x x
Vậy ta sẽ đi giải phương trình
2
4 1 3 5 2 0x x x x
để tìm
B
,
giống như một hành trình để đi tìm người thân :
Ta viết biểu thức
2
4 1 3 5 2 0x x x x
lên máy tính
Ấn SOLVE để tìm nghiệm, máy hỏi
?X
.
Nhập
10
để tìm nghiệm gần
10
nhất.
Máy cho nghiệm
1.395643924 x
Lưu nghiệm này vào B bằng cách ấn X + Shift STO + B
Tương tự tìm nghiệm gần
2.5
nhất
Máy cho nghiệm
1.395643924 x
Tương tự tìm nghiệm gần
6
nhất
Máy vẫn cho nghiệm
1.395643924 x
Vậy phương trình
2
4 1 3 5 2 0x x x x
chỉ có nghiệm duy nhất là
xB
.
Để kiểm chứng
,AB
có phải “họ hàng” với nhau không, ta thành thử thấy
1
2
AB
Mà
AB
nên
2
1 21
24
A B (A B)
A


Kết luận : Nghiệm của phương trình
2
4 1 3 5 2 0x x x x
là
1 21
4
x

▶ Phân tích hướng giải:
Ta thấy : Khi
1 21
4
x

thì
1 21
5 2 2
2
xx

Vậy ta chỉ cần nhân liên hợp
5 2 2xx
.
▶ Cách 1 : Nhân liên hợp hoàn toàn:
Ta có :
2
2
2
22
4 1 3 5 2 0
4 2 5 3 5 2 2 0
4 2 5 0
5 2 2
4 2 5 3 5 2 0
3
2
x x x x
x x x x x x
xx
xx
x x x x x
x
x
x




Ta dễ dàng thấy rằng :
2
2
2
52
1 27
3 5 2 0
4 2 16
2
x
x x x x x x







Vậy bài toán được giải quyết hoàn toàn.
▶ Cách 2 : Phân tích thành nhân tử:
Ta có :
2
2
4 1 3 5 2 0
52 22 3 5 2 0
x x x x
x x x x x x
Sau đó tương tự làm như cách 1.
Một số bài tập tương tự :
1.
2
4 2 3 4 2 3 x x x x
2.
3 2 2
2 16 48 13 5 15 3 x x x x x x
3.
3 2 2
4 3 6 2 2 1 2 x x x x x x
THỦ THUẬT 3 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
GIẢI PHƯƠNG TRÌNH BẬC 4
Bài 1: Giải Phương Trình:
2
4 8 2 3 1x x x
(đề thi thử Đại Học THPT Lưu Hoàng – Ưng Hoàng – Hà Nội năm 2013)
Điều kiện xác định:



3
;
2
x
.
▶ Ý tưởng :
Ta cần giải phương trình bậc 4 sau :
22
4 8 1 2 3 0( x x ) x
▶ Thực hiện :
Sử dụng Thủ Thuật Rút Gọn Biểu Thức ta được :
2
2
4 3 2
4 8 1 2 3 0
16 64 56 14 2 0
x x x
x x x x
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được các
nghiệm được gán vào
,,A B C
như sau :
0 280776406
2 395643924
0 1043560763
A.
B.
C.

Tìm trong
,,A B C
, cặp nào là “họ hàng” với nhau bằng cách thành
thử các tổng
,, A B B C C A
:
2 114867518
5
2
0 1764203298
A B ,
BC
C A ,

Vậy
,BC
là “họ hàng” với nhau rồi.
Vậy thành thử tiếp ta thấy :
5
2
1
4
BC
BC

Suy ra
,BC
là nghiệm của phương trình :
22
51
0 4 10 1 0
24
x x x x
Sử dụng Thủ Thuật Rút Gọn Biểu Thức ta được :
4 3 2
2
2
16 64 56 14 2
4 6 2
4 10 1
x x x x
xx
xx

Kết luận :
4 3 2
22
22
16 64 56 14 2
4 6 2 4 10 1
2 2 3 1 4 10 1
x x x x
x x x x
x x x x
▶ Phân tích hướng giải:
Bằng việc sử dụng kết hợp các thủ thuật ở trên, ta có được lời giải ngắn gọn
như sau :
▶ Cách 1 : Bình phương hai vế:
Ta có :
2
2
4 3 2
2
2
2
4 8 1 2 3 0
16 64 56 14 2 0
2 2 3 1
4 8 2
4 10 1 0
31
x x x
x x x x
x x x
x x x x

▶ Cách 2 : Phân tích thành nhân tử:
Ta có :
2
2 2 2 3 2 1 2
4
3
8 2 3 1
0xx
x x x
xx
Một số bài tập tương tự :
1.
2
4 12 9 2 2 1 1 x x x x
2.
2
2 9 12 4 7 3 x x x x
3.
2
6 9 1 7 5 2 x x x x
4.
2
3 14 10 2 0 x x x
Bài 2: Giải Phương Trình:
2
2 2 4 4 2 9 16x x x
(đề thi thử Đại Học lần 3 THPT Quỳnh Lưu 1 – Nghệ An năm 2013)
Điều kiện xác định:



3
;
2
x
.
▶ Ý tưởng :
Ta lần lượt bình phương hai vế để được phương trình bậc 4 :
22
22
2
22
2
4 2 4 16 2 16 8
2 2 4 4 2 9 16
2 9 16
16 8 2 9 8 32
256 8 2 9 8 32
x x x x
x x x
x x x
x x x

Vậy công việc của chúng ta là giải phương trình bậc 4 sau :
2
22
256 8 2 9 8 32 0x x x
▶ Thực hiện :
Không như bài 1, ta có thể bỏ qua bước rút gọn biểu thức.
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được các
nghiệm được gán vào
,AB
như sau :
1 885618083
1 885618083
A.
B.

Dễ thấy
0AB
nên
,AB
rất có thể là “họ hàng” với nhau rồi.
Vậy thành thử tiếp ta thấy :
0
32
9
AB
AB


Suy ra
,AB
là nghiệm của phương trình :
22
32
0 9 32 0
9
xx
Sử dụng Thủ Thuật Rút Gọn Biểu Thức ta được :
2
22
2
2
256 8 2 9 8 32
9 16 32
9 32
x x x
xx
x
Kết luận :
2
22
22
256 8 2 9 8 32
9 32 9 16 32
x x x
x x x
▶ Phân tích hướng giải:
Ta vẫn sẽ có hai cách giải cho bài toán trên như sau :
▶ Cách 1 : Bình phương hai vế:
Ta có :
22
22
2
22
22
2
4 2 4 16 2 16 8 2 9 16
16 8 2 9 8 32
256 8 2 9 8 32
9 32 9 16 3
2 2 4 4 2 9 16
20
x x x x
x x x
x x x
xx
x x x
x
▶ Cách 2 : Phân tích thành nhân tử:
Ta có :
22
22
22
2
4 2 4 16 2 16 8
2 2 4 4 2 9 1
2 9 16
16 8 2 9 8 32
2 8 2 8 8
6
202
xx
x
xx
x x x
xx
x
x
x
x
Một số bài tập tương tự :
1.
2
3 1 6 1 9 60 29 x x x x
2.
34
2 2 2 5
5
x x x
3.
2
9
2 4 3 1 2 1
7
x x x x
4.
2
27
1 1 16
2
x x x
Bài 3: Giải Phương Trình:
3
4 1 3 2
5
x
xx
(đề thi thử Đại Học THPT Phan Bội Châu – Phú Yên năm 2013)
Điều kiện xác định:



3
;
2
x
.
▶ Ý tưởng :
Ta lần lượt bình phương hai vế để được phương trình bậc 4 :
2
2
2
5 4 1 3 2 3
169 34 50 4 1 3 2
169 34 2500 4 1 3 2
x x x
x x x x
x x x x
Vậy công việc của chúng ta là giải phương trình bậc 4 sau :
2
2
169 34 2500 4 1 3 2 0x x x x
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được 2 nghiệm
là :
3
2
A
B

Vậy nhân tử của bài toán sẽ là :
32xx
Ta cần tìm thương của biểu thức :
2
2
169 34 2500 4 1 3 2
32
x x x x
fx
xx

Tuy nhiên, sử dụng Thủ Thuật Rút Gọn Biểu Thức lại không được
ổn vì hệ số của đa thức quá to.
Nếu không gán giá trị cho
1000x
được thì ta sử dụng
lim
để
chắc chắn nhất
Cách tìm
lim
bằng máy tính CASIO chỉ đơn giản là gán cho
x
là
một số cực to. Ví dụ như
10
10x
.
Ta thấy
()fx
sẽ là một tam thức bậc 2 nên ta có thể đặt :
2
f x ax bx c
Ta tìm hệ số
,,abc
bằng cách lấy :
Tìm
a
:
2
1
x
fx
a lim
x


Tìm
b
:
2
339
x
f x ax
b lim
x

Tìm
c
:
2
1026c f x ax bx
Kết luận :
2
2
2
169 34 2500 4 1 3 2
339 1026
32
x x x x
xx
xx

▶ Phân tích hướng giải:
Lưu ý rằng :
2
339 1026 3 342x x x x
Do đó, ta cũng sẽ có hai cách giải cho bài toán trên như sau :
▶ Cách 1 : Bình phương hai vế:
Ta có :
2
2
2
2
5 4 1 3 2 3
169 34 50 4 1 3 2
169 34 2500 4 1 3 2
2 342 3 0
x x x
x x x x
x x x x
x x x
▶ Cách 2 : Phân tích thành nhân tử:
Ta có :
3
4 1 3 2
5
4 1 3 2 4 1 3 2
4 1 3 2
5
1
4 1 3 2 4 1 3 2 5 0
5
x
xx
x x x x
xx
x x x x
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự :
1.
3 2 1 2 0 x x x
2.
2
3 2 25 1 56 0 x x x
3.
6 6 2 3 2 3 1 0 x x x
4.
5 7 6 13 2 2 0 xx
THỦ THUẬT 4 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ MỘT ẨN
Bài 1: Giải Bất Phương Trình:
4
21
2
1
2 4 18 0
2
log x log x
(đề thi thử Đại Học khối A lần 1 THPT Chuyên ĐH Vinh – Nghệ An năm 2013)
Điều kiện xác định:



2;18x
.
▶ Ý tưởng :
Ta có:
4
21
2
4
4
4
22
4 18
2 4 18
2
1
2 4 1
2
0
0
4
8
2
log x log x
log x l x
xx
g
t
o
t
với
4
18tx
và
4
0 20t;
Ta cần phân tích thành nhân tử biểu thức :
2
4
4 20tt
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được các
nghiệm như sau :
0 466823165
2
A.
B

Chắc chắn biểu thức sẽ có nhân tử
2t
Sử dụng Thủ Thuật Rút Gọn Biểu Thức ta được :
4
32
2
4 20
2
2 5 2
t
t t t
tt
Kết luận :
3
2
4
2
2 5 2
4 20
2
tt
tt t t


▶ Phân tích hướng giải:
Với điều kiện
4
0 20t
nên
32
4
2 5 2 0 0 20t t t t ;
. Vậy ta có lời
giải như sau :
▶ Lời giải : Bình phương hai vế:
Đặt
4
18tx
với
4
0 20t;
. Khi đó :
4
4
21
2
4
2
2
2
3
4
4
2
1
2 4 18 0
2
2 4 18
2 4 18
20 4
4 20 0
4
20
4
24
2 5 2
22
log x log x
log x log
t
x
xx
tt
tt
t
t
t
t
tt
x


Một số bài tập tương tự :
1.
4
5 1 1 xx
2.
2
4
2 2 6 6 x x x
3.
4
3
17 11 2 x x x
4.
4
5 6 2 13 xx
Bài 2: Giải Bất Phương Trình:
32
3 4 4 1 0x x x x
(đề thi thử Đại Học khối A + B lần 1 THPT Ba Đình – Hà Nội năm 2013)
Điều kiện xác định:

1;x
.
▶ Ý tưởng :
Thông thường, ta có hai cách để đưa về đa thức bậc 6 :
Cách 1 : Bình phương hai vế.
Cách này không khả quan lắm vì chúng ta chưa thể bình phương
ngay được do bài toán này là bất phương trình.
Cách 2 : Đặt ẩn phụ
1yx
.
Cách này khá là ổn vì chúng ta không cẩn để ý lắm đến dấu của bất
phương trình
Vậy ta được :
32
32
2 2 2
3 4 4 1 0
1 3 1 4 1 4 0
x ( x x ) x
y y y y
Ta cần phân tích thành nhân tử biểu thức :
32
2 2 2
1 3 1 4 1 4y y y y
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được các
nghiệm như sau :
2 414213562
1 618033988
0 414213562
A.
B.
C.

Thành thử thấy
2
1
AB
AB

nên nhân tử của bài toán này là :
2
21yy
Sử dụng Thủ Thuật Rút Gọn Biểu Thức ta được :
32
2 2 2
4 3 2
2
1 3 1 4 1 4
41
21
y y y y
y y y y
yy




Sử dụng Thủ Thuật Giải Phương Trình Bậc 4 ta được :
4 3 2 2 2
4 1 1 2 1y y y y y y y y
Kết luận :
32
2 2 2 2 2 2
1 3 1 4 1 4 1 2 1y y y y (y y )(y y )
▶ Phân tích hướng giải:
Ta có lời giải như sau :
▶ Cách 1 : Đặt ẩn phụ hoàn toàn:
Đặt
1yx
với
0y
. Khi đó bất phương trình trở thành :
32
2 2 2
2 2 2
0
12
1 5 1 5
22
15
0
1 3 1 4 1 4
2
0
1 2 1
y y y y
(y y
y
y
y
)(y y )


▶ Cách 2 : Đặt ẩn phụ không hoàn toàn:
Đặt
1yx
với
0y
. Khi đó bất phương trình trở thành :
32
3 2 2
2
3 4 4 1 0
3 4 0
20
20
x x x x
x x y y
x y x y
xy
xy

▶ Cách 3 : Phân tích thành nhân tử:
Ta có :
32
2
3 4 4 1 0
12
20
1
01
1
x x x x
x x x x
xx
xx

Một số bài tập tương tự :
1.
3
2
33 13 3 0 x x x x
2.
3 2 2
2 7 9 6 1 x x x x x x
3.
2
2 4 3 4 2 16 3 0 x x x x
4.
3 2 2
2 14 2 13 1 0 x x x
THỦ THUẬT 5 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ HAI ẨN
Bài 1: Giải Hệ Phương Trình:
3 2 3 2
22
3 9 22 3 9
1
2
x x x y y y
xyxy

(đề thi Đại Học khối A + A1 năm 2012)
▶ Ý tưởng :
Đa phần các bài tập hệ phương trình mà có phương trình là đa thức bậc 3
ẩn
x
hoặc
y
, không chứa các hạng tử như
22
, , ,...xy x y xy
thì phương trình
đó rất có thể phân tích thành nhân tử được.
Ta sẽ thử phân tích thành nhân tử phương trình sau :
3 2 3 2
3 9 22 3 9 0x x x y y y
Coi như đây là phương trình bậc 3 ẩn
x
, ta sẽ giải phương trình khi
1000y
▶ Thực hiện :
Gán
1000y
Vào tính năng giải phương trình bậc 3 trong MODE
EQN
Lần lượt nhập hệ số của phương trình bậc 3 :
32
1 3 9 22 3 9; ; ; y y y


Coi như ta giải phương trình bậc 3 :
32
3 9 1002990978 0 x x x
Máy tính trả về các nghiệm :
1
2
3
1002
499 5 886 8845
499 5 886 8845
x
x . . I
x . . I
Vì
1002 2y
nên ta được
2xy
là nhân tử của bài toán
Thực hiện phép chia đa thức 2 ẩn bằng dùng
lim
:
3 2 3 2
3 9 22 3 9
2
x x x y y y
fx
xy

Nhận thấy
()fx
sẽ là một tam thức bậc 2 nên
fx
sẽ có dạng
2
ax bx c
với:
2
2
22
1
999 1
1 1000989 11
x
x
fx
a lim
x
f x x
b lim y
x
c f x x y x y y




Vậy ta được :
22
2
3 2 2
2
3
3 9 22 3 9
2
1 11
11
x x x y y y
x y x y y
xx
xy
y y x y
Kết luận :
2
32
2
23
3 9 22 3 9
2 11
x x x y y y
y x xy y x yx

❓ Làm thế nào để biết được phương trình 2 ẩn không phân tích được?
Cách làm trên là cách nhanh nhất để biết được khi nào phương trình 2 ẩn
không phân tích được. Ví dụ như đối với phương trình :
22
1
0
2
y xx y
Tương tự, ta thử cho
1000y
và nhận được giá trị của
x
là :
1
2
0 5 1000 4995
0 5 1000 4995
x . . I
x . . I


Nghiệm này lẻ nên chắc chắn phương trình này không thể có nhân tử dạng
ax by c
với
,,abc
Vậy điều kiện để phương trình không thể phân tích nhân tử dạng
ax by c
với
,,abc
là :
i) Phương trình có hệ số không quá lớn.
ii) Cho
1000y
, giải phương trình ta thấy phương trình không có
nghiệm hữu tỷ.
Bạn đọc có thể thử nghiệm với phương trình :
a)
22
11 0x xy y x y
b)
3 2 3 2
3 9 21 3 9x x x y y y
▶ Phân tích hướng giải:
Thực ra chỉ cần biết nhân tử
2xy
, ta đã có thể có nhiều cách giải cho
bài toán này rồi.
Nhưng việc giải quyết nốt nhân tử còn lại có vẻ hơi khó khăn :
22
11 0x xy y x y
Thủ Thuật Sử Dụng CASIO Để Giải Hệ Phương Trình sẽ giúp bạn.
▶ Cách 1 : Phân tích thành nhân tử:
Ta có :
3 2 3
22
22
2
2 11 0
20
11
3 9 22 3 9
0
20
y x xy y x y
xy
x xy y
x x x y y
x
y
y
x
x
y
Do
2
2 2 2 2
1 1 81
2 11 3 0
2 2 4
x xy y x y x y x y x y
▶ Cách 2 : Đặt ẩn phụ + Hàm đặc trưng:
Ta đặt
2ty
(mục đích để
xt
). Vậy ta luôn có :
3 2 3 2
32
32
3 2 3 2
3 9 22 3 9
3 9 22 2 3 2 9 2
3 9 22 3 9 22
x x x y y y
x x x t t t
x x x t t t
Vì
22
22
1 1 1
1
2 2 2
x y x yxy
nên ta được
13
11
11
22
13
x;
x , y
t;

Xét hàm đặc trưng :
32
3 9 22f k k k k
với
13k ( , )
. Khi đó ta có :
3 1 3 0 1 3f' k k k k ;
Từ đó ta dễ dàng tìm được
xt
. Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự :
1.
2
3
2
32
2
3 2 8 12
1
x x y y
xy

2.
3 2 3 2
22
8 28 12 32 2
1
2x x x y
xy
y
y
y
x

3.
2
2
4 4 3 2
4 1 2
16 32 24 2 12 3
xy
x y y y x y
4.
3 2 3 2
22
3 2 3 3 7 11 6
2 3 2
x xy y xy y x y
x xy y x y
Bài 2: Giải Hệ Phương Trình:
2
3 3 2
1 2 2 1
8 3 4 2 2 0
x y x
y x y y x

(đề thi thử Đại Học lần 2 THPT Lê Văn Hưu – Thanh Hóa năm 2011)
▶ Ý tưởng :
Ta sẽ thử phân tích thành nhân tử phương trình sau :
3 3 2
8 2 3 4 2 0x x yy y
Coi như đây là phương trình bậc 3 ẩn
x
, ta sẽ giải phương trình khi
1000y
▶ Thực hiện :
Gán
1000y
Vào tính năng giải phương trình bậc 3 trong MODE
EQN
Lần lượt nhập hệ số của phương trình bậc 3 :
32
8 0 2 3 4 2; ; ; y y y


Máy tính trả về các nghiệm :
1
2
3
500 5
250 25 433 446
250 25 433 446
x.
x . . I
x . . I
Vì
1
500.5
2
y
nên ta được
21xy
là nhân tử của bài toán
Thực hiện phép chia đa thức 2 ẩn bằng dùng
lim
:
3 3 2
8 2 3 4 2
21
x x y y
fx
xy
y
Nhận thấy
()fx
sẽ là một tam thức bậc 2 nên
fx
sẽ có dạng
2
ax bx c
với:
2
2
22
4
4
2002 2 2
2 2 1002002 2 2
x
x
fx
a lim
x
f x x
b lim y
x
c f x x y x y y



Vậy ta được :
2
32
2
2
3
2
21
4 2 2 2 2
4 2 2
8 2 3 4 2
22
xy
x y x y y
x y xy x y
x x y y y

Kết luận :
2
2
3
2
3
8 2 3 4 2
4 2 22 21 2
x x y y y
xy x xy y x y

▶ Phân tích hướng giải:
Ta giải quyết nốt
22
4 2 2 2 2 0x xy y x y
bằng cách :
2
2
2
2
1
4 2 2
3
4 1 1 0
4
2 12
4
xx xy y x yyy
Sau đó sử dụng Thủ Thuật Giải Phương Trình Vô Tỷ để giải quyết
phương trình vô tỷ còn lại.
Ta cũng có thể xét hàm đặc trưng với bài toán này.
▶ Cách 1 : Phân tích thành nhân tử:
Ta có :
22
2
3 3 2
2
8 2 3 4 2
4 2 2 22 1 0
2
2
42
10
2 1 0
2 2 2 0
x xy
x x y y y
xy
xy
x
y x y
x xy y x y
y
Do
2
2
2
2
1
4 2 2
3
4 1 1 0
4
2 12
4
xx xy y x yyy
Khi đó phương trình
2
1 2 2 1x y x
trở thành :
2
2 2 2 1
1 2 1 1 2 1 0x
x
x
x
xx
x

▶ Cách 2 : Đặt ẩn phụ + Hàm đặc trưng:
Ta đặt
1
2
t
x
(mục đích để
yt
). Vậy ta luôn có :
3 3 2
3
32
3 2 3 2
8 3 4 2 2 0
11
8 3 4 2 2 0
22
3 4 3 4
y x y y x
tt
y y y
y y y t t t

Xét hàm đặc trưng :
32
3 4f k k k k
với
k
. Khi đó ta có :
2
3 6 4 0f' k k k k
Từ đó ta dễ dàng tìm được
xt
. Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự :
1.
2
3 3 2
5 19 1 3 2 1 0
8 6 16 20 24 0
x y x x
x y y x y
2.
3 2 3 2 2
22
3 2 3 3 3 1
1
0
x
x xy y x y x
y xy
3.
4 2 2 4 3 2 2 2
4 17 4 8 2 04
3
x x y y x xy
x xy
xy
y

4.
3 3 2 2
22
72 9 112 55 60 113 67 0
8 3 5 7 3 2
x y x y x y
x x y x x y
Bài 3: Giải Hệ Phương Trình:
3 3 2
3
7 3 12 6 1
4 1 3 2 4
x y xy x y x x
x y x y
(đề thi thử Đại Học lần 1 THPT Cù Huy Cận – Hà Tĩnh năm 2013)
▶ Ý tưởng :
Ta sẽ thử phân tích thành nhân tử phương trình sau :
3 2 2
2
3
33
0
7 3 12 6
7 3 12 6
3
1
10x y x y x
x y xy x y x
y
x
▶ Thực hiện :
Gán
1000y
Vào tính năng giải phương trình bậc 3 trong MODE
EQN
Lần lượt nhập hệ số của phương trình bậc 3 :
23
7 3 12 6 3 1; y ; y ; y
Máy tính trả về các nghiệm :
1
2
3
999
286 071 247 312
286 071 247 312
x
x . . I
x . . I



Vì
999 1 y
nên ta được
1xy
là nhân tử của bài toán
Thực hiện phép chia đa thức 2 ẩn bằng dùng
lim
:
3 2 2 3
2
7 3 12 6 3 1
1
x ( y )x ( y )x y
f x ax bx c
xy

Với :
2
2
22
7
7
4005 4 5
7 4 5 1001001 1
x
x
f(x)
a lim
x
f(x) x
b lim y
x
c f(x) x y x y y



Vậy ta được :
3 2 2 3
22
22
7 3 12 6 3 1
1
7 4 5 1
7 4 5 1
x ( y )x ( y )x y
xy
x y x y y
x y xy x y

Kết luận :
3 2 2 3
22
7 3 12 6 3 1
1 7 4 5 1
x ( y )x ( y )x y
x y x y xy x y
▶ Phân tích hướng giải:
Ta giải quyết nốt
22
4 07 5 1x y xy x y
bằng cách :
22
22
11
7 4 5 1 2 3
22
0x y xy x y x y x
Ta cũng có thể xét hàm đặc trưng với bài toán này. Lưu ý là đề bài cho
3 xy x y
nên ta nghĩ tới việc lấy
3
xy
. Khi đó thì
21 x y x
.
▶ Cách 1 : Phân tích thành nhân tử:
Ta có :
3 3 2
22
22
7 3 12 6
1 7 4 5 1 0
10
7 4 5 1 0
1
x y x y xy x y
xy
x y xy x y
x y xy x y x x

Nếu
10 xy
thì phương trình
3
4 1 3 2 4x y x y
trở thành :
3
3 2 2 4 xx
Do
3
3 2 2 4 f x x x
đồng biến vì
2
3
11
'
22
32

fx
x
x
Suy ra
2x
là nghiệm duy nhất của phương trình
3
3 2 2 4 xx
▶ Cách 2 : Nhóm hợp lý:
3 3 2
3
3
7 3 12 6 1
21
1
x y xy x y x x
x x y
xy
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự :
1.
3 3 2
3
2 6 14 10 3
3 2 2 2
x y x x y xy x y
x y y x x
2.
3 3 2
3
4
23
1 9 2 7 1
2
70
2x y y x y
x y x y
xy x y


3.
2 2 2
4 12 12 19 13
11
x y x y x x y
x y y
4.
4 4 3 2 2
4 5 2
2 2 2 1 3 0
x y x x y x
x y x y
Bài 4: Cho hàm số
3 2 2 2
2 1 2 1 1 1y x ( m )x (m m )x m ( )
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số
1()
khi
0m
.
b) Tìm
m
để đồ thị
1()
cắt trục hoành tại 3 điểm
A,B,C
phân biệt (
A
là
điểm cố định) sao cho
1 2 1 2
2(k k ) x x
, trong đó
12
k ,k
là hệ số góc của tiếp
tuyến với
1()
tại
B,C
;
12
x ,x
là hoành độ của điểm cực trị của
1()
.
(đề thi thử Đại Học lần 2 THPT Quỳnh Lưu 4 – Nghệ An năm 2013)
▶ Ý tưởng :
Đề bài cho rằng
A
cố định nên hoành độ
A
là hằng số.
Vậy phương trình
3 2 2 2
2 1 2 1 1 0x ( m )x (m m )x m
tồn tại một
nghiệm là hằng số.
Nghiệm vụ của chúng ta là phân tích thành nhân tử phương trình :
3 2 2 2
2 1 2 1 1 0x ( m )x (m m )x m
▶ Thực hiện :
Gán
1000m
Vào tính năng giải phương trình bậc 3 trong MODE
EQN
Lần lượt nhập hệ số của phương trình bậc 3 :
22
1 2 1 2 1 1; m ; m m ; m
Máy tính trả về các nghiệm :
1
2
3
1
999
1001
x
x
x


Vì
999 1
1001 1
m
m
nên nhân tử của bài toán là
1
1
1


x
xm
xm
Vì hệ số của
3
x
là
1
nên ta có :
3 2 2 2
2 1 2 1 1
1 1 1
x ( m )x (m m )x m
x x m x m
Kết luận :
3 2 2 2
2 1 2 1 1
1 1 1
x ( m )x (m m )x m
x x m x m
▶ Phân tích hướng giải:
Khi biết 3 nghiệm của phương trình bậc 3, ta tìm được tọa độ của 3 điểm.
Căn cứ theo giả thiết, ta sẽ có lời giải của bài toán.
Sử dụng Thủ Thuật Rút Gọn Biểu Thức là một lợi thế.
▶ Lời giải : Phân tích thành nhân tử:
Ta có :
3 2 2 2
2 1 2 1 1 0
1 1 1 0
x ( m )x (m m )x m
x x m x m
Vậy
y
cắt
Ox
tại 3 điểm phân biệt khi và chỉ khi
1 1 1m, m,
là 3 số
phân biệt hay
0m
và
2m
.
Suy ra
1 0 1 0 1 0A( , );B( m, );C( m, )
. Theo giả thiết thì:
22
1
22
2
3 1 2 2 1 1 2 1 2
3 1 2 2 1 1 2 1 2 4
k ( m) ( m )( m) m m m
k ( m) ( m )( m) m m m
Vậy
2
1 2 1 2
21
2 8 1 26
3
mm
k k x x m

(thỏa mãn)
Một số bài tập tương tự :
1.
3 2 2 3 2
3 7 3 4 4 0 x m x xm m m m
2.
3 2 2
4 2 12 8 0 x xm m x
3.
3 2 2 3 2
4 4 28 1 24 4 6 1 0 x x m x m m m
4.
3 2 3
5 2 6 4 0 x m x m m
Bài 5: Giải hệ phương trình :
4 2 2
22
4 4 2
2 6 23
x y y
yy
x
x x
(đề thi thử Đại Học lần 2 THPT Đông Anh – Hà Nội năm 2013)
▶ Ý tưởng :
Thử phân tích thành nhân tử từng phương trình của hệ phương trình, ta
thấy không phân tích được. Đây là một dạng toán khác với các bài tập trên,
khi mà ta phải lấy
12PT kPT
để phân tích thành nhân tử.
▶ Thực hiện :
Sử dụng Thủ Thuật Giải Hệ Phương Trình ta tìm được
2k
Ta cần phân tích thành nhân tử biểu thức :
4 2 2 2 2
4 4 2 2 2 6 23 0x y y y yxxx
Đặt
2
xt
và gán
1000y
, ta làm như các ví dụ trên.
Kết luận :
4 2 2 2 2
22
4 4 2 2 2 6 23
12 4
x y y y x y
x y x y
xx
▶ Phân tích hướng giải:
Ta có thể trình bày trực tiếp lời giải bằng việc lấy
1 2 2PT PT
rồi phân
tích thành nhân tử.
▶ Lời giải : Phân tích thành nhân tử:
Ta có :
4 2 2 2 2
22
4 4 2 2 2 6 23 0
12 4 0
x y y y x y
x y x
xx
y
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự :
1.
22
22
2 2 1 0
4 6 2 1 0
x xy y x
x xy y x
2.
22
2
2 2 1 0
3 5 1 0
x y x y
x xy x y
3.
22
2
10
5 12 7 5 0
x xy y x y
x xy x y
4.
22
22
4 4 6 3 0
4 4 4 6 0
x xy y x y
x xy y x y
THỦ THUẬT 6 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
GIẢI PHƯƠNG TRÌNH VÔ TỶ
Bài 1: Giải Hệ Phương Trình:
3 3 2
2 2 2
6 12 16 0
4 3 4 3 10 0
x y y x
x x y y y x

(đề thi thử Đại Học – Bà Rịa Vũng Tàu năm 2014)
▶ Ý tưởng :
Tuy là một hệ phương trình trong Thủ Thuật Giải Phương Trình Vô Tỷ,
nhưng nó lại mang ý nghĩa lớn về việc quan trọng của phương pháp giải
phương trình vô tỷ. Chắc hẳn bạn đọc thắc mắc về việc một phương trình
vô tỷ lại được phân tích “ảo diệu” như một số ví dụ trên. Thủ Thuật Giải
Phương Trình Vô Tỷ sẽ giúp bạn hiểu được phần nào cách giải phương
trình vô tỷ bằng máy tính CASIO.
Đối với bài toán trên, sử dụng Thủ Thuật Phân Tích Đa Thức Thành
Nhân Tử Hai Ẩn ta được :
3 3 2
3
3
6 12 16 0
12 2 12 2
2
2
x y y x
x x y y
xy
yx
(vì
22x
và
04y
)
Vấn đề của chúng ta là ở phương trình sau khi thế
2yx
:
22
3 4 3 4x x x x
❓ Làm thế nào để phân tích phương trình này?
Giả sử phương trình có nhân tử
2
4 x ax b
với
a,b
.
Nhân tử này chứa nghiệm của bài toán. Ta chắc chắn tìm được
,ab
nếu
như ta biết được :
Một nghiệm vô tỷ dạng
mn
p
Hoặc hai nghiệm hữu tỷ
Các ví dụ sau sẽ làm rõ vấn đề của bài toán.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
22
3 4 3 4x x x x
có nghiệm
2x 
Nghiệm
2x 
sẽ thỏa mãn nhân tử
2
4 x ax b
với mọi
a,b
. Tức là
2
40x ax b
khi
2x 
Khi đó ta luôn có
2 2 0 1 0a b a,b ;
(vì
a,b
)
Kết luận : Nhân tử của bài toán này là
2
4 xx
❓ Làm thế nào để tìm được nhân tử còn lại?
Có khá nhiều cách để chia biểu thức chứa căn bằng CASIO.
Nếu bạn đọc chưa có kinh nghiệm, hãy cứ bình tĩnh nhóm hợp lý theo cách
cách mà chuyên đề này hoặc nhiều tài liệu khác gọi là “nhân liên hợp
không hoàn toàn”.
Nếu bạn đọc đã quen với việc giải phương trình vô tỷ, bạn đọc hãy đợi
cuốn sau của tác giả để nâng cao khả năng sử dụng máy tính CASIO trong
giải toán.
▶ Phân tích hướng giải:
Nhân liên hợp không hoàn toàn tức là không nhân liên hợp trực tiếp mà sẽ
giữ lại căn thức :
▶ Lời giải : Nhân liên hợp không hoàn toàn:
Ta có
22x
và
04y
nên ta được :
3 3 2
3
3
6 12 16 0
12 2 12 2
x y y x
x x y y
Xét
3
( ) 12f t t t
với
22 t
ta được
2
'( ) 3 12 0 2;2 f t t t
.
Vậy
()ft
nghịch biến và liên tục trên
2;2
. Do đó ta được
2xy
.
Suy ra :
22
22
2 2 2
22
3 4 3 4
3 4 2 4
3 4 4 4
4 4 3 0
x x x x
x x x x
x x x x x x x
x x x
Một số bài tập tương tự :
1.
3 2 2 2
3 3 2
2 1 1
0x x y x xy y x y
yx
2.
3 3 2
9 3 24 18
5 1 2 4 6 0
0
2
x y y x y
y x x y y
3.
4 4 3 3
2
16 32 4 16 8 0
15
x y x y x y
x y x y
4.
55
5
22
1 2 2 1
6 3 4 2 4 3 3 3 2 1
x y x y
x x y x y x y x x

Bài 2: Giải Phương Trình:
2
2 3 2 4 2 1x x x x
▶ Ý tưởng :
Tất cả các phương trình dạng một căn thức
ax b
đều có một lời giải cực
nhanh, cực chính xác và không kém phần thú vị. Đó là phân tích thành
nhân tử.
Cách nhanh nhất để phân tích thành nhân tử đó là đặt ẩn phụ
21tx
như cách làm dưới đây :
▶ Thực hiện :
Đặt
21tx
suy ra
2
1
2
t
x
Thế vào phương trình ta được :
2
22
2
11
2 3 1 4
22
tt
(t )t

Sử dụng Thủ Thuật Phân Tích Đa Thức Thành Nhân Tử ta được :
2
22
22
2
1 1 1
2 3 1 4 1 3
2 2 4
tt
(t )t t t

Thế ngược lại
21tx
ta được :
22
22
11
1 3 2 1 1 2 1 3
44
t t x x
Vậy tóm lại ta được :
2
22
22
2
1 1 1
2 3 1 4 2 1 1 2 1 3
2 2 4
tt
(t )t x x

Kết luận :
22
2
1
2 3 2 4 2 1 2 1 1 2 1 3
4
x x x x x x
▶ Phân tích hướng giải:
Có rất rất nhiều cách giải cho dạng toán này. Bạn đọc có thể suy nghĩ thêm
các cách làm cho phong phú. Sau đó có thể đối chiếu với các bài tập dưới
đây.
▶ Lời giải : Phân tích thành nhân tử:
Ta có :
2
22
2 3 2 4 2 1
1
2 1 1 2 1 3 0
4
x x x x
xx
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự :
1.
2
7 16 3 13 2 0 x x x x
2.
22
3 5 2 3 2 2 x x x x x
3.
2
2 2 7 3 4 2 x x x x
4.
2
9 111 60 30 2 3 1 x x x x
Bài 3: Giải Phương Trình:
2
3 1 2 1 0 x x x
▶ Ý tưởng :
Tương tự Bài 2, ta đặt ẩn phụ để phân tích thành nhân tử. Tuy nhiên, để
mở rộng phạm vi của phương pháp, ta có thể làm theo hướng của Bài 1.
▶ Thực hiện :
Đặt
1tx
suy ra
2
1xt
Thế vào phương trình ta được :
2
22
01 3 1 1 2tt t
Sử dụng Thủ Thuật Phân Tích Đa Thức Thành Nhân Tử ta được :
2
2 2 2 2
1 3 1 1 2 1 1t t t tt tt
Thế ngược lại
1tx
ta được :
22
11
1 1 1 1 1 1
1 1 2
t t t t
x x x x
x x x x
Kết luận :
2
3 1 2 1 1 2 1x x x x x x x
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương
trình
2
3 1 2 1 0 x x x
có nghiệm là
55
2
x
Gọi nhân tử của bài toán là
1 x ax b
thì khi đó :
10
3 5 5 5
0
22
1 5 5 5
0
22
1 5 2 1 5 0
1 0 1
1 5 2 0 2






x ax b
ab
ab
a b a
aa
a b b
Kết luận : Nhân tử của bài toán này là
12xx
▶ Phân tích hướng giải:
Có rất nhiều cách giải, bạn đọc theo dõi ở dưới đây :
▶ Cách 1 : Bình phương hai vế:
Ta có :
2
2
2
2
4 3 2
22
3 1 2 1 0
3 1 2 1
3 1 4 1
6 11 10 5 0
1 5 5 0
x x x
x x x
x x x
x x x x
x x x x
▶ Cách 2 : Đặt ẩn phụ hoàn toàn:
Ta đặt
1tx
với
0t
ta được
2
1xt
. Vậy phương trình trở thành :
2
22
42
22
1 3 1 1 2 0
2 1 0
1 1 0
ttt
t t t
t t t t
▶ Cách 3 : Phân tích thành nhân tử:
Ta có :
2
3 1 2 1 0 1 2 1 0 x x x x x x x
▶ Cách 4 : Nhân liên hợp hoàn toàn:
Nếu
2 1 0 xx
thì không thỏa mãn phương trình.
Nếu
2 1 0 xx
thì :
2
2
2
2
3 1 2 1 0
5 5 2 2 1 0
2
5 5 1 0
21
5 5 1 0
x x x
x x x x
xx
xx
x x x x



▶ Cách 5 : Đặt ẩn phụ không hoàn toàn:
Ta đặt
1tx
với
0t
ta được
2
1xt
. Vậy phương trình trở thành :
22
2 2 0
20x t x
x t t
t
x
▶ Cách 6 : Nhân liên hợp không hoàn toàn:
Ta có :
2
2
3 1 2 1 0
5 5 2 2 1 0
2 1 2 1 2 2 1 0
1 2 1 0
x x x
x x x x
x x x x x x
x x x x
▶ Cách 7 : Đặt ẩn phụ đưa về hệ phương trình:
Ta đặt
12 yx
. Khi đó ta được hệ phương trình :
2
2
2
2
21
4 5 0
3 2 5 0
3 1 2 2 0


yx
y y x
x x y
x x y
Vậy ta được :
22
4 5 3 2 5 0 20 yxy xx yy y x x
Một số bài tập tương tự :
1.
2
2 11 7 1 x x x x
2.
2
2 9 11 1 x x x x
3.
2
2 5 6 5 2 2 1 0 x x x x
4.
2
6 15 22 5 22 2 0 x x x x
Bài 4: Giải Phương Trình:
2
2 2 3 2 1 0x x x x
▶ Ý tưởng :
Tạm bỏ qua ý tưởng đặt ẩn phụ, ta thử giải bài toán này bằng cách tìm
nhân tử.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương
trình
2
2 2 3 2 1 0x x x x
có nghiệm là
22x
Ta tìm nhân tử
21 x ax b
nhanh chóng hơn bằng cách :
Khi
22x 
thì
2 1 1 2 1xx
Kết luận : Nhân tử của bài toán này là
2 1 1xx
▶ Phân tích hướng giải:
Có rất nhiều cách giải, bạn đọc theo dõi ở dưới đây :
▶ Cách 1 : Phân tích thành nhân tử:
Ta có :
2
2 2 3 2 1 0
2 1 2 1 2 1 1 0
x x x x
x x x x
▶ Cách 2 : Nhân liên hợp hoàn toàn:
Nếu
2 1 1 0 xx
thì không thỏa mãn phương trình.
Nếu
2 1 1 0 xx
thì :
2
2
2
2
2 2 3 2 1 0
4 2 3 2 1 1 0
3
4 2 1 0
2 1 1
4 2 2 1 2 1 0
x x x x
x x x x x
x
xx
xx
x x x x



▶ Cách 3 : Đặt ẩn phụ không hoàn toàn:
Ta có :
2
2
2 2 3 2 1 0
4 2 3 2 1 1 0
2 1 1 2 1 1 3 2 1 1 0
2 1 1 2 1 2 1 0
x x x x
x x x x x
x x x x x x x
x x x x
▶ Cách 4 : Đặt ẩn phụ đưa về hệ phương trình:
Ta đặt
2 1 1 yx
. Khi đó ta được hệ phương trình :
2
2
2 2 2 0
2 3 4 2 0
y y x
x xy x
Vậy ta được :
22
2 2 2 2 3 4 2 0 2 2 0 y y x x xy x x y x y
Một số bài tập tương tự :
1.
2
6 11 6 3 2 0 x x x x
2.
2
9 13 2 9 6 1 0 x x x x
3.
2
3 3 20 8 10 4 0 x x x x
4.
2
9 15 18 6 3 4 0 x x x
Bài 5: Giải Phương Trình:
2
3 4 1 1 0 x x x x
▶ Ý tưởng :
Dạng toán một căn thức
ax b
hay ở chỗ :
Nếu phương trình có nghiệm
0
xx
thì chắc chắn phương trình sẽ có
nhân tử
0
ax b ax b
.
Tuy nhiên, để tổng quát với những dạng toán khác, ta luôn tìm được nhân
tử nếu biết trước 2 nghiệm hữu tỷ của bài toán.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương
trình
2
3 4 1 1 0 x x x x
có nghiệm là
1x
và
3x
Ta tìm nhân tử
1x ax b
chứa cả hai nghiệm
1x
và
3x
.
Vậy là
10 x ax b
khi
1x
hoặc
3x
. Suy ra :
00
11
;;
2 3 0
22



ab
ab
ab
Vậy nhân tử của chúng ta là
11
1
22



xx
Kết luận : Nhân tử của bài toán này là
2 1 1xx
▶ Phân tích hướng giải:
Tương tự các ví dụ trước, ta có các hướng giải chính như sau :
▶ Cách 1 : Phân tích thành nhân tử không hoàn toàn:
Ta có :
2
3 4 1 1 0
2 1 1 3 1 2 0
x x x x
x x x x
▶ Cách 2 : Nhân liên hợp hoàn toàn:
Nếu
2 1 1 0 xx
thì không thỏa mãn phương trình.
Nếu
2 1 1 0 xx
thì :
2
2
3 4 1 1 0
3 9 1
3 1 2 1 1 0
2 2 2
31
1 3 0
2
2 2 1 1
1 3 3 1 2 0




x x x x
x x x x x
x
xx
xx
x x x x
▶ Cách 3 : Đặt ẩn phụ không hoàn toàn:
Ta có :
2
2
3 4 1 1 0
3 9 1
3 1 2 1 1 0
2 2 2
31
2 1 1 2 1 1 1 2 1 1 0
22
2 1 1 3 1 2 0
x x x x
x x x x x
x x x x x x x
x x x x
▶ Cách 4 : Đặt ẩn phụ đưa về hệ phương trình:
Ta đặt
2 1 1 yx
. Khi đó ta được hệ phương trình :
2
2
2
2
1 5 1 9
1
2 4 3 0
1
0
3 4 1 1 0
2 2 2
2
41
2




x xy x y
x x x
x
y
y y x
y
Vậy ta được :
2 2
2 3 2 4 3 0
2 3 7 0
1 5 1 9
2 2 2 2




x y y x
x y x y
xy x y
▶ Cách 5 : Phân tích thành nhân tử hoàn toàn:
Theo bổ đề ở đầu bài thì chắc chắn phương trình này sẽ có 2 nhân tử là
1 1 1x
và
1 3 1x
Vậy nhân tử của bài toán này là
1 1 2xx
. Ta được :
2
3 4 1 1 0
1 1 2 2 3 1 0
x x x x
x x x x
Một số bài tập tương tự :
1.
2
2 3 2 1 1 x x x x
2.
2
2 15 5 7 5 2 1 x x x x
3.
2
3 22 25 8 17 5 x x x x
4.
2
12 46 41 19 27 2 3 x x x x
Bài 6: Giải Phương Trình:
2
2 5 3 3 1 3 1 0 x x x x
▶ Ý tưởng :
Ta vẫn đi tìm nghiệm trước khi giải mỗi bài toán.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương
trình
2
2 5 3 3 1 3 1 0 x x x x
có nghiệm duy nhất là
7
4
x
Ta có thể sử dụng bổ đề ở Bài 5 để tìm nhân tử.
Tuy nhiên, để tổng quát với những dạng toán khác, ta có thể tìm
nhân tử
31 x ax b
bằng phương pháp Đổi Dấu Trước Căn
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương
trình
2
2 5 3 3 1 3 1 0 x x x x
có các nghiệm là :
0;5 2 7;5 2 7x
Khi
5 2 7x
thì
1
3 1 16 6 7 3 7
2
x
x
. Vậy nhân
tử của phương trình
2
2 5 3 3 1 3 1 0 x x x x
là :
2 3 1 1 xx
Vậy không đổi dấu trước căn nữa, ta sẽ được nhân tử của phương
trình
2
2 5 3 3 1 3 1 0 x x x x
là :
2 3 1 1xx
Kết luận : Nhân tử của bài toán này là
2 3 1 1xx
▶ Phân tích hướng giải:
Đối với những bài toán có nghiệm duy nhất, chúng ta thường nghĩ đến 3
hướng chính như sau :
Nhân liên hợp
Đạo hàm
Bất đẳng thức, đánh giá
Chúng ta thử xem các hướng đó giúp ích được gì cho chúng ta không :
▶ Cách 1 : Nhân liên hợp hoàn toàn:
Ta có :
2
2
2 5 3 3 1 3 1 0
5 21 5
2 3 1 3 1 0
2 2 2
1 4 7
19
3 4 7 0
22
2 3 1 5
19
4 7 3 0
2
2 3 1 5










x x x x
x x x x
xx
xx
x
xx
x
▶ Cách 2 : Đạo hàm: (Tham Khảo)
Xét hàm số :
2
2 5 3 3 1 3 1 f x x x x x
với
1
,
3



x
.
Khi đó :
3 9 1
' 4 5
2
31
x
f x x
x
và
3
9 9 7
'' 4
4
31

x
fx
x
.
Suy ra
1
'' 0
3
f x x
. Vậy
'0fx
có tối đa một nghiệm.
Dễ thấy
' 0 ' 1 0ff
nên tồn tại
0
0,1x
để
0
'0fx
.
Nếu
0
xx
thì
0fx
có tối đa một nghiệm. Chỉ ra nghiệm này là
7
4
x
Nếu
0
1
3
xx
thì
1
1
3
x
. Suy ra :
1 1 10
, 1 0
3 3 9



f x Max f f f
Vậy
0fx
không có nghiệm trong khoảng
0
1
,
3


x
Kết luận :
7
4
x
.
▶ Cách 3 : Bất đẳng thức, đánh giá:
Nếu
7
4
x
thì :
22
2
7 21
2 5 3 3 1 3 1 2 5 3 3 1 1
44
21 1
2 5 4 3 4 7 0
88



x x x x x x
x x x x
Nếu
7
1
4
x
thì :
22
2
21
2 5 3 3 1 3 1 2 5 3 3 1 1
4
5 21 1
2 3 4 7 0
2 2 2
x x x x x x x
x x x x
Nếu
1
1
3
x
thì :
22
2 5 3 3 1 3 1 2 5 3 2 1 3 0 x x x x x x x x
▶ Cách 4 : Phân tích thành nhân tử không hoàn toàn:
Ta có :
2
2 5 3 3 1 3 1 0
2 3 1 1 3 1 2 1 0
x x x x
x x x x
▶ Cách 5 : Phân tích thành nhân tử không hoàn toàn:
Ta có :
2
2 5 3 3 1 3 1 0
1
7 3 3 3 1 0
3
2 3 1 5
xx
x
xx
x x x
▶ Cách 6 : Phân tích thành nhân tử hoàn toàn:
Ta có :
2
2 5 3 3 1 3 1 0
1
2 3 1 5 3 1 1 2 3 1 1 0
3
x x x x
x x x x
Một số bài tập tương tự :
1.
2
3 2 2 1 1 0 x x x x
2.
2
2 5 4 5 4 2 1 0 x x x x
3.
3
2 1 2 0 x x x x x
4.
22
2 3 1 3 x x x x x
Bài 7: Giải Phương Trình:
2
11 7 3 2 1 2 1 0 x x x x
▶ Ý tưởng :
Ta tìm nghiệm của phương trình để tìm nhân tử.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương
trình
2
11 7 3 2 1 2 1 0 x x x x
có tập nghiệm là
23 10 5,2 2
Với mỗi nghiệm, ta được nhân tử tương ứng là
2 1 1 xx
và
2
21
55



x
x
Bậc của phương trình là bậc 2 nên ta sẽ có :
2
11 7 3 2 1 2 1
2
2 1 1 2 1
55



x x x x
x
k x x x
Thử một vài giá trị ta thấy
5k
Kết luận :
2
2
11 7 3 2 1 2 1 5 2 1 1 2 1
55



x
x x x x x x x
▶ Phân tích hướng giải:
Ta cũng có rất nhiều cách làm cho bài toán này. Tuy nhiên cách làm ngắn
gọn như sau :
▶ Lời giải : Phân tích thành nhân tử :
Ta có :
2
11 7 3 2 1 2 1 0
2 1 1 5 2 1 2 0
x x x x
x x x x
Một số bài tập tương tự :
1.
2
2 10 10 3 2 1 0 x x x x
2.
2
2 8 4 3 1 2 1 0 x x x x
3.
2
2 19 18 2 2 0 x x x x
4.
2
12 5 1 5 2 0 x x x x
Bài 8: Giải Phương Trình:
2
6 10 10 13 1 2 0 x x x x
▶ Ý tưởng :
Ta tìm nghiệm của phương trình để tìm nhân tử.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương
trình
2
6 10 10 13 1 2 0 x x x x
có tập nghiệm là
5 2 22
2;
9





Với nghiệm
5 2 22
9
x
, ta được nhân tử tương ứng là
2 2 3 1 xx
Kết luận : Nhân tử của bài toán này là
2 2 3 1 xx
▶ Phân tích hướng giải:
Ta cũng có thể tìm nhân tử
22x 
vì nó chứa nghiệm
2x
.
▶ Cách 1 : Phân tích thành nhân tử không hoàn toàn:
Ta có :
2
6 10 10 13 1 2
3 2 2 2 2 2
0
3 1 0
x x x x
x x x x
▶ Cách 2 : Phân tích thành nhân tử hoàn toàn:
Ta có :
2
6 10 10 13 1 2
2 2 6 4 2 9 0
2 2 2 2 1 3 0
0
2 2 1
x x x x
x x x x
x x x x
Một số bài tập tương tự :
1.
2
8 14 2 0 x x x
2.
2
6 3 12 5 11 2 x x x x
3.
2
15 55 28 37 7 5 2 x x x x
4.
2
3 18 28 8 28 3 x x x x
Bài 9: Giải Phương Trình:
2
10 13 7 19 5 1 0 x x x x
▶ Ý tưởng :
Ta tìm nghiệm của phương trình để tìm nhân tử.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương
trình
2
10 13 7 19 5 1 0 x x x x
có tập nghiệm là
5 3 17 3 2 21
;
8 25


Nhân tử tương ứng là
2 1 5 1 xx
và
3 1 2 1 xx
Kết luận : Nhân tử của bài toán này là
2 1 5 1 xx
và
3 1 2 1 xx
▶ Phân tích hướng giải:
Lời giải sẽ vô cùng ngắn gọn :
▶ Lời giải : Phân tích thành nhân tử:
Ta có :
2
10 13 7 19 5 1 0
2 1 5 1 3 1 2 1 0
x x x x
x x x x
Một số bài tập tương tự :
1.
2
2 19 40 2 3 3 x x x x
2.
2
2 19 16 2 3 3 x x x x
3.
2
12 5 1 5 3 x x x x
4.
2
15 26 2 4 4 x x x x
Bài 10: Giải Phương Trình:
22
9 12 2 3 2 9 1 0 x x x x x
▶ Ý tưởng :
Đây là một ví dụ điển hình cho việc không tốt của phương pháp Bình
Phương Hai Vế. Mọi bài toán dạng này đều có thể phân tích thành nhân tử
nên bạn đọc không cần lo lắng nếu gặp bài toán tương tự.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương
trình
22
9 12 2 3 2 9 1 0 x x x x x
có tập nghiệm là
23 3 21 23 3 21
;
66






Nhân tử tương ứng là
9 1 3 2 xx
Kết luận : Nhân tử của bài toán này là
9 1 3 2 xx
▶ Phân tích hướng giải:
Chúng ta thử giải bài toán này dưới dạng nhiều hướng đi khác nhau. Thử
xem cách nào phù hợp với chúng ta nhất.
▶Cách 1 : Bình phương hai vế:
Ta có :
22
22
22
22
5 4 3 2
3 2 2
2
32
9 12 2 3 2 9 1 0
9 12 2 3 2 9 1
9 12 2 3 2 9 1
9 78 154 94 69 85 0
1 9 69 85 0
9 69 85 0
10
x x x x x
x x x x x
x x x x x
x x x x x
x x x x
xx
xx
Xét hàm số
32
1 f x x x
với
1x
. Ta được :
2
' 3 2 3 2 0 1 f x x x x x x
Vậy ta chứng minh được phương trình
0fx
có tối đa một nghiệm.
Chỉ ra nghiệm này là
33
2 116 12 93 116 12 93
6
x
và thấy nó
không thỏa mãn phương trình ban đầu.
Kết luận :
23 3 21
6
x
.
▶Cách 2 : Nhân liên hợp không hoàn toàn:
Ta có :
22
2
32
2
9 12 2 3 2 9 1 0
23 85 1
3 2 9 9 1 3 2 0
3 9 9
1
9 1 3 2 9 1 3 2
9
1
3 2 9 9 1 3 2 0
9
9 1 3 2 1 1 0
9 1 3 2 0
x x x x x
xx
x x x x x
x x x x x
x x x x
x x x x
xx
▶Cách 3 : Nhân liên hợp hoàn toàn:
Ta có :
22
2
32
22
2
2
2
2
2
9 12 2 3 2 9 1 0
23 85 1
3 2 9 9 1 3 2 0
3 9 9
3 2 9 9 69 85
11
9 69 85 0
99
9 1 3 2
1 3 2 9
9 69 85 0
9
9 1 3 2
9 69 85 1 1
0
9 1 3 2
9 69 85 0





x x x x x
xx
x x x x x
x x x x
x x x
xx
xx
x x x
xx
x x x x
xx
xx
▶Cách 4 : Phân tích thành nhân tử:
Ta có :
22
9 12 2 3 2 9 1 0
9 1 3 2 1 1 0
9 1 3 2 0
x x x x x
x x x x
xx
❓ Tại sao lại sinh ra nghiệm
33
2 116 12 93 116 12 93
6
x
?
Bản chất của phương pháp bình phương hai vế là việc giải cả 2 phương
trình :
22
9 12 2 3 2 9 1 0 x x x x x
22
9 12 2 3 2 9 1 0 x x x x x
Và nghiệm
33
2 116 12 93 116 12 93
6
x
là của phương trình dưới
Một số bài tập tương tự :
1.
22
4 5 4 2 2 x x x x x
2.
22
3 4 1 2 1 x x x x x
3.
32
5 5 3 2 1 1 x x x x x
4.
32
2 11 23 31 13 2 3 x x x x x
Bài 11: Giải Phương Trình:
3 2 2
7 16 6 8 1 0 x x x x x x
▶ Ý tưởng :
Tương tự tất cả các bài toán khác, chúng ta thử tìm nghiệm của bài toán để
định hướng giải.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương
trình
3 2 2
7 16 6 8 1 0 x x x x x x
có nghiệm duy nhất
là
5x
.
Thử nhân liên hợp, ta thấy :
3 2 2
2
2
7 16 6 8 1 0
8
5 4 2 0
12





x x x x x x
xx
x x x
x
Tuy nhiên,
2
2
8
4 2 0
12


xx
xx
x
lại có nghiệm
5x
.
Đặt
3 2 2
7 16 6 8 1f x x x x x x x
Thử bằng Mode TABLE hoặc gán trực tiếp CALC, ta thấy :
x
1
2
3
4
5
6
7
10
>10
()fx
4
12
8.8284
3.0717
0
4.8065
22.7173
208
>0
Vậy đây là một bài toán nghiệm bội kép
5x
.
Kết luận : Bài toán bội kép
5x
và chắc chắn chứa nhân tử
2
12x
▶ Phân tích hướng giải:
Ta nhận thấy
3 2 2
7 16 6 8 1 0 f x x x x x x x
nên ta có
thể dùng bất đẳng thức.
Ngoài ra, ta vẫn có thể tìm nhân tử của bài toán dưới dạng tổng quát (cho
cả những bài toán nhiều căn, căn bậc cao) tương tự cách làm sau :
Giả sử nhân tử của bài toán là
1x ax b
Khi đó
10f x x ax b
có nghiệm bội kép
5x
Khi đó
,ab
phải thỏa mãn hệ phương trình sau :
1
1
'(5) 0
0
4
4
(5) 0 3
2 5 0
4
a
f
a
f
ab
b






Kết luận : Nhân tử của bài toán là
13
1
44
xx



.
Ta còn một hướng đi khác, đó là bất đẳng thức, đánh giá.
Ta thấy rằng :
x
1
2
3
4
5
6
7
10
>10
()fx
4
12
8.8284
3.0717
0
4.8065
22.7173
208
>0
Vậy chứng tỏ là rất có thể
( ) 0fx
với mọi
1x
▶Cách 1 : Nhân liên hợp hoàn toàn:
Ta có :
3 2 2
3 2 2
2
7 16 6 8 1 0
3 15 75 1 3
8 1 0
4 2 4 4 4
31
50
4
4 4 1 3
5








x x x x x x
x x x x x x x
xx
xx
x
▶Cách 2 : Nhân liên hợp không hoàn toàn:
Ta có :
3 2 2
3 2 2
2
2
7 16 6 8 1 0
3 15 75 1 3
8 1 0
4 2 4 4 4
1 3 1 3
12 1 1
4 4 4 4
13
8 1 0
44
13
1 4 8 8 12 1 0
44
13
10
44









x x x x x x
x x x x x x x
x x x x x
x x x x
x x x x x
x
x
x
▶Cách 3 : Phân tích thành nhân tử không hoàn toàn:
Ta có :
3 2 2
2
2
7 16 6 8 1 0
1 2 2 2 3 1 0
x x x x x x
x x x x x
▶Cách 4 : Phân tích thành nhân tử hoàn toàn:
Ta có :
3 2 2
22
7 16 6 8 1 0
11 01 1 2
x x x x x x
x x x x
▶Cách 5 : Bất đẳng thức, đánh giá:
Ta có :
3 2 2
7 16 6 ( 1)( 6 10) 4 0 x x x x x x
với mọi
1x
nên suy
ra
2
80 xx
. Do
14
1
4


x
x
theo BĐT Cauchy nên ta được :
3 2 2
3 2 2
2
7 16 6 8 1
14
7 16 6 8 .
4
3
5 0 1
4
x x x x x x
x
x x x x x
x x x

▶Cách 6 : Đạo hàm:
Đặt
3 2 2
7 16 6 8 1f x x x x x x x
với
1x
Ta có
2
5 3 2
53
' 3 14 16 2 3 8
2 1 2 1
2 6 16 1 5 3 2 1 2 7 1 6 2
2 1 2 1
xx
x
f x x x x x
xx
x x x x x x x x
xx







Vậy
2
2
'( ) 0
5
12
x
x
fx
x
x

(vì
7 1 6 2 0 1x x x
)
Vẽ bảng biến thiên ta được
( ) (5) 0f x f
Vậy
( ) 0fx
khi và chỉ khi
5x
.
Một số bài tập tương tự :
1.
2
2 5 5 3 1 2 x x x x
2.
3 2 2
3 6 4 2 3 1 3 2 x x x x x x
3.
3 2 2
2 2 1 1 3 1 x x x x x x
4.
2
32
8 12 4 2 1 x x x x x
Bài 12: Giải Phương Trình:
2
2
28
1 2 2
23


xx
xx
xx
(đề thi THPT Quốc Gia năm 2015)
▶ Ý tưởng :
Là một bài thi trong đề thi THPT Quốc Gia, nhiều bạn bị mất điểm vì
không giải quyết trọn vẹn được bài toán này.
Có rất nhiều cách để có được lời giải, chúng ta thử khám phá lần lượt.
▶ Thực hiện :
Dễ dàng ta thấy
2
2 8 4 2
2 2 2 2 2
x x x x
x x x
. Vậy ta được :
2
2
2
28
1 2 2
23
4 2 2 2 2 1 2 3 2 2


xx
xx
xx
x x x x x x x
Thứ ta cần giải quyết là giải phương trình sau :
2
2
32
4 2 2 1 2 3
1 2 3 2 4 4 2 0
5 4 2 0
x x x x x
x x x x x x
x x x x x
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được :
Phương trình
32
5 4 2 0x x x x x
có nghiệm
3.30277563A
Phương trình
32
5 4 2 0 x x x x x
có nghiệm
0.30277563B
Thành thử ta thấy
3AB
.
Nghiệm của phương trình ban đầu là :
2
3 13
22
A B A B
x

Khi
3 13
2
x
thì
7 13 1 13
21
22
xx

.
Kết luận : Nhân tử của bài toán này là
21xx
▶ Phân tích hướng giải:
Sẽ có rất rất nhiều cách giải cho bài toán này và lời giải sẽ nhanh chóng
được tìm ra nếu ta sử dụng CASIO một cách thành thạo. Bạn đọc có thể suy
nghĩ thêm.
▶Cách 1 : Bình phương hai vế:
Ta có :
32
2
2
32
2 4 3 2
2
5 4 2 0
5 4 2
3 1 3 7 0
3 1 0

x x x x x
x x x x x
x x x x x x
xx
(do
22
4 3 2 2
27 2 8
3 7 2 0
2 4 9 3
x
x x x x x x
)
▶Cách 2 : Nhân liên hợp không hoàn toàn:
Ta có :
32
32
2
2
5 4 2 0
5 4 1 4 2 1
1 3 1 4 2 1
1 2 1 2 1 4 2 1 0
2 1 3 1 2 0
x x x x x
x x x x x x x x
x x x x x x
x x x x x x x x
x x x x x x
▶Cách 3 : Phân tích thành nhân tử:
Ta có :
32
2
5 4 2 0
2 1 3 1 2 0
x x x x x
x x x x x x
(Vì
2
2
3 1 2 2 1 2 2 2 1 3 0 x x x x x x x
)
▶Cách 4 : Hàm đặc trưng kiểu 1:
Ta đặt
2ax
và
1bx
với
0a
và
1b
. Ta có :
22
2
2
2 2 4 1
22
2
2
3
a a b
xx
b
x x x
▶Cách 5 : Hàm đặc trưng kiểu 2:
Ta có :
32
32
2
5 4 2
3 4 2 2
2 3 1 4 2 2
x x x x x
x x x x x
x x x x x
Xét hàm số
2
22f t t t
với
t
thì
2
3 4 2 0f' t t t t
.
Hàm số cũng liên tục trên . Vậy :
2
10
3 13
2 1 2 1
2
21
x
f x f x x x x
xx

▶Cách 6 : Đạo hàm:
▶Cách 7 : Đặt ẩn phụ hoàn toàn:
▶Cách 8 : Đặt ẩn phụ không hoàn toàn:
▶Cách 9 : Nhân liên hợp hoàn toàn:
▶Cách 10 : Đặt ẩn phụ đưa về hệ phương trình:
▶Cách 11 : Đánh giá, bất đẳng thức:
▶Cách 12 : Hàm đặc trưng kiểu 3:
❓ Tại sao lại có các lời giải trên ?
Thực sự thì các lời giải này tương tự nhau nên việc tìm ra mấu chốt của bài
toán sẽ đưa đến các lời giải như trên. Kể cả là Cách 4, Cách 5, Cách 12.
Quan trọng là bạn đọc tư duy như thế nào cho hiệu quả. Hãy thử động
não. Nếu bạn đọc quá tò mò thì hãy kiên nhẫn xem các bài tập ví dụ tiếp
theo.
Đó là cách giải quyết hầu hết các bài toán dạng :
32
ax bx cx d mx n px q
Để biến đổi phương trình về dạng :
f ex f f ux v ex f ux v
Gợi ý :
ex f ux v
là nhân tử của bài toán.
Một số bài tập tương tự :
1.
32
3 9 8 2 x x x x x
2.
32
6 13 2 2 1 0 x x x x x
3.
32
4 12 13 21 32 36 1 x x x x x
4.
32
2 9 37 18 32 14 2 1 x x x x x
Sau đây là một số vấn đề mở rộng về việc ứng dụng của phương pháp giải
phương trình vô tỷ bằng CASIO :
Giải bất phương trình vô tỷ
Tìm biểu thức cần nhân liên hợp
Bất đẳng thức
Hàm đặc trưng (cách giải tổng quát cho bài toán THPT Quốc Gia 2015)
Đặt ẩn phụ không hoàn toàn
Đặt ẩn phụ đưa về hệ phương trình
Bài 13: Giải Bất Phương Trình:
2
2 3 4 1 2 x x x x
▶ Ý tưởng :
Có lẽ bây giờ nhìn lại bài toán này, bạn đọc đã hình dung được rất nhiều
cách làm. Lời giải ngắn gọn nhất và dễ biến đổi nhất là phương pháp phân
tích thành nhân tử.
▶ Thực hiện :
Sử dụng máy tính CASIO ta được nhân tử của bài toán này là
23 xx
▶ Phân tích hướng giải:
Ta coi bất phương trình như phương trình.
▶ Lời giải : Phân tích thành nhân tử:
Ta có :
2
2 3 2 1 0
2
2 3 4 1 2
3
x x x x x
x
xx
x
xx

Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự :
1.
2
3 2 1 2 2 1 x x x x
2.
22
5 6 1 2 3 1 2 x x x x x
3.
22
6 6 2 5 12 5 x x x x
4.
2
4
21
1 2 3
x
x
x
Bài 14: Giải Bất Phương Trình:
3 2 2
2 3 2 3 5 4 1 x x x x x
▶ Ý tưởng :
Ta cũng có thể sử dụng CASIO để tìm biểu thức cần nhân liên hợp cho bài
toán này.
▶ Thực hiện :
Sử dụng máy tính CASIO ta được nhân tử của bài toán này là
1 2 1
1 1 1 1
2 3 3
x x x x
▶ Phân tích hướng giải:
Ta sẽ nhóm theo nhân tử
21
1
33



xx
vừa tìm được.
▶ Lời giải : Nhân liên hợp:
Ta có :
3 2 2
22
2
2 3 2 3 5 4 1
4 13 10 2 1
3 5 4 1
3 3 3 3 3
1 3 5 4
4 5 2 0
21
3
91
33
4 5 2 0













x x x x x
x x x x x x
xx
xx
xx
xx
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự :
1.
3 2 2
2 26 20 6 16 4 1 0 x x x x x x
2.
2 3 2
9 3 2 3 18 x x x x
3.
2 3 2
5 25 16 1 15 34 14 x x x x x x
4.
32
1
5 5 2
2
x x x x x
Bài 15: Giải Bất Phương Trình:
22
3 7 3 5 1 0 x x x x x
▶ Ý tưởng :
Tương tự bài 14, ta cũng có thể tìm được biểu thức cần nhân liên hợp với
1x
▶ Thực hiện :
Sử dụng máy tính CASIO ta được nhân tử của bài toán này là
12 xx
▶ Phân tích hướng giải:
Để nhân liên hợp, ta cần xét một số điều kiện :
▶ Lời giải : Nhân liên hợp:
Ta có : Nếu
5 13
1 2 0
2
x x x
thì thoả mãn
Nếu
5 13
1 2 0
2
x x x
thì :
22
3 2 2
22
2
2
2
2
2
3 7 3 5 1 0
4 2 3 3 5 1 2 0
3 5 5 3
1 5 3 0
12
35
5 3 1 0
12
5 3 1 1 2 3
0
12
5 3 0
x x x x x
x x x x x x x
x x x x
x x x
xx
xx
x x x
xx
x x x x x
xx
xx






Nếu
5 13
1 2 0
2
x x x
thì tương tự.
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự :
1.
5 4 4
2 1 2 1 x x x x x x
2.
3 2 2
3 7 4 3 3 2 2 0 x x x x x x
3.
3 2 2
7 16 4 3 4 1 5 2 0 x x x x x x
4.
3 2 2
5 1 3 5 2 1 0 x x x x x x
Bài 16: Giải Phương Trình:
3 2 2
4 11 10 2 9 2 3x x x x x x
▶ Ý tưởng :
Ta sẽ sử dụng CASIO để kiểm tra xem bài toán này có sử dụng bất đẳng
thức được không.
▶ Thực hiện :
Thứ nhất, sử dụng máy tính cầm tay ta thấy phương trình này có nghiệm
duy nhất là
3 2 4.41421356 x
Thứ hai, ta thử khi
1.5,2,4,4.4,4.5,5,10,1000,...x
thì ta thấy :
3 2 2
3
4 11 10 2 9 2 3 0
2
x x x x x x x
Vậy ta sẽ chứng minh
3 2 2
4 11 10 2 9 2 3 0x x x x x x
▶ Phân tích hướng giải:
Ta thấy nghiệm là
32x
là điểm rơi, vậy thì khi đó :
2 3 1 2 2xx
Để ý rằng khi
3
2
x
(theo ĐKXĐ) thì
3
4 11 10 0x x x
, từ đó ta có lời
giải như sau :
▶ Lời giải : Bất đẳng thức:
ĐKXĐ:
3
2
x
. Khi đó :
3 2 2
71
4 11 10 2 3 4 10 29 0
88
x x x x x x
Vậy suy ra
2
2 9 0 10 1 2x x x
. Do đó :
2
22
1
2 2 3 2 2 3 2 1 2 3 2
22
x
x x x x x x x
x
Từ đó :
2
2
3 2 2
2
2
2
2 9 1
4 11 10 2 9 2 3
22
67
0 6 7 0
22
x x x
x x x x x x
x
xx
xx
x

Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự :
1.
2
3 4 2 1 0 x x x
2.
4 3 2 3
3 10 48 32 4 12 1 x x x x x x
3.
42
2
31
18 9 3 2
36 4
xx
x x x
4.
6 2 4 3
13 6 16 2 10 2 x x x x x x x
Bài 17: Giải Phương Trình:
32
5 4 2x x x x x
▶ Ý tưởng :
Ta đã có rất nhiều cách để làm bài toán này. Tuy nhiên, để có một lời giải
ngắn gọn như cách 4, cách 5, cách 12 thì ta phải tìm được biểu thức của
hàm đặc trưng. Sử dụng máy tính CASIO cũng sẽ giúp ích được cho chúng
ta tìm hàm đặc trưng.
▶ Thực hiện :
Sử dụng CASIO, ta tìm được nhân tử là
21xx
. Vậy ta cần tìm hàm
đặc trưng sao cho
21f x f x
.
Vì hệ số của
2x
là
2
4 2 2xx
là bất di bất dịch rồi nên ta biến
đổi như sau :
32
32
2
32
5 4 2
5 4 4 2
1 4 5 2 2 2
x x x x x
x x x k x x x k
x x k x k x x k



▶ Phân tích hướng giải:
Hàm đặc trưng của bài toán này sẽ có dạng :
2
2f t t t k
bởi vì vế
phải ta có
2fx
rồi
Vậy để
21f x f x
thì vế trái sẽ phải thỏa mãn :
32
2
32
3 2 3 2
1 4 5 1
1 4 5 1 1 2
1 4 5 3 2 5 3 3
2
x x k x k f x x
x x k x k x k x x
x x k x k x k x k x k x
k

▶ Lời giải : Hàm đặc trưng:
ĐKXĐ :
2x
. Ta có :
32
32
2
5 4 2
3 4 2 2
2 3 1 4 2 2
x x x x x
x x x x x
x x x x x
Xét hàm số
2
22f t t t
với
t
thì
2
3 4 2 0f' t t t t
Hàm số cũng liên tục trên . Vậy :
2
10
3 13
2 1 2 1
2
21
x
f x f x x x x
xx

Một số bài tập tương tự :
1.
32
2 4 5 25 16 50 3 x x x x x
2.
3
2 23 45 16 18 2 x x x x
3.
3
8 11 6 3 3 2 xx x x
4.
32
2 2 11 31 2 19 3 x x x x x
Bài 18: Giải Phương Trình:
32
6 12 12 4 2 0x x x x x
▶ Ý tưởng :
Ta sẽ làm tương tự bài 17.
▶ Thực hiện :
Sử dụng CASIO, ta tìm được nhân tử của bài toán là
23xx
.
Ta có :
32
32
6 12 12 4 2
6 12 12 4 4 2
x x x x x
x x k x k x x k
▶ Phân tích hướng giải:
Vì
2
4 2 6xx
nên nhân tử của chúng ta có dạng :
2
6f t t t k
với
k
thỏa mãn
2
32
3 2 3 2
6 12 12 4 3 6 3
6
23
12 12 4 9 6 33 15 45
3
x x k x k x x k x
x
f x f x x
x k x k x k x k x k x
k


▶ Lời giải : Hàm đặc trưng:
ĐKXĐ :
2x
. Ta có :
32
32
2
2
6 12 12 4 2
6 15 4 2 3
3 3 3 6 2 3 2 6
32
x x x x x
x x x x x
x x x x
xx



Lời giải chi tiết dành cho bạn đọc.
Bài 19: Giải Phương Trình:
32
2 5 5 2 5 2 1x x x x x
▶ Ý tưởng :
Ta sẽ làm tương tự bài 17.
▶ Thực hiện :
Sử dụng CASIO, ta tìm được nhân tử của bài toán là
2 1 1xx
.
Ta có :
32
32
2 5 5 2 5 2 1
2 5 5 2 5 2 5 2 1
x x x x x
x x x x k x x k
▶ Phân tích hướng giải:
Ta cần tìm
2
6f t t t k
với
k
thỏa mãn đẳng thức sau với mọi
x
32
2
2 5 5 2 5 2 5 2 1
2 1 1
1 6 1
x x x x k x x k
f x f x
x x k
Ta được
1k
▶ Lời giải : Hàm đặc trưng:
ĐKXĐ :
1
2
x
. Ta có :
32
32
2
2
2 5 5 2 5 2 1
2 7 2 5 2 1 1
1 1 1 6 2 1 1 2 1 6
1 2 1
x x x x x
x x x x x
x x x x
xx



Lời giải chi tiết dành cho bạn đọc.
Bài 20: Giải Phương Trình:
32
8 40 72 58 8 3x x x x x
▶ Ý tưởng :
Ta sẽ làm tương tự bài 17.
▶ Thực hiện :
Sử dụng CASIO, ta tìm được nhân tử của bài toán là :
51
3 3 2 2 3
22
x x x x



Hay gọn hơn là
3 2 4xx
.
▶ Phân tích hướng giải:
Cần tìm hàm
2
5f t t t k
sao cho
3 2 4f x f x x
. Hay :
32
8 40 72 58 8 8 4332x x x k fxx x x k f x
Vì biểu thức đúng với mọi
x
nên mình cho
0x
ta được :
2
8 58 4 4 5 4 2k f k k
Thử lại thấy thỏa mãn.
▶ Lời giải : Hàm đặc trưng:
ĐKXĐ :
3x
. Ta có :
32
2
2
8 40 72 58
5
83
2 4 5 2 4 2 3 3 2
2 4 3
x x x x x
x x x x
xx



Lời giải chi tiết dành cho bạn đọc.
Bài 21: Giải Phương Trình:
3 2 2
2 3 5 2 5 7 2 2 1 0x x x x x x
▶ Ý tưởng :
Ta sẽ sử dụng phương pháp đặt ẩn phụ không hoàn toàn để giải quyết bài
toán.
▶ Thực hiện :
Sử dụng máy tính cầm tay CASIO ta được 2 nhân tử của bài toán
này là :
2 1 2 xx
2 1 2 3 xx
Sử dụng máy tính cầm tay CASIO để chia biểu thức ta được :
3 2 2
2 3 5 2 5 7 2 2 1
2 1 1
2 1 2 3 2 1 2
x x x x x x
xx
x x x x
Từ đó ta đặt
21xa
thì :
3 2 2
3 2 2 3 2
2 3 5 2 5 7 2 2 1
1 2 2 3
2 5 5 4 9 1 4 6
x x x x x x
a x a x a x
x a x a a x a a a
Kết luận :
3 2 2
2 3 5 2 5 7 2 2 1 1 2 2 3x x x x x x a x a x a x
▶ Phân tích hướng giải:
Ta chỉ cần trình bày ngược lại với những gì chúng ta làm
▶ Lời giải : Đặt ẩn phụ không hoàn toàn:
ĐKXĐ :
1
2
x
. Đặt
21ax
với
0a
thì :
3 2 2
3 2 2 3 2
2 3 5 2 5 7 2 2 1 0
2 5 5 4 9 1 4 6 0
1 2 2 3 0
x x x x x x
x a x a a x a a a
a x a x a x
Bài 22: Giải Phương Trình:
3 2 2
3 2 4 2 6 2 0x x x x x x
▶ Ý tưởng :
Ta sẽ thử đặt ẩn phụ để đưa về hệ phương trình
▶ Thực hiện :
Sử dụng máy tính cầm tay CASIO ta được 2 nhân tử của bài toán
này là :
23xx
Vậy ta đặt
2ax
và
3bx
suy ra
2
1ab
và :
3 2 2
3 2 2
2 3 2
3 2 4 2 6 2
3 3 3 2 3 4 3 2 3 6
8 9 6 11 2
x x x x x x
b b b b b a
b b a b b b
Hệ phương trình của chúng ta sẽ là :
2
2 3 2
10
8 9 6 11 2 0
ab
b b a b b b
Vì ta luôn có
ab
nên chỉ cần làm mất hệ số tự do, tức
2 (1) (2)PT PT
là ta có lời giải rồi.
Kết luận : Lấy
2 (1) (2)PT PT
rồi phân tích thành nhân tử.
▶ Phân tích hướng giải:
Tuy lời giải này hơi dài nhưng cũng khá hay. Chúng ta cùng thử phương
pháp đặt ẩn phụ giải hệ phương trình
▶ Lời giải : Đặt ẩn phụ đưa về hệ phương trình:
ĐKXĐ :
2x
. Khi đó đặt
2ax
và
3bx
với
0a
và
1b
suy ra
3 2 2
3 2 2
2 3 2
3 2 4 2 6 2
3 3 3 2 3 4 3 2 3 6
8 9 6 11 2
x x x x x x
b b b b b a
b b a b b b
Vậy ta có hệ phương trình :
2
2 3 2
10
8 9 6 11 2 0
ab
b b a b b b
Lấy
2 (1) (2)PT PT
ta được :
2 3 2 2
2
8 9 6 9 2
6 9 2
3
0
0
0
b b a b b b a
a b b b a
ab
a
b
(vì
22
6 9 2 ( 3) 2 0 b b a b a
)
Lời giải chi tiết dành cho bạn đọc.
Bài 23: Giải Phương Trình:
22
2 1 2 2 0x x x x
▶ Ý tưởng :
Tuy đây là một dạng toán khó hơn dạng ban đầu một tẹo nhưng ý tưởng
vẫn là tìm nhân tử.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
22
2 1 2 2 0x x x x
có nghiệm
A 0.215250436
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
22
2 1 2 2 0x x x x
có nghiệm
B -1.54858377
Vì
4
3
AB
nên
2
27
23
A B A B
A


Nghiệm của bài toán này là
27
3
x

. Khi đó :
2
29 4 7 1 2 7
2 2 1
93
xx
Kết luận : Nhân tử của bài toán này là
2
2 2 1xx
▶ Phân tích hướng giải:
Ta chủ yếu dùng các cách sau cho dạng toán này :
Nhân liên hợp
Phân tích thành nhân tử
Đạo hàm, hàm số
Đánh giá, bất đẳng thức
Đặt ẩn phụ đưa về hệ phương trình
Phương pháp bình phương hai vế nhiều khi không sử dụng được để giải
bất phương trình hoặc nó có nguy cơ tiềm ẩn nghiệm lẻ.
▶Cách 1 : Nhân liên hợp hoàn toàn:
Ta có :
2
2 2 2
2 1 2 2 0 1 2 2 0x x x x x x x x
Vì vậy :
22
22
2
2
2
2 1 2 2 0
3 4 1 2 2 2 1 0
2
3 4 1 1 0
2 2 1
3 4 1 0
x x x x
x x x x x
x
xx
xx
xx




(vì
2
22
2 2 1
1 0 0
2 2 1 2 2 1
xx
x
x x x x

)
27
3
x


(vì
0x
)
Vậy
27
3
x

.
▶Cách 2 : Nhân liên hợp không hoàn toàn:
Ta có :
22
22
2 2 2
22
2 1 2 2 0
3 4 1 2 2 2 1 0
2 2 1 2 2 1 2 2 2 1 0
2 2 1 2 1 0
x x x x
x x x x x
x x x x x x x
x x x
2
2 2 1xx
(vì
2
2 1 0xx
)
2
2
2
3 4 1 0
2 2 1 2 7
3
2 1 0
2 1 0
xx
xx
x
x
x




Vậy
27
3
x

.
▶Cách 3 : Phân tích thành nhân tử:
Ta có :
22
22
2 1 2 2 0
2 1 2 2 1 0
x x x x
x x x
▶Cách 4 : Đạo hàm:
Xét hàm
22
2 1 2 2f x x x x x
trên .
Khi đó ta có :
2
2
41
22
2
x
f' x x
x
. Vậy suy ra :
2
2
22
4 3 2
1
0
1 2 4 1
1
3 2 5 4 2 0
x
f' x
x x x
x
x x x x

Vậy phương trình
0f ' x
vô nghiệm. Suy ra
0fx
có tối đa 1 nghiệm.
Dễ thấy
27
0
3
f





nên
27
3
x

là nghiệm duy nhất của bài toán.
▶Cách 5 : Đánh giá, bất đẳng thức:
Ta thấy :
2
2
2
2 1 0
27
2 2 1 0
3
2 2 1
x
x x x
xx


.
Tương tự thì :
2
27
2 2 1 0
3
x x x

.
Lại có
2
2 2 2
2 1 2 2 1 2 2 0x x x x x x x x
. Vậy :
Nếu
27
3
x

thì :
2 2 2 2
2 1 2 2 2 1 2 2 1 3 4 1 0x x x x x x x x x x
Nếu
27
0
3
x


thì :
2 2 2 2
2 1 2 2 2 1 2 2 1 3 4 1 0x x x x x x x x x x
Nếu
27
3
x

thì thỏa mãn.
Vậy
27
3
x

.
▶Cách 6 : Đặt ẩn phụ đưa về hệ phương trình:
Đặt
2
2 2 1xy
(mục đích là để
xy
). Ta được hệ phương trình :
2
2
2
22
2
2 2 1
2 1 2 2 1
4 4 1 0
4 4 1 0
xy
x x x y
x y y
x xy x
Để mất hệ số tự do, ta lấy
(1) (2)PT PT
rồi phân tích nhân tử, chắc chắn
sẽ có nhân tử
xy
vì ta ép nó phải như vậy mà. Thử nhé :
2 2 2
4 4 1 4 4 1 0
4 1 0
x y y x xy x
y x y
Lời giải chi tiết dành cho bạn đọc.
❓Tại sao không đưa về hệ phương trình đối xứng như một số giáo viên
hay giảng dạy?
Là người nghiên cứu lâu năm nên mình hiểu bản chất của việc đưa về hệ
phương trình đối xứng. Lấy một ví dụ, mình là Bùi Thế Việt sinh ngày
13/02/1997 nên mình sẽ tự tạo ra một hệ phương trình đối xứng như sau :
2
2
13 2 7
13 2 7
x x y xy
y y x xy
Và sau đây là bài toán suy ra từ hệ phương trình trên :
Bài toán: Giải Phương Trình:
22
47 131 26 7 2 49 190 169 0x x x x x
▶Lời giải: Đặt ẩn phụ đưa về hệ phương trình đối xứng :
Đặt
2
49 190 169 2 7 13x x y x
ta được hệ phương trình :
2
2
2
2
2
2
2
49 190 169 2 7 13
47 131 26 7 2 2 7 13 0
28 4 8 52 0
14 2 2
1
6
3 2 7
13 2
4
7
0
x x y x
x x x y x
xy y x y
xy
x x y xy
y y x
xy
y
x
x
❓Tại sao bài toán này có thể đưa về hệ phương trình đối xứng?
Thực chất không hẳn bài toán nào cũng có thể đưa được về hệ phương
trình đối xứng. Bản chất là việc đặt
2
49 190 169x x ax by c
và biến
đổi phương trình dưới dạng
0x y x y k
nhưng nhiều bài toán
chưa chắc có thể biến đổi như vậy được. Cách tốt nhất để giải những bài
toán dạng này là phân tích thành nhân tử hoặc nhân liên hợp, đánh giá :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
22
47 131 26 7 2 49 190 169 0x x x x x
có tập nghiệm
5 11 2 13
0
22
;;






Nhân tử của bài toán sẽ là :
2
49 190 169 5 13x x x
chứa cặp nghiệm
5
0
2
;



2
49 190 169 9 9x x x
chứa nghiệm
11 2 13
2






Lời giải bài toán trên chỉ là :
22
22
47 131 26 7 2 49 190 169 0
2 49 190 169 5 13 49 190 169 9 9 0
x x x x x
x x x x x x
Bài 24: Giải Phương Trình:
22
5 4 1 1 3 1 0x x x x x
▶ Ý tưởng :
Ta vẫn sẽ có những cách sau nhờ phương pháp tìm nhân tử
Nhân liên hợp
Phân tích thành nhân tử
Đạo hàm, hàm số
Đánh giá, bất đẳng thức
Đặt ẩn phụ đưa về hệ phương trình
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
22
5 4 1 1 3 1 0x x x x x
có tập nghiệm
1
0
3
;



Gọi nhân tử của bài toán là
2
31x x ax b
. Khi đó :
10
2
11
1
0
33
b
a
b
ab




Kết luận : Nhân tử của bài toán này là
2
3 1 2 1x x x
▶ Phân tích hướng giải:
Vẫn sẽ có khá nhiều cách làm như bài toán trước.
▶Cách 1 : Nhân liên hợp hoàn toàn:
Ta có :
22
2
5 4 1 1 3 1 0
1
3 1 1 0
3 1 2 1
x x x x x
x
xx
x x x




▶Cách 2 : Nhân liên hợp không hoàn toàn:
Ta có :
22
22
22
2
22
5 4 1 1 3 1 0
3 1 3 1 2 1
3 1 2 1 3 1 2 1
1 3 1 2 1 0
3 1 2 1 3 1 3 2 0
x x x x x
x x x x x x
x x x x x x
x x x x
x x x x x x
▶Cách 3 : Phân tích thành nhân tử:
Ta có :
22
22
5 4 1 1 3 1 0
3 1 2 1 3 1 3 2 0
x x x x x
x x x x x x
▶Cách 4 : Đạo hàm, hàm số:
Ta đặt :
22
5 4 1 1 3 1f x x x x x x
suy ra :
2
2
32
3
2
5
2
4 11 5
10 4
2 3 1
8 36 39 7
10
4 3 1
15 1
8 3 1
xx
f' x x
xx
x x x
f'' x
xx
x
f''' x
xx





▶Cách 5 : Đánh giá, bất đẳng thức:
Ta có :
2
2
1
0
3
3 1 2 1
35
2
0
3 1 2 1
3 5 1
23
x
x x x
x
x
x x x
x


▶Cách 6 : Đặt ẩn phụ đưa về hệ phương trình:
Ta có : Đặt
2
3 1 2 1x x y
ta được hệ phương trình :
22
2
4 3 4 0
5 2 3 2 0
x y x y
x xy x y
Bài toán này không có hệ số tự do nên ta phải làm kiểu khác.
Cho
xy
ta được :
2 2 2
22
4 3 4 3
5 2 3 2 3
x y x y y y
x xy x y y y
.
Để triệt tiêu thì ta phải lấy
(1) (2)PT PT
. Vậy lấy
(1) (2)PT PT
ta được :
2 2 2
4 3 4 5 2 3 2 0
2 3 2 3 0
x y x y x xy x y
x y x y
Bài 25: Giải Phương Trình:
3 2 2 2
7 7 5 14 13 3 2 8 0x x x x x x x
▶ Ý tưởng :
Ta dựa vào nghiệm của phương trình để giải quyết bài toán này.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
3 2 2 2
7 7 5 14 13 3 2 8 0x x x x x x x
có nghiệm
duy nhất
1
8
x
Kết luận : Phương trình có nghiệm duy nhất
1
8
x
▶ Phân tích hướng giải:
Với những bài toán có nghiệm duy nhất, ta thử các phương pháp sau :
Nhân liên hợp
Đạo hàm
Bất đẳng thức, đánh giá
▶Cách 1 : Nhân liên hợp hoàn toàn:
Khi
1
8
x
thì
2
23
28
8
xx
nên ta sẽ có lời giải như sau :
3 2 2 2
2
3 2 2
2
2
2
7 7 5 14 13 3 2 8 0
33 339
43 23
7 13 3 2 8
8 8 8 8
8 17 13 3
1
8 1 7 5 43 0
8
8 2 8 23
x x x x x x x
xx
x x x x x
x x x
x x x
xx







Cách này khó khăn rồi. Để giải tiếp ta phải đánh giá phương trình :
2 2 2
7 5 43 8 2 8 23 8 17 13 3 0x x x x x x x
Thứ nhất, ta luôn có :
2
7 5 43 0x x x
Thứ hai, ta thấy :
2
2 8 2
7
x
x x x
(bạn đọc tự chứng minh)
Nếu
20
7
x

thì
2
8 17 13 3 0x x x
, suy ra :
2 2 2
7 5 43 8 2 8 23 8 17 13 3 0x x x x x x x
Nếu
20
7
x

thì
2 2 2
22
2
2
7 5 43 8 2 8 23 8 17 13 3
7 5 43 8 2 23 8 17 13 3
7
2560 3424
1728
77
2560 107 109511
0
7 160 70
x x x x x x x
x
x x x x x
xx
x









▶Cách 2 : Đạo hàm:
Xét hàm số :
3 2 2 2
7 7 5 14 13 3 2 8f x x x x x x x x
Ta có :
32
2
2
3 21 26 107
21 14 5
28
x x x
f' x x x
xx

.
Lại một thử thách nữa đến với chúng ta.
Chúng ta cần giải phương trình sau :
3 2 2 2
3 21 26 107 21 14 5 2 8 0x x x x x x x
Thử một vài giá trị bằng máy tính cầm tay, ta thấy :
3 2 2 2
3 21 26 107 21 14 5 2 8 0x x x x x x x x
.
Có lẽ ta phải làm tương tự cách 1 thôi :
Thứ nhất, ta luôn có :
2
21 14 5 0x x x
.
Vậy ta có :
Nếu
20
7
x

thì
32
3 21 26 107 0x x x
, suy ra :
3 2 2 2
3 21 26 107 21 14 5 2 8 0x x x x x x x x
Nếu
20
7
x

thì :
3 2 2 2
3 2 2
2
2
3 21 26 107 21 14 5 2 8
3 21 26 107 21 14 5 2
7
383
65 117
7
383 1343891
65 0
910 12740
x x x x x x x
x
x x x x x
x
x
x






▶Cách 3 : Đánh giá, bất đẳng thức:
Phương trình
3 2 2 2
7 7 5 14 13 3 2 8 0x x x x x x x
có nghiệm
duy nhất
1
8
x
.
Đánh giá theo
2
28xx
thì được nhưng còn
2
13 3xx
thì sao ?
Ta chưa biết dấu của
2
13 3xx
. Ta sẽ xét cả dấu của nó nữa :
Nếu
13 181
2
x
thì
2
2
13 3 0
2 8 7 78
xx
x x x
. Khi đó :
3 2 2 2
3 2 2
2
2
7 7 5 14 13 3 2 8
7 7 5 14 13 3 7 78
176 988 248
176 13 3 1300 280 0
x x x x x x x
x x x x x x
xx
x x x
Nếu
1 13 181
82
x

thì
2
2
13 3 0
23
28
8
xx
xx
. Khi đó :
3 2 2 2
3 2 2
2
7 7 5 14 13 3 2 8
23
7 7 5 14 13 3
8
1
7 5 43 0
8
x x x x x x x
x x x x x
x x x



Nếu
13 181 1
28
x

thì
2
2
13 3 0
23
28
8
xx
xx
. Khi đó :
3 2 2 2
3 2 2
2
7 7 5 14 13 3 2 8
23
7 7 5 14 13 3
8
1
7 5 43 0
8
x x x x x x x
x x x x x
x x x



Nếu
13 181
2
x
thì
2
2
13 3 0
2 8 0
0
xx
xx
x
. Khi đó :
3 2 2 2
32
7 7 5 14 13 3 2 8
7 7 5 14 0
x x x x x x x
x x x
Bài toán được giải quyết hoàn toàn.
▶Cách 4 : Phân tích thành nhân tử:
Phương trình
3 2 2 2
7 7 5 14 13 3 2 8 0x x x x x x x
có nghiệm
duy nhất
1
8
x
và nhân tử
2
28x x ax b
Phương trình
3 2 2 2
7 7 5 14 13 3 2 8 0x x x x x x x
có nghiệm
duy nhất
2
3
x 
và nhân tử
2
28x x ax b
(vì ta đổi dấu trước
căn nên nhân tử cũng có căn đổi dấu).
Vậy :
23 1
0
7
88
8 2 2
0
33
ab
a
b
ab



Nhân tử của bài toán là :
2
2 8 7 2x x x
Sử dụng máy tính cầm tay để phân tích thành nhân tử, ta được lời giải :
3 2 2 2
2 2 2
2
7 7 5 14 13 3 2 8 0
2 8 7 2 2 2 8 1 0
2 8 7 2 0
1
8
x x x x x x x
x x x x x x x
x x x
x

Lời giải chi tiết dành cho bạn đọc.
❓Tại sao bài toán này có thể phân tích thành nhân tử khi có nghiệm duy
nhất?
Như chúng ta đã biết, chúng ta chắc chắn tìm được nhân tử của bài toán
nếu biết 2 nghiệm hữu tỷ hoặc 1 nghiệm vô tỷ dạng
ab
.
Tuy nhiên, đối với nghiệm duy nhất thì tùy từng bài mới có thể phân tích
thành nhân tử được.
Cách tốt nhất để thử xem bài toán có phân tích thành nhân tử khi có
nghiệm duy nhất là phương pháp đổi dấu trước căn.
Nếu bài toán sau khi đổi căn mà có nghiệm vô tỷ dạng
ab
hoặc
nghiệm hữu tỷ thì chắc chắn phương trình ban đầu có thể phân tích thành
nhân tử được. Nếu không thì ta nên làm cách khác cho bài toán
Bài 26: Giải Phương Trình:
2 2 2
5 4 2 2 2 1 0x x x x x x
▶ Ý tưởng :
Ta dựa vào nghiệm của phương trình để giải quyết bài toán này.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
2 2 2
5 4 2 2 2 1 0x x x x x x
có nghiệm
0 6403882032A.
và
0 1569296691B.
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
2 2 2
5 4 2 2 2 1 0x x x x x x
có nghiệm
0 3903882032C.
và
1 593070331D.
và
1E
Thấy
AC
nên
2
1 17
28
A C (A C)
A


Thấy
BD
nên
2
7 33
28
B D B D)
B


Từ đó ta tìm ra được các nhân tử là :
2
2 2 3x x x
và
2
2 2 3 2x x x
Kết luận : Phương trình có hai nhân tử là :
2
2 2 3x x x
và
2
2 2 3 2x x x
▶ Phân tích hướng giải:
Ta dùng thủ thuật CASIO để chia biểu thức, ta được :
▶Lời giải : Phân tích thành nhân tử:
Ta có :
2 2 2
2 2 2
5 4 2 2 2 1 0
1
2 2 3 2 2 3 2 2 2 1 0
2
x x x x x x
x x x x x x x x
Bài 27: Giải Phương Trình:
3 2 2 2
4 4 4 8 1 0x x x x x
▶ Ý tưởng :
Ta cũng dựa vào nghiệm của phương trình để giải quyết bài toán này.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
3 2 2 2
4 4 4 8 1 0x x x x x
có nghiệm
4
3
x
và
12
5
x 
Gọi nhân tử của bài toán là
2
1x ax b
thì :
2
54
1
0
1
33
1 2 0
4
13 12
4
2
0
55
ab
a
xx
b
ab




Kết luận : Phương trình có nhân tử là
2
1
12
4
xx



▶ Phân tích hướng giải:
Ta dùng thủ thuật CASIO để chia biểu thức hoặc sử dụng phương pháp
nhân liên hợp không hoàn toàn:
▶Lời giải : Nhân liên hợp không hoàn toàn:
Ta có :
3 2 2 2
2 2 3 2 2
22
2 2 2 2
2
2
22
4 4 4 8 1 0
4 8 1 2 4 4 4 8 2
44
4 8 1 2
4
4 8 1 2 4 1 2 1 2
44
15
4
4 1 8 1
12
4
0
4
x x x x x
xx
x x x x x x x
x
x
x
x x x
x x x
x x x x x
x x x x



Bài 28: Giải Phương Trình:
22
4 4 3 2 0x x x x x
▶ Ý tưởng :
Ta dựa vào nghiệm của phương trình để tìm nhân tử của bài toán.
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
22
4 4 3 2 0x x x x x
có nghiệm
2
5
x
và
0 2637626160x A .
.
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
22
4 4 3 2 0x x x x x
có nghiệm
1 263762616B.
Vì
2
3 21
26
A B (A B)
A B A

Gọi nhân tử là
2
2x x ax b
thì :
2
2
21 3 21
0 2 2 1 0
1
36
a
a b x x x
b



Kết luận : Phương trình có nhân tử là
2
2 2 1x x x
▶ Phân tích hướng giải:
Tương tự các bài toán trước, ta cũng sẽ nhanh chóng có lời giải bằng cách
phân tích thành nhân tử
▶Lời giải : Phân tích thành nhân tử:
Ta có :
22
22
2 2 1
42
2
3
2
4
0
0x
x x x x
x
x
xx
x
x


Bài 29: Giải Phương Trình:
2
2 14 2 1 3 1 11 1 0x x x x
▶ Ý tưởng :
Tuy đây là một dạng toán khó hơn nhưng ý tưởng vẫn là phương pháp tìm
nhân tử
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
2
2 14 2 1 3 1 11 1 0x x x x
có nghiệm
65
16
x
và
5
4
x
.
Gọi nhân tử là
11x a x b
thì :
79
5
0
5
44
1 1 2 0
3
13
3
2
0
22
ab
a
xx
b
ab




Kết luận : Phương trình có nhân tử là
3 1 5 1 6xx
▶ Phân tích hướng giải:
Ta có thể sử dụng máy tính CASIO để chia biểu thức. Lời giải sẽ nhanh
chóng được tìm ra :
▶Cách 1 : Nhân liên hợp không hoàn toàn:
Ta có :
2
5 16
1 1 2 3 2 1
33
5
1 1 2
2 14 2 1 3 1 11 1 0
70
20 1
3
32
55
1 1 2 1 1 2
33
3 1 5 1
1
3
6 1 1 1 0
3
x x x
x
x x x x
xx
x x x x
x
x
xx
x
x






▶Cách 2 : Phân tích thành nhân tử:
Ta có :
2
2 14 2 1 3 1 11 1 0
1 3 1 5 1 1 2 0
x x x x
x x x x
Bài 30: Giải Phương Trình:
2
9 2 6 1 5 1 8 1x x x x
▶ Ý tưởng :
Ta sẽ tìm nhân tử dạng
11x a x b
của phương trình trên
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
2
9 2 6 1 5 1 8 1x x x x
có nghiệm
0 9921567416A.
và
0 9921567416B.
Vì
2
37
28
A B (A B)
A B A
Gọi nhân tử là
11x a x b
thì :
1 0 1
3
1 1 0
3 3 3
2
0
4 4 2
aa
xx
a b b





Kết luận : Phương trình có nhân tử là
2 1 2 1 3xx
▶ Phân tích hướng giải:
Ta làm tương tự bài trên:
▶Lời giải : Phân tích thành nhân tử:
Ta có :
2
2 1 2 1 3 1 2
9 2 6 1 5 1 8 1
1 1 0
x x x
x x x
x
x
Bài 31: Giải Phương Trình:
2
3 10 3 2 6 2 4 4 0x x x x
▶ Ý tưởng :
Ta sẽ tìm nhân tử dạng
22x a x b
của phương trình trên
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
2
3 10 3 2 6 2 4 4 0x x x x
có nghiệm duy nhất
6
5
x
.
Khi
6
5
x
thì
45
2
5
x
và
25
2
5
x
Gọi nhân tử là
22x a x b
thì :
4 5 2 5
0
55
a
b
với
a,b
suy ra
20(a;b) ( ; )
Kết luận : Phương trình có nhân tử là
2 2 2xx
▶ Phân tích hướng giải:
Ta sẽ sử dụng máy tính CASIO để chia biểu thức:
▶Lời giải : Phân tích thành nhân tử:
Ta có :
2
3 10 3 2 6 2 4 4 0
2 2 2 2 2 2 3 0
x x x x
x x x x
Bài 32: Giải Phương Trình:
32 8 2 4 4 015 7x x x x x
▶ Ý tưởng :
Ta sẽ tìm nhân tử dạng
24x a x b
của phương trình trên
▶ Thực hiện :
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
32 8 2 4 4 015 7x x x x x
có nghiệm duy nhất
2 133974596A.
.
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
32 8 2 4 4 015 7x x x x x
có nghiệm duy nhất
3 663836718B.
.
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
32 8 2 4 4 015 7x x x x x
vô nghiệm.
Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình
32 8 2 4 4 015 7x x x x x
có nghiệm
3 866025404C.
và
2 096163282D.
Thành thử
A B,A C,A D
ta thấy :
2
63
22
A C (A C)
A C A
Gọi nhân tử là
24x a x b
thì :
1
1 3 1 3
0 2 4 1 0
1
22
a
a b x x
b

Kết luận : Phương trình có nhân tử là
2 4 1xx
▶ Phân tích hướng giải:
Ta sẽ sử dụng máy tính CASIO để chia biểu thức:
▶Lời giải : Phân tích thành nhân tử:
Ta có :
32 8 2 4 4 015 7
2 4 1 3 4 4 2 8 2 4 4 0
x x x x x
x x x x x x x
THỦ THUẬT 7 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
GIẢI HỆ PHƯƠNG TRÌNH
Bài 1: Giải Hệ Phương Trình:
22
2
40
20
x y y
y xy x y
▶ Ý tưởng :
Ý tưởng của chúng ta rất đơn giản : lấy
12PT( ) kPT( )
rồi phân tích thành
nhân tử
❓ Làm thế nào để tìm được
k
?
Có khá nhiều cách để tìm được
k
. Đối với dạng
toán này thì có cách khác:
22
1 1 1 1 1 1
22
2 2 2 2 2 2
0
0
a x b y c xy d x e y f
a x b y c xy d x e y f
Khi đó đặt
k
sẽ là nghiệm của phương trình :
2 2 2
4cde abf ae bd fc
Với :
12
12
12
12
12
12
a a ka
b b kb
c c kc
d d kd
e e ke
f f kf






▶ Thực hiện :
Áp dụng công thức :
2 2 2
4cde abf ae bd fc
Ta có :
2
2
22
4 1 4 2 1
1 1 4 2
k k k k
k k k k k
Ta được 3 nghiệm là
5
13
2
k ;k ;k
Với :
1
1
1
42
a
bk
ck
dk
ek
fk

Kết luận : Ta lấy
12PT( ) PT( )
hoặc
2 1 5 2PT( ) PT( )
hoặc
1 3 2PT( ) PT( )
rồi
phân tích thành nhân tử
❓ Nếu không tìm được
k
hoặc
k
lẻ thì sao?
99,99% sẽ tìm được
k
. Nếu
k
lẻ thì chứng tỏ bài toán có lẽ sai đề hoặc là
không phù hợp. Tuy nhiên một số bài toán cho
2; 3;...k
thì ta cũng có
thể áp dụng công thức trên.
▶ Phân tích hướng giải:
Việc phân tích thành nhân tử bằng CASIO là một lợi thế không hề nhỏ.
▶ Cách 1 : Phân tích thành nhân tử:
Lấy
12PT( ) PT( )
ta được:
2 1 0(x )(x y )
▶ Cách 2 : Phân tích thành nhân tử:
Lấy
2 1 5 2PT( ) PT( )
ta được:
2 2 3 1 0(x y )( x y )
▶ Cách 3 : Phân tích thành nhân tử:
Lấy
1 3 2PT( ) PT( )
ta được:
2 2 1 0(x y )(x y )
Bài 2: Giải Hệ Phương Trình:
22
2
16 4 12
8 4 28 5 18
x xy y
x xy x y
(đề thi Học Sinh Giỏi lớp 12 – TP Hồ Chí Minh năm 2014)
▶ Ý tưởng :
Ta sẽ tìm
k
bằng công thức.
▶ Thực hiện :
Áp dụng công thức :
2 2 2
4cde abf ae bd fc
Ta có :
2
2
22
4 16 8 12 18 140 4 4
25 16 8 784 4 4 12 18
k k k k
k k k k k
Ta được nghiệm là
2k
Với :
16 8
1
44
28
5
12 18
ak
b
ck
dk
ek
fk




Kết luận : Ta lấy
1 2 2PT PT
rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta sẽ sử dụng thủ thuật phân tích thành nhân tử 2 ẩn để giải quyết bài toán
▶ Lời giải : Phân tích thành nhân tử:
Lấy
1 2 2PT( ) PT( )
ta được:
4 4 8 6 0x y x y
Bài 3: Giải Hệ Phương Trình:
3 3 2
22
3 15 18 36
2 2 2 6 3 0
x y x x y
x y x y
▶ Ý tưởng :
Ta sẽ tìm
k
không bằng công thức
2 2 2
4cde abf ae bd fc
mà sử dụng
mối liên hệ giữa các nghiệm
,xy
giống như cách giải phương trình vô tỷ.
▶ Thực hiện :
Tìm nghiệm của hệ phương trình bằng CASIO ta được các bộ
nghiệm là :
3 3 1 5
2 2 2 2
(x, y) , ; ,
Giả sử
x ay b
suy ra
33
1
22
3
1 5 3
22
ab
a
xy
b
ab


Khi
3xy
thì :
3 3 2
22
3 15 18 36 3 2 3 2 5
2 2 2 6 3 2 3 2 5
x y x x y y y
x y x y y y
Suy ra
1 3 2PT PT
Kết luận : Ta lấy
1 3 2PT PT
rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta sẽ chỉ cần nói
1 3 2PT PT
mà không phải trình bày dài dòng như
trên.
▶ Lời giải : Phân tích thành nhân tử:
Lấy
1 3 2PT( ) PT( )
ta được:
3 3 2 2 2
22
3 15 18 36 3 2 2 2 6 3 0
3 3 9 0
30
x y x x y x y x y
(x y )(x xy y y )
xy
Vì :
22
2
2
22
2 2 2 6 3
3 4 29
3 9 1 0
2 4 3 3
x y x y
y
(x xy y y ) x y






Lời giải chi tiết dành cho bạn đọc.
Bài 4: Giải Hệ Phương Trình:
22
22
2 9 0
0
1
x y x y xy
x x y x
▶ Ý tưởng :
Ta làm tương tự bài 3.
▶ Thực hiện :
Tìm nghiệm của hệ phương trình bằng CASIO ta được các bộ
nghiệm là :
1 2 2 1(x,y) ( , );( , )
Mối liên hệ giữa
x
và
y
là
3xy
Khi
3xy
thì :
22
22
12 9 6 1
3 1 2
2xx
x
y x y y
y x y xy y y
Suy ra
2 1 2PT( ) PT( )
Kết luận : Ta lấy
2 1 2PT( ) PT( )
rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta sẽ sử dụng thủ thuật phân tích thành nhân tử 2 ẩn để giải toán.
▶ Lời giải : Phân tích thành nhân tử:
Lấy
2 1 2PT( ) PT( )
ta được:
2
3 2 4 0
3
(x y )(x xy x y )
xy
Vì :
22
2
2
2
2
3 7 3 10
2 4 0
2 2 4 7 7
x xy y x y
y
x xy x y x y






Lời giải chi tiết dành cho bạn đọc.
Bài 5: Giải Hệ Phương Trình:
3 2 3
3
4 12 9 6 5
xy x y
x x x y y
▶ Ý tưởng :
Ta làm tương tự bài 3.
▶ Thực hiện :
Tìm nghiệm của hệ phương trình bằng CASIO ta được các bộ
nghiệm là :
3 17 1 17
42
(x, y) ,




Mối liên hệ giữa
x
và
y
là
1
2
y
x 
Khi
1
2
y
x 
thì :
2
3 2 3 2
1
34
2
3
4 12 9 6 5 1 4
2
xy x y y y
x x x y y y y y
Suy ra
3 1 1 2(y )PT( ) PT( )
Kết luận : Ta lấy
3 1 1 2(y )PT( ) PT( )
rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta làm tương tự các bài toán trước :
▶ Lời giải : Phân tích thành nhân tử:
Lấy
3 1 1 2(y )PT( ) PT( )
ta được:
2
1 2 2 0(x y )( x y )
Lời giải chi tiết dành cho bạn đọc.
Bài 6: Giải Hệ Phương Trình:
33
22
91
4 3 16 9
xy
x y x y

▶ Ý tưởng :
Ta làm tương tự bài 3.
▶ Thực hiện :
Tìm nghiệm của hệ phương trình bằng CASIO ta được các bộ
nghiệm là :
4 3 3 4(x,y) ( , );( , )
Mối liên hệ giữa
x
và
y
là
7xy
Khi
7xy
thì :
33
22
91 21 4 3
4 3 16 9 7 4 3
x y y y
x y x y y y
Suy ra
1 3 2 0PT( ) PT( )
Kết luận : Ta lấy
1 3 2PT( ) PT( )
rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta làm tương tự các bài toán trước :
▶ Cách 1 : Hàm đặc trưng:
Lấy
1 3 2PT( ) PT( )
ta được:
32
32
12 48 7 12 7 48 7x x x y y y
Xét hàm đặc trưng:
2
32
12 48 3 4 0f t t t t f ' t t
Lời giải chi tiết dành cho bạn đọc.
▶ Cách 2 : Phân tích thành nhân tử:
Lấy
1 3 2PT( ) PT( )
ta được:
3 2 3 2
22
22
12 48 7 12 7 48 7
7 5 2 13 0
53
7 3 0
2 2 2 2
x x x ( y) ( y) ( y)
x y x xy y x y
yy
x y x




Lời giải chi tiết dành cho bạn đọc.
Bài 7: Giải Hệ Phương Trình:
22
32
3 9 9
2 20 20
x xy x y y
x x y x y
▶ Ý tưởng :
Ta làm tương tự bài 3.
▶ Thực hiện :
Tìm nghiệm của hệ phương trình bằng CASIO ta được các bộ
nghiệm là :
0 0 2 1(x,y) ( , );( , )
Mối liên hệ giữa
x
và
y
là
2xy
Khi
2xy
thì :
22
32
3 9 9 9 1
2 20 20 20 1 1
x xy x y y y y
x x y x y y y y

Suy ra
20 1 1 9 2 0(y )PT( ) PT( )
Kết luận : Ta lấy
20 1 1 9 2(y )PT( ) PT( )
rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta phải làm thêm một hệ phương trình nữa:
▶ Cách 1 : Phân tích thành nhân tử:
Lấy
20 1 1 9 2(y )PT( ) PT( )
ta được:
22
2 18 10 15 60 80 0(x y)( x y xy x y)
Lấy
8 1 3PT( ) PT( )
ta được:
2 222
18 10 15 608 80 0
24
3
0
9
32
9x xy x y x y xy x y
x y x
y
y


Lời giải chi tiết dành cho bạn đọc.
▶ Cách 2 : Phân tích thành nhân tử:
Lấy
4 2 5 1 9 2x y PT( ) PT( )
ta được:
2 3 2 2 4 0y x x y x y
Lời giải chi tiết dành cho bạn đọc.
THỦ THUẬT 8 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
TÍNH NGUYÊN HÀM, TÍCH PHÂN
Bài 1: Tính Tích Phân:
2
2
3
2
2
1x
x dx
I
▶ Ý tưởng :
Ta cần viết dưới dạng:
2 22
2
2
11
11
1
x a b c d
fx
xx
xx
x


với
a,b,c,d
.
Khi đó ta sẽ tìm
, , ,a b c d
bằng
lim
▶ Thực hiện :
Ta lần lượt tìm
lim
của các biểu thức sau :
2
1
2
1
2
1
2
1
1
1
4
1
1
4
1
1
1
4
1
1
4
1
x
x
x
x
a lim f x x
a
b lim f x x
x
c lim f x x
c
d lim f x x
x










Kết luận : Ta được :
2
222
2
1 1 1 1
4
1
1 4 1
4 1 4 1
x
x
x
x
xx


▶ Phân tích hướng giải:
Công việc của chúng ta đơn giản rồi. Chúng ta sẽ tách như trên và tính tích
phân từng phần
▶ Lời giải : Tích phân tổng:
Ta có :
33
2
22
22
3
2
2
2
1 1 1 1
4 1 4 1
4 1 4 1
1 1 1 1 3 7
11
4 1 1 4 2
1
48
x dx
I dx
xx
xx
ln x ln x ln
xx
x











Bài 2: Tính Tích Phân:
3
2
0
2
tanxdx
I
cos x
(đề thi thử Đại Học lần 2 THPT Kim Thành 2 – Hải Dương năm 2013)
▶ Ý tưởng :
Đặt
t cosx
thì
dt sinxdx
. Đổi cận ta được:
1
3
2
1
0
2
2
2 2
tan xdx d
tt
t
I
cos x

Ta cần viết dưới dạng :
22
2
1
22
a b c
ft
tt
ttt
▶ Thực hiện :
Ta lần lượt tìm
lim
của các biểu thức sau :
2
2
2
2
0
1
1
2
2
1
4
2
2
4
t
t
t
a lim f t t
b lim f t t
t
c lim f t
a
t








Kết luận : Ta được :
2 2
1 1 1
4
222
42
1
tt
tt t

▶ Phân tích hướng giải:
Ta sẽ trình bày như sau :
▶ Lời giải : Tích phân tổng:
Ta đặt
t cosx
thì
dt sinxdx
. Khi đó :
11
3
22
11
0
22
1
1
2
2
1 1 1
4 4 2
2 2 2
1 1 5 1
2
2 2 4 3 30
2
11
44
tan xdx
dt
dt
I
tt
cosx t
ln t ln t
t
l
t
t
n









Bài 3: Tính Tích Phân:
5
2
5
1
2
1
1x
x dx
I
x
▶ Ý tưởng :
Đặt
5 4
5dt xt dx x
. Vậy:
5
2 32
5
1
22
1
1
1
1
5
1
1
x dx
t dt
I
x
tt
x


Đặt
2 2
1
1
1
1
a b c
f
t
t
tt
t t t


với
a,b,c
. Ta sẽ đi tìm
a,b,c
▶ Thực hiện :
Ta lần lượt tìm
lim
của các biểu thức sau :
2
1
2
1
0
1
11
1
1
2
t
t
t
a
a lim f t t
b lim f t t
t
c lim f t t









Kết luận : Ta được :
2 2
2 1 1
1
1
1
1
tt
t
t tt
▶ Phân tích hướng giải:
Ta sẽ trình bày như sau :
▶ Lời giải : Tích phân tổng:
Ta đặt
5 4
5dt xt dx x
. Khi đó :
5
2 32 32
2
5
1 1 1
32
22
1
1
1
1 1 2 1 1
5 5 1
11
1
1 2 1 64 31
1
5 1 5 33 165
x dx
t dt
I dt
tt
t t t
x
ln t ln ln
x
t
t








Bài 4: Tính Tích Phân:
2
5
2
4
3
33
3 1 1xx
x
Ix
x
d

▶ Ý tưởng :
Đặt :
2
23232
3 1 1
33
31
33 1
1
x a b c d e f
f(x)
x x x
x
x x
xx
x


▶ Thực hiện :
Ta lần lượt tìm
lim
của các biểu thức sau :
3
2
3
3
2
1
2
3
3
1
1
32
3
3
2
3
4
3
32
33
12
15
1
8
1
1
1
8
9
x
x
x
x
x
x
b
c
d
a lim f x x
a
b lim f x x
x
a
lim f x x
xx
lim f x x
d
lim f x x
x
fl
e
im f x x














Kết luận : Ta được :
2
323 2 2
33 3 9 2 2 15 1
3 1 1 1
3 8 1 8 1
2 3 4 3
x
x x x
xxx x x x




▶ Phân tích hướng giải:
Ta sẽ trình bày như sau :
▶ Lời giải : Tích phân tổng:
Ta có :
5
2
4
3
5
32
4
5
2
4
2
2
33
3 9 2 2 15 1
3 8 1 8 1
2 3 4 3
3 9 2 15 1
2 3 1 1
4 3 1 8 8
43
15 7 1 35
2 3 5
84
3
8
1
1
84
1
x
I dx
dx
x x x
xx
ln x ln x ln x
xx
x
ln
x
ln ln
xx
x











Bài 5: Tính Tích Phân:
2
2
3
2
1
11xx
I dx

▶ Ý tưởng :
Đặt :
22 2
2
1
1
111
1
ab
xx
c
f(x)
x
x
x
▶ Thực hiện :
Ta lần lượt tìm
lim
của các biểu thức sau :
2
1
2
1
1
1
1
2
1
1
2
x
x
a lim f x
b lim f x
x
x
a
x





Ta sẽ tìm
c
như sau : Xét
1000x
thì :
2
2
2
2
1
1 50
2
11
0
1
1
a b x
x
x
c
x
xx





Kết luận : Ta được :
2
2
2
2
1 1 1
21
21
2111xx
x
x
x
x

▶ Phân tích hướng giải:
Ta sẽ trình bày như sau :
▶ Lời giải : Tích phân tổng:
Ta có :
33
2
2
22
3
2
2
2
2
1 1 1
21
21
21
1 1 1 1 2
11
2 1 2 4 4 4
11
x
I dx dx
x
x
x
ln
ln|x | ln|x
xx
|
x







Bài 6: Tính Tích Phân:
2
1
3
22
0
21
1 2 3
x x x
xx
I dx
x

▶ Ý tưởng :
Đặt :
32
2
22
2
21
1 2
3
3
12
x x x
x
x x x
ab
f(x)
xx

▶ Thực hiện :
Ta đã biết
i
,
12i
lần lượt là nghiệm của
2
10x 
,
2
2 3 0xx
Ta lần lượt tìm
lim
của các biểu thức sau :
2
2
12
1 0 25 0 25
2 3 1 1 060660172
1 1 1
4 4 4
31
3 2 3 7
11
4 4 4
xi
xi
lim f x , , i
b lim f x x , i
ax
x
i
x
x
x
a
bi

Kết luận : Ta được :
32
2 222
21
1
1 3 7
4 1 4 223 3
xx
xx
x x x
x x x x




▶ Phân tích hướng giải:
Ta sẽ trình bày như sau :
▶ Lời giải : Tích phân tổng:
Ta có :
11
22
00
1
2
3
2
0
2
22
1 3 7
4 1 4 2 3
1 1 3 2 2
1 2 3 1
8 4 8 2
2 2 2 2
2
16 2 2
21
1
22
23
2
xx
I dx dx
x x x
ln x arctan x ln x x arctan x
ln
arctan
x x x
x x x
arctan















THỦ THUẬT 9 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
GIẢI BẤT ĐẲNG THỨC
Bài 1: Cho
0a,b,c
và
3a b c
. Tìm GTLN của:
2 2 2
3 3 3
4 1 4 1 4 1
1 1 1
a b c
P
a b c
▶ Ý tưởng :
Ta cần tìm
k,m
sao cho:
3
2
41
1
a
ka m
a

với mọi
0a
.
Dấu bằng khi và chỉ khi
0
1aa
.
Để tổng quát vấn đề, ta cần tìm
k,m
sao cho
f(x) mg(x) k
hoặc
f(x) mg(x) k
với mọi
x
Khi đó
,km
sẽ là nghiệm của hệ phương trình sau :
00
00
f x kg x m
f' x k'g x

Với
0
xx
là điểm rơi.
▶ Thực hiện :
Ta sẽ tìm
k
một cách nhanh chóng bằng cách :
2
3
1
4 1 1
4
1
x
d
x
x
k
dx




Và
m
sẽ được tìm bằng cách :
0
0
3
0
2
41
9
4
1
a
m ka
a
Với
0
1a
là điểm rơi của bài toán
Ta sẽ phân tích thành nhân tử
3
2
4 1 9
4
1
aa
a

để chứng minh nó
không dương với mọi
0a
.
Kết luận : Ta luôn có:
3
3
2
22
11 5 1
4 1 9
00
4
1
41
(a a )(a )
aa
a
a
a

▶ Phân tích hướng giải:
Ta sẽ làm tương tự với
,bc
rồi cộng lại là ra đáp án :
▶ Lời giải : Bất đẳng thức:
Ta có :
3
22
22
3
3
11 5 1
4 1 9 4 1 9
0
44
11
41
(a a )(a )
a a a a
a
aa
a

Chứng minh tương tự ta có
3
2
4 1 9
4
1
bb
b

và
3
2
4 1 9
4
1
cc
c

, suy ra:
2 2 2
3 3 3
4 1 4 1 4 1 9 9 9 15
4 4 4 2
1 1 1
a b c a b c
P
a b c
.
Vậy
15
2
max
P
khi và chỉ khi
1a b c
Bài 2: Cho
0a,b,c
. Chứng minh rằng:
3 3 3 3 3 3
2 2 2 2 2 2
2 2 2
4
2 2 2
b c a
a b c
ab b bc c ca
a b c
a b c a

▶ Ý tưởng :
Ta cần tìm
k,m
sao cho:
3 3 3
2 2 2
2 2 1
2 2 1
b
ka m
ax
a
b kx
b x
m
a b x

với
mọi
a xb
.
▶ Thực hiện :
Ta sẽ tìm
,km
bằng cách :
33
0
22
0
1
0
0
2 1 2 1
19 15
16 16
2 1 2 1
x
x
d
k m kx
dx
xx
x
xx





Ta sẽ phân tích thành nhân tử
33
22
2
19 15
16
2
a b
ab
ab ba

Kết luận : Ta luôn có:
2
33
22
22
33
22
6
2
19 15
00
16
2
16 2
2
19 15
16
2
a b a b
b
ab
a,b
ab
a
a
a
b
a ab b
b
ab
ab ba





▶ Phân tích hướng giải:
Ta sẽ làm tương tự với
,bc
rồi cộng lại là ra đáp án :
▶ Lời giải : Bất đẳng thức:
Ta có :
2
33
22
22
33
22
6
2
19 15
00
16
2
16 2
2
19 15
16
2
a b a b
b
ab
a,b
ab
a
a
a
b
a ab b
b
ab
ab ba





Chứng minh tương tự ta có :
33
22
2
19 15
16
2
b c
bc
bc cb

và
33
22
2
19 15
16
2
c a
ca
ca ac

Suy ra:
3 3 3 3 3 3
2 2 2 2 2 2
2 2 2
4
2 2 2
b c a
a b c
ab b bc c ca
a b c
a b c a

.
Bài 3: Cho
0a,b,c
thỏa mãn
1abc
. Tim GTNN của:
2 2 2
2 2 2
1 1 1
1 1 1
a b c
P
a(a ) b(b ) c(c )
▶ Ý tưởng :
Ta thấy
lnabc lna lnb lnc
nên ta tìm
k,m
sao cho :
2
2
1
1
a
k ln a m
a(a )

Dấu đẳng thức khi
1a.
▶ Thực hiện :
Tương tự bài toán trước, ta tìm được
1
2
k 
và
1
2
m
.
Ta cần chứng minh
2
2
1 1 1
00
22
1
a
f(a) ln a a
a(a )
Kết luận : Ta sẽ chứng minh
2
2
1 1 1
00
22
1
a
f(a) lna a
a(a )
▶ Phân tích hướng giải:
Ta chứng minh bằng đạo hàm là cách tốt nhất:
▶ Lời giải : Bất đẳng thức:
Ta có bổ đề :
2
2
1 1 1
00
22
1
a
f(a) lna a
a(a )
Chứng minh :
32
32
33
22
1 2 7 2
31
1
2
1 2 1
a a a a
a a a
f'(a)
a
a a a a

Vậy
01f'(a) a
và
f'(a)
đổi dấu từ âm sang dương khi đi qua
1
Suy ra
10f(a) f( )
(đpcm).
Chứng minh tương tự, suy ra:
2 2 2
2 2 2
1 1 1 3 1 3 3
2 2 2 2 2
1 1 1
a b c ln abc
P lna ln b ln c
a(a ) b(b ) c(c )
Vậy
3
1
2
min
P a b c
Bài 4: Cho
0a,b,c
thỏa mãn
3a b c
. Chứng minh rằng:
2 2 2
2 2 2
1 1 1
a b c
a b c
▶ Ý tưởng :
Ta cần tìm
k,m
sao cho
2
2
1
a ka m
a
▶ Thực hiện :
Tương tự bài toán trước, ta tìm được
44k ,m
.
Ta cần chứng minh
2
2
1
44f(a) a a
a
Tuy nhiên
2
2
2
22
2 1 1
1
4 4 0
a a a
aa
aa
.
BĐT này chỉ đúng nếu
0 1 2a
Kết luận : Ta sẽ chia các trường hợp để áp dụng :
2
2
2
22
2 1 1
1
4 4 0
a a a
aa
aa
▶ Phân tích hướng giải:
Ta sẽ làm như sau :
▶ Lời giải : Bất đẳng thức:
Không mất tính tổng quát giả sử
a b c
TH1:
12a b c
thì vô lý
TH2:
12a b c
thì vô lý
TH3:
12a b c
thì
2 3 2 2c b c a
suy ra
22
2
c
. Còn
3 2 2 2b b c
Dễ thấy
f(a)
đồng biến trên
0( , )
nên ta có:
2 2 80
3 2 2 10 2 0
29
f(a) f(b) f(c) f( ) f f




TH4:
12a b c
thì
2
2
2
22
2 1 1
1
4 4 0
a a a
aa
aa
luôn
đúng
Vậy
4 12 0f(a) f(b) f(c) (a b c)
Tóm lại BĐT được chứng minh
Bài 5: Cho
0x,y,z
thỏa mãn
2 4 7 2x y z xyz
. Tìm GTNN của:
P x y z
▶ Ý tưởng :
Nếu bạn đọc đã từng xem đáp án chính thức, lời giải của bài toán này rất
khó để thực hiện. Tuy nhiên, chúng ta có cách khác dễ dàng hơn rất nhiều
chỉ cần sử dụng máy tính CASIO.
Ta sẽ đi tìm điểm rơi của bài toán. Cách tìm điểm rơi bằng phương pháp
nhân tử Lagrange.
▶ Thực hiện :
Xét hàm
2 4 7 2f(x,y,z) x y z k( x y z xyz)
. Ta có hệ:
17
2
12
1 2 2 0
1 4 2 0
1 7 2 0
2 4 7 2
4
2
14
8 14 1
2
1 2 1 4 1
2 4 7
2
78
k
xy
k
k
yz
k
k
zx
k
yz xz x
k( yz)
k( xz)
k( yx)
x y z xyz
k k k
k
k
y
kk





Từ đó ta được
15
56
2
xy , yz ,zx
hay
5
32
2
(x, y,z) , ,



Kết luận : Điểm rơi của bài toán là
5
32
2
(x, y,z) , ,



▶ Phân tích hướng giải:
Ta sẽ áp dụng bất đẳng thức Cauchy với điểm rơi có sẵn :
▶ Lời giải : Phương pháp nhân tử Lagrange:
Ta có :
3
33
7 7 105 5 5 15 3 3 15 15
12 10 8 12 8 2 10 8 4 4
7 7 105 5 5 15 3 3 15 15 15
3 3 3
12 10 8 12 8 2 10 8 4 4 2
P x y x z y z
xy xz yz
x y x z y z
xy xz yz



Vậy
5
32
22
15
min
P (x, y,z) , ,



| 1/104
| | Tải xuống

Có thể bạn quan tâm:

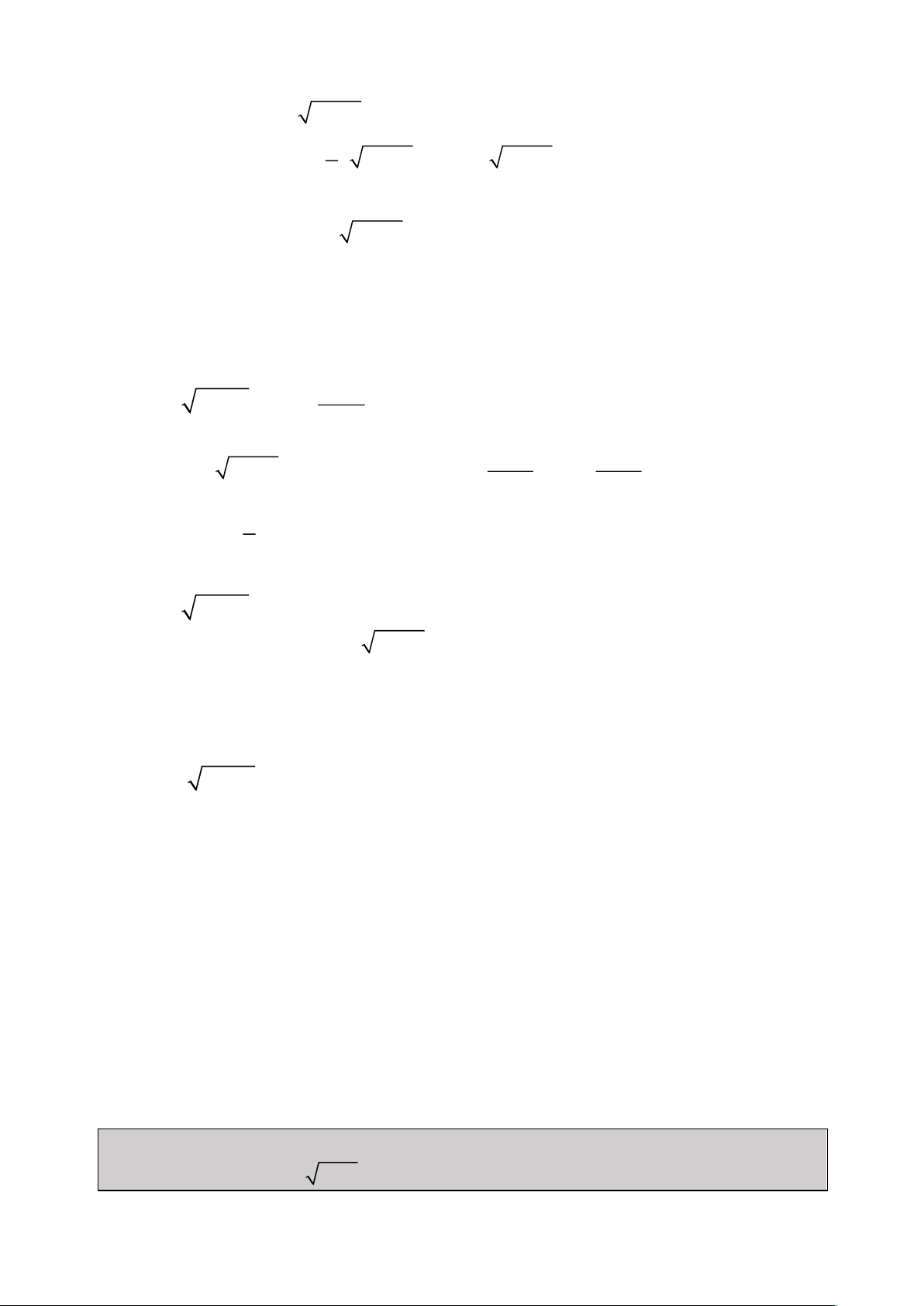
Preview text:

KỸ NĂNG SỬ DỤNG CASIO TRONG GIẢI TOÁN
(Bùi Thế Việt – THPT Chuyên Thái Bình)
Trong các dụng cụ học tập được phép mang vào phòng thi trong các kỳ thi
đại học, kỳ thi THPT Quốc Gia thì máy tính cầm tay là dụng cụ không thể
thiếu giúp chúng ta tính toán nhanh chóng.
Tuy nhiên, máy tính cầm tay sẽ là trợ thủ đắc lực để giải toán, đặc biệt là
giải Phương Trình, Hệ Phương Trình, Bất Phương Trình, ... hay kể cả là Bất Đẳng Thức.
Mình (tác giá - Bùi Thế Việt) là một người rất đam mê với những kỹ năng,
thủ thuật sử dụng máy tính cầm tay trong giải toán. Mình đã áp dụng nó
vào đề thi THPT Quốc Gia 2015. Chỉ trong 3 – 5 phút, mình đã đưa ra lời
giải chính xác cho câu Phương Trình Vô Tỷ và cũng chỉ gần 1 giờ, mình đã
hoàn thành xong bài làm với điểm số tuyệt đối, là 1 trong 85/671.149 người được điểm tối đa.
Vậy sử dụng sao cho hiệu quả ? Hãy đến với chuyên đề Kỹ Năng Sử Dụng CASIO Trong Giải Toán.
Chuyên đề này chưa phải là tất cả những Thủ Thuật mà mình đưa tới cho
bạn đọc. Tuy không nhiều nhưng các thủ thuật dưới đây sẽ mang tới sự kỳ
diệu mà chiếc máy tính CASIO có thể mang lại.
Chuyên đề sẽ giới thiệu 8 thủ thuật CASIO hay dùng trong việc giải toán :
 Thủ thuật sử dụng CASIO để rút gọn biểu thức
 Thủ thuật sử dụng CASIO để giải phương trình bậc 4
 Thủ thuật sử dụng CASIO để tìm nghiệm phương trình
 Thủ thuật sử dụng CASIO để phân tích đa thức thành nhân tử một ẩn
 Thủ thuật sử dụng CASIO để phân tích đa thức thành nhân tử hai ẩn
 Thủ thuật sử dụng CASIO để giải hệ phương trình
 Thủ thuật sử dụng CASIO để tích nguyên hàm, tích phân
 Thủ thuật sử dụng CASIO để giải bất đẳng thức
THỦ THUẬT 1 : THỦ THUẬT SỬ DỤNG CASIO
ĐỂ RÚT GỌN BIỂU THỨC
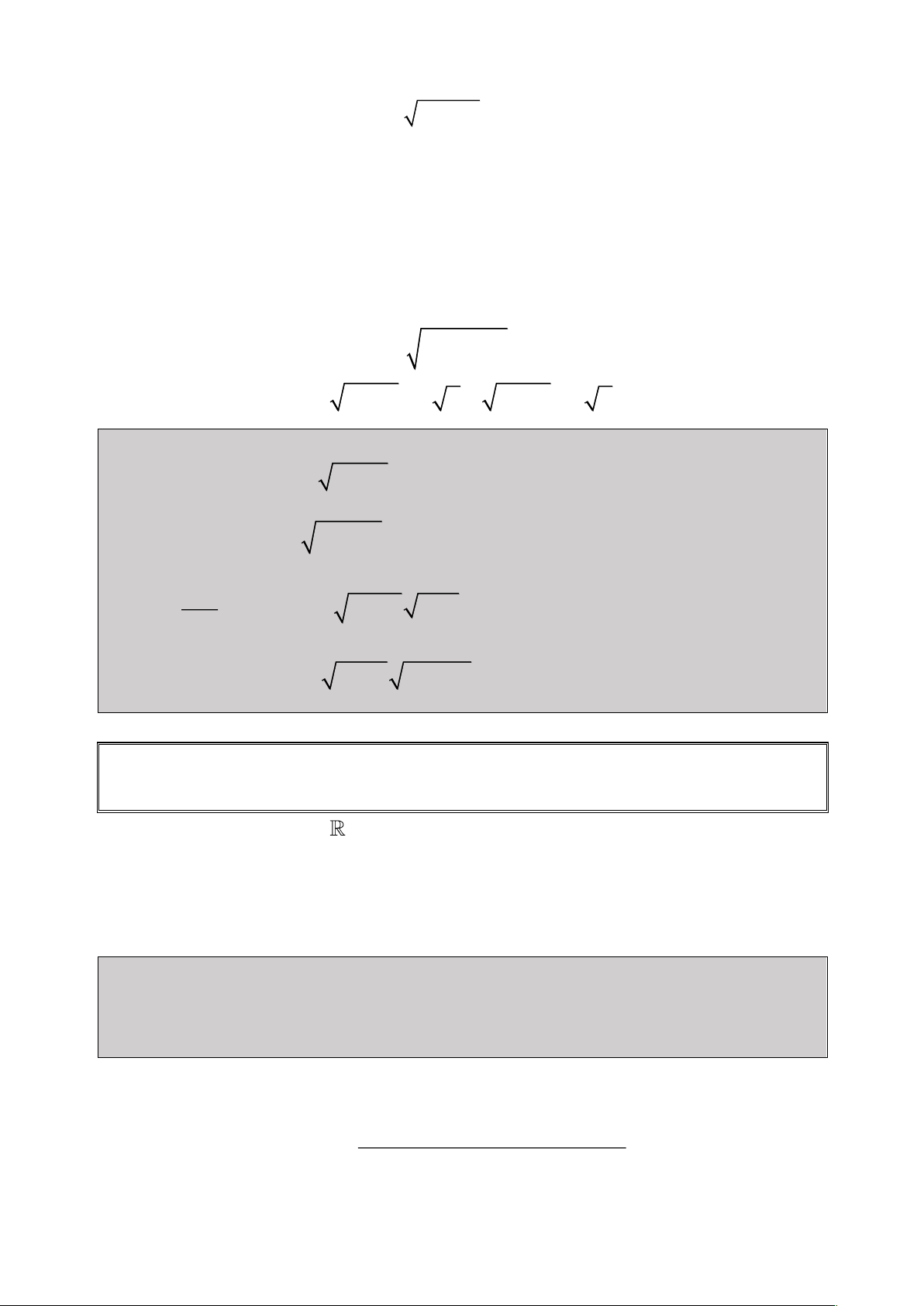
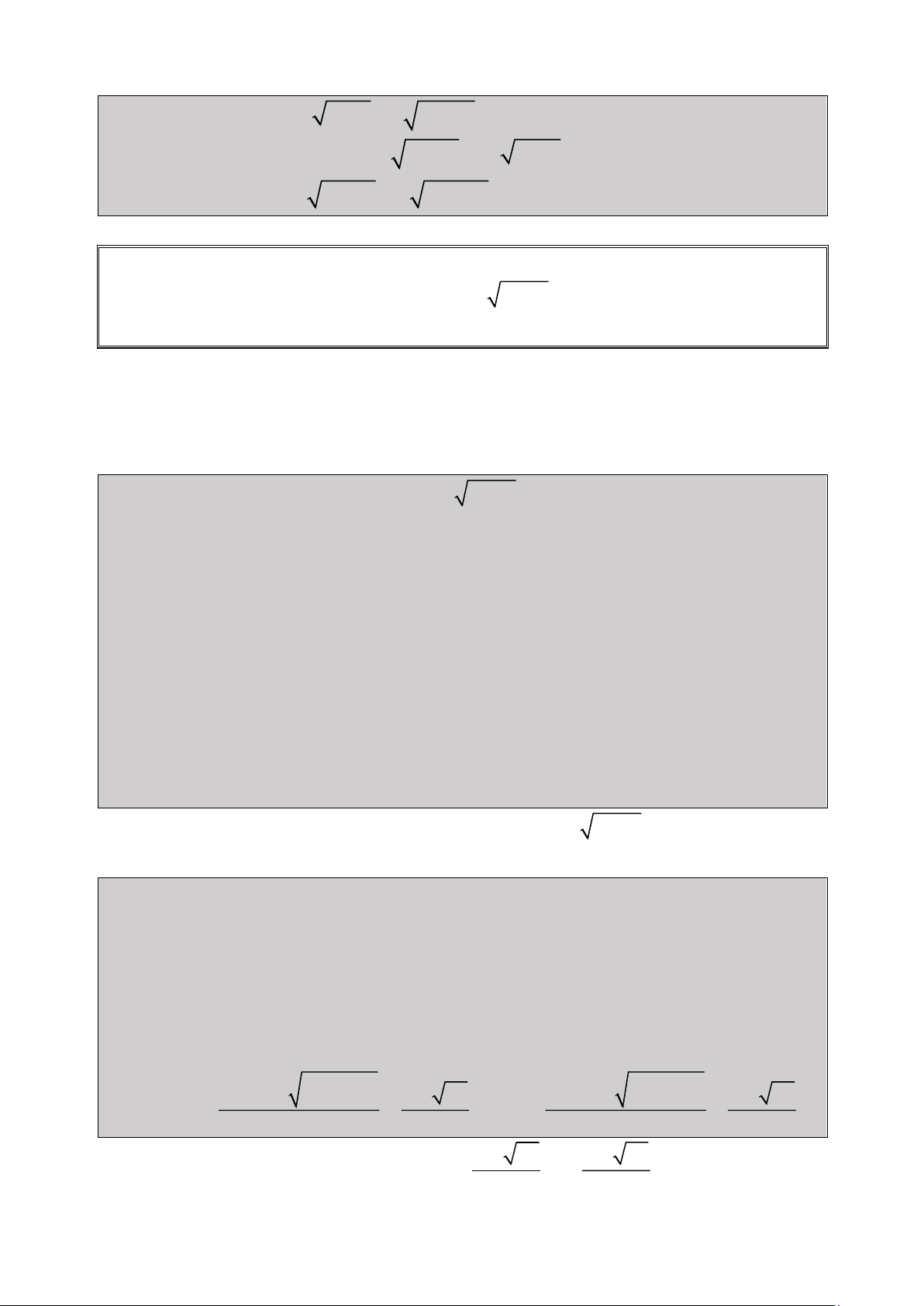
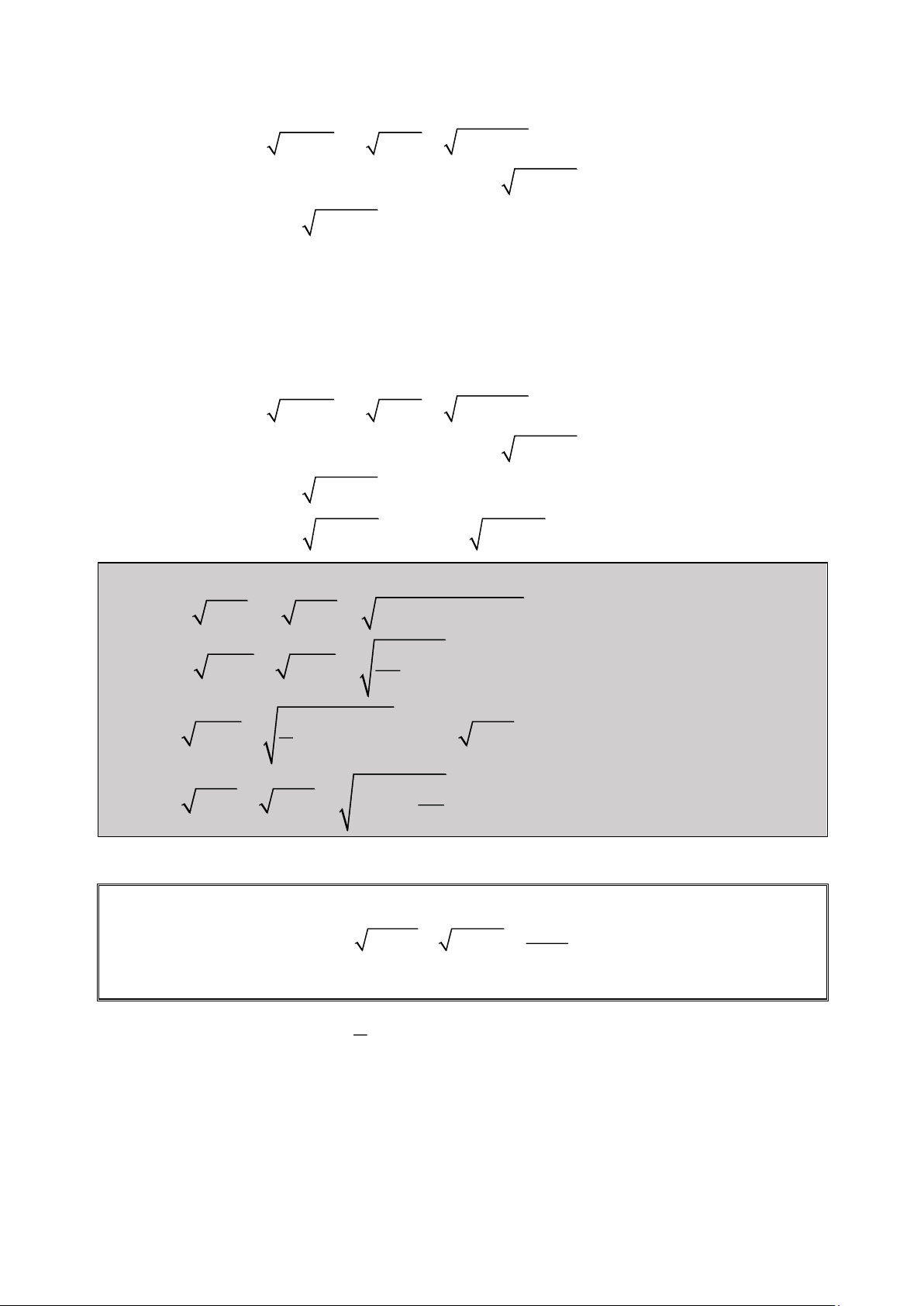
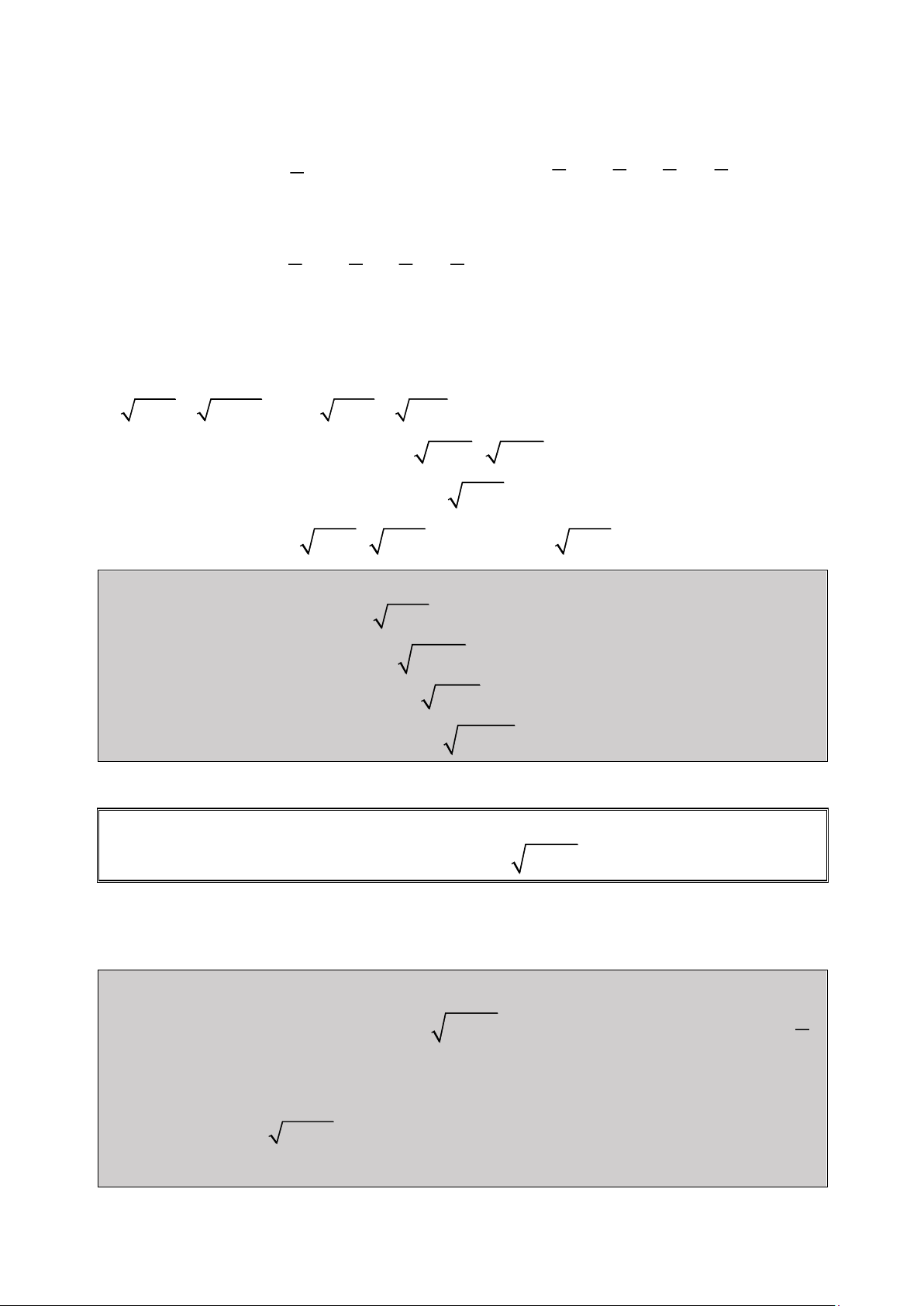
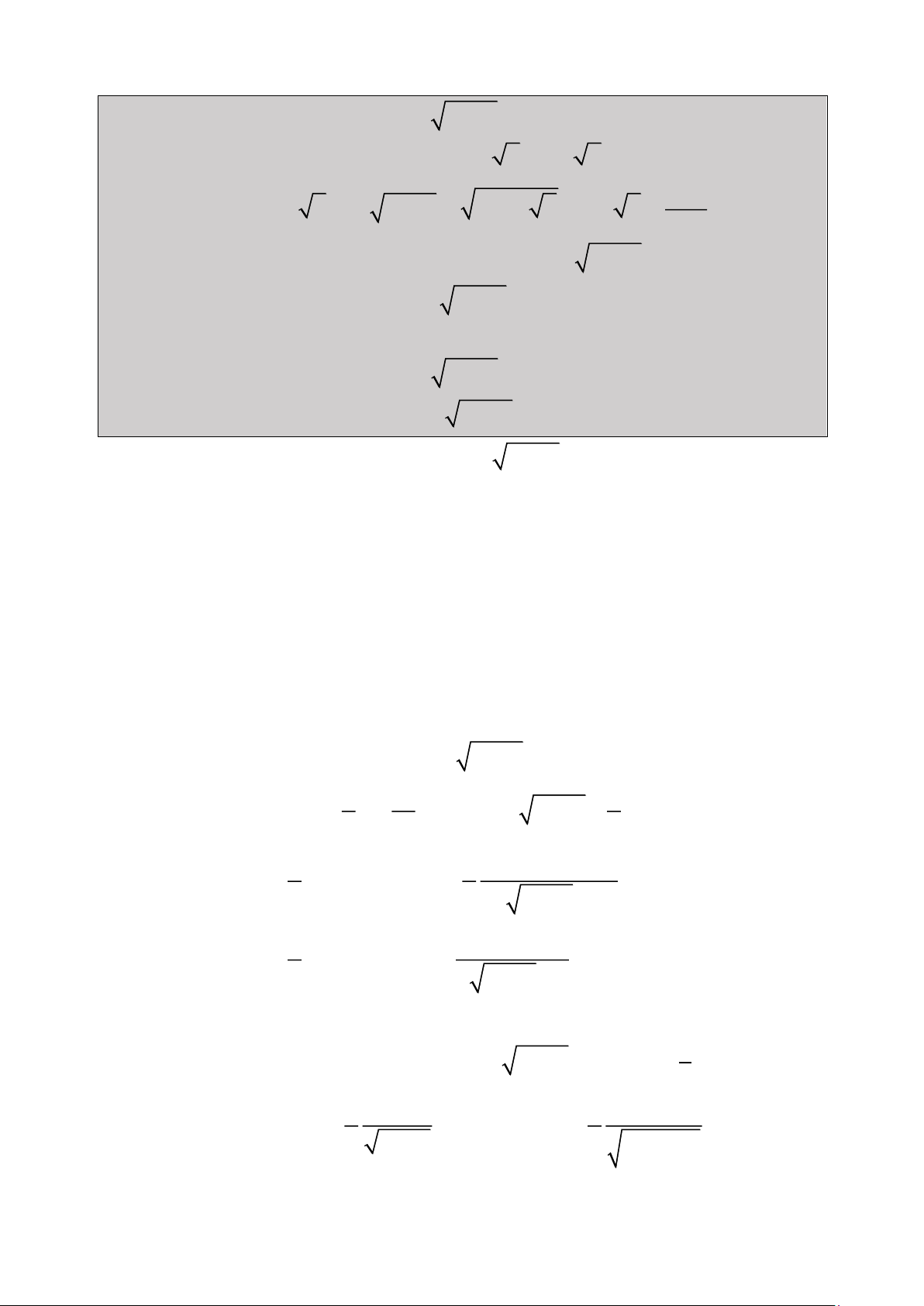
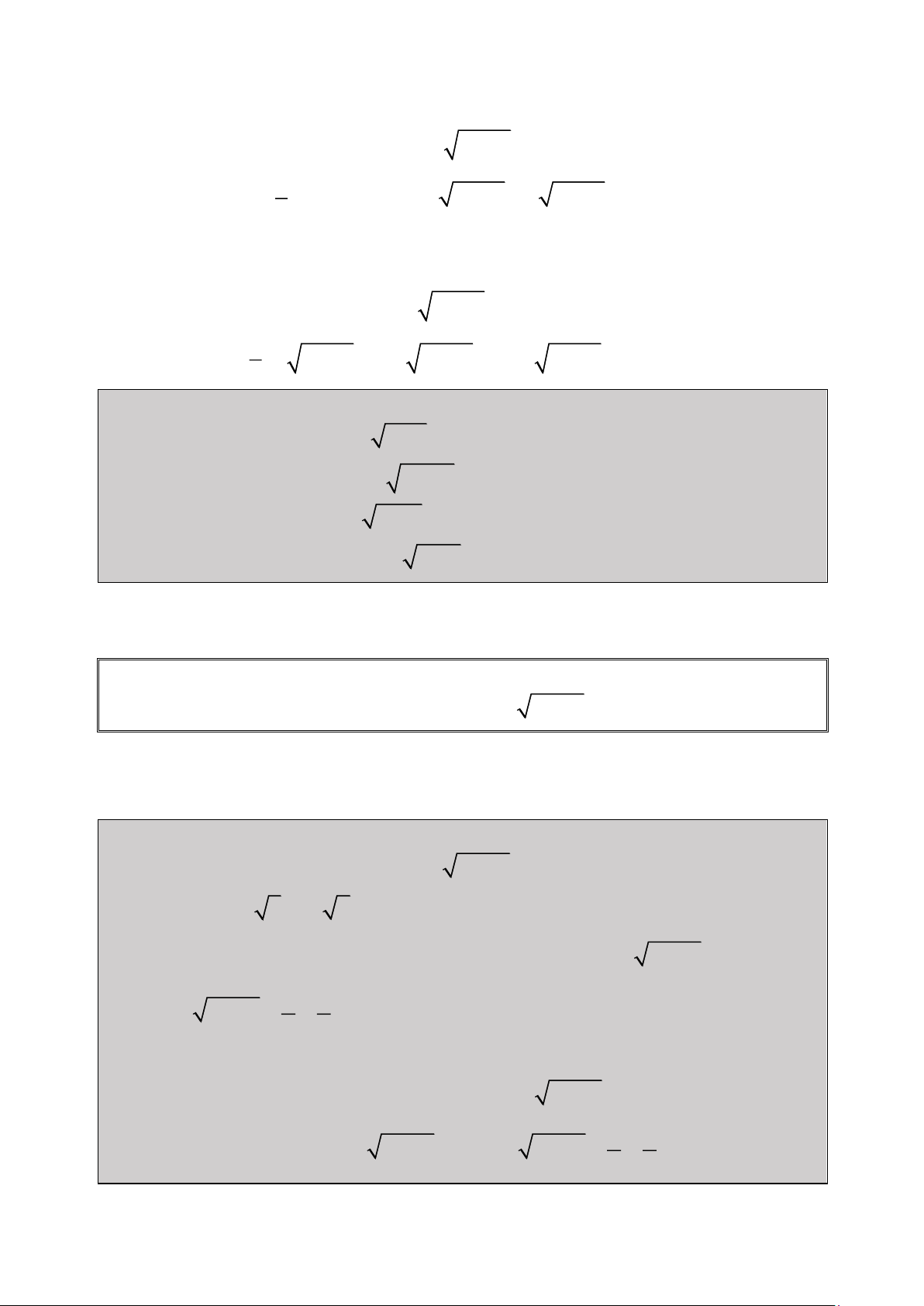
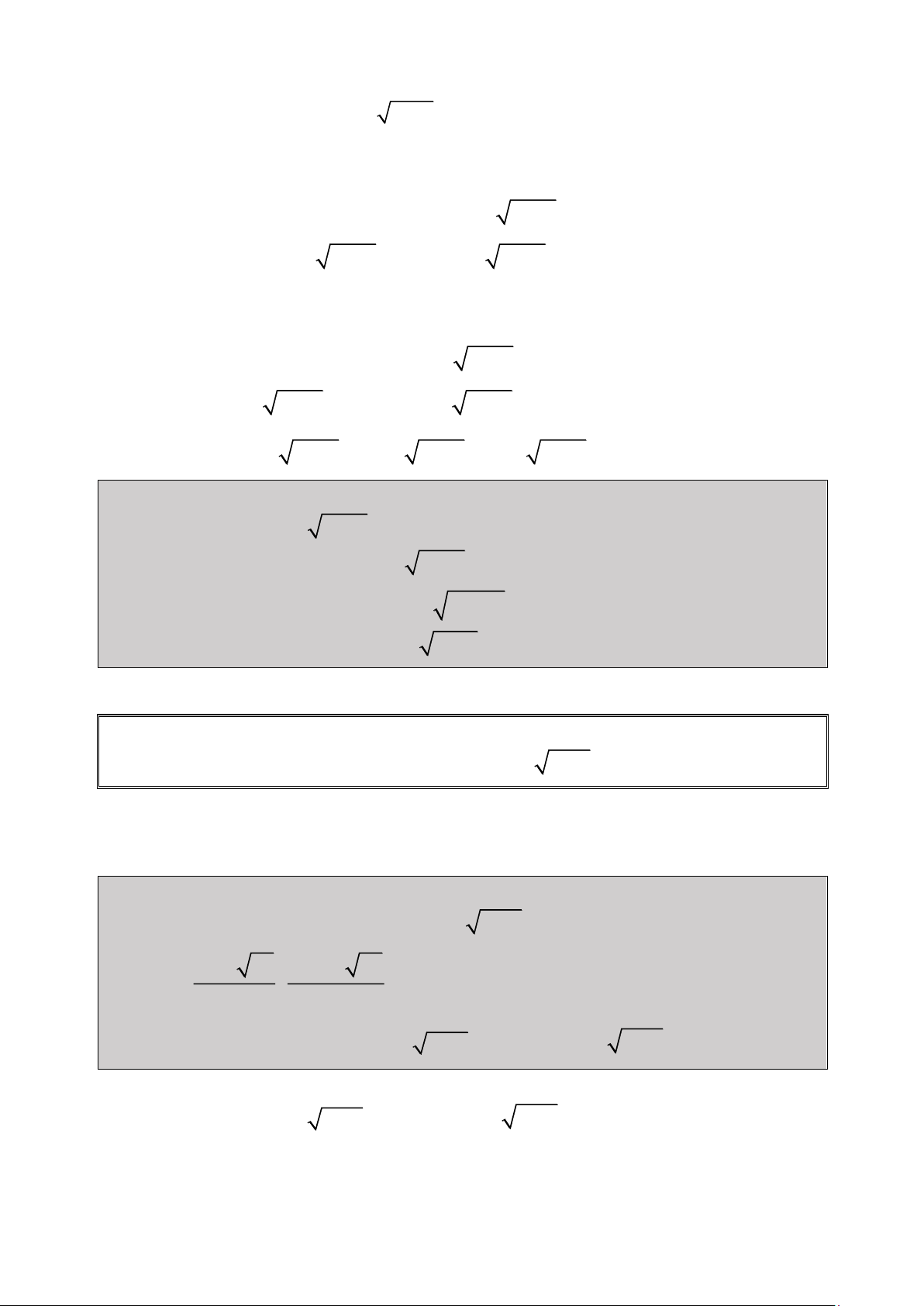
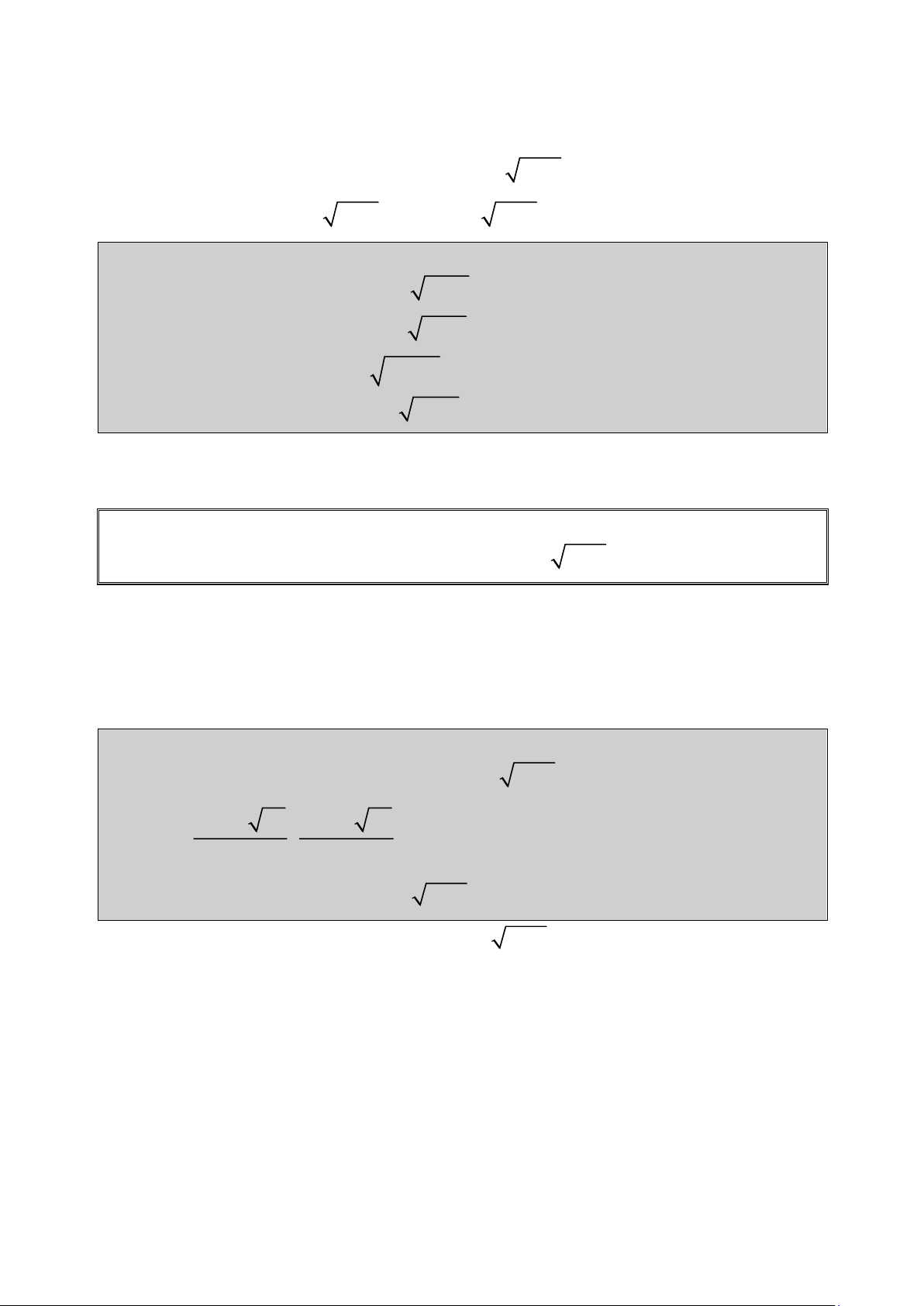
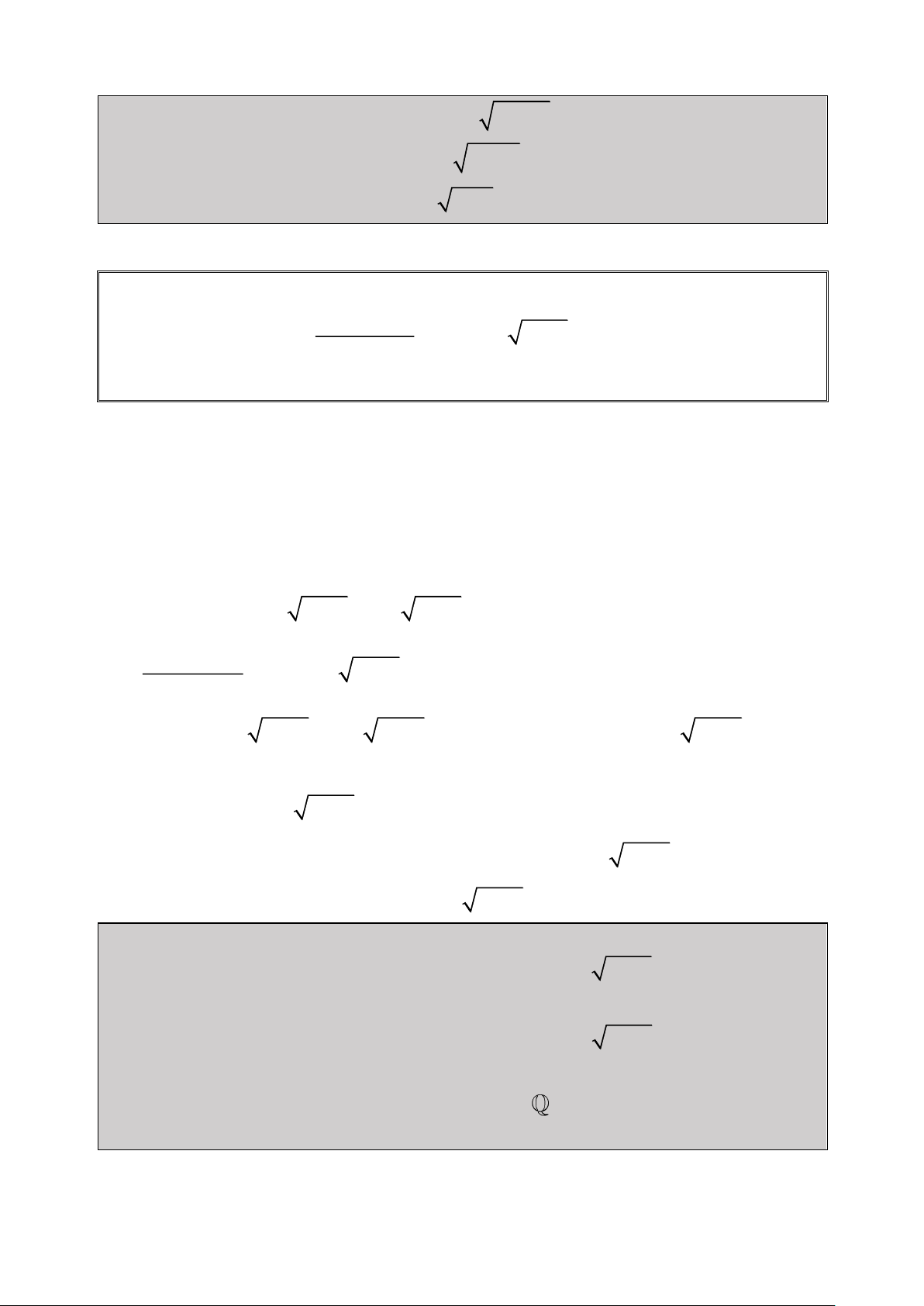
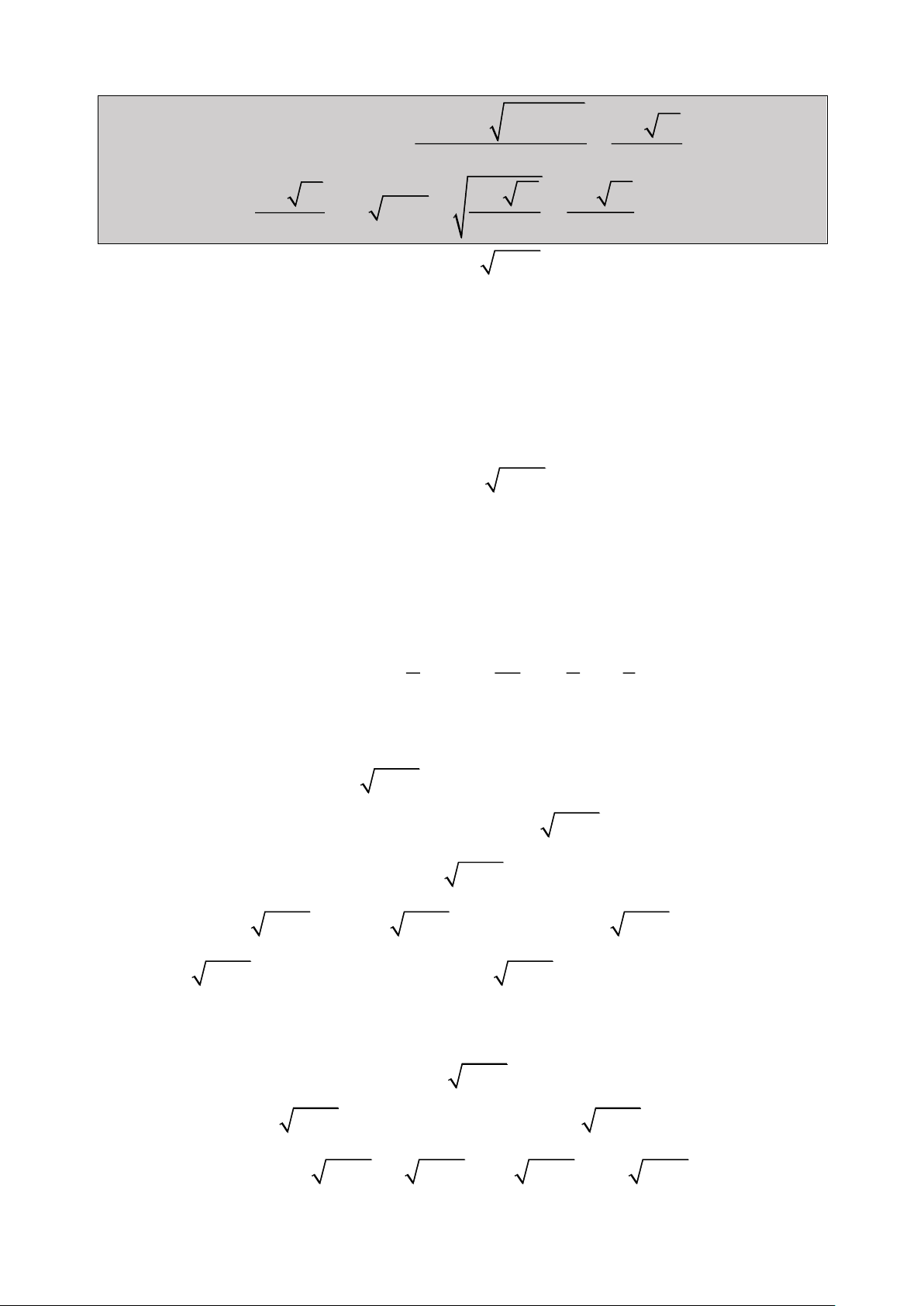
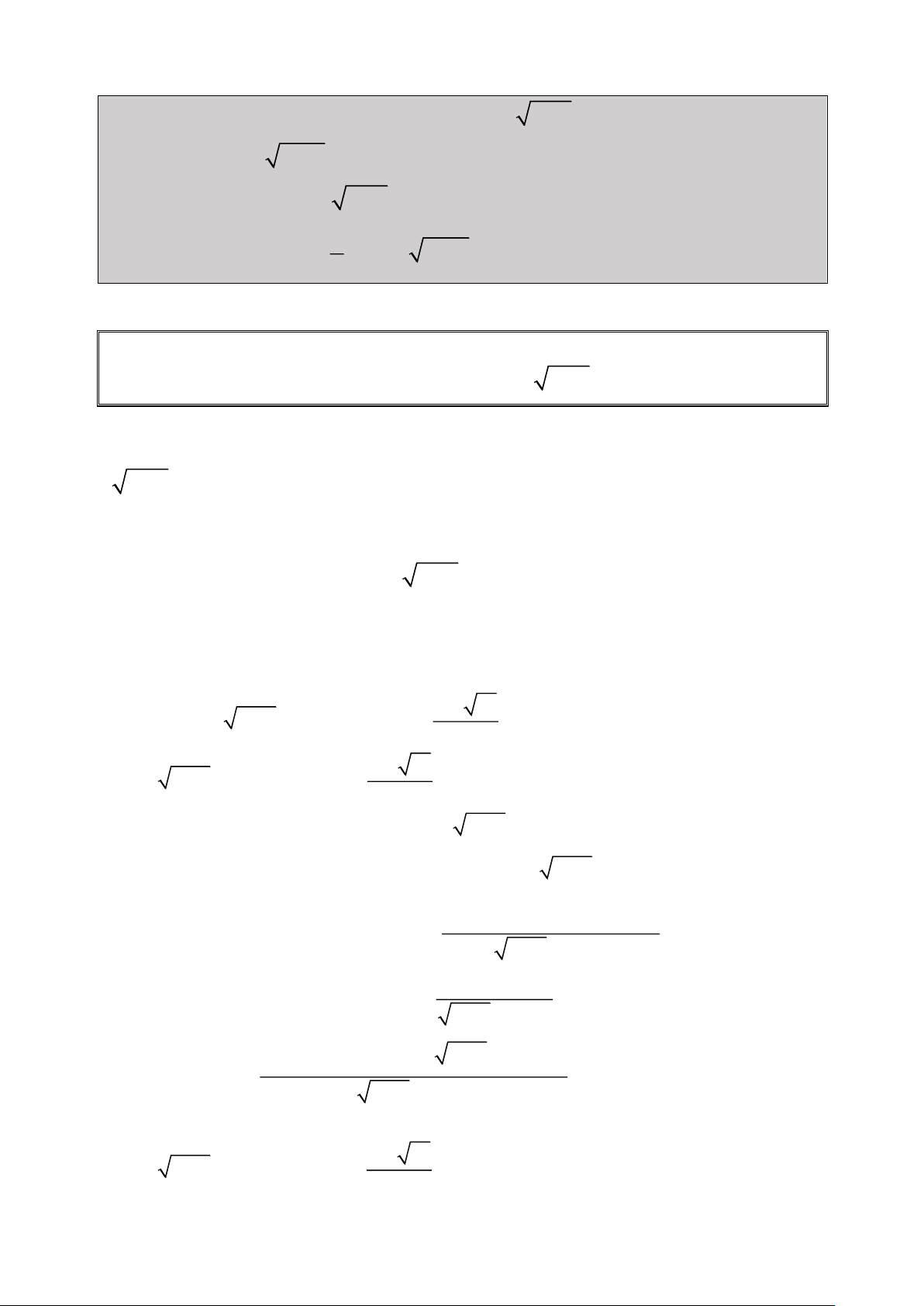
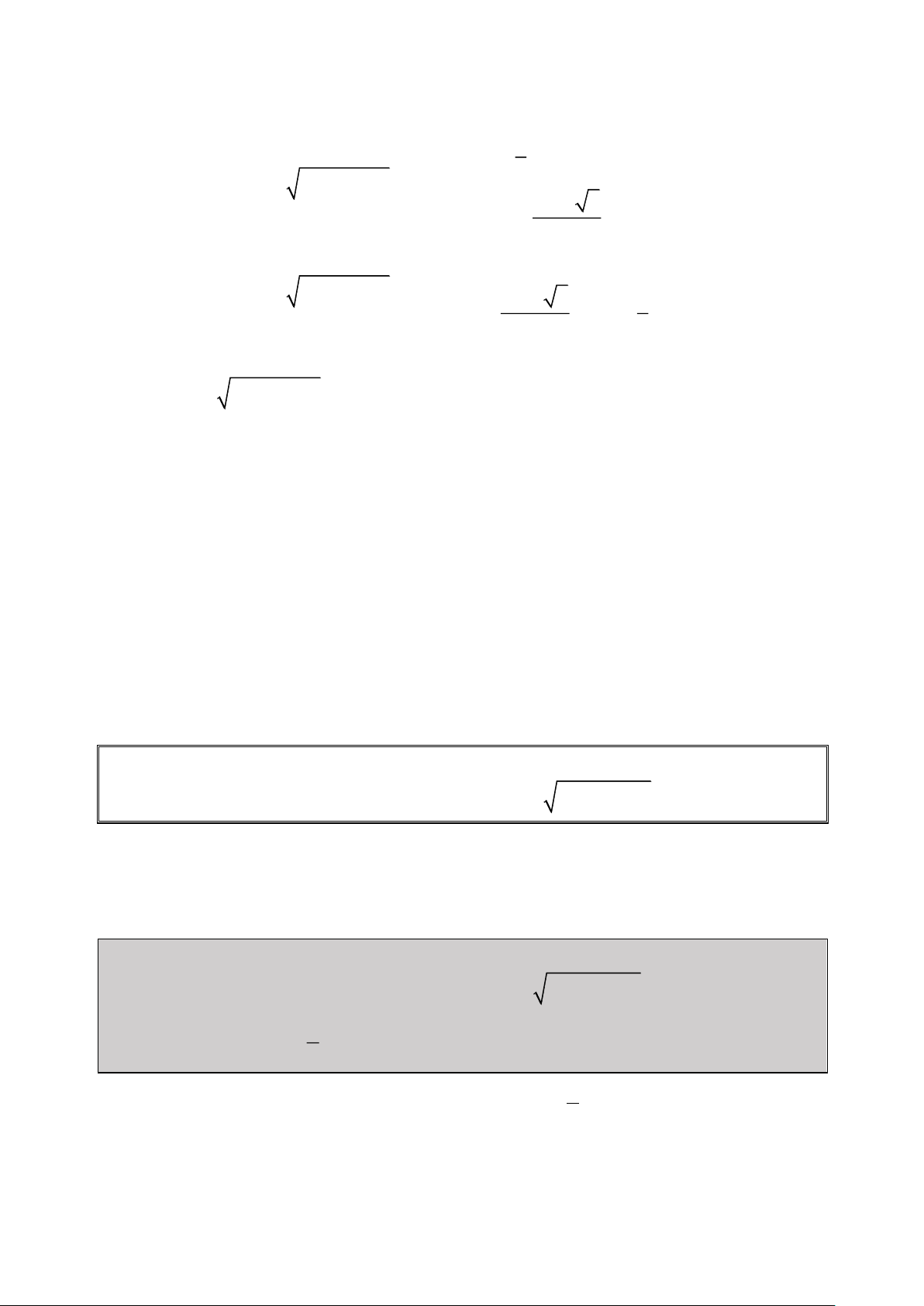
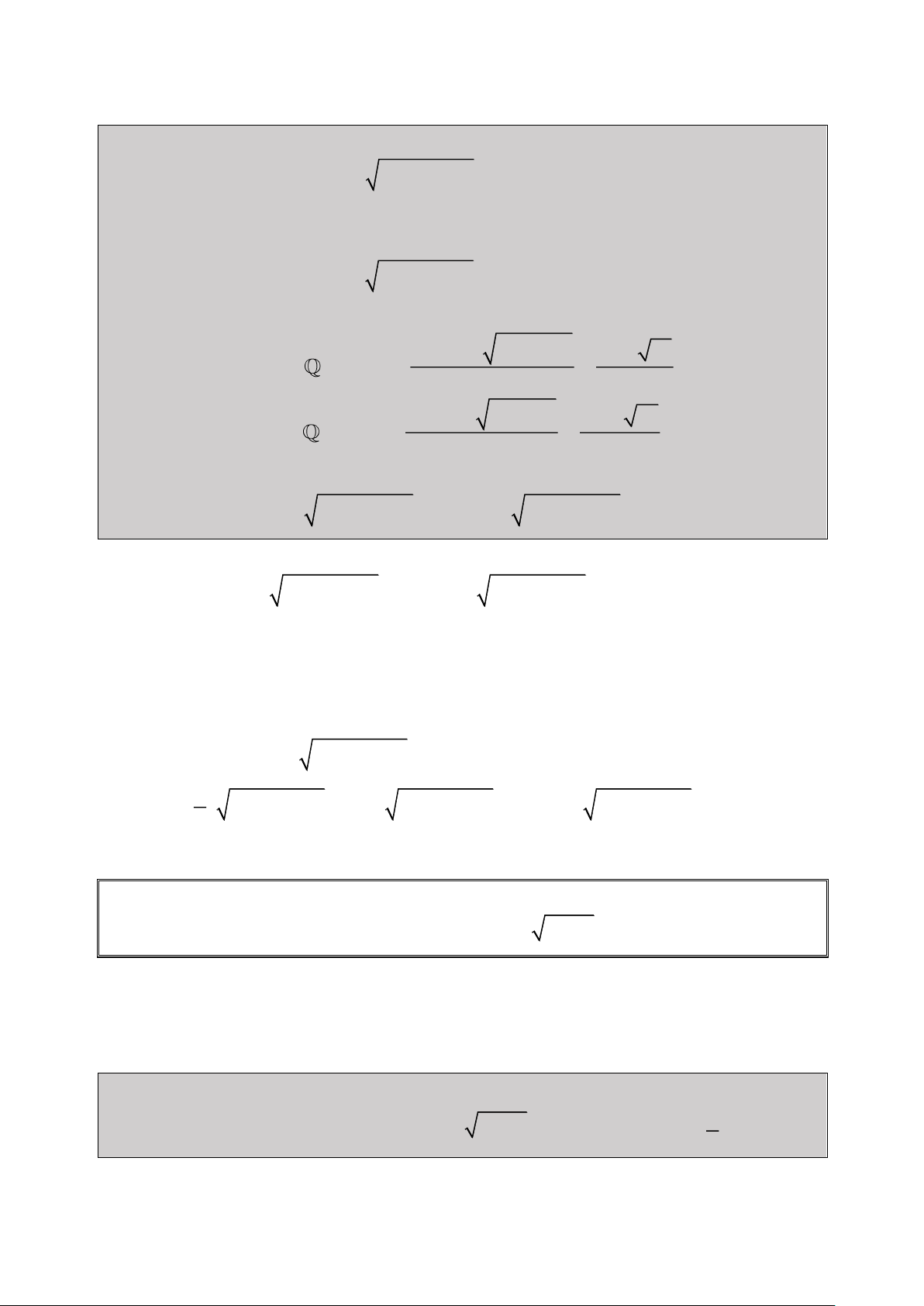
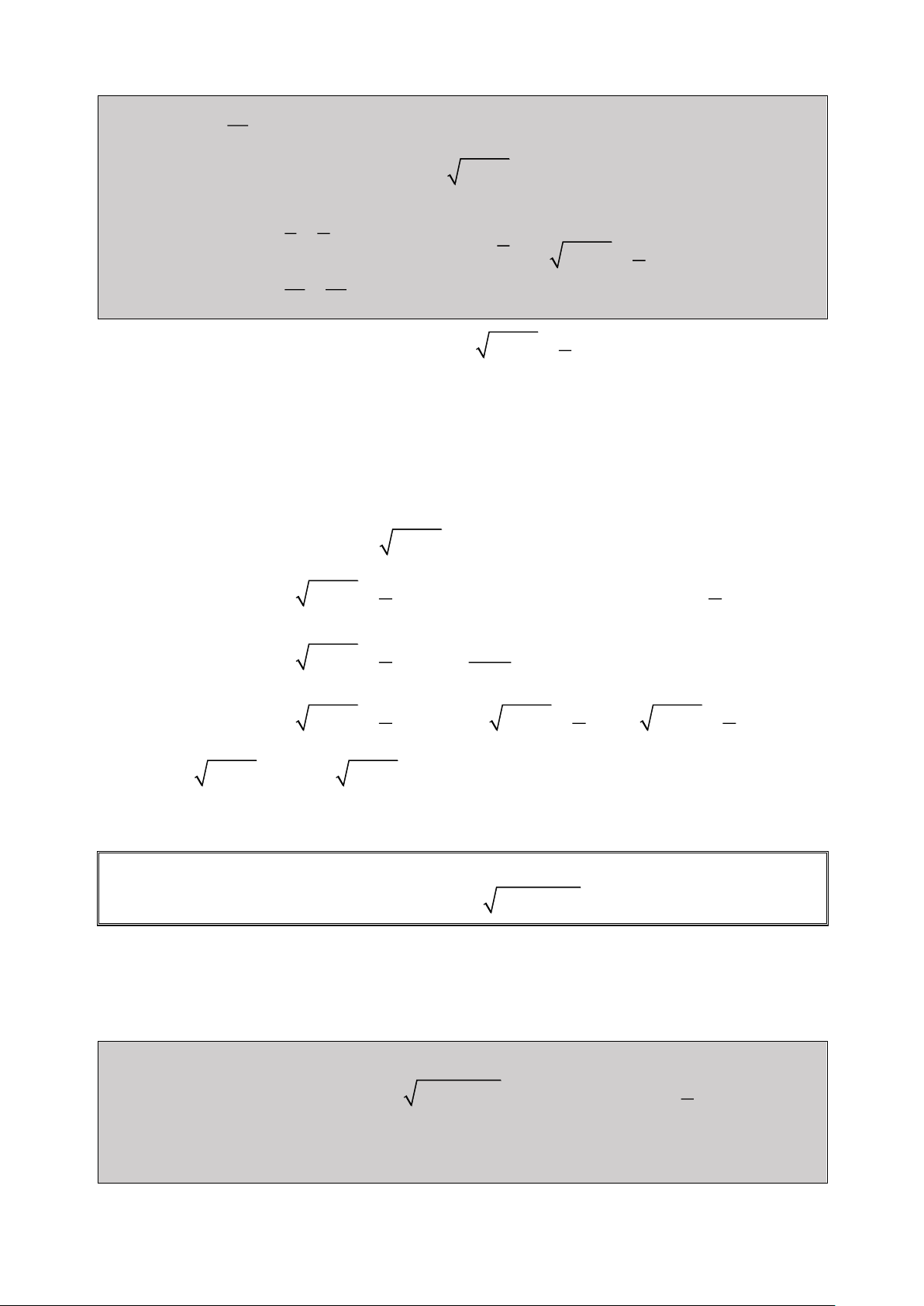
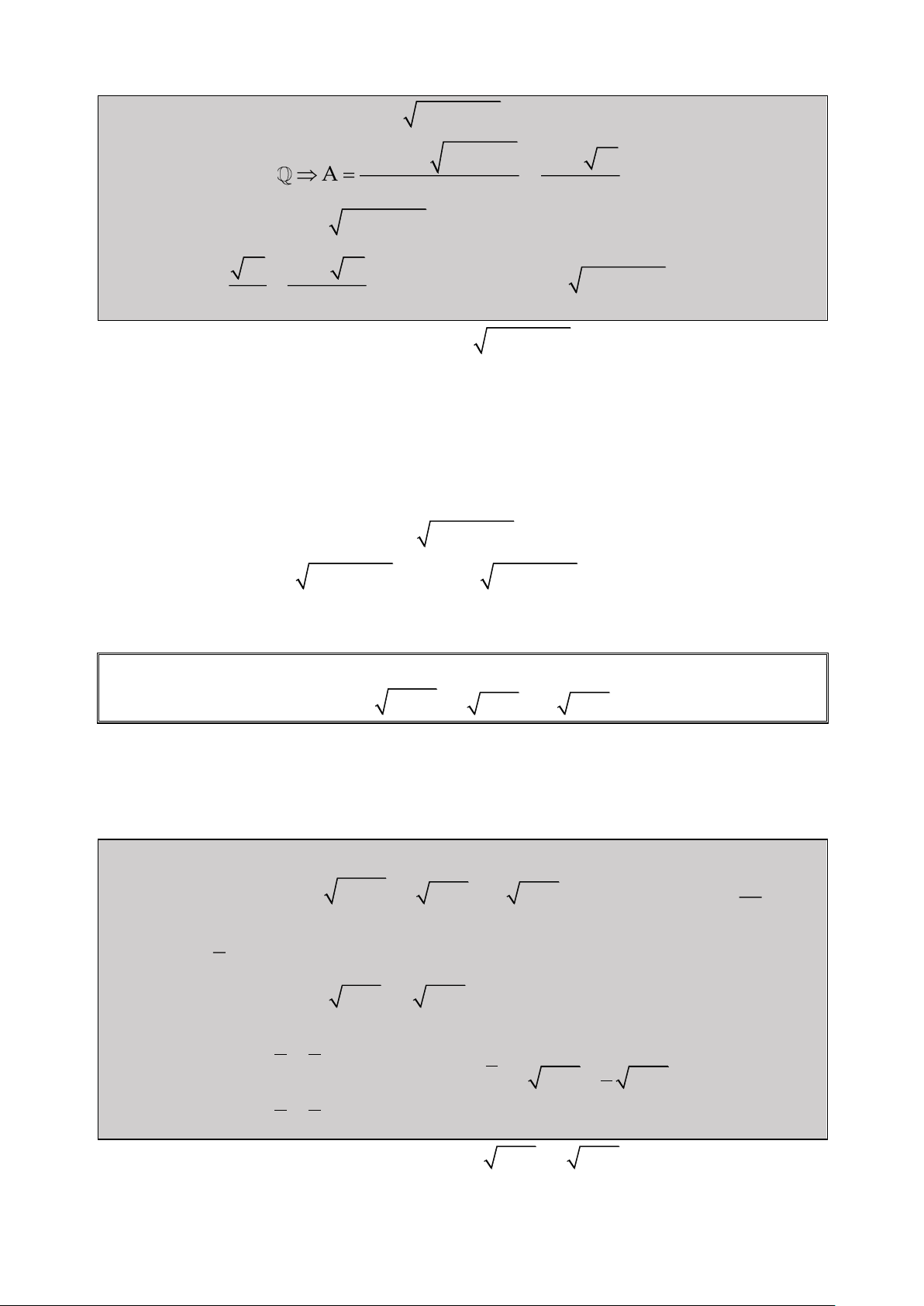
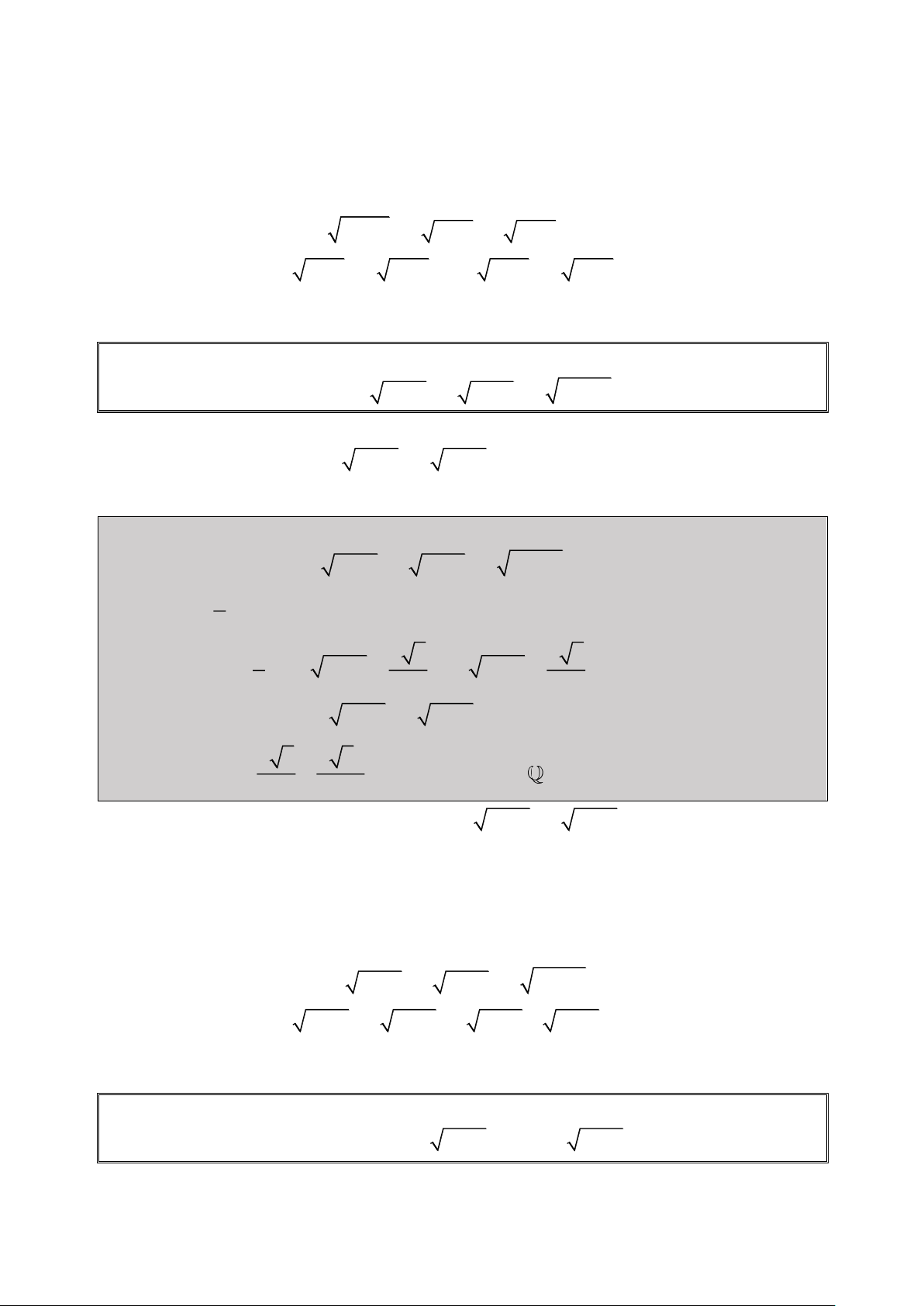
Bài 1: Giải Phương trình: 2
2x 1  x  3x 1  0
(đề thi Đại Học khối D năm 2006)  1 
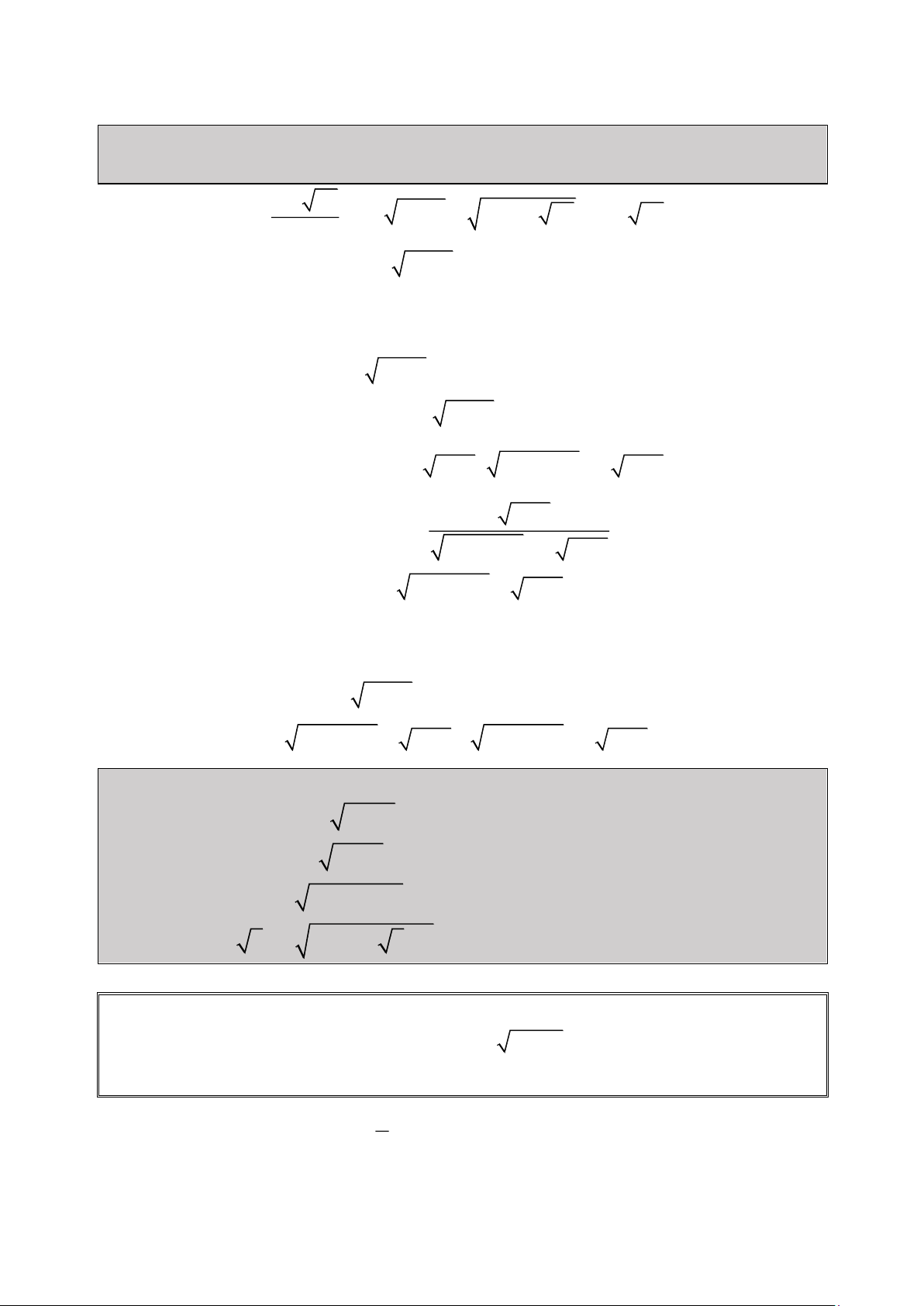
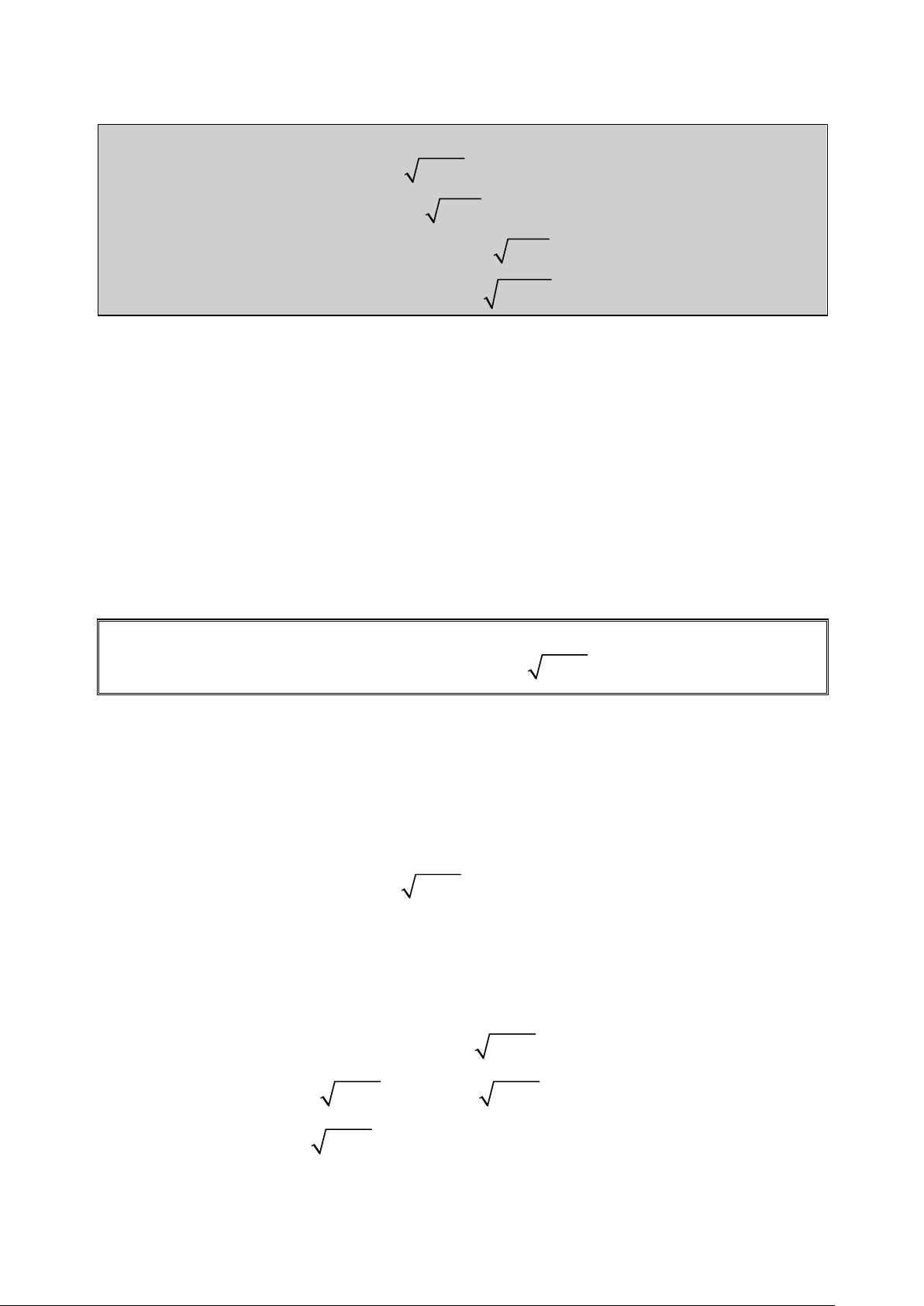
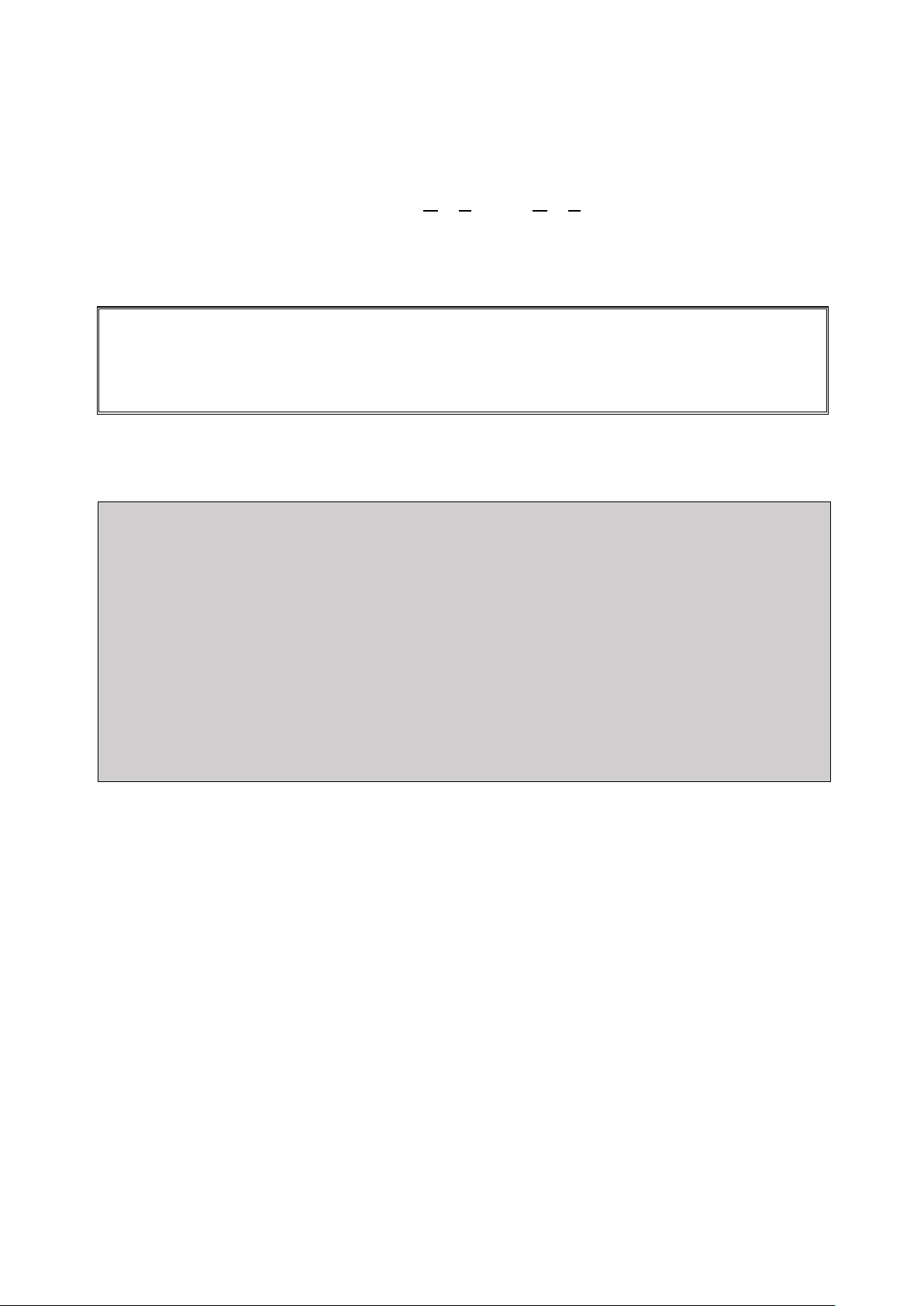
Điều kiện xác định: x  ;    .  2 
Thông thường với dạng toán này, ta sẽ bình phương hoặc đặt ẩn để đưa về phương trình bậc 4.
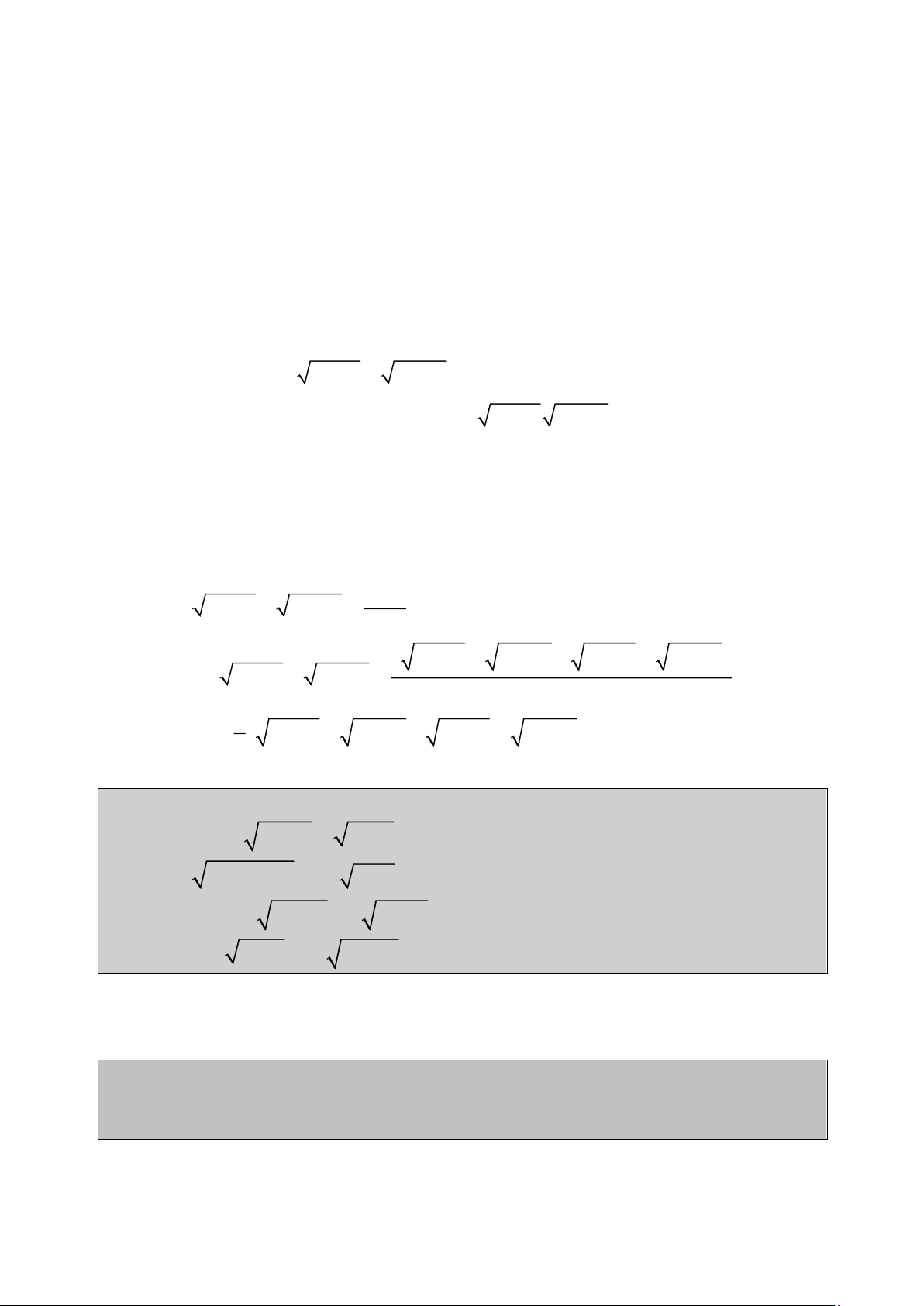
Hướng 1 : Bình phương hai vế : 2
2x 1  x  3x 1  0 2 2
 2x 1 (x  3x 1)  0 4 3 2
 x  6x 11x  8x  2  0 2  t 1
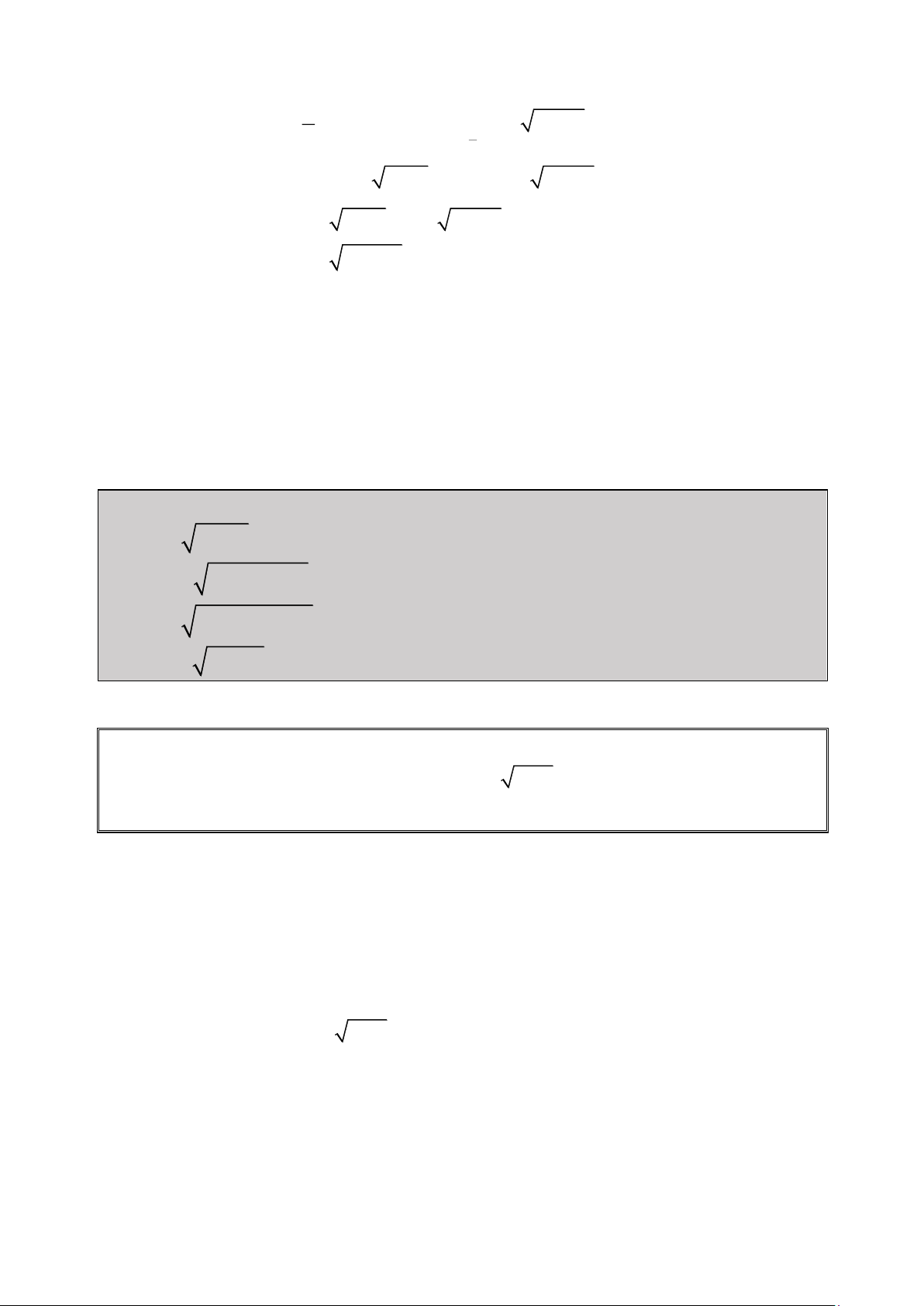
Hướng 2 : Đặt ẩn phụ : Đặt t  2x 1  0  x  ta được : 2 2
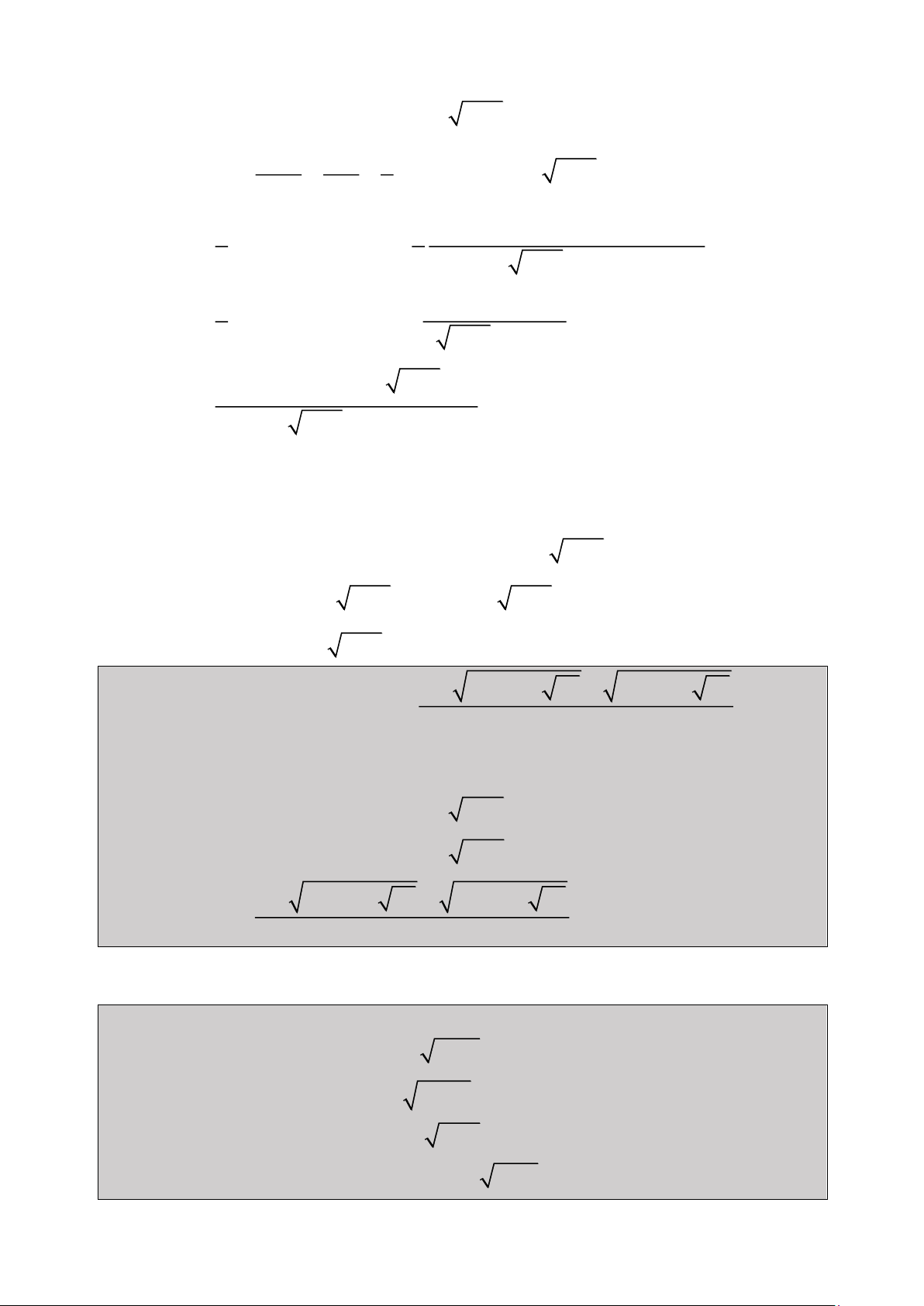
2x 1  x  3x 1  0 2 2 2  t 1  t 1  t     3  1  0 2 2     4 t 2 1   t  t   0 4 4
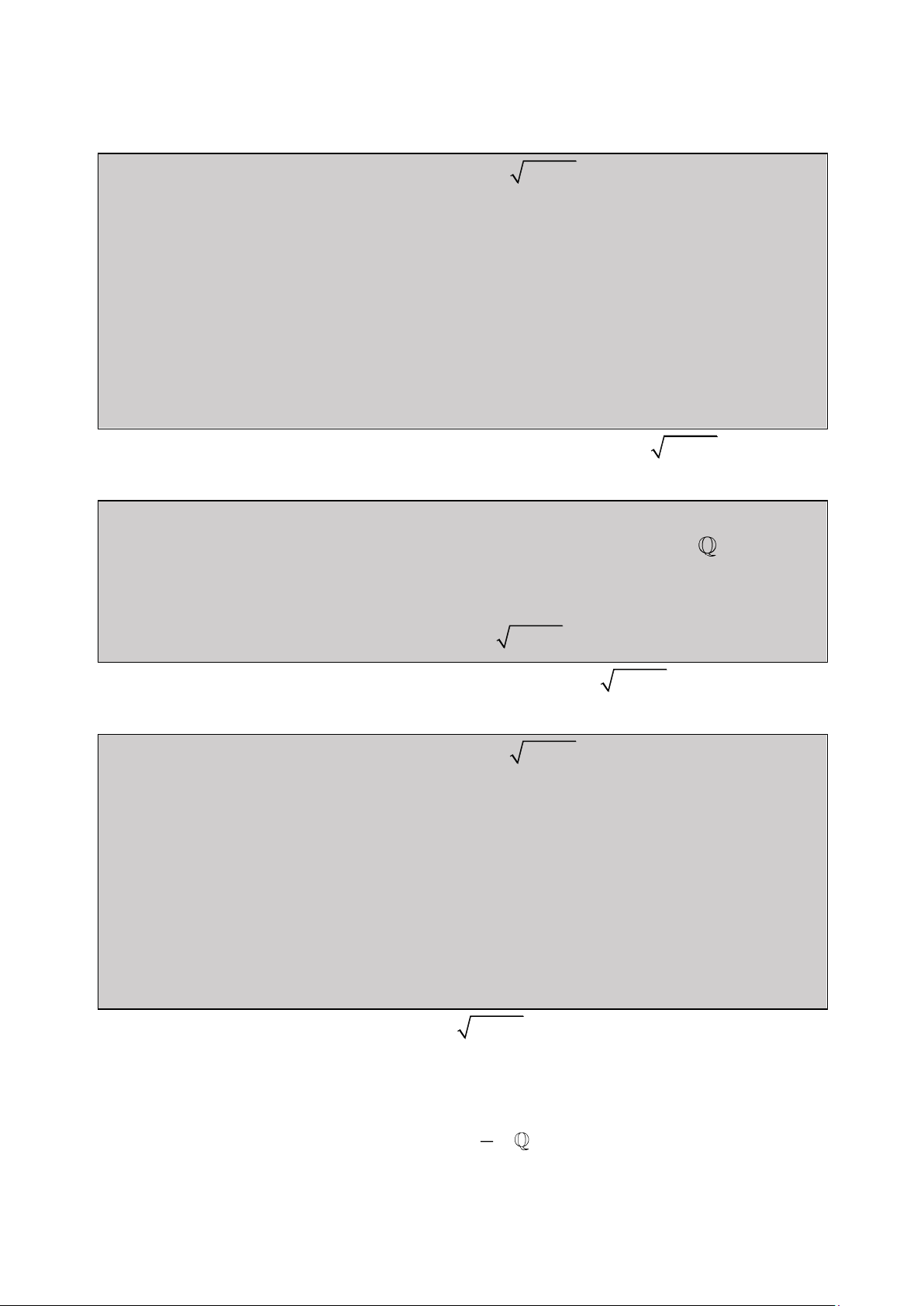
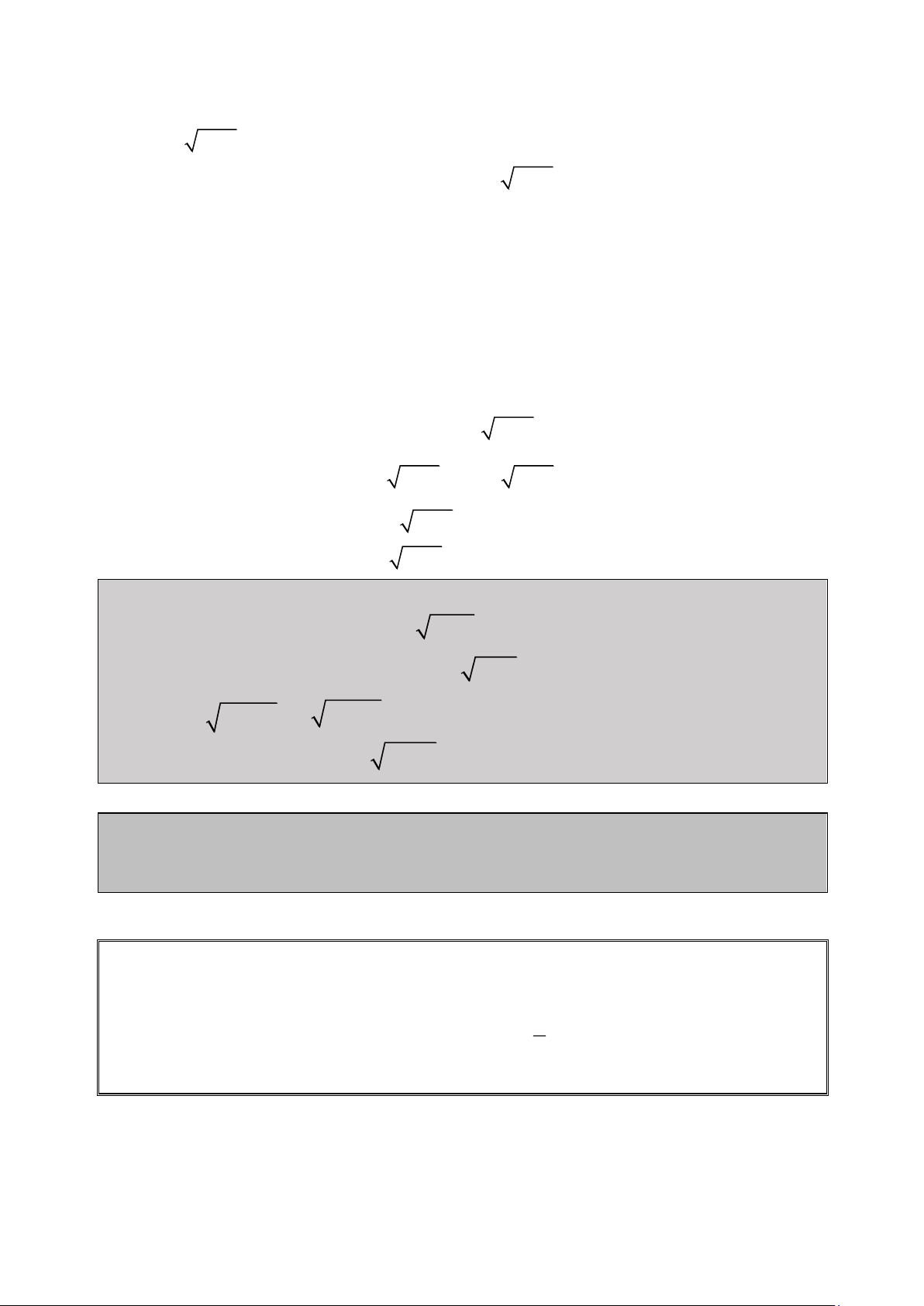
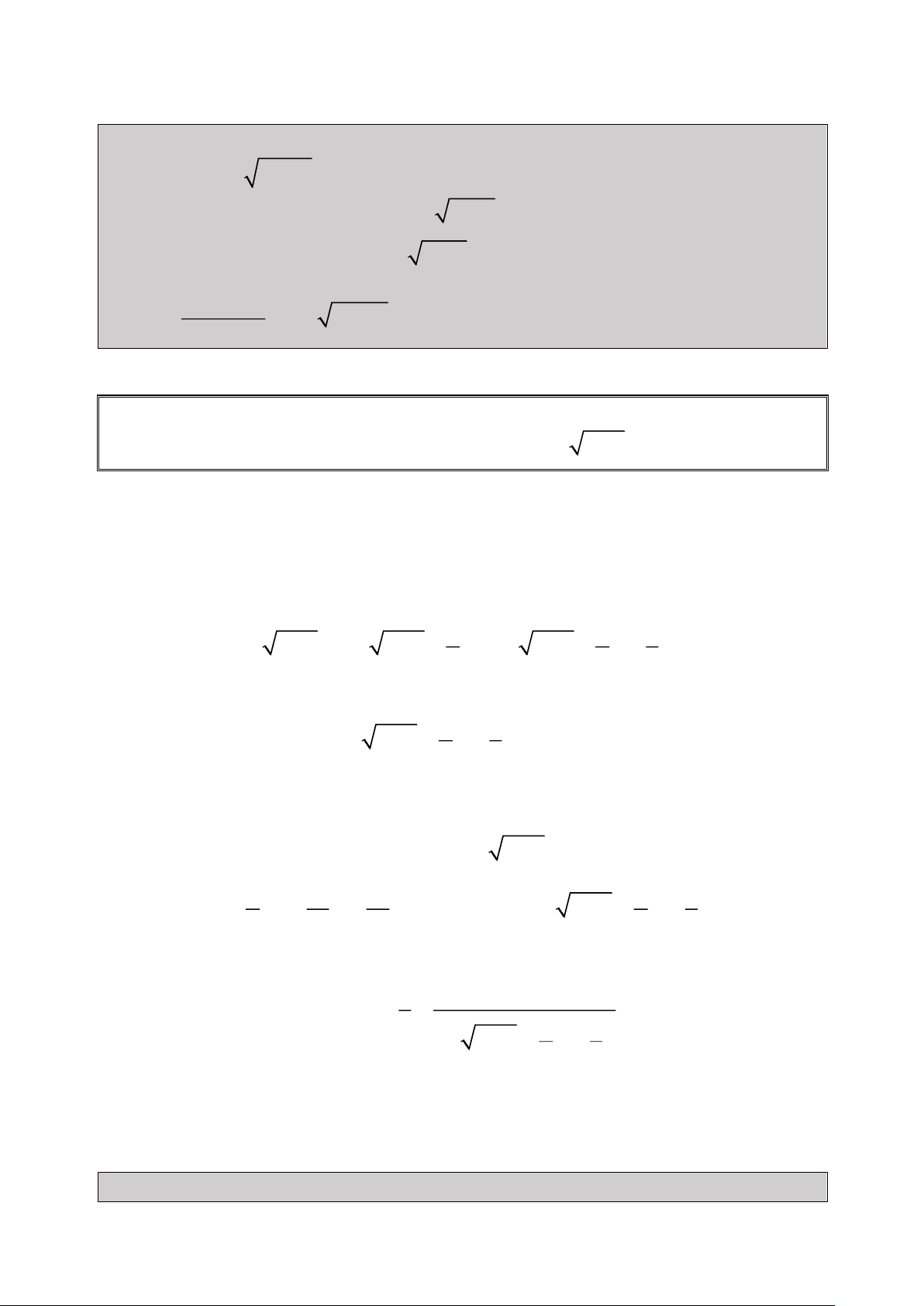
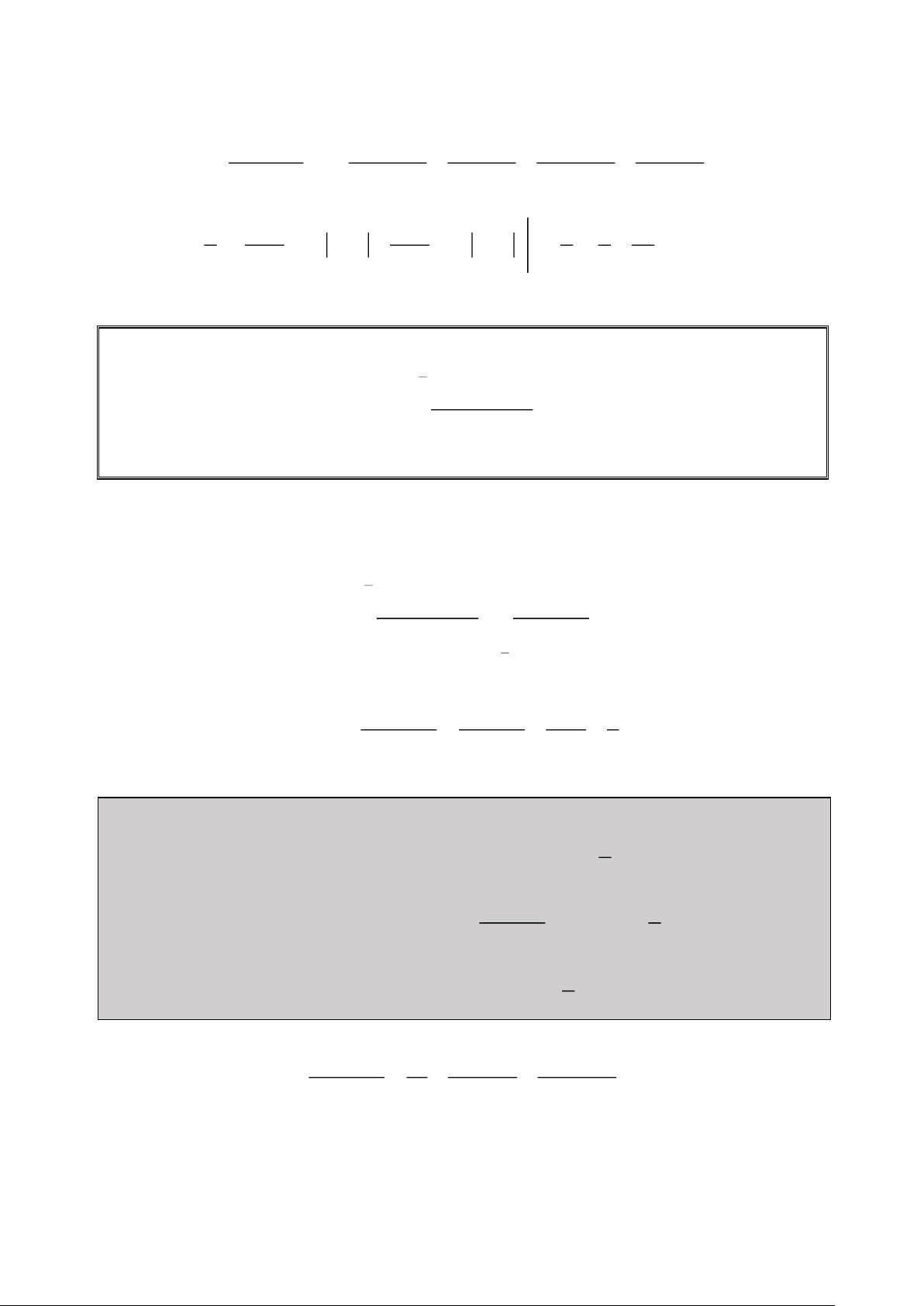
❓ Làm thế nào để rút gọn biểu thức một cách nhanh chóng : 2 2 4 3 2 2x 1 ( x
  3x 1)  x  6x 11x  8x  2 2 2 2 4  t 1  t 1 t 2 1 t     3  1  t  t  2 2 4 4    
Nếu bạn chưa biết Thủ Thuật Sử Dụng Casio Để Rút Gọn Biểu Thức,
chắc hẳn bạn sẽ phải kỳ công ngồi nháp. Và đôi khi bạn cũng sẽ gặp những sai sót.
Tuy nhiên, nếu bạn sử dụng CASIO, mọi chuyện sẽ đơn giản hơn bạn nghĩ. ▶ Ý tưởng :
Ta sẽ xét biểu thức khi x 1000 . Dựa vào chữ số hàng đơn vị, hàng nghìn,
hàng triệu, hàng tỷ, ... ta sẽ tìm được hệ số tương ứng với hệ số tự do, hệ số x , hệ số 2 x , hệ số 3 x , ... Ví dụ xét : 3 2
f(x)  ax  bx  cx  d thì 9
f (1000)  a00b00c00d  10 a f 1000 Suy ra a  . 9 10
❓ Làm thế nào để tính giá trị biểu thức khi x 1000 .
Cách nhanh nhất là sử dụng phím CALC để gán giá trị
Ví dụ khi ta nhập một biểu thức ẩn X , ta ấn CALC và cho X 1000 và ấn
“=” thì máy tính sẽ hiển thị kết quả của biểu thức khi X 1000
Để hiểu rõ hơn, vui lòng xem cách làm dưới đây.
▶ Thực hiện :
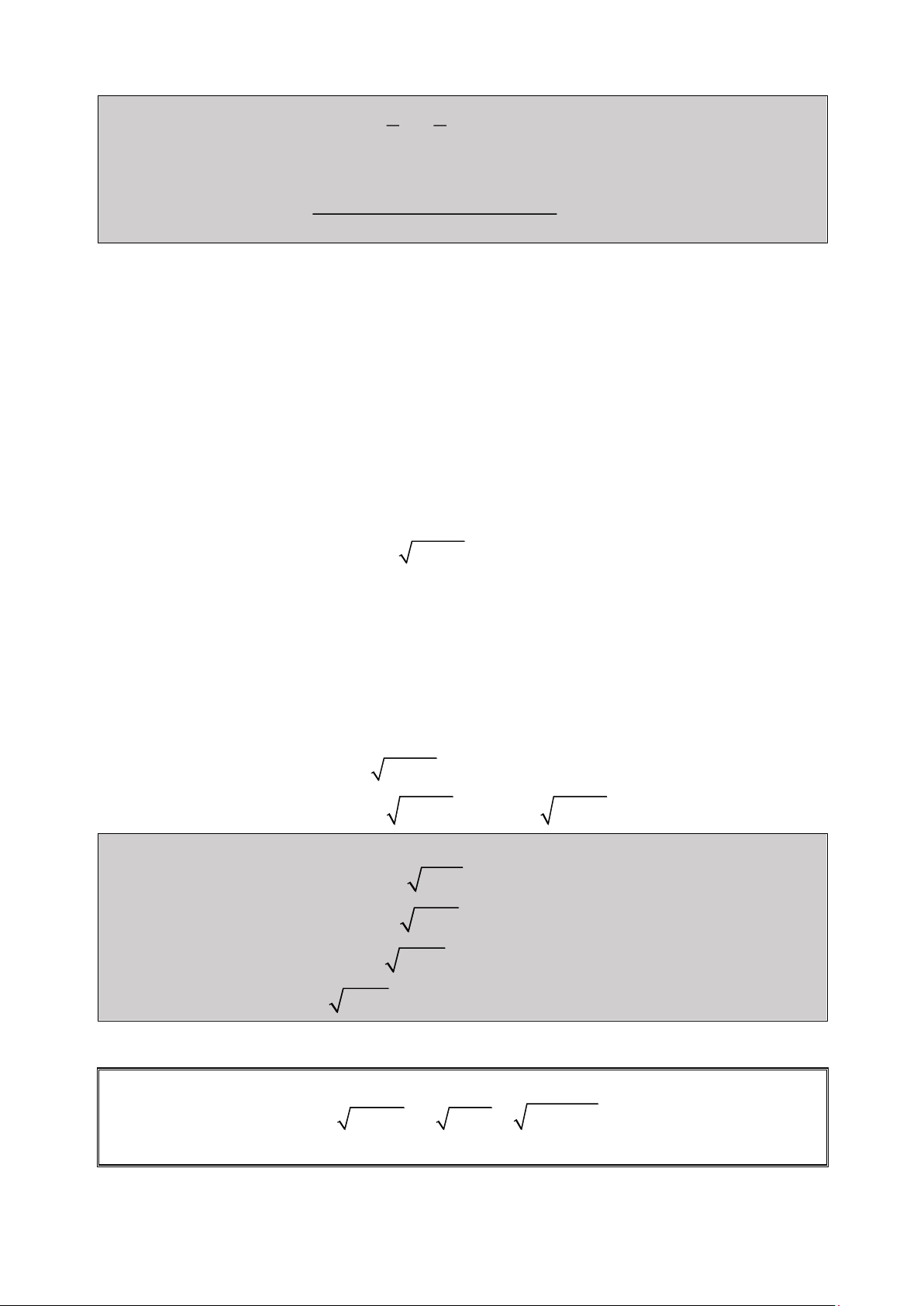
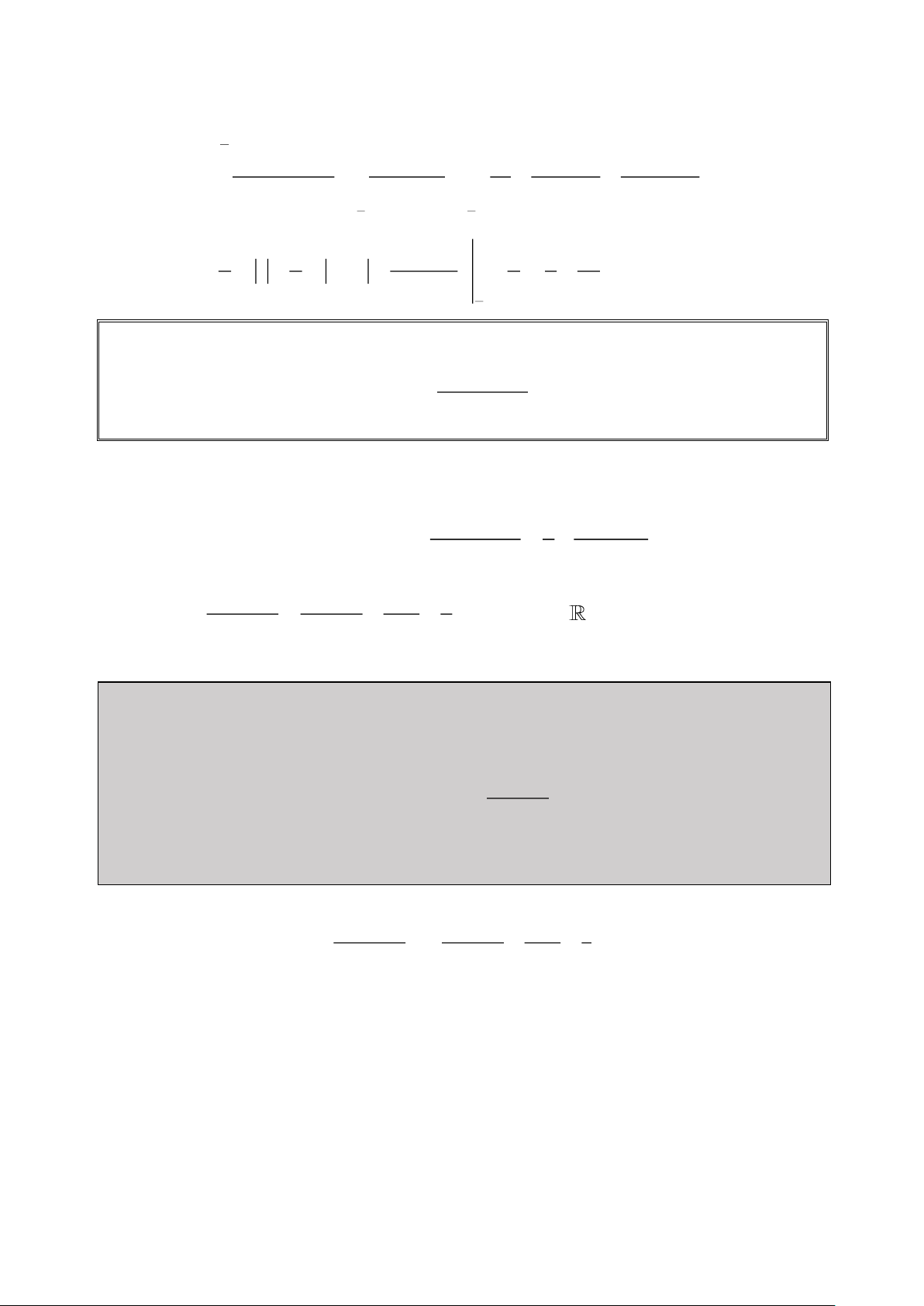
a) Ta muốn rút gọn biểu thức 2 2 f(x)  2x 1( x
  3x 1) , ta lần lượt tính như sau: Ta có : f 1000 11 12 4  9  ,9401099210  10   x f 1000 4 9 3
 x  5989007998  610  6x f 1000 4 3 6 2  x  6x  10  992002  11  10  11  x f 1000 4 3 2 3
 x  6x 11x  7998  810  8x f 1000 4 3 2
 x  6x 11x  8x  2   f x 4 3 2
 x  6x 11x  8x  2
Vậy đáp số: x   x  x  2 2 4 3 2 2 1 3 1
 x  6x 11x  8x  2 . 2 2 2  x 1  x 1
b) Ta muốn rút gọn biểu thức f x  x     3  1 , ta sẽ 2 2    
nhân biểu thức trên với 4 để hệ số của f (x) đều là số nguyên. Ta có : 4f 1000 11 12 4
 9,9999600410 10  x 4f 1000 4 6 2  x  3  996001  4  10  4  x 4f 1000 4 2 3
 x  4x  3999  410  4x 4f 1000 4 2  x  4x  4x  1   4f x 4 2  x  4x  4x 1  f x 4 x 2 1   x  x  4 4 2 2 2 4  x 1  x 1 x 1 Vậy đáp số: 2 x     3  1   x  x  . 2 2 4 4    
▶ Phân tích hướng giải:
❓ Làm thế nào để giải quyết nốt bài toán trên ?
Hãy từ từ, đọc hết chuyên đề này rồi xem lại bài toán trên, chắc chắn bạn
đọc sẽ có cái nhìn hoàn toàn khác về những bài tập dạng này.
Hãy thử xem qua các lời giải sau :
▶ Cách 1 : Nhân liên hợp hoàn toàn: Ta có : 2
2x 1  x  3x 1  0  x  
1 x  2   2x 1   1  0     x   2 1  x  2   0   2x 1 1        x   2x 1 1 1  x 1   0   2  x 1 1   x 2  2   1 1       2x 1    0 2 1  
▶ Cách 2 : Nhân liên hợp không hoàn toàn: Ta có : 2
2x 1  x  3x  1  0  x  
1 x  2   2x 1   1  0 1   2x 1   1  2x 1  
1 x  2   2x 1   1  0 2 1   2x 1   1  2x 1   1 x  2  2  0 2 1   2x 1   1  2x 1   1 x   1  2x 1   1  0 2 1     x   x   2 2 1 1 1 2  x 1 1  0  2  2x 1 1  1   2x 1   1 x  
1  2x 1 1 2  2x 1 1 2   0 2
▶ Cách 3 : Phân tích thành nhân tử không hoàn toàn: 2
2x 1  x  3x 1  0   2x 1  x   1  2x 1  x  0
▶ Cách 4 : Phân tích thành nhân tử hoàn toàn: 2
2x 1  x  3x 1  0 1   2x 1  x   1  2x 1  2 1  0 2
▶ Cách 5 : Bình phương hai vế: 2
2x 1  x  3x 1  0
 2x 1  x  3x  2 2 1
 x  4x  2x  2 2 1  0
▶ Cách 6 : Đặt ẩn phụ hoàn toàn: 2 1 Đặt  2 1   t t x x . Vậy ta có : 2 2 2 2  t    t   2 1 1
2x 1  x  3x 1  0  t     3  1  0 2 2     1  t  2t   1 t  2 2 1  0 4
▶ Cách 7 : Đặt ẩn phụ không toàn toàn:
Đặt t  2x 1 . Vậy ta có : 2
2x 1  x  3x 1  0 2 2  x  t  x  t
 t  xt  x   1  0
▶ Cách 8 : Đặt ẩn phụ đưa về hệ phương trình:
Đặt y  2x 1 . Ta có hệ phương trình :  2
x  3x  1  y  0   2
y  2x  1   0
Lấy PT (1)  PT (2) ta được :
 2x 3x1 y 2y 2x10
 x y  
1 x y  0
8 cách làm trên tuy có khác nhau về cách trình bày nhưng về bản chất thì
giống nhau. Đó là cùng xuất phát từ một thứ gọi là “nhân tử”. Khi có nhân
tử, chúng ta biết được biểu thức nào cần nhóm để đặt ẩn phụ, nhân liên
hợp, phân tích nhân tử. Để hiểu rõ hơn, bạn đọc hãy đọc các thủ thuật tiếp
theo rồi quay lại xem bài toán này và thử làm những bài tập tương tự.
Một số bài tập tương tự : 1. 2
x  2x  2  x x 1  0 2. 2
2x 15x  2  6x   11 2x 1 3. 2
x  24x  35  
4 2x  7 x  2 4. 2
4x 13x 14  4 x  2 3x  2
Bài 2: Giải phương trình: x  2 3 4  6 x  3x 13
(đề thi thử Đại Học lần 3 khối B THPT Ngô Gia Tự – Bắc Ninh năm 2013)
Điều kiện xác định: x    0,  . ▶ Ý tưởng :
Tương tự bài 1, ta cũng sẽ sử dụng máy tính CASIO để rút gọn phương trình bậc 4 sau : f x  x   2 2     3 4 13 36 x  3x   ▶ Thực hiện :
Ta làm các bước như bài 1 : Ta có : f 1000 11 12 4  9,800699410 10  x f 1000 4 10 9 3  x  1
 ,99300599910  2010  20x f 1000 4 3 6 2
 x  20x  69940009  7010  70x f 1000 4 3 2 3  x  20x  70x  59
 991  6010  60x f 1000 4 3 2
 x  20x  70x  60x  9  f 1000 4 3 2
 x  20x  70x  60x  9 2 2
Kết luận : x       3x  x 4 3 2 4 13 36 3
 x  20x  70x  60x  9  
▶ Phân tích hướng giải :
Vậy bài toán đã cho chỉ đơn giản là việc giải phương trình bậc 4 : 4 3 2
x  20x  70x  60x  9  0
Cách giải phương trình bậc 4 bằng máy tính cầm tay ở các thủ thuật tiếp theo.
Ngoài ra có vô vàn cách giải khác tương tự như bài 1. Tuy nhiên chúng ta
nên để ý cách giải phương trình này bằng việc phân tích nhân tử vì đó là ý
tưởng ra đề của rất nhiều bài toán khó.
▶ Cách 1 : Bình phương hai vế: Ta có : x  42 3  6 x  3x 13  x  4 2 2 13  36 3 x  3x  0   4 3 2
 x  20x  70x  60x  9  0  x   1 x  3 2 x 16x  3  0
▶ Cách 2 : Phân tích thành nhân tử: Ta có :
x  42 6 x 2x 3 13
  2x 3 4 x 2x 3 2 x
Một số bài tập tương tự : 1. 2 3
x 15x 1  8 x x 2. 2 3
x  2x  3  x  3x 2 7x 3.
13x  8  8 2x 1 x 1  0 8 4. 2 2 2
4x  6x 1  4 x 1 x  2x
Bài 3: Giải phương trình: 5 4 3 2
x  6x  7x  29x 16x  2  0
Điều kiện xác định: x . ▶ Ý tưởng :
Thông thường những bài tập giải phương trình kiểu này thường có một
hướng giải nhanh gọn. Đó là “Phân Tích Thành Nhân Tử”.
Muốn phân tích được thì ta phải biết được nhân tử của bài toán.
❓ Làm thế nào để tìm ra nhân tử của bài toán ?
Bằng thủ thuật CASIO, ta dễ dàng tìm ra nhân tử của bài toán này là
 2x 6x2. Nhưng để tìm được thì bạn đọc hãy đợi tới các thủ thuật sau.
Tóm lại là ta muốn tìm nhân tử còn lại của bài toán, hay chính là thương của phép chia : 5 4 3 2      f x x 6x 7x 29x 16x 2  2 x  6x  2
▶ Thực hiện: 5 4 3 2
x  6x  7x  29x 16x  2 Ta coi biểu thức
chỉ là một đa thức ẩn x và 2 x  6x  2 làm tương tự bài 1 : f 1000 9 3  999995001 10  x f 1000 3 3  x  4999   5  10  5  x f 1000 3  x  5x 1 Vậy ta được : 5 4 3 2
x  6x  7x  29x 16x  2 3  x  5x 1 2 x  6x  2
▶ Phân tích hướng giải:
Sau khi chia đa thức, ta được : 5 4 3 2 x  x  x  x  x    3 x  x   2 6 7 29 16 2 5 1 x  6x  2
Để giải phương trình bậc 3 : 3
x  5x 1 0 thì hãy đón xem thủ thuật giải
phương trình bậc 3 ở dưới
Vậy ta có lời giải như sau : ▶ Lời giải : Ta có : 5 4 3 2
x  6x  7x  29x 16x  2  0   3 x  5x   1  2 x  6x  2  0 Xét đa thức : g x 3  x  5x 1
Vì g(x) bậc 3 nên g(x)  0 có tối đa 3 nghiệm. Chỉ ra 3 nghiệm này là :     2 1 3 15 x  15 o c s  arccos    1 3  3  50            2 1 3 15 2 x  15 o c s  arccos      2 3  3  50  3            2 1 3 15 2 x  15 o c s  arccos      3 3  3  50  3     
Bài toán được giải quyết hoàn toàn.
Hy vọng qua 3 bài toán cơ bản trên, bạn đọc hình dung được lợi ích của
việc sử dụng máy tính cầm tay trong việc rút gọn biểu thức khi giải toán.
Một số bài tập tương tự : 1. 4 3 2
x  2x  6x x  2  0 2. 5 4 2
x x  3x x  2  0 3. 5 4 3 2
2x  2x  5x  2x  4x  2  0 4. 6 5 4 3 2
x  6x  7x  24x  72x  64x 16  0
THỦ THUẬT 2 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
TÌM NGHIỆM PHƯƠNG TRÌNH
Bài 1: Giải Bất Phương Trình: 2
300x  40x  2  10x 1  3 10x  0 1  x  1 x  2
(đề thi thử Đại Học lần 2 THPT Quỳnh Lưu 1 – Nghệ An năm 2013)  1 3 
Điều kiện xác định: x   ;  /   0 . 10 10 
▶ Ý tưởng :   Ta luôn có :  x   x    x   x 1 3 1 1 2 1 1  2 x   ;   10 10
Quan trọng nhất bây giờ là giải quyết bất phương trình : 2
300x  40x  2  10x 1  3 10x  0
Thông thường với dạng toán này, ta sẽ nhân liên hợp với nghiệm của bài toán.
❓ Làm thế nào để tìm các nghiệm của phương trình : 2
300x  40x  2  10x 1  3 10x  0
Sử dụng phím SOLVE để tìm nghiệm, nhưng có lẽ với một số bạn, phím
SOLVE cho ta đúng một nghiệm của bài toán. Vậy với bài toán có nhiều
nghiệm thì sao ? Làm thế nào để biết bài toán chỉ có một nghiệm duy nhất ?
Để hiểu rõ hơn, bạn đọc hãy xem cách làm dưới đây :
▶ Thực hiện :  Ta viết biểu thức 2
300x  40x  2  10x 1  3 10x  0 lên máy tính
 Ấn SOLVE để tìm nghiệm, máy hỏi X ? .  1 1 Nhập để tìm nghiệm gần nhất. 10 10  1
Máy cho nghiệm x  0.2  5
 Ấn SOLVE để tìm nghiệm, máy hỏi X ? .  3 3 Nhập để tìm nghiệm gần nhất. 10 10  1
Máy cho nghiệm x  0.2  5
Vậy ta có thể kết luận : Phương trình 1 2
300x  40x  2  10x 1  3 10x  0 có nghiệm duy nhất x  . 5
▶ Phân tích hướng giải: 1 Khi biết x
là nghiệm duy nhất của phương trình, ta chắc chắn sử dụng 5
được phương pháp nhân liên hợp. Ngoài ra, nếu bạn đọc thủ thuật giải
phương trình vô tỷ bằng CASIO, ta có thể có thêm những cách làm khác.
▶ Cách 1 : Nhân liên hợp hoàn toàn: Ta có : 2
300x  40x  2  10x 1  3 10x  0     x   1 1 10 2 30  x  2    0   10x 1 1 3 10x 1      x   10x 1 1 10 2 30x 1    0   10  x 1 1 3 10x 1
▶ Cách 2 : Phân tích thành nhân tử: Ta có : 2
300x  40x  2  10x 1  3 10x  0 2
 300x  40x  3  3 10x   10x 1   1  0
 1 310x 30x  2 310x  30x  3   10x 1   1  0         x x   30 2 3 10x 30x 3 1 10 2     0  1 3 10x 10x 1 1               x   x   30 1 3 10x 30x 2 10x 1 10 2     0  1 3 10x 10x 1 1     
Một số bài tập tương tự : 1. 2
x  2x  2  2 2x 1  2  x  0 2. 3
x  2x  7  2 x  3  3 2x  5  0 3. 2
x 11x 12  
3 x  2 4x 1 11 x  2  0 4. 3 2 2
x x 14  6 x  5  2 10  x  0
Bài 2: Giải Phương Trình: xx   3 2 2  3 x 1
(đề thi thử Đại Học lần 1 Khối D THPT Tuy Phước – Bình Định năm 2013)
Điều kiện xác định: x     1, . ▶ Ý tưởng :
Tương tự bài 1, ta sẽ tìm nghiệm để nhân liên hợp thử xem.
▶ Thực hiện :
 Ta viết biểu thức xx   3 2
2  3 x 1  0 lên máy tính
 Ấn SOLVE để tìm nghiệm, máy hỏi X ? .  Nhập 1
 để tìm nghiệm gần 1  nhất.
 Máy cho nghiệm x  0  .541381265
 Lưu nghiệm này vào A bằng cách ấn X + Shift STO + A
 Tương tự tìm nghiệm gần 10 nhất
 Máy cho nghiệm x  . 5 54138 6 12 5
 Lưu nghiệm này vào B bằng cách ấn X + Shift STO + B
 Tương tự tìm nghiệm gần 2.5 nhất
 Máy cho nghiệm x  . 5 54138 6 12 5
 Đây chính là nghiệm B
Vậy ta có thể kết luận : Phương trình xx   3 2
2  3 x 1  0 có hai nghiệm
là x A và x B .
❓ Làm thế nào để viết nghiệm ,
A B dưới dạng vô tỷ ?
Đơn giản chỉ cần làm một trong hai cách sau : A   B   5 Cách 1 : ta thấy  . AB  3  
 A,B là nghiệm của phương trình : 2 X  5X  3  0
 Cách 2 : ta thấy A B nên ta luôn có : A  B  A  B2 5  37 A  B  A  B2  A   5 37 và B   2 2 2 2 5  37 5  37
Ta được 2 nghiệm của bài toán này là : và . 2 2
▶ Phân tích hướng giải:
❓ Làm thế nào để nhân liên hợp với nghiệm vô tỷ ?
Rất đơn giản, hãy xem cách làm dưới đây : 5  37 Ta thấy : khi x  thì 3
x 1  8614 37  7  37  2x  2 2
Vậy ta chỉ cần nhân liên hợp  3 x 1  2x  2 .
▶ Cách 1 : Nhân liên hợp hoàn toàn: Ta có : 2xx  2 3  3 x 1 2
 2x 10x  6  3 3x 1 2x  2 2
 2x 10x  6  3 x 1 2x  x 1 2 x 1    x   2 x  x   3 1 5 3  2    0   2  x  x 1  2 x 1    2 x  5x  3 2
x  x 1  x 1  0
▶ Cách 2 : Phân tích thành nhân tử: Ta có : 2xx  2 3  3 x 1   2
2 x  x 1  x 1 2
x  x 1  2 x 1  0
Một số bài tập tương tự : 1. 2 3
x 16x 14  2 x 1  0 2. 2 3
2x  5x 1 7 x 1  0 3. 2 4 2 x  5x 1
x x 1  0 4. 4
8x  4 3  3 x  4x 3 1  0
Bài 3: Giải Phương Trình: x 2 4x  
1  x  3 5  2x  0
(đề thi thử Đại Học lần 1 Khối A + A1 THPT Tuy Phước – Bình Định năm 2013)  5 
Điều kiện xác định: x    ;  .  2 
▶ Ý tưởng :
Tương tự bài 1, ta vẫn sẽ tìm nghiệm để nhân liên hợp.
▶ Thực hiện :
 Ta viết biểu thức x 2 4x  
1  x  3 5  2x  0 lên máy tính
 Ấn SOLVE để tìm nghiệm, máy hỏi X ? .  Nhập 10
 để tìm nghiệm gần 10  nhất.
 Máy cho nghiệm x  0.895643923
 Lưu nghiệm này vào A bằng cách ấn X + Shift STO + A
 Tương tự tìm nghiệm gần 2.5 nhất
 Máy cho nghiệm x  0.895643923
 Tương tự tìm nghiệm gần 6  nhất
 Máy vẫn cho nghiệm x  0.895643923
Vậy ta có thể kết luận : Phương trình x 2 4x  
1  x  3 5  2x  0 chỉ có
nghiệm duy nhất là x A .
❓ Làm thế nào để viết nghiệm A dưới dạng vô tỷ ?
Tương tự bài 2, ta cũng sẽ tìm số vô tỷ B để thỏa mãn A B  . Nhưng
B sẽ không thỏa mãn phương trình ban đầu, mà thỏa mãn phương trình
khi đã đổi dấu trước căn. Tức B là nghiệm của phương trình : x 2 4x  
1  x  3 5  2x  0
Vậy ta sẽ đi giải phương trình x 2 4x  
1  x  3 5  2x  0 để tìm B ,
giống như một hành trình để đi tìm người thân :
 Ta viết biểu thức x 2 4x  
1  x  3 5  2x  0 lên máy tính
 Ấn SOLVE để tìm nghiệm, máy hỏi X ? .  Nhập 10
 để tìm nghiệm gần 10  nhất.
 Máy cho nghiệm x  1  .395643924
 Lưu nghiệm này vào B bằng cách ấn X + Shift STO + B
 Tương tự tìm nghiệm gần 2.5 nhất
 Máy cho nghiệm x  1  .395643924
 Tương tự tìm nghiệm gần 6  nhất
 Máy vẫn cho nghiệm x  1  .395643924 Vậy phương trình x 2 4x  
1  x  3 5  2x  0 chỉ có nghiệm duy nhất là x B . Để kiểm chứng ,
A B có phải “họ hàng” với nhau không, ta thành thử thấy 1 A  B    2 2 A  B  (A  B) 1   21
Mà A B nên A   2 4
Kết luận : Nghiệm của phương trình x 2 4x  
1  x  3 5  2x  0 là 1   21 x  4
▶ Phân tích hướng giải: 1   21 1   21 Ta thấy : Khi x  thì 5  2x   2x 4 2
Vậy ta chỉ cần nhân liên hợp  5  2x  2x .
▶ Cách 1 : Nhân liên hợp hoàn toàn: Ta có : x 2 4x  
1  x  3 5  2x  0  x 2
4x  2x  5  x  3 5  2x  2x  0     x  2 3 4x  2x  5 x   0   5  2x  2x    2 4x  2x  5 2
2x x  3  x 5  2x   0 Ta dễ dàng thấy rằng : 2 2  1   5  2x  2 27
2x x  3  x 5  2x   x      x   0 4  2    16  
Vậy bài toán được giải quyết hoàn toàn.
▶ Cách 2 : Phân tích thành nhân tử: Ta có : x 2 4x  
1  x  3 5  2x  0   5 2x  2x 2
2x x  3  x 5  2x   0
Sau đó tương tự làm như cách 1.
Một số bài tập tương tự : 1. 2
4x  2x  3  4x 2x  3 2. 3 2 x x x   2 2 16 48
13x  5x 15 x  3 3. 3 2
x x x   2 4 3 6
2 2x x   1 x  2
THỦ THUẬT 3 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
GIẢI PHƯƠNG TRÌNH BẬC 4
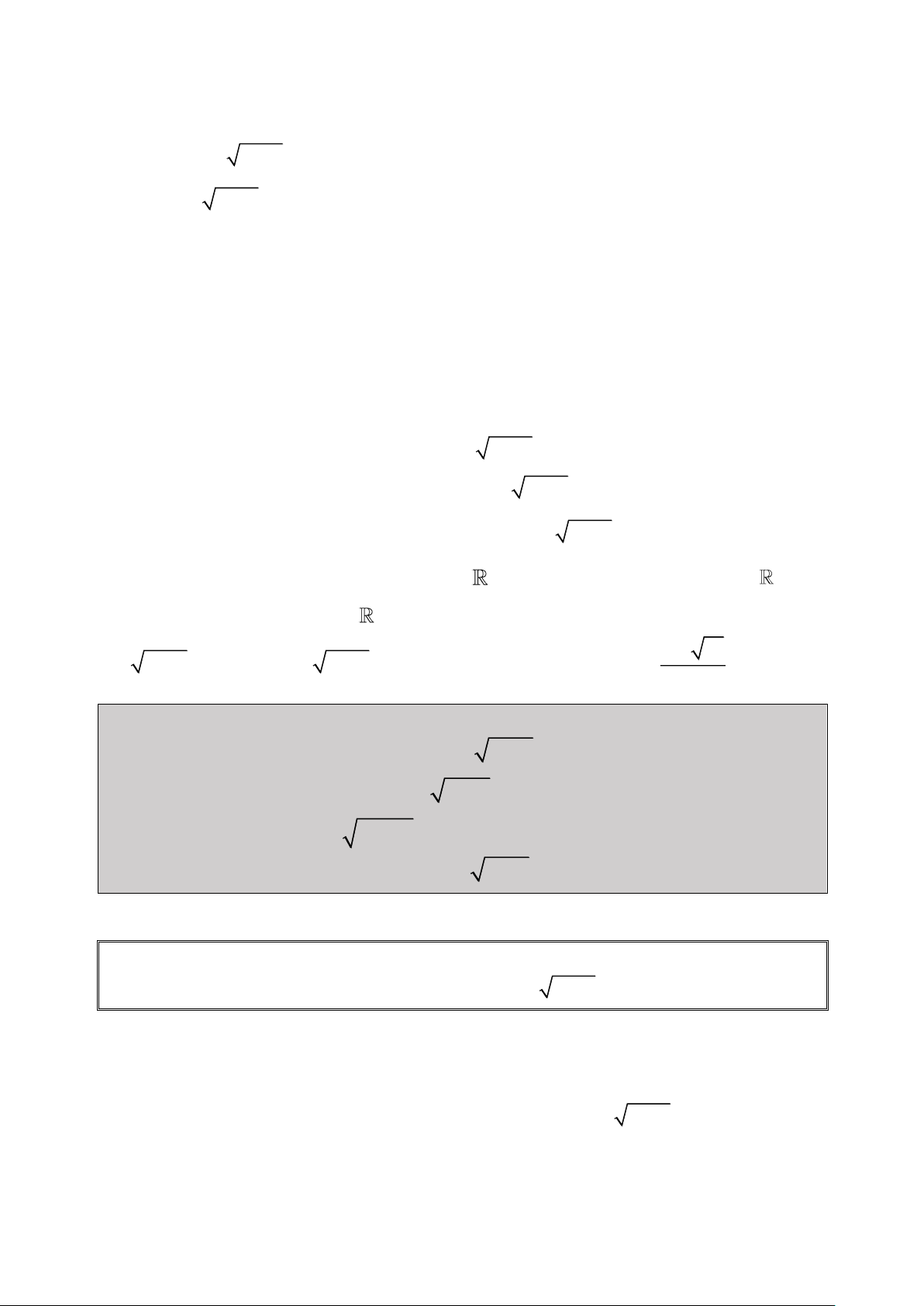
Bài 1: Giải Phương Trình: 2 4x  8x  2x  3 1
(đề thi thử Đại Học THPT Lưu Hoàng – Ưng Hoàng – Hà Nội năm 2013)  3 
Điều kiện xác định: x   ;    .  2  ▶ Ý tưởng :
Ta cần giải phương trình bậc 4 sau : 2 2
(4x 8x 1)  2x  3  0
▶ Thực hiện :
 Sử dụng Thủ Thuật Rút Gọn Biểu Thức ta được : 4x 8x 2 2 1  2x  3  0 4 3 2
16x  64x  56x 14x  2  0
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được các nghiệm được gán vào , A , B C như sau : A   0  2 . 80776406   B  2 3 . 95643924  C  0 1 . 043560763  Tìm trong , A ,
B C , cặp nào là “họ hàng” với nhau bằng cách thành
thử các tổng A  ,
B B C,C A :  A  B  2 114 , 867518  5  B  C   2  C  A  0  176 , 4203298  Vậy ,
B C là “họ hàng” với nhau rồi.
 Vậy thành thử tiếp ta thấy :  5 B  C   2  1  BC   4 Suy ra ,
B C là nghiệm của phương trình : 2 5 1 2
x  x   0  4x 10x 1  0 2 4
 Sử dụng Thủ Thuật Rút Gọn Biểu Thức ta được : 4 3 2
16x  64x  56x 14x  2 2  4x  6x  2 2 4x 10x 1 Kết luận : 4 3 2
16x  64x  56x  14x  2   2 4x  6x  2 2 4x 10x   1  2 2 2x  3x   1  2 4x 10x   1
▶ Phân tích hướng giải:
Bằng việc sử dụng kết hợp các thủ thuật ở trên, ta có được lời giải ngắn gọn như sau :
▶ Cách 1 : Bình phương hai vế: Ta có : 2 4x  8x  2x  3  1  4x 8x  2 2 1  2x  3  0 4 3 2
 16x  64x  56x 14x  2  0  2 2 2x  3x   1  2 4x 10x   1  0
▶ Cách 2 : Phân tích thành nhân tử: Ta có : 2 4x  8x  2x  3  1
 2x  2  2x  32x 1 2x  3  0
Một số bài tập tương tự : 1. 2
4x 12x  9  22x   1 x 1 2. 2
2x  9x 12  4x  7 x  3 3. 2
6x  9x 1  7x  5 x  2 4. 2
x  3x 14 10 2  x  0
Bài 2: Giải Phương Trình: 2
2 2x  4  4 2  x  9x 16
(đề thi thử Đại Học lần 3 THPT Quỳnh Lưu 1 – Nghệ An năm 2013)  3 
Điều kiện xác định: x   ;    .  2  ▶ Ý tưởng :
Ta lần lượt bình phương hai vế để được phương trình bậc 4 : 2
2 2x  4  4 2  x  9x 16
 42x  4 162  x 2 2 16 8  2x  9x 16 2 2
 16 8  2x  9x  8x  32
 2568  2x   9x 8x  322 2 2
Vậy công việc của chúng ta là giải phương trình bậc 4 sau :
  x  x  x 2 2 2 256 8 2 9 8 32  0
▶ Thực hiện :
 Không như bài 1, ta có thể bỏ qua bước rút gọn biểu thức.
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được các nghiệm được gán vào , A B như sau : A   1  8 . 85618083  B 1 8 . 85618083
 Dễ thấy A  B  0 nên ,
A B rất có thể là “họ hàng” với nhau rồi.
 Vậy thành thử tiếp ta thấy : A   B  0   32 AB    9 Suy ra ,
A B là nghiệm của phương trình : 2 32 2 x   0  9x  32  0 9
 Sử dụng Thủ Thuật Rút Gọn Biểu Thức ta được :
2568  2x   9x  8x  322 2 2 2  9x 16x  32 2 9x  32 Kết luận :
2568  2x   9x  8x  322 2 2   2 9x  32 2 9x 16x  32
▶ Phân tích hướng giải:
Ta vẫn sẽ có hai cách giải cho bài toán trên như sau :
▶ Cách 1 : Bình phương hai vế: Ta có : 2
2 2x  4  4 2  x  9x 16
 42x  4 162  x 2 2 16 8  2x  9x 16 2 2
 16 8  2x  9x  8x  32
 2568  2x   9x  8x  322 2 2   2 9x  32 2 9x 16x  32  0
▶ Cách 2 : Phân tích thành nhân tử: Ta có : 2
2 2x  4  4 2  x  9x 16
 42x  4 162  x 2 2 16 8  2x  9x 16 2 2
 16 8  2x  9x  8x  32   2 2 8  2x  x  8 2 2 8  2x  x  0
Một số bài tập tương tự : 1. 2
3 x 1  6 x 1  9
x  60x  29 34
2. 2 2  x  2  x   5x 5 9 3. 2 x  2 
x  4x  3 1  2 x 1 7 27 4. 2
1 x  1 x  16x  2
Bài 3: Giải Phương Trình: x  3 4x 1  3x  2  5
(đề thi thử Đại Học THPT Phan Bội Châu – Phú Yên năm 2013)  3 
Điều kiện xác định: x   ;    .  2  ▶ Ý tưởng :
Ta lần lượt bình phương hai vế để được phương trình bậc 4 :
5 4x 1  3x  2   x  3 2  x 169x  34  50  4x 1 3x  2  x 169x  342 2  25004x   1 3x  2
Vậy công việc của chúng ta là giải phương trình bậc 4 sau : x  x 2 2 169 34  25004x   1 3x  2  0
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được 2 nghiệm là : A   3   B  2
 Vậy nhân tử của bài toán sẽ là : x  3x  2
 Ta cần tìm thương của biểu thức : x  x 2 2 169 34  25004x   1 3x  2 f x  x  3x  2
Tuy nhiên, sử dụng Thủ Thuật Rút Gọn Biểu Thức lại không được
ổn vì hệ số của đa thức quá to.
Nếu không gán giá trị cho x  1000 được thì ta sử dụng lim để chắc chắn nhất
Cách tìm lim bằng máy tính CASIO chỉ đơn giản là gán cho x là
một số cực to. Ví dụ như 10 x  10 .
Ta thấy f (x) sẽ là một tam thức bậc 2 nên ta có thể đặt :   2 f x  ax  bx  c Ta tìm hệ số , a ,
b c bằng cách lấy :  Tìm a : f x a  lim 1 2 x x  Tìm b : f x 2  ax b  lim  339  x x  Tìm c : c  f x 2  ax  bx  1026 Kết luận : x 169x342 2  25004x   1 3x  2 2     x  x   x 339x 1026 3 2
▶ Phân tích hướng giải: Lưu ý rằng : 2
x  339x 1026  x  3x  342
Do đó, ta cũng sẽ có hai cách giải cho bài toán trên như sau :
▶ Cách 1 : Bình phương hai vế: Ta có :
5 4x 1  3x  2   x  3 2  x 169x  34  5  0 4x 1 3x  2  x 169x  342 2  25004x   1 3x  2
 x  2x  342x  32  0
▶ Cách 2 : Phân tích thành nhân tử: Ta có : x  3 4x 1  3x  2 
5 4x1 3x2 4x1 3x2  4x 1  3x  2  5 1
   4x 1  3x  2 4x 1  3x  2 5  0 5
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự : 1.
x  3  2x 1  x  2  0 2. 2
3 x x  2  25 x 1  56  0 3.
x  6  6 2x  3  2 3x 1  0
4. 5  7 x  6 13 2x  2  0
THỦ THUẬT 4 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ MỘT ẨN
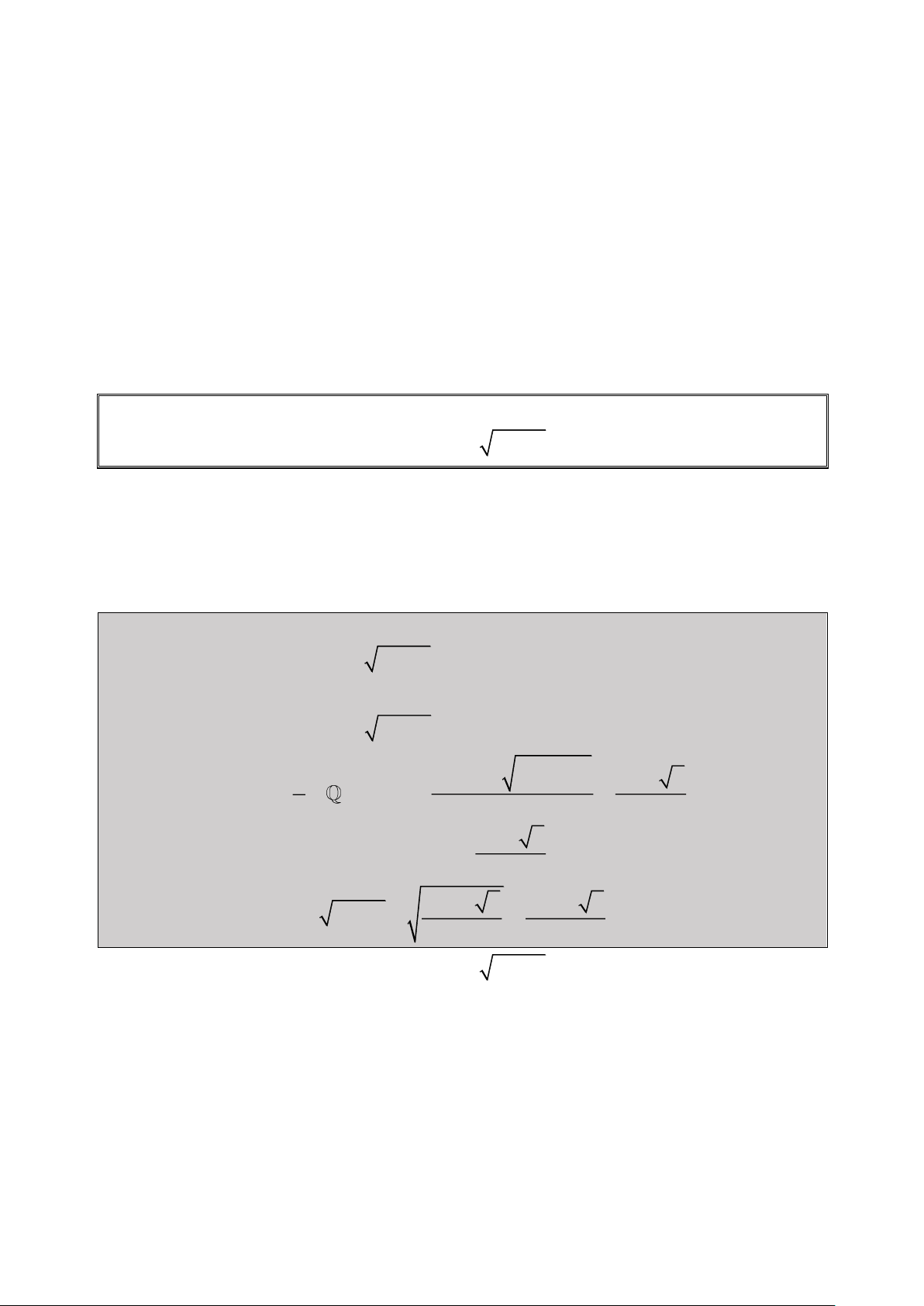
Bài 1: Giải Bất Phương Trình:
1 log 2  x  log  4 4  18  x  0 2 1  2 2
(đề thi thử Đại Học khối A lần 1 THPT Chuyên ĐH Vinh – Nghệ An năm 2013)
Điều kiện xác định: x  2;18   . ▶ Ý tưởng : Ta có:
1 log 2  x  log  4 4  18  x  0 2 1  2 2  log 2  x  l g o 4  18  x 2 2  4  4  2  x  4  18  x 4  20  t  4  t với 4 t  18  x và 4 t  0; 20  
Ta cần phân tích thành nhân tử biểu thức :   t2 4 4  20  t
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được các nghiệm như sau : A   0  4 . 66823165  B  2
 Chắc chắn biểu thức sẽ có nhân tử t  2
 Sử dụng Thủ Thuật Rút Gọn Biểu Thức ta được : 4  t2 4  20  t 3 2  t  2t  5t  2 t  2 Kết luận : 4  t2 4  20  t   3 2
t  2t  5t  2t  2
▶ Phân tích hướng giải: Với điều kiện 4 0  t  20 nên 3 2 4 t  2t  5t  2  0 t   0; 20  . Vậy ta có lời giải như sau :
▶ Lời giải : Bình phương hai vế: Đặt 4 t  18  x với 4 t  0; 20  . Khi đó :
1 log 2  x  log  4 4  18  x  0 2 1  2 2  log 2  x  log 4  18  x 2 2  4  4  2  x  4  18  x 4  20  t  4  t   4  t2 4  20  t  0  t4  3 2
 t  2t  5t  2t  2 0  t4  2  t  4  2   x  2
Một số bài tập tương tự : 1.
4 5x 1  x 1 2. 2 4
2 2x x  6  x  6 3. 4
3 x 17 x 11  x  2 4. 4
5 6x  2  x  13
Bài 2: Giải Bất Phương Trình: 3 x   2
3x  4x  4 x 1  0
(đề thi thử Đại Học khối A + B lần 1 THPT Ba Đình – Hà Nội năm 2013)
Điều kiện xác định: x     1; . ▶ Ý tưởng :
Thông thường, ta có hai cách để đưa về đa thức bậc 6 :
Cách 1 : Bình phương hai vế.
 Cách này không khả quan lắm vì chúng ta chưa thể bình phương
ngay được do bài toán này là bất phương trình.
Cách 2 : Đặt ẩn phụ y  x 1 .
 Cách này khá là ổn vì chúng ta không cẩn để ý lắm đến dấu của bất phương trình Vậy ta được : 3 2
x  (3x  4x  4) x 1  0  y  3 1  3y  2 2 2 1  4 2 y   1  4y  0
Ta cần phân tích thành nhân tử biểu thức :
y  3  y  2 2 2   2 1 3 1 4 y   1  4y
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được các nghiệm như sau : A   2  4 . 14213562   B 1 6 . 18033988   C  0 4 . 14213562 A   B    2 Thành thử thấy 
nên nhân tử của bài toán này là : AB  1    2y  2y 1
 Sử dụng Thủ Thuật Rút Gọn Biểu Thức ta được : y 3   1  3  y  2 2 2 1  4 2 y   1  4 y   4 3 2  y  y  4y  y 1 2 y  2y 1
 Sử dụng Thủ Thuật Giải Phương Trình Bậc 4 ta được : 4 3 2
y  y  y  y    2 y  y   2 4 1 1 y  2y   1 Kết luận :
y  3  y  2 2 2   2 y     2 2 2 1 3 1 4 1
4 y  (y  y 1)(y  2y 1)
▶ Phân tích hướng giải:
Ta có lời giải như sau :
▶ Cách 1 : Đặt ẩn phụ hoàn toàn:
Đặt y  x 1 với y  0 . Khi đó bất phương trình trở thành : y  3 1  3y  2 2 2 1  4 2 y   1  4y  0 2 2 2
 (y  y 1)(y  2y 1)  0 y  1   2   1 5 1  5  y   2 2 1  5  0  y  2
▶ Cách 2 : Đặt ẩn phụ không hoàn toàn:
Đặt y  x 1 với y  0 . Khi đó bất phương trình trở thành : 3 x   2
3x  4x  4 x 1  0 3  x   2 2 3x  4y  y  0
 x  yx  2y2  0 x  2y  0  x   y
▶ Cách 3 : Phân tích thành nhân tử: Ta có : 3 x   2
3x  4x  4 x 1  0
 x  x 1x  2 x 12  0 x  2 x 1  0  x x1
Một số bài tập tương tự : 3
1.  x  3    2 3
x x 13 x  3  0 2. 3 2
x x x    2 2 7 9
x x  6 x 1 3. 2
2x 4x  3  4 x  2 16x  3  0 4. 3 x    2 x   2 2 14 2 13 x 1  0
THỦ THUẬT 5 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ HAI ẨN
Bài 1: Giải Hệ Phương Trình: 3 2 3 2
x  3x  9x  22  y  3y  9y   2 2 1  x  y  x  y   2
(đề thi Đại Học khối A + A1 năm 2012)
▶ Ý tưởng :
Đa phần các bài tập hệ phương trình mà có phương trình là đa thức bậc 3
ẩn x hoặc y , không chứa các hạng tử như 2 2
xy, x y, xy ,... thì phương trình
đó rất có thể phân tích thành nhân tử được.
Ta sẽ thử phân tích thành nhân tử phương trình sau : 3 2 x  x  x    3 2 3 9 22 y  3y  9y  0
Coi như đây là phương trình bậc 3 ẩn x , ta sẽ giải phương trình khi y  1000
▶ Thực hiện :  Gán y 1000
 Vào tính năng giải phương trình bậc 3 trong MODE EQN
 Lần lượt nhập hệ số của phương trình bậc 3 :  ; ;  3 2 1 3
9 ; 22  y  3y  9y  
 Coi như ta giải phương trình bậc 3 : 3 2
x  3x  9x 1002990978  0
 Máy tính trả về các nghiệm : x 1002 1  x  4  99 5 .  886 8 . 845I 2  x  4  99 5 .  886 8 . 845I 3
 Vì 1002  y  2 nên ta được  x y  2 là nhân tử của bài toán
 Thực hiện phép chia đa thức 2 ẩn bằng dùng lim : 3 2 x  x  x    3 2 3 9 22 y  3y  9y f x  x  y  2
 Nhận thấy f (x) sẽ là một tam thức bậc 2 nên f x sẽ có dạng 2 ax  bx  c với:  f x  a  lim 1 2 x x   f x 2  x  b  lim  999  y 1 x x  c  fx 2  x  y   2
1 x  1000989  y  y 11    Vậy ta được : 3 2
x  3x  9x  22   3 2 y  3y  9y x  y  2 2  x  y   2 1 x  y  y 11 2 2
 x  xy  y  x  y 11 Kết luận : 3 2
x  3x  9x  22   3 2 y  3y  9y  x  y  2 2 2
x  xy  y  x  y 1  1
❓ Làm thế nào để biết được phương trình 2 ẩn không phân tích được?
Cách làm trên là cách nhanh nhất để biết được khi nào phương trình 2 ẩn
không phân tích được. Ví dụ như đối với phương trình : 2 2 1 x  y  x  y   0 2
Tương tự, ta thử cho y  1000 và nhận được giá trị của x là : x  0 5 . 1000.4995I 1  x  0 5 . 1000 4 . 995I 2
Nghiệm này lẻ nên chắc chắn phương trình này không thể có nhân tử dạng
ax by c với ,a ,bc
Vậy điều kiện để phương trình không thể phân tích nhân tử dạng
ax by c với ,a ,bc là :
i) Phương trình có hệ số không quá lớn.
ii) Cho y  1000, giải phương trình ta thấy phương trình không có nghiệm hữu tỷ.
Bạn đọc có thể thử nghiệm với phương trình : a) 2 2
x  xy  y  x  y 11  0 b) 3 2 3 2
x  3x  9x  21  y  3y  9y
▶ Phân tích hướng giải:
Thực ra chỉ cần biết nhân tử  x y  2 , ta đã có thể có nhiều cách giải cho bài toán này rồi.
Nhưng việc giải quyết nốt nhân tử còn lại có vẻ hơi khó khăn : 2 2
x  xy  y  x  y 11  0
Thủ Thuật Sử Dụng CASIO Để Giải Hệ Phương Trình sẽ giúp bạn.
▶ Cách 1 : Phân tích thành nhân tử: Ta có : 3 2 3 2
x  3x  9x  22  y  3y  9y  x  y  2 2 2
x  xy  y  x  y 1  1  0 x  y  2  0   2 2
x  xy  y  x  y 11 0  x  y  2  0    
Do x  xy  y  x  y   2 2 2 2 2 1 1 81 2
11  3x  y  x  y    x  y    0   2   2  4
▶ Cách 2 : Đặt ẩn phụ + Hàm đặc trưng:
Ta đặt t y  2 (mục đích để x t ). Vậy ta luôn có : 3 2 3 2
x  3x  9x  22  y  3y  9y
 x  3x  9x  22  t  23  3t  22 3 2  9t  2 3 2 3 2
 x  3x  9x  22  t  3t  9t  22 2 2     Vì 2 2 1 1 1
x  y  x  y   x     y  1  nên ta được 2  2   2  x 1  ;3 1 1  1
  x  ,y  1  2 2 t    1  ;3
Xét hàm đặc trưng : f k  3 2
 k  3k  9k  22 với k( 1  ,3) . Khi đó ta có : f'k  3k   1 k   3  0 k   1  ;  3
Từ đó ta dễ dàng tìm được x t . Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự : 3 3 2
x 3x  2  8y 12y 1.  2 2 x  2y 1 3 2 3 2 8
 x  28x 12x  32  y  y  22y 2.  2 2 x  y  xy 1 
 x  42  y  2 1  2 3.  4 4 3 2
x 16y  32y  24y  2x 12y  3 3 2 3 2
x 3xy  2y 3xy  3y  7x 11y  6 4.  2 2
x  xy  y  2x  3y  2
Bài 2: Giải Hệ Phương Trình: 2  x  y 1  2 2x 1  3 3 2
y 8x  3y  4y  2x  2  0
(đề thi thử Đại Học lần 2 THPT Lê Văn Hưu – Thanh Hóa năm 2011) ▶ Ý tưởng :
Ta sẽ thử phân tích thành nhân tử phương trình sau : 3 x  x   3 2 8 2 y  3y  4y  2  0
Coi như đây là phương trình bậc 3 ẩn x , ta sẽ giải phương trình khi y  1000
▶ Thực hiện :  Gán y 1000
 Vào tính năng giải phương trình bậc 3 trong MODE EQN
 Lần lượt nhập hệ số của phương trình bậc 3 :  ; ;  3 2 8 0
2 ; y  3y  4y  2  
 Máy tính trả về các nghiệm : x  500 5 . 1  x  2  50 2 . 5  433 4 . 46I 2  x  2  50 2 . 5  433 4 . 46I 3   1 Vì 500.5  y
nên ta được 2x y  
1 là nhân tử của bài toán 2
 Thực hiện phép chia đa thức 2 ẩn bằng dùng lim : 3 x  x   3 2 8 2 y  3y  4y  2 f x  2x  y 1
 Nhận thấy f (x) sẽ là một tam thức bậc 2 nên f x sẽ có dạng 2 ax  bx  c với:  f x  a  lim  4 2 x x   f x 2  4x  b  lim  2002  2y  2 x x  c  fx 2  x  2y  2 2
x 1002002  y  2y  2    Vậy ta được : 3 8x  2x   3 2 y  3y  4y  2 2x  y 1 2  4x  2y  2 2 x  y  2y  2 2 2
 4x  y  2xy  2x  2y  2 Kết luận : 3 8x  2x   3 2 y  3y  4y  2  2x  y   1  2 2
4x  2xy  y  2x  2y  2
▶ Phân tích hướng giải:
Ta giải quyết nốt 2 2
4x  2xy  y  2x  2y  2  0 bằng cách : 2 1 3
4x  2xy  y  2x  2y  2  4x  y   1  y  2 2 2 1 1  0 4 4
Sau đó sử dụng Thủ Thuật Giải Phương Trình Vô Tỷ để giải quyết
phương trình vô tỷ còn lại.
Ta cũng có thể xét hàm đặc trưng với bài toán này.
▶ Cách 1 : Phân tích thành nhân tử: Ta có : 3 3 2
8x  2x  y  3y  4y  2  2x  y   1  2 2
4x  2xy  y  2x  2y  2  0 2x  y 1  0   2 2 4
 x  2xy  y  2x  2y  2  0  2x  y 1 0 1 2 3 2 Do 2 2
4x  2xy  y  2x  2y  2  4x  y   1  y   1 1  0 4 4 Khi đó phương trình 2
x  y 1  2 2x 1 trở thành : 2 x  2x  2 2x 1
 x 1 2x 1x 1 2x 1  0
▶ Cách 2 : Đặt ẩn phụ + Hàm đặc trưng: 1 Ta đặt  t x
(mục đích để y t ). Vậy ta luôn có : 2 3 3 2
y  8x  3y  4y  2x  2  0 3  t    t   3 1 2 1  y  8  3   y  4y  2  2  0    2   2  3 2 3 2
 y  3y  4y  t  3t  4t
Xét hàm đặc trưng : f k  3 2
 k  3k  4k với k . Khi đó ta có : f'k 2  3k  6k  4  0 k  
Từ đó ta dễ dàng tìm được x t . Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự : 2
 x  5y 19x 1 3 2x 1  0 1.  3 3 2 8
 x  y  6y 16x  20y  24  0 3 2 3 2 2
x 3xy  2y  3x 3y  3x 1 0 2.  2 2  x  y  xy 1   x  y  xy  3 3.  4 2 2 4 3 2 2 2 4
 x 17x y  4y  8x  2xy  4x  y  0 3 3 2 2
72x  9y 112x  55y  60x 113y  67  0  4.  2  8x  3x  5y   7x  3 2 x  2y
Bài 3: Giải Hệ Phương Trình: 3 3
7x  y  3xyx  y 2 12x  6x 1  3 
4x  y 1  3x  2y  4 
(đề thi thử Đại Học lần 1 THPT Cù Huy Cận – Hà Tĩnh năm 2013) ▶ Ý tưởng :
Ta sẽ thử phân tích thành nhân tử phương trình sau : 3 3 7x  y  3xyx  y 2 12x  6x 1 0 3  7x  3y 12 2 x   2 6  3y  3 x  y 1  0
▶ Thực hiện :  Gán y 1000
 Vào tính năng giải phương trình bậc 3 trong MODE EQN
 Lần lượt nhập hệ số của phương trình bậc 3 :  ; y   2 3 7 3
12 ; 6  3y  ; y 1    
 Máy tính trả về các nghiệm : x  999  1  x  286 0 . 71 247 3 . 12I 2  x  286 0 . 71 247 3 . 12I 3  Vì 9
 99  y 1 nên ta được x y  
1 là nhân tử của bài toán
 Thực hiện phép chia đa thức 2 ẩn bằng dùng lim : 3 2 2 3       f x 7x (3y 12)x (6 3y )x y 1 2   ax  bx  c x  y 1 Với :  f(x) a  lim  7  2 x x  2  f(x)  7x  b  lim  4005   4y  5 x x  2
c  f(x)  7x  4y  5 2 x 1001001  y  y 1    Vậy ta được : 3 2 2 3
7x  (3y 12)x  (6  3y )x  y 1 x  y 1 2  7x  4y  5 2 x  y  y 1 2 2
 7x  y  4xy  5x  y 1 Kết luận : 3 2 2 3
7x  (3y 12)x  (6  3y )x  y 1  x  y   1  2 2
7x  y  4xy  5x  y   1
▶ Phân tích hướng giải:
Ta giải quyết nốt 2 2
7x  y  4xy  5x  y  1  0 bằng cách : 2 2     2 2 1 1
7x  y  4xy  5x  y 1  2  x  y   3   x   0   2   2 
Ta cũng có thể xét hàm đặc trưng với bài toán này. Lưu ý là đề bài cho
3xy x y nên ta nghĩ tới việc lấy  x y3 
. Khi đó thì x y  2x 1.
▶ Cách 1 : Phân tích thành nhân tử: Ta có : 3 3 7x  y  3xy x  y 2 12x  6x 1  x  y   1  2 2
7x  y  4xy  5x  y   1  0 x  y 1  0   2 2 7
 x  y  4xy  5x  y 1  0
Nếu x y 1  0 thì phương trình 3 4x  y 1  3x  2y  4 trở thành : 3 3x  2  x  2  4 1 1 Do f x 3
 3x  2  x  2  4 đồng biến vì f 'x    x  2 3 2 x  2 3 2
Suy ra x  2 là nghiệm duy nhất của phương trình 3 3x  2  x  2  4
▶ Cách 2 : Nhóm hợp lý: 3 3 7x  y  3xy x  y 2 12x  6x 1  2x  3 1  x  y3  x  y 1
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự : 3 3 2
2x  y  6x 14x  y 10 3xyx  y 1.  3 
3x  y  y  2x  2 x  2  3 3
x  y  xyx  y  2 2  2y  3x  y  2 2.  4 3 
x  y 1  9 2x  y  7 17  0    x  y   2 2 x  y  2 4 12 12x 19x 13y 3.  x  y  y 1 1  4 4 3 2 2
 x  y  4x  5x  y  2x
4.  x2y 2 2x y130  Bài 4: Cho hàm số 3 2 2 2
y  x  (2m 1)x  (m  2m 1)x  m 1 1 ( )
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số 1 ( ) khi m  0 . b) Tìm m để đồ thị 1
( ) cắt trục hoành tại 3 điểm A,B,C phân biệt ( A là
điểm cố định) sao cho 2(k  k )  x x , trong đó k ,k là hệ số góc của tiếp 1 2 1 2 1 2 tuyến với 1
( ) tại B,C ; x ,x là hoành độ của điểm cực trị của 1 ( ). 1 2
(đề thi thử Đại Học lần 2 THPT Quỳnh Lưu 4 – Nghệ An năm 2013) ▶ Ý tưởng :
Đề bài cho rằng A cố định nên hoành độ A là hằng số. Vậy phương trình 3 2 2 2
x  (2m 1)x  (m  2m 1)x  m 1 0 tồn tại một nghiệm là hằng số.
Nghiệm vụ của chúng ta là phân tích thành nhân tử phương trình : 3 2 2 2
x  (2m 1)x  (m  2m 1)x  m 1 0
▶ Thực hiện :  Gán m 1000
 Vào tính năng giải phương trình bậc 3 trong MODE EQN
 Lần lượt nhập hệ số của phương trình bậc 3 :  ; m   2 2 1 2
1 ; m  2m 1 ; m  1    
 Máy tính trả về các nghiệm : x 1 1  x  999  2 x  1001   3   x   1  9  99  m 1   Vì 
nên nhân tử của bài toán là 
x m   1  1  001  m 1   x m  1  Vì hệ số của 3 x là 1 nên ta có : 3 2 2 2
x  (2m 1)x  (m  2m 1)x  m 1  x   1 x  m   1 x  m   1 Kết luận : 3 2 2 2
x  (2m 1)x  (m  2m 1)x  m 1  x   1 x  m   1 x  m   1
▶ Phân tích hướng giải:
Khi biết 3 nghiệm của phương trình bậc 3, ta tìm được tọa độ của 3 điểm.
Căn cứ theo giả thiết, ta sẽ có lời giải của bài toán.
Sử dụng Thủ Thuật Rút Gọn Biểu Thức là một lợi thế.
▶ Lời giải : Phân tích thành nhân tử: Ta có : 3 2 2 2
x  (2m 1)x  (m  2m 1)x  m 1  0  x   1 x  m   1 x  m   1  0
Vậy y cắt Ox tại 3 điểm phân biệt khi và chỉ khi 1 m, 1   m 1 , là 3 số
phân biệt hay m  0 và m  2 . Suy ra A 1 ( ,0);B 1 (  m,0);C( 1
  m,0) . Theo giả thiết thì: 2 2  k  3 1 (  m)  2(2m 1) 1
(  m)  m  2m 1  2  m 1  2 2 k  3( 1   m)  2(2m 1)( 1
  m)  m  2m 1 2m  4 2 m  2m 1 Vậy 2k  k  2  x x  8 
 m 1 26 (thỏa mãn) 1 2 1 2 3
Một số bài tập tương tự : 1. 3
x  m   2 2 3 2 3
7 x  3xm m m  4m  4  0 2. 3 2 2
4x xm  2m 12x  8  0 3. 3 2 x x   2 m   3 2 4 4 28
1 x  24m  4m  6m 1  0 4. 3
x  m   2 3
5 x  2m  6m  4  0
Bài 5: Giải hệ phương trình : 4 2 2
x  4x  y  4y  2  2 2
 x y  2x  6y  23
(đề thi thử Đại Học lần 2 THPT Đông Anh – Hà Nội năm 2013) ▶ Ý tưởng :
Thử phân tích thành nhân tử từng phương trình của hệ phương trình, ta
thấy không phân tích được. Đây là một dạng toán khác với các bài tập trên,
khi mà ta phải lấy PT 
1  kPT2 để phân tích thành nhân tử.
▶ Thực hiện :
 Sử dụng Thủ Thuật Giải Hệ Phương Trình ta tìm được k  2
 Ta cần phân tích thành nhân tử biểu thức : 4 2 2
x  x  y  y    2 2 4 4 2
2 x y  2x  6y  23  0  Đặt 2
x t và gán y  1000, ta làm như các ví dụ trên. Kết luận : 4 2 2
x  4x  y  4y  2  2 2 2 x y  2x  6y  23   2 x  y 12 2 x  y  4
▶ Phân tích hướng giải:
Ta có thể trình bày trực tiếp lời giải bằng việc lấy PT   1  2PT 2 rồi phân tích thành nhân tử.
▶ Lời giải : Phân tích thành nhân tử: Ta có : 4 2 2
x  4x  y  4y  2  2 2 2
x y  2x  6y  23  0   2 x  y 12 2 x  y  4  0
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự : 2 2
 x  2xy  y  2x 1 0 1.  2 2
x  4xy  6y  2x 1 0 2 2
2x  2y  x  y 1 0 2.  2 3
 x  xy  x  5y 1  0 2 2
x  xy  y  x  y 1 0 3.  2
x  5xy 12x  7y  5  0 2 2
 x  4xy  4y  6x  3y  0 4.  2 2
x  xy  4y  4x  4y  6  0
THỦ THUẬT 6 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
GIẢI PHƯƠNG TRÌNH VÔ TỶ
Bài 1: Giải Hệ Phương Trình: 3 3 2 
x  y  6y 12x 16  0   2 2 2
x 4  x  3 4y  y  3y 10  x  0 
(đề thi thử Đại Học – Bà Rịa Vũng Tàu năm 2014) ▶ Ý tưởng :
Tuy là một hệ phương trình trong Thủ Thuật Giải Phương Trình Vô Tỷ,
nhưng nó lại mang ý nghĩa lớn về việc quan trọng của phương pháp giải
phương trình vô tỷ. Chắc hẳn bạn đọc thắc mắc về việc một phương trình
vô tỷ lại được phân tích “ảo diệu” như một số ví dụ trên. Thủ Thuật Giải
Phương Trình Vô Tỷ sẽ giúp bạn hiểu được phần nào cách giải phương
trình vô tỷ bằng máy tính CASIO.
Đối với bài toán trên, sử dụng Thủ Thuật Phân Tích Đa Thức Thành
Nhân Tử Hai Ẩn ta được : 3 3 2
x  y  6y 12x 16  0
 x 12x  y  23 3 12y  2  x  y  2  y  x  2 (vì 2
  x  2 và 0  y  4)
Vấn đề của chúng ta là ở phương trình sau khi thế y x  2 : x   2 2 3 4  x  x  3x  4
❓ Làm thế nào để phân tích phương trình này?
Giả sử phương trình có nhân tử  2
4  x  ax  b với a,b .
Nhân tử này chứa nghiệm của bài toán. Ta chắc chắn tìm được , a b nếu như ta biết được : m   n Một nghiệm vô tỷ dạng p
 Hoặc hai nghiệm hữu tỷ
Các ví dụ sau sẽ làm rõ vấn đề của bài toán.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương trình x   2 2 3
4  x  x  3x  4 có nghiệm x   2
 Nghiệm x   2 sẽ thỏa mãn nhân tử  2
4  x  ax  b với mọi a,b . Tức là 2
4  x  ax  b  0 khi x   2
 Khi đó ta luôn có 2  2a  b  0  a,b  1;0 (vì a,b )
Kết luận : Nhân tử của bài toán này là  2 4  x  x
❓ Làm thế nào để tìm được nhân tử còn lại?
Có khá nhiều cách để chia biểu thức chứa căn bằng CASIO.
Nếu bạn đọc chưa có kinh nghiệm, hãy cứ bình tĩnh nhóm hợp lý theo cách
cách mà chuyên đề này hoặc nhiều tài liệu khác gọi là “nhân liên hợp không hoàn toàn”.
Nếu bạn đọc đã quen với việc giải phương trình vô tỷ, bạn đọc hãy đợi
cuốn sau của tác giả để nâng cao khả năng sử dụng máy tính CASIO trong giải toán.
▶ Phân tích hướng giải:
Nhân liên hợp không hoàn toàn tức là không nhân liên hợp trực tiếp mà sẽ giữ lại căn thức :
▶ Lời giải : Nhân liên hợp không hoàn toàn: Ta có 2
  x  2 và 0  y  4 nên ta được : 3 3 2
x  y  6y 12x 16  0
 x 12x  y  23 3 12y  2 Xét 3
f (t)  t 12t với 2
  t  2 ta được 2
f '(t)  3t 12  0t  2  ;2 .
Vậy f (t) nghịch biến và liên tục trên 2; 2 . Do đó ta được x y  2. Suy ra : x 3 2 2 4  x  x  3x  4  x  3 2 4  x  x 2  2x  4  x  3 2 4  x  x   2 4  x  x 2 4  x  x   2 4  x  x 2 4  x  3  0
Một số bài tập tương tự : 3 2 2 2
x  x y 3x 3xy  y  2x  y  0 1.  y  2 1  x 1  3 3 2 
x  y  9y  3x  24y 18  0 2. y 5 
 x 1  x  2 y  4  2y  6  0 4 4 3 3 1
 6x  y  32x  4y 16x 8y  0  3.  2  x  y 1  x  y  5   x  5
1  y  25  x  y  25 1 4.  2 x  6x  3y  4   2x  4 3y 2 3x  3  2y  x x 1
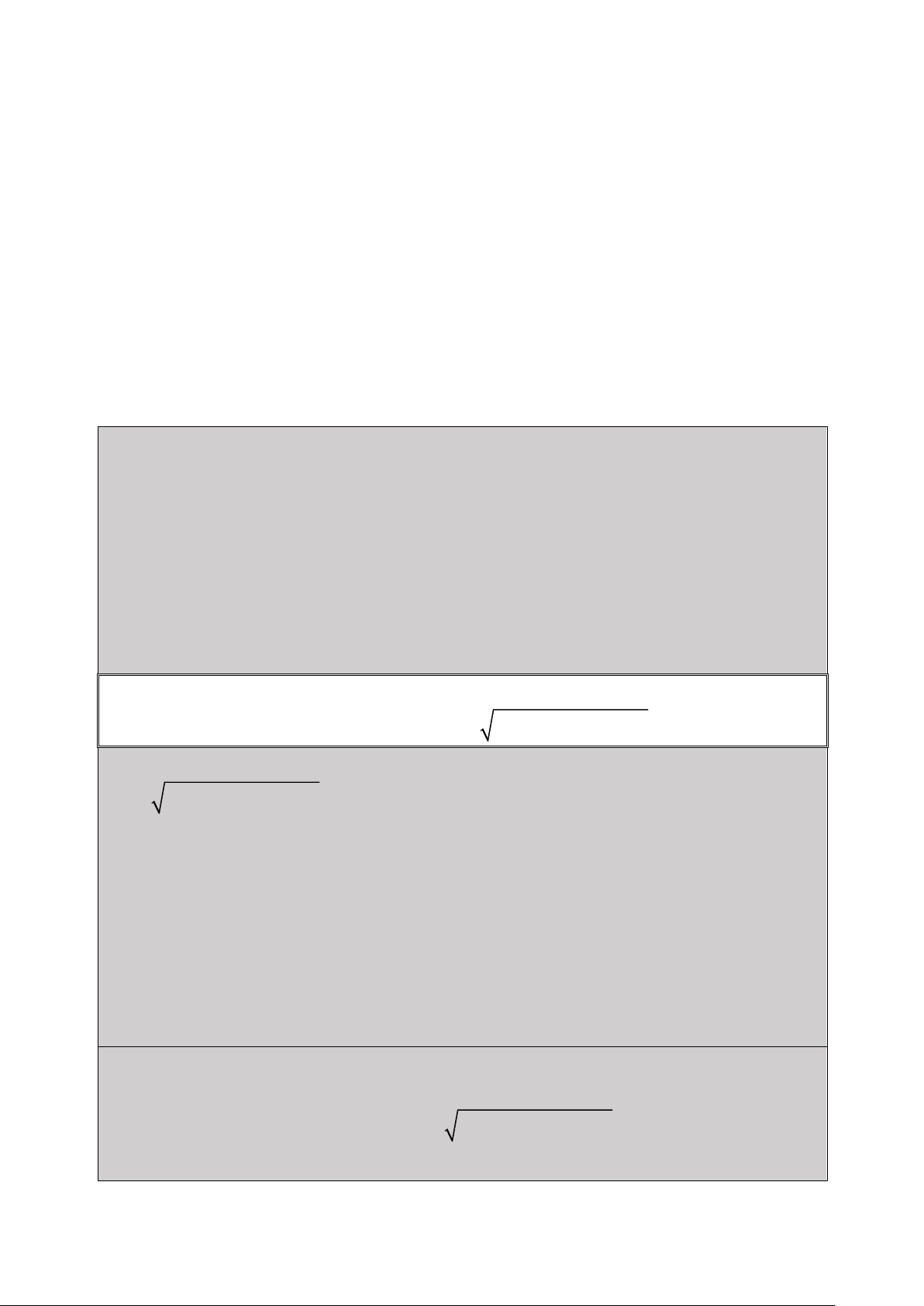
Bài 2: Giải Phương Trình: 2
x  2x  3  2x  4 2x 1
▶ Ý tưởng :
Tất cả các phương trình dạng một căn thức ax  b đều có một lời giải cực
nhanh, cực chính xác và không kém phần thú vị. Đó là phân tích thành nhân tử.
Cách nhanh nhất để phân tích thành nhân tử đó là đặt ẩn phụ t  2x 1
như cách làm dưới đây :
▶ Thực hiện : 2   t 1
Đặt t  2x 1 suy ra x  2
 Thế vào phương trình ta được : 2 2 2  t 1  t 1 2    2   3  (t 1 4)t 2 2    
 Sử dụng Thủ Thuật Phân Tích Đa Thức Thành Nhân Tử ta được : 2 2 2  t 1  t 1 1    2
  3  (t 1 4)t  t  2 1 t  32 2 2 2 4    
 Thế ngược lại t  2x 1 ta được : 1 t   t   1 1 3   2x 1  2 1  2x 1  32 2 2 4 4
 Vậy tóm lại ta được : 2 2 2  t 1  t 1 1    2
  3  (t 1 4)t   2x 1  2 1  2x 1  32 2 2 2 4     2 2 1 Kết luận : 2
x  2x  3  2x  4 2x 1   2x 1   1  2x 1  3 4
▶ Phân tích hướng giải:
Có rất rất nhiều cách giải cho dạng toán này. Bạn đọc có thể suy nghĩ thêm
các cách làm cho phong phú. Sau đó có thể đối chiếu với các bài tập dưới đây.
▶ Lời giải : Phân tích thành nhân tử: Ta có : 2
x  2x  3  2x  4 2x 1 1   2x 1  2 1  2x 1  32  0 4
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự : 1. 2
x  7 x 16  3x 13 x  2  0 2. 2 x x    2 3 5 2
x  3x  2 x  2 3. 2
2x  2x  7  3x  4 x  2 4. 2
9x 111x  60  30 x  2 3x 1
Bài 3: Giải Phương Trình: 2
x  3x 1 2 x 1  0 ▶ Ý tưởng :
Tương tự Bài 2, ta đặt ẩn phụ để phân tích thành nhân tử. Tuy nhiên, để
mở rộng phạm vi của phương pháp, ta có thể làm theo hướng của Bài 1.
▶ Thực hiện :
 Đặt t  x 1 suy ra 2 x  t 1
 Thế vào phương trình ta được : t  2 2 1   2 3 t   1  1  2t  0
 Sử dụng Thủ Thuật Phân Tích Đa Thức Thành Nhân Tử ta được : t  2 2
  2t     t   2t  t   2 1 3 1 1 2 1 t  t   1
 Thế ngược lại t  x 1 ta được :  2t t   2 1 t  t   1
 x 1 x 1   1 x 1 x 1   1
 x  x 1x  x 1  2 Kết luận : 2
x  3x 1 2 x 1  x  x 1x  2  x 1
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương 5  5 trình 2
x  3x 1 2 x 1  0 có nghiệm là x  2
 Gọi nhân tử của bài toán là  x 1  ax b thì khi đó :
x 1  ax b  0 3  5 5  5   a b  0 2 2 1 5 5  5   a b  0 2 2
 1 5a  2b  a   1 5  0 a 1  0 a  1      1
  5a  2b  0 b  2
Kết luận : Nhân tử của bài toán này là  x 1  x  2
▶ Phân tích hướng giải:
Có rất nhiều cách giải, bạn đọc theo dõi ở dưới đây :
▶ Cách 1 : Bình phương hai vế: Ta có : 2
x  3x 1 2 x 1  0 2  x  3x 1  2 x 1  x  3x  2 2 1  4x   1 4 3 2
 x  6x 11x 10x  5  0   2 x  x   1  2 x  5x  5  0
▶ Cách 2 : Đặt ẩn phụ hoàn toàn:
Ta đặt t  x 1 với t  0 ta được 2
x  t 1. Vậy phương trình trở thành : t  2 2 1   2 3 t   1  1  2t  0 4 2  t  t  2t 1  0   2t  t   1  2 t  t   1  0
▶ Cách 3 : Phân tích thành nhân tử: Ta có : 2
x  3x 1 2 x 1  0   x x 1 x  2  x 1  0
▶ Cách 4 : Nhân liên hợp hoàn toàn:
Nếu x  2  x 1  0 thì không thỏa mãn phương trình.
Nếu x  2  x 1  0 thì : 2
x  3x 1 2 x 1  0 2
x  5x  5  2x  2 x 1  0    2  2
x  5x  5 1  0   
x  2  x 1    2
x  5x  5x x 1  0
▶ Cách 5 : Đặt ẩn phụ không hoàn toàn:
Ta đặt t  x 1 với t  0 ta được 2
x  t 1. Vậy phương trình trở thành : 2 2 x  t  2x  2t  0
 x  tx  2  t  0
▶ Cách 6 : Nhân liên hợp không hoàn toàn: Ta có : 2
x  3x 1 2 x 1  0 2
x  5x  5  2x  2 x 1  0
 x  2 x 1x  2 x 1 2x  2 x 1  0
 x x 1x  2 x 1  0
▶ Cách 7 : Đặt ẩn phụ đưa về hệ phương trình: Ta đặt y
x 1  2 . Khi đó ta được hệ phương trình :   y 22 2  x 1
y  4y x  5  0    2
x  3x 1 2   y  2 2  0
x 3x  2y  5  0 Vậy ta được :
 2y y x  2 4 5
x  3x  2 y  5  0   y x x y  2  0
Một số bài tập tương tự : 1. 2
2x x 11   x  7 x 1 2. 2
2x x  9   x   11 x 1 3. 2
2x  5x  6  
5 x  2 2x 1  0 4. 2
6x 15x  22  5x  22 x  2  0
Bài 4: Giải Phương Trình: 2
2x  x  2  3x 2x 1  0 ▶ Ý tưởng :
Tạm bỏ qua ý tưởng đặt ẩn phụ, ta thử giải bài toán này bằng cách tìm nhân tử.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương trình 2
2x  x  2  3x 2x 1  0 có nghiệm là x  2  2
 Ta tìm nhân tử  2x 1  ax b nhanh chóng hơn bằng cách : Khi x  2  2 thì 2x 1 1 2  x 1
Kết luận : Nhân tử của bài toán này là  2x 1  x   1
▶ Phân tích hướng giải:
Có rất nhiều cách giải, bạn đọc theo dõi ở dưới đây :
▶ Cách 1 : Phân tích thành nhân tử: Ta có : 2
2x  x  2  3x 2x 1  0   2x 1  2x   1  2x 1  x   1  0
▶ Cách 2 : Nhân liên hợp hoàn toàn:
Nếu 2x 1  x 1  0 thì không thỏa mãn phương trình.
Nếu 2x 1  x 1  0 thì : 2
2x x  2  3x 2x 1  0 2
 x  4x  2  3x 2x 1 x   1  0    3x  2
x  4x  2 1  0   
2x 1  x 1    2
x  4x  2 2x 1  2x   1  0
▶ Cách 3 : Đặt ẩn phụ không hoàn toàn: Ta có : 2
2x x  2  3x 2x 1  0 2
 x  4x  2  3x 2x 1 x   1  0
  2x 1 x  
1  2x 1  x  
1  3x  2x 1  x   1  0
  2x 1 x  
1  2x 1  2x   1  0
▶ Cách 4 : Đặt ẩn phụ đưa về hệ phương trình:
Ta đặt y  2x 1 1. Khi đó ta được hệ phương trình : 2
y  2y  2x  2  0  2
2x 3xy  4x  2  0 Vậy ta được :
 2y y x  2 2 2 2
2x  3xy  4x  2  0   x y2x y  2  0
Một số bài tập tương tự : 1. 2
6x 11x   x  6 3x  2  0 2. 2
9x 13x  2  9x  6 x 1  0 3. 2
3x  3x  20  8x 10 x  4  0 4. 2
9x 15x 18  6 3x  4  0
Bài 5: Giải Phương Trình: 2
x  3x  4   x   1 x 1  0 ▶ Ý tưởng :
Dạng toán một căn thức ax b hay ở chỗ :
Nếu phương trình có nghiệm x x
thì chắc chắn phương trình sẽ có 0
nhân tử  ax b ax b . 0 
Tuy nhiên, để tổng quát với những dạng toán khác, ta luôn tìm được nhân
tử nếu biết trước 2 nghiệm hữu tỷ của bài toán.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương trình 2
x  3x  4   x   1
x 1  0 có nghiệm là x  1  và x  3
 Ta tìm nhân tử  x 1  ax b chứa cả hai nghiệm x  1  và x  3.
 Vậy là x 1  ax b  0 khi x  1
 hoặc x  3. Suy ra :
0  a b  0  a b  1 1   ;   ;  
2  3a b  0  2 2     1 1
Vậy nhân tử của chúng ta là x 1  x     2 2 
Kết luận : Nhân tử của bài toán này là 2 x 1  x   1
▶ Phân tích hướng giải:
Tương tự các ví dụ trước, ta có các hướng giải chính như sau :
▶ Cách 1 : Phân tích thành nhân tử không hoàn toàn: Ta có : 2
x  3x  4   x   1 x 1  0
 2 x 1 x  
1 3 x 1  x  2  0
▶ Cách 2 : Nhân liên hợp hoàn toàn:
Nếu 2 x 1  x 1  0 thì không thỏa mãn phương trình.
Nếu 2 x 1  x 1  0 thì : 2
x  3x  4   x   1 x 1  0 3 9 1 2
x  3x   x  
1 2 x 1  x   1  0 2 2 2  
x x  3 x 1 1 3   x x       0 2 2 2 1 1        x  
1  x  33 x 1  x  2  0
▶ Cách 3 : Đặt ẩn phụ không hoàn toàn: Ta có : 2
x  3x  4   x   1 x 1  0 3 9 1 2
x  3x   x  
1 2 x 1  x   1  0 2 2 2 3
   x   x   x   x   1 2 1 1 2 1 1  x  
1 2 x 1  x   1  0 2 2
 2 x 1 x  
1 3 x 1  x  2  0
▶ Cách 4 : Đặt ẩn phụ đưa về hệ phương trình:
Ta đặt y  2 x 1 1. Khi đó ta được hệ phương trình :   y  2 1  4x   2 1
y  2y  4x 3  0     1 
x  3x  4   x   1  y   1 5 1 9 2 2 1  0 x xy x y 0        2  2 2 2 2 Vậy ta được :  1 5 1 9  2 x xy x y      2 2
3 y  2 y  4x  3  0  2 2 2 2 
 x y2x  3y  7  0
▶ Cách 5 : Phân tích thành nhân tử hoàn toàn:
Theo bổ đề ở đầu bài thì chắc chắn phương trình này sẽ có 2 nhân tử là  x1 1
 1 và  x 1  31
Vậy nhân tử của bài toán này là x 1  x 1  2 . Ta được : 2
x  3x  4   x   1 x 1  0
x 1 x 1 2x  23 x 1  0
Một số bài tập tương tự : 1. 2
x  2x  3  2x   1 x 1 2. 2
2x 15x  5  7x  5 2x 1 3. 2
3x  22x  25  8x 17 x  5 4. 2
12x  46x  41  19x  27 2x  3
Bài 6: Giải Phương Trình: 2
2x  5x  3   3 x   1 3x 1  0 ▶ Ý tưởng :
Ta vẫn đi tìm nghiệm trước khi giải mỗi bài toán.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương 7 trình 2
2x  5x  3   3 x   1
3x 1  0 có nghiệm duy nhất là x  4
 Ta có thể sử dụng bổ đề ở Bài 5 để tìm nhân tử.
 Tuy nhiên, để tổng quát với những dạng toán khác, ta có thể tìm
nhân tử  3x 1  ax b bằng phương pháp Đổi Dấu Trước Căn
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương trình 2
2x  5x  3   3 x   1
3x 1  0 có các nghiệm là :
x  0;5  2 7;5  2 7   1
Khi x  5  2 7 thì 3 1  16  6 7  3  7  x x . Vậy nhân 2 tử của phương trình 2
2x  5x  3   3 x   1 3x 1  0 là :
2 3x1x 1
 Vậy không đổi dấu trước căn nữa, ta sẽ được nhân tử của phương trình 2
2x  5x  3   3 x   1 3x 1  0 là :  2 
3x 1  x   1
Kết luận : Nhân tử của bài toán này là 2 3x 1  x   1
▶ Phân tích hướng giải:
Đối với những bài toán có nghiệm duy nhất, chúng ta thường nghĩ đến 3 hướng chính như sau :  Nhân liên hợp  Đạo hàm
 Bất đẳng thức, đánh giá
Chúng ta thử xem các hướng đó giúp ích được gì cho chúng ta không :
▶ Cách 1 : Nhân liên hợp hoàn toàn: Ta có : 2
2x  5x  3   3 x   1 3x 1  0 5 21  5  2  2x x    3 x   1 3x 1   0   2 2  2  1  x x  
x  34x  7 9   1 4 7   0 2 2 2 3x 1  5 1  x   9   4 7  x  3    0 2   2 3x 1  5  
▶ Cách 2 : Đạo hàm: (Tham Khảo)  1 
Xét hàm số : f x 2
 2x  5x  3   3 x   1
3x 1 với x   ,    .  3  x  9 9x  7
Khi đó : f x 3 9 1 '  4x  5 
và f '  x  4  . 2 3x 1 4 3x  3 1
Suy ra f x 1 '  0 x
   . Vậy f ' x  0 có tối đa một nghiệm. 3
Dễ thấy f '0 f ' 
1  0 nên tồn tại x  0,1 để f ' x  0 . 0  0   7
Nếu x x thì f x  0 có tối đa một nghiệm. Chỉ ra nghiệm này là x  0 4 1 1
Nếu   x x thì   x  1 . Suy ra : 0 3 3 f x   1 
Max f    f    1  10 , 1   f     0     3    3  9  1 
Vậy f x  0 không có nghiệm trong khoảng  ,  x0   3  7 Kết luận : x  . 4
▶ Cách 3 : Bất đẳng thức, đánh giá: 7 Nếu x  thì : 4  7  21 2
2x  5x  3   3 x   2 1
3x 1  2x  5x  3  3 1 1    4  4 21 1 2
 2x  5x
 4x  34x  7  0 8 8 7 Nếu 1  x  thì : 4 21 2
2x  5x  3   3 x   2 1
3x 1  2x  5x  3   3 x   1 1 4 5 21 1 2  2x x
 x  34x  7  0 2 2 2 1
Nếu   x  1 thì : 3 2
x x    x   2 2 5 3 3 1
3x 1  2x  5x  3  2x   1  x  3  0
▶ Cách 4 : Phân tích thành nhân tử không hoàn toàn: Ta có : 2
2x  5x  3   3 x   1 3x 1  0
 2 3x 1 x  
1  3x 1  2x   1  0
▶ Cách 5 : Phân tích thành nhân tử không hoàn toàn: Ta có : 2
2x  5x  3   3 x   1 3x 1  0 1
 7x 3x 3 3x 12 3x 15  0 3
▶ Cách 6 : Phân tích thành nhân tử hoàn toàn: Ta có : 2
2x  5x  3   3 x   1 3x 1  0 1
 2 3x 15 3x 1 
1 2 3x 1  x   1  0 3
Một số bài tập tương tự : 1. 2
x  3x  2   2 x   1 x 1  0 2. 2
2x  5x  4  5x  4 2x 1  0 3. 3
x x  2  x x   1 x  2  0 4. 2
x x    2 2 3 x x   1 x  3
Bài 7: Giải Phương Trình: 2
x 11x  7  32x   1 2x 1  0 ▶ Ý tưởng :
Ta tìm nghiệm của phương trình để tìm nhân tử.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương trình 2
x 11x  7  32x   1
2x 1  0 có tập nghiệm là 2310 5,2 2
 Với mỗi nghiệm, ta được nhân tử tương ứng là  2x 1  x   1 và  x 2  2x 1      5 5 
 Bậc của phương trình là bậc 2 nên ta sẽ có : 2
x 11x  7  32x   1 2x 1 k
x   x   x 2   2 1 1 2x 1      5 5 
 Thử một vài giá trị ta thấy k  5 Kết luận :  x 2  2
x 11x  7  32x   1
2x 1  5 2x 1  x   1 2x 1      5 5 
▶ Phân tích hướng giải:
Ta cũng có rất nhiều cách làm cho bài toán này. Tuy nhiên cách làm ngắn gọn như sau :
▶ Lời giải : Phân tích thành nhân tử : Ta có : 2
x 11x  7  32x   1 2x 1  0
  2x 1 x  
1 5 2x 1  x  2  0
Một số bài tập tương tự : 1. 2
2x 10x 10  
3 x  2 x 1  0 2. 2
2x  8x  4   3 x   1 2x 1  0 3. 2
2x 19x 18  x 2x  2  0 4. 2
x 12x  5   x   1 5x  2  0
Bài 8: Giải Phương Trình: 2
6x 10x 10  13x   1 x  2  0 ▶ Ý tưởng :
Ta tìm nghiệm của phương trình để tìm nhân tử.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương trình 2
6x 10x 10  13x   1
x  2  0 có tập nghiệm là  5 2 22  2;   9     5 2 22 Với nghiệm x
, ta được nhân tử tương ứng là 9
2 x2 3x 1
Kết luận : Nhân tử của bài toán này là 2 x  2  3x   1
▶ Phân tích hướng giải:
Ta cũng có thể tìm nhân tử  x  2  2 vì nó chứa nghiệm x  2 .
▶ Cách 1 : Phân tích thành nhân tử không hoàn toàn: Ta có : 2
6x 10x 10  13x   1 x  2  0
 3 x  2  2x  22 x  2 3x   1  0
▶ Cách 2 : Phân tích thành nhân tử hoàn toàn: Ta có : 2
6x 10x 10  13x   1 x  2  0
  x  2  2 6x  4 x  2  x 9  0
  x  2  22 x  2  
1 2 x  2  3x   1  0
Một số bài tập tương tự : 1. 2
x  8x 14  x  2  0 2. 2
6x  3x 12  5x 1  1 x  2 3. 2
15x  55x  28  37x  7 5x  2 4. 2
3x 18x  28  8x  28 x  3
Bài 9: Giải Phương Trình: 2
10x 13x  7  19x  5 x 1  0 ▶ Ý tưởng :
Ta tìm nghiệm của phương trình để tìm nhân tử.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương trình 2
10x 13x  7  19x  5 x 1  0 có tập nghiệm là 5 3 17 3   2 21  ;   8 25  
 Nhân tử tương ứng là 2 x 1 5x  
1 và 3 x 1  2x   1
Kết luận : Nhân tử của bài toán này là
2 x15x 1 và 3 x12x 1
▶ Phân tích hướng giải:
Lời giải sẽ vô cùng ngắn gọn :
▶ Lời giải : Phân tích thành nhân tử: Ta có : 2
10x 13x  7  19x  5 x 1  0
 2 x 15x  
1 3 x 1  2x   1  0
Một số bài tập tương tự : 1. 2
2x 19x  40  2 x  3 x  3 2. 2
2x 19x 16  
2 x  3 x  3 3. 2
x 12x  5   x   1 5x  3 4. 2
x 15x  26  2 x  4 x  4
Bài 10: Giải Phương Trình: 2 x x    2 9 12 2
3x  2x  9 x 1  0 ▶ Ý tưởng :
Đây là một ví dụ điển hình cho việc không tốt của phương pháp Bình
Phương Hai Vế. Mọi bài toán dạng này đều có thể phân tích thành nhân tử
nên bạn đọc không cần lo lắng nếu gặp bài toán tương tự.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương trình 2 x x    2 9 12 2
3x  2x  9 x 1  0 có tập nghiệm là
233 21 23 3 21  ;   6 6  
 Nhân tử tương ứng là 9 x 1 3x  2
Kết luận : Nhân tử của bài toán này là 9 x 1  3x  2
▶ Phân tích hướng giải:
Chúng ta thử giải bài toán này dưới dạng nhiều hướng đi khác nhau. Thử
xem cách nào phù hợp với chúng ta nhất.
▶Cách 1 : Bình phương hai vế: Ta có : 2
9x 12x  2   2
3x  2x  9 x 1  0 2
 9x 12x  2   2
3x  2x  9 x 1
 9x 12x  22  3x  2x 92 2 2 x   1 5 4 3 2
 9x  78x 154x  94x  69x 85  0   3 2 x x   1  2
9x  69x  85  0 2
9x  69x  85  0   3 2
x x 1  0
Xét hàm số f x 3 2
x x 1 với x 1. Ta được : f x 2 '
 3x  2x x 3x  2  0x 1
Vậy ta chứng minh được phương trình f x  0 có tối đa một nghiệm. 3 3
2  116 12 93  116 12 93
Chỉ ra nghiệm này là x  và thấy nó 6
không thỏa mãn phương trình ban đầu. 23  3 21 Kết luận : x  . 6
▶Cách 2 : Nhân liên hợp không hoàn toàn: Ta có : 2
9x 12x  2   2
3x  2x  9 x 1  0 2 23x 85x 1 3  x     2
3x  2x  99 x 1  3x  2  0 3 9 9 1
  x9 x 13x  29 x 13x  2 9 1   2
3x  2x  99 x 1  3x  2  0 9
 9 x 13x  2x x 1  1  0
 9 x 1  3x  2  0
▶Cách 3 : Nhân liên hợp hoàn toàn: Ta có : 2
9x 12x  2   2
3x  2x  9 x 1  0 2 23x 85x 1 3  x     2
3x  2x  99 x 1  3x  2  0 3 9 9 x x x x x  
9x  69x  85  2 3 2 9 2 9 69 85 1 1 2    0 9 9
9 x 1  3x  2 1    x x  
9x  69x  85 2 3 2 9 2  x    0 9 
9 x 1  3x  2   2
9x  69x  85x x 1   1   0
9 x 1  3x  2 2
 9x  69x  85  0
▶Cách 4 : Phân tích thành nhân tử: Ta có : 2 x x    2 9 12 2
3x  2x  9 x 1  0
 9 x 13x  2x x 1  1  0
 9 x 1  3x  2  0 3 3     ❓ 2 116 12 93 116 12 93
Tại sao lại sinh ra nghiệm x  ? 6
Bản chất của phương pháp bình phương hai vế là việc giải cả 2 phương trình :  2 x x    2 9 12 2
3x  2x  9 x 1  0  2 x x    2 9 12 2
3x  2x  9 x 1  0 3 3
2  116 12 93  116 12 93 Và nghiệm x
là của phương trình dưới 6
Một số bài tập tương tự : 1. 2
x x    2 4 5
x  4x  2 x  2 2. 2
x x    2 3 x  4x   1 2x 1 3. 3 2
x  5x  5x  3  2x   1 x 1 4. 3 2
2x 11x  23x  31  
13 x  2 x  3
Bài 11: Giải Phương Trình: 3 2 x x x    2 7 16 6
x x  8 x 1  0 ▶ Ý tưởng :
Tương tự tất cả các bài toán khác, chúng ta thử tìm nghiệm của bài toán để định hướng giải.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được phương trình 3 2 x x x    2 7 16 6
x x  8 x 1  0 có nghiệm duy nhất là x  5.
 Thử nhân liên hợp, ta thấy : 3 2
x  7 x 16x  6   2
x x  8 x 1  0    x x   x  5 2 8 2
x  4x  2    0  x 1  2  2 x x   8 Tuy nhiên, 2
x  4x  2 
 0 lại có nghiệm x  5. x 1  2
 Đặt f x 3 2
x x x    2 7 16 6
x x  8 x 1
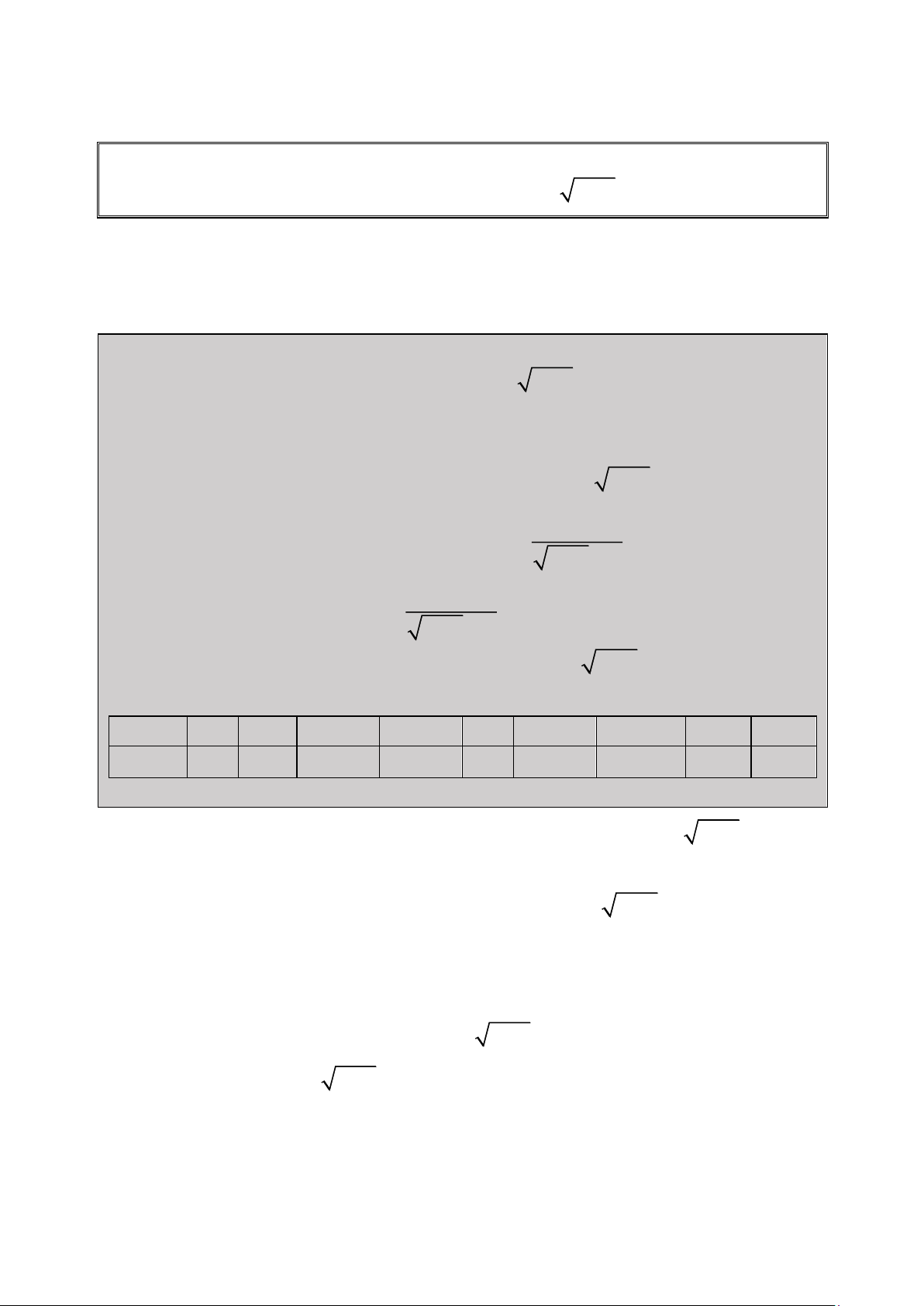
 Thử bằng Mode TABLE hoặc gán trực tiếp CALC, ta thấy : x 1 2 3 4 5 6 7 10 >10 f (x) 4 12 8.8284 3.0717 0 4.8065 22.7173 208 >0
 Vậy đây là một bài toán nghiệm bội kép x  5.
Kết luận : Bài toán bội kép x  5 và chắc chắn chứa nhân tử  x   2 1 2
▶ Phân tích hướng giải:
Ta nhận thấy f x 3 2
x x x    2 7 16 6
x x  8 x 1  0 nên ta có
thể dùng bất đẳng thức.
Ngoài ra, ta vẫn có thể tìm nhân tử của bài toán dưới dạng tổng quát (cho
cả những bài toán nhiều căn, căn bậc cao) tương tự cách làm sau :
 Giả sử nhân tử của bài toán là  x 1  ax b
 Khi đó f x  x 1  ax b  0 có nghiệm bội kép x  5  Khi đó ,
a b phải thỏa mãn hệ phương trình sau :  1 1 a    f '(5)  0   a  0  4   4    f (5)  0 3
25a b  0 b     4  1 3 
Kết luận : Nhân tử của bài toán là x 1  x    .  4 4 
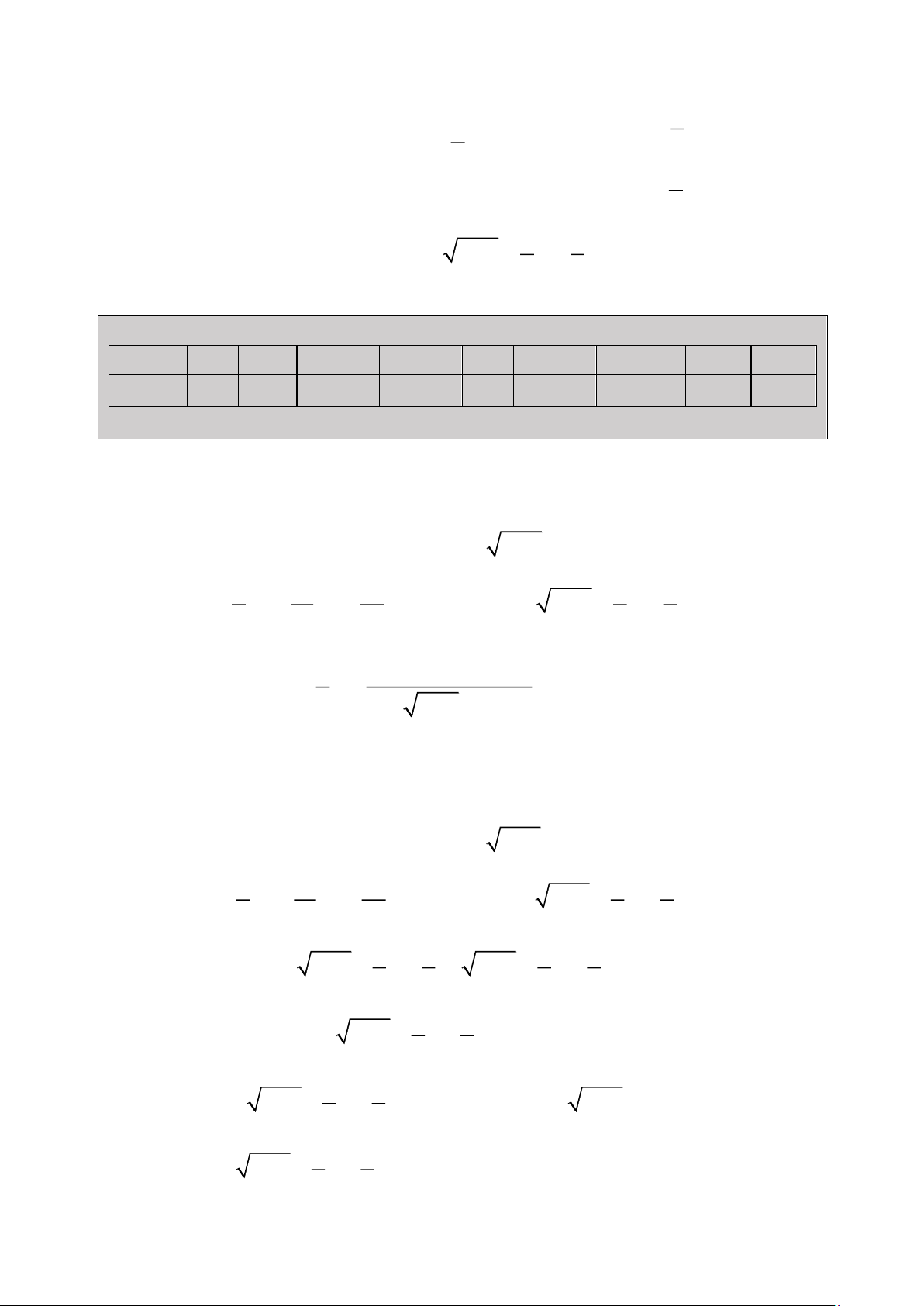
Ta còn một hướng đi khác, đó là bất đẳng thức, đánh giá.  Ta thấy rằng : x 1 2 3 4 5 6 7 10 >10 f (x) 4 12 8.8284 3.0717 0 4.8065 22.7173 208 >0
 Vậy chứng tỏ là rất có thể f (x)  0 với mọi x 1
▶Cách 1 : Nhân liên hợp hoàn toàn: Ta có : 3 2
x  7x 16x  6   2
x x  8 x 1  0 3 15 75  1 3  3 2  x x x   2 x x  8 x 1  x   0   4 2 4  4 4    x 2 3 1 5  x x x      0 4 4 4 1 3        x  5
▶Cách 2 : Nhân liên hợp không hoàn toàn: Ta có : 3 2
x  7x 16x  6   2
x x  8 x 1  0 3 15 75  1 3  3 2  x x x   2 x x  8 x 1  x   0   4 2 4  4 4   1 3  1 3   1  2x x 1  x x 1  x      4 4  4 4    1 3  2 x x  8 x 1  x   0    4 4   1 3   x 1  x    2
4x  8x  8 12x x 1  0  4 4  1 3
x 1  x   0 4 4
▶Cách 3 : Phân tích thành nhân tử không hoàn toàn: Ta có : 3 2
x  7x 16x  6   2
x x  8 x 1  0
  x 122  2x  2x 23x x 1  0
▶Cách 4 : Phân tích thành nhân tử hoàn toàn: Ta có : 3 2
x  7x 16x  6   2
x x  8 x 1  0
 x x 1 x 1 2
1  x 1  22  0
▶Cách 5 : Bất đẳng thức, đánh giá: Ta có : 3 2 2
x  7x 16x  6  (x 1)(x  6x 10)  4  0 với mọi x 1 nên suy 1 4 ra 2
x x  8  0 . Do 1  x x
theo BĐT Cauchy nên ta được : 4 3 2
x  7 x 16x  6   2
x x  8 x 1 x 1 4 3 2
x  7x 16x  6   2
x x  8. 4 3
xx  52  0 x  1 4
▶Cách 6 : Đạo hàm:
Đặt f x 3 2
x x x    2 7 16 6
x x  8 x 1 với x 1 Ta có x x   x   f ' x 5 3 2 5 3 2   
 3x 14x 16 
 x  2 3x 8   2 x 1  2 x 1 
x  2 6x16 x15x3 x2 x127 x16x2   2 x 1 2 x 1 x  2 x  2
Vậy f '(x)  0    
(vì 7 x 1  6x  2  0 x  1)  x 1  2 x  5
Vẽ bảng biến thiên ta được f ( )
x f (5)  0
Vậy f (x)  0 khi và chỉ khi x  5.
Một số bài tập tương tự : 1. 2
2x  5x  5  3x   1 x  2 2. 3 2
x x x    2 3 6 4
2x  3x   1 3x  2 3. 3 2
x x x    2 2 2 1 x x   1 3x 1
4. x x x   x  2 3 2 8 12 4 2 x 1
Bài 12: Giải Phương Trình: 2
x  2x  8  x 1 x  2  2 2    x  2x  3
(đề thi THPT Quốc Gia năm 2015) ▶ Ý tưởng :
Là một bài thi trong đề thi THPT Quốc Gia, nhiều bạn bị mất điểm vì
không giải quyết trọn vẹn được bài toán này.
Có rất nhiều cách để có được lời giải, chúng ta thử khám phá lần lượt.
▶ Thực hiện : 2
x  2x 8  x  4x  2  Dễ dàng ta thấy  . Vậy ta được : x  2  2 
 x2 2 x2 2
x  2x  8  x 1 x  2  2 2    x  2x  3
 x  4 x  2  2 x  2  2  x   1  2
x  2x  3 x  2  2
Thứ ta cần giải quyết là giải phương trình sau :
x  4 x 2  2  x 1 2x 2x3  x   1  2
x  2x  3  2 x  4   x  4 x  2  0 3 2
x x x  5  x  4 x  2  0
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta được :  Phương trình 3 2
x x x  5   x  4 x  2  0 có nghiệm A  3.30277563  Phương trình 3 2
x x x  5   x  4 x  2  0 có nghiệm B  0  .30277563
 Thành thử ta thấy AB  3 .
 Nghiệm của phương trình ban đầu là :
A B   A B2 3  13 x   2 2     3 13 7 13 1 13 Khi x  thì x  2    x 1. 2 2 2
Kết luận : Nhân tử của bài toán này là  x  2  x   1
▶ Phân tích hướng giải:
Sẽ có rất rất nhiều cách giải cho bài toán này và lời giải sẽ nhanh chóng
được tìm ra nếu ta sử dụng CASIO một cách thành thạo. Bạn đọc có thể suy nghĩ thêm.
▶Cách 1 : Bình phương hai vế: Ta có : 3 2
x x x  5   x  4 x  2  0
 x x x 52  x  42 3 2 x  2   2 x  3x   1  4 3 2
x x  3x x  7  0 2
x  3x 1  0 2 2  x  27 2  8 (do 4 3 2 2
x x  3x x  7  x   2  x    0     )  2  4  9  3
▶Cách 2 : Nhân liên hợp không hoàn toàn: Ta có : 3 2
x x x  5   x  4 x  2  0 3 2
x x x  5  x  4x  
1   x  4 x  2  x   1  x   1  2 x  3x  
1   x  4 x  2  x   1  x  
1  x  2  x  
1  x  2  x  
1   x  4 x  2  x   1  0
  x  2  x   1  2
x x  3   x   1 x  2   0
▶Cách 3 : Phân tích thành nhân tử: Ta có : 3 2
x x x  5   x  4 x  2  0
  x  2  x   1  2
x x  3   x   1 x  2   0
(Vì x x    x   x    x    x    x   2 2 3 1 2 2 1 2 2 2 1  3  0 )
▶Cách 4 : Hàm đặc trưng kiểu 1:
Ta đặt a x  2 và b x 1 với a  0 và b  1  . Ta có :
x2 2x4x 1 2x 2x3  a  2 2
a  2  b  2 2 b  2
▶Cách 5 : Hàm đặc trưng kiểu 2: Ta có : 3 2
x  x  x  5  x  4 x  2 3 2
 x  x  x  3  x  4 x  2  2   2 x  2x  3x  
1  x  4 x  2  2
Xét hàm số f t   2
t  2t  2 với t thì f't 2  3t  4t  2  0 t   .
Hàm số cũng liên tục trên . Vậy :    x     f x  f x   1 0 3 13 2 1  x  2  x 1    x  x  2   x  2 1 2
▶Cách 6 : Đạo hàm:
▶Cách 7 : Đặt ẩn phụ hoàn toàn:
▶Cách 8 : Đặt ẩn phụ không hoàn toàn:
▶Cách 9 : Nhân liên hợp hoàn toàn:
▶Cách 10 : Đặt ẩn phụ đưa về hệ phương trình:
▶Cách 11 : Đánh giá, bất đẳng thức:
▶Cách 12 : Hàm đặc trưng kiểu 3:
❓ Tại sao lại có các lời giải trên ?
Thực sự thì các lời giải này tương tự nhau nên việc tìm ra mấu chốt của bài
toán sẽ đưa đến các lời giải như trên. Kể cả là Cách 4, Cách 5, Cách 12.
Quan trọng là bạn đọc tư duy như thế nào cho hiệu quả. Hãy thử động
não. Nếu bạn đọc quá tò mò thì hãy kiên nhẫn xem các bài tập ví dụ tiếp theo.
Đó là cách giải quyết hầu hết các bài toán dạng : 3 2
ax  bx  cx  d  mx  n px  q
Để biến đổi phương trình về dạng :
f ex  f  f  ux  v   ex  f  ux  v
Gợi ý : ex  f  ux  v là nhân tử của bài toán.
Một số bài tập tương tự : 1. 3 2
x x  3x  9   x  8 x  2 2. 3 2
x  6x 13x  2   x  2 x 1  0 3. 3 2
4x 12x 13x  21  32x  36 x 1 4. 3 2
2x  9x  37 x 18  32x 14 2x 1
Sau đây là một số vấn đề mở rộng về việc ứng dụng của phương pháp giải
phương trình vô tỷ bằng CASIO :
 Giải bất phương trình vô tỷ
 Tìm biểu thức cần nhân liên hợp  Bất đẳng thức
 Hàm đặc trưng (cách giải tổng quát cho bài toán THPT Quốc Gia 2015)
 Đặt ẩn phụ không hoàn toàn
 Đặt ẩn phụ đưa về hệ phương trình
Bài 13: Giải Bất Phương Trình: x    2 2 3 x  4x   1 x  2 ▶ Ý tưởng :
Có lẽ bây giờ nhìn lại bài toán này, bạn đọc đã hình dung được rất nhiều
cách làm. Lời giải ngắn gọn nhất và dễ biến đổi nhất là phương pháp phân tích thành nhân tử. ▶ Thực hiện :
Sử dụng máy tính CASIO ta được nhân tử của bài toán này là
x2  x3
▶ Phân tích hướng giải:
Ta coi bất phương trình như phương trình.
▶ Lời giải : Phân tích thành nhân tử: Ta có : 2x  3   2 x  4x   1 x  2
  x  2  x 3x x  2  x   1  0
x  2  x  3
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự : 1.  x   2 3
2x 1  2x  2x 1 2. 2
x x    2 5 6 1
2x  3x   1 x  2 3. 2 x    2 6 6
2x  5x 12 x  5 2  x  2 1 4. 1 2x  3 4 x
Bài 14: Giải Bất Phương Trình: 3 2
x x    2 2 3 2
3x  5x  4 x 1 ▶ Ý tưởng :
Ta cũng có thể sử dụng CASIO để tìm biểu thức cần nhân liên hợp cho bài toán này. ▶ Thực hiện :
Sử dụng máy tính CASIO ta được nhân tử của bài toán này là  x   1   2 1  1 1 x 1   x 1  x       2   3 3 
▶ Phân tích hướng giải:  2 1  Ta sẽ nhóm theo nhân tử x 1  x    vừa tìm được.  3 3 
▶ Lời giải : Nhân liên hợp: Ta có : 3 2
2x  3x  2   2
3x  5x  4 x 1 4 13 10  2 1  2  x x    2
3x  5x  4 x 1  x    3 3 3  3 3     
  x  x   2 1 3x  5x  4 4 5 2     0  3  2 1   9 x 1  x        3 3  
 4x  5x  2  0
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự : 1. 3 2 x x x    2 2 26 20
6x 16x  4 x 1  0 2.  2x   3 2 9 3
x  2  3x x 18 3.  2 x x   3 2 5 25 16
x 1  x 15x  34x 14 1 4. 3 2
x x x  5   x  5 x  2 2
Bài 15: Giải Bất Phương Trình: 2
x x    2 3 7
x  3x  5 x 1  0 ▶ Ý tưởng :
Tương tự bài 14, ta cũng có thể tìm được biểu thức cần nhân liên hợp với x 1 ▶ Thực hiện :
Sử dụng máy tính CASIO ta được nhân tử của bài toán này là
x1 x2
▶ Phân tích hướng giải:
Để nhân liên hợp, ta cần xét một số điều kiện :
▶ Lời giải : Nhân liên hợp: 5  13
Ta có : Nếu x 1  x  2  0  x  thì thoả mãn 2 5  13
Nếu x 1  x  2  0  x  thì : 2 2 x  3x  7   2 x  3x  5 x 1  0 3 2
 x  4x  2x  3   2
x  3x  5 x 1  x  2  0 2 2         x x x x x 1  3 5 5 3 2 x  5x  3      0 x 1  x  2    x  x   x  5x  3 2 3 5 2  x 1   0   x  1  x  2 
 2x 5x3 x 1 x12x3   0 x 1  x  2 2  x  5x  3  0 5  13
Nếu x 1  x  2  0  x  thì tương tự. 2
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự : 1. 5 4
x x x    4 2 1
x x  2 x 1 2. 3 2
x x x    2 3 7 4
3x  3x  2 x  2  0 3. 3 2 x x x    2 7 16 4
3x  4x   1 5x  2  0 4. 3 2
x x x    2 5 1
3x  5x  2 x 1  0
Bài 16: Giải Phương Trình: 3 2 x  x  x    2 4 11 10 x  2x  9 2x  3 ▶ Ý tưởng :
Ta sẽ sử dụng CASIO để kiểm tra xem bài toán này có sử dụng bất đẳng thức được không. ▶ Thực hiện :
Thứ nhất, sử dụng máy tính cầm tay ta thấy phương trình này có nghiệm
duy nhất là x  3  2  4.41421356
Thứ hai, ta thử khi x 1.5, 2, 4, 4.4, 4.5,5,10,1000,... thì ta thấy : 3 2 x  x  x    2 x  x   3 4 11 10 2 9 2x  3  0 x   2 Vậy ta sẽ chứng minh 3 2 x  x  x    2 4 11 10
x  2x  9 2x  3  0
▶ Phân tích hướng giải:
Ta thấy nghiệm là x  3  2 là điểm rơi, vậy thì khi đó :
2x  3  1  2  x  2 3 Để ý rằng khi x  (theo ĐKXĐ) thì 3
x  4x 11x 10  0 , từ đó ta có lời 2 giải như sau :
▶ Lời giải : Bất đẳng thức: 3 7 1 ĐKXĐ: x  . Khi đó : 3 2
x  4x 11x 10   2x  3 2 4x 10x  29  0 2 8 8 Vậy suy ra 2
x  2x  9  0  x  10 1  2 . Do đó : 2 
x  x    x   x   x 2  x  2   1 2 2 3 2 2 3 2 1  2x  3     x   x 2 2 2 Từ đó : 2 x  x  x 
x  4x 11x 10  x  2x  9  2 2 9 1 3 2 2   2x  3  2x  2 x 6x72 2 2        x   0 x 6x 7 0 2 2
Lời giải chi tiết dành cho bạn đọc.
Một số bài tập tương tự : 1. 2
x  3x  4  2 x 1  0 2. 4 3 2 x x x x    3 3 10 48 32
4 x 12 x 1 4 2 x 31x 3. 2 
18x  9  3x x  2 36 4 4. 6 2 x x x   x 4 3 13 6 16 2
x x 10 x  2
Bài 17: Giải Phương Trình: 3 2
x  x  x  5  x  4 x  2 ▶ Ý tưởng :
Ta đã có rất nhiều cách để làm bài toán này. Tuy nhiên, để có một lời giải
ngắn gọn như cách 4, cách 5, cách 12 thì ta phải tìm được biểu thức của
hàm đặc trưng. Sử dụng máy tính CASIO cũng sẽ giúp ích được cho chúng ta tìm hàm đặc trưng. ▶ Thực hiện :
Sử dụng CASIO, ta tìm được nhân tử là
x  2  x 1. Vậy ta cần tìm hàm
đặc trưng sao cho f  x  2   f x   1 .
Vì hệ số của x  2 là x    x  2 4 2
 2 là bất di bất dịch rồi nên ta biến đổi như sau : 3 2
x  x  x  5  x  4 x  2 3 2
 x  x  x  5  k x  4  x  4 x  2  k x x k      
1 x  4k  5   x  22 3 2  2 x  2  k  
▶ Phân tích hướng giải:
Hàm đặc trưng của bài toán này sẽ có dạng : f t   2
t  2t  k bởi vì vế
phải ta có f  x  2 rồi
Vậy để f  x  2   f x  
1 thì vế trái sẽ phải thỏa mãn : 3 2 x  x  k  
1 x  4k  5  f x   1 x   x  x  k  
1 x  4k  5  x 1 k x  2 3 2 1  2 x  3 2  x  x  k   3
1 x  4k  5  x  k  3 2
x  2k  5x  3k  3 x   k  2
▶ Lời giải : Hàm đặc trưng:
ĐKXĐ : x  2  . Ta có : 3 2
x  x  x  5  x  4 x  2 3 2
 x  x  x  3  x  4 x  2  2   2 x  2x  3x  
1  x  4 x  2  2
Xét hàm số f t   2
t  2t  2 với t thì f't 2  3t  4t  2  0 t  
Hàm số cũng liên tục trên . Vậy :    x     f x  f x   1 0 3 13 2 1  x  2  x 1    x  x  2   x  2 1 2
Một số bài tập tương tự : 1. 3 2
2x  4x  5x  25  16x  50 x  3 2. 3
2x  23x  45  16x 18 x  2 3. 3
8x 11x  6  3x 3x  2 4. 3 2
2x  2x 11x  31  2x 19 x  3
Bài 18: Giải Phương Trình: 3 2
x  6x 12x 12  x  4 x  2  0 ▶ Ý tưởng :
Ta sẽ làm tương tự bài 17. ▶ Thực hiện :
Sử dụng CASIO, ta tìm được nhân tử của bài toán là  x  2  x  3 . Ta có : 3 2
x  6x 12x 12  x  4 x  2 3 2
 x  6x  12  kx 12  4k  x  4 x  2  k
▶ Phân tích hướng giải: Vì x    x  2 4 2
 6 nên nhân tử của chúng ta có dạng :
f t   2t  6t  k với k thỏa mãn
f  x  2  f3 x x 
 x  6x  12  kx 12  4k  3 x2 3 2  63 x  k x  3 2
 x  6x  12  k 3
x 12  4k  x  k  9 2
x  6k  33x 15k  45 x   k  3 
▶ Lời giải : Hàm đặc trưng:
ĐKXĐ : x  2 . Ta có : 3 2
x  6x 12x 12  x  4 x  2 3 2
 x  6x 15x  x  4 x  2 3   
 3  x  33 x  6   x  2 3 x  22 2  6    3  x  x  2
Lời giải chi tiết dành cho bạn đọc.
Bài 19: Giải Phương Trình: 3 2
x  2x  5x  5  2x  5 2x 1 ▶ Ý tưởng :
Ta sẽ làm tương tự bài 17. ▶ Thực hiện :
Sử dụng CASIO, ta tìm được nhân tử của bài toán là  2x 1  x   1 . Ta có : 3 2
x  2x  5x  5  2x  5 2x 1 3 2
 x  2x  5x  5  2x  5k  2x  5 2x 1  k
▶ Phân tích hướng giải:
Ta cần tìm f t   2
t  6t  k với k thỏa mãn đẳng thức sau với mọi x 3 2
x  2x  5x  5  2x  5k  2x  5 2x 1  k
 f  2x 1  fx   1  x  2 1  6x 1 k Ta được k 1
▶ Lời giải : Hàm đặc trưng: 1 ĐKXĐ : x  . Ta có : 2 3 2
x  2x  5x  5  2x  5 2x 1 3 2
 x  2x  7x  2x  5 2x 1   1 x    1  1 x   1
 6   2x 1  1 2x 12 2  6    x 1 2x 1
Lời giải chi tiết dành cho bạn đọc.
Bài 20: Giải Phương Trình: 3 2
8x  40x  72x  58  x  8 x  3 ▶ Ý tưởng :
Ta sẽ làm tương tự bài 17. ▶ Thực hiện :
Sử dụng CASIO, ta tìm được nhân tử của bài toán là :  5 
 x    x    1 3 3 2  x  2  x  3  2  2
Hay gọn hơn là  x  3  2x  4 .
▶ Phân tích hướng giải:
Cần tìm hàm f t   2
t  5t  k sao cho f x  3  f2x  4 x  . Hay : 3 2
8x  40x  72x  58  k x  8  x  8 x  3  k  f  x  3  f 2x  4
Vì biểu thức đúng với mọi x nên mình cho x  0 ta được : k 
 f     2 8 58 4 4  5 4   k  k  2
Thử lại thấy thỏa mãn.
▶ Lời giải : Hàm đặc trưng:
ĐKXĐ : x  3  . Ta có : 3 2
8x  40x  72x  58  x  8 x  3   
 2x  42  52x  4  2   x  32  5 x  3  2    2x  4  x  3
Lời giải chi tiết dành cho bạn đọc.
Bài 21: Giải Phương Trình: 3 2 x  x  x    2 2 3 5 2
5x  7x  2 2x 1  0 ▶ Ý tưởng :
Ta sẽ sử dụng phương pháp đặt ẩn phụ không hoàn toàn để giải quyết bài toán.
▶ Thực hiện :
 Sử dụng máy tính cầm tay CASIO ta được 2 nhân tử của bài toán này là :
  2x 1  x  2
  2x 1  2x 3
 Sử dụng máy tính cầm tay CASIO để chia biểu thức ta được : 3 2 x  x  x    2 2 3 5 2 5x  7x  2 2x 1     
x   x   x   x   2x 1 x 1 2 1 2 3 2 1 2
 Từ đó ta đặt 2x 1  a thì : 3 2
2x  3x  5x  2   2 5x  7x  2 2x 1  a  x  
1 a  x  2a  2x  3 3  2x  5a  5 2 x   2 4a  9a   3 2 1 x  a  4a  a  6 Kết luận : 3 2 x  x  x    2 2 3 5 2
5x  7x  2 2x 1  a  x  
1 a  x  2a  2x  3
▶ Phân tích hướng giải:
Ta chỉ cần trình bày ngược lại với những gì chúng ta làm
▶ Lời giải : Đặt ẩn phụ không hoàn toàn: 1 ĐKXĐ : x  
. Đặt a  2x 1 với a  0 thì : 2 3 2
2x  3x  5x  2   2
5x  7x  2 2x 1  0 3  2x  5a  5 2 x   2 4a  9a   3 2
1 x  a  4a  a  6  0  a  x  
1 a  x  2a  2x  3  0
Bài 22: Giải Phương Trình: 3 2 x  x  x    2 3 2 4
x  2x  6 x  2  0 ▶ Ý tưởng :
Ta sẽ thử đặt ẩn phụ để đưa về hệ phương trình
▶ Thực hiện :
 Sử dụng máy tính cầm tay CASIO ta được 2 nhân tử của bài toán này là :  x2 x3
 Vậy ta đặt a x  2 và b  3 x suy ra 2
a b 1 và : 3 2
x  3x  2x  4   2 x  2x  6 x  2  3  b3  
3 3  b2  23  b  4  3  b2  23  b  6a   2 b  8b  9 3 2 a  b  6b 11b  2
 Hệ phương trình của chúng ta sẽ là : 2 a  b 1 0  2  b  8b  9   3 2
a  b  6b 11b  2  0
 Vì ta luôn có a b nên chỉ cần làm mất hệ số tự do, tức
2PT (1)  PT (2) là ta có lời giải rồi.
Kết luận : Lấy 2PT (1)  PT (2) rồi phân tích thành nhân tử.
▶ Phân tích hướng giải:
Tuy lời giải này hơi dài nhưng cũng khá hay. Chúng ta cùng thử phương
pháp đặt ẩn phụ giải hệ phương trình
▶ Lời giải : Đặt ẩn phụ đưa về hệ phương trình:
ĐKXĐ : x  2 . Khi đó đặt a x  2 và b  3  x với a  0 và b 1 suy ra 3 2
x  3x  2x  4   2 x  2x  6 x  2  3  b3  
3 3  b2  23  b  4  3  b2  23  b  6a   2 b  8b  9 3 2 a  b  6b 11b  2 2 a  b 1 0 
Vậy ta có hệ phương trình :  2  b  8b  9   3 2
a  b  6b 11b  2  0
Lấy 2PT (1)  PT (2) ta được :  2b 8b9 3 2 2
a  b  6b  9b  2a  0  a  b 2 b  6b  9  2a  0 a  b   a  0  b  3 (vì 2 2
b  6b  9  2a  (b  3)  2a  0 )
Lời giải chi tiết dành cho bạn đọc.
Bài 23: Giải Phương Trình: 2 2
x  2x 1 2x x  2  0 ▶ Ý tưởng :
Tuy đây là một dạng toán khó hơn dạng ban đầu một tẹo nhưng ý tưởng vẫn là tìm nhân tử.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương trình 2 2
x  2x 1 2x x  2  0 có nghiệm A  0.215250436
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương trình 2 2
x  2x 1 2x x  2  0 có nghiệm B  -1.54858377 A  B  A  B2    4 2 7
Vì A  B    nên A   3 2 3    2 7
Nghiệm của bài toán này là x  . Khi đó : 3    2 29 4 7 1 2 7 x  2    2x 1 9 3
Kết luận : Nhân tử của bài toán này là  2 x  2  2x  1
▶ Phân tích hướng giải:
Ta chủ yếu dùng các cách sau cho dạng toán này :  Nhân liên hợp
 Phân tích thành nhân tử  Đạo hàm, hàm số
 Đánh giá, bất đẳng thức
 Đặt ẩn phụ đưa về hệ phương trình
Phương pháp bình phương hai vế nhiều khi không sử dụng được để giải
bất phương trình hoặc nó có nguy cơ tiềm ẩn nghiệm lẻ.
▶Cách 1 : Nhân liên hợp hoàn toàn:
Ta có : x  x   x x    x  2 2 2 2 2 1 2 2 0 1  2x x  2  x  0 Vì vậy : 2 2
x  2x 1 2x x  2  0 2
 3x  4x 1 2x 2x  2  2x  1  0    x  2 x  x   2 3 4 1 1   0   2  x  2  2x 1 2  3x  4x 1  0 2 2x x  2 1 (vì 1   0 x   0 ) 2 2 x  2  2x 1 x  2  2x 1 2   7  x  (vì x  0 ) 3 2   7 Vậy x  . 3
▶Cách 2 : Nhân liên hợp không hoàn toàn: Ta có : 2 2
x  2x 1 2x x  2  0 2  3x  4x 1 2x 2 x  2  2x  1  0
  2x  2  2x  1 2
x  2  2x  1  2x 2 x  2  2x  1  0
  2x  2  2x  1 2 x  2  1  0 2  x  2  2x 1 (vì 2 x  2 1  0 x   ) 2
x  2  2x  2 2 1 3  x  4x 1 0 2   7      x  2  x 1 0 2  x 1 0 3 2   7 Vậy x  . 3
▶Cách 3 : Phân tích thành nhân tử: Ta có : 2 2
x  2x 1 2x x  2  0
  2x  2  1 2x  2  2x  1  0
▶Cách 4 : Đạo hàm: Xét hàm f x 2 2
 x  2x 1 2x x  2 trên . 4 2 x   1
Khi đó ta có : f 'x  2x  2  . Vậy suy ra : 2 x  2 x 1 
f'x  0  x 1 x 24x   2 2 2 2 1 x 1   4 3 2 3
 x  2x  5x  4x  2  0
Vậy phương trình f 'x  0 vô nghiệm. Suy ra f x  0 có tối đa 1 nghiệm.  2   7  2   7 Dễ thấy f    0   nên x 
là nghiệm duy nhất của bài toán. 3   3
▶Cách 5 : Đánh giá, bất đẳng thức: 2x 1  0  2   7 Ta thấy : 2
x  2  2x 1 0    x  . x  2   2x  2 2 1 3   Tương tự thì : 2 2 7
x  2  2x 1  0  x  . 3
Lại có x  x   x x   x  2 2 2 2 2 1 2 2 1
 2x x  2  x  0 . Vậy : 2   7 Nếu x  thì : 3 2 2 2
x  x   x x   x  x   x x   2 2 1 2 2 2 1 2 2 1  3  x  4x 1 0 2   7 Nếu 0  x  thì : 3 2 2 2
x  x   x x   x  x   x x   2 2 1 2 2 2 1 2 2 1  3  x  4x 1  0 2   7 Nếu x  thì thỏa mãn. 3 2   7 Vậy x  . 3
▶Cách 6 : Đặt ẩn phụ đưa về hệ phương trình: Đặt 2
x  2  2y 1 (mục đích là để x y ). Ta được hệ phương trình :
x  2  2y  2 2 1  2 x  2x 1  2x  2y  1 2 2
x  4y  4y 1 0   2
x  4xy  4x 1 0
Để mất hệ số tự do, ta lấy PT (1)  PT (2) rồi phân tích nhân tử, chắc chắn
sẽ có nhân tử  x y vì ta ép nó phải như vậy mà. Thử nhé :  2 2
x  y  y     2 4 4 1 x  4xy  4x   1  0  4y   1 x  y  0
Lời giải chi tiết dành cho bạn đọc.
❓Tại sao không đưa về hệ phương trình đối xứng như một số giáo viên hay giảng dạy?
Là người nghiên cứu lâu năm nên mình hiểu bản chất của việc đưa về hệ
phương trình đối xứng. Lấy một ví dụ, mình là Bùi Thế Việt sinh ngày
13/02/1997 nên mình sẽ tự tạo ra một hệ phương trình đối xứng như sau : 2 x 13x  2y  7xy  2 y 13y  2x  7xy
Và sau đây là bài toán suy ra từ hệ phương trình trên :
Bài toán: Giải Phương Trình: 2 x  x    x   2 47 131 26 7 2 49x 190x 169  0
▶Lời giải: Đặt ẩn phụ đưa về hệ phương trình đối xứng : Đặt 2
49x 190x 169  2y  7x 13 ta được hệ phương trình :
49x 190x 169  2y  7x 132 2  2 47x 131x  26  
7x  22y  7x 13  0 2
28xy  4y 8x  52y  0   2 14
 xy  2x  26x  4y  0 2 x 13x  2y  7xy   2 y 13y  2x  7 y x
❓Tại sao bài toán này có thể đưa về hệ phương trình đối xứng?
Thực chất không hẳn bài toán nào cũng có thể đưa được về hệ phương
trình đối xứng. Bản chất là việc đặt 2
49x 190x 169  ax  by  c và biến
đổi phương trình dưới dạng x  yx  y  k  0 nhưng nhiều bài toán
chưa chắc có thể biến đổi như vậy được. Cách tốt nhất để giải những bài
toán dạng này là phân tích thành nhân tử hoặc nhân liên hợp, đánh giá :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương trình 2 x  x    x   2 47 131 26 7 2
49x 190x 169  0 có tập nghiệm  5 1  1 2 13  0; ;   2 2  
 Nhân tử của bài toán sẽ là :     2 5
49x 190x 169  5x 13 chứa cặp nghiệm 0;   2      2 11 2 13
49x 190x 169  9x  9 chứa nghiệm    2  
Lời giải bài toán trên chỉ là : 2
47x 131x  26  7x  2 2 49x 190x 169  0  2 2
49x 190x 169  5x 13 2
49x 190x 169  9x  9  0
Bài 24: Giải Phương Trình: 2 x  x   x   2 5 4 1 1 x  3x 1  0 ▶ Ý tưởng :
Ta vẫn sẽ có những cách sau nhờ phương pháp tìm nhân tử  Nhân liên hợp
 Phân tích thành nhân tử  Đạo hàm, hàm số
 Đánh giá, bất đẳng thức
 Đặt ẩn phụ đưa về hệ phương trình
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương  1  trình 2 x  x   x   2 5 4 1 1
x  3x 1  0 có tập nghiệm 0;   3
 Gọi nhân tử của bài toán là  2
x  3x 1  ax  b. Khi đó : 1   b  0  a  2  1 1    a  b  0  b  1  3 3
Kết luận : Nhân tử của bài toán này là  2 x  3x 1  2x  1
▶ Phân tích hướng giải:
Vẫn sẽ có khá nhiều cách làm như bài toán trước.
▶Cách 1 : Nhân liên hợp hoàn toàn: Ta có : 2
5x  4x 1  x   2 1 x  3x 1  0     x x   x 1 3 1 1    0 2  x 3x 1 2x 1       
▶Cách 2 : Nhân liên hợp không hoàn toàn: Ta có : 2
5x  4x 1  x   2 1 x  3x 1  0 2  3x  x  x   1  2 x  3x 1  2x  1
  2x 3x 1 2x  1 2x 3x 1 2x  1 x   1  2
x  3x 1  2x  1  0
  2x 3x 1 2x  1 2x 3x 13x  2  0
▶Cách 3 : Phân tích thành nhân tử: Ta có : 2 5x  4x 1 x   2 1 x  3x 1  0
  2x 3x 1 2x  1 2x 3x 13x  2  0
▶Cách 4 : Đạo hàm, hàm số: Ta đặt : f x 2
 x  x   x   2 5 4 1 1 x  3x 1 suy ra : 2   f'x 4x 11x 5 10x  4  2 2 x  3x 1     f' x 3 2 8x 36x 39x 7 10  4 x  3x  3 2 1   f' 'x 15x  1  8 x  3x  5 2 1
▶Cách 5 : Đánh giá, bất đẳng thức: Ta có :   1   x  0   2 3
 x  3x 1  2x 1    3   5  x     2  x  0  2  x   3x 1  2x 1  3   5 1    x      2 3
▶Cách 6 : Đặt ẩn phụ đưa về hệ phương trình: Ta có : Đặt 2
x  3x 1  2y 1 ta được hệ phương trình : 2 2
x  4y  3x  4y  0  2 5
 x  2xy  3x  2y  0
Bài toán này không có hệ số tự do nên ta phải làm kiểu khác. 2 2 2
x  4y  3x  4y  3  y  y
Cho x y ta được :  . 2 2 5
 x  2xy  3x  2y  3y  y
Để triệt tiêu thì ta phải lấy PT (1)  PT (2) . Vậy lấy PT (1)  PT (2) ta được :  2 2
x  y  x  y   2 4 3 4
5x  2xy  3x  2y  0
 2x  y3x  2y  3  0
Bài 25: Giải Phương Trình: 3 2 x  x  x    2 x  x   2 7 7 5 14 13 3 x  2x  8  0 ▶ Ý tưởng :
Ta dựa vào nghiệm của phương trình để giải quyết bài toán này.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương trình 3 2 x  x  x    2 x  x   2 7 7 5 14 13 3
x  2x  8  0 có nghiệm 1 duy nhất x  8 1
Kết luận : Phương trình có nghiệm duy nhất x  8
▶ Phân tích hướng giải:
Với những bài toán có nghiệm duy nhất, ta thử các phương pháp sau :  Nhân liên hợp  Đạo hàm
 Bất đẳng thức, đánh giá
▶Cách 1 : Nhân liên hợp hoàn toàn: 1 Khi x  thì 2 23 x  2x  8 
nên ta sẽ có lời giải như sau : 8 8 3 2
7x  7x  5x 14   2 x 13x  3 2 x  2x  8  0 2 33x 339x   3 43  x      2 x  x   2 23 7 13 3 x  2x  8    8 8 8  8  
8x 17 2x 13x 3  1 2   8x   1  7x  5x  43    0 2 8  8 x 2x 8 23      
Cách này khó khăn rồi. Để giải tiếp ta phải đánh giá phương trình :
 2x  x  2x  x   x  2 7 5 43 8 2 8 23 8 17 x 13x  3  0 Thứ nhất, ta luôn có : 2 7x  5x  43  0 x   x Thứ hai, ta thấy : 2 x  2x  8   2 x  
(bạn đọc tự chứng minh) 7 x Nếu
 2  0 thì  x   2 8
17 x 13x  3  0 , suy ra :
7  2x  x  2x x   x  2 7 5 43 8 2 8 23 8 17 x 13x  3  0 x Nếu  2  0 thì 7  2 7x  5x  43 2
8 x  2x  8  23  8x 17 2 x 13x  3     x   2 7x  5x  43 8  2  23      8x 17 2 x 13x  3   7   2 2560x 3424x   1728 7 7 2 2560  107  109511   x    0  7  160  70
▶Cách 2 : Đạo hàm:
Xét hàm số : f x 3 2
 x  x  x    2 x  x   2 7 7 5 14 13 3 x  2x  8 3 2 3x  21x  26x 107 Ta có : f 'x 2  21x 14x  5  . 2 x  2x  8
Lại một thử thách nữa đến với chúng ta.
Chúng ta cần giải phương trình sau : 3 2 x  x  x    2 x  x   2 3 21 26 107 21 14 5 x  2x  8  0
Thử một vài giá trị bằng máy tính cầm tay, ta thấy : 3 2 x  x  x    2 x  x   2 3 21 26 107 21 14 5 x  2x  8  0 x   .
Có lẽ ta phải làm tương tự cách 1 thôi : Thứ nhất, ta luôn có : 2 21x 14x  5  0 x   . Vậy ta có : x Nếu  2  0 thì 3 2
3x  21x  26x 107  0 , suy ra : 7 3 2 x  x  x    2 x  x   2 3 21 26 107 21 14 5 x  2x  8  0 x   x Nếu  2  0 thì : 7 3 2
3x  21x  26x 107   2 21x 14x  5 2 x  2x  8  x  3 2
 3x  21x  26x 107   2 21x 14x  5  2    7  383x 2  6  5x  117 7 2  383  1343891  6  5x    0   910  12740
▶Cách 3 : Đánh giá, bất đẳng thức: Phương trình 3 2 x  x  x    2 x  x   2 7 7 5 14 13 3
x  2x  8  0 có nghiệm 1 duy nhất x  . 8 Đánh giá theo 2
x  2x  8 thì được nhưng còn  2 x 13x  3 thì sao ?
Ta chưa biết dấu của  2
x 13x  3 . Ta sẽ xét cả dấu của nó nữa : 2  13  181 x 13x  3  0  Nếu x  thì  . Khi đó : 2 2
 x  2x  8  7x  78  3 2
7x  7x  5x 14   2 x 13x  3 2 x  2x  8 3 2
 7x  7x  5x 14   2
x 13x  37x  78 2 176x  988x  248 176 2
x 13x  3 1300x  280  0 2 x 13x  3  0 1 13  181  Nếu  x  thì  23 . Khi đó : 8 2 2  x  2x  8   8 3 2
7x  7x  5x 14   2 x 13x  3 2 x  2x  8 3 2 23  7x  7x  5x 14   2x 13x3 8  1   x   2 7x  5x  43  0  8  2 x 13x  3  0 13  181 1  Nếu  x  thì  23 . Khi đó : 2 8 2  x  2x  8   8 3 2
7x  7x  5x 14   2 x 13x  3 2 x  2x  8 3 2 23  7x  7x  5x 14   2x 13x3 8  1   x   2 7x  5x  43  0  8  2 x 13x  3  0  13  181  Nếu x  thì 2
 x  2x  8  0 . Khi đó : 2 x  0  3 2
7x  7x  5x 14   2 x 13x  3 2 x  2x  8 3 2
 7x  7x  5x 14  0
Bài toán được giải quyết hoàn toàn.
▶Cách 4 : Phân tích thành nhân tử: Phương trình 3 2 x  x  x    2 x  x   2 7 7 5 14 13 3
x  2x  8  0 có nghiệm 1 duy nhất x  và nhân tử  2 x  2x  8  ax  b 8 Phương trình 3 2 x  x  x    2 x  x   2 7 7 5 14 13 3
x  2x  8  0 có nghiệm 2 duy nhất x   và nhân tử  2
 x  2x  8  ax  b (vì ta đổi dấu trước 3
căn nên nhân tử cũng có căn đổi dấu). 23 1  a  b  0  a  7  Vậy : 8 8    8 2  b  2    a  b  0  3 3
Nhân tử của bài toán là :  2 x  2x  8  7x  2
Sử dụng máy tính cầm tay để phân tích thành nhân tử, ta được lời giải : 3 2
7x  7x  5x 14   2 x 13x  3 2 x  2x  8  0
  2x  2x 8 7x  2 2 2
2 x  2x  8  x  x   1  0 2
 x  2x  8  7x  2  0 1  x  8
Lời giải chi tiết dành cho bạn đọc.
❓Tại sao bài toán này có thể phân tích thành nhân tử khi có nghiệm duy nhất?
Như chúng ta đã biết, chúng ta chắc chắn tìm được nhân tử của bài toán
nếu biết 2 nghiệm hữu tỷ hoặc 1 nghiệm vô tỷ dạng a b .
Tuy nhiên, đối với nghiệm duy nhất thì tùy từng bài mới có thể phân tích thành nhân tử được.
Cách tốt nhất để thử xem bài toán có phân tích thành nhân tử khi có
nghiệm duy nhất là phương pháp đổi dấu trước căn.
Nếu bài toán sau khi đổi căn mà có nghiệm vô tỷ dạng a b hoặc
nghiệm hữu tỷ thì chắc chắn phương trình ban đầu có thể phân tích thành
nhân tử được. Nếu không thì ta nên làm cách khác cho bài toán
Bài 26: Giải Phương Trình: 2 x   2 x  x 2 5 4
x  2x  2  2x 1  0 ▶ Ý tưởng :
Ta dựa vào nghiệm của phương trình để giải quyết bài toán này.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương trình 2 x   2 x  x 2 5 4
x  2x  2  2x 1  0 có nghiệm A  0  6 . 403882032 và B  0  1 . 569296691
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương trình 2 x   2 x  x 2 5 4
x  2x  2  2x 1  0 có nghiệm C  0 3 . 903882032 và D  1  5 . 93070331 và E 1 2 A  C  (A  C)    1 17 Thấy A  C nên A   2 8 2 B  D  B  D)    7 33 Thấy B  D nên B   2 8
 Từ đó ta tìm ra được các nhân tử là :
 2x 2x23x và  2x 2x23x2
Kết luận : Phương trình có hai nhân tử là :
 2x 2x23x và  2x 2x23x2
▶ Phân tích hướng giải:
Ta dùng thủ thuật CASIO để chia biểu thức, ta được :
▶Lời giải : Phân tích thành nhân tử: Ta có : 2 5x   2 4 x  x 2
x  2x  2  2x 1  0 1   2 x  2x  2  3x 2
x  2x  2  3x  2 2 x  2x  2  1  0 2
Bài 27: Giải Phương Trình: 3 2 x  x    2 x  x   2 4 4 4 8 x 1  0 ▶ Ý tưởng :
Ta cũng dựa vào nghiệm của phương trình để giải quyết bài toán này.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương 4 trình 3 2 x  x    2 x  x   2 4 4 4 8
x 1  0 có nghiệm x  và 3 12 x   5
 Gọi nhân tử của bài toán là  2 x 1  ax  b thì : 5 4  a  b  0  1 3 3 a  2 1    4  x  1  x  2  0 13 12 4
  a  b  0 b  2   5 5  
Kết luận : Phương trình có nhân tử là 2 1  x 1  x  2  4 
▶ Phân tích hướng giải:
Ta dùng thủ thuật CASIO để chia biểu thức hoặc sử dụng phương pháp
nhân liên hợp không hoàn toàn:
▶Lời giải : Nhân liên hợp không hoàn toàn: Ta có : 3 2 x  4x  4   2 4x  x  8 2 x 1  0    x   x  2 4x  x  8 2 3 2  x 1   2    x  4x  4   2 4x  x  8  2    4   4    2  x  15x 2 4x  x  8 2  x 1   2   12  4  x  4  4    x   x  x  2 4x  x  8 2 2 2  x 1   2  4  
 x 1   2 x 1   2  4   4  4    2 4 x  1  x  8 2 2 x 1  x   0
Bài 28: Giải Phương Trình: 2 x  x   x   2 4 4 3 x  x  2  0 ▶ Ý tưởng :
Ta dựa vào nghiệm của phương trình để tìm nhân tử của bài toán.
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương 2 trình 2 x  x   x   2 4 4 3
x  x  2  0 có nghiệm x  và 5 x  A  0 2 . 637626160 .
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương trình 2 x  x   x   2 4 4 3
x  x  2  0 có nghiệm B  1  2 . 63762616 2 A  B  (A  B)    3 21 Vì A  B   A   2 6  Gọi nhân tử là  2
x  x  2  ax  b thì : 21 3   21 a  2  2  a  b  0  
 x  x  2  2x 1 0 3 6 b  1  
Kết luận : Phương trình có nhân tử là  2 x  x  2  2x  1
▶ Phân tích hướng giải:
Tương tự các bài toán trước, ta cũng sẽ nhanh chóng có lời giải bằng cách phân tích thành nhân tử
▶Lời giải : Phân tích thành nhân tử: Ta có : 2
x  4x  4  x  3 2 x  x  2  0   2
x  x  2  2x  1 2
x  x  2  x  2  0
Bài 29: Giải Phương Trình: 2
2x 14  2 x 1  3 x 1 11 x 1  0 ▶ Ý tưởng :
Tuy đây là một dạng toán khó hơn nhưng ý tưởng vẫn là phương pháp tìm nhân tử
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương 65 trình 2
2x 14  2 x 1  3 x 1 11 x 1  0 có nghiệm x  và 16 5 x  . 4
 Gọi nhân tử là  x 1  a x 1  b thì : 7 9  a  b  0  5 4 4 a   5    3  x 1  x 1  2  0 1 3 3
  a  b  0 b  2 2 2
Kết luận : Phương trình có nhân tử là 3 x 1  5 x 1  6
▶ Phân tích hướng giải:
Ta có thể sử dụng máy tính CASIO để chia biểu thức. Lời giải sẽ nhanh chóng được tìm ra :
▶Cách 1 : Nhân liên hợp không hoàn toàn: Ta có : 2
2x 14  2 x 1  3 x 1 11 x  1  0  5   x   x     x  16 70 1 1 2 3 2 1    x   20 x 1  3  3 3  5    x 1 
x 1  23 2 x 1  3   5  5   3   x 1  x 1  2 x 1  x 1  2  3  3 
 3 x 1  5 x 1  6 x 1  x 1   1  0
▶Cách 2 : Phân tích thành nhân tử: Ta có : 2
2x 14  2 x 1  3 x 1 11 x 1  0
  x 1 3 x 1  5 x 1  x 1  2  0
Bài 30: Giải Phương Trình: 2
9  2x  6 1  x  5 1  x  8 1  x ▶ Ý tưởng :
Ta sẽ tìm nhân tử dạng  1 x  a 1 x  b của phương trình trên
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương trình 2
9  2x  6 1  x  5 1  x  8 1  x có nghiệm A  0 9 . 921567416 và B  0  9 . 921567416 2 A  B  (A  B)  3 7 Vì A  B   A   2 8
 Gọi nhân tử là  1 x  a 1 x  b thì : a 1  0 a 1   3 3 3   3  x 1  x 1   0  a  b  0 b   2   4 4  2
Kết luận : Phương trình có nhân tử là 2 1 x  2 x 1  3
▶ Phân tích hướng giải:
Ta làm tương tự bài trên:
▶Lời giải : Phân tích thành nhân tử: Ta có : 2
9  2x  6 1 x  5 1 x  8 1 x
 2 1 x  2 x 1 3 1 x  2 x 1   1  0
Bài 31: Giải Phương Trình: 2
3x 10  3 2  x  6 2  x  4 4  x  0 ▶ Ý tưởng :
Ta sẽ tìm nhân tử dạng  2  x  a 2  x  b của phương trình trên
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương trình 2
3x 10  3 2  x  6 2  x  4 4  x  0 có nghiệm duy nhất 6 x  . 5  6 4 5 2 5 Khi x  thì 2  x  và 2  x  5 5 5
 Gọi nhân tử là  2  x  a 2  x  b thì : 4 5 2 5a 
 b  0 với a,b suy ra (a;b)  ( 2  ;0) 5 5
Kết luận : Phương trình có nhân tử là  2  x  2 2  x 
▶ Phân tích hướng giải:
Ta sẽ sử dụng máy tính CASIO để chia biểu thức:
▶Lời giải : Phân tích thành nhân tử: Ta có : 2
3x 10  3 2  x  6 2  x  4 4  x  0
  2  x  2 2  x2 2  x  2  x  3  0
Bài 32: Giải Phương Trình:
15x  32  7x  8 x  2  x  4 4  x  0
▶ Ý tưởng :
Ta sẽ tìm nhân tử dạng  x  2  a 4  x  b của phương trình trên
▶ Thực hiện :
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình 15x  32  7x  8 x  2  x  4 4  x  0 có nghiệm duy nhất A  2 1 . 33974596 .
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình 15x  32  7x  8 x  2  x  4 4  x  0 có nghiệm duy nhất B  3 6 . 63836718 .
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình 15x  32  7x  8 x  2  x  4 4  x  0 vô nghiệm.
 Sử dụng Thủ Thuật Tìm Nghiệm Phương Trình ta thấy phương
trình 15x  32  7x  8 x  2  x  4 4  x  0 có nghiệm C  3 8 . 66025404 và D  2 0 . 96163282
 Thành thử A  B,A  C,A  D ta thấy : 2 A  C  (A  C) 6  3 A  C  A   2 2
 Gọi nhân tử là  x  2  a 4  x  b thì : 1   3 1 3 a  1   a  b  0  
 x  2  4  x 1 0 2 2 b 1
Kết luận : Phương trình có nhân tử là  x  2  4  x   1
▶ Phân tích hướng giải:
Ta sẽ sử dụng máy tính CASIO để chia biểu thức:
▶Lời giải : Phân tích thành nhân tử: Ta có :
15x  32  7x  8 x  2  x  4 4  x  0
  x  2  4  x  
1 3x  4 4  x x  2  8 x  2  4 4  x   0
THỦ THUẬT 7 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
GIẢI HỆ PHƯƠNG TRÌNH
Bài 1: Giải Hệ Phương Trình: 2 2
x  y  y  4  0  2
y  xy  x  y  2  0 ▶ Ý tưởng :
Ý tưởng của chúng ta rất đơn giản : lấy PT 1
( )  kPT(2) rồi phân tích thành nhân tử
❓ Làm thế nào để tìm được k ? Với :
Có khá nhiều cách để tìm được k . Đối với dạng  a  a  ka 1 2 
toán này thì có cách khác: b  b  kb 1 2  2 2
 a x  b y  c xy  d x  e y  f  0  c  c  kc 1 1 1 1 1 1  1 2  2 2
a x  b y  c xy  d x  e y  f  0 d  d  kd 2 2 2 2 2 2  1 2 
Khi đó đặt k sẽ là nghiệm của phương trình : e  e  ke 1 2  2 2 2
cde  4abf  ae  bd  fc  f  f  kf 1 2
▶ Thực hiện :  Áp dụng công thức : Với : 2 2 2
cde  4abf  ae  bd  fc  a 1   Ta có : b  1   k  4 1   k 4   2k 2  k  1   k  c  k      1   k2   1   k 2 2 k  k  4   2k d k   e  1   k  5
Ta được 3 nghiệm là k  1;k  ;k  3  2 f  4   2k Kết luận : Ta lấy PT 1 ( )  PT(2) hoặc 2PT 1 ( )  5PT(2) hoặc PT 1 ( )  3PT(2) rồi phân tích thành nhân tử
❓ Nếu không tìm được k hoặc k lẻ thì sao?
99,99% sẽ tìm được k . Nếu k lẻ thì chứng tỏ bài toán có lẽ sai đề hoặc là
không phù hợp. Tuy nhiên một số bài toán cho k  2; 3;... thì ta cũng có
thể áp dụng công thức trên.
▶ Phân tích hướng giải:
Việc phân tích thành nhân tử bằng CASIO là một lợi thế không hề nhỏ.
▶ Cách 1 : Phân tích thành nhân tử: Lấy PT 1
( )  PT(2) ta được: (x  2)(x  y 1)  0
▶ Cách 2 : Phân tích thành nhân tử: Lấy 2PT 1
( )  5PT(2) ta được: (x  y  2)(2x  3y 1)  0
▶ Cách 3 : Phân tích thành nhân tử: Lấy PT 1
( )  3PT(2) ta được: (x  2y  2)(x  y 1)  0
Bài 2: Giải Hệ Phương Trình: 2 2 1  6x  4xy  y 12  2 8
 x  4xy  28x  5y  1  8
(đề thi Học Sinh Giỏi lớp 12 – TP Hồ Chí Minh năm 2014) ▶ Ý tưởng :
Ta sẽ tìm k bằng công thức.
▶ Thực hiện :  Áp dụng công thức : Với : 2 2 2
cde  4abf  ae  bd  fc  a 16  8k   Ta có : b 1  416  8k 1
 2 18k 1404  4k 2 k  c  4  4k     2 
5 16  8k k  784k  4  4k2 2 2  1  2 18k d 28k    e   k
Ta được nghiệm là k  2 5  f  1  2 18k
Kết luận : Ta lấy PT  
1  2PT 2 rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta sẽ sử dụng thủ thuật phân tích thành nhân tử 2 ẩn để giải quyết bài toán
▶ Lời giải : Phân tích thành nhân tử: Lấy PT 1
( )  2PT(2) ta được: 4x  y  48x  y  6  0
Bài 3: Giải Hệ Phương Trình: 3 3 2
x  y  3x 15x 18y  36  2 2 2
 x  2y  2x  6y  3  0 ▶ Ý tưởng :
Ta sẽ tìm k không bằng công thức 2 2 2
cde  4abf  ae  bd  fc mà sử dụng
mối liên hệ giữa các nghiệm ,
x y giống như cách giải phương trình vô tỷ.
▶ Thực hiện :
 Tìm nghiệm của hệ phương trình bằng CASIO ta được các bộ nghiệm là :  3 3   1 5  (x,y)   , ;     ,   2 2   2 2   3 3   a  b  a 1
 Giả sử x  ay  b suy ra 2 2     x  y  3 1 5  b  3    a  b  2 2  Khi x  y  3 thì : 3 3 2
x  y 3x 15x 18y 36  3
 2y  32y  5  2 2
2x  2y  2x  6y  3   2y 32y 5  Suy ra PT  1  3  PT2
Kết luận : Ta lấy PT  
1  3PT 2 rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta sẽ chỉ cần nói PT  
1  3PT 2 mà không phải trình bày dài dòng như trên.
▶ Lời giải : Phân tích thành nhân tử: Lấy PT 1 ( )  3PT(2) ta được:  3 3 2
x  y  3x 15x 18y  36  3 2 2
2x  2y  2x  6y  3  0 2 2
 (x  y  3)(x  xy  y  3y  9)  0  x  y  3  0 Vì : 2 2 2x  2y  2x  6y  3 2 2  y    2 2 3 4 29
 (x  xy  y  3y  9)  x 1    y    0   2  4 3  3
Lời giải chi tiết dành cho bạn đọc.
Bài 4: Giải Hệ Phương Trình: 2 2
x  y  x  y  xy  0   x   2 2 x  y   2 1  9x  0 ▶ Ý tưởng :
Ta làm tương tự bài 3.
▶ Thực hiện :
 Tìm nghiệm của hệ phương trình bằng CASIO ta được các bộ nghiệm là : (x,y)  1 ( ,2);(2 1 , )
 Mối liên hệ giữa x và y là x  3 y  Khi x  3 y thì : 2 2
x  y  x  y  xy  3  y  1y  2  x   2 2
x  y  12  9x  6y   1 y  2  Suy ra 2PT 1 ( )  PT(2) Kết luận : Ta lấy 2PT 1
( )  PT(2) rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta sẽ sử dụng thủ thuật phân tích thành nhân tử 2 ẩn để giải toán.
▶ Lời giải : Phân tích thành nhân tử: Lấy 2PT 1 ( )  PT(2) ta được: 2
(x  y  3)(x  xy  x  2y  4)  0  x  y  3 Vì : 2 2 2 x  xy  y  x  y     
 x  xy  x  y   2 2 y 2 3 7 3 10 2 4   x      y    0   2 2  4  7  7
Lời giải chi tiết dành cho bạn đọc.
Bài 5: Giải Hệ Phương Trình: xy  x  y  3  3 2 3 4
 x 12x  9x  y  6y  5 ▶ Ý tưởng :
Ta làm tương tự bài 3.
▶ Thực hiện :
 Tìm nghiệm của hệ phương trình bằng CASIO ta được các bộ nghiệm là :  3   17 1 17  (x,y)   ,    4 2    y
Mối liên hệ giữa x và y là x  1 2  y Khi x  1 thì : 2  1 xy  x  y  3    2y y4  2  3 2 3 3
4x 12x  9x  y  6y  5  y  1 2 y  y  4  2  Suy ra 3(y 1)PT 1 ( )  PT(2)
Kết luận : Ta lấy 3(y 1)PT 1
( )  PT(2) rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta làm tương tự các bài toán trước :
▶ Lời giải : Phân tích thành nhân tử: Lấy 3(y 1)PT 1 ( )  PT(2) ta được: 2 (
 x  y 1)(2x  y  2)  0
Lời giải chi tiết dành cho bạn đọc.
Bài 6: Giải Hệ Phương Trình: 3 3 x  y  91  2 2 4  x  3y 16x  9y ▶ Ý tưởng :
Ta làm tương tự bài 3.
▶ Thực hiện :
 Tìm nghiệm của hệ phương trình bằng CASIO ta được các bộ nghiệm là : (x,y)  (4,3); 3 ( ,4)
 Mối liên hệ giữa x và y là x  7  y  Khi x  7  y thì : 3 3 x  y 91 2  1 y  4y  3  2 2
4x  3y 16x  9y  7  y  4y 3  Suy ra PT 1 ( )  3PT(2)  0 Kết luận : Ta lấy PT 1
( )  3PT(2) rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta làm tương tự các bài toán trước :
▶ Cách 1 : Hàm đặc trưng: Lấy PT 1 ( )  3PT(2) ta được: x  x 
x    y3    y2 3 2 12 48 7 12 7  487  y
Xét hàm đặc trưng: f t  t 
t  t  f't  t  2 3 2 12 48 3 4  0
Lời giải chi tiết dành cho bạn đọc.
▶ Cách 2 : Phân tích thành nhân tử: Lấy PT 1 ( )  3PT(2) ta được: 3 2 3 2
x 12x  48x  (7  y) 12(7  y)  48(7  y)  x  y  7 2 2
x  xy  y  5x  2y 13  0 2 2         x  y   y 5 y 3 7   x    3    0     2 2 2 2       
Lời giải chi tiết dành cho bạn đọc.
Bài 7: Giải Hệ Phương Trình: 2 2 3
 x  xy  9x  y  9y  3 2 2  x  x y  20x  20y ▶ Ý tưởng :
Ta làm tương tự bài 3.
▶ Thực hiện :
 Tìm nghiệm của hệ phương trình bằng CASIO ta được các bộ nghiệm là : (x,y)  (0,0);(2, 1  )
 Mối liên hệ giữa x và y là x  2  y  Khi x  2  y thì : 2 3  x  xy    2
9x  y  9y  9yy   1  3 2x    2xy20x20y  2  0yy   1 y   1  Suy ra 20(y 1)PT 1 ( )  9PT(2)  0
Kết luận : Ta lấy 20(y 1)PT 1
( )  9PT(2) rồi phân tích thành nhân tử
▶ Phân tích hướng giải:
Ta phải làm thêm một hệ phương trình nữa:
▶ Cách 1 : Phân tích thành nhân tử: Lấy 20(y 1)PT 1 ( )  9PT(2) ta được: 2 2 (x  2y) 18
( x 10y 15xy  60x  80y)  0 Lấy 8PT 1 ( )  PT 3 ( ) ta được: 8 2 2
3x  xy  9x  y  9y   2 2
18x 10y 15xy  60x  80y  0
 2x  y  43x  2y  0
Lời giải chi tiết dành cho bạn đọc.
▶ Cách 2 : Phân tích thành nhân tử:
Lấy 42x  y  5PT 1 ( )  9PT(2) ta được:
2y  x3x2y2x y 4  0
Lời giải chi tiết dành cho bạn đọc.
THỦ THUẬT 8 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
TÍNH NGUYÊN HÀM, TÍCH PHÂN
Bài 1: Tính Tích Phân: 3 2 x dx I    2 x 2 2 1
▶ Ý tưởng : 2 x a b c d
Ta cần viết dưới dạng: f x       với x  2     1 x 2 1 x 1 x 2 2 1 x 1 a,b,c,d . Khi đó ta sẽ tìm , a , b , c d bằng lim
▶ Thực hiện :
 Ta lần lượt tìm lim của các biểu thức sau : 
a  lim f xx  2 1 1   x 1  4          a b lim f x  x   1  x    x  1 2 1 1   4   
c  lim f xx  2 1 1   x 1  4         c d lim f x  x   1    x    x  1 2 1 1   4  Kết luận : Ta được : 2 x 1 1 1 1      x  2 2     1 4x 2 1 4x  1 4x 2 1 4x  1
▶ Phân tích hướng giải:
Công việc của chúng ta đơn giản rồi. Chúng ta sẽ tách như trên và tính tích phân từng phần
▶ Lời giải : Tích phân tổng: Ta có : 3 3 2 x dx   1 1 1 1 I       d  x   2 2 x        1 4 x 1 4 x 1 4 x 1 4 x 1 2 
 2  2    2   3 1  1 1  1 3 7    ln x 1   ln x 1  ln    4  x 1 x 1  4 2 48 2
Bài 2: Tính Tích Phân:  3 tan xdx I   cosx22 0
(đề thi thử Đại Học lần 2 THPT Kim Thành 2 – Hải Dương năm 2013) ▶ Ý tưởng :
Đặt t  cosx thì dt  sin xdx . Đổi cận ta được:  3 1 tan xdx dt I     2 cosx  2 t t  2 0  2 1   2
Ta cần viết dưới dạng :   1 a b c f t    
tt  22 t  22 t  2 t
▶ Thực hiện :
 Ta lần lượt tìm lim của các biểu thức sau : 
a  lim f tt  22 1    t 2  2     a  b  lim  f t  t  2 1   t    t 22 2   4    c  lim f t 1 t   t0 4 Kết luận : Ta được : 1 1 1 1   
tt  22 4t 4t  2 2t  22
▶ Phân tích hướng giải:
Ta sẽ trình bày như sau :
▶ Lời giải : Tích phân tổng:
Ta đặt t  cosx thì dt  sin xdx . Khi đó :  3 1 1 tan xdx dt   1 1 1 I       dt    2 cosx  2 t t 2  4t 4 t  2 2 t  2   0  2       2 1 1  2 2 1  1 1 1  1 5 1
  ln t  ln t  2    ln   4 4 2  t 2   1 4 3 30  2
Bài 3: Tính Tích Phân:  5 2 1 x dx I   x 2 5  1 1 x 
▶ Ý tưởng :  5 2 1 x  32 dx 1 1 tdt Đặt 5 4 t  x  dt  5x x d . Vậy: I     x 2 2 5 5 1  x t 1 t 1  1   1  t a b c Đặt f t   
 với a,b,c . Ta sẽ đi tìm a,b,c
t1 t2 1 t2 1 t t
▶ Thực hiện :
 Ta lần lượt tìm lim của các biểu thức sau : 
a  lim f t1 t2  2   t 1      b  lim  f t a  1 t   t    1 t 1 2 1     c  lim f tt 1  t0  Kết luận : Ta được : 1  t 2 1 1     t1 t2 1 t2 1 t t
▶ Phân tích hướng giải:
Ta sẽ trình bày như sau :
▶ Lời giải : Tích phân tổng: Ta đặt 5 4 t  x  dt  5x x d . Khi đó :  5 2 1 x  32 dx    1 1 t 32 dt 1 2 1 1 I            x dt       1 x 2 5 t1 t2 5  1 t2 5 1 t t 1 1 1  32 1  2  1 64 31   ln 1 t  ln t  ln    5  t 1  5 33 165 1
Bài 4: Tính Tích Phân: 5 2 x  33 I  x d  3 x  3 x 1 x 1 4    2   ▶ Ý tưởng : Đặt : 2 x  33 a b c d e f f(x)        x  3 x  2 3 1 x   1
x 33 x 32 x 3 x  2 1 x 1 x 1
▶ Thực hiện :
 Ta lần lượt tìm lim của các biểu thức sau : 
a  lim f xx  3 3 3    x3 2          a b lim f x   9 x  32  x3    x 33   4       limfx a b c   x  3  2   x3  x 33 x 32        
d  lim f xx  2 1  2 x 1       e     d lim f x  x   15 1  x 1     x 2 1   8   
f  lim f xx   1 1   x 1  8 Kết luận : Ta được : 2 x  33 3  9 2 2 15 1       x 33 x  2 1 x   1 2x  33 4x  32 x  3 x  2 1 8x   1 8x   1
▶ Phân tích hướng giải:
Ta sẽ trình bày như sau :
▶ Lời giải : Tích phân tổng: Ta có : 5 2 x  33 I  dx  3 2 x  3 x 1 x 1 4       5   3  9 2 2 15 1        dx 
 2x33 4x32 2 x  3 x 1 8 x 1 8 x 1  4        5   3 9 2 15 1     ln x    ln x   ln x    4  x  3 2 3 1 1 2 4x  3 x 1 8 8   4 15 7 1 35  ln 2  ln3  ln5  8 4 8 8 4
Bài 5: Tính Tích Phân: 3 1 I  dx  x1 x 1 2  2  2  ▶ Ý tưởng : Đặt : 1 a b c f(x)     x  2 1 x   1 x  2 2 2 1 x 1 x 1
▶ Thực hiện :
 Ta lần lượt tìm lim của các biểu thức sau :
a  limfxx  2 1 1   x 1  2    a  b  limfx  x   1    x    x  1 2 1 1   2 
 Ta sẽ tìm c như sau : Xét x 1000 thì :   1 a b x 2 c      x 1  500  2 2    x   1 
 2x  1 x 1 x1 2  Kết luận : Ta được : 1 1 1 x    x  2 1  2 x   1 2x  2 1 2x   1 2 2 x   1
▶ Phân tích hướng giải:
Ta sẽ trình bày như sau :
▶ Lời giải : Tích phân tổng: Ta có : 3 3   1 1 1 x I  dx     d  x   x  2 1  2 x   1  2x  2 1 2x   1 2   2x 1  2 2  3  1 1 1  ln 2 1 2              x   ln|x 1| ln|x 1| 2 1 2 4 4 4  2
Bài 6: Tính Tích Phân: 1 3 2 x  2x  x 1 I    dx 2 x   1  2 x  2x  3 0  ▶ Ý tưởng : Đặt : 3 2 x  2x  x 1 a b f(x)     2 x   1  2 x  2x  3 2 2 x 1 x  2x  3
▶ Thực hiện :  Ta đã biết i , 1
  2i lần lượt là nghiệm của 2 x 1 0 , 2 x  2x  3  0
 Ta lần lượt tìm lim của các biểu thức sau : a  limfx 2 x   1  0  ,25  0,25i  xi  b  lim f x 2
x  2x  3 11,060660172i  x 1   2i  1 1 1   x a    i   4 4 4   3 2 3  x   1 3x  7 b 1 i 1   4 4 4 Kết luận : Ta được : 3 2 x  2x  x 1 x 1 3x  7    2 x   1  2 x  2x  3 4 2 x   1 4 2 x  2x  3
▶ Phân tích hướng giải:
Ta sẽ trình bày như sau :
▶ Lời giải : Tích phân tổng: Ta có : 1 1 3 2 x    2x  x 1 x 1 3x  7 I    dx    d  x  2 x   1  2 x  2x  3  4   2 x   1 4 2 x  2x  3  0 0  1  1     ln 2 x   1 3  arctan x  ln 2 x  x   2 2 1 2 3  arctan  x   1      8 4 8 2 2     0  ln 2 2 2 2     arctan 2  arctan 16 2 2 2 2
THỦ THUẬT 9 : THỦ THUẬT SỬ DỤNG CASIO ĐỂ
GIẢI BẤT ĐẲNG THỨC
Bài 1: Cho a,b,c  0 và a  b  c  3 . Tìm GTLN của: 2 2 2 4a 1 4b 1 4c 1 P    3 3 3 a 1 b 1 c 1
▶ Ý tưởng : 2 4a 1 Ta cần tìm k,m sao cho:
 ka  m với mọi a  0. 3 a 1
Dấu bằng khi và chỉ khi a  a 1. 0
Để tổng quát vấn đề, ta cần tìm k,m sao cho
f(x)  mg(x)  k hoặc f(x)  mg(x)  k với mọi x
Khi đó k, m sẽ là nghiệm của hệ phương trình sau : f x  kg x   m 0   0   f'  x  k'g x 0   0 
Với x  x là điểm rơi. 0
▶ Thực hiện :
 Ta sẽ tìm k một cách nhanh chóng bằng cách : 2 d  4x 1 1 k     3 dx  x 1 4  x 1
 Và m sẽ được tìm bằng cách : 2 4a 1 9 0 m   ka  3 0 a 1 4 0
Với a  1 là điểm rơi của bài toán 0 2    4a 1 a 9
Ta sẽ phân tích thành nhân tử  để chứng minh nó 3 a 1 4
không dương với mọi a  0 . Kết luận : Ta luôn có: 2 2 2 4a 1 a  9 (a 11a  5)(a 1)     0 a   0 3 a 1 4 4 3 a   1
▶ Phân tích hướng giải:
Ta sẽ làm tương tự với ,
b c rồi cộng lại là ra đáp án :
▶ Lời giải : Bất đẳng thức: Ta có : 2 2 2 2 4a 1 a  9 (a 11a  5)(a 1) 4a 1 a  9     a   0   3 a 1 4 4 3 a   3 1 a 1 4 2 4b 1 b  9 2 4c 1 c  9
Chứng minh tương tự ta có  và  , suy ra: 3 b 1 4 3 c 1 4 2 2 2 4a 1 4b 1 4c 1 a  9 b  9 c  9 15 P        . 3 3 3 a 1 b 1 c 1 4 4 4 2 15 Vậy    m P  ax khi và chỉ khi a b c 1 2
Bài 2: Cho a,b,c  0 . Chứng minh rằng: 3 3 3 3 3 3 2a  b 2b  c 2c  a a  b  c    2 2 2 2 2 2 2a  ab  b 2b  bc  c 2c  ca  a 4
▶ Ý tưởng : 3 3 3 2a  b 2x 1 Ta cần tìm k,m sao cho:  ka  mb   kx  m với 2 2 2 2a  b a  b 2x  x 1 mọi a  xb .
▶ Thực hiện :
 Ta sẽ tìm k,m bằng cách : 3 3 d  2x 1  19 2x 1 15 0 k      m   kx    2  2 0 dx 2  x  x 1 16 2  x  x 1 16 0 0 x 1  3 3    2a b 19a 15b
Ta sẽ phân tích thành nhân tử  2 2 2a  ab  b 16 Kết luận : Ta luôn có: 2a  b 19a 15b 6a  ba  b2 3 3     0 a  ,b  0 2 2 2a  ab  b 16 16 2 2 2a  ab  b  3 3 2a  b 19a 15b   2 2 2a  ab  b 16
▶ Phân tích hướng giải:
Ta sẽ làm tương tự với ,
b c rồi cộng lại là ra đáp án :
▶ Lời giải : Bất đẳng thức: Ta có : 2a  b 19a 15b 6a  ba  b2 3 3     0 a  ,b  0 2 2 2a  ab  b 16 16 2 2 2a  ab  b  3 3 2a  b 19a 15b   2 2 2a  ab  b 16
Chứng minh tương tự ta có : 3 3 2b  c 19b 15c 3 3    2c a 19c 15a và  2 2 2b  bc  c 16 2 2 2c  ca  a 16 Suy ra: 3 3 3 3 3 3 2a  b 2b  c 2c  a a  b  c    . 2 2 2 2 2 2 2a  ab  b 2b  bc  c 2c  ca  a 4
Bài 3: Cho a,b,c  0 thỏa mãn abc 1. Tim GTNN của: 2 2 2 a 1 b 1 c 1 P    2 2 2 a(a 1) b(b 1) c(c 1) ▶ Ý tưởng :
Ta thấy lnabc  lna  ln b  ln c nên ta tìm k,m sao cho : 2 a 1  klna m 2 a(a 1)
Dấu đẳng thức khi a 1.
▶ Thực hiện :  1 1
Tương tự bài toán trước, ta tìm được k   và m  . 2 2 2   a 1 1 1 Ta cần chứng minh f(a)   ln a   0 a   0 2 a(a 1) 2 2 2 a 1 1 1
Kết luận : Ta sẽ chứng minh f(a)   ln a   0 a   0 2 a(a 1) 2 2
▶ Phân tích hướng giải:
Ta chứng minh bằng đạo hàm là cách tốt nhất:
▶ Lời giải : Bất đẳng thức: Ta có bổ đề : 2 a 1 1 1 f(a)   ln a   0 a   0 2 a(a 1) 2 2 Chứng minh : a  a  a  a   1  3 2 3 2 a  2a  7a  2 3 1 1  f'(a)     a  3 1 a 2a 2a  3 2 2 1 a
Vậy f'(a)  0  a 1 và f'(a) đổi dấu từ âm sang dương khi đi qua 1 Suy ra f(a)  f 1 ( )  0 (đpcm).
Chứng minh tương tự, suy ra: 2 2 2 a 1 b 1 c 1 3 1 P   
  lna  ln b  ln c 3 lnabc 3    2 2 2 a(a 1) b(b 1) c(c 1) 2 2 2 2 2 3 Vậy P   a  b  c 1 min 2
Bài 4: Cho a,b,c  0 thỏa mãn a  b  c  3 . Chứng minh rằng: 2 2 2 1 1 1 a  b  c    2 2 2 a b c
▶ Ý tưởng : 1 Ta cần tìm k,m sao cho 2 a   ka  m 2 a
▶ Thực hiện :
 Tương tự bài toán trước, ta tìm được k  4,m  4  .  1 Ta cần chứng minh 2 f(a)  a   4a  4 2 a a  2a 1 a 1 2 1   2 2  Tuy nhiên a   4a  4   0 . 2 2 a a
 BĐT này chỉ đúng nếu 0  a 1 2
Kết luận : Ta sẽ chia các trường hợp để áp dụng : 1 a 2a 1a 2 2 1 2 a   4a  4   0 2 2 a a
▶ Phân tích hướng giải:
Ta sẽ làm như sau :
▶ Lời giải : Bất đẳng thức:
Không mất tính tổng quát giả sử a  b  c
TH1: a  b  c 1 2 thì vô lý
TH2: a  b 1 2  c thì vô lý 2  2
TH3: a 1 2  b  c thì 2c  b  c  3  a  2  2 suy ra c  . Còn 2
b  b  c  3 2  2  2
Dễ thấy f(a) đồng biến trên (0,) nên ta có:   
f(a)  f(b)  f(c)  f( )  f    2 2 80 3 2 2  f    10 2  0   2 9   a  2a 1 a 1 2 1   2 2
TH4: 1 2  a  b  c thì a   4a  4   0 luôn 2 2 a a đúng
Vậy f(a)  f(b)  f(c)  4(a  b  c) 12  0
Tóm lại BĐT được chứng minh
Bài 5: Cho x, y,z  0 thỏa mãn 2x  4y  7z  2xyz . Tìm GTNN của: P  x  y  z ▶ Ý tưởng :
Nếu bạn đọc đã từng xem đáp án chính thức, lời giải của bài toán này rất
khó để thực hiện. Tuy nhiên, chúng ta có cách khác dễ dàng hơn rất nhiều
chỉ cần sử dụng máy tính CASIO.
Ta sẽ đi tìm điểm rơi của bài toán. Cách tìm điểm rơi bằng phương pháp nhân tử Lagrange.
▶ Thực hiện :
 Xét hàm f(x,y,z)  x  y  z  k(2x  4y  7z  2xyz). Ta có hệ:  1  7k xy   2k   1 k(2  2yz)  0 1  2  k  yz   1 k(4  2xz)  0  2k    1  k(7  2yx)  0 1  4k   zx  2  x  4y  7z  2xyz  k  2 4 7     2 yz xz xy 4k 8k 14k 1     2  k  1  2k 1  4k 1  7k 8  15  5  Từ đó ta được xy 
, yz  5,zx 6 hay (x, y,z)  3  , ,2 2  2   5 
Kết luận : Điểm rơi của bài toán là (x, y,z)  3  , ,2  2 
▶ Phân tích hướng giải:
Ta sẽ áp dụng bất đẳng thức Cauchy với điểm rơi có sẵn :
▶ Lời giải : Phương pháp nhân tử Lagrange: Ta có :  7 7 105   5 5 15   3 3 15  15 P   x  y     x  z     y  z    12 10 8  xy  12 8 2xz  10 8 4  yz 4  7 7 105 5 5 15 3 3 15 15 15 3  33 x  y   3 x  z   33 y  z    12 10 8xy 12 8 2xz 10 8 4yz 4 2 15  5  Vậy P   (x,y,z)  3  , ,2 min  2  2 