lOMoARcPSD|45315597 Kiểm Tra
Môn: Xác suất và thống kê toán học Thời gian: 45 phút
Câu 1. Một thùng trái cây gồm 100 quả trong đó có 70 quả cam. Xác suất để lấy được một quả cam bằng a) 0, 03 b) 0, 3 c) 0, 07 d) 0, 7
Câu 2. Cho A, B là hai biến cố. Biết rằng P(A) = 0, 5, p(B) = 0, 4 và P(AB) = 0, 2. Tính P(A + B)? a) 0, 9 b) 0, 7 c) 0, 5 d) 0, 4
Câu 3. Công thức xác suất nào dưới đây không chính xác:
a) P( A + B) = P( A) + P(B) − P( AB)
b) P( AB) = P( A).P(B| A) với P( A) > 0 c) P( A) = 1 − P( A) d) P( A + B) = P( A) + P(B)
Câu 4. Một lớp sinh viên học toán gồm 60 sinh viên trong đó có 15 sinh viên nữ. Chọn ngẫu nhiên 3 bạn
sinh viên biết rằng khả năng được chọn của mỗi bạn là như nhau. Xác suất để chọn được đúng 2 bạn nữ
trong 3 bạn được chọn bằng C2 + C1 A2 + A1 C2 C1 A2 A1 15 45 15 45 15 45 15 45 a) b) c) d) C3 A3 C3 A3 60 60 60 60
Câu 5. Cho A, B là hai biến cố của cùng một phép thử ngẫu nhiên. Công thức nào sau đây sai:
a) P(B) = P( A)P(B| A) + P( A)P(B| A) b) P(B A) = 1 − P(B A) c) P(B A) = P(B) − P(B A)
d) P( A) = P(B)P( A|B) + P(B)P( A|B)
Câu 6. Trong một ký túc xá của trường đại học có tỉ lệ thích xem đá đóng là 60%. Chọn ngẫu nhiên độc
lập 10 bạn trong ký túc. Xác suất để trong 10 bạn có đúng 5 bạn thích xem đá bóng bằng a) C5 (0, 6)5.(0, 4)5 b) C5 ((0, 6)5 + (0, 4)5) 10 10 c) (0, 6)5 + (0, 4)5 d) (0, 6)5.(0, 4)5
Câu 7. Lô 1 có hai loại sản phẩm là chính phẩm và phế phẩm. Lô 2 gồm 6 phế phẩm và 193 chính phẩm.
Chọn ngẫu nhiên một sản phẩm ở lô 1 và đưa vào lô 2. Từ lô 2 lấy ngẫu nhiên một sản phẩm. Xác suất
để sản phẩm lấy ra từ lô 2 là chính phẩm biết rằng sản phẩm đưa vào lô 2 từ lô 1 là phế phẩm bằng: 193 193 7 7 a) b) c) d) 200 199 200 199
Câu 8. Trọng lượng ( đơn vị: kg) của một bao gạo là một biến ngẫu nhiên X có phân phối chuẩn. Biết
rằng trọng lượng trung bình là 50 kg và độ lệch chuẩn về trọng lượng là 0,4 kg. Khi đó EX và DX bằng a) EX=50, DX=0,4 b) EX=50, DX=0,16 c) EX=0,4, DX=50 d) EX=0,4, DX=2500 Trang 1
Downloaded by H?u mai (maihauhaumai@gmail.com) lOMoARcPSD|45315597
Câu 9. Cho X là biến ngẫu nhiên liên tục có phân phối chuẩn N(4; 0, 25). Ta ký hiệu Φ(x) là hàm phân
phối chuẩn tắc và µ, σ lần lượt là giá trị trung bình và độ lệch chuẩn của X. Khẳng định nào dưới đây không đúng. b − 4! a − 4!
a) µ = 4, P(a < X < b) = Φ − Φ σ σ a − µ !
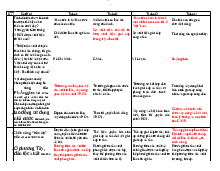
b)σ = 0, 5, P(X ≥ a) = 1 − Φ 0, 5
c) µ = 4, P(a ≤ X ≤ b) = Φ(b) − Φ(a) b − 4!
d) σ2 = 0, 25, P(X < b) = Φ 0, 5
Câu 10. Cho X là biến ngẫu nhiên rời rạc có bảng phân phối xác suất như sau X=x −2 1 1, 5 4 . P(X=x) 0, 3 0, 2 0, 4 0, 1
Gọi F(x) là hàm phân phối xác suất của X. Khi đó giá trị của F(1) bằng a) 0, 5 b) 0, 2 c) 0, 3 d) 0
Câu 11. Cho X là biến ngẫu nhiên liên tục có hàm phân phối xác suất được cho bởi công thức    0 nếu x ≤ 1  F(x) =  .  1   1 − nếu x > 1  x
Khi đó P(1 ≤ X ≤ 3) bằng 2 1 a) 0 b) c) không xác định d) 3 3
Câu 12. Cho X là biến ngẫu nhiên liên tục có hàm phân phối xác suất được cho bởi công thức   0 nếu x ≤ 1      !   1 F(x) = k 1 −
nếu 1 < x ≤ 2 (với k là tham số thực).    x       1 nếu x > 2 Giá trị của k bằng 1 a)k = b)k = 2 c)k = 0 d)k = −2 2 Trang 2
Downloaded by H?u mai (maihauhaumai@gmail.com) lOMoARcPSD|45315597
Câu 13. Cho X là biến ngẫu nhiên liên tục có hàm mật độ xác suất được cho bởi công thức   0 nếu x < [0, 2]   f (x) =  .  x3    nếu x ∈ [0, 2]  4
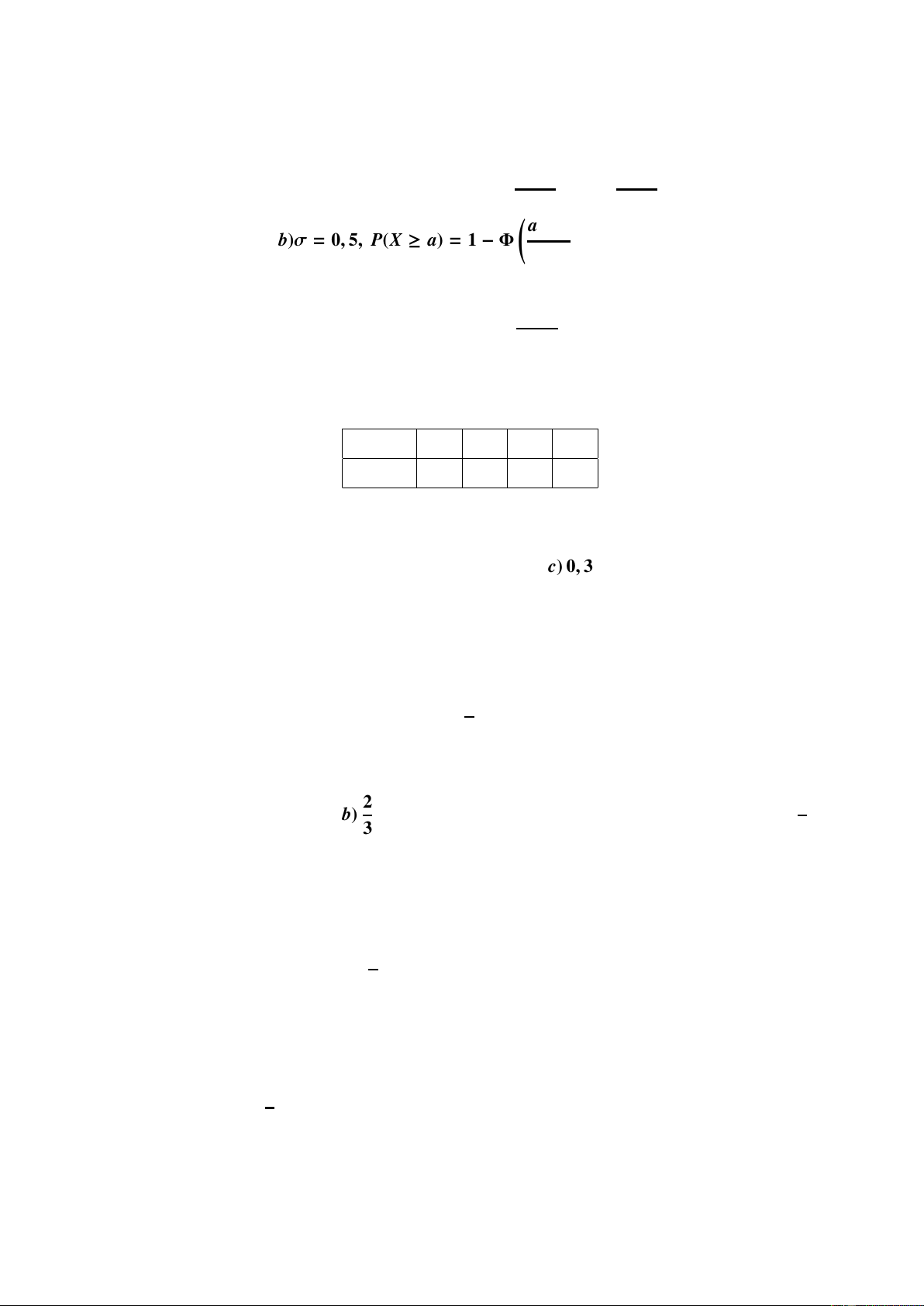
Hàm phân phối xác suất F(x) của X được cho bởi công thức 3x2 x4 a) F(x) = , với mọi x ∈ R b) F(x) = , với mọi x ∈ R 4 16      0 nếu x ≤ 0 0 nếu x ≤ 0            3x2   x4 c) F(x) =  nếu 0 < x ≤ 2 d) F(x) =  nếu 0 < x ≤ 2       4  16         1 nếu   x > 2  1 nếu x > 2
Câu 14. Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau X=x -2 -1,5 0 2 3 P(X=x) 0,3 0,1 0,2 0,1 0,3 Kỳ vọng của X bằng a) 1, 5 b) − 1, 5 c) 0, 35 d) − 0, 35
Câu 15. Cho X là biến ngẫu nhiên liên tục có hàm phân phối xác suất là F(x) có đạo hàm liên tục tại
mọi x và hàm mật độ xác suất là f(x). Giả thiết thêm X có kỳ vọng hữu hạn. Công thức nào dưới đây sai: +∞ x +∞ Z Z Z a) F0(x) = f (x) với mọi x b) EX = x f (x)dx c) F(x) = f (t)d t d) EX = xF(x)dx −∞ −∞ −∞
Câu 16. Cho hàm mật độ của biến ngẫu nhiên liên tục X có dạng     a(1 − x2) nếu x ∈ [−1, 1]  f (x) = 
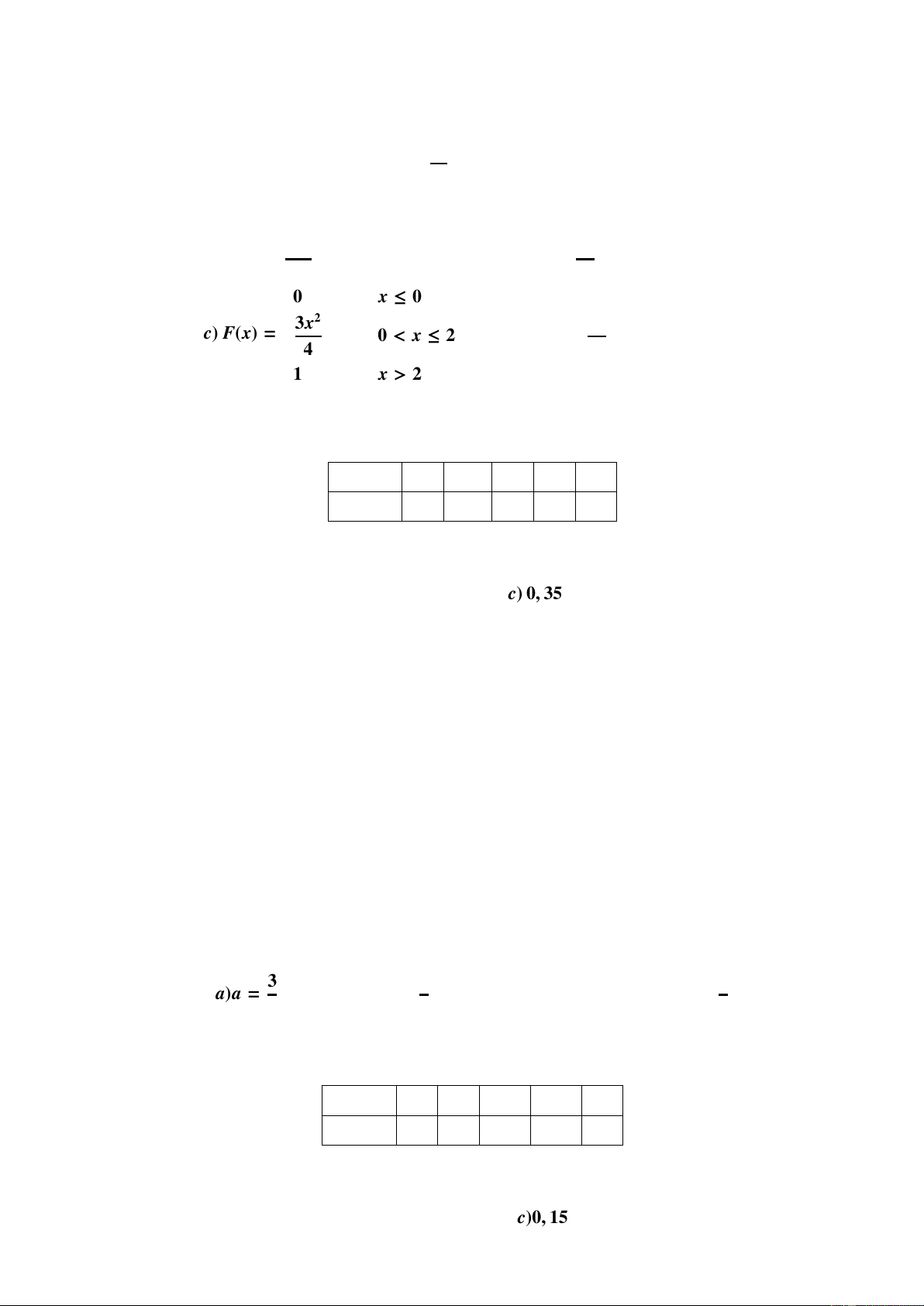
(với a là tham số thực).    0 nếu x < [−1  , 1] Chọn khẳng định đúng? 3 1 4 a)a = b)a = c)a = 2 d)a = 4 2 3
Câu 17. Cho biến ngẫu nhiên X có bảng phân phối xác suất X=x -1 2 3 4 4,5 P(X=x) 0,3 0,1 0,15 0,25 0,2
Xác suất để 2 < X < 4 bằng a)0, 25 b)0, 4 c)0, 15 d)0, 5 Trang 3
Downloaded by H?u mai (maihauhaumai@gmail.com) lOMoARcPSD|45315597
Câu 18. Sản phẩm do máy A sản xuất gồm hai loại là chính phẩm và phế phẩm. Tỷ lệ phế phẩm của máy
A là 5%. Lấy ngẫu nhiên 12 sảnphẩm của máy A một cách độc lập. Xác suất để trong 12 sản phẩm được
lấy ra có ít nhất 2 phế phẩm là a) Xấp xỉ 0, 45964 b)0, 45964 c)0, 11836 d) Xấp xỉ 0, 11836
Câu 19. Sản phẩm của nhà máy X được sản xuất bởi hai máy I và II. Tỷ lệ đóng góp sản phẩm trong
tổng sản phẩm được sản xuất bởi nhà máy của máy I và máy II lần lượt là 55% và 45%. Tỷ lệ sản phẩm
không đạt tiêu chuẩn do máy I và máy II sản xuất lần lượt là 4% và 3%. Lấy ngẫu nhiên một sản phẩm
kiểm tra. Xác suất để lấy được sản phẩm đạt tiêu chuẩn là a)0, 97 b)0, 9645 c)0, 965 d)0, 96
Câu 20. Tiến hành gieo một quân xúc xắc n lần độc lập (n ∈ N∗) . Biết rằng xác suất để xuất hiện đúng
2 lần mặt 6 chấm là 25 . Biết rằng φ là ký hiệu của tập rỗng. Chọn khẳng định đúng trong các khẳng 216 định sau: a)n = 7 b)n = 4 c)n = 12 d)n ∈ φ
- - - - - - - - - - - - - - - - - - - HẾT - - - - - - - - - - - - - - - - - - - Trang 4
Downloaded by H?u mai (maihauhaumai@gmail.com)