lOMoAR cPSD| 45903860 APPLIED STATISTICS COURSE CODE: ENEE1006IU Lecture 14:
Chapter 8: Time series analysis and forecasting
(3 credits: 2 is for lecture, 1 is for lab-work) 1 lOMoAR cPSD| 45903860
CHAPTER 8: TIME SERIES ANALYSIS AND FORECASTING •8.1. Time series patterns •8.2. Forecast accuracy •8.3. Trend projection
•8.4. Time series decomposition 2 lOMoAR cPSD| 45903860 8.1. TIME SERIES PATTERNS
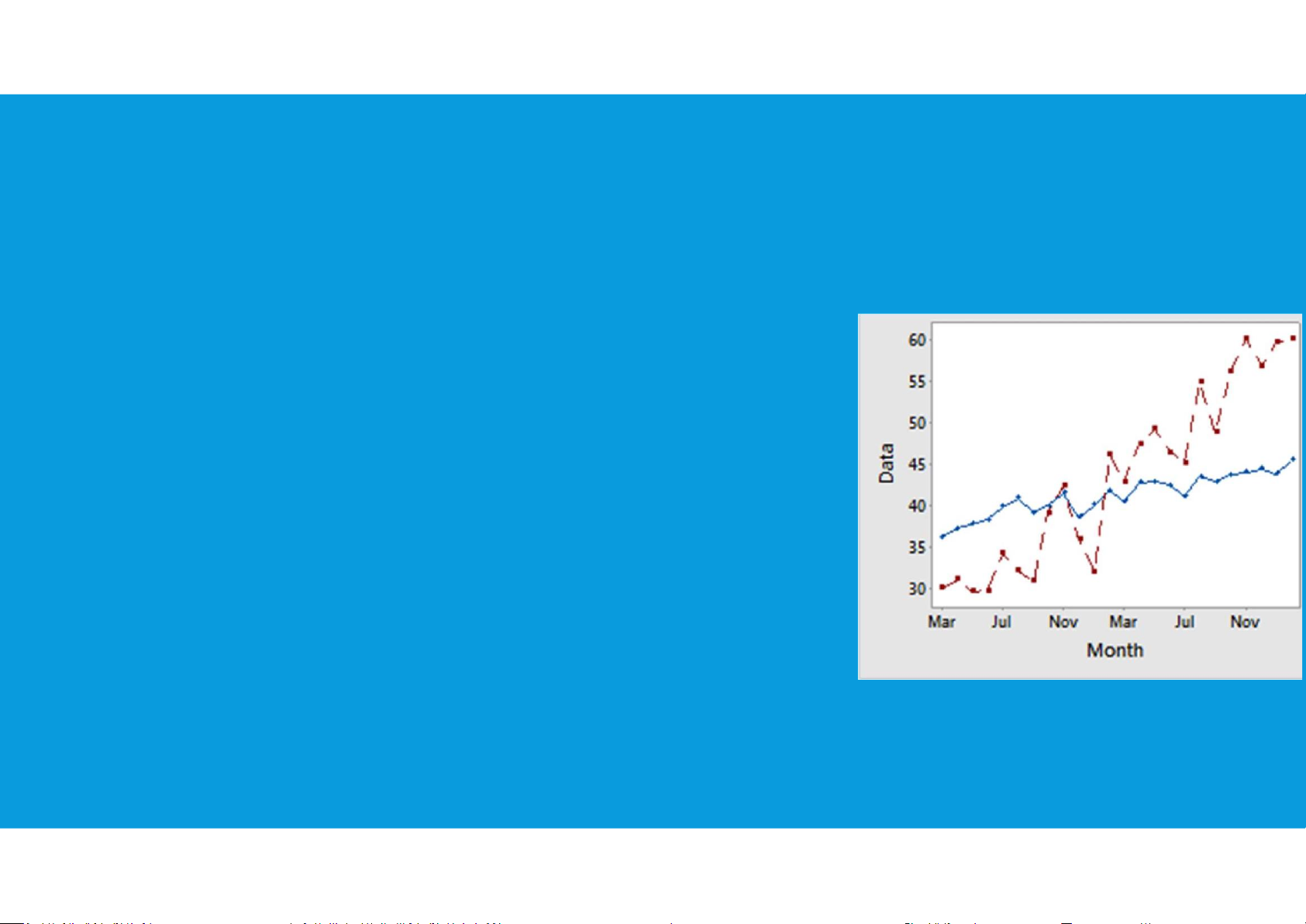
•A time series is a sequence of observations on a variable measured at successive
points in time or over successive periods of time.
•The pattern of the data is an important factor in
understanding how the time series has behaved in the past.
•To identify the underlying pattern in the data, a
useful first step is to construct a time series plot.
•A time series plot is a graphical presentation of the
relationship between time and the time series
variable; time is on the horizontal axis and the time
series values are shown on the vertical axis. 3 lOMoAR cPSD| 45903860 8.1. TIME SERIES PATTERNS 4 lOMoAR cPSD| 45903860
•Horizontal Pattern: a horizontal pattern exists when the data fluctuate around a constant mean
•Trend Pattern: a trend is usually the result of long-term factors; gradual
shifts or movements to relatively higher or lower values over a longer period of time
•Seasonal Pattern: Seasonal patterns are recognized by seeing the same
repeating patterns over successive periods of time 5 lOMoAR cPSD| 45903860 8.1. TIME SERIES PATTERNS
•Trend and Seasonal Pattern: in such
cases we need to use a forecasting
method that has the capability to deal
with both trend and seasonality
•Cyclical Pattern: a cyclical pattern exists
if the time series plot shows an
alternating sequence of points below
and above the trend line lasting more
than one year. cyclical effects are often 6 lOMoAR cPSD| 45903860
combined with long-term trend effects and referred to as trend-cycle effects 8.2. FORECAST ACCURACY •Principles of Forecasting:
Many types of forecasting models that differ in complexity and amount of data & way they generate forecasts:
1. Forecasts are rarely perfect
2. Forecasts are more accurate for grouped data than for individual items
3. Forecast are more accurate for shorter than longer time periods 7 lOMoAR cPSD| 45903860 TYPES OF FORECASTING METHODS
•Decide what needs to be forecast
Level of detail, units of analysis & time horizon required
•Evaluate and analyze appropriate data
Identify needed data & whether it’s available
•Select and test the forecasting model
Cost, ease of use & accuracy •Generate the forecast
•Monitor forecast accuracy over time TYPES OF FORECASTING METHODS
•Forecasting methods are classified into two groups: 8 lOMoAR cPSD| 45903860
•Qualitative methods – judgmental methods Forecasts generated subjectively by the forecaster Educated guesses •Quantitative methods – based on mathematical modeling Forecasts generated through mathematical modeling QUANTITATIVE METHODS •Time Series Models: 9 lOMoAR cPSD| 45903860
Assumes information needed to generate a forecast is contained in a time series of data
Assumes the future will follow same patterns as the past
•Causal Models or Associative Models:
Explores cause-and-effect relationships
Uses leading indicators to predict the future
Housing starts and appliance sales TIME SERIES MODELS
•Forecaster looks for data patterns as
Data = historic pattern + random variation
•Historic pattern to be forecasted:
Level (long-term average) – data fluctuates around a constant mean
Trend – data exhibits an increasing or decreasing pattern 10 lOMoAR cPSD| 45903860
Seasonality – any pattern that regularly repeats itself and is of a constant length
Cycle – patterns created by economic fluctuations
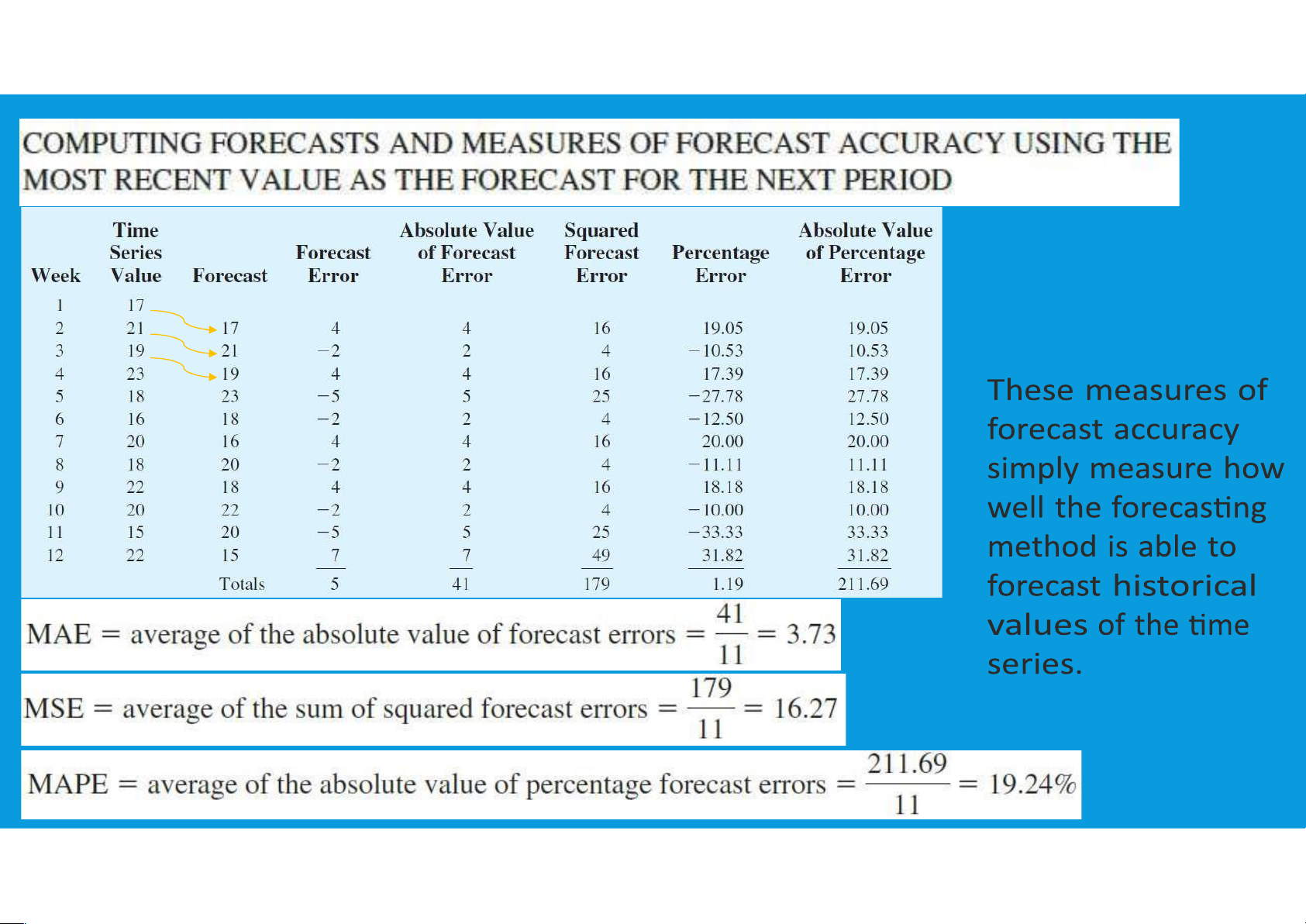
•Random Variation cannot be predicted TIME SERIES MODELS •Naive: Ft 1 At
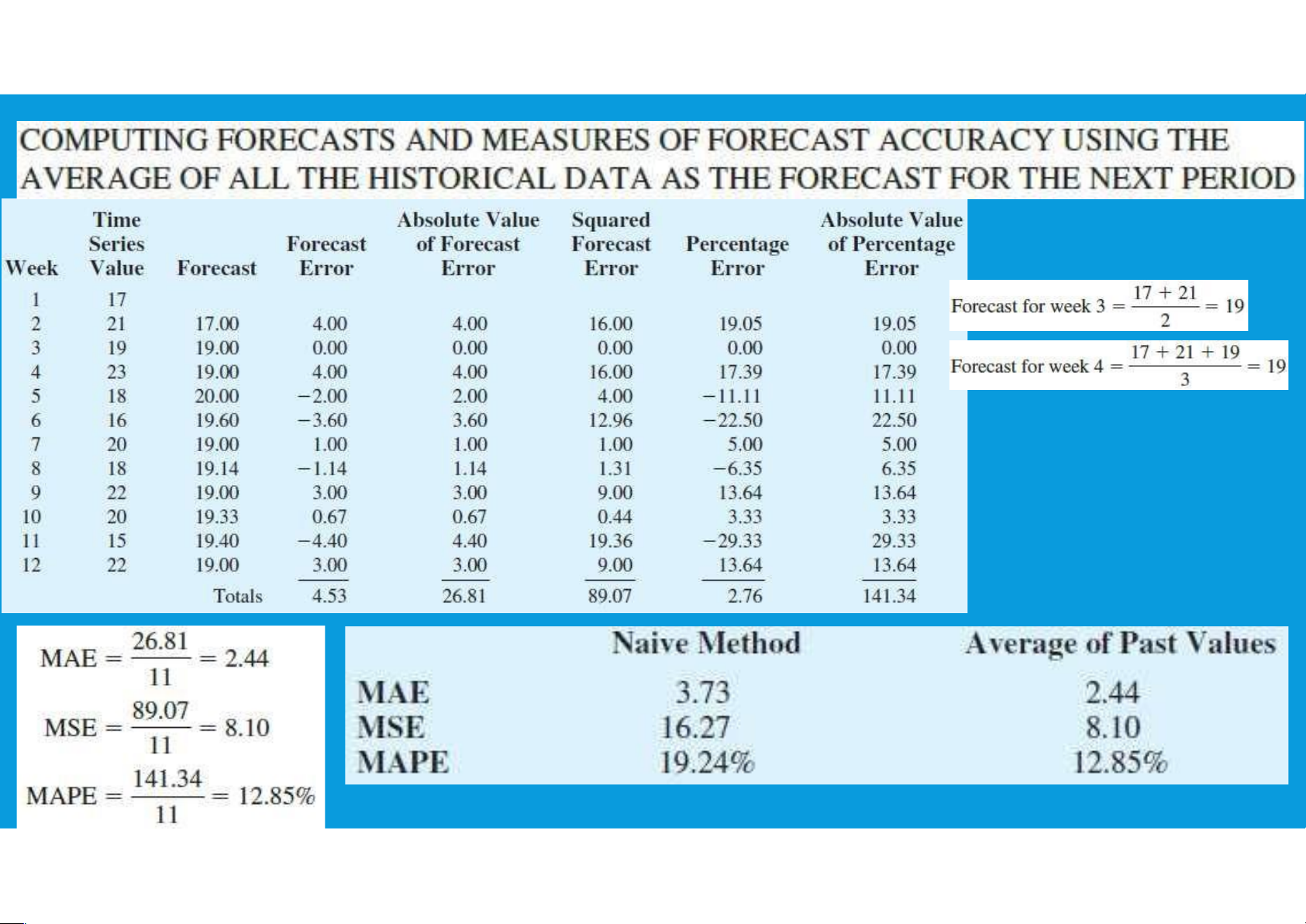
The forecast is equal to the actual value observed during the last period – good for level patterns •Simple Mean: Ft 1 At /n
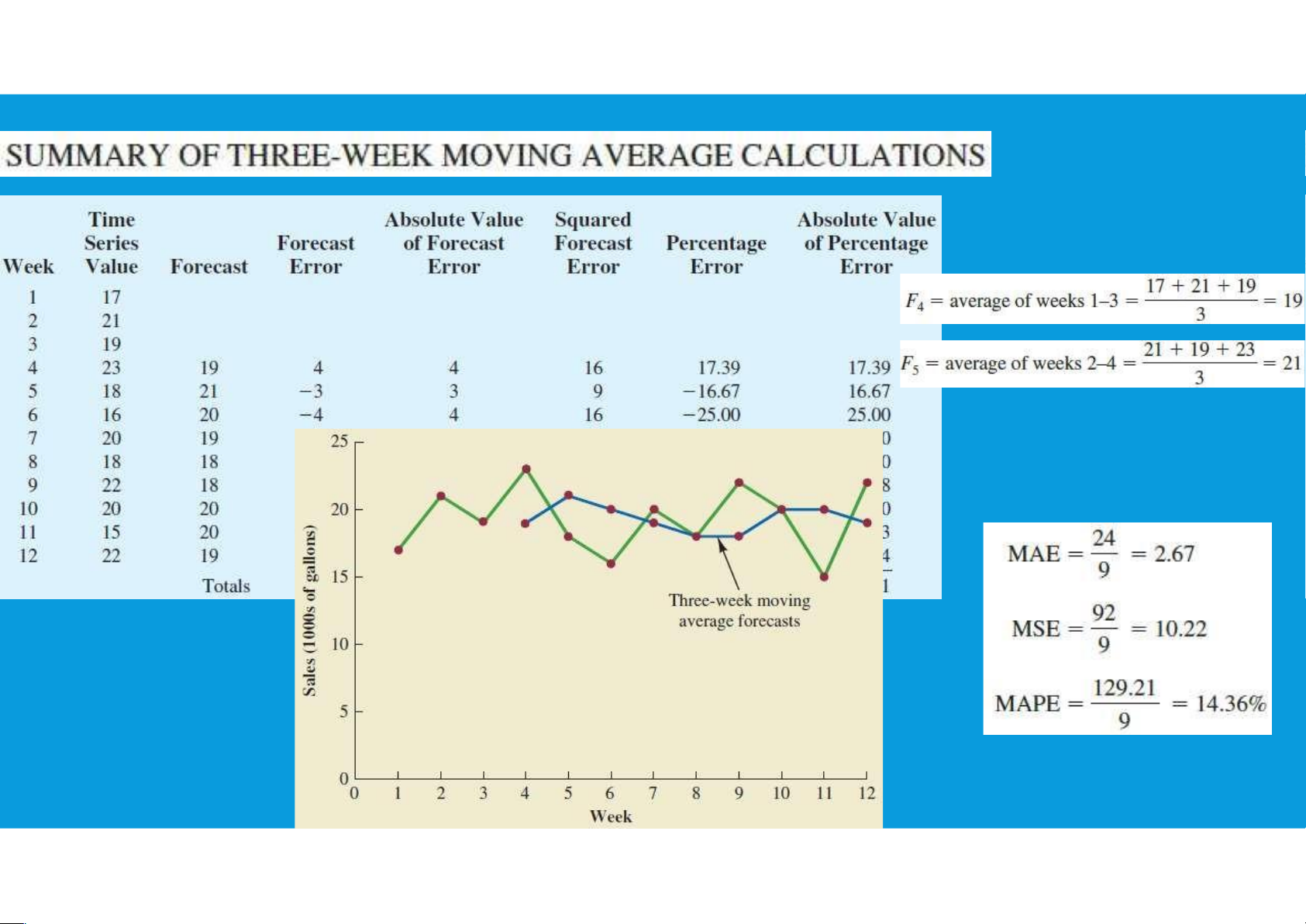
The average of all available data - good for level patterns 11 lOMoAR cPSD| 45903860 •Moving Average: Ft 1 At /n
The average value over a set time period (e.g.: the last four weeks)
Each new forecast drops the oldest data point & adds a new observation
More responsive to a trend but still lags behind actual data TIME SERIES MODELS
•Weighted Moving Average: Ft 1 CtAt
•All weights must add to 100% or 1.00
e.g. Ct =0.5, Ct-1 =0.3, Ct-2 =0.2 (weights add to 1.0) 12 lOMoAR cPSD| 45903860
•Allows emphasizing one period over others; above indicates more weight on recent data (Ct=0.5)
•Differs from the simple moving average that weighs all periods equally more responsive to trends TIME SERIES MODELS •Exponential Smoothing: Ft 1 αAt 1 α Ft
Most frequently used time series method because of ease of use and minimal amount of data needed
•Need just three pieces of data to start:
Last period’s forecast (Ft) 13 lOMoAR cPSD| 45903860
Last periods actual value (At)
Select value of smoothing coefficient, α,between 0 and 1.0
•If no last period forecast is available, average the last few periods or use naive method
•Higher α values (e.g. 0.7 or 0.8) may place too much weight on last period’s random variation MEASURING FORECAST ERROR
•Forecasts are never perfect
•Need to know how much we should rely on our chosen forecasting method •Measuring forecast error: 14 lOMoAR cPSD| 45903860 Et At Ft
•Note that over-forecasts = negative errors and under-forecasts = positive errors
MEASURING FORECASTING ACCURACY
•Mean Absolute Deviation (MAD) •Mean Square Error (MSE)
measures the total error in a forecast Penalizes larger errors without regard to sign •Tracking Signal
•Cumulative Forecast Error (CFE) Measures if your model
Measures any bias in the forecast is working MAD actual forecast n 15 lOMoAR cPSD| 45903860 CFE actual forecast MSE n actual - forecast 2 TS CFE MAD 16 lOMoAR cPSD| 45903860 17 lOMoAR cPSD| 45903860 18 lOMoAR cPSD| 45903860 19 lOMoAR cPSD| 45903860 HOMEWORKS (1) Note: Each table for each method
Compute the forecasts and measures of forecast accuracy, using: 20