Lecture 6: Chapter 4: Probability and Distribution | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ CHí Minh
Random experiments, counting rules, and assigning probabilities. Events and their probabilities. Some basic relationships of probability. Conditional probability. Bayes’ theorem 4.1. INTRODUCTION TO PROBABILITY. Random experiments. A random experiment is a process that generates well-defined experimental outcomes. On any single repetition or trial, the outcome that occurs is determined completely by chance. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Môn: Applied statistics (ENEE1006IU)
Trường: Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Applied statistics (ENEE1006IU)
Trường:
Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
lOMoAR cPSD| 45903860 APPLIED STATISTICS COURSE CODE: ENEE1006IU Lecture 6:
Chapter 4: Probability and Distribution
(3 credits: 2 is for lecture, 1 is for lab-work) 1 lOMoAR cPSD| 45903860
4.1. INTRODUCTION TO PROBABILITY
•Random experiments, counting rules, and assigning probabilities
•Events and their probabilities
•Some basic relationships of probability •Conditional probability •Bayes’ theorem
4.1. INTRODUCTION TO PROBABILITY •Random experiments: 2 lOMoAR cPSD| 45903860
A random experiment is a process that generates well-defined experimental
outcomes. On any single repetition or trial, the outcome that occurs is
determined completely by chance.
By specifying all the possible experimental outcomes, we identify the sample
space for a random experiment.
The sample space for a random experiment is the set of all experimental outcomes.
An experimental outcome is also called a sample point to identify it as an element of the sample space.
4.1. INTRODUCTION TO PROBABILITY •Random experiments: lOMoAR cPSD| 45903860
4.1. INTRODUCTION TO PROBABILITY •Counting rules: 4 lOMoAR cPSD| 45903860
Being able to identify and count the experimental outcomes is a necessary step in assigning probabilities. Three useful counting rules:
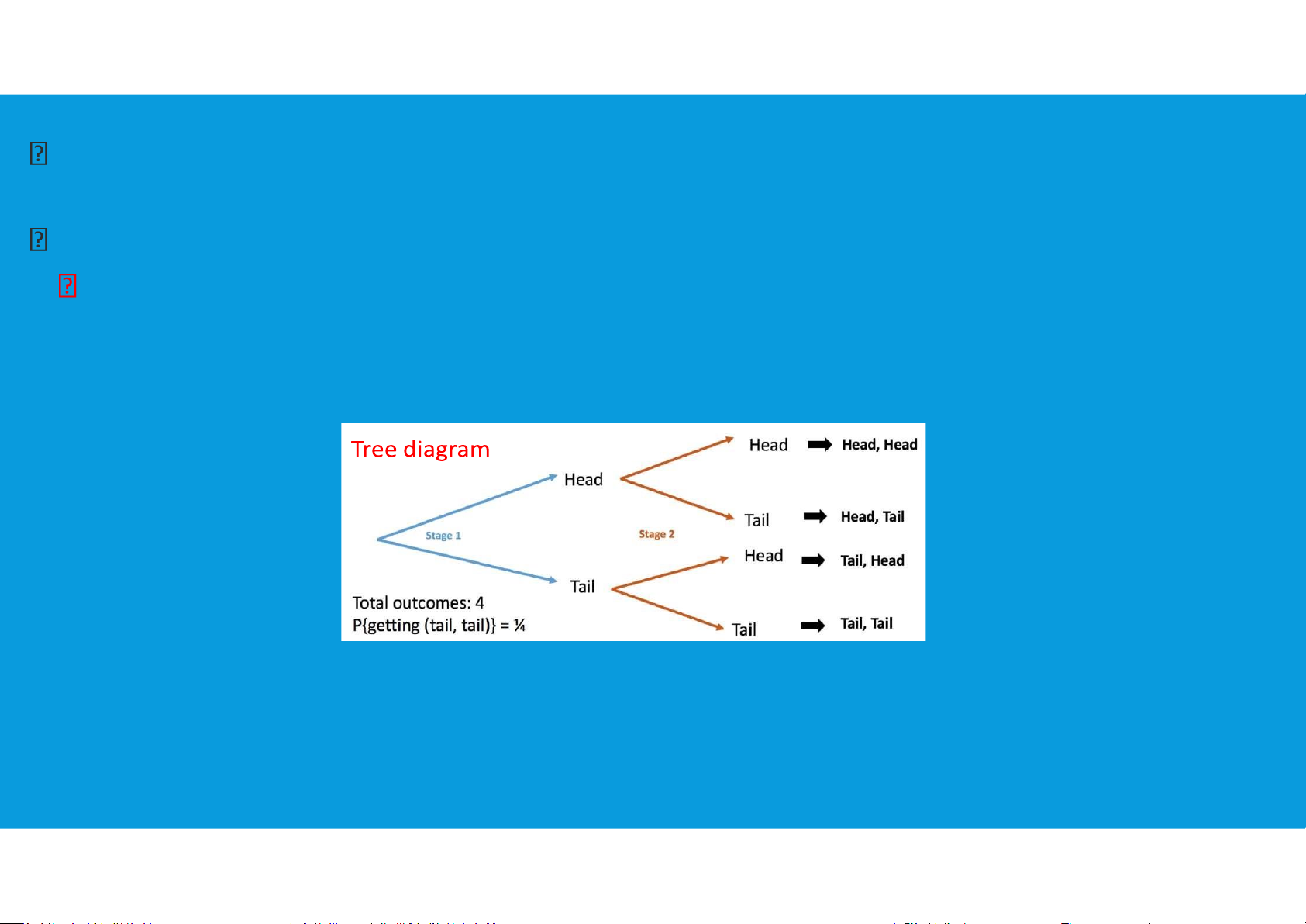
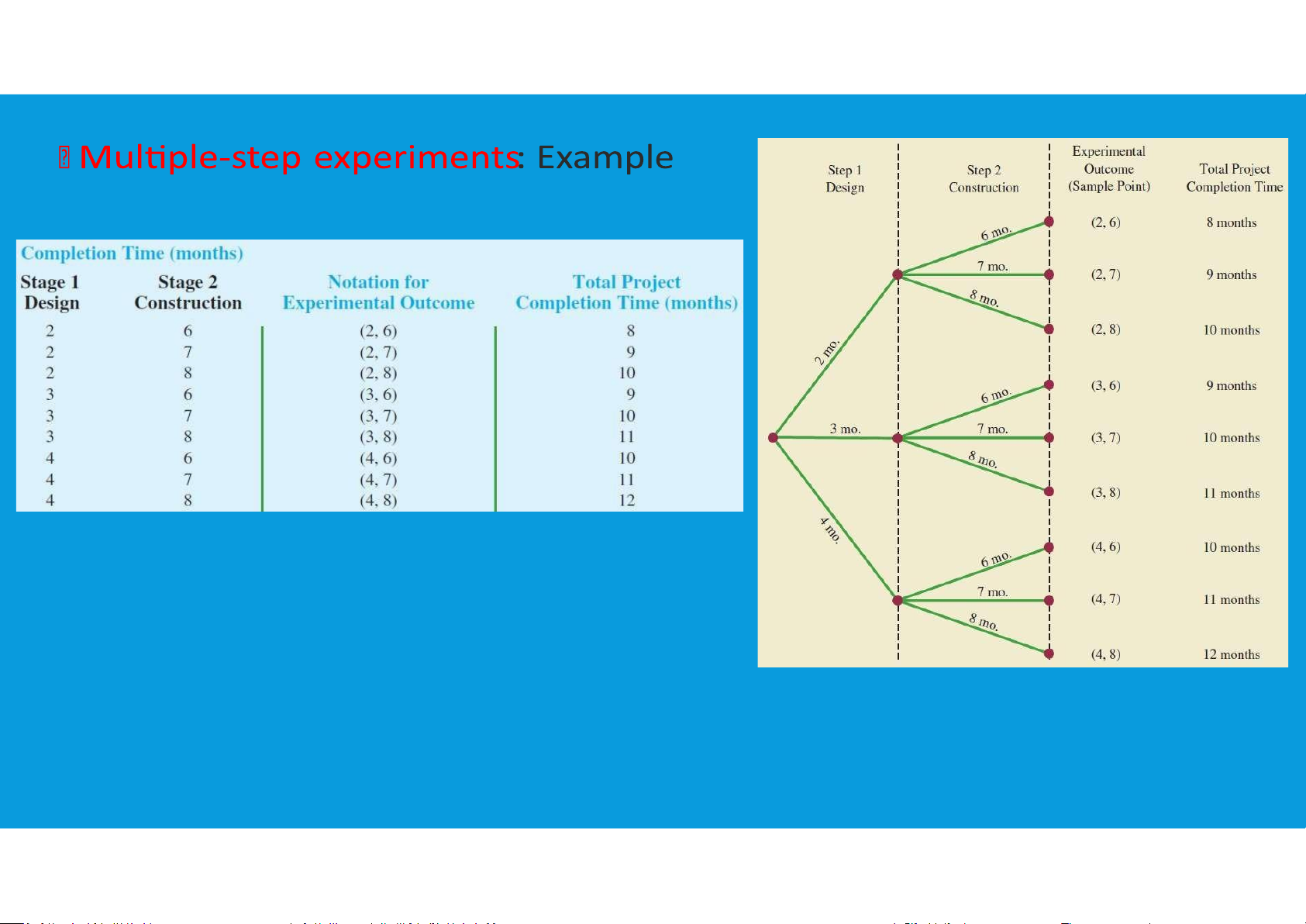
Multiple-step experiments: If an experiment can be described as a sequence of k
steps with n1 possible outcomes on the first step, n2 possible outcomes on the
second step, and so on, then the total number of experimental outcomes is given by (n1)*(n2)* . . . *(nk).
4.1. INTRODUCTION TO PROBABILITY •Counting rules: lOMoAR cPSD| 45903860
4.1. INTRODUCTION TO PROBABILITY 6 lOMoAR cPSD| 45903860 •Counting rules:
Combinations: allows one to count the number of experimental outcomes when the
experiment involves selecting n objects from a set of N objects.
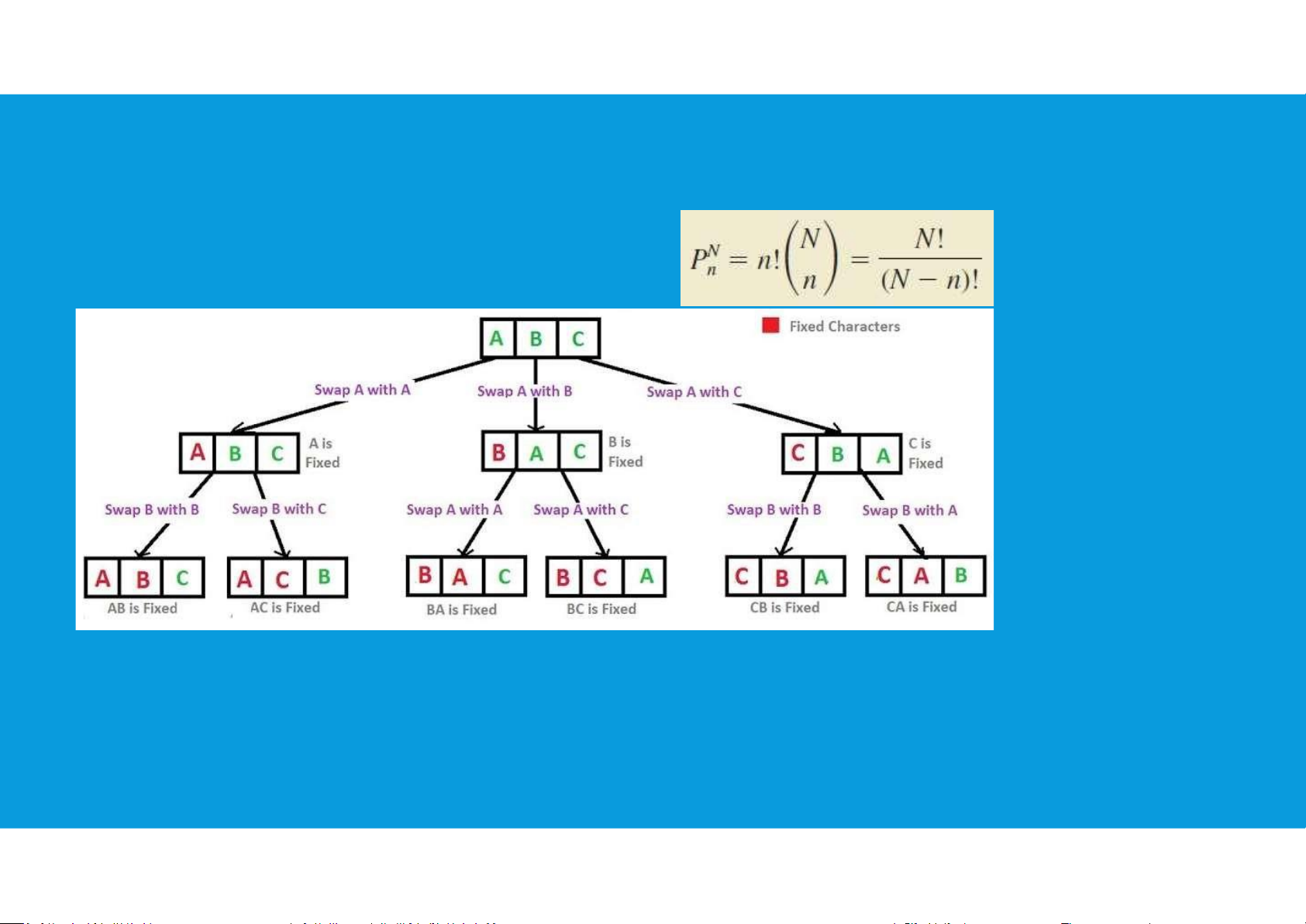
The notation ! means factorial; for example, 5 factorial is 5! = (5)(4)(3)(2)(1) = 120 4.1. INTRODUCTION TO PROBABILITY •Counting rules: Permutations: allows one to compute the number of
experimental outcomes when n objects are to be selected from a set of N objects lOMoAR cPSD| 45903860
where the order of selection is important. The same n objects selected in a different
order are considered a different experimental outcome. 8 lOMoAR cPSD| 45903860
4.1. INTRODUCTION TO PROBABILITY •Assigning probabilities:
The three approaches most frequently used are the classical, relative frequency, and subjective methods.
Regardless of the method used, two basic requirements for assigning probabilities must be met. lOMoAR cPSD| 45903860
4.1. INTRODUCTION TO PROBABILITY •Assigning probabilities:
The classical method of assigning probabilities is appropriate when all the
experimental outcomes are equally likely.
When using this approach, the two basic requirements for assigning
probabilities are automatically satisfied.
If n experimental outcomes are possible,
a probability of 1/n is assigned to each experimental outcome
4.1. INTRODUCTION TO PROBABILITY •Assigning probabilities: 10 lOMoAR cPSD| 45903860
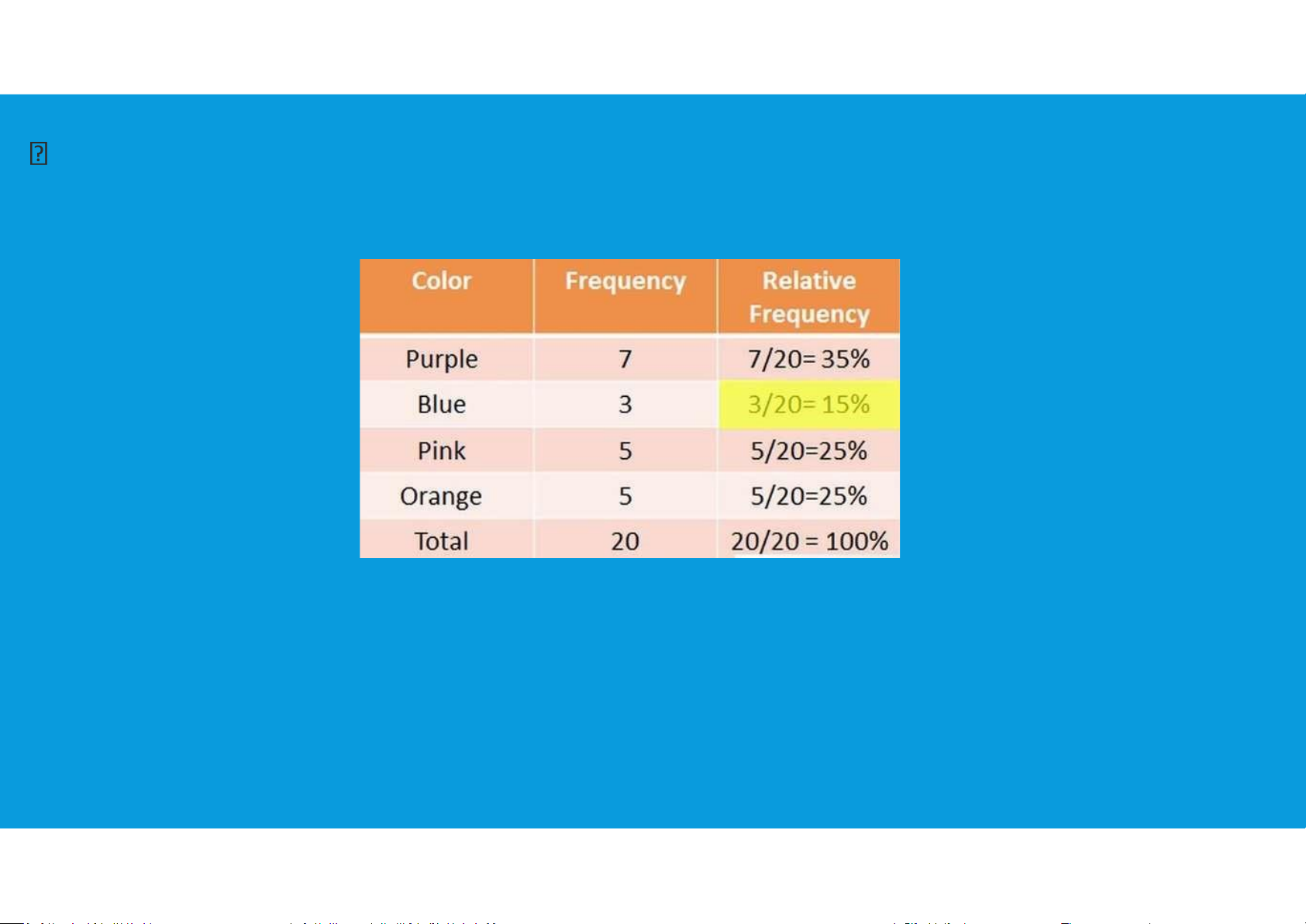
The relative frequency method of assigning probabilities is appropriate when data are
available to estimate the proportion of the time the experimental outcome will occur
if the experiment is repeated a large number of times.
When using this approach, the two basic requirements for assigning probabilities are automatically satisfied.
4.1. INTRODUCTION TO PROBABILITY •Assigning probabilities: lOMoAR cPSD| 45903860
The subjective method of assigning probabilities is most appropriate when one
cannot realistically assume that the experimental outcomes are equally likely and
when little relevant data are available.
4.1. INTRODUCTION TO PROBABILITY
•Events and their probabilities: 12 lOMoAR cPSD| 45903860
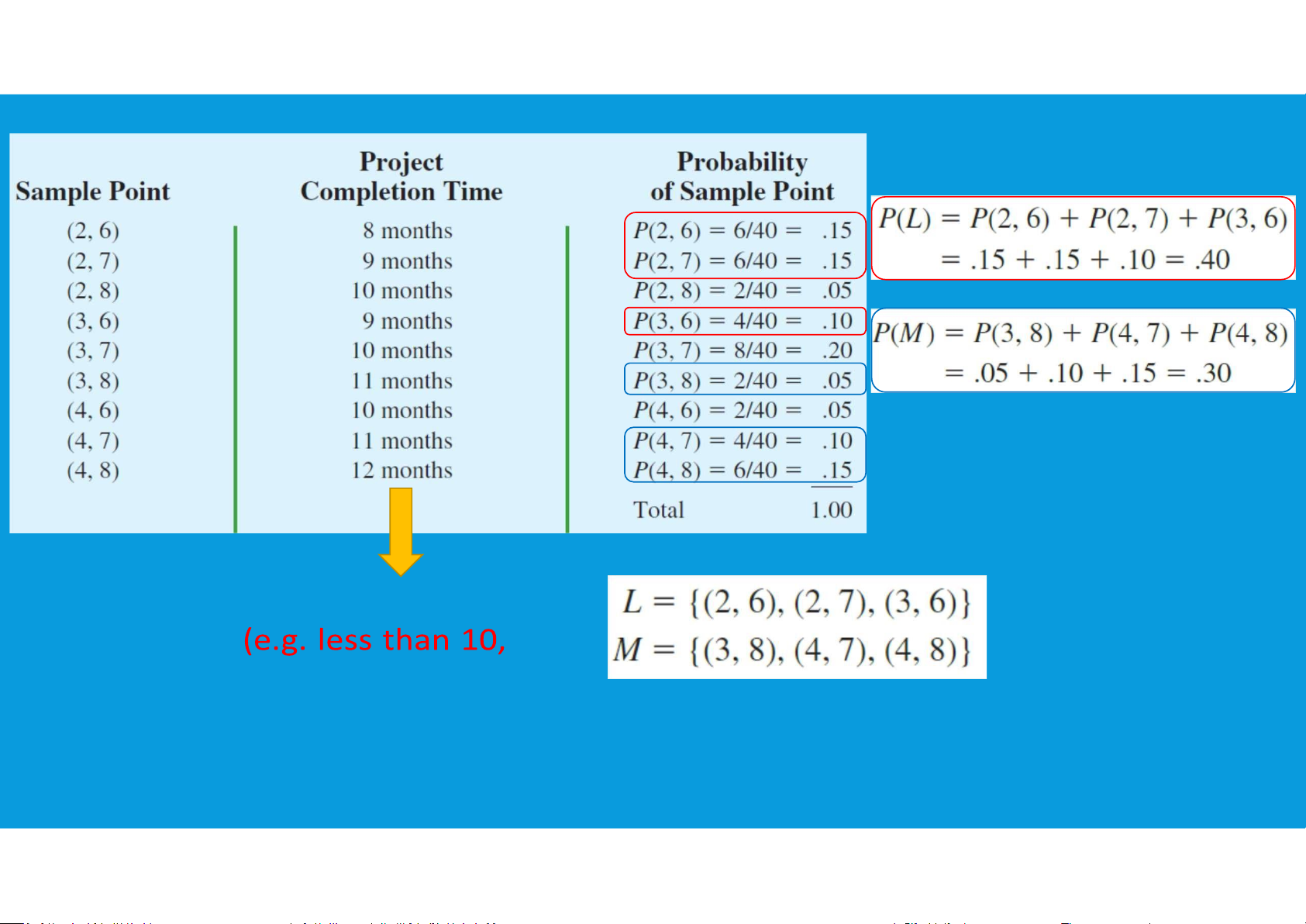
An event is a collection of sample points.
The probability of any event is equal to the sum of the probabilities of the sample points in the event.
calculate the probability of a particular event by adding the probabilities of the
sample points (experimental outcomes) that make up the event.
4.1. INTRODUCTION TO PROBABILITY
•Events and their probabilities: lOMoAR cPSD| 45903860 Events equal 10, more than 10, etc.)
4.1. INTRODUCTION TO PROBABILITY 14 lOMoAR cPSD| 45903860
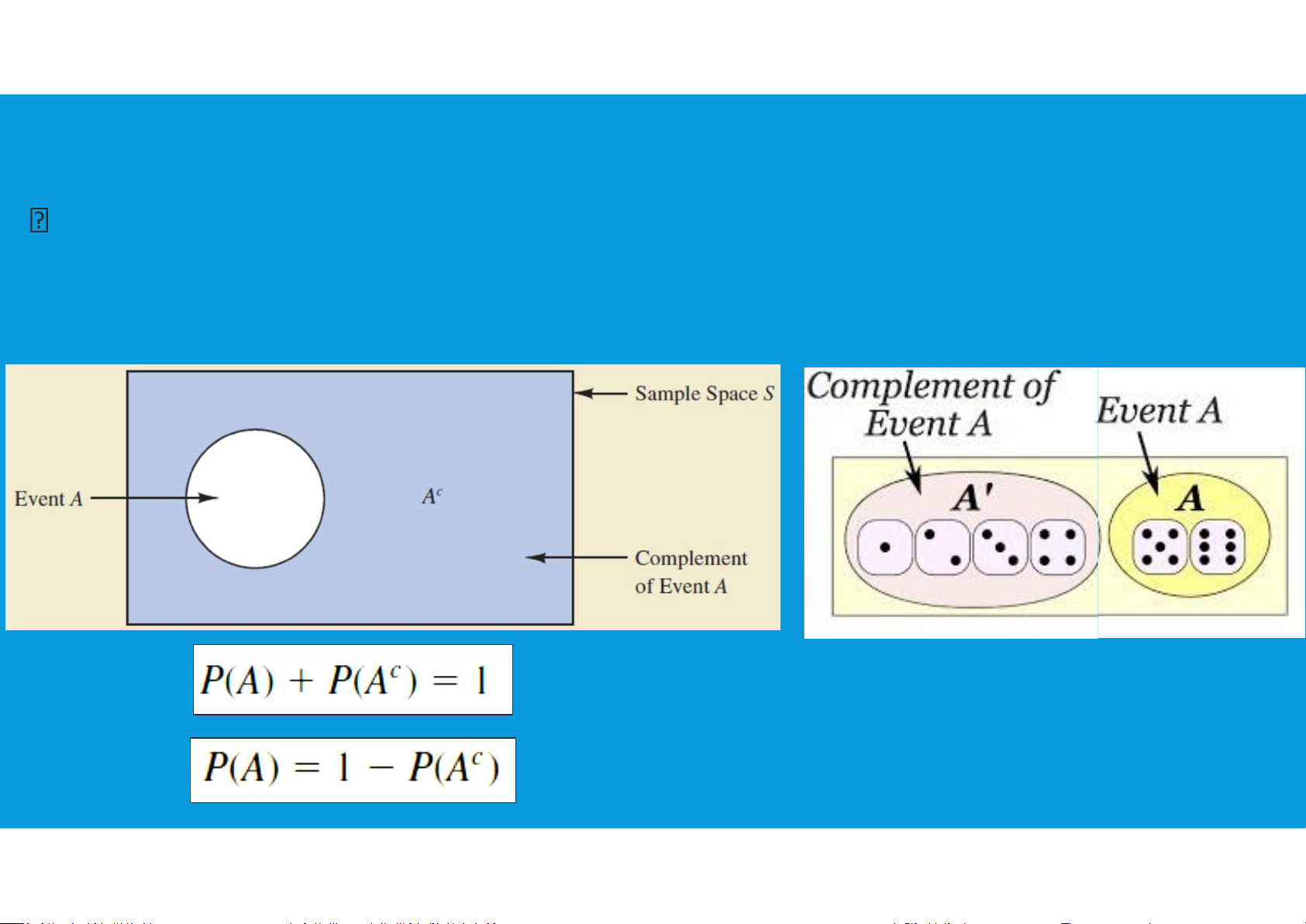
•Some basic relationships of probability:
The complement of A is defined to be the event consisting of all sample points
that are not in A. The complement of a is denoted by Ac. lOMoAR cPSD| 45903860
4.1. INTRODUCTION TO PROBABILITY
•Some basic relationships of probability:
Addition Law: is helpful when we are interested in knowing the probability that
at least one of two events occurs. That is, with events A and B we are interested
in knowing the probability that event A or event B or both occur.
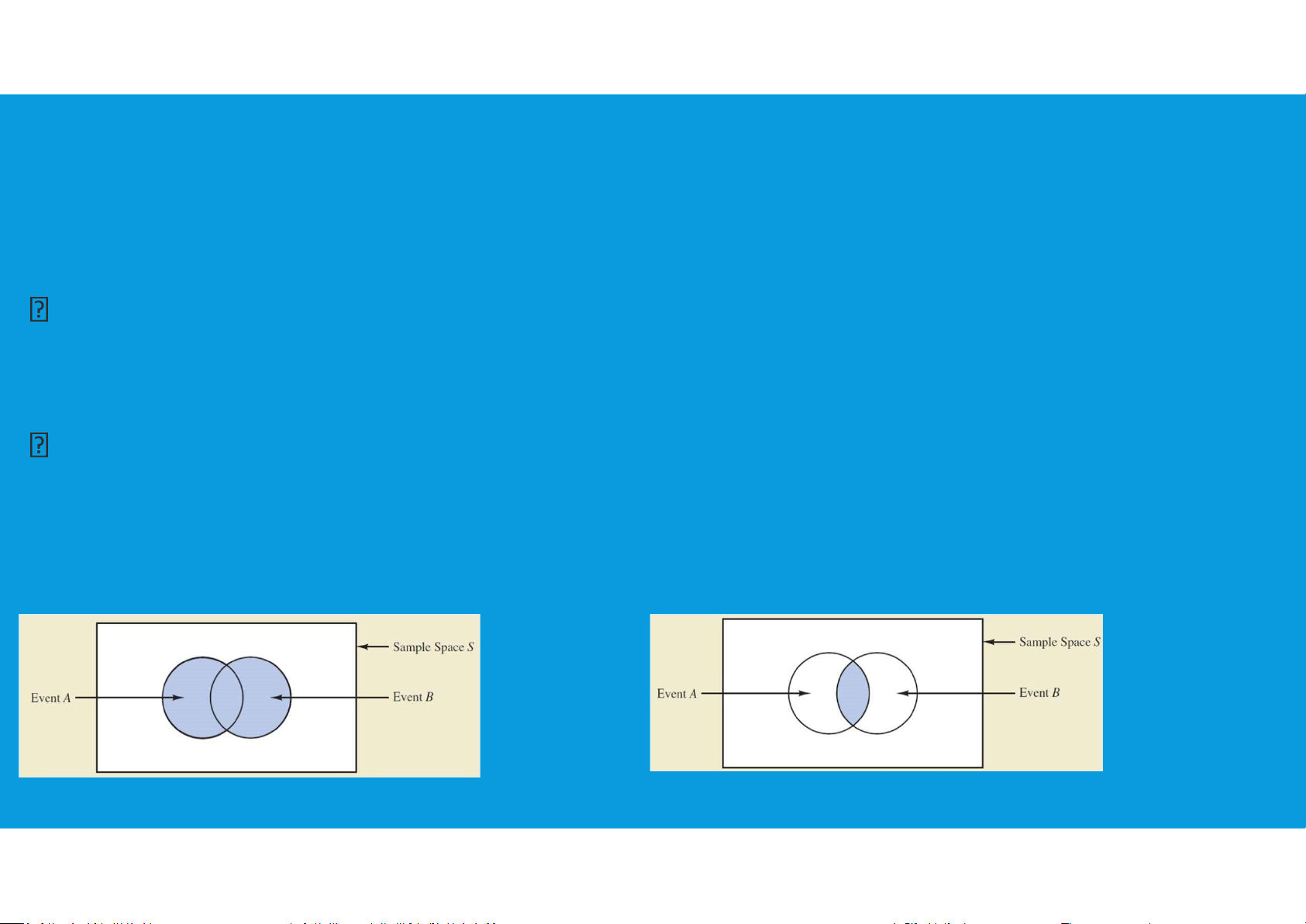
Addition Law: two concepts related to the combination of events: the union of
events and the intersection of events.
-The union of A and B is the event containing all
-The intersection of A and B is the event containing
sample points belonging to A or B or both. The
the sample points belonging to both A and B. The union is denoted by A U B.
intersection is denoted by A ∩ B. 16 lOMoAR cPSD| 45903860
4.1. INTRODUCTION TO PROBABILITY
•Some basic relationships of probability:
The addition law provides a way to compute the probability that event A or
event B or both occur. In other words, the addition law is used to compute the
probability of the union of two events. lOMoAR cPSD| 45903860
4.1. INTRODUCTION TO PROBABILITY
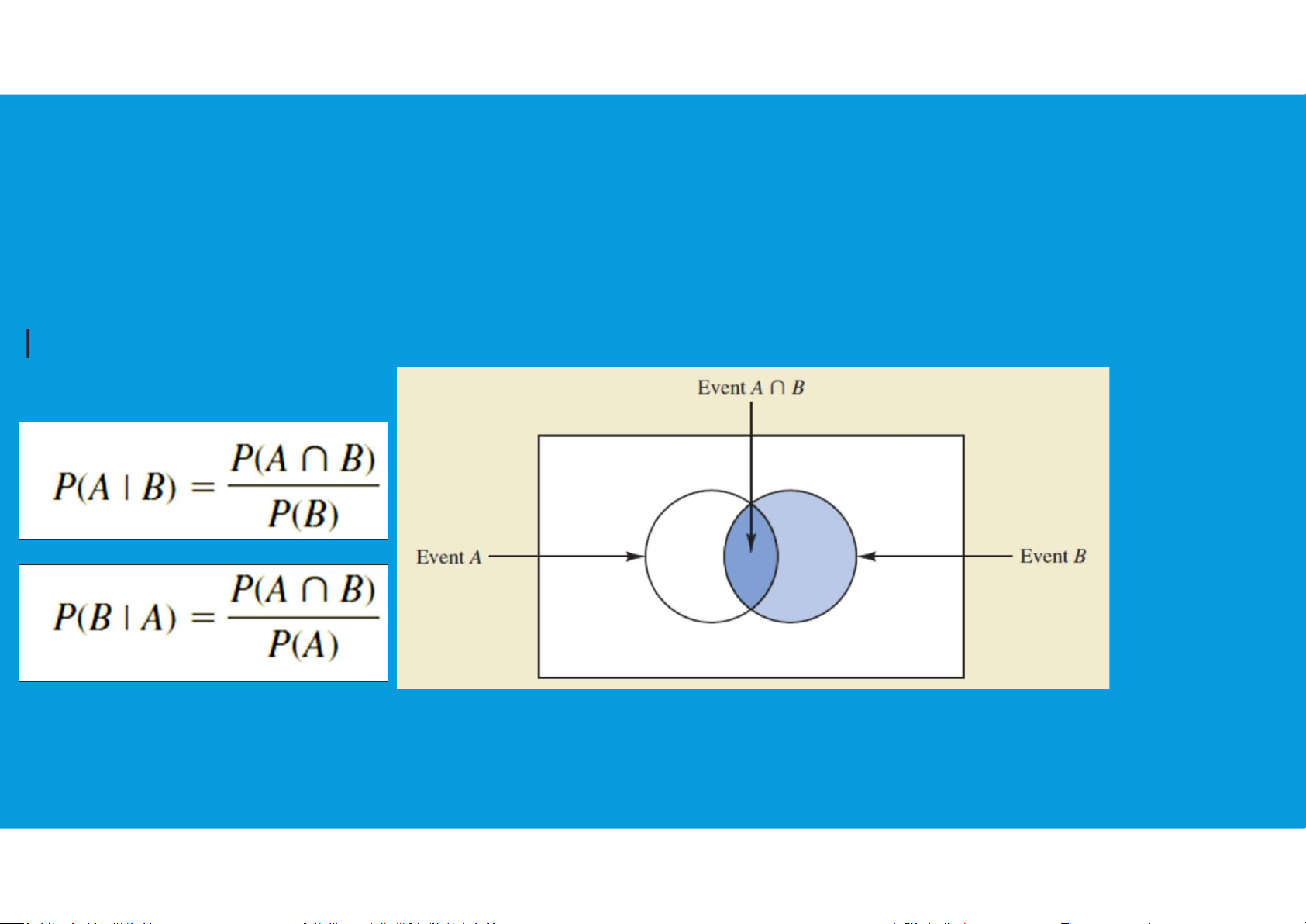
•Conditional probability: Suppose we have an event A with 18 lOMoAR cPSD| 45903860
probability P(A). If we obtain new information and learn that A related event,
denoted by B, already occurred, we will want to take advantage of this
information by calculating a new probability for event A.
•This new probability of event A is called a conditional probability and is written P(A
B) (“the probability of A given B”)
4.1. INTRODUCTION TO PROBABILITY lOMoAR cPSD| 45903860 20