Lí thuyết chương 1 Đại số vecto | Toán ứng dụng

Chương 1 Đại số vectơ 1.1 Định nghĩa vectơ 1.1.1
Quan hệ tương đương trên tập hợp
Định nghĩa 1.1.1. Cho hai tập hợp A và B. Một quan hệ hai ngôi từ A vào
B là một tập con R của tập tích Descartes A × B. Ta dùng ký hiệu a R b để
chỉ mọi cặp (a, b) ∈ R. Một quan hệ hai ngôi từ A vào chính nó được gọi là một quan hệ trên A.
Ví dụ 1.1.2. Nhắc lại một vài ví dụ quen thuộc.
a) Quan hệ ≤ là một quan hệ trên tập hợp các số thực R.
b) Quan hệ chia hết là một quan hệ trên tập hợp các số nguyên Z.
c) Với mọi số nguyên dương n, quan hệ đồng dư modulo n là một quan hệ
trên tập hợp các số nguyên Z.
Định nghĩa 1.1.3. Quan hệ R trên tập hợp A được gọi là một quan hệ tương
đương nếu nó thỏa mãn ba tính chất phản xạ, đối xứng và bắc cầu. Điều này
nghĩa là, với mọi a, b, c ∈ A, ta phải có: a) (Phản xạ) a R a,
b) (Đối xứng) Nếu a R b thì b R a,
c) (Bắc cầu) Nếu a R b và b R c thì a R c.
Ví dụ 1.1.4. Quan hệ đồng dư modulo n là một quan hệ tương đương trên tập hợp Z. 5
Chương 1. Đại số vectơ
Ví dụ 1.1.5. Quan hệ ≤ trên R, quan hệ chia hết trên Z không phải là các quan hệ tương đương.
Mệnh đề 1.1.6. Cho ∼ là một quan hệ tương đương trên tập hợp A. Với mọi
a ∈ A, tập hợp a := {x ∈ A | a ∼ x} được gọi là lớp tương đương của phần tử a.
Xét hai phần tử a, b bất kỳ của A. Khi đó, các lớp tương đương a và b hoặc rời
nhau hoặc trùng nhau.
Chứng minh. Ta có thể chỉ ra rằng: • Nếu a ∼ b thì a = b.
• Nếu a 6∼ b thì a ∩ b = ∅.
Mệnh đề được chứng minh.
Hệ quả 1.1.7. Quan hệ tương đương ∼ cảm sinh một phân hoạch của tập hợp
A bởi các lớp tương đương. Nói nôm na, tập hợp A bị tách thành hợp rời rạc
của các tập hợp con; trong đó, các phần tử thuộc cùng một tập hợp con thì
tương đương với nhau, còn các phần tử thuộc các tập con khác nhau thì không
tương đương với nhau. Ký hiệu A/∼:= {a | a ∈ A}.
Chứng minh. Hệ quả được suy trực tiếp từ sự thật rằng: a ∼ b khi và chỉ khi a = b.
Ví dụ 1.1.8. Quan hệ đồng dư modulo 2 trên tập các số nguyên Z là một quan
hệ tương đương. Quan hệ này cảm sinh một phân hoạch của tập các số nguyên
thành hai tập con rời nhau: tập hợp các số nguyên lẻ (đồng dư 1 modulo 2) và
tập hợp các số nguyên chẵn (đồng dư 0 modulo 2). Tập thương của Z bởi quan
hệ tương đương này, ký hiệu là Z/2, chỉ bao gồm hai phần tử 0 và 1.
Ví dụ 1.1.9. Một cách tổng quát, khi xét quan hệ đồng dư modulo n trên Z,
ta thu được tập thương Z/n = {0,1,..., n − 1}. Trong đó, k ký hiệu tập con của Z
gồm tất cả các số nguyên đồng dư với k modulo n. 1.1.2 Vectơ hình học
Thông qua các đoạn thẳng định hướng, ta sẽ đưa ra định nghĩa chính xác của
các vectơ hình học trong mặt phẳng và trong không gian.
Quy ước 1.1.10. Các định nghĩa và tính chất sau đây, nếu không nhấn mạnh
ngữ cảnh cụ thể, ta hiểu là đang xét hoặc trong mặt phẳng, hoặc trong không gian. 6
1.1. Định nghĩa vectơ
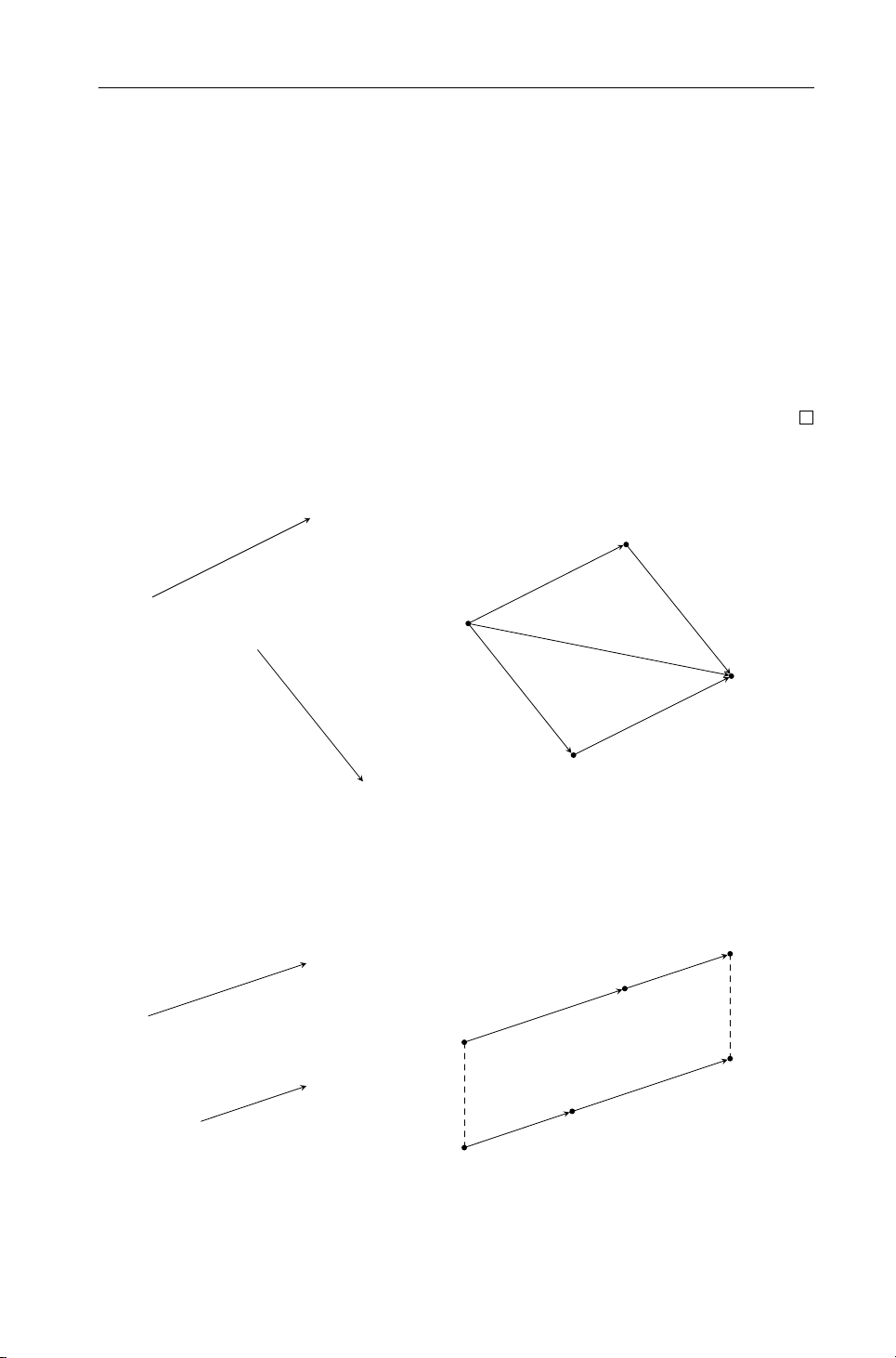
Định nghĩa 1.1.11. Cho hai điểm P và Q bất kỳ. Ta ký hiệu [P,Q] là đoạn
thẳng định hướng đi từ P đến Q. Trong đó, điểm P gọi là ngọn, điểm Q gọi
là gốc, đường thẳng PQ gọi là giá (hoặc phương).
a) Hai đoạn thẳng định hướng gọi là cộng được với nhau nếu gốc đoạn này
trùng với ngọn của điểm kia. Cụ thể, ta định nghĩa [P,Q]+[Q, R] = [P, R].
b) Với mọi số thực α, ta định nghĩa phép nhân α[P,Q] = [P,Q0]. Trong đó,
Q0 nằm trên tia PQ nếu α > 0, nằm trên tia đối của tia PQ nếu α < 0, sao cho PQ0 = |α|PQ. Q P
Hình 1.1: Đoạn thẳng định hướng [P,Q].
Định nghĩa 1.1.12. Hai đoạn thẳng định hướng được gọi là cùng phương
nếu chúng có giá song song hoặc trùng nhau.
Định nghĩa 1.1.13. Cho hai đoạn thẳng định hướng [P,Q] và [P0,Q0] cùng
phương. Vẽ đường thẳng d bất kỳ song song với cả PQ và P0Q0. Trên d vẽ một
điểm O bất kỳ, và vẽ hai điểm M, N sao cho OPQM và OP0Q0N là các hình
bình hành. Khi đó, [P,Q] và [P0,Q0] được gọi là cùng hướng nếu điểm O nằm
ngoài đoạn thẳng MN, được gọi là ngược hướng nếu điểm O nằm giữa M và N.
Định nghĩa 1.1.14. Đoạn thẳng định hướng [P,Q] được gọi là tương đương
(hoặc bằng) với đoạn thẳng định hướng [P0,Q0], và ký hiệu là [P,Q] ∼ [P0,Q0],
nếu chúng có cùng hướng và cùng độ dài. C
Định lý 1.1.15. Trên tập hợp các đoạn thẳng định hướng, quan hệ ∼ định
nghĩa trong 1.1.14 là một quan hệ tương đương.
Chứng minh. Dễ dàng kiểm tra quan hệ này thỏa mãn ba điều kiện của một quan hệ tương đương.
Định nghĩa 1.1.16. Lớp tương đương của mỗi đoạn thẳng định hướng được
gọi là một vectơ (hình học). Cụ thể, lớp tương đương của đoạn thẳng định # »
hướng [P,Q] là một vectơ được ký hiệu bởi PQ. 7
Chương 1. Đại số vectơ
Ký hiệu 1.1.17. Ký hiệu S2 là tập hợp tất cả các đoạn thẳng định hướng trong
mặt phẳng. Tập thương S2/∼ là tập hợp tất cả các vectơ trong mặt phẳng, được
ký hiệu là V2. Tương tự, ta ký hiệu S3 là tập hợp tất cả các đoạn thẳng định
hướng trong không gian, và V3 là tập hợp tất cả các vectơ trong không gian. # »
Nhận xét 1.1.18. Một cách nôm na, vectơ PQ là tập hợp các đoạn thẳng định
hướng tương đương với [P,Q]. Như vậy, khi nhắc đến vectơ, người ta chỉ cần # »
quan tâm đến ba yếu tố: phương, hướng và độ dài. Độ dài của vectơ PQ bằng # »
độ dài đoạn thẳng PQ, và được ký hiệu bởi |PQ|.
Định nghĩa 1.1.16 của vectơ phù hợp với định nghĩa “ngây thơ” được học
ở trường phổ thông. Một bài tập nhỏ dành cho người đọc là tự chiêm nghiệm
lại tính đúng đắn của các tính chất của vectơ đã học ở trường phổ thông (hai
vectơ bằng nhau, phép cộng vectơ, nhân vectơ với một số, . . . ) theo định nghĩa
mới bên trên. Để minh họa, ta xét ví dụ bên dưới. # » # »
Ví dụ 1.1.19. Ta có PQ = P0Q0 nếu và chỉ nếu [P,Q] ∼ [P0,Q0]. 1.2 Không gian vectơ 1.2.1
Các phép toán tuyến tính trên vectơ
Từ các phép toán trên đoạn thẳng định hướng, ta xây dựng được phép cộng
hai vectơ và phép nhân vectơ với một số thực.
Mệnh đề và định nghĩa 1.2.1. Với mọi điểm P,Q, R và mọi α ∈ R, các định
nghĩa sau đây là định nghĩa tốt: # » # » # » a) PQ + QR = PR. # » # »
b) αPQ = PQ0, trong đó Q0 xác định thỏa α[P,Q] = [P,Q0].
Chứng minh. Ý thứ nhất được chứng minh như sau. Lấy các điểm P0, Q0, R0 # » # » # » # »
sao cho PQ = P0Q0 và QR = Q0R0. Điều này nghĩa là [P,Q] ∼ [P0,Q0] và [Q, R] ∼
[Q0, R0]. Từ đây ta suy ra [P, R] ∼ [P0, R0] (bài toán hình học thuần túy), tức là # » # » P R = P0R0.
Ý thứ hai được chứng minh tương tự.
Mệnh đề 1.2.2. Mọi vectơ #» u và #»
v đều có thể cộng được với nhau. Hơn nữa, #» #» #» #» u + v = v + u . 8
1.2. Không gian vectơ
Chứng minh. Chọn điểm P bất kỳ. Vẽ điểm Q sao cho đoạn thẳng định hướng #» #» # »
[P, Q] có cùng phương, cùng hướng, cùng độ dài với vectơ u . Khi đó, u = PQ. #» # » #» #»
Tương tự như vậy, vẽ điểm R sao cho v = QR. Như vậy ta thu được, u + v = # » # » # » PQ + QR = PR. # »
Để kết thúc chứng minh, ta chỉ cần chỉ ra rằng vectơ PR không phụ thuộc
vào việc chọn điểm P. Thật vậy, chọn một điểm P0 bất kỳ, theo cách tương tự, #» #» # »
ta thu được ba điểm P0, Q0, R0 mà u + v = P0R0. Tuy nhiên, vì [P, R] ∼ [P0, R0] # » # » nên PR = P0R0.
Tính giao hoán của phép cộng được suy ra khi lý luận trên các đoạn thẳng
định hướng. Mệnh đề được chứng minh. #» Q u P #» R v Q0
Hình 1.2: Phép cộng hai vectơ khác phương. R #» u Q P #» R0 v Q0 P0
Hình 1.3: Phép cộng hai vectơ cùng phương. 9
Chương 1. Đại số vectơ 1.2.2
Các tính chất của không gian vectơ
Định lý 1.2.3. Phép cộng hai vectơ và phép nhân vectơ với số thực có 8 tính
chất cơ bản sau đây: a) Với mọi #» #» #» #» #» #» #» u , #» v và #»
w, ta có ( u + v ) + w = u + ( v + w). b) Với mọi #» #» #» #» u và #» v , ta có #» u + v = v + u . #» #» #»
c) Tồn tại duy nhất vectơ không #» #» 0 để #»
u + 0 = 0 + u = u với mọi #» u . #» d) Mọi vectơ #» #» #» #» #»
u đều có phần tử đối, ký hiệu là − u , để #»
u +(− u ) = (− u )+ u = 0 . e) Với mọi #» #» #» u , #»
v và mọi α ∈ R, ta có α( u + v ) = α#» u + α#» v . f) Với mọi #» #»
u và mọi α,β ∈ R, ta có (α + β) u = α#» u + β#» u . g) Với mọi #» #»
u và mọi α,β ∈ R, ta có (αβ) u = α(β#» u ). h) Với mọi #» #» #»
u , ta có 1 u = u . #»
Chứng minh. Vectơ không 0 là lớp tương đương của đoạn thẳng định hướng # » # »
mà điểm ngọn trùng với điểm gốc. Vectơ đối của PQ là vectơ QP. Các tính chất
còn lại được kiểm chứng khi làm việc trên các đoạn thẳng định hướng.
Định nghĩa 1.2.4. Nhờ định lý 1.2.3, phép trừ hai vectơ được định nghĩa bởi #» #» #» #» u − v := u + (− v ).
Định nghĩa 1.2.5. Các tập hợp V2 và V3 (xem định nghĩa 1.1.16) được trang bị
hai phép toán: phép toán cộng các vectơ bất kỳ và phép toán nhân một vectơ
bất kỳ với một số thực. Các phép toán này thỏa mãn 8 tính chất đã nêu trong
định lý 1.2.3. Khi đó, các tập hợp V2 và V3 lần lượt được gọi là không gian
vectơ thực trên mặt phẳng và trong không gian.
Nhận xét 1.2.6. Định nghĩa không gian vectơ trong đại số tuyến tính được
tổng quát hóa từ định nghĩa 1.2.5. Theo đó, một tập hợp V bất kỳ sẽ được gọi
là một không gian vectơ thực (hoặc phức) nếu nó được trang bị phép cộng các
phần tử của V , và phép nhân một phần tử của V với một số thực (hoặc phức)
sao cho thỏa mãn 8 tính chất như trong định lý 1.2.3. 10
1.2. Không gian vectơ 1.2.3
Cơ sở của không gian vectơ Định nghĩa 1.2.7. # » # » # »
Các vectơ u1, u2,..., un được gọi là đồng phẳng nếu tồn
tại các đoạn thẳng định hướng đại diện cho các vectơ này sao cho chúng cùng
nằm trên một mặt phẳng. #»
Định lý 1.2.8. Trong không gian cho hai vectơ #» u , #»
v khác vectơ 0 và không
cùng phương. Khi đó, vectơ #»
s đồng phẳng với #» u và #»
v khi và chỉ khi tồn tại
duy nhất các số thực α và β sao cho
#»s = α#»u+β#»v. Chứng minh. #» #» #»
Trường hợp s cùng phương với u hoặc v được chứng minh trực
tiếp dùng định nghĩa phép nhân một số thực với một vectơ. #» #» #»
Đối với trường hợp s khác phương với cả u và v , ta dùng sự thật rằng: ba
điểm trong không gian luôn đồng phẳng, cho nên ba cạnh của một tam giác #» #» #»
luôn đồng phẳng. Thật vậy, ta biểu diễn ba vectơ s , u , v bởi các đoạn thẳng
định hướng chung gốc và đồng phẳng. Dùng quy tắc hình bình hành ta có thể
xác định được các hệ số α và β. Tiếp theo, ta chứng minh tính duy nhất của
các hệ số này bằng phản chứng. Giả sử có hai phân tích khác nhau, khi đó α#» u + β#» v = α0 #» u + β0 #» v . #» #»
Điều này dẫn tới điều vô lý là u và v cùng phương. Kết thúc chứng minh. #»
Hệ quả 1.2.9. Trên mặt phẳng cho hai vectơ #» u , #»
v khác vectơ 0 và không cùng
phương. Khi đó, với mọi vectơ #»
s trên mặt phẳng đều tồn tại duy nhất các số
thực α và β sao cho
#»s = α#»u+β#»v.
Chứng minh. Suy trực tiếp từ định lý 1.2.8. #»
Định lý 1.2.10. Trong không gian cho ba vectơ #» u , #» v , #»
w khác vectơ 0 và
không đồng phẳng. Khi đó, mọi vectơ #»
s trong không gian đều được phân tích
một cách duy nhất thành tổ hợp tuyến tính của các vectơ #» u , #» v và #» w. Nói cách
khác, tồn tại duy nhất các số thực α, β và γ sao cho
#»s = α#»u+β#»v+γ#»w. Chứng minh. #» #» #» #»
Trường hợp s đồng phẳng với hai trong ba vectơ u , v và w
được quy về định lý 1.2.8. Với trường hợp còn lại, ta dùng quy tắc hình hộp để
xác định các hệ số α, β và γ. Ta chứng minh tính duy nhất của phân tích bằng
phản chứng. Giả sử có hai phân tích khác nhau, khi đó α#» u + β#» v + γ#» w = α0 #» u + β0 #» v + γ0 #» w. 11
Chương 1. Đại số vectơ #» #» #»
Điều này dẫn tới sự vô lý là u , v và w đồng phẳng. Kết thúc chứng minh.
Định nghĩa 1.2.11. Ta có các định nghĩa sau đây: #»
a) Tập hợp gồm hai vectơ bất kỳ trên mặt phẳng, khác 0 và không cùng
phương, được gọi là một cơ sở của V2. Do đó, V2 được gọi là không gian vectơ thực hai chiều. #»
b) Tập hợp gồm ba vectơ bất kỳ trong không gian, khác vectơ 0 và không
đồng phẳng, được gọi là một cơ sở của V3. Do đó, V3 được gọi là không gian vectơ thực ba chiều. 1.3
Bổ sung về các phép toán trên vectơ
Ngoài các phép toán tuyến tính trên vectơ, trong mục này chúng ta sẽ xem
xét một vài phép toán khác có ứng dụng quan trọng trong hình học là tích vô
hướng và tích hữu hướng. Tích vô hướng được dùng để diễn đạt các đại lượng
độ dài và góc. Trong khi đó, tích hữu hướng của hai vectơ thể hiện vùng diện
tích của hình bình hành (có thể suy biến) “tựa” trên hai vectơ đó. 1.3.1 Tích vô hướng Định nghĩa 1.3.1. #» #»
Cho hai vectơ u và v . Tích vô hướng của chúng, ký hiệu #» #»
là u . v , được định nghĩa bởi #» #» #» #» #» #»
u . v = | u |.| v |.cos( u , v ) #» #» #» #» #» #»
trong đó ( u , v ) là góc (không định hướng) giữa hai vectơ u và v , với ( u , v ) ∈ [0, π].
Mệnh đề 1.3.2. Điều kiện cần và đủ để hai vectơ vuông góc với nhau là tích
vô hướng của chúng bằng không. Chứng minh. #» #»
Vectơ u vuông góc với vectơ v khi và chỉ khi góc giữa chúng π #» #» bằng
. Điều này xảy ra khi và chỉ khi u . v = 0. 2
Nhận xét 1.3.3. Các đại lượng độ dài và góc có thể được biểu diễn theo ngôn
ngữ tích vô hướng như sau: #» #» a) | u |2 = u 2. #» #» #» #» u . v b) cos( u , v ) = p#» #» . u 2. v 2 12
1.3. Bổ sung về các phép toán trên vectơ
Định lý 1.3.4. Tích vô hướng của hai vectơ có các tính chất cơ bản sau đây: #» a) Với mọi #» u đều có #»
u 2 ≥ 0. Hơn nữa, #»
u 2 = 0 khi và chỉ khi #» u = 0 . b) Với mọi #» #» #» #» u và #» v , ta có #» u . v = v . u . c) Với mọi #» #» #» #» u , #»
v và mọi α ∈ R, ta có (α#»
u ). v = α( u . v ).
Chứng minh. Các tính chất này được suy ra trực tiếp của định nghĩa tích vô hướng. #» Định nghĩa 1.3.5. #» #» #»
Cho hai vectơ u và v thỏa u 6= 0 . Khi đó, vectơ #» #» #» #» #» v u , v ) u . v P | | cos( #» #» #» #» u ( v ) := #» u = #» u | u | u 2 #» #»
được gọi là hình chiếu trực chuẩn của vectơ v trên phương u . Nhận xét 1.3.6. #» #» Vectơ P #»
u ( v ) là một vectơ cùng phương với u . #»
Mệnh đề 1.3.7. Cho hai vectơ #» #» #» #» u và #» v thỏa #» u 6= 0 . Khi đó, #» u . v = u .P #» u ( v ).
Chứng minh. Ta biến đổi #» #» #» #» #» #» u . v #» #» #» u .P #» u ( v ) = P #» u ( v ). u = #» u 2 = u . v . | u |2
Đây chính là điều phải chứng minh.
Mệnh đề 1.3.8. Các phép toán tuyến tính được bảo toàn qua phép chiếu trực chuẩn. Cụ thể: a) Nếu #» #» #» #» u = v thì P #» w ( u ) = P #» w ( v ). b) P #» #» #» #» #» w ( u + v ) = P #» w ( u ) + P #» w ( v ). c) P #» #» w (α #» u ) = αP #» w ( u ).
Chứng minh. Dùng định nghĩa của hình chiếu trực chuẩn như trong 1.3.5.
Định lý 1.3.9. Tích vô hướng có tính chất phân phối đối với phép cộng. Cụ thể, với mọi #» u , #» v và #» w, ta có #» #» #» #» #» #» #» u .( v + w) = u . v + u .w. #» #» Chứng minh. #» #»
Nếu u = 0 , kết quả là hiển nhiên. Ta xét trường hợp u 6= 0 .
Dùng các mệnh đề 1.3.7 và 1.3.8, ta thu được #» #» #» #» #» #» #» #» #» u .( v + w) = u .P #» u ( v + w) = u . (P #» u ( v ) + P #» u (w)) . (1.1) 13
Chương 1. Đại số vectơ Mặt khác, ta cũng có #» #» #» #» #» #» #» #» u . v + u .w = u .P #» u ( v ) + u .P #» u (w). (1.2)
Vế phải của các phương trình (1.1) và (1.2) là các tích vô hướng của các vectơ
cùng phương. Do đó, để chứng minh tính chất phân phối của tích vô hướng #» #» #»
với phép cộng, đủ để chỉ ra nó đúng cho các vectơ u , v , w cùng phương. Kết
quả được suy ra từ tính chất phân phối của phép nhân đối với phép cộng trên
các đoạn thẳng định hướng. Người đọc có thể tự kiểm chứng bằng cách chia ra ba trường hợp: #» #» #»
a) u cùng hướng với cả v và w; #» #» #»
b) u ngược hướng với cả v và w; #» #» #»
c) u cùng hướng với v nhưng ngược hướng với w. Kết thúc chứng minh. #»
Hệ quả 1.3.10. Cho hai vectơ #» u và #» v thỏa #»
u 6= 0 . Khi đó tồn tại duy nhất phân tích #» #» #» v = v1 + v2 sao cho #»
v1 cùng phương với #» u , và #»
v2 trực chuẩn với #» u . Chứng minh. #» #»
Điều kiện v1 cùng phương với u đồng nghĩa với việc tồn tại số #»
thực α để v1 = α#»
u . Khi đó, phân tích như trong mệnh đề, nếu tồn tại, sẽ kéo #» #»
theo sự kiện vectơ ( v − α#»
u ) trực chuẩn với u . Theo mệnh đề 1.3.2, điều này nghĩa là #» #» #» #» u . v ( v − α#»
u ) u = 0 ⇔ α = #» . | u |2 #» #» #» #»
Lúc này, các vectơ v1 và v2 hoàn toàn được xác định, trong đó v1 = P #» u ( v ). 1.3.2
Tích hữu hướng và tích hỗn tạp
Trong không gian ta có thể định hướng bộ ba vectơ bằng các khái niệm tam
diện thuận và nghịch như sau: Định nghĩa 1.3.11. #» #» #»
Bộ ba vectơ có thứ tự ( u , v , w) được gọi là một tam diện thuận #» #»
nếu khi để bàn tay phải sao cho ngón cái là u , ngón trỏ là v thì ngón #»
giữa là w (chiều của các vectơ là chiều hướng từ lòng bàn tay ra đầu ngón
tay). Trường hợp ngược lại được gọi là một tam diện nghịch. 14
1.3. Bổ sung về các phép toán trên vectơ Ví dụ 1.3.12. #» #» #»
Xét các vectơ u , v , w như trong hình vẽ bên dưới. Khi đó, bộ ba #» #» #» #» #» #»
( u , v , w) làm thành một tam diện thuận, trong khi ( v , u , w) là một tam diện nghịch. #» w #» v #» u Định nghĩa 1.3.13. #» #» #» #»
Cho hai vectơ u và v . Tích hữu hướng của u và v là #» #»
một vectơ, ký hiệu là u ∧ v , được xác định như sau: #» #» #» #»
a) u ∧ v vuông góc với cả u và v . #» #» #» #»
b) Bộ ba ( u , v , u ∧ v ) tạo thành một tam diện thuận. #» #» #» #»
c) | u ∧ v | = | u |.| v |.sinθ, trong đó 0 ≤ θ ≤ π là góc (không định hướng) giữa #» #» hai vectơ u và v .
Mệnh đề 1.3.14. Điều kiện cần và đủ để hai vectơ cùng phương là tích hữu #»
hướng của chúng bằng vectơ 0 .
Chứng minh. Đủ để chỉ ra độ dài của tích hữu hướng bằng 0.
Định lý 1.3.15. Tích hữu hướng của hai vectơ có các tính chất cơ bản sau đây: a) Với mọi #» #» #» #» u và #» v , ta có #» u ∧ v = − v ∧ u . b) Với mọi #» #» #» #» #» #» #» u , #» v và #» w, ta có #»
u ∧ ( v + w) = u ∧ v + u ∧ w. c) Với mọi #» #» #» #» u và #»
v , ta có (α#»
u ) ∧ v = α( u ∧ v ).
Để chứng minh định lý 1.3.15, ta cần bổ đề sau:
Bổ đề 1.3.16. Cho ba vectơ #» #» #» #» #» #» u , #» v và #» w. Khi đó, #»
u .( v ∧ w) = ( u ∧ v ).w. 15
Chương 1. Đại số vectơ
Chứng minh. Định nghĩa 1.3.13 nói rằng hình bình hành tựa trên hai vectơ #» #» #» #»
v và w có diện tích bằng | v ∧ w|. Do đó, dùng mệnh đề 1.3.7 ta suy ra rằng #» #» #»
| u .( v ∧ w)| chính là thể tích V của hình hộp (có thể suy biến) tựa trên ba vectơ #» #» #»
u , v và w. Tương tự như vậy ta cũng lý luận rằng thể tích V của hình hộp #» #» #»
nêu trên bằng với |( u ∧ v ).w|. Như vậy ta có #» #» #» #» #» #»
| u .( v ∧ w)| = |( u ∧ v ).w| = V . #» #» #» #» #» #» #»
Hơn nữa, khi ( u , v , w) tạo thành một tam diện thuận thì u .( v ∧ w) = ( u ∧ #» #» #» #» #» #» #» #»
v ).w = V . Ngược lại, nếu ( u , v , w) là một tam diện nghịch thì u .( v ∧ w) = #» #» #» ( u ∧ v ).w = −V .
Định nghĩa 1.3.17. Đại lượng #» #» #» #» #» #» #» #» #»
[ u , v , w] := u .( v ∧ w) = ( u ∧ v ).w #» #» #»
được gọi là tích hỗn tạp của ba vectơ u , v và w.
Chứng minh của bổ đề 1.3.16 kéo theo sự thật rằng:
Hệ quả 1.3.18. Ba vectơ đồng phẳng khi và chỉ khi tích hỗn tạp của chúng bằng 0.
Để kết thúc mục này, ta đưa ra sau đây một chứng minh cho định lý 1.3.15.
Chứng minh định lý 1.3.15. Các tính chất 1 và 3 được suy trực tiếp từ định #» #» #» #» #»
nghĩa của tích hữu hướng. Đối với tính chất thứ hai, đặt s = u ∧ ( v + w) − u ∧ #» #» #» #» #»
v − u ∧ w. Ta phải chứng minh s = 0 . Thật vậy, #» #» #» #» #» #» #» #» #»
s 2 = s [ u ∧ ( v + w) − u ∧ v − u ∧ w] #» #» #» #» #» #» #» #» #» #»
= [ s , u , v + w] − [ s , u , v ] − [ s , u , w] (tính phân phối của tích vô hướng) #» #» #» #» #» #» #» #» #» #»
= ( s ∧ u )( v + w) − ( s ∧ u ) v − ( s ∧ u ) v (định nghĩa tích hỗn tạp) #» #» #» #» #» #» #» #»
= ( s ∧ u )( v + w) − ( s ∧ u )( v + w) (tính phân phối của tích vô hướng) = 0. #» #»
Từ đây ắt phải có s = 0 . Ta thu được điều cần chứng minh. 1.3.3
Không gian vectơ Euclide và đại số vectơ
Định nghĩa 1.3.19. Một không gian vectơ nếu được trang bị thêm tích vô
hướng được gọi là một không gian vectơ Euclide, nếu được trang bị tích
hữu hướng thì được gọi là một đại số vectơ.
Ví dụ 1.3.20. V2 là một không gian vectơ Euclide, V3 là một đại số vectơ Eu- clide. 16