Tài liệu tham khảo. Hướng dẫn đề thi cuối kì Toán HK1 . Khoa học ứng dụng

TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
ĐỀ THI CUỐI KỲ I NĂM HỌC 25-26 THÀNH PHỐ HỒ CHÍ MINH Môn: TOÁN 1 (ĐỢT 1) KHOA KHOA HỌC ỨNG DỤNG Mã môn học: MATH132401 BỘ MÔN TOÁN
Ngày thi: 28/10/2025. Thời gian: 90 phút.
Được sử dụng tài liệu là 1 tờ A4 viết tay.
Câu 1 (1.0 điểm). Cho hai hàm số f  x 1 sin  x , g  x 2
 3x  3x  2 . Giải phương trình
g f x  2 .  4x 1 1  , neu x  0
Câu 2 (2.0 điểm). Cho f  x   x . b    2 x  sin x  3x  , m neu x  0
(a) Xác định các giá trị của b và m để hàm số f  x liên tục tại x  0 .
(b) Với b  0 và m  2 , hãy xét tính khả vi của hàm số tại x  0 .
Câu 3 (1.0 điểm). Viết phương trình tiếp tuyến với đường cong C có phương trình 5 3 x  xy  y  x 4 ln
 y  1, tại P 1;  1 .
Câu 4 (1.0 điểm). Áp suất khí (tính bằng Pa) trong buồng nén biến thiên theo thể tích V  3 m  theo công 500 dV thức P V  
. Biết thể tích khí đang tăng với tốc độ   3
0.04 m s tại thời điểm 3 V  2 m . Tìm 2 V 1 dt
tốc độ thay đổi của áp suất P tại thời điểm đó.
Câu 5 (1.5 điểm). Một công ty sản xuất dự định chế tạo một bồn chứa dầu hình trụ có đáy kín nhưng không
nắp, với thể tích yêu cầu là 3
V  100 m . Chi phí vật liệu làm đáy bồn có giá 2 triệu đồng/ 2 m , còn chi phí
vật liệu làm thành bồn là 3 triệu đồng/ 2
m . Hãy xác định kích thước của bồn (bán kính đáy và chiều cao)
sao cho tổng chi phí vật liệu là nhỏ nhất, và tính chi phí tối thiểu đó. (Cho biết thể tích và diện tích thành
bên của hình trụ có chiều cao h và bán kính đáy r lần lượt là 2 V   r h và S  2 rh ). bên
Câu 6 (1.5 điểm). Tìm cực trị tương đối của hàm số      2 2 x U x x e .
Câu 7 (2.0 điểm). Một tách cà phê ban đầu có nhiệt độ 90C được đặt trong một căn phòng có nhiệt độ
không đổi là 20C . Sau 5 phút, nhiệt độ của tách cà phê là 60C . Kí hiệu T t là nhiệt độ tách cà phê
sau t phút. Theo định luật làm nguội của Newton, sự thay đổi nhiệt độ tách cà phê được mô tả theo phương trình vi phân dT  k T T a  dt
trong đó k là một hằng số và T là nhiệt độ căn phòng. a
(a) Xác định hàm nhiệt độ T t .
(b) Tính nhiệt độ trung bình của tách cà phê trong 10 phút đầu tiên. 1/2
Số hiệu: BM1/QT-PDBCL-RĐTV
Ghi chú: Cán bộ coi thi không giải thích đề thi.
Chuẩn đầu ra của học phần (Về kiến thức) Nội dung KT
CLO1: Giải thích được các khái niệm về hàm số, hàm ngược, hàm siêu việt, vẽ đồ thị, Câu 1, 2, 3, 4,
liên tục, đạo hàm, vi phân và tích phân. 5, 6, 7
CLO2: Tính được các giới hạn, đạo hàm, vi phân của một hàm số, tính tích phân cơ Câu 2, 3, 4, 5, bản. 6, 7, 8
CLO3: Xây dựng được mô hình toán học sử dụng đạo hàm để giải quyết các yêu cầu Câu 4, 5, 7
về tốc độ thay đổi và tối ưu trong đời sống, vật lý và kỹ thuật.
CLO4: Giải được phương trình vi phân tách biến. Câu 7
TP.HCM, ngày 21 tháng 10 năm $2025$ Trưởng bộ môn toán [Chữ ký] Phạm Văn Hiển 2/2
Số hiệu: BM1/QT-PDBCL-RĐTV LỜI GIẢI THAM KHẢO
SV làm theo cách khác, nếu đúng vẫn chấm điểm bình thường
ĐÁP ÁN CHỈ MANG TÍNH CHẤT THAM KHẢO
Câu 1 (1.0 điểm). Cho hai hàm số f  x 1 sin  x , g  x 2
 3x  3x  2 . Giải phương trình
g f x  2 . Lời giải:
Tập xác định: D   1  ,  1 và D   f  1, 1 x
Phương trình  g f  x    g  f  2 2  2
  3 f  3 f  2  2   f x 1  0 sin x  0 x  0        f   x 1  1 sin x 1 x  sin1
Vậy tập nghiệm của phương trình là: S  0,sin  1  4x 1 1  , neu x  0
Câu 2 (2.0 điểm). Cho f  x   x . b    2 x  sin x  3x  , m neu x  0
(a) Xác định các giá trị của b và m để hàm số f  x liên tục tại x  0 .
(b) Với b  0 và m  2 , hãy xét tính khả vi của hàm số tại x  0 . Lời giải:
(a) Xác định các giá trị của b và m để hàm số f  x liên tục tại x  0 .
f  x liên tục tại x  0  f 0  lim f  x  lim f  x (1) x 0 x 0   Ta có: f 0  m (2)
Cũng có: lim f  x  lim b          2 x sin x 3x m m  (3) x0 x0 4x 1 1 2 Và lim f  x L'h  lim  lim  2 (4) x 0 x 0 x 0 x     4x 1 Từ  
1 ,2,3,4 suy ra để f  x liên tục tại x  0  m  2, b   
(b) Với b  0 và m  2 , hãy xét tính khả vi của hàm số tại x  0  4x 1 1  , neu x  0
Với b  0 và m  2 suy ra f  x liên tục tại x  0 và f  x   x 3  x  2, neu x  0 f x  f 0  3x  2  2 3x Xét: f '0       lim  lim  lim  3 x0  x0 x0 x 0 x  x 3/2
Số hiệu: BM1/QT-PDBCL-RĐTV 4x 1 1 2  2  2 f x  f 0  4x 1 1 2x Và: f       L'h x 4x 1 ' 0  lim  lim  lim  lim    2 x0  x0 x0 x0 x 0 x x  2x       x  1 4x 11 4x 1 1 4 1    f   4 ' 0  lim  lim  lim  2 x0 x0 x 4x 1  x 1 4x 1 x0 4x 1  1 4x 1 4x 1 Do: f '0  f '0 
 f x không khả vi tại x  0
Câu 3 (1.0 điểm). Viết phương trình tiếp tuyến với đường cong C có phương trình 5 3 x  xy  y  x 4 ln
 y  1, tại P 1;  1 . Lời giải: Từ 5 3 x  xy  y  x 4 ln
 y  1 ta đặt: F x y 5 3  x  xy  y x 4 , ln  y 1  0 4 3 y 5x  y  y dy F Suy ra: 4 3 2  5   ,  3  ln   3  4 x x F x y F xy x y      x y 2 x dx F 3xy  ln x  y y   3 4 dy F
Hệ số góc của tiếp tuyến: x k     3 dx F P1;  1 y
Phương trình tiếp tuyến: y  3 x   1 1  3x  4
Câu 4 (1.0 điểm). Áp suất khí (tính bằng Pa) trong buồng nén biến thiên theo thể tích V  3 m  theo công 500 dV thức P V  
. Biết thể tích khí đang tăng với tốc độ   3
0.04 m s tại thời điểm 3 V  2 m . Tìm 2 V 1 dt
tốc độ thay đổi của áp suất P tại thời điểm đó. Lời giải: 500
Lấy vi phân 2 vế của phương trình P V   theo thời gian t s : 2 V 1 dP 1000V dV Phương trình     dt   2 2 1 dt V dV dP 1000 16 Theo đề:   3 0.04 m s và 3 V  2 m khi đó:   
0.04   Pa s dt dt 25 5 V 2 16
Vậy, áp suất đang giảm với tốc độ: Pa s 5
Mỗi phép toán thiếu đơn vị thì bị trừ 0,1 điểm
Câu 5 (1.5 điểm). Một công ty sản xuất dự định chế tạo một bồn chứa dầu hình trụ có đáy kín nhưng không
nắp, với thể tích yêu cầu là 3
V  100 m . Chi phí vật liệu làm đáy bồn có giá 2 triệu đồng/ 2 m , còn chi phí
vật liệu làm thành bồn là 3 triệu đồng/ 2
m . Hãy xác định kích thước của bồn (bán kính đáy và chiều cao)
sao cho tổng chi phí vật liệu là nhỏ nhất, và tính chi phí tối thiểu đó. (Cho biết thể tích và diện tích thành
bên của hình trụ có chiều cao h và bán kính đáy r lần lượt là 2 V   r h và S  2 rh ). bên 4/2
Số hiệu: BM1/QT-PDBCL-RĐTV Lời giải: 100 Theo đề ta có: 2
V   r h  100  h  m 2   r 100 300 Hàm chi phí: C r 2 2 2 2S 3S 2 r 3 2 rh 2 r 6 2           r  (triệu đồng), day bên   r  r  với r  0 300 600 Xét: C 'r 3 2    2r   0  r  150  ,Và: C 'r 2    2   0, r   0 2     r  3  r  2 Nên min C r  C  khi 3 r  150 m 3  h  150 m  3150 3 2 6 150 r 0 3
Vậy chi phí thấp nhất (tối thiểu) cần dùng là: 3 2 6 150 (triệu đồng) 2
với hai kích thước hình trụ 3 r  150 m 3 , h  150 m 3
Mỗi phép toán thiếu đơn vị thì bị trừ 0,1 điểm
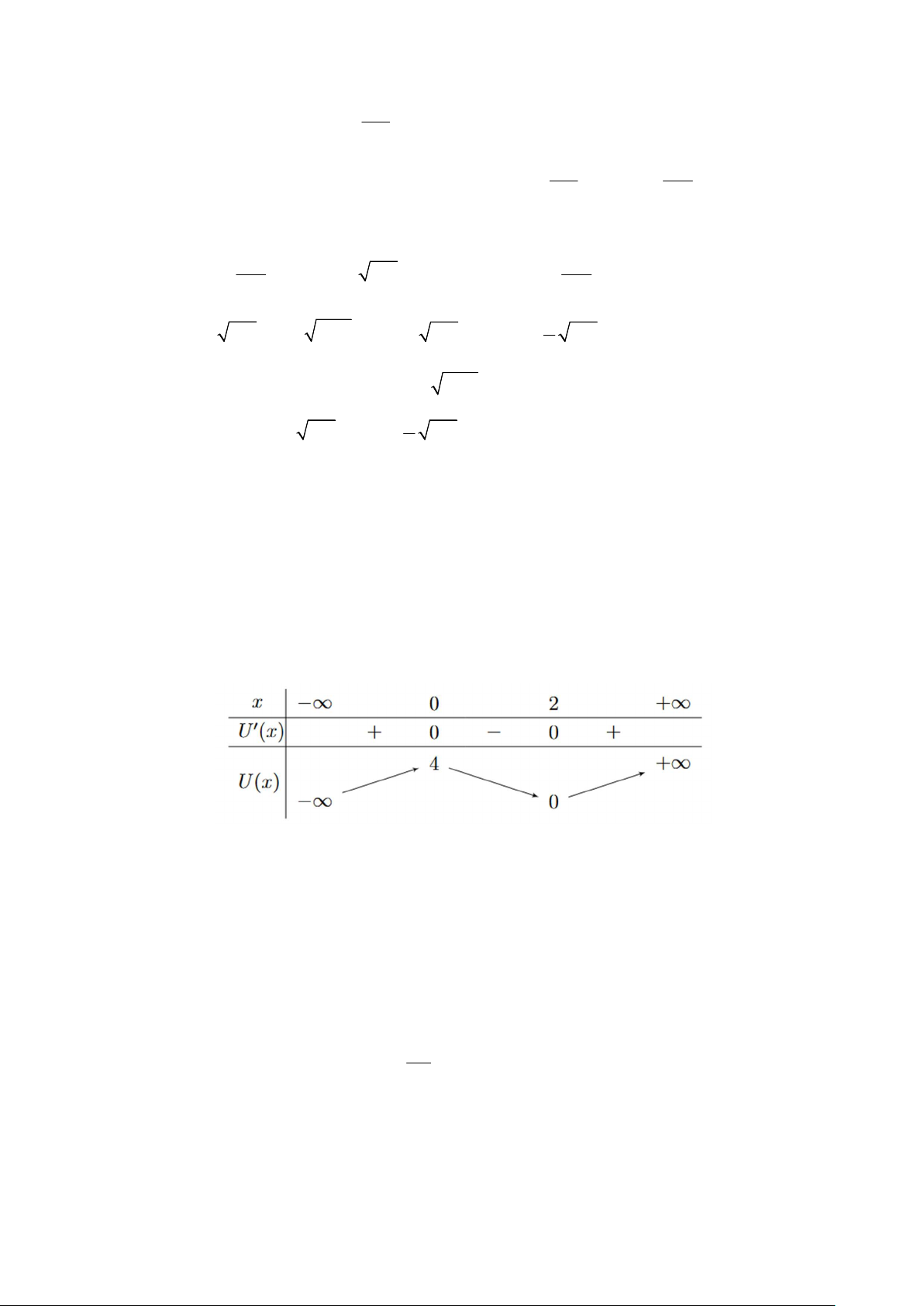
Câu 6 (1.5 điểm). Tìm cực trị tương đối của hàm số      2 2 x U x x e . Lời giải: Tập xác định: D   U x
Đạo hàm: '     2 x U x x x e Bảng biến thiên:
Từ bảng biến thiên suy ra hàm số đạt cực cực đại tương đối tại x  0 với f 0  4 và đạt cực tiểu tương
đối tại x  2 với f 2  0
Câu 7 (2.0 điểm). Một tách cà phê ban đầu có nhiệt độ 90C được đặt trong một căn phòng có nhiệt độ
không đổi là 20C . Sau 5 phút, nhiệt độ của tách cà phê là 60C . Kí hiệu T t là nhiệt độ tách cà phê
sau t phút. Theo định luật làm nguội của Newton, sự thay đổi nhiệt độ tách cà phê được mô tả theo phương trình vi phân dT  k T T a  dt
trong đó k là một hằng số và T là nhiệt độ căn phòng. a
(a) Xác định hàm nhiệt độ T t .
(b) Tính nhiệt độ trung bình của tách cà phê trong 10 phút đầu tiên. 5/2
Số hiệu: BM1/QT-PDBCL-RĐTV Lời giải:
(a) Xác định hàm nhiệt độ T t . Từ đề ta có: T
20C,T 0 90C,T 5 60    C a dT dT dT Khi đó:  k T T   kdt   kdt  C  T   kt  C a  ln 20   dt T  20 T  20    kt T t  Ce  20 T    C   70 0  C  20  90  Mà    T  5 1 4 5k  Ce  20  60 k  ln  5 7  1 4  ln t   Vậy: T t  5 7 70e    20
(b) Tính nhiệt độ trung bình của tách cà phê trong 10 phút đầu tiên. 10   10 10  1 4  10  1 4   1 4 1              T  T t dt   e    dt   e    dt      e   t    TB   ln t ln t ln 1 5 t 165 1 5 7 5 7 5 7 70 20 7 2 2 20 10  0 10 4 49 4 0 0    0    ln  ln  7  7 0 6/2
Số hiệu: BM1/QT-PDBCL-RĐTV