Luyện kỹ năng Toán 10 trắc nghiệm hệ thức lượng tam giác thường

Tài liệu gồm 32 trang, được biên soạn bởi thầy giáo Đặng Công Đức (Giang Sơn), tuyển chọn các bài tập luyện kỹ năng môn Toán 10 trắc nghiệm hệ thức lượng tam giác thường mức độ cơ bản – vận dụng – vận dụng cao, kết hợp ba bộ sách giáo khoa Toán 10 chương trình mới: Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống. Mời bạn đọc đón xem!

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

32 trang 1 tháng trước

Tác giả:

Profile Lê Phương
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
L
L
U
U
Y
Y
Ệ
Ệ
N
N
K
K
Ỹ
Ỹ
N
N
Ă
Ă
N
N
G
G
T
T
O
O
Á
Á
N
N
1
1
0
0
T
T
H
H
P
P
T
T
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
H
H
Ệ
Ệ
T
T
H
H
Ứ
Ứ
C
C
L
L
Ư
Ư
Ợ
Ợ
N
N
G
G
T
T
A
A
M
M
G
G
I
I
Á
Á
C
C
T
T
H
H
Ư
Ư
Ờ
Ờ
N
N
G
G
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
–
–
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
–
–
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
C
C
A
A
O
O
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
Đ
Đ
Á
Á
P
P
Á
Á
N
N
C
C
H
H
I
I
T
T
I
I
Ế
Ế
T
T
P
P
D
D
F
F
B
B
Ạ
Ạ
N
N
Đ
Đ
Ọ
Ọ
C
C
V
V
U
U
I
I
L
L
Ò
Ò
N
N
G
G
L
L
I
I
Ê
Ê
N
N
H
H
Ệ
Ệ
T
T
Á
Á
C
C
G
G
I
I
Ả
Ả
:
:
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
9
9
8
8
0
0
2
2
1
1
9
9
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
7
7
/
/
2
2
0
0
2
2
4
4
2
L
L
U
U
Y
Y
Ệ
Ệ
N
N
K
K
Ỹ
Ỹ
N
N
Ă
Ă
N
N
G
G
T
T
O
O
Á
Á
N
N
1
1
0
0
T
T
H
H
P
P
T
T
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
H
H
Ệ
Ệ
T
T
H
H
Ứ
Ứ
C
C
L
L
Ư
Ư
Ợ
Ợ
N
N
G
G
T
T
A
A
M
M
G
G
I
I
Á
Á
C
C
T
T
H
H
Ư
Ư
Ờ
Ờ
N
N
G
G
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
–
–
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
–
–
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
C
C
A
A
O
O
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
DUNG
LƯỢNG
NỘI DUNG BÀI TẬP
3 FILE
1 file 2 trang
CƠ BẢN GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
3 FILE
1 file 2 trang
CƠ BẢN ĐỊNH LÝ SIN, ĐỊNH LÝ COSIN, GIẢI TAM GIÁC
3 FILE
1 file 2 trang
VẬN DỤNG GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
3 FILE
1 file 2 trang
VẬN DỤNG ĐỊNH LÝ SIN, ĐỊNH LÝ COSIN, GIẢI TAM GIÁC
3 FILE
1 file 2 trang
VẬN DỤNG CAO GÓC LƯỢNG GIÁC, HỆ THỨC LƯỢNG
TAM GIÁC THƯỜNG
3
HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN CƠ BẢN P1)
_______________________________
Câu 1. Giá trị của
o o
cos 60 sin 30
bằng bao nhiêu?
A.
3
2
B.
3
C.
3
3
D.
1
.
Câu 2. Giá trị của
o o
tan 30 cot 30
bằng bao nhiêu?
A.
4
3
B.
C.
2
3
D.
2
Câu 3. Trong các đẳng thức sau đây, đẳng thức nào sai?
A.
o o
sin 0 cos 0 1
B.
o o
sin90 cos90 1
C.
o o
sin180 cos180 1
D.
o o
sin 60 cos60 1
Câu 4. Trong các khẳng định sau, khẳng định nào sai?
A.
o o
cos60 sin30
. B.
o o
cos60 sin120
. C.
o o
cos30 sin120
. D.
o o
sin 60 cos120
.
Câu 5. Đẳng thức nào sau đây sai?
A.
o o
sin 45 sin 45 2
. B.
o o
sin30 cos60 1
.
C.
o o
sin 60 cos150 0
. D.
o o
sin120 cos30 0
.
Câu 6. Giá trị
o o
cos 45 sin 45
bằng bao nhiêu?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 7. Trong các đẳng thức sau, đẳng thức nào đúng?
A.
o
sin 180 cos
. B.
o
sin 180 sin
.
C.
o
sin 180 sin
. D.
o
sin 180 cos
.
Câu 8. Trong các đẳng thức sau, đẳng thức nào sai?
A.
o o
sin 0 cos0 0
. B.
o o
sin 90 cos90 1
.
C.
o o
sin180 cos180 1
. D.
o o
3 1
sin 60 cos 60
2
.
Câu 9. Cho
là góc tù. Điều khẳng định nào sau đây là đúng?
A.
sin 0
. B.
cos 0
. C.
tan 0
. D.
cot 0
.
Câu 10. Giá trị của
o o o o
sin 36 cos 6 sin126 cos 84
E
là
A.
1
2
. B.
3
2
. C.
1
. D.
1
.
Câu 11. Trên nửa đường tròn đơn vị cho điểm
M
sao cho
xoM
như hình bên. Tìm mệnh đề đúng.
A.
os 0
c
. B.
os 0
c
. C.
os 0
c
. D.
os 1
c
.
Câu 12. Cho góc
x
thoả
0 0
0 90
x
. Trong các mệnh đề sau, mệnh đề nào sai?
A.
sin 0
x
B.
cos 0
x
C.
tan 0x
D.
cot 0
x
Câu 13. Giá trị của biểu thức
0 0 0 0
tan ttan 9 27 63 tan 1 an 8
bằng
A.
2
. B.
4
. C.
2
. D.
1
2
.
Câu 14. Cho
tan 2 90 180
thì
cos
có giá trị bằng :
4
A.
1
5
. B.
1
5
. C.
3
5
. D.
3
5
.
Câu 15. Giá trị của
2 2 2 2
cos 73 cos 87 cos 3 cos 17
B
là
A.
2
. B.
2
. C.
2
. D.
1
.
Câu 16. Cho
tan 2
. Giá trị của
3sin cos
sin cos
A
là:
A.
5
. B.
5
3
. C.
7
. D.
7
3
.
Câu 17. Cho
1
cos
2
x
. Tính biểu thức
2 2
3sin 4 cosP x x
A.
13
4
. B.
7
4
. C.
11
4
. D.
15
4
.
Câu 18. Biết
1
cos
3
. Giá trị đúng của biểu thức
2 2
sin 3cos
P
là:
A.
1
3
. B.
10
9
. C.
11
9
. D.
4
3
.
Câu 19. Cho biết
1
tan
2
. Tính
cot
.
A.
cot 2
. B.
cot 2
. C.
1
cot
4
. D.
1
cot
2
.
Câu 20. Trên nửa đường tròn đơn vị cho điểm
M
sao cho
xoM
như hình bên. Tìm mệnh đề đúng.
A.
sin 0
. B.
sin 0
. C.
sin 0
. D.
sin 1
.
Câu 21. Cho
là góc tù và
5
sin
13
. Giá trị của biểu thức
3sin 2 cos
là
A.
3
. B.
9
13
. C.
3
. D.
9
13
.
Câu 22. Cho biết
sin cos
a
. Giá trị của
sin .cos
bằng bao nhiêu?
A.
2
sin .cos
a
. B.
sin .cos 2a
.
C.
2
1
sin .cos
2
a
. D.
2
1
sin .cos
2
a
.
Câu 23. Cho biết
2
cos
3
. Tính giá trị của biểu thức
cot 3 tan
2cot tan
E
?
A.
19
13
. B.
19
13
. C.
25
13
. D.
25
13
Câu 24. Cho biết
2
cos
3
. Giá trị của biểu thức
cot 3 tan
2 cot tan
E
bằng bao nhiêu?
A.
25
3
. B.
11
13
. C.
11
3
. D.
25
13
.
Câu 25. Trong các hệ thức sau hệ thức nào đúng?
A.
2 2
sin cos 1
. B.
2 2
sin cos 1
2
.
C.
2 2
sin cos 1
. D.
2 2
sin 2 cos 2 1
.
5
HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN CƠ BẢN P2)
_______________________________
Câu 1. Đẳng thức nào sau đây đúng?
A.
o
tan 180 tana a
. B.
o
cos 180 cosa a
.
C.
o
sin 180 sina a
. D.
o
cot 180 cota a
.
Câu 2. Trên nửa đường tròn đơn vị cho điểm
M
sao cho
xoM
như hình bên. Tìm mệnh đề đúng.
A.
sin 0
. B.
sin 0
. C.
sin 0
. D.
sin 1
.
Câu 3. Trong các đẳng thức sau đây, đẳng thức nào đúng?
A.
sin 180 sin
. B.
cos 180 cos
C.
tan 180 tan
. D.
cot 180 cot
Câu 4. Cho
và
là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
A.
sin sin
. B.
cos cos
. C.
tan tan
. D.
cot cot
.
Câu 5. Cho góc
tù. Điều khẳng định nào sau đây là đúng?
A.
sin 0
. B.
cos 0
. C.
tan 0
. D.
cot 0
.
Câu 6. Hai góc nhọn
và
phụ nhau, hệ thức nào sau đây là sai?
A.
sin cos
. B.
tan cot
. C.
1
cot
cot
. D.
cos sin
.
Câu 7. Trên nửa đường tròn đơn vị cho điểm
M
sao cho
xoM
như hình bên. Tìm mệnh đề đúng.
A.
0
0
tan
x
y
. B.
0
0
tan
y
x
. C.
tan
o
x
. D.
0
tan
y
.
Câu 8. Đơn giản biểu thức
2 2 2
1 sin cot 1 cotG x x x
.
A.
2
sin x
. B.
2
cos x
. C.
1
cos x
. D.
cos x
.
Câu 9. Đơn giản biểu thức
sin
cot
1 cos
x
E x
x
ta được
A.
sin x
. B.
1
cos x
. C.
1
sin x
. D.
cos x
.
Câu 10. Khẳng định nào sau đây là sai?
6
A.
2 2
sin cos 1
. B.
2
2
1
1 cot sin 0
sin
.
C.
tan .cot 1 sin .cos 0
. D.
2
2
1
1 tan cos 0
cos
.
Câu 11. Bất đẳng thức nào dưới đây là đúng?
A.
sin90 sin100
. B.
cos95 cos100
. C.
tan 85 tan125
. D.
cos145 cos125
.
Câu 12. Cho
3
sin , 90 180
5
. Tính
cot 180P
A.
3
4
P
. B.
3
4
P
. C.
4
3
P
. D.
4
3
P
.
Câu 13. Cho góc
thỏa mãn
0 180
,
1 2
cos , sin
3 3
. Khẳng định nào sau đây sai?
A.
tan 2
. B.
2
cot
2
.
C.
2
sin 180
3
. D.
1
cos 180
3
.
Câu 14. Cho biết
2
cos
3
. Tính
tan
?
A.
5
4
. B.
5
2
. C.
5
2
. D.
5
2
.
Câu 15. Cho biết
1
tan
2
. Tính
cot
.
A.
cot 2
. B.
cot 2
. C.
1
cot
4
. D.
1
cot
2
.
Câu 16. Đẳng thức nào sau đây là sai?
A.
1 cos sin
0 , 180
sin 1 cos
x x
x x
x x
. B.
1
tan cot 0 , 90 ,180
sin cos
x x x
x x
C.
2 2
2 2
1
tan cot 2 0 , 90 ,180
sin cos
x x x
x x
D.
2 2
sin 2 cos 2 2
x x
.
Câu 17. Biểu thức
2 2 2 2
tan sin tan sinx x x x
có giá trị bằng
A.
1
. B.
0
. C.
2
. D.
1
.
Câu 18.
cos
bằng bao nhiêu nếu
1
cot
2
?
A.
5
5
. B.
5
2
. C.
5
5
. D.
1
3
.
Câu 19. Nếu
tan 3
thì
cos
bằng bao nhiêu?
A.
10
10
. B.
1
3
. C.
10
10
. D.
10
10
.
Câu 20. Cho
là góc tù và
5
sin
13
. Giá trị của biểu thức
3sin 2cos
là
A.
9
13
. B.
3
. C.
9
13
. D.
3
.
Câu 21. Biết
cot , 0
a a
. Tính
cos
.
A.
2
cos
1
a
a
. B.
2
1
cos
1
a
. C.
2
1
cos
1
a
. D.
2
cos
1
a
a
.
Câu 22. Cho
là góc tù và
4
sin
5
. Giá trị của biểu thức
2sin cosA
bằng
A.
7
5
. B.
7
5
. C.
1
. D.
11
5
.
____________________________
7
LƯỢNG GIÁC LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN CƠ BẢN P3)
_______________________________
Câu 1. Cho góc
90 ;180 .
Khẳng định nào sau đây đúng?
A.
sin
và
cot
cùng dấu. B. Tích
sin .cot
mang dấu âm.
C. Tích
sin .cos
mang dấu dương. D.
sin
và
tan
cùng dấu.
Câu 2. Cho
là góc tù. Mệnh đề nào đúng trong các mệnh đề sau?
A.
tan 0.
B.
cot 0.
C.
sin 0.
D.
cos 0.
Câu 3. Cho
0º 90º
. Khẳng định nào sau đây đúng?
A.
cot 90º tan
. B.
cos 90º sin
.
C.
sin 90º cos
. D.
tan 90º cot
.
Câu 4. Trong các khẳng định sau, khẳng định nào sai?
A.
cos 60 sin30
. B.
cos60 sin120
. C.
cos30 sin120
. D.
sin 60 cos120
.
Câu 5. Đẳng thức nào sau đây sai?
A.
sin 45 sin 45 2
. B.
sin30 cos60 1
.
C.
sin 60 cos150 0
. D.
sin120 cos30 0
.
Câu 6. Cho hai góc nhọn
và
(
)
. Khẳng định nào sau đây là sai?
A.
cos cos
. B.
sin sin
. C.
tan tan 0
. D.
cot cot
.
Câu 7. Cho 4 góc có các điểm biểu diễn trên nửa đường tròn đơn vị thứ tự là
, , ,A B C D
như hình vẽ.
Hỏi trong 4 góc đó có bao nhiêu góc có giá trị lượng giác cosin là một số dương?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 8. Đơn giản biểu thức
2 2 2
1 sin cot 1 cotG x x x
.
A.
2
sin x
. B.
2
cos x
. C.
1
cos x
. D.
cos x
.
Câu 9. Cho
ABC
vuông tại
A
, góc
B
bằng
30
. Khẳng định nào sau đây là sai?
A.
1
cos
3
B
. B.
3
sin
2
C
. C.
1
cos
2
C
. D.
1
sin
2
B
Câu 10. Công thức nào sau đây sai
A.
2
2
1
1 tan
cos
x
x
B.
2
2
1
1 cot
sin
x
x
C.
2
2
2
1 tan
cos
x
x
D.
2 2
tan .cot 1x x
Câu 11. Cho 4 góc có các điểm biểu diễn trên nửa đường tròn đơn vị thứ tự là
, , ,A B C D
như hình vẽ.
Hỏi trong 4 góc đó có bao nhiêu góc có giá trị lượng giác sin là một số dương?
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 12. Cho góc
thỏa mãn
1
cos
3
. Giá trị của biểu thức
1
sin
cos
P
bằng
A.
9 2 2
3
. B.
4 3
2
. C.
3 2 2
3
. D.
.
Câu 13. Giá trị của
2 2 2 2
cos 73 cos 87 cos 3 cos 17
B
là
8
A.
2
. B.
2
. C.
2
. D.
1
.
Câu 14. Giá trị của biểu thức
2 2 2 2
sin 51 sin 55 sin 39 sin 35
A
là
A.
3
. B.
4
. C.
1
. D.
2
.
Câu 15. Cho biết
3
sin .
3 5
Giá trị của
2 2
3sin 5cos
3 3
P
bằng bao nhiêu?
A.
105
.
25
P
B.
107
.
25
P
C.
109
.
25
P
D.
111
.
25
P
Câu 16. Cho biết
2
cos
3
. Giá trị của biểu thức
cot 3tan
2cot tan
E
bằng bao nhiêu?
A.
25
3
. B.
11
13
. C.
11
3
. D.
25
13
.
Câu 17. Biết
1
cos
3
. Giá trị đúng của biểu thức
2 2
sin 3 cos
P
là:
A.
11
9
. B.
4
3
. C.
1
3
. D.
10
9
.
Câu 18. Cho
1
3
cot
. Giá trị của biểu thức
3sin 4cos
2sin 5cos
A
là:
A.
15
13
. B.
13
. C.
15
13
. D.
13
.
Câu 19. Rút gọn biểu thức
2
1
2sin .cos
sin x
P
x x
ta được
A.
1
tan
2
P x
. B.
1
cot
2
P x
. C.
2cotP x
. D.
2 tanP x
.
Câu 20. Trên nửa đường tròn đơn vị cho điểm
M
sao cho
xoM
như hình bên. Tìm mệnh đề đúng.
A.
os 0
c
. B.
os 0
c
. C.
os 0
c
. D.
os 1
c
.
Câu 21. Cho
, ,A B C
là ba góc trong tam giác
ABC
, chọn mệnh đề đúng trong các mệnh đề sau:
A.
sin sin
C A B
. B.
cos cos
C A B
.
C.
cot cot
C A B
. D.
tan tan
C A B
.
Câu 22. Rút gọn biểu thức
2
1 sin
2sin .cos
x
P
x x
ta được
A.
1
tan
2
P x
. B.
1
cot
2
P x
. C.
2cotP x
. D.
2 tanP x
.
Câu 23. Biểu thức:
4 2 2 2
cos cos sin sinf x x x x x
có giá trị bằng
A.
1
. B.
2
. C.
2
. D.
1
.
Câu 24. Biểu thức
2 2 2 2
tan sin tan sinx x x x
có giá trị bằng
A.
1
. B.
0
. C.
2
. D.
1
.
Câu 25. Cho biết
2
cos
3
. Tính giá trị của biểu thức
cot 3tan
2cot tan
E
?
A.
19
13
. B.
19
13
. C.
25
13
. D.
25
13
_________________________________
9
HỆ THỨC LƯỢNG TRONG TAM GIÁC THƯỜNG LỚP 10 THPT
ĐỊNH LÝ SIN, ĐỊNH LÝ COSIN, GIẢI TAM GIÁC
(LỚP BÀI TOÁN CƠ BẢN P1)
________________________________________________
Câu 1. Cho tam giác
ABC
, mệnh đề nào sau đây đúng?
A.
2 2 2
2 cosa b c bc A
B.
2 2 2
2 cosa b c bc A
C.
2 2 2
2 cosa b c bc C
D.
2 2 2
2 cosa b c bc B
Câu 2. Tính diện tích tam giác
ABC
, biết
7, 8, 6
a b c
.
A.
21 15
4
S
B.
5 15
2
S
C.
5 15
4
S
D.
15
2
S
Câu 3. Cho tam giác
ABC
, chọn công thức đúng ?
A.
2 2 2
2 . cos
AB AC BC AC AB C
. B.
2 2 2
2 . cos
AB AC BC AC BC C
.
C.
2 2 2
2 . cos
AB AC BC AC BC C
. D.
2 2 2
2 . cos
AB AC BC AC BC C
.
Câu 4. Định lý sin được phát biểu là
A.
2 .
sin sin sinC
a b c
R
A B
B.
2
2sin 2sin 2sinC
a b c
R
A B
C.
sin sin sinC
a b c
R
A B
D.
2 2 2
.
sin sin sinC
a b c
R
A B
Câu 5. Cho
ABC
thỏa mãn :
2cos 2
B
. Khi đó:
A.
0
30 .
B
B.
0
60 .
B
C.
0
45 .
B
D.
0
75 .
B
Câu 6. Cho
ABC
vuông tại
B
và có
0
25
C
. Số đo của góc
A
là:
A.
0
65 .
A
B.
0
60 .
A
C.
0
155 .
A
D.
0
75 .
A
Câu 7. Công thức diện tích nào sau đây đúng
A.
2 sin sin sinS bc A ca B ab C
B.
sin sin sinS bc A ca B ab C
C.
1 1 1
sin sin sin
3 3 3
S bc A ca B ab C
D.
2 sin 2 sin 2 sinS bc A ca B ab C
Câu 8. Cho tam giác
ABC
có
3
7; 5;cos
5
b c A
. Diện tích tam giác
ABC
bằng
A.10 B. 14 C. 15 D. 18
Câu 9. Cho
ABC
có
0
6, 8, 60
b c A
. Độ dài cạnh
a
là:
A.
2 13.
B.
3 12.
C.
2 37.
D.
20.
Câu 10. Một tam giác giải được nếu biết :
A. Độ dài
3
cạnh B. Độ dài
2
cạnh và
1
góc bất kỳ
C. Số đo
3
góc D. Độ dài
1
cạnh và
2
góc bất kỳ
Câu 11. Chọn công thức đúng trong các đáp án sau:
A.
1
sin .
2
S bc A
B.
1
sin .
2
S ac A
C.
1
sin .
2
S bc B
D.
sin .S bc B
Câu 12. đây là công thức Heron (tính diện tích tam giác với độ dài 3 cạnh cho trước).
A.
S p p a p b p c
B.
2
S p p a p b p c
C.
2
S p p a p b p c
D.
S p p a p b p c
Câu 13. Tam giác
ABC
có
5, 7, 8AB BC CA
. Số đo góc
A
bằng:
A.
30 .
B.
45 .
C.
60 .
D.
90 .
Câu 14. Tam giác
ABC
có
2, 1AB AC
và
60A
. Tính độ dài cạnh
BC
.
A.
1.BC
B.
2.BC
C.
2.
BC
D.
3.
BC
Câu 15. Tam giác
ABC
có
2, 3
AB AC
và
45C
. Tính độ dài cạnh
BC
.
A.
5.
BC
B.
6 2
.
2
BC
C.
6 2
.
2
BC
D.
6.
BC
Câu 16. Trong tam giác
ABC
công thức nào sau đây có thể dùng để tính
cos A
?
A.
2 2 2
cos .
2
c a b
A
ca
.
B.
2 2 2
cos .
2
b c a
A
bc
.
10
C.
2 2 2
cos .
2
a b c
A
ab
. D.
2 2 2
cos .
2
a b c
A
ac
.
Câu 17. Cho tam giác
ABC
có
120
A
. Chọn khẳng định đúng.
A.
2 2 2
3a b c bc
B.
2 2 2
a b c bc
. C.
2 2 2
3a b c bc
. D.
2 2 2
a b c bc
.
Câu 18. Cho tam giác
ABC
có góc
120
A
,
8, 5
b c
. Khi đó số đo của
B
gần nhất với số nào sau đây?
A.
71 35'
B.
30 37 '
. C.
45 12 '
. D.
37 35'
.
Câu 19. Cho
ABC
có
6, 8, 10.
a b c
Diện tích
S
của tam giác trên là:
A.
48.
B.
24.
 C.
12.
 D.
30.

Câu 20. Tính diện tích tam giác
ABC
có
12; 8; 30
AB AC BAC
.
A.
24 2
B. 48 C. 24 D.
24 3
Câu 21. Cho tam giác
ABC
có
ˆ
ˆ
75 , 45
B C
và
50
BC
. Tính độ dài cạnh
AB
.
A.
24 2
B. 48 C. 24 D.
40,8
Câu 22. Cho tam giác
ABC
có
6, 7, 8
AB AC BC
. Giá trị
cos A
bằng bao nhiêu?
A.
0,5
B.
1
4
C.
1
3
D.
3
4
Câu 23. Tính số đo góc A của tam giác
ABC
biết
2 2 2
2a b c bc
.
A.
60
B.
45
C.
135
D.
150
Câu 24. Cho tam giác
ABC
có
2 2 2
3b c a bc
. Lựa chọn mệnh đề đúng
A.
100 50BAC
B.
150ABC ACB
C.
160ABC
D.
60BAC
Câu 25. Tam giác
ABC
có
60 , 45
B C
và
5AB
. Tính độ dài cạnh
AC
.
A.
5 6
.
2
AC
B.
5 3.
AC
C.
5 2.
AC
D.
10.AC
Câu 26. Tam giác
ABC
có
2; 6; 1 3
a b c
thì bán kính R của đường tròn ngoại tiếp là
A. 1 B.
2
C.
2
2
D.
3
Câu 27. Tính bán kính ra của đường tròn nội tiếp tam giác ABC biết độ dài ba cạnh là 13, 14, 15.
A. 2 B. 3 C. 4 D.
2
Câu 28. Tam giác
ABC
có độ dài ba cạnh thỏa mãn đẳng thức
3a b c a b c ab
. Số đo của góc C
khi đó là
A.
60
B.
120
C.
45
D.
30
Câu 29. Cho hình bình hành
ABCD
có
3
AD
,
5
AB
và đường chéo
5
AC
. Đường chéo
BD
có độ dài
bằng bao nhiêu ?
A.
43
. B.
2 13
. C.
8
. D.
8 3
.
Câu 30. Tam giác
ABC
có
75 ; 45
A B
. Tính
AB
AC
.
A.
5
3
AB
AC
B.
6
2
AB
AC
C.
5
6
AB
AC
D.
11
7
AB
AC
Câu 31. Tam giác với ba cạnh là
5;12;13
có bán kính đường tròn ngoại tiếp là ?
A.
6.
B.
8.
C.
13
2
. D.
11
2
.
Câu 32. Cho tam giác
ABC
thoả mãn :
2 2 2
3b c a bc
. Khi đó :
A.
0
30 .
A
B.
0
45 .
A
C.
0
60 .
A
D.
0
75
A
.
Câu 33. Tam giác
ABC
có
16,8
a
;
0
56 13'
B
;
0
71
C
. Cạnh
c
bằng bao nhiêu?
A.
29,9.
B.
14,1.
C.
17,5.
D.
19,9.
________________________________
11
HỆ THỨC LƯỢNG TRONG TAM GIÁC THƯỜNG LỚP 10 THPT
ĐỊNH LÝ SIN, ĐỊNH LÝ COSIN, GIẢI TAM GIÁC
(LỚP BÀI TOÁN CƠ BẢN P2)
________________________________________
Câu 1. Cho tam giác
ABC
nhọn có
2 cos 2
B
. Tính góc
B
.
A.
0
30 .
B
B.
0
60 .
B
C.
0
45 .
B
D.
0
75 .
B
Câu 2. Cho tam giác
ABC
có
29
AC
;
80 ; 35
A C
. Tính độ dài cạnh
BC
( làm tròn kết quả đến hàng
phần mười) .
A.
31,5
B.
31,2
C.
32,6
D.
30,6
Câu 3. Cho tam giác
ABC
có
14; 16
AC BC
;
72
B
. Tính góc
C
(làm tròn kết quả đến độ).
A.
0
53
B.
0
55
C.
0
45
D.
0
46
Câu 4. Cho tam giác
ABC
có
26; 29; 35
AB AC BC
. Tính góc
A
(làm tròn kết quả đến độ).
A.
0
53
B.
0
79
C.
0
45
D.
0
70
Câu 5. Cho
ABC
có
0
2, 6, 135 .
a b C
Diện tích của tam giác là:
A.
4
. B.
6 2
. C.
3 2
. D.
4 3
.
Câu 6. Cho tam giác ABC có
4; 7; 9AB BC CA
. Tính
cos A
.
A.0,5 B.
2
3
C.
2
3
D.
1
3
Câu 7. Cho
ABC
có
BC a
,
120
BAC
. Bán kính đường tròn ngoại tiếp
ABC
là
A.
3
2
a
R
. B.
2
a
R
. C.
3
3
a
R
. D.
R a
.
Câu 8. Tam giác
ABC
có
8
a
,
3
c
,
60
B
. Độ dài cạnh
b
bằng bao nhiêu?
A.
49
. B.
97
. C.
7
. D.
61
.
Câu 9. Cho
ABC
có
4
a
,
5
c
,
150
B
. Tính diện tích tam giác
ABC
.
A.
10
S
. B.
10 3
S
. C.
5
S
. D.
5 3
S
.
Câu 10. Một tam giác có ba cạnh là
52
,
56
,
60
. Bán kính đường tròn ngoại tiếp tam giác đó là
A.
65
4
. B.
40
. C.
32,5
. D.
65,8
.
Câu 11. Tam giác
ABC
có góc
A
nhọn,
5
AB
,
8
AC
, diện tích bằng
12.
Tính độ dài cạnh
.BC
A.
2 3
. B.
4
. C.
5
. D.
3 2
.
Câu 12. Tam giác
ABC
có
75 , 45
A B
,
2
AC
. Tính cạnh
AB
.
A.
2
2
. B.
6
. C.
6
2
. D.
6
3
.
Câu 13. Tính diện tích tam giác
ABC
, biết
3
7, 5,cos
5
b c A
.
A.
14
. B.
13
. C.
15
. D.
16
.
Câu 14. Tính diện tích tam giác
ABC
, biết
3, 4, 5
AB AC BC
.
A.
6
. B.
9
. C.
12
. D.
10
.
Câu 15. Tam giác
ABC
có
60
B
,
45
C
,
3
AB
. Tính cạnh
AC
.
A.
3 6
2
. B.
3 2
2
. C.
6
. D.
2 6
3
.
Câu 16. Tam giác
ABC
có các góc
75 , 45
A B
. Tính tỉ số
AB
AC
.
A.
6
3
. B.
6
. C.
6
2
. D.
1, 2
.
Câu 17. Tính bán kính đường tròn ngoại tiếp tam giác
ABC
biết
AB c
và
os( )
1
c
3
A B
.
12
A.
2
2
c
. B.
3 2
8
c
. C.
9 2
8
c
. D.
3
2
c
.
Câu 18. Tam giác
ABC
có các góc
105
A
,
45
B
. Tính tỉ số
AB
AC
.
A.
2
2
. B.
2
. C.
2
2
. D.
6
3
.
Câu 19. Tam giác
ABC
có
4AB
,
5
AC
,
6
BC
. Tính
cos( )B C
.
A.
1
8
. B.
1
4
. C.
–0,125
. D.
0, 75
.
Câu 20. Tam giác có ba cạnh lần lượt là
2,3, 4
. Góc bé nhất của tam giác có sin bằng bao nhiêu?
A.
15
8
. B.
7
8
. C.
1
2
. D.
14
8
.
Câu 21. Tam giác có ba cạnh lần lượt là
3
,
8
,
9
. Góc lớn nhất của tam giác có cosin bằng bao nhiêu?
A.
1
6
. B.
1
6
. C.
17
4
. D.
4
25
.
Câu 22. Cho tam giác
ABC
. Khẳng định nào sau đây là đúng ?
A.
1
. .
2
ABC
S a b c
. B.
sin
a
R
A
.
C.
2 2 2
cos
2
b c a
B
bc
. D.
2 2 2
2
2 2
4
c
b a c
m
.
Câu 23. Cho
ABC
có
84, 13, 14, 15.
S a b c
Độ dài bán kính đường tròn ngoại tiếp
R
của tam giác trên là:
A.
8,125.
B.
130.
C.
8.
D.
8,5.
Câu 24. Tam giác
ABC
có
4, 30 , 75
AC BAC ACB
. Tính diện tích tam giác
ABC
.
A.
8
ABC
S
. B.
4 3
ABC
S
. C.
4
ABC
S
. D.
8 3
ABC
S
.
Câu 25. Tam giác
ABC
có
3, 6, 60
AB AC BAC
. Tính độ dài đường cao
a
h
của tam giác.
A.
3 3
a
h
. B.
3
a
h
. C.
3
a
h
. D.
3
2
a
h
.
Câu 26. Tam giác
ABC
có
4, 60
AC ACB
. Tính độ dài đường cao
h
xuất phát từ đỉnh
A
của tam giác.
A.
2 3
h
. B.
4 3
h
. C.
2h
. D.
4h
.
Câu 27. Tam giác
ABC
có
21, 17, 10
a b c
. Gọi
'B
là hình chiếu vuông góc của
B
trên cạnh
AC
.
Tính
'BB
.
A.
' 8BB
. B.
84
'
5
BB
. C.
168
'
17
BB
. D.
84
'
17
BB
.
Câu 28. Tam giác
ABC
có
8AB
cm,
18AC
cm và có diện tích bằng
64
2
cm
. Giá trị
sin A
bằng:
A.
3
sin
2
A
. B.
3
sin
8
A
. C.
4
sin
5
A
. D.
8
sin
9
A
.
Câu 29. Nếu tam giác
ABC
có
2 2 2
BC AC AB
thì
A.
A
là góc tù. B.
A
là góc vuông.
C.
A
là góc nhọn. D.
A
là góc nhỏ nhất.
Câu 30. Cho tam giác
ABC
có
26; 38
AB AC
;
60
BAC
. Tính độ dài cạnh
BC
( làm tròn kết quả đến
hàng phần mười) .
A.
33,6
B.
32,6
C.
31,6
D.
30,6
Câu 31. Cho tam giác
ABC
có BC = 10,
30BAC
và bán kính đường tròn ngoại tiếp là R. Mệnh đề nào sau
đây đúng ?
A.
9
R
B.
13 15
R
C.
10
R
D.
4 8
R
_________________________________
13
HỆ THỨC LƯỢNG TRONG TAM GIÁC THƯỜNG LỚP 10 THPT
ĐỊNH LÝ SIN, ĐỊNH LÝ COSIN, GIẢI TAM GIÁC
(LỚP BÀI TOÁN CƠ BẢN P3)
________________________________________
Câu 1. Trong các công thức sau, công thức nào đúng?
A.
1
sin .
2
S bc B
B.
1
sin .
2
S bc A
C.
1
sin .
2
S ab B
D.
1
sin
2
S ac C
Câu 2. Cho tam giác
ABC
có
0
4, 3, 30
AB AC BAC
. Diện tích tam giác
ABC
bằng
A.
3.
S
B.
4 3.
S
C.
6 3.
S
D.
6
S
.
Câu 3. Tính diện tích tam giác
ABC
biết
3, 5, 6
AB BC CA
.
A.
56
. B.
48
. C.
6
. D.
8
.
Câu 4. Cho tam giác
ABC
có
3
AB
,
4
AC
,
5
BC
. Bán kính đường tròn nội tiếp tam giác bằng?
A.
8
9
. B.
4
5
. C.
3
4
. D.
1
.
Câu 5. Cho tam giác
ABC
với
BC a
,
AC b
,
AB c
. Đẳng thức nào sai?
A.
2 2 2
2 cosb a c ac B
B.
2 2 2
2 cosa b c bc A
.
C.
2 2 2
2 cosc b a ab C
. D.
2 2 2
2 cosc b a ab C
.
Câu 6. Cho
ABC
có
0
6, 8, 60
b c A
. Độ dài cạnh
a
là.
A.
2 13.
B.
3 12.
C.
2 37.
D.
20.
Câu 7. Cho tam giác
ABC
có
2 2 2
0
a b c
. Khi đó :
A.
0
90
C
B.
0
90
C
C.
0
90
C
D. Không thể kết luận được gì về
C
.
Câu 8. Cho tam giác
ABC
với
7BC cm
,
9AC cm
,
4AB cm
. Tính
cos A
A.
2
cos
3
A
. B.
1
cos
2
A
. C.
1
cos
3
A
. D.
2
cos
3
A
.
Câu 10. Cho tam giác
ABC
với
, ,
BC a AC b AB c
. Khẳng định nào sau đây đúng?
A.
2 cosa R A
. B.
2 sina R A
. C.
2 tana R A
. D.
sina R A
.
Câu 11. Cho tam giác
ABC
có
45
B
, cạnh
cm
22AC
. Bán kính
R
của đường tròn ngoại tiếp tam giác
ABC
bằng
A.
1cm
R
. B.
2 cm
R
. C.
4 cm
R
. D.
3 cm
R
.
Câu 12. Cho tam giác
ABC
có góc
0 0
ˆ
ˆ
60 ,C 45
B
, cạnh
4AB
. Tính độ dài cạnh
AC
.
A.
2 6
. B.
6
2
. C.
4 6
3
. D.
3 6
4
.
Câu 13. Tam giác ABC có
2 2 2
2( ) 1993
b c a
. Độ dài trung tuyến kẻ từ A của tam giác là
A. 498,25 B. 996,5 C. 120 D. 1993
Lời giải
Câu 14. Cho tam giác
ABC
có
4, 6, 8
a b c
. Khi đó diện tích của tam giác là:
A.
9 15.
B.
3 15.
C.
105.
D.
2
15.
3
Câu 15. Tam giác với ba cạnh là
5;12;13
có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu ?
A.
2.
B.
2 2.
C.
2 3.
D.
3.
Câu 16. Cho
ABC
có
0
60 , 8, 5.
B a c
Độ dài cạnh
b
bằng:
A.
7.
B.
129.
C.
49.
D.
129
.
Câu 17. Cho tam giác
ABC
. Tìm công thức sai:
A.
2 .
sin
a
R
A
B.
sin .
2
a
A
R
C.
sin 2 .b B R
D.
sin
sin .
c A
C
a
Câu 18. Cho tam giác
ABC
. Đẳng thức nào sai ?
A.
sin( 2 ) sin 3 .A B C C
B.
cos sin
2 2
B C A
.
14
C.
sin( ) sin .A B C
D.
2
cos sin
2 2
A B C C
.
Câu 19. Tam giác
ABC
có
cos B
bằng biểu thức nào sau đây?
A.
2 2 2
.
2
b c a
bc
B.
2
1 sin .B
C.
cos( ).A C
D.
2 2 2
.
2
a c b
ac
Câu 20. Cho tam giác
ABC
có các góc
0 0
ˆ
ˆ
120 ,C 40
B
, cạnh
5BC cm
. Tính độ dài cạnh
AB
(làm tròn kết
quả đến hàng đơn vị).
A.
7cm
. B.
8cm
. C.
9cm
. D.
10cm
.
Câu 21. Cho
ABC
có
0
4, 5, 150 .
a c B
Diện tích của tam giác là:
A.
5 3
. B.
10
. C.
5
. D.
10 3
.
Câu 22. Cho tam giác
ABC
có
4, 7, 9
AB BC AC
. Diện tích tam giác
ABC
bằng
A.
6.
S
B.
8 3.
S
C.
5 6.
S
D.
6 5
S
.
Câu 23. Tính diện tích tam giác có ba cạnh lần lượt là
3
,
2
và 1.
A.
3
. B.
2
2
. C.
6
2
. D.
3
2
.
Câu 24. Tam giác ABC có
45 , 6, 75
A c B
. Độ dài đường cao
b
h
bằng
A.
3 2
B.
3
2
C.
6 2
D.
2 3
Câu 24. Tam giác ABC có
45 ; 6; 75
A c B
. Độ dài bán kính đường tròn ngoại tiếp của tam giác bằng
A.
8 3
B.
2 3
C.
6 3
D.
4 3
Câu 25. Cho tam giác ABC có
3 2
a b c
h h h
. Lựa chọn mệnh đề đúng
A.
2 1 1
sin sin sinA B C
B.
1 1 2
sin sin sinA B C
C.
3 2 1
sin sin sinA B C
D.
1 2 3
sin sin sinA B C
Câu 26. Chọn công thức đúng trong các đáp án sau:
A.
1
sin .
2
S bc A
B.
1
sin .
2
S ac A
C.
1
sin .
2
S bc B
D.
1
sin .
2
S C bc C
Câu 27. Tính diện tích tam giác có ba cạnh lần lượt là
5
,
12
,
13
.
A.
34
. B.
7 5
. C.
60
. D.
30
.
Câu 28. Tam giác có ba cạnh lần lượt là
1
,
2
,
5
. Tính độ dài đường cao ứng với cạnh lớn nhất
A.
2 5
5
. B.
2 5
3
. C.
1
. D.
1,3
.
Câu 29. Cho tam giác
ABC
có
0
6, 8, 60
AB AC A
. Tính
BC
A.
2 13.
BC
B.
52.
BC
C.
2 37.
BC
D.
148.
BC
Câu 30. Cho tam giác
ABC
có
0 0
5, 60 , 45
AB B C
. Tính
AC
A.
5 2.
AC
B.
10.
AC
C.
5 6
.
2
AC
D.
5 3.
AC
Câu 31. Cho tam giác
ABC
có
0
5, 2, 45
AB AC C
. Tính
BC
A.
3.
BC
B.
2.
BC
C.
3.
BC
D.
2.
BC
Câu 32. Cho tam giác
ABC
có
5, 7, 8
AB BC AC
. Tính số đo của góc
A
A.
0
90 .
B.
0
45 .
C.
0
60 .
D.
0
30 .
Câu 33. Cho tam giác
ABC
có
0 0
45 , 6, 75
A c B
. Tính độ dài cạnh
BC
A.
3 6
B.
3
.
2
C.
2 6.
D.
2 3.
15
HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN VẬN DỤNG P1)
_______________________________
Câu 1. Rút gọn biểu thức sau
2 2
2
cot cos sin .cos
cot cot
x x x x
A
x x
A.
4A
. B.
2A
. C.
1A
. D.
3
A
.
Câu 2. Biểu thức
2
cot tan
a a
bằng
A.
2 2
1 1
sin cos
. B.
2 2
cot tana a
. C.
2 2
1 1
sin cos
. D.
2 2
cot tan 2
a a
.
Câu 3. Biểu thức
4 4 6 6
3 sin cos 2 sin cos
f x x x x x
có giá trị bằng:
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 4. Đẳng thức nào sau đây là sai?
A.
1 cos sin
0 , 180
sin 1 cos
x x
x x
x x
B.
1
tan cot 0 ,90 ,180
sin cos
x x x
x x
C.
2 2
2 2
1
tan cot 2 0 , 90 ,180
sin cos
x x x
x x
D.
2 2
sin 2 cos 2 2
x x
.
Câu 5. Tìm giá trị nhỏ nhất của biểu thức
2
tan 2 tan 5y x x
.
A. 4 B. 7 C. 5 D. 3
Câu 6. Giá trị của biểu thức
2 0 2 0 2 0 2 0 2 0
0 2 0
sin 90 cos 120 cos 0 60 cot 135
sin 30 cos 60
tg g
E
bằng
A.1 B. 2 C.
1
3
D.
3
7
Câu 7. Tổng
o o o o o2 2 2 2
o
2 2
sin 2 sin 4 sin 6 ... sin 84 sin 86 sin 88
bằng
A.
21
. B.
23
. C.
22
. D.
24
.
Câu 8. Tính
2 0 2 0 2 0 2 0
sin 20 cos 40 ... cos 160 sin 180
N
A.
4
B.
1
C.
2
D.
3
Câu 9. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
cos 3y x
.
A. 4 B. 2 C. 6 D. 7
Câu 10. Đẳng thức nào sau đây là đúng ?
A.
4 4 2 2
sin cos 1 2sin cos .
x x x x
B.
4 4
sin cos 1.x x
C.
6 6 2 2
sin cos 1 3sin cos .
x x x x
D.
4 4 2 2
sin cos sin cos .x x x x
Câu 11. Cho biết
3cos sin 1
,
o o
0 90
Giá trị của
tan
bằng
A.
4
tan
3
B.
3
tan
4
C.
4
tan
5
D.
5
tan
4
Câu 12. Cho biết
0 0
2 cos 2 sin 2, 0 90 .
Tính giá trị của
cot .
A.
5
cot
4
B.
3
cot
4
C.
2
cot
4
D.
2
cot
2
Câu 13. Cho biết
1
cos sin .
3
Giá trị của
2 2
tan cot
P
bằng bao nhiêu?
A.
5
4
P
. B.
7
4
P
. C.
9
4
P
. D.
11
4
P
.
Câu 14. Biết
sin cos 2
a a
. Hỏi giá trị của
4 4
sin cosa a
bằng bao nhiêu?
A.
3
2
. B.
1
2
. C.
1
. D.
0
.
Câu 15. Cho
tan cot m
. Tìm
m
để
2 2
tan cot 7
.
A.
9
m
. B.
3
m
. C.
3
m
. D.
3
m
.
Câu 16. Cho
2
cos 2sin (1 sin ) 2(1 sin ) 1
.
(1 sin )cos (1 sin ) cos 1 sin 3
x x x x
x x x x x
. Tính
cos x
.
16
A.
1
3
B.
2
3
C.
1
5
D. 1
Câu 17. Giá trị của
o o o o o
tan 5 .tan10 .tan15 ...tan 80 . tan 85
A
là
A.
2
. B.
1
. C.
0
. D.
1
.
Câu 18. Cho
tan cot 2x x
. Tính
3 3
tan cotx x
.
A.4 B. 2 C. 5 D. 1
Câu 19. Kết quả rút gọn biểu thức
1 1
cos 1 tan 1 tan
cos cos
x x x
x x
bằng
A.
2
B.
2 tan x
C.
2cot x
D.
2sin x
Câu 20. Cho góc
x
thỏa mãn
0 0
0 180
x
và
tan 3
x
, giá trị của biểu thức
2 2
2 2
sin 2 cos 1
3sin cos 1
x x
A
x x
là
A.
7
6
. B.
6
7
. C.
2
3
. D.
3
2
.
Câu 21. Cho
sin cos
x x m
. Tính theo
m
giá trị của
sin .cosM x x
.
A.
2
1
m
. B.
2
1
2
m
. C.
2
1
2
m
. D.
2
1
m
.
Câu 22. Cho góc
x
thỏa mãn
4
cot
3
x
. Tính giá trị của biểu thức:
2
3 sin 2cos
sin cos 4sin
x x
B
x x x
.
A.
415
48
B.
11
48
C.
123
48
D. 1
Câu 23. Cho tam giác
ABC
thỏa:
2sin sin 1
A B C
. Nhận dạng tam giác
ABC
.
A.Cân tại A B. Vuông tại A C. Vuông tại C D. Đều
Câu 24. Cho biết
1
sin cos .
5
Giá trị của
4 4
sin cos
P
bằng bao nhiêu?
A.
15
5
P
B.
17
5
P
C.
19
5
P
D.
21
5
P
Câu 25. Cho
, ,A B C
là ba góc trong tam giác
ABC
. Tính giá trị của biểu thức sau:
sin .cos cos .sin
P A B C A B C
A.
0
P
. B.
1P
. C.
1P
. D.
2P
.
Câu 26. Cho
, ,A B C
là ba góc trong tam giác
ABC
. Tính giá trị của biểu thức sau:
2 2
180
cos 180 cos tan .tan
2 2 2 2
B A C B A C
P
A.
1P
. B.
1P
. C.
2P
. D.
0
P
.
Câu 27. Đẳng thức nào sau đây là sai?
A.
2 2
(cos sin ) (cos sin ) 2,x x x x x
.
B.
2 2 2 2
tan sin tan sin , 90
x x x x x
.
C.
4 4 2 2
sin cos 1 2sin cos ,x x x x x
.
D.
6 6 2 2
sin cos 1 3sin cos ,x x x x x
.
Câu 28. Kết quả rút gọn của biểu thức
2
sin tan
1
cos 1
a a
a
bằng
A.
2
. B.
1 tan
. C.
2
1
cos
. D.
2
1
sin
.
Câu 29. Tính giá trị biểu thức
3 3
sin 5cos
sin 2cos
a a
C
a a
khi
tan 2
a
.
A.
15
2
. B.
32
5
. C.
35
6
. D.
4
.
________________________
17
HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN VẬN DỤNG P2)
_______________________________
Câu 1. Biểu thức:
4 2 2 2
cos cos sin sinf x x x x x
có giá trị bằng
A.
1
. B.
2
. C.
2
. D.
1
.
Câu 2. Trong các mệnh đề sau, mệnh đề nào sai?
A.
2
sin cos 12sin cosx x x x
. B.
4 4 2 2
sin cos 12sin cosx x x x
.
C.
2
sin cos 1 2sin cosx x x x
. D.
6 6 2 2
sin cos 1sin cosx x x x
.
Câu 3. Tìm tổng giá trị nhỏ nhất và giá trị lớn nhất của
3sin 4cosM x x
.
A.3 B. 2 C. 4 D. 0
Câu 4. Cho
tan 2
x
. Tìm giá trị m sao cho
2 2
2 2
sin 2sin cos cos
0,44
3sin 4sin cos 5cos
x x x m x
x x x x
.
A.
3
m
B.
4
m
C.
5
m
D.
6
m
Câu 5. Cho hai góc
,x y
thỏa mãn
2 2
tan tan ;cot cot
3 3
x y x y
. Tính giá trị
tan .tanx y
.
A. 2 B.
2 3
C.
3
D. – 1
Câu 6. Kết quả rút gọn biểu thức
2 2 2 2
2 2
tan cos cot sin
sin cos
x x x x
Q
x x
bằng
A.
xsin
1
B.
xcos
1
C. 2 D. – 2
Câu 7. Cho
0
2 2 4
2 2
0
4
sin cos cos
cos sin sin
0 180
x x x
A x
x x x
. Chọn mệnh đề đúng trong các mệnh đề sau.
A.
4
tanA x
. B.
sin cos
sin
x x
A
x
. C.
4
cotA x
. D.
2
cotA x
.
Câu 8. Giả sử
4 4
1
3sin cos
2
x x
thì
4 4
sin 3cos
x x
có giá trị bằng :
A. 1. B. 2. C. 3. D. 4.
Câu 9. Giả sử
2 2
2 2
tan sin
tan
cot os
n
x x
x
x c x
( giả thiết biểu thức có nghĩa). Khi đó n có giá trị là
A.
3
. B.
6
. C.
5
. D.
4
.
Câu 10. Biểu thức
2 2 2 2 2
sin .tan 4sin tan 3cosa a a a a
không phụ thuộc vào a và có giá trị bằng
A.
6
. B.
5
. C.
3
. D.
4
.
Câu 11. Cho 4 góc
1 2 3 4
; ; ;
có các điểm biểu diễn trên nửa đường tròn đơn vị thứ tự là
, , ,A B C D
như
hình vẽ.
Khẳng định nào sau đây là khẳng định đúng?
A.
1 3 4
cos cos cos
. B.
2 1 4
cos cos cos
.
C.
3 2 4
cos cos cos
. D.
2 4 3
cos cos cos
.
Câu 12. Cho
2
cos
3
. Tính
tan 3cot
tan cot
A
.
A.
17
9
B.
11
9
C.
10
9
D.
7
9
18
Câu 13. Cho
tan cot 2
x x
, tính
2 2
4sin cos
tan cot
x x
x x
.
A.3 B. 1 C. 2 D. – 2
Câu 14. Cho tam giác
,ABC
,khẳng định nào sau đây sai?
A.
sin sinA B C
. B.
sin cos
2 2
A C B
.
C.
cos cosA B C
. D.
cos sin
2 2
A C B
.
Câu 15. Biết
, ,A B C
là các góc của tam giác
,ABC
khi đó
A.
sin sin .C A B
B.
cos cos .C A B
C.
tan tan .C A B
D.
cot cot .C A B
Câu 16. Cho tam giác
ABC
. Khẳng định nào sau đây là sai ?
A.
sin cos .
2 2
A C B
B.
cos sin .
2 2
A C B
C.
sin sin .A B C
D.
cos cos .A B C
Câu 17. Đơn giản biểu thức
sin
cot
1 cos
x
E x
x
ta được
A.
sin x
. B.
1
cos x
. C.
1
sin x
. D.
cos x
.
Câu 18. Rút gọn biểu thức sau
2 2
2
cot cos sin .cos
cot
cot
x x x x
A
x
x
.
A.
1A
. B.
2A
. C.
3
A
. D.
4A
.
Câu 19. Cho hai góc
,x y
thỏa mãn
0 , 90
x y
và thỏa mãn
2 2
tan tan 2;cot cot 2
x y x y
. Biểu thức
5 tan 6 tanx y
nhận giá trị bằng
A.10 B. 11 C. 8 D. 7
Câu 20. Cho
tan 2
. Giá trị của
3 3
sin cos
sin 3cos 2 sin
B
gần nhất với
A.0,086 B. 0,072 C. 0,094 D. 0,065
Câu 21. Biết
sin cos
x x m
. Khi đó giá trị biểu thức
4 4
sin cosx x
theo
m
là
A.
2 4
3 2
2
m m
A
B.
2 4
3 3
2
m m
A
C.
2 4
1 2
2
m m
A
D.
2 4
4
3 2
m m
A
Câu 22. Giá trị của biểu thức
o o o o o
tan1 tan 2 tan 3 ...tan 88 tan 89
A
là
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 23. Cho hai góc nhọn
a
và
b
. Biết
1
cos
3
a
và
1
cos
4
b
. Tính giá trị
2 2
(cos cos ) (sin sin ) .P a b a b
A.
119
144
B.
59
144
C.
129
144
D.
19
144
Câu 24. Cho
4
tan
3
x
và
2
x
. Giá trị của biểu thức
2
2
sin cos
sin cos
x x
M
x x
bằng
A.
31
11
B.
32
11
C.
5
11
D.
6
13
Câu 25. Cho
3cos sin 1,0 90
. Tính giá trị của
tan
.
A.
4
3
B.
2
3
C.
5
3
D.
8
3
Câu 26. Cho
1
sin cos
5
. Tính giá trị của
4 4
sin cos
P
.
A.
17
5
B.
17
15
C.
2 17
5
D.
17
10
_____________________________
19
HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN VẬN DỤNG P3)
_______________________________
Câu 1. Cho
4
sin ,
5
với
90 180
. Tính giá trị của
3
sin cos
cos
M
A.
25
27
M
B.
175
27
M
. C.
35
27
M
. D.
25
27
M
.
Câu 2. Cho tam giác
ABC
, tính giá trị biểu thức
sin .cos cos .sin
P A B C A B C
A.
0
. B.
1
. C.
1
. D.
2
.
Câu 3. Cho
tan 2
x
. Tính
2 2
2 2
2sin 5sin .cos cos
2sin sin .cos cos
x x x x
A
x x x x
A.
1
11
A
B.
11A
C.
1
11
A
D.
11A
Câu 4. Cho 4 góc
1 2 3 4
; ; ;
có các điểm biểu diễn trên nửa đường tròn đơn vị thứ tự là
, , ,A B C D
như hình
vẽ.
Khẳng định nào sau đây là khẳng định đúng?
A.
1 3 4
sin sin sin
. B.
4 1 2
sin sin sin
.
C.
4 3 2
sin sin sin
. D.
2 4 3
sin sin sin
.
Câu 5. Cho
tan cot 3.
Tính giá trị của biểu thức sau:
2 2
tan cot
A
.
A.
12A
. B.
11A
. C.
13
A
. D.
5
A
.
Câu 6. Biết
sin cos 2
a a
. Hỏi giá trị của
4 4
sin cosa a
bằng bao nhiêu?
A.
3
2
. B.
1
2
. C.
1
. D.
0
.
Câu 7. Cho điểm
1 2 2
;
3 3
M
trên nửa đường tròn đơn vị. Gọi góc
xOM
với
M
là điểm đối xứng với
M
qua trục
Oy
. Giá trị lượng giác của
tan
là
A.
1
tan
2 2
. B.
tan 2 2
.
C.
2 2 1
tan
3
. D.
2 2
tan
9
.
Câu 8. Biết rằng
3 2
3
cos sin
tan tan tan
cos
x x
x a x b x c
x
.Tínhgiátrị
a b c
.
A.4 B.3 C.2 D.6
Câu 9. Cho tam giác
ABC
. Kết quả rút gọn biểu thức
3 3
sin cos
cos
2 2
.tan
sin
cos sin
2 2
B B
A C
B
A C A C
B
là
A.2 B.3 C.0 D.1
Suy ra điều phải chứng minh.
Câu 10. Giá trị biểu thức
o 2 2 2o
sin(90 ) cos(180 ) sin (1 tan ) tanA x x x x x
không phụ thuộc vào biến và
có giá trị bằng
20
A.3 B. 2 C. 4 D. 0
Câu 11. Kết quả rút gọn biểu thức
1 1 1
. 2
sin 1 cos 1 cos
B
x x x
là
A.
2
2 cot x
B.
2 sin x
C.
3 cos x
D.
2 sin 2x
Câu 12. Tính
cos10 cos30 cos50 ... cos150 cos170
A
.
A.
0
. B.
2
. C.
1
. D.
1
.
Câu 13. Giá trị biểu thức
4 2 4 4 2 4
sin 6cos 3cos cos 6sin 3sinP x x x x x x
không phụ thuộc vào
x
.
Giá trị đó bằng
A.2 B. 3 C. 4 D. 1
Câu 14. Cho góc
xOM
với điểm
1 2 2
;
3 3
M
trên nửa đường tròn đơn vị. Giá trị lượng giác của
cot
là
A.
1
cot
2 2
. B.
cot 2 2
.
C.
2 2 1
cot
3
. D.
2 2
cot
9
.
Câu 15. Kết quả rút gọn biểu thức
2
2
2 2 2
1 tan
1
4 tan 4sin cos
x
A
x x x
bằng
A.0 B. – 1 C. 1 D. 2
Câu 16. Cho
0 0 0 0
cos 60 5cos 120 6.sin 60 .cot 60
H x x x x
0 0
0 90
x
. Chọn mệnh đề
đúng trong các mệnh đề sau.
A.
1H
. B.
1
3
H
. C.
3
H
. D.
0
H
.
Câu 17. Cho
0 0
tan 3 0 180
a a
. Khi đó
2 2
2 2
sin 2sin .cos 2cos
2sin 3sin .cos 4cos
a a a a
B
a a a a
bằng
A.
1
31
. B.
5
14
. C.
2
13
. D.
5
12
.
Câu 18. Cho
1
sin
3
a
. Giá trị của biểu thức
cot tan
tan 2cot
a a
A
a a
bằng
A.
1
9
. B.
7
9
. C.
17
81
. D.
7
17
.
Câu 19. Cho
2 0 2 0 2 0 2 0
cos 10 cos 20 cos 30 ... cos 180
D
. Chọn mệnh đề đúng trong các mệnh đề sau.
A.
0
D
. B.
8
D
. C.
2022
D
. D.
18
D
.
Câu 20. Cho biết
cot 5
. Tính giá trị của
2
2cos 5sin cos 1
E
?
A.
10
26
. B.
100
26
. C.
50
26
. D.
101
26
.
Câu 21. Cho
0 0
3
sin cos 0 180
4
x x x
. Biểu thức
sin cosB x x
bằng
A.
3
4
. B.
23
16
. C.
23
4
. D.
9
16
.
Câu 22. Biểu thức
sin 180 2cos 90 cos .tan 90
E x x x x x
sau khi thu gọn bằng với biểu thức
nào trong 4 biểu thức dưới đây:
A.
0
A
. B.
2sinB x
. C.
sinC x
. D.
2cosD x
.
Câu 23. Trong mặt phẳng tọa độ
Oxy
, cho điểm
M
nằm trên nửa đường tròn đơn vị. Điểm
M
có tung độ và
hoành độ đều dương, góc
xOM
có thể là
A.
100
. B.
80
. C.
120
. D.
140
.
_________________________________
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
--------------------------------------------------------------------------------------------
LUYỆN KỸ NĂNG TOÁN 10 THPT
TRẮC NGHIỆM HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG
CƠ BẢN – VẬN DỤNG – VẬN DỤNG CAO
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
ĐÁP ÁN CHI TIẾT PDF BẠN ĐỌC VUI LÒNG LIÊN HỆ TÁC GIẢ:
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 7/2024 1
LUYỆN KỸ NĂNG TOÁN 10 THPT
TRẮC NGHIỆM HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG
CƠ BẢN – VẬN DỤNG – VẬN DỤNG CAO
__________________________________________ DUNG NỘI DUNG BÀI TẬP LƯỢNG 3 FILE
CƠ BẢN GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ 1 file 2 trang 3 FILE
CƠ BẢN ĐỊNH LÝ SIN, ĐỊNH LÝ COSIN, GIẢI TAM GIÁC 1 file 2 trang 3 FILE
VẬN DỤNG GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ 1 file 2 trang 3 FILE
VẬN DỤNG ĐỊNH LÝ SIN, ĐỊNH LÝ COSIN, GIẢI TAM GIÁC 1 file 2 trang 3 FILE
VẬN DỤNG CAO GÓC LƯỢNG GIÁC, HỆ THỨC LƯỢNG 1 file 2 trang TAM GIÁC THƯỜNG 2
HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN CƠ BẢN P1)
_______________________________
Câu 1. Giá trị của o o
cos 60  sin 30 bằng bao nhiêu? 3 3 A. B. 3 C. D. 1. 2 3
Câu 2. Giá trị của o o
tan 30  cot 30 bằng bao nhiêu? 4 1 3 2 A. B. C. D. 2 3 3 3
Câu 3. Trong các đẳng thức sau đây, đẳng thức nào sai? A. o o sin 0  cos 0  1 B. o o sin 90  cos 90  1 C. o o sin180  cos180  1  D. o o sin 60  cos 60  1
Câu 4. Trong các khẳng định sau, khẳng định nào sai? A. o o cos 60  sin 30 . B. o o cos 60  sin120 . C. o o cos 30  sin120 . D. o o sin 60   cos120 .
Câu 5. Đẳng thức nào sau đây sai? A. o o sin 45  sin 45  2 . B. o o sin 30  cos 60  1. C. o o sin 60  cos150  0 . D. o o sin120  cos30  0 . Câu 6. Giá trị o o
cos 45  sin 45 bằng bao nhiêu? A. 1. B. 2 . C. 3 . D. 0 .
Câu 7. Trong các đẳng thức sau, đẳng thức nào đúng? A.  o
sin 180      cos . B.  o
sin 180     sin . C.  o
sin 180     sin . D.  o
sin 180     cos .
Câu 8. Trong các đẳng thức sau, đẳng thức nào sai? A. o o sin 0  cos 0  0 . B. o o sin 90  cos 90  1 . 3  1 C. o o sin180  cos180  1 . D. o o sin 60  cos 60  . 2
Câu 9. Cho  là góc tù. Điều khẳng định nào sau đây là đúng? A. sin  0 . B. cos  0 . C. tan  0 . D. cot  0 .
Câu 10. Giá trị của o o o o
E  sin 36 cos 6 sin126 cos 84 là 1 3 A. . B. . C. 1. D. 1  . 2 2 
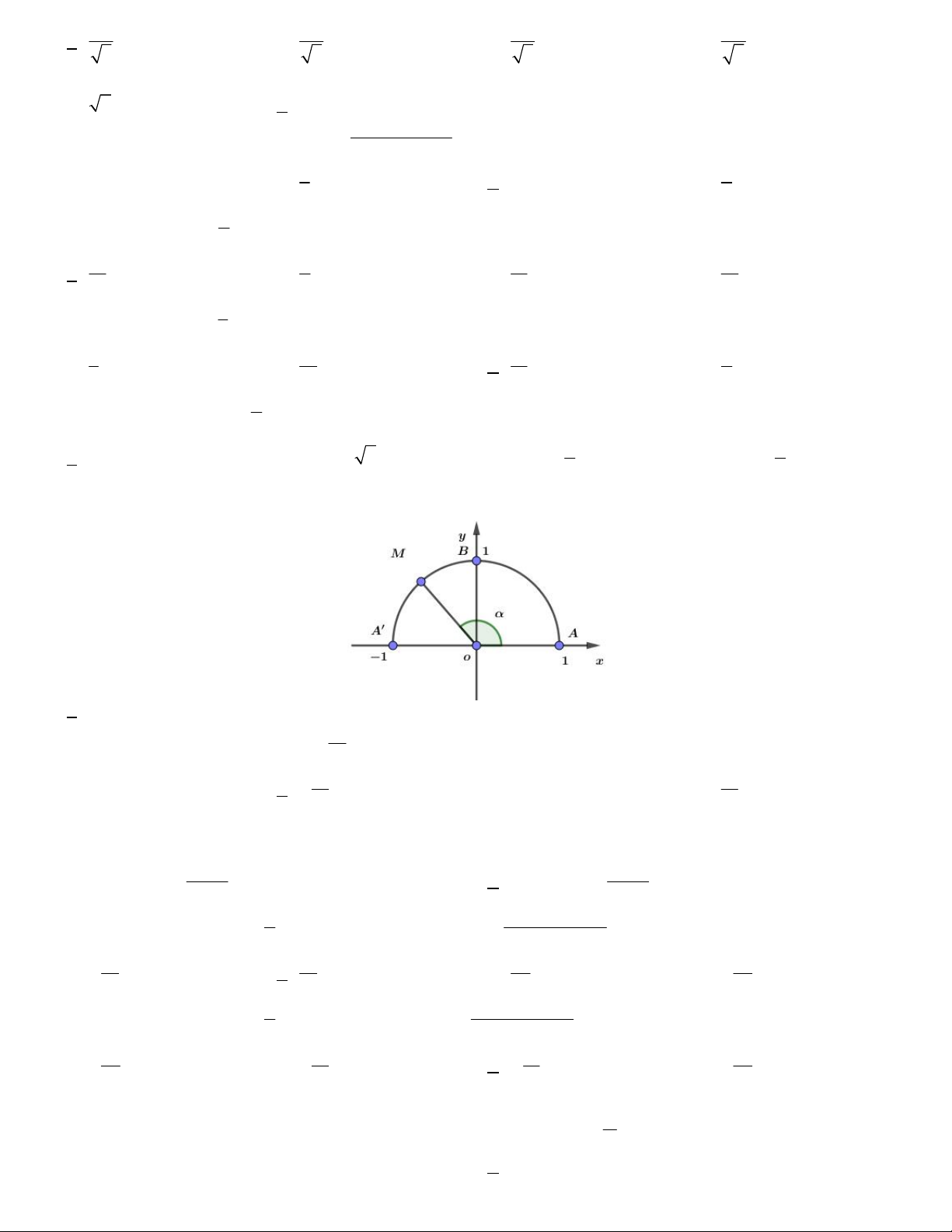
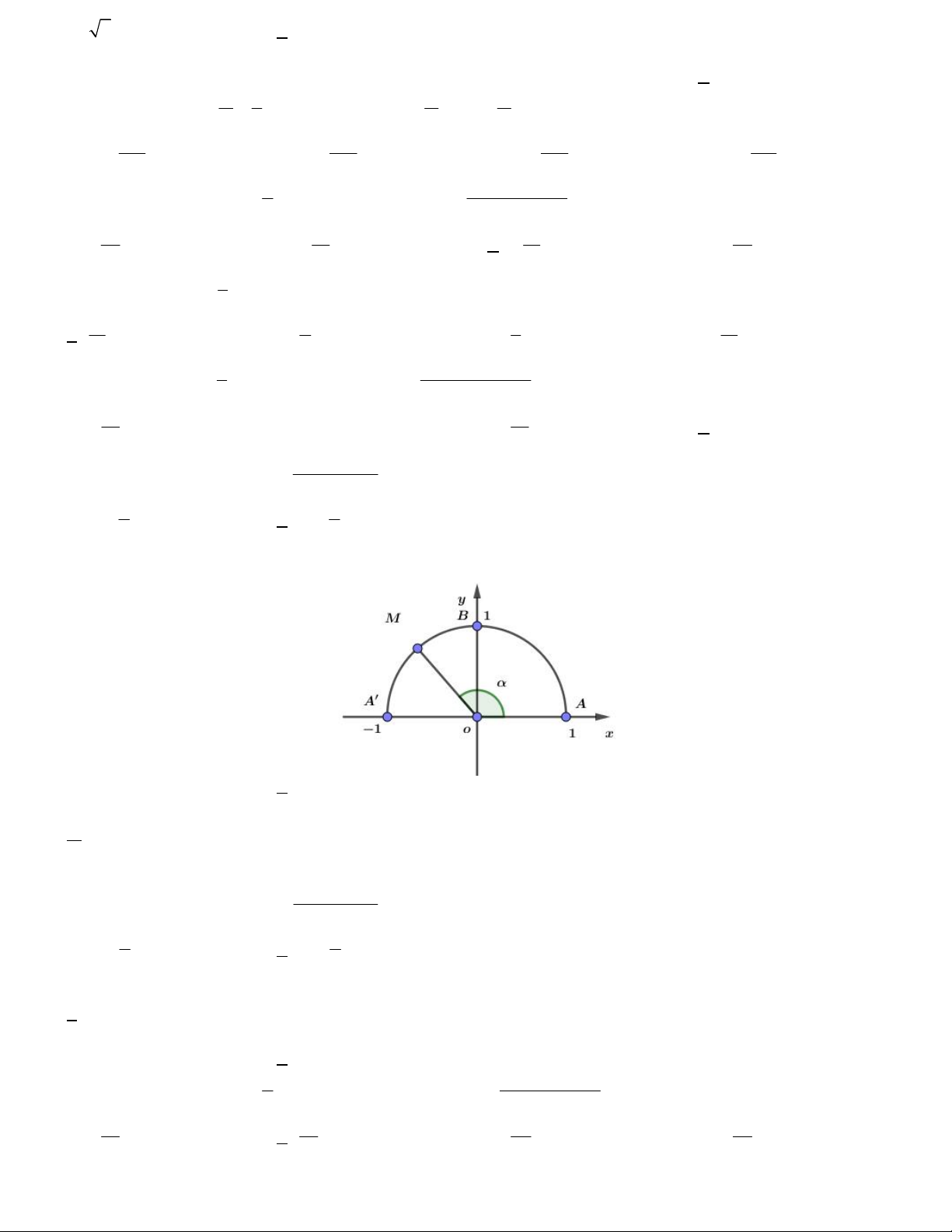
Câu 11. Trên nửa đường tròn đơn vị cho điểm M sao cho xoM   như hình bên. Tìm mệnh đề đúng. A. cos  0 . B. cos  0 . C. cos  0 . D. cos  1.
Câu 12. Cho góc x thoả 0 0
0  x  90 . Trong các mệnh đề sau, mệnh đề nào sai? A. sin x  0 B. cos x  0 C. tan x  0 D. cot x  0
Câu 13. Giá trị của biểu thức 0 0 0 0
tan 9  tan 27  tan 63  tan 1 8 bằng 1 A. 2 . B. 4 . C. 2 . D. . 2
Câu 14. Cho tan  2 
90   180  thì cos có giá trị bằng : 3 1 1 3 3 A. . B. . C. . D. . 5 5 5 5
Câu 15. Giá trị của 2  2  2  2 B cos 73 cos 87 cos 3 cos 17     là A. 2 . B. 2 . C. 2  . D. 1. 3sin   cos
Câu 16. Cho tan  2 . Giá trị của A  là: sin   cos 5 7 A. 5 . B. . C. 7 . D. . 3 3 1
Câu 17. Cho cos x  . Tính biểu thức 2 2
P  3 sin x  4 cos x 2 13 7 11 15 A. . B. . C. . D. . 4 4 4 4 1
Câu 18. Biết cos 
. Giá trị đúng của biểu thức 2 2
P  sin   3 cos  là: 3 1 10 11 4 A. . B. . C. . D. . 3 9 9 3 1
Câu 19. Cho biết tan   . Tính cot  . 2 1 1 A. cot   2 . B. cot   2 . C. cot   . D. cot   . 4 2 
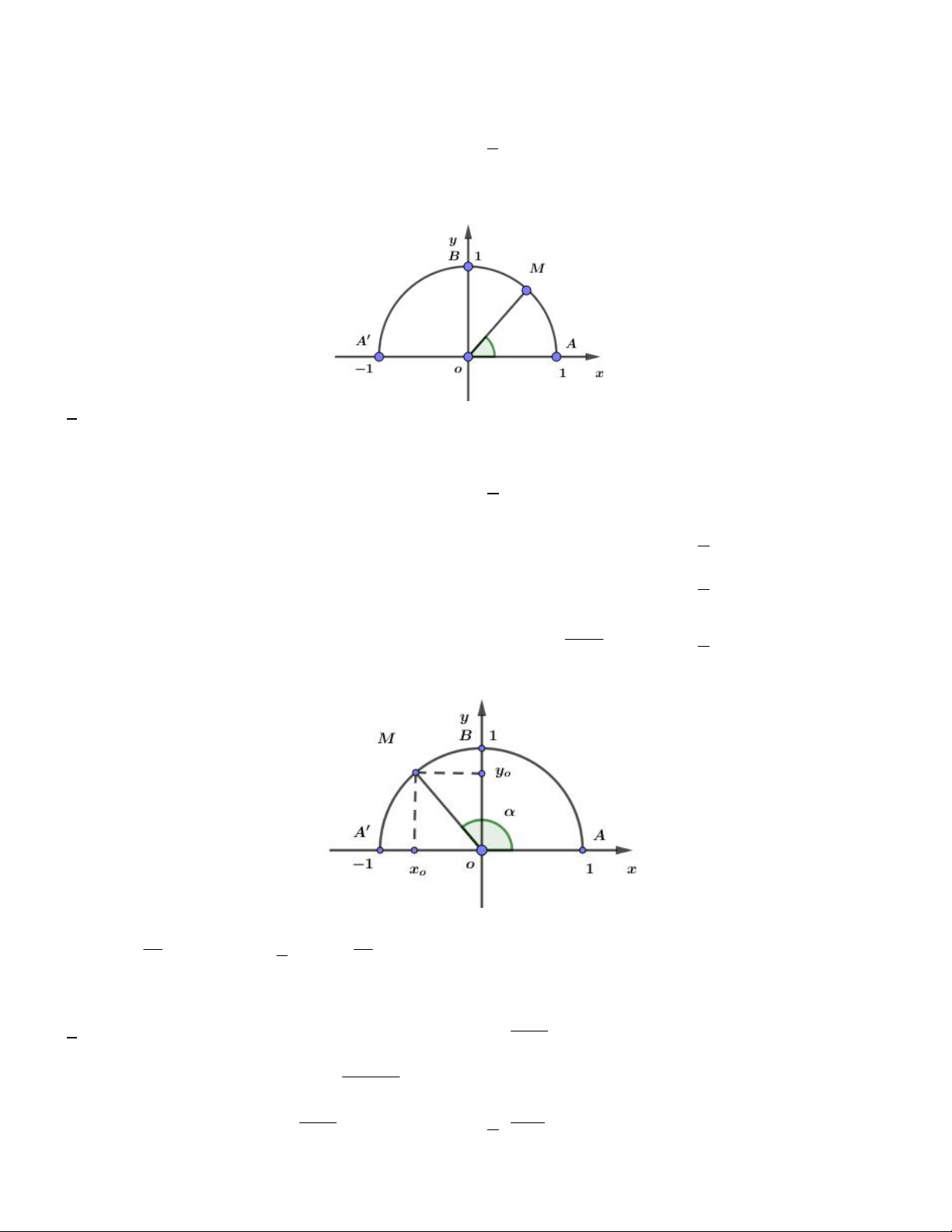
Câu 20. Trên nửa đường tròn đơn vị cho điểm M sao cho xoM   như hình bên. Tìm mệnh đề đúng. A. sin   0 . B. sin   0 . C. sin   0 . D. sin   1. 5
Câu 21. Cho  là góc tù và sin  
. Giá trị của biểu thức 3sin   2 cos là 13 9 9 A. 3. B.  . C. 3  . D. . 13 13
Câu 22. Cho biết sin   cos  a . Giá trị của sin .cos bằng bao nhiêu? A. 2
sin  .cos   a .
B. sin .cos  2a . 2 1  a 2 a  1 C. sin .cos  . D. sin .cos  . 2 2 2 cot   3 tan 
Câu 23. Cho biết cos  
. Tính giá trị của biểu thức E  ? 3 2 cot   tan  19 19 25 25 A.  . B. . C. . D.  13 13 13 13 2 cot   3 tan 
Câu 24. Cho biết cos  
. Giá trị của biểu thức E  bằng bao nhiêu? 3 2 cot   tan  25 11 11 25 A.  . B.  . C.  . D.  . 3 13 3 13
Câu 25. Trong các hệ thức sau hệ thức nào đúng?  A. 2 2 sin   cos   1. B. 2 2 sin   cos  1. 2 C. 2 2 sin   cos   1. D. 2 2 sin 2  cos 2  1 . 4
HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN CƠ BẢN P2)
_______________________________
Câu 1. Đẳng thức nào sau đây đúng? A.  o
tan 180  a    tan a . B.  o
cos 180  a   cos a . C.  o
sin 180  a   sin a . D.  o
cot 180  a    cot a . 
Câu 2. Trên nửa đường tròn đơn vị cho điểm M sao cho xoM   như hình bên. Tìm mệnh đề đúng. A. sin   0 . B. sin   0 . C. sin   0 . D. sin   1.
Câu 3. Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin 180     sin .
B. cos 180    cos
C. tan 180    tan .
D. cot 180     cot
Câu 4. Cho  và  là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai? A. sin  sin  . B. cos   cos  . C. tan   tan  . D. cot   cot  .
Câu 5. Cho góc  tù. Điều khẳng định nào sau đây là đúng? A. sin  0 . B. cos  0 . C. tan  0 . D. cot   0 .
Câu 6. Hai góc nhọn  và  phụ nhau, hệ thức nào sau đây là sai? 1 A. sin  cos  . B. tan  cot  . C. cot   . D. cos  sin  . cot  
Câu 7. Trên nửa đường tròn đơn vị cho điểm M sao cho xoM   như hình bên. Tìm mệnh đề đúng. x y A. 0 tan   . B. 0 tan   . C. tan   x . D. tan   y . y x o 0 0 0
Câu 8. Đơn giản biểu thức G   2  x 2 2 1 sin
cot x 1 cot x . 1 A. 2 sin x . B. 2 cos x . C. . D. cos x . cos x sin x
Câu 9. Đơn giản biểu thức E  cot x  ta được 1 cos x 1 1 A. sin x . B. . C. . D. cos x . cos x sin x
Câu 10. Khẳng định nào sau đây là sai? 5 1 A. 2 2 sin   cos   1. B. 2 1 cot   sin  0 . 2   sin  1 C. tan.cot   1
 sin.cos  0 . D. 2 1 tan   cos  0 . 2   cos 
Câu 11. Bất đẳng thức nào dưới đây là đúng? A. sin 90 sin100  . B. cos 95 cos100  . C. tan 85 tan125  . D. cos145 cos125  . 3 Câu 12. Cho sin ,90  180   
 . Tính P cot180    5 3 3 4 4 A. P  . B. P   . C. P   . D. P  . 4 4 3 3 1 2
Câu 13. Cho góc  thỏa mãn 0  180   , cos   , sin 
. Khẳng định nào sau đây sai? 3 3 2 A. tan    2 . B. cot    . 2 C.     2 sin 180   . D.     1 cos 180  . 3 3 2
Câu 14. Cho biết cos   . Tính tan ? 3 5 5 5 5 A. . B.  . C. . D.  . 4 2 2 2 1
Câu 15. Cho biết tan   . Tính cot . 2 1 1 A. cot   2 . B. cot   2 . C. cot   . D. cot   . 4 2
Câu 16. Đẳng thức nào sau đây là sai? 1  cos x sin x 1 A. 
x  0, x  180  . B. tan x cot xx 0,90,180     sin x 1  cos x sin x cos x 1 C. 2 2 tan x cot x 2 x 0 , 90 ,180     D. 2 2
sin 2x  cos 2x  2 . 2 2   sin x cos x Câu 17. Biểu thức 2 2 2 2
tan x sin x  tan x  sin x có giá trị bằng A. 1  . B. 0 . C. 2 . D. 1. 1
Câu 18. cos bằng bao nhiêu nếu cot    ? 2 5 5 5 1 A.  . B. . C.  . D.  . 5 2 5 3
Câu 19. Nếu tan  3 thì cos bằng bao nhiêu? 10 1 10 10 A.  . B. . C.  . D. . 10 3 10 10 5
Câu 20. Cho  là góc tù và sin  
. Giá trị của biểu thức 3sin  2cos là 13 9 9 A. . B. 3. C.  . D. 3  . 13 13
Câu 21. Biết cot   a, a  0 . Tính cos . a 1 1 a A. cos  . B. cos  . C. cos   . D. cos   . 2 1 a 2 1 a 2 1 a 2 1 a 4
Câu 22. Cho  là góc tù và sin  
. Giá trị của biểu thức A  2sin  cos bằng 5 7 7 11 A. . B. . C. 1. D. . 5 5 5
____________________________ 6
LƯỢNG GIÁC LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN CƠ BẢN P3)
_______________________________
Câu 1. Cho góc  90 ;
 180. Khẳng định nào sau đây đúng?
A. sin và cot  cùng dấu.
B. Tích sin.cot mang dấu âm.
C. Tích sin.cos mang dấu dương.
D. sin và tan  cùng dấu.
Câu 2. Cho  là góc tù. Mệnh đề nào đúng trong các mệnh đề sau? A. tan  0. B. cot   0. C. sin   0. D. cos  0.
Câu 3. Cho 0º    90º . Khẳng định nào sau đây đúng? A. cot 90º      tan . B. cos 90º     sin . C. sin 90º     cos . D. tan 90º     cot .
Câu 4. Trong các khẳng định sau, khẳng định nào sai? A. cos 60 sin 30  . B. cos 60 sin120  . C. cos 30 sin120  . D. sin 60 cos120   .
Câu 5. Đẳng thức nào sau đây sai? A. sin 45 sin 45   2 . B. sin 30 cos 60  1. C. sin 60 cos150   0 . D. sin120 cos 30   0 .
Câu 6. Cho hai góc nhọn  và  (   ) . Khẳng định nào sau đây là sai? A. cos  cos  . B. sin  sin  . C. tan  tan   0 . D. cot   cot  .
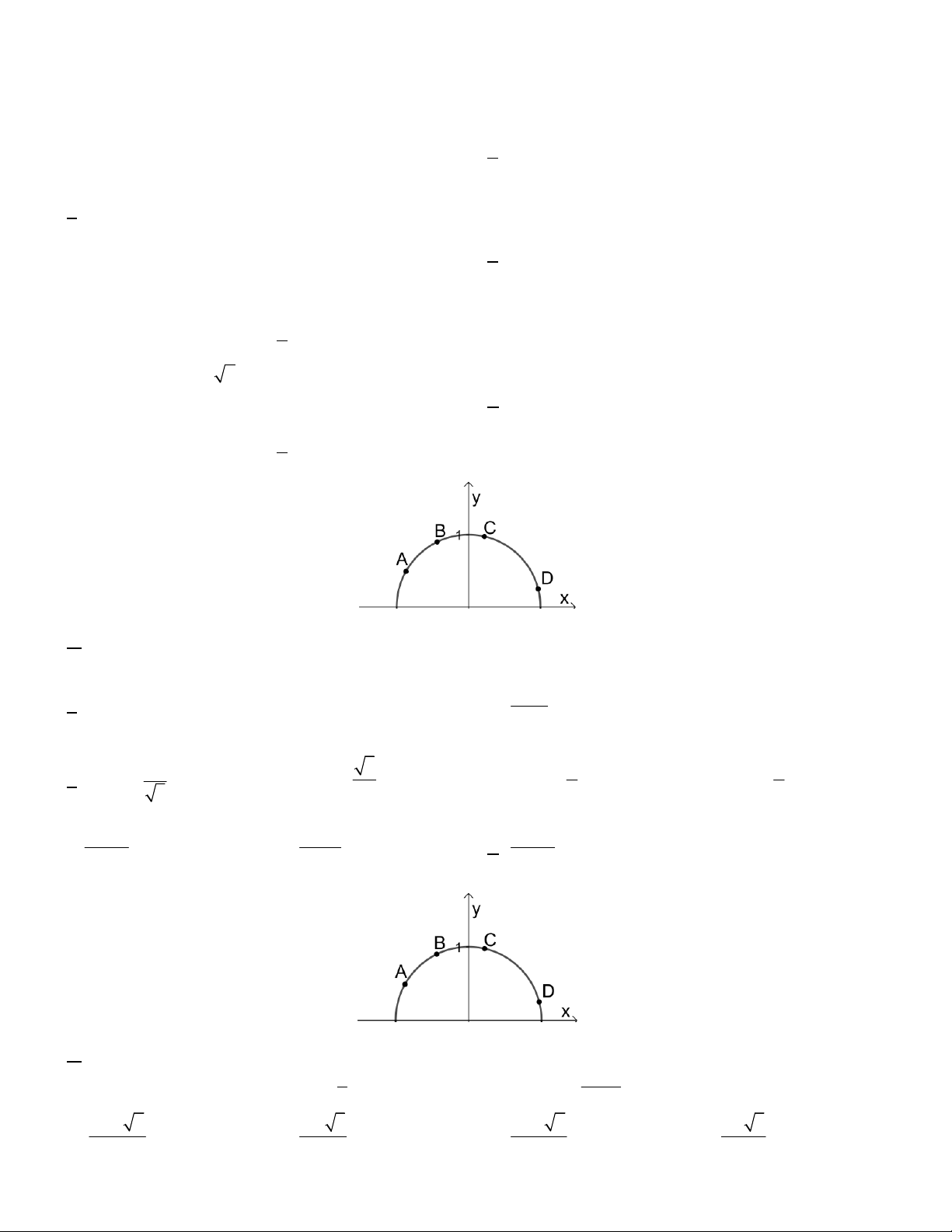
Câu 7. Cho 4 góc có các điểm biểu diễn trên nửa đường tròn đơn vị thứ tự là ,
A B,C, D như hình vẽ.
Hỏi trong 4 góc đó có bao nhiêu góc có giá trị lượng giác cosin là một số dương? A. 2 . B. 3 . C. 1. D. 4 .
Câu 8. Đơn giản biểu thức G   2  x 2 2 1 sin
cot x  1  cot x . 1 A. 2 sin x . B. 2 cos x . C. . D. cos x . cos x
Câu 9. Cho ABC vuông tại A , góc B bằng 30 . Khẳng định nào sau đây là sai? 1 3 1 1 A. cos B  . B. sin C  . C. cos C  . D. sin B  3 2 2 2
Câu 10. Công thức nào sau đây sai 1 1 2 A. 2  1 tan x B. 2  1 cot x C. 2  1 tan x D. 2 2 tan . x cot x  1 2 cos x 2 sin x 2 cos x
Câu 11. Cho 4 góc có các điểm biểu diễn trên nửa đường tròn đơn vị thứ tự là ,
A B,C, D như hình vẽ.
Hỏi trong 4 góc đó có bao nhiêu góc có giá trị lượng giác sin là một số dương? A. 4. B. 3 . C. 2 . D. 1. 1 1
Câu 12. Cho góc  thỏa mãn cos  . Giá trị của biểu thức Psin   bằng 3 cos 9  2 2 4  3 3  2 2 1 3 A. . B. . C. . D. . 3 2 3 2
Câu 13. Giá trị của 2  2  2  2 B cos 73 cos 87 cos 3 cos 17     là 7 A. 2 . B. 2 . C. 2  . D. 1.
Câu 14. Giá trị của biểu thức 2  2  2  2 A sin 51 sin 55 sin 39 sin 35     là A. 3 . B. 4 . C. 1. D. 2 .  3   Câu 15. Cho biết sin  . Giá trị của 2 2 P  3sin  5cos bằng bao nhiêu? 3 5 3 3 105 107 109 111 A. P  . B. P  . C. P  . D. P  . 25 25 25 25 2 cot  3 tan
Câu 16. Cho biết cos  
. Giá trị của biểu thức E  bằng bao nhiêu? 3 2 cot  tan 25 11 11 25 A.  . B.  . C.  . D.  . 3 13 3 13 1
Câu 17. Biết cos 
. Giá trị đúng của biểu thức 2 2
P  sin   3 cos  là: 3 11 4 1 10 A. . B. . C. . D. . 9 3 3 9 1 3sin  4 cos
Câu 18. Cho cot 
. Giá trị của biểu thức A  là: 3 2sin  5cos 15 15 A.  . B. 1  3 . C. . D. 13 . 13 13 2 1 sin x
Câu 19. Rút gọn biểu thức P  ta được 2 sin . x cos x 1 1 A. P  tan x . B. P  cot x .
C. P  2 cot x .
D. P  2 tan x . 2 2 
Câu 20. Trên nửa đường tròn đơn vị cho điểm M sao cho xoM   như hình bên. Tìm mệnh đề đúng. A. cos  0 . B. cos  0 . C. cos  0 . D. cos  1. Câu 21. Cho , A ,
B C là ba góc trong tam giác ABC , chọn mệnh đề đúng trong các mệnh đề sau:
A. sin C  sin  A B .
B. cos C  cos  A B .
C. cot C  cot  A B .
D. tan C  tan  A B . 2 1  sin x
Câu 22. Rút gọn biểu thức P  ta được 2 sin . x cos x 1 1 A. P  tan x . B. P  cot x .
C. P  2 cot x .
D. P  2 tan x . 2 2
Câu 23. Biểu thức: f x 4 2 2 2
 cos x  cos x sin x  sin x có giá trị bằng A. 1. B. 2 . C. 2  . D. 1  . Câu 24. Biểu thức 2 2 2 2
tan x sin x  tan x  sin x có giá trị bằng A. 1  . B. 0 . C. 2 . D. 1. 2 cot  3 tan
Câu 25. Cho biết cos  
. Tính giá trị của biểu thức E  ? 3 2 cot  tan 19 19 25 25 A.  . B. . C. . D.  13 13 13 13
_________________________________ 8
HỆ THỨC LƯỢNG TRONG TAM GIÁC THƯỜNG LỚP 10 THPT
ĐỊNH LÝ SIN, ĐỊNH LÝ COSIN, GIẢI TAM GIÁC
(LỚP BÀI TOÁN CƠ BẢN P1)
________________________________________________
Câu 1. Cho tam giác ABC , mệnh đề nào sau đây đúng? A. 2 2 2
a b c  2bc cos A B. 2 2 2
a b c  2bc cos A C. 2 2 2
a b c  2bc cos C D. 2 2 2
a b c  2bc cos B
Câu 2. Tính diện tích tam giác ABC , biết a  7, b  8, c  6 . 21 15 5 15 5 15 15 A. S  B. S  C. S  D. S  4 2 4 2
Câu 3. Cho tam giác ABC , chọn công thức đúng ? A. 2 2 2
AB AC BC  2 AC.AB cos C . B. 2 2 2
AB AC BC  2 AC.BC cos C . C. 2 2 2
AB AC BC  2 AC.BC cos C . D. 2 2 2
AB AC BC  2 AC.BC  cos C .
Câu 4. Định lý sin được phát biểu là a b c a b c A.    2 . R B.    2R sin A sin B sinC 2 sin A 2 sin B 2 sinC a b c 2a 2b 2c C.    R D.    . R sin A sin B sinC sin A sin B sinC
Câu 5. Cho ABC thỏa mãn : 2 cos B  2 . Khi đó: A. 0 B  30 . B. 0 B  60 . C. 0 B  45 . D. 0 B  75 .
Câu 6. Cho ABC vuông tại B và có  0
C  25 . Số đo của góc A là: A. 0 A  65 . B. 0 A  60 . C. 0 A 155 . D. 0 A  75 .
Câu 7. Công thức diện tích nào sau đây đúng
A. 2S bc sin A ca sin B ab sin C
B. S bc sin A ca sin B ab sin C 1 1 1 C. S bc sin A ca sin B ab sin C
D. S  2bc sin A  2ca sin B  2ab sin C 3 3 3 3
Câu 8. Cho tam giác A
BC có b  7;c  5; cos A
. Diện tích tam giác ABC bằng 5 A.10 B. 14 C. 15 D. 18
Câu 9. Cho ABC có  0
b  6, c  8, A  60 . Độ dài cạnh a là: A. 2 13. B. 3 12. C. 2 37. D. 20.
Câu 10. Một tam giác giải được nếu biết : A. Độ dài 3 cạnh
B. Độ dài 2 cạnh và 1 góc bất kỳ C. Số đo 3 góc
D. Độ dài 1 cạnh và 2 góc bất kỳ
Câu 11. Chọn công thức đúng trong các đáp án sau: 1 1 1 A. S bc sin A. B. S ac sin A. C. S bc sin B.
D. S bc sin B . 2 2 2
Câu 12. đây là công thức Heron (tính diện tích tam giác với độ dài 3 cạnh cho trước). A. S
p p a p b p c
B. S  2 p p a p b p c C. S
2 p p a p b p c D. S
p p a p b p c 
Câu 13. Tam giác ABC có AB  5, BC  7, CA  8. Số đo góc A bằng: A. 30 .  B. 45 .  C. 60 .  D. 90 .  
Câu 14. Tam giác ABC có AB  2, AC  1 và A  60 . Tính độ dài cạnh BC . A. BC  1. B. BC  2. C. BC  2. D. BC  3. 
Câu 15. Tam giác ABC có AB
2, AC  3 và C  45 . Tính độ dài cạnh BC . 6  2 6  2 A. BC  5. B. BC  . C. BC  . D. BC  6. 2 2
Câu 16. Trong tam giác ABC công thức nào sau đây có thể dùng để tính cos A ? 2 2 2
c a b 2 2 2
b c a A. cos A  . B. cos A  .. 2ca 2bc . 9 2 2 2
a b c 2 2 2
a b c C. cos A  .. D. cos A  .. 2ab 2ac
Câu 17. Cho tam giác ABC có 
A  120 . Chọn khẳng định đúng. A. 2 2 2
a b c  3bc B. 2 2 2
a b c bc . C. 2 2 2
a b c  3bc . D. 2 2 2
a b c bc . 
Câu 18. Cho tam giác ABC có góc A  120 , b  8, c  5 . Khi đó số đo của 
B gần nhất với số nào sau đây? A. 71 35  ' B. 30 3  7 ' . C. 4512 ' . D. 37 35  ' . Câu 19. Cho ABC c
ó a  6, b  8, c  10. Diện tích S của tam giác trên là: A. 48. B. 24. C. 12. D. 30. 
Câu 20. Tính diện tích tam giác ABC có AB  12; AC  8; BAC  30 . A. 24 2 B. 48 C. 24 D. 24 3
Câu 21. Cho tam giác ABC có ˆ  ˆ B 75 , C 45  
và BC  50 . Tính độ dài cạnh AB . A. 24 2 B. 48 C. 24 D. 40,8
Câu 22. Cho tam giác ABC có AB  6, AC  7, BC  8 . Giá trị cos A bằng bao nhiêu? 1 1 3 A. 0, 5 B. C. D. 4 3 4
Câu 23. Tính số đo góc A của tam giác ABC biết 2 2 2
a b c  2bc . A. 60 B. 45 C. 135 D. 150
Câu 24. Cho tam giác ABC có 2 2 2
b c a  3bc . Lựa chọn mệnh đề đúng           A.100  BAC  50
B. ABC ACB  150 C. ABC  160 D. BAC  60  
Câu 25. Tam giác ABC có B  60 ,
C  45 và AB  5 . Tính độ dài cạnh AC . 5 6 A. AC  . B. AC  5 3. C. AC  5 2. D. AC  10. 2
Câu 26. Tam giác ABC có a  2;b
6;c  1 3 thì bán kính R của đường tròn ngoại tiếp là 2 A. 1 B. 2 C. D. 3 2
Câu 27. Tính bán kính ra của đường tròn nội tiếp tam giác ABC biết độ dài ba cạnh là 13, 14, 15. A. 2 B. 3 C. 4 D. 2
Câu 28. Tam giác ABC có độ dài ba cạnh thỏa mãn đẳng thức a b ca b c  3ab . Số đo của góc C khi đó là A. 60 B. 120 C. 45 D. 30
Câu 29. Cho hình bình hành ABCD có AD  3 , AB  5 và đường chéo AC  5 . Đường chéo BD có độ dài bằng bao nhiêu ? A. 43 . B. 2 13 . C. 8 . D. 8 3 .   AB
Câu 30. Tam giác ABC có A  75 ; B  45 . Tính . AC AB 5 AB 6 AB 5 AB 11 A.  B.  C.  D.  AC 3 AC 2 AC 6 AC 7
Câu 31. Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn ngoại tiếp là ? 13 11 A. 6. B. 8. C. . D. . 2 2
Câu 32. Cho tam giác ABC thoả mãn : 2 2 2
b c a  3bc . Khi đó : A. 0 A  30 . B. 0 A  45 . C. 0 A  60 . D. 0 A  75 .  
Câu 33. Tam giác ABC có a  16,8 ; 0 B  56 13' ; 0
C  71 . Cạnh c bằng bao nhiêu? A. 29,9. B. 14,1. C. 17,5. D. 19,9.
________________________________ 10
HỆ THỨC LƯỢNG TRONG TAM GIÁC THƯỜNG LỚP 10 THPT
ĐỊNH LÝ SIN, ĐỊNH LÝ COSIN, GIẢI TAM GIÁC
(LỚP BÀI TOÁN CƠ BẢN P2)
________________________________________
Câu 1. Cho tam giác ABC nhọn có 2 cos B  2 . Tính góc B .     A. 0 B  30 . B. 0 B  60 . C. 0 B  45 . D. 0 B  75 .
Câu 2. Cho tam giác ABC có AC  29 ;   A  80 ;
C  35 . Tính độ dài cạnh BC ( làm tròn kết quả đến hàng phần mười) . A. 31,5 B. 31, 2 C. 32,6 D. 30,6 
Câu 3. Cho tam giác ABC có AC  14; BC  16 ; 
B  72 . Tính góc C (làm tròn kết quả đến độ). A. 0 53 B. 0 55 C. 0 45 D. 0 46
Câu 4. Cho tam giác ABC có AB  26; AC  29; BC  35 . Tính góc A (làm tròn kết quả đến độ). A. 0 53 B. 0 79 C. 0 45 D. 0 70 
Câu 5. Cho ABC có 0
a  2, b  6, C  135 . Diện tích của tam giác là: A. 4 . B. 6 2 . C. 3 2 . D. 4 3 .
Câu 6. Cho tam giác ABC có AB  4; BC  7;CA  9 . Tính cos A . 2 2 1 A.0,5 B. C.  D. 3 3 3 
Câu 7. Cho ABC có BC a , BAC  120 . Bán kính đường tròn ngoại tiếp ABC là a 3 a a 3 A. R  . B. R  . C. R  . D. R a . 2 2 3 
Câu 8. Tam giác ABC có a  8 , c  3 , B  60 . Độ dài cạnh b bằng bao nhiêu? A. 49 . B. 97 . C. 7 . D. 61 . 
Câu 9. Cho ABC có a  4 , c  5 , B  150 . Tính diện tích tam giác ABC . A. S  10 . B. S  10 3 . C. S  5 . D. S  5 3 .
Câu 10. Một tam giác có ba cạnh là 52 , 56 , 60 . Bán kính đường tròn ngoại tiếp tam giác đó là 65 A. . B. 40 . C. 32,5 . D. 65,8 . 4
Câu 11. Tam giác ABC có góc A nhọn, AB  5 , AC  8 , diện tích bằng 12. Tính độ dài cạnh B . C A. 2 3 . B. 4 . C. 5 . D. 3 2 .  
Câu 12. Tam giác ABC có A  75 ,
B  45 , AC  2 . Tính cạnh AB . 2 6 6 A. . B. 6 . C. . D. . 2 2 3 3
Câu 13. Tính diện tích tam giác ABC , biết b  7, c  5, cos A  . 5 A. 14 . B. 13 . C. 15 . D. 16 .
Câu 14. Tính diện tích tam giác ABC , biết AB  3, AC  4, BC  5 . A. 6 . B. 9 . C. 12 . D. 10 .  
Câu 15. Tam giác ABC có B  60 , C  45 , AB  3 . Tính cạnh AC . 3 6 3 2 2 6 A. . B. . C. 6 . D. . 2 2 3   AB
Câu 16. Tam giác ABC có các góc A  75 ,
B  45 . Tính tỉ số . AC 6 6 A. . B. 6 . C. . D. 1, 2 . 3 2 1
Câu 17. Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB c và os c ( A B)  . 3 11 c 2 3c 2 9c 2 3c A. . B. . C. . D. . 2 8 8 2   AB
Câu 18. Tam giác ABC có các góc A  105 , B  45 . Tính tỉ số . AC 2 2 6 A. . B. 2 . C. . D. . 2 2 3
Câu 19. Tam giác ABC có AB  4 , AC  5 , BC  6 . Tính cos(B C) . 1 1 A. . B.  . C. –0,125 . D. 0, 75 . 8 4
Câu 20. Tam giác có ba cạnh lần lượt là 2, 3, 4 . Góc bé nhất của tam giác có sin bằng bao nhiêu? 15 7 1 14 A. . B. . C. . D. . 8 8 2 8
Câu 21. Tam giác có ba cạnh lần lượt là 3 , 8 , 9 . Góc lớn nhất của tam giác có cosin bằng bao nhiêu? 1 1 17 4 A. . B.  . C. . D.  . 6 6 4 25
Câu 22. Cho tam giác ABC . Khẳng định nào sau đây là đúng ? 1 a A. S . a . ABC b c   . B.  R . 2 sin A 2 2 2
b c a 2 2 2
b a c C. cos B  . D. 2 2 2 c m  . 2bc 4
Câu 23. Cho ABC có S  84, a 13,b  14,c  15. Độ dài bán kính đường tròn ngoại tiếp R của tam giác trên là: A. 8,125. B. 130. C. 8. D. 8,5.  
Câu 24. Tam giác ABC có AC  4, BAC  30 ,
ACB  75 . Tính diện tích tam giác ABC . A. S  8 . B. S  4 3 . C. S  4 . D. S  8 3 . ABCABC ABCABC
Câu 25. Tam giác ABC có AB  3, AC  6, BAC  60 . Tính độ dài đường cao h của tam giác. a 3 A. h  3 3 . B. h  3 . C. h  3 . D. h  . a a a a 2 
Câu 26. Tam giác ABC có AC  4, ACB  60 . Tính độ dài đường cao h xuất phát từ đỉnh A của tam giác. A. h  2 3 . B. h  4 3 . C. h  2 . D. h  4 .
Câu 27. Tam giác ABC có a  21, b  17, c  10 . Gọi B ' là hình chiếu vuông góc của B trên cạnh AC . Tính BB ' . 84 168 84 A. BB '  8. B. BB '  . C. BB '  . D. BB '  . 5 17 17
Câu 28. Tam giác ABC có AB  8 cm, AC  18 cm và có diện tích bằng 64 2
cm . Giá trị sin A bằng: 3 3 4 8 A. sin A  . B. sin A  . C. sin A  . D. sin A  . 2 8 5 9
Câu 29. Nếu tam giác ABC có 2 2 2
BC AC AB thì   A. A là góc tù. B. A là góc vuông.   C. A là góc nhọn.
D. A là góc nhỏ nhất.
Câu 30. Cho tam giác ABC có AB  26; AC  38 ; 
BAC  60 . Tính độ dài cạnh BC ( làm tròn kết quả đến hàng phần mười) . A. 33,6 B. 32,6 C. 31,6 D. 30,6  
Câu 31. Cho tam giác ABC có BC = 10, BAC  30 và bán kính đường tròn ngoại tiếp là R. Mệnh đề nào sau đây đúng ? A. R  9 B. 13  R  15 C. R  10 D. 4  R  8
_________________________________ 12
HỆ THỨC LƯỢNG TRONG TAM GIÁC THƯỜNG LỚP 10 THPT
ĐỊNH LÝ SIN, ĐỊNH LÝ COSIN, GIẢI TAM GIÁC
(LỚP BÀI TOÁN CƠ BẢN P3)
________________________________________
Câu 1. Trong các công thức sau, công thức nào đúng? 1 1 1 1 A. S bc sin . B B. S bc sin . A C. S ab sin . B D. S ac sin C 2 2 2 2 
Câu 2. Cho tam giác ABC có 0
AB  4, AC  3, BAC  30 . Diện tích tam giác ABC bằng A. S  3. B. S  4 3. C. S  6 3. D. S  6 .
Câu 3. Tính diện tích tam giác ABC biết AB  3, BC  5, CA  6 . A. 56 . B. 48 . C. 6 . D. 8 .
Câu 4. Cho tam giác ABC có AB  3 , AC  4 , BC  5 . Bán kính đường tròn nội tiếp tam giác bằng? 8 4 3 A. . B. . C. . D. 1 . 9 5 4
Câu 5. Cho tam giác ABC với BC a , AC b , AB c . Đẳng thức nào sai? A. 2 2 2
b a c  2ac cos B B. 2 2 2
a b c  2bc cos A . C. 2 2 2
c b a  2ab cos C . D. 2 2 2
c b a  2ab cos C . 
Câu 6. Cho ABC có 0
b  6,c  8, A  60 . Độ dài cạnh a là. A. 2 13. B. 3 12. C. 2 37. D. 20.
Câu 7. Cho tam giác ABC có 2 2 2
a b c  0 . Khi đó : A.  0 C  90 B.  0 C  90 C.  0 C  90
D. Không thể kết luận được gì về  C .
Câu 8. Cho tam giác ABC với BC  7 cm , AC  9cm , AB  4 cm . Tính cos A 2 1 1 2 A. cos A   . B. cos A  . C. cos A  . D. cos A  . 3 2 3 3
Câu 10. Cho tam giác ABC với BC a, AC b, AB c . Khẳng định nào sau đây đúng?
A. a  2R cos A .
B. a  2R sin A .
C. a  2R tan A .
D. a R sin A . 
Câu 11. Cho tam giác ABC có B  45 , cạnh AC  2 2 cm . Bán kính R của đường tròn ngoại tiếp tam giác ABC bằng A. R  1 cm . B. R  2 cm . C. R  4 cm . D. R  3 cm .
Câu 12. Cho tam giác ABC có góc 0 0 ˆ ˆ
B  60 , C  45 , cạnh AB  4 . Tính độ dài cạnh AC . 6 4 6 3 6 A. 2 6 . B. . C. . D. . 2 3 4
Câu 13. Tam giác ABC có 2 2 2
2(b c )  a  1993 . Độ dài trung tuyến kẻ từ A của tam giác là A. 498,25 B. 996,5 C. 120 D. 1993 Lời giải
Câu 14. Cho tam giác ABC có a  4,b  6,c  8 . Khi đó diện tích của tam giác là: 2 A. 9 15. B. 3 15. C. 105. D. 15. 3
Câu 15. Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu ? A. 2. B. 2 2. C. 2 3. D. 3.
Câu 16. Cho ABC có 0
B  60 , a  8, c  5. Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 .
Câu 17. Cho tam giác ABC . Tìm công thức sai: a a c sin A A.  2R . B. sin A  .
C. b sin B  2R. D. sin C  . sin A 2R a
Câu 18. Cho tam giác ABC . Đẳng thức nào sai ? B C A
A. sin(A B  2C)  sin 3C. B. cos  sin . 2 2 13
A B  2C C
C. sin( A B)  sin C. D. cos  sin . 2 2
Câu 19. Tam giác ABC có cos B bằng biểu thức nào sau đây? 2 2 2
b c a 2 2 2
a c b A. . B. 2 1 sin B .
C. cos( A C). D. . 2bc 2ac
Câu 20. Cho tam giác ABC có các góc 0 0 ˆ ˆ
B  120 , C  40 , cạnh BC  5cm . Tính độ dài cạnh AB (làm tròn kết
quả đến hàng đơn vị). A. 7cm . B. 8cm . C. 9cm . D. 10cm . 
Câu 21. Cho ABC có 0
a  4, c  5, B  150 . Diện tích của tam giác là: A. 5 3 . B. 10 . C. 5 . D. 10 3 .
Câu 22. Cho tam giác ABC có AB  4, BC  7, AC  9 . Diện tích tam giác ABC bằng A. S  6. B. S  8 3. C. S  5 6. D. S  6 5 .
Câu 23. Tính diện tích tam giác có ba cạnh lần lượt là 3 , 2 và 1. 2 6 3 A. 3 . B. . C. . D. . 2 2 2    
Câu 24. Tam giác ABC có A  45 , c  6, B  75 . Độ dài đường cao h bằng b 3 A. 3 2 B. C. 6 2 D. 2 3 2    
Câu 24. Tam giác ABC có A  45 ;c  6; B  75 . Độ dài bán kính đường tròn ngoại tiếp của tam giác bằng A. 8 3 B. 2 3 C. 6 3 D. 4 3
Câu 25. Cho tam giác ABC có 3h  2h h . Lựa chọn mệnh đề đúng a b c 2 1 1 1 1 2 A.   B.   sin A sin B sin C sin A sin B sin C 3 2 1 1 2 3 C.   D.   sin A sin B sin C sin A sin B sin C
Câu 26. Chọn công thức đúng trong các đáp án sau: 1 1 1 1 A. S bc sin A. B. S ac sin A. C. S bc sin B . D. S C bc sin C . 2 2 2 2
Câu 27. Tính diện tích tam giác có ba cạnh lần lượt là 5 , 12 , 13 . A. 34 . B. 7 5 . C. 60 . D. 30 .
Câu 28. Tam giác có ba cạnh lần lượt là 1, 2 , 5 . Tính độ dài đường cao ứng với cạnh lớn nhất 2 5 2 5 A. . B. . C. 1. D. 1, 3 . 5 3 
Câu 29. Cho tam giác ABC có 0
AB  6, AC  8, A  60 . Tính BC A. BC  2 13. B. BC  52. C. BC  2 37. D. BC  148.  0 
Câu 30. Cho tam giác ABC có 0
AB  5, B  60 ,C  45 . Tính AC 5 6 A. AC  5 2. B. AC  10. C. AC  . D. AC  5 3. 2 
Câu 31. Cho tam giác ABC có 0
AB  5, AC  2, C  45 . Tính BC A. BC  3. B. BC  2. C. BC  3. D. BC  2.
Câu 32. Cho tam giác ABC có AB  5, BC  7, AC  8 . Tính số đo của góc A A. 0 90 . B. 0 45 . C. 0 60 . D. 0 30 .  0 
Câu 33. Cho tam giác ABC có 0
A  45 , c  6, B  75 . Tính độ dài cạnh BC 3 A. 3 6 B. . C. 2 6. D. 2 3. 2 14
HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN VẬN DỤNG P1)
_______________________________ 2 2 cot x  cos x sin . x cos x
Câu 1. Rút gọn biểu thức sau A   2 cot x cot x A. A  4 . B. A  2 . C. A  1 . D. A  3 .
Câu 2. Biểu thức  a a2 cot tan bằng 1 1 1 1 A.  . B. 2 2
cot a  tan a . C.  . D. 2 2
cot a tan a  2 . 2 2 sin  cos  2 2 sin  cos 
Câu 3. Biểu thức f x   4 4 x x   6 6 3 sin cos
2 sin x  cos x có giá trị bằng: A. 1. B. 2 . C. 3  . D. 0 .
Câu 4. Đẳng thức nào sau đây là sai? 1 cos x sin x 1 A. 
x  0, x 180  B. tan x cot xx 0,90,180     sin x 1 cos x sin x cos x 1 C. 2 2 tan x cot x 2 x 0, 90 ,180     D. 2 2
sin 2x  cos 2x  2 . 2 2   sin x cos x
Câu 5. Tìm giá trị nhỏ nhất của biểu thức 2
y  tan x  2 tan x  5 . A. 4 B. 7 C. 5 D. 3 2 0 2 0 2 0 2 0 2 0
sin 90  cos 120  cos 0  tg 60  cot g 135
Câu 6. Giá trị của biểu thức E  bằng 0 2 0 sin 30  cos 60 1 3 A.1 B. 2 C. D. 3 7 Câu 7. Tổng 2 o 2 o 2 o 2 o 2 o 2 o
sin 2  sin 4  sin 6  ...  sin 84  sin 86  sin 88 bằng A. 21. B. 23. C. 22 . D. 24 . Câu 8. Tính 2 0 2 0 2 0 2 0
N  sin 20  cos 40  ...  cos 160  sin 180 A. 4 B. 1 C. 2 D. 3
Câu 9. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của biểu thức y  cos x  3 . A. 4 B. 2 C. 6 D. 7
Câu 10. Đẳng thức nào sau đây là đúng ? A. 4 4 2 2
sin x  cos x 1 2sin x cos . x B. 4 4
sin x  cos x  1. C. 6 6 2 2
sin x  cos x 1 3sin x cos . x D. 4 4 2 2
sin x  cos x  sin x  cos x. o o
Câu 11. Cho biết 3cos  sin  1, 0    90 Giá trị của tan  bằng 4 3 4 5 A. tan  B. tan  C. tan  D. tan  3 4 5 4 Câu 12. Cho biết 0 0
2 cos  2 sin   2, 0    90 . Tính giá trị của cot . 5 3 2 2 A. cot   B. cot   C. cot   D. cot   4 4 4 2 1
Câu 13. Cho biết cos  sin   . Giá trị của 2 2 P
tan   cot  bằng bao nhiêu? 3 5 7 9 11 A. P  . B. P  . C. P  . D. P  . 4 4 4 4
Câu 14. Biết sin a  cos a  2 . Hỏi giá trị của 4 4
sin a  cos a bằng bao nhiêu? 3 1 A. . B. . C. 1. D. 0 . 2 2 2 2
Câu 15. Cho tan   cot   m . Tìm m để tan   cot   7 . A. m  9 . B. m  3 . C. m  3  . D. m  3  . 2
cos x  2sin x(1  sin x) 2(1 sin x) 1 Câu 16. Cho .  . Tính cos x .
(1 sin x) cos x  (1 sin x) cos x 1 sin x 3 15 1 2 1 A. B. C. D. 1 3 3 5
Câu 17. Giá trị của o o o o o
A  tan 5 . tan10 . tan15 ... tan 80 . tan 85 là A. 2 . B. 1. C. 0 . D. 1  .
Câu 18. Cho tan x  cot x  2 . Tính 3 3
tan x  cot x . A.4 B. 2 C. 5 D. 1  1  1 
Câu 19. Kết quả rút gọn biểu thức cos x 1   tan x 1  tan x    bằng  cos x  cos x  A. 2 B. 2 tan x C. 2 cot x D. 2sin x 2 2
sin x  2 cos x 1
Câu 20. Cho góc x thỏa mãn 0 0
0  x  180 và tan x  3 , giá trị của biểu thức A  là 2 2
3sin x  cos x 1 7 6 2 3 A. . B. . C. . D. . 6 7 3 2
Câu 21. Cho sin x  cos x m . Tính theo m giá trị của M  sin . x cos x . 2 m 1 2 m 1 A. 2 m 1 . B. . C. . D. 2 m 1. 2 2 4 3
sin x  2 cos x
Câu 22. Cho góc x thỏa mãn cot x
. Tính giá trị của biểu thức: B   . 3 2 sin x cos x  4sin x 415 11 123 A. B. C. D. 1 48 48 48
Câu 23. Cho tam giác ABC thỏa: 2 sin A  sin  B C  1 . Nhận dạng tam giác ABC . A.Cân tại A B. Vuông tại A C. Vuông tại C D. Đều 1
Câu 24. Cho biết sin   cos  . Giá trị của 4 4
P  sin   cos  bằng bao nhiêu? 5 15 17 19 21 A. P  B. P  C. P  D. P  5 5 5 5 Câu 25. Cho ,
A B, C là ba góc trong tam giác ABC . Tính giá trị của biểu thức sau: P  sin .
A cos  B C   cos .
A sin  B C  A. P  0 . B. P  1 . C. P  1. D. P  2 . Câu 26. Cho , A ,
B C là ba góc trong tam giác ABC . Tính giá trị của biểu thức sau:  B   180      A C B A C 2 2 P  cos 180   cos  tan . tan      2  2 2 2   A. P  1  . B. P  1 . C. P  2 . D. P  0 .
Câu 27. Đẳng thức nào sau đây là sai? A. 2 2
(cos x  sin x)  (cos x  sin x)  2, x  . B. 2 2 2 2
tan x  sin x  tan x sin x, x   90 . C. 4 4 2 2
sin x  cos x  1 2sin x cos x, x  . D. 6 6 2 2
sin x  cos x  1 3sin x cos x, x  . 2
 sin a  tan a
Câu 28. Kết quả rút gọn của biểu thức 1   bằng  cos a 1  1 1 A. 2 . B. 1 tan . C. . D. . 2 cos  2 sin  sin a  5cos a
Câu 29. Tính giá trị biểu thức C  khi tan a  2 . 3 3
sin a  2 cos a 15 32 35 A. . B. . C. . D. 4 . 2 5 6
________________________ 16
HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN VẬN DỤNG P2)
_______________________________
Câu 1. Biểu thức: f x 4 2 2 2
 cos x  cos x sin x  sin x có giá trị bằng A. 1. B. 2 . C. 2  . D. 1  .
Câu 2. Trong các mệnh đề sau, mệnh đề nào sai? A.  x x2 sin cos
 12 sin x cos x . B. 4 4 2 2
sin x  cos x  12 sin x cos x . C.  x x2 sin cos
 1  2 sin x cos x . D. 6 6 2 2
sin x  cos x  1sin x cos x .
Câu 3. Tìm tổng giá trị nhỏ nhất và giá trị lớn nhất của M  3sin x  4 cos x . A.3 B. 2 C. 4 D. 0 2 2
sin x  2 sin x cos x m cos x
Câu 4. Cho tan x  2 . Tìm giá trị m sao cho  0, 44 . 2 2
3sin x  4 sin x cos x  5 cos x A. m  3 B. m  4 C. m  5 D. m  6 2 2
Câu 5. Cho hai góc x, y thỏa mãn tan x  tan y
;cot x  cot y   . Tính giá trị tan . x tan y . 3 3 A. 2 B. 2  3 C.  3 D. – 1 2 2 2 2 tan x  cos x cot x  sin x
Câu 6. Kết quả rút gọn biểu thức Q   bằng 2 2 sin x cos x 1 1 A. B. C. 2 D. – 2 sin x cos x 2 2 4
sin x  cos x  cos x Câu 7. Cho 0 A
0  x 180 . Chọn mệnh đề đúng trong các mệnh đề sau. 2 2 4  0 
cos x  sin x  sin x sin x  cos x A. 4 A  tan x . B. A  . C. 4 A  cot x . D. 2 Acot x. sin x Câu 8. Giả sử 4 4 1
3sin x  cos x  thì 4 4
sin x  3cos x có giá trị bằng : 2 A. 1. B. 2. C. 3. D. 4. 2 2 tan x  sin x Câu 9. Giả sử
 tann x ( giả thiết biểu thức có nghĩa). Khi đó n có giá trị là 2 2 cot x  os c x A. 3 . B. 6 . C. 5 . D. 4 . Câu 10. Biểu thức 2 2 2 2 2 sin .
a tan a  4sin a  tan a  3cos a không phụ thuộc vào a và có giá trị bằng A. 6 . B. 5 . C. 3 . D. 4 .
Câu 11. Cho 4 góc  ; ; ; có các điểm biểu diễn trên nửa đường tròn đơn vị thứ tự là ,
A B,C, D như 1 2 3 4 hình vẽ.
Khẳng định nào sau đây là khẳng định đúng?
A. cos  cos  cos .
B. cos  cos  cos . 1 3 4 2 1 4
C. cos  cos  cos .
D. cos  cos  cos . 3 2 4 2 4 3 2 tan   3cot  Câu 12. Cho cos  . Tính A  . 3 tan   cot  17 11 10 7 A. B. C. D. 9 9 9 9 17 4 sin x cos x
Câu 13. Cho tan x  cot x  2 , tính . 2 2 tan x  cot x A.3 B. 1 C. 2 D. – 2
Câu 14. Cho tam giác ABC, ,khẳng định nào sau đây sai?  AC B
A. sin  A B  sin C . B. sin  cos   .  2  2  A C B
C. cos  A B  cos C . D. cos  sin .    2  2 Câu 15. Biết ,
A B, C là các góc của tam giác ABC, khi đó
A. sin C  sin A B.
B. cosC  cosA B.
C. tan C  tan A B.
D. cot C   cot A B.
Câu 16. Cho tam giác ABC . Khẳng định nào sau đây là sai ? A C B A C B A. sin  cos . B. cos  sin .
C. sin A B  sinC.
D. cosA B  cosC. 2 2 2 2 sin x
Câu 17. Đơn giản biểu thức E  cot x  ta được 1 cos x 1 1 A. sin x . B. . C. . D. cos x . cos x sin x 2 2 cot x  cos x sin . x cos x
Câu 18. Rút gọn biểu thức sau A   . 2 cot x cot x A. A 1. B. A  2 . C. A  3 . D. A  4 . 
Câu 19. Cho hai góc x, y thỏa mãn 0  x, y  90 và thỏa mãn 2 2
tan x  tan y  2; cot x  cot y  2 . Biểu thức
5 tan x  6 tan y nhận giá trị bằng A.10 B. 11 C. 8 D. 7 sin   cos
Câu 20. Cho tan  
2 . Giá trị của B  gần nhất với 3 3
sin   3cos   2 sin  A.0,086 B. 0,072 C. 0,094 D. 0,065
Câu 21. Biết sin x  cos x m . Khi đó giá trị biểu thức 4 4
sin x  cos x theo m là 2 4 3  2m m 2 4 3  3m m A. A  B. A  2 2 2 4 1 2m m 2 4 3  2m m C. A  D. A  2 4
Câu 22. Giá trị của biểu thức o o o o o
A  tan1 tan 2 tan 3 ... tan 88 tan 89 là A. 0 . B. 2 . C. 3. D. 1. 1 1
Câu 23. Cho hai góc nhọn a và b . Biết cos a  và cos b  . Tính giá trị 2 2
P  (cos a  cos b)  (sin a sin b) . 3 4 119 59 129 19 A.  B.  C.  D.  144 144 144 144 4  2 sin x  cos x
Câu 24. Cho tan x   và
x   . Giá trị của biểu thức M  bằng 3 2 2 sin x  cos x 31 32 5 6 A. B. C. D. 11 11 11 13 Câu 25. Cho 3cos sin  1, 0  90    
. Tính giá trị của tan  . 4 2 5 8 A. B. C. D. 3 3 3 3 1
Câu 26. Cho sin   cos  . Tính giá trị của 4 4
P  sin   cos  . 5 17 17 2 17 17 A. B. C. D. 5 15 5 10
_____________________________ 18
HỆ THỨC LƯỢNG TAM GIÁC THƯỜNG LỚP 10 THPT
GIÁ TRỊ LƯỢNG GIÁC GÓC TỪ 0 ĐẾN 180 ĐỘ
(LỚP BÀI TOÁN VẬN DỤNG P3)
_______________________________ 4 sin   cos Câu 1. Cho sin  
, với 90    180 . Tính giá trị của M  5 3 cos  25 175 35 25 A. M  B. M  . C. M  . D. M   . 27 27 27 27
Câu 2. Cho tam giác ABC , tính giá trị biểu thức P  sin .
A cos  B C   cos .
A sin  B C  A. 0 . B. 1. C. 1  . D. 2 . 2 2 2sin x  5sin .
x cos x  cos x
Câu 3. Cho tan x  2 . Tính A  2 2 2sin x  sin .
x cos x  cos x 1 1 A. A  B. A  11  C. A   D. A  11 11 11
Câu 4. Cho 4 góc  ; ; ; có các điểm biểu diễn trên nửa đường tròn đơn vị thứ tự là ,
A B,C, D như hình 1 2 3 4 vẽ.
Khẳng định nào sau đây là khẳng định đúng?
A. sin  sin  sin .
B. sin   sin   sin  . 1 3 4 4 1 2
C. sin   sin  sin .
D. sin   sin   sin  . 4 3 2 2 4 3
Câu 5. Cho tan   cot   3. Tính giá trị của biểu thức sau: 2 2
A  tan   cot  . A. A  12. B. A  11. C. A  13 . D. A  5 .
Câu 6. Biết sin a  cos a  2 . Hỏi giá trị của 4 4
sin a  cos a bằng bao nhiêu? 3 1 A. . B. . C. 1  . D. 0 . 2 2  1 2 2 
Câu 7. Cho điểm M   ;
 trên nửa đường tròn đơn vị. Gọi góc 
  xOM  với M  là điểm đối xứng với  3 3   
M qua trục Oy . Giá trị lượng giác của tan là 1 A. tan  . B. tan  2 2 . 2 2 2 2 1 2 2 C. tan   . D. tan  . 3 9 cos x  sin x
Câu 8. Biết rằng 3 2
 tan x a tan x b tan x c . Tính giá trị a b c . 3 cos x A.4 B. 3 C. 2 D. 6 3 B 3 B sin cos
cos  A C
Câu 9. Cho tam giác ABC . Kết quả rút gọn biểu thức 2 2   . tan B là  A C   A C  sin B cos sin      2   2  A.2 B. 3 C. 0 D. 1
Suy ra điều phải chứng minh.
Câu 10. Giá trị biểu thức o o 2 2 2
A  sin(90  x)  cos(180  x)  sin x(1 tan x)  tan x không phụ thuộc vào biến và có giá trị bằng 19 A.3 B. 2 C. 4 D. 0 1 1 1
Câu 11. Kết quả rút gọn biểu thức B  .   2 là sin x 1  cos x 1  cos x A. 2 2 cot x B. 2 sin x C. 3 cos x D. 2 sin 2x
Câu 12. Tính A  cos10  cos 30  cos 50  ...  cos150  cos170 . A. 0 . B. 2 . C. 1  . D. 1.
Câu 13. Giá trị biểu thức 4 2 4 4 2 4
P  sin x  6 cos x  3cos x  cos x  6 sin x  3sin x không phụ thuộc vào x . Giá trị đó bằng A.2 B. 3 C. 4 D. 1  1 2 2  Câu 14. Cho góc 
  xOM với điểm M  ;
 trên nửa đường tròn đơn vị. Giá trị lượng giác của cot  là  3 3    1 A. cot   . B. cot   2 2 . 2 2 2 2 1 2 2 C. cot   . D. cot   . 3 9 1 tan x2 2 1
Câu 15. Kết quả rút gọn biểu thức A   bằng 2 2 2 4 tan x 4 sin x cos x A.0 B. – 1 C. 1 D. 2
Câu 16. Cho H   0 x     0  x   0 x    0 cos 60 5cos 120 6.sin
60 .cot x  60   0 0
0  x  90  . Chọn mệnh đề
đúng trong các mệnh đề sau. 1  A. H  1  . B. H  . C. H  . D. H  0. 3 3 2 2 sin a  2sin .
a cos a  2cos a Câu 17. Cho a    0 0 tan
3 0  a  180  . Khi đó B  bằng 2 2 2sin a  3sin .
a cos a  4cos a 1 5 2 5 A. . B. . C. . D. . 31 14 13 12 1 cot a  tan a
Câu 18. Cho sin a
. Giá trị của biểu thức A  bằng 3 tan a  2cot a 1 7 17 7 A. . B. . C. . D. . 9 9 81 17 Câu 19. Cho 2 0 2 0 2 0 2 0
D  cos 10  cos 20  cos 30 ...  cos 180 . Chọn mệnh đề đúng trong các mệnh đề sau. A. D  0 . B. D  8. C. D  2022 . D. D 18 .
Câu 20. Cho biết cot   5 . Tính giá trị của 2
E  2 cos   5sin  cos 1? 10 100 50 101 A. . B. . C. . D. . 26 26 26 26 3
Câu 21. Cho sin x  cos x   0 0
0  x  180  . Biểu thức B  sin x  cos x bằng 4 3 23 23 9 A. . B. . C. . D. . 4 16 4 16
Câu 22. Biểu thức E  sin 180  x  2cos 90  x  cos .
x tan x x  90 sau khi thu gọn bằng với biểu thức
nào trong 4 biểu thức dưới đây: A. A  0 . B. B  2  sin x .
C. C  sin x . D. D  2  cos x .
Câu 23. Trong mặt phẳng tọa độ Oxy , cho điểm M nằm trên nửa đường tròn đơn vị. Điểm M có tung độ và 
hoành độ đều dương, góc xOM có thể là A. 100 . B. 80 . C. 120 . D. 140 .
_________________________________ 20