Luyện kỹ năng trắc nghiệm đúng – sai tổng hợp chủ đề lượng giác

Tài liệu gồm 18 trang, được biên soạn bởi thầy giáo Đặng Công Đức (Giang Sơn), tuyển chọn các bài tập rèn luyện kỹ năng giải toán trắc nghiệm định dạng đúng – sai tổng hợp chủ đề hàm số lượng giác và phương trình lượng giác môn Toán 11 THPT, kết hợp ba bộ sách giáo khoa Toán 11 chương trình mới: Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống. Mời bạn đọc đón xem!

45 23 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

26 trang 1 tháng trước

Tác giả:

Profile Lê Phương
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
L
L
U
U
Y
Y
Ệ
Ệ
N
N
K
K
Ỹ
Ỹ
N
N
Ă
Ă
N
N
G
G
T
T
O
O
Á
Á
N
N
1
1
1
1
T
T
H
H
P
P
T
T
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
Đ
Đ
Ú
Ú
N
N
G
G
,
,
S
S
A
A
I
I
T
T
Ổ
Ổ
N
N
G
G
H
H
Ợ
Ợ
P
P
C
C
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
L
L
Ư
Ư
Ợ
Ợ
N
N
G
G
G
G
I
I
Á
Á
C
C
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
Đ
Đ
Á
Á
P
P
Á
Á
N
N
C
C
H
H
I
I
T
T
I
I
Ế
Ế
T
T
P
P
D
D
F
F
B
B
Ạ
Ạ
N
N
Đ
Đ
Ọ
Ọ
C
C
V
V
U
U
I
I
L
L
Ò
Ò
N
N
G
G
L
L
I
I
Ê
Ê
N
N
H
H
Ệ
Ệ
T
T
Á
Á
C
C
G
G
I
I
Ả
Ả
:
:
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
9
9
8
8
0
0
2
2
1
1
9
9
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
7
7
/
/
2
2
0
0
2
2
4
4
2
L
L
U
U
Y
Y
Ệ
Ệ
N
N
K
K
Ỹ
Ỹ
N
N
Ă
Ă
N
N
G
G
T
T
O
O
Á
Á
N
N
1
1
1
1
T
T
H
H
P
P
T
T
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
Đ
Đ
Ú
Ú
N
N
G
G
,
,
S
S
A
A
I
I
T
T
Ổ
Ổ
N
N
G
G
H
H
Ợ
Ợ
P
P
C
C
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
L
L
Ư
Ư
Ợ
Ợ
N
N
G
G
G
G
I
I
Á
Á
C
C
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
–
–
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
–
–
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
C
C
A
A
O
O
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
DUNG
LƯỢNG
NỘI DUNG BÀI TẬP
6 FILE
1 file 4 trang
TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG LƯỢNG GIÁC
3
LƯỢNG GIÁC LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG P1
_________________________________
Câu 1. Tính được các giá trị lượng giác của góc
2
3
k
(biết
k
). Xác định tính đúng, sai của các
khẳng định
a)
3
sin
2
b)
1
cos
2
c)
tan 3
d)
3sin 2 2
Câu 2. Hình vẽ bên là vòng tròn lượng giác gốc A, trong đó
là hình vuông,
1
45
AOM
. Xét góc
lượng giác
có điểm đầu là điểm A, điểm cuối là điểm bất kỳ nào đó trên vòng tròn lượng giác
Xác định tính đúng, sai của các khẳng định
a) Tại điểm cuối B thì
sin 1
.
b) Tại điểm cuối
3
M
thì
2sin 3cos 1
.
c) Hai điểm
2 3
,M M
là điểm biểu diễn đầy đủ nghiệm của phương trình lượng giác
2
sin
2
x
.
d) Khi di chuyển điểm cuối
1 2
M M
thì
tan
tăng dần.
Câu 3. Cho hàm số
cos2 cosf x x x
. Xác định tính đúng, sai của các khẳng định
a)
Hàm số có chu kỳ tuần hoàn là
2
.
b)
Hàm số là hàm số chẵn.
c)
Hàm số có giá trị nhỏ nhất là một số lớn hơn – 2.
d)
Phương trình
0
f x
có tổng tất cả các nghiệm trong khoảng
0;2
là
7
6
T
Câu 4. Cho biết
1
sin
3
và
2
. Xác định tính đúng, sai của các khẳng định
a)
2 2
cos
3
b)
4 2
sin 2
9
c)
7
cos2
9
d)
22
sin 3
27
Câu 5. Cho đồ thị hàm số lượng giác
y f x
như hình vẽ. Xác định đúng, sai của các khẳng định
a)
1
f
. b)
cosy x
.
c)
2023 2024 2
f f
. c) Phương trình
2
3
f x
có 45 nghiệm trong khoảng
0;50
.
Câu 6. Cho phương trình lượng giác
1
sin 2
2
x
(*). Xác định tính đúng, sai của các khẳng định
a) Phương trình (*) tương đương
sin 2 sin
6
x
b) Trong khoảng
0;
phương trình có 3 nghiệm
c) Tổng các nghiệm của phương trình trong khoảng
0;
bằng
3
2
d) Trong khoảng
0;
phương trình có nghiệm lớn nhất bằng
11
12
4
Câu 7. Cho hàm số
3
( ) | tan | 3f x x x x
. Xác định tính đúng, sai của các khẳng định
a) Tập xác định của hàm số:
\ ,
2
D k k
. b)
( ) ( ).
f f
c) Hàm số đã cho đối xứng qua gốc tọa độ
0;0
O
d) Hàm số đã cho là hàm số chẵn.
Câu 8. Cho phương trình lượng giác
tan 2 15 1
x
(*). Xác định tính đúng, sai của các khẳng định
a) Phương trình (*) có nghiệm
30 90 ( )
x k k
b) Phương trình có nghiệm âm lớn nhất bằng
30
c) Tổng các nghiệm của phương trình trong khoảng
180 ;90
bằng
180
d) Trong khoảng
180 ;90
phương trình có nghiệm lớn nhất bằng
60
Câu 9. Cho hàm số
( ) 2cos 1f x x
và
( ) sin tang x x x
. Xác định tính đúng, sai của các khẳng định
a) Tập xác định hàm số
f x
:
D
.
b) Hàm số
f x
là hàm tuần hoàn.
c) Tập xác định hàm số
g x
:
\
3
D k k
.
d) Hàm số
g x
là hàm không tuần hoàn.
Câu 10. Cho hàm số lượng giác
2
sin 4
f x x
. Xác định tính đúng, sai của các khẳng định
a)
5 cos2f x x
.
b)
Hàm số đã cho là hàm số chẵn và có chu kỳ bằng
.
c)
Đồ thị hàm số đã cho luôn nằm trong khoảng giữa hai đường thẳng cách nhau một khoảng bằng 1.
d)
Phương trình
5sinf x x
có 1 điểm biểu diễn trên vòng tròn lượng giác.
Câu 11. Cho
2
sin ,
3 2
. Xác định tính đúng, sai của các khẳng định
a)
5
cos
3
b)
2 5
tan
5
c)
5 2 3
cos
3 6
d)
10 2 2
cos
4 6
Câu 12. Cho hàm số
( ) tanf x x
và
2
sin 2
( ) cot
2
x
g x x
. Xác định tính đúng, sai của các khẳng định
a) Tập xác định hàm số
f x
:
\
2
D k k
.
b) Hàm số
f x
là hàm không tuần hoàn.
c) Tập xác định hàm số
g x
:
\{ }
D k k
.
d) Hàm số
g x
là hàm tuần hoàn.
Câu 13. Cho hàm số
2
( ) sin cos 1f x x x
. Khi đó;
a) Tập xác định của hàm số
D
b) Hàm số đã cho là hàm số chẵn.
c) Hàm số có giá trị nhỏ nhất là một số lớn hơn – 2.
d) Phương trình
0
f x
có 5 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
Câu 14. Cho hàm số
2 3cosf x x
và
sin cosg x x x
. Xác định tính đúng, sai của các khẳng định
a) Giá trị lớn nhất của hàm số
f x
bằng 5
5
b) Hàm số
f x
đạt giá trị nhỏ nhất khi
2 ( )
x k k
c) Giá trị lớn nhất của hàm số
g x
bằng
2
d) Hàm số
g x
đạt giá trị nhỏ nhất khi
3
2 ( ).
4
x k k
Câu 15. Cho phương trình lượng giác
1
cot3
3
x
(*). Xác định tính đúng, sai của các khẳng định
a) Phương trình (*) tương đương
6
cot3 cotx
b) Phương trình (*) có nghiệm
( )
9 3
x k k
c) Tổng các nghiệm của phương trình trong khoảng
;0
2
bằng
5
9
d) Phương trình có nghiệm dương nhỏ nhất bằng
2
9
Câu 16. Cho biết
12
cos
13
x
và
3
2
x
; Xác định tính đúng, sai của các khẳng định
a)
sin 0
x
b)
5
sin
13
x
c)
5
cot
12
x
d)
5 12 3
sin
3 26
x
Câu 16. Cho hàm số lượng giác
sin 2 3cosf x x x
. Xác định tính đúng, sai của các khẳng định
a) Hàm số đã cho có chu kỳ tuần hoàn
2
.
b) Hàm số không thể biểu thị theo hàm số bậc hai của
cos ,sinx x
.
c)
4,f x x
.
d) Phương trình
0
f x
có 1 nghiệm trong khoảng
0;
?
Câu 17. Cho các hàm số sau:
( ) 2 cos3 1f x x
;
( ) | 2sin 2 | | 2sin 2|
g x x x
. Khi đó:
a) Tập xác định hàm số
f x
là:
D
. b) Hàm số
f x
đã cho là hàm số chẵn.
c) Tập xác định hàm số
g x
là:
D
. d) Hàm số
g x
đã cho là hàm số lẻ.
Câu 18. Cho biết
tan 2
x
và
0 90
x
. Xác định tính đúng, sai của các khẳng định
a)
cos 0
x
b)
3
cos
3
x
c)
6
sin
3
x
d)
3 6
cos 30
6
x
Câu 19. Cho hàm số lượng giác
2
2sin 2 5sin 2 2
f x x x
.
a) Hàm số có chu kỳ tuần hoàn là
2
.
b) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số là một số lớn hơn 9.
c) Hai phương trình
2; sin 2 0
f x x
là hai phương trình tương đương.
d) Giải phương trình
0
f x
ta thu được 4 điểm biểu diễn trên vòng tròn lượng giác.
Câu 20. Tìm được tập giá trị các hàm số sau trên tập xác định của chúng:
a) Hàm số
3siny x
có tập giá trị là
[ 3;3]
T
.
b) Hàm số
2cos 1y x
có tập giá trị là
[ 3;1]
T
.
c) Hàm số
2030 4cosy x
có tập giá trị là
[2026;2034]
T
.
d) Hàm số
2
sin 4sin 1y x x
có tập giá trị là
[ 3;3]
T
.
Câu 21. Biết
8 5
sin ,tan
17 12
a b
và
a
,
b
là các góc nhọn. Xác định tính đúng, sai của các khẳng định
a)
8
tan
15
a
b)
21
sin( )
221
a b
c)
14
cos( )
22
a b
d)
17
tan( ) .
14
a b
Câu 22. Cho phương trình lượng giác
3 3 tan 2 0
3
x
. Xác định tính đúng, sai của các khẳng định
6
a) Phương trình có nghiệm
,
6 2
k
x k
.
b) Phương trình có nghiệm âm lớn nhất bằng
3
c) Khi
2
4 3
x
thì phương trình có ba nghiệm
d) Tổng các nghiệm của phương trình trong khoảng
2
;
4 3
bằng
6
Câu 23. Chiều cao
h m
của một cabin trên vòng quay vào thời điểm
t
giây sau khi bắt đầu chuyển động được
cho bởi công thức
30 20sin
25 3
t
h t
. Xác định tính đúng, sai của các khẳng định
a) Chu kỳ tuần hoàn của chuyển động là
50s.
b)
Chiềucaolớnnhấtcủacabinlà
50m
.
c) Tại thời điểm
175
6
t s
thì chiều cao cabin bằng
10m
.
d) Sau 12,5 giây thì cabin đạt độ cao 40 m lần đầu tiên?
Câu 24. Cho hàm số
3.cos5 2sin3 .cos2f x x x x
. Xác định tính đúng, sai của các khẳng định
a)
Hàm số đã cho là hàm số lượng giác.
b)
Hàm số đã cho có chu kỳ tuần hoàn
2
5
T
.
c)
Hàm số đã cho có giá trị lớn nhất là một số nguyên tố.
d)
Tổng của nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
sinf x x
là
9
.
Câu 25. Biết
0 , ,
2 4
a b a b
và
tan tan 3 2 2
a b
. Xác định tính đúng, sai của các khẳng định
a)
tan tan 2 2 2.
a b
b)
tan 1 2
a
c)
tan 1 2
b
d)
tan tan 2 2 2.
a b
Câu 26. Cho
3
cot 3, 2
2
x x
. Xác định tính đúng, sai của các khẳng định
a)
10
sin
10
x
b)
3
cos
10
x
c)
4 10
sin
3 5
x
d)
3
tan
3 3
x
Câu 27. Xét tính đúng - sai của các đẳng thức sau:
a)
3 1
sin sin cos
6 2 2
x x x
.
b)
4sin .sin 2 .sin3 sin 4 sin 2 sin6x x x x x x
.
c)
1 sin 2 cos 2 2 2 sin .cos .
4
x x x x
.
d)
2 2 2
sin 2sin .sin .cos sin cosx a x x a a x a
.
Câu 28. Cho các hàm số sau:
2
( ) 5 3sinf x x
;
( ) tan cosg x x x x
. Khi đó:
a) Tập xác định hàm số
f x
là:
D
.
b) Hàm số
f x
đã cho là hàm số lẻ.
c) Tập xác định hàm số
g x
là:
\
2
D k k
.
d) Hàm số
g x
đã cho là hàm số lẻ.
___________________________
7
LƯỢNG GIÁC LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG P2
_________________________________
Câu 1. Cho
2 5
cos ,2
5 2
, xác định tính đúng, sai của các khẳng định
a)
21
sin
5
b)
4 21
sin 2
25
c)
17
cos 2
25
d)
4 21
tan 2
17
Câu 2. Cho một góc lượng giác
,
Ox Ou
có số đo
250
và một góc lượng giác
,
Ox Ov
có số đo
270
.
Xét tính đúng - sai của các phát biểu sau:
a) Số đo góc lượng giác
,
Ou Ox
bằng
250 360
k
,
k
.
b) Số đo góc lượng giác
,
Ov Ox
bằng
270 360
k
,
k
.
c) Số đo một góc lượng giác
,
Ou Ov
bằng
20
.
d) Số đo một góc lượng giác
,
Ou Ov
theo đơn vị radian bằng
9
.
Câu 3. Cho phương trình lượng giác
1
sin
2
x
, khi đó:
a) Phương trình tương đương
sin sin
6
x
b) Phương trình có nghiệm là:
7
2 ; 2 ( )
6 6
x k x k k
.
c) Phương trình có nghiệm âm lớn nhất bằng
3
d) Số nghiệm của phương trình trong khoảng
;
là ba nghiệm
Câu 4. Cho hàm số
4 4
sin cos
2 2
x x
f x
. Xét tính đúng, sai của các mệnh đề
a) Đồ thị hàm số đi qua điểm
0;1
A
.
b) Hàm số có chu kỳ bằng
T
.
c) Hàm số có giá trị lớn nhất bằng 1.
d) Tổng tất cả các nghiệm thuộc khoảng
0;2
của phương trình
5
8
f x
là
6
.
Câu 5. Tìm được tập xác định của hàm số. Khi đó:
a) Hàm số
cot 3
4
y x
xác định khi
( )
12 3
k
x k
b) Hàm số
sin 1y x
có tập xác định là
D
.
c) Hàm số
sin
2 cos
x
y
x
có tập xác định là
D
.
d) Hàm số
tan 2 cot 2y x x
xác định khi
cos 2 0
sin 2 0
x
x
Câu 6. Từ một vị trí ban đầu trong không gian, vệ tinh
X
chuyển động theo quỹ đạo là một đường tròn quanh
Trái Đất và luôn cách tâm Trái Đất một khoảng bằng
9200km
. Sau 2 giờ thì vệ tinh
X
hoàn thành hết một vòng
di chuyển.
a) Quãng đường vệ tinh
X
chuyển động được sau 1 giờ là:
28902,65( ).km
b) Quãng đường vệ tinh
X
chuyển động được sau 1,5 giờ là:
43353,98( )km
c) Sau khoảng 5,3 giờ thì
X
di chuyển được quãng đường
240000km
d) Giả sử vệ tinh di chuyển theo chiều dương của đường tròn, sau 4,5 giờ thì vệ tinh vẽ nên một góc
9
2
rad?
Câu 7. Cho hai đồ thị hàm số
sin
4
y x
và
siny x
, khi đó:
8
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số:
sin sin
4
x x
b) Hoành độ giao điểm của hai đồ thị là
3
( )
8
x k k
c) Khi
[0;2 ]
x
thì hai đồ thị hàm số cắt nhau tại ba điểm
d) Khi
[0;2 ]
x
thì toạ độ giao điểm của hai đồ thị hàm số là:
5 5 7 7
;sin , ;sin
8 8 8 8
.
Câu 8. Một vật dao động xung quanh vị trí cân bằng theo phương trình
1,5cos
4
t
x
; trong đó
t
là thời gian
được tính bằng giây và quãng đường
| |h x
được tính bằng mét là khoảng cách theo phương ngang của chất
điểm đối với vị trí cân bằng. Khi đó:
a) Vật ở xa vị trí cân bằng nhất nghĩa là
1,5h m
.
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất
c) Khi vật ở vị trí cân bằng thì
cos 0
4
t
d) Trong khoảng từ 0 đến 20 giây thì vật đi qua vị trí cân bằng 4 lần?
Câu 9. Cho hình vẽ sau:
Xét tính đúng – sai của các phát biểu sau:
a) Số đo góc lượng giác
( , )OM OA
là
π
sđ(OM,OA)= +k2
π(k )
3
.
b)
s
đ(ON,OA)=sđ(ON,OM)-sđ(OA,OM)
.
c) Độ dài cung tròn AM lớn là:
2
3
AM
l
.
d) Hai điểm
,M N
biểu diễn các cung có số đo là:
( )
3
x k k
.
Câu 10. Cho
1
sin ,
5 2
x x
. Xác định tính đúng, sai của các khẳng định
a)
4 6
sin 2 .
5
x
b)
23
cos2
25
x
c)
20 6
tan 2
3
x
d)
23 6
cot 2
120
x
Câu 11. Cho biết
3 4
sin ,cos
5 5
. Xét
sin sin( )
2
A
;
cos( ) cot
2
B
.
Xác định tính đúng, sai của các khẳng định
9
a)
cos sin
A
b)
cos tan
B
c)
27
20
A B
d)
29
20
A B
Câu 12. Cho hai hàm số lượng giác
cos
cos sin ;
sin
x
f x x x g x
x
2
1 2
.
a)
sin cos
sin cos
x x
g x
x x
.
b) Hàm số
f x
có chu kỳ tuần hoàn
T 2
.
c) Hàm số
f x
có giá trị lớn nhất bằng
2
.
d) Phương trình
f x g x
có 4 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
Câu 13. Cho
cot 2
x
. Tính được các biểu thức
1 2
2
2sin 3cos 2
,
3sin 2cos cos sin cos
x x
B B
x x x x x
, khi đó:
a) Vì
cot 2
x
nên
sin 0
x
. b)
1
8
B
c)
2
5
B
d)
1 2
13
B B
Câu 14. Từ một vị trí ban đầu trong không gian, vệ tinh
X
chuyển động theo quỹ đạo là một đường tròn quanh
Trái Đất và luôn cách tâm Trái Đất một khoảng bằng
9200km
. Sau 2 giờ thì vệ tinh
X
hoàn thành hết một vòng
di chuyển. Xác định tính đúng, sai của các khẳng định
a) Quãng đường vệ tinh
X
chuyển động được sau 1 giờ là:
28902,65( ).km
b) Quãng đường vệ tinh
X
chuyển động được sau 1,5 giờ là:
43353,98( )km
c) Sau khoảng 5,3 giờ thì
X
di chuyển được quãng đường
240000km
d) Giả sử vệ tinh di chuyển theo chiều dương của đường tròn, sau 4,5 giờ thì vệ tinh vẽ nên một góc
9
2
rad?
Câu 15. Biết:
5
cos2 ,0 90
9
. Xác định tính đúng, sai của các khẳng định
a)
28
sin
9
b)
53
cos
9
c)
371
tan
53
d)
371
cot
14
Câu 16. Cho phương trình lượng giác
3
sin 3
3 2
x
a) Phương trình có nghiệm
2
9 3
( )
2
3 3
x k
k
x k
b) Phương trình có nghiệm âm lớn nhất bằng
2
9
c) Trên khoảng
0;
2
phương trình đã cho có 3 nghiệm
d) Tổng các nghiệm của phương trình trong khoảng
0;
2
bằng
7
9
Câu 17. Cho hai hàm số
2
3 ; cos 2f x x x g x x
. Xét tính đúng – sai của các mệnh đề sau:
a) Đồ thị hàm số
f x
đi qua điểm
1; 2
.
b) Hàm số
2
g x
có chu kỳ
2
T
.
c) Hàm số
g x
có giá trị lớn nhất bằng 1.
d) Phương trình
. 0
f x g x
có 4 nghiệm thực.
Câu 18. Cho hai hàm số
2 2
3 2 , sin 4 2f x x x g x x x
. Xét tính đúng, sai của các mệnh đề
a) Hàm số
f x
không đi qua điểm nào có hoành độ bằng 3.
b) Hàm số
g x
có tập xác định
.
10
c) Hàm số
g x
có đồ thị nằm phía trên đường thẳng
2
y
.
d) Phương trình
. 0
f x g x
có 13 nghiệm thực.
Câu 19. Cho góc lượng giác
có số đo theo đơn vị rađian là
3
4
. Xét tính đúng – sai của các mệnh đề
a) Góc lượng giác
có số đo theo đơn vị độ là
155
.
b) Điểm biểu diễn góc lượng giác
là điểm
M
trên đường tròn lượng giác thuộc góc phần tư thứ I.
c) Góc lượng giác
5
4
có cùng điểm biểu diễn trên đường tròn lượng giác với góc
.
d) Góc lượng giác
855
có cùng điểm biểu diễn trên đường tròn lượng giác với góc
.
Câu 20. Cho
0
2
. Xét tính đúng – sai của các mệnh đề
a)
cos( ) 0
A
; b)
tan( ) 0
B
;
c)
2
sin 0
5
C
; d)
3
cos 0
8
D
.
Câu 21. Cho hàm số
2
cos 1 2sin
2cos sin 1
x x
f x
x x
. Xét tính đúng – sai của các mệnh đề
a)
cos
sin 1
x
f x
x
.
b) Đồ thị hàm số đi qua điểm
0;1
.
c) Hàm số đã cho là hàm số chẵn.
d) Phương trình
3
f x
có 5 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
Câu 22. Cho hàm số
2
sin sin sin 2
f x x m x x
.
a) Phương trình
0
f x
đã cho luôn có nghiệm với mọi giá trị
m
.
b) Có 2 giá trị nguyên
m
để phương trình
0
f x
có nghiệm
3
;2
2
.
c) Với
1
m
, hàm số đã cho có giá trị nhỏ nhất bằng 0.
d)
0 0 0
2024 ,f x f x x
.
Câu 23. Cho hàm số
cos2 cos y f x x
x
. Xét tính đúng - sai của các phát biểu sau:
a) Tập xác định của hàm số trên là
.
b) Hàm số trên là hàm số chẵn.
c) Đặt
cost x
thì hàm số trở thành
2
2 1y f t t
x
.
d) Giá trị nhỏ nhất của hàm số trên là
0
.
Câu 24. Xét tính đúng - sai của các phát biểu độc lập
a) Tập xác định của hàm số
sin 2y x
là
.
b) Tập xác định của hàm số
tan 2
3
y x
là:
5
\
12
k
,
k
.
c) Đường cong trong hình dưới là đồ thị của hàm số
sinx
y
.
x
y
π
-1
1
3π
2
-
3π
2
π
2
-
π
2
-π
O
e) Giá trị lớn nhất của hàm số
2
sin cos 2
y x x
là
13
4
.
________________________
11
LƯỢNG GIÁC LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG P3
_________________________________
Câu 1. Tính được các giá trị lượng giác của góc
, biết:
2 10 3
tan ,
9 2
. Khi đó:
a)
9
cot
2 10
b)
9
cos
11
c)
cos 0
sin 0
d)
2 10
sin
11
Câu 2. Xét hai hàm số
2
4cos 3; 2sin 1f x x g x x
. Xét tính đúng, sai của các phát biểu sau
a) Đồ thị hàm số
g x
đi qua điểm
;3
2
.
b) Hàm số
f x
là hàm số chẵn và có chu kỳ
T
.
c) Giá trị lớn nhất của hàm số
f x g x
là một số nguyên.
d) Hai phương trình
0; 0
f x g x
có 2 nghiệm chung trên khoảng
3
;
2 2
.
Câu 3. Đồ thị như hình sau là của một trong bốn hàm số
cos ; sin ; sin 2 ; cos2f x x f x x f x x f x x
Xét tính đúng, sai của các khẳng định
a)
cosf x x
.
b) Hàm số đã cho có chu kỳ
2
T
.
c) Hàm số đã cho có giá trị lớn nhất bằng 1.
d) Phương trình
1
3
f x
có 8 nghiệm trong khoảng
0;10
.
Câu 4. Xét hàm số
sin sin 7 sin 3 sin5f x x x x x
. Xét tính đúng, sai của các khẳng định
a) Hàm số đã cho có tập xác định
.
b) Hàm số đã cho là hàm số chẵn và có chu kỳ
2T
.
c) Hàm số có thể viết lại thành
3
4cos 2 5cos2f x x x
.
d) Phương trình
0
f x
có 7 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
Câu 5. Cho hàm số
cos 2 cos .f x x x
Xét tính đúng, sai của các phát biểu sau:
a) Hàm số đã cho là hàm số chẵn và có chu kỳ
T
.
b) Đồ thị hàm số không đi qua điểm
0;2
.
c) Phương trình
3
1 0
f x
tương đương với phương trình
3
cos (8cos 1)
0
3cos 1
x x
x
.
d) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho bằng
13
8
.
Câu 6. Cho hàm số lượng giác
sin
4
f x x
. Xét tính đúng, sai của các phát biểu sau:
a) Hàm số đã cho là hàm số lẻ và có chu kỳ của hàm số là một số lớn hơn 5.
b) Đồ thị hàm số đi qua điểm
2
0;
2
.
c) Phương trình
3
1
f x
có 1 nghiệm thuộc đoạn
;2
.
d) Giá trị nhỏ nhất của hàm số
2 2cosg x f x x
bằng
2
.
Câu 7. Cho phương trình
sin 2
x m
. Xét tính đúng, sai của các phát biểu sau:
a) Với
0
m
, phương trình có nghiệm là
2
k
x
.
12
b) Phương trình có nghiệm là
3
x
khi
1
2
m
.
c) Phương trình có nghiệm khi
1;1
m
.
d) Phương trình có hai nghiệm phân biệt trên
0;
2
khi
0;1
m
.
Câu 8. Cho phương trình lượng giác
2cos 1 0
3
x m
, trong đó
m
là tham số. Xét tính đúng - sai
của các phát biểu sau:
a)
6
là nghiệm của phương trình khi và chỉ khi
1
m
.
b) Khi
0
m
phương trình có tập nghiệm là
2 ; 2
3
k k k
.
c) Tập các giá trị của
m
để phương trình có nghiệm là
1;1
.
d) Khi
1
m
phương trình có 6 nghiệm trong đoạn
0;6
.
Câu 9. Xét tính đúng/sai của các mệnh đề sau:
a)
180
1 rad; 1rad .
180
b) Một cung của đường tròn bán kính
R
và có số đo
rad thì có độ dài
l R
.
c) Với ba tia
, ,Ou Ov Ow
bất kì, ta có
0
, , , 360
sđ Ou Ov sđ Ov Ow sđ Ou Ow k
,
k
.
d) Cho
5OA cm
. Chu vi hình vẽ sau đây bằng
10
Câu 10. Cho phương trình lượng giác
2sin 3 0
12
x
, khi đó:
a) Phương trình tương đương
sin sin
12 3
x
b) Phương trình có nghiệm là:
7
2 ; 2 ( )
4 12
x k x k k
.
c) Phương trình có nghiệm âm lớn nhất bằng
4
d) Số nghiệm của phương trình trong khoảng
;
là hai nghiệm
Câu 11. Cho
3
cos
4
a
;
sin 0
a
;
3
sin
5
b
;
cos 0
b
. Xét tính đúng – sai của các phát biểu sau:
a) Giá trị của
7
tan
3
a
.
b) Giá trị của
2
cot
3
b
.
c) Giá trị của
cos2 cos2a b
thuộc khoảng
1
;1
2
.
d) Giá trị của
cos
a b
thuộc khoảng
1 1
;
2 3
.
Câu 12. Cho hàm số
sin cos2f x x x
. Xét tính đúng, sai của các phát biểu sau:
a) Hàm số đã cho có tập xác định
.
b) Hàm số đã cho có chu kỳ
2
T
.
c) Hàm số đã cho có giá trị lớn nhất là một số nguyên.
13
d) Phương trình
0
f x
có ít hơn 27 nghiệm thuộc đoạn
0;20
.
Câu 13. Xét tính đúng – sai của các mệnh đề sau:
a) Cho góc hình học
75
uOv
. Công thức số đo tổng quát của góc lượng giác
,
Ou Ov
là
75 .360 ,k k
.
b) Cho một góc lượng giác
,
Ox Ou
có số đo
50
và một góc lượng giác
,
Ox Ov
có số đo
125
. Số đo
của góc lượng giác
,
Ou Ov
bằng
175 360 ,k k
.
c) Trên đồng hồ hình dưới đây, kim phút đang chỉ đúng số 2. Đến lúc 13 giờ 30 phút thì kim phút đã quay được
một góc lượng giác có số đo bằng
480
.
d) Trong hình dưới, cánh quạt được chia thành 3 phần bằng nhau.
28
AOD
. Công thức số đo tổng quát của
góc lượng giác
,
Ox OC
bằng
148 .360
k
.
Câu 14. Xét sự biến thiên của hàm số
sin cos . y x x
Xét tính đúng, sai của các khẳng định
a) Hàm số đã cho có chu kỳ
2
T
.
b) Hàm số đã cho đồng biến trên khoảng
3
4 4
; .

c) Hàm số đã cho có tập giá trị là
1 1; .
d) Phương trình
0
y
có 6 nghiệm thỏa mãn bất phương trình
2
20 19 0
x x
.
Câu 15. Cho vòng tròn lượng giác như hình vẽ. Điểm
0 0
;M x y
là điểm cuối biểu diễn góc lượng giác
. Xét
tính đúng, sai của các khẳng định
.
a) Nếu
0 0
3
0 0, 0
2
x y
. b)
sin 2024 sin
.
14
c)
4 4
0 0
1
x y
. d)Tại điểm
thì
1
tan
3
.
Câu 16. Xét tính đúng - sai của các phát biểu sau:
a)
sin sin cos cos sina b a b a b
.
b)
0 0 0 0 0
sin31 .cos12 cos12 .sin31 sin19 .
c)
Cho
4
cos , ;0
5 2
x x
. Giá trị của
sin 2x
là
24
25
.
d) Cho
1
sin
3
và
2
. Biết giá trị của
1 6
cos
6
a
b
với
,a b
thì
4
a b
.
Câu 17. Xét tính đúng - sai của các mệnh đề sau:
a)
2
1 sin 2
sin
2
x
x
b) Nếu
1
cos
3
thì
7
cos2
9
c) Nếu
3
sin
4
x
với
0;
2
x
thì
3 7
sin 2
8
x
d) Cho
2
cos
3
với
;0
2
biết
tan
4
a b c
.
, , , 0
a b c c
Khi đó
0
a b c
.
Câu 18. Cho
1 1
tan ,0 ; tan ,0
2 2 3 2
a a b b
. Xét tính đúng - sai của các phát biểu sau:
a)
cot 2
a
. b)
tan( ) 1
a b
. c)
tan( ) 7
a b
. d)
2 5
sin( 2 )
25
a b
.
Câu 19. Cho hai hàm số
tan ; tan 3f x x g x x
. Xét tính đúng, sai của các phát biểu sau:
a) Hàm số
f x
xác định khi
sin 1x
.
b) Hai hàm số đều là hàm số lẻ và có cùng chu kỳ tuần hoàn.
c)
sin
cos3
x
g x f x
x
.
d) Tổng các nghiệm trong đoạn
0;30
của phương trình
3 3
0
f x g x
là một số lớn hơn 145.
Câu 20. Xét hàm số
cos3 sinf x x x
. Xét tính đúng, sai của các phát biểu sau:
a)
Hàm số đã cho là hàm số không chẵn, không lẻ.
b)
Hàm số
cos3f x x
có khoảng đồng biến
2 ; 2 ,
2 2
k k k
.
c)
Hàm số đã cho có chu kỳ
2
T
.
d)
Phương trình
2
0
f x
có 5 nghiệm thuộc đoạn
;
2 2
.
Câu 21. Cho hàm số
2sin 4 1
3
f x x
. Xét tính đúng, sai của các khẳng định
a) Hàm số đã cho là hàm số lẻ.
b) Hàm số đã cho có giá trị lớn nhất bằng 1.
c) Hàm số đã cho có chu kỳ
2
T
.
d) Nghiệm dương nhỏ nhất của phương trình
0
f x
thuộc khoảng
;
9 6
.
Câu 22. Cho hàm số
sin cosf x m x x
. Xét tính đúng, sai của các khẳng định
a)
Hàm số đã cho có chu kỳ
2
T
.
b)
Hàm số đã cho luôn là hàm số không chẵn, không lẻ.
c)
Đồ thị hàm số đã cho đi qua điểm
0; 1
với mọi giá trị
m
.
d)
Phương trình
1
f x
luôn luôn có nghiệm với mọi giá trị
m
.
__________________________________
15
LƯỢNG GIÁC LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG P4
_________________________________
Câu 1. Tính được các giá trị lượng giác của góc
, biết:
tan 2,0
2
. Khi đó
a)
1
cot
2
b)
2
1
cos
5
c)
5
cos
5
d)
2 5
sin
5
Câu 2. Cho hàm số
2cos 1 cos 2
f x x x
. Xét tính đúng, sai của các khẳng định
a)
cos 2 5cos 3f x x x
.
b) Hàm số đã cho là hàm số chẵn.
c) Hàm số đã cho có chu kỳ
2
T
.
d) Phương trình
0
f x
có đúng 4 nghiệm thuộc đoạn
2 ;2
.
Câu 3. Cho hàm số
2
cos sin 1y x x
. Xét tính đúng, sai của các khẳng định
a) Hàm số đã cho là hàm số không chẵn, không lẻ.
b) Hàm số đã cho có đồ thị nằm phía trên trục hoành.
c) Phương trình
2
y
có bốn điểm biểu diễn nghiệm trên vòng tròn lượng giác.
d) Giá trị lớn nhất của hàm số bằng
9
4
.
Câu 4. Cho vòng tròn lượng giác như hình vẽ, M và N đối xứng qua trục và
60
MOx
.
y
x
N
M
O
-1
-1
1
1
a)
2
MON
radian.
b) Điểm M biểu diễn nghiệm của phương trình
3
sin
2
x
.
c) Giả sử M, N di động ở nửa bên phải vòng tròn lượng giác, khi đó diện tích tam giác MON lớn nhất
khi
60
MON
.
d) Hai điểm
M
và N biểu diễn đầy đủ nghiệm của phương trình
2
1
sin
2 4
x
.
Câu 5. Cho hàm số
2cos 2 1f x x
. Xét tính đúng, sai của các khẳng định
a) Hàm số đã cho có chu kỳ
2
T
.
b) Bất phương trình
2
4cos 5f x x
nghiệm đúng với mọi giá trị
x
.
c) Đồ thị hàm số luôn nằm phía dưới đồ thị hàm số
2
2 3
g x x x
.
d) Nghiệm lớn nhất của phương trình
2
0
f x
x x
là một số lớn hơn
5
.
Câu 6. Cho góc
0 180
thỏa mãn
tan 3
. Xét tính đúng, sai của các khẳng định
a)
1
cot
3
. b)
cos 0
.
16
c)
3 10
sin
10
. d)
2sin 3cos 3
3sin 2cos 11
P
.
Câu 7. Cho phương trình lượng giác
2sin 2
x
. Xét tính đúng, sai của các khẳng định
a) Phương trình tương đương
sin sin
4
x
b) Phương trình có nghiệm là:
3
2 ; 2 ( )
3 4
x k x k k
.
c) Phương trình có nghiệm dương nhỏ nhất bằng
4
.
d) Phương trình có 2 nghiệm trong khoảng
;
2 2
.
Câu 8. Tìm được tập xác định của hàm số. Xét tính đúng, sai của các khẳng định
a) Hàm số
cot 3
4
y x
xác định khi
( )
12 3
k
x k
b) Hàm số
sin 1y x
có tập xác định là
D
.
c) Hàm số
sin
2 cos
x
y
x
có tập xác định là
D
.
d) Hàm số
tan 2 cot 2y x x
xác định khi
cos2 0
sin 2 0
x
x
Câu 9. Cho
tan 2
. Xét tính đúng - sai của các phát biểu sau:
a)
1
cot
2
.
b) Khi
0
2
thì
5
cos
5
.
c) Giá trị của biểu thức
3 3
sin cos 5
sin 3cos 2sin 31
B
d) Nếu
4 4
sin cos 1
a b a b
thì
8 8
3 3 3 3
sin cos 1
A
a b a b
.
Câu 10. Cho hàm số
2cos 1
cos 2
x
y
x
. Xét tính đúng, sai của các khẳng định
a) Đồ thị hàm số đã cho đi qua điểm
0; 3
.
b) Hàm số đã cho là hàm số chẵn và có tập xác định
.
c) Phương trình
1y
vô nghiệm.
d) Gọi
M
,
m
tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số thì
9 1
M m
.
Câu 11. Cho hai hàm số
cos cos 2 cos3
x xx
x
f
và
2cos 2 2sin 1
g x x x
. Xét tính đúng, sai của
các khẳng định
a) Hàm số đã cho là hàm số chẵn.
b) Hàm số đã cho có chu kỳ
5
T
.
c)
f x g x
.
d) Phương trình
0
f x
có 6 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
Câu 12. Cho hai hàm số
2cot 2 3cot 3 ; tan 2f x x x g x x
. Xét tính đúng, sai của các khẳng định
a) Hàm số
f x
là hàm số lẻ.
b) Hàm số
g x
có chu kỳ
T
.
c) Hàm số
g x
có một khoảng đồng biến là
;
4 4
.
d) Phương trình
5 5
f x g x
vô nghiệm.
17
Câu 13. Cho hàm số
2
2sin 1 2sin 2 1 ; 3 4cosf x x x g x x
. Xét tính đúng, sai của các khẳng
định
a) Hàm số
f x
là hàm số lẻ.
b) Hàm số
g x
có chu kỳ
2
T
.
c) Đồ thị hàm số
g x
luôn nằm phía dưới hoặc tiếp xúc đường thẳng
1
y
.
d) Tổng các nghiệm trên đoạn
;
của phương trình
f x g x
bằng
.
Câu 14. Cho
2
sin
3
,
2
, xét tính đúng, sai của các mệnh đề sau
a)
cos 0
. b)
5
cos
3
.
c)
5 5
sin
2 3
. d) Giá trị của biểu thức
2
5 tan
1 tan
P
là
10
9
.
Câu 15. Cho vòng tròn lượng giác như hình vẽ. Xét tính đúng, sai của các khẳng định
a) Giá trị
sin
tăng dần khi điểm cuối góc lượng giác di chuyển theo hướng
B B
.
b) Hai điểm
,A A
biểu diễn đầy đủ các nghiệm của phương trình
sin 0
x
.
c) Điểm D biểu diễn các góc lượng giác
5
2
6
k
.
d) Bốn điểm
, , ,C D E F
biểu diễn đầy đủ các nghiệm của phương trình
2cos2 1x
.
Câu 16. Cho góc
thỏa mãn
0
2
và
cot 3
. Xét tính đúng - sai của các phát biểu sau:
a)
sin 0
b)
10
sin
10
c)
3 3
sin 10
3sin 2 21
cos
cos osc
d)
2
2
17 7 13
t
0
an tan cot cot 7
4 2 4
2
Câu 17. Cho các hàm số sau
2
( ) 2| cos |; ( ) 1 3sinf x x g x x
. Xét tính đúng, sai của các khẳng định
a) Giá trị lớn nhất của hàm số
f x
bằng 2 b) Giá trị nhỏ nhất của hàm số
f x
bằng 0
c) Giá trị lớn nhất của hàm số
g x
bằng 2 d) Giá trị nhỏ nhất của hàm số
g x
bằng
2
Câu 18. Cho
0 90
. Xét được dấu của các biểu thức sau. Khi đó:
a)
sin 90 0
A
; b)
cos 45 0
B
;
c)
tan 270 0
C
; d)
cos 2 90 0
D
.
Câu 19. Cho các hàm số sau
( ) sinf x x
và
( ) cosg x x
. Xét tính đúng, sai của các khẳng định
18
a) Hàm số
( ) sinf x x
đồng biến trên khoảng
;
2 2
b) Hàm số
( )f x
nghịch biến trên khoảng
3 5
;
4 4
.
c) Hàm số
( )g x
nghịch biến trên khoảng
(0; )
.
d) Hàm số
( )g x
đồng biến trên khoảng
25 13
;
6 3
.
Câu 20. Biến đổi được các biểu thức sau về dạng tích. Xét tính đúng, sai của các khẳng định
a)
cos 3 cos 2 cos 2 cos 3x x x x
b)
sin 3 sin 2 2sin 2 cos
2
x
x x x
;
c)
5 3
cos 4 cos 2sin sin
2 2
x x
x x
d)
sin 5 sin 2 cos 3 sin 2x x x x
Câu 21. Cho hàm số
2 sinf x x
và
3sin cos 2
g x x x
. Khi đó:
a) Giá trị lớn nhất của hàm số
f x
bằng
3
b) Phương trình
2
g x
có nhiều hơn 5 nghiệm trên khoảng
0; 4
.
c) Giá trị lớn nhất của hàm số
g x
bằng 4
d) Giá trị nhỏ nhất của hàm số
g x
bằng 0
Câu 22. Cho các hàm số
( ) 3 2 sinf x x
; và
1
( ) tan cos
2 3
x
g x x
, khi đó:
a) Hàm số
f x
có tập xác định là:
D
. b) Hàm số
f x
đã cho là hàm tuần hoàn.
c) Hàm số
g x
xác định khi
2 ( )
x k k
. d) Hàm số
g x
đã cho là hàm không tuần hoàn.
Câu 23. Cho biết
1
cos2
4
và
3
2
. Xét tính đúng, sai của các khẳng định
a)
sin 0,cos 0
b)
10
sin
4
c)
6
cos
4
d)
15
cot
5
Câu 24. Cho các hàm số
3
( ) 3sinf x x
;
( ) 5cos 2
3
g x x
. Xét tính đúng, sai của các khẳng định
a) Tập xác định hàm số
f x
là:
D
.
b) Hàm số
f x
đã cho là hàm số chẵn.
c) Đồ thị hàm số
g x
luôn nằm phía trên hoặc tiếp xúc đường thẳng
5
y
.
d) Hàm số
g x
đã cho là hàm số lẻ.
Câu 25. Trên miền
;
đồ thị hàm số
sinf x x
như hình vẽ. Xét tính đúng, sai của các khẳng định
a) Đồ thị hàm số đi qua gốc tọa độ.
b) Hàm số nghịch biến trên
;0
.
c) Giá trị nhỏ nhất của hàm số trên
;
2 5
bằng – 1.
d) Phương trình
1
4
f x
có 6 nghiệm trên
0;3
.
_______________________________________
19
LƯỢNG GIÁC LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG P5
_________________________________
Câu 1. Tính được các giá trị lượng giác của góc
, biết:
tan 2,0
2
. Khi đó
a)
1
cot
2
b)
2
1
cos
5
c)
5
cos
5
d)
2 5
sin
5
Câu 2. Cho hàm số
2cos 1 cos 2
f x x x
. Xét tính đúng, sai của các khẳng định
e)
cos 2 5cos 3f x x x
.
f) Hàm số đã cho là hàm số chẵn.
g) Hàm số đã cho có chu kỳ
2
T
.
h) Phương trình
0
f x
có đúng 4 nghiệm thuộc đoạn
2 ;2
.
Câu 3. Cho hàm số
2
cos sin 1y x x
. Xét tính đúng, sai của các khẳng định
e) Hàm số đã cho là hàm số không chẵn, không lẻ.
f) Hàm số đã cho có đồ thị nằm phía trên trục hoành.
g) Phương trình
2
y
có bốn điểm biểu diễn nghiệm trên vòng tròn lượng giác.
h) Giá trị lớn nhất của hàm số bằng
9
4
.
Câu 4. Cho vòng tròn lượng giác như hình vẽ, M và N đối xứng qua trục và
60
MOx
.
y
x
N
M
O
-1
-1
1
1
e)
2
MON
radian.
f) Điểm M biểu diễn nghiệm của phương trình
3
sin
2
x
.
g) Giả sử M, N di động ở nửa bên phải vòng tròn lượng giác, khi đó diện tích tam giác MON lớn nhất
khi
60
MON
.
h) Hai điểm
M
và N biểu diễn đầy đủ nghiệm của phương trình
2
1
sin
2 4
x
.
Câu 5. Cho hàm số
2cos 2 1f x x
. Xét tính đúng, sai của các khẳng định
e) Hàm số đã cho có chu kỳ
2
T
.
f) Bất phương trình
2
4cos 5f x x
nghiệm đúng với mọi giá trị
x
.
g) Đồ thị hàm số luôn nằm phía dưới đồ thị hàm số
2
2 3
g x x x
.
h) Nghiệm lớn nhất của phương trình
2
0
f x
x x
là một số lớn hơn
5
.
Câu 6. Cho góc
0 180
thỏa mãn
tan 3
. Xét tính đúng, sai của các khẳng định
a)
1
cot
3
. b)
cos 0
.
20
c)
3 10
sin
10
. d)
2sin 3cos 3
3sin 2cos 11
P
.
Câu 7. Cho phương trình lượng giác
2sin 2
x
. Xét tính đúng, sai của các khẳng định
a) Phương trình tương đương
sin sin
4
x
b) Phương trình có nghiệm là:
3
2 ; 2 ( )
3 4
x k x k k
.
c) Phương trình có nghiệm dương nhỏ nhất bằng
4
.
d) Phương trình có 2 nghiệm trong khoảng
;
2 2
.
Câu 8. Tìm được tập xác định của hàm số. Xét tính đúng, sai của các khẳng định
a) Hàm số
cot 3
4
y x
xác định khi
( )
12 3
k
x k
b) Hàm số
sin 1y x
có tập xác định là
D
.
c) Hàm số
sin
2 cos
x
y
x
có tập xác định là
D
.
d) Hàm số
tan 2 cot 2y x x
xác định khi
cos2 0
sin 2 0
x
x
Câu 9. Cho
tan 2
. Xét tính đúng - sai của các phát biểu sau:
a)
1
cot
2
.
b) Khi
0
2
thì
5
cos
5
.
c) Giá trị của biểu thức
3 3
sin cos 5
sin 3cos 2sin 31
B
d) Nếu
4 4
sin cos 1
a b a b
thì
8 8
3 3 3 3
sin cos 1
A
a b a b
.
Câu 10. Cho hàm số
2cos 1
cos 2
x
y
x
. Xét tính đúng, sai của các khẳng định
e) Đồ thị hàm số đã cho đi qua điểm
0; 3
.
f) Hàm số đã cho là hàm số chẵn và có tập xác định
.
g) Phương trình
1y
vô nghiệm.
h) Gọi
M
,
m
tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số thì
9 1
M m
.
Câu 11. Cho hai hàm số
cos cos 2 cos3
x xx
x
f
và
2cos 2 2sin 1
g x x x
. Xét tính đúng, sai của
các khẳng định
e) Hàm số đã cho là hàm số chẵn.
f) Hàm số đã cho có chu kỳ
5
T
.
g)
f x g x
.
h) Phương trình
0
f x
có 6 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
Câu 12. Cho hai hàm số
2cot 2 3cot 3 ; tan 2f x x x g x x
. Xét tính đúng, sai của các khẳng định
e) Hàm số
f x
là hàm số lẻ.
f) Hàm số
g x
có chu kỳ
T
.
g) Hàm số
g x
có một khoảng đồng biến là
;
4 4
.
h) Phương trình
5 5
f x g x
vô nghiệm.
| 1/26
| | Tải xuống

Có thể bạn quan tâm:

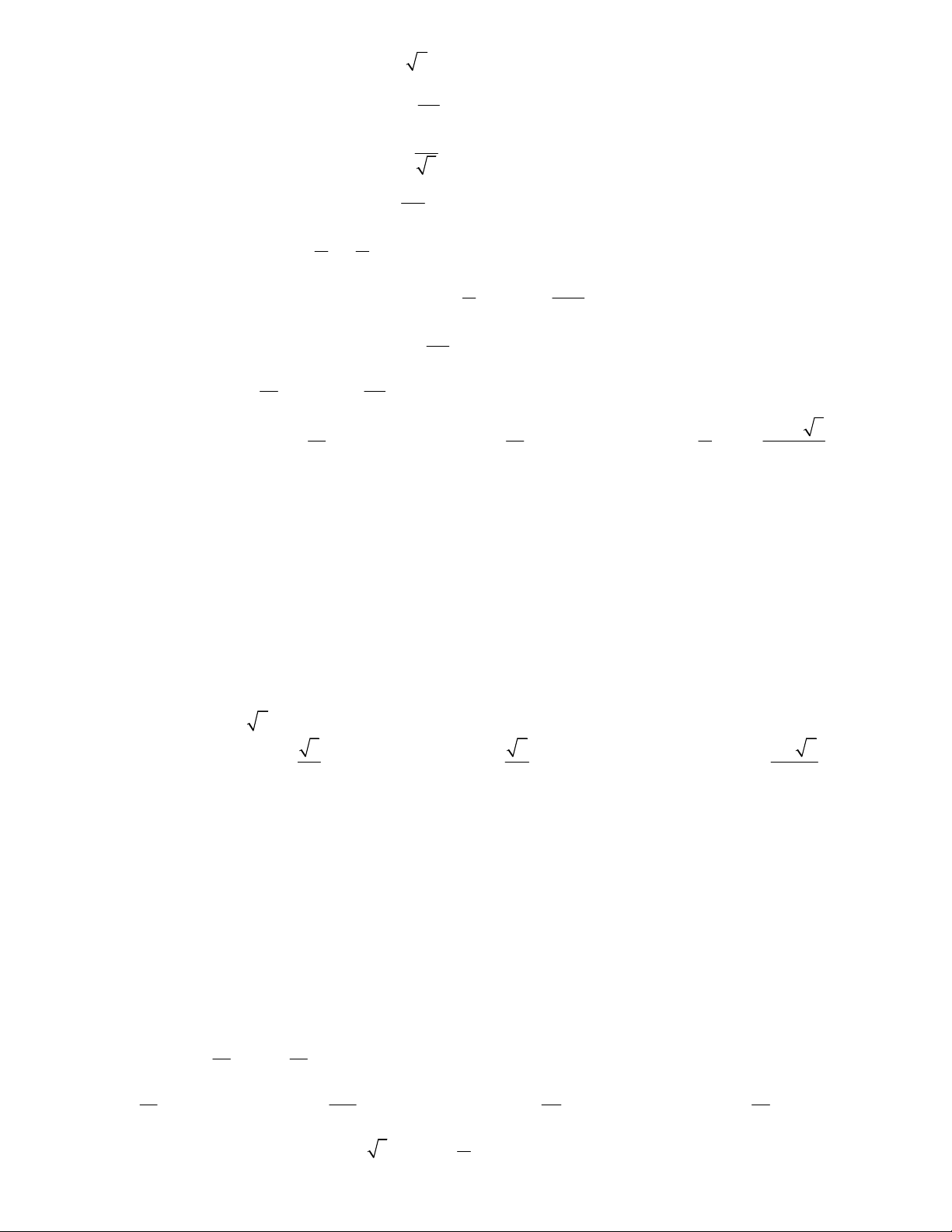
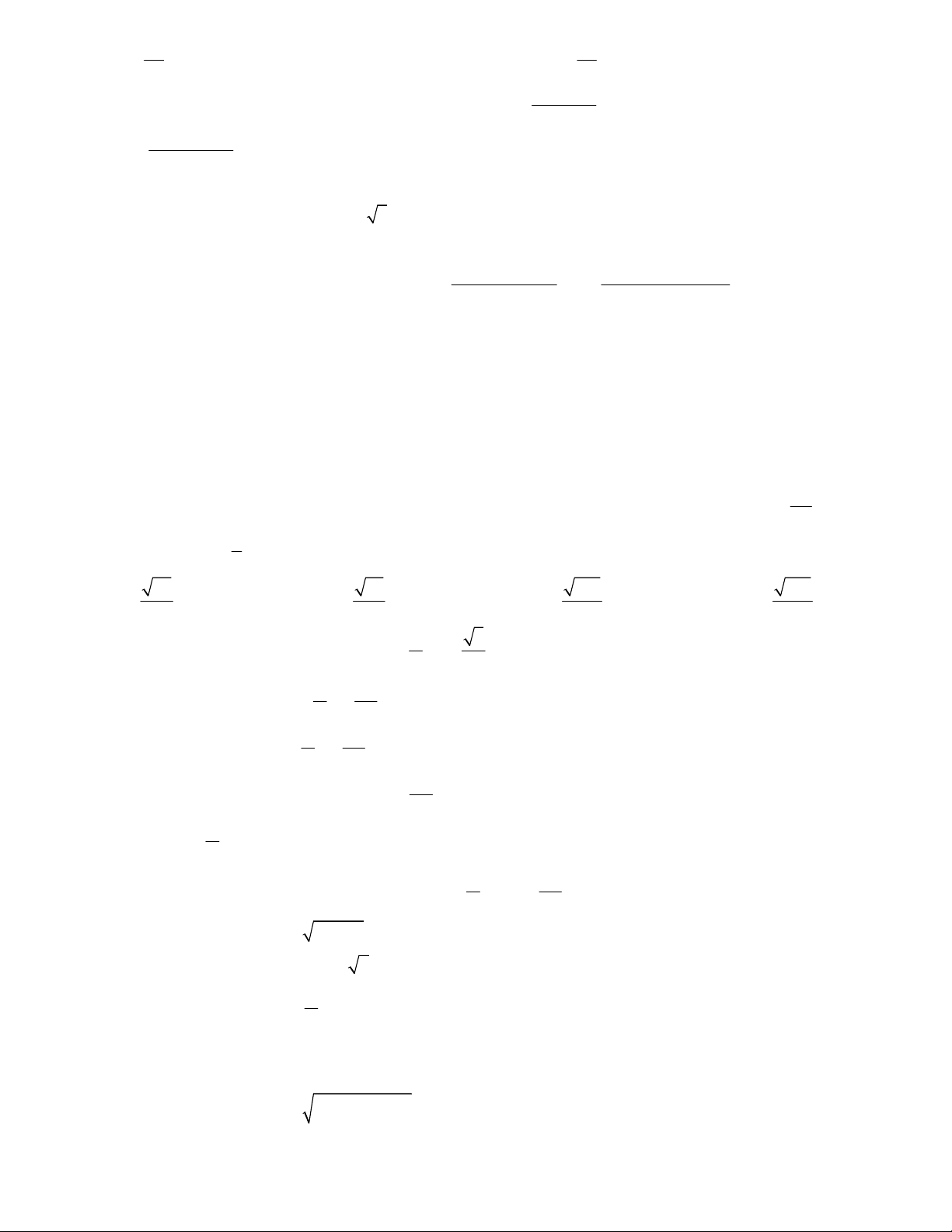
Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
--------------------------------------------------------------------------------------------
LUYỆN KỸ NĂNG TOÁN 11 THPT
TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG LƯỢNG GIÁC
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
ĐÁP ÁN CHI TIẾT PDF BẠN ĐỌC VUI LÒNG LIÊN HỆ TÁC GIẢ:
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 7/2024 1
LUYỆN KỸ NĂNG TOÁN 11 THPT
TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG LƯỢNG GIÁC
CƠ BẢN – VẬN DỤNG – VẬN DỤNG CAO
__________________________________________ DUNG NỘI DUNG BÀI TẬP LƯỢNG 6 FILE
TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG LƯỢNG GIÁC 1 file 4 trang 2
LƯỢNG GIÁC LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG P1
_________________________________ 
Câu 1. Tính được các giá trị lượng giác của góc  
k 2 (biết k   ). Xác định tính đúng, sai của các 3 khẳng định 3 1 a) sin    b) cos   c) tan  3 d) 3sin 2  2 2 2 
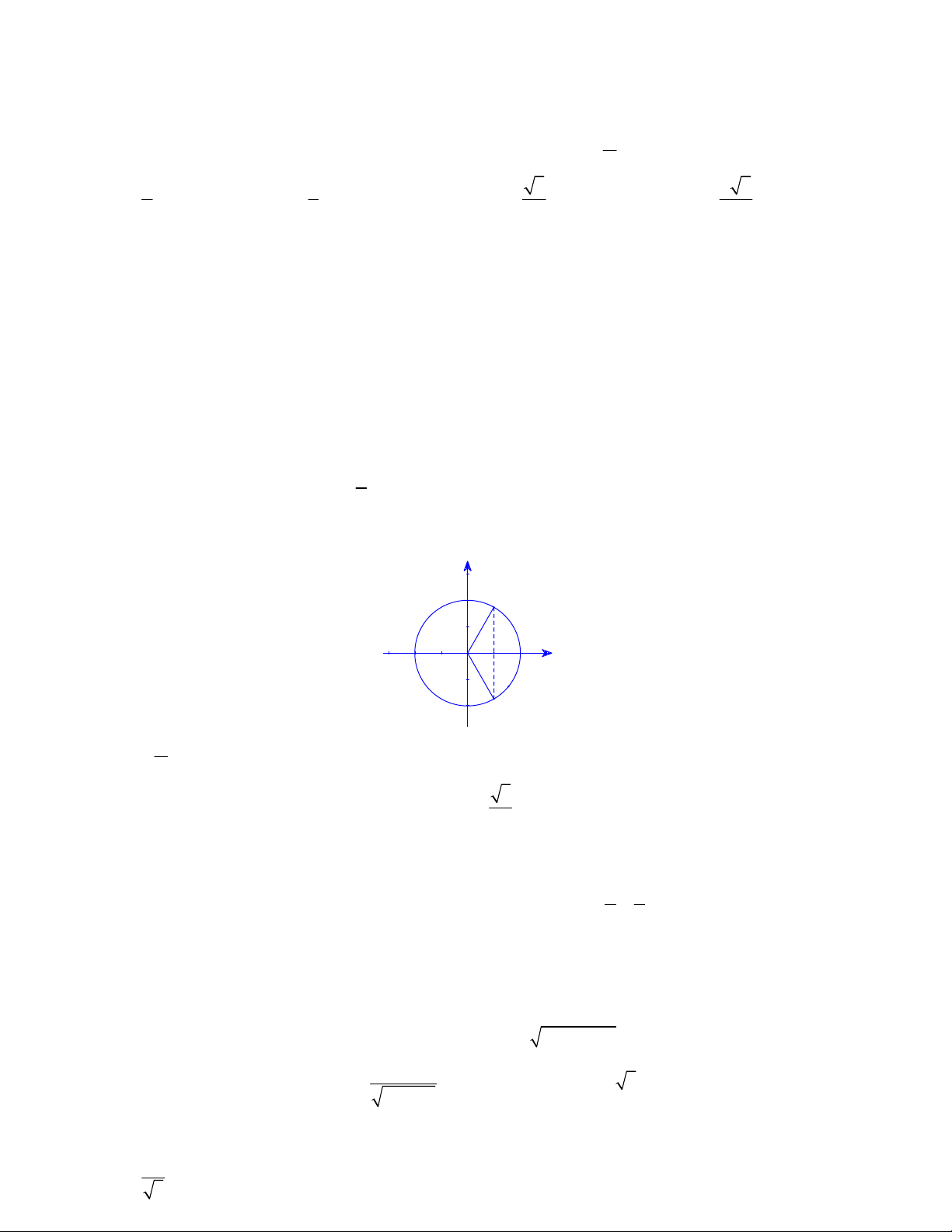
Câu 2. Hình vẽ bên là vòng tròn lượng giác gốc A, trong đó M M M M là hình vuông, AOM  45 . Xét góc 1 2 3 4 1
lượng giác  có điểm đầu là điểm A, điểm cuối là điểm bất kỳ nào đó trên vòng tròn lượng giác
Xác định tính đúng, sai của các khẳng định
a) Tại điểm cuối B thì sin   1.
b) Tại điểm cuối M thì 2 sin   3cos  1 . 3 2
c) Hai điểm M , M là điểm biểu diễn đầy đủ nghiệm của phương trình lượng giác sin x  . 2 3 2
d) Khi di chuyển điểm cuối M M thì tan  tăng dần. 1 2
Câu 3. Cho hàm số f x  cos 2x  cos x . Xác định tính đúng, sai của các khẳng định
a) Hàm số có chu kỳ tuần hoàn là 2 .
b) Hàm số là hàm số chẵn.
c) Hàm số có giá trị nhỏ nhất là một số lớn hơn – 2. 7
d) Phương trình f x  0 có tổng tất cả các nghiệm trong khoảng 0; 2  là T  6 1 
Câu 4. Cho biết sin  và
    . Xác định tính đúng, sai của các khẳng định 3 2 2 2 4 2 7 22 a) cos   b) sin 2   c) cos 2  d) sin 3  3 9 9 27
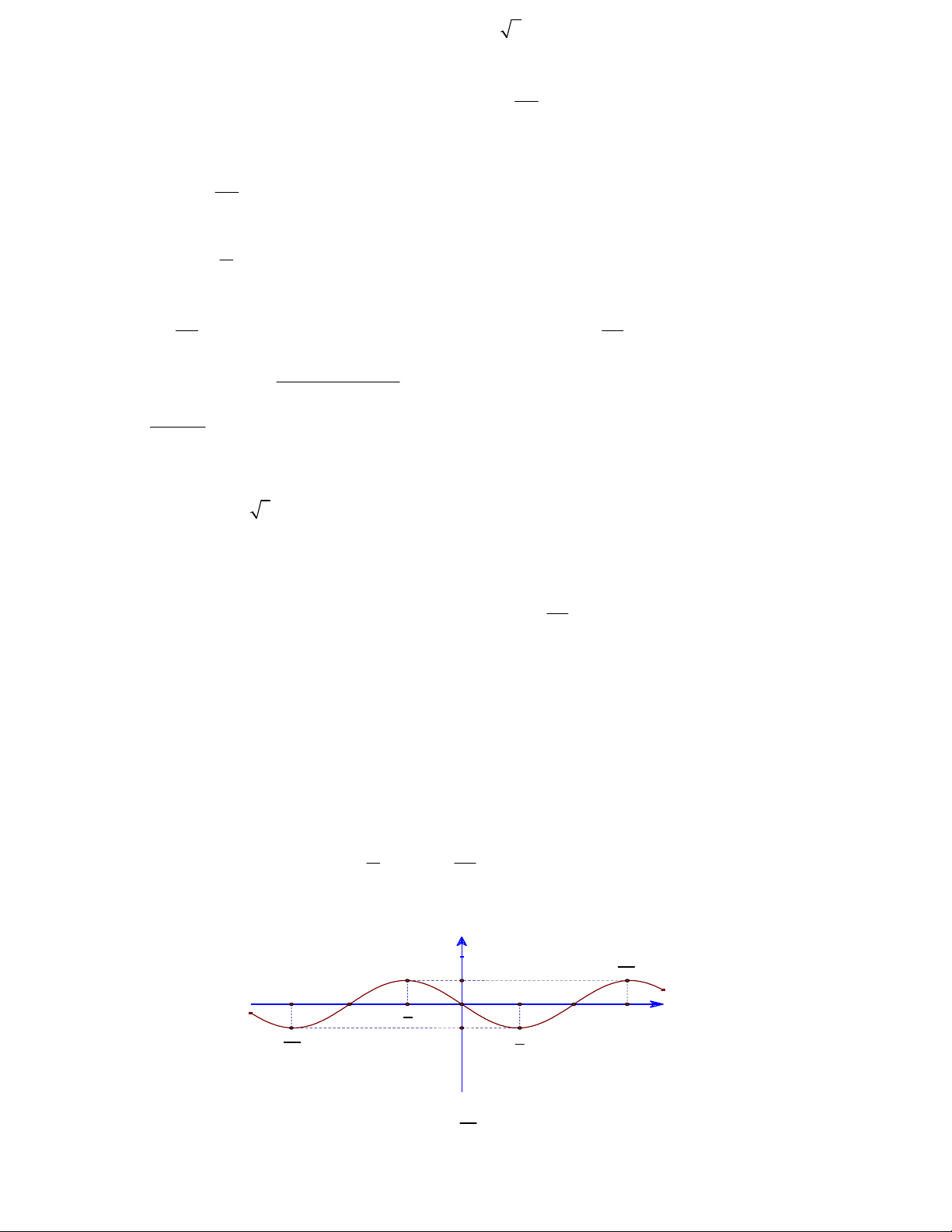
Câu 5. Cho đồ thị hàm số lượng giác y f x như hình vẽ. Xác định đúng, sai của các khẳng định
a) f    1.
b) y  cos x . 2
c) f 2023  f 2024  2 .
c) Phương trình f x 
có 45 nghiệm trong khoảng 0;50  . 3 1
Câu 6. Cho phương trình lượng giác sin 2x  
(*). Xác định tính đúng, sai của các khẳng định 2 
a) Phương trình (*) tương đương sin 2x  sin 6
b) Trong khoảng 0;  phương trình có 3 nghiệm 3
c) Tổng các nghiệm của phương trình trong khoảng 0;  bằng 2 11
d) Trong khoảng 0;  phương trình có nghiệm lớn nhất bằng 12 3 Câu 7. Cho hàm số 3 f (x) |
 tan x |  x  3x . Xác định tính đúng, sai của các khẳng định  
a) Tập xác định của hàm số: D   \   k , k  . b) f ( 
 )   f ( ).  2 
c) Hàm số đã cho đối xứng qua gốc tọa độ O 0;0
d) Hàm số đã cho là hàm số chẵn.
Câu 8. Cho phương trình lượng giác tan 2x 15 
 1 (*). Xác định tính đúng, sai của các khẳng định
a) Phương trình (*) có nghiệm x 30 k90   (k  ) 
b) Phương trình có nghiệm âm lớn nhất bằng 30
c) Tổng các nghiệm của phương trình trong khoảng  1  80 ;  90 bằng 180 d) Trong khoảng  1  80 ;
 90 phương trình có nghiệm lớn nhất bằng 60
Câu 9. Cho hàm số f (x)  2 cos x 1 và g(x)  sin x  tan x . Xác định tính đúng, sai của các khẳng định
a) Tập xác định hàm số f x : D   .
b) Hàm số f x là hàm tuần hoàn.  
c) Tập xác định hàm số g x : D   \   kk   .  3 
d) Hàm số g x là hàm không tuần hoàn.
Câu 10. Cho hàm số lượng giác f x 2
 sin x  4 . Xác định tính đúng, sai của các khẳng định
a) f x  5  cos 2x .
b) Hàm số đã cho là hàm số chẵn và có chu kỳ bằng  .
c) Đồ thị hàm số đã cho luôn nằm trong khoảng giữa hai đường thẳng cách nhau một khoảng bằng 1.
d) Phương trình f x  5sin x có 1 điểm biểu diễn trên vòng tròn lượng giác. 2  Câu 11. Cho sin  ,
    . Xác định tính đúng, sai của các khẳng định 3 2 5 2 5 a) cos   b) tan    3 5    5  2 3    10  2 2 c) cos      d) cos       3  6  4  6 sin 2x
Câu 12. Cho hàm số f (x)  tan x và 2
g(x)  cot x
. Xác định tính đúng, sai của các khẳng định 2  
a) Tập xác định hàm số f x : D   \   kk   .  2 
b) Hàm số f x là hàm không tuần hoàn.
c) Tập xác định hàm số g x : D   \ {kk  }  .
d) Hàm số g x là hàm tuần hoàn. Câu 13. Cho hàm số 2
f (x)  sin x  cos x 1. Khi đó;
a) Tập xác định của hàm số D  
b) Hàm số đã cho là hàm số chẵn.
c) Hàm số có giá trị nhỏ nhất là một số lớn hơn – 2.
d) Phương trình f x  0 có 5 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
Câu 14. Cho hàm số f x  2  3cos x và g x  sin x  cos x . Xác định tính đúng, sai của các khẳng định
a) Giá trị lớn nhất của hàm số f x bằng 5 4
b) Hàm số f x đạt giá trị nhỏ nhất khi x    k2 (k )
c) Giá trị lớn nhất của hàm số g x bằng  2 3
d) Hàm số g x đạt giá trị nhỏ nhất khi x  
k 2 (k  ). 4 1
Câu 15. Cho phương trình lượng giác cot 3x  
(*). Xác định tính đúng, sai của các khẳng định 3    
a) Phương trình (*) tương đương cot 3x  cot    6   
b) Phương trình (*) có nghiệm x   k (k  ) 9 3    5
c) Tổng các nghiệm của phương trình trong khoảng  ; 0   bằng  2  9 2
d) Phương trình có nghiệm dương nhỏ nhất bằng 9 12 3
Câu 16. Cho biết cos x   và   x
; Xác định tính đúng, sai của các khẳng định 13 2 5 5    5 12 3 a) sin x  0 b) sin x   c) cot x  d) sin  x    13 12  3  26
Câu 16. Cho hàm số lượng giác f x  sin 2x  3cos x . Xác định tính đúng, sai của các khẳng định
a) Hàm số đã cho có chu kỳ tuần hoàn 2 .
b) Hàm số không thể biểu thị theo hàm số bậc hai của cos x, sin x .
c) f x  4, x  .
d) Phương trình f x  0 có 1 nghiệm trong khoảng 0;  ?
Câu 17. Cho các hàm số sau: f (x)  2 cos 3x 1 ; g(x) |
 2 sin x  2 |  | 2sin x  2 |. Khi đó:
a) Tập xác định hàm số f x là: D   .
b) Hàm số f x đã cho là hàm số chẵn.
c) Tập xác định hàm số g x là: D   .
d) Hàm số g x đã cho là hàm số lẻ.
Câu 18. Cho biết tan x  2 và 0 x 90  
. Xác định tính đúng, sai của các khẳng định 3 6  a) cos x  0 b) cos x  c) sin x  d) x    3 6 cos 30  3 3 6
Câu 19. Cho hàm số lượng giác f x 2
 2sin 2x  5sin 2x  2 .
a) Hàm số có chu kỳ tuần hoàn là 2 .
b) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số là một số lớn hơn 9.
c) Hai phương trình f x  2; sin 2x  0 là hai phương trình tương đương.
d) Giải phương trình f x  0 ta thu được 4 điểm biểu diễn trên vòng tròn lượng giác.
Câu 20. Tìm được tập giá trị các hàm số sau trên tập xác định của chúng:
a) Hàm số y  3sin x có tập giá trị là T  [3; 3] .
b) Hàm số y  2 cos x 1có tập giá trị là T  [3;1].
c) Hàm số y  2030  4 cos x có tập giá trị là T  [2026; 2034]. d) Hàm số 2
y  sin x  4sin x 1có tập giá trị là T  [3;3] . 8 5
Câu 21. Biết sin a  , tan b
và a , b là các góc nhọn. Xác định tính đúng, sai của các khẳng định 17 12 8 21 14 17 a) tan a
b) sin(a b) 
c) cos(a b) 
d) tan(a b)  . 15 221 22 14   
Câu 22. Cho phương trình lượng giác 3  3 tan 2x   0  
. Xác định tính đúng, sai của các khẳng định  3  5  k
a) Phương trình có nghiệm x   , k   . 6 2 
b) Phương trình có nghiệm âm lớn nhất bằng  3   2 c) Khi  x
thì phương trình có ba nghiệm 4 3    2  
d) Tổng các nghiệm của phương trình trong khoảng ;   bằng  4 3  6
Câu 23. Chiều cao h m của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động được   t  
cho bởi công thức h t   30  20sin  
 . Xác định tính đúng, sai của các khẳng định  25 3 
a) Chu kỳ tuần hoàn của chuyển động là 50s.
b) Chiều cao lớn nhất của cabin là 50m . 175
c) Tại thời điểm t
s thì chiều cao cabin bằng 10m . 6
d) Sau 12,5 giây thì cabin đạt độ cao 40 m lần đầu tiên?
Câu 24. Cho hàm số f x  3.cos 5x  2sin 3 .
x cos 2x . Xác định tính đúng, sai của các khẳng định
a) Hàm số đã cho là hàm số lượng giác. 2
b) Hàm số đã cho có chu kỳ tuần hoàn T  . 5
c) Hàm số đã cho có giá trị lớn nhất là một số nguyên tố.  
d) Tổng của nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình f x  sin x là . 9  
Câu 25. Biết 0  a,b  , a b
và tan a tan b  3 2 2 . Xác định tính đúng, sai của các khẳng định 2 4
a) tan a  tan b  2  2 2. b) tan a  1   2 c) tan b  1   2
d) tan a  tan b  2   2 2. 3
Câu 26. Cho cot x   3,
x  2 . Xác định tính đúng, sai của các khẳng định 2 10 3 a) sin x   b) cos x  10 10  4   10    3 c) sin  x    d) tan x      3  5  3  3
Câu 27. Xét tính đúng - sai của các đẳng thức sau:    3 1 a) sin x   sin x  cos x   .  6  2 2 b) 4sin . x sin 2 .
x sin 3x  sin 4x  sin 2x  sin 6x .   
c) 1 sin 2x  cos 2x  2 2 sin . x cos x  .   .  4  d) 2 x  a x 2 x a  a x 2 sin 2sin .sin .cos sin  cos a .
Câu 28. Cho các hàm số sau: 2
f (x)  5  3sin x ; g(x)  tan x x cos x . Khi đó:
a) Tập xác định hàm số f x là: D   .
b) Hàm số f x đã cho là hàm số lẻ.  
c) Tập xác định hàm số g x là: D   \   kk   .  2 
d) Hàm số g x đã cho là hàm số lẻ.
___________________________ 6
LƯỢNG GIÁC LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG P2
_________________________________ 2 5 Câu 1. Cho cos  , 2   
, xác định tính đúng, sai của các khẳng định 5 2 21 4 21 17 4  21 a) sin   b) sin 2  c) cos 2   d) tan 2  5 25 25 17
Câu 2. Cho một góc lượng giác O ,
x Ou có số đo 250 và một góc lượng giác Ox,Ov có số đo 2  70 .
Xét tính đúng - sai của các phát biểu sau:
a) Số đo góc lượng giác  Ou,Ox bằng 2
 50  k360 , k   .
b) Số đo góc lượng giác Ov,Ox bằng 270  k360 , k  .
c) Số đo một góc lượng giác Ou,Ov bằng 2  0 . 
d) Số đo một góc lượng giác Ou,Ov theo đơn vị radian bằng . 9 1
Câu 3. Cho phương trình lượng giác sin x   , khi đó: 2   
a) Phương trình tương đương sin x  sin    6   7
b) Phương trình có nghiệm là: x  
k 2 ; x
k 2 (k  ) . 6 6 
c) Phương trình có nghiệm âm lớn nhất bằng  3
d) Số nghiệm của phương trình trong khoảng    ;  là ba nghiệm x x
Câu 4. Cho hàm số f x 4 4  sin  cos
. Xét tính đúng, sai của các mệnh đề 2 2
a) Đồ thị hàm số đi qua điểm A0  ;1 .
b) Hàm số có chu kỳ bằng T   .
c) Hàm số có giá trị lớn nhất bằng 1. 5
d) Tổng tất cả các nghiệm thuộc khoảng 0;2  của phương trình f x  là 6 . 8
Câu 5. Tìm được tập xác định của hàm số. Khi đó:     k
a) Hàm số y  cot 3x  
 xác định khi x   (k  )  4  12 3
b) Hàm số y  sin x 1 có tập xác định là D   . sin x c) Hàm số y
có tập xác định là D   . 2  cos x cos 2x  0
d) Hàm số y  tan 2x  cot 2x xác định khi  sin 2x  0 
Câu 6. Từ một vị trí ban đầu trong không gian, vệ tinh X chuyển động theo quỹ đạo là một đường tròn quanh
Trái Đất và luôn cách tâm Trái Đất một khoảng bằng 9200 km . Sau 2 giờ thì vệ tinh X hoàn thành hết một vòng di chuyển.
a) Quãng đường vệ tinh X chuyển động được sau 1 giờ là:  28902, 65( km).
b) Quãng đường vệ tinh X chuyển động được sau 1,5 giờ là:  43353, 98( km)
c) Sau khoảng 5,3 giờ thì X di chuyển được quãng đường 240000 km 9
d) Giả sử vệ tinh di chuyển theo chiều dương của đường tròn, sau 4,5 giờ thì vệ tinh vẽ nên một góc rad? 2   
Câu 7. Cho hai đồ thị hàm số y  sin x  
 và y  sin x , khi đó:  4  7   
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số: sin x   sin x    4  3
b) Hoành độ giao điểm của hai đồ thị là x
k (k  ) 8
c) Khi x [0; 2 ] thì hai đồ thị hàm số cắt nhau tại ba điểm  5 5   7 7 
d) Khi x [0; 2 ] thì toạ độ giao điểm của hai đồ thị hàm số là: ;sin , ;sin     .  8 8   8 8   t 
Câu 8. Một vật dao động xung quanh vị trí cân bằng theo phương trình x  1, 5cos 
 ; trong đó t là thời gian  4 
được tính bằng giây và quãng đường h |
x | được tính bằng mét là khoảng cách theo phương ngang của chất
điểm đối với vị trí cân bằng. Khi đó:
a) Vật ở xa vị trí cân bằng nhất nghĩa là h  1, 5 m .
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất  t 
c) Khi vật ở vị trí cân bằng thì cos  0    4 
d) Trong khoảng từ 0 đến 20 giây thì vật đi qua vị trí cân bằng 4 lần?
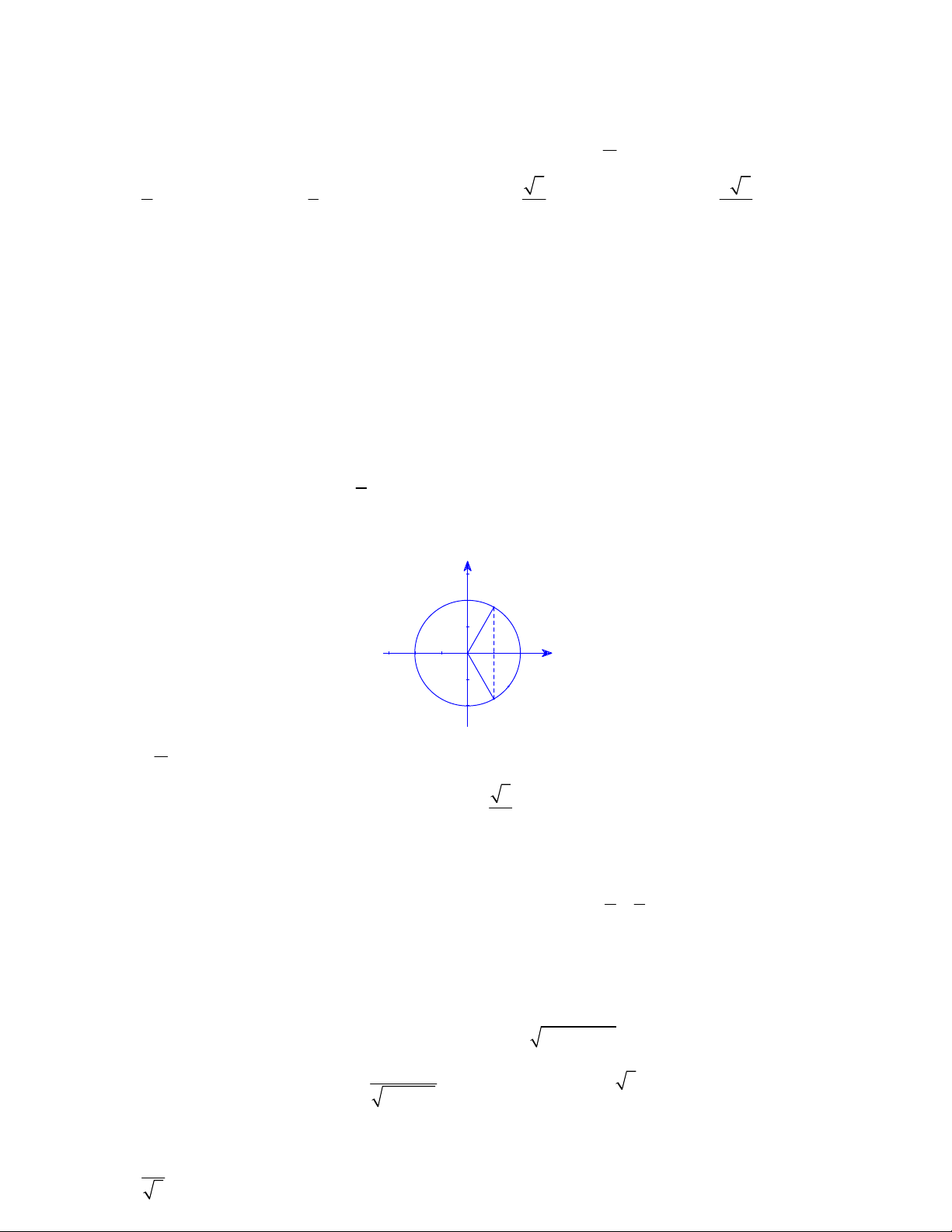
Câu 9. Cho hình vẽ sau:
Xét tính đúng – sai của các phát biểu sau: π
a) Số đo góc lượng giác (OM ,O ) A là sđ(OM,OA)= +k2π (k  ) . 3
b) sđ(ON,OA) = sđ(ON,OM) - sđ(OA,OM) . 2
c) Độ dài cung tròn AM lớn là: l  . AM 3 
d) Hai điểm M , N biểu diễn các cung có số đo là: x
k (k  ) . 3 1 
Câu 10. Cho sin x  ,
x   . Xác định tính đúng, sai của các khẳng định 5 2 4 6 23 20 6 23 6 a) sin 2x  . b) cos 2x  c) tan 2x  d) cot 2x  5 25 3 120 3 4      
Câu 11. Cho biết sin   , cos   . Xét A  sin    sin(   )  
; B  cos(  )  cot    . 5 5  2   2 
Xác định tính đúng, sai của các khẳng định 8
a) A  cos  sin
b) B  cos  tan 27 29 c) A B
d) A B   20 20 cos 2x
Câu 12. Cho hai hàm số lượng giác f x  cos x  sin ; x g x  . 1  sin 2x sin x  cos x
a) g x  . sin x  cos x
b) Hàm số f x có chu kỳ tuần hoàn T  2.
c) Hàm số f x có giá trị lớn nhất bằng 2 .
d) Phương trình f x  g x có 4 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
2 sin x  3cos x 2
Câu 13. Cho cot x  2 . Tính được các biểu thức B  , B  , khi đó: 1 2 2
3sin x  2 cos x
cos x  sin x cos x
a) Vì cot x  2 nên sin x  0 . b) B  8 1 c) B  5  d) B B  1  3 2 1 2
Câu 14. Từ một vị trí ban đầu trong không gian, vệ tinh X chuyển động theo quỹ đạo là một đường tròn quanh
Trái Đất và luôn cách tâm Trái Đất một khoảng bằng 9200 km . Sau 2 giờ thì vệ tinh X hoàn thành hết một vòng
di chuyển. Xác định tính đúng, sai của các khẳng định
a) Quãng đường vệ tinh X chuyển động được sau 1 giờ là:  28902, 65( km).
b) Quãng đường vệ tinh X chuyển động được sau 1,5 giờ là:  43353, 98( km)
c) Sau khoảng 5,3 giờ thì X di chuyển được quãng đường 240000 km 9
d) Giả sử vệ tinh di chuyển theo chiều dương của đường tròn, sau 4,5 giờ thì vệ tinh vẽ nên một góc rad? 2 5
Câu 15. Biết: cos 2 , 0  90   
. Xác định tính đúng, sai của các khẳng định 9 28 53 371 371 a) sin   b) cos  c) tan   d) cot   9 9 53 14    3
Câu 16. Cho phương trình lượng giác sin 3x       3  2   2 x    k  9 3
a) Phương trình có nghiệm  (k  )  2 x   k  3 3 2
b) Phương trình có nghiệm âm lớn nhất bằng  9    c) Trên khoảng 0; 
 phương trình đã cho có 3 nghiệm  2     7
d) Tổng các nghiệm của phương trình trong khoảng 0;   bằng  2  9
Câu 17. Cho hai hàm số f x 2
 3x x ; g x  cos 2x . Xét tính đúng – sai của các mệnh đề sau:
a) Đồ thị hàm số f x đi qua điểm 1; 2  .  b) Hàm số 2
g x có chu kỳ T  . 2
c) Hàm số g x có giá trị lớn nhất bằng 1.
d) Phương trình f x.g x  0 có 4 nghiệm thực.
Câu 18. Cho hai hàm số f x   2
x x   g x    2 3 2 , sin
4x  2x . Xét tính đúng, sai của các mệnh đề
a) Hàm số f x không đi qua điểm nào có hoành độ bằng 3.
b) Hàm số g x có tập xác định  . 9
c) Hàm số g x có đồ thị nằm phía trên đường thẳng y   2 .
d) Phương trình f x.g x  0 có 13 nghiệm thực. 3
Câu 19. Cho góc lượng giác  có số đo theo đơn vị rađian là
. Xét tính đúng – sai của các mệnh đề 4
a) Góc lượng giác  có số đo theo đơn vị độ là 155 .
b) Điểm biểu diễn góc lượng giác  là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ I. 5 c) Góc lượng giác 
có cùng điểm biểu diễn trên đường tròn lượng giác với góc  . 4
d) Góc lượng giác 855 có cùng điểm biểu diễn trên đường tròn lượng giác với góc  . 
Câu 20. Cho 0   
. Xét tính đúng – sai của các mệnh đề 2
a) A  cos(   )  0 ;
b) B  tan(   )  0 ;  2   3  c) C  sin    0   ; d) D  cos    0   .  5   8 
cos x 1 2sin x
Câu 21. Cho hàm số f x 
. Xét tính đúng – sai của các mệnh đề 2
2 cos x  sin x 1 cos x
a) f x  . sin x 1
b) Đồ thị hàm số đi qua điểm 0;  1 .
c) Hàm số đã cho là hàm số chẵn.
d) Phương trình f x  3 có 5 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
Câu 22. Cho hàm số f x   x m 2 sin
sin x  sin x  2 .
a) Phương trình f x  0 đã cho luôn có nghiệm với mọi giá trị m . 3 
b) Có 2 giá trị nguyên m để phương trình f x  0 có nghiệm  ; 2  . 2   
c) Với m  1, hàm số đã cho có giá trị nhỏ nhất bằng 0.
d) f x f x  2024 , x  . 0   0  0
Câu 23. Cho hàm số y f x  cos 2x  cos x . Xét tính đúng - sai của các phát biểu sau:
a) Tập xác định của hàm số trên là  .
b) Hàm số trên là hàm số chẵn.
c) Đặt t  cos x thì hàm số trở thành y f x 2
 2t t 1 .
d) Giá trị nhỏ nhất của hàm số trên là 0 .
Câu 24. Xét tính đúng - sai của các phát biểu độc lập
a) Tập xác định của hàm số y  sin 2x là  .    5 
b) Tập xác định của hàm số y  tan 2x    là:  \ 
k  , k .  3   12 
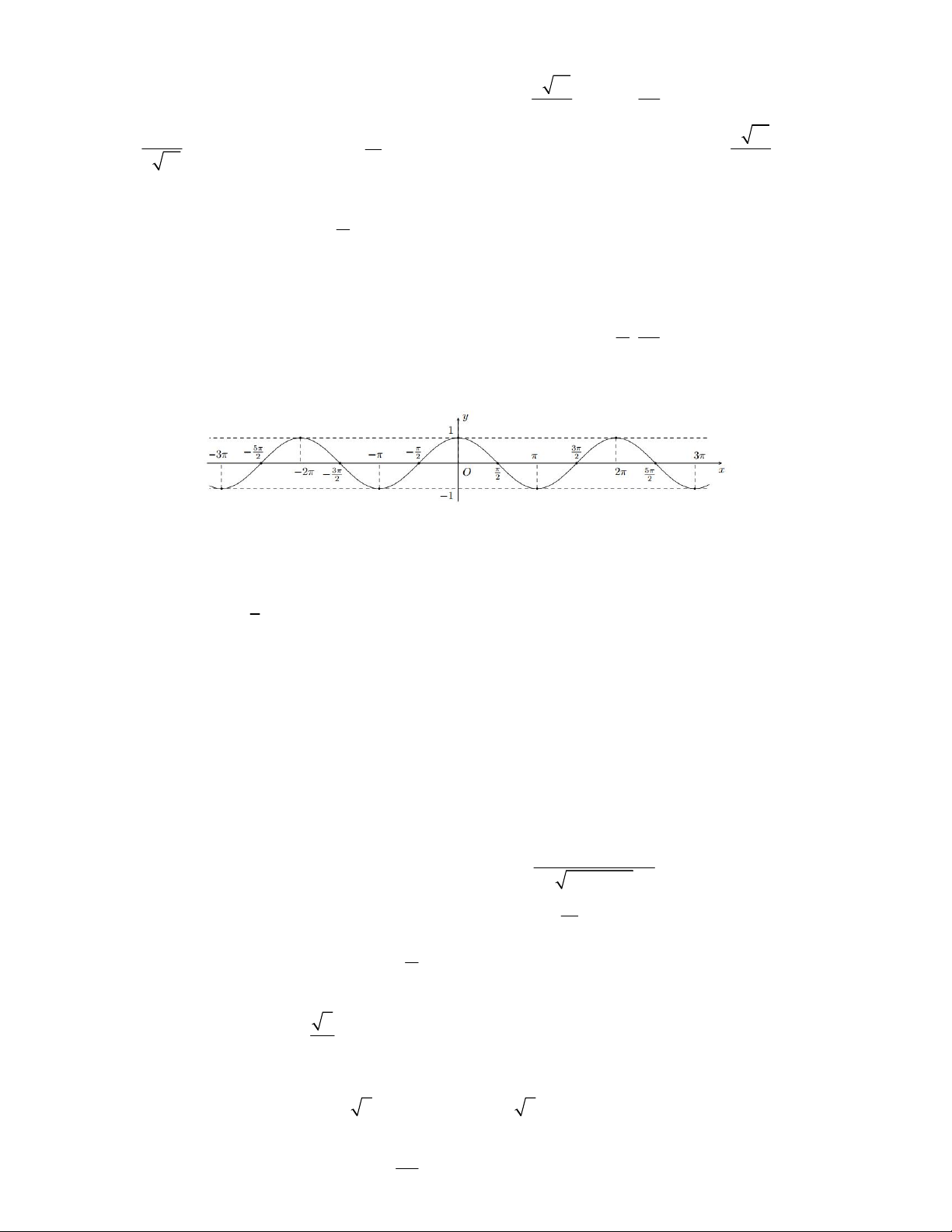
c) Đường cong trong hình dưới là đồ thị của hàm số y   s inx . y 3π 1 2 x π -π O π - 2 3π -1 π - 2 2 13
e) Giá trị lớn nhất của hàm số 2
y  sin x  cos x  2 là . 4
________________________ 10
LƯỢNG GIÁC LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG P3
_________________________________ 2 10 3
Câu 1. Tính được các giá trị lượng giác của góc  , biết: tan   ,    . Khi đó: 9 2 9 9 cos  0 2 10 a) cot   b) cos   c)  d) sin   2 10 11 sin   0  11
Câu 2. Xét hai hàm số f x 2
 4 cos x  3; g x  2sin x 1. Xét tính đúng, sai của các phát biểu sau   
a) Đồ thị hàm số g x đi qua điểm ;3   .  2 
b) Hàm số f x là hàm số chẵn và có chu kỳ T   .
c) Giá trị lớn nhất của hàm số f x  g x là một số nguyên.   3 
d) Hai phương trình f x  0; g x  0 có 2 nghiệm chung trên khoảng  ;   .  2 2 
Câu 3. Đồ thị như hình sau là của một trong bốn hàm số
f x  cos x; f x  sin ; x
f x  sin 2 ; x
f x  cos 2x
Xét tính đúng, sai của các khẳng định
a) f x  cos x .
b) Hàm số đã cho có chu kỳ T  2 .
c) Hàm số đã cho có giá trị lớn nhất bằng 1. 1
d) Phương trình f x  có 8 nghiệm trong khoảng 0;10  . 3
Câu 4. Xét hàm số f x  sin x sin 7x  sin 3x sin 5x . Xét tính đúng, sai của các khẳng định
a) Hàm số đã cho có tập xác định  .
b) Hàm số đã cho là hàm số chẵn và có chu kỳ T  2 .
c) Hàm số có thể viết lại thành f x 3
 4 cos 2x  5 cos 2x .
d) Phương trình f x  0 có 7 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
Câu 5. Cho hàm số f x  cos 2x  cos .
x Xét tính đúng, sai của các phát biểu sau:
a) Hàm số đã cho là hàm số chẵn và có chu kỳ T   .
b) Đồ thị hàm số không đi qua điểm 0; 2 . 3
cos x(8 cos x 1)
c) Phương trình  f x 3 1  0  
tương đương với phương trình  0 . 3cos x 1 13
d) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho bằng . 8   
Câu 6. Cho hàm số lượng giác f x  sin x  
 . Xét tính đúng, sai của các phát biểu sau:  4 
a) Hàm số đã cho là hàm số lẻ và có chu kỳ của hàm số là một số lớn hơn 5.  2 
b) Đồ thị hàm số đi qua điểm  0;  .  2    c) Phương trình 3
f x  1 có 1 nghiệm thuộc đoạn  ;2  .
d) Giá trị nhỏ nhất của hàm số g x  2 f x  2 cos x bằng 2 .
Câu 7. Cho phương trình sin 2x m . Xét tính đúng, sai của các phát biểu sau: k
a) Với m  0 , phương trình có nghiệm là x  . 2 11  1
b) Phương trình có nghiệm là x  khi m  . 3 2
c) Phương trình có nghiệm khi m   1   ;1 .   
d) Phương trình có hai nghiệm phân biệt trên 0;   khi m  0;  1 .  2    
Câu 8. Cho phương trình lượng giác 2 cos x   m 1  0  
, trong đó m   là tham số. Xét tính đúng - sai  3  của các phát biểu sau:  a)
là nghiệm của phương trình khi và chỉ khi m  1. 6  
b) Khi m  0 phương trình có tập nghiệm là   k2 ;   k2  k   .  3 
c) Tập các giá trị của m để phương trình có nghiệm là  1  ;  1 .
d) Khi m  1 phương trình có 6 nghiệm trong đoạn 0;6  .
Câu 9. Xét tính đúng/sai của các mệnh đề sau:     180  a) 1  rad; 1rad  .   180   
b) Một cung của đường tròn bán kính R và có số đo  rad thì có độ dài l   R .
c) Với ba tia Ou, Ov, Ow bất kì, ta có sđ Ou Ov  sđ Ov Ow  sđ Ou Ow 0 , , ,
k360 , k   .
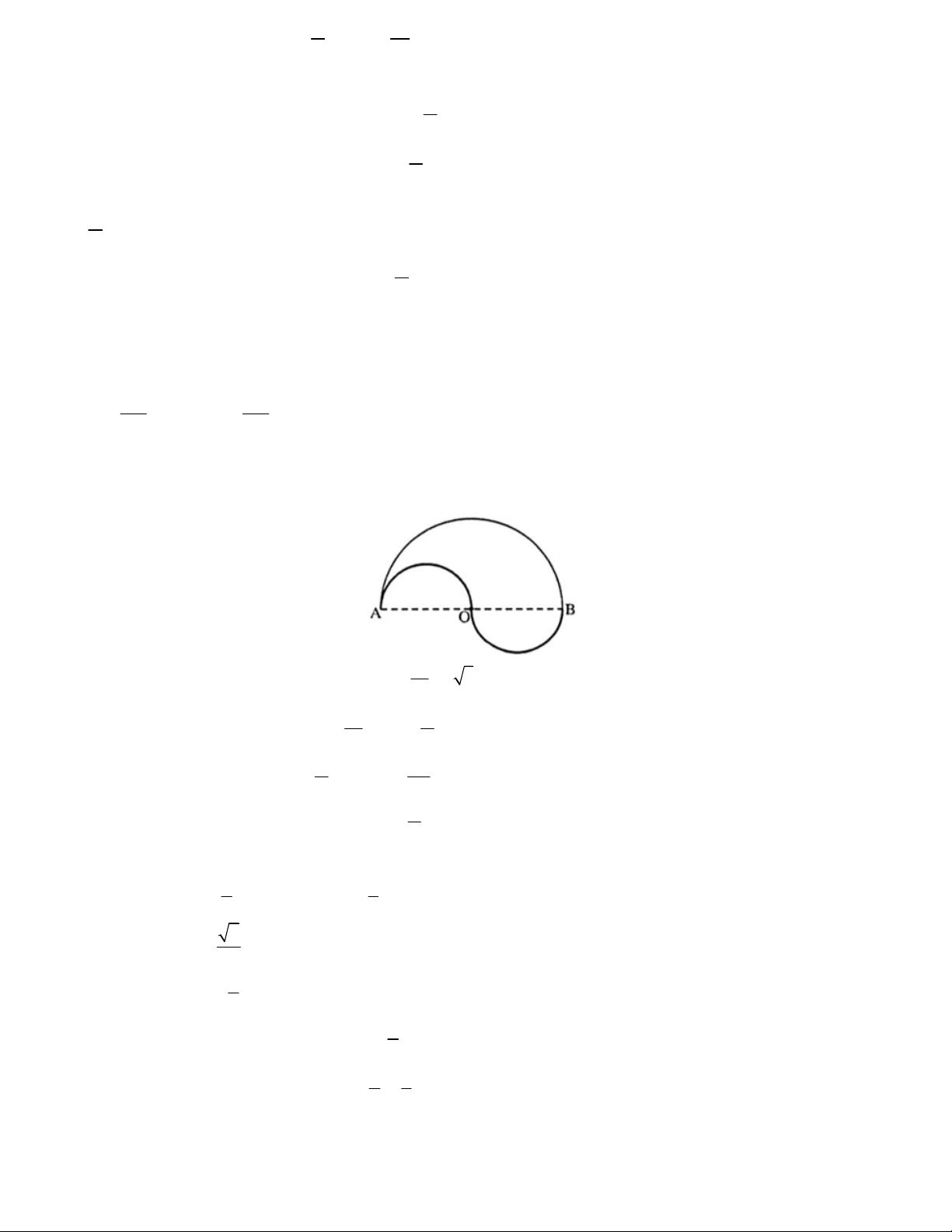
d) Cho OA  5cm . Chu vi hình vẽ sau đây bằng 10   
Câu 10. Cho phương trình lượng giác 2 sin x   3  0   , khi đó:  12       
a) Phương trình tương đương sin x   sin      12   3   7
b) Phương trình có nghiệm là: x
k 2 ; x
k 2 (k  ) . 4 12 
c) Phương trình có nghiệm âm lớn nhất bằng  4
d) Số nghiệm của phương trình trong khoảng    ;  là hai nghiệm 3 3
Câu 11. Cho cos a
; sin a  0 ; sin b
; cos b  0 . Xét tính đúng – sai của các phát biểu sau: 4 5 7
a) Giá trị của tan a  . 3 2
b) Giá trị của cot b   . 3  1 
c) Giá trị của cos 2a  cos 2b thuộc khoảng ;1 .    2   1 1 
d) Giá trị của cos a b thuộc khoảng  ;    .  2 3 
Câu 12. Cho hàm số f x  sin x  cos 2x . Xét tính đúng, sai của các phát biểu sau:
a) Hàm số đã cho có tập xác định  .
b) Hàm số đã cho có chu kỳ T  2 .
c) Hàm số đã cho có giá trị lớn nhất là một số nguyên. 12
d) Phương trình f x  0 có ít hơn 27 nghiệm thuộc đoạn0;20 .
Câu 13. Xét tính đúng – sai của các mệnh đề sau: 
a) Cho góc hình học uOv  75 . Công thức số đo tổng quát của góc lượng giác Ou, Ov là
75  k.360 , k   .
b) Cho một góc lượng giác Ox ,Ou có số đo 50 và một góc lượng giác Ox ,Ov có số đo 1  25 . Số đo
của góc lượng giác Ou ,Ov bằng 175  k360 ,  k   .
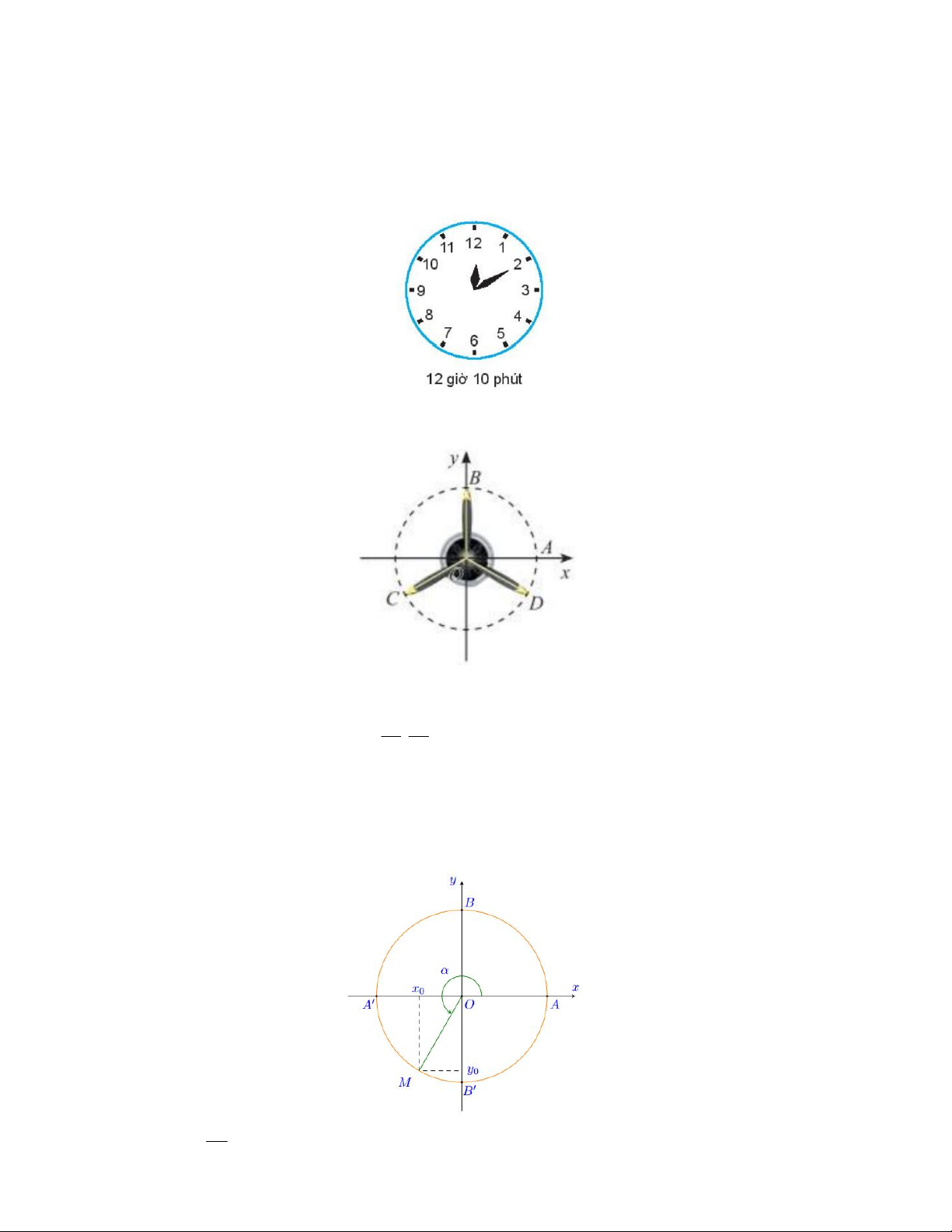
c) Trên đồng hồ hình dưới đây, kim phút đang chỉ đúng số 2. Đến lúc 13 giờ 30 phút thì kim phút đã quay được
một góc lượng giác có số đo bằng 480 . 
d) Trong hình dưới, cánh quạt được chia thành 3 phần bằng nhau. AOD  28 . Công thức số đo tổng quát của
góc lượng giác Ox, OC  bằng 148  k.360 .
Câu 14. Xét sự biến thiên của hàm số y  sin x  cos .
x Xét tính đúng, sai của các khẳng định
a) Hàm số đã cho có chu kỳ T  2 .  3  
b) Hàm số đã cho đồng biến trên khoảng ; .   4 4  
c) Hàm số đã cho có tập giá trị là 1; 1 .  
d) Phương trình y  0 có 6 nghiệm thỏa mãn bất phương trình 2
x  20x 19  0 .
Câu 15. Cho vòng tròn lượng giác như hình vẽ. Điểm M x ; y là điểm cuối biểu diễn góc lượng giác  . Xét 0 0 
tính đúng, sai của các khẳng định . 3 a) Nếu 0   
x  0, y  0 .
b) sin   2024   sin . 0 0 2 13 1 c) 4 4 x y  1.
d)Tại điểm M 2x ;3x thì tan  . 0 0  0 0 3
Câu 16. Xét tính đúng - sai của các phát biểu sau:
a) sin a b  sin a cos b  cos a sin b . b) 0 0 0 0 0
sin 31 .cos12  cos12 .sin 31  sin19 . 4    24 c) Cho cos x  , x   ;0 
 . Giá trị của sin 2x là  . 5  2  25 1     1 a 6 d) Cho sin   và
    . Biết giá trị của cos      với ,
a b thì a b  4 . 3 2  6  b
Câu 17. Xét tính đúng - sai của các mệnh đề sau: 1 sin 2x a) 2 sin x  2 1 7 b) Nếu cos  thì cos 2   3 9 3    3 7 c) Nếu sin x  với x  0;   thì sin 2x  4  2  8 2       d) Cho cos  với    ; 0   biết tan    a b c   . a, , b c  ,
c  0 Khi đó a b c  0 . 3  2   4  1  1 
Câu 18. Cho tan a  , 0  a
; tan b  , 0  b
. Xét tính đúng - sai của các phát biểu sau: 2 2 3 2 2 5 a) cot a  2 . b) tan(a  ) b 1. c) tan(a  ) b  7 .
d) sin(a  2b)   . 25
Câu 19. Cho hai hàm số f x  tan ; x
g x  tan 3x . Xét tính đúng, sai của các phát biểu sau:
a) Hàm số f x xác định khi sin x  1 .
b) Hai hàm số đều là hàm số lẻ và có cùng chu kỳ tuần hoàn. sin x
c) g x  f x  . cos 3x
d) Tổng các nghiệm trong đoạn 0;30 của phương trình 3 f x 3
g x  0 là một số lớn hơn 145.
Câu 20. Xét hàm số f x  cos 3x  sin x . Xét tính đúng, sai của các phát biểu sau:
a) Hàm số đã cho là hàm số không chẵn, không lẻ.    
b) Hàm số f x  cos 3x có khoảng đồng biến   k 2 ;
k 2 , k     .  2 2 
c) Hàm số đã cho có chu kỳ T  2 .     d) Phương trình 2
f x  0 có 5 nghiệm thuộc đoạn  ;  . 2 2      
Câu 21. Cho hàm số f x  2sin 4x  1  
. Xét tính đúng, sai của các khẳng định  3 
a) Hàm số đã cho là hàm số lẻ.
b) Hàm số đã cho có giá trị lớn nhất bằng 1.
c) Hàm số đã cho có chu kỳ T  2 .    
d) Nghiệm dương nhỏ nhất của phương trình f x  0 thuộc khoảng ;   .  9 6 
Câu 22. Cho hàm số f x  m sin x  cos x . Xét tính đúng, sai của các khẳng định
a) Hàm số đã cho có chu kỳ T  2 .
b) Hàm số đã cho luôn là hàm số không chẵn, không lẻ.
c) Đồ thị hàm số đã cho đi qua điểm 0;  1 
với mọi giá trị m .
d) Phương trình f x  1luôn luôn có nghiệm với mọi giá trị m .
__________________________________ 14
LƯỢNG GIÁC LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG P4
_________________________________
Câu 1. Tính được các giá trị lượng giác của góc  , biết: tan   2, 0    . Khi đó 2 1 1 5 2 5 a) cot   b) 2 cos   c) cos   d) sin   2 5 5 5
Câu 2. Cho hàm số f x  2 cos x  
1 cos x  2 . Xét tính đúng, sai của các khẳng định
a) f x  cos 2x  5cos x  3 .
b) Hàm số đã cho là hàm số chẵn.
c) Hàm số đã cho có chu kỳ T  2 .
d) Phương trình f x  0 có đúng 4 nghiệm thuộc đoạn  2   ; 2  . Câu 3. Cho hàm số 2
y  cos x  sin x 1. Xét tính đúng, sai của các khẳng định
a) Hàm số đã cho là hàm số không chẵn, không lẻ.
b) Hàm số đã cho có đồ thị nằm phía trên trục hoành.
c) Phương trình y  2 có bốn điểm biểu diễn nghiệm trên vòng tròn lượng giác. 9
d) Giá trị lớn nhất của hàm số bằng . 4 
Câu 4. Cho vòng tròn lượng giác như hình vẽ, M và N đối xứng qua trục và MOx  60 . y 1 M x -1 O 1 N -1  a)  MON  radian. 2 3
b) Điểm M biểu diễn nghiệm của phương trình sin x  . 2
c) Giả sử M, N di động ở nửa bên phải vòng tròn lượng giác, khi đó diện tích tam giác MON lớn nhất khi  MON  60 . x 1
d) Hai điểm M và N biểu diễn đầy đủ nghiệm của phương trình 2 sin  . 2 4
Câu 5. Cho hàm số f x  2 cos 2x 1 . Xét tính đúng, sai của các khẳng định
a) Hàm số đã cho có chu kỳ T  2 .
b) Bất phương trình f x 2
 4 cos x  5 nghiệm đúng với mọi giá trị x   .
c) Đồ thị hàm số luôn nằm phía dưới đồ thị hàm số g x 2 
x  2x  3 . f x
d) Nghiệm lớn nhất của phương trình
 0 là một số lớn hơn 5 . 2 x   x
Câu 6. Cho góc  0    180 thỏa mãn tan  3 . Xét tính đúng, sai của các khẳng định 1 a) cot   . b) cos  0 . 3 15 3 10 2sin 3cos 3  c) sin   . d) P   . 10 3sin  2cos 11
Câu 7. Cho phương trình lượng giác 2 sin x
2 . Xét tính đúng, sai của các khẳng định 
a) Phương trình tương đương sin x  sin 4  3
b) Phương trình có nghiệm là: x
k 2 ; x
k 2 (k  ) . 3 4 
c) Phương trình có nghiệm dương nhỏ nhất bằng . 4    
d) Phương trình có 2 nghiệm trong khoảng  ;   .  2 2 
Câu 8. Tìm được tập xác định của hàm số. Xét tính đúng, sai của các khẳng định     k
a) Hàm số y  cot 3x  
 xác định khi x   (k  )  4  12 3
b) Hàm số y  sin x 1 có tập xác định là D   . sin x c) Hàm số y
có tập xác định là D   . 2  cos x cos 2x  0
d) Hàm số y  tan 2 x  cot 2 x xác định khi  sin 2x  0 
Câu 9. Cho tan  2 . Xét tính đúng - sai của các phát biểu sau: 1 a) cot   . 2  5 b) Khi 0    thì cos   . 2 5 sin   cos 5
c) Giá trị của biểu thức B   3 3
sin   3cos   2 sin  31 4 4 sin  cos  1 8 8 sin  cos  1 d) Nếu   thì A    . a b a b 3 3 3 3 a b a b 2 cos x 1
Câu 10. Cho hàm số y
. Xét tính đúng, sai của các khẳng định cos x  2
a) Đồ thị hàm số đã cho đi qua điểm 0;3 .
b) Hàm số đã cho là hàm số chẵn và có tập xác định  .
c) Phương trình y  1vô nghiệm.
d) Gọi M , m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số thì 9M m  1  .
Câu 11. Cho hai hàm số f x  cos x  cos 2x  cos 3x và g x  2 cos 2x 2sin x  
1 . Xét tính đúng, sai của các khẳng định
a) Hàm số đã cho là hàm số chẵn.
b) Hàm số đã cho có chu kỳ T  5 .
f x  g x c) .
d) Phương trình f x  0 có 6 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
Câu 12. Cho hai hàm số f x  2 cot 2x  3cot 3 ; x
g x  tan 2x . Xét tính đúng, sai của các khẳng định
a) Hàm số f x là hàm số lẻ.
b) Hàm số g x có chu kỳ T   .    
c) Hàm số g x có một khoảng đồng biến là  ;   .  4 4  d) Phương trình 5   5 f
x g x vô nghiệm. 16
Câu 13. Cho hàm số f x   x   x   g x 2 2 sin 1 2 sin 2 1 ;
 3  4 cos x . Xét tính đúng, sai của các khẳng định
a) Hàm số f x là hàm số lẻ. 
b) Hàm số g x có chu kỳ T  . 2
c) Đồ thị hàm số g x luôn nằm phía dưới hoặc tiếp xúc đường thẳng y  1.
d) Tổng các nghiệm trên đoạn  
 ;  của phương trình f x  g x bằng  . 2 
Câu 14. Cho sin   ,
    , xét tính đúng, sai của các mệnh đề sau 3 2  5 a) cos  0 . b) cos  . 3  5  5 5 tan  10 c) sin      .
d) Giá trị của biểu thức P  là . 2  2  3 1 tan  9
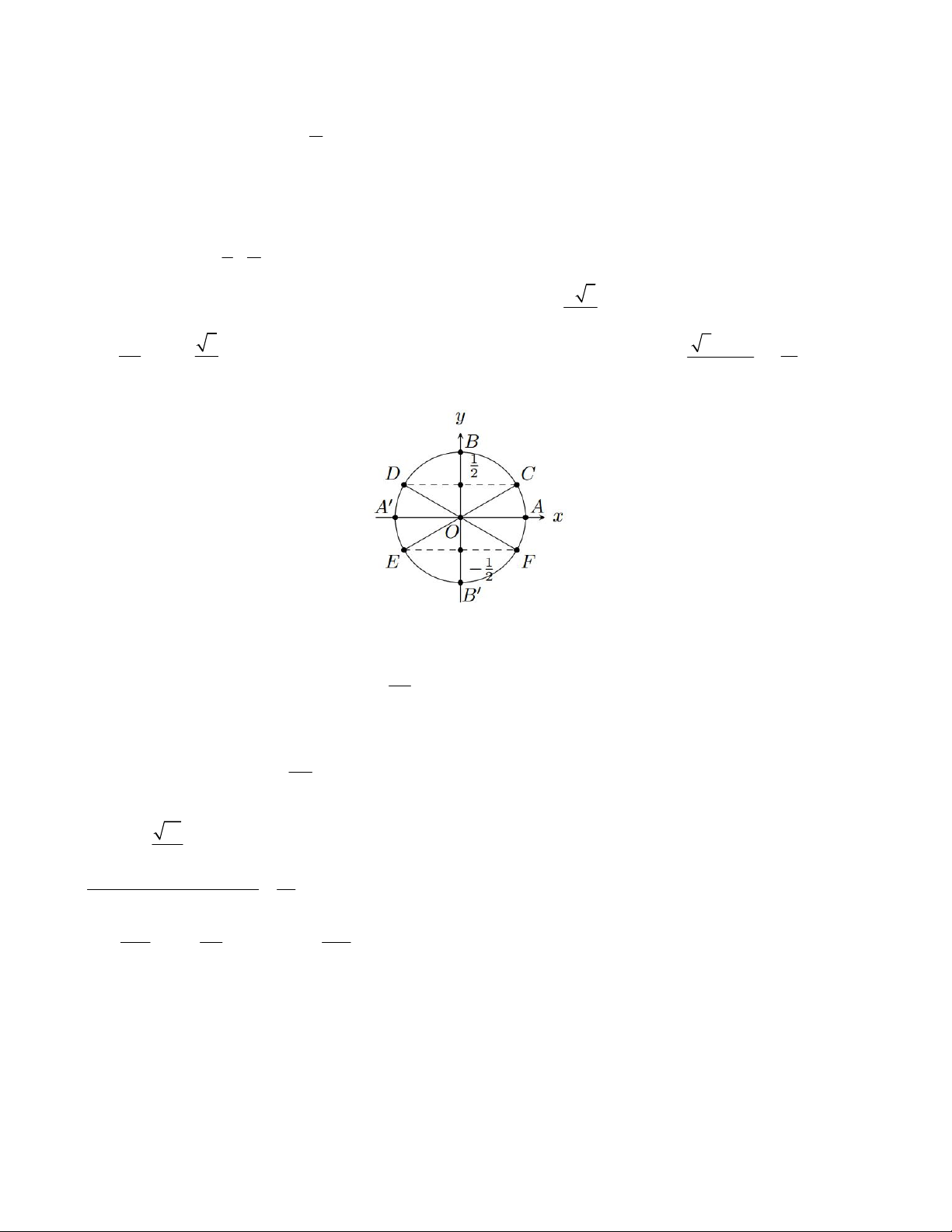
Câu 15. Cho vòng tròn lượng giác như hình vẽ. Xét tính đúng, sai của các khẳng định
a) Giá trị sin tăng dần khi điểm cuối góc lượng giác di chuyển theo hướng B  B .
b) Hai điểm A , A biểu diễn đầy đủ các nghiệm của phương trình sin x  0. 5
c) Điểm D biểu diễn các góc lượng giác  k 2 . 6
d) Bốn điểm C, D, E, F biểu diễn đầy đủ các nghiệm của phương trình 2cos 2x 1.  
Câu 16. Cho góc  thỏa mãn    0 và cot  3
 . Xét tính đúng - sai của các phát biểu sau: 2 a) sin  0 10 b) sin    10 cos  sin  10 c)  3 3 cos   3sin   2 os c  21 2 2  17  7   13  d) tan  tan   cot  cot    7    0 2 4 2    4     
Câu 17. Cho các hàm số sau 2
f (x)  2 | cos x |; g(x)  1 3sin x . Xét tính đúng, sai của các khẳng định
a) Giá trị lớn nhất của hàm số f x bằng 2
b) Giá trị nhỏ nhất của hàm số f x bằng 0
c) Giá trị lớn nhất của hàm số g x bằng 2
d) Giá trị nhỏ nhất của hàm số g x bằng 2  Câu 18. Cho 0  90  
. Xét được dấu của các biểu thức sau. Khi đó: a) A sin  90     0 ; b) B cos  45     0 ; c) C tan 270      0 ; d) D cos 2 90     0 .
Câu 19. Cho các hàm số sau f ( x)  sin x và g ( x)  cos x . Xét tính đúng, sai của các khẳng định 17    
a) Hàm số f (x)  sin x đồng biến trên khoảng  ;    2 2   3 5 
b) Hàm số f ( x) nghịch biến trên khoảng ;   .  4 4 
c) Hàm số g ( x) nghịch biến trên khoảng (0; ) .  25 13 
d) Hàm số g ( x) đồng biến trên khoảng ;   .  6 3 
Câu 20. Biến đổi được các biểu thức sau về dạng tích. Xét tính đúng, sai của các khẳng định x
a) cos 3 x  cos x  2 cos 2 x  cos 3 x
b) sin 3x  sin 2x  2 sin 2x cos ; 2 5x 3x
c) cos 4x  cos x  2 sin sin
d) sin 5 x  sin x  2 cos 3 x sin 2 x 2 2
Câu 21. Cho hàm số f x  2sin x và g x  3sin x cos x  2 . Khi đó:
a) Giá trị lớn nhất của hàm số f x  bằng 3
b) Phương trình g x   2 có nhiều hơn 5 nghiệm trên khoảng 0; 4  .
c) Giá trị lớn nhất của hàm số g x  bằng 4
d) Giá trị nhỏ nhất của hàm số g x  bằng 0 x 1
Câu 22. Cho các hàm số f ( x) 
3  2 sin x ; và g ( x)  tan  cos x , khi đó: 2 3
a) Hàm số f x  có tập xác định là: D   .
b) Hàm số f x  đã cho là hàm tuần hoàn.
c) Hàm số g x  xác định khi x k2(k  )  .
d) Hàm số g x  đã cho là hàm không tuần hoàn. 1 3
Câu 23. Cho biết cos 2   và    
. Xét tính đúng, sai của các khẳng định 4 2 10 6 15 a) sin  0, cos  0 b) sin  c) cos  d) cot  4 4 5   
Câu 24. Cho các hàm số 3
f (x)  3sin x ; g( ) x  5  cos 2x  
 . Xét tính đúng, sai của các khẳng định  3 
a) Tập xác định hàm số f x  là: D   .
b) Hàm số f x  đã cho là hàm số chẵn.
c) Đồ thị hàm số g x  luôn nằm phía trên hoặc tiếp xúc đường thẳng y  5  .
d) Hàm số g x  đã cho là hàm số lẻ.
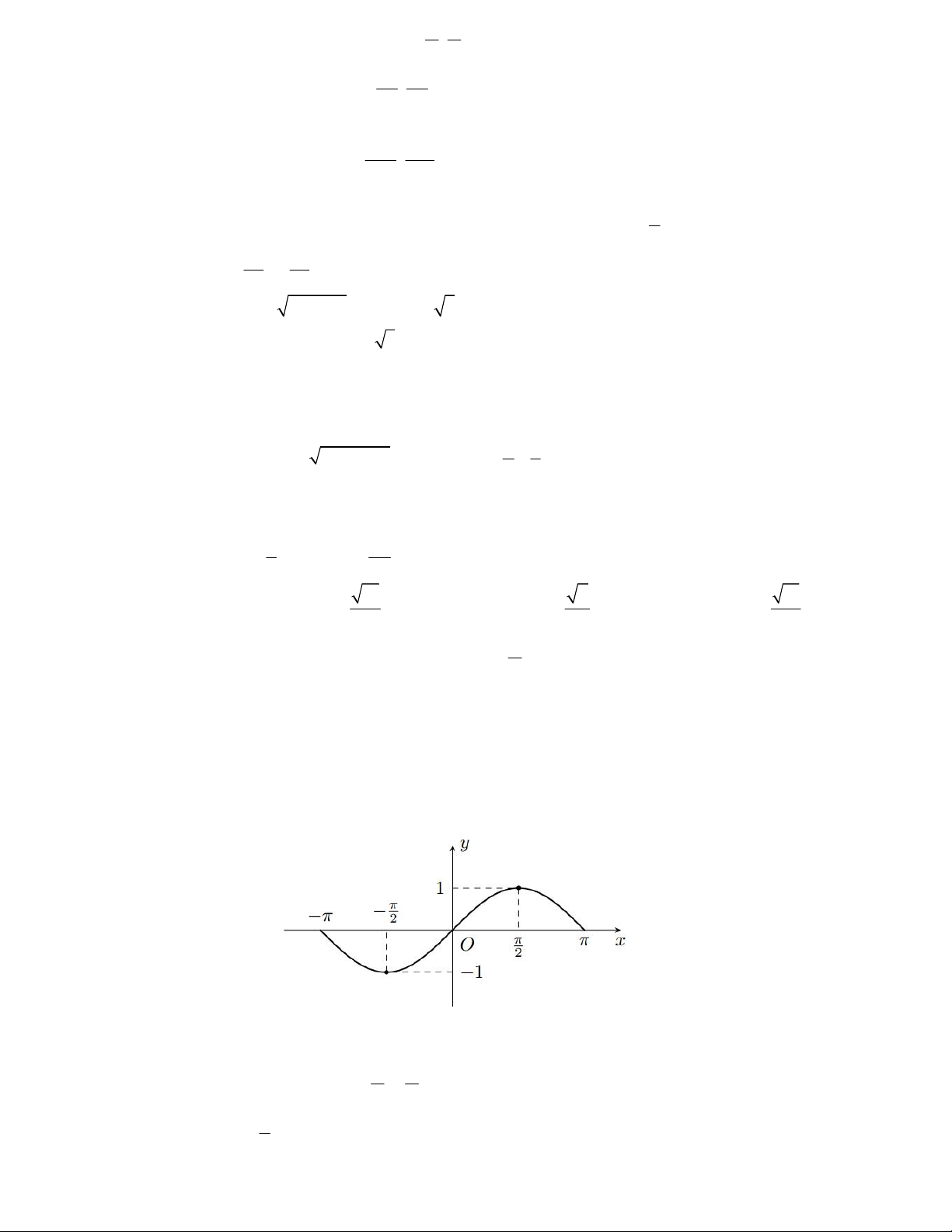
Câu 25. Trên miền  
 ;  đồ thị hàm số f x  sin x như hình vẽ. Xét tính đúng, sai của các khẳng định
a) Đồ thị hàm số đi qua gốc tọa độ.
b) Hàm số nghịch biến trên    ; 0 .    
c) Giá trị nhỏ nhất của hàm số trên  ;   bằng – 1. 2 5    1
d) Phương trình f x  có 6 nghiệm trên 0;3  . 4
_______________________________________ 18
LƯỢNG GIÁC LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG, SAI TỔNG HỢP CHƯƠNG P5
_________________________________
Câu 1. Tính được các giá trị lượng giác của góc  , biết: tan   2, 0    . Khi đó 2 1 1 5 2 5 a) cot   b) 2 cos   c) cos   d) sin   2 5 5 5
Câu 2. Cho hàm số f x  2 cos x  
1 cos x  2 . Xét tính đúng, sai của các khẳng định
e) f x  cos 2x  5cos x  3 .
f) Hàm số đã cho là hàm số chẵn.
g) Hàm số đã cho có chu kỳ T  2 .
h) Phương trình f x  0 có đúng 4 nghiệm thuộc đoạn  2   ; 2  . Câu 3. Cho hàm số 2
y  cos x  sin x 1. Xét tính đúng, sai của các khẳng định
e) Hàm số đã cho là hàm số không chẵn, không lẻ.
f) Hàm số đã cho có đồ thị nằm phía trên trục hoành.
g) Phương trình y  2 có bốn điểm biểu diễn nghiệm trên vòng tròn lượng giác. 9
h) Giá trị lớn nhất của hàm số bằng . 4 
Câu 4. Cho vòng tròn lượng giác như hình vẽ, M và N đối xứng qua trục và MOx  60 . y 1 M x -1 O 1 N -1  e)  MON  radian. 2 3
f) Điểm M biểu diễn nghiệm của phương trình sin x  . 2
g) Giả sử M, N di động ở nửa bên phải vòng tròn lượng giác, khi đó diện tích tam giác MON lớn nhất khi  MON  60 . x 1
h) Hai điểm M và N biểu diễn đầy đủ nghiệm của phương trình 2 sin  . 2 4
Câu 5. Cho hàm số f x  2 cos 2x 1 . Xét tính đúng, sai của các khẳng định
e) Hàm số đã cho có chu kỳ T  2 .
f) Bất phương trình f x 2
 4 cos x  5 nghiệm đúng với mọi giá trị x   .
g) Đồ thị hàm số luôn nằm phía dưới đồ thị hàm số g x 2 
x  2x  3 . f x
h) Nghiệm lớn nhất của phương trình
 0 là một số lớn hơn 5 . 2 x   x
Câu 6. Cho góc  0    180 thỏa mãn tan  3 . Xét tính đúng, sai của các khẳng định 1 a) cot   . b) cos  0 . 3 19 3 10 2sin 3cos 3  c) sin   . d) P   . 10 3sin  2cos 11
Câu 7. Cho phương trình lượng giác 2 sin x
2 . Xét tính đúng, sai của các khẳng định 
a) Phương trình tương đương sin x  sin 4  3
b) Phương trình có nghiệm là: x
k 2 ; x
k 2 (k  ) . 3 4 
c) Phương trình có nghiệm dương nhỏ nhất bằng . 4    
d) Phương trình có 2 nghiệm trong khoảng  ;   .  2 2 
Câu 8. Tìm được tập xác định của hàm số. Xét tính đúng, sai của các khẳng định     k
a) Hàm số y  cot 3x  
 xác định khi x   (k  )  4  12 3
b) Hàm số y  sin x 1 có tập xác định là D   . sin x c) Hàm số y
có tập xác định là D   . 2  cos x cos 2x  0
d) Hàm số y  tan 2 x  cot 2 x xác định khi  sin 2x  0 
Câu 9. Cho tan  2 . Xét tính đúng - sai của các phát biểu sau: 1 a) cot   . 2  5 b) Khi 0    thì cos   . 2 5 sin   cos 5
c) Giá trị của biểu thức B   3 3
sin   3cos   2 sin  31 4 4 sin  cos  1 8 8 sin  cos  1 d) Nếu   thì A    . a b a b 3 3 3 3 a b a b 2 cos x 1
Câu 10. Cho hàm số y
. Xét tính đúng, sai của các khẳng định cos x  2
e) Đồ thị hàm số đã cho đi qua điểm 0;3 .
f) Hàm số đã cho là hàm số chẵn và có tập xác định  .
g) Phương trình y  1vô nghiệm.
h) Gọi M , m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số thì 9M m  1  .
Câu 11. Cho hai hàm số f x  cos x  cos 2x  cos 3x và g x  2 cos 2x 2sin x  
1 . Xét tính đúng, sai của các khẳng định
e) Hàm số đã cho là hàm số chẵn.
f) Hàm số đã cho có chu kỳ T  5 .
f x  g x g) .
h) Phương trình f x  0 có 6 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
Câu 12. Cho hai hàm số f x  2 cot 2x  3cot 3 ; x
g x  tan 2x . Xét tính đúng, sai của các khẳng định
e) Hàm số f x là hàm số lẻ.
f) Hàm số g x có chu kỳ T   .    
g) Hàm số g x có một khoảng đồng biến là  ;   .  4 4  h) Phương trình 5   5 f
x g x vô nghiệm. 20