38 trang 6 lượt tải

Luyện kỹ năng trắc nghiệm đúng – sai và trả lời ngắn đạo hàm và ứng dụng

12

Tài liệu gồm 38 trang, được biên soạn bởi thầy giáo Đặng Công Đức (Giang Sơn), tuyển chọn các bài tập rèn luyện kỹ năng giải toán trắc nghiệm đúng – sai và trắc nghiệm trả lời ngắn chủ đề đạo hàm và ứng dụng môn Toán 11 THPT.

Chủ đề: Tài liệu chung Toán 11 85 tài liệu

Môn: Toán 11 3.6 K tài liệu

Tác giả:

Profile

Linh Đan

1 tháng trước
Danh sách Quiz
/38
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
L
L
U
U
Y
Y
Ệ
Ệ
N
N
K
K
Ỹ
Ỹ
N
N
Ă
Ă
N
N
G
G
T
T
O
O
Á
Á
N
N
1
1
1
1
T
T
H
H
P
P
T
T
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
Đ
Đ
Ú
Ú
N
N
G
G
,
,
S
S
A
A
I
I
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
T
T
R
R
Ả
Ả
L
L
Ờ
Ờ
I
I
N
N
G
G
Ắ
Ắ
N
N
Đ
Đ
Ạ
Ạ
O
O
H
H
À
À
M
M
V
V
À
À
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
Đ
Đ
Á
Á
P
P
Á
Á
N
N
C
C
H
H
I
I
T
T
I
I
Ế
Ế
T
T
P
P
D
D
F
F
B
B
Ạ
Ạ
N
N
Đ
Đ
Ọ
Ọ
C
C
V
V
U
U
I
I
L
L
Ò
Ò
N
N
G
G
L
L
I
I
Ê
Ê
N
N
H
H
Ệ
Ệ
T
T
Á
Á
C
C
G
G
I
I
Ả
Ả
:
:
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
9
9
8
8
0
0
2
2
1
1
9
9
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
3
3
/
/
2
2
0
0
2
2
5
5
2
L
L
U
U
Y
Y
Ệ
Ệ
N
N
K
K
Ỹ
Ỹ
N
N
Ă
Ă
N
N
G
G
T
T
O
O
Á
Á
N
N
1
1
1
1
T
T
H
H
P
P
T
T
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
Đ
Đ
Ú
Ú
N
N
G
G
,
,
S
S
A
A
I
I
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
T
T
R
R
Ả
Ả
L
L
Ờ
Ờ
I
I
N
N
G
G
Ắ
Ắ
N
N
Đ
Đ
Ạ
Ạ
O
O
H
H
À
À
M
M
V
V
À
À
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
DUNG
LƯỢNG
NỘI DUNG BÀI TẬP
1 FILE
14 trang
TRẮC NGHIỆM ĐÚNG, SAI ĐẠO HÀM (THUẦN TÚY)
1 FILE
8 trang
TRẮC NGHIỆM ĐÚNG, SAI ĐẠO HÀM (ỨNG DỤNG THỰC TẾ)
1 FILE
10 trang
TRẮC NGHIỆM TRẢ LỜI NGẮN ĐẠO HÀM (THUẦN TÚY)
1 FILE
6 trang
TRẮC NGHIỆM TRẢ LỜI NGẮN ĐẠO HÀM (ỨNG DỤNG THỰC TẾ)
3
ĐẠO HÀM LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG SAI (THUẦN TÚY)
______________________________
Câu 1. Dùng định nghĩa để tính đạo hàm của hàm số
2
( ) 2y f x x x
tại điểm
0
1
x
. Khi đó:
a)
1
( ) (1)
(1) lim
1
x
f x f
f
x
b)
2
1
2 3
(1) lim
1
x
x x
f
x
c)
1
(1) lim 4
x
f x
d)
(1) 5
f a a
Câu 2. Dùng định nghĩa để tính đạo hàm của hàm số
( )
x
f x
tại điểm
0
0
x
ta được
(0)
f a
. Xét tính
đúng, sai của các khẳng định sau
a)
0
( ) (0)
lim
0
0
x
f
f x f
x
b)
0
'
4
l0 im
1
x
x
f
c) Phương trình
3 3
x
có nghiệm bằng
2
x a
d)
log 9 3
a
Câu 3. Dùng định nghĩa để tính đạo hàm của hàm số
3
( ) 2f x x
. Khi đó:
a) Với bất kì
0
x
:
0
0
0
0
( )
lim
x x
f
f
x f x
x
x
x
b)
(1) 6
f
c) Giá trị nhỏ nhất của
f x f x
là một số lớn hơn – 7.
d) Tiếp tuyến của đồ thị tại điểm có hoành độ
0
x
cắt trục hoành tại điểm có hoành độ dương.
Câu 4. Dùng định nghĩa để tính đạo hàm của hàm số
2
( )
1
f x
x
với
1x
. Khi đó:
a) Với bất kì
0
1
x
, ta có:
0
0
0
2
lim
(1 ) 1
x x
f
x
x
x
b)
(2) 2
f
c)
1
(3)
3
f
d)
3
(2) (3)
2
f f
Câu 5. Cho hàm số
3
( ) 2y f x x
có đồ thị
( )C
và điểm
M
thuộc
( )C
có hoành độ
0
1
x
. Xét tính đúng,
sai của các khẳng định
a) Phương trình
2
6 1
x f x x f
có hai nghiệm phân biệt cùng dương.
b) Tiếp tuyến của
( )C
tại
M
cắt đồ thị hàm số
2
8 7 4
y x x
tại hai điểm phân biệt có tổng hoành độ
bằng 5.
c) Tiếp tuyến của
( )C
tại
M
cắt đường thẳng
: 3d y x
tại điểm có hoành độ bằng 4.
d) Tiếp tuyến của
( )C
tại
M
vuông góc với đường thẳng
1
:
6
y x
.
Câu 6. Cho hàm số
2
( )
1
f x
x
có đồ thị là đường cong
( )C
và xét điểm
(3; 1) ( )M C
. Xét tính đúng, sai
của các mệnh đề
a)Đạo hàm của hàm số luôn nhận giá trị dương với mọi giá trị
1x
.
b) Tiếp tuyến của
( )C
tại điểm
M
song song với đường thẳng
y x
c)
2
3
2
(1 2 )f x
x
.
d) Tiếp tuyến của đường cong tại điểm
0 0
;N x y
tạo với hai trục tọa độ một tam giác vuông cân, khi đó
2
0 0
2 1
x x
.
4
Câu 7. Cho hàm số
2cosy f x x x
và
a) Vi phân của hàm số là
1 4sin cos
2 2
x x
dy dx
.
b) Tập giá trị của hàm số
f x
là một đoạn có độ dài bằng 4.
c) Phương trình
3cos 1f x x
có 2 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
c) Tồn tại 2 điểm có hoành độ
0;2
sao cho tiếp tuyến của đồ thị hàm số tại điểm đó song song với đường
thẳng
2 2024
y x
.
Câu 8. Cho hàm số
2
3 1y x x
có đồ thị
( )C
. Xét tiếp tuyến của
( )C
tại giao điểm của
( )C
với trục tung.
Xét tính đúng, sai của các mệnh đề
a) Phương trình
3 4 17
y y y
có hai nghiệm phân biệt với tổng hai nghiệm bằng 5.
b) Tiếp tuyến đã cho đi qua điểm
1;3
A
.
c) Tiếp tuyến đã cho cắt đường thẳng
2 1y x
tại điểm có hoành độ bằng
0
d) Tiếp tuyến đã cho tiếp xúc với đồ thị hàm số
4 2
4
y x x
tại tiếp điểm có tung độ nhỏ hơn 3.
Câu 9. Cho hàm số
sin
x
y e x
. Xét tính đúng, sai của các khẳng định
a) Vi phân của hàm số là
cos sin
x
x x
dy dx
e
.
b)
cos
x x
y e ye x
.
c) Tồn tại đúng 2 giá trị nguyên m để phương trình
2
x
y e m
có nghiệm.
d)
2 2 0
y y y
.
Câu 10. Xét đồ thị hàm số
9
1
x
f x
x
và đường thẳng
d
là tiếp tuyến vuông góc với đường thẳng
: 2 2 0
d x y
. Xét tính đúng, sai của các mệnh đề
a) Có hai phương trình tiếp tuyến
d
thỏa mãn bài toán.
b) Một trong hai tiếp tuyến đi qua điểm
1;5
A
.
c)
2
2
2
8(2 1)
2
3
x
f x x
x x
.
d)Tồn tại ba tiếp tuyến của đồ thị hàm số tạo với hai trục tọa độ một tam giác cân.
Câu 11. Cho hàm số
4
.
x
y x e
. Xét tính đúng sai của các mệnh đề sau
a)Tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1 có hệ số góc
4
5k e
.
b)
4
' 4
x
y e y
.
c)Phương trình
2
' 1 4 2
x
y x e
có đúng 1 nghiệm dương
d) Hàm số đã cho có đạo hàm cấp hai
4
.
x
y a bx e
với
2 2
41
a b
.
Câu 13. Cho hàm số
2
2
y x x
. Xét tính đúng sai của các mệnh đề sau
a)
3
. 1 0
y y
b)
3
. 1
y y
c)
3 2
1
( 2 ).y x x y
y
. d)
3
2
1
2
y
x x
.
Câu 14. Cho hàm số
3 2
2 6 1
f x x x m
. Xét tính đúng sai của các mệnh đề
a)
2
' 6 6f x x x
.
b)
2 2 10
f f
.
c) Giá trị nhỏ nhất của
'f x
bằng – 7.
d) Tồn tại hai giá trị
,a b
thỏa mãn
0
f a f b
thì có 7 số nguyên
m
để
,
f a f b
trái dấu.
Câu 15. Cho hàm của hàm số
3 2
3 5f x x x x
. Xét tính đúng sai của các mệnh đề sau
5
a)
2
3 6 1,f x x x x
b)
1 2
f
c)
1 2;0
f x x
d)
2 1
f x x
Câu 16. Cho hàm của hàm số
2 1
1
x
f x
x
. Xét tính đúng sai của các mệnh đề sau
a)
2
3
, 1
1
f x x
x
b)
0 3
f
c)
0 1
f x x
d) Phương trình
1
3
f x
có nghiệm duy nhất.
Câu 17. Cho hàm số
3 2
1y x ax bx
thỏa mãn
0 1 1
y y
. Xét tính đúng sai của các mệnh đề
a)
2
3 2
y x ax b
. b)
0
a b
.
c) Giá trị nhỏ nhất của
2 2
a b
bằng 1. d)
1 2
y
.
Câu 18. Cho hàm của hàm số
sin2f x x
. Xét tính đúng sai của các mệnh đề sau
a)
cos2 ,f x x x
b)
2
2
f
c)
4; 4 ,f x x
d)
2 2,f x x
Câu 19. Cho hàm của hàm số
2
x
f x
. Xét tính đúng sai của các mệnh đề sau
a)
2 ln2,
x
f x x
.
b)
2,f x x
.
c) Phương trình
x
f x e
có nghiệm duy nhất thuộc khoảng
0;1
.
d)
1 2ln 2
f
.
Câu 20. Cho hai hàm số
2
1f x x x
và
3g x x
. Xét tính đúng sai của các mệnh đề sau
a)
2 1f x x
.
b)
.
f x g x
có giá trị nhỏ nhất bằng 2.
c)
17,f g x x
.
d).
2 1000 1
f m g m
.
Câu 21. Cho hàm số
2
( )
x
y ax bx c e
với
0
b
. Xét tính đúng sai của các mệnh đề sau
a) Đạo hàm của hàm số đã cho bằng
2
(2 )
x
ax a b x b c e
.
b)
1 3 2
y a b c e
.
c) Khi hàm số có đạo hàm bằng có đạo hàm là
2
3
x
y ax ax b c e
thì
a b
.
d) Khi hàm số có đạo hàm là
2
3 1
x
y ax a x b c e
thì biểu thức
9
M a
b
có giá trị nhỏ nhất bằng
7.
Câu 22. Cho hàm số
3 2
1
( 6) 1
3
y f x x mx m x
. Xét tính đúng, sai của các khẳng định
a)Vi phân của hàm số đã cho là
2
2 6
dy x mx m dx
.
b) Tồn tại bao 4 giá trị nguyên m thuộc
10;10
để phương trình
0
y
vô nghiệm.
c) Tiếp tuyến của đồ thị hàm số có hệ số góc nhỏ nhất tại điểm có hoành độ
x m
.
6
d)Đạo hàm cấp hai của hàm số hợp
x
f e
là
3 2
3 6 ( 6)
x x x
e me m e
.
Câu 23. Đạo hàm
f x F x
của hàm số
3 2
9
6
2
F x x x mx
có bảng xét dấu sau đây.
Xét tính đúng sai của các mệnh đề sau
a)
2
3 9
f x x x m
.
b)
7 (1) 9
F
.
c) Đạo hàm của hàm số hợp đạt giá trị nhỏ nhất bằng
27
8
.
d) Tiếp tuyến của đồ thị hàm số
f x
tại điểm có hoành độ bằng 2 cắt trục tung tại điểm có tung độ lớn hơn – 5.
Câu 24. Cho hai hàm số
3
1
f x
x
và
2
2
x
g x
x
. Xét tính đúng sai của các mệnh đề sau
a)
2
3
, 1
1
f x x
x
.
b)
2
2
4
' , 2
2
x x
g x x
x
.
c)
. ' ' . ' , \ 1; 2
f x g x f x g x x
.
d) Phương trình
2
3 1 0
f x x
có nghiệm duy nhất
2; 1
.
Câu 25. Cho bốn hàm số
sinf x x
,
cosg x x
,
tanh x x
và
cotk x x
.
Xét tính đúng sai của các mệnh đề sau
a)
cos ,f x x x
. b)
1;1 ,g x x

.
c)
2
1
' ,
cos 2
h x x k k
x
. d)
' ' tan 1k x h x x
.
Câu 26. Cho
y
là hàm số của
x
thỏa mãn phương trình
siny x
.
Xét tính đúng sai của các mệnh đề sau
a) Đạo hàm của hàm số
y
là
cos
y x
.
b) Tồn tại 2 giá trị nguyên m để phương trình
y y m
có nghiệm.
c) Đạo hàm cấp hai của hàm số
y
là
2
sin

y x
.
d) Giá trị nhỏ nhất của hàm số
2
y y
là một số lớn hơn 2.
Câu 27. Cho hàm số
1
3y x
x
. Xét tính đúng sai của các mệnh đề sau
a) Phương trình
0
y
có hai nghiệm phân biệt đối nhau.
b)
2
2 6x y xy x
.
c)Hàm số
y y
có giá trị nhỏ nhất 3 bằng với
0
x
.
d)
2
3 2 6
x y xy y

.
Câu 28. Cho hàm số
3 2
3 2 4
y x x m m
. Xét tính đúng sai của các mệnh đề sau
a)
0
y
có hai nghiệm phân biệt.
b)
2
3 3y m m
.
c)
y
đạt giá trị lớn nhất tại
0
x
.
d) Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 có đặc điểm song song với trục hoành và cách trục
hoành một khoảng không vượt quá 5.
Câu 29. Cho hàm số
2 sin 3cosy f x x x
. Xét tính đúng sai của các mệnh đề sau
a)
' 2 cos 3 sin ,f x x x x
.
7
b) Nếu
thỏa mãn
0
f
thì
12
tan 2
5
.
c) Hàm số
f x

có giá trị lớn nhất là một số nguyên.
d) Phương trình
0
f x
có 4 nghiệm phân biệt thuộc khoảng
0; 4
.
Câu 30. Cho hàm số
2 1
1
x
y f x
x
. Xét tính đúng sai của các mệnh đề sau
a)
2
3
' , \ 1
1
f x x
x
.
b) Tồn tại tiếp tuyến của đồ thị hàm số mà tiếp tuyến đó có hệ số góc bằng
2023
.
c) Phương trình
6
f x

có nghiệm lớn hơn
2
.
d) Điều kiện tham số để phương trình
'f x kf x
có hai nghiệm phân biệt là
3
8
k
.
Câu 31. Cho hàm số
3 2
1
( ) 4 6
3
f x x x mx
. Xét tính đúng, sai của các khẳng định
a) Với
0
m
, phương trình
0
f x
có hai nghiệm phân biệt với tổng bằng 6.
b) Khi tiếp tuyến của đồ thị hàm số có hệ số góc nhỏ nhất thì hoành độ tiếp điểm bằng 4.
c)
2 8
x x
f e e
.
d) Nếu có hai số
,a b
phân biệt thỏa mãn điều kiện
0
f a f b
và
2 3 22
a b
. thì
3 3
f
.
Câu 32. Cho hàm số
2 3 khi 1
1
khi 1
x x
f x
x
x
. Xét tính đúng sai của các mệnh đề sau
a) Hàm số
f x
liên tục tại
1x
.
b) Hàm số
f x
có đạo hàm tại
1x
.
c) Hàm số
f x
liên tục tại
1x
và hàm số
f x
cũng có đạo hàm tại
1x
.
d) Hàm số
f x
không có đạo hàm tại
1x
.
Câu 33. Cho hàm số
2
4
f x x
và
3 2g x x
. Xét tính đúng sai của các mệnh đề sau
a) Vi phân hàm số
2
4
f x x
là
2
4
x
dx
x
.
b) Đạo hàm của hàm số
f x
tại
3
x
bằng
3 5
5
.
c) Đạo hàm của hàm số
f g x
tại
3
x
bằng
7 5
5
.
d) Đạo hàm của hàm số
g f x
tại
3
x
bằng
3 5
5
.
Câu 34. Cho hai hàm số
3 2
3 1f x x x mx
và
2
5
g x x mx m
. Xét tính đúng, sai của các khẳng
định
a)
1 3
f m
.
b) Phương trình
f x g x
có tổng tất cả các nghiệm nhỏ hơn 3.
c)
2
3 6
f g x g x g x m
.
d) Biết
0
m
là giá trị của tham số
m
để hai số phân biệt
1 2
,x x
thỏa mãn
1 2
0
f x f x
và
2 2
1 2 1 2
13
x x x x
. Khi đó
0
15; 7
m
Câu 35. Cho hàm số
3 2
1
3 2
x mx
f x
có đồ thị là đường cong
m
C
. Xét tính đúng, sai của các khẳng định
sau
a)Phương trình
0
y
luôn luôn có nghiệm.
8
b)
2
2 2f m m
.
c) Gọi A là điểm thuộc đồ thị, A có hoành độ bằng 1. Với
4m
thì tiếp tuyến tại A song song với đường thẳng
5y x
.
d)Xét hàm số
2
2 3
g x f x x
, với
2
m
thì phương trình
0
g x
có hai nghiệm phân biệt.
Câu 36. Cho hàm số
3 2 2
3 2 4 2
f x x x mx m
. Xét tính đúng, sai của các khẳng định sau
a).
2
9 4 4f x x x m
.
b) Phương trình
0
f x
có hai nghiệm phân biệt khi
1
19
m
.
c) Điều kiện tham số
m
để
f x
luôn dương với mọi
0;x
là
0
m
.
d)
2 4 2
1 2 9 24 13 4f x x x x m
.
Câu 37. Cho hàm số
sin
x
y e x
. Xét tính đúng, sai của các khẳng định
a).
1
2
y y y
b)
(sin cos )
x
y e x x
c)Phương trình
5 sin
x
y e x
có 4 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
d)
2 cos
x
y e x
.
Câu 38. Cho hàm số
1
x
y xe
. Xét tính đúng, sai của các khẳng định
a)
2
x y xy y
b)
1
1
1
x
y e
x
c)
3
0
x y xy y
d)
3
2 3 0
x y xy y
Câu 39. Cho hàm số
2
1
3
x
y f x
x
. Khi đó:
a)
2
2
cos 6 cos 1
cos
(cos 3)
x x
f x
x
.
b) Tổng các nghiệm của phương trình
' 0
y
bằng
6
.
c) Đồ thị của hàm số
'y
đi qua điểm
3
1;
2
A
.
d) Tiếp tuyến
d
của đồ thị hàm số tại điểm có hoành độ bằng 1 cắt đường phân giác góc phần tư thứ nhất tại
điểm có hoành độ lớn hơn 1.
Câu 40. Cho hàm số
2
1
1
y f x
x
. Xét tính đúng, sai của các khẳng định
a)Vi phân của hàm số là
2 2
( 1) 1
x
dy dx
x x
.
b) Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 2 đi qua điểm
3 5
3;
25
.
c)
sin cos
tan
cos
x x
f x
x
.
d)
3 5
'' ' 3
xy y x y
Câu 41. Cho hàm số
2
3
4 2 3
2
x
y f x x x
có đồ thị
( )C
. Xét tính đúng – sai của các mệnh đề
a) Biết
2
'
y ax bx c
khi đó
10
a b c
.
b) Phương trình
y y m

có hai nghiệm phân biệt có tổng bình phương bằng 10 thì giá trị tham số m thu
được là một số nguyên.
9
c)
2
cos 12cos cos 2
xf x x
.
d) Phương trình tiếp tuyến của đồ thị
( )C
tại điểm giao điểm với trục tung song song với đường thẳng
2
2
y x m
với m là tham số.
Câu 42. Cho hàm số
2
3f x x x
có đồ thị
C
và hàm số
lng x x
. Xét tính Đúng – Sai của mỗi khẳng
định sau
a)
2
1 1
1
3 2
1 lim lim 1
1 1
x x
f x f
x x
f
x x
b) Tiếp tuyến của đồ thị
C
tại điểm có hoành độ
1x
có phương trình:
1y x
.
c) Bất phương trình
3
g x
có tập nghiệm
1
;
3
.
d) Đặt
.
h x f x g x
, khi đó phương trình
2
2. .
h x x x h x
có nghiệm thuộc khoảng
1;1
.
Câu 43. Cho hàm số
4
1
y
x
. Xét tiếp tuyến của đồ thị hàm số
4
1
y
x
tại điểm có hoành độ
0
1
x
. Xét
tính đúng, sai của các mệnh đề
a) Hệ số góc của tiếp tuyến bằng
1.
b) Tiếp tuyến đi qua điểm
1;2
M
.
c) Tiếp tuyến cắt đường thẳng
2 1y x
tại điểm có hoành độ bằng
4
3
.
d) Tồn tại 3 đường tiếp tuyến
d
của đồ thị hàm số mà
d
tạo với hai trục tọa độ một tam giác vuông
OAB
thỏa
mãn
4OA OB
.
Câu 44. Cho hàm số
2
x x
y f x e
. Xét tính đúng, sai của các khẳng định
a) Vi phân của hàm số là
2
2 1
x x
dy x e dx
.
b) Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 cắt parabol
2
y x
tại hai điểm phân biệt nằm về
hai phía trục tung.
c) Phương trình
0
f x
có hai nghiệm
1
x
,
2
x
thỏa mãn
1 2
1
.
4
x x
.
d)
2
sin 2 sin 2
sin 2 cos 2 sin 4
x x
f x x x e
.
Câu 45. Cho hàm số
2
2
y f x x x
. Xét tính đúng, sai của các mệnh đề
a)Vi phân của hàm số là
2
1
2
x
dy dx
x x
.
b)Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 song song với đường thẳng
2
3
x
y
.
c)
3 2
2
4 3 2
2 3 6 2
2 3 2
x x x
f x x
x x x x
.
d) Giá trị biểu thức
3 2
. 2 .
M y y x x y x
là một số nguyên tố.
Câu 46. Cho hàm số
siny f x x x
. Xét tính đúng, sai của các khẳng định
a)Vi phân của hàm số đã cho là
cos sin
dy x x x dx
.
b)
2 2sinxy y xy x
.
c)
4 cos sinxy y xy x x x
.
d)Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
2
x
có phương trình
2
3
2 4
y x
.
Câu 47. Cho hàm số
2
3
4 2 3
2
x
y x x
, biết
2
'
y ax bx c
. Khi đó:
a)
10
a b c
b) Phương trình
' 0
y
có hai nghiệm phân biệt
10
c) Đồ thị hàm số
'y
cắt trục tung tại điểm
0; 2
d) Đồ thị hàm số
'y
cắt đường thẳng
3
y
tại hai điểm phân biệt
Câu 48. Cho hàm số
4 2
1
4 3 2y x x x
x
. Khi đó:
a)
3
' 1
2
y
b) Đồ thị của hàm số
'y
đi qua điểm
3
1;
2
A
c)
3597
' 4
16
y
d) Điểm
M
thuộc đồ thị
( )C
của hàm số
4 2
1
4 3 2y x x x
x
có hoành độ
0
1
x
. Khi đó, phương trình
tiếp tuyến của
( )C
tại
M
vuông góc với đường thẳng
2
3
y x
Câu 49. Cho hàm số
3
2 1
x
y
x
. Khi đó:
a)
' 0 7
y
b) Đồ thị của hàm số
'y
đi qua điểm
7
1;
3
A
c)
' 1 ' 2
y y
d) Điểm
M
thuộc đồ thị
( )C
của hàm số
3
2 1
x
y
x
có hoành độ
0
0
x
. Khi đó, phương trình tiếp tuyến của
( )C
tại
M
song song với đường thẳng
7 2024
y x
Câu 50. Cho hàm số
2
1
3
x
y
x
. Khi đó:
a)
3
' 1
2
y
b) Tổng các nghiệm của phương trình
' 0
y
bằng
6
c) Đồ thị của hàm số
'y
đi qua điểm
3
1;
2
A
d)
' 1 ' 2
y y
.
Câu 51. Cho hàm số
2
( 2 3) 3 1
y x x x
. Khi đó:
a)
' 1 31
y
b) Tổng các nghiệm của phương trình
' 0
y
bằng
3
c) Đồ thị của hàm số
'y
đi qua điểm
0; 7
A
d)
' 1 ' 2
y y
Câu 52. Cho hàm số
(2 3)(4 1)
y x x
. Khi đó:
a)
' 1 13
y
b)
' 1 ' 25 22
y y
c) Đồ thị của hàm số
'y
đi qua điểm
25; 9
A
.
d)
' 1 ' 2
y y
Câu 53. Cho hàm số
3
1
y f x x
. Dùng định nghĩa đạo hàm tính đạo hàm của hàm số
f x
tại
2
x
.
Khi đó các mệnh đề sau đúng hay sai?
a) Có
2
2
lim ' 2
2
x
f x f
f
x
.
11
b) Với
0
h
, ta có
0
2 2
lim 10
h
f h f
h
.
c) Tiếp tuyến của đồ thị hàm số
y f x
tại điểm
2;7
M
có hệ số góc là
12
.
d)
2
2 2
lim ' 2 2
2
x
f x xf
f
x
.
Lời giải
a) Đúng
b) Sai
c) Đúng
d) Sai
a) Theo định nghĩa đạo hàm ta có
2
2
lim ' 2
2
x
f x f
f
x
nên suy ra mệnh đề đúng.
b) Ta có:
3 2
2
0 0 0
2 2
6 12
lim lim lim 6 12 12.
h h h
f h f
h h h
h h
h h
Suy ra mệnh đề sai.
c) Ta có
2;7
M
thuộc đồ thị của hàm số
y f x
, nên tiếp tuyến của đồ thị hàm số tại M có hệ số góc là
' 2 12.
f
Suy ra mệnh đề đúng.
d) Ta có:
2 2
2 2
2 2
2 2 2 2 2 2 2 2
lim lim
2 2
2 2 2 2 2 2
lim lim
2 2
2
2
2lim 2 .lim 2 ' 2 2
2 2
x x
x x
x x
f x xf f x f f xf
x x
f x f f xf
x x
f x f
x
f f f
x x
Suy ra mệnh đề sai
Câu 54. Cho hàm số
y f x
có đồ thị
C
, biết
3 5, ' 3 6
f f
.
Các mệnh đề sau đúng hay sai?
a) Có
3
3
lim 9
3
x
f x f
x
.
b) Tiếp tuyến của
C
tại điểm có hoành độ bằng
3
song song với đường thẳng
3 7 0.
x y
c) Tiếp tuyến của
C
tại điểm
3; 3
M f
có phương trình là
6 10
y x
.
d) Tiếp tuyến của
C
tại điểm
3; 3
M f
cách điểm
6; 11
I
một khoảng bằng
6
.
Lời giải
a) Sai
b) Sai
c) Sai
d) Sai
a) Ta có:
3
3
lim ' 3 6
3
x
f x f
f
x
suy ra mệnh đề sai
b Tiếp tuyến của
C
tại điểm có hoành độ bằng
3
hệ số góc
' 3 6
f
đường thẳng
3 7 0 3 7
x y y x
có hệ số góc bằng
3
.
Suy ra mệnh đề sai
c) Tiếp tuyến của
C
tại điểm
3; 3
M f
có phương trình là
3 ' 3 3 5 6 3 6 13
y f f x y x y x
. Suy ra mệnh đề sai.
d) Tiếp tuyến của
C
tại điểm
3; 3
M f
là
: 6 10 6 10 0
y x x y
2 2
6.6 11 10
; 37
6 1
d I
. Suy ra mệnh đề sai
Câu 55. Cho hàm số
2
3 6
y f x x x
có đồ thị
C
. Xét phương trình tiếp tuyến của
C
tại giao điểm
I
của
C
với trục tung. Các mệnh đề sau đúng hay sai?
a) Tiếp tuyến có hệ số góc
3
.
b) Giao điểm của tiếp tuyến này với trục hoành có hoành độ lớn hơn
3
.
c) Tiếp tuyến này cắt các trục
,Ox Oy
tại A, B và diện tích
ABC
là
12
.
d) Tiếp tuyến này đi qua tâm đường tròn đường kính
OD
với
6;6
D
.
12
Câu 56. Cho hàm số
2 1
1
x
y
x
có đồ thị
C
và đường thằng
: 3 5y x
. Các mệnh đề sau đúng hay sai?
a) Có một tiếp tuyến của
C
song song với
.
b) Các tiếp tuyến của
C
luôn có hệ số góc âm.
c) Có đúng hai tiếp tuyến của
C
vuông góc với
.
d) Tiếp tuyến của
C
có hệ số góc
k
thoả phương
3
4 0
k
có hoành độ tiếp điểm dương đi qua
1 1
;
2 6
K
.
Câu 57. Cho hàm số
3
1
y f x
x
. Các mệnh đề sau đúng hay sai?
a) Có
2
3
'
1
f x
x
.
b) Có
' 2 3
f
.
c) Luôn có tiếp tuyến của
C
song song với đường thẳng
3 5y x
.
d) Bất phương trình
1
' 0
12
f x
có tích của nghiệm nguyên âm nhỏ nhất và nghiệm nguyên dương lớn nhất
là
30
.
Câu 58. Dùng định nghĩa để tính đạo hàm của hàm số
2
( ) 3y f x x x
tại điểm
0
1
x
. Các mệnh đề sau
đúng hay sai?
a)
1
( ) (1)
(1) lim
1
'
x
f x f
f
x
.
b)
2
1
3 4
(1) lim
1
'
x
x x
f
x
.
c)
1
lim 4
' 1
x
f x
.
d)
6
'(1)f a a
.
Câu 60. Cho hàm số
3
( ) 2y f x x
có đồ thị
( )C
và điểm
M
thuộc
( )C
có hoành độ
0
1
x
. Các mệnh đề
sau đúng hay sai?
a) Hệ số góc của tiếp tuyến của
( )C
tại điểm
M
bằng
6
b) Phương trình tiếp tuyến của
( )C
tại
M
đi qua điểm
0; 4
A
.
c) Phương trình tiếp tuyến của
( )C
tại
M
cắt đường thẳng
: 3d y x
tại điểm có hoành độ bằng 4.
d) Phương trình tiếp tuyến của
( )C
tại
M
vuông góc với đường thẳng
1
:
6
y x
.
Câu 61. Cho hàm số
f x
xác định trên
( ; )a b
tại
0
( ; )
x
a b
. Các mệnh đề sau đúng hay sai?
a)
0
0
0
0
lim
x x
f x f x
f x
x x
.
b) Nếu
6 ( ; )a b
và
2
6f
thì
6
6
lim 6
6
x
f x f
x
.
c) Hàm số
3 2
2f x x x
có
3 2
2
2
lim 4
2
2
x
x x
f
x
.
d) Hàm số
2
1
x
f x
x
có
2
2
lim 0
( 1)( 2
2
)
x
x
f
x x
.
Câu 62. Dùng định nghĩa để tính đạo hàm của hàm số
3
1
( ) 4f x x
. Các mệnh đề sau đúng hay sai?
a) Với bất kì
0
x
:
0
0
0
0
( )
lim
x x
f
f
x f x
x
x x
.
b)
(1) 12
f
.
c)
5
( )
( 5) l
5
im
5

x
f x f
f
x
.
13
d)
2
a > 0.
f a
Câu 63. Dùng định nghĩa để tính đạo hàm của hàm số
2
( )
1
x
f x
x
tại điểm
0
0
x
ta được
(0)
f a
. Các
mệnh đề sau đúng hay sai?
a)
0
( ) (0)
lim
0
0
x
f
f x f
x
. b)
0
'
4
l0 im
1
x
x
f
.
c)
3
3
16
f
. d)
2 4
f
.
Câu 64. Cho hàm số
3
( ) 2y f x x
có đồ thị
( )C
và điểm
M
thuộc
( )C
có hoành độ
0
1
x
. Các mệnh đề
sau đúng hay sai?
a) Hệ số góc của tiếp tuyến của
( )C
tại điểm
M
bằng
6
.
b) Phương trình tiếp tuyến của
( )C
tại
M
đi qua điểm
0; 4
A
.
c) Phương trình tiếp tuyến của
( )C
tại
M
cắt đường thẳng
: 3d y x
tại điểm có hoành độ bằng 4.
d) Phương trình tiếp tuyến của
( )C
tại
M
vuông góc với đường thẳng
1
:
6
y x
.
Câu 65. Cho hàm số
3
5
( ) 2
3
f x x x
.Các mệnh đề sau đúng hay sai?
a) Với bất kì
0
x
:
0
0
0
0
( )
lim
x x
f
f
x f x
x
x
x
.
b)
2
5 2f x x x
.
c)
1 7
f
.
d) Giả sử
3
5
( ) 2
3
f x x x
là phương trình chuyển động của một chất điểm
( )f x
tính bằng mét
,m
x
tính bằng
giây
s
. Gia tốc a của chất điểm tại thời điểm
5x s
là
2
50 / . = a m s
Câu 66. Cho hàm số
2
4y x x
. Các mệnh đề sau đúng hay sai?
a) Đạo hàm của hàm số
2
4y x x
tại điểm
0
1
x
bằng
4
.
b) Hệ số góc của tiếp tuyến của đồ thị hàm số đã cho tại điểm
0
0
x
bằng
2
.
c) Phương trình tiếp tuyến của parabol tại điểm
0
1
x
là
2 1y x
.
d) Phương trình tiếp tuyến của parabol tại điểm có tung độ
0
4
y
là
2 1y x
.
Câu 67. Cho bất phương
2 5 8
x y
. Các mệnh đề sau đúng hay sai? Cho hàm số
4
y f x x
. Các mệnh
đề sau đúng hay sai?
a) Đạo hàm của hàm số tại điểm
0
1
x
là
( 1) 4
f
b) Giao điểm của đồ thị hàm số với trục tung là
(0;0)
O
.
c) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng
1
là
4 3.
y x
d) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hệ số góc bằng 4 là
4 1y x
.
Câu 68. Cho hàm số
3 2
3 2.
y x x
Các mệnh đề sau đúng hay sai?
a) Đạo hàm của hàm số tại điểm
0
1
x
bằng
4
.
b) Hệ số góc của tiếp tuyến tại điểm
0
0
x
bằng
0
.
c) Phương trình tiếp tuyến của đồ thị hàm số song song với đường thẳng
9 7y x
là
9 25.
y x
d) Phương trình tiếp tuyến của đồ thị hàm số vuông góc với đường thẳng
1
45
y x
là
45 173; 45 83.
y x y x
Câu 69. Cho hàm số
3
y x
. Các mệnh đề sau đúng hay sai?
a) Đạo hàm của hàm số tại điểm
0
2
x
bằng
4
.
b) Hệ số góc của tiếp tuyến tại điểm
0
1
x
bằng
1
.
c) Phương trình tiếp tuyến của đồ thị hàm số tại điểm
1; 1
là
3 2.
y x
d) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ bằng 8 là
12 16.
y x
Câu 70. Cho hàm số
3 2
2 3 4 1y x x x
. Các mệnh đề sau đúng hay sai?
14
a) Có
2
6 6 4
y x x
.
b)
( 3) 67
y
.
c) Phương trình tiếp tuyến của đồ thị hàm số tại điểm
1; 2
M
là
4 2
y x
.
d) Một vật chuyển động có phương trình là
3 2
( ) 2 3 4 1 ( )s t t t t m
trong đó
t
là thời gian tính bằng giây, thì
vận tốc tức thời của vật tại thời điểm
3( )t s
bằng
2
40 /s
m
.
Câu 71. Cho hàm số
cos sin cos 2 .f x x x x
Các mệnh đề sau đúng hay sai?
a) Có
sin cos 2sin 2 .f x x x x
.
b)
3 3 1
3 2
f
.
c) Có
2 ( ) 2.sin 2 2
f x x
d) Phương trình
1
f x
tương đương với phương trình
sin 1 cos 1 0.
x x
Câu 72. Cho hàm số
26 10
( )
5
x
f x
x
.
Các mệnh đề sau đúng hay sai?
a) Hàm số luôn xác định với mọi
x
.
b)
120
(2)
49
f
.
c) Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm
5;14
M
bằng
5
6
d) Dân số (tính theo nghìn người) của một thành phố được cho bởi công thức
26 10
( )
5
t
f t
t
, trong đó
t
(được
tính bằng năm) là khoảng thời gian tính từ năm 2015. Thì tốc độ tăng dân số
( )f t
trong năm 2025 của thành
phố đó là
8
5
Câu 73. Cho hàm số
2
3
3
x x
y
.
Các mệnh đề sau đúng hay sai?
a) Hàm số đã cho là hàm hợp của hai hàm số
2
3u x x
và
3
u
y
.
b) Có
1
2
3
y
c) Có
0, 2;y x
d) Phương trình
.ln 3 0
y y
có nghiệm duy nhất
Câu 74. Cho hàm số
3
4 2
3
6
x
y x x x
, biết
2
y ax bx c
. Khi đó:
a)
10
a b c
.
b) Phương trình
0
y
có hai nghiệm phân biệt.
c) Đồ thị hàm số
y y x
cắt trục tung tại điểm
0; 2
.
d) Đồ thị hàm số
y y x
cắt đường thẳng
3
y
tại hai điểm phân biệt.
Câu 75. Cho hàm số
3 2
1
2 1
3
y x x x
có đồ thị là
C
. Các mệnh đề sau đúng hay sai?
a)
'(1) 1
y
.
b)
2
'
y ax bx c
khi đó
5
a b c
.
c) Đồ thị hàm số
'y
đi qua điểm
2;3
M
.
d) Bất phương trình
' 1
y
có
3
nghiệm nguyên .
Câu 76. Cho hàm số
2 1
( )
1
x
y f x
x
có đồ thị
C
. Các mệnh đề sau đúng hay sai?
a)
'(2) 1
y
.
b)
' 0, 1y x
.
c) Đồ thị hàm số
'y
đi qua điểm
2;3
M
.
d) Phương trình tiếp tuyến của
C
song song với đường thẳng
3y x
là
3 1y x
và
3 11.
y x
15
Câu 77. Cho hàm số
2
4 4
1
x x
y
x
. Các mệnh đề sau đúng hay sai?
a) Tập xác định của hàm số đã cho là
\{1}.
b) Đồ thị hàm số
y
cắt trục tung tại điểm có tung độ bằng
4
.
c)
'(3) '(2)
y y
.
d) Tập nghiệm của bất phương trình
' 0
y
là
0;1
.
Câu 78. Cho hàm số
2
2 .f x x x
Các mệnh đề sau đúng hay sai?
a) Hàm số
f x
xác định khi
2
2 0.
x x
b)
2
'
2
ax b
f x
x x
, khi đó
2
a b
.
c) Phương trình
' 0
f x
có nghiệm
1
2
x
.
d) Tập nghiệm
S
của bất phương trình
'
f x f x
có
3
giá trị nguyên.
Câu 79. Cho hàm số
4 2
1
4 3 2y x x x
x
. Các mệnh đề sau đúng hay sai?
a)
3
1
2
y
.
b) Đồ thị của hàm số
y
đi qua điểm
3
1;
2
A
.
c) Đồ thị của hàm số
y
đi qua điểm
3597
4;
16
B
.
d) Điểm
M
thuộc đồ thị
( )C
của hàm số
4 2
1
4 3 2y x x x
x
có hoành độ
0
1
x
. Khi đó, phương trình
tiếp tuyến của
( )C
tại
M
vuông góc với đường thẳng
2
3
y x
.
Câu 80. Cho hàm số
3
2 1
x
y
x
. Các mệnh đề sau đúng hay sai?
a)
0 7
y
.
b) Đồ thị của hàm số
'y
đi qua điểm
7
1;
3
A
.
c)
1 2
y y
.
d) Điểm
M
thuộc đồ thị
( )C
của hàm số
3
2 1
x
y
x
có hoành độ
0
0
x
. Khi đó, phương trình tiếp tuyến của
( )C
tại
M
song song với đường thẳng
7 2024
y x
.
Câu 81. Cho hàm số
2
1
3
x
y
x
. Các mệnh đề sau đúng hay sai?
a)
3
1
2
y
.
b) Tổng các nghiệm của phương trình
0
y
bằng
6
.
c) Đồ thị của hàm số
y
đi qua điểm
3
1;
2
A
.
d)
1 2
y y
.
Câu 82. Cho hàm số
3
2
2 3
3
x
f x mx m x
. Xét tính đúng sai của các mệnh đề sau.
a) Đạo hàm của hàm số là
2
2 2
f x x mx m
.
b) Với
2
m
thì phương trình
' 0
f x
có một nghiệm
2
x
.
c)
2
m
thì bất phương trình
' 0
f x
có hai nghiệm nguyên phân biệt.
16
d) Số các giá trị nguyên của tham số
m
để
' 0
f x
với mọi
x
là
4
.
Câu 83. Hàm số
2 1x
y
x m
, với
m
là tham số. Các mệnh đề sau đúng hay sai?
a) Khi
2
m
thì hàm của hàm số là
2
5
, , 2
2
y x x
x
.
b) Với
x m
, hàm số có đạo hàm
2
2 1
m
y
x m
.
c) Với
m
thì phương trình
0
y
vô nghiệm.
d) Có duy nhất một giá trị nguyên âm của
m
để
0, 4;y x

.
Câu 84. Cho hàm số
2
( ) ln( 1) 2024
y f x x x
. Khi đó các mệnh đề sau đúng hay sai?
a)
2
1
1
1
f x
x
.
b)
0 1
f
.
c) Phương trình
0
f x
có hai nghiệm phân biêt.
d) Hàm số
y f x
có giá trị nhỏ nhất bằng
2
.
Câu 85. Cho hàm số
3 2
1
6 3
3
mx
y x m x
có đạo hàm là
y
. Khi đó:
a) Với
1
m
thì
1 6
y
.
b) Với
1
m
thì
10
y x
khi
3;1
x
.
c) Với
; 2 3;m
thì phương trình
0
y
có hai nghiệm phân biệt.
d) Tổng tất cả các giá trị của
m
để phương trình
0
y
có hai nghiệm phân biệt là
1 2
,x x
thỏa mãn
2 2
1 2
30
xx
là
4
.
Câu 86. Cho hàm số
2 1
5
x
y
x
có đồ thị
C
. Các mệnh đề sau đúng hay sai?
a) Hàm số có tập xác định
\ 5
D
.
b)
2
11
,
5
y x
x
.
c)
4 11
y
.
d) Diện tích tam giác tạo bởi tiếp tuyến của
C
tại điểm có hoành độ bằng
6
và hai trục tọa độ bằng
283
Câu 87. Cho hàm số
3
1 1y f x x m x
có đạo hàm
y
(với
m
là tham số ). Các mệnh đề sau đúng
hay sai?
a) Với
4
m
thì
1 0
f
.
b)Với
1
m
thì
5
f x
khi
1
x
.
c) Với
0
m
thì
6 1f x x
khi
; 2 0;x
 
.
d)Với
1
m
thì đạo hàm của hàm số
2 1
y f x
luôn dương với mọi
x
thuộc
.
Câu 88. Cho hàm số
lnf x x x
có đồ thị
C
. Các mệnh đề sau đúng hay sai?
a)
1
f x x
x
.
b)
f
1 1
.
c) Phương trình
2
f x
có một nghiệm nguyên dương.
d) Tiếp tuyến của đồ thị
C
tại điểm có hoành độ
0
x e
có phương trình
2 2y x e
.
______________________________
17
ĐẠO HÀM LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG SAI (ỨNG DỤNG THỰC TẾ)
_____________________________
Câu 1. Một chất điểm chuyển động thẳng xác định bởi phương trình
( )S t
, với
( )S t
là quãng đường có đơn vị là
( )m
. Các mệnh đề sau đúng hay sai?
a) Vận tốc của chất điểm được xác định bởi công thức
( )V S t
.
b) Gia tốc của chất điểm được xác định bởi công thức
( ) ( )a t V t
.
c) Vận tốc của chất điểm tại thời điểm
2
t
giây là
(2) (2)V S
.
d) Gia tốc của chất điểm tại thời điểm
2
t
giây là
(2) (2)
a S
.
Câu 2. Một viên đạn được bắn lên cao theo phương thẳng đứng có phương trình chuyền động
2
2 196 4,9s t t t
,
trong đó
0, ( )t t s
là thời gian chuyển động,
( )s m
là độ cao so với mặt đất.
Xét tính đúng sai của các mệnh đề sau
a) Sau
20s
kể từ khi bắn thì viên đạn đạt được độ cao
1962m
.
b) Vận tốc tức thời của viên đạn ngay khi viên đạn được bắn ra là
196 /m s
c) Vận tốc tức thời của viên đạn khi viên đạn đạt được độ cao
1962m
là
5 /m s
.
d) Tại thời điểm viên đạn đạt vận tốc tức thời bằng 98 m/s thì viên đạn đang ở độ cao
1472m
so với mặt đất.
Câu 3. Một tài xế đang lái xe ô tô, ngay khi phát hiện có vật cản phía trước đã phanh gấp lại nhưng vẫn xảy ra
va chạm, chiếc ô tô để lại vết trượt dài 20,4 m (được tính từ lúc bắt đầu đạp phanh đền khi xảy ra va chạm).
Trong quá trình đạp phanh, ô tô chuyển động theo phương trình
2
5
( ) 20
2
s t t t
, trong do
s
(đơn vị mét) 1à
độ dài quãng đường đi được sau khi phanh,
t
(đơn vị giây) là thời gian tính từ lúc bắt đầu phanh (
0 4t
).
Xét tính đúng sai của các mệnh đề sau
a) Vận tốc tức thời của ô tô ngay khi đạp phanh là
20( / )m s
b) Xe ô tô trên chưa chạy quá tốc độ, (tốc độ giới hạn cho phép là 70 km/h).
c) Thời điểm xảy ra va chạm cách thời điểm bắt đầu đạp phanh
6,8
giây
d) Vận tốc tức thời của ô tô ngay khi xảy ra va chạm là
14( / )m s
Câu 4. Phương trình chuyển động của một hạt được cho bởi công thức
10 2 sin 4
4
s t t
, trong đó
s
tính bằng centimet và
t
được tính bằng giây. Xét tính đúng sai của các mệnh đề sau
a) Gia tốc của hạt tại thời điểm
3t
giây là
2
16
2
cm/s
b) Vận tốc của hạt tại thời điểm
3t
giây là
2
cm/s
.
c) Vận tốc lớn nhất của hạt đạt được là
4 2
cm/s
.
d) Gia tốc nhỏ nhất của hạt đạt được là
2
16
2
cm/s
.
Câu 5. Một vật chuyển động trên đường thẳng được xác định bởi công thức
3 2
( ) 3 7 2s t t t t
, trong đó
0t
và tính bằng giây và
s
là quãng đường chuyển động được của vật trong
t
giây tính bằng mét. Xét tính
đúng, sai của các khẳng định sau
a) Tốc độ của vật tại thời điểm
2t
là
7( / )m s
b) Gia tốc của vật tại thời điểm
2t
là
2
6 /m s
c) Gia tốc của vật tại thời điểm mà vận tốc của chuyển động bằng
2
16 /m s
là
2
10 /m s
d) Thời điểm
1t
(giây) tại đó vận tốc của chuyển động đạt giá trị nhỏ nhất.
Câu 6. Một chất điểm chuyển động có quãng đường
S
được xác định bởi phương trình:
3 2
1
3
3
S t t t t
trong đó
0,t t
được tính bằng giây và
S
được tính bằng mét. Các mệnh đề sau đúng hay sai?
a) Phương trình vận tốc tức thời của chất điểm là
2
2 3v t t t
.
b) Tại thời điểm bắt đầu chuyển động, gia tốc tức thời của chất điểm bị triệt tiêu.
c) Tại thời điểm vận tốc tức thời của chất điểm nhỏ nhất, chất điểm chuyển động được quãng đường dài
14
3
mét.
d) Khi gia tốc tức thời của chất điểm không dương, vận tốc tức thời của chất điểm dao động trong phạm vi
2
m/s đến
3
m/s.
18
Câu 7. Một chất điểm bắt đầu chuyển động theo phương trình
3 2
2 3 5 8s t t t t
, trong đó
0t
, t tính
bằng giây và
s t
tính bằng mét. Các mệnh đề sau đúng hay sai?
a) Gia tốc tức thời của chất điểm là
2
12 6 /a t t m s
.
b) Gia tốc tức thời của chất điểm tại thời điểm
5t s
là
2
54 /m s
.
c) Gia tốc tức thời của chất điểm tại thời điểm vận tốc đạt giá trị nhỏ nhất là
2
0 /m s
.
d) Khi gia tốc bằng
2
6 /m s
thì quãng đường chất điểm di chuyển được là
12m
.
Câu 8. Một chất điểm rơi tự do với phương trình chuyển động được xác định bởi hàm số
2
1
( )
2
S t gt
. Với
2
( 10 / )g m s
ở độ cao
125m
. Các mệnh đề sau đúng hay sai?
a) Vận tốc của chất điểm tại thời điểm
1
2
t
giây là
2
1
2
1 1
1
2 8
( ) lim
1
2
2
x
gt g
S
t
.
b) Nếu
2
2
1
2
2
lim 2
2
x
gt g
g
t
thì chất điểm đạt vận tốc là
2
.
c) Vận tốc của chất điểm được xác định bởi công thức
( ) ( )
V t S t gt
.
d) Khi chạm đất thì chất điểm đạt vận tốc
( ) 40 /V t m s
.
Câu 9. Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát, có phương trình
chuyển động
2cos 1
2 6
x t t
, trong đó t tính bằng giây và
x t
tính bằng centimét. Các mệnh đề sau
đúng hay sai?
a) Gia tốc tức thời của con lắc là
2 2
cos /
2 6
x t t cm s
.
b) Gia tốc tức thời của con lắc tại thời điểm
2t s
là
2
2
3
2 /
2
x cm s
.
c) Gia tốc tức thời của con lắc tại thời điểm vận tốc đạt giá trị lớn nhất
2
0 /cm s
.
d) Khi gia tốc tức thời của con lắc đạt lớn nhất thì con lắc cách vị trí ban đầu
2cm
.
Câu 10. Một chất điểm chuyển động theo phương trình
3sin 2 cos 2s t t t
với
t
(giây) là khoảng thời gian
tính từ khi vật bắt đầu chuyển động và
s
(mét) là quãng đường vật đi được trong thời gian đó. Các mệnh đề
sau đúng hay sai?
a) Vận tốc tức thời tại thời điểm
8
t
giây của chuyển động bằng
2 m/s
8
v
.
b) Gia tốc tức thời tại thời điểm
t
giây của chuyển động bằng
12sin 2 4cos 2a t t t
.
c) Gia tốc tức thời tại thời điểm
4
t
giây của chuyển động bằng
2
4 m/s
4
a
.
d) Gia tốc của chuyển động đạt giá trị lớn nhất bằng
4 10
.
Câu 11. Cho chuyển động xác định bởi phương trình
3 2
3 9 27
t tS t t
. Trong đó
t
tính bằng giây (s) và
S
tính bằng mét (m). Các mệnh đề sau đúng hay sai?
a) Đạo hàm cấp một của hàm số đã cho là
2
6 9
' 3S t t
t
.
b) Vận tốc tức thời tại thời điểm
3
t
giây của chuyển động bằng
3 40m/s
v
.
c) Gia tốc tức thời tại thời điểm
4t
giây của chuyển động bằng
2
4 24 /a m s
.
d) Gia tốc của chuyển động tại thời điểm vận tốc triệt tiêu là
2
12 /m s
.
Câu 12. Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một đường cong có dạng parabol
(H.9.6a), đoạn dốc lên
1
L
và đoạn dốc xuống
2
L
là phần đường thẳng có hệ số góc lần lượt là
0, 5
và
0,75
.
Để tàu lượn chạy êm và không bị đổi hướng đột ngột,
1
L
và
2
L
phải có những tiếp tuyến của cung parabol tại
19
các điểm chuyển tiếp
P
và
Q
(H.9.6b). Giả sử gốc tọa độ đặt tại
P
và phương trình của parabol là
2
y ax bx c
, trong đó
x
tính bằng mét. Các mệnh đề sau đúng hay sai?
a)
0
c
.
b)
0,5
b
.
c) Giả sử khoảng cách theo phương ngang giữa
P
và
Q
là
40
. Khi đó
1
64
a
.
d) Giả sử khoảng cách theo phương ngang giữa
P
và
Q
là
40
. Chênh lệch độ cao giữa hai điểm chuyển tiếp
P
và
Q
bằng
5
.
Câu 13. Một chất điểm chuyển động thẳng xác định bởi phương trình
3 2
1
( ) 3 2 6
3
S t t t t
, với
( )S t
là
quãng đường có đơn vị là
( )m
. Các mệnh đề sau đúng hay sai?
a) Vận tốc của chất điểm được xác định bởi công thức
2
( ) 6 2V t t t
.
b) Tại thời điểm
2
t
giây chất điểm đạt vận tốc lớn nhất.
c) Chất điểm đạt vận tốc lớn nhất là
( ) 7( / )V t m s
.
d) Khi chất điểm đạt vận tốc lớn thì vật chuyển động được quãng đường là
18 ( )m
.
Câu 14. Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng
parabol (H.9.6a), đoạn dốc lên
1
L
và đoạn dốc xuống
2
L
là những phần đường thẳng có hệ số góc lần lượt là
0, 5
và
0,75
. Để tàu lượn chạy êm và không bị đổi hướng đột ngột,
1
L
và
2
L
phải là những tiếp tuyến của
cung parabol tại các điểm chuyển tiếp
P
và
Q
(H.9.6b). Giả sử gốc toạ độ đặt tại
P
và phương trình của
parabol là
2
y ax bx c
, trong đó
x
tính bằng mét.
Các mệnh đề sau đúng hay sai?
a) Ta có:
0
c
.
b)
(0) 0,5
y b
.
c) Giả sử khoảng cách theo phương ngang giữa
P
và
Q
là
40m
. Khi đó
64
a
d) Chênh lệch độ cao giữa hai điểm chuyển
P
và
Q
là
5( ).m
Câu 15. Một vật chuyển động trên một đường được xác định bởi công thức
3 2
( ) 3 7 2s t t t t
, trong đó
0t
và tính bằng giây và
s
là quãng đường chuyển động được của vật trong
t
giây tính bằng mét. Các mệnh
đề sau đúng hay sai?
a) Vận tốc của vật tại thời điểm
2t
là
7( / )m s
.
b) Gia tốc của vật tại thời điểm
2t
là
2
6 /m s
.
c) Gia tốc của vật tại thời điểm mà vận tốc của chuyển động bằng
16 /m s
là
2
10 /m s
.
d) Thời điểm
1t
(giây) tại đó vận tốc của chuyển động đạt giá trị nhỏ nhất.
20
Câu 16. Một con lắc lò xo dao động điều hoà theo phương ngang trên mặt phẳng không ma sát, có phương
trình dao động
2 3
10sin 3
3 5
x t t
, trong đó
x
tính bằng centimét và thời gian
t
tính bằng giây. Các
mệnh đề sau đúng hay sai?
a) [NB]
0 12,5
x
(làm tròn kết quả đến một chữ số thập phân).
b)
20 2 3
' s
3 3 5
x t co t
.
c) Vận tốc của con lắc tại thời điểm
8t s
là
20,5(cm/s)
(Làm tròn đến một chữ số thập phân).
d) Thời điểm đầu tiên mà vận tốc của con lắc bằng
0
là
1,35( )s
.
Câu 17. Một vật chuyển động trên đường thẳng được xác định bởi công thức
3 2
( ) 3 7 2s t t t t
, trong đó
0t
tính bằng giây và
s
là quãng đường chuyển động được của vật trong
t
giây tính bằng mét. Các mệnh đề
sau đúng hay sai?
a) Tốc độ của vật tại thời điểm
2t
là
7( / )m s
.
b) Gia tốc của vật tại thời điểm
2t
là
2
6 /m s
.
c) Gia tốc của vật tại thời điểm mà vận tốc của chuyển động bằng
2
16 /m s
là
2
10 /m s
.
d) Thời điểm
1t
(giây) tại đó vận tốc của chuyển động đạt giá trị nhỏ nhất.
Câu 18. Số dân của một thị trấn sau
t
năm kề từ năm
1970
được ước tính bởi công thức
26 10
5
t
f t
t
(
f t
được tính bằng nghìn người). Các khẳng định sau đúng hay sai?
a) Số dân của thị trấn vào đầu năm
1980
là
18
nghìn người.
b) Số dân của thị trấn vào đầu năm
1995
là
23
nghìn người.
c) Xem
f t
là một hàm số xác định trên nửa khoảng
0;

, đạo hàm của hàm số
f t
biểu thị tốc độ tăng
dân số của thị trấn (tính bằng nghìn nguời/năm) có công thức là:
2
120
5
f t
t
.
d) Hàm số
f t
nghịch biến trên
0;

.
Câu 19. Số dân của một thành phố sau
t
năm kể từ năm 1980 được ước tính bởi công thức
30 20
6
t
f t
t
,
f t
được tính bằng nghìn người. Các khẳng định sau đây đúng hay sai?
a) Số dân của thành phố vào năm 2025 (kết quả làm tròn tới hàng phần nghìn) là
26,863
nghìn người.
b) Số dân của thành phố có thể vượt quá 30 nghìn người.
c) Xem
f t
là một hàm số xác định trên nửa khoảng
0;

thì hình vẽ sau đây là đồ thị của hàm số
f t
d) Đạo hàm của hàm số
f t
biểu thị tốc độ tăng dân số của thành phố (tính bằng nghìn người/năm) thì tốc độ
tăng dân số của thành phố vào năm 2002 nhỏ hơn tốc độ tăng dân số của thành phố vào năm 2025.
Câu 20. Trong thí nghiệm y học, người ta cấy
1000
vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm,
người ta xác định số lượng vi khuẩn thay đổi theo thời gian bởi công thức:
2
100
1000
100
t
N t
t
(con). Trong
đó
t
là thời gian tính bằng giây. Các khẳng định sau đúng hay sai?
a) Số lượng vi khuẩn tại thời điểm
10
giây sau khi cấy là
1005
con.

Tài liệu khác của Toán 11

Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
--------------------------------------------------------------------------------------------
LUYỆN KỸ NĂNG TOÁN 11 THPT
TRẮC NGHIỆM ĐÚNG, SAI
TRẮC NGHIỆM TRẢ LỜI NGẮN
ĐẠO HÀM VÀ ỨNG DỤNG
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
ĐÁP ÁN CHI TIẾT PDF BẠN ĐỌC VUI LÒNG LIÊN HỆ TÁC GIẢ:
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 3/2025 1
LUYỆN KỸ NĂNG TOÁN 11 THPT
TRẮC NGHIỆM ĐÚNG, SAI
TRẮC NGHIỆM TRẢ LỜI NGẮN
ĐẠO HÀM VÀ ỨNG DỤNG
___________________________ DUNG NỘI DUNG BÀI TẬP LƯỢNG 1 FILE
TRẮC NGHIỆM ĐÚNG, SAI ĐẠO HÀM (THUẦN TÚY) 14 trang 1 FILE
TRẮC NGHIỆM ĐÚNG, SAI ĐẠO HÀM (ỨNG DỤNG THỰC TẾ) 8 trang 1 FILE
TRẮC NGHIỆM TRẢ LỜI NGẮN ĐẠO HÀM (THUẦN TÚY) 10 trang 1 FILE
TRẮC NGHIỆM TRẢ LỜI NGẮN ĐẠO HÀM (ỨNG DỤNG THỰC TẾ) 6 trang 2
ĐẠO HÀM LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG SAI (THUẦN TÚY)
______________________________
Câu 1. Dùng định nghĩa để tính đạo hàm của hàm số 2
y f (x)  x  2x tại điểm x  1. Khi đó: 0  2    x 2x 3  f (x) f (1) a) f (1)  lim b) f (1)  lim x 1  x 1 x 1  x 1
c) f  (1)  lim  x  4
d) f  (1)  a a  5 x 1  x  2
Câu 2. Dùng định nghĩa để tính đạo hàm của hàm số f (x) 
tại điểm x  0 ta được f  (0)  a . Xét tính x 1 0
đúng, sai của các khẳng định sau  4  f (x) f (0) a) f 0  lim b) ' f 0  lim x0 x  0 x0 x 1
c) Phương trình 3x  3 có nghiệm bằng x a  2 d) log 9  3 a
Câu 3. Dùng định nghĩa để tính đạo hàm của hàm số 3
f (x)  2x . Khi đó:
f (x)  f   x0 
a) Với bất kì x : f x  lim 0  0 xx0 x x0 b) f  (1)  6 
c) Giá trị nhỏ nhất của f  x  f x là một số lớn hơn – 7.
d) Tiếp tuyến của đồ thị tại điểm có hoành độ x cắt trục hoành tại điểm có hoành độ dương. 0 2
Câu 4. Dùng định nghĩa để tính đạo hàm của hàm số f (x) 
với x  1. Khi đó: 1 x  2
a) Với bất kì x  1, ta có: f x  lim 0  0 x 0
x (1 x) 1 x0  b) f  (2)  2 1 c) f  (3)  3   3
d) f (2)  f (3)  2 Câu 5. Cho hàm số 3
y f (x)  2x có đồ thị (C ) và điểm M thuộc (C ) có hoành độ x  1. Xét tính đúng, 0
sai của các khẳng định a) Phương trình 2
x f  x  6x f  
1 có hai nghiệm phân biệt cùng dương.
b) Tiếp tuyến của (C ) tại M cắt đồ thị hàm số 2
y x  8  7x  4 tại hai điểm phân biệt có tổng hoành độ bằng 5.
c) Tiếp tuyến của (C ) tại M cắt đường thẳng d : y  3x tại điểm có hoành độ bằng 4. 1
d) Tiếp tuyến của (C ) tại M vuông góc với đường thẳng  : y   x . 6 2
Câu 6. Cho hàm số f (x) 
có đồ thị là đường cong (C ) và xét điểm M (3; 1
 ) (C) . Xét tính đúng, sai 1 x của các mệnh đề
a)Đạo hàm của hàm số luôn nhận giá trị dương với mọi giá trị x  1. 1 5
b) Tiếp tuyến của (C ) tại điểm M song song với đường thẳng y   x  2 2  2 c) 2
f (1 2x )     . 3 x
d) Tiếp tuyến của đường cong tại điểm N x ; y tạo với hai trục tọa độ một tam giác vuông cân, khi đó 0 0  2 x  2x  1. 0 0 3
Câu 7. Cho hàm số y f x  x  2cos x và  x x
a) Vi phân của hàm số là dy  1 4sin cos dx   .  2 2 
b) Tập giá trị của hàm số f  x là một đoạn có độ dài bằng 4.
c) Phương trình f  x  3cos x 1có 2 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
c) Tồn tại 2 điểm có hoành độ  0; 2  sao cho tiếp tuyến của đồ thị hàm số tại điểm đó song song với đường
thẳng y  2x  2024 . Câu 8. Cho hàm số 2
y x  3x 1 có đồ thị (C ) . Xét tiếp tuyến của (C ) tại giao điểm của (C ) với trục tung.
Xét tính đúng, sai của các mệnh đề
a) Phương trình 3y  4 y  y 17 có hai nghiệm phân biệt với tổng hai nghiệm bằng 5.
b) Tiếp tuyến đã cho đi qua điểm  A 1;  3 .
c) Tiếp tuyến đã cho cắt đường thẳng y  2x 1 tại điểm có hoành độ bằng 0
d) Tiếp tuyến đã cho tiếp xúc với đồ thị hàm số 4 2
y x x  4 tại tiếp điểm có tung độ nhỏ hơn 3. Câu 9. Cho hàm số  x y e
sin x . Xét tính đúng, sai của các khẳng định cos x  sin x
a) Vi phân của hàm số là dy dx . x e b) x x y e
ye   cos x .
c) Tồn tại đúng 2 giá trị nguyên m để phương trình x y e   2m có nghiệm.
d) y  2 y  2 y  0 . x  9
Câu 10. Xét đồ thị hàm số f x 
và đường thẳng d  là tiếp tuyến vuông góc với đường thẳng x 1
d : x  2y  2  0 . Xét tính đúng, sai của các mệnh đề
a) Có hai phương trình tiếp tuyến d  thỏa mãn bài toán.
b) Một trong hai tiếp tuyến đi qua điểm  A 1;  5 .  8  (2x 1) c)  f  2
x x  2  .  
x x  32 2
d)Tồn tại ba tiếp tuyến của đồ thị hàm số tạo với hai trục tọa độ một tam giác cân. Câu 11. Cho hàm số 4  . x y
x e . Xét tính đúng sai của các mệnh đề sau
a)Tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1 có hệ số góc 4 k  5e . b) 4 ' x y e  4 y . c)Phương trình     2 ' 1 4 x y x e
 2 có đúng 1 nghiệm dương
d) Hàm số đã cho có đạo hàm cấp hai      4 . x y a bx e với 2 2 a b  41. Câu 13. Cho hàm số 2
y  2x x . Xét tính đúng sai của các mệnh đề sau a) 3
y .y 1  0 b) 3
y .y  1 1 1  c) 3 2
y  (x  2x ).y   . d) y  . y  2xx 3 2
Câu 14. Cho hàm số f x 3 2
 2x  6x m  1 . Xét tính đúng sai của các mệnh đề a) f x 2 '  6x  6x .
b) f 2  f 2  10 .
c) Giá trị nhỏ nhất của f ' x bằng – 7.
d) Tồn tại hai giá trị a,b thỏa mãn f a  f b  0 thì có 7 số nguyên m để f a, f b trái dấu.
Câu 15. Cho hàm của hàm số f x 3 2
x 3x x 5. Xét tính đúng sai của các mệnh đề sau 4 a) f  x 2
 3x 6x 1, x   b) f   1  2
c) f  x 1 x 2  ;  0
d) f  x  2   x  1  2x 1
Câu 16. Cho hàm của hàm số f x 
. Xét tính đúng sai của các mệnh đề sau x 1 3
a) f  x  , x   1   x  2 1 b) f   0  3
c) f  x  0  x  1  1
d) Phương trình f   x  có nghiệm duy nhất. 3 Câu 17. Cho hàm số 3 2
y x ax bx 1 thỏa mãn y 0  y 
1  1. Xét tính đúng sai của các mệnh đề a) 2
y  3x  2ax b .
b) a b  0 .
c) Giá trị nhỏ nhất của 2 2
a b bằng 1. d) y   1  2 .
Câu 18. Cho hàm của hàm số f x  sin 2x . Xét tính đúng sai của các mệnh đề sau   
a) f  x  cos 2 , x x   b) f   2    2 
c) f  x  4  ; 4, x  d) 2
  f  x  2, x  
Câu 19. Cho hàm của hàm số   2x f x
. Xét tính đúng sai của các mệnh đề sau x
a) f  x  2 ln 2, x  .
b) f  x  2, x  . c) Phương trình   x f
x e có nghiệm duy nhất thuộc khoảng 0  ;1 . d) f   1  2ln 2 .
Câu 20. Cho hai hàm số f x 2
x x 1 và g x   3 x . Xét tính đúng sai của các mệnh đề sau
a) f   x   2 x  1. 
b)  f x.g x 
 có giá trị nhỏ nhất bằng 2. 
c)  f g x 17, x    .
d). f  m  2  g 1000  m  1. Câu 21. Cho hàm số 2  (   ) x y ax bx
c e với b  0 . Xét tính đúng sai của các mệnh đề sau 2
a) Đạo hàm của hàm số đã cho bằng   (2  ) x ax
a b x b ce   .
b) y 1  3a  2b c e . 2       
c) Khi hàm số có đạo hàm bằng có đạo hàm là 3 x y ax ax b c e 
 thì a b . 2         9
d) Khi hàm số có đạo hàm là  3  1 x y ax a x b c e
 thì biểu thức M a có giá trị nhỏ nhất bằng b 7. 1
Câu 22. Cho hàm số y f x 3 2 
x mx  (m  6)x 1. Xét tính đúng, sai của các khẳng định 3
a)Vi phân của hàm số đã cho là dy   2
x  2mx m  6 dx .
b) Tồn tại bao 4 giá trị nguyên m thuộc 10;10  để phương trình y  0vô nghiệm.
c) Tiếp tuyến của đồ thị hàm số có hệ số góc nhỏ nhất tại điểm có hoành độ x  m . 5
d)Đạo hàm cấp hai của hàm số hợp   x
f e  là 3x 2 3  6 x  (  6) x e me m e .   9
Câu 23. Đạo hàm f x   F   x  của hàm số F x 3 2  x
x mx  6 có bảng xét dấu sau đây. 2
Xét tính đúng sai của các mệnh đề sau a) f x 2
 3x  9x m . b) 7  F(1)  9 . 27
c) Đạo hàm của hàm số hợp đạt giá trị nhỏ nhất bằng  . 8
d) Tiếp tuyến của đồ thị hàm số f x tại điểm có hoành độ bằng 2 cắt trục tung tại điểm có tung độ lớn hơn – 5. 2 3 x
Câu 24. Cho hai hàm số f x  
và gx 
. Xét tính đúng sai của các mệnh đề sau x  1 x 2 3
a) f  x   , x   1  .  x  2 1 2 x  4x
b) g x '  , x   2    .  x  22
c)  f x.g x '  f ' x.g ' x, x   \ 1  ;  2    . 
d) Phương trình  f  2 x  3x  
1   0 có nghiệm duy nhất .    2;   1
Câu 25. Cho bốn hàm số f x  sin x , g x   cos x , h x   tan x và k x   cot x .
Xét tính đúng sai của các mệnh đề sau
a) f   x   cos x, x   .
b) g   x   1;  1 , x   . 1 
c) h x '  , x   kk
k x  '  h x  '  tan x 1    . d)     2       . cos x 2
Câu 26. Cho y là hàm số của x thỏa mãn phương trình y  sin x .
Xét tính đúng sai của các mệnh đề sau
a) Đạo hàm của hàm số y là  y  cos x .
b) Tồn tại 2 giá trị nguyên m để phương trình y y  mcó nghiệm.
c) Đạo hàm cấp hai của hàm số y là 2
y   sin x .
d) Giá trị nhỏ nhất của hàm số 2y  ylà một số lớn hơn 2. 1
Câu 27. Cho hàm số y  3x
. Xét tính đúng sai của các mệnh đề sau x
a) Phương trình y  0 có hai nghiệm phân biệt đối nhau. b) 2
x y  2xy  6x .
c)Hàm số y y có giá trị nhỏ nhất 3 bằng với x  0 . d) 2
x y  3xy  2 y  6 . Câu 28. Cho hàm số 3 2
y  x  3x m  2m  4 . Xét tính đúng sai của các mệnh đề sau
a) y  0 có hai nghiệm phân biệt. b) y m  2  3  3m .
c) y đạt giá trị lớn nhất tại x  0 .
d) Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 có đặc điểm song song với trục hoành và cách trục
hoành một khoảng không vượt quá 5.
Câu 29. Cho hàm số y f x   2 sin x  3cos x . Xét tính đúng sai của các mệnh đề sau
a) f ' x   2 cos x  3sin x,x   . 6 12
b) Nếu  thỏa mãn f     0 thì tan 2  . 5
c) Hàm số f   x  có giá trị lớn nhất là một số nguyên.
d) Phương trình f   x   0 có 4 nghiệm phân biệt thuộc khoảng 0; 4  . 2 x  1
Câu 30. Cho hàm số y f x 
. Xét tính đúng sai của các mệnh đề sau x 1 3
a) f ' x  , x   \ 1 . 2    x   1
b) Tồn tại tiếp tuyến của đồ thị hàm số mà tiếp tuyến đó có hệ số góc bằng  2023 .
c) Phương trình f   x   6 có nghiệm lớn hơn 2 . 3
d) Điều kiện tham số để phương trình f x   kf ' x  có hai nghiệm phân biệt là k  . 8 1 Câu 31. Cho hàm số 3 2 f (x) 
x  4x mx  6 . Xét tính đúng, sai của các khẳng định 3
a) Với m  0 , phương trình f  x  0 có hai nghiệm phân biệt với tổng bằng 6.
b) Khi tiếp tuyến của đồ thị hàm số có hệ số góc nhỏ nhất thì hoành độ tiếp điểm bằng 4. 
c)   x   2 x f e e  8 .   d) Nếu có hai số ,
a bphân biệt thỏa mãn điều kiện f a   f b   0 và 2a  3b  22 . thì f 3  3  .  2x  3 khi x  1 
Câu 32. Cho hàm số f x   1
. Xét tính đúng sai của các mệnh đề sau  khi x  1   x
a) Hàm số f x  liên tục tại x  1 .
b) Hàm số f x  có đạo hàm tại x  1 .
c) Hàm số f x  liên tục tại x  1 và hàm số f x  cũng có đạo hàm tại x  1 .
d) Hàm số f x  không có đạo hàm tại x  1 .
Câu 33. Cho hàm số f x 2
x  4 và g x  3x  2 . Xét tính đúng sai của các mệnh đề sau x
a) Vi phân hàm số f x 2  x  4 là dx . 2 x  4 3 5
b) Đạo hàm của hàm số f x tại x  3 bằng . 5 7 5
c) Đạo hàm của hàm số f g x 
 tại x  3 bằng . 5 3 5
d) Đạo hàm của hàm số g f x 
 tại x  3 bằng . 5
Câu 34. Cho hai hàm số f x  3 2
x  3 x m x  1 và g x  2
x mx m  5 . Xét tính đúng, sai của các khẳng định
a) f  1  m  3 .
b) Phương trình f   x   g   x  có tổng tất cả các nghiệm nhỏ hơn 3. 
c)  f g x 2
  3g x 6g x  m   .
d) Biết m là giá trị của tham số m để hai số phân biệt x , x thỏa mãn f   x f x  0 và 1   2  0 1 2 2 2 x x
x x  13 . Khi đó m  15; 7 0   1 2 1 2 3 2 x mx
Câu 35. Cho hàm số f x  
1có đồ thị là đường cong C
. Xét tính đúng, sai của các khẳng định m  3 2 sau
a)Phương trình y  0luôn luôn có nghiệm. 7
b) f   m  2 2  2m .
c) Gọi A là điểm thuộc đồ thị, A có hoành độ bằng 1. Với m   4 thì tiếp tuyến tại A song song với đường thẳng y  5x. 2
d)Xét hàm số g x  f x  2x  
3 , với m  2 thì phương trình g x  0 có hai nghiệm phân biệt.
Câu 36. Cho hàm số f x  3 2 2
 3x  2 x  4mx m  2 . Xét tính đúng, sai của các khẳng định sau
a). f   x  2
 9 x  4 x  4m . 1
b) Phương trình f   x   0 có hai nghiệm phân biệt khi m   . 19
c) Điều kiện tham số m để f  x luôn dương với mọi x  0;   là m  0 .  d)  f  2
x    x 4 2 1 2
9x  24x 13  4m   . Câu 37. Cho hàm số x
y e sin x . Xét tính đúng, sai của các khẳng định 1
a). y  y y  2 b) x
y  e (sin x  cos x)
c)Phương trình   5 x y
e sin x có 4 điểm biểu diễn nghiệm trên vòng tròn lượng giác. d)   2 x y e cos x . 1  Câu 38. Cho hàm số x y xe
. Xét tính đúng, sai của các khẳng định a) 2
x y  xy y 1   1  b) x y  e 1    x  c) 3
x y  xy  y  0 d) 3
x y  2xy  3y  0 2 x 1
Câu 39. Cho hàm số y f x  . Khi đó: x  3 2
cos x  6 cos x 1 
a)  f cos x    . 2 (cos x  3)
b) Tổng các nghiệm của phương trình y'  0 bằng  6 .  3 
c) Đồ thị của hàm số y' đi qua điểm A 1;    .  2 
d) Tiếp tuyến d của đồ thị hàm số tại điểm có hoành độ bằng 1 cắt đường phân giác góc phần tư thứ nhất tại
điểm có hoành độ lớn hơn 1. 1
Câu 40. Cho hàm số y f x 
. Xét tính đúng, sai của các khẳng định 2 x 1 x
a)Vi phân của hàm số là dy dx . 2 2 (x 1) x 1  3 5 
b) Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 2 đi qua điểm 3;   . 25    sin x cos x
c) f tan x  . cos x d) 3 5
xy '  y ' 3x y 2 x
Câu 41. Cho hàm số y f x 3  4x
 2x  3 có đồ thị ( )
C . Xét tính đúng – sai của các mệnh đề 2 a) Biết 2
y '  ax bx c khi đó a b c  10  .
b) Phương trình y  y  m có hai nghiệm phân biệt có tổng bình phương bằng 10 thì giá trị tham số m thu
được là một số nguyên. 8 c)  f x  2 cos
  12 cos x cos x  2    .
d) Phương trình tiếp tuyến của đồ thị ( )
C tại điểm giao điểm với trục tung song song với đường thẳng 2 y  2
x m với m là tham số.
Câu 42. Cho hàm số f x  2
x  3x có đồ thị C  và hàm số g x   ln x . Xét tính Đúng – Sai của mỗi khẳng định sau
f x  f   2 1 x 3x  2 a) f   1  lim  lim  1  x 1  x 1 x 1  x 1
b) Tiếp tuyến của đồ thị C  tại điểm có hoành độ x  1 có phương trình: y x  1  .  1 
c) Bất phương trình g   x   3 có tập nghiệm  ;    .  3 
d) Đặt h x   f x .g x  , khi đó phương trình h x  2 2.
x x.h  x  có nghiệm thuộc khoảng   1;1 . 4 4
Câu 43. Cho hàm số y
. Xét tiếp tuyến của đồ thị hàm số y
tại điểm có hoành độ x  1. Xét x 1 x 1 0
tính đúng, sai của các mệnh đề
a) Hệ số góc của tiếp tuyến bằng 1.
b) Tiếp tuyến đi qua điểm M  1  ;  2 . 4
c) Tiếp tuyến cắt đường thẳng y  2x 1 tại điểm có hoành độ bằng . 3
d) Tồn tại 3 đường tiếp tuyến d của đồ thị hàm số mà d tạo với hai trục tọa độ một tam giác vuông OAB thỏa
mãn OA  4OB . Câu 44. Cho hàm số   2 x x y f x e   
. Xét tính đúng, sai của các khẳng định
a) Vi phân của hàm số là     2 2 1 xx dy x e dx .
b) Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 cắt parabol 2
y x tại hai điểm phân biệt nằm về hai phía trục tung. 1
c) Phương trình f  x  0 có hai nghiệm x , x thỏa mãn x .x   . 1 2 1 2 4 d)          2 sin 2 sin 2 sin 2 cos 2 sin 4 x x f x x x e    .
Câu 45. Cho hàm số y f x 2
 2x x . Xét tính đúng, sai của các mệnh đề 1 x
a)Vi phân của hàm số là dy dx . 2 x  2x 2x
b)Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 song song với đường thẳng y   3 . 3 3 2 
2x  3x  6x  2 c)  f  2 x x   .   4 3 2
x  2x  3x  2x d) Giá trị biểu thức 3 2
M y .y 
x  2x.y x là một số nguyên tố.
Câu 46. Cho hàm số y f x  x sin x . Xét tính đúng, sai của các khẳng định
a)Vi phân của hàm số đã cho là dy   x cos x  sin xdx .
b) xy  2 y  xy  2  sin x .
c) xy  y  xy  4x cos x  sin x .  2  3
d)Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x
có phương trình y   x  . 2 2 4 2 x Câu 47. Cho hàm số 3 y  4x   2x  3 , biết 2
y '  ax bx c . Khi đó: 2
a) a b c  1  0
b) Phương trình y '  0 có hai nghiệm phân biệt 9
c) Đồ thị hàm số y ' cắt trục tung tại điểm 0; 2
d) Đồ thị hàm số y ' cắt đường thẳng y  3 tại hai điểm phân biệt 1 Câu 48. Cho hàm số 4 2
y x  4x  3 x  2  . Khi đó: x 3 a) y '  1   2  3 
b) Đồ thị của hàm số y ' đi qua điểm A 1;    2  3597 c) y '4  16 1
d) Điểm M thuộc đồ thị (C) của hàm số 4 2
y x  4x  3 x  2 
có hoành độ x  1. Khi đó, phương trình x 0 2
tiếp tuyến của (C) tại M vuông góc với đường thẳng y x 3 x  3
Câu 49. Cho hàm số y  . Khi đó: 2x 1 a) y '0  7  7 
b) Đồ thị của hàm số y ' đi qua điểm A 1;    3  c) y '  1  y '2 x  3
d) Điểm M thuộc đồ thị (C) của hàm số y
có hoành độ x  0 . Khi đó, phương trình tiếp tuyến của 2x 1 0
(C) tại M song song với đường thẳng y  7x  2024 2 x 1
Câu 50. Cho hàm số y  . Khi đó: x  3 3 a) y '  1  2
b) Tổng các nghiệm của phương trình y '  0 bằng 6  3 
c) Đồ thị của hàm số y ' đi qua điểm A 1;     2  d) y '  1  y '2 .
Câu 51. Cho hàm số y   x   2 ( 2
3) x  3x   1 . Khi đó: a) y '  1  3  1
b) Tổng các nghiệm của phương trình y '  0 bằng 3
c) Đồ thị của hàm số y ' đi qua điểm A0;7 d) y '  1  y '2
Câu 52. Cho hàm số y  (2 x  3)(4 x 1) . Khi đó: a) y '  1  13 b) y ' 
1  y '25  22
c) Đồ thị của hàm số y ' đi qua điểm A25; 9   . d) y '  1  y '2
Câu 53. Cho hàm số y f x 3
x 1. Dùng định nghĩa đạo hàm tính đạo hàm của hàm số f x tại x  2 .
Khi đó các mệnh đề sau đúng hay sai?
f x  f 2 a) Có lim  f '2 . x2 x  2 10
f 2  h  f 2
b) Với h  0 , ta có lim  10 . h0 h
c) Tiếp tuyến của đồ thị hàm số y f x tại điểm M 2;7 có hệ số góc là 12 .
2 f x  xf 2 d) lim  f '2  2 . x2 x  2 Lời giải a) Đúng b) Sai c) Đúng d) Sai
f x  f 2
a) Theo định nghĩa đạo hàm ta có lim
f '2 nên suy ra mệnh đề đúng. x2 x  2
f 2  h  f 2 3 2
h  6h 12h b) Ta có: lim  lim  lim  2
h  6h 12  12. h0 h0 h0 h h Suy ra mệnh đề sai.
c) Ta có M 2;7 thuộc đồ thị của hàm số y f x , nên tiếp tuyến của đồ thị hàm số tại M có hệ số góc là f '2  12. Suy ra mệnh đề đúng. d) Ta có:
2 f x  xf 2
2 f x  2 f 2  2 f 2  xf 2 lim  lim x2 x2 x  2 x  2
2 f x  2 f 2
2 f 2  xf 2  lim  lim x2 x2 x  2 x  2
f x  f 2 2  x  2 lim  f 2.lim
 2 f '2  f 2 x2 x2 x  2 x  2 Suy ra mệnh đề sai
Câu 54. Cho hàm số y f x có đồ thịC  , biết f 3  5, f '3  6 . Các mệnh đề sau đúng hay sai?
f x  f 3 a) Có lim  9 . x 3  x  3
b) Tiếp tuyến của C  tại điểm có hoành độ bằng 3 song song với đường thẳng 3x y  7  0.
c) Tiếp tuyến của C  tại điểm M 3; f 3 có phương trình là y  6x 10 .
d) Tiếp tuyến của C  tại điểm M 3; f 3 cách điểm I 6; 1   1 một khoảng bằng 6 . Lời giải a) Sai b) Sai c) Sai d) Sai
f x  f 3 a) Ta có: lim
f '3  6 suy ra mệnh đề sai x 3  x  3
b Tiếp tuyến của C  tại điểm có hoành độ bằng 3 hệ số góc f '3  6
đường thẳng 3x y  7  0  y  3x  7 có hệ số góc bằng 3 . Suy ra mệnh đề sai
c) Tiếp tuyến của C  tại điểm M 3; f 3 có phương trình là
y f 3  f '3 x  3  y  5  6 x  3  y  6x 13. Suy ra mệnh đề sai.
d) Tiếp tuyến của C  tại điểm M 3; f 3 là 6.6   1   1 10
 : y  6x  10  6x y  10  0 d I;  
 37 . Suy ra mệnh đề sai 2 2 6 1
Câu 55. Cho hàm số y f x 2
x  3x  6 có đồ thị C . Xét phương trình tiếp tuyến của C  tại giao điểm I
của C  với trục tung. Các mệnh đề sau đúng hay sai?
a) Tiếp tuyến có hệ số góc 3 .
b) Giao điểm của tiếp tuyến này với trục hoành có hoành độ lớn hơn 3.
c) Tiếp tuyến này cắt các trục Ox, Oy tại A, B và diện tích ABC là 12 .
d) Tiếp tuyến này đi qua tâm đường tròn đường kính OD với D  6  ;6 . 11 2x 1
Câu 56. Cho hàm số y
có đồ thị C  và đường thằng  : y  3x  5 . Các mệnh đề sau đúng hay sai? x 1
a) Có một tiếp tuyến của C  song song với  .
b) Các tiếp tuyến của C  luôn có hệ số góc âm.
c) Có đúng hai tiếp tuyến của C  vuông góc với  . 3  1 1  
d) Tiếp tuyến của C  có hệ số góc k thoả phương  4  0 có hoành độ tiếp điểm dương đi qua K ;   . k  2 6  3
Câu 57. Cho hàm số y f x 
. Các mệnh đề sau đúng hay sai? x 1 3
a) Có f ' x   .  x  2 1
b) Có f '2  3.
c) Luôn có tiếp tuyến của C  song song với đường thẳng y  3x  5 . 1
d) Bất phương trình f ' x 
 0 có tích của nghiệm nguyên âm nhỏ nhất và nghiệm nguyên dương lớn nhất 12 là 30 .
Câu 58. Dùng định nghĩa để tính đạo hàm của hàm số 2
y f (x)  x  3x tại điểm x  1. Các mệnh đề sau 0 đúng hay sai?
f (x)  f (1) a) f ( ' 1)  lim . x 1  x 1 2 x  3x  4 b) f ( ' 1)  lim . x 1  x 1 c) f ' 
1  lim  x  4 . x 1 
d) f '(1)  a a  6 . Câu 60. Cho hàm số 3
y f (x)  2x có đồ thị (C) và điểm M thuộc (C) có hoành độ x  1. Các mệnh đề 0 sau đúng hay sai?
a) Hệ số góc của tiếp tuyến của (C) tại điểm M bằng 6
b) Phương trình tiếp tuyến của (C) tại M đi qua điểm A0; 4 .
c) Phương trình tiếp tuyến của (C) tại M cắt đường thẳng d : y  3x tại điểm có hoành độ bằng 4. 1
d) Phương trình tiếp tuyến của (C) tại M vuông góc với đường thẳng  : y   x . 6
Câu 61. Cho hàm số f  
x xác định trên ( ; a )
b tại x  ( ; a )
b . Các mệnh đề sau đúng hay sai? 0 f  
x f x0
a) f x  lim . 0  xx  0 x x0 f   x f   6 b) Nếu 6  ( ; a )
b và f   6  2 thì lim  6. x6 x 6 x  2x c) Hàm số f   3 2
x x 2x có f   3 2 2  lim  4 . x2 x2 xx  2 d) Hàm số f   2 x  có f   2  lim  0. x 1
x2 (x 1)(x2)
Câu 62. Dùng định nghĩa để tính đạo hàm của hàm số 3 f (x)  4
x 1. Các mệnh đề sau đúng hay sai?
f (x )  f x  0  
a) Với bất kì x : f x  lim . 0  0 xx0 x x0 b) f  (1)  1  2 .
f (x)  f    5 c) f ( 5  )  lim . x 5  x  5 12
d) f 2 a a> 0. x  2
Câu 63. Dùng định nghĩa để tính đạo hàm của hàm số f (x) 
tại điểm x  0 ta được f  (0)  a . Các x 1 0
mệnh đề sau đúng hay sai?  4  f (x) f (0) a) f 0  lim . b) ' f 0  lim . x0 x  0 x0 x 1 c) f    3 3  . d) f   2    4  . 16 Câu 64. Cho hàm số 3
y f (x)  2x có đồ thị (C) và điểm M thuộc (C) có hoành độ x  1  . Các mệnh đề 0 sau đúng hay sai?
a) Hệ số góc của tiếp tuyến của (C) tại điểm M bằng 6 .
b) Phương trình tiếp tuyến của (C) tại M đi qua điểm A 0; 4 .
c) Phương trình tiếp tuyến của (C) tại M cắt đường thẳng d : y  3x tại điểm có hoành độ bằng 4. 1
d) Phương trình tiếp tuyến của (C) tại M vuông góc với đường thẳng  : y   x . 6 5 Câu 65. Cho hàm số 3 f (x) 
x  2x .Các mệnh đề sau đúng hay sai? 3
f (x)  f   x0 
a) Với bất kì x : f x  lim . 0  0 xx0 x x0 b) f  x 2 5  x 2  x . c) f   1 7  . 5 d) Giả sử 3 f (x) 
x  2x là phương trình chuyển động của một chất điểm f (x) tính bằng mét m, x tính bằng 3
giây  s  . Gia tốc a của chất điểm tại thời điểm x 5
  s  là a =  2 50 m / s . Câu 66. Cho hàm số 2
y  x  4x . Các mệnh đề sau đúng hay sai?
a) Đạo hàm của hàm số 2
y  x  4x tại điểm x  1 bằng 4 . 0
b) Hệ số góc của tiếp tuyến của đồ thị hàm số đã cho tại điểm x  0 bằng 2 . 0
c) Phương trình tiếp tuyến của parabol tại điểm x  1 là y  2x  1. 0
d) Phương trình tiếp tuyến của parabol tại điểm có tung độ y  4 là y  2x  1. 0
Câu 67. Cho bất phương 2x  5 y  8 . Các mệnh đề sau đúng hay sai? Cho hàm số    4 y
f x x . Các mệnh đề sau đúng hay sai?
a) Đạo hàm của hàm số tại điểm x  1 là f (  1)  4 0
b) Giao điểm của đồ thị hàm số với trục tung là O(0; 0) .
c) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 là y  4x  3.
d) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hệ số góc bằng 4 là y  4x 1. Câu 68. Cho hàm số 3 2
y x  3x  2. Các mệnh đề sau đúng hay sai?
a) Đạo hàm của hàm số tại điểm x  1 bằng 4 . 0
b) Hệ số góc của tiếp tuyến tại điểm x  0 bằng 0 . 0
c) Phương trình tiếp tuyến của đồ thị hàm số song song với đường thẳng y  9x  7 là y  9x  25. 1
d) Phương trình tiếp tuyến của đồ thị hàm số vuông góc với đường thẳng y   x là 45
y  45x 173; y  45x  83. Câu 69. Cho hàm số 3
y x . Các mệnh đề sau đúng hay sai?
a) Đạo hàm của hàm số tại điểm x  2 bằng 4 . 0
b) Hệ số góc của tiếp tuyến tại điểm x  1 bằng 1. 0
c) Phương trình tiếp tuyến của đồ thị hàm số tại điểm  1  ;  
1 là y  3x  2.
d) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có tung độ bằng 8 là y  12x 16. Câu 70. Cho hàm số 3 2
y  2x  3x  4x 1. Các mệnh đề sau đúng hay sai? 13 a) Có 2
y  6x  6x  4 . b) y (  3  )  67 .
c) Phương trình tiếp tuyến của đồ thị hàm số tại điểm M 1; 2 là y  4x  2 .
d) Một vật chuyển động có phương trình là 3 2
s(t)  2t  3t  4t 1 (m) trong đó t là thời gian tính bằng giây, thì
vận tốc tức thời của vật tại thời điểm t  3(s) bằng  2 40 m/s  .
Câu 71. Cho hàm số f x   cos x  sin x  cos 2 .
x Các mệnh đề sau đúng hay sai?
a) Có f  x   sin x  cos x  2sin 2 . x .    3 3 1 b) f     .  3  2 c) Có  2  f (
x)  2.sin 2x  2
d) Phương trình f  x  1 tương đương với phương trình sin x   1 cos x   1  0. 26x 10
Câu 72. Cho hàm số f (x) 
. Các mệnh đề sau đúng hay sai? x  5
a) Hàm số luôn xác định với mọi x   . 120 b) f (  2)  . 49 5
c) Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm M 5;14 bằng 6 26t 10
d) Dân số (tính theo nghìn người) của một thành phố được cho bởi công thức f (t) 
, trong đó t (được t  5
tính bằng năm) là khoảng thời gian tính từ năm 2015. Thì tốc độ tăng dân số f (
t) trong năm 2025 của thành 8 phố đó là 5 2 Câu 73. Cho hàm số 3 3x x y  
. Các mệnh đề sau đúng hay sai?
a) Hàm số đã cho là hàm hợp của hai hàm số 2
u x  3x và 3u y  . 1
b) Có y 2  3
c) Có y  0 , x  2;  
d) Phương trình y  .
y ln 3  0 có nghiệm duy nhất 3 x Câu 74. Cho hàm số 4 2 y  x
x  3x , biết 2
y  ax bx c . Khi đó: 6
a) a b c  1  0 .
b) Phương trình y  0 có hai nghiệm phân biệt.
c) Đồ thị hàm số y y  x cắt trục tung tại điểm 0; 2   .
d) Đồ thị hàm số y y  x cắt đường thẳng y  3 tại hai điểm phân biệt. 1 Câu 75. Cho hàm số 3 2 y
x x  2x 1 có đồ thị là C  . Các mệnh đề sau đúng hay sai? 3 a) y '(1)  1. b) 2
y '  ax bx c khi đó a b c  5  .
c) Đồ thị hàm số y ' đi qua điểm M 2;3 .
d) Bất phương trình y '  1 có 3 nghiệm nguyên . 2x 1
Câu 76. Cho hàm số y f (x) 
có đồ thị C  . Các mệnh đề sau đúng hay sai? x 1 a) y '(2) 1. b) y '  0, x   1.
c) Đồ thị hàm số y ' đi qua điểm M  2  ;3 .
d) Phương trình tiếp tuyến của C  song song với đường thẳng y  3
x là y  3
x 1 và y  3x 11. 14 2 x  4x  4
Câu 77. Cho hàm số y
. Các mệnh đề sau đúng hay sai? x 1
a) Tập xác định của hàm số đã cho là  \{1}.
b) Đồ thị hàm số y cắt trục tung tại điểm có tung độ bằng 4 .
c) y '(3)  y '(2) .
d) Tập nghiệm của bất phương trình y '  0 là 0  ;1 .
Câu 78. Cho hàm số f x 2
x 2x. Các mệnh đề sau đúng hay sai?
a) Hàm số f x xác định khi 2 x  2x  0. ax b
b) f 'x 
, khi đó a b  2 . 2 x  2x 1
c) Phương trình f 'x  0 có nghiệm x  . 2
d) Tập nghiệm S của bất phương trình f 'x  f x có 3 giá trị nguyên. 1 Câu 79. Cho hàm số 4 2
y x  4x  3 x  2 
. Các mệnh đề sau đúng hay sai? x 3 a) y  1   . 2  3 
b) Đồ thị của hàm số y đi qua điểm A 1;   .  2   3597 
c) Đồ thị của hàm số y đi qua điểm B 4;   .  16  1
d) Điểm M thuộc đồ thị (C) của hàm số 4 2
y x  4x  3 x  2 
có hoành độ x  1. Khi đó, phương trình x 0 2
tiếp tuyến của (C) tại M vuông góc với đường thẳng y x . 3 x  3
Câu 80. Cho hàm số y
. Các mệnh đề sau đúng hay sai? 2x 1 a) y0  7 .  7 
b) Đồ thị của hàm số y ' đi qua điểm A 1;   .  3  c) y  1  y2 . x  3
d) Điểm M thuộc đồ thị (C) của hàm số y
có hoành độ x  0 . Khi đó, phương trình tiếp tuyến của 2x 1 0
(C) tại M song song với đường thẳng y  7x  2024 . 2 x 1
Câu 81. Cho hàm số y
. Các mệnh đề sau đúng hay sai? x  3 3 a) y  1  . 2
b) Tổng các nghiệm của phương trình y  0 bằng 6 .  3 
c) Đồ thị của hàm số y đi qua điểm A 1;    .  2  d) y  1  y2 . 3 x
Câu 82. Cho hàm số f x 2 
mx  m  2 x  3 . Xét tính đúng sai của các mệnh đề sau. 3
a) Đạo hàm của hàm số là f  x 2
x  2mx m  2 . b) Với m  2
 thì phương trình f ' x  0 có một nghiệm x  2 . c) m  2
 thì bất phương trình f ' x  0 có hai nghiệm nguyên phân biệt. 15
d) Số các giá trị nguyên của tham số m để f ' x  0 với mọi x  là 4 . 2x 1
Câu 83. Hàm số y
, với m là tham số. Các mệnh đề sau đúng hay sai? x m 5
a) Khi m  2 thì hàm của hàm số là y  , x   , x  2 .  x  22 2m 1 b) Với x
  m , hàm số có đạo hàm y  .  x m2 c) Với m
   thì phương trình y  0 vô nghiệm.
d) Có duy nhất một giá trị nguyên âm của m để y  0, x   4;  . Câu 84. Cho hàm số 2
y f (x)  ln(x 1)  x  2024 . Khi đó các mệnh đề sau đúng hay sai? 1
a) f  x  1 . 2 x 1 b) f 0  1.
c) Phương trình f  x  0 có hai nghiệm phân biêt.
d) Hàm số y f  x có giá trị nhỏ nhất bằng 2 . 1 Câu 85. Cho hàm số 3 2 y
x mx  m  6 x  3 có đạo hàm là y . Khi đó: 3
a) Với m  1 thì y  1  6 .
b) Với m  1 thì y x  10 khi x  3   ;1 . c) Với m   ;  2
   3;  thì phương trình y  0 có hai nghiệm phân biệt.
d) Tổng tất cả các giá trị của m để phương trình y  0 có hai nghiệm phân biệt là x , x thỏa mãn 2 2 x x  30 1 2 1 2 là 4 . 2x 1
Câu 86. Cho hàm số y
có đồ thị C . Các mệnh đề sau đúng hay sai? x  5
a) Hàm số có tập xác định D   \   5 . 11 b) y  , x    .  x  52 c) y 4    11.
d) Diện tích tam giác tạo bởi tiếp tuyến của C  tại điểm có hoành độ bằng 6 và hai trục tọa độ bằng 283
Câu 87. Cho hàm số y f x 3
x  m  
1 x 1 có đạo hàm y (với m là tham số ). Các mệnh đề sau đúng hay sai?
a) Với m  4 thì f   1  0 .
b)Với m  1 thì f  x  5 khi x   1 .
c) Với m  0 thì f  x  6
x 1 khi x  ;  2  0; .
d)Với m  1 thì đạo hàm của hàm số y f 2x  
1 luôn dương với mọi x thuộc  .
Câu 88. Cho hàm số f x  x ln x có đồ thị C  . Các mệnh đề sau đúng hay sai? 1
a) f  x  x  . x b) f   1  1.
c) Phương trình f  x  2 có một nghiệm nguyên dương.
d) Tiếp tuyến của đồ thị C  tại điểm có hoành độ x e có phương trình y  2x  2e . 0
______________________________ 16
ĐẠO HÀM LỚP 11 THPT
LỚP BÀI TOÁN TRẮC NGHIỆM ĐÚNG SAI (ỨNG DỤNG THỰC TẾ)
_____________________________
Câu 1. Một chất điểm chuyển động thẳng xác định bởi phương trình ( S t) , với (
S t) là quãng đường có đơn vị là ( )
m . Các mệnh đề sau đúng hay sai?
a) Vận tốc của chất điểm được xác định bởi công thức V S(t) .
b) Gia tốc của chất điểm được xác định bởi công thức (
a t)  V (t) .
c) Vận tốc của chất điểm tại thời điểm t  2 giây là V(2)  ( S 2) .
d) Gia tốc của chất điểm tại thời điểm t  2 giây là (
a 2)  S (2) .
Câu 2. Một viên đạn được bắn lên cao theo phương thẳng đứng có phương trình chuyền động st 2
 2  196t  4,9t ,
trong đó t  0, t(s) là thời gian chuyển động, s(m) là độ cao so với mặt đất.
Xét tính đúng sai của các mệnh đề sau
a) Sau 20s kể từ khi bắn thì viên đạn đạt được độ cao 1962m .
b) Vận tốc tức thời của viên đạn ngay khi viên đạn được bắn ra là 196m / s
c) Vận tốc tức thời của viên đạn khi viên đạn đạt được độ cao 1962m là 5m / s .
d) Tại thời điểm viên đạn đạt vận tốc tức thời bằng 98 m/s thì viên đạn đang ở độ cao 1472m so với mặt đất.
Câu 3. Một tài xế đang lái xe ô tô, ngay khi phát hiện có vật cản phía trước đã phanh gấp lại nhưng vẫn xảy ra
va chạm, chiếc ô tô để lại vết trượt dài 20,4 m (được tính từ lúc bắt đầu đạp phanh đền khi xảy ra va chạm). 5
Trong quá trình đạp phanh, ô tô chuyển động theo phương trình 2
s(t)  20t
t , trong do s (đơn vị mét) 1à 2
độ dài quãng đường đi được sau khi phanh, t (đơn vị giây) là thời gian tính từ lúc bắt đầu phanh ( 0  t  4 ).
Xét tính đúng sai của các mệnh đề sau
a) Vận tốc tức thời của ô tô ngay khi đạp phanh là 20(m / ) s
b) Xe ô tô trên chưa chạy quá tốc độ, (tốc độ giới hạn cho phép là 70 km/h).
c) Thời điểm xảy ra va chạm cách thời điểm bắt đầu đạp phanh 6,8giây
d) Vận tốc tức thời của ô tô ngay khi xảy ra va chạm là 14(m / s)   
Câu 4. Phương trình chuyển động của một hạt được cho bởi công thức s t   10  2 sin  4 t   , trong đó  4 
s tính bằng centimet và t được tính bằng giây. Xét tính đúng sai của các mệnh đề sau
a) Gia tốc của hạt tại thời điểm t  3 giây là 2 16 2 cm/s
b) Vận tốc của hạt tại thời điểm t  3 giây là 2 cm/s .
c) Vận tốc lớn nhất của hạt đạt được là 4 2 cm/s .
d) Gia tốc nhỏ nhất của hạt đạt được là 2 16 2 cm/s .
Câu 5. Một vật chuyển động trên đường thẳng được xác định bởi công thức 3 2
s(t)  t  3t  7t  2 , trong đó
t  0 và tính bằng giây và s là quãng đường chuyển động được của vật trong t giây tính bằng mét. Xét tính
đúng, sai của các khẳng định sau
a) Tốc độ của vật tại thời điểm t  2 là 7( m / ) s 2
b) Gia tốc của vật tại thời điểm t  2 là 6 m/ s  2 2
c) Gia tốc của vật tại thời điểm mà vận tốc của chuyển động bằng 16 m / s là 10 m / s
d) Thời điểm t  1 (giây) tại đó vận tốc của chuyển động đạt giá trị nhỏ nhất. 1
Câu 6. Một chất điểm chuyển động có quãng đường S được xác định bởi phương trình: S t  3 2
t t  3t 3
trong đó t  0, t được tính bằng giây và S được tính bằng mét. Các mệnh đề sau đúng hay sai?
a) Phương trình vận tốc tức thời của chất điểm là v t  2
t  2t  3 .
b) Tại thời điểm bắt đầu chuyển động, gia tốc tức thời của chất điểm bị triệt tiêu. 14
c) Tại thời điểm vận tốc tức thời của chất điểm nhỏ nhất, chất điểm chuyển động được quãng đường dài 3 mét.
d) Khi gia tốc tức thời của chất điểm không dương, vận tốc tức thời của chất điểm dao động trong phạm vi 2
m/s đến 3 m/s. 17
Câu 7. Một chất điểm bắt đầu chuyển động theo phương trình s t  3 2
 2t  3t  5t  8 , trong đó t  0 , t tính
bằng giây và s t tính bằng mét. Các mệnh đề sau đúng hay sai?
a) Gia tốc tức thời của chất điểm là a t   t   2 12 6 m / s  .
b) Gia tốc tức thời của chất điểm tại thời điểm t  5 s là  2 54 m / s  .
c) Gia tốc tức thời của chất điểm tại thời điểm vận tốc đạt giá trị nhỏ nhất là  2 0 m / s  . d) Khi gia tốc bằng  2
6 m / s  thì quãng đường chất điểm di chuyển được là 12m. 1
Câu 8. Một chất điểm rơi tự do với phương trình chuyển động được xác định bởi hàm số 2 (
S t)  gt . Với 2 2
(g10m/ s ) ở độ cao 125m . Các mệnh đề sau đúng hay sai? 1 1 2  1 gt g 1
a) Vận tốc của chất điểm tại thời điểm t  giây là 2 8 S (  )  lim . 2 1 2 x 1 2 t  2 1 2 gt  2g b) Nếu 2 lim
 2gthì chất điểm đạt vận tốc là 2. x2 t  2
c) Vận tốc của chất điểm được xác định bởi công thức V(t)  S(t)  gt .
d) Khi chạm đất thì chất điểm đạt vận tốc V(t)  40m/ s .
Câu 9. Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát, có phương trình    
chuyển động x t   2 cos t  1  
, trong đó t tính bằng giây và x t  tính bằng centimét. Các mệnh đề sau  2 6  đúng hay sai?    
a) Gia tốc tức thời của con lắc là x t  2    t     2 cos cm / s  .  2 6  2 3
b) Gia tốc tức thời của con lắc tại thời điểm t  2 s là x 2   2 cm / s  . 2
c) Gia tốc tức thời của con lắc tại thời điểm vận tốc đạt giá trị lớn nhất  2 0 cm / s  .
d) Khi gia tốc tức thời của con lắc đạt lớn nhất thì con lắc cách vị trí ban đầu 2cm .
Câu 10. Một chất điểm chuyển động theo phương trình s t   3sin 2t  cos 2t với t (giây) là khoảng thời gian
tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Các mệnh đề sau đúng hay sai?    
a) Vận tốc tức thời tại thời điểm t
giây của chuyển động bằng v  2 m/s   . 8  8 
b) Gia tốc tức thời tại thời điểm t giây của chuyển động bằng a t   12sin 2t  4 cos 2t .    
c) Gia tốc tức thời tại thời điểm t
giây của chuyển động bằng 2 a  4  m/s   . 4  4 
d) Gia tốc của chuyển động đạt giá trị lớn nhất bằng 4 10 .
Câu 11. Cho chuyển động xác định bởi phương trình S t  3 2
t  3t  9t  27 . Trong đó t tính bằng giây (s) và
S tính bằng mét (m). Các mệnh đề sau đúng hay sai?
a) Đạo hàm cấp một của hàm số đã cho là S 't  2
 3t  6t  9 .
b) Vận tốc tức thời tại thời điểm t  3 giây của chuyển động bằng v 3  40 m/s .
c) Gia tốc tức thời tại thời điểm t  4 giây của chuyển động bằng a   2
4  24 m / s .
d) Gia tốc của chuyển động tại thời điểm vận tốc triệt tiêu là 2 12 m / s .
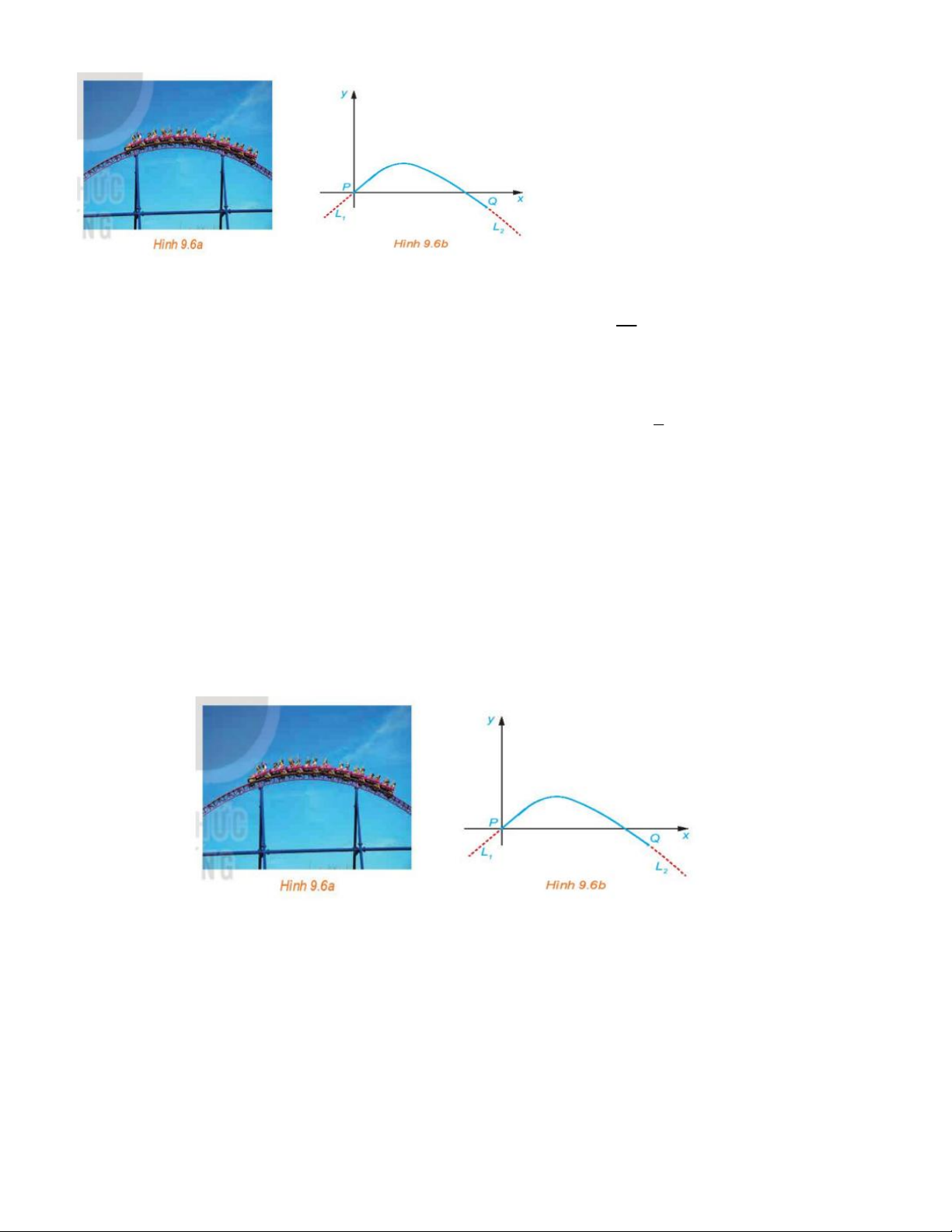
Câu 12. Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một đường cong có dạng parabol
(H.9.6a), đoạn dốc lên L và đoạn dốc xuống L là phần đường thẳng có hệ số góc lần lượt là 0, 5 và 0, 75 . 1 2
Để tàu lượn chạy êm và không bị đổi hướng đột ngột, L và L phải có những tiếp tuyến của cung parabol tại 1 2 18
các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc tọa độ đặt tại P và phương trình của parabol là 2
y ax bx c , trong đó x tính bằng mét. Các mệnh đề sau đúng hay sai? a) c  0 . b) b  0, 5 . 1
c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 . Khi đó a  . 64
d) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 . Chênh lệch độ cao giữa hai điểm chuyển tiếp
P và Q bằng 5 . 1
Câu 13. Một chất điểm chuyển động thẳng xác định bởi phương trình 3 2 (
S t)   t 3t 2t  6, với ( S t) là 3
quãng đường có đơn vị là ( )
m . Các mệnh đề sau đúng hay sai?
a) Vận tốc của chất điểm được xác định bởi công thức 2
V(t)  t  6t2.
b) Tại thời điểm t  2 giây chất điểm đạt vận tốc lớn nhất.
c) Chất điểm đạt vận tốc lớn nhất là V(t)  7(m/ ) s .
d) Khi chất điểm đạt vận tốc lớn thì vật chuyển động được quãng đường là 18 (m) .
Câu 14. Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng
parabol (H.9.6a), đoạn dốc lên L và đoạn dốc xuống L là những phần đường thẳng có hệ số góc lần lượt là 1 2
0, 5 và 0, 75 . Để tàu lượn chạy êm và không bị đổi hướng đột ngột, L và L phải là những tiếp tuyến của 1 2
cung parabol tại các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc toạ độ đặt tại P và phương trình của parabol là 2
y ax bx c , trong đó x tính bằng mét.
Các mệnh đề sau đúng hay sai? a) Ta có: c  0 .
b) y (0)  b  0, 5 .
c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 m . Khi đó a  6  4
d) Chênh lệch độ cao giữa hai điểm chuyển P và Q là 5( ) m .
Câu 15. Một vật chuyển động trên một đường được xác định bởi công thức 3 2
s(t)  t  3t  7t  2 , trong đó
t  0 và tính bằng giây và s là quãng đường chuyển động được của vật trong t giây tính bằng mét. Các mệnh đề sau đúng hay sai?
a) Vận tốc của vật tại thời điểm t  2 là 7( m / s) .
b) Gia tốc của vật tại thời điểm t  2 là  2 6 m / s  .
c) Gia tốc của vật tại thời điểm mà vận tốc của chuyển động bằng 16 m / s là  2 10 m / s  .
d) Thời điểm t  1 (giây) tại đó vận tốc của chuyển động đạt giá trị nhỏ nhất. 19
Câu 16. Một con lắc lò xo dao động điều hoà theo phương ngang trên mặt phẳng không ma sát, có phương  2 3 
trình dao động x t   10sin t   3  
, trong đó x tính bằng centimét và thời gian t tính bằng giây. Các  3 5 
mệnh đề sau đúng hay sai? a) [NB] x 
0 12,5(làm tròn kết quả đến một chữ số thập phân). 20  2 3 
b) x 't   co s t    . 3  3 5 
c) Vận tốc của con lắc tại thời điểm t  8s là 20, 5 (cm/s) (Làm tròn đến một chữ số thập phân).
d) Thời điểm đầu tiên mà vận tốc của con lắc bằng 0 là 1, 35(s) .
Câu 17. Một vật chuyển động trên đường thẳng được xác định bởi công thức 3 2
s(t)  t  3t  7t  2 , trong đó
t  0 tính bằng giây và s là quãng đường chuyển động được của vật trong t giây tính bằng mét. Các mệnh đề sau đúng hay sai?
a) Tốc độ của vật tại thời điểm t  2 là 7( m / s) .
b) Gia tốc của vật tại thời điểm t  2 là  2 6 m / s  .
c) Gia tốc của vật tại thời điểm mà vận tốc của chuyển động bằng 2 16 m / s là  2 10 m / s  .
d) Thời điểm t  1 (giây) tại đó vận tốc của chuyển động đạt giá trị nhỏ nhất. 26t  10
Câu 18. Số dân của một thị trấn sau t năm kề từ năm 1970 được ước tính bởi công thức f t   t  5
( f t  được tính bằng nghìn người). Các khẳng định sau đúng hay sai?
a) Số dân của thị trấn vào đầu năm 1980 là 18 nghìn người.
b) Số dân của thị trấn vào đầu năm 1995 là 23 nghìn người.
c) Xem f t  là một hàm số xác định trên nửa khoảng 0;  , đạo hàm của hàm số f t  biểu thị tốc độ tăng
dân số của thị trấn (tính bằng nghìn nguời/năm) có công thức là: 120
f  t   . t  52
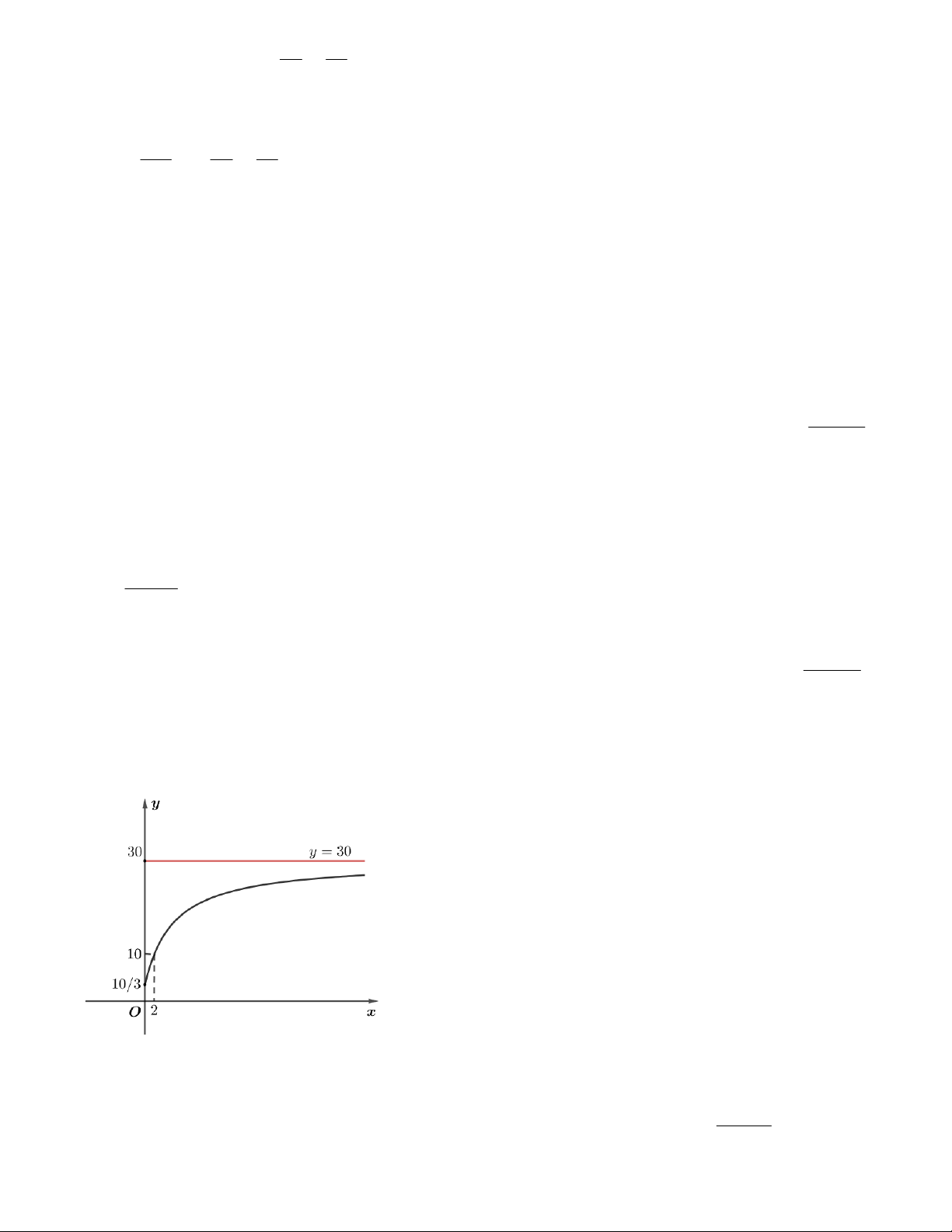
d) Hàm số f t  nghịch biến trên 0;  . 30t  20
Câu 19. Số dân của một thành phố sau t năm kể từ năm 1980 được ước tính bởi công thức f t   , t  6
f t  được tính bằng nghìn người. Các khẳng định sau đây đúng hay sai?
a) Số dân của thành phố vào năm 2025 (kết quả làm tròn tới hàng phần nghìn) là 26,863 nghìn người.
b) Số dân của thành phố có thể vượt quá 30 nghìn người.
c) Xem f t  là một hàm số xác định trên nửa khoảng 0;  thì hình vẽ sau đây là đồ thị của hàm số f t
d) Đạo hàm của hàm số f t  biểu thị tốc độ tăng dân số của thành phố (tính bằng nghìn người/năm) thì tốc độ
tăng dân số của thành phố vào năm 2002 nhỏ hơn tốc độ tăng dân số của thành phố vào năm 2025.
Câu 20. Trong thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, 100t
người ta xác định số lượng vi khuẩn thay đổi theo thời gian bởi công thức: N t  1000  (con). Trong 2 100  t
đó t là thời gian tính bằng giây. Các khẳng định sau đúng hay sai?
a) Số lượng vi khuẩn tại thời điểm 10 giây sau khi cấy là 1005 con. 20

Tài liệu liên quan: