Luyện tập chung Bài 21-22 | Bài giảng PowerPoint Toán 8 | Kết nối tri thức

+ Phân thức đại số là gì? cho ví dụ.
Phân thức đại số là một biểu thức có dạng trong
đó A, B là hai đa thức và B khác đa thức 0. A là tử, B là mẫu 2x  1 Ví dụ : 2 3x  4x 1
Điều kiện xác định của phân thức là gì?
Điều kiện xác định của phân thức là điều kiện của
biến để giá trị của mẫu thức B khác 0
Để tính giá trị của phân thức tại những giá
trị cho trước của biến ta thực hiện như thế nào?
Để tính giá trị của phân thức tại những giá trị cho
trước của biến ta thay các giá trị cho trước của biến
vào phân thức rồi tính giá trị của biểu thức số vừa nhận được.
http://tieuhoc.info – Pham Khac
Lap Kien Bai Primary School – 2015
Nêu tính chất cơ bản của phân thức?
+ Tính chất cơ bản của phân thức
- Nếu nhân cả tử và mẫu của 1 phân thức với cùng 1
đa thức khác 0 thì được 1 phân thức bằng phân thức đã cho A A.M =  M 0   B B.M
- Nếu tử và mẫu của phân thức có nhân tử chung thì
khi chia cả tử và mẫu cho nhân tử chung đó ta được
một phân thức bằng phân thức đã cho
A A : N (N là nhân tử chung) = B B : N
http://tieuhoc.info – Pham Khac
Lap Kien Bai Primary School – 2015
Nêu cách rút gọn phân thức?
Cách rút gọn phân thức:
Muốn rút gọn một phân thức đại số ta làm như sau:
- Phân tích tử và mẫu của phân thức (nếu cần) để tìm nhân tử chung
- Chia cả tử và mẫu cho nhân tử chung đó
http://tieuhoc.info – Pham Khac
Lap Kien Bai Primary School – 2015
Nêu cách quy đồng mẫu thức nhiều phân thức?
Cách quy đồng mẫu thức nhiều phân thức
B1: Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung .
B2: Tìm nhân tử phụ của mỗi mẫu thức.
B3: Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
http://tieuhoc.info – Pham Khac
Lap Kien Bai Primary School – 2015 1. Ví dụ 1. 2 Cho phân thức: x  4 P  x  2
a) Viết điều kiện xác định của P
b) Rút gọn P và kí hiệu Q là phân thức nhận được
c) Kiểm tra x = 13 có thỏa mãn điều kiện xác định của P hay
không. Tính giá trị của P và Q tại x = 13 rồi so sánh hai kết quả G Giiải ải
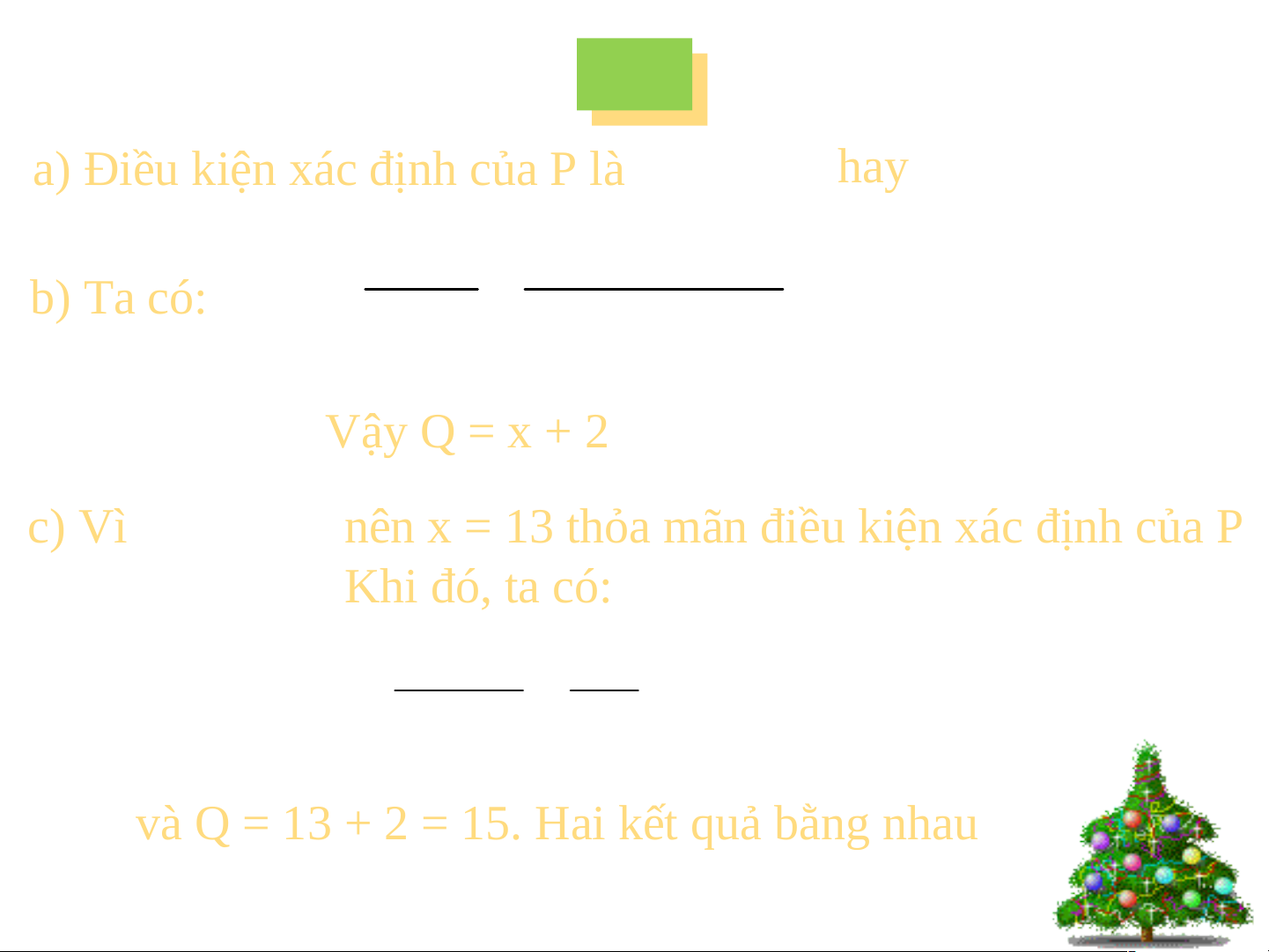
a) Điều kiện xác định của P là x  2 0  hay x 2 
a) Điều kiện xác định của P là hay 2
x  4  x  2  x  2 b) Ta có: P   x   2 b) Ta có: x  2 x  2 V V ậy Q ậy Q = = x + x + 2 2 c) Vì x 13  2  c) Vì nên x = nên x = 13 t 13 t hỏa m hỏa m ãn đi ãn đi ều k ều kiiện xác ện xác đị đị nh của P nh của P K K h hii đ đ ó, t ó, t a có: a có: 2 13  4 165 P   1  5 13  2 11 và Q và Q = = 13 + 13 + 2 = 2 = 15. H 15. H a aii kết kết quả bằng nh quả bằng n au hau C C hú ý hú ý
Khi tính giá trị của một phân thức tại giá trị đã cho của
biến thỏa mãn điều kiện xác định, ta nên rút gọn phân thức
rồi thay giá trị đã cho của biến vào phân thức đã rút gọn 2. Ví dụ 2. T T H H Ả Ả O O L L U U Ậ Ậ N N N N H H Ó Ó M M
Bạn Nam vẽ lá cờ Tổ Quốc là một hình chữ nhật có chiều
rộng 12cm và chiều dài 19cm.
a) Viết phân thức biểu thị tỉ số giữa chiều rộng và chiều
dài của hình chữ nhật nhận đượckhi tăng mỗi cạnh của hình
chữ nhật đã vẽ thêm x (cm)
b) Tính giá trị của phân thức trong câu a tại x = 2 và cho
biết hình chữ nhật đó có đảm bảo tỉ lệ tiêu chuẩn
2 : 3 của quốc kì Việt Nam không? G Giiả ảii a) a) K K hi hi ttăng m ăng m ỗ ỗii cạ cạ nh x ( nh x ( cm cm )) t t hì hì hì hì nh chữ nh c nhật hữ nhật m m ớ ớii có có chi chi ều r ều ộng và rộng v chi à chi ều dài ều dài l l ần ần llượt ượt l l à ( à ( 12 12 + + x) x) ((c c m m )) và và ( ( 19 19 + + x) x) ((cm cm )).. T Tỉỉ số gi số gi ữa chi ữa chi ều r ều ộng và chi rộng và chi ều ều dài dài của hì của hì nh nh 12  x chữ nhật chữ nhật m m ới ới llà: à: 1 9  x 12  2 14 2
b) Giá trị của phân thức tại x = 2 là  
b) Giá trị của phân thức tại x = 2 là 19  2 21 3 V Vìì vậ vậ y h y hìình nh chữ nhật
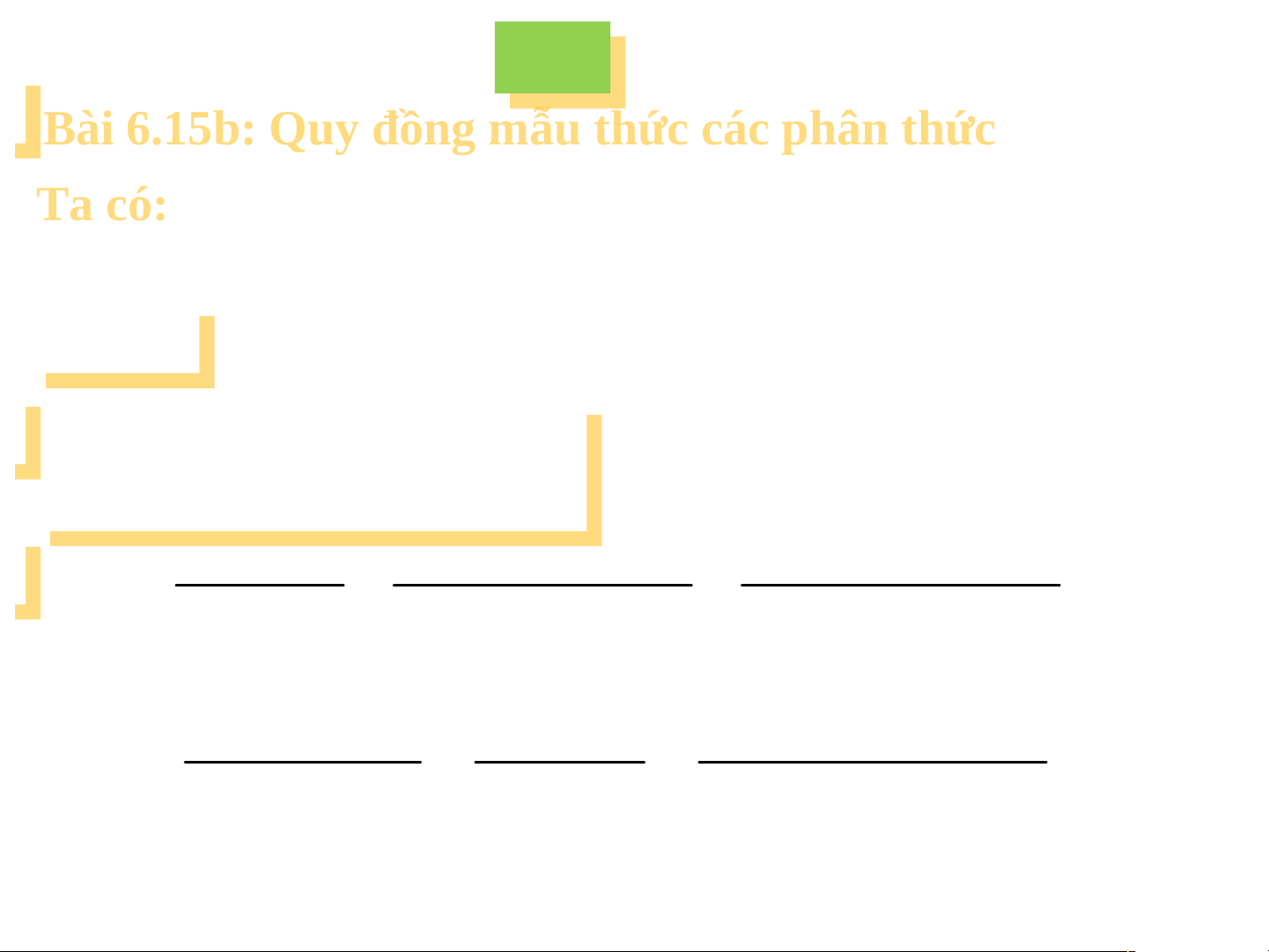
chữ nhật đó đảm đó đảm bảo bảo ttỉỉ llệ t ệ tiiêu chuẩn 2: êu chuẩn 2: 3 3 của của quốc kì quốc kì V Viiệt ệt N N am am L L U U Y Y Ệ Ệ N N T T Ậ Ậ P P B B ài ài 6.15 6 b: .15b: Q Q uy đồng m uy đồng m ẫu t ẫu t hức hức các p các hân t phân t hức hức 9 1 2 4x và  36 2 và x  6x  9 3 x  4x
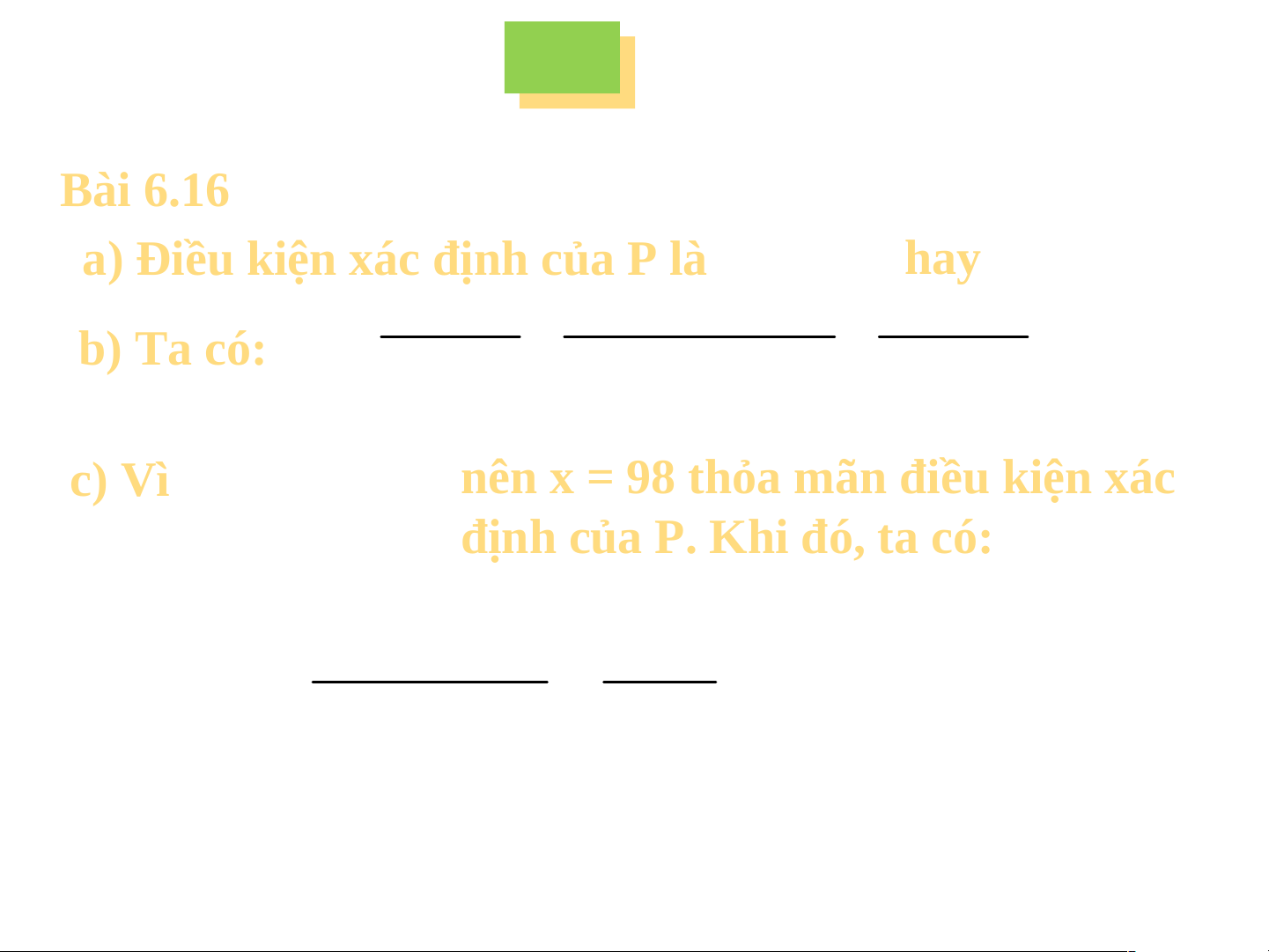
Bài 6.16. Cho phân thức P 
Bài 6.16. Cho phân thức  x  2 2 a) a) V Viiết ết đi đi ều ki ều ki ện xác ện xác đị đị nh c nh ủa phân t của phân t hức hức b) b) R R út út gọ g n phâ ọn phâ n t n t hức hức P P c) c) T Tíính g nh giiá t á t rị rị của phâ của phâ n t n t hức hức đã ch đã o t cho t ại ại x = x = 98 98 G Giiải ải B B ài ài 6.15 6.1 b: 5b: Q Q uy đồng m uy đồng m ẫu t ẫu t hức hức các các phân t phân t hức hức 2 T T a có: a có:    2 4x 36 4 x  9 4
  x  3  x  3       2 2 x 6x 9 x 3 MT MT C C ::   2 4 x 3  x  3 N N T T P: P: < < x + x + 3> 3> ;; < < 4( 4( x – 3) x – 3) > > Q Q Đ Đ :: 9 9 9 x  3   2 4x  36
4 x  3  x  3 4 x  32  x  3 1 1 4 x  3   2 x  6x  9  x  3 2
4 x  3 2  x  3 G Giiả ảii B B ài ài 6.16 6.16
a) Điều kiện xác định của P là x  2 0  hay x  2
a) Điều kiện xác định của P là hay 3 x  4x
x  x  2  x  2 x x  2 b) Ta có: P    b) Ta có:  x  2 2  x  22 x  2 c) Vì x 9  8  2 c) Vì nên x = nên x = 98 t 98 t hỏa m hỏa m ãn đi ãn đi ều ki ều ki ện xác ện xác đị đị nh c nh ủa P. của P. K K hi hi đó, t đó, t a c a ó: có: 98 98  2 9408 P   9  4,08 98  2 100 V V Ậ Ậ N N D D Ụ Ụ N N G G
Bài tập 6.18 SGK trang 14.
Lúc 6 giờ sáng, Bác Vinh lái ô tô xuất phát từ Hà Nội
đi huyện Tĩnh Gia(Thanh Hóa). Khi đến Phủ Lý (Hà Nam),
cách Hà Nội khoảng 60km, Bác Vinh dừng lại ăn sáng trong
20 phút. Sau đó, bác Vinh tiếp tục đi về Tĩnh Gia và phải
tăng vận tốc thêm 10km/h để đến nơi đúng giờ dự định.
a) Gọi x (km/h) là vận tốc của ô tô đi trên quãng
đường Hà Nội – Phủ Lý. Hãy viết các phân thức biểu thị
thời gian bác Vinh chạy xe trên các quãng đường Hà Nội –
Phủ Lý và Phủ Lý – Tĩnh Gia, Biết rằng quãng đường Hà
Nội – Tĩnh Gia có chiều dài khoảng 200km
b) Nếu vận tốc ô tô đi trên quãng đường Hà Nội –
Phủ Lý là 60km/h thì bác Vinh đến Tĩnh gia lúc mấy giờ. G Giiả ảii a) a) T T hời hời g giian ch an ạy xe
chạy xe quãng đường H
quãng đường H à N à N ội ội - - Phủ L Phủ L ý l ý l à à 60 (giờ). x Q Q uãng đường P
uãng đường P hủ L hủ L ý - ý - T Tĩĩnh G nh Giia l a l à 20 à 20 0 – 60 = 0 – 60 = 14 1 0km 40km N N ên ên tthời hời g giian chạ an chạ y xe y xe quãn quã g đường Phủ ng đường P L hủ L ý - ý - T Tĩĩnh nh G Giia a 140 ( ( vậ v n t ận t ốc t ốc t ăng 10 km ăng 10 km//h) h) llà à (giờ). x 10 G Giiả ảii b) b) N N ếu vận t ếu vận t ốc ốc ô t ô t ô t ô t rên quãng rên quã đường ng đường H H à N à N ội ội -- Phủ Phủ L L ý l ý l à à 60 km 60 km//h, t h, t ức l ức l à x = à x = 60 60 tthì hì t t hời hời g giian xe an đi xe đi ttừ ừ H H à N à N ội ội đến đến T Tĩĩnh G nh Giia ( a ( không
không kể cả dùng nghỉ
kể cả dùng nghỉ 20 2 phút 0 phút )) llà à 60 140  1   2 3  60 60 10 T T hời hời g giian xe an đi xe đi ttừ ừ H H à N à N ội ội đến T đến Tĩĩnh G nh Giia kể
a kể cả dừng nghỉ cả dừng nghỉ 20 p 20 hút phút llà 3 gi à 3 gi ờ 20 phút ờ 20 phút :: V V ậy xe ậy xe xuất xuất phát phát l l úc ú 6 g c 6 giiờ sáng ờ sáng nên nê xe n xe đến T đến Tĩĩnh G nh Giia a llúc úc 9 g 9 giiờ ờ 20 2 phút 0 phút..
HƯỚNG DẪN VỀ NHÀ
- Ghi nhớ kiến thức trong bài.
- Hoàn thành các bài tập trong SGK, bài 6.17; 6.19 (trang 14 SGK).
- Chuẩn bị bài mới “Phép cộng và phép trừ
phân thức đại số”.
Document Outline

• PowerPoint Presentation
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22