26 trang 3 lượt tải

Luyện tập chung Toán 11 THPT đạo hàm và ứng dụng

6

Tài liệu gồm 26 trang, được biên soạn bởi thầy giáo Đặng Công Đức (Giang Sơn), tuyển chọn các bài tập luyện tập chung môn Toán 11 THPT chủ đề đạo hàm và ứng dụng (kết hợp 3 bộ sách giáo khoa Toán 11: Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống).

Chủ đề: Tài liệu chung Toán 11 85 tài liệu

Môn: Toán 11 3.6 K tài liệu

Tác giả:

Profile

Linh Đan

1 tháng trước
Danh sách Quiz
/26
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
L
L
U
U
Y
Y
Ệ
Ệ
N
N
T
T
Ậ
Ậ
P
P
C
C
H
H
U
U
N
N
G
G
T
T
O
O
Á
Á
N
N
1
1
1
1
T
T
H
H
P
P
T
T
Đ
Đ
Ạ
Ạ
O
O
H
H
À
À
M
M
V
V
À
À
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
Đ
Đ
Á
Á
P
P
Á
Á
N
N
C
C
H
H
I
I
T
T
I
I
Ế
Ế
T
T
P
P
D
D
F
F
B
B
Ạ
Ạ
N
N
Đ
Đ
Ọ
Ọ
C
C
V
V
U
U
I
I
L
L
Ò
Ò
N
N
G
G
L
L
I
I
Ê
Ê
N
N
H
H
Ệ
Ệ
T
T
Á
Á
C
C
G
G
I
I
Ả
Ả
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
9
9
8
8
0
0
2
2
1
1
9
9
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
2
2
/
/
2
2
0
0
2
2
5
5
2
L
L
U
U
Y
Y
Ệ
Ệ
N
N
T
T
Ậ
Ậ
P
P
C
C
H
H
U
U
N
N
G
G
T
T
O
O
Á
Á
N
N
1
1
1
1
T
T
H
H
P
P
T
T
Đ
Đ
Ạ
Ạ
O
O
H
H
À
À
M
M
V
V
À
À
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
DUNG
LƯỢNG
NỘI DUNG
8 FILE
1 file 3 trang
LUYỆN TẬP CHUNG
Đ
Đ
Ạ
Ạ
O
O
H
H
À
À
M
M
V
V
À
À
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
3
ĐẠO HÀM LỚP 11 THPT
(LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P1_ĐÁP ÁN)
_______________________________
TRẮC NGHIỆM ABCD
Câu 1. Cho hàm số
3
2
f x x x m
, giá trị của
1
f
bằng
A. 6 . B. 8 . C. 3 . D. 2 .
Câu 2. Tính đạo hàm của hàm số
2
logy x
A.
ln 2
'y
x
B.
1
'
y
x
. C.
'
ln 2
x
y
. D.
'
y
.
Câu 3. Tìm hàm số
y F x
có bảng xét dấu đạo hàm
y f x
như sau
A.
3
( 2)
y x
B.
2
4 4
y x x
C.
3 2
6 9 4
y x x x
D.
3
2( 2)
y x
Câu 4. Cho hàm số
3 2
3 5y x x mx
. Tìm giá trị tham số m để
1 4
y
.
A.
5
m
B.
4
m
C.
3
m
D.
2
m
Câu 5. Tính đạo hàm của hàm số
4 3
y x
.
A.
2
4 3
y
x
B.
4
4 3
y
x
C.
1
2 4 3
y
x
D.
1
4 3
y
x
Câu 6. Tìm vi phân của hàm số
sin 2y x
.
A.
2cos2
dy xdx
B.
cos2
dy xdx
C.
sin 2
dy xdx
D.
2sin 2
dy xdx
Câu 7. Cho hàm số
3
3y x x
có đồ thị
C
.Hệ số góc
k
của tiếp tuyến với đồ thị
C
tại điểm có tung độ
bằng
4
là:
A.
0
k
B.
2
k
C.
6
k
D.
9
k
Câu 8. Cho hàm số
2
sin
2
x
y
. Tính đạo hàm của hàm số đã cho.
A.
1
' sin
2
y x
B.
' sin2y x
C.
' 2sin2y x
D.
' siny x
Câu 9. Cho hàm số
3 2
8y x x mx
. Có bao nhiêu số nguyên dương m sao cho
1 0
y
.
A.10 B. 4 C. 9 D. 8
Câu 10. Hàm số
3 2
1y x mx nx
thỏa mãn điều kiện
(1) 6; (2) 17
y y
. Tính
m n
.
A.3 B. 0 C. 1 D. 2
Câu 11. Hàm số
2
2
x x
y
có đạo hàm là
A.
2
2 .ln 2
x x
. B.
2
(2 1).2 .ln 2
x x
x
. C.
2
2 1
( ).2
x x
x x
. D.
2
(2 1).2
x x
x
.
Câu 12. Một chất điểm dao động điều hòa theo phương trình
3cos 2
3
S t cm
. Tìm gia tốc tức thời của
chất điểm tại thời điểm
2t s
.
A.
2
59,22 /cm s
. B.
2
59,22 /cm s
. C.
2
18,85 /cm s
. D.
2
18,85 /cm s
.
4
TRẮC NGHIỆM ĐÚNG, SAI
Câu 1. Cho hàm số
4
.
x
y x e
. Xét tính đúng sai của các mệnh đề sau
a)
4
' 4 4 .
x
y x e
b)
4
' 4
x
y e y
.
c)
' 0 1
y
.
d)
4
' 1 5.y e
.
Câu 2. Một viên đạn được bắn lên cao theo phương thẳng đứng có phương trình chuyền động
2
2 196 4,9s t t t
,
trong đó
0, ( )t t s
là thời gian chuyển động,
( )s m
là độ cao so với mặt đất.
Xét tính đúng sai của các mệnh đề sau
a) Sau
20s
kể từ khi bắn thì viên đạn đạt được độ cao
1962m
.
b) Vận tốc tức thời của viên đạn ngay khi viên đạn được bắn ra là
196 /m s
c) Vận tốc tức thời của viên đạn khi viên đạn đạt được độ cao
1962m
là
5 /m s
.
d) Tại thời điểm viên đạn đạt vận tốc tức thời bằng 98 m/s thì viên đạn đang ở độ cao
1472m
so với mặt đất.
Câu 3. Cho hàm số
2
2
y x x
. Xét tính đúng sai của các mệnh đề sau
a)
3
. 1 0
y y
b)
3
. 1
y y
c)
3 2
1
( 2 ).y x x y
y
.
d)
3
2
1
2
y
x x
.
Câu 4. Cho hàm số
4
3 2
3 2
3
4 2
x m
y f x mx x
trong đó
m
là tham số. Các mệnh đề sau đúng hay
sai?
a)
3 2
3 3 2f x x mx m x
.
b) Kết quả của
1
6
f
không phụ thuộc vào tham số
m
.
c) Với
1
m
, ta có
2 27
f
.
d) Có hai giá trị dương của tham số
m
thỏa mãn phương trình
0
f x
có hai nghiệm phân biệt sao cho tổng
bình phương của hai nghiệm đó bằng
26
9
.
5
TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. Một chất điểm chuyển động theo phương trình
3 2
S 2t 18t 2t 1
, trong đó
t
tính bằng giây
s
và
S
tính bằng mét
m
. Tính thời gian vận tốc chất điểm đạt giá trị lớn nhất.
Câu 2. Một vật chuyển động theo phương trình
3 2
2
s t t mt
(đơn vị: mét). Biết rằng tại thời điểm
10t s
vận tốc của chuyển động bị triệt tiêu. Tìm gia tốc của chuyển động tại thời điểm
2t s
.
Câu 3. Cho hàm số
f x
thỏa mãn
2
2
1 1 .
xf x x f x f x
với mọi
x
dương. Biết
1 1 1
f f
. Giá trị
2
2
f
gần nhất số nguyên nào
Câu 4. Có bao nhiêu giá trị nguyên âm của tham số
m
để hàm số
4
1 3
4 2
y x mx
x
có đạo hàm không âm
trên khoảng
0;
.
C
C
â
â
u
u
5
5
.
.
C
C
á
á
c
c
h
h
à
à
m
m
s
s
ố
ố
2
2
, ,
f x
y f x y f x y
f x
l
l
ầ
ầ
n
n
l
l
ư
ư
ợ
ợ
t
t
c
c
ó
ó
c
c
á
á
c
c
đ
đ
ồ
ồ
t
t
h
h
ị
ị
1 2 3
, ,C C C
.
.
H
H
ệ
ệ
s
s
ố
ố
g
g
ó
ó
c
c
t
t
i
i
ế
ế
p
p
t
t
u
u
y
y
ế
ế
n
n
t
t
ạ
ạ
i
i
đ
đ
i
i
ể
ể
m
m
c
c
ó
ó
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
b
b
ằ
ằ
n
n
g
g
1
1
c
c
ủ
ủ
a
a
1 2 3
, ,C C C
(
(
t
t
ư
ư
ơ
ơ
n
n
g
g
ứ
ứ
n
n
g
g
)
)
l
l
ầ
ầ
n
n
l
l
ư
ư
ợ
ợ
t
t
l
l
à
à
1 2 3
, ,k k k
k
k
h
h
á
á
c
c
0
0
v
v
à
à
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
1 2 3
2 3k k k
.
.
T
T
í
í
n
n
h
h
1f
.
.
Câu 6. Cho hàm số
4 3 2
y mx nx px qx r
, , , ,m n p q r
. Hàm số
y f x
có đồ thị như hình vẽ
bên.
Tìm giá trị nhỏ nhất của biểu thức
2018
f x r
S
m
.
6
ĐẠO HÀM LỚP 11 THPT
(LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P2)
_______________________________
TRẮC NGHIỆM ABCD
Câu 1. Cho hàm số
3 2
3 5y x x mx
. Tìm giá trị tham số m để
1 4
y
.
A.
5
m
B.
4
m
C.
3
m
D.
2
m
Câu 2. Tìm đạo hàm của hàm số
logy x
.
A.
ln10
y
x
B.
1
ln10
y
x
C.
1
10ln
y
x
D.
1
y
x
Câu 3. Tính vi phân
2
2x 2
d x
.
A.
2
(2x 2) x
2x 2
d
x
B.
2
( 1) x
2 2x 2
x d
x
C.
2
( 1) x
2x 2
x d
x
D.
2
( 1) x
2x 2
x d
x
Câu 4. Tìm số nghiệm của phương trình
2
ln(2 5 ) 0
x x
.
A.2 B. 1 C. 0 D. 3
Câu 5. Vi phân của
là :
A.
2
5
d d .
cos 5
x
y x
x
B.
2
5
d d .
sin 5
y x
x
C.
2
5
d d .
cos 5
y x
x
D.
2
5
d d .
cos 5
y x
x
Câu 6. Cho hàm số
2 1
1
x
f x
x
. Tồn tại bao nhiêu giá trị nguyên x để
4
27
( 1)
f x
x
?
A. 2 B. 1 C. 3 D. 4
Câu 7. Hàm số
F x
có bảng xét dấu đạo hàm
f x
như hình vẽ
Tồn tại bao nhiêu số nguyên x thỏa mãn
2
2 3 0
x x F x
.
A.4 B. 1 C. 3 D. 2
Câu 8. Cho hàm số
2
3 6
2
x x
y
x
. Tính số nghiệm nguyên của bất phương trình
0
y
.
A.3 B. 5 C. 2 D. 4
Câu 9. Một vật giao động điều hòa có phương trình quảng đường phụ thuộc thời gian
sin
s A t
. Trong
đó
, ,
A
là hằng số,
t
là thời gian. Khi đó biểu thức vận tốc của vật là?
A.
cos
v A t
. B.
cos
v A t
. C.
cos
v A t
. D.
cos
v A t
.
Câu 10. Cho hàm số
.2
3
1
23
xxy
đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là
nghiệm của phương trình
0
y
là:
A.
3
7
xy
B.
3
7
xy
C.
3
7
xy
D.
xy
3
7
Câu 11. Một chất điểm chuyển động theo quy luật
3 2
6s t t t
với
t
là thời gian tính từ lúc bắt đầu chuyển
động,
s t
là quãng đường đi được trong khoảng thời gian
t
. Tính thời điểm
t
tại đó vận tốc đạt giá trị lớn nhất.
A.3s B. 2s C. 4s D. 3,5s
Câu 12. Hàm số xác định trên R thỏa mãn
3
3
lim 3
3
x
f x f
x
. Hỏi phương trình
2
4 3
x x f
có tổng
bình phương các nghiệm là bao nhiêu ?
A. 20 B. 22 C. 37 D. 11
7
TRẮC NGHIỆM ĐÚNG, SAI
Câu 1. Cho hàm số
3 2
2 6 1
f x x x m
. Xét tính đúng sai của các mệnh đề
a)
2
' 6 6f x x x
.
b)
2 2 10
f f
.
c) Giá trị nhỏ nhất của
'f x
bằng – 7.
d) Tồn tại hai giá trị
,a b
thỏa mãn
0
f a f b
thì có 7 số nguyên
m
để
,
f a f b
trái dấu.
Câu 2. Cho hàm số
3
( ) 2y f x x
có đồ thị
( )C
và điểm
M
thuộc
( )C
có hoành độ
0
1
x
. Xét tính đúng,
sai của các khẳng định
a) Phương trình
2
6 1
x f x x f
có hai nghiệm phân biệt cùng dương.
b) Tiếp tuyến của
( )C
tại
M
cắt đồ thị hàm số
2
8 7 4
y x x
tại hai điểm phân biệt có tổng hoành độ
bằng 5.
c) Tiếp tuyến của
( )C
tại
M
cắt đường thẳng
: 3d y x
tại điểm có hoành độ bằng 4.
d) Tiếp tuyến của
( )C
tại
M
vuông góc với đường thẳng
1
:
6
y x
.
Câu 3. Cho hàm số
2
2
y f x x x
. Xét tính đúng, sai của các mệnh đề
a)Vi phân của hàm số là
2
1
2
x
dy dx
x x
.
b)Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 song song với đường thẳng
2
3
3
x
y
.
c)
3 2
2
4 3 2
2 3 6 2
2 3 2
x x x
f x x
x x x x
.
d) Giá trị biểu thức
3 2
. 2 .
M y y x x y x
là một số nguyên tố.
Câu 4. Cho hai hàm số
3 2
3 1f x x x mx
và
2
5
g x x mx m
. Xét tính đúng, sai của các khẳng
định
a)
1 3
f m
.
b) Phương trình
f x g x
có tổng tất cả các nghiệm nhỏ hơn 3.
c)
2
3 6
f g x g x g x m
.
d) Biết
0
m
là giá trị của tham số
m
để hai số phân biệt
1 2
,x x
thỏa mãn
1 2
0
f x f x
và
2 2
1 2 1 2
13
x x x x
. Khi đó
0
15; 7
m
8
TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. Cho hàm số
3 2
1
2 1
3
y x x x
có đồ thị là
C
. Tiếp tuyến của
C
tại điểm
1
1;
3
M
cắt đường
thẳng
5
3
x
tại điểm có tung độ bằng bao nhiêu ?
Câu 2. Cho hàm số
3 2
3
2 2 3 1,
2
y m x m x x m
là tham số. Số các giá trị nguyên
m
để
0,y x
là bao nhiêu ?
Câu 3. Cho hàm số
f x
có đạo hàm trên
thỏa mãn
2 1 e
x
x f x x f x
và
1
0
2
f
. Giá trị
6 2
f
gần nhất số nguyên nào
Câu 4. Cho biết điện lượng truyền trong dây dẫn theo thời gian biểu thị bởi hàm số
2
( ) 2
Q t t t
, trong đó
t
được tính bằng giây và
Q
được tính theo Culông. Tính cường độ dòng điện tại thời điểm
4( )t s
.
Câu 5. Một chất điểm chuyển động thẳng xác định bởi phương trình
2
1
( )
2
s t t
, trong đó
t
là thời gian tính bằng
giây và
s
là quãng đường đi được trong
t
giây tính bằng mét. Tính vận tốc tức thời của chất điểm tại
5t
.
Câu 6. Một quả bóng được thả rơi tự do từ đài quan sát trên sân thượng của toà nhà Landmark 81 (Thành phố
Hồ Chí Minh) cao
461,3m
xuống mặt đất, với phương trình chuyển động
2
( ) 4,9s t t
. Tính vận tốc của quả
bóng khi nó chạm đất, bỏ qua sức cản không khí. (Đơn vị
/m s
, kết quả gần đúng làm tròn đến hàng phần
chục)
9
ĐẠO HÀM LỚP 11 THPT
(LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P3
_______________________________
TRẮC NGHIỆM ABCD
Câu 1. Tính đạo hàm của hàm số
13
x
y
A.
13
ln13
x
y
B.
1
.13
x
y x
C.
13 ln13
x
y
D.
13
x
y
Câu 2. Cho hàm số
3 2
3 1f x x mx x
. Tìm giá trị tham số m sao cho
1 18
f
.
A.
2
m
B.
2
m
C.
3
m
D.
4
m
Câu 3. Cho hàm số
2
ln 5
f x x x
. Tìm tập nghiệm
S
của phương trình
0
f x
.
A.
S
. B.
5
2
S
.
C.
0; 5
S
. D.
;0 5;
 
S
.
Câu 4. Biết rằng hàm số
f x
xác định và có đạo hàm. Tính vi phân hàm số
sin 2x
f
.
A.
2 2 sin 2
os x x xc f d
B.
4 2 sin 2
os x x xc f d
C.
6 2 sin 2
os x x xc f d
D.
sin 2 sin 2
x x xf d
Câu 5. Cho hàm số
2
1
y x x
. Tìm số nghiệm dương của phương trình
2
1
1
x
y
x
.
A.3 B. 2 C. 1 D. 0
Câu 6. Cho hàm số
( ) 2
f x x
có đạo hàm là
f x
, hàm số
( ) 4 sin
4
x
g x x
có đạo hàm là
g x
. Tính
giá trị biểu thức
2 . 2
P f g
.
A.
1P
. B.
16
16
P
. C.
1
4
P
. D.
16
P
.
Câu 7. Vi phân của hàm số
3 2
5 1
3 2
x x
y x
là
A.
2
6
dy x x dx
. B.
2
5
dy x x
.
C.
3 2
5
3 2
x x
dy dx
. D.
2
5
dy x x dx
.
Câu 8. Cho hàm số
2
cos 3y x
. Tính vi phân của hàm số.
A.
d 3cos3 sin3 dy x x x
. B.
d 6cos3 sin3 dy x x x
.
C.
d 2cos3 sin3 dy x x x
. D.
d 3sin 6 dy x x
.
Câu 9. Đồ thị hàm số
sin cosy x x
tiếp xúc với đường thẳng nào sau đây
A.
1y
B.
2
y
C.
3
y
D.
2
y
Câu 10. Gọi
0 0
;M x y
là điểm trên đồ thị hàm số
3 2
3 1
y x x
mà tiếp tuyến tại đó có hệ số góc bé nhất
trong các tiếp tuyến của đồ thị hàm số. Khi đó
2 2
0 0
x y
bằng
A.
29
. B.
10
. C.
26
. D.
1
.
Câu 11. Một chất điểm chuyển động thẳng xác định bởi phương trình
3 2
2 4 1s t t t
trong đó
t
tính bằng
giây,
s
tính bằng mét. Tìm thời điểm mà vận tốc của chất điểm bằng
24 /m s
.
A.
6 s
t
. B.
3 s
t
. C.
2 s
t
. D.
5 s
t
.
Câu 12. Giá trị biểu thức
0 1 2
2 3 4 ... ( 2)
n
n n n n
C C C n C
bằng
A.
1
( 4)2
n
n
B.
1
( 3)2
n
n
C.
1
( 5)2
n
n
D.
1
( 6)2
n
n
10
TRẮC NGHIỆM ĐÚNG, SAI
Câu 1. Cho hàm số
2cosy f x x x
và
a) Vi phân của hàm số là
1 4sin cos
2 2
x x
dy dx
.
b) Tập giá trị của hàm số
f x
là một đoạn có độ dài bằng 4.
c) Phương trình
3cos 1f x x
có 2 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
c) Tồn tại 2 điểm có hoành độ
0;2
sao cho tiếp tuyến của đồ thị hàm số tại điểm đó song song với đường
thẳng
2 2024
y x
.
Câu 2. Cho hàm số
sin
x
y e x
. Xét tính đúng, sai của các khẳng định
a) Vi phân của hàm số là
cos sin
x
x x
dy dx
e
.
b)
cos
x x
y e ye x
.
c) Tồn tại đúng 2 giá trị nguyên m để phương trình
2
x
y e m
có nghiệm.
d)
2 2 0
y y y
.
Câu 3. Cho hàm số
2
3 1y x x
có đồ thị
( )C
. Xét tiếp tuyến của
( )C
tại giao điểm của
( )C
với trục tung.
Xét tính đúng, sai của các mệnh đề
a) Phương trình
3 4 17
y y y
có hai nghiệm phân biệt với tổng hai nghiệm bằng 5.
b) Tiếp tuyến đã cho đi qua điểm
1;3
A
.
c) Tiếp tuyến đã cho cắt đường thẳng
2 1y x
tại điểm có hoành độ bằng
0
d) Tiếp tuyến đã cho tiếp xúc với đồ thị hàm số
4 2
4
y x x
tại tiếp điểm có tung độ nhỏ hơn 3.
Câu 4. Phương trình chuyển động của một hạt được cho bởi công thức
10 2 sin 4
4
s t t
, trong đó
s
tính bằng centimet và
t
được tính bằng giây. Xét tính đúng sai của các mệnh đề sau
a) Gia tốc của hạt tại thời điểm
3t
giây là
2
16
2
cm/s
b) Vận tốc của hạt tại thời điểm
3t
giây là
2
cm/s
.
c) Vận tốc lớn nhất của hạt đạt được là
4 2
cm/s
.
d) Gia tốc nhỏ nhất của hạt đạt được là
2
16
2
cm/s
.
11
TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. Cho hàm số
2018
ln
1
x
f x
x
. Tính tổng
1 2 ... 2018
S f f f
thu được phân số tối giản
,
a
a b
b
. Tính
2
b a
.
Câu 2. Giả sử hàm số
y f x
liên tục, nhận giá trị dương trên
0;

và thỏa mãn
1 1
f
,
. 3 1f x f x x
, với mọi
0
x
.
Giá trị
3
5 3 5f f
gần nhất số nguyên nào ?
Câu 3. Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
2
ln 1
2
x
y mx x
có đạo hàm
không âm trên khoảng
1;

?
Câu 4. Người ta xây dựng một cây cầu vượt giao thông hình parabol nối hai điểm có khoảng cách là
400m
. Độ
dốc của mặt cầu không vượt quá
10
(độ dốc tại một điểm được xác định bởi góc giữa phương tiếp xúc với mặt
cầu và phương ngang). Tính chiều cao giới hạn từ đỉnh cầu đến mặt đường (làm tròn kết quả đến chũ số thập
phân thứ nhất).
Câu 5. Một chất điểm chuyển động có vận tốc tức thời
v t
phụ thuộc vào thời gian
t
theo hàm số
4 2
8 500
v t t t
. Trong khoảng thời gian
0t
đến
5t
chất điểm đạt vận tốc lớn nhất tại thời điểm bao
nhiêu giây
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
3
2018y x x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
(
(
C
C
)
)
.
.
X
X
é
é
t
t
đ
đ
i
i
ể
ể
m
m
1
A
c
c
ó
ó
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
1
1
x
t
t
h
h
u
u
ộ
ộ
c
c
(
(
C
C
)
)
.
.
T
T
i
i
ế
ế
p
p
t
t
u
u
y
y
ế
ế
n
n
c
c
ủ
ủ
a
a
(
(
C
C
)
)
t
t
ạ
ạ
i
i
1
A
c
c
ắ
ắ
t
t
(
(
C
C
)
)
t
t
ạ
ạ
i
i
đ
đ
i
i
ể
ể
m
m
t
t
h
h
ứ
ứ
h
h
a
a
i
i
2 1
A A
c
c
ó
ó
t
t
ọ
ọ
a
a
đ
đ
ộ
ộ
2 2
;x y
.
.
T
T
i
i
ế
ế
p
p
t
t
u
u
y
y
ế
ế
n
n
c
c
ủ
ủ
a
a
(
(
C
C
)
)
t
t
ạ
ạ
i
i
2
A
c
c
ắ
ắ
t
t
(
(
C
C
)
)
t
t
ạ
ạ
i
i
đ
đ
i
i
ể
ể
m
m
t
t
h
h
ứ
ứ
h
h
a
a
i
i
3 2
A A
c
c
ó
ó
t
t
ọ
ọ
a
a
đ
đ
ộ
ộ
3 3
;x y
.
.
C
C
ứ
ứ
t
t
i
i
ế
ế
p
p
t
t
ụ
ụ
c
c
n
n
h
h
ư
ư
t
t
h
h
ế
ế
,
,
t
t
i
i
ế
ế
p
p
t
t
u
u
y
y
ế
ế
n
n
c
c
ủ
ủ
a
a
(
(
C
C
)
)
t
t
ạ
ạ
i
i
1n
A
c
c
ắ
ắ
t
t
(
(
C
C
)
)
t
t
ạ
ạ
i
i
đ
đ
i
i
ể
ể
m
m
t
t
ọ
ọ
a
a
đ
đ
ộ
ộ
1n n
A A
c
c
ó
ó
t
t
ọ
ọ
a
a
đ
đ
ộ
ộ
;
n n
x y
.
.
T
T
ì
ì
m
m
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
d
d
ư
ư
ơ
ơ
n
n
g
g
n
n
b
b
i
i
ế
ế
t
t
2019
2018 2 0
n n
x y
.
.
12
ĐẠO HÀM LỚP 11 THPT
LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P4_ĐÁP ÁN
_______________________________
TRẮC NGHIỆM ABCD
Câu 1. Cho hàm số
2023
x
y f x
. Giá trị của
' 2
f
bằng
A.
2
' 2 2023
f
. B.
2
'(2) 2023 .ln 2023
f
.
C.
2
2023
'
ln 2023
f x
. D.
2
ln 2023
'
2023
f x
.
Câu 2. Gọi a là nghiệm của phương trình
2
1
0
4 3x x
. Khi đó khẳng định nào sau đây sai
A.
2
3 11
a a
B.
2
7
a a
C.
2
4
a a
D.
2
5 13
a a
Câu 3. Cho hàm số
2
1
2
x
y f x
. Giá trị của
' 1
f
bằng
A.
' 1 6ln 2
f
. B.
'(1) 7 ln 2
f
. C.
'(1) 8ln 2
f
. D.
'(1) 9ln 2
f
.
Câu 4. Đạo hàm của hàm số
2
sin 5f x x
là
A.
( ) 2sin 5f x x
. B.
( ) 5sin10f x x
.
C.
( ) 10sin10f x x
. D.
( ) 5sin10f x x
.
Câu 5. Cho hàm số
3 2
3 5y x mx x
với
m
là tham số. Tìm tập hợp
M
tất cả các giá trị của
m
để
0
y
có hai nghiệm phân biệt.
A.
3;3
M
. B.
; 3 3;M
 
.
C.
M
. D.
; 3 3;M
 
.
Câu 6. Cho hàm số
3 2
3 1 f x x x x
. Giá trị
1
f
bằng:
A. 0 . B. 1. C. 2. D. 3.
Câu 7. Hàm số
2
1
2 5
y
x x
có đạo hàm là
2
2
2 5
ax b
y
x x
.. Giá trị của
P a b
là:
A.
4P
B.
2P
C.
2 P
D.
0
P
Câu 8. Tính đạo hàm của hàm số
2
log 2 1
y x
.
A.
2
2 1 ln 2
y
x
. B.
1
2 1 ln 2
y
x
. C.
2
2 1
y
x
. D.
1
2 1
y
x
.
Câu 9. Tính tổng các nghiệm thực của phương trình
2
4 6
0
2
x x
x
.
A.3 B. – 4 C. – 2 D. – 1
Câu 10. Cho hàm số
4 5
f x g x
. Tính
1
g
biết rằng
1 1; 1 2
g f
.
A.1 B. 2 C. 3 D. 4
Câu 11. Một chất điểm chuyển động có phương trình
3 2
4s t t t
(
t
là thời gian tính bằng giây). Gia tốc
của chuyển động tại thời điểm vận tốc đạt giá trị lớn nhất là
A.
6
. B.
0
. C.
2
. D.
4
.
C
C
â
â
u
u
1
1
2
2
.
.
C
C
h
h
o
o
c
c
á
á
c
c
h
h
à
à
m
m
s
s
ố
ố
2
3 4
2
2 1 , ,
3 2
f x
y f x y f x y
f x
l
l
ầ
ầ
n
n
l
l
ư
ư
ợ
ợ
t
t
c
c
ó
ó
c
c
á
á
c
c
đ
đ
ồ
ồ
t
t
h
h
ị
ị
1 2 3
, ,C C C
.
.
H
H
ệ
ệ
s
s
ố
ố
g
g
ó
ó
c
c
t
t
i
i
ế
ế
p
p
t
t
u
u
y
y
ế
ế
n
n
t
t
ạ
ạ
i
i
đ
đ
i
i
ể
ể
m
m
c
c
ó
ó
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
b
b
ằ
ằ
n
n
g
g
1
1
c
c
ủ
ủ
a
a
1 2 3
, ,C C C
(
(
t
t
ư
ư
ơ
ơ
n
n
g
g
ứ
ứ
n
n
g
g
)
)
l
l
ầ
ầ
n
n
l
l
ư
ư
ợ
ợ
t
t
l
l
à
à
1 2 3
, ,k k k
k
k
h
h
á
á
c
c
0
0
v
v
à
à
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
đ
đ
i
i
ề
ề
u
u
k
k
i
i
ệ
ệ
n
n
1 2 3
5 6k k k
.
.
T
T
í
í
n
n
h
h
1f
.
.
A
A
.
.
15
1
11
f
B
B
.
.
12
1
13
f
C
C
.
.
6
1
23
f
D
D
.
.
1
1
5
f
13
TRẮC NGHIỆM ĐÚNG, SAI
Câu 1. Biết
y
là hàm số của
x
thỏa mãn phương trình
1 lnxy y
. Xét tính đúng sai của các mệnh đề sau.
a) Đạo hàm của hàm số
y
là
2
1
y
y
xy
.
b)
2
1
0y
e
.
c) Đạo hàm cấp hai của hàm số
y
là
2
2
2 1
1
yy xy y y xy
y
xy
.
d)
3
3
0y
e
.
Câu 2. Một tài xế đang lái xe ô tô, ngay khi phát hiện có vật cản phía trước đã phanh gấp lại nhưng vẫn xảy ra
va chạm, chiếc ô tô để lại vết trượt dài 20,4 m (được tính từ lúc bắt đầu đạp phanh đền khi xảy ra va chạm).
Trong quá trình đạp phanh, ô tô chuyển động theo phương trình
2
5
( ) 20
2
s t t t
, trong do
s
(đơn vị mét) 1à
độ dài quãng đường đi được sau khi phanh,
t
(đơn vị giây) là thời gian tính từ lúc bắt đầu phanh (
0 4t
).
Xét tính đúng sai của các mệnh đề sau
a) Vận tốc tức thời của ô tô ngay khi đạp phanh là
20( / )m s
b) Xe ô tô trên chưa chạy quá tốc độ, (tốc độ giới hạn cho phép là 70 km/h).
c) Thời điểm xảy ra va chạm cách thời điểm bắt đầu đạp phanh
6,8
giây
d) Vận tốc tức thời của ô tô ngay khi xảy ra va chạm là
14( / )m s
Câu 3. Cho hàm số
1
3 2
y f x
x
. Các mệnh đề sau đúng hay sai?
a)
3
8
"
3 2
f x
x
.
b)
' 1 " 1 6
f f
.
c)
3
" 0,
2
f x x
.
d)
3
8
"
3 2
x
x
f e
e
.
Câu 4. Cho hàm số
3
( ) 2y f x x
có đồ thị
( )C
và điểm
M
thuộc
( )C
có hoành độ
0
1
x
. Xét tính đúng,
sai của các khẳng định
a) Phương trình
2
6 1
x f x x f
có hai nghiệm phân biệt cùng dương.
b) Tiếp tuyến của
( )C
tại
M
cắt đồ thị hàm số
2
8 7 4
y x x
tại hai điểm phân biệt có tổng hoành độ
bằng 5.
c) Tiếp tuyến của
( )C
tại
M
cắt đường thẳng
: 3d y x
tại điểm có hoành độ bằng 4.
d) Tiếp tuyến của
( )C
tại
M
vuông góc với đường thẳng
1
:
6
y x
.
14
TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. Cho đa thức
( ) (1 2 )
n
f x x
2 *
0 1 2
n
n
a a x a x a x n N
. Tìm hệ số
2
a
, biết rằng
1 2
2 13122
n
a a na n
.
Câu 2. Cho hàm số
y f x
có đạo hàm trên
thỏa mãn
3
1 3 2
f x x x
. Tìm giá trị nhỏ nhất của biểu
thức
2 3 4
P f x f x
.
Câu 3. Hàm số
y f x
có đạo hàm liên tục trên
1;2
và
1 4
f
và
3 2
2 3f x xf x x x
. Giá trị
2
f
là số nguyên nào ?
Câu 4. Một chiếc ô tô đang chạy thì người lái xe đã phanh gấp lại vì gặp phải vật cản phía trước nhưng vẫn xảy
ra va chạm, chiếc ô tô để lại vết trượt dài
15,5m
(được tính từ lúc bắt đầu đạp phanh cho đến khi xảy ra va
chạm). Trong quá trình đạp phanh, ô tô chuyển động theo phương trình
2
3
( ) 15
2
s t t t
, trong đó
s
(đơn vị:
m
) là độ dài quãng đường đi được sau khi phanh và
t
(đơn vị: giây) thời gian tính từ lúc bắt đầu đạp phanh
0 5
t
. Vận tốc tức thời của ô tô ngay khi xảy ra va chạm là
Câu 5. Dân số của Việt Nam sau t năm tính từ năm 2023 được dự đoán theo công thức với
( )N t
tính theo đơn
vị triệu người :
( ) 100. ,0 50
at
N t e t
. Biết rằng đạo hàm của hàm số
( )N t
biểu thị tốc độ gia tăng dân số
của Việt Nam ( đơn vị là triệu người/ năm). Vào năm 2066 thì tốc độ gia tăng dân số hơn 2 triệu người/ năm.
Hỏi vào năm 2080 thì tốc độ gia tăng dân số là bao nhiêu?
Câu 6. Cho các hàm số
y f x
,
y g x
,
f x
y
g x
. Nếu hệ số góc tiếp tuyến của các đồ thị hàm số đã
cho tại điểm có hoành độ
0
x
bằng nhau và khác không thì giá trị lớn nhất của
0
f x
bằng bao nhiêu ?
15
ĐẠO HÀM LỚP 11 THPT
(LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P5_ĐÁP ÁN)
_______________________________
TRẮC NGHIỆM ABCD
Câu 1. Tìm nghiệm của đạo hàm
y
biết rằng
2
6 5y x x
.
A.
3
x
B.
2
x
C.
4
x
D.
1x
Câu 2. Tính đạo hàm của hàm số
4 2
5 5 6y x x x
.
A.
3
20 10 6y x x
B.
3
20 10 6
y x x
C.
3
20 10y x x
D.
3
20 10 6y x x
Câu 3. Tính tổng các hệ số đối với đạo hàm của hàm số
2
3
4
2
f x x x
.
A.4 B. 9 C. 5 D. 7
Câu 4. Đạo hàm của hàm số
3 4
2 1
x
f x
x
tại điểm
1
x
là
A.
11
3
. B.
1
5
. C. – 11. D.
11
9
.
Câu 5. Đạo hàm của hàm số
2
2 1 0
y x x x
là
A.
2
10 1
2
x
y
x
. B.
2y x
. C.
2
6 1
2
x
y
x
. D.
4 1
2
x
y
x
.
Câu 6. Cho hàm số
2
6 19
y x x
. Có bao nhiêu số nguyên âm x thỏa mãn
0
y
.
A.3 B. 2 C. 1 D. 4
Câu 7. Tính đạo hàm của hàm số
x
1
2 ln
e
x
y x
.
A.
1 1
2 ln 2 ln
e
x
x
y x
x
. B.
1
2 ln 2 e
x x
y
x
.
C.
x
1 1
2 ln2
e
x
y
x
. D.
x
1
2 ln 2 e
x
y
x
.
Câu 8. Một vật chuyển động có phương trình
4 3 2
3 3 2 1 m
S t t t t
, t là thời gian tính bằng giây. Gia tốc
của vật tại thời điểm
st 3
là
A.
2
48m/s .
B.
2
28m/s .
C.
2
18m/s .
D.
2
54m/s .
Câu 9. Cho hàm số
3 2
3 1f x x x mx
. Biết
0
m
là giá trị của tham số
m
để hai số phân biệt
1 2
,x x
thỏa
mãn
1 2
0
f x f x
và
2 2
1 2 1 2
13
x x x x
. Mệnh đề nào dưới đây đúng?
A.
0
1;7
m
. B.
0
7;10
m
. C.
0
15; 7
m
. D.
0
7; 1
m
.
Câu 10. Xét hàm số
2
1 cos 2y f x x
. Chọn câu đúng:
A.
2
sin 4
d ( ) d
2 1 cos 2
x
f x x
x
. B.
2
sin 4
d ( ) d
1 cos 2
x
f x x
x
.
C.
2
cos 2
d ( ) d
1 cos 2
x
f x x
x
. D.
2
sin 2
d ( ) d
2 1 cos 2
x
f x x
x
.
Câu 11. Cho hàm số
3 2
2 ( 2) 1y mx mx m x
. Tìm tất cả các giá trị của tham số thực
m
để phương trình
0
y
vô nghiệm.
A.
( ;6) (0; )
m
 
. B.
6;0
m
. C.
6;0
m
. D.
6;0
m
.
C
C
â
â
u
u
1
1
2
2
.
.
Cho hàm số
y f x
,
y g x
,
3
1
f x
y
g x
. Hệ số góc của các tiếp tuyến của đồ thị các hàm số
đã cho tại điểm có hoành độ
1x
bằng nhau và khác
0
. Khẳng định nào dưới đây đúng?
A.
1 3
f
. B.
1 3
f
. C.
11
1
4
f
. D.
11
1
4
f
.
16
TRẮC NGHIỆM ĐÚNG, SAI
Câu 1. Cho hàm số
( ) sin 2
3
f x x
và
( ) 5 cos3g x x
. Các mệnh đề sau đúng hay sai?
a) Đạo hàm của hàm số
( )f x
trên
là
( ) cos 2
3
f x x
.
b) Đạo hàm của hàm số
( )g x
trên
là
( ) 3sin3g x x
.
c) Tất cả các nghiệm của phương trình
3 ( ) 2 ( )f x g x
là
5
2
6
x k
( )
k
.
d) Gọi
( ) ( ) sin6h x g x x
, giá trị lớn nhất của hàm
( )h x
bằng
3
.
Câu 2. Cho hàm số
1
( )
1
x
f x
x
. Các mệnh đề sau đúng hay sai?
a) Đạo hàm của hàm số
1
( )
1
x
f x
x
tại
0
3
x
là
3
1
2
1
(3) lim
2
x
x
x
f
x
.
b) Đạo hàm của hàm số
1
( )
1
x
f x
x
là
2
2
( )
( 1)
f x
x
.
c) Nếu
0
1
1
1
lim 2
x
x
x
x
thì
(0) 2
f
.
d) Hệ số góc của tiếp tuyến tại điểm có hoành độ
0
2
x
là
(2) 2
f
.
Câu 3. Chuyển động của một vật có phương trình là
( ) 4.cos 2
12
s t t m
, với
t
là thời gian tính bằng
giây. Khi đó, các mệnh đề sau đúng hay sai?
a) Sau 5 giây vật đi được quãng đường là
3,86 ( )m
b) Vận tốc tức thời của vật theo thời gian là
( ) 8 .sin 2
12
v t t
c) Tại thời điểm
5
( )
6
t s
, vận tốc của vật là
11,6 ( /s)m
d) Vận tốc lớn nhất của vật đạt
25,13 ( / )m s
Câu 4. Cho hàm số
2
( )
x
y ax bx c e
với
0
b
.
a) Đạo hàm của hàm số đã cho bằng
2
(2 )
x
ax a b x b c e
.
b)
1 3 2
y a b c e
.
c) Khi hàm số có đạo hàm bằng có đạo hàm là
2
3
x
y ax ax b c e
thì
a b
.
d) Khi hàm số có đạo hàm là
2
3 1
x
y ax a x b c e
thì biểu thức
9
M a
b
có giá trị nhỏ nhất là một
số nhỏ hơn 8.
17
TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. Cho hàm số
2
1, 0
1, 0
ax bx x
f x
ax b x
. Khi hàm số
f x
có đạo hàm tại
0
0
x
. Hãy tính giá trị tổng
2T a b
(kết quả là số nguyên).
Câu 2. Cho hàm số
1
.ln 4 2 .
ln 4
x
f x
Giá trị tổng
1 2 3 2023
' ' ' ... ' .
2024 2024 2024 2024
S f f f f
gần nhất số chính phương nào
Câu 3. Cho hàm số
3 4
khi 0
4
1
khi 0
4
x
x
f x
x
. Khi đó
16 0
f
là số nguyên nào ?
Câu 4. Phương trình chuyển động của một chất điểm được biểu thị bởi công thức
2 3
4 2 4 2S t t t t
, trong
đó
0t
và
t
tính bằng giây
s
,
S t
tính bằng mét
m
. Tìm gia tốc
a
của chất điểm tại thời điểm
5t s
.
C
C
â
â
u
u
5
5
.
.
Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô
hình hoá bằng hàm số
0,75t
a
P t
b e
, trong đó thời gian
t
được tính bằng giờ. Tại thời điểm ban đầu
0t
,
quần thể có
20
tế bào và tăng với tốc độ
12
tế bào/giờ. Theo mô hình này, quần thể nấm men về lâu dài tăng
nhưng không vượt quá là bao nhiêu tế bào?
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
c
c
á
á
c
c
h
h
à
à
m
m
s
s
ố
ố
2 3
2 , 6 ,
3 4
f x
y f x y f x y
f x
l
l
ầ
ầ
n
n
l
l
ư
ư
ợ
ợ
t
t
c
c
ó
ó
c
c
á
á
c
c
đ
đ
ồ
ồ
t
t
h
h
ị
ị
1 2 3
, ,C C C
.
.
H
H
ệ
ệ
s
s
ố
ố
g
g
ó
ó
c
c
t
t
i
i
ế
ế
p
p
t
t
u
u
y
y
ế
ế
n
n
t
t
ạ
ạ
i
i
đ
đ
i
i
ể
ể
m
m
c
c
ó
ó
h
h
o
o
à
à
n
n
h
h
đ
đ
ộ
ộ
b
b
ằ
ằ
n
n
g
g
2
2
c
c
ủ
ủ
a
a
1 2 3
, ,C C C
(
(
t
t
ư
ư
ơ
ơ
n
n
g
g
ứ
ứ
n
n
g
g
)
)
l
l
ầ
ầ
n
n
l
l
ư
ư
ợ
ợ
t
t
l
l
à
à
1 2 3
, ,k k k
k
k
h
h
á
á
c
c
0
0
v
v
à
à
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
đ
đ
i
i
ề
ề
u
u
k
k
i
i
ệ
ệ
n
n
1 2 3
3 4 5k k k
.
.
T
T
í
í
n
n
h
h
g
g
i
i
á
á
t
t
r
r
ị
ị
6 2
f
(kết quả là số nguyên)
18
ĐẠO HÀM LỚP 11 THPT
(LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P6)
_______________________________
TRẮC NGHIỆM ABCD
Câu 1. Cho các hàm số:
3 3 3 3
4 ; 6 ; 4 5; 4 10
y x x y x x y x x y x x
.
Trong các hàm số trên, có bao nhiêu hàm số có đạo hàm
2
3 4
y x
?
A.3 B. 4 C. 2 D. 1
Câu 2. Sử dụng công thức đạo hàm tích, đạo hàm của hàm số
3 2
( 4 )( 7)
y x x x
bằng
A.
2 2 3
2(3 4)( 7) ( 4 ).2x x x x x
B.
2 2 3
(3 4)( 7) ( 4 ).x x x x x
C.
2 2 3
(3 4)( 7) ( 4 ).2x x x x x
D.
2 2 3
(3 4)( 7) ( 4 ).2x x x x x
Câu 3. Cho hàm số
( ) cos 2sin 3 1f x a x x x
. Tìm
a
để phương trình
( ) 0
f x
có nghiệm.
A.
5
a
. B.
5
a
. C.
5
a
. D.
5
a
.
Câu 4. Có bao nhiêu số nguyên m nhỏ hơn 10 để mọi tiếp tuyến của đồ thị hàm số
1
3
x
y
x m
luôn có hệ số
góc dương
A.9 B. 7 C. 6 D. 5
Câu 5. Tính đạo hàm của hàm số
2
9
log 1
y x
.
A.
2
1
1 ln 9
y
x
. B.
2
1 ln 3
x
y
x
. C.
2
2 ln9
1
x
y
x
. D.
2
2ln 3
1
y
x
.
Câu 6. Biết rằng đạo hàm của hàm số
7
4
ax
y
x b
bằng
2
4
ab
x b
. Khi đó giá trị tích
ab
bằng
A.10 B. 14 C. 12 D. 10
Câu 7. Cho hàm số
2x
y e
. Nghiệm của phương trình
4
x
y e
nằm trong khoảng nào
A.
0;1
B.
3
1;
2
C.
3
;2
2
D.
2;3
Câu 8. Đồ thị hàm số
sin cosy x x
tiếp xúc với đường thẳng nào sau đây
A.
1y
B.
2
y
C.
3
y
D.
2
y
Câu 9. Cho
4 2
1 3 4
: 3 3
4 2
m
m
C y x x m
. Gọi
m
A C
có hoành độ
1
. Tìm
m
để tiếp tuyến tại
A
song song với đường thẳng
: 6 2017 ?d y x
A.
3.m
B.
3.m
C.
5.m
D.
0.m
Câu 10. Một chất điểm chuyển động thẳng có phương trình
3 2
5 9 3s t t t
(
t
là thời gian tính bằng giây
s
,
s
là đường đi tính bằng mét
m
. Gia tốc của chất điểm tại thời điểm
0
3t s
là
A.
2
8 /m s
. B.
2
6 /m s
. C.
2
12 /m s
. D.
2
16 /m s
.
Câu 11. Cho các hàm số
f x
,
g x
,
h x
có đạo hàm trên
và thỏa mãn
2
3 2 3
f x g x h x
với mọi
x
,
8 5
g
,
1 3
h
. Giá trị
2
f
bằng
A.
2
. B.
3
. C.
5
. D.
5
.
Câu 12. Với
0
b
, hàm số
2
( )
x
ax bx c e
có đạo hàm là
2
3 1
x
y ax a x b c e
. Tìm giá trị nhỏ nhất
của biểu thức
9
M a
b
.
A.4 B. 5 C. 6 D. 7
19
TRẮC NGHIỆM ĐÚNG, SAI
Câu 1. Cho hàm số
.sin2
x
y f x e x
. Các mệnh đề sau đúng hay sai?
a)
" 4cos 2 2sin 2
x
f x e x x
b)
" 0 4
f
.
c)
2 ' " 5
f x f x f x
.
d)
2
2 4 4cos 4 3sin 4
x
f x e x x
.
Câu 2. Cho hàm số
ln 2 4
y f x x
. Các mệnh đề sau đúng hay sai?
a) Tập xác định của hàm số
y f x
là
2;D

.
b)
0
y x D
.
c) Tổng các nghiệm của phương trình
1
y
là
4
.
d) Có
1
giá trị thực của tham số
m
để phương trình
2 0
y y m
có hai nghiệm
1 2
,x x
sao cho tổng của
chúng bằng
5
.
Câu 3. Cho hàm số
sin 2y x
. Các khẳng định sau đúng hay sai?
a) Đạo hàm cấp 2 của hàm số là
2sin 2y x
.
b)
0
4
y
.
c)
4 0
y y

.
d) Phương trình
cos 4 1 0
y x
có 5 nghiệm phân biệt thuộc đoạn
;
.
Câu 4. Một vật chuyển động trên đường thẳng được xác định bởi công thức
3 2
( ) 3 7 2s t t t t
, trong đó
0t
và tính bằng giây và
s
là quãng đường chuyển động được của vật trong
t
giây tính bằng mét. Xét tính
đúng, sai của các khẳng định sau
a) Tốc độ của vật tại thời điểm
2t
là
7( / )m s
b) Gia tốc của vật tại thời điểm
2t
là
2
6 /m s
c) Gia tốc của vật tại thời điểm mà vận tốc của chuyển động bằng
2
16 /m s
là
2
10 /m s
d) Thời điểm
1t
(giây) tại đó vận tốc của chuyển động đạt giá trị nhỏ nhất.
20
TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. Tính đạo hàm của hàm số
1 1 1 1 1 1
cos
2 2 2 2 2 2
y x
với
0;
x
ta thu được kết quả
1
sin
x
a b
trong đó
,a b
. Tính
a b
.
C
C
â
â
u
u
2
2
.
.
C
C
h
h
o
o
c
c
á
á
c
c
h
h
à
à
m
m
s
s
ố
ố
6
, ,
9 2
f x
f x g x h x
g x
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
0
f m g m h m
.
.
G
G
i
i
á
á
t
t
r
r
ị
ị
l
l
ớ
ớ
n
n
n
n
h
h
ấ
ấ
t
t
c
c
ủ
ủ
a
a
8
f m
l
l
à
à
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
n
n
à
à
o
o
Câu 3. Cho hàm số
ln
x
f x e m
. Tìm số thực dương
m
sao cho
' ' 1 1
f x f x
. Khi đó
2
10 9m m
gần nhất số nguyên nào
Câu 4. Cho hàm số
2
1
x
y
x
có đồ thị
( )C
và điểm
( ;1)A a
. Gọi
S
là tập hợp tất cả các giá trị thực của
tham số
a
để có đúng một tiếp tuyến của
( )C
đi qua
A
. Tổng tất cả các giá trị các phần tử của
S
là
Câu 5. Một vật chuyển động theo quy luật
3 2
1
6
2
s t t
với
t
(giây)là khoảng thời gian từ khi vật bắt đầu
chuyển động và
s
(mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian 6 giây, kể
từ lúc bắt đầu chuyển động, vận tốc lớn nhất vật đạt được bằng bao nhiêu?
Câu 6. Năm 2010, dân số ở một tỉnh H là
1038229
người. Tính đến năm 2015, dân số của tỉnh đó là
người. Cho biết dân số của tỉnh H được ước tính theo công thức
.
.
N r
S N Ae
(trong đó
A
là
dân số của năm lấy làm mốc,
S
là dân số sau
N
năm,
r
là tỉ lệ tăng dân số hàng năm được làm tròn đến
hàng phần nghìn). Tốc độ gia tăng dân số (người/năm) vào thời điểm sau 1 năm kể từ năm
2010
được xác
định bởi hàm số
'S N
. Tốc độ gia tăng dân số của tỉnh H vào năm
2025
là bao nhiêu (làm tròn kết quả đến
hàng đơn vị theo đơn vị người/năm), biết tỉ lệ tăng dân số hàng năm không đổi.

Tài liệu khác của Toán 11

Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
------------------------------------------------------------------------------------------
LUYỆN TẬP CHUNG TOÁN 11 THPT
ĐẠO HÀM VÀ ỨNG DỤNG
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
ĐÁP ÁN CHI TIẾT PDF BẠN ĐỌC VUI LÒNG LIÊN HỆ TÁC GIẢ
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 2/2025 1
LUYỆN TẬP CHUNG TOÁN 11 THPT
ĐẠO HÀM VÀ ỨNG DỤNG
__________________________ DUNG NỘI DUNG LƯỢNG 8 FILE LUYỆN TẬP CHUNG 1 file 3 trang
ĐẠO HÀM VÀ ỨNG DỤNG 2
ĐẠO HÀM LỚP 11 THPT
(LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P1_ĐÁP ÁN)
_______________________________ TRẮC NGHIỆM ABCD
Câu 1. Cho hàm số f x 3
x  2x m , giá trị của f    1 bằng A. 6 . B. 8 . C. 3 . D. 2 .
Câu 2. Tính đạo hàm của hàm số y  log x 2 ln 2 1 x 1 A. y '  B. y '  . C. y '  . D. y '  . x x ln 2 x ln 2
Câu 3. Tìm hàm số y F x có bảng xét dấu đạo hàm y  f x như sau A. 3 y  (x  2) B. 2
y x  4x  4 C. 3 2
y x  6x  9x  4 D. 3
y  2(x  2) Câu 4. Cho hàm số 3 2
y x  3x mx  5 . Tìm giá trị tham số m để y  1  4 . A. m  5 B. m  4 C. m  3 D. m  2
Câu 5. Tính đạo hàm của hàm số y  4x  3 . 2 4 1 1 A. y  B. y  C. y  D. y  4x  3 4x  3 2 4x  3 4x  3
Câu 6. Tìm vi phân của hàm số y  sin 2x .
A. dy  2 cos 2xdx
B. dy  cos 2xdx
C. dy  sin 2xdx
D. dy  2 sin 2xdx Câu 7. Cho hàm số 3
y x  3x có đồ thị C  .Hệ số góc k của tiếp tuyến với đồ thị C  tại điểm có tung độ bằng 4 là: A. k  0 B. k  2  C. k  6 D. k  9 x 2
Câu 8. Cho hàm số y  sin
. Tính đạo hàm của hàm số đã cho. 2 1 A. y '  sin x
B. y '  sin 2x
C. y '  2sin 2x
D. y '  sin x 2 Câu 9. Cho hàm số 3 2
y x x mx  8 . Có bao nhiêu số nguyên dương m sao cho y  1  0 . A.10 B. 4 C. 9 D. 8 Câu 10. Hàm số 3 2
y x mx nx 1thỏa mãn điều kiện y (  1)  6; y (
 2)  17 . Tính m n . A.3 B. 0 C. 1 D. 2 2 Câu 11. Hàm số 2x x y   có đạo hàm là 2 2 2 2
A. 2x x.ln 2 . B. (2 1).2x . x x   ln 2 . C. 2 1 ( ).2x x x x    . D. (2 1).2x x x   .   
Câu 12. Một chất điểm dao động điều hòa theo phương trình S  3cos 2 t  
 cm . Tìm gia tốc tức thời của  3 
chất điểm tại thời điểm t  2s . A. 2 59, 22 cm / s . B. 2 59  , 22 cm / s . C. 2 18,85 cm / s . D. 2 1
 8,85 cm / s . 3
TRẮC NGHIỆM ĐÚNG, SAI Câu 1. Cho hàm số 4  . x y
x e . Xét tính đúng sai của các mệnh đề sau a)     4 ' 4 4 . x y x e b) 4 ' x y e  4 y .
c) y '0  1. d) y   4
' 1  5.e .
Câu 2. Một viên đạn được bắn lên cao theo phương thẳng đứng có phương trình chuyền động s t  2
 2  196t  4,9t ,
trong đó t  0, t(s) là thời gian chuyển động, s(m) là độ cao so với mặt đất.
Xét tính đúng sai của các mệnh đề sau
a) Sau 20s kể từ khi bắn thì viên đạn đạt được độ cao 1962m .
b) Vận tốc tức thời của viên đạn ngay khi viên đạn được bắn ra là 196m / s
c) Vận tốc tức thời của viên đạn khi viên đạn đạt được độ cao 1962m là 5m / s .
d) Tại thời điểm viên đạn đạt vận tốc tức thời bằng 98 m/s thì viên đạn đang ở độ cao 1472m so với mặt đất. Câu 3. Cho hàm số 2
y  2x x . Xét tính đúng sai của các mệnh đề sau a) 3
y .y 1  0 b) 3
y .y  1 1 c) 3 2
y  (x  2x ).y   . y 1  d) y  .  2xx 3 2 4 3x m  2
Câu 4. Cho hàm số y f x 3 2   mx
x  3 trong đó m là tham số. Các mệnh đề sau đúng hay 4 2 sai? a) f  x 3 2
 3x  3mx  m  2 x .  1 
b) Kết quả của f    không phụ thuộc vào tham số m .  6 
c) Với m  1, ta có f  2  27 .
d) Có hai giá trị dương của tham số m thỏa mãn phương trình f   x  0 có hai nghiệm phân biệt sao cho tổng 26
bình phương của hai nghiệm đó bằng . 9 4
TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. Một chất điểm chuyển động theo phương trình 3 2 S  2
 t 18t  2t 1, trong đó t tính bằng giây s và
S tính bằng mét m . Tính thời gian vận tốc chất điểm đạt giá trị lớn nhất.
Câu 2. Một vật chuyển động theo phương trình s t  3 2
t mt  2 (đơn vị: mét). Biết rằng tại thời điểm
t  10s vận tốc của chuyển động bị triệt tiêu. Tìm gia tốc của chuyển động tại thời điểm t  2s . 2 Câu 3. Cho hàm số
f x thỏa mãn xf  x 2  1  x 1
  f x. f   x   
 với mọi x dương. Biết f   1  f   1  1 . Giá trị 2
f 2 gần nhất số nguyên nào 1 3
Câu 4. Có bao nhiêu giá trị nguyên âm của tham số m để hàm số 4 y x mx  có đạo hàm không âm 4 2x
trên khoảng 0;   . f x 2
Câu 5. Các hàm số y f x, y f x    , y
lần lượt có các đồ thị C , C , C . Hệ số góc tiếp tuyến 1 2 3 f  2 x
tại điểm có hoành độ bằng 1 của C , C ,C (tương ứng) lần lượt là k , k , k khác 0 và thỏa mãn k  2k  3k . 1 2 3 1 2 3 1 2 3 Tính f   1 . Câu 6. Cho hàm số 4 3 2
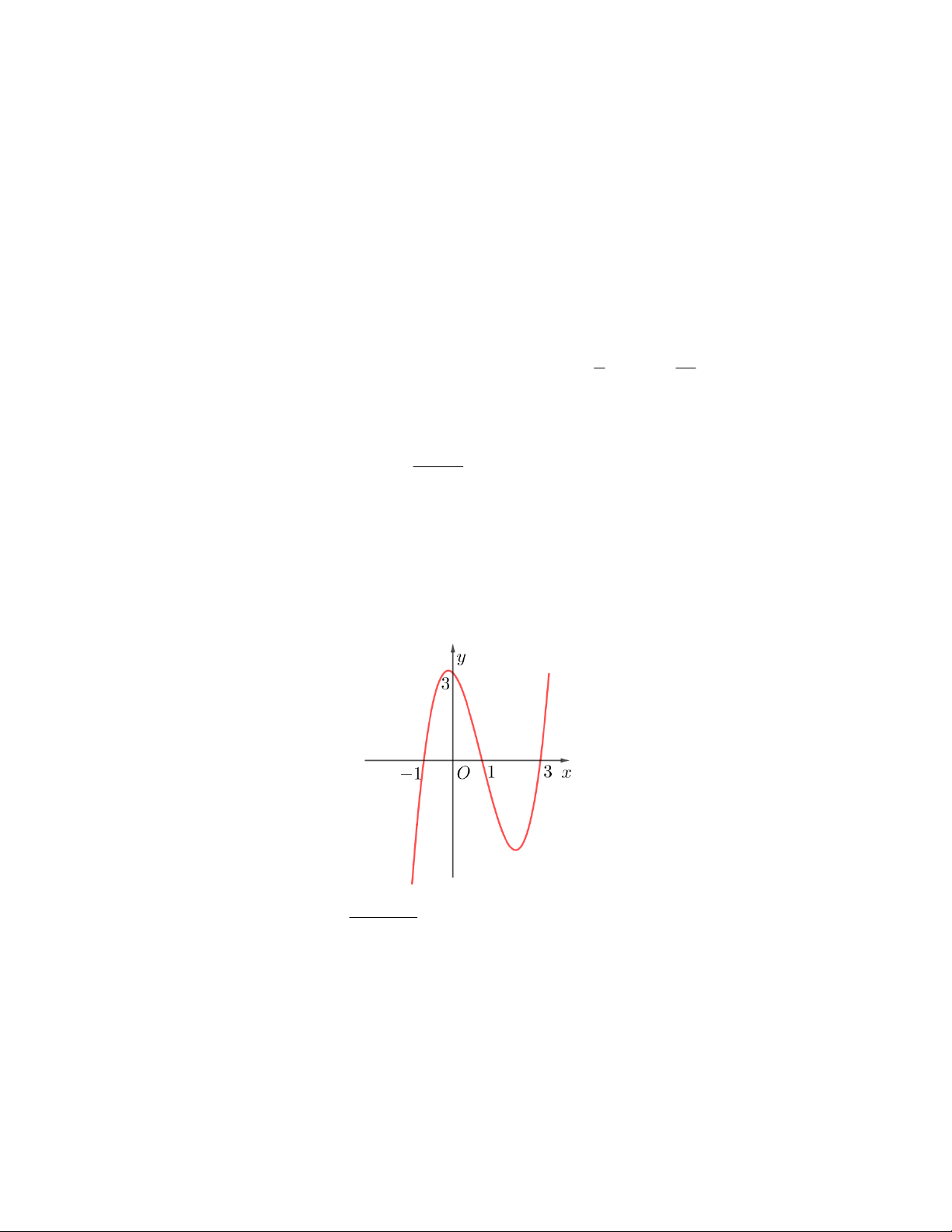
y mx nx px qx r m,n, p, q, r   . Hàm số y f  x có đồ thị như hình vẽ bên.
f x  r
Tìm giá trị nhỏ nhất của biểu thức S   2018. m 5
ĐẠO HÀM LỚP 11 THPT
(LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P2)
_______________________________ TRẮC NGHIỆM ABCD Câu 1. Cho hàm số 3 2
y x  3x mx  5 . Tìm giá trị tham số m để y  1  4 . A. m  5 B. m  4 C. m  3 D. m  2
Câu 2. Tìm đạo hàm của hàm số y  log x . ln10 1 1 1 A. y  B. y  C. y  D. y  x x ln10 10ln x x
Câu 3. Tính vi phân d  2 x  2x  2 . (2x  2) x d (x 1) x d (x 1) x d (x 1) x d A. B. C. D. 2 x  2x  2 2 2 x  2x  2 2 x  2x  2 2 x  2x  2 
Câu 4. Tìm số nghiệm của phương trình 2
ln(2x 5x)  0   . A.2 B. 1 C. 0 D. 3
Câu 5. Vi phân của y  tan 5x là : 5x 5 5 5 A. dy  d . x B. dy   d . x C. dy  d . x D. dy   d . x 2 cos 5x 2 sin 5x 2 cos 5x 2 cos 5x 2x 1 27
Câu 6. Cho hàm số f x 
. Tồn tại bao nhiêu giá trị nguyên x để f  x  ? x 1 4 (x 1) A. 2 B. 1 C. 3 D. 4
Câu 7. Hàm số F x có bảng xét dấu đạo hàm f x như hình vẽ
Tồn tại bao nhiêu số nguyên x thỏa mãn  2
x  2x  3 F x  0 . A.4 B. 1 C. 3 D. 2 2 x  3x  6
Câu 8. Cho hàm số y
. Tính số nghiệm nguyên của bất phương trình y  0 . x  2 A.3 B. 5 C. 2 D. 4
Câu 9. Một vật giao động điều hòa có phương trình quảng đường phụ thuộc thời gian s  si
A n t   . Trong đó ,
A , là hằng số, t là thời gian. Khi đó biểu thức vận tốc của vật là? A. v  c
A os t   . B. v   
A cos t   . C. v  
A cos t   . D. v   c
A os t   . 1 Câu 10. Cho hàm số 3 2 y
x x  2. đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là 3
nghiệm của phương trình y  0 là: 7 7 7 7
A. y  x  B. y x
C. y  x  D. y x 3 3 3 3
Câu 11. Một chất điểm chuyển động theo quy luật s t  3 2  t
  6t với t là thời gian tính từ lúc bắt đầu chuyển
động, s t  là quãng đường đi được trong khoảng thời gian t . Tính thời điểm t tại đó vận tốc đạt giá trị lớn nhất. A.3s B. 2s C. 4s D. 3,5s
f x  f 3
Câu 12. Hàm số xác định trên R thỏa mãn lim  3. Hỏi phương trình 2
x  4x f 3 có tổng x 3  x  3
bình phương các nghiệm là bao nhiêu ? A. 20 B. 22 C. 37 D. 11 6 TRẮC NGHIỆM ĐÚNG, SAI
Câu 1. Cho hàm số f x 3 2
 2x  6 x m  1 . Xét tính đúng sai của các mệnh đề a) f x 2 '  6x  6x .
b) f 2  f 2  10 .
c) Giá trị nhỏ nhất của f ' x bằng – 7.
d) Tồn tại hai giá trị a, b thỏa mãn f a  f b  0 thì có 7 số nguyên m để f a, f b trái dấu. Câu 2. Cho hàm số 3
y f (x)  2x có đồ thị (C ) và điểm M thuộc (C ) có hoành độ x  1  . Xét tính đúng, 0
sai của các khẳng định a) Phương trình 2
x f  x  6x f  
1 có hai nghiệm phân biệt cùng dương.
b) Tiếp tuyến của (C ) tại M cắt đồ thị hàm số 2
y x  8  7x  4 tại hai điểm phân biệt có tổng hoành độ bằng 5.
c) Tiếp tuyến của (C ) tại M cắt đường thẳng d : y  3x tại điểm có hoành độ bằng 4. 1
d) Tiếp tuyến của (C ) tại M vuông góc với đường thẳng  : y   x . 6
Câu 3. Cho hàm số y f x 2
 2x x . Xét tính đúng, sai của các mệnh đề 1 x
a)Vi phân của hàm số là dy dx . 2 x  2x 2x
b)Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 song song với đường thẳng y   3 . 3 3 2 
2x  3x  6x  2 c)  f  2 x x   .   4 3 2
x  2x  3x  2x d) Giá trị biểu thức 3 2
M y .y  x  2x.y x là một số nguyên tố.
Câu 4. Cho hai hàm số f x  3 2
x  3 x m x  1 và g x  2
x mx m  5 . Xét tính đúng, sai của các khẳng định
a) f  1  m  3 .
b) Phương trình f   x   g   x  có tổng tất cả các nghiệm nhỏ hơn 3. 
c)  f g x 2
  3g x 6g x  m   .
d) Biết m là giá trị của tham số m để hai số phân biệt x , x thỏa mãn f   x f x  0 và 1   2  0 1 2 2 2 x x
x x  13 . Khi đó m  15; 7 0   1 2 1 2 7
TRẮC NGHIỆM TRẢ LỜI NGẮN 1  1  Câu 1. Cho hàm số 3 2 y
x x  2x 1 có đồ thị là C  . Tiếp tuyến của C  tại điểm M 1;   cắt đường 3  3  5 thẳng x
tại điểm có tung độ bằng bao nhiêu ? 3 3
Câu 2. Cho hàm số y  m  2 3 x  m  2 2
x  3x 1, m là tham số. Số các giá trị nguyên m để 2 y  0, x   là bao nhiêu ? 1
Câu 3. Cho hàm số f x có đạo hàm trên  thỏa mãn   2       1     ex x f x x f x và f 0  . Giá trị 2
6 f 2 gần nhất số nguyên nào
Câu 4. Cho biết điện lượng truyền trong dây dẫn theo thời gian biểu thị bởi hàm số 2
Q(t)  2t t , trong đó t
được tính bằng giây và Q được tính theo Culông. Tính cường độ dòng điện tại thời điểm t  4( s) . 1
Câu 5. Một chất điểm chuyển động thẳng xác định bởi phương trình 2 s(t) 
t , trong đó t là thời gian tính bằng 2
giây và s là quãng đường đi được trong t giây tính bằng mét. Tính vận tốc tức thời của chất điểm tại t  5 .
Câu 6. Một quả bóng được thả rơi tự do từ đài quan sát trên sân thượng của toà nhà Landmark 81 (Thành phố
Hồ Chí Minh) cao 461,3 m xuống mặt đất, với phương trình chuyển động 2
s(t)  4,9t . Tính vận tốc của quả
bóng khi nó chạm đất, bỏ qua sức cản không khí. (Đơn vị m / s , kết quả gần đúng làm tròn đến hàng phần chục) 8
ĐẠO HÀM LỚP 11 THPT
(LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P3
_______________________________ TRẮC NGHIỆM ABCD
Câu 1. Tính đạo hàm của hàm số 13x y  13x A. y  B. 1 .13x y x    C. 13x y  ln13 D. 13x y  ln13
Câu 2. Cho hàm số f x 3 2
x  3mx x 1. Tìm giá trị tham số m sao cho f   1  18 . A. m  2  B. m  2 C. m  3 D. m  4
Câu 3. Cho hàm số f x   2
ln x  5x . Tìm tập nghiệm S của phương trình f  x  0 .  5  A. S   . B. S   .  2  C. S  0;  5 . D. S   ;
 0  5;  .
Câu 4. Biết rằng hàm số f x xác định và có đạo hàm. Tính vi phân hàm số f sin 2x . A. 2 o c 2
s x f sin 2xd x B. 4 o c 2
s x f sin 2xd x C. 6 o c 2
s x f sin 2xd x
D. sin 2x f sin 2xd x x 1 Câu 5. Cho hàm số 2
y x x 1 . Tìm số nghiệm dương của phương trình y  . 2 x 1 A.3 B. 2 C. 1 D. 0 x
Câu 6. Cho hàm số f (x) 
x  2 có đạo hàm là f x, hàm số g(x)  4x  sin
có đạo hàm là g x. Tính 4
giá trị biểu thức P f   2 .g  2 . 16 1 A. P  1. B. P  . C. P  . D. P  . 16 4 16 3 2 x x
Câu 7. Vi phân của hàm số y    5x  1 3 2 là A. dy   2
x x  6 dx . B. 2
dy x x  5 . 3 2  x x  C. dy    5 dx 2   .
D. dy   x x  5 dx . 3 2   Câu 8. Cho hàm số 2
y  cos 3x . Tính vi phân của hàm số.
A. dy  3cos3x sin 3 d x x .
B. dy  6cos 3x sin 3 d x x . C. dy  2  cos3x sin 3 d x x . D. dy  3  sin 6 d x x .
Câu 9. Đồ thị hàm số y  sin x  cos x tiếp xúc với đường thẳng nào sau đây A. y  1 B. y  2 C. y   3 D. y  2
Câu 10. Gọi M x ; y là điểm trên đồ thị hàm số 3 2
y x 3x 1
 mà tiếp tuyến tại đó có hệ số góc bé nhất 0 0 
trong các tiếp tuyến của đồ thị hàm số. Khi đó 2 2 x y bằng 0 0 A. 29 . B. 10 . C. 26 . D. 1.
Câu 11. Một chất điểm chuyển động thẳng xác định bởi phương trình 3 2
s t  2t  4t 1 trong đó t tính bằng
giây, s tính bằng mét. Tìm thời điểm mà vận tốc của chất điểm bằng 24m / s . A. t  6s . B. t  3s . C. t  2s . D. t  5s .
Câu 12. Giá trị biểu thức 0 1 2
2C  3C  4C  ...  (n  2) n C bằng n n n n A. 1 ( 4)2n n   B. 1 ( 3)2n n   C. 1 ( 5)2n n   D. 1 ( 6)2n n   9 TRẮC NGHIỆM ĐÚNG, SAI
Câu 1. Cho hàm số y f x  x  2cos x và  x x
a) Vi phân của hàm số là dy  1 4 sin cos dx   .  2 2 
b) Tập giá trị của hàm số f  x là một đoạn có độ dài bằng 4.
c) Phương trình f  x  3cos x 1có 2 điểm biểu diễn nghiệm trên vòng tròn lượng giác.
c) Tồn tại 2 điểm có hoành độ  0;2  sao cho tiếp tuyến của đồ thị hàm số tại điểm đó song song với đường
thẳng y  2x  2024 . Câu 2. Cho hàm số  x
y e sin x . Xét tính đúng, sai của các khẳng định cos x  sin x
a) Vi phân của hàm số là dy dx . x e b) x x y e
ye   cos x .
c) Tồn tại đúng 2 giá trị nguyên m để phương trình x y e   2m có nghiệm.
d) y  2 y  2 y  0 . Câu 3. Cho hàm số 2
y x  3x 1 có đồ thị (C ) . Xét tiếp tuyến của (C ) tại giao điểm của (C ) với trục tung.
Xét tính đúng, sai của các mệnh đề
a) Phương trình 3y  4 y  y 17 có hai nghiệm phân biệt với tổng hai nghiệm bằng 5.
b) Tiếp tuyến đã cho đi qua điểm A1;  3 .
c) Tiếp tuyến đã cho cắt đường thẳng y  2x 1 tại điểm có hoành độ bằng 0
d) Tiếp tuyến đã cho tiếp xúc với đồ thị hàm số 4 2
y x x  4 tại tiếp điểm có tung độ nhỏ hơn 3.   
Câu 4. Phương trình chuyển động của một hạt được cho bởi công thức s t   10  2 sin  4 t   , trong đó  4 
s tính bằng centimet và t được tính bằng giây. Xét tính đúng sai của các mệnh đề sau
a) Gia tốc của hạt tại thời điểm t  3 giây là 2 1  6 2 cm/s
b) Vận tốc của hạt tại thời điểm t  3 giây là 2 cm/s .
c) Vận tốc lớn nhất của hạt đạt được là 4 2 cm/s .
d) Gia tốc nhỏ nhất của hạt đạt được là 2 1  6 2 cm/s . 10
TRẮC NGHIỆM TRẢ LỜI NGẮN 2018x
Câu 1. Cho hàm số f x  ln
. Tính tổng S f  
1  f 2 ... f 2018 thu được phân số tối giản x 1
a a,b . Tính 2b a . b
Câu 2. Giả sử hàm số y f x liên tục, nhận giá trị dương trên 0;  và thỏa mãn f  
1  1, f x  f  x. 3x 1, với mọi x  0 . Giá trị 3
f 5  3 f 5 gần nhất số nguyên nào ? 2 x
Câu 3. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y
mx  ln  x   1 có đạo hàm 2
không âm trên khoảng 1;  ?
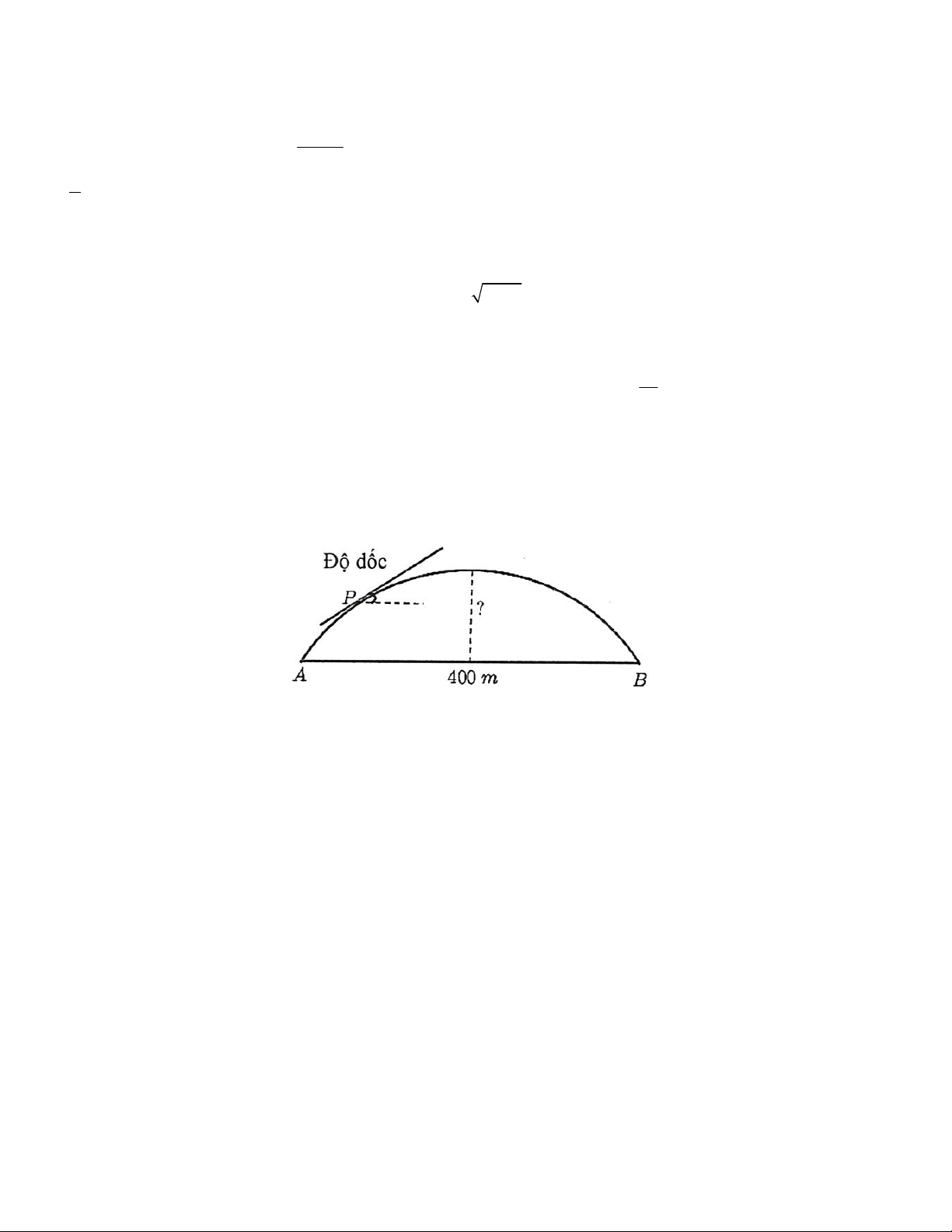
Câu 4. Người ta xây dựng một cây cầu vượt giao thông hình parabol nối hai điểm có khoảng cách là 400 m . Độ
dốc của mặt cầu không vượt quá 10 (độ dốc tại một điểm được xác định bởi góc giữa phương tiếp xúc với mặt
cầu và phương ngang). Tính chiều cao giới hạn từ đỉnh cầu đến mặt đường (làm tròn kết quả đến chũ số thập phân thứ nhất).
Câu 5. Một chất điểm chuyển động có vận tốc tức thời v t phụ thuộc vào thời gian t theo hàm số v t 4 2  t
  8t  500 . Trong khoảng thời gian t  0 đến t  5 chất điểm đạt vận tốc lớn nhất tại thời điểm bao nhiêu giây Câu 6. Cho hàm số 3
y x  2018x có đồ thị (C). Xét điểm A có hoành độ x  1 thuộc (C). Tiếp tuyến của (C) 1 1
tại A cắt (C) tại điểm thứ hai A A có tọa độ  x ; y
. Tiếp tuyến của (C) tại A cắt (C) tại điểm thứ hai 2 2  1 2 1 2
A A có tọa độ  x ; y . Cứ tiếp tục như thế, tiếp tuyến của (C) tại A cắt (C) tại điểm tọa độ A A có 3 3  3 2 n 1  n n 1 
tọa độ  x ; y
. Tìm giá trị nguyên dương n biết 2019
2018x y  2  0 . n n n n 11
ĐẠO HÀM LỚP 11 THPT
LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P4_ĐÁP ÁN
_______________________________ TRẮC NGHIỆM ABCD Câu 1. Cho hàm số     2023x y f x
. Giá trị của f '2 bằng A. f   2 ' 2  2023 . B. 2
f '(2)  2023 .ln 2023. 2 2023 ln 2023
C. f ' x  .
D. f ' x  . ln 2023 2 2023 1   
Câu 2. Gọi a là nghiệm của phương trình  0 
. Khi đó khẳng định nào sau đây sai 2 
x  4x  3  A. 2 a  3a  11 B. 2 a a  7 C. 2 a a  4 D. 2 a  5a  13 Câu 3. Cho hàm số   2 1 2x y f x   
. Giá trị của f '  1 bằng A. f '  1  6 ln 2 . B. f '(1)  7 ln 2 . C. f '(1)  8 ln 2 . D. f '(1)  9 ln 2 .
Câu 4. Đạo hàm của hàm số f x 2  sin 5x là A. f (
x)  2 sin 5x . B. f (
x)  5sin10x . C. f (
x)  10 sin10x . D. f (
x)  5sin10x . Câu 5. Cho hàm số 3 2
y x mx  3x  5 với m là tham số. Tìm tập hợp M tất cả các giá trị của m để y  0
có hai nghiệm phân biệt. A. M   3  ;3 . B. M   ;    3 3;  . C. M   . D. M   ;  3    3;  .
Câu 6. Cho hàm số f x 3 2
x  3x x 1. Giá trị f    1 bằng: A. 0 . B. 1. C. 2. D. 3. 1 ax b
Câu 7. Hàm số y
có đạo hàm là y 
.. Giá trị của P a b là: 2 x  2x  5
x x  2 2 2 5 A. P  4 B. P  2 C. P  2 D. P  0
Câu 8. Tính đạo hàm của hàm số y  log 2x 1 . 2   2 1 2 1 A. y  . B. y  . C. y  . D. y  . 2x   1 ln 2 2x   1 ln 2 2x 1 2x 1 2 
x  4x  6 
Câu 9. Tính tổng các nghiệm thực của phương trình  0   . x  2   A.3 B. – 4 C. – 2 D. – 1
Câu 10. Cho hàm số f x  4g x  5 . Tính g 
1 biết rằng g   1  1; f   1  2 . A.1 B. 2 C. 3 D. 4
Câu 11. Một chất điểm chuyển động có phương trình 3 2
s  t t t  4 ( t là thời gian tính bằng giây). Gia tốc
của chuyển động tại thời điểm vận tốc đạt giá trị lớn nhất là A. 6 . B. 0 . C. 2 . D. 4 . f  2 x 3 4 
Câu 12. Cho các hàm số y f 2x  
1 , y f x , y
lần lượt có các đồ thị C , C ,C . Hệ số 1 2 3 f  2 3x  2
góc tiếp tuyến tại điểm có hoành độ bằng 1 của C , C ,C (tương ứng) lần lượt là k , k , k khác 0 và thỏa mãn 1 2 3 1 2 3
điều kiện k  5k  6k . Tính f   1 . 1 2 3 15 12 6 1 A. f   1  B. f   1   C. f   1   D. f   1   11 13 23 5 12 TRẮC NGHIỆM ĐÚNG, SAI
Câu 1. Biết y là hàm số của x thỏa mãn phương trình xy  1 ln y . Xét tính đúng sai của các mệnh đề sau. 2 y
a) Đạo hàm của hàm số y là y  . 1 xy 1 b) y0  . 2 e
2 yy1 xy 2
y y xy
c) Đạo hàm cấp hai của hàm số y là y  . 1 xy2 3 d) y 0  . 3 e
Câu 2. Một tài xế đang lái xe ô tô, ngay khi phát hiện có vật cản phía trước đã phanh gấp lại nhưng vẫn xảy ra
va chạm, chiếc ô tô để lại vết trượt dài 20,4 m (được tính từ lúc bắt đầu đạp phanh đền khi xảy ra va chạm). 5
Trong quá trình đạp phanh, ô tô chuyển động theo phương trình 2
s(t)  20t
t , trong do s (đơn vị mét) 1à 2
độ dài quãng đường đi được sau khi phanh, t (đơn vị giây) là thời gian tính từ lúc bắt đầu phanh ( 0  t  4 ).
Xét tính đúng sai của các mệnh đề sau
a) Vận tốc tức thời của ô tô ngay khi đạp phanh là 20(m / ) s
b) Xe ô tô trên chưa chạy quá tốc độ, (tốc độ giới hạn cho phép là 70 km/h).
c) Thời điểm xảy ra va chạm cách thời điểm bắt đầu đạp phanh 6,8giây
d) Vận tốc tức thời của ô tô ngay khi xảy ra va chạm là 14(m / s) 1
Câu 3. Cho hàm số y f x 
. Các mệnh đề sau đúng hay sai? 3  2x 8
a) f " x  . 3 2x3 b) f '  1  f "  1  6 . 3
c) f " x  0, x   . 2 x 8
d) f "e   . 3 2 x e 3 Câu 4. Cho hàm số 3
y f (x)  2x có đồ thị (C ) và điểm M thuộc (C ) có hoành độ x  1. Xét tính đúng, 0
sai của các khẳng định a) Phương trình 2
x f  x  6x f  
1 có hai nghiệm phân biệt cùng dương.
b) Tiếp tuyến của (C ) tại M cắt đồ thị hàm số 2
y x  8  7x  4 tại hai điểm phân biệt có tổng hoành độ bằng 5.
c) Tiếp tuyến của (C ) tại M cắt đường thẳng d : y  3x tại điểm có hoành độ bằng 4. 1
d) Tiếp tuyến của (C ) tại M vuông góc với đường thẳng  : y   x . 6 13
TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. Cho đa thức ( )  (1 2 )n f x x 2 n
a a x a x   a x n N
. Tìm hệ số a , biết rằng n  * 0 1 2  2
a  2a   na  13122n . 1 2 n
Câu 2. Cho hàm số y f x có đạo hàm trên  thỏa mãn f x   3
1  x  3x  2 . Tìm giá trị nhỏ nhất của biểu
thức P  2 f  x  3 f  x  4 .
Câu 3. Hàm số y f x có đạo hàm liên tục trên 1; 2 và f  
1  4 và f x  xf  x 3 2
 2x  3x . Giá trị
f 2 là số nguyên nào ?
Câu 4. Một chiếc ô tô đang chạy thì người lái xe đã phanh gấp lại vì gặp phải vật cản phía trước nhưng vẫn xảy
ra va chạm, chiếc ô tô để lại vết trượt dài 15, 5m (được tính từ lúc bắt đầu đạp phanh cho đến khi xảy ra va 3
chạm). Trong quá trình đạp phanh, ô tô chuyển động theo phương trình 2
s(t)   t 15t , trong đó s (đơn vị: 2
m ) là độ dài quãng đường đi được sau khi phanh và t (đơn vị: giây) thời gian tính từ lúc bắt đầu đạp phanh
0  t  5 . Vận tốc tức thời của ô tô ngay khi xảy ra va chạm là
Câu 5. Dân số của Việt Nam sau t năm tính từ năm 2023 được dự đoán theo công thức với N (t) tính theo đơn vị triệu người : ( )  100. at N t
e , 0  t  50 . Biết rằng đạo hàm của hàm số N (t) biểu thị tốc độ gia tăng dân số
của Việt Nam ( đơn vị là triệu người/ năm). Vào năm 2066 thì tốc độ gia tăng dân số hơn 2 triệu người/ năm.
Hỏi vào năm 2080 thì tốc độ gia tăng dân số là bao nhiêu? f x
Câu 6. Cho các hàm số y f x , y g x , y
. Nếu hệ số góc tiếp tuyến của các đồ thị hàm số đã g x
cho tại điểm có hoành độ x bằng nhau và khác không thì giá trị lớn nhất của f x bằng bao nhiêu ? 0  0 14
ĐẠO HÀM LỚP 11 THPT
(LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P5_ĐÁP ÁN)
_______________________________ TRẮC NGHIỆM ABCD
Câu 1. Tìm nghiệm của đạo hàm y biết rằng 2
y x  6x  5 . A. x  3 B. x  2 C. x  4 D. x  1
Câu 2. Tính đạo hàm của hàm số 4 2
y  5x  5x  6x . A. 3
y  20x 10x  6 B. 3
y  20x 10x  6 C. 3
y  20x 10x D. 3
y  20x 10x  6 3
Câu 3. Tính tổng các hệ số đối với đạo hàm của hàm số f x 2  4x x . 2 A.4 B. 9 C. 5 D. 7 3  x  4
Câu 4. Đạo hàm của hàm số f x  tại điểm x  1  là 2x 1 11 1 11 A.  . B. . C. – 11. D.  . 3 5 9
Câu 5. Đạo hàm của hàm số y   2 2x   1
x x  0 là 2 10x 1 2 6x 1 4x 1 A. y  .
B. y  2 x . C. y  . D. y  . 2 x 2 x 2 x Câu 6. Cho hàm số 2 y
x  6x 19 . Có bao nhiêu số nguyên âm x thỏa mãn y  0 . A.3 B. 2 C. 1 D. 4 x 1
Câu 7. Tính đạo hàm của hàm số y  2 ln x  . x e x  1  1 x 1 A. y  2
 ln 2ln x   x   . B. y  2 ln 2   e .  x  ex x x 1 x 1 1 C. y  2 ln 2  . D. x y  2 ln 2   e . x x e x
Câu 8. Một vật chuyển động có phương trình 4 3 2
S t  3t 3t  2t 1 m , t là thời gian tính bằng giây. Gia tốc
của vật tại thời điểm t s 3 là A. 2 48 m/s . B. 2 28 m/s . C. 2 18 m/s . D. 2 54 m/s .
Câu 9. Cho hàm số f x 3 2
x  3x mx 1. Biết m là giá trị của tham số m để hai số phân biệt x , x thỏa 0 1 2
mãn f  x f x  0 và 2 2
x x x x  13 . Mệnh đề nào dưới đây đúng? 1   2  1 2 1 2 A. m  1; 7 . B. m  7;10 . C. m  15; 7 . D. m  7; 1 . 0   0   0   0  
Câu 10. Xét hàm số y f x 2
 1 cos 2x . Chọn câu đúng:  sin 4x  sin 4x A. df (x)  dx . B. df (x)  dx . 2 2 1 cos 2x 2 1 cos 2x cos 2x  sin 2x C. df (x)  dx . D. df (x)  dx . 2 1 cos 2x 2 2 1 cos 2x Câu 11. Cho hàm số 3 2
y mx  2mx  (m  2)x 1. Tìm tất cả các giá trị của tham số thực m để phương trình
y  0 vô nghiệm. A. m  ( ;  6)  (0; ) .
B. m  6;0 .
C. m 6; 0 . D. m 6; 0. f x  3
Câu 12. Cho hàm số y f x , y g x , y
. Hệ số góc của các tiếp tuyến của đồ thị các hàm số g x 1
đã cho tại điểm có hoành độ x  1 bằng nhau và khác 0. Khẳng định nào dưới đây đúng? 11 11 A. f   1  3 . B. f   1  3 . C. f   1   . D. f   1   . 4 4 15 TRẮC NGHIỆM ĐÚNG, SAI   
Câu 1. Cho hàm số f (x)  sin 2x    và g( )
x  5  cos3x . Các mệnh đề sau đúng hay sai?  3    
a) Đạo hàm của hàm số f (x) trên  là f (
x)  cos 2x    .  3 
b) Đạo hàm của hàm số g( )
x trên  là g (  x)  3  sin 3x . 5
c) Tất cả các nghiệm của phương trình 3 f (  x)  2g (
x) là x  
k 2 (k   ) . 6 d) Gọi (
h x)  g(x)  sin 6x , giá trị lớn nhất của hàm h (  x) bằng 3 . x 1
Câu 2. Cho hàm số f ( ) x
. Các mệnh đề sau đúng hay sai? x 1 x 12 x 1 x1
a) Đạo hàm của hàm số f ( ) x
tại x  3 là f (  3)  lim . x1 0 x3 x2 x 1 2
b) Đạo hàm của hàm số f ( ) x  là f (  ) x   . x1 2 (x1) x 11  c) Nếu x 1 lim  2
 thì f (0)  2 . x0 x
d) Hệ số góc của tiếp tuyến tại điểm có hoành độ x  2 là f (2)  2 . 0   
Câu 3. Chuyển động của một vật có phương trình là s(t)  4.cos 2 t  
 m , với t là thời gian tính bằng  12 
giây. Khi đó, các mệnh đề sau đúng hay sai?
a) Sau 5 giây vật đi được quãng đường là 3,86 (m)   
b) Vận tốc tức thời của vật theo thời gian là v(t)  8 .sin 2 t     12  5
c) Tại thời điểm t
(s) , vận tốc của vật là 11, 6 (m/s) 6
d) Vận tốc lớn nhất của vật đạt 25,13 (m/s) Câu 4. Cho hàm số 2  (   ) x y ax bx
c e với b  0 . 2
a) Đạo hàm của hàm số đã cho bằng   (2  ) x ax
a b x b ce   .
b) y 1  3a  2b c e . 2       
c) Khi hàm số có đạo hàm bằng có đạo hàm là 3 x y ax ax b c e 
 thì a b . 2         9
d) Khi hàm số có đạo hàm là  3  1 x y ax a x b c e
 thì biểu thức M a có giá trị nhỏ nhất là một b số nhỏ hơn 8. 16
TRẮC NGHIỆM TRẢ LỜI NGẮN 2
ax bx 1, x  0
Câu 1. Cho hàm số f x  
. Khi hàm số f x có đạo hàm tại x  0 . Hãy tính giá trị tổng 0
ax b 1, x  0 
T a  2b (kết quả là số nguyên). 1 Câu 2. Cho hàm số   .ln 4x f x   2. ln 4  1   2   3   2023 
Giá trị tổng S f '  f '  f '  ...  f ' .       
 gần nhất số chính phương nào  2024   2024   2024   2024 
3  4  x khi x  0  
Câu 3. Cho hàm số f x 4  
. Khi đó 16 f 0 là số nguyên nào ? 1  khi x  0   4
Câu 4. Phương trình chuyển động của một chất điểm được biểu thị bởi công thức S t  2 3
 4  2t  4t  2t , trong
đó t  0 và t tính bằng giây  s , S t  tính bằng mét m . Tìm gia tốc a của chất điểm tại thời điểm t  5s .
Câu 5. Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô a
hình hoá bằng hàm số P t  
, trong đó thời gian t được tính bằng giờ. Tại thời điểm ban đầu t  0, 0,75t b e
quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Theo mô hình này, quần thể nấm men về lâu dài tăng
nhưng không vượt quá là bao nhiêu tế bào? f x 2 3
Câu 6. Cho các hàm số y f x  2, y f x  6   , y
lần lượt có các đồ thị C , C ,C . Hệ số f 3x  4 1 2 3
góc tiếp tuyến tại điểm có hoành độ bằng 2 của C , C ,C (tương ứng) lần lượt là k , k , k khác 0 và thỏa mãn 1 2 3 1 2 3
điều kiện 3k  4k  5k . Tính giá trị 6 f 2 (kết quả là số nguyên) 1 2 3 17
ĐẠO HÀM LỚP 11 THPT
(LỚP BÀI TOÁN LUYỆN TẬP CHUNG_P6)
_______________________________ TRẮC NGHIỆM ABCD
Câu 1. Cho các hàm số: 3 3 3 3 y x  4 ; x y x  6 ; x
y x  4x  5;
y x  4x 10 .
Trong các hàm số trên, có bao nhiêu hàm số có đạo hàm 2
y  3x  4 ? A.3 B. 4 C. 2 D. 1
Câu 2. Sử dụng công thức đạo hàm tích, đạo hàm của hàm số 3 2
y  (x  4x)(x  7) bằng A. 2 2 3
2(3x  4)(x  7)  (x  4x).2x B. 2 2 3
(3x  4)(x  7)  (x  4x).x C. 2 2 3
(3x  4)(x  7)  (x  4x).2x D. 2 2 3
(3x  4)(x  7)  (x  4x).2x
Câu 3. Cho hàm số f (x)  a cos x  2 sin x  3x 1. Tìm a để phương trình f (
x)  0 có nghiệm. A. a  5 . B. a  5 . C. a  5 . D. a  5 . x 1
Câu 4. Có bao nhiêu số nguyên m nhỏ hơn 10 để mọi tiếp tuyến của đồ thị hàm số y  luôn có hệ số x  3m góc dương A.9 B. 7 C. 6 D. 5
Câu 5. Tính đạo hàm của hàm số y  log  2 x 1 . 9  1 x 2x ln 9 2 ln 3 A. y  . B. y  . C. y  . D. y  .  2 x   1 ln 9  2 x   1 ln 3 2 x 1 2 x 1 ax  7 ab
Câu 6. Biết rằng đạo hàm của hàm số y  bằng
. Khi đó giá trị tích ab bằng 4x bx b2 4 A.10 B. 14 C. 12 D. 10 Câu 7. Cho hàm số 2 x
y e . Nghiệm của phương trình   4 x y
e nằm trong khoảng nào  3   3  A. 0;  1 B. 1;   C. ;2   D. 2;3  2   2 
Câu 8. Đồ thị hàm số y  sin x  cos x tiếp xúc với đường thẳng nào sau đây A. y  1 B. y  2 C. y   3 D. y  2 1 3m 4 Câu 9. Cho C y x x m
. Gọi A  C có hoành độ 1 . Tìm m để tiếp tuyến tại A m m   :  4  2  3  3 4 2
song song với đường thẳng d : y  6x  2017 ? A. m  3. B. m  3. C. m  5. D. m  0.
Câu 10. Một chất điểm chuyển động thẳng có phương trình 3 2
s t  5t  9t  3( t là thời gian tính bằng giây s ,
s là đường đi tính bằng mét m . Gia tốc của chất điểm tại thời điểm t  3 s là 0   A. 2 8 m / s . B. 2 6 m / s . C. 2 12 m / s . D. 2 16 m / s .
Câu 11. Cho các hàm số f x , g x , h x có đạo hàm trên  2
f x g 3x  2  h x  3 và thỏa mãn      
với mọi x   , g8  5, h 
1  3 . Giá trị f 2 bằng A.  2 . B.  3 . C.  5 . D. 5 .
Câu 12. Với b  0 , hàm số 2 (   ) x ax
bx c e có đạo hàm là 2      3   1 x y ax a
x b ce
 . Tìm giá trị nhỏ nhất của biểu thức 9 M a  . b A.4 B. 5 C. 6 D. 7 18 TRẮC NGHIỆM ĐÚNG, SAI Câu 1. Cho hàm số    x y
f x e .sin 2x . Các mệnh đề sau đúng hay sai? a) "  x f
x e 4 cos 2x  2sin 2x b) f "0  4 .
c) 2 f ' x  f " x  5 f x . d)     2 2   4 x f x
e 4 cos 4x  3sin 4x   .
Câu 2. Cho hàm số y f x  ln 2x  4 . Các mệnh đề sau đúng hay sai?
a) Tập xác định của hàm số y f x là D  2;  . b) y  0 x   D .
c) Tổng các nghiệm của phương trình y  1  là 4 .
d) Có 1 giá trị thực của tham số m để phương trình y  y  m  2  0 có hai nghiệm x , x sao cho tổng của 1 2 chúng bằng 5 .
Câu 3. Cho hàm số y  sin 2x . Các khẳng định sau đúng hay sai?
a) Đạo hàm cấp 2 của hàm số là y  2 sin 2x .    b) y  0   .  4 
c) y  4 y  0 .
d) Phương trình y  cos 4x 1  0 có 5 nghiệm phân biệt thuộc đoạn    ;  .
Câu 4. Một vật chuyển động trên đường thẳng được xác định bởi công thức 3 2
s(t)  t  3t  7t  2 , trong đó
t  0 và tính bằng giây và s là quãng đường chuyển động được của vật trong t giây tính bằng mét. Xét tính
đúng, sai của các khẳng định sau
a) Tốc độ của vật tại thời điểm t  2 là 7( m / ) s 2
b) Gia tốc của vật tại thời điểm t  2 là 6 m/ s  2 2
c) Gia tốc của vật tại thời điểm mà vận tốc của chuyển động bằng 16 m / s là 10 m / s
d) Thời điểm t  1 (giây) tại đó vận tốc của chuyển động đạt giá trị nhỏ nhất. 19
TRẮC NGHIỆM TRẢ LỜI NGẮN 1 1 1 1 1 1 1 x
Câu 1. Tính đạo hàm của hàm số y    
cos x với x 0;  ta thu được kết quả sin 2 2 2 2 2 2 a b
trong đó a, b   . Tính a b . f x  6
Câu 2. Cho các hàm số f x, g x, hx 
thỏa mãn f m  gm  hm  0 . Giá trị lớn
9  2g x
nhất của 8 f m là số nguyên nào Câu 3. Cho hàm số    ln  x f x
e m . Tìm số thực dương m sao cho f ' x  f '1 x  1. Khi đó 2
m 10m  9 gần nhất số nguyên nào x  2
Câu 4. Cho hàm số y
có đồ thị (C) và điểm ( A ;
a 1) . Gọi S là tập hợp tất cả các giá trị thực của x  1
tham số a để có đúng một tiếp tuyến của (C) đi qua A . Tổng tất cả các giá trị các phần tử của S là 1
Câu 5. Một vật chuyển động theo quy luật 3 2
s   t  6t với t (giây)là khoảng thời gian từ khi vật bắt đầu 2
chuyển động và s (mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian 6 giây, kể
từ lúc bắt đầu chuyển động, vận tốc lớn nhất vật đạt được bằng bao nhiêu?
Câu 6. Năm 2010, dân số ở một tỉnh H là 1038229 người. Tính đến năm 2015, dân số của tỉnh đó là
1153600 người. Cho biết dân số của tỉnh H được ước tính theo công thức   .  . N r S N A e (trong đó A là
dân số của năm lấy làm mốc, S là dân số sau N năm, r là tỉ lệ tăng dân số hàng năm được làm tròn đến
hàng phần nghìn). Tốc độ gia tăng dân số (người/năm) vào thời điểm sau 1 năm kể từ năm 2010 được xác
định bởi hàm số S ' N  . Tốc độ gia tăng dân số của tỉnh H vào năm 2025 là bao nhiêu (làm tròn kết quả đến
hàng đơn vị theo đơn vị người/năm), biết tỉ lệ tăng dân số hàng năm không đổi. 20

Tài liệu liên quan: