Lý thuyết Chương 1 Mạng không gian, chỉ số Miller môn Cơ sở dữ liệu | Đại học sư phạm Hà Nội

lOMoAR cPSD| 40551442 PHYS 304: Cơ sở Vật lí chất rắn Bộ môn Vật lí Chất rắn – Điện tử Khoa Vật lí – Trường Đại học Sư Phạm Hà Nội #1 Chương 1 Lý thuyết 1. Phân biệt mạng không gian và mạng tinh thể 2. Kể tên của 7 hệ tinh thể và viết các hằng số mạng tương ứng.
3. Có bao nhiêu phép đối xứng của
mạng không gian? Định nghĩa các phép đối xứng đó. 4. Qui tắc xây dựng các ô mạng Bravais 5. Phân biệt ô sơ cấp và ô đơn vị 6. Viết công thức tính chỉ số Miller cho đường thẳng và mặt phẳng mạng Bài tập Mạng không gian Bài 1.1 Đồng oxit (CuO2 là một trong những chất siêu dẫn nhiệt độ cao) có cấu trúc tinh thể dạng 2D như hình 1.1a. Giả sử
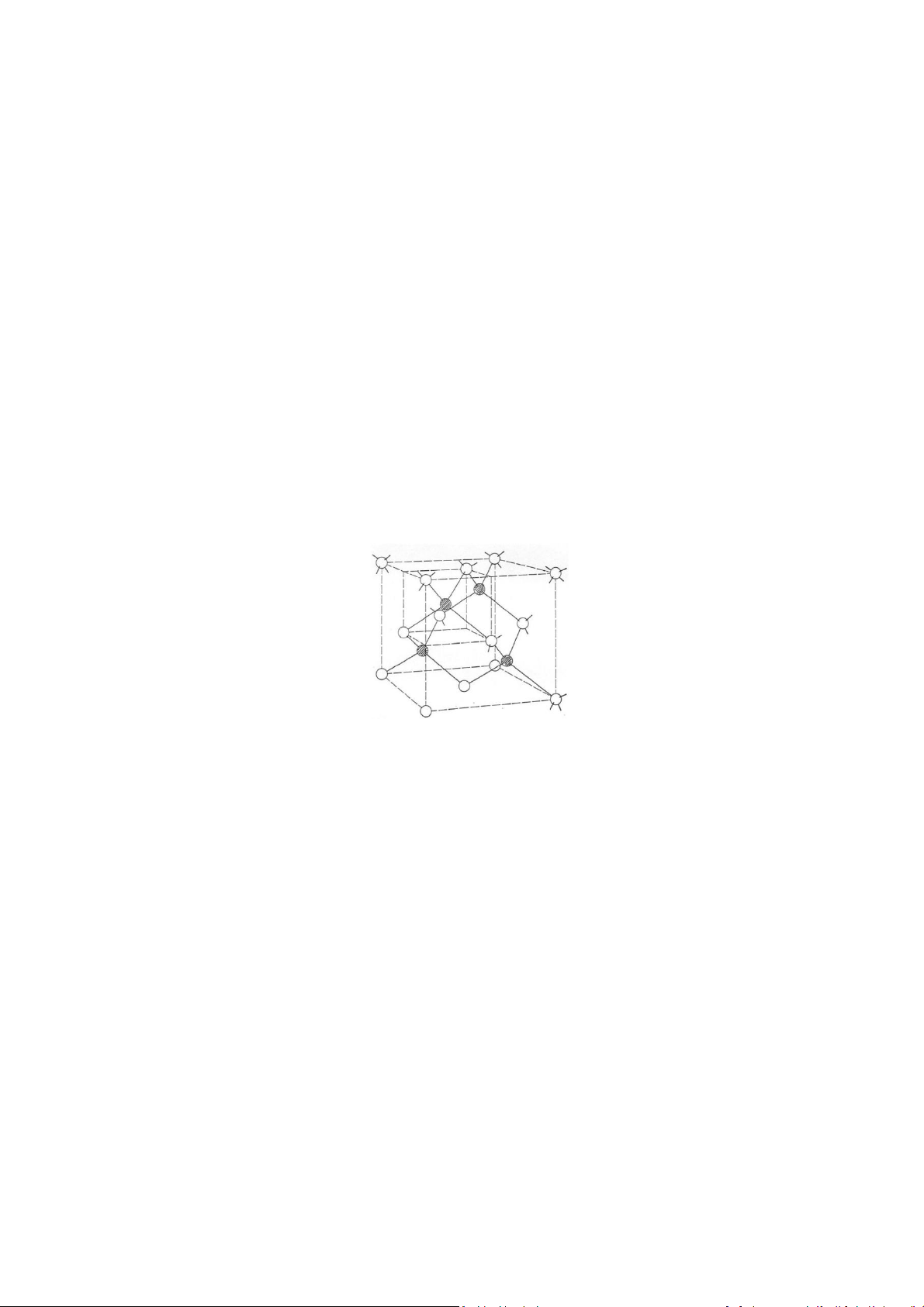
rằng khoảng cách giữa các nguyên tử đồng (hình tròn đặc) là a. Hình 1.1: Cấu trúc mạng 2D của ôxit đồng (a) và cấu trúc mạng 2D của LaCuO (b) a. Xây dựng mạng không gian 2D của CuO2 và vẽ các vector cơ sở khả dĩ. b. Chỉ rõ ô đơn vị và “gốc” của mạng này. c. Tinh thể LaCuO có dạng tương tự CuO2 nhưng không hoàn toàn đồng phẳng. Vị trí “+” là nguyên tử bị nâng lên, vị trí “-” là nguyên tử bị hạ xuống so với mặt phẳng chính. Hãy chỉ ra ô sơ cấp và gốc của mạng tinh 1 lOMoAR cPSD| 40551442 thể này. Xác định trên hình vẽ các hằng số mạng của mạng tinh thể đã cho (Hình 1.1b). Bài 1.2 Hãy vẽ ô sơ cấp, xác định số phối vị trong mạng tinh thể lập phương đơn giản, lập phương tâm khối, lập phương tâm mặt và lục giác. Bài 1.3 Tìm hệ số lấp đầy của một số cấu trúc tinh thể: lập phương tâm mặt, lập phương tâm khối và tinh thể kim cương. Coi rằng các nguyên tử trong tinh thể là các quả cầu cứng. Bài 1.4 Gallium Arsenide (GaAs) có cấu trúc tương tự kim cương (hình 1.2). Biết Ga
biểu diễn bằng hình tròn đặc, còn As được biểu diễn bởi hình tròn rỗng. Hình 1.2: Cấu trúc mạng của GaAs a) Tính số nguyên tử trong một ô đơn vị.
b) Mạng không gian của cấu trúc này là loại gì? c) Chọn bộ 3 vector cơ sở biểu diễn ô sơ cấp của mạng này. Viết câu trả lời dưới dạng các vector trên hệ tọa độ Descartes. Có bao nhiêu nguyên tử trong ô sơ cấp này. Bài 1.5 Chứng minh rằng các mạng không gian chỉ có thể có các trục quay 2, 3, 4 và 6, không thể có trục quay bậc 5 và cao hơn 6. Các chỉ số Miller lOMoAR cPSD| 40551442 Bài 1.6
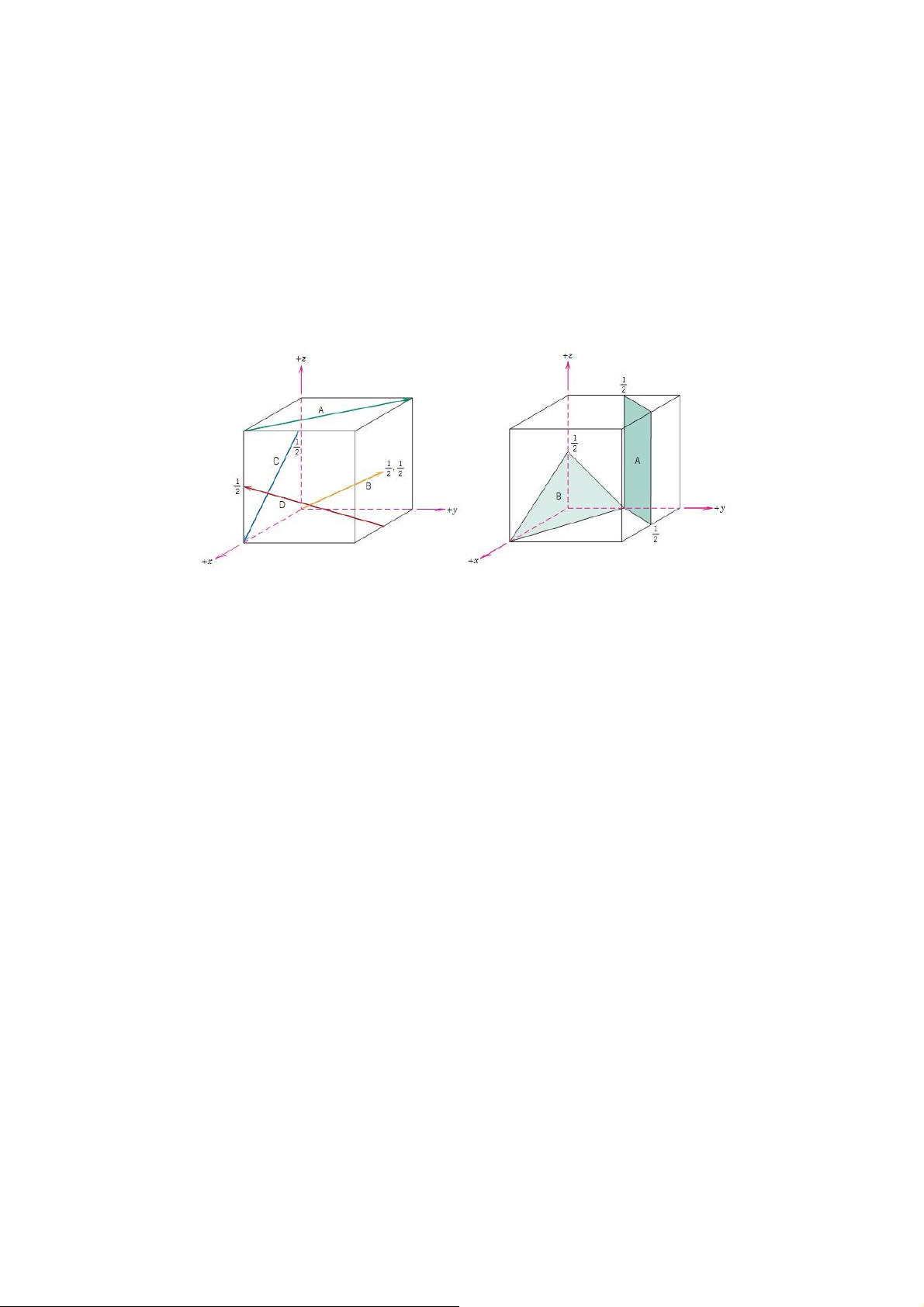
Chứng minh rằng trong mạng lập phương, phương [hkl] luôn vuông góc với mặt phẳng (hkl). Với các mạng khác, điều đó có đúng không? Bài 1.7 Xác định chỉ số Miller của các đường thẳng và mặt
phẳng mạng được biểu diễn trên hình 1.4. Hình 1.4 Một số cấu trúc tinh thể Bài 1.8 𝛼 − 𝐶𝑜 có cấu trúc lục giác xếp chặt (HCP) với hằng số mạng là 𝑎 = 2.51Å 𝑣à 𝑐 = 4,07Å. 𝛽 − 𝐶𝑜 có cấu trúc lập phương tâm mặt (FCC) với hằng số mạng là 3,55Å. Hãy tính bán kính của nguyên tử Co và so sánh hệ số lấp đầy của hai mạng trên. Bài 1.9 Sodium (Na) chuyển từ cấu trúc BCC sang HCP tại nhiệt độ 23K. Giả sử rằng khối lượng riêng của Sodium là không đổi và tỉ số c/a là lí tưởng. Hãy tính hằng số mạng a của cấu trúc lục giác biết rằng hằng số mạng a’ trong cấu trúc lập phương tâm khối của Sodium là 𝑎′ = 4,23Å. Bài 1.10 Tinh thể CsCl có cấu trúc lập phương đơn giản với gốc gồm một ion Cs+ ở đỉnh của hình lập phương và một ion Cl- nằm tâm hình lập phương. Bán kính của ion Cs+ và ion Cl- lần lượt là ra và rb. Chứng minh lOMoAR cPSD| 40551442 rằng các nguyên tử nằm trên đường chéo chính của mạng lập phương không thể chạm nhau nếu tỉ số rb lớn hơn 1,37. ra Bài 1.11 Indi có cấu trúc tứ giác (tetragonal), hằng số mạng là a = 0,325 nm và c= 0,495 nm. a) Cho biết hệ số lấp đầy của tinh thể là 0,69 và bán kính nguyên tử là 0,1625 nm. Hãy xác định số nguyên tử Indi trong một ô mạng.
b) Khối lượng nguyên tử của Indi là 114,82. Hãy tính khối lượng riêng của Indi. Bài 1.12 Xác định số nguyên tử sắt (Fe) có trong một ô mạng lập phương. Cho biết hằng số mạng là a = 2,87 Å, khối lượng nguyên tử của sắt là A = 55,84 và khối lượng riêng r = 7800 kg/m3. Cho biết rõ hơn về cấu trúc mạng tinh thể của sắt. Hãy tính bán kính của một nguyên tử Fe nếu giả sử rằng trong cấu trúc trên các nguyên tử Fe được coi như những quả cầu xếp cho chạm vào nhau. Bài 1.13 Urani có cấu trúc trực thoi với các hằng số mạng a, b, c lần lượt là: 0,286; 0,587 và 0,495 nm. Cho biết khối lượng riêng, khối lượng nguyên tử và bán kính nguyên tử Urani lần lượt là: 19,05 g/cm3, 238,03 và 0,1385 nm. Hãy tính hệ số lấp đầy của tinh thể Urani.