











Preview text:
lOMoARcPSD| 36149638
CHỦ ĐỀ 3: CHẤT RẮN VÀ CHẤT LƯU
3.1. Sự sắp xếp nguyên tử và các ại lượng ặc trưng của vật chất
3.1.1 Sự sắp xếp nguyên tử trong chất rắn, lỏng, khí 3.1.2 Ứng suất, ộ
biến dạng, khối lượng riêng
Nếu bạn bóp một quả bóng cao su, nó sẽ bị biến dạng.
Đại lượng ặc trưng cho lực mà bạn tác dụng khi bóp quả bóng ược gọi là ứng suất, còn ại
lượng ặc trưng cho mức ộ biến dạng của quả bóng ược gọi là ộ biến dạng.
Điều này có nghĩa là khi ứng suất ược ặt vào một vật do một tác nhân bên ngoài, vật ó sẽ
áp ứng lại bằng cách chịu biến dạng. Như vậy ứng suất gây ra biến dạng.
Ứng suất
Để vật rắn dễ biến dạng hơn, lực cần phải ặt vào một diện tích nhỏ.
Ví dụ một lực tác dụng lên một cái cọc ở ầu nhọn có diện tích nhỏ sẽ làm cho nó biến dạng
nhiều hơn, so với cũng lực ó tác dụng lên ầu tù của cọc có diện tích lớn hơn.
Do ó ứng suất có liên quan với tỉ số của lực và diện tích của bề mặt mà lực ó tác dụng:
ứng suất = lực/diện tích
Như vậy ứng suất là lực trên một ơn vị diện tích. Trong hệ SI, ơn vị của ứng suất là N/m2
và ược gọi là pascan (Pa): 1Pa = 1N/m2
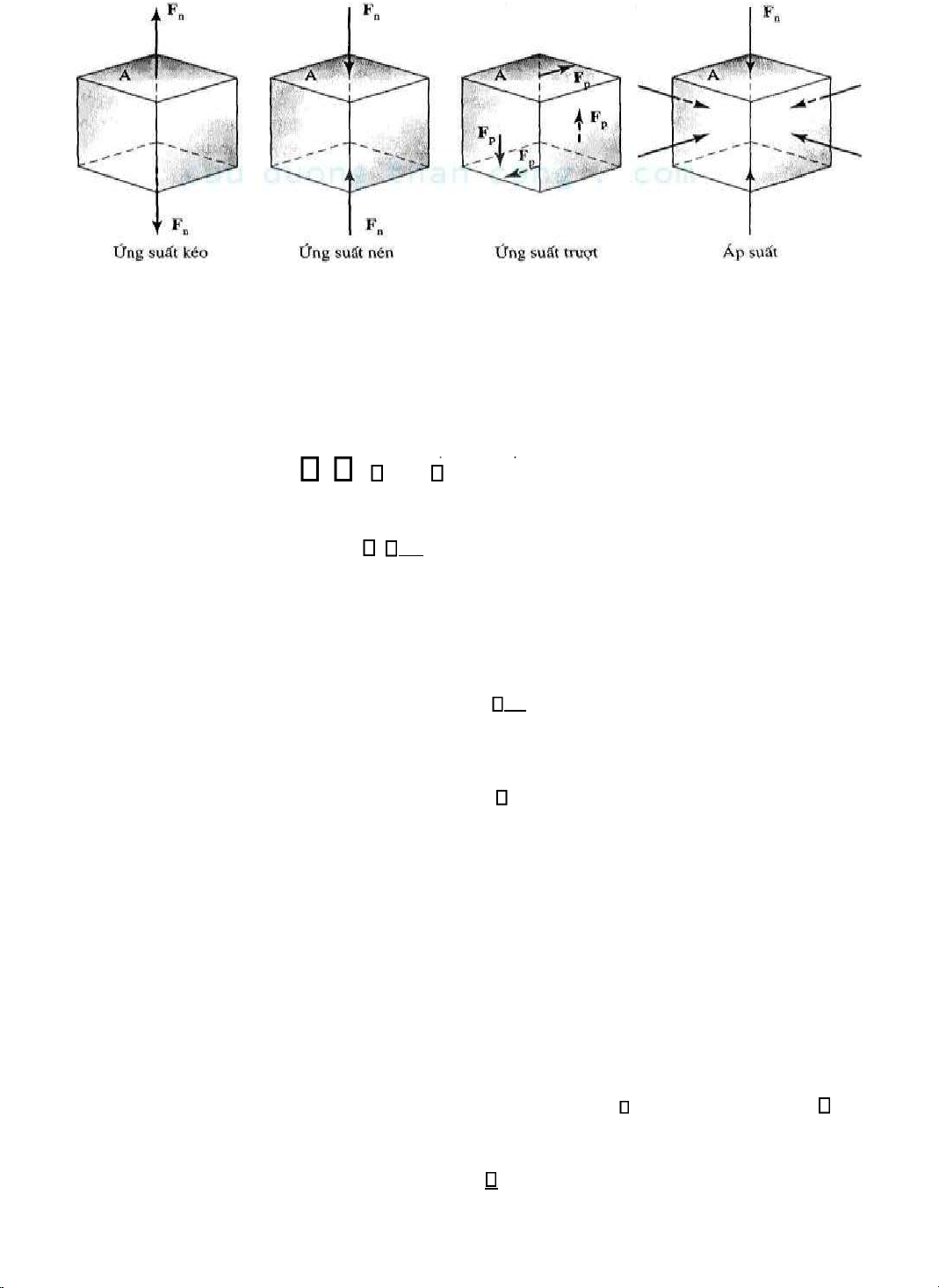
Vì lực có thể tác dụng lên một mặt theo một số cách khác nhau, nên cũng có một số loại
ứng suất như ược minh hoạ trên hình 3-1. Mỗi lực ược biểu diễn trên hình 3-1 ược phân bố ều
trên diện tích mà nó tác dụng.
Loại ứng suất ược cho trên hình 3-la ược gọi là ứng suất kéo. Với ứng suất kéo, hai lực -
ều có ộ lớn là Fn - ược ặt vào hai mặt ối diện của vật rắn, chẳng hạn như khối lập phương trên
hình vẽ. Các lực này ều vuông góc với mặt và hướng ra phía ngoài mặt mà nó tác dụng, ứng suất
kéo có xu hướng kéo giãn vật ra. Như vậy ứng suất kéo k ược ịnh nghĩa như sau: Fn k (3-1) A
Ớ ây A là diện tích của một mặt. Giả sử rằng Fn 50N A; 10mm2 10 4 2m . Khi ó k FAn10
50 4 2Nm 5.105N m/ 2 5.105Pa.
Nếu mỗi lực pháp tuyến ều có hướng i vào phía trong bề mặt mà nó tác dụng (hình 31b)
thì khi ó ứng suất gọi là ứng suất nén. Ứng suất nén có xu hướng ép vật lại. Ứng suất nén là: n Fn A lOMoARcPSD| 36149638
Hình 3-1: (a) và (b): Nếu lực là pháp tuyến (vuông góc) với bề mặt, thì ứng suất ược gọi
là ứng suất kéo hoặc ứng suất nén. (c) Nếu lực song song với bề mặt thì ứng suất gọi là ứng suất
trượt, (d) Nếu cùng lực ó nhưng ược ặt vuông góc với tất cả các mặt thì ược gọi là áp suất.
Ứng suất trượt ược biểu diễn trên hình 3-lc. Trong trường hợp này có bốn lực, mỗi lực
có ộ lớn Fp ược ặt song song với các mặt của khối lập phương. ít nhất cần phải có bốn lực ể giữ
vật ó ở trạng thái cân bằng (
F 0; M 0;). Ứng suất trượt bằng: Fp t (3-2) A
Loại ứng suất ược gọi là áp suất ược cho trên hình 3-1d. Trên mỗi mặt của vật rắn, lực tác
dụng ều vuông góc và có hướng i vào phía trong mặt mà nó tác dụng. Áp suất p bằng: F p n (3-3) A
Áp suất thường gặp là áp suất khí quyển trên bất cứ bể mặt nào ặt trong nó. Ở mực nước
biển, giá trị của áp suất khí quyển là 1,01.105 Pa 101kPa . Độ lớn của lực do khí quyển tác
dụng lên một mảng da hình vuông với kích thước l0mm trên cơ thể bạn là Fn = pA = (101kPa)(10mm)2 = 10N.
Độ biến dạng
Độ biến dạng là ộ o sự biến dạng của một vật rắn khi có một ứng suất ặt lên nó.
Sự biến dạng của vật rắn phụ thuộc vào ứng suất và loại vật liệu. Một vật liệu ẳng hướng
(có các tính chất theo mọi hướng ều như nhau), chẳng hạn như thủy tinh, sẽ "phản ứng" ối với
ứng suất một cách như nhau theo tất cả các phương. Trái lại, gỗ sẽ "phản ứng" khác nhau nếu ứng
suất kéo ặt dọc theo thớ gỗ hay ngang thớ gỗ.
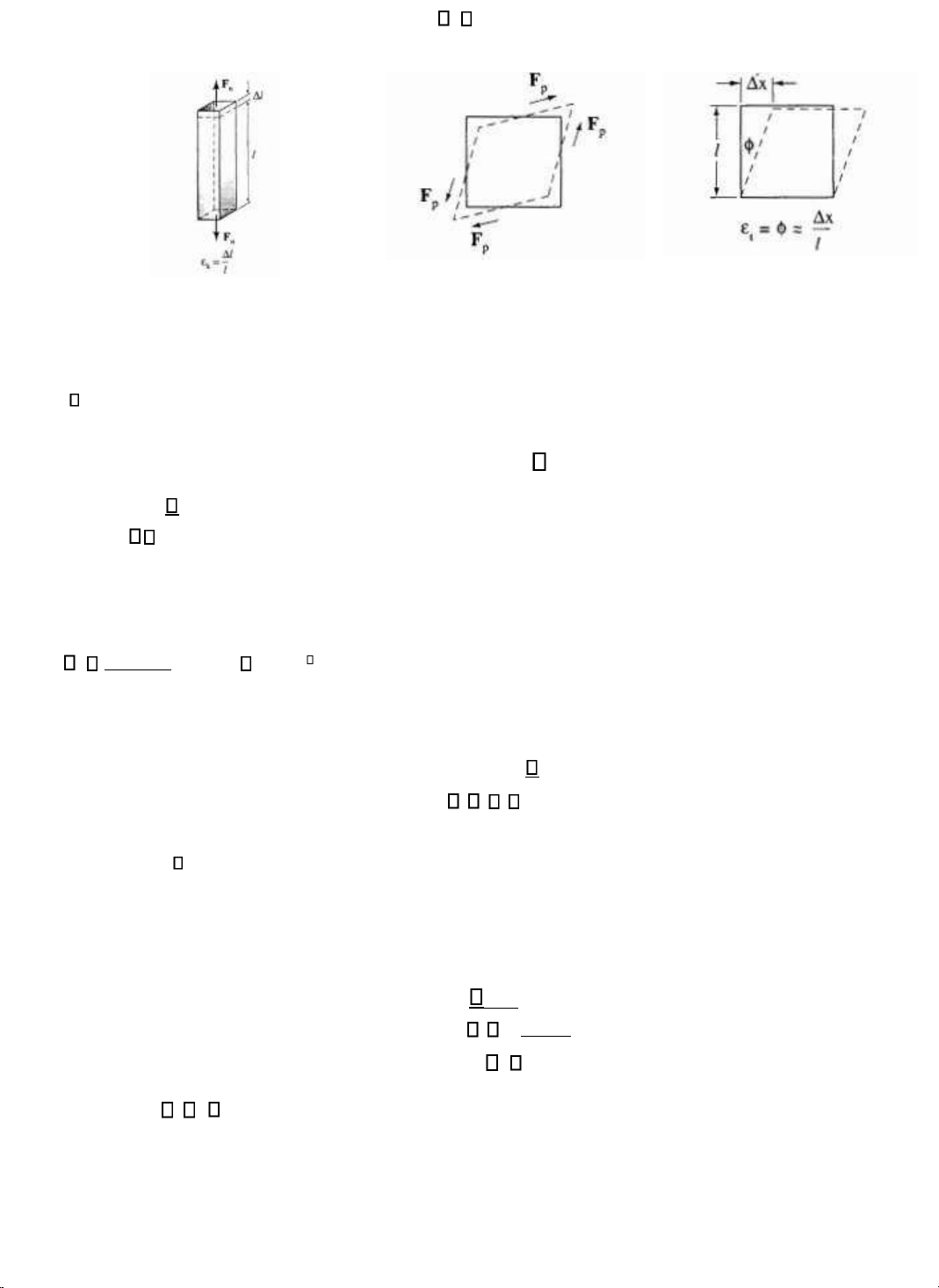
Hình 10-2a cho thấy sự biến dạng của vật rắn khi có ứng suất kéo ặt vào. Vật rắn ược kéo
giãn dài ra và chiều dài ban ầu l của nó cũng tăng thêm một oạn l . Độ biến dạng kéo k ược ịnh nghĩa bởi: l lOMoARcPSD| 36149638 k (3-4) l (a) (b) (c)
Hình 3-2. (a) Độ biến dạng kéo ược ịnh nghĩa như thương số của ộ tăng chiền dài
l do có ứng suất kéo và chiền dài ban dần l. (b) Khi có ứng suất trượt tác dụng vật bị biến dạng,
(c) Xoay vật chịu ứng suất sao cho một cạnh của nó trùng với vị trí của vật không chịu ứng suất sẽ
cho phép ta ịnh nghĩa biếu dạng trượt là góc . Đối với biến dạng trượt thông x thường . l
Vì ộ biến dạng là tỉ số của hai ộ dài nên nó là không thứ nguyên và không có ơn vị.
Chẳng hạn nếu một dây cáp có chiều dài 12m ược kéo dãn 6mm thì ộ biến dạng kéo là 0,006m k
5.10 . 4 Sự "phản ứng" của một vật rắn ồng nhất và ẳng hướng ối với ứng 12m
suất trượt (hình 3-2b) ược gọi là ộ biến dạng trượt và ược ịnh nghĩa bởi: x t l
Ở ây x là ộ dịch chuyển của góc khối lập phương ra khỏi vị trí vuông góc như ta thấy
trên hình 3-2c. Độ biến dạng trượt cũng không có thứ nguyên.
Suất Young E biểu diễn mối quan hệ tuyến tính ó giữa ứng suất pháp tuyến và ộ biến dạng: k Fn / A E k l l/ hay k
E k . Suất Young có thứ nguyên [lực] [diện tích] -1 và trong hệ SI có ơn vị là
pascan (Pa). Một sợi dây thép có giá trị E lớn, trong khi một dây cao su kéo giãn dễ dàng có giá
trị E nhỏ. Xem bảng 3-1.
Suất trượt S biểu diễn mối quan hệ giữa ứng suất trượt với ộ biến dạng trượt: lOMoARcPSD| 36149638 t Fp / A S t x l/ hay t
S t . Suất trượt cũng có thứ nguyên là [lực] [diện tích]-1 và trong hệ SI có ơn vị là pascan (Pa).
Một vật rắn chống lại sự xoắn mạnh mẽ sẽ có giá trị S lớn. Như bạn có thể thấy trong bảng
3-1, giá trị của E và S lớn thường xảy ra với cùng một vật rắn.
Suất nén B liên hệ sự thay ổi tỉ số của thể tích với sự thay ổi của áp suất: B
V dp p dV V V/
B cho biết cần một áp suất bao nhiêu ể nén một chất tới tỉ lệ thể tích ã cho. Thể tích của
một chất lỏng hoặc chất khí cũng có thể thay ổi nếu áp suất tác dụng lên chúng thay ổi.
Bảng 3-1 cũng cho giá trị của suất nén ối với một số chất lỏng, chất khí cũng như chất rắn. Chú
ý rằng một chất khí iển hình (thường là dễ nén) có suất nén nhỏ hơn rất nhiều một chất lỏng
(thường khó nén hơn nhiều).
Bảng 3-1. Các hằng số àn hồi của một số vật liệu1 Vật liệu E (GPa) s (GPa) B (GPa) Nhôm 70 30 70 Đồng thau 91 36 61 Đồng 110 44 140 Chì 15 5,6 7,7 Thép 200 84 160 Tungsten 390 150 200 Xương 15 80 Bêtông 25 Kim cương 1120 450 540 Thuỷ tinh 55 23 31 Nước á 14 3 8 Gỗ (dọc thớ) (ngang 10 thớ) 1 Thuỷ ngân 0 0 27 Nước 0 0 2,2
1 Tất cả các giá trị ều cho với ơn vị Gpa=109Pa lOMoARcPSD| 36149638
Đa số các chất khí ở nhiệt ộ 0 0 104
phòng và áp suất khí quyển
Ví dụ 3-1: Ứng suất và ộ biến dạng trong một dây thép.
Một dây kéo gỗ bằng thép buộc vào một cây gỗ rồi ược kéo bởi một máy kéo. Biết rằng
dây có ường kính 12,5mm và chiều dài giữa máy kéo và gỗ là 10,5m. Biết rằng lực cần thiết ể
kéo cây gỗ có ộ lớn bằng 9500N. Hãy xác ịnh (a) ứng suất trong dây và (b) ộ biến dạng của dây.
(c) Dây sẽ bị giãn một oạn bằng bao nhiêu khi cây gỗ bị kéo?
Giải: (a) Theo ịnh nghĩa của ứng suất kéo: k FAn (69500,25mmN )2 77MPa.
(b) Độ biến dạng ược tìm bằng cách dùng kết quả của câu (a) và giá trị suất Young của thép cho trong bảng 3-1. k k k 77MPa 3,9.10 . 4 E k E 200GPa l
(c) Từ ịnh nghĩa của ộ biến dạng , ta tìm ượ k c dộ giãn của dây: l
l kl (3,9.10 )(10, 4 5 )m 4,1mm
Mặc dù sự thay ổi này của chiều dài là có thể o ược nhưng chưa ủ ể người kéo gỗ nhận thấy ược.
Khối lượng riêng
Khi chúng ta nói sắt "nặng" hơn nhôm là ta muốn nói gì? Chúng ta không muốn nói rằng
bất kì mẩu sắt nào cũng nặng hơn mẩu nhôm nào, mà chúng ta muốn nói rằng với thể tích như
nhau thì sắt nặng hơn nhôm và do ó có khối lượng lớn hơn nhôm. Điều này ược thể hiện trong ại
lượng khối lượng riêng hay còn gọi là mật ộ khối lượng hay mật ộ của một m chất: V
Ở ây m là khối lượng và V là thể tích. Thứ nguyên của khối lượng riêng là [khối lượng][thể
tích]-1 và trong hệ SI nó có ơn vị là kg/m . Khối lượng riêng gần úng của một số chất ược cho
trong bảng 3-2. Như ta sẽ thấy trong mục sau, áp suất trong chất lưu ở một ộ sâu ã cho ược xác
ịnh bởi mật ộ (khối lượng riêng) của chất lưu tại ó.
Vì nước óng vai trò to lớn trong cuộc sống hàng ngày, nên người ta thường so sánh khối
lượng riêng của một vật liệu với khối lượng riêng của nước bằng cách lấy tỉ số của chúng. Tỉ số lOMoARcPSD| 36149638
này ược gọi là tỉ trọng của vật liệu ó2. Vì tỉ trọng là tí số của hai ại lượng có cùng thứ nguyên
nên nó không có thứ nguyên.
Ví dụ tỉ trọng của gỗ ược xác ịnh từ khối lượng riêng của gỗ và nước cho trong bảng 0,7.103kg m/ 3 3-2: 1,00.10 3kg m/ 3 0,7.
Tỉ trọng thường ược dùng trong thương mại nhiều hơn là dùng trong khoa học. Các iều
kiện quy ịnh cho các chất lỏng dùng cho acquy và cho các loại rượu nho thường ược ặc trưng bởi tỉ trọng.
Bảng 3-2: Khối lượng riêng gần úng của một số vật liệu3 Khối lượng Vật liệu Vật liệu Khối lượng riêng Kg/m3 riêng Kg/m3 Nhôrn 2,7.103 Máu 1.05.103 Đồng 8,9.103 Rượu êtylic 0,81.103 Vàng 19,3.103 Thuỷ ngân 13,6.103 Iridi 22,6.103 Nước l,00.103 Sắt hoặc 7,8.103 Nước biển 1,03.103 Chì 11,3.103 Glycerin l,26.103 Platin 21,4. 103 Không khí 1,29 Tungsten 19,3. 103 Heli 0,179 Hi ro 0,090 Xương 1,8.1O3 Hơi nước (100°C) 0,6 Bêtông 2,4.103 Kim cương 3,5.103
Không gian giữa các vì sao 3.10-22 Thuỷ tinh 2,6.103 Mặt Trời (trung bình) 1,4.103 Nước á 0,92.103 Trái Đất (trung bình) 5,5.103
2 Tên gọi này không thật chính xác vì tỉ số trên không có liên quan gì ến trọng trường cả
3 nếu không ghi chú khác, các giá trị ều ược o ở nhiệt ộ phòng và áo suất khí quyển hoặc ở những vùng bên ngoài trái ất lOMoARcPSD| 36149638 Gỗ 0,7. 103 Sao nơtron 1017
Ví dụ 3-2: Mật ộ của silic
Một khối silic hình chữ nhật có kích thước 120mm 165mm 265mmvà có khối lượng 11,8kg.
(a) Tính mật ộ (khối lượng riêng) của silic. (b) Xác ịnh tỉ trọng của silic. Giải: (a)
Thể tích của khối silic bằng:
V (0,120 )(0,165 )(0,255 )m m m 5,05.10 3 3m
Như vậy mật ộ của silic bằng: Vm
5,05.1011,8kg 3 3m 2,34.103kg m/ 3. (b)
Tỉ trọng của silic là tỉ số của mật ộ silic và mật ộ nước, bằng: 2,34.103kg m/ 3 3 3m 2,34. 1,00.10
3.2. Tĩnh học chất lưu
3.2.1 Áp suất tại một iểm trong lòng chất lỏng
Nếu một ứng suất trượt ược ặt vào một chất lỏng hoặc chất khí, nó sẽ tiếp tục biến dạng hoặc chảy.
Chất lưu tĩnh sẽ không có ứng suất trượt.
Trên bất kỳ bề mặt nào giới hạn một chất lưu ở trạng thái ứng yên, lực ều phải là pháp
tuyến ối với bề mặt ó. Có nghĩa là ứng suất trong chất lưu là áp suất p.
Áp suất ở trong một chất lưu ứng yên không phụ thuộc vào sự ịnh hướng của bề mặt mà nó tác dụng.
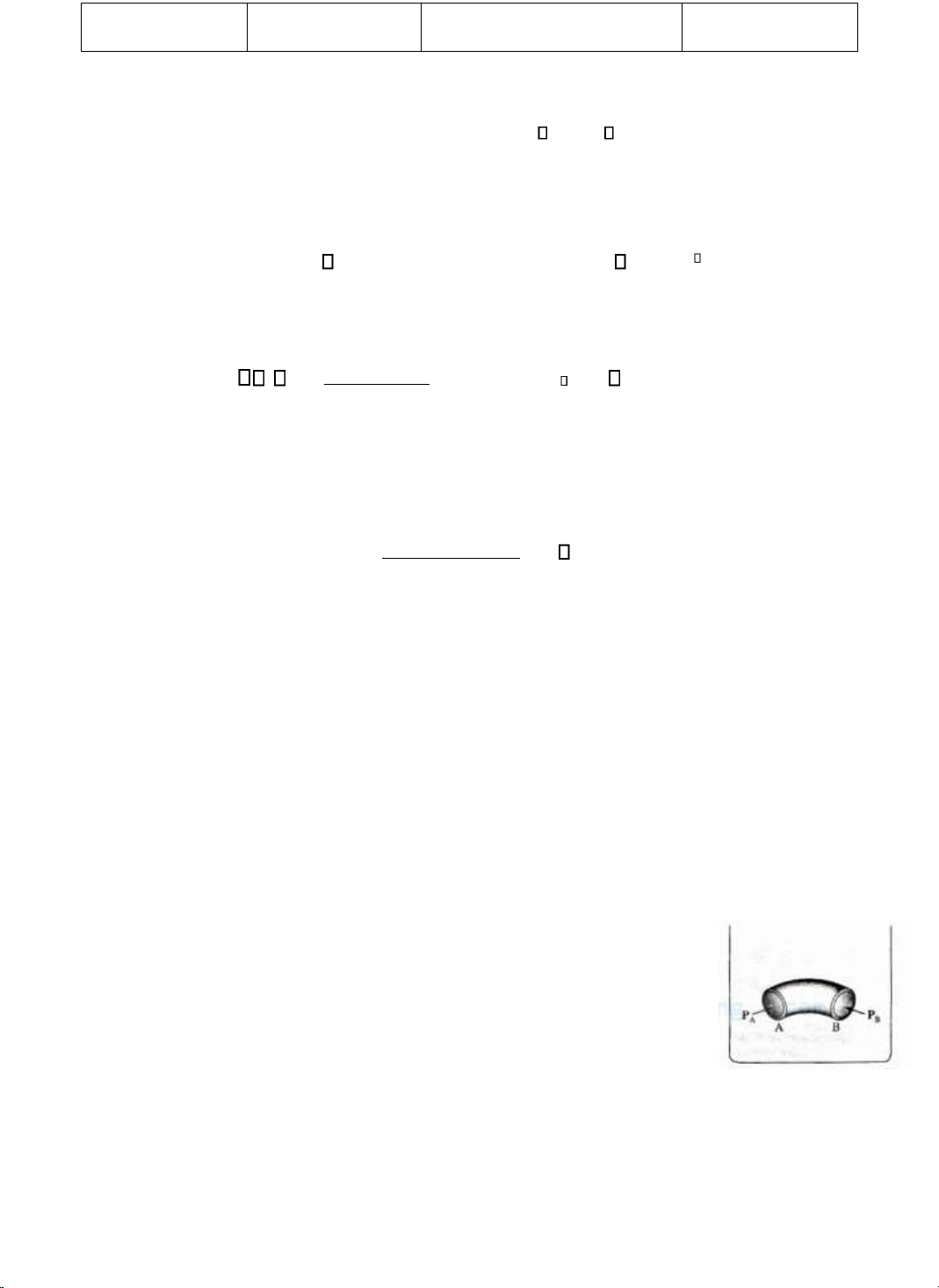
Ví dụ: Có một oạn ống uốn cong nhỏ ược treo nằm ngang trong một
chất lưu (Hình 3-3). Nếu có bất cứ sự chênh lệch áp suất nào ở hai ầu ống
lập tức chất lưu sẽ chảy, iều này trái với giả thiết chất lưu ứng yên.
Vì hai ầu ống có sự ịnh hướng bất kỳ nên ta kết luận: áp
suất chất lưu ở một bình ộ là như nhau theo mọi hướng. Hình 3-3 lOMoARcPSD| 36149638
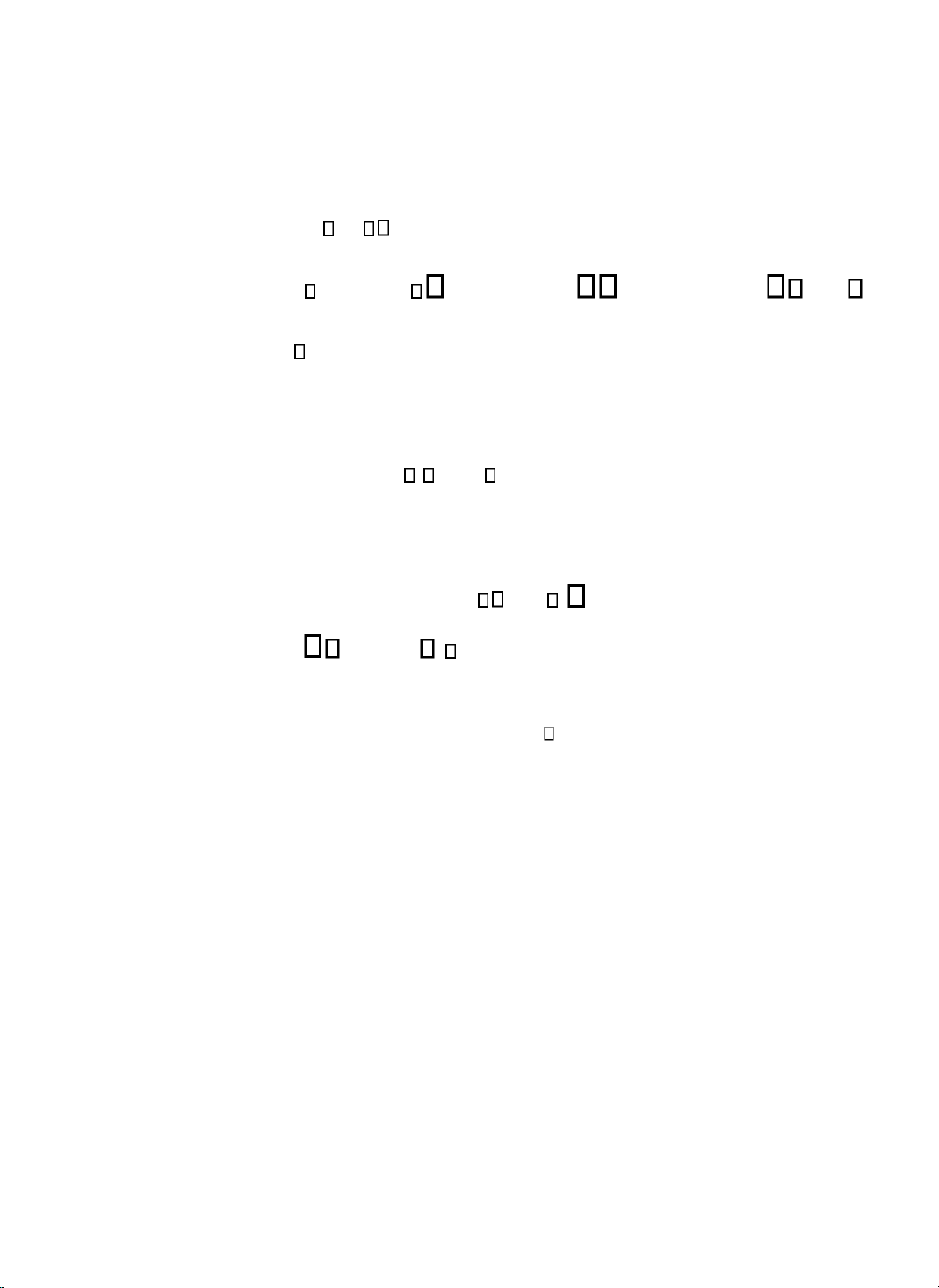
Chất lưu không tác dụng lực căng hay lực kéo lên một vật, ở
trạng thái tĩnh nó chỉ có một xu hướng là nén lên mọi mặt của một
vật bất kỳ ặt trong nó (Hình 3-4).
Hình 3-4: lực nén của chất lưu lên
một vật ặt trong nó
Áp suất của chất lưu có thể ược o bằng một dụng cụ rất ơn
giản. Dụng cụ o áp suất ược cấu tạo bằng một xi-lanh rỗng ược hút
chân không nối với một pittông nhẹ bằng một lò xo. Ta có thể thấy
cấu tạo của nó ở (Hình 3-5). Hình 3-
5: Dụng cụ o áp suất chất lưu
Khi nhúng dụng cụ o áp suất này vào chất lưu cần khảo sát thì chất lưu sẽ nén một lực F
lên mặt bên ngoài của pittông. Lò xo bên dưới cũng sẽ bị nén theo cho ến khi lực nén F của chất
lưu cân bằng với lực àn hồi của lò xo. Đo ộ lớn của lực àn hồi thì ta sẽ biết giá trị của lực nén F.
Tổng quát, áp suất của chất lưu chính là lực nén của chất lưu ó lên một ơn vị diện tích
của bề mặt vật khác ặt trong nó. Công thức tính áp suất khi ó là: p F A
Nếu áp suất thay ổi trên toàn bề mặt của vật bị nén thì khi ó áp suất tại vi trí của diện tích nhỏ dA sẽ là: p
dF dF pdA dA
Vì vậy, lực tác dụng của chất lưu lên toàn diện tích bề mặt A của vật là: F dF pdA
Đơn vị ó áp suất trong hệ SI là (N/m2) hay pascal (Pa): 1Pa N m 1 / 2
3.2.2 Sự thay ổi áp suất theo ộ sâu – Định luật Pascal
Sự thay ổi áp suất theo ộ sâu
Mặc dù áp suất trong một chất lưu ứng yên là như nhau ối với một mức ngang ã cho nhưng
áp suất bị thay ổi theo vị trí thẳng ứng vì có trọng lượng của chất lưu. lOMoARcPSD| 36149638
Tất cả thợ lặn ều biết ược rằng áp suất nước tăng theo ộ sâu. Trong khi áp suất khí quyển
lại giảm theo ộ cao. Đó là lý do tại sao khi càng lên cao thì máy bay phải tạo thêm áp lực lên
khoang chứa ể các hành khách trong ó ều không cảm nhận ược sự thay ổi áp suất.
Bây giờ chúng ta sẽ khảo sát xem tại sao áp suất lại tăng theo ộ sâu?
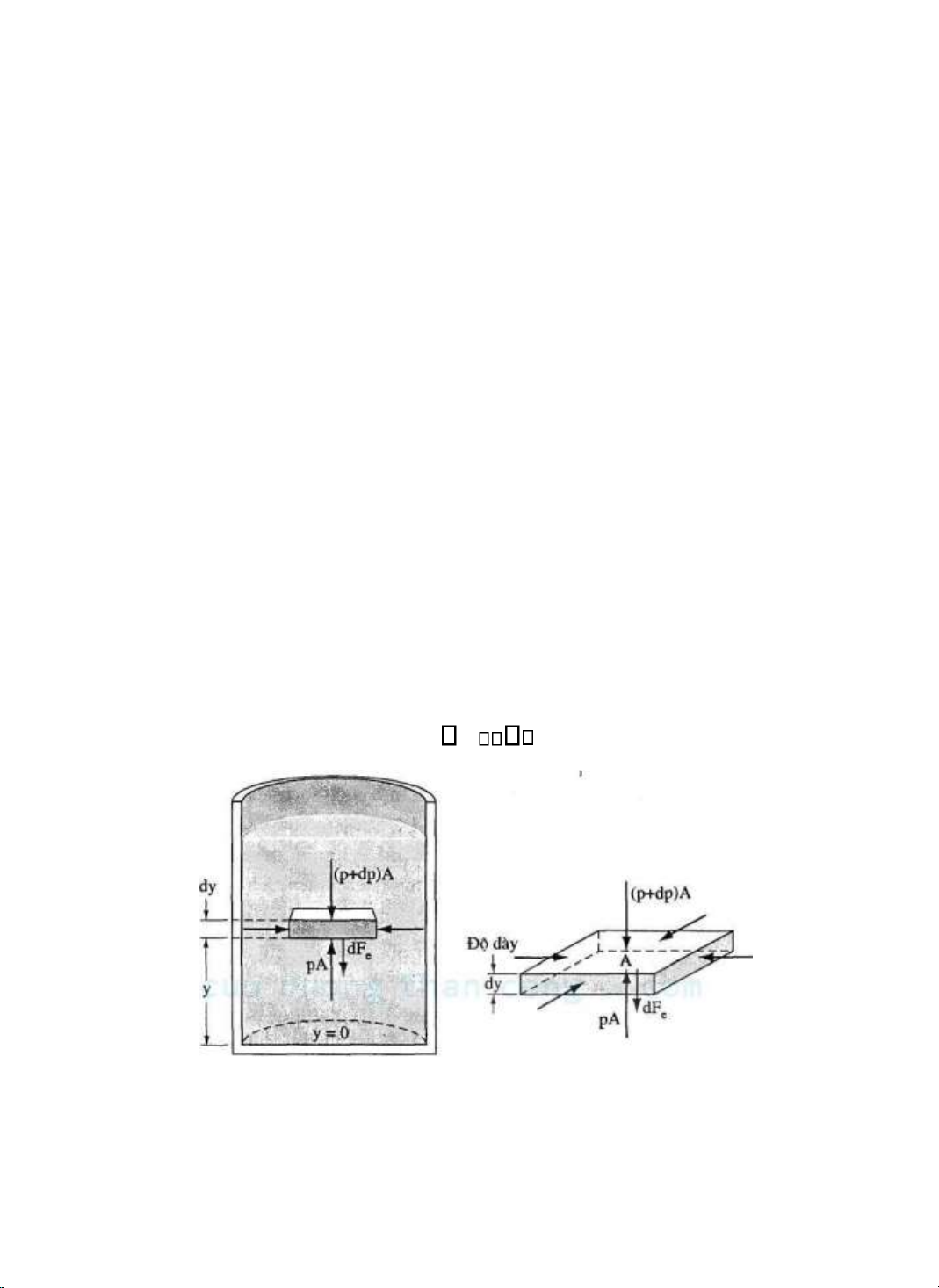
Ta hãy xét một yếu tố nhỏ của chất lưu như cho trên hình 3-6. Yếu tố này ược ịnh vị theo
phương thẳng ứng bởi toạ ộ y và có ộ dày vô cùng bé dy. Áp suất của chất lưu bao quanh tác dụng
lên yếu tố ó các lực. Vì áp suất theo phương ngang là như nhau nên tổng hợp các lực nằm ngang
bằng 0. Theo phương thẳng ứng có ba lực tác dụng lên yếu tố: lực hấp dẫn tác dụng bởi Trái Đất
dFe, lực có ộ lớn pA tác dụng từ phía dưới lên mặt dưới của yếu tố và lực có ộ lớn (p +dp)A tác
dụng từ phía trên xuống mặt trên của yếu tố. Vì chất lưu ở trạng thái cân bằng nên tổng hợp của
các lực này cũng bằng 0: pA - (p + dp)A - dFe = 0 hay: Adp = - dFe
Điều này có nghĩa là hiệu áp suất phải có giá trị sao cho nó cân bằng ược với trọng lượng của yếu tố chất lưu.
Bây giờ thay dFe = (dm)g = (pdV)g = pgAdy, trong ó dm là khối lượng của yếu tố chất
lưu có thể tích dV = Ady, ta sẽ có: dp = - pgdy (3-5)
Nguyên nhân của hiệu áp suất này là sự cần thiết phải giữ yếu tố chất lưu chống lại ược
trọng lượng của nó. Vì y ược o theo phương thẳng ứng hướng lên trên nên dấu trừ ở ây chỉ ra rằng
áp suất giảm khi ộ cao so với áy tăng lên.
Để xác ịnh hiệu áp suất giữa hai mức sâu (hay cao) trong chất lưu, ta cần tích phân
phương trình (3-5). Nếu kí hiệu p1 và p2 là áp suất tại các ộ cao y1 và y2 tương ứng, ta có: p2 y2 dp gdy p1 y1
Hình 3-6. Các lực tác dụng lên một yếu tố chất lưu ở trạng thái cân bằng. lOMoARcPSD| 36149638
Một chất lỏng iển hình thường có suất nén B lớn, do ó nó gần như không chịu nén. Điều
này có nghĩa là mật ộ của chất lỏng về căn bản không phụ thuộc vào áp suất, do ó không phụ
thuộc vào vị trí trong chất lỏng.
Khi ó p cùng g, có thể ưa ra ngoài dấu tích phân và ta ược: p p 2 1 g y y 2 1
Nếu mặt thoáng của chất lỏng ở y2, nơi áp suất có giá trọ p2 = p0 thì áp suất p1 = p ở ộ sâu h = y
2 – y1 sẽ thỏa mãn phương trình p0 p gh hay:
p p0 gh (3-6)
Như vật áp suất tăng tuyến tính trong một chất lỏng không chịu nén.
Ví dụ 3-3: Áp suất áy biển
Hãy xác ịnh áp suất ở áy biển tại nơi có ộ sâu 3000m. Cho áp suất ớ bề mặt ại dương là áp
suất khí quyển 1,01.105 Pa. Giải.
Từ bảng 3-2 ta thấy nước biển có mật ộ bằng 1,03.103kg/m3. Vậy theo phương trình (3- 6): p 1,01.105Pa 1,03.103kgm. 3 9,8N kg/ 3,00.103m 3,0.107Pa.
tức là lớn gần gấp 300 lần áp suất khí quyển. Vì áp suất lớn ghê gớm như vậy nên việc
khảo sát những vùng sâu dưới biển cần phải có những con tàu thiết kế ặc biệt ược gọi là tiềm thuỷ ĩnh.
Định luật Pascal
Ta cũng nhận thấy áp suất chất lưu là như nhau tại mọi iểm có cùng ộ sâu và không phụ
thuộc vào hình dạng vật chứa.
Nếu áp suất trên mặt thoáng của chất lỏng là p0 ược tăng thêm một lượng bằng p, thì khi
ó phương trình (3-6) cho thấy rằng, áp suất tại một iểm tuỳ ý có ộ sâu h so với mặt thoáng cũng
sẽ tăng một lượng p. Kết quả này ược gọi là ịnh luật Pascal:
Áp suất ặt vào một khối chất lưu ứng yên không chịu nén, ược nhốt kín, sẽ ược truyền nguyên
vẹn ến mọi phần của chất lưu ó.
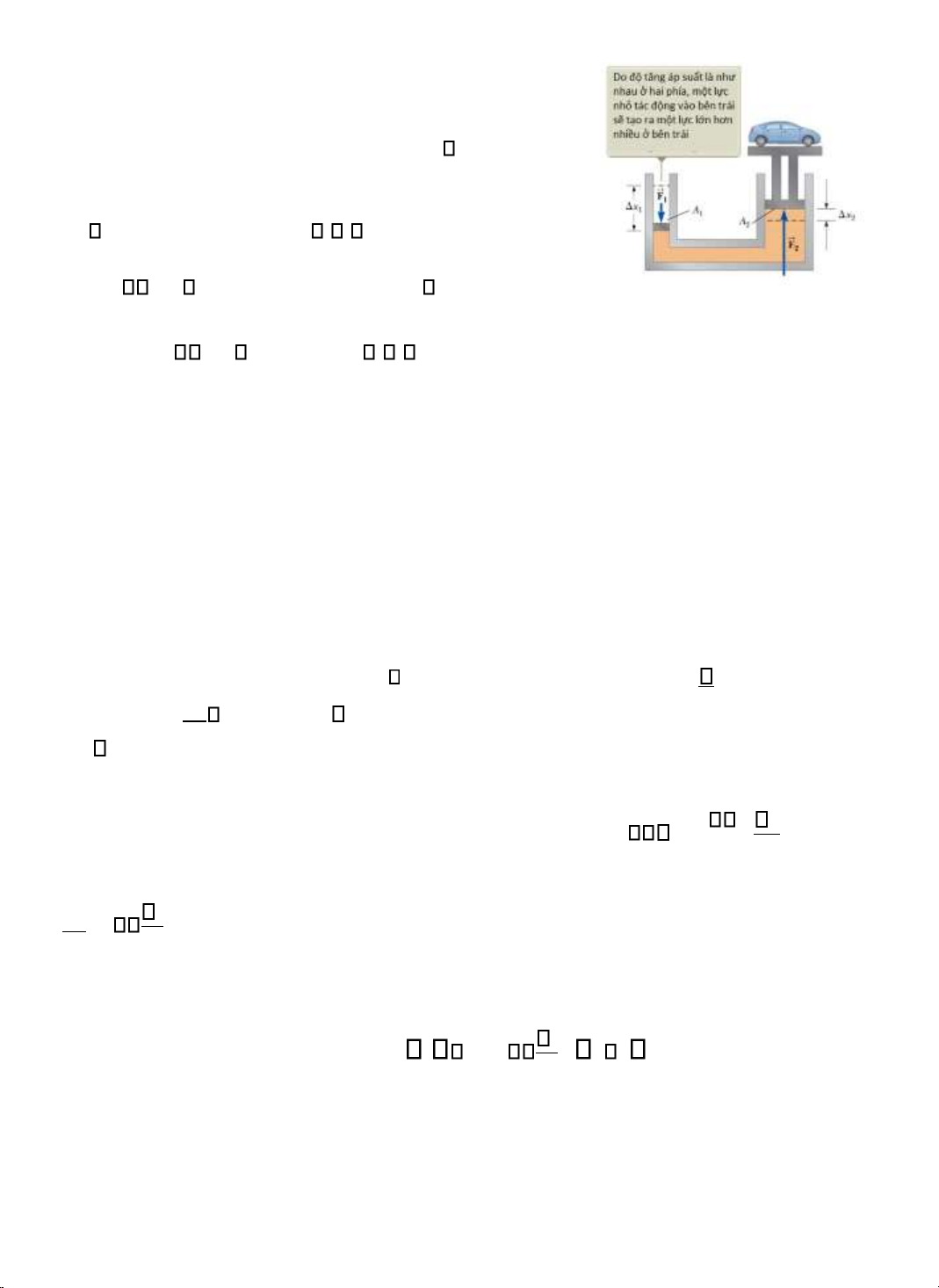
Máy ép thuỷ lực (thẳng góc) là một thiết bị minh hoạ tuyệt vời cho ịnh luật Pascal. Hình 3-7.
Một lực nhỏ F1 tác ộng vào piston nhỏ bên trái với diện tích bề mặt A1. Áp lực ược truyền
qua một chất lỏng không thể nén ến piston bên phải với diện tích bề mặt A2 lớn hơn. Bởi vì áp
suất phải giống nhau ở cả hai bên nên p = F1 / A1 = F2 / A2. Do ó, lực F2 lớn hơn lực F1 với hệ số tỉ lệ là A2/A1. lOMoARcPSD| 36149638
Bằng cách thiết kế một máy ép thủy lực với các diện tích thích hợp A1 và A2, ta có thể thu
ược một lực lớn ở ầu ra từ một lực nhỏ ở ầu vào.
Bởi vì chất lỏng không ược thêm vào hoặc tháo
ra khỏi hệ thống, thể tích chất lỏng ược ẩy xuống bên trái trong
Hình 3-7 khi piston di chuyển xuống dưới A1. x1 bằng thể tích
chất lỏng bị ẩy lên bên phải khi piston phải di chuyển lên trên A2. x2. Tức là,
A1. x1A2. x2; do ó, A 2 / A1
x1 / x2. Chúng ta ã biết, A2 / A1 F2 / F1.
Hình 3-7: sơ ồ máy ép thủy Do ó, F2 / F1
x1 / x2 , vì vậy F1. x1F2. x2. lực
Mỗi bên của phương trình này là công của lực tác ộng lên piston tương ứng. Do ó, công
của lực F1 trên piston ầu vào bằng công của lực F2 trên piston ầu ra, vì nó phải bảo tồn năng lượng.
Các ứng dụng khác của ịnh luật Pascal: phanh thủy lực, nâng xe hơi, òn bẩy thủy lực, xe nâng hàng.
Chất lưu chịu nén
Nếu chất lưu chịu nén áng kể thì hệ thức giữa mật ộ và chiều cao trong chất lưu cần phải
biết trước khi tích phân phương trình (3-6). Đối với nhiều chất khí, chẳng hạn như không khí, còn
có một hệ thức giữa áp suất p và mật ộ khi nhiệt ộ ược xem là không ổi: p
. Ở ây p0 và 0 tương ứng là áp suất và mật ộ ở iểm quy chiếu, ví dụ tại y = 0 p0 0 p
chẳng hạn. Phương trình (3-5) bây giờ ược viết thành dp gdy 0 gdy hay: p0 dp g 0
dy. Phương trình này có thể ược tích phân từ mức quy chiếu y = 0 ến mức cao h: p p0 g ln p h ln p 0 0 h 0 p0 Hay: lOMoARcPSD| 36149638 g p h 0 h ln p0 p0 Hay: 0g p h
p e0. p0 h (3-7)
Như vậy áp suất chất lưu chịu nén giảm với ộ cao theo hàm e-mũ.
3.2.3 Phương pháp o áp suất khí quyển
Áp suất khí quyển là một thông số quan trọng luôn ược ề cập ến trong các chương trình
dự báo thời tiết. Giá trị của áp suất khí quyển này thay ổi theo từng vùng, từng thời iểm chứ
không phải là giá trị áp suất khí quyển chuẩn p0 không ổi mà ta ã ề cập ở mục trên. Vậy, áp suất
khí quyển này ược o như nào?
Khí áp kế Torricelli
Một trong những khí áp kế phổ biến (hay còn gọi là phong vũ biểu) ã ược chế tạo bởi nhà
bác học Evangelista Torricelli (1608–1647) là dụng cụ dùng ể o áp suất khí quyển.
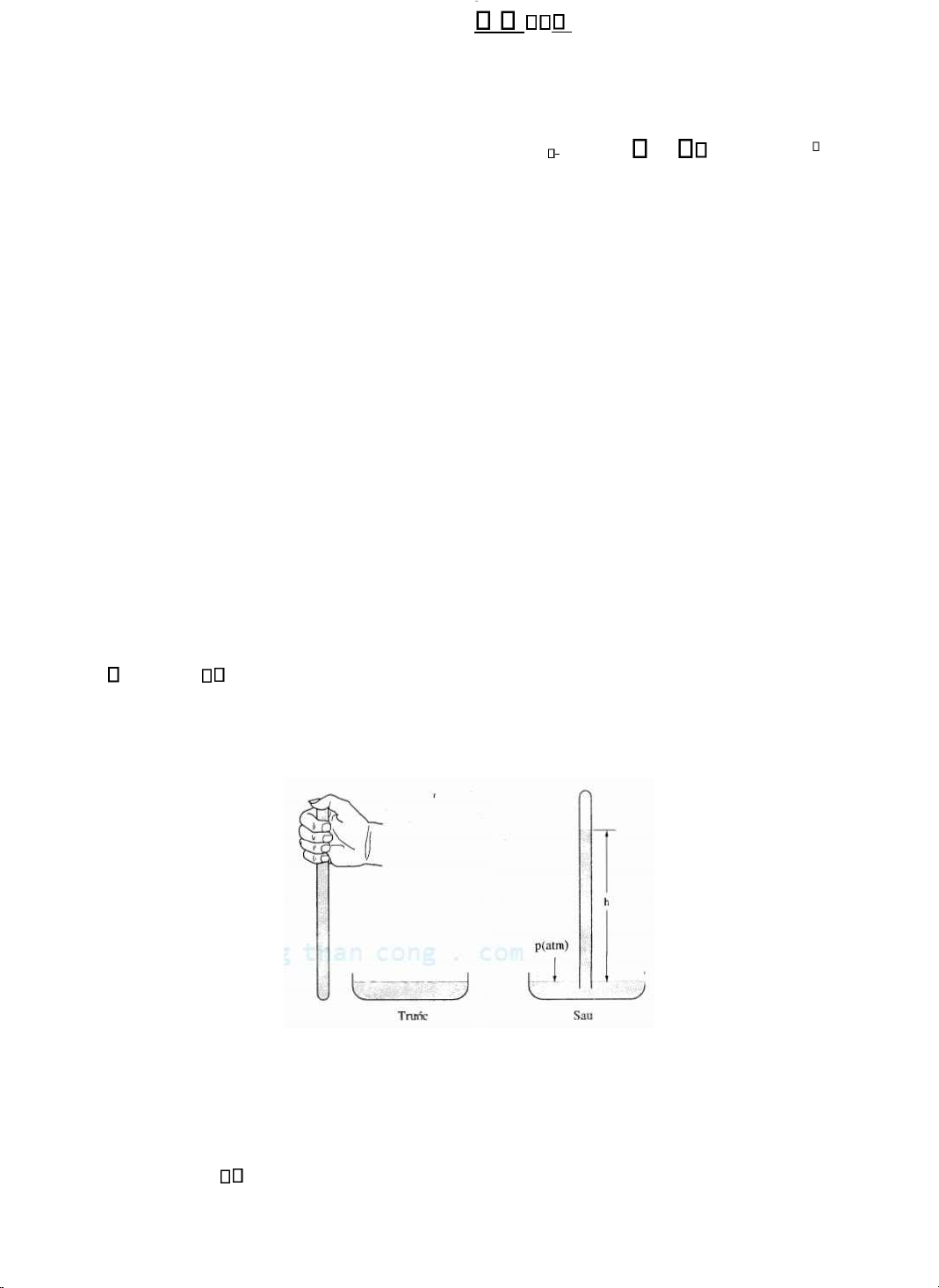
Một khí áp kế ơn giản bao gồm một ống chứa ầy thuỷ ngân ược ặt lộn ngược với ầu hở
nhúng trong một chậu cũng ựng thuỷ ngân (hình 3-8). Mức thủy ngân trong ống sẽ giảm cho tới
khi ạt trạng thái cân bằng, sao cho ỉnh của cột thuỷ ngân có ộ cao h so với mặt thuỷ ngân trong
chậu. Không gian trong ống ở trên thuỷ ngân gần như là chân không. Một lượng nhỏ hơi thuỷ
ngân ở ó có áp suất nhỏ hơn một phần triệu áp suất khí quyển. Do ó, trong phương trình (3-6) ta ặt p 0 0 và patm
Hg gh. Điều này có nghĩa là áp suất của khí quyển có thể ỡ ược một cột thuỷ
ngân có ộ cao bằng h. Nói một cách khác, trọng lượng của cột thuỷ ngân úng bằng trọng lượng
của cột không khí có cùng tiết diện nhưng có ộ cao tới tận ỉnh của tầng khí quyển.
Hình 3-8. Khí áp kế. Một ống chứa dầy thuỷ ngán ược dốc ngược và nhúng vào một chậu thuỷ
ngân. Mức ĩhuỷ ngân trong ống sẽ tụt xuống tới dộ cao h tuỳ thuộc vào áp suất khí quyến. Vì áp
suất khí quyển tiêu chuẩn bằng 760mmHg, nên ống phải dài hơn 760mm. Vì patm
Hg gh nên áp suất tỉ lệ với chiều cao h của cột thuỷ ngân. Tại mức nước biển lOMoARcPSD| 36149638 p p atm atm 1,01.105Pa và h
760mm,ây là kết quả tính trung bình vì còn phụ thuộc vào Hg g
thời tiết. Trước kia áp suất khí quyển thường ược o bằng phương pháp này và ơn vị o thường lấy
là milimét thuỷ ngân (mmHg) hay torr (Itorr là áp suất của một cột thuỷ ngân cao 1mm). Chẳng
hạn huyết áp thường ược o bằng ơn vị milimét thuỷ ngân. Khí áp kế chữ U
Áp suất của một chất khí trong một bình có thể
ược o bằng một áp kế như cho trên hình 3-9. Một ống
hình chữ U chứa một chất lỏng, chẳng hạn như thuỷ
ngân (Hg) có thể dâng lên các mức khác nhau ở một
phía. Áp suất ở iểm A là áp suất khí quyển patm vì ống
hở ở A. Theo phương trình (3-6), áp suất trong chất lỏng của áp kế ở B bằng patm
gh với là mật ộ của chất Hình 3-9. Áp kế chữ U.
lỏng trong áp kế. Áp suất ở iểm C cũng Áp suất toàn phần p ược gọi là áp suất tuyệt chính là
áp suất ớ B vì chúng cùng nằm ở ối, trong khi ó p g p patm
gh ược một mức (ngang). Vậy
áp suất p trong bình gọi là áp suất (theo) áp kế. cầu ở hình 3-9 là: p patm gh
Ví dụ 3-4: Áp suất theo áp kế
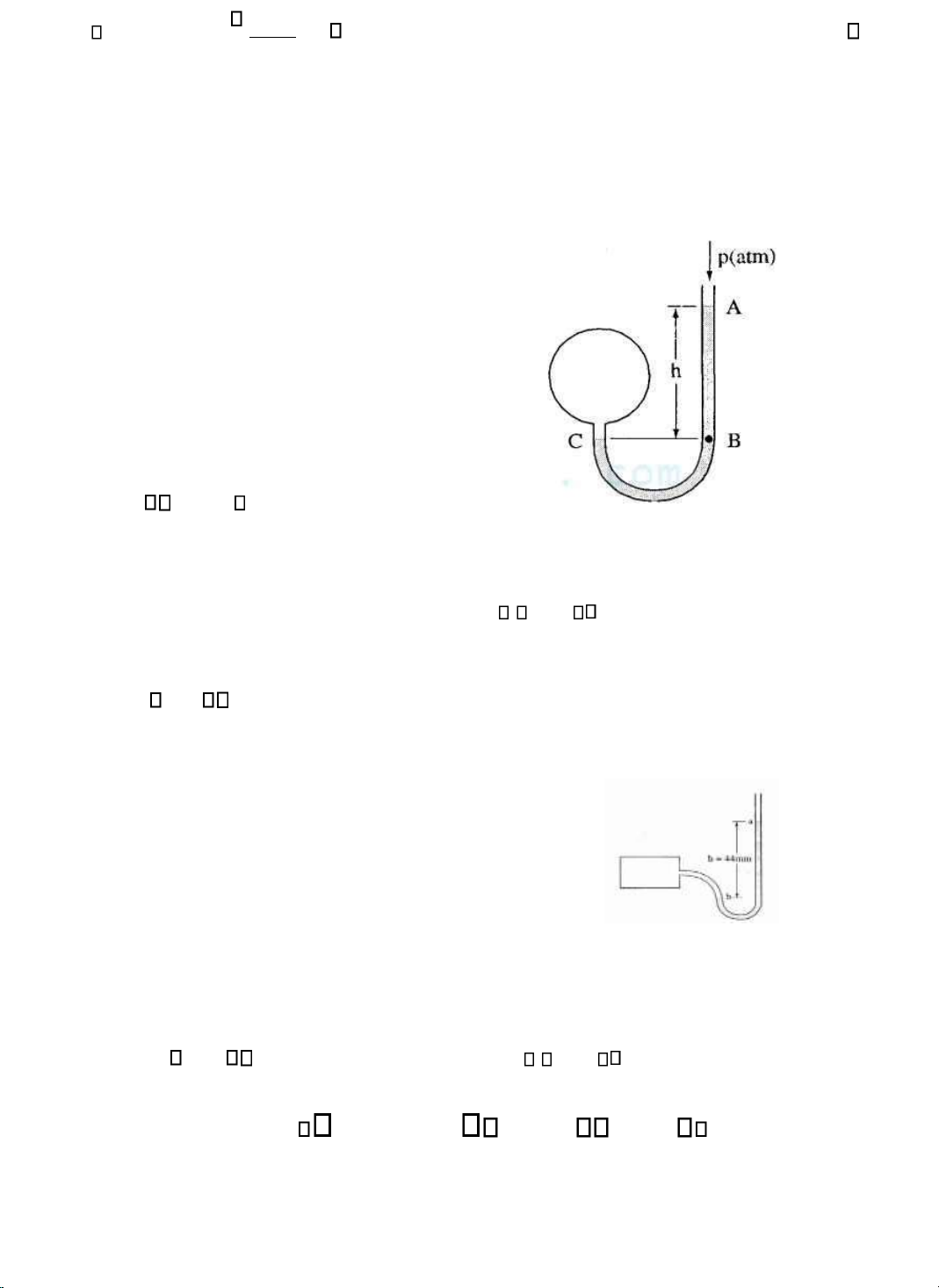
Một áp kế thuỷ ngân nối với một bình chứa khí như cho
trên hình 3-10. Xác ịnh áp suất theo áp kế tại các iểm a và b và
ở một iểm bất kì trong bình. Hình 3-10 Giải.
Tại iểm a áp suất bằng áp suất khí quyển vì vậy áp suất theo áp kế ở a bằng 0. Ớ iểm b, áp suất bằng p b patm
gh do ó áp suất theo áp kế là pbg pb patm gh bằng: pbg 13,6.103kg m/3 9,8N kg/ 0,044m 5,9kPa.
Bên trong bình, áp suất gần như tại b vì mật ộ không khí nhỏ tới mức sự thay ổi áp suất từ
b tới inh của bình có thể bỏ qua. lOMoARcPSD| 36149638
Ví dụ 3-5: Áp suất tính theo ơn vị torr.
(a) Xác ịnh áp suất tuyệt ối ở áy một hồ 1 nước ngọt sâu 6,2m. (b) Tính áp suất theo áp kế
ở ó. (c) Biểu diễn kết quả ở câu (b) theo ơn vị torr (không phải ơn vị trong hệ SI). Giải: (a)
Áp suất tuyệt ối p bằng: p p atm gh 1,01.105Pa 1,00.103kg m/ 3 9,8N s/ 2 6,2m 1,62.105Pa.
Cần lưu ý rằng pg ối với nước vào cỡ 104N/m3, nên cứ xuống sâu thêm lOm nước, áp suất
lại tăng 103Pa tức là cỡ 1at. (b)
Áp suất theo khí áp là: p ứ g p patm
6,1.104Pa. (c) Áp suất pg ng
với chiều cao h của cột thủy ngân: p g 6,1.104Pa h H gg 3kg m/ 3 9,8N kg/ 460mm. 13,6.10
Vì áp suất 1 torr ứng với áp suất 1 mmHg nên: p g 460 torr.
3.2.4 Lực nổi và ịnh luật Archimedes
Theo truyền thuyết, Hiero - vua của xứ Syracuse - ra lệnh chế tạo một vương miện mới.
Nhưng khi nhận chiếc vương miện vừa làm xong ông ã không hài lòng. Ông ngờ rằng người thợ
kim hoàn ã pha thêm bạc vào thay cho vàng ròng.
Nhà vua bèn hỏi người bạn của mình là nhà toán học Archimedes rằng liệu có thể xác ịnh
ược chiếc vương miện có làm hoàn toàn bằng vàng ròng mà không phải cắt vụn ra hay không?
Một lần khi vẫn ang còn trăn trở về bài toán ó, ông bước vào buồng tắm. Sau khi ã thả
mình trong bổn tắm ầy nước ông chợt nhận ra rằng lượng nước tràn ra do ông vừa chiếm chỗ úng
bằng thể tích phần cơ thể ông ngập trong nước. Truyền thuyết, còn kể rằng Archimedes vừa hét
to "Eureka!" (Tôi tìm ra rồi!) vừa nhảy ra khỏi bồn tắm và chạy lao ra phố. Điều mà ông vừa phát
hiện ra ó là có thể tìm ược thể tích của một vật có hình dạng phức tạp bằng cách nhúng nó vào trong nước.
Sau ó bằng cách so sánh trọng lượng của vương miện với trọng lượng của khối vàng ròng
có cùng thể tích ông có thể xác ịnh ược chiếc vương miện có phải làm bằng vàng nguyên chất
hay không. Theo truyền thuyết, người thợ kim hoàn quả thật ã gian dối và ã bị hành quyết! lOMoARcPSD| 36149638
Mặc dù câu chuyện trên có thể không có thật nhưng úng là Archimedes ã có viết cuốn
sách "Về các vật nổi", trong ó ông ã xác lập những nguyên lí chung của thủy tĩnh học. Trong số
những nguyên lí ó có một ịnh luật sau này mang tên ông, ược phát biểu như sau:
Một vật ược nhúng một phần hoặc toàn bộ trong một chất lưu sẽ chịu tác dụng một lực ẩy
có ộ lớn bằng trọng lượng của khối chất lưu bị chiếm chỗ và hướng lên trên dọc theo ường thẳng
ứng i qua trọng tâm của khôi chất lưu ó.
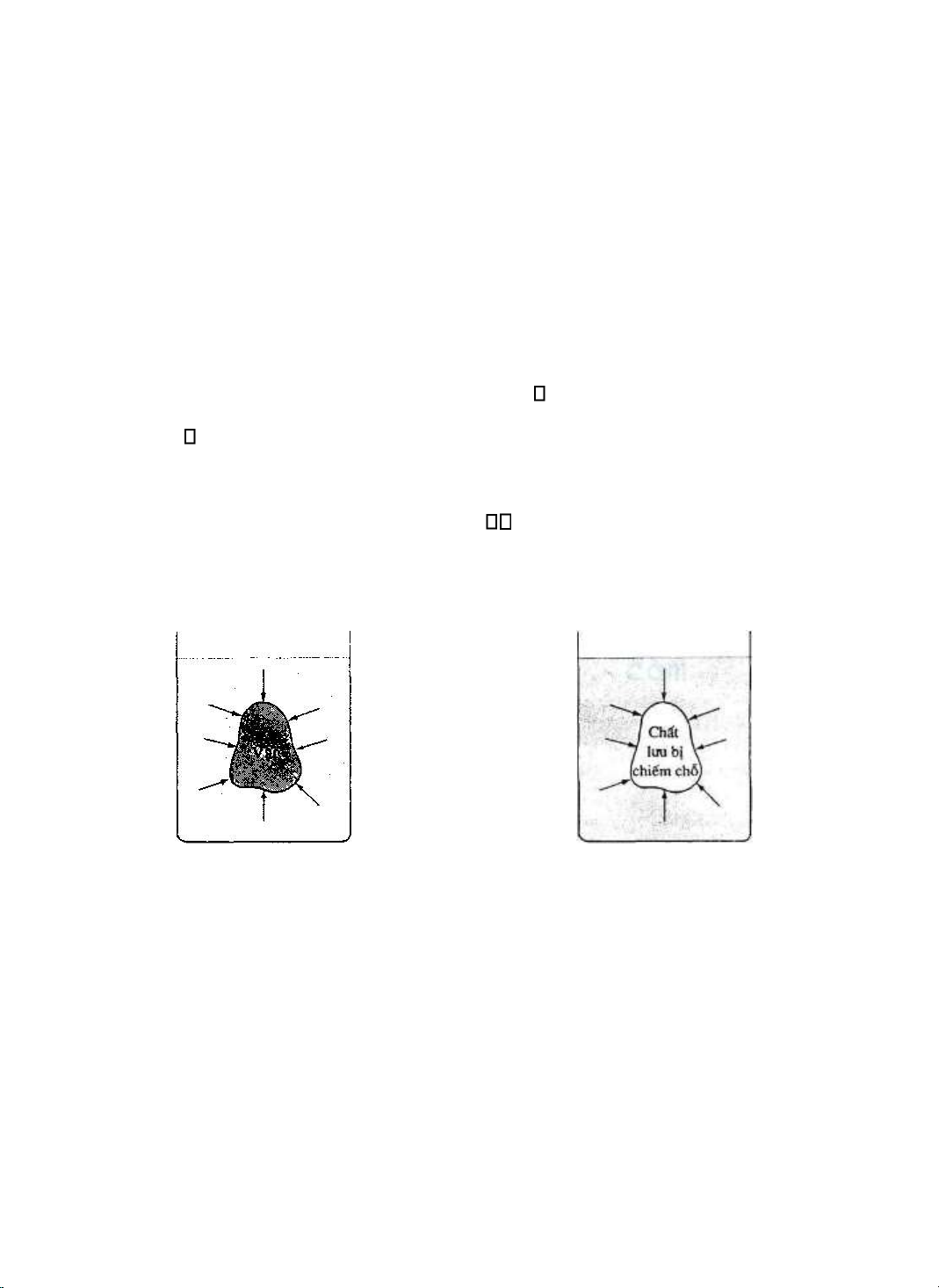
Để thấy ịnh luật Archimedes ược suy ra từ ịnh luật II Newton như thế nào, ta hãy xét một
vật ứng yên trong khi ược nhúng vào một chất lưu như hình 3-11. Áp suất của chất lưu bao quanh
sẽ tác dụng các lực lên vật ó và lực tổng hợp tác dụng lên vật bởi chất lưu chính là lực ẩy
Archimedes. Nhưng chính lực ó cũng tác dụng lên khối chất lưu trước khi bị vật ó chiếm chỗ. Vì
khối chất lưu trước khi bị chiếm chỗ ở trạng thái cân bằng tịnh tiến và cân bằng quay, do ó chất
lưu bao quanh phải cung cấp một lực ẩy hướng lên ể cân bằng với trọng lượng của khối chất lưu ó.
Vì khối lượng của khối chất lưu bị chiếm chỗ là V , nên trọng lượng của khối chất lưu ó
có ộ lớn bằng gV và ó cũng là ộ lớn của lực ẩy Archimedes FB tác dụng lên một vật bất kì ược nhúng vào chất lưu ó: FB gV
FB là ộ lớn của lực nổi, ρ là mật ộ khối lượng của chất lưu, g là gia tốc trọng trường
và V là thể tích của khối chất lưu bị vật chiếm chỗ.
Hình 3-11. Lực ẩy Archimedes tác dụng lên vật úng bằng lực tác dụng lên khối chất lưu
bị vật ó chiếm chỗ. lOMoARcPSD| 36149638
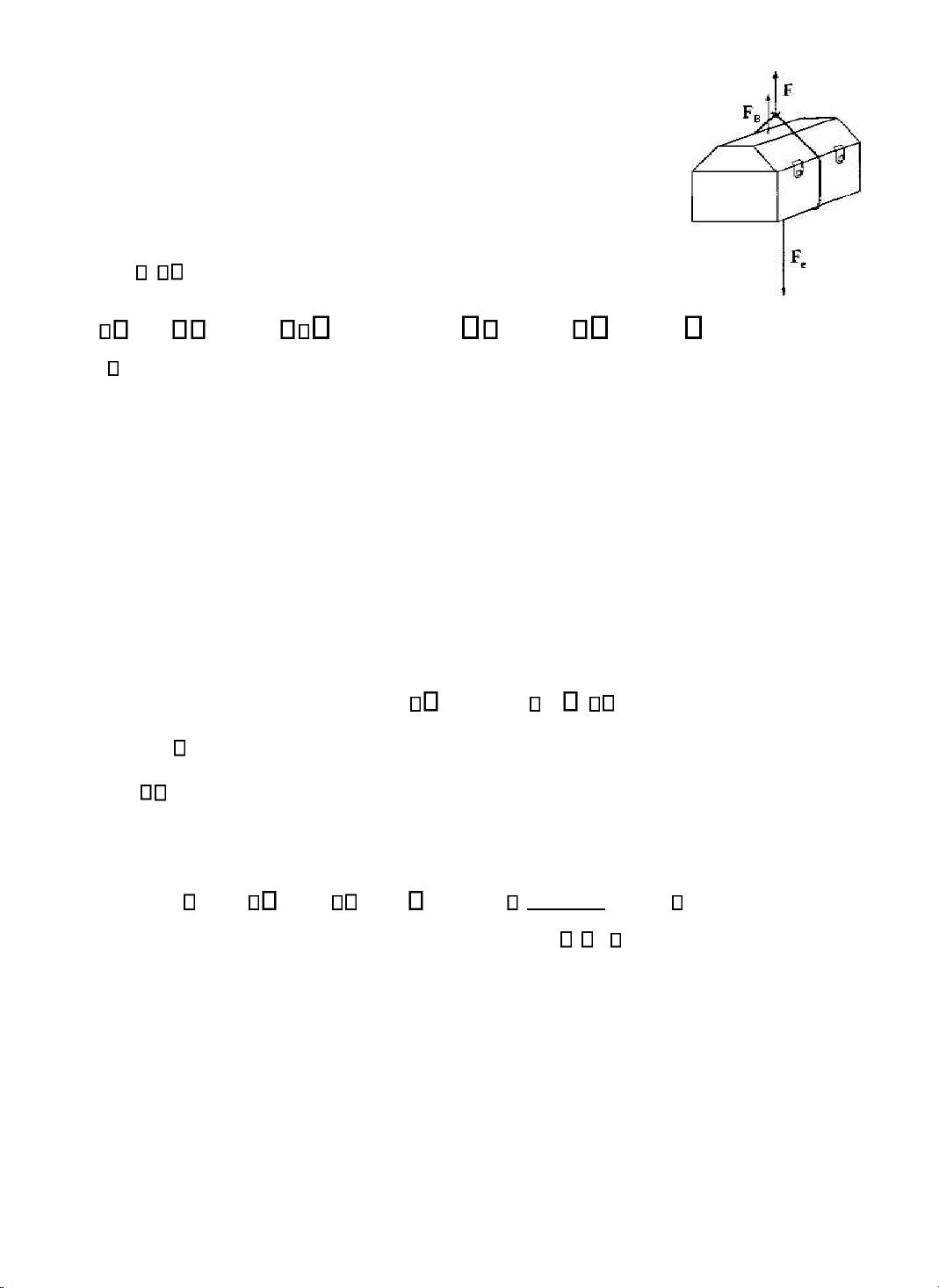
Ví dụ 3-6: lực ẩy Archimedes tác dụng lên một hòm châu báu
Một hòm châu báu nặng 92kg và có thể tích 0,031m3 nằm ở áy ại dương. Cần phải có một
lực bằng bao nhiêu ể nâng ược nó lên? Giải.
Các lực tác dụng lên hòm ược chỉ rõ trên hình 3-12. Lực kéo
F và lực ẩy Archimedes FB hướng lên cần phải cân bằng với trọng lượng
Fc hướng xuống, do ó: F mg gV 92kg 9,8N kg/ 1,03.103 kg m/3 9,8N kg/ 0,031m3 590N. Hình 3-12
Vì 590N là trọng lượng của 60kg (trong không khí) nên việc nâng hòm châu báu trên cũng
tựa như ỡ một hòm nặng 60kg trên mặt nước.
Ví dụ 3-7: Khí cầu Heli
Xác ịnh thể tích khí heli cần thiết ể khinh khí cầu lơ lửng trên không trung, biết rằng khinh
khí cầu là rỗng và trang thiết bị trên ó có khối lượng 390kg. Giải.
Lực ẩy Archimedes tác dụng lên khí cầu do không khí bị chiếm chỗ phải bằng và
ngược chiều với trọng lượng của khí cầu cùng với các thiết bị trên ó cộng với khí heli. Vậy F B 390kg m g He kkgV
ở ây kk là mật ộ không khí. Nhưng khối lượng của heli phụ thuộc vào thể tích của khí cầu: mHe
HeV . Chú ý rằng ở ây ta ã giả thiết thể tích của khí cầu lúc xẹp và thể tích các thiết
bị là nhỏ không áng kể. khi ó kk gV 390kg HeV g hay: V 390kg 350m3. kk He
Ở ây ta giả thiết không khí và khí heli ở áp suất khí quyển.
3.3. Động lực học chất lưu
Ở các nội dung trước, ta ã khảo sát chất lưu ở trạng thái tĩnh. Trong ề mục này ta sẽ khảo
sát chất lưu ở trạng thái chuyển ộng. Khi một chất lưu chuyển ộng thì chuyển ộng của nó sẽ thuộc
một trong hai loại: chuyển ộng thành dòng (lớp) (hình 3-13) hay chuyển ộng rối (hình 3-14). lOMoARcPSD| 36149638
Hình 3-13: Chuyển ộng thành lớp Hình 3-14: Khói thuốc chuyển ộng của chất khí
khi xe chuyển ộng trong sự chảy thành dòng ở phía dưới và trong hầm trong sự
chảy rối ở phía trên.
Các chất lưu chuyển ộng phức tạp hơn rất nhiều so với các chất lưu ứng yên. Sự mô tả
chất lưu chuyển ộng òi hỏi phải biết về vận tốc chất lưu cũng như áp suất và mật ộ tại tất cả các iểm.
Hình 3-14 minh hoạ phần nào sự phức tạp ấy. Các hạt khói tạo cho ta hình ảnh trực quan
về không khí chuyển ộng. Ở gần ầu iếu thuốc lá ang cháy, bức tranh khá phẳng lặng và gần như
không thay ổi theo thời gian. Ở cao hơn bức tranh trở nên phức tạp hơn và biến ổi theo thời gian.
Loại biến ổi theo thời gian này ược gọi là sự chảy rối (tức là có những cuộn xoáy).
Trước ây, ôi khi bạn ược giao cho một bài toán và người ta nói cho biết: bỏ qua ma sát.
Một iều ược chấp nhận ngầm là nếu bạn kể cả ma sát, thì bài toán sẽ thành khó. Đó cũng là trường
hợp ở ây. Chuyển ộng của các chất lưu thực là phức tạp và chưa ược hiểu ầy ủ. Thay vào ó, chúng
ta nghiên cứu chuyển ộng của một chất lưu lý tưởng, nghiên cứu ơn giản về mặt toán học. Tuy các
kết quả của chúng ta không thể hoàn toàn phù hợp với cách xử sự của các chất lưu thực, chúng
vẫn khá gần, ủ ể có thể sử dụng ược. Ở ây ta nêu bốn giả ịnh về chất lưu lý tưởng.
Sự chảy ổn ịnh
Trong sự chảy ổn ịnh, hay sự chảy thành lớp, vận tốc của chất lưu tại bất kỳ iểm cố ịnh nào cũng
không thay ổi theo thời gian, cả về ộ lớn lẫn hướng. Dòng nước nhẹ nhàng chảy gần tâm của một
dòng yên tĩnh là dòng ổn ịnh, nhưng dòng chảy qua một loạt ghềnh thác thì không. Hình 3-14 cho
thấy sự chuyển từ một dòng ổn ịnh sang một dòng không ổn ịnh. Tốc ộ của các hạt khói tăng dần
khi chúng lên cao, và ến một tốc ộ tới hạn nào ó thì dòng thay ổi tính chất, từ dòng ổn ịnh sang không ổn ịnh.
Chất lưu không chịu nén
Chúng ta giả ịnh, như ta vừa làm ối với chất lưu tĩnh, rằng chất lưu lý tưởng của ta không
chịu nén. Nghĩa là khối lượng riêng của nó có giá trị không ổi. lOMoARcPSD| 36149638
Chất lưu không nhớt
Nói một cách ại khái, thì ộ nhớt của một chất lưu là số o sức chống lại của chất lưu ối với
sự chảy. Thí dụ, mật ong ặc chống lại sự chuyển ộng nhiều hơn nước, do ó ta nói rằng mật ong
nhớt hơn mước. Sự nhớt tương tự như ma sát giữa các chất rắn.
Cả hai ều là cơ chế, nhờ ó mà năng lượng của vật chuyển ộng biến ổi thành nhiệt năng.
Khi không có ma sát, một khối á có thể lướt với tốc ộ không ổi trên một mặt nằm ngang. Cũng
bằng cách ấy, một vật chuyển ộng qua một chất lưu không nhớt cũng không chịu lực cản nhớt
nào, tức là không có lực ma sát do sự nhớt sinh ra. Lord Rayleigh ã vạch ra rằng, trong một chất
lưu lý tưởng, thì chân vịt tàu thủy không làm việc ược, nhưng một mặt khác, cái tàu (một khi ẫ
ẩy cho chạy) lại không cần chân vịt.
Dòng không xoáy (rối)
Khi thả một hạt bụi nhỏ xíu, cho chuyển ộng cùng chất lưu. Mặc dù vật thử có thể (hoặc
không) chuyển ộng trên một ường tròn thì trong dòng không xoáy, vật thử không quay quanh bất
kỳ trục nào i qua khối tâm của nó.
3.3.1 Khái niệm ường dòng, ống dòng Đường dòng
Một ví dụ về dòng chảy không rối và ở trạng thái ổn ịnh ược cho trên hình 3-15. Dòng
chảy nói chung i từ trái sang phải hình vẽ. Những ường sẫm minh hoạ bức tranh dòng chảy ược
tạo bởi các hạt thuốc nhuộm ược bơm vào chất lưu. Những ường này ược gọi là các ường dòng.
Đường dòng là ường vạch nên bởi một phần tử rất nhỏ của chất lưu, mà ta có thể gọi là
một hạt chất lưu.
Khi chất lưu chuyển ộng, tốc ộ của nó có thể thay ổi cả về ộ lớn lẫn về hướng. Vì các ường
dòng cho thấy các hạt chất lưu chuyển ộng như thế nào, nên chúng ược vẽ tại mọi iểm sao cho
luôn luôn song song với vận tốc của chất lưu tại iểm ó như trên hình 3-16.
Hình 3-15: Các dòng chất lưu chảy qua Hình 3-16: Một ường dòng trong chất lưu
một mạng các khối trụ. Các
chuyển ộng. Tại mỗi iểm, ường dòng
ường dòng chỉ ường i của các hạt thuốc hướng song song với vận tốc chất lưu tại
nhuộm dã ược bơm vào dòng. iểm ó. lOMoARcPSD| 36149638 Ống dòng
Các ường dòng có thể vẽ sao cho chúng bao quanh
một ống dòng. Vì ường dòng song song với vận tốc chất lưu
tại mọi iểm của nó, nên chất lưu chỉ chảy dọc theo ống và
không có phần chất lưu nào chảy qua thành của ống dòng ó.
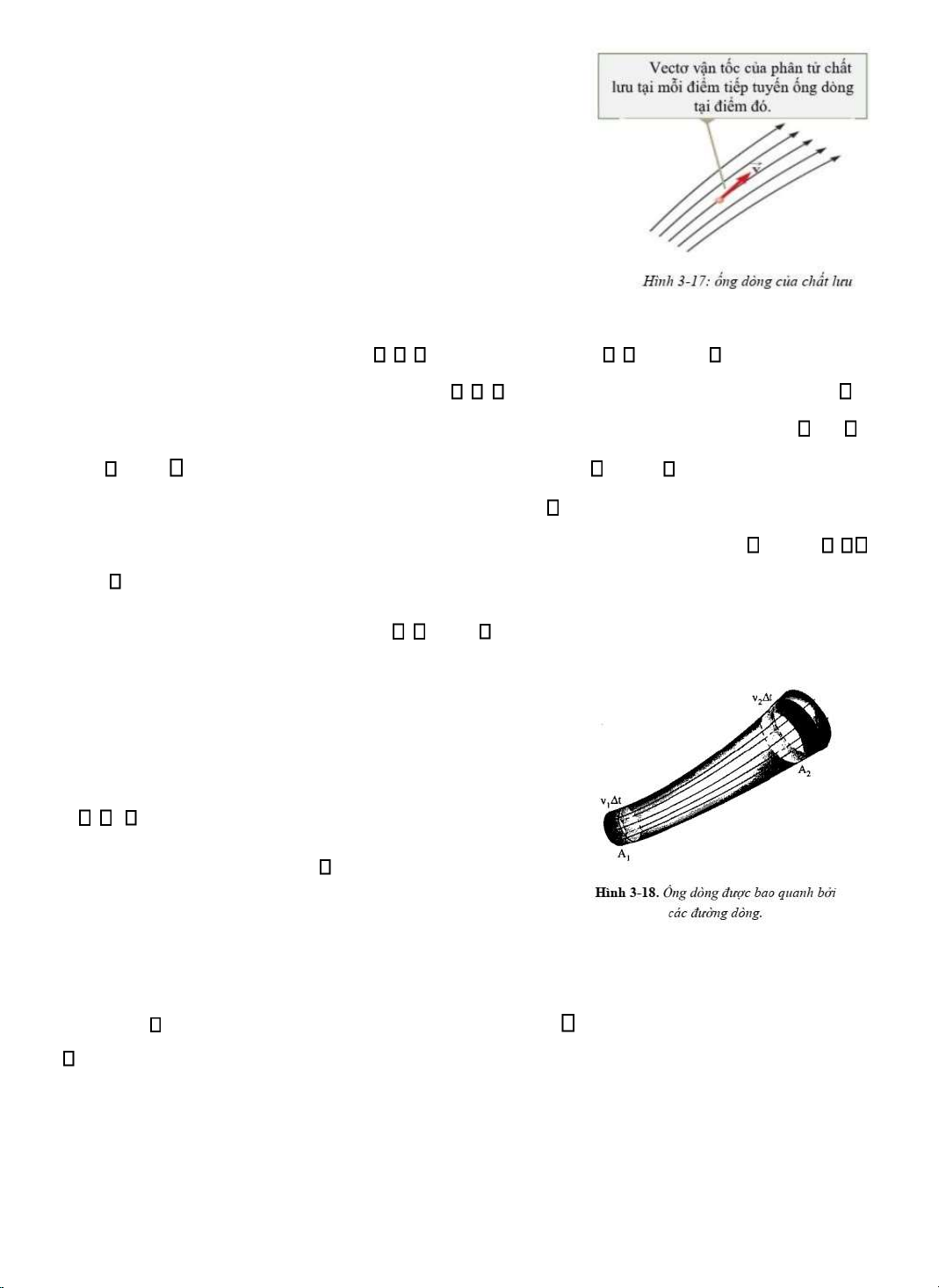
Ống dòng là ường cong sao cho tiếp tuyến với nó tại
mỗi iểm trùng với phương của vecto vận tốc của phân tử chất
lưu tại iểm ó (hình 3-17).
3.3.2 Phương trình liên tục – bảo toàn khối lượng
Xét một yếu tố chất lưu i vào ở ầu dưới của ống trong hình 3-18. Thể tích của yếu tố này bằng diện tích A
1 nhân với chiều dài
l v t1 của oạn ống ó: V Av t1 1 . Chúng ta ã chọn
chiều dài của phần tử ang xét là khoảng cách l v t1 mà chất lưu i ược trong thời gian t ở
ầu ó của ống, do ó khối lượng của chất lưu i vào ống ở ầu dưới trong khoảng thời gian t là 1 1 1Av t
, với là mật ộ của chất lưu ở ó. Lí luận tương tự cho 2 A v2 2 t là khối lượng của chất
lưu i ra khỏi ầu trên của ống trong chính khoảng thời gian t . Vì chất lưu không ược tích tụ trong
ống khi chảy ở trạng thái ổn ịnh nên khối lượng i vào phải bằng khối lượng i ra: 1Av t1 1 2 A v2 2 t hay: 1Av1 1 2 A v22 (3-8)
Phương trình này ược gọi là phương trình liên tục,
nó biểu diễn sự bảo toàn khối lượng trong dòng chảy ổn ịnh.
Tiếp theo nếu chúng ta giả thiết rằng chất lưu là
không chịu nén hay tương ương là có mật ộ không ổi, khi ó 1 2 và: Av 1 1 A v2 2 (3- 9)
Đây là một giả thiết tốt ối với nước hoặc thậm chí
khá tốt ối với dòng không khí chảy quanh cánh máy bay, hay trong các ống dẫn khí nóng - lạnh
vì ở ó áp suất không thay ổi nhiều. Tích vA cho lưu lượng theo thể tích và ược biểu diễn bằng kí
hiệu Q vA . Nhân lưu lượng theo thể tích vA với mật ộ ta ược lưu lượng theo khối lượng:
vA, ó là khối lượng chất lưu i qua A
trong một ơn vị thời gian. lOMoARcPSD| 36149638
Ví dụ 3-8: lưu lượng trong ống
(a) Một ường dẫn nước nối từ ống có bán kính 12,5mm với ống có bán kính 9mm. Nếu tốc
ộ của nước trong ống 12,5mm là l,8m/s thì tốc ộ nước trong ống nhỏ
bằng bao nhiêu (hình 3-19)? (b) Tính lưu lượng theo thể tích và (c)
lưu lượng theo khối lượng. Giả thiết rằng r =12,5mm nước không chịu nén. Hình 3-19 Giải:
(a) Dùng phương trình liên tục cho chất lưu không chịu nén, phương trình 10-9 ta có: v 2 AvA1 12 v1 rr1222 3,5m s/ .
(b) Lưu lượng theo thể tích là: Q Av 1 1 Av2 2 [ 12,5.10 3m 2] 1 ,8m s/ 8,8.10 4 3m s/ .
(c) Lưu lượng theo khối lượng là:
1 1 1Av 2 2 2Av 1,0.103kg m/3 8,8.10 4 3m s/ 0,88kg s/ .
3.3.3 Phương trình Bernoulli và các ứng dụng của ộng lực học chất lưu
Phương trình Bernoulli – bảo toàn năng lượng
Phương trình liên tục biểu diễn sự bảo toàn khối lượng cho ta một hệ thức giữa mật ộ
và vận tốc v của chất lưu dọc theo dòng chảy. Đối với chất lưu không chịu nén, vA là một hằng
số. Dùng phương pháp công và năng lượng, ta có thể rút ra một biểu thức khác liên hệ những biến số ó với áp suất.
Chúng ta vẫn giới hạn chỉ xét dòng chảy ổn ịnh trong ó không có công ược thực hiện bởi
các lực không bảo toàn. Trong mục sau, ta sẽ mô tả ngắn gọn tác dụng của các lực không bảo toàn ó.
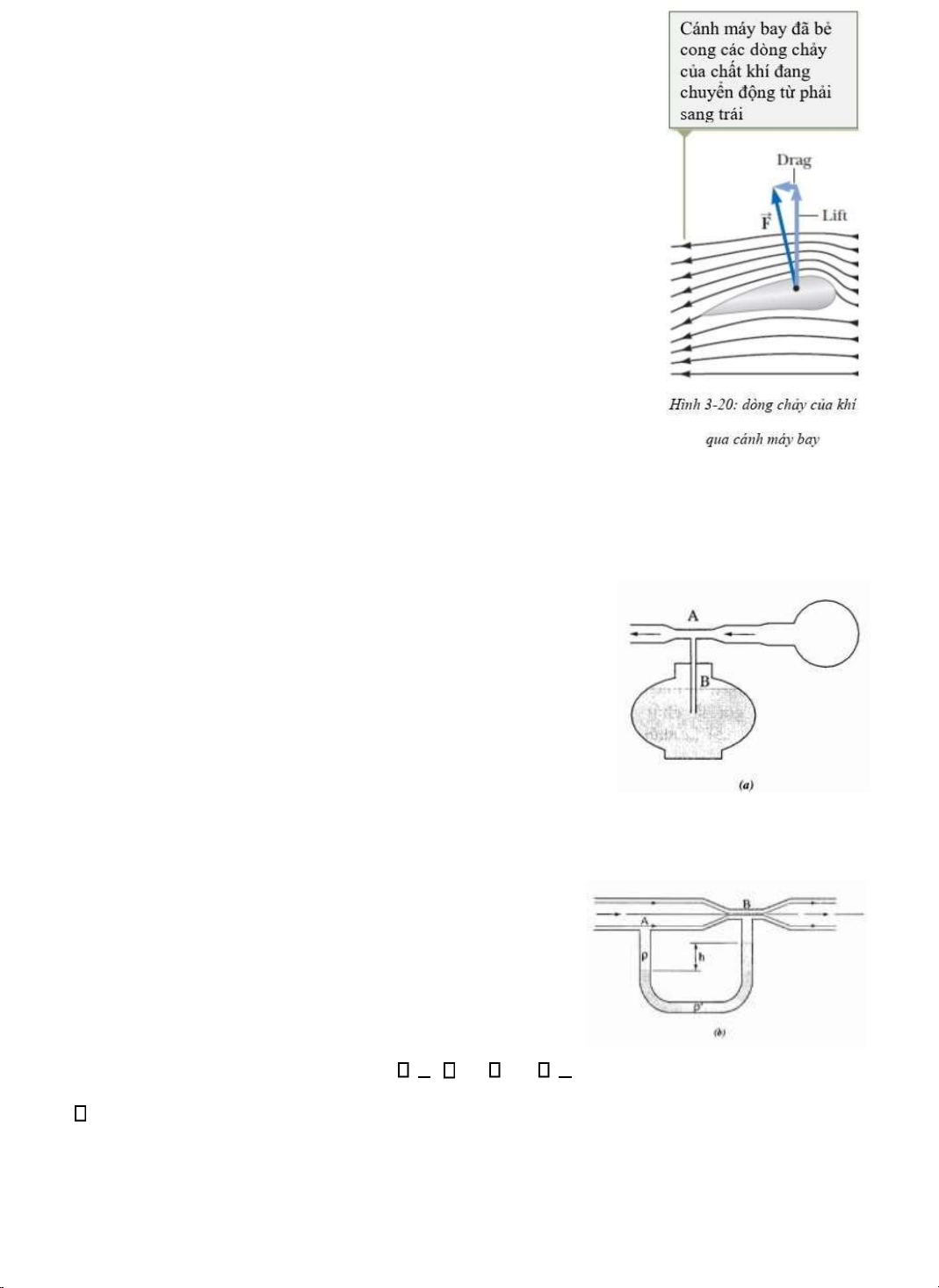
Tốc ộ của dòng chảy, chiều cao của chất
lưu và áp suất có thể thay ổi dọc theo một ường
dòng, chẳng hạn như các vị trí 1 và 2 trong hình 3-20.
Ta hãy xét công ược thực hiện trong
khoảng thời gian ngắn t trên chất lưu ban ầu ở
trong vùng ược giới hạn bởi A A1, 2 và ống dòng.
Lực tác dụng lên biên A1bởi chất lưu ở
phía sau nó là p A1 1. Công thực hiện bởi lực Hình
3-20. Dòng chảy dọc theo ống dòng. Thể tích này trong thời gian t là tích của lực ó với AV trong lOMoARcPSD| 36149638
các vùng tô sầm khoảng cách mà chất lưu i ược trong thời bằng: V v A t 1 1 v A t2 2 . Khối
lượng của hai gian t ;v t 1 Vậy W1 p Av t1 1 1
. vùng này ền bằng m V.
Tương tự, ở A2 áp suất cũng thực hiện công W2
p Av2 2 2 t. Chú ý rằng, ở A1 công ược
thực hiện trên chất lưu còn ở A2 công ược thực hiện bởi chất lưu, do ó có sự khác biệt về dấu. Vậy
tổng công thực hiện trên chất lưu là: W W 1 W2p Av t1 1 1 p Av2 2 2 t.
Từ phương trình liên tục ối với chất lưu không chịu nén, ta có v A1 1 v A2 2 , do ó V v A t ' ' 1 1 v A t2 2
.là thể tích giữa A1 và A1 hoặc A2 và A2 . Đó chính là thể tích chất lưu
i vào ở một ầu và i ra ở ầu kia trong khoảng thời gian t . Vậy, tổng công tác dụng lên chất lưu
có thể viết dưới dạng: W p p 1 2 V.
Theo ịnh luật bảo toàn năng lượng, công này úng bằng sự thay ổi cơ năng của chất lưu
ban ầu ược giới hạn bởi A1và A2 . Vì dòng chảy là ổn ịnh nên các tính chất của chất lưu trong vùng giới hạn bởi A '
1 và A2 là không thay ổi. Tuy nhiên có sự thay ổi cơ năng trong vùng mới bị chiếm
giữa A2 và A ' '
2 và trong vùng giữa A1 và A1mới bị bỏ lại. Vì thể tích của cả hai vùng này ều là V và
mật ộ không ổi nên khối lượng của hai vùng này cũng bằng nhau và m v
bằng m V . Thế năng ược cho bởi
m gy và ộng năng bởi 2 . Như vậy sự biến thiên cơ năng là: E m gy 2 12 m v 22 m gy 1 12 m v 12
Theo ịnh luật bảo toàn năng lượng: p 1 p2 V
m gy 2 12 m v 22 m gy 1 12 m v 12 lOMoARcPSD| 36149638 m
Chia hai vế cho V và lưu ý rằng , ta có: V p p 1 2 gy2 1 v22 gy1 1 v12 2 2
Sắp xếp lại các số hạng sao cho mỗi vế chỉ chứa một loại chỉ số ta ược: 1 1 p 2 2 1 gy1 v1 p2 gy2 v2 (3-10) 2 2 Hay p
gy v2 constant Với:
- p là áp suất chất lưu tại một iểm bất kỳ trong dòng chảy.
- ρ là mật ộ khối lượng của chất lưu.
- y là ộ cao của tiết diện ó.
- ν là vận tốc dòng chảy tại tiết iện ó.
Phương trình này ược gọi là phương trình Becnoulli, nó ược phát biểu lần ầu tiên trong
cuốn Thuỷ ộng lực học của ông xuất bản năm 1738. Chú ý rằng khi rút ra phương trình Becnoulli,
chúng ta ã giả thiết dòng là ổn ịnh, không chảy rối và bảo toàn năng lượng của chất lưu không chịu nén.
Trong trường hợp chất lỏng ứng yên, khi óv 1 v2
0 và phương trình Bernoulli tương
ương với phương trình (3-6) cho mọi sự biến thiên của áp suất theo chiều sâu trong chất lưu ứng yên.
Phương trình Bernoulli cùng với phương trình liên tục (3-9) có thể ược dùng ể giải một số
loại bài toán về dòng chất lưu. Sau ây chúng ta cùng i tìm hiểu các ứng dụng của nó.
Các ứng dụng của ộng lực học chất lưu Dòng chảy của khí qua cánh máy bay
Lý thuyết ộng lực học chất lưu có thể giúp ta giải thích ược các hiện tượng liên quan
chuyển ộng của các vật thể trong chất lưu. lOMoARcPSD| 36149638
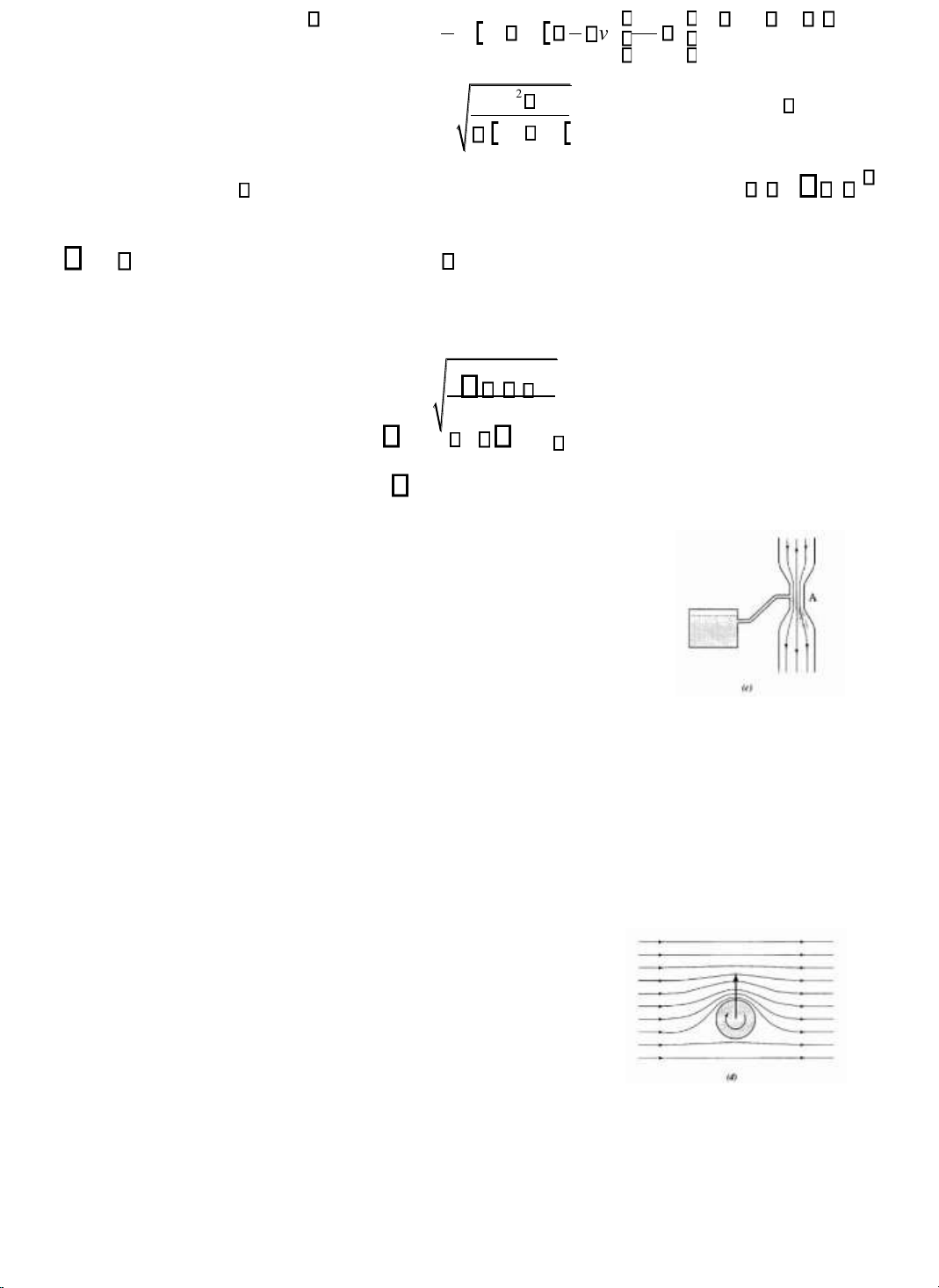
Đầu tiên ta sẽ khảo sát dòng khí chuyển ộng qua cánh máy
bay có hình ảnh các ường dòng như hình 3-21. Giả sử dòng khí ang
chuyển ộng theo phương ngang từ phải sang trái với vận tốc 𝑣1. Khi
gặp cánh máy bay, do ộ nghiêng của cánh dòng chảy của chất khí bị
bẻ cong lõm xuống với vận tốc 𝑣2. Cánh máy bay ã tác dụng một
lực lên dòng khí và theo ịnh luật III Newton, dòng khí này cũng tác
dụng ngược lại lên máy bay một lực 𝐹 cùng ộ lớn nhưng ngược
chiều. Lực này ược phân tích thành 2 thành phần là lực nâng và lực
cản. Lực nâng tác dụng vào cánh máy bay sẽ phụ thuộc vào các yếu
tố như: tốc ộ của máy bay, diện tích của cánh, ộ cong của cách máy
bay và góc giữa cánh máy bay so với phương ngang. Độ cong của
cánh máy bay phải ược thiết kế sao nhằm làm cho áp suất khí ở
phía trên cánh máy bay nhỏ hơn phía dưới tuân theo ịnh luật
Bernoulli. Chính sự chênh lệch áp suất này ã giúp nâng cánh máy
bay lên. Khi góc chênh lệch giữa cánh máy bay và phương ngang
tăng thì sẽ làm xuất hiện các dòng chảy xoáy làm giảm lực nâng.
Một cách tổng quát, khi một vật thể chuyển ộng xuyên qua
một chất lưu thì nó sẽ bẻ cong các dòng chảy làm sinh ra lực nâng tác dụng lên vật ó. Một vài
yếu tố ảnh hưởng lên lực nâng này là: hình dạng của vật, sự ịnh hướng của vật so với dòng
chảy, chuyển ộng xoáy và kết cấu bề mặt của vật thể ó.
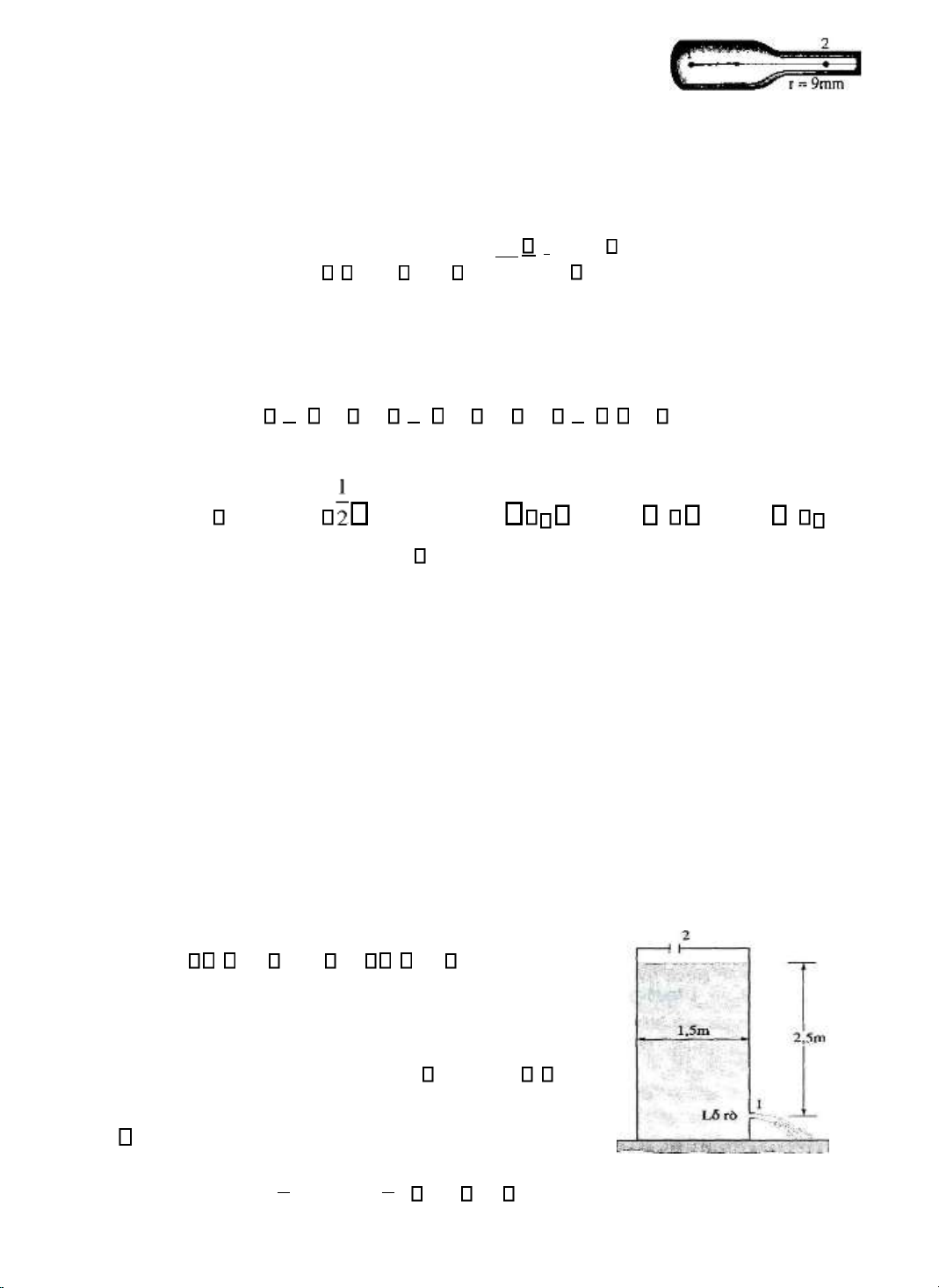
Hình a cho thấy một bình phun nước hoa.
Những dụng cụ tương tự ược dùng ể phun sơn hoặc thuốc
trừ sâu. Khi bóp quả bóp của lọ phun nước hoa, không khí sẽ
phóng qua cái cổ hẹp của bình phun. Nếu nước hoa có mật ộ như
của nước, tốc ộ không khí khoảng 17m/s trong oạn ống (cổ) hẹp
sẽ làm tụt áp suất ở iểm A làm cho áp suất khí quyển ẩy nước
hoa lên cao 2cm dọc theo ống dẫn ến chỗ cổ hẹp.
Ống hút mà các bác sĩ nha khoa thường dùng ể làm sạch
nước bọt trong miệng cũng có một oạn ống hẹp với tốc ộ dòng
nước cao ể tạo áp suất thấp hơn áp suất khí quyển.
Hình b Lưu lượng kế Venturi
Sự hạ thấp của áp suất nhờ tốc ộ của chất lưu cũng là
cơ sở ể chế tạo lưu lượng kế Venturi (hình b). Lưu lượng kế
Venturi là một dụng cụ ể o tốc ộ chảy của một chất lưu. Đầu
A có tiết diện A, ầu B có tiết diện a (A > a), theo phương trình
liên tục ta có: VAA = vBa (vA < VB). Mặt
khác theo phương trình Bernoulli: p 1 2 A vA pB 1 v 2 B . 2 2
vì vA < vB nên áp suất pA > pB. Hiệu áp suất giữa A và B là: lOMoARcPSD| 36149638 2 1 1 2 2 2 A
p p p v v v 1 A B B A A 2 2 2 a 2
Từ ó suy ra vận tốc tại ầu 2 ap A là: vA 2 2 A a
trong ó hiệu áp suất p ược o thông qua ộ chênh lệch h của cột chất lỏng bằng: p '
gh; là khối lượng riêng của chất lưu còn ' là khối lượng riêng của chất lỏng trong ống. Công
thức trên viết lại bằng: 2 ' gh vA a A a2 2
Nhiều bộ chế hoà khí của ôtô cũng có một ống hẹp, gọi là ống
Venturi (hình c). Mục ích của nó là nhằm hạ thấp áp suất ở iểm A sao
cho xăng chạy tới sẽ hoà với dòng không khí dẫn tới buồng ốt của ộng cơ.
Trong giông bão và khi có gió lớn, không khí lao thành dòng sát
các toà nhà làm cho áp suất bên ngoài toà nhà thấp hơn áp suất của
không khí tĩnh ở bên trong nhà. Điều ó thường làm cho các cửa sổ bật mở ra phía ngoài: chứ
không phải vào trong. Tương tự các ống khói cũng thường có một dòng khí hút nhỏ thậm chí
phía dưới không ốt lửa, bởi vì gió vẫn thổi ngang qua ống khói, trong khi không khí ở bên trong
nhà vẫn là dừng. Nếu bạn quan sát một lò sưởi (bằng củi) vào một êm cả gió, bạn sẽ dễ dàng quan
sát ược hiệu ứng Bernoulli.
Hình d biểu diễn một hình trụ quay trong một chất lưu chuyển ộng.
Nếu hình trụ cuốn theo một số chất lưu i theo nó thì bức
tranh ường dòng kết quả sẽ như ược cho trên hình. Điều này làm
cho tốc ộ của chất lưu bên trên hình trụ sẽ cao hơn bên dưới nó
và do ó áp suất phía trên hình trụ sẽ thấp hơn phía dưới nó. Kết
quả sẽ có một lực tác dụng lên hình trụ theo hướng vuông góc với
hướng chuyển ộng của chất lưu (trong trường họp ang xét lực này
hướng lên phía trên của trang giấy). Hiện tượng này ược gọi là
hiệu ứng Magnus. lOMoARcPSD| 36149638
Ví dụ 3-9: biến thiên áp suất dọc theo một ống nằm ngang
Nước ( ược xem như một chất lưu không chịu nén và có ộ nhớt
nhỏ không áng kể) chảy qua một ống nằm ngang của hình 3-
19. Ở iểm 1 áp suất theo áp kế bằng 51kPa và tốc dộ là 1,8m/s. Xác r =12,5mm ịnh tốc ộ và áp suất
theo áp kế ở iểm 2. Giải.
Tốc ộ ở iểm 2 có thể tìm từ phương trình liên tục ối với chất lưu không chịu nén: A 1 r12 v A1 1 v A2 2 v 2 v1 v1 2
3,5m s/ . A2 r1
Áp suất ở iểm 2 khi ó có thể tìm ược từ phương trình Bernoulli. Vì y1 = y2 nên: p 1 1 v12 p2 1 v22 p2 p1 1 v12 1 v22 2 2 2 2 5,1.104 Pa 1,00.103 kg m/3 1,8m s/ 2 3,5m s/ 2 4,7.104 Pa.
Thoạt nhìn có cảm giác như là nghịch lí vì áp suất ở 2 lại thấp hơn ở 1. Nhưng nếu bạn
chú ý rằng, chất lỏng cần phải ược gia tốc giữa 1 và 2 nên rõ ràng là áp suất ở 1 phải cao hơn áp
suất ở 2. Thậm chí nếu chất lưu có ộ nhớt nhỏ, các lực xuất hiện do ộ nhớt của chất lưu có thể
nhỏ so với các lực cần ể gia tốc chất lưu và p2 vẫn có thể nhỏ hơn p1.
Từ ví dụ này ta thấy rằng khi ộ cao không ổi, tốc ộ trong chất lưu càng cao kéo theo áp
suất càng thấp và tốc ộ càng thấp thì áp suất càng cao.
Ví dụ 3-10: lỗ rò trong ống ứng
Một ường ống thẳng ứng có ường kính trong là 1,5m có một lỗ rò ường kính 15mm ở một
bên và dưới mức nước trong ống là 2,5m (hình 3-21). Xác ịnh vận tốc của nước phun ra từ lỗ rò ó. Giải.
Áp dụng phương trình Bemoulli cho các iểm 1 và 2 ta có: p 1 gy1 1v12 p2 gy2 1 v22 2 2
Điểm 1 ở ngay phía ngoài lỗ với dòng nước phụt ra có tốc ộ v1
và iểm 2 là iểm bất kì ở mặt nước trong ống. Cả hai iểm ều
có áp suất là áp suất khí quyển, sao cho p 1 p2 hay p1 p2
0. Thay các giá trị này vào phương trình Bemoulli và chia hai vế cho , ta ược: 1 1 gy1 v12 gy2 v22
Hình 3-21: Nước rò từ ống đứng. lOMoARcPSD| 36149638 2 2
Vìv A2 2 v A1 1, tốc ộ v2 của nước ở iểm 2 có thể bỏ qua so với tốc ộ v1. (Thật vậy: v 2 v1 A1 0,015m2 2 v1 0,00010 v1 0 ). A2 1,5m
Vậy tốc ộ của dòng nước phun ra từ lỗ rò bằng: v 2 1 2g y 2 y1 2 9
,8m s/ 2 2,5m 49m s2 / 2.
Lấy căn bậc hai của hai vế ta ược: v 1 7m s/ .
Ví dụ 3-11: áp suất trong ường dẫn nước
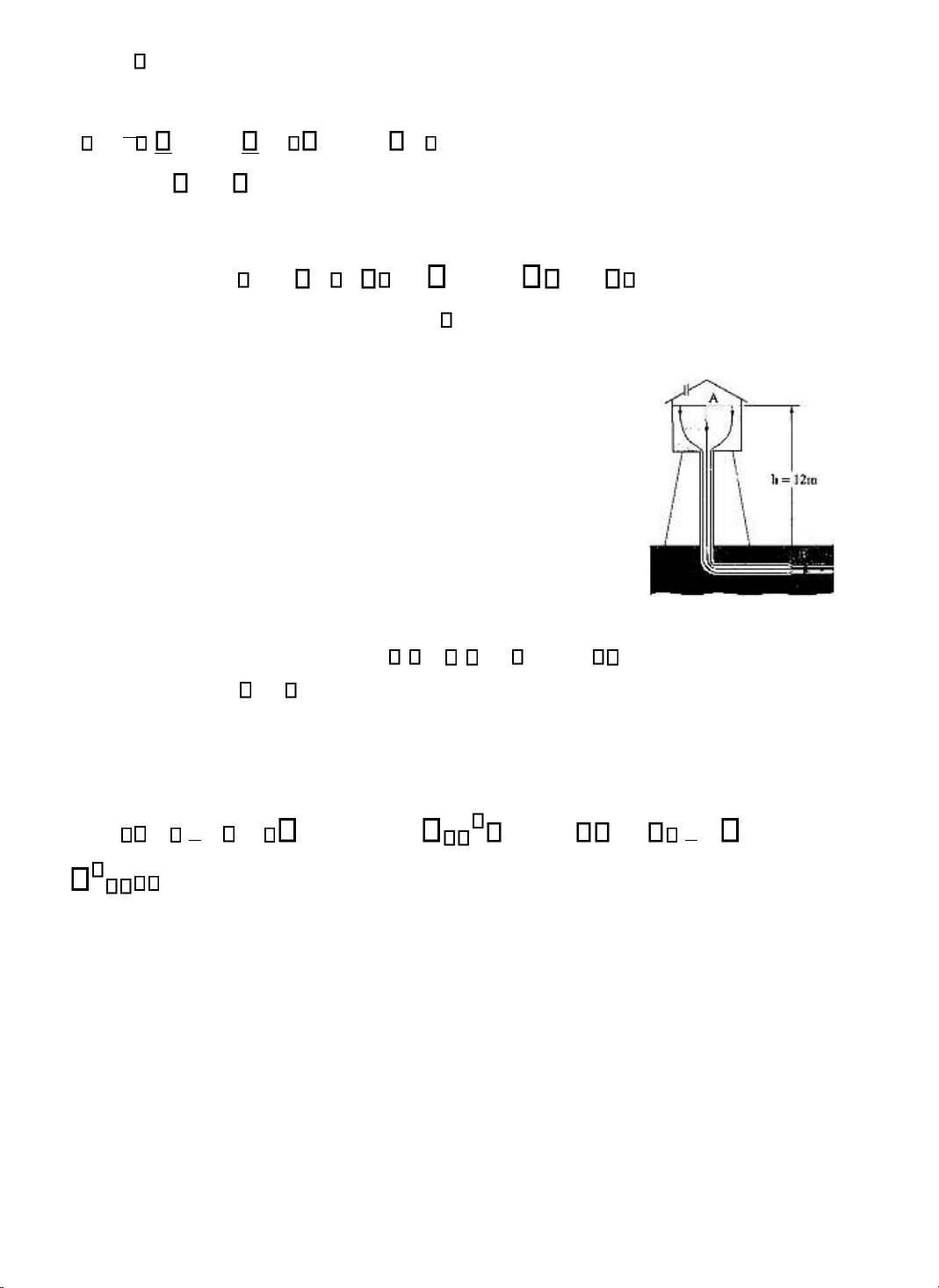
Một hệ thống cấp nước dùng một bể nước ể tích trữ phòng
khi cần dùng ã có sẵn. Nếu mức nước trong bể ở iểm A trong hình
3-22 cao 12m so với ường dẫn nước chính và tốc ộ trong ường dẫn
nước chính ở iểm B là 16m/s, hãy xác ịnh áp suất theo áp kế ở các iểm A và B. Giải.
Tại iểm A, áp suất theo áp kế bằng 0 vì bể ể hở ối với khí quyển. Áp
dụng phương trình Bernoulli tại A và B: Hình 3-22 1 2 p 2 A
gyB 1 vB pB gy B vB 2 2
Tốc ộ vA của nước trong bể lớn có thể xem như bằng 0 và h = yA - yB = 12m. Vậy: p 2 B gh 12 vB 1,00.103kg m/3 9,8N kg/ 12m 12 16m s/ 2 1,0.104Pa.
Áp suất theo áp kế trong ường ống là âm! Điều này có nghĩa là áp suất tuyệt ối trong ường
ống nhỏ hơn áp suất khí quyển. Trong thiết kế hệ thống dẫn nước, tình hình như vậy nên tránh,
vì nếu có một lỗ rò trong ống thì nước bẩn trong ất có thể sẽ lọt vào. Trong hệ thống dẫn nước
thật, dòng thường là chảy rối và hiếm khi có vận tốc vượt quá 3m/s.
3.4. Sự chảy của chất lỏng thực
Các mục trên ề cập ến sự chảy của một chất lưu lý tưởng, mà tính chất chủ yếu là có ộ
nhớt bằng không. Mọi chất lưu thực ều nhớt, và tính chất này có ảnh hưởng quan trọng ến hành
vi của chúng. Ta xét một số ví dụ sau: lOMoARcPSD| 36149638 Lớp biên
Một hiệu quả quan trọng của tính nhớt, là khi có chuyển ộng tương ối giữa một chất lưu và một
chất rắn, thì các phân tử chất lưu ở gần mặt chất rắn có xu hướng gắn vào mặt nó. Xu hướng này
giảm nhanh theo khoảng cách tới mặt. lớp chất lưu thể hiện xu hướng chống lại chuyển ộng ược
gọi là lớp biên. Sự tồn tại của một lớp biện có nhiều hệ quả quen thuộc.
Thí dụ, ta có thể chờ ợi rằng bụi bẩn không bám vào cánh của một cái quạt ang quay, nhưng nó
vẫn bám. Lí do là không khí ở ngay gần mặt cánh quạt không chuyển ộng ối với cánh quạt, nên ở
ó không có cơ chế nào ể “thổi bay” các hạt bụi bẩn. Cũng vì lí do ó, bạn không thể thổi bay hết
bụi trên mặt bàn mà bạn phải lau nó mới i. Một vài tấm vải lau ĩa thì tác dụng có hiệu quả hơn
khi chỉ rửa ĩa ơn thuần. Nước chảy trong lòng suối ở sườn núi không phải là nguyên nhân ầu tiên
khiến lòng suối bị khoét ra trong á. Lớp biên là cho nước bì tù ọng nhiều nhất tại các iểm tiếp xúc
với lòng suối; chính là các hạt á chuyên chở bởi dòng suối có tác dụng ục khoét chủ yếu. Sự kéo theo
Con cầy ang ào hang ở dưới một ồng cỏ phẳng. Để thông
gió cho hang, nó xây một cái ụ quanh một cửa hang, như trên hình
vẽ. Khi một cơn gió nhẹ thổi ngang qua ồng cỏ, phí trên ụ, thì gió
kéo theo và ưa các phân tử không khí ở miệng ụ i xa. Nhờ có lớp
biên của không khí phủ trên mặt bằng phẳng ở cửa dưới của hang,
gió ở ó chuyển ộng chậm hơn, và ít bị cuốn theo hơn. Vì không
khí ở ụ bị cuốn i nhiều hơn nên không khí bị cưỡng bức vào qua
cửa hang dưới, thỏi qua hang và thoát ra khỏi cửa có ụ, và do ó thông gió cho hang.
Bạn có thể chứng minh sự cuốn theo bằng cách thổi một
dòng không khí qua một mảnh giấy ặt ngay sát dưới môi dưới.
Không khí trong dòng khí có áp suất là áp suất khí quyển (nó có
tốc ộ, không phải vì áp suất của nó giảm mà vì phổi của bạn cho
nó tốc ộ ấy). Khi không khí thổi qua khúc giấy ở gần, nó cuốn theo
các phân tử không khí ở giữa dòng khí và mảnh giấy và ưa chúng
i, làm cho áp suất tại ó giảm. Khi ó, áp suất khí quyển dưới mảnh
giấy buộc mảnh giấy phải nâng cao lên.
3.4.1 Hiện tượng nội ma sát và ịnh luật Newton
Hiện tượng nội ma sát
Thường thì các lực không bảo toàn trong chất lưu không thể bỏ qua như chúng ta ã làm
cho tới nay. Những lực này làm tiêu tán cơ năng của chất lưu thành nội năng của nó hệt như lực
ma sát làm tiêu tán năng lượng của một vật trượt trên một bề mặt thành nội năng của vật và bề ■^s mặt ó.
Chất lưu có những lực tiêu tán như thế ược gọi là chất lưu nhớt. lOMoARcPSD| 36149638
Nếu ộ nhớt của chất lưu không nhỏ tới mức có thể bỏ qua ược, thì cơ năng của nó không
bảo toàn và phương trình Bernoulli không còn áp dụng ược nữa. Khi một chất lưu nhớt chảy trong
một ống tiết diện ều nằm ngang, áp suất sẽ giảm dọc theo ường dòng như ược minh hoạ trên hình 3-23. Hình 3-24.
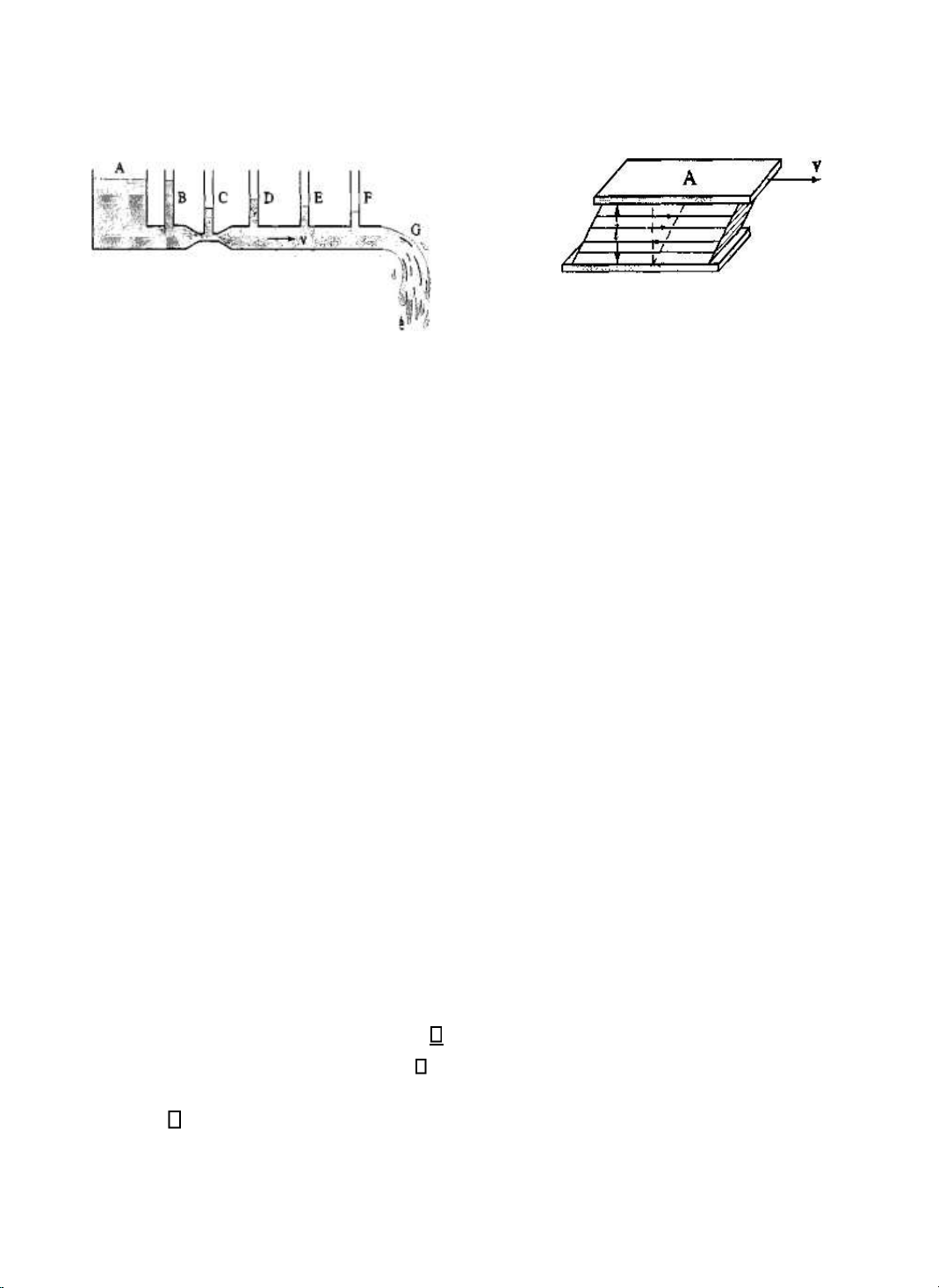
Khi tấm trên ược kéo chậm, chất lưu nhớ
t giữa hai tấm sẽ chảy thành các lớp với vận tốc tỉ lệ với
khoảng cách từ lớp ến
Hình 3-23. Dòng chảy của chất lưu
tấm ứng yên ở áy, như ược chỉ bằng chiều
dài các mũi tên trên hình.
Thí nghiệm như hình 3-24 ược dùng ể nghiên cứu ộ nhớt của các chất lưu. Tấm trên
chuyển ộng với tốc ộ thấp, không ổi ở ỉnh của chất lưu. Các thí nghiệm ều chứng tỏ rằng ối với
a số chất lưu, vận tốc của chất lưu tại các iểm ở giữa hai tấm của hình 3-24 biến thiên một cách
tuyến tính theo khoảng cách tính ến tấm ứng yên ở áy.
Các chất lưu mà thành phần nằm ngang của lực cần thiết làm tấm trên chuyển ộng tỉ lệ
thuận với tốc ộ của tấm ược gọi là chất lưu Newton.
Nước và không khí là những ví dụ gần úng của chất lưu Newton. Một số chất dẻo và thể
huyền phù như máu và hỗn hợp nước với ất sét là những ví dụ về chất lưu không Newton.
Đối với chúng, ộ lớn của lực cần thiết ể làm cho tấm trên chuyển ộng phải tỉ lệ với bình
phương tốc ộ. Ở các tốc ộ cao, dòng chảy trở thành chảy rối và trở nên rất phức tạp trong tất cả các chất lưu.
Độ lớn của lực F tác dụng lên tấm chuyển ộng ược tìm bằng thực nghiệm và thấy rằng nó
không chỉ phụ thuộc vào vận tốc v của tấm chuyển ộng mà còn tỉ lệ với diện tích của tấm A và tỉ
lệ nghịch với khoảng cách l giữa tấm chuyển ộng và tấm ứng yên: Av F (3-11) l
Ở ây là một hằng số tỉ lệ và ược gọi là ộ nhớt. Đơn vị của ộ nhớt trong hệ SI là lOMoARcPSD| 36149638
Nsm. . 2 hay Pa s. . Độ nhớt của a số các chất lưu ều phụ thuộc vào nhiệt ộ. Ví dụ, ộ nhớt của
nước giảm từ khoảng 2.10 3Ns m. / 2ở nhiệt ộ óng băng (0°C) tới khoảng3.10 3Ns m. / 2ở nhiệt ộ
sôi (100°C). Các khí thông thường, như không khí chẳng hạn, có ộ nhớt khoảng
2.10 5Ns m. / 2 trong khoảng nhiệt ộ ó.
Bảng sau ây chỉ ra ộ nhớt của một vài chất lưu: Chất lưu Nhiệt ộ (0C)
Độ nhớt (10-3N.s.m-2) Không khí 20 0,018 Nước 40 0,653 Nước 20 1,003 Dầu xe máy (SAE 10) 30 200 Glyxerin 20 1490 Thuỷ ngân 20 1,554 3.4.2 Chuyển
ộng của chất lỏng thực qua ống tròn nằm ngang. Công thức Poiseuill
Bức tranh chuyển ộng của chất lưu cho trên hình 3-24 ược gọi là sự chảy thành lớp. Mỗi
một lớp ều tác dụng một lực lên lớp ở cạnh nó. Nhưng vì dòng chảy không rối nên các lớp không trộn vào nhau.
Với chất lưu nhớt chảy trong một ống tiết diện ều nằm ngang, áp suất sẽ giảm dọc theo
ống. Hiệu áp suất giữa hai iểm p1 và p2 (hình 3-25) ược tính theo công thức Poiseuille: Q L p p 1 2 8 R4 (3-12)
trong ó Q là lưu lượng theo thể tích ( ơn vị m/s), là ộ nhớt, L là chiếu dài giữa hai iểm p1 và p2,
R là bán kính của ường ống. Từ công thức (3-12) có thể tính ược lưu lượng theo thể tích: p R 4 Q (3-13) 8 L
Ví dụ 3 -12: Các hiệu ứng xơ cứng ộng mạch.
Giả sử rằng sự xơ cứng ộng mạch làm giảm bán kính các mạch máu tim xuống 2 lần. Hỏi
tim phải làm tăng hiệu áp suất lên bao nhiêu lần ể giữ cho lưu lượng máu là không ổi? Giả sử
rằng máu là một chất lỏng Newton và chảy theo lớp. Giải. lOMoARcPSD| 36149638
Vì lưu lượng tỉ lệ với luỹ thừa bậc bốn của bán kính, do ó sự giảm bán kính xuống hai
lần sẽ làm giảm lượng máu xuống 24 lần, tức 16 lần. Lưu lượng máu lại tỉ lệ bậc nhất với hiệu áp
suất, vì vậy ể giữ cho lưu lượng không ổi, tim phải làm tăng hiệu áp suất lên 16 lần.
Thực tế, máu không phải là chất lỏng Newton và sự chảy của máu không phải hoàn toàn
là không rối (xoáy), nên kết quả trên chỉ là gần úng. Tuy nhiên, nó minh hoạ cho những vấn ề
nghiêm trọng mà sự xơ cứng ộng mạch ặt ra cho chúng ta.




