Thông tin
Quiz

Lý thuyết đồ thị hiện đại | Trường Đại học Sư phạm Hà Nội

Lý thuyết đồ thị hiện đại | Trường Đại học Sư phạm Hà Nộivới những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống.

Môn:

Chuyên đề Toán 48 tài liệu

Trường:

Đại học Sư Phạm Hà Nội 2.1 K tài liệu

Thông tin:

23 trang 11 tháng trước

Tác giả:

Kim Oanh

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Lý thuyết đồ thị hiện đại | Trường Đại học Sư phạm Hà Nội

54 27 lượt tải Tải xuống

Lý thuy hi ết đồ thị ện đại

( n) cơ bả

Trương Phước Nhân, 27/10/2019

01. Các khái ni n Chủ đề ệm cơ bả

02. C p ghép Chủ đề ặ

03. Tính liên thông Chủ đề

0 ph ng Chủ đề 4. Đồ thị ẳ

05. Bài toán tô màu Chủ đề đồ thị

06. M ng v n t i Chủ đề ạ ậ ả

07. C u trúc con c c Chủ đề ấ ủa đồ thị dày đặ

08. C u trúc con c Chủ đề ấ ủa đồ thị thưa

09. D c a lý thuy t Ramsey Chủ đề ạng đồ thị ủ ế

10 Hamilton Chủ đề . Đồ thị

ng u nhiên Chủ đề 11. Đồ thị ẫ

12. Cây khung - T p s p th t t Chủ đề ậ ắ ứ ự ốt

N i dung c a bài vi t này nh m m u m k lý thuy thông d ng ộ ủ ế ằ ục đích giới thiệ ột số ết quả ết mang tính ụ

nh trong các ng d ng c ất ứ ụ ủa lý thuyết đồ thị hiện đại.

Chủ 01. Các khái ni n đề ệm cơ bả

1.1. Đồ thị

Đồ thị

là m p ột cặ

 

,V E

g m m nh ồ ột tập đỉ

và m p c nh ột tậ ạ

sao cho

E V

 

 

t n t cức là các phầ ử ủa

- t p con c p là các 2 ậ ủa tậ

Các ph n t c p ầ ử ủa tậ

nh c được gọ ỉi là các đ ủa đồ thị

, còn ph n t ccác ầ ử ủa

i là các được gọ

cạnh của

Đồ thị

c bi u di n tr c quan b ng cách s d ng các ch u di n cho các thường đượ ể ễ ự ằ ử ụ ấm tròn để biể ễ

đỉ ố ộ ộ ủ ồ ịnh và n i hai chấm tròn lại bằng m t cung n o thành mếu như chúng tạ t cạnh c a đ th

trên t nh Đồ thị ập đỉ

 

1,...,7V 

v p c nh ới tậ ạ

         

 

1,2 , 1,5 , 2,5 , 3,4 , 5,7E 

T nh c ập các đỉ ủa đồ thị

u là thường được kí hiệ

 

V G

, còn t p các c ậ ạnh thì được

kí hi u là ệ

 

E G

S nh c ố các đỉ ủa đồ thị

i là c a nó, kí hi u bđược gọ bậc ủ ệ ởi

; còn số các c c ạnh của nó đượ

kí hi u là ệ

Đồ thị

i là ho tùy thu c vào bđược gọ hữu hạn ặc vô hạn ộ ậc

c a nó. ủ

ng t n i dung bài vi t này n u không có gi i thích gì thêm thì m nh là Lưu ý rằ rong toàn bộ ộ ế ế ả ặc đỉ đang

kh h u h n. ảo sát các đồ thị ữ ạ

nh Đỉ

v nh được gọi là liên thuộc ới cạ

n u ế

v e

, t nh ức là đỉ

là m ột đầu mút nào đó của

cạnh

C nh ạ

 

,x y

c kí hi u l ng thường đượ ệ ại dưới dạ

(hoặc

). Nếu

x X

và

y Y

thì

được gọi

là một

X Y

c nh. T p h p g m t các ạ ậ ợ ồ ất cả

X Y

c nh trong t p ạ ậ

u là được kí hiệ

 

,E X Y

n ti ng ta kí hi u Để thuậ ện trong quá trình trình bày, thông thườ ệ

 

,E x X

và

 

,E X y

thay cho

 

 

,E x X

và

 

 

,E X y

. T p h p g nh trong ậ ợ ồm t t cấ ả các cạ

nh n ậ

làm m c kí hi u ột đầu mút đượ ệ

là

 

E v

nh Hai đỉ

,x y

i là (ho n u được gọ liên hợp ặc láng giềng) ế

là m nh c ột cạ ủa đồ thị

nh phân biHai cạ ệt

,e f

p n u chúng có chung m u mút. được gọi là liên hợ ế ột đầ

N u t nh c a m ế ất cả các đỉ ủ ộ ồt đ thị

u liên h đề ợp đôi một với nhau thì đồ thị

được gọi là

đầy đủ.

M trên ột đồ thị đầy đủ

c kí hi u là đỉnh thường đượ ệ

; đồ ị th

i là m thường được gọ ột

tam giác.

M p h nh (ho t không liên h p v ột tậ ợp các đỉ ặc các cạnh) đôi mộ ợ ới nhau được gọi là độc l pậ

(hoặc ổn định).

Cho trước hai đồ thị

 

,G V E

và

 

,G V E

  



Đồ thị

và



ng c u, kí hi u được gọi là đẳ ấ ệ

G G



, n u t n t i m t song ánh ế ồ ạ ộ

:V V







sao cho

   

xy E x y E

 



  

v i mớ ọi

,x y V

Ánh xạ



i là m n u được gọ ột phép đẳng cấu; ế

G G





thì



i là m được gọ ột tự uđẳng cấ .

n u m t qu suy lu p lu Thực tế ế ột kế ả ận nào đó củ ột đồa ta đúng trên m thị thì lậ ận đó cũng sẽ đúng

trên các đồ ị đẳ th ng cấu với nó nên thường ta không quá đặt nặng việc phải phân bi ng ệt các đồ thị đẳ

cấu v i nhau. ớ

ng kí hi u Do đó ta thườ ệ

G G





i cách kí hi u hơn so vớ ệ

G G



Cho trước hai đồ thị

 

,G V E

và

 

,G V E

  

Đặt

 

: ;G G V V E E

  

   

và

 

: ,G G V V E E

  

   

N u ế

G G

  

thì

và



. được gọi là phân bi tệ

N u ế

V V





và

E E





thì



là m cột đồ thị con ủa

(ho ặc đồ thị

chứa đồ thị



N u ế

G G





và



nh chứa t các cất cả ạ

xy E

với

,x y V





thì



c g i là mđượ ọ ột đồ con cthị ảm

sinh của

; t p ậ



được gọi là khung



trong

, kí hi u ệ

G G V

  

 

u Do đó, nế

U V

nh thì là một tập các đỉ

G U

 

 

con trên t nh chính là đồ thị ập đỉ

v nh ới các cạ

chính là các c a ạnh củ

mà có c u n m trong ả hai đầu mút đề ằ

N u ế

G G





và



là khung c a ủ

, tức là

V V





, thì



i là cđược gọ đồ con khungthị ủa

N u ế

là m nh b ột tập đỉ ất kì củ ồa đ thị

thì ta kí hi u ệ

:G U G V U

  

 

Nói cách khác,

G U

chính là đồ thị thu được từ đồ thị

b nh nằng cách xóa đi tất cả các đỉ ằm

trong

và các c nh liên thu i chúng. ạ ộc vớ

N u ế

 

U v

n ti ng kí hi u thì để thuậ ện trong trình bày ta thườ ệ

G v

thay cho

 

G v

N u ế

F V

 

 

u thì ta kí hiệ

 

: ,G F V E F  \

và

 

: ,G F V E F  

n ti n khi trình bày các k t qu , ng kí hi u Tương tự như ở trên, để thuậ ệ ế ả ta thườ ệ

G e

và

G e

thay

cho cách viết

 

G e

và

 

G e

Đồ thị

i là ) theo m t tính chđược gọ tối cđại – ạnh (hoặc t i cố tiểu – ạnh ộ ất

u b n thân nào đó nế ả

a mãn tính chthỏ ất

nhưng không có đồ thị

G xy

(hoặc

G xy

) nào thỏa mãn tính chất

trong

đó

,x y

nh không liên h p b t kì c là hai đỉ ợ ấ ủ ồa đ thị

ng tro khái ni ) theo m t tính chLưu ý rằ ng cách định nghĩa ệm t iố ại đ (hoặc t uối tiể ộ ất

nêu trên th t ậ

ra chính là ta đang xem xét phầ ể ệ con đã đư c đn tử tối đại và tối ti u trên quan h đồ thị ợ ịnh nghĩa

trướ ộc đó; còn khi ta nói m t t i tiập các đỉnh (hoặc tập các cạnh) là tối đại (hoặc tố ểu) thì ta đang xem

xét trên quan h ng. ệ bao hàm thông thườ

N u ế

và



phân bi t thì là hai đồ thị ệ

G G





kí hi ệu cho đồ thị nhận được từ

G G





b ng cách ằ

n nh cối t t cấ ả các đỉ ủa

v nh c ới t t cấ ả các đỉ ủa đồ thị



Phần bù

của

là m trên t nh ột đồ thị ập đỉ

p c nh là có tậ ạ

V E

 

 

Đồ thị tuy n tínhế

 

L G

của

là m có t nh là ột đồ thị ập đỉ

nh sao cho hai đỉ

,x y E

p vliên hợ ới

nhau khi và ch khi ỉ

,x y

nh liên h p trong là hai đỉ ợ

1.2. B c c a m ậ ủ ột đỉnh

Cho trước đồ thị

 

,G V E

u Kí hiệ

 

N v

n là ( hoặc đơn giả

 

N v

) là tập t các láng gi ng c nh ất cả ề ủ ỉa đ

trong đồ thị

V i m i t p ớ ọ ậ

U V

, t p các láng gi ng c nh ậ ề ủa tập đỉ

, kí hi u là ệ

 

N U

, p t t c ng là tậ ấ ả các láng giề

n m trong ằ

V U\

c nh n m trong t p ủ ỉa các đ ằ ậ

Bậc

 

d v

n là ( hoặc đơn giả

 

d v

) của m nh ột đỉ

chính là s ố

 

N v

, t ng s nh ức là bằ ố các đỉ

láng giềng c nh ủ ỉa đ

. M nh có b nh cô l p. ộ ỉt đ ậc bằng 0 được gọi là đỉ ậ

S ố

   

 

: minG d v v V



 |

cđược gọi là b c nh tậ ỏ nhấ ủa

, s ố

   

 

: maxG d v v V  |

được

g c a ọi là b tậc lớn nhấ ủ

N u t nh cế ất cả các đỉ ủa

u có bđề ậc

thì

được là

- u uđề ( ho n là ặc đơn giả đề ).

M 3- i là m . ột đồ thị đều được gọ ột khối lập phương

S ố

 

v V

d v

d G







c được gọi là b c trung bìnhậ ủa đồ thị

D dàng nh n th y r ng ễ ậ ấ ằ

     

G d G G



  

B c trung bình c a m phân b c a các c nh trên t nh ậ ủ ột đồ thị là thước đo giúp ta đánh giá sự ố ủ ạ ừng đỉ

của mộ ồt đ thị.

y, b ng cách kí hi uThật vậ ằ ệ

 





s gi c nh trên s nh c là tỉ ố ữa số ạ ố đỉ ủ ồa đ thị

ta nh n ậ thấy r ng ằ

   

G d G





u tính t ng (Nế ổ

 

v V

d v





nh ctheo t t cấ ả các bậc đỉ ủa

thì m nh chúng ta tính l p l i chính xác ỗi cạ ặ ạ

hai l m n cho m u mút c nh này) ần: ỗi lầ ỗi đầ ủa cạ

Do đó

   

1 1

2 2

v V

E d v d G V



 



, nên

   

G d G





N u m nh l có nhi u c nh trên m nh, ế ột đồ thị có b c nhậ ỏ ất đủ ớn thì nó cũng sẽ ề ạ ột đỉ

b ởi vì

     

1 1

2 2

G d G G

 

 

c l i m có th c trung bình r n m c dù b a nó là Nhưng ngượ ạ ột đồ thị ể có bậ ất lớ ặ ậc nhỏ nhất củ

khá nh . ỏ

Tuy nhiên nh có b l n không hoàn toàn phân tácn gi nh có b , t c là m các đỉ ậc đủ ớ ữa các đỉ ậc nhỏ ứ ọ ồi đ

thị

đều s t m có b c trung bình không nh c trung bình c ẽ chứa ít nhấ ột đồ thị con ậ ỏ hơn bậ ủ ồa đ thị

và b nh n b c nh nh ậc nhỏ ất của nó cũng không nhỏ hơn phân nửa lầ ậ ỏ ất củ ồa đ thị

K t qu 1.2 ế ả

M ọi đồ thị

t m u ch a m con có ít nhấ ột cạnh đề ứ ột đồ thị

sao cho

     

H H G

  

 

xây d ng Ý tưởng để ự

t ừ đồ thị

r n: xóa d nh có b cho ất đơn giả ta sẽ ần đi tất cả các đỉ ậc nhỏ

đế ỉ ớ ịn khi ch còn lại các đỉ ậc đủnh có b l n c ủa đồ th

M t câu h i mà ta ph i quy c khi trình bày phép ch ng minh c ộ ỏ ải giả ết trướ ứ ủa ta đó là :

i u ki n c nh “Đ ề ệ ủa bậc đỉ

 

d v

nh là gì để khi ta xóa đi đỉ

m giá tr cthì không làm giả ị ủa

 



?”

Câu tr l i cho câu hả ờ ỏi này đó chính là

   

d v G





yThật vậ , khi nh ta xóa đi đỉ

mà

   

d v G





s nh b gi còn s nh githì ố các đỉ ị ảm đi 1 ố các cạ ảm đi

t t quá ối đa không vượ

 

d v

Khi đó,

 

   

 

E G d v

E G

d G d G v

V V



   





   

d v d G

t s Do đó, ỉ ố



gi c nh trên s nh s không b gi m. ữa số ạ ố đỉ ẽ ị ả

Chứng minh k t qu 1.1. ế ả

Đầu tiên ta xây d ng m con c m sinh ự ột dãy các đồ thị ả

0 1

...G G G  

b ng ằ như sau:

u “Nế

có m nh ộ ỉt đ

có b c ậ

   

i i

d v G





thì ta đặt

i i i

G G v



 

; trong trường hợp ngược lại, ta

kết thúc quá trình xây dựng và đặt

H G

”.

nh Theo cách chọn đỉ

   

1i i

G G

 





v i mớ ọi

Do đó,

   

H G

 



M t khác, ặ

 

0K G

 

 

, nên không có b con mà ta xây d ng ất kì đồ thị nào trong dãy đồ thị ự

theo phương pháp trình bày ở ị ỗ trên là đồ th r ng, tức là

H  

Điều đó có nghĩa đồ thị

a ít nh t m nh không phù h p v u ki n nêu trong thucó chứ ấ ột đỉ ợ ới điề ệ ật

toán, tức là

   

H H

 



. □

1.3. Đường đi và chu trình

Đường đi

 

,P V E

m v nh là ột đồ thị ới tập đỉ

 

0 1

, ,...,

V x x x

và t p c nh ậ ạ

 

0 1 1 2 1

, ,...,

k k

E x x x x x x





trong đó tất cả các đỉnh

t phân bi đều đôi mộ ệt.

nh Khi đó, hai đỉ

và

gọi là được liên kết bởi đường đi

i là các cvà được gọ đầu mút ủa

;

các đỉnh

1 1

,...,

x x



i là các cđược gọ đỉnh trong ủa đường đi

S nh c a m c dài ố các cạ ủ ột đường đi được gọi là chiều dài ủa nó và đường đi có độ

được

kí hi u là ệ

ng Lưu ý rằ

nh n giá tr b ng 0, t c là có thể ậ ị ằ ứ

P K

Đường đi

P P

trong đồ thị

ng ta kí hi u m nh c a nó, ch ng h nThông thườ ệ ột đường đi bởi các đỉ ủ ẳ ạ

0 1

...

P x x x

, và

g i mọ là ột

đường đi từ

đến

( hoặc gi a ữ

và

Với

0 i j k  

, kí hi u: ệ

: ...

i i

Px x x

: ...

i i k

x P x x

: ...

i j i j

x Px x x

và

1 2 1

: ...

P x x x





0 1

: ...

P x x x





: ...

i i k

x P x x





1 1

: ...

o o

j i j

x P x x x

 



n ti n trong viĐể thuậ ệ ệc trình bày các phép chứng minh n hóa các cách kí hita thường đơn giả ệu các

đường đi.

ng h n, n u h p Chẳ ạ ế ợ

Px xQy yR 

của ba đường đi

xQy

cũng là một đường đi thì ta có

thể n hóa cách kí hi u thành đơn giả ệ

PxQyR

Đường

,P Q

và

xPyQz

C c hai t nh ho trướ ập đỉ

,A B

, đường đi

...

P x x

i là mđược gọ ột đường đi

A B

n u ế

   

V P A x 

và

   

V P B x 

n hóa cách kí hi ng kí hi u mĐể đơn giả ệu ta thườ ệ ột đường đi

 

a B

bởi

a B

Hai hay nhi i là n chúng ch nh ều đường đi được gọ độc lập ếu không có đường đi nào trong số ứa đỉ

trong của một trong các đường đi còn lại.

Hai đường đi

a b

p khi và ch được gọ ội là đ c lậ ỉ

,a b

là c t cặp đỉnh chung duy nhấ ủa chúng.

c m Cho trướ ộ ồt đ thị con

, đường đi

được gọi là

- đường đi n u ế

khác r ng và giao cỗ ủa

đường đi

v ớ ồi đ thị

u mút c a nó. chính là các đầ ủ

c mCho trướ ột đường đi

 

0 1

... 3

P x x k



 

Khi đó, đồ thị

1 0k

P x x





c g i là m . đượ ọ ột chu trình

B ng cách kí hi gi t tính ph p ta ằ ệu tương tự như đã đối với các đường đi, thông thường để ảm bớ ức tạ

thườ ộ ủng kí hiệu m t chu trình b nh cởi dãy các đỉ a nó. Chẳng hạn, chu trình

c kí hi u lthường đượ ệ ại

dưới dạng

0 1 0

...

x x x



a m t chu trình chính là s c nh (ho nh) c t chu trình có Chiều dài củ ộ ố ạ ặc số đỉ ủa chính chu trình đó; mộ

độ dài

i là mthường được gọ ột

- chu trình và kí hi u bệ ởi

dài nh a m Độ nhỏ ất củ ột chu trình chứa trong đồ thị

c được gọi là girth ủ ồa đ thị

và kí hi u là ệ

 

g G

; t c t chu trình chđộ dài l n nhớ ấ ủa mộ ứa trong đồ thị

. được gọi là circumference

C nh n nh không liên h p nhau c c g i là m c ạ ối hai đỉ ợ ủa chu trình đượ ọ ột dây cung ủa chu trình đó.

con c m sinh c Đồ thị ả ủ ồa đ thị

ng m m m sinh c có dạ ột chu trình được gọi là ột chu trình cả ủa

đồ ị th

Chu trình

v i dây cung ớ

và các chu trình c m sinh ả

6 4

,C C

N u m nh l n thì nó s a m t chu trình có chi u dài ế ột đồ thị có b c nhậ ỏ ất đủ ớ ẽ chứ ột đường đi và mộ ề

khá l n: ớ

K t qu 1.3.1. ế ả

M i ọ đồ thị

u ch a m u dài b ng đề ứ ột đường đi có chiề ằ

 



và m t chu trình có chi u dài tộ ề ối

thiểu b ng ằ

 





Chứng minh k t qu 1.3.1. ế ả

G ỉa sử

...

x x

u dài c là đường đi có chiề ực đại trong đồ thị

các láng gi ng c nh Khi đó, tất cả ề ủa đỉ

u phđề ải nằm trên đường đi này.

Do đó,

   

k d x G



 

ng th u gĐồ ời, nế ọi

 

0 1i k  

s nh nh t sao cho là chỉ ố ỏ ấ

 

i k

x x E G

Khi đó,

...

i k i

x x x

là m t chu trình và chi u dài c a nó t u là b ng ộ ề ủ ối thiể ằ

 





. □

Khoảng cách

 

d x y

( hoặc

 

,d x y

) giữa hai đỉnh

,x y

u dài c được định nghĩa là chiề ủa

đường đi

x y

nh nh t ch ỏ ấ ứa trong đồ thị

; trong trư t đườ ợng h p không có mộ ờng đi

x y

nào như

thế thì ta đặt

 

, :

d x y  

ng cách l n nh nh b Khoả ớ ất giữa hai đỉ ất kì củ ồa đ thị

được gọi là đường kính của

kí hi u bệ ởi

 

diam G

K t qu 1.3.2. ế ả

M ọi đồ thị

a ít nh t m u thcó chứ ấ ột chu trình đề ỏa mãn đánh giá

   

2 1g G diam G 

ng minh k t qu 1.3.2. Chứ ế ả

G ỉa sử

dài nh nh c ch là chu trình có độ ỏ ất đượ ứa trong đồ thị

N u ế

   

2 2g G diam G 

thì

nh mà kho ng cách gi nh này trong chứa hai đỉ ả ữa hai đỉ

n là lớ

hơn hoặc bằng

 

1diam G 

ng kính, kho ng cách gi Theo định nghĩa về đườ ả ữa hai đỉnh này trong đồ thị

ph i nh ả ỏ hơn so với

kho ng cách c ả ủa chúng khi tính trong đồ thị

n nhnên đường đi ngắ ất

n nh trên không th ối hai đỉ ể

là m ộ ồt đ thị con của

Do đó, đường đi

ph a mải chứ ột

- ng đường đi có dạ

xPy

B ng cách v dài nh trong s ằ ới đường đi có độ ỏ ố hai đường đi

x y

trong

, ta thu được một chu

trình có chiều dài còn nh chu trình ỏ hơn cả

, mâu thu n v thiẫ ới giả ết

dài nh là chu trình có độ ỏ

nh ất được chứa trong đồ thị

. □

nh Đỉ

c được gọi là tâm ủ ồa đ thị

n u kho ng cách l n nh nh ế ả ớ ất từ đỉ

n t nh còn lđế ất cả các đỉ ại

là nhỏ nhất.

c Khoảng cách này được gọi là bán kính ủa đồ thị

, kí hi u bệ ởi

 

rad G

Do đó,

 

   

 

min max ,

x V G y V G

rad G d x y

 



. n nhiên, Hiể

     

2rad G diam G rad G 

ng kính và bán kính không có m i liên h p v nh Đườ ố ệ trực tiế ới bậc nhỏ ất hoặc

b ậc trung bình.

ng kính và bán kính l i có liên h m t thi i b c l n nh Tuy nhiên, đườ ạ ệ ậ ết vớ ậ ớ ất:

có b l n ch ng kính và bán kính nh n u b n nh t c a nó là “Đồ thị ậc ớ ỉ có thể có đườ ỏ ế ậc lớ ấ ủ

đủ ớn”. l

K t qu 1.3.3. ế ả

c Cho trướ đồ thị

có bán kính nh c b ng ỏ hơn hoặ ằ

và b n nh t nh c b ng ậc lớ ấ ỏ hơn hoặ ằ

Khi đó,

a không quá chứ

kd

nh. đỉ

Chứng minh k t qu 1.3.3. ế ả

G ỉa sử

là tâm của

và kí hi u ệ

p t nh c là tậ ất cả các đỉ ủa đồ thị

có kho nh ảng cách đến đỉ

đúng bằng

Khi đó,

 

V G D



và

1D 

M t khác, t gi ặ ừ ả thiết

 

G d 

1i i

D d D





v i mớ ọi

1,...,i k

B p toán h c ta d dàng ch ng minh r ng ằng phương pháp quy nạ ọ ễ ứ ằ

D d

v i mớ ọi

1,...,i k

Do đó,

1 1

i k

G d kd



   



. □

Dây truy n dài ề có độ

trong đồ thị

là m t dãy ộ

0 0 1 1 1

...

k k

v e v e e v



g nh và các c nh cồm các đỉ ạ ủa

s p x p luân phiên nhau sao cho ắ ế

 

i i i

e v v





v i mớ ọi

1,..., 1i k 

; trong trường h p ợ

0 k

v v

thì xích

đượ ọc g i là đóng.

N u t nh c a m t phân biế ất cả các đỉ ủ ột xích đôi mộ ệt thì xích đó chính là mộ ờng đi trong t đư

1.4. Tính liên thông

Đồ thị

i là n nh b i nhau bđược gọ liên thông ếu hai đỉ ất kì của nó đều được nối vớ ởi một đường đi

nào đó trong

N u ế

 

U V G

và

G U

 

 

liên thông thì là đồ thị

i là được gọ t p liên thông trong ậ

K t qu 1.4.1. ế ả

liên thông Cho trước đồ thị

n t i m l nh c Khi đó, tồ ạ ột phép đánh số ại các đỉ ủ ồa đ thị dưới dạng

,...,

v v

sao cho

,...,

i i

G G v v

 

 

luôn th là đồ ị ớ liên thông v i mọi

Ch ng minh k t qu 1.4.1.ứ ế ả

ra m t cách xây d nh a mãn yêu c bài b ng Ta sẽ chỉ ộ ựng phép đánh số các đỉ thỏ ầu đề ằ

phương pháp đệ qui.

n xét Nhậ

1 1

G G v

 



 

liên thông. luôn là một đồ thị

s nh Giả ử đã tìm được các đỉ

,...,

v v

c ủ ồa đ thị

sao cho

,...,

i i

G G v v

 

 

liên thông luôn là đồ thị

v i mớ ọi

1,..., 2i n 

n t i m nh Khi đó, tồ ạ ộ ỉt đ

v G G 

M t khác, do ặ

là m liên thông nên t n t i một đồ thị ồ ạ ột đường đi

v v

Đặt



nh cu i cùng clà đỉ ố ủa đường đi

n m trong ằ

G G

nh Khi đó, đỉ



có ít nh t là m t láng gi ng n m trong ấ ộ ề ằ

D dàng ch ễ ứng minh được rằng đồ thị

1 1 1

,...,

i i

G G v v

 

 

 

liên thông. cũng là một đồ thị □

Cho trước đồ thị

 

,G V E

con Đồ thị

của

n u được gọi là thành ph n liên thôngầ ế

con liên thông clà đồ thị ực đại

được chứa trong

T p ậ

X V E 

nh được gọi là tách các tập đỉ

,A B

n u v i mế ớ ọi đường đi

A B

chứa trong

u đề

chứa ít nhất m nh hoột đỉ ặc một cạnh thu c tộ ập

u này ch ng t r ng Điề ứ ỏ ằ

A B X 

t p Hơn nữa, ậ

được gọi là tách

(hoặc

clà t p táchậ ủa

) nếu

tách hai đỉnh nào đó của

G X

trong

M i là n t thành ph n liên thông. ột đỉnh được gọ đỉnh khớp ếu nó tách hai đỉnh nào đó trong cùng mộ ầ

M g i là n u mút c a chính mình. ột cạnh được ọ cạnh cầu ếu nó tách hai đầ ủ

u này ch ng t r ng c nh c u không th n m trên b t k m t chu trình trong m . Điề ứ ỏ ằ ạ ầ ể ằ ấ ỳ ộ ột đồ thị

Đồ ị ỉ ớ th với các đ nh kh p

, , ,v x y w

và c nh c u ạ ầ

e xy

Đồ thị

i là được gọ

- liên thông n u ế

G k

và

G X

liên thông v i m i t p là đồ thị ớ ọ ậ

X V

sao cho

X k

, t nh nào c ức là không có hai đỉ ủa đồ thị

c tách bđượ ởi ít hơn

nh còn l đỉ ại.

b t kì luôn là Đồ thị ấ

- 1- ng. liên thông; đồ thị liên thông chính là đồ thị liên thông thông thườ

S nguyên ố

l n nh t sao cho ớ ấ

là m ộ ồt đ thị

- i là liên thông được gọ chỉ s liên thông ố

 



của đồ thị

Khi đó,

 





n u và ch n u ế ỉ ế

không liên thông holà đồ thị ặc

G K

, và

 

K n



 

với

1n 

N u ế

1G 

và

G F

liên thông v i m i t p là đồ thị ớ ọ ậ

F E

sao cho

F l

thì

đượ ọc g i là

- liên thông cạnh.

S nguyên ố

l n nhớ ất sao cho

là m ộ ồt đ thị

- liên thông cạnh

 



c ủa đồ thị

Khi đó,

 





n u và ch n u ế ỉ ế

không liên thông. là đồ thị

Đồ ị th

với

   

4G G

 

 

; đồ ị th

với

 





và

 





D dàng ch ng, ễ ứng minh được rằ

     

G G G

  

 

v i m ớ ọi đồ thị

có ch s liên thông l n s kéo theo b t c n. Do đó một đồ thị ỉ ố ớ ẽ ậc nhỏ nhấ ủ ồa đ thị đó càng lớ

i, m nh n không kéo theo ch s liên thông (ho s liên thông Ngược lạ ộ ồt đ thị có b c nhậ ỏ ất lớ ỉ ố ặc chỉ ố

cạnh) của nó phải lớn.

Nhưng tuy nhiên giả ẫn đế thiết này lại d n sự tồn tại của một đồ thị con có chỉ số liên thông lớn của

nó:

K t qu 1.4.2. (Mader) ế ả

M c trung bình l ng ọi đồ thị có bậ ớn hơn hoặc bằ

u ch t m con đề ứa ít nhấ ộ ồt đ thị

- liên thông.

Chứng minh k t qu 1.4.2. ế ả

N u ế

 

0,1k 

nh là hi n nhiên. thì khẳng đị ể

Không m t tính t ng quát ta có th xét ấ ổ ể

2k 

và xét m ột đồ thị

 

,G V E

a mãn gi thỏ ả thiết của bài

toán v i ớ

:V n

và

:E m

n hóa phép ch ng minh quy n s ng minh m nh t ng quátĐể đơn giả ứ ạp của bài toán, ta ẽ chứ ột khẳng đị ổ

hơn:

s “Giả ử đồ thị

 

,G V E

a mãn: thỏ

2 1n k 

;

ii)

  

2 3 1 1m k n k    

Khi đó,

t m chứa ít nhấ ộ ồt đ thị con

- liên thông.”

nh này th t s m nh c n ch ng minh, t u ki n và (ii) có (Khẳng đị ậ ự ạnh hơn khẳng đị ầ ứ ức là các điề ệ (i) thể

được suy ra d dàng t ễ ừ

 

4d G k

i) vì

   

4n G d G k   

ii) vì

 

m d G n kn 

)

ng minh kh nh v a nêu b p toán h c theo s nh Ta chứ ẳng đị ừ ằng phương pháp quy nạ ọ ố đỉ

N u ế

2 1n k 

thì

 

k n n 

, nên

 

m n n 

u ki n ii). (theo điề ệ

Do đó,

1n k

G K K



 

(đpcm).

Bấm Tải xuống để xem toàn bộ.

| 1/23

| | Tải xuống

Preview text:

Lý thuyết đồ thị hiện đại (cơ bản)
Trương Phước Nhân, 27/10/2019
Chủ đề 01. Các khái niệm cơ bản Chủ đề 02. Cặp ghép
Chủ đề 03. Tính liên thông
Chủ đề 04. Đồ thị phẳng
Chủ đề 05. Bài toán tô màu đồ thị
Chủ đề 06. Mạng vận tải
Chủ đề 07. Cấu trúc con của đồ thị dày đặc
Chủ đề 08. Cấu trúc con của đồ thị thưa
Chủ đề 09. Dạng đồ thị của lý thuyết Ramsey
Chủ đề 10. Đồ thị Hamilton
Chủ đề 11. Đồ thị ngẫu nhiên
Chủ đề 12. Cây khung - Tập sắp thứ tự tốt
Nội dung của bài viết này nhằm mục đích giới thiệu một số kết quả lý thuyết mang tín h thông dụng
nhất trong các ứng dụng của lý thuyết đồ thị hiện đại.
Chủ đề 01. Các khái niệm cơ bản
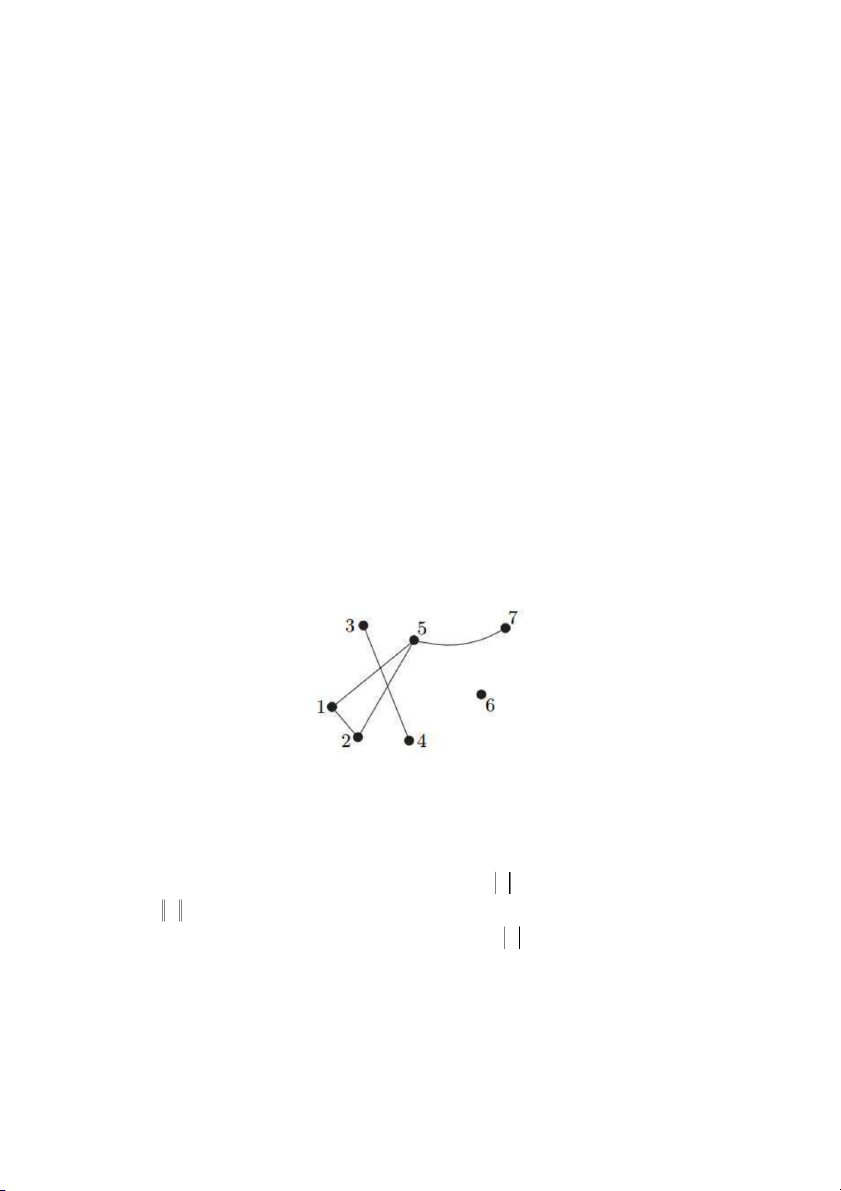
1.1. Đồ thị 2
Đồ thị G là một cặp V,E gồm một tập đỉnh V và một tập cạnh E sao ch oE  V     ,
tức là các phần tử của
E là các 2- tập con của tập V . Các phần tử của tập
V được gọi là các ỉ
đ nh của đồ thị G , còn các phần tử của
E được gọi là các cạnh của G .
Đồ thị G thường được biểu diễn trực quan bằng cách sử dụng các chấm tròn để biểu diễn cho các
đỉnh và nối hai chấm tròn lại bằng một cung nếu như chúng tạo thành một cạnh của đồ t G . ị h
Đồ thị trên tập đỉnh V  1,...,  7 với tập cạnh E  
 1, 2 ,1, 5 ,2, 5 ,3, 4 ,5, 7.
Tập các đỉnh của đồ thị G thường được kí hiệu là V G , còn tập các cạnh thì được
kí hiệu là E G .
Số các đỉnh của đồ thị G được gọi là bậc của nó, kí hiệu bởi
G ; còn số các cạnh của nó được kí hiệu là G .
Đồ thị G được gọi là hữu hạn hoặc vô hạn tùy thuộc vào bậc G của nó.
Lưu ý rằng trong toàn bộ nội dung bài viết này nếu không có giải thích gì thêm thì mặc đỉnh là đang
khảo sát các đồ thị hữu hạn.
Đỉnh v được gọi là liên thuộc với cạnh v nếu ve , tức là đỉnh v là một đầu mút nào đó của cạnh v . Cạnh x, 
y thường được kí hiệu lại dưới dạng xy (hoặc yx ). Nếu x  X và y Y thì xy được gọi
là một X Y cạnh. Tập hợp gồm tất cả các
X  Y cạnh trong tập E được kí hiệu là E X,Y  .
Để thuận tiện trong quá trình trình bày, thông thường ta kí hiệu E x,X  và E X,y  thay cho E 
 x,X và EX , y . Tập hợp gồm tất cả các cạnh trongE nhận v làm một đầu mút được kí hiệu là E v .
Hai đỉnh x,y được gọi là liên hợp (hoặc láng giềng) nếu
xy là một cạnh của đồ thị G . Hai cạnh phân biệt ,
e f được gọi là liên hợp nếu chúng có chung một đầu mút.
Nếu tất cả các đỉnh của một ồ đ thị
G đều liên hợp đôi một với nhau thì đồ thị G được gọi là đầy đủ.
Một đồ thị đầy đủ trên n đỉnh thường được kí hiệu là K ; đồ t ị
h K thường được gọi là một n 3 tam giác.
Một tập hợp các đỉnh (hoặc các cạnh) đôi một không liên hợp với nhau được gọi là độc lập
(hoặc ổn định).
Cho trước hai đồ thị G  V,E và GV ,E  .
Đồ thị G và G được gọi là đẳng cấu, kí hiệu G G , nếu tồn tại một song ánh  :V V
sao cho xy E   xy E với mọi x,yV .
Ánh xạ  được gọi là một phép đẳng cấu; nếu
G  G thì  được gọi là một tự đẳng cấu.
Thực tế nếu một kết quả suy luận nào đó của ta đúng trên một đồ thị thì lập luận đó cũng sẽ đúng
trên các đồ thị đẳng cấu với nó nên thường ta không quá đặt nặng việc phải phân biệt các đồ thị đẳng cấu với nhau.
Do đó ta thường kí hiệu G  G hơn so với cách kí hiệu G G .
Cho trước hai đồ thị G  V,E và GV ,E  .
Đặt G G: V V ;E E và GG: V V ,E  E .
Nếu G G   thì G và G được gọi là phân biệt.
Nếu V  V và E  E thì G là một đồ thị con của G (hoặc đồ thị G chứa đồ thị G).
Nếu G  G và G chứa tất cả các cạnh
xy  E với x,y V thì G được gọi là một đồ thị con cảm
sinh của G ; tập V được gọi là khung G trong G , kí hiệu G  G V     .
Do đó, nếu U  V là một tập các đỉnh thì G U  
  chính là đồ thị con trên tập đỉnh U với các cạnh chính là các cạnh của
G mà có cả hai đầu mút đều nằm trong U .
Nếu G  G và V là khung của G, tức là V  V , thì G được gọi là đồ thị con khung của G .
Nếu U là một tập đỉnh bất kì của đồ thị
G thì ta kí hiệu G  U : GV \U   .
Nói cách khác, G U chính là đồ thị thu được từ đồ thị G bằng cách xóa đi tất cả các đỉnh nằm
trong U và các cạnh liên thuộc với chúng. Nếu U   
v thì để thuận tiện trong trình bày ta thường kí hiệu G  v thay cho G   v . 2 Nếu F  V  
  thì ta kí hiệu G  F :V,E \ F và G  F : V,E  F .
Tương tự như ở trên, để thuận tiện khi trình bày các kết quả, ta thường kí hiệu
G  e và G  e thay
cho cách viết G  
e và G    e .
Đồ thị G được gọi là tối đại – cạn
h (hoặc tối tiểu – cạnh) theo một tính chất
P nào đó nếu bản thân
G thỏa mãn tính chất
P nhưng không có đồ thị G  xy (hoặc G  xy ) nào thỏa mãn tính chất P trong
đó x,y là hai đỉnh không liên hợp bất kì của đồ thị G .
Lưu ý rằng trong cách định nghĩa khái niệm tối ạ
đ i (hoặc tối tiểu) theo một tính chất P nêu trên thật
ra chính là ta đang xem xét phần tử tối đại và tối t ể
i u trên quan hệ đồ thị con đã được định nghĩa
trước đó; còn khi ta nói một tập các đỉnh (hoặc tập các cạnh) là tối đại (hoặc tối tiểu) thì ta đang xem
xét trên quan hệ bao hàm thông thường.
Nếu G và G là hai đồ thị phân biệt thì G G kí hiệu cho đồ thị nhận được từ G G bằng cách
nối tất cả các đỉnh của G với tất cả các đỉnh của đồ thị G. 2
Phần bù G của G là một đồ thị trên tập đỉnh V có tập cạnh là V E   \ .
Đồ thị tuyến tính L G của G là một đồ thị có tập đỉnh là E sao cho hai đỉnh x,yE liên hợp với
nhau khi và chỉ khi x,y là hai đỉnh liên hợp trong G .
1.2. Bậc của một đỉnh
Cho trước đồ thị G  V,E .
Kí hiệu N v ( hoặc đơn giản là N v ) là tập tất cả các láng giềng của đỉnhv trong đồ thị G . G  
Với mọi tập U  V , tập các láng giềng của tập đỉnh
U , kí hiệu là N U  , là tập tất cả các láng giềng
nằm trong V \U của các đỉnh nằm trong tập U .
Bậc d v ( hoặc đơn giản là d v ) của một đỉnh v chính là số N v , tức là bằng số các đỉnh G  
láng giềng của đỉnh v . Một ỉ
đ nh có bậc bằng 0 được gọi là đỉnh cô lập. Số    G : mi  n d  v | v 
V được gọi là bậc nhỏ nhất của G , số  
G : maxd 
v | v V được
gọi là bậc lớn nhất của G .
Nếu tất cả các đỉnh của G đều có bậc k thì G được là k - đều ( hoặc đơn giản là đều).
Một đồ thị 3- đều được gọi là một khối lập phương. dv
Số d G : vV 
được gọi là bậc trung bình của đồ thị G . V
Dễ dàng nhận thấy rằng G  d G  G .
Bậc trung bình của một đồ thị là thước đo giúp ta đánh giá sự phân bố của các cạnh trên từng đỉnh của một ồ đ thị. E
Thật vậy, bằng cách kí hiệu  G :
là tỉ số giữa số cạnh trên số đỉnh của đồ thị G , V 1
ta nhận thấy rằng  G d G. 2 (Nếu tính tổng d
 v theo tất cả các bậc đỉnh của
G thì mỗi cạnh chúng ta tính lặp lại chính xác v V 
hai lần: mỗi lần cho mỗi đầu mút của cạnh này) 1 1 1
Do đó E  dv  dG , nên  G  dG . 2 2 V 2 v V 
Nếu một đồ thị có bậc nhỏ nhất đủ lớn thì nó cũng sẽ có nhiều cạnh trên một đỉnh, 1 1
bởi v ì G  d G   G . 2 2
Nhưng ngược lại một đồ thị có thể có bậc trung bình rất lớn mặc dù bậc nhỏ nhất của nó là khá nhỏ.
Tuy nhiên các đỉnh có bậc đủ lớn không hoàn toàn phân tácn giữa các đỉnh có bậc nhỏ, tức là mọi ồ đ
thị G đều sẽ chứa ít nhất một đồ thị con có bậc trung bình không nhỏ hơn bậc trung bình của đồ G thị
và bậc nhỏ nhất của nó cũng không nhỏ hơn phân nửa lần bậc nhỏ nhất của đồ thị G :
Kết quả 1.2
Mọi đồ thị G có ít nhất một cạnh đều chứa một đồ thị con H sao cho
 H   H   G.
Ý tưởng để xây dựng H từ đồ thị G rất đơn giản: ta sẽ xóa dần đi tất cả các đỉnh có bậc nhỏ cho
đến khi chỉ còn lại các đỉnh có bậc đủ lớn của đồ t ị h G .
Một câu hỏi mà ta phải giải quyết trước khi trình bày phép chứng minh của ta đó là :
“Điều kiện của bậc đỉnh d v là gì để khi ta xóa đi đỉnh v thì không làm giảm giá trị của G ?”
Câu trả lời cho câu hỏi này đó chính là
dv  G .
Thật vậy, khi ta xóa đi đỉnh v mà d v  G th ìsố các đỉnh bị giảm đi
1 còn số các cạnh giảm đi
tối đa không vượt quá d v . Khi đó, 2 EG
2 EG  dv d G 
 d G v  V V 1 1
 d v  d G 2
Do đó, tỉ số  giữa số cạnh trên số đỉnh sẽ không bị giảm.
Chứng minh kết quả 1.1.
Đầu tiên ta xây dựng một dãy các đồ thị con cảm sinh
G  G  G  ... bằng như sau: 0 1
“Nếu G có một ỉ
đ nh v có bậc d v   G thì ta đặt G : G  v ; trong trường hợp ngược lại, ta i   i i i i 1  i i
kết thúc quá trình xây dựng và đặt H : G ”. i
Theo cách chọn đỉnhv ,  G   G với mọi i. i 1    i  i
Do đó,  H   G. Mặt khác,   1
K   0   G, nên không có bất kì đồ thị nào trong dãy đồ thị con mà ta xây dựng
theo phương pháp trình bày ở trên là đồ t ị
h rỗng, tức là H   .
Điều đó có nghĩa đồ thị H có chứa ít nhất một đỉnh không phù hợp với điều kiện nêu trong thuật
toán, tức là  H    H  . □
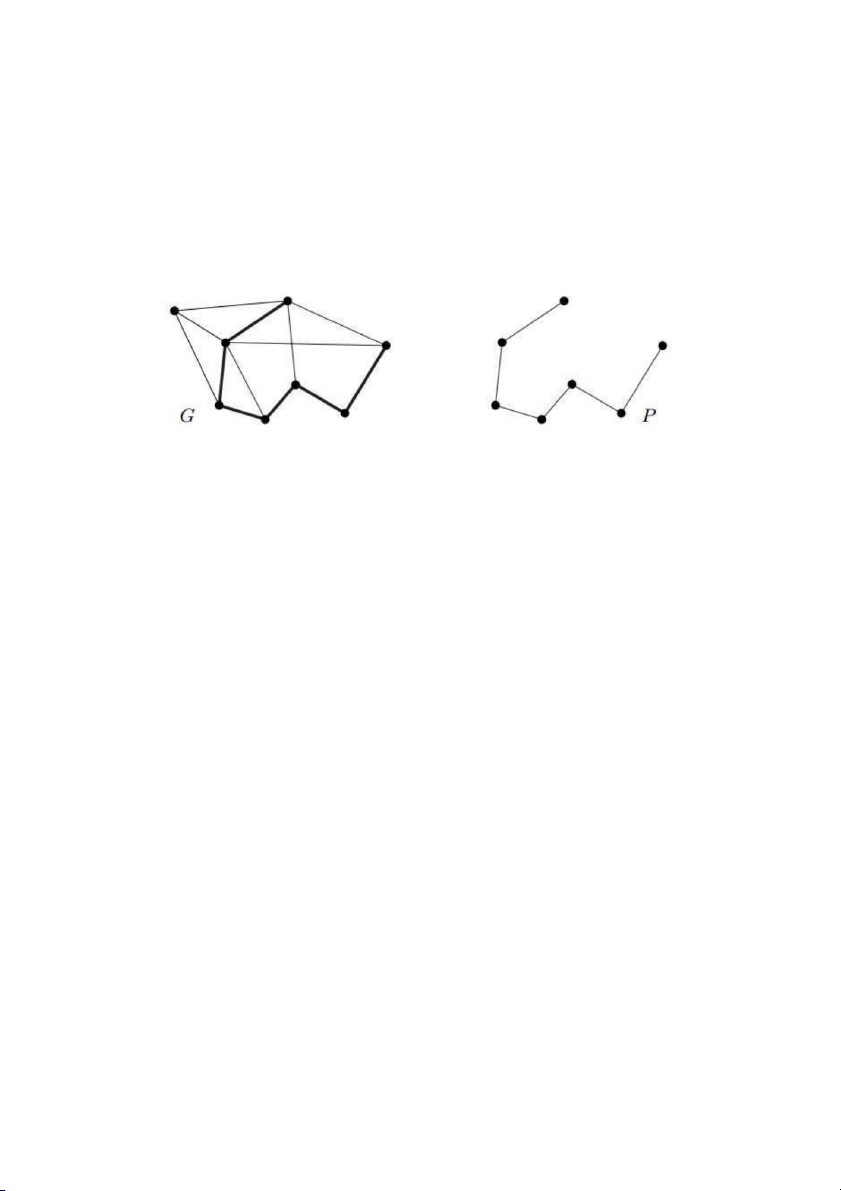
1.3. Đường đi và chu trình
Đường đ i P V,E l
à một đồ thị với tập đỉnh V  x ,x ,..., và tập cạnh 0 1 xk 
E  x x ,x x ,...,x x trong đó tất cả các đỉnh 0 1 1 2
v đều đôi một phân biệt. k 1  k  i
Khi đó, hai đỉnh x và x gọi là được liên kết bởi đường đi P và được gọi là các đầu mút của P ; 0 k
các đỉnh x ,..., x được gọi là các đỉnh trong của đường đi P . 1 k 1 
Số các cạnh của một đường đi được gọi là chiều dà icủa nó và đường đi có độ dà k i được kí hiệu là P . k
Lưu ý rằng k có thể nhận giá trị bằng 0, tức là P 1  K . 0 Đường đi P  trong đồ thị G . 6 P
Thông thường ta kí hiệu một đường đi bởi các đỉnh của nó, chẳng hạ
Pn x x ... , vàP gọi l à một 0 1 xk
đường đi từ x đến x ( hoặc giữa x và x ). 0 k 0 k
Với 0  i  j  k , kí hiệu: P
x : x ...x i 0 i
x P : x ...x i i k
x Px : x ... x i j i j và o P : x x ... 1 2 xk 1 o P x
i : x ...x 0 i 1 o
x P : x ...x i i 1  k o o x .
i P x : x ...x j i 1  j 1 
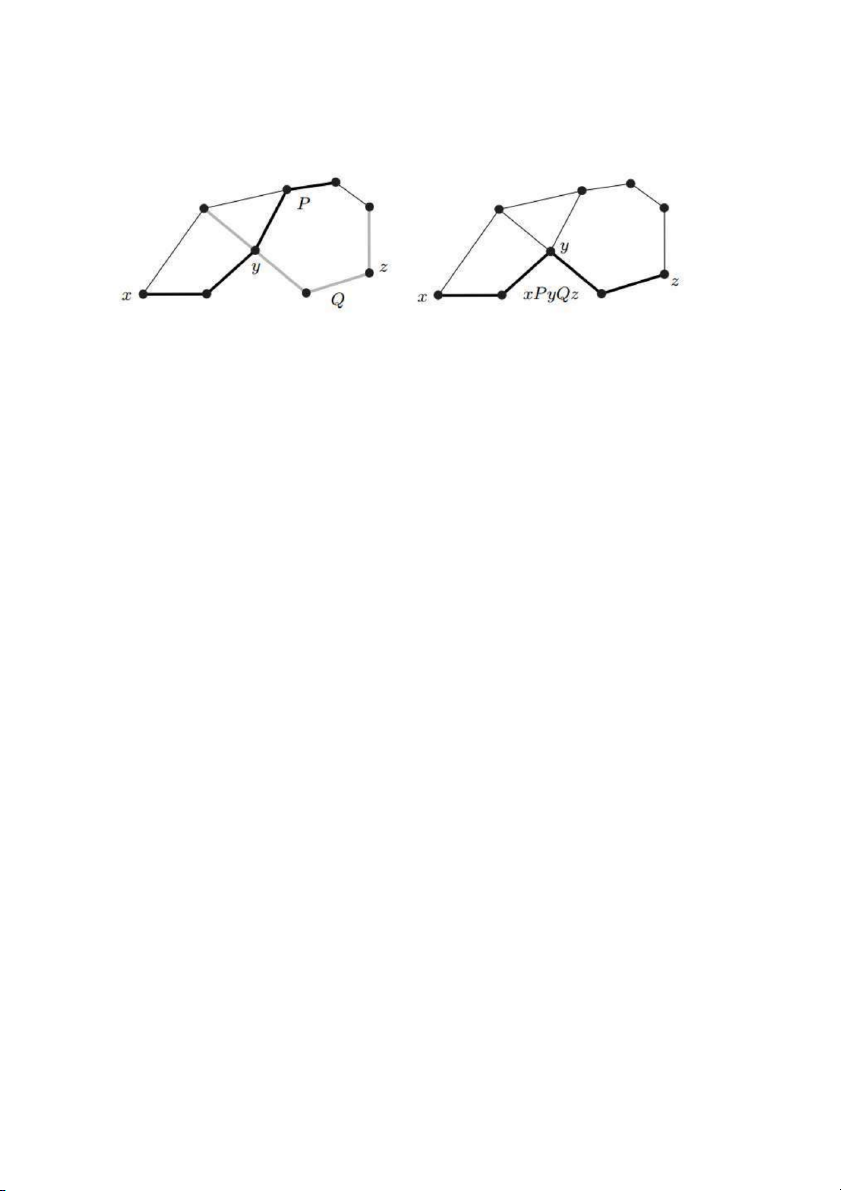
Để thuận tiện trong việc trình bày các phép chứng minh ta thường đơn giản hóa các cách kí hiệu các đường đi. Chẳng hạn, nếu hợp
Px  xQy  yR của ba đường đi Px , xQy , yR cũng là một đường đi thì ta có
thể đơn giản hóa cách kí hiệu thành P xQyR.
Đường P,Q và xPyQz .
Cho trước hai tập đỉnh ,
A B , đường đi P  x ... được gọi là m  0 x
ột đường đi A B k
nếu V P A  x và V P B  x . k  0 
Để đơn giản hóa cách kí hiệu ta thường kí hiệu một đường đ i 
a  B bởi a  B .
Hai hay nhiều đường đi được gọi là độc lập nếu không có đường đi nào trong số chúng chứa đỉnh
trong của một trong các đường đi còn lại.
Hai đường đi a  b được gọi là ộ đ c lập khi và chỉ ,
a b là cặp đỉnh chung duy nhất của chúng. Cho trước một ồ
đ thị con H , đường đi P được gọi là H - đường đi nếu P khác rỗng và giao của
đường đi P với ồ
đ thị H chính là các đầu mút của nó.
Cho trước một đường đi P  x ...x k  3 . 0 k 1   
Khi đó, đồ thị P x x được gọi là một chu trình. k 1  0
Bằng cách kí hiệu tương tự như đã đối với các đường đi, thông thường để giảm bớt tính phức tạp ta
thường kí hiệu một chu trình bởi dãy các đỉnh của nó. Chẳng hạn, chu trìn C h
t hường được kí hiệu lại
dưới dạng x ...x x . 0 k1 0
Chiều dài của một chu trình chính là số cạnh (hoặc số đỉnh) của chính chu trình đó; một chu trình có
độ dài k thường được gọi là một k- chu trình và kí hiệu bởi C . k
Độ dài nhỏ nhất của một chu trình chứa trong đồ th
Gị được gọi là girth của đồ thị G và kí hiệu là
g G ; độ dài lớn nhất của một chu trình chứa trong đồ thị
G được gọi là circumference.
Cạnh nối hai đỉnh không liên hợp nhau của chu trình được gọi là một dây cung của chu trình đó.
Đồ thị con cảm sinh của đồ thị
G có dạng một chu trình được gọi là một chu trình cảm sinh của đồ t ị h G .
Chu trình C với dây cung xy và các chu trình cảm sinh C ,C . 8 6 4
Nếu một đồ thị có bậc nhỏ nhất đủ lớn thì nó sẽ chứa một đường đi và một chu trình có chiều dài khá lớn:
Kết quả 1.3.1.
Mọi đồ thị G đều chứa một đường đi có chiều dài bằng
 G và một chu trình có chiều dài tối
thiểu bằng  G 1.
Chứng minh kết quả 1.3.1.
Gỉa sử x ...x là đường đi có chiều dài cực đại trong đồ thị 0 G . k
Khi đó, tất cả các láng giềng của đỉnhx đều phải nằm trên đường đi này. k
Do đó, k  d x   G . k   
Đồng thời, nếu gọi 0  i  k  
1 là chỉ số nhỏ nhất sao cho
x x  E G . i k  
Khi đó, x ...x x là một chu trình và chiều dài của nó tối thiểu là bằn
 g G 1. □ i k i
Khoảng cách d x,y ( hoặc d x,y ) giữa hai đỉnh x,y được định nghĩa là chiều dài của G 
đường đi x  y nhỏ nhất chứa trong đồ thị G ; trong trường hợp không có một đường đi x  y nào như
thế thì ta đặt d x,y :  . G
Khoảng cách lớn nhất giữa hai đỉnh bất kì của đồ thị
G được gọi là đường kính của G ,
kí hiệu bởi diam G .
Kết quả 1.3.2.
Mọi đồ thị G có chứa ít nhất một chu trình đều thỏa mãn đánh giá
g G  2diam G 1 .
Chứng minh kết quả 1.3.2.
Gỉa sử C là chu trình có độ dài nhỏ nhất được chứa trong đồ thị G .
Nếu g G  2diam G  2 thì C chứa hai đỉnh mà khoảng cách giữa hai đỉnh này tron Cg là lớn
hơn hoặc bằng diamG1.
Theo định nghĩa về đường kính, khoảng cách giữa hai đỉnh này trong đồ thị
G phải nhỏ hơn so với
khoảng cách của chúng khi tính trong đồ thị
C nên đường đi ngắn nhất P nối hai đỉnh trên không thể là một ồ đ thị con của C .
Do đó, đường đi P phải chứa một C - đường đi có dạng xPy .
Bằng cách với đường đi có độ dài nhỏ trong số hai đường đi
x  y trong C , ta thu được một chu
trình có chiều dài còn nhỏ hơn cả chu trình
C , mâu thuẫn với giả thiết C là chu trình có độ dài nhỏ
nhất được chứa trong đồ thị G . □
Đỉnh v được gọi là tâm của đồ thị G nếu khoảng cách lớn nhất từ đỉnh
v đến tất cả các đỉnh còn lại là nhỏ nhất.
Khoảng cách này được gọi là bán kính của đồ thị
G , kí hiệu bởi rad G .
Do đó, rad G  min max d  ,
x y . Hiển nhiên, radG  diamG  2radG . G  x V  G y V  G
Đường kính và bán kính không có mối liên hệ trực tiếp với bậc nhỏ nhất hoặc bậc trung bình.
Tuy nhiên, đường kính và bán kính lại có liên hệ mật thiết với bậc lớn nhất:
“Đồ thị có bậc lớn chỉ có thể có đường kính và bán kính nhỏ nếu bậc lớn nhất của nó là đủ lớn”.
Kết quả 1.3.3.
Cho trước đồ thị G có bán kính nhỏ hơn hoặc bằngk và bậc lớn nhất nhỏ hơn hoặc bằng d .
Khi đó, G chứa không quá 1 k  kd đỉnh.
Chứng minh kết quả 1.3.3.
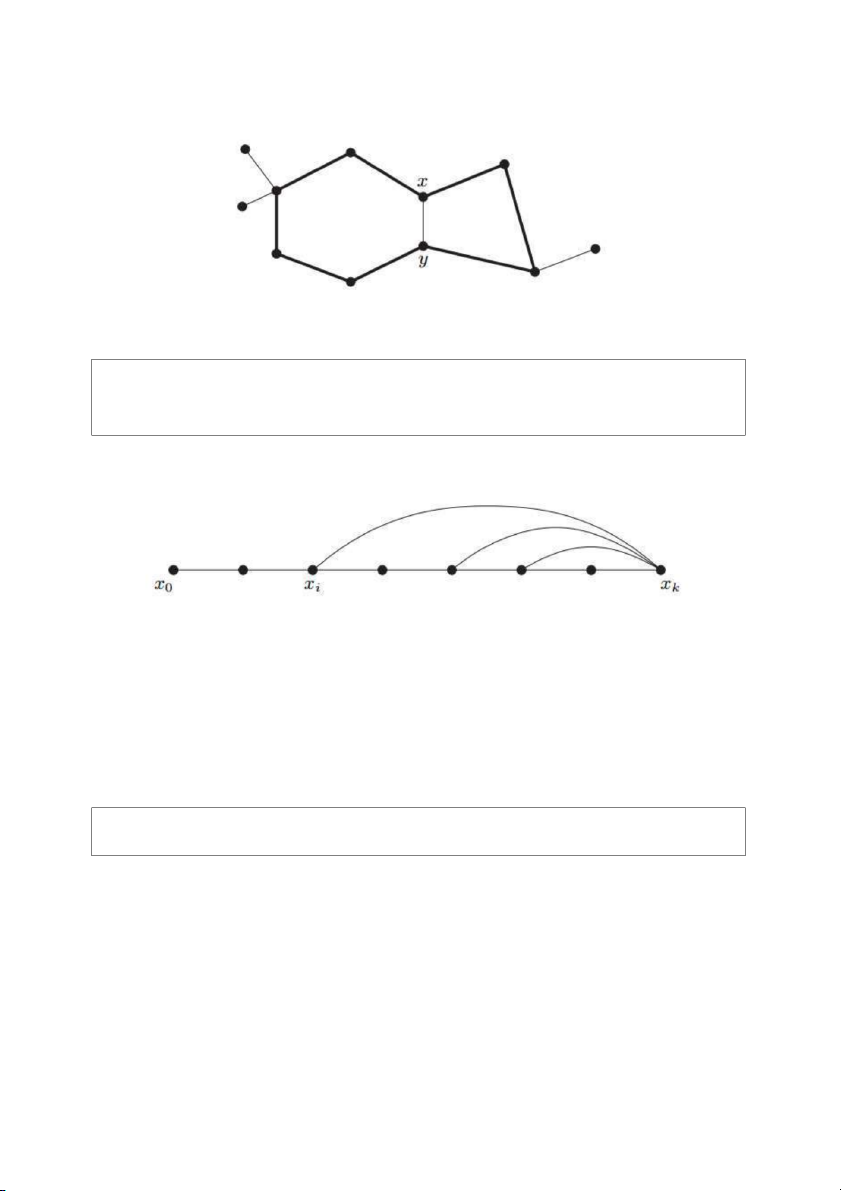
Gỉa sử z là tâm của G và kí hiệu D là tập tất cả các đỉnh của đồ thị G có khoảng cách đến đỉnh z i đúng bằng i . k
Khi đó, V G  D và D  1. i 0 i 0
Mặt khác, từ giả thiết G  d , D  d D với mọi i 1,...,k . i i 1 
Bằng phương pháp quy nạp toán học ta dễ dàng chứng minh rằng D i
 d với mọi i  1,...,k . i k Do đó, G 1 i  d 1 k  kd . □ i 1 
Dây truyền có độ dài k trong đồ thị G là một dãy v e v e ...e v gồm các đỉnh và các cạnh của G 0 0 1 1 k 1  k
sắp xếp luân phiên nhau sao cheo  v ,v với mọi i 1,...,k 1; trong trường hợp v  v thì xích i i i 1   0 k
được gọi là đóng.
Nếu tất cả các đỉnh của một xích đôi một phân biệt thì xích đó chính là một đ ờng ư đi trong G . 1.4. Tính liên thông
Đồ thị G được gọi là liên thông nếu hai đỉnh bất kì của nó đều được nối với nhau bởi một đường đi nào đó trong G.
Nếu U  V G và G U  
  là đồ thị liên thông thì U được gọi là tập liên thông trong G .
Kết quả 1.4.1.
Cho trước đồ thị liên thông G .
Khi đó, tồn tại một phép đánh số lại các đỉnh của đồ thị dưới dạng v ,...,v sao cho G  G v ,...,v  1 n i  1 i 
luôn là đồ thị liên thông với mọi i.
Chứng minh kết quả 1.4.1.
Ta sẽ chỉ ra một cách xây dựng phép đánh số các đỉnh thỏa mãn yêu cầu đề bài bằng phương pháp đệ qui.
Nhận xét G  G v  luôn là một đồ thị 1  1 liên thông.
Giả sử đã tìm được các đỉnh v ,..., th
G  G v ,...,v  1
v của đồ ị G sao cho luôn là đồ thị i i  1 i  liên thông
với mọi i  1,...,n  2 .
Khi đó, tồn tại một đỉnh v G  G . i
Mặt khác, do G là một đồ thị liên thông nên tồn tại một đường điv  P . 1 v
Đặt v là đỉnh cuối cùng của đường đi P nằm trong G  G . i 1  i
Khi đó, đỉnh v có ít nhất là một láng giềng nằm trong G . i 1 i
Dễ dàng chứng minh được rằng đồ thị G  Gv ,..., v  cũng là một đồ thị □ i 1   1 i 1   liên thông.
Cho trước đồ thị G  V,E.
Đồ thị con H của G được gọi là thành phần liên thông nếu H là đồ thị con liên thông cực đại
được chứa trong G .
Tập X  V  E được gọi là tách các tập đỉnh ,
A B nếu với mọi đường đi A  B chứa trong G đều
chứa ít nhất một đỉnh hoặc một cạnh thuộc tập X .
Điều này chứng tỏ rằng
A  B  X .
Hơn nữa, tập X được gọi là tách G (hoặc X là tập tách của G ) nếu X tách hai đỉnh nào đó của
G  X trong G.
Một đỉnh được gọi là đỉnh khớp nếu nó tách hai đỉnh nào đó trong cùng một thành phần liên thông.
Một cạnh được gọi là cạnh cầu nếu nó tách hai đầu mút của chính mình.
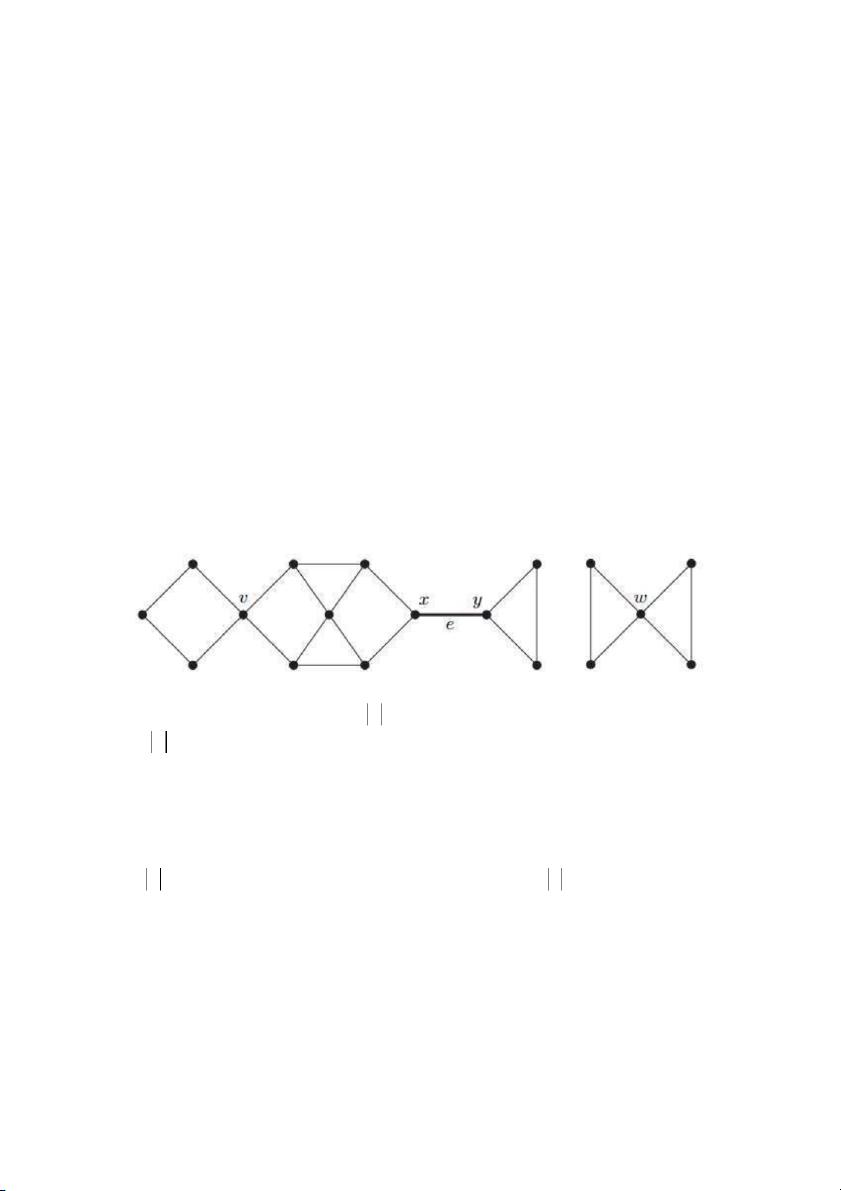
Điều này chứng tỏ rằng cạnh cầu không thể nằm trên bất kỳ một chu trình trong một đồ thị. Đồ t ị h với các đỉnh khớp , v , x ,
y w và cạnh cầu e  xy .
Đồ thị G được gọi là k - liên thông nếu G  k và G  X là đồ thị liên thông với mọi tập X  V
sao cho X  k , tức là không có hai đỉnh nào của đồ thị
G được tách bởi ít hơn k đỉnh còn lại.
Đồ thị bất kì luôn là 0- liên thông; đồ thị 1- liên thông chính là đồ thị liên thông thông thường.
Số nguyên k lớn nhất sao cho G là một ồ
đ thị k - liên thông được gọi là chỉ số liên thông  G của đồ thị G .
Khi đó,  G  0 nếu và chỉ nếu G là đồ thị không liên thông hoặc G 
, và   K  n  n  1 1 K với n  1.
Nếu G  1 và G  F là đồ thị liên thông với mọi tập F  E sao cho F  l thì G
được gọi là l - liên thông cạnh.
Số nguyên l lớn nhất sao cho G là một ồ
đ thị l - liên thông cạnh  G của đồ thị G .
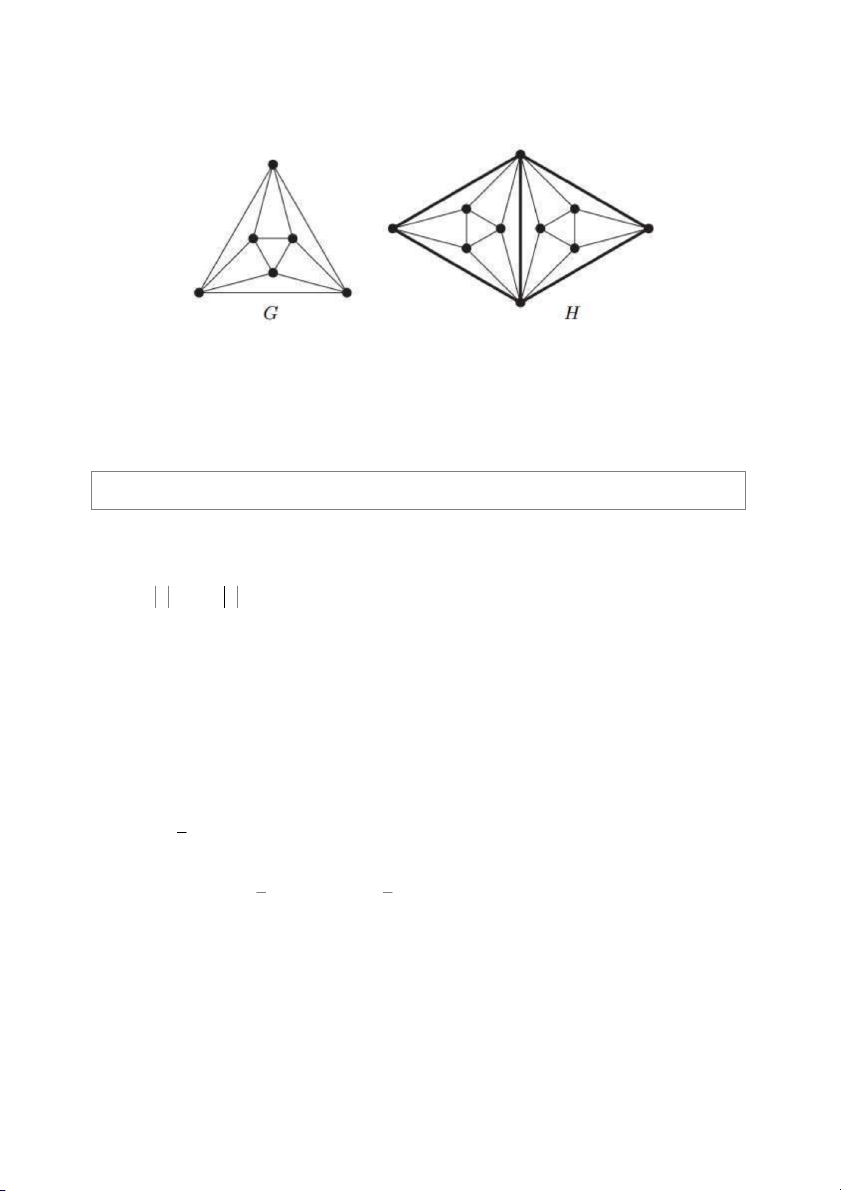
Khi đó,  G  0 nếu và chỉ nếu G là đồ thị không liên thông. Đồ t ị
h G với  G   G  4 ; đồ t ị
h H với   H  2 và  H  4 .
Dễ dàng chứng minh được rằng,
 G  G  G với mọi đồ thị G.
Do đó một đồ thị có chỉ số liên thông lớn sẽ kéo theo bậc nhỏ nhất của đồ thị đó càng lớn. Ngược lại, một ồ
đ thị có bậc nhỏ nhất lớn không kéo theo chỉ số liên thông (hoặc chỉ số liên thông
cạnh) của nó phải lớn.
Nhưng tuy nhiên giả thiết này lại ẫ
d n đến sự tồn tại của một đồ thị con có chỉ số liên thông lớn của nó:
Kết quả 1.4.2. (Mader)
Mọi đồ thị có bậc trung bình lớn hơn hoặc bằng
4 k đều chứa ít nhất một ồ
đ thị conk - liên thông .
Chứng minh kết quả 1.4.2. Nếu k 0, 
1 thì khẳng định là hiển nhiên.
Không mất tính tổng quát ta có thể xé k t
 2 và xét một đồ thị G  V,E thỏa mãn giả thiết của bài toán với V :  n và E :  m .
Để đơn giản hóa phép chứng minh quy nạp của bài toán, ta sẽ chứng minh một khẳng định tổng quát hơn:
“Giả sử đồ thị G  V,E  thỏa mãn:
i) n  2k 1;
i ) m  2k 3n  k   1 1.
Khi đó, G chứa ít nhất một ồ đ thị con k - liên thông.”
(Khẳng định này thật sự mạnh hơn khẳng định cần chứng minh, tức là các điều kiện (i) và (i ) có thể
được suy ra dễ dàng từ
d G  4k :
i) vì n    G  d  G  4k , 1
i ) vì m  d Gn  2 ) 2 kn
Ta chứng minh khẳng định vừa nêu bằng phương pháp quy nạp toán học theo số đỉ n n . h 1 1
Nếu n  2k 1 thì k  n n  
1 , nên m  n n   1 (theo điều kiện i ). 2 2
Do đó, G  K  K (đpcm). n k 1 