Lý thuyết đồng dạng và phương pháp phân tích thứ nguyên | Bài giảng môn quá trình thiết bị | Đại học Bách khoa hà nội

CH#3400
Quá$trình và$thiết$bị$công$nghệ$hoá$học$I
Lý#thuyết#đồng#dạng#và#
phương#pháp#phân#tích#thứ#nguyên Dimensional Analysis
Giảng&viên:&Nguyễn&Minh&Tân
Tan.nguyenminh@hust.edu.vn&
Bộ&môn&QT>TB&CN&Hóa&học&&&Thực&phẩm
Trường&Đại&học&Bách&khoa&Hà&nội
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
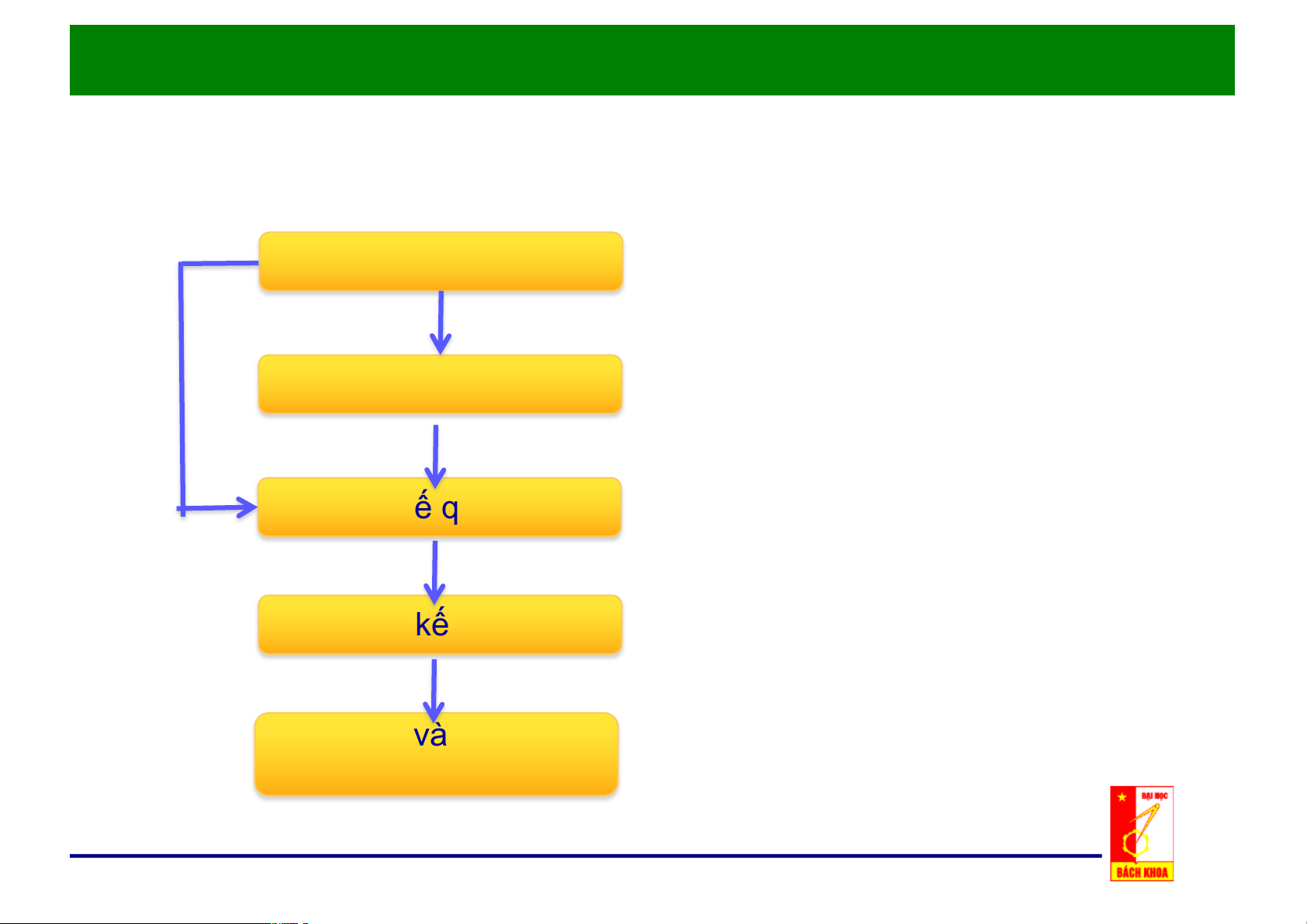
Các$bước$phát$triển$công$nghệ$mới
Phát triển nguyên lý sản xuất Thí$nghiệm$trong$PTN sản phẩm mới
Xác định các số liệu quá trình, Thiết$bị$thí$nghiệm
tính chất nguyên liệu, đánh
giá tác động môi trường, nghiên cứu tính kinh tế Thiết$kế$quá$trình
Thiết kế dây chuyền thiết bị,
thiết bị điều khiển quá trình, Thiết$kế$thiết$bị thiết kế thiết bị
Thiết kế mặt bằng, lắp đặt, vận hành Chế$tạo$và$vận$hành$ thiết$bị
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
I.#Thuyết#đồng#dạng
1.1.#Khái#niệm#về#đồng#dạng
- Phương trình vi phân mô tả diễn biến quá trình ưới dạng mô hình toán học
- Nghiệm của phương trình vi phân chứa các hằng số tích phân đặc trưng
cho đối tượng cụ thể, được xác định nhờ các thực nghiệm và các điều kiện
biên (điều kiện đơn trị): + Kích thước hình học + Điều kiện không gian
+ Thời gian tồn tại quá trình
+ Thông số vật lý của các chất tham gia quá trình
+ Ảnh hưởng tương hỗ của môi trường xung quanh -
Phương pháp nghiên cứu quá trình và thiết bị bằng mô hình thực
nghiệm gọi là phương pháp mô hình -
Lý thuyết đồng dạng dựa trên các mô hình
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên Thuyết'đồng'dạng
Những&điều&kiện&đồng&dạng
Các hiện tượng đồng dạng nhau khi tỷ lệ của các đại lượng tượng tự đặc
trưng của chúng là đại lượng không đổi theo 4 điều kiện sau:
+ Đồng dạng hình học: hai vật đồng dạng về hình học khi kích thước
tương ứng song song với nhau và có tỷ lệ không đổi
+ Đồng dạng về thời gian: Tỷ lệ giữa các khoảng thời gian mà những
điểm hay những phân tử của hệ thống đồng dạng chuyển động theo
những quĩ đạo đồng dạng hình học là một hằng số
+ Đồng dạng vật lý: Những thông số vật lý của hai điểm hay hai phần
tử tương ứng trong hệ thống đồng dạng về không gian và thời gian
có tỷ lệ giữa những đại lượng cùng loại là một hằng số
+ Đồng dạng về điều kiện đầu và điều kiện biên: những điều kiện
đầu và điều kiện biên của hai hệ đồng dạng nhau cũng đồng dạng.
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
I.#Thuyết#đồng#dạng
Định%số%đồng%dạng%và%chuẩn%số%đồng%dạng -
Hằng số đồng dạng là tỉ lệ giữa hai đại lượng tương ứng của hai hệ khác nhau -
Tỉ lệ giữa hai đại lượng giống nhau tại hai điểm khác nhau của cùng
một hệ thống gọi là định số đồng dạng -
Định số đồng dạng cấu tạo từ các địa lượng cùng loại gọi là định số đơn hệ -
Định số đồng dạng cấu tạo bởi các đại lượng khác nhau không cùng loại
gọi là chuẩn số đồng dạng Định luật Niu tơn
Chuẩn số số Niu tơn dw ! F = m F ! = idem d mw
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
Các$chuẩn$số$đồng$dạng
- Lý thuyết đồng dạng cho phép biến đổi phương
trình vi phân mô tả một quá trình thành một phương trình chuẩn số
- Các quá trình vận chuyển chất lỏng, truyền nhiệt,
chuyển khối,… đều có thể được biểu thị qua chuẩn số đồng dạng
- Mỗi chuẩn số đồng dạng đều phản ánh một hiện
tượng và mang tên người đã lập ra nó
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
I.#Thuyết#đồng#dạng
Các$Định$lý$đồng$dạng -
Định lý 1: Các chuẩn số đồng dạng tương ứng của các hiện tượng
đồng dạng với nhau có cùng trị số F! F! 1 1 1 1 m w F ! 1 1 = 1 2 2 hay = 1 F ! m w 2 2 1 1 m w m w 2 2 2 2 Rút ra Chỉ số đồng a a dạng Trong đó F ! = 1 = C F ! w m 1 = a 1 ; = a 1 ; = a 1 ; = a a a F ! w m F ! w m m w 2 2 2 2
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
I.#Thuyết#đồng#dạng
Các$Định$lý$đồng$dạng -
Định lý 2: Mỗi phương trình biểu thị cho mối liên hệ giữa các đại
lượng đặc trưng cho một quá trình vật lý nào đó đều có thể viết dưới
dạng một hàm của các chuẩn số đồng dạng
f (K , K , K ,..., K = 1 2 3 n ) 0 Phương trình chuẩn số -
Định lý 3: Các hiện tượng được coi là đồng dạng với nhau nếu các
điều kiện đơn trị đồng dạng với nhau và những chuẩn số xác định
được cấu tạo từ chúng có trị số như nhau
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
Thứ$nguyên$và$đơn$vị
Thứ nguyên/Dimension: Thứ nguyên của một đại lượng là một tính
chất vật lí mà đại lượng đó mô tả/ A measure of a physical quantity
Đơn vị/Unit: Đơn vị đo lường là bất kỳ một đại lượng vật lý, hay tổng
quát là một khái niệm, nào có thể so sánh được, ở điều kiện tiêu chuẩn
(thường không thay đổi theo thời gian) dùng để làm mốc so sánh cho các
đại lượng cùng loại trong đo lường/A way to assign a number to that dimension.
Có 7 loại thứ nguyên cơ bản/ There are seven primary dimensions : 1. Mass/khối lượng m (kg) 2. Length/Chiều dài L (m) 3. Time/Thời gian t (sec) 4. Temperature/nhiệt độ T (K) 5. Current/ Dòng điện I (A)
6. Amount of Light/ lượng ánh sáng C (cd)
7. Amount of matter/ Lượng vật chất N (mol)
Tất cả thứ nguyên dẫn xuất đều có thể được tạo bởi các tổ hợp của các thứ nguyên cơ bản
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
Thứ$nguyên$và$đơn$vị
Thứ nguyên của tốc độ
Thứ nguyên của gia tốc
Thứ nguyên của lực
Thứ nguyên của công
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
Định luật đồng nhất thứ nguyên: Các thừa số trong phép cộng phải có cùng thứ nguyên
Không thể cộng một quả cam với 2 quả táo
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
Định luật đồng nhất thứ nguyên: Các thừa số trong phép cộng phải có cùng thứ nguyên Phương trình Bernoulli
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
Phương trình của các đại lượng không thứ nguyên : Nếu ta chia mỗi
thừa số của một phương trình với tập hợp các biến số và hằng số
(mà tích của nó có cùng thứ nguyên thì ta sẽ thu được Phương trình
của các đại lượng không thứ nguyên
Most of which are named after a notable scientist or engineer (e.g.,
the Reynolds number and the Froude number).
Chia 2 vế của pt Bernoulli
cho 1 đại lượng áp suất (ví
dụ: P!), ta thu được phương
trình của các đại lượng không thứ nguyên (phương trình chuẩn số).
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
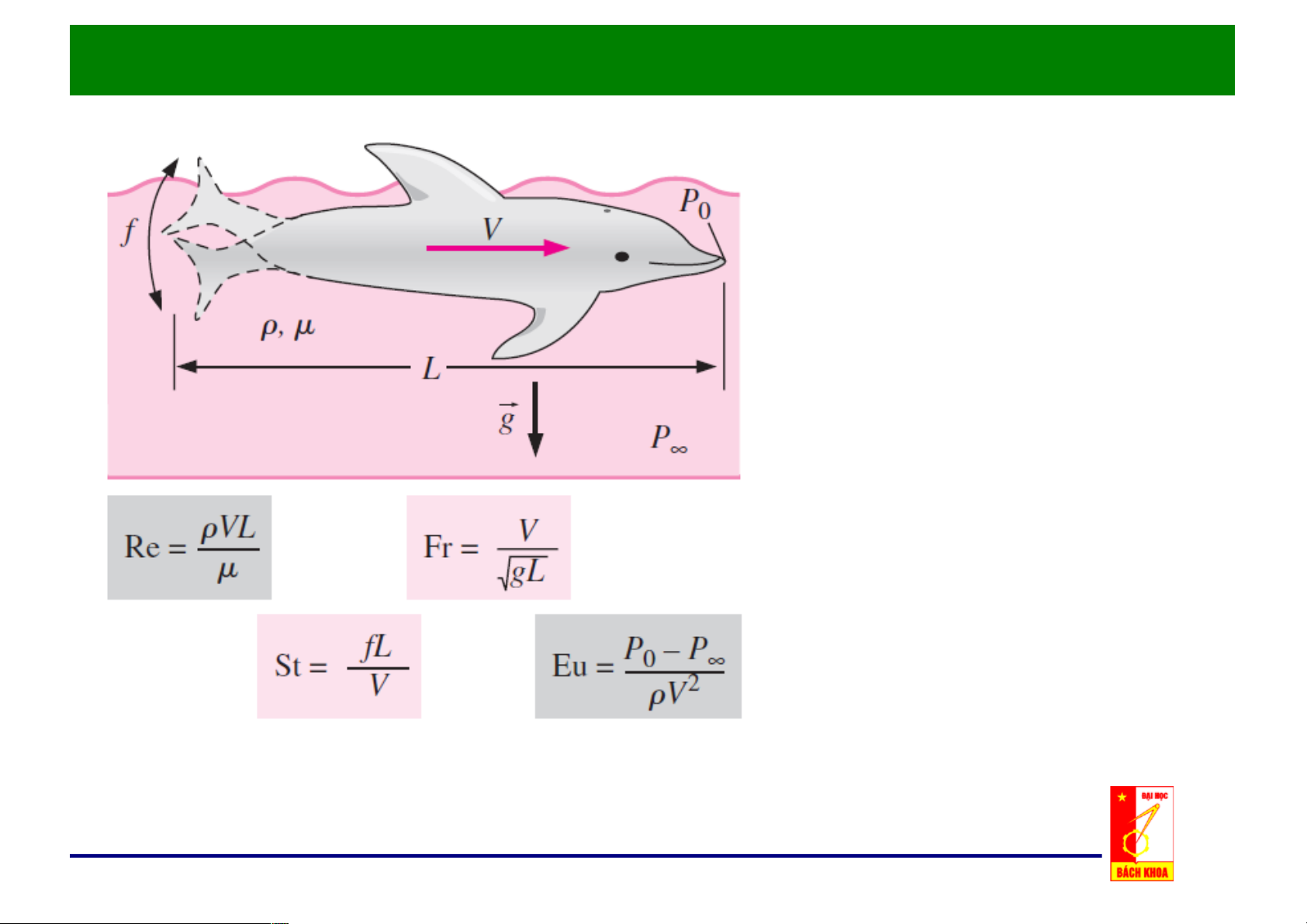
Trong các bài toán thuỷ lực
với một bề mặt tự do, thường
có các đại lượng sau: chiều dài
đặc trưng L, vận tốc đặc trưng
V, tần số đặc trưng f, chênh
lệch áp suất P0 ! P". Khi phân
tích thứ nguyên các số hạng
của pt vi phân chất lỏng
chuyển động, thu nhận được 4
chuẩn số đại lượng không thứ
nguyên: chuẩn số Reynolds,
chuẩn số Froude, chuẩn số
Strouhal, và chuẩn số Euler
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
Trong cơ học chất lỏng/Fluid Mechanics
• Chuẩn số Reynolds/ The Reynolds number (Re): là một đại lượng
không thứ nguyên đại diện cho tỉ lệ giữa độ nhớt và lực quán tính.
•Chuẩn số Froude /The Froude number (Fr) là một đại lượng không
thứ nguyên đại diện cho tỉ lệ giữa quán tính của vật với lực trọng
trường. Trong cơ học chất lỏng, chuẩn số Froude được sử dụng để xác
định trở lực của vật nhúng 1 phần trong chất lỏng chuyển động trong
chất lỏng, cho phép so sánh các vật thể có kichx thước khác nhau thác
tất định điện trở của một đối tượng Nhiều ngập di chuyển qua nước, và
cho phép so sánh các đối tượng của các kích cỡ khác nhau.
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
Trong cơ học chất lỏng/Fluid Mechanics,
•Chuẩn số Strouhal/The Strouhal number (St) là một đại
lượng không thứ nguyên mô tả dòng chảy dao động.
•Chuẩn số Euler/ The Euler number (Eu) là một đại lượng
không thứ nguyên mô tả mối quan hệ giữa tổn thất áp suất
và động năng. Đối với dòng chảy lý tưởng không có ma sát thì chuẩn số Euler = 1
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
Nhiệm&vụ&của&phương&pháp&phân&tích&thứ& nguyên
1. Lập chuẩn số độc lập cho một quá trình cần nghiên cứu
2. Nếu quá trình được mô tả từ một pt vi phân thì các
chuẩn số sẽ được lập trực tiếp từ chúng
3. Phân tích thứ nguyên là phương pháp để từ những
thứ nguyên của các đại lượng tham gia quá trình
đưa ra ít nhất các thông số ảnh hưởng mới, là
những đại lượng không thứ nguyên
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên Định%lý%π
- Quan hệ hàm số giữa n biến số của một hiện tượng
(quá trình) mà các biến số này có m đơn vị cơ bản
của thứ nguyên có thể lập n-m tích lũy thừa không
thứ nguyên của các biến ấy.
- Có n-m chuẩn số đồng dạng
- Nếu có quan hệ : f(x1,x2, x3) =0 giữa các đại lượng
ảnh hưởng thì cũng có dạng g(π1,π2, π3) =0
- Tích lũy thừa không thứ nguyên
πj – chuẩn số không thứ nguyên j=1,2,…s
n số lượng các biến ảnh hưởng n
m – số đơn vị được dùng " = k x j ! Pk k =1
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
Vận$dụng$thực$tiễn$của$phân$tích$thứ$nguyên
- Lý thuyết đồng dạng cho phép biến đổi phương
trình vi phân mô tả một quá trình thành một phương trình chuẩn số
- Các quá trình vận chuyển chất lỏng, truyền nhiệt,
chuyển khối,… đều có thể được biểu thị qua chuẩn số đồng dạng
- Mỗi chuẩn số đồng dạng đều phản ánh một hiện
tượng và mang tên người đã lập ra nó
Thuyết đồng dạng & Phương pháp phân tích thứ nguyên
Vận$dụng$thực$tiễn$của$phân$tích$thứ$nguyên
- Phân tích thứ nguyên để: tạo ra các chuẩn số đồng dạng
- Quan hệ giữa các chuẩn số được xác định bằng thực nghiệm
- Yêu cầu quá trình xác định bằng thực nghiệm:
- giảm tối đa các điểm đo,
- đảm bảo độ chính xác cần thiết
- n-m chuẩn số độc lập được xác định từ phương trình
vi phân tuyến tính với nhiều phương pháp Phép thử hệ thống Nguyên tắc Kramer
Dùng đại lượng chuẩn (làm đại lượng dẫn)
Cấu tạo từ các thông số vật lý
Lập từ phương trình vi phân