Lý thuyết, phương pháp giải toán và bài tập phép quay – Lê Bá Bảo

Tài liệu gồm 23 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, tổng hợp lý thuyết, hướng dẫn phương pháp giải toán và tuyển chọn bài tập trắc nghiệm – tự luận 

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

23 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 1
(+)
M'
M
O
A
B
B'
O
(+)
(+)
O
d'
d
B'
A'
B
A
(+)
R = R'
R'
R
I'
I
O
ABC =
A'B'C'
C'
B'
A'
C
B
A
(+)
O
Chủ đề 2: PHÉP QUAY
I- LÝ THUYẾT:
1. Định nghĩa: Cho điểm O và góc lượng giác
.
Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành
điểm M’ sao cho
'OM OM
và góc lượng giác
; ' .
OM OM
Ký hiệu:
O;
Q
2. Nhận xét:
a) PhÐp quay t©m O gãc quay 2 , lµ phÐp ®ång nhÊt.
b) PhÐp quay t©m O gãc quay 2 1 , lµ phÐp ®èi xøng t©m O.

a k k
a k k
3. Tính chất:
Tính chất 1:
;
;
'
, : ' '
'
PhÐp quay b¶o toµn kho¶ng c¸ch gi÷a hai ®iÓm bÊt kú PhÐp dêi h×nh
O
O
Q A A
A B A B AB
Q B B
Tính chất 2: Phép quay:
1. Bảo toàn tính thẳng hàng và thứ tự của các điểm tương ứng.
2. Biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.
3. Biến đường thẳng thành đường thẳng.
4. Biến tam giác thành tam giác bằng nó.( trực tâm
trực tâm, trọng tâm
trọng
tâm). Góc thành góc bằng nó.
5. Biến đường tròn thành đường tròn có cùng bán kính (
'
'
II
RR
).
4. Một số kết quả và dấu hiệu sử dụng phép quay để giải toán
0
0
0
0
90
90
60
60
;
;
;
;
;
()
a. ABC c©n t¹i A: ( ) . §Æc biÖt: ABC vu«ng c©n t¹i A:
()
()
b. Chøng minh ABC ®Òu:
()
c. Chøng minh ABCD víi O lµ g®iÓm 2 ®êng chÐo lµ h×nh vu

A
A
A
A
B
Q B C
Q B C
Q B C
Q B C
Q C A
0
0
45
45
;
;
( )
«ng:
( )
O
O
Q A B
Q B C
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 2
* MỘT SỐ KẾT QUẢ CẦN LƯU Ý:
1) Ảnh của điểm qua phép quay
00
;90 ; 90
,
OO
QQ
:
Điểm
;
MM
M x y
:
0
0
;90
; 90
'
( ) '( '; '):
'
'
( ) '( '; '):
'
M
O
M
M
O
M
xy
Q M M x y
yx
xy
Q M M x y
yx


2) Giả sử phép quay
;I
Q
biến đường thẳng d thành d’:
Khi đó:
0
0 0 0
0 90 ; '
90 180 ; ' 180
dd
dd


3) Các phương pháp xác định ảnh của đường thẳng d qua
;I
Q
:
Phương pháp 1: Chọn 2 điểm bất kì. Đường thẳng ảnh đi qua 2 ảnh tương ứng.
;
;
;
( ) '
, : ( ) ' ' '
( ) '
I
I
I
Q A A
A B d Q d d A B
Q B B
Phương pháp 2: Chọn 1 điểm A thuộc đường thẳng. Xác định ảnh A’.
Đường thẳng ảnh d’ đi qua A’ và hợp với d một góc
.
Phương pháp 3:
Gồm 2 bước:
Bước 1: Chọn
Hd
với
IH d
. Xác định
;
( ) '
I
Q H H
.
Bước 2: Đường thẳng d’ cần tìm đi qua H’ và vuông góc với IH’.
II- LUYỆN TẬP :
Bài tập 1: Cho điểm
22
(1;2), : 1 0, (C): 2 4 1 0M x y x y x y
. Xác định tọa độ điểm A’,
//
, ( )C
lần lượt là ảnh của M,
, (C)
qua:
a) Phép quay tâm O, góc quay
0
90
.
b) Phép quay tâm O, góc quay
0
90

.
Gợi ý:
a) Ta có:
0
/
;90
( ) ( 2;1)
O
Q M M
.
Dễ thấy :
Qua phép quay
0
;90O
Q
, hình chữ nhật OAMB có ảnh
Là hình chữ nhật OA’M’B’.
Ta có:
0
0
0
/
;90
/
;90
/
;90
( ) (0;1)
( ) ( 2;1)
( ) ( 2;0)

O
O
O
Q A A
Q M M
Q B B
* Kỷ năng xác định ảnh của đường thẳng qua phép quay tâm O, góc quay
0
90
.
Phương pháp 1: Chọn 2 điểm bất kì trên
, xác định ảnh tương ứng. Đường thẳng
/
cần tìm là
đường thẳng qua hai ảnh.
Chọn
(1;2), (0;1) MB
d'
d
H'
H
I
-2
1
2
1
x
y
A'
B'
M'
M
B
A
O
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 3
Ta có:
0
0
//
;90
/ / /
//
;90
( ) ( 2;1)
( ) ( 1;0)
O
O
Q M M
MN
Q N N
.
Đường thẳng
/
đi qua điểm
'( 2;1)M
và có 1 vtcp
' ' (1; 1)MN
Vậy
/
2
:
1
xt
t
yt


Phương pháp 2: Sử dụng mối quan hệ về góc giữa d và d’
Gọi
/
là ảnh của đường thẳng
qua
0
;90O
Q
. Suy ra:
//
:0 x y m
Chọn
0
//
;90
(1;2) ( ) ( 2;1)
O
M Q M M
Ta có:
2 1 0 1mm
.
Vậy
/
: 1 0 xy
Phương pháp 3: Sử dụng quỹ tích:
0
;90
( ) ' '
O
M Q M M
Gọi
0
/
;90
''
( ; ) ( ) ( '; '):
''
O
x y x y
M x y Q M M x y
y x y x



Lúc đó:
'; ' ' ' 1 0 ' ' 1 0M y x y x x y
Vậy
/
: 1 0 xy
Nhận xét: Trong 3 phương pháp trên,
- Phương pháp 1 tỏ ra hiệu quả cho tất cả các phép biến hình (dù dài dòng).
* Xác định ảnh của đường tròn:
Phương pháp 1: Theo tính chất của phép quay: Biến đường tròn thành đường tròn có cùng bán kính.
Ta có
(1;2)
;
2
:
M
C M R
R
0
/
;90
( ) ( 2;1)
O
Q M M
là tâm của đường tròn ảnh
/
C
.
Vậy đường tròn
/
C
:
22
2 1 4xy
Phương pháp 2: Sử dụng quỹ tích.
Gọi
0
/
;90
''
( ; ) ( ) ( '; '):
''
O
x y x y
M x y C Q M M x y
y x y x



Lúc đó:
22
'; ' ' ' 2 ' 4 ' 1 0M y x C y x y x
22
( ') ( ') 4 ' 2 ' 1 0x y x y
Vậy
/ 2 2
: 4 2 1 0 C x y x y
Hoàn toàn tương tự, giải quyết yêu cầu b.
PHẦN KIẾN THỨC ĐỌC THÊM:
CÔNG THỨC TỌA ĐỘ VỚI PHÉP QUAY VỚI
TÂM VÀ GÓC QUAY BẤT KÌ
Đặt vấn đề:
Trong Hình học 10, Đai số 10 và 11, lý thuyết về lượng giác một cách cơ bản thì chúng ta đã
thừa nhận:
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 4
Với mỗi góc lượng giác
bất kì.
Xác định trên (C) điểm M sao cho:
xOM
Lúc đó:
;
MM
M x y
, ta thừa nhận:
sin ; ; ; cos tan = cot =
MM
MM
MM
yx
yx
xy

Hay:
;sincosM

(*)
Sở dĩ có cách biễu diễn (*) vì đường tròn lượng giác có bán kính
1R
.
Và thực chất đây là cách biểu diễn đơn giản nhất đối với hệ tọa độ cực gốc O, có góc và bán kính R
bất kì.
TỔNG QUÁT: Đối với hệ tọa độ cực: gốc O có góc
và bán kính R bất kì.
Điểm M với góc lượng giác
xOM
, thì ta có:
; sincosM R R

Bài tập 2: Cho điểm
22
(1;2), : 1 0, (C): 2 4 1 0M x y x y x y
. Xác định tọa độ điểm M’,
//
, ( )C
lần lượt là ảnh của M,
, (C)
qua phép quay tâm O, góc quay
2

k
.
Gợi ý:
Giả sử góc lượng giác
0
;Ox OM
. Khi đó, góc lượng giác
/
0
;Ox OM


Vậy điểm
00
; sin5cos 5M

Do đó:
0
0
0
0
1
1
5
2
sin 2
sin
5
cos
5cos
5


và điểm
/
00
); sin( )5cos( 5M

nên:
0 0 0
0 0 0
) . sin .sin 2sin
sin( ) sin . .sin 2 sin
5cos( 5 cos cos cos
5 5 cos cos cos
Vậy điểm
/
2sin ;2 sincos cosM

(y.c.b.t)
Hoàn toàn tương tự như yêu cầu trên, độc giả tự giải quyết.
Bài tập 3: Cho điểm
(1;2), ( 2;3)IM
. Xác định tọa độ điểm M’ là ảnh của M qua phép quay tâm I,
góc quay
2

k
.
Gợi ý:
* Trước hết ta tìm điểm N sao cho
ON IM
:
Giả sử điểm
( ; )N x y
, khi đó:
21
( 3;1)
32
x
ON IM N
y

* Gọi N’ là ảnh của
( 3;1)N
qua
;I
Q
, khi đó do M’ là ảnh của M qua
;I
Q
và
ON IM
nên
//
ON IM
.
* Bây giờ, ta tính tọa độ của điểm N’. Giả sử, góc lượng giác
0
;Ox ON
. Khi đó, góc lượng giác
/
0
;.

Ox OM
Vậy điểm
00
; sin5cos 5M

O
K
H
x
y
M
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 5
Do đó:
0
0
0
0
3
3
10
1
sin 1
sin
10
cos
10cos
10



và điểm
/
00
); sin( )10cos( 10N

nên:
0 0 0
0 0 0
) . sin .sin 3 sin
sin( ) sin . .sin 3sin
10cos( 10 cos cos cos
10 10 cos cos cos
Suy ra: điểm
/
sin ; 3sin3cos cosN
* Giả sử:
/
( '; ')M x y
thì
/
( 1; 2)IM x y
Do
//
1 sin
.
2 3sin
3cos
os



x
ON IM
y
Do đó:
/
1 sin ;2 3sin3cos cosM
(y.c.b.t)
Bài tập 4:
Cho ®êng th¼ng d vµ ®iÓm O cè ®Þnh kh«ng thuéc d, M lµ ®iÓm di ®éng trªn d.
H·y t×m tËp hîp c¸c ®iÓm N sao cho OMN ®Òu.
Gợi ý: Biểu diễn điểm N theo M thông qua phép quay
0
60
Do tam giác OMN đều nên tồn tại hai phép quay:
0
0
;60
; 60
()
()
O
O
Q M N
Q M N
Do M thuộc đường thẳng d nên N thuộc vào
đường thẳng d’, d’’ lần lượt là ảnh của d qua
0
;60O
Q
và
0
; 60O
Q
.
Vậy quỹ tích cần tìm là 2 đường thẳng d’ và d’’.
Tương tự:
Bài tập 5:
Cho ®trßn (C) vµ ®iÓm O cè ®Þnh kh«ng thuéc (C), M lµ ®iÓm di ®éng trªn (C).
H·y t×m tËp hîp c¸c ®iÓm N sao cho OMN vu«ng c©n t¹i O.
Gợi ý: Biểu diễn điểm N theo M thông qua phép quay
0
90
Bài tập 6: Cho 2 tam giác vuông cân ABC và ADE (như hình vẽ). Gọi G và G’ lần lượt là trọng tâm
các tam giác ABD và ACE. Chứng minh tam giác AGG’ vuông cân.
Gợi ý: Xây dựng phép quay tâm A góc quay
0
90
biến G thành G’.
Xét phép quay:
0
;90A
Q
có :
0
0
;90
;90
()
()
A
A
Q B C
Q D E
Suy ra:
0
;90
()
A
Q ABD ACE
. Do G và G’ lần lượt là trọng tâm các tam giác ABD và ACE nên
theo tính chất của phép quay:
0
;90
0
'
( ) '
' 90
A
AG AG
Q G G
GAG

Vậy tam giác AGG’ vuông cân. (đ.p.c.m)
d''
d'
d
N
N
O
M
60
0
60
0
A
B
C
D
E
G'
G
E
D
C
B
A
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 6
Bài tập 7:
Cho ba ®iÓm A, B, C theo thø tù trªn th¼ng hµng. VÏ cïng mét phÝa hai tam gi¸c
®Òu ABE, BCF. Gäi M vµ N t¬ng øng lµ hai trung ®iÓm cña AF vµ CE. Chøng minh r»ng:
BMN lµ tam gi¸c ®Òu.
Gợi ý: Xây dựng phép quay tâm B góc quay
0
60
biến N thành M.
Xét phép quay:
0
;60B
Q
có :
0
0
;60
;60
()
()
B
B
Q C F
Q E A
Suy ra:
0
;60
()
B
Q CE FA
.
Do N và M lần lượt là trung điểm các cạnh CE và AF nên theo
tính chất của phép quay:
0
;60
0
()
60
B
BN BM
Q N M
MBN

Vậy tam giác BMN đều. (đ.p.c.m)
Bài tập 8: Cho tam giác ABC. Dựng về phía ngoài tam giác các hình vuông BCIJ, ACMN, ABEF và
gọi O, P, Q lần lượt là tâm của của chúng.
a) Gọi D là trung điểm của AB. Chứng minh rằng:
DOP
vuông cân tại D.
b) Chứng minh rằng:
AO PQ vµ AO=PQ.
Gợi ý: Xây dựng phép quay tâm D góc quay
0
90
biến O thành P, hoặc sử dụng mối quan hệ hình học
liên quan.
a) Xét phép quay
0
;90C
Q
0
0
0
;90
;90
;90
()
()
()
C
C
C
Q M A
Q MB MI
Q B I

(1)
MB AI
MB AI
Dễ thấy, DP là đường trung bình của các tamgiác ABM
nên:
1
2
//
DP BM
DP BM
(2)
Tương tự, DO là đường trung bình của tam giác ABI nên:
1
2
//
DO AI
DO AI
(3)
Từ (1), (2) và (3) suy ra:
DO DP
DO DP
hay
DOP
vuông cân tại D. (đ.p.c.m)
b) Theo câu a,
DOP
vuông cân tại D nên
0
;90
()
D
Q O P
(*)
Mặt khác:
0
;90
()
D
Q A Q
(**)
Từ (*) và (**) suy ra:
0
;90
()
D
AO QP
Q AO QP
AO QP

(đ.p.c.m)
M
N
F
E
A
B
C
D
Q
P
O
J
I
B
A
C
F
N
M
E
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 7
Bài tập 9:
Cho tø gi¸c låi ABCD. VÒ phÝa ngoµi tø gi¸c dùng c¸c tam gi¸c ®Òu ABM, CDP.
VÒ phÝa trong tø gi¸c dùng hai tam gi¸c ®Òu BCN vµ ADK.CMR: MNPK lµ h×nh b×nh hµnh.
Gợi ý:
Xét phép quay
0
;60B
Q
:
0
0
;60
;60
()
()
B
B
Q M A
Q N C
0
;60
( ) (1)
B
Q MN AC MN AC
Xét phép quay
0
;60D
Q
:
0
0
;60
;60
()
()
D
D
Q K A
Q P C
0
;60
( ) (2)
D
Q KP AC KP AC
Từ (1) và (2) suy ra:
MN KP
(*)
Tương tự, chứng minh được
MK PN
(**)
Từ (*) và (**) suy ra: MKNP là hình bình hành (đ.p.c.m)
Bài tập 10: Cho 2 hình vuông ABCD và BEFG. Gọi M, N lần lượt là trung điểm của AG và CE.
Chứng minh rằng: Tam giác BMN vuông cân.
Gợi ý: Xây dựng phép quay tâm B góc quay
0
90
biến N thành M.
Xét phép quay:
0
;90B
Q
có :
0
0
;90
;90
()
()
B
B
Q C A
Q E G
Suy ra:
0
;90
()
B
Q CE AG
.
Do N và M lần lượt là trung điểm các cạnh CE và AG
nên theo tính chất của phép quay:
0
;90
0
()
90
B
BN BM
Q N M
MBN

Vậy tam giác MBN vuông cân. (đ.p.c.m)
Bài tập 11:
1 1 1
VÒ phÝa ngoµi tam gi¸c ABC, dùng ba tam gi¸c ®Òu BCA , ACB , ABC .
1 1 1
Chøng minh r»ng: AA , BB , CC ®ång quy.
Gợi ý: Sử dụng tính chất phép quay: Bảo toàn tính thẳng hàng và thứ tự của 3 điểm bất kì.
Giả sử:
11
AA CC I
. Cần chỉ rõ:
11
hay , , I BB B I B
thẳng hàng.
Thật vậy, xét phép quay
0
;60B
Q
:
0
0
1
;60
1
;60
()
()
B
B
Q A C
Q A C
11
0
1
0
11
60
; 60
AA CC
AIC
AA CC
(1)
Lấy trên
1
IC
điểm E sao cho:
AI EI
(2)
Từ (1) và (2) suy ra:
AEI
là tam giác đều.
K
N
M
P
D
A
B
C
M
N
G
F
E
D
B
C
A
E
I
B
1
C
1
A
1
A
B
C
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 8
Lúc đó, xét phép quay
0
;60A
Q
:
0
0
0
;60
1
;60
1
;60
()
()
()
A
A
A
Q E I
Q C B
Q C B
Do
1
, , E C C
thẳng hàng nên theo tính chất của phép quay:
1
, , I B B
thẳng hàng. Điều này chứng tỏ
1 1 1
AA , BB , CC ®ång quy.
(đ.p.c.m)
Bài tập 12: Cho tam giác ABC. Trên các cạnh AB và BC, về phía ngoài tam giác, dựng 2 hình vuông
ABMN và BCPQ. Chứng minh rằng: Các tâm của hình vuông này cùng với 2 trung điểm của MQ,
AC tạo thành 1 hình vuông.
Gợi ý:
Gọi
1
O
và
3
O
lần lượt là tâm 2 hình vuông ABMN và BCPQ, còn
2
O
và
4
O
lần lượt là trung điểm
của AC , MQ.
Xét phép quay
0
;90B
Q
:
0
0
0
;90
;90
;90
()
()
()
B
B
B
Q M A
MC AQ
Q MC AQ
Q C Q MC AQ


(1)
Dễ thấy:
1 2 2 3 3 4 4 1
, , , O O O O O O O O
lần lượt là đường
trung bình của các tam giác MAC, ACQ, MCQ, MAQ.
Suy ra:
12
12
//
1
2
O O MC
O O MC
(2) và
23
23
//
1
2
O O AQ
O O AQ
(3)
Từ (1), (2) và (3) suy ra:
1 2 2 3
1 2 2 3
(*)
O O O O
O O O O
Tương tự, do
34
34
//
1
2
O O MC
O O MC
(4) và
41
41
//
1
2
O O AQ
O O AQ
(5)
Từ (1), (4) và (5) suy ra:
3 4 4 1
3 4 4 1
(**)
O O O O
O O O O
Từ (*), (**) suy ra:
1 2 3 4
O O O O
là hình vuông. (đ.p.c.m)
Bài tập 13: Cho điểm A và 2 đường tròn (C), (C’) phân biệt. Dựng theo chiều dương tam giác đều
ABC, biết đỉnh B, C lần lượt nằm trên (C) và (C’).
Gợi ý:
Phân tích: Do tam giác ABC đều nên:
0
0
;60
( )
; 60
A
AB AC
Q B C
AB AC
Cách dựng:
- Dựng đường tròn (C’’) là ảnh của (C) qua
0
;60A
Q
.
- Xác định giao điểm
( ') ( '')C C C
.
- Thực hiện phép quay
0
; 60
()
A
Q C B
O
4
O
3
O
2
O
1
N
M
Q
P
B
A
C
O'
O
(C'')
(C')
(C)
C'
B'
C
B
A
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 9
Biện luận: Nghiệm bài toán tùy thuộc số giao điểm của (C’’) và (C’).
Bài tập 14: Cho 2 đường thẳng a, b song song và một điểm G không nằm trên chúng. Xác định tam
giác đều ABC có
, A a B b
và G là trọng tâm tam giác ABC.
Gợi ý:
Phân tích: Giả sử đã dựng được
ABC
thỏa đk.
Ta có:
0
120
GA GB GC
AGB BGC CGA

Suy ra:
0
;120
( )
G
Q A B
Cách dựng:
- Dựng a’ là ảnh của a qua
0
;120G
Q
.
- Xác định
'B a b
.
- Các đỉnh A, C là ảnh của B qua
00
;120 ; 120
,
GG
QQ
Biện luận: Bài toán luôn có 1 nghiệm hình.
Bài tập 15: Cho tam giác ABC và vẽ phía ngoài hai hình vuông ABMN, ACPQ.
a) Chứng minh :
BQ CN
và
BQ CN
.
b) Gọi O, O’ lần lượt là tâm của các hình vuông ABMN, ACPQ. Chứng minh rằng: Tam giác
OIO’ vuông cân.
Gợi ý:
a) Xét phép quay
0
; 90A
Q
:
0
0
; 90
; 90
()
()
A
A
Q B N
Q Q C
0
; 90
()
A
BQ NC
Q BQ NC
BQ NC
(đ.p.c.m)
b) Ta có: OI và O’I lần lượt là đường trung bình của
các tam giác BNC và BCQ nên suy ra:
//
(1)
1
2
OI NC
OI NC
và
' //
(2)
1
'
2
O I BQ
O I BQ
Theo câu a, và từ (1), (2) suy ra:
'
'
OI O I
OI O I
. Vậy tam giác OIO’ vuông cân. (đ.p.c.m)
Bài tập 16: Cho 2 đường tròn (O) và (O’) bằng nhau và cắt nhau ở A và B. Từ điểm I cố định kẻ cát
tuyến di động IMN với (O), MB và NB cắt (O’) tại M’, N’.
Chứng minh rằng: Đường thẳng M’N’ luôn đi qua 1 điểm cố định.
Gợi ý: Gọi
;'AO AO
.
Xét phép quay
;A
Q
:
;
;
( ) '
( ) ( ')
'
A
A
Q O O
Q O O
RR

Vì MM’ và NN’ qua B nên:
; ' ; ' ; 'AO AO AM AM AN AN
a'
b
a
G
120
0
C
A
B
I
C
A
B
P
Q
M
N
O
O'
I'
I
M'
N'
O'
A
B
M
N
O
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 10
Lúc đó:
;
;
;
( ) '
( ) ' '
( ) '
A
A
A
Q M M
Q MN M N
Q N N

Do MN đi qua điểm I cố định nên M’N’ đi qua điểm cố định I’ là ảnh của I qua
;A
Q
.
Bài tập 17: Chứng minh rằng: Các đoạn thẳng nối tâm các hình vuông dựng trên các cạnh của một
hình bình hành về phía ngoài, hợp thành một hình vuông.
Gợi ý:
Gọi
1 2 3 4
, , , I I I I
lần lượt là tâm của các hình vuông cạnh AB, BC, CD, DA
Xét phép quay
0
2
;90I
Q
:
0
2
;90
()
I
Q B C
(1)
Do
13
I BA I CD
nên
31
I C BI
. (2)
Mặt khác:
0
31
31
45
//
DCI ABI
I C BI
DC AB


(3)
Từ (1), (2) và (3) suy ra:
0
2
1 2 2 3
13
;90
1 2 2 3
()
I
I I I I
Q I I
I I I I

Lý luận tương tự ta có
1 4 4 3
I I I I
và
1 4 4 3
I I I I
. Vậy
1 2 3 4
I I I I
là hình vuông. (đ.p.c.m)
III- BÀI TẬP TỰ LUẬN - TỰ LUYỆN:
00
( ;90 ) ( ;60 )
1) Cho tam gi¸c ABC. X¸c ®Þnh ¶nh cña ABC qua c¸c phÐp quay:
a) a)
2) Cho h×nh vu«ng ABCD víi O lµ t©m. Gäi M, N lÇn lît lµ trung ®iÓm c
AA
QQ
00
(0;90 ) ( ; 90 )
ña AB, AD. X¸c
®Þnh ¶nh cña AMN qua phÐp quay:
a) a)
O
QQ
00
;90 ; 90
3) Trong mÆt ph¼ng cho c¸c ®iÓm (0;3), (-2;0), (1;4). X¸c ®Þnh to¹ ®é c¸c ®iÓm A',B', C'
lÇn lît lµ ¶nh cña A, B, C qua:
a) b)
4) Cho
OO
A B C
QQ
0
22
;90 ; 90
®êng th¼ng : 4 2 0 vµ ®êng trßn (C): 4 2 0. X¸c ®Þnh
ph¬ng tr×nh ', (C') lÇn lît lµ ¶nh cña vµ (C) qua phÐp quay:
a) b)
OO
x y x y x y
QQ

0
5) Cho n÷a ®êng trßn t©m O vµ ®êng kÝnh BC. §iÓm A ch¹y trªn n÷a ®êng trßn ®ã.
Dùng vÒ phÝa ngoµi cña ABC h×nh vu«ng ABEF. Chøng minh r»ng: E ch¹y trªn n÷a ®êng
trßn cè ®Þnh.
6) Cho ®êng th¼ng d vµ
®iÓm O cè ®Þnh kh«ng thuéc d, M lµ ®iÓm di ®éng trªn d. H·y t×m
tËp hîp c¸c ®iÓm N sao cho OMN ®Òu.
7) Cho 2 ®êng trßn (O) vµ (O') b»ng nhau vµ c¾t nhau t¹i A, B. Tõ 1 ®iÓm I cè ®Þnh kÎ c¸t tuyÕn
di
®éng IMN víi (O), MB vµ NB lÇn lît c¾t (O') t¹i M', N'. CMR: M'N' lu«n ®i qua 1 ®iÓm cè ®Þnh.
I
4
I
3
I
2
I
1
D
C
B
A
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 11
8) Cho ba ®iÓm A, B, C theo thø tù trªn th¼ng hµng. VÏ cïng mét phÝa, dùng hai tam gi¸c
®Òu ABE, BCF. Gäi M vµ N t¬ng øng lµ hai trung ®iÓm cña AF vµ CE. Chøng minh r»ng:
BMN lµ tam gi¸c ®Òu.
9) Cho tam gi¸c ABC. Qua ®iÓm A dùng hai tam gi¸c vu«ng c©n ABE vµ ACF. Gäi M lµ trung
®iÓm cña BC vµ gi¶ sö AM FE=H. Chøng minh r»ng: AH lµ ®êng cao cña AEF.
10) Cho tø gi¸c låi ABCD. VÒ phÝa ngoµi

tø gi¸c dùng c¸c tam gi¸c ®Òu ABM, CDP. VÒ phÝa
trong tø gi¸c dùng hai tam gi¸c ®Òu BCN vµ ADK. Chøng minh: MNPK lµ h×nh b×nh hµnh.
11) Cho tam gi¸c ABC. VÒ phÝa ngoµi tam gi¸c, dùng ba tam gi¸c ®Òu BC
1 1 1
1 1 1
A , ACB , ABC .
Chøng minh r»ng: AA , BB , CC ®ång quy.
12) Cho tam gi¸c ABC. Dùng vÒ phÝa ngoµi tam gi¸c c¸c h×nh vu«ng BCIJ, ACMN, ABEF vµ
gäi O, P, Q lÇn lît lµ t©m cña chóng.
a) Gäi D lµ trung ®iÓm cña AB. Chøng minh r»ng: DOP vu«ng c©n t¹i D.
b) Chøng minh r»ng: AO PQ vµ AO=PQ.
13) Cho tam gi¸c ABC. Trªn c¸c c¹nh AB vµ BC, vÒ phÝa ngoµi tam gi¸c dùng 2 h×nh vu«ng
ABMN, BCPQ. Chøng minh r»ng: C¸c t©m cña h×nh vu«ng nµy cïng víi 2 trung ®iÓm cña
MQ, AC t¹o thµnh 1 h×nh vu«ng.
III- BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho hai điểm phân biệt
,AB
và
là góc lượng giác bất kì. Biết
11
;;
,,
OO
Q A A Q B B


khẳng định nào sau đây đúng?
A.
11
.A B AB
B.
11
.A B AB
C.
11
.A B AB
D.
11
.A B AB
Câu 2: Cho tam giác đều
ABC
(thứ tự đỉnh theo chiều dương lượng giác), khẳng định nào sau đây sai?
A.
;
3
.
A
Q B C



B.
;
3
.
A
Q C B



C.
7
;
3
.
A
Q C B



D.
7
;
3
.
A
Q C B



Câu 3: Gọi hình vuông
ABCD
tâm
O
(các đỉnh theo thứ tự theo chiều ngược chiều kim đồng hồ).
Khẳng định nào sau đây đúng?
A.
0
O;90
.Q B A
B.
0
O;90
.Q B C
C.
0
O;90
.Q B O
D.
0
O;90
.Q B D
Câu 4: Cho hình vuông
MNPQ
(thứ tự các đỉnh cùng chiều quay của kim đồng hồ). Phép quay nào
sau đây biến điểm
M
thành điểm
.P
A. Phép quay tâm
Q
góc
90 .
B. Phép quay tâm
Q
góc
45 .
C. Phép quay tâm
Q
góc
45 .
D. Phép quay tâm
Q
góc
90 .
Câu 5: Trong mặt phẳng với hệ tọa độ
,Oxy
cho điểm
1;2 .A
Khẳng định nào sau đây đúng?
A.
3
;
2
2;1 .
O
Q A A




B.
3
;
2
2; 1 .
O
Q A A




C.
3
;
2
1; 2 .
O
Q A A



D.
3
;
2
2; 1 .
O
Q A A



Câu 6: Có bao nhiêu phép quay với góc quay
00
0 360

biến tam giác đều cho trước thành
chính nó?
A.
0.
B.
1.
C.
2.
D.
4.
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 12
Câu 7: Biết thực hiện liên tiếp hai phép quay
;I
Q
và
;
, 2 , 2 , ,
I
Q k k k k

ta được phép
đồng nhất. Khẳng định nào sau đây đúng?
A.
2 , .kk
B.
2 , .kk
C.
2 , .
2
kk
C.
2 , .
2
kk
Câu 8: Phép biến hình nào sau đây không có tính chất: “Biến một đường thẳng thành một đường
thẳng song song hoặc trùng với nó”?
A. Phép đồng nhất. B. Phép vị tự. C. Phép quay bất kì. D. Phép tịnh tiến.
Câu 9: Cho đường thẳng
và điểm
.I 
Phép quay tâm
I
với góc quay
nào sau đây thì biến
đường thẳng thành chính nó?
A.
0
60 .
B.
0
90 .
C.
0
180 .
D.
0
360 .
Câu 10: Phép quay tâm
I
góc quay
90
biến đường thẳng
d
thành đường thẳng
d
. Khẳng định nào
sau đây là đúng?
A.
dd
. B.
//dd
. C.
dd
. D.
, 45 .dd

Câu 11: Trong mặt phẳng với hệ tọa độ
,Oxy
ảnh của điểm
3; 4B
qua phép quay tâm
,O
góc quay
0
90 ,
có tọa độ là
A.
4;3 .
B.
4; 3 .
C.
3;4 .
D.
4; 3 .
Câu 12: Trong mặt phẳng với hệ tọa độ
Oxy
, cho điểm
0;3M
. Xác định tọa độ điểm
M
là ảnh của
điểm
M
qua phép quay tâm
0;0O
, góc quay
270

.
A.
3;0 .M
B.
3;3 .M
C.
0; 3 .M
D.
3;0 .M
Câu 13: Trong mặt phẳng với hệ tọa độ
Oxy
, phép quay tâm
2;1I
, góc quay
0
120
, biến điểm
1;9M
thành điểm
'M
có tọa độ là
A.
1 5 3 2 3 3
;
22
M




. B.
5 8 3 6 3
;
22
M

.
C.
5 8 3 2 2 3
;
22
M




. D.
1 5 3 6 3
;.
22
M


Câu 14: Cho
3;4M
. Tìm ảnh của điểm
M
qua phép quay tâm
O
góc quay
0
30
.
A.
3 3 3
' ; 2 3
22
M




. B.
' 2; 2 3M
.
C.
33
' ;2 3
2
M




. D.
3 3 3
' 2; 2 3
22
M





.
Câu 15: Trong mặt phẳng
Oxy
, cho điểm
1;1M
. Hỏi các điểm sau điểm nào là ảnh của
M
qua phép
quay tâm
O
, góc
45
?
A.
–1;1M
. B.
1;0M
. C.
2;0M
. D.
0; 2M
.
Câu 16: Trong mặt phẳng với hệ tọa độ
,Oxy
cho đường thẳng
: 2 1 0.xy
Ảnh của đường thẳng
qua phép quay tâm
,O
góc quay
0
90
là đường thẳng có phương trình
A.
2 1 0.xy
B.
2 2 0.xy
C.
2 2 0.xy
D.
2 1 0.xy
Câu 17: Trong mặt phẳng với hệ tọa độ
,Oxy
phép quay tâm
O
, góc quay
0
90
biến đường tròn
22
: 4 6 3 0C x y x y
thành đường tròn
C
có phương trình nào sau đây?
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 13
A.
22
: 3 2 16.C x y
B.
22
: 3 2 16.C x y
C.
22
: 2 3 16.C x y
D.
22
: 2 3 16.C x y
Câu 18: Trong mặt phẳng với hệ tọa độ
,Oxy
cho đường tròn
2
2
: 1 5.C x y
Xác định phương
trình đường tròn
C
là ảnh của đường tròn
C
qua phép quay tâm
,O
góc quay
0
90 .
A.
2
2
1 5.xy
B.
2
2
1 5.xy
C.
22
1 1 5.xy
D.
2
2
1 5.xy
Câu 19: Cho tam giác đều
ABC
có
G
là trọng tâm (hình vẽ bên). Khẳng định
nào sau đây đúng?
A.
,120
.
G
Q B A
B.
,60
.
G
Q B A
C.
,120
.
G
Q A B
D.
,6
.
G
Q A B
G
A
B
C
Câu 20: Có bao nhiêu phép quay với góc quay
với
;



biến hình vuông thành chính nó?
A.
1.
B.
2.
C.
3.
D.
5.
Câu 21: Trong mặt phẳng, tìm ảnh của điểm
2; 1A
qua phép quay tâm
O
, góc quay
90 .
A.
1; 2 .M
B.
1;2 .N
C.
1;2 .P
D.
2;1 .Q
Câu 22: Trong mặt phẳng, cho đường thẳng
: 2 1 0xy
. Xác định ảnh của
qua phép quay tâm
O
(
O
là gốc tọa độ), góc quay
90
.
A.
2 1 0.xy
B.
2 1 0.xy
C.
2 1 0.xy
D.
2 1 0.xy
Câu 23: Về phía ngoài tam giác
ABC
, dựng các hình vuông
ABMN
và
ACPQ
. Gọi
,IJ
lần lượt là tâm các hình vuông
ABMN
và
ACPQ
;
E
là trung điểm
BC
(tham khảo hình
vẽ). Khẳng định nào sau đây sai?
A.
EIJ
vuông cân. B.
.BQ CN
C.
.AE MP
D.
.BQ CN
E
J
I
Q
P
N
M
C
B
A
Câu 24: Trong mặt phẳng, cho hai điểm
1; 3 , 2;1AB
. Gọi
,MN
lần lượt là ảnh của
,AB
qua phép
dời hình bằng cách thực hiện liếp tiếp phép tịnh tiến theo vectơ
3; 1v 
và phép quay tâm
O
, góc quay
90
. Viết phương trình đường thẳng
MN
.
A.
4 20 0.xy
B.
4 20 0.xy
C.
4 12 0.xy
D.
4 5 0.xy
Câu 25: Cho tam giác đều
ABC
cạnh
a
có
G
là trọng tâm. Gọi tam giác
MNP
là ảnh của tam giác
ABC
qua phép dời hình bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ
BC
và phép
quay tâm
G
, góc quay
90
. Tính độ dài
.GM
A.
3
.
3
a
B.
23
.
3
a
C.
7
.
2
a
D.
7.a
Câu 26: Cho tam giác đều
ABC
. Hãy xác định góc quay của phép quay tâm
A
biến
B
thành điểm
C
.
A.
30

. B.
90

. C.
120
. D.
0
60

hoặc
0
60
.
Câu 27: Cho hai hình vuông
ABCD
và
BEFG
như hình bên. Tìm
ảnh của tam giác
ABG
qua phép quay tâm
B
, góc quay
90
.
A.
BCD
. B.
CBE
.
C.
ABD
. D.
DCG
.
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 14
Câu 28: Trong mặt phẳng với hệ tọa độ
,Oxy
cho vectơ
3; 2v 
và điểm
1;4 .M
Xác định tọa độ
ảnh của điểm
M
qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm
,O
góc quay
0
90
và phép tịnh tiến theo vectơ
.v
A.
1; 3 .
B.
7; 1 .
C.
2; 6 .
D.
4;2 .
Câu 29: Trong mặt phẳng
Oxy
, cho đường thẳng
: 2 3 9 0d x y
. Viết phương trình của đường thẳng
'd
là ảnh của đường thẳng
d
qua phép quay tâm
O
góc
0
90
.
A.
2 3 9 0xy
. B.
3 2 9 0xy
. C.
3 2 9 0xy
. D.
2 3 9 0xy
.
Câu 30: Trong mặt phẳng tọa độ
Oxy
, cho hai đường thẳng
: 4 3 5 0d x y
và
' : 7 4 0d x y
. Nếu
có phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc quay
với
0 180
là góc nào sau đây?
A.
120
. B.
60
. C.
90
. D.
45
.
Câu 31: Có bao nhiêu điểm biến thành chính nó qua phép quay tâm
O
góc với
2k
(
k
là một
số nguyên)?
A.
0
. B.
1
. C.
2
. D. Vô số.
Câu 32: Cho hình chữ nhật có
O
là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm
O
góc quay
,
02


biến hình chữ nhật trên thành chính nó?
A.Không có. B.Hai. C.Ba. D.Bốn.
Câu 33: Trong mặt phẳng Oxy, cho điểm
( 3;6)B
. Tìm toạ độ điểm E sao cho B là ảnh của E qua phép
quay tâm O góc quay
0
90
.
A.
E(6;3).
B.
E( 3; 6).
C.
E( 6; 3).
D.
E(3;6).
Câu 34: Trong mặt phẳng tọa độ
Oxy
cho phép quay tâm
O
biến điểm
1; 0A
thành điểm
0;1 .A
Khi đó nó biến điểm
1; 1M
thành điểm
A.
1; 1M

. B.
1;1M
. C.
1;1M
. D.
1; 0M
.
Câu 35: Trong mặt phẳng với hệ tọa độ
Oxy
, phép quay tâm
4; 3I
góc quay
180
biến đường thẳng
: 5 0d x y
thành đường thẳng
d
có phương trình
A.
30xy
. B.
30xy
. C.
50xy
. D.
30xy
.
Câu 36: Trong mặt phẳng
Oxy
, cho đường tròn
22
: 4 10 4 0C x y x y
. Viết phương trình
đường tròn
C
biết
C
là ảnh của
C
qua phép quay với tâm quay là gốc tọa độ
O
và góc
quay bằng
270
.
A.
22
: 10 4 4 0C x y x y
. B.
22
: 10 4 4 0C x y x y
.
C.
22
: 10 4 4 0C x y x y
. D.
22
: 10 4 4 0C x y x y
.
Câu 37: Cho lục giác đều
ABCDEF
tâm
O
như hình bên. Tam giác
EOD
là ảnh của tam giác
AOF
qua
phép quay tâm
O
góc quay . Tìm .
O
F
E
D
C
B
A
A.
o
60 .
B.
o
60 .
C.
o
120 .
D.
o
120 .
_______________HẾT_______________
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 15
LỜI GIẢI CHI TIẾT
Câu 1: Cho hai điểm phân biệt
,AB
và
là góc lượng giác bất kì. Biết
11
;;
,,
OO
Q A A Q B B


khẳng định nào sau đây đúng?
A.
11
.A B AB
B.
11
.A B AB
C.
11
.A B AB
D.
11
.A B AB
Lời giải:
Phép quay là phép dời hình nên bảo toàn khoảng cách giữa hai điểm bất kì.
Chọn đáp án D.
Câu 2: Cho tam giác đều
ABC
(thứ tự đỉnh theo chiều dương lượng giác), khẳng định nào sau đây sai?
A.
;
3
.
A
Q B C



B.
;
3
.
A
Q C B



C.
7
;
3
.
A
Q C B



D.
7
;
3
.
A
Q C B



Lời giải:
Ta có:
7
;
3
.
A
Q C B



Vậy C sai.
Chọn đáp án C.
Câu 3: Gọi hình vuông
ABCD
tâm
O
(các đỉnh theo thứ tự theo chiều ngược chiều kim đồng hồ).
Khẳng định nào sau đây đúng?
A.
0
O;90
.Q B A
B.
0
O;90
.Q B C
C.
0
O;90
.Q B O
D.
0
O;90
.Q B D
Lời giải:
0
O;90
Q B C
vậy B đúng.
Chọn đáp án B.
Câu 4: Cho hình vuông
MNPQ
(thứ tự các đỉnh cùng chiều quay của kim đồng hồ). Phép quay nào
sau đây biến điểm
M
thành điểm
.P
A. Phép quay tâm
Q
góc
90 .
B. Phép quay tâm
Q
góc
45 .
C. Phép quay tâm
Q
góc
45 .
D. Phép quay tâm
Q
góc
90 .
Lời giải:
Dễ thấy
, 90
.
Q
Q M P

Chọn đáp án A.
Q
P
N
M
Câu 5: Trong mặt phẳng với hệ tọa độ
,Oxy
cho điểm
1;2 .A
Khẳng định nào sau đây đúng?
A.
3
;
2
2;1 .
O
Q A A




B.
3
;
2
2; 1 .
O
Q A A




C.
3
;
2
1; 2 .
O
Q A A



D.
3
;
2
2; 1 .
O
Q A A



Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 16
Lời giải:
Ta có:
3
;;
22
2; 1 .
OO
Q A Q A A

Chọn đáp án B.
Câu 6: Có bao nhiêu phép quay với góc quay
00
0 360

biến tam giác đều cho trước thành
chính nó?
A.
0.
B.
1.
C.
2.
D.
4.
Lời giải:
Tồn tại hai phép quay với góc quay
00
0 360

:
+)
0
;120
.
G
Q ABC ABC
+)
0
;240
.
G
Q ABC ABC
Với
G
là trọng tâm tam giác
.ABC
120
0
G
A
B
C
Chọn đáp án C.
Câu 7: Biết thực hiện liên tiếp hai phép quay
;I
Q
và
;
, 2 , 2 , ,
I
Q k k k k

ta được phép
đồng nhất. Khẳng định nào sau đây đúng?
A.
2 , .kk
B.
2 , .kk
C.
2 , .
2
kk
C.
2 , .
2
kk
Lời giải:
Khi
2,kk
thì thực hiện liên tiếp hai
phép quay
;I
Q
và
;
, 2 , 2 , ,
I
Q k k k k

ta được phép đồng nhất.
Chọn đáp án B.
2
π
-
α
α
M'
I
M
≡
M''
Câu 8: Phép biến hình nào sau đây không có tính chất: “Biến một đường thẳng thành một đường
thẳng song song hoặc trùng với nó”?
A. Phép đồng nhất. B. Phép vị tự. C. Phép quay bất kì. D. Phép tịnh tiến.
Lời giải:
Phép quay với góc quay
2k

hoặc
2,kk
biến một đường thẳng thành một
đường thẳng song song hoặc trùng với nó.
Chọn đáp án C.
Câu 9: Cho đường thẳng
và điểm
.I 
Phép quay tâm
I
với góc quay
nào sau đây thì biến
đường thẳng thành chính nó?
A.
0
60 .
B.
0
90 .
C.
0
180 .
D.
0
360 .
Lời giải:
;60
; 60
I
Q
. Vậy A sai
;90O
Q

. Vậy B sai
//
;180O
Q

. Vậy C sai
;360O
Q

. Vậy D đúng
Chọn đáp án D.
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 17
Câu 10: Phép quay tâm
I
góc quay
90
biến đường thẳng
d
thành đường thẳng
d
. Khẳng định nào
sau đây là đúng?
A.
dd
. B.
//dd
. C.
dd
. D.
, 45 .dd

Lời giải:
Chọn đáp án A.
Câu 11: Trong mặt phẳng với hệ tọa độ
,Oxy
ảnh của điểm
3; 4B
qua phép quay tâm
,O
góc quay
0
90 ,
có tọa độ là
A.
4;3 .
B.
4; 3 .
C.
3;4 .
D.
4; 3 .
Lời giải:
; 90
4
4; 3
3
BB
O
BB
xy
Q B B B
yx


.
Chọn đáp án B.
Câu 12: Trong mặt phẳng với hệ tọa độ
Oxy
, cho điểm
0;3M
. Xác định tọa độ điểm
M
là ảnh của
điểm
M
qua phép quay tâm
0;0O
, góc quay
270

.
A.
3;0 .M
B.
3;3 .M
C.
0; 3 .M
D.
3;0 .M
Lời giải:
Chọn đáp án D.
Câu 13: Trong mặt phẳng với hệ tọa độ
Oxy
, phép quay tâm
2;1I
, góc quay
0
120
, biến điểm
1;9M
thành điểm
'M
có tọa độ là
A.
1 5 3 2 3 3
;
22
M




. B.
5 8 3 6 3
;
22
M

.
C.
5 8 3 2 2 3
;
22
M




. D.
1 5 3 6 3
;.
22
M


Lời giải:
Giả sử
';M x y

. Ta có:
00
00
cos120 sin120
.
sin120 cos120
x x a y b a
y x a y b b
Thay
1; 9; 2; 1x y a b
, ta có
5 8 3 6 3
;
22
M

.
Chọn đáp án B.
Câu 14: Cho
3;4M
. Tìm ảnh của điểm
M
qua phép quay tâm
O
góc quay
0
30
.
A.
3 3 3
' ; 2 3
22
M




. B.
' 2; 2 3M
.
C.
33
' ;2 3
2
M




. D.
3 3 3
' 2; 2 3
22
M





.
Lời giải:
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 18
Gọi
0
;30
' '; '
O
M x y Q
.Áp dụng biểu thức tọa độ
' cos sin
' sin cos
x x y
y x y
ta có
00
00
33
' 3cos 30 4sin 30 2
2
3
' 3sin 30 4cos 30 2 3
2
x
y
3 3 3
' 2; 2 3
22
M




.
Chọn đáp án D.
Câu 15: Trong mặt phẳng
Oxy
, cho điểm
1;1M
. Hỏi các điểm sau điểm nào là ảnh của
M
qua phép
quay tâm
O
, góc
45
?
A.
–1;1M
. B.
1;0M
. C.
2;0M
. D.
0; 2M
.
Lời giải:
+ Thay biểu thức tọa độ của phép quay tâm
O
góc quay
45
ta có:
.cos45 .sin 45 cos45 sin45 0
.sin45 .cos45 sin45 cos45 2
o o o o
o o o o
x x y
y x y
.
Vậy
0; 2M
.
Chọn đáp án D.
Câu 16: Trong mặt phẳng với hệ tọa độ
,Oxy
cho đường thẳng
: 2 1 0.xy
Ảnh của đường thẳng
qua phép quay tâm
,O
góc quay
0
90
là đường thẳng có phương trình
A.
2 1 0.xy
B.
2 2 0.xy
C.
2 2 0.xy
D.
2 1 0.xy
Lời giải:
Gọi
;M x y d
,
; 90 ; 90
;
OO
Q Q M M M
M M M M
M M M M
x y y x
y x x y









, thay vào phương trình đường thẳng
2. 1 0 : 2 1 0
MM
y x x y

.
Chọn đáp án D.
Câu 17: Trong mặt phẳng với hệ tọa độ
,Oxy
phép quay tâm
O
, góc quay
0
90
biến đường tròn
22
: 4 6 3 0C x y x y
thành đường tròn
C
có phương trình nào sau đây?
A.
22
: 3 2 16.C x y
B.
22
: 3 2 16.C x y
C.
22
: 2 3 16.C x y
D.
22
: 2 3 16.C x y
Lời giải:
Đường tròn
2; 3 ,I
bán kính
4.R
Ta có:
0
;90
3;2 :
O
Q I I
Tâm đường tròn
.C
Đường tròn
C
có tâm
3;2 ,I
bán kính
4RR

nên có phương trình:
22
3 2 16.xy
Chọn đáp án A.
Câu 18: Trong mặt phẳng với hệ tọa độ
,Oxy
cho đường tròn
2
2
: 1 5.C x y
Xác định phương
trình đường tròn
C
là ảnh của đường tròn
C
qua phép quay tâm
,O
góc quay
0
90 .
A.
2
2
1 5.xy
B.
2
2
1 5.xy
C.
22
1 1 5.xy
D.
2
2
1 5.xy
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 19
Lời giải:
Đường tròn
C
có tâm
1;0 ,I
bán kính
5.R
Ta có:
0
; 90
0;1 .
O
Q I I
Đường tròn
C
có tâm
0;1I
, bán kính
5,RR

có phương trình:
2
2
1 5.xy
Chọn đáp án B.
Câu 19: Cho tam giác đều
ABC
có
G
là trọng tâm (hình vẽ bên). Khẳng định
nào sau đây đúng?
A.
,120
.
G
Q B A
B.
,60
.
G
Q B A
C.
,120
.
G
Q A B
D.
,6
.
G
Q A B
G
A
B
C
Lời giải:
Ta có
,120
.
G
Q A B
Chọn đáp án C.
Câu 20: Có bao nhiêu phép quay với góc quay
với
;



biến hình vuông thành chính nó?
A.
1.
B.
2.
C.
3.
D.
5.
Lời giải:
Gọi
O
là tâm của hình vuông. Khi đó phép quay tâm
O
,
góc quay
với
; ;0; ;
22




biến hình vuông thành
chính nó.
Chọn đáp án D.
Câu 21: Trong mặt phẳng, tìm ảnh của điểm
2; 1A
qua phép quay tâm
O
, góc quay
90 .
A.
1; 2 .M
B.
1;2 .N
C.
1;2 .P
D.
2;1 .Q
Lời giải:
Biểu thức tọa độ của phép quay tâm
O
, góc quay
90
biến
;M x y
thành
;M x y
:
xy
yx

.
Suy ra
,90
1;2 .
O
Q A N
Chọn đáp án B.
Câu 22: Trong mặt phẳng, cho đường thẳng
: 2 1 0xy
. Xác định ảnh của
qua phép quay tâm
O
(
O
là gốc tọa độ), góc quay
90
.
A.
2 1 0.xy
B.
2 1 0.xy
C.
2 1 0.xy
D.
2 1 0.xy
Lời giải:
Lấy
1;0M
,
1;1N
nằm trên
.
Biểu thức tọa độ của phép quay tâm
O
, góc quay
90
biến
;M x y
thành
;M x y
:
xy
yx

.
Khi đó
, 90 , 90
0;1 , 1; 1
OO
Q M M Q N N

và
, 90O
Q

.
Suy ra
đi qua hai điểm
,MN

. Do đó
: 2 1 0.xy
Chọn đáp án D.
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 20
Câu 23: Về phía ngoài tam giác
ABC
, dựng các hình vuông
ABMN
và
ACPQ
. Gọi
,IJ
lần lượt là tâm các hình vuông
ABMN
và
ACPQ
;
E
là trung điểm
BC
(tham khảo hình
vẽ). Khẳng định nào sau đây sai?
A.
EIJ
vuông cân. B.
.BQ CN
C.
.AE MP
D.
.BQ CN
E
J
I
Q
P
N
M
C
B
A
Lời giải:
Xét phép quay tâm
A
, góc quay
90
.
Ta có
,90 ,90 ,90
,
A A A
Q N B Q C Q Q NC BQ
.
Suy ra
BQ CN
và
.BQ CN
BCN
có
EI
là đường trung bình nên
//EI CN
và
1
2
EI CN
.
CBQ
có
EJ
là đường trung bình nên
//EJ BQ
và
1
2
EJ BQ
.
Suy ra
EI EJ
và
EI EJ
EIJ
vuông cân tại
.E
Chọn đáp án C.
E
J
I
Q
P
N
M
C
B
A
Câu 24: Trong mặt phẳng, cho hai điểm
1; 3 , 2;1AB
. Gọi
,MN
lần lượt là ảnh của
,AB
qua phép
dời hình bằng cách thực hiện liếp tiếp phép tịnh tiến theo vectơ
3; 1v 
và phép quay tâm
O
, góc quay
90
. Viết phương trình đường thẳng
MN
.
A.
4 20 0.xy
B.
4 20 0.xy
C.
4 12 0.xy
D.
4 5 0.xy
Lời giải:
Ta có
4; 4 , 5;0
vv
T A C T B D
,
,90 ,90
4;4 , 0;5 .
OO
Q C M Q D N


Suy ra
: 4 20 0.MN x y
Chọn đáp án B.
Câu 25: Cho tam giác đều
ABC
cạnh
a
có
G
là trọng tâm. Gọi tam giác
MNP
là ảnh của tam giác
ABC
qua phép dời hình bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ
BC
và phép
quay tâm
G
, góc quay
90
. Tính độ dài
.GM
A.
3
.
3
a
B.
23
.
3
a
C.
7
.
2
a
D.
7.a
Lời giải:
Phép tịnh tiến theo vectơ
BC
biến
ABC
thành
DCE
.
Phép quay tâm
G
, góc quay
90
biến
DCE
thành
MNP
.
Gọi
,IJ
lần lượt là trọng tâm của
DCE
và
MNP
.
Ta có
BC
GI aT G I 
,
,90G
GI GJ aQ I J
.
,90
,
2 3 3
, . .
3 2 3
G
BC
MJ AG MJ AG
aa
T AG DI Q DI MJ
Suy ra
2
2
3 2 3
.
33
aa
MG a




Chọn đáp án B.
E
D
J
G
P
N
M
C
B
I
A
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 21
Câu 26: Cho tam giác đều
ABC
. Hãy xác định góc quay của phép quay tâm
A
biến
B
thành điểm
C
.
A.
30

. B.
90

. C.
120
. D.
0
60

hoặc
0
60
.
Lời giải:
Ta có:
( , ) 60
AB AC
AB AC
nên
( ; 60 )
()
A
Q B C

.
Chọn đáp án D.
Câu 27: Cho hai hình vuông
ABCD
và
BEFG
như hình bên. Tìm
ảnh của tam giác
ABG
qua phép quay tâm
B
, góc quay
90
.
A.
BCD
. B.
CBE
.
C.
ABD
. D.
DCG
.
Lời giải:
Ta có:
, 90 , 90 , 90
,,
B B B
Q B B Q A C Q G E
hay ảnh của tam giác
ABG
qua phép quay
tâm
B
, góc quay
90
là tam giác
CBE
.
Chọn đáp án B.
Câu 28: Trong mặt phẳng với hệ tọa độ
,Oxy
cho vectơ
3; 2v 
và điểm
1;4 .M
Xác định tọa độ
ảnh của điểm
M
qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm
,O
góc quay
0
90
và phép tịnh tiến theo vectơ
.v
A.
1; 3 .
B.
7; 1 .
C.
2; 6 .
D.
4;2 .
Lời giải:
Ta có:
0
1
;90
4; 1
O
Q M M
và
12
1; 3 .
v
T M M
Chọn đáp án A.
Câu 29: Trong mặt phẳng
Oxy
, cho đường thẳng
: 2 3 9 0d x y
. Viết phương trình của đường thẳng
'd
là ảnh của đường thẳng
d
qua phép quay tâm
O
góc
0
90
.
A.
2 3 9 0xy
. B.
3 2 9 0xy
. C.
3 2 9 0xy
. D.
2 3 9 0xy
.
Lời giải:
Gọi
;M x y d
;
0
(O;90 )
'( '; ') QM x y M
Ta có:
00
00
' .cos90 .sin90 ' '
'; '
''
' .sin90 .cos90
x x y x y x y
M y x
y x y x
y x y



.
Có:
'; ' : 2 3 9 0 2 ' 3 ' 9 0M y x d x y y x
Vậy phương trình
'd
cần tìm là :
3 2 9 0xy
Chọn đáp án B.
Câu 30: Trong mặt phẳng tọa độ
Oxy
, cho hai đường thẳng
: 4 3 5 0d x y
và
' : 7 4 0d x y
. Nếu
có phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc quay
với
0 180
là góc nào sau đây?
A.
120
. B.
60
. C.
90
. D.
45
.
Lời giải:
Hai đường thẳng
d
và
'd
có vecto pháp tuyến lần lượt là
4;3
d
n
và
'
1;7
d
n
.
Ta có:
'
'
'
.
4.1 3.7
2
cos , ' cos , .
2
5.5 2
.
dd
dd
dd
nn
d d n n
nn
Suy ra
, ' 45dd 
.
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 22
Vì
,'dd
hoặc
, ' 180dd
nên
45

hoặc
135

.
Chọn đáp án D.
Câu 31: Có bao nhiêu điểm biến thành chính nó qua phép quay tâm
O
góc với
2k
(
k
là một
số nguyên)?
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải:
Điểm đó chính là tâm quay
O
.
Chọn đáp án B.
Câu 32: Cho hình chữ nhật có
O
là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm
O
góc quay
,
02


biến hình chữ nhật trên thành chính nó?
A.Không có. B.Hai. C.Ba. D.Bốn.
Lời giải:
Có 2 phép quay tâm
O
góc
,
02


biến tam giác trên thành chính nó là các phép quay
với góc quay bằng:
,
2
.
Chọn đáp án B.
Câu 33: Trong mặt phẳng Oxy, cho điểm
( 3;6)B
. Tìm toạ độ điểm E sao cho B là ảnh của E qua phép
quay tâm O góc quay
0
90
.
A.
E(6;3).
B.
E( 3; 6).
C.
E( 6; 3).
D.
E(3;6).
Lời giải:
Điểm
( 6; 3)E 
.
Chọn đáp án C.
Câu 34: Trong mặt phẳng tọa độ
Oxy
cho phép quay tâm
O
biến điểm
1; 0A
thành điểm
0;1 .A
Khi đó nó biến điểm
1; 1M
thành điểm
A.
1; 1M

. B.
1;1M
. C.
1;1M
. D.
1; 0M
.
Lời giải:
Từ giả thiết, kết hợp với hình vẽ ta thấy góc quay là
2
.
Khi đó phép quay tâm
O
góc quay
2
biến điểm
1; 1M
thành điểm
1;1M
.
Chọn đáp án B.
Câu 35: Trong mặt phẳng với hệ tọa độ
Oxy
, phép quay tâm
4; 3I
góc quay
180
biến đường thẳng
: 5 0d x y
thành đường thẳng
d
có phương trình
A.
30xy
. B.
30xy
. C.
50xy
. D.
30xy
.
Lời giải:
-1
1
1
M'
M
A'
A
O
x
y
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 23
Ta có phép quay
o
;180I
Q
là phép đối xứng tâm
I
Vì
Id
nên nếu
I
Đ d d
thì
//dd
, suy ra phương trình
: 0 5d x y m m
.
Xét
0;5
8; 11 .
4; 3

I
Md
Đ M M M
I
Cho
8; 11Md


3m
. Vậy
: 3 0d x y
.
Chọn đáp án B.
Câu 36: Trong mặt phẳng
Oxy
, cho đường tròn
22
: 4 10 4 0C x y x y
. Viết phương trình
đường tròn
C
biết
C
là ảnh của
C
qua phép quay với tâm quay là gốc tọa độ
O
và góc
quay bằng
270
.
A.
22
: 10 4 4 0C x y x y
. B.
22
: 10 4 4 0C x y x y
.
C.
22
: 10 4 4 0C x y x y
. D.
22
: 10 4 4 0C x y x y
.
Lời giải:
Đường tròn
C
có tâm
2; 5I
, bán kính
4 25 4 5R
.
Ta có
,270O
C Q C
, 90O
C Q C

,90O
C Q C
.
Do đó
,90O
I Q I
. Vì đây là phép quay
90
nên
5
2
II
II
xy
yx

, suy ra
5;2I
.
Bán kính đường tròn
C
là
5RR

.
Vậy
22
: 5 2 25C x y
22
: 10 4 4 0C x y x y
.
Chọn đáp án B.
Câu 37: Cho lục giác đều
ABCDEF
tâm
O
như hình bên. Tam giác
EOD
là ảnh của tam giác
AOF
qua
phép quay tâm
O
góc quay . Tìm .
O
F
E
D
C
B
A
A.
o
60 .
B.
o
60 .
C.
o
120 .
D.
o
120 .
Lời giải:
; 120O
Q O O
,
; 120O
Q A F
.
; 120O
Q F D
.
Chọn đáp án B.
| 1/23
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11 Chủ đề 2: PHÉP QUAY I- LÝ THUYẾT: M' (+)
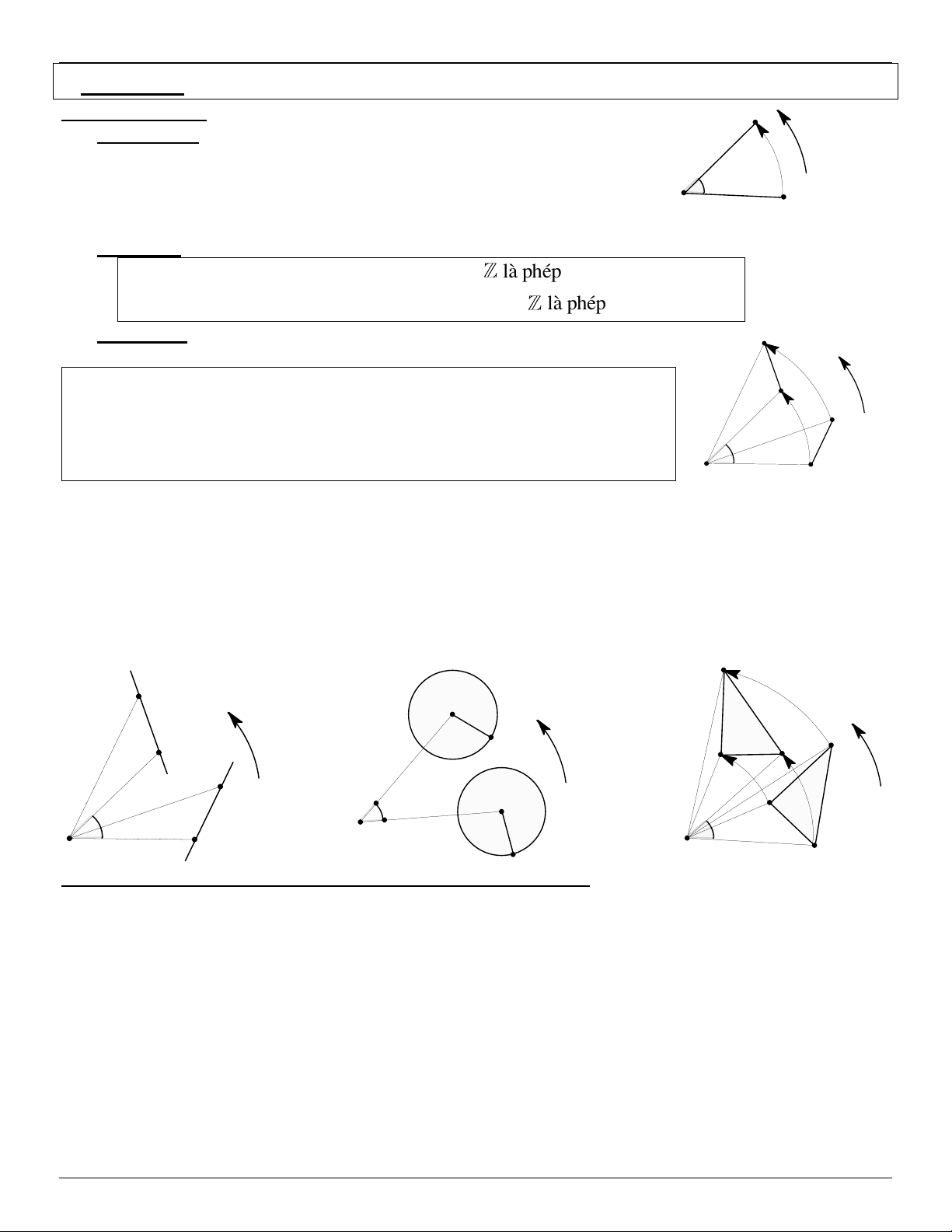
1. Định nghĩa: Cho điểm O và góc lượng giác  .
Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành
điểm M’ sao cho OM OM ' và góc lượng giác OM ;OM '  .  O M Ký hiệu: Q O;   2. Nhận xét:
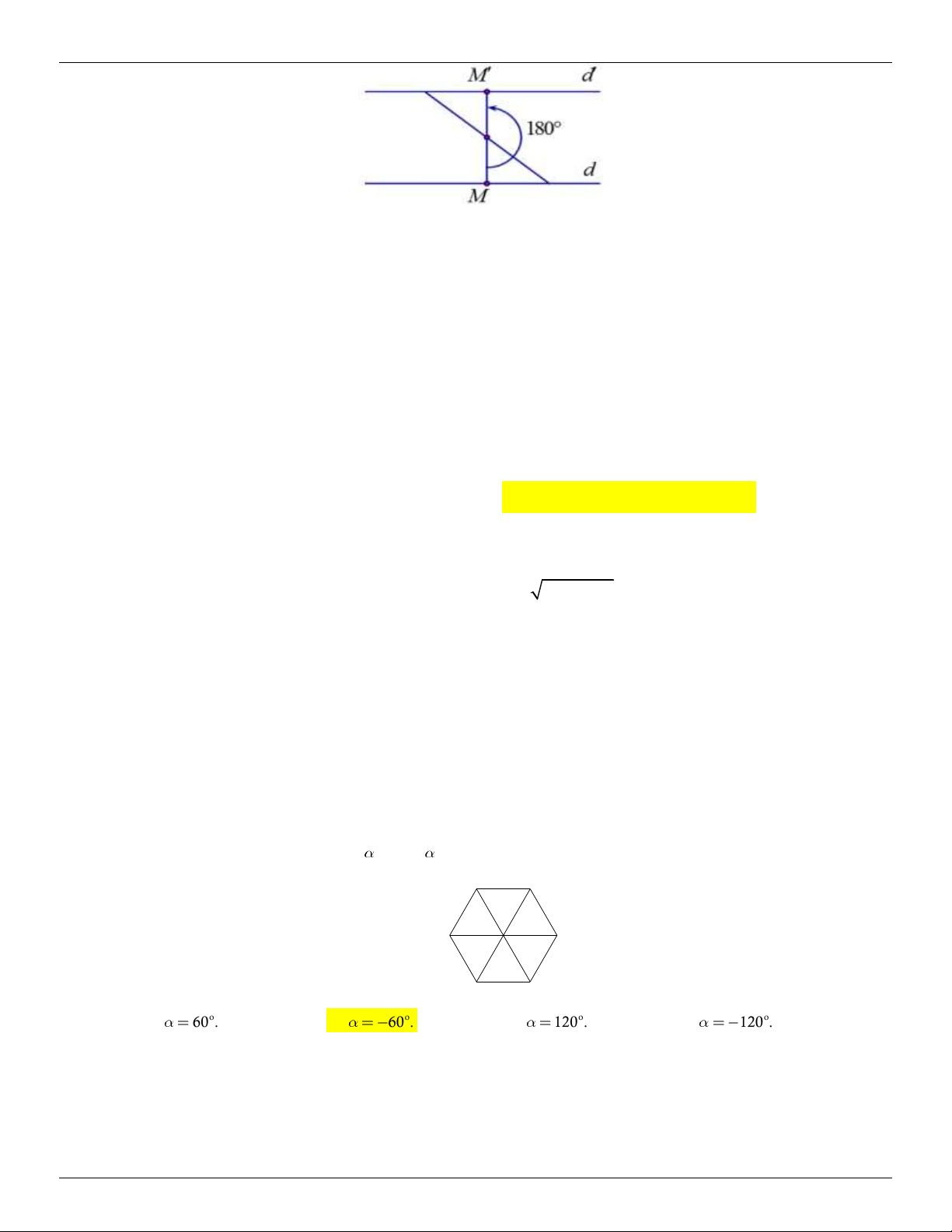
a) PhÐp quay t©m O gãc quay a k2 , k  lµ phÐp ®ång nhÊt.
b) PhÐp quay t©m O gãc quay a  2k  
1  , k  lµ phÐp ®èi xøng t©m O. 3. Tính chất: B' Tính chất 1: (+) A'Q A A'  O;      , A : B
A' B '  AB Q B B '  O;   B    
 PhÐp quay b¶o toµn kho¶ng c¸ch gi÷a hai ®iÓm bÊt kú PhÐp dêi h×nh O A
Tính chất 2: Phép quay:
1. Bảo toàn tính thẳng hàng và thứ tự của các điểm tương ứng.
2. Biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.
3. Biến đường thẳng thành đường thẳng.
4. Biến tam giác thành tam giác bằng nó.( trực tâm 
 trực tâm, trọng tâm   trọng
tâm). Góc thành góc bằng nó. I   I '
5. Biến đường tròn thành đường tròn có cùng bán kính ( ). d'R R ' B' B' I' (+) R' (+) (+) A' A' B d C' B I   O C RO A O R = R'A ABC = A'B'C'
4. Một số kết quả và dấu hiệu sử dụng phép quay để giải toán  Q (B)  C 0 A 90 ;  a. ABC c©n t¹i A:      Q (B)  . C §Æc biÖt: AB  C vu«ng c©n t¹i A:  A;  Q B C   ( )  0 A; 90    Q (B)  C 0 A 60 ;  b. Chøng minh ABC ®Òu:     Q C A   ( )  0 B 60 ;     Q ( ) A B 0 O 45 ; 
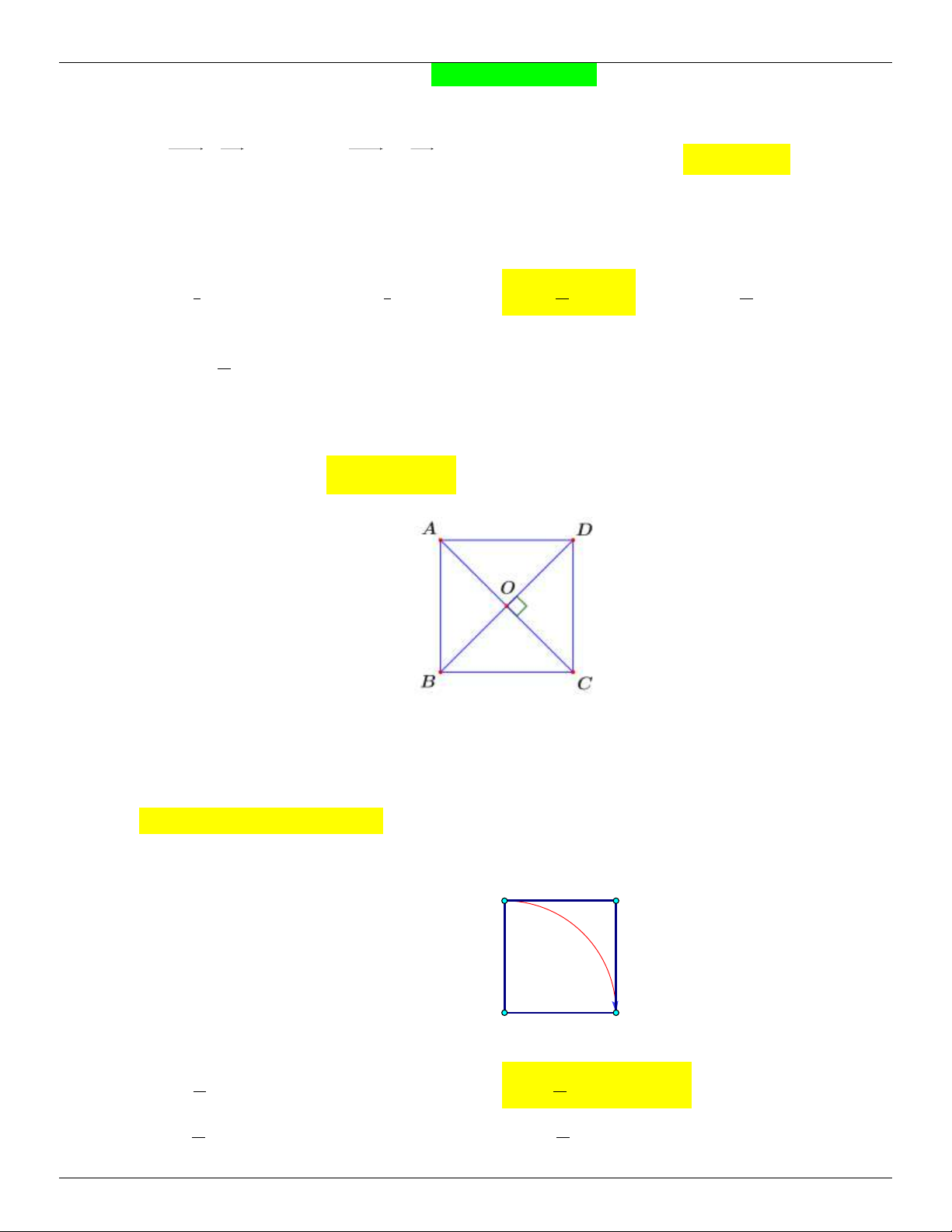
c. Chøng minh ABCD víi O lµ g®iÓm 2 ®­êng chÐo  lµ h×nh vu«ng:   Q B C   ( )  0 O 45 ; 
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 1
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
* MỘT SỐ KẾT QUẢ CẦN LƯU Ý:
1) Ảnh của điểm qua phép quay Q , Q : 0 O   0 ;90 O; 9  0   x'  yM   Q
(M )  M '(x '; y ') :  0 O;90  y '  x   M
Điểm M x ; y : M M   x'  yM    Q
(M )  M '(x '; y ') :  0 O; 90   y '  x   M
2) Giả sử phép quay Q
biến đường thẳng d thành d’: I ;  0
0    90  d;d '   Khi đó:  0 0 90    180   d;d ' 0  180 
3) Các phương pháp xác định ảnh của đường thẳng d qua Q : I ; 
Phương pháp 1: Chọn 2 điểm bất kì. Đường thẳng ảnh đi qua 2 ảnh tương ứng.   Q ( ) A A' I ;  ,
A B d :    Q
(d )  d '  A' B ' I ;    Q (B)  B ' I ; 
Phương pháp 2: Chọn 1 điểm A thuộc đường thẳng. Xác định ảnh A’. d I
Đường thẳng ảnh d’ đi qua A’ và hợp với d một góc . Phương pháp 3: Gồm 2 bước: H d'
Bước 1: Chọn H d với IH d . Xác định  Q (H )  H ' . I ;  H' Bước 2: 
Đường thẳng d’ cần tìm đi qua H’ và vuông góc với IH’. II- LUYỆN TẬP :
Bài tập 1: Cho điểm 2 2 M(1;2), :
x y 1  0, (C): x y  2x  4y 1  0 . Xác định tọa độ điểm A’, / /
 , (C ) lần lượt là ảnh của M, , (C) qua:
a) Phép quay tâm O, góc quay 0   90 .
b) Phép quay tâm O, góc quay 0   90  . Gợi ý: a) Ta có: /  Q (M)  M ( 2  ;1). 0 O;90  Dễ thấy : y Qua phép quay  Q
, hình chữ nhật OAMB có ảnh B 0 O;90  M 2
Là hình chữ nhật OA’M’B’. M' A' 1 /    Q ( ) A A (0;1) 0 O;90  Ta có: /   Q (M)  M ( 2  ;1) -2 1 x /  0 O;90   O Q B B B' A   ( )  ( 2  ;0) 0 O;90 
* Kỷ năng xác định ảnh của đường thẳng qua phép quay tâm O, góc quay 0   90 .
Phương pháp 1: Chọn 2 điểm bất kì trên , xác định ảnh tương ứng. Đường thẳng /  cần tìm là
đường thẳng qua hai ảnh.
Chọn M (1; 2), B(0;1)  
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 2
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11 / /    Q (M )  M ( 2  ;1)   0 O;90  Ta có: / / /     M N . / /  Q (N )  N ( 1  ;0)   0 O;90  Đường thẳng /
 đi qua điểm M '( 2
 ;1) và có 1 vtcp M ' N '  (1; 1  ) x  2   t Vậy /  :  t   y 1 t
Phương pháp 2: Sử dụng mối quan hệ về góc giữa d và d’ Gọi /
 là ảnh của đường thẳng  qua Q . Suy ra: / /
     : x y m  0 0 O;90  Chọn / /
M (1; 2)     Q (M )  M ( 2  ;1)  0 O;90  Ta có: 2
 1 m  0  m  1. Vậy /
 : x y 1  0
Phương pháp 3: Sử dụng quỹ tích: M     Q
(M )  M '  ' 0 O;90  x'  yx y ' Gọi / M ( ; x y)     Q
(M )  M (x '; y ') :    0 O;90  y '  xy  x'
Lúc đó: M y ';x'    y '  x' 1  0  x' y '1  0 Vậy /
 : x y 1  0
Nhận xét: Trong 3 phương pháp trên,
- Phương pháp 1 tỏ ra hiệu quả cho tất cả các phép biến hình (dù dài dòng).
* Xác định ảnh của đường tròn:
Phương pháp 1: Theo tính chất của phép quay: Biến đường tròn thành đường tròn có cùng bán kính. M
Ta có C   M R (1; 2) ; :  R  2 / /  Q (M )  M ( 2
 ;1) là tâm của đường tròn ảnh C  . 0 O;90  Vậy đường tròn  / 2 2
C  :  x  2   y   1  4
Phương pháp 2: Sử dụng quỹ tích. x'  yx y ' Gọi M ( ;
x y)  C  /  Q
(M )  M (x '; y ') :    0 O;90  y '  xy  x'
Lúc đó: M y x C   y 2  x 2 '; ' ' '
 2 y'  4x' 1  0 2 2
 (x')  (y ')  4x' 2y '1  0 Vậy  / C  2 2
: x y  4x  2 y 1  0
Hoàn toàn tương tự, giải quyết yêu cầu b.
PHẦN KIẾN THỨC ĐỌC THÊM:
CÔNG THỨC TỌA ĐỘ VỚI PHÉP QUAY VỚI
TÂM VÀ GÓC QUAY BẤT KÌ Đặt vấn đề:
Trong Hình học 10, Đai số 10 và 11, lý thuyết về lượng giác một cách cơ bản thì chúng ta đã thừa nhận:
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 3
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11 y
Với mỗi góc lượng giác  bất kì. M H
 Xác định trên (C) điểm M sao cho: xOM   
 Lúc đó: M x ; y , ta thừa nhận: M M x K O y x
sin  y ; cos  x ; tan = M ; cot = M M M x y M M
Hay: M cos;sin  (*)
Sở dĩ có cách biễu diễn (*) vì đường tròn lượng giác có bán kính R  1.
Và thực chất đây là cách biểu diễn đơn giản nhất đối với hệ tọa độ cực gốc O, có góc và bán kính R bất kì.
TỔNG QUÁT: Đối với hệ tọa độ cực: gốc O có góc  và bán kính R bất kì.
Điểm M với góc lượng giác xOM   , thì ta có: M  c
R os; R sin 
Bài tập 2: Cho điểm 2 2 M(1;2), :
x y 1  0, (C): x y  2x  4y 1  0 . Xác định tọa độ điểm M’, / /
 , (C ) lần lượt là ảnh của M, , (C) qua phép quay tâm O, góc quay   k2 . Gợi ý:
Giả sử góc lượng giác O ;
x OM    . Khi đó, góc lượng giác  / O ;
x OM      0 0
Vậy điểm M  5cos ; 5sin 0 0   1 cos    0  5cos  1  Do đó: 0 5    và điểm /
M  5cos( ); 5sin( ) 0 0     2 5 sin 2   0 sin  0  5
 5cos( )  5 cos .cos  sin .sin  cos  2sin  0  0 0  nên: 
 5 sin( )  5 sin .cos  cos .sin  2cos  sin  0  0 0  Vậy điểm /
M cos  2sin;2cos  sin  (y.c.b.t)
Hoàn toàn tương tự như yêu cầu trên, độc giả tự giải quyết.
Bài tập 3: Cho điểm I(1;2), M( 2
 ;3) . Xác định tọa độ điểm M’ là ảnh của M qua phép quay tâm I,
góc quay   k2 . Gợi ý:
* Trước hết ta tìm điểm N sao cho ON IM : x  2  1
Giả sử điểm N ( ;
x y) , khi đó: ON IM    N( 3  ;1) y  3  2
* Gọi N’ là ảnh của N (3;1) qua  Q
, khi đó do M’ là ảnh của M qua Q
và ON IM nên I ;  I;  / / ON IM .
* Bây giờ, ta tính tọa độ của điểm N’. Giả sử, góc lượng giác  ;
Ox ON    . Khi đó, góc lượng giác 0  / O ;
x OM     . 0
Vậy điểm M  5cos ; 5sin 0 0 
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 4
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11  3  cos    0  10cos  3   Do đó: 0 10    và điểm /
N  10cos( ); 10 sin( ) 0 0     1 10 sin 1   0 sin  0  10
 10cos( )  10 cos .cos  sin .sin  3  cos  sin  0  0 0  nên: 
 10 sin( )  10 sin .cos  cos .sin  cos  3sin  0  0 0  Suy ra: điểm / N  3
 cos  sin;cos  3sin  * Giả sử: /
M (x '; y ') thì /
IM  (x 1; y  2) x 1  3  cos  sin Do / /
ON IM   . Do đó: /
M 1 3cos  sin;2  cos  3sin  (y.c.b.t)
y  2  os  3sin
Bài tập 4: Cho ®­êng th¼ng d vµ ®iÓm O cè ®Þnh kh«ng thuéc d, M lµ ®iÓm di ®éng trªn d.
H·y t×m tËp hîp c¸c ®iÓm N sao cho O  MN ®Òu.
Gợi ý: Biểu diễn điểm N theo M thông qua phép quay 0 60 d d'
Do tam giác OMN đều nên tồn tại hai phép quay: N  Q (M)  N M 0 O;60   d''600   Q (M)  N 0 O; 60   600
Do M thuộc đường thẳng d nên N thuộc vào O N
đường thẳng d’, d’’ lần lượt là ảnh của d qua  Q và Q . 0 O;60   0 O; 60  
Vậy quỹ tích cần tìm là 2 đường thẳng d’ và d’’. Tương tự:
Bài tập 5: Cho ®trßn (C) vµ ®iÓm O cè ®Þnh kh«ng thuéc (C), M lµ ®iÓm di ®éng trªn (C).
H·y t×m tËp hîp c¸c ®iÓm N sao cho O  MN vu«ng c©n t¹i O.
Gợi ý: Biểu diễn điểm N theo M thông qua phép quay 0 90
Bài tập 6: Cho 2 tam giác vuông cân ABC và ADE (như hình vẽ). Gọi G và G’ lần lượt là trọng tâm
các tam giác ABD và ACE. Chứng minh tam giác AGG’ vuông cân.
Gợi ý: Xây dựng phép quay tâm A góc quay 0
90 biến G thành G’. C    Q (B)  C 0 D A;90  Xét phép quay:  Q có :  0 A;90    Q ( ) D E 0 A;90  E A B Suy ra:  Q ( AB ) D A
CE . Do G và G’ lần lượt là trọng tâm các tam giác ABD và ACE nên 0 A;90  CAG AG ' 
theo tính chất của phép quay:  Q
(G)  G '   0 D A;90  0 GAG '  90
Vậy tam giác AGG’ vuông cân. (đ.p.c G' .m) G E B A
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 5
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Bài tập 7: Cho ba ®iÓm A, B, C theo thø tù trªn th¼ng hµng. VÏ cïng mét phÝa hai tam gi¸c
®Òu ABE, BCF. Gäi M vµ N t­¬ng øng lµ hai trung ®iÓm cña AF vµ CE. Chøng minh r»ng: BMN lµ tam gi¸c ®Òu.
Gợi ý: Xây dựng phép quay tâm B góc quay 0 60 biến N thành M. E    Q (C)  F 0 B;60  F Xét phép quay:  Q có :  0 B;60   N   Q (E)  A 0 B;60  M Suy ra:  Q (CE)  FA . 0 B;60 
Do N và M lần lượt là trung điểm các cạnh CE và AF nên theo A B C BN BM
tính chất của phép quay:  Q
(N)  M   0 B;60  0 MBN  60
Vậy tam giác BMN đều. (đ.p.c.m)
Bài tập 8: Cho tam giác ABC. Dựng về phía ngoài tam giác các hình vuông BCIJ, ACMN, ABEF và
gọi O, P, Q lần lượt là tâm của của chúng.
a) Gọi D là trung điểm của AB. Chứng minh rằng: DOP vuông cân tại D.
b) Chứng minh rằng: AO  PQ vµ AO=PQ.
Gợi ý: Xây dựng phép quay tâm D góc quay 0
90 biến O thành P, hoặc sử dụng mối quan hệ hình học liên quan. a) Xét phép quay  Q 0 C;90     Q (M)  A 0 C;90  MB AI      Q (MB)  MI  (1) 0 C;90   MB AI   Q (B) I 0 C;90 
Dễ thấy, DP là đường trung bình của các tamgiác ABM N  1 DP BM nên:  2 (2)  MDP // BM P F A
Tương tự, DO là đường trung bình của tam giác ABI nên:  D 1 QDO AIE 2 (3) B C DO// AIDO DP
Từ (1), (2) và (3) suy ra:  O
hay DOP vuông cân tại D. (đ.p.c.m) DO DP J I
b) Theo câu a, DOP vuông cân tại D nên  Q ( ) O P (*) 0 D;90  Mặt khác:  Q ( ) A Q (**) 0 D;90  AO QP Từ (*) và (**) suy ra:  Q (A ) O QP   (đ.p.c.m) 0 D;90  AO QP
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 6
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Bài tập 9: Cho tø gi¸c låi ABCD. VÒ phÝa ngoµi tø gi¸c dùng c¸c tam gi¸c ®Òu ABM, CDP.
VÒ phÝa trong tø gi¸c dùng hai tam gi¸c ®Òu BCN vµ ADK.CMR: MNPK lµ h×nh b×nh hµnh. Gợi ý:    Q (M)  A 0 B;60  B Xét phép quay  Q :  M C 0 B;60    Q (N)  C K 0 B;60    Q
(MN)  AC MN AC (1) 0 B;60   N P   Q (K)  A 0 D;60  A Xét phép quay  Q :  0 D;60    Q (P)  C 0 D;60  D   Q
(KP)  AC KP AC (2) 0 D;60 
Từ (1) và (2) suy ra: MN KP (*)
Tương tự, chứng minh được MK PN (**)
Từ (*) và (**) suy ra: MKNP là hình bình hành (đ.p.c.m)
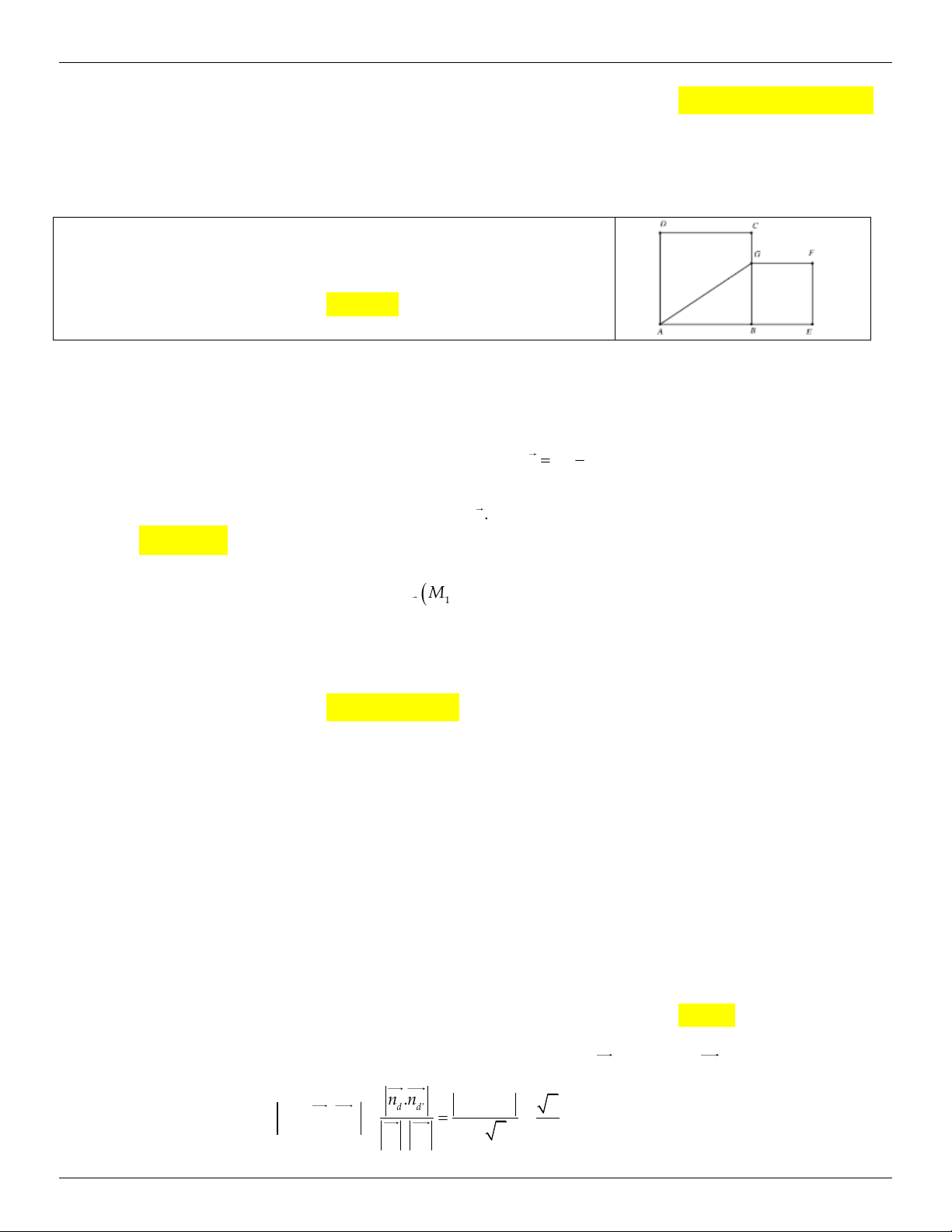
Bài tập 10: Cho 2 hình vuông ABCD và BEFG. Gọi M, N lần lượt là trung điểm của AG và CE.
Chứng minh rằng: Tam giác BMN vuông cân.
Gợi ý: Xây dựng phép quay tâm B góc quay 0 90 biến N thành M. C    Q (C)  A 0 B;90  B Xét phép quay:  Q có :  0 B;90  N   Q (E)  G 0 B;90  D Suy ra:  Q (CE)  AG . 0 B;90  E A M
G Do N và M lần lượt là trung điểm các cạnh CE và AG
nên theo tính chất của phép quay: BN BMFQ
(N)  M   0 B;90  0 MBN  90
Vậy tam giác MBN vuông cân. (đ.p.c.m)
Bài tập 11: VÒ phÝa ngoµi tam gi¸c ABC, dùng ba tam gi¸c ®Òu BCA , ACB , ABC . 1 1 1
Chøng minh r»ng: AA , BB , CC ®ång quy. 1 1 1
Gợi ý: Sử dụng tính chất phép quay: Bảo toàn tính thẳng hàng và thứ tự của 3 điểm bất kì.
Giả sử: AA CC I . Cần chỉ rõ: I BB hay B, I, B thẳng hàng. 1 1 1 1 B1    Q (A )  C 0 B  1 ;60 Thật vậy, xét phép quay AQ :  0 C B;60  1E   Q ( ) A C 0 B  1 ;60 IAA CC  1 1 C B 0      AIC (1)  AA ;CC   60 1 0  60 1 1
Lấy trên IC điểm E sao cho: AI EI (2) 1
Từ (1) và (2) suy ra: AEI là tam giác đều. A1
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 7
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11    Q (E)  I 0 A;60   Lúc đó, xét phép quay  Q : Q  (C )  B 0 A;60   0 A  1 ;60     Q (C)  B 0 A  1 ;60 Do E, ,
C C thẳng hàng nên theo tính chất của phép quay: I, B , B thẳng hàng. Điều này chứng tỏ 1 1
AA , BB , CC ®ång quy. (đ.p.c.m) 1 1 1
Bài tập 12: Cho tam giác ABC. Trên các cạnh AB và BC, về phía ngoài tam giác, dựng 2 hình vuông
ABMN và BCPQ. Chứng minh rằng: Các tâm của hình vuông này cùng với 2 trung điểm của MQ,
AC tạo thành 1 hình vuông. Gợi ý:
Gọi O và O lần lượt là tâm 2 hình vuông ABMN và BCPQ, còn O và O lần lượt là trung điểm 1 3 2 4 của AC , MQ.    Q (M)  A 0 B;90  MC AQ Xét phép quay  Q :   Q
(MC)  AQ   (1) 0 B;90    0 B;90    Q (C) QMC AQ 0 B;90 
Dễ thấy: O O , O O , O O , O O lần lượt là đường 1 2 2 3 3 4 4 1
trung bình của các tam giác MAC, ACQ, MCQ, MAQ. M OO // MC OO // AQ O 1 2  2 3  4 Suy ra:  1 (2) và  1 (3) N Q O O MCO O AQ 1 2   2 2 3  2 O1O O O O Từ (1), (2) và (3) suy ra: 1 2 2 3  (*) P O O O OO3 1 2 2 3 B OO // MC OO // AQ 3 4  4 1  Tương tự, do  1 (4) và  1 (5) A C O2 O O MCO O AQ 3 4   2 4 1  2 O O O O Từ (1), (4) và (5) suy ra: 3 4 4 1  (**) O O O O  3 4 4 1
Từ (*), (**) suy ra: O O O O là hình vuông. (đ.p.c.m) 1 2 3 4
Bài tập 13: Cho điểm A và 2 đường tròn (C), (C’) phân biệt. Dựng theo chiều dương tam giác đều
ABC, biết đỉnh B, C lần lượt nằm trên (C) và (C’). Gợi ý:
Phân tích: Do tam giác ABC đều nên: AB ACA      Q B C AB; AC    ( ) 0 0 ;60   60 A B (C'') (C') Cách dựng: C O'
- Dựng đường tròn (C’’) là ảnh của (C) qua  Q . 0 A;60  O
- Xác định giao điểm C  (C ')  (C '') . B' - Thực hiện phép quay  Q (C)  B (C) C' 0 A; 6  0 
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 8
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Biện luận: Nghiệm bài toán tùy thuộc số giao điểm của (C’’) và (C’).
Bài tập 14: Cho 2 đường thẳng a, b song song và một điểm G không nằm trên chúng. Xác định tam
giác đều ABC có A  ,
a B b và G là trọng tâm tam giác ABC. Gợi ý:
Phân tích: Giả sử đã dựng được ABC thỏa đk. a'
GA GB GC  Ta có:  A 0  a
AGB BGC CGA  120 Suy ra:  Q ( ) A B 0 1200 G;120  C Cách dựng: G
- Dựng a’ là ảnh của a qua  Q . 0 G ;120  b
- Xác định B a ' b . B
- Các đỉnh A, C là ảnh của B qua  Q , Q 0 G   0 ;120 G; 1  20 
Biện luận: Bài toán luôn có 1 nghiệm hình.
Bài tập 15: Cho tam giác ABC và vẽ phía ngoài hai hình vuông ABMN, ACPQ.
a) Chứng minh : BQ CN và BQ CN .
b) Gọi O, O’ lần lượt là tâm của các hình vuông ABMN, ACPQ. Chứng minh rằng: Tam giác OIO’ vuông cân. Gợi ý:    Q (B)  N N 0 A; 90   a) Xét phép quay  Q :  0 A; 90 
  Q (Q)C 0 A; 90   M QBQ NC O  Q
(BQ)  NC   (đ.p.c.m) 0 A; 9  0  BQ NC A P b) Ta có: OI và O’I O'
lần lượt là đường trung bình của
các tam giác BNC và BCQ nên suy ra: OI  // NCC
O' I // BQB I  (1) 1 và  (2) 1 OI NCO' I BQ   2  2 O
I O' I
Theo câu a, và từ (1), (2) suy ra: 
. Vậy tam giác OIO’ vuông cân. (đ.p.c.m) O
I O' I
Bài tập 16: Cho 2 đường tròn (O) và (O’) bằng nhau và cắt nhau ở A và B. Từ điểm I cố định kẻ cát
tuyến di động IMN với (O), MB và NB cắt (O’) tại M’, N’.
Chứng minh rằng: Đường thẳng M’N’ luôn đi qua 1 điểm cố định.
Gợi ý: Gọi  A ; O AO'   . AN   Q ( ) O O' A;   Xét phép quay   Q ( ) O  (O') A;    Q : A;    R R' N' O' M'
I' Vì MM’ và NN’ qua B nên: OA ;
O AO'   AM; AM '   AN; AN ' B M I
Lớp Toán thầy LÊ BÁ BẢO
- Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 9
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11   Q (M)  M ' A;  Lúc đó:    Q
(MN)  M 'N ' A;    Q (N)  N ' A; 
Do MN đi qua điểm I cố định nên M’N’ đi qua điểm cố định I’ là ảnh của I qua  Q . A; 
Bài tập 17: Chứng minh rằng: Các đoạn thẳng nối tâm các hình vuông dựng trên các cạnh của một
hình bình hành về phía ngoài, hợp thành một hình vuông. Gợi ý:
Gọi I , I , I , I lần lượt là tâm của các hình vuông cạnh AB, BC, CD, DA 1 2 3 4 I2 Xét phép quay  Q : Q (B)  C (1) 0 I ;90  0 I ;90 2  2  Do IBA I
CD nên I C BI . (2) I1 C 1 3 3 1 B 0    Mặt khác: DCI ABI 45 D I 3 1 
I C BI (3) 3 A 3 1 DC // ABI I I I Từ (1), (2) và (3) suy ra: 1 2 2 3 I4Q
(I )  I   0 1 3 I ;90 2  I I I I  1 2 2 3
Lý luận tương tự ta có I I I I và I I I I . Vậy I I I I là hình vuông. (đ.p.c.m) 1 4 4 3 1 4 4 3 1 2 3 4
III- BÀI TẬP TỰ LUẬN - TỰ LUYỆN:
1) Cho tam gi¸c ABC. X¸c ®Þnh ¶nh cña AB  C qua c¸c phÐp quay: a) Q a) Q 0 0 ( A;90 ) ( A;60 )
2) Cho h×nh vu«ng ABCD víi O lµ t©m. Gäi M, N lÇn l­ît lµ trung ®iÓm cña AB, AD. X¸c ®Þnh ¶nh cña AMN  qua phÐp quay: a) Q a) Q 0 0 (0;90 ) (O; 90  )
3) Trong mÆt ph¼ng cho c¸c ®iÓm (
A 0;3), B(-2;0), C(1;4). X¸c ®Þnh to¹ ®é c¸c ®iÓm A',B', C'
lÇn l­ît lµ ¶nh cña A, B, C qua: a)  Q b) Q 0 O   0 ;90 O; 90   4) Cho 2 2 ®­êng th¼ng :
x  4y  2  0 vµ ®­êng trßn (C): x y  4x  2y  0. X¸c ®Þnh ph­¬ng tr×nh '
 , (C') lÇn l­ît lµ ¶nh cña  vµ (C) qua phÐp quay: a)  Q b) Q 0 O;90  O; 90  0 
5) Cho n÷a ®­êng trßn t©m O vµ ®­êng kÝnh BC. §iÓm A ch¹y trªn n÷a ®­êng trßn ®ã. Dùng vÒ phÝa ngoµi cña AB 
C h×nh vu«ng ABEF. Chøng minh r»ng: E ch¹y trªn n÷a ®­êng trßn cè ®Þnh.
6) Cho ®­êng th¼ng d vµ ®iÓm O cè ®Þnh kh«ng thuéc d, M lµ ®iÓm di ®éng trªn d. H·y t×m
tËp hîp c¸c ®iÓm N sao cho OMN  ®Òu.
7) Cho 2 ®­êng trßn (O) vµ (O') b»ng nhau vµ c¾t nhau t¹i A, B. Tõ 1 ®iÓm I cè ®Þnh kÎ c¸t tuyÕn
di ®éng IMN víi (O), MB vµ NB lÇn l­ît c¾t (O') t¹i M', N'. CMR: M'N' lu«n ®i qua 1 ®iÓm cè ®Þnh.
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 10
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
8) Cho ba ®iÓm A, B, C theo thø tù trªn th¼ng hµng. VÏ cïng mét phÝa, dùng hai tam gi¸c
®Òu ABE, BCF. Gäi M vµ N t­¬ng øng lµ hai trung ®iÓm cña AF vµ CE. Chøng minh r»ng: BMN lµ tam gi¸c ®Òu.
9) Cho tam gi¸c ABC. Qua ®iÓm A dùng hai tam gi¸c vu«ng c©n ABE vµ ACF. Gäi M lµ trung
®iÓm cña BC vµ gi¶ sö AM  FE=H. Chøng minh r»ng: AH lµ ®­êng cao cña AE  F.
10) Cho tø gi¸c låi ABCD. VÒ phÝa ngoµi tø gi¸c dùng c¸c tam gi¸c ®Òu ABM, CDP. VÒ phÝa
trong tø gi¸c dùng hai tam gi¸c ®Òu BCN vµ ADK. Chøng minh: MNPK lµ h×nh b×nh hµnh.
11) Cho tam gi¸c ABC. VÒ phÝa ngoµi tam gi¸c, dùng ba tam gi¸c ®Òu BCA , ACB , ABC . 1 1 1
Chøng minh r»ng: AA , BB , CC ®ång quy. 1 1 1
12) Cho tam gi¸c ABC. Dùng vÒ phÝa ngoµi tam gi¸c c¸c h×nh vu«ng BCIJ, ACMN, ABEF vµ
gäi O, P, Q lÇn l­ît lµ t©m cña chóng.
a) Gäi D lµ trung ®iÓm cña AB. Chøng minh r»ng: D  OP vu«ng c©n t¹i D.
b) Chøng minh r»ng: AO  PQ vµ AO=PQ.
13) Cho tam gi¸c ABC. Trªn c¸c c¹nh AB vµ BC, vÒ phÝa ngoµi tam gi¸c dùng 2 h×nh vu«ng
ABMN, BCPQ. Chøng minh r»ng: C¸c t©m cña h×nh vu«ng nµy cïng víi 2 trung ®iÓm cña
MQ, AC t¹o thµnh 1 h×nh vu«ng.
III- BÀI TẬP TRẮC NGHIỆM Câu 1:
Cho hai điểm phân biệt A, B và  là góc lượng giác bất kì. Biết Q
A A , Q B B , O;   1 O;       1
khẳng định nào sau đây đúng? A. A B A . B
B. A B  A . B C. A B A . B D. A B A . B 1 1 1 1 1 1 1 1 Câu 2:
Cho tam giác đều ABC (thứ tự đỉnh theo chiều dương lượng giác), khẳng định nào sau đây sai? A. Q  B. Q  C. Q C  . B D. Q C  . B  7     7      C      BC. . B   A;   A;   A;   A;   3   3   3   3  Câu 3:
Gọi hình vuông ABCD tâm O (các đỉnh theo thứ tự theo chiều ngược chiều kim đồng hồ).
Khẳng định nào sau đây đúng? A.  Q B  . A B. Q B C. C. Q B  . O D. Q B  . D 0 O;90     0 O;90     0 O;90     0 O;90    Câu 4:
Cho hình vuông MNPQ (thứ tự các đỉnh cùng chiều quay của kim đồng hồ). Phép quay nào
sau đây biến điểm M thành điểm P.
A. Phép quay tâm Q góc 90 . 
B. Phép quay tâm Q góc 45 . 
C. Phép quay tâm Q góc 45 . 
D. Phép quay tâm Q góc 90 .  Câu 5:
Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A1; 2. Khẳng định nào sau đây đúng? A. Q A A 2  ;1 . B. Q A A 2; 1  .  3       3      O;  O;   2   2  C. Q A A 1  ; 2  . D. Q A A 2  ; 1  .  3       3      O;  O;   2   2  Câu 6:
Có bao nhiêu phép quay với góc quay   0 0
0    360  biến tam giác đều cho trước thành chính nó? A. 0. B. 1. C. 2. D. 4.
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 11
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11 Câu 7:
Biết thực hiện liên tiếp hai phép quay Q ,         
k2 , k 2 , k,k ta được phép I ;   Q và I ;   
đồng nhất. Khẳng định nào sau đây đúng?
A.       k2 , k  .
B.     k2 , k  .   C.    
k2 , k . C.    
k2 , k . 2 2 Câu 8:
Phép biến hình nào sau đây không có tính chất: “Biến một đường thẳng thành một đường
thẳng song song hoặc trùng với nó”? A. Phép đồng nhất. B. Phép vị tự.
C. Phép quay bất kì. D. Phép tịnh tiến. Câu 9:
Cho đường thẳng  và điểm I  . Phép quay tâm I với góc quay  nào sau đây thì biến
đường thẳng thành chính nó? A. 0   60 . B. 0   90 . C. 0   180 . D. 0   360 .
Câu 10: Phép quay tâm I góc quay 90 biến đường thẳng d thành đường thẳng d . Khẳng định nào sau đây là đúng? A. d d . B. d / /d . C. d d .
D. d,d  45 . 
Câu 11: Trong mặt phẳng với hệ tọa độ Oxy, ảnh của điểm B3;4 qua phép quay tâm O, góc quay 0 90 , có tọa độ là A. 4; 3. B. 4; 3  . C. 3; 4. D. 4; 3.
Câu 12: Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M 0; 3 . Xác định tọa độ điểm M là ảnh của
điểm M qua phép quay tâm O0;0 , góc quay   270 . A. M 3  ;0. B. M 3  ;3. C. M0; 3  . D. M3;0.
Câu 13: Trong mặt phẳng với hệ tọa độ Oxy , phép quay tâm I 2;1 , góc quay 0
120 , biến điểm M 1;9
thành điểm M ' có tọa độ là  1 5 3 2   3 3   5  8 3 6   3  A. M ;    . B. M  ;  . 2 2      2 2    5  8 3 2   2 3   1 5 3 6   3  C. M ;    . D. M  ; . 2 2      2 2  
Câu 14: Cho M 3; 4 . Tìm ảnh của điểm M qua phép quay tâm O góc quay 0 30 .  3 3 3  A. M ' ;  2 3   . B. M ' 2  ; 2 3 . 2 2     3 3   3 3 3  C. M ' ; 2 3   . D. M '  2;  2 3  . 2      2 2  
Câu 15: Trong mặt phẳng Oxy , cho điểm M 1; 
1 . Hỏi các điểm sau điểm nào là ảnh của M qua phép
quay tâm O , góc 45 ? A. M  –1  ;1 . B. M 1;0 . C. M  2;0 . D. M 0; 2  .
Câu 16: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng  : 2x y  1  0. Ảnh của đường thẳng
 qua phép quay tâm O, góc quay 0
90 là đường thẳng có phương trình
A. x  2y  1  0.
B. 2x y  2  0.
C. 2x y  2  0.
D. x  2y  1  0.
Câu 17: Trong mặt phẳng với hệ tọa độ Oxy, phép quay tâm O , góc quay 0 90 biến đường tròn C 2 2
: x y  4x  6y  3  0 thành đường tròn C có phương trình nào sau đây?
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 12
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11 2 2 2 2
A. C : x  3  y  2  16.
B. C : x  3  y  2  16. 2 2 2 2
C. C : x  2  y  3  16.
D. C : x  2  y  3  16.
Câu 18: Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn C x  2 2 :
1  y  5. Xác định phương
trình đường tròn C là ảnh của đường tròn C qua phép quay tâm O, góc quay 0 90 . 2 2
A. x  y  2 2 1  5.
B. x  y  2 2 1  5.
C. x  1  y  1  5. D. x  2 2 1  y  5.
Câu 19: Cho tam giác đều ABC có G là trọng tâm (hình vẽ bên). Khẳng định A nào sau đây đúng? A. Q B  . A B. Q B  . A G ,60   G ,120       G C. Q A  . B D. Q A  . B G ,6   G ,120       B C
Câu 20: Có bao nhiêu phép quay với góc quay  với      ;  
 biến hình vuông thành chính nó? A. 1. B. 2. C. 3. D. 5.
Câu 21: Trong mặt phẳng, tìm ảnh của điểm A2; 
1 qua phép quay tâm O , góc quay 90 .  A. M 1; 2  . B. N 1; 2. C. P 1; 2. D. Q2;1.
Câu 22: Trong mặt phẳng, cho đường thẳng  : x  2y  1  0 . Xác định ảnh của  qua phép quay tâm
O ( O là gốc tọa độ), góc quay 90 .
A. x  2y  1  0.
B. 2x y  1  0.
C. 2x y  1  0.
D. 2x y  1  0.
Câu 23: Về phía ngoài tam giác ABC , dựng các hình vuông Q
ABMN và ACPQ . Gọi I , J lần lượt là tâm các hình vuông
ABMN và ACPQ ; E là trung điểm BC (tham khảo hình N
vẽ). Khẳng định nào sau đây sai? A J P
A. EIJ vuông cân. B. BQ CN. I M C. AE MP. D. BQ CN. B E C
Câu 24: Trong mặt phẳng, cho hai điểm A1;3 , B 2; 
1 . Gọi M, N lần lượt là ảnh của A, B qua phép
dời hình bằng cách thực hiện liếp tiếp phép tịnh tiến theo vectơ v  3; 1   và phép quay tâm
O , góc quay 90 . Viết phương trình đường thẳng MN .
A. x  4y  20  0.
B. x  4y  20  0.
C. 4x y  12  0.
D. 4x y  5  0.
Câu 25: Cho tam giác đều ABC cạnh a có G là trọng tâm. Gọi tam giác MNP là ảnh của tam giác
ABC qua phép dời hình bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ BC và phép
quay tâm G , góc quay 90 . Tính độ dài GM. a 3 2a 3 a 7 A. . B. . C. . D. a 7. 3 3 2
Câu 26: Cho tam giác đều ABC . Hãy xác định góc quay của phép quay tâm A biến B thành điểm C . A.   30 . B.   90 . C.   120   . D. 0   60 hoặc 0   60 .
Câu 27: Cho hai hình vuông ABCD và BEFG như hình bên. Tìm
ảnh của tam giác ABG qua phép quay tâm B , góc quay 90 . A. BCD . B. CBE . C. ABD . D. DCG .
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 13
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Câu 28: Trong mặt phẳng với hệ tọa độ Oxy, cho vectơ v  3; 2
  và điểm M 1
 ; 4. Xác định tọa độ
ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O, góc quay 0
90 và phép tịnh tiến theo vectơ v. A. 1; 3. B. 7; 1  . C. 2; 6. D. 4; 2.
Câu 29: Trong mặt phẳng Oxy , cho đường thẳng d : 2x  3y  9  0 . Viết phương trình của đường thẳng
d ' là ảnh của đường thẳng d qua phép quay tâm O góc 0 90 .
A. 2x  3y  9  0 .
B. 3x  2y  9  0 .
C. 3x  2y  9  0 .
D. 2x  3y  9  0 .
Câu 30: Trong mặt phẳng tọa độ Oxy , cho hai đường thẳng d : 4x  3y  5  0 và d' : x  7y  4  0 . Nếu
có phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc quay  với
0  180 là góc nào sau đây? A. 120 . B. 60 . C. 90 . D. 45 .
Câu 31: Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O góc với
k2 ( k là một số nguyên)? A. 0 . B. 1 . C. 2 . D. Vô số.
Câu 32: Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc quay  ,
0    2 biến hình chữ nhật trên thành chính nó? A.Không có. B.Hai. C.Ba. D.Bốn.
Câu 33: Trong mặt phẳng Oxy, cho điểm B(3; 6) . Tìm toạ độ điểm E sao cho B là ảnh của E qua phép quay tâm O góc quay 0 90 . A. E(6;3). B. E( 3  ; 6)  . C. E( 6  ; 3  ). D. E(3; 6).
Câu 34: Trong mặt phẳng tọa độ Oxy cho phép quay tâm O biến điểm A1; 0 thành điểm A0;  1 .
Khi đó nó biến điểm M 1;  1 thành điểm A. M  1  ;  1 . B. M 1;  1 . C. M  1  ;  1 . D. M 1; 0 .
Câu 35: Trong mặt phẳng với hệ tọa độ Oxy , phép quay tâm I 4; 3
  góc quay 180 biến đường thẳng
d : x y  5  0 thành đường thẳng d  có phương trình
A. x y  3  0 .
B. x y  3  0 .
C. x y  5  0 .
D. x y  3  0 .
Câu 36: Trong mặt phẳng Oxy , cho đường tròn C 2 2
: x y  4x 10 y  4  0 . Viết phương trình
đường tròn C  biết C là ảnh của C  qua phép quay với tâm quay là gốc tọa độ O và góc quay bằng 270 . A. C  2 2
: x y 10x  4 y  4  0 . B. C  2 2
: x y 10x  4 y  4  0 . C. C  2 2
: x y 10x  4 y  4  0 . D. C  2 2
: x y 10x  4 y  4  0 .
Câu 37: Cho lục giác đều ABCDEF tâm O như hình bên. Tam giác EOD là ảnh của tam giác AOF qua
phép quay tâm O góc quay . Tìm . A B O F C E D A. o 60 . B. o 60 . C. o 120 . D. o 120 .
_______________HẾT_______________
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 14
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
LỜI GIẢI CHI TIẾT Câu 1:
Cho hai điểm phân biệt A, B và  là góc lượng giác bất kì. Biết Q
A A , Q B B , O;   1 O;       1
khẳng định nào sau đây đúng? A. A B A . B
B. A B  A . B C. A B A . B D. A B A . B 1 1 1 1 1 1 1 1 Lời giải:
Phép quay là phép dời hình nên bảo toàn khoảng cách giữa hai điểm bất kì.
Chọn đáp án D. Câu 2:
Cho tam giác đều ABC (thứ tự đỉnh theo chiều dương lượng giác), khẳng định nào sau đây sai? A. Q  B. Q  C. Q C  . B D. Q C  . B  7     7      C      BC. . B   A;   A;   A;   A;   3   3   3   3  Lời giải: Ta có: Q C  .
B Vậy C sai.  7     A;   3 
Chọn đáp án C. Câu 3:
Gọi hình vuông ABCD tâm O (các đỉnh theo thứ tự theo chiều ngược chiều kim đồng hồ).
Khẳng định nào sau đây đúng? A.  Q B  . A B. Q B C. C. Q B  . O D. Q B  . D 0 O;90     0 O;90     0 O;90     0 O;90    Lời giải:   Q
B C vậy B đúng. 0 O;90   
Chọn đáp án B. Câu 4:
Cho hình vuông MNPQ (thứ tự các đỉnh cùng chiều quay của kim đồng hồ). Phép quay nào
sau đây biến điểm M thành điểm P.
A. Phép quay tâm Q góc 90 . 
B. Phép quay tâm Q góc 45 . 
C. Phép quay tâm Q góc 45 . 
D. Phép quay tâm Q góc 90 .  Lời giải: Dễ thấy Q M  . P M N Q, 9  0    
Chọn đáp án A. Q P Câu 5:
Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A1; 2. Khẳng định nào sau đây đúng? A. Q A A 2  ;1 . B. Q A A 2; 1  .  3       3      O;  O;   2   2  C. Q A A 1  ; 2  .      D. Q A A 2; 1 .  3      3      O;  O;   2   2 
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 15
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11 Lời giải: Ta có: Q A Q A A 2; 1  .  3          O;  O;   2   2 
Chọn đáp án B. Câu 6:
Có bao nhiêu phép quay với góc quay   0 0
0    360  biến tam giác đều cho trước thành chính nó? A. 0. B. 1. C. 2. D. 4. Lời giải:
Tồn tại hai phép quay với góc quay   0 0 0    360  : A +)  Q ABC ABC . 0 G;120      1200 +)  Q ABC ABC . 0 G;240      G Với B
G là trọng tâm tam giác ABC. C
Chọn đáp án C. Câu 7:
Biết thực hiện liên tiếp hai phép quay Q ,         
k2 , k 2 , k,k ta được phép I ;   Q và I ;   
đồng nhất. Khẳng định nào sau đây đúng?
A.       k2 , k  .
B.     k2 , k  .   C.    
k2 , k . C.    
k2 , k . 2 2 Lời giải:
Khi     k2 , k   thì thực hiện liên tiếp hai M' phép quay Q ,         
k2 , k 2 , k,k I ;   Q và I ;   
ta được phép đồng nhất.
Chọn đáp án B. 2π-α α I M≡M'' Câu 8:
Phép biến hình nào sau đây không có tính chất: “Biến một đường thẳng thành một đường
thẳng song song hoặc trùng với nó”? A. Phép đồng nhất. B. Phép vị tự.
C. Phép quay bất kì. D. Phép tịnh tiến. Lời giải:
Phép quay với góc quay   k2 hoặc     k2 , k   biến một đường thẳng thành một
đường thẳng song song hoặc trùng với nó.
Chọn đáp án C. Câu 9:
Cho đường thẳng  và điểm I  . Phép quay tâm I với góc quay  nào sau đây thì biến
đường thẳng thành chính nó? A. 0   60 . B. 0   90 . C. 0   180 . D. 0   360 . Lời giải: Q
    ;  60     . Vậy A sai I ; 60        Q
       . Vậy B sai O; 90      Q
      . Vậy C sai O      // ;180  Q
       . Vậy D đúng O; 360    
Chọn đáp án D.
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 16
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Câu 10: Phép quay tâm I góc quay 90 biến đường thẳng d thành đường thẳng d . Khẳng định nào sau đây là đúng? A. d d . B. d / /d . C. d d .
D. d,d  45 .  Lời giải:
Chọn đáp án A.
Câu 11: Trong mặt phẳng với hệ tọa độ Oxy, ảnh của điểm B3;4 qua phép quay tâm O, góc quay 0 90 , có tọa độ là A. 4; 3. B. 4; 3  . C. 3; 4. D. 4; 3. Lời giải:      x y 4 B B Q
B B    B 4  ; 3 . O; 90       y     x 3 B B
Chọn đáp án B.
Câu 12: Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M 0; 3 . Xác định tọa độ điểm M là ảnh của
điểm M qua phép quay tâm O0;0 , góc quay   270 . A. M 3  ;0. B. M 3  ;3. C. M0; 3  . D. M3;0. Lời giải:
Chọn đáp án D.
Câu 13: Trong mặt phẳng với hệ tọa độ Oxy , phép quay tâm I 2;1 , góc quay 0
120 , biến điểm M 1;9
thành điểm M ' có tọa độ là  1 5 3 2   3 3   5  8 3 6   3  A. M ;    . B. M  ;  . 2 2      2 2    5  8 3 2   2 3   1 5 3 6   3  C. M ;    . D. M  ; . 2 2      2 2   Lời giải:
x  x a 0
cos120  y b 0 sin120  a
Giả sử M 'x ; y . Ta có:  y   x a . 0
sin120  y b 0 cos120   b  5  8 3 6   3 
Thay x  1; y  9; a  2; b  1 , ta có M ;   . 2 2   
Chọn đáp án B.
Câu 14: Cho M 3; 4 . Tìm ảnh của điểm M qua phép quay tâm O góc quay 0 30 .  3 3 3  A. M ' ;  2 3   . B. M ' 2  ; 2 3 . 2 2     3 3   3 3 3  C. M ' ; 2 3   . D. M '  2;  2 3  . 2      2 2   Lời giải:
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 17
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
x'  xcos  y sin 
Gọi M 'x'; y'   Q
.Áp dụng biểu thức tọa độ  ta có 0 O;30 
y '  x sin   y cos    0 0 3 3
x'  3cos 30  4 sin 30   2    2 3 3 3   M '  2;  2 3  .   2 2  0 0 3
y '  3 sin 30  4 cos 30   2 3    2
Chọn đáp án D.
Câu 15: Trong mặt phẳng Oxy , cho điểm M 1; 
1 . Hỏi các điểm sau điểm nào là ảnh của M qua phép
quay tâm O , góc 45 ? A. M  –1  ;1 . B. M 1;0 . C. M  2;0 . D. M 0; 2  . Lời giải:
+ Thay biểu thức tọa độ của phép quay tâm O góc quay 45 ta có:
x  .xcos45o  .ysin 45o  cos45o sin 45o  0  .
y  .xsin 45o  .
y cos 45o  sin 45o  cos 45o  2
Vậy M 0; 2  .
Chọn đáp án D.
Câu 16: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng  : 2x y  1  0. Ảnh của đường thẳng
 qua phép quay tâm O, góc quay 0
90 là đường thẳng có phương trình
A. x  2y  1  0.
B. 2x y  2  0.
C. 2x y  2  0.
D. x  2y  1  0. Lời giải:
 Gọi Mx; yd , Q    ;Q
M M  M  O; 90   O; 90       x     y y x M M M M    
, thay vào phương trình đường thẳng y        x x y M MM M   2.y           x  1 0 :x 2y 1 0 . M M
Chọn đáp án D.
Câu 17: Trong mặt phẳng với hệ tọa độ Oxy, phép quay tâm O , góc quay 0 90 biến đường tròn C 2 2
: x y  4x  6y  3  0 thành đường tròn C có phương trình nào sau đây? 2 2 2 2
A. C : x  3  y  2  16.
B. C : x  3  y  2  16. 2 2 2 2
C. C : x  2  y  3  16.
D. C : x  2  y  3  16. Lời giải:
Đường tròn I 2; 3
 , bán kính R  4. Ta có:  Q
I I 3; 2 : Tâm đường tròn C. 0 O;90     
Đường tròn C có tâm I3; 2 , bán kính R  R  4 nên có phương trình:
x  2 y  2 3 2  16.
Chọn đáp án A.
Câu 18: Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn C x  2 2 :
1  y  5. Xác định phương
trình đường tròn C là ảnh của đường tròn C qua phép quay tâm O, góc quay 0 90 . 2 2
A. x  y  2 2 1  5.
B. x  y  2 2 1  5.
C. x  1  y  1  5. D. x  2 2 1  y  5.
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 18
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11 Lời giải:
Đường tròn C có tâm I 1;0 , bán kính R  5. Ta có:  Q
I I 0;1 . 0 O; 9  0     
Đường tròn C có tâm I0;1 , bán kính R  R  5, có phương trình: x  y  2 2 1  5.
Chọn đáp án B.
Câu 19: Cho tam giác đều ABC có G là trọng tâm (hình vẽ bên). Khẳng định A nào sau đây đúng? A. Q B  . A B. Q B  . A G ,60   G ,120       G C. Q A  . B D. Q A  . B G ,6   G ,120       B C Lời giải: Ta có Q A  . B G ,120    
Chọn đáp án C.
Câu 20: Có bao nhiêu phép quay với góc quay  với      ;  
 biến hình vuông thành chính nó? A. 1. B. 2. C. 3. D. 5. Lời giải:
Gọi O là tâm của hình vuông. Khi đó phép quay tâm O ,    
góc quay  với    
 ; ;0; ;  biến hình vuông thành  2 2  chính nó.
Chọn đáp án D.
Câu 21: Trong mặt phẳng, tìm ảnh của điểm A2; 
1 qua phép quay tâm O , góc quay 90 .  A. M 1; 2  . B. N 1; 2. C. P 1; 2. D. Q2;1. Lời giải: x  y
Biểu thức tọa độ của phép quay tâm O , góc quay 90 biến M x; y thành Mx ; y :  . y   x Suy ra Q A N 1; 2 . O ,90      
Chọn đáp án B.
Câu 22: Trong mặt phẳng, cho đường thẳng  : x  2y  1  0 . Xác định ảnh của  qua phép quay tâm
O ( O là gốc tọa độ), góc quay 90 .
A. x  2y  1  0.
B. 2x y  1  0.
C. 2x y  1  0.
D. 2x y  1  0. Lời giải:
Lấy M 1;0 , N 1;1 nằm trên  . x  y
Biểu thức tọa độ của phép quay tâm O , góc quay 90 biến M x; y thành Mx ; y :  . y    x Khi đó Q
M M 0;1 , Q N N 1; 1  và Q    . O , 90     O, 9  0  
  O, 90          
Suy ra  đi qua hai điểm M, N . Do đó  : 2x y  1  0.
Chọn đáp án D.
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 19
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Câu 23: Về phía ngoài tam giác ABC , dựng các hình vuông Q
ABMN và ACPQ . Gọi I , J lần lượt là tâm các hình vuông N
ABMN và ACPQ ; E là trung điểm BC (tham khảo hình A J P
vẽ). Khẳng định nào sau đây sai? I M
A. EIJ vuông cân. B. BQ CN. C. B C AE MP. D. BQ CN. E Lời giải:
Xét phép quay tâm A , góc quay 90 . Q Ta có Q
N B, Q
C Q Q NC BQ . A,90   A,90   A,90         N
Suy ra BQ CN và BQ CN.  A P
BCN có EI là đường trung bình nên EI // CN và J I 1 M EI CN . 2  B C
CBQ có EJ là đường trung bình nên EJ // BQ và E 1 EJ BQ . 2
Suy ra EI EJ và EI EJ  EIJ vuông cân tại E.
Chọn đáp án C.
Câu 24: Trong mặt phẳng, cho hai điểm A1;3 , B 2; 
1 . Gọi M, N lần lượt là ảnh của A, B qua phép
dời hình bằng cách thực hiện liếp tiếp phép tịnh tiến theo vectơ v  3; 1   và phép quay tâm
O , góc quay 90 . Viết phương trình đường thẳng MN .
A. x  4y  20  0.
B. x  4y  20  0.
C. 4x y  12  0.
D. 4x y  5  0. Lời giải:
Ta có T A  C 4; 4
 , T B  D5;0 , Q
C M 4; 4 , Q D N 0; 5 . O ,90     O,90     v v     
Suy ra MN : x  4y  20  0.
Chọn đáp án B.
Câu 25: Cho tam giác đều ABC cạnh a có G là trọng tâm. Gọi tam giác MNP là ảnh của tam giác
ABC qua phép dời hình bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ BC và phép
quay tâm G , góc quay 90 . Tính độ dài GM. a 3 2a 3 a 7 A. . B. . C. . D. a 7. 3 3 2 Lời giải: P
Phép tịnh tiến theo vectơ BC biến ABC thành DCE .
Phép quay tâm G , góc quay 90 biến DCE thành MNP . J M
Gọi I, J lần lượt là trọng tâm của DCE và MNP . D A
Ta có T G  I N
GI a , Q
I J GI GJ a . G ,90   BC   I T AG 2 a 3 a 3  DI, Q
DI MJ MJ AG, MJ AG  .  . G BC G,90     3 2 3 E B C 2  a a Suy ra 2 3 2 3 MG a     .  3  3  
Chọn đáp án B.
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 20
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Câu 26: Cho tam giác đều ABC . Hãy xác định góc quay của phép quay tâm A biến B thành điểm C . A.   30 . B.   90 . C.   120   . D. 0   60 hoặc 0   60 . Lời giải: AB AC Ta có:  nên Q (B)  C . (AB, AC)  6  0    ( A; 60 )
Chọn đáp án D.
Câu 27: Cho hai hình vuông ABCD và BEFG như hình bên. Tìm
ảnh của tam giác ABG qua phép quay tâm B , góc quay 90 . A. BCD . B. CBE . C. ABD . D. DCG . Lời giải: Ta có: Q B B,Q A C,Q
G E hay ảnh của tam giác ABG qua phép quay B, 9  0   B, 9  0   B, 9  0        
tâm B , góc quay 90 là tam giác CBE .
Chọn đáp án B.
Câu 28: Trong mặt phẳng với hệ tọa độ Oxy, cho vectơ v  3; 2
  và điểm M 1
 ; 4. Xác định tọa độ
ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O, góc quay 0
90 và phép tịnh tiến theo vectơ v. A. 1; 3. B. 7; 1  . C. 2; 6. D. 4; 2. Lời giải: Ta có:  Q M M 4  ; 1
 và T M M 1  ; 3  . v 1  2   0 O;90    1  
Chọn đáp án A.
Câu 29: Trong mặt phẳng Oxy , cho đường thẳng d : 2x  3y  9  0 . Viết phương trình của đường thẳng
d ' là ảnh của đường thẳng d qua phép quay tâm O góc 0 90 .
A. 2x  3y  9  0 .
B. 3x  2y  9  0 .
C. 3x  2y  9  0 .
D. 2x  3y  9  0 . Lời giải:
Gọi M x; yd ; M'(x'; y')  Q M 0   (O;90 ) 0 0 x'  . x cos90  . y sin 90 x'  yx y' Ta có:     
My';x' . 0 0 y'  . x sin 90  . y cos90 y'  xy  x'
Có: M y'; x'd : 2x  3y  9  0  2y' 3x' 9  0
Vậy phương trình d ' cần tìm là : 3x  2y  9  0
Chọn đáp án B.
Câu 30: Trong mặt phẳng tọa độ Oxy , cho hai đường thẳng d : 4x  3y  5  0 và d' : x  7y  4  0 . Nếu
có phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc quay  với
0  180 là góc nào sau đây? A. 120 . B. 60 . C. 90 . D. 45 . Lời giải:
Hai đường thẳng d và d ' có vecto pháp tuyến lần lượt là n  4; 3 và n  1;7 . d'   dn .nd d 4.1 3.7 2
Ta có: cosd,d'  cosn ,n   
Suy ra d,d'  45 . d d  ' . ' n . n 5.5 2 2 d d'
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 21
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11
Vì d,d'   hoặc d,d'  180  nên   45 hoặc   135 .
Chọn đáp án D.
Câu 31: Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O góc với
k2 ( k là một số nguyên)? A. 0 . B. 1 . C. 2 . D. Vô số. Lời giải:
Điểm đó chính là tâm quay O .
Chọn đáp án B.
Câu 32: Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc quay  ,
0    2 biến hình chữ nhật trên thành chính nó? A.Không có. B.Hai. C.Ba. D.Bốn. Lời giải:
Có 2 phép quay tâm O góc  , 0    2 biến tam giác trên thành chính nó là các phép quay
với góc quay bằng:  , 2 .
Chọn đáp án B.
Câu 33: Trong mặt phẳng Oxy, cho điểm B(3; 6) . Tìm toạ độ điểm E sao cho B là ảnh của E qua phép quay tâm O góc quay 0 90 . A. E(6;3). B. E( 3  ; 6)  . C. E( 6  ; 3  ). D. E(3; 6). Lời giải:
Điểm E(6;3) .
Chọn đáp án C.
Câu 34: Trong mặt phẳng tọa độ Oxy cho phép quay tâm O biến điểm A1; 0 thành điểm A0;  1 .
Khi đó nó biến điểm M 1;  1 thành điểm A. M  1  ;  1 . B. M 1;  1 . C. M  1  ;  1 . D. M 1; 0 . Lời giải: y A' M' 1 x O A 1 -1 M
Từ giả thiết, kết hợp với hình vẽ ta thấy góc quay là . 2 
Khi đó phép quay tâm O góc quay
biến điểm M 1;  
1 thành điểm M 1;  1 . 2
Chọn đáp án B.
Câu 35: Trong mặt phẳng với hệ tọa độ Oxy , phép quay tâm I 4; 3
  góc quay 180 biến đường thẳng
d : x y  5  0 thành đường thẳng d  có phương trình
A. x y  3  0 .
B. x y  3  0 .
C. x y  5  0 .
D. x y  3  0 . Lời giải:
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 22
Chuyên đề PHÉP BIẾN HÌNH TRONG MẶT PHẲNG Hình Học 11 Ta có phép quay  Q
là phép đối xứng tâm I o I ;180 
Vì I d nên nếu Đ d d thì d / /d  , suy ra phương trình d : x y m  0m  5   . I  
M 0;5d  Xét Đ M M M Cho M 8; 1  
1  d  m  3 . Vậy d  : x y  3  0 . I
    8;1  1 .  I 4; 3
Chọn đáp án B.
Câu 36: Trong mặt phẳng Oxy , cho đường tròn C 2 2
: x y  4x 10 y  4  0 . Viết phương trình
đường tròn C  biết C là ảnh của C  qua phép quay với tâm quay là gốc tọa độ O và góc quay bằng 270 . A. C  2 2
: x y 10x  4 y  4  0 . B. C  2 2
: x y 10x  4 y  4  0 . C. C  2 2
: x y 10x  4 y  4  0 . D. C  2 2
: x y 10x  4 y  4  0 . Lời giải:
Đường tròn C có tâm I2;  5 , bán kính R  4  25  4  5 .
Ta có C  Q C
 C  Q C
 C   Q C . O,90   O, 90   O, 270        
x  y   5 Do đó I Q
I  . Vì đây là phép quay 90 nên I I
, suy ra I 5; 2 . O,90     y x    2 I I
Bán kính đường tròn C  là R R  5 . 2 2
Vậy C  :  x  5   y  2  25  C  2 2
: x y 10x  4 y  4  0 .
Chọn đáp án B.
Câu 37: Cho lục giác đều ABCDEF tâm O như hình bên. Tam giác EOD là ảnh của tam giác AOF qua
phép quay tâm O góc quay . Tìm . A B O F C E D A. o 60 . B. o 60 . C. o 120 . D. o 120 . Lời giải: Q
O O , Q
A F . Q F D . O; 1  20   O; 1  20   O; 1  20        
Chọn đáp án B.
Lớp Toán thầy LÊ BÁ BẢO - Số 4 Kiệt 116 Nguyễn Lộ Trạch (TP Huế)_Trung tâm KM10 Hương Trà 0935.785.115 23