Lý thuyết "Quy luật 8 - Quy luật phân phối Student"
Tài liệu gồm 3 trangbao gồm các kiến thức cơ bản liên quan: "Quy luật 8 - Quy luật phân phối Student" giúp bạn ôn luyện và nắm vững kiến thức. Mời bạn đọc đón xem!
Preview text:
lOMoARcPSD|35973522 Quy luật 8:
QUY LUẬT PHÂN PHỐI STUDENT I. Lý thuyết: 1. Định nghĩa:
- Biến ngẫu nhiên liên tục T được gọi là phân phối theo quy luật
student với n tự do, ký hiệu là T ~ T(n) nếu hàm mật độ xác suất có dạng:
( với -∞ < t < +∞) Trong đó: = là hàm Gamma
- Đồ thị hàm ) có dạng: ) 0 t
Hàm mật độ phân phối T(n) Chú ý:
* Phân phối student còn được gọi là phân phối t. Phân phối t có
một giá trị mode và đối xứng qua đường thẳng t=0
* Khi số bậc tự do n khá lớn, phân phối t sẽ xấp xỉ phân phối
chuẩn hóa N(0,1) Do đó, nếu n khá lớn(n>= 30), ta có thể dùng
phân phối chuẩn hóa thay cho phân phối t. Tuy nhiên, khi số bậc
tự do không lớn(<30), phân phối t khác xa so với phân phối
chuẩn giới hạn (nói dễ hiểu, nếu n >= 30, có thể dùng phân
phối chuẩn hóa thay cho phân phối t, còn n < 30 thì không.)
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522
2. Các số đặc trưng chính:
- Kỳ vọng: E(T) = 0 (n>1)
- Phương sai sai: Var(T) = (n>2)
3. Phân vị (giá trị giới hạn)
Cho ĐLNN T~T(n), khi đó, với 0 < α < 1 cho trước giá trị
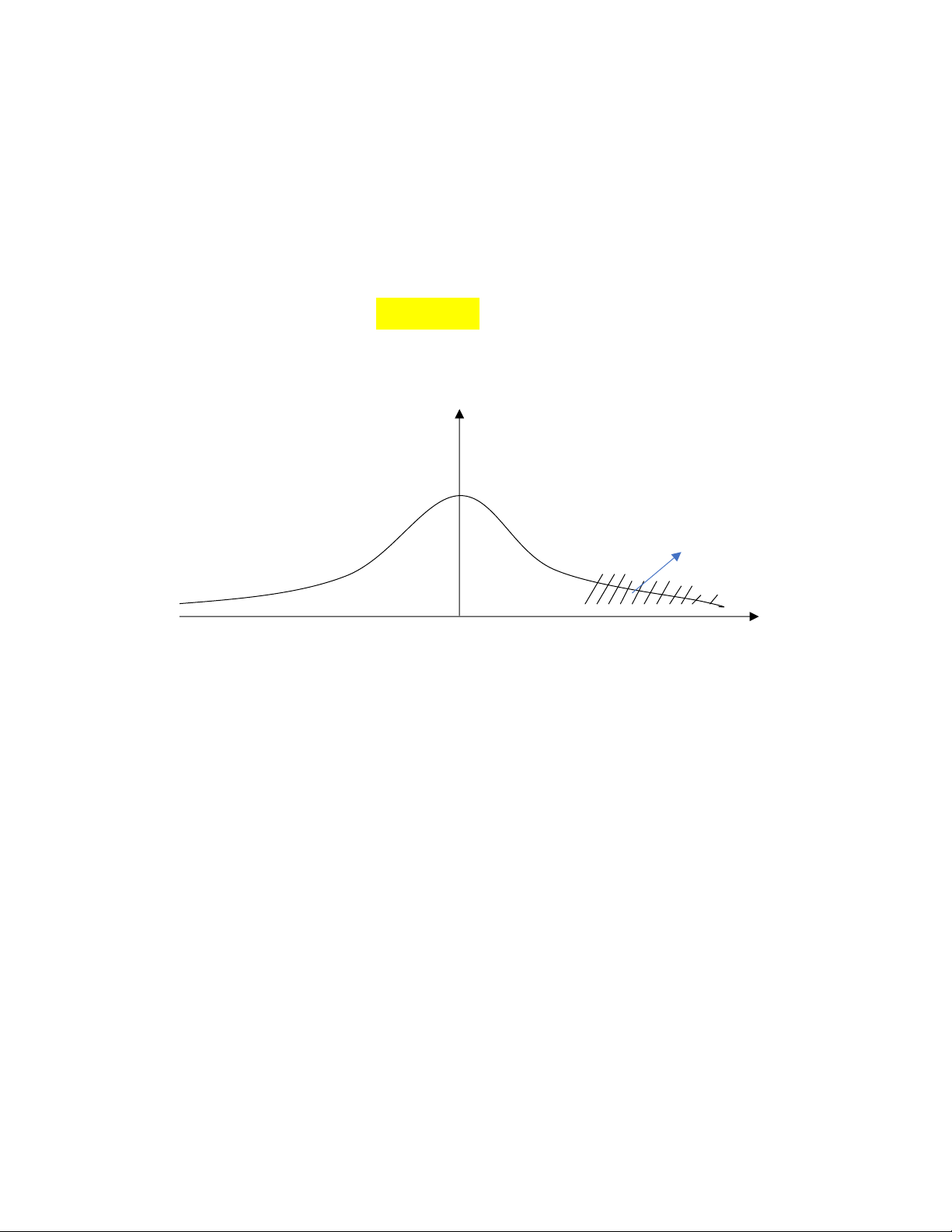
của ĐLNN T thỏa mãn P(T >) = được gọi là giá trị phân vị student mức . ) 0 t
Phân vị student mức CHÚ Ý:
- Vì phân phối t là phân phối đối xứng, nên: =
- Nếu n>30, có thể đùng phân phối chuẩn hóa N(0,1) thay thế
cho phân phối student và =
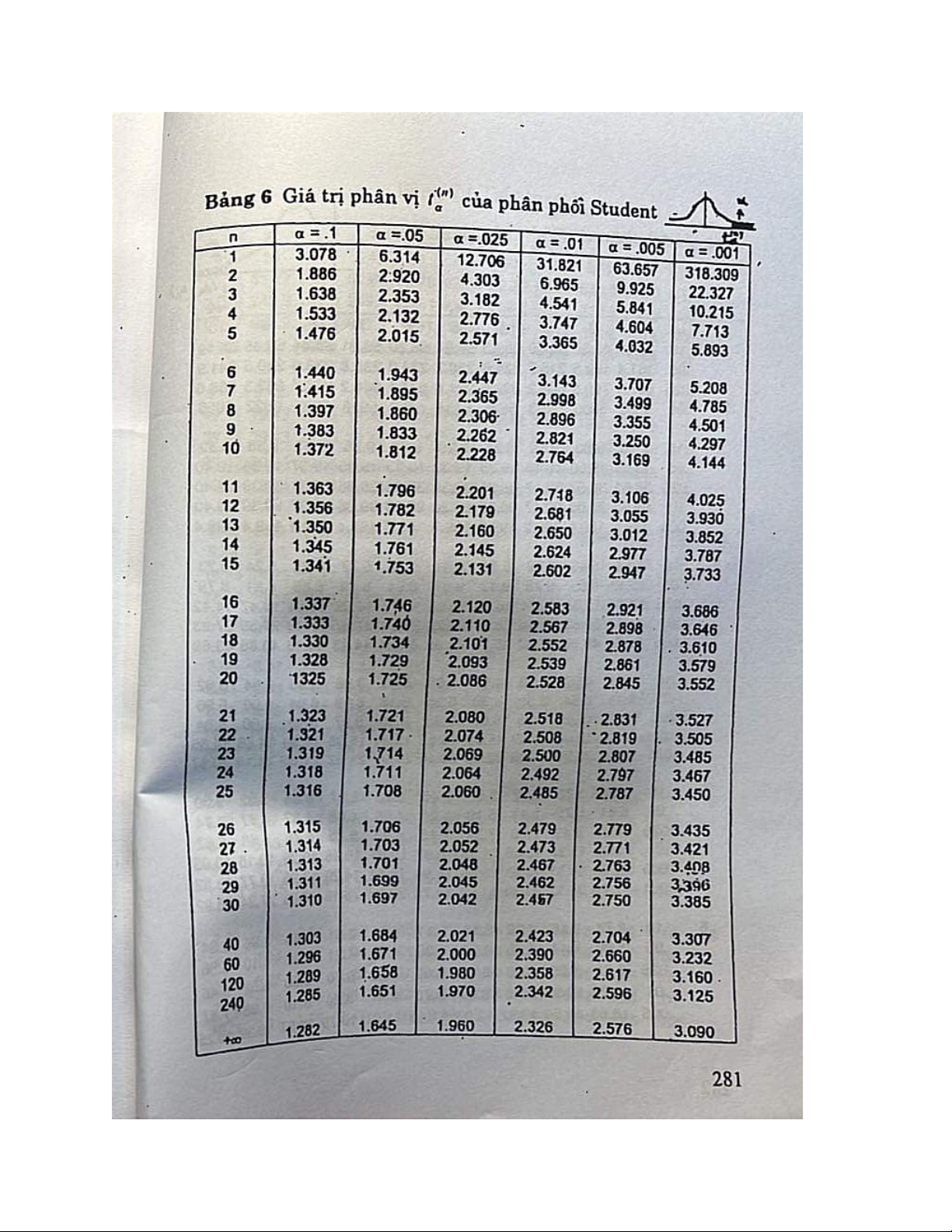
- Các giá trị phân vị ứng với n và được cho ở bảng phụ lục 6.
(<30 tra bảng ppt, >30 tra bảng pp chuẩn hóa)
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com) lOMoARcPSD|35973522
Downloaded by Di?p ??ng Ng?c (tanphatthpt@gmail.com)