Lý Thuyết Trò Chơi Trong Độc Quyền Nhóm | Bài thảo luận kinh tế vi mô

TRƯỜNG ĐẠI HỌC THƯƠNG MẠI KHOA KINH TẾ BÀI THẢO LUẬN
Học phần Kinh tế vi mô 2
ĐỀ TÀI: PHÂN TÍCH LÝ THUYẾT TRÒ CHƠI TRONG CÁC CHIẾN
LƯỢC CẠNH TRANH CỦA CÁC DOANH NGHIỆP ĐỘC QUYỀN
NHÓM VÀ NGHIÊN CỨU CÁC CASE STUDY ĐIỂN HÌNH Mã lớp học phần: 242_MIEC0311_02 Giảng viên hướng dẫn: Hồ Thị Mai Sương Nhóm thực hiện: 6 Hà Nội, tháng 4 năm 2025 1 LỜI CẢM ƠN
Lời đầu tiên, Nhóm 6 xin được gửi lời cảm ơn chân thành nhất đến giảng viên
Hồ Thị Mai Sương. Trong quá trình học tập và tìm hiểu môn Kinh tế vi mô 2 nhóm đã
nhận được rất nhiều sự quan tâm, giúp đỡ, hưỡng dẫn tâm huyết và tận tình của cô. Cô
đã giúp nhóm em tích lũy thêm nhiều kiến thức về môn học này để có thể hoàn thành
được bài tiểu luận về đề tài “Phân tích lý thuyết trò chơi trong các chiến lược cạnh tranh
của các doanh nghiệp độc quyền nhóm và nghiên cứu các case study điển hình”.
Trong quá trình làm bài chắc chắn khó tránh khỏi những thiếu sót. Do đó, nhóm
em kính mong nhận được những lời góp ý của cô để bài tiểu luận của em ngày càng hoàn thiện hơn.
Chúng em xin chân thành cảm ơn! 2 MỤC LỤC
DANH MỤC BẢNG BIỂU . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
DANH MỤC SƠ ĐỒ, HÌNH VẼ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
LỜI MỞ ĐẦU . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
CHƯƠNG 1. CƠ SỞ LÝ LUẬN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.1. Độc quyền nhóm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.1.1. Các đặc trưng cơ bản của độc quyền nhóm . . . . . . . . . . . . . . . . . . . . . . . . 8
1.1.2. Các mô hình cạnh tranh của doanh nghiệp độc quyền nhóm . . . . . . . . . . 9
1.2. Lý thuyết trò chơi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.2.1. Khái niệm và lịch sử ra đời . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.2.2. Xác định cân bằng Nash trong trò chơi đồng thời . . . . . . . . . . . . . . . . . . 16
1.2.3. Xác định cân bằng Nash trong trò chơi tuần tự . . . . . . . . . . . . . . . . . . . . 20
CHƯƠNG 2. PHÂN TÍCH CASE STUDY ĐIỂN HÌNH . . . . . . . . . . . . . . . . . . . . 23
2.1. Case study 1- Cạnh tranh giá trong ngành công nghiệp viễn thông . . . . . . 23
2.1.1. Bối cảnh nghiên cứu tình huống . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
2.1.2. Phân tích và đánh giá tình huống . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.2. Case study 2- Cạnh tranh sản lượng trong ngành hàng không . . . . . . . . . . 33
2.2.1. Bối cảnh nghiên cứu tình huống . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.2.2. Phân tích và đánh giá tình huống . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
KẾT LUẬN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
TÀI LIỆU THAM KHẢO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 3
DANH MỤC BẢNG BIỂU
Bảng 2.2.Thị phần thuê bao di động của Việt Nam giai đoạn 2007 -2011. . . . . . . . . . 30 4
DANH MỤC SƠ ĐỒ, HÌNH VẼ
Hình 1.1 Đường phản ứng tốt nhất của hai hãng trong mô hình Cournot . . . . . . . . . . . 10
Hình 1.2. Đường phản ứng tốt nhất của hai hãng trong mô hình Bertrand khi sản phầm
khác biệt và hai hãng ra quyết định đồng thời . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
Hình 1.3. Ma trận lợi ích khi mỗi người chơi đều có chiến lược ưu thế . . . . . . . . . . . . 16
Hình 1.4. Lựa chọn của người chơi khi có chiến lược bị lấn át . . . . . . . . . . . . . . . . . . 17
Hình 1.5. Phân tích phản ứng tốt nhất tìm cân bằng Nash . . . . . . . . . . . . . . . . . . . . . . 19
Hình 1.6. Quyết định gia nhập thị trường của hãng B và phản ứng của hãng A nếu hai
hãng ra quyết định đồng thời . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
Hình 1.7. Cây trò chơi của hai hãng A và B khi quyết định gia nhập thị trường. . . . . . 21
Hình 2.1. Cây trò chơi của hai doanh nghiệp Viettel và VNPT khi quyết định chiến lược
định giá thấp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
Hình 2.2. Ma trận lợi ích giữa 2 hãng khi mỗi hãng đều có chiến lược ưu thế (tỷ đồng)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
Hình 2.3. Cây trò chơi của hai hãng Vietnam Airlines và Vietjet Air khi quyết định mở
rộng chuyến bay. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 5 LỜI MỞ ĐẦU
1. Tính cấp thiết nghiên cứu của đề tài
Trong bối cảnh nền kinh tế thị trường ngày càng phát triển theo hướng cạnh tranh
mạnh mẽ, các doanh nghiệp không còn hoạt động một cách đơn lẻ hay ngẫu nhiên, mà
luôn phải đối mặt với các đối thủ có chiến lược và hành vi được tính toán kỹ lưỡng. Đặc
biệt, trong những ngành có ít doanh nghiệp cùng hoạt động – hay còn gọi là thị trường
độc quyền nhóm – hành động của một doanh nghiệp có thể gây ảnh hưởng đáng kể đến
lợi ích của doanh nghiệp còn lại, và ngược lại. Chính vì thế, việc hiểu và dự đoán được
hành vi chiến lược của các đối thủ cạnh tranh trở thành yếu tố sống còn đối với mọi
doanh nghiệp trong môi trường như vậy.
Lý thuyết trò chơi, với công cụ phân tích hành vi chiến lược dựa trên mô hình toán
học, cung cấp một nền tảng vững chắc để lý giải và dự đoán các quyết định kinh tế giữa
các tác nhân có tương tác với nhau. Việc ứng dụng lý thuyết trò chơi, đặc biệt là các khái
niệm như cân bằng Nash, vào trong phân tích chiến lược cạnh tranh của các doanh
nghiệp hoạt động trong thị trường độc quyền nhóm không chỉ mang lại cái nhìn trực
quan và logic về hành vi chiến lược mà còn giúp doanh nghiệp xây dựng kế hoạch hành
động tối ưu trong thực tế.
Đặc biệt, ở các ngành như viễn thông và hàng không, nơi có số lượng doanh nghiệp
tham gia tương đối ít, rào cản gia nhập cao và mức độ tương tác cạnh tranh rất rõ ràng,
việc nghiên cứu chiến lược cạnh tranh thông qua lăng kính của lý thuyết trò chơi càng
trở nên cần thiết. Sự cạnh tranh về giá, sản lượng, hoặc động thái gia nhập – rút lui khỏi
thị trường đều là những biểu hiện rõ ràng của trò chơi chiến lược trong kinh tế học hiện
đại. Do đó, việc phân tích các tình huống thực tế trong những ngành này dưới góc độ lý
thuyết trò chơi sẽ góp phần quan trọng trong việc lý giải hành vi của doanh nghiệp, nâng
cao năng lực cạnh tranh, đồng thời tạo ra hàm ý chính sách cho cơ quan quản lý nhà
nước nhằm định hướng thị trường vận hành hiệu quả và lành mạnh hơn.
Với tất cả những lý do trên, có thể khẳng định rằng việc nghiên cứu đề tài “Phân
tích lý thuyết trò chơi trong các chiến lược cạnh tranh của các doanh nghiệp độc quyền
nhóm và nghiên cứu các case study điển hình” là hoàn toàn cấp thiết cả về mặt lý luận
lẫn thực tiễn trong bối cảnh kinh tế hiện nay.
2. Đối tượng, mục tiêu và phạm vi nghiên cứu
- Đối tượng nghiên cứu: Hành vi cạnh tranh giữa các doanh nghiệp trong thị trường độc quyền nhóm. 6
- Mục tiêu nghiên cứu: Phân tích các mô hình trò chơi chiến lược được áp dụng trong
thực tiễn cạnh tranh tại Việt Nam, từ đó đề xuất các chiến lược tối ưu.
- Phạm vi nghiên cứu: Tập trung vào hai ngành tiêu biểu là viễn thông và hàng không tại Việt Nam.
3. Kết cấu đề tài nghiên cứu
Bài tiểu luận gồm 2 chương chính:
Chương 1: Cơ sở lý luận
Chương 2: Phân tích các case study điển hình 7
CHƯƠNG 1. CƠ SỞ LÝ LUẬN
1.1. Độc quyền nhóm
1.1.1. Các đặc trưng cơ bản của độc quyền nhóm
Đặc trưng cơ bản của một ngành độc quyền nhóm là sự phụ thuộc lẫn nhau giữa
các hãng trên thị trường. Mỗi khi ra quyết định về sản lượng, giá cả hay các quyết định
kinh doanh có liên quan khác, mỗi doanh nghiệp đều phải cân nhắc xem quyết định của
mình có ảnh hưởng gì đến các quyết định của các đối thủ, khiến cho các đối thủ phản
ứng như thế nào. Trong trường hợp này, việc luôn luôn phải tính đến hành vi của các đối
thủ làm cho quá trình ra quyết định của các hãng trở nên khó khăn và phụ thuộc vào nhau.
Tính phụ thuộc lẫn nhau của các doanh nghiệp là đặc điểm nổi bật của thị trường
độc quyền nhóm. Nó xuất phát từ quy mô tương đối lớn của mỗi doanh nghiệp trong
điều kiện số lượng doanh nghiệp hạn chế. Trong bối cảnh này, hành vi của mỗi doanh
nghiệp đều tác động đến lợi ích kinh doanh của các đối thủ. Điều đó không xảy ra trên
thị trường độc quyền thuần túy, vì thực tế doanh nghiệp độc quyền không có đối thủ.
Trên thị trường cạnh tranh hoàn hảo, số lượng doanh nghiệp nhiều, quy mô doanh nghiệp
nhỏ, việc thay đổi sản lượng của mỗi doanh nghiệp riêng biệt không tác động gì được
đến kết cục chung của thị trường cũng như đối thủ. Các doanh nghiệp cạnh tranh hoàn
hảo lại là những người chấp nhận giá, do đó, trên thực tế, chúng không có khả năng theo
đuổi cũng như không cần thiết phải theo đuổi một chính sách giá cả riêng. Sau này,
chúng ta sẽ thấy, trên thị trường cạnh tranh có tính chất độc quyền, do cũng có rất nhiều
doanh nghiệp quy mô nhỏ cùng hoạt động nên hành vi của một doanh nghiệp riêng biệt
cũng hầu như không ảnh hưởng đến các doanh nghiệp khác. Chỉ trên thị trường độc
quyền nhóm, những phản ứng có thể của các đối thủ mới được các doanh nghiệp xem
như một biến số quan trọng cần tính đến mỗi khi ra quyết định. Trên thị trường độc
quyền nhóm, khả năng các đối thủ cũng sẽ giảm giá theo có thể lôi cuốn các doanh
nghiệp vào một cuộc cạnh tranh giá cả mà thường thì mọi doanh nghiệp đều bị thua
thiệt. Về cơ bản, thị trường độc quyền nhóm là một thị trường có những đặc trưng cơ bản sau:
- Có một số ít các hãng cung ứng phần lớn hoặc toàn bộ sản lượng của thị trường.
Số lượng các hãng trên thị trường độc quyền nhóm từ 2 hãng trở lên.
- Sản phẩm hàng hóa có thế đồng nhất hoặc không đồng nhất.
- Có rào cản lớn về việc gia nhập vào thị trường. Điều này có nghĩa là các hãng
không tự do gia nhập vào thị trường này giống thị trường cạnh tranh hoàn hảo
hay thị trường cạnh tranh độc quyền được. Các hãng sẽ gặp một số trở ngại gia 8
nhập thị trường, như đã phân tích ở thị trường độc quyền thuần túy đã đề cập đến ở chương 4.
- Một đặc điểm riêng có của thị trường độc quyền nhóm mà không tồn tại trong 3
cấu trúc thị trường còn lại, đó là tính phụ thuộc lẫn nhau giữa các hãng là rất lớn,
tức là mọi quyết định về giá, sản lượng, chiến lược kinh doanh... của một hãng
trên thị trường sẽ đều ảnh hưởng đến kết quả kinh doanh của các hãng khác.
Một số thị trường độc quyền nhóm điển hình như thị trường dịch vụ hàng không. Ở
Việt Nam, dịch vụ hàng không về vận chuyển hành khách hiện nay được cung ứng bởi
các hãng Hàng không quốc gia Việt Nam (Vietnam Airline), Vietjet Air, Vietnam Pacific
Airline, Bamboo Airline. Hay lĩnh vực dịch vụ ngân hàng, viễn thông, sản xuất thép, sản
xuất xe ô tô, điện thoại di động...
1.1.2. Các mô hình cạnh tranh của doanh nghiệp độc quyền nhóm
1.1.2.1. Mô hình Cournot
Mô hình Cournot phân tích hành vi của các hãng độc quyền trong thị trường song
độc quyền (thị trường độc quyền chỉ có 2 hãng cạnh tranh với nhau) cạnh tranh với nhau
về sản lượng. Giả thiết của mô hình này như sau:
- Hai hãng này sản xuất ra những sản phẩm đồng nhất và đều biết về đường cầu của thị trường.
- Hai hãng phải đưa ra quyết định cần sản xuất bao nhiêu đơn vị sản phẩm và ra
quyết định trong hoàn cảnh không biết đối thủ cạnh tranh của mình sẽ sản xuất
bao nhiêu đơn vị sản phẩm. Tình huống này trong thị trường độc quyền nhóm là
tình huống mà các hãng phải ra quyết định đồng thời với đối thủ, khi chưa biết
đối thủ của mình quyết định như thế nào.
Bản chất của mô hình Cournot là mỗi hãng sẽ dự báo về mức sản lượng của hãng
đối thủ và từ đó đưa ra quyết định về mức sản lượng của hãng mình để tối đa hóa lợi nhuận.
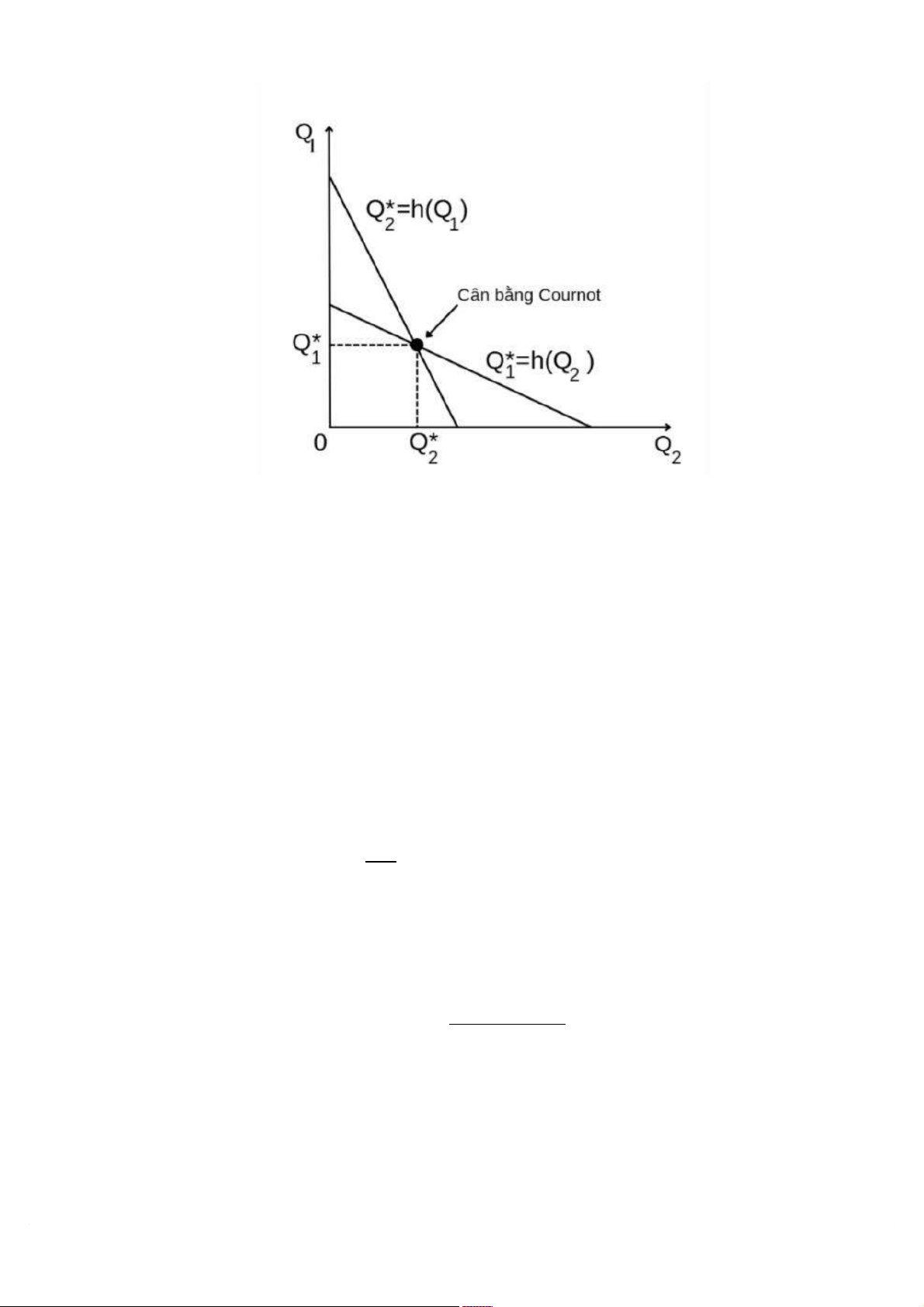
Giao điểm của hai đường phản ứng thể hiện điểm cân bằng thị trường, người ta gọi
đây là cân bằng Cournot. Tại trạng thái này, mỗi hãng đều đã đưa ra quyết định lựa chọn
sản lượng tốt nhất cho hãng mình trên cơ sở dự báo đúng về sản lượng của hãng đối thủ.
Cân bằng Cournot chính là cân bằng Nash, là một trường hợp đặc biệt của cân bằng Nash. 9
Hình 1.1 Đường phản ứng tốt nhất của hai hãng trong mô hình Cournot
Giả sử có hai hãng trong một thị trường cùng sản xuất một loại sản phẩm đồng nhất.
Hàm cầu của thị trường có dạng là P = a - b.Q, trong đó Q là sản lượng của thị trường
và bằng tổng sản lượng của hãng 1 và hãng 2 (Q = Q1 + Q2). Hàm chi phí của hãng 1
là TC1= f (Q1) và TC2 = f (Q2).
Khi đó hàm lợi nhuận của mỗi hãng là:
π1 = P. Q1 - TC1= (a – bQ1 – bQ2). Q1- TC1
π2 = P. Q2 - TC2= (a – bQ1 – bQ2). Q2- TC2
Điều kiện để hãng 1 tối đa hóa lợi nhuận là: ∂π1
𝜕𝑄1 = 0 → a – 2bQ1 – MC1 = 0
Từ đây, ta rút ra mối quan hệ giữa mức sản lượng mà hãng 1 sẽ sản xuất phụ
thuộc vào mức sản lượng của hãng 2, và đây chính là phương trình đường phản ứng của hãng 1 là: Q1= a – bQ2 – MC1 2𝑏 10
Làm tương tự, ta có thể xây dựng phương trình đường phản ứng của hãng 2 như sau: Q2= a – bQ1 – MC2 2𝑏
Cân bằng Cournot xảy ra tại giao điểm của hai đường phản ứng. Khi đó, thế Q2
ở phương trình đường phần ứng của hãng 2 vào phương trình đường phản ứng của hãng
1 và ngược lại thì chúng ta sẽ tính ra được sản lượng của hai hãng tại điểm cân bằng.
Trong trường hợp đơn giản, giả sử mức chi phí cận biên của hai hãng đều bằng
nhau và đều bằng c, khi đó, phương trình đường phản ứng của hãng 1 và 2 là: Q1= a – bQ2 – c 2𝑏 Q2= a – bQ1 – c 2𝑏
Cân bằng Cournot xảy ra tại giao điểm của hai đường phản ứng, từ đây ta tính
được sản lượng của hai hãng: Q ∗ = a−c 1∗ = Q2 3𝑏
Như vậy cân bằng Cournot (hay cũng là cân bằng Nash) trong trường hợp này là: (a − 3 c 𝑏 ; a − c 3𝑏 )
Tại cân bằng Cournot, tổng sản lượng của thị trường là: ∗ = 2(a−c) Q = Q1∗+ 𝑄2 3𝑏
1.1.2.2. Mô hình Stackelberg
Mô hình Stackelberg khác với mô hình Cournot ở chỗ, nêu trong mô hình
Cournot là hai hãng cạnh tranh với nhau về sản phẩm và ra quyết định đồng thời, thì
trong mô hình Stackelberg hai hãng lại ra quyết định tuần tự, tức là một hãng ra quyết
định trước và sau đó hãng đối thủ mới ra quyết định sản lượng của mình.
Giả sử có một thị trường song độc quyền gồm hãng 1 và hãng 2 cùng phải ra
quyết định trong việc xác định sản lượng mà hãng sẽ bán. Sản phẩm của hai hãng là
đồng nhất, hai hãng hoạt động độc lập và thông tin thị trường là hoàn hảo. Hãng 1 là 11
hãng ra quyết định sản lượng trước, và một khi được quyết định thì quyết định này là
không thể thay đổi. Tiếp đó hãng 2 sẽ quan sát hãng 1 và quyết định sản lượng mà hãng
mình sẽ sản xuất căn cứ vào sản lượng của hãng 1. Đường cầu của thị trường là P = a -
b.Q với Q = Q1 + Q2. Để đơn giản, giả sử, hai hãng có chi phí cận biên không đổi đều
bằng c và không có chi phí cố định.
Khi đó hàm lợi nhuận của mỗi hãng là
π1 = P. Q1 - cQ1= (a – bQ1 – bQ2). Q1- cQ1
π2 = P. Q2 - cQ2= (a – bQ1 – bQ2). Q2- cQ2
Áp dụng điều kiện tối đa hóa lợi nhuận đối với hãng 2, ta có đường phản ứng của hãng 2 là: Q2= a – bQ1 – 𝑐 2𝑏
Thay thế Q 2 vào phương trình lợi nhuận của hãng 1:
π1 = (a - bQ1 - b a – bQ1 – 𝑐 2𝑏 ). Q1 - cQ1
Áp dụng điều kiện tối đa hóa lợi nhuận đối với hãng 1, ta tính được mức sản
lượng tối ưu của hãng 1 là: Q∗ = a−c 1 2𝑏
Thay thế Q*1 vào phương trình sản lượng của hãng 2, xác định được mức sản
lượng tối ưu đối với hãng 2: Q∗ = a−c 2 4𝑏 1.1.2.3. Mô hình Bertrand
Trong một số trường hợp, cạnh tranh về giá có vẻ hợp lý hơn cạnh tranh về sản
lượng, đặc biệt là trong ngắn hạn. Mô hình Bertrand là mô hình độc quyền nhóm nhưng
các hãng cạnh tranh nhau về giá cả. Có ba trường hợp:
Trường hợp thứ nhất. Sản phẩm đồng nhất
Giả sử có hai hãng 1 và 2 trong một ngành cùng sản xuất một loại sản phẩm đồng
nhất. Hai hãng có mức chi phí cận biên như nhau là c và đều không có chi phí cố định.
Mỗi hãng coi giá của hãng đối thủ là cố định và ra quyết định đặt giá đồng thời. Hàm 12
cầu thị trường là P = a – bQ. Khi các hãng giả định rằng giá của hãng khác là cố định,
mỗi hãng sẽ cố gắng đặt giá thấp hơn so với giá đối thủ đặt một chút ít (để có được toàn
bộ thị trường). Cân bằng của thị trường đạt được khi cả hai hãng đều đặt giá bằng chi
phí biên P = MC = c. Cả hai hãng đều thu được lợi nhuận kinh tế bằng 0
Trường hợp thứ hai. Sản phẩm khác biệt - quyết định giá đồng thời
Giả sử có một thị trường với hai hãng cạnh tranh đồng thời về giá cả. Mức giá
của hai hãng tương ứng là P1 và P2. Phương trình đường cầu cho mỗi hãng là: Q1 = a - P1 + bP2 Q2 = a- P2 + bP1 với b ≥ 0.
Chi phí cận biên của mỗi hãng là cố định và đều bằng c
Đường phản ứng của hãng 1 là: P1= a + bP2+ 𝑐 2
Đường phản ứng của hãng 2 là: P2= a + bP1+ 𝑐 2
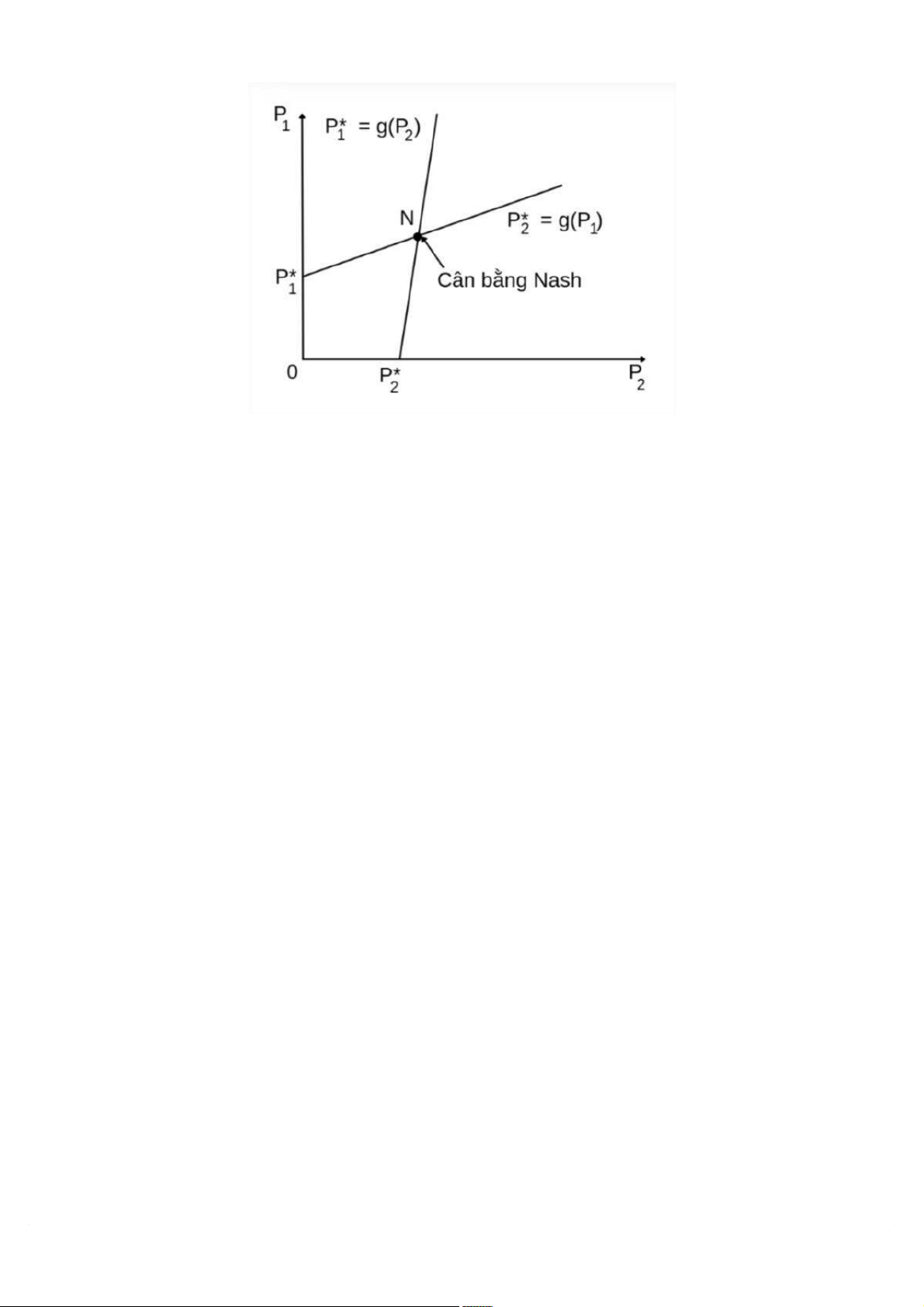
Trong trường hợp này, thị trường sẽ cân bằng tại giao điểm của hai đường phản
ứng, là điểm N trên đồ thị. Bởi vì điểm N vừa nằm trên đường phản ứng của hãng 1 và
vừa nằm trên đường phản ứng của hãng 2, điều đó có nghĩa là mỗi hãng đều đã ra quyết
định về giá giúp cho hãng mình tối đa hóa lợi nhuận trên cơ sở dự báo đúng về mức giá
của hãng đối thủ. Và do đã tối đa hóa lợi nhuận, mỗi hãng không có động cơ để thay đổi
quyết định của mình và thị trường đạt trạng thái cân bằng. Cân bằng này gọi là cân bằng
Bertrand và nó cũng chính là một trường hợp đặc biệt của cân bằng Nash. 13
Hình 1.2. Đường phản ứng tốt nhất của hai hãng trong mô hình Bertrand khi sản phầm
khác biệt và hai hãng ra quyết định đồng thời
Trường hợp thứ ba. Sản phẩm khác biệt- quyết định gia không đồng thời
Giả sử có một thị trường với hai hãng cạnh tranh về giá cả. Mức giá của hai hãng
tương ứng là P1 và P2. Phương trình đường cầu cho mỗi hãng là: Q 1 = a -P1 + bP2 Q2 = a - P2 + bP1 với b ≥ 0
Chi phí cận biên của mỗi hãng là cố định và đều bằng c
Hãng 1 quyết định về giá trước, sau đó hãng 2 căn cứ vào mức giá của hãng 1 để
đưa ra quyết định về giá cho hãng. Trường hợp này chúng ta thực hiện giống như đối
với mô hình Stackelberg, chỉ khác biệt là mô hình Stackelberg thì hai hãng cạnh tranh
về sản lượng, còn ở đây là cạnh tranh về giá.
1.2. Lý thuyết trò chơi
1.2.1. Khái niệm và lịch sử ra đời
Lý thuyết trò chơi hay còn gọi là “Game Theory”, lý thuyết này từ lâu đã trở
thành một lĩnh vực trong kinh tế học nói chung. Bởi nó có tính ứng dụng rộng rãi trong
kinh tế học vi mô, vĩ mô, tài chính, quản trị, ngân hàng, thương mại quốc tế, chính trị,
khoa học về chiến tranh, ngoại giao hầu hết ở các môi trường có tính tương tác chiến lược cao. 14
Những người đã tiên phong đặt nền móng cho lý thuyết này chính là nhà toán
học John von Neumann, John Nash và nhà kinh tế học Oskar Morgenstern. Mặc dù, khởi
nguồn của lý thuyết lại là toán học ứng dụng và phát triển như công cụ nghiên cứu kinh
tế học hành vi, nhưng đến hiện nay lý thuyết này còn được sử dụng trong nhiều ngành
như tâm lý học và logic, sinh học, triết học…
Cho đến hiện tại, lý thuyết trò chơi được coi là một nhánh của toán học ứng dụng,
trong đó nó sử dụng các mô hình để nghiên cứu các tình huống chiến thuật mà tại đó
những người tham gia cố gắng để tối đa hóa kết quả thu được của mình, có tình đến
hành động và phản ứng của các đối thủ khác. Trong kinh tế học, lý thuyết trò chơi được
ứng dụng rộng rãi trong phân tích hành vi của các hãng hoạt động trên thị trường nhóm.
Một số khái niệm cơ bản trong lý thuyết trò chơi:
• Trò chơi là một tình huống mà trong đó người chơi (người tham gia) đưa ra quyết
định chiến lược, có tính đến hành động và phản ứng của các đối thủ. Và họ sẽ
hành động theo cách, nếu tôi tin rằng các đối thủ cạnh tranh của tôi là người có
lý trí và hành động để đạt được kết quả tối ưu thì tôi phải tính đến hành vi của họ
như thế nào khi ra quyết định tối ưu cho mình.
• Người chơi là những người tham gia vào tình huống đó (hay là trò chơi), và hành
động của họ có tác động đến kết quả của những người khác.
• Chiến lược là nguyên tắc hoặc kế hoạch hành động trong khi tiến hành trò chơi.
• Kết cục là giá trị tương ứng với một kết quả có thể xảy ra, nó phản ảnh lợi ích
thu được của mỗi người chơi phụ thuộc vào chiến lược của người chơi đó và cả
chiến lược của những người chơi khác trong trò chơi.
Trong lý thuyết trò chơi, người ta chia ra trò chơi đồng thời và trò chơi tuần tự. Trò
chơi đồng thời là trò chơi mà trong đó những người chơi ra quyết định chiến lược mà
không biết đến quyết định của đối phương. Đồng thời ở đây không có nghĩa là phải ra
quyết định tại cùng một thời điểm mà chỉ có ý nghĩa rằng người chơi này không biết đến
quyết định của người chơi khác. Còn trò chơi tuần tự là trò chơi mà một người chơi ra
quyết định trước, người chơi tiếp theo sẽ ra quyết định căn cứ vào quyết định của người đi trước.
Trong trò chơi mà các bên ra quyết định chiến lược này, chúng ta có một số giả định nghiên cứu sau:
• Một là những người chơi là những người có lý trí. Mục đích của những người
chơi đều là tối đa hóa kết cục của bản thân họ, họ là những người biết tính toán hoàn hảo. 15
• Hai là những người chơi đều có hiểu biết chung về trò chơi và về đối thủ.
Kết cục cuối cùng của trò chơi là mỗi bên ra quyết định nhằm tối đa hóa kết cục
của bản thân trên cơ sở dự báo đúng hoặc biết trước về hành động của đối thủ. Như vậy,
để giải quyết trò chơi, chúng ta sẽ đi tìm cân bằng Nash. Cân bằng Nash là một tập hợp
các chiến lược (hay hành động) trong đó mỗi người chơi đã làm điều tốt nhất có thể cho
mình, trên cơ sở dự báo đúng hoặc biết trước về hành động của đối thủ. Ở trạng thái này,
mỗi người chơi không có động cơ xa rời chiến lược (hay hành động) của mình, vì đã đạt
được kết cục tốt nhất, và vì thế các chiến lược hay hành động của người chơi ở trạng
thái cân bằng Nash được gọi là chiến lược ổn định.
1.2.2. Xác định cân bằng Nash trong trò chơi đồng thời
Đối với trò chơi đồng thời ta sử dụng ma trận lợi ích để tìm cân bằng Nash. Ma
trận lợi ích là một bảng số liệu mà trong đó sẽ cho biết kết cục của mỗi người chơi tương
ứng với các chiến lược mà người chơi đó và người chơi đối thủ. Mỗi ô của ma trận lợi
ích sẽ thể hiện kết cục của hai người chơi tương ứng với từng lựa chọn chiến lược của
họ. Để phân tích cân bằng Nash trong trò chơi đồng thời ta xét 3 trường hợp:
Trường hợp thứ nhất. Khi người chơi có chiến lược ưu thế
Giả sử tình huống nghiên cứu của chúng ta là nghiên cứu về hành vi của 2 hãng
đang cạnh tranh với nhau trên thị trưởng song độc quyền, mỗi hãng có 2 lựa chọn chiến
lược là thực hiện quảng cáo hoặc không thực hiện quảng cáo. Do mỗi người chơi đều có
2 lựa chọn chiến lược, nên ma trận này sẽ có hai hàng và hai cột. Giả sử chúng ta thể
hiện chiến lược của hãng A ở dòng và của hãng B ở cột . Trong mỗi ô sẽ có 2 con số,
con số đẳng trước thể hiện kết cục của hãng A và con số đằng sau thể hiện kết cục của hãng B. Hãng B Quảng cáo Không quảng cáo Hãng A Quảng cáo 16 ; 16 20 ; 15 Không quảng cáo 15 ; 20 18 ; 18
Hình 1.3. Ma trận lợi ích khi mỗi người chơi đều có chiến lược ưu thế
Trong ô thứ nhất, con số 16 đằng trước thể hiện kết cục của hãng A (lợi nhuận
của hãng A) trong trường hợp cả hai hãng đều lựa chọn thực hiện quảng cáo. Trong ví 16
dụ này. nếu cả hai hãng cùng quảng cáo thì lợi nhuận của mỗi hãng đều là 16 trong khi
đó nếu cả hai hãng cùng thực hiện không quảng cáo thì lợi nhuận cho mỗi hãng là 18.
Còn nếu 1 hãng quảng cáo và hãng kia không quảng cáo thì hãng quảng cáo sẽ chiếm
lĩnh nhiều thị trưởng hơn và đạt lợi nhuận 20 trong khi hãng không quảng cáo chỉ đạt lợi nhuận 15.
Nếu hãng B thực hiện quảng cáo, thì phản ứng tốt nhất của hãng A là thực hiện
quảng cáo. Chúng ta nhìn vào cột đầu tiên của ma trận thì sẽ thấy nếu hãng A quảng cáo
sẽ thu được lợi nhuận là 16, còn không quảng cáo thì chỉ thu được lợi nhuận 15 thấp
hơn, do vậy hãng A sẽ chọn quảng cáo. Còn nếu hãng B không quảng cáo thì quyết định
tốt nhất của hãng A cũng vẫn là thực hiện quảng cáo (lợi nhuận 20 lớn hơn mức lợi
nhuận 18 khi không quảng cáo). Như vậy ta có thể thấy rằng quyết định tốt nhất của
hãng A là quảng cáo bất kể hãng B ra quyết định như thế nào. Chiến lược quảng cáo của
hãng A được gọi là chiến lược ưu thế. Phân tích tương tự cho hãng B ta cũng thấy rằng
bất kể hãng A ra quyết định như thế nào thì quyết định mang lại lợi nhuận cao nhất cho
hãng B cũng là thực hiện quảng cáo.
Trong một trò chơi mà cả hai người đều có chiến lược ưu thế thì cân bằng Nash
sẽ xảy ra khi mỗi người đều lựa chọn chiến lược như thế của mình. Do đó kết cục cả hai
hãng A và hãng B đều lựa chọn chiến lược ưu thế của mình là quảng cáo.
Trường hợp thứ 2. Khi người chơi có chiến lược bị lấn át
Giả sử có hai hãng là hãng X và hãng Y, mỗi hãng đều có 3 lựa chọn chiến lược,
đó là mở rộng quy mô sản xuất, giữ nguyên quy mô hoặc thu hẹp quy mô sản xuất. Kết
cục lợi nhuận theo năm của mỗi hãng được thể hiện như trên ma trận lợi ích. Hãng B Mỏ rộng Giữ nguyên Thu hẹp Mở rộng 0 ; 0 12 ; 8 18 ; 9 Hãng A Giữ nguyên 8 ; 12 16 ; 16 20 ; 15 Thu hẹp 9 ; 18 15 ; 20 18 ; 18
Hình 1.4. Lựa chọn của người chơi khi có chiến lược bị lấn át 17
Chúng ta phân tích phản ứng tốt nhất của hãng X:
Nếu hãng Y mở rộng quy mô, quyết định tốt nhất đối với hãng X sẽ là thu hẹp
quy mô (vì có lợi nhuận cao nhất là 9 triệu USD, so với 8 triệu nếu giữ nguyên và hòa
vốn nếu cũng thực hiện mở rộng).
Nếu hãng Y giữ nguyên quy mô sản xuất thì quyết định tốt nhất của hãng X cũng là giữ nguyên quy mô.
Nếu hãng Y thu hẹp quy mô sản xuất thì quyết định mang lại kết cục tốt nhất cho
hãng X là thu hẹp quy mô.
Tùy theo quyết định của hãng Y mà hãng X chọn giữ nguyên quy mô hoặc thu
hẹp quy mô. Như vậy hãng X không có chiến lược ưu thế là chiến lược luôn được lựa
chọn. Chúng ta cũng thấy rằng hãng X không bao giờ lựa chọn chiến lược mở rộng quy
mô, bất kể sự lựa chọn của hãng Y như thế nào. Chiến lược mở rộng quy mô đối với
hãng X được gọi là chiến lược bị lấn át.
Chúng ta phân tích đến lựa chọn của hãng Y.
Nếu hãng X thực hiện việc mở rộng quy mô, thì quyết định tốt nhất cho hãng Y là thu hẹp quy mô.
Nếu hãng X thực hiện giữ nguyên quy mô sản xuất thì quyết định tốt nhất cho
hãng Y cũng là giữ nguyên quy mô.
Và khi hãng X thực hiện thu hẹp quy mô sản xuất thì quyết định tốt nhất cho hãng Y là giữ nguyên quy mô.
Đối với hãng Y trong ví dụ này cũng không có chiến lược ưu thế, nhưng lại cũng
có chiến lược bị lấn át, đó là chiến lược mở rộng quy mô, là chiến lược mà hãng Y không
bao giờ lựa chọn bất kể hãng X quyết định như thế nào.
Vậy trong trường hợp người chơi có chiến lược bị lấn át thì chúng ta tìm ra cân
bằng Nash bằng cách loại bỏ chiến lược bị lấn át (do chiến lược này không được chọn),
tương ứng khi đó chúng ta sẽ xóa dòng hoặc cột tương ứng với chiến lược bị lấn át đó,
từ đó kích cỡ ma trận sẽ được giảm xuống, và cứ lặp lại như vậy cho đến khi xác định được điểm cân bằng.
Trong ví dụ trên, do cả hai hãng đều có chiến lược bị lấn át là mở rộng quy mô,
ta sẽ loại bỏ chiến lược này khỏi ma trận lợi ích và làm cho ma trận này chỉ có lại 2 hàng
và 2 cột, mỗi hãng chỉ còn chiến lược là giữ nguyên quy mô hoặc thu hẹp quy mô. Khi
ma trận lợi ích được giảm kích thước, đối với hãng X, ta lại thấy rằng chiến lược thu
hẹp quy mô lại trở thành chiến lược bị lấn át và ta xóa chiến lược này khỏi ma trận. Cuối 18
cùng khi hãng X chọn chiến lược giữ nguyên quy mô thì Y cũng sẽ chọn giữ nguyên
quy mô và kết cục của trò chơi là (giữ nguyên quy mô; giữ nguyên quy mô)
Trường hợp thứ ba. Khi người chơi không có chiến lược ưu thế cũng như chiến lược bị lấn át
Giả sử có hai hãng cạnh tranh với nhau, trong trường hợp thông thường mỗi hãng
có thể đạt được lợi nhuận là 45.000 USD. Hai hãng tăng dự kiến đầu tư và nghiên cứu
triển khai với chi phí là 45.000 USD. Nghiên cứu triển khai chỉ thành công khi cả hai
hãng cùng thực hiện và nếu nghiên cứu triển khai thành công mỗi hãng sẽ kiếm được
95.000 USD. Còn nếu một hãng đầu tư và nghiên cứu phát triển khai hãng còn lại không
đầu tư thì hãng đầu tư sẽ không còn lợi nhuận, hãng không đầu tư vẫn giữ nguyên mức lợi nhuận là 45.000 USD. Hãng B Đầu tư Không đầu tư Hãng A Đầu tư 50 ; 50 0 ; 45 Không đầu tư 45 ; 6 45 ; 45
Hình 1.5. Phân tích phản ứng tốt nhất tìm cân bằng Nash
Nếu hãng B đầu tư thì quyết định tốt nhất cho hãng A cũng là đầu tư, nhưng nếu
hãng B không đầu tư thì quyết định tốt nhất cho hãng A lại là không đầu tư. Điều này có
nghĩa là hãng A không có chiến lược ưu thế cũng như chiến lược bị lấn át.
Tương tự như vậy hãng B cũng không có chiến lược ưu thế cũng như chiến lược
bị lấn át. Để tìm cân bằng Nash trong trường hợp này chúng ta tìm đến tập hợp chiến
lược có phản ứng tốt nhất của cả hai hãng.
Cụ thể là ở ô A, khi hãng B đầu tư thì phản ứng tốt nhất của hãng A cũng là đầu
tư, và khi hãng A đầu tư, phản ứng tốt nhất của hãng B là đầu tư. Như vậy, tại ô A xảy
ra phản ứng tốt nhất của cả hai hãng, tương tự như vậy với ô D trên đồ thị, khi cả hai
hãng cùng không đầu tư cũng xảy ra phản ứng tốt nhất của hai hãng.
Với tình huống này, có tới hai cân bằng Nash, đó là cả hai hãng cùng đầu tư và
cả hai hãng cùng không đầu tư với kết cục tương ứng là (50; 50) và (45; 45). Hai tập
hợp chiến lược của hai người chơi này là cân bằng Nash, bởi vì tập hợp chiến lược đó
có tính chất ổn định. Nếu cả hai hãng đã lựa chọn chiến lược như vậy thì sẽ đạt được kết 19
cục tốt nhất trong tình huống đó rồi, và không có động cơ thay đổi chiến lược của mình
nữa. Trong trường hợp trò chơi có nhiều hơn một cân bằng Nash thì kết cục trong thực
tế sẽ không biết được người chơi lựa chọn thế nào, chỉ biết rằng nếu cả hai người chơi
cùng chọn vào ô phản ứng tốt nhất của cả hai người chơi thì sẽ đạt được trạng thái cân bằng.
1.2.3. Xác định cân bằng Nash trong trò chơi tuần tự
Trong nhiều tình huống thực tế, các quyết định chiến lược không diễn ra đồng
thời mà xảy ra theo trình tự thời gian. Khi một người chơi hành động trước, và người
chơi còn lại đưa ra phản ứng sau khi đã quan sát được hành vi của đối phương, trò chơi
đó được gọi là trò chơi tuần tự. Việc xác định cân bằng Nash trong trò chơi tuần tự đòi
hỏi một công cụ phân tích khác so với trò chơi đồng thời – đó là cây trò chơi kết hợp
với phương pháp suy luận ngược.
Để xác định cân bằng Nash trong trò chơi tuần tự, ta sử dụng phương pháp
quy hồi ngược (backward induction). Phương pháp này bao gồm các bước:
1. Xác định hành động tối ưu của người chơi đi sau, giả định rằng họ đã biết được
hành động của người chơi đi trước.
2. Người chơi đi trước sẽ dự đoán phản ứng của người chơi sau và chọn hành động tối ưu cho mình.
3. Từ đó xác định được chiến lược tối ưu cho cả hai bên, đảm bảo rằng không ai có
động lực để đơn phương thay đổi chiến lược – chính là cân bằng Nash tuần tự
Ví dụ điển hình là mô hình Stackelberg trong kinh tế học công nghiệp, nơi doanh
nghiệp dẫn đầu chọn sản lượng trước và doanh nghiệp đi sau phản ứng lại, giúp cả hai
đạt trạng thái cân bằng.
Giả sử trên thị trường hiện tại chỉ có một doanh nghiệp duy nhất là hãng A đang
hoạt động. Một doanh nghiệp mới – hãng B – đang cân nhắc gia nhập thị trường này.
Nếu hãng B tham gia, điều đó sẽ làm giảm thị phần của hãng A và kéo theo lợi nhuận
của hãng A cũng bị sụt giảm. Khi đứng trước tình huống này, hãng A có thể lựa chọn
một trong hai phản ứng: hoặc không làm gì, chấp nhận sự cạnh tranh từ hãng B và chia
sẻ thị phần; hoặc chủ động đe dọa giảm giá để khiến hãng B không đạt được lợi nhuận,
qua đó khiến hãng B phải từ bỏ ý định gia nhập thị trường. Ngược lại, hãng B cũng có
hai lựa chọn: hoặc quyết định gia nhập thị trường, hoặc ở ngoài cuộc để tránh rủi ro 20