Lý thuyết trường điện từ | Môn Điện từ học 1 - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58702377
TRƯỜNG ĐIỆN TỪ - ELECTROMAGNETIC FIELD THEORY Số tiết: 45
Tài liệu tham khảo
1. Kiều Khắc Lâu, LÝ THUYẾT TRƯỜNG ĐIỆN TỪ, GD, 2006
2. Ngô Nhật Ảnh, TRƯỜNG ĐIỆN TỪ, ĐHBK TPHCM, 1995
3. Nguyễn Hoàng Phương, GIÁO TRÌNH LÝ THUYẾT TRƯỜNG, GD, 1978 Chương 0
MỘT SỐ CÔNG THỨC TOÁN HỌC 1. Vector a a ,a ,ax y z ia x ja y ka z b b ,b ,bx y z ibx jb y kbz c c ,c ,cx yz icx jcy kc z • a.b a bx x a by y a bz z i j k • a a b y by
a z i a b y z a bz y j a b z x a bx z k a b a x bx x y a by x bz • a.b a b cos a,b • a b c lOMoAR cPSD| 58702377 Phương: c a,b Chiều:
theo qui tắc vặn nút chai Độ lớn: c a b sin a,b • a b c b. a.c c. a.b 2. Toán tử nabla , , x y z 3. Gradient gradU .U i U j U k U x y z 4. Divergence diva .a a x a y a z x y z 5. Rotary i j k a z a i y x y z y z rota a a a a x y z j azx axz k axy ayx Số phức Hàm mũ ez ex iy ex cosy isin y
Hàm mũ là một hàm tuần hoàn có chu kì là 2 i. Thực vậy, ta có lOMoAR cPSD| 58702377 e2k i cos2k isin 2k 1 Suy ra ez 2k i e .ez 2k i ez Công thức Euler eiy = cosy +isiny
Khi đó số phức z = r ei = r(cos +isin )
Phương trình vi phân tuyến tính cấp hai
Phương trình vi phân từ trường cấp hai là phương trình bậc nhất đối với hàm chưa biết
và các đạo hàm của nó: y a y1 a y2 f(x) (1) Trong đó:
a1, a2 và f(x) là các hàm của biến độc lập x
f(x) = 0 (1) gọi là phương trình tuyến tính thuần nhất f(x) 0 (1)
gọi là phương trình tuyến tính không thuần nhất a1, a2 const (1)
gọi là phương trình tuyến tính có hệ số không đổi
Phương trình vi phân tuyến tính cấp hai thuần nhất
Phương trình vi phân từ trường cấp hai thuần nhất có dạng: y a y1 a y2 0 (2)
a1, a2 là các hàm của biến x
Định lí 1. Nếu y1 = y1(x) và y2 = y2(x) là 2 nghiệm của (2) thì y = C1y1 + C2y2
(trong đó C1, C2 là 2 hằng số tuỳ ý) cũng là nghiệm của phương trình ấy.
y x1 const , ngược lại là phụ
Hai hàm y1(x) và y2(x) là độc lập tuyến tính khi y2 x thuộc tuyến tính lOMoAR cPSD| 58702377
Định lí 2. Nếu y1(x) và y2(x) là 2 nghiệm độc lập tuyến tính của phương trình vi
phân từ trường cấp hai thuần nhất (2) thì y = C1y1 + C2y2 (trong đó C1, C2 là 2 hằng
số tuỳ ý) là nghiệm tổng quát của phương trình ấy.
Định lí 3. Nếu đã biết một nghiệm riêng y1(x) của phương trình vi phân từ trường
cấp hai thuần nhất (2) thì có thể tìm được một nghiệm riêng y2(x) của phương
trình đó, độc lập tuyến tính với y1(x) bằng cách đặt y2(x) = y1(x).u(x)
Phương trình vi phân tuyến tính cấp hai không thuần nhất
Phương trình vi phân từ trường cấp hai là phương trình bậc nhất đối với hàm chưa biết
và các đạo hàm của nó: y a y1 a y2 f (x) (3)
Trong đó: a1 và a2 là các hàm của biến độc lập x; f(x) 0
Định lí 1. Nghiệm tổng quát của phương trình không thuần nhất (3) bằng nghiệm
tổng quát của phương trình thuần nhất (2) tương ứng và một nghiệm riêng nào đó
của phương trình không thuần nhất (3). Định lí 2. Cho phương trình không thuần nhất y a y1 a y2 f (x)1 f (x)2 (4)
Nếu y1(x) là nghiệm riêng của phương trình y a y1 a y2 f (x)1 (5)
và y2(x) là nghiệm riêng của phương trình y a y1 a y2 f (x)2 (6)
thì y(x) = y1(x) + y2(x) cũng là nghiệm riêng của phương trình (4)
Phương trình vi phân tuyến tính cấp hai có hệ số không đổi
Phương trình vi phân từ trường cấp hai thuần nhất có dạng: y py qy 0 (7) p, q là các hằng số
Giả sử nghiệm riêng của (7) có dạng y ekx (8)
Trong đó: k là hằng số sẽ được xác định Suy ra lOMoAR cPSD| 58702377 y kekx , y k e2 kx Thay (9) (8) và (9) vào (7) ta có e (10) kx k2 pk q 0 Vì ekx  0 nên k2 pk q 0 (11)
Nếu k thoả mãn (11) thì y = ekx là một nghiệm riêng của phương trình vi
phân (7). Phương trình (11) gọi là phương trình đặc trưng của phương trình vi phân (7)
Nhận xét: Phương trình đặc trưng (7) là phương trình bậc 2 có 2 nghiệm k1 và k2 như sau
- k1 và k2 là 2 số thực khác nhau, khi đó 2 nghiệm riêng của phương trình vi phân (7) là y1 ek x , (12) 1 y2 ek x2
Hai nghiệm riêng (12) là độc lập từ trường vì (13) y1 e k1 k2 x const y2
Do đó nghiệm tổng quát của phương trình vi phân (7) là y y1 y2 C e1 k x 1 C e2 k x2 (14)
- k1 và k2 là 2 số thực trùng nhau: k1 = k2
Hai nghiệm riêng độc lập từ trường: y1 ek x1 , y2 xek x1
Nghiệm tổng quát của phương trình vi phân (7) là y C e1 k x (15) 1 C xe2k x1 C1 C x e2 k x1
- k1 và k2 là 2 số phức liên hợp: k1 = + i và k2 = - i Hai
nghiệm riêng của phương trình vi phân (7) là y1 e i x e e x i x (16) y2 e i x e e x i x Theo công thức Euler ta có ei x cos x isin x lOMoAR cPSD| 58702377 i x cos x isin x (17) e Suy ra y1 e e x i x e x cos x isin x
(18) y2 e e x i x e x cos x isin x
Nếu y và y là 2 nghiệm của phương trình vi phân (7) thì các hàm 1 2 y y y1 1 2 e x cos x 2 (19) y y y2 1 2 e x sin x 2i
cũng là nghiệm của phương trình vi phân (7) và độc lập từ trường vì y y 12 tg x const (20)
Do đó nghiệm tổng quát của phương trình vi phân (7) là y C e x x 1
cos x C e2 sin x e x C cos x1 C sin x2 (21) Chương 1 CÁC ĐỊNH LUẬT
VÀ NGUYÊN LÍ CƠ BẢN CỦA TRƯỜNG ĐIỆN TỪ
1.1. Các đại lượng đặc trưng cho trường điện từ
1.1.1. Vector cường độ điện trường
• Điện trường được đặc trưng bởi lực tác dụng lên điện tích đặt trong điện trường F qE (1.1) Hay: lOMoAR cPSD| 58702377 F (1.2) E q
• Cđđt E tại một điểm bất kì trong điện trường là đại lượng vector có trị số bằng
lực tác dụng lên một đơn vị điện tích điểm dương đặt tại điểm đó
• Lực tác dụng giữa 2 đt điểm Q và q F 4 Qq 0 r r02 (1.3)
- 0 8,854.10 12 F/m - hằng số điện
- - độ điện thẩm tương đối
- r0 - vector đơn vị chỉ phương
• Hệ đt điểm q ,q ,...,q1 2 n E i 1 n E i 4 1 0 i 1 n q rri 0ii 2 (1.4)
r0i - các vector đơn vị chỉ phương
• Trong thực tế hệ thường là dây mảnh, mặt phẳng hay khối hình học, do đó: 1 r El 0 l ldl r 2 4 (1.5) 1 r (1.6) ES 4 SdS r 2 0 S 1 r (1.7) dV EV 4 V r 2 0 V lOMoAR cPSD| 58702377
1.1.2. Vector điện cảm
Để đơn giản khi tính toán đối với các môi trường khác nhau, người ta sử dụng vector điện cảm D D 0E (1.8)
1.1.3. Vector từ cảm
• Từ trường được đặc trưng bởi tác dụng lực của từ trường lên điện tích chuyển động hay
dòng điện theo định luật Lorentz F qv B (1.9)
• Từ trường do phần tử dòng điện Idl tạo ra được xác định bởi định luật thực nghiệm BVL (1.10) dB 02 Idl r 4 r
- 0 4 .10 7 1,257.10 6 H/m - hằng số từ -
- độ từ thẩm tương đối
Từ trường của dây dẫn có chiều dài l (1.11) 0 Idl r B 4 r2 l
1.1.4. Vector cường độ từ trường
Để đơn giản khi tính toán đối với các môi trường khác nhau, người ta sử
dụng vector cường độ từ trường H lOMoAR cPSD| 58702377 B (1.12) H 0
1.2. Định luật Ohm và định luật bảo toàn điện tích
1.2.1. Định luật Ohm dạng vi phân
• Cường độ dòng điện I chạy qua mặt S đặt vuông góc với nó bằng lượng điện tích q chuyển
qua mặt S trong một đơn vị thời gian dq (1.13) I dt
Dấu trừ chỉ dòng điện I được xem là dương khi q giảm
• Để mô tả đầy đủ sự chuyển động của các hạt mang điện trong môi trường dẫn điện, người
ta đưa ra khái niệm mật độ dòng điện J n ev0 v E (1.14)
dạng vi phân của định luật Ohm
- n0 - mật độ hạt điện có điện tích e
- - mật độ điện khối
- v - vận tốc dịch chuyển của các hạt điện - - điện dẫn suất
• Dòng điện qua mặt S được tính theo I dI JdS EdS (1.15) S S S
• Một vật dẫn dạng khối lập phương cạnh L, 2 mặt đối diện nối với nguồn áp U, ta có 2 và R L )
(lưu ý: áp dụng c/t S = L S L lOMoAR cPSD| 58702377 U (1.16) I S EdS ES ( L)(EL) LU R
dạng thông thường của định luật Ohm
Vì E và dS cùng chiều, đặt 1 (1.17) RL
- điện dẫn suất có đơn vị là 1/ m
1.2.2. Định luật bảo toàn điện tích
• Điện tích có thể phân bố liên tục hay gián đoạn, không tự sinh ra và cũng
không tự mất đi, dịch chuyển từ vùng này sang vùng khác và tạo nên dòng điện.
• Lượng điện tích đi ra khỏi mặt kín S bao quanh thể tích V bằng lượng điện tích
giảm đi từ thể tích V đó.
• Giả sử trong thể tích V được bao quanh bởi mặt S, ta có Q dV (1.18) V lOMoAR cPSD| 58702377
sau thời gian dt lượng điện tích trong V giảm đi dQ dQ d (1.19) I dV dt dt V Mặt khác (1.20) I JdS S Suy ra (1.21) S JdS V t dV Theo định lý OG (1.22) S JdS V .J dV V t dV Suy ra (1.23) .J 0 t
Đây là dạng vi phân của định luật bảo toàn điện tích hay phương trình liên tục.
1.3. Các đặc trưng cơ bản của môi trường
Các đặc trưng cơ bản của môi trường: , , Các phương trình: (1.24) D 0 E (1.25) B H 0
gọi là các phương trình vật chất •
, , cường độ trường : môi trường tuyến tính •
, , const : môi trường đồng nhất và đẳng hướng •
, , theo các hướng khác nhau có giá trị không đổi khác nhau: môi trường
không đẳng hướng. Khi đó , biểu diễn bằng các tensor có dạng như bảng lOMoAR cPSD| 58702377
số. Chẳng hạn ferrite bị từ hoá hoặc plasma bị từ hoá là các môi trường không
đẳng hướng khi truyền sóng điện từ •
, , vị trí : môi trường không đồng nhất
Trong tự nhiên đa số các chất có > 1 và là môi trường tuyến tính.
Xecnhec có >> 1 : môi trường phi tuyến
> 1 : chất thuận từ : các kim loại kiềm, Al, NO, Phương trình, O, N, không
khí, ebonic, các nguyên tố đất hiếm
< 1 : chất nghịch từ : các khí hiếm, các ion như Na+, Cl- có các lớp electron
giống như khí hiếm, và các chất khác như Pb, Zn, Si, Ge, S, CO2, H2O, thuỷ tinh,
đa số các hợp chất hữu cơ
>> 1 : chất sắt từ : môi trường phi tuyến : Fe, Ni, Co, Gd, hợp kim các
nguyên tố sắt từ hoặc không sắt từ Fe-Ni, Fe-Ni-Al. Độ từ hoá của chất sắt từ lớn
hơn độ từ hoá của chất nghịch từ và thuận từ hàng trăm triệu lần.
• Căn cứ vào độ dẫn điện riêng : chất dẫn điện, chất bán dẫn và chất cách điện hay điện môi
Chất dẫn điện: > 104 1/ m, = : chất dẫn điện lý tưởng
Chất bán dẫn: 10-10 < < 104
Chất cách điện: < 10-10, = 0 : điện môi lý tưởng
Không khí là điện môi lý tưởng: = = 1, = 0
1.4. Định lí Ostrogradski-Gauss đối với điện trường
• Được tìm ra bằng thực nghiệm, là cơ sở của các phương trình Maxwell
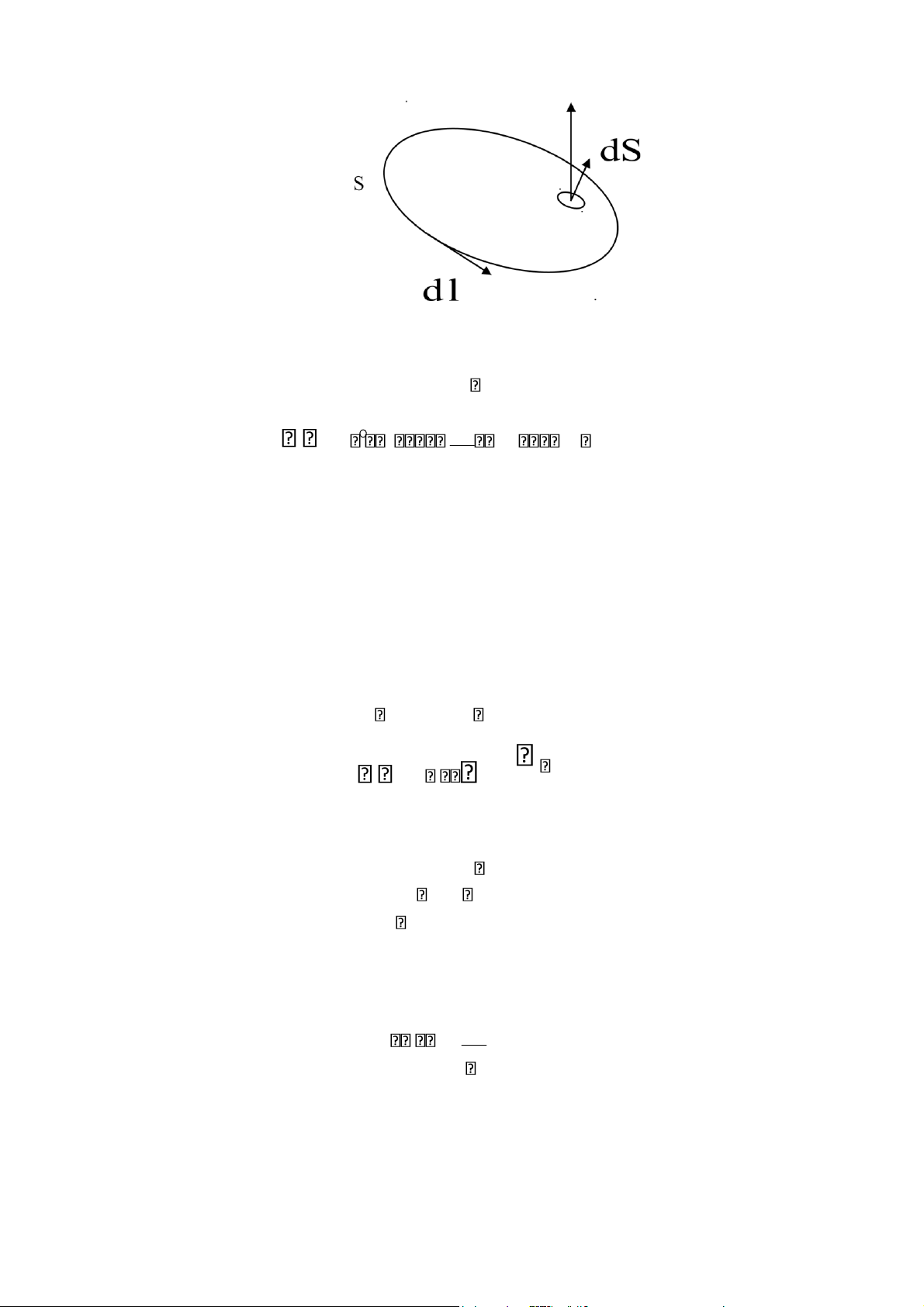
• Thông lượng của vector điện cảm D qua mặt S là đại lượng vô hướng được xác định bởi tích phân E DdS (1.26) S lOMoAR cPSD| 58702377 dS D r d S
dS : vi phân diện tích theo hướng pháp tuyến ngoài
dS.cos(D,dS) : hình chiếu của S lên phương D
Xét một mặt kín S bao quanh điện tích điểm q, tính thông lượng của
D do q tạo ra qua mặt kín S, ta có q.dS.cos D,dS q (1.27) d DdS 2 d 4 r 4
d là vi phân góc khối từ điện tích q nhìn toàn bộ diện tích dS
Thông lượng của D qua toàn mặt kín S là q (1.28) S DdS 4 d q
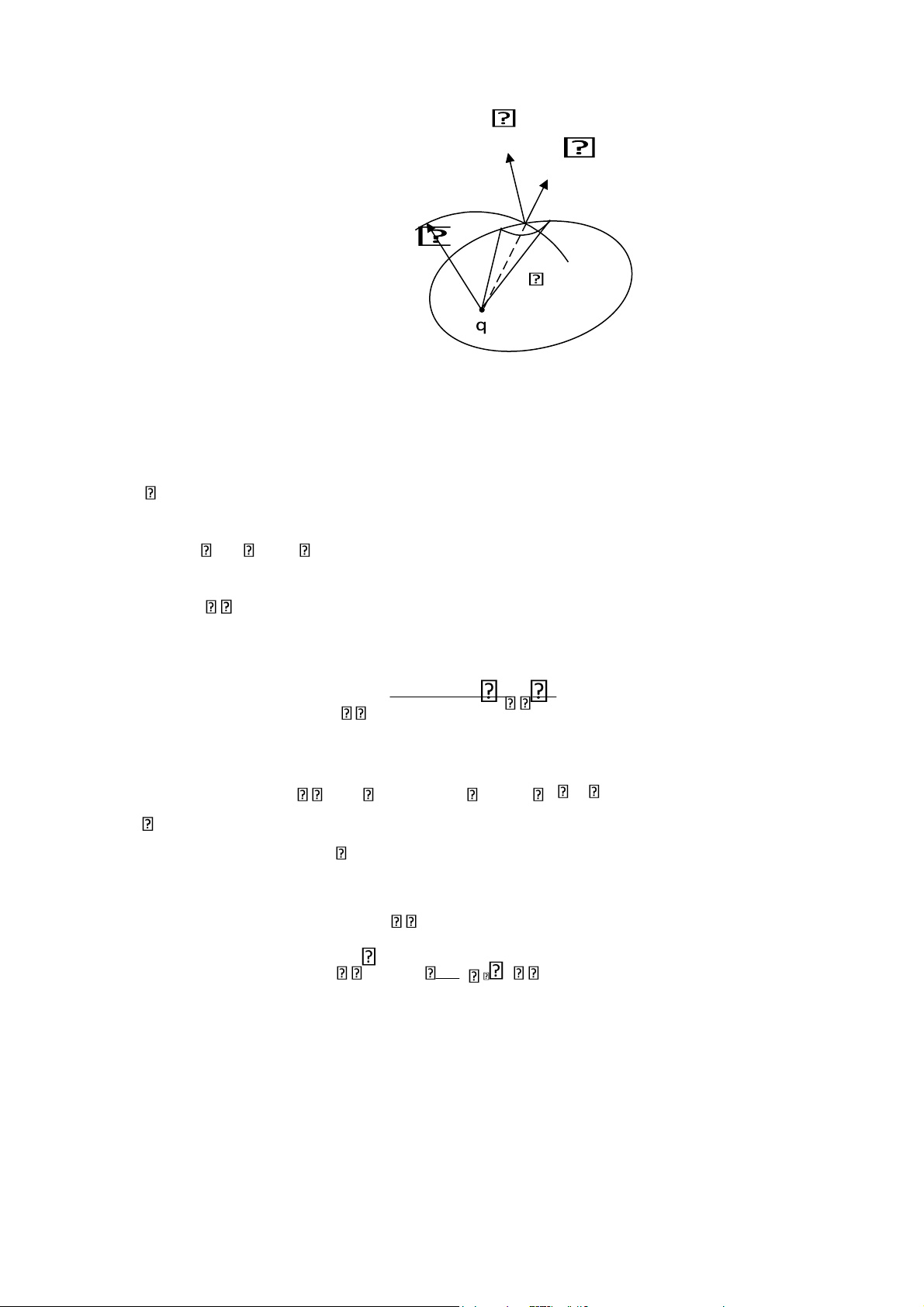
• Xét trường hợp điện tích điểm q nằm ngoài mặt kín S. Từ điện tích q nhìn toàn
mặt S dưới một góc khối nào đó. Mặt S có thể chia thành 2 nửa S và S' (có
giao tuyến là AB). Pháp tuyến ngoài của S và S' sẽ có chiều ngược nhau.
Do đó tích phân trên S và S' có cùng giá trị nhưng trái dấu. Khi đó thông lOMoAR cPSD| 58702377
lượng của D qua toàn mặt kín S bằng 0. A D dS B q
• Xét hệ điện tích điểm q1, q2, ..., qn đặt trong mặt kín S, ta có D n D i (1.29) i 1
Thông lượng của D do hệ q1, q2, ..., qn gây ra qua toàn mặt kín S DdS n D dS i n qi (1.30) Q S i 1 S i 1
Vậy: Thông lượng của vector điện cảm D qua mặt kín S bất kỳ bằng tổng đại
số các điện tích nằm trong thể tích V được bao quanh bởi S
Lưu ý: Vì Q là tổng đại số các điện tích q1, q2, ..., qn, do đó có thể âm hoặc dương
• Nếu trong thể tích V được bao quanh bởi S có mật độ điện khối  thì được tính theo E DdS dV Q (1.31) S V
Các công thức (1.30) và (1.31) là dạng toán học của định lí
OstrogradskiGauss đối với điện trường.
Nguyên lý liên tục của từ thông lOMoAR cPSD| 58702377
• Thực nghiệm đã chứng tỏ đường sức từ là khép kín dù nguồn tạo ra nó là dòng
điện hay nam châm. Tìm biểu thức toán học biểu diễn cho tính chất này
• Giả sử có mặt kín S tuỳ ý nằm trong từ trường với vector từ cảm B. Thông
lượng của B qua mặt kín S bằng tổng số các đường sức từ đi qua mặt S này.
Do đường sức từ khép kín nên số đường sức từ đi vào thể tích V bằng số đường sức
từ đi ra khỏi thể tích V đó. Vì vậy thông lượng của B được tính theo M BdS 0 (1.32) S
Công thức (1.32) gọi là nguyên lý liên tục của từ thông. Đây là một phương
trình cơ bản của trường điện từ
1.5. Luận điểm thứ nhất - Phương trình Maxwell-Faraday
Khi đặt vòng dây kín trong một từ trường biến thiên thì trong vòng dây này xh dòng
điện cảm ứng. Chứng tỏ trong vòng dây có một điện trường E có chiều là chiều
của dòng điện cảm ứng đó.
Thí nghiệm với các vòng dây làm bằng các chất khác nhau, trong điều kiện
nhiệt độ khác nhau đều có kết quả tương tự. Chứng tỏ vòng dây dẫn không phải
là nguyên nhân gây ra điện trường mà chỉ là phương tiện giúp chỉ ra sự có mặt
của điện trường đó. Điện trường này cũng không phải là điện trường tĩnh vì đường
sức của điện trường tĩnh là đường cong hở. Điện trường tĩnh không làm cho hạt
điện dịch chuyển theo đường cong kín để tạo thành dòng điện được (vì hoá ra
trong điện trường tĩnh không cần tốn công mà vẫn sinh ra năng lượng điện !).
Muốn cho các hạt điện dịch chuyển theo đường cong kín để tạo thành dòng điện
thì công phải khác 0, có nghĩa là qEdl 0 (1.33) lOMoAR cPSD| 58702377
l và đ.sức của điện trường này phải là các đ.cong
kín và gọi là điện trường xoáy.
Phát biểu luận điểm I: Bất kì một từ trường nào biến đổi theo thời gian cũng
tạo ra một điện trường xoáy.
Thiết lập phương trình Maxwell-Faraday:
Theo định luật cảm ứng điện từ của Faraday, sức điện động cảm ứng xh trong một vòng
dây kim loại kín về trị số bằng tốc độ biến thiên của từ thông đi qua diện tích của vòng dây d (1.34) ec dt
Dấu (-) phản ảnh sức điện động cảm ứng trong vòng dây tạo ra dòng điện
cảm ứng có chiều sao cho chống lại sự biến thiên của từ thông  BdS (1.35)
S là thông lượng của vector từ cảm B qua
S được bao bởi vòng dây. Suy ra d d dB B (1.36) ec dt dt BdS dt dS S t dS S S
Hoặc biểu diễn sức điện động cảm ứng ec theo lưu số của vector cường độ điện trường E ec Edl (1.37) l
Chiều của vòng dây kín l lấy ngược chiều kim đồng hồ khi nhìn nó từ ngọn của B lOMoAR cPSD| 58702377 B
Vì vòng dây kín l đứng yên nên theo các công thức (1.35), (1.36), (1.37) ta có l Edl S Bt dS (1.38)
Đây là phương trình Maxwell-Faraday dưới dạng tích phân, cũng là một
phương trình cơ bản của trường điện từ.
Vậy: Lưu số của vector cường độ điện trường xoáy dọc theo một đường cong
kín bất kì bằng về giá trị tuyệt đối nhưng trái dấu với tốc độ biến thiên theo thời
gian của từ thông gửi qua diện tích giới hạn bởi đường cong kín đó.
Theo giải tích vector (công thức Green-Stock) (1.39) Edl E dS l S
Theo các phương trình (1.38) và (1.39) B (1.40) E t
Đây là phương trình Maxwell-Faraday dưới dạng vi phân, có thể áp dụng đối
với từng điểm một trong không gian có từ trường biến thiên. lOMoAR cPSD| 58702377
1.6. Luận điểm thứ hai - Phương trình Maxwell-Ampere
Theo luận điểm I, từ trường biến thiên theo thời gian sinh ra điện trường
xoáy. Vậy ngược lại điện trường biến thiên có sinh ra từ trường không ? Để đảm
bảo tính đối xứng trong mối liện hệ giữa điện trường và từ trường, Maxwell đưa ra luận điểm II:
Bất kì một điện trường nào biến thiên theo thời gian cũng tạo ra một từ trường.
(Đã chứng minh bằng thực nghiệm)
Lưu ý: điện trường nói chung có thể không p.bố đồng đều trong không gian,
có nghĩa là thay đổi từ điểm này sang điểm khác, nhưng theo luận điểm II sự biến
thiên của điện trường theo không gian không tạo ra từ trường, chỉ có sự biến
thiên của điện trường theo thời gian mới tạo ra từ trường.
Thiết lập phương trình Maxwell-Ampere:
Theo nguyên lí tác dụng từ của dòng điện và định luật Biot-Savart-Laplace,
Ampere phát biểu định luật dòng điện toàn phần:
Lưu số của vector cường độ từ trường H dọc theo một đường cong kín bất kì bằng
tổng đại số các dòng điện đi qua diện tích bao bởi đường cong này Hdl n Ii I (1.41) l i 1 dS I i J S dl lOMoAR cPSD| 58702377
Dòng điện I đi qua diện tích S có thể phân bố liên tục hoặc gián đoạn.
Nếu dòng điện qua mặt S có phân bố liên tục với mật độ dòng điện J thì Hdl JdS (1.42) l S
Định luật dòng điện toàn phần cũng là một phương trình cơ bản của trường điện từ
Khái niệm về dòng điện dịch
Căn cứ vào định luật cảm ứng điện từ của Faraday và định luật dòng điện toàn phần của
Ampere, Maxwell bằng lý thuyết đã chỉ ra sự tác dụng tương hỗ giữa đt và từ trường cùng với
việc đưa ra khái niệm mới về dòng điện dịch. Dòng điện dịch có mật độ được tính theo công thức D E P (1.43) Jd 0 Jd0 JdP t t t Trong đó: P JdP
- mật độ dòng điện p.cực trong điện môi do sự xê dịch của các t điện tích E Jd0 0
- điện trường biến thiên trong chân không và gọi là mật độ dòng t điện dịch
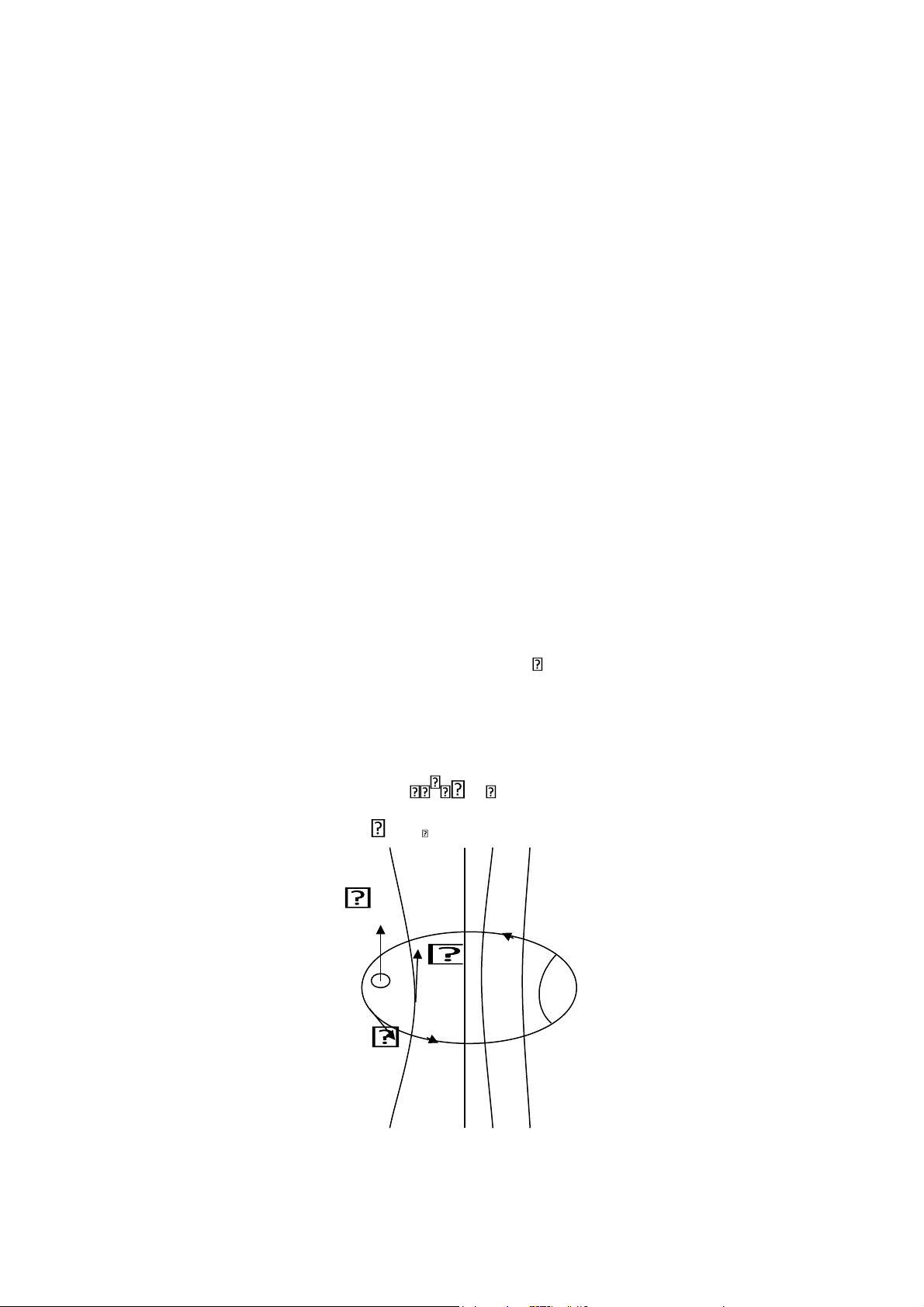
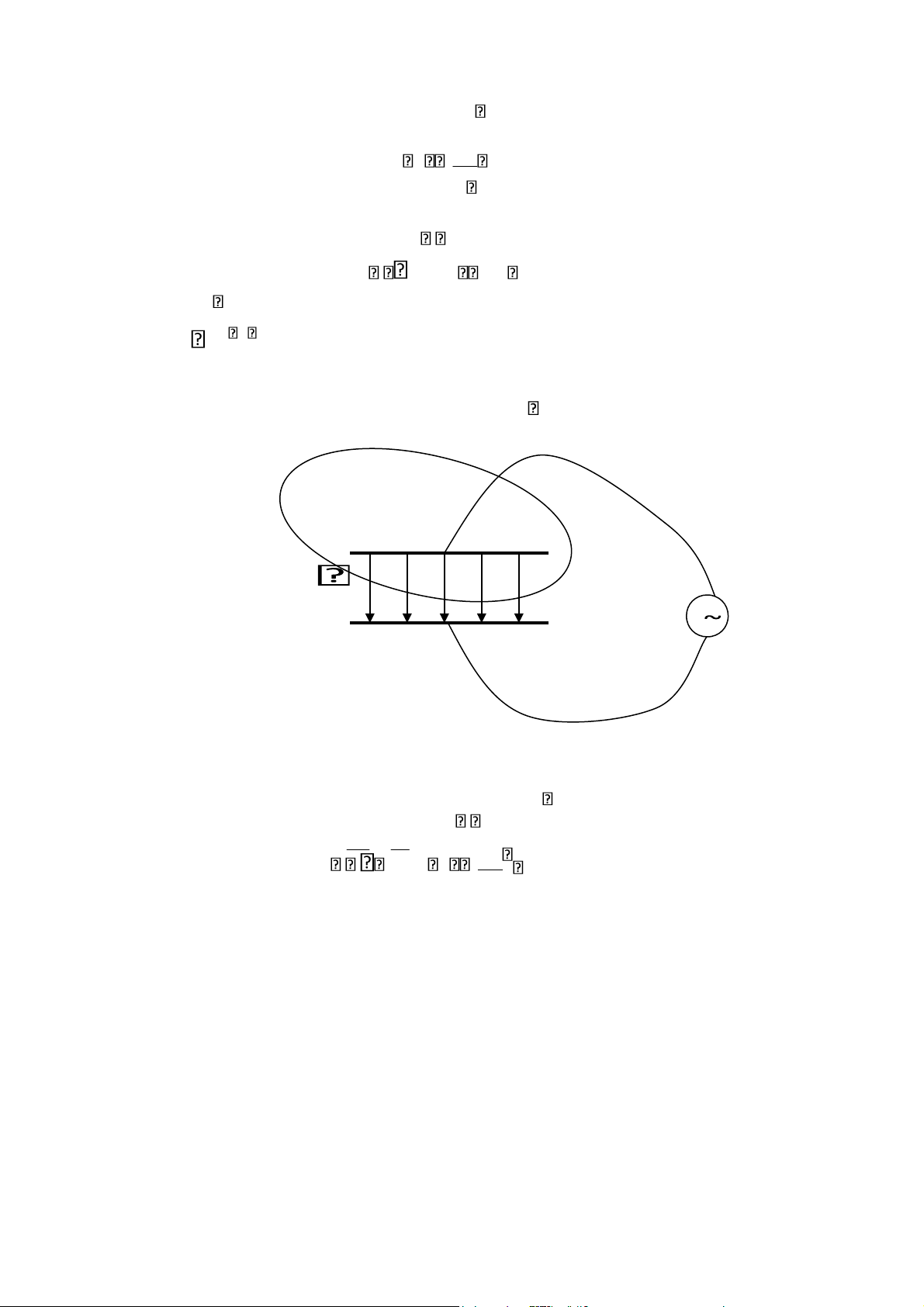
Để chứng minh sự tồn tại của dòng điện dịch, xét thí dụ sau: có một mặt kín
S bao quanh 1 trong 2 bản của tụ điện. Do có điện áp xoay chiều đặt vào tụ điện
nên giữa 2 bản tụ có điện trường biến thiên E và dòng điện biến thiên chạy qua tụ.
Dòng điện này chính là dòng điện dịch trong chân không vì giữa 2 bản tụ không tồn
tại điện tích chuyển động và có giá trị: lOMoAR cPSD| 58702377 (1.44) E Id0 S 0 t Theo định luật Gauss (1.45) q 0EdS 0ES S
dS S vì điện trường chỉ tồn tại giữa 2 bản tụ S
Đối với môi trường chân không, ta có: = 1 S + q S' E - q
Dòng điện dẫn chạy trong dây dẫn nối với tụ có giá trị bằng (1.46) dq d E I 0EdS S 0 t dt dt S Suy ra I = Id0 (1.47)
Vậy: dòng điện dịch chạy giữa 2 bản tụ bằng dòng điện dẫn chạy ở mạch ngoài tụ điện.
Bằng cách bổ sung dòng điện dịch vào vế phải của phương trình (1.42), ta có