LÝ THUYẾT TƯƠNG QUAN VÀ HÀM HỒI QUY | Xác suất thống kê | Trường Đại học Bách khoa Hà Nội

LÝ THUYẾT TƯƠNG QUAN VÀ HÀM HỒI QUY
1. MỐI QUAN HỆ GIỮA 2 ĐẠI LƯỢNG NGẪU NHIÊN
Khi khảo sát hai biến ngẫu nhiên X và Y ta thấy giữa chúng có thể có một số quan hệ sau:
• X và Y độc lập với nhau, tức là việc nhận giá trị của biến ngẫu nhiên này không
ảnh hưởng đến việc nhận giá của biến ngẫu nhiên kia.
• X và Y có mối phụ thuộc hàm số Y = (  X )
• X và Y có sự phụ thuộc tương quan và phụ thuộc không tương quan (được biểu
hiện thông qua rất nhiều quan sát). Ví dụ lấy ngẫu nhiên 100 người xếp theo thứ
tự từ thấp đến cao thì nói chung chiều cao càng cao thì trọng lượng càng lớn.
Nhưng với trường hợp riêng lẻ thì chưa chắc đúng (có thể người thấp nhưng trọng
lượng lại cao). Rõ ràng là với chiều cao biết trước thì không thể khẳng định người
đó nặng bao nhiêu, tuy nhiên sử dụng quan hệ tương quan có thể chỉ ra trọng
lượng bao nhiêu là bình thường với chiều cao như vậy. 2. HỆ SỐ TƯƠNG QUAN
2.1. Hiệp phương sai (covariance)
Hiệp phương sai của 2 biến ngẫu nhiên X và Y được xác định bởi: cov(X ,Y ) = {
E [X − E(X )][Y − E(Y )]}
Công thức tính : cov(X ,Y) = E(XY) − E(X ).E(Y) Nhận xét:
• Xét quan hệ của X và Y là dạng có xu thế đồng biến hay nghịch biến.
• Nếu cov(X,Y) = 0 thì ta nói 2 biến ngẫu nhiên X và Y không tương quan.
• Nếu X và Y độc lập thì X và Y không tương quan
• cov(X, X ) =V(X )
2.2. Hệ số tương quan
Hệ số tương quan của 2 bnn X và Y, ký hiệu r , được xác định bởi công thức: X ,Y cov(X ,Y ) r = X ,Y  . X Y
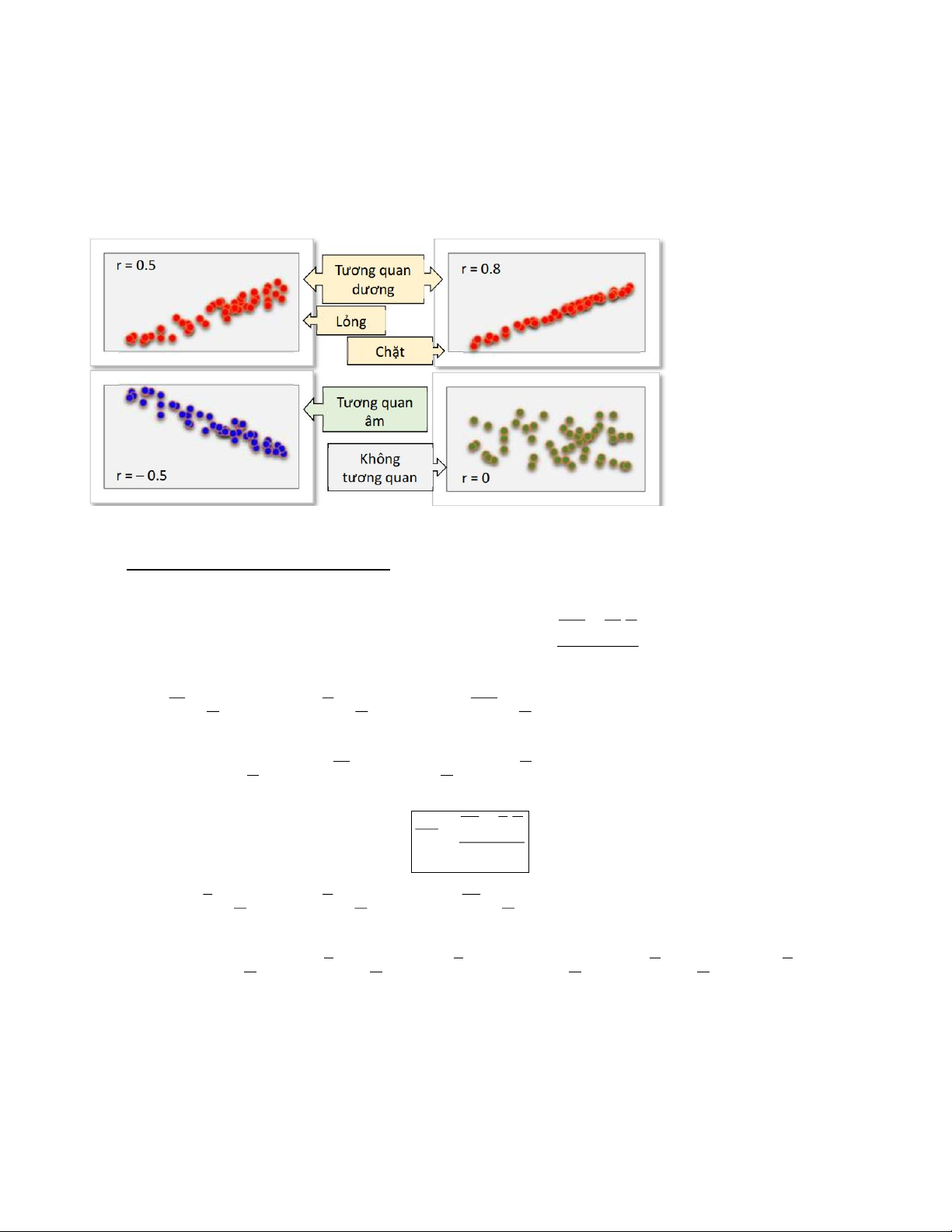
Hệ số tương quan đo mức độ phụ thuộc tuyến tính giữa X và Y. r
> 0 thì Y có xu thế tăng khi X tăng X ,Y r
< 0 thì Y có xu thế giảm khi X tăng X ,Y | r
| > 0,7 thì coi như X và Y có quan hệ tuyến tính: Y = aX + b. X ,Y
2.3. Ước lượng hệ số tương quan
Lập mẫu ngẫu nhiên (X ,Y ),(X ,Y ),...,(X ,Y ) 1 1 2 2 n n −
Để ước lượng hệ số tương quan ta dùng thống kê XY X .Y R = S .S X Y n n n Với 1 1 1 X =
X , Y = Y , XY = X Y i i i i n = n = n i 1 i 1 i 1 = 1 n 1 n 2 2 2 2 S =
(X − X) , S = (Y −Y) X i Y i n = n i 1 i 1 = xy −
Với mẫu số liệu cụ thể ta tính được . x y r = XY s .s X Y n n n trong đ 1 1 1 ó: x = x y = y xy = x y i i i i n = n = n i 1 i 1 i 1 = 1 n 1 n 1 n 1 n 2 2 2 2 2 2 2 2 s =
(x − x) = x −(x) , s = (y − y) = y −(y) X i i Y i i n = n = n = n i 1 i 1 i 1 i 1 = Tính chất: • |r|  1
• Nếu |r| = 1 thì X và Y có quan hệ tuyến tính
• Nếu |r| càng lớn thì sự phụ thuộc tương quan tuyến tính giữa X và Y càng chặt chẽ
• Nếu r = 0 thì X và Y không tương quan
• Nếu r > 0 thì X và Y có tương quan thuận (X tăng thì Y có xu thế tăng),
• nếu r < 0 thì X và Y có tương quan nghịch (X tăng thì Y có xu thế giảm) 3. HỒI QUY
3.1. Kỳ vọng có điều kiện
 Biến ngẫu nhiên rời rạc
Kỳ vọng có điều kiện của biến ngẫu nhiên Y với điều kiện X = x là: m
E(Y | x) =  y P(X = x,Y = y ) j j j 1 =
Tương tự kỳ vọng có điều kiện của biến ngẫu nhiên X với điều kiện Y = y là: m
E( X | y) =  x P(X = x ,Y = y) i i i 1 =
 Biến ngẫu nhiên liên tục +
E(Y | x) = .
y f ( y | x)dy − +
E( X | y) = .
x f (x | y)dx −
Trong đó hai hàm mật độ có điều kiện được tính như sau: f (x, y) f ( , x y)
f (x | y) =
f ( y | x) = f ( y) f (x) Y X 3.2. Hàm hồi quy
Trong thực tế ta thường gặp 2 bnn X, Y có mối liên hệ với nhau, trong đó việc
khảo sát X thì dễ còn khảo sát Y thì khó hơn thậm chí không thể khảo sát được. Ta muốn tìm mối liên hệ (
 X ) nào đó giữa X và Y, nếu biết X ta có thể dự đoán được Y.
Giả sử biết X, nếu dự đoán bằng (
 X ) thì trung bình của bình phương sai số phạm phải là 2 [ E Y − (  X )] .
Vấn đề đặt ra là tìm (
 X ) như thế nào để 2 [ E Y − (
 X )] nhỏ nhất (phương pháp bình
phương sai số cực tiểu hay phương pháp bình phương sai số nhỏ nhất). Kết quả thu được: (
 X ) = E(Y | X ) thì 2 [ E Y − (  X )] nhỏ nhất. (
 X ) = E(Y | X ) được gọi là phương trình hồi quy hay phương trình tương quan.
3.3. Xác định hàm hồi quy
Giả sử X và Y có quan hệ tuyến tính E(Y | X ) = AX + B
Dựa vào n cặp số liệu (x , y ),(x , y ),...,(x , y ) của (X ,Y) ta tìm hàm y = ax + b để ước 1 1 2 2 n n
lượng cho hàm Y = AX + B .
Với dữ liệu thu được (x , y ) khi đó giá trị y = ax + b là dự báo cho y . i i i i i
Sai số của xấp xỉ:  = y − y = y − ax − b i i i i i
Phương pháp bình phương cực tiểu: tìm a và b sao cho n n 2 2 F( , a ) b =  = y ax b min. i ( − − ) i i i 1 = i 1 = n n n n  F   2 = 2
− x (y − ax −b) = 0 . a  x + .
b  x =  x y  i i i  i i i i  a   Suy ra: i 1 = i 1 = i 1 = i 1 =    n n n F    = 2
− (y − ax −b) = 0 .
a  x + nb =  y i i i i  b   i 1 =  i 1= i 1 =
Giải phương trình ta được nghiệm:  n  n   n  . n  x y − x y i i  .  
i    i  i 1 =
 i 1=   i 1=  a = 2  n  n  2  x − x i   i   i 1 =  i 1=    n n  n   n  2 x . y x x y i  − i  . 
i    i i   i 1 = i 1 =
 i 1=   i 1=  b = hay b = y − . a x 2  n  n  2 . n  x −  x i   i   i 1 =  i 1=  1 n 1 n x = x y = y i  i n n i 1 = i 1 =
CHƯƠNG V. QUY HOẠCH THỰC NGHIỆM §1. ĐỊNH NGHĨA QHTN
1.1. Định nghĩa: qui hoạch thực nghiệm là tập hợp các tác động nhằm đưa ra chiến thuật
làm thực nghiệm từ giai đoạn đầu đến giai đoạn kết thúc của quá trình nghiên cứu đối
tượng (từ nhận thông tin mô phỏng đến việc tạo ra mô hình toán, xác định các điều kiện
tối ưu), trong điều kiện đã hoặc chưa hiểu biết đầy đủ về cơ chế của đối tượng.
Đối tượng của quy hoạch thực nghiệm trong các ngành công nghệ: Là một quá trình
hoặc hiện tượng nào đó có những tính chất, đặc điểm chưa biết cần nghiên cứu. Người
nghiên cứu có thể chưa hiểu biết đầy đủ về đối tượng, nhưng đã có một số thông tin tiên
nghiệm dù chỉ là sự liệt kê sơ lược những thông tin biến đổi, ảnh hưởng đến tính chất
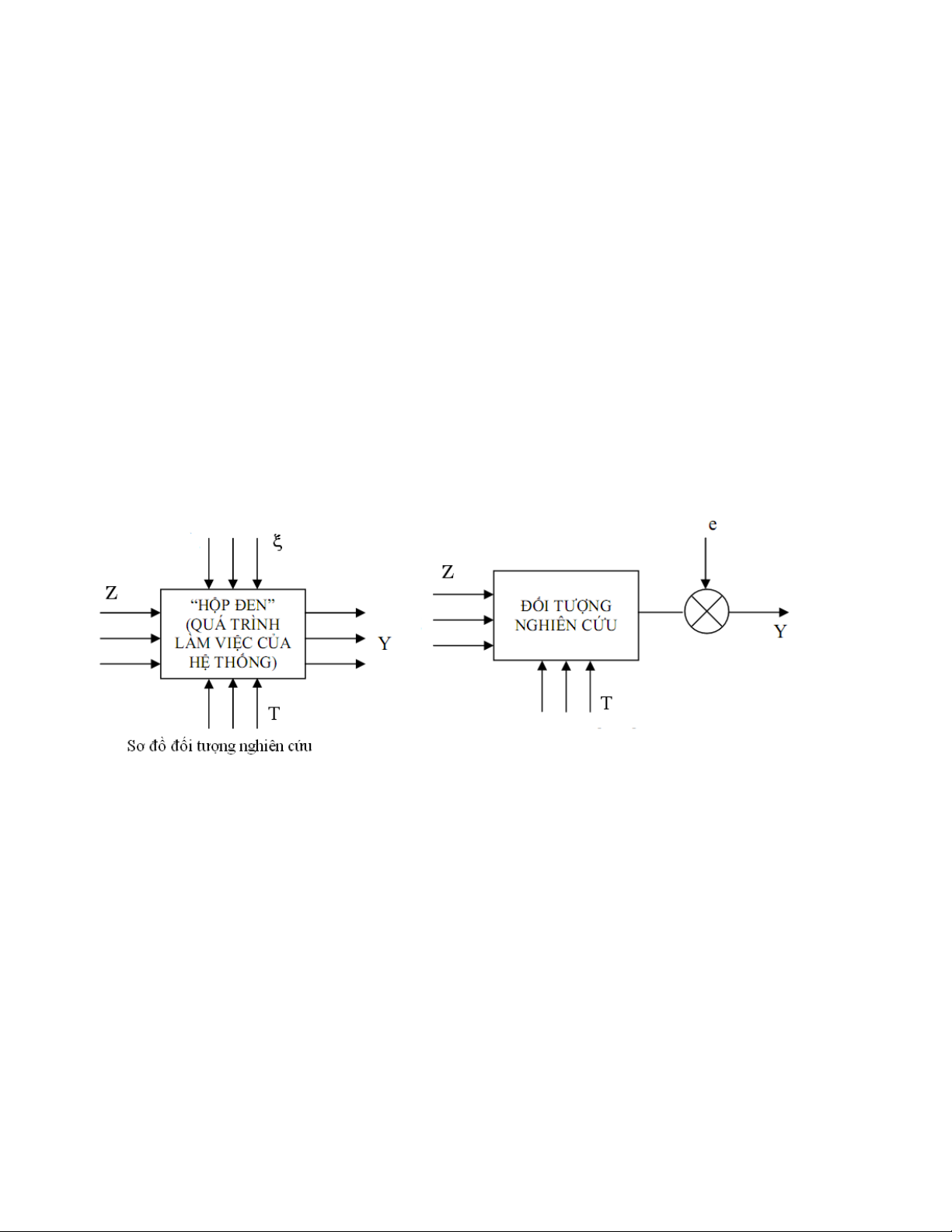
đối tượng. Có thể hình dung chúng như một “hộp đen” trong hệ thống điều khiển gồm
các tín hiệu đầu vào và đầu ra.
Thông thường ta muốn xây dựng được hàm f: Y = f (Z , Z ,..., Z ) 1 2 k
Chúng ta chỉ xét f là dạng hàm tuyến tính.
- Các tín hiệu đầu vào được chia thành ba nhóm:
1) Các biến kiểm tra được và điều khiển được, mà người nghiên cứu có thể điều chỉnh
theo dự định, biểu diễn bằng vectơ: Z = [z , z ,..., z ] 1 2 k
2) Các biến kiểm tra được nhưng không điều khiển được, biểu diễn bằng vectơ:
T = (t ,t ,...,t ) 1 2 m
3) Các biến không kiểm tra được và không điều khiển được, biểu diễn bằng
vectơ:  = [ , ,..., ] 1 2 p
1.2. Các nguyên tắc cơ bản của qui hoạch thực nghiệm
Đầu tiên ta sẽ phải hạn chế miền mà các biến nhận: Tìm miền để Z nhận giá trị. i min Z [Z ;Zmax ] i i i
1.2.1. Nguyên tắc không lấy toàn bộ trạng thái đầu vào
Để có thông tin toàn diện về tính chất hàm mục tiêu về nguyên tắc cần tiến hành
vô số các thực nghiệm trong miền qui hoạch.
Ví dụ, trong trường hợp có hai yếu tố, nếu cho mỗi yếu tố biến đổi liên tục từ -1
đến +1 thì miền thực nghiệm sẽ là hình vuông chứa vô số điểm M (z , z ) đặc trưng cho 1 2 trạng thái đầu vào.
Về lý thuyết nếu không tiến hành tất cả các thực nghiệm đó thì có thể bỏ sót đặc
điểm nào đó của hàm mục tiêu, tuy nhiên thực tế không thể thực hiện được điều đó. Do
vậy người nghiên cứu chỉ có thể lấy những giá trị rời rạc (thường chọn theo mắt lưới),
chọn mức biến đổi nào đó cho các yếu tố. Sự lựa chọn này cần có cơ sở khoa học, nó
gắn liền với sự lựa chọn dạng hàm, tức là dạng mô phỏng của bề mặt đáp ứng. Dạng
hàm thông thường là bậc một hoặc bậc hai.
1.2.2. Nguyên tắc phức tạp dần mô hình toán học
Y = b + b Z + b Z + ... + b Z đây là mô hình tuyến tính đơn giản nhất. 0 1 1 2 2 k k
Y = b + b Z + b Z + ... + b Z + b Z Z + b Z Z + ... là mô hình tuyến tính phức tạp hơn 0 1 1 2 2 k k 12 1 2 13 1 3 2 2
Y = b + b Z + b Z + ...+ b Z + b Z Z + b Z Z + ...+ b Z + b Z + ... 0 1 2 2 2 k k 12 1 2 13 1 3 11 1 22 2
Khi chưa có thông tin ban đầu về các tính chất của hàm mục tiêu, thì không nên
xây dựng mô hình phức tạp của đối tượng để tránh chi phí vô ích về thời gian, phương
tiện vật chất nếu không dùng đến mô hình đó. Vì thế lý thuyết qui hoạch thực nghiệm
hướng dẫn nên bắt đầu từ những mô hình đơn giản nhất, ứng với những thông tin ban
đầu đã có về đối tượng. Logic tiến hành thực nghiệm là nên làm ít thí nghiệm để có mô
hình đơn giản (ví dụ mô hình tuyến tính), kiểm tra tính phù hợp của mô hình:
- Nếu mô hình phù hợp, đạt yêu cầu thì dừng lại, hoặc cải tiến;
- Nếu mô hình không phù hợp thì tiến hành giai đoạn tiếp theo của thực nghiệm: làm
những thí nghiệm mới, bổ sung để rồi nhận được mô hình phức tạp hơn (ví dụ mô hình
phi tuyến), kiểm tra mô hình mới cho đến khi đạt được mô hình hữu dụng.
1.2.3. Nguyên tắc đối chứng với nhiễu
Độ chính xác của mô hình phải tương xứng với cường độ nhiễu ngẫu nhiên mà
chúng tác động lên kết quả đo hàm mục tiêu. Trong cùng điều kiện như nhau, độ nhiễu
càng nhỏ thì mô hình càng phải chính xác, phải phức tạp hơn.
Bằng các công cụ tính toán thống kê, người ta đã xây dựng hoàn chỉnh các qui
trình chuẩn theo các tiêu chuẩn thống kê để giải quyết các nhiệm vụ xác định tính phù
hợp của mô hình tìm được, hiệu chỉnh dạng mô hình, kiểm tra tính đúng đắn của các giả
thiết, các tiên đề mà dựa vào đó tìm ra các mô hình.
1.2.4. Nguyên tắc ngẫu nhiên hóa.
Ta phải chủ động tạo các tình huống ngẫu nhiên trong thực nghiệm. Ví dụ là ngẫu
nhiên hóa trình tự các thí nghiệm tiến hành.
1.2.5. Nguyên tắc tối ưu.
Đây là nguyên tắc trung tâm trong lý thuyết QHTN. Theo đó kế hoạch thực
nghiệm cần phải có những tính chất tối ưu cụ thể theo quan điểm của một hay một nhóm
các tiêu chuẩn tối ưu đã xác định trước. Các tiêu chuẩn đó thường được xây dựng khác
nhau thông qua ngôn ngữ toán học. Nói chung xu hướng là: Ít thí nghiệm hơn – nhiều
thông tin hơn – chất lượng kết quả cao hơn.
1.3. Kế hoạch thực nghiệm
1.3.1. Xác định miền giới hạn
Mục tiêu là xác định tham số đầu vào Z để tiến hành các thí nghiệm, muốn vậy phải xác
định được miền mà các biến z có thể nhận giá trị: min max z  z  z . j j j j
Sau đó dựa vào miền giới hạn đó để tạo ra kế hoạch thực nghiệm bao gồm các điểm
(phương án) thí nghiệm. Một điểm (phương án) thí nghiệm là một bộ giá trị cụ thể của
các giá trị đầu vào Z. Tại điểm thứ i của kế hoạch ta có một bộ số liệu đầu vào của Z:
(z , z ,..., z ) 1 i i 2 ik
với k là số yếu tố đầu vào
i = 1, 2,..., N là điểm thí nghiệm thứ i của kế hoạch
N là số điểm thí nghiệm của kế hoạch
1.3.2. Các mức yếu tố
Các giá trị cụ thể của các thành phần của Z được ấn định tại 1 điểm kế hoạch được gọi là
các mức yếu tố. Một số mức thường gặp: mức trên, mức dưới, mức cơ sở, … Mức cơ sở 0 0 0 0
Z = (z , z ,..., z ) là một điểm thí nghiệm được quan tâm đặc biệt, thông 1 2 k
thường nó được gọi là tâm kế hoạch vì trong vùng quanh nó phân bố toàn bộ các điểm max min z + z
kế hoạch. Công thức xác định mức cơ sở như sau: 0 j j z = j 2 mức trên: max z j mức dưới: min z j mức cơ sở: 0 z j
1.3.3. Giá trị mã hóa
Do khi thu thập số liệu về các biến đầu vào có thể xảy ra tình huống có thứ nguyên khác
nhau, điều này dẫn đến khó khăn trong xử lý. Để khắc phục người ta quy đổi số liệu về
giá trị mã hóa (là giá trị không có thứ nguyên). 0 z − z max min z − z Công thức biến đổi: j j x = với j j z  = j z  j 2 j
Như vậy theo tỷ lệ quy chuẩn, mức cơ sở mã hóa của yếu tố đầu vào là 0 x = 0 j
Còn với các điểm thí nghiệm khác ta có: 1 −  x 1 j
✓ Mức trên ( x =1) ký hiệu là “+” j
✓ Mức cơ sở ( x = 0 ) ký hiệu là 0 j
✓ Mức dưới ( x = 1
− ) ký hiệu là “–” j
Sau khi mã hóa, hàm chúng ta quan tâm có dạng :
Y = b + b X + b X + ... + b X 0 1 1 2 2 k k
1.3.4. Ma trận thực nghiệm
Ma trận thực nghiệm là dạng mô tả chuẩn các điều kiện tiến hành thí nghiệm (các điểm
thí nghiệm) theo bảng chữ nhật, mỗi hàng là một thí nghiệm, các cột ứng với các yếu tố đầu vào.
Có 2 ma trận thực nghiệm: theo giá trị thực tế Z và theo giá trị mã hóa X. N0 Z Z … Z y 1 2 k 1 z z … z y 11 12 1k 1 2 z z … z y 21 22 2k 2 … … … … … … N z z … z y N 1 N 2 Nk N
§2. PHƯƠNG PHÁP BÌNH PHƯƠNG CỰC TIỂU 2.1. Đặt bài toán.
Bài toán đưa ra là cần nghiên cứu về biến y trong một hệ thống, trong đó y phụ thuộc
vào các yếu tố độc lập x , x ,..., x có thể điều khiển được và biến  không điều khiển 1 2 k
được (người ta thường gọi là nhiễu). Mối quan hệ:
y = f (x , x ,..., x ,  ,  ,...,  ) +  1 2 k 1 2 m
với dạng hàm f đã biết nhưng chưa biết các tham số  , ,..., và E( )  = 0 1 2 m
Để tìm mối quan hệ của y và x , x ,..., x ta làm N thí nghiệm ta được bảng số liệu: 1 2 k N0 x x … x y 1 2 k 1 x x … x y 11 12 1k 1 2 x x … x y 21 22 2 k 2 … … … … … … N x x … x y N 1 N 2 Nk N
Một điểm thí nghiệm là một bộ số liệu (x , x ,..., x ) . i1 i 2 ik
Đối với mỗi bài toán cụ thể, các điểm thí nghiệm chỉ có thể chạy trên một miền xác định k H 
gọi là miền quy hoạch. Bài toán đặt ra:
Trên cơ sở các số liệu thu được, ta tìm một hàm số
y = f (x , x ,..., x ) (6.1) 1 2 k
biểu diễn gần đúng tốt nhất hàm y = f (x , x ,..., x , , ,..., ) là giá trị thay thế cho y. 1 2 k 1 2 m
Phương trình (6.1) được gọi là phương trình hồi quy thực nghiệm.
Để giải quyết bài toán người ta sử dụng phương pháp bình phương cực tiểu. Mục đích là
xác định các tham số  , ,..., sao cho cực tiểu bình phương sai số. 1 2 m N 2
(y − y ) → min (LS) i i i 1 =
trong đó y (i = 1,.., N) là các kết quả thí nghiệm i
y = f (x , x ,..., x ,  ,  ,...,  ) (i = 1,.., N ) là các giá trị lý thuyết. i i1 i 2 ik 1 2 m
Vì các tham số  , ,..., chưa biết nên tổng bình phương sai số là một hàm của các 1 2 m N tham số đó: 2
S( , ,..., ) = (y − y ) → min 1 2 m i i i 1 = 
Từ đó suy ra S = 0 (i = 1,..,m) . Ta cố gắng xác định các hệ số dựa vào các phương i trình này.
2.2. Trường hợp hàm tuyến tính. (TH đặc biệt)
Xét bài toán với quan hệ y =  +  x +  x + ...+  x +  0 1 1 2 2 k k với E( )
 = 0 và y =  +  x +  x + ...+  x 0 1 1 2 2 k k
Bảng số liệu thí nghiệm N0 x x x … x y 0 1 2 k 1 1 x x … x y 11 12 1k 1 2 1 x x … x y 21 22 2 k 2 … ... … … … … … N 1 x x … x y N 1 N 2 Nk N
Suy ra: y =  x +  x +  x + ... +  x với quy ước x = 1 i 0 i 0 1 i1 2 i 2 k ik i 0
Bài toán đặt ra: Xác định các hệ số  = b sao cho: j j N N k 2 2
S( , , ,..., ) = (y − y ) = (y −  x ) → min 0 1 2 k i i i j ij i 1 = i 1 = i=0 
Dựa vào điều kiện cực trị ta có: S = 0 (i = 0,..,k) i N k N k S     
= 2 −x (y −  x ) = 0   x (y −  x ) = 0 (i = 0,..,k)  (6.2) ij i j ij   ij i j ij       j i 1 = i=0 i 1 = i=0    1 x x ... x   y  0 11 12 1k 1        1 x x ... x y Đặt 1 21 22 2k 2        = X = Y =  ...  ... ... ... ... ...  ...         1 x x ... x     y k N1 N 2 Nk  N 
Khi đó hệ (6.2) trở thành T
X (Y − X )  = 0 Suy ra T T
X X  = X Y , nếu tồn tại ma trận nghịch đảo T 1
(X X )− ta sẽ thu được kết quả: T 1 ( )−  = ( T X X X Y )
§3. QUY HOẠCH TRỰC GIAO
3.1. Quy hoạch trực giao và tính chất
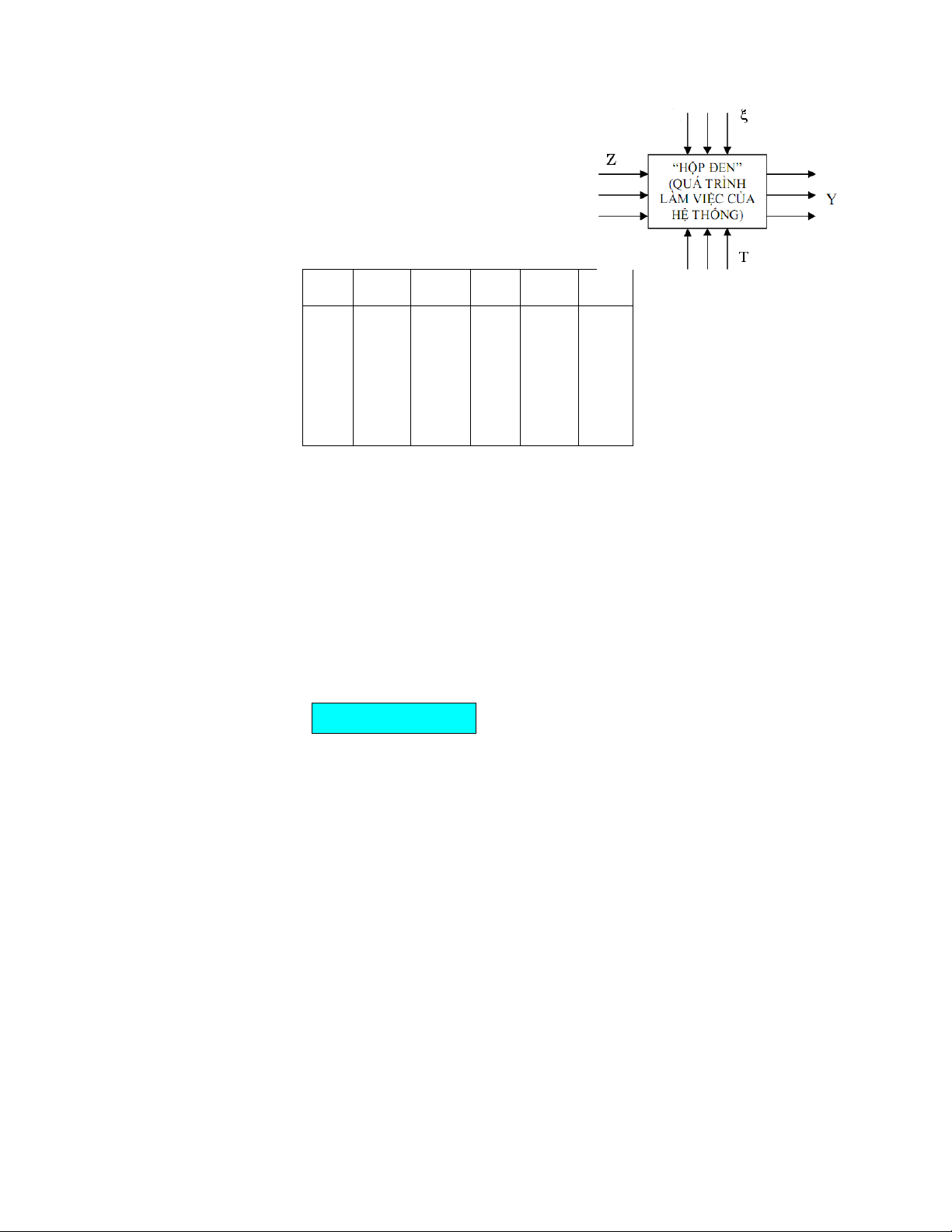
3.1.1. Mở đầu. Xét mô hình:
Làm N thí nghiệm để đo Y, ta được bảng số liệu: N0 x x … x y 1 2 k 1 x x … x y 11 12 1k 1 2 x x … x y 21 22 2 k 2 … … … … … … N x x … x y N 1 N 2 Nk N Xét mô hình:
y =  +  x +  x + ... +  x +  (6.3) 0 1 1 2 2 k k Với 2  ~ N(0; ) (6.4)
Đặt y =  +  x +  x + ...+  x (6.5) 0 1 1 2 2 k k
Ta thấy ngay E(y) = E(y) . (6.5) gọi là mô hình hồi quy lý thuyết
Ta sử dụng số liệu ở bảng trên và sử dụng phương pháp bình phương cực tiểu ta thu
được ước lượng điểm cho  = (  ... )T chính là véctơ B với công thức tính: 0 1 k T 1 ( )− = ( T B X X X Y ) (6.6) b   1 x x ... x   y  0 11 12 1k 1       b 1 x x ... x y Trong đó 1 21 22 2k 2       B = X = Y =  ...  ... ... ... ... ...  ...        b 1 x x ... x     y k N1 N 2 Nk  N 
Tính được B thay vào (6.3) ta thu được:
y = b + b x + b x + ... + b x (6.7) 0 1 1 2 2 k k
(6.7) gọi là mô hình hồi quy thực nghiệm
Vấn đề đặt ra: liệu có thể bố trí thí nghiệm sao cho: • Số thí nghiệm ít • Tính toán gọn
• Đảm bảo độ chính xác.
3.1.2. Định nghĩa quy hoạch trực giao
Quy hoạch trực giao là quy hoạch bố trí các thí nghiệm sao cho ma trận:  1 x x ... x  11 12 1k   1 x x ... x 21 22 2k X   =  ... ... ... ... ...    1 x x ... x  N1 N 2 Nk  có t/c: ma trận tích T
X X có các giá trị không nằm trên đường chéo chính đều bằng 0 N Từ đó suy ra: x = 0 ij i 1 = N x .x = 0 j   k ij ik i 1 = N Nếu đặt 2 2 2
c = N ; c = x
j = 1,.., k ta có: 0 j ij i 1 = 2 c 0 ... 0  2 1/ c 0 ... 0  0   0   2 0 c ... 0 2 0 1 / c ... 0 T  1    X X = = C  T 1 − 1 − 1  ( X X ) = C = ... ... ... ...      ... ... ... ...    2    0 0 ... c  2 0 0 ... 1 / c k   k  N   N   1  y   y   i  2 i c i 1 =  o i 1 =   1 1 ... 1  y    1 N       1 N  x x ... x y x y       x y  T 11 21 N1 2 i1 i T 1 − T 2 i1 i X Y = =
Suy ra B = ( X X ) ( X Y ) = c i 1 =   1 i 1=  ... ... ... ...  ...        ...   ...  x x ... x y        1k 2k Nk k N     1 N  x y  x y ik i    2 ik i  c i 1 =   k i 1= 
3.2. Quy hoạch trực giao cấp I
3.2.1. Định nghĩa
Quy hoạch trực giao cấp 1 là quy hoạch trực giao thỏa mãn: 2 c = N j = 0,1,..., k j N
(Điều này tương ứng với việc 2 2
c =  x = N hay nói cách khác ta luôn có | x |=1) j ij ij i 1 =
3.2.2. Các bước thực hiện quy hoạch trực giao cấp 1:
1. Xác định miền biến thiên: min max z  z  z j j j max min z + z
Tâm quy hoạch 0 j j z = j 2
2. Chọn dạng phương trình hồi quy:
Mã hóa số liệu: 0 max min
x = 2(z − z ) /(z − z ) j j j j j
Chọn dạng tuyến tính: y = b + b x + b x + ...+ b x 0 1 1 2 2 k k hoặc dạng:
y = b + b x + b x + ... + b x + b x x + ... + b x x , ... 0 1 1 2 2 k k 12 1 2 k 1 − ,k k 1 − k
3. Thực hiện N thí nghiệm với 2k N =
, xác định các hệ số hồi quy bằng phương pháp
bình phương cực tiểu − . = ( ) 1 T T B X X X Y
4. Kiểm định sự có nghĩa của các hệ số hồi quy (xét bi = 0 hay khác 0)
5. Kiểm định sự có nghĩa của phương trình hồi quy. (kiểm tra mô hình có dùng được?)
Ưu điểm của ma trận trực giao cấp I:
- Khi loại bỏ những hệ số không có nghĩa sẽ không phải tính lại các hệ số có nghĩa.
- Phương sai các hệ số b trong phương trình hồi qui có giá trị tối thiểu.
- Tâm phương án thông tin nhiều nhất → chỉ lần thực nghiệm lặp ở tâm thực nghiệm là đủ.
Xét mô hình (6.3): y =  +  x +  x + ... +  x +  0 1 1 2 2 k k
• hệ số hồi quy xác định bởi công thức:  1 N b =  y  0 i  N i 1 =  1 N b =  x y j = 1,..., k j ij i  N i 1 =
• Kiểm định sự có nghĩa của các hệ số hồi quy b . j H : = 0  j i) Cặp giả thuyết 0  H :  0  1 j
người ta sẽ chọn giải pháp lặp n lần thí nghiệm tại mức cơ sở (tại tâm). Khi đó ta tính 0 như sau: n n 0 0 1 i 1 2 i 2 y =  y  s =
(y − y ) (phương sai mẫu hiệu chỉnh) 0 0 ts 0 0 n = n − i 1 0 1 0 i 1 = 2
s : phương sai tái sinh: chính là mức độ phân tán dữ liệu của hệ thống ts 2
s : phương sai tái hiện th b −  b Chọn thống kê j j j t = =
~ t(n −1) với H đúng bj 0 s s 0 bj bj 
Với mức ý nghĩa  tra bảng student ta được t = t(n −1,1− )  0 2
Miền bác bỏ H : W = (− ;  t
− ) (t ;+) 0    b b
iii) Giá trị quan sát j j t = = N bj s s bj ts Ta xác định được 2 2 1 s s .{C − =
} . Với quy hoạch trực giao cấp I ta có: bj ts jj 1 s 2 2 s = s . ts  s = bj ts bj N N
Nếu | t | t ta chấp nhận H hay là ta có hệ số tương ứng b bằng 0 bj  0 j
Nếu | t | t ta bác bỏ H hay là ta có hệ số tương ứng b khác 0 bj  0 j
• Kiểm định sự phù hợp của phương trình hồi quy y = b + b x + b x +...+ b x (*) 0 1 1 2 2 k k
Dùng thí nghiệm lặp để tính 2
s ước lượng cho 2
 không phụ thuộc dạng của y . ts
- Độ dư là hiệu giữa giá trị thực nghiệm thu được với giá trị tính được theo phương trình
hồi qui của các thông số tối ưu.
- Phương sai tìm được trên cơ sở tổng bình phương các độ dư gọi là phương sai dư, được kí hiệu là 2 s . du
- Phương sai dư là ước lượng của 2
 phụ thuộc dạng của phương trình hồi quy (*). 1 N 2 2 s = (y − y ) du i i N − L i 1 =
y được tính thông qua điểm thí nghiệm thứ i và dựa vào phương trình hồi quy (*) i
N là số điểm thí nghiệm ( 2k N = )
L là số hệ số hồi quy có nghĩa trong phương trình hồi quy
Nếu y phù hợp với mô hình thì hai phương sai bằng nhau.
Người ta làm n thí nghiệm lặp tại tâm 0 2 2
H : s = s Cặp giả thuyết: 0 du ts  2 2
H : s  s  1 du ts 2 Chọn thống kê sdu F =
~ Fisher với bậc tự do ở tử là (N – L), bậc mẫu là n −1 2 s 0 ts 2 N
Từ đó tính được giá trị quan sát s 1 du F = với 2 2 s = (y − y ) 2 s du i i N − L ts i 1 =
Chọn mức ý nghĩa , tra bảng ta tìm được F (phân vị trên của Fisher bậc tự do (N – L)
và n −1 mức ): F = F ( ;  N − ;
L n −1) : phân vị trên mức a 0  0
Nếu F  F  chấp nhận 
H  mô hình phù hợp 0
Nếu F  F  bác bỏ 
H  mô hình không phù hợp 0
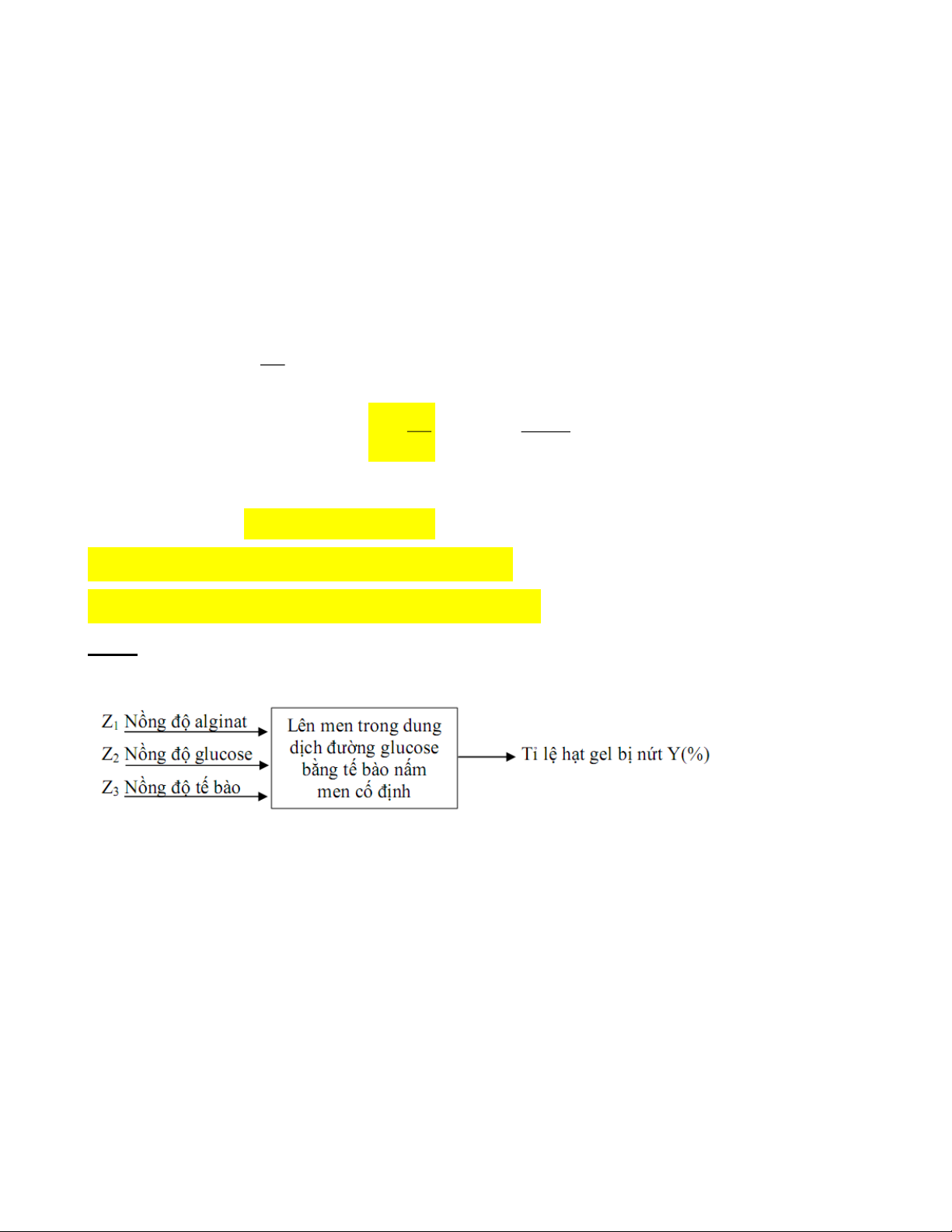
Ví dụ: Nghiên cứu tối ưu hóa quá trình cố định tế bào nấm men bằng Alginat để lên men rượu
Các yếu tố ảnh hưởng đến mạng lưới gel: nồng độ alginat, nồng độ glucose, nồng độ tế bào.
Sau quá trình lên men, vớt các hạt gel ra và xác định tỷ lệ (%) hạt gel bị nứt. Tỷ lệ hạt
gel bị nứt càng thấp càng tốt nghĩa là hạt gel càng chắc càng tốt.
Sau khi tiến hành các thí nghiệm thăm dò, tác giả chọn vùng khảo sát như sau: Z1 = 1% – 4% Z2 = 10% – 18% Z3 = 10% – 20%
Phương án quy hoạch thực nghiệm: phương pháp trực giao cấp 1
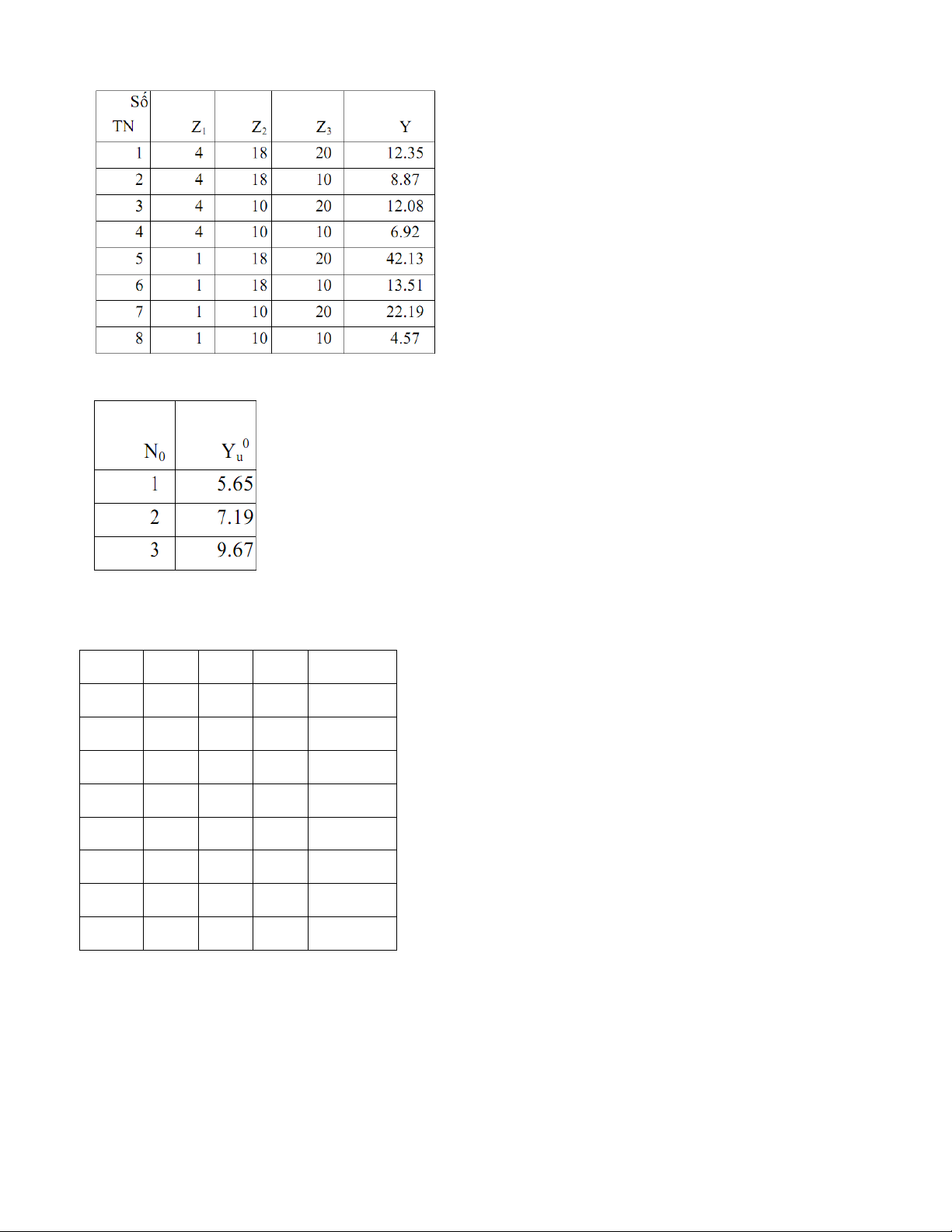
Thí nghiệm lặp tại tâm 0 Z = (2,5;14;15)
Phương trình hồi quy dạng: Y = b + b X + b X + b X 0 1 1 2 2 3 3 Mã hóa dữ liệu x1 x2 x3 y 1 1 1 1 12.35 2 1 1 -1 8.87 3 1 -1 1 12.08 4 1 -1 -1 6.92 5 -1 1 1 42.13 6 -1 1 -1 13.51 7 -1 -1 1 22.19 8 -1 -1 -1 4.57 1 1 1 1   ...      1 1 1 1 −     b  1 1 1 − 1    0       b 1 1 1 − 1 − 1       B = X = Y = T − T =  1 B ( X X ) X Y b  1 1 − 1 1    2         b   1 1 − 1 1 −    3     1 1 − 1 − 1         1 1 − 1 − 1 −  .... Bước 3
y = b0 + b1*x1 + b2*x2 + b3*x3 + b12*x1*x2 TN x1 x2 x3 y x1*y x2*y x3*y 1 1 1 1 12.35 12.35 12.35 12.35 2 1 1 -1 8.87 8.87 8.87 -8.87 3 1 -1 1 12.08 12.08 -12.08 12.08 4 1 -1 -1 6.92 6.92 -6.92 -6.92 5 -1 1 1 42.13 -42.13 42.13 42.13 6 -1 1 -1 13.51 -13.51 13.51 -13.51 7 -1 -1 1 22.19 -22.19 -22.19 22.19 8 -1 -1 -1 4.57 -4.57 -4.57 -4.57 TB cộng 15.3275 -5.2725 3.8875 6.86 b0 b1 b2 b3
Theo phương pháp bình phương cực tiểu ta tính được:
b = 15.3275; b = 5
− .2725; b = 3.8875; b = 6.86 0 1 2 3
y^ = 15.3275 – 5.2725*x1 + 3.8875*x2 + 6.86*x3
Bước 4: Kiểm định hệ số bằng 0 hay khác 0
n = 3 số liệu của y tại tâm: 5.65 ; 7.19 ; 9.67 ta tính được: 0 0 1 n i 2 s =
(y − y ) = 2.0282 ts o 0 n −1 0 i 1 = b Giá trị quan sát: j t = N ta được: bj sts
t = 21.3746; t = 7
− .3536 ; t = 5.4212 ; t = 9.5665 0 b 1 b 2 b 3 b 
Ngưỡng t = t(n −1;1− ) = t(2;0.975) = 4.3  0 2
Do tất cả các giá trị quan sát đều có trị tuyệt đối lớn hơn ngưỡng, nên tất cả các hệ số khác 0.
Mô hình sẽ có dạng: y^ = 15.3275 – 5.2725*x1 + 3.8875*x2 + 6.86*x3. L = 4
Bước 5: Kiểm định sự phù hợp của mô hình x1 x2 x3 y y^ (y-y^)^2 1 1 1 12.35 20.8025 71.44476 1 1 -1 8.87 7.0825 3.195156 1 -1 1 12.08 13.0275 0.897756 1 -1 -1 6.92 -0.6925 57.95016 -1 1 1 42.13 31.3475 116.2623 -1 1 -1 13.51 17.6275 16.95381 -1 -1 1 22.19 23.5725 1.911306 -1 -1 -1 4.57 9.8525 27.90481 1 N Ta có 2 2 s =
(y − y ) = 74.13 du i i N − L i 1 = 2 s Giá trị quan sát du F = =18.02 2 sts
Ngưỡng: F = F(N − ;
L n −1; ) = F (4; 2;0.05) = 19.2468  0
Do F  F nên mô hình phù hợp.
3.2.3. Một số mô hình mở rộng từ quy hoạch trực giao cấp I
Đối với qui hoạch thực nghiệm, những phương trình hồi qui cấp I thường chọn các khai
triển của đa thức có dạng tổng quát như sau:
y = b + b x + b x + ... + b x + b x x +  b x x x 0 1 1 2 2 k k ij i j ijl i j l i j
i jl i
Bằng cách đặt x = x x và x = x x x ta sẽ đưa được phương trình về dạng tuyến tính, ij i j ijl i j l
chỉ có điểm khác là giá trị của các biến vừa đặt tính được thông qua k biến ban đầu.
Hoàn toàn tương tự ta tính được các hệ số của phương trình hồi quy như sau: