Lý thuyết về chuỗi thời gian - Lý thuyết Xác suất | Đại học Sư Phạm Hà Nội
Lý thuyết về chuỗi thời gian - Lý thuyết Xác suất | Đại học Sư Phạm Hà Nội giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực
Môn: Lý thuyết xác suất (MATH 233)
Trường: Đại học Sư Phạm Hà Nội
Thông tin:
Tác giả:
Preview text:
Mục lục 1 Mở đầu 3
1.1 Một số ví dụ về Chuỗi thời gian . . . . . . . . . . . . . . . . . . . . . . . 3
1.2 Mục tiêu của Phân tích Chuỗi thời gian . . . . . . . . . . . . . . . . . . 7
1.3 Một vài mô hình Chuỗi thời gian đơn giản . . . . . . . . . . . . . . . . . 8
1.3.1 Một vài mô hình có trung bình mẫu bằng 0 . . . . . . . . . . . . 9
1.3.2 Các mô hình với Tính xu hướng và Tính mùa vụ . . . . . . . . . 10
1.3.3 Một cách tiếp cận chung cho Mô hình Chuỗi thời gian . . . . . . 14
1.4 Các mô hình dừng và hàm tự tương quan . . . . . . . . . . . . . . . . . 15
1.4.1 Hàm tự tương quan mẫu . . . . . . . . . . . . . . . . . . . . . . . 18
1.4.2 Mô hình cho dữ liệu Hồ Huron . . . . . . . . . . . . . . . . . . . . 20
1.5 Ước lượng và Triệt tiêu thành phần Mùa vụ và thành phần Xu hướng . 22
1.5.1 Ước Lượng và Triệt tiêu thành phần xu hướng khi không có
thành phần mùa vụ . . . . . . . . . . . . . . . . . . . . . . . . . . 23
1.5.2 Ước lượng và loại bỏ cả tính xu hướng và tính mùa vụ . . . . . . 29
1.6 Kiểm tra chuỗi nhiễu ước lượng . . . . . . . . . . . . . . . . . . . . . . . 33 2 QUÁ TRÌNH DỪNG 42
2.1 Các tính chất cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
2.2 Quá trình tuyến tính . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
2.3 Mở đầu về quá trình ARMA . . . . . . . . . . . . . . . . . . . . . . . . . . 50
2.4 Tính chất của trung bình mẫu và hàm tự tương quan . . . . . . . . . . 52
2.4.1 Ước lượng cho µ . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
2.4.2 Ước lượng của γ(·) và ρ(·) . . . . . . . . . . . . . . . . . . . . . . . 54
2.5 Dự báo chuỗi thời gian dừng . . . . . . . . . . . . . . . . . . . . . . . . . 58
2.5.1 Dự đoán bậc hai của các biến ngẫu nhiên . . . . . . . . . . . . . 60
2.5.2 Toán tử dự báo P (· | W) . . . . . . . . . . . . . . . . . . . . . . . . 61
2.5.3 Thuật toán Durbin-Levinson . . . . . . . . . . . . . . . . . . . . . 62
2.5.4 Thuật toán đổi mới . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
2.5.5 Tính toán hồi qui cho dự báo h bước . . . . . . . . . . . . . . . . 67
2.5.6 Dự đoán một quá trình dừng theo quá khứ vô hạn . . . . . . . . 68
2.5.7 Sự xác định của ˜
PnXn+h . . . . . . . . . . . . . . . . . . . . . . . . 68
2.6 Phân tách Wold . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69 3 Mô hình ARMA 73
3.1 Quá trình ARMA(p, q) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
3.2 ACF và PACF của quá trình ARMA(p, q) . . . . . . . . . . . . . . . . . . . 77
3.2.1 Tính toán cho ACVF . . . . . . . . . . . . . . . . . . . . . . . . . . 77
3.2.2 Hàm tự tương quan . . . . . . . . . . . . . . . . . . . . . . . . . . 82 1
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN
3.2.3 Hàm tự tương quan từng phần . . . . . . . . . . . . . . . . . . . . 83
3.2.4 Các ví dụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
3.3 Dự báo quá trình ARMA . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
3.3.1 Dự báo h-bước của quá trình ARMA(p, q) . . . . . . . . . . . . . . 91
Bài giảng Phân tích chuỗi thời gian 2
CHƯƠNG 1 Mở đầu
Trong chương này, ta sẽ được giới thiệu một vài ý tưởng cơ bản của phân tích chuỗi
thời gian và các quá trình ngẫu nhiên. Ta cũng sẽ chú trọng vào các khái niệm về tính
dừng, đồng phương sai và các hàm đồng phương sai mẫu. Đồng thời, sách cũng sẽ
đưa ra một vài kỹ thuật tiêu chuẩn cho việc ước lượng và triệt tiêu tính xu hướng và
tính mùa vụ (trong một khoảng thời gian đã biết) từ một chuỗi thời gian quan quan sát
được. Những kỹ thuật này sẽ được mô tả thông qua bộ dữ liệu trong Mục 1.1. Các tính
toán trong các ví dụ có thể được thực hiện bằng việc sử dụng các gói chuỗi thời gian
ITSM, hiện đã có phiên bản chuyên nghiệp trên các trang http://extras. springer.com.
Các bộ dữ liệu được bao gồm trong các tệp với tên kết thúc bằng .TSM. Ví dụ, thống
kê lượng rượu vang đỏ Úc đã bán sẽ được đặt tên là WINE.TSM. Phần lớn các chủ đề
được đề cập đến trong chương này sẽ được nhắc lại và phát triển kỹ hơn ở phần còn
lại của cuốn sách. Những bạn đọc chưa được làm quen với các khái niệm về biến ngẫu
nhiên và véctơ ngẫu nhiên có thể đọc trước Phụ lục A.
1.1 Một số ví dụ về Chuỗi thời gian
Một chuỗi thời gian là một tập hợp các quan sát xt, trong đó mỗi quan sát được
thực hiện tại một điểm thời gian t. Một chuỗi thời gian thời gian rời rạc (dạng mà ta
đề cập chủ yếu trong cuốn sách này) là một chuỗi thời gian mà tập hợp T0 các điểm
thời gian của các quan sát là rời rạc, ví dụ như trong trường hợp các quan sát được
thực hiện tại các mốc thời gian cố định. Ta thu được các chuỗi thời gian thời gian
liên tục khi các quan sát được thực hiện trên cả một khoảng thời gian, ví dụ như T0 = [0, 1].
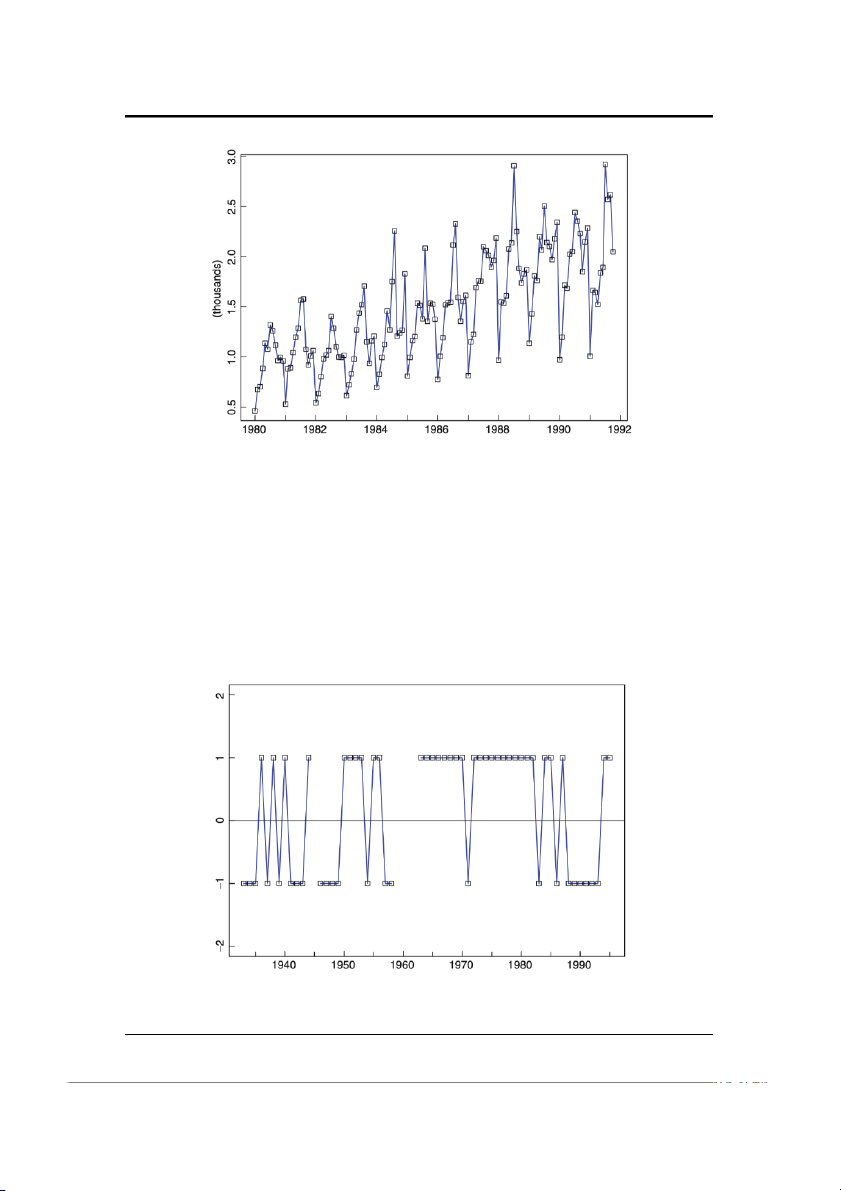
Ví dụ 1.1.1 (Lượng rượu vang đỏ Úc đã bán; WINE.TSM). Hình 1-1 mô tả lượng
rượu vang đỏ Úc bán được hàng tháng (tính theo đơn vị kiloliters) từ Tháng 1 năm
1980 đến Tháng 10 năm 1991. Trong trường hợp này, tập T0 bao gồm 142 mốc
thời điểm {( Tháng 1 năm 1980), (Tháng 2 năm 1980), ...,(Tháng 10 năm 1991)}.
Cho tập hợp gồm n quan sát được thực hiện tại các mốc thời gian cách đều nhau,
để thuận tiện, không mất tính tổng quát, ta giả sử rằng tập các mốc thời gian T0
là tập các số nguyên {1, 2, . . . , n}. Trong ví dụ đang xét, ta tính thời gian theo các
tháng với Tháng 1 năm 1980 như tháng thứ 1. Khi đó, T0 là tập {1, 2, . . . , 142}. Ta
thấy từ biểu đồ rằng lượng hàng bán được có mẫu theo xu hướng tăng và tính mùa
vụ đạt đỉnh vào tháng 7 và xuống thấp vào tháng 1. Để vẽ mô tả được dữ liệu sử
dụng ITSM, ta chạy chương trình bằng cách kích đúp vào biểu tượng ITSM rồi chọn
File>Project>Open>Univariate, nhấn OK và chọn tệp WINE.TSM. Khi đó, biểu đồ mô
tả dữ liệu sẽ xuất hiện trên màn hình. 3
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN
Hình 1-1: Lượng rượu vang đỏ Úc đã bán trong khoảng 01/1980-10/1991
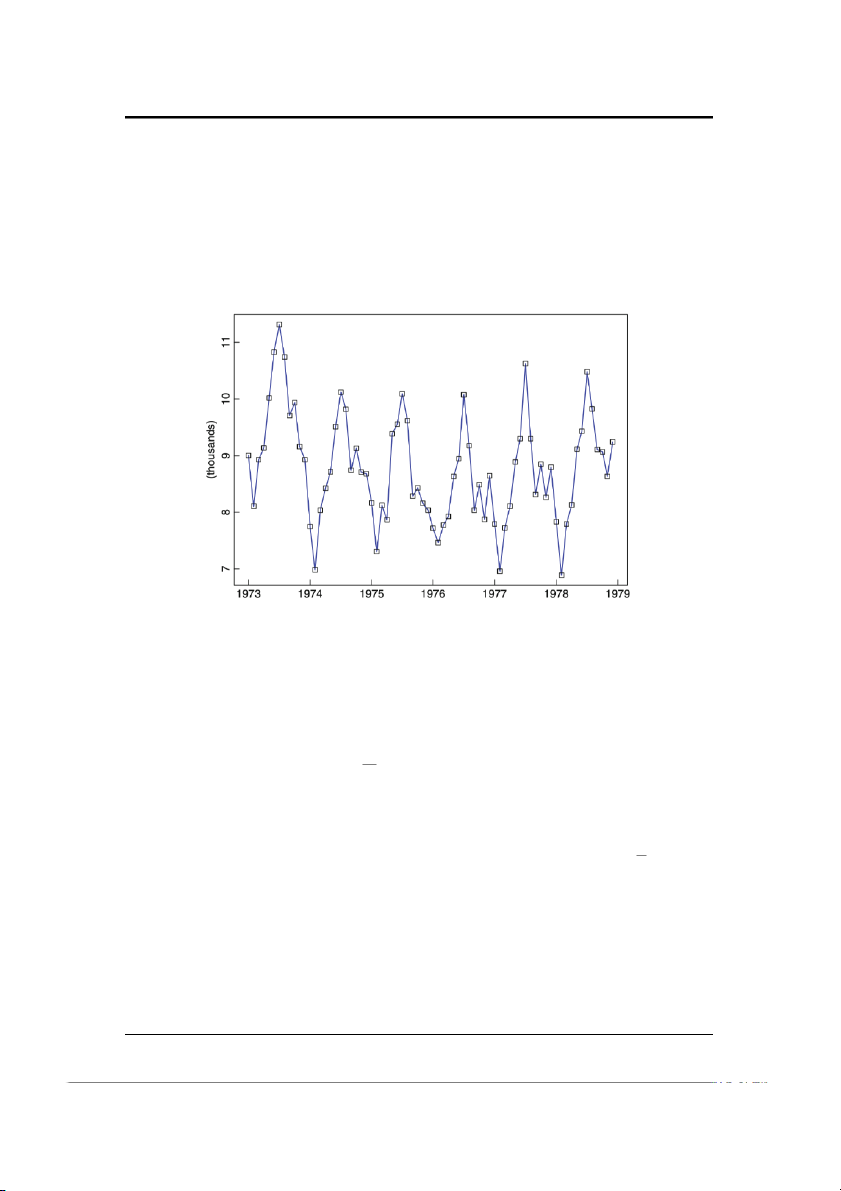
Ví dụ 1.1.2 (Trận đấu bóng chày All-Star, 1933-1995). Hình 1-2 mô tả kết quả của
các trận đấu all-star bằng cách vẽ các điểm xt, trong đó (1
nếu đội bóng thuộc Liên đoàn quốc gia thắng trong năm t, xt = −1
nếu đội bóng thuộc giải Nhà nghề Mỹ thắng trong năm t.
Đây là một chuỗi chỉ có thể nhận hai giá trị, 1 và −1. Dữ liệu cũng có một vài
giá trị bị khuyết, bởi không có trận đấu nào vào năm 1945, và chỉ có hai trận đấu
trong các năm từ 1959-1962.
Hình 1-2: Kết của các trận đấu bóng chày All-Star, 1933-1995
Bài giảng Phân tích chuỗi thời gian 4
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN
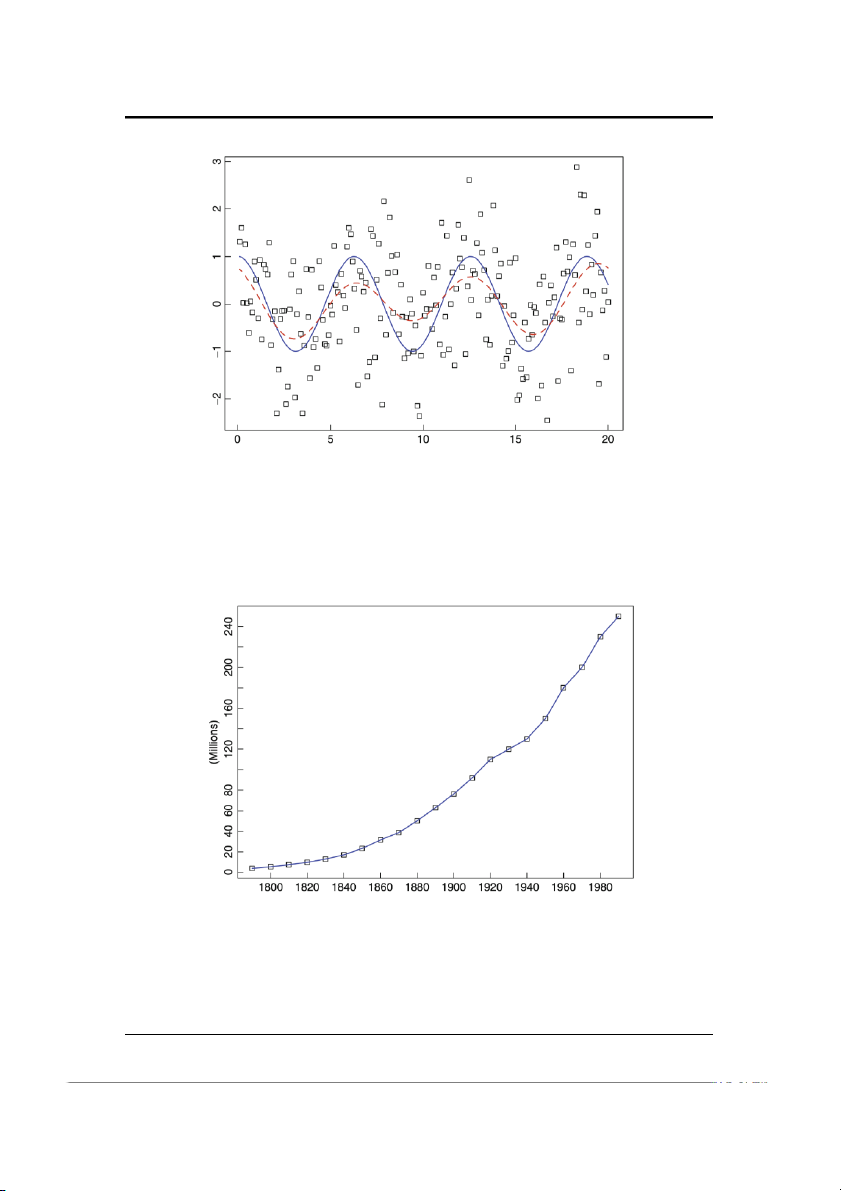
Ví dụ 1.1.3 (Tử vong do tai nạn, U.S.A., 1973-1978; DEATHS.TSM). Tương tự như
trong ví dụ về lượng rượu đã bán, biểu đồ mô tả số người tử vong do tai nạn hàng
tháng cho thấy tính mùa vụ mạnh, với số lượng cao nhất hàng năm rơi vào Tháng
7 và số lượng thấp nhất hàng năm rơi vào Tháng 2. Trong Hình 1-3, ta thấy yếu tố
xu hướng không rõ ràng như trong ví dụ về rượu. Trong Mục ??, ta sẽ xét bài toán
biểu diễn số liệu như tổng của xu hướng, thành phần mùa vụ và phần dư.
Hình 1-2: Số liệu về tử vong do tai nạn, 1973-1978
Ví dụ 1.1.4 (Vấn đề dò tín hiệu; SIGNAL.TSM). Hình 1-4 cho biết các giá trị mô phỏng của chuỗi t Xt = cos + N , . . . , , 10 t, t = 1, 2 200
trong đó {Nt} là một dãy các biến ngẫu nhiên độc lập có cùng phân phối chuẩn,
với kỳ vọng bằng 0 và phương sai bằng 0.25. Một chuỗi như vậy thường được hiểu
như tín hiệu cùng với nhiễu, trong đó tín hiệu là hàm trơn S t = cos t ở trong 10
trường hợp này. Trong trường hợp ta chỉ được cho dữ liệu về Xt, làm thể nào ta có
thể xác định thành phần tín hiệu chưa biết? Có rất nhiều cách tiếp cận cho vấn đề
này, tương ứng với các giả thiết khác nhau cho tín hiệu và nhiễu. Một cách tiếp cận
đơn giản là làm trơn dữ liệu bằng cách viết Xt thành tổng sóng sin của các chuỗi
khác (xem Mục ??) và loại bỏ các thành phần có tần số lớn. Nếu ta làm điều này với
các giá trị {Xt} trong Hình 1-4 và chỉ giữ lại 3.5% thấp nhất của các tần số, ta thu
được ước lượng cho tín hiệu, được mô tả bằng đường nét đứt màu đỏ trong Hình
1-4. Hình dáng sóng của tín hiệu là khá gần với hình dáng của tín hiệu thật trong
trường hợp này, mặc dù biên độ là nhỏ hơn. 5
Bài giảng Phân tích chuỗi thời gian
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN
Hình 1-4: Chuỗi {Xt} của Ví dụ 1.1.4
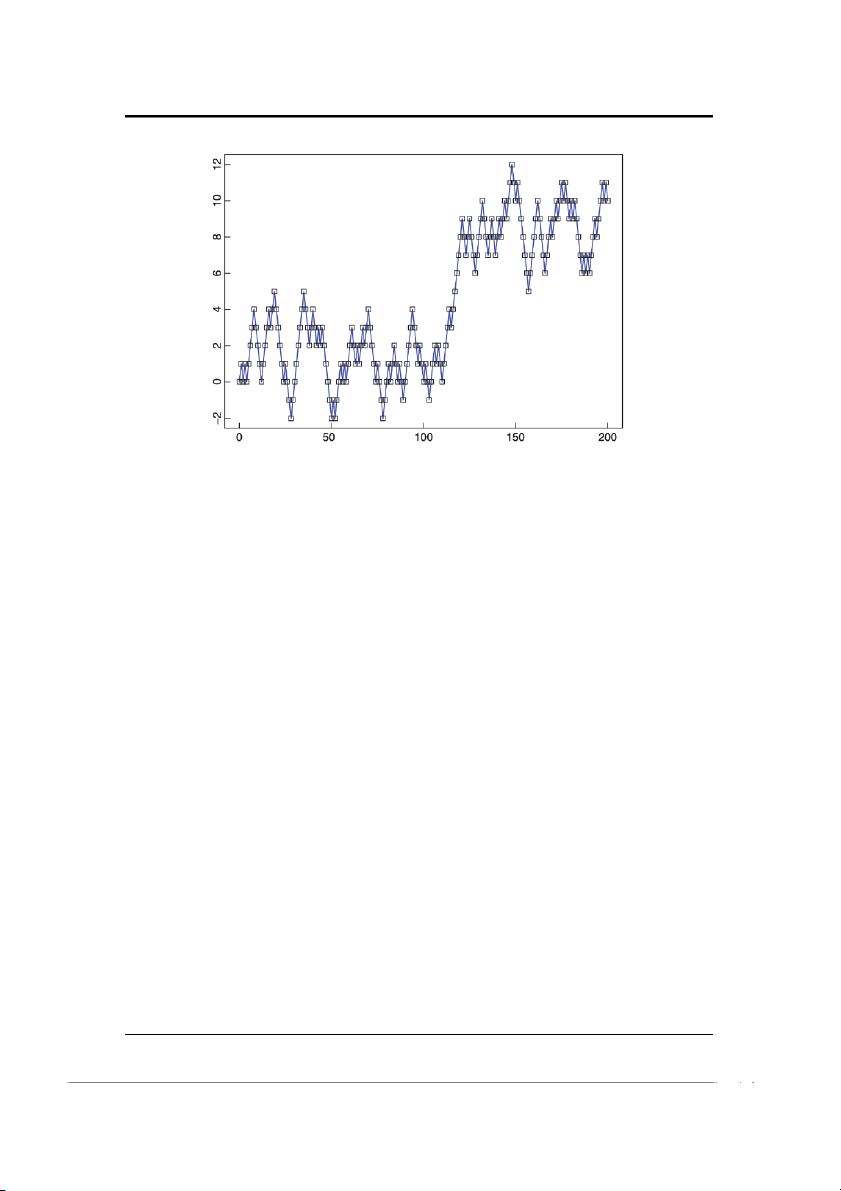
Ví dụ 1.1.5 (Dân số nước Mỹ, 1790-1990; USPOP.TSM). Dân số của nước Mỹ, được
đo trong các khoảng thời gian 10 năm, được mô tả trong Hình 1-5. Biểu đồ gợi ý
khả năng khớp xu hướng bậc hai hoặc xu hướng mũ cho dữ liệu. Chúng ta sẽ tìm
hiểu điều này kỹ hơn ở Mục 1.3
Hình 1-5: Dân số của nước Mỹ trong 10 năm, giai đoạn 1790-1990
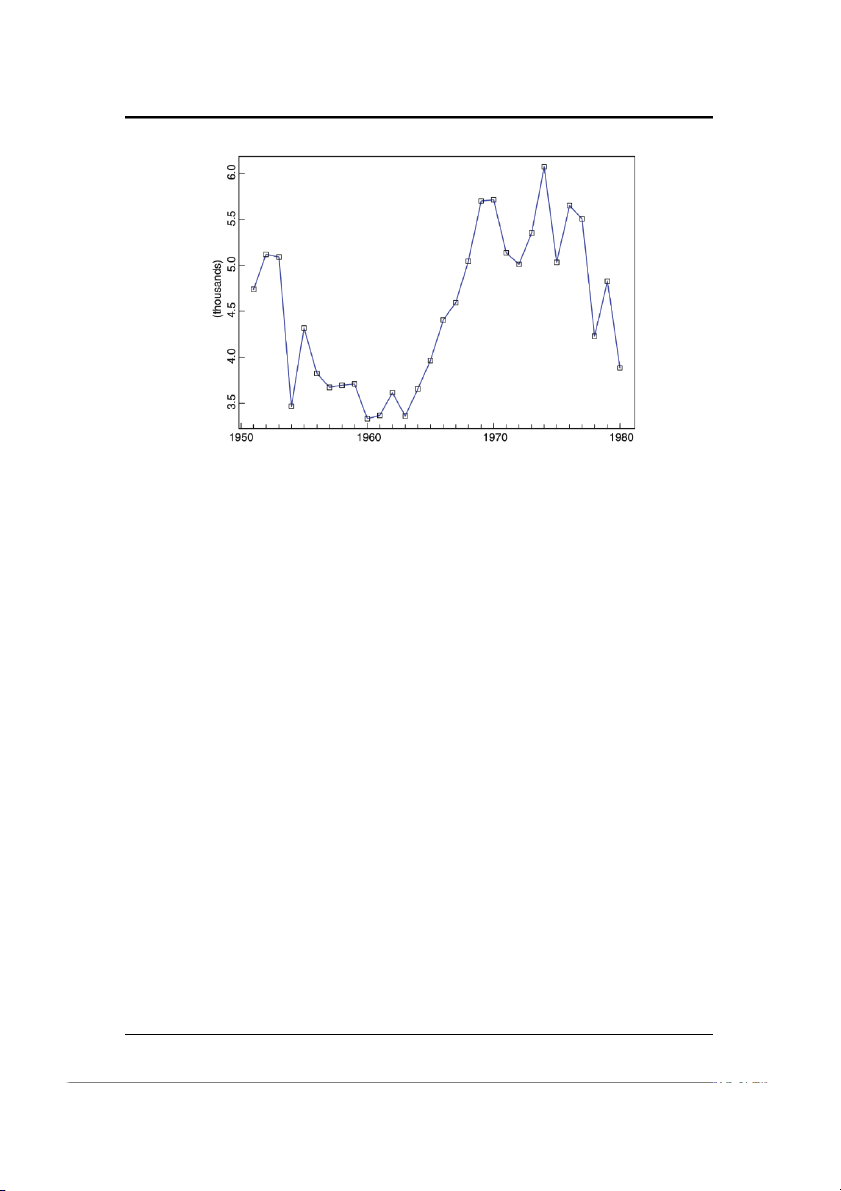
Ví dụ 1.1.6 (Số các cuộc đình công tại nước Mỹ, 1951-1980; STRIKES.TSM). Số
lượng các cuộc đình công hàng năm ở Hoa Kỳ trong những năm 1951-1980 được
thể hiện trong Hình 1-6. Chúng dường như dao động thất thường ở một mức độ thay đổi chậm.
Bài giảng Phân tích chuỗi thời gian 6
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN
Hình 1-6: Các cuộc đình công tại nước Mỹ, 1951-1980
1.2 Mục tiêu của Phân tích Chuỗi thời gian
Các ví dụ được xem xét trong Mục 1.1 là một số ít trong vô số chuỗi thời gian gặp
phải trong các lĩnh vực kỹ thuật, khoa học, xã hội học và kinh tế. Mục đích của
chúng ta trong tài liệu này là nghiên cứu các kỹ thuật đưa ra suy luận từ những
chuỗi như vậy. Tuy nhiên, trước khi có thể làm điều này, ta cần phải thiết lập một
mô hình xác suất giả định để biểu diễn dữ liệu. Sau khi chọn được họ mô hình phù
hợp, chúng ta có thể ước tính các tham số, kiểm tra mức độ phù hợp của dữ liệu
và có thể sử dụng mô hình phù hợp để hiểu hơn về cơ chế tạo ra chuỗi.
Mô hình này có thể được sử dụng để cung cấp một mô tả ngắn gọn về dữ liệu.
Ví dụ, chúng ta có thể biểu diễn dữ liệu về số ca tử vong do tai nạn trong Ví dụ
1.1.3 dưới dạng tổng của một xu hướng cụ thể, các thành phần mùa vụ và các yếu
tố ngẫu nhiên. Để giải thích các số liệu thống kê kinh tế như số liệu thất nghiệp,
điều quan trọng là phải nhận ra sự hiện diện của các thành phần mùa vụ và loại
bỏ chúng để không nhầm lẫn chúng với các xu hướng dài hạn. Quá trình này được
gọi là điều chỉnh tính mùa vụ. Các ứng dụng khác của mô hình chuỗi thời gian bao
gồm tách (hoặc lọc) nhiễu khỏi tín hiệu như trong Ví dụ 1.1.4, dự đoán giá trị tương
lai của chuỗi chẳng hạn như doanh số bán rượu vang đỏ trong Ví dụ 1.1.1 hoặc
dữ liệu dân số trong Ví dụ 1.1.5, kiểm tra các giả thuyết như sự nóng lên toàn cầu
bằng cách sử dụng dữ liệu nhiệt độ được ghi lại, dự đoán một chuỗi từ quan sát của
một chuỗi khác, ví dụ: dự đoán doanh số bán hàng trong tương lai bằng cách sử
dụng dữ liệu chi tiêu quảng cáo và kiểm soát giá trị tương lai của chuỗi bằng cách
điều chỉnh các tham số. Mô hình chuỗi thời gian cũng hữu ích trong nghiên cứu mô
phỏng. Ví dụ, hiệu suất của một hồ chứa phụ thuộc rất nhiều vào lượng nước đầu
vào ngẫu nhiên hàng ngày của hệ thống. Nếu chúng được mô hình hóa dưới dạng
chuỗi thời gian thì chúng ta có thể sử dụng mô hình phù hợp để mô phỏng một số
lượng lớn các chuỗi đầu vào hàng ngày độc lập. Biết được quy mô và phương thức
hoạt động của hồ chứa, chúng ta có thể xác định được tỷ lệ đầu vào mô phỏng gây
ra cạn nước hồ chứa trong một khoảng thời gian nhất định. Tỷ lệ này sau đó sẽ là 7
Bài giảng Phân tích chuỗi thời gian
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN
ước tính về xác suất cạn kiệt của hồ chứa tại một thời điểm nào đó trong khoảng thời gian nhất định.
1.3 Một vài mô hình Chuỗi thời gian đơn giản
Một phần quan trọng của việc phân tích chuỗi thời gian là việc lựa chọn mô hình
xác suất (hoặc lớp mô hình) phù hợp cho dữ liệu. Để có thể xem xét đến tính chất
không dự đoán được của các quan sát trong tương lai, điều tự nhiên là giả sử rằng
mỗi quan sát xt là giá trị thực tế của một biến ngẫu nhiên Xt nào đó.
Định nghĩa 1.3.1. Mô hình chuỗi thời gian cho dữ liệu được quan sát {xt} là
đặc tả của các phân phối đồng thời (hoặc có thể chỉ là kỳ vọng và hiệp phương
sai) của một dãy các biến ngẫu nhiên {Xt} trong đó {xt} được mặc định các giá trị quan sát được.
Chú ý 1.3.2. Chúng ta sẽ thường xuyên sử dụng thuật ngữ chuỗi thời gian để chỉ
cả dữ liệu và quá trình chúng là các giá trị quan sát được.
Một mô hình chuỗi thời gian xác suất hoàn chỉnh cho dãy các biến ngẫu nhiên
{X1, X2, . . .} sẽ chỉ ra tất cả các phân phối đồng thời của các vectơ ngẫu nhiên (X 0
1, . . . , Xn) , n = 1, 2, . . . hoặc tương đương là tất cả các xác suất có dạng
P [X1 ≤ x1, . . . , Xn ≤ xn] ,
−∞ < x1, . . . , xn < ∞, n = 1, 2, . . . .
Sự chỉ rõ ra như vậy hiếm khi được sử dụng trong phân tích chuỗi thời gian (trừ
khi dữ liệu được tạo ra bởi một số cơ chế đơn giản đã được hiểu rõ), vì nói chung
nó sẽ chứa quá nhiều tham số để có thể ước tính từ dữ liệu có sẵn. Thay vào đó, ta
sẽ chỉ xác định các moment bậc nhất và bậc hai của phân phối đồng thời, nói cách
khác, các giá trị kỳ vọng EXt và các kỳ vọng tích E (Xt+hXt) , t = 1, 2, . . . , h = 0, 1, 2, . . .,
những cái mà tập trung vào các tính chất của dãy {Xt} mà chỉ phụ thuộc vào chúng.
Những tính chất như vậy của {Xt} được gọi là các tính chất bậc hai. Trong trường
hợp cụ thể khi tất cả các phân phối đồng thời là chuẩn nhiều chiều, các tính chất
bậc hai của {Xt} xác định hoàn toàn các phân phối đồng thời và do đó đưa ra các
tính chất xác suất đầy đủ của chuỗi. Nói chung, chúng ta sẽ mất đi một lượng thông
tin nhất định khi nhìn vào chuỗi thời gian qua “lăng kính bậc hai”; tuy nhiên, như
chúng ta sẽ thấy trong Chương 2, lý thuyết dự đoán tuyến tính sai số bình phương
nhỏ nhất chỉ phụ thuộc vào các tính chất bậc hai, do đó cung cấp thêm bằng chứng
cho việc sử dụng các tính chất bậc hai của các mô hình chuỗi thời gian.
Hình 1-7 cho thấy một giá trị có thể quan sát được của {St, t = 1, . . . , 200}, trong
đó {St} là dãy các biến ngẫu nhiên được chỉ ra trong Ví dụ 1.3.5 dưới đây. Trong
hầu hết các bài toán thực tế liên quan đến chuỗi thời gian, chúng ta chỉ có một tập
các giá trị quan sát được duy nhất. Ví dụ, chỉ có một quan sát duy nhất về lượng
mưa hàng năm ở Fort Collins trong những năm 1900-1996, nhưng ta hình dung
rằng đó là một trong nhiều chuỗi đã có thể xảy ra. Trong các ví dụ sau đây, ta sẽ
được giới thiệu một số mô hình chuỗi thời gian đơn giản. Một trong những mục tiêu
của ta là mở rộng danh mục này để có thể sử dụng một loạt các mô hình nhằm cố
gắng khớp với các quan sát của một tập dữ liệu cho trước nào đó.
Bài giảng Phân tích chuỗi thời gian 8
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN
1.3.1 Một vài mô hình có trung bình mẫu bằng 0
Ví dụ 1.3.3 (Nhiễu độc lập cùng phân phối). Có lẽ mô hình đơn giản nhất cho chuỗi
thời gian là mô hình trong đó không có thành phần xu hướng hoặc mùa vụ và trong
đó các quan sát là các biến ngẫu nhiên độc lập và có cùng phân phối (iid) với giá trị
trung bình bằng 0. Ta gọi các biến ngẫu nhiên như vậy X1, X2, . . . là nhiễu độc lập
cùng phân phối. Theo định nghĩa, ta có thể viết, với mọi số nguyên dương n và các số thực x1, . . . , xn,
P [X1 ≤ x1, . . . , Xn ≤ xn] = P [X1 ≤ x1] · · · P [Xn ≤ xn] = F (x1) · · · F (xn) ,
trong đó F (·) là hàm phân phối tích lũy (xem Mục A.1) của từng biến ngẫu nhiên
được cùng phân phối X1, X2, . . . Trong mô hình này, không có sự phụ thuộc giữa các
quan sát. Cụ thể, với mọi h ≥ 1 và mọi x, x1, . . . , xn,
P [Xn+h ≤ x | X1 = x1, . . . , Xn = xn] = P [Xn+h ≤ x] ,
cho thấy rằng thông tin về X1, . . . , Xn không có giá trị để dự đoán về Xn+h. Cho
các giá trị của X1, . . . , Xn, hàm f làm tối thiểu hóa sai số bình phương trung bình
E (Xn+h − f (X1, . . . , Xn))2 trên thực tế là hàm đồng nhất 0 (xem Bài tập 1.2). Mặc
dù điều này có nghĩa là nhiễu độc lập cùng phân phối là một quá trình khá nhàm
chán đối với người dự báo, nhưng nó đóng một vai trò quan trọng như một nền
móng cho các mô hình chuỗi thời gian phức tạp hơn.
Ví dụ 1.3.4 (Chuỗi nhị phân). Ta xét một ví dụ về nhiễu độc lập cùng phân phối,
cho dãy các biến ngẫu nhiên độc lập cùng phân phối {Xt, t = 1, 2, . . .,} với P [Xt = 1] = p, P [Xt = −1] = 1 − p,
trong đó p = 1. Chuỗi thời gian thu được bằng cách tung đồng xu liên tục và ghi 2
+1 cho mỗi mặt ngửa và -1 cho mỗi mặt sấp thường được mô hình hóa như một
quan sát của quá trình này. Một cách tiên nghiệm, ta có thể xét một mô hình cho
các trận đấu bóng chày all-star trong Ví dụ 1.1.2. Tuy nhiên, ngay cả khi xem xét
sơ qua kết quả từ năm 1963-1982, cho thấy Liên đoàn Quốc gia thắng 19 trên 20
trận, đã gây nên một nghi ngờ về giả thuyết P [Xt = 1] = 1. 2
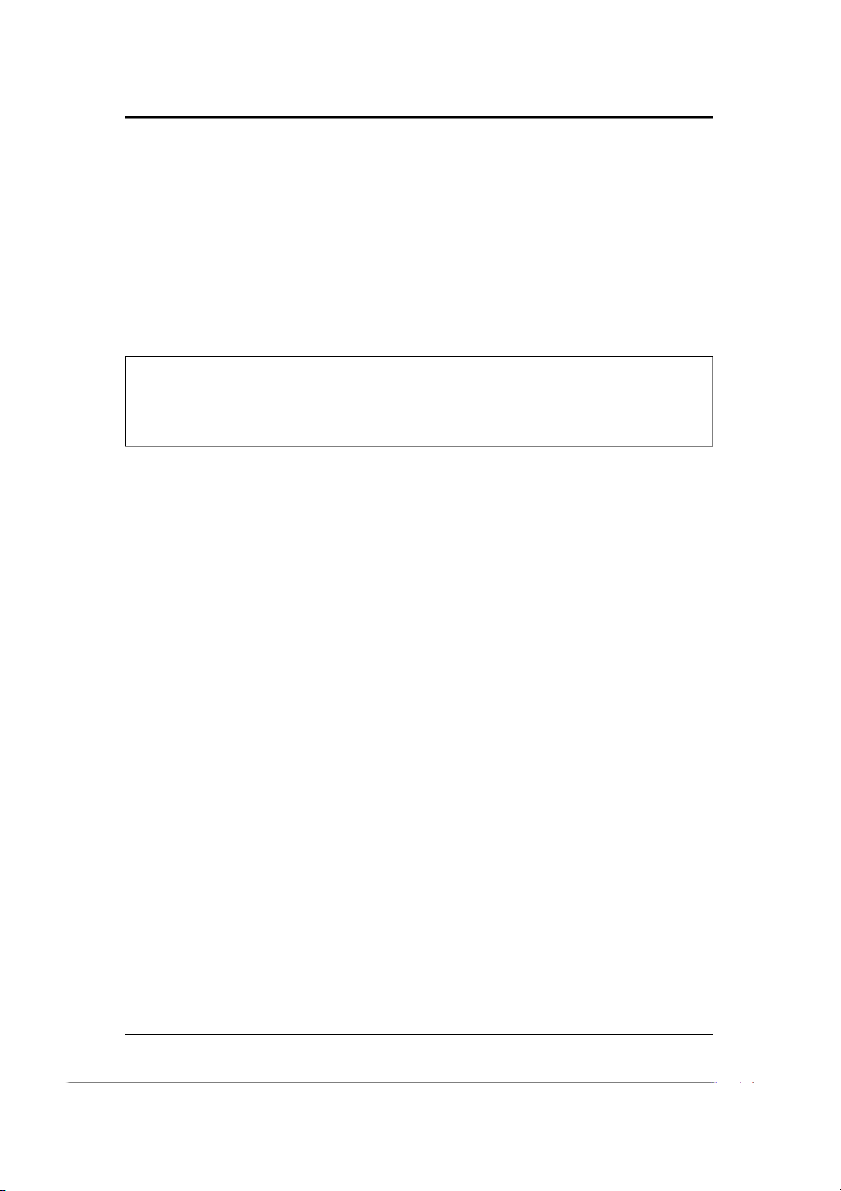
Ví dụ 1.3.5 (Du động ngẫu nhiên). Du động ngẫu nhiên {St, t = 0, 1, 2, . . .} (bắt đầu
từ 0) thu được bằng cách tính tổng tích lũy (hoặc "lấy tích phân") các biến ngẫu
nhiên độc lập cùng phân phối. Do đó, Du động ngẫu nhiên có giá trị trung bình
bằng 0 thu được bằng cách đặt S0 = 0 và St = X1 + X2 + · · · + Xt, với t = 1, 2, . . . ,
trong đó {Xt} là nhiễu độc lập cùng phân phối. Nếu {Xt} là một quá trình nhị trong
Ví dụ 1.3.4, thì {St, t = 0, 1, 2, . . .,} được gọi là một Du động ngẫu nhiên đối xứng đơn
giản. Bước đi này có thể được xem là vị trí của một người đi bộ bắt đầu ở vị trí 0
tại thời điểm 0 và tại mỗi thời điểm nguyên, người đó tung một đồng xu công bằng,
bước một đơn vị sang phải mỗi khi xuất hiện mặt ngửa và một đơn vị sang trái cho
mỗi mặt sấp. Một quan sát có kích thước 200 của một Du động ngẫu nhiên đối
xứng đơn giản được mô tả trong Hình 1-7. Lưu ý rằng kết quả của việc tung đồng
xu có thể được phục hồi từ {St, t = 0, 1, . . .} bằng cách lấy sai phân. Do đó, kết quả
của lần tung t có thể được xác định từ St − St . −1 = Xt 9
Bài giảng Phân tích chuỗi thời gian
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN
Hình 1-7: Một quan sát về du động ngẫu nhiên đơn giản {St, t = 0, 1, 2, ..., 200}
1.3.2 Các mô hình với Tính xu hướng và Tính mùa vụ
Trong một số ví dụ về chuỗi thời gian ở Mục 1.1, dữ liệu có xu hướng rõ ràng. Xu
hướng ngày càng tăng rõ ràng ở cả doanh số bán rượu vang đỏ của Úc (Hình 1-1)
và dân số của nước Mỹ (Hình 1-5). Trong cả hai trường hợp, mô hình có trung bình
bằng 0 cho dữ liệu là không phù hợp. Biểu đồ dữ liệu dân số, không chứa thành
phần tuần hoàn rõ ràng, gợi ý rằng ta nên thử một mô hình có dạng Xt = mt + Yt,
trong đó mt là một hàm thay đổi chậm được gọi là thành phần xu hướng và Yt có giá
trị trung bình bằng 0. Một kỹ thuật hữu ích để ước tính mt là phương pháp bình
phương nhỏ nhất (một số phương pháp khác sẽ được đề cập đến trong trong Mục ??).
Trong phương pháp bình phương tối thiểu, chúng ta cố gắng khớp một họ hàm tham số, ví dụ, m 2 t = a0 + a1t + a2t , (1.1)
cho dữ liệu {x1, . . . , xn} bằng cách chọn các tham số, trong hình minh họa này a0, a1
và a2, để làm tối thiểu hóa Pn (x t=1
t − mt)2. Phương pháp khớp đường cong này được
gọi là hồi quy bình phương nhỏ nhất và có thể được thực hiện bằng chương trình
ITSM và chọn Regression option.
Ví dụ 1.3.6 (dân số nước Mỹ, 1790-1990). Để khớp một hàm có dạng (1.3.1) với
dữ liệu dân số được hiển thị trong Hình 1-5, chúng ta đặt lại nhãn cho trục thời
gian sao cho t = 1 tương ứng với năm 1790 và t = 21 tương ứng với năm 1990.
Chạy phần mềm ITSM, chọn File>Project>Open>Univariate, và mở tệp USPOP.TSM.
Sau đó, chọn Regression>Specify, chọn Polynomial Regression với bậc bằng 2, nhấn
chọn OK. Cuối cùng, chọn tùy chọn Regression>Estimation>Least Squares, sẽ cho
ta ước lượng tham số như sau cho mô hình (1.3.1):
Bài giảng Phân tích chuỗi thời gian 10
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN ˆa0 = 6.9579 × 106, ˆa 6 1 = −2.1599 × 10 , và ˆa2 = 6.5063 × 105
Hình 1-8: Dân số nước Mỹ cho thấy xu hướng bậc 2 được khớp bởi phương pháp
bình phương tối thiểu
Biểu đồ của hàm ước lượng được hiển thị với dữ liệu gốc trong Hình 1-8. Các giá
trị ước tính của quá trình nhiễu Yt, 1 ≤ t ≤ 21, là phần dư thu được bằng cách trừ ˆ
mt = ˆa0 + ˆa1t + ˆa2t2 từ xt.
Thành phần xu hướng ước lượng ˆ
m >< /t cung cấp cho chúng ta một yếu tố dự
báo tự nhiên về các giá trị tương lai của Xt. Ví dụ, nếu chúng ta ước lượng nhiễu
Y22 bằng giá trị trung bình của nó, tức là bằng 0, thì (1.1) sẽ đưa ra dân số Hoa Kỳ ước tính cho năm 2000 là ˆ m 6 5 2
22 = 6.9579 × 10 − 2.1599 × 106 × 22 + 6.5063 × 10 × 22 = 274.35 × 106.
Tuy nhiên, nếu các phần dư {Yt} có sự tương quan lớn, chúng ta có thể sử dụng
các giá trị của chúng để đưa ra ước lượng tốt hơn về Y22 và cho dân số X22 vào năm 2000.
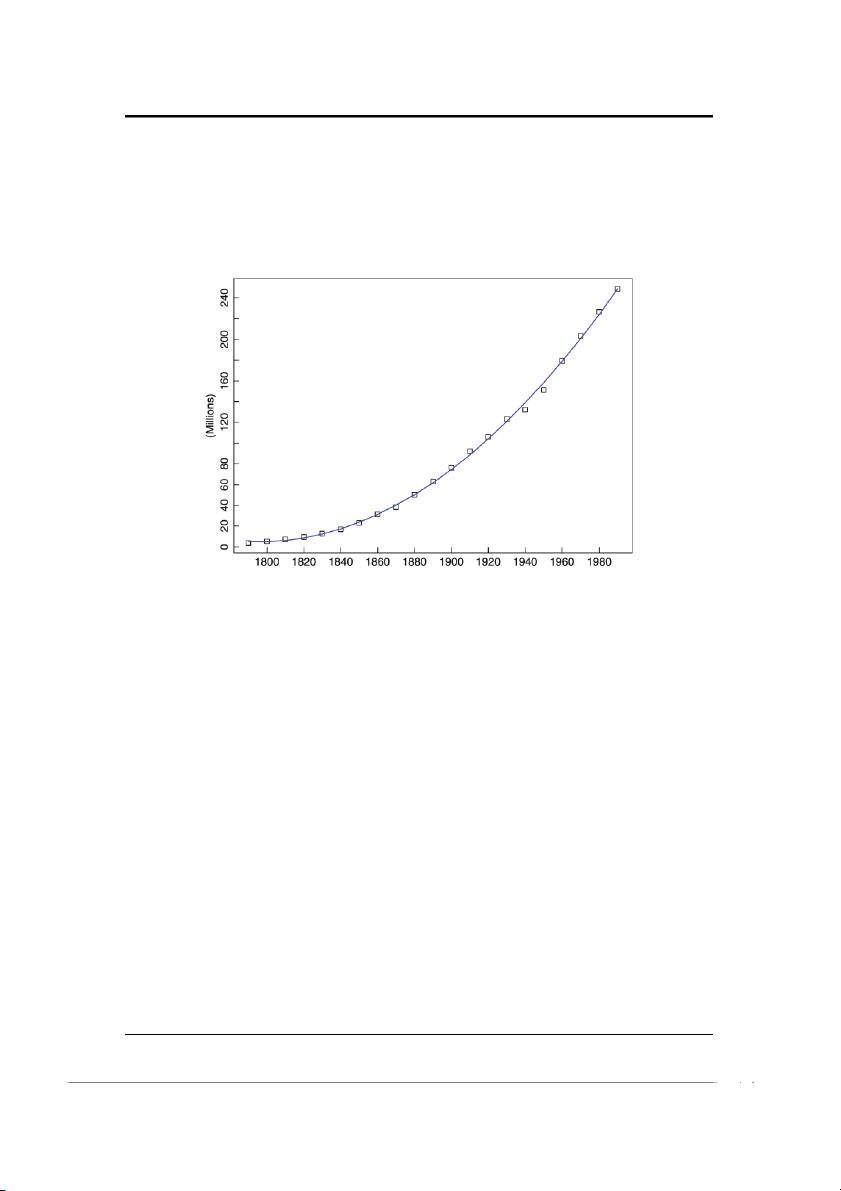
Ví dụ 1.3.7 (Độ cao mực nước của Hồ Huron 1875-1972; LAKE.DAT). Biểu đồ mực
nước tính bằng feet của Hồ Huron (giảm 570) trong những năm 1875-1972 được
hiển thị trong Hình 1-9. Do mực nước hồ dường như giảm với tốc độ gần như tuyến
tính, ITSM đã được sử dụng để khớp với mô hình có dạng Xt = a0 + a1t + Yt, t = 1, . . . , 98 (1.2)
(với trục thời gian được đặt lại như trong Ví dụ 1.3.6). Ước lượng bình phương tối
thiểu của các giá trị tham số là ˆa0 = 10.202 and ˆa1 = −0.0242. 11
Bài giảng Phân tích chuỗi thời gian
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN
Hình 1-9: Mực nước hồ Huron cho thấy tính tuyến tính phù hợp với phương pháp
bình phương tối thiểu
(Đường bình phương nhỏ nhất thu được, ˆa0 + ˆa1t, cũng được hiển thị trong Hình
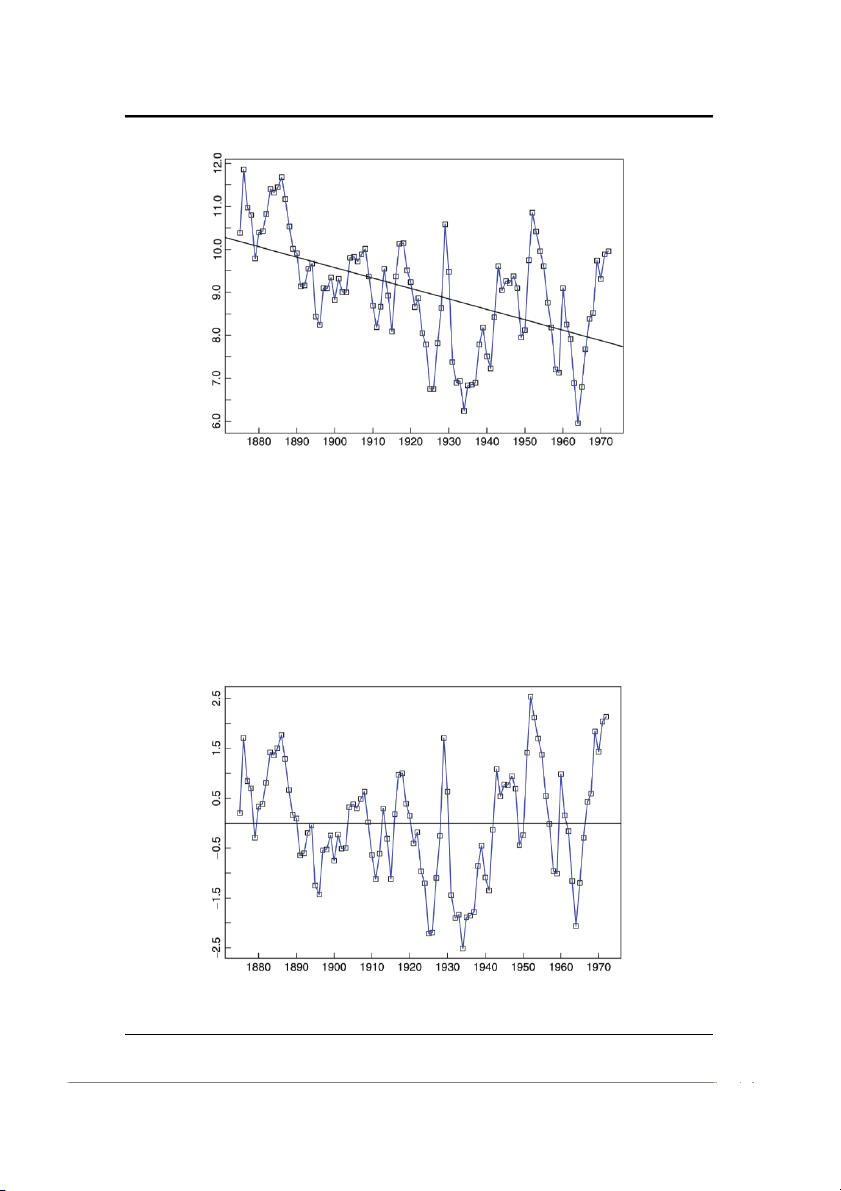
1-9). Các ước tính cho nhiễu, Yt, trong mô hình (1.2) là phần dư thu được bằng
cách trừ đi đường bình phương nhỏ nhất khỏi xt và được vẽ trong Hình 1-10. Có
hai đặc điểm thú vị của đồ thị phần dư. Đầu tiên là không có bất kỳ xu hướng rõ
ràng nào. Thứ hai là độ mịn của đồ thị. (Đặc biệt, có những đoạn phần dư dài có
cùng dấu. Điều này sẽ rất khó xảy ra nếu phần dư là những quan sát về nhiễu độc
lập cùng phân phối có giá trị trung bình bằng 0). Độ trơn của đồ thị chuỗi thời gian
nói chung biểu thị sự tồn tại của một dạng phụ thuộc nào đó giữa các quan sát.
Hình 1-10: Phần dư từ việc lắp đường thẳng vào dữ liệu của hồ Huron trong Hình 1-9
Bài giảng Phân tích chuỗi thời gian 12
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN
Sự phụ thuộc như vậy có thể được sử dụng để tạo thuận lợi cho việc dự báo giá trị
tương lai của chuỗi. Nếu chúng ta giả sử tính hợp lệ của mô hình được trang bị với
số dư độc lập cùng phân phối {Yt}, thì dự đoán sai số bình phương trung bình nhỏ
nhất của số dư (Y99) tiếp theo sẽ bằng 0 (theo Bài tập 1.2). Tuy nhiên, Hình 1-10
gợi ý rõ ràng rằng Y99 sẽ dương.
Vậy thì làm cách nào để chúng ta định lượng sự phụ thuộc và làm cách nào để
xây dựng các mô hình dự báo kết hợp sự phụ thuộc trong trường hợp cụ thể? Để
giải quyết những câu hỏi này, Mục 1.4 giới thiệu hàm tự tương quan như một thước
đo sự phụ thuộc và các quá trình dừng như một nhóm các mô hình hữu ích thể
hiện nhiều cấu trúc phụ thuộc khác nhau. Hồi quy Điều hòa
Nhiều chuỗi thời gian bị ảnh hưởng bởi các yếu tố mùa vụ như thời tiết, ảnh hưởng
của chúng có thể được mô hình hóa bằng một thành phần tuần hoàn với khoảng
thời gian cố định đã biết. Ví dụ, chuỗi số ca tử vong do tai nạn (Hình 1-3) cho thấy
mô hình lặp lại hàng năm với đỉnh điểm vào tháng 7 và chạm đáy vào tháng 2, gợi
ý rõ ràng về yếu tố mùa vụ theo chu kỳ 12 tháng. Để thể hiện yếu tố mùa vụ như
vậy, có tính đến nhiễu nhưng giả sử rằng sẽ không có xu hướng, chúng ta có thể
sử dụng mô hình đơn giản, Xt = st + Yt,
trong đó st là một hàm tuần hoàn theo t với chu kỳ d (st−d = st). Một lựa chọn hợp lý
cho st là tổng các sóng điều hòa (hoặc sóng hình sin) được cho bởi k X st = a0 +
(aj cos (λjt) + bj sin (λjt)) , (1.3) j=1
trong đó a0, a1, . . . , ak và b1, . . . , bk là các tham số chưa biết và λ1, . . . , λk là các tần số cố
định, mỗi số là bội số nguyên của 2π/d. Để thực hiện hồi quy điều hòa bằng ITSM,
chọn Regression>Specify, tích vào hai ô vuông, Include intercept term và Harmonic
Regression. Sau đó xác định số điều hòa [k trong phương trình (1.3)] và nhập k
chỉ số Fourier có giá trị nguyên f1, . . . , fk. Đối với sóng hình sin có chu kỳ d, ta đặt
f1 = n/d, trong đó n là số lượng quan sát trong chuỗi thời gian. (Nếu n/d không phải
là số nguyên, ta sẽ xóa một vài quan sát từ đầu chuỗi để biến nó thành số nguyên).
Tiếp theo, k − 1 chỉ số Fourier khác phải là bội số nguyên dương của chỉ số đầu
tiên, tương ứng với tính điều hòa của sóng hình sin cơ bản với chu kỳ d. Do đó,
để khớp một sóng hình sin với chu kỳ 365 với 365 quan sát hàng ngày, ta sẽ chọn
k = 1 và f1 = 1. Để khớp một tổ hợp tuyến tính của các sóng hình sin với các chu
kỳ 365/j, j = 1, . . . , 4, ta sẽ chọn k = 4 và fj = j, j = 1, . . . , 4. Một khi k và các tần
số f1, . . . , fk đã được xác định, nhấn chọn OK và chọn Regression>Estimation>Least
Squares để thu được các hệ số cần tính. Để xem hàm ước lượng phù hợp với dữ
liệu như thế nào, chọn Regression>Show fit.
Ví dụ 1.3.8 (Tử vong do tai nạn). Để khớp tổng của hai sóng điều hòa có chu
kỳ 12 tháng và 6 tháng với dữ liệu tử vong do tai nạn hàng tháng x1, . . . , xn với
n = 72, ta chọn k = 2, f1 = n/12 = 6 và f2 = n/6 = 12. Sử dụng ITSM như mô tả
ở trên, chúng ta thu được hàm ước lượng như trong Hình 1-11. Như có thể thấy
từ hình, tính tuần hoàn của chuỗi được mô tả khá tốt bởi hàm ước lượng này.
Trong thực tế, cần thử nghiệm một số cách kết hợp các sóng điều hòa khác nhau 13
Bài giảng Phân tích chuỗi thời gian
BM Toán Ứng dụng - Khoa Toán Tin - ĐHSPHN
để tìm ra ước lượng hợp lý cho thành phần mùa vụ. Chương trình ITSM cũng cho
phép ước lượng một tổ hợp tuyến tính của xu hướng điều hòa và xu hướng đa
thứcbằng cách chọn cả Harmonic Regression và Polynomial Regression trong phần
Regression>Specificationdialog. Các phương pháp khác để giải quyết sự tính mùa
vụ của xu hướng được mô tả trong Mục ??.
Hình 1-11: Thành phần điều hòa ước lượng của dữ liệu tử vong do tai nạn từ ITSM
1.3.3 Một cách tiếp cận chung cho Mô hình Chuỗi thời gian
Các ví dụ ở phần trước minh họa một cách tiếp cận chung để phân tích chuỗi thời
gian là cơ sở cho phần lớn nội dung trong cuốn sách này. Trước khi giới thiệu các
ý tưởng về sự phụ thuộc và tính dừng, chúng tôi phác thảo cách tiếp cận này để
cung cấp cho người đọc một cái nhìn tổng quan về cách thức mà các ý tưởng khác
nhau của chương này khớp với nhau.
• Vẽ chuỗi và kiểm tra các đặc điểm chính của biểu đồ, đặc biệt kiểm tra xem có (a) xu hướng, (b) thành phần mùa vụ,
(c) bất kỳ thay đổi đột ngột nào,
(d) các quan sát ngoại lai.
• Loại bỏ các thành phần xu hướng và mùa vụ để có được phần dư ổn định (như
định nghĩa ở Mục 1.4). Để đạt được mục tiêu này đôi khi cần phải áp dụng
một phép biến đổi sơ bộ cho dữ liệu. Ví dụ, nếu độ lớn của các dao động dường
như tăng gần như tuyến tính theo cấp độ của chuỗi, thì chuỗi được chuyển
đổi {ln X1, . . . , ln Xn} sẽ có những biến động có cường độ ổn định hơn. Ví dụ,
xem Hình 1-1 và 1-17. (Nếu một số dữ liệu âm, hãy thêm hằng số dương vào
từng giá trị dữ liệu để đảm bảo rằng tất cả các giá trị đều dương trước khi
lấy logarit). Có một số cách để loại bỏ xu hướng và tính thời vụ (xem Mục ??),
một số cách liên quan đến việc ước tính các thành phần và trừ chúng khỏi dữ
liệu, và một số cách khác tùy thuộc vào việc lấy sai phân dữ liệu, tức là thay
Bài giảng Phân tích chuỗi thời gian 14