Lý thuyết Véctơ lực môn Cơ học cơ sở | Học viện kỹ thuật quân sự

Những tháp vô tuyến được giữ ổn định bởi các sợi cáp, chúng tác dụng các lực lên tháp qua
những điểm nối với tháp. Trong chương này, sẽ trình bày cách biểu diễn các lực đó bằng các véctơ đề các. 18 2 VÉCTƠ LỰC
Mục đích của chương
 Trình bày cách hợp lực và phân tích lực thành các thành phần theo quy tắc hình bình hành.
 Biểu diễn lực và vị trí đặt lực dưới dạng véc tơ Đề các, trình bầy cách xác định phương
chiều và độ lớn của véctơ lực.
 Giới thiệu tích vô hướng để xác định góc giữa hai véctơ hay là xác định hình chiếu của
véc tơ lên một véc tơ khác.
2.1 Vô hướng và véctơ
Hầu hết các đại lượng vật lý trong cơ học có thể được biểu diễn toán học bằng các vô hướng và các véctơ.
Vô hướng. Một đại lượng mô tả bởi một số âm hoặc dương được gọi là một vô hướng.
Chẳng hạn như khối lượng, thể tích, hay chiều dài là các đại lượng vô hướng thường sử dụng
trong tĩnh học. Trong cuốn sách này, các vô hướng được biểu thị bởi các chữ cái in nghiêng,
ví dụ như vô hướng A.
Véctơ. Một véctơ là một đại lượng mà có cả trị số và phương chiều. Trong tĩnh học các
đại lượng véctơ thường xuyên gặp như vị trí, lực, và mômen. Nói chung một véctơ được biểu
diễn bằng một chữ cái với một mũi tên trên đầu, ví dụ như là A . Trị số được viết là A hoặc
viết đơn giản A. Trong quyển sách này các véctơ sẽ được biểu diễn bằng các chữ cái đậm, ví
dụ A được sử dụng để ký hiệu véctơ “A”. Giá trị của nó luôn luôn là một đại lượng dương,
biểu diễn bằng chữ cái in nghiêng, được viết là |A|, hoặc đơn giản là A khi nó được hiểu là một vô hướng dương.
Một véctơ được biểu diễn hình học
bằng một mũi tên, nó được sử dụng để
định nghĩa độ lớn, phương và chiều của
một véctơ. Giá trị của véctơ là độ dài của
mũi tên, phương được xác định bởi góc
giữa một trục tham chiếu với đường tác
dụng của mũi tên, và chiều được biểu thị
bởi chiều của mũi tên. Ví dụ véctơ A (hình
2-1) có độ lớn 4 đơn vị, có phương hợp
với phương ngang theo chiều ngược chiều Hình 2-1
kim đồng hồ một góc 200, và có chiều
hướng lên về phía phải. Điểm O là gốc của
véctơ, điểm P là ngọn hay đỉnh của véctơ. 19
2.2 Phép tính véctơ
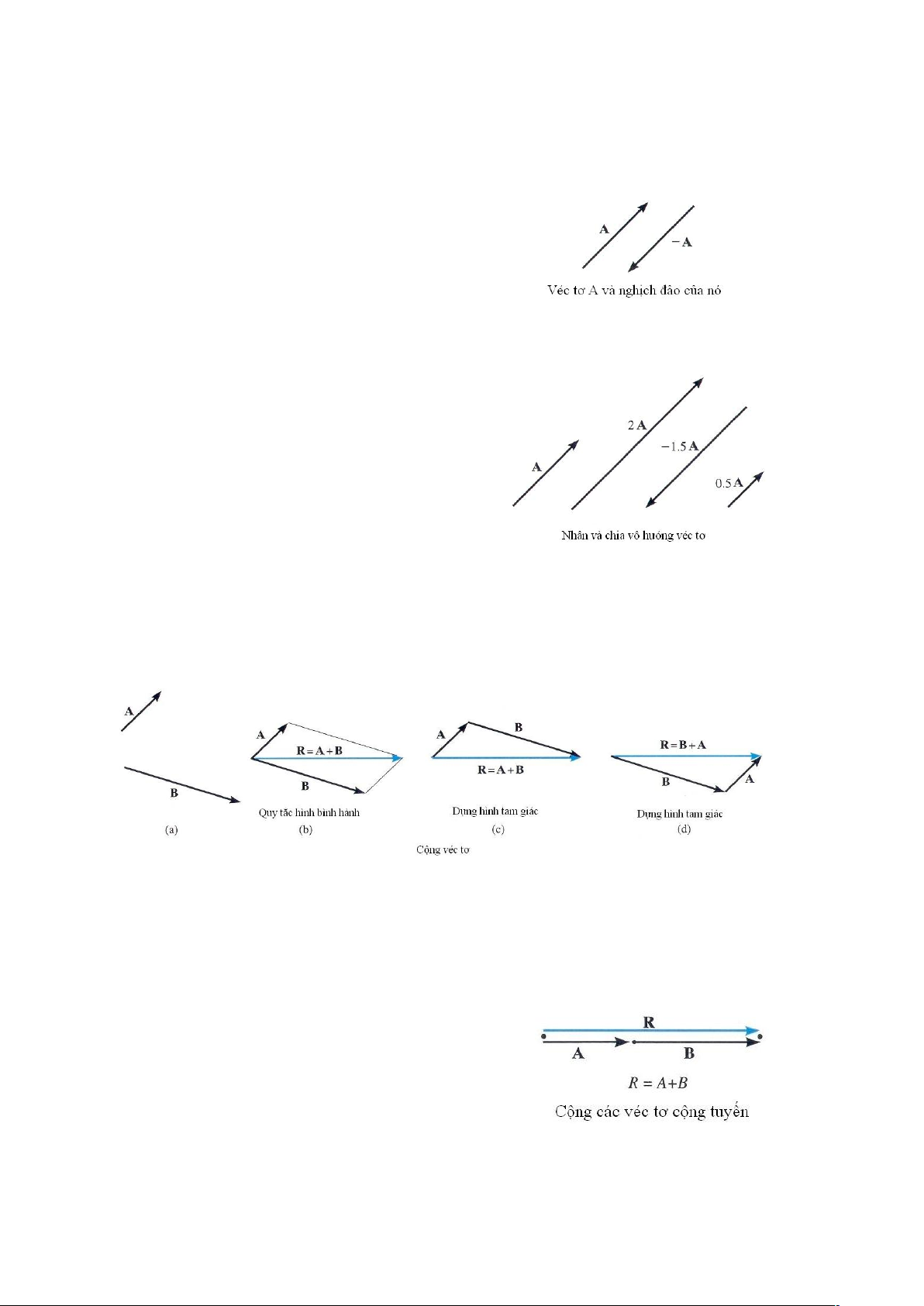
Nhân và chia một véctơ cho một vô hướng. Tích
số giữa véctơ A và vô hướng a, viết là aA, là một
véctơ có độ lớn |aA|, chiều của aA cùng chiều với A
nếu a dương, và ngược chiều với A nếu a âm. Trong
trường hợp đặc biệt, ta sẽ thu được véctơ ngược chiều
nếu nhân một véctơ với vô hướng (–1) , hình 2-2. Chia
một véctơ cho một vô hướng có thể được xác định Hình 2-2
bằng cách sử dụng quy tắc nhân, từ A/a = (1/a)A,
a ≠ 0. Các ví dụ minh hoạ của các phép tính được chỉ ra trên hình 2-3.
Phép cộng véctơ. Hai véctơ A và B chẳng hạn là
véc tơ lực hay véc tơ định vị (hình 2-4a), có thể cộng
thành một véctơ tổng R = A + B bằng cách sử dụng
quy tắc hình bình hành. Để thực hiện, đặt hai véctơ A
và B tại cùng điểm gốc của chúng (hình 2-4b). Từ đầu
mút của các véctơ vẽ các đường thẳng song song với
véctơ kia, các đường này cắt nhau tại một điểm, do đó Hình 2-3
có các cạnh còn lại của hình bình hành. Từ hình vẽ,
véctơ tổng R là đường chéo của hình bình hành, đó là đường kéo dài nối từ gốc của A và B
tới giao điểm của các đường thẳng song song. Hình 2-4
Ta cũng có thể cộng hai véctơ A và B sử dụng cách dựng hình tam giác, đây là một
trường hợp đặc biệt của quy tắc hình bình hành, nhờ đó véc tơ B được cộng với véctơ A
theo cách “nối điểm đầu với điểm cuối”, tức là nối điểm đầu của véctơ A với điểm cuối của
véctơ B, hình 2-4c. Véctơ tổng R là véctơ được nối từ
gốc của véctơ A tới ngọn của véctơ B. Bằng cách tương
tự, véctơ R có thể thu được nhờ cộng véctơ A với véctơ
B, hình 2-4d. Khi so sánh hai trường hợp trên thấy hai
kết quả giống nhau, do đó phép cộng véctơ có tính chất
giao hoán, R = A + B = B + A.
Trường hợp đặc biệt, nếu A và B là hai véctơ cộng Hình 2-5 20
tuyến (collinear), tức là cả hai véctơ có cùng đường tác dụng, quy tắc hình bình hành đưa về
phép cộng đại số hay phép cộng vô hướng R = A + B, hình 2-5.
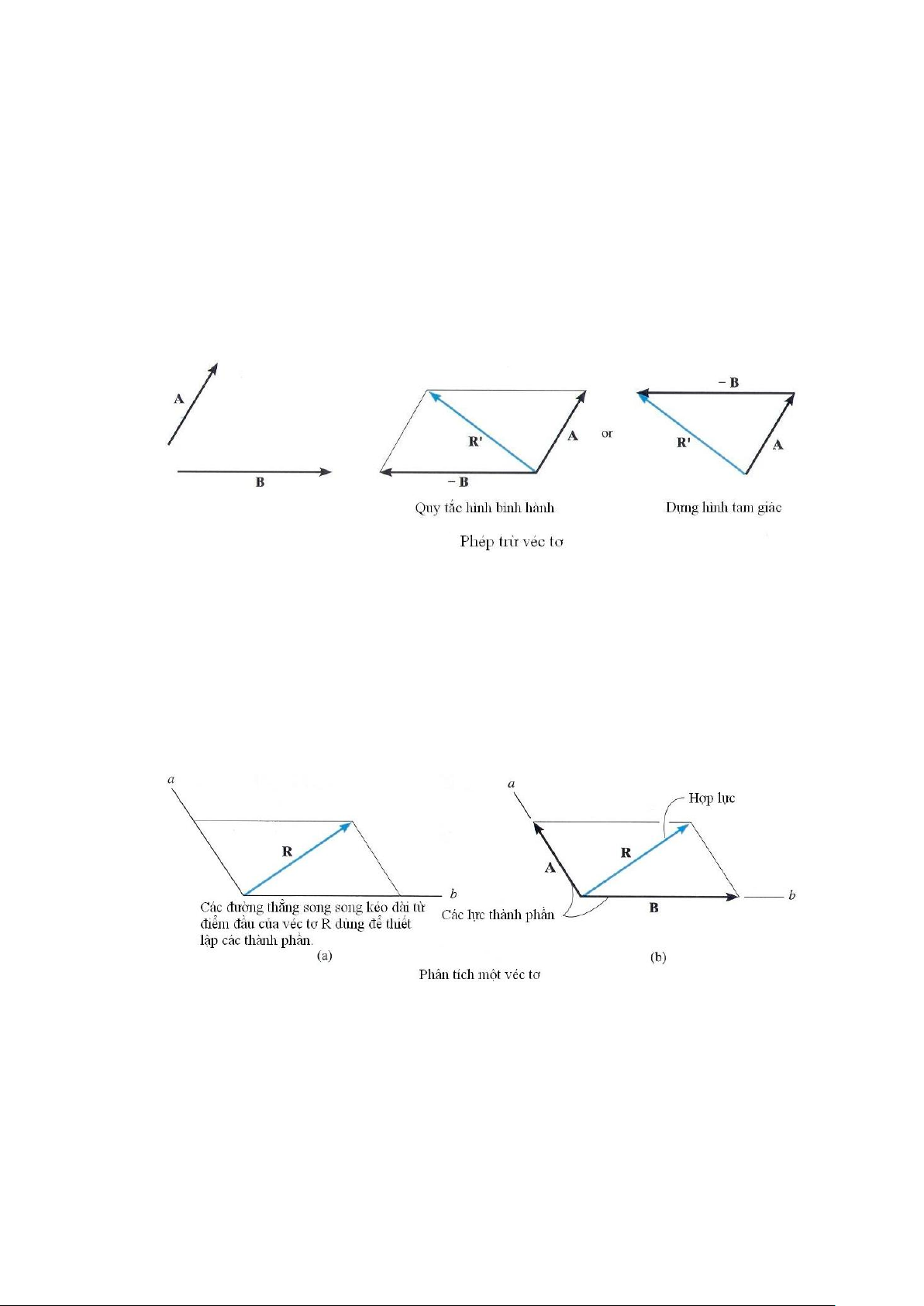
Phép trừ véctơ. Hiệu hai véctơ A và B được biểu diễn như sau:
R = A – B = A + (–B)
Véctơ tổng này được biểu diễn trên hình vẽ, hình 2-6. Cho nên phép trừ của hai véctơ
được định nghĩa như là một trường hợp đặc biệt của phép cộng véctơ, vì vậy các quy tắc của
phép cộng véctơ cũng được áp dụng cho phép trừ véctơ. Hình 2-6
Phân tích véctơ. Bằng cách sử dụng quy tắc hình bình hành ta có thể phân tích một véctơ
ra thành hai thành phần theo hai phương biết trước. Ví dụ, véctơ R (hình 2-7a) được phân tích
ra hai thành phần có đường tác dụng dọc theo các đường a và b. Đường thứ nhất bắt đầu từ
ngọn của véctơ R kẻ song song với a và kéo dài tới b. Tương tự, đường thứ 2 kẻ song song
với b bắt đầu từ ngọn của R kéo dài tới đường a (hình 2-7a). Từ đó thu được hai thành phần
véctơ của R là A và B theo hai phương a và b như hình vẽ (hình 2-7b). Hình 2-7
2.3 Phép cộng véctơ lực
Từ thực nghiệm đã chỉ ra rằng lực là một đại lượng véctơ vì nó được xác định bởi trị số,
phương và chiều và vì thế nó cộng được với nhau theo quy tắc hình bình hành. Hai bài toán
thường gặp trong tĩnh học bao gồm hoặc đi xác định véctơ hợp lực của hệ lực hoặc phân tích 21
một lực đã biết ra thành hai thành phần. Như đã đề cập trong phần 2.2, cả hai vấn đề này đều
cần sử dụng quy tắc hình bình hành.
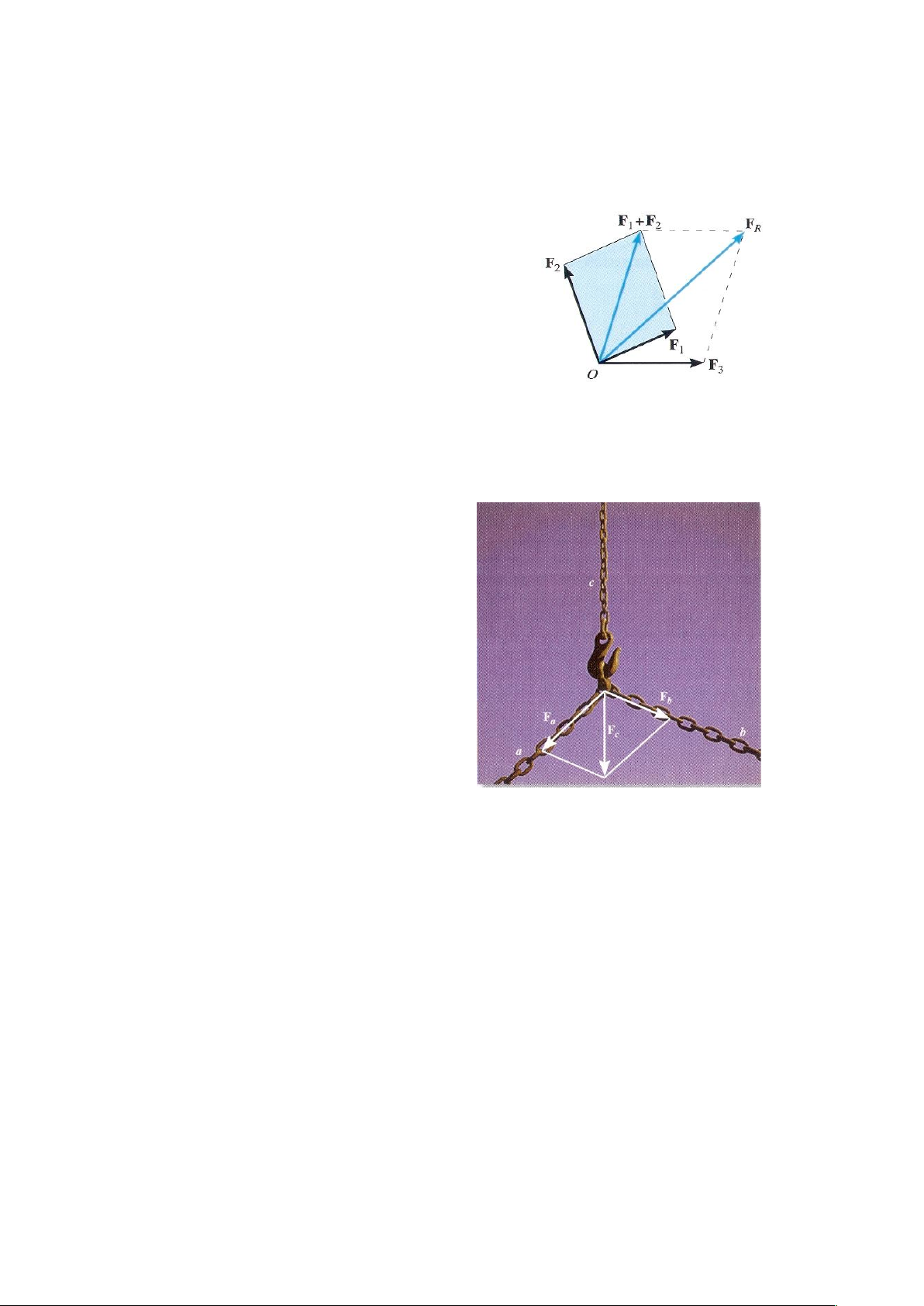
Nếu có nhiều hơn hai lực được cộng lại, lần lượt áp
dụng quy tắc hình bình hành ta có thể thu được véctơ hợp
lực. Ví dụ, nếu có 3 lực F1, F2, F3 đặt tại điểm O, hình 2-8,
hợp của hai lực đầu tiên được xác định là véctơ F1 + F2,
sau đó cộng véctơ này với véctơ lực thứ 3 là F3, ta có hợp
lực của hệ ba lực trên là FR = (F1 + F2) + F3. Như ở trên khi
sử dụng quy tắc hình bình hành để cộng các lực, thường
phụ thuộc vào các phép tính hình học và phép tính lượng
giác để xác định độ lớn và phương của hợp lực. Do đó để Hình 2-8
thay thế và để cho vấn đề trở nên đơn giản hơn người ta
đưa vào “phương pháp chiếu”, phương pháp này sẽ được
giải thích trong phần 2.4.
Nếu ta biết lực Fa và Fb của hai dây xích a và b tác
dụng lên móc treo bởi dây xích c, ta có thể xác định
được hợp lực của chúng là Fc bằng cách sử dụng quy
tắc hình bình hành. Ở đây vẽ các đường thẳng song
song với các dây xích a và b từ đầu mút của lực Fa và
Fb thu được một hình bình hành như trên hình vẽ, từ
đó xác định được Fc.
Tương tự, nếu biết lực Fc của dây xích c, khi đó
hai thành phần của nó là Fa và Fb có đường tác dụng là
a và b, có thể được xác định nhờ sử dụng quy tắc hình
bình hành. Khi đó xuất phát từ ngọn của Fc kẻ các
đường thẳng song song với các đường a và b thu được
hình bình hành, từ đó xác định được Fa và Fb.
CÁC BƯỚC PHÂN TÍCH
Các bài toán sử dụng phép cộng của hai véctơ có thể được giải như sau:
Quy tắc hình bình hành
 Vẽ các véc tơ có cùng gốc sau đó biểu diễn véctơ tổng theo qui tắc hình bình hành.
 Theo quy tắc hình bình hành cộng hai véctơ lực, thì véctơ hợp lực chính là véctơ
đường chéo của hình bình hành.
 Nếu phân tích một lực ra thành hai lực thành phần từ gốc của nó theo phương của hai
trục, từ mút của của nó vẽ các đường thẳng song song với các trục ta thu được hình
bình hành. Hai cạnh của hình bình hành biểu diễn hai lực thành phần.
 Biểu diễn các trị số và các góc của tất cả lực trên sơ đồ và chỉ ra hai đại lượng chưa biết cần xác định. 22
Hình học lượng giác
 Vẽ lại một nửa hình bình hành để minh họa một hình
tam giác mô tả cộng véctơ “ngọn tới gốc” của các lực thành phần.
 Trị số của véctơ hợp lực có thể được xác định từ định
lý hàm số cosines, và phương của nó được xác định từ
định lý hàm số sines, hình 2-9.
 Trị số của hai lực thành phần được xác định từ định lý hàm số sines, hình 2-9. Hình 2-9
CÁC ĐIỂM QUAN TRỌNG
 Một vô hướng là một số âm hoặc một số dương.
 Một véctơ là một đại lượng đặc trưng bởi trị số, phương và chiều.
 Nhân hoặc chia một véctơ cho một vô hướng sẽ làm thay đổi độ lớn của véctơ, chiều
của véctơ sẽ thay đổi (ngược chiều) nếu vô hướng đó là âm.
 Trong trường hợp đặc biệt, nếu các véctơ cộng tuyến (trên cùng một đường thẳng), thì
véctơ tổng được tính theo phép cộng đại số hay phép cộng vô hướng.
Ví dụ 2-1. Đinh ốc như trên hình vẽ (hình 2-10a) chịu tác dụng của hai lực F1 và F2. Xác
định trị số và phương của véctơ hợp lực của hai lực trên. Hình 2-10 Bài giải
Quy tắc hình bình hành. Áp dụng quy tắc hình bình hành cộng hai véctơ F1, F2 biểu
diễn như trên hình vẽ (hình 2-10b). Hai đại lượng chưa biết là trị số của véctơ hợp lực FR và góc  (theta).
Hình học lượng giác. Từ hình 2-10b, vẽ tam giác véctơ, hình 2-10c. Trị số FR được xác
định từ định lý hàm số cosines: 23 2 2 0
F  (100 N)  (150 N)  2(100 N)(150 N)cos115 R
 10000  22500  30000( 0  .4226)  212.6 N  213 N
Áp dụng định lý hàm số sine xác định góc , sử dụng giá trị tính toán được của FR. 150 N 212,6 N  150 N => sin   (0.9063) =>  = 39,80 0 sin  sin115 212.6 N
Do đó, góc  hợp bởi véctơ FR với phương ngang là: 0 0 0
  39.8 15.0  54.8 
Chú ý: Các kết quả tính được có vẻ là đúng, vì hình 2-10b cho thấy lực FR có độ lớn lớn hơn
hai lực thành phần và có phương nằm giữa hai lực thành phần.
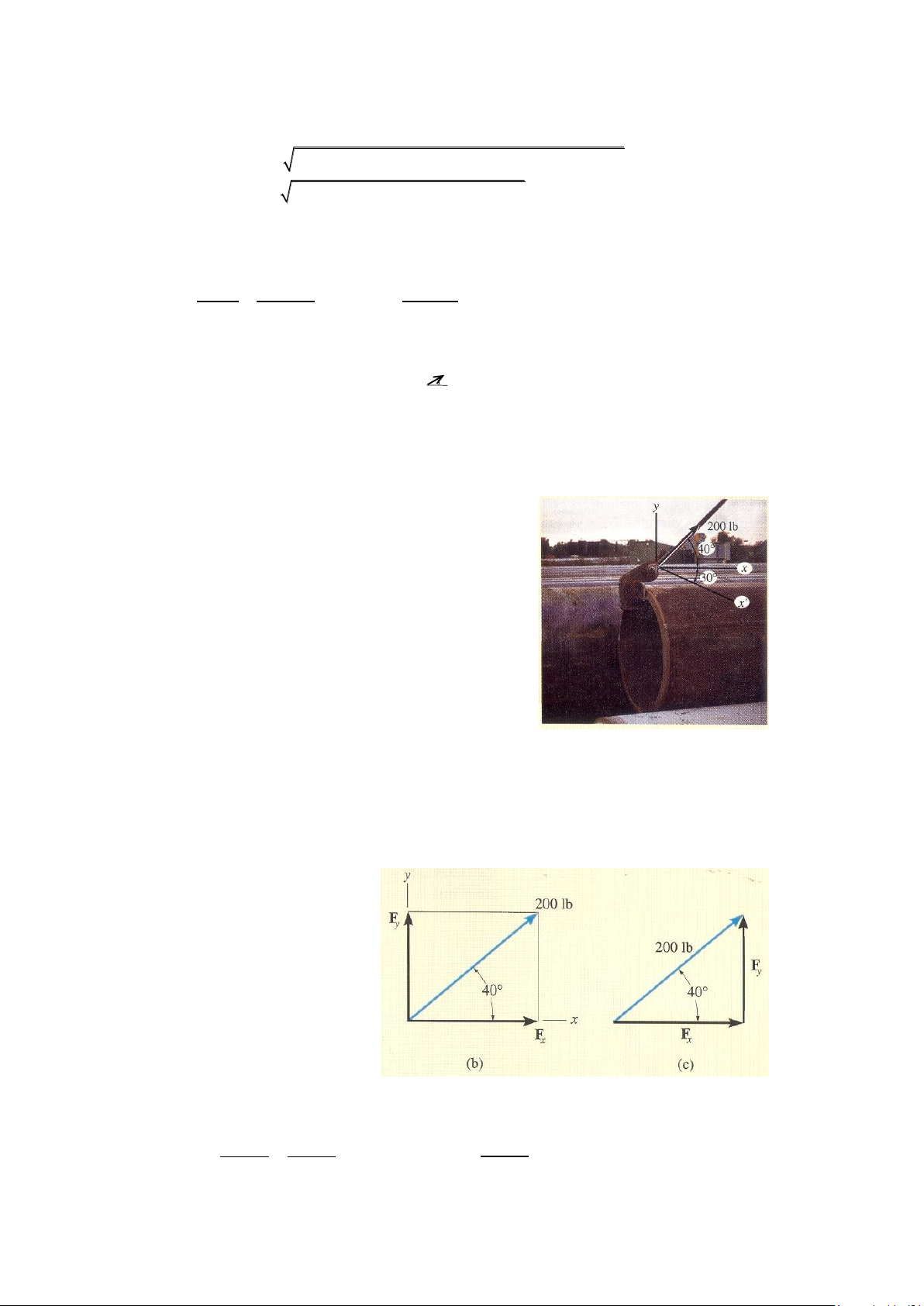
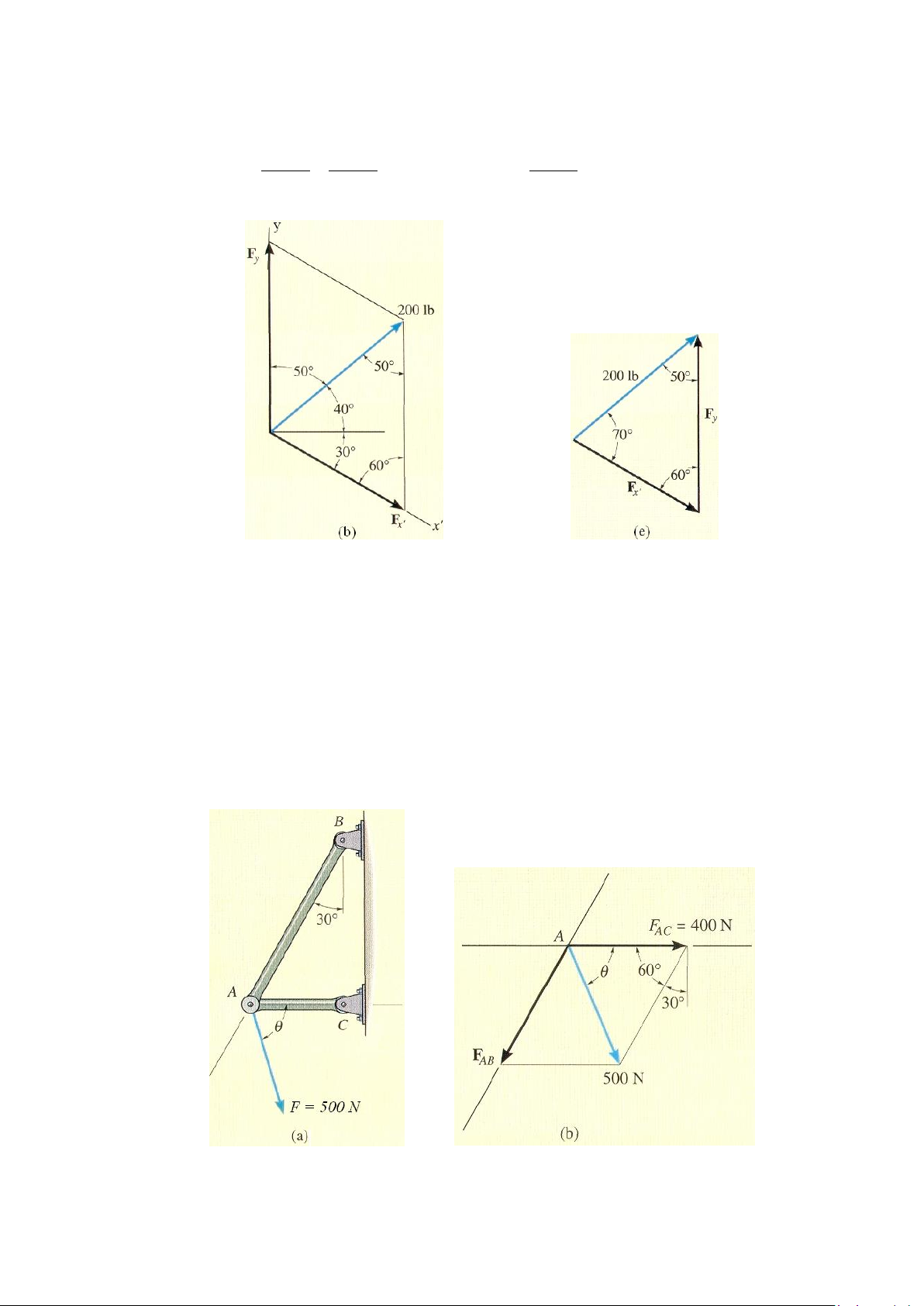
Ví dụ 2-2. Phân tích lực có độ lớn 200 lb tác dụng lên
một đường ống, hình 2-11a, ra thành các thành phần (a)
theo phương x và y, và (b) theo phương x và y. Bài giải
Sử dụng quy tắc hình bình hành để phân tích lực F ra
thành hai thành phần trong hai trường hợp, sau đó vẽ tam
giác véctơ để xác định các giá trị lực thành phần nhờ hình học lượng giác.
Phần (a). Véctơ tổng hợp F = Fx + Fy được biểu diễn Hình 2-11a
trên hình 2-11b. Trong trường hợp đặc biệt, chú ý rằng độ
dài của các lực thành phần được vẽ theo tỷ lệ dọc theo trục
x và y như sau, vẽ các đường thẳng bắt đầu từ ngọn của F
song song với trục x và y theo quy tắc hình bình hành. Từ
tam giác véctơ (hình 2-11c), ta có: 0 F  200lbcos 40 153lb x 0 F  200lbsin 40 129lb y
Phần (b). Véctơ hợp lực F = Fx
+ Fy biểu diễn trên hình 2-11d. Theo
quy tắc hình bình hành xác định
được Fx và Fy. Áp dụng định lý
hàm số sines, từ tam giác véctơ Hình 2-11b, c (hình 2-11d), ta có: F 0    200lb sin 50 x  => F  lb    200 177 lb 0 0 sin 50 sin 60 x 0  sin 60  24 F 0   y 200lb  sin 70 => F  200 lb   217 lb 0 0 sin 70 sin 60 y 0  sin 60  Hình 2-11b, e
Chú ý: Bản vẽ phác thảo đúng tỷ lệ sẽ cho ta liên tưởng về mối quan hệ giữa độ lớn của các
lực thành phần, như kết quả tính được.
Ví dụ 2-3. Lực F tác dụng lên dàn như trên hình 2-12a có độ lớn 500 N và nó được phân
tích ra thành hai thành phần tác dụng dọc theo thanh AB và AC. Xác định góc  hợp bởi
phương của lực F và phương ngang như hình vẽ, sao cho thành phần FAC có chiều từ A tới C
và có độ lớn là 400 N. Hình 2-12a, b 25 Bài giải
Theo quy tắc hình bình hành, véctơ F được phân tích thành hai thành phần FAC và FAB
được biểu diễn như trên hình vẽ, hình 2-12b. Theo tam giác véctơ, hình 2-12c, sử dụng định
lý hàm số sines góc  được xác định như sau: 400 N 500 N  400 N   => 0 sin  
sin 60  0.6928 =>  = 43.90 0   sin  sin 60  500 N 
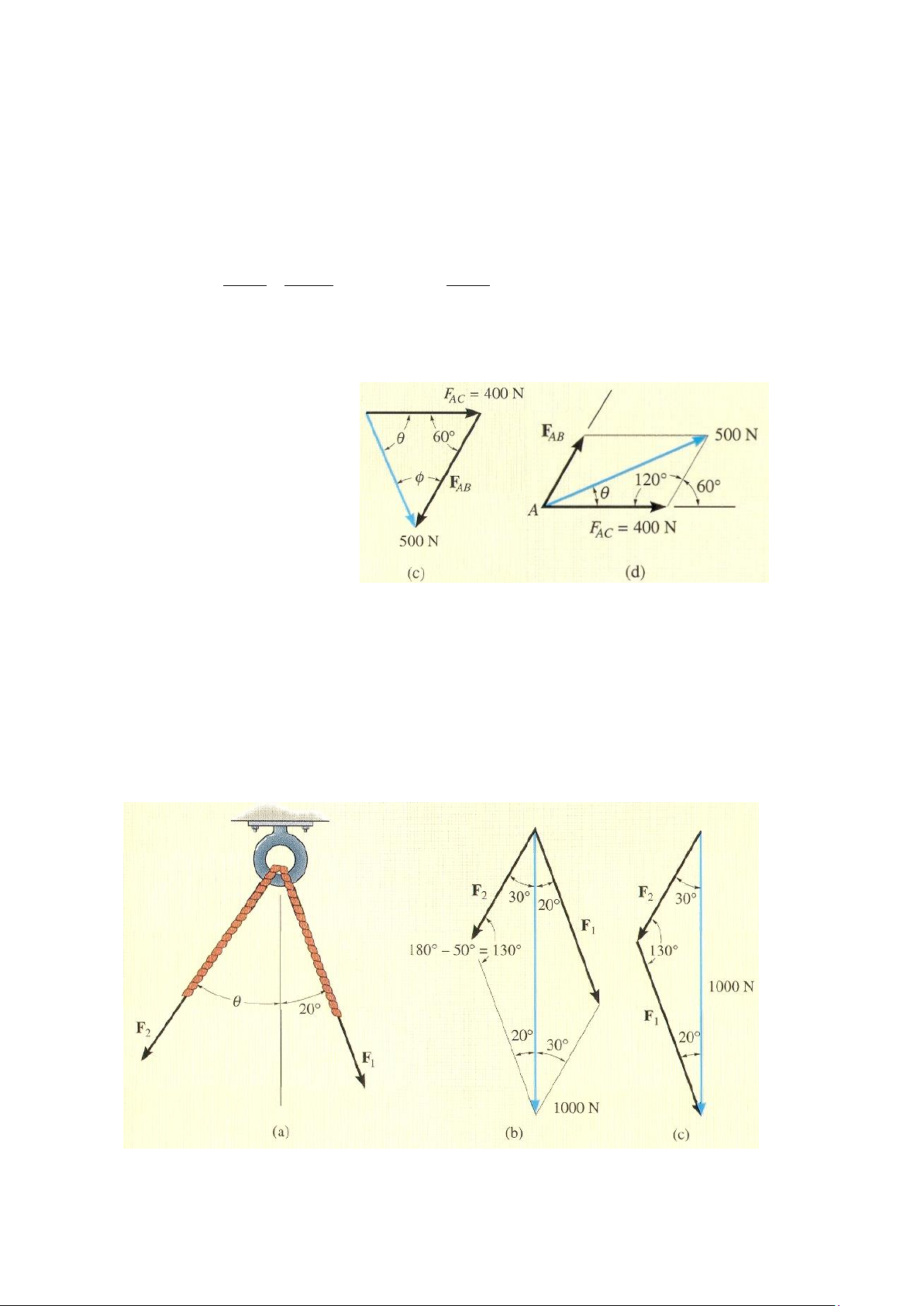
Khi đó, ta có:  = 1800 – 600 – 43.90 = 76.10
Áp dụng định lý hàm số
cosine ta sẽ xác định được giá
trị của lực thành phần FAB:
FAB = 561 N. Kết quả này cho
thấy các lực thành phần đôi khi lớn hơn hợp lực
Chú ý: Nếu lực F có phương
hợp với phương ngang một góc
 về phía trên (hình 2-12d), và
thành phần FAC có độ lớn như Hình 2-12c, d
yêu cầu. Chứng minh rằng
 = 16.10 và FAB có độ lớn 161 N.
Ví dụ 2-4. Vòng treo như hình vẽ 2-13a chịu tác dụng của hai lực F1 và F2. Nếu hợp lực
của chúng có độ lớn 1 kN, có phương thẳng đứng hướng xuống dưới. Xác định (a) độ lớn của
F1 và F2 nếu góc  = 300, và (b) độ lớn của F1 và F2 nếu độ lớn F2 đạt cực tiểu. Hình 2-13 26 Bài giải
Phần (a). Theo quy tắc hình bình hành, véctơ hợp lực biểu diễn như hình vẽ 2-13b. Từ
tam giác véctơ, hình 2-13c, theo định lý hàm số sine ta có độ lớn F1 và F2: F 1000 N 1  => F 0 0 1 = 653 N sin 30 sin130 F 1000 N 2  => F 0 0 2 = 446 N sin 20 sin130
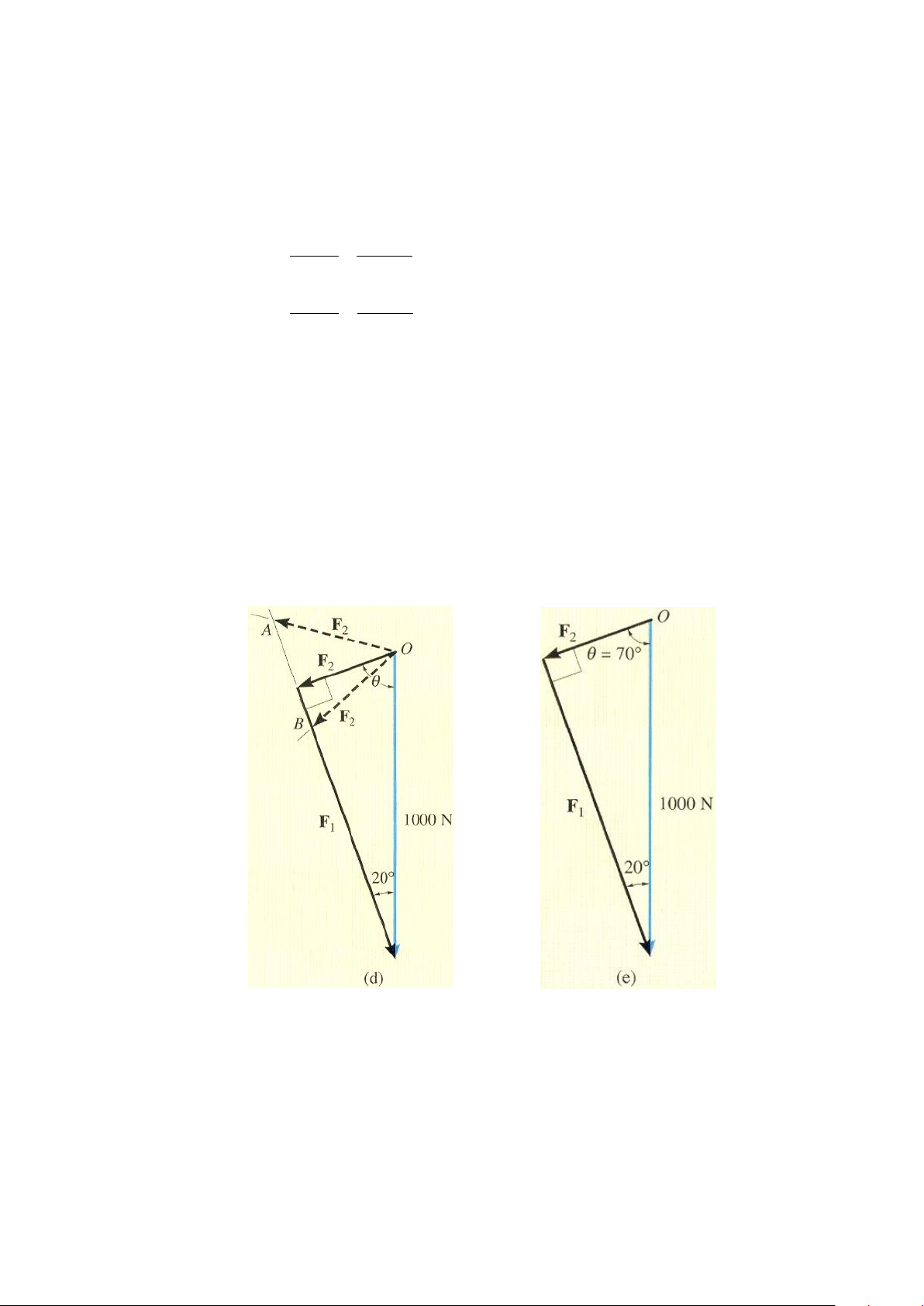
Phần (b). Nếu góc  không được xác định rõ, khi đó theo tam giác véctơ, hình 1-13d, có
nhiều cách cộng F2 với F1 để thu được hợp lực có độ lớn 1000 N. Trong trường hợp đặc biệt,
độ lớn nhỏ nhất của F2 sẽ tìm được khi đường tác dụng của F2 có phương vuông góc với
phương (đường tác dụng) của F1, ngoài ra bất kỳ một phương nào khác ví dụ như OA hoặc
OB đều thu được F2 có trị số lớn hơn. Đo đó, góc  = 900 – 200 = 700, F2 sẽ đạt giá trị nhỏ
nhất. Khi đó, từ tam giác véctơ, hình 2-13e, ta có: 0 F 1000sin 70 N  940 N 1 0 F 1000cos70  342 N 2 Hình 2-13d, e 27 BÀI TẬP
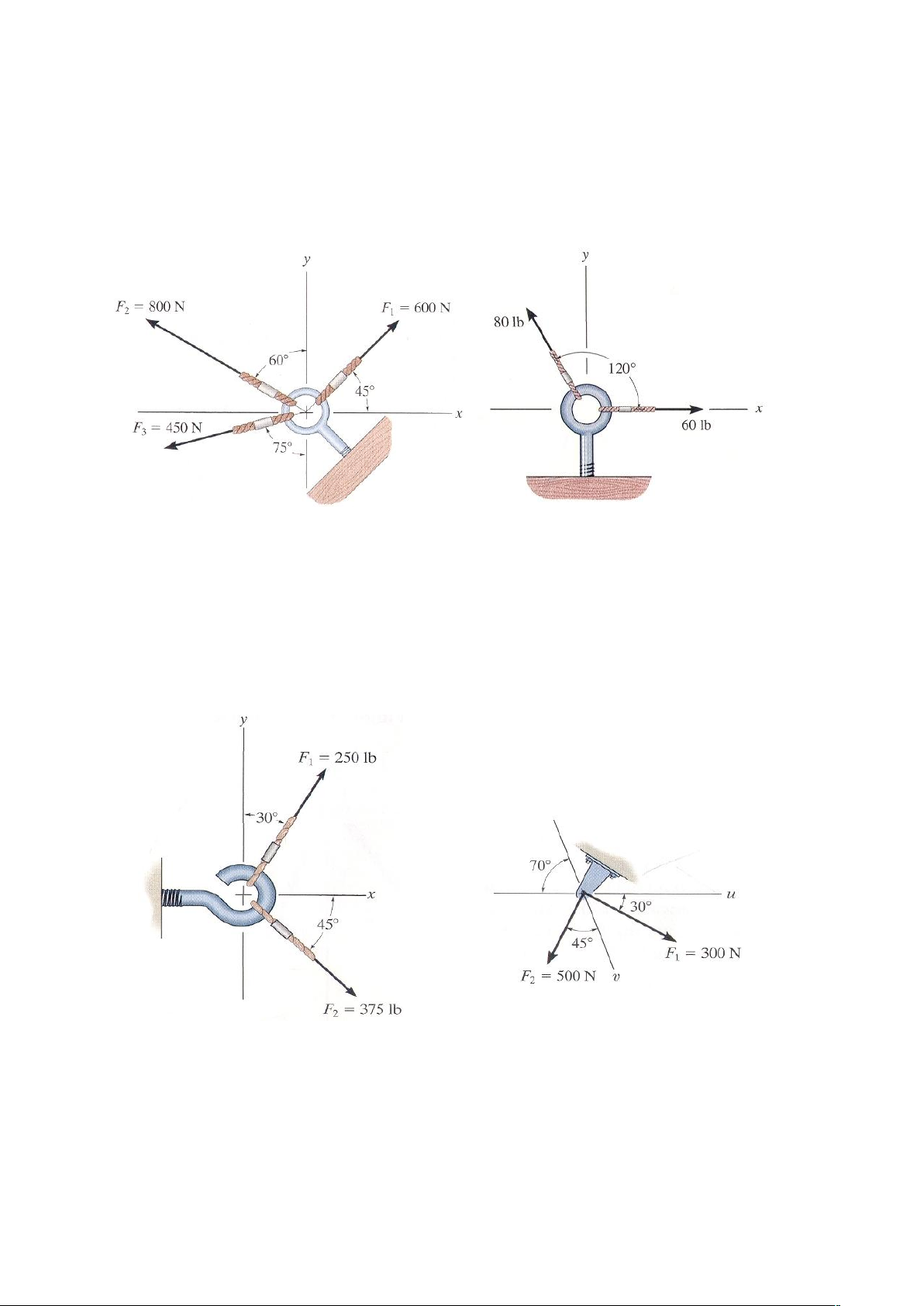
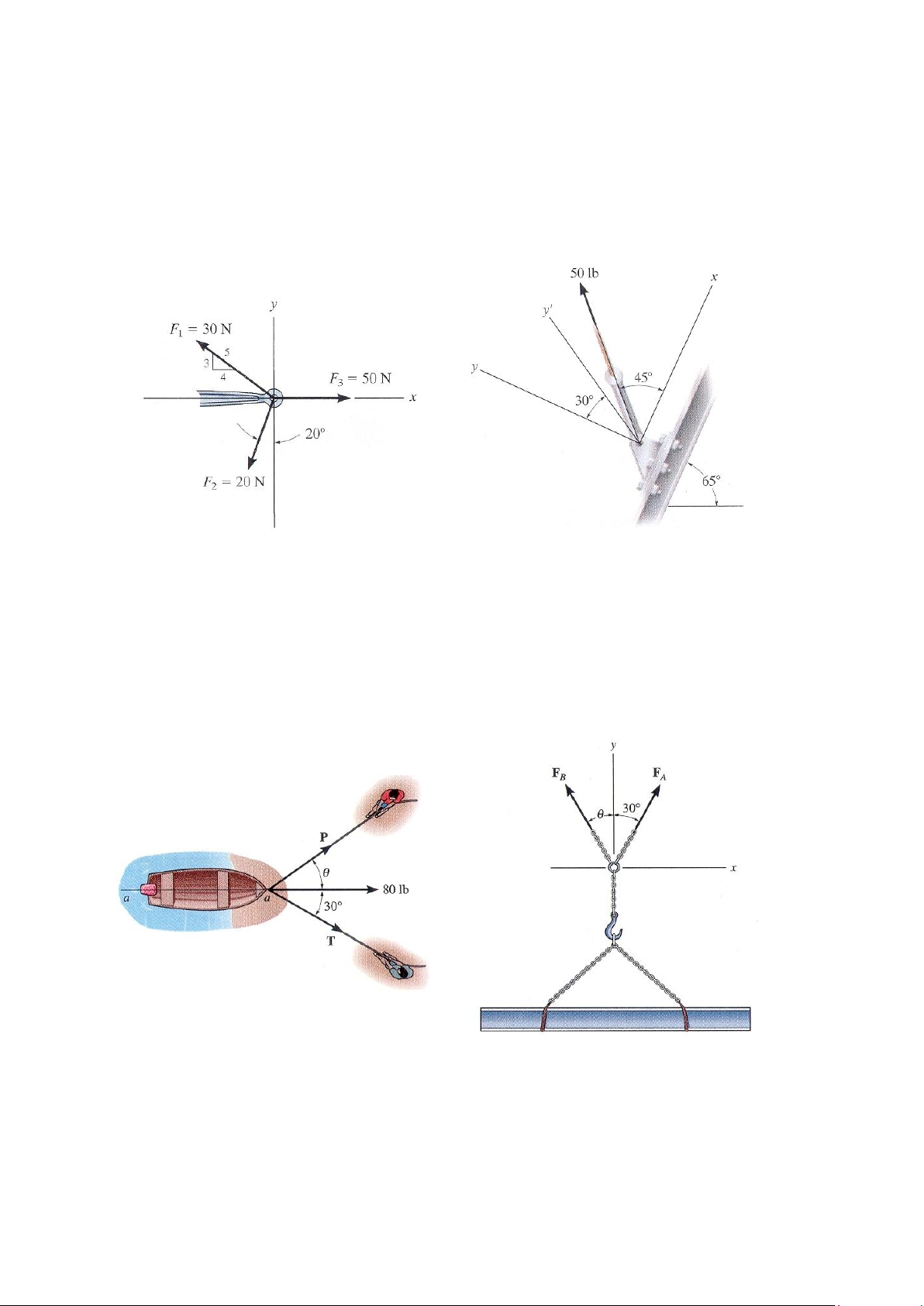
2-1. Xác định trị số của véctơ hợp lực FR = F1 + F2 và phương chiều của nó, theo chiều
ngược chiều kim đồng hồ so với chiều dương trục x. Bài tập 2-1 Bài tập 2-2
2-2. Xác định trị số của véctơ hợp lực, phương của hợp lực (góc giữa đường tác dụng của
véctơ hợp lực với phương ngang x). Hình 2-2.
2-3. Xác định trị số của véctơ hợp lực FR = F1 + F2 và phương chiều của nó, theo chiều
ngược chiều kim đồng hồ so với chiều dương trục x. Bài tập 2-3 Bài tập 2-4/5/6
*2-4. Xác định trị số của véctơ hợp lực FR = F1 + F2 và phương chiều của nó, theo chiều
cùng chiều kim đồng hồ so với chiều dương trục u.
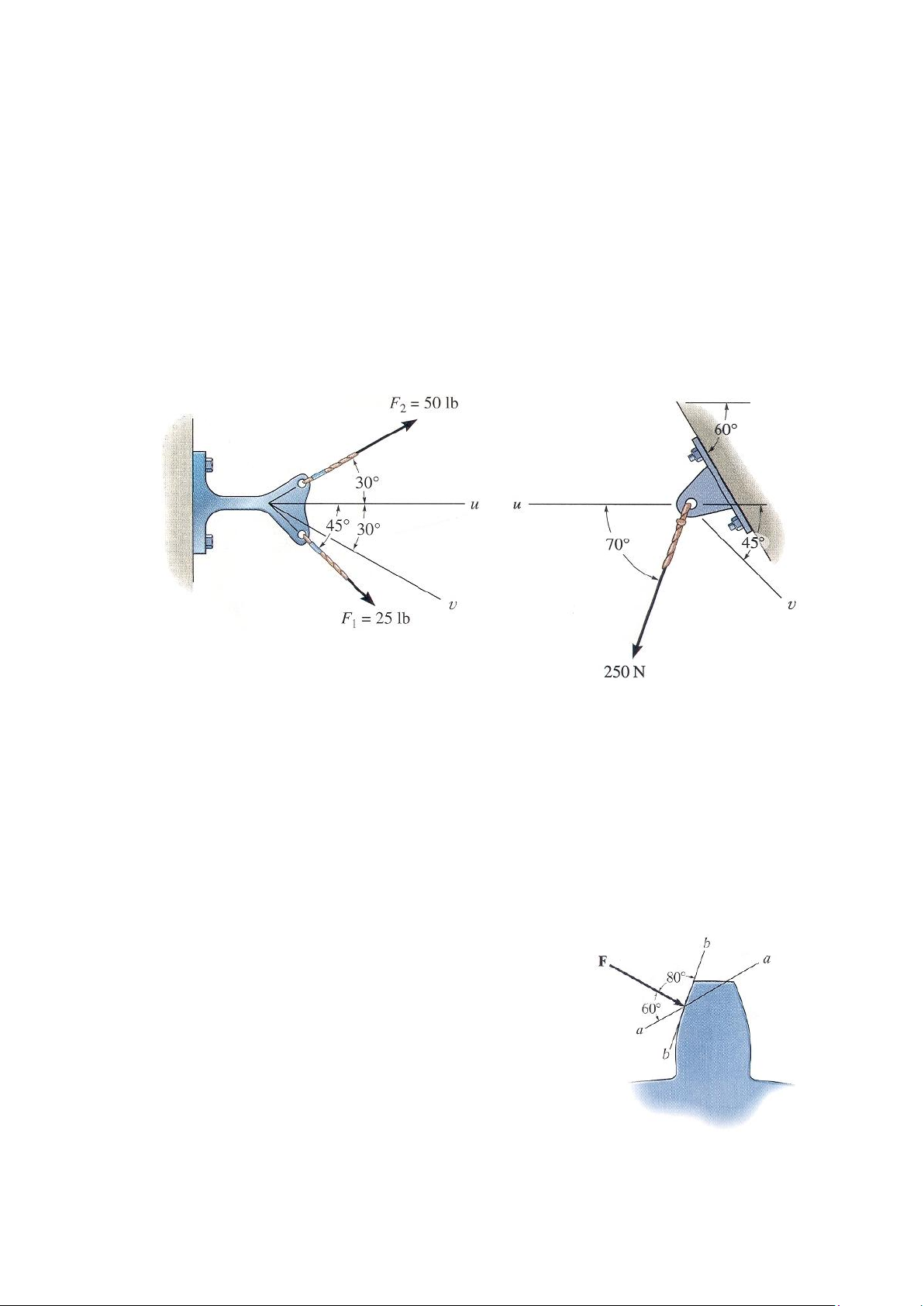
2-5. Phân tích lực F1 thành hai thành phần theo hai phương u, v và xác định độ lớn của chúng. 28
2-6. Phân tích lực F2 thành hai thành phần theo hai phương u, v và xác định độ lớn của chúng.
2-7. Xác định trị số, phương (góc giữa đường tác dụng của véctơ hợp lực với phương u),
chiều của véctơ hợp lực FR = F1 + F2, biết F1, F2 cho trên hình vẽ 2-7.
*2-8. Phân tích lực F1 ra hai thành phần với các đường tác dụng dọc theo phương u và v.
Xác định các lực thành phần.
2-9. Phân tích lực F2 ra hai thành phần có đướng tác dụng theo phương u và v. Xác định các lực thành phần. Bài tập 2-7/8/9 Bài tập 2-10
2-10. Xác định các lực thành phần của lực có độ lớn 250 N có phương chiều như trên
hình vẽ với đường tác dụng của các lực thành phần dọc theo trục u và v.
2-11. Cho lực tác dụng lên răng của một bánh răng có độ lớn là F = 20 lb như trên hình
vẽ. Hãy phân tích lực F thành hai thành phần theo hai phương aa và bb.
*2-12. Nếu thành phần của lực F tác dụng lên răng theo phương aa có độ lớn là 30 lb.
Hãy xác định độ lớn của lực F và thành phần của nó theo phương bb.
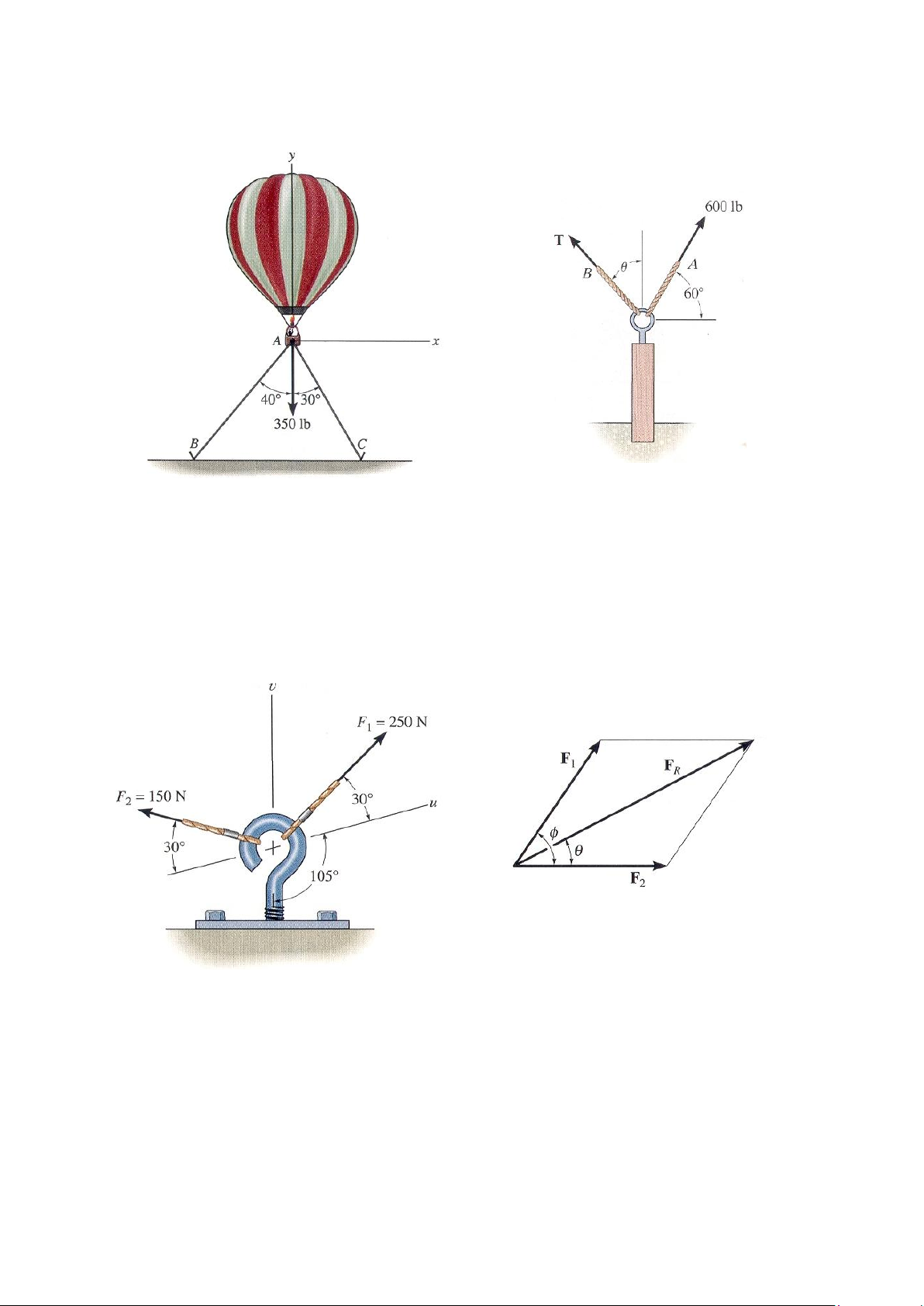
2-13. Hợp lực có phương thẳng đứng xuống dưới cần
thiết để giữ cho khí cầu đứng yên tại chỗ có độ lớn 350 lb,
hình 2-13. Hãy phân tích lực này ra thành các thành phần
theo phương của dây AB và AC, và xác định độ lớn của các lực thành phần.
2-14. Một chiếc cột được rút khỏi mặt đất nhờ sử dụng
hai sợi dây thừng A và B. Dây A chịu tác dụng của một lực
có độ lớn 600 lb, có phương hợp với phương ngang một góc
600. Nếu véctơ hợp lực tác dụng lên cột có độ lớn 1200 lb
theo phương thẳng đứng hướng lên trên, hãy xác định lực T
của dây B tương ứng với góc  như hình vẽ. Bài tập 2-11/12 29 Bài tập 2-13 Bài tập 2-14
2-15. Phân tích lực F1 ra các thành phần dọc theo phương của trục u và v và xác định độ lớn của chúng.
*2-16. Phân tích lực F2 ra các thành phần dọc theo phương trục u và v. Xác định độ lớn
của các lực thành phần. Bài tập 2-15/16 Bài tập 2-17
2-17. Xác định độ lớn và phương của véctơ hợp lực FR. Biểu diễn kết quả theo độ lớn của
các lực thành phần F1 và F2 và góc .
2-18. Cho sức căng của các dây cáp là 400 N, hình 2-18, xác định trị số và phương của
véctơ hợp lực tác dụng lên pulli. Biết góc  giữa phương của véctơ hợp lực với phương ngang
x là góc giữa đường AB kéo dài từ đầu mút của các bulông A, B với phương x. 30
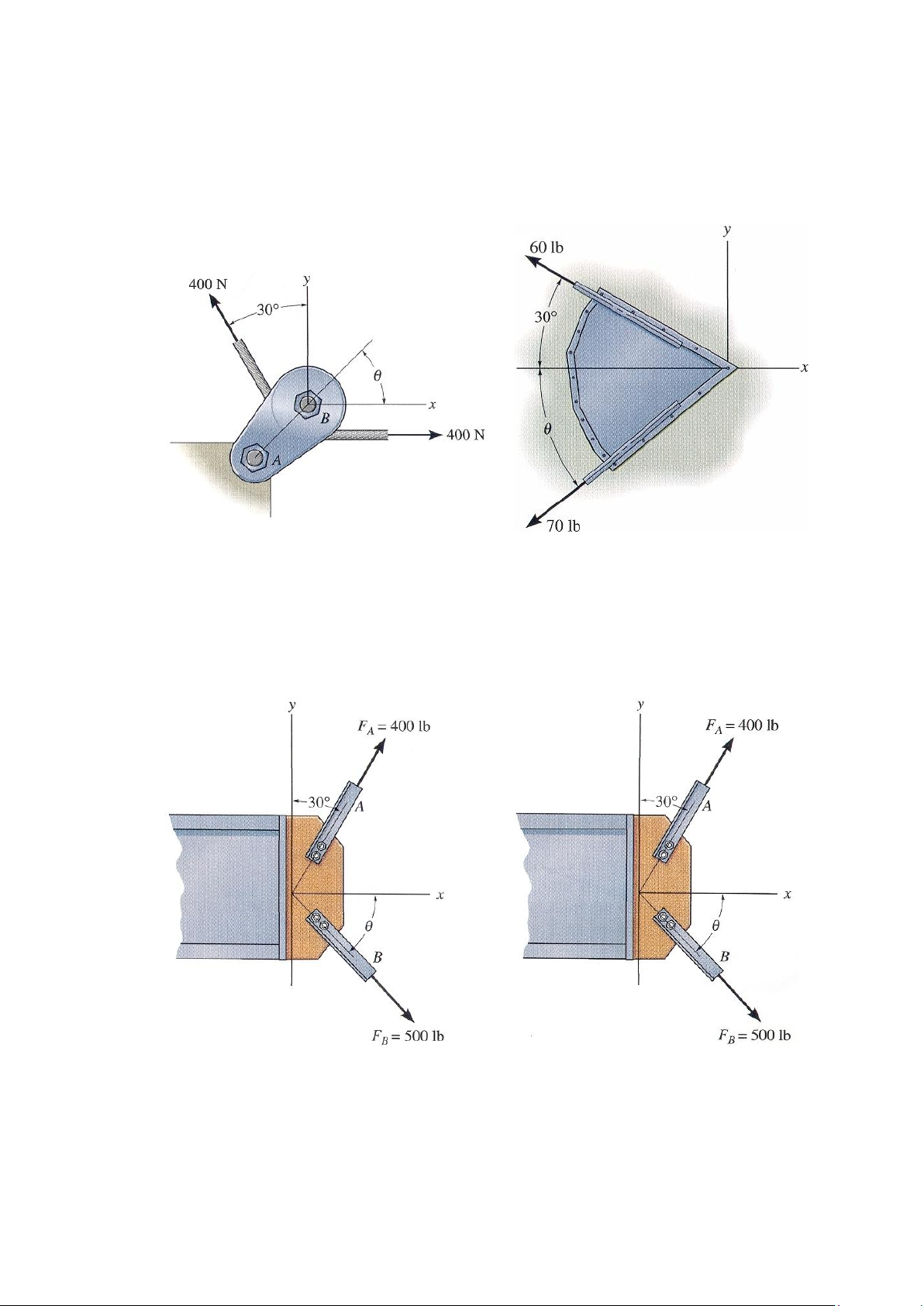
2-19. Giá consơn được bắt đinh tán với tấm cố định (hình 2-19) chịu tác dụng của hai lực.
Xác định góc  hợp bởi véctơ hợp lực với trục ngang x (theo chiều âm của trục), xác định độ
lớn của véctơ lực tổng hợp. Bài tập 2-18 Bài tập 2-19
*2-20. Tấm mỏng chịu tác dụng của các lực dọc theo các thanh A và B như hình vẽ 2-20.
Cho góc  = 600, xác định trị số của véctơ hợp lực và phương của nó (góc giữa đường tác
dụng với chiều dương trục x theo chiều cùng chiều kim đồng hồ). Bài tập 2-20 Bài tập 2-21
2-21. Xác định góc  giữa thanh B với trục x nếu véctơ hợp lực của các lực tác dụng lên
các thanh A, B là FA, FB có chiều theo chiều dương của trục x. Khi đó hãy xác định độ lớn của véctơ hợp lực. 31
2-22. Xác định trị số và phương chiều của véctơ hợp lực của ba lực FR = F1 + F2 + F3
theo cách sau: Đầu tiên tìm hợp lực F = F1 + F2 sau đó tìm FR = F + F3.
2-23. Xác định trị số và phương chiều của véctơ hợp lực của ba lực FR = F1 + F2 + F3
theo cách sau: Đầu tiên tìm hợp lực F = F2 + F3 sau đó tìm FR = F + F1. Bài tập 2-22/23 Bài tập 2-24
*2-24. Hãy phân tích lực có độ lớn 50 lb thành các thành phần tác dụng theo (a) các trục
x, y và (b) các trục x, y như hình vẽ.
2-25. Con thuyền được kéo vào bờ nhờ hai sợi dây như hình vẽ 2-25. Xác định độ lớn của
các lực thành phần T và P tác dụng theo mỗi sợi dây được phân tích từ véctơ hợp lực có độ
lớn 80 lb, có phương dọc theo đường sống aa của thuyền như hình vẽ. Lấy  = 400. Bài tập 2-25/26 Bài tập 2-27/28
2-26. Con thuyền được kéo vào bời nhờ hai sợi dây, nếu véctơ hợp lực có độ lớn là 80 lb,
có phương dọc theo đường sống aa của thuyền như hình vẽ. Xác định trị số của các lực T và
P tác dụng theo mỗi sợi dây và góc  sao cho giá trị của lực P đạt nhỏ nhất, biết T hợp với
phương aa một góc 300. 32
2-27. Dầm được kéo lên nhờ hai dây xích như hình vẽ 2-27. Xác định độ lớn của các lực
FA và FB tác dụng theo phương của mỗi dây xích, biết hợp lực của chúng có độ lớn 600 N và
có phương theo chiều dương trục y. Lấy  = 450.
*2-28. Dầm được kéo lên nhờ hai dây xích, hình 2-28. Biết véctơ hợp lực có độ lớn là 600
N, có phương dọc trục y theo chiều dương. Xác độ lớn của các lực thành phần FA và FB tác
dụng dọc theo mỗi dây xích và góc  giữa phương của FB với trục y sao cho lực FB có giá trị
nhỏ nhất. Biết FA có phương hợp với trục y một góc 300.
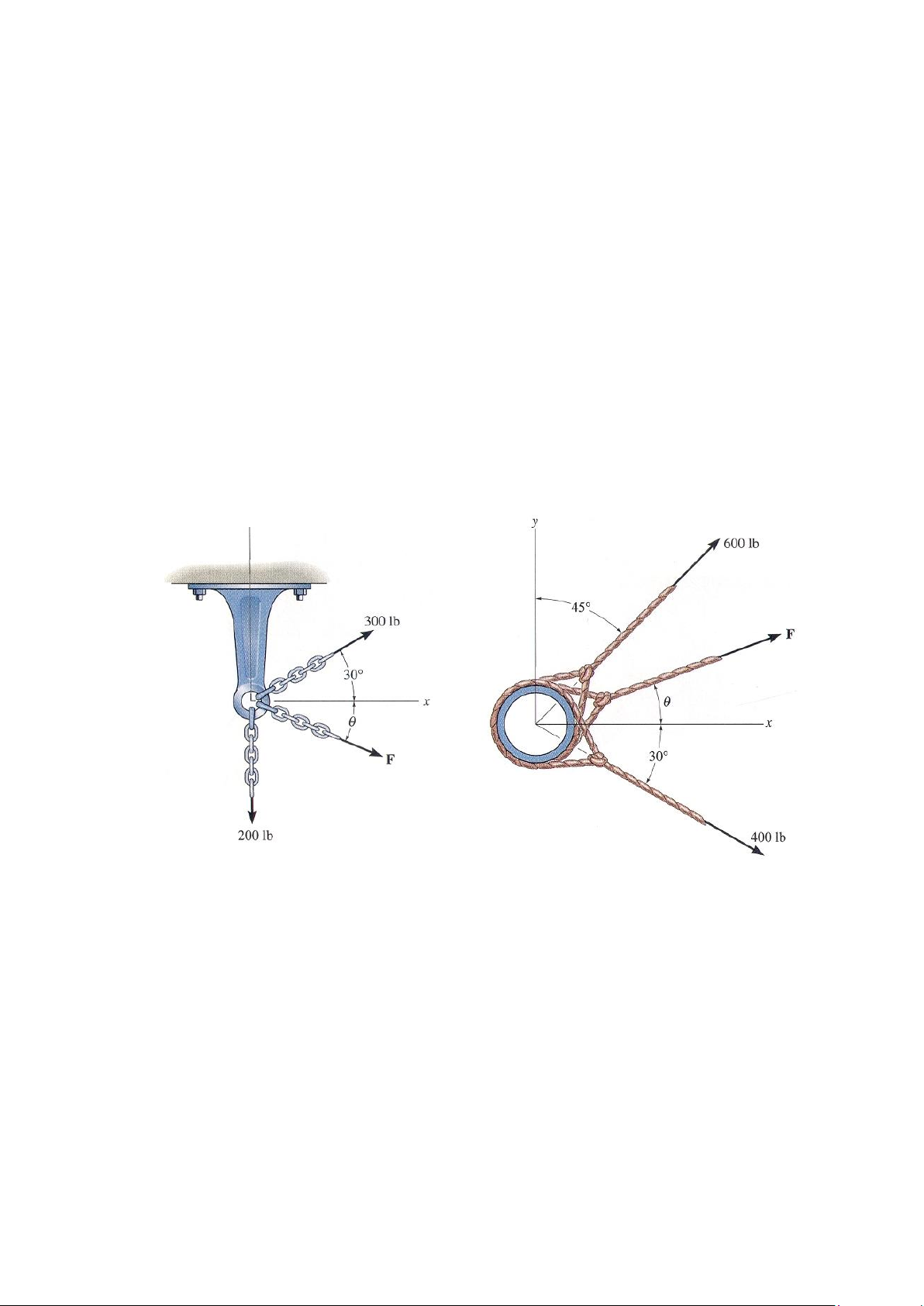
2-29. Ba dây xích tác dụng lên tấm, biết rằng hợp lực tác dụng lên tấm của chúng có độ
lớn 500 lb. Biết hai dây xích tác dụng lên tấm các lực đã biết, hình 2-29. Xác định góc  hợp
bởi phương của lực thứ ba F với trục x theo chiều kim đồng hồ nếu giá trị của nó đạt nhỏ
nhất. Cho các lực nằm trong cùng một mặt phẳng x-y. Xác định trị số của lực F.
Gợi ý: Đầu tiên đi xác định hợp lực của hai lực đã biết, lực thứ ba F có đường tác dụng
trùng với đường tác dụng của hợp lực hai lực đã biết. Bài tập 2-29 Bài tập 2-30
2-30. Ba dây cáp kéo một đường ống tạo ra hợp lực có độ lớn 900 lb. Cho biết hai lực kéo
của hai dây cáp, hình 2-30. Xác định góc  hợp bởi phương của lực thứ ba F với phương
ngang sao cho lực thứ ba có giá trị nhỏ nhất, và hãy xác định giá trị của lực F khi đó. Cho các
lực nằm trong cùng một mặt phẳng x-y. Xác định giá trị của lực F khi đó.
Gợi ý: Đầu tiên đi xác định hợp lực của hai lực đã biết. 33